4 ESO MATEMÀTIQUES B
 José Colera J., M.ª José Oliveira G., Ignacio Gaztelu A., Ramón Colera C., Rosario García P., Ana Aicardo B.
José Colera J., M.ª José Oliveira G., Ignacio Gaztelu A., Ramón Colera C., Rosario García P., Ana Aicardo B.

 José Colera J., M.ª José Oliveira G., Ignacio Gaztelu A., Ramón Colera C., Rosario García P., Ana Aicardo B.
José Colera J., M.ª José Oliveira G., Ignacio Gaztelu A., Ramón Colera C., Rosario García P., Ana Aicardo B.
• Fes un esquema, un gràfic o una taula que t’ajude a organitzar les dades
• En els problemes geomètrics, fes un dibuix
• Experimenta, tempteja, posa exemples... conjectura i comprova...
• Investiga
1. Nombres irracionals
2. Nombres reals: la recta real
3. Trams de la recta real: intervals i semirectes
4. Arrels i radicals
5. Nombres aproximats. Errors
6. Nombres en notació científica. Control de l’error
7. Logaritmes
Exercicis i problemes resolts
Exercicis i problemes
1. Polinomis. Operacions
2. Regla de Ruffini
3. Arrel d’un polinomi. Recerca d’arrels
4. Factorització de polinomis
5. Divisibilitat de polinomis
6. Fraccions algebraiques
2.
3.
4.
1. Semblança
2. Homotècia
3. Rectangles de dimensions interessants
4. Semblança de triangles
5. La semblança en els triangles rectangles
6. Semblança de triangles rectangles en cossos geomètrics
Exercicis i problemes resolts
Exercicis i problemes
Taller de matemàtiques
Autoavaluació
1. Raons trigonomètriques d’un angle agut
2. Relacions trigonomètriques fonamentals
3. La calculadora en trigonometria
4. Raons trigonomètriques de 0° a 360°
5. Angles de mesures qualssevol.
Raons trigonomètriques
6. Resolució de triangles rectangles
7. Resolució de triangles no rectangles
8. Uns teoremes molt interessants
Exercicis i problemes resolts
Exercicis i problemes
Taller de matemàtiques
Autoavaluació
134
1. Vectors en el pla
2.
3.
4. Punt mitjà d’un segment
6.
7.
1. L’estadística i els seus mètodes
2. Taules de freqüències
3. Paràmetres estadístics: x i σ
4. Paràmetres de posició per a dades aïllades
5. Paràmetres de posició per a dades agrupades
6. Diagrames de caixa
7. Estadística inferencial
8. Estadística en els mitjans de comunicació Exercicis i problemes resolts
Exercicis i problemes
Taller de matemàtiques Autoavaluació
1. Distribucions bidimensionals
2. El valor de la correlació
3. La recta de regressió per a fer estimacions
4. Reflexionem: la correlació significa causa-efecte?
5. Distribucions bidimensionals amb calculadora
Exercicis i problemes resolts
Exercicis i problemes Taller de matemàtiques
1. Estratègies basades en el producte
2. Variacions i permutacions (importa l’ordre)
3. Quan no hi influïx l’ordre. Combinacions
4. Un triangle numèric interessant
5. Fórmula de Newton
Exercicis i problemes resolts
Exercicis i problemes
1. Esdeveniments aleatoris
2. Probabilitats dels esdeveniments. Propietats
3. Probabilitats en experiències simples
4. Probabilitats en experiències compostes
5. Composició d’experiències independents
6. Composició d’experiències dependents
7. Taules de contingència
Exercicis i problemes resolts
Exercicis i problemes
268
286
308
El concepte de funció ha anat evolucionant i perfilant-se al llarg del temps. Quins requisits se li ha anat exigint a aquest concepte?
— Una funció relaciona dues variables.
— Les funcions descriuen fenòmens naturals.

— Les relacions funcionals poden ser descrites mitjançant fórmules (relacions algebraiques).
— Les funcions poden ser representades gràficament.
Les següents són algunes de les contribucions més importants per a perfilar el paper de les funcions i la seua definició formal:
• Nicolau Oresme (segle xiv) va ser el primer a descriure les lleis de la naturalesa com a relacions de dependència entre dues variables.
• Galileu (segle xvi) va usar per primera vegada l’experimentació (va dissenyar, va experimentar, va mirar, va anotar) per a establir numèricament aquestes relacions.
• Descartes (segle xvii), amb l’algebrització de la geometria, va propiciar que les funcions pogueren ser representades gràficament.
• Leibniz (segle xvii), el 1673, va usar per primera vegada la paraula funció per a designar aquest tipus de relacions.

• Euler (segle xviii) va anar perfilant el concepte, al qual va donar precisió i generalitat. Va presentar una definició general molt rigorosa, que no dista molt de la que usem actualment. Va aportar la nomenclatura f (x).
• Dirichlet (segle xix) va ampliar el concepte de funció admetent, finalment, que una relació entre dues variables pot ser funció encara que no hi haja una expressió analítica que la descriga.

Un rellotge de sol no és exacte pel fet que la Terra, en el seu moviment al voltant del Sol, no va sempre a la mateixa velocitat.
El gràfic següent mostra en quants minuts s’avança o es retarda el rellotge de sol en el transcurs d’un any.
A partir d’aquest, ens podem fer infinitat de preguntes:
En quina data s’avança més?
En quina data es retarda més?
Què passarà l’any següent? I a l’altre?
Aquest comportament es repetix cada any. Recorda que aquesta mena de funcions s’anomena periòdiques

En l’Europa del segle xvi, la influència d’Aristòtil (filòsof del segle IV aC) era extraordinària i les seues creences no es qüestionaven. Segons Aristòtil, si es deixen caure dos cossos de pesos diferents, el més pesant arribarà abans al sòl. Es conta que Galileu, sent professor novençà de la Universitat de Pisa, va desmuntar aquesta creença mitjançant una experiència pública: va deixar caure dos objectes metàl·lics de pesos molt diferents des de la torre de Pisa. Van caure simultàniament. D’aquesta manera va demostrar les seues tesis però va ser expulsat de la universitat. És possible que en l’anècdota anterior hi haja molt de mite. No obstant això, sí que és cert que va experimentar sobre la caiguda d’un cos per un pla inclinat, controlant distàncies i temps.
1. a) Explica per què és periòdica la funció que descriu els avançaments o retards del rellotge de sol al llarg de l’any.
b) Indica en quines dates és exacte..
2. Es deixa caure una bola per un raïl lleument inclinat i es mesura la distància que recorre en diferents temps:
a) Representa les dades anteriors sobre una quadrícula com la que tens a l’esquerra. Usa’ls per a obtindre la corba corresponent.
b) Comprova que els valors obtinguts responen (amb molt bona aproximació) a la següent relació: e = 10t 2
Una funció lliga dues variables numèriques que, habitualment, s’anomenen x i y :
x és la variable independent. y és la variable dependent.
La relació entre les variables mitjançant la funció f associa a cada valor de x un únic valor de y. S’expressa així: y = f (x )
Per a visualitzar el comportament d’una funció, recorrem a la seua representació gràfica.
Es diu domini de definició d’una funció, f , i es designa per Dom f, el conjunt de valors de x per als quals existix la funció.
Es diu recorregut de f el conjunt de valors que pren la funció. És a dir, el conjunt de valors de y per als quals hi ha una x tal que f (x) = y.
EXERCICI RESOLT
Explicar per què és funció la relació següent:
Càrrega el teu mòbil al 100 % i apunta cada 15 min el percentatge de càrrega que té, fins que s’esgote totalment.
PENSA I PRACTICA
Es lliguen dues variables: el temps, t, mesurat en minuts, i el percentatge, p, de bateria. La primera és la variable independent. La segona és la variable dependent.
En cada instant, el mòbil té un percentatge de càrrega. És a dir, per a cada valor de t hi ha un únic valor de p
Per tant, p és una funció que depén de t: p = f (t).
1 Aquest gràfic descriu l’evolució de la producció mundial de plàstics (en milions de tones anuals).
268 367 produccin de plàstic (tm) any
2 Indica el domini i el recorregut d’aquestes funcions:

a) Quines són les dues variables?
b) Explica per què és una funció.
➜ anayaeducacion.es Concepte de funció. 187
c) Quines són el domini de definició i el recorregut?
El gràfic d’una funció permet apreciar-ne el comportament global amb un simple colp d’ull.

Tant en l’estudi de les matemàtiques com en altres ciències o en la vida quotidiana, ens trobem freqüentment amb funcions.
Les funcions ens vénen donades de molt diverses formes: mitjançant el seu gràfic, per una taula de valors, per una fórmula o mitjançant una descripció verbal (enunciat).
La funció de la dreta ve donada pel gràfic. Descriu el consum d’aigua en un centre d’estudis al llarg d’un dia laborable.
Com millor es pot apreciar el comportament global d’una funció és mitjançant la seua representació gràfica. Per això, sempre que pretenguem analitzar una funció, intentarem representar-la gràficament, qualsevol que siga la forma en la qual, en principi, ens vinga donada.
Quan una funció ve donada per un enunciat o una descripció, la idea que ens en podem fer és, quasi sempre, quantitativament poc precisa. Però si l’enunciat s’acompanya amb dades numèriques, la funció pot quedar perfectament determinada. Vegem dos exemples de funcions que relacionen l’altura sobre el nivell del mar amb el temps transcorregut :
• Fèlix va eixir al matí de la seua casa de camp, va seguir un camí que portava al cim d’una muntanya, va menjar dalt i va tornar a poqueta nit.
• Maria va eixir de sa casa, a la platja, a les 9 a.m. Va caminar 45 min fins al cim d’un turó que està a 250 m d’altura sobre el nivell del mar, es va quedar 10 minuts contemplant les vistes i va tardar 30 min a tornar a casa.
1 Analitzem el gràfic de dalt.
a) Quant temps es mesura el consum d’aigua en el centre d’estudis?
b) Durant quines hores el consum d’aigua és nul?
c) Quan és creixent el consum? Quan és decreixent?
d) A quines hores s’aconseguixen els valors màxims i els valors mínims de consum d’aigua? Quins són aquests valors?
2 Fixa’t en les funcions altura sobre el nivell del mar - temps transcorregut que s’han descrit més amunt referents a les excursions fetes per Fèlix i Maria.
a) Representa el gràfic corresponent a Fèlix.
b) Representa el gràfic corresponent a Maria.
c) Si comparares els dos gràfics anteriors amb els dels teus companys, quins serien més pareguts, els de Fèlix o els de Maria?
Explica per què.
Algú que guanye 54 000 €:
• Se situa en la 3a fila.
• Pels primers 45 000 € ha de pagar 7 250 €, i per la resta (54 000 € – 45 000 € = 9 000 €) ha de pagar el 35 %.
35 % de 9 000 € = 3 150 €
• Per tant, ha de pagar:
7 250 € + 3 150 € = 10 400 €
Amb freqüència se’ns donen els valors d’una funció mitjançant una taula en la qual s’obtenen directament les dades buscades. No obstant això, en altres casos cal efectuar complexos càlculs per obtindre el que es busca.
|Exemple: la taula per al pagament a Hisenda
Observem aquesta taula amb la qual es calcula el que cada persona (contribuent) ha de pagar a Hisenda (quota íntegra) en funció del que va guanyar l’últim any menys els descomptes legalment admesos (base liquidable).
Obtindre la quota íntegra que correspon a cada una de les següents bases liquidables:
a) 9 500 €
b) 25 000 €
c) 50 000 €
d) 85 000 €
nota: La taula que maneja l’agència tributària és d’aquest tipus, però més complexa.
L’ús d’aquesta taula està exemplificat en el marge. Però el significat és aquest:
• Els guanys de 0 a 10 000 € no paguen res (0 %).
• Pel guanyat entre 10 000 € i 25 000 €, es paga el 15 %.
• Pel guanyat entre 25 000 € i 45 000 €, es paga el 25 %.
• Pel guanyat entre 45 000 € i 70 000 €, es paga el 35 %.
• Pel guanyat per damunt de 70 000 €, es paga el 45 %.
Per tant, el que ha de pagar algú que guanye 54 000 € es calcularia així:
a) Aquesta quantitat correspon a la primera fila. Per tant, no es paga res.
b) La quota corresponent a aquesta quantitat es troba directament, sense càlculs, en la fila 2a → Quota: 2 250 €
c) Ens situem en la 3a fila. Pels primers 45 000 € cal pagar 7 250 €. Pels
5 000 € restants, cal pagar el 35 %, que són 1 750 €. Per tant, caldrà pagar 7 250 € + 1 750 € = 9 000 €.
d) Ens situem en l’última fila. Pels primers 70 000 € cal pagar 16 000 €. Pels 15 000 € restants, cal pagar el 45 %, és a dir, 6 750 €. Per tant, cal pagar, en total, 16 000 € + 6 750 € = 22 750 €.
➜ anayaeducacion.es Funcions
3 Troba la quota íntegra que correspon a cada una de les següents bases liquidables:
a) 12 000 € b) 20 000 € c) 45 000 € d) 100 000 €
4 La segona columna de la taula de dalt es pot obtindre a partir de la resta de les dades que hi ha en aquesta. Explica com.
definides mitjançant taules de valors.
L’expressió analítica és la forma més precisa i operativa de donar una funció. Però per a visualitzar-la es requerix un minuciós estudi posterior. Vegem alguns exemples:
|Exemple 1
Una bola que es deixa caure per un pla lleument inclinat porta una acceleració de 20 cm/s2. La distància, e, en centímetres, que recorre en funció del temps, t, en segons, ve donada per la fórmula e = 10t 2 .
|Exemple 2
El volum d’una esfera en funció del seu radi és: V = 3 4 πr 3 (r en cm, V en cm3)
|Exemple 3
El període, T, d’un cert pèndol ve donat en funció de la longitud, l (en m), per la fórmula T = l 2
El període és el temps, en segons, que tarda a fer una oscil·lació, anada i tornada.
|Exemple 4
L’augment, A, de la mida d’un objecte que es mira a través d’una lupa éss A = d 2 2 –. d : distància de la lupa a l’objecte, en cm. A: augment (nombre pel qual es multiplica la mida real).


5 En l’exemple 1, calcula la distància que recorre la bola en 1, 2, 3, 4 i 5 segons. A quin temps correspon una distància de 2 m?
En l’exemple 2, troba el volum d’una esfera de radi 5 cm i el radi d’una esfera de volum 800 cm 3 .
6 Troba (exemple 3) el període d’un pèndol d’1 m de llarg. Quina és la longitud d’un pèndol amb un període de 6 segons?
7 Calcula la mida aparent, A, d’un objecte (exemple 4) per als següents valors de d : 0; 0,5; 1; 1,5; 1,9; 1,99
Per a d = 4 s’obté A = –1. Això vol dir que l’objecte es veu de la mateixa mida, però invertit. Interpreta els valors de A per a d : 10; 5; 2,5; 2,1; 2,01
NOTACIÓ
Si Dom f és el conjunt de tots els reals excepte x = –3, podem expressar-ho mitjançant la unió de intervals, (– ∞, –3) ∪ (–3, +∞), o així: Dom f = Á – {–3}
En la funció y = x 2 podem donar a x un valor qualsevol i obtindrem el corresponent valor de y. Diem que aquesta funció està definida en tot Á o bé que el seu domini de definició és Á o (–∞, +∞).
No obstant això, en la funció y = x no podem donar a x valors negatius. El seu domini de definició és [0, +∞).
Per què es restringix el domini de definició?
Dom f pot quedar restringit per una de les causes següents:
Impossibilitat de realitzar alguna operació. Això passa si en f (x) hi ha:
• Denominadors. Els valors que fan zero un denominador no estan en el domini de definició.
Per exemple, per a f (x) = x 3 1 + , el domini és el conjunt de tots els reals excepte x = –3. És a dir, Dom f = (–∞, –3) ∪ (–3, +∞).
• Arrels quadrades. No estan en el domini de definició els valors que fan que l’expressió dins de l’arrel siga negativa.
Per exemple, per a f (x) = x 2 – , els valors x < 2 no estan en el domini de definició. Per tant, Dom f = [2, +∞).
Context real del qual s’ha extret la funció
Per exemple, si A = l 2 representa l’àrea d’un quadrat en funció del costat, el domini és (0, +∞), ja que la longitud del costat ha de ser un nombre positiu.
Voluntat de qui proposa la funció.
Així, podem referir-nos a la funció y = 2x definida en (0, 4] sense més raó que el fet que vulguem fer-ho.
➜ anayaeducacion.es

Reforça el càlcul de dominis.
EXERCICI RESOLT
Trobar el domini de definició de les funcions donades per les seues expressions analítiques:
a) y = xx28 1 2
b) y = x5 +
Quan no es diu el contrari, el domini de definició és tan ampli com permeten les operacions que componen l’expressió analítica de la funció.
el denominador, de manera que no pertanyen al domini de definició.
PENSA I PRACTICA
1 Troba el domini de definició de les funcions següents:
Observa en aquest gràfic del valor de l’euríbor el 2022, la importància dels punts de tall amb els eixos.
• El tall amb l’eix Y correspon al valor al començament de l’any.
• El tall amb l’eix X mostra quan deixa de ser negatiu.
Els punts de tall d’una funció amb l’eix X en la majoria dels casos indiquen el canvi de signe dels valors que pren (abans del punt de tall eren positius i després passen a ser negatius, o viceversa). Per aquest i altres motius és important conéixer aquests puntss.
Quan una funció ve donada mitjançant una expressió analítica, y = f (x), és fàcil trobar els punts de tall amb els eixos:
• Per trobar on talla l’eix X, fem que f (x) = 0.
• Una funció snomés pot tallar una vegada a l’eix Y, es troba amb f (0).
Calcular els punts de tall amb els eixos de f (x) = x 3 – 4x 2 + x + 6
Per trobar els punts de tall amb l’eix X, fem f (x) = 0. x 3 – 4x 2 + x + 6 = 0 → x1 = –1, x2 = 2, x3 = 3
La funció talla l’eix X en els punts (–1, 0), (2, 0) i (3, 0).

El punt de tall amb l’eix Y es troba calculant f (0).
f (0) = 6, és a dir, talla l’eix Y en el punt (0, 6).
El signe d’una funció pot ser positiu o negatiu. Si la funció està per damunt de l’eix X, els valors seran positius i, si està per davall, negatius.
Per estudiar el signe d’una funció f (x), resolem dues inequacions:
• f (x) > 0, en la solució de la qual (interval o unió d’intervals) f (x) serà positiva.
• f (x) < 0, en la solució de la qual la funció serà negativa.
Estudiar el signe d’aquesta funció:
f (x) = x 3 – 4x 2 + x + 6
Sabem que la funció s’anul·la en x1 = –1, x2 = 2, x3 = 3, per la qual cosa els intervals a estudiar són:
• En (–∞, –1), com que f (–2) = –20 < 0 → negativa
• En (–1, 2), com que f (0) = 6 > 0 → positiva
• En (2, 3), com que f (2,5) = –0,875 < 0 → negativa
• En (3, +∞), com que f (4) = 10 > 0 → positiva
Atenció: Si la funció tinguera una discontinuïtat en un cert punt, x = a, caldria tindre en compte aquesta abscissa per a estudiar els intervals.
PENSA I PRACTICA
1 Troba els punts de tall amb els eixos d’aquestes funcions:
a) f (x) = 3x – 2 b) f (x) = x 2 + x – 6
c) f (x) = x 3 – 2x 2 – x + 2 d) f (x) = x 2 + 2x + 1
2 Estudia el signe de les funcions de l’exercici anterior.
3 Troba els punts de tall amb els eixos i estudia el signe de la funció f (x) = xx 6 1 –2 + .
OBSERVA
Les línies temporals com la temperatura són contínues, però la funció del preu de l’habitatge està feta de punts que s’unixen amb una línia per veure l’evolució.
En una funció contínua, a «xicotetes» variacions de la x corresponen variacions també «xicotetes» de la y. Mentre que en els punts de discontinuïtat (amb salt) una xicoteta variació de la x (un minut més a l’aparcament) pot produir una variació gran (2 €) en la y.
OBSERVA
() y x xx x xx x 2 2 2 2 –––– 2 == =

És a dir, y = x si x ≠ 2, perquè no podem dividir per zero. Per això deixem un buit en aquest punt.
PENSA I PRACTICA
La funció del marge és contínua en tot el seu domini de definició. No obstant això, les tres funcions següents són discontínues: a
a) c) b) a a
Per què són discontínues?
a) Presenta un salt en el punt d’abscissa a.
b) Té branques infinites en el punt a. És a dir, els valors de la funció creixen indefinidament quan la x s’aproxima a a.
c) Li falta un punt. És a dir, no està definida en x = a.
Una funció és contínua quan no presenta discontinuïtats de cap tipus. Una funció és contínua en un interval [a, b ] si no hi presenta cap discontinuïtat.
Hi ha molts aparcaments que continuen cobrant «per hores». Això vol dir que només per entrar ja es paga 1 h. Si s’està 1h i 10 min es paguen 2 h. El primer dels dos gràfics següents descriu aquesta forma de pagament. És una funció amb diversos punts de discontinuïtat per salts.
Els usuaris preferixen que les tarifes es regisquen per la funció el gràfic de la qual és la 2 . Evidentment, és contínua.
Les funcions següents presenten discontinuïtats:
Aquesta perquè té branques infinites. I aquesta perquè li falta un punt.
➜ anayaeducacion.es Funcions contínues i discontínues.
1 Construïx una funció similar a la 1 , però per al cas que es pague 1 € cada mitja hora. Quina de les opcions de pagament et pareix més justa?
2 Analitza la funció 3 per a valors «pròxims a 2». Comprova que quan x val 1,9; 1,99; 1,999; 2,01; 2,001, la y pren valors «molt grans».
EXERCICI RESOLT

Indicar els intervals en els quals és creixent i en els quals és decreixent la funció de la dreta donada gràficament.
PENSA I PRACTICA
El temps de son (hores al dia dormint) de les persones en els dos primers anys de vida és una funció decreixent (a més edat, menys hores de son).
Com saps, les funcions s’analitzen d’esquerra a dreta: com evolucionen els valors de y en augmentar els valors de x. Donem, per tant, les definicions següents: Una funció f és creixent en un interval quan:
x2 > x1, aleshores f (x2) > f (x1)
Anàlogament, la funció f és decreixent en un interval quan:
x2 > x1, aleshores f (x2) < f (x1)
Una funció pot ser creixent en uns intervals i decreixent en uns altres.

La funció està definida en l’interval [–7, 11].
És creixent en els intervals (–7, –3) i (1, 11).

És decreixent en l’interval (–3, 1).
1 Observa la funció de la dreta i indica en quins intervals és creixent i en quins és decreixent.
(Suposarem que si la funció està definida només en els intervals en els quals la veus dibuixada).
La taxa de variació absoluta ens dona el canvi que una variable presenta d’un cert moment a un altre posterior. Per exemple, si el salari mensual mínim interprofessional el 2018 va ser de 735,90 € i el 2022 va ser de 1 000 €, en el període 2018-2022 ha tingut una pujada o variació absoluta de 264,10 €
La taxa de variació relativa en un interval de temps és el quocient entre la variació absoluta i el valor que va prendre la variable en el moment inicial. El resultat es dona en tant per cent. Així, la variació relativa del salari mensual mínim interprofessional en el període 2018-2022 és:
Per a mesurar la rapidesa de variació (augment o disminució) d’una funció en un interval, s’usa la taxa de variació mitjana o TVM.
S’anomena taxa de variació mitjana de la funció f en l’interval [a, b ] el quocient entre la variació de la funció i la longitud de l’interval.
TVM de f en [a, b ] = () () ba fb fa ––
Observa que la TVM de f en [a, b ] és el pendent del segment AB.
, , 735 90
264 10 = 0,3589, és a dir, un augment del 35,89 %.
1 Calcular la taxa de variació mitjana de la funció donada gràficament a la dreta en els intervals
5] i [5, 8].
Si f és creixent en [a, b ], aleshores TVM de f en [a, b ] > 0, i si f és decreixent en [a, b ], aleshores TVM de f en [a, b ] < 0. Atenció! No té per què ocórrer el contrari, és a dir, si la TVM de f en un interval [a, b ] és positiva la funció no té per què ser creixent en aquest interval, pot ser una part creixent i una altra decreixent (com ocorre en l’exemple resolt 2 a continuació).
En la figura veiem que:
2 a) Trobar la TVM de la funció y = x2 – 4x + 5 en els intervals [2, 4] i [0, 3].
b) Com és la funció en cada un d’aquests intervals?
b) Observant el gràfic veiem que la funció és creixent en l’interval [2, 4]. Observa que, encara que la TVM en l’interval [0, 3] és negativa, la funció té en aquest interval una part decreixent (interval [0, 2]) i una altra creixent (interval [2, 3]).
2 Troba la taxa de variació mitjana (TVM) de la funció f representada, en els intervals [1, 3], [3, 6], [6, 8], [8, 9] i [3, 9].
➜ anayaeducacion.es Taxa de variació mitjana.
3 Troba la TVM de la funció y = x 2 – 4x + 5 (exercici resolt 2) en [0, 2], [1, 3] i [1, 4].
4 Troba la TVM de les funcions següents en [–1, 1], [0, 3] i [2, 5].
a) y = 2x – 2 b) y = x3 – 2x + 1 c) y = –3
El gràfic de l’esquerra mostra l’evolució del pes d’un jove durant 3 anys de la seua vida. Als 16 anys pesava uns 50 kg. Augmenta el pes fins a uns 55 kg. A partir d’ací, baixa fins a 52 kg, però es recupera i el pes augmenta fins als 70 kg, que va pesar amb 19 anys.
No hi ha dubte que el pes mínim durant aquests tres anys va ser amb 16 anys, i el màxim amb 19 anys, però hi ha dos moments en els quals aconseguix un màxim relatiu (55 kg) i un mínim relatiu (52 kg).
Una funció té un màxim relatiu en un punt quan en aquest la funció pren un valor major que en els punts pròxims. En tal cas, la funció és creixent fins al màxim i decreixent a partir d’aquest.
Anàlogament, si f té un mínim relatiu en un punt, és decreixent abans del punt i creixent a partir d’aquest.
La funció pot prendre en altres punts valors majors que un màxim relatiu i menors que un mínim relatiu. El major valor d’una funció en un interval s’anomena màxim absolut. Anàlogament, el menor valor d’una funció en un interval s’anomena mínim absolut.
1 Indicar quins són els màxims i els mínims de la funció següent.
2 Trobar els màxims i mínims d’aquesta funció.
1 Observa la funció representada a la dreta i indica quins són els màxims i els mínims (relatius i absoluts).
Té un màxim relatiu en el punt d’abscissa –3. El valor és 2. Té un mínim relatiu en (1, –5).
El màxim absolut coincidix amb el màxim relatiu. Té un mínim absolut en (–7, –6).
Té un màxim relatiu en (–3, 4) i dos mínims relatius en (–5, 3) i en (5, –2). El mínim absolut coincidix amb un dels mínims relatius, (5, –2). Té dos màxims absoluts: (–8, 5) i (8, 5).
Aquestes tendències es coneixen com a límits de funcions. En batxillerat aprendràs a reconéixer-les i a calcular-les a partir de les seues expressions analítiques.
1 En netejar el congelador, ha quedat en un got un tros de gel. Representar el gràfic de la variació de la temperatura d’aquesta aigua sabent que el gel ix del congelador a –10 °C, i tarda mitja hora a posar-se a 0 °C i 2 h més a descongelar-se. La temperatura exterior és de 20 °C.
2 A quant tendix el volum d’un cub quan creix la seua aresta?
Un paracaigudista salta d’un avió a una determinada altura. La seua velocitat creix molt ràpidament al principi, però segons passa el temps, tendix a estabilitzar-se a causa del fet que la força del fregament de l’aire s’iguala a la gravetat. Aquest és el gràfic de la funció que relaciona la velocitat amb el temps:

Observem que la velocitat a partir d’un cert moment s’estabilitza al voltant d’un valor. Podem afirmar que:
En passar el temps, la velocitat tendix a 55 m/s (198 km/h).
Hi ha funcions en què, encara que només en coneguem un tros, podem predir com es comporten lluny de l’interval en què han estat estudiades, perquè tenen branques amb una tendència molt clara.
El gel puja la seua temperatura fins a arribar a 0 °C. A partir d’ací, es descongela a poc a poc mantenint la temperatura de 0 °C fins que es liqua per complet. Després, augmenta la temperatura de l’aigua que tendix a igualar-se amb la de l’habitació en la qual es troba.
El volum d’un cub en funció de la seua aresta és V = l 3. Com més gran siga l’aresta, més gran serà el volum.
És a dir, el volum creix indefinidament. Això s’expressa de la manera següent:
Quan l’aresta creix indefinidament, el volum tendeix a infinit.

En aquest gràfic es representa el començament d’una funció periòdica de període 7. Esbrinar els valors d’aquesta funció en els punts d’abscisses a = 10; b = 19 ; c
En el marge s’ha representat la variació de l’altura d’una cabina d’una roda de fira quan aquesta fa una volta. Tarda mig minut (30 segons), i en aquest temps puja, arriba al punt més alt, baixa i arriba a terra. Però aquest moviment es repetix una vegada i una altra. La seua representació gràfica és aquesta:
En aquesta funció, el que passa en l’interval [0, 30] es repetix reiteradament. Es tracta d’una funció periòdica de període 30.
Funció periòdica és aquella el comportament de la qual es repetix cada vegada que la variable independent recorre un cert interval. La longitud d’aquest interval s’anomena període.
= 10 → f (10) = f (3) = 3 (ja que 10 = 7 · 1 + 3, i cada 7 unitats es repetix el valor de la funció)
→ f (19) = f (5) = 4 (ja que 19 = 7 · 2 + 5)
c = 418,5 → f (418,5) = f (5,5) = 3 (ja que 418,5 = 7 · 59 + 5,5)
d = 1 778 → f (1 778) = f (0) = 0 (ja que 1 778 = 7 · 254)
1 La quantitat de radioactivitat que posseïx una substància es reduïx a la meitat cada any. El gràfic adjunt descriu la quantitat de radioactivitat que hi ha en una porció d’aquesta substància en transcórrer el temps.
A quant tendix la radioactivitat amb el pas del temps?
2 La cisterna d’uns serveis públics s’ompli i es buida, automàticament, cada dos minuts, seguint el ritme del gràfic adjunt.
a) Dibuixa el gràfic corresponent a 10 min.
b) Quanta aigua hi ha a la cisterna en els instants següents?
I) 17 min II) 40 min 30 s
III) 1 h 9 min 30 s
La ciència està plena de funcions en les quals les variacions de les causes influïxen proporcionalment en les variacions dels efectes. Totes aquestes funcions es diuen lineals i es representen mitjançant rectes. Vegem-ne un exemple:
Si d’un moll pengem diferents pesos, es produïxen diversos allargaments. És a dir, la longitud del moll és funció del pes que s’hi penja. I és interessant destacar que aquesta funció és lineal.
En concret, suposem que el moll sense estirar mesura 30 cm i que s’allarga 15 cm per cada quilogram que hi pengem. La relació és: y = 30 + 15x (y: longitud en cm; x: pes en kg)
El domini de definició d’aquesta funció és [0, 6], suposant que per a pesos de més de 6 kg el moll es deteriora.
y = mx
Les funcions de proporcionalitat es representen mitjançant rectes que passen per l’origen. Descriuen una proporció entre els valors de les dues variables. El pendent de la recta és la raó de proporcionalitat, m.
Per exemple, l’espai recorregut a velocitat constant, v, en funció del temps és: e = v · t, doonnde v és el pendent de la recta que relaciona e amb t.
Funció constant: y = n

Es representa mitjançant una recta paral·lela a l’eix X El pendent és 0.
La recta y = 0 coincidix amb l’eix X.
Per exemple, la distància d’un satèl·lit artificial a la Terra és constant, no depén del temps, t. L’equació seria d = 36 000, d: distància, en km; t: temps, que no apareix en l’equació.
Expressió general de la funció lineal: y = mx + n
La representació és una recta de pendent m que talla l’eix Y en el punt (0, n). El nombre n s’anomena ordenada en l’origen.
Per exemple, la recta F = 32 + 1,8C, representada en el marge, permet passar de graus centígrads, C, a graus Fahrenheit, F.

➜ Representa una recta i escriu l’equació a partir d’un punt i el pendent.
Aquesta fórmula és molt útil. Aprén a usar-la!
Amb molta freqüència hem d’escriure l’equació d’una recta de la qual en coneixem un punt i el pendent. La donem a continuació:
Punt: P (x0, y0) Pendent: m Equació: y = y0 + m(x – x0)
justificació
• y = y0 + m (x – x0) és una expressió de 1r grau. Per tant, és una recta.
• El coeficient de la x és m. Per tant, el pendent és m.
• Si donem a x el valor x0 → y = y0 + m (x0 – x0) = y0 + m · 0 = y0. Per a x = x0 hem obtingut y = y0, és a dir, passa per (x0, y0).
❚ Recta donada peR dos punts
Per trobar l’equació de la recta que passa per dos punts, procedim així:
➜ Representa una recta i escriune la equació a partir de dos punts.
Trobar l’equació de cada una de les rectes següents:
a) Passa per (–5, 7) i té un pendent de 5 –3 .
b) Passa per (–2, 7) y per (4, 5).
• A partir dels dos punts, n’obtenim el pendent.
• Amb el pendent i un dels punts, n’obtenim l’equació.
➜ anayaeducacion.es Repassa l’equació punt-pendent.
a) Equació: y = 7 – 5 3 (x + 5). Això ja és l’equació de la recta.
Podem simplificar-la: y = 7 – 5 3 x – 5 3 · 5 → y = 4 – 5 3 x
b) Comencem trobant-ne el pendent: m = 42() 57 6 2 3 1 ––– ==
Equació de la recta que passa per (–2, 7) i el pendent de la qual és – 3 1 : y = 7 – 3 1 (x + 2) → y = 3 19 – 3 1 x
1 Representa les funcions següents:
a) y = 2x b) y = 3 2 x c) y = – 4 1 x d) y = –3 7 x
2 Representa.
a) y = 3 b) y = –2 c) y = 0 d) y = –5
3 Representa aquestes funcions:
a) y = 2x – 3 b) y = 3 2 x + 2
c) y = – 4 1 x + 5 d) y = –3x – 1
4 Un objecte mòbil, en l’instant inicial, està a 3 m de l’origen i se n’allunya amb una velocitat de 2 m/s. Troba l’equació de la seua distància a l’origen en funció del temps i representa-la.
➜ anayaeducacion.es Calcula el pendent d’una recta.
5 El preu de les creïlles al mercat és d’1 €/kg, i el de les tomaques, 2 €/kg.
a) Escriu l’equació del cost d’una bossa de creïlles en funció del pes.
b) Escriu l’equació del cost d’una bossa de tomaques en funció del pes.
c) Representa les funcions anteriors.
6 Amb les dades que se’t donen, troba l’equació de cada una de les rectes següents:
a) Passa per (–3, –5) i té un pendent de 9 4 .
b) Passa per (0, –3) i té un pendent de 4.
c) Passa per (3, –5) i per (–4, 7).

El curs passat vam fer una suau introducció a l’estudi de les paràboles. Ara repassarem allò i avançarem una mica en el seu tractament.
Observa les paràboles següents amb les seues respectives equacions:
Analitzant-les, podem realitzar les afirmacions següents:
Les funcions y = ax 2 + bx + c, amb a ≠ 0, anomenades quadràtiques, es representen totes mitjançant paràboles i són contínues en tot Á.
Cada una d’aquestes paràboles té un eix paral·lel a l’eix Y.
La seua forma depén de a, coeficient de x 2, de la manera següent:
• Si dues funcions quadràtiques tenen el mateix coeficient de x 2, les seues paràboles corresponents són idèntiques, encara que poden estar situades en posicions diferents.
• Si a > 0, tenen les branques cap amunt, i si a < 0, cap avall.
• Com més gran siga |a |, més estilitzada és la paràbola.
La calculadora ens permet elaborar, de manera ràpida i eficient, una taula de valors corresponent a qualsevol funció, en l’interval que vulguem i amb els increments desitjats. Observa com ho fem per a la funció y = –x 2 + 3x + 4.

Es tria 3:Taula en l’opció de �. Apareix f (x) i, a continuació, s’introduïx l’expressió. Tin en compte que per a escriure la x cal prémer les tecles x )
x ) x + 3 x ) + 4= Apareix aquesta pantalla, on has d’indicar el primer i l’últim valor de x i la grandària del pas:
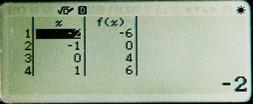
Per a representar una funció quadràtica donada per la seua equació, només cal obtindre uns quants dels seus punts. Començarem calculant el vèrtex de la paràbola, per a trobar, després, alguns punts que l’envolten.
• Trobem l’abscissa del vèrtex de la paràbola y = ax 2 + bx + c → x0 = – a b 2
• Calculem el valor de la funció en algunes abscisses pròximes al vèrtex.
• Els talls amb els eixos poden vindre’ns bé per a la representació:
— Amb l’eix X, es resol l’equació ax 2 + bx + c = 0.
— Amb l’eix Y, és el (0, c ).
Representar la paràbola d’equació y = –x 2 + 3x + 4.
Obtenim el vèrtex:
Abscissa: x0 = – 2 3 – = 1,5 → Ordenada: f (1,5) = 6,25 → Vèrtex: (1,5; 6,25)
Obtenim punts pròxims al vèrtex:
En el nostre cas, com el vèrtex està en x = 1,5, li donem els valors de –2 a 5 i anem d’1 en 1 (pas).
Per veure els valors que no ixen, has de moure’t cap avall amb el cursor.
Podem observar que, a causa de la simetria de la paràbola respecte al seu eix, les ordenades dels punts que estan a la mateixa distància del vèrtex coincidixen. És a dir, com que el vèrtex està en x = 1,5, llavors f (1) = f (2); f (0) = f (3)…
Vegem que – x 2 + 3x + 4 = 0 té dues solucions, x = –1 i x = 4; i que f (0) = 4. Però aquests punts de tall amb els eixos ja apareixen en la taula.
1 Associa cada un dels coeficients de la x 2 amb la paràbola corresponent:
• a = –1
• a = 2
• a = –3 1
➜ anayaeducacion.es Representa funcions quadràtiques.
2 Representa les paràboles següents:
a) y = x 2 – 2x + 2 b) y = –2x 2 – 2x – 3
c) y = 3 1 x 2 + x – 2 d) y = –x 2 + 4
e) y = –2 1 x 2 + 2 f ) y = 3x 2 + 6x + 4
3 Dibuixa en la teua llibreta la representació gràfica d’aquestes funcions quadràtiques:
a) y = (x – 1) · (x – 3) b) y = 2(x – 2)2
c) y = 2 1 (x + 2) · (x – 2) d) y = (x – 1)2 + 5
1 Domini de definició
Indicar quin és el domini de definició d’aquesta funció:
y = 36xx 9 –2 +
L’arrel quadrada es pot calcular si l’expressió davall de l’arrel és positiva o 0.
Resolem 3x 2 + 6x – 9 = 0 → x1 = –3, x2 = 1. I estudiem el signe en els intervals (– ∞, –3), (–3, 1) i (1, +∞).
• Si x ≤ –3 → 3x 2 + 6x – 9 ≥ 0
• Si –3 < x < 1 → 3x 2 + 6x – 9 < 0
• Si x ≥ 1 → 3x 2 + 6x – 9 ≥ 0
Fes-ho tu Calcula el domini de definició de la funció següent: y = xx 21420 2 +
2 Gràfic d’una funció discontínua
Donat el gràfic de la dreta:
a) Trobar-ne el domini.
b) En quins punts talla els eixos? Estudiar el signe de la funció.
c) Trobar la TVM en els intervals [−4, −2] i [0, 1]. És creixent o decreixent en aquests intervals?
d) Indicar els punts de discontinuïtat de la funció. Quin tipus de discontinuïtat presenta en cada un?
Per tant, podem donar a x qualsevol valor menor o igual que –3 o bé qualsevol valor major o igual que 1.
Per tant, el domini d’aquesta funció, f, és: Dom f = (– ∞, –3] ∪ [1, +∞)
Representem y = 3x 2 + 6y – 9 perquè es veja clar on és positiu i negatiu el radicand. Atenció! Aquest no és el gràfic de f (x).
a) La funció no està definida en x = −1, ni en x = 5. El seu domini és Dom = [–4, –1) ∪ (–1, 5).
b) Talla l’eix X en els punts (−4, 0), (1/2, 0) i (3, 0). Està per damunt de l’eix X, després és positiva en els intervals [–4, –1), (−1, 1/2) i (3, 5) i negativa en l’interval (1/2, 3).
c) TVM [−4, −2] = () () () ff 2 24 4 2 10 2 1 –––==
TVM [0, 1] = 10 12 3 –– = Mirant el gràfic, veiem que és creixent en [−4, −2] i decreixent en [0, 1].
d) Té dues discontinuïtats: en x = −1 presenta una branca infinita i en x = 3 un salt.
Fes-ho tu Digues els intervals de creixement i decreixement de la funció anterior.
3 Obtenció de l’equació d’una paràbola a partir del vèrtex i un dels punts
Trobar l’equació de la paràbola el vèrtex de la qual és (3, –1) sabent que passa pel punt (2, –2).
Representar-la en uns eixos de coordenades.
Fes-ho tu Troba l’equació de la paràbola el vèrtex de la qual està en el punt (–2, –9) i que passa per (0, 1).
Una paràbola qualsevol és y = ax 2 + bx + c.
El valor de l’abscissa del vèrtex és x = 3.
Per tant: –b/2a = 3 8 b = –6a (*)
La paràbola passa per (3, –1) i (2, –2):
La
Interpretació de gràfics. Característiques
1 Aquest és el gràfic de l’evolució de la temperatura d’un malalt:
4 Aquesta taula mostra les reserves d’aigua d’un embassament durant tres anys. Tenim les dades concretes en cinc moments de cada any:
a) Quant temps va estar en observació?
b) En quin dia la temperatura aconseguix un màxim? I un mínim? Quina temperatura aconseguix?
c) En quins intervals de temps creix la temperatura i en quins decreix?
d) Troba la TVM en l’interval [3,5; 5].
e) A què tendix la temperatura en passar el temps?
2 Traiem de la nevera un got amb aigua. Aquest gràfic mostra la temperatura en passar el temps:
a) Dibuixa els gràfics corresponents als tres anys de la funció Nre. de setmanes - Reserva en uns mateixos eixos. Descriu-les.
b) Segons les dades, en quin mes i any va haver-hi més reserva? I menys?
c) Quin n’és el domini?
d) Amb aquestes dades, podem saber el recorregut de cada funció?
5 Un triangle isòsceles té 20 cm de perímetre. Anomena x el costat desigual i y els costats iguals.
a) Fes una taula de valors i, a partir d’aquesta, escriu la funció que relaciona el valor de y amb el de x.
b) Quin n’és el domini de definició?
Domini de definició
a) Quina temperatura hi ha dins de la nevera? I fora?
b) Traiem del microones un got amb aigua a 98 °C. Traça el gràfic de la temperatura en passar el temps.
3 La pressió atmosfèrica a nivell de la mar és, de mitjana, la que exercix una columna de mercuri de 760 mm. Se sol expressar com 760 mm de Hg.
En el gràfic s’aprecia com varia en augmentar l’altura.
a) A quant tendix la pressió quan l’altura augmenta?
b) Quina pressió patix l’exterior d’un avió que vola a 10 km d’altura?
6 Troba el domini de definició en cada un dels casos següents:
a) y = x2 – 1 b) y = xx 5 2 2 + c) y = 2 3 x3 + 7x – 2
d) y = x 3 1 –e) y = x x 210 –3 + f) y = x x 1 21 –2 +
g) y = x 2 –h) y = xx x 6 1 ––2 + i ) y = xx 1 –2
j) y = x 7 + k) y = x 1– l) y = x 39 –
m) y = x– n) y = x 34
3 ñ) y = 1 – 5 x 22 +
Funcions lineals i quadràtiques
7 Representa les següents funcions lineals:
a) y = 2x – 3 b) y = 7 4 x
c) y = x 5 –+310 d) y = 2,5
8 Calcula en cada cas l’equació de la recta i representa-la.
a) P (0, 0), m = 1 b) P (2, –1), m = 0
c) A (–2, 1), m = 2 1 d) A (1, 3), m = –3 5
9 Troba, en cada cas, l’equació de la recta que passa pels punts A i B:
a) A (3, 0), B (5, 0) b) A (–2, – 4), B (2, –3)
c) A (0, –3), B (3, 0) d) A (0, –5), B (–3, 1)
10 Calcula l’equació d’aquestes funcions lineals:
B C D
11 Associa cada gràfic a la seua expressió.
a) y = x 2
b) y = –x 2 + 3
c) y = (x – 3)2
12 Fes una taula de valors donant a x valors enters de l’interval [−4, 4] per representar les funcions següents:
a) y = x 2 + 1 b) y = –x 2 + 4
c) y = –3x 2 d) y = 0,4x 2
13 Troba l’equació, en cada cas, i representa-la:
a) Recta que passa per (2, –3) i és paral·lela a la recta que passa per (1, –2) i (– 4, 3).
b) Funció de proporcionalitat que passa pel punt (– 4, 2).
c) Funció constant que passa per (18; –1,5).
14 Troba, en cada cas, el vèrtex de la paràbola, indicant si és màxim o mínim, i els punts de tall amb els eixos. Representa-les.
a) y = 8 – x 2 b) y = 4 + (3 – x)2
c) y = –x 2 – 2x + 4 d) y = xx3
15 Representa, sobre els mateixos eixos, les funcions donades en cada apartat i troba’n els punts de tall.
a) yx yx 2 –2 = = * b) yx yx 4 2 –2 = = *
Resol els sistemes d’equacions dels apartats a) i b) i comprova que els punts de tall que has trobat són les solucions.
16 L’òrbita del cometa Halley és una el·lipse molt excèntrica, un dels focus de la qual és el Sol. Aquesta funció relaciona la distància del cometa al Sol amb el temps:
distància al sol (UA)
1755 1832 1909 1986
any
a) És una funció periòdica? Quin n’és el període?
b) En quin any tornarà a acostar-se al Sol?
17 Aquest és el gràfic de l’evolució dels tres primers atletes a arribar a la meta en una carrera de 1 000 m: distància (m)
a) Quant hi va tardar cada un?
b) En quins moments s’han avançat els uns als altres?
c) Quina va ser la velocitat mitjana de cada un en la primera meitat de la carrera? I en la segona?
18 a) Troba la TVM d’aquesta funció en els intervals [0, 4], [5, 7], [−4, 0] i [−2, 4].
b) Digues en quins intervals és creixent i en quins decreixent.
c) Indica’n els punts de tall amb els eixos i estudia el signe de la funció.
Troba el valor dels paràmetres desconeguts perquè les rectes i els punts complisquen les condicions demanades. Representa-les.
a) Que la recta que passa pels punts (4, 0) i (–2, a) tinga pendent –1.
b) Que la recta y = bx + 2 passe pel punt (–3, 4).
c) Que les rectes d’equacions y = 3x + c i y = cx + 3 es tallen en el punt d’ordenada 2. Quina és l’abscissa corresponent?
d) Que els punts (d, –2) i (4, e) pertanguen a la recta d’equació y = x 2 1 3 –.
20 Troba la TVM de y = 3x 3 + 9x 2 – 3x – 9 en els intervals [–2, 0], [–1, 0], [–3, –1] i [0, 1].
21 Troba els dominis de definició de:
f (x) = x 9 –2 g (x) = xx67 –2 + h(x) = x 4– 2 j(x) = xx23 –2 ++
22 Calcula el vèrtex, l’eix de simetria i els punts de tall amb els eixos (si els té) d’aquestes paràboles:
a) y = 2x 2 b) y = 2(x – 5)2
c) y = 2(x – 5)2 + 2 d) y = –x 2 + 1
e) y = –(x + 1)2 + 1 f) y = –3x + 2x 2
23 Recorda que la fórmula del volum d’un cilindre és V = πr 2h.
a) Escriu la funció que relaciona el volum d’un cilindre de 1 cm de radi amb l’altura.
b) Indica la funció que relaciona el volum d’un cilindre de 1 cm d’altura amb el radi de la base.
c) Calcula el volum d’un cilindre d’1 cm de radi per a altures de 1, 2, 3, 4 i 5 cm. Representa’n la funció.
d) Troba el volum d’un cilindre d’1 cm d’altura per a radis de 1, 2, 3, 4 i 5 cm. Representa’n la funció.
e) Quina altura té un cilindre d’1 cm de radi el volum de la qual és 37,68 cm3?
f ) Quina radi té un cilindre d’1 cm d’altura el volum de la qual és 803,84 cm3?
23
temperatura (°C)
24 Observa les següents gràfics de funcions: 2 –12
a) Relaciona cada corba amb aquests enunciats sobre la temperatura d’un got d’aigua:
I. Quan passa de la taula a la nevera.
II. Quan es trau de la nevera i es deixa a la taula.
III. Quan passa de la taula al congelador.
b) A quina temperatura està la casa? I el congelador? I la nevera?
25 Observa aquest gràfic en el qual, sent xica, segons la teua edat i la teua altura, pots saber, de manera aproximada, en quin percentil d’alçada estàs:
Anna, de 15 anys i 170 cm, es troba en el percentil 90. És a dir, que és més alta que el 90 % de la població i, per tant, més baixa que el 10 %.
a) Estima el percentil d’aquestes altres xiques:
• Ester: 13 anys; 160 cm • Èrica: 11 anys; 135 cm
• Maria: 8 anys; 117 cm • Marta: 12 anys; 150 cm
b) Si Olívia està en el percentil 75 i té 13 anys, quina en serà l’altura?
c) Quina edat té Leonor si amb 105 cm d’altura està en el percentil 25?
26 Troba l’equació de la funció quadràtica el gràfic de la qual, una paràbola, passa per (0, 0), (1, –3) i (5, 5).
27 Aquesta funció relaciona l’espai recorregut per una moto amb el temps.
a) A quina distància està l’àrea de descans?
b) Troba la TVM en els intervals [0, 9], [0, 5] i [6, 9].
c) Quina és la velocitat mitjana en el primer tram abans del descans? I en el segon? Quina relació hi ha entre les velocitats mitjanes i les TVM de l’apartat anterior?
d) Troba la velocitat mitjana del viatge.
28 Un cos, en caiguda lliure, adquirix una velocitat que augmenta uns 35 km/h cada segon. Deixem caure una bola de ferro des dalt d’un penya-segat.
a) Escriu l’expressió analítica de la funció que relaciona el temps des que es va deixar caure amb la velocitat a la qual cau.
b) Representa-la en uns eixos.
c) Suposant que la bola no es frena amb l’aire, quina velocitat portarà als 3 s? I als 10 s?
d) Si la bola xoca contra el sòl a una velocitat de 420 km/h, quant ha tardat a caure?
29 L’altura, h, a la qual es troba en cada instant, t, una fletxa que llancem amb l’arc cap amunt amb una velocitat de 40 m/s és h = 40t – 5t 2 .
a) Representa gràficament la funció.
b) Digues quin n’és el domini de definició.
c) En quin moment aconseguix l’altura màxima? Quina és aquesta altura?
d) En quin moment es clava la fletxa al sòl?
e) En quin interval de temps la fletxa està a una altura superior a 35 metres?
30 Resol analíticament i gràficament aquests siste-
32 Observa aquests gràfics funcions discontínues i contesta en cada una d’aquestes:
31 a) Calcula b i c perquè el vèrtex de la paràbola y = x 2 + bx + c estiga en el punt (3, 1).
b) Quin n’és l’eix de simetria?
c) Quins en són els punts de tall amb els eixos?
a) Quins són els punts de discontinuïtat? Explica la raó de discontinuïtat en cada punt.
b) Quin n’és el domini de definició?
c) Indica, si té, els màxims i els mínims relatius.
d) En quins intervals és creixent? I decreixent?
33 Enguany, Verònica ha aconseguit collir de la seua producció 240 kg d’alvocats que hui es vendrien a 1,20 €/kg. A partir d’ara, cada dia que passa es fan malbé 4 kg, però el preu augmenta 0,10 €/kg. Quan ha de vendre els alvocats per obtindre el màxim benefici? Quin serà aquest benefici?
34 Amb un rectangle de cartolina de 50 cm × 20 cm, volem fabricar una caixa amb tapadora.
a) Escriu el volum en funció de x, V (x).
b) Donant valors a x, representa el gràfic de V (x).
c) Quin és el domini de V (x)?
35 Donada la següent funció periòdica:
Dona’n el període i els valors de la funció en x = 1;
36 Troba l’expressió analítica corresponent a cada una de les paràboles representades:
37 Dibuixa i escriu l’equació, en cada cas, de les paràboles que complixen aquestes condicions:
a) L’eix és x = 2, el coeficient de la x 2 és –1 i talla l’eix X en un sol punt.
b) Té el vèrtex en el punt (3, –2) i té la mateixa forma que y = x 2
c) Té el vèrtex en l’origen de coordenades i passa pel punt (–3, –18).
38 Dibuixa un quadrat ABCD de 7 cm de costat. Sobre el costat AB, marca un punt P que diste x de A, i dibuixa un nou quadrat PQRS inscrit en l’anterior.
a) Observa que si x = 3 cm, AS = 7 – 3 = 4 cm. Quant mesura PS ? Quina és l’àrea del nou quadrat?
b) Quina és la funció que relaciona x amb l’àrea del quadrat? Indica’n el domini.
c) Usa una escala adequada en cada eix i representa-la.
39 Una funció, f (x), és periòdica de període 5, i la seua TVM en [1, 3] és 1.
a) Què podem dir de la TVM de la funció en l’interval [6, 8]? I en l’interval [11, 13]?
b) Quina TVM té la funció en [3, 6]?
c) Quina és la taxa de variació mitjana de la funció en l’interval [4, 9]? I en [8, 43]?
40 En una piscina hi ha un trampolí a 6 m de l’aigua. Des d’allí, deixem caure una pilota rodant i cau a l’aigua a 10 m de la vertical del trampolí. La trajectòria és una paràbola amb vèrtex en el punt de caiguda.
a) Pren O com a origen i troba l’equació de la trajectòria de la pilota des que ix del trampolí fins que toca l’aigua.
41 Observa que el gràfic de y = f (x) talla l’eix X en x = –2, x = 0 i x = 4. Pren valors positius en els intervals
(–2, 0) i (4, +∞), i negatius en (– ∞, –2) i (0, 4).
Tenint això en compte, podem afirmar que:
• El domini de definició de la funció y = ()fx 1 és Á – {–2, 0, 4}.
• El domini de definició de la funció y = ()fx és [–2, 0] ∪ [4, +∞).
Raonant de manera similar, digues el domini de definició de y = ()fx 1 i y = ()fx , per a les següents funcions donades pels gràfics:
m
b) Dona’n el domini de definició.
10 m
a) Y X
a) Y X
Y X
Y X
b) Y X
d)
c) Y X
c) Y X
d)
b) Y X
42 Digues, raonadament, si és vertadera o falsa:
a) Si una funció és discontínua en un punt, aquest punt no pertany al domini de definició.
b) Si un punt no pertany al domini de definició d’una funció, aquesta no pot ser contínua en aquest.
c) Una funció periòdica sempre és contínua.
d) El pendent d’una recta és la TVM de qualsevol dels seus intervals.
e) La TVM d’una funció periòdica en qualsevol interval de longitud igual al període és 0.
f ) Si en una paràbola la TVM d’un interval és 0, el vèrtex està en el punt mitjà d’aquest interval.
g) Totes les funcions no lineals tenen almenys un màxim o un mínim relatiu.
h) Si una funció periòdica és decreixent en tot el seu domini, aleshores no és contínua.
Un autobús arranca de la parada i, a poc a poc, va guanyant velocitat. Àlvar, Beatriu i Carolina han quedat fora en el moment de l’eixida i cada un intenta accedir a l’autobús de manera diferent.
• Àlvar s’ha despistat i ha de córrer per aconseguir-ho.
• Beatriu, que està a 80 m per davant de l’autobús en el moment que aquest arranca, decidix esperar-lo i agafar-lo quan passe al seu costat.
• Carolina arriba tan tard que la porten amb motocicleta fins que aconseguix acostar-s’hi.
Aquestes són les representacions gràfiques d’aquests quatre moviments (el de l’autobús i els dels tres passatgers):



Podem fer-nos preguntes relatives a cada un d’ells per separat:
• Quant tarda l’autobús a recórrer els primers 80 m? I els següents 80 m? Quina distància ha recorregut als 10 s?
• A quina velocitat corre cada un dels viatgers?
Però més interessants són les preguntes que relacionen dos gràfics:
• Quant tarda l’autobús a arribar fins a Beatriu? Quina és la seua velocitat en aquest instant? Li resultarà possible a Beatriu pujar a aquesta velocitat?
• Quan i on aconseguix Àlvar abastar l’autobús? Quines velocitats porten l’autobús i Àlvar en aquest moment? Li resultarà fàcil accedir a l’autobús?
L’equació del moviment de l’autobús en els primers segons és , yt 1 48 2 = Comprova que l’equació del moviment de Carolina és y = 20(t – 18) i troba les equacions d’Àlvar i Beatriu.
Respon les mateixes preguntes que es van plantejar abans a partir de les quatre equacions.
Per esbrinar la velocitat dels passatgers, dividix l’espai recorregut entre el temps emprat. La velocitat de l’autobús en cada instant pots obtindre-la aproximadament.
1 Observa el valor d’una empresa des que es va fundar.
valor (milions d’euros) temps (mesos)
4 8 12 16 20 24
a) Quin n’era el valor en el moment de l’obertura?
b) A quant es va reduir el seu valor després de 4 mesos?
c) Quina és la TVM en l’interval [4, 12]? Dona el resultat en milers d’euros per mes.
d) Descriu si té màxims o mínims relatius.
e) Quina sembla la tendència per als pròxims mesos?
2 Observa el gràfic i respon:
a) Indica’n el domini i el recorregut.
c) Digues quins són els punts de tall amb els eixos.
d) Estudia’n el signe.
3 Troba el domini de definició d’aquestes funcions:
a) j (x) = x2 – 16 b) f (x) = x 48 + c) g (x) = x 7 1 –
d) h(x) = xx215 –2 + e) ()fx 1 f ) () () x h fx
4 Representa cada una d’aquestes rectes i, en el cas que no estiga donada per la seua expressió analítica, escriu-la.
a) y = 2x + 3 b) y = 2 – x 2 3
c) Passa per (–2, 1) i té pendent m = 1/2.











d) Passa pels punts (2, 5) i (4, 3).
e) Passa per l’origen de coordenades i és paral·lela a la recta y = 2x – 1.

f ) Funció de proporcionalitat que passa per (–3, 5).
g) Funció constant que passa per (2, –2).

5 Troba el vèrtex d’aquestes paràboles i representa-les:

a) y = x 2 2 – 2 b) y = x 2 + 4x – 5
c) y = (5 – x)(x + 1) d) y = –(x – 3)2 – 1
➜ anayaeducacion.es Resolucions d’aquests exercicis.
6 a) Troba la paràbola que passa per (0, 0), (1, 6) i (–1, −2).
b) Quin n’és el vèrtex? És un màxim o un mínim?
c) Indica en quin interval creix i en quin decreix.
7 Calcula la TVM de la funció d’equació y = x 2 + 4x – 5 en els intervals [–5, 2], [–2, 1] i [1, 2].
8 Amb un llistó de fusta de 3 metres de llarg, volem fabricar un marc per a un quadre.
a) Si la base del quadre mesurara 0,5 m, quant mesuraria l’altura? I la superfície?
b) Quina és l’expressió que ens dona la superfície, S, per a una base qualsevol, b ? Representa-la.
c) Per a quin valor de la base s’obté la superfície màxima? Quant val aquesta superfície?
9 Observa aquesta funció periòdica:
a) Quin n’és el període?
b) Troba els seus valors en: x = 0; x = –6; x = –3; x = 2; x = 4; x = 40; x = –40; x = 42.
10 En el quadrat ABCD, per a cada punt P de la diagonal AC es forma un rectangle.
a) Anomena x la distància de P a AB i escriu la funció que relaciona aquesta distància amb l’àrea del rectangle.
b) Digues el seu domini i representa-la.
SITUACIÓ D’APRENENTATGE
REFLEXIONA
Revisa els aspectes treballats i planteja solucions als problemes que es detecten.
Per a això, descarrega d’anayaeducacion.es la rúbrica corresponent, reflexiona de manera individual i compartix en grup.
Fes l’autoavaluació competencial inclosa en anayaeducacion.es.
Les nocions relatives a les distribucions bidimensionals sorgixen d’estudis realitzats en biologia.

• Adolf Quetelet (1796-1874) va ser el primer matemàtic interessat per les relacions estadístiques entre variables. Va realitzar algunes anàlisis sobre la relació entre diferents característiques de l’ésser humà. Va estudiar, per exemple, la relació entre l’edat i l’altura de les persones de 0 a 30 anys.

• Francis Galton (1822-1911) es va interessar per la influència que algunes característiques dels pares pogueren tindre sobre les dels fills, a instàncies del seu cosí Charles Darwin.
Com que no va considerar que fora factible experimentar amb persones i mancava de dades suficients per a extraure conclusions relatives a elles, va recórrer a l’experimentació amb pésols, estudiant la distribució dels pesos de dues generacions de llavors. En les seues conclusions va encunyar el terme regressió. L’índex de correlació li va servir per a descriure similituds degudes al parentiu.
• Karl Pearson (1857-1936) va continuar el treball de Galton. Per primera vegada va considerar i va descriure el significat del coeficient de correlació negatiu. Va dissenyar i va posar en pràctica mètodes matemàtics rigorosos amb els quals va poder usar la correlació per a inferir valors d’una variable a partir dels de l’altra. També va estendre l’estudi de la correlació a més de dues variables.

Què és una distribució bidimensional?
Un grup de biòlegs està estudiant una població de flamencs. Per a això, prenen mesures d’algunes de les seues característiques anatòmiques. En mesurar les envergadures de les ales el conjunt de resultats és una distribució estadística d’una variable (unidimensional). També és unidimensional la distribució dels ses pesos. Però si atenen conjuntament les dues variables (envergadura i pes), s’obté una distribució bidimensional. El grau de relació que existix entre aquestes s’anomena correlació.
Relació funcional i relació estadística. El rebut del gas
En el cost mensual del gas intervenen dos conceptes:
– Una quantitat fixa de 18 € al mes (lloguer de comptador i terme de potència).
– El consum, expressat en kWh, a 0,125 € el kWh.
En la taula següent apareixen dades corresponents a huit habitatges: el consum de gas, el cost del rebut i el nombre de persones que habiten en cada una:
Usuari: Matilde Kurgans Rodríguez
3,00 €
• Les variables x i y de la taula anterior complixen la relació y = 0,125x + 18. És una relació funcional, perquè donat un valor de x, s’hi obté, de manera exacta, un únic valor de y
• Les variables n i y també estan relacionades (a més persones a la casa, cal esperar que hi haja més despesa en consum de gas). No obstant això, no és una relació funcional. Coneixent el nombre de persones que habita en un habitatge no podem saber la despesa en gas. Aquest tipus de relacions estadístiques (no funcionals) s’estudiaran en la unitat present.
1. En l’exemple del consum del gas:
a) Observa en el gràfic (I) que el punt corresponent al primer habitatge està sobre la recta.
Comprova que també els altres.
b) D’un habitatge ens diuen que s’han consumit 500 kWh. Sabries calcular, exactament, a quant ascendix el rebut del gas?
c) Comprova que els punts senyalats en el gràfic (II) del marge són els sis primers de la distribució que relaciona n amb y Representa els restants.
Observa com, a la vista d’aquests punts, podríem aventurar-nos a dir alguna cosa sobre la despesa de gas en un habitatge amb 7 persones, però correríem el risc que fora erroni.
estudiants nota en M nota en F
A l’esquerra tens les notes de deu estudiants (a, b, c…) d’una classe en dues assignatures: Matemàtiques (M) i Física (F).

Hi ha dues variables. Cada individu té, per tant, dos valors associats: la seua nota en M i la seua nota en F. Per això es tracta d’una distribució bidimensional
Si representem cada estudiant mitjançant un punt les coordenades del qual són les seues respectives notes en M i en F, obtindrem el gràfic adjunt, anomenat núvol de punts o diagrama de dispersió. El punt (9, 6), per exemple, correspon a l’estudiant f , i el (2, 1), al i.
Observant les notes d’aquests estudiants, apreciem una clara relació entre aquestes: a notes baixes en una assignatura li corresponen, quasi sempre, notes baixes en l’altra; i això mateix passa amb les notes mitjanes o altes. Com a conseqüència d’això, els punts del núvol estan en una franja estreta. Direm que hi ha correlació entre les dues variables.
Podem traçar, a ull, una recta que s’ajuste al núvol de punts, com la que apareix en el gràfic de l’esquerra
Es diu recta de regressió i marca la tendència del núvol
En resum:
• Si a cada un dels individus d’un col·lectiu li assignem dos valors, corresponents a dues variables x i y, tenim una distribució bidimensional. La representació gràfica de la distribució dóna lloc a un conjunt de punts anomenat núvol de punts o diagrama de dispersió.
• Quan hi ha una certa relació estadística entre els valors de la distribució, es diu que hi ha correlació entre les variables. Aquesta correlació s’aprecia perquè el núvol de punts és relativament estret i, en aquest cas, es pot traçar una recta que s’hi adapta. Es diu recta de regressió.
1 Identifica els restants punts del diagrama de dispersió de l’exemple de les notes en matemàtiques i en física.
Vegem una altra distribució bidimensional: les notes dels mateixos deu estudiants (a, b, c…) en Matemàtiques, M, i en l’assignatura de Valencià, V. I comparem el núvol de punts d’aquesta distribució bidimensional MV amb la que hem vist en la pàgina anterior, M-F
És evident que la correlació entre M i F és més forta que la correlació entre M i V, ja que en la primera, els punts estan més estrets al voltant de la recta de regressió que en la segona
La correlació entre dues variables pot ser més o menys forta segons que els punts del núvol estiguen més o menys propers a la recta de regressió.
Una jugadora de bàsquet fa 10 llançaments a cistella des d’una distància d’1 m, altres 10 des de 2 m, i així successivament fins a 8 m. En cada cas ha pres nota del nombre d’encistellades. Si observem, en el marge, el núvol de punts, veiem que la correlació és forta però negativa, ja que a més distància, menys encistellades.
Una correlació és positiva quan en augmentar una variable, x, tendix a augmentar l’altra variable, y .
Una correlació és negativa quan en augmentar x, tendix a disminuir y
coRRelació positiva
coRRelació negativa
El signe de la correlació coincidix amb el signe del pendent de la recta de regressió
EXERCICI RESOLT
Aquesta és la taula dels 15 primers classificats en una lliga de futbol:
equip j g e p f c pts
A 34 22 5 7 59 37 71
B 34 20 9 5 53 30 69
C 34 20 8 6 62 28 68
D 34 17 8 9 53 47 59
E
a) En relacionar els punts obtinguts (Pts) amb els partits guanyats (G), és lògic que hi haja una correlació positiva (com més partits guanya un equip, més punts té). En representar-la, apreciem en el núvol de punts una correlació positiva forta.
F 34 14 9 11 43 35 51
G 34 12 11 11 50 41 47
H 34 13 8 13 42 43 47
I 34 11 11 12 41 35 44
J 34 12 8 14 45 47 44
K 34 10 13 11 42 44 43
L 34 10 12 12 42 38 42
M 34 11 8 15 34 47 41
N 34 11 7 16 44 60 40
O 34 11 6 17 30 44 39
Les columnes signifiquen:
• J: Partits jugats
• G: Partits guanyats
• E: Partits empatats
• P: Partits perduts
• F: Total de gols marcats (a favor)
• C: Total de gols rebuts (en contra)
• Pts: Punts obtinguts
Analitzar les següents distribucions bidimensionals, representar-les i, quan la correlació siga forta, traçar-hi la recta de regressió:
a) Pts - G b) Pts - P c) Pts - E
b) Si relacionem els punts obtinguts (Pts) amb els partits perduts (P), també és lògic que hi haja una correlació negativa (com més partits perda un equip, menys punts té).
Representem el núvol de punts i veiem que hi ha una correlació negativa forta.
c) Entre els punts obtinguts (Pts) i els partits empatats (E) no s’aprecia correlació, és a dir, tant hi ha molts o pocs empats entre els equips amb més punts o amb els quals tenen menys punts.
2 En cada una de les següents distribucions bidimensionals, intenta, sense representar-la, estimar si la correlació serà positiva o negativa, forta o feble. Després, representa-la mitjançant el núvol de punts, traça-hi a ull la recta de regressió i corrobora o modifica les teues estimacions.
➜ anayaeducacion.es Interpreta un núvol de punts.
a) G - F b) Pts - F
c) F - C
d) Pts - Posició en la taula
En la posició posar 1 al primer, 2 al segon, i així.
3 Busca, en un periòdic o en Internet, una taula com l’anterior, d’actualitat, i estudia distribucions com les que hem vist en aquesta pàgina.
Per estudiar alguns efectes de l’altitud, un grup de deu estudiants aficionats a la investigació científica ha dut a terme un experiment. Cada un d’ells ha pujat a una altura diferent, al (m), a la mateixa muntanya i ha obtingut mesures sobre:
pla. Nombre de plantes d’una certa espècie en 1 dam 2 . pRe. Pressió atmosfèrica, en mm. pul. Pulsacions per minut del mateix experimentador. Aquests són els resultatss: al pla pre pul
i. altuRa - nombRe de plantes No s’aprecia correlació.
Sembla que si s’haguera fet en l’interval d’altures 0 m a 750 m, la correlació hauria sigut bastant alta
I també que si ens quedem amb l’interval 700 m – 2 000 m, la correlació hauria sigut negativa i també alta.
1 343 12 650 89
1 550 3 630 80
1 820 0 610 85
2 184 2 580 92
Relacionar cada una de les tres variables amb l’altura sobre el nivell del mar, representant els núvols de punts i avaluant-ne la correlació.
La correlació és positiva i mitjanament forta, ja que els punts no estan molt estrets al voltant de la recta
És lògic que siga negativa, perquè en augmentar l’altitud, la pressió disminuïx.
La correlació és positiva i mitjanament forta, ja que els punts no estan molt estrets al voltant de la recta
Les pulsacions creixen a més altura, ja que hi ha menys oxigen i el cor necessita bombejar més quantitat de sang.
4 En les següents distribucions bidimensionals referents als teus companys i companyes de classe, estima si la correlació serà positiva o negativa, molt forta, forta, dèbil o quasi nul·la:
a) Mesura d’un pam - Mesura del peu.
b) Nombre d’hores setmanals d’estudi - Nombre d’hores setmanals mirant la televisió
c) Nombre d’hores setmanals d’estudi - Nombre de suspesos en l’última avaluació.
d) Estatura - Pes.
e) Nota en matemàtiques en l’últim examen - Nombre d’assignatures suspeses en l’última avaluació
f ) Pes - Nota en Matemàtiques
g) Alçada mitjana dels pares - Alçada de l’alumne.
h) Distància de casa al centre d’estudis - Temps mitjà que tarda a arribar-hi.
i) Nombre de llibres llegits a l’any - Nombre d’assignatures suspeses en l’última avaluació.
➜ Troba el coeficient de correlació de dos conjunts de dades.
Igual que per a la mitjana (x – ) o per a la desviació típica (σ), també hi ha una fórmula per a trobar el valor de la correlació d’una distribució bidimensional a partir de les dades de la taula. En aquest curs no la trobarem mitjançant la fórmula ni aprendrem a obtindre-la amb calculadora, però sí que ens familiaritzarem amb la gamma de valors que pot prendre

El valor de la correlació es denomina coeficient de correlació i es designa amb la lletra r.
El major valor de r es dóna quan els punts estan alineats (relació funcional). En aquest cas, el valor de r és 1 o –1, segons siga positiva o negativa. Per tant, els valors que pot prendre r oscil·len entre –1 i 1.
r = 1
Atenció ! En un núvol de punts, el valor del pendent de la recta de regressió (1, 1/3, –1/2, –2) no té res a veure amb el valor de la correlació. Només ens fixem en el signe del pendent (positiu o negatiu).
r = –1
Observa els núvols de punts següents i en cada un fixa’t en la relació entre el valor de r i com de «junts» o de «separats» es troben els punts respecte a la seua recta de regressió.
r = 0,99
r = 0,86
r = 0,59
r = –0,92
1 Els següents nombres són els valors absoluts dels coeficients de correlació, r, de les distribucions bidimensionals representades a la dreta: 0,75 0,47 0,92 0,97
Assigna cada un a la seua, canviant el signe quan convinga.
r = –0,77
r = –0,41
➜ anayaeducacion.es Coeficient de correlació.
Aquesta taula mostra algunes variables socioeconòmiques dels districtes del centre d’una gran ciutat.
Di rpc Est Pa Ca
A 16,5 14 58 22
B 17,5 12 42 22
C 21 12 35 7
D 25 11 33 9
E 26,5 12 34 13
F 20 9 54 27
G 23 12 34 24
H 12 8 60 28
I 10,5 7 67 34
J 10 4 72 29
K 10 4 79 37
L 13,5 8 57 24
M 15 9 51 23
Les columnes signifiquen:
• Di: Districte
• RPC: Renda per càpita (en milers d’euros)
• Est: Nre. de persones amb estudis universitaris per cada mil habitants
• Pa: Nre. de desocupats per cada mil habitants
• Ca: Nre. de cases d’apostes
Analitzar aquestes distribucions:
a) RPC - Ca
b) RPC - Est
c) RPC - Des
Sabent que les correlacions són, no respectivament, 0,76; –0,92 i –0,80, estimar quin correspon a cada distribució.
a) Podríem pensar que com més alta siga la renda per càpita major nombre de cases d’apostes hi haurà en el districte, no obstant això, és tot el contrari. Observa com en els districtes amb menys renda per càpita sol haver-hi més cases d’apostes que en aquells la renda dels quals per càpita és major. Com veus, la correlació és relativament alta i negativa.
b) Segons les dades, sembla que com més renda per càpita té el districte, hi ha més percentatge de persones amb estudis universitaris.
Atés que aquest fenomen no és una regla fixa, hi ha moltes excepcions (en barris amb rendes per càpita mitjanes –ni altes, ni baixes– el percentatge de persones amb estudis universitaris és igual o major que en els barris amb rendes altes), la correlació, en aquest cas, com pots apreciar-hi, no és tan alta.
c) En els barris més empobrits, desgraciadament, sol haver-hi major percentatge de desocupats.
Si observes la representació sembla clar que els punts estan bastant agrupats al voltant de la recta, per la qual cosa el coeficient de correlació és major.
nre. de cases d’apostes
cada mil habitants)
A la vista dels tres gràfics, la correlació corresponent a la primera (RPC - Ca) és –0,80; a la segona (RPC - Est), 0,76; i a la tercera (RPC - Des), –0,92.
2 Representa el núvol de punts i traça-hi a ull la recta de regressió de la distribució bidimensional Est - Des de l’exercici resolt anterior.
3 Indica quin d’aquests valors s’ajusta millor al valor de la correlació de la distribució de l’exercici 2. 0,80 –0,5 –0,97 0,2 –0,81 –1
3
A l’estimació que fem de la variable y per a un cert valor de x a partir de la recta de regressió l’anomenem y ^ .
Servix la recta de regressió per a estimar el valor de y que correspon a un nou individu del qual es coneix el valor de x ? Per descomptat que podem fer l’estimació, però, quin grau de fiabilitat té?
Sembla raonable pensar que com més forta siga la correlació, més fiable serà l’estimació, però, hi influïxen altres factors? Abans d’extraure conclusions definitives, vegem uns exemples.

|
La longitud d’un rail de via de tren a 0 °C és de 10 m. La taula del marge ens mostra els allargaments, A (en mm), a diferents temperatures, T (en °C). A partir de les dades de la taula, ens preguntem per l’allargament que s’obtindria per a temperatures de 30 °C i 100 °C.
El primer que fem és representar les dades en un núvol de punts. Observem en el marge que s’ajusten quasi exactament a una recta, recta de regressió traçada en blau. Per la qual cosa donem per cert que el coeficient de correlació és molt proper a 1 Obtenim l’equació de la recta de regressió. Com que passa per (0, 0) i (50, 6), la seua equació és y = 50 6 x → y = 0,12x.
Per a 30 °C obtenim y ^(30) = 3,6 mm, i per a 100 °C, y ^(100) = 12 mm. Les dues estimacions poden ser molt fiables, sobretot la primera, ja que el valor de la temperatura està en el tram dels valors controlats. En la segona estimació la temperatura està fora de l’interval de valors, però poc allunyada.
|Exemple 2
Les estatures, E (en cm), i els pesos, P (en kg), de 8 jugadors de bàsquet vénen donats en la taula del marge Volem estimar, mitjançant la recta de regressió, el pes d’un nou fitxatge l’alçada del qual és de 208 cm. Per a això, representem les dades i la recta de regressió i trobem gràficament el pes que correspon a 208 cm:
y ^(208) = 106
En aquest cas, la correlació no és tan alta com en l’anterior, per això, seria més prudent que diguérem que el pes que correspon a 208 cm és relativament proper a 106; per exemple, entre 102 kg i 110 k.
1 Estima, amb les dades de l’exemple 1, l’allargament corresponent a una temperatura de 45 ºC. Consideres fiable l’estimació?
2 Estima, amb les dades de l’exemple 2, el pes d’un nou jugador l’estatura del qual siga de 180 cm. Consideres fiable l’estimació?
L’estimació és molt millor com més gran és |r |.
L’estimació només s’ha de fer per a valors de x pròxims a les dadess.
La recta de regressió per a fer estimacions.
Tornem a l’exemple del grup d’estudiants de l’exercici resolt de la pàgina 221 en què es relacionava l’altura amb la pressió atmosfèrica.
Calcular l’equació de la recta de regressió suposant que passa pels punts primer i últim de la taula.
Estimar la pressió atmosfèrica que correspon a altures de 600 m, 3 000 m i 5 000 m.
Com de fiable és cada una de les estimacions?
Quines garanties d’èxit tenim quan fem estimacions basant-nos en la recta de regressió?
Com hem vist en els exemples anteriors, la seguretat en la previsió serà major com major siga el coeficient de correlació en valor absolut. És a dir:
• Si |r | és proper a 1 es podrà dir que, probablement, el valor real serà proper a la nostra previsió.
• Si |r | és xicotet, hem d’abstindre-nos de fer previsions.
Però encara per a valors grans de |r |, les previsions poden ser molt insegures si el punt de la recta de regressió sobre el qual fem l’estimació està molt allunyat dels punts coneguts. En l’exemple 1 de la pàgina anterior, considerem bastant segures les previsions d’allargament que vam fer per a temperatures de 30 °C i 100 °C. Molt menys segurs hauríem d’estar si, a partir de la fórmula, pretenguérem fer estimacions per a 500 ºC; probablement es cometrien errors importants.
Trobem l’equació de la recta de regressió suposant que passa pels punts (0, 760) i (2 184, 580):
Efectuem les estimacions: y ^(600) = 710,6 y ^(3 000) = 512,8 y ^(5 000) = 348
Estimem, quasi amb absoluta seguretat, una pressió atmosfèrica d’uns 710 mm a una altitud de 600 m. També és molt fiable una estimació
512 mm a una altitud de 3 000 m.
No obstant això, no hem de confiar en l’estimació de la pressió a 5 000 m, ja que les observacions de què disposem (en les quals es basen els nostres càlculs) són molt llunyanes a aquesta altitud.
3 Estima, mitjançant la recta de regressió, la pressió corresponent a 1 000 m. És fiable l’estimació?
➜ anayaeducacion.es Estimació amb la recta de regressió.
4 Estima la pressió corresponent a una altitud de 6 000 m. Comenta com de fiable és aquesta estimació.
Un mal ús de l’estadística
Imagina un titular de premsa com el que veus en el marge, i imagina també que en l’article corresponent s’al·ludix a un estudi estadístic del qual es deduïx una alta correlació entre el sou mitjà dels obrers durant una sèrie d’anys i la despesa en begudes alcohòliques en els mateixos anys. Podem, fins i tot, imaginar que aquest «estudi» s’aplica a un segment molt concret de la població (per exemple, els immigrants).
La manipulació que subjau en aquest suposat estudi és evident: es pretén donar la falsa idea que la millora dels sous es malgasta en begudes alcohòliques. La realitat és una altra: amb el pas del temps, i la inflació, pugen els sous així com els preus de tot (també els de les begudes alcohòliques).

A pesar d’exemples com aquest, per fortuna, l’ús que en general es fa de les estadístiques és veraç i constructiu.

Un bon estudi estadístic requerix moltes cauteles i afinar tant en el disseny de l’experiència com en la interpretació dels resultats obtinguts..
En les ciències experimentals i en les ciències socials es recorre amb freqüència a l’estadística en general i a la correlació en particular. Per exemple:
Per estudiar l’eficàcia d’un adob, se seleccionen diverses parcel·les amb característiques molt similars: tipus de terra, hores de reg, tipus de llavor, moment de la plantació, hores de sol… D’aquesta manera es podran relacionar les dues variables: quantitat d’adob-nivell de producció sense que el resultat es veja pertorbat per aquelles altres variables que estem controlant.
Vegem uns curiosos exemples en els quals hi ha una indubtable correlació entre dues variables i, no obstant això, la possible relació causa-efecte és molt discutible.
• És fàcil demostrar que els xiquets amb peus grans lligen millor que els que tenen peus xicotets. Influïx la grandària del peu en la capacitat per a la lectura?

Individus: 200 xiquets presos a l’atzar en un col·legi. Variables: x → grandària del peu; y → nivell de lectura.

• S’ha constatat que, als pobles d’una certa comarca, com més nius de cigonya hi ha a les teulades, més naixements de xiquets es produïxen. Tenen, per tant, rea a veure les cigonyes amb els naixements?
Individus: 43 pobles d’una certa comarca. Variables: x → nombre de cigonyes en les teulades; y → nombre de naixements a l’any.
• Un estudi va demostrar que en els anys en què més rogatives o processons hi havia per a demanar pluges, menys plovia. Serà que als sants els irriten les rogatives?
Individus: cada un dels últims 30 anys. Variables: x → nre. de rogatives demanant pluja al llarg de l’any; y → L/m2 de pluja recollits en l’any.
En el primer cas hi ha una variable intermèdia, l’edat, que es relaciona amb les altres dues, clar! En el segon, la variable intermèdia és la grandària dels pobles I en el tercer, la relació causa-efecte és la contrària: a menys pluja, més rogatives

nota en M nota en F

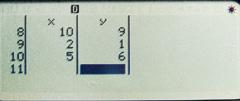

Al llarg d’aquesta unitat hem pretés que et familiaritzes amb la idea de correlació: per a què servix, on s’usa, com s’interpreta, etc. I, també, que sigues capaç de ferte a la idea del valor que pot prendre la correlació entre dues variables donades mitjançant un núvol de punts o una taula de valors. Aquesta destresa és el símptoma que domines amb desimboltura aquesta teoria. No obstant això, el valor de la correlació també es pot trobar amb la calculadora. Potser t’abellisca aprendre a fer-ho per comprovar algun dels exercicis resolts «a ull».
Posem la calculadora en menú «Distribució bidimensional» de la manera següent: menú → 6:Estadística → 2: y = a+bx (Distribució bidimensional).

Ara anem introduint valors en el caseller corresponent.
Vegem, per exemple com s’introduïxen els 10 parells de valors de la primera distribució que hem vist en aquesta unitat (mira-la en el marge).
En primer lloc, s’introduïx la dada corresponent al primer element de la variable x (Nota en Matemàtiques), que és just on està ombrejat.
Després d’escriure la dada, es prem la tecla = perquè s’inserisca en el seu lloc. A continuació, s’introduïx la segona dada, i així fins al dècim. Després, amb ajuda dels cursors, ens situem en el primer element de la variable y (Nota en Física) i fem el mateix amb les altres deu dades.
Una vegada completada la taula, per obtindre la correlació entre les dues variables, premem i seleccionem 4:Càlc regressió. Apareix en la pantalla el valor de r. En aquest cas, hem obtingut r = 0,876356092 ≈ 0,88.

La pantalla ens dona també els valors a i b, que són, respectivament, l’ordenada en l’origen i el pendent de la recta de regressió (observa el núvol de punts amb la seua corresponent recta de regressió en el marge).
Trobem ara amb la calculadora, en aquest altre exemple de la pàgina 271, la correlació dels llançaments a cistella amb les distàncies des de les quals es llança (veure taula en el marge).
Introduïm els 8 parells de dades i procedim de la mateixa forma que en l’exemple anterior per obtindre la correlació: r = –0,941583818 ≈ –0,94
En aquest cas, la recta de regressió és y = 10,9 – 1,5x.
➜
1 Ajuda’t de la calculadora per comprovar si està bé la correlació corresponent a cada núvol de punts de l’exemple de la pàgina 274. Fes el mateix amb les correlacions de l’exercici 1 de la mateixa pàgina.
2 Calcula el coeficient de correlació entre la longitud d’un raïl de via de tren i la temperatura de l’exemple de la pàgina 276. Comprova que la recta de regressió és, aproximadament, y = 0,12x
1 Temps a Vigo
Aquesta taula mostra la temperatura mitjana, T (en °C), la pluja, P (en mm), i les hores de sol, S, a Vigo al llarg d’un any:
7 125 104 f 10,4 106 93
mç 11,3 97 134
ab 13,1 78 166
mg 14 64 182
jn 17,1 25 197
jl 20,4 35 223
ag 18,3 38 263
s 18,7 84 181
o 16,9 135 151
n 13,4 155 83
d 11,5 131 60
Estudiar les tres possibles distribucions bidimensionals i assignar a cada una el valor de la seua correlació pres dels següents: r = –0,86 r = –0,59 r = 0,77
D’un moll pengem pesos. Aquesta taula ens dóna les masses, M (en g), i els allargaments, A (en cm):
a) Representar els punts i traçar la recta de regressió.
b) És raonable que la correlació siga 0,999?
c) Estimar els allargaments per a 40 g, 100 g, 250 g, 350 g i 3 kg.
Fes-ho tu Estima l’allargament per a masses de 190 g i 5 kg i indica la fiabilitat d’ambdues estimacions.
A la vista de les tres representacions gràfiques, podem assignar a cada distribució la seua correlació:
0,77
les Illes Cíes (Vigo) en aquest any:
Relaciona aquesta variable amb cada una de les anteriors mitjançant núvols de punts. Indica si la correlació és més o menys forta en cada una.
b) La correlació és 0,999, ja que els punts estan pràcticament sobre la recta.
c) Les estimacions per a masses de 40 g, 100 g, 250 g i 350 g són allargaments d’11 cm, 29 cm, 72 cm i 102 cm, respectivament. Tot i que la correlació és molt forta, no seria gens fiable l’estimació que férem per a una massa de 3 kg, ja que aquest valor està extraordinàriament allunyat del tram que controlem.
1 Per a cada un dels casos següents:
— Digues si es tracta d’una distribució bidimensional.
— Indica quines són les variables que es relacionen.
— Indica si es tracta d’una relació funcional o d’una relació estadística.
a) Grandària de l’habitatge - Despesa en calefacció.
b) Nombre de persones que viuen en una casa - Litres d’aigua consumits en un mes.
c) Metres cúbics de gas consumits en una casa - Cost del rebut del gas.
d) Longitud d’un pam en un estudiant - Número de calçat que usa.
e) Nombre de metges i metgesses per cada mil habitants - Índex de mortalitat infantil.
f) Velocitat amb què es llança una pilota cap amuntAltura que aconseguix.
2 En cada un dels apartats de l’exercici anterior, estima si la correlació serà positiva o negativa, forta o feble.
3 Aquests són els resultats que hem obtingut en mesurar les hores de son diàries de diversos bebés de diferents edats (en mesos):
edat 1 3 6 12 18 12 18 24
hores 16 15 14 13 14 14 12 13
a) És una distribució bidimensional? Quines són les variables que es relacionen? I els individus?
b) És una relació estadística o funcional?
c) Representa el núvol de punts.
d) Indica si la correlació és positiva o negativa, forta o feble.
e) Tria un dels valors següents per al coeficient de correlació: 0,81; –0,24; –0,79; 0,32.
4 Representa el diagrama de dispersió corresponent a la següent distribució i digues quin d’aquests valors pot ser el seu coeficient de correlació:
r = 1 r = –0,25 r = –1 r = –0,63
5 Els nombres 0,2; –0,9; –0,7 i 0,6 corresponen als coeficients de correlació de les següents distribucions bidimensionals. Assigna a cada un dels gràfics el seu: a) b)
6 a) Traça, a ull, en el quadern la recta de regressió corresponent a cada una de les següents distribucions bidimensionals:
b) Quins d’elles tenen correlació positiva i quins tenen correlació negativa?
c) Ordena de menor a major les correlacions de les quatre (en valor absolut).
En primer lloc, la que presenta correlació més feble, i, en últim lloc, aquella la correlació de la qual és més forta.
7 Una de les distribucions de l’exercici anterior presenta una relació funcional.
a) De quina es tracta?
b) Quina és l’expressió analítica de la funció que relaciona les dues variables?
8 Representa el núvol de punts d’aquesta distribució i estima quin d’aquests tres pot ser el seu coeficient de correlació: r = 0,98; r = –0,51; r = 0,57.
x 0 1 2 3 3 4 5 6 7 8 9 y 1 4 6 2 4 8 6 5 3 6 9
Després, pots comprovar el resultat, si et sembla, amb ajuda de la calculadora.
9 Les alçades de 10 xiques (xi ) i les de les seues respectives mares (yi ) són:
Representa els valors sobre paper quadriculat mitjançant un núvol de punts, traça-hi a ull la recta de regressió i digues si la correlació és positiva o negativa i més o menys forta del que esperaves.
10 Els coeficients de correlació d’aquestes distribucions bidimensionals són, en valor absolut: 0,55; 0,75; 0,87 i 0,96. Assigna a cada una el seu, canviant el signe quan siga procedent: a) b) c) d)
12 S’ha fet un estudi amb ratolins per veure els augments de pes (en g) mensuals que produïxen unes certes substàncies A, B i C (en mg diaris). Les dades obtingudes venen donades en aquesta taula:
augMent de pes si la substància és b
de pes si la substància és
11 Traça-hi la recta de regressió de les distribucions
a) i c) de l’exercici anterior i estima, en cada una, els valors que corresponen a x = 0 i a x = 10. En quin són més fiables les estimacions?
Els resultats negatius volen dir que en lloc d’augmentar, el pes disminuïx.
a) Representa el núvol de punts de cada distribució.
b) Indica, en cada cas, si la correlació és positiva o negativa i forta o feble.
c) A la vista dels resultats, fes un breu informe sobre les conseqüències d’administrar cada una de les substàncies.
13 Un ús excessiu del mòbil té alguns inconvenients; per exemple, influïx negativament en el son. S’ha preguntat a 10 joves pel nombre d’hores que usen el mòbil diàriament i les hores que solen dormir cada nit. Aquests són els resultats:
hores de Mòbil 1 2 5 3 2 5 3 1 2 4 hores de son 10 8 4 7 9 5 6 8 6 7
b) Dibuixa-hi, a ull, la recta de regressió.
c) Quin d’aquests valors és el coeficient de correlació?
d) Sobre la recta, estima el nombre d’hores de son per a un altre estudiant que usa el mòbil 4 h diàries.
Aquesta taula reflectix el nombre d’accidents de trànsit mortals en 15 províncies espanyoles (2018):
16 Les distàncies mitjanes dels planetes al Sol i els temps que tarden a fer una volta completa al voltant del mateix son:

a) Representa el núvol de punts, indicant si la correlació és positiva o negativa, forta o feble.
b) Quin d’aquests valors indica la correlació? 0,78; 0,98; –0,82; 0,43. Comprova-ho amb la calculadora.
c) Traça-hi a ull la recta de regressió i estima els accidents en via interurbana en una província que haja tingut 55 en via urbana.
15 Llig aquestes dades d’alguns països d’Àfrica (2020):
S’han pres com a unitats:
• La distància mitjana entre la Terra i el Sol: 1 UA = 150 milions de quilòmetres
• Un any terrestre.
a) Representa el núvol de punts i estima r.
b) Troba amb la calculadora el valor del coeficient de correlació i l’equació de la recta de regressió.
c) Si existira un planeta la distància del qual al Sol fora de 3,5 UA, quin seria el seu temps de revolució? Podríem estar segurs d’aquesta estimació?
d) Indica el temps de revolució d’un hipotètic planeta la distància del qual al Sol fora de 60 UA. Seria una estimació raonable?
17 Amb les dades del problema anterior, elabora una taula amb els cubs de les distàncies (d 3) dels planetes al Sol i els quadrats dels temps de revolució (t 2) i estudia la correlació entre els dos valors. És una relació funcional? (Busca en el llibre de física la tercera llei de Kepler).
a) Representa les dades i estima quin creus que és el seu coeficient de correlació: 0,99; –0,90; 0,85; –0,52.
b) Traça-hi a ull la recta de regressió i amb aquesta estima quina mortalitat infantil li correspon a un país l’esperança de vida del qual en nàixer fora de 75 anys.
c) Comprova amb la calculadora el coeficient de correlació i la recta de regressió.
Troba el període de Plutó, un objecte transneptunià (amb la categoria de planeta nan) que fins al 2006 es considerava el nové planeta del sistema solar. La seua distància al Sol és d’unes 40 UA.
En aquesta unitat hem aprés a dibuixar i interpretar la recta que millor s’emmotla a un núvol de punts (regressió lineal). No obstant això, hi ha casos en els quals el núvol de punts corresponent a una distribució bidimensional adopta formes com les que veus a la dreta (exponencial, logarítmica, polinòmica…).
Existixen mètodes de matemàtica superior que permeten trobar tant les equacions de la recta de regressió com les de les altres corbes, i valorar el grau d’aproximació del núvol de punts a la corba trobada.
Mesurem la desigualtat: corbes de Lorenz i índex de Gini
Els gràfics del marge s’anomenen corbes de Lorenz i representen la distribució de la riquesa entre la població de tres països diferents.
La verda passa pel punt (75, 10), això significa que en aquest país el 75 % més pobre posseïx un 10 % de la riquesa total. També passa per (96, 50), és a dir, el 4 % dels més rics posseïxen el 50 % de la riquesa total.
Analitza els tres gràfics representats i indica quin correspon a un país utòpic (tots tenen la mateixa riquesa); quin a un país molt injust, i quin, a un país moderadament just.
A vegades, en lloc de comparar amb gràfics, resulta més operatiu i més precís fer-ho amb nombres. Per aquest motiu va aparéixer el coeficient de Gini, que va ser una mesura desenvolupada per l’estadístic italià Corrado Gini el 1912.
L’índex de Gini és un nombre comprés entre 0 i 1: si fora 0, estaríem enfront d’una perfecta igualtat (tots tenen el mateix) i si fora 1, la desigualtat seria absoluta (un té tot i els altres, res).
Per a mesurar-ho podem usar les corbes de Lorenz. Si prenem l’àrea davall de la diagonal del quadrat com 1/2 (àrea d’un triangle rectangle de base i altura 1), el coeficient de Gini serà l’àrea que hi ha entre la bisectriu i la corba de Lorenz dividit per 1/2, és a dir, multiplicada per 2. El coeficient de Gini se sol expressar com un percentatge, d’aquesta manera se’l coneix com índex de Gini.
Espanya el 2021 tenia un índex de Gini de 33. Observa com estaven aleshores alguns altres països del món: Noruega: 25; Uruguai: 40; Brasil: 49; Tanzània: 40; Índia: 35; Estats Units: 42. Els països amb major i menor índex de Gini són, respectivament, Sud-àfrica amb 63 i Eslovàquia amb 23. Tin en compte que els menors índexs de Gini no coincidixen exactament amb els països més desenvolupats, ni els majors amb els menys desenvolupats, encara que segurament hi ha una certa correlació.
investiga
Busca en Internet i fes una taula amb dades, com, per exemple, PIB, nivell de felicitat, esperança de vida i índex de Gini, de països més i menys desenvolupats. Després, estudia la correlació que hi ha entre diversos parells de variables i trau conclusions.
1 De les següents distribucions bidimensionals, digues en quins casos la correlació és positiva, en quins és negativa i en quins no veus correlació:
a) Altura d’una persona - Grandària del seu gos.
b) Distància d’un viatge d’avió - Preu del bitllet.
c) Latitud d’un lloc de l’hemisferi nord - Temperatura mitjana anual.
d) Altura - Pressió atmosfèrica.
e) Profunditat de la mar - Pressió de l’aigua.
2 Associa a cada una de les distribucions bidimensionals de l’exercici anterior una d’aquestes correlacions:
r = –1 r = 0,83 r = –0,92 r = 0,23 r = 1





3 Associa cada núvol de punts amb una de les correlacions següents:
r = 1 r = –0,83 r = 0,97 r = 0,18
➜ anayaeducacion.es Resolucions d’aquests exercicis.
5 S’han anotat les hores d’estudi de 10 estudiants de 4t A per preparar un examen de Matemàtiques, i la nota obtinguda en aquesta prova. Aquests són els resultats:
a) Representa les dades en un núvol de punts.
b) Traça-hi a ull la seua corresponent recta de regressió.
c) Quin d’aquests valors és el coeficient de correlació?
r = 0,64 r = 0,96 r = –0,87 r = 0,25



d) Si et sembla, pots trobar el valor de r amb la calculadora.
6 Sabem que la recta de regressió corresponent a les dades de l’exercici anterior té l’equació següent:
y = 4,04 + 1,12x
a) Estima quina nota obtindria un estudiant que haguera dedicat 3,5 hores a preparar l’examen. I si no haguera estudiat res (0 hores)?
b) Consideres fiables aquestes estimacions? Explica per què.





7 La correlació entre les temperatures mitjanes mensuals d’una ciutat i el temps mitjà que els seus habitants es queden a casa els caps de setmana és de –0,89. Et sembla raonable aquest valor? Explica-ho.
Serà positiva o negativa la correlació entre la pluja caiguda mensualment a la Corunya i el temps mitjà d’estada a casa els caps de setmana?
4 Aquests són les altures (en cm) i la talla del peu dels components de l’equip de judo de l’institut.

SITUACIÓ D’APRENENTATGE
a) Quines variables que es relacionen en aquesta distribució bidimensional?
b) Representa el núvol de punts.

c) És una relació estadística o funcional?
d) Traça-hi a ull la recta de regressió.
Revisa els aspectes treballats i planteja solucions als problemes que es detecten.
Per a això, descarrega d’anayaeducacion.es la rúbrica corresponent, reflexiona de manera individual i compartix en grup.
Fes l’autoavaluació competencial inclosa en anayaeducacion.es.
Reservats tots els drets. El contingut d’aquesta obra està protegit per la llei, que estableix penes de presó, multes o ambdues ensems, ultra les indemnitzacions corresponents per danys i perjuís, per a aquells qui reproduïren, plagiaren, distribuïren o comunicaren públicament, en tot o en part, una obra literària, artística o científica, o la seua transformació, interpretació o execució artística fixada en qualsevol tipus de suport o comunicada per qualsevol mitjà sense autorització prèvia.
© GRUPO ANAYA, S.A., 2022 - C/ Valentín Beato, 21 - 28037 Madrid.