Mundua helburu: Matematika 2. DBH. Lagina

2

PROIEKTU DIGITALA DAUKA DBH

1. hiruhilekoa

MATEMATIKA

José Colera J., Ignacio Gaztelu A., Ramón Colera C.

Aurkibidea

Entrenatu problemak ebatziz 10

1. Antolatu informazioa eta planifikatu ebazpena

2. Adierazi datuak eskematikoki

3. Iritzira kalkulatu

4. Jokatu sistematikoki

Problemak

Ikasketa-egoera

Itzala uzten duten erronkak: Aritmetika 22

1 Z enbaki arruntak eta

1. Zenbaki arrunten multzoa

2. Zatigarritasun-erlazioa

3. Zenbaki lehenak eta konposatuak

4. Multiplo komunetako txikiena

5. Zatitzaile komunetako handiena

6. Zenbaki osoen Z multzoa

7. Eragiketak zenbaki osoekin

8. Zenbaki osoen berreketak

9. Zenbaki oso baten erro karratua

Ariketak eta problemak

Matematika-lantegia

Autoebaluazioa

osoak 24

4 P roportzionaltasuna

1. Arrazoiak eta proportzioak

2. Magnitude zuzenean proportzionalak

3. Magnitude alderantziz proportzionalak

4. Proportzionaltasun konposatuko problemak

5. Banaketa proportzionalen problemak

eta problemak

2 Zenbaki hamartarrak eta zatikiak 48

1. Zenbaki hamartarrak

2. Eragiketak zenbaki hamartarrekin

3. Zenbaki hamartarrarren erro karratua

4. Zatikiak

5. Zatikiak eta zenbaki hamartarrak

Ariketak eta problemak Matematika-lantegia

3 Eragiketak zatikiekin

1. Zatikiak batzea eta kentzea

2. Zatikiak biderkatzea eta zatitzea

3. Problemak zatikiekin

4. Berreketak eta zatikiak Ariketak eta problemak

6

1. Ehunekoak. Kontzeptua

2. Ehunekoen problemak

3. Bankuko interesak

4. Beste problema aritmetiko batzuk

7

1. Zertarako balio du aljebrak?

2. Adierazpen aljebraikoak

3. Polinomioak

4. Biderkadura nabarmenak

eta problemak

1. Ekuazioak: esanahia eta erabilgarritasuna

2. Ekuazioak: elementuak eta nomenklatura

3. Gaiak iraultzea

4. Ekuazio sinpleak ebaztea

5. Izendatzailedun ekuazioak

6. Lehen mailako ekuazioak ebazteko prozedura orokorra

7. Problemak ekuazioekin ebaztea

8. Bigarren mailako ekuazioak

9. Bigarren mailako ekuazioak ebaztea

Ariketak eta problemak

Matematika-lantegia

Autoebaluazioa

8 Ekuazio-sistemak

1. Bi ezezaguneko lehen mailako ekuazioak

2. Ekuazio linealen sistemak

3. Sistema linealak ebazteko metodoak

180

4. Problemak ebaztea ekuazio-sistemen laguntzaz

Ariketak eta problemak

Matematika-lantegia

Autoebaluazioa

Ikasketa-egoera. Matematikako notaren kalkulua 200

Ikasketa-egoera

Itzala

9 Pitagorasen teorema

1. Pitagorasen teorema

2. Alde bat zenbat den kalkulatzea

beste biak zenbat diren jakinik

3. Pitagorasen teoremaren erabilerak

Ariketak eta problemak

Matematika-lantegia

Autoebaluazioa

10 A ntzekotasuna

1. Antzeko irudiak

2. Planoak, mapak eta maketak

3. Irudi antzekoak eraikitzea

4. Talesen teorema

5. Triangelu zuzenen arteko antzekotasuna

6. Triangeluen antzekotasunaren erabilerak

Ariketak eta problemak

Matematika-lantegia Autoebaluazioa

11 G orputz geometrikoak

1. Prismak

2. Piramideak

3. Piramide-enborrak

4. Poliedro erregularrak

5. Poliedroen sekzio lauak

6. Zilindroak

7. Konoak

8. Kono-enborrak

9. Esferak Ariketak eta problemak

220

1. Bolumen-unitateak

2. Cavalieriren printzipioa

3. Prismaren eta zilindroaren bolumenak

4. Piramidearen eta piramide-enborraren bolumenak

5. Konoaren eta kono-enborraren bolumena

6. Esferaren bolumena Ariketak eta problemak

242

1. Funtzio kontzeptua

2. Goratzea eta beheratzea

3. Balio-taulen bidez emandako funtzioak

4. Ekuazioaren bidez emandako funtzioak

5. Proportzionaltasun-funtzioak: y = mx

6. Zuzen baten malda

7. Funtzio linealak: y = mx + n

8. Funtzio konstanteak: y = k

eta problemak

1. Gertakari aleatorioak

2. Gertakari baten probabilitatea

3. Probabilitateak esleitzea esperientzia erregularretan

4. Probabilitateak kalkulatzeko estrategia batzuk Ariketak eta problemak

Honelakoa da zure liburua

HASIERAKO UNITATEA: ENTRENATU PROBLEMAK EBATZIZ

Antolatu informazioa eta planifikatu ebazpena

2 m bider 3 m neurriko alfonbra bat laukizuzen-itxurako gela baten erdian jarrita dago, eta lurraren laurdena estaltzen du. Alfonbraren ertzik luzeenak hormatik

1 m-ra daude. Hormatik zenbatera daude ertzik laburrenak?

Problemak ebazteko estrategiak, horien bitartez soluzioa lortzeko, modu errazagoan.

Pentsatu eta saiatu ebazten. Unitatean zehar landutako estrategiak praktikatzeko problemak.

ITZALA UZTEN DUTEN ERRONKAK

Entrenatu problemak ebatziz

BENETAKO PROBLEMAK Ondo dakizunez, ariketa eta problema tipikoez gain (horiek ebazteko teknika zehatzak dagoeneko badakizkizu), beste problema zailago batzuk ere badira, nondik nora jo jakitea hain erraz ez dutenak, eta buruari eraginda ere ederki kostatzen direnak. Benetako problema horiei helduko diegu, hain zuzen ere, hurrengo orrialdeetan.

NOLA AURRE EGIN BENETAKO PROBLEMA BATI?

Hasteko: • Ulertu enuntziatua ondo. Baliteke hainbat bider irakurri behar izatea. Irudikatu behar baduzu, irudikatu. Egin ideiak antolatzen lagunduko dizun eskema bat. Zein dira datuak?, hau da, zer dakigu? (Beharrezkoak dira datu guztiak? Beharbada batzuek ez dute ezer gaineratzen). • Zer galdetzen da? Argi dago? Ikusten duzu zer erlazio dagoen datuekin?

10

EBAZPENA Ez dakizu nondik hasi? Saiatu iritzira kalkulatzen. Ebatzi kasu partikularren bat edo asmatu antzeko problema bat, baina datu errazagoak izango dituena. Saiatu gogoratzen antzeko problemaren bat landu duzun. Jokatu sistematikoki: erreparatu dakizunari eta tarteko urratsei, baina nora iritsi behar duzun begi-bistatik galdu gabe. Bidea zein den badakizula uste baduzu, aurrera! Eta ez atzera, ez aurrera, geratzen bazara, ez dio ardura. Zoaz berriro hasierara.

ETA AZKENEAN Soluzioa lortu duzunean, egiaztatu arrazoizkoa eta zentzuzkoa dela. Azaldu jarraitutako prozesua. Jarri izena urrats bakoitzean lortu duzunari. Hurrengo orrialde hauetan, estrategia horietako batzuk erabiliko ditugu.

→ a = 24 4 = 6 m 6 = 3 + 2x denez, orduan x = 1,5 m. Beraz, ertzik laburrenak hormatik 1,5 m-ra daude.

PENTSATU ETA SAIATU EBAZTEN

1 Makina batek 5 torloju egiten ditu minutuko. Astelehenetik ostegunera, 8 h eta 13 h bitartean eta 15 h eta 17 h bitartean egoten da martxan, eta ostiraletan, 8 h eta 14 h bitartean. 25 000 torlojuko eskariari erantzuteko, asteazkenean, maiatzaren 24ko goizeko 11tan jarri dute martxan makina. Noiz amaituko du eskaria?

Hasierako testutik abiatuta, ariketa eta problema bereizten ikasiko duzu, eta benetako problema bat ebazteko jarraitu beharreko oinarrizko urratsak zein diren ezarriko dituzu.

UNITATEAREN HASIERA

Erabili dakizuna eta ebatzi Malen eta Xabi bizikletan entrenatzera joan dira.

2 Motorzale bat etxetik irten da zita batera joateko. Kon turatu da 60 km/h-ra joanda ordu-laurden berandu iritsiko dela, baina 100 km/h-ra joanda ordu-laurden lehenago helduko dela. Etxetik zer distantziatara joan behar du? 60 km/h-ra joanda, zitaren lekutik zer distantziatara egongo da zitaren orduan? 100 km/h-ra joanda, behar baino zenbat kilometro gehiago egingo ditu abiadura horretan jarraituz gero? Beraz, zenbat kilometro gehiago egiten ditu

MULTZOA GEOMETRIA

9. Pitagorasen teorema

10. Antzekotasuna 11. Gorputz geometrikoak 12. Bolumenaren neurria

Urte asko daramatzazu irudi geometrikoak ikusten eta horiei buruz arrazoitzen. Planotik espaziora eta espaziotik planora joanda, jarraitu duzun ibilbide intuitibo eta kontzeptuala interesgarria eta aberasgarria izango zitzaizun ziurrenik. Ikasturte honetan, bide zoragarri horretan aurrera beste pauso bat egingo duzu. Pitagorasen teoremarekin topo egingo duzu berriro, eta haren aplikazioak praktikatuko dituzu planoan zein espazioan. Forma bera izateagatik erlazio interesgarriak partekatzen dituzten irudiei buruz arrazoituko duzu. Zer gertatzen da beren azalerekin?

Eta beren bolumenekin?

Eta ikusiko duzu ezagutzen dituzun gorputz geometrikoek propietate berri eta harrigarriak dituztela, adibidez, planoen bidez ebakitzen direnean.

202

Proportzionaltasuna

Proportzionaltasunaren kontzeptua kultura guztien aztarnetan agertzen da, hasieran problemekin eta egoera praktikoekin lotuta: hiru pegarrek bi zahagi betetzen dituzte; sei pegarrek lau betetzen dituzte...

Gaur egunera arte iritsi diren lehen zibilizazio haietako taulatxo edo papiro batzuek proportzionaltasunari buruzko problemak dituzte: salgaien trukea, banaketa proportzionalak... Adibidez, Rhindeko papiroan (K.a. 1650), gai desberdinei buruzko 87 problema matematiko aurkitu ziren dokumentu egiptoarrean, honako problema hau dago: 10 litro koipek urtebete iraun behar badute, zenbat gantz erabil daiteke egun batean? Antzinako Grezian, matematikariek proportzionaltasunari buruz hausnartu zuten, proportzionaltasunaren legeak eta erlazioak aztertuz. Hau da, egoera zehatzetatik independentea zen gorputz teoriko bat formalizatu eta eraikitzen hasi ziren.

Nahikotxo geroago, Errenazimentuan, merkataritzaren garapenak beste bultzada bat eman zion proportzionaltasunari, eta matematika komertzialaren aurrerapenean gauzatu zen: deskontuak, zorrak, epeak... Hilabetez 100 dobloi uzten badizkizut, 106 itzuliko dizkidazu. Urtebetez 200 dobloi eskatzen badizkidazu, itzuliko didazu... Gaur egun, matematikan, proportzionaltasunari buruzko egitura teoriko bat dago, adibide edo egoera partikularrak alde batera utzita, argi eta garbi erakusten dituena proportzionaltasunaren kontzeptuak, lege orokorrak eta erlazioak. Unitate honetan, eduki horien oinarriak aurkituko dituzu. Ondoren, goragoko mailetan, jakintza hori osatzen joango zara, eta eguneroko egoera askotan aplikatu ahal izango dituzu, hala nola: erostea, banatzea, aurreikustea, espekulatzea, zenbaketak egitea...

Malenek, tarteka, belozimetroari eta kilometro-kontagailuari begiratu dio, eta pedalei eragiten doala, kalkulu batzuk egiten aritu da. 1. Hogei minutuan 5 km egin baditut, eta erritmo berean jarraitzen badut, zer distantzia egingo dut ordubetean?

2. Zenbateko batezbesteko abiadura adieraziko du belozimetroak?

3. Abiadura horretan, zenbat denbora beharko dut kilometro bat egiteko? Eta auzoko herrira heltzeko, jakinda 12 kilometrora dagoela?

AURITZ 12 km

4. Zenbat denbora beharko du Malenen eta Xabiren bide beretik doan traktore batek auzoko herriraino heltzeko, bi lagunek daramaten abiadura halako hirura aurreratu baditu? Eta 60 km/h-ra aurreratu dituen furgoneta batek?

95 94

IKERKETA Ermita zaharberritzeko lanak Ermita bat zaharberritzeko eta egokitzeko lanei ekingo zaie, jakinda baseliza hori Maiderren eta Telmoren aitona-amonak bizi diren herriko ondare kultural, erlijioso eta afektiboa dela.

ERRONKA Eraikinaren zaharberritzea nola egin erabakitzeko nahitaezkoak diren aurretiazko kalkulu eta estimazioetako batzuk egitea:

Teilatuaren azalera. Estalki osoa konpontzeko. Hormen eta sabaien kanpoko eta barruko azalerak. Konpontzeko, pintatzeko, eta abar. Barruko bolumena. Instalatu beharreko berokuntza-sistema mota eta kostua estimatzeko.

Aurreko egoera adibide gisa proposatu da, baina irekia da eta nahi bezala egokitu daiteke. Adibidez: planteatu liteke barrualdea eta kanpoaldea ez bereiztea, emandako neurri batzuetatik abiatzea, beste eraikin eredu bat aukeratzea (ikastetxea, kiroldegia, etab.), maketa bat eraikitzea eraikuntza-joko

203

Ikaskuntza-egoera, eduki-multzo bakoitzerako bat; unitate horietan landu dituzun ezagutzak, trebetasunak eta jarrerak erabili beharra izango duzu, eta zure gaitasunak eskuratzen eta garatzen lagunduko dizute.

Unitate bakoitzaren hasieran, gai horretan ikasiko dituzun edukiei buruzko sarrera historiko labur bat ageri da.

Motibazioari eragiteko ariketasorta bat ere proposatzen da, aldez aurretik dituzun ezagutzak azaleratzeko.

Proiektuaren GAKOekin lotuta dauden baliabideak

Honelakoa da zure proiektu digitala

Proiektu honek ikasturteko eduki guztiak eskaintzen dizkizu, bai liburu digitalaren bidez, bai era askotako baliabideen bidez.

Ikasteko beste modu bat ezagutuko duzu, erraza, intuitiboa eta edozein plataforma eta gailurekin bateragarria.

Nola sartu?

Zure liburuko lehenbiziko orrialdearekin batera aurkituko dituzu proiektu digitalean sartzeko behar dituzun argibide guztiak.

Zenbaki arruntak zibilizazio guztietan erabili izan dira, Antzinarotik, eguneroko jarduerak errazteko: zenbatzea, neurtzea, merkaturatzea, eraikitzea... (matematika praktikoa). Grekoak haratago joan ziren: matematika landu zuten, jakitearen plazer hutsagatik (matematika teorikoa). Pitagorasek (K.a. vi mendea) eta bere dizipuluek oso modu berezian gurtu zituzten zenbakiak. Haien arabera, zenbakiek dena arautzen eta gobernatzen zuten: musika, planeten mugimendua, geometria… Zenbakien propietateak eta erlazioak aztertu zituzten, eta sailkapenak egin zituzten, geroago Euklidesek Elementuak izeneko sortaren vii liburuan jasotakoak.

Zenbaki negatiboak arruntak baino askoz geroago sortu ziren, merkataritzaren beharrei erantzuteko eta zeroa erabiltzen zuten zenbakikuntza-sistemak agertu ondoren. Izan ere, zeroa ezinbesteko elementua izan zen zenbaki negatiboak eraikitzeko. Dena dela, lehenengoz sistematizatuta mendean agertu ziren, idazki hinduetan, eguneroko gai eta jarduerei lotuta; hala nola edukitzea eta zor izatea alderatzeko. «Ezerezari kendutako zorra ondasun bihurtzen da.» (Zor bat barkatzen badizute, saldoak hobera egiten du.) «Ezerezari kendutako ondasuna zor bihurtzen da.» (Kredituan erosiz gero, saldoak

Erabili dakizuna eta ebatzi Lagun-kuadrilla bateko neska-mutil batzuk saskibaloi-ligako berdina egiten ari dira. Saskibaloi-liga hemezortzi talderen artean Talde bakoitzak orrialde bikoitz bat betetzen du albumean, eta mo, entrenatzailearen kromo bat eta klubaren ezkutuarena beste

1. Markelek 73 kromo zituen atzo albumean, eta errepikatutako tzeko. Gaur bosna kromoko hiru pakete erosi ditu, eta dagoeneko sei jokalari tokatu zaizkio. Gero, Maiderrekin 13 kromo trukatu dituenak eman, eta falta zaizkionak bildu. Erantzun ondorengo galdera hauei, agertzen diren ordenan, bakoitza eskuineko adierazpenen artean dagokionarekin. a) Zenbat kromo ditu guztira bildumak? b) Zenbat orrialde ditu albumak, kontuan izanda lehenengoan aurkibidea ageri dela, eta azkenekoan, kredituak?

c) Zenbat kromotan hobetu da gaur Markelen bilduma? d) Errepikatu gabeko zenbat kromo ditu orain? e) Errepikatutako zenbat geratu zaizkio? f) Zenbat falta zaizkio oraindik bilduma osatzeko?

2. Kermanek 42 kromo ditu errepikatuta, eta lodiera bereko piloak pilo bakoitzean 5 kromo baino gehiago eta 10 baino gutxiago modutan egin dezake?

3. Kermanek dio 250 kromo lortzen baditu, eta tartean errepikatutakorik albumeko 13 orrialde beteta izango dituela. Baina Ainara ez beharbada bakar bat ere ez duela beteta izango esan dio. Peruk rren batzuk beteko dituela, hiruzpalau, baina zail ikusten du Hiruretako zein uste duzu dabilela zuzen? Azaldu.

4. Nereari oso kromo gutxi falta zaizkio bilduma osatzeko, dagoeneko eta. Albumeko zenbat orri bete dituela gutxienez ziurtatu gehienez?

Zenbaki arruntak eta osoak

Zer eskaintzen dizu?

Era askotako baliabideak ditu; paperezko liburuaren erreprodukzioa baino askoz gehiago da.

Honakoak egiteko aukera izango duzu:

Ariketak egin

ariketa elkarreragileak

Aztertu

laburpen elkarreragileak, eskemak...

Ikasi

audioak, bideoak, Game Room-ak...

Ebaluatu

autoebaluazioa, portfolioa...

Nolakoa da?

Erantzun globala era askotako hezkuntza-ingurune baterako.

Intuitiboa

Zuk erraz erabiltzeko modukoa.

Gailu anitzekoa

Edozein gailu motatan (ordenagailuan, tabletan, smartphonean…) egokitzen eta ikusten da, pantailaren edozein tamaina eta bereizmenetan.

Deskargagarria

Aukera ematen du Interneteko konexiorik gabe lan egiteko eta gailu batean baino gehiagotan deskargatzeko.

Sinkronizagarria

Erabiltzaileak egiten dituen aldaketak berez sinkronizatzen dira, lan egiteko erabilitako edozein gailu konektatzean.

Unibertsala

Bateragarria da ikastetxeetan gehien erabiltzen diren sistema eragileekin, ikaskuntzako inguru birtualekin (IIB) eta hezkuntza-plataformekin (LMS).

Hasi aurretik

Ezagutu zure erronkak

IKASKETA-EGOERA

NOLAKOAK DIRA?

Ikaskuntza-egoerei buruzko bost proposamen dira:

• Ezagutza, jarrera eta trebetasunei eragiteko pentsatuak, eta jakintza-trukea eta zure gaitasunen garapena sustatuko dutenak.

• 2030erako Garapen Jasangarrirako Helburuekin konprometituta daudenak.

• Zure mundu errealetik eta esperientziatik hurbil daudenak eta errespetatuko dituztenak.

• Aurrera eraman beharko dituzun lanen eta jardueren egitura argi eta erraza ematen dutenak.

NOLA LAN EGINGO DUZU?

BLOKE BAKOITZAREN HASIERAN HAU AURKITUKO DUZU:

EDUKI-MULTZOA OSATZEN DUTEN UNITATEETAN AURKITUKO DUZUNA:

Ekuazio-sistemak problemak ebazteko tresna indartsuak dira. Aztertu arretaz ondoren eskaintzen zaizkizun adibideak. Antzeko problema motak ebazteko eredutzat har ditzakezun adibideak dira. 1. problema Sare eta Anje neba-arrebak dira. Kulunkan, Anjek lepoan 3 kiloko motxila badu orekatzen dira. Eta biak alde batera jarrita, motxilarik gabe, 87 kilo dituen aitarekin orekatzen dira. Zer pisu du bakoitzak? 3 kg 87 kg

tek 80 km-ra dagoen helmuga batera bidaltzeak 33,75 ERRONKA Edozein bidalketaren kostua kalkulatzeko gai izatea, jakinda zein diren pisua, gunerainoko distantzia eta enkargua betetzeko adostutako epea. Entrega estandarrek astebeteko epean kilometroko zer gastu duten kalkulatzea. Entrega estandarretan astebeteko epean kilo bakoitzeko kostua zein den kalkulatzea. Entrega-epeen aldaketengatik, ibilgailu bereziengatik, eta abarrengatik egon litezkeen karguak eta deskontuak kalkulatzeko prozedurak ezartzea. Kasu bakoitzeko kostu orokorra kalkulatzeko formulak diseinatzea. Aurreko egoera adibide gisa proposatu da, baina egoera irekia da eta, beraz, nahi beste aldaketa egin daitezke datuetan eta eskaeretan (enkargu-kopuruaren araberako eskaintzak eta beherapenak kontuan hartzea, etab.) zein

-

Problemak ebaztea ekuazio-sistemen laguntzaz 4 y + 3) + 2 + 3 87 = 84 y = 42 = 42 3 x = 45 IDEIAK FINKATZEKO

Problemako elementuak eta koefizienteak aljebraikoki identifikatuko ditugu.

kimikako nota kalkulatzeko, kontuan hartzen da azterketetako noten

xy yx 175 dd =+ * → laborategia →

ditugu. Multzo honetako 5. unitatean, horiek interpretatzeko eta horiekin lotutako egoerak ebazteko trebetasunak hobetuko dituzu.

MULTZOA PROPORTZIONALTASUNA 93 92 Magnitudeen proportzionaltasunarekin lotuta dagoen arrazoiketa matematikoa berezkoa da gure buruan, gure pentsamoldean: langilekopuru bikoitzak bi aldiz handiagoa den harresia eraiki du, edo harresi bera denboraren erdian altxatuko du; kontsumoa herena murrizten badugu, gastuak ere herena jaitsiko dira… Proportzionaltasuna arautzen duten arauen azterketan sakontzeak eta problema zehatzetan zuzen aplikatzeko moduak lantzeak nabarmen handitzen du mundu errealarekin lotutako problemak ebazteko gure ahalmena. Eguneroko bizipenak ehunekoen aipamenez josita

• Motibazioari eragiteko testu bat, blokea osatzen duten unitateekin erlazionatuta dauden erronken testuingurua azalduko dizuna.

• Ikaskuntza-egoera bati buruzko proposamena.

• Proposatutako egoerari dagokion ikaskuntzasegida.

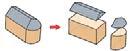
IDEIAK FINKATZEKO Aztertu eta ebatzi: Apalategiaren zer zati betetzen du kutxak etzanda dagoenean? Eta zutik dagoenean?

48 cm 42 cm 4 Hiru boligrafo eta errotuladore bat erosi, eta 6 € ordaindu ditut. Nire lagun Errosek 9,25 € ordainduta, bi boligrafo eta hiru errotuladore erosi ditu. Zenbat balio du boligrafo batek? Eta errotuladore batek? € € Fruta-dendan, bezero batek kilo bat laranja eta bi kilo sagar erosi, eta 3,90 ordaindu ditu. Beste bezero batek, hiru kilo laranja eta kilo bat sagar erosi, eta 5,70 € ordaindu ditu. Zenbat balio du kilo bat laranjak? Eta kilo bat sagarrek? 1 kg laranja € 1 kg sagar y € 6 Aurreko astean, zinemako bi sarrera eta poltsa bat krispeta 10 € ordaindu genituen. Gaur, zinemako lau sarrera eta hiru poltsa krispeta 22 € ordaindu ditugu. Zenbat balio du sarrera batek? Eta poltsa bat krispetak?

d d d d d dd d d d d d d d dd d d

• Multzo bakoitzeko erronka aurrera eramateko beharko dituzun oinarrizko ezagutzak ulertzen eta erabiltzen lagunduko dizuten ariketak.

ZEIN DIRA?

• Aldagaiak paketerian, bigarren eduki-multzorako.

• Matematikako notaren kalkulua, hirugarren edukimultzorako.

• Ermita zaharberritzeko lanak, laugarren eduki-multzorako.

• Gentzanek bidaia egin du, bosgarren eduki-multzorako.

UNITATEEN AMAIERAKO ORRIALDEETAN AURKITUKO DUZUNA:

AUTOEBALUAZIOA anayaharitza.es Ariketa hauen ebazpena.

EDUKI-MULTZOAREN AMAIERAN AURKITUKO DUZUNA:

40ren %

IRAKURRI ETA INFORMATU Interes konposatua Unitate honetan ikasi duzu zer irabazi (Interes → sortzen duen inbertitutako edo mailegatutako kapital batek K ), ehuneko jakin batean ezarrita dagoenean (Korritua → % k denbora tarte batez ). Interes mota horri sinplea deritzo, eta dirua erabiltzeko klabeak ikasten eta lantzen hasteko balio izan dizu. Baina praktikan, formula askoz konplexuagoak erabiltzen dira. Pentsatu K kantitate bat urteko % 3an ezarri dugula, eta bankuarekin hitzartu dugula irabaziak urte bakoitzaren amaieran batuko direla kontuan K (urtearen hasieran) K K 100 31 K + 0,3 K = 1,03 K (urtearen amaieran) Beraz, kontuan urte bakoitzaren amaieran dagoen dirua hasieran zegoenaren % 103 bihurtzen da. Hau da, urtez urte haziz doa. 1. urtea 2. urtea 3. urtea Kalkulatu buruz. a) 220ren % 50 b) 60ren % 25 c) 40ren % 75 d) 370en % 10 e) 500en % 20 40ren % 5 2 Osatu taula zure koadernoan. % 25 % 140 3/20 zk hamartarra 0,800,07 Kalkulatu. a) 80ren % 65 b) 3 200en % 4 c) 160ren % 16 d) 38ren % 150 e) 300en % 0,5 f) 50en % 1,5 4 Kalkulatu kasu hauetako bakoitzean. a) -ren % 50 = 12 b) -ren %25 = 8 c) -ren % 10= 7 d) -ren % 75= 30 e) -ren % 5 = 18 f) -ren % 20= 12 5 Ogi batek 2,50 € balio zuen, baina % 4 garestitu da gaur. Zenbat balio du orain? 6 36 000 litro zituen ur-depositu batetik % 15 gastatu dugu. Zenbat litro gelditzen dira? 7 30 neska-mutileko ikasgela batean, gaur 6 ez dira etorri. Zer ehunekok huts egin du? Ospitale batek 210 ohe ditu beteta, hau da, ohe guztien % 84. Zenbat ohe ditu ospitaleak guztira?

1,03 1,03 1,03 55 balio zuen jertse bat % 20 merkatu dute. Zenbat balio du orain? 10 Autobus-billetea % garestitu da gaur,

aurrena urtea urtea 3. urtea 1,03 (1,03) (1,03) Ikusten duzunez, zaildu egiten da kontua. Bada, pentsatu zer izango den irabaziak hilabetez hilabete batzen direnean kontuan. Dirua baldintza horietan ezartzen denean, interesa konposatua dela

eta orain 2,10 € balio du. Zenbat balio zuen atzo? 11 % 15 merkeago zegoen alkandora bat 34 € ordaindu dugu. Zenbat balio zuen beherapenaren aurretik? Kalkulatu zer interes sortzen duen 6 €-ko kapitalak, % 2,5ean ezarrita badago banku batean 8 hilabetez. 13 3,20 €/L balio duen oliba-olioaren zenbat litro nahastu behar dira 1,60 €/L balio duen ekilore-olioaren 150 litrorekin nahastearen prezioa 2,60 €/L izateko?

15 Txorrota batek orduan betetzen du depositu bat. Beste txorrota batek orduan betetzen du depositu bera. Zenbat denboratan beteko da depositua bi txorrotak aldi berean irekiz gero?

HAUSNARTU Berrikusi landutako alderdiak eta eman konponbidea hautemandako arazoei. Horretarako, deskargatu dagokion errubrika anayaharitza.es webgunetik, egin gogoeta banaka eta bateratze-lana taldean. PROBATU ZURE KONPETENTZIAK Egin anayaharitza.es webgunean ageri den konpetentzien autoebaluazioa.

• Zure gaitasunak ebaluatzeko proposamen bat, anayaharitza.es webgunetik jaitsi dezakezuna.

Ikerketa Paketeria-enpresa batek, bere zerbitzuen kostuak ezartzeko, kontuan hartzen ditu paketeen pisua, entrega-gunerainoko dagoen distantzia, entrega-epea, eta egin ditzakeen beherapenak edo aparteko motiboengatik egon litezkeen kargak.

Hasierako datuak Pakete bat garraiatu eta entregatzeko kostuaren barruan, kargu bat finkoa da, eta horri gehitu behar zaizkio pisuarekiko

proportzionala den kopuru bat eta entrega-distantziarekiko proportzionala den beste kopuru bat. Gainera, kostu osoa entrega-epearekiko alderantziz proportzionala da, eta epe hori izan liteke estandarra (7 egun) edo premiazkoa (24 h edo 48 h). Kargu finkoak honako taula honetan bildu dira: (kg) 5 kg edo gutxiago 5 kg baino gehiago eta 10 kg edo gutxiago 10 kg baino gehiago eta 20 kg edo gutxiago 20 kg baino gehiago 5 kg-ko pakete bat bidaltzeak, entrega-epea astebetekoa izanik eta entrega-gunea 25 km-ra egonda, 17,25 € balio du. Baina bezero beraren beste bidalketa berdin batek 80 km-ra dagoen helmuga batera bidaltzeak 33,75 Helburua Edozein bidalketaren kostua kalkulatu nahi dugu. Adibidez: Zenbat balioko du 6,5 kiloko pakete bat 32 km-ra dagoen toki batera 48 orduko epean bidaltzeak? lantegi dituzu, baita horiek Abiatu gaitezen 1. Kalkula dezagun, bi bidalketetako paketea berdina dela jakinda, zenbateko igoera dagoen kostuan kilometroko, entrega estandarretan, astebeteko epean. Hasierako datuak kontuan hartuz gero: Aldea km-etan → 80 25 55 Aldea kostuan 33,75 17,25 16,50 € 16,50 55 0,30 €/km Bidalketaren kostua 0,30 € igotzen da kilometroko. Kalkula dezagun kostuaren igoera kiloko, entrega estandarretan. 5 kilo 25 km-ra entregatuz gero, pisuari dagokion kostuaren zatia hau da: pisuari dagokion kargua = kostu osoa kargu finkoa distantziari dagokion kargua 17,25 25 0,3 3,75 € Kostuaren igoera kiloko hau da: 3,75 0,75 €/kg 3. Kalkula dezagun zenbat balio duen 6,5 kiloko pakete bat 32 km-ra bidaltzeak, astebeteko epean. Kostua 10 + 0,3 32 + 0,75 6,5 24,475 24,48 € Pakete hori bidaltzeak, aipatutako baldintzetan, 24,48 balio du. Kalkula dezagun zenbat balio duen 6,5 kiloko pakete bat 32 km-ra bidaltzeak, 48 orduko epean. – Zazpi eguneko epean 24,475 – Egun bateko epean → 24,475 7 – Bi eguneko epean (24,475 7) 85,6625 85,66 € Pakete bera 48 h-ko epean bidaltzeak 85,66 € balio du. 5. Praktikatu dezagun lortutakoa. a) Zenbat balioko du 45 kg-ko kaxa bat bilketa-tokitik 60 km-ra dagoen helbide batera bidaltzeak, tarifa estandarrarekin?

Enpresak % 7,5 kargatzen du bidalketa hozkailu-garraioan egin behar bada, eta % 5eko beherapena ezartzen du hilabete berean 10 zerbitzutik gora kontratatu badira. a) Zenbat kostatuko da hozkailu-furgoneta batean 15 kg-ko bidalketa bat egitea 25 km-ra eta 24 orduko epean? Eta 15 kg-ko pakete baten bidalketa estandar bat egitea, ohikoa den bezero batentzat, 25 km-ra eta aipatutako beherapenarekin? (I) C 15 + 0,3 D + 0,75 P (II) (15 0,3 + 0,75 2 (III) C (15 0,3 D + 0,75 P) 7 2

131 130

• Interesgarri iruditu dakizkizukeen beste erronka batzuk.

• Diagnosi-tresnen proposamenak, anayaharitza.es webgunetik jaitsi daitezkeenak.

• Amaierako profilaren errubrika, anayaharitza.es webgunetik jaitsi daitezkeenak, lortu dituzun gaitasunak autoebaluatzeko.

MULTZOA ARITMETIKA

1. Zenbaki arruntak eta osoak

2. Zenbaki hamartarrak eta zatikiak

3. Eragiketak zatikiekin

Zenbakiek gure mundu fisikoarekin lotutako fenomeno guztiak ordenatzeko, zenbatzeko, neurtzeko, kodetzeko… balio digute. Zenbakien arteko erlazioen bidez, gai gara unibertsoaren alderdi asko esploratzeko.

Eduki-multzo honetan zehar, gure zenbakikuntza-sistema hamartar-posizionala aztertuko duzu, eta eraginkortasun txikiagoko baina historikoki garrantzitsuak izandako beste zenbakikuntza-sistema batzuekin alderatu ahal izango duzu.

Zatigarritasuna eta haren aplikazioak berrikusiko dituzu, zenbakiak, zatikiak eta hamartarrak hobeto ulertu eta maneiatuko dituzu, eta problemak ebazteko behar bezala erabiliko dituzu.

ERRONKA

Lo-orduak

Pertsonek bizitzan zehar egiten dituzten lo-orduen azterketa/analisia egin nahi da: guztira lo egindako orduak, etapa bakoitzaren garrantzia…

Jarraibiderako iradokizunak

• Egin plan bat: erabaki zer jakin nahi den eta zer urrats egingo diren hori lortzeko.

• Zehaztu zer iturritatik eta zer modutan lortuko dituzun datuak: inkestak, argitalpenak, adituei kontsulta eginda, senideei eta abar.

• Aukera bat da Interneten bilatzea zenbat lo-ordu gomendatzen dituzten adituek. Baina, kasu honetan, interesgarriagoa da, agian, norberaren bitartekoekin ikertzea eta, edonola ere, zure emaitzak adituen emaitzekin alderatzea.

• Balioztatu pertsona batek bere bizitza osoan eta bizitzako etapa bakoitzean zenbat ordu lo egiten dituen.

• Zehaztu gutxienez hiru etapa; adibidez, haurtzaroa, gaztaroa eta zahartzaroa. Dena dela, hori baino banaketa zorrotzagoa ere egin liteke.

• Ezarri etapa batzuen eta besteen arteko erlazioak eta konparazioak, eta egin beharrezko datuak lortzeko modua emango dizuten kalkuluak.

• Azaldu modu argian prozesuak, emaitzak eta ondorioak.

oharra: Ikasturte honetan planteatuko diren ikaskuntza-egoera guztiak bezala, hasiera batean irekia izango da, bai jarraitu beharreko planari dagokionez, bai beharrezko informazioa lortzeko moduari dagokionez.

Gainera, jarraibide edo iradokizun batzuk proposatuko dira egoera horien garapena gidatzeko.

Multzoaren amaieran, 90. eta 91. orrialdeetan, ebatzi beharreko eredu bat aurkituko duzu, adibide gisa, zuk gauzatu duzunarekin alderatzeko.

1

Zenbaki arruntak eta osoak

Zenbaki arruntak zibilizazio guztietan erabili izan dira, Antzinarotik, eguneroko jarduerak errazteko: zenbatzea, neurtzea, merkaturatzea, eraikitzea... (matematika praktikoa). Grekoak haratago joan ziren: matematika landu zuten, jakitearen plazer hutsagatik (matematika teorikoa).

Pitagorasek (K.a. vi. mendea) eta bere dizipuluek oso modu berezian gurtu zituzten zenbakiak. Haien arabera, zenbakiek dena arautzen eta gobernatzen zuten: musika, planeten mugimendua, geometria…

Zenbakien propietateak eta erlazioak aztertu zituzten, eta sailkapenak egin zituzten, geroago Euklidesek Elementuak izeneko sortaren vii. liburuan jasotakoak.

Zenbaki negatiboak arruntak baino askoz geroago sortu ziren, merkataritzaren beharrei erantzuteko eta zeroa erabiltzen zuten zenbakikuntza-sistemak agertu ondoren. Izan ere, zeroa ezinbesteko elementua izan zen zenbaki negatiboak eraikitzeko.

Dena dela, lehenengoz sistematizatuta vii. mendean agertu ziren, idazki hinduetan, eguneroko gai eta jarduerei lotuta; hala nola edukitzea eta zor izatea alderatzeko.

«Ezerezari kendutako zorra ondasun bihurtzen da.» (Zor bat barkatzen badizute, saldoak hobera egiten du.)

«Ezerezari kendutako ondasuna zor bihurtzen da » (Kredituan erosiz gero, saldoak okerrera egiten du.)

Europan arabiarrei esker zabaldu ziren zenbakiok, baina oso astiro eta ez toki guztietan berdin. xvi mendetik aurrera, matematikari askok teorizatu zuten zenbaki negatiboei buruz, baina zenbaki oso negatiboen multzoa matematikako gai moduan xix mendearen amaieran onartu zen azkenean.

Erabili dakizuna eta ebatzi

Lagun-kuadrilla bateko neska-mutil batzuk saskibaloi-ligako kromoen bilduma berdina egiten ari dira. Saskibaloi-liga hemezortzi talderen artean jokatzen dute.

Talde bakoitzak orrialde bikoitz bat betetzen du albumean, eta jokalarien 16 kromo, entrenatzailearen kromo bat eta klubaren ezkutuarena beste bat izaten ditu.

1. Markelek 73 kromo zituen atzo albumean, eta errepikatutako 27 kromo, trukatzeko. Gaur bosna kromoko hiru pakete erosi ditu, eta dagoeneko bazeuzkan sei jokalari tokatu zaizkio. Gero, Maiderrekin 13 kromo trukatu ditu: errepikatuta dituenak eman, eta falta zaizkionak bildu.

Erantzun ondorengo galdera hauei, agertzen diren ordenan, eta lotu erantzun bakoitza eskuineko adierazpenen artean dagokionarekin.

a) Zenbat kromo ditu guztira bildumak?

b) Zenbat orrialde ditu albumak, kontuan izanda lehenengoan aurkibidea ageri dela, eta azkenekoan, kredituak?

c) Zenbat kromotan hobetu da gaur Markelen bilduma?

d) Errepikatu gabeko zenbat kromo ditu orain?

e) Errepikatutako zenbat geratu zaizkio?

f) Zenbat falta zaizkio oraindik bilduma osatzeko?

2. Kermanek 42 kromo ditu errepikatuta, eta lodiera bereko piloak egin nahi ditu, pilo bakoitzean 5 kromo baino gehiago eta 10 baino gutxiago jarrita. Zenbat modutan egin dezake?

3. Kermanek dio 250 kromo lortzen baditu, eta tartean errepikatutakorik ez badu, albumeko 13 orrialde beteta izango dituela. Baina Ainara ez dago ados, eta beharbada bakar bat ere ez duela beteta izango esan dio. Peruk uste du bakarren batzuk beteko dituela, hiruzpalau, baina zail ikusten du gehiago betetzea. Hiruretako zein uste duzu dabilela zuzen? Azaldu.

4. Nereari oso kromo gutxi falta zaizkio bilduma osatzeko, dagoeneko 310 ditu eta. Albumeko zenbat orri bete dituela gutxienez ziurtatu dezakegu? Eta gehienez?

MAIEN ZENBAKIKUNTZA

Ikertu maien zenbakikuntza-sistemaren arauak eta ezaugarriak. → 238

Zenbaki arrunten multzoa 1

Gauzak banaka zenbatzeko erabiltzen ditugun zenbakiak zenbaki arruntak dira.

Zenbaki arrunten multzoa N letraren bidez adierazten da, ordenatuta dago eta hasiera du, baina ez azkenik.

N = {0, 1, 2, 3, 4, …}

Zenbaki arruntak zenbakien zuzenean adierazten dira, ordenan.

01234 10

Zenbaki Sistema Hamartarra

Zibilizazioaren hasieratik, kulturek zenbaki arruntak adierazteko hainbat era asmatu dituzte: zenbaki-sistemak dira.

E H U 2 3 8

20 · (2 · 5 + 1) + 1 · (3 · 5 + 3) = = 220 + 18 = 238

egiptoar erromatar hamartar zenbakikuntza zenbakikuntza zenbakikuntza

Guk Zenbaki Sistema Hamartarra (ZSH) erabiltzen dugu. Sistema hori Indian asmatu zen eta arabiarrek zabaldu zuten Mediterraneoan zehar, islamiar mundua hedatu zen denboran, viii. mendetik aurrera.

ZSH posizioaren araberakoa da, zifraren balioa zenbakiaren barruan hartzen duen kokapenak zehazten duelako. hmm mm em hm m e h u

KONTUAN IZAN

Hasieran, eskuetako hatzen bidez zenbatzen zen; 10 zenbakia horregatik da zenbakikuntza-sistema hamartarraren oinarri.

Eta hamartarra da, edozein ordenatako hamar unitatek goragoko hurrengo ordenako unitate bat balio dutelako.

1 EM = 10 HM = 100 M = 1 000 E = 10 000 H = 100 000 U

Ondorioz, zenbaki bat ondorengo adibide honek erakusten duen moduan deskonposatu daiteke (deskonposizio polinomikoa):

Sistema hirurogeitarra

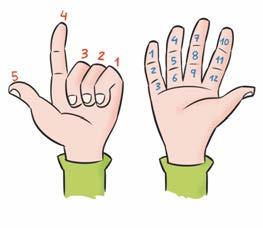
Guk hamarnaka zenbatzen dugun eran (sistema hamartarra), beste kultura batzuek hirurogeinaka zenbatu dute historian zehar (sistema hirurogeitarra).

Oinarritzat 60 zenbakia hartzea, seguruenik, zenbatzeko falangeak erabiltzetik dator: hatz erakusle, erdiko hatz, eraztun-hatz eta hatz txikiko 12 falangeak, eta, gidari gisa, hatz lodia. Eta zenbatutako kopurua beste eskuko hatzekin eramango zuten.

❚ denbora eta angeluen anplitudea neurtzea

Gaur egun, sistema hirurogeitarra denbora eta angeluen anplitudea neurtzeko erabiltzen da. Magnitude horietan, unitate bakoitza beheragoko ordenako 60 unitatetan zatitzen da.

5 x 12 = 60

➜ anayaharitza.es Pasatu forma konplexura edo ez-konplexura.

Kontuan izan minutuen eta segundoen idazkerak ez direla berdinak bi magnitudeetan.

❚ adierazpen konplexuak eta ez-konplexuak

Gogoratu magnitude bati dagozkion kantitateen neurriak adieraz daitezkeela aldi berean hainbat unitate erabiliz (forma konplexua) edo unitate bakar bat erabiliz (forma ez-konplexua).

forma konplexua forma ez-konplexua 1 h 15 min

IDEIAK

Kopiatu koadernoan eta osatu.

1 Pasatu forma konplexura. a)

2 Pasatu 2 ordu eta 24 minutu forma ez-konplexura (lehenengo, minututara, eta, gero, segundotara).

a) Minututara pasatzea: 2 h 24 min → (2 · 60 + 24) min = (… + …) min = … min

b) Segundotara pasatzea: 2 h 24 min → (2 · 3 600 + 24 · …) s = … s

ZATIGARRITASUNA 24 7 3 3 (zehaztugabea)

24 ez da zatigarria 7rekin 24 8 0 3 (zehatza)

24 zatigarria da 8rekin

Zatigarritasun-erlazioa 2

Multiploak eta zatitzaileak

Bi zenbaki zatigarritasun-erlazioaren bidez lotuta daude, horien arteko zatidura zehatza baldin bada.

|Adibidea

60 20 0 3 → 60 zatigarria da 20rekin. 60multiploada20rena 20zatitzaileada60rena )

a : b zatiketa zehatza izanez gero

a da b-ren multiploa.

b da a-ren zatitzailea.

Zenbaki baten multiploak eta zatitzaileak

• Zenbaki baten multiploek kopuru zehatzean hartzen dute zenbaki hori barnean, eta jatorrizko zenbakia edozein zenbaki arruntekin biderkatuz lortzen dira.

|Adibidea

12ren lehenengo multiploak kalkulatuko ditugu:

12REN MULTIPLOAK

12 · 1 = 12 12 · 2 = 24

• Zenbaki batek infinitu multiplo ditu.

• Zenbaki guztiak dira bere buruaren eta unitatearen multiploak. → a · 1 = a a da 1en multiploa. a da a-ren multiploa.

• Zenbaki baten zatitzaileak kopuru zehatzean daude zenbakiaren barruan eta, ondorioz, zatiketa eginda zatidura zehatza lortzen da.

12 · 3 = 36 12 · 4 = 48

KONTUAN IZAN

n · 0 = 0

• Zeroa edozein zenbakiren multiplotzat jo genezake.

• Zeroak multiplo bakarra du: zeroa bera.

|Adibidea

12ren zatitzaileak kalkulatuko ditugu: 12 1 12 2 12 3

➜ anayaharitza.es Aurkitu

12ren zatitzaileak honako hauek dira: 1 - 2 - 3 - 4 - 6 - 12

Kontuan izan pareka doazela.

• Zenbakiek zatitzaile-kopuru mugatua dute.

• Zenbakiek bi zatitzaile dituzte gutxienez: zenbaki bera eta unitatea.

zenbaki baten multiploak eta zatitzaileak.

KONTUAN IZAN

Zenbait zifratako zenbaki bat beti deskonposatu daiteke 2ren multiplo bat gehi unitateen zifra eginda: 128 = 120 + 8

2ren multiploa unitateen zifra

KONTUAN IZAN

Bederatziz osatutako zenbakiak 3ren eta 9ren multiploak dira. 9 = 9 · 1 = 3 · 3

Zenbaki baten multiploen propietate bat

Konturatzen bazara, 12ren bi multiplo batuz gero 12ren beste multiplo bat lortzen da. 36 + 60 = 12 · 3 + 12 · 5 = 12 · (3 + 5) = 12 · 8 = 96

a zenbaki baten bi multiploren batura a-ren beste multiplo bat da m · a + n · a = (m + n) · a

Zatigarritasun-irizpideak

Zatigarritasun-irizpideak dira zenbaki bat 2, 3, 5, 11… eta abarren multiploa den azkar jakiteko modua ematen diguten erregela oso sinple batzuk.

❚ zatigarria 2rekin, 5ekin eta 10ekin

Ondo dakizun moduan:

• Zenbaki bat 2ren multiploa da 0, 2, 4, 6 edo 8 amaitzen bada.

• Zenbaki bat 5en multiploa da 0 edo 5 amaitzen bada.

• Zenbaki bat 10en multiploa da 0 amaitzen bada.

❚ zatigarria 3rekin eta 9rekin

Zenbait zifra dituen zenbaki bat beti deskonposatu daiteke honela: 3ren multiplo bat, gehi zenbakiaren zifren batura:

99

3ren multiploa zifren batuketa

Lehenengo batugaia 3ren multiploa da. Goian ikusitako propietatearen arabera, zenbakia 3ren multiploa izateko, bigarren batugaiak ere hala izan behar du. Eta arrazoitze berak balio du 9ren multiploetarako.

• Zenbaki bat 3ren multiploa da bere zifren batura 3ren multiploa bada.

• Zenbaki bat 9ren multiploa da bere zifren batura 9ren multiploa bada.

❚ zatigarria 11rekin

Zenbait zifratako zenbaki bat beti deskonposatu daiteke honela: 11ren multiplo bat, gehi zenbakiaren zifrak txandaka batu eta kenduta lortutako emaitza:

649 = 600 = 594 + 6 40 = 44 – 4 9 = 9 = (594 + 44) + (6 – 4 + 9)

11ren multiploa zifren arteko batuketa eta kenketa

Lehenengo batugaia 11ren multiploa da. Zenbakia 11ren multiploa izateko, bigarren batugaiak ere hala izan behar du.

Zenbaki bat 11ren multiploa da toki bakoitietan dituen zifren batura ken toki bikoitietan dituen zifren batura (edo alderantziz) 11ren multiploa bada.

Laukiko zenbaki guztiak 11ren multiploak dira. Egiaztatu.

IDEIAK FINKATZEKO

Kopiatu koadernoan eta osatu.

1 Zatitu, behatu eta erantzun.

a) 173 zenbakia 19ren multiploa da? Eta 228?

b) 43 zenbakia 516ren zatitzailea da? Eta 743?

2 Idatzi 13ren lehenengo zortzi multiploak.

42ren

4 Bilatu 14 zenbakiak 250 eta 300 bitartean dituen multiplo guztiak.

14 zenbakiak 250 eta 300 bitartean dituen multiploak hauek dira: …

PRAKTIKATZEKO

1 Idatzi:

a) 20ren lehenengo bost multiploak.

b) 20ren zatitzaile guztiak.

2 Idatzi 36 zenbaki laukizuzen moduan adierazteko modu guztiak.

36 = 3 · 12

Zer erlazio dute 36ren zatitzaileekin?

3 Idatzi biderkadura moduan 60 duten zenbaki-pare guztiak.

4 Bilatu:

a) 7 zenbakiak 100 eta 150 bitartean dituen multiploak.

b) 13 zenbakiak 1 000ren ostean duen lehenengo multiploa.

5 Kopiatu, inguratu bikoitiak eta zirriborratu 3ren multiploak.

45 - 67 - 74 - 96 - 143 - 138 - 251 - 309 - 488

6 Zer balio hartu behar ditu a zifrak zenbakia izan dadin:

5 6 a

a) 2ren multiploa. b) 3ren multiploa.

c) 5en multiploa. d) 9ren multiploa.

7 Hautatu, zenbaki hauen artean, 11ren multiploak. 286 611 913 1 804 2 444 3 333

8 Behatu, kopiatu koadernoan eta osatu.

a) n = 2 · 3 · k = 6 · k → n zenbakia 2ren eta 3ren multiploa bada, 6ren multiploa ere bada.

b) m = 2 · 5 · k = 10 · k → m zenbakia 2ren eta 5en multiploa bada, …en multiploa ere bada.

c) p = 15 · k = 3 · 5 · k → p zenbakia 15en multiploa bada, …ren eta …en multiploa ere bada.

GOGORATU

Hona hemen 100 baino txikiagoak diren zenbaki lehenak:

2 3 5 7 11

13 17 19 23 29

31 37 41 43 47

53 59 61 67 71

73 79 83 89 97

Zenbaki lehenak eta konposatuak 3

• Zenbaki batzuk biderketa moduan deskonposatu daitezke: 40 = 8 · 5 = 2 · 2 · 2 · 5

40 zenbaki konposatua dela diogu.

• Beste zenbaki batzuek bi zatitzaile baino ez dituzte, adibidez, 13 zenbakiak: 13 eta 1. Beraz, ezin dira biderketa moduan gehiago deskonposatu: 13 = 13 · 1 → ezin da gehiago deskonposatu

13 zenbaki lehena dela diogu.

• Biderkagaietan deskonposatu ezin den zenbakia zenbaki lehena da.

• Zenbaki lehenak bi zatitzaile baino ez ditu: bere burua eta unitatea.

• Lehenak ez diren zenbakiak konposatuak dira.

Zenbaki bat biderkagai lehenetan deskonposatzea

GOGORATU

Zenbaki bat biderkagai lehenetan deskonposatzeko, jokatu ordenan, zatigarritasun-irizpideak kontuan izanda.

2rekin zatigarria 594 2 297 3

3rekin zatigarria 99 3 33 3

11rekin zatigarria 11 11 1

➜ anayaharitza.es Gogoratu nola deskonposatu behar diren zenbakiak biderkagai lehenetan.

PRAKTIKATZEKO

Zenbaki bat biderkagaietan deskonposatzean, deskonposizio-maila handiena lortzen da biderkagai guztiak lehenak direnean.

Zenbaki bat biderkagai lehenetan deskonposatzeko, komeni da ordenan jokatzea. Aztertu nola deskonposatu dugun 594 zenbakia:

1 Honako zenbaki hauen artean, bereizi lehenak eta konposatuak.

3 Deskonposatu honako zenbaki hauek biderkagai lehenetan.

a) 84 b) 130 c) 160 d) 594

e) 720 f ) 975 g) 2 340 h) 5 220

4 Eragiketarik egin gabe, idatzi faktorizatuta:

2 Kopiatu eta osatu biderkagaietan deskonposatzeko prozesuak.

a) 12ren hiru multiplo = 22 · 3.

b) 75en zatitzaile guztiak = 3 · 5 · 5.

5 Kontuan hartuz m = 22 · 3 · 5 eta n = 23 · 3 direla, idatzi:

a) m-ren eta n-ren hiru multiplo komun.

b) m-ren eta n-ren hiru zatitzaile komun.

PRAKTIKATZEKO

1 Kalkulatu buruz.

Multiplo komunetako txikiena 4

, b, c, … zenbait zenbakiren multiplo komunetako txikiena da zenbaki horiek dituzten multiplo komunen artean txikiena, eta honela idazten da: m. k. t. (a, b, c, …).

Multiplo komunetako txikiena kalkulatzea

m.k.t. (a, b, c, …) lortzeko, a, b, c… biderkagai lehenetan deskonposatu eta biderkagai guztiak erabiliko ditugu, baina ezinbesteko aldiz.

|Adibidea

200 eta 240 zenbakien multiplo komunetako txikiena kalkulatuko dugu.

• Aurrena, zenbakiak biderkagai lehenetan deskonposatuko ditugu:

200 = 23 · 52 240 = 24 · 3 · 5

• Gero, biderkagai egokiak hautatuko ditugu: 200en guztiak, 240ren guztiak, baina ezinbesteko aldiz soilik:

Zenbait zenbakiren multiplo komunetako txikiena kalkulatzeko:

• Deskonposatu zenbakiak biderkagai lehenetan.

• Aukeratu biderkagai lehen guztiak, komunak direnak eta ez direnak, eta jaso horietako bakoitza aukeran duen berretzaileetan handienera.

EBATZITAKO PROBLEMA

Kiroletako oinetakoak egiten dituen lantegi batean, 100 cm-ko kordoiak dituzten zapatilak egiten dituzte (200 cm pareak) eta 120 cm-ko kordoiak dituzten botak (240 cm pareak).

Zer luzera izan behar du karrete batek, baldin eta zapatila-pareen kopuru zehatz bati eta bota-pareen kopuru zehatz bati kordoia jartzeko adina izan behar badu?

m. k. t. (200, 240) = 1 200

Soluzioa: Karreteak 1 200 cm (12 m) izan behar ditu, edo kantitate horren multiploren bat: 12 - 24 - 36… metro.

a) m. k. t. (3, 5) b) m. k. t. (6, 11)

c) m. k. t. (10, 15) d) m. k. t. (10, 25)

e) m. k. t. (30, 40) f ) m. k. t. (50, 100)

2 Kalkulatu.

a) m. k. t. (18, 24) b) m. k. t. (21, 35)

c) m. k. t. (72, 90) d) m. k. t. (90, 120)

e) m. k. t. (60, 72, 90) f ) m k t. (50, 75, 100)

3 Supermerkatu batean 36 egunean behin egiten dute inbentarioa, eta apalategiak 24 egunean behin berrantolatzen dituzte. Zenbatean behin bat egiten dituzte bi lanak egun berean?

4 Bi gurpilek, 24 hagineko batek eta 32 hagineko beste batek, akoplatuta biratzen dute engranaje bat martxan jartzean. Zenbat bira emango ditu gurpil bakoitzak berriz ere hasierako posizioan geratu arte?

Zatitzaile komunetako handiena 5

a, b, c, … zenbait zenbakiren zatitzaile komunetako handiena da zenbaki horiek komunean dituzten zatitzaileen artean handiena, eta honela idazten da:

z. k. h. (a, b, c, …)

Zatitzaile komunetako handiena kalkulatzea

z. k. h. (a, b, c, …) kalkulatuko dugu a, b, c, … zenbakiek komunean dituzten biderkagai lehen guztiak erabilita.

|Adibidea

200 eta 240 zenbakien zatitzaile komunetako handiena kalkulatuko dugu.

• Lehenengo, zenbakiak biderkagai lehenetan deskonposatuko ditugu: 200 = 23 · 52 240 = 24 · 3 · 5

• Gero, komunean dituzten biderkagaiak hautatuko ditugu:

= 23 · 5 = 40

Zenbait zenbakiren zatitzaile komunetako handiena kalkulatzeko:

• Deskonposatu zenbakiak biderkagai lehenetan.

• Aukeratu komunak diren biderkagai lehenak soilik, eta jaso horietako bakoitza aukeran dauden berretzaileetan txikienera.

EBATZITAKO PROBLEMA

Arotz batek 200 cm-ko ohol bat eta 240 cm-ko beste bat zati berdinetan ebaki nahi ditu, ahalik eta handienetan eta ohol zatirik utzi gabe. Zer luzera izan behar dute ebakitako zatiek?

z. k. h. (200, 240) = 40

Soluzioa: Zatiek 40 cm-ko luzera izan behar dute.

PRAKTIKATZEKO

1 Kalkulatu buruz.

a) z. k. h. (4, 6) b) z. k. h. (6, 8)

c) z. k. h. (5, 10) d) z. k. h. (15, 20)

e) z. k. h. (18, 24) f ) z. k. h. (50, 75)

2 Nekazari batek 248 cm × 250 cm neurriko arlo bat erabiliko du hazitoki moduan, laukizuzen-itxurakoa. Baina karratuetan banatuta nahi du, denak berdinak eta ahalik eta handienak.

Zer neurri izango du hazitokiko karratu bakoitzak?

➜ anayaharitza.es Praktikatu m.k.t. eta z.k.h. kalkulatzea.

3 Kalkulatu.

a) z. k. h. (24, 36) b) z. k. h. (28, 42)

c) z. k. h. (63, 99) d) z. k. h. (90, 126)

e) z. k. h. (165, 275) f ) z. k. h. (360, 450)

4 Olio-biltegi baten jabeak 885 litro oliba-olio eta 705 litro ekilore-olio gorde nahi ditu, txanbil berdinak eta ahalik eta handienak erabilita. Zer edukiera izan behar dute txanbilek denak beteta egoteko eta oliorik sobera ez geratzeko?

KONTUAN IZAN

Zenbakiaren balio absolutua zenbakien zuzenean zerora duen distantzia da.

Zenbaki osoen Z multzoa 6

Zenbaki arrunten N multzoa hartuz gero, eta zeroa alde batera utzita, +a elementu bakoitzeko zeinu negatiboko –a elementu bat eransten badugu, multzo berri bat lortuko dugu; multzo horri zenbaki osoen multzoa esaten zaio matematikan, eta Z letraren bidez adierazten da.

Zenbaki osoen balio absolutua eta aurkakoa

• Zenbaki oso baten balio absolutua da zeinua kenduta lortzen den zenbaki arrunta, eta bi barraren artean idatziz adierazten da.

balio absolutua

• Zenbaki oso baten aurkakoa da balio absolutu bera baina kontrako zeinua duen beste zenbaki oso bat.

|Adibideak

(+7)-ren aurkakoa → (–7) (–7)-ren aurkakoa → (+7)

Z multzoko ordena

Zenbaki osoen multzoa zenbakien zuzenean adierazten da, ordenan: …–6–5–4–3–2–10+1+2+3+4+5+6…

Argi ikusten denez, zuzeneko edozein zenbaki da ezkerrera dituenak baino handiagoa, eta eskuinera dituenak baino txikiagoa.

• Edozein zenbaki positibo zero baino handiagoa da, eta zeroa, edozein zenbaki negatibo baino handiagoa.

ADIBIDEAK (–7) < 0 < (+1)

(–12) < (–9) < (–2)

PRAKTIKATZEKO

• Zenbaki negatiboak zenbaki positiboen kontrara ordenatzen dira. Zenbaki negatibo handiena da balio absoluturik txikiena duena.

1 Idatzi honako zenbaki hauetako bakoitzaren balio absolutua eta aurkakoa.

a) –3

b) +8

c) –11

d) +23 e) –37 f ) +60

2 Ordenatu txikitik handira.

–7, –13, +8, –1, +1, +5, 0, +10, –24

3 Zuzena ala okerra?

a) Edozein zenbaki oso arrunta ere bada.

b) Edozein zenbaki arrunt osoa da.

c) Negatiboek baino ez dute aurkakoa.

d) Aurkako bi zenbaki osok balio absolutu bera dute.

Eragiketak zenbaki osoekin 7

Zenbaki osoen batuketa eta kenketa

Gogoratu zenbaki osoen adierazpenak ebazteko oinarrizko erregela batzuk:

Bi zenbaki batzeko (kentzeko):

• Zeinu bera badute, balio absolutuen batuketa egin eta batugaien zeinua jartzen da. +4 + 7 = +11 –3 – 6 = –9

• Zeinu desberdina badute, balio absolutuen kenketa egin eta balio absolutu handiena duenaren zeinua jartzen da. – 4 + 10 = +6 +3 – 8 = –5

Bi zenbaki positibo eta negatibo baino gehiagoren arteko eragiketak egiteko, bi bide jarraitu ditzakegu:

• Eragiketak urratsez urrats egitea, agertzen doazen neurrian.

• Positiboak alde batetik eta negatiboak bestetik multzokatzea. Gero, eragiketak egitea.

IDEIAK FINKATZEKO

1 Irakurri, hausnartu eta osatu koadernoan.

a) Aurrena 5 € eta gero 3 € eman badizkidate 8 € gehiago ditut.

+5 + 3 = …

c) 0 € eman badizkidate, eta 3 € kendu badizkidate … € … ditut.

+10 – 3 = …

2 Kopiatu eta osatu, adierazpen bera bi modutan ebazteko.

3 – 7 – 5 + 8 = – 5 + 8 = + 8 = …

PRAKTIKATZEKO

1 Kalkulatu buruz.

a) 5 – 7 b) 2 – 9 c) –1 – 9

d) –12 + 17 e) –22 + 10 f ) –12 – 13

2 Ebatzi.

a) 10 – 3 + 5 b) 2 – 9 + 1 c) 16 – 4 – 6

d) 7 – 10 – 3 e) –7 – 8 + 5 f ) –5 + 8 + 4

g) –8 + 2 + 3 h) –1 – 2 – 3 i) –7 – 3 – 4

b) Aurrena 4 € eta gero 2 € gastatu baditut … € gutxiago izango ditut.

–4 – 2 = …

d) 3 € jaso baditut eta 7 € gastatu, … € … ditut.

+3 – 7 = …

3 – 7 – 5 + 8 = 3 + 8 – 7 – 5 = +11 – = …

3 Kalkulatu.

a) 3 – 7 + 2 – 5

b) 2 – 6 + 9 – 3 + 4

c) 7 – 10 – 5 + 4 + 6 – 1

d) – 6 + 4 – 3 – 2 – 8 + 5

e) 12 + 5 – 17 – 11 + 20 – 13

f ) 16 – 22 + 24 – 31 + 12 – 15

Eragiketak zenbaki osoekin

➜ anayaharitza.es Eragiketak zenbaki osoekin.

Batuketak, kenketak eta parentesiak

Hausnartu bankuko kontu korronte bati buruzko honako enuntziatu hauei buruz:

• 25 €-ko txeke bat ingresatu badut, 25 € gehiago egongo dira. → +(+25) = +25

• 18 €-ko faktura bat ordaidu badut, 18 € gutxiago egongo dira. → +(–18) = –18

• 55 €-ko txeke bat atera badut, 55 € gutxiago egongo dira. → –(+55) = –55

• 60 €-ko faktura bat atzera bota badut, 60 € gehiago egongo dira. → –(–60) = +60

• Aurrean plus zeinua duen parentesi bat kentzean, parentesi barruko zeinuak ez dira aldatzen.

• Aurrean minus zeinua duen parentesi bat kentzean, parentesi barruko zeinuak aldatzen dira: plusen tokian minus, eta minusen tokian plus. |Adibideak

+ 8 – 2) = –3 + 8 – 2

+ 8 – 2) = +3 – 8 + 2

IDEIAK FINKATZEKO

3 Kopiatu eta osatu, adierazpen bera bi modutan ebazteko.

a) Aurrena, parentesiak kenduta.

(7 – 10) – (2 – 5 + 4 – 9) = 7 – – 2 + – + = 7 + 5 + 9 – – – = 21 – = …

b) Aurrena, parentesi barruko eragiketak eginda.

(7 – 10) – (2 – 5 + 4 – 9) = (–3) – ( – ) = (–3) – (– ) = …

PRAKTIKATZEKO

4 Kendu parentesiak eta kalkulatu.

a) (–3) – (+4) – (–8)

b) –(–5) + (–6) – (–3)

c) (+8) – (+6) + (–7) – (–4)

d) –(–3) – (+2) + (–9) + (+7)

5 Ebatzi, parentesiak kenduta.

a) (4 – 9) – (5 – 8)

b) –(1 – 6) + (4 – 7)

c) 4 – (8 + 2) – (3 – 13)

d) 12 + (8 – 15) – (5 + 8)

e) 22 – (7 – 11 – 3) – 13

6 Ebatzi, aurrena parentesi barruko eragiketak eginda.

a) (2 – 6) + (4 – 8)

b) (8 – 10) – (12 – 7)

c) 15 – (2 – 5 + 8) + (6 – 9)

d) (8 – 6) – (3 – 7 – 2) + (1 – 8 + 2)

e) (5 – 16) – (7 – 3 – 6) – (9 – 13 – 5)

7 Ebatzi bi modutan, adibidean bezala.

• 10 – (13 – 7) = 10 – (+6) = 10 – 6 = 4

10 – (13 – 7) = 10 – 13 + 7 = 17 – 13 = 4

a) 15 – (12 – 8)

b) 9 – (20 – 6)

c) 8 – (15 – 12) d) 6 – (13 – 2)

e) 15 – (6 – 9 + 5) f ) 21 – (3 – 10 + 11 + 6)

8 Kalkulatu.

a) 7 – [1 + (9 – 13)] b) –9 + [8 – (13 – 4)]

c) 12 – [6 – (15 – 8)] d) –17 + [9 – (3 – 10)]

e) 2 + [6 – (4 – 2 + 9)] f ) 15 – [9 – (5 – 11 + 7)]

9 Ebatzi.

a) (2 – 9) – [5 + (8 – 12) – 7]

b) 13 – [15 – (6 – 8) + (5 – 9)]

c) 8 – [(6 – 11) + (2 – 5) – (7 – 10)]

d) (13 – 21) – [12 + (6 – 9 + 2) – 15]

e) [4 + (6 – 9 – 13)] – [5 – (8 + 2 – 18)]

f) [10 – (21 – 14)] – [5 + (17 – 11 + 6)]

Zenbaki osoak biderkatzea

Bi zenbaki osoren biderkadura zenbat den kalkulatzeko, kontuan hartu biderketa bat dela batugai beraren batuketa bat:

(+3) · (– 6) = Hiru bider batuko dugu (– 6):

+(– 6) + (– 6) + (– 6) = – 6 – 6 – 6 = –18

(–3) · (– 6) = Hiru bider kenduko dugu (– 6):

–(– 6) – (– 6) – (– 6) = +6 + 6 + 6 = +18

Hala ere, azkar biderkatzeko, honako erregela hau aplikatzen da:

zeinuen erregela

Bi zenbaki osoren biderkadura:

• Positiboa da, biderkagaiek zeinu bera izanez gero.

• Negatiboa da, biderkagaiek zeinu desberdinak izanez gero.

(+) : (+) = +

(-) : (-) = +

(+) : (-) = -

(-) : (+) = -

PRAKTIKATZEKO

10 Biderkatu.

Zenbaki osoak zatitzea

4) = –24 (– 4) · (+8) = –32

Zenbaki osoen arteko zatiketak zenbaki arrunten arteko zatiketak dituen erlazio berberak ditu.

(+4) · (+6) = +24 (+24) : (+4) = +6

(– 4) · (– 6) = +24 (+24) : (– 4) = – 6

(+4) · (– 6) = –24

(–24) : (+4) = – 6

(–24) : (– 6) = +4

Zatiketan, biderketan bezala aplikatzen da zeinuen erregela..

a) (+10) · (–2) b) (– 4) · (–9)

c) (–7) · (+5) d) (+11) · (+7)

11 Erreparatu adibideei eta biderkatu adierazitako bi moduetan.

• (–3) · (+2) · (–5) = (– 6) · (–5) = +30

(–3) · (+2) · (–5) = (–3) · (–10) = +30

a) (–2) · (–3) · (+4) b) (–1) · (+2) · (–5)

c) (+4) · (–3) · (+2) d) (– 6) · (–2) · (–5)

12 Egin honako zatiketa hauek.

a) (–18) : (+3) b) (–15) : (–5)

c) (+36) : (–9) d) (–30) : (–10)

e) (–52) : (+13) f ) (+22) : (+11)

13 Kopiatu, osatu eta konparatu. Zer ikusten duzu?

(+60) : [(–30) : (–2)] = (+60) : [+15] =

[(+60) : (–30)] : (–2) = [ ] : (–2) =

14 Kalkulatu zenbat balio duen x-k kasu bakoitzean.

a) (–18) : x = +6 b) (+4) · x = –36

c) x · (–13) = +91 d) x : (–11) = +5

➜ anayaharitza.es Praktikatu zenbaki osoen biderketa eta zatiketa.

Eragiketak

zenbaki osoekin

Eragiketa konbinatuak

Aztertu eragiketak zer ordenan egin ditugun honako adierazpen konbinatu hauen balioak kalkulatzeko:

(–18) : (11 – 9 – 5) + 5 · (6 – 8)

• Aurrena, parentesi barruko eragiketak. ⎯⎯→ (–18) : (–3) + 5 · (–2)

• Gero, biderketak eta zatiketak. ⎯⎯→ (+6) + (–10)

• Amaitzeko, batuketak eta kenketak. ⎯⎯→ 6 – 10 = – 4

IDEIAK FINKATZEKO

4 Kopiatu honako adierazpen hau, osatu eta lortu bere balioa:

(6 – 9 + 2) · (–5) + 3 · (2 – 6) + 4 = = ( ) · (–5) + 3 · ( ) + 4 = = ( ) + ( ) + 4 = – + 4 =

PRAKTIKATZEKO

15 Kalkulatu, adibideetan bezala.

• 15 – 8 · 3 = 15 – 24 = –9

• 18 : 6 – 5 = 3 – 5 = –2

a) 18 – 5 · 3 b) 6 – 4 · 2

c) 7 · 2 – 16

e) 5 – 30 : 6

d) 18 – 15 : 3

f ) 20 : 2 – 11

16 Kalkulatu, adibidean bezala.

• 21 – 4 · 6 + 12 : 3 = 21 – 24 + 4 = 25 – 24 = 1

a) 20 – 4 · 7 + 11 b) 12 – 6 · 5 + 4 · 2

c) 15 – 20 : 5 – 3 d) 6 – 10 : 2 – 14 : 7

e) 5 · 3 – 4 · 4 + 2 · 6 f ) 7 · 3 – 5 · 4 + 18 : 6

17 Erreparatu adibideari eta kalkulatu kasu hauek.

• (–3) · (– 4) + (– 6) · 3 = (+12) + (–18) = 12 – 18 = – 6

a) 5 · (–8) – (+9) · 4

b) 32 : (–8) – (–20) : 5

c) (–2) · (–9) + (–5) · (+4)

d) (+25) : (–5) + (–16) : (+4)

e) (+6) · (–7) + (–50) : (–2)

f ) (+56) : (–8) – (–12) · (+3)

(6 – 9 + 2) · (–5) + 3 · (2 – 6) + 4

( ) (–5) + 3 · ( ) + 4

( ) + ( ) + 4 – + 4 =

18 EBATZITAKO ARIKETA (– 2) · [ 11 + 3 · ( 5 – 7) ] – 3 · ( 8 – 11 )

= = (–2) · [11 + 3 · (–2)] – 3 · (–3) = = (–2) · [11 – 6] + 9 = (–2) · [+5] + 9 = –10 + 9 = –1

+9 +5

19 Kalkulatu.

a) 28 : (–7) – (–6) · [23 – 5 · (9 – 4)]

b) (–2) · (7 – 11) – [12 – (6 – 8)] : (–7)

20 3.8 helburua. Idatzi OMEren arabera 14 urteko neska-mutilek astean gehienez eta gutxienez lo egin beharreko orduen arteko aldea islatzen duen adierazpen aritmetiko bat, eta ebatzi. OMEren arabera, nerabe batek 9 eta 11 ordu bitartean lo egin behar ditu egunean.

ULERTU ETA APLIKATU ERRONKA

KONTUAN IZAN

10n = 10 · 10 · … · 10

n biderkagai ↓

10n = 100 … 0

n zero

Zenbaki osoen berreketak 8

Gogoan izan berreketa bat biderkagai beraren biderketa bat dela: berretzailea

berrekizuna = a · a · a · … · a n adiz

KONTUAN IZAN

[(–2) + (–3)]2 = [–5]2 = +25

(–2)2 + (–3)2 = 4 + 9 = +13

Batuketa (edo kenketa) baten berreketa ez da batugaien berreketen batuketaren parekoa.

|Adibideak

• (+4)2 = (+4) · (+4) = +16

• (–3)4 = (–3) · (–3) · (–3) · (–3) = +81

• (–3)5 = (–3) · (–3) · (–3) · (–3) · (–3) = –243

Zenbaki negatiboen berreketak

Zenbaki negatibo baten ondoz ondoko berreketetan, emaitza positiboak eta negatiboak lortzen dira txandaka: (–3)1 = –3 (–3)2 = +9 (–3)3 = –27 (–3)4 = +81

Zenbaki negatibo bat berretuz gero:

• Berretzailea bikoitia izanez gero, emaitza positiboa da. (– a)n (bikoitia) → positiboa

• Berretzailea bakoitia izanez gero, emaitza negatiboa da. (– a)n (bakoitia) → negatiboa

Berreketen propietateak

Honako propietate hauek funtsezkoak dira berreketen kalkuluak egiteko. Ikasi buruz eta aztertu arretaz adibideetako bakoitza.

❚ biderketa baten berreketa

Biderketa baten berreketa eta biderkagaien berreketen arteko biderketa berdinak dira.

[(–2) (+5)]3 = (–2)3 (+5)3

[–10]3 (–8) · (+125)

–1 000 –1 000

❚ zatiketa baten berreketa

Zatiketa baten berreketa eta zatikizunaren eta zatitzailearen berreketen arteko zatiketa berdinak dira.

[(–10) : (+5)]3 = (–10)3 : (+5)3

(–2)3 (–1 000) : (+125)

–8 –8

❚ berrekizun bereko berreketen arteko biderketa

Berrekizun bereko bi berreketa biderkatzeko, berretzaileak batzen dira.

(–10)2 · (–10)3 = (–10)2 + 3 = (–10)5

(+100) · (–1 000)

–100 000

❚ berrekizun bereko berreketen arteko zatiketa

Berrekizun bereko bi berreketa zatitzeko, berretzaileen arteko kenketa egiten da. (–10)5 : (–10)3 = (–10)5 – 3 = (–10)2

(–100 000) : (–1 000)

❚ berreketa baten berreketa

Berreketa bat berretzeko, berretzaileak biderkatzen dira.

PRAKTIKATZEKO

1 Idatzi biderketa moduan, ahal izanez gero, eta kalkulatu.

a) (–1)7 b) (–5)2 c) (–10)5

d) (–7)3 e) (–1)0 f ) (–7)0

2 Kalkulatu lau eragiketako kalkulagailuaren bidez, adibidean bezala.

• 125 → 12**==== → {∫“¢°°«“}

a) (–11)3 b) 175 c) (–27)4

3 Laburtu berreketa bakarrera, adibideetan bezala.

• 25 · (–3)5 = [2 · (–3)]5 = (– 6)5

• (–15)4 : (+3)4 = [(–15) : (+3)]4 = (–5)4 = 54

a) 32 · 42 b) (–2)3 · 43

c) (+15)3 : (–5)3 d) (–20)2 : (– 4)2

4 Laburtu a m · a n = a m + n propietatea erabiliz.

a) x 2 · x 3 b) a 4 · a 4 c) z 5 · z

5 Laburtu berreketa bakarrera.

a) (–2)5 · 27 b) (–2)3 · (+2)6

c) (–12)2 · (+12)2 d) (+9)4 · (–9)2

6 Laburtu a m : a n = a m – n propietatea erabiliz.

a) x 7 : x 4 b) a 7 : a 2 c) z 8 : z 3

7 Laburtu berreketa bakarrera.

a) (–7)8 : (–7)5 b) 109 : (–10)4

c) 124 : (–12) d) (– 4)10 : (+4)6

8 Erabili (a m)n = a m · n propietatea, eta laburtu.

a) (x 3)2 b) (a 3)3 c) (z 6)3

9 Kopiatu koadernoan eta osatu.

a) (32)4 = 3 b) [(–2)4]3 = (–2)

c) [(+5)2]2 = (+5) d) [(– 6)3]5 = (– 6)

10 Laburtu adibidean bezala.

• (a 6 · a 4) : a 7 = a 10 : a 7 = a 3

a) (x 5 · x 2) : x 4 b) m 7 : (m 2 · m 3)

c) (a · a 6) : (a 2 · a 4) d) (z 5 · z 3) : (z 4 · z 2)

11 Egin eragiketak eta kalkulatu.

a) 106 : (54 · 24) b) (–12)7 : [(–3)5 · 45]

c) [(–9)5 . (–2)5] : 184 d) [57 · (– 4)7] : 204

PRAKTIKATZEKO

Zenbaki oso baten erro karratua 9

• Gogoratu erro karratua karratura jasotzearen alderantzizko eragiketa dela. a = b ⇔ b 2 = a

• Erro karratu osoa duten zenbakiei karratu perfektu esaten zaie.

|Adibideak

497= ⇔ 749 2 =

40020= ⇔ 20400 2 = 4 49 eta 400 karratu perfektuak dira

Zenbaki positibo batek bi erro karratu ditu, bata positiboa eta bestea negatiboa.

16ren erro karratuak 4 eta – 4 dira. 4 → izan ere, 42 = +16 – 4 → izan ere, (– 4)2 = +16

Baina kontuan izan, hitzarmenez, 16 jartzen dugunean, soluzio positiboaz ari garela. Soluzio negatiboa kontuan hartzeko, minus zeinua jarri behar dugu aurrean. 16 = +4 – 16 = – 4

Zenbaki negatiboek ez dute erro karraturik.

() = x ⇔ x 2 = –16 → Ezinezkoa

() → Ez da existitzen, ez dagoela karratura jasota emaitza negatiboa emango duen zenbakirik.

Beste erro batzuk

Erro karratuaz gain, bitik gorako errotzaileak dituzten erroak lor ditzakegu.

Orokorrean:

1 Kalkulatu, egonez gero, zenbat diren honako erro hauek.

a) () b) () c) () 25+

d) () e) () f ) ()

2 Egin gogoeta eta kalkulatu, egonez gero.

d)

MENDERATZEN DUZU OINARRIZKOA?

Zenbakikuntza-sistemak

1 Hona hemen zenbaki bat bi zenbakikuntza-sistematan adierazita:

Zenbakikuntzasistema egiptoarra.

Zenbakikuntzasistema maia.

a) Azaldu zer esanahi duten ikurrek kasu bakoitzean.

b) Idatzi, bi sistemetan, aurreko eta osteko zenbakiak.

2 Kopiatu eta osatu.

a) 2 300 M = … E b) 4 800 H = … M

c) 2 EM = ….. M d) 700 M = … HM

3 Kopiatu, kalkulatu eta osatu.

a) 1 h 13 min 27 s → … s

b) 587 min → … h … min

c) 6 542 s → … h … min … s

Multiploak eta zatitzaileak

4 Erantzun eta arrazoitu erantzuna.

a) 132 multiploa da 11rena? Eta 11 zatitzailea 132rena?

b) 574 multiploa da 14rena? Eta 27 zatitzailea 1 542rena?

5 Kalkulatu.

a) 10en aurreneko bost multiploak.

b) 13ren aurreneko bost multiploak.

c) 23ren zatitzaile guztiak.

d) 32ren zatitzaile guztiak.

6 Hausnartu eta erantzun.

a) Zenbaki baten hiru zatitzaile handienak 20, 30 eta 60 dira. Zer zenbakiri buruz ari gara?

b) Zenbaki baten hiru multiplorik txikienak 12, 24 eta 36 dira. Zer zenbaki da?

Zenbaki lehenak eta konposatuak

7 Idatzi.

a) Aurreneko hamar zenbaki lehenak.

b) Bi zifrako zenbaki lehen handiena eta hiru zifrako lehen txikiena.

8 Kopiatu zenbaki hauek eta osatu, biderkagai lehenetan deskonposatzeko.

1 400 = 2 · · 1 485 = · · 11

9 Deskonposatu ahalik eta biderkagai kopuru gehienetan.

a) 378 b) 1 144 c) 1 872

Multiplo komunetako txikiena eta zatitzaile komunetako handiena

10 Kalkulatu buruz.

a) m. k. t. (2, 3) b) m. k. t. (6, 9)

c) m. k. t. (4, 10) d) m. k. t. (6, 10)

e) m. k. t. (6, 12) f ) m. k. t. (12, 18)

11 Kalkulatu buruz.

a) z. k. h. (4, 8) b) b) z. k. h. (6, 9)

c) z. k. h. (10, 15) d) z. k. h. (12, 16)

e) z. k. h. (16, 24) f ) z. k. h. (18, 24)

12 Kalkulatu.

a) m.k.t. (24, 36) b) z.k.h. (24, 36)

c) m.k.t. (28, 42) d) z.k.h. (28, 42)

e) m.k.t. (45, 75) f ) z.k.h. (45, 75)

Zenbaki osoak

13 Ordenatu txikienetik handienera. – 6, +8, –16, –3, +12, –7, +4, +15, –11

Zenbaki osoen batuketa eta kenketa

14 Egin eragiketak.

a) 5 – 8 – 4 + 3 – 6 + 9

b) 10 – 11 + 7 – 13 + 15 – 6

c) 9 – 2 – 7 – 11 + 3 + 18 – 10

d) –7 – 15 + 8 + 10 – 9 – 6 + 11

15 Kalkulatu.

a) 15 + (8 – 6) b) 11 – (2 + 8)

c) 6 + (2 – 8) – (1 + 7)

d) (13 – 11) – (10 + 7) – (2 – 10)

Zenbaki osoen biderketa eta zatiketa

16 Egin eragiketak zeinuen erregela erabilita.

a) (– 4) · (+7) b) (–21) : (+3)

c) (– 6) · (–8) d) (+30) : (+5)

e) (+10) · (+5) f ) (– 63) : (–9)

g) (–9) · (–5) h) (+112) : (–14)

17 Kopiatu eta osatu.

a) (–3) · (…) = –15 b) (– 28) : (…) = –4

c) (…) · (– 4) = +32 d) (…) : (+5) = +10

e) (+20) · (…) = +60 f ) (…) : (–7) = +8

Eragiketa konbinatuak zenbaki osoekin

18 Kalkulatu.

a) 5 – 4 · 3 b) 2 · 9 – 7

c) 4 · 5 – 6 · 3 d) 2 · 8 – 4 · 5

e) 16 – 4 · 7 + 2 · 5 – 19 f ) 5 · 6 – 21 – 3 · 7 + 12

19 Ebatzi.

a) 7 · (6 – 4) b) (7 – 10) · 2

c) (– 3) · (7 – 6) d) (10 – 4) · (– 2)

e) 6 · (5 – 3) + 2 · (2 – 7) f ) 5 · (–3 – 1) – 4 · (9 – 7)

Zenbaki osoen berreketak

20 Kalkulatu.

a) (–5)4 b) (+4)5 c) (– 6)3

d) (+7)3 e) (–8)2 f ) (–10)7

g) (+3)0 h) (–6)0 i) (–10)0

21 Adierazi zenbaki bakar baten berreketa moduan.

a) 104 : 54 b) 127 : (– 4)7

c) (–9)6 : 36 d) 26 · 26

e) (– 4)5 · (–2)5 f ) 24 · (–5)4

22 Laburtu berreketa bakarrera.

a) x2 · x4 b) m4 · m3 c) x6 · x

d) m8 : m5 e) x3 : x f ) m5 : m5

g) (x3)2 h) (m5)2 i) (x 2)2

Zenbaki osoen erro karratua

23 Kalkulatu, existitzen baldin bada.

a) 49 b) 7 2 c) 49–

d) 15 2 e) 225 f )

g) 2500 h) 50 2 i )

ENTRENATU ETA PRAKTIKATU

24 Beheko segida horretan, aurreko hamar zenbaki arruntak daude, sistema bitarrean idatzita (1 eta 0 zeinuak soilik erabiltzen dituen sisteman):

0 - 1 - 10 - 11 - 100 - 101 - 110 - 111 - 1000 - 1001

Idatzi hurrengo hamarrak.

25 Kopiatu zenbaki hauek eta hautatu:

1 000 2 007 4 829 5 511 6 005

a) 2ren multiploak. b) 3ren multiploak.

c) 5en multiploak. d) 11ren multiploak.

26 Idatzi.

a) 50 eta 60 arteko zenbaki lehenak.

b) 80 eta 100 arteko zenbaki lehenak.

c) 100etik gorako aurreneko hiru zenbaki lehenak.

27 Kalkulatu.

a) m. k. t. (12, 15) b) m. k. t. (24, 60)

c) m. k. t. (48, 54) d) m. k. t. (90, 150)

e) m. k. t. (6, 10, 15) f ) m. k. t. (8, 12, 18)

28 Kalkulatu.

a) z. k. h. (36, 45) b) z. k. h. (48, 72)

c) z. k. h. (105, 120) d) z. k. h. (135, 180)

e) z. k. h. (8, 12, 16) f ) z. k. h. (45, 60, 105)

29 Idatzi laukizuzen honen erpinen koordenatuak, eta marraztu M erpina (1, 0) puntuan daukan laukizuzen berdin bat.

30 Egin eragiketak.

a) 16 + [3 – 9 – (11 – 4)]

b) 8 – [(6 – 9) – (7 – 13)]

c) (6 – 15) – [1 – (1 – 5 – 4)]

d) (2 – 12 + 7) – [(4 – 10) – (5 – 15)]

e) [9 – (5 – 17)] – [11 – (6 – 13)]

31 Kalkulatu.

a) (–2) · [(+3) · (–2)] b) [(+5) · (–3)] · (+2)

c) (+6) : [(–30) : (–15)] d) [(+40) : (– 4)] : (–5)

e) (–5) · [(–18) : (– 6)] f ) [(–8) · (+3)] : (– 4)

g) [(–21) : 7] · [8 : (– 4)] h) [6 · (–10)] : [(–5) · 6]

32 Kalkulatu, eta aztertu nola aldatzen den emaitza parentesien posizioaren arabera.

a) 17 – 6 · 2 b) (17 – 6) · 2

c) (–10) – 2 · (–3) d) [(–10) – 2] · (–3)

e) (–3) · (+5) + (–2) f ) (–3) · [(+5) + (–2)]

33 Egin eragiketak.

a) 5 · [11 – 4 · (11 – 7)] b) (– 4) · [12 + 3 · (5 – 8)]

c) 6 · [18 + (– 4) · (9 – 4)] – 13

d) 4 – (–2) · [–8 – 3 · (5 – 7)]

e) 6 · (7 – 11) + (–5) · [5 · (8 – 2) – 4 · (9 – 4)]

34 Laburtu berreketa bakarrera.

EBATZI PROBLEMA ERRAZAK

Zenbaki arrunten problemak

40 14 urteko pertsona batek 9 eta 11 ordu lo egin behar ditu OMEren arabera, eta 40 urteko batek, 7 eta 9 ordu bitartean. Zer alde egongo da, urte oso bateko lo-orduei dagokienez, 14 urteko nerabe baten eta 40 urteko heldu baten artean?

41 156 dantzariko konpainia baten koreografian, dantzariak errenkada eta zutabetan jartzen dira. Errenkadako 20 dantzari gehiago badago zutabeko baino, zenbat errekada eta zutabe daude?

42 50 cm × 65 cm neurriko kartoi mehe bat daukagu, eta karratu-itxurako fitxak egiteko ebakiko dugu, ahalik eta handienak.

Zer aldea izango du fitxa bakoitzak?

43 Balantza baten eskuineko platertxoan 30 gramoko zurezko dadoak jarri ditugu, eta ezkerrekoan, 36 gramoko kristalezko puxtarriak.

Balantza orekan dagoela jakinda, eta jarri ditugun dadoak eta puxtarriak guztira 15 baino gehiago ez direla:

35 Erreparatu adibideari eta laburtu.

() xx x · 63 23 2 == = x 3

a) () x 22 b) () m 32 c) () a 42

d) x 4 e) m 6 f ) a 8

HAUSNARTU, APLIKATU, ADIERAZI

36 Bilatu 427ren bi zifrako zatitzaile bat.

37 50etik beherako zenbaki bat 6ren eta 7ren multiploa da. Zer zenbaki da?

38 20 pertsonako multzoa errenkada eta zutabe kopuru zehatzetan antolatu daiteke. Adibidez, lau errenkada eta bost zutabetan. 13 pertsonako multzoa, berriz, errenkada bakarrean jar daiteke.

Bilatu, 150 pertsonatik 170era bitartean izanda, zein diren soilik errenkada bakarrean antolatu daitezkeen pertsona multzoak.

39 Hiru zifrako zenbaki bat 150en multiploa eta 2 100en zatitzailea da. Zer zenbaki izan daiteke?

a) Zenbat pisu jarri dugu platertxo bakoitzean?

b) Zenbat dado eta zenbat puxtarri erabili ditugu?

44 Lantegi batetik bi kamioi irten dira hozkailu mota berdinekin beteta. Lehenengoak 481 kiloko zama eraman du, eta bigarrenak, 555 kilokoa. Zer pisu du hozkailu bakoitzak eta zenbat hozkailu eraman ditu kamioi bakoitzak?

45 Kable-kiribil batek 150 m baino gehiago eta 200 m baino gutxiago ditu. Zein da kablearen luzera zehatza, jakinda 15 m-ko zatietan zein 18 m-ko zatietan moztu, ez dela kablerik geratzen?

46 Udal batek, kontsumo ekologikoaren alde egiteko, aisialdirako baratzeak eskaini dizkie herritarrei. Horretarako, lursail karratu bat 15 m × 20 m neurriko arloetan banatu du. Zer neurri ditu lursailak, udalak 50 arlotan banatu duela jakinda?

47 Gozotegi bateko labean 2 400 madalena eta

2 640 mantekado egin dituzte, eta ale-kopuru berdineko poltsatan sartu, baina produktuak nahastu gabe. Zenbat ale jarri dituzte poltsa bakoitzean, jakinda 10 baino gehiago eta 15 baino gutxiago direla?

Problemak zenbaki osoekin

48 Marraztu koordenatu-ardatz batzuk eta

A (–2, 0) eta B (4, 2) puntuak.

Irudikatu erpin moduan bi puntu horiek dituzten karratu guztiak (hiru dira).

Amaitzeko, idatzi karratu horietako bakoitzaren erpinen koordenatuak.

51 Bi zenbaki osoren batura 3 da, eta kendura, 7. Zein dira bi zenbaki horiek?

52 Bi zenbaki osoren batura –22 da, eta zenbaki horien balio absolutuen batura, 70. Zein dira zenbaki horiek?

APUR BAT GEHIAGO PENTSATZEKO

53 Gozotegi bateko labean madalenak egin dituzte gaur. Gero, dozena erdiko poltsatan sartu dituzte, eta bi geratu zaizkie sobera.

49 –50etik hasi eta +50era bitarteko zenbaki oso guztiak idatzi nahi izanez gero, zenbat aldiz erabili behar da 7 zifra? Eta 5? Eta 3?

50 EBATZITAKO ARIKETA

Bi zenbaki osoren batura minus bost da (–5), eta kendura, hemeretzi (+19).

Zein dira bi zenbaki oso horiek?

Adibide erraz batekin probatuko dugu

6 eta 4 zenbakiak hartuko ditugu:

5 aleko poltsak egin izan balituzte, hiru geratuko ziren sobera, baina 8 aleko poltsak eginda, ez zen bat bera ere geratuko. 40 poltsa baino apur bat gehiago bete dituztela jakinda, zenbat madalena egin dituzte labean gaur?

54 Atletismo talde bateko kideek adostu dute entrenatzaileari 130 € balio duen kronometro bat ematea opari.

—Pena da pisu, disko eta xabalina jaurtitzaileek oparian ez parte hartzea! —esan du kapitainak—. Hiru gehiago bagina, bakoitzak 3 € gutxiago ipini beharko genuke.

Zenbat taldekide bildu dira oparia egiteko, jakinda kide bakoitzak euroen kantitate osoa jarri behar izan duela, zentimorik gabe?

10

2–64 += = 3 → 10 – 2 = 8 → 8 : 2 = 4 ← (txikiena)

Bi zenbakien baturari bi zenbakien kendura kenduz gero, txikienaren bikoitza lortuko dugu.

(a + b) – (a – b) = a + b – a + b = 2 · b

Jatorrizko problema ebatziko dugu

– Batura (–5) da eta kendura (+19) da.

– Batura ken kendura txikienaren bikoitza da:

(–5) – (+19) = –5 – 19 = –24 (txikienaren bikoitza)

Txikiena da: (–24) : 2 = –12

Handiena da: –12 + 19 = 7

Egiaztatu.

55 Nebarekin joan naiz amarentzat aukeratu dugun oparia erostera. Nebak dio, bere partea jarri ondoren, 10  € geratuko zaizkiola. Hori entzunda, nik mailegua eskatu diot, niri 5 € falta zaizkit eta nire partea jartzeko. Zenbat balio du opariak, biok dugun dirua batuta guztira 85 € ditugula jakinda?

56 Bi kontu-korronte ditut banku berean. Lehenengoan bigarrenean baino 200 € gehiago daude, baina batetik bestera dirua pasatu eta berdinduta utziko banitu, bakoitzean 20 € egongo lirateke. Zenbat diru daukat kontu bakoitzean?

Erabili grafiko hau laguntzeko:

Beste aukera bat da 50 . problema berrikusi eta galdera honi erantzutea: zein da bi kontuen batura eta zenbat aldea edo kendura?

Matematika-lantegia

IRAKURRI ETA INFORMATU

Lehenak eta antzinakoak

Zenbaki lehenek Antzinarotik eman zuten arreta. Horren froga argi bat Kristo baino ia hirurehun urte lehenago jaio zen Eratostenesen lanetan daukagu.

Baina hori ez da ezer! Antzinago ere, duela 20 000 urte, Zairen, historiaurreko gizakiren batek zenbaki batzuk markatu zituen hezur batean.

Ez dakigu zer adierazten duten, baina ezkerrekoak 10 eta 20 bitarteko zenbaki lehenak dira! Nola gelditu zara?

19 17 + + + 13 11 = 60

IKERTU

Zenbaki perfektuak

Pitagorikoen arabera, zenbaki bat perfektua da bere zatitzaile propioen baturarekin bat egiten badu. Adibidez, 6 zenbakiak:

6ren zatitzaile propioak 1, 2, 3 dira (6 ere 6ren zatitzailea da, baina ez da propioa).

1 + 2 + 3 = 6

• 25 eta 30 artean beste zenbaki perfektu bat dago. Gauza zara aurkitzeko?

Zenbaki lagunak

Pitagorikoek bi zenbaki lagunak zirela zioten zenbaki baten zatitzaile propioen baturak beste zenbakia ematen zuenean.

Bren zatitzaileen batura

Bren zatitzaileen batura

• 220 zenbakiak lagun bat du. Gauza zara aurkitzeko?

ERAGIN BURUARI

Kromoak

• Alazne kromo-bilduma bat egiten ari da, eta kromo berriak lortu ahala albumean itsasten ditu. Oraingoz, jarrita dituenak hiru aldiz gehiago dira errepikatuta dituenak eta aldatzeko erabiliko dituenak baino. Errepikatuta dituenen ordez ez dituenak lortuko balitu, hiru aldiz gehiago izango lirateke jarritako kromoak hutsik dituen tokiak baino. Hutsik dauden tokiak 15 baino gehiago eta 20 baino gutxiago badira, zenbat kromo ditu bildumak?

Irudian Ishangoko hezurraren ikuspegi bat ageri da, Bruselako Natura Zientzien Historia Museoan dago.

AUTOEBALUAZIOA

1 Idatzi:

a) 17ren aurreneko lau multiploak.

b) 72ren zatitzaile guztiak.

2 Bilatu:

a) 1 000ren osteko 17ren lehenengo multiploa.

b) 415en zatitzailea den bi zifrako zenbaki bat.

3 Idatzi 20 eta 40 arteko zenbaki lehenak.

4 Adierazi zenbaki hauetako zein diren 2ren multiploak, zein 3renak, zein 5enak eta zein 10enak: 897 - 765 - 990 - 2 713 - 6 077 - 6 324 - 7 005

5 Kopiatu zure koadernoan, eta deskonposatu biderkagai lehenetan 150 eta 225 zenbakiak. 150 = 2 · · · 225 = 3 · · ·

6 Kalkulatu.

a) z. k. h. (150, 225)

b) m. k. t. (150, 225)

7 Kalkulatu.

a) 6 – 11 + (9 – 13) b) 2 – (5 – 8)

c) (7 – 15) – (6 – 2) d) 5 – [2 – (3 – 2)]

8 Kalkulatu.

a) 4 · 5 – 3 · (–2) + 5 · (–8) – 4 · (–3)

b) (10 – 3 · 6) – 2 · [5 + 3 · (4 – 7)]

c) 10 – 10 · [– 6 + 5 · (– 4 + 7 – 3)]

9 Laburtu berreketa bakarrera.

a) a 3 : b 3 b) a 5 : b 5 c) a 4 . a 2

d) x 6 x 4 e) (x 3)3 f ) (–5)7 : (–5)5

10 Arropa-denda batek kamiseta-partida bat salgai jarri du, denak prezio berean. Lehenengo egunean hainbat saldu ditu, 221 € bilduta guztira, eta bigarren egunean, oraindik gehiago, 272 € bilduta. Zenbat uste duzu balio duela kamiseta bakoitzak?

➜ anayaharitza.es

11 100 m-ko zabalera eta 120 m-ko luzera duen laukizuzen-itxurako lursail bat ahalik eta arlo karratu handienetan zatitu nahi dugu. Zer luzera izan behar du arlo bakoitzaren aldeak?

12 Lantegi batean 45 segundoan behin gas-balbula baten ihesa entzuten da, eta 60 segundoan behin gabi baten kolpea. Bi soinuak aldi berean entzun berri baditugu, zenbat denbora barru entzungo ditugu biak batera berriro?

13 Pilo batean 45 cm-ko ertza duten kuboak metatu ditugu, eta, ondoan, 60 cm-ko ertza duten kubo batzuk. Zer altueratan bat egingo dute hirugarrenez bi dorreen gailurrek?

14 Bi zenbaki osoren batura 4 da, eta zenbaki horien balio absolutuen batura, 16. Zer zenbaki dira?

15 Erreparatu karratuari. A

a) Idatzi A, B, C, D erpinen eta M zentroaren koordenatuak.

b) Pentsa M-ren inguruan biratzen duzula, eta A erpina Al (4, 2) puntuan geratu dela. Idatzi Al , B l , C l eta D l erpin berrien koordenatuak.

IKASKUNTZA-EGOERA

HAUSNARTU

Berrikusi landutako alderdiak eta eman konponbidea hautemandako arazoei. Horretarako, deskargatu dagokion errubrika anayaharitza.es webgunetik, egin gogoeta banaka eta bateratze-lana taldean.

PROBATU ZURE KONPETENTZIAK

Egin anayaharitza.es webgunean ageri den konpetentzien autoebaluazioa.

Ariketa hauen ebazpena.

© GRUPO ANAYA, S.A., 2023 - C/ Valentín Beato, nº 21 - 28037 Madrid.

Reservados todos los derechos. El contenido de esta obra está protegido por la Ley, que establece penas de prisión y/o multas, además de las correspondientes indemnizaciones por daños y perjuicios, para quienes reprodujeren, plagiaren, distribuyeren o comunicaren públicamente, en todo o en parte, una obra literaria, artística o científica, o su transformación, interpretación o ejecución artística fijada en cualquier tipo de soporte o comunicada a través de cualquier medio, sin la preceptiva autorización.