Mundua helburu: Matematika B Aukera 4. DBH. Lagina

4

PROIEKTU DIGITALA DAUKA DBH

1. hiruhilekoa

MATEMATIKA B AUKERA

José Colera J., M.ª José Oliveira G., Ignacio Gaztelu A., Ramón Colera C., Rosario García P., Ana Aicardo B.

Aurkibidea

Trebatu problemak ebatziz 10

• Egin datuak antolatzen lagunduko dizun eskema bat, grafiko bat edo taula bat

• Problema geometrikoetan, egin irudi bat!

• Esperimentatu, kalkulatu iritzira, jarri adibideak… Egin aieruak eta egiaztatu

• Ikertu

Problemak

Berrikusi eta sakondu problema aritmetikoak

IKASKUNTZA-EGOERA

1 Z enbaki errealak 34

1. Zenbaki irrazionalak

2. Zenbaki errealak: zuzen erreala

3. Zuzen errealeko zatiak: tarteak eta zuzenerdiak

4. Erroak eta errotzaileak

5. Zenbaki hurbilduak. Erroreak

6. Zenbakiak idazkera zientifikoan. Errorearen kontrola

7. Logaritmoak

Ebatzitako ariketak eta problemak

Ariketak eta problemak

Matematika-lantegia

Autoebaluazioa

2 P olinomioak eta zatiki aljebraikoak 60

1. Polinomioak. Eragiketak

2. Ruffiniren erregela

3. Polinomio baten erroa. Erroak bilatu

4. Polinomioen faktorizazioa

5. Polinomioen zatigarritasuna

6. Zatiki aljebraikoak

Ebatzitako ariketak eta problemak

Ariketak eta problemak

Matematika-lantegia

5

1. Ekuazioak

2. Ekuazio-sistemak

3. Ezezagun bateko inekuazioak

4. Bi ezezaguneko ekuazio linealak

eta problemak

1. Antzekotasuna

2. Homotezia

3. Neurri interesgarriko laukizuzenak

4. Triangeluen antzekotasuna

5. Antzekotasuna triangelu angeluzuzenetan

6. Triangelu angeluzuzenen antzekotasuna gorputz geometrikoetan Ebatzitako ariketak eta problemak

Ariketak eta problemak

1. Angelu zorrotz baten arrazoi trigonometrikoak

2. Oinarrizko erlazio trigonometrikoak

3. Kalkulagailua trigonometrian

4. 0° -360° arteko arrazoi trigonometrikoak

5. Edozein neurritako angeluak. Arrazoi trigonometrikoak

6. Triangelu angeluzuzenen ebazpena

7. Zuzenak ez diren triangeluen ebazpena

8. Teorema oso interesgarri batzuk

Ebatzitako ariketak eta problemak

Ariketak eta problemak

Matematika-lantegia

Autoebaluazioa

6 Geometria analitikoa

1. Bektoreak planoan

2. Eragiketak bektoreekin

3. Puntuak adierazten dituzten bektoreak

4. Zuzenki baten erdiko puntua

5. Puntu lerrokatuak

6. Zuzenaren ekuazioak

158

7. Zuzenak. Paralelotasuna eta perpendikulartasuna

8. Koordenatu-ardatzekiko zuzen paraleloak

9. Bi zuzenen posizio erlatiboak

10. Bi punturen arteko distantzia

11. Zirkunferentzia ekuazioa

12. Mugimendu batzuen azterketa

Ebatzitako ariketak eta problemak Ariketak eta problemak

7 F untzioak I

1. Oinarrizko kontzeptuak

2. Nola adierazten dira funtzioak

3. Definizio-eremua

4. Ebaki-puntuak ardatzekin. Funtzio baten zeinua

5. Funtzio jarraituak. Etenak

6. Funtzio baten aldaketak

7. Joera eta periodikotasuna

8. Funtzio linealak

9. Funtzio koadratikoak

Ebatzitako ariketak eta problemak Ariketak eta problemak

Matematika-lantegia

8 F untzioak II

1. Zatika definitutako funtzioak

2. Funtzio errodunak

3. Alderantzizko proportzionaltasuneko funtzioak

4. Funtzio esponentzialak

5. Funtzio logaritmikoak

6. Funtzio trigonometrikoak. Radiana

Ebatzitako ariketak eta problemak

Ariketak eta problemak

Matematika-lantegia Autoebaluazioa

Ikaskuntza-egoera. Landare populazioak 236

IKASKUNTZA-EGOERA

Itzala uzten duten erronkak:

9 Estadistika 240

1. Estatistika eta haren metodoak

2. Maiztasun-taulak

3. Parametro estatistikoak: x eta σ

4. Posizio-parametroak datu bakanetarako

5. Posizio-parametroak datu multzokatuetarakok

6. Kaxa-diagramak

7. Estatistika inferentziala

8. Estatistika komunikabideetan

Ebatzitako ariketak eta problemak

Ariketak eta problemak

Matematika-lantegia Autoebaluazioa

10 Banaketa bidimentsionalak

1. Banaketa bidimentsionalak

2. Korrelazioaren balioa

3. Erregresio-zuzena estimazioak egiteko

4. Hausnartu: korrelazioak

kausa-efektua esan nahi du?

5. Banaketa bidimentsionalak kalkulagailuarekin

Ebatzitako ariketak eta problemak

Ariketak eta problemak

Matematika-lantegia

Autoebaluazioa

11 Konbinatoria

1. Biderketan oinarritutako estrategiak

2. Aldakuntzak eta permutazioak (ordenak ardura dio)

3. Ordenak eraginik ez duenean. Konbinazioak

4. Zenbakizko triangelu interesgarri bat

5. Newtonen formula

Ebatzitako ariketak eta problemak

Ariketak eta problemak

Matematika-lantegia

Autoebaluazioa

12 Probabilitateen kalkulua 308

1. Zorizko gertaerak

2. Gertaeren probabilitateak. Propietateak

3. Probabilitateak saiakuntza bakunetan

4. Probabilitateak saiakuntza konposatuetan

5. Saiakuntza askeen konposizioa

6. Mendeko saiakuntzen konposizioa

7. Kontingentzia-taulak

Ebatzitako ariketak eta problemak

Ariketak eta problemak

Matematika-lantegia

Autoebaluazioa

Ikaskuntza-egoera. Loteria klasikoen antzekoak 330

Honelakoa da zure proiektu digitala

Proiektu honek ikasturteko eduki guztiak eskaintzen dizkizu, bai liburu digitalaren bidez, bai era askotako baliabideen bidez.

Ikasteko beste modu bat ezagutuko duzu, erraza, intuitiboa eta edozein plataforma eta gailurekin bateragarria.

Nola sartu?

Zure liburuko lehenbiziko orrialdearekin batera aurkituko dituzu proiektu digitalean sartzeko behar dituzun argibide guztiak.

— Funtzioek naturako fenomenoak deskribatzen dituzte. — Erlazio funtzionalak formulen bidez deskribatu daitezke (erlazio aljebraikoak). — Funtzioak grafikoki adierazi daitezke. Hona hemen funtzioen zeregina eta definizio formala zehazteko egin diren ekarpen garrantzitsuenetako batzuk: Nicole d’Oresme (xiv mendea): lehena izan zen naturako legeak bi aldagairen arteko mendekotasunerlazio moduan deskribatzen. • Galileo (xvi mendea): lehena izan zen esperimentazioa erabiltzen (diseinatu, esperimentatu, behatu eta idatzi) erlazio horiek zenbakiz zehazteko.

Descartes xvii mendea): geometriaren bere aljebraizazioaren bidez, funtzioak grafikoki adierazi ahal izateko modua ekarri zuen. Leibniz mendea): 1673an, lehenengoz erabili zuen funtzio hitza erlazio mota hauek izendatzeko. Euler xviii mendea): kontzeptua zehaztu zuen, eta zorroztasuna eta orokortasuna eman zion. Definizio orokor

Erabili dakizuna eta ebatzi Funtzioaren adibide bat Eguzki-erlojua ez da zehatza, Lurra ez baita beti abiadura berean ren inguruan egiten duen mugimenduan. Hurrengo grafikoak erakusten du zenbat minututan aurreratzen den eguzki-erlojua urtebetean. Grafiko horretatik abiatuta, egin ditzakegu: Zer datatan aurreratzen da Zer datatan atzeratzen da gehien? Zer gertatuko da datorren urtean? goan? Jokabide hori urtero errepikatzen izan funtzio mota hauei periodikoak zaiela.

Zer abiadurarekin erortzen dira objektuak? mendeko Europan, Aristotelesen (K.a. iv mendeko filosofoa) zen eta haren sinesmenak ez ziren zalantzan jartzen. Aristotelesek berdineko bi gorputz erortzen utziz gero, astunena lehenago Kontatzen dutenez, Galileok, Pisako Unibertsitatean irakasle lanetan goela, jendaurreko esperimentu baten bidez zapuztu zuen uste objektu, oso pisu desberdinekoak,utzi zituen erortzen Pisako dorretik. erori ziren, eta bere tesiak frogatzea lortu zuen, baina unibertsitatetik Litekeena da aurreko pasadizoak mitotik asko izatea. Hala ere, putz bat plano inklinatu batetik nola erortzen den esperimentatu tantziak eta denborak kontrolatuz. ❚ Hausnartu 1. a) Azaldu zergatik den periodikoa eguzki-erlojuak urtean zehar tuen aurreratzeak eta atzeratzeak deskribatzen dituen funtzioa. b) Adierazi zer datatan den zehatza. 2. Bola bat apur bat inklinatuta dagoen errail batetik behera erortzen eta hainbat denboratan zer distantzia egin duen neurtu da: DENBORA, (s-tan) 0 0,5 11,522,533,544,55 DISTANTZIA, e (cm-tan) 02,5102240 63 a) Adierazi aurreko datu horiek ezkerrean duzun koadrikularen batean. Erabili datuak egoera horri dagokion kurba lortzeko. b) Egiaztatu lortutako balioek honako erlazio honi dagozkiola

Zer eskaintzen dizu?

Era askotako baliabideak ditu; paperezko liburuaren erreprodukzioa baino askoz gehiago da.

Honakoak egiteko aukera izango duzu:

Ariketak egin

ariketa elkarreragileak

Aztertu

laburpen elkarreragileak, eskemak...

Ikasi

audioak, bideoak, Game Room-ak...

Ebaluatu

autoebaluazioa, portfolioa...

Nolakoa da?

Erantzun globala era askotako hezkuntza-ingurune baterako.

Intuitiboa

Zuk erraz erabiltzeko modukoa.

Gailu anitzekoa

Edozein gailu motatan (ordenagailuan, tabletan, smartphonean…) egokitzen eta ikusten da, pantailaren edozein tamaina eta bereizmenetan.

Deskargagarria

Aukera ematen du Interneteko konexiorik gabe lan egiteko eta gailu batean baino gehiagotan deskargatzeko.

Sinkronizagarria

Erabiltzaileak egiten dituen aldaketak berez sinkronizatzen dira, lan egiteko erabilitako edozein gailu konektatzean.

Unibertsala

Bateragarria da ikastetxeetan gehien erabiltzen diren sistema eragileekin, ikaskuntzako inguru birtualekin (IIB) eta hezkuntza-plataformekin (LMS).

Hasi aurretik

Ezagutu zure erronkak

IKASKUNTZA-EGOERA

NOLAKOAK DIRA?

Ikaskuntza-egoerei buruzko lau proposamen dira:

• Ezagutza, jarrera eta trebetasunei eragiteko pentsatuak, eta jakintza-trukea eta zure gaitasunen garapena sustatuko dutenak.

• 2030erako Garapen Jasangarrirako Helburuekin konprometituta daudenak.

• Zure mundu errealetik eta esperientziatik hurbil daudenak eta errespetatuko dituztenak.

• Aurrera eraman beharko dituzun lanen eta jardueren egitura argi eta erraza ematen dutenak.

NOLA LAN EGINGO DUZU?

BLOKE BAKOITZAREN HASIERAN

HAU AURKITUKO DUZU:

LANDARE POPULAZIOAK Gazte talde batek eskualde jakin bateko landarediarekin zerikusia duten gai Landare-espezie jakin baten kasuan, aztertu nahi dute zer eragin duenhektareako dagoen ale-kopuruan Horretarako, hektarea bakoitzeko landare-kopurua zenbatuko dute, altitudearen arabera, eta lortutako datuetara gutxi gorabehera egokituko den funtzioa lortu nahi dute. Zuhaitz espezie jakin bateko basoen hazkundea ere aztertu nahi dute. Informazioa bildu dute, eta ondorioztatu dute espezie horren baso-masaren hazkunde-tasa, baldintza egokietan, % 40koa dela mende bakoitzean. Hurrengo mendeetan, milaka urteetan erritmo horretan haziko balitz, hurbil dagoen baso txiki batekin zer gertatuko litzatekeen jakin nahi dute. Zenbat denbora beharko litzateke 100 bider hazteko? Eta 1  000 bider hazteko?... Horretarako, dagokion funtzioa aztertu behar dute: funtzio hori = 1,4

MULTZOA

FUNTZIOAK

7. Funtzioak 8. Funtzioak

Magnitudeen arteko erlazioak modu dotore eta praktikoan deskribatzen dira funtzioen lengoaiaren bidez. Funtzio mota desberdinek (lineala, koadratikoa, erroduna, alderantzizko proportzionaltasunekoa, esponentziala, logaritmikoa, trigonometrikoa…) askotariko egoerak modelizatzeko balio dute, eta, beraz, oso lagungarriak dira denetariko eta Oinarrizko funtzio moten propietateekin eta grafikoekin ohitzen goazen neurrian, orduan eta erraztasun handiagoa eskuratuko dugu naturan, gizartean, teknikan, zientzian… gertatzen diren erlazioen interpretazioa eta tratamendua egiteko.

EDUKI-MULTZOA OSATZEN DUTEN UNITATEETAN AURKITUKO DUZUNA:

ponentziala da, igarotako mende-kopurua izanik, eta, dagokion baso-masa, unitate gisa behaketaren unean dagoena hartuta. Asmoa da baso txiki horrek hurrengo 2 500 urteetan izango duen

ERRONKA Datu-taula batetik abiatuta, funtzio bat bere balioetara ondo hurbiltzen den aztertzeko eskatuko dizuegu, eta funtzio horren laguntzaz beste batzuk estimatzeko. 1,4 funtzioaren grafikoa irudikatuz, argi ikusi beharko duzue ohiko koordenatu kartesiarrak ez direla egokiak funtzio hori tarte zabal batean aztertzeko ([0, 25]). Paper erdilogaritmikoa ezagutuko duzue, eta gero eta handiagoak diren funtzioak adierazteko nola erabiltzen den landuko duzue, eta, zehazki adierazteko. Konturatuko zarete adierazpen mota honekin balio baxuak eta altuak fidagarritasun berarekin ageri direla. Hasieran esponentzialki hazten diren, gero pixkanaka moteltzen doazen, eta, azkenerako, guztiz egonkortzen diren populazioak interpretatzen ikasiko duzue. funtzio logistikoa ezagutu eta aztertuko duzue.

187 186

• Motibazioari eragiteko testu bat, blokea osatzen duten unitateekin erlazionatuta dauden erronken testuingurua azalduko dizuna.

• Ikaskuntza-egoera bati buruzko proposamena.

• Proposatutako egoerari dagokion ikaskuntzasegida.

D-ren koordenatuak, jakinda B puntuaren simetrikoa dela M-rekiko. b) Egiaztatu ABC triangelua angeluzuzena dela. c) Zer lauki mota da ABCD Arrazoitu. 56 A(3, –2), B(9, 0) eta C(–3, 6) triangeluan, aurkitu: a) A-tik eta BC-ren erdigunetik igarotzen den zuzeb) -tik abiatzen den erdibidekoaren ekuazioa. c) Goiko bi zuzenen ebaki-puntua (triangeluaren barizentroa). Futbol-zelai honetan, koadrikula bakoitzak m-ko aldea du. Gorrien eta Horien arteko partida jokatuko da.

Q

a) Adierazi zer koordenatu dituzten lerrokatuta dauden hiru jokalari horiek eta lerrokatuta dauden hiru gorriek. b) Zer distantzia dago atezain horiaren eta c) Zein da erdiko zirkuluaren ekuazioa? Adierazi, horrez gain, hegalen ekuazioak. d) Pentsatu baloia Q jokalariak duela. Adierazi baloiak H ate barrura sartzean egiten duen ibilbidea zehazten duen zuzen baten ekuazioa. (Aukera asko daude).

58 Egiaztatu A (1, 3), B (4, 1) eta C (3, 11/4) erpinak dituen triangelua isoszelea dela, eta kalkulatu alde desberdinaren gaineko altueraren neurria. 59 Itsas estazio batetik, radar batean bi ontzi ageri dira. Bata P (4, 3) puntuan dago, eta (5, 2) bektorearen norabideari jarraitzen dio; besteak 4x – 10y = 17 zuzenaren norabideari jarraitzen dio. Egin lezakete talka?

60 yt 2 1– zuzena izanda, kalkulatu ABzenkiaren luzera puntuak zuzenak koordenatu-ardatzekin dituen ebaki-puntuak izanik. 61 A (0, 4) eta B (–1, 0) puntuak paralelogramo baten ondoz ondoko erpinak dira, eta badakigu diagonalek M (2, 1) puntuan elkar ebakitzen dutela. Lortu C D erpinen koordenatuak. Kalkulatu puntu baten koordenatuak, jakinda abzisa ordenatuaren berdina duela, eta A (2, 0) eta B (0, 4) puntuetatik distantzia berera dagoela.

Ariketak eta problemak HAU ERE EGIN DEZAKEZU 68 Kalkulatu A (–1, 5) puntuak – 2 + 1 = zuzenarekiko duen simetrikoa. Laguntza: 176. orrialdeko ebatzitako 1. ariketa antzekoa da. 69 Egiaztatu analitikoki B(6, 4) puntua A(–2, 2) puntuaren simetrikoa dela 4 y – 11 = 0 zuzenarekiko. 70 a) Idatzi zer baldintza bete behar duen edozein puntuk (–1, 3) eta (4, –2) puntuetatik distantzia berera egoteko. b) Egiaztatu AB zuzenkiaren erdigunetik igarotzen den zuzen bat lortzen duzula, eta AB zuzenarekiko perpendikularra dela AB-ren erdibitzailea). Zehaztu 4 + 7 0 zuzeneko zer puntu den A(2, 1) eta B (1, –3) puntuekiko distantziakidea. 72 B (3, 1) eta D (–5, –3) puntuak dira A erpina abzisa-ardatzean daukan erronbo baten aurkako erpinak. Aurkitu A C erpinen koordenatuak. 73 Aurkitu zirkunferentzia honen zentroa eta erradioa: + y – 10x 8y + 5 0 -ko gaiak eta -koak bereiziko ditugu: x – 10 + …) + + 8 + …) + = 0 Osatu egingo dugu, parentesi bakoitzaren barruan binomio baten karratua agertu dadin:

63 A(–1, 2), B(–3, –2) eta C(5, 2) erpineko triangeluan, kalkulatu: a) AC aldeak erdigunean duen zuzen perpendikularraren ekuazioa AC-ren erdibitzailea). b) AB-ren erdibitzailearen ekuazioa. c) Erdibitzaileen ebaki-puntua (triangeluaren zirkunzentroa). d) ABC triangeluan zirkunskribatutako zirkunferentziaren ekuazioa. Laguntza: 176. orrialdeko ebatzitako 3. ariketa antze64 Frogatu erpin hauek dituen laukia, A (4, 2), B (–2, 5), C (–5, 2) eta D (–2, –4) trapezio isoszele bat dela, eta kalkulatu bere perimetroa. 65 Idatzi PQ diametroa duen zirkunferentziaren ekuazioa, P (–5, 2) eta Q (3, –6) izanik. 66 Aurkitu ( 3) = 29 zirkunferentziak lehenengo koadranteko erdikariarekin dituen ebakipuntuak. 67 Kalkulatu -ren balioa (–3, puntua zirkunferentzia honetakoa izateko: 1) + + 2) = 25.

5) puntu bat eta parabola bat emanda, T P = P' T P' = P'' T F F' eta T (F' F'' esango diegu. a) Aurkitu P''-ren koordenatuak eta F''-ren ekuazioa. b) Egiaztatu P'' F'' bat datozela P pun= (7, –4) bektoreko T translazioa ezarrita lortzen den emaitzarekin. 78 S eta dira ardatz moduan, hurrenez hurren, X ardatza, = 4 zuzena eta dituzten simetriak. P(5, –3) puntua y 4 = 0 zuzena izanda: a) = P' P' = P'' = r' r' = r'' direla jakinda, egiaztatu P'' eta r'' bat datozela P-ri -ri O(0, 0) zentroa eta 90°-ko angelua duen B bira ezartzean lortutako emaitzarekin b) S P = P' (P' = P'' S r' S r' = r'' direla jakinda, egiaztatu eta r' bat datozela P-ri eta -ri (0, 8) bektoreko T translazio bat ezartzean lortutako emaitzarekin. ULERTU DUZU? HAUSNARTU Zuzena ala okerra? Arrazoitu zure erantzunak. a) Norabide bereko bi bektore ezin dira batu. b) Aurkako bi bektorek norabide bera dute. c) bada, eta < 0, orduan

bide desberdinekoak dira. d) bada, orduan modulu berekoak dira. e) + 25 = 0 ekuazioak zirkunferentzia bat adierazten du. 3 = 0 zuzena perpendikularra da 3 1 zuzenarekiko. by = adierazpena zuzen baten ekuazioa da. Esan nolakoa den kasu hauetako bakoitzean: a) = 0 b) b = 0 c) 0 d) = 0, = 81 1 bi zuzen perpendikularrak badira, baldintza hauetako zein beteko dituzte bere maldek? a) 1 b) c) 1 = –1 d) = –1

• Multzo bakoitzeko erronka aurrera eramateko beharko dituzun oinarrizko ezagutzak ulertzen eta erabiltzen lagunduko dizuten ariketak.

ZEIN DIRA?

• Zenbaki kamuflatuak, lehenengo eduki-multzorako.

• Ikasketa-bidaia, bigarren eduki-multzorako.

• Landare populazioak, hirugarren eduki-multzorako.

• Loteria klasikoen antzekoak, laugarren eduki-multzorako.

UNITATEEN AMAIERAKO ORRIALDEETAN AURKITUKO DUZUNA:

Matematika-lantegia

IKERTU

AUTOEBALUAZIOA

EDUKI-MULTZOAREN AMAIERAN AURKITUKO DUZUNA:

Barraskilo maiteminduak Lurrean, 1 m-ko aldea duen karratu bateko A, B, C, D lau erpinetako bakoitzean barraskilo bat dago. Lau animaliatxoak maiteminduta daude. Ze poliiiiita! Baina, bai gauza bitxia: haietako bakoitza hurrengoarekin maiteminduta dago: • A-k B maite du; • B-k C maite du; • C-k, D • eta D-k, A. Aldi berean eta abiadura berean mugitzen hasi dira, minutuko 10 cm-an, bakoitza maite duen horren norabidean.

A C

D

A(1, 4), B(3, 3), C(–2, 5) eta D(0, –3) puntuak emanda, aurkitu bektore hauen koordenatuak: a) AB b) CD c) AC d) BD 2 (4, –2) eta (–2, –1) bektoreak izanda: a) Adierazi 2 1 3 bektoreak eta horien koordenatuak. b) Kalkulatu 23 bektorearen koordenatuak. a) (2, –6), (3, 1) eta (–5, 5) bektoreak emanda, kalkulatu -ren balioak wuxy egiaztatu dadin.

10 Adierazi, kasu hauetako bakoitzean, malda eta igarotzen duen puntuetako bat, eta, gero, irudikatu. a) OX = (3, 4) + (2, –1) b) y 1 = 0 c) xt yt 23 d) 23 1 –

10 cm

ZER KURBARI JARRAITZEN DIOTE Barraskiloen mugimendua imitatzeko, ondoren ageri den marrazki honen modukoa egin dezakezu: Simulazio bat da, eta barraskilo bakoitzak 10 cm egiten ditu aurrera norabide egokian, eta, ondoren, bat-batean norabidea aldatzen du bere maitearen bila. Hau da, norabidea etengabe aldatzen joan beharrean, 10 cm-tik 10 cm-ra egiten dute. Egin marrazkia 1:10 eskalan (10 cm-ko karratua eta 1 cm-ko aurrerapena). Kurba mota hauei jazarpen-kurbak esaten zaie, eta matematika asko jakin behar da bere ekuazioa lortzeko.

Zentzuzkoa dirudi, simetria bidez, karratuaren zentroan topo egitea.

Galdera horri erantzuteko, apur bat egokituko dugu ariketa: pentsatu kartoi handi bat dugula, bertan karratua irudikatu dugula eta lurzoruan jarri dugula. Barraskiloak gainean daude. Mugitzen hasten diren unean, kartoia mugituko dugu, baina B barraskiloa lurzoruko toki berean utziz (kartoiarekiko mugituko dugu, baina ez lurzoruarekiko). Argi dago A-k AB lerroari jarraitzen diola lurzoruarekiko. Topo egiten dutenerako, A-k 1 m egina izango du 10 minutuan. Eta, beraz, gainerakoek ere bai.

b) Kalkulatu zein izan behar den k-ren balioa p( ,) k 3 bektoreak bektorearen norabide bera izan dezan. Aurkitu zein den -ren balioa A (1, –5), B (3, 0) (6, puntuak lerrokatuta egoteko. (1, 4), (3, 6), (–1, –2) eta (–3, 2) puntuak izanda, adierazi bikote hauen erdigunea: a) A b) c) A C d) C Aurreko ariketako puntuak izanda, aurkitu A puntuaren simetrikoa puntu hauetako bakoitzarekiko: a) B b) C c) D d) O(0, 0) 7 Asmatu hiru puntu lerrokatu, A B C AB BC bete dadin. Idatzi puntu horietatik igarotzen den zuzenaren ekuazio esplizitua eta orokorra. (–2, –3) eta (4, 3) muturreko zuzenkian, aurkitu P-ren koordenatuak, baldin eta APAB 3 2 bada. 9 Lortu zuzen hauetako bakoitzaren ekuazio bektoriala, parametrikoak, jarraitua, esplizitua eta orokorra: a) (3, –2)-tik igarotzen da eta bere norabide-bekd(–1, 5) da. b) X ardatzarekiko paraleloa da eta (3, –5) puntutik igarotzen da. c) ardatzarekiko paraleloa da eta (–4, –2)-tik igarotzen da. d) zuzenarekiko perpendikularra da eta (3, –1)-etik igarotzen da. e) + 4 0 zuzenarekiko perpendikularra da eta koordenatuen jatorritik igarotzen da.

11 A(2, 1) eta B(6, 4) triangelu baten erpinak dira. M(0,5; –1) puntua -ren erdigunea dela jakinda, kalkulatu AC -ren koordenatuak eta triangeluaren perimetroa. 12 A(–2, 2), B(0, 7) eta C(6, 4) erpineko triangeluan, aurkiB-tik abiatzen diren erdibidekoaren ekuazioa eta altuera. 13 Aurkitu zentroa C(0, –3) puntuan duen eta A(3, 0) puntutik igarotzen den zirkunferentziaren ekuazioa. 14 Aurkitu zirkunferentzia hauetako bakoitzaren zentroa eta erradioa, eta irudikatu: a) 6 – 10 + 25 = 0 b) 4 – 2 + = 0 c) + 4 15 Esan honako zuzen bikote hauen posizio erlatiboa: a) y + 4 b) = 3 2 OX = (–1, 3) + (1, –1) c) xt yt 12 11 y 1 4 –

Berrikusi landutako alderdiak eta eman konponbidea hautemandako arazoei. Horretarako, deskargatu dagokion errubrika haritza.es webgunetik, egin gogoeta banaka eta bateratzelana taldean. PROBATU ZURE KONPETENTZIAK Egin anayaharitza.es webgunean ageri den konpetentzien autoebaluazioa.

• Zure gaitasunak ebaluatzeko proposamen bat, anayaharitza.es webgunetik jaitsi dezakezuna.

Bartzelonako erdigunean ibiltzeko, erreferentzia-sistema kartesiar bat eraiki dute planoaren gainean, koordenatu-zentro gisa Tetuango plaza eta 133 m-ko aldea duen lauki bat hartuta. Kontuan izanik Tetuango plazatik ateratzen direla beti (koordenatuen jatorria):

Kalkulatu zein izan behar den -ren balioa Natur Zientzien Museora OX = (4, 3)  + Adierazi zer kaletan (edo bidegurutzetan) dagoen La Pedrerak, Familia Santuak eta Catalunya Plazak osatzen duten triangeluaren barizentroa. Glòries dorrera iritsi dira. Ze forma ederra duen! Ba al zenekien bere sekzio bertikalak parabolak direla? Zer altuera izango du? Kalkulatzeko, m-ko altuera duen teodolito bat egin dute (bilatu tutorialetan nola egin) eta neurriak hartu dituzte. Teodolitoa hartuta jarri diren tokitik, dorrearen punturik altuena horizontalarekiko 70°-ko angelupean ikusten dute. Eta gero, urrundu egin dira, baina justu 50°-ko angelupean ikusteko adina bakarrik.

DIMETRODONEN BIZKAR-HEGALA ETA BESTE BITXIKERIA BATZUK Natur Zientzien Museoan dinosauroen eta desagertutako beste animalia handi batzuen erakusketa bat dago. Deigarria egin zaie, batez ere,kar-hegala. Gidariak esan die hegal handi horrek termorreguladore lanak egiten zituela: «eguzki-plaka» gisa erabiltzen zuten berotu beharra zutenean, eguzkitik energia hartzeko; edo freskatzeko, bero handiko uneetan. Baina beste galdera bat ere bueltaka zuten buruan: zergatik zeukaten animalia handi horiek bakarrik erradiadore bitxi eta artifizial hori, eta ez txikienek? Galdera horrek beste gogoeta hau ekarri zien: Irradiazioa larruazalaren bidez egiten da eta, beraz, larruaren azalerarekiko proportzionala da, hau da, larruaren luzeraren karratuarekiko proportzionala. Erabiliko den beroa, berriz, gorputzaren bolumen osoan banatuko denez, larruaren luzeraren kuboarekiko proportzionala da. Animalia handietan, azalera ez da nahikoa hain bolumen handiaren beharrak asetzeko, eta konponbide bat da azalera handitzea bizkar-hegal gisa (azalera nabarmen handitzen da, bolumena ia handitu gabe); hori da dimetrodonen kasua. Antzeko mekanismoa dira elefanteen belarri handiak, freskatzeko erabiltzen dituzte. Ikus ditzagun azalera-bolumena erlazioa nabarmentzeko galdera batzuk: Zergatik jaten dute ugaztun txikiek gehiago (pisuarekiko proportzioan) handiek baino? Bilatu, adibidez, saguari eta lehoiari buruzko datuak. Eguzkiak pertsona batek baino bero handiagoa igortzen du, noski! Izan ere, Eguzkiak 9,46 10 cal igortzen ditu segundoko, eta pertsona batek, 3 10 cal. – Alderatu zer bero-kantitate igortzen duten azalera-unitateko (1 dm do bakoitzean, eguzkiak eta pertsona batek. Datuak: Eguzkiaren erradioa: 696 340 km; pertsona baten azalera: m gutxi gorabehera. – Eta orain konparatu Eguzkiak eta 80 litroko bolumena duen pertsona batek bolumen unitateko igortzen duten-bero kantitatea Eta harritu emaitza ikusita. Alderatu hidrogeno-atomo baten tamaina eguzki-sistemaren tamainarekin, sistema txikitu eta eguzkia protoi baten tamainaren parekoa eginez. Eguzkitik zer distantziatara legoke Neptuno Eguzkia dm Gulliverren bidaiak ipuinean, liliputarrek 15 cm-ko garaiera zuten, eta Gulliverrek, 180 cm-koa. Liliputeko erregeak sagar bat jango balu, zenbat eman beharko lizkioke Gulliverri bere tamainarekiko proportzioan kantitate berdina jan dezan? Pentsatu erregeak urrezko dobloi balio duen kapa daramala, eta Gulliverri haren tamainarekiko proportzionala den kapa oparitu nahi diola. Zenbat balioko du? Orain egin zuk Bilatu neurri-desberdintasunek egoera harrigarriak sortarazten dituzten beste kasu batzuk. Ikertu animalia handien tamainak dituen mugei buruz. Aztertu zergatik bizi

Bazenekien badaudela giza gorputzaren beroa baliatzen duten eraikinetako klimatizazio-sistemak? Munduan hainbat lekutan jarri dira abian; esaterako, Stockholmeko Geltoki Zentralean, trenak egunero hartzen duen jendetzaren beroa erabiltzen dute, hodien bitartez bideratuta, inguruko eraikinak berotzeko. Bilatu energia-iturri hain

Banaka edo

Deskargatu anayaharitza.es webgunetik erronka honi dagozkion zure gaitasunak berrikusteko errubrika bat. Autoebaluatu proiektuaren zure planifikazioa; horretarako, deskargatu zereginen planifikazioari buruzko itua. Zer moduz talde-lana? Balorazioa egiteko, erabili anayaharitza.es webgunean dagoen koebaluazio-itua.

185 184

• Interesgarri iruditu dakizkizukeen beste erronka batzuk.

• Diagnosi-tresnen proposamenak, anayaharitza.es webgunetik jaitsi daitezkeenak.

• Amaierako profilaren errubrika, anayaharitza.es webgunetik jaitsi daitezkeenak, lortu dituzun gaitasunak autoebaluatzeko.

MULTZOA ARITMETIKA ETA ALJEBRA

1. Zenbaki errealak

2. Polinomioak eta zatiki aljebraikoak

3. Ekuazioak, inekuazioak eta sistemak

Zenbakizko egituren ordenari eta erregulartasunari erreparatuta, zenbakizko mekanismoen ahalmena eta zehaztasuna aintzat hartuta, edertasuna eta eraginkortasuna baino ez ditugu aurkituko zenbakien eremuan zehar egindako txango orotan.

Hizkuntza aljebraikoak, hizkuntza argi eta moldakorrak, aritmetikaren zerbitzura jarrita, orokortasuna ematen du enuntziatuen azalpenean eta arintasuna prozedura eta metodoetan.

Horrez gain, aljebrak bere aldetik ere aukera ematen du era guztietako problema askori erraz eta dotore aurre egiteko.

ZENBAKI KAMUFLATUAK

5 + 2 − 3 idazten badugu, argi dago emaitza 4 dela. Zenbaki hori, 4 zenbakia, apur bat kamuflatuta dago batuketan, baina erraz aurkitzeko moduan. Beste hau, ordea, askoz gordeago dago: 2 + 1 + 1 2 + 1 4 + 1 8 + …

Ondo dakizun moduan, a1 = 2 eta r = 1/2 dituen progresio geometriko bateko gaien arteko batuketa batura da. Beraz, batura hau da:

Batura = a1 1 r = 2 1 1 2

= 4

Zenbakiak mozorrotzeko edo kamuflatzeko hainbat modu landuko ditugu, horietako batzuk oso bitxiak. Esate baterako hau:

• Antzik hartzen al diozu urrezko zenbakiari Fibonacciren segidaren barruan?

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144...

• Lortu daiteke π zenbakia batuketa infinitu honen emaitza eginez? 4 4 3 + 4 5 4 7 + 4 9 4 11 + 4 13 4 15 +

• Eta infinituraino luzatzen den zatiki-kate honetan eragiketak eginda, pentsatuko zenuen azken emaitza zenbaki erraz bat dela: 2 Zatiki mota horri zatiki jarraitua esaten zaio.

Labur esanda, zenbakiak adierazpen konplikatu eta zailen bidez kamuflatzeko hainbat modu daude. Adierazpen horietan murgildu eta gordetzen duten zenbakia bilatzea lan entretenigarria da eta, zenbaitetan, zirraragarria ere bai.

ERRONKA

• Tresna digital baten laguntzarekin, edo aljebra modu adimentsuan erabili eta behin eta berriz eragiketak eginez, nahaste-borraste algoritmiko horietan eta beste batzuetan ezkutatuta dauden zenbakiak aurkituko dituzue. Eta erronka joko dizuegu, zeuek ere antzeko egoerak diseinatu eta asmatzeko, zenbakien ezkutaketa-joko honetan.

• Jolas dibertigarri bat proposatuko dizuegu: segida bateko hasierako elementuetako batzuk eman, eta hurrengo gaia zein den aurkitzea. Ez hori bakarrik: segida zenbakizkoa denean eta soluzioa lortu ahal izateko araurik sumatzen ez denean, polinomio bat sortzen ikasiko duzue, zalantzarik izango ez duen arrazoizko erantzun bat lortzeko.

Zer zenbaki uste duzu estaltzen duela autoak?

Zenbaki errealak

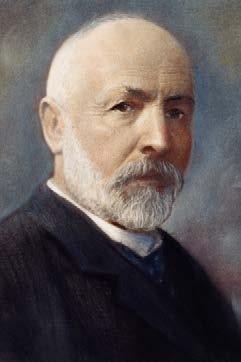
Zenbaki arruntak zibilizazio guztiek erabili izan dituzte antzina-antzinatik.

Negatiboen eta, batez ere, zeroaren papera pentsatu eta finkatzea zailagoa izan zen. Horregatik, zenbaki osoak ez ziren guztiz formalizatu vii. mendearen amaiera arte, Indian. Handik iritsi zitzaizkigun ix mendean, arabiar kulturaren bidez, zenbakikuntza-sistema hamartarposizionalarekin batera.

Zatikiak oso antzinatik erabiltzen hasi ziren, baina gaur egun ematen diegun moduko erabilera xiv. mendean finkatu zen.

Zenbaki irrazionalak pitagorikoek aurkitu eta identifikatu zituzten, gure aroaren aurreko v. mendean, gutxi gorabehera. Hala ere, ia 2 000 urtez ez ziren zenbaki moduan tratatu, magnitude geometriko moduan baizik.

Zenbaki arrazionalak eta irrazionalak egitura eta ezaugarri oso interesgarriak dituen multzo bakar baten partaide gisa hartzea oso ideia berria da. Zenbaki errealaren kontzeptua, orain erabiltzen dugun bezala, funtzioei buruzko azterketek aurrera egin ahala sortu eta eraiki zen. Behin betiko formalizazioa, 1871n, Cantor alemaniarrari zor zaio.

Georg Cantor (1845-1918)

Erabili dakizuna eta ebatzi

π zenbakia Antzinaroan

π zenbakia irrazionala da. Baina historian zehar hainbat balio arrazional eman izan zaizkio. Hona hemen horietako batzuk:

Antzinako Egipto (K.a. xx. mendea g.g.b.)

Antzinako Babilonia (K.a. xx. mendea g.g.b.)

Arkimedes (K.a. iii. mendea)

Tolomeo (ii. mendea)

Liu Hiu (v. mendea)

Zenbaki moten antolamendua

3,16

25/8

22/7

377/120

355/113

Ezagutzen ditugun zenbaki-multzoak oso ondo egituratuta daude:

• Arruntak, N

• Arruntei bere aurkakoak erantsiz gero (negatiboak), zenbaki osoen multzoa lortzen dugu, Z

• Osoei zatikizko zenbakiak erantsiz gero, arrazionalak lortzen ditugu, Q

• Arrazionalei ez-arrazionalak eransten badizkiegu, lortuko dugu ondo egituratutako multzo bat?

❚ Hausnartu

1. a) Idatzi hiru zenbaki arrunt eta arruntak ez diren hiru zenbaki oso.

b) Idatzi osoak ez diren hiru zenbaki arrazional eta arrazionalak ez diren hiru zenbaki.

c) Kokatu aurreko ataletako zenbakiak zure koadernoan, goian ageri den moduko eskema batean.

2. π-ren balioa 3,14159265359… dela jakinda, goian ikusi ditugun hurbilketa bakoitzean, eman egindako errorearen kota bat

Adibidez: 377 120 = 1 3,141666… 3,141592…

Errorea 1 hamar milaren baino txikiagoa da: errorea < 0,0001

KONTUAN IZAN

Karratu perfektuak biderkagai lehenetan deskonposatzean, zenbaki lehen bakoitza aldi kopuru bikoitian dago.

Adibidez:

Zenbaki irrazionalak

Zenbaki arrazionalak dira bi zenbaki osoren arteko zatiki moduan jar daitezkeenak. Horien adierazpen hamartarra zehatza edo periodikoa da.

Zenbaki irrazionalak ez-arrazionalak dira; hau da, bi zenbaki osoren zatiki moduan jar ezin daitezkeenak. Horien adierazpen hamartarra infinitua eta ezperiodikoa da. Adibidez, π = 3,14159265359…

Infinitu zenbaki irrazional daude, eta horietako zenbait oso interesgarriak dira. Ikus ditzagun batzuk.

Karratuaren diagonala: 2 zenbakia

Pitagorasen teoremak 1eko aldea duen karratu baten diagonalaren balioa ematen digu: d =  11 2 22+=

Irrazionala dela egiaztatuko dugu; hau da, ezin dela bi zenbaki osoren arteko zatiketa moduan jarri. Absurdora eramanda egingo dugu (badela pentsatu, eta absurdo batera heltzen garela ikusiko dugu).

— 2 arrazionala dela pentsatuko dugu.

— Arrazionala bada, bi zenbaki osoren arteko zatiketa moduan jarri ahalko da:

b a 2=

— Bi atalak ber bi egingo ditugu: 2 =  b a 2 2 → a2 = 2b2

N = 22 · 3 · 53

N 2 = (22 · 3 · 53)2 = 24 · 32 · 56

Berretzaile guztiak bikoitiak dira.

b 2 karratu perfektua denez, 2 biderkagaia aldi-kopuru bikoitian du. Beraz, 2b 2 denean, 2 biderkagaia aldi-kopuru bakoitian egongo da; eta hori ezinezkoa da, 2b 2 = a 2 baita, beste karratu perfektu bat. Hau da arrazoitu duguna: « 2 arrazionaltzat hartuta, absurdo batera heldu gara». Horrela, absurdora eramanda, 2 ez dela arrazionala frogatu dugu.

Erroen bidez adierazten diren beste irrazional batzuk

2 -ren kasuan bezala, p karratu perfektua ez bada, p irrazionala da.

p ez bada n-garren berreketa zehatz bat, p n zenbaki irrazional bat da.

Adibidez, 8 , 9 3 eta 10 5 zenbaki irrazionalak dira

Zenbaki arrazional baten eta irrazional baten arteko eragiketak egitean, emaitza zenbaki irrazional bat da (zerorekin biderkatzen dugunean izan ezik).

Adibidez, 2  + 3, 4 –  10 5 , 9 3  : 7 irrazionalak dira.

Froga dezagun 4 –  10 5 irrazionala dela, 10 5 ere hala dela oinarritzat hartuz.

— Demagun N = 4 –  10 5 → 10 5  = 4 – N

— SN arrazionala balitz, 4 – N ere hala litzateke. Hau da, 10 5 arrazionala litzateke, eta hori gezurra da

1 Frogatu honako zenbaki hauek irrazionalak direla: a) 3

IZAR PITAGORIKOA

Urrezko zenbakia: Φ =  √5 + 1 2

Aldea unitate bateko luzerakoa duen pentagono baten diagonala ( 5 + 1) : 2 zenbakia da; argi dagoenez, zenbaki irrazional bat. Hori da, hain zuzen ere, historian irrazionaltzat onartu zen lehenengo zenbakia.

Pentagono erregular baten bost diagonalekin eraturiko irudi hau pitagorikoen ikurra zen.

Artista greziarrek bereziki harmoniatsuak jo zituzten Φ zenbakian oinarritutako proportzioak. Horregatik, Φ zenbakiari urrezko zenbakia deitu zioten.

Izena, Φ (fi, grekoko «F» letra) Fidias izenaren hasierako letra da; izan ere, K.a. v. mendeko eskultore greziar honek behin eta berriro erabili zuen proportzio hori.

anayaharitza.es

π zenbakiari eta beste irrazional batzuei buruzko bitxikeriak.

KONTUAN IZAN

2 , 5 , Φ eta beste zenbaki irrazional batzuk ez bezala, π zenbakia ezin da era zehatzean adierazi zuzen errealean.

π zenbakia

Ondo dakizunez π zirkunferentzia baten luzeraren eta diametroaren arteko erlazioa da. Zenbaki hori duela askotik ezagutzen eta erabiltzen duzu.

Zenbaki irrazionala da, eta, beraz, infinitu zifra hamartar ez-periodiko ditu

π letra «P»-ri dagokion grekoko ordaina da. Zergatik izen hori? Grekozko perifereia hitzak zirkunferentzia esan nahi duelako (zirkuluaren periferia).

e zenbakia

Matematikan oso garrantzitsua den beste zenbaki irrazional bat e zenbakia da. Historiako karisma handieneko matematikari baten omenez deitu zioten horrela, Leonhard Eulerren omenez.

Zenbaki horren balio hurbildua 2,7182… da, eta oraindik aurrera egoera askotan aurkituko dugu:

— Animalia-edo landare-populazio baten hazkunde-prozesua deskribatzeko, funtzio esponentzial bat erabiltzen da eta bertan e zenbakia ageri da.

Baita substantzia erradioaktibo batean, denbora aurrera joan ahala, geratzen den erradioaktibitate-hondarra deskribatzeko ere.

— Eta kate bat, kable bat, soka bat… muturrak altuera berean jarrita zintzilikatzen badugu, eratzen den kurba (katenaria) ere e zenbakiarekin deskribatzen da.

4

1 Laukizuzen honek berezitasun bat du: karratu bat kentzen badiogu, geratzen den laukizuzena hasierakoaren antzekoa da.

Frogatu alde handia x = Φ dela.

3 Egiaztatu Φ urrezko zenbakia irrazionala dela.

KONTUAN IZAN

Badira zenbakien beste multzo batzuk ere, beharbada beste ikasturte batzuetan ikasiko dituzunak; baina Á multzoak zenbakien zuzena betetzen du eta ez du hutsarterik uzten, ondoren ikusiko dugun bezala.

Zenbaki errealak: zuzen erreala

Zenbaki arrazionalek eta irrazionalek osatzen duten multzoa zenbaki errealen multzoa da eta Á idatzita adierazten dugu.

Hau da, bai arrazionalak bai irrazionalak zenbaki errealak dira. Eta horiek zenbaki guztiak dira. Á multzoarekin, zenbakien multzoari buruzko taula osatu dezakegu:

NOTAZIOA

x edozein zenbaki arrunt bada, x ∈ N adieraziko dugu; osoa bada, x ∈ Z; arrazionala bada, x ∈ Q; eta erreala bada, x ∈ Á.

Zenbaki errealekin arrazionalekin egiten ditugun eragiketa berdinak egin ditzakegu: batuketak, kenketak, biderketak eta zatiketak (zerorekin izan ezik), eta propietate berdinak dituzte.

BEHATU

Zatikizko bi zenbakiren batura ez da zertan zatiki bat izan. Adibidez:

3 1 3 5 3 6 2 += =

Eta bi oso negatiboren arteko biderketa eginda, emaitza ez da oso negatibo bat. Adibidez: (–2) · (–3) = 6

Horrez gain, edozein errotzailetako erroak ere lor ditzakegu (zenbaki negatiboen errotzaile bikoitiko erroak izan ezik), eta emaitzak zenbaki erreala izaten jarraituko du. Zenbaki arrazionalen kasuan ez zen hori gertatzen.

Ikusten duzunez, N, Z, Q multzoak, baita Á multzoa ere, multzo itxiak dira batuketa eta biderketaren kasuan; hau da, multzo horietako bateko bi elementuren batuketa zein biderketa eginda, multzo bereko beste elementu bat lortuko dugu. Oso negatiboen, zatikizkoen eta irrazionalen kasuan ez da halakorik gertatzen: bi irrazionalen arteko batura arrazional bat izan daiteke (adibidez: (1 + 2 ) + (3 – 2 ) = 4), eta bi irrazionalen arteko biderkadura ere arrazional bat izan daiteke (adibidez: 28 ·  = 4).

Zuzen erreala

Zenbaki arrazionalek, ondo dakizunez, bete-bete egiten dute zenbakien zuzena; hau da, zuzenaren tarte bakoitzean infinitu zenbaki arrazional daude, berdin dio tartea oso txikia bada ere. Hala ere, eta bitxia dirudien arren, zenbakion artean infinitu hutsarte daude. Hutsarte horiek zenbaki irrazionalek betetzen dituzte, eta denek batera zenbakien zuzena osatzen dute.

EZ AHAZTU

Zuzen erreala osoa da; hau da, zuzeneko puntu bakoitzari zenbaki erreal bat dagokio eta zenbaki erreal bakoitzari zuzeneko puntu bat dagokio.

Zuzen batean jatorri bat kokatzen badugu (zeroa, 0) eta unitate-luzera zehazten badugu, zuzeneko puntu bakoitzari zenbaki arrazional edo irrazional bat egokituko zaio. Hau da, zuzeneko puntu bakoitzari zenbaki erreal bat dagokio. Horregatik, zenbakien zuzenari zuzen erreal esaten diogu.

Zenbaki erreal guztiak zuzenean kokatu ondoren, bi zenbakiren artean infinitu arrazional eta infinitu irrazional daudela ziurta dezakegu, bi zenbaki horiek osooso hurbil egon arren.

ADIBIDEA

5 zenbakiaren adierazpena:

Zenbakiak zuzen errealean adieraztea

❚ zatikizko zenbakiak talesen teoremaren bidez adieraztea

Aztertu nola kokatuko dugun zuzen errealaren gainean 5 14 zenbakia Talesen teorema erabiliz: 5 14  = 2 +  5 4 0

❚ erroak pitagorasen teoremaren bidez adieraztea

Prozedura honek n kalkulatzeko modua ematen du, n ∈ N edozein dela ere: Adibidez: 32 1 2 2 =+ `j

10 =+3122

Hala ere, zenbaki erreal gehienak ezin dira zehatz adierazi prozedura horien bidez. Adibidez, nola adierazi 842 5 zenbakia? Normalena adierazpen hurbildua egitea izango da.

❚ zenbaki errealen adierazpen Hurbildua

Adierazpen hamartarraren bidez emandako zenbaki erreal baten adierazpena guk nahi bezain hurbildua izango da. Adibidez, 842 5 = 3,8464…:

PENTSATU ETA PRAKTIKATU

Ikusten duzunez, handiagotze bakoitzean aurreko azpi-tartea hamar zatitan banatu eta horietako batekin geratu gara. Azken batean, bila gabiltzan zenbakira guk nahi adina hurbiltzen gara.

Zenbaki errealak, kasuaren arabera, modu zehatzean edo nahi adina hurbilduta adieraz ditzakegu zuzen errealean.

1 a) Arrazoitu adierazitako puntua 21 dela.

2 Zer zenbaki da geziarekin markatu dugun hori?

b) Adierazi 27  (27 = 36 – 9) eta 40 (40 = 36 + 4).

Adierazi modu berean 2,716 zenbakia.

Zuzen errealeko zatiak: tarteak eta zuzenerdiak

Zientziaren munduan, aldagai jakin bat zer eremutan den baliozkoa zehaztu beharra egoten da sarritan. Adibidez, «3 s eta 11 s arteko denbora-tartean». Horretarako, zuzen errealeko zenbait zati nomenklatura egokia erabiliz izendatzen ikasi behar dugu.

Tarte irekia

TARTE IREKIA

(a, b) = {x ∈ Á / a < x < b} a b

Aurreko adierazpena honela irakurtzen da:

hauen multzoa

{ x ∈ Á / a < x < b }

x zenbaki

errealak

non eta a baino handiagoak

TARTE

eta b baino txikiagoak diren

(a, b) tarte irekia a-ren eta b-ren artean dauden zenbaki guztien multzoa da, a eta b barnean hartu gabe: { x ∈ Á / a < x < b }.

Honela adierazten da: a b

Adibidez, (–2, 1) tartea –2ren eta 1en artean dauden zenbaki guztiek eratzen dute, –2 eta 1 multzo horretatik kanpo utziz: { x ∈ Á / –2 < x < 1}.

Beste adibide bat: 15 cm × 10 cm-ko neurria duen kartoi zati batekin kutxa bat eraikitzeko, erpinetan lau karratu berdin ebaki behar ditugu, eta, gero, tolestu. Horretarako, karratu horien aldeak 5 cm baino txikiagoa izan behar du → (0, 5). 15 cm

Tarte itxia

[a, b] tarte itxia a-ren eta b-ren artean dauden zenbaki guztien multzoa da, a eta b barnean hartuta: { x ∈ Á / a ≤ x ≤ b }.

Honela adierazten da: a b

Adibidez, [–2, 1] tartea –2 eta 1 arteko zenbaki erreal guztiek eratzen dute, –2 eta 1 ere kontuan hartuz: {x ∈ Á / –2 ≤ x ≤ 1}.

Beste adibide bat: 2 kg edo gehiagoko pisua duten eta 5 kg-tik pasatzen ez diren paketeak baino ez ditugu onartzen → [2, 5].

Tarte erdi-irekia

TARTE ERDI-IREKIA (a, b] = {x ∈ Á / a < x ≤ b} a b [a, b) = {x ∈ Á / a ≤ x < b} a b

BEHATU

• Zer zenbaki dagozkio {x ∈ Z / –2 < x ≤ 4} tarteari?

• Zer desberdintzak adierazten ditu [–2, 0) tartean dauden zenbaki osoak?

• (a, b] tartea a-ren eta b-ren artean dauden zenbaki guztien multzoa da, b ere kontuan hartuz, baina a ez: {x ∈ Á / a < x ≤ b }.

Honela adierazten da: a b

• [a, b) tartea a-ren eta b-ren artean dauden zenbaki guztien multzoa da, a ere kontuan hartuz, baina b ez: {x ∈ Á / a ≤ x < b }.

Honela adierazten da: a b

Adibidez, (3, 4] tartea 3ren eta 4ren artean dauden zenbaki guztien multzoa da, 4 barnean hartuz, baina 3 ez: {x ∈ Á / 3 < x ≤ 4}.

Beste adibide bat: haurtzaindegi honetan 1 urte beteta duten, baina 4 urteak bete gabe dituzten umeak baino ez dituzte onartzen → [1, 4).

ZUZENERDIAK

(– ∞ , a) = {x ∈ Á / x < a}

a (– ∞ , a] = {x ∈ Á / x ≤ a} a (a, +∞) = {x ∈ Á / x > a} a [a, +∞) = {x ∈ Á / x ≥ a} a

Zuzenerdiak eta zuzen erreala

(– ∞, a) tartea a baino zenbaki txikiagoek osatzen dute: { x ∈ Á / x < a}.

(– ∞, a] tartea a baino zenbaki txikiagoek eta a-k berak osatzen dute: { x ∈ Á / x ≤ a}.

(a, +∞) tartea a baino zenbaki handiagoek osatzen dute: { x ∈ Á / x > a}.

[a, +∞) tartea a baino zenbaki handiagoek eta a-k berak osatzen dute:

{ x ∈ Á / x ≥ a}.

• (– ∞, 2) tartea { x ∈ Á / x < 2} multzoa da → 2

• [2, +∞) tartea { x ∈ Á / x ≥ 2} multzoa da → 2

BEHATU

Bi tarte edo zuzenerdiren bilketa adierazteko ∪ erabiltzen da:

(–∞, 2) ∪ (0, 5] = (–∞, 5]

Bi tarte edo zuzenerdiren ebaketa adierazteko ∩ erabiltzen da:

(–∞, 2) ∩ (0, 5] = (0, 2)

EBATZITAKO ARIKETAK

1 Idatzi tarteen bidez eta irudikatu:

a) 2 < x ≤ 3 b) x ≤ 1

c) x > 0

2 Idatzi desberdintzen bidez eta irudikatu:

a) [–2, 0] b) [–1, +∞)

c) (0, 1)

3 x-ren zer baliotarako da baliozkoa ondorengo adierazpen hau?

(x2) () x3 –+

PENTSATU ETA PRAKTIKATU

• Botoa emateko, 18 urte beteta izan behar dira → [18, +∞). Jakina, testuinguru horretan +∞ erlatibizatu egin behar da.

Zuzen erreala bera ere honela adierazten da tarte baten bidez: Á = (– ∞, +∞).

Baldintza zehatz bat betetzen duen zenbakirik ez dagoenean, multzo huts baten bidez adierazten da, eta multzo horren ikurra ∅ da. Esaterako, x 2 < 0 betetzen duten x zenbakiak multzo huts honi dagozkio: {x ∈ Á / x 2 < 0} = ∅.

a) (2, 3] tarte erdi-irekia

b) (– ∞, 1] zuzenerdia

c) (0, +∞) zuzenerdia

a) { x ∈ Á / –2 ≤ x ≤ 0} –2 0

b) { x ∈ Á / x ≥ –1} –1

c) { x ∈ Á / 0 < x < 1} 0 1

Erro karratua kalkulatzeko, errokizuna zero edo positiboa izan behar da. Eta hori gertatzen da biderkagaietako bat zero denean, biak negatiboak direnean edo biak positiboak direnean. Hau da, x ≤ –2 bada edo x ≥ 3 bada.

(–∞, –2] ∪ [3, +∞) –3 –2 –1 0 1 2 3 4

1 Idatzi honako multzo hauek tarteen bidez eta irudikatu kasu bakoitzean zehaztutako baldintzak betetzen dituzten zenbakiak:

a) 5 eta 6 arteko zenbakiak, bi muturrak barne.

b) 7 baino zenbaki handiagoak.

c) –5 zenbakia edo –5 baino txikiagoak.

➜ anayaharitza.es Tarteak zuzen errealean.

2 Idatzi tarteen bidez eta irudikatu.

a) { x ∈ Á / 3 ≤ x < 5} b) { x ∈ Á / x ≥ 0}

c) { x ∈ Á / –3 < x < 1} d) { x ∈ Á / x < 8}

3 Idatzi desberdintzen bidez eta irudikatu.

a) (–1, 4] b) [0, 6] c) (–∞, – 4) d) [9, +∞)

BURUZKO KALKULUA

1. Esan zein den k-ren balioa kasu hauetan: a) k 3  = 2 b) 2433 k = c) k 3 2 4 = d) 10242 k =

2. Kalkulatu erro hauek: a) 3 b) 32 5 c) 5 d) 0 8

e) 81 4 f ) 125 3 ADI

4

Erroak eta errotzaileak

a zenbaki baten n-garren erroa esaten zaio eta a n idazten da honako baldintza hau betetzen duen b zenbakiari:

a n  = b baldin eta bn = a a n erroa da; a, errokizuna, eta n, erroaren errotzailea.

Horrelako adierazpenak erabili behar dituzunean, batzuetan zenbakizko balioa kalkulatu beharko duzu. Horretarako, definizioa hartu beharko duzu kontuan (alboan proposatzen diren ariketa horietan bezala), edo kalkulagailua erabili beharko duzu. Beste batzuetan, berriz, erroa bere horretan utzi beharko duzu, edo sinplifikatu, edo beste erro batzuekin eragiketak egin, etab.

Erroen berezitasun batzuk

• a ≥ 0 bada, a n existitzen da, n edozein dela ere.

• a < 0 bada, errotzaile bakoitia duten erroak baino ez dira existitzen.

• 4 zenbakiak bi erro karratu baditu ere, 4 idaztean, erro positiboaz ari gara: 4  = 2.

Orokorrean, a zenbaki positibo batek bi erro karratu ditu: a eta – a .

Erroen forma esponentziala

Erroak berreketa moduan adieraz daitezke:

➜ anayaharitza.es Berreketen propietateak gogoratzeko ariketak.

PENTSATU ETA PRAKTIKATU

1 Adierazi honako erro hauek berreketen bidez:

2 Kalkulatu.

41/2

82/3

3 Adierazi erroen bidez.

x 7/9

1251/3

645/6

6251/4

) 363/2

2.

Erroen eragiketak

Erroek trebe eta bizkor ezagutzen eta erabiltzen jakin behar ditugun propietateak dituzte. Orrialde honen eta hurrengoaren alboko tartekietan jarriko ditugu. Propietate horiek guztiak berreketen propietate ezagunen ondorio zuzenak dira. Eta arreta berezia jarriko diegu propietate horiei esker lortzen diren eragiketei.

❚ erroak sinplifikatzea

Erroak berreketa moduan adieraziz gero, batzuetan sinplifikatu egin daitezkeela ikusiko dugu. Adibidez: 93 33 3 // 4 2 4 2412 = ===

1. propietatea erabili dugu (ikusi alboan).

❚ erroak errotzaile komunera laburtzea

Errotzaile desberdina duten bi erro konparatu nahi ditugunean, beti ez da erraza izaten. Errotzaile berarekin adierazten baditugu, askoz errazagoa da. Egia esan, izendatzaile komunera laburtzea besterik ez da.

Adibidez, 586 3 eta 70 konparatzeko:

1. propietatea erabili dugu berriro (ikusi alboan).

❚ biderkagaiak errotik kanpo ateratzea

Erro batzuk sinplifikatzeko eta erroen arteko batuketak eta kenketak egiteko, batzuetan biderkagaiak errotik kanpora atera beharko ditugu. Ikus ditzagun adibide

2. propietatea erabili dugu (ikusi alboan).

❚ errotzaile bereko erroen biderketa eta zatiketa

Adibidez: ·15201520300·== (2. propietatea, ikusi alboan)

(3. propietatea, ikusi alboan)

❚ errotzaile desberdineko erroen biderketa eta zatiketa Errotzaile desberdina duten erroak biderkatzeko edo zatitzeko, berretzaile komunera laburtu behar ditugu:

1., 2. eta 3. propietateak ezarri ditugu (ikusi alboan).

5. PROPIETATEA aa · n m mn = , izan ere:

GOGOAN IZAN

Erro berdinak baino ezin dira batu.

❚ erro baten berreketa

4. propietatea erabili dugu (ikusi alboan).

❚ erro baten erroa

Adibidez:

➜ anayaharitza.es Erroei buruz dakizuna indartzeko ariketak.

PENTSATU ETA PRAKTIKATU

4 Sinplifikatu.

5. propietatea erabili dugu (ikusi alboan).

❚ erroen batuketak eta kenketak

Bi erro desberdin ezin dira elkarrekin batu, horien adierazpen hamartar hurbilduak lortzen ez baditugu. Batuketa egiteko, erroek berdinak izan behar dute.

Adibidez:

77 –3 + 4 Hurbilduz baino ezin dira eragiketak egin; edo, bestela, adierazita utzi behar dira.

32

Honako adierazpen hauek, berriz, sinplifikatu daitezke:

75 11175–55 +=

Batzuetan, erroen arteko batuketa sinplifikatu daitekeela ez da argi ikusten. Beraz, lehenengo, ahal diren biderkagai guztiak errotik kanpora aterako ditugu, edo erroak sinplifikatuko ditugu. Adibidez: 321850

a) x 9 12 b) x 8 12 c) y 10 5

d) 8 6 e) 64 9 f ) 81 8

5 Zein da kasu hauetan bietako handiena?

a) 31 4 eta 13 3

b) 51 3 eta 132650 9

6 Laburtu. a) · 22 3 5 b)

7 Atera errotik atera litezkeen biderkagai guztiak. a)

9 Egin eragiketak.

Izendatzailea arrazionalizatzea

AZTERTU

2  = 1,4142…

Zailagoa da hau egitea: 1,00000000 1,4142 0100600 0,7071… 016060 01918

hau egitea baino: 1,4142… 2 014 0,7071… 02 0

Eta emaitza bera lortzen dugu.

GOGOAN IZAN

Arrazionalizatzea arrazionala ez dena arrazional egitea da.

Antzina, gaur egungo kalkulurako tresnak ez zeudenean, lan handia egin behar izaten zen eragiketak arintzeko eta errazteko metodoak lortzeko. Adibidez, 2 1 zuzenean kalkula daiteke eskuz ( 2 -ren zenbait zifra kalkulatu, eta, gero, 1 zati emaitza hori egin). Baina kalkulu horiek asko errazten dira honako hau kontuan hartuta: · ·2 1 2 12 2 2 2 ==

Eragiketa bi eratara egiten baduzu, ikusiko duzu izendatzailetik erroa kentzea askoz errazagoa eta erosoagoa dela (ikusi alboan).

Gaur egun kalkulurako ditugun tresna eraginkorrekin beharrizanik ez badago ere, oraindik ohitura dago problemen azken emaitzak izendatzailean errorik ez duten zenbakizko adierazpenen bidez emateko.

Izendatzailetik erroak kentzeko erabiltzen dugun prozesuari izendatzailearen arrazionalizazioa esaten zaio.

Kasu guztietan galdera hau egingo dugu: zer adierazpenekin biderkatu behar dut izendatzailea biderkadurak errorik izan ez dezan? Adierazpen hori zein den aurkitu ondoren, azken emaitza aldatu ez dadin, zenbakitzailea ere adierazpen horrekin biderkatuko dugu

KONTUAN IZAN

• (a + b ) · (a – b ) = a 2  – b 2

• ab – adierazpenari ab + adierazpenaren konjugatua esaten zaio.

Eta alderantziz: ab + da ab –adierazpenaren konjugatua

PENTSATU ETA PRAKTIKATU

10 Arrazionalizatu izendatzaileak.

Eragiketa batzuk errazagoak dira eragiketak egiten hasi aurretik arrazionalizatzen baditugu.

beste erro batzuk. Adibidez:

3.

AZTERTU

a) 34 m neurriak 2 zifra esangarri ditu.

b) 0,0863 hm3 neurriak 3 zifra esangarri ditu.

c) 53 000 L neurriak 2 zifra esangarri ditu, azkeneko zeroek zenbakia izendatzeko baino ez baitute balio. Hobe da 53 milaka litro jartzea.

AZTERTU

Zenbaki hurbilduak. Erroreak

Hurbilketak eta erroreak

Aplikazio praktikoetan zenbaki hurbilduak erabiltzen dira. Gogora ditzagun zenbaki hurbilduen erabilera kontrolatzeko kontzeptu eta prozedura batzuk.

Zifra esangarriak zenbaki hurbilduak adierazteko erabiltzen direnak dira. Zehatzak direla dakigunak eta transmititu nahi den horretarako garrantzitsuak direnak baino ez ditugu erabili behar

Adibidez, igerileku baten edukiera 718900 L -koa dela neurtu badugu, arrazoizkoa izango da 719 m3 dituela esatea, 3 zifra esangarri bakarrik erabiliz. Baina neurketa oso zehatza izan ez bada, egokiena 720 m3 esatea izango da; edo, hobeto, 72 hamarka m3.

a) :34m Erroreabsolut< 0, 5m

Neurketa ua

Neurri hurbildu baten errore absolutua balio errealaren eta balio hurbilduaren arteko kenketaren emaitza da.

Z [ \

] ] ] ]

Neurketa Hauda

b) :0,0863 hm Erroreabs. <0,00005 hm ,erroreabs. <50m

3 3 3

Errore absolutua = |Balio erreala – Balio hurbildua|

c) :L L 53 500 Neurketamilesde Erroreabsolutua< *

AZTERTU

Aurreko neurrien errore erlatiboak hauek dira:

a) E.e. <  , 34 05  < 0,015 = % 1,5

b) E.e. <  , , 00863 000005  < 0,0006 = % 0,06

c) E.e. <  53000 500  < 0,0095 < 0,01 = % 1

EBATZITAKO ARIKETAK

1 Adierazi honako kantitate hauek zifra esangarrien arrazoizko kopurua erabiliz:

a) Pinakoteka bat ikustera urtebetean joandako bisitariak: 183 594.

b) Manifestazio bateko parte-hartzaileak: 234 590.

c) 1 dm3 prestakinean dagoen bakterio kopurua: 302 593 847.

Balio erreala, orokorrean, ezezaguna da. Beraz, errore absolutua ere ezezaguna da. Garrantzitsuena errore hori mugatzea da, borneak jartzea: errore absolutua ... baino txikiagoa da. Errore absolutuaren bornea erabilitako azken zifra esangarritik abiatuta lortzen da.

Aurreko adibidean (igerilekuaren edukiera: 719 m3), azken zifra esangarriak (9 zifra) m3-en unitateak adierazten ditu. Errore absolutua metro kubiko erdia baino txikiagoa izango da (errorea < 0,5 m3).

Errore erlatiboa errore absolutuaren eta balio errealaren arteko zatiketaren emaitza da. Zenbat eta zifra esangarri gehiago erabili, orduan eta txikiagoa da. Errore erlatiboa ehunekotan ere adierazten da (%)

Adibidean, errore erlatiboa , 719 05 < 0,0007 = % 0,07 baino txikiagoa da

a) Arrazoizkoa da bisitarien kopurua hain zehatz ematea; izan ere, museora sartzeko sarrera ordaindu behar izaten da, eta, jakina, diru-sarrerak zenbatu egiten dira. Beraz, 183 594 izango da saldutako sarreren kopurua.

Dena dela, informazioa norako den kontuan hartuz, zifra sinplifikatu egin daiteke: «ia berrehun mila», «ehun eta laurogei mila baino gehiago» esatea ontzat emango dugu.

b) Ezinezkoa da inork manifestazio batera joan direnak hain zehatz zenbatzea. Zifra ez da «puztu» edo «murriztu» behar arrazoi sektarioengatik, baina ezin liteke balioztatzea horrenbeste zehaztu. Adibidez, «berrehun mila baino gehiago» esatea arrazoizkoa litzateke; baita «200 000 eta 250 000 artean» esatea ere

c) Horrelako kantitateetan, zifra esangarri bat edo gehienez ere bi zehaztu daitezke: 3 ehunka milioi edo 30 hamarka milioi bakterio

2 Eman aurreko ariketako kantitateetako bakoitza balioztatzean egin den errore absolutuaren borne bat eta errore erlatiboaren borne bat.

a) Bisitarien kopurua 180 mila izan dela esaten badugu (edo hobeto, 18 hamarka mila), 183 594 – 180 000 = 3 594 pertsonako errore absolutua egin dugu. Guk bisitarien kantitate zehatza dakigunez, errore hori justu zenbatekoa den jakin dezakegu. Baina gure informazioa jasotzen duenak (18 hamarka mila) onartu beharko du errorea izan daitekeela erabiltzen ez den lehenengo zifraren 5 unitaterainokoa: 5 000 pertsonako errorea. Laburbilduz:

Balioztatzea: 180 mila

Errore absolutua < 5 000

Errore erlatiboa <  180000 5000  < 0,028 < 0,03 → E.e. < 0,03 = % 3

b) Balioztatzea: 200 000

Errore absolutua < 50 000

Errore erlatiboa <  200000 50000  = 0,25 = % 25

c) Balioztatzea: 3 ehunka milioi = 300 milioi

Errore absolutua < 0,5 hamarka milioi = 5 milioi

Error relativo <  300 5  < 0,017 < 0,02 → E.e. < 0,02 = % 2

PENTSATU ETA PRAKTIKATU

1 Zuzena ala okerra? Arrazoitu erantzunak.

a) Igerileku batean 147 253 892 milaka tanta ur sartzen direla esatea zuzena da neurketak oso zehatz egin badira.

b) Igerileku batean 147 253 892 milaka tanta ur sartzen direla esatea ez da arrazoizkoa, ezinezkoa baita neurketa hain zehatz egitea. Askoz zentzuzkoagoa izango litzateke 15 hamarka mila milioi tanta sartzen direla esate.

c) Igerilekuan sartzen den tanta kopurua 15 hamarka mila milioikoa dela zuzen estimatu badugu, egiten gabiltzan errore absolutua hamarka mila milioi erdi baino txikiagoa da; hau da, E. abs. < 5 000 000 000 tanta.

d) Neurketa batean egindako errore erlatiboa 0,019 baino txikiagoa bada % 19 baino txikiagoa dela esan dezakegu.

e) Neurketa batean egindako errore erlatiboa 0,019 baino txikiagoa bada, % 2 baino txikiagoa dela esan dezakegu.

f ) Kalkulagailuak π = 3,14159265 dela diosku. π = 3,14 hartzen badugu, egindako errore absolutua 0,00159266 baino txikiagoa dela baiezta dezakegu; baina arrazoizkoagoa da E. abs. < 0,0016 dela esatea, edo, bestela, E. abs. < 0,002 dela.

2 Azaldu zergatik ez den arrazoizkoa zaku batean 11 892 583 ale arroz daudela esatea.

Adierazi modu egokian eta mugatu adierazpen horrekin egindako errore absolutua eta errore erlatiboa.

3 Eman π = 3,1416 hartzean egiten den errore erlatiboaren borne bat eta errore erlatiboaren beste borne bat.

LANDU

Adierazi zenbaki hauek idazkera zientifikoan:

a) 340 000 b) 0,00000319

c) 25 · 106 d) 0,04 · 109

e) 480 · 10– 8 f ) 0,05 · 10– 8

Zenbakiak idazkera zientifikoan. Errorearen kontrola

3,845 · 1015 eta 9,8 · 10–11 zenbakiak idazkera zientifikoan emanda daude:

Bi biderkagairen bidez adierazita daude: bata zenbaki hamartarra da, eta bestea, 10en berreketa bat.

• Zenbaki hamartarra da 1 edo 1 baino handiagoa, eta 10 baino txikiagoa

• 10en berreketak berretzaile osoa du.

Lehenengoa, 3,845 · 1015 = 3845000000000000, zenbaki «handia» da Bigarrena, 9,8 · 10–11 = 0,000000000098, zenbaki «txikia» da. notazio Honen onurak

Izenak berak adierazten duen moduan, notazio hau zehaztasuna behar duten testuinguruetan erabiltzeko pentsatuta dago, sekula ez hizkuntza arruntean. Pentsatu zer izango litzatekeen horrela hitz egingo banegu:

— Zenbat seme-alaba dituzu? → 5 · 100

— Zenbat neska-mutil daude zure ikastetxean? → 6,74 · 102

— Badituzue 2,5 · 10–4 m-ko lodierako orratzak?

Argi dago ez dugula horrela hitz egiten. Izan ere, notazio hau ez da elkarrekin egunerokoan komunikatzeko.

Aldiz adierazteko modu hori oso erosoa da kantitate hurbildu oso handiekin edo oso txikiekin lan egiteko, izan ere:

• Begi kolpe batean erraz hautematen da zenbakiaren «tamaina»; bigarren biderkagaiari erreparatu behar diogu eta 10en berretzaileak emango digu horren berri.

• Agerikoa da kantitatea zenbateko zehaztasunez ematen den. Zenbat eta zifra esangarri gehiago lehenengo biderkagaiak, orduan eta zehatzago zenbakia.

JAKIN-MINA

Beharbada inoiz honelako azalpenen bat ikusiko duzu:

Zenbaki oso bat zero batekin edo gehiagorekin amaitzen bada, zenbat zifra esangarri dituen zehazteko, komeni da notazio zientifikoan adieraztea. Dena dela, zero horiek zifra esangarri moduan aintzat hartu behar direla adierazteko beste modu bat da koma bat jartzea zenbakiaren amaieran. Beraz:

3 200 zenbakiak 2 zifra esangarri ditu.

3 200, erako zenbakiak 4 zifra esangarri ditu.

Ez da komunitate zientifikoak onartuta duen erregela bat (eta liburu honetan ez dugu erabiliko), baina irakasleak uste badu baliozkoa dela gai hau argitzeko, zergatik ez erabili?

Adibidez, 7,6 · 108 eta 7,603 · 108 parekoak dira, gutxi gorabehera («oso antzeko tamaina» dute), baina bigarrena zehaztasun handiagoz emanda dago, lau zifra esangarri baititu, eta lehenengoak, berriz, bi baino ez.

Eragiketak notazio zientifikoan dauden zenbakiekin

Kalkulagailuarekin, oso erraz egiten dira eragiketak notazio zientifikoan. Gogoan izan zenbaki bat notazio zientifikoan idazteko, � tekla erabiltzen dela. Esate baterako, 7,6 · 108 → 7,6 � 8; 2,5 · 10–4 → 2,5 �f 4. Baina «eskuz» egin nahi badugu, arretaz jokatu behar dugu.

❚ biderketa eta zatiketa

Eragiketak bereizita egiten dira, osagai hamartarrak alde batetik, eta 10eko berreketak beste batetik. Gero, emaitza berriz osatzen da, notazio zientifikoaren formatua hartzeko. Adibidez:

(3,25 · 105) · (4,6 · 1011) = (3,25 · 4,6) · (105 · 1011) = 14,95 · 1016 = 1,495 · 1017 (3,25 · 105) : (4,6 · 1011) = (3,25 : 4,6) · (105 : 1011) = 0,7065 · 10–6 = 7,065 · 10–7 Ikusten duzunez, 3,25 : 4,6 kasuko zatiduran lau zifra esangarri hartuta konformatu gara. Problemaren testuinguruak bestelako zehaztasunik ematen ez badigu, modu subjektiboan erabaki beharko dugu.

ADI

Honako zenbaki hauekin ematen dugun informazioa ez da kasu guztietan berdina:

2,5 · 102; 2,50 · 102; 2,500 · 102

Zenbaki hamartarraren amaieran eransten diren zeroek balio dute zenbat zifra kontrolatzen diren adierazteko.

EBATZITAKO ARIKETA

Txinan 1 400 milioi pertsona bizi direla esan digute.

a) Adierazi kantitate hori notazio zientifikoan.

b) Kantitate zehatza ala hurbildua da?

c) Eman errore absolutuaren borne bat, datua nola adierazi den kontuan hartuz.

d) Eman errore erlatiboaren borne bat.

❚ batuketa eta kenketa

Batugaiak prestatu behar ditugu, denek 10eko berreketa bera izan dezaten eta biderkagai komun moduan jarri ahal izateko. Gero, batuketa egin ondoren, emaitza berriro antolatuko dugu notazio zientifikoan. Adibidez:

3,7 · 1011 + 5,83 · 108 – 4 · 109 =  3 700 · 108 + 5,83 · 108 – 40 · 108 =  = 3 665,83 · 108 = 3,66583 · 1011

Edo bestela:

3,7 · 1011 + 5,83 · 108 – 4 · 109 = 3,7 · 1011 + 0,00583 · 1011 – 0,04 · 1011 = = 3,66583 · 1011

Notazio zientifikoan emandako zenbakietako

errorearen kontrola

«Biltegian 2 500 zaku irin daude» esaten badigute, baliteke hori kantitate hurbildua izatea, eta benetan dakiguna izatea 25 ehunka zaku inguru daudela, eta errorea dela ehuneko baten erdia (50 zaku) baino txikiagoa. Edo 250 hamarreko zaku daudela, eta errorea dela hamarreko baten erdia (5 zaku) baino txikiagoa. Notazio zientifikoan, adierazpenak ez du zalantzarako biderik ematen: 2,5 · 102 emanda, bi zifra esangarri baino ez daude. Eta hiru badira, 2,50 · 102 idatziko dugu.

a) 1 400 milioi bizilagun = 1,4 · 109 bizilagun

b) Argi dago zenbaki hurbildua dela, ezinezkoa baita hain kantitate handi, sakabanatu eta aldakorra hain zehatz kalkulatzea.

c) eta d) 1 400 milioi esaten digutenean, lehenengo bi zifrak kontrolatuta daudela pentsatu behar dugu. Eta baliteke, gainera, ondoren ematen diren zeroetakoren bat ere kontrolatuta egotea

Neurketan lehenengo bi zifrak baino ez badaude kontrolatuta:

Neurketa: 14 ehunka milioi pertsona

Errore absolutua < 0,5 ehunka milioi = 50 000 000

Errore erlatiboa < 0,5/14 < 0,036 = % 3,6

Neurketan kantitatearen lehenengo zeroa ere kontrolatuta badago:

Neurketa: 140 hamarka milioi pertsona. Kasu honetan, honela jar daiteke idazkera zientifikoan: 1,40 · 109. Eta koma dezimalaren osteko 0 horrek zifra esangarri hori kontrolatuta dagoela adierazten du Errore absolutua < 0,5 hamarka milioi = 5 000 000

Errore erlatiboa < 0,5/140 < 0,0036 = % 0,36

PENTSATU ETA PRAKTIKATU

1 Egin eragiketak. Gero, egiaztatu kalkulagailuarekin:

a) (6,4 · 105) · (5,2 · 10– 6)

b) (2,52 · 104) : (4 · 10– 6)

c) 7,92 · 106 + 3,58 · 107

d) 6,43 · 1010 + 8,113 · 1012 – 8 · 1011

2 Lurretik Eguzkiraino 149 000 000 km daude.

a) Adierazi idazkera zientifikoan.

b) Adierazi cm-tan, bi zifra esangarri emanez.

c) Adierazi cm-tan, lau zifra esangarri emanez.

d) Mugatu errore absolutua eta erlatiboa aurreko hiru kasuetan.

23 = 8 berdintza honela jar daiteke: log2 8 = 3. log2 8 honela irakurtzen da: «logaritmoa 2 oinarrian 8».

Modu berean, hau esan dezakegu: log5 125 = 3, izan ere, 53 = 125

log5 5 2 1 = , izan ere, 51/2 =  5

log10 1 000 000 = 6, izan ere, 106 = 1 000 000 log10 0,0001 = – 4, izan ere, 10– 4 = 1/104 = 0,0001

a oinarriko P > 0 zenbaki baten logaritmoa esaten zaio, eta log a P idazten da, P lortzeko a oinarriari ezarri behar zaion berretzaileari (a > 0 eta a ≠ 1). log a P = x ⇔ a x  = P

Logaritmoen propietateak

1. Bi logaritmo erraz log a a = 1 log a 1 = 0

Oinarriaren logaritmoa 1 da, eta 1en logaritmoa 0 da, oinarria edozein dela ere.

2. Biderketak eta zatiketak log a (P · Q ) = log a P + log a Q log a Q P  = log a P – log a Q

Biderketa baten logaritmoa da biderkagaien logaritmoen arteko batuketa. Zatiketa baten logaritmoa da zatikizunaren eta zatitzailearen logaritmoen arteko kenketa. Adibidez: log2 loglog log 2 84 842–3 22 3 2 =+

3. Berreketak eta erroak log a P k  = k log a P log a lo gP n P 1 n a =

Berreketa baten logaritmoa (P k edo PP / n n 1 = ) da berretzailea bider berrekizunaren logaritmoa.

4. Oinarri aldaketak log b P =  log log b P a

a

a oinarriko logaritmoak kalkulatzen jakinez gero, formula honi esker, b edozein oinarritako logaritmoak kalkula ditzakegu.

LOGARITMO HAMARTARREN GARRANTZIA

Erreparatu bi zenbaki hauei:

A = 6 748 B = 67,48 = A/100

log B = log (A/100) = log A – log 100 = = log A – 2

Horrek esan nahi du bi logaritmoek zati hamartar berdina dutela.

Logaritmoen tauletan, 6 748ren logaritmoaren zati hamartarra bilatu behar zen eta, gero, zati osoa erantsi, kontuan hartuta 6 748; 67,48 edo 67 480 000 zen.

Historia apur bat

Kalkulagailuak agertu baino mende batzuk lehenago, logaritmoak asmatu ziren eskuz egin beharreko eragiketa izugarri luzeak arintzeko. Eta nola egiten zen hori? Biderketak eta zatiketak batuketa eta kenketa bihurtuz (argi dago bigarren eragiketa horiek askoz erosoagoak direla). Horretarako, taula handi batzuk erabiltzen z (liburu oso lodietan emanak), eta taula horietan biderkagaien logaritmo hamartarrak bilduta zeuden, modu zehatzean edo oso hurbilduan.

Eta logaritmo nepertarren papera zein izan zen orduan? Zenbaki askoren logaritmo hamartarrak eskuz lortzeak eskatzen zuen prozesu izugarri neketsu horretan, e zenbakia berez sortu zen, eta, ondorioz, baita logaritmo nepertarrak ere. Hau da, logaritmo nepertarrak izan ziren logaritmo hamartarren balioak modu naturalean lortzeko tresna, praktikan erabili behar zirenak hamartarrak baitziren. Nepertarrei logaritmo naturalak deitu zitzaien, eta hamartarrei logaritmo arruntak. Baina gaur egun kalkulagailuak baditugu, zertarako logaritmoak? Apur bat kulturagatik, eta beste apur bat logaritmoekin topo egingo dugulako sinplifikazio aljebraikoetan (adibidez, ekuazio mota batzuk ebazteko) eta zientziaren edo teknikaren mundutik ateratako adierazpen funtzionaletan.

Logaritmoak kalkulagailuarekin

Dakizunez, gaur egun erabiltzen ditugun kalkulagailuek logaritmoak kalkulatzeko hiru tekla dituzte: , j eta . Lehenengo biak erraz aurki daitezke. Hirugarrena (logaritmo hamartarra), aldiz, ezkutuagoa dago eta bigarren funtzio gisa agertzen da; erabiltzeko, s sakatu behar da.

Logaritmoa 10 eta e ez den oinarri batean lortzeko, kalkulagailu berrietan j tekla erantsi dute. Hala ere, batzuetan hobe izan daiteke oinarri-aldaketari buruzko 4. propietatera jotzea (ikusi 50. orrialdea) tekla hori erabiltzea baino. Horretarako, hobe da ln erabiltzea, zuzeneko tekla bat baita. Ikus ditzagun, adibide batekin, egiteko dauden bi moduak:

• log 5 2 → jí 2 ””5 = 4,64385619

•

EBATZITAKO ARIKETA

Aurkitu, kalkulagailua erabilita, honako logaritmo hauek, bi moduetan: j tekla erabilita eta oinarri-aldaketa eginda.

PENTSATU ETA PRAKTIKATU

4 Erabili j eta teklak honako logaritmo hauek aurreko ariketa ebatzian ikusi ditugun bi moduetan kalkulatzeko:

Ebatzitako ariketak eta problemak

1 Tarteak

Adierazi tarte moduan honako desberdintza hauetako bakoitza egiaztatzen duten zenbakiak:

a) ≤ x 5 b) x 24 <+

c) Nola adierazi beharko litzateke a) ataleko desberdintzaren aurkakoa?

Egin zuk

Adierazi tarteen bidez.

a) ≤ x 31 – b) x 23 >+

a) x 5 = bada → x 5= edo x 5–=

Beraz: ≤ x 5 → ≤ x –≤55 → [, ] x –55 !

b) x +=24 bada → x +=24 edo x 24 – += → x 2= edo x 6–=

Beraz: x 24 <+ → x –<62 < → () ,x –62 !

c) a) ataleko desberdintzaren aurkakoa x 5> da. Tarteen bilketa baten bidez adierazten da.

A = 12 211122 11 + esango diogu, eta bi atalak karratura jasoko ditugu.

osoa dela.

3 Logaritmoak

Aurkitu x-ren balioa kasu hauetako bakoitzean:

a) 3 = 5 + log x

b) logx 36 = 2

c) log x + 2log 5 = 2

Kasu guztietan logaritmoaren definizioa erabiliko dugu:

a) 3 – 5 = log x → x = 10–2

b) x 2 = 36 → x = 6 (x = – 6 ez da baliozkoa)

c) Logaritmoaren propietateak erabiliko ditugu: log x + log 52 = 2 → log (x · 52) = 2 → 25x = 102 → x = 4

Egin zuk Kalkulatu x kasu hauetan: a) log3 x =  2 1 b) 2log x – log 4 = –2

4 Interesak, erroreak eta logaritmoak

Inbertitzaile batek 2 · 106 -ko gordailua egin du, urteko

Dirua atera duenean, 2,43 · 10 6 eman dizkiote gutxi gorabehera.

a) Eman hurbilketa horren

erlatiboaren eta absolutuaren borne bana.

b) Zenbat urtez utzi zuen dirua bankuan?

(*) Logaritmoak hartuko ditugu bi ataletan n bakantzeko.

Ariketak eta problemak

MENDERATZEN DUZU OINARRIZKOA?

Zenbaki-multzoak

1 Zenbaki hauek ditugu: // ,, 23 3567 17 1826 1618 ;; ;; ;; !

a) Zein dira osoak?

b) Badago arrunta den zenbakirik?

c) Eta irrazionalik?

2 a) Sailkatu, arrazionalak edo irrazionalak diren kontuan izanda.

;, ;; ;; ;π e 2 3 08 74 3 7 2 1 2 3 !

b) Ordenatu txikienetik handienera.

c) Zein dira zenbaki errealak?

3 Eman29– eta8– arteko zenbaki oso bat, arrazional bat, osoa ez den zenbaki bat eta irrazional bat.

4 Adierazi zer zenbaki-multzotakoa (N, Z, Q edo

Á) izan litekeen honako zenbaki hauetako bakoitza; adierazi aukera guztiak:

π , 7 4 6 13 52 152 2 13 –; ;; ;; ; + !

Tarteak eta zuzenerdiak

5 Adierazi zuzen errealean honako tarte eta zuzenerdi hauetako bakoitza:

A = [–2, 4] B = (1, 6) C = [–7, –3)

D = (0, 5] E = (– ∞, 1] F = (–1, +∞)

6 Idatzi honako zenbaki-multzo hauetako bakoitza tarte edo zuzenerdi moduan:

a) 2 baino handiagoak eta 7 baino txikiagoak.

b) –1 eta 3 bitartekoak, bi muturrak barne.

c) 5 edo 5 baino handiagoak.

d) 10 baino txikiagoak.

7 Irudikatu grafikoki eta adierazi tarte edo zuzenerdi moduan honako desberdintza hauetako bakoitza:

a) –3 ≤ x ≤ 2 b) 5 < x c) x ≥ –2

d) –2 ≤ x < 3/2 e) 4 < x < 4,1 f ) –3 ≤ x

8 Adierazi tarte edo zuzenerdi moduan, eta desberdintza moduan, honako zenbaki-multzo hauetako bakoitza:

a) –1 0 3 b)

Berreketak, erroak eta erroketak

9 Kalkulatu honako adierazpen hauen balioak: a) 25 / 52 b) () / 43 c) 81 , 02 5– d) 8 6 8

10 Adierazi berreketa moduan.

a)

11 Jarri erro moduan.

a) 51/2 b) (–3)2/3 c) 3 4 / 13cm

d) (a 3)1/4 e) (a 1/2)1/3 f ) (a –1)3/5

12 Adierazi honako zenbaki hauetako bakoitza 2ren berreketa baten bidez, eta, gero, egin biderketa:

a) 16 / 32 3 –`j b) 4 6 c) 2 1 eo

13 Adierazi honako erro hauek zatikizko berretzailea duten berreketen bidez, eta sinplifikatu:

a) aa 2 5 b) x x 2 3 c) a 1 3 4

14 Sinplifikatu.

a) 3 2 4 b) a 8 12 c) a 15 5

d) ab24 8 e) a 8 4 3 f ) ab69 3

Zenbaki hurbilduak. Notazio zientifikoa

15 Aurkitu honako hurbilketa hauetako bakoitzaren errore absolutua eta erlatiboa:

a) 3 41 , bi zifra hamartarrekin

b) 72 , zifra hamartar batekin

c) 17 123 , ehunenetara

16 Eman hauteskunde batzuetako boto-kopuruari buruz egin diren hurbilketa hauen errore absolutuaren borne bat eta errore erlatiboaren borne bat:

a) 348 milaka boto b) 5 632 000

c) 890 000 d) 78945

e) 9 milioi f ) 134 milaka

17 Kalkulatu buruz.

a) (1,5 · 107) · (2 · 105) b) (3 · 106) : (2 · 1011)

c) (4 · 10–7) : (2 · 10–12) d) 410 8

Egin eskuz, notazio zientifikoa erabilita, eta eman egindako errore absolutuaren kota bat.

a) (3,5 · 107) · (4 · 108) b) (5 · 10–8) · (2,5 · 105)

c) (1,2 · 107) : (5 · 10–6) d) (6 · 10–7)2

Logaritmoak

19 Erabili logaritmoaren definizioa eta kalkulatu.

a) log2 64 b) log2 16 c) log2 4 1

d) log2 2 e) log3 243 f ) log3 27 1

g) log3 9 3 h) log 0,001 i) log5 0,2

20 Kalkulatu honako logaritmo hauen oinarriak:

a) logb 64 = 3 b) logb 100 = 2

c) logb 243 = 5 d) logb 625 = 4

21 Aurkitu kalkulagailua erabilita.

a) log4 23,4 b) log3 543 c) log5 0,06

d) log6 20,8 e) log5 123 f ) log2 0,872

ENTRENATU ETA PRAKTIKATU

22 Kokatu zenbakiak behean ikusten duzun moduko

diagrama batean:

1; , 723 # ; 1 – 2 ; 3,5; 9 11 ; 4 1 ; 6 ; π 4 ; –104

23 a) Zer zenbaki irrazional adierazten dituzte A, B, C eta D puntuek? 3 01DCBA

1 2

b) Adierazi 8 eta 11

24 a) Esan ondorengo zenbaki hauetako zein dauden A = [–3, 7) edo B = (5, +∞) tarteetan:

–3; 10; 0,5; 7; – 4; 5 ; , 63 ! ; π; 5 27 ; 48 ; 1 – 2

b) Honako tarte hauetako zeinek adierazten ditu A-n eta B -n dauden zenbakiak ?

(–3, 5) [2, 7) [5, 7] (5, 7)

c) Adierazi A ∪ B eta A ∩ B tarte moduan eta desberdintza moduan.

25 Adierazi markatutako zenbaki-multzoak tarteen bilketa moduan, ∪ ikurra erabilita:

a) –4

c) 3 6 d) –1

26 Sinplifikatu.

a) a 15 5 b)

27 Adierazi berreketa moduan eta kalkulatu x kasuetako bakoitzean, bi ataletako berretzaileak berdinduz:

28 Biderkatu eta sinplifikatu.

29 Atera erroetatik ahal dituzun biderkagai guztiak.

errotzaile komunera eta adierazi emaitzak erro bakar batekin

erroan eta sinplifikatu errokizuna.

Ariketak eta problemak

36 Arrazionalizatu, eta sinplifikatu, egin badaiteke.

a) 13 3 + b) 12 12 –+ c) a a 1+

d) 22 11 3+ e) ab a 2 4 32 4 f ) 5 5 3 3–+

37 Adierazi analisi hauetako zer emaitza dauden erreferentzia-balioen tartetik kanpo:

Emaitzak Erreferentzia-balioak Unitateak

Leukozitoak 3,16 (3,5-11) × 103 µL

Hematieak 5,87 (4,3-5,9) × 106 µL

Plaketak 1,9 (1,50-4,50) × 105 µL

Kreatinina 0,68 (0,7-1,3) × 105 mg/dL

38 Kalkulatu logaritmoaren definizioa erabilita. log4 163 + log4 2 + log 0,0001 + log 100

39 log x = 1,3 eta log y = 0,8 badira, kalkulatu:

a) log (x · y) b) log () xy c) log x y 2 d) log y x

42 –= adierazpena emanda, aldatu logaritmoak hartuta eta propietateak ezarrita, ebatzitako adibidean egin den bezala

xy

a) xy M 10 3 2 = b) N xy z 23 = c) P y x 2 3 =

EBATZI PROBLEMA ERRAZAK

41 Aurkitu x-ren zer baliotarako kalkulatu daitezkeen honako erro hauek:

a) x 7– b) x 5– c) x– d) x 1 2 +

42 M zentroko eta r erradioko ingurunea esaten zaio zentrotzat M eta mutur moduan M –  r eta

M + r dituen tarte irekiari, eta I(M, r) izendatzen da.

Adibidez: E(0, 2) = (–2, 2) eta E(2, 3) = (–1, 5)

Adierazi honako ingurune hauek tarte moduan:

a) E(0, 1) b) E(0, 3) c) E(3, 5) d) E(–2; 1,5)

e) E(–3; 0,3) f ) E(2,1; 3) g) E(–0,2; 5,3)

43 Adierazi honako tarte hauetako bakoitza I(M, r) motako ingurune moduan:

a) (–3, 3) b) (2, 4) c) (0, 6) d) (–1, 4)

e) (–3, 2) f ) (0; 7,5) g) (–5; –2,2) h) (1,2; 4,7)

44 Adierazi M logaritmorik gabe. (Kontuan izan log M = log k bada, orduan M = k).

a) () loglog log Mx x 32 –=+

b) () loglog loglog Mx y 13 – =+ +

c) () lnlnlnln Mx yx22=+3– +

45 Ortoedro baten neurriak, zentimetrotan, 81827 ## dira. Kalkulatu:

a) Azalera osoa. Eman balio zehatza, erroekin.

b) Diagonalaren luzera. Adierazi neurri hau erroekin eta zifra hamartar batekin hurbilduta.

c) Kalkulatu aurreko puntuko hurbilketan egin diren errore absolutua eta errore erlatiboa.

46 Triangelu isoszele batean, desberdina den aldearen luzera 53 cm da, eta alde horri dagokion altuera da alde horren laurdena. Kalkulatu triangeluaren perimetroa. Adierazi erroekin.

APUR BAT GEHIAGO PENTSATZEKO

47 Esne Bidearen diametroa 105 700 argi-urtekoa da, eta argi-urte bat 1,461 · 1012 km dira.

a) Zenbat kilometroko diametroa du gure galaxiak?

b) Zenbat milurteko beharko lituzke espazio-ontzi batek gure galaxia zeharkatzeko, 2 000 km/s-ko abiaduran?

c) Elektroi baten diametroa 4 · 10–15 m-koa dela jakinda, zenbat elektroi jarri beharko lirateke erreskadan Esne Bidea inguratzeko? (Pentsatu zirkunferentzia bat dela).

48 Kalkulatu ertza 8 cm-koa duen tetraedro erregular baten altuera. h h/3 2h/3

h 6 6 2 2

50 Egiaztatu honako bi hexagono hauen azaleren arteko erlazioa 4/3 dela. (Kontuan izan hexagono bakoitza 6 triangelu aldekidetan banatu daitekeela).

51 Adierazi tarte moduan honako desberdintza hauetako bakoitza egiaztatzen duten zenbakiak:

a) | x | < 3 b) | x  – 1| ≤ 5 c) | x + 3| < 4

Nola adieraziko zenituzke aurreko desberdintza horien aurkakoak egiaztatzen dituzten zenbakiak? Hau da: | x | ≥ 3 | x  – 1| > 5 | x + 3| ≥ 4

ULERTU ETA APLIKATU ERRONKA

52 Kalkulatu zatiki eran. 1 1 1 2 1 1 1 + + +

a) 2ren ordez jarri 1 + 1/2 eta egin eragiketak berriro. Egin prozesu hori beste behin.

b) Egiaztatu emaitzetako zenbakitzaileak eta izendatzaileak Fibonacciren segidako gaiak direla.

c) Zer baliotara hurbiltzen dira lortutako zatidurak?

57 2 cm-ko aldea duen karratu batetik abiatuta, ABFE laukizuzena eraiki dugu.

Urrezko laukizuzen bat da?

Egiaztatu bere aldeen zatidura Φ urrezko zenbakia dela.

58 Urrezko zenbakiak ekuazio hau betetzen du:

Φ2  – Φ – 1 = 0

Hortik abiatuta, egiaztatu honako berdintza hauek:

a) Φ2  = Φ + 1 b) Φ – 1 =  1 U

c) Φ3 = 2Φ + 1 d) Φ4 = 3Φ + 2

ULERTU DUZU? HAUSNARTU

59 Zuzena ala okerra? Azaldu eta jarri adibideak.

a) Zenbaki irrazional batzuk ez dira errealak.

b) Bi zenbaki arrazionalen artean infinitu irrazional daude.

c) Zenbaki hamartar periodiko baten alderantzizkoa hamartar zehatz bat izan daiteke.

d) 0,83 · 109 zenbakia ez dago notazio zientifikoan.

60 4 ≥ loglogab2–33 bada, zer erlazio egon behar da a-ren eta b-ren artean?

53 a) Adierazi honako segida honetako gaiak berreketa moduan:

… aa a 13131313131312;; 3 == ==

b) Egiaztatu berretzaileak arrazoia 1/2 duen progresio geometriko bateko gaien batura direla.

c) Zer baliotara hurbiltzen da segida hori?

54 Bankuan diru-kantitate bat gordailuan uzten badut urteko % 3an, zenbat urte igaro beharko dira kantitate hori hirukoizteko?

HAU ERE EGIN DEZAKEZU

55 Egiaztatu ezin dela kalkulagailua erabili 5129 · 463 lortzeko, zenbaki handiegia delako. Erabili berreketen propietateak eta adierazi notazio zientifikoan.

56 Kalkulatu zein den x-ren balioa honako adierazpen hauetako bakoitzean:

a)ogxlogl2237 =+ b) 75 63 x =+

61 Aztertu m zuzen errealean adierazteko modu hau. Arrazoitu. m

62 x zenbakia [–1, 3) tartekoa bada, eta y zenbakia, (0, 4] tartekoa, azaldu zer tartetan egon daitekeen x + y.

Eta x – y ?

63 Azaldu honako berdintza hauek zuzenak ala okerrak diren:

a) log (a · b) = log a · log b

b) log b a bl  = log a – log b

c) loglogaa 3 1 3 =

d) log (a 2  · b ) = 2(log a + log b )

ULERTU ETA APLIKATU ERRONKA

Matematika-lantegia

IRAKURRI ETA INFORMATU

Urrezko laukizuzenak

Laukizuzen bat urrezkoa dela esaten dugu bere aldeek proportzio jainkotiarra dutenean; hau da, unitatetzat alde txikia hartuta, alde handiaren neurria urrezko zenbakia denean Φ =  2 1 5+  = 1,618…

Laukizuzen mota hauek propietate bitxi bat dute: alde handiaren gainean karratu bat erantsiz gero, urrezko beste laukizuzen bat lortzen da. Egiaztatu:

Eta karratuak erantsiz jarraitzen baduzu, gero eta handiagoak, urrezko laukizuzenen segida bat lortuko duzu, eta horien gainean zirkunferentzia-arkuz eratutako espiral eder bat eraiki liteke:

maskorra.

Oso espiral ezaguna da eta matematiketan lantzen da (espiral isogonala edo espiral geometrikoa). Baina harrigarriena da berez agertzen dela, modu naturalean, hainbat landare- eta animalia-espezietan (loreak, fruituak, moluskuen maskorretan, etab.).

• Eraiki espiralaren ondoz ondoko erradioen segida, aintzat hartuta eransten diren karratuen aldeekin bat datozela:

Leonardo Pisakoa (1170-1250)

Fibonacci ere esaten zioten (gizon onaren semea).

Bere aita merkataria eta Pisako kontsula izan zen Bugia hirian, gaur egungo Aljerian.

Horri esker arabiarren matematika ikasi zuen, batik bat zenbakikuntza hamartarra, eta Europan barneratzen lagundu zuen.

Berak deskribatu zuen inork baino lehenago segida ospetsu hau: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …

Ikusten duzu erlaziorik segida horren eta Fibonacciren segidaren artean?

Segida horretan gaietako bakoitza aurreko biak batuta lortzen da. Fibonacciren segidak oso erlazio estua du urrezko zenbakiarekin, Φ

1 a) Sailkatu honako zenbaki hauek arruntak, osoak, arrazionalak eta errealak diren kontuan izanda:

3 4 6 – ; 2π; , log 05 2 ; , 347 # ;

2,03333…; 81 ; 4 3 ; / 53 ; – 13/9; – 8

b) Adierazi zein diren irrazionalak.

c) Ordenatu txikienetik handienera.

2 Adierazi zer zenbaki adierazten dituzten A, B, C eta D puntuek. 1 0

2 12 A D B C 3

3 Taula honetan bilduta dago EBko herrialde batzuetako biztanleria eta urteko BPGa milioika eurotan.

7 Egin eragiketak eta sinplifikatu.

a) () 3 32 3 2 + b) 54 26 150 –+

c) 50 5 2 2 – d) 23 10 2–

8 Kalkulatu, logaritmoaren definizioa ezarrita edo kalkulagailua erabilita.

a) log3 9 1 3 b) log2 32 1 2 4 cm

9 Aurkitu zein den x-ren balioa kasu hauetako bakoitzean:

a) logx 73 – 2 = b) log 202 x = c) loglogx51 +=

10 Lortu 6 m2-ko azalera duen karratu batean inskribatutako eta zirkunskribatutako zirkunferentzien artean geratzen den koroa zirkularraren azalera. Eman balio zehatza.

11 10 cm-ko aldea duen karratu batean, erpin bakoitzean triangelu angeluzuzen isoszele bat ebaki dugu, eta oktogono erregular bat lortu dugu.

a) Adierazi notazio zientifikoan, eta kalkulatu bakoitzaren per capita BPGa. Aurkitu kasu bakoitzeko, errore absolutuaren borne bat eta erlatiboaren borne bat.

b) Zer ehuneko da Estoniako BPGa Espainia, Finlandia eta Frantziakoaren aldean?

4 a) Idatzi zenbaki-multzo hauek tarte moduan, eta adierazi grafikoki:

i) ≤ x –<27 ii) x 1–> iii) | x | < 4

b) Idatzi tarte hauek desberdintza moduan:

A = [–3, 4) B = (–∞ , 3 )

c) Adierazi A ∪ B eta A ∩ B tarte moduan eta desberdintza moduan.

5 Adierazi berreketen bidez:

6 Atera errotik atera litezkeen biderkagai guztiak.

a) Lortu oktogonoaren aldearen neurri zehatza.

b) Kalkulatu azalera. c) Lortu erradioa.

IKASKUNTZA-EGOERA

HAUSNARTU

Berrikusi landutako alderdiak eta eman konponbidea hautemandako arazoei.

Horretarako, deskargatu dagokion errubrika anayaharitza.es webgunetik, egin gogoeta banaka eta bateratzelana taldean.

PROBATU ZURE KONPETENTZIAK

Egin anayaharitza.es webgunean ageri den konpetentzien autoebaluazioa.

AUTOEBALUAZIOA ➜ anayaharitza.es Ariketa hauen ebazpena.

© GRUPO ANAYA, S.A., 2023 - C/ Valentín Beato, nº 21 - 28037 Madrid.

Reservados todos los derechos. El contenido de esta obra está protegido por la Ley, que establece penas de prisión y/o multas, además de las correspondientes indemnizaciones por daños y perjuicios, para quienes reprodujeren, plagiaren, distribuyeren o comunicaren públicamente, en todo o en parte, una obra literaria, artística o científica, o su transformación, interpretación o ejecución artística fijada en cualquier tipo de soporte o comunicada a través de cualquier medio, sin la preceptiva autorización.