Mundua helburu: Matematika A Aukera 4. DBH. Lagina by Grupo Anaya, S.A.

LIZENTZIA

4

1. MATEMATIKA A AUKERA

José Colera J., M.ª José Oliveira G., Ignacio Gaztelu A., Ramón Colera C., Ana Aicardo B. hiruhilekoa

DAUKA

12HILEKO

PROIEKTU DIGITALA

DBH Munduahelburu

LAGINA

Aurkibidea

Ikasturteko oinarrizko jakintzak

• Egin datuak antolatzen lagunduko dizun eskema bat, grafiko bat edo taula bat

• Problema geometrikoetan, egin irudi bat!

• Esperimentatu, kalkulatu iritzira, jarri adibideak… Egin aieruak eta egiaztatu

• Ikertu

Problemak

Berrikusi eta sakondu problema aritmetikoak IKASKUNTZA-EGOERA

1 Zenbaki arruntak, osoak

1. Zenbaki arruntak

2. Zenbaki osoak

3. Zatikiak

4. Eragiketak zatikiekin

5. Problemak zatikiekin

6. Berreketak

Ariketak eta problemak

Autoebaluazioa

Bitxikeria matematikoak

2 Zenbaki hamartarrak 48

1. Zenbakikuntza-sistema hamartarraren garrantzia

2. Zenbaki hamartar motak

3. Hamartarretik zatikira igarotzea

4. Kantitate hurbilduak. Erroreak

5. Notazio zientifikoa

Ariketak eta problemak

Autoebaluazioa

Bitxikeria matematikoak

3 Zenbaki errealak 62

1. Zenbaki irrazionalak

2. Zenbaki errealak: zuzen erreala

3. Zuzen errealaren zatiak: tarteak eta zuzenerdiak

4. Erroak eta errotzaileak

Ariketak eta problemak

Autoebaluazioa

Bitxikeria matematikoak

IKASKUNTZA-EGOERA

1. Monomioak eta polinomioak. Zenbakizko balioa

2. Polinomioen arteko eragiketak

3. Polinomio zati (x a) egitea

4. Polinomio baten erroak

5. Polinomioen faktorizazioa

6. Ekuazioetarako prestatzen Ariketak eta problemak

1. Ekuazioa. Ekuazio baten soluzioa

2. Lehen mailako ekuazioak

3. Bigarren mailako ekuazioak

4. Beste ekuazio mota batzuk

Ariketak eta problemak

Autoebaluazioa

Bitxikeria matematikoak 6

1. Ekuazio-sistema linealak

2. Ekuazio-sistemen ebazpena

3. Ekuazio linealen sistema konplexuagoak

4. Sistema ez-linealak

5. Problemak sistemen bidez ebaztea

6. Ezezagun bateko inekuazioak

Ariketak eta problemak

Autoebaluazioa

Bitxikeria matematikoak

IKASKUNTZA-EGOERA

Aljebra 78

Polinomioak 80

Itzala uzten duten erronkak:

Autoebaluazioa Bitxikeria matematikoak

Ekuazioak 96

Ekuazio-sistemak eta inekuazioak 112

Merkatu ekologiko eta jasangarria 130

IKASKUNTZA-EGOERA

Trebatu problemak ebatziz

Itzala uzten duten erronkak: Aritmetika 32

zatikizkoak

eta

Karismadun hiru zenbaki

7 Funtzioak. Ezaugarriak

1. Oinarrizko kontzeptuak

2. Nola adierazten dira funtzioak?

3. Ebaki-puntuak ardatzekin. Funtzio baten zeinua

4. Funtzio jarraituak. Etenak

5. Funtzio baten aldaketak

6. Joera eta periodikotasuna

eta problemak

8 Oinarrizko funtzioak

1. Funtzio linealak

2. Funtzio koadratikoak

3. Funtzio errodunak

4. Alderantzizko proportzionaltasuneko funtzioak

5. Funtzio esponentzialak

eta problemak

1. Oinarrizko kontzeptuak

2. Maiztasun-taulak

3. Parametro estatistikoak: x eta σ

4. Posizio-parametroak

5. Kaxa-diagramak

6. Estatistika inferentziala

7. Estatistika komunikabideetan Ariketak

1. Banaketa bidimentsionalak

2. Korrelazioaren balioa

3. Erregresio-zuzena estimazioak egiteko

4. Hausnartu: Korrelazioak kausa-efektua adierazten du?

5. Banaketa bidimentsionalak kalkulagailuarekin

Ariketak eta problemak

Autoebaluazioa

Bitxikeria matematikoak

1. Antzekotasuna

2. Homotezia

3. Neurri interesgarriko laukizuzenak

4. Triangeluen antzekotasuna

5. Triangelu angeluzuzenen antzekotasuna

1. Probabilitateak lortzea: esperimentazioa ala kalkulu matematikoa?

2. Ausazko gertaerak

3. Gertaera baten probabilitatea

4. Gertaera baten probabilitatea lortzea

5. Esperientzia konposatuak. Probabilitatea

6. Kontingentzia-taulak

Ariketak eta problemak

Autoebaluazioa

IKASKUNTZA-EGOERA Itzala uzten duten erronkak: Funtzioak eta geometria 132

134

Ariketak

Autoebaluazioa Bitxikeria matematikoak

150

Ariketak

Autoebaluazioa Bitxikeria matematikoak

Antzekotasuna. Erabilerak 166

Autoebaluazioa Bitxikeria matematikoak IKASKUNTZA-EGOERA Ikerketa biologikoak 184

Itzala uzten duten erronkak: Estatistika eta probabilitatea 186 10 E statistika 188

Ariketak eta problemak

IKASKUNTZA-EGOERA

eta

Autoebaluazioa Bitxikeria matematikoak 11 Banaketa bidimentsionalak

problemak

208

Probabilitatea

222

IKASKUNTZA-EGOERA Loteriak eta zorizko beste joko batzuk 236

Bitxikeria matematikoak

Zenbaki arruntak, osoak eta zatikizkoak

Zenbaki osoen jatorria

Zibilizazio guztiek erabili izan dituzten zenbaki arruntak, antzinatetik hasita. Egiptoarrek, babiloniarrek, greziarrek, erromatarrek, txinatarrek, indiarrek, arabiarrek, maiek… oso sistema desberdinak erabili izan dituzte, gauza batzuetan elkarren antzekoak eta beste batzuetan oso bestelakoak.

Eragiketak arintasun handiagoz egiteko modua eman zuen sistema posizional bat lortzea mendeetako lanaren fruitu izan zen. Zailagoa izan zen zenbaki negatiboak ulertu eta onartzea, eta zer esanik ez zeroa.

Beraz, zenbaki osoen multzoak ez zuen gorputzik hartu vii . mendearen amaiera arte, Indian. Guregana ix . mendean heldu zen arabiarren bidez, zenbakisistema hamartar-posizionalarekin batera.

Zatikiak

Zatikiak oso antzinatik erabili izan dira unitatearen zatiak adierazteko. Babilonian zatiki hirurogeitarrak erabiltzen zituzten (izendatzaileak 60ren berreketak ziren), eta gaur egun ere oraindik erabiltzen dugu nomenklatura hori angeluen neurrietan eta denboraren neurrietan.

Egiptoarrek zatiki unitarioak baino ez zituzten erabiltzen (zenbakitzailean bat zenbakia zuten zatikiak: 1 2 , 1 3 , 1 4 , 1 5 , … eo . Harrigarria bada ere, 2 5 adieraz-

teko ez zuten 1 5 + 1 5 idazten, 1 3 + 1 15 baizik; izan ere, zatiki bakoitza behin baino ez zuten jartzen Are harrigarriagoa da nomenklatura horrek hainbat mende iraun izatea. Zatikiak gaur egun erabiltzen ditugun moduan ez ziren finkatu xiv. mendera arte.

1 34

GOGORATU

Zenbaki kardinalek zenbatzeko balio dute, eta ordinalek, ordenatzeko.

Adibidez, «Lasterketako 8 finalistetatik, Mario hirugarren heldu da» baieztapenean, 8 zenbakia kardinala da, eta 3, ordinala.

Zenbaki arruntak 1

Guztia zenbatzen dugu: gela batean dauden ikasleak, zoru batean dauden lauzen kopurua, edota poker-sorta batean batekoak ordenatzeko zenbat modu dauden. Zenbatzeko zenbaki arruntak erabiltzen ditugu. Dakizunez, 0, 1, 2, 3, …, 10, 11, 12, … 99, 100, 101, … dira. Infinitu zenbaki daude. Eta horien guztien multzoa izendatzeko N erabiltzen dugu. Ordenatuta daudenez, zuzen baten gainean irudika ditzakegu:

0 1 2 3 4 5 6 7 8 9 10 11

Zenbaki arruntek zenbakitzeko ere balio dute. Adibidez, Oihane Goikoetxea ikasgelako zerrendan hamahirugarrena dela esaten dugu.

Batuketa eta biderketa

Zenbaki arruntak batu eta biderkatu egin daitezke; eragiketa horien emaitza ere zenbaki arrunt bat da.

Gogoan izan a ∙ b + c eta a + b ∙ c adierazpenetan biderketa batuketa baino lehen egin behar dela. Lehentasuna batuketari eman nahi diogunean, parentesi artean adierazi behar dugu: a ∙ (b + c), (a + b) ∙ c

Zatiketa

ADIBIDEA

100 elementu 7 indibiduoren artean banatzean, zatiduran 14 lortzen dugu (indibiduo bakoitzari 14 elementu dagozkio) eta hondarrean 2 (2 elementu geratzen dira banatu gabe).

Zenbaki arrunten arteko zatiketak banaketa adierazten du. 100 : 5 = 20 zatiketa interpretatzean, esan dezakegu 100 elementu (zatikizuna) 5 zatitan (zatitzailea) banatu direla, eta parte bakoitzari 20 elementu (zatidura) dagozkiola. Banaketa eginda aukeran genituen elementu guztiak erabili baditugu, kasu honetan bezala, zatiketa zehatza dela esaten dugu. Baina banaketa egin eta elementuren bat sobera geratu bada, zatiketa osoa dela esaten dugu. Kasu horretan, zatiduraz gain hondarra ere lortzen dugu.

Berreketa eta erroketa

Ondo dakizun moduan, zenbaki arrunten berreketa bat da, azken batean, biderkagai beraren biderketa bat. Adibidez: 74 = 7 ∙ 7 ∙ 7 ∙ 7. Hori jakinda, berehala lortzen ditugu berreketaren propietateak.

Erroketa da berreketaren kontrako eragiketa. 74 = 2 401 bada, orduan

2 401 7 4 4 4 = = 7. N multzoan erro osoek soilik dute zentzua.

PENTSATU ETA PRAKTIKATU

1 Kalkulatu.

a) Asteko zer egun izango da 357 egun barru?

(23)2 d) 2 () 3 2

3 375 3

000 000

2 Gaur astelehena da. Bihar… izango da. Etzi … izango

25 egun barru… izango da.

b) Asteko zer egun izango da 7a + 3 egun igaro ondoren, a edozein zenbaki arrunt bada?

c) Nola adieraziko zenuke, orokorrean, larunbata izateko igaro diren egunen kopurua?

35 U 1

f) 1

33 ∙ 23 ∙

(2 ∙ 5)6

da.

Zenbaki osoak 2

Batzuetan, kantitate negatiboak erabili behar izaten dira. Ikus ditzagun adibide batzuk:

• –5 °C-ra egoteak esan nahi du zeroz azpitik 5 °C-ra gaudela.

• Bankuan –108 €-ko saldoa izateak esan nahi du 108 € zor direla…

Dakizun moduan, oso negatiboek, arruntekin batera, zenbaki osoen multzoa eratzen dute, eta multzo hori adierazteko Z erabiltzen da. Zenbaki osoekin batuketak eta biderketak egin, eta zenbaki osoak lortzen dira. Gainera, arruntekin gertatzen den ez bezala, bi zenbaki osoren arteko kenketa eginda beste zenbaki oso bat lortzen da.

Zenbaki osoak honela adierazten dira zuzenean:

Zuzenaren gaineko ordena hori-irizpide honi jarraituta egiten da:

• Arruntak (zeroa eta oso positiboak) lehendik ordenatuta zeuden.

• Zenbaki arruntak oso negatiboak baino handiagoak dira.

• a eta b zenbaki arruntak badira, eta a < b bada, orduan –a > –b

Zenbaki oso baten balio absolutua

Zenbaki baten balio absolutua da zenbaki horren magnitudea, zeinua alde batera utzita. Honela idazten da: | x |, eta honetara definitzen da:

• Zenbaki arrunt baten balio absolutua zenbakia bera da: | 5 | = 5, | 0 | = 0

• Zenbaki negatibo baten balio absolutua bere aurkakoa da: | –27 | = 27

• Grafikoki, zenbaki baten balio absolutua da 0-raino duen distantzia: |– 4| = 4 |3| = 3 144444424444443144424443 – 4 0 3

Zenbaki osoen eragiketak egiteko erregelak

• Zenbaki positiboen eta negatiboen batuketak egiteko, batzuk eta besteak multzokatuko ditugu, lortutako emaitzen kenketa egingo dugu, eta balio absolutu handiena duenaren zeinua jarriko diogu.

• Parentesi baten aurrean minus zeinua agertzen bada, parentesia kentzean barruko batugai guztien zeinuak aldatu behar dira.

• Zenbaki osoak biderkatzeko, «zeinuen erregela» gogoratuko dugu:

PENTSATU ETA PRAKTIKATU

1 Ordenatu txikienetik handienera: –4, 19, 7, 0, –6

2 Kalkulatu.

a) | | –3 | | b) | | 5 + (3 – 11) | |

d) | 5 + | 3 – 11 | | e) | 30 – (–20 – 9) |

3 Kalkulatu.

a) (1 – 4) – (5 – 3) – (–6)

b) –3(4 – 2) – 4(3 – 8)

c) (–2)3 + (–3)4 – 52

d) 15 – 4(3 – 6) – 2[4 – 5(2 – 3)]

–7 … – 6 –5 – 4 –3 –2 –1 0 1 2 3 4 5 6 7 8 …

+ ∙

= + + ∙ – = – – ∙ + = – – ∙ – = +

GOGORATU

Zenbaki osoak zatiki eran adieraz dai-

Zatikiak 3

Zatikizko zenbakiak neurriak adierazteko

Neurtzeko, unitatea zatitu egin behar izaten da. Hortik sortu zen zatikizko zenbakiaren ideia: unitatearen erdia, bostena, milarena...

Zatikizko zenbakien adierazpenak zatikiak dira.

Honako hauek zatikizko zenbakiak dira: ,,,,

Zatiki horietan guztietan, zenbakitzailea izendatzailea baino txikiagoa da eta, beraz, unitatearen zatiak dira denak. Zatiki propioak dira.

2 3 , 3 7 – eta 4 19 bezalako zenbakiak ere zatikizkoak dira, eta zenbaki oso baten eta zatiki propio baten batuketaren bidez adieraz daitezke (zenbaki mistoak):

Zatikizko zenbakiak zenbaki osoekin batera adieraz daitezke zuzenean

BURUZKO KALKULUA

1. Sinplifikatu zatiki hauek:

15 10 b) 8 6

21 14

44 33

18 12

17 34

100 75

26 52

2. Aurreko bederatzi zatiki horiek hirunaka baliokideak dira. Sailkatu.

3. Idatzi 500 300 zatikiaren sei zatiki baliokide

Zein da horien guztien zatiki laburtezina?

PENTSATU ETA PRAKTIKATU

Zatikizko zenbakiek, zenbaki osoekin batera, zenbaki arrazionalen multzoa osatzen dute, eta multzo hori Q letrarekin izendatzen dugu.

Q multzoko elementuen ezaugarri bat zatiki eran adieraz daitezkeela da.

Zatikien sinplifikazioa. Zatiki baliokideak

Gogoan izan zatiki bat sinplifikatzea dela zenbakitzailea eta izendatzailea zenbaki oso berarekin zatitzea.

Sinplifikatu ezin den zatikia laburtezina dela esaten dugu.

Bi zatiki baliokideak dira sinplifikatzean zatiki laburtezin bera ematen badute.

1 Adierazi oso baten eta zatiki baten arteko batuketa moduan. a) 9 40 b) 5 86 c) 10 127 d) 12 127 e) 8 43 –

2 Lortu zatiki laburtezina a) 21 18 b) 35 14 c) 36 42 d) 56 14 e) 200 75

3 Kopiatu zuzena koadernoan eta adierazi zatikiak, gutxi gorabehera.

37 U 1

2 1 5 1 5 3 7 4 100 1 1 000 145

2 3 1 2 1 =+ 3 7 2 3 1 =+dn 4 4 19 4 3 =+

3 4 5 2 1 0 –7 3 = 1 + 1 2 3 2 — = 4 + 3 4 19 4 –4 –5 –3 –2 –1 = –2 –1 3

Adibidez: 24 28 6 7 = 6 15 2 5 2 5 – == 7 500 5 000 3 2 =

35 –10 eta 28 8 –baliokideak dira: 35 10 7 2 7 2 – == 28 8 7 2 7 2 – ==

Adibidez,

tezke:

1 4

12 === =

2 4

)

–2 –1 0 1 2 3 ,, ,,,, 5 13 9 18 5 7 4 11 20 11 10 7 10 17 ➜

anayaharitza.es Praktikatu zatiki laburtezina kalkulatzea.

Eragiketak zatikiekin 4

Zatikien batuketa

Izendatzaile bera duten zatikien batuketa egitea oso erraza da: zenbakitzaileen arteko batuketa egin behar da, eta izendatzailea bere horretan utzi.

Izendatzaile desberdina duten zatikien batuketa (eta kenketa) egiteko, izendatzaile bera har dezaten, zatiki baliokideak bilatu eta bihurtu egin behar ditugu.

Zatikien biderketa

Gauza baten laurden baten herena da gauza horren hamabirena: ·

Modu berean arrazoituta, honako hau ikusten dugu:

Bi zatikiren biderketa eginda, emaitza beste zatiki bat da, izendatzaile moduan jatorrizko zatikien izendatzaileen biderkadura duena, eta zenbakitzaile moduan, zenbakitzaileen biderkadura: · · b a d c bd ac ·=

Kantitate baten zatikia zatikien biderketaren kasu partikular bat da; izan ere, ondo dakizun moduan, zenbaki oso bat adieraz daiteke izendatzailean unitatea duen zatiki baten bidez, zenbakitzaile moduan zenbakia bera jarrita.

Esate baterako: Anderrek aurreztuta zituen 1 260 €-tik 3 2 gastatu ditu ikasturte amaierako bidaia ordaintzeko. Beraz, bidaia honenbeste kostatu zaio: ··

Zatiki baten alderantzizkoa. Zatikien zatiketa

4 zenbakiaren alderantzizkoa 4 1 da. Eta kontrara, 4 1 zenbakiaren alderantzizkoa 4 da.

3 zatikiaren alderantzizkoa 3 5 da. Eta kontrara.

0 ez den gainerako zatiki orok, b a , alderantzikoa du, a b , eta hau betetzen da: a ba b = 1.

Bi zatikiren zatiketa kalkulatzeko, lehenengoaren eta bigarrenaren alderantzizkoaren arteko biderketa egiten da:

5 3 4 3 4 5 45 4 1 5 20 15 20 16 20 100 20 15 16 100 20 69 –– –+= += += + =

Adibidez:

11 3 1 412

2 4 5 34 25 12 10 5 36 · · == =

1 260 3 2 1 1 260 3 2 3 2

520 == = 840 €

· : b a d c b a b a c d c d · · == Adibidez: : 21 10 7 2 21 2 10 7 42 70 3 5 · == =

BURUZKO KALKULUA

3 2 6 1 + b) 3 2 6 1 –

3 2 4 3 d) 3 9 4

3 1 f )

3 4

e) 1 :

: 7

3 2

4 3 en 3 2 j) 600en 3 2 4 3 ·

5 1 en 2 1 l) 800en 5 3 en 2 1

g) 600en

600en

d) 3 1 4 3 5 4 1 20 1 – + dn >

3 Laburtu zatiki bakarrera. a) :: 11 12 3 33 16 dn b) 3 5 14 13 26 21 ··dn

c) : 39 11 13 3 9 22 dn d) : 10 7 5 9 7 3 dn 4 Kalkulatu.

39 U 1

b) 4 3 7 8 46 –+

d) 1 2 1 4 1 8 ++

21 5 1 4 + dn

4 3 2 10 13 – + c) 1 3 1 6 1 –+dn

PENTSATU ETA PRAKTIKATU 1 Kalkulatu. a) 4 3 11 3 7 –+

c) 9 3 7 6 2 5 –+dn

e) 1 2 1 3 1 –+dn

2 Kalkulatu. a) 2 1 4 1 8 1 ++ b)

581en

c) 580en 20 11 5 Kalkulatu

duen. a) 3 1 en 2 1 b) 4 1 en 3 2 c) 5 3 en 9 5 6 Kalkulatu. a) 1 9 10 5 1 4 1 · ++dn b) : 1 2 1 3 1 4 1 2 3 + dn c) () 12 5 7 1 2 10 1 ·– –· < F d) () 3 1 9 2 2 6 5 2 7 5 – + d d n n > H e) : 5 4 3 2 10 1 1 15 7 – d d n n f ) : 4 1 7 3 15 2 1 5 2 d d n n > > H H 7 Kalkulatu. a) ·· 5 3 2 3 2 5 ––b) 4 3 1 2 1 4 3 1 – –+ dn c) () () 3 3 2 3 4 5 6 53 1 – –d d n n d) · –1 15 7 5 4 3 2 10 1 –

ARIKETA Kalkulatu. a) 5 3 10 3 3 2 2 1 –

b) 270en 9 5 c) 8 15 en 5 2 d) :· 7 9 6 3 2 cm e) :( )· 9 2 5 1 4 1 2 10 1 ·–+ cm > < H F a) 5 3 10 3 3 2 2 1 –dn > H = 5 3 10 3 3 2 2 1 5 3 10 3 3 2 2 1 += += < F = 30 18 30 9 30 20 30 15 30 18 92015 30 14 15 7 += + == b) 1 270 9 5 9 150 270 5 · == c) 8 15 5 2 58 40 30 4 3 15 2 · · == = d) :: 7 9 6 3 2 7 9 1 6 3 2 42 9 3 2 14 2 14 2 7 1 3 3 · ··· = === = ddnn e) :( ) 9 2 5 1 4 1 2 10 1 ·– · + dn > < H F = :: 2 20 10 2 20 2 10 2 2 1 9 9 · – –– == < F

a) 275en 5 1 b)

7 3

zer zatiki ematen

EBATZITAKO

cm >H

Problemak zatikiekin 5

❚ 1. problema

Hiri batean 120 000 biztanle zeuden 2000. urtean. Lehenengo hamar urteetan biztanleria 4/15 hazi zen, eta ondorengo hamar urteetan, 9/16. Zenbat biztanle zeuden 2020an?

Lehenengo hamar urteetan:

120 000ren 15 4 = (120 000 : 15) · 4 = 32 000

KONTUAN IZAN

Zatikia eta zatia jakin eta kopuru osoa kalkulatzeko, zatia zenbakitzailearekin zatitu eta izendatzailearekin biderkatu behar da.

T-ren 5 3 = 48

T = (48 : 3) · 5 = 80

➜ anayaharitza.es Praktikatu zatikien problemei buruzko ebazpena. 600 ? 150

Saldutakoak Salzeko

2010ean 120 000 + 32 000 = 152 000 biztanle zeuden. Ondorengo hamar urteetan:

152 000ren 16 9 = (152 000 : 16) · 9 = 85 500

2020an 152 000 + 85 500 = 237 500 biztanle zeuden.

❚ 2. problema

GKE batek lasterketa solidario bat antolatu du, eta, dirua biltzeko, kamiseta-sorta bat jarri du salgai. Astebetean 600 kamiseta saldu dituzte; hau da, kamiseta guztien 4/7. Zenbat kamisetako sorta da?

Sorta osatzen duten kamiseta guztien kopuruari T esaten badiogu:

050

KONTUAN IZAN

Osotasun bat adierazten duten zatikien arteko batura unitatea da (osotasuna).

b a d c f e 1 ++ = b a d c f e 1– +=bl

Mutilak Nesnak

Laburbilduz: T = (600 : 4) · 7 = 1 050

1 050 kamisetako sorta da.

❚ 3. problema

Exekutibo batek kapitalaren heren bat pentsio-funts batean ezarri du, hiru bostenak akzioetan inbertitu ditu, eta gainerako 3 836 euroak kontu korrontean dauzka. Zenbat diru du guztira?

Inbertitutako zatia: Kontu korrontean duen zatia:

Guztira duen dirua: 3 836 · 15 = 57 540 €

❚ 4. problema

36 ikasleko gela batean 2/3 mutilak dira. Nesken 3/4 musikako eskoletara joaten dira. Ikasle guztien zer zati hartzen dute musikara doazen neskek? Zenbat dira?

2 mutilak dira → 3 1 neskak dira

Musikara doazen nesken zatia:

== Gelako ikasleen

Musikara doazen neskak: 36ren 4 1 = 36 : 4 = 9

T-ren 7 4 = 600 → T-ren 7 1 = 600 : 4 = 150 → T-ren 7 7 = 150 · 7 = 1

3 1 5 3 15 59 15 14 += + = → 1 15 14 15 15 15 14 15 1 ==

3 1 en 4 3 = · 3 1 4 3 12 3 4

4 1

KONTUAN IZAN

Kantitate baten zatikia kalkulatzeko, zatikiaren eta kantitatearen arteko biderketa egiten dugu.

b a -ren · d c b a d c =

❚ 5. problema

Hiru lagunek sari bat banatu dute: lehenengoak sariaren 2/5 eraman ditu; bigarrenak, geratu denaren 5/9; eta hirugarrenak, 92 €. Zenbatekoa zen saria?

Lehenengoak sariaren 5 2 eraman ditu; 5 3 geratzen dira.

Bigarrenak sariaren 5 3 en 9 5 eraman ditu = 3 5 · 9 5 = 9 3 = 3 1

Lehenengoak eta bigarrenak sariaren 5 2 3 1 15 65 15 11 += + = eraman dituzte.

Hirugarrenak sariaren 15 15 15 11 15 4 –= eraman ditu. 15

4 dira, 92 €; 15 1 da, 92 : 4 = 23 €; eta 15 15 dira, 23 · 15 = 345 €

Beraz, saria (92 : 4) · 15 = 345 €-koa zen.

PENTSATU ETA PRAKTIKATU

1 Lursail bat hiru zatitan banatu dute. Zatietako bi lursail osoaren 2/5 eta 1/3 dira. Zein da zati handiena?

2 Aurreko probleman, lursailak 240 m2 baditu, zer azalera hartzen du zatietako bakoitzak?

3 Ikasgela bateko mutilen 2/5ek betaurrekoak dituzte. Gela horretan 36 ikasle daude eta 7/12 neskak dira. Zenbat mutilek dituzte betaurrekoak?

4 Gorkak asteko sariaren 2/7 musikan gastatu du, eta 1/5 liburutan. Sariaren zer zati gastatu du? Zer zati geratzen zaio?

5 Fruta-denda batean, goizean, dendako frutaren 3/5 saldu dute eta, arratsaldean, geratzen zenaren erdia.

a) Zer zati geratu zaie saldu gabe?

b) Hasieran 750 kg bazeuden, zenbat kilo fruta saldu dituzte?

6 1 500 €-ko soldata batetik, seirena jatekoan gastatzen da; hipoteka ordaintzeko, berriz, jatekoan baino 350 € gehiago. Soldataren zer zati geratzen da beste gauza batzuetarako?

7 Merkatuko postua itxi duenean, meloi saltzaileak hau erabili du buruan:

«Gaur hainbeste meloi saldu ditut. Hamaika baino ez zaizkit gelditu; hau da, saldu ditudanen hamarrena». Zenbat meloi zituen hasieran saltzeko?

8 Bulego batek 297 000 €-ko aurrekontua du urte osorako. Gastu finkoak aurrekontuaren bostena izango dira, eta gainerakoaren 2/11 ekipamendu eta tresnerian erabili beharko dira. Zenbat geratuko zaie beste gastu batzuetarako?

9 Klub batek 1 200 sarrera ditu partida baterako. Sarreren 3/5 zaleei salduko dizkie, eta geratzen direnen 5/8, beste taldekoei. Zenbat sarrera geratuko dira leihatilan saltzeko?

10 Dentista batek 1 h eta 3/4 egiten ditu bere kontsultan egunero. Egunean 15 pertsona hartzen baditu, orduaren zer zati egiten du bakoitzarekin? Zenbat minutu dira?

11 Lauren arteko banaketa: A-k eta B-k osotasunaren 2/7 eta 13/21 hartu dituzte, hurrenez hurren. C-k, gainerakoaren 7/10. Eta D-k, 390 €. Zenbat diru banatu da?

12 Txirrindulari batek ibilbidearen 2/3 eginda zituela utzi du lasterketa. 10 kilometro gehiago eginda, ibilbidearen hiru laurdenak egingo zituen. Zenbat kilometro egin dituzte helmugaratu direnek?

13 Sei lagunen artean zazpigarren batentzako oparia erosi dute. Ordaintzeko orduan, batek dirurik ez duela eta, besteetako bakoitzak 1,50 euro gehiago ipini behar izan du. Zenbat balio zuen opariak?

41 U 1

1 ° 2 ° 3 ° 1.a 2.a 3.a

ARE ERRAZAGO

Kalkulatu buruz:

a) 22 b) (–2)2 c) 23

d) (–2)3 e) 52 f) (–10)3

g) 17 h) (–1)7 i) 104

j) (–10)4 k) (–5)4 l) (–3)3

Berreketak 6

Berrekizun osoa eta berretzaile oso positiboa

EBATZITAKO ARIKETAK

1 Kalkulatu berreketa hauek:

3 2, –3 2, (–3) 2, –(–3) 2

2 3, –2 3, (–2) 3, –(–2) 3

1 28, –1 28, (–1) 105, –(–1) 105

2 Sinplifikatu.

a) 3 5 · 2 3 · 2 2

b) (5 2) 3 · 2 2 2 8

3 Egin eragiketak.

(–3 + 1) 3 + (5 – 8) 4 · (–1) 9 –

– (–5) 2 · (–1) 4

PENTSATU ETA PRAKTIKATU

1 Kalkulatu berreketa hauek:

32 = 9

Gogoratu: aa aa a ·· ·…· aldiz

n n

= 12 3 a da berrekizuna; n, berretzailea.

Esate baterako: 24 = 2 · 2 · 2 · 2 = 16 (–2)4 = (–2) · (–2) · (–2) · (–2) = 16 25 = 2 · 2 · 2 · 2 · 2 = 32 (–2)5 = (–2) · (–2) · (–2) · (–2) · (–2) = –32

• a positiboa bada, an positiboa da n edozein dela ere.

• a negatiboa bada: n n( bikoitia → an positiboa. Adibidez, (–2)4 = 16. bakoitia → an negatiboa. Adibidez, (–2)5 = –32.

❚ berreketen propietateak

(–2)3 · (–2)5 = (–2)3 + 5 = (–2)8

64 = (2 · 3)4 = 24 · 34

(–2)5 = (–1 · 2)5 = (–1)5 · 25 = –25

(53)4 = 53 · 4 = 512

bada, a a a n m mn –= Adibidez: 10 10 10 10

7 74 3 –==

–32 = –9 (–3)2 = 9 –(–3)2 = –9

23 = 8 –23 = –8 (–2)3 = –8 –(–2)3 = –(–8) = 8 128 = 1 –128 = –1 (–1)105 = –1 –(–1)105 = –(–1) = 1

a) 35 · 23 · 22 = 35 · (23 · 22) = 35 · 25 = (3 · 2)5 = 65

b) (52)3 · 2 2 2 8 = 52 · 3 · 28 – 2 = 56 · 26 = (5 · 2)6 = 106

(–3 + 1)3 + (5 – 8)4 · (–1)9 – (–5)2 · (–1)4 = (–2)3 + (–3)4 · (–1) – 52 · 1 =

= –8 – 81 – 25 = 114

3 Egin eragiketa hauek:

a) –105 b) (–10)5 c) (–10)6 d) –(–10)5

e) (–1)100 f) –106 g) –16 h) –(–1)101

2 Sinplifikatu: 5 · [( )] () () 3 33 ––33 58 4

a) [(1 – 7) – (8 – 3) – (–2)5] · [15 + (–11)]2

b) (7 – 3) · [4 – (–3)] + (5 – 1)2 · [6 – (–3)4]

c) (–3)2 – (–33) + 52 · (–5)2 – [2 – (–3)4 · (–2)]

d) 17 – (–4)(–3 + 6) – 2[4 – 5(2 – 3)7]2

1. a m · a n = a m + n Adibidez:

2. (a · b)m = a m · b m Adibidez:

3. (a m)n = a m · n Adibidez:

4. m > n

Berrekizun arrazionala eta berretzaile osoa

Aurreko orrialdean, berretzaile oso positiboa duten berreketak berrikusi ditugu. Orain, berretzailea zero edo zenbaki oso negatibo bat duten berreketak landuko ditugu. a

EBATZITAKO ARIKETAK

2 Laburtu berreketa bakarrera: a) (3–5) · (34) = 3–5 + 4 = 3–1 b) 3–2 · 5–2 = (3 · 5)–2 = 15–2

c) (105)–3 = 105 · (–3) = 10–15

PENTSATU ETA PRAKTIKATU

4 Ordenatu txikienetik handienera. 2–3, 2–1, 20, 2–2, 2– 4, (–2)–3, (–2)–1

5 Kalkulatu berreketa hauen balioa: a) 5–1 b)

43 U 1

0 = 1, baldin eta a ≠ 0 bada. a –n = a 1 n . Beraz, a –1 = a 1 b a a b –1 = bl b a a b a b n n n n –== b c l m Adibidez: 10–1 = ,; , 10 1 01 5 2 2 5 2 5 4 25 625 2 2 2 2 –== == = c c m m BEHATU a a aa n n nn 0 –== a a 1 n n = Beraz, a 0 = 1 izan behar da. aa a aa 1 nn nn 0 0– –== = GOGORATU 1. a m · a n = a m + n 2. (a · b)m = a m · b m 3. (a m)n = a m · n 4. a a a n m mn –= 5. b a b a m m m = bl

balioa: a) 5 2 –3cm = , 5 8 125 15 625 2 3 == cm b) 10 1 –5cm = 105 = 100 000 c) 0, 125 1 2cm = 82 = 64 d) · 5 3 5 3 22 –ccmm = 5 3 5 3 1 22 0 –==ccmm

Kalkulatu honako berreketa hauen

4 1 4 12 3 3

e) : 2 1 2 1 22 – = 2 2 22 2 2 22 4 ––== f ) 4 2 3 4 –– = () 2 2 2 2 22 () 23 4 6 4 46 2 –––––== =

d) 123 · 4–3 = 123 ·

= cm = 33

2–3 c) (– 6)0 d) 2 1 –2cm e) 3 2 –1cm f ) 4 1 –2 g) 10 1 –1cm h) 2 5 2 –1 cm >H i) 0,2– 4 6 Adierazi berrekizunean 3 duen berreketa batekin ·( )· 3 1 3 1 3 1 33 12 3 25 7 – cc c mm m

Adierazi berrekizunean 2 duen berreketa baten bidez. a) 4–2 b) 8 1 –2cm c) () · 2 48 33 11 8 Laburtu eta adierazi berreketa moduan. a) () 7 –7 2 4 –b) : 55 1 24 c) · · 23 62 21 42 ––d) · 2 1 2 1 3 2 3 2 ––ccmm e) ·( ) 5 1 5 3 2 32 – eo f ) 9 3 3 4 ––g) · 2 510 2 22 –h) · · 15 8 12 5 21 25 ––i) () 5 3 10 9 32 5 ·· · 7 4 2 72 33 – c e m o

Ariketak eta problemak

MENDERATZEN DUZU OINARRIZKOA?

Zenbaki osoak

1 Kalkulatu adibidean egin den moduan.

• 6 – 2 – 8 + 4 – 7 + 3 = (6 + 4 + 3) – (2 + 8 + 7) = = 13 – 17 = –4

a) 7 + 2 + 5 – 9 – 1 – 6

b) 8 – 4 + 3 – 7 + 8 – 5 + 2

c) –6 + 4 – 10 – 2 + 9 – 7 + 1

d) 13 – 5 – 11 + 6 – 15 + 6

e) 11 – 7 – 8 – 2 + 5 – 4 + 8

2 Kendu parentesiak eta kalkulatu.

a) (+5) + (–4)

b) (+3) – (–7)

c) (–2) + (–9) – (–3)

d) (–5) – (+3) – (–10)

e) –(+6) – (– 4) + (–7)

f) –(–3) – (–1) – (–5)

3 Kalkulatu.

a) 5 + (–3) – (–2) + (4 – 6) – [3 – (6 – 4)]

b) (3 + 6 – 11) · (4 – 2 – 9) · (–1)

c) 5 · [8 – (2 + 3)] – (–4) · [6 – (2 + 7)]

d) (–7) · [4 · (3 – 8) – 5 · (8 – 5)]

Zatikiak. Eragiketak

4 Adierazi oso baten eta zatiki baten arteko batuketa moduan.

a) 3 5 b) 3 8 c) 6 17 d) 5 24 e) –12 37 f) 10 43

5 Lortu, kasu hauetako bakoitzean, zatiki laburtezina.

a) 27 12 b) 14 4 c) 6 –2 d) 30 18 e) –30

6 Kalkulatu buruz.

a) 8 7 en erdia.

b) 5 9 en herena.

c) –4ren bostenaren erdia.

d) 3 2 en erdiaren hirukoitza.

7 Kalkulatu buruz.

a) 21en 3 4 b) 10en 2 5

c) 1 milioiren 10 3 d) Ehun milaren 20 7

8 Kalkulatu buruz.

a) 400en bi bosten.

b) Zer zenbakiren bi bosten den 160.

c) 140ren hiru zazpiren.

d) Zer zenbakiren bost seiren den 25.

9 Adierazi orduaren zatiki moduan:

a) 15 minutu b) 20 minutu

c) 10 minutu d) 1 minutu

e) 120 segundos f) 1 segundo

10 Aurkitu guztizkoa kasu hauetako bakoitzean.

a) Aurrekontuaren 5 3 dira 351 €

b) Ikastetxean daudenen 7 6 dira 492 ikasle.

c) Jauregiaren azaleraren 8 5 dira 2 850 m2.

Berreketak

11 Kendu parentesiak eta sinplifikatu.

–

40 f)

7 –

() [( )] 5 5 ––6 32 b) () 3 9 –4 2

[(–3) 5 : (–3) 3]2 d) [2 4 · (–2) 2] : (–4) 3 12 Laburtu adibidean bezala. • () [( )] () () 16 8 64 42 22 22 2 22 22 2 ·–·· ·–·· · ·· 2 23 43 2 62 3 46 12 6 == = 2 2 2 10 19 9 == a) () 32 –2432 b) ·( ) 25 5 125 –22 c) () · 3 39 52 24 13 Kalkulatu. a) () () 6 6 ––3 23 2 b) 9 · () 3 –1 4 4 2 c) 1 35 5 · 24 3 d) () () · 6 23 2 3 6 4 10 e) () () 6 –·23 –4 55 f ) () · · 1 2 5 10 –43 54

ENTRENATU ETA PRAKTIKATU

14 Kalkulatu.

a) 16 – 3 · [8 – 2 · (5 – 6)]

b) 2 + 8 : [14 – 5 · (6 – 4)]

c) 30 : [12 · (4 – 6) – 6 · (4 – 7)]

d) 4 · [5 – (2 – 6)] – 3 · [8 – (4 – 7)]

e) 3 · (6 – 9) – 7 · [10 + 3 · 5 – 3 · (5 + 4)]

f) 2 · (5 – 9 · [7 + 3 · (5 – 7)]) + 6

15 Kalkulatu.

a) |(2 – 3) – (1 – 7) – 5| · [–(11 + (–4))]

b) (1 – 4) · 3 + (7 – 5) · |5 + 2 · (–3)|

c) (–2) + 3 · (–2) + |4 · (–6) – [1 – 3 · (–2)]|

d) 5 – |(–2) · |– 4 + 5|| – 2[4 – |–2| · |2 – 3|]

e) |–2 – |(–2) · (–4)| · (–5 + 4)| – |–1 + 3| · (–2)

16 Kalkulatu.

a) 30 ikasleren 2/5en 1/3.

b) 42 ibilgailuren erdien 4/7.

c) Urte bateko asteen laurdenen 7/13.

d) Apirileko egunen heren baten 3/5.

17 Aurkitu zer zatiki geratzen den guztizkoari kentzean:

22 Kalkulatu.

a) (–2)4

18 Aurkitu guztizkoa kasu hauetako bakoitzean:

a) Aurrekontuaren 3/5 dira 351 €.

b) Ikastetxean daudenen 6/7 dira 492 ikasle.

c) Jauregiaren azaleraren 5/8 dira 2 850 m2

19 Laburtu zatiki bakarrera.

20 Adierazi zenbakien zuzenean.

45 U 1

a) 1 2 ren 8 3 b) 5 2 ren 7 1 c) 3 2 ren 10 1 d) 4 3 ren 8 5

1 2 4 3

a) 5 3 4

5 2 1 –++ ccmm

1 3 1 4 3 2 1 3 1 4 1 ++ + c c c m m m

4 3 2 1

5 3 3 1 1

20 3 ++ c

m m >H

;; ; ; 3 2 4 3 2 1 5 6 10 3 – –

a) ·· 4 3 9 8 6 5 –– cm b) : 1 2 1 8 1 3 7 1 –++ ccmm c) –2 1 14 3 4 3 2 1 8 1 –+ cm d) · : 3 5 6 7 2 3 3 5 –cm

21 Kalkulatu.

c) (–2)3 d)

e) 2–3 f) (–2)–3

(–1)16 h) (–1)17 i) (–1)8

23 Kalkulatu. a) 3 5 –2cm b) 7 3 ––1cm c) 6 1 ––2cm d) 2 1 –3cm e) 3 4 3cm f ) 4 1 ––3cm 24 Laburtu. a) () 3 3 ––3 2 b) 3 2 2 –3 2 4 c c m m c) : 2 1 4 1 3 2 c c m m d) : 2 55 2 23ccmm e) · () 69 23 4 –32 32 2 f) 2 1 3 2 –cm >H 25 Kalkulatu. a)

b) ·· () 5 2 5 1 2 3 25 –1 2 – –+ c c m m c) 5 3 2 5 3 2 –1 2 3 – –– c c c m m m d) : 2 3 4 7 8 9 4 5 3 2 c c m m e) 2 3 4 3 3 1 9 7 4 2 1 – –+ c c m m f ) 4 1 12 7 4 5 2 5 4 1 4 ––1 + c c c m m m 26 Laburtu. a) 91··26 23 4 2 b) ·· 32 5 44524 ·· 34 c) 12 827 · 1 1 ––

b) –24

–23

723

–3 · (4 – 2)–2 + 10 · (5)–1

EBATZI PROBLEMA ERRAZAK

27 Izozkailu bateko tenperatura 2 °C jaisten da 3 minutuan behin, –18 °C-ra arte. Zer denbora behar du –12 °C-ra iristeko, piztean 16 °C-an badago?

28 Aristoteles K.a. 322. urtean hil zen, eta 62 urte bizi izan zen. Zer urtetan jaio zen?

29 510 litro ardo dituen upel batekin, 3/4 litroko zenbat botila bete ditzakegu? Eta litro eta erdiko zenbat?

30 5/2 litroko txanbil batekin 25 edalontzi betetzen dira. Litroaren zer zati sartzen da edalontzi bakoitzean?

31 3/4 litroko botila batetik, bostena edan dugu. Litroaren zer zati geratzen da?

32 a) Rafak diruaren 2/3 arropa erosteko gastatu du, eta 1/4 jatekoa erosteko. Diruaren zer zati gastatu du?

b) Zer zati geratzen zaio gastatzeko?

c) 180 € bazituen, zenbat ez du gastatu?

33 Lursail batean, 4/5 garitarako erabiltzen da, eta gainerakoa, 100 m2, artoa ereiteko. Zer azalera du sailak?

34 Pilota batek, punpa bakoitzean, aurretik izandako altueraren 2/3 hartzen du. Hiru punpa egin ondoren, 2 m-ra iritsi da. Zer altueratatik erori da?

35 Lorezain batek lorategiaren 2/5 ureztatzen du egunean. Zenbat egunetan ureztatuko du lorategi osoa? Zenbat irabaziko du, eguneko 50 € kobratzen badu?

36 Fruta- eta barazki-postu batean, egun oso batean egindako salmenten 5/6 frutei dagozkie. Eta frutak salduta bildutako diruaren 3/8 laranjekin lortu dute. Laranjak salduta 89 € bildu badituzte, zenbat diru bildu dute postuan egun osoan?

37 Pellori, hileko soldata gordinetik, zortziren bat PFEZrako kentzen diote, eta hamarren bat, Gizarte Segurantzarako. Soldata garbia 1 302 € bada, zein da hileko soldata gordina

38 Ikasgela batean, ikasleen 3/7 zientzia-museora joan dira, eta 2/5, kontzertu batera.

a) Nora joan da ikasle gehiago?

b) 6 ikasle ez badira txango batera ere joan, zenbat ikasle dira gelan?

39 Depositu batean, astelehenean 3 000 litro ur zeuden eta beteta zegoen. Asteartean deposituaren 1/6 erabili zen. Asteazkenean, 1 250 litro. Zer zati geratzen da?

APUR BAT GEHIAGO PENTSATZEKO

40 Lur-arlo batetik, azaleraren 2/3 saldu ziren aurrena, eta, gero, geratzen zen zatiaren 2/3. Udalak parke publiko bat egiteko desjabetu du geratzen zen 3 200 m2-ko zatia. Zenbateko azalera du lur-arloak?

41 Langile batek 1 ordu eta hiru ordu-laurdenean etxe bateko zoruaren 3/5 leundu ditu. 10 a. m. zirenean hasi bada, zer ordutan amaituko du leuntzen zoru guztia?

42 Tren batek 3 ordu eta laurdenean egiten ditu 918 km-ko ibilbide baten 5/9.

a) Kalkulatu zer denboratan egiten duen ibilbide osoa abiadura horretan.

b) Zenbatekoa da batezbesteko abiadura?

HAU ERE EGIN DEZAKEZU

43 Oilo batek, 4 eguneko 3 arrautza jarri ditu batez beste zortzi astez, eta hurrengo hamabi asteetan, 6 eguneko 5 arrautza batez beste. Zenbat arrautza jarri ditu batez beste egunean aldikada horretan?

44 Tapizatzeko oihal bat, garbitzen denean, 3/20 txikitzen da luzeran eta 7/25 zabaleran. Zabaleran 125 cm dituen oihal pieza baten zenbat metro erosi behar dira 39,9 m2-ko azalera estaltzeko?

45 Saltzaile ibiltari batek laranja saski bat darama. Bisitatu duen lehen etxean, laranjen erdiak saldu ditu. Bigarren etxean, geratzen zitzaizkion laranjen erdiak saldu ditu. Hirugarren eta laugarren etxeetan, beste horrenbeste gertatu zaio, eta horrekin, zeramatzan laranja guztiak saldu ditu. Zenbat laranja zeramatzan? oharra: Ez du laranjarik zatitu.

46 Zenbaki baten zatitzaile lehenak dira zenbakia bera ez den gainerako zatitzaile guztiak (1 ere zenbatuta). Zenbaki bati perfektua esaten zaio bere zatitzaile lehen guztien baturarekin bat badator. Aurkitu honako zenbaki hauetako zein diren perfektuak: 4, 6, 60, 100

Ariketak eta problemak

ULERTU ETA APLIKATU ERRONKA

AUTOEBALUAZIOA

1 Ebatzi.

a) |4 – |–7|| b) 1 – |3 + |–4|| c) 8 – |–11|

2 Egin eragiketa hauek:

a) 20 – 4 · (6 – 2 · 2 – 5)

b) 12 + (–3) · [16 – 4 · 9 – 6 · 5]

c) 2 · [–1 + (1 – 3)] – 2 · [5 – (2 – 5)]

3 Banandu zati osoa, honela: 1 =+ 2

➜ anayaharitza.es Ariketa hauen ebazpena.

6 Pilota batek, punpa bakoitzean, aurretik zuen altueraren 2/5 galtzen du. Erortzen utzi dugun altueraren zer zati harrapatuko du lau punpa eman ondoren?

7 Bilkura batera joan diren pertsona guztietatik, 1/6 Europakoak dira; 1/3, Asiakoak; 2/5, Amerikakoak, eta gainerakoak, Afrikakoak. Europako 60 ordezkari daudela jakinda, zenbat dira Afrikakoak?

8 Ibilgailu batek goizean egin du bete behar duen bidearen 3/8, eta arratsaldean geratzen zaionaren 2/3. Jakinda helmuga 130 km-ra duela oraindik:

a) Zenbat kilometro ditu bide osoak?

b) Zenbat denbora (ordu eta minutuetan) beharko du itzulerako bidea egiteko, 120 km/h-ra joanda?

IKASKUNTZA-EGOERA

HAUSNARTU

Berrikusi landutako alderdiak eta eman konponbidea hautemandako arazoei. Horretarako, deskargatu dagokion errubrika anayaharitza.es webgunetik, egin gogoeta banaka eta bateratze-lana taldean.

PROBATU ZURE KONPETENTZIAK

Egin anayaharitza.es webgunean ageri den konpetentzien autoebaluazioa.

BITXIKERIA MATEMATIKOAK

Erlazionatu

Fibonacci deitzen zitzaion («gizon onaren semea» esan nahi du). Aita Pisako merkatari eta kontsul izan zen Bugian, gaur egungo Aljerian. Horri esker, arabiarren matematika ikasi zuen, batez ere zenbakikuntza-sistema hamartarra, eta Europan sartzen lagundu zuen.

Berak deskribatu zuen lehen aldiz segida ospetsu hau: 1, 1, 2, 3, 5, 8, 13,… Segida horretan, gaietako bakoitza aurreko biak batuta lortzen da.

Irudikatu espiral hau paper koadrikulatu batean, eta saiatu apur bat handiagoa egiten.

Badakizu azaltzen zer erlazio duen Fibonacciren segidarekin?

Zenbaki perfektuak

Ikusi dugunez (46. ariketa), zenbaki perfektu bat da bere zatitzaile lehenen baturarekin bat datorrena. 48 zenbaki perfektu baino ez dira ezagutzen, eta bat bera ere ez da bakoitia. Infinitu daudela uste da, baina oraindik ezin izan da ziurtatu.

47 U 1

2 1 a) 4 7 b)

7 3 c) 5 45 d) –5 48 e) 10 93 f) 11 310 g) 44 405 h) –621 2 437 4 Kalkulatu. a) ++ –20 17 5 2 4 1 10 7 b) + –0 7 12 1 5 2 dn c) –· –· – 1 5 3 10 3 2 1 2 3 5 dn > H d) ––() 2 7 5 4 4 3 5 8 1 3 2 –d d n n

–

a) () () · 3 46 2· 10 32 32 4 b) () () () 52 110 ·––· 45 34 c) () · 2 32 6 –· 5 32 2 d) ·· 5 1 3 2 4 3 1 3 –2–cc c mm m e) 1 3 2 3 2 5 3 3 · 1 2 – –+ c c m m

5 Aurkitu adierazpen bakoitzaren balioa:

Leonardo Pisakoa (1179-1250)

ULERTU ETA APLIKATU ERRONKA

Zenbaki hamartarrak

Gure zenbaki-sistema sinplea eta oso erabilgarria da. Hamartarra eta posizionala dela esaten dugu.

Antzinako zibilizazio gehienek, baita oso primitiboek ere, zenbaketa hamartarreko sistema izan zuten (edozein kopuru 10 sinbolo edo zifra bakarrik erabiliz irudikatuta). Zergatik? Zalantzarik gabe, eskuetako atzamarrengatik: kopuruak izendatzen eta kontuak egiten laguntzen dute, eta hamar ditugu.

Gure sistemak bi ezaugarri garrantzitsu eta bereizgarri ditu beste sistema batzuen aldean: posizionala da, eta zero zifrak gainerako zifrek ez bezalako berezitasun batzuk ditu.

Zero zenbakia, hasiera batean, kantitaterik gabeko posizioa adierazteko erabili zen. Gerora lortu zuen gainerako zifren maila bera. Eta askoz geroago hartu zuten zenbakitzat.

Hainbat zibilizazio saiatu ziren ildo horretan, baina Indian lortu zuten, vii. mendean. Dena dela, aurkikuntza pozgarri hori arabiarren matematikak ekarri zigun ix . mendean.

Zenbakikuntza-sistema hamartar-posizional hori Europan, hasieran, zenbaki osoak izendatzeko soilik erabili zen. xvi. mendean, unitatearen zatiak kuantifikatzeko ere zabaldu zen.

Zenbakikuntza-sistema hamartarraren garrantzia

Grezia klasikoko jakintsuak geometra handiak izan ziren, baina aritmetika arloan oso aurrerapen gutxi egin zituzten. Zergatik? Bada, euren zenbaki-sistema (erromatar sistemaren oso antzekoa) txarra zelako.

Zuk badakizu zenbaki erromatarrak nola idazten diren. Sistema batukorra da. Adibidez, 1347 honela idazten da: MCCCXLVII

… eta horrek esan nahi du → 1 000 + 100 + 100 + 100 + (50 – 10) + 5 + 1 + 1

Zenbakiak adierazteko modu hori, gogaikarria eta nekagarria ez ezik, zaila ere bada zenbakiak konparatzeko eta eragiketak egiteko.

Zenbakikuntza-sistema hamartarraren onurak

Zenbakikuntza-sistema hamartarra posizionala da, eta aurrerapen handia izan zen beste sistemen aldean, zenbakiak errazago irakurri, idatzi eta konparatzeko modua eta eragiketak erosoago egiteko bidea ekarri baitzuen. Ziurtatu hala dela honako adibideak aztertu eta ondoren ageri diren galderei erantzunez:

|Adibideak

• Taula honetan, munduko hiru herrialde populatuenek 2023/01/01ean izango duten biztanleria estimatu da:

a) Idatzi irakurtzen den moduan: Zenbat biztanle ditu AEBk?

b) Zer herrialdek du biztanle gehiago, Indiak ala Txinak? Zenbat gehiago?

c) Biribildu ehun milioikoetara Txina, India eta AEBren biztanleriak.

• Autonomia erkidego bateko langabezia-indizeak izandako hileko aldakuntza: Martxoan → % 1,089 Apirilean → – % 1,11

d) Bi hilabete horietako zeinetan izan du aldakuntza handiagoa langabeziak?

e) Zer hiletan igo da gehiago langabezia?

f)Zer alde dago martxoko eta apirileko aldakuntzen artean?

Beheko bi kantitateak Lurraren masarena (L) eta hidrogeno-atomo baten masarena (H) dira. Biak dauden zifra guztiekin eta idazkera laburtuan adierazita:

L → 5 980 000 000 000 000 000 000 000 kg = 5,98 · 1024 kg

H → 0,000 000 000 000 000 000 000 001 660 kg = 1,66 · 10–24 kg

g) Bi idazkera horietako zein iruditzen zaizu egokiagoa zenbaki mota horietarako? Azaldu zergatik.

49 U 2

herrialdea biztanle-

Txina 1 448 471 000 India 1 425 263 000 AEB 334 805 000

kopurua

GOGORATU

Zatiketa batean, badakigu hondarra zatitzailea baino txikiagoa izan behar dela. Beraz, gehienez egon litezkeen hondarren kopurua zatitzaileak berak mugatzen du.

zatikizuna 3 … zatidura

hondarra (0, 1, 2)

Beraz, beti helduko gara 0 hondarrera, edo bestela hondarrak mugarik gabe

errepikatuko dira.

• Esandako horren arabera, zatiki oro bihur liteke hamartar zehatza edo periodikoa, zenbakitzailea izendatzailearekin zatituta.

Zenbaki hamartar motak 2

Ekarri gogora zenbaki hamartar motak, eta aztertu zer ezaugarri dituzten zatiki batetik lortzen diren hamartarrek, eta zein zehatza ez den erro batetik lortzen direnek.

Hamartar zehatza

• , 40 13 0 325 =

13,0 40

0,325

Hamartar periodiko purua

• , 33 41 124 = #

PENTSATU ETA PRAKTIKATU

1 Pasatu forma hamartarrera.

Hamartar periodiko mistoa

• , 15 32 21 3 = !

32 15 020 2,133… 050 050 05

Infinitu zifra ez-periodiko dituen hamartarra

• 7 = 2,6457513…, 5 3 = 1,7099759…, 100 5 = 2,5118864…

Zehatza ez den edozein errok infinitu zenbaki hamartar ez-periodiko ditu. Zenbaki horiek ezin dira adierazi zatiki moduan eta, beraz, irrazionalak dira.

➜

a) 6 5 b) 16 3 c) 2 d) 22 7 e) 2 1

2 Zer esan dezakezu kasu bakoitzari dagokion hamartarrari buruz?

a) 9 5 b) 9 4 c) 9 5 9 4 – d) 9 5 9 4 +

3 Ondoren proposatutako probleman, jarri m-ren eta p-ren ordez zenbaki osoak, eta lortu, kasu bakoitzean, hamartar zehatz bat, periodiko puru bat eta periodiko misto bat:

Mendizale batek m metro egiten ditu p urratsetan.

Zenbat metro egiten ditu urrats bakoitzean?

1,00

Zatidurak zifra hamartarren kopuru mugatu bat du, eta hondarra 0 da. Hamartar zehatz bat lortu dugu, 0,325. 200 00

41 33 080 1,242… 140 080 14

Zatidurak zifra hamartarren kopuru mugagabea du, eta periodikoki errepikatzen dira. Hamartar periodiko purua lortu dugu, , 124 # . Errepikatzen diren zifrei periodo esaten zaie.

Hasieran, errepikatzen ez den zati hamartar bat dago. Hortik aurrera, zatidurako zifrak periodikoki errepikatzen dira. Hamartar periodiko mistoa lortu dugu, , 21 3 !

anayaharitza.es Praktikatu zatikitik zenbaki hamartarrera igarotzea.

KALKULAGAILUAREKIN

Gogoan izan kalkulagailuan hamartar periodiko bat idazteko teklak erabili behar dituzula.

5 . 4 91 = 5,4 91 #

Hamartarretik zatikira igarotzea 3

Hamartar zehatzak

Zenbaki hamartar zehatz bat zatiki moduan adieraztea oso erraza da. Nahikoa da zuzen interpretatzen jakitea. Adibidez:

Hamartar periodiko puruak

Hamartar periodikoak zatikira igarotzea ez da horren erraza. Aztertu arretaz ondorengo adibide hau, eta egin zeuk, prozesua ondo ulertuta: Adieraz dezagun , 384 # zatiki eran:

Emaitza hamartar eran (zehatza zein periodikoa) emanda, Ë tekla sakatzean, dagokion zatiki sortzailea lortuko dugu: 990

Hamartar periodiko mistoak

5 437

Adieraz

,2 134 # zatiki eran:

Bider 10 egingo dugu, hamartar periodiko puru bat lortzeko.

Orain, aurrekoa bider 100 egingo dugu, zati hamartar bera duen beste bat lortzeko.

Kenketa eginez, zati hamartarra ezabatu eta zenbaki oso bat lortuko dugu.

Bai hamartar zehatzak, bai periodikoak zatiki eran jar daitezke. Hau da, zenbaki arrazionalak dira.

• Infinitu zifra ez-periodiko dituzten hamartarrak, hau da, 2 , 9 3 , π, 13,04004000400004…, bezalako irrazionalak ezin dira zatiki eran adierazi.

PENTSATU ETA PRAKTIKATU

1 Osatu prozesua honako hamartar hauek zatiki eran adierazteko:

2 Identifikatu honako zenbaki hauetako zein diren arrazionalak eta aurkitu zer zatiki dagokien:

a) 6,78 b) , 678 # c) , 67 8 !

d) 59,83 # e) 0,004 f) , 0004 !

f) π = 3,101001000100001… g) , 00 04 #

i) π = 3,14159265359… j) , 31416 #

51 U 2

a) 1,4 = 10 14 b) 7,395 = 1 000 7 395 c) 0,0008 = 1 000 0 8

,… ,… N N100 3 848484 384 848484 = = ) Kenketa eginda: 100N – N = 384 – 3 → 99N = 381 → N = , 384 99 381 = #

dezagun

Z [ \ ] ] ] ] ] ] ] ] ] N = 00 1,2343434… 10N = 0 012,343434… 1 000N = 1 234,343434…

1 000N – 10N = 1 234 – 12 → 990N = 1 222 → N = , 12 34 990 1 222 = #

a) , ,… ,… N N 5 893893 5 893 1000 5 893893 893 = = ) & b) ,… ,… ,… , N N N 3 45454545 13 45454545 01345 100 10 000 0 13454545 1 45 = = = Z [ \ ] ] ] #

KONTUAN IZAN

Zifra esangarriak zenbaki hurbilduak adierazteko erabiltzen diren zenbakiak dira

Eman beharreko informazioari begira ezinbestekoak diren zifrak baino ez dira erabili behar

Kantitate hurbilduak. Erroreak 4

Neurri erreala eta neurri hurbildua

Bai magnitudeak zuzenean neurtzean eta bai zeharka egindako neurketetan ere, kantitate hurbilduak erabiltzen ditugu. Zenbaitetan, beste aukerarik ez dugulako, eta beste batzuetan, erosoagoa eta praktikoagoa delako.

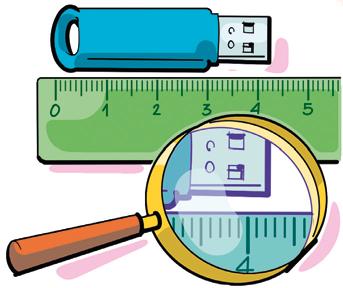
• Zer luzera du alboan ikusten duzun pendriveak?

Erregelak ez ditu bereizten milimetroa baino txikiagoak diren luzerak. Beraz, ez dakigu neurri zehatza. Hala ere, hau ziurtatu dezakegu:

4,2 cm < l < 4,3 cm

Esan genezake pendriveak 4,2 cm edo 42 mm dituela gutxi gorabehera.

• Zer luzera du 8 metroko hodi bat hiru zati berdinetan banatuta eratzen diren zatietako bakoitzak?

Hodiaren luzera (8 metro) zati 3 egitean, hamartar periodiko bat lortzen dugu:

k = 8 : 3 = , 26 ! m = 266,666… cm

Zati bakoitzak, gutxi gorabehera, 2,67 metro edo 267 zentimetro dituela esango dugu.

• Adierazi honako kantitate hauek zifra esangarrien zentzuzko kopurua erabiliz:

a) Museo batek urtebetean hartu duen bisitari-kopurua: 183 594.

Kantitate hori zifra guztiekin eman daiteke; izan ere, museora sartzeko sarrera ordaindu behar denez, sarrerak zenbatu egiten dira:

183 594 bisitari

Dena dela, zenbait informazio edo argibide ematean, sinplifikatu egin daiteke: «ia berrehun mila» edo «ehun eta laurogei mila baino gehiago».

180 000 < bisitariak < 200 000

b) Manifestazio batean bildu den pertsona-kopurua: 234 590.

Ezinezkoa da inork manifestazioan bildu diren guztiak hainbesteko zehaztasunez zenbatzea.

Zentzuzkoena «berrehun mila baino gehiago» esatea litzateke. 200 000 < manifestariak

PENTSATU ETA PRAKTIKATU

1 Hurbildu honako kantitate hauek zifra esangarrien kopuru egokia erabiliz:

a) Iberiar penintsularen azalera: 583 254 km2.

b) Etxe-agentzia baten webguneak astean batez beste izaten dituen bisitak: 13 585.

c) Kilo bat arrozetan dagoen ale-kopurua: 11 892 583.

d) Kostako herri batera abuztuan joan diren turisten kopurua: 87 721.

e) Litro bat esne 6 edalontzitan banatu eta edalontzi bakoitzean sartu den esne-kantitatea.

f ) Kilo bat urrerekin egin diren 12 kateetako bakoitzaren pisua.

8 m k k k

l l ≈

4,2 cm

l ≈ 4,2 cm

neurri erreala → Ezezaguna

hurbilketa → 4,2 cm

errore erreala → Ezezaguna

errorearen bornea → 1 mm

Errore-bornea 1 mm da, ezkerreko muturra hartu dugulako modu arbitrarioan.

Errore absolutua

Neurri hurbildu baten errore absolutua balio errealaren eta balio hurbilduaren arteko aldea da, balio absolutuan.

errore absolutua = | balio erreala – balio hurbildua |

Balio zehatza, normalean, ez da ezaguna izaten. Beraz, egiten den errore absolutua ere ez dakigu zenbatekoa den. Baina garrantzitsuena mugatzea da: Errore absolutua … baino txikiagoa da

Pendrivearen kasuan, errorea mugatuta dago: 1 mm baino txikiagoa da.

Biribiltzea eta errore absolutuaren bornea

Gogoan izan biribiltzea unitate-ordena zehatz batera hurbiltzea dela, handiagora zein txikiagora; beti ere kontuan hartuz ezabatutako lehenengo zifra 5 baino handiagoa edo txikiagoa den.

Beraz, milakoetara biribiltzen dugunean adibidez:

81 394

81 629

EBATZITAKO

ARIKETA

Eman honako balioztatze hauen errore absolutuaren borne bat:

a) Hodi-zati bakoitzaren luzera: 266, 6 " cm → 267 cm

b) Museo batera joandako bisitariak: 183 594 → 180 000

c) Manifestariak: 234 590 → 200 000

PENTSATU ETA PRAKTIKATU

Hodi-zatia → 266,7 cm

Museoko bisitariak → 184 000

Manifestariak → 230 000

81 000

REDONDEO BIRIBILTZEA 4 errorea < 500

82 000

Egindako errorea 5 ehuneko baino txikiagoa da. Beraz, biribiltzean errore absolutuaren bornea 500ekoa dela diogu.

Biribildu dugunean, errore absolutuaren bornea izan da erabili ez dugun lehenengo zifraren ordenako 5 unitatekoa.

a) 266,666… cm → 267,000 cm

Ezabatutako lehenengo zifra

Erabili ez den lehenengo zifra zentimetro hamarrenen ordenakoa da (milimetroak). Beraz, errore absolutua 5 milimetro baino txikiagoa da:

errore absolutua < 0,5 cm = 5 mm

b) 183 594 → 180 000

Ezabatutako lehenengo zifra

errore absolutua < 5 000

c) 234 590 → 200 000

Ezabatutako lehenengo zifra

errore absolutua < 50 000

2 Zer borne emango zenuke errore absoluturako, aurreko ariketan honako hurbilketa hauek hartuz gero?

3 Eman honako biribiltze hauen errore absolutuaren borne bat:

23 483 215 → 23 000 000 0,0034826 → 0,0035

4 Eman aurreko orrialdeko 1. ariketako balioztatze bakoitzaren errore absolutuaren borne bat.

53 U 2

500 500 81 629 81 000 82 000 81 394

hurbilketa → 170 cm garai da.

errore absolutua < 5 cm

errore erlatiboa < , 170 5 003 <

hurbilketa → 173 cm garai da.

errore absolutua < 0,5 mm

errore erlatiboa < , , 173 05 0 003 <

Errore erlatiboa

Errore absolutuak ez digu ematen neurketaren «zehaztasunari» buruzko informazio guztia, honako adibide hauetan argi ikusiko duzunez:

bi hiriren arteko distantzia → 126 km (errore absolutua < 0,5 km)

ibai baten zabalera → 13 m (errore absolutua < 0,5 m)

Errore absolutua askoz handiagoa da lehenengo neurketan (0,5 km > 0,5 m) bigarrenean baino. Hala ere, bigarrena askoz nabarmenagoa da; izan ere, 13 m neurtu eta 0,5 m-ko akatsa egitea 126 km neurtu eta 0,5 km-ko akatsa egitea baino gehiago da.

Argi eta garbi ikusten da hori errore absolutua distantziarekin zatitzean eta, ondorioz, unitateko egin den errorea lortzean. Hau da, errore erlatiboa lortzean: , , 126 05 0 004 ≈ , , 13 05 004 ≈

Errore erlatiboa ezezaguna da errore absolutua ezezaguna bada. Baina kasu honetan ere errorearen tamainari borneak ezar diezazkiokegu.

Errore erlatiboa errore absolutuaren eta balio errealaren arteko zatidura da.

ERRORE ERLATIBOA BALIOERREALA ERRORE ABSOLUTUA =

Zenbat eta zifra esangarri gehiago erabili, orduan eta txikiagoa da errore erlatiboa.

EBATZITAKO ARIKETA

Eman balioztatze hauen errore erlatibo bat:

a) Hodi-zati bakoitzaren luzera: 266, 6 " cm → 267 cm

b) Museoko bisitariak: 183 594 → 180 000

c) Manifestariak: 234 590 → 200 000

PENTSATU ETA PRAKTIKATU

5 Begoñak baskula bat erosi du. Nola dabilen azaltzeko argibideetan, adibide hau ageri da: 62,7 kg ≤ pisu erreala < 62,8 kg

a) Zenbateko errore absolutua darabil baskulak?

b) Baskulak markatzen duenez, Begoñak 52,3 kg-ko pisua du, eta senarrak, 85,4 kg-koa. Eman pisaldi bakoitzerako errore erlatiboaren borne bat.

6 Eman aurreko orrialdeko 4. ariketako balioztapenetan egindako errore erlatiboen borne bat.

7 Zuzena ala okerra?

a) Errore erlatiboa bat baino txikiagoa da beti.

b) Zenbat eta txikiagoa errore absolutua, orduan eta zehatzagoa neurketa

c) Zenbat eta handiagoa errore erlatiboa, orduan eta handiagoa neurketaren zehaztasuna ere.

d) Errore absolutua ez da inoiz erlatiboa baino txikiagoa.

hurbilduak. Erroreak 4

Kantitate

a) , RBILKETA ERRORE ABSOLUTUA HU 267 05 cm cm < 3 errore erlatiboa < , 267 05 < 0,002 b) RBILKETA ERRORE ABSOLUTUA HU 180 000 5 000 < 3 errore erlatiboa < 5 000 180 000 < 0,028 c) RBILKETA ERRORE ABSOLUTUA HU 200 000 50 000 < 3 errore erlatiboa < 2 50 000 00 000 < 0,25 → → →

➜ anayaharitza.es Praktikatu erroreen kalkulua.

GOGORATU

Notazio zientifikoa 5

Iparrizarra

Notazio zientifikoan emanda dauden zenbakiek bi biderkagai dituzte: zenbaki hamartar bat eta 10en berreketa bat.

• Zenbaki hamartarra 1 edo 1 baino handiagoa eta 10 baino txikiagoa da.

• 10en berreketak berretzaile osoa du.

Lurretik Alfa Centaurira dagoen distantzia A = 41 300 000 000 000 km da, eta Iparrizarrera dagoena, B = 4 070 000 000 000 000 km. Jakingo zenuke esaten, boteprontoan, bi distantzietako zein den handiagoa?

Argi dago zeroak zenbatu behar ditugula hori jakiteko, eta lan hori geldoa eta nekosoa dela. Gainera, nabarmena da ohiko idazkera praktikotasun gutxikoa dela zenbaki handiak erabiltzeko.

Zifrak zenbatuta, zenbakiak notazio zientifikoan adieraz ditzakegu:

41310 10 407 A· B· 1 15

3 = = 4 Orain argi dago B > A dela.

, ,

Notazio hau askoz praktikoagoa eta erabilgarriagoa da.

Notazio zientifikoa oso zenbaki txikiekin ere erabiltzen da:

0,000000000098 = ,, 100 000 000 000 98 10 98 11 = = 9,8 · 10–11

Zifra asko dituzten zenbakietan, arrazoizkoa izaten da lehenengoak bakarrik erabiltzea, eta horrek erraztu egiten du hurbilketak notazio zientifikoan adieraztea.

Adibidez: Txinako biztanleria: 1 406 828 000 biztanle

hurbilketa → 1 400 milioi → 1,4 · 109

errore absolutua < 50 milioi → 5 · 107

laburbilduz: Notazio zientifikoa oso erosoa da oso kantitate handiak edo oso txikiak adierazteko, bi arrazoirengatik:

• Berehala igartzen da zenbakiaren tamaina, nahikoa da 10en berretzaileari erreparatzea.

• Argi geratzen da kantitatea zenbateko zehaztasunez ematen den: erabilitako zifra guztiak zifra esangarriak dira.

Adibidez, Lurretik Eguzkira dagoen distantzia 1,50 · 108 km-koa dela esanda, eta

Uranotik Neptunora dagoena 1,7 · 109 km-koa, bi gauza argi daude:

— Bigarren distantzia lehenengoa baino handiagoa da.

— Lehenengo neurria zehaztasun handiagoz eman da bigarrena baino.

PENTSATU ETA PRAKTIKATU

1 Adierazi zifra guztiekin.

a) 2,63 · 108 b) 5,8 · 10–7

2 Idatzi notazio zientifikoan, hiru zifra esangarrirekin.

a) 262 930 080 080 000 b) 2 361 · 109

c) 0,000000001586 d) 0,256 · 10–10

3 Adierazi gramotan, notazio zientifikoa erabilita.

a) Lurraren masa: 5 974 trilioi tona.

b) Elektroi baten masa: 9,10 · 10–31 kilo.

4 Datu hau kontuan izanda:

Indiako biztanleria: 1 425 263 000 biztanle

Hartu hiru zifra esangarriko hurbilketa bat, eta eman errore absolutuaren kota bat eta errore erlatiboaren beste bat.

5 Lurraren bolumena hau da, gutxi gorabehera:

1 083 210 000 000 km3

Adierazi metro kubikotan, hiru zifra esangarrirekin, eta eman errore absolutuaren kota bat eta errore erlatiboaren beste bat.

55 U 2

↓

Alfa Centauri

magnitude- ordenak giga 109 mega 106 kilo 103 hekto 102 deka 10 dezi 10–1 zenti 10–2 mili 10–3 mikro 10–6 nano 10–9

GOGORATU

• · 10 10 10 mn mn = +

105 · 108 = 1013

• : 10 10 10 mn mn –=

1011 : 108 = 103

107 : 10–3 = 1010

Eragiketak idazkera zientifikoan emandako zenbakiekin

Idazkera zientifikoan dauden zenbakien eragiketak egitean, normal jokatuko dugu, baina zenbaki bakoitza eratzen bi biderkagai daudela kontuan hartuz: adierazpen hamartarra eta 10en berreketa:

• Biderketa eta zatiketa berehala kalkulatzen dira, ohiko prozedurak erabiliz: (4,25 · 109) · (5,6 · 107) = (4,25 · 5,6) · (109 · 107) = 23,8 · 1016

Idazkera zientifikoan → 23,8 · 1016 = 2,38 · 1017

• Batuketa eta kenketa egiteko, batugaiak prestatu behar ditugu: 10eko berrekizun izan behar dute denek, biderkagai komun moduan jartzeko:

1,43 · 108 + 5,2 · 107 = 14,3 · 107 + 5,2 · 107 = (14,3 + 5,2) · 107 = = 19,5 · 107 = 1,95 · 108

EBATZITAKO ARIKETAK

1 Zer masa da handiagoa, Lurrarena ala Artizarrarena eta Merkuriorena batuta?

Datuak bilatuko ditugu (planeten masak):

merkurio → 3,30 · 1023 kg artizarra → 4,8 · 1024 kg

lurra → 5,97 · 1024 kg

merkurioren masa + artizarraren masa: 3,30 · 1023 + 4,8 · 1024 = 0,33 · 1024 + 4,8 · 1024 = 5,13 · 1024

Lurraren masa aurreko batura horrekin konparatuko dugu: 5,97 · 1024 > 5,13 · 1024

Soluzioa: Lurraren masa handiagoa da beste bienak batuta baino.

2 Zenbat bider sartzen da Lurra Eguzkiaren barruan?

anayaharitza.es Eragiketak notazio zientifikoan emandako zenbakiekin.

PENTSATU ETA PRAKTIKATU

6 Kalkulatu.

Datuak bilatuko ditugu (Eguzkiaren eta Lurraren bolumenak):

eguzkia → 1,4123 · 1018 km3 lurra → 1,0833 · 1012 km3

Bi datuen arteko zatiketa egingo dugu:

Soluzioa: Eguzkiaren barruan milioi bat eta hirurehun mila Lur sartzen dira, gutxi gorabehera.

a) 2,25 · 1015 – 3,44 · 1014 b) 1,05 · 10–9 + 1,8 · 10–9

c) 1,8 · 1011 · 1,4 · 10 – 4 d) 4,25 · 106 : 1,7 · 10 –9

e) ,· ,· 46010 62110 6 –7 f) ,· ,· ,· 41 10 95 10 34 10 –11 78

7 Vilargia = 2,20 · 1010 km3 eta Milargia = 7,35 · 1022 kg badira:

a) Zenbat aldiz sartuko litzateke Ilargia Lurraren barruan?

b) Zenbat Ilargi elkartu beharko lirateke Lurraren masa lortzeko?

8 Ikusi dugunez Lurretik Alfa Centaurira 4,13 · 1013 km daude. Jakinda argiak 300 000 km/s-ra bidaiatzen duela, Alfa Centauriko izarretako bat lehertuko balitz, zenbat denbora barru jakingo genuke Lurrean?

9 Avogadroren zenbakia (6,022 · 1023) da edozein substantziaren mol batean dagoen molekula-kopurua. Hau da, mol batean, 6,022 · 1023 molekula daude.

a) Mol bat urek 18 g-ko pisua badu, zer masa du molekula bakoitzak?

b) Zenbat molekula daude 1 g uretan?

Notazio zientifikoa

,· ,· , , ·≈ ,· 1 0833 10 1 4123 10 1 0833 1 4123 10 130101 300 000 12 18 18 12 6 –==

➜

Ariketak eta problemak

MENDERATZEN DUZU OINARRIZKOA?

Zenbaki hamartarraren eta zatikiaren arteko erlazioa

1 Kalkulatu buruz zatiki bakoitzari dagokion zenbaki hamartarra:

a) 4 3 b) 5 1 c) 5 8 d) 10 17

e) 100 15 f ) 2 45 g) 20 7 h) 25 31

2 Adierazi zenbaki hamartar moduan, eta ordenatu txikienetik handienera. 1 8 3 500 6 251 2 000 1500 147 140 21 2 3

3 Sailkatu zenbaki arrazional hauek kontuan izanda hamartar zehatzak eta hamartar periodikoak diren:

a) 8 13 b) 27 139 c) 11 25

d) 250 9 e) 66 131 f ) 18 223

4 Adierazi zatiki laburtezin moduan.

a) 1,321 b) , 24 ! c) 0,008 d) , 554 #

e) , 235 # f ) , 00 36 # g) 0, 945 & h) , 0116 ! Egiaztatu emaitzak kalkulagailuarekin.

5 Adierazi zatiki laburtezin moduan.

a) 2,075 b) , 070 # c) , 05 3 ! d) , 054 # e) 0,008

f) 0, 003 & g) , 0116 ! h) 12,48 i) , 04 27 # j) , 013 #

Zenbaki hurbilduak. Erroreak

6 Hurbildu ehunenetara.

a) 0,318 b) 3,2414 c) 18,073

d) 71 100 e) 13 25 f ) 7 65

7 Egin eragiketak kalkulagailuarekin, eta hurbildu emaitzak adierazitako unitate-ordenara.

a) 23,4 ! + (2,192 · 2,18) milarenetara

b) 2,37 – ,, 1, 1240 2 564 + ehunenetara

c) 0,19 · 152,5 – 18,4 ! hamarrenetara

8 Kalkulatu.

a) Aurreko ariketako hurbilketa bakoitzean egindako errore absolutua.

b) Kasu bakoitzean egindako errore erlatiboaren borne bat.

9 Adierazi zifra esangarrien kopuru egokia erabilita.

a) Telebista-saio baten audientzia: 3 017 849 ikus-entzule.

b) Birus baten tamaina: 0,008375 mm.

c) 157-ren emaitza.

d) Auto baten prezioa: 18 753 €

e) Udal baten aurrekontua: 987 245 €.

f) Ordezkari izateko hautagai batek jasotako botoen ehunekoa: % 37,285.

g) Urtegi baten edukiera: 3 733 827 000 L.

10 Kalkulatu, aurreko ariketako ataletako bakoitzean, hurbilketa moduan emandako kantitateen errore absolutua eta errore erlatiboa.

11 Idatzi zenbaki hauetako bakoitzaren hurbilketa bat, bost milaren baino gutxiagoko errorearekin:

a) 5,7468 b) 12,5271 c) 8,0018

Notazio zientifikoa

12 Adierazi 10en berreketa baten bidez.

a) 1 000 b) 1 000 000 c) 1 000 000 000

d) 0,001 e) 0,000001 f ) 0,000000001

g) 10 000 1 h) , 01 1 i) 0, 001 1

13 Adierazi zenbaki hamartar batekin.

a) 105 b) 10–5 c) 10–6 d) 10 1 4

e) 10 1 2 f) 1 : 103 g) 1 : 10–2 h) 10 1 –4

14 Adierazi zein izan behar den n-ren balioa berdintza hauetako bakoitza egiaztatzeko:

a) 0,0000000023 = 2,3 · 10n

b) 87,1 · 10–6 = 8,71 · 10n

c) 1 250 000 = 1,25 · 10n

d) 254,2 · 104 = 2,542 · 10n

e) 0,000015 · 10–2 = 1,5 · 10n

15 Adierazi bi zifrarekin.

a) 6,25 · 10 8 b) 2,7 · 10 –4 c) 3 · 10 –6

d) 5,18 · 1014 e) 3,215 · 10–9 f ) –4 · 10–7

U 2

Ariketak eta problemak

16 Idatzi notazio zientifikoan.

a) 4 230 000 000 b) 0,00000004 c) 84 300

d) 0,000572 e) 0,00724 f ) 500 821

g) 35 594 h) 585 000 000 i) 0,23

17 Ordenatu txikienetik handienera. Horretarako, adierazi notazio zientifikoan adierazita ez daudenak.

a) 1,58 · 1026; 160 · 1023; 95 · 1018; 600 000 · 1020

b) 37,2 · 1011; 241,7 · 1010; 0,0084 · 1015; 1013

c) 273 · 10–15; 0,43 · 10–10; 10–12; 10–13

18 Laburtu.

a) · 10 10 10 6 52 b) · 10 10 10 8 24

c) · · 10 10 10 10 48 57 d) · 10 10 10 10 23 01

19 Kalkulatu buruz.

a) (1,5 · 107) · (2 · 105) b) (3 · 106) : (2 · 10–3)

c) (4 · 10–12) : (2 · 10–4) d) · 910 4

e) (2 · 10–3)3 f ) 810 6 –

20 Kalkulatu arkatza eta papera erabilita, adierazi notazio zientifikoan eta egiaztatu kalkulagailuarekin.

a) (3,5 · 107) · (4 · 108) b) (5 · 10–8) · (2,5 · 105)

c) (1,2 · 107) : (5 · 10–6) d) (6 · 10–7)2

e) · 121 10 6 – f ) (5 · 104)3

21 Kalkulatu notazio zientifikoa erabilita, eta egiaztatu, gero, kalkulagailuarekin.

a) 5,3 · 108 – 3 · 1010 b) 3 · 10–5 + 8,2 · 10–6

c) 3,1 · 1012 + 2 · 1010 d) 6 · 10–9 – 5 · 10–8

ENTRENATU ETA PRAKTIKATU

22 Egiaztatu, zatiki eran jarrita, honako zenbaki hamarta hauek zenbaki osoei dagozkiela: ,; ,; ,; , 19 29 79 11 9 !! !!

Lortutako emaitza kontuan izanda, zer zenbaki oso dagokio 126, 9 ! -ri?

23 Ordenatu txikienetik handienera.

5,53; , 553 # ; , 55 3 ! ; 5,5; 5,56; , 55 !

24 Esan zenbaki hauetako zein diren arrazionalak; hau da, zein adieraz daitezkeen zatiki moduan:

3,45; , 1003 ! ; 2 ; 2 + 5 ; π; 1, 117 &

25 Adierazi notazio zientifikoan eta kalkulatu.

a) (75 800)4 : (12 000)2

b) ·, ,· 1 520 000 0 00302 0 000541 10 318 000

26 Erabili kalkulagailua eragiketak egiteko, eta adierazi emaitza bi eta hiru zifra esangarrirekin:

a) (4,5 · 10 12) · (8,37 · 10 –4)

b) (8,4 · 10 11) : (3,2 · 10 –6)

c) (7,8 · 10 –7) 3

27 Egiaztatu, zatikira igarota, eragiketa hauen emaitza zenbaki oso bat dela:

a) 61,, 73 82 + ## b) ,: ,4360 16 ##

c) 26,, 99 3 + ! d) ,: ,, 14 15 01 + !

28 Egin eragiketak.

a) , 3 4 06 + ! b) 0, 5 1 9 + ! c) ,, 0 02871 + ##

d) 02,, 80 72 + ## e) ,, : 02 01 !! f) ,, · 0072 !!

g) ,, 0 15 6 + ! h) :0, 15 3 ! i) ·0, 11 45 #

29 Idatzi kasu bakoitzean emandako zenbakien artean dagoen hamartar zehatz bat eta hamartar periodiko bat:

a) 3,5 eta 3,6 b) , 34 ! eta , 35 !

c) , 32 5 ! eta , 32 56 # d) , 02 31 –# eta , –0229 !

30 Erabili kalkulagailua eta adierazi modu hamartarrean zatiki hauek:

Aztertu izendatzaileak eta arrazoitu zer baldintza bete behar duen zatiki batek hamartar zehatza edo periodikoa bihurtu ahal izateko.

31 Zatiketa egin gabe, esan honako zatiki hauetako zeinek ematen duen hamartar periodiko bat. Gero, lortu horien guztien adierazpen hamartarra:

a) 3 1 b) 4 5 c) 14 7

d) 20 5 e) 20 1 f) 60 2

32 Esan zein den, zenbaki hauetako bakoitza modu hamartarrean adieraziz gero, hogeigarren tokian dagoen zifra hamartarra:

a) 111 47 b) 990 123 c) 13 45

,, ,,, 5 179 6 23 8 59 20 129 9 425 7 45

33 Kontuan izanda 1 9 = 0,111… = , 01 ! dela, adierazi adierazpen hauek zatiki moduan:

a) , 02 ! b) , 03 !

c) , 04 ! d) , 05 !

e) , 06 ! f) , 07 !

34 , 04 ! = 9 4 denez, adierazi zatiki moduan, adibidean egin den bezala:

• 1, 4 ! = 1 + 0, 4 ! = 1 + = 9 4 9 13

a) , 24 ! b) , 34 ! c) , 00 4 ! d) , 10 4 ! e) , 20 4 !

35 2,5 eta 2,6 zenbakiak n = 7 18 balioaren bi hurbilketa dira.

a) Kalkulatu errore absolutua kasuetako bakoitzean. Bietako zein dago n-tik hurbilago?

b) Kalkulatu errore erlatiboaren borne bat kasu bakoitzean.

36 Adierazi, kasu bakoitzean, zein hurbilketatan egin den errore absolutu txikiena:

a) , 137 # ≈ , ,

13 14 b) 6 17 ≈ , ,

28 29

37 Munduko horma bertikal handienak 1 573 m eta

1 577 m bitartean ditu, eta pertsona baten batezbesteko garaiera 1,67 m eta 1,68 m artekoa da. Konparatu bi neurketen errore absolutuak eta erlatiboak.

38 Adierazi kantitate hauek zifra esangarrien zentzuzko kopurua emanez:

a) Planetako ozeano guztien ur bolumen osoa 1 285 657 000 km3-koa da.

b) Espainiar estatuaren azalera 504 782 km2-koa da.

c) Munduko zuhaitzik altuenak 111,55 m ditu.

d) Espazio-ontzi baten masa 2 960 194 kg-koa da.

e) Lurraren bolumena 1 083 208 840 000 km3-koa da.

f) 2 505 378 € tokatu zaizkio loterian.

g) Nire bizitza osoan 1 357 421 m egin ditut oinez.

h) Edalontzi batean 857 321 432 tanta ur sartzen dira.

39 Eman aurreko ariketako kantitateetako bakoitza biribiltzean egindako errore absolutuaren borne bat eta errore erlatiboaren beste bat.

40 Adierazi notazio zientifikoan.

a) Futbol-ligako jardunaldi bati buruzko kinieletan bildutakoa: 1 628 000 €

b) Orratz-buru baten diametroa, m-tan: 0,1 mm.

c) Hezkuntza arloaren aurrekontua, eurotan: 525 mila milioi €

d) Odol-zelulen diametroa, m-tan: 0,00075 mm.

41 Manifestazio batera 850 000 pertsona joan dira.

a) Adierazi kantitatea notazio zientifikoan.

b) Kantitate zehatza da ala hurbildua?

c) Eman hiru zifra esangarri hartzean egindako errore absolutuaren borne bat eta errore erlatiboaren beste bat.

42 Eskualde batean, azpiegituretarako 3 430 milioi euroko aurrekontua bideratu dute.

a) Adierazi kantitate hori notazio zientifikoan.

b) Eman bi zifra esangarri hartuta egindako errore absolutuaren borne bat eta errore erlatiboaren beste bat.

EBATZI PROBLEMA ERRAZAK

43 Duela 7 urte 17 500 €-an erositako auto bat 5 800 €-an saltzen da gaur. Zenbat kostatu da eguneko? Eman zure erantzunean egindako errore absolutuaren borne bat eta errore erlatiboaren beste bat.

44 Alderantzizko bi problema.

a) Txirrindulari bat 22,7 km/h-ko abiaduran doa. Zein da bere abiadura metro segundoko?

b) Oinezko batek segundoko bi urrats ematen ditu, eta urrats bakoitzean 0,85 m aurreratzen ditu. Zer abiadura darama kilometro ordutan?

45 Mendizale batek txango batean eman dituen urratsak zenbatu ditu, eta 100 metroko tarte bakoitza banderatxo batekin seinalatu du.

100 metroan → 123 urrats

500 metroan → 622 urrats

Kilometro batean → 1 214 urrats

Zenbat egiten du aurrera, batez beste, urrats bakoitzean?

Zer datu erabili duzu? Azaldu zergatik.

U 2 59

46 Herrialde bateko ur-kontsumoa 142 litrokoa da, gutxi gorabehera, biztanleko eta eguneko.

51 Aztertu erregaien prezioei buruzko kartel hau:

a) Zer distantzia egingo du 6 L/100 km kontsumitzen dituen auto batek 95eko berun gabeko gasolinan 70 € gastatu baditu? Eta gasolina 98ko berun gabea bada?

Zein da biztanleria osoaren urteko kontsumoa, metro kubikotan? Adierazi emaitza notazio zientifikoan, errore absolutuaren borne batekin eta errore erlatiboaren beste batekin.

47 Gidari batek autoaren erreserba-argia piztu bezain laster betetzen du depositua beti. Atzo 54,8 litro bota zizkion, eta argia 912 km egin ondoren piztu da.

a) Zenbat ordaindu zuen gasolina, 1,55 €/L balio badu?

b) Zein da autoaren erregai-gastua? (litro/100 km)

c) Zein da kostua, eurotan, 100 km-ko?

48 Botilaratzeko makina batek 5 botila freskagarri betetzen ditu 1,55 segundoko. Zenbat denboratan beteko du 20 000 botilako sorta?

49 a) Eguzkiaren masa 330 000 bider da Lurrarena, eta Lurraren masa 5,97 · 1021 t da. Adierazi notazio zientifikoan Eguzkiaren masa, kg-tan.

b) Argiaren abiadura 300 000 km/s-koa da. Adierazi km/h-tan, notazio zientifikoa erabilita.

c) Ilea 4,4 · 10–7 cm/s-ko abiaduran hazten bada, zenbat denbora beharko du 1 cm luzatzeko? Eta metro bat?

APUR BAT GEHIAGO PENTSATZEKO

50 Ganaduarentzako jatekoa egiten duen lantegi batean, pentsu jakin bat osagai hauekin eta kantitate eta prezio hauetan prestatzen du:

kantitatea prezioa

artoa 1,75 t 178 /t

garagarra 2,150 t 164 /t

koltza 0,5 t 327 /t

zahia 0,85 t 275 /t

arrain - irina 250 kg 1,58 /kg

Gero, pentsua 20 kiloko zakuetan bildu eta saltzen dute. Zegan dago zaku bakoitza?

b) Zer gastu egin du A gasolioan 5,2 L/100 km kontsumitzen dituen beste ibilgailu batek, erregai horrekin 580 km egin dituela jakinda?

52 Existitzen den izaki bizidun txikiena birus bat da eta 10–18 g-ko pisua du; eta handiena balea urdina da eta, 138 t-ko pisua du, gutxi gorabehera Zenbat birus beharko genituzke balearen pisua berdintzeko?

53 50 kg hareatan 3 · 106 pikor badaude, zenbat harea-pikor egongo dira tona batean?

54 Txerto baten dosia 0,05 cm3 da. 100 000 000 bakterio baditu cm3 bakoitzeko, zenbat bakterio daude dosi batean? Adierazi notazio zientifikoan.

55 Astroen arteko distantziak neurtzeko, neurri-unitate moduan argi-urtea erabiltzen da; hau da, argiak urte batean egiten duen distantzia, 3 · 105 km/s-ko abiaduran joanda.

a) Aurkitu zenbat kilometro diren argi-urte bat.

b) Esne Bideak, gure galaxiak, ehun mila argi-urteko diametroa du. Adierazi kilometrotan.

56 Kalkulatu zenbat denbora behar duen argiak Eguzkitik Lurreraino iristeko, jakinda Eguzkitik 1,5 · 108 km-ra gaudela. (Gogoan izan argiaren abiadura 3 · 105 km/s dela).

57 Bi ispilu paralelo jarri ditugu, bata bestetik metro batera, eta izpi bat zuzendu dugu ispiluetako batetik perpendikular. Kalkulatu zenbat aldiz errebotatzen duen (islatzen den) izpiak bi ispiluetan ordubetean.

58 Material baten dilatazio-koefizienteak adierazten digu zein den material horren luzera-unitate baten luzamendua tenperatura Celsius gradu bat handitzen den bakoitzeko.

Erantzun hurrengo galderei, jakinda kobrearen dilatazio-koefizientea 1,7 · 10–5 dela.

a) Zenbat luzatuko da 100 m-ko kobrezko kable bat tenperatura 8 °C-tik 22 °C-ra igotzean?

b) Zenbat uzkurtuko da 45 °C-tik 11 °C-ra jaitsiz gero?

Ariketak eta problemak

beste

batzuk 375

95eko berun gabea 1,720 /L 98ko berun gabea 1,876 /L A gasolioa 1,624 /L A+ gasolioa 1,723 /L B gasolioa 1,155 /L

AUTOEBALUAZIOA

1 Adierazi honako zenbaki hauetako zein jar daitezkeen zatiki moduan, eta idatz itzazu, egin daitezkeenetan:

18,6 3 + 5 π 2 10,3 ! 12, 6 ! 7 3 6,12

2 Aurkitu zatiki bakoitzari dagokion zenbaki hamartarra:

a) 11 4 b) 100 3 447 c) 3 19 d) 85 11 e) 134 5

3 Adierazi zifra esangarrien kopuru egokia emanez, eta kalkulatu kasu bakoitzean egindako errore absolutua eta errore erlatiboa:

a) Garaje-plaza baten prezioa: 19 350 €.

b) 910 berreketaren emaitza.

c) Irratsaio baten entzule-kopurua: 2 970 350.

➜ anayaharitza.es Ariketa hauen ebazpena.

6 a) Adierazi notazio zientifikoan. Gero, kalkulagailuaren laguntzaz, adierazi emaitza hiru zifra esangarrirekin. , 15 000 25 10 0 00007 7

b) Adierazi emaitza hurbiltzean egindako errore absolutuaren borne bat eta errore erlatiboaren beste bat.

7 Konglomeratu-ohol bat erosiko dugu, 1,20 m × 2,80 m neurrikoa.

a) Zenbat kostatuko zaigu 13,5 €/m2 balio badu?

b) Katalogoan iragartzen dutenez, konglomeratua 7 kg/m2 motakoa da. Zer pisu izango du oholak?

c) Jabeak konglomeratu-ohola 40 €-an utzi badigu, zenbat kostatu zaigu metro karratua?

IKASKUNTZA-EGOERA

4 Adierazi zenbat zifra esangarri dituen beheko testuan ageri diren hurbilketetako bakoitzak, eta eman bakoitzaren errore absolutuaren borne bat eta errore erlatiboaren beste bat:

Duela 30 min, 800 m2-ko lursaila duen 120 m2-ko etxe bat alokatu dut 1 200 €-an hilean.

5 Adierazi notazio zientifikoan, eta esan zenbat zifra esangarri erabili diren kasu bakoitzean.

a) Errusiaren azalera: 17 000 000 km2

b) AEBko BPGa: 20 500 000 000 000 €

c) Elektroi baten lodiera: 0,0000000000000001 m

d) Koronabirus baten diametroa: 0,000000013 m

BITXIKERIA MATEMATIKOAK

Eman iritzia: hamartarra ala osoa?

Kalkulatu honako hamartar periodiko puru honen zatiki sortzailea:

0,999999…

Egin emaitzari buruzko gogoeta. Zentzuzkoa iruditzen zaizu?

Arrazoitu zure erantzuna.

HAUSNARTU

Berrikusi landutako alderdiak eta eman konponbidea hautemandako arazoei.

Horretarako, deskargatu dagokion errubrika anayaharitza.es webgunetik, egin gogoeta banaka eta bateratzelana taldean.

PROBATU ZURE KONPETENTZIAK

Egin anayaharitza.es webgunean ageri den konpetentzien autoebaluazioa.

Batezbesteko pisua

Nekazari batek hogei zaku gariz bete du gurdia. Zaku bakoitzak 35,5 kg ditu batez beste.

Gaua ostatu batean egin du, eta ostalariari jenerotan ordaindu dio. Horretarako, lehenengo zakutik 1 kg gari hartu du, bigarrenetik 2 kg, hirugarrenetik 3 kg, eta horrela jarraitu du, azkenera arte. Zer pisu dute batez beste orain zakuek?

U 2 61

Eskubide guztiak gordeta. Legeak lan honen edukia babestu eta espetxe-zigorrak edota isunak eta kalte-galeren ondoriozko kalte-ordainak ezartzen ditu honako hauentzat: edozein literatura-lan, artelan zein zientzia-lan, edo horren eraldaketa, interpretazioa edo gauzapena (edozein euskarritan finkatuta edo edozein eratan komunikatuta), oso-osorik edo zati batean, baimenik gabe erreproduzitu, plagiatu, banatu edo komunikatzen dutenentzat.