Operación mundo: Physics and Chemistry 3. Secondary DF (muestra)

DUAL FOCUS

3 SECONDARY EDUCATION PHYSICS AND CHEMISTRY ANDALUSIA

5

THE FORCES AND THEIR EFFECTS

Take action!

Can you find the value of gravity where you live?

FORCES

SCAN THE CODE TO FIND OUT ABOUT THE CHALLENGE

• By contact

• At a distance

Deformation

Changes in the state of movement produce allows the classification of are measured with some common ones are which is directly proportional to

• Plastics

• Elastics

• Position

• Trajectory

• Distance travelled

• Displacement

• Speed

• Velocity

• Acceleration

Contact surfaces Mass

exercised by act through act through act through

Frictional

we may study their effects with

Hooke’s Law

Newton’s Laws

Coulomb’s Law Law of universal gravitation

Threads, cables, ropes

Elastic objects

Contact surfaces

FOCUS O N ENGLISH

Listening and Speaking

Listen and repeat the most important terms of this unit, paying attention to their pronunciation.

Reading and Writing

Read the outline on forces and their effects and write a sentence in your notebook that summarises the content of each branch.

Forces 1

1.1 Effects of forces

A force is any cause that has the effect of changing the state of motion of an object or deforming it.

Effects of forces

Changes in the state of motion

When acting on an object, a force can

Moves it, if it is stationary.

Stops it, if it is moving.

1.2 Resultant force

Curves the motion.

What are forces?

What are their effects on objects?

Deformation

Depending on how the objects react, we distinguish between

Elastic objects

Regain their shape when the force stops acting.

It is possible to apply several forces on an object at once, and the resultant, or net, force is the vector sum of all the individual forces. If the net force on an object is zero, the effect is the same as if there were no forces acting on it.

1.3 Contact and at-a-distance forces

Contact forces are the forces that are exerted when objects collide, rub against each another or push against each other. However, there are forces in nature, such as those that act between the planets and the Sun, or electrical currents and magnets, that act at a distance, without contact.

1 Speaking. Name which of the following examples involve forces that produce obvious deformations, and which involve noticeable changes in the state of motion:

a) Turning the steering wheel of a moving motorcar.

b) Driving on a bumpy road.

c) Stepping on the accelerator of a motorcar.

d) Sitting in the passenger seat.

2 Speaking. Discuss with your classmates whether the following statement is correct: “A force can be applied

Plastic objects

Remain deformed after the force stops acting.

Vocabulary

Force - State of motionDeformation - Elastic - PlasticVector - Resultant - Net - Contact forces - At-a-distance forces

to an object without deforming it or changing its state of motion”.

3 Writing. Indicate whether the following sentences are true and correct in your notebook the false statements:

a) When a motorcar drives around a curve, we cannot know if there are forces applied on it.

b) For an object to be in motion, a constant force must act on it.

c) Contact forces can only produce deformations in the objects on which they act.

Everyday forces

Weight

Frictional forces

Oppose the movement of objects and stop them when they move. In this group are frictional force and air resistance.

Collision force

The force that two objects exert on each other when they collide.

The force with which the Earth attracts all objects on its surface.

The weight of an object of mass m is: P = m · g where g is the gravity of our planet, 9.8 N/kg.

What forces may we encounter?

What are the effects of these forces?

Normal

The force that a surface exerts on the objects that rest on it, preventing them from passing through it.

Elastic force

The force that all elastic objects can exert on themselves, causing them to return to their original shape. When an object is suspended from a spring, the elastic force prevents the spring from stretching completely, so that, at equilibrium, P = F e

4 Writing. When a motorcar moves along the road, the engine applies a forward force to it, by which it travels. But there are three other forces acting on it. Draw a picture of the motorcar with the forces and explain each one.

5 A person weighs 588 N on Earth.

a) Draw the forces acting on it at rest.

b) What is its mass?

c) How much would it weigh on the Moon, if the gravity there is 1.6 N/kg?

Tension

The force that threads, ropes, cables can exert on objects attached to one end when we pull on the other end.

6 Speaking. Of the forces studied on this page, which are contact forces and which are at-a-distance forces?

7 Writing. Do you see any mistakes in the following sentence: “My brother weighs 90 kg”. If so, reconstruct the sentence to make it physically correct.

Vocabulary

Friction – Rubbing - Resistance - Weight - MassGravity - Normal - Tension - Elastic - Collision

Motion 3

3.1 Position, trajectory and distance travelled

Motion is defined as the change of position of a moving object relative to a reference frame. Therefore, motion is a relative concept depending on the reference frame we take.

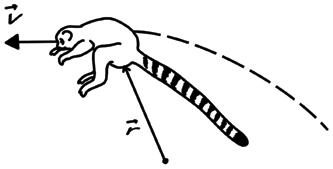
Let’s study the magnitudes of the movement on the map below:

1

The position vector indicates the position of the object relative to the chosen origin. For example, the position of the treasure relative to the tree is " rtree

The position vector of the treasure with respect to the rock is " rrock

What is motion?

What magnitudes measures it and how do we study changes in it?

4

The position vector of the hare with respect to the spring is changing.

5

3

The position vector of the treasure with respect to the tortoise, " rtortoise , changes as the tortoise moves. We could also say that the treasure is moving with respect to the tortoise.

The trajectory is the line formed by all the points to which the position vector has pointed.

6

The distance travelled, e, is the distance the object travels along the trajectory.

8 With the scale used in the image and the data in it, indicate the position of the treasure with respect to:

a) The tree.

b) The rock.

c) The spring.

9 Speaking. Specify which of the following terms corresponds to each of the statements: position vector, displacement, distance travelled, trajectory.

a) The distance travelled by an object measured along its trajectory.

7

The displacement vector, d " , is the vector that joins the initial position with the final position. Its modulus, || d " , d, is called the displacement, and will always be less than or equal to the distance travelled.

b) The succession of points through which a moving object passes.

c) The position of the object at each instant.

d) Distance separating the initial and final positions.

10 Writing. Complete the following sentence in your notebook: “The .... is measured along the .... so it will always be .... or equal to the .... ”.

11 If the tortoise were to move in a straight line to the left, draw in your notebook what the path of the treasure would look like with respect to the tortoise.

Vocabulary

Reference system - Motion - Position - Trajectory - Distance travelled - Displacement

3.2

Speed and velocity are different physical quantities. The tells us the average rate at which a moving object travels through space along its trajectory. The moving object would have moved if it had gone in a straight line in the same direction as the displacement vector.

The average velocity, m " v , is defined as the displacement, d " , per unit time t : " v t d m = " 1

3

The instantaneous velocity, or velocity, v " , is the average velocity calculated over a very small time interval.

3.3 Uniform rectilinear motion

It is the motion of an object on a straight trajectory at constant speed. The distance travelled is proportional to the time. If we represent the initial position with s0 and the final position by s, we have that, e = s – s0, and we can write the equation of the uniform rectilinear motion:

v t ss ss vt – 0 0 == + "

Problem solved

1 A motorcar is moving along a straight road at 90 km/h. At a certain instant it passes kilometre marker 21. Calculate:

a) How long it will take to pass kilometre 30.

b) Its position 2 minutes after passing that point.

Let us express speed in IS:

a) We use the equation of uniform rectilinear motion, s = s0 + v · t: 30 000 = 21 000 + 25 · t � min t s 25 30 00021000 360 6 –== =

b) Two minutes later t = 6 + 2 = 8 min = 480 s will have elapsed. Substitute this time into the equation of uniform rectilinear motion:

s = s0 + v · t = 21 000 + 25 · 480 = 33 000 m = 33 km

The average speed, vm, is the distance travelled, e, per unit tim, t: v t e m = 2

The instantaneous speed, or speed, v, is the average speed in a tiny interval of time. It is equal to the instantaneous speed modulus: vv = " 4

Vocabulary

Speed - Velocity - Time intervalUniform rectilinear motion

12 Writing. What does it mean that the average speed of a moving object is 5 m/s? What if the average speed were 5 m/s to the south?

13 Speaking. If a moving object has moved for 10 s with an average speed of 2 m/s, how much distance has it travelled? Can we figure out its displacement?

14 A motorbike is travelling along a straight road at a constant speed of 72 km/h when it passes the 28-kilometre mark. Where was it going 15 minutes earlier?

3.4 Acceleration in rectilinear movement

In rectilinear movements, the speed of a moving object can change. Acceleration is the quantity that measures the rate of these changes.

The average acceleration, am, is defined as the change in speed per unit time:

The instantaneous acceleration, a, is an average acceleration measured over a very small time interval.

By convention, a positive acceleration indicates that the object’s speed is increasing, and a negative acceleration indicates the speed is decreasing.

3.5 Vertical free fall

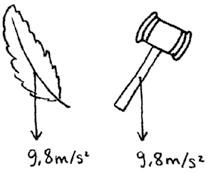
An object in vertical free fall is an object that is dropped or thrown vertically. These objects move with constant acceleration, the acceleration of gravity, which on Earth is 9.8 m/s2. Therefore, an object in free fall accelerates (or slows down) by 9.8 m/s every second.

15 The graph of the speed of a moving object is:

If vi = 5 m/s and vf = 30 m/s, the change in speed is 25 m/s. Since it has occurred over 5 s, on average, it changed 5 m/s every s.

Specify which of the following statements are true:

a) The moving object moves with constant speed.

b) The average speed of the movement is zero.

c) The object has positive acceleration until t = 10 s, and then it has negative acceleration.

d) The initial and final positions coincide.

e) The acceleration in the first section is 0.5 m/s 2 , and in the second, –2 m/s 2 .

16 How fast would you have to throw a ball vertically upwards such that it would stop moving after one second? Express the result in km/h.

17 If we throw a brick downwards at 5 m/s and hits the ground at 13.6 m/s, how long did it fall?

18 If we throw an object upwards at 12 m/s, how fast will it be at t = 2 s?

19 Reading. Read the following paragraph and answer:

“The position of an object in a reference frame may have positive or negative values, depending on whether it is to the right or to the left of the origin of the reference frame, respectively”.

Of the other quantities studied (distance travelled, speed and acceleration), which can take positive or negative values, and which cannot? Explain your answer.

We have previously seen that elastic objects recover their shape when the force that deforms them stops acting. This is because the deformation they undergo is related to the elastic force that then restores the object’s shape:

The elastic force, F e, is proportional to the deformation, Δl, undergone by the elastic system: F e  =  –k · Δl

Elongation, Δl, is how much the object has been stretched or compressed.

How do we study deformations?

Is there a relationship between the deformation of an object and the force applied, and between this and the force that restores the original shape?

The minus sign indicates that the elastic force acts in the opposite direction to the deformation.

The constant k is called the elastic constant and depends on the properties of the elastic system.

Problem solved

2 A 10 cm spring stretches to 12 cm when a force of 8 N acts on it. Find:

a) The elastic constant of the spring.

b) What much it will stretch when F = 12 N.

a) The elastic constant is calculated using Hooke’s law:

Δl = 12 cm – 10 cm = 2 cm

As the system is in equilibrium, the magnitudes of the force and the elastic force are equal:

b) Knowing the elastic constant, we can calculate a spring’s elongation under any force:

== ==

Therefore, the length of the stretched spring will be:

l

10 cm + 3 cm = 13 cm

In equilibrium, the force applied to deform the spring is equal to the elastic force that tries to restore the spring to its original shape. If a mass hanging from the spring forces the spring to stretch twice as much, then the elastic force exerted by the spring also doubles.

20 A Hooke’s constant of k  = 200 N/m means that a force of 200 N will deform a spring by 1 m. How much will the same spring deform if you double the force?

21 An object weighing 1.5 kg hangs from a fixed spring, and we measure an elongation of 4 cm.

a) What is the value of the Hooke’s constant k?

b) How much will the spring stretch if we hang 900 g on it?

Vocabulary Elastic force - Deformation Elongation - Equilibrium

Newton’s laws 5

In 1687, Isaac Newton stated the laws relating forces to motion.

5.1. Law of inertia

Newton recovered an idea stated earlier by Galileo in his first law:

If no forces act on an object, or the net force is zero, the object is necessarily at rest or in uniform rectilinear motion.

5.2 Fundamental law of dynamics

This second law reveals what happens when the net force is not zero:

If an object is acted upon by a net force, it experiences an acceleration, proportional to the force, in the same direction as the force:

F = m · a

5.3 Law of action and reaction

Newton’s third law states that there are no isolated forces in nature:

Two interacting objects exert equal forces on each other in opposite directions. Each force is applied to one of the bodies, so these forces never cancel each other out.

22 Listening. Listen to the text about Galileo that you will find in anayaeducacion.es and complete the following sentences in your notebook with the missing words:

a) Before Galileo people thought that the .... state of objects was .... and that for an object to be in motion it was necessary for a .... to act on it.

b) ..thought that an object could .... naturally without any .... acting on it.

c) According to .... first law, an object on which no .... acts is necessarily at .... or in ....

How are forces related to motion?

What are the laws of motion?

Accelerate

In a horizontal plane, the object should neither accelerate nor slow down. If it ends up stopping, it is due to friction.

The greater the mass, the more the object resists changing its state of motion (the smaller its acceleration). F a

The bullet exerts a force on the barrel equal to that exerted by the barrel on the bullet, but their effects are different.

23 Writing. Write the following sentence in your notebook, correcting any errors you find: “When an object is accelerated, it experiences more force the greater the mass of the object. So, the greater the mass of the object, the greater the acceleration with which it falls to the surface of the Earth.”

24 Speaking. Explain what happens to the passengers on a bus when the bus:

a) Brakes.

b) Turns right.

c) Travels in a straight line without changing its speed.

Gravitational and electrical forces

6.1 Law of universal gravitation

Any two objects attract each other with a force directly proportional to the product of their masses and inversely proportional to the square of the distance between them:

This law explains the force of mutual attraction between any two objects, for example, between the Earth and the Moon or between the Earth and

We call this force the force of gravity.

In the case of an object on the surface of the Earth, we call it weight: FbT = P

6.2 Coulomb’s Law

What types of interactions are there?

What laws explain them?

Vocabulary

Gravity - Gravitation - Electric force

- Mutual attractionDirect and inverse proportionality

According to Newton’s third law, the force exerted by the Earth on the Moon, " FLT , is opposite to the force exerted by the Moon on the Earth, " FTL

If the charges have the same sign, they repel each other, and if they have different signs, they attract.

The electric force is directly proportional to the product of the charges and inversely proportional to the square of the distance separating them:

25 Two electrons separated by a distance r interact both gravitationally and electrically. Compare the two forces.

Data: G = 6,67 · 10–11 N · m2 · kg–2; K = 9 · 109 N · m2 · C–2; m e = 9,1 · 10 –31 kg; e = 1,602 · 10 –19 C.

26 Make a table showing the similarities and differences between gravitational and electrostatic forces.

27 How will the force of gravity between two masses change if we move them apart to twice their initial distance?

The final challenge

Take action!

Gravity on Earth

Are you able to experimentally obtain the value of gravity where you live?

Group work. Organise the class into small working groups and discuss the following questions, searching the Internet for the information you need (always use trustworthy sites):

• The facts that the Earth is not homogeneous, that its shape is not perfectly spherical and that it is rotating mean that gravity can have different values at different points on the surface. What do you think are the effects of each factor?

• How can we measure its value experimentally? Find at least two ways (with what you have studied in the unit, you could deduce one of them). After answering these questions, measure gravity by both methods.

Procedure

When taking measurements, remember that every measurement has errors. To reduce errors, when you measure a physical quantity, you should take at least three measurements and use the arithmetic mean of the individual measurements as the value. Note down the information that may be relevant and note the usefulness of tables to organise the data.

Results and conclusions

You have probably obtained similar, but not identical, values for gravity by both methods. Discuss in each group the following questions: How many decimal places do you think you should use to express your results? Which method do you think is more reliable?

Afterwards, discuss in the classroom to answer the following questions:

1 It is likely that the different working groups have obtained different values for gravity. Why might that be?

2 If we were to decide as a class, what value of gravity would be the most appropriate?

Galileo Galilei was the first scientist to prove experimentally that all objects fall with the same acceleration.

3 Organise yourselves to look up information and explain the relationship of gravimetry to what you have just done.

4 Together, prepare a slide show to tell your classmates from other classes in the school about your experience. You can also do this by putting up posters with the information in the school corridors.

SECONDARY EDUCATION 3 DUAL FOCUS

PHYSICS AND CHEMISTRY

Index

THE FORCES AND THEIR EFFECTS 5

The force quantity

The interactions of matter force it to change its motion or become deformed, the causes of these effects are forces and we measure them in newtons (SI).

A body does not have force rather it has energy, and thanks to that it can exert forces on other bodies.

Force:

Force is anything that produces deformations and changes in the state of motion.

1 Choose the correct statement about forces:

a) Objects have force, and therefore can produce deformations.

b) Objects do not have force, but they can exert forces on each other.

Contact and at-a-distance forces

Vector character

When we talk about a force we must also state in which direction it is applied. These types of quantities are called vector quantities and are represented by vectors.

We call the quantities that we knew about up to now (such as temperature) scalar quantities.

The forces exerted when an object collides with another, when objects are rubbed, pushed, etc. are contact forces.

At-a-distance forces occur without the need for physical contact, such as the gravitational pull between the planets and the Sun, etc.

2 In the following situations, indicate whether the forces act by contact or at-a-distance:

a) A magnet sticks to the refrigerator door.

b) The wind propels the sail of a ship.

c) A fruit falls from a tree.

3 Fill in the gaps in your notebook with the missing words:

.... quantities require specifying the .... in which they act. For example, force, .... and .... .

When we deform an elastic body by applying a force (F ), an elastic force appears (Fe) which is the same as that which we apply but in the opposite direction: Fe = F

We have two categories depending on how the objects become deformed:

• Elastic body: it recovers its original shape when the force that was keeping it deformed stops; examples are springs, hair ties, etc.

• Plastic body: it remains deformed once the force that was deforming it stops acting. Clay and plasticine are plastic materials.

4 Indicate whether the following objects are elastic or plastic:

a) Dough made from flour and water that, after kneading, is circular and flat.

b) The front shock absorber of a bicycle, which causes the handlebars to sink when riding over a pothole.

Friction forces

There are forces that stop the bodies in motion due to the interaction of these bodies with the environment. These forces are called friction forces, R.

We can subdivide these forces into rubbing forces (caused by the ground) and air or water resistance etc.

Friction is the force that slows down an object that slides on the ground. Do you think we could walk if friction didn’t exist?

Collisions

When two bodies collide they exert forces on one another, deforming the other body and changing its motion in a very short period of time.

6 When a moving object collides with a fixed object, which of the two objects exerts the force?

a) The one that was in motion before the crash, since the other had no force because it was still.

b) The one that was still, because it forces the other object to stop.

c) Both objects, since forces are interactions between two objects.

Weight, P, is the force that a body undergoes due to gravitational pull. Like all forces, we measure it in newtons and it is proportional to mass.

P = m · g

7 In your notebook, correct any errors in the following sentence:

As my weight is 65 kg, when I wear a 5 kg backpack, the total weight will be 70 kgs.

When a body hangs from a rope, there is a force that counteracts the weight, which we call tension.

9 If the lamp in the picture weighs 50 N, what is the tension?

The normal force is the force that solid surfaces, such as the ground, exert on bodies supported by them. It is always perpendicular to the surface and prevents the object from penetrating it.

8 Indicate in which direction the normal force acts when you lean a ladder against a wall.

Elastic force is present in many situations and it will appear with the deformation of any body, like when hanging a weight from a spring.

10 In addition to elastic force, what other forces act on the ball when it is in contact with the ground?

Position and trajectory

Reference systems

The first thing to do to study the rest or motion of an object is to decide on the reference system to use, to be able to specify where the object is (its position) and what it is moving towards.

11 A reference system is: a) A point that we take as a reference to measure the position of objects. b) A scaled representation of the reality that we take as a reference.

If the object is in motion, it has a trajectory, which is the succession of positions it occupies over time. When the trajectory is a straight line, we call the motion rectilinear.

12 Complete the following sentence in your notebook: The .... of a object with respect to a .... system indicates .... the object is in relation to it. The .... is the succession of .... through which a moving object has passed.

Uniform rectilinear motion:

Rectilinear movements

Is a rectilinear motion in which the velocity remains constant; therefore, there is no acceleration.

x = x0 + v · t

Rectilinear motion with constant acceleration:

When an object is left free at a certain height, it is observed to fall vertically towards the ground with increasing speed (free fall). However, if we throw it upwards, the object slows down until it finally stops (free ascent) and immediately begins to fall.

v = v0 + a · t

g = 9,8 m/s2

13 Indicate whether the following sentences are true or false, and correct the false ones:

a) In uniform motion, the speed increases constantly.

b) In an upward vertical throw, the acceleration decreases until the object stops. The object then falls with constant speed.

c) Free fall is a type of vertical motion in which the acceleration is constant and equal to 9.8 m/s2

Newton’s 1st and 2nd laws

Newton’s 1st law, or the law of inertia, explains that the natural state of objects is rest or uniform rectilinear motion, and they tend to conserve it unless a force acts on them.

Newton’s 2nd law, law of dynamics, objects experience an when subjected to a same direction as the former.

Newton’s 3rd law, or law of action and reaction, explains that forces equal in magnitude but in opposite directions.

F1 = F2

14 Indicate which Newton’s law each statement corresponds to:

a) If the force exerted on a mass is doubled, the acceleration of the mass is doubled.

Elastic force:

b) An object at rest shall remain in that state until a net force acts on it..

c) When pushing a wall, the wall exerts an opposite force on our hand of the same magnitude.

Hooke’s law

Elastic force is directly proportional to the deformation of an elastic body. In other words, elastic force is opposite of the force causing the deformation. In mathematical terms:

F = k · Δl

k is what we call the elastic constant, which is characteristic of each elastic body.

15 When hanging a 0.5 kg mass from a spring, we observe that the spring lengthens by 1 cm. How long will it be if we double the mass? Choose the correct explanation:

a) The elastic force is proportional to the deformation.

b) The greater the mass that hangs from a spring, the less force the spring exerts to regain its shape, and that is why it stretches more.

10 kg F

What is gravitational force?

The mutual force by which two bodies of masses M and m, separated by a distance, r, from centre to centre, are attracted, is directly proportional to the product of the masses of the bodies and inversely proportional to the square of the distance that separates them:

Universal gravitational constant

16 If the distance between the Earth and the Moon were doubled, how much would the gravitational force between them change?

a) It would double.

b) It would be halved.

c) It would decrease to one quarter.

Weight and gravity

• The force of gravity Fg is the one that causes bodies to fall.

• Weight is the force of gravity exerted by a planet:

= Pm g

The gravity by which any object falls to the surface of a planet is:

= g R G M 2

17 As you know, weight is a force. What physical magnitude is gravity, g ? What is its value on the surface of the Earth?

Coulomb’s Law

The force by which two charges interact, q and Q, separated by a distance, r, from centre to centre, is directly proportional to the product of its charges and inversely proportional to the distance that separates them:

= F

e 2

r Qq K

If the charges are of different signs they attract each other and if they are of the same sign they repel each other.

18 Two charges repel each other with a force of 10 N. If the sign of both charges is changed and one of them doubles in value, the charges:

a) Repel each other with twice the force.

b) They attract twice as strongly.

c) Force ceases to act.

Constant K is around 20 orders of magnitude greater than constant G. Electrostatic force is much stronger than gravitational force.