Mundua helburu: Matematika II 2. Batxilergoa. Lagina

MATEMATIKA II BATXILERGOA 2

12HILEKO LIZENTZIA

DIGITALA

Aurkibidea Ikasturteko oinarrizko jakintzak

4 S istemak determinanteen

1. Rouchéren teorema

2. Cramerren erregela

3. Cramerren erregela edozein sistematan aplikatu

4. Sistema homogeneoak

5. Sistemak determinanteen bidez eztabaidatu

6. Ekuazio-sistema baten forma matriziala

Ariketak eta problemak

Autoebaluazioa

Unibertsitatera sartzeko probarako: I. multzoa

I. multzoaren autoebaluazioa

I.

1. Ekuazio linealen sistemak

2. Ekuazio linealen sistema baten soluzio posibleak

3. Sistema mailakatuak

4. Gaussen metodoa

5. Ekuazio-sistemen eztabaida Ariketak eta problemak Autoebaluazioa

2

1. Nomenklatura. Definizioak

2. Eragiketak matrizeekin

3. Matrizeen arteko eragiketen propietateak

4. Matrize karratuak

5. Matrize bateko errenkaden arteko erlazio linealak

6. Matrize baten heina Ariketak eta problemak Autoebaluazioa

3 D eterminanteak

1. Bi ordenako determinanteak

2. Hiru ordenako determinanteak

3. Edozein ordenatako determinanteak

4. Minor osagarria eta adjuntua

5. Determinantea lerro bateko elementuetatik abiatuta garatu

6. Edozein ordenatako determinanteak kalkulatzeko metodoa

7. Matrize baten heina, minorretatik abiatuta

8. Matrize baten alderantzizkoa

lortzeko beste metodo bat

Ariketak eta problemak

Autoebaluazioa

II.

MULTZOA. Geometria

5 Bektoreak espazioan

1. Eragiketak bektoreekin

2. Bektore baten adierazpen analitikoa.

3. Bektoreen biderketa eskalarra

4. Biderketa bektoriala

5. Hiru bektoreren arteko biderketa mistoa

Ariketak eta problemak

6

1. Erreferentzia-sistema espazioan

2. Bektoreak geometriako problemetan erabili

3. Zuzenaren ekuazioak

4. Bi zuzenen posizio erlatiboak

5. Planoaren ekuazioak

6. Plano bat zehazteko moduak

7. Plano eta zuzenen posizio erlatiboak

8. Ekuazioen hizkuntza: aldagaiak, parametroak…

Ariketak eta problemak Autoebaluazioa

7

1. Zuzen eta planoen arteko angeluen neurria

2. Puntu, zuzen eta planoen arteko distantziak

3. Azaleren eta bolumenen neurriak

4. Leku geometrikoak espazioan

Ariketak eta problemak

Autoebaluazioa

Unibertsitatera sartzeko probarako: II. multzoa

II. multzoaren autoebaluazioa

130

150

III. MULTZOA. Analisia

8 F untzioen limiteak.

J arraitutasuna 212

1. Funtzioen limiteen ideia grafikoa

2. Teoria apur bat: ikas dezagun limiteak definitzen

3. Limiteen eragiketa errazak

4. Indeterminazioak

5. Infinituen konparazioa

6. Limiteen kalkulua x → +∞ denean

7. Limiteen kalkulua x → –∞ denean

8. Funtzio baten limitea puntu batean. Jarraitasuna

9. Limiteen kalkulua x → c denean

10. Limiteak kalkulatzeko ahalmen handiko tresna

11. Jarraitutasuna tarte batean

Ariketak eta problemak Autoebaluazioa

9 Deribatuak 246

1. Funtzio baten deribatua puntu batean

2. Funtzio deribatua

3. Deribazio-erregelak

4. Funtzio baten deribatua, alderantzizkoarena jakinda

5. Funtzio inplizitu baten deribatua

6. Deribazio logaritmikoa

7. Deribazio-formulak modu arrazoituan lortu

8. Funtzio baten diferentziala

Ariketak eta problemak

Autoebaluazioa

10

Deribatuen erabilerak

1. Kurba batekiko zuzen ukitzailea

2. Funtzio baten goratzea eta beheratzea puntu batean

3. Funtzio baten maximo eta minimo erlatiboak

4. Bigarren deribatutik ateratako informazioa

5. Funtzioen optimizazioa

6. Bi teorema garrantzitsu

7. Batezbesteko balioaren teoremaren erabilera teorikoak

Ariketak eta problemak

Autoebaluazioa

11

Funtzioen adierazpena

1. Kurbak eraikitzeko oinarrizko elementuak

2. Balio absolutua funtzioen adierazpenean

3. Funtzio polinomikoen adierazpena

4. Funtzio arrazionalen adierazpena

5. Beste funtzio mota batzuen adierazpena

Ariketak eta problemak

Autoebaluazioa

12 Ja torrizkoen kalkulua

1. Jatorrizkoak.

Kalkulatzeko oinarrizko erregelak

2. Berehalako integralen adierazpen konposatua

3. «Zatika» integratu

4. Funtzio arrazionalen integrazioa

Ariketak eta problemak

Autoebaluazioa

13 Integral de finitua

1. Kurba baten azpiko azalera

2. Funtzioa [a, b] tartean integragarri izateko baldintza bat

3. Integralaren propietateak

4. Integrala eta deribatuarekin duen erlazioa

5. Barrowen erregela

6. Azalerak integralen bidez kalkulatzea

7. Biraketa-gorputz baten bolumena

Ariketak eta problemak

Autoebaluazioa

Unibertsitatera sartzeko probarako: III. multzoa

III. multzoaren autoebaluazioa

IV. MULTZOA. Probabilitatea

14 Zo ria eta probabilitatea

1. Zorizko saiakuntzak. Gertaerak

2. Maiztasuna eta probabilitatea

3. Laplaceren legea

4. Probabilitate baldintzatua. Gertaera askeak

5. Proba konposatuak

6. Probabilitate osoa

7. «A posteriori» probabilitateak.

330

276

Bayesen formula

Ariketak eta problemak

Autoebaluazioa

15 Pr obabilitate-banaketak

1. Banaketa estatistikoak

2. Aldagai diskretuko probabilitate-banaketak

3. Banaketa binomiala

4. Aldagai jarraituko probabilitate-banaketak

5. Banaketa normala

6. Banaketa binomiala normalera hurbiltzen da

Ariketak eta problemak

Autoebaluazioa

302

Unibertsitatera sartzeko probarako: IV. multzoa

IV. multzoaren autoebaluazioa

360

Honelakoa da zure liburua

Hasteko

Liburua hastean aurkituko duzun lehenengoa da problemak ebazte unitate bat.

Problemak ebatzi Zer da benetako problema bat? Dagoeneko hainbat ikasturtetan ikusiko zenuenez, zure liburuan problemak ebatzi izeneko atala agertzen da. Atal horretan, problema berezi batzuk lantzen dira, problema bitxiak. Horiek ebazteko, garrantzitsuena ez da asko jakitea; horiek ebazteko, garrantzitsuena ondo pentsatzen jakitea da. Benetako problema horiek argi eta garbi bereizten dira ariketa soiletatik. Aurrean benetako problema bat daukagunean, gutxi gorabehera badakigu egoera horretan nora joan nahi dugun, baina ez dakigu nola iritsi. Hain zuzen ere, hori izango da zailtasunik handiena: egoera argitzea eta helburura eramango gaituen bide egokiren bat aurkitzea Benetako problemak ebazten jakiteko, trebea izan behar da oso. Baina hori pazientzia eta ekina izanda lortzen da: ausarta izan eta hainbat eratako problemak landu behar dira, eta horietatik guztietatik ahalik eta onunarik handiena ateratzen ahalegindu behar dugu, ebaztea lortu zein lortu ez Hurrengo orrialdeetan, problemak ebazten lagunduko dizuten pentsamenduestrategia batzuk emango dizkizugu. Lan horri begira emaitza onak izaten dituzten jokatzeko moduak dira. Horrez gainera, ageri diren ariketek estrategiak errazago landu eta barneratzen lagunduko dizute. Atal honetan proposatu diren problemetako batzuk errazak irudituko zaizkizu; beste batzuk, ez hain errazak; eta beste batzuk, berriz, oso-oso zailak. Baina denetatik aterako duzu probetxua eta, beharbada, probetxurik handiena zailenak iruditu zaizkizun horietatik lortuko duzu, pentsatzeko bide eta metodo gehiago saiatu beharko baitituzu. Ez dezazula pentsatu problemak ebazten egiten duzun denbora alperrekoa dela. Ebaztea lortzen ez baduzu ere, denbora hori ondo baino hobeto erabilitakoa izango da beti Problemen ebazpenean ageri diren etapak Problema ulertzea Arretaz irakurri behar dugu. Zenbait kasutan, eskema bat erabiliko dugu. Argi izan behar dugu zer dakigun, zer eskatzen zaigun eta baldintzak zein diren.

Ebazte-plan bat pentsatzea Hau da faserik zailena. Problema asko ebazteak ondorio argi bat du: baliabide egokiak bereganatuko ditugu problema berriak trebe ebazteko. Problemak ebazteko estrategiak atalean baliabide horietako batzuk deskribatzen dira. Pentsatutako plana gauzatzea Plana ondo pentsatuta badago, aurrera ateratzea eta emaitza lortzea nahiko erraza izaten da. Dena dela, normalena izaten da aldez aurretik pentsatutako bidea moldatu eta plana egokitu behar izatea.

Eduki-multzo bakoitzaren amaieran unibertsitatera sartzeko proba prestatzeko argibideak aurkituko dituzu.

Unibertsitatera sartzeko probarako II. multzoa Geometria Geometriaren atala landu duzunean, hainbat problema mota ebazteko modua ematen duten oinarrizko kontzeptu eta teknikak ikasi dituzu. Gogoratu ditzagun horietako batzuk.

Eduki-multzo bakoitzaren amaieran autoebaluazio luze bat aurkituko duzu, multzoko unitate guztien edukiak berrikusteko.

Problemei aurre egiteko jarraibideak eta urratsak emango dizkizugu.

Planoarekiko perpendikularra den bektore bat bilatu behar duzu. Nola? Planoarekiko paralelo izango diren bi bektoretatik abiatuta. Horietako bat da zuzenaren norabide-bektorea, (1, –4, 3). Beste bat, P-tik zuzeneko A(1, 0, –1) puntura doan bektorea. Etab.

modu dituzu:

Hainbat estrategia erakutsiko dizkizugu, eta estrategia horiek erabiltzeko problemak planteatuko dizkizugu.

Multzoko autoebaluazioa

Autoebaluazioa II. multzoa Geometria anayaharitza.es

Zehaztu modulua 2 duten bektore guztien artean u (1, –1, –1) (–1, 2, 1) bektoreekiko ortogonalak direnak.

2 (2, 0, 0), (1, 0, –1) eta (–2, 3, 2) bektoreak izanda, kalkulatu: a) bektoreek zehaztutako paralelogramoaren azalera. b) bektoreek eratzen duten angelua. c) u v eta w bektoreek eraturiko paralelepipedoaren bolumena.

3 a) Kalkulatu a (2, 0, 0) bektorearen b (2, 2, 0) gaineko proiekzioaren koordenatuak. b) Aurkitu b gaineko proiekzioaren luzera.

4 Lortu xy yz 0 2 – * zuzenaren norabide-bektorea eta idatzi bere ekuazio parametrikoak 5 Lortu plano baten ekuazioa, jakinda A (0, –1, 3) eta

B (2, –1, 1) muturrak dituen zuzenkiarekiko perpendikularra dela eta zuzenki horren erdigunetik igarotzen dela.

6 Kalkulatu triangelu baten azalera, jakinda bere erpinak direla

2 + 2 – 2 = 0 planoak koordenatu-ardatzekin dituen ebaki-puntuak.

7 Idatzi Z ardatza perpendikular ebakitzen duen eta P (1, 2, 3) puntutik igarotzen den zuzenaren ekuazioa. 8 Zuzen hauek ditugu: 20 0 –– * xb yz 3 3 * a) Zehaztu b 0 zer baliorekin izango diren eta paraleloak. b) Ba al dago ≠ eta b ≠ 0 baliorik zuzenak bat etor daitezen?

9 Zehaztu zein izan behar den k-ren balioa planokideak izateko. Idatzi, ondoren, zuzen horiek

emanda, jarraibideak emanda…

Hemen, unibertsitatera sartzeko probetan agertzen diren eduki batzuen azalpen labur bat ikusi ahal izango duzu, aurreko urteetako ariketa eta problema batzuekin batera.

Liburua lau multzotan banatuta dago: Aljebra; Geometria; Analisia; Probabilitatea.

Honelakoa da zure proiektu digitala

Proiektu honek ikasturteko eduki guztiak eskaintzen dizkizu, bai liburu digitalaren bidez, bai era askotako baliabideen bidez.

Ikasteko beste modu bat ezagutuko duzu, erraza, intuitiboa eta edozein plataforma eta gailurekin bateragarria.

Nola sartu?

Zure liburuko lehenbiziko orrialdearekin batera aurkituko dituzu proiektu digitalean sartzeko behar dituzun argibide guztiak.

2 3 5

Ekuazio linealen sistema baten soluzio posibleak 2

Ekuazio-sistema batek soluzioa izan dezake (bateragarria edo baliteke soluziorik ez izatea (bateraezina). Sistema bateragarriek soluzio bat izan dezakete determinatuak edo infinitu so- luzio izan ditzakete indeterminatuak). Bi ezezaguneko ekuazio-sistemak Honako sistema hauek eta horien interpretazio geometrikoak aztertuko ditugu 2 3 3 5 9 4 –+= 4 Ekuazio-sistema honen soluzioa = 3, = 1 da. Horrek esan nahi du bi zuzenek (3, 1) puntuan ebakitzen dutela elkar Beraz, sistema bateragarria determinatua da.

2 3 5

x

KONTUAN IZAN Sistema bat bateragarria edo bateraezina dela esan beharrean, zuzenago izango litzateke zehaztea sistema eratzen duten ekuazioak bateragarriak direla (hau da, denek soluzio komun bat dutela) edo bateraezinak direla (ez dagoela denena den soluzio komunik). Dena dela, hemen erabilitako nomenklatura orokorrean onartuta dagoena da.

11 20 8 –––++ * Hiru planoek puntu batean ebakitzen dute elkar. bateragarri determinatua da Soluzioa: = 1, y = 7, = –2

] ] ] ]

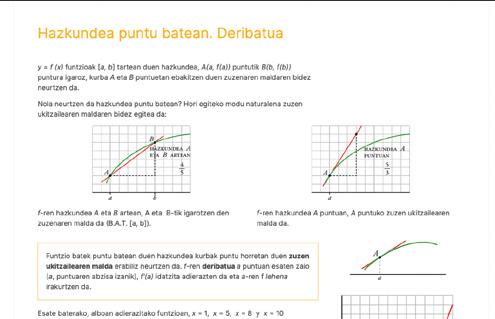
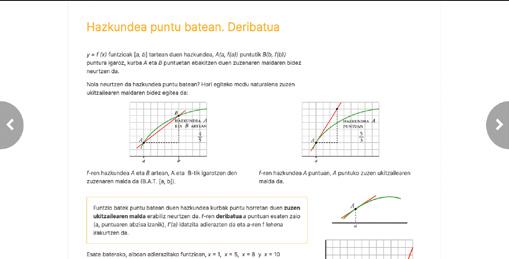
38

y y y

3 5 2

9 4 13 –– 4 Sistema hau aurrekoaren berdina da ia; izan ere, aurreneko bi ekuazioak berdinak dira, eta hirugarrena aurreko bi horiek atalez atal batuta lortzen da Zuzen berria (marrazkian beltza dena) (3, 1) puntutik igarotzen da eta puntu ho- rretan ebakitzen dute elkar hiru zuzenek. Beraz, sistema hori ere bateragarria eta determinatua da.

• 2 4 3 6 9 184 Bi ekuazioek gauza bera diote. Horietako baten soluzio bakoitza bestearena ere bada. Bi zuzenak bat datoz. Hau da, zuzen bera dira Sistema bateragarria eta indeterminatua da.

x y y 2 4 3 6 9 12 + 4 Ekuazioek kontrakoa diote. Ez dute soluzio berdinik. Geometrikoki, bi zuzenak paraleloak dira, puntu batean ere ez baitute bat egiten Sistema honek ez du soluziorik. Bateraezina da. Ebazten saiatzen garenean, zen- tzugabeko adierazpenak lortzen ditugu x y y y

3 5 2

9 4 6 – 4 Sistema hau bigarren sistemaren oso antzekoa da; hirugarren ekuazioko gai askea baino ez da aldatzen. Baina hori dela eta, ez da beste biek elkar ebakitzen duten (3, 1) puntutik igarotzen. Ez dago hiru puntuek bat egiten duten punturik. Beraz, sistema hau bateraezina da.

–

+

7 3 2 5

–––

+

x x y y z 2

Laugarren ekuazioa beste hiruren batura da. kion planoa (horia) komunean duten puntutik da. Sistema bateragarri determinatua da Soluzioa: = 1, y = 7, z = –2 x x

y y 2 4 7

3 2 5 4

–––––

11 20 8 3 20 9

––+= * Hirugarren ekuazioak, beste bien batura denez, telako informaziorik eransten sistemari. Sistema rri indeterminatua da Soluzioa: Planoek elkar ebakitzen duten zuzeneko guztiak dira sistemaren soluzio. • 2 32

Z [ ] ] Laugarren ekuazioak beste hiruren baturaren esaten du. Plano hori (horia) ez da beste hiruren puntutik igarotzen. Sistema bateraezina da Ez du soluziorik x y y y 11 20 3

Pentsatu eta praktikatu

z z ––– + * Hirugarren ekuazioak kontra egiten dio beste lortzen denari. Sistema bateraezina da Ez du soluziorik Ebatzi eta interpretatu geometrikoki honako ekuazio-sis- tema hauek a) x y y y

2 32 2 32 1 4 3 + * b) x y y y2

y y z 6 0 0 – * d) xy y z 6 1 1 –++ *

11 6 1 7 – * c) x

2 a) b) c) d)

Zer eskaintzen dizu?

Era askotako baliabideak ditu; paperezko liburuaren erreprodukzioa baino askoz gehiago da.

Honakoak egiteko aukera izango duzu:

Ariketak egin

ariketa elkarreragileak

Aztertu

laburpen elkarreragileak, eskemak...

Ikasi

audioak, bideoak, Game Room-ak...

Ebaluatu

autoebaluazioa, portfolioa...

Nolakoa da?

Erantzun globala era askotako hezkuntza-ingurune baterako.

Intuitiboa

Zuk erraz erabiltzeko modukoa.

Gailu anitzekoa

Edozein gailu motatan (ordenagailuan, tabletan, smartphonean…) egokitzen eta ikusten da, pantailaren edozein tamaina eta bereizmenetan.

Deskargagarria

Aukera ematen du Interneteko konexiorik gabe lan egiteko eta gailu batean baino gehiagotan deskargatzeko.

Sinkronizagarria

Erabiltzaileak egiten dituen aldaketak berez sinkronizatzen dira, lan egiteko erabilitako edozein gailu konektatzean.

Unibertsala

Bateragarria da ikastetxeetan gehien erabiltzen diren sistema eragileekin, ikaskuntzako inguru birtualekin (IIB) eta hezkuntza-plataformekin (LMS).

IKASKUNTZA-EGOERAK ERRONKAK ITZALA UZTEN DUEN

Eta honek, zertarako balio du?

Galdera hori behin eta berriro egiten da Matematikako eskoletan, urtez urte. Eta atzetik etorri ohi den azalpena luzea izaten da: matematikak nonahi daude, baita naturan ere; denerako balio dute; ia edozein diziplinatan erabiltzen dira... Baina noiz erabiliko ditut benetako zerbaitetan?

Tira. Ikasgelan ikasten diren kontzeptuak eta tresnak erabilgarriak izan daitezen, ez dira beti arazo errealetan zuzenean aplikatzeko modukoak izan behar. Matematika ikasteak balio du, batez ere, egitura mentalak sortzeko, edozein motatako problemei aurre egiteko estrategiak sortzeko, eta, gainera, zentzu kritikoa garatzeko.

Eta gozatzeko ere bai. Bai, hala da. Baita problema on bat modu autonomoan ebazteak ematen duen poza sentitzeko ere.

Jarraian aurkezten diren ikaskuntza-egoeretan aurkituko dituzu problema errealak, sinplifikatuak, ezagutzen dituzun tresnekin ebatz daitezkeenak, edota ikasturtean zehar eskuratuko dituzunekin. Eta, jakina, ikerketak ere topatuko dituzu, landutako ezagutzak integratzeko, teoriak eraikitzen eta hipotesiak baieztatzen edo ezeztatzen parte hartzeko, dela eskuan boligrafoa hartuta, dela ordenagailu edo kalkulagailu erabilita.

Helburu horrekin. anayaharitza.es webgunean eduki-multzo desberdinekin lotutako erronkak aurkituko dituzu, hemen aurkezten dizkizugun hauek bezalakoak; eta horiei aurre egin beharko diezu, taldean edo banaka, zeure ikaskuntza propioa eraikitzeko. Horretarako, dagoeneko dakizunaren eta ezagutza berrien arteko beharrezko loturak ezarri beharko dituzu.

Piztu

Piztu zure burua eta ekarri gogora urte hauetan zehar eskuratu dituzun eduki guztiak. Eduki horiek izango dira erronka ebazteko beharko dituzun ikaskuntza berriak eraikitzen hasteko oinarria.

Planifikatu

Planifikatu zure ikaskuntza eraikitzeko eta gaitasunak garatzeko prozesua. Erabili eskura dituzun iturriak eta baliabideak.

Ebaluatu

Ebaluatu eta berrikusi jarraitu duzun prozesua, eta laburbildu ikasi duzun guztia. Lortu duzu zure helburura iristea? Nola sentitu zara?

Aurre egin

Erronka hauei aurre egitea lagungarri izango duzu egitura mentalak sortzeko, egoeren ereduak egiten ikasteko, azaltzeko, argudiatzeko, arrazoitzeko, problema berriei modu sistematiko eta sendoan aurre egiteko, egungo mundua ulertzeko, eta matematikaz, bere metodoen, formen, egituren, sortze-prozesuen eta historiaren edertasunaz gozatzeko.

TRANSFORMAZIOAK PLANOAN MATRIZEEN LAGUNTZAZ

DBHko 3. mailan, planoan izaten diren mugimenduak ikasi zenituen: translazioak, biraketak eta simetriak, eta horien konposizioak. Eta 4. mailan, homoteziak. Unitate honetan berriro erabiliko dituzu eskuartean transformazio horiek, baina, orain, matrize batzuk izango dira puntuak, zuzenak eta kurbak eraldatzeko erabiliko ditugun bitartekoak.

• Planoko transformazio bakoitzari 3 × 3 matrize bat dagokio, matrizearen azkeneko errenkada (0 0 1) izanik beti. Adibidez, (a, b) bektoreko translazio batik dagokion matrizea hau da:

POLIEDRO ERREGULARRAK, ORAIN, ANALITIKOKI

Duela urte askotatik ezagutzen dituzun poliedro erregularrek propietate oso interesgarriak dituzte, eta horietako asko aurreko ikasturteetan aztertu dituzu geometria klasikoaren laguntzaz (Pitagoras, antzekotasuna, azalerak eta bolumenak kalkulatzeko formulak, etab.). Orain, geometría analíticari buruz ikasiko duzunarekin, zure bilaketa hobetu ahal izango duzu, eta poliedro batzuk erpinen koordenatuak emanez deskribatuko dituzu. Horri esker, modua izango duzu:

• Distantziak kalkulatzeko (puntuen artean, zuzenen artean, puntuetatik planoetarakoak, etab.).

• Zuzenen ekuazioak lortzeko (ertzak).

• Perpendikulartasunak egiaztatzeko.

• Bi transformazio konposatzeko, dagozkien matrizeak biderkatzen dira.

• Planoko (x, y) puntu bakoitza honelako zutabematrize baten bidez deskribatzen da:

• Azalerak eta bolumenak kalkulatzeko.

• Sekzio oso interesgarriak aurkitu edo balioztatzeko, behean duzun honelakoak, esaterako.

• (x, y) puntu bat transformatzeko, transformaziomatrizea puntuaren zutabe-matrizearekin biderkatu behar da. Adibidez:

Bada, horrela jokatuta, ibilbide oso interesgarria egin daiteke ezagun ditugun transformazioetan barrena. Eta, horrez gainera, Geogebra erabiltzera animatzen bazara, transformazioak konbinatu eta diseinu original mordoa sortu ahal izango dituzu.

Jardun honetan, geometria klasikoaren bidez lortutako emaitzak eta erlazioak kontrastatuko ditugu geometria analitikoaren erabileraren ondorioz lortutako pareko emaitzekin. Adibidez, tetraedro baten bolumena modu klasikoan lortzeko modua (1/3 Aoinarria · h) konparatuko dugu biderketa mistoaren bidez analitikoki lortutako emaitzarekin.

E (6 3, 6, 0)

B (0, 12, 0)

A (0, 0, 0)

KURBAK ETA GAINAZALAK ESPAZIOAN

Planoak eta zuzenak espazioan deskribatzeko, ekuazio inplizituak (2x y + z = 6) eta parametrikoak erabiliko dituzu:

ZENBAT SALGAI EROSIKO DUGU ASTE HONETAN? NOLA KUDEATU JATETXE BATEKO GENEROA

Ikasturte honetan neurri txikiko matrizeak ikusiko dituzu; oro har, ez dira 5 errenkada edo zutabe baino handiagoak izango. Dena dela, matrizeen erabileretako bat da zenbakizko datu kopuru handiak erabiltzea, horietatik informazioa ateratzeko. Hori matrize-eragiketa soil batzuen bidez lor daiteke. Eragiketa horiek guk egin ditzakegu edo, atsegin handiz, ordenagailu batek egingo dizkigu.

Horrez gainera, pilota bat (esfera) edo errugbiko baloi bat (elipsoidea) beren ekuazioen bidez deskribatzen ere ikasiko duzu.

Gidatu egingo zaitugu, parametroek jokatzen duten paperari buruzko gogoeta eginez eta behar bezala erabiliz, beste kurba eta gainazal espazial askoren ekuazioak lor ditzazun:

Eskailera kiribil baten baranda edo mailak, malguki bat, donuts bat edo zela bat.

Matrizeak erabiliko ditugu hainbat gosariren osagaiak, astebetean zer kantitate kontsumitzea espero den edota prezioak zein diren. Azken batean, lortu nahi duguna da astean erabiltzen diren osagaien kopuru osoa, eta zenbat balio duten.

Matrizeak erabilita, prozesua egituratu eta sistematizatu egiten da; horrela, astero, kontsumitu nahi diren errazioak aldatuz, automatikoki lortzen da produktuen eta prezioen azken emaitza.

Nahi izanez gero, ibilbide hori GeoGebrak lagunduta egingo duzu; horrek prozesu batzuk erraztuko dizkizu eta, zalantzarik gabe, adierazpen liluragarriak egiteko aukera emango dizu.

DISEINUKO BOTILAK (DISEINU MATEMATIKODUNAK)

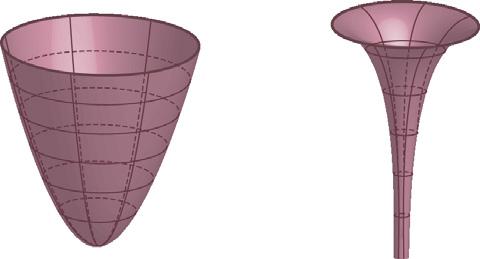
Ezagun dituzu biraketa-gorputz geometriko batzuen bolumenak kalkulatzeko formulak: zilindroak, konoak, esferak... Baina oraingoz ez dakizu nola lortu beste batzuenak, adibidez, paraboloidearenak eta hiperboloidearenak.

Gainera, biraketa-gorputz batzuen azalerak lortzen ikasiko duzu.

Integralek bi bolumen horiek kalkulatzeko aukera emango dizute, eta dagoeneko ezagutzen dituzunenak: zilindroa, konoa, kono-enborra eta esfera. Baita beste edozein biraketa-gorputzenak ere, baldin eta gorputza sortzeko erabilitako funtzioaren karratua integratzen badakizu.

Are gehiago, matematikaren mundu abstraktuan sartuko zara, infinituaren erabilerak paradoxa oso interesgarria sortzen duen munduan:

Luzera infinituko tronpeta honek azalera infinitua du.

Ontzi-diseinatzaile bihurtuko zara: funtzioei buruz dakizuna erabiliko duzu biraketa-solido alternatiboak, politak edo klasikoak sortzen dituzten zatiak modelatzeko. Merkataritzan gehien erabiltzen diren bolumenak gordetzeko izan behar dituzten dimentsioak kalkulatuko dituzu.

Horrek esan nahi du letoizko xafla fin batekin eraiki nahiko bagenu, kostua amaigabea izango litzatekeela, infinitua. Baina bolumena mugatua du!! Beraz, kostu neurritsu batekin objektu trinkoa eraikiko ligukete. Nola liteke gutxiago kostatzea tronpeta trinko bat egitea tronpeta biltzen duen azala baino?! Hori ere ikasiko duzu.

ETA HAINBAT GAUZA GEHIAGO…

• Banaketa binomial eta normalak galdera soziologikoak argitzeko oso erabilgarriak direla ikusiko duzu.

• Kalkulu diferentzialaren eta integralaren alderdi intuiziozkoena aztertuko duzu, ardatz moduan trenen mugimenduak eta mundu praktikotik ateratako beste egoera batzuk hartuz.

• Infinitura jo ideia oso ñabardura desberdinekin erabiltzen duten funtzioak egin eta aztertuko dituzu…

Problemak ebatzi

Zer da benetako problema bat?

Dagoeneko hainbat ikasturtetan ikusiko zenuenez, zure liburuan problemak ebatzi izeneko atala agertzen da. Atal horretan, problema berezi batzuk lantzen dira, problema bitxiak. Horiek ebazteko, garrantzitsuena ez da asko jakitea; horiek ebazteko, garrantzitsuena ondo pentsatzen jakitea da. Benetako problema horiek argi eta garbi bereizten dira ariketa soiletatik.

Aurrean benetako problema bat daukagunean, gutxi gorabehera badakigu egoera horretan nora joan nahi dugun, baina ez dakigu nola iritsi. Hain zuzen ere, hori izango da zailtasunik handiena: egoera argitzea eta helburura eramango gaituen bide egokiren bat aurkitzea

Benetako problemak ebazten jakiteko, trebea izan behar da oso. Baina hori pazientzia eta ekina izanda lortzen da: ausarta izan eta hainbat eratako problemak landu behar dira, eta horietatik guztietatik ahalik eta onunarik handiena ateratzen ahalegindu behar dugu, ebaztea lortu zein lortu ez

Hurrengo orrialdeetan, problemak ebazten lagunduko dizuten pentsamenduestrategia batzuk emango dizkizugu. Lan horri begira emaitza onak izaten dituzten jokatzeko moduak dira. Horrez gainera, ageri diren ariketek estrategiak errazago landu eta barneratzen lagunduko dizute.

Atal honetan proposatu diren problemetako batzuk errazak irudituko zaizkizu; beste batzuk, ez hain errazak; eta beste batzuk, berriz, oso-oso zailak. Baina denetatik aterako duzu probetxua eta, beharbada, probetxurik handiena zailenak iruditu zaizkizun horietatik lortuko duzu, pentsatzeko bide eta metodo gehiago saiatu beharko baitituzu. Ez dezazula pentsatu problemak ebazten egiten duzun denbora alperrekoa dela. Ebaztea lortzen ez baduzu ere, denbora hori ondo baino hobeto erabilitakoa izango da beti

Problemen ebazpenean ageri diren etapak

Problema ulertzea

Arretaz irakurri behar dugu. Zenbait kasutan, eskema bat erabiliko dugu. Argi izan behar dugu zer dakigun, zer eskatzen zaigun eta baldintzak zein diren.

Ebazte-plan bat pentsatzea

Hau da faserik zailena. Problema asko ebazteak ondorio argi bat du: baliabide egokiak bereganatuko ditugu problema berriak trebe ebazteko. Problemak ebazteko estrategiak atalean baliabide horietako batzuk deskribatzen dira.

Pentsatutako plana gauzatzea

Plana ondo pentsatuta badago, aurrera ateratzea eta emaitza lortzea nahiko erraza izaten da. Dena dela, normalena izaten da aldez aurretik pentsatutako bidea moldatu eta plana egokitu behar izatea.

Lortutako soluzioari buruz hausnartzea

Oso urrats garrantzitsua da problemen ebazpena hobetzeko.

— Lortutako soluzioa zentzuzkoa eta arrazoizkoa den ziurtatu behar da.

— Jarraitutako prozesuari buruzko gogoeta egin behar da, zertan hobetu daitekeen ikusi…

— Problema horrekin lotuta dauden beste batzuk planteatzea komeni izango da, agian: errazagoak, konplexuagoak…

Problemak ebazteko aholku batzuk (jarrerak)

• Ondo ulertu problemako termino guztiak.

Ziurtatu datu guztiak eta esaldi guztiak ulertzen dituzula. Zer eskatzen den, zertan oinarritu zaitezkeen... Enuntziatua zail samarra bada, saiatu zeure buruari edo beste pertsona bati azaltzen

• Jarri lanean buruko baliabide guztiak. Jarri zeure arreta oso-osoa egiten ari zaren horretan, problemak ebaztea buruzko jarduera konplexua baita.

Pazientzia dosi handia beharko duzu eta ekina izan beharko duzu. Ez etsi lehenengo zailtasunarekin topo egiten duzunean. Problema bakoitzak bere denbora behar du

• Ebatzi berriro zailenak izan diren problemak.

Problema bat ebazteko laguntza behar izan baduzu, saiatu problema hori berori zeure kabuz ebazten arratsalde horretan bertan. Eta berriro gero, handik egun batzuetara.

• Egin ebazteko beste bide batzuei buruzko gogoeta.

Zurea izan ez den beste ebazpide bat erakutsi badizute, agertu interesa eta saiatu bide hori ulertzen. Gero, saiatu beste bide horri jarraituta ebazten

• Atera probetxua problema onei.

Problema onak ikasteko iturri emankorra dira. Problema bat «berriro egitea», idazketa hobetuz, urratsen bat zehaztuz, laburbideren bat erabiliz... ez da inondik ere denbora alperrik galtzea, ariketa bikaina baizik

Problema interesgarria bada, aukera izango duzu beharbada beste hauetarako:

— Problema orokortzeko.

— Antzeko beste bat asmatzeko (errazagoa zein zailagoa).

— Baldintza jakin bat ezabatuz gero, edo beste bat gehituz gero zer gertatuko litzatekeen galdetzeko

• Trukatu ondorioak ikaskideekin.

Problemak bakarka pentsatu beharrekoak dira. Kasu batzuetan bakarrik izango du zentzua taldean lantzeak; adibidez, soluziora heltzen lagunduko diguten ideien bila ari garenean. Baina hori ere bakarkako lanaren ondoren egin beharrekoa da (taldeari lagundu ahal izateko, prest egon beharra dago, eta prestakuntza horrek bakarkako saiakera eskatzen du).

Baina behin problema ebatzi ondoren, ideiak trukatzea probetxu handikoa izango da. Eta oso onuragarria izango da ohitura hori sistematiko bihurtzea

Estrategia batzuen azterketa

Haztamuka ibili, kasu guztiak sistematikoki aztertu

Kasu askotan haztamuka jo behar izango dugu, agertzen zaizkigun aukera guztiak kasuz kasu aztertu beharko ditugu. Baina bilaketa hori egitean, ezinbestekoak izango dira urrats hauek:

• Lehenengo eta behin, ikerketa-eremua mugatu behar dugu, problema zentzuz, ikuspuntu egokiaren arabera aztertzeko.

• Bilaketan oso sistematikoak izan behar dugu.

Ebatzitako problema

Sei zifrako zenbaki baten lehenengo digitua 1 da. Zifra hori beste muturrera eraman (hau da, eskuinean jarri) eta gainerako zifren ordena berdin utziz gero, zenbaki berria (hori ere sei zifrakoa) lehenengo zenbakia halako hiru da

Zein da hasierako zenbakia?

• Hasierako zenbakiari A esango diogu, eta zenbaki berriari, B:

A : 1 __ a __ b __ c __ d __ e __ eta B : a __ b __ c __ d __ e __ 1

B zenbakia A halako hiru izan behar da

• Ikus dezagun emaitzaren azken zifran zer aukera ager daitezkeen, digitua 3rekin biderkatzen dugula kontuan hartuz:

A-ren azkeneko zifra 0 1

B-ren azkeneko zifra = 3A 0 3 6

(Ikusten duzunez, 3A kasuan ez da zifrarik errepikatzen).

• B-ren azkeneko zifra 1 bada, A-ren azkeneko zifra 7 baino ezin da izan (aztertu taula: 3 · 7 = 21): e = 7. Beraz, B-ren azken-aurreko zifra ere 7 izango da:

A : 1 a b c d 7 eta B : a b c d 7 1

• B-ren azken-aurreko zifra 7 bada, A-ren azken-aurreko zifra 5 izan behar da (kontuan izan 3 · 5 + 2 = 17 dela; gehi 2 egin behar dugu, aurretik 21 lortu eta bururako bi eraman behar ditugulako): d = 5

Orain arte hau daukagu: A : 1 __ a __ b __ c __ 5 __ 7 __ eta B : a __ b __ c __ 5 __ 7 __ 1

• Amaitu zuk arrazoiketa, eta lortu bila gabiltzan zenbakia 142 857 dela

Adi! Ebazteko beste modu bat.

Modua dago problema hau era azkar eta dotoreagoan ebazteko. Begira:

1 a b c d e = 100 000 + a b c d e a b c d e 1 = 10 · (a b c d e) + 1

anayaharitza.es Berrikusketa: problemak kasu posible guztiak aztertuta ebaztea.

Deitu a b c d e = x eta erlazionatu aljebraikoki bi kantitateak: 10x + 1 = 3 · (100 000 + x )

Amaitu zuk ebazpena.

1 Hardy matematikaria bisitan joan zitzaion behin ospitalera Ramanujan matematikari indiarrari, eta hau esan zion: «1 729 zenbakiko taxian etorri naiz. Hori bai, hori, gatzik gabeko zenbakia!». «Baita zera ere!» —erantzun zion Ramanujanek—, «Oso zenbaki interesgarria da: bi kuboren arteko batura moduan bi modu desberdinetan adieraz daitekeen zenbaki txikiena da». Frogatu hala dela

2 Jarraian doazen lau zenbaki osoren arteko biderkadura

7 590 024 da. Zein dira zenbaki horiek?

3 Aurkitu honako desberdintza hau betetzen duen n zenbaki oso handiena zein den: n 200 < 5300.

4 45 amaitzen diren lau zifrako zenbat zenbaki dira 45en multiploak? Badago 45ekin hasten den baten bat? Azaldu zure erantzuna.

5 Zenbat da 60 000 eta 70 000 arteko zenbaki palindromo guztien arteko batura?

6 1 000tik beherako zenbat zenbakitan da 7 digituen arteko batura?

7 Zein da 3 857105 zenbakiaren azkeneko digitua (unitateen zifra)?

Eskema, marrazki edo diagrama bat egin

Eskema on bat beti izaten da lagungarria problemak ebazteko. Eta zenbait kasutan, izugarri errazten du ebazpenean zer bide hartu behar den eta nondik nora jo behar den erabakitzeko

Gainera, problema bat beste baten antzekoa bada, antzeko eskema erabil daiteke.

Ebatzitako problema

Soldadu talde bat desfilatzen ari da 30 m-ko luzera duen ilara eratuz. Sarjentua azkeneko soldaduaren parean doa, baina pausoa azkartu eta ilararen bururaino heldu da. Orduan, buelta erdia eman, eta erritmoa aldatu gabe, berriro ere azkenekoaren ondoan jarri da Zer distantzia egin du sarjentuak denbora-tarte horretan, jakinda pelotoiak 20 m aurreratu dituela bitarte

Ilarak d egiten duenean aurrera, sarjentuak 30 + d egiten du.

Ilarak 20 – d egitean aurrera, sarjentuak 30 – (20 – d) = 10 + d egiten du atzera.

Sarjentuak eta pelotoiak bi denbora-tartetan egiten dituzten zatiak proportzionalak dira. Beraz:

Pentsatu eta praktikatu

8 Aurreko problema horretan, zer distantzia egingo du sarjentuak soldaduen ilarak 40 m egiten baditu aurrera?

9 Motor batek 5 L gasolina kontsumitzen ditu beheko errepideko bi puntuetako bakoitzaren arteko zatia egiteko. Deposituan 10 L sartzen direla eta eserlekuan 5 L-ko bidoia eraman daitekeela jakinda, nola egingo dugu errepide hori osorik motorrarekin zeharkatzeko? (G gasolindegietan motorraren depositua bete eta 5 L -ko bidoiak eros daitezke). Zenbat litro gasolina behar ditugu gasolindegi batetik n tartera dagoen beste gasolindegi bateraino heltzeko? Lau tarte egiteko, aurrena bidoi bat uztera joan beharko dugu ibilbideko tarteko punturen batera. Problema hori bost tarteko errepide baten kasuan ebazteko, lagungarri izango da lau tarteko errepide baten kasua ebaztea lehenengo?

10 Beduino batek ur-putzurik ez duen 150 km-ko basamortua zeharkatu nahi du. Dromedario gainean joango da, baina animaliak 50 km egin ditzake egunean, gainean beduinoa, horren jatekoa eta 50 kg-ko zama daramatzala. Hori bai!, iluntzean 25 litro ur edan behar ditu.

Baldintza horietan, hiru egun behar ditu ibilaldia egiteko. Zenbat egun beharko ditu 200 km-ko basamortua zeharkatzeko? Eta 250 km-koa balitz?… Eta...? Distantzia horietarako, beduinoak erabiltzen duen estrategia da bidean zehar ur-ontziak uztea, eta iritsi ahala hartzen joatea.

Ebazten duzunean, idatzi soluzioa problema landu ez duen edonork ulertzeko moduan.

11 Ontzi batean alkohol eta ur nahastea dago, 3tik 7ko proportzioan. Beste ontzi batean ere nahaste bera dago, baina 2tik 3ko proportzioan. Kalkulatu 3tik 5eko proportzioa duen alkohola-ura nahastearen 12 burruntzali lortzeko zenbat burruntzali atera behar ditugun ontzi bakoitzetik

Zuhaitz-diagrama erabili

Estrategia hau «eskema, irudi edo diagrama bat egitea» aholkatzen duen estrategiaren parte da. Baina hain da garrantzitsua, atal oso bat merezi du

Ebatzitako problema

Athleticek eta Errealak launa berdindu dute (4-4). Emaitza horretara modu askotan heldu ahal izan dira. Adibidez: 0-1, 1-1, 2-1, 3-1, 3-2, 3-3, 3-4, 4-4.

Zenbat modutan heldu ahal izan dira 4-4 emaitzara?

Prozesu osoa deskribatuko dugu, golez gol:

Ikusten duzunez, guztira 70 bide daude emaitza horretara heltzeko

Emaitza partzialetako bakoitzean aurrera egiteko bi modu daude, lau lortu denetan izan ezik. Horrez gain, oraindik zero duten emaitzak kenduta, beste guztiak bi egoeratatik lortutakoak izan daitezke. Adibidez, 3-2 emaitzaren aurretik, 3-1 emaitza edo 2-2 egon daitezke

Eskuineko grafikoan, emaitzetako bakoitzera heltzeko guztira zenbat bide dauden agertzen dira zenbatuta. Zenbakietako bakoitza gainean dituen bi zenbakiak batuta lortzen da; adibidez:

anayaharitza.es Berrikusketa: problemak ebazteko eskemak, irudiak edo diagramak egitea.

Pentsatu eta praktikatu

12 Zenbat modutan hel gaitezke 5-0 emaitzara? Zenbat modutan 4-1 emaitzara? Beraz, zenbat modutan 5-1 emaitzara?

31 emaitzarabidetatik helgaitezke

22 emaitzarabidetatik helgaitezke 4 6

Beraz, 3-2 emaitzara 4 + 6 = 10 bidetatik hel gaitezke.

13 Partidaren amaierako emaitzaz gain (4-4), tartean 3-1 emaitza egon dela jakinda, zenbat modu daude azkeneko markagailu horretara heltzeko?

Ebatzitako problema

Saioa gorriz adierazita dagoen ibilbideari jarraituz joan da autoan A puntutik B-ra

Koadrikula behean ageri den moduan jarri eta aztertzen badugu, erraz ikusten da aurreko orrialdean zenbatzeko erabili dugun eredu bera erabil dezakegula oraingoan ere, ezta?

Baina beste ibilbide asko ere har zitzakeen

a) Zenbat? (Eskuinerantz eta beherantz baino ezin da joan).

b) Eta lehenengo G gasolindegitik igaro nahi badu depositua betetzeko?

14 Saskibaloi-partida batean, emaitza 8-0 da une honetan. Badakigu ez dutela hirukorik sartu (puntu 1 eta 2ko saskiratzeak baino ez dituzte egin); beraz, zenbat modutan heldu ahal izan dira emaitza horretara? (Ziurtatu 34 modu direla).

16 Egiaztatu saskibaloi partida batean une batean 4-4 emaitza badugu, horraino 784 modutan heldu ahal izan garela (kontuan hartu 1, 2 eta 3 puntuko saskiratzeak egon ahal izan direla).

17 Enarak eta Manuk 40na euro jokatu dituzte joko batean: hiru partida irabazten dituen lehenengoa izango da garaile. Baina halako batean, jokoa bertan behera utzi behar dute. Une horretaraino Enarak partida bat irabazi du eta Manuk bat ere ez

Nola banatu beharko dute dirua?

15 Kalkulatu zenbat modutan hel gaitezkeen 4-4 emaitzara saskibaloi partida batean, hirukorik sartu gabe. Guk, hemen, zenbaketaren hasiera adierazi dugu:

18 Kristina eta Gontzal ping-pong txapelketa baten finalera heldu dira. Jarraian 3 partida edo txandaka 4 partida irabazten dituena izango da txapeldun.

Egin partidetako emaitza posible guztiak erakutsiko dituen zuhaitz-diagrama bat

Jarraitu zeuk eta egiaztatu, harrigarria badirudi ere, 556 modu daudela

Pentsatu eta praktikatu

Jarraitu zeuk eta egiaztatu soluzioak hauek direla: a) 126 eta b) 40.

Idazkera egokia aukeratu, ezezagunak egoki izendatu

Problema batzuek itxuraz oso zailak dirudite; baina ariketa errazak izan daitezke, idazkera egokia aukeratzen trebeak bagara

Enuntziatuak hizkuntza aljebraikoan jarri behar ditugunean, batzuetan ezezagunak modu batean baino gehiagotan aukeratzeko modua egoten da. Oso garrantzitsua da onuragarria den modua aukeratzen jakitea.

Ebatzitako problema

Eskailera mekaniko batek n maila ditu ikusgai, eta abiadura konstantean doaz beherantz.

Andoni eta Koldo eskaileretan behera doaz, eurak ere abiadura konstantean.

Baina Koldok Andonik daraman abiadura halako bi dakar

Koldok 27 maila jaitsi ditu beheraino heltzeko, eta Andonik, 18 maila.

Zenbat eskailera-maila, n, daude ikusgai?

Koldok 27 maila jaisten dituen denboran, eskaileraren mekanismoak n – 27 jaisten ditu.

Era berean, Andonik 18 maila jaisten dituen denboran, eskailerak n – 18 jaisten ditu.

anayaharitza.es Berrikusketa: idazkera egokia aukeratzea eskatzen duten problemen ebazpena.

Pentsatu eta praktikatu

Jaitsierako abiadurei honela esaten badiegu:

Andonirena; 2a, Koldorena; b, eskailerarena.

Berdintza horietatik hau lortzen dugu:

Eskailerak 54 maila ditu ikusgai.

egiaztapena:

Koldok 27 maila jaisten dituen denboran, eskailerak beste 27 jaisten ditu. Hau da, eskailerak Koldoren abiadura bera darama, eta Andoniren abiadura halako bi Beraz, Andonik 18 maila jaisten dituen denboran, eskailerak maila horiek halako bi jaisten ditu: 36

19 Eskailera mekaniko batean, Andreak Marta bere ahizpak baino 10 bider bizkorrago igotzen ditu mailak. Andreak

40 maila igo behar izan ditu goraino heltzeko. Marta

10 maila igota heldu da goraino.

Zenbat maila ditu ikusgai eskailera zati horrek?

20 Ebatzi honako ekuazio-sistema hau aldagai-aldaketa egokia eginez:

Ebatzitako problema

Felipek 30 s-an igotzen ditu metroko eskailera-tarte bat, eta guztira 60 maila igotzen ditu

Isidrok 36 s behar ditu eskailera-tarte bera igotzeko, eta guztira 48 maila igotzen ditu.

Egun batean, eskailerako mekanismoa ez dabil. Zenbat denbora beharko du bakoitzak goraino igotzeko?

Eskaileraren mekanismoaren abiadurari v esango diogu (maila-kopurua segundoko).

vkopurua6030 =+

vkopurua4836 =+60 maila, 30 s 48 maila, 36 s maila mailaikusgai

FELIPE: ISIDRO: ikusgai 4

Hortik lortzen dugun ekuazioa ebatziko dugu: 60 + 30v = 48 + 36v → 6v = 12 → v = 2 maila/s

Ikusgai diren mailen kop. = 60 + 30 · 2 = 120

Feliperen abiadura 30 60 = 2 maila/s da.

Isidroren abiadura 36 48 3 4 = maila/s da.

Beraz: Felipek 120 maila igotzeko behar duen denbora → 2 120 = 60 s = 1 min

Isidrok behar duen denbora → / 43 120 = 90 s = 1 min eta erdi

21 Leirek 10 s behar ditu 50 maila jaitsi eta eskailera mekanikoaren zati bat egiteko. Eider mantsoago doa, eta 20 s-an eskailera zati bereko 30 maila jaisten ditu. Zenbat maila ditu eskailera zati horrek?

Zenbat denbora beharko luke bakoitzak zati hori jaisteko, mekanismoa hondatuta egongo balitz?

24 Ebatzi honako sistema hau:

22 Markelek 60 maila igotzen ditu goraka doazen eskailera mekanikoetatik igotzen denean. Baina beheraka datozenetatik igotzen bada, orduan 120 maila igotzen ditu

Zenbat maila dituzte ikusgai eskailera zati horiek? (Bi zatiek luzera bera dutela pentsatu behar dugu, eta abiadurak ere berdinak direla).

23 Esterrek 20 pauso ematen ditu abiadura konstantean mugitzen den zinta garraiagailu bat zeharkatzeko. Abiadura berean baina kontrako noranzkoan joanez gero, 60 pauso eman behar ditu zinta zeharkatzeko. Zenbat pauso eman beharko ditu zinta geldi badago? Konparatu Esterren eta zintaren abiadurak

25 Ebatzi ekuazio hau, aldagai-aldaketa egokia eginez:

26 Lau zifrako zenbaki palindromo guztiek dute 1 ez den zatitzaile komun bat. Zein da?

27 Aztertu:

Egia al da jarraian doazen lau zenbaki arrunten arteko biderkadura karratu perfektu bat ken 1 dela beti? Horrela bada, adierazi karratu hori biderkagaien funtzioan.

* Ikusten duzunez, gakoa idazkera egokia aukeratzea da, jarraian doazen lau zenbaki arrunten arteko biderkadura gehi 1 eginda karratu perfektu bat lortzeko

Pentsatu eta praktikatu

Problema diofantikoak

Ekuazio diofantikoak dira zenbait aldagaiz osatuta dauden soluzio osoak dituzten ekuazio aljebraikoak

Ekuazio diofantikoak ageri den polinomioaren mailaren arabera sailkatzen dira: linealak izan daitezke, koadratikoak…

Ikus ditzagun ekuazio diofantikoak dituzten problema batzuen adibideak.

Ebatzitako problema

Iragarrita dago elurte handi bat etorriko dela, eta, ikastetxe batean, egoerari aurre egiteko prestatzea erabaki dute. Beraz, palak, hartxintxar-zakuak eta gatz-poltsak erosi dituzte. 25 €, 5 € eta 0,25 € balio dute, hurrenez hurren. 500 € justu gastatu dituzte, eta, hori da kasualitatea!, palak, zakuak eta poltsak zenbatuta, guztira 500 objektu erosi dituzte.

Aurkitu objektu mota bakoitzeko zenbat erosi dituzten.

Planteamendua idaztean ekuazio diofantikoak ematen dituen problema tipikoa da. Kasu honetan, hiru ezezaguneko bi ekuazio lineal dituen sistema bat daukagu: x → gatz-poltsen kop.

19ren multiplo bakarra da 114 = 19 · 6.

28 Litxarreria-denda batean 100 gozoki erosi eta 5 euro ordaindu ditut. Erregaliz handiek 50 zentimo balio dute; gominolek, 10 zentimo, eta erregaliz-gozokiek, 1 zentimo. Mota bakoitzeko zenbat gozoki erosi ditut?

29 Anek 100 euro gastatu ditu bazar bateko 40 gauza erosita. 1 €, 4 € eta 12 €-ko gauzak baino saltzen ez badituzte, prezio bakoitzeko zenbat gauza erosi ditu?

30 Antoniok 3 pesoko billeteak baino ez ditu, eta lanparadendan 5 pesoko billeteak baino ez daude. Nola egingo du 19 peso balio duen lanpara bat ordaintzeko?

31 Mamenek koloretako arkatzen 10 kaxa erosi ditu: batzuetan 5 arkatz daude; beste batzuetan, 10 arkatz, eta beste batzuetan, 25 arkatz. Guztira koloretako 90 arkatz baditu, mota bakoitzeko zenbat kaxa erosi ditu?

32 Poltsiko batean hiru motatako txanponak ditugu: 5, 20 eta 50 zentimokoak. Guztira, 2 euro eta 85 zentimoko balioa (285 zentimo) duten 12 txanpon ditugu. Mota bakoitzeko zenbat txanpon ditugu?

33 Lau zenbakiren arteko biderkadura eta zenbaki horien berorien arteko batura berdinak dira: 6,75. Zenbakietako bat 1 bada, zein dira beste zenbakiak?

• Zenbakiak hauek dira: 1; x; y; z = 5,75 – x – y.

• 6,75 = 33 · 2 1 2dn (Ikusten duzunez, izendatzailean 4 bat dago).

• Zenbaki osoak erabiltzeko, honela jar ditzakegu: x' = 4x, y' = 4y, z' = 4z = 23 – x' – y'

• Biderkadura hau da: x' · y' · (23 – x' – y' ) = 24 · 33; eta hortik aurrera, problema diofantiko bat da

Egiaztapen matematikoa

Prozesu deduktiboa

Arrazoibide deduktiboa arrazoitzeko modu nagusia da. Funtsean, egiaztatuta dauden egia batzuetatik abiatu, eta, bide logiko bati jarraituz, baliozko beste emaitza berri bat lortzea da

Zehatzago aztertuko dugu

Proposizioak

Proposizio bat zalantzarako tarterik uzten ez duen baieztapen argia da; egia ala gezurra izan daiteke, baina zalantzarik gabe bata edo bestea da

Adibidez: «Triangelu aldekide guztiek angeluak berdinak dituzte» egia da «Triangelu aldekide guztiak laukizuzenak dira» gezurra da.

Sarritan, aldagai baten mendekoak diren proposizioak erabiltzen dira.

Adibidez: «x zenbaki lehena da». x-ren balioaren arabera, proposizioa egia ala gezurra izango da

Aldagai baten edo gehiagoren mendekoak diren proposizioak proposizio-familiak dira. Aldagaien balio bakoitzerako proposizio zehatz bat lortuko dugu; eta hori egia ala gezurra izango da

Proposizio batzuk oso zailak dira eta kostatu egiten da egiaztatzea

Adibidez: x zenbaki erreala bada eta ax 2 + bx + c = 0 betetzen badu, orduan:

= a bac b 2 4 2 + edo bestela x = a bb ac 2 4 –2

Proposizio konplexu bat proposizio sinpleagoen bidez adieraz daiteke, zenbait eragiketa eginda.

Proposizioak dituzten eragiketak lantzea eta lortzen diren proposizioen egiazkotasuna aztertzea oso interesgarria eta erraza da, baina luzea; eta, horregatik, orrialde hauen helburuetatik kanpo dago. Beraz, inplikazioa baino ez dugu ikusiko; hau da, arrazoibide deduktiborako behar diren oinarrizko proposizioen arteko eragiketa.

Inplikazioa

A proposizio batek ondoriotzat B beste proposizio bat ekartzen badu, A-k B inplikatzen duela esaten da, eta honela adierazten da:

A ⇒ B

Kasu horretan, A egia bada, orduan B ere egia da.

Adibidez: A : «x aldagaia 6ren multiploa da»; B : «x aldagaia 2ren multiploa da»

Argi dago A ⇒ B; izan ere, «x 6ren multiploa bada, orduan x 2ren multiploa da».

Beraz, A egia bada (adibidez, x = 12 bada), B ere egia da.

ERREPARATU

Proposizio bati buruz egia ala gezurra den erabaki beharko dugu; hau da, honelako funtzio bat existitzen da: {proposizioak} → {E, G}

INPLIKAZIO BAT ADIERAZI

Hainbat modu daude:

• A ⇒ B

• A bada, orduan B.

• A baldintza nahikoa da B gertatzeko.

• A gertatzen bada, B ere bai.

Inplikazio-kateak

A ⇒ B eta B ⇒ C badira, orduan A ⇒ C.

Orokorrean:

A1 ⇒ A2 bada, eta A2 ⇒ A3 bada, eta A3 ⇒ A4 bada … eta An – 1 ⇒ An bada, orduan, A1 ⇒ An

Adibidez: A: «n3 – n = (n – 1) n (n + 1)»

B: «n3 – n ondoz ondoko hiru zenbaki arrunten arteko biderkadura da».

C: «n3 – n hiru zenbaki arrunten arteko biderkadura da, kontuan izanda horietako bat bikoitia dela eta beste bat 3ren multiploa».

D: «n3 – n kenketaren emaitza 6ren multiploa da».

A ⇒ B eta B ⇒ C eta C ⇒ D direnez, orduan A ⇒ D da

Eta A egia denez, D ere egia dela ondorioztatzen dugu.

Metodo deduktiboa, egiaztapena egiteko

X proposizioa egia dela egiaztatu nahi dugu. Horretarako, honela joka dezakegu:

A proposizio batetik abiatuko gara, inplikazio hori egia dela jakinda. Inplikazio baten bidez, B beste proposizio bat ere egia dela lortuko dugu (A egia bada eta

A ⇒ B bada, orduan B ere egia da). Eta, horrela, hurrenez hurren, inplikaziokate baten bidez, X proposiziora helduko gara. Era horretara, X egia dela frogatuko dugu

Ebatzitako problema

Lortu bigarren mailako ekuazio bat ebazteko formula; hau da, egiaztatu honako hau egia

+ x = 0, a ≠ 0 orduan, beste hau ere egia dela:

HIZTEGIA

Eskuinean deskribatu dugun erregela deduktiboari, hau da, «A egia bada, eta, gainera A ⇒ B bada, orduan B ere egia da» erregelari, modus ponens esaten zaio.

a-rekin biderkatuko dugu guztia, x 2-ko gaia karratu perfektua izan dadin

4rekin biderkatuko dugu guztia, bigarren gaia biderkadura bikoitz bat izan dadin.

b 2 batuko dugu bi ataletan, lehenengo atalean batuketa baten karratua eratzeko

4ac bigarren atalera igaroko dugu

Erro karratua aterako dugu bi ataletan, horietako batek zeinu bikoitza izango duela ahaztu gabe.

Azkenik, x askatuko dugu.

Ebatzitako problema

Egiaztatu honako propietate hau:

B'A' da CAB triangeluko AB aldearekiko paraleloa eta erdia. Beraz:

B'A' // AB eta BA'' AB 2 =

Bi erdibidekoren arteko P ebaki-puntuak bi segmentutan ebakitzen ditu erdibidekoak, eta horietako bat bestea halako bi da:

·' PA PA 2 = 'PPBB 2· =

PA-ren erdiko puntuari M esango diogu, eta PB-ren erdiko puntuari, N.

Beraz, MN da PAB triangeluko AB aldearekiko paraleloa eta erdia.

Ondorioz:

MN // AB eta MN AB 2 =

B'A' eta MN berdinak eta paraleloak direla frogatu dugu. Beraz, B'A'NM laukia paralelogramo bat da eta horren diagonalek erdiko puntuetan ebakitzen dute elkar:

'' PM PA PN PB eta ==

Ondorioa: ·· '' PA PA PB PB 22 eta ==

Pentsatu

1 Ondorioztatu x 2 – mx + n = 0 motako ekuazioetan x askatzeko formula bat, urratsez urrats joanda eta ondo arrazoituta.

2 Egiaztatu ax 2 + bx + c = 0 ekuazioaren erroak x1 eta x2 badira, orduan x1 + x2 = –a b eta x1 · x2 = a c direla.

3 n zenbakiren (x1, x2, x3, …, xn) batezbesteko aritmetikoa x bada, egiaztatu honako hau: () () n xx n x x ––ii 2 2 2 = //

4 Aztertu honako berdintza hauek: 22 + 32 + 62 = 72

32 + 42 + 122 = 132 42 + 52 + 202 = 212 …

a) Orokortu emaitza

b) Frogatu baliozkoak direla

5 Frogatu triangelu baten hiru erdibidekoek puntu batean ebakitzen dutela elkar.

6 Frogatu triangelu baten angeluen batura 180° dela

7 Frogatu zirkunferentzierdi batean inskribaturiko angelua zuzena dela, derrigorrean.

8 Kontuan izanda C triangelu angeluzuzen bat dela, egiaztatu irudiaren gainean honako hau:

9 Egiaztatu gorriz margotuta dagoen gainazalaren azalera eta urdinarena berdinak direla:

10 Triangelu angeluzuzen batean, a eta b katetoak dira eta c hipotenusa da. Esan h altuerari

Egiaztatu h, (c + h) eta (a + b) aldeak dituen triangelua angeluzuzena dela

Baliokidetasuna

A ⇒ B bada, eta, gainera, B ⇒ A bada, orduan A ⇔ B jar dezakegu eta bi proposizioak baliokideak direla esaten dugu.

Adibidez: A : «x triangeluak hiru angeluak berdinak ditu».

B : «x triangeluak hiru aldeak berdinak ditu».

A ⇒ B, «triangelu batek hiru angeluak berdinak baditu, orduan, hiru aldeak ere berdinak ditu»

B ⇒ A, «triangelu batek hiru aldeak berdinak baditu, orduan, hiru angeluak ere berdinak ditu»

Beraz, A ⇔ B. A eta B proposizioak baliokideak dira.

Hau esaten dugu: «Triangelu batek hiru angeluak berdinak ditu, baldin eta hiru aldeak berdinak baditu, orduan bakarrik».

Edo, bestela: «Triangelu batek hiru aldeak berdinak izateko, baldintza beharrezkoa eta nahikoa da hiru angeluak berdinak izatea»

Baliokidetasun-kate baten bidez egiaztatzea

Batzuetan, ez da erraza izaten frogatu nahi dugun X proposizioraino eramango gaituzten proposizioen katea aurkitzea. Baina gerta liteke errazago frogatzen den proposizio baliokide bat aurkitzen jakitea. Bada, hortik abiatuta, X-ren egiazko baliokide batera helduko gara. Ikus dezagun nola:

X ⇔ A ⇔ B ⇔ C bada eta C egia bada, orduan C ⇒ B ⇒ A ⇒ X da, eta, beraz, X egia da.

Ebatzitako problema

a eta b bi zenbaki erreal dira eta

a · b > 0 betetzen dute.

Egiaztatu ≥ b a a b 2 + dela.

Azkeneko desberdintza hori egia da; izan ere, zenbakitzailea karratua denez, 0 baino handiagoa edo berdina da; eta izendatzailea 0 baino handiagoa da, hipotesiaren arabera (enuntziatuan hala esaten delako).

Baliokidetasun-kateak, atzekoz aurrera irakurtzen badugu, lehenengo desberdintza ere egia dela erakusten digu.

Pentsatu eta praktikatu

11 Egiaztatu:

12 Egiaztatu:

Absurdoaren bidezko metodoa

Matematiketan, proposizio bat aldi berean egia eta gezurra dela egiaztatzen dugunean, absurdora eraman dugula esaten dugu. Baina egoera hori ezin denez onartu, horraino heltzeko baldintzak gezurra izango dira:

X proposizio bat egiaztatzeko, proposizio horren ezeztapena (X ez) egiatzat jo dezakegu. Bide horretatik absurdora eramaten badugu:

X ez ⇒ absurdoa

orduan, (X ez) gezurra izango da, eta, beraz, X egia izan behar da

Absurdora eramatearen metodoak, beraz, proposizio baten ezeztapena erabiltzen du proposizio hori egia ala gezurra den egiaztatzeko

Ebatzitako problemak

KONTRAJARRERA

Ezeztapen batetik abiatuta egiten den beste egiaztapen-metodo bat da. Inplikazioen arteko baliokidetasunak erabiltzen ditus:

X ⇒ Y eta Y ez ⇒ X ez

Hau da, X-k Y inplikatzen duela egiaztatzeko, (Y ez) proposizioak (X ez) inplikatzen duela frogatzen da.

Egiaztatu infinitu zenbaki lehen daudela Jo dezagun enuntziatuak dioena ez dela egia; hau da, pentsa dezagun zenbaki lehenen kopuru finitua dagoela: 2, 3, 5, 7, 11, 13, 17, …, P. Azkeneko zenbaki hori, P, zenbaki lehenik handiena izango litzateke

Zenbaki lehen guztiekin, honako zenbaki hau osatuko dugu:

N = (2 · 3 · 5 · 7 · 11 · 13 · 17 · … · P ) + 1

N izango da «zenbaki lehen guztien arteko biderketa, gehi 1».

Eta N ezin dugu zatitu ez 2rekin, ez 3rekin, ez 5ekin, …, ez P-rekin. Beraz, horrek N zenbaki lehen bat dela adieraziko luke. Baina gure planteamenduan, zenbaki lehenetan handiena P zen.

Zenbaki lehenen kopuru finitua dagoela onartuz gero, kontraesan batera heldu gara. Beraz, argi dago zenbaki lehenen kopurua infinitua dela.

O zentroa eta r erradioa dituen zirkunferentzia eta t zuzena ditugu. Zirkunferentziak eta zuzenak T puntuan bakarrik bat egiten badute, egiaztatu t zuzena OT erradioarekiko perpendikularra dela.

Pentsa dezagun OT ez dela t-rekiko perpendikularra. O-tik t-ra doan perpendikularra marraztuko dugu : OS.

' ST ST = betetzen duen T' puntu bat hartuko dugu.

OST eta 'OST bi triangeluak berdinak dira, angeluzuzenak direlako eta katetoak berdinak dituztelako. Beraz, horien hipotenusak ere berdinak dira. Horrek esan nahi du OT' = r (erradioa) eta, beraz, T' zirkunferentziako puntu bat dela.

Baina ez al dugu esan zuzenak eta zirkunferentziak T puntuan bakarrik bat egiten dutela? Kontraesana dago!

Beraz, OT perpendikularra izan behar da t-rekiko.

Pentsatu eta praktikatu

1 Egiaztatu a eta b osoak badira eta a + a 2 + a 3 = b + b 2 betetzen bada, orduan a bikoitia dela

2 Bi zuzen planokide (ez datoz bat) planoko beste zuzen batekiko perpendikularrak badira, orduan bi zuzen horiek paraleloak dira.

3 a) Egiaztatu a eta b arrazionalak badira eta c irrazionala bada, orduan a + b · c irrazionala delal.

b) Egiaztatu 5 irrazionala dela eta, beraz, 3 – 2 5 ere hala dela.

Indukzio-metodoa osoa

P (n) propietate bat n edozein zenbaki arrunten kasuan egia dela frogatu nahi dugu. Horretarako, honela jokatuko dugu:

a) n = 1 kasurako egia dela frogatuko dugu: P (1) egia da

b) n-ren balio jakin baterako egia balitz, n + 1 hurrengo baliorako ere egia izango litzatekela frogatuko dugu. Beraz, hau frogatuko dugu:

«P (n) egia da ⇒ P (n + 1) egia da»

[Ikusten duzunez, ez dugu esaten P (n) egia dela; egia balitz, orduan P (n + 1) ere egia litzatekeela esaten dugu].

P (n) egia ⇒ P (n + 1) egia

P (1) egia ⇒ P (2) egia ⇒ P (3) egia ⇒ …

Ebatzitako problema

Egiaztatu honako hau:

12 + 2 2 + 32 + … + n 2 =

= () () nn n 6 12 1 ++

Berdintza egia da n = 1 denean; izan ere:

12 = () () 6 11 12 1 ++

n-ren balio jakin baterako egia dela onartuko dugu, eta hortik, n + 1 hurrengo baliorako ere egia dela atera behar dugu:

Egiaztatu 2 2n – 1 multiploa dela

3rena, n edozein zenbaki arrunt dela ere

Azkeneko adierazpena egiaztatu nahi dugun berdintzako bigarren atala da, baina n-ren lekuan n + 1 jarrita. Beraz, bete egiten da n + 1 kasurako

n = 1 denean, 22 – 1 = 3 da eta, beraz, 3ren multiploa da.

22n – 1 kenketaren emaitza 3ren multiploa dela onartuko dugu. Ikus dezagun

22(n + 1) – 1 kenketarena ere hala den: 22(n + 1) – 1 = 22n + 2 – 1 = 22n · 4 – 1 = 4 · 22n – 1 =

Pentsatu eta praktikatu

1 Erabili indukzio osoaren metodoa honako berdintza hauek egiaztatzeko: a) (1 + 2 + … + n)2 = 13 + 23 + … + n 3 b) 2

c) 13 + 23 + … + n 3 = ()nn 4 1 22 +

batura 7ren multiploa da

20) biderkadura 48ren multiploa da, n bikoitia bada

Usategiaren printzipioa

Printzipio bat ukatu ezin den egia bat da eta beste ondorio batzuk lortzeko abiapuntu moduan balio du.

«Usategiaren printzipioa» Dirichletek diseinatu zuen eta honela enuntziatu daiteke: «21 usoko multzoa usategi batek dituen 20 zuloetatik sartu bada, ziurra da bi uso gutxienez zulo beretik sartu direla». Begi bistako enuntziatu erraz hori egiaztapen askoren oinarri da, tartean egiaztapen sakon batzuena.

Ebatzitako problema

Jai batean 50 pertsona daude

Egiaztatu bi pertsonak, gutxienez, lagun-kopuru bera duela jaira joandakoen artean.

Honela jokatuko dugu: — A izenekoa B-ren laguna bada, orduan B izenekoa A-ren laguna da. — Norbera ez da bere buruaren lagun.

Hori kontuan izanda, jaira bildu diren 50 pertsona horietako bakoitzak honenbeste lagun izan ditzake: 0, 1, 2, 3, …, 49. Jakina, baten batek lagunik ez badu, ezin da egon 49 lagun izango dituenik; hau da, ezin da egon bere burua kenduta beste guztien lagun izango denik. Beraz, 0 badago, 49 ezin da egon; eta 49 badago, 0 ezin da egon.

Horrek esan nahi du 49 aukera baino ez dagoela jaira bildu diren 50 lagunentzat. Usategiaren printzipioa erabiliz, lagun-kopuru bera duten bi pertsona egon behar dira gutxienez jaian.

1 450 ikasleko institutu batean, gutxienez bi ikaslek egun berean egiten dituzte urteak. Egiaztatu hala dela.

2 Kreditu-txartelen «zenbaki sekretuak» lau digiturekin eratzen dira. Adibidez, zenbaki sekretu horietako batzuk 2704, 0012, 9461 izan daitezke. Frogatu Espainiako estatuan kode bera duten bi kreditu-txartel gutxienez badaudela.

3 Ziurta dezakezu Euskal Autonomia Erkidegoan buruan ile kopuru bera duten bi pertsona gutxienez badaudela? Arrazoitu erantzuna.

4 ABC triangelu aldekide bat da eta aldea 2 cm-koa du. Egiaztatu triangelu barruko bost puntu aukeratzen baditugu, bi puntu gutxienez bata bestetik 1 cm baino gutxiagora egongo direla.

5 35 m-ko aldea duen larre karratu batean 26 ardi sartu ditugu bazkatzera.

Frogatu bi ardi gutxienez bata bestetik 10 m-ra baino gutxiagora egongo direla beti.

6 Behean ageri den 4 × 6 neurriko koadrikulan, karratuetako batzuk margotu ditugu eta beste batzuk zuri utzi ditugu.

Hori modu askotan egin daiteke. Saiatu lau erpinak kolore berekoak dituen laukizuzenik zehazteko modurik emango ez digun aukeraren bat (guk margotu dugun horretan ez da hori gertatzen, gorriz adierazita ageri diren lau karratuetan ikusten denez).

4 × 7 neurriko koadrikula batean, beti agertuko zaigu kolore bereko erpinak dituen laukizuzenen bat. Egiaztatu hala dela.

Pentsatu eta praktikatu

Trebatzeko problemak

Ondoren proposatzen ditugun problema guztiak www.anayaharitza.es webgunean ebatzita daude. Horietako askotan, gainera, laguntza batzuk ematen dira hasieran, ebazpenean nondik nora jo jakiteko. Problema bat ebaztera zoazenean, lehenengo saia zaitez zeure kontura ebazten. Modurik aurkitzen ez baduzu, erabili ematen zaizun laguntza. Eta, azkenik, konparatu webguneak ematen dizun ebazpena eta zuk lortutakoa. Problema hauek guztiak (edo ia guztiak) multzokatuta ageri dira antzeko beste problema batzuekin batera. Multzo bakoitzeko lehenengoa gorriz adierazita dago, eta hurrengoak, urdinez. Adibidez, 1 eta 2 problemek multzo bat osatzen dute; 1 problemaren ebazpenak 2 problema ebazten lagunduko dizu.

1 Nire armairuko kutxan 6 galtzerdi gris eta 8 beltz ditut, denak solte. Gaur gaueko jairako kolore bereko galtzerdiak jantzi nahi ditut, baina bonbilla erre da eta ez dut ezer ikusten. Zenbat galtzerdi hartu beharko ditut kolore bereko bi ditudala ziurtatzeko?

2 Poltsa batean hogei bola gorri, hamar berde eta bost beltz ditut. Bolak banan bana ateratzen baditut, zenbat ateraldi egin beharko ditut kolore bereko lau bola izango ditudala ziurtatzeko?

3 Oihan baten erdian bi herri daude: E eta G esango diegu. E-ko bizilagunek egia esaten dute beti, eta G-koek, gezurra. Bi herriak bata bestetik hurbil daudenez, normala izaten da E-koak G-n egotea, eta G-koak E-n egotea. Oihanean galdu den esploratzaile bat herrietako batera heldu da, baina ez daki zeinetara. Bizilagun bat gelditu eta hau galdetu dio:

— Hemengoa zara?

Zergatik jakingo dugu erantzun horrekin ziur E herrian ala G herrian dagoen? Deskribatu soluziora heltzeko jarraitu duzun prozesua, eta arrazoitu urratsetako bakoitza.

4 Sei robot hizketan dabiltza psikiatraren itxaron-gelan. Gaitz, arraro bat dute guztiek: gezurra baino ez dute esaten, ala egia baino ez. Ederto ezagutzen dute elkar denek, eta txandaka hau esan dute:

— Hemen, egia dioen bakarra dago.

— Batek, gutxienez, egia dio hemen

— Egia dioten bi baino ez daude.

— Bik, gutxienez, egia diote.

— Egia dioten hiru baino ez daude.

— Hiruk, gutxienez, egia diote.

Zeinek diote egia eta zeinek gezurra?

5 Bost atleta entrenatzailearekin hizketan ari dira azkeneko lasterketan lortutako emaitzari buruz:

karmele: Oraingoan Amaiaren aurretik heldu naiz.

amaia: Tina Erroseren ondoren heldu da.

tina: Errosek ez du irabazi.

errose: Karmele laugarren heldu da

leire: Gaur egun ederra zegoen korrika egiteko

Zer ordenatan heldu dira?

6 Txanpon-jokoan ari naiz sei lagunekin, eta psikologiako nire dohainei esker, ondorio hau atera dut:

— Lau jokalarik bina txanpon atera dituzte.

— Andonik eta Beak txanpon-kopuru bera atera dute, eta Danik eta Elenak ere kopuru bera.

— Karmelek Elenak baino txanpon gehiago atera ditu, baina Beak baino gutxiago.

Zer zenbaki esan behar dut nik denon artean guztira zenbat txanpon ditugun asmatu eta, horrela, jokoa irabazteko?

7 Dantza-areto bat neska-mutilez beteta dago. Bikoteka dantzan ari dira, neska eta mutil jarrita. Une batean, mutilen 6/11 nesken 4/5ekin dantzan aritu dira. Neska-mutilen zer proportzio egon da dantzan egin gabe une horretan? Mutilen zer proportzio eta nesken zer proportzio dago?

8 300 eta 400 arkatz artean ditugu, eta hainbat kaxa. Kaxa bakoitzean 7 arkatz sartzen dira. Halako batean konturatu gara kaxen 5/6 betetzeko arkatzen 3/5 erabili ditugula. Zenbat kaxa gehiago beharko ditugu arkatz guztiak gordetzeko?

9 Bidaia batean, bi turistak urdaiazpikoak eta gaztak erosi nahi dituzte. Autobuseko gidariak eskatu die erosketak ez daitezela izan 40 kg baino gehiagokoak. Beraz, turista bakoitzak zehatz erosi ditu 40 kg. Bien artean, pisu bereko 5 urdaiazpiko eta pisu bereko 5 gazta daramatzate. Batek hiru aldiz urdaiazpiko gehiago erosi ditu gaztak baino, eta besteak, bi aldiz gazta gehiago urdaiazpikoak baino. Zer pisu du urdaiazpiko bakoitzak eta gazta bakoitzak?

10 Segalari talde batek bi arlotako belarra ebaki behar du. Arloetako baten azalera bestearena halako bi da. Segalari guztiak arlo handian aritu dira egun erdiz, eta beste egun erdian, erdiek arlo handian lan egiten dute, eta beste erdiek, txikian. Hurrengo egunean, arlo txikian ebakitzeko falta zen belarra segalari bakarrak ebaki du, egun osoko lanaldian. Zenbat segalarik osatzen dute taldea?

11 Azeri batek 2 jauzi eta 1/3 egiten ditu segundoko. Halako batean, segundoko 4 jauzi eta 1/2 egiten dituen txakur bat atzetik hasi zaio, baina ordurako azeriak txakurrak baino 30 jauzi eta 3/4 gehiago daramatza eginda. Zenbat denbora beharko du txakurrak azeria harrapatzeko, txakurraren 3 jauzi azeriaren 2 jauzi adina direla jakinda?

12 Anek eta Mikelek hitzordua adostu dute arratsaldeko zortzietarako. Aneren erlojua 10 min atzeratuta dago,, baina berak uste du 5 min aurreratuta dagoela. Mikelek, berriz, 5 min dauka erlojua aurreratuta, baina berak uste du 10 minutu atzeratuta duela. Zer ordutan helduko da bakoitza?

13 Oihal-saltzaile batek % 44 irabazten izan du kostuaren gainetik. Baina, egun batean konturatu da oihalak neurtzeko metro batek akatsa zuela, eta hori konpondu duenean irabaziak % 50 handitu ditu. Zenbat neurtzen zuen metro tranposoak?

14 Zer zenbaki falta da azkeneko triangeluan?

17 Ebatzi honako ekuazio hau aldagai-aldaketa egokia eginez: (x 2 – 6x + 9)2 – 10(x – 3)2 + 9 = 0

18 Kalkulatu Paul txikiaren altuera:

99 cm

19 Dantzaldi batean 20 pertsona daude. Mutil eta neska jarrita ari dira dantzan. Anak 7 mutilekin egin du dantza; Loreak, 8rekin; Saioak, 9rekin, … Jonek, guztiekin. Zenbat mutil eta zenbat neska daude?

20 Aita batek seme-alaben artean banatu du artaldea

• Zaharrenari ardi bat eta geratzen direnen 1/7 eman dio.

• Bigarrenari, bi ardi eta geratzen direnen 1/7.

• Hirugarrenari, hiru ardi eta geratzen direnen 1/7.

• Eta horrela jarraitu du, gazteenera heldu arte. Horrela jokatuta, denek herentzia bera hartu dute eta ez da ardirik sobra geratu. Zenbat neba-arreba dira? Zenbat ardi zeuden taldean?

21 Virginiak koloretako arkatzen 17 kaxa erosi ditu: batzuetan 12 arkatz datoz; beste batzuetan, 8; eta beste batzuetan, 5 arkatz. Guztira koloretako 121 arkatz baditu, mota bakoitzeko zenbat kaxa erosi ditu?

15 Aurkitu honako sistema honen soluzioak:

22 Poltsiko batean hiru motatako txanponak ditugu: 5, 20 eta 50 zentimokoak. 20 txanpon ditugu guztira, eta 4 euro eta 15 zentimoko (415 zentimo) balioa. Mota bakoitzeko zenbat txanpon ditugu?

16 Triangelu honetan, zirkulu barruko zenbakia da berarekin lotuta dituen erpinetako zenbakien

Lege horri jarraituz, zer balio adierazi behar ditugu triangelu honen erpinetan? Eta laukizuzen honetakoetan?

23 Estherrek laguntza eskatu dio Koldo lagunari, taberna batetik eskatu dizkioten kanapeak prestatzen laguntzeko. Bien artean 1 h 40 minutu behar izan dituzte, eta Koldok 50 kanape prestatu ditu. Hurrengo egunean, Estherrek Maiderri eskatu dio laguntza, eskaera berdintsua prestatzeko. Bien artean 2 h 5 min behar izan dituzte, eta Maiderrek 25 kanape prestatu ditu. Zenbat kanape ditu eskaerak? Zenbat denbora beharko lukete Estherrek, Koldok eta Maiderrek eskari osoa prestatzeko, bakarka egingo balute?

Trebatzeko problemak

24 Bi baserritar oiloak saltzen ibili dira merkatuan eta biek diru-kantitate bera poltsikoratu dute

— Nik zuk jarri dituzun prezioan saldu izan banitu oiloak —esan dio lehenengoak bigarrenari— 100 ezkutu irabaziko nituen.

— Nik zuk jarritako prezioan saldu izan banitu oiloak, 36 ezkutu baino ez nituen irabaziko —esan dio bigarrenak. Zenbat oilo saldu ditu bakoitzak, kontuan izanda guztira ez direla dozenara iritsi?

25 Nekazari batek triangelu-itxurako lursail bat du, eta lursail horren alde bakoitzaren parean, karratu-itxurako beste bat. Karratu-itxurako lursailek 4 225 m2, 1 369 m2 eta 5 594 m2 badituzte, zer azalera du triangelu-itxurakoak?

26 Ortoedro baten aurpegiek 35 cm2, 60 cm2 eta 84 cm2-ko azalera dute.

a) Zein da ortoedroaren bolumena?

b) Eta diagonalaren luzera?

27 Pentsa 20 triangelu angeluzuzen berdin ebaki ditugula, eta katetoek 2 cm eta 1 cm-ko luzera dutela. Hori egin ondoren, denak elkarrekin jarri ditugu bata bestearen alboan, karratu bat eratzeko. Erraza dirudi, ezta? Saiatu zu.

30 Zirkulu bat inskribatu dugu 4 cm-ko aldea duen karratu batean. Gero, zirkulu horren barruan karratu bat inskribatu dugu, eta horren barruan, beste zirkulu bat. Eta horrela jarraitu dugu, mugarik gabe

Kalkulatu, bai ilunduta dagoen azalera, bai zuri geratu den zatiarena.

31 Berdinak diren bi karratu planoan mugitzen ari dira. Karratuetako baten erpinetako bat beste karratuaren zentroan badago, zer posiziotan izango da maximoa bi karratuen arteko ebakidura-azalera?

32 Irudiko erronboak 120 cm2-ko azalera du, eta diagonalen arteko zatidura 2,4 da. Kalkulatu inskribaturiko zirkuluaren azalera

r

33 Lurzoruan dagoen esfera batek 10 m-ko itzala proiektatzen du lurra ukitzen duen puntutik. Une horretan bertan, 1 m-ko altuera duen poste bertikal batek 1 m-ko itzala egiten du. Kalkulatu esferaren erradioa.

28 Hiru lagunek pizza bat erostea erabaki dute. Lagunetako bat geometra bikaina da, eta diametroa hiru zati berdinetan zatitu ondoren, irudian zehaztuta ageri diren zatietan banatu du pizza. Bidezkoa da banaketa hori? Arrazoitu ezazu

29 Kalkulatu 10 cm-ko aldea duen pentagono erregularra zatitzean egin ditugun hiru triangelu horietako bakoitzaren azalera

34 Hondartzako baloi handi bat daukagu, 100 cm-ko erradiokoa, eta lurzoruarekin angelu zuzena eratzen duen horma baten kontra jarri dugu.

r = 100 cm

Zenbateko erradioa izango du hormaren, lurzoruaren eta hondartzako baloiaren artean sar daitekeen pilotarik handienak?

35 Erregela, konpasa eta kartaboia erabiliz, marraztu triangelu bat, kontuan hartuz aldearen luzera a dela, eta alde horren muturretatik abiatzen bi erdibidekoen luzerak, mb eta mc

45 a) Frogatu badaudela 1 000 baino kendura handiagoa duten ondoz ondoko bi zenbaki lehen.

b) Egiaztatu, m oso handia izanda ere, badaudela m baino kendura handiagoa ematen duten ondoz ondoko bi zenbaki lehen. (Hau da, ondoz ondoko m zenbaki konposatu daudela).

46 A, B, C, D > 0 denean, beti betetzen da honako desberdintza hau?

36 a) Azaldu, 1 eta 10 arteko sei zenbaki arrunt hartuz gero, zergatik den ziurra horietako biren arteko batura 11 dela.

b) Asmatu antzeko problema bat 55 eta 111 bitarteko zenbaki arruntak erabiliz, eta ebatzi.

37 1 · 2 · 3 · 4 · … · 48 · 49 · 50 zenbakia oso handia da

a) Zenbatgarren lekuan dago, unitateetatik abiatuta, zero ez den lehenengo digitua?

b) Zein da digitu hori?

38 Esan zein den honako zenbaki hauetako bakoitzaren azkeneko digitua (unitateen zifra):

a) 284559 b) 328100 c) 153153

39 248 – 1 kenketaren emaitza 60 eta 70 arteko bi zenbakirekin zatitu daiteke. Zein dira zenbaki horiek?

40 1856. urtean, batetik mila milioira arteko zenbakien karratuak biltzen dituen liburua argitaratu zen (oso liburu lodia). Zertarako? Bada, biderkatzeko! Zuri dagokizu nola egiten den aurkitzea eta azaltzea. Horretarako, erlazionatu bi zenbakiren m · n biderkadura eta m + n eta m – n eragiketen karratuen arteko kendura. Azaldu nola erabili beharko litzatekeen «karratuen liburua» bi zenbaki oso handiren arteko biderkadura (adibidez, 57 839 · 8 756) eragiketa errazagoen bidez kalkulatzeko.

41 Zein da handiagoa, log3 108 edo log5 375?

* Deskonposatu zenbakiak biderkagaietan.

42 Zenbaki hau osoa da. Zein da? || 40 257402 57 +

Egiaztapenak

43 Egiaztatu honako hauek:

a) m bakoitia bada, orduan m 2 + 1 ez da 4ren multiploa.

b) l, m, n ondoz ondoko zenbaki osoak badira, orduan l 2 + m 2 + n 2 batuketaren emaitza 24ren multiploa da.

44 Egiaztatu zenbaki arrunten artean 365 dela bakarra kalkulatu daitekeenajarraian doazen hiru zenbakiren karratuen arteko batuketa eginda, eta, horrez gain, hurrengo bi zenbakien karratuen arteko batuketa eginda.

(1 + A)2 (1 + B )2 (1 + C )2 (1 + D )2 ≥ 24 ABCD

47 a eta b ondoz ondoko bi zenbaki oso badira, orduan: a 2 + b 2 + (ab )2

batuketaren emaitza karratu perfektua izango da beti. Zergatik?

Egiaztapen geometrikoak

48 ACDB paralelogramoan, , AP CR BQ DS == . Egiaztatu PQRS ere paralelogramo bat dela.

49 Egiaztatu triangelu isoszele guztietan betetzen dela hau: angelu berdinen aurkako kanpo-angeluaren erdikaria alde desberdinarekiko paraleloa da.

50 Egiaztatu honako hau: angelu baten erdikariaren edozein puntutik angeluaren alde batekiko paralelo bat marraztuz gero, eratzen den triangelua isoszelea da.

Trebatzeko problemak

51 ABCD paralelogramo batean, Q puntua AD-ren erdiko puntua da, eta P puntua, CB-ren erdiko puntua. Egiaztatu BQ eta DP zuzenkiek hiru zati berdinetan zatitzen dutela AC

57 a eta b bi zenbaki desberdin eta positibo direla jakinda, egiaztatu honako berdintza hau: ab ab ab 2 2 > + +

58 m ≥ 0 eta n ≥ 0 badira, egiaztatu ≤ mn mn 22 ++22

Absurdora eramatea eta kontrajarrera

59 Egiaztatu aurreko ariketan egiaztatutako bera, baina absurdora eramanez.

52 ABC triangeluko AB aldean P edozein puntu adierazi dugu. Gero, , AW WP PX XB == , , AZ ZC BY YC == zehaztu ditugu. Egiaztatu W XY Z = dela.

60 Egiaztatu x + x 1 ≥ 2 dela x zenbaki erreal positibo guztien kasuan.

61 a, b zenbakiak ≠, ab ab 2 + betetzen duten zenbaki erreal positiboak badira, orduan a ≠ b.

62 Egiaztatu a, b, c hiru zenbaki bakoiti badira, orduan ax 2 + bx + c = 0 ekuazioak ezin duela erro arrazionalik izan

Indukzio-metodoa

53 Triangelu berdea eta gorria plano banatan daude, π eta σ. Paraleloak dira? Hori argitzeko, baliogarria da triangeluek aldeak paraleloak dituztela jakitea?

Kuboaren BE diagonalak P eta Q puntuetan ebakitzen ditu bi plano horiek. Frogatu zenezake BP PQ QE == betetzen den?

Horretarako, aurkitu BADG tetraedroaren BP altuera, jakinda bere bolumena kuboaren bolumenaren 1/6 dela. (Zergatik?)

54 Egiaztatu α = β + γ dela irudi honetan. a b c

Egiaztatzeko, saiatu koadrikula honen moduko bat erabiltzen.

Baliokidetasun-katea

55 Egiaztatu x zenbaki erreal ororen kasuan honako hau betetzen dela: x 2 + 1 ≥ 2x

56 Egiaztatu bi zenbaki erreal positiboren batezbesteko aritmetikoa batezbesteko geometrikoaren berdina edo handiagoa dela. Hau da: ≥ xy xy 2 +

63 Egiaztatu n 3 + 5n batuketaren emaitza 6ren multiploa dela n-ren balio arrunt guztien kasuan.

64 Indukzio osoaren metodoa erabiliz, egiaztatu:

a) 2n > 2n + 1 da n ≥ 3 zenbaki arrunten kasuan.

b) 1 · 4 + 2 · 7 + 3 · 10 + … + n · (3n + 1) = n · (n + 1)2 da n zenbaki arrunt guztien kasuan.

65 Erabili indukzio osoaren metodoa honako berdintza hauek egiaztatzeko n zenbaki arrunta denerako:

a) 1 + 3 + 6 + 10 + … + () () () nn nn n 2 1 6 12 + = ++

b) ·· · ()nn n n 12 1 23 1 34 1 1 1 1 ++ ++ + = +

66 Aztertu berdintza hauek: 1 = 1

1 – 4 = –(1 + 2)

1 – 4 + 9 = 1 + 2 + 3

…

Zer erregela orokorri jarraitzen diote? Adierazi idazkera egokia erabiliz eta egiaztatu

67 Egiaztatu 62n – 1 kenketaren emaitza 35ekin zatitu daitekeela n-ren balioa (arrunta) edozein dela ere

68 Egiaztatu n ∈ bada, orduan n 5 – 5n 3 + 4n eragiketaren emaitza 120ren multiploa dela.

69 Egiaztatu indukzio bidez: 12 + 32 + 52 + … + (2n – 1)2 = () () nn n 6 21 22 1 –+

I. multzoa

ALJEBRA

1. Ekuazio-sistemak. Gaussen metodoa

2. Matrizeen aljebra

3. Determinanteak

4. Sistemak determinanteen bidez ebaztea

1

Ekuazio-sistemak. Gaussen metodoa

Gaussek erabilitako metodoa

xix. mendearen hasieran, Gaussek Palas asteroidea behatu zuen. Eta lortutako neurketetatik abiatuta, sei ezezaguneko sei ekuazio zituen sistema batera heldu zen. Sistema hori ebazteko, gaur egun «Gaussen metodoa» esaten diogun prozedura diseinatu zuen.

Hogeita bat mende lehenago, Txinan Matematiken arteari buruzko bederatzi kapituluak liburua argitaratu zen. Zortzigarrenean, honako problema hau ageri da: Hiru zereal mota daude. Lehenengoaren hiru fardo, bigarrenaren bi fardo eta hirugarrenaren fardo bat hartuz gero, 39 neurri izango ditugu. Lehenengoaren bi fardo, bigarrenaren hiru eta hirugarrenaren bat hartuta, 34 neurri. Eta lehenengoaren fardo bat, bigarrenaren bi eta hirugarrenaren hiru hartuta, 26 neurri. Zenbat neurri zereal daude zereal mota bakoitzaren fardo batean?

Eta, ebazteko, honako hau egiten dute aipaturiko liburu horretan:

Zenbakiak taula batean jarri (ekuazio bakoitza zutabe batean deskribatzen da, enuntziatuko azkenengotik hasita):

Zutabeekin aldaketak eginez, ezkerreko taula beste hau bihurtzen da:

Eta eskuineko taulatik, berehala eta hurrenez hurren, fardo bakoitzeko zerealaren neurri-kopurua lortzen da.

Bi prozedurak zein antzekoak diren ikusita, gaur egun Gaussen metodo esaten diogun horri, beharbada, «Chui-Chang Suan-Shuren metodo» esan beharko genioke (hori baita egilea ezagun ez duen liburu horren izenburua txineraz).

«Matematiken arteari buruzko bederatzi kapituluak» liburuko orrialde bat.

Gaussen egunkari zientifikoa

Carl Friedrich Gauss (1777-1855) historian izan den matematikaririk handiena da askorentzat, eta «matematikarien printzea» ezizenez ere esaten diote. Matematikaren arlo bat bera ere ez zuen utzi landu gabe. Baina bitxia badirudi ere, ez zen bere aurkikuntzak argitara ateratzeko zalea

19 urte zituela, Euklidesen garaitik ebatzi gabe zegoen geometriako problema bat ebazteko prozedura lortu zuen. Egiaztapen bikaina egin zuen, teknika aljebraikoak erabili baitzituen ebazteko (berrikuntza handia izan zen geometriako problema bat prozedura aljebraikoen bidez ebaztea).

20 markoko zilarrezko txanpona, Alemaniako Errepublika Demokratikoa zenekoa, Gaussen omenez.

Aurkikuntza egin, eta berekin zeraman egunkari txikian zehaztu zuen egun horretan bertan, 19 orri baino ez zituen eskuliburu batean. Koadernotxo hori urte askotan erabili zuen, eta 146 ohar idatzi zituen guztira. Horietako azkena, 1814. urtean, oharrak egiten hasi eta 17 urtera. Bertan ageri diren ideien kopurua eta sakontasuna kontuan hartuz, matematiken historian izan den dokumentu baliotsuenetako bat dela esan dezakegu.

Gaussen zientzia-egunkariaren orrialdea.

EBATZI

Zereal-fardoak

Koadernotxo hori erabakigarria izan da jenio horren pentsaera ezagutzeko, baina ez zen argitaratu 1898. urtera arte; hau da, Gauss hil eta berrogeita hiru urte geroago arte

Zereal-fardoen problema txinatarrarekin batera zenbakien bi taula ageri dira. Lehenengoak enuntziatutik lortzen diren ekuazioak deskribatzen ditu. Ekuazioen koefizienteak zutabeetako zenbakiak direla kontuan izanda, sistema honela geratzen da:

a) Idatzi bigarren taulari dagokion ekuazio-sistema. Ikusten duzunez, sistema hau oso erraza da ebazten: 1. ekuaziotik z-ren balioa lortu, eta horrekin, bigarren ekuazioan, y lortzen da. Amaitzeko, 3. ekuaziotik x lortzen da. Soluzioa: x = 37/4, y = 17/4, z = 11/4.

b) Egiaztatu soluzio hau baliozkoa dela hasierako sisteman.

Zer aldaketa egin zioten ezkerreko taulari eskuinekoa lortzeko? Begira:

(2. taulako 1. zutabea) = 15 · (1.a) – 12 · (2.a) + 3 · (3.a)

(2. taulako 2. zutabea) = 3 · (2.a) – 2 · (1.a)

(1.a), (2.a) eta (3.a) lehenengo taulako zutabeak dira.

Lehenengo taulako zutabeekin bigarren taulakoak lortzeko hemen egiten diren eragiketek zailak badirudite ere, unitate honetan lan hori egiteko metodo errazago bat ikasiko duzu.

Ekuazio linealen sistemak

Ekuazio lineala

Honako ekuazio hauek linealak dira:

2x – 3 = 0 5x + 4y = 20 3x + 2y + 6z = 6 5x – 3y + z – 5t = 0

Denek dute berezitasun bat: 1. mailako ekuazio polinomikoak dira. Hau da, ezezagunak ez daude berretzaileetara jasota, ez daude elkar biderkatzen, ez erro barruan, ez izendatzailean…

Beste ekuazio hauek, berriz, ez dira linealak:

2x – 3y + z = 5 3xy – 2z = 0 x + 2y – sen z = 1

Ekuazio lineala ezezagun bat edo gehiago dituen lehenengo mailako ekuazio polinomikoa da.

• Planoan mugitzen bagara, bi ezezagun izango ditugu: x, y. Bi ezezagun edo ezezagun bakarra dituen ekuazio lineal batek zuzen bat adierazten du planoan. Zuzeneko puntuak ekuazioaren soluzioak dira.

Adibidez, 5x + 4y = 20 da XY planoko zuzen bat. (4, 0), (0, 5), (–2; 7,5), (3; 1,25) puntuak zuzenekoak dira, eta, beraz, ekuazioaren soluzioak dira

x = 3 edo y = 5 ekuazioek ere zuzenak adierazten dituzte.

• Hiru ezezagun dituen (edo hiru ezezagunetakoren bat) ekuazio lineal batek plano bat adierazten du espazioan. Planoko puntuak ekuazioaren soluzioak dira.

Adibidez, 3x + 2y + 6z = 6 plano bat da hiru dimentsioko espazioan. (2, 0, 0), (0, 3, 0), (0, 0, 1), (1, 1, 1/6) puntuak planokoak dira, eta, beraz, ekuazioaren soluzioak dira.

5x + 4y = 20, x = 3 edo y = 5 ekuazioak ere planoak dira

Ekuazio baliokideak

Bi ekuazio baliokideak dira soluzio bera dutenean (edo soluzio berak dituztenean).

Ekuazio bateko bi atalak zero ez den zenbaki berarekin biderkatzen edo zatitzen baditugu, lortuko dugun ekuazioa eta hasierakoa baliokideak dira.

Adibidez:

x y 4 5 + = 1 eta 5x + 4y = 20 baliokideak dira (zuzen bera adierazten dute).

30x + 20y + 60z = 60 eta 3x + 2y + 6z = 6 baliokideak dira (plano bera adierazten dute).

Ekuazio linealen sistemak

Zenbait ekuazio batera ematen badira euren soluzio komuna edo komunak zehazteko, ekuazio-sistema bat eratzen dutela esaten dugu.

• Bi ezezaguneko ekuazio linealen sistema batek zuzen multzo bat adierazten du. Sistema ebazten badugu, zuzen horiek punturen bat berdina duten zehaztu eta puntu hori kokatuko dugu

• Sistema bateko ekuazioek hiru ezezagun badituzte, planoak adierazten dituzte. Sistema ebaztea da plano horiek guztiek berdina duten puntua edo puntuak aurkitzea.

SISTEMA

Ekuazio-sistemak oso interesgarriak dira, eta horiek landuko ditugu unitate honetan eta hurrengoetan. Horregatik, aurrerantzean, «ekuazio-sistema» edo, besterik gabe, «sistema» erabiltzen dugunean, «ekuazio linealen sistema» adierazi nahiko dugu.

bi ezezaguneko ekuazio linealak

hiru ezezaguneko ekuazio linealak

➜ Marraztu planoak eta zuzenak.

Sistema baliokideak

Bi ekuazio-sistema baliokideak dira soluzio berdinak badituzte

Bi sistema baliokide izan daitezke, nahiz eta sistemak eratzen dituzten ekuazioak baliokideak izan ez

Adibidez: x x y y 5 2 3 16 3 ––= = + 4 eta x x y y 513 1 + + = = 4 baliokideak dira, biek ere soluzio bakar

hau baitute: x = 3, y = –2

Aldaketak ekuazio-sistema batean

Sistema batetik beste sistema baliokide batera pasatzeko egindako aldaketa guztiak baliozkoak dira. Adibidez, honako hauek:

1 Ekuazioetako baten bi atalak zero ez den zenbaki batekin biderkatzea edo zatitzea

x xy z z y 3 25 53 –– + + = = 4 (2.a) · 3 ⎯⎯→ x x y y z z 3 3 5 63 3 15 –– + + = = 4

2 Ageri diren ekuazioen konbinazio lineala den ekuazio bat eranstea, edo, aitzitik, ageri direnen konbinazio lineala den ekuazio bat kentzea.

x xy z z y 3 25 53 –– + + = = 4 (1.a) – 3 · (2.a)

EKUAZIOEN KONBINAZIO LINEALA

x x y y y

35 2 11 4

3 5 12 –– + + = = = 4

z z z

3 Ekuazioetako baten ordez zenbaki batekin biderkaturiko beste ekuazio bat batzean lortzen den emaitza jartzea

Ekuazioen konbinazio lineala esaten diogu ekuazioetako bakoitza zenbaki batekin biderkatu eta atalez atal batzean lortzen dugun emaitzari.

ADI!

Sistemaren soluzioak aldatzen ez dituzten aldaketei baliozko aldaketa esaten zaie

Ekuazioen sistemak ebaztean, baliozkoak ez ezik «komenigarriak» ere badiren aldaketak egin behar ditugu; hau da, soluziora hurbilduko gaituzten aldaketak. Horretarako, batez ere, hemen deskribatu ditugun 1 eta 3 aldaketak erabiliko ditugu

1 Zuzena ala okerra?

a) (x, y) bi ezezagun dituen ekuazio-sistema batean, x + y = 4 ekuazioak, besteak beste, (3, 1) soluzioa du

b) (x, y, z) hiru ezezagun dituen sistema batean, x + y = 4 ekuazioak ez du zentzurik

c) (x, y, z) hiru ezezagun dituen sistema batean, x + y = 4 ekuazioak zentzua du. Plano bat adierazten du, eta sistema horren soluzio batzuk hauek dira: (3, 1, 0), (3, 1, 7), (3, 1, – 4).

d) Planoan bagaude (x, y bi ezezagunekin), y = 0 ekuazioak X ardatza adierazten du

e) Espazioan bagaude (x, y, z hiru ezezagunekin), y = 0 ekuazioak XZ planoa adierazten du

2 Azaldu zergatik diren baliokideak sistema-pare hauek, ebazpena egin gabe:

➜ Bi eta hiru dimentsioko ekuaziosistemak.

Ekuazio-sistema batek soluzioa izan dezake (bateragarria) edo baliteke soluziorik ez izatea (bateraezina).

Sistema bateragarriek soluzio bat izan dezakete (determinatuak) edo infinitu soluzio izan ditzakete (indeterminatuak).

Bi ezezaguneko ekuazio-sistemak

Honako sistema hauek eta horien interpretazio geometrikoak aztertuko ditugu:

• x x y y 2 3 3 5 9 4 –+= = 4 Ekuazio-sistema honen soluzioa x = 3, y = 1 da. Horrek esan nahi du bi zuzenek (3, 1) puntuan ebakitzen dutela elkar.

Beraz, sistema bateragarria eta determinatua da.

KONTUAN IZAN

Sistema bat bateragarria edo bateraezina dela esan beharrean, zuzenago izango litzateke zehaztea sistema eratzen duten ekuazioak bateragarriak direla (hau da, denek soluzio komun bat dutela) edo bateraezinak direla (ez dagoela denena den soluzio komunik). Dena dela, hemen erabilitako nomenklatura orokorrean onartuta dagoena da.

2 3 5

x x

2

3 5 2 –

+= = = 4 Sistema hau aurrekoaren berdina da ia; izan ere, aurreneko bi ekuazioak berdinak dira, eta hirugarrena aurreko bi horiek atalez atal batuta lortzen da

y y y

9 4 13 –

y y

Bi ekuazioek gauza bera diote. Horietako baten soluzio bakoitza bestearena ere bada. Bi zuzenak bat datoz. Hau da, zuzen bera dira

4 3

• x x x y y y 2 3 5 3 5 2 9 4 6 –+= = = 4

Sistema hau bigarren sistemaren oso antzekoa da; hirugarren ekuazioko gai askea baino ez da aldatzen. Baina hori dela eta, ez da beste biek elkar ebakitzen duten (3, 1) puntutik igarotzen. Ez dago hiru zuzenek bat egiten duten punturik.

Beraz, sistema hau bateraezina da.

2 2x+3y=9 3x–5y=4 2x+3y=9 3x–5y=4 5x –2y = 13 2x+3y=9 4x+6y=18 2x+3y=9 4x+6y=12 2x+3y=9 3x–5y=4 5x –2y = –6

Hiru ezezaguneko ekuazio-sistemak

Azter ditzagun honako sistema hauek eta horiei dagozkien interpretazio geometrikoak:

➜ Sortu mota desberdinetako ekuazio-sistemak.

Hiru planoek puntu batean ebakitzen dute elkar. Sistema bateragarri determinatua da

x = 1, y = 7, z = –2

Laugarren ekuazioa beste hiruren batura da. Horri dagokion planoa (horia) komunean duten puntutik igarotzen da. Sistema bateragarri determinatua da

x = 1, y = 7, z = –2

Laugarren ekuazioak beste hiruren baturaren kontrakoa esaten du. Plano hori (horia) ez da beste hiruren ebakipuntutik igarotzen. Sistema bateraezina da

Hirugarren ekuazioak, beste bien batura denez, ez dio bestelako informaziorik eransten sistemari. Sistema bateragarri indeterminatua da Soluzioa: Planoek elkar ebakitzen duten zuzeneko puntu guztiak dira sistemaren soluzio.

Hirugarren ekuazioak kontra egiten dio beste biak batuta lortzen denari. Sistema bateraezina da

1 Ebatzi eta interpretatu geometrikoki honako ekuazio-sistema hauek:

2 a) Ebatzi sistema hau: x x y y 23 4 –+= = *

b) Erantsi hirugarren ekuazio bat sistema bateragarria izaten jarraitzeko

c) Erantsi hirugarren ekuazio bat sistema bateraezina izateko

d) Interpretatu geometrikoki kasu bakoitzean egin duzuna

Sistema mailakatuak

• Honako sistema hauek oso errazak dira ebazteko:

P ROPOSAMENA

Ebatzi urratsez urrats honako hiru sistema hauetako bakoitza.

Behetik gora joanda, ezezagun bakoitzaren balioa lortuko dugu, eta aurreko ekuazioetan ordezkatzen badugu, prozesuarekin aurrera jarraitu ahal izango dugu. Sistema mota hauei mailakatu esaten zaie

• Beste sistema hau ere mailakatua da. Ekuazioak baino ezezagun gehiago dituenez, ezezagunetako bat bigarren atalera igaroko dugu, eta gainerakoak horren funtzioan kalkulatuko ditugu:

(3.a) z = 11 – 3t

(2.a) y = 8 – z = 8 – (11 – 3t) = –3 + 3t

(1.a) x = 5 + t – 2y = 5 + t – 2(–3 + 3t) = 11 – 5t

Ezezagun guztiak t-ren funtzioan jarrita daudenez, t parametrotzat hartuko dugu, balio aldakor bat emango diogu. t = λ esaten badiogu, honela geldituko da:

x = 11 – 5λ y = –3 + 3λ z = 11 – 3λ t = λ

λ-ri ematen diogun zenbakizko balio bakoitzerako, balio horri dagozkion x, y, z eta t-ren balioak lortuko ditugu. Adibidez:

λ = 0 denean, x = 11, y = –3, z = 11, t = 0 lortzen dugu.

λ = 1 denean, x = 6, y = 0, z = 8, t = 1 lortzen dugu.

• Hain agerikoa izan ez arren, honako sistema hau ere mailakatua da:

IDAZKERA

λ (lambda), μ (mu), ν (nu) parametro moduan erabiltzen diren letra grekoak dira.

x x

–++

y y yz

= = =

35 2 11 4 14

b b b b Argi dago 2. ekuazioan y bakandu dezakegula, 1. ekuazioan x, eta, azkenik, 3. ekuazioan z

_ ` a

Sistema hauei ere mailakatu esango diegu, nahiz eta itxura aldetik ematen ez duten

1 Identifikatu honako sistema hauek mailakatu gisa eta eba-

2 Mailakatuak dira sistema hauek? Ebatzi:

Nola pasatu sistema batetik beste sistema baliokide mailakatu batera Ikus dezagun nola pasatu sistema batetik mailakatua den beste sistema baliokide batera, ebatzitako adibide batzuen bidez

Ebatzitako ariketa

1 Bihurtu sistema hauek sistema mai-

1

koefizienteak oso lagungarriak dira aldaketa errazak egiteko

Orain badaukagu sistema modu mailakatuan jarrita. Aldaketak(*) egin dira, argi dagoenez, y-ren koefizienteak berdintzeko, eta, horrela, zatikiak erabili beharrik gabe ezabatu ahal

Ebazpena:

3 Bihurtu sistema hauek mailakatu eta ebatzi

➜ Adierazi sistema mailakatu batera transformatzeko faseak.

Gaussen metodoa

Aurreko orrialdean ekuazio linealen sistema bat sistema mailakatu bihurtzeko ikusi eta erabili dugun prozedura Gaussen metodoa da. Metodo hori errazago erabiliko dugu ezezagunak alde batera utzi eta zenbakiak bakarrik erabiltzen baditugu (koefizienteak eta gai askeak), matrize eran jarrita

Ikus dezagun nola ebatz daitekeen aurreko orrialdeko bigarren adibidea:

MATRIZEAK

Zenbaki-kaxa hauek, matrize izenekoak, hurrengo unitatean landu eta ikasiko ditugu sakonago. Hemen ekuazio-sistema bateko koefizienteen euskarri moduan erabiliko ditugu, besterik gabe.

Prozesuan parte hartzen duten matrize horietako bakoitza ekuazio-sistema bati dagokio. Azkena mailakatua da eta, beraz, oso erraz ebazten da.

Gaussen metodoa da ekuazio linealen sistema bat sistema mailakatu bihurtzea. Horretarako, «zeroak egin» behar ditugu, ekuazioei oinarrizko bi aldaketa eginez:

• Ekuazio bat zero ez den zenbaki batekin biderkatzea.

• Ekuazio bat zenbaki batekin biderkatutako beste ekuazio batekin batzea.

Prozesu hori askoz errazagoa eta erosoagoa da ekuazioak erabili beharrean zenbakiak bakarrik erabiltzen baditugu —koefizienteak eta gai askeak— matrizetan egituratuta

Prozesuaren amaieran, edo tarteko urratsen batean, honako kasu hauetakoren bat aurki dezakegu:

a) Zeroen errenkada bat. Ekuazio hutsal bati dagokio eta, beraz, bazter utz dezakegu:

(0 0 … 0 0 ) ⇔ 0x + 0y + … + 0t = 0

b) Bi errenkada berdin edo proportzional. Ekuazio baliokideei dagozkie eta, beraz, horietako bat bazter utz dezakegu:

→ 015 26 …………

c) Azkeneko zenbakia kenduta —gai askeari dagokiona— besteak zero dituen errenkada bat:

(0 0 … 0 ) ⇔ 0x + 0y + … + 0t =

( zero ez den zenbaki bat da)

Argi dago ekuazio hori ezinezkoa dela. Ebatzi ezin den ekuazio bat duten kasu hauek sistema bateraezintzat joko ditugu segituan

E KUAZIO HUTSALA

0x + 0y + 0z = 0 ekuazioak azalkeria bat, hutsaltasun bat adierazten du. Zenbakien edozein hirukote izango da ekuazio horren soluzio. Ekuazio hutsal esaten zaio.

1 Zuzena ala okerra?

a) Sistema bateraezin batek sistema mailakatu bateragarria eman dezake, Gaussen metodoa aplikatu ondoren. Edo alderantziz

b) Gaussen metodoa erabili ondoren azkenean lortzen dugun sistema mailakatua hasierako sistemaren mota berekoa da; izan ere, emandako urrats guztiek sistema bat beste sistema baliokide bat bihurtzen dute.

Ekuazio-sistema motak

Gaussen metodoak modua ematen du ekuazio linealen edozein sistema horren baliokide izango den sistema mailakatu bat bihurtzeko

Hasierako sistema bateragarria den (determinatua zein indeterminatua) edo bateraezina den jakiteko, prozesuaren amaieran lortzen dugun sistema mailakatuaren itxurari begiratuko diogu. Honako kasu hauetako bat gerta daiteke:

I. f 0 0 0 0 0 0

zero ez den zenbaki bat edozein zenbaki

Ekuazio baliozkoak ezezagunak adina izango dira. Urratsez urrats joanda, ezezagun bakoitzerako zenbakizko balio bat lortuko dugu.

Beraz, sistema bateragarri determinatua da.

II.

SISTEMA HOMOGENEOAK

Sistema homogeneo bat da gai independente guztiak zero dituen sistema:

Ekuazio baliozkoak ezezagunak baino gutxiago dira. Sobera dauden ezezagunak bigarren atalera igaroko ditugu, eta, beraz, besteen balioa horien funtzioan emango dugu

Sistema bateragarri indeterminatua da. Sistema horren soluzio orokorra bigarren atalera igarotako ezezagunak adina parametroren bidez emango dugu.

III.

Adierazitako ekuazio hori ezin da inoiz bete Sistema bateraezina da.

Argi dago sistema homogeneo bateko ekuazio guztiek daukatela soluzio moduan, gutxienez, soluzio hutsala, x = 0, y = 0, z = 0. Beraz, sistema homogeneoak beti dira bateragarriak.

1 Ebatzi honako sistema hau Gaussen

2

honako sistema hau Gaussen

Ekuazio-sistemen eztabaida

Aztertu ekuazio linealen honako sistema hau:

Egia esan, ekuazio-sistema bat izan beharrean sistemen multzo bat da, k parametroaren balio bakoitzerako ekuazio-sistema desberdin bat baitago

Infinitu sistema horietatik, batzuk bateragarriak izango dira beharbada, eta beste batzuk, bateraezinak. Parametroaren «mendekoa» den sistema eztabaidatzea da sistema hori era batekoa edo bestekoa k-ren zer baliorekin izango den jakitea.

Parametro baten edo gehiagoren mendekoa den ekuazio-sistema bat eztabaidatzea hau da: sistema hori bateragarria edo bateraezina parametroen zer baliorekin izango den identifikatzea, determinatua edo indeterminatua zer kasuetan den ere bereiziz

4. unitatean ekuazio-sistema linealak Gaussen metodoa ez den beste metodo batekin ebazten ikasiko dugu. Prozedura berri hori, oro har, erosoagoa da sistemak eztabaidatzeko. Dena dela, Gaussen metodoak ere sistemak eztabaidatzeko modua ematen du. Ikus dezagun ebatzitako ariketa baten bidez.

denean, ebatzi:

Gaussen metodoa erabiliko dugu:

• k = 1 bada, azkeneko errenkada (0 0 0 1 ) da. Sistema bateraezina da.

orduan:

Hau da, k ≠ 1 denean, sistema bateragarri determinatua da

32 2 + +

Soluzioa: ,, k kk k kk k k 1 21 1

Kontuan hartu: Ez daude infinitu soluzio, infinitu sistema baizik: k-ren balio bakoitzerako sistema bat. Eta sistema horietako bakoitzak soluzio bakarra du, k = 1 kasuari dagokionak izan ezik. Horrek ez dauka soluziorik. Adibidez, k = 2 kasurako, hau da sistema:

Ebatzitako ariketa 1 Eztabaidatu ekuazio-sistema hauek

2 Eztabaidatu ekuazio-sistema hauek k-ren funtzioan:

➜ Adierazi parametro baten araberakoa den sistema bat.

Ebatzitako ariketak eta problemak

Ebatzi eta interpretatu geometrikoki honako ekuazio-sistema hauek:

a) Hiru aldagai daudenez, x, y, z, ekuazio bakoitza espazioko plano bat da. Lehenengo bi ekuazioen ordena aldatuko dugu, lehenengo koefizientea 1 izan dadin:

EGIN ZUK

Ebatzi eta interpretatu geometrikoki honako ekuazio-sistema hauek:

Soluzioak: (1 + λ, λ, –1 – λ)

Sistemak zuzen batean elkar ebakitzen duten lau plano adierazten ditu.

b) Ezezagunen koefiziente bat bera ere ez denez 1, erreferentzia moduan lehenengo ekuazioa hartuko dugu:

ezin da inoiz bete. Sistema bateraezina da,

Sisteman ez dagoenez plano paraleloen bikoterik, binaka hiru zuzenetan elkar ebakitzen duten hiru plano adierazten ditu.

c) Bi aldagai baino ez daudenez, x eta y, ekuazio bakoitza planoko zuzen bat da. Erreferentzia moduan bigarren errenkada hartuko dugu:

Azkenengo bi errenkadak alde batera utzi, eta hau geratzen zaigu:

Soluzioa: (3/4, –1/4)

Sistemak (3/4, –1/4) puntuan elkar ebakitzen duten lau zuzen adierazten ditu.

1. Gaussen metodoa

2. Gaussen metodoa ekuazio-sistema linealak eztabaidatzeko erabiltzea

Eztabaidatu eta ebatzi sistema hauek, beraietan ageri den parametroaren funtzioan, Gaussen metodoa erabilita. Eman, kasuetako bakoitzean, interpretazio geometriko bat:

Ekuazioen ordena aldatuko dugu.

EGIN ZUK

Eztabaidatu eta ebatzi, parametroaren funtzioan, Gaussen metodoa erabilita. Eman interpretazio geometrikoak.

• m = 1 bada, azkenengo errenkada (0 0 0 0) da eta kendu daiteke. Sistema bateragarri indeterminatua da, ezezagun gehiago dituelako ekuazioak baino. Parametro baten mendekoak diren infinitu soluzio ditu. xz yz y 0

32 44 0

––= = = 4 Soluzioak: x = 2 – 3λ, y = 4 – 4λ, z = λ

Zuzen bat komunean duten hiru plano adierazten dituzte.

• m ≠ 1 bada, sistema bateragarri determinatua da. ()

xz yz y m

–––

32 44 0 1

= = = 4 Soluzioa: x = – 1, y = 0, z = 1

Hiru planoek (–1, 0, 1) puntuan ebakitzen dute elkar.

Bigarren ekuazioan y-ren koefizientea baliogabetzen duten balioak aurkituko ditugu: 1 – m 2 = 0 → m = ± 1

• m = –1 bada, bigarren ekuazioa 0 · y = 2 izango da. Sistema bateraezina da. Bi zuzen paralelo dira.

• m = 1 bada, bigarren ekuazioa, 0 · y = 0, ezabatu daiteke. Sistema bateragarri indeterminatua da. x + y = 0 ekuazioa baino ez zaigu geratzen, eta, ebazteko, y parametrotzat joko dugu. Soluzioak hauek dira: (–λ, λ). Bi zuzenak bat datoz.

• m ≠ ±1 bada, sistema bateragarri determinatua da. m-ren balio bakoitzerako, sistema bat daukagu, eta soluzio bakar bat:

puntu batean ebakitzen dute elkar.

a-ren balio bakoitzerako, sistema desberdin bat daukagu, soluzio bakar batekin: (0, 0, 0). Koordenatu ardatzean elkar ebakitzen duten hiru plano dira.

Ebatzitako ariketak eta problemak

3. Ekuazioak baino ezezagun gehiago dituzten sistemak

Ebatzi eta interpretatu geometrikoki honako sistema hauek:

a) xy z xy z 31 22 3 –+= += *

b) xy z xy z 24 62 23 1 ––+= += *

Sistema hauek (ekuazioak baino ezezagun gehiago dituztenak) ez daukate inoiz soluzio bakarra. Infinitu soluzio izan ditzakete, edo bat bera ere ez.

a) z bigarren atalera igaro eta z = λ egingo dugu (parametroa). Horrela, sistemak ekuazioak adina ezezagun izango ditu.

EGIN ZUK

Ebatzi eta interpretatu geometrikoki honako ekuazio-sistema hauek:

a) xy z yz 24 0 ––+= = *

b) xy z xy z 23 36 31 ––+= += *

Pertsona batek 60 000 € inbertitu ditu A, B eta C hiru enpresatan, eta 6 000 €-ko irabaziak lortu ditu. A eta B enpresetan inbertitu duenaren batura k aldiz izan da C enpresan inbertitutakoa, eta irabaziak % 5ekoak izan dira A-n, % 10ekoak B-n eta % 20koak C-n.

a) Planteatu ekuazio-sistema bat enpresa bakoitzean zenbat diru inbertitu duen jakiteko.

b) Aztertu bere bateragarritasuna eta ebatzi k = 5 kasurako, baldin eta ahal bada.

EGIN ZUK

A, B eta C-ren artean guztira daukaten dirua A eta B-ren artean daukatenaren % 150 da, eta A eta C-ren artean daukatenaren bikoitza. C-k duen dirua A-k duenaren bikoitza bada, jakin dezakegu zenbat diru duen bakoitzak?

xy

xy 31 23 2 –m m += + += +

(1.a) (2.a) – 2 · (1.a) xy y 31 55 m += + =

Sistemaren soluzioak (–2 + λ, 1, λ) dira. Parametro baten mendekoak direnez, zuzen bat eratzen duten infinitu soluzio daude.

λ-ren balio bakoitzerako soluzio bat lortzen dugu.

Zuzen batean elkar ebakitzen duten bi plano dira.

Soluzioen egiaztapena:

() 23 1 22 12 –3 mm mm ++ = ++ =

b) Bi ekuazioek plano bera adierazten dute, bata bestearen bikoitza baita. Bigarren ekuazioa baino ez dugu hartuko, eta hiru ezezagun dituenez, bi parametro behar ditugu ebazteko.

z eta y bigarren atalera igaroko ditugu, x = 1 + 2y – 3z, eta y = λ eta z = μ egingo dugu.

Sistemaren soluzioak (1 + 2λ – 3μ, λ, μ) dira. Sistemak infinitu soluzio ditu. Planoak bat datoz.

4. Problemak eztabaidatzea eta ebaztea

a) Ekuazio-sistema bat planteatuko dugu, problemako baldintzak aintzat hartuta. x da A enpresan inbertitutako dirua, y da B-n inbertitutakoa, eta z, C-n inbertitutakoa.

b) Bateragarritasuna aztertzeko, hirugarren ekuazioa sinplifikatuko dugu eta gai independenteak milaka eurotan adieraziko ditugu.

Bigarren ekuazioan ikusten dugunez, k = –1 bada, (0z = –60) ekuazioak ez du soluziorik. Beraz, k ≠ –1 izan behar da; eta k problema honetan zenbaki positibo bat izan behar denez (k aldiz), esango dugu sistema bateragarria dela baldin eta k > 0 bada.

1. Parametro bateko eta soluzio bakarreko sistemak

a) Gaussen metodoa ezartzean, sistema mailakatu bat lortuko duzu, eta hirugarren ekuazioa (m + 1)z = 8 da.

+ + *

–+ +

Zehaztu zer baldintza bete behar duen m-k ekuazio horrek soluzioa izan dezan.

z z mz 2 2

2.

y y y

= = =

22 1 3 5

b) Ebatzi sistema, bateragarri determinatua egiten duten m-ren balioetarako.

b) Adierazi z-ren balioa m-ren funtzioan, eta lortu x-ren eta y-ren balioak, horiek ere m-ren funtzioan

Soluzioa:

a) m ≠ −1 bada, sistema bateragarri determinatua da. m ≠ −1 den balio bakoitzerako, soluzio bakarra duen sistema desberdin bat daukagu.

b) x = –1; y = m m 1 7–+ ; z = m 1 8 +

Sistema bateragarri indeterminatu baten soluzio berdinak dituen sistema bat

*

–– –+= =

3. Sistema bateragarria

xy z xy z xy z xy az a 1 22 3 22 ––++ = ++ = ++ = += *

4. Sistema bateragarria

• Frogatu S sistema bateragarri indeterminatua dela, eta lortu bere soluzioak.

• Idatzi sistema berriaren matrizea eta ezarri Gaussen metodoa.

• Zehaztu zein izan behar den k-ren balioa ekuazio berria hutsala izan eta ezabatu ahal izateko.

• Egiaztatu S-ren soluzioek hirugarren ekuazioa egiaztatzen dutela lortu duzun k-ren baliorako.

Soluzioa: k = –8 denean, soluzioak dira (1 + 5λ, 3λ, λ) zuzeneko puntuak.

• Egiaztatu, Gaussen metodoa erabilita, lehenengo hiru ekuazioak soilik dituen sistema bateragarria dela, eta laugarrenarekin bateragarri izaten jarraitzen duela a-ren edozein baliotarako.

• Zein izan behar da a-ren balioa laugarren ekuazioa ekuazio hutsala izateko?

• Ezabatu ekuazio hutsalak eta ebatzi sistema, bateragarri indeterminatua eta bateragarri determinatua den kasuetan.

• Aukeratu egokiro parametro moduan hartuko duzun ezezaguna.

Soluzioa: a = –1 bada, bateragarri indeterminatua da, eta soluzioa ,, 3 1 3 4 – mm dn da.

a ≠ –1 bada, bateragarri determinatua da, eta soluzioa ,, 3 1 3 1 1 dn da.

10

xmy mx y m

• Ezarri Gaussen metodoa, eta 2. ekuaziorako (1 – m2)y = –(1 + m) lortuko duzu.

• Zer baldintza bete behar du m-k sistemak soluzioa izan dezan?

• Zehaztu m-ren zer baliok bihurtzen duten ekuazio hori bateraezin edo ekuazio hutsal bat.

• Sistemak planoko bi zuzen adierazten ditu, komunean puntu bat izan dezaketenak, puntu bat ere ez, edo infinitu puntu.

Soluzioa: m ≠ ±1 bada, bateragarri determinatua da, eta soluzioa , mm 1 1 1 1 –

–––

m ≠ ±1 balio bakoitzerako, puntu batean elkar ebakitzen duten bi zuzen lortzen ditugu.

m = 1 bada, sistema bateraezina da. Bi zuzen paralelo dira.

m = –1 bada, sistema bateragarri indeterminatua da. Zuzenak bat datoz.

Gidatutako ariketak eta problemak

Proposatutako ariketak eta problemak

Praktikatzeko

Ekuazio-sistema linealen ebazpena eta interpretazio geometrikoa

1 Ebatzi eta interpretatu geometrikoki honako sistema hauek:

Gaussen metodoa

7 Ebatzi Gaussen

8

2 Ebatzi eta interpretatu geometrikoki.

3 Arrazoitu honako sistema hauek soluziorik duten, eta interpretatu geometrikoki. Ebatzi, egin litekeen kasuetan.

9 Ebatzi, ahal izanez gero, honako sistema hauek:

6 Idatzi hiru ekuazioko eta bi ezezaguneko sistema bat, soluziorik ez duena, eta interpretatu geometrikoki.

10 Aztertu eta ebatzi Gaussen metodoaren bidez.

11 Sailkatu honako sistema hauek bateragarriak edo bateraezinak diren kontuan izanda:

12 Aztertu eta ebatzi Gaussen metodoaren bidez:

23

Ekuazio-sistemak eztabaidatzea

13 Eztabaidatu honako sistema hauek m parametroaren balioen arabera:

Ebazteko

19 Sailkatu honako sistema hauek, kontuan izanda a-ren balioen arabera zenbat soluzio dituzten, eta ebatzi a = 2 kasuan:

a) x x y y y z az 2 1 3 2 ––

14 Eztabaidatu honako sistema hauek eta ebatzi, egin litekeenean:

+ + *

15 Ebatzi honako sistema hauetako bakoitza bateragarri egingo

16 Eztabaidatu sistema hauek k-ren balioen arabera, eta ebatzi, egin litekeenean:

17 Eztabaidatu honako ekuazio-sistema hauek parametroaren balioen funtzioan:

18 Eztabaidatu eta ebatzi parametroaren funtzioan:

= = =

1 2

y y y a a 2 4 4 10

b) Ebatzi bateragarri determinatua den kasuetan.

21 a) Aztertu sistema λ-ren balioen arabera: x x x y y

+ + = = =

2 2 0 –m m + + *

b) Ebatzi λ = 3 kasurako.

2 5 2 52

1 3 ––– + + + = = =

y z z zm

*

= = = *

x x

+ + +

+ + +

z z az 2 5 34 0 0 0 6

a) Ondorioztatu a-ren zer baliorekin daukan sistemak (0, 0, 0) soluzioa soilik.

b) Ebatzi sistema infinitu soluzio dituen kasuan.

25 Itsasontzi batek 400 ibilgailu (autoak, kamioiak eta motorrak) garraiatzen ditu. 5 kamioiko 2 motor daude. Eta autoak gainerako ibilgailuen 9/7 dira. Mota bakoitzeko zenbat ibilgailu garraiatzen ditu itsasontziak?

Proposatutako ariketak eta problemak

26 Autobus batek 60 bidaiari daramatza, baina hiru tarifa motarekin. Bidaiari batzuek billete osoa ordaindu dute, hau da, 1,2 euro. Bidaiarien beste multzo batek billetearen balioaren % 80 ordaindu dute, eta hirugarren multzo batek, % 50. Atzo autobusak 46,56 euro bildu zituen billeteak salduta. Kalkulatu zenbat bidaiari joan diren tarifa mota bakoitzarekin, jakinda deskontu handiena duten bidaiariak bi aldiz gehiago direla gainerako bidaiariak baino.

27 Denda batean, bi jaka eta blusa bat erosi eta 200 € ordaindu dugu. Dendara itzuli eta jaka bat eta praka-pare bat erosten baditugu, eta blusa itzuli, 100 € ordainduko dugu. Zenbat ordainduko dugu bost jaka, praka-pare bat eta blusa bat erosita?

28 Kutxazain automatiko batek 95 billete ditu guztira, 10, 20 eta m eurokoak. Badakigu kutxazainean 2 000 € daudela, eta 10 euroko billeteen kopurua bi aldiz handiagoa dela 20 euroko billeteen kopurua baino.

a) Planteatu problemaren baldintzak adierazten dituen ekuazio-sistema bat. Frogatu m ∈{5, 50, 100} bada, sistema bateragarri determinatua dela.

b) Egon litezke 5 edo 100 euroko billeteak kutxazainean?

c) Ebatzi sistema m = 50 kasurako.

29 Irenek A enpresako 200 akzio erosi ditu, B enpresako 150, eta C-ko 100. Guztira 3 300 € ordaindu du. Jesusek 3 750 € gastatu ditu A enpresako 50 akzio, B-ko 120 eta C-ko 240 erosteko. Datu horiekin, jakin dezakegu akzio bakoitzaren prezioa zein den? Eta akzio bakoitzaren prezioa kopuru oso bat bada, 1 € eta 12 € bitartekoa, biak barne?

30 Pertsona batek 6 000 €-ko irabaziak lortu ditu 60 000 € inbertituta hiru enpresatan: A, B eta C. A eta B enpresetan guztira inbertitutakoa m aldiz izan da C-n inbertitutakoa, eta irabaziak % 5ekoak izan dira A-n, % 10ekoak B-n eta % 20koak C-n.

a) Planteatu ekuazio-sistema bat enpresa bakoitzean zenbat diru inbertitu den jakiteko.

b) Frogatu m > 0 bada sistema bateragarri determinatua dela.

c) Aurkitu soluzioa m = 5 kasurako.

31 Biltegi batek A, B eta C hiru markak egiten duten produktu jakin bat banatzen du. A markak 250 gramoko kaxatan ontziratzen du, eta 10 €-an saldu; B markak 500 gramoko kaxatan ontziratzen du, eta 18 €-an saldu; eta C markak 1 kiloko kaxatan ontziratzen du, eta 33 €-an saldu. Biltegian bezero bati produktu horren 2,5 kilo saldu dizkiote, 100 €-an. Jakinda guztira 5 kaxa saldu dizkiotela, kalkulatu mota bakoitzeko zenbat kaxa erosi dituen. Soluziorik al du problemak?

32 Kafetegi batean, A mahaikoek 6 kafe eta 3 tostada eskatu dituzte eta 12 € ordaindu dute, eta B mahaikoek, 6 kafe eta m tostada eskatuta, 13,60 € ordaindu dute.

a) Planteatu ekuazio-sistema bat, x eta y ezezagunak kafearen prezioa eta tostadaren prezioa izanik, hurrenez hurren.

b) m-ren zer baliotarako dauka soluzioa aurreko sistemak? Soluziorik egonez gero, bakarra izango da beti? Eskatu ahal izan dituzte B mahaikoek 4 tostada? Erantzuna baietz bada, zenbat balio du kafe batek?

33 Lagun batzuek, atzo, 4 freskagarri, 3 ogitarteko eta 5 izozki eskatu zituen taberna batean, eta 30,60 € ordaindu zuten guztira. Aurreko egun batean, 2 freskagarri, ogitarteko bat eta 2 izozki erosita, 12,30 € ordaindu zuten.

a) Gaur ere taberna horretan izan dira, eta 6 freskagarri, 5 ogitarteko eta 8 izozki eskatu dituzte. Zenbat ordainduko dute? Arrazoitu zure erantzuna.

b) Freskagarri batek, ogitarteko batek eta izozki batek 8,20 € balio badute, zein da bakoitzaren prezioa banaka?

34 Lantegi batean, goizeko txandan kontsumitu dituzten erregai-tonak m aldiz dira arratsaldeko txandan kontsumitutako tonak.

Gainera, badakigu arratsaldeko txandan m tona gutxiago kontsumitzen dituztela goizeko txandan baino.

a) Planteatu eta eztabaidatu problema hori m-ren funtzioan.

b) Izan liteke goizeko txandan bi aldiz erregai gehiago kontsumitzea arratsaldeko txandan baino?

c) m = 2 dela pentsatuz gero, zenbat kontsumitzen da arratsaldeko txandan?

35 Herrialde batek A, B eta C hiru markatako 21 000 ibilgailu inportatu ditu, 10 000, 15 000 eta 20 000 euroan, hurrenez hurren. Ibilgailuak 322 milioi euro kostatu dira guztira. Badakigu 21 000 ibilgailu daudela, B markakoak eta k aldiz A markakoak zenbatuta.

a) Planteatu sistema bat problemaren baldintzekin, marka bakoitzeko ibilgailu-kopuruaren funtzioan.

b) Ebatzi sistema k = 3 kasurako.

c) Egiaztatu sistemak ez duela soluziorik k = 2 kasuan.

Galdera teorikoak

36 Zuzena ala okerra? Arrazoitu eta jarri adibideak.

a) Bi ezezaguneko bi ekuazio dituen eta bateragarri indeterminatua den sistema bati ekuazio bat erantsita, sistema hori bateragarri determinatua bihur dezakegu, edo bateraezina.

b) Hiru ezezaguneko hiru ekuazio dituen eta bateragarri determinatua den sistema bati ekuazio bat erantsita, sistema hori bateragarri indeterminatua bihur dezakegu.

c) xy za

xy za 2 24 22 1 22 ––+= += + * sistema bateraezina da a-ren balioa edozein dela ere

d) x x y y a b 32 –+= = * sistema bateragarri indeterminatua da a-ren

eta b-ren edozein baliotarako

e) Sistema bateragarri determinatu bat eta bateragarri indeterminatu bat baliokideak izan daitezke.

37 Erantsi ekuazio bat xy z xy z22 1 22 3 ––+= += * sistemari, bihurtu dadin:

a) bateraezina. b) bateragarri determinatua.

c) bateragarri indeterminatua.

AUTOEBALUAZIOA

1 Ebatzi eta interpretatu sistema hauek geometrikoki:

Sakontzeko

38 a-ren zer baliotarako da sistema hau bateraezina?

2 Eztabaidatu sistema hau eta ebatzi, ahal denean:

• Izan daiteke bateragarri indeterminatua a = 2 baliorako?

• Ebatzi a = 2 den kasuan.

• a ≠ 1 eta a ≠ 2 bada, izan daiteke bateragarri determinatua?

39 Ekuazio-sistema hau edukita:

a) Arrazoitu parametroen a = 0, b = 1, c = 2 balioetarako sistema bateragarria dela.

b) Zehaztu zein izan behar diren a, b eta c parametroen balioak (x, y, z) = (1, 2, 3) sistemaren soluzioa dela egiaztatzeko.

c) Arrazoitu soluzio hori bakarra den ala ez den.

4 Ekuazio hauek ditugu: xy z xy

a) Erantsi ekuazio bat sistema bateraezina izan dadin.

b) Erantsi ekuazio bat bateragarri determinatua izan dadin.

c) Erantsi ekuazio bat bateragarri indeterminatua izan dadin.

Arrazoitu zer prozedura erabili duzun kasu bakoitzean.

5 Ekuazio linealen sistema hau daukagu:

3 Kutxazain automatiko batean 1 330 € daude, 10 €, 20 € eta m €-ko billeteetan. Badakigu guztira 97 billete daudela, eta 10 €-koak bi aldiz gehiago daudela 20 €-koak baino.

a) Planteatu ekuazio-sistema bat mota bakoitzeko zenbat billete dauden jakiteko.

b) Frogatu m ∈{5, 50, 100, 200} bada sistema bateragarri determinatua dela, eta ebatzi ezazu m = 50 kasuan.

c) Arrazoitu kutxazainean 100 €-ko billeterik egon daitekeen.

a) Aurkitu sistema bateraezin egingo duen a -ren balio bat.

b) Eztabaidatu ba al dagoen sistema bateragarri determinatua egiten duen a-ren baliorik.

c) Ebatzi sistema a = 0 kasuan.

➜ anayaharitza.es Ariketa hauen ebazpena.

Matrizeen aljebra 2

Aljebra modernoa

xix. mendearen aurretik, matematikak arduratzen ziren, funtsean, zenbakiez (aritmetika) eta irudiez (geometria). Aljebra bi ikasgaietarako tresna baliagarria zen, eta oso erabilgarria izan zen, bai alderdi praktikoetan, bai zientifikoetan. xix. mendearen hasieran, matematikaren beste adar batzuetan bezala, aljebraren barruan ere ideia eta joera berriak garatu ziren. Ondorioz, aljebraren xede gisa agertu ziren matrizeak, determinanteak, bektoreak...

Hamilton eta koaternioiak

xix. mendearen hasieran sortu ziren ideia berriak zenbaki konplexuetan oinarrituta sortu ziren. Gogora ekar dezagun a + bi zenbaki konplexu bat dela, funtsean, ( a , b ) zenbaki erreal pare bat. Eta 1 modulua eta α argumentua dituen zenbaki konplexu batekin biderkatuz gero lortzen den emaitza, geometrikoki, α angeluko bira gisa interpretatzen dela. Beraz, zenbaki errealen bikoteekin egiten diren eragiketak planoko transformazioekin erlazionatuta badaude, zergatik ez aztertu zenbaki errealen hirukoteetatik sortzen den aljebra?

Hamilton (1805-1865) saiatu zen a + bi + cj formako hirukoekin egindako eragiketei zentzua ematen, eta, horretarako, i eta j aldagaiei i irudizko unitatearen antzeko funtzioa eman zien, baina ez zuen lortu horrek funtzionatzea. Hamabost urteko ibilbide luzearen eta saiakera askok huts egin ondoren, 1843ko egun batean, emaztearekin Dublingo zubi batean paseatzen ari zela, ideia bat bururatu zitzaion: hirukoen ordez, a + bi + cj + dk formako laukoteak erabiltzea. Primeran funtzionatu zuen. Hamiltonek berak «koaternioi» deitu zien interpretazio geometriko emankorra zuten egitura aljebraikodun zenbakizko laukote horiei. Horrela, eremu handia ireki zien aljebrari bereziki eta zientziei oro har. Adibidez, koaternioiek higiduraren dinamika hiru dimentsiotan deskribatzeko balio dutenez, hainbat arlotan erabili izan dira: errealitate birtualetako grafikoetan, bideo-jokoen programazioan, robotikan, espazio-denboraren geometriaren azterketan, abiazio komertzialaren nahiz transbordadore espazialen hegaldi- software an… Hamilton matematikari bikaina izan zen, baina ekarpen nabarmenak egin zizkion fisikari ere (optika, dinamika, mekanika). Haurra baino ez zela hainbat hizkuntza menderatzen zituen, eta talentu goiztiartzat hartu zuten. Filosofiarekiko eta literaturarekiko interes handia izan zuen beti, eta unibertsitatean hain ospe handia lortu omen zuen, ezen «lorategietako belarra zapaltzen uzten zioten», nahiz eta erabat debekatuta zegoen. Seguru aski, noizbait, bere hausnarketetan murgildurik, konturatu gabe belar gainean ibili zen, eta, jakina, inor ez zen ausartu ezer aurpegiratzera.

William Rowan Hamilton

Matrizeak

Matrizeak, zenbakien kutxa laukizuzenen bidez adierazita, oso antzinatik erabiltzen dira. Txinatarrek, K.a. ii. mendean, tauletan jasotzen zituzten hiru ezezaguneko hiru ekuazio linealeko sistemen zenbakizko elementuak. Eta zenbaki horien transformazioen bidez, soluziora iristen ziren.

Beraz, esan genezake, matrizeen eremua sortu aurretik ere matrizeak garatuta eta finkatuta zeudela, baina notazioa, berez, 1843an erabili zuen lehen aldiz Cayleyk. Entitate independente gisa hartu zituen, eta matrizeen aljebra garatu zuen (batuketa eta biderketa, unitate-matrizea, matrize nulua, matrize baten alderantzizko matrizea). Lehena izan zen matrizeak sakon aztertzen eta haiei buruzko artikuluak argitaratzen, eta, beraz, matrizeen teoriaren sortzailetzat hartzen da. 1858an teoria horri buruzko memoria bat argitaratu zuen, matrizearen lehen definizio abstraktua jasotzen duena.

Arthur Cayley (1821-1895)

«Matrize» izena Cayleyren lagun handi batek asmatu zuen 1850ean, Sylvesterrek.

EBATZI

Apalategi modularrak

Enpresa batek apalategi modularren hiru modelo saltzen ditu (A1, A2, A3), eta horiek, era berean, lau modulu-motaz osatuta daude: M1, M2, M3, M4.

Apalategi-modelo bakoitza zer moduluk eratzen duten eskuineko grafikoan ageri da deskribatuta.

Informazio hori alboko taularen bitartez ere adierazi daiteke.

Era berean, moduluak hainbat osagaiz osatuta daude: finkapen-elementuak O1, zurezko pieza handiak O2, eta zurezko pieza txikiak O3.

Adierazi taula baten bitartez moduluen osagaiei buruzko diagraman bildutako informazioa.

Zenbakizko taula hauek matrizeak dira:

Ikusten duzun moduan, errenkadak eta zutabeak dituzten laukizuzen-itxurako kaxak dira.

Lehenengoa 3 errenkada eta 4 zutabe dituen matrize bat da. Hau da, 3 × 4 dimentsioa du.

Bigarrena 1 × 5 dimentsioko matrize bat da (1 errenkada, 5 zutabe). Matrize mota horri errenkada-bektore esaten zaio, eta goiko hori 5 dimentsioko errenkadabektore bat da.

Hirugarrena 4 dimentsioko zutabe-bektore bat da (4 × 1 matrizea da).

Laugarrena 3 × 3 dimentsioko matrize bat da. 3 ordenako matrize karratu esaten zaio

• Matrizeak laukizuzen-itxurako zenbakizko taulak dira:

Honako hau m errenkada eta n zutabe dituen matrizea da. m × n dimentsiokoa da.

aij elementuak zenbaki errealak dira (aij ∈ Á).

Matrize generiko bat izendatzean, aurreko horren modukoa, elementu bakoitzean bi azpi-indize idazten dira, zer errenkadatakoa eta zer zutabetakoa den zehazteko. Esaterako, a23 gaia bigarren errenkadan eta hirugarren zutabean dago. Dena dela, goiko matrize hori sinplifikatzeko, honela izendatu dezakegu:

() a ,, ,, ij jn im 1 1 … = = edo, bestela, A = (aij)m, n edo, besterik gabe, (aij)

m = n bada, matrizea karratua dela esaten dugu

• Bi matrize berdinak dira dimentsio berekoak direnean eta, gainera, elementuz elementu berdinak direnean:

() () Aa Bb , ,

= = 4 A = B ⇔ aij = bij

ij mn ij mn

• A = (aij)m, n matrize baten matrize iraulia da At = (aji)n, m beste matrize bat, eta lortzen da A matrizean errenkaden tokian zutabeak jarrita, eta zutabeen tokian errenkadak. A matrizearen iraulia izendatzeko A' ere erabiltzen da; hau da, At = A'

• A matrize bati simetrikoa deitzen zaio baldin eta At = A bada. Matrize bat simetrikoa izateko, nahitaez karratua izan behar da.

• Eskuineko matrizeari triangeluarra esaten zaio, karratua delako eta diagonal nagusiaren azpian dauden elementu guztiak zero direlako:

Aztertu honako adibide hauek:

3. COVID-19aren pandemiari buruzko jarraipenaren barruan, lau herritan astebetean izan diren kutsatze-kopuruak, ospitaleratze berriak eta altak zenbatu ditugu.

HAUSNARTU

3. adibidea oso xalo eta sinplea da, baina aukera daukagu egoera errealagoa irudikatzeko, kontuan hartuz gero, esaterako, positibo faltsuak, gaixoek izan dezaketen sintometako bakoitza, eta abar. Eta, beste alde batetik, aintzat hartuta herri multzo handi bat. Matrize itzel bat izango litzateke, errenkada eta zutabe ugari dituena.

Argi dago datuek 4 errenkadako eta 3 zutabeko matrizea osatzen dutela.

4. Enpresa bateko zuzendari emakumezkoak asteko egun bakoitzean beste zeregin batzuetan zenbat ordu egin dituen zenbatu du:

Ordenagailuek aukera ematen dute mota horretako matrizeak gordetzeko, baita haiekin eragiketak egiteko ere.

× 5 matrize bat da. 1 Idatzi matrize hauen matrize irauliak:

2 Idatzi X t = X beteko duen X matrize bat; hau da, simetrikoa izango dena.

3 Idatzi honako egoera hau deskribatuko duen matrize bat:

Eragiketak matrizeekin

Matrizeak batu egin daitezke, zenbaki batekin biderkatu daitezke, edota beren artean biderkatu daitezke. Ondoren ikusiko duzunez, eragiketa horietako bakoitzak berezitasun eta interpretazio propioak ditu:

Matrizeen arteko batuketa

Bi matrizeren arteko batuketa egiteko, dimentsio bera izan behar dute. Dimentsio berekoak direnean, elementuz elementu batu behar dira:

(aij)m, n + (bij)m, n = (aij + bij)m, n

➜ Eragiketak matrizeekin.

matrizeak ezin dira batu, ez direlako dimentsio berekoak

3. Aurreko orrialdeko 3. adibidean pandemiak iraun duen aste guztiei dagozkien kutsatze-kopuruen, ospitaleratzeen eta ospitaleetako alten matrizeak bagenitu, horien batura izango litzateke pandemiak iraun duen bitartean aipatutako herrietan guztira izandako kutsatzeak, ospitaleratzeak eta ospitale-altak biltzen dituen matrize bat.

Zenbaki baten eta matrize baten arteko biderketa

Zenbaki bat matrize batekin biderkatzeko, matrizeko elementu bakoitza zenbakiarekin biderkatu behar da: k · (aij)m, n = (kaij)m, n

2. Aurreko orrialdeko 4. adibidean, enpresako zuzendariak uste badu hilabete jakin bat osatzen duten lau asteak gutxi gorabehera berdinak izango direla, hileko dedikazioaren matrizea lortzeko, nahikoa izango da asteko dedikazioaren matrizea bider 4 egitea.

Pentsatu eta praktikatu

1 Matrize hauek izanda:

Errenkada-matrize baten eta zutabe-matrize baten arteko biderketa

Dimentsio bera duten errenkada-bektore baten eta zutabe-bektore baten arteko biderketaren emaitza bi matrizeak elementuz elementu biderkatu eta batuta lortzen den zenbaki bat da:

OHARRA

Definizio horrek errenkada-bektore bat zutabe-bektore batekin biderkatzean balio du, baina ez biderkagaien ordena alderantzizkoa denean.

2 Dibisak trukatzeko bulego batean prezio hauek eskaintzen dituzte gaur:

1 $ = 0,85 €

1 ¥ = 0,008 €

Enpresari batek euroak behar ditu. Dibisa-bulegora 70 $, 20 € eta 15

¥-rekin heldu bada, zenbat eurorekin irtengo da?

3 Unitatearen hasierako «Apalategi modularrak» probleman, A1 motako apalategi bat egiteko O2 motako zenbat osagai behar diren jakin nahi dugu.

Konturatzen bazara, guztira eurotara aldatutako kopurua errenkada-bektore baten eta zutabe-bektore baten arteko biderketa eginda lortu daiteke: (,

Bulegotik 79,62 €-rekin irtengo da.

Argi dago ariketa hau matrizeak erabili gabe ebatz zitekeela.

Honela egin dezakegu:

A1 apalategiko (M1, M2, M3, M4) modulu-kopurua: (1 2 1 0)

O2 osagaien kopurua moduluetako bakoitzean:

Nola idatz liteke kalkulu hori matrizeen bitartez?

Osagaien kopuru osoa:

1 Egin F · C biderketa:

Ebatzitako ariketak

Matrizeen biderketa

A eta B bi matrize izanda, A · B biderketa egiteko, lehenengoaren zutabe-kopuruak bat etorri behar du bigarrenaren errenkada-kopuruarekin.

Hori gertatzen bada, A · B = C biderkadura beste matrize bat da, eta horren elementuak lehenengoaren errenkada-bektore bakoitza bigarrenaren zutabe-bektore bakoitzarekin biderkatuta lortzen dira, honela:

() () Aa Bb , ,

= = 4 A · B = C = (cij)m,p

ik mn kj np

cij da A-ko i errenkadaren eta B-ko j zutabearen arteko biderkadura:

OSO GARRANTZITSUA

Matrizeen A · B biderketa egiteko nahitaezkoa da A-ren errenkada bakoitzeko bektoreak B-ren zutabe bakoitzeko bektoreen dimentsio berekoak izatea.

A · B = C (m, n) (n, p) (m, p)

Lortu dugun C matrizeak A-k adina errenkada (m) eta B-k adina zubate (p) ditu

Aztertu, adibide hauen bidez, nola egiten den matrizeen arteko biderketa:

ZUTABE-BEKTOREA BIDER

2. Jostailu-enpresa batek hiru kutxa tematiko saltzen ditu, barnean pertsonaiak, garraiobideak, osagarriak eta txabolak dituztela.

A matrizea: kutxa tematiko bakoitzak (pirata-ontzia, Po; etxaldea, Et; eta ospitalea, O) zenbat pertsonaia, Pe; garraiobide, Ga; osagarri, Og; eta txabola, Tx; dituen.

B matrizea: Zer prezio duen, eurotan, osagaietako bakoitzak bi fabrika desberdinetan, F1 eta F2.

Ikusten duzunez, C · F biderkadura 4 × 4 dimentsioko matrize bat da. Kalkula ezazu.

A · B matrizeak zehazten du zer prezio duen kutxa tematikoetako bakoitzak fabriketako bakoitzean.

Adibidez, 57 kantitateak esan nahi du F2 fabrikak 57 € kobratuko duela pirata-ontziaren kutxa tematikoa egitea.

➜ anayaharitza.es

Matrizeen eragiketa konbinatuak indartzeko ariketak.

Ebatzitako ariketak

1 Unitatearen hasieran emandako «Apalategi modularrak» problema grafiko honen bidez laburbildu genezake:

Apalategiak Moduluak Osagaiak

Erabili matrizeen biderketa apalategiko modulu bakoitzak mota bakoitzeko zenbat osagai behar dituen lortzeko, apalategia zer moduluk osatzen duten kontuan hartuta.

2 Truke-bulego batean hiru txanpon motarekin lan egiten dute: euroak, dolarrak eta yenak. Edozein txanponetako kantitateak hartzen dituzte, eta kanbioa ere edozein txanponetan ematen dituzte.

1 € = 1,18 ↔ 1 $ = 0,85 €

1 € = 125 ¥ ↔ 1 ¥ = 0,0080 €

1 $ = 106 ¥ ↔ 1 ¥ = 0,0094 $

Bezero batek 15 $, 27 € eta 2 500 ¥

ditu. Zenbateko kapitala du dolarretan? Eta zenbatekoa eurotan? Eta

A apalategi bakoitza M zer moduluk eratzen duten deskribatzen duten grafikoak A matrizean daude laburbilduta.

M modulu bakoitza O zer osagaik eratzen duten deskribatzen duten grafikoak B matrizean daude laburbilduta.

Pentsatu eta praktikatu

Txanpon trukea erakusten duen taula honako hau da:

dezagun 15

€ eta 2 500 yenen txanpon-trukearen emaitza, hiru txanponetan.

truke trukerako trukearen emaitza matrizea kantitateak txanpon desberdinetan

2 Egin honako matrize hauen artean egin daitezkeen biderketa guztiak:

3 Saiatu 3 × 3 dimentsioko I3 matrize bat lortzen, kontuan izanda A (3 × 3) edozein matrize karraturekin biderkatuta berdin geldituko dela.

Hau da: A · I3 = I3 · A = A

Aurreko berdintza hori egiaztatzen duen I3 matrizeari 3 ordenako unitate-matrize esaten zaio.

Bere fisonomia zein den dakizunean, edozein ordenatako unitate-matrizea lortzen jakingo duzu.

Matrizeen arteko eragiketen propietateak

Matrizeen eragiketek oso egitura interesgarria ematen dieten propietate batzuk dituzte. Ikus ditzagun.

Matrizeen arteko batuketaren propietateak

m × n dimentsioko matrizeak batu egin daitezke eta emaitza m × n dimentsioko beste matrize bat da. Gainera, batuketak propietate hauek betetzen ditu:

1. Elkartze-propietatea: (A + B ) + C = A + (B + C )

2. Trukatze-propietatea: A + B = B + A

3. Elementu neutroa: elementu guztiak 0 dituen 0m,n matrizea m × n dimentsioko beste edozein matrizerekin batuz gero, bigarren matrize hori berdin uzten du; hau da, A + 0 = 0 + A = A

4. A matrize orok –A aurkakoa du: A = (aij ) matrizearen aurkakoa –A = (–aij ) da; izan ere, (aij ) + (–aij ) = (aij – aij ) = (0) = 0.

KONTUAN IZAN

Propietate trukakorrak parentesiak kentzeko modua ematen du:

MATRIZE ANTISIMETRIKOA

Matrize karratu baten aurkakoa eta iraulia berdinak direnean, antisimetrikoa dela esaten da. Adibidez:

Lau propietate horiek laburbiltzeko esaten da m × n dimentsioko matrizeen Mm,n multzoa talde abeldarra dela batuketari dagokionez.

Zenbaki eta matrizeen arteko biderketaren propietateak

a, b ∈ Á eta A, B ∈ Mm,n badira, honako propietate hauek betetzen dira:

1. Elkartze-propietatea: a · (b · A) = (a · b) · A

2. I. motako banatzea: (a + b) · A = a · A + b · A

3. II. motako banatzea: a · (A + B) = a · A + a · B

4. Bider 1 zenbakia: 1 · A = A

1 Egiaztatu zenbakien eta matrizeen arteko biderketaren 1. propietatea:

NOMENKLATURA

Elementuen multzo bat talde abeldarra dela esaten dugu, baldin eta elementu horien artean honako propietateak betetzen dituen eragiketa bat definitzen badute:

• Elkarkorra.

• Trukakorra.

• Elementu neutroa.

• Aurkako gaia.

1 Egiaztatu zenbakien eta matrizeen arteko biderketaren 2. eta 3. propietateak, matrize hauek erabilita:

Matrizeen arteko biderketaren propietateak

1. Elkartze-propietatea: (Am,n · Bn,p) · Cp,q = Am,n · (Bn,p · Cp,q)

Propietate honek modua ematen digu parentesiak kentzeko zenbait matrize biderkatzen ditugunean (beti ere, dimentsioak kontuan hartuz, matrizeetako bakoitza hurrengoarekin «biderkagarria» bada).

2. Matrizeen arteko biderketa ez da trukakorra.

Horrek esan nahi du biderkatu behar diren matrizeak ageri diren ordenan idatzi behar ditugula. Eta, beraz, honelako adierazpenak erabiliko ditugu:

«M matrizea ezkerretik (edo eskuinetik) biderkatuta dago A matrizearekin».

1 Egiaztatu elkartze-propietatea kasu hauetarako:

OSO GARRANTZITSUA

Matrizeetan, orokorrean, A · B eta B · A ez dira berdinak.

2 Egiaztatu matrizeen arteko biderketa ez dela trukakorra, adibide batzuk erabiliz.

• A matrizea 3 × 2 ordenakoa bada, eta B matrizea 2 × 4 ordenakoa, A · B egin daiteke, baina B · A, ez.

•

A · B eta B · A egin daitezke, baina

· B da 3 × 3 dimentsiokoa, eta B · A da 2 × 2 dimentsiokoa •

3. Banatze-propietateak

A, B, C, D matrizeak eragiketak egiteko moduko dimentsiokoak badira, honako propietate hauek betetzen dira:

2 Egiaztatu banatze-propietateak honako matrize hauetarako:

Matrize karratuak

Ordena jakin bateko matrizeak, Mn,n, elkarrekin batu daitezke, baita zenbaki batekin biderkatu ere. Baina, horrez gain, elkarrekin biderkatu daitezke. Eragiketa horiek orain arte ikasitako propietate guztiak betetzen dituzte, eta besteren bat

(aij)n,n matrize karratu baten a11, a22, …, ann elementuek diagonal nagusia eratzen dute. Eta diagonal nagusiko elementuak 1 eta gainerako guztiak 0 dituen In matrizeak honako propietate hau du:

∈ Mn,n edozein dela ere, A · In = In · A = A. Horregatik esaten dugu In unitatematrizea dela

NOMENKLATURA

Unitate-matrizeari identitate-matrize ere esaten zaio.

Matrize baten alderantzizkoa

Mn,n multzoan biderketa definiturik dagoenez (hau da, n ordenako bi matrize karraturen arteko biderkadura n ordenako beste matrize karratu bat denez), eta, gainera, unitate-matrizea existitzen denez, derrigorrezkoa dirudi galdera hau egitea: matrize karratu guztiek alderantzizkoa dute? Hau da, A matrize karratu bat emanda, existitzen da A · A–1 = A–1 · A = I betetzen duen A–1 beste matrize bat? Adibidez:

NOMENKLATURA

Alderantzizkoa duten matrize karratuei erregular esaten zaie.

Alderantzizkorik ez duten matrize karratuei singular esaten zaie.

Erantzuna ezetz da. Matrize karratu batzuek badute alderantzizkoa, baina beste batzuek ez. Ondoren azalduko dugun metodoak matrize baten alderantzizkoa lortzeko balio du (baldin eta alderantzizkorik badu), edo alderantzizkorik ez duela jakiteko

Matrize baten alderantzizkoa, Gaussen metodoaren bidez

A matrize baten A–1 alderantzizkoa lortzeko, A matrizeari unitate-matrizea lortzeko ezarri beharreko aldaketa berberak egingo dizkiogu I unitate-matrizeari.

( I | A–1 )

Praktikan, A matrizea jarri, eta eskuinean I matrizea idatziko dugu. A matrizea I bihurtzeko egin beharreko aldaketak egingo ditugu. Ondorioz, I matrizearen eskuinera lortuko dugun matrizea A–1 da. Egindako aldaketa guztiak izango dira aurreko ikasturtean ekuazio-sistema bat Gaussen metodoaren bidez ebazteko egiten genituenak. Ezkerreko aldean zeroen errenkada bat ageri bada, A matrizeak ez du alderantzizkorik.

➜ anayaharitza.es

Gaussen metodoak matrize baten alderantzizkoa lortzeko balio duela justifikatzea.

➜ Matrize baten alderantzizkoa.

Ebatzitako ariketak

matrizeak ez du

1 Kalkulatu honako matrize hauetako bakoitzaren alderantzizkoa Gaussen metodoa erabiliz, edo aurkitu alderantzizkorik ez duela:

Kalkulatu honako matrizeetako bakoitzaren alderantzizkoa, edo aurkitu ez duela:

Pentsatu eta praktikatu

n ordenako matrize karratuen aljebra

n ordena jakin bateko matrize karratuen Mn,n multzoan, bi barne-eragiketa daude (n ordenako bi matrize karraturen batuketa zein biderketaren emaitza ordena bereko beste matrize karratu bat da), eta kanpo-eragiketa bat (zenbaki erreal baten eta matrize karratu baten biderketaren emaitza ordena bereko beste matrize karratu bat da).

• barne-eragiketen propietateak

A, B, C, I ordena bereko matrize karratuak dira.

batuketa biderketa

elkarketa (A + B) + C = A + (B + C ) (A · B) · C = A · (B · C )

trukaketa A + B = B + A Ez

elementu neutroa 0; A + 0 = 0 + A = A I; A · I = I · A = A

elementu simetrikoa A-ren aurkakoa –A da. A + (–A ) = (–A ) + A = 0

Matrize batzuek  A–1

alderantzizkoa dute:

A · A–1 = A–1 · A = I

banaketa A · (B + C ) = A · B + A · C, (B + C ) · A = B · A + C · A

Propietate horiei esker, n × n ordenako A, B, C matrizeak jakinda eta X matrize ezezaguna edukita, AX + B = C motako ekuazioak honela ebatz ditzakegu (A matrizeak alderantzizkoa izan behar du):

AX + B = C → AX = C – B → A–1(AX ) = A–1(C – B) → X = A–1(C – B)

• kanpo-eragiketaren propietateak

A, B matrizeak dira, eta a, b, zenbaki errealak.

elkarketa (a · b) · A = a · (b · A)

banaketa (a + b) · A = a · A + b · A a · (A + B) = a · A + a · B

1 zenbakiarekin biderkatzea 1 · A = A

Propietate hauek guztiak Mn,n multzoari aljebra izeneko egitura ematen diote. Ondorioz, erraz egin daitezke elementuen arteko eragiketak.

BARNE-ERAGIKETA

Matrizeen arteko batuketa zein biderketa barne-eragiketak dira, Mn,n multzoko elementuen (matrizeak) arteko eragiketak egiten direlako eta emaitza ere Mn,n multzoko elementua delako.

➜ anayaharitza.es

Matrize karratuen eragiketa konbinatuak indartzeko ariketak.

KANPO-ERAGIKETA

Zenbaki baten eta matrize baten arteko biderketa kanpo-eragiketa bat da, Á eta Mn,n multzo desberdinetako elementuen arteko eragiketa baita.

1 Ebatzi AX + B = C matrize-ekuazioa, honako hau jakinda:

A = 2 5 3 1 eo B = 3 1 1 1 –eo

C = 17 5 24 26 –eo

Ebatzitako ariketak

2 Ebatzi matrize-ekuazioen sistema hau:

X X Y Y A B 2 3 3 –+ = = )

honako hau kontuan hartuz:

A = 20 2 5 15 ––––

B = 23 4 17 15 –

eta X eta Y ezezagunak 2 × 2 ordenako matrizeak direla jakinda.

Oso egokia da laburketa-metodoa ezartzea. Horretarako, bi berdintzak atalez atal

tuko ditugu

Lehenengo ekuazioan ordezkatuko dugu:

3 Matrize hauek izanda:

A = 1 2 0 7 eo B = 1 4 5 1 ––

egiaztatu honako hauek:

a) A · (B + C ) = (A · B) + (A · C )

b) (A + B) · C = (A · C ) + (B · C )

c) A · (B · C ) = (A · B) · C

4 A = 3 5 0 –1 eo eta B = 0 1 6 –3 eo dira.

=

0 1 eo

8 Egin beheko eragiketa horiek, matrizeak honako hauek

izanda: A = 1 0 2 3 eo B = 4 3 7 0 –eo C = 1 3 1 2 –eo

a) (A · B) + (A · C )

b) (A – B) · C

c) A · B · C

9 A = 1 0 2 1 eo matrizea izanda, egiaztatu (A – I )2 = 0 dela.

Aurkitu honako hau betetzen duen X matrizea: 3 · X – 2 · A = 5 · B

5 Aurkitu ondorengo hau betetzen duten 2 × 2 ordenako A eta B bi matrize: 2A + B = 1 2 4 0 eo A – B = 1 1 2 0 –eo

6 Aurkitu honako hau egiaztatzen duten X eta Y bi matrize: 2X – 3Y = 1 4 5 2 eo X – Y = 1 3 0 6 –eo

7 Esan nolakoa izan behar den honako baldintza hau betetzen duen X matrizea: X ·

10 Aurkitu matrize hauen alderantzizkoa: a)

c)

11

b)

c)

Matrize bateko errenkaden arteko erlazio linealak

Matrizeak oso laguntza garrantzitsua dira ekuazio-sistemak lantzeko, aztertzeko eta ebazteko. Horretarako, matrize baten heina interpretatu eta maneiatu behar da, eta kontzeptu hori hurrengo atalean ikasi eta erabiliko dugu.

Bidea prestatzeko, atal honetan matrize baten errenkaden (edo zutabeen) artean egon daitezkeen erlazioak aztertuko ditugu, eta hori guztia espazio bektorialaren kontzeptuaren barruan oinarrituko dugu.

Eremu bektoriala

V multzo bat daukagu, eta multzo horretako elementuen artean (bektore esango diegu) baldintza jakin batzuk betetzen dituzten bi eragiketa zehaztuta daude:

• V -ko bi elementuren arteko batuketa (+)

Bi bektoreren batura beste bektore bat da.

baldin eta u , v ∈ V, orduan u + v ∈ V.

• zenbaki batekin biderkatzea (·)

Zenbaki erreal baten eta bektore baten biderkadura beste bektore bat da. a ∈ Á eta u ∈ V, orduan a · u ∈ V

Horrez gainera, eragiketa horiek zenbait propietate betetzen badituzte, V multzoak + eta · (V, +, ·) eragiketekin batera espazio bektoriala eratzen duela esaten da.

• bektoreen konbinazio lineala

Eragiketa hauen bidez, bektore batzuetatik abiatuta beste batzuk lor daitezke. Adibidez, a, b, c zenbaki errealak badira eta u , v , w bektoreak badira, orduan a u + b v +c w bektore berri bat da. Esaten da u , v , w -ren konbinazio lineala dela.

• independentzia lineala

Zenbait bektore linealki independenteak (L.I.) dira bat bera ere ezin bada jarri gainerakoen konbinazio lineal moduan.

W = { v 1, v 2, v 3, …, v n} bektore-multzo bat da. W-ren heina esaten zaio multzo horretan dauden bektore linealki independenteen kopuru maximoari.

Zenbaki errealen n-koteak

(3, –5, 1) hirukote bat da. Bi hirukote honela batu daitezke: (3, –5, 1) + (7, 0, 4) = (10, –5, 5). Emaitza beste hirukote bat da. Hirukote bat zenbaki batekin biderkatu daiteke, honela: ,, –2 ·( ,, ) 35 1 –= 5 2 5 6 5 2 cm Emaitza hirukote bat da.

• Zenbaki errealen hirukote guztien multzoak (Á3) espazio bektorial bat eratzen du goian aipatutako eragiketekin batera: batuketa eta zenbaki erreal batekin biderkatzea.

• Beste horrenbeste esan genezake bikoteei buruz: (2, –1), (3, 4), (0, 5), …

• Baita laukoteei buruz ere: (0, –1, 3, 7), (4, 1/3, –2, 0), (0, 1, 0, 1), …

Oro har, (a1, a2, …, an) ∈ Án n-kote guztien multzoa, + eta · eragiketekin batera, espazio bektorial bat da.

BEKTOREAK EZ DIRA «GEZITXOAK» SOILIK

Bektorea gezi gisa adierazteak espazio bektorialaren ideia sortzen du: propietate jakin batzuk betetzen dituzten eragiketak zehaztuta dituzten bektoreen multzoa. Baina badira eragiketa eta propietate berberak dituzten «beste izate matematiko batzuk». Horregatik, espazio bektorialaren definizioa «gezi» bilduma bat baino askoz ideia zabalagoa eta irekiagoa da.

➜ anayaharitza.es Espazio bektoriala. Propietateak.

n-koteen mendekotasun eta independentzia lineala

(2, 3) eta (6, 9) bikoteak linealki mendekoak (L.M.) dira, (6, 9) = 3 · (2, 3) baita. Aldiz, (2, 3) eta (6, 8) bikoteak linealki independenteak dira, bietako bat ere ez ezin baita lortu bestea zenbaki batekin biderkatuta. Ikus dezagun hala dela, matrizeetako bat bestetik abiatuta jartzen saiatuta:

(6, 8) = a · (2, 3) = (2a, 3a) → / aa aa 62 3 83 83 == == 4 → → Ezin da!!

• Ziurra da hiru bikote linealki mendekoak direla. Adibidez, hauek:

(2, 3), (–1, 4), (14, –1). Hala direla egiaztatzeko, hau idatziko dugu: (14, –1) = a(2, 3) + b(–1, 4) = (2a – b, 3a + 4b)

Hortik sistema hau lortzen dugu: ab ab 214 34 1 ––

= += 4

Hau da, (14, –1) = 5 · (2, 3) + (– 4) · (–1, 4)

Soluzioak: a = 5, b = –4

• Arrazoitze bera erabiliko dugu (1, 2, 0), (0, 3, 4) eta (1, 0, 1) hirukoteak linealki independenteak direla egiaztatzeko. (0, 3, 4) ezin da jarri (1, 2, 0) eta (1, 0, 1) hirukoteen konbinazio lineal moduan.

(0, 3, 4) = a(1, 2, 0) + b(1, 0, 1) = (a + b, 2a, b)

Baina a + b = 3/2 + 4 ≠ 0. Sistemak ez du soluziorik.

• Ziurra da lau hirukote linealki mendekoak direla. Egiaztatu hauen kasuan: (1, 2, 0), (0, 3, 4), (1, 0, 1), (5, 1, –1). Berdintza hau ezartzen baduzu: (5, 1, –1) = a (1, 2, 0) + b (0, 3, 4) + c(1, 0, 1), soluzio hau lortuko duzu: a = 2, b = –1 eta c = 3.

• Eta berriro arrazoitze bera erabilita, lau laukote independenteak izan daitezke, baina bost ziurra da mendekoak direla. Egiaztatu laukote hauen kasuan: (1, 0, 0, 0), (0, 1, 0, 0), (0, 0, 1, 0), (0, 0, 0, 1) eta (7, 2, –4, 3).

Oro har, n-kote linealki independenteen kopuru maximoa n da. Hau da, n-tik gora

n-kote baditugu, ziurra da linealki mendekoak direla.

n-kote linealki independenteak ezartzeko modurik argiena hau da: (1, 0, 0, …, 0), (0, 1, 0, …, 0), (0, 0, 1, …, 0), …, (0, 0, 0, …, 1)

Pentsatu eta praktikatu

1 Adierazi kasu hauetako bakoitzeko matrizeak mendekoak ala independenteak diren.

a) (2, 3) eta (–4, 6) b) (1, –3) eta (–2, 6)

c) (1, 2), (–3, –4) eta (5, 6) d) (–2, –3, 0) eta (2, 3, 1)

2 Egiaztatu (2, 3, –1) ezin dela jarri (1, 2, 5) eta (0, –1, 2) hirukoteen konbinazio lineal moduan.

3 Egiaztatu (2, –1, 0), (1, 0, –1), (–2, 3, 1) eta (2, –3, 1) hirukoteak L.M. direla. Horretarako, aurkitu zein diren a, b eta c-ren balioak berdintza honetan: (2, –3, 1) = a(2, –1, 0) + b(1, 0, –1) + c(–2, 3, 1)

4 Zuzena ala okerra?

a) Gerta liteke lau bikote linealki independenteak izatea.

b) Edozein hiru hirukote hartuta, L.I. dira.

c) Edozein lau hirukote hartuta, ziurra da L.M. direla.

d) Bi laukote L.I. izan daitezke, baina lau laukote ziurra da linealki mendekoak direla.

e) (1, 0, 0, 0, 0), (0, 2, 0, 0, 0), (0, 0, –2, 0, 0), (0, 0, 0, 0, 1/2) eta (0, 0, 0, 3 , 0) boskoteak L.I. dira.

f) n-kote multzo bat linealki mendekoa da baldin eta multzoko baten batek koordenatu guztiak zero baditu.

Matrize baten heina

Matrize bateko errenkaden artean (baita zutabeen artean ere) mendekotasun linealeko erlazioak egon litezke, eta horrelako erlaziorik dagoen jakitea oso garrantzitsua da ekuazio-sistemak aztertzerakoan.

• errenkada-bektoreak matrize batean

Matrize baten errenkadak bektoretzat har daitezke. Eta baliteke linealki independenteak (L.I.) izatea, edota batzuk besteen mendekoak izatea linealki. Esate baterako:

A = 2 1 3 0 1 4 4 5 –fp Bere bi errenkadak L.I. dira.

B = f 5 6 1 11

1 3 17 2

(3.a) = 5 · (1.a) – 4 · (2.a) (4.a) = (1.a) + (2.a)

–– p Lehenengo bi errenkadak L.I. dira. Beste biak lehenengoen mendekoak dira linealki:

p Lehenengo bi errenkadak L.I. dira. Hirugarrena linealki bi horien mendekoa da:

(3.a) = (1.a) – (2.a)

A matrize baten heina, hein (A), da linealki independenteak diren errenkaden kopurua.

Horren arabera, aurreko hiru matrizeen heina 2 da:

hein(A) = 2, hein(B) = 2, hein(C) = 2

• zutabe-bektoreak matrize batean

Matrize baten zutabeak ere bektoretzat har daitezke. Eta matrize baten heina definitzeko, L.I. diren zutabe-kopurua har dezakegu. Baina zalantza gelditzen zaigu definizio honek ez ote duen nolabait aurrekoaren kontrakoa esaten. Hau da: izan liteke desberdina matrize batean L.I. diren errenkada-kopurua eta L.I. diren zutabe-kopurua? Hurrengo teoremak erakusten duenez, ezin liteke.

Teorema

Matrize batean, L.I. diren errenkaden kopurua bat dator L.I. diren zutabeen kopuruarekin. Horren arabera, matrize baten heina da L.I. diren errenkaden edo zutabeen kopurua.

Goiko A, B, C hiru matrizeen heina 2 denez, guztiek dituzten linealki independenteak diren bi zutabe. Hala da:

— A-n, lehenengo bi zutabeak L.I. dira, eta (3.a) = 4 · (1.a) – 3 · (2.a), (4.a) = 5 · (1.a) – 2 · (2.a).

— B-n, bi zutabeak L.I. dira.

— C-n, lehenengo biak L.I. dira, eta (3.a) = –1 · (1.a) – 1 · (2.a).

DIMENTSIOA ETA HEINA

3 × 5 matrize baten heina 3 da gehienez. Orokorrean, m × n matrize baten heina, gehienez, m edo n bi zenbakietan txikiena da.

2. unitatean, matrize baten heina modu eraginkorragoan lortzen ikasiko dugu. Horretarako, tresna matematiko berri bat erabiliko dugu: determinanteak

➜ anayaharitza.es Matrize batean linealki independenteak diren errenkaden kopurua linealki independenteak diren zutabeen kopuruarekin bat datorrela erakusteko egiaztapena.

➜ Matrize baten heina lortzea.

Matrize baten heina Gaussen metodoaren bidez lortzea

1. unitatean ikusi genuen bezala, ekuazio linealen sistema bat Gaussen metodoaren bitartez ebaztea da sistema horri ezartzea sistema mailakatua bihurtuko duten zenbait aldaketa.

Edozein matrize hartu (ez du derrigorrez ekuazio-sistema batekin lotuta egon behar) eta Gaussen metodoan bezala jokatzen badugu, egiten dugun aldaketa bakoitzak ez du matrizearen heina aldatzen; izan ere, aldatu dugun errenkadak mendekotasun edo independentzia lineal bera izaten jarraituko du gainerako errenkadekin.

Beraz, matrize baten heina zein den lortzeko, «zeroak egin» ditzakegu, Gaussen metodoan bezala. Azkenean lortzen dugun matrize mailakatuaren heina da (0 0 … 0) ez diren errenkaden kopurua, jakina 1

ALDERANTZIZKO MATRIZEA

Orain, honako irizpide hau eman dezakegu: n ordenako matrize karratu batek alderantzizkoa du baldin eta horren heina n bada; hau da, matrizearen errenkada guztiak L.I. badira.

Heina 4 da, lau errenkadak baitira L.I. Erraza da konturatzea n-kote mailakatu hauek L.I. direla, bakar bat ere ezin baita jarri besteen konbinazio lineal moduan. Beraz, matrize baten heina lortzeko, transformatu egingo dugu modu mailakatuan jarri arte.

Aurkitu matrize honen heina:

Ebatzitako ariketak eta problemak

1. Matrizeak eta grafikoak. Interpretazioa

A herrialde batean nazioarteko hiru aireportu daude, A1, A2, A3, eta B herrialde batean, lau aireportu, B1, B2, B3, B4

Astelehenean A-tik B-ra joan nahi duen pertsona batek honako hegaldi hauek ditu aukeran:

a) A eta B artean dauden hegaldiei buruzko informazioa ematen digun M matrizea hau da:

2

3 B4

matrize horrek adierazten ditu B herrialdetik C herrialdera asteartean joateko dauden hegaldiak.

a) Idatzi astelehenean A eta B artean dauden hegaldiak adierazten dituen matrizea.

b) Adierazi, grafiko baten bidez, asteartean B eta C artean dauden hegaldiei buruzko informazioa.

c) Irudikatu A eta C artean dauden hegaldi guztien artean B-tik pasatzen direnak deskribatzen dituen grafikoa.

d) Erabili matrizeen biderketa, eta lortu A aireportu bakoitzetik C aireportu bakoitzera B-ko aireporturen batetik igarota joateko dauden hegaldien konbinazio-kopurua.

d) Aurreko grafikoak deskribatzen ditu A-ko aireportu bakoitzetik B-koetara dauden hegaldiak (M matrizean laburbilduta daude), eta B-ko bakoitzetik C-koetara daudenak (N matrizean laburbilduta daude). M · N biderkadura-matrizeak adierazten du A-ko aireportu bakoitzetik C-ko aireportu bakoitzera B-koren batetik igarota dauden konbinazioen kopurua.

Ikusten duzunez, M · N matrizea dagokio c) ataleko erantzunaren grafikoari.

2. Eragiketak matrizeekin. Berdintza

Aurkitu 2 ordenako A eta B bi matrize karratu, honako hau betetzen dutenak:

• Bi matrizeen batura da 2 ordenako identitate-matrizea.

• A – B kenketa eginda, C = 1 2 3 4 eo -ren matrize iraulia lortzen da

EGIN ZUK

A = x y 2 3 –fp da. Aurkitu zein izan

behar diren x-ren eta y-ren balioak

A2 = A bete dadin. Matrize horiei idenpotenteak esaten zaie.

A eta B matrizeetako elementuei izena jarriko diegu:

Adierazitako eragiketak egin, eta emaitzak idatziko ditugu:

Soluzioa:

Bila gabiltzan matrizeak hauek dira:

3. Matrize alderantzikatu eta irauli berdinak

A = f a b 0

0 1 0

0 0 1 p matrizea izanda, kalkulatu zein izan behar diren a-ren eta b-ren balioak A matrizearen alderantzikatua bat etortzeko irauliarekin.

A matrizearen alderantzikatua irauliaren berdina bada, ortogonala dela esaten da.

EGIN ZUK

lortu dugun matrizeko gai bakoitza I matrizean toki hori betetzen duenarekin berdinduko dugu. 2 2 + p A · A t = I → f a ab ab b 0 1 0

eta 0 0 1

3 0 1 p = f a ab ab b 0 1 0

EGIN ZUK

matrizea:

X

A

∙

=

t

C

0 0 0 1 p → A · A t = f a b 0 1 0

A = (–1, 0 ,1), B = (3, 0, 1) eta

C = (4, –2, 0) matrizeak emanda, kalkulatu BtAX + C t = X betetzen duen X matrizea.

2 2

0 0 0 0 1

1 11

4. Matrize baten eta bere irauliaren dimentsioak

2 2 + p = f 0 0 1 0

0 0 1

ortogonala izateko. 0 p · f ab 0 0 01 0

10 p Elementuz elementu berdindu, eta lortutako sistema ebatziko dugu: a b

0 0 1

= += ab 0 = * → Soluzioak dira a = ±1; b = 0 Baldintza betetzen duten bi matrize daude, f 0 0 1 0

B

dugu:

B · B =

Kontuan

biderkadura

10 p eta f 1 0 0

0 0 1

(2A – I ) · (2A – I ) = 4A 2 – 2AI – I 2A + I 2

hartuz A 2 = A dela, 2AI = I 2A dela eta I 2 = I dela,

· B = 4

A – 4A +

0 1 0

0 0 1

– p

EGIN ZUK. Egiaztatu A 2 = A + I bada, orduan A alderantzikagarria dela (alderantzikagarria izatea erregularra izatea da).

Ebatzitako ariketak eta problemak

6. Matrizedun ekuazioak

Matrize hauek ditugu:

A = 4 3 5 4 eo B = 0 1 1 0 eo

a) Aurkitu behekoa betetzen duen X matrizea:

AX + B = I

b) A matrizea dugu:

A = 1 30 3 eo

Kalkulatu honako ekuazio hau betetzen duen X matrizea:

XA – 2X = A

a) Bila gabiltzan matrizea X = a c b d eo da. Bi modutan lor dezakegu: horren elementuak hartu eta AX + B = I berdintzako eragiketak eginez, bi ezezaguneko bi ekuazioko sistema lortu arte; edo X bakanduta, A-ren alderantzizko matrizearekin egoki biderkatu ondoren

Lehenengo metodoa

Beraz, X = 1 1 1 1

Bigarren metodoa

AX + B = I → AX = I – B → (*) A –1 AX = A –1 (I – B) → → IX = A –1 (I – B) → X = A –1 (I – B)

(*) Bi atalak A –1 matrizearekin biderkatuko ditugu ezkerretik A matrizearen alderantzizkoa Gaussen metodoa erabiliz kalkuluko dugu:

EGIN ZUK

Matrize karratu hauek emanda:

A = 2 3 1 2 eo eta B = 1 2 0 3 eo

aurkitu honako hau betetzen duen X matrizea:

AXA = 2BA

b) X bakanduko dugu, lehenengo atalean biderkagai komuna aterata eta kontuan izanda honako hau: 2X = 2XI = 2IX → X(A – 2I) = A.

Bi atalak bider (A – 2I )–1 egingo ditugu eskuinetik.

Horretarako, (A – 2I ) = 1 11 0

7. Biderkagai komuna. Alderantzizko matrizea

A matrize karratu bat da eta A2 + 2A = 3I betetzen du, I identitate-matrize bat izanik.

a) Aurkitu zein izan behar diren a-ren eta

b-ren balioak ekuazio hau bete dadin: A–1 = a A + b I.

b) Kalkulatu zein izan behar diren p-ren eta

q-ren balioak A4 = p A + q I bete dadin.

EGIN ZUK

Adierazi M –1 matrizea M-ren eta I-ren

funtzioan, jakinda M berdintza hau betetzen duen matrize karratu bat dela:

kalkulatuko dugu, eta bere alderantzizkoa,

a) Emandako baldintzan, I bakanduko dugu:

Biderkagai komun moduan

aterata, matrize bat lortuko dugu, ez zenbaki bat; beraz, 2I idatziko dugu. Gainera, kortxete artean dagoen adierazpena A matrizearen alderantzizkoa da, bien arteko biderkadura unitate-matrizea baita.

Bakandu X eta kalkulatu.

8. Matrize baten berreketa

1 0 1

A = f 0 1 0 0 1

1 p matrizea eta n ∈N

emanda, kalkulatu A-ren n-garren berretura.

EGIN ZUK

A = 1 3 0 1 eo matrizea eta n edozein zenbaki arrunt ditugu.

a) Kalkulatu A n

b) Aurkitu A 50 – A 20

n berretzailearen kasuan ere erregela berari jarraitzen diola onartuko dugu; hau da:

An-ren adierazpen hori An + 1 kasurako ere baliozkoa dela egiaztatu badugu, orduan baliozkoa da edozein n-tarako (indukzio-metodoa).

9. Matrize bat beste biren alderantzizkoekin biderkatuta bakantzea

a) Bakandu X matrizea C(A + X) B = I ekuazioan.

b) Lortu X matrizea, A = 3 1 4 2 eo ,

B =  1 0 1 1 eo eta C = 1 1 0 1 eo direla jakinda.

EGIN ZUK

Aurkitu AXB = A +  B egiaztatzen

duen X matrizea, A = 1 0 1 1 –eo eta

B = 4 1 1 0 –eo izanik.

10. Matrize baten heina

Aztertu zein den M matrizearen heina a-ren balioen arabera. Ba al dago hein (M) = 1 egingo duen a-ren baliorik? M =

2 1 01 p

EGIN ZUK

Aztertu B-ren barrutia m parametroaren arabera:

a) C –1 matrizearekin biderkatuko dugu ezkerretik, eta B –1 matrizearekin eskuinetik. C –1C(A + X )BB –1 = C –1

M matrizea zero posible guztiak egiteko moduan aldatuko dugu:

M matrizearen heina ezin da 1 izan a-ren balio batekin ere, lehenengo bi errenkadak linealki independenteak direlako a edozein dela ere

Gidatutako ariketak eta problemak

1. Matrizedun ekuazioa

Kalkulatu x, y, z honako hau kontuan izanda:

· x y zy x z 11 5 0 0 5 = e f e o p o

2. Matrize bat bakantzea

Zehaztu AXA – B = 0 betetzen duen X matrizea, kontuan izanda:

A = 3 2 1 1 eo , B =  5 1 2 3 –eo

eta 2 ordenako matrize nulua 0 dela.

3. Matrize trukagarriak

A = 1 2 1 0 eo matrizea izanda, lortu

A-rekin trukagarriak diren B matrize guztiak; hau da, A · B = B · A betetzen dutenak.

Idatzi bi parametroren funtzioan eta jarri adibide bat.

• Bihurtu berdintza hori ekuazio-sistema bat, lehenengo ataleko matrizeen biderketa eginez eta elementuz elementu bigarren ataleko matrizearekin berdinduz.

• Ebatzi lortu duzun sistema hori

Soluzioa: Lau soluzio daude: (2, 2, –1), (2, –2, 1), (–2, 2, 1), (–2, –2, –1).

• X bakantzeko, pasatu B bigarren atalera eta biderkatu berdintza hori A –1 matrizearekin eskuinetik eta ezkerretik.

• Aurkitu A –1, definizioa erabiliz (A · A –1 = I ) edo Gaussen metodoaren bidez.

Soluzioa: X = 4 3 3 2 –eo

• B matrizeak 2 ordenako matrize karratu bat izan behar du, eta elementu ezezagunekoa; adibidez, a c b d eo . Bete behar duen baldintza da AB = BA.

• Toki bera betetzen duten elementuak biderkatu eta berdinduta, lau ezezaguneko bi ekuazio dituen sistema bat lortuko duzu, infinitu soluzioduna. Hartu c eta d, eta adierazi a-ren eta b-ren funtzioan.

Soluzioa: A-rekin trukagarriak diren matrizeak dira B = a b b ab2–eo , a, b ∈Á.

Adibidez, a = 1 eta b = 2 badira, orduan, B = 1 4 2 –1 eo

A = 17 1 29 17 0

emanda, kalkulatu:

a) A2, A3, A4, …, A8 matrizeak.

b) Honako hau betetzen duten m eta n zenbaki errealak:

(A + I)3 = mI + nA

A = 2 0 0 –1 eo eta B =  8 6 9 7 ––eo matrizeak izanda, aurkitu XAX –1 = B betetzen duen X matrizea.

a) Egin A · A biderketa, lortu A2, eta kalkuluak eginda lortzen duzun emaitza biderkatu berriro A-rekin, A3 lortzeko. Aurreko emaitza horietatik abiatuta, gainerako berreketak lor ditzakezu zenbakizko biderketak egin gabe.

b) (A + I)3 kalkulatzeko, kontuan izan I 2 = I dela, eta erabili aurreko atalean lortutako emaitza. Koefizienteak berdinduta, m eta n lortuko dituzu

Soluzioa: a) A2 = –I, A3 = –A, A4 = I, A5 = A, A6 = –I, A7 = –A, A8 = I

b) m = –2, n = 2

• Biderkatu ekuazioaren bi atalak X matrizearekin eskuinetik.

• Hartu X = a c b d eo, eta biderkatu A eta B matrizeak X-rekin, ordena egokian. Bi ekuazio-sistema lortuko dituzu; bata, a-rekin eta c-rekin, eta bestea, b-rekin eta d-rekin

• Egiaztatu bi sistemak indeterminatuak direla. Adierazi c ezezaguna a-ren funtzioan, eta b ezezaguna d-ren funtzioan, eta idatzi X matrizea a-ren eta b-ren funtzioan

Soluzioa: X = / a a b b 23 eo matrizean a ≠ 0 eta b ≠ 0 betetzen duten infinitu soluzio daude X –1 existitzeko. Adibidez, a = 3 eta b = 1 egiten badugu, orduan X = 3 2 1 1 eo

4. Matrize baten berreketak

5. Infinitu soluzioko ekuazioa

Proposatutako ariketak eta problemak

Trebatzeko

Eragiketak matrizeekin

1 Matrize hauek emanda: A =  1 2 3 0 –eo B =  2 0 10 14 –eo C =  f 1 2

Kalkulatu, ahal bada, beste hauek:

2 10 3 –– p

a) A ∙ B b) B ∙ C c) At ∙ C d) A ∙ B ∙ C e) B + C ∙ At

2 A = f 3 3 2

9 Fabrikatzaile batek hiru zuku mota ekoizten ditu: klasikoa, A; azukrerik gabea, B; eta esneduna, C. Zuku-mota bakoitza lau neurritan saltzen du (1/4 L, 1/3 L, 1/2 L eta 1 L), ondorengo prezio hauetan, eurotan:

• 1/4 L-ko neurria ( 0,5 ; 0,4 ; 0,6)

• 1/3 L-ko neurria (0,8 ; 0,75 ; 0,9)

• 1/2 L-ko neurria (1; 0,9 ; 1,2 )

• 1 L-ko neurria (1,5 ; 1,2 ; 1,75)

0 1 0

8 6 5 ––– p izanda, egiaztatu (A +  I )2 = 0 dela, eta adierazi A 2 matrizea A-ren eta I-ren konbinazio lineal gisa.

3 a) Egiaztatu A 2 = 2A – I dela, A =

I matrizea 3 ordenako unitate-matrizea izanda.

b) Erabili aurreko berdintza hori A 4 kalkulatzeko.

4 A = 1 2 1 1 eo matrizea emanda, aurkitu AB = BA betetzen duten B matrizeak

5 Ebatzi matrizeen bidez emandako honako sistema hau:

Egun batean ekoizten dituen ontziak matrize honen bidez adierazita daude:

1/4 L 1/3 L 1/2 L 1 L

M = A B C f 300 250 150

500 300 600

250 200 150

200 150 100 p

a) Idatzi prezioak adierazten dituen N matrize bat.

b) Kalkulatu MN matrizearen diagonal nagusiko elementuak, eta azaldu zer esanahi duten.

c) Egizu gauza bera NM matrizeko diagonal nagusiko elementuen kasuan.

Matrize karratuak. Alderantzizko matrizea

10 Honako matrize hauek emanda:

A =  2 3 1 2 –eo B =  0 4 1 –2 eo

kalkulatu:

a) A · B b) B · A c) B –1

7 A = x y 1 –1 fp matrizea izanik.

a) Kalkulatu A 2 .

b) Zehaztu x-ren eta y-ren balioak A 2 =  x 1 2

izanik.

6 Kalkulatu A matrizearekin trukagarria den X matrize bat; hau da, A · X = X · A betetzen duena, A = 1

d) (A + B )(A – B ) e) A 2  – B 2 f ) (A + B )2

11 A =  1 0 1 2 –eo matrizea emanda, aurkitu honako matrize hauetako zein den horren alderantzizkoa:

M =  / / / / 32 12 32 12 eo N =  / / 1 0 12 12 eo

8 Hizkuntza-eskola batean, ingeles, frantses eta txinerako ikasleak lau mailatan banatuta daude, A matrizeak adierazten duen moduan. Gainera, klase horiek hizkuntza-laborategia duten geletan edo ez dutenetan eman daitezke. Eskola-ordu bakoitzaren prezioa B matrizeak adierazten du.

12 Erabili Gaussen metodoa honako matrize hauetako bakoitzaren matrize alderantzizkoa lortzeko: A =  1 1 2 0 –eo B =  1 2 0 4 –eo C = f 1 0 0

13 a) A =  f 0 0 0

2 0 0

nulua dela

Kalkulatu zer diru irabazten duen eskolak hizkuntza bakoitzeko klase-ordu bakoitzagatik, laborategia duen edo ez duen kontuan izanda.

0 1 1

1 0 1 p

– p matrizea izanda, frogatu A 3 matrize

1 1 0

b) Gero, egiaztatu I + A + A 2 matrizea I – A matrizearen alderantzizkoa dela.

Proposatutako ariketak eta problemak

Ekuazio matrizialak

14 Kalkulatu honako baldintza hauek betetzen dituzten X eta Y matrizeak:

XY A XY B 23+= += * , jakinda A = 4 10 5 eo eta B = 0 1 1 0 eo

15 Beheko A eta B matrizeak izanda, eta 2X – B 2 = A · B betetzen dela jakinik, kalkulatu X.

A = f 1 1 0

0 1 0

1 0 2 p B = f 1 1 0

16 Honako matrize hauek emanda:

0 1 0

1 1 0

0 0 1 p matrizea emanda, kalkulatu A –1

Aurkitu AX + 2A = I egiaztatzen duen X matrizea.

22 A =  3 2 1 0 eo , B =  1 1 2 1 –eo eta C = 3 1 1 2 –eo matrizeak ditugu.

a) Bakandu X matrizea XA – B = XC ekuazioan.

b) Kalkulatu X

– p

1 1 1

A =  11 01 –eo B =  1 3 –11 eo C =  1 1 10 eo

aurkitu AX – A = B – C betetzen duen X matrizea.

23 A = 2 3 3 5 ––eo eta B = 1 9 4 5 ––eo matrizeak emanda:

a) Kalkulatu 2X – Y = A eta X – 3Y = B egiaztatzen dituzten X eta Y matrizeak.

b) Aurkitu B + ZA – B t = 3I betetzen duen Z matrizea, I matrizea 2 ordenako unitate-matrizea izanik.

Matrize baten heina

24 Aztertu honako matrize hauen heina:

[

= AB 4 –+ = \

e e o o ] ] ] ] ]

18 M =  1 1 5 3 –eo eta N = 1 3 0 0 eo matrizeak izanda, aurkitu honako baldintza hauek betetzen dituzten X eta Y bi

matrize:

19 Matrize hauek izanda: A

B =  2 2 1 2

C = f 1 0 2 2 2 0 –– p

a) Kalkulatu B –1 Gaussen metodoaren bidez.

A = 1 2 2 4 3 6 4 8 –––eo B = 1 1 3 0 0 0 –eo C = f 1 2 12 2 4 24 3 6 36 –––– p D = f 1 2 3 2 4 6 3 0 0 p E = f 1 0 0 0 2 1 3 0 0 0 3 1 p F = f 0 1 0 0 0 1 1 0 0 p

A = f 1 2 1 1 3 1 1 5 6 2 11 29 – p B = f 2 4 6 1 2 3 3 1 2 – p C = f 1 1 1 3 3 5 1 7 1 3 1 5 1 3 1 5 – p D = f 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ––––– p

d) Zer dimentsiotakoa izan behar du N matrizeak C tN matrize karratua izateko?

–eo ,

–eo eta C =

1 1

0

A = f m 1 2 2 2 1 1 2 1 –– p B = f m m 1 2 4 1 4 10 1 2 p C =  m m m m 2 1 1 –+ eo D = f m m 1 0 2 0 0 1 0 1 ––2 p E =  mm 2 1 11 ––eo F = f m m m 2 0 0 0 1 0 1 ––– p

Ebazteko

27 Kalkulatu A n eta B n, honako hauek jakinda:

34 Kalkulatu A matrizearekin trukagarria den X matrize bat; alegia, A · X = X · A betetzen duena, A = 1 0 1 1 eo izanik.

17 1 0

A = f // 1 0 0

17 0 1 p B = 1 0 0 3 eo

Gero, kalkulatu A 2 + 2A –1 · X

35 A = 1 1 24 –eo eta B = 0 2 –11 eo matrizeak ditugu. Zehaztu

28 A = f 4 3 3

1 1 0 –––

5 4 4

– p matrizea emanda, kalkulatu A 2 , A 3 , …, A 128 .

29 Zehaztu, ahal bada, (A – kI )2 matrizea nulua egingo duen k-ren balio bat, kontuan hartuta honako hau:

A = f 0 1 1

BXB = 2BA betetzen duen X matrizea.

36 A eta B honela definituriko bi matrize dira:

A = f 5 2 0

2 5 0

0 0 1 p B = f a c b c 00

0 0 1 p

1 0 1

2 2 3 – – p

30 Aztertu honako matrize hauen heina zein den k parametroaren balioaren arabera:

a) Aurkitu zer baldintza bete behar duten a, b, c koefizienteek A · B = B · A bete dadin.

b) a = b = c = 1 denean, kalkulatu B 10 zein den.

37 Matrize karratu bat ortogonala dela esaten dugu horren alderantzizkoa eta iraulia bat datozenean.

Kalkulatu zein izan behar diren x-ren eta y-ren balioak A matrize hau ortogonala izateko:

38 Matrize hauek ditugu:

31 A = 1 1 0 1 –eo izanda, aurkitu XA + A t = 2I betetzen duen X matrizea.

Aurkitu AXB = I2 betetzen duen X matrizea.

39 Matrize hauek emanda:

a) m-ren zer baliotarako existitzen da B –1? m = 1 kasurako, kalkulatu B –1 .

b) m = 1 kasurako, aurkitu X · B + C = D betetzen duen X matrizea.

33 A = f 2 2 3

izanda:

1 3 3

1 2 –2 p eta I (3 ordenako unitate-matrizea)

a) Kalkulatu (A – I )2 eta A(A – I ) matrizeak.

b) Arrazoitu A matrizea alderantzikagarria dela.

c) Egiaztatu ez dela existitzen A – I matrizearen alderantzizkoa.

d) Zehaztu zer balio izan behar duen λ parametro errealak A –1 = λ(A – 2I ) egiaztatzeko.

Aurkitu, baldin eta existitzen bada, AX + B = A2 betetzen duen X matrizea.

40 Aurkitu X 2 = 2X ekuazio matriziala betetzen duten X = a bc 0 eo matrize guztiak, a, b ∈ Á izanik.

42 Aurkitu AX + B = 3X egiaztatzen duen X matrizea,

Proposatutako ariketak eta problemak

43 a) Askatu X matrizea AXA + B = B(2A + I ) berdintzan.

b) Kalkulatu X matrizea A = 1 0 1 1 –eo eta B =  1 1 2 1 eo diren kasuan.

44 A = f 1 3 5

50 Ba al dago modurik A 2 matrize nulua izateko, A matrize ez-nulua izanik? Erantzuna baietz bada, eman adibide bat.

51 Egiaztatu A ta B alderantzikagarriak badira (A ∙ B)–1 = = B –1 ∙ A–1 betetzen dela.

0 1 1

0 1 2 ––

p matrizea emanda, aurkitu XA + A = A –1

ekuazioa betetzen duen X matrizea.

45 1.3 helburua. Ospitale bateko Zaintza Intentsiboen Unitatean (ZIU), pazienteak bere egoeraren arabera sailkatzen dituzte: kritikoak, larriak eta egonkorrak. Barne-medikuntzako mediku batek egunero aztertzen du egoera, pazientearen bilakaera kontuan izanik. Paziente bat egoera batetik bestera igarotzeko probabilitatea honako grafo honek adierazten du:

a) Idatzi probabilitateen matrizea.

b) Egun jakin batean ZIUan 20 gaixo kritiko, 35 larri eta 30 egonkor badaude, zein da hurrengo egunerako espero litekeen banaketa?

46 a) Egiaztatu A matrizea A 2 = 2A – I betetzen duen matrize karratua bada, I identitate-matrizea izanik, orduan A alderantzikagarria dela. Zein da A –1 matrizearen adierazpena?

b) Erabili aurreko atal hori A =

52 2 ordenako A matrize karratu baten aztarna da azt (A) = a11 + + a22. Frogatu A eta B matrizeak 2 ordenako bi matrize karratu badira, orduan azt (A · B) = azt (B · A) dela.

53 Frogatu A idenpotentea bada, orduan I – A ere badela. (Matrize bat idenpotentea da A2 = A bada).

54 Zuzena ala okerra? Arrazoitu zure erantzuna eta jarri adibideak.

a) A matrizea 2 × 2 neurrikoa bada eta heina 2 badu, heina ez da aldatuko errenkada bat edo zutabe bat erantsiz gero.

b) X – AX = B bada, orduan X = (I – A)–1B

c) A = 1 3 2 1 ––eo bada, orduan (A + I )2 = 6I.

d) AB = BA ordena bereko bi matrize karratu badira, orduan (AB)t = At B t

e) Heina 3 duen 3 errenkadako eta 3 zutabeko matrize bati errenkada bat eta zutabe bat ezabatzen badizkiogu, orduan bere heina 2 izango da.

f ) (A t = –A ) matrize asimetriko batean, diagonal nagusiko elementu guztiak 0 dira.

1 –

––– p matrizearen alderantzizkoa kalkulatzeko

Galdera teorikoak

47 A(3 × 2); B(2 × 4); C(4 × 4); D(2 × 1) matrizeak ditugu.

a) Justifikatu honako biderketa hauetako zein egin daitezkeen:

AB AC BC CD AD

b) Baten bat matrize karratua da?

48 A matrizea 2 × 3 dimentsiokoa da. Existitzen da B matrizeren bat A · B errenkada bakarreko matrizea izateko? Eta B · A?

Jarri kasu bakoitzerako adibide bat.

49 Egiaztatu A matrize karratu bat bada, beti betetzen duela honako hau:

a) A + At simetrikoa da.

b) A − At antisimetrikoa da. (Kontuan izan B matrizea antisimetrikoa dela baldin eta B = −Bt bada).

1 4 5

2 3 5

g) M = f k

4 1 1 –2 p matrizearen heina 3 da, baldin eta k = 0 bada

3 2 5

h) A matrize erregular bat bada eta (B – C )A = 0 (matrize nulua), ziurtatu dezakegu B = C dela.

Sakontzeko

55 Askatu X matrizea (X + A)2 = X 2 + XA + I2 berdintzan, eta

lortu X matrizea A = 1 1 2 0 –eo kasuan

56 Frogatu A matrize erregular bat bada, XA 2 + BA = A 2 ekuazioan X askatzean X = I – BA –1 lortzen dela.

57 A eta B ordena bereko bi matrize karratu dira. A · B = A ·  C berdintzatik, ezin da ondorioztatu, oro har, B = C dela.

Frogatu baieztapen hori. Horretarako, bilatu A · B = A · C betetzen duten B eta C bi matrize desberdin, kontuan

izanik A = 1 1 1 1 eo dela

58 Aurkitu 2 ordenako matrize karratu bat, I eta –I matrizeen berdina izango ez dena eta alderantzizko matrizea eta iraulia berdinak dituena.

59 Lortu antisimetrikoa izango den 2 ordenako matrize baten forma orokorra.

60 a) A matrizea n ordenako matrize erregular bat bada eta AB + BA = 0 betetzen duen B matrize bat existitzen bada, frogatu BA –1 + A –1B = 0 dela.

b) A = 3 4 2 3 eo bada, aurkitu AB + BA = 0 betetzen duen B ≠ 0 matrize bat.

61 Matrize hauek ditugu:

62 Matrize karratu bat k baturako matrize magikoa da errenkada bakoitzeko, zutabe bakoitzeko eta bi diagonaletako elementuen baturak k direnean kasu guztietan.

Zein da k-ren balioa matrize magiko bat antisimetrikoa bada? Aurkitu 3 ordenako matrize magiko antisimetriko guztiak.

63 Lortu 3 ordenako matrize magiko simetriko guztiak k = 0 kasurako.

A = f a a b

1 0 00

0 0 p B = f 0 4 0

1 0 0 –– p C = f x y z p, a, b ∈ Á

4 2 2

a) Zehaztu a-ren eta b-ren zer baliorekin den A matrizea erregularra; hau da, zer baliorekin duen alderantzizkoa.

b) Aurkitu a-ren eta b-ren zer baliorekin betetzen den A = A–1 .

c) a = 2 eta b = 2 kasuan, kalkulatu AC = BC betetzen duten C matrizeak.

64 Lortu 3 ordenako matrize magiko simetriko guztiak k = 3 kasurako.

65 A matrize karratuak A 2 – 2A = 3I berdintza egiaztatzen du.

a) Egiaztatu A alderantzikagarria dela, eta adierazi A –1 matrizea A-ren eta I-ren funtzioan.

b) Adierazi A 3 matrizea A-ren eta I-ren konbinazio lineal moduan.

c) Aurkitu A 2 – 2A = 3I egiaztatzen duten 2 ordenako matrize simetriko guztiak.

1 Aztertu honako matrize honek izango duen heina a parametroaren balioen arabera:

7 a) Aurkitu honako matrize honen alderantzizkoa:

A = f 1 0 2

2 1 1

1 1 0 p

2 A(3 × 3); C(3 × 2) eta D(2 × 2) matrizeak ditugu. Zer dimentsio izan behar du B matrizeak AB = CD ekuazioa matrizialak zentzua izateko?

3 Egiaztatu A matrizea 2 ordenako matrize karratu bat bada, orduan (A t )2 = (A 2) t dela.

4 A = 1 5 0 1 eo matrizea izanda, kalkulatu A n

5 Zehaztu AX = XA betetzen duten A matrize guztiak, kontuan izanda X = 1 1 1 1 eo dela.

6 C = 1 1 2 1 eo matrizea izanda, aurkitu honako ekuazio hauek

egiaztatzen dituzten X eta Y bi matrize:

b) Ebatzi 2XA + B = A t ekuazioa, kontuan izanda: B = f 1 0 2

0 2 1

1 3 0

8 Arrazoitu matrize honi errenkada bat erantsita heina 4 izango duen matrize berri bat lortu dezakegun:

9 Kontsumitzaile-elkarte batek oinarrizko lau produktuk hiru supermerkatutan dituzten prezioak (eurotan) konparatu nahi ditu. Honako datu hauek lortu dituzte:

Familia batek aukeratutako dendaren arabera izan duen gastua konparatzeko, astean produktu bakoitzaren zenbat ale erosi diren hartuko dugu kontuan. Eta dagozkien kantitateak dira 2, 1, 3, 4.

Egin matrizeen eragiketak, familia bakoitzak, aukeratutako dendaren arabera, astean izan dituen gastuak konparatzeko.

anayaharitza.es Ariketa hauen ebazpena.

Determinanteak 3

Aitzindariak

Matrizeen teoria, kontzeptuei dagokienez, determinanteen oinarria da. Matrize izena Sylvesterrek sortu zuen, eta, hain zuzen ere, determinanteekiko duen «amatasun» erlazioari egiten dio erreferentzia. Dena dela, literatura matematikoan, determinanteak matrizeak baino mende bat lehenago agertu ziren. Historialari gehienek bat egiten dute esatean determinanteak sistematiko erabili zituen lehenengoa Leibniz izan zela. Hain zuzen ere, 1693an, determinanteen algoritmoaren baliokidea erabili zuen ekuazio-sistemak ebazteko. Hala ere, batzuen ustez, aurretik Seki Kowa japoniarrak erabili zituen, 10 urte lehenago. Eta Colin McLaurinek (1730) eta Gabriel Cramerrek (1750) ere erabili zituzten, ekuazio-sistemak ondo egituratutako tratamenduen bidez ebazteko, eta, 1772an, Alexandre Vandermondek determinanteen azterketa sistematikoa egin zuen lehen aldiz.

Formalizazioa eta zabalkundea

Determinanteak eta matrizeak arreta handiz aztertu ziren xix. mendean. Baina ez zuten berrikuntzarik ekarri maila teorikoan, eta berrikuntza bakarra hizkuntza arlokoa izan zen. Dena dela, bi arloak ere oso tresna erabilgarriak dira. Lagrangek esan zuen bezala: «Ondo eraikita dagoen hizkuntzaren onura hain da handia, ezen notazio sinplifikatua teoria sakonen iturri bihurtzen baita askotan». Determinanteen teoriari ekarpen handienak, xix. mendean, Cauchy frantsesak egin zizkion, eta matematikaren beste adar batzuekin egin zuen bezala, determinanteen teoria modu sistematiko, zorrotz eta dotorean jorratu zuen. Cauchyk 1812an Institute de Francen azaldu zuen memoria batean argitaratu zituen bere emaitzak. Ordutik aurrera, aplikazio askotan erabili zituen: uhinen hedapena, geometriako problemak, fisikako problemak… Berak sortu zuen «determinante» terminoa. Baina zer determinatzen du determinante batek? Unitate honetan ikusiko dugun bezala, determinantearen balioak zehazten du sistema batek soluzioa duen ala ez duen.

Cayley eta Sylvester matematikari ingelesek nabarmen lagundu zuten teoria hori garatzen: nomenklatura hobetu zuten, barra bertikal bikoitza ezarri zuten determinanteak izendatzeko, eta determinanteen erabilera-eremua zabaldu zuten.

Seki Kowa (1642-1708)

James Joseph Sylvester (1814-1897)

Cayley eta Sylvester

Arthur Cayley (1821-1895) matematikari emankorrenetako bat izan zen Euler eta Cauchyrekin batera. Merkatari aberatsen familia batekoa zen; izan zituen maisuek laster antzeman zuten oso gaitasun handiko ikaslea zela, eta aita konbentzitu zuten Cambridgeko Trinity Collegen sartzen utz ziezaion. Gerora, han jarraitu zuen irakasle, harik eta lana utzi zuen arte, elizgizon bihurtzeko baldintza ezarri ziotelako irakaskuntzan jarraitu ahal izateko. Abokatutzan aritu zen orduan, baina matematikarako zuen zaletasuna alde batera utzi gabe. Lege kontuek aspertu egiten zuten ordea, eta, hamalau urtez epaitegietan aritu ondoren, Cambridgera itzuli zen irakasle.

Cayleyren artikulu askotan beste matematikari handi ingeles baten inspirazioa ageri da: James Joseph Sylvester (1814-1897). Elkarrekin harreman bikaina izan zuten bizitza osoan. Sylvester pertsona xelebrea zen, «jakintsu distraitua» topikoaren adibide ona.

Cayleyk eta Sylvesterrek, matematikan ez ezik, garrantzizko beste alderdi batzuetan ere eragina izan zuten; hala nola Cambridgeko Unibertsitateko Erdi Aroko pentsamoldea aldatzen laguntzeko, emakumeak ikasle gisa onartzeari dagokionez. Izan ere, Sylvesterren lehenengo ikasletako bat, eta nabarmenenetakoa, Florence Nightingale izan zen, urte batzuk geroago ospitaleetako baldintzak eta, oro har, arreta medikoa hobetzeko egindako ekarpenagatik nabarmenduko zena.

EBATZI

2 ordenako determinanteak

Unitatea garatzean ikusiko dugunez, 2 ordenako matrize baten determinantea zenbaki bat da, eta lortzen da matrizeko elementuak gurutzean biderkatuta eta emaitzen kenketa eginda, honela:

Eta zergatik izen hori? Zer «determinatzen du» determinante batek?

Hasteko, bi ekuazio-sistema hauek ebatziko ditugu:

Koefizienteen matrizeak hauek dira:

Determinanteak hauek dira: det A1 = –9 eta det A2 = 0

Ikusten duzunez, S1 sistemak soluzio bakarra du, eta koefiziente-matrizearen determinantea 0 ez beste edozein zenbaki da; S2 sistemak, berriz, ez du soluziorik, eta determinantea 0 da. Beti gertatuko da hori?

• Ebatzi sistema hauek eta kalkulatu koefiziente-matrize bakoitzaren determinantea:

29

Adibide horietatik ondorioztatzen denez, soluzio bakarreko sistemetan, koefiziente-matrizearen determinantea zero ez den zenbaki bat da. Eta gainerako sistemetan, bateraezinak edo indeterminatuak direnetan, determinantea zero da. Beraz, determinanteek «determinatzen dute» sistemak soluzio bakarra izatea ala ez izatea. Horregatik dira hain garrantzitsuak.

Bi ordenako determinanteak

Matrize karratu baten determinantea matrizeko elementuekin eragiketa jakin batzuk eginez lortzen den zenbaki bat da. Unitatean zehar, gero eta ordena handiagoko matrizeen determinanteak kalkulatzen ikasiko dugu. Hasteko, bi ordenako matrizeak landuko ditugu.

Bi ordenako A a a a a 11 21 12 22 = eo matrize karratu baten determinantea honela lortzen den zenbaki bat da:

det A = a11 a22 – a21 a12

A matrizearen determinantea izendatzeko, modu hauetako edozein erabiliko dugu: det A, det a a a a 11 21 12 22 eo , | A |, a a a a 11 21 12 22

Ebatzitako ariketak

1 Kalkulatu A = 7 2 5 11

matrizearen determinantea, eta egiaztatu bat datorrela matrize irauliaren determinantearekin.

1 Kalkulatu 3 7 0 0 –.

AZTERTU det A

KALKULATZEKO ERREGELA

• Batugai bakoitzean, errenkada bakoitzeko biderkagai bat eta zutabe bakoitzeko bat dago.

• Horiek dira aurreko baldintza horrekin lor daitezkeen biderkadura bakarrak.

• Batugaietako batek + zeinua du, eta besteak, –. a21 a22

a11 a12

Determinantearen emaitza zero da, zutabeetako baten bi elementuak zero dira eta.

Bigarren determinantearen errenkadak lehenengo determinanteko errenkaden berdinak direnez, baina lekuz aldatuta, batugaiek zeinua aldatzen dute; beraz, azkeneko emaitza berdina da, baina zeinuz aldatuta

1 A matrizea 2 × 2 dimentsiokoa izanik, arrazoitu baieztapen hauek zuzenak ala okerrak diren:

a) | A | = 0 izateko, matrizearen lau elementuek 0 izan behar dute.

b) A matrizearen bigarren zutabeko bi elementuak 0 badira, orduan | A | = 0.

c) A matrizearen bi errenkadak bat badatoz, orduan | A | = 0.

d) a c b d = –15 bada, orduan c a d b = 15.

e) m n 3 7 = 43 bada, orduan m n 30 70 = 430.

2 Kalkulatu determinante hauen balioa, eta esan zergatik diren zero horietako batzuk:

Hiru ordenako determinanteak

➜ Matrize baten determinantea.

• Batugai bakoitzean errenkada bakoitzeko biderkagai bat eta zutabe bakoitzeko bat dago. Hori egiaztatzeko, kontuan hartu batugai bakoitzean hiru elementu daudela. Lehenengo azpi-indizeak (errenkadenak) 1 2 3 dira beti. Bigarren azpiindizeak ere 1 2 3 dira, hainbat modutan ordenatuta.

• Errenkada bakoitzeko eta zutabe bakoitzeko elementu batekin egin daitezkeen biderkagai guztiak daude; izan ere, zutabeen azpi-indizeak 1, 2, 3 zenbakien permutazio guztiak dira. 3! = 6 daude

• Batugaien erdiek + zeinua dute, eta beste erdiek, – zeinua. Sei batugai horiek gogoratzea oso erraza da Sarrusen erregela esaten zaion honako erregela mnemotekniko honekin:

+ zeinuko batugaiak – zeinuko batugaiak

Ebatzitako

1 Kalkulatu honako determinante

Beren zeinuarekin: 5 – 24 + 0 = –19 Minus zeinuarekin: –(140 + 9 + 0) = –149

Beraz, determinantea hau da: –19 – 149 = –168

b) Matrize triangeluarretan, determinantearen garapenean nulua ez den batugai bakarra diagonal nagusiarena da. Beraz:

BEHATU

1 1 2 3 3 2 2 2 1 3 3 1 3 3 1 2 2 1

Determinanteen propietateak

1. Matrize baten determinantea eta matrize horren irauliarena berdinak dira: |A| = |At |

2. Matrize karratu batek zeroen lerro bat (errenkada zein zutabea) badu, horren determinantea zero da.

Izan ere, batugai guztietan agertuko da lerro horretako elementuren bat biderkagai moduan. Beraz, batugai guztiak nuluak dira.

3. Matrize karratu bateko bi lerro paralelo trukatzen baditugu, matrize horren determinanteak zeinua aldatzen du.

ADI!

Propietate hauek guztiek n ordenako edozein determinanteren kasuan balio dute. Modu orokorrean enuntziatuta daude, baina 3 ordenako determinanteen adibideak erabiliz azaldu ditugu. Horietako batzuen kasuan, alboan, determinantearen ordena edozein dela ere baliozkoa dela egiaztatzen da.

Batugaiak berdinak dira, baina zeinuak aldatuta dituzte.

4. Matrize karratu batek bi lerro paralelo berdin baditu, matrize horren determinantea zero da.

4.AREN EGIAZTAPENA

Berdinak diren bi lerroak trukatzen badira, matrize horren determinanteak berdin jarraituko du. Baina 3. propietatearen arabera, zeinua aldatu beharko luke. 0 da zeinua aldatuta ere berdin gelditzen den zenbaki bakarra.

Batugaietako bakoitza plus zeinuarekin dago behin, eta minus zeinuarekin beste behin.

5. Matrize karratu baten lerro bateko (errenkada zein zutabe) elementu guztiak zenbaki berarekin biderkatzen baditugu, matrize horren determinantea ere zenbaki horrekin biderkatuko da

5.AREN EGIAZTAPENA

Batugai bakoitzak biderkagai bat k-rekin biderkatuta du. Beraz, batura osoa geratuko da k-rekin biderkatuta (k biderkagai komuna da).

6. Matrize karratu batek bi errenkada (edo zutabe) proportzionalak baditu, matrize horren determinantea zero da

6.AREN EGIAZTAPENA

Nahikoa da 5. propietatea aplikatzea eta determinantetik proportzionaltasun-biderkagaia ateratzea. Hori eginda, bi lerro berdin geratzen zaizkigu, eta 4. propietatea erabiliz, determinantea baliogabetu egiten da.

8. Matrize baten lerro bati gainerako paraleloen konbinazio lineal bat batzen badiogu, matrizearen determinantea ez da aldatzen

9. Matrize batean lerroetako bat gainerako paraleloen konbinazio lineala bada, orduan matrize horren determinantea zero da. Eta, alderantziz: determinante bat zero bada, errenkadaren bat (eta zutaberen bat) gainerakoen konbinazio lineala da.

10. Bi matrizeren arteko biderketaren determinantea matrize horien determinanteen arteko biderketa da: | A · B | = | A | · | B |

9.AREN EGIAZTAPENA

Zenbait determinanteren batuketa moduan deskonposatu daiteke, eta determinante horietako bakoitza zero da, bi lerro proportzional izateagatik.

1 Egiaztatu emaitza hau, garapena

2 Frogatu honako hauek:

a) I identitate-matrizea bada, orduan | I | = 1

b) A matrize erregular bat bada, orduan | A –1 | =

arrazoitu honako baieztapen hauek zuzenak ala okerrak

a) |A| = 0, hirugarren zutabea lehenengo bien batura delako.

b) |B| = 0, hirugarren zutabea lehenengo bien kendura delako.

c) |C| = 0, hirugarren zutabea lehenengo bien biderkadura delako.

Ebatzitako ariketak

Edozein ordenatako determinanteak

n × n matrize baten determinantea lortzeko, n elementuko biderketa posible guztiak batu behar ditugu, errenkada bakoitzeko elementu bat eta zutabe bakoitzeko bat hartuz, haien zeinuarekin edo zeinua aldatuta, irizpide jakin baten arabera

Azter dezagun aurreko definizio hori:

• Determinante bat garatzen dugunean, batugai asko agertzen dira, eta horietako bakoitza n biderkagairen arteko biderketa da: a1σ(1) a2σ(2) an σ(n) 1, 2, …, n lehenengo azpi-indizeek errenkadei egiten diete erreferentzia. σ(1), σ(2), …, σ(n) bigarren azpi-indizeek zutabeei egiten diete erreferentzia, eta 1, 2, …, n zenbakien permutazio bat dira (σ esaten diegu). Beraz, errenkada bakoitzeko elementu bat eta zutabe bakoitzeko elementu bat dago biderkatzen.

• Zenbat batugai daude? 1, 2, …, n zenbakiekin egin daitezkeen permutazioak adina. Hau da, n! batugai.

• Zer zeinu darama batugai bakoitzak? + edo – , σ permutazioaren propietate jakin bat kontuan hartuz. Ikus dezagun propietate hori

Batugai bakoitzaren zeinua

a1σ(1) a2σ(2) an σ(n) batugaian, n biderkagaiak errenkadetako indizeen arabera ordenatuta daude (1. azpi-indizea). Bigarren azpi-indizeek, σ(1), σ(2), …, σ(n), zutabeei egiten diete erreferentzia, eta σ da (1, 2, …, n) elementuen permutazioa. σ(i ) adierazpenak ematen digu σ permutazioan i lekua betetzen duen elementua.

Permutazio batean, elementuak binaka jarri eta hasierako kokapenean duten ordena bera gordetzen badute, segidan daudela diogu; eta ordena aldatuta badute, alderantzikatuta daudela. Zutabeetako indizeen permutazioek alderantzikatze-kopuru bikoitia badute, batugaiak bere zeinua gordezten du (+), eta bakoitia bada, zeinua aldatzen du (-).

Adibidez, 4 × 4 determinante batean, a13 a21 a34 a42 batugaiak ordenatuta ditu errenkaden indizeak (1, 2, 3, 4). Zutabeen indizeak (3, 1, 4, 2) permutazio bat dira. Azter dezagun zenbat alderantzikatze dituen:

3 alderantzikatuta dago 1ekin eta 2rekin → (2 alderantzikatze)

1 segidan dago ondorengoekin → (0 alderantzikatze)

4 alderantzikatuta dago 2rekin 2 → (1 alderantzikatze)

Guztira 3 alderantzikatze daude, kopuru bakoitia. Beraz, batugai horrek zeinua aldatuko du →

Determinantearen definizioa honela geratzen da:

alderantzikatze-kop.

P (n) adierazpenak esan nahi du batugai bakoitza lortzen dela (1, …, n) elementuen permutazio batetik.

KONTUAN IZAN

2 ordenako eta 3 ordenako determinanteak definitzeko, erraz bistaratu ahal izateko moduko erregela batzuk eman dira (gurutzean biderkatzea, Sarrusen erregela), gogoan hartzeko zer batugaik parte hartzen duten eta zer zeinu dagozkien.

Orrialde honetan emango dugun definizio orokorrak interes teorikoa du huts-hutsean. Irakurri gabe utzita ere, gaiari dagozkion gainerako atalak arazorik gabe ulertuko dira, eta nahikoak izango dira determinanteak trebe erabiltzeko.

ADIBIDEA

n = 4 kasuan, batugaian:

a13 a21 a34 a42 errenkaden azpi-indizeak (1, 2, 3, 4) dira, eta zutabeen azpi-indizeek (3, 1, 4, 2) permutazioa eratzen dute. Hau da, σ(1) = 3, σ(2) = 1, σ(3) = 4, σ(4) = 2.

DETERMINANTEEN PROPIETATEAK

Lehenago esan dugun bezala, aurreko atalean 3 ordenako determinanteetarako enuntziaturiko hamar propietateek edozein ordenatako determinanteetarako balio dute.

ADI

Definizio zail hau ez da batere erosoa eragiketak egiteko orduan. 3 baino ordena handiagoko determinanteak kalkulatzeko, propietate berri bat eta bertan oinarritutako prozedura lortuko ditugu hurrengo atalean.

Ebatzitako ariketak

1 Egiaztatu honako biderketa hau a24 · a33 · a12 · a51 · a45

5 ordenako determinante baten batugaietako bat dela, eta aurkitu zer zeinu dagokion

Bost biderkagaiak errenkadetako indizeak kontuan hartuz ordenatuko ditugu: a12 · a24 · a33 · a45 · a51

Zutabeen indizeak (2, 4, 3, 5, 1) dira, eta hori (1, 2, 3, 4, 5) elementuen permutazio bat da. Beraz, determinantearen garapeneko batugaietako bat da. Ikus dezagun zer zeinu duen. Alderantzikatzeak zenbatuko ditugu:

• 2 alderantzikatuta dago 1ekin → 1 alderantzikatze

• 4 alderantzikatuta dago 3rekin eta 1ekin → 2 alderantzikatze

• 3 alderantzikatuta dago 1ekin → 1 alderantzikatze

• 5 alderantzikatuta dago 1ekin → 1 alderantzikatze

Guztira, 5 alderantzikatze daude, bakoitia. Beraz, minus zeinua (–) dagokio

a) 3. errenkadako elementu guztiak zero dira.

Beraz, 2. propietatearen arabera, determinantea zero da.

b) Laugarren zutabea lehenengoa bider –2 eginez lortzen da. Hau da, 1. eta 4. zutabeak proportzionalak dira.

Determinantea 0 da, 6. propietatea kontuan hartuz.

Errenkada eta zutabe bakoitzean 0 ez den elementu bakarra dago. Beraz, 4! = 24 batugaien artean, bakarra dago zero ez dena (gainerakoetan 0 biderkagai bat baitago):

5 · (–2) · 3 · 7

Ikus dezagun zer zeinu dagokion. a13 · a24 · a31 · a42 batugaia da. Errenkadetako (1, 2, 3, 4) indizeak ordenatuta daude. Zutabeen indizeak (3, 4, 1, 2) dira

3 → bi alderantzikatze; 4 → bi alderantzikatze; 1 → 0 alderantzikatze Guztira, 4 alderantzikatze daude, bikoitia. Beraz, bere zeinuarekin jarraituko du; eta determinantearen balioa 5 · (–2) · 3 · 7 = –210 da.

Pentsatu eta praktikatu

1 Zuzena ala okerra? 4 × 4 ordenako A matrize batean, 16 elementuak zenbaki positiboak dira:

a) | A | determinantearen garapenean 4! = 4 · 3 · 2 · 1 = 24 batugai daude, denak positiboak.

b) | A | determinantearen garapenean 12 batugai positibo eta 12 negatibo daude.

c) | A | determinantea zenbaki positibo bat da, ziur.

d) | –A | = | A |.

2 a) Zenbat batugai ditu 5 ordenako | aij | determinantearen garapenak?

b) Egiaztatu horietako bat a41 · a32 · a55 · a24 · a13 dela. Zer zeinu du?

3 Kalkulatu honako determinante hauen balioak:

Minor osagarria eta adjuntua

Matrize batean r errenkada eta r zutabe hautatuz gero, horien gurutzaketan dauden elementuek r ordenako azpimatrize karratu bat eratzen dute. Azpimatrize horren determinanteari deitzen zaio jatorrizko matrizearen r ordenako minorra.

n × n matrize karratu batean aij elementu bat nabarmendu eta dagozkion errenkada eta zutabea ezabatzen baditugu, (n – 1) × (n – 1) azpimatrize bat lortuko dugu. Horren determinantea n – 1 ordenako minor bat da, aij elementuaren minor osagarri esaten zaio, eta izendatzeko, αij erabiltzen da

aij-ren adjuntua Aij = (–1)i + j · αij zenbakia da; hau da, minor osagarria, bere zeinuarekin edo alderantzizko zeinuarekin, i + j bikoitia edo bakoitia den kontuan hartuz.

1 Aurkitu M matrizearen bi ordenako bi minor eta hiru ordenako beste bi minor.

1. eta 4. errenkadak eta 2. eta 4. zutabeak hautatu ditugu. Hautatu dugun 2 ordenako minorra, beraz, hau da:

elementuaren minor osagarria hau

2

32

32 = –198 da.

a12, a33 eta a43 elementuen minor osagarriak eta adjuntuak.

Ebatzitako ariketa

Aurkitu

Determinantea lerro bateko elementuetatik abiatuta garatu

Determinanteen bi propietate berri ikasiko ditugu. Lehenengoa oso lagungarria da 3 baino ordena handiagoko determinanteak kalkulatzeko.

11. Matrize karratu baten errenkada edo zutabe bateko elementuak horien adjuntuekin biderkatzen baditugu eta emaitzak batzen baditugu, hasierako matrizearen determinantea lortuko dugu. Kasu horretan, determinantea lerro horretako elementuetatik abiatuta garatu dela esaten da

3 ordenako determinante bat bigarren errenkadako elementuetatik abiatuta garatzea hau da:

(*) 2. errenkadako elementuetatik abiatuta «garatu» nahi dugunez, errenkada horretako elementuak biderkagai komun moduan aterako ditugu

Ebatzitako

1 Kalkulatu honako matrize honen determinantea

a)

zutabea:

a) 3. zutabetik abiatuta garatuz.

|

3 Kalkulatu

12. Errenkada bateko (edo zutabe bateko) elementuak paraleloa den beste bateko adjuntuekin biderkatu eta emaitzak batzen baditugu, batura zero da

Adibidez, a21 A31 + a22 A32 + a23 A33 = 0

Kasu zehatz honen egiaztapena

(*) Goian dagoena beheko determinantearen garapena da hirugarren errenkadako elementuetatik abiatuta, eta horregatik jar dezakegu berdintza hor

(**) Determinanteak bi errenkada berdin ditu eta, beraz, zero da

1 Matrize hau izanda

1. zutabeko elementuen adjuntuak lortuko ditugu:

egiaztatu honako hau: 2. zutabeko elementuak 1. zutabeko elementuen adjuntuekin biderkatu eta emaitzak batuz gero, batura zero da

Pentsatu

diguten batuketa egingo dugu:

da: emaitza 0 da, 12. propietatearen ondorioz.

b) Kalkulatu 3. zutabeko elementuen eta 2. zutabean dagozkien adjuntuen arteko biderkadura guztien batuketa

7 2 8 –

1 6 4 –

Egiaztatu zazpi kasuetan emaitza bera lortzen duzula

2 Matrize hau dugu.

f 3 5 9

c) Arrazoitu zergatik diren zero aurreko bi emaitzak

1 6 4 –– p

7 2 8

a) Kalkulatu 1. errenkadako elementuen eta 3. errenkadan dagozkien adjuntuen arteko biderkadura guztien batuketa.

a) 7 4 3 1 0 0 7 0 3 4 6 1 4 7 9 9 –b) 3 1 0 2 1 4 3 0 1 1 2 0 3 4 5 2 ––c) 0 1 2 0 0 1 0 2 3 1 3 0 4 0 5 1 d) 3 5 0 8 1 6 1 6 4 2 3 7 0 0 0 1 –

Ebatzitako ariketa

Edozein ordenatako determinanteak kalkulatzeko metodoa

Ikusi dugunez, ordena handiko determinanteak kalkulatzeko, oso lagungarria da zenbait zero dituen errenkadaren bat edukitzea; zenbat eta gehiago, hobeto. Baina zerorik ez badu, zer? Kasu horretan, «zeroak egingo ditugu». Zeroak egitea da matrize baten heina lortzearen parekoa; eta heina lortzea, era berean, ekuazio-sistemak Gaussen metodoaren bidez (1. unitatean landu dugu) ebaztearen parekoa da. Kasu honetan, determinanteetan, 8. propietate sinplifikatua erabiliko dugu: Lerro bati horren paralelo baten eta zenbaki baten arteko biderkadura batuz gero, determinantea ez da aldatzen.

Ebatzitako ariketa

1 Kalkulatu honako determinante hauek, lerroren batean zeroak eginez:

a) Determinantea 2. zutabeko elementuetatik abiatuta garatuko dugu, zutabe horretan zero bat dagoelako, eta, areago: «zeroak egiteko modua» errazten duen bateko bat ere

3 × 3 determinanteetan ere komeni liteke «zeroak egitea».

(*) Urrats hau egiten da «zeroak egiteko» balioko digun –1 bat lortzeko. Ikusten duzunez,

1 Kalkulatu honako determinante hauek:

Matrize baten heina, minorretatik abiatuta

Aurreko unitatean ikusi dugunez, matrize baten heina linealki independenteak dituen errenkaden (edo zutabeen) kopurua da. Definizio horrek modua ematen digu heinak Gaussen metodoaren bidez lortzeko

Orain, determinanteak heinak kalkulatzeko erabili nahi ditugu. Horretarako, 9. propietatea gogoratuko dugu:

Matrize karratu baten determinantea zero izateko baldintza beharrezkoa eta nahikoa da errenkadak (edo zutabeak) linealki mendekoak izatea; hau da, horietako bat besteen konbinazio lineal moduan jarri ahal izatea: | A | = 0 ⇔ A matrizearen errenkadak linealki mendekoak dira

Edo, bestela: | A | ≠ 0 ⇔ matrizearen errenkadak linealki independenteak dira

Propietate honek matrize baten heinari buruzko beste definizio bat ematen digu:

Matrize baten heina da nuluak ez diren bere minorren ordena maximoa. • Adibidez: A

Gorriz adierazita dagoen azpimatrizearen determinanteak –105 balio du (egiaztatu). 0 ez beste zenbaki bat denez, bere hiru errenkadak L.I. direla ziurtatu dezakegu. Beraz, A-ren lehenengo hiru errenkadak ere L.I. dira, eta A-ren heina 3 da gutxienez [hein(A) ≥ 3].

A-ren kasuan 4 ordenako bost minor daude (4naka hartutako 5 zutaberen konbinazio-kopurua). Baina bostak nuluak dira. Horrek esan nahi du A-ren laugarren errenkada linealki menpekoa dela lehenengo hirurekiko. A-ren heina ez da 4. Beraz, hein(A) = 3 da, eta hori da gorriz adierazitako minorraren ordena; izan ere, goragoko ordenako minorrak denak nuluak dira. • Beste adibide bat:

1 0 3 5 eo

matrizearen determinantea zero ez den beste zenbaki bat da. Beraz, lehenengo bi errenkadak linealki independenteak dira

Hiru ordenako minorrak kalkulatzen baditugu, denak zero direla ikusiko dugu. Beraz, lau ordenakoak eta bost ordenakoak ere zero dira. Matrizearen heina 2 da.

Matrize horretan 3 ordenako 200 minor daudela kontuan hartuz, denak kalkulatzeko lana izugarria da. Hurrengo orrialdean, matrize baten heina modu sinplifikatuan lortzeko metodo bat ikusiko dugu.

Matrize baten heina.

Matrize baten heina minorretatik abiatuta lortzeko metodoa

Matrize baten «minor» kopurua izugarri handia da. Bitxikeria moduan, jakizu 4 × 5 matrize batek 2 ordenako 60 minor, 3 ordenako 40 minor eta 4 ordenako 5 minor dituela. Eta zentzugabea litzateke heina jakiteko horiek guztiak kalkulatu behar izatea. Adibide baten bidez deskribatuko dugun ondorengo metodoak matrize baten heina nahiko bizkor kalkulatzeko modua ematen digu.

➜ anayaharitza.es

Parametro baten mendekoa den matrize baten heina kalkulatzeko sakontze praktikoa, ariketa eta guzti

Lehenengo, nulua ez den bi ordenako minor bat nabarmenduko dugu (hori begiz jota egin daiteke). Ahalik eta errazena hartzen ahaleginduko gara, geroago kalkulatu beharko ditugun ordena handiagoko determinante askotan parte hartuko du eta.

da A matrizearen lehenengo bi erren-

Ikus dezagun hirugarren errenkada linealki mendekoa den horiekiko. Horretarako –3 eta –2 bi elementu berriak erantsiko dizkiogu, eta bi zutabe horiek dituzten 3 ordenako minor guztiak kalkulatuko ditugu, horietakoren bat zero ez den ikusteko:

Denak zero direnez, hirugarren errenkada lehenengo bien konbinazio lineala dela esan dezakegu.

(Hiru minor horietakoren bat nulua ez balitz, hirugarren errenkada ez litzateke L.I. izango beste biekiko. Oinarri moduan 3 ordenako minor hori hartuko genuke eta hiru zutabeak laugarren errenkadako elementuekin zabalduko genituzke. Horrela, lau elementuko hiru zutabe lortuko genituzke. Beste zutabe bat erantsiz gero, 4 ordenako minorren bat nulua ez den aztertuko genuke).

Orain, laugarren errenkadarekin hirugarrenarekin egindakoa egingo dugu. Horrela lortzen ditugun 3 ordenako hiru minorrak zero dira. Beraz, laugarren errenkada ere lehenengo bien konbinazio lineala da.

Matrizearen heina bi da (nulua ez den minor baten ordena maximoa, edo, bestela esanda, L.I. diren errenkaden kopuru maximoa).

1 Kalkulatu honako matrize honen

Ebatzitako ariketa

1 Kalkulatu honako matrize hauen heinak:

Pentsatu eta praktikatu

Matrize baten alderantzizkoa lortzeko beste metodo bat

Aurreko unitatean, matrize baten alderantzizkoa Gaussen metodoa erabiliz lortzen ikasi dugu. Baina determinanteak eta horien propietateak jakinda, alderantzizkoa beste modu batean lor dezakegu.

A = (ai j ) matrize karratu bat erregularra izateko, hau da, alderantzizkoa izan dezan, nahitaezkoa eta nahikoa da horren determinantea

➜ Matrize baten alderantzizkoa.

Horrela definiturik dagoen matrizea A-ren alderantzizkoa dela frogatzeko, A · A –1 = (pi j ) biderketa egin eta unitate-matrizea dela egiaztatuko dugu; hau da, diagonal nagusiko p ii elementu bakoitza bateko bat dela eta gainerako elementuak zero direla. Hori frogatzeko, p22 eta p23 kalkulatuko ditugu:

ERREPARATU

Ai j matrizea ai j elementuaren adjuntua da. Ikusten duzunez, A –1 matrizean elementu bakoitzaren ordez horren adjuntua jartzean sortzen den matrize iraulia ageri da. Horregatik jarri dugu (Aj i ).

Emaitza bera lortzen dugu diagonal nagusiko beste edozein elementutarako:

(*) 11. PROPIETATEA

Errenkada bateko elementuen eta dagozkien adjuntuen arteko biderkaduren batura |A| da.

Eta, orokorrean, i ≠ j bada, pi j = 0.

• Beraz, hau frogatu dugu: A · A –1 = In (n dimentsioko unitate-matrizea )

Kontuz! A = (a i j ) matrize erregular baten alderantzizkoa || ·( ) A A 1 ji dela baieztatu dugu. Eta bi matrizeen biderketa eginda, hala dela egiaztatu dugu. Dena dela, matrize horretara nola iritsi garen galdetu behar diogu geure buruari. Modu konstruktiboan lortzeko, hurrengo unitatean ikasiko ditugun tresna batzuk behar ditugu. Bertan egingo dugu, beraz.

(**) 12. PROPIETATEA

Errenkada bateko elementuen eta paralelo bati dagozkion adjuntuen arteko biderkaduren batura 0 da.

Matrize baten alderantzizkoa kalkulatzeko erregela praktikoa

Matrize baten alderantzizkoa lortzeko, honako urrats hauek ematea iradokitzen dugu:

|

| aurkituko dugu, eta nulua ez bada bakarrik egingo dugu aurrera.

(1) Matrize berri bat eratuko dugu, elementu bakoitzaren minor osagarriekin

(2) Zeinua aldatuko dugu txandaka, adjuntuak lortzeko

(3) (A i j )t = (A j i ) matrizea irauliko dugu.

(4) Elementu bakoitza zati | A | egingo dugu. Zatigarriak ez badira, erosoagoa da

1 biderkagai komun moduan ateratzea.

2  ×  2 MATRIZE BATEN ALDERANTZIZKOA

A

(1)

1 Kalkulatu matrize hauetako bakoitzaren alderantzizkoa:

2 Kalkulatu matrize hauen alderantzizkoak:

Ebatzitako ariketak eta problemak

1. 4 ordenako determinante bat kalkulatzea

Aurkitu, a-ren funtzioan, honako determinante honen balioa:

Kalkulatu determinante honen balioa

(1) Batu 2., 3. eta 4. zutabeak lehenengoari.

(2) Atera 4a + 1 faktore komuna, 1. zutabetik.

(3) 1. zutabeari jarraituta garatuz gero, azken determinantearen balioa da diagonal nagusiko elementuen biderkadura, izan ere matrize triangeluar bati dagokio.

2. Determinanteen propietateak

Erabili determinanteen propietateak honako berdintza hau egiaztatzeko:

Lehenengo errenkada eta lehenengo zutabea a-ren multiploak dira:

7 bada, kalkulatu honako determinante hauen balioak, garapena egin gabe:

Ekuazio bat ebaztea

Kalkulatu x-ren balioa, |2B| = 160 dela jakinda eta B matrizea hau izanda:

2B matrizea B-ren elementu guztiak bider 2 eginda lortzen da. Beraz, errenkada guztiak bider 2 eginda egongo direnez, hau betetzen da:

3.

4. Determinante baten balioa beste baten baliotik abiatuta ondorioztatzea

= bada, aurkitu:

(1) 5 biderkagai komun moduan atera dugu.

(2) Hirugarren errenkada beste bietako bakoitzarekin batu dugu.

(3) Errenkaden bi permutazio egin ditugu. Determinanteak ez du zeinua aldatz.

5. Parametro baten mendeko matrize baten heina. Matrize-ekuazioa

Matrize hauek ditugu:

a) Aztertu ondorengo matrize honen heina k parametroaren balioen arabera:

∙ Bt + kI

b) Kalkulatu A ∙ Bt · X – X = 2I egiaztatzen duen X matrizea.

kalkulatu

b) X askatzeko, (A · Bt – I ) · X = 2I biderkagai komuna aterako dugu, eta bi atalak ezkerretik bider (A · Bt – I)–1 egingo ditugu. (A · Bt – I) matrizea a) atalekoa bezalakoa da, baina k = –1 izanik. Ziurtatu dezakegu bere heina 3 dela, alderantzikagarria, eta alderantzizko matrizea kalkulatu dezakegu.

Aurkitu AX = BC egiaztatzen duen X

(1) Batuketaren karratua garatu dugu, 1. errenkadako elementu bakoitzean.

(2) 1. errenkadari kendu diogu 2.aren bikoitza gehi 3.a.

Ebatzitako ariketak eta problemak

6. Berdintza bat egiaztatzea

Egiaztatu A = a c b d eo bada, hau betetzen dela: A 2 – (a + d)A + | A | I = 0

I matrizea 2 ordenako unitate-matrizea izanik, eta 0 matrizea, 2 ordenako matrize nulua

EGIN ZUK

Egiaztatu badagoela A matrize karratu bat, 2 ordenakoa, simetrikoa, | A | = –7 duena eta hau betetzen duena:

f

22 22 ++ + + ++

eo = 0 0 0 0

ad bc ––

7. Parametro baten mendekoa den matrize baten heina aztertzea

–7

a –

• a ≠ –1 kasuan, hein (M) = 3; izan ere, lehenengo hiru zutabeek eraturiko 3 ordenako minorra ez da 0

1 2 4 0 1 1 3 0 6 ––= – 6 – 6 + 12 = 0 1 2 4 0 1 1 1 2 4 ––= 0

Hirugarren errenkada beste bien konbinazio lineala dela egiaztatu dugu.

Beraz, hein (M ) = 2; izan ere, 1 2 0 –1 ≠ 0.

Aztertu honako matrize hauek zer hein duten k parametroaren balioen arabera :

M = f k k 1 36 4 3 9 6 2 6 4 –––––– p

b)

|N | = () a a aa a a a 41 2 1 2 1 0 2 2 1 2 3 1 –12 –––+= = – 4(a – 2) – (a + 2)(–a2 + 3a – 2) = a3 – a2 – 8a + 12 = 0 a a 2 –3 = = • a ≠ 2 eta a ≠ –3 badira → hein (N ) = 4 a = 2 denean → N = f 1 2 4 1 2 2 0 2 4 0 4 0 1 2 3 1 ––––– p; eta a = –3 denean → N = f 16 0 4 0 1 0 1 3 2 3 1 1 3 3 2 –––– p. • a = 2 bada → hein (N ) = 2; izan

ere,

2.arekiko proportzionala da, eta

8. Determinanteen propietateak eta matrize baten heina

B matrizea 3 × 3 ordenako edozein matrize da. Esan honako baieztapen hauek zuzenak ala okerrak diren, erantzunak arrazoituz:

a) hein (B) = 2 bada, orduan hein (B2) = 2.

b) hein (B) = 3 bada, orduan hein (B3) = 3

c) hein (B) = 3 bada, orduan hein (B–1) = 3.

EGIN ZUK

A eta B matrizeak 2 ordenako bi matrize karratu badira, eta hein (A) = 2 eta hein (B ) = 1 badira, honako baieztapen hauetako zein betetzen da beti?:

a) hein (A + B ) = 3

b) hein (A + B ) ≤ 2

c) hein (A + B ) > 1

a) Okerra da. hein (B ) = 2 bada, orduan | B | = 0 eta | B 2| = | B | · | B | = 0 dira.

Horrek adierazten digu, hein (B 2) ≤ 2 dela.

Eta B 2 matrizearen heina 1 izan daiteke, adibide honek erakusten duen moduan:

(B ) = 2 eta hein (B 2) = 1

b) Zuzena da. hein (B ) = 3 bada, orduan

9. Alderantzizko matrizea kalkulatzea

a) Adierazi zein izan behar den m-ren balioa A alderantzikagarria izateko.

b) Ebatzi XA – B t = C ekuazio matriziala m = 0 kasurako. EGIN ZUK

a) Aurkitu a-ren zer baliorekin den erregularra A

b) a = 2 denean, aurkitu A matrizearen alderantzizkoa

Gidatutako ariketak eta problemak

1. Determinanteen propietateak

c1, c2 eta c3 3 ordenako matrize karratu baten 1., 2. eta 3. zutabeak badira, eta |c1 c2 c3| = 7 betetzen badute, kalkulatu:

a) |c3 c1 c2 |

b) | 3c1 c2 + c1 – c3 |

c) |c1 + 2c3 c2 2c3 – c1 |

a) Ikusten duzunez, 2. eta 3. zutabeak trukatu egin dira; eta gero, 1. eta 2. zutabeak.

b) Kontuan izan zenbakiekin biderkatu diren bi zutabe daudela.

c) Gogoan izan lerro bati zenbaki batekin biderkaturiko beste lerro bat batzean, determinantearen balioa ez dela aldatzen

Soluzioa:

a) 7 b) –21 c) 28

2. Determinante bat duen ekuazioa ebaztea

Aztertu zenbat soluzio erreal dituen honako ekuazio honek a-ren balioen arabera:

• Determinantea garatzeko, batu lehenengo zutabeari beste hirurak eta, gero, atera biderkagai komuna lehenengo zutabe horretatik. Kendu lehenengo errenkada beste hirurei, eta matrize diagonal baten determinantera helduko zara

• Ekuazioa ebazteko, berdindu biderkagai bakoitza zerorekin eta kontuan hartu a-ren zeinua

Soluzioa:

a = 0 bada → x = 0; a > 0 bada → x = ± a ; a < 0 bada → x = ± a–3

3. Matrize baten elementuak determinatzea

Honako matrize hauek izanda:

A = 2 0 1 1 eo B = b a c 2 2 3 –+ eo

zehaztu zein izan behar diren a, b eta c-ren balioak |B| = 8 eta AB = BA izateko.

4. Bi parametroren

Aztertu honako matrize honen heina:

• Garatu | B |, eta lortzen duzun adierazpena berdin 8 egin.

• Kalkulatu AB eta BA biderkadurak, eta berdindu itzazu gaiz gai.

• Ekuazio-sistema bat lortuko duzu, eta horren soluzioak bila gabiltzan balioak izango dira.

Soluzioa: a = 1, b = –2, c = 4

• Kontuan hartu zein den matrizeak izan dezakeen hein maximoa

• Kalkulatu lehenengo hiru errenkadek eta zutabeek eratutako minorra baliogabetuko duen a-ren balioa zein den, eta zehaztu zein den B-ren heina minor hori zero ez denean.

• Aurkitu zein den 1., 3. eta 4. zutabeek eratutako minorra baliogabetuko duen b-ren balioa.

• Aztertu zer baldintza bete behar diren hein (B ) = 2 izateko.

Soluzioa: a ≠ –1 bada edo b ≠ –2, hein (B ) = 3. a = –1 eta b = –2 badira, hein (B ) = 2.

a) Lortu | A | = 0 beteko duten m-ren balioak.

matrizea izanda:

a) Kalkulatu m-ren zer baliorekin izango duen A matrizeak alderantzizkoa.

b) m = 1 denean, kalkulatu zein den XA + X – 2A = 0 egiaztatzen duen X matrizea.

b) • Ekuazioan, igaro 2A bigarren atalera eta atera X biderkagai komun moduan. Horretarako, kontuan izan X = XI dela

• Biderkatu bi atalak matrize egokiarekin, X askatzeko. Gogoan izan matrizeen arteko biderketa ez dela trukakorra; beraz, erabaki ezkerretik edo eskuinetik biderkatu behar duzun.

Soluzioa:

a) A erregularra da m ≠ 0 eta m ≠ 2 denean. b) X =

mendeko matrize baten heina

5. Ekuazio matrizial bat ebaztea

Proposatutako ariketak eta problemak

Praktikatzeko

Determinanteak. Propietateak

1 Ebatzi honako ekuazio hauek:

2 Aurkitu 4 ordenako honako determinante hauetako bakoitzaren

6 a x b y c z 1 7 2

111 = 5 dela jakinda, kalkulatu honako determinante hauen balioak: 1 7 2 ++ + b) ca zx bc yz c z

3 Kalkulatu determinante hauen balioak:

4 m p n q = –5 bada, zein da determinante hauetako bakoitzaren balioa? Arrazoitu erantzunak:

n pq q ++33 b) p q m n c) n q m p 3 3 ––d) p q m n 2 2 e) / mp nm mq 1 f ) mm p p 5 5

00 1 ––––c) x ax x

1 2 2

b) 1 7 2

1 2 2

y by y

1 2 2

z cz z

–––

3 3 3

–++ + d) a b c

+ + +

3 3 3

x y z

7 Erabili honako determinante hau garatzeko propietateak, eta kalkulatu bere balioa:

x x x x x x x x x 21 2 25 32 34 36 3 + + + + + + 8 a)

Ebatzi | A | = 0

9 Aurkitu honako matrize hauen heinak:

a) A = f 3 6 1 4 5 10 0 5 1 2 1 0 – p b) B = f 1 4 1 2 5 0 3 6 0 1 2 3 1 1 4 – p c) C = f 2 0 0 2 1 0 2 0 0 2 1 1 0 1 0 0 –––– p d) D = f 1 0 2 2 1 7 0 1 3 3 2 0 ––– p

a) A = f a 2 1 3 1 1 1 0 –2 p b) B = f a a 1 1 1 2 1 0 2 2 ––– p

c)

C = f a a 2 3 1 3 1 4 2 –– p d) D = f a a 1 1 1 1 1 1 1 – p

heina 3 baino txikiagoa.

Proposatutako ariketak eta problemak

12 Aztertu honako matrize hauen heinak a parametroaren balioaren

17 Honako matrize hau emanda: M

a) Adierazi M-ren heina λ-ren balioen arabera.

b) Aztertu λ-ren zer baliotarako existitzen den M–1 .

c) Aurkitu M–1, baldin eta existitzen bada, λ = –2 denean.

13

14 Aztertu honako matrize hauen heinak a parametroaren balioen

18 Aurkitu t parametroaren zer baliorekin ez diren erregularrak A eta B matrizeak, eta kalkulatu:

a) A –1 , t = 1 bada. b) B –1 , t = 2 bada. A =

Alderantzizko matrizea. Matrize-ekuazioak

15 Aurkitu matrize hauetako bakoitzaren alderantzizkoa:

20

16 a) Kalkulatu matrize hauetako bakoitzaren alderantzizkoa:

b) Ebatzi AX = B eta XB = A ekuazioak, A eta B aurreko ataleko matrizeak izanik.

emanda, aurkitu:

a) x-ren zer baliorekin duen A matrizeak alderantzizkoa.

b) A-ren alderantzizkoa x = 2 denean.

c) Zein den b ∈ Á balioa, bA matrizeak 1 determinantea izateko.

22 A = f 2 2 3

1 3 3

1 2 2 p matrizea emanda:

a) Kalkulatu A (2I – A ).

b) Arrazoitu A eta 2I – A matrizeen alderantzizkoak existitzen diren.

c) k-ren zer baliorekin egiaztatzen da A –1 = kI – A ?

23 Matrize hauek izanda: A = 2 1 0

aurkitu (AB t + C )X = D egiaztatzen duen X matrizea.

24 Aurkitu X, jakinda 3AX = B betetzen dela, eta hauek izanda:

Ebazteko

25 Ebatzi honako ekuazio hauek:

30 Honako matrize hauek izanda:

A = f m m m 1 1 11

1 0 1 – p B = f 1 2 0

26 Aztertu honako matrize hauen heinak bakoitzak duen parametroaren balioen arabera:

27 Kalkulatu honako matrize hauen heinak t parametroaren

a) m-ren zer baliotarako existitzen da A –1?

b) m = 1 denean, aurkitu X matrizea, jakinda XA + B = C betetzen duela.

29 A = k 1 01 2 1 –eo eta B = f k 0 1 3 1 2 p matrizeak ditugu.

a) Zehaztu k-ren zer baliorekin duen AB matrizeak alderantzizkoa.

b) Ebatzi ABX = 3I ekuazioa k = 0 den kasuan, eta I matrizea 2 ordenako unitate-matrizea izanik.

– p

1 0 1

a) Kalkulatu m-ren zer baliorekin existitzen den A–1 .

b) m = 2 denean, aurkitu X matrizea, jakinda hau egiaztatzen duela: AX – BBt = I

31 Egiaztatu determinanteen propietateak erabiliz.

a) a a ab ab b b 2 11 2 1

22 + = (a – b )3

1 1 1

b) a a a a a

1 22 0 21 –2 2 2 = (a 2 – 1)2

32 n ordenako matrize hau emanda: An = f

kalkulatu A2, A3 eta A5-en determinanteak.

33 A = f 1 1 0

0 1 0

0 0 1 p matrizea izanda:

a) Aurkitu A n-ren adierazpen orokorra, n edozein zenbaki arrunt izanik.

b) Arrazoitu A n matrizeak alderantzizkoa duela n ≥ 1 betetzen duen edozein baliotarako, eta kalkulatu alderantzizko matrize hori.

34 Matrize hau emanda: A = f 5 4 3

4 2 2

3 2 1 p

Kalkulatu ondorengo hau betetzen duen X matrizea: AX = (A–1 At + I)2

35 A = f a a a

b b c c c 2 30 3 4 – p matrizea dugu, eta badakigu a, b eta

c ez direla nuluak.

a) Zehaztu linealki independenteak ez diren A-ren zutabekopurua.

b) Kalkulatu A-ren heina.

Proposatutako ariketak eta problemak

36 Aztertu zein den honako matrize honen heina a, b eta c balioetarako.

M = f a bc b ac c ab

55 5 ++ + p

37 Kalkulatu, egin daitekeen kasuetan, matrizearen alderantzizkoa:

A = f cos α sin α 0

–sin α cos α 0

Galdera teorikoak

0 0 1 p

38 Zuzena ala okerra? Arrazoitu erantzunak eta jarri adibideak.

a) Baldin eta c1, c2 eta c3 badira 3 ordenako matrize karratu baten 1., 2. eta 3. zutabeak, eta |c1 c2 c3| = 5 betetzen badute, orduan:

i) |c2 2c3 c1| = 10

ii) |c1 + c2 c2 – c1 c3| = 0

iii) |c1 + c3 c2 c3 + c1| = 5

iv) |–c2 2c1 – c3 c3 + c2| = 10

b) Baldin eta B matrizea 3 ordenako matrize karratu bat bada, eta bere determinantea 4 bada, orduan:

i) |5B | = 20 ii) | B 2| = 16 iii) | B –1| = 1/4

c) Baldin eta A matrizea A 2 = 2A – I betetzen duen matrize karratua bada, orduan A alderantzikagarria da eta A –1 = 2I – A da.

d ) A eta B bi matrize erregular dira eta AXB = A + B egiaztatzen dute; beraz, X = A –1 + B –1 .

39 Arrazoitu galdera hauei eman diezun erantzuna:

a) |M| = 3 eta |2M| = 48 badira, zein da M matrizearen heina?

b) A matrizea 4 ordenako matrize karratua bada eta |2A| = 80 bada, zenbat balio du A-ren determinanteak?

c) A eta B matrizeak 3 ordenako bi matrize karratu dira eta |AB| = 5 da. Zein da A-ren heina? Eta B-rena?

40 Honako biderketa hauetako zein da 4 ordenako determinante baten garapenekoa?

a) a12 · a23 · a31 · a42

b) a14 · a41 · a23 · a32

41 A matrize karratua 4 ordenakoa bada, jakin dezakezu zein den a21 A11 + a22 A12 + a23 A13 + a24 A14 baturaren balioa matrizearen elementuak zein diren jakin gabe?

42 A = a m b n c p fp matrizearen heina 2 bada, zein izango da B-ren heina?

B = f ma nb pc

m a n b p c 22 2 – p

43 4 ordenako A eta B matrizeak emanda, eta | A | = 3 eta

| B | = 2 izanik, kalkulatu |A –1|, | B t A | eta |(AB –1) t |.

44 a) Definitu zeri esaten zaion matrize baten heina.

b)Esan honako baieztapen hauetako zein diren zuzenak, eta arrazoitu erantzuna:

i) hein (A) = hein (–A) (–A da A-ren aurkako matrizea).

ii) hein (A) = hein (At ) (At da A-ren matrize transposatua).

iii) hein (A + B ) = hein (A) + hein (B )

iv) hein (A 2) = [hein (A)]2

v) hein (A) = hein (A –1) baldin eta A-k alderantzizkoa badu (A –1 da A-ren alderantzizko matrizea).

45 Idatzi 2 ordenako A eta B bi matrize, jakinda:

a) det (A + B ) ≠ det (A) + det (B )

b) det (A + B) = det (A) + det (B )

46 M da 2 ordenako matrize karratu bat. Zer baldintza bete behar dute matrize horren elementuek |M + I| = |M| + |I| bete dadin?

47 3 ordenako M matrize karratu baten determinanteak 4 balio badu, kalkulatu:

a) hein (5M ) b) hein (M 2) c) |(M –1)2|

48 3 × 3 matrize baten determinantea 5en multiploa da. Arrazoitu honako baieztapen hauek zuzenak ala okerrak diren:

a) Errenkadetako batean elementu guztiak 5en multiploak dira.

b) Elementu guztiak 5en multiploak dira.

c) Matrizearen heina 3 da.

d) Matrizeak ez du alderantzizkorik.

* Determinante honen izena Vandermonderena da. 50 Egiaztatu, garatu gabe,

51 Idatzi 3 errenkadako eta 3 zutabeko matrize bat, 3 elementu nulu dituena eta 2 ordenako minorretako bat ere ez duena nulua.

52 Zehaztu, 2 ordenako matrize karratuen artean, baldintza hauek betetzen dituztenak: elementu guztiak zenbaki osoak, determinantearen balioa –1, eta alderantzizkoa eta iraulia berdinak.

* Egin A · A t = I eta |A | = –1. Soluzioak 4 dira.

53 a) Aztertu M-ren heina a-ren eta b-ren balioen arabera.

a) Aurkitu a-ren zer baliorekin den M alderantzikagarria.

b) Kalkulatu M-ren alderantzizkoa a = 0 denean.

c) Ebatzi XM = N ekuazioa a = 0 kasurako.

55 A = f 2 3 2

1 0 1

0 4 1

– p matrizea kontuan izanda:

a) Aurkitu (Aij ) matrizea.

20 0

M = f ab a a ba ba

+ p

0 0 ––

b) Kalkulatu M –1 matrizea a = 1, b = –1 kasuan.

c) Arrazoitu MX + 2X = M ekuazioak soluziorik duen

a = 1, b = –1 kasuan.

54 Honako matrize hauek emanda:

1 Aurkitu a-ren zer baliorekin ez den erregularra A matrizea.

2 Kalkulatu determinante honen balioa, emaitza faktorizatuta emanez:

3 M = a a 1 5 4 –eo matrizea emanda, kalkulatu:

a) a-ren zer baliorekin ez den alderantzikagarria M.

b) a = 4 denean, aurkitu N = Mt M –1 betetzen duen N matrize bat.

c) Ebatzi MX – M 2 = Mt matrize-ekuazioa a = 4 kasuan.

b) Frogatu A · (Aij )t = f || || ||

0 0

A A A 0 0

0 0 p dela.

c) Zer erlazio dago |A | eta |(Aij )|-ren artean?

56 A da 3 ordenako matrize karratu bat, |A | ≠ 0 izanik. Bilatu zer erlazio dagoen |A | eta |(Aij )|-ren artean. Horretarako, kontuan izan aurreko problemako b) atala eta |A · B | = |A | · |B | dela.

57 A bada n ordenako matrize karratu bat, eman |(Aij )|-ren balioa |A |-ren funtzioan.

4 Baldin eta c1, c2, c3 badira matrize baten zutabe-bektoreak

a) Zehaztu t-ren zer baliorekin den erregularra A matrizea.

b) t = 1 kasuan, aurkitu AXA –1 = B egiaztatzen duen X matrizea.

7 a-ren zer baliorekin egiaztatzen da |

4

Sistemak determinanteen

bidez ebaztea

Ekuazio-sistemak ebazteko tresna berriak

Ekuazio-sistemen ebazpena Gaussen metodoa erabiliz jorratu izan dugu, baina alderdi batzuetan ebazpen hori hobetu egiten da aurreko unitateetan ikasi ditugun tresna batzuk erabiliz gero: matrizeak eta determinanteak.

Badago bi matrizeren heina aurkitu eta sistema bat bateragarria den ala ez den jakiteko modua ematen digun emaitza garrantzitsu bat. Rouchéren teorema da.

Ekuazio linealen sistema baten soluzioak determinanteen bidez aurkitzeko prozedurari

Cramerren erregela deitzen zaio. Gaussen metodoaren aldean, bi abantaila nabarmen ditu: askoz ere eraginkorragoa da parametro bat edo gehiago dituzten sistemak eztabaidatzeko, eta, soluzioetan, ezezagun bakoitzaren balioa gainerakoena ezagutu gabe lor daiteke.

Determinanteak ekuazio-sistemak ebazteko

Gabriel Cramer (1704-1752) matematikari suitzarra oso goiztiarra izan zen: 18 urterekin doktoratu zen, eta 20 urterekin Genevako Unibertsitateko irakasle izan zen. Ekuazio-sistemak ebazteko bere erregela ospetsua 1750ean argitaratu zuen.

Aurrekariak

— Cardanok, xvi. mendearen erdialdera, 2 × 2 sistemak ebazteko prozedura bat deskribatu zuen Ars magna bere lanean, eta funtsean bat dator Cramerren erregelarekin (determinanteak definitu ez bazituen ere, bere metodoan inplizituki ageri da 2  × 2 determinantearen ideia).

Leibniz ere gerora Cramerren erregela izango zen horretara hurbildu zen ekuazio-sistemei buruz egindako ikerketetan.

1730ean, MacLaurinek Cramerren erregela 2 × 2 eta 3 × 3 sistemetarako probatu zuen Aljebraren tratatua bere lanean (1748an argitaratu zen, hil eta bi urtera). 4 × 4 sistemak nola landu beharko liratekeen adierazten duten oharrak ere egin zituen.

Eugène Rouché (1832-1910) matematikari frantsesak 1875ean argitaratu zuen bere teorema; dena dela, teorema horren egiletza zalantzan jarri zuen beste matematikari frantses batek: Fontené. Berak egiaztapena lehenago eman zuela baieztatzen zuen.

Gabriel Cramer

Colin MacLaurin (1698-1746)

EBATZI

2 × 2 sistemak determinanteen bidez ebaztea

Lortu dezagun bi ezezaguneko bi ekuazio dituen sistema baten soluzio orokorra:

()

() ax ay c ax ay c 1 2 11 12 1 21 22 2

+= += 4

Egin dezagun lehenengo ekuazioa bider a22 eta bigarrena bider a12:

aa xa ay ca aa xa ay ca 11 212221 22 21 12 22 12 212 2 += += 3

Bi berdintzen kenketa eginda: (

12 y ezabatuta, x askatuko dugu bere balioa lortzeko. Modu berean lortuko dugu y-ren balioa ere.

Sistemaren soluzioa, beraz, hau da: x aa aa ca ca ––11 22 21 12 1222 12 = aa aa y ac ac ––11 22 21 12 12 1121 =

Soluzio horretan hiru zenbaki ageri dira: izendatzaile komuna eta bi zenbakitzaile. Zenbaki horiek honako matrize hauen determinanteak dira:

Lehenengoa, A, sistemako koefizienteen matrizea da. Beste biak lortzen dira A matrizean, dagokion ezezagunaren koefizienteen ordez, gai independenteak jarrita.

Beraz, soluzioa honela adierazi daiteke:

• Ebatzi, aurreko erregela hori erabilita, ekuazio-sistema hauek:

Egiaztatu soluzioa kasuetako bakoitzean.

3 × 3 sistemetara zabaltzea

• Nolakoa uste duzu izango dela hiru ezezaguneko hiru ekuazio dituen sistema baten soluzioa aurreko erregela horren arabera? Idatzi kasu horri dagozkion formulak, eta erabili honako ekuazio-sistema hauek ebazteko:

Rouchéren teorema

1. unitatean ikusi dugun moduan, Gaussen metodoak modua ematen du sistema bat bateragarria den ala ez den jakiteko.

Orain azalduko dugun prozedura honek ere modua ematen digu bi matrizeren heinetan oinarritu eta sistema bat bateragarria den jakiteko. Prozedura hau da: sistemak soluzioa badu, gai askeen zutabea jar daiteke koefiziente-matrizeko zutabeen arteko konbinazio lineal moduan.

Rouchéren teorema

Honako sistema honek soluzioa izan dezan

hau da baldintza nahikoa eta beharrezkoa: A koefiziente-matrizearen heina bat etortzea A’ matrize zabalduaren heinarekin.

ADIBIDEA Erreparatu

Egiaztapena

Sistema zutabe-bektoreen arteko konbinazio lineal moduan jar dezakegu:

Argi ikusten den moduan, sistemak soluzioa badu, gai askeen zutabea A matrizeko zutabeen arteko konbinazio lineal moduan jartzeko modua ematen duten x1, x2, x3, …, xn zenbaki batzuk existitzen dira. Beraz, A matrizeari (ci ) zutabea eranstean, matrizeak ez du heina handiagotzen. Hau da, sistemak soluzioa badu, orduan: hein (A’ ) = hein (A)

Kontrako arrazoitzea antzekoa da: hein (A’ ) = hein (A) bada, (ci ) zutabea gainerakoen arteko konbinazio lineala da, eta, beraz, existitzen dira (ai1), (ai2), (ai3), …, (ain ) bektoreekin biderkatuz gero emaitza moduan (ci ) bektorea ematen duten x1, x2, x3, …, xn zenbaki batzuk. Horrela, bada, x1, x2, x3, …, xn zenbaki horiek sistemaren soluzio dira

hein (A) eta hein (A' )-ren arteko erlazioa sistema bateraezin batean

Sistema bateraezina bada, hein (A) ≠ hein (A’ ) da. A’ matrizeak A matrizeak baino zutabe bat gehiago duenez, horren heina unitate bat handiagoa baino ezin da izan. Beraz, sistema bateraezina bada, hein (A’ ) = hein (A) + 1.

Ebatzitako ariketa

1 Erabili Rouchéren teorema honako sistema hauek bateragarriak edo bateraezinak diren jakiteko:

A | = –2 ≠ 0. Beraz, hein (A) = 3. A' matrizeak hiru errenkada baino ez dituenez, horren heina ezin da izan 3 baino handiagoa. Horrek esan nahi du, hein (A) = hein (A' ). Sistema bateragarria da.

b) x x x

2 43

y y y

z z

= =

––––+ +

0 1 4

laukizuzen gorrian nabarmendutako minorra ez baita

c) Sistema hau eta aurrekoa, hirugarren ekuazioko gai askean izan ezik, gainerakoan berdinak dira.

hein (A) = hein (A' ) = 2 dela egiaztatu daiteke. Sistema bateragarria da.

d) A' matrize karratu bat denez, horren determinantea aurkituko dugu: | A' | = 60 ≠ 0. Beraz, hein (A' ) = 3. A matrizeak bi zutabe baino ez dituenez, hein (A) = 2. Beraz, hein (A) = 2 ≠ hein (A’ ) = 3, eta sistema bateraezina da.

1 Erabili Rouchéren teorema honako sistema hauek bateragarriak ala bateraezinak diren jakiteko:

2 Aurreko ariketako prozesu berari jarraituta, esan honako sistema hauek bateragarriak ala bateraezinak diren:

Cramerren erregela

Cramerren erregela berehalako erabilera praktikoa duen teorema da. n ezezagun dituzten n ekuazioko sistema baten soluzioa lortzeko balio du. n = 4 kasurako enuntziatu eta frogatuko dugu. Gero, hortik abiatuta, berehala lortzen da edozein n-tarako orokortzea

4 ezezaguneko 4 ekuazio dituen sistema bat dugu:

(A)

hein (A' ) da. Beraz, sistema bateragarria da

CRAMER EDO GAUSS?

Sistema bat Gaussen metodoaren bidez ebazteko, ezinbestekoa da triangelatzea eta ezezagunen balioak kateatuta lortzea bata bestearen atzean.

Cramerren erregelak, ostera, ezezagun baten balioa gainerakoak lortu gabe kalkulatzeko modua ematen du. Zenbait kasutan, hori abantaila handia da.

Adierazpen horretan, Ax matrizea hau da: A matrizeko x-ren koefiziente-zutabearen lekuan gai askeen zutabea jarrita lortzen dena. Eta modu berean lortzen dira Ay , Az , At ere: A matrizean, dagokion ezezagunaren koefiziente-zutabearen ordez gai askeena jarrita

1 Enuntziatu Cramerren erregela hiru ezezaguneko hiru ekuazio dituen sistema baterako.

2 Ebatzi honako ekuazio-sistema hau Cramerren erregela

Cramerren erregelaren egiaztapena

Ezezagunetako bakoitza askatu behar dugu. Lehenengo, x askatuko dugu. x askatzeko, y, z, t ezabatu behar ditugu. Hori egiteko, (1), (2), (3), (4) esango diegun lau ekuazioak x-ren koefizienteen adjuntuekin biderkatuko ditugu :

Batuketa eginda lortuko dugun berdintza zatika aztertuko dugu: x-ren koefizientea hau da: a11

41 = |A| y-ren koefizientea hau da:

a12A11 + a22A21 + a32A31 + a42A41 = 0

Era berean, argi ikusten denez, z-ren eta t-ren koefizienteak zero dira.

Gai askea hau da:

c1A11 + c2A21 + c3A31 + c4A41

Eta hori da A matrizean x-ren koefiziente-zutabearen ordez gai askeen zutabea jartzean lortzen den Ax matrizearen determinantea:

GOGORATU

• a11A11 + a21A21 + … adierazpena A-ren determinantearen garapena da lehenengo zutabeko elementuetatik abiatuta.

• a12A11 + a22A21 + … adierazpena da A matrizearen zutabe bateko elementuen eta beste zutabe batekoen adjuntuen arteko biderkaduren arteko batuketa.

Beraz, 0 balio du.

Laburbilduz:

(1) · A11 + (2) · A21 + (3) · A31 + (4) · A41 batuketa egitean, hau lortzen dugu: | A | x + 0y + 0z + 0t = | Ax |

| A | ≠ 0 denez, x askatu eta hau lortzen dugu: x = || || A A x

y askatzeko (1), (2), (3), (4) ekuazioak bider A12, A22, A32, A42 egin beharko genituzke, hurrenez hurren. z eta t askatzeko ere berdin jokatuko dugu, eta hau lortuko dugu:

➜ anayaharitza.es

Aurreko unitatean, matrize karratu baten alderantzizkoaren adierazpena eman genuen. Adierazpen horren baliozkotasuna egiaztatu genuen, baina modu konstruktiboan nola

lortzen zen ez genuen ikusi. Orain, Cramerren erregelaren bidez, egiaztapen hori lortzeko moduan gaude

Pentsatu eta praktikatu

3 Egiaztatu Cramerren erregela hiru ezezaguneko hiru ekuazio dituen sistema baterako

Jokatu orrialde honetan egin dugun moduan

Cramerren erregela edozein sistematan aplikatu

Cramerren erregelak, printzipioz, |A| ≠ 0 betetzen duten (n × n) sistema karratuetarako baino ez du balio (sistema horiei «Cramerrenak» esaten zaie). Dena dela, edozein sistema bateragarriri aplika dakioke, ondoren ikusiko dugun moduan.

n ezezaguneko m ekuazio dituen sistema bat daukagu, bateragarria. Demagun hein (A) = hein (A' ) = r dela, eta r < m, r < n direla. Horrek esan nahi du koefiziente-matrizeak zero ez den r ordenako minor bat duela. Idazkera hori sinplifikatzeko, minorra A matrizearen ezkerreko ertzean dagoela pentsatuko dugu; hau da, lehenengo r errenkaden eta lehenengo r zutabeen ebakidurak eratzen duela:

(*) Ezabatu egiten dira, aurreko r ekuazioen K.L. baitira

Sistema hori, beraz, beste honen baliokidea da:

Sistema hori Cramerrena da, eta gai askeak «sobera» dauden ezezagunen (xr +1, …, xn) funtzioan emanda daude. Beraz, soluzioa n – r parametroaren araberakoa da.

• r = m bada, ekuazio guztiak dira erabilgarriak (bat bera ere ez dago «sobera»).

• r = n < m, bada, zenbait ekuazio «sobera» daude, baina ezabatzen ditugunean, n ezezaguneko n ekuazio dituen Cramerren sistema bat geratzen da, determinatua.

Ebatzitako ariketak

1 Aztertu eta ebatzi honako sistema hau:

hein (A) kalkulatu:

Zutabeen artean honako erlazio hauek ikusten ditugu: (3.a) = –(2.a) (4.a) = (2.a) – (1.a)

Beraz, A matrizeak bi zutabe baino ez ditu L.I.

Hau da, hein (A) = 2

Sistema homogeneoak

Kasu honetan, ekuazio-sistemen mota berezi bat aztertuko dugu, 1. unitatean jada ikusi genuena: gai independente guztiak zero dituzten sistemak.

Gai aske guztiak zero dituzten ekuazio-sistemei homogeneo esaten zaie.

Honako bi propietate hauek dituzte bereizgarri:

Sistema homogeneo baten soluzioa x = 0, y = 0, z = 0, t = 0, … da, eta hori ziurra da. Soluzio hutsala esaten zaio.

Sistema homogeneo batek beste soluzio batzuk izan ditzan, nahikoa eta beharrezkoa da honako hau:

hein (A) < ezezagun-kopurua

direla esan nahi du. Baten bat sobera dago. Ikus dezagun

dugu → hein (A) = 2

Beraz, lehenengo bi ekuazioak independenteak dira; hirugarren ekuazio ezabatu eta z bigarren atalera pasatu dezakegu:

Sistemak determinanteen bidez eztabaidatu

1. unitatean ikusi genuen zer den parametro baten mendekoak diren ekuazioen sistema bat eztabaidatzea, eta eztabaidatu genituen sistema batzuk Gaussen metodoa erabilita. Oraingo honetan determinanteen laguntzaz egingo dugu, eta konturatuko gara modu honetara egitea erosoagoa dela.

Ebatzitako ariketak

1 Eztabaidatu eta ebatzi ekuazio-sistema hauek, a parametroaren balioen

1

| A | faktorizatu dugu, parametroaren zer baliorekin baliogabetzen den errazago ikusteko. Kasu horiek dira aparteko arretaz aztertu behar ditugunak.

• a = 1

Sistema ekuazio bakarrera laburtu dugu: x + y + z = 1. Beraz, indeterminatua da. Horren soluzioa lortzeko, balio parametriko bat eman behar diegu ezezagunetako biri, eta beste ezezaguna horien funtzioan jarri behar dugu.

• a ≠ 1, a ≠ –2

a-ren balio bakoitzerako (1 eta –2 ez diren balioetarako), sistema bateragarria eta determinatua da

| Ax |, | Ay |, | Az | kalkulatuko ditugu: | Ax | = | Ay | = | Az | = (a – 1)2

Beraz, soluzioa hau da:

➜ anayaharitza.es

Ekuazio-sistemen eztabaida indartzeko ariketak.

2 Eztabaidatu eta ebatzi honako ekuazio-sistema hau k-ren balioen arabera:

Gogora dezagun horrek ez duela esan nahi infinitu soluzio daudenik. a-ren balio bakoitzerako soluzio bakarra duen sistema bat dago. Adibidez, a = 0 kasuan, sistemaren ekuazioa da x = 1/2, y = 1/2, z = 1/2.

Oraingoan komeni zaigu | A' | kalkulatzea eta 0rekin berdintzea. Kasu horietan bakarrik izango da sistema bateragarria. |

• k = 2 bada, hein (A) = hein (A' ) = 2. Sistema bateragarri determinatua da.

Soluzioa: x = 6, y = 1

• k = –31 bada, hein (A) = hein (A' ) = 2. Sistema bateragarri determinatua da.

Soluzioa: x = –3/5, y = 38/5

• k ≠ 2 eta k ≠ –31 badira, sistema bateraezina da; izan ere, hein (A' ) = 3 ≠ hein (A) = 2.

➜ Parametrodun matrize baten determinantea.

Ebatzitako ariketak

3 Eztabaidatu eta ebatzi honako sistema hau, ahal denean:

Homogeneoa denez, sistema kasu guztietan da bateragarria; beti izango du, gutxienez, x = 0, y = 0, z = 0 soluzioa. Gainera, ekuazio-kopurua ezezagun-kopurua baino txikiagoa denez, sistema beti da indeterminatua

x x my y z mz 2 3 60 0 –

+ += =

Azter dezagun A matrizearen heina m-ren funtzioan:

m 2 13 –= 6 + m → Baliogabetu egiten da m = – 6 denean.

m 2 1 6 –= –2m – 6 → Baliogabetu egiten da m = –3 denean.

Bi determinanteak baliogabetuko dituen m-ren baliorik ez dagoenez, A matrizearen heina 2 da kasu guztietan. Beraz, sistema bateragarri indeterminatua da eta bi ekuazioak dira baliagarriak, berdin dio m-ren balioa zein den

• m ≠ –

➜ anayaharitza.es Bi soluzioak bat datoz.

4 Eztabaidatu eta ebatzi, egin litekeenean, honako sistema hau:

() () x x y y 1 1 3

m mm m + += =

–

Kontuz! λ sistemarako parametro bat da. Sistema indeterminatua denean, beste parametro bat erabili beharko dugu soluzioak deskribatzeko.

Pentsatu

1 Eztabaidatu eta ebatzi

•

6

y

dugu

Soluzioa: x = –3λ, y = λ, z = 0 ohar garrantzitsua. Problema orain arte ikusitakoarekin ebatzi da. Dena dela, arrazoizkoa da galdetzea soluzio berdinak lortuko ote genituzkeen erreferentzia moduan m = –3 balioa hartuz gero. Egin dezagun:

• m ≠ –3 denean, lortzen dugu x = m m 26 18 –2 + μ, y = μ, z = m m 26 6 + + μ 4 2. soluzioa

• m = –3 kasuan: x = –3μ, y = 0, z = μ Bada, egiaztatu dugunez, bi soluzioak bat datoz. Webgunean kasuistika horren analisi sakona ageri da.

| A | = λ2 – 4 = (λ – 2)(λ + 2) → Baliogabetu egiten da λ = 2 kasuan eta λ = –2 kasuan. Nahi izanez gero, egiaztatu honako emaitzetako bakoitza.

• λ = 2: hein (A) = 1 ≠ hein (A' ) = 2. Sistema bateraezina da.

• λ = –2: hein (A) = hein (A' ) = 1. Sistema bateragarri indeterminatua da.

Soluzioak: x = –2 – 3k, y = k

• λ ≠ 2 eta λ ≠ –2: hein (A) = hein (A' ) = 2. Sistema bateragarri determinatua da.

Soluzioa: x = () 4 2 2 –

–––2 m mm m m + = , y = 2 ––m m (λ bakoitzerako, soluzio bakarreko sistema bat dago).

2 Eztabaidatu eta ebatzi honako ekuazio-sistema hau, a parametroaren funtzioan:

() () () ax ax y ay 1 11 0 0 ––+ ++ = = *

Ekuazio-sistema baten forma matriziala

Ekuazio-sistema batek hiru matrize ditu berarekin lotuta: koefizienteena, ezezagunena eta gai askeena. Adibidez:

HISTORIAKO OHARRA

1858an Cayleyk ikusi zuen «sistema lineal baten koefiziente-matrizea har daitekeela aldagaien gainean jokatzen duen eragiletzat; a zenbakiak ax lortzeko x ezezagunari eragiten dion bezala».

Sistema hori modu matrizialean honela adieraz daiteke:

A matrizeak alderantzizkoa badu, X honela askatu ahal izango dugu:

denez (egiaztatu), hau lortuko dugu:

n ezezaguneko n ekuazio dituen sistema bat modu matrizialean honela adieraz daiteke: AX = C

A matrizea da ezezagunen koefizienteekin eratuta dagoen m × n matrize bat

X matrizea da ezezagunek eratzen duten n × 1 zutabe-matrize bat

C matrizea da gai askeek eratzen duten m × 1 zutabe-matrize bat

A matrize erregularra bada, sistemaren soluzioa honela lor daiteke: X = A–1 · C

1 Ebatzi matrizeen bidez honako siste-

1 Adierazi modu matrizialean eta ebatzi (kontuan izan aurreko unitateko 78. orrialdean proposatutako 1. ariketa).

eta ebatzi

➜ Ebatzi sistemak matrizeen bidez.

Ebatzitako ariketak eta problemak

1. Sistemak Rouchéren teorema erabiliz eztabaidatzea

Eztabaidatu sistema hauek eta ebatzi bateragarriak direnean. Eman kasu bakoitzaren interpretazio geometriko bat:

1 badira, hein (A) = 3 = hein (A'

EGIN ZUK

Eztabaidatu honako ekuazio-sistema hauek eta ebatzi bateragarriak direnean:

errenkada berdin daudenez, hein (A' ) = 2 = hein (A). Beraz, sistema bateragarri indeterminatua d.

matrizean

da

geometrikoa: m ≠ 0 eta m ≠ 1 badira, puntu batean elkar ebakitzen duten hiru plano dira. m = 0 bada, planoek zuzen batean ebakitzen dute elkar. m = 1 bada, planoak binaka ebakitzen dute elkar.

b) Lehenengo, A'-ren heina aztertu behar dugu, 4 izan daiteke eta:

• a ≠ 2 bada, hein (A' ) = 4 > hein (A) sistema bateraezina da.

a = 2 bada, hein (A' ) < 4.

Sistema bateragarri determinatua da. Ebazteko, lehenengo hiru ekuazioak hartuko ditugu, zero ez den minor bat eratzen baitute; eta Cramerren erregela aplikatuta, hau lortzen dugu:

x = 1, y = 1, z = 1

Interpretazio geometrikoa: a ≠ 2 bada, binaka elkar ebakitzen duten lau plano dira. a = 2 bada, planoek puntu batean ebakitzen dute elkar.

2.

parametroren mendeko sistemak

Eztabaidatu honako ekuazio-sistema hau a eta b parametroen funtzioan:

+ + *

ay y y

EGIN ZUK

mx x x

z z zb 3 8

3 1 ––+ +

2 4

= = =

Eztabaidatu honako sistema hau eta ebatzi m-ren eta n-ren balioen arabera:

• 2 1 4

1 1 1

2 3 8

3 1 –– p 1 1 2 –3 ≠ 0 denez → hein (A) = 2. b

+ + + 2 1 4 –= 6 – 3a = 0 → a = 2

= = = a ≠ 2 bada, b-ren edozein baliotarako, hein (A) = hein (A' ) = 3. Sistema bateragarri determinatua da • A' = f b

1 1 1

2 3 8

3 1 –= 25 – 5b = 0 → b = 5 • a = 2 eta b = 5 badira, hein (A) = hein (A' ) = 2 < ezezagun-kop. Sistema bateragarri indeterminatua da • a = 2 eta b ≠ 5 badira, hein (A) = 2 ≠ hein (A' ) =

3.

Sistema bateraezina da Ekuazio-sistema hau daukagu: f m m m 1 0 1 2 0

1 1 2

––– p f x y z p = f 0 0 0 p

a) Zein izan behar da m-ren balioa sistemak soluzio bat baino gehiago izan dezan?

b) Ebatzi m = 1 kasuan.

EGIN ZUK

m = 1 edo m = 4/3 bada, hein (A) = hein (A' ) < 3. Sistema bateragarri indeterminatua da. Infinitu soluzio ditu.

m ≠ 1 eta m ≠ 4/3 bada, hein (A) = hein (A' ) = 3. Sistemak soluzio bakarra du. Sistema homogeneo bat denez, soluzioa (0, 0, 0) da, soluzio hutsala.

x x y y ay z z z 3 3 4 0 0 0 – + + + + + = = =

x

Soluzioa:

x = –2λ, y = λ, z = λ

4. Ekuazioak baino ezezagun gehiago dituzten sistemak

Honako ekuazio-sistema hau emanda:

x x x

a) Izan daiteke bateraezina?

b) Ebatzi m = 0 kasuan.

Eztabaidatu ekuazio-sistema hau, eta ebatzi a = 0 kasuan:

• m = 1 bada,

1 1 2 2 1 11 0 2 ––≠ 0 →

hein (A) = 2 eta hein (A' ) = 3. Sistema bateraezina da.

b) m = 0 bada, sistemak infinitu soluzio ditu, eta Cramerren erregela erabilita ebatziko dugu, z bigarren atalera igaroz z = λ parametro moduan.

Soluzioak hauek dira:

x

3

Bi

3. Sistema homogeneoak

Gidatutako ariketak eta problemak

1.

Sistema bateragarria parametroaren edozein baliotarako

a) Egiaztatu ez dela existitzen a-ren baliorik hein (A) ≠ hein (A' ) betetzen duenik.

= = = *

y ay y

++ + +

z z az

+

a a 2 2 2 ––

a) Egiaztatu bateragarria dela a-ren edozein baliotarako.

b) Aurkitu a-ren balio guztietarako soluzioak.

b) Aurkitu a-ren zer baliorekin den zero A-ren determinantea, eta, beraz, zer baliorekin den bateragarri indeterminatua sistema, eta adierazi soluzioa parametro batekiko. Erabili Cramerren erregela soluzioak a-ren funtzioan lortzeko gainerako balioetarako.

Soluzioa:

a) a ≠ –1 kasuan, hein (A) = hein (A' ) = 3. Bateragarri determinatua da.

a = –1 kasuan, hein (A) = hein (A' ) = 2. Bateragarri indeterminatua da.

b) a = –1 kasuan, soluzioak (3 – 2m, 4 – 3m, m) dira.

eo

2.

Matrize forman emandako sistema bat eztabaidatzea

1

• Aurkitu koefiziente-matrizearen determinantea eta lortu zer baliorekin egiten den zero.

• Aurkitu koefiziente-matrizearen eta matrize zabalduaren heinak, eta alderatu.

Soluzioa:

X = x y z

3. Sistema matriziala

z m m m 12 –

m = 1 bada, ekuazio guztiak berdinak dira. Sistema bateragarri indeterminatua da. m = – 2 bada, hein (A) = 2 ≠ hein (A' ) = 3. Sistema bateraezina da. m ≠ 1 eta m ≠ – 2 bada, sistema bateragarri determinatua da.

• Deitu X bila gabiltzan matrizeari, jakinda hau bete behar duela: X = A–1B. Kontuan izan zein izan behar den X-ren dimentsioa berdintza hori egiaztatu dadin.

• Biderkatu bi atalak A-rekin, ezkerretik. Soluzio moduan X matrizea duen ekuazio-sistema bat lortuko duzu.

• Ebatzi sistema hori, Cramerren erregela erabiliz, m parametroaren funtzioan.

Soluzioa: A–1B = 1 1 1 fp

4. Sistema bateragarri indeterminatu baten soluzio berdinak dituen sistema bat

*

x x y y z z 2 2 3 0 + + + = =

• Egiaztatu hasierako sistemak hein (A) = hein (A') egiaztatzen duela. Ebatzi.

• stema berriak soluzio horiek izan ditzan, erantsitko ekuazioa izan behar da lehenengo bien konbinazio lineala. Beraz, eratzen dituzun 3 ordenako minorrek nuluak izan behar dute.

• Nulua ez den 2 ordenako minor batetik abiatuta, eratu 3 ordenako bi minor 3. errenkadarekin eta 4. zutabearekin, batek m eta besteak n barne izateko moduan.

• 0rekin berdintzean, m-ren eta n-ren balioak lortuko dituzu.

Soluzioa: m = 2 3 ; n = 2 –1 . Sistemaren soluzioak hauek dira: (–1 – λ, λ + 2, λ).

A = 2 1

() x mx mx y y mz z

Ekuazio-sistema hau emanda:

Proposatutako ariketak eta problemak

Rouchéren teorema. Cramerren erregela

1 Erabili Rouchéren teorema honako sistema hauek bateragarriak edo bateraezinak diren jakiteko. Ebatz itzazu, egin daitekeenean.

6 Eztabaidatu honako sistema homogeneo hauek a parametroaren funtzioan:

2 Ebatzi honako sistema hauek Cramerren erregela erabilita:

7 Eztabaidatu sistema hauek m parametroaren balioen arabera:

3 Aztertu eta ebatzi sistema hauek, egin daitekeenean:

Sistema baten matrize forma

8 Adierazi matrize forman eta ebatzi alderantzizko matrizea erabilita:

9 Idatzi sistema hauek ohiko forman, eta ebatzi, baldin eta ebatzi badaitezke:

1 34`

12 1 ` j matrizeak emanda, kalkulatu zein izan behar den k-ren balioa xA  +  y B = 4C ekuazio-sistema bateragarria izateko, eta ebatzi kasu horretan.

Proposatutako ariketak eta problemak

Ebazteko

12 Aztertu eta ebatzi honako sistema hauek, eta interpretatu geometrikoki: a) () xy z mx ym

12

13 Eztabaidatu eta ebatzi honako sistema hauek:

17 Liburu-denda bateko jabeak 84 liburu bi preziotan saldu ditu: batzuk 5m euroan, eta beste batzuk, 4m euroan, eta salmenta horiekin 3 105 euro bildu ditu.

a) Planteatu ekuazio-sistema bat, x eta y ezezagunak mota bakoitzetik saldutako liburuen kopuruak izanik, eta aztertu bere bateragarritasuna.

b) Izan liteke liburuak, hurrenez hurren, 45 eta 36 euroan saltzea?

c) Ebatzi sistema m = 9 kasurako. Mota bakoitzeko zenbat liburu saldu zituen?

18 288 pertsonako talde bat daukagu, 18 eta 25 urte bitartekoak, eta sailkatuta daude ikasleak, langileak edo langabeak diren kontuan hartuta. Badakigu bost ikasleko hiru landun daudela, eta lanik gabe daudenak beste guztien % 80 direla.

a) Planteatu egoera horri dagokion ekuazio-sistema.

a) eta c) kasuetan, parametro bat behar baduzu ebazteko, ezin diozu λ deitu, parametro hori sistemarena baita.

14 Ekuazio-sistema hau daukagu:

a) Arrazoitu parametroen a = 0, b = 1, c = 2 balioetarako sistema bateragarria dela.

b) Zehaztu zein izan behar diren a, b eta c parametroen balioak (x, y, z) = (1, 2, 3) sistemaren soluzioa dela egiaztatu dadin.

c) Arrazoitu soluzio hori bakarra den ala ez den.

15 Eztabaidatu honako sistema hauek parametroaren funtzioan, eta ebatzi bateragarriak direnean:

b) Zenbat ikasle, landun eta langabe daude?

19 Euro bateko zenbait txanpon ditugu, hiru multzotan jarrita. Hirugarren pilotik bigarrenera hamabi txanpon eraman ditugu, eta, ondoren, bigarrenetik lehenengora hamar txanpon. Hori eginda, hiru piloek txanpon-kantitate bera dute.

a) Enuntziatuan emandako datuekin, zehaztu dezakegu zenbat txanpon zeuden hasieran piloetako bakoitzean? Arrazoitu erantzuna.

b) Zehaztu zenbat txanpon zeuden hasieran pilo bakoitzean, jakinda guztira 51 txanpon zeudela.

Galdera teorikoak

20 Lau ekuazio eta hiru ezezagun dituen sistema homogeneo baten koefiziente-matrizearen heina 3 da. Zer esan dezakezu soluzioari buruz?

Arrazoitu zure erantzuna.

21 Lau ekuazio eta lau ezezagun dituen sistema batean hein (A ) = hein (A' ) = 2 egiaztatzen bada, erabil daiteke Cramerren erregela?

16 Gitarra elektrikoak egiten dituen enpresa batek 325 aleko eskari bat bete behar du. Gitarrak bidaltzeko 3 kaxa mota erabiliko dituzte (A, B eta C), 5, 10 eta 15 alerako tokia dutenak, hurrenez hurren. Guztira 35 kaxa prestatu dituzte. Badakigu, gainera, A eta B motako kaxa guztiak kontuan hartuta, 6 bider gehiago direla C motako kaxak baino.

a) Planteatu ekuazio-sistema bat, eskariari erantzuteko mota bakoitzeko zenbat kaxa erabil daitezkeen kalkulatzeko.

b) Aztertu sistema horren bateragarritasuna eta ebatzi.

Erantzuna baietz bada, azaldu zer aldaketa egin behar diren sisteman erregela hori ezarri ahal izateko.

22 Ezezagunak adina ekuazio dituen sistema batean, koefiziente-matrizearen determinantea 0 da. Erantzun, arrazoituta, honako galdera hauei:

a) Izan daiteke bateragarria?

b) Izan dezake soluzio bakarra?

c) Noiz izango da bateraezina?

2 1 3 – p, B = f a b

Sakontzeko

c p eta C = f a b

a) x x x x y y y y z z z t t t t a 3 5 2 32 2 4 3 1 2 ––––+ + + + + + + = = = = Z [ \ ] ] ] ] ] b) ax ay ay z z z az t t t t 2 1 1 2 0 –––+ + + += = = = Z [ \ ] ] ] ] ]

27 Eztabaidatu honako sistema hauek:

24 Sailkatu honako sistema hau m-ren balioen arabera, eta ebatzi soluzioa duenean:

2 –2 *

32 25 4 33

xy z xy z xy z mm

++ = ++ = ++

=

25 Eztabaidatu, a eta b parametroen funtzioan, honako ekuazio-sistema hau: xayz xy z xy zb

––++ = = ++ = *

28 Aztertu honako plano hauek zer posizio erlatibo duten a  parametroak hartzen duen balioaren arabera:

2 Eztabaidatu honako sistema hau, eta ebatzi sistema bateragarri indeterminatu egiten duten a-ren balioetarako eta a = 0 kasurako:

*

5 Eztabaidatu honako sistema homogeneo hau eta ebatzi soluzioa duenean. Interpretatu geometrikoki.

xy y z x x x y y z kz 2 3 2 3 0 0 0 0 + + + + + + + = = = = Z [ \ ] ] ] ]

*

–––

+= += +=

xy za ax yz a xayz 23 22 6

3 a) Eztabaidatu ekuazio linealen sistema hau λ parametroaren balioen arabera:

m m + + + +

a) Planteatu ekuazio-sistema bat eta arrazoitu m-ren zer baliotarako den bateragarri determinatua.

z z z

= = =

1 1 1 –

b) Ebatzi λ = 1 kasurako.

a) () x x ax ay y y z az z a a a 2 –21 + + + + + + = = = + + * b) x x y y y z z z a 2 3 1 1 2 ––––+ = = = = Z [ \ ] ] ] ] ] AUTOEBALUAZIOA ➜

b) Zein izan daitezke m-ren balioak problemak soluzioa izateko? Kalkulatu soluzioa m = 4 kasurako.

7 Eztabaidatu eta ebatzi honako sistema hauek:

Unibertsitatera sartzeko probarako

I. multzoa: Aljebra

Menderatzen dituzu matrizeen propietateak eta eragiketak?

Argi duzu zer egin daitekeen eta zer ez?

Badakizu zer estrategia erabil ditzakezun matrizeen berdintza batean ezezaguna bakantzeko?

Ondorengo adierazpen hauetako zein dagokio A–1 matrizeari, hau da, A-ren alderantzizkoari?

a) A d c b a 1 –

–eo b) a c b d –

–eo

c) d c b a –

–eo d) A d c b a 1 eo

Teknika hauekin eta beste zenbaitekin, ariketa eta problema mordoa ebatzi ahal izango dituzu.

Badakizu determinanteak erabiltzen ekuazio-sistemak eztabaidatu eta ebazteko, parametrodunak zein parametro gabeak izan?

Ezagutzen duzu Rouchéren teorema?

Menderatzen duzu Cramerren erregela eta nola erabiltzen den?

A da 3 ezezaguneko ekuazio-sistema baten koefizienteen matrizea, eta Al , bere matrize zabaldua. Erlazionatu ezkerreko errenkada bakoitza eskuinean dagokionarekin.

a) Hein (A) = Hein ( Al ) < 3

b) Hein (A) < Hein ( Al ) = 3 III) Infinitu soluzio

c) Hein (A) = Hein ( Al ) = 3 III) Soluziorik ez

d) Hein (A) = Hein ( Al ) < 2 III) Soluzio bat

e) Hein (A) < Hein ( Al ) < 3

Ariketen eta problemen adibideak

Aurkitu ditzakezun aljebrako ariketak problemak ugariak eta era askotakoak dira.

■ Aztertu bi hauek. Ebazteko ezinbestekoa da ondo menderatzea matrizeak, beren eragiketak eta propietateak.

Aurkitu A · X · B = I betetzen duen X matrizea, hau jakinda:

2 Matrize hauek ditugu:

■ Edo ekuazio-sistemen ebazpenean oinarritutako beste hauek jakitea:

1 Honako ekuazio-sistema hau daukagu: () ()

a. Kalkulatu ondorengo matrize hau: ()

b. Zehaztu ondorengo hau egiaztatzen duen X matrizearen errenkada- eta zutabe-kopurua: X · At = Bt

c. Arrazoitu At matrize alderantzikagarria den, eta kalkulatu X matrizea.

Lehenengoa erraz ebazten da, A-ren eta B-ren alderantzizkoak aurkitu eta horiekin behar bezala biderkatuta, hasierako berdintzan:

Bigarrena zailtxoagoa da, eta matrizeen zenbait propietate eta eragiketari buruzko ezagutzak erabili behar dira.

Problema hauek ebazteko behar izan diren teknikak ezkerrean berrikusita ageri direnak dira.

anayaharitza.es webgunean hau aurkituko duzu:

• Aljebrako oinarrizko teknika horiek ikasteko bide bat, arintasuna eskuratu dezazun teknika horiek ulertzeko, erabiltzeko eta aplikatzeko.

• Unibertsitatera sartzeko proben problema-bilduma bat, ebatzitakoak, proposatutakoak, laguntza eta guzti emanda, jarraibideak emanda…

Z [ \

] ] ] ] ] ] ] ]

22 12 21 1

xy z xa yaza xaya z

––+= ++ = ++ +=

a. Eztabaidatu a-ren balioen arabera.

b. Badago sistemak infinitu soluzio izateko a -ren baliorik? Erantzuna baietz bada, ebatzi.

2 Berotegi bat eraiki nahi da haziak hazteko, tenperatura, hezetasuna eta airearen konposizioa kontrolatuta. Berotegi barrura hornitu beharreko aireak % 78 nitrogenoa izan behar du, % 21 oxigenoa eta % 1 argona.

a. Berotegiaren edukiera 2 000 litrokoa bada, zehaztu zenbat litro nitrogeno, zenbat litro oxigeno eta zenbat litro argon behar diren.

b. Airea hornitzeko, hiru nahaste gaseoso daude, A, B eta C, eta horien konposizioa erantsitako taulan ageri da. Lortu nahasketa bakoitzetik zer kantitate erabili behar den berotegia eskatutako konposizioa duen airearekin betetzeko.

nahastea nitrogenoa oxigenoa argona

A % 80 % 20 % 0

B % 70 % 20 % 10

C % 60 % 40 % 0

Lehenengoa oso teknikoa da, eta A-ren eta Al -ren heinak konparatu behar dira, A -ren kalkulutik abiatuta.

Bigarrenean, oztopo bakarra da enuntziatua zuzen interpretatzea, eta ebazteko zailtasunik ez duen ekuaziosistema bat planteatzea.

Autoebaluazioa

I. multzoa : Aljebra ➜ anayaharitza.es

1 A = 5 2 3 3 eo , B = x x 2 1 eo eta C = 0 1 1 4 ––eo izanda:

a) Aurkitu zein izan behar den x-ren balioa B 2 = A bete dadin.

b) Kalkulatu zein izan behar den x-ren balioa B + C = A–1 izateko.

c) Aurkitu x-ren zer baliok egiaztatuko duen A – B + 2 1 C = 3I

ez-nuluk egiaztatzen duten AX = mX, m-ren balioren baterako.

1 0 1

2 M = m m

––+

0 1 1

1 0 1

matrizea izanda:

a) Aztertu, Gauss erabilita eta determinanteekin, M-ren heina m-ren balioen arabera.

b) Kalkulatu M-ren alderantzizkoa m = 1 denean.

3 Aurkitu A · At = 2 2 2 4 ––eo betetzen duten A = x y 1 0 fp erako matrizeak.

4 Askatu X matrizea AX – 2X = B ekuazio-matrizean, eta aurkitu bere balioa, A = 1 1 1 2 –eo eta B = 3 6 0 3 –eo direla jakinda.

5 A = 2 2 5 –1 eo matrizea emanda, aurkitu m-ren eta n-ren zer baliok egiaztatuko duten A 2 + mA + nI = 0

6 A = 1 1 1 –1 eo matrizea daukagu:

a) Egiaztatu A 2 = 2I dela, eta kalkulatu A –1 propietate hori erabilita.

b) Kalkulatu A 13

7 Matrize hauek ditugu: A = 11 0 30 2 ––fp B =

11 A = 0 1 1 –1 eo matrizea izanda, lortu A-rekin trukagarriak diren B matrize guztiak, hau da, A · B = B · A egiaztatzen dutenak.

12 Frogatu, garapena egin gabe, honako hau:

13 Ebatzi honako ekuazio-sistema lineal hauek, egin ahal badira, eta interpretatu geometrikoki:

14 Eztabaidatu eta ebatzi sistema hau, m-ren balioen arabera, bi modutan: Gauss erabilita eta determinanteak erabilita.

15 Sistema hau daukagu:

+= +=

Aurkitu ondorengo sistema hau egiaztatzen duten X eta Y matrizeak: XY A XY B 2 32 2 1 –

8 4. mailako M matrize karratu baten 1., 2., 3. eta 4. zutabeak

C1, C2, C3 eta C4 badira, eta |M | = –3 bada, kalkulatu:

a) M 3 1 b) |M –1| c) |C1, 2C2 + C4, C4, C3|

Adierazi, kasuetako bakoitzean, zer propietate erabili dituzun.

9 Idatzi AX = B sistemaren ekuazio linealak, kontuan izanda A =

eta B = f 11 5 2 p direla, eta ebatzi.

Aurkitu al dezakegu sistema bateraezina egingo duen a-ren baliorik? Eta bateragarri determinatua egingo duenik?

Arrazoitu zure erantzunak.

16 a) Egiaztatu sistema hau bateragarri indeterminatua dela:

b) Arrazoitu bateragarri determinatua bihurtuko duen ekuazio berri bat erantsi dakiokeen. Eta bateraezin egingo duena?

Ariketa hauen ebazpena.

II. multzoa

GEOMETRIA

5. Bektoreak espazioan

6. Puntuak, zuzenak eta planoak espazioak

7. Problema metrikoak

Bektoreak espazioan 5

Geometria greziarra

Matematika Tales Miletokoarekin hasi zen, K.a. vi. mendearen hasieran, gaur egun ulertzen dugun moduan: egia batzuk beste batzuetatik modu logikoan ondorioztatzen dituen pentsamendu-sistema baten gisa. Eta indartsuen garatu zen matematikako adarra geometria izan zen, gailurra K.a. iii. mendean lortuz, Euklides, Arkimedes eta Apoloniorekin. Geometria greziar hori ondo gorde zuten India, Persia eta Arabiako matematikaren munduan, Europa Mendebaldeko kulturak gainbehera egin zuen mende luzeetan.

Geometria aljebrarekin bat eginik

Euklides tradizio aristotelikoaren jarraitzaile zen, baina tradizio hark magnitudeak eta zenbakiak objektu bereizitzat hartzen zituen, eta Euklidesek bien arteko erlazioa ezarri nahi izan zuen. Dena dela, hori lortzeko xvii. mendearen hasierara arte itxaron behar izan zen: Descartesek zenbakien artean erabiltzen ziren antzeko eragiketak definitu zituen magnitudeetarako ere. Horretarako, magnitude berri bat asmatu zuen, eta unitate deitu zion.

xv. eta xvi. mendeetan, aljebraren garapenak eta aljebraren kalkulu sinbolikoak lortutako heldutasunak abantailazko posizioan jarri zituzten Descartes eta Fermat xvii. mendean, eta jakin zuten posizio hori erabiltzen greziar geometriako problema klasikoak hizkuntza aljebraikora itzultzeko, geometria analitikoa sortuz. Horrela, aukera eta problemen mundu berri bat ireki zen, bai geometriarako, bai aljebrarako. Eta elkarreragin horrek, gainera, nabarmen bultzatu zuen analisi infinitesimalaren garapena.

Esparruen eta pertsonen (Fermat, Descartes, Pascal, Newton, Leibniz, Huygens, Bernoullitarrak...) bat egite horri esker, xvii. mendea pribilegiatua izan zen pentsamendu matematikoaren bilakaerari dagokionez.

René Descartes (1596-1650)

Pierre Fermat (1601-1665)

Bektoreak

Bektorearen kontzeptua xvii. mendearen amaieratik erabili zen norabidea eta noranzkoa zuten magnitudeak irudikatzeko eta konposatzeko, hala nola indarra eta abiadura.

Baina tratamendu bektorial baten lehen zantzuak xvii. mendearen hasierakoak dira, matematikari batzuek fenomeno fisikoak hizkuntza matematikoaren bidez deskribatzeko beharra ikusi zutenean. Galileo Galilei (1564-1642) aitzindaria izan zen lan horretan. Higidura parabolikoaren ibilbidea mugimendu horizontal batek eta bertikal batek osatzen zutela identifikatu zuen. Hori deskribatzeko, bi higidurak «batuketa» eragiketa berri baten bidez konbinatu behar ziren, ezin baitzen egin ordura arte ezagutzen ziren bitartekoen bidez; metodo berri bat behar zen.

Isaac Newtonek (1642-1727) Galileok hasitako ikerketa jarraitu zuen, eta, indar-paralelogramoaren adierazpenaren bidez, matematikoki adierazi zuen gorputz bati ezarritako bi indar indibidualen batuketaren emaitza. Bi indarrek aldi berean gorputz baten gainean eragiten dutenean, indar erresultantea paralelogramo baten diagonalaren bidez deskribatu daitekeela ezarri zuen, eta paralelogramoaren aldeek indar indibidualak deskribatzen dituztela. Nahiz eta Newtonek ez zuen bektorearen nozioa gaur egun ezagutzen dugun bezala erabili, oso hurbileko ideia bat erabili zuen indarraren kontzeptuan.

Ia mende bat geroago, Lagrangek koordenatuak sartu zituen bektoreen mundura, eta, ondorioz, magnitude bektorialak aritmetizatu zituen.

xix. mendean, bektoreekin zerikusia duten mugarri garrantzitsuenen artean, aipatzekoak dira Gaussek zenbaki konplexuak irudikatzeko erabili zituela, bektore-aljebra bat garatu zela 1832 eta 1837 urteen artean (egungo kalkulu bektorialaren baliokidea, Giusto Bellavitisen eskutik), edo Hermann Grassmannek 1844tik aurrera garatutako bektoreen teoria espazio n-dimentsionaletara orokortu zela. Eta ezin aipatu gabe utzi William Hamilton, xx. mendearen erdialdera bektore izena lehenengoz erabili zuena.

EBATZI

Ortoedro baten diagonala eta paralelepipedo baten bolumena

1 Adierazi ortoedro baten diagonala a, b eta c bere dimentsioen funtzioan

2 Kalkulatu paralelepipedo baten bolumena a, b eta c dimentsioen eta α eta β angeluen funtzioan

Eragiketak bektoreekin

Bektoreek espazioan dituzten ezaugarriak, baita eragiketak ere, eta planoan dituztenak berdinak dira, eta azken horiek badakizkigu aurreko ikasturtetik. Gogora ditzagun:

AB bektorea jatorria A-n eta muturra B-n duen zuzenki orientatua da.

AB -ren modulua A-tik B-ra dagoen distantzia da. Honela izendatzen da: | AB |

AB -ren norabidea A eta B hartzen dituen zuzenaren eta horrekiko paralelo diren zuzen guztien norabidea da.

Norabide bakoitzak elkarren aurkako bi noranzko ditu: A-tik B-rakoa, eta B-tik A-rakoa

Bi bektore berdinak dira modulu bera, norabide bera eta noranzko bera dutenean (ekipolente ere deitzen zaie).

Bektore bat erabili nahi dugunean, haren lekuan, berdinak dituen bektore guztien artean edozein har dezakegu. Aukera horietako bakoitza bektore finko bat da. Eta denak dira bektore askea esaten zaion bektore bakarraren ordezkariak.

Bektoreak adierazteko, letrak erabiltzen dira gainean gezia jarrita, u , v , w , y , z , …, edo ordezkarietako baten bidez adierazten dira, jatorria eta muturra izendatuz eta gainean gezitxo bat jarrita: AB .

Bektore baten eta zenbaki baten arteko biderkadura

k ≠ 0 zenbaki baten eta v bektore baten arteko biderkadura beste bektore bat da: k · v (edo, besterik gabe, k v ). Eta ezaugarri hauek ditu:

• Norabidea: v bektorearena

• Noranzkoa: v -ren berdina edo alderantzizkoa, k positiboa edo negatiboa den aintzat hartuta, hurrenez hurren.

• Modulua: v -ren moduluaren eta k-ren balio absolutuaren arteko biderketa

|k v | = |k | | v |

0 v biderkadura zero bektorea da, 0 . Jatorria eta muturra leku berean dituen bektorea da, eta, beraz, horren modulua zero da. Ez du norabiderik

–1 v bektorea izendatzeko – v erabiltzen dugu, eta v -ren aurkakoa esaten diogu.

Bektore unitarioak

Modulua 1 duten bektoreei bektore unitario esaten diegu.

1

v bektorea v -ren norabide eta noranzko bera dituen bektore unitario bat da.

v bektorea v -ren norabide bera baina kontrako noranzkoa duen bektore unitarioa da.

A jatorria eta B muturra dituen bektorea.

NOMENKLATURA

k 1 v biderkadura k 1 zenbakia v bektorearekin biderkatuta lortzen da. Dena dela, batzuetan, v bektorea k-rekin zatituta lortzen dela esaten da (berez txarto esanda egon arren). Esapide zuzena ez bada ere, horretara esatea onartzen da hizkuntza kolokialean. Hori bai, k v ez da inoiz jartzen.

➜ Bektoreak GeoGebrarekin.

Bi bektoreren arteko batuketa eta kenketa

• u eta v bi bektoreren arteko batuketa egiteko, v bektorea u -ren jarraian jarri behar dugu, v -ren jatorriak u -ren muturrarekin bat egiteko moduan. Batura, uv + , jatorria u -rena eta muturra v -rena dituen bektorea da.

• Bi bektoreren arteko u– v kenketa egiteko, u -ri v -ren aurkakoa batzen zaio:

u– vu (– v) =+

Paralelogramoaren erregela

u eta v jatorri berean ezartzen baditugu eta paralelogramoa osatzen badugu, orduan:

• u -ren eta v -ren jatorri bera duen diagonala uv + batura-bektorea da

• v -ren muturretik u -ren muturrera doan diagonala u– v da.

u – v

u v u + v

Eraikuntza horrek bektoreek norabide desberdinak badituzte baino ez du balio. Norabide bera dutenean, bai batura eta bai kendura hutsalak dira.

Hiru bektoreren arteko batuketa

Paralelepipedoaren erregela

u, veta w hiru bektore jatorri berean jarriko ditugu; u + v batuketa egingo dugu, eta hortik lortzen dugun uv + bektoreari w batuko diogu, paralelogramoaren erregela erabiliz. Hori eginda, uv w ++ ` j bektorea lortuko dugu. Orduan:

• uv w ++ ` j batura-bektorea paralelepipedoaren diagonala da Eraikuntza honek balio du u, vw eta bektoreak planokideak ez badira; hau da, plano berean ez badaude.

Bektoreen eragiketen propietateak

bektoreen batuketa 1 elkarketa uv wu vw ++ =+ + ``jj 2 trukaketa uv vu += + 3 bektore nulua v0 v += 4 alderantzizko bektorea v–()v0 +=

Propietate horiek guztiek espazio bektorialeko egitura ematen diote bektore-multzoari. (2. unitateko 5. paragrafoan espazio bektoriala aztertzen da).

1 a · (b · v ) = (ab ) · v propietateak zenbaki eta bektoreen arteko biderketa zenbakien arteko biderketarekin erlazionatzen du.

a) Agertzen diren lau biderketa horietatik, zein dira lehen motakoak eta zein bigarrenekoak?

b) Interpretatu propietate hori, a = 3, b = –2 eta v paper gainean adierazitako edozein bektore dela kontuan hartuz

2 (a + b) · v = a · v + b · v banatze-propietateak erlazionatu egiten ditu zenbakien batuketa eta bektoreen batuketa.

a) Agertzen diren bi batuketa horietatik, esan zein den mota batekoa eta zein bestekoa.

b) Interpretatu propietate hori, a = 3, b = 5 eta v paper gainean adierazitako bektore bat direla kontuan hartuz.

Pentsatu eta praktikatu

Bektore baten adierazpen analitikoa

2. unitatean, edozein espazio bektorialetako elementuak kontuan hartu, eta konbinazio lineala eta bektoreen arteko mendekotasun eta independentzia lineala zer diren definitu genuen. Unitate honetan, zehaztu egingo ditugu kontzeptu horiek bektoreetarako; hau da, «segmentu orientatuen» kasuan.

Bektoreen konbinazio lineala

x, y, z , …, w zenbait bektore eta a, b, c, …, l, beste horrenbeste zenbaki emanda, … ab cl xy zw ++ ++ adierazpenari bektoreen konbinazio lineala esaten zaio

Adibidez: 4 x + 2 y , –2 xy + konbinazioak x eta y bektoreen konbinazio linealak dira

Mendekotasun eta independentzia lineala

Zenbait bektore linealki mendekoak direla esaten dugu bektore horietakoren bat gainerakoen konbinazio lineal moduan jar badaiteke. Horrela ez denean, hau da, bektore bat ere ezin denean gainerakoen konbinazio lineal moduan jarri, linealki independenteak direla esaten dugu.

Adibidez:

1. Lerrokatuta dauden bi bektore linealki mendekoak dira

v = 1,5u

2. Lerrokatuta ez dauden bi bektore linealki independenteak dira

3. Hiru bektore planokide (plano berean daudenak) linealki mendekoak dira.

y

= 2x + 3z

y = 2x + 3z x

Oinarria

u v z

Planokideak ez diren x , y , z hiru bektore linealki independenteak dira eta, gainera, espazioko beste edozein bektore modu bakarrean jar daiteke horien konbinazio lineal moduan. Hori dela eta, oinarri bat eratzen dutela esaten dugu.

B = ( x , y , z )

Planokideak ez diren edozein hiru bektorek hiru dimentsioko espazio bektorialeko oinarri bat eratzen dute

Hiru bektoreak elkarrekiko perpendikularrak badira, oinarri ortogonala eratzen dutela esaten dugu. Horrez gainera, 1 modulua badu, oinarria ortonormala dela esaten da.

Bektore batek oinarri batekiko dituen koordenatuak

B = ( x , y , z ) oinarria emanda, v edozein bektore modu bakarrean jar daiteke bere elementuen konbinazio lineal moduan:

ab c vx yz =+ +

a, b, c zenbakiak v -ren koordenatuak dira B-rekiko.

Honela adierazten da: v = (a, b, c ), edo bestela, v (a, b, c ).

B = ( x , y , z ) oinarriko elementuen koordenatuak hauek dira:

x (1, 0, 0), y (0, 1, 0), z (0, 0, 1)

Zero-bektorearen koordenatuak 0 (0, 0, 0) dira edozein oinarritan

Eragiketak koordenatuekin

Ondo dakizunez, bektoreen koordenatuek «zentzuz» jokatzen dute eragiketak egiten ditugunean. Zehaztu dezagun esandako hori:

(, ,) xy z u 11 1 (, ,) xy z v 22 2

• batuketa: (, ,) xx yy zz uv 12 12 12 += ++ +

uv + bektorearen koordenatuak u -ren koordenatuak eta v -ren koordenatuak

batuta lortzen dira.

• zenbaki batekin biderkatzea: k u = (kx1, ky1, kz1)

k u bektorearen koordenatuak k bider u -ren koordenatuak eginda lortzen dira

• konbinazio lineala: a u + b v = (ax1 + bx2, ay1 + by2, az1 + bz2)

Emaitza horien ondorioz, oso erosoa izango da bektoreak landu behar ditugunean horien koordenatuak erabiltzea

Ebatzitako ariketa

1 x , y , z , w bektoreen koordenatuak hauek dira oinarri jakin batekiko:

x (1, –2, 0), y (0, –1, 3)

z (1, 0, –5), w (–1, 1, 0)

Aurkitu zein diren a, b eta c, honako hau betetzeko:

a x + b y + c z = w

Pentsatu eta praktikatu

ADI

B = ( x , y , z ) oinarri bat bada, orduan:

• v edozein bektore jar liteke x , y eta z bektoreen konbinazio lineal gisa.

• Hori egiteko modu bakarra dago; hau da, a, b eta c bakarrak dira.

a (1, –2, 0) + b (0, –1, 3) + c (1, 0, –5) = (–1, 1, 0) →

→ (a + c, –2a – b, 3b – 5c ) = (–1, 1, 0)

Koordenatuz koordenatu berdintzen baditugu, hiru ezezaguneko hiru ekuazio dituen sistema bat lortuko dugu:

ac ab bc

1 21 35 0

––

+= = = 4 Sistema hori ebatzita, hau lortzen dugu: a = 2, b = –5, c = –3

1 u (–3, 5, 1), v (7, 4, –2) badira, aurkitu honako hauen koordenatuak:

a) 2 u b) 0 v c) – u

d) 2 u + v e) u – v f ) 5 u – 3 v

2 Bektore hauek ditugu:

x (1, –5, 2), y (3, 4, –1), z (6, 3, –5), w (24, –26, – 6)

Aurkitu zein diren a, b, c honako hau betetzeko:

a x + b y + c z = w

Bektoreen biderketa eskalarra

Normala denez, biderketa eskalarrak espazioan duen definizioa, propietateak eta erabilerak bat datoz planoan dituenekin (eta horiek badakizkigu iazko ikasturtetik).

Gogora ditzagun:

u eta v ( u ≠ 0, v ≠ 0) bi bektoreren biderketa eskalarra honako hau da: || || (, ) • cos uv uv uv = %

|| u eta || v zenbaki positiboak dira. Beraz, uv • zenbaki positiboa edo negatiboa izango da, u eta || v bektoreek eratzen duten angeluaren arabera:

• (, ) uv % zorrotza bada, cos (, ) uv % > 0 ⇒ uv • positiboa da.

• (, ) uv % zorrotza bada, cos (, ) uv % < 0 ⇒ uv • negatiboa da.

Oinarrizko propietatea

u = 0 edo v = 0 badira, orduan uv • = 0 da. Baina bektore bat bera ere ez bada zero-bektorea, cos (, ) uv % = 0 denean bakarrik izango da zero biderketa eskalarra; hau da, u ⊥ v bada

Nuluak ez diren bi bektoreren arteko biderketa eskalarra bektoreak perpendikularrak direnean bakarrik izango da zero:

u ≠ 0 eta v ≠ 0

uv • = 0 ⇔ u ⊥ v

Modulua, angelua, proiekzioa

• Bektore baten modulua: ||uu u • = || || (, )| |· || cos 1 uu uu uu uu • 22 == = %

• Bi bektoreren arteko angelua: (, ) || || cos u uv uv • v= %

(Nahikoa da biderketa eskalarraren adierazpenean cos (, ) uv % askatzea).

• v -ren gaineko u -ren proiekzio-bektorea || v uv v • 2 da.

Gogoan izan () proy u v = || (, )| | || || || cos uu vu uv uv v ••uv == % dela AB zuzenkiaren

luzera, eta angelua zorrotza edo kamutsa den aintzat hartuta, + edo – izango dela.

Zenbaki hori v -ren norabide eta noranzko bera dituen || 1 v v bektore unitarioa-

rekin biderkatzen badugu, proiekzio-bektorea lortuko dugu.

HIZKUNTZA

Eskalar hitzak zenbakia esan nahi du, bektore hitzarekin kontrajarrita.

Horregatik esaten zaio horrela bektoreen arteko biderketa horri, emaitza zenbaki bat delako.

NOMENKLATURA

Oraindik aurrera ez dugu punturik jarriko zenbaki baten eta bektore baten arteko biderketa adieraztean. Puntua biderketa eskalarraren kasuan baino ez dugu erabiliko. u u

Eragiketak biderketa eskalarrarekin. Propietateak

Bektoreen arteko biderketa eskalarra bektoreen arteko gainerako eragiketekin erlazionatzean, zenbait propietate betetzen dira. Ikusi genituen aurreko ikasturtean, baina berriro gogoratuko ditugu orain:

1. Trukatze-propietatea: • uv vu • =

2. Elkartze-propietatea: λ( u • v ) = (λ u ) • v = u • (λ v )

3. Banatze-propietatea: • u( vw)u vu w •• += +

Biderketa eskalarraren adierazpen analitikoa

B (i ,j ,k) oinarria ortonormala bada, honako hau betetzen da: • ii

Emaitza horiek guztiak begi-bistakoak dira, kontuan hartuz i , j , k elkarrekiko perpendikularrak direla eta honako hau betetzen dela:

u -ren eta v -ren koordenatuak (, ,) xy z u 11 1 eta (, ,) xy z v 22 2 badira B (i ,j ,k) oinarri ortonormal batekiko, orduan bere biderketa eskalarra hau da:

uv • = x1 x2 + y1 y2 + z1 z2 Egiaztapena uv

i + y2 j + z2 k ) (=*) = (x1 x2) ( i • i ) + (y1 y2) ( j • j ) + (z1 z2) ( k • k ) + + (x1 y2) ( i • j ) + (x1 z2) ( i • k ) + (y1 x2) ( i • j ) +

+ (y1 z2) ( j • k ) + (z1 x2) ( i • k ) + (z1 y2) ( j • k )(=**)

= x1 x2 + y1 y2 + z1 z2

Pentsatu eta praktikatu

PROPIETATEAK

(*) Biderketa eskalarraren banatze- eta elkartze-propietateak aplikatu dira, baita zenbakien batuketaren elkartze- eta trukatze-propietateak ere, batugaiak berrantolatzeko.

(**) Kontuan hartu da oinarri ortonormal batean hau betetzen dela:

ii 1 • = jj 1 • = kk 1 • =

ij 0 • = ik 0 • = jk 0 • =

1 Hiru bektorek u (3, –1, 5), v (4, 5, 11), w (–2, k, 3) koordenatuak dituzte oinarri ortonormal batekiko.

a) Kalkulatu uv • .

b) Aurkitu zein izan behar den k-ren balioa v eta w perpendikularrak izateko.

aurreko emaitza batzuen laburpen praktikoa

• (, ,) xy z u 11 1 , (, ,) xy z v 22 2 , (, ) uv % bi bektoreren arteko biderketa eskalarra, (, ) uv % = α izanik:

KONTUAN HARTU

Hemendik aurrera, erabiliko dugun oinarria ortonormala dela onartuko dugu.

• (, ,) xy z u 11 1 bektore baten modulua:

• (, ,) xy z u 11 1 , (, ,) xy z v 22 2 bi bektoreren arteko α angelua:

• (, ,) xy z u 11 1 bektorearen proiekzioa (, ,) xy z v 22 2 bektorearen gainean:

1 Eman bektore honekiko bektore perpendikular bat:

v (3, –1, 5)

Hasteko, problema modu orokorrean planteatuko dugu: • uv = 0 berdintza betetzen duen v (α, β, γ) bektore bat aurkitu behar dugu; hau da:

(α, β, γ) • (3, –1, 5) = 0 ⇔ 3α – β + 5γ = 0

Hiru ezezaguneko ekuazio horrek infinitu soluzio ditu; adibidez:

(1, –2, –1), (2, 11, 1), …

Baina v -rekiko perpendikularra den bektore bat azkar lortzeko modu erraz bat dago: bi koordenatu lekuz aldatzea, eta, horrez gain, horietako bat zeinuz ere aldatzea. Beste koordenatua zero egingo dugu

v (3, –1, 5) (α, β, γ)

u (1, 3, 0) (–β, α, 0)

Argi dagoenez, (3, –1, 5) • (1, 3, 0) = 0 da.

Modu berean lortuko ditugu (5, 0, –3) eta (0, 5, 1); horiek ere, v -rekiko perpendikularrak

Ebatzitako ariketak

➜ Biderketa eskalarra.

2 Bektore hauek ditugu oinarri ortonormal batekiko:

u (3, – 4, 12) v (5, –2, – 6)

Kalkulatu:

a) • uv

b) || ||uv eta

c) , () uv %

d) v -ren gaineko u -ren proiekzioa.

e) Zein izan behar da x-ren balioa

w (7, x, –2) perpendikularra izateko u -rekiko?

Horrek esan nahi du u -ren proiekzio-bektoreak 6,078 modulua duela v -ren norabide berean, eta v -ren kontrako noranzkoa duela.

gaineko u -ren proiekzio-bektorea

3 Lortu w (3, –1, 2)-rekiko eta v (1, 0, 3)-rekiko bektore perpendikular bat.

u -rekiko eta v -rekiko perpendikularra den w (x, y, z ) bektore baten koordenatuak aurkitu nahi ditugu:

Hiru ezezaguneko bi ekuazio dituen sistema homogeneo bat da, 2 heinekoa; izan ere, u eta v linealki independenteak dira. Ezezagunetako bat bigarren atalera igaroko dugu:

Pentsatu eta praktikatu

xy z

xz 32 –3 = = 3

Sistema horrek infinitu soluzio proportzional ditu. Horietako bat x = 3, y = 7, z = –1 da.

Hau da, bila gabiltzan bektorea (3, 7, –1) edo horrekiko edozein paralelo izan daiteke. aDi: Hurrengo atalean, hori baino metodo eraginkorragoa ikasiko dugu bi bektorerekiko perpendikularra den bektore bat lortzeko

2 u (5, –1, 2), v (–1, 2, –2) bektoreak izanda, kalkulatu:

a) uv • b) ||uv|| eta c) (, ) uv %

d) v -ren gaineko u -ren proiekzioa eta u -ren gaineko

v -ren proiekzioa. (Zuzenkia eta bektorea)

e) Zein izan behar da x-ren balioa (7, 2, x ) bektorea

u -rekiko perpendikularra izateko?

3 Lortu elkarrekiko paraleloak ez diren hiru bektore, baina beste bektore honekiko perpendikularrak direnak:

v (3, 2, 7)

4 Aurkitu behean emandako bi bektore horiekiko perpendikularra den bektore bat:

u (5, –1, 2) v (–1, 2, –2)

Ebatzitako ariketak

Biderketa bektoriala

u eta v bi bektoreren arteko biderketa bektoriala u × v beste bektore bat da eta honela definitzen da:

• u eta v linealki independenteak badira, u × v bektoreak ezaugarri hauek ditu:

— Modulua: | u × v | = ||uv|| sin (, ) uv %

— Norabidea: u -rekiko eta v -rekiko perpendikularra.

— Noranzkoa: (, ) uv % < 180° bada, gorantz

(, ) uv % > 180° bada, beherantz.

(Angelua noranzko positiboan hartuko dugu; hau da, erlojuko orratzen higiduraren kontrara)

• u eta v linealki mendekoak badira, hau da, horietakoren bat 0 bada edo norabide bera badute, orduan u × v = 0

Propietateak

1. u × v biderketa bektorialaren modulua u eta v bektoreek zehazten duten paralelogramoaren azalera adinakoa da.

Horren egiaztapena berehala lortzen da, paralelogramoaren altuera | v | sin α dela kontuan hartuz. (Ikusi alboko grafikoa).

2. u × v = – v × u

Izan ere, modulu bera, norabide bera eta aurkako noranzkoa dute, erraz egiaztatzen denez

3. u × u = 0 da beti, u edozein dela ere

4. B (i ,j ,k) oinarriko bektoreek hau betetzen dute: i × j = k , j × k = i , k × i = j .

5. (a u ) × v = a ( u × v ) = u × (a v )

Erraz egiaztatzen da, biderketa bektorialaren definiziotik abiatuta.

6. Biderketa bektorialak ez du elkartze-propietatea. Orokorrean, ( u × v ) × w eta u × ( v × w ) ez dira berdinak. Adibidez:

7. u × v biderketaren adierazpen analitikoa. (, ,) xy z u 11 1 , (, ,) xy z v 22 2 badira, orduan:

8. Biderketa bektorialaren banatze-propietatea, bektoreen arteko batuketari dagokionez.

u × ( v + w ) = u × v + u × w

➜ Biderketa bektoriala.

Joseph-Louis Lagrangek (1736-1813) ekarpen nabarmena egin zuen bektoreen tratamendu aljebraikoan.

aurreko emaitza batzuen laburpen praktikoa

• (, ,) xy z u 11 1 , (, ,) xy z v 22 2 bi bektoreren arteko biderketa bektoriala. Koordenatuak hauek dira:

• u eta v bektoreek zehaztutako paralelogramoaren azalera lortzeko, u × v biderketaren modulua kalkulatuko dugu.

• Lerrokatuta ez dauden u eta v bi bektoreren bektore perpendikularra lortzeko, u × v kalkulatuko dugu.

Ebatzitako ariketak

1

a) Kalkulatu u (3, –5, 1) eta v (4, 7, 6) bektoreen arteko biderketa bektoriala

b) Egiaztatu biderketa hori bektore horietako bakoitzarekiko perpendikularra dela.

a) Adierazpen analitikoa erabiliko dugu biderketa bektoriala kalkulatzeko

u

(–37, –14, 41)

b) u × v biderketa u -rekiko perpendikularra izateko, biderketa eskalarrak zero izan behar du:

(3, –5, 1) • (–37, –14, 41) = 3 · (–37) – 5 · (–14) + 1 · 41 = 0

Modu berean, u × v ⊥ v izateko:

(4, 7, 6) • (–37, –14, 41) = 4 · (–37) + 7 · (–14) + 6 · 41 = 0

Beraz, u × v perpendikularra da u -rekiko eta v -rekiko.

2 Kalkulatu triangelu gorriaren azalera.

u(3, –5, 1)

u eta v bektoreek zehazturiko paralelogramoaren azalera kalkulatuko dugu.

Paralelogramoaren azalera = | u × v | = |(–37, –14, 41)| = = 37 14 41 3 246 22 2 ++ = = 56,97 u2

Triangeluaren azalera lortutako emaitzaren erdia izango da

v(4, 7, 6)

3 Aurkitu u (3, –5, 1) eta v (4, 7, 6) bektoreekiko perpendikularra den bektore bat.

Triangeluaren azalera = 2 1 Paralelogramoaren azalera = 28,49 u2

u eta v bektoreekiko perpendikularra den bektorea bi horien arteko biderketa bektoriala da:

u × v = (–37, –14, 41)

edo horren beste edozein bektore proportzional.

Pentsatu eta praktikatu

1 Kalkulatu u (3, 7, – 6) eta v (4, 1, –2) bektoreen biderketa bektoriala.

2 Aurkitu bi bektore hauekiko perpendikularra den bektore bat: u (3, 7, – 6) v (4, 1, –2)

3 Aurkitu bektore hauek zehazten duten triangeluaren azalera:

u (3, 7, – 6) v (4, 1, –2)

Hiru bektoreren arteko biderketa mistoa

u , v , w bektoreen arteko biderketa mistoa esaten zaio, eta [ u , v , w ] izendatzen dugu, eragiketa hauek eginez lortzen dugun zenbakiari: [ u , v , w ] = u • ( v × w ). Interpretazio geometrikoa [

renproiekzioaveta wbektoreekdefinitzenduten paralelogramoarenazalera veta wbektoreekdefinitutakoplanoarekiko perpendikularraren gainekou

kdefinitutako kdefinitutako- - u, veta w paralelepipedoaren oinarriarenazalera u, veta w paralelepipedoaren altuera

= u , v eta w bektoreek zehazturiko paralelepipedoaren bolumena.

Biderketa mistoaren ko [ v , w ] balio absolutua da u , v eta w bektoreek definitutako paralelepipedoaren bolumena.

Nola eragiten dio bektoreen ordenak biderketa mistoari?

Bai interpretazio geometrikoak, bai adierazpen analitikoak aukera ematen dute ondorioztatzeko kortxete barruko bektoreak permutatzen baditugu, gehienez ere emaitzaren zeinua aldatzen dela, baina ez haren balio absolutua. Beraz, bolumenak kalkulatzeko, edozein ordenatan jarritako bektoreen biderketa mistoaren balio absolutua hartuko dugu.

Ebatzitako ariketa

1 Aurkitu u (–5, 1, 7), v (4, 7, 3) eta

w (1, 0, 4) bektoreek definitutako paralelepipedoaren bolumena. [ u , v , w ] = 5 4 1

Pentsatu eta praktikatu

1 7 0

7 3

= –202 Beraz, paralelepipedoaren bolumena 202 u3 da

1 Kalkulatu honako bektore hauek zehazten duten paralelepipedoaren bolumena: u (3, –5, 1) v (7, 4, 2) w (0, 6, 1)

2 Kalkulatu zein izan behar den x-ren balioa u (3, –5, 1), v (7, 4, 2) eta z (1, 14, x) bektoreak planokideak izateko (hau da, zehazten duten paralelepipedoaren bolumena zero izateko).

1. Bektoreen konbinazio lineala

Honako bektore hauek izanda:

u (a, 1 + a, 2a), v (a, 1, a), w (1, a, 1)

a) Kalkulatu zein izan behar den a-ren balioa u , v eta w bektoreak linealki mendekoak izateko.

b) Aztertu c (3, 3, 0) bektorea linealki mendekoa den u , v eta w bektoreekiko a = 2 kasuan.

c) Arrazoitu a = 0 kasuan u • ( v × w ) = 0 berdintza betetzen den

EGIN ZUK

Bektore hauek emanda:

u (1, –3, 2), v (–2, 6, – 4), w (2, 0, 1)

a) Adierazi, ahal izanez gero, u bektorea v -ren eta w -ren konbinazio lineal moduan.

b) u , v eta w bektoreak linealki mendekoak ala independenteak dira?

2. Bektore perpendikularrak

Bektore hauek emanda:

u (3, 2, –2), v (–1, m, 4)

a) Aurkitu m-ren zer baliorekin izango diren u + v eta u – v bektoreak ortogonalak.

b) m = 1 kasuan, aurkitu u -rekiko eta v -rekiko perpendikularra den eta modulua 9 duen bektore bat.

a) Linealki mendekoak badira, bektoreetako bat gutxienez besteen konbinazio moduan jarri ahal izango da. Kasu horretan, eratzen duten matrizearen heinak 3 baino txikiagoa izan behar du

, v , w bektoreak linealki mendekoak dira

b) a = 2 kasuan, u , v eta w bektoreak linealki independenteak dira. 3-koak diren hiru bektore linealki independente direnez, 3-ko oinarri bat eratzen dute. Beraz, beste edozein bektore horien mendekoa izango da linealki; hain zuzen ere,

3, 0).

dezagun konbinazio lineala

3 w .

c) u • ( v × w ) = [ u , v , w ] = 0 da a = 0 kasuan. a) puntuan frogatu dugu.

a) Kalkulatu u + v eta u – v bektoreen koordenatuak:

u + v = (3, 2, –2) + (–1, m, 4) = (2, 2 + m, 2)

u – v = (3, 2, –2) – (–1, m, 4) = (4, 2 – m, – 6)

Ortogonalak izateko, bektoreen arteko biderketa eskalarrak zero izan behar du:

b) m = 1 kasuan → v = (–1, 1, 4)

u -rekiko eta v -rekiko perpendikularra den bektorea emandako bektoreen biderketa bektoriala eginez lortuko dugu: u × v

5)

EGIN ZUK

a) Aztertu a (2, –1, 0) eta b (1, –2, –1) bektoreak ortogonalak diren

b) Aztertu a -rekiko eta b -rekiko perpendikularra den bektore unitario bat.

Modulua kalkulatuko dugu: |(10, –10, 5)|

da u -rekiko eta v -rekiko, eta mo-

Beraz, ,, 9 3 2 3 2 3 1 –dn = (6, – 6, 3) bektoreak modulua 9 du, eta u eta v bektoreekiko perpendikularra da

Ebatzitako ariketak eta problemak

3. Biderketa eskalar eta bektorialak

u eta v bektoreen biderketa eskalarra, jakinik | u | = 4 eta | v | = 12 moduluak dituztela, –24 da. Kalkulatu:

a) u eta v bektoreek eraturiko angelua.

b) (– v ) • u c) | u × v |

d) ( u × v ) • v

e) ( u × v ) • ( v × u )

EGIN ZUK

Aurreko ariketako bektore berdinak erabilita, aurkitu:

a) v • ( u + v )

b) ( u + v ) • ( u – v )

4. Oinarria eta koordenatuak

e1, e2, e3 dira 3-rekiko linealki independenteak diren hiru bektore.

a) Linealki independenteak al dira hurrengo bektoreak ere?

u = e1 – e3

v = e2 + e3

w = e1 – e2 + e3

b) Kalkulatu u × v eta egiaztatu emaitza ortogonala dela u eta v bektoreekiko.

EGIN ZUK

Aurreko enuntziatuko datuekin, kalkulatu honako hau:

u , – v , u × v ]

5. Proiekzio-bektorea

a) u (–2, 0, 1), v (a, b, 6), w (2, 1, –2), bektoreak emanda, aurkitu zein izan behar diren a-ren eta b-ren balioak u eta v perpendikularrak izan daitezen, eta v -ren w gaineko proiekzioak 2 modulua izan dezan.

b) Zein dira v -ren w gaineko proiekzioaren koordenatuak?

a) Biderketa eskalarraren definiziotik, eratzen duten angelua lortzen dugu:

b)

c) Biderketa bektorialaren moduluaren definizioa ezarriko dugu:

24 3

d) ( u × v ) • v da bi bektore perpendikularren biderketa eskalarra; beraz, bere biderkadura eskalarra 0 da.

e) v × u = –( u × v ) denez, orduan ( u × v ) • ( v × u ) da bi bektore kontrajarriren biderketa eskalarra:

(24 3 )2 (–1) = –1 728

a) e 1, e 2, e 3 bektoreek 3 oinarri bat eratzen dute.

u , v eta w bektoreen koordenatuak oinarri horretan hauek dira:

u (1, 0, –1) v (0, 1, 1) w (1, –1, 1)

u , v , w bektoreen mendekotasun lineala aztertuko dugu:

Beraz, u , v eta w linealki independenteak dira.

b) u × v = 10 1

k – = ij k –+ → u × v = (1, –1, 1)

Frogatu dezagun u × v perpendikularra dela u eta v -rekiko:

b) v -ren w gaineko proiekzioa 2 denez, eta w  = 3, v -ren w gaineko proiekzio-

6. Bektore planokideak

u (1, –1, 2) eta v (3, 1, –1) emanda, aurkitu zer bektore diren u -rekiko perpendikularrak, eta u -rekin eta v -rekin planokideak

EGIN ZUK

a) Aurkitu zein izan behar den m-ren balioa u (2, 3, 0), v (1, m, –1) eta w (–2, 0, 6) bektoreak planokideak izateko.

b) Aztertu emandako bektore bikoteren bat perpendikularra den m-ren balio horretarako.

w (x, y, z) honako hau betetzen duen bektore bat da:

• w ⊥ u → (x, y, z) • (1, –1, 2) = x – y + 2z = 0

• w bektorea planokidea da u -rekin eta v -rekin; hau da, bektore horiek zehazten duten paralelepipedoaren bolumena zero da → [ u , v , w ]

Bi baldintza horiekin eraturiko sistema ebatziko dugu:

xy z xy z 20 74 0 ––+= ++ = 4 → xz y xz y 2 47 += += 4 Soluzioa: (3t, t, –t ), t ≠ 0 izanik

Emandako baldintzak betetzen dituzten infinitu bektore daude. (3t, t, –t ) formakoak dira, t ≠ 0 izanik, eta v bektorearekiko paraleloak.

7. Baldintza jakin batzuk dituen bektorea aurkitzea

Aurkitu v (1, 0, 1) bektorearekiko perpendikularrak diren eta ,, w 2 1 2 2 2 1

bektorearekin 60°-ko angelua eratzen duten 3-ko bektore unitarioak

EGIN ZUK

Bektore hauek emanda:

u(3, –2, 3) , v (4, –2, – 4)

aurkitu | u |, | v |, (, ) uv % eta v -ren gaineko u -ren proiekzio-bektorea

Gidatutako ariketak eta problemak

1.

Kalkulatu s bektorearen modulua, jakinda a eta b bektoreen batura dela, eta | a | = 8, | b | = 6 direla eta 75°-ko angelua osatzen dutela.

2.

Kalkulatu zein izan behar den m-ren balioa a (3, 0, 1), b (0, m, –1) eta a × b bektoreek 49 u3-ko bolumena izango duen paralelepipedo bat zehaztu dezaten.

• Marraztu s bektorea, a eta b aldeak dituen paralelogramoan erregela aplikatuta.

• Kalkulatu s diagonalaren aurkako angelua.

• Aplikatu kosinuaren teorema s -ren modulua lortzeko.

Soluzioa: | s | ≈ 11,2 75º s b a

• Lortu a × b bektorearen koordenatuak m-ren funtzioan.

• Lortu paralelepipedoaren bolumena, a , b eta a × b bektoreen biderketa mistoaren balio absolutua kalkulatuz

• Berdindu bolumen hori 49rekin. Bi soluzio lortuko dituzu

Soluzioa: m = 2, m = –2

ABCD tetraedro erregular bat da, a ertzekoa. Egiaztatu honako hau:

a) a AB AC AC AD AD AB 2 •• • 2 == =

b) Aurkako ertzak ortogonalak dira.

a) Irudikatu tetraedro bat, eta jarri izena erpinei. Eskatzen diren biderketa eskalarrak lortzeko, kontuan izan zer neurtzen duten tetraedroaren ertzek eta binaka eratzen dituzten angeluek

b) Aurkako bi ertz AB eta CD dira, adibidez. Bi horien biderketa eskalarra lortzeko, adierazi CD ertza AD eta AC ertzen funtzioan eta erabili banatze-propietatea.

a (1, –1, 0), b (0, 1, –3), c (0, 2, –1) eta d (7, – 4, 5) bektoreak emanda:

a) Arrazoitu hurrengo multzo hauetako zein den oinarri bat:

B1 = { , ab }, B2 = { ,, , ab cd } edo

B3 = ,, {} ab c .

b) Zehaztu zein diren d -ren koordenatuak oinarri horretan.

a) Gogoan izan zenbat bektorek eratzen duten hiru dimentsioko espazio bektorialaren oinarri bat eta zer baldintza bete behar duten horien artean.

b) Adierazi d oinarriko bektoreen konbinazio lineal moduan, eta zehaztu zein diren konbinazio lineal horren koefizienteak.

Soluzioa:

a) B3 da oinarria. b) d 7,, 5 13 5 14 –dn

Kubo baten erpin batean hiru indar daude ezarrita, f 1, f 2 eta f 3, erpin horretatik igarotzen diren hiru aurpegien diagonalen arabera zuzenduta. Indar horien moduluak 1, 2 eta 3 badira, hurrenez hurren, kalkulatu zein den erresultantearen modulua.

• Hiru bektoreren arteko ( f 1 + f 2 + f 3) batura-bektorearen modulua kalkulatu nahi dugu. Kontuan izan modulu horren karratua fff 2 ++ 13 batura bere buruarekin biderkatzean lortzen den biderketa eskalarra dela

• Gogoan izan kubo baten ondoz ondoko bi aurpegietako diagonalek 60°-ko angelua eratzen dutela; izan ere, horien muturrak lotuz gero, triangelu aldekide bat lortzen da Soluzioa: | f 1 + f 2 + f 3| = 5

Bi bektoreren batura-bektorea

Paralelepipedo baten bolumena

3. Tetraedro erregularra

5. Bektore baten modulua

4. Oinarri eta koordenatuak

Proposatutako ariketak eta problemak

Trebatzeko

Mendekotasun eta independentzia lineala. Oinarria eta koordenatuak

1 a) Egiaztatu u = (1, 1, –1), v = (2, 1, 0) eta w = (–2, –1, 3) bektoreek oinarri bat osatzen dutela.

b) Aurkitu a = (1, 2, 1) eta b = (–1, 0, 2) bektoreen koordenatuak oinarri horrekiko.

2 Honako bektore-multzo hauetako zein dira oinarri bat?

Arrazoitu erantzunak:

A = {(1, 2, 1), (1, 0, 1), (2, 2, 2)}

B = {(1, 1, 1), (1, 0, 1), (1, 1, 0), (0, 0, 1)}

C = {(–3, 2, 1), (1, 2, –1), (1, 0, 1)}

3 Egiaztatu x (3, –1, 0) bektorea ezin dela adierazi u (1, 2, –1) eta v (2, –3, 5) bektoreen konbinazio lineal moduan.

x , u eta v linealki independenteak dira?

4 Egiaztatu a (1, 2, 3), b (2, 1, 3), c (1, 0, 1) bektoreetako edozein adieraz daitekeela beste bien K.L. moduan.

5 Zehaztu m-ren eta n-ren balioak honako bektore-multzo hauek linealki mendekoak izateko:

a) u (m, –3, 2), v (2, 3, m), w (4, 6, –4)

b) u (3, 2, 5), v (2, 4, 7), w (1, –1, n)

6 a) a parametroaren zein baliotarako da oinarri bat S = {(1, 1, 1), (a, 1, 1), (1, a, 0)} bektore-multzoa?

b) a = 2 kasurako, aurkitu, ahal baldin bada, (0, 1, 0) bektoreak oinarri horrekiko dituen koordenatuak.

7 Zer erlazio egon behar da m eta n artean u (m, –1 , 0 ), v ( 2, 0, n) eta w (1, 1, –2) bektoreak linealki menpekoak izan daitezen?

8 Frogatu (1, a, b), (0, 1, c), (0, 0, 1) bektoreak linealki independenteak direla a, b eta c edozein dela ere.

Bektoreen biderketa

9 Oinarri ortonormal batean, a (1, 2, 2) eta b (–4, 5, –3) ditugu. Kalkulatu:

a) a b b) | a | eta | b | c) )(a,b \

d) ( a + b ) ⋅ ( a – b ) e) a × b f ) | a × b |

g) b -ren gaineko a -ren proiekzio-zuzenkia.

h) a -ren gaineko b -ren proiekzio-bektorea.

10 Bektore hauek emanda: ai jk m =+ + eta b–2i 4j k m =+ + aurkitu zein izan behar den m-ren balioa a eta b bektoreak izan daitezen...

a) paraleloak. b) ortogonalak. c) | a | = 4

11 Aurkitu v (1, –1, 2) bektorearen gaineko u (3, 1, 2) bektorearen proiekzio-bektorea

12 a (1, 2, 3) eta b (2, –2, 1) ortogonalak dira? Ez badira, aurkitu zer angelu eratzen duten

13 Aztertu u bektorea ,, 2 1 2 1 0 cm unitarioa den. Ez bada, aurkitu u bektorearen norabide bereko bi bektore unitarioren koordenatuak.

14 u2 i–=+jk eta v– i3 j2 k =+ + emanda, egiaztatu u × v eta v × u bektoreak aurkakoak direla eta lortu horien modulua Zein da u eta v -k zehaztutako triangeluaren azalera?

15 u = (1, –1, 0) eta v = (2, 0, 1) bektoreak emanda, aurkitu u eta v bektoreekiko ortogonala den bektore bat, unitarioa dena, eta u eta v bektoreekiko ortogonala den bektore bat, modulua 24 duena.

16 Kalkulatu zer angelu eratzen duten kasu hauetako bakoitzean emandako bektoreek.

a) u = (1, –3, 2) eta v = (1, 0, –1)

b) u = (3, 4, 0) eta v = (4, 0, 2)

c) u = (2, –4, 0) eta v = (–1, 2, 0)

17 Kalkulatu kasu hauetako bakoitzean ageri diren hiru bektoreen biderketa mistoa:

a) u (1, –3, 2), v (1, 0, –1), w (2, 3, 0)

b) u (3, 2, 1), v (1, –2, 0), w (– 4, 1, 1)

c) u (1, 2, –1), v (3, 0, 2), w (–1, 4, –4)

Kalkulatu kasu bakoitzeko hiru bektoreek zehazten duten paralelepipedoaren bolumena ere.

18 Kalkulatu u (1, 2, 3), v (–2, 1, 0) eta w = u × v bektoreek zehazturiko paralelepipedoaren bolumena. Arrazoitu zergatik den emaitza | u × v |2

19 Kalkulatu honako bektore hauek zehazten duten tetraedroaren bolumena:

a (3, –1, 1), b (1, 7, 2), c (2, 1, –4)

20 a (1, 2, –1) eta b (1, 3, 0) bektoreak emanda, egiaztatu a × b bektorea a + b eta a – b bektoreekiko perpendikularra dela.

Proposatutako ariketak eta problemak

Ebazteko

21 Bektore hauek ditugu: u (1, –1, 3), v (1, 0, –1), w (m, 1, 0)

a) Kalkulatu m-ren zer baliorekin diren ortogonalak u eta w

b) Esan m-ren zer baliorekin diren linealki independenteak u , v eta w

c) m = 1 kasuan, idatzi s (3, 0, 2) bektorea u , v eta w bektoreen konbinazio lineal moduan.

22 u = (–1, 4, 8) eta v = (1, 2, –2) bektoreak ditugu:

a) Frogatu u eta v bektoreek eraturiko angelua 90° baino handiagoa dela.

b) Kalkulatu u eta v bektoreekiko perpendikularra izan eta modulua 1 duen bektore bat.

23 a) Egiaztatu u (3, –2, 1) eta v (4, 3, –6) bektoreek zehazturiko paralelogramoa laukizuzen bat dela

b) Kalkulatu horren azalera, oinarria altuerarekin biderkatuz, eta egiaztatu emaitza bera lortuko duzula | u × v | eginda.

24 Bektore hauek izanda: u 1 (2, 0, 0), u 2 (0, 1, –3), u 3 = a u 1 + b u 2, zer erlazio bete behar dute a eta b parametroek u 3 ortogonala izateko v (1, 1, 1) bektorearekiko?

25 Kalkulatu v (1, 2, 3) eta w (1, –1, 1) bektoreekiko ortogonala izan eta [ u , v , w ] = 19 betetzen duen u bektore baten koordenatuak

26 a) Zehaztu zein izan behar den a-ren balioa (–2, a, a), (a, –2, a) eta (a, a, –2) bektoreak linealki mendekoak izateko

b) Lortu, kasu horietan, bektoreen arteko mendekotasunerlazio bat

27 Aurkitu zein izan behar den b-ren balioa u = (1, b, 2) eta

v = (–1, 1, 2) bektoreek 60°-ko angelua eratu dezaten.

28 u eta v bi bektoreei buruz, badakigu | u | = 12; | v | = 10 ; | u – v | = 20 direla. Kalkulatu:

a) u v

b) u eta v bektoreek eratzen duten angelua.

c) u eta u – v bektoreek eratzen duten angelua.

* Begiratu ebatzitako 8. problema.

29 Kalkulatu a-ren eta b-ren balioak u = (a, 1, b) eta

v = (–2, a, 1) bektoreak ortogonalak izateko, eta haien moduluak berdinak izan daitezen.

30 u eta v bi bektoreri buruz badakigu ortogonalak direla eta

| u | = 6 eta | v | = 10 direla. Kalkulatu | u + v | eta | u – v |

31 u = (1, –3, 2), v = (1, 0, –1) eta w = (2, 1, 3) bektoreak emanda, kalkulatu:

a) Hiru bektore horiek zehazten duten paralelepipedoaren bolumena.

b) Paralelepipedo horren altueraren neurria, oinarri gisa u eta v bektoreek zehaztutako aurpegia hartuz.

32 u (1, –1, 0), v (0, 1, 2) eta w (k + 1, 2k, 2 – 3k) bektoreak izanda, esan k-ren zer baliorekin…

a) izango diren u , v eta w planokideak.

b) izango den w bektorea u eta v bektoreekiko perpendikularra.

c) izango den u , v eta w bektoreak ertz moduan dituen tetraedroaren bolumena 1/6.

33 Honako bektore hauek emanda: u (1, 0, –1), v (0, a + 1, 0), w (1, 1, a – 1)

a) Aurkitu a-ren zer baliorekin diren linealki mendekoak u , v eta w bektoreak

b) Aztertu c (1, 2, 3) bektorea linealki mendekoa den u , v eta w bektoreekiko, a = 2 kasuan

c) Arrazoitu a = 1 kasuan u • ( v × w ) = 0 berdintza betetzen den

34 Aurkitu v (1, –2, 3) bektorearen norabide bera duen bektore bat, kontuan izanda w (–2, 4, –1) bektorearekin 25 u2-ko azalera duen paralelogramo bat eratzen duela.

35 Aurkitu a (2, –1, 1) eta b (1, 0, 3) bektoreekin planokidea eta c (2, 3, 0)-rekiko ortogonala den v bektorea

36 a eta b bektoreak ditugu | a | = 4 eta | b | = 2 betetzen dutenak, )(a,b \ = 60° izanik. Kalkulatu | a + b | eta | a – b |

Galdera teorikoak

37 a) Zein da multzo honetan dagoen bektore linealki independenteen kopurua?

S = {(1, 1, 1), (0, 2, 1), (2, 0, –3), (–1, 1, 2)}

b) Nulua ez den bektore batek hiru osagaiak berdinak ditu. Idatzi daiteke S -ren lehenengo bi bektoreen konbinazio lineal moduan?

c) Ba al dago bektorerik, lehen bi osagaiak 1 izanik, S-ren bigarren eta hirugarren bektoreen konbinazio lineal gisa jar daitekeenik?

38 Biderketa eskalarra erabiliz, frogatu a ⊥ b eta a ⊥ c badira, orduan a ⊥ (m b + n c ) dela.

39 Nolakoak izan behar dute u eta v bi bektorek u + v batuketa u – v kenketarekiko perpendikularra izateko?

40 a) u v = u w bada, ziurta genezake v = w dela?

b) a × b = a × c bada, nahitaez izan behar da b = c ? Arrazoitu zure erantzunak eta jarri adibideak.

41 a) Egon daitezke u v = 3, | u | = 1, | v | = 2 betetzen duten u eta v bi bektore?

b) Bi bektorek | u v | = | u | | v | betetzen badute, zer esan dezakezu eratzen duten angeluaz?

42 Zuzena ala okerra? Arrazoitu zure erantzunak eta jarri adibideak.

a) a (2, –3, 0) eta b (1, 0, –2) bektoreekiko planokideak eta c (–1, 1, – 4) bektorearekiko ortogonalak diren infinitu bektore daude.

b) | a | = 5, | b | = 3 badira eta a eta b bektoreek eratzen duten angelua 60°-koa bada, orduan | a + b | = 8 da.

c) u eta v edozein bi bektore badira, u × ( u + v ) + + v × ( u + v ) = 0 berdintza betetzen da.

d) Bi bektore perpendikularrak badira, biderketa bektoriala nulua da.

e) a , b eta 2 a – 3 b bektoreen biderketa mistoa 0 da, a eta b bektoreak edozein direla ere.

f) Bi bektore ortogonal linealki independenteak dira beti.

43 a , b eta c hiru bektore linealki independenteak badira, ziurtatu al dezakegu a + b , a – b , a + b – c bektoreak ere hala direla? Arrazoitu zure erantzuna.

Sakontzeko

44 a , b , c linealki independenteak dira. Esan, arrazoiak emanez, biderketa misto hauetako zein den 0: [ a + c , a – c , a + b + c ], [ a + c , b , a + b ], [ a – c , c – b , b – a ]

45 u eta v bektoreei buruz badakigu u + v = a , 2 u – 3 v  =  b betetzen dutela, a (2, –1, 0) eta b (1, 3, –1) izanik. Aurkitu u eta v bektoreek eratzen duten angelua.

46 u , v eta w bektoreek honako baldintza hauek betetzen dituzte: | u | = 5, | v | = 4, | w | = 7, u + v + w = 0

Kalkulatu u v + u w + v w

47 u eta v bektoreak ditugu, eta | u | = 6; | v | = 8 ; | u – v | = 10 dira. Kalkulatu [ u × v , u , v ] biderketa mistoa.

48 u eta v bi bektore ortogonal eta unitarioak dira. Kalkulatu zein izan behar den a parametroaren balioa u + a v eta u – a v bektoreek 60°-ko angelua eratzeko.

49 Frogatu u eta v edozein bi bektore badira, orduan: ( u v )2 + | u × v |2 = | u |2 | v |2

50 Frogatu ( u – v ) × ( u + v ) = 2( u × v ) dela, u eta v edozein direla ere.

1 a) Kalkulatu a, b eta c parametroak, a u + b v + c w = =  0 bete dadin. Kontuan hartu u (1, –1, 0), v (0, 1, 2), w (–2, 0, 1) direla.

b) u , v eta w bektoreek oinarri bat eratzen dute?

c) Egin badaiteke, idatzi r (1, 1, 1) bektorea u , v eta w bektoreen konbinazio lineal moduan.

2 u(3, –2, 3) eta v (4, –2, – 4) bektoreak ditugu. Aurkitu | u |, | v |, (, ) uv % eta v -ren gaineko u -ren proiekzio bektorea

3 u (3, – 4, 0) eta v (m, 0, 7) bektoreak izanda:

a) Kalkulatu m-ren balioa u eta v bektoreak perpendikularrak izan daitezen.

b) Aurkitu u eta v bektoreekiko perpendikularra den w

c) Lortu, hurrenez hurren u -ren, v -ren eta w -ren norabide bera izango duten u ', v ', w ' hiru bektore unitario.

d) u ', v ' eta w ' bektoreek oinarri ortonormala eratzen dute?

4 a) Esan zer erlazio egon behar den a-ren eta b-ren artean u (1, 2, –1), v (0, 1, a) eta w (3, b, 0) bektoreak planokideak izateko.

b) a = 3 kasuan, kalkulatu zein izan behar den b-ren balioa u , v eta w bektoreek zehazten duten paralelepipedoaren bolumena 10 u3 izateko

5 Kalkulatu zein izan behar den m-ren balioa a (2, –1, 4) eta b (0, 3, m) bektoreek zehazten duten triangeluaren azalera 35 u2 izateko.

6 Aurkitu (3, –1, 0) bektorearekiko perpendikularra izan eta (0, 0, 1)-rekin 60°-ko angelua eratzen duen bektore bat, modulua 10 duela jakinda.

7 {, ,} xy z Á3-ko oinarria da. Kalkulatu m-ren balioa xy z u–=+ , mx y2 v= + , ym z w–3=+ bektoreek 1 u3-ko bolumena duen tetraedro bat zehaztu dezaten.

6

Puntuak, zuzenak eta planoak espazioan

Geometria analitikoa

Geometria Analitikoaren asmatzaileek, Descartesek eta Fermatek (xvii. mendea), interes handia zuten gainazalen azterketari buruz, baina arreta gutxi jarri zioten, eta, batez ere, kurba lauak landu zituzten. xviii. mendean garatu zen espazioaren geometria analitikoa. Clairaut, Euler eta Lagrange izan ziren aitzindariak.

Geometra moduan maila bikaina eta bokazio pedagogikoa zuelako, Monge (1746-1818) jo daiteke geometria analitiko tridimentsionalaren benetako aitatzat: hainbeste libururen artean, bat Pariseko Eskola Politeknikoko bere ikasleentzat argitaratu zuen, eta, bertan, espazioko geometria analitikoa ia-ia gaur ezagutzen dugun moduan garatu zuen.

Geometria ez-euklidearrak

xiv. mendearen lehenengo erdian, hogeita hiru mende baino gehiagoko problema geometriko sakon bat argia ikusten hasi zen. Euklidesek geometriaren eraikin logikoa oinarritzeko proposatu zituen postulatuen artean (hau da, aho batez onartzen diren «ageriko» baieztapenen artean), bosgarrenak, gainerako guztiek ez bezala, ez zirudien inondik inora ere «agerikoa»: «Bi zuzen ebakitzen dituen beste batek barne-angeluak eratzen baditu bi horiekin (zuzenaren alde beretik), eta barne-angelu horien batura bi angelu zuzenena baino txikiagoa bada, orduan bi zuzenek, mugagabe luzatuz gero, bat egingo dute angeluen arteko batura bi angelu zuzenena baino txikiagoa den aldetik».

Hainbat eta hainbat mendetan aritu ziren matematikariak pentsatzen, derrigorrez onartu behar ote zen hain baieztapen konplikatua konbentzioz, geometria eraikitzeko. Ez ote zegoen beste biderik

Horretarako saiakerak egon ziren, hainbeste gainera. Matematikarien pentsamendu kolektiboak xix. mendearen lehenengo erdian lortu zuen nahikoa heldutasun izatea; eta ordurako, bakoitzak bere aldetik, baina ia aldi berean, Gaussek Alemanian, Bolyaik Hungarian eta Lobatxevskik Errusian, soluzioa aurkitu zuten: Euklidesen bosgarren postulatuaren ezeztapenean oinarrituriko beste geometria batzuk eraiki zitezkeen Geometria ez-euklidearrak jaio ziren. Matematikaren munduan iraultza eragin zuten, eta, denborarekin, aldaketa izugarria ekarri zuten giza ezagutzaren teoriari buruzko pentsamendu filosofikoan

Parisko Eskola Politeknikoa.

Geometria horien esanahia

Euklidesen bosgarren postulatua berak proposatutakoa baino modu errazagoan proposatu daiteke: «Planoko r zuzenetik kanpo dagoen P puntu batetik zuzen horrekiko paralelo bat eta bakarra marraztu daiteke». Hau da, P-tik igarotzen den eta r ebakitzen ez duen zuzen bakarra dago

Geometria ez-euklidearrak Euklidesen gainerako postulatu guztiak onartuz eta bosgarren hori ukatuz eraiki daitezke. Eta hori bi modutan egin daiteke:

(1) P puntutik abiatuta ezin da marraztu r ebakiko ez duen zuzenik

(2) P puntutik abiatuta r ebakiko ez duten zuzen bat baino gehiago marraztu daitezke

Oinarri horien gainean eraiki ziren geometria berriak, Geometria euklidearra bezain sendoak (ez dute kontraesanik)

Aitzindarien etsipena

Etsigarria izan behar da, benetan, mundu berri bat aurkitu eta inork ez sinestea, nahiz eta ahaleginak eta bi egin aurkikuntza hori zabaltzeko

Geometria ez-euklidearraren aitzindari izan ziren Lobatxevski eta Bolyai matematikarien karrerek argi erakusten dute ideia berriek zer zail izaten duten barneratzea gizakiaren buru kolektiboaren inertziaz. Dena dela, Lobatxevski eta Bolyai garai hartan gorenean zeuden matematika zentroetan egon izan balira, Errusiako Kazanen eta garai hartan Hungaria eta gaur egun Errumania den txoko batean egon beharrean, beharbada ideia berri horiek azkarrago iritsi eta zabalduko ziren.

EBATZI

Geometria eliptikoa

Geometria ez-euklidearra izan daitekeen horietako bati eliptiko esaten zaio. Eta horren bertsio erraz bat gainazal esferiko baten gainean garatzen da. Kasu honetan, «zuzenak» zirkunferentzia maximoak izango dira (gainazal esferikoak zentrotik igarotzen den plano batekin dituen ebaketak).

Geometria horrek Euklidesen lehenengo lau postulatuak betetzen ditu.

Egiaztatu honako hauek:

a) Bi «zuzenek» elkar ebakitzen dute beti

b) «Zuzen» batetik kanpo dagoen puntu batetik ezin da marraztu lehenengo zuzen hori ebakiko ez duen «zuzenik»

c) Geometria eliptiko honetan ez da betetzen Euklidesen bosgarren postulatu

Nikolai Lobatxevski (1792-1856)

Geometria eliptikoaren triangelua

Erreferentzia-sistema espazioan

Bektoreak oso tresna lagungarriak dira espazioko geometrian. Beraz, unitate hau hasteko, bektoreetatik abiatu eta erreferentzia-sistema bat eraikiko dugu, puntuak adierazteko lehenengo, eta, irudi espazialak gero

Espazioko erreferentzia-sistema bat da R = {O, { ij,, k }} multzoa, eta osagai hauek ditu:

• Jatorri izeneko puntu finko bat, O.

• Bektoreentzako oinarri bat, B = { ij,, k }.

Espazioko P puntu bakoitzari OP bektorea esleitzen zaio (, ,) OP ab c koordenatuduna

POSIZIO-BEKTOREA

OP bektoreari esaten zaio P puntuaren posizio-bektorea.

Horren arabera, planoko P puntu bakoitzak (a, b, c ) koordenatu batzuk ditu R erreferentzia-sistemarekiko. Honela idatziko dugu: P (a, b, c). Eta alderantziz: koordenatuen hiruko bakoitzari puntu bakarra dagokio espazioan.

Koordenatu-ardatzei X, Y, Z esango diegu. Oinarriko bektoreekiko zuzen paraleloak dira, eta O jatorritik igarotzen dira

KONTUAN HARTU

Aurreratzean, darabilgun oinarria ortonormala dela onartuko dugu; hau da, 1 modulua duten eta elkarrekiko perpendikularrak diren bektoreekin eratutakoa.

1 Adierazi P (3, 5, 4) puntua.

1. Koordenatuak kontuan hartuz, P1, P2, P3 puntuak lortuko ditugu.

2. Koordenatuen plano bakoitzean paralelogramoak osatzen baditugu, P', P'', P''' lortuko ditugu

3. Paraleloak marraztuko ditugu P', P'', P''' puntuetatik hiru ardatzetara. Hirurek ebakiko dute elkar P puntuan.

Pentsatu

1 Adierazi hurrengo puntu hauek:

P (5, 2, 3), Q (3, –2, 5), R (1, 4, 0)

S (3, 0, 4), T (0, 6, 3), U (0, 0, 4)

2 Kokatu P puntu bat erreferentzia-sistema baten gainean. Proiektatu puntu hori (P') XY planoaren gainean (ikusten duzunez P'-ren proiekzioa ez da unibokoa, zure gogoaren araberakoa baizik). Jarraitu prozesua P-ren koordenatuak zehaztu arte.

Ebatzitako ariketa

eta praktikatu

Bektoreak geometriako problemetan erabili

Bi puntu lotzen dituen bektorearen koordenatuak

Gogoan izan PQ OQ OP – = dela. Beraz:

P (x1, y1, z1) eta Q (x2, y2, z2) lotzen dituen bektorearen koordenatuak hauek dira: (, ,) xx yy zz PQ – 21 21 21

Q P PQ ren koordenatuak ren koordenatuak –ren koordenatuak bektorea muturra jatorria =

Adibidez, P eta Q puntuak P (3, –5, 8), Q (1, 7, – 4) badira:

(, (),) (, ,) PQ 13 75 48 21212 – = =

QP = (3 – 1, –5 – 7, 8 – (– 4)) = (2, –12, 12)

Hiru puntu lerrokatuta daudela egiaztatu

A (x1, y1, z1), B (x2, y2, z2) eta C (x3, y3, z3) puntuak lerrokatuta daude AB eta BC bektoreek norabide bera badute. Puntuen koordenatuak proportzionalak direnean beti gertatzen da hori; hau da, baldin eta: xx xx yy yy zz zz –

Adibidez, A (5, –1, – 4), B (3, 3, 2) eta C (2, 5, 5) puntuak lerrokatuta dauden ikusteko, (, ,) AB 24 6 – eta (, ,) BC 12 3 – bektoreek koordenatu proportzionalak dituzten aztertuko dugu.

1 2 2 4 3 6 ––== = 2 denez, proportzionaltasuna dago, eta, beraz, AB // BC dela baiezta dezakegu, eta A, B eta C lerrokatuta daudela

Zuzenki baten erdiko puntua

Paralelogramo baten diagonalek erdiko puntuetan elkar ebakitzen dute. Alboko irudian, OS OA OB =+ da diagonal horietako bat:

() OM OS OA OB 2 1 2 1 == += ,, xx yy zz 22 2 12 12 12 + + + dn

A (x1, y1, z1) eta B (x2, y2, z2) muturrak dituen zuzenki baten M erdiko puntuaren koordenatuak hauek dira: M ,, xx yy zz 22 2 12 12 12 + + + dn

Adibidez, A (7, –1, 4) eta B (1, 5, –3) muturrak dituen zuzenki baten erdiko puntua hau da:

➜ Puntuak, posizio-bektoreak eta bektoreak.

Puntu batek beste batekiko duen simetrikoa

P puntuak Q puntuarekiko duen simetrikoa P' da, Q puntua PP' zuzenkiaren erdiko puntua bada. Beraz, P (x1, y1, z1) eta Q (x2, y2, z2) badira, P' (α, β, γ)-ren koordenatuak honako berdintza hauetatik lortzen dira:

Adibidez, P (5, –1, 2) puntuak Q (7, 0, 3)-rekiko duen simetrikoa lortzeko, puntu simetriko horri P' (α, β, γ) esango diogu eta kontuan hartuko dugu Q puntua PP' -ren erdiko puntua dela:

Ebatzitako ariketak

1 Kalkulatu zein izan behar diren m-ren eta n-ren balioak P (4, –1, 3), Q (3, 5, 1) eta R (0, m, n) lerrokatuta egoteko

2 Aurkitu P (7, 4, –2) puntuak Q (3, –11, 7)-rekiko duen P' simetrikoa

3 Aurkitu A (7, –2, 11) eta B (10, 7, 5) muturreko zuzenkia hiru zati berdinetan zatituko duten M eta N bi puntu

AM = — AB 3 1

M N

A(7, –2, 11)

AB = (3, 9, – 6)

B(10, 7, 5)

AM AB 3 1 = = (1, 3, –2)

OM OA AM =+ = (7, –2, 11) + (1, 3, –2) = = (8, 1, 9)

ON OA AN OA AM2 =+ =+ = (7, –2, 11) + (2, 6, – 4) = (9, 4, 7)

M eta N puntuen koordenatuak M (8, 1, 9) eta N (9, 4, 7) dira.

Pentsatu eta praktikatu

1 Kalkulatu m-ren eta n-ren balioak P(7, –1, m), Q(8, 6, 3) eta R(10, n, 9) puntuak lerrokatuta egoteko.

2 Aurkitu A(1, –3, 5), B(0, 7, 2) eta C(–1, 5, 6) erpineko triangeluaren aldeetako erdiko puntuen koordenatuak.

3 A(–3, 5, 11) eta B(3, 5, –1) puntuak emanda:

a) Aurkitu AB zuzenkiaren erdiko puntua.

b) Aurkitu B puntuak A-rekiko duen simetrikoa.

c) Lortu AM = 2MB beteko duen AB-ko M puntu bat

d) Lortu NB = 3AN beteko duen AB-ko N puntu bat

Ekuazio bektoriala

r zuzen bat bektorialki zehaztuta dago honako hauek jakinez gero:

• r zuzeneko P puntu bat; horrek OP = p jakitea dakar, posizio-bektorea.

• r-rekiko paraleloa den d bektore bat, norabide-bektorea.

Irudian ikusten dugunez, p , p + d , p – d , p + 2 d , … bektoreak jatorria O puntuan dutela kokatuz gero, mutur bat zuzenaren gainean izango dute denek. Orokorrean, p + λ d bektorea izango da jatorria O puntuan ezarri eta X muturra zuzenaren gainean duen bektorea. Horrela, r -ren ekuazio bektoriala lortuko dugu :

• O koordenatuen jatorria da

• X zuzeneko puntu aldakor bat da

r : OX = p + λ d

• p posizio-bektorea da, zuzenaren gainean kokatzen gaituena

• d norabide-bektore bat da, zuzenarekiko paraleloa

• λ parametro bat da. λ aldatzean (λ ∈ Á), X puntuak zuzena ibiltzen du

Ekuazio parametrikoak

Ekuazio bektorialean bektoreen lekuan koordenatuak jartzen baditugu, honela geratuko zaigu:

(x, y, z) = (p1, p2, p3) + λ (d1, d2, d3)

Aldagai bakoitza bere aldetik adieraziz gero, r -ren ekuazio parametrikoak lortuko

ditugu:

• (x, y, z) dira r-ko puntu generiko baten koordenatuak

• (p1, p2, p3) dira r-ko puntu zehatz baten koordenatuak

• (d1, d2, d3) dira r-rekiko bektore paralelo baten koordenatuak

• λ parametro bat da. λ-ren balio bakoitzerako r-ko (x, y, z) puntu bat lortzen da

Adibidez, lor ditzagun irudiko r zuzenaren ekuazio bektoriala eta ekuazio parametrikoak.

P (3, 5, 8) puntua zuzenekoa da. Beraz, p = OP (3, 5, 8) posizio-bektorea da d (2, 6, 4) bektorea r-rekiko paraleloa da. Beraz, norabide-bektore bat da.

3 X r O P(3,

λ edozein dela ere, OX pd m =+ bektoreak X muturra r zuzenaren gainean dauka; hau da, X mugitu egiten da r gainean, λ aldatzean Á-ren balio guztiak hartuz.

5, 8)

Ekuazio bektoriala: OX = p + λ d

Bektoreen lekuan koordenatuak jarriz gero:

(x, y, z) = (3, 5, 8) + λ(2, 6, 4)

32 56 84 =+ =+ =+ *

m m m

➜

Zuzen baten ekuazioa.

6, 4)

Zuzenaren ekuazio jarraitua

Ekuazio parametrikoetako bakoitzean λ parametroa askaztuz gero, hau lortzen dugu:

λ = ,, d xp d yp d zp – – –1 1 2 2 3 3 mm==

Berdintza horietako bigarren atalak berdinduz gero, zuzenaren forma jarraitua lortuko dugu d xp d yp d zp – – –1 1 2 2 3 3 == (x, y, z) da zuzeneko puntu orokor bat, (p1, p2, p3) da posizio-bektorea, eta (d1, d2, d3) da norabide-bektore bat

Adibidez, OP (3, 5, 8) posizio-bektorea eta d (2, 6, 4) norabide-bektorea dituen aurreko orrialdeko adibideko r zuzenaren ekuazio jarraitua hau da:

x y z 2 3 6 5 4 8 –––==

Batzuetan, zuzena forma jarraituan emanda dagoenean, zeroren bat izaten du izendatzailean. Adierazpen hori ez da onargarria aritmetikoki, baina onar daiteke adierazpen sinboliko moduan: izendatzaileak zuzenaren norabide-bektorearen koordenatuak dira.

Adibidez, P (3, –1, 4) puntutik igarotzen den eta d (2, –5, 0)-rekiko paraleloa den s zuzenak forma jarraitu hau du:

: x y z s 2 3 5 1 0 4 –––= + =

Lehenengo berdintzak benetako proportzio bat adierazten du. Baina hirugarren zatikiak izaera sinbolikoa baino ez du: r-rekiko paraleloak diren bektore guztiek hirugarren koordenatua zero dutela adierazten du. Hau da, zuzeneko puntu guztien hirugarren koordenatua konstantea da: z = 4.

Zuzenaren ekuazioaren forma inplizitua

4. unitatean ikusi dugun moduan, ax + by + cz + d = 0 ekuazio lineal batek plano bat adierazten du, eta horietako bik eratzen duten sistema plano horietako biren arteko ebaketa da

ADI!

Honela adierazpenak:

matematikoki ez dira zuzenak. Testuinguru honetan adierazpen sinboliko modura onartzen dira: (2, –5, 0) bektorea (norabide-bektorea) zuzenarekiko paraleloa dela adierazten du.

ERREPARATU

Koefiziente-matrize baten heina 2 bada, hau da, baldin eta (a, b, c) ≠ λ(a' , b' , c' ) bada, orduan ebaketa zuzen bat da eta forma inplizituan dagoela esaten dugu. 1

honako zuzen hauek forma in-

Zuzen baten ekuazioaren forma jarraituko bi berdintzetako bakoitzak plano baten ekuazioa zehazten du.

a) λ ezabatuko dugu, x-ren eta z -ren adierazpenak erabiliz:

Ebatzitako ariketak

2 Lortu P (0, 1, –3) puntutik igarotzen den eta d (1, –5, 0) bektorearekiko paraleloa den zuzenaren ekuazio parametrikoak, jarraitua eta inplizitua

Ekuazio bektoriala OX OP d m =+ da. Bektoreen lekuan koordenatuak jarriz gero, hau lortzen dugu: (x, y, z) = (0, 1, –3) + λ(1, –5, 0) = (λ, 1 – 5λ, –3)

3 Lortu A (1, 7, 3) eta B (2, –1, – 8) puntuetatik igarotzen den zuzenaren ekuazio parametrikoak eta aurkitu zuzen horretako beste bi puntu.

4 Zuzen hau emanda:

ekuazio parametrikoak: x y z 15 3 ––

Z [ \

m m = = =

] ] ] forma jarraitua: x y z 15 1 0 3 ––== +

Ekuazio inplizitu bat z = –3 da; hau da, z + 3 = 0.

Bestea lortzeko, λ lehenengo bi ekuazio parametrikoetatik ezabatu dezakegu, edo ekuazio jarraituko lehenengo berdintzatik

forma inplizitua: xy z 51 30 = += 3 → xy z 51 0 30 –+= += 3

• Zuzenaren posizio-bektore moduan OA (1, 7, 3) hartuko dugu, eta norabidebektore moduan, AB (1, – 8, –11)

Ekuazio parametrikoak hauek dira: x y z

Z [ \

] ] ]

=+ = =

1 78 311 ––

m m m

• Zuzeneko puntuak lortzeko, λ-ri balioak emango dizkiogu:

λ = –1 denean → x = 0, y = 15, z = 14. Puntu hau lortzen dugu: (0, 15, 14).

λ = 2 denean → x = 3, y = –9, z = –19. Puntu hau lortzen dugu: (3, –9, –19).

Ikusten duzunez, λ = 0 eta λ = 1 denean, hurrenez hurren, A eta B lortzen dira.

A. Argi dago zuzenekoa dela. λ = 0 kasuan lortzen da.

r : x y z

Z [ \

] ] ]

m m = =+ =

––

3 23 1

Aztertu puntu hauetakoren bat

r -koa den:

A (3, 2, –1) B (–2, 17, –1)

C (1, 5, 0) D (2, 8, –1)

B Lehenengo koordenatuaren kasuan: –2 = 3 – λ → λ = 5. Ikus dezagun λ = 5 kasuan beste koordenatuak lortzen diren:

· y z 23 517 –1 =+ = = 3 Jakina, B ∈ r

C Argi dago ez dela zuzenekoa; izan ere, z ≠ –1.

D Lehenengo koordenatuaren kasuan: 2 = 3 – λ → λ = 1

Bigarren koordenatuan ordezkatuko dugu: y = 2 + 3 · 1 = 5 ≠ 8

Ez, puntu hori D ∉ r

Pentsatu eta praktikatu

1 Lortu beheko puntu horietatik igarotzen den zuzenaren ekuazio parametrikoak, forma jarraituan jarritako ekuazioa eta ekuazio inplizituak:

A (–5, 3, 7) eta B (2, –3, 3)

2 Aurreko zuzena kontuan hartuta, aurkitu A eta B izango ez diren beste sei puntu.

3 Aztertu ondoren emango ditugun puntu hauek r zuzenekoak diren:

Bi zuzenen posizio erlatiboak

r eta s bi zuzenen ekuazioak ematen dizkigutenean, lau kasu hauetako bat izango dugu esku artean:

KOINTZIDENTEAK

• Norabide bera

• Puntu komun bat

PARALELOAK

• Norabide bera

• Puntu komunik ez

ELKAR EBAKITZEN DUTE

• Norabide desberdina

• Puntu komun bat

Honako zuzen hauen posizio erlatiboak aztertuko ditugu:

r: OX = p + λ d s: OX = p' + λ d'

Bere norabide-bektoreak paraleloak badira ( d // d ')

ELKAR GURUTZATZEN DUTE

• Norabide desberdina

• Puntu komunik ez

Kasu horretan zuzenak bat datoz edo paraleloak dira. Hori argitzeko, r-ko puntu bat hartuko dugu (adibidez P ) eta s-koa den ala ez den aztertuko dugu.

• P ∈ s → lzuzenak bat datoz (hau da, zuzen bera dira).

• P ∉ s → zuzenak paraleloak dira.

Argi dago, baietz. Beraz, zuzenak bat datoz. Zuzen bera dira.

Norabide-bektoreak paraleloak ez badira ( d ez paraleloa d '-rekiko)

Kasu honetan hirugarren bektore bat erabiliko dugu, PP' , zuzen batetik bestera doana.

• r eta s zuzenek elkar ebakitzen badute, d , d ' eta PP' bektoreak planokideak dira; hau da, linealki mendekoak dira.

• r eta s zuzenek elkar gurutzatzen badute, d , d ' eta PP' bektoreak ez dira planokideak; hau da, linealki independenteak dira.

d , d ' eta PP' bektoreak linealki independenteak diren ala ez diren jakiteko, hiru bektore horien koordenatuek eratzen duten M' matrizearen determinantea zero den ala ez den aztertu behar dugu: M'

det (M' ) = 0 bada, r eta s zuzenek elkar ebakitzen dute.

det (M' ) ≠ 0 bada, r eta s zuzenek elkar gurutzatzen dute.

➜

d'

r

s P

PP' = OP' – OP

P' d

Marraztu zuzenak eta erabaki bere posizio erlatiboa.

Clariaut (1713-1765) geometria analitikoaren aitzindarietako bat izan zen.

Ebatzitako ariketak

1 Aztertu honako zuzen bikote hauen posizio erlatiboa

d (–5, 1, –1) eta d '(10, –2, 2) bektoreen koordenatuak proportzionalak dira; beraz, r eta s zuzenek norabide bera dute

r

2 Nolakoak dira r eta s zuzenak ?

r

EGIN ZUK

Aztertu honako zuzen hauen posizio

Zuzen bera diren ala ez diren ikusteko, r zuzeneko (3, 2, 5) puntua s -ren ekuazio parametrikoetan ordezkatuko dugu:

lortu ditugun balioak ez datoz bat. Beraz, (3, 2, 5) puntua ez da s-koa.

Zuzenak paraleloak dira

d (–3, 5, 1) eta d '(–1, 1, 0) norabide-bektoreen koordenatuak ez dira proportzionalak. Beraz, zuzenek elkar ebakitzen dute edo elkar gurutzatzen dute

PP' bektore bat aurkituko dugu, r-ko P puntu batetik s-ko P' puntu batera doana.

P (2, 3, 0), P' (1, 0, 5) → PP' (–1, –3, 5)

Ikus dezagun d , d ' eta PP' bektoreak planokideak diren ala ez diren:

3 5 1

1 1 0

1 3 5 – = –15 + 3 + 1 + 25 = 14 ≠ 0

r

3 Aztertu honako zuzen hauen posizio erlatiboa:

Beraz, zuzenek elkar gurutzatzen dute

EGIN ZUK

Aztertu honako zuzen hauen posizio

erlatiboa:

PP'

r P'(1, 0, 5)

d d'

s

P(2, 3, 0) (–3, 5, 1) (–1, –3, 5) (–1, 1, 0)

Zuzenek norabide desberdinak dituzte; izan ere, d (–3, 5, 1) ez da d '(–1, 2, 0)-rekiko paraleloa.

Zutabetzat bi bektore horiek dituen determinantea, eta P (2, 3, 0) ∈ r eta P' (1, 0, 5) ∈ s puntuak lotzen dituen bektorea zero da

3 5 1

1 2 0

21 30 05

–––= 0 → Hiru bektoreak planokideak dira.

Beraz, zuzenek elkar ebakitzen dute.

Zer puntutan ebakitzen duten elkar ikusteko, ekuazio parametrikoak koordenatuz koordenatu berdinduko ditugu. (Ohar garrantzitsua: enuntziatuan bi zuzenak parametro berarekin ematen badira ere, aldi berean erabiltzean, parametro desberdinak idatzi behar ditugu).

Berdinketa eginez: 23

Hau lortzen dugu: λ = 5, μ = 14

Ebaki-puntua lortzeko, λ = 5 hartuko dugu r -ren ekuazioetan :

4 (–13, 28, 5) puntuan ebakitzen dute elkar.

Puntu bera lortzen dugu s zuzenean μ = 14 eginez gero. (Gogoan izan s zuzenean λ-ren lekuan μ jarri dugula)

Planoaren ekuazioak

Ekuazio bektoriala

π plano bat bektorialki zehaztuta dago honako elementu hauek badakizkigu:

• π planoko P puntu bat. Izan ere, hortik, posizio-bektore esaten diogun OP = p bektorea dakigu.

• Planoarekiko paraleloak diren eta elkarrekiko independenteak diren u eta v bi bektore.

p bektoreak planoko P puntu batean kokatzen gaitu. λ u + μ v konbinazioak, alboko grafikoak erakusten duen moduan, P puntutik π planoko X edozein puntutara joateko modua ematen digu

Eta, horrela, planoaren ekuazio bektoriala lortuko dugu:

• X da planoko puntu generiko bat

• p da planoaren gainean kokatzen gaituen posiziobektore bat

π: OX = p + λ u + μ v

• u eta v dira planoarekiko bektore paraleloak eta linealki independenteak

• λ eta μ dira parametroak

Ekuazio parametrikoak

Zuzenen kasuan bezala, ekuazio bektorialeko bektoreen lekuan horien koordenatuak jartzen baditugu, planoaren ekuazio parametrikoak lortuko ditugu.

λ eta μ, parametroei ematen diegun balio-pare bakoitzeko, π-ko puntu baten koordenatuak lortzen ditugu.

Ekuazio inplizitua

Ekuazio parametrikoetan λ eta μ parametroak ezabatzen baditugu, ekuazio bakarra lortuko dugu. Planoaren ekuazio inplizitua esaten zaio, eta era honetakoa da:

ax + by + cz + d = 0

Ekuazio inplizitua ekuazio parametrikoetatik abiatuta lortzeko, hurrengo sistema honetatik λ eta μ ezabatu behar ditugu (ikusten duzunez, λ eta μ ezezagunak dira).

KONTUAN HARTU

Planoaren ekuazio bektoriala koordenatuen bidez idatziz gero, itxura honetakoa da:

➜ anayaharitza.es

Indartzeko ariketak: plano baten ekuazio parametrikoak ekuazio inplizituetara igarotzea.

ERREPARATU

Planteaturiko sistemak hiru ekuazio eta bi ezezagun (λ, μ) ditu.

Sistemak soluzioa izan dezan, matrize zabalduaren determinantea zero izan behar da; hau da:

Hau da, (x, y, z) planoko puntu bat bada, aurreko ekuazio-sistema horrek soluzioa du (hori betetzen duten λ eta μ existitzen dira) eta, ondorioz, matrizearen determinantea zero da. Zerorekin berdindutako determinantea, beraz, planoaren ekuazio inplizitua da.

HIZTEGIA

Planoaren ekuazio inplizituari ekuazio orokor ere esaten zaio.

Ekuazio inplizitua, planoarekiko bektore normal batetik abiatuta

Plano bati buruz ezagun baditugu P0(x0, y0, z0) puntu bat eta n (a, b, c) bektore normal bat, orduan planoa zehaztuta dago eta bere ekuazioa hau da:

a(x – x0) + b(y – y0) + c(z – z0) = 0

Bada, X (x, y, z) planoko puntu bat bada, PX 0 (x – x0, y – y0, z – z0) bektorea planoarekiko paraleloa da eta, beraz, n -rekiko perpendikularra, (edo, bestela, 0 bektorea da). Edonola ere, hau betetzen da:

(a, b, c) • (x – x0, y – y0, z – z0) = 0 ⇒ a (x – x0) + b (y – y0) + c (z – z0) = 0

Alderantziz: ax + by + cz + d = 0 (1) plano baten ekuazioa bada, (a, b, c) koordenatuko bektorea plano horrekiko perpendikularra da.

Izan ere, P0(x0, y0, z0) planoko puntu zehatz bat bada, honako hau betetzen da:

ax0 + by0 + cz0 + d = 0 (2)

Bi ekuazioen arteko kenketa eginez, (1) – (2), hau lortzen dugu:

a (x – x0) + b (y – y0) + c (z – z0) = 0 ⇔ (a, b, c) • (x – x0, y – y0, z – z0) = 0

Hau da, (a, b, c) perpendikularra da (x – x0, y – y0, z – z0) bektorearekiko, eta, beraz, planoarekiko.

Ebatzitako ariketak

1 Aurkitu P (2, 3, 5) puntutik igarotzen den eta u (–1, –2, –3) eta v (1, 3, 5) bektoreekiko paraleloa den π planoaren ekuazioa.

2 Hona hemen forma inplizituan emandako zuzen bat; hau da, bi planoren arteko ebaketa moduan:

r : xy z xz 32 54 0 38 0 –+= ++ = )

Aurkitu r-rekiko bektore paralelo bat.

Pentsatu eta praktikatu

n bektore normalak planoaren orientazioa zehazten du

➜ Planoaren ekuazioak

u × v = (–1, 2, –1) da planoarekiko bektore normal bat. Beraz, planoaren ekuazioa hau da:

–1(x – 2) + 2(y – 3) – 1(z – 5) = 0

π: x – 2y + z – 1 = 0

Planoaren ekuazio parametrikoetatik abiatuta ere ebatz liteke. Baina eraginkorragoa da aurreko ebazpen hori.

n = u × v u v r1 r2

Zuzen horretako bi puntu lortu litezke, P1 eta P2. Eta PP12 bektorea paraleloa da r-rekiko. Baina askoz eraginkorragoa da biderketa bektorialean oinarritutako beste metodo hau erabiltzea:

= = 4 → (3, –2, 5) × (–1, 0, 3) // r P r

(3, –2, 5) (–1, 0, 3)

r zuzena zehazten duten planoei π1 eta π2 esango diegu.

(, ,) π

(3, –2, 5) × (–1, 0, 3) r

1 Aurkitu P(2, –1, 3) puntutik igarotzen den eta u (1, 0, 4) eta v (0, 4, 7) bektoreekiko perpendikularra den planoaren ekuazio inplizitua.

b) Aurkitu planoarekiko bektore normala, eta, horrekin, idatzi ekuazioa.

2 Zehaztu bi planoren arteko ebaketa moduan adierazita dagoen honako zuzen honekiko bektore paralelo bat:

xy z yz 54 40 23 12 0 –+= += *

a) Bektore normalen bidez.

b) Zuzeneko bi puntu lortuz.

Plano bat zehazteko moduak

Plano baten ekuazioa berehala zehaztu daiteke P0 (x0, y0, z0) ∈ π puntu bat eta n (a, b, c) ⊥ π bektore normal bat ezagututa:

π: a(x – x0) + b(y – y0) + c (z – z0) = 0

Hainbat egoeraren bitartez heldu gaitezke horraino, oso modu errazean. Ikus ditzagun batzuk:

• Elkar ebakitzen duten eta planokoak diren bi zuzen izanda Zuzenetako bakoitza puntu baten eta norabide-bektore baten bidez zehaztuta dago:

r1: P1, d 1 r2: P2, d 2 d 1 eta d 2 erabilita, bektore normal bat lortuko dugu: n = d 1 × d 2 . Bi puntuetako bat hartuta, P1 edo P2, eta bektore normala, n , planoaren ekuazioa lortuko dugu.

• Planoko puntu bat eta planoarekiko paraleloak diren eta elkar gurutzatzen duten bi zuzen izanda

Aurreko kasuaren antzekoa da: zuzenen norabide-bektoreen bitartez bektore normala lortzen dugu: n = d 1 × d 2

• Planoan dauden eta elkarrekiko paraleloak diren bi zuzen izanda

r1: P1, d 1 r2: P2, d 2 d 1 // d 2

P P12 bektorea planoarekiko paraleloa da (planoan dago). Bektore horrek, d 1 bektorearekin batera, modua ematen digu bektore normala lortzeko: n = P P12 × d 1 . Eta hortik, n eta bi puntuetako bat (P1 edo P2) erabilita, planoaren ekuazioa lortzen dugu.

• Lerrokatuta ez dauden planoko hiru puntu izanda, P1, P2 eta P3 Ikus ditzagun egoera hau ebazteko hiru modu:

• P P12 eta P P13 bektoreak planoarekiko paraleloak dira. Beraz, planoarekiko bektore normal bat da n = P P12 × P P13 .

n eta hiru puntuetako bat erabilita, planoaren ekuazioa lortzen dugu.

• P1(x1, y1, z1), P2(x2, y2, z2) eta P3(x3, y3, z3) puntuak π planoko puntu finkoak badira, eta X(x, y, z) puntua π-ko puntu generiko bat bada, orduan XP1 , P P12 eta P P13 bektoreak planokideak izan behar dira eta, beraz, beren koordenatuen matrizearen determinantea 0 izan behar da. Hona

Orain, transformatu dezagun determinantea.

BEHATU

Hiru puntutatik igarotzen den planoaren ekuazioa adierazteko modu bitxi honetara heldu gara.

Errenkada bat eta zutabe bat erantsi ditugu. Horren elementuetatik garatuta, jatorrizko determinantea lortuko dugu.

1., 3. eta 4. errenkadei 2. errenkada batu diegu.

• Ikus dezagun beste zer modutan lor dezakegun planoko hiru puntutatik abiatuta planoaren ekuazioa, ax + by + cz +

x3, y3, z3) puntuek ekuazio hori betetzen dute, beraz:

y2, z2) eta

parametro baten mendeko soluzioa du Parametroari balio bat emanda, a, b, c eta d lortzen dira eta, beraz, planoaren ekuazioa.

Ebatzitako ariketak

1 Aurkitu π planoaren ekuazioa, jakinda barne hartzen duela zuzen hau:

1 zuzenari buruz badakigu P1(3, –1, –4) eta d 1 (5, –2, 0).

r2-rekiko bektore paralelo bat aurkitu behar dugu.

d 2 = (1, 1, –3) × (2, –1, 0) = (–3, –6, –3) // π

Proportzional bat hartuko dugu: (1, 2, 1) // π

d 1 eta d 2 -rekiko perpendikularra den bektore bat bilatuko dugu, hau da, π-rekiko perpendikularra.

n = (5, –2, 0) × (1, 2, 1) = (–2, –5, 12) ⊥ π

π: –2(x – 3) – 5(y + 1) + 12(z + 4) = 0

2 Kalkulatu honako zuzen hauek barne hartzen dituen π planoaren ekuazioa: r1

Ba al dago benetan bi zuzenak barne hartzen dituen planoren bat? Hori gertatzeko, elkar ebaki behar dute edo paraleloak izan behar dute (elkar gurutzatzen badute, ez dago horrelako planorik).

Ikus dezagun: d 1 (–5, 3, 1) // r1; d 2 (10, –6, –2) // r2; d 2 = –2 d 1 . Beraz, r1 // r2

Zuzenak paraleloak dira. Lortu dezagun zer planok hartzen dituen bere barnean. P1(2, –1, 0) eta P2(3, 0, 11) ∈π, P P12 = (1, 1, 11) // π d 1 × P P12 = (–5, 3, 1) × (1, 1, 11) = (32, 56, –8) ⊥ π

Har dezagun bektore paralelo bat: (4, 7, –1)

Planoaren ekuazioa da π: 4(x – 2) + 7(y + 1) – z = 0.

3 Lortu honako hiru puntuak barne hartzen dituen π planoaren ekuazioa:

P(1, –3, 0), Q(2, 7, 4), R(0, 4, 5)

PQ (1, 10, 4) // π, PR (–1, 7, 5) // π, PQ × PR = (22, –9, 17) ⊥ π (Puntuak lerrokatuta baleude, ziur aski konturatuko ginen PQ eta PR bektoreen koordenatuak ikustean. Baina konturatu ezean, orain argi izango genuke, biderketa bektoriala (0, 0, 0)).

π: 22(x – 1) – 9(y + 3) + 17z = 0 → π: 22x – 9y + 17z – 49 = 0

Nahi izanez gero, problema hau beste prozeduretako edozein erabilita ere emaitza hori lortzen dela egiazta dezakezu.

Pentsatu eta praktikatu

1 Aurkitu zuzen hauek barne hartzen dituen planoaren ekuazioa:

2 Zehaztu hiru puntu hauek hartzen dituen planoa:

P1(2, 0, 1)

P2(2, –1, 1)

P3(1, –1, –1)

Egizu lehen ikusitako hiru prozeduren bidez.

Bi plano

Bi planok elkar ebaki dezakete, paraleloak izan daitezke edo bat etor daitezke. Planoaren ekuazio inplizituek eratzen duten sistematik abiatuta: '' '' ax by cz d ax by cz d 0 0 ++ +=

matrize hauek lortzen ditugu: M = '' ' a a b b c c eo eta M' = '' '' a a b b c c d d

Matrize horien heinak aztertuta, soluzioei buruzko informazioa lortuko dugu; hau da, bi planoen puntu komunak zein diren jakingo dugu, eta, beraz, planoen posizio erlatiboa zein den

• hein (M ) = hein (M' ) = 1 bada, orduan (a, b, c, d ) proportzionalak dira (a', b', c' , d' )-rekiko, eta sistemak soluzioa du: plano bera dira.

• hein (M ) = 1 eta hein (M' ) = 2 badira, hau da, (a, b, c) koefizienteak proportzionalak badira (a', b', c' )-rekiko, baina gai independenteak proportzionaltasunerlazioa gordetzen ez badu, sistemak ez du soluziorik: planoak paraleloak dira.

• hein (M ) = hein (M' ) = 2 bada, hau da, (a, b, c) eta (a', b', c' ) koefizienteak proportzionalak ez badira, sistemak soluzioa du, baina planoak ez datoz bat: zuzen batean elkar ebakitzen dute.

Zuzena eta planoa

r zuzen baten eta π plano baten posizio erlatiboa aztertzeko, komeni da kontuan hartzea d bektorea (r-ren norabidea ) eta n bektorea (planoarekiko normala).

• d ⊥ n ( d • n = 0) bada, orduan zuzena planoan dago edo planoarekiko paraleloa da. Hori jakiteko, zuzeneko puntu bat hartu eta planokoa den aztertuko dugu.

• d ez bada perpendikularra n -rekiko ( d • n ≠ 0), orduan r zuzenak π ebakitzen du.

Ebaki-puntua lortzeko, beren ekuazioek eratzen duten sistema ebatziko dugu.

Adibidez:

π: 2x + 5y – 3z + 10 = 0, r : x y z 0 3 3 1 5

π-rekiko bektore normala: n (2, 5, –3)

r -ren norabide-bektorea: d (0, 3, 5)

n • d = (2, 5, –3)

• (0, 3, 5) = 15 – 15 = 0

Beraz, r zuze-rekiko paraleloa da edo plano horretakoa da. Zer den jakiteko, P (3, –1, 0) ∈ r puntua π planokoa den aztertuko dugu: 2 · 3 + 5(–1) – 3 · 0 + 10 = 11 ≠ 0

Hau da, P ∉ π da, eta, beraz, r zuzena π-rekiko paraleloa da.

Ebatzitako ariketak

1 Aztertu honako plano hauen posizio erlatiboa:

Begi bistakoa da koefizienteak proportzionalak direla, baina gai independenteak ez duela proportzionaltasun-erlazioa gordetzen; hau da: hein

Beraz, planoak paraleloak dira.

Zuzenaren (–2, –1, 6) norabide-bektorea ez da (1, –3, 5) bektore normalarekiko perpendikularra. Beraz, zuzenak puntu batean ebakitzen du planoa. Puntu hori lortzeko, zuzeneko puntu orokorraren koordenatuak planoaren ekuazioan ordezkatuko ditugu:

] ] ]

32 1 46 = = =+

––m m m Z [ \

3 Aztertu zer posizio erlatibo duten zuzen honek

x y z

7 5 0 2 0 3 ––== +

3 – 2λ – 3(1 – λ) + 5(4 + 6λ) + 11 = 0

Ekuazio horren soluzioa λ = –1 da. Horrek esan nahi du zuzenak λ = –1 parametroaren balioari dagokion puntuan ebakitzen duela planoa: () () ()

x y z

== == =+ =

32 15 11 2 46 12

1

π: 2x – y + 3z = 8 r : x y z 23 –13 –m m m =+ =+ = *

_ ` a

b b b Ebaki-puntua: (5, 2, –2)

(7, 0, 0)//r (2, –1, 1) ⊥ π (7, 0, 0) · (2, –1, 1) = 14 ≠ 0

Beraz, r zuzenak π ebakitzen du. Lor dezagun ebaki-puntua:

Zuzenak y – 2 = 0, z + 3 = 0 ekuazioak ematen ditu. Hau da, y = 2, z = –3. (Zuzena y = 2, z = –3 planoen ebaketa da. Beraz, X ardatzarekiko paraleloa da).

Planoaren ekuazioan ordezkatuz:

2x – 2 + (–3) + 11 = 0 → hau lortzen dugu: x = –3

Beraz, zuzenak eta planoak (–3, 2, –3) puntuan ebakitzen dute elkar.

oharra: Zuzenaren ekuaziotik abiatu eta zuzen hori zehazten duten bi planoak zein diren lortzeko, lehenengo adierazpena beste bietako bakoitzarekin parekatu behar dugu; baina azken horiek euren artean ez. Bestela, sinplifikazioan dena ezabatuko dugu.

Ikusten duzunez, «izendatzailean» zero duten «zatikiak» dituen planoaren ekuazioa lortzeko, zatikiaren «zenbakitzailea» berdin zero egin behar dugu. (Zorrotz jokatuta, erabiltzen ditugunak ez dira zatikiak eta ez dute zenbakitzailerik edo izendatzailerik. Horregatik idatzi ditugu hitzok komatxoen artean).

xy

z

xy

Ekuazioen hizkuntza: aldagaiak, parametroak…

Ekuazio inplizituak

Hiru dimentsioko espazioan, ekuazio batek gainazal bat deskribatzen du:

xy z xy z

22 0 22 0

++ = += = → planoak dira

xy z 25 22 2 ++ = → esfera bat da

xy 9 22+= → zilindro bat da

Ekuazio bakoitza aldagaien arteko murrizketa bat da. Ekuazio batean aldagai bat ez egoteak esan nahi du aldagai horrek ez duela murrizketarik eta, beraz, mugitzeko askatasun osoa duela

Lerro bat bi gainazalen arteko ebaketa moduan adieraz daiteke, bi ekuazioko sistema baten bidez:

xy z z 22 2 0 ++ = = ) → zuzen bat da, bi planoren ebaketa

xy z z 25 0 22 2 ++ = = ) → zirkunferentzia bat da, esfera baten eta plano baten ebaketa

xy z 25 0 22+= = ) → zirkunferentzia berdina da, zilindro baten eta plano baten ebaketa

Ekuazio parametrikoak

Ekuazio parametrikoek aldagai bakoitzaren jokabidea adierazten dute modu esplizituan. Parametro bakoitza askatasun maila bat da. Parametro bat duten ekuazio parametrikoek lerro bat deskribatzen dute; bi parametro dituztenek, gainazal bat

Parametro bat aldagaietako batean baino ez bada agertzen, aldagai hori aske mugitzen da, gainerakoak kontuan hartu gabe:

= =

3

zuzen bat da (gorria), parametro bakarra baitu.

zuzen berdea da, baina

plano berdea da, bi parametro baititu.

Á3-ko elementua askatasun maila

Baina hau ere plano bat izan arren, ez da aurrekoa bezain argi ikusten. (Ala bai? x eta y batzen baditugu, x + y = 4 lortzen dugu. Hori ekuazio inplizitua da, eta erraz ikusten da!)

➜ Beste azalera batzuen definizioa.

Ebatzitako ariketa

1 Idatzi honako irudi hauen ekuazio parametrikoak eta inplizituak:

a) Y ardatza b) XY planoa

c) Y, Z ardatzen zuzen erdikaria

a) Ez x eta ez z ez dira 0. Dena dela, y aske mugitzen da. x y z

Ekuazio inplizituak parametrikoetatik lortzen dira: x z 0 0 = = ) Hau da, bi plano horien ebaketa da.

b) x eta y aske eta bata bestearekiko independente mugitzen dira. Bakoitza, parametro bat da. z zero da.

d)

EGIN ZUK

Idatzi honako irudi hauen ekuazio parametrikoak eta inplizituak:

a) Z ardatza b) XZ planoa

c) X, Y ardatzen zuzen erdikaria.

d) Z

Azken ekuazioa, z = 0, planoaren ekuazio inplizitua da.

c) x zero da, eta y eta z aldi berean mugitzen dira, balio bera hartuta.

Ekuazio inplizituak: x yz 0 = = *

d) x aske mugitzen da. y eta z aldi berean mugitzen dira, balio bera hartuta baina zeinu desberdinekoak.

1 Idatzi honako irudi hauen ekuazio inplizituak eta parametrikoak: 2 Adierazi grafikoki honako ekuazio hauen bidez emandako irudiak:

Ebatzitako ariketak eta problemak

1. Forma inplizituan emandako zuzen baten norabide-bektorea

Zehaztu s zuzenaren ekuazioa, jakinda (0, 2, −4) puntutik igarotzen dela eta honako zuzen honekiko paraleloa dela:

r : xy z xy z 53 21 32 4 – += +=

Adierazi s bi planoren arteko ebaketa moduan.

Problemaren analisia: s zuzenak r-ren norabide bera izango du. Ekuazio inplizituen bidez emandako zuzen baten norabide-bektorea lortuko dugu, bi modutan:

1) Planoek eratzen duten sistema ebatzita.

2) Planoen bektore normalekiko perpendikularra den bektore bat lortuta.

1) xy

Edo, bestela, har dezakegu d( ,, ) 02 3 r = Forma hau hartzea komeni da norabide-bektoreaz gain puntu bat ere behar dugunean.

EGIN ZUK

Egiaztatu honako plano hauek

α: x – y + z – 4 = 0

β: 2x + y – z + 1 = 0

elkar ebakitzen dutela, eta aurkitu zehazten duten zuzenaren ekuazio parametrikoak.

2) r -ren norabide-bektorea: n × n ' = (5, –3, 2) × (1, 3, –2) = (0, 12, 18) d r = (0, 2, 3) har dezakegu. Prozedura hau errazagoa da norabide-bektorea baino ez badugu behar. s-ren ekuazio parametrikoak:

y

s-ren ekuazioa, planoen arteko ebaketa moduan: x yz

2. Zuzen bat perpendikular ebakitzen duen zuzena

Idatzi s zuzenaren ekuazio jarraitua, jakinda plano honetakoa dela:

π: x – 2y + z = 4

eta perpendikular ebakitzen duela zuzen hau:

r : xy z xy z 10 33 0 += +=

EGIN ZUK

Zuzen hau izanik:

Problemaren analisia: s zuzena π planoan badago eta r-rekiko perpendikularra bada, orduan s igaroko da r-ren eta π-ren arteko ebaki-puntutik. s-ren norabide-bektorea perpendikularra da π-ren bektore normalarekiko, planoan dagoelako, eta r norabide-bektorearekiko.

r-ren eta π-ren ebaki-puntua lortzeko, r adieraziko dugu ekuazio parametrikoen bidez, eta π planoaren ekuazioan ordezkatuko ditugu. Hortik, d r ere lortuko dugu.

r-ren parametrikoak lortuko ditugu, sistema parametro baten funtzioan ebatzita:

r -ren ekuazio parametrikoak :

2 32 ––= = = *

yt zt

π-ren ekuazioan ordezkatuko ditugu: (2 – t ) – 2(3 – 2t ) + t = 4 → t = 2 → P (0, –1, 2)

r: x y z

Z [ \

Zehaztu:

12 3 –5

m m = =+ =

] ] ] eta P (5, 5, 1) puntua.

a) P-tik igaro eta r-rekiko perpendikularra den planoaren ekuazioa. planoaren ekuazioa.

b) P-tik igaro eta r perpendikular ebakitzen duen zuzenaren ekuazioa.

Oharra: Ebaki-puntua r-ren eta π-ren ekuazioek eratzen duten sistema ebatzita ere lor dezakegu.

s-ren norabide-bektorea lortzeko, biderketa bektorial hau kalkulatuko dugu: n = (1, –2, 1), π-ren bektore normala, bider d r = (−1, −2, 1), ekuazio parametrikoak idaztean lortu dugun r-ren norabide-bektorea.

P puntuarekin eta d s bektorearekin, s -ren ekuazioa jarraitua daukagu: x y

3. Erronbo baten erpina

P(7, 4, 2), Q(1, 2, −2) eta R(2, 1, −3) puntuak ditugu. Horietako bat erronbo baten zentroa da, eta beste biak, erpinak. Kalkulatu ezagutzen ez ditugun erpinen koordenatuak.

Badakigu erronbo baten diagonalek elkar ebakitzen dutela erdigunean eta perpendikularrak direla. Egiaztatuko dugunez, puntu bat ere ez da beste bi puntuek zehazten duten zuzenkiaren erdigunea.

Erpinak ez dira aurrez aurrekoak, ondoz ondokoak baizik.

dezagun PQ , PR eta QR bektoreen artetik zer bektore-pare diren ortogonalak.

= (–6, –2,

EGIN ZUK

A (1, 2, 3), B (–2, 1, 0) eta C (a, a, 2), puntuak izanda, aurkitu zein izan behar den a-ren balioa AB eta AC bektoreak ortogonalak izateko. a-ren balio horretarako, puntuetako bat erronboaren zentroa da, eta beste biak, erpinak. Aurkitu erpin guztien koordenatuak.

4. Bi zuzenen posizio erlatiboak. Zuzenok hartzen dituen planoa

Honako zuzen hauek emanda:

r : xy z xz 6 3 –+= += )

s: x y z 1 1 6 1 2 –= + =

a) Aztertu bere posizio erlatiboa. Elkar ebakitzen badute, aurkitu ebaki-puntua.

b) Aurkitu barne hartzen dituen planoaren ekuazioa.

EGIN ZUK

Zuzen hauek izanda:

r : x y z 3 5 2 1 4 2 ––– + ==

s : xy z xy z 22 50 2110 –++ += ++ = *

a) Aztertu bere posizio erlatiboa.

b) Aurkitu zuzen horiek barne hartzen dituen planoa.

Q puntua erronboaren zentroa da. Beste bi erpinak dira R-ren eta P-ren simetrikoak Q-rekiko. A(x, y, z) eta B(x', y', z') esango diegu.

a) r eta s zuzenen posizioa jakiteko, aurrena, bi zuzenen norabide-bektoreak paraleloak diren ikusiko dugu:

= =+ = * → d( ,, ) 12 1 – r = s:

x y

→

0, beraz, r eta s zuzenek elkar ebakitzen dute. Ebaki-puntua lortzeko, r-ren eta s-ren ekuazio parametrikoak berdinduko ditugu:

=+

r

+=

Ebatzitako ariketak eta problemak

5. Bi zuzenen posizio erlatiboa parametro baten funtzioan

Aztertu, a-ren funtzioan, honako zuzen hauen posizio erlatiboa:

Problemaren analisia: Ebazteko bi prozedura erabil ditzakegu:

r : x y z

EGIN ZUK

Z [ \

] ] ]

=+ = =+

53 1 64 –m m m

s: ax yz xy z 32 12 25 6 ––+= +=

Aztertu honako zuzen hauen posizio erlatiboa m-ren balioen arabera:

r : x m y z 1 2 1 1 4 ––––==

s : x y z

=+ = = *

12 22 –2

m m m

1) d r , d s eta RS bektoreen koordenatuek eratzen duten matrizearen heina aztertzea a-ren balioaren arabera, R ∈ r eta S ∈ s izanik.

2) r zuzeneko puntu orokor baten koordenatuak s zuzenaren ekuazioetan ordezkatzea, eta aztertzea a-ren zer baliorekin duten zuzenek punturen bat komuna.

1) r zuzena R (5, 1, 6)-tik igarotzen da eta d r (3, –1, 4) norabide-bektorea du.

s zuzenaren norabide-bektorea hau da: d s = (a, 3, –2) × (2, 5, –1) = (7, a – 4, 5a – 6).

s-ko puntu bat bilatzeko, x = 0 egin eta ebatziko dugu:

x = 0 → yz yz 32 12 56 ––= = 4 y = 0, z = – 6 → S (0, 0, – 6) ∈ s → RS (–5, –1, –12)

Orain, M = ( d r , d s , RS ) = f aa 3 7 5

4 56 12 –

––––– p matrizearen heina aztertuko dugu.

1 4 1

| M | = –96 + 24a = 0 ⇔ a = 4. Beraz:

• a = 4 bada, hein (M ) = 2, bektoreak planokideak dira eta zuzenek elkar ebakitzen dute

• a ≠ 4 bada, hein (M ) = 3, zuzenek elkar gurutzatzen dute

2) s-ren ekuazioetan, x, y, z-ren lekuan r-ren parametrikoak jarriko ditugu:

() () () () () () a 53 31 26 412 25 35 16 46 mm m mm m ++ +=

2. ekuazioan, λ = 1 lortzen dugu.1. ekuazioan ordezkatuz, hau lortzen dugu: a = 4

• a = 4 bada, bi zuzenek puntu bat komuna dute. Puntu hori kalkulatzeko, r-ren parametrikoek λ = 1 denean zer balio duten jakin behar dugu. Puntu hori (8, 0, 10) da

• a ≠ 4 bada, zuzenek ez dute puntu bat ere berdina: elkar gurutzatzen dute

6. Hiru planoren posizio erlatiboak parametroen funtzioan

Honako plano hauek emanda:

α: x + y + z = m

β: x – y = 0

γ: 3x + y + nz = 0

Aztertu bere posizio erlatiboa m-ren eta n -ren funtzioan, eta adierazi zer kasutan zehazten duten prisma bat.

EGIN ZUK

Aztertu plano hauen posizio erlatiboa a-ren balioen arabera.

nan un prisma?

Hiru planoen ekuazioek eratzen duten sistema aztertuko dugu:

• n ≠ 2 bada, hein (A) = hein (A' ) = 3, eta, beraz, sistema bateragarri determinatua da m-ren balioa edozein dela ere. m-ren eta n ≠ 2 balio bakoitzerako, puntu batean elkar ebakitzen duten hiru plano desberdin lortuko ditugu.

• n = 2 bada, hein (A) = 2. Azter dezagun A'-ren heina.

• n = 2 eta m = 0 badira, hein (A) = hein (A' ) = 2, sistema bateragarri indeterminatua da. Infinitu soluzio ditu, planoek zuzen batean elkar ebakitzen dute.

• n = 2 eta m ≠ 0 badira, hein (A) = 2 eta hein (A' ) = 3, sistema bateraezina da. Hiru planoek ez dute punturik komunean. Ez dagoenez bat egiten duen planorik, ezta plano paralelorik ere, kasu honetan prisma bat zehazten dute.

7. Plano bat zehaztea

Idatzi α planoaren ekuazioa, jakinda r zuzena barne hartzen duela, eta π planoa ebakitzen duela OXY planoarekiko paraleloa den s zuzen batean.

Problemaren analisia:

1) α planoak r hartzen duenez, r-ko edozein puntu α-koa izango da. Gainera, r-ren norabide-bektorea α-rekiko paraleloa den bektore bat da.

2) α planoak s zuzena ere hartzen du; zuzen horren norabide-bektorea perpendikularra da OXY eta π planoen bektore normalekiko

1) r-ren puntu bat eta norabide-bektorea bilatuko ditugu : P (1, 3, 0) ∈ r d r (0, 0, 1)//α

2) d s perpendikularra da n π (1, 1, 1)-rekiko, eta ' n (0, 0, 1) bektorea z = 0 ekuazioa duen OXY planoaren bektore normala da.

Beraz, ' dn n s π # = = (1, 1, 1) × (0, 0, 1) = (1, –1, 0)//α

P puntuarekin eta d r eta d s bektoreekin, α planoaren ekuazioa idatziko dugu:

EGIN ZUK. Aurkitu plano baten ekuazioa, jakinda r :

zuzena barne hartzen

duela, eta π: 2x – y – z = 3 planoa y = 0 planoarekiko paraleloa den zuzen batean ebakitzen duela

8. Zuzenaren eta planoaren posizioa

a) Zehaztu zein izan behar diren a-ren eta b-ren balioak π: 2x + y + az = b planoak zuzen hau barne har dezan:

r : xy z xy z 1 20 ++ = += *

b) a-ren eta b-ren zer baliorekin da r zuzena π-rekiko paraleloa?

c) Zer baliorekin ebakitzen du r zuzenak π? Aurkitu ebaki-puntua a = 0 eta b = 7 kasuan.

EGIN ZUK

a) Aztertu zuzen honen

a) Baldintza betetzeko, planoaren bektore normala eta zuzenaren norabide bektorea perpendikularrak izan behar dira:

n = (2, 1, a) d = (1, 1, 1) × (–1, –2, 1) = (3, –2, –1)

n · d = 0 → 6 – 2 – a = 0 → a = 4

Beraz, a = 4 bada, zuzena paraleloa da edo planoan dago. a ≠ 4 bada, zuzenak planoa ebakitzen du.

r-ko edozein puntu π-koa izan behar da.

z = 0 egingo dugu puntu bat lortzeko:

P (2, –1, 0) ∈ r → P ∈ π → 2 · 2 + 1 (–1) + 4 · 0 = b → b = 3

b) r zuzena π-rekiko paraleloa izango da a = 4 eta b ≠ 3 badira (hau da, zuzeneko puntu bat planoan ez badago).

c) r zuzenak π ebakiko du a ≠ 4 bada eta b-k edozein balio hartzen badu

=+ = = *

12 –2

r : xt yt z

eta π: ax + 3y – z = 0 planoaren arteko posizio erlatiboak, a-ren balioen arabera

b) Aurkitu r-ren eta π-ren arteko ebaki-puntua a = 1 kasuan

Ebaki-puntua lortzeko, r parametrikoen bidez adieraziko dugu:

r : x y z

23 12 –

m m m

Q (2 + 3λ, –1 – 2λ, – λ)

= = * Bila gabiltzan puntua era honetakoa da:

Q ∈ π egingo dugu, a = 0 eta b = 7 izanik:

2(2 + 3λ) – 1 – 2λ = 7 → λ = 1

r zuzenaren ekuazioan ordezkatu eta Q(5, –3, –1) puntua lortuko dugu.

Ebatzitako ariketak eta problemak

9. Bi zuzen ebakitzen dituen zuzena

Aurkitu P(1, 0, –1) puntutik igaro eta r eta s ebakitzen dituen zuzena, bi zuzen horien ekuazioak hauek izanik:

Problemaren analisia:

A ebazpena. Bila gabiltzan zuzenari t esango diogu. r eta t zuzenek elkar ebakitzen badute, d r , d t eta RP (R ∈ r) bektoreak planokideak dira. Antzeko baldintza bete behar da s eta t zuzenek elkar ebakitzeko. Bi baldintza horiek kontuan izanda, norabide-bektore bat lor dezakegu: d t bektorea, t-rena. Bektore horrekin eta P puntuarekin, t-ren ekuazioa idatziko dugu. B ebazpena. t-ren ekuazioa lortzeko beste modu bat da bi planoren arteko ebaketa moduan hartzea: r zuzena eta P puntua hartzen dituen α planoa, eta s zuzena eta P puntua hartzen dituen β planoa. A ebazpena

• r-ren eta s-ren posizio erlatiboa aztertuko dugu. Horretarako, r parametrikoetan adieraziko dugu.

r: xy z xy z 32 10 24 0 ––++ = ++ = ( Ebatzita ⎯⎯→ x y z 55 97

s : x y z

EGIN ZUK

Aurkitu P (2, –1, 1) puntutik igarotzen den eta honako zuzen hauek ebakitzen dituen zuzena:

3 1

m m m

=+ = =+ * → S (3, 0, 1) ∈s d s (1, 1, 1)

hein ( d r , d s , RS ) = hein f 1 1 3

5 1 5

= = = * → R (0, –5, –9) ∈r d r (1, –5, –7)

m m m

d r(1, –5, –7), d s(1, 1, 1), RS = (3 – 0, 0 + 5, 1 + 9) = (3, 5, 10)

7 1 10 p = 3 → Bi zuzenek elkar gurutzatzen dute.

• Aurkitu P-tik igaro eta r eta s ebakitzen dituen t zuzena:

t-ren norabide-bektoreari d t (a, b, c) deituko diogu.

d t , d r eta RP (1, 5, 8) planokideak dira → ab c 1 1 5 5 7 8 = 0

d t , d s eta SP (–2, 0, –2) planokideak dira → ab c 1 2 1 0 1 2 = 0

→ ab c ac 32 0 0 –+= = 3 Sistema honen soluzio bat da a = 3, b = 1, c = 3. Beraz, t-ren norabide-bektore bat da (3, 1, 3).

B ebazpena

Z [ \

t-ren ekuazioak: x y z

] ] ]

=+ = =+

13 –13

m m m

t zuzena zehazten dute α planoak (r zuzena eta P puntua barne hartzen ditu) eta β planoak (s zuzena eta P puntua barne hartzen ditu).

t-ko puntu bat hartu eta X(x, y, z) esango diogu. Beraz, XP = (x – 1, y, z + 1).

α planoa: XP , d r eta RP bektoreek zehaztuta. Ekuazio hau du:

β planoa: XP , d s eta SP bektoreek zehaztuta.

hau dudu:

Hortik, t adieraziko dugu α eta β planoen ebaketa moduan. t:

1. Zuzenki bat hiru zati berdinetan zatitzen duten puntuak

Aurkitu AB zuzenkia hiru zati berdinetan zatitzen duten puntuen koordenatuak, A (5, –1, 6), B (– 4, 4, 6) direla jakinda

• Marraztu AB eta adierazi hiru zati berdinetan zatituko duten P eta Q puntuak P-ren koordenatuak lortzeko, kontuan izan OP OA AP =+ dela, O koordenatuen jatorria eta (/ ) AP AB 13 = izanik. Kalkulatu bektore horien koordenatuak eta egin eragiketak OP -ren koordenatuak lortu arte; hau da, P puntuaren koordenatuak.

• Q beste puntua PB zuzenkiaren erdiko puntua da.

Soluzioa: P (2, 2/3, 6), Q (–1, 7/3, 6)

r zuzena P (1, –1, 1) puntutik igarotzen bada eta horren norabide-bektorea (1, 2, –2) bada, badago r zuzena π: 2x + 3y + 4z = a planokoa egingo duen a-ren baliorik? Erantzuna baietz bada, aurkitu a-ren balio hori; eta ezetz bada, arrazoitu erantzuna

• P puntuarekin eta emandako bektorearekin, deskribatu r zuzenaren ekuazio parametrikoak. Zein dira r -ko puntu orokor baten koordenatuak ?

r zuzena π planoaren barruan egoteko, zuzeneko puntu guztiek bete behar dute plano horretako ekuazioa.

• Ordezkatu r-ko puntu orokorraren koordenatuak π planoaren ekuazioan eta egiaztatu a-ren balio jakin batekin ekuazioa betetzen duten infinitu puntu daudela

Soluzioa: a = 3 bada, r zuzeneko puntuek π planoaren ekuazioa betetzen dute

3. Zuzen bat ebaki, puntu batetik igaro eta plano baten barruan dagoen zuzena

Aurkitu A (1, –1, 0)-tik igarotzen den, π: x + y = 0 planoaren barruan dagoen eta s : x = y = z zuzena ebakitzen duen r zuzenaren ekuazioa

4. Bi zuzenen posizio erlatiboa

r zuzena P (1, –1, –2) puntutik igarotzen da eta π: ax + 2y + 3z + 6 = 0 planoarekiko perpendikularra da; eta s zuzena A (1, 0, 0) eta B (–1, –3, –4) puntuetatik igarotzen da.

a) Kalkulatu zein izan behar den a-ren balioa r eta s zuzenek elkar ebakitzeko

b) Aurkitu a horretarako ebaki-puntua.

c) Zein izango litzateke bi zuzenen posizioa a-k lortu dugun balio horren ordez beste bat hartuko balu?

• r -ko puntu bat ezagutzen dugu; r-ko beste puntu bat aterako dugu, hortik ekuazioa lortzeko. r zuzena π planoan dago eta s ebakitzen du; beraz, s zuzenak π ebakitzen du, r eta s zuzenek elkar ebakitzen duten puntu berean

• Idatzi s-ren ekuazio parametrikoak eta aurkitu s-ren eta π-ren arteko ebaki-puntua. Puntu horrekin eta A puntuarekin, lortu eskatutako zuzenaren ekuazioak

Soluzioa: r : x = –λ; y = λ; z = 0

a) Zuzenek elkar ebakitzeko, r-ren, s-ren eta AP bektorearen norabide-bektoreak planokideak izan behar dira. r-ren norabide-bektorea π planoaren bektore normala da, eta a-ren mendekoa da. Aurkitu zein izan behar den a-ren balioa hein (, ,) AP ddrs < 3 izateko

b) Idatzi r eta s zuzenen ekuazio parametrikoak, bi parametroak adierazteko letra desberdina erabiliz Ebatzi r eta s zuzenen ekuazioek osatutako sistema, eta egiaztatu r-ko eta s-ko puntu bera lortzen duzula kalkulatutako parametroen balioetarako.

c) Egiaztatu d r eta d s bektoreak paraleloak izan daitezkeen a-ren balioren batekin.

Soluzioa: a) a = 1 b) Q (3, 3, 4) c) r-k eta s-k elkar gurutzatzen dute a ≠ 1 bada.

A (1, 1, 1), B (1, 0, 0) eta C (0, 2, 1) puntuak ditugu. r zuzena A eta B puntuetatik igarotzen da, eta π planoa C-tik igaro eta r-rekiko perpendikularra da. Aurkitu r-ren eta π-ren arteko ebaki-puntua.

• Idatzi A eta B puntuetatik igarotzen den zuzenaren ekuazio parametrikoak π planoak r-rekiko perpendikular izan behar duenez, r-ren AB norabide-bektorea planoaren bektore normala da. Beraz, π planoko a, b eta c koefizienteak dakizkigu.

• d gai independentea lortzeko, kontuan izan C puntuak π planoaren ekuazioa bete behar duela. Kalkulatu r-ren eta π-ren arteko ebaki-puntua, π-ren ekuazioan r-ren parametrikoak ordezkatuz

Soluzioa: P (1, 3/2, 3/2)

2. Plano baten barruko zuzena

5. Zuzen eta plano baten ebaketa

Proposatutako ariketak eta problemak

Trebatzeko

Puntuak eta bektoreak

1 A(1, 3, –1), B(2, 0, 2) eta C(4, –1, –3) puntuak paralelogramo baten ondoz ondoko erpinak dira. Aurkitu D laugarren erpina eta paralelogramoaren zentroa.

2 Aurkitu A(–2, 3, 0) puntuak M(1, –1, 2) puntuarekiko duen simetrikoa.

3 Kalkulatu a, b eta c-ren balioak, A(a, 0, b) eta B(3, c, 1) puntuak simetrikoak izan daitezen M(3, –2, 1)-rekiko.

4 a) A(2, 1, –1), B(−1 , 4 , −7) eta C(4 , −1, 3) puntuak emanda, aztertu lerrokatuta dauden.

b) Lerrokatuta badaude, aztertu D(1, 2, −2) puntua lerrokatuta dagoen A, B eta C-rekin.

5 Kalkulatu zein izan behar diren a-ren eta b-ren balioak

A(1, 2, –1), B(3, 0, –2) eta C(4, a, b) puntuak lerrokatuta egoteko

6 AB zuzenkia emanda, eta A (–2, 1, 0) eta B (1, 3, –2) direla jakinda, aurkitu AP AB 3 1 = eta AQ AB 3 2 = beteko duten P eta Q puntuak

7 Aurkitu P eta Q puntuak, AQ = AB 5 3 eta AP AQ 3 2 = betetzen direla eta A(2, 0, 1) eta B(7, 5, –4) direla jakinda.

Zuzenak

8 Idatzi honako zuzen hauen ekuazio parametrikoak eta inplizituak:

a) A (–3, 2, 1) eta B (–5/2, 3/2, 0) puntuetatik igarotzen da.

b) A (0, 1, –1) puntutik igarotzen da eta B (1, 1, –1) eta C (2, 0, 1) puntutik igarotzen den zuzenarekiko paraleloa da.

9 Idatzi A (1, 0, 1), B (–2, 0, 1) eta C (0, 3, 1) erpinak dituen triangeluko aldeen ekuazio inplizituak.

10 Aztertu P(3, 1, 0), Q(0, –5, 1) eta R(6, –5, 1) puntuetatik igarotzen den zuzenik existitzen den.

11 Idatzi koordenatu-ardatzen ekuazio parametrikoak eta ekuazio inplizituak.

12 Idatzi A(–4, 2, 5) puntutik igarotzen den eta Z ardatzarekiko paraleloa den zuzenaren ekuazioak.

13 Idatzi P(1, –3, 0) puntutik igarotzen den eta uv # bektorearekiko paraleloa den zuzenaren ekuazioak, u (1, –1, 2) eta v (2, 0, 0) direla jakinda.

14 Aurkitu honako zuzen hauen ekuazio parametrikoak:

r : xy z xy z 23 0 20 += += ( s : xy z yz 23 0 32 10 –+= += (

15 Idatzi r zuzenaren ekuazioa bi planoren ebaketa moduan, jakinik r igarotzen dela P(1, 0, −2) puntutik eta paraleloa dela zuzen honekiko s: z == x y 21 1 –+ .

16 Aurkitu r´ eta s´ zuzenen ekuazio parametrikoak, jakinda A(−2, 0, 1) puntutik igarotzen direla eta, hurrenez hurren, r eta s zuzenekiko paraleloak direla.

r : xy z xy z 23 0 20 += += ( s : xy z yz 23 0 32 10 –+= += (

17 Aztertu honako zuzen hauen posizio erlatiboa eta aurkitu ebaki-puntua, egin ahal den kasuetan:

18 Kalkulatu zein izan behar den a-ren balioa r eta s zuzenek elkar ebakitzeko:

zein den r eta s zuzenen ebaki-puntua, kalkulatu duzun a-ren baliorako.

=+ =+ = *

s :

x

n

Planoak

22 Idatzi honako plano hauetako bakoitzaren ekuazio inplizitua:

a) A(1, –3, 2) puntuak eta u (2, 1, 0) eta v (–1, 0, 3) bektoreek zehazten dute.

b) P(2, –3, 1) puntutik igarotzen da eta bektore normala n (5, –3, –4) du.

c) x y z 21 1 3

= + = zuzenarekiko perpendikularra da eta (1, 0, 1) puntutik igarotzen da.

23 Idatzi plano hauen ekuazio parametrikoak:

a) z = 3 b) x = –1 c) y = 2

24 Zein da x = –1 planoaren bektore normala? Idatzi plano horrekiko perpendikularra den zuzen baten ekuazioak, jakinda A(2, 3, 0) puntutik igarotzen dela.

25 Kalkulatu m-ren eta n-ren zer baliorekin izango diren paraleloak honako plano hauek:

α: mx + y – 3z – 1 = 0 β: 2x + ny – z – 3 = 0

Etor al daitezke bat α eta β?

26 A (0, 1, –2), B (1, 2, 0), C (0, 0, 1) eta D (1, 0, m ) puntuak ditugu.

Kalkulatu zein izan behar den m-ren balioa lau puntuak planokideak izateko.

27 Idatzi A(1, 2, 0), B(0, 1, 2), C(2, −1, 3) eta D(1, 0, 1) puntuetatik igarotzen den zuzenarekiko paraleloa den zuzena barne hartzen duen planoaren ekuazioa.

28 Idatzi π planoaren ekuazio parametrikoak, jakinda

A(−1, 5, 0) eta B(0, 1, 1) puntuetatik igarotzen dela eta zuzen honekiko paraleloa dela:

r : xy yz 32 30 23 10 –+= = (

29 Plano hauek izanda:

π: mx + 2y – 3z – 1 = 0 eta π': 2x – 4y + 6z + 5 = 0 esan m-ren zer baliorekin izango diren planoak:

a) Paraleloak. b) Perpendikularrak.

30 Aurkitu r : xy xy 26 0 32 40 ––+= += ( zuzenarekiko perpendikularra den eta P (1, – 4, 2) puntutik igarotzen den planoaren ekuazioa.

31 Egiaztatu x y z 2 3 3 2 ––== zuzenak x – 2y + z = 1 planoa ebakitzen duela, eta aurkitu ebaki-puntua.

32 Zuzen hauek ditugu:

r : x yz 2 1 2 –– == s : x xy z 2 25 11 ––= = *

a) Egiaztatu r eta s paraleloak direla.

b) Aurkitu r eta s barne hartzen dituen planoaren ekuazio inplizitua.

33 Aurkitu zuzen batek eta puntu batek zehazturiko planoaren ekuazioa, honako kasu hauetan:

a) P(2, 1, 2) eta r: x – 2 = y z 13 3 4 ––––=

b) A(1, 0, 1) eta r : xy z xy z 10 22 0 22 1 ––++ = += + (

34 Aztertu kasu hauetako bakoitzean ageri diren hiru planoen posizio erlatiboak:

a) π1: x + 2y – z – 3 = 0 b) π1: 2x – y + z – 3 = 0 π2: 3y + 2z – 1 = 0 π2: x – y + z – 2 = 0 π3: x + y + z – 2 = 0 π3: 3x – y + z – 4 = 0

c) π1: x – y + z – 1 = 0 d) π1: x + y – 2z = 0 π2: 3x + y – 2z = 0 π2: –x + y + z + 1 = 0 π3: 2x + 2y – 3z + 4 = 0

3: 2x – z + 2 = 0

35 Aztertu s zuzenaren eta π planoaren posizio erlatiboak honako kasu hauetan:

a) s: x y z 0 1

= = =+ * π: 2x – y + 3z = 6 b) s: x y 3 2 = = * π: z = 1

0– m m

36 Idatzi xt yt zt

1 –12 =+ =+ = * zuzena hartzen duen eta 2x + y – z – 2 = 0

planoarekiko perpendikularra den planoaren ekuazioa

37 Idatzi r zuzena barne hartzen duen eta s zuzenarekiko paraleloa den planoaren ekuazioa.

s : xy z xy z 0 20 –= += ( r : x 2 1 –= y = 2 – z

38 2x + ay + z = 2 planoa eta r(x, y, z) = (0, 0, 0) + λ(2, 1, 1) zuzena ditugu.

a) Zehaztu zein izan behar den a parametroa, zuzena perpendikularra izateko planoarekiko.

b) Aurkitu zein izan behar den a-ren balioa, zuzena paraleloa izateko planoarekiko.

39 x − y + 3 = 0 eta 2x + y − z = 0 planoak izanda, aurkitu bi planoekiko paraleloa den eta P(2, 2, 3) puntutik igarotzen den zuzenaren ekuazioa.

40 π: 2x – 3y + z = 0 planoa eta r : x y z 1 1 1 2 2 1 –––== +

zuzena ditugu Idatzi r zuzena barne hartzen duen eta π

planoarekiko perpendikularra den planoaren ekuazioa

Proposatutako ariketak eta problemak

Ebazteko

41 Beheko ekuazioak dituzten r eta s zuzenak ditugu:

r : x – 1 = y = 1 – z eta s : xy xz 24 2 –= = + '

a) Aurkitu zuzenen arteko ebaki-puntua.

b) Zehaztu r eta s barne hartzen dituen planoaren ekuazioa.

42 π: x + z = 4 planoa eta P (1, 1, 0) puntua izanda, lortu:

a) P barne hartzen duen eta π planoarekiko paraleloa den planoaren ekuazioa.

b) P puntutik igarotzen den eta π planoarekiko perpendikularra den r zuzenaren ekuazio parametrikoak.

Zein da r zuzenaren eta lortutako planoaren posizio erlatiboa?

43 Kalkulatu zein izan behar den m-ren balioa honako plano hauek binaka elkar ebaki dezaten:

α: x – 3y – 2z – 2 = 0

β: –2x + y – z – 3 = 0

π: 5x + 5z = m

44 α: 2x + ay + 4z + 25 = 0 planoa

emanda, kalkulatu a-ren zer baliorekin egongo den zuzena planoaren barruan.

45 Idatzi P (1, 1, 1) puntutik igaro eta honako zuzenak ebakiko dituen zuzenaren ekuazio jarraitua:

r : xy z xy z 1 22 0 ++ = ++ =

y z 21 2 1 1 –== +

46 Kalkulatu zein izan behar den b-ren balioa r eta s zuzenek elkar ebakitzeko. Lortu ebaki-puntua eta barne hartzen dituen planoaren ekuazioa:

r : x y z 2 1 3 5 2 1 ––= + = + s : x yb z 4 12 1 –––==

47 A(1, 1, 1), B(1, −1, −1) puntuak izanik, kalkulatu:

a) π planoaren ekuazioa, jakinda A eta B plano horrekiko simetrikoak direla.

b) C eta D puntuak, jakinda AB zuzenkia hiru zati berdinetan zatitzen dutela.

48 Zuzen hauek izanda,

r : y xz x y 2 213 2 = += ( s : xy xz z y 24 3 2 ––+= = + (

eta A(0, 0, 3) puntua, aurkitu A-tik igaro eta r eta s zuzenekiko paraleloa den planoaren ekuazio orokorra.

49 A(1, 1, 1) eta B(3, 1, 2) puntuek zehazten duten r zuzena eta beste zuzen hau izanda:

s : xz y 21 0 20 –= =

aztertu horien posizio erlatiboak eta idatzi biak hartzen dituen planoaren ekuazioa, baldin eta planorik badago

50 Aurkitu A(1, 3, 2) eta B(–2, 5, 0) puntuetatik igarotzen den planoaren ekuazioa, jakinda zuzen honekiko paraleloa dela:

x y z

= =+ =

3 2 23

– m m m

51 A (2, 1, –1), B (1, 0, 1) eta C (0, 1, –3) paralelogramo baten ondoz ondoko hiru erpin dira.

a) Aurkitu D laugarren erpina.

b) Zehaztu paralelogramoaren zentrotik igarotzen den eta zentroa barne hartzen duen planoarekiko perpendikularra den zuzenaren ekuazioa.

52 r : x y z 1 2 1 31 –== + zuzena, P(3, 1, −1) puntua eta

π: 2x + y – z = 0 planoa ditugu. Aurkitu P eta Q puntuetatik igarotzen den zuzenaren ekuazio parametrikoak, jakinik Q puntua dela r zuzenaren eta P barne hartzen duen π-rekiko plano paraleloaren arteko ebaki-puntua.

53 r : m x z y 1 2 1 4 1 –––== eta π: x + y + kz = 0 planoak izanda, aurkitu m eta k, hau bete dadin:

a) r zuzena π planoarekiko perpendikularra izatea.

b) r zuzena π planoan egotea.

54 A(2, −1, 1) eta B(−2, 3, 1) puntuak izanda:

a) Idatzi A eta B puntuetatik igarotzen den r zuzenaren ekuazio parametrikoak.

b) Zehaztu s zuzenaren ekuazioa, jakinda r-rekiko perpendikularra dela eta P(−4, 17, 0) puntutik igarotzen dela.

c) Aurkitu A eta B simetriko egiten dituen planoaren ekuazioa.

55 Aurkitu P(0, −2 , 1) puntutik igaro eta honako zuzenak ebakitzen dituen zuzenaren ekuazio jarraitua:

r : xy z xy z 2 2 2 –1 += = ( s : x y z 2 1 1 4 3 1 + = + = +

56 Plano hauek ditugu:

π1: x + y = 1 π2: my + z = 0

π3: x + (m + 1)y + mz = m + 1

a) Zein izan behar da m-ren balioa, puntu komunik izan ez dezaten?

b) Zehaztu zein den planoen posizio erlatiboa m = 0 denean.

57 r : xy z xz 30 23 0 ––+= += ) zuzena eta ax – y + 4z – 2 = 0 ekua-

zioa dituen planoa ditugu.

a) Kalkulatu a-ren balioa r zuzena planoarekiko paraleloa izateko.

b) Ba al dago r zuzena planoarekiko perpendikular egingo duen a-ren baliorik?

58 Honako zuzen eta plano hauek ditugu:

r : xz yz 23 0 40 – += = * π: x + 2y + 3z – 1 = 0

Aurkitu π planoko P (2, 1, –1) puntutik igarotzen den eta r-rekiko perpendikularra den s zuzenaren ekuazioa.

59 a) Aztertu honako zuzen eta plano hauen posizio erlatiboa:

r : x y 3 2 = = * π: z = 1

b) Aurkitu r-rekiko perpendikularra den eta r-ren eta π-ren arteko ebaki-puntutik igarotzen den zuzen baten ekuazioa, baldin eta existitzen bada.

60 a) Zuzen hau dugu: r : xy xz 25 0 20 –= += )

Idatzi r zuzena barnean hartzen duen eta koordenatuen jatorritik igarotzen den π planoaren ekuazioa.

b) Aurkitu P (1, 1, 1) puntutik igarotzen den eta π-rekiko perpendikularra den zuzenaren ekuazioa.

61 Idatzi A (1, –3, 2) eta B (0, 1, 1) puntuetatik igarotzen den planoaren ekuazioa, jakinda zuzen honekiko paraleloa dela: r : xy yz 32 10 23 30

62 A eta B puntuen koordenatuak A (3, 4, 1 + 2a) eta

B (–3, a, 0) dira. Kalkulatu A-tik eta B-tik igarotzen den zuzenaren ekuazio parametrikoak. Ba al dago a-ren baliorik zuzen horrek R (9, 4, 6) puntua barne hartzeko?

63 r : x y z 2 1 2 3 ––

== zuzena eta (2, −5, 1) puntutik igaro eta (−1, 0, −1) norabidea duen s zuzena izanda:

a) Aztertu r eta s zuzenen posizio erlatiboa.

b) Idatzi r-rekiko paraleloa izan eta s barne hartzen duen plano baten ekuazioa.

c) Idatzi r-rekiko perpendikularra izan eta koordenatuen jatorritik igarotzen den plano baten ekuazioa.

64 Aurkitu A (1, 1, 1) puntutik igaro, π: x – y + z – 3 = 0 planoarekiko paraleloa izan eta s : x y 1 3 = = * ebakitzen duen zuzenaren ekuazioa.

65 Aztertu α: mx – y + 2 = 0 eta β: 2x + 3y = 0 planoen posizio erlatiboa, m parametroaren arabera.

66 Kalkulatu P(1, 2, 3) puntuak π: −x + z = 0 planoarekiko duen puntu simetrikoa.

67 r : xy xz 30 23 0 ––+= += ) eta s : x = y + 1 = z 2 2 – zuzenak ditugu.

a) Aurkitu r eta s barne hartzen dituen planoaren ekuazioa.

b) Lortu P(0, −1, 2) puntutik igaro eta r perpendikular ebakitzen duen zuzena.

c) Zehaztu zer balio izan behar duten a eta b parametroek s zuzena plano honetan egoteko: π: x – 2y + az = b

68 α: x + y + z = 0 eta β planoak ditugu. Bere ebaketa

r : x xz y yz 0 0 ++ = += + * zuzena da.

Aurkitu β planoaren ekuazioa, jakinik A(1, 1, 1) ∈ β

69 a) Egiaztatu zuzen hauek:

ez dutela elkar ebakitzen eta ez direla paraleloak.

b) Aurkitu r barne hartzen duen eta s-rekiko paraleloa den α planoaren ekuazioa, baita s barne hartu eta r-rekiko paraleloa den β planoarena ere. Nolakoak dira elkarrekiko α eta β?

70 r eta s adierazpen hauen bidez definituriko zuzenak dira:

r : mx = y – 1 = z + 3 eta s : x y z 2 1 2 3 ––+ ==

a) Aurkitu zein izan behar den m parametroaren balioa r eta s perpendikularrak izateko.

b) Arrazoitu m-ren zer baliorekin izango diren r eta s paraleloak.

71 P (1, –2, 1) puntua, π: 2x – 4y + z = 15 planoa eta

r : x y z 2 1 1 2 –=+ = zuzena izanda:

a) Aurkitu P puntutik igarotzen den eta r barne hartzen duen planoaren ekuazioa.

b) Aurkitu P-tik igaro, π-rekiko paraleloa izan eta r ebakitzen duen zuzenaren ekuazioak.

72 π: ax + y + z = a eta π': x – ay + az = –1 planoak izanda, egiaztatu zuzen batean ebakitzen dutela elkar, a parametroak edozein balio hartzen duela ere. Lortu zuzen horren norabide-bektorea parametro horren funtzioan.

Proposatutako ariketak eta problemak

73 u = (2, 3, 5), v = (6, –3, 2), w = (4, –6, 3), p = (8, 0, a) bektoreak eta plano hauek izanda:

π: (x, y, z) = (1, 2, 3) + λ u + μ v

π': (x, y, z) = (1, 2, 3) + λ w + μ p aztertu π eta π' planoen posizio erlatiboa, a-ren balioen arabera.

74 Aurkitu P (2, 0, –1) puntutik igarotzen den r zuzenaren ekuazioak, jakinda beste zuzen hauek ebakitzen dituela:

s1: x y z 2 2 1 2 1 1 –––== + s2: xy yz 40 33 0 –++ = += *

75 Aztertu planoaren eta honako zuzen hauen arteko posizio erlatiboak, a-ren balioen arabera:

π: x + ay – z = 1 r : xy az xy za 22 1 ––+= = *

76 Zuzen hauek ditugu:

r : xy ax z 36 0 33 0 ––+= += ) s : xaya yz 21 4 24 0 = = *

a) a-ren zer baliorekin egongo dira zuzen horiek plano baten barruan? Edo ez dago hori betetzen duen parametrorik? Hori betetzen duen parametroa badago, idatzi plano horren ekuazioa.

b) a-ren zer baliorekin izango dira zuzenak paraleloak? Eta a-ren zer baliorekin elkar gurutzatuko dute?

Galdera teorikoak

77 Zuzena ala okerra? Arrazoitu erantzunak.

a) x + 14y + 11z + 12 = 0 planoa x y z 5 3 2 1 3 ––= + = zuzenarekiko paraleloa da.

b) Aurreko ataleko planoak barnean hartzen du zuzen hau: x y z 3 2 1 1 1 ––– = + =

c) Bi plano ebakitzailek zehazten duten zuzenaren norabide-bektorea bi plano horien bektore normalekiko paraleloa da.

d) r eta s zuzenek elkar gurutzatzen badute, puntu jakin batetik igaro eta r eta s ebakitzen dituen zuzen bat existitzen da.

e) Zuzen baten norabide-bektorea plano baten bektore normalarekiko perpendikularra ez bada, zuzenak eta planoak elkar ebakitzen dute.

f ) α eta β planoak paraleloak badira eta π planoak ebaki egiten baditu, orduan hiru planoek eratzen duten ekuazio-sistema bateragarri indeterminatua da.

78 a) Azaldu nola lortzen diren plano baten ekuazio parametrikoak ekuazio inplizitutik abiatuz. Azaldu

planoa erabiliz.

b) Zer egin behar da ekuazioan ez bada ezezagunetako bat ageri? Azaldu π': 2x – z + 8 = 0 planoa erabiliz.

79 r zuzena eta bertako P puntu bat izanda, puntu horretan r-rekiko perpendikularrak diren zenbat zuzen marraztu litezke?

80 π plano bat eta bertako Q puntu bat ditugu. Plano barruan dauden eta puntu horretatik igarotzen diren zenbat zuzen marraztu litezke? Eta Q-tik igarotzen diren π-rekiko zenbat zuzen perpendikular?

81 Zein dira zuzen honen ekuazio inplizituak?: x y z 0 4 0 3 2 1 – –= + =

Lortu liteke zuzen horren ekuazio jarraitua bere ekuazio inplizituetatik abiatuta?

82 π1 eta π2 bi plano paralelo dira; eta r1 eta r2, hurrenez hurren, π1 eta π2 planoen barruan dauden bi zuzen. Ziurta dezakegu r1 eta r2 paraleloak direla?

83 A (x1, y1, z1) eta B (x2, y2, z2) puntuak ax + by + cz + d = 0 planokoak dira. Frogatu analitikoki AB bektorea n (a, b, c) bektorearekiko perpendikularra dela.

84 Zer baldintza bete behar dute hiru puntuk plano bat zehazteko? Arrazoitu A (1, 2, 3), B (2, 3, 4) eta C (5, 6, 7) puntuak barne hartzen dituzten infinitu plano daudela.

85 Zuzen eta plano hauek ditugu:

r : '' '' ax by cz d ax by cz d 0 0 ++ += += ++ * π: a''x + b''y + c''z + d'' = 0

a) Zer esanahi geometriko du zuzenaren eta planoaren ekuazioak elkartuz lortzen den sistema bateragarria dela esateak?

b) Eta sistema bateragarri indeterminatua dela esateak?

86 Deskribatu eta adierazi honako irudi hauetako bakoitza:

a) y = 3 b) x z 0 0 = = ) c) x = y = z

d) x y z

= = = * e) x y z 0

0 3 m

m n = = = * f ) x y z

= = = *

0 3 0

g) xt yt z

=+ =+ = * zuzena 2x – y + mz = 3 ekuazioa duen planoaren barruan dago, m-ren balioa edozein dela ere.

12 2 0

87 a) Egiaztatu ardatzak A (a, 0, 0), B (0, b, 0) eta C (0, 0, c) puntuetan ebakitzen dituen planoaren ekuazioa a x b y c z 1 ++ = eran idatz daitekeela, a, b eta c nuluak ez badira.

b) Erabili esamolde hori 14x + 35y + 10z = 70 planoak ardatzekin dituen ebaki-puntuak aurkitzeko.

Sakontzeko

88 Esan zer baldintza bete behar duten a, b, c eta d parametroek π: ax + by + cz + d = 0 planoa izan dadin:

a) XY planoarekiko paralelo.

b) XY planoarekiko perpendikular.

c) Z ardatzarekiko paralelo.

d) X ardatzarekiko perpendikular.

1 2 –3 *

=+ =+ =+

zuzena izan dadin:

a) XZ planoarekiko paraleloa.

b) XY planoarekiko perpendikularra.

c) X ardatzarekiko paraleloa.

r1: x yz 1 = = * r2: x yz 2 2 = =

* r

91 (1 + 2k)x + (1 – k)y + (1 + 3k)z + 2k – 1 = 0 ekuazioak plano multzo bat adierazten du. k-ren balio bakoitzerako plano bat lortuko dugu. Frogatu denek hartzen dutela barnean r zuzen bera, eta aurkitu horren ekuazio parametrikoak.

92 Plano-sorta

r : : : xy z xy z 23 40 21 0 –r v += ++ = * zuzena da π eta σ planoen

ebaketa. r barne hartzen duten plano guztien multzoari r ertzeko plano-sorta esaten zaio, eta adierazpen analitiko

hau du: a(2x + 3y – z – 4) + b(x – 2y + z + 1) = 0 r

a eta b parametroen balio-bikote bakoitzerako (a = 0 eta

b = 0 kasuan izan ezik), sortako plano bat lortzen da.

a) Aurkitu (0, 0)-tik pasatzen denaren planoa.

b) k-ren zer baliorekin da sortako plano bat perpendikularra t : x y k z 35 2 –== zuzenarekiko? Zein da plano hori?

c) Aurkitu aurreko sorta horretako plano guztietakoak diren bi puntu.

d) Idatzi ertz moduan s : x y z 3 5 2 1 1 3 –––= + = zuzena duen plano-sortaren adierazpena

e) Sorta honen planoetatik zein dago (0, 0) baino urrunago?

AUTOEBALUAZIOA ➜ anayaharitza.es

1 P (1, 2, 3) eta Q (1, –1, 3) puntuetatik igarotzen den r zuzena eta A (1, 0, 1), B (2, –1, 3) eta C (4, 1, 0) puntuak barne hartzen dituen planoa ditugu.

a) Aurkitu zuzenaren eta planoaren ekuazio inplizituak eta aztertu haien posizio erlatiboa.

b) Kalkulatu, ahal bada, haien ebakidura-puntua.

2 A(1, –1, 1) eta B(2, 2, 2) puntuak izanda, aurkitu A eta B puntuak simetriko egiten dituen planoaren ekuazioa.

3 Idatzi r : x y z

=+ =

23 1 m m m

=

Ariketa hauen ebazpena.

r : x y z 7 17 0 1 2 8 –––== s : x y zk 15 4 2 19 m m m =+ = =+ Z [ \ ] ] ]

α

: 2x + y + z – 1 = 0 β: x + y – z – m = 0 γ: x + mz

–

4 Zehaztu A (1, 1, 1)-tik igaro, π: x – y + z – 3 = 0 planoarekiko paralelo izan eta s : x y 1 3 = = * ebakitzen duen zuzena.

r1: x y z 1 5 22 m m = =+ =+ * r2: x y z 7 15 3 7 ––m m = =+ = Z [ \ ] ] ]

r

Problema metrikoak 7

Geometria metrikoa

Aurreko unitatean, zuzenen eta planoen ekuazio motez gain, paralelotasunari, ebaketari eta intzidentziari buruzko problemak ikusi ditugu (puntu hau zuzen horretan dago?, zuzen hau plano horretakoa da?). Horiek guztiak —paralelotasuna, ebaketa eta intzidentzia— propietate afinak dira. Neurrien arteko erlazioak (angeluak, distantziak, azalerak, bolumenak) propietate metrikoak dira.

Geometria metrikoaren garapenean, Mongeren eta horren ikasleen ekarpenez gain, lorpen aipagarrienak hauek dira: puntu batetik plano batera dagoen distantzia kalkulatzeko formula (Lagrange) eta paralelepipedo baten bolumenarena (Cauchy).

Pedro Puig Adam (1900-1960) matematikari espainiar handi eta didakta apartak arlo honetan klasikoa den lana idatzi zuen: Geometria Metrikoa

Geometria modernoagoak

Geometriaren oraintsuko bilakaerak hainbat bidetatik egin du aurrera:

• xix. mendearen amaieran, geometria analitiko klasikoaren barruan, eboluzio bide berriak garatu ziren, eta, adibidez, hortik sortu zen adarretako bat geometria aljebraikoa da, gaur egun zenbakien teoriari dagokionez oso inplikazio garrantzitsuak dituen geometria mota.

• Geometria diferentziala ere analisia eta geometria uztartuta sortu zen. Geometria mota honen aplikazioak fisikaren arloarekin lotuta daude, batez ere erlatibitatearen teoriarekin.

• Geometriaren beste modu bat topologia da. Hasieran, zenbait aldaketa ezarri eta apurtu ez, baina plastilinazkoak balira bezala itxuraz aldatzen ziren irudien propietateak landu zituen geometria mota honek. Adibidez, zirkunferentzia bat eta triangelu bat topologikoki berdinak dira, bata bestea bihur dezakegulako hautsi edo itsatsi gabe. Baina zirkunferentzia bat eta zuzenki bat ez dira berdinak, tipologikoki, itsatsi edo zatitu egin beharko liratekeelako bata bestea bihurtzeko.

Pedro Puig Adam (1900-1960)

Gaspard Monge, geometria deskriptiboaren aita

Matematika ez da, inolaz ere, askok uste bezain zientzia aseptikoa, hotza eta munduko zereginetatik hain urrunekoa. Batzuetan gerra bezalako gai gorrotagarriekin zuzenean lotuta egoten da. Hori izan zen, hain zuen, 17 urteko gazte baten aurkikuntza geometriko garrantzitsuen kasua, nahiz eta Frantziako Estatuak 30 urte baino gehiagoz isilpean gorde zuen.

Gaspard Mongek (1746-1818) hiri baten eskala handiko mapa bat egin zuen 1762ko bere oporraldian. Horretarako, behaketa-metodo eta -tresna originalak diseinatu zituen, eta egindako lan horri esker, delineatzaile gisa sartu zen Mézièresko Eskola Militarrean. Han zegoela, gotorleku bateko kanoientzako kokaleku onena aurkitzeko zeregina agindu zioten, baina esku artean oso datu gutxi zituela. Mongek kalkulu-metodo astunak erabili beharrean (orduan erabiltzen zirenak), huts-hutsean geometrikoak ziren prozedurak erabili zituen. Eta hain azkar ebatzi zuen problema, ezen komandanteak baztertu egin zuen, «harropuzkeria» bat zela pentsatuz. Baina handik gutxira, metodo berri horien balioaz ohartu ziren, eta 1795era arte sekretu militarra izan ziren. Ordura arte egon zen Monge metodohoriek Parisko Eskola Politeknikoan irakasteko baimenik gabe. Gaur egun geometria deskriptiboa deritzoguna garatu zuen, irudi tridimentsionalak bi dimentsioko azalera batean irudikatzeko aukera ematen duen geometria. Antolatzaile trebea ere izan zen, eta Itsas Armadako ministro izatera iritsi zen. Napoleonen lagun mina izan zen, eta harekin batera igo zen boterera. Egiptora ere lagundu zuen Napoleon, baita Fourier ere, kultur espedizio ospetsuan. Erori ere Napoleonekin batera erori zen 1814an, eta 1818an hil zen Parisen.

EBATZI

Distantziak kalkulatu

1. Gogoratu nola lortzen den ortoedro baten diagonala ortoedroaren neurrietatik abiatuta, eta kalkulatu A (4, –2, –7) eta B (7, 2, 5) puntuen arteko distantzia

2. Kalkulatu P (8, 6, 12) puntutik r zuzenera dagoen distantzia. Lortu, lehenengo, puntu horretatik igaro eta zuzenarekiko perpendikularra izango den planoaren ekuazioa.

2 1 72 – m m *

= = =+

3. P (4, 35, 70) puntutik π planora dagoen distantzia lortzeko, lehenengo aurkitu P-tik igarotzen den eta π planoarekiko perpendikularra den zuzen baten ekuazioak

π: 5y + 12z – 1 = 0

A P P r B r X Y Z

Zuzen eta planoen arteko angeluen neurria

Zuzenen arteko, planoen arteko eta zuzenen eta planoen arteko angeluak aztertzeko, elementu bakoitzaren norabidea bereiziko duen bektore bat behar dugu. Zuzenaren kasuan, norabide-bektoreak du zeregin hori, jakina; planoaren kasuan, bektore normalak.

n d

r r

n d r r

→ d bektoreak zuzenaren norabidea zehazten du

→ n bektoreak planoaren norabidea zehazten du, π-rekiko perpendikularra den norabide bakarra dago eta

Angeluak neurtzeko, formula hau erabiliko dugu:

cos α = | | • || | | u u v v

Eta hortik, u eta v bektoreek edo u eta – v bektoreek eratzen duten angelurik txikiena lor dezakegu.

Bi zuzenen arteko angelua

r eta r' bi zuzenen arteko α angelua zuzen horien d eta d ' norabide-bektoreek eratzen duten angelua da. Adierazpen honen bidez lortzen da:

cos α = || |'| |'| dd dd •

Bi planoren arteko angelua

π eta π ' bi planok eraturiko α angelua horien n eta ' n bektore normalek eratzen duten angelua da:

' n n • n n

cos α = || || || '

Zuzen baten eta plano baten arteko angelua

Zuzen baten eta plano baten arteko angelua zuzenak planoaren gaineko bere proiekzioarekin eratzen duen angelua da; hau da, zuzenak planoaren norabide normalarekin eratzen duen angeluaren osagarria

Zuzenaren norabide-bektorea d bada eta planoarekiko bektore normala n bada, r eta π arteko α angelua honela lortuko dugu:

cos (90° – α) = sin α = || || || n n • d d

Ebatzitako ariketak

1 Aurkitu honako zuzen hauek eratzen duten angelua:

r-ren norabide-bektorea d (5, 3, –1) da.

s zuzenaren norabide-bektorea da zuzen hori zehazten duten planoen bektore normalen arteko biderketa bektoriala:

d ' = (2, 3, –5) × (1, –2, 0) = (–10, –5, –7) Beraz,

2 Aurkitu honako plano hauen arteko angelua:

π: x – 2y + 4z = 0

π': 2x – y + 3 = 0

3 Esan zer angelu eratzen duten zuzen honek

r : x y z 2 3 5 1 1 1 –––= + =

eta plano honek

π: 2x – 5y + 7z – 11 = 0 ?

Bektore normalak n (1, –2, 4) eta ' n (2, –1, 0) dira:

cos α = |( ,, )( ,, )| • 14 16 12 42 10 105 4 41 0 ++ = ++ = 0,39036 → α = 67° 1'

Bila gabiltzan angeluari α esango diogu.

Beraz, 90° – α da d -ren eta n -ren norabideek eratzen duten angelua, noranzkoak aintzat hartu gabe.

d (2, 5, –1) // r

n (2, –5, 7) ⊥ π

cos (90° – α) = || || || n n • d d = || 30 4257 78 = 0,5788

90° – α = arc cos (0,5788) = 54° 38'

α = (, ) r r % = 90° – 54° 38' = 35° 22'

Edo bestela, zuzenean:

sin α = || || || n n • d d = 0,5788 → α = 35° 22'

Pentsatu eta praktikatu

1 Aurkitu r eta s zuzenen arteko angelua :

r : x y z

3 Honako plano hauek emanda:

π1: x + 2y + 3z + 6 = 0

–

m m = =+ =

35 23 1

s : xy z xy 23 0 24 0

2 Kalkulatu zein den zuzen honek r :

+

y

z + 1 = 0 planoarekin eratzen duen angelua.

π2: –x – y + 2z – 1 = 0

π3: x – 2y + z = 0

a) Aurkitu zer angelu eratzen duten π1-ek eta π2-k.

b) Kalkulatu zer angelu eratzen duten π2-k eta π3-k.

c) Zehaztu zer angelu eratzen duten r : 1 2

r r ) zuzenak eta

π3 planoak.

d) Zer angelu eratzen dute r : 1

r r

eta s : 2

r r ) zuzenek?

Puntu, zuzen eta planoen arteko distantziak

Bi punturen arteko distantzia

P1(x1, y1, z1) eta P2(x2, y2, z2) bi punturen arteko distantzia PP12 bektorearen modulua da:

dist (P1, P2) = || () () () xx yy zz PP – 12 21 2 21 2 21 2 =+ +

Adibidez, P (5, –1, 7) eta Q (4, 5, –11) arteko distantzia hau da:

dist (P, Q ) = () () () 45 51 11 7 361 –22 2 ++ += = 19 u

Puntu baten eta zuzen baten arteko distantzia

P puntu batetik r zuzen baterako distantzia puntu hori zuzenarekin lotzen duen zuzenki perpendikularraren luzerari esaten zaio; hau da, P-tik zuzenaren gaineko P' proiekziora dagoen distantziari.

dist (P, r ) = dist (P, P' )

Ikus dezagun P-tik r-rainoko distantzia kalkulatzeko metodo batzuk.

• plano perpendikularraren metodoa

• P-tik igaro eta r-rekiko perpendikularra den π planoa lortuko dugu.

• Bila gabiltzan P' puntua π-ren eta r-ren arteko ebaketa izango da

• Eta hortik, kalkuluak eginda: dist (P, r ) = dist (P, P' )

• puntu orokorraren metodoa

r zuzeneko R puntu orokor batek λ parametro baten mendeko koordenatuak ditu. PR zuzenkia r-rekiko perpendikular egiten badugu, λ-ren balioa lortuko dugu eta, hortik, P' jakingo dugu. Horretarako:

• r zuzenaren parametrikoak idatziko ditugu (horrela jarrita ez badaude)

• R lortuko dugu, λ-ren mendeko koordenatuak erabiliz. PR lortuko dugu.

• PR ⊥ r egingo dugu, biderketa eskalarra erabiliz: • PR d = 0. Horrela, λ ezezaguna duen ekuazioa lortuko dugu eta hori izango da ebatzi beharrekoa

• Ekuazioaren soluzioan lortzen dugun λ-ren balioak P' puntuaren koordenatuak emango dizkigu

• biderketa bektorialaren metodoa: distantziaren kalkulua

Alboko irudiko paralelogramoaren azalera || RP d # da. Paralelogramoaren azalera oinarriaren || d luzerarekin zatitzen badugu, altuera lortzen dugu. Beraz, P eta r arteko distantzia berehala lortuko dugu:

dist (P, r ) = ||

|| RP d d Oinarria Azalera # =

Metodo honen bidez, berehala kalkula daiteke P-tik r-rako distantzia, aldez aurretik P' puntua (P-ren r gaineko proiekzioa) lortu beharrik gabe.

dist (P1, P2) = ortoedroaren diagonala

P1-etik P2-ra dagoen distantzia da ortoedroaren diagonalaren luzera.

«AURREZ AURREKO PUNTUA» P'

r P

P' puntua da P puntuak r gainean duen proiekzioa, eta ikasle batek aurrez aurreko puntua esan zion. Ondo jarritako izena iruditu zaigu. r

➜ Puntu baten eta zuzen baten arteko distantzia aurkitzeko urratsak.

dist (P, r ) = h =

Ebatzitako ariketa

1 Kalkulatu P (5, –1, 6) puntutik zuzen honetara dagoen distantzia:

plano perpendikularraren metodoa

r

➜

[ \

––m m m ] ] ]

= = =+

• P (5, –1, 6) puntutik igaro eta r-rekiko perpendikularra den π planoa.

π-rekiko bektore normala r -ren norabide-bektorea da : (,21,) 1 nd==

d(–2, –1, 1)

P' P(5, –1, 6) r

π planoa: –2(x – 5) – (y + 1) + (z – 6) = 0 → 2x + y – z – 3 = 0

• π-ren eta r-ren ebaketa

r-ren koordenatuak π-ren ekuazioan ordezkatuko ditugu, λ lortzeko:

2(1 – 2λ) + (–λ) – (5 + λ) – 3 = 0 → λ = –1

Sakondu: «distantzia minimoaren» metodoa.

Pentsatu eta praktikatu

Z [ \

] ] ]

x y z

λ = –1 → () () ()

== == =+ =

12 13 11 51 4 –

• Eskatutako distantzia:

b b b → P' (3, 1, 4)

_ ` a

dist (P, r ) = dist (P, P' ) = () () () 53 11 64 12 22 2 ++ = u

puntu orokorraren metodoa

R (1 – 2λ, –λ, 5 + λ) puntua r zuzeneko puntu orokorra da.

RP = (4 + 2λ, –1 + λ, 1 – λ) bektorea aldakorra da, λ parametroaren mendekoa baita.

RP bektorea λ-ren zer baliorekin izango den r-rekiko perpendikularra bilatuko dugu. Hau da, RP d • = 0 egingo dugu:

(–2, –1, 1) • (4 + 2λ, –1 + λ, 1 – λ) = 0

–2(4 + 2λ) – 1(–1 + λ) + (1 – λ) = 0

Soluzioa hau da: λ = –1.

biderketa bektorialaren metodoa

RP d # = (0, – 6, – 6)

|| RP d # = 06++=22672

|| d = 41 16 ++ =

dist (P, r ) = || || RP d d Oinarria

r R P

R (1, 0, 5), P (5, –1, 6) → RP = (4, –1, 1), d = (–2, –1, 1)

P'

P (5, –1, 6)

RP(4,–1,1) d(–2, –1, 1)

Azalera # = = 6 72 12 = u r

R(1, 0, 5)

1 Kalkulatu, arrazoituz, P(5, 6, 6) puntutik r : (5λ, 2 – λ, λ) zuzenera dagoen distantzia

Egizu ikasi dituzun hiru metodoak erabiliz

Puntu batetik plano baterako distantzia

Ikus dezagun puntu batetik plano baterako distantzia lortzeko bi modu

• zuzen perpendikularraren metodoa

P-tik π-ra dagoen distantzia P-tik planoaren gaineko bere proiekziora dagoena da: dist (P, π) = dist (P, P' )

Aurrez aurreko puntua lortzeko, P' puntu batetik zuzen baterainoko distantzia kalkulatu dugunean bezala jokatuko dugu.

• P-tik igaro eta π-rekiko perpendikularra den r zuzena lortuko dugu.

• P' puntua r-ren eta π-ren arteko ebaki-puntua da.

• formula zuzenean erabiltzea

Dena dela, prozesu hori guztia askoz laburrago egin dezakegu, puntu batetik plano baterainoko distantzia kalkulatzeko formula eroso bat dago eta:

π: ax + by + cz + d = 0 planoa eta P (x0, y0, z0) puntua ditugu. P puntuaren π gaineko proiekzioari P' esango diogu. Planoko Q (α, β, γ) puntu bat hartuko dugu. dist (P, π) = || || ' PP QR = = ( QP -ren n gaineko proiekzioa) =

)| |( )| ab c ax by cz ab c ax by cz ab c 22 2 00 0 22 2 00 0 ab ca bc ++ ++ = ++ ++ ++ (α, β, γ) planokoa denez, aα + bβ + cγ + d = 0 betetzen da, eta, beraz, aα + bβ + cγ = –d

Goian ordezkatuz, azkenean hau lortzen dugu: dist (P, π) = || ab c ax by cz d 22 2 00 0 ++ ++ +

1 Kalkulatu P (–2, – 6, 11) puntutik

π: x – 3y + 5z – 1 = 0 planorako distantzia.

• P -tik igaro eta π-rekiko perpendikularra den zuzena : r :

r-ren eta π-ren arteko ebaketa: (–2 + λ) – 3(– 6 – 3λ) + 5(11 + 5λ) – 1 = 0 → λ = –2 λ = –2 kasuan, P' (–4, 0, 1) puntuaren koordenatuak lortzen ditugu. Beraz, (, ,) . PP' 26 10 = dist (P, π) = dist (P, P' ) = || () () PP' 26 10 140 235 22 2 =+ += = u

• Formula erabiliz: dist (P, π) = () |( )| 13 5 23 65 11 1 35 70 235 –22 2 ++ + == u

Pentsatu eta praktikatu

2 Kalkulatu P-tik π-ra dagoen distantzia, zuzen perpendikularraren metodoa erabiliz eta formula aplikatuz

P (11, 7, 9) π: 3x + 4z + 6 = 0

3 Kalkulatu zer distantzia dagoen P (5, –3, 8) eta

Q 73,, 2 5 dn puntuetatik π: 5x – 11y + 2z – 7 = 0 planora, formula erabiliz

Zuzen batetik plano baterako distantzia

r-ren norabide-bektoreari d deitzen diogu, eta π-rekiko bektore normalari n

• d ez bada n -rekiko perpendikularra ( d • n ≠ 0), orduan r zuzenak π ebakitzen du dist (r, π) distantzia zero da

• d perpendikularra bada n -rekiko ( d • n = 0), orduan r paraleloa da π-rekiko edo plano horretan dago. Bai kasu batean eta bai bestean, r zuzeneko P puntu bat hartu eta : dist (r, π) = dist (P, π)

Bi planoren arteko distantzia

π eta π' planoekiko bektore normalei n eta ' n esango diegu.

• n bektorea ' n -rekiko paraleloa ez bada, orduan planoek elkar ebakitzen dute eta distantzia zero da

• n bektorea ' n -rekiko paraleloa bada, orduan π eta π' planoek bat egiten dute edo paraleloak dira. Kasu batean eta bestean, π planoko P puntu bat hartu eta: dist (π, π') = dist (P, π')

1 Kalkulatu zer distantzia dagoen zuzen honetatik:

2 Kalkulatu zer distantzia dagoen plano honetatik:

π: x – 5y + 2z – 19 = 0

plano honetara:

σ: 2x – 10y + 4z = 0

Pentsatu eta praktikatu

Zuzena planoarekiko paraleloa denez edo plano horren barruan dagoenez, r zuzenetik π-rako distantzia lortzeko, r-ko edozein puntutik π-rako distantzia

P (3, 1, –2) ∈ r puntua hartuko dugu:

dugu

Zuzena planoarekiko paraleloa da. Distantzia 2,41 unitatekoa da

Bi planoak paraleloak dira, koefizienteak proportzionalak dituzte eta. Beraz, planoen arteko distantzia da horietako baten edozein puntutik beste planora dagoen distantzia

P (2, –1, 6) puntua π planokoa da (egiaztatu).

Beraz:

4 Kalkulatu zer distantzia dagoen r zuzenaren eta π planoaren artean:

5 Kalkulatu bi plano hauen arteko distantzia:

π: y – 5z + 4 = 0

π': 2y – 10z = 0

Bi zuzenen arteko distantzia

d eta d' bektoreak dituzten r eta s bi zuzenen arteko distantzia kalkulatzean, bi kasu izan ditzakegu:

• d bektorea d' -rekiko paraleloa bada, zuzen bera dira edo paraleloak dira. Orduan, r-tik s-rako distantzia lortzeko, r-ko P puntu bat bilatu eta dist (r, s) = dist (P, s) egingo dugu kasu guztietan

Puntu batetik zuzen baterainoko distantzia 180. orrialdean landu dugu.

• d ez bada paraleloa d' -rekiko, eta ez bada agerikoa zuzenek elkar ebakitzen dutela, orduan r-tik s-ra dagoen distantzia lortzeko, honako prozedura hauetako edozein erabil dezakegu. Distantzia hori zero bada, r eta s zuzenek elkar ebakitzen dutela ondorioztatuko dugu.

• plano paraleloaren metodoa

s-rekiko paraleloa den eta r barne hartzen duen π planoa lortuko dugu. Eta, hortik: dist (r, s ) = dist (s, π) = dist (s-ko edozein puntu, π)

• biderketa mistoaren metodoa

π planoak barnean hartzen du r zuzena eta paraleloa da s-rekiko. R da r-ko edozein puntu, eta S da s-ko edozein puntu. Beraz, RS bektorea r-tik s-ra doa.

d (r-ren norabide-bektorea), d' (s-ren norabide-bektorea) eta RS bektoreek paralelepipedo bat zehazten dute. Horren h altuera da s zuzenetik π planora dagoen distantzia; hau da, bila gabiltzan s eta r arteko distantzia.

Baina altuera bolumenaren eta oinarriaren azaleraren arteko zatidura ere bada.

• Paralelepipedoaren bolumena da |[ d , d' , RS ]| (biderketa mistoa).

• Oinarriko paralelogramoaren azalera da | d × d' | (biderketa bektorialaren modulua). Beraz, bila gabiltzan distantzia hau da:

dist (r, s ) = dist (S, π) = h = Oinarriaren azalera

Paralelepipedoarenbolumena = paralelogramo |'| |[ ,',]| RS Área Volumenparalelepípedo dd dd # =

• bektore aldakorraren metodoa

R puntua r-ko puntu orokor bat da. Horren koordenatuak λ-ren araberakoak dira.

S puntua s-ko puntu orokor bat da. Horren koordenatuak μ-ren araberakoak dira

RS bektoreak jatorria r zuzenean du, eta muturra, s zuzenean. Horren koordenatuak bi parametroren araberakoak izango dira: λ eta μ.

RS behartuko dugu r-rekiko eta s-rekiko perpendikularra izatera; horretarako, bider d eta bider d' eginez lortzen diren biderketa eskalarrak berdin 0 izan behar dira. Bi biderketa horiek eratzen dute bi ezezaguneko bi ekuazioko sistema bat.

Sistema hori ebatzita, λ eta μ lortuko ditugu, eta horiekin, R0 ∈ r eta S0 ∈ s; eta horien kasuan, RS00 perpendikularra da r-rekiko eta s-rekiko. Beraz: dist (r, s ) = dist (R0, S0)

Metodo honen bitartez, zuzenen arteko distantzia aurkitzeaz gain, komunean duten perpendikularra ere lortzen dugu.

1 Kalkulatu honako zuzen hauen arteko distantzia:

Aurkitu dezagun r barne hartzen duen eta s -rekiko paraleloa den π planoa:

s : x y z ] ] ]

m m Z [ \

43 3 54 –m m m

5 1 82 =+ = =+

(, ,) //

(, ,) // r s 10 2 31 4 – 4 Beraz, (1, 0, 2) × (3, –1, 4) = (2, 2, –1) perpendikularra da π-rekiko.

= 0 → π: 2x + 2y – z = 0 dist

biderketa mistoaren metodoa dist (r, s) = dist (π, s) =

=

S(4, 3, 5) 4 0 1

z –

3,

5), π] = |· ·| 44 1 24 23 5 3 9 3 –++ + == u

d'(3, –1, 4)

dist (r, s ) = 3 9 3 = u

bektore aldakorraren metodoa

r -ko puntu generikoa : R (5 + λ, –1, 8 + 2λ)

,,'

d dd dd # = r s r

λ eta μ jarriko dugu, aldi berean bi zuzen erabiltzean, bakoitzak bere parametroa izan behar baitu.

Jatorria r zuzenean eta muturra s zuenean duen bektore generiko bat hau da:

RS = (4 + 3μ – 5 – λ, 3 – μ + 1, 5 + 4μ – 8 – 2λ) = = (–1 + 3μ – λ, 4 – μ, –3 + 4μ – 2λ)

RS bektore posible guztien artean, bi zuzenekiko perpendikularra dena bilatuko dugu:

(, ,) (, ,) RS RS 10 20 75 11 0 31 40 19 11 26 0 – • • mn mn =+ = =+ = 4 → → (, ,) (, ,) RS RS 10 20 75 11 0 31 40 19 11 26 0 – • • mn mn =+ = =+ = 4

Soluzioa da λ = 3, μ = 2. Balio horiek r eta s zuzenetan ordezkatuta, R0 eta S0 puntuak lortuko ditugu:

(, ,) (, ,) R S 81 14 10113 – 0 0 4

dist

(r, s) = dist (R0,

S

Metodo hau aurrekoa baino zailagoa da, baina oso baliagarria da r-tik s-rako distantziaz gain bi zuzen horien perpendikular komuna lortu nahi denean, alegia, R0 eta S0 puntuetatik igarotzen den zuzena.

2 Aurkitu honako zuzen hauen arteko distantzia:

• Bektore aldakorraren metodoa erabilita ebatziko dugu.

R(10 + 7λ, –2 – 3λ, 9 + 4λ) da r zuzeneko puntu aldakor bat.

S(7 – 2μ, –5 + 3μ, 5) da s zuzeneko puntu aldakor bat. Adi! λ ez den beste parametro bat jarri dugu, r zuzenean erabilitakotik bereizteko.

SR (3 + 7λ+ 2μ, 3 – 3λ– 3μ, 4 + 4λ) bektoreak jatorria s zuzenean du, eta muturra, r zuzenean.

SR bektore posible guztien artean, bi zuzenekiko perpendikularra dena bilatuko dugu:

00 323130 ––• •

= = mn mn =+ += == 4

Ekuazio sistema horren soluzioa λ = –1, μ = 2 da.

λ = –1 balioa r zuzenean ordezkatuta, R0(3, 1, 5) lortzen dugu.

μ = 2 balioa s zuzenean ordezkatuta (enuntziatura joanez gero, λ = 2 egingo dugu s-n), S0(3, 1, 5) lortzen dugu. Puntu bera da!

Beraz, bi zuzenek (3, 1, 5) puntuan elkar ebakitzen dutela lortu dugu eta, beraz, zuzenen arteko distantzia 0 dela.

S (7, –5, 5)

RS (–3, –3, – 4)

R (10, –2, 9)

d' (–2, 3, 0) '

d (7, –3, 4)

s r

• Problema hori berori biderketa mistoaren metodoa erabilita ebatziko dugu. d , d' , RS -ren biderketa mistoa: [, '] , RS 4

7 2 3

–

3 3 3

4 00 dd –––

Paralelepipedoaren bolumena 0 bada, zuzenen arteko distantzia 0 da.

Beraz, zuzenek elkar ebakitzen dute. Metodo honekin ebaki-puntua lortzen ez badugu ere, nahi izanez gero, aurkitu dezakegu.

r eta s zuzenen ebaki-puntua lortzeko, bi zuzenen koordenatuak berdinduko ditugu:

Sistema horren soluzioa λ = –1, μ = 2 da. λ = –1 balioa r zuzenean edo μ = 2 balioa s zuzenean ordezkatuz gero, (3, 1, 5) puntu bera lortuko dugu; eta hori da ebaki-puntua.

6 Kalkulatu emandako bi zuzen hauen arteko distantzia, ikasitako hiru metodoak erabilita:

Ebatzitako ariketak

Azaleren eta bolumenen neurriak

5. unitatean, bektoreak landu genituenean, paralelogramo baten azalera biderketa bektoriala erabiliz kalkulatu genuen, eta paralelepipedo baten bolumena, biderketa mistoa erabiliz. Unitate honetan, emaitza horiek distantziak kalkulatzeko erabili ditugu, eta, orain, bi formula lortzeko hartuko ditugu berriro esku artean; triangelu baten azalera eta tetraedro baten bolumena

Triangelu baten azalera, hiru erpinak jakinda

ABC & -ren azalera || ABCABAC 2 1 # = &

Adibidea. A (–5, 2, 1), B (1, 7, 5), C (–1, 0, 4) badira.

(, ,)

(, ,) AB AC AB AC 65 4 42 3 23232 –# = 4

(, ,)

Triangeluaren

Tetraedro baten bolumena, lau erpinak jakinda

Gogoan izan tetraedro baten bolumena irudi horri dagokion paralelepipedoaren bolumenaren seirena dela (aztertu alboan ageri den arrazoiketa)

Horrez gain, kontuan izan behar dugu paralelepipedo baten bolumena irudia zehazten duten hiru bektoreen arteko biderketa mistoaren balio absolutua dela. Beraz, ondorio hau ateratzen dugu:

A, B, C, D erpineko tetraedroaren bolumena = |[ ,, ]| AB

Erpinen koordenatuak A (x1, y1, z1), B (x2, y2, z2),

C (x3, y3, z3), D (x4, y4, z4) badira, bolumenaren balio absolutuak adierazpen hau izango du:

(2., 3. eta 4. errenkadei 1.a kenduz gero, biderketa mistoaren adierazpena ikusiko duzu).

Paralelepipedo erdia bolumen bereko hiru piramidetan (tetraedroak) deskonposatzen da. I = II ; izan ere, oinarritzat azalera bera duten ADB eta BDE triangeluak hartuz gero, altuerak ere bat dator, C baita berdina duten aurkako erpina.

Modu berean, ii = iii

1 Kalkulatu tetraedro baten bolumena, erpinak hauek direla jakinda:

A (3, 5, 7), B (1, 0, –1),

C (7, –1, 4) eta D (11, 4, – 6).

Erabiltzeko errazenak B erpinaren koordenatuak direnez, B erpina hartuko dugu hiru bektoreen jatorritzat:

BA (2, 5, 8) BC (6, –1, 5) BD (10, 4, –5) ABCD-ren

1 Kalkulatu erpinak honako puntu hauetan dituen triangeluaren azalera: A (1, 3, 5), B (2, 5, 8) eta C (5, 1, –1).

2 Kalkulatu A (2, 1, 4), B (1, 0, 2), C (4, 3, 2) eta D (1, 5, 6) erpinak dituen tetraedroaren bolumena

Pentsatu eta praktikatu

Leku geometrikoak espazioan

Leku geometrikoek (L.G.) espazioan duten esanahia, bai eta tratamendu analitikoa ere, planoan dutenaren antzekoa da.

Plano erdibitzailea

Zuzenki baten plano erdibitzailea zuzenkiak erdiko puntuan duen plano perpendikularrari esaten zaio. Zuzenkiaren bi muturretatik distantzia berera dauden espazioko puntu guztien leku geometrikoa da:

dist (X, A ) = dist (X, B )

Planoerdi erdikaria

Planoerdi erdikaria angelu diedro bat bi angelu berdinetan zatitzen duenari esaten zaio. Angelu diedroa eratzen duten planoerdietatik distantzia berera dauden puntuen leku geometrikoa da:

dist (X, π) = dist (X, π')

Kontuan izan bi planok, elkar ebakitzen dutenean, lau angelu diedro zehazten dituztela eta, beraz, bi plano erdikari daudela

1 Aurkitu A (1, –3, 4) eta B (5, 1, –2) puntuetatik distantzia berera dauden espazioko puntuen L.G.

Hau betetzen duten X (x, y, z ) puntuak bilatu behar ditugu: dist (X, A) = dist (X, B ):

() () () () () () xy zx yz 13 45 12 22 22 22 ++ += ++ +

Ber bi egin, garatu eta sinplifikatu ondoren, ekuazio hau lortuko dugu: 2x + 2y – 3z – 1 = 0.

AB (4, 4, – 6)-rekiko perpendikularra den plano bat da; izan ere, n (2, 2, –3) bektore normala bektore horrekiko proportzionala da eta AB-ren erdiko puntutik igarotzen da: M (3, –1, 1). Beraz, AB zuzenkiaren plano erdibitzailea da

2 Aurkitu π eta π' planoetatik distantzia berera dauden espazioko puntuen L.G.:

π: x + y – 1 = 0

π': y – z – 1 = 0

Pentsatu eta praktikatu

dist (X, π) = dist (X, π') → || || xy yz 2 1 2 1 – + =

Balio absolutuak kentzean, ± zeinu bikoitza ageri da:

x + y – 1 = y – z – 1 → x + z = 0 (σ)

x + y – 1 = –(y – z – 1) → x + 2y – z – 2 = 0 (σ')

Leku geometrikoa σ eta σ' bi planok eratzen dute:

• r zuzenean elkar ebakitzen dute, π eta π' planoek bezala. Beren ekuazio inplizituak, beraz, hauek dira: r : xy yz 10 10 –+= = *

• Gainera σ eta σ' perpendikularrak dira, horien bektore normalak ere hala baitira; izan ere: (1, 0, 1) • (1, 2, –1) = 0

1 Aurkitu ondoren ageri diren bikote hauetatik distantzia berera dauden puntuen L.G.:

a) A (4, –1, 7) eta B (–2, 5, 1)

b) π: x + y + z – 2 = 0 eta π': x – y + z – 2 = 0

c) π: x – 3y + 2z – 8 = 0 eta π': x

Angelu diedroa, bi planoerdiz osatutakoa, eta angelu horren planoerdi erdikaria

Gainazal esferikoa

Gainazal esferikoa da Q zentroraino r distantzia konstantea duten espazioko puntuen leku geometrikoa

Zirkunferentziak planoan duen ekuazioak eta esferak espazioan duen ekuazioak antz handia dute, eta, beraz, hemen emaitza batzuk baino ez ditugu adieraziko, bestelako azalpenik eman gabe

Q (x0, y0, z0) zentroa eta r erradioa dituen gainazal esferiko bateko X (x, y, z,) puntuek honako baldintza hau betetzen dute: || r QX =

Q (x0, y0, z0) zentroa eta r erradioa duen gainazal esferikoa :

(x – x0)2 + (y – y0)2 + (z – z0)2 = r 2

Aurreko berdintza hori garatuz, mota honetako adierazpenera helduko gara:

x 2 + y 2 + z 2 + Ax + By + Cz + D = 0

Eta alderantziz, mota honetako ekuazio bat Q ,, AB C 22 2 –dn zentroa eta r = AB C D 22 2 –22 2 ++dd d nn n erradioa dituen gainazal esferiko bati dagokio, baldin eta errokizuna positiboa bada.

Q (x0, y0, z0) X (x, y, z) r

1 Aztertu ea ekuazio hau, x 2 + y 2 + z 2 – 4x + 6z – 12 = 0

gainazal esferiko bati dagokion, eta, hala bada, adierazi zein diren zentroa eta erradioa.

2 Gainazal esferiko honek: (x – 3)2 + (y + 2)2 + (z – 1)2 = 25

eta plano honek: 2x – 2y + z – 2 = 0

zirkunferentzia batean elkar ebakitzen dute.

Aurkitu erradioa.

r = AB C D 22 2 –22 2 ++dd d nn n = 23 12 25 5 22++ == u

5eko erradioa eta Q ,, AB C 22 2 –dn = (2, 0, –3) zentroa dituen gainazal esferikoa da.

Gainazal esferikoak zentroa Q (3, –2, 1) puntuan dauka, eta bere erradioa R = 5 u da.

Q-tik planorako distantzia hau da:

d = |· ·( )| 22 1 23 22 12 3 –22++ + = u

Beraz, zirkunferentziaren erradioa hau da:

r Q d

Pentsatu eta praktikatu

2 Aztertu x2 + y2 + z2 + 2x – 10y + 25 = 0 ekuazioa gainazal esferiko bati dagokion, eta, hala bada, aurkitu zentroa eta erradioa.

3 Kalkulatu 4x – 3z – 3 = 0 planoak (x – 2)2 + (y + 5)2 + z2 = = 169 ebakitzean eraturiko zirkunferentziaren erradioa.

4 Aurkitu O (0, 0, 0) eta Q (10, 0, 0) puntuetarainoko distantzien karratuen arteko batura 68 u duten espazioko puntuen leku geometrikoa

Kalkuluak egin ondoren, egiaztatu gainazal hori (5, 0, 0) zentroa eta 3 u erradioa duen esfera bat dela.

5 Aurkitu zentroa O(5, –1, 3) puntuan duen eta 4x + 4y – 2z + 11 = 0 ekuazioko planoarekiko ukitzailea den gainazal esferikoaren ekuazioa.

➜ Gainazal esferikoa

Elipsoidea

• planoan. Elipsea da foku izeneko F eta F ' bi puntu finkoetarainoko distantzien batura k konstantea duten P (x, y) puntuen leku geometrikoa: PF + ' PF = k.

Fokuak F '(–c, 0) eta F(c, 0) badira, orduan elipsearen ekuazioa hau da: + ,non /eta a x b y ak ba c 12 –2 2 2 2 22 == =

• espazioan. Elipsoidea da F eta F ' bi puntu finkoetarainoko distantzien batura k konstantea duten P (x, y, z) puntuen leku geometrikoa.

Fokuak F' (–c, 0, 0) eta F(c, 0, 0) badira, elipsoidearen ekuazioak forma hau hartzen du: + 1 = a x b yz 2 2 2 22 +

1 Aurkitu F (3, 0, 0) eta

F ' (–3, 0, 0) fokuetarainoko distantzien batura 10 duten puntuen leku geometrikoa.

Bila gabiltzan X (x, y, z) puntuek hau bete behar dute: dist (X, F ) = dist (X, F ' ) = 10.

() () xy zx yz 310 3–22 22 22 ++ ++ ++ =

xx yz xx yz 69 10 69 22 22 22 ++ ++ =+ ++

Aurreko adierazpena karratura jaso eta gaiak sinplifikatzen baditugu, hau lortzen dugu:

12x – 100 = –20 xx yz 69 –22 2 ++ +

Berriro karratura jaso eta sinplifikatuta:

16x 2 + 25y 2 + 25z 2 = 400

Zati 400 eginez:

Paraboloidea

• planoan. Parabola bat da puntu finko batetik, F (fokua), eta zuzen finko batetik, d (zuzentzailea) distantzia berera dauden P(x, y) puntuen leku geometrikoa. Fokua

F ,0 p 2 cm bada, eta zuzentzailea, d: x = –p 2 , parabolaren ekuazioa da: y2 = 2px

• espazioan. Paraboloide bat da F puntu finko batetik eta π plano finko batetik

distantzia berera dauden P(x, y, z) puntuen leku geometrikoa. F ,,00 p 2 cm bada

eta π: x = –p 2 bada, orduan paraboloidearen ekuazioa da y2 + z2 = 2px

1 Aurkitu π: z = –1 planotik eta F (0, 0, 1) puntutik distantzia berera

baten ekuazioaren oso antzekoa da.

Ebatzitako ariketa

➜ anayaharitza.es Konikoen berrikusketa sakona.

Hiperboloidea

• planoan. Hiperbola bat da foku izeneko F eta F ' bi puntu finkoetarainoko distantzien arteko kenketaren balio absolutu moduan k konstantea duten P (x, y) puntuen leku geometrikoa, k: | PF –' PF | = k.

Fokuak F '(–c, 0) eta F(c, 0) badira, orduan hiperbolaren ekuazioa hau da: ,non /. eta a x b y ak bc a 12 2 2 2 2 22 == =

Alboko irudiko zuzen puntudunak hiperbolaren asintotak dira.

• espazioan. Hiperboloide bat da F eta F ' (fokuak) bi puntu finkoetarainoko distantzien kendura k konstantea duten P(x, y, z) puntuen leku geometrikoa.

Fokuak F '(–c, 0, 0) eta F(c, 0, 0) badira, hiperboloidearen ekuazioa hau da:

1 Aurkitu beheko baldintza betetzen duten P(x, y, z) puntuen leku geometrikoa: | PF –' PF | = 8 non F(0, 5, 0) eta F' (0, –5, 0).

Berriro ere karratura jasoko dugu, eta sinplifikatu:

y2 – 16x2 – 16z2 = 144

Zati 144 egingo dugu bi ataletan:

Pentsatu

Lortu, ondorengo ariketetako bakoitzean, adierazitako baldintza beteko duten P (x, y, z) puntuen leku geometrikoaren ekuazioa:

6 F (0, 3, 0) eta F ' (0, –3, 0) puntuetarainoko distantzien batura 10 u da.

7 F (0, 0, 5) eta F ' (0, 0, –5) puntuetarainoko distantzien batura 26 u da.

8 F (5, 0, 0) eta F ' (–5, 0, 0) puntuetaraino distantzien batura 26 u da.

9 F (0, 1, 0) puntutik eta π: y = –1 planotik distantzia berera daude.

10 F (1/4, 0, 0) puntutik eta π: x = –1/4 planotik distantzia berera daude.

11 F (0, 0, 5) eta F ' (0, 0, –5) puntuetarainoko distantzien kendura 8 u da.

12 | PF –' PF | = 10 betetzen dute, non F (0, 13, 0) eta F ' (0, –13, 0).

13 O (0, 0, 0) eta Q (10, 0, 0) puntuetarainoko distantzien karratuen kendura 40 u da.

14 P (0, 0, –6) eta Q (0, 0, 6) puntuetarainoko distantzien karratuen batura 90 u da.

15 P (0, 0, –6) eta Q (0, 0, 6) puntuetarainoko distantzien karratuen kendura 72 u da.

Zer erlazio dago leku geometriko honen eta aurreko ariketako leku geometrikoaren artean?

Ebatzitako ariketak eta problemak

Zehaztu zein den A (–3, 1, –7) puntuaren simetrikoa honako zuzen honekiko:

Problemaren analisia π planoa lortuko dugu, r zuzenarekiko perpendikularra eta A puntua barne hartzen duena. r zuzenaren eta π planoaren arteko ebaketa M puntua da, A puntuaren eta A' simetrikoaren artekoa.

M lortzeko beste modu bat da r zuzeneko puntu generiko moduan adieraztea eta AM eta d r ortogonalak direla ezartzea.

• A barne hartzen duen eta r-rekiko perpendikularra den π planoa aurkituko dugu : nd r = (1, 2, 2) → π: 1(x + 3) + 2(y – 1) + 2(z + 7)

• r zuzenaren eta π planoaren ebaki-puntua: (–1 + λ) + 2(3 + 2λ) + 2(–1 + 2λ) + 15 = 0 9λ + 18 = 0 → λ = –2 → M (–3, –1, –5)

r M A A' r

Aurkitu zein den A (1, –1, 1) puntuaren simetrikoa honako zuzen honekiko:

• A' (α, β, γ) puntua A-ren simetrikoa da M-rekiko: ,, 2 3 2 1 2 7 –– a b c +

= (–3, –1, –5) → A' (–3, –3, –3)

M lortzeko beste modu bat

M puntua r-koa da. Koordenatu hauek ditu: (–1 + λ, 3 + 2λ, –1 + 2λ).

• AM d r = 0, hortik λ = –2 lortzen dugu, eta, beraz, M(–3, –1, –5).

2. Puntu, zuzen eta planoen arteko distantzia

r: y z 1 0 = = ) eta Q(1, 1, 1) izanda:

a) Aurkitu dist (P, Q) = 1 u betetzen duen r zuzeneko P puntu bat.

b) Zehaztu plano baten ekuazioa, jakinda Q ∈ π dela eta dist (P, Q) = dist (P, π) betetzen dela.

EGIN ZUK

Aurkitu β: x – 2y + 3z + 12 = 0 planotik 14 5 u distantziara egongo den

r: (x, y, z) = (0, −2, 1) + λ(−1, 2, −3) .

a) r -ko edozein puntu P (λ, 1, 0) itxurakoa da. P puntuak hau bete behar du: dist (P, Q) = | PQ | = 1

PQ = (1 – λ, 0, 1) → | PQ | = ()10 1 –22 2 m ++ = 1 → (1 – λ)2 = 0 → λ= 1

Bila gabiltzan puntua P (1, 1, 0) da.

Idatzi r zuzenak π planoaren gainean duen proiekzioaren ekuazio inplizituak:

Z

] π

EGIN ZUK

[

= = = \

1 2 –m m m

Aurkitu aurreko r zuzenak

π: x + 2y – 5z – 1 = 0 planoaren gainean duen proiekzioa.

P Q r

b) dist (P, Q) = dist (P, π) bada, orduan PQ izan behar da π planoarekiko perpendikularra.

n PQ π = = (0, 0, 1)

Planoaren ekuazioa π: 0 · x + 0 · y + 1 · z + d = 0

Hau dakigunez, Q ∈ π : 1 + d = 0 → d = −1, eta, beraz, π: z – 1 = 0

n π (2, –3, 1) // σ; d r (–1, –1, 2) // σ; nd r π #

= (–5,

r' :

1. Puntu baten simetrikoa zuzen batekiko

3. Zuzen baten plano baten gaineko proiekzioa

Zehaztu zein den r: x + 2 = y = z − 2 zuzenak π: x + z + 2 = 0 planoarekiko duen r' simetrikoa.

Problemaren analisia Azter dezagun r eta π-ren posizioa. r-ren simetrikoa igarotzen da r eta π-ren ebaki-puntutik, baldin eta existitzen bada, baita r-ko beste edozein puntuk π-rekiko duen puntu simetrikotik.

EGIN ZUK

Aurkitu r : == x y z 01 2 2 1 –+ zuzenak π: 2x – y + z − 6 = 0 planoarekiko duen r' zuzen simetrikoaren ekuazioa.

• r zuzenaren eta π planoaren posizioa: d r = (1, 1, 1); n π = (1, 0, 1) → d r ∙ n π = 1 + 1 = = 2 ≠ 0. r-ren norabide-bektorea eta planoaren bektore normala ez dira perpendikularrak, eta, beraz, zuzenak ez du planoa ebakitzen.

• Q puntua kalkulatuko dugu, r eta π-ren ebaki-puntua:

* M Q r

Aztertu r eta s zuzenen arteko posizio erlatiboa, eta aurkitu bere arteko distantzia.

-ko puntu generiko bat da Pr (–2 + λ, λ, 2 + λ).

Pr puntua π planoaren ekuazioan ordezkatuko dugu, eta, horrela, ebaki-puntua lortuko dugu:

–2 + λ + 2 + λ + 2 = 0 → λ = –1 → Q(–3, –1, 1), eta r eta r' bi zuzenena da.

• Q ez den r-ko beste edozein puntuk π-ren gainean duen proiekzio ortogonala lortuko dugu. r-ko beste puntu bat aurkitzeko, esaterako λ = 2 hartu eta P (0, 2, 4) lortuko dugu. P puntutik π-rekiko perpendikularra den s zuzenaren ekuazioa hau da: d s = n π = (1, 0, 1) → s: x y z 2 4

= = =+

+ *

4 m m

s zuzenaren eta π planoaren M ebaki-puntua lortzeko, s-ko puntu generiko bat ordezkatuko dugu π-ren ekuazioan. Hau da, λ + 4 + λ+ 2 = 0 → λ = –3 M(−3, 2, 1) da PP ' zuzenkiaren erdigunea, P ' puntua P (0, 2, 4)-ren simetrikoa izanik π planoarekiko.

• P' (x, y, z) puntuaren koordenatuak lortuko ditugu:

P' (–6, 2, –2)

– m m m r'

=+ = =+ r P P'

• Amaitzeko, bila gabiltzan r ' zuzenaren ekuazioa kalkulatuko dugu, kontuan izanda Q (–3, –1, 1) eta P '(–6, 2, –2) puntuetatik igarotzen dela:

3 1 1

Z [ \

r : x y z

] ] ]

= =+ =

m m m

s : xy yz 21 0 0 = += *

EGIN ZUK

Kalkulatu zuzenen arteko distantzia:

r : x – 1 = –y = z + 3

s : 3 – x = y + 4 = –z + 2

• s-ren norabide-bektorea lortuko dugu: d s = (1, –2, 0) × (0, 1, 1) = (–2, –1, 1) d r (2, 1, –1) d s (–2, –1, 1) → d r = – d s r eta s zuzenek norabide bera dute.

A (0, 1, 3) ∈ r baina A ∉ s → r eta s paraleloak dira. B

A r s ds

• Biderketa bektoriala erabilita, zehaztu dezagun d s bektoreak eta r-ko A puntu bat s-ko B puntu batekin lotzen duen beste edozein bektorek zehazten duten paralelogramoaren azalera. Azalera oinarriarekin zatitzean, | d s |, paralelogramoaren altuera lortuko dugu; hau da, A-tik s-ra dagoen distantzia, eta, beraz, r-tik s-ra dagoena. s-ko puntu bat hartuko dugu, z = 0 eginez: B (1, 0, 0). Har dezagun A (0, 1, 3) ∈ r

( ,,) ( ,,) (, ) || || |( ,, )| |( ,, )| B distA s AB AB 100 113 21 1 45 3 6 50 3 53 d d s s # == == 4

4. Zuzen baten simetrikoa plano batekiko

5. Zuzen paraleloen arteko distantzia

Ebatzitako ariketak eta problemak

6. Elkar gurutzatzen duten zuzenen arteko distantzia

Ekuazio hauek dituzten zuzenak izanda:

r : xy z xy z 54 22 5 ––+= = *

s : xy z 5 4 = = )

a) Arrazoitu r eta s zuzenek elkar gurutzatzen dutela.

b) Kalkulatu, arrazoituz, r eta s zuzenen arteko distantzia.

c) Zehaztu r eta s zuzenekiko paraleloa eta distantziakidea den planoaren ekuazioa.

EGIN ZUK

a) Egiaztatu r eta s zuzenek elkar gurutzatzen dutela eta kalkulatu horien arteko distantzia.

r : x y z 1 1 1 2 3 ––+= = +

Problemaren analisia. r eta s zuzenen arteko distantzia kalkulatzeko, plano paraleloaren metodoa erabiliko dugu: r barne hartu eta s-rekiko paraleloa den β planoa aurkituko dugu. s-ko edozein puntutik β planora dagoen tartea da bila gabiltzan distantzia.

a) d r (–1, 1, – 4); P (0, 3, –1) ∈ r ; d s (–1, –1, 0); Q (0, 5, 4) ∈ s : d r , d s eta PQ (0, 2, 5) planokideak diren aztertuko dugu

= 18 ≠ 0 → Bektoreak linealki independenteak dira, ez daude plano berean; beraz, r eta s zuzenek elkar gurutzatzen dute.

b) r barne hartu eta s -rekiko paraleloa den β planoa:

P (0, 3, –1) ∈ r

c) Bila gabiltzan π planoa paraleloa izan behar denez r eta s-rekiko, eta, beraz, β-rekiko, forma hau izango du: –2

s : xt yt zt 1 2–

= =+ = *

b) Aurkitu r eta s zuzenekiko paraleloak izan eta s-tik 14 -ko distantziara dauden planoen ekuazioa.

7. Puntu distantziakideak

Ekuazio hauek dituzten planoak izanda:

α: x – y + z = 0 eta β: x + y – z = 2

a) Aurkitu A (1, 2, 3) puntutik igarotzen den eta bi plano horietako bat ere ebakitzen ez duen r zuzenaren ekuazioa.

b) Zehaztu R (1, 0, 0) eta S (1, 2, 4) puntuetatik distantzia berera dagoen r zuzeneko P puntua.

EGIN ZUK

Demagun γ plano bat dugula, β-rekiko paraleloa eta s barne hartzen duena. Har dezagun γ planoko puntu bat, adibidez, s-ko Q(0, 5, 4) puntua, eta β planoko beste bat, esaterako, r-ko P(0, 3, –1) puntua, eta PQ zuzenkiaren erdigunea lortuko dugu: M(0, 4, 3/2).

a) Azter dezagun α eta β planoen posizioa.

n a (1, –1, 1) eta n b (1, 1, –1) ez direnez proportzionalak, planoak ez dira paraleloak, eta, beraz, s zuzen batean ebakitzen dute elkar.

Egiaztatu dezagun A puntua ez dagoela planoetako batean ere: 1 − 2 + 3 ≠ 0 1 + 2 – 3 ≠ 2

A puntutik igarotzen den r zuzena ez dago planoetako batean ere, eta ebaki ere ez ditu egiten; beraz, bi planoekiko paraleloa izan behar da. Norabide-bektorea da zehazten duten zuzenarekiko paraleloa; hau da: d r = n a × n b = (0, 2, 2) = 2(0, 1, 1)

= =+ =+

5 3 22

m

m m =+ = = *

B(1, 0, 1) eta C(2, 4, −2)-rekiko.

A eta d r izanda, r-ren ekuazio parametrikoak idatziko ditugu: x y z *

b) P(1, 2 + λ, 3 + λ) da honako hau bete behar duen r-ko puntu bat PR PS = →

P(1, 1, 2) da bila gabiltzan puntua.

8.

gurutzatzen duten bi zuzenekiko zuzen perpendikularra

Egiaztatu zuzen hauek

r : x y z

Z [ \

= =+ =

1 5 m m

Z [ \

] ] ] s : x y z

] ] ]

73 5 7 –m m =+ =+ =

elkar ebakitzen dutela, eta, ondoren, aurkitu biekiko perpendikularra den zuzenaren ekuazioa. s r

t a b

Problemaren analisia t zuzena bi planoren arteko ebaketa moduan adieraziko dugu: α planoa, r zuzena eta d r × d s bektorea barne hartzen dituena, eta β planoa, s zuzena eta d r × d s bektorea barne hartzen dituena. r eta s zuzenen posizio erlatiboa

r eta s : zuzenekiko perpendikularra : bi planoren arteko ebaketa

Bila gabiltzan t zuzena perpendikularra denez r-rekiko eta s-rekiko, bere norabide-bektorea hau da: dd d tr s # = = (0, 1, 1) × (3, 1, 0) = (–1, 3, –3) α

r eta t barne hartzen ditu:

Beraz, t zuzena hau da: xy z xy

EGIN ZUK

Zuzen hauek ditugu:

r : z x y 2 3 11 1 – –==

Beste metodo bat: r-tik s-ra doan bektore aldakorra

= = = *

s : x y z ––

m m m

Aurkitu zer puntuk zehazten duten bi zuzenen arteko distantzia minimoa eta komunean duten perpendikularraren ekuazioa.

eta s zuzenetan ordezkatuta, R (1, 3, –2), S (4, – 6, 7) lortzen ditugu.

eta

puntuetatik igarotzen den zuzena perpendikular komuna da.

Biderketa bektorialaren metodoa erabiliko dugu: dist (S,

edozein puntu hartuko dugu, adibidez R (2, 0, 0), eta

S(λ, – λ, 0); beraz, RS (λ – 2, – λ, 0). Eta d r (–1, 1, 1) denez:

-ko puntu generiko

Bila gabiltzan puntua, beraz, S(1, –1, 0) da.

Elkar

9. Zuzen batetik puntu baterainoko distantzia

Ebatzitako ariketak eta problemak

10. Leku geometrikoak

Plano hauek emanda:

α: z = 0 eta β: x – 2y + 2z – 5 = 0

aurkitu:

a) α planotik 2 unitateko distantziara dauden β planoko puntuen leku geometrikoa.

b) α eta β planoetatik distantzia berera dauden puntuen leku geometrikoa.

c) β-tik α-tik baino bi aldiz distantzia handiagora dauden r zuzeneko puntuak.

a) α planoko puntu generikoen forma P (x, y, 0) da. P puntutik β planorako dagoen distantzia kalkulatuko dugu, eta 2rekin berdindu. dist (

Beraz, bila gabiltzan puntuek erlazio horietako bat bete behar dute eta, gainera, z = 0 planoaren barruan egon behar dute.

Bi zuzen dira: r : xy z 2110 0 = = ) eta s : xy z 21 0 0 –+ = = )

b) P (x, y, z) deituko diogu dist (P, α) = dist (P, β) betetzen duen puntuari:

z – 5 → x – 2y + 5z – 5 = 0

α eta β planoek eratzen duten angelu diedroaren plano erdikariak dira.

c) r-ko puntu generiko bat P (1 + 2t, t, –t ) formakoa da eta dist (P, β) = 2dist (P, α) bete behar du.

EGIN ZUK

Aurkitu A (0, 2, 1)-rainoko distantzia B (–1, 3, –2)-rainokoa baino bi aldiz handiagoa duten puntuen L.G.

11. Esfera

a) Idatzi A (1, –3, 4), B (1, –5, 2), C (1, –3, 0) puntuetatik igarotzen den eta zentroa x + y + z = 0 planoan duen esferaren ekuazioa.

b) Zein da esfera horrek A puntuan duen plano ukitzailearen ekuazioa?

bi plano lortu ditugu

zentroa: U (1, –3, 2)

Esferaren erradioa = dist (U, A ) = 2

Esferaren ekuazioa: (x – 1)2 + (y + 3)2 + (z – 2)2 = 4

b) A puntuan ukitzailea den α planoaren bektore normala UA da: UA = (0, 0, 2)

α planoa:

Q (–2, 2, 1) puntuak eta v (1, 1, 1) bektoreak zehazten duten zuzeneko puntu guztien artean, aurkitu zein den P (1, 3, 0) puntutik hurbilen dagoena. Kalkulatu P puntutik zuzenera zer distantzia dagoen.

Zehaztu zer erlazio bete behar duten a eta b parametroek, P (a, 1, b) puntutik A (1, 1, 1), B (1, 0, 0) eta

C (0, 2, 1) puntuek zehazten duten planorako distantzia 1 izateko.

• Aurkitu r-rekiko perpendikularra den eta P-tik igarotzen den π planoaren ekuazioa r-ren eta π-ren arteko ebaki-puntuari A esan: puntu hori aurkitzeko, ordezkatu r-ren ekuazio parametrikoak π-ren ekuazioan

• P-tik r-ra dagoen distantzia eta P-tik A-ra dagoena berdinak dira

Soluzioa: A (–1, 3, 2), dist (P, r ) = 2 2 u.

• Idatzi A, B eta C puntuetatik igarotzen den π planoaren ekuazio inplizitua. Horretarako, hartu AB eta AC bektoreak eta emandako puntu horietakoren bat

• P-tik π-rako distantziaren adierazpena berdin 1 egin

• Balio absolutua duen ekuazio bat lortuko duzu eta, beraz, bi soluzio agertuko dira. Soluzioa: a – b = 3 edo, bestela, a – b = – 3 .

Q (3, –1, 4) puntua eta zuzen hau ditugu:

14

a) Aurkitu Q-tik r zuzenera zer distantzia dagoen

b) Arrazoitu Q-tik igarotzen den eta (1, –1, 1) norabide-bektorea duen s zuzenak ez duela r ebakitzen

c) Kalkulatu r eta s arteko distantzia

4.

Aurkitu P (2, –1, 1) puntutik igarotzen den eta r zuzena perpendikularrean ebakitzen duen s zuzenaren ekuazioa:

a) Aurkitu P puntu bat eta r-ren norabide-bektorea, d r . Zatitu d r eta PQ bektoreek eratzen duten paralelogramoaren azalera oinarriaren neurriarekin, eta dist (Q, r) lortuko duzu

b) Egiaztatu d r , d s eta PQ bektoreak linealki independenteak direla eta, beraz, ez direla planokideak.

c) r eta s zuzenek elkar gurutzatzen dutenez, horien arteko distantzia aurkitzeko, zatitu d r , d s eta PQ bektoreek eratzen duten paralelepipedoaren bolumena d r eta d s bektoreek eraturiko oinarriaren azalerarekin

a) Kalkulatu kubo baten bolumena, jakinik erpinak bi plano hauetan dituela:

α: 4x + 6y – 12z + 1 = 0

β: –2x – 3y + 6z – 5 = 0

b) A(2, 1, 3) eta B(1, 2, 3) puntuak

ABCD karratu baten ondoz ondoko bi puntu dira. C puntua β eta π: x – y + z = 2 planoetan dago.

Aurkitu C eta D.

Problema ebazteko bi metodo erabil ditzakegu:

I) s zuzena bi planoren arteko ebaketa da: α planoa, r-rekiko perpendikularra eta P barne hartzen duena ; β planoa, r eta P barne hartzen dituena.

II) r-rekiko perpendikularra den eta P barne hartzen duen α planoa aurkitu ondoren, lortu r zuzenaren eta α planoaren arteko Q ebaki-puntua. P eta Q puntuek s zuzena zehazten dute

Soluzioa: (x, y, z) = (2, –1, 1) + λ (8, 2, – 4)

a) Egiaztatu α eta β planoen arteko distantzia. Aurkitu kuboko ertzaren luzera, hau da, α eta β planoen arteko distantzia.

b) AB eta BC bektoreek perpendikularrak izan behar dute. Horrez gainera, badakigu C ∈ β eta C ∈ π direla.

Hiru ekuazioko sistema bat lortuko duzu, eta horren soluzioa C-ren koordenatuei dagokie.

AB = DC bektore-berdintzarekin, aurkitu D-ren koordenatuak.

Soluzioa: a) V = 0,27 u3 b) C (2, 3, 3); D (3, 2, 3)

1. Zuzen batetik hurbilen dagoen puntua

2. Puntu batetik plano baterako distantzia

3. Zuzenen arteko distantzia

Zuzen batekiko zuzen perpendikularra

5. Kubo baten bolumena eta karratu baten erpinak

Proposatutako ariketak eta problemak

Trebatzeko Angeluak

1 Aurkitu zein den r eta s zuzenek kasu hauetako bakoitzean eratzen duten angelua. Lehenengo, aztertu elkar ebakitzen duten:

a) r : x y z

9 Aurkitu r zuzenetik π planora zer distantzia dagoen kasu hauetako bakoitzean:

––

52 43 2

m m m

= =+ = * s : x y z

= =+ = *

5 45 – m m m

b) r : xy z xy z 54 22 5 ––+= = * s : xy z 5 5 –= = )

2 Aurkitu zer angelu eratzen duten kasu hauetako bakoitzeko zuzenak eta planoak:

a) r : x y z 2 1 4 3 2 –+ = + =

b) r : x = λ, y = 1 + 2λ, z = –2

c) r : x y z 2 1 1 3 1 ––==

: x – 2y – z + 1 = 0

: 2x – y + z = 0

: x + z = 17

3 Kalkulatu kasu hauetako bakoitzeko plano-bikoteak zer angelu eratzen duen:

a) α: z = 3 β: x – y + 2z + 4 = 0

b) α: 2x + y – 3 = 0 β: x + z – 1 = 0

c) α: x – 2y + z = 0 β: z = 0

4 Kalkulatu ondorengo erpinak dituzten triangeluen hiru angeluak:

a) A (0, 0, 0), B (1, 2, 1), C (3, 1, 1)

b) A (2, 7, 3), B (1, 2, 5), C (–1, –2, 5)

5 Kalkulatu zein izan behar den m-ren balioa r eta s zuzenek angelu hauek eratzeko:

a) 90°

b) 60°

r : x y z 1 2 1 1 1 ––––== s: x y m z 1 1 –– ==

Distantziak

6 Kalkulatu zer distantzia dagoen Q (2, –1, 0) puntutik

P (2, 0, 4) puntua eta beheko zuzena barne hartzen dituen

planora: s : == x y z 2 3 3 2 0 4 ––

7 Kalkulatu honako plano-bikote hauen arteko distantzia:

a) π1: x – 2y + 3 = 0; π2: 2x – 4y + 1 = 0

b) π1: 3x – 2y + z – 2 = 0; π2: 2x – y + z = –5

8 Kalkulatu, kasu hauetako bakoitzean, P eta π planoaren arteko distantzia:

a) P (0, 1, 3)

b) P (2, 0, 1)

π: x – y – 2z + 3 = 0

π: x + y – 2z = 0

c) P (3, – 4, 1) π: y = 3

d) r: x– 1 = = z y 2 1 1 1 –––s : x = y m 1 –= z – 1

Z [ \

=+ = =+

24 3 m m m

] ] ] b) r : x y z

32 5 4

m m

=+ = =+ * π: 3x – 4y – 3 = 0 π: 7x – 2y – z + 1 = 0 10 r : x y z

Z [ \

=+ =+ =

4 2 13

m m m

] ] ] zuzena

eta P(3, 1, 6) puntua izanda:

a) Idatzi π plano baten ekuazioa, jakinda r-rekiko perpendikularra dela eta P barne hartzen duela.

b) Aurkitu Q puntua, r eta π-ren arteko ebaki-puntua.

c) Kalkulatu P-tik Q-rako distantzia.

11 Aurkitu aurreko problemako zuzenaren eta puntuaren arteko distantzia d r eta PR bektoreen biderketa bektoriala erabilita, jakinda R dela r-ko edozein puntu.

12 Zer distantzia dago P (2, 2, –11) puntuaren eta zuzen honen artean?

r : x y z 912 13 65 m m m =+ = =+ Z [ \ ] ] ] 13 r: x y z 2 1 3 3 1 ––= + = zuzena eta A(5,

a) Kalkulatu A puntutik r zuzenera dagoen distantzia.

14 Kalkulatu zer distantzia dagoen bi zuzen hauen artean: r : x y z Z

] s : x y z 212 19 4 – m m m = =+ =+

4 10 3 95 ] ]

Horretarako, jarraitu urrats hauei:

1) Aurkitu r zuzena barne hartzen duen eta s zuzenarekiko paraleloa den π planoa.

2) Kalkulatu s-ko puntu batetik (nahi duzunetik) π planora zer distantzia dagoen.

16 Kalkulatu zer distantzia dagoen zuzen hauen artean: r

Horretarako, egin honako hau:

1) Aurkitu PQ bektorea, kontuan hartuz P eta Q puntuak, hurrenez hurren, r eta s zuzenetakoak direla.

2) Kalkulatu PQ bektoreak eta r-ren eta s-ren norabide-bektoreek zehazten duten paralelepipedoaren V bolumena.

3) Kalkulatu r-ren eta s-ren norabide-bektoreek zehazten duten paralelogramoaren A azalera.

4) r-tik s-ra dagoen distantzia bat dator V zati A egitean lortzen dugun emaitzarekin.

17 Egiaztatu honako zuzen hauek elkar gurutzatzen dutela, eta kalkulatu haien arteko distantzia.

Leku geometrikoak. Esfera

23 Arrazoitu ekuazio hauetako zein diren esferenak eta, horien kasuan, adierazi zentroa eta erradioa zein diren:

a) x2 + y2 – 2x + 4y – 8 = 0

b) 2x2 – 2y2 + 2z2 + 4x – 16 = 0

c) 2x2 + 2y2 + 2z2 + 4x – 16 = 0

d) x2 + y2 + z2 + 2x – 2y + 8 = 0

e) 3x2 + 3y2 + 3z2 + 6x – 12z – 3 = 0

24 Idatzi honako esfera hauen ekuazioak:

a) (1, 0, –5) zentroa eta 1 erradioa.

b) AB diametroa, A(3, –4, 2), B(5, 2, 0) izanik.

c) (4, –2, 3) zentroa eta x – z = 0 planoarekiko ukitzailea.

d) (3, –1, 2) zentroa eta YZ planoarekiko ukitzailea.

25 Aurkitu (2, –1, 4) punturainoko distantzia 7 duten puntuen leku geometrikoa.

Azalerak eta bolumenak

18 Kalkulatu ABC triangeluaren azalera kasu hauetako bakoitzean:

a) A(2, 7, 3), B(1, –5, 4), C(7, 0, 11)

b) A(3, –7, 4), B(–1, 2, 5), C(–5, 11, 6)

Arrazoitu bigarrenaren soluzioa.

19 Kalkulatu beheko erpinak dituzten tetraedroen bolumenak:

a) (2, 1, 4); (1, 0, 2); (4, 3, 2); (1, 5, 6)

b) (4, 1, 2); (2, 0, 1); (2, 3, 4); (6, 5, 1)

20 Kalkulatu koordenatu-ardatzek eta beheko planoak zehazten duten tetraedroaren bolumena:

π: 6x – 5y + 3z – 30 = 0

21 Aurkitu r : x y z 2 3 3 4 4 –+ == zuzenarekiko perpendikularra den eta (–1, 1, 0) puntutik igarotzen den π planoaren ekuazioa, eta kalkulatu π planoak eta hiru koordenatu-planoek zehazten duten irudiaren bolumena

22 P (0, 3, 8) eta Q (2, 1, 6) muturrak dituen zuzenkiaren erdigunetik igarotzen den plano perpendikularrak A, B eta C puntuetan ebakitzen ditu koordenatu-ardatzak.

Aurkitu ABC triangeluaren azalera.

26 Aurkitu A (–2, 3, 4)-rainoko distantzia B (3, –1, –2)-rainoko distantzia baino bi aldiz handiagoa duten puntuen leku geometrikoa.

27 A (4, 2, 0) eta B (2, 6, –4) puntuak emanda, aurkitu PA eta PB perpendikular egiten dituzten P puntuen leku geometrikoa.

28 Aurkitu honako plano hauetatik distantzia berera dauden puntuen leku geometrikoa:

π1: x + y – z = 1 eta π2: x – y + z = 1

Ebazteko

29 π: 2x – 3y + z = 8 planoa eta P (−1, 2, 0) puntua ditugu. Kalkulatu.

a) P-tik igarotzen den eta π-rekiko perpendikularra den zuzen baten ekuazioak.

b) P puntutik π planora dagoen d distantzia.

c) P-tik d distantzia berera dagoen π-rekiko plano paralelo baten ekuazioa.

30 a) Aurkitu π planoaren ekuazioa, jakinda barne hartzen duela r : xy z xy z 10 20 –++ = ++ = * zuzena eta σ: 2x – y + 3z + 1 = 0 planoarekiko perpendikularra dela.

b) Lortu π eta σ planoek zehazten duten zuzenaren ekuazio parametrikoak.

c) Aurkitu r zuzenak σ planoarekin eratzen duen angelua.

Proposatutako ariketak eta problemak

31 r : xz yz 23 0 40 – += = * eta π: x + 2y + 3z – 1 = 0 badira, aurkitu

π planoaren barruan dagoen, P(2, 1, –1) puntutik igarotzen den eta r-rekiko perpendikularra den zuzen baten ekuazioa.

32 a) Aurkitu A, B, C puntuak, jakinda r : x – 12 = y z 6 3 2 6 –+ = zuzenekoak direla eta (x = 0; y = 0; z = 0) plano koordenatuetan kokatuta daudela.

b) Zehaztu A, B, C puntuetako zein dagoen beste bien artean.

33 Zehaztu zuzen hauek komuna duten zuzen perpendikularra:

r : xy z xy 4 27 += + += * s : x y 20 30 –= += *

34 a) Aurkitu zein izan behar den p, baldin eta r1 eta r2 zuzenen norabideak perpendikularrak izatea nahi badugu:

r1: x y z 4 2 1 2 ––== r2: x p yp z 1 1 13 3 ––––==

b) Egiaztatu elkar ebakitzen dutela. Aurkitu ebaki-puntua eta zuzenak barne hartzen dituen planoaren ekuazioa.

35 Idatzi (1, 2, 1) puntutik igaro eta beheko zuzena perpendikularrean ebakitzen duen zuzenaren ekuazioa:

r : xy z xz 1 2 = += )

36 ABC triangeluaren erpinak 2x + y – 3z = 6 planoak koordenatu-ardatzekin dituen ebaki-puntuak dira. Aurkitu Y ardatzean dagoen B puntutik abiatzen den altueraren ekuazioa.

37 Zehaztu σ: x – 2y + 3z + 6 = 0 planoarekiko paraleloa den eta jatorritik 12 unitatera dagoen π planoaren ekuazioa.

38 P(1, 0, –1), Q(2, 1, 1) puntuak eta r : x – 5 = y = z 2 2 –+ zuzena izanda, aurkitu:

a) P-ren puntu simetrikoa r-rekiko.

b) P eta Q puntuetatik distantzia berera dagoen r-ko puntua.

39 a) Idatzi r eta s perpendikular ebakitzen dituen zuzenaren ekuazioak:

r : x y z

40 a) Aurkitu zein izan behar den k, r : x y z 2 –m m m

Z [ \

= = =

] ] ] zuzenak eta π: x – y + kz = 3 planoak

60°-ko angelua eratzeko.

b) k = 0 kasuan, kalkulatu zein izan litezkeen a-ren balioak P (a, a, a) distantzia berera egoteko r zuzenetik eta π planotik.

41 r : x 2 1 –= y + 1 = z + 1 zuzena eta π: x – y = 0 planoa ditugu. Kalkulatu zer azalera duen zuzenaren eta planoaren arteko ebaki-puntuak, P (1, −1, 1) puntuak eta puntu horren plano gaineko proiekzio ortogonalak eratzen duten triangeluak.

42 r : x y z m 1 2 1 4 1 –––== zuzena eta π: x + y + kz = 0 planoa ditugu. Aurkitu zein izan behar diren m-ren eta k-ren balioak kasu hauek betetzeko:

a) zuzena perpendikularra izateko planoarekiko.

b) zuzena planoan egoteko.

43 Aurkitu zein diren P(1, 2, 3) puntuaren simetrikoak α: x – 3y – 2z + 4 = 0 planoarekiko eta zuzen honekiko: r : xy xz 30 40 ––+= = )

44 π da 9x + 12y + 20z = 180 ekuazioko planoa. Aurkitu:

a) π-rekiko paraleloak izan eta 4 unitateko distantziara dauden plano paraleloen ekuazioak.

b) π planoak OX, OY, OZ ardatzekin hurrenez hurren dituen A, B, C ebaki-puntuak, eta AB eta AC bektoreek osatzen duten angelua.

c) Erpin moduan O koordenatuen jatorria eta A, B eta C puntuak dituen tetraedroaren bolumena

45 Idatzi jatorritik hurbilen (1, 3, 2) puntua duen planoaren ekuazioa.

46 Drone bat P (2 , –3, 1) puntuan dago, eta, zuzen eramanda, π: 3x + 4z + 15 = 0 planoko punturik hurbilenera bideratu nahi dugu.

a) Kalkulatu droneak jarraitu behar duen zuzenaren ekuazio parametrikoa.

b) Aurkitu dronea iritsiko den planoko puntu horren koordenatuak.

3 25 0

––m m =+ =+ = * s : x y z

= =+ =+ *

3 64 2 – m m

b) Kalkulatu zer distantzia dagoen r eta s artean.

47 Irudikatu 6 unitateko aldea duen kubo bat, erpin bat jatorrian jarriz, eta ondoz ondoko beste hiru erpinak, koordenatu-ardatzen gainean. Kalkulatu kuboaren diagonal batetik aurpegi bateko diagonalera egongo den gutxieneko distantzia, kontuan hartuz diagonalen zuzenek elkar gurutzatzen dutela.

48 a) r : xy xz 0 0 –+= = ) zuzena izanda, zer puntu egongo dira

π: 2x – y + 2z + 1 = 0 planotik 3 1 u-ra.

b) Lortu aurreko atalean aurkitutako puntuetatik 3 1 u-ra egongo diren π planoko puntuak

49 A(–1, 3, –1), B(–3, 1, –7) eta C(0, 5, 1) puntuak izanda:

a) Frogatu triangelu baten erpinak direla.

b) Kalkulatu B puntuak eta horren AC gaineko proiekzioak zehazten duten zuzenkiaren luzera.

50 Karratu batek aldeetako bat r : xy z xy z 32 20 22 0 –++ = += * zuzenean

du, eta beste bat, s : x y z 2 3 1 1 2 5 ––––== + zuzenean.

a) Kalkulatu karratuaren azalera.

b) Karratuaren erpinetako bat (0, 0, 0) bada, zein da r zuzenean dagoen beste erpina?

51 Aurkitu zein den P(3, 1, 4) puntutik hurbilen dagoen

x – z = 3 planoaren puntua, baita P puntu horren eta emandako planoaren arteko distantzia ere.

52 P(2, 1, –1), Q(1, 4, 1) eta R(1, 3, 1) puntuak izanda:

a) Egiaztatu ez daudela lerrokatuta, eta kalkulatu zehazten duten triangeluaren azalera.

b) V(1, 1, –1) puntutik P, Q eta R puntuetako bakoitzera zuzenak marraztuz gero, piramide bat zehaztuko dugu. Kalkulatu piramide horren altuera eta bolumena.

53 Jakinda r' dela honako zuzen honek

r : x y z 2 1 1 1 2 2 –––==

α: x – 3y + 2z + 12 = 0 planoaren gainean duen r ' proiekzio ortogonala, idatzi zer ekuazio duen.

54 A(3, 0, 0), B(0, 3, 0) eta C(0, 0, 3) puntuak tetraedro baten hiru erpin dira. D laugarren erpina dago

P (1, 1, 1) puntutik igarotzen den eta A, B, C puntuek zehazten duten π planoarekiko perpendikularra den r zuzenean. Aurkitu D puntuaren koordenatuak, jakinda tetraedroaren bolumena 18 u3 dela.

55 Aurkitu A(1, –1, 0) eta B(2, 3, –4) puntuetatik distantzia berera dauden P(x, y, z) puntuen leku geometrikoa. Egiaztatu AB -rekiko perpendikularra den plano bat lortzen duzula eta AB-ren erdiko puntutik igarotzen dela.

56 r zuzena eta π planoa ditugu:

r : xy z xy z 22 22 20 – –++ = += * π: ax + y + z – b = 0

a) Kalkulatu a eta b zein izan behar diren, π planoak barne har dezan r zuzena.

b) Zehaztu a-ren eta b-ren balioak, r paraleloa izateko π planoarekiko

57 Zentroa C(1, 1, –1) puntuan eta aldeetako bat beheko zuzenaren gainean dituen karratu bat daukagu:

r : x y z 1 2 1 1 0 1 –––==

a) Idatzi karratu hori dagoen planoaren ekuazioa.

b) Kalkulatu karratuaren aldearen luzera.

58 Ondoko irudian, kalkulatu zer

angelu eratzen duten BC zuzenak eta

B puntua AD aldearen erdiko puntuarekin lotzen duen zuzenak A

59 r : xy z xy 32 10 10 –+= += * zuzena daukagu.

a) Zehaztu zein den r perpendikular ebaki eta (0, 2, 2) puntutik igarotzen den s zuzenaren ekuazioa, eta r eta s zuzenen arteko P ebaki-puntuaren koordenatuak.

b) Aurkitu r eta s zuzenak barne hartzen dituen π planoaren ekuazioa, eta P-tik igarota π planoarekiko perpendikularra den t zuzenaren ekuazioa.

c) Q puntua t-ko edozein puntu bada, kalkulurik egin gabe, azaldu zer erlazio dagoen Q-tik r-ra, s-ra eta π-ra dauden distantzien artean.

60 Aurkitu zein den koordenatuen jatorritik 1 u distantziara dagoen mx + y + z – (m + 1) = 0 familiako planoa.

61 a) Zehaztu zein izan behar diren a eta b parametroen balioak, hiru plano hauek zuzen berean ebaki dezaten elkar:

π1: x + ay + z = 0

π2: x + y – 2z = b

π3: –2x + y + z = –2

b) Aurkitu koordenatuen jatorriak zer simetriko daukan hiru planoen zuzen komunarekiko.

62 A (0, 0, 0) eta B (1, 1, 1) triangelu baten bi erpin dira, eta

C hirugarren erpina r : xy z 2 1 = = ) zuzenean dago. Trian-

geluaren azalera / 22 u2 bada, zein izan daitezke C-ren koordenatuak ?

Proposatutako ariketak eta problemak

63 Aurkitu beheko bi planoetatik distantzia berera dauden

r : x y z 2 1 1 1 3 –= + = zuzeneko puntuak:

Galdera teorikoak

76 Zuzena ala okerra? Arrazoitu erantzuna eta eman adibideak.

] ] ]

–=+ =+ =+

3 6 n

––m mn Z [ \

64 A(1, 3, −1), B (1, 5, 4), C (2, 0, 2) izanda, aurkitu zein den A , B , C puntuekin batera 7 u3-ko bolumena duen tetraedro bat eratzen duten puntuen leku geometrikoa.

65 a) Aurkitu α: 3x + y – 2z + 1 = 0 eta β: x – 3y + 2z – 3 = 0 planoetatik distantzia berera dauden puntuen leku geometrikoa.

66 Aurkitu 2x – y + 2z = 2 x = y planotik 1 unitateko distantziara dauden x = y planoko puntu guztien leku geometrikoaren ekuazioak. Deskribatu lortutako irudia.

67 a) Idatzi x2 + y2 + z2 – 2x – 4y + 4 = 0 esferak P(1, 2, 1) puntuan duen plano ukitzailearen ekuazioa.

b) Zer puntu da P-rekiko diametralki aurkakoa emandako esfera horretan?

68 Aurkitu x – 2z – 8 = 0 eta 2x – z + 5 = 0 planoekiko ukitzailea den esferaren ekuazioa, zentroa zuzen honetan badu:

a) ax + by + cz + d = 0 ekuazioak plano bat adierazten du:

I) a = 0 eta b = 0 badira, XY planoarekiko perpendikularra da.

II) b = 0 eta c = 0 badira, YZ planoarekiko paraleloa da.

III) a = 0 eta c = 0 badira, Y ardatzarekiko perpendikularra da.

b) x + y – 2z – 5 = 0 planoaren eta x = y = z zuzenaren arteko distantzia ezin da kalkulatu.

c) Zuzen hauen ebaki-puntua ezin da lortu:

r : x y z 2 1 6 21 6 23 ––––== s : x y z 2 3 2 23 4 ––= + =

d) A (x1, y1, z1) puntua π: ax + by + cz + d = 0 planoan badago eta B (x2, y2, z2) puntuak AB • (a, b, c) = 0 betetzen badu, orduan B ∈ π

e) Zuzen bat perpendikularra bada plano batean dagoen zuzen batekiko, plano horrekiko perpendikularra ere bada beti.

f) α: x + y – z = 1 eta β: x – y + z = −2 planoen arteko distantzia 0 da.

*

r : x y 2 0 – = =

70 Aurkitu r = 27 erradioa duen, P(1, 2, −3) puntutik igarotzen den eta zentroa r: x = y + 1 = z zuzenean duen esferaren ekuazioa.

g) Elkar gurutzatzen duten bi zuzenek eratzen duten angelua da zuzen horien plano beraren gaineko proiekzio ortogonalek eratzen duten angeluaren berdina.

h) α eta β planoek zuzen batean elkar ebakitzen badute, ez dago α eta β-rekiko distantziakidea den planorik.

i) x 2 + y 2 + z 2 + 2x –2y + 8 = 0 ekuazioa esfera bati dagokio.

77 Zehaztu P (x0, y0, z0) edozein puntuk koordenatu planoen gainean duen proiekzio ortogonala.

78 Zer baldintza bete behar du P (x, y, z) edozein puntuk P-tik A(1, 0, 0) eta B (0, 0, 1) puntuetara dagoen distantzia berdina izateko? Zer adierazten du baldintza horrek?

72 Aurkitu (0, 0, 3)-tik eta z = –3 planotik distantzia berera dauden espazioko puntuen leku geometrikoa.

73 Aurkitu (0, 5, 0) eta (0, –5, 0) puntuetarainoko distantzien arteko kendura 4 duten puntuen leku geometrikoa.

74 a) Idatzi A(4, 1, –3) eta B(3, 2, 1) puntuetatik igaro eta zentroa

x y z 2 8 1 3 1 4 –––== + zuzenean duen esferaren ekuazioa

b) Zein da esfera horrek B puntuan duen plano ukitzailearen ekuazioa?

75 Idatzi esfera baten ekuazioa, jakinda zentroa r : xy z x 4 1 –+= += )

zuzenean duela eta x – y + 2z – 4 = 0 planoarekiko ukitzailea

dela P(3, 1, 1) puntuan.

Sakontzeko

79 r zuzena A puntuak eta d r norabide-bektoreak zehazten dute, eta s zuzena, B puntuak eta d s bektoreak. r eta s zuzenek elkar gurutzatzen badute:

a) Arrazoitu dist (r, s) = || |[ ,, ]| AB dd dd rs

rs # berdintza.

b) Arrazoitu r-rekiko eta s-rekiko perpendikular komuna

hau dela:

(, ,)

# # = =

(, ,) det det AX BX 0 0 dd d dd d rr s sr s *

80 P(1, –1, 3), Q(1, 2, 1) eta R (1, 0, –1) dira. Aurkitu P, Q eta R puntuek zehazturiko planoaren barruko zer S puntuk eratuko duten P, Q, R eta S erpineko paralelogramoa.

81 P(1, –1, 1) eta Q(3, –3, 3) puntuak dira x + y = 0 planoarekiko perpendikularra den plano baten barruan dagoen karratu baten aurkako bi erpin. Aurkitu gainerako erpinak eta kalkulatu karratuaren perimetroa.

82 Aurkitu x y z 25 16 9 1 2 2 2 ++ = gainazalak hiru plano koordenatuekin dituen ebaki-puntuak. Zer irudi lortu duzu? Zer izen du emandako gainazalak?

83 Aurkitu honako elipsoide honen zentroa eta ardatzen luzerak: 2x 2 + 3y 2 + z 2 – 8x + 6y – 4z – 3 = 0.

84 x 2 + y 2 + z 2 – 2x – 4y + 4z – 7 = 0, ekuazioa emanda, aztertu nola osatu ditugun zuriuneak C zentroa eta r erradioa dituen gainazal esferiko baten adierazpena lortzeko:

(x 2 – 2x + 1) + (y 2 – 4y + 4) + (z 2 + 4z + 4) – 7 = 1 + 4 + 4 →

→ (x – 1)2 + (y – 2)2 + (z + 2)2 = 16 → C(1, 2, –2); R = 4

Egin gauza bera beste ekuazio hauen kasuan:

a) x 2 + y 2 + z 2 – 4x + 6y – 12 = 0

b) x 2 + y 2 + z 2 – 2x + 2z + 1 = 0

c) x 2 + y 2 + z 2 – 4y + 2z – 4 = 0

d) x 2 + y 2 + z 2 – 2x – 2y + 2z + 7 = 0

Zer gertatzen da zero edo zero baino txikiagoa den erradioa lortuz gero?

85 Adierazi zertan datzan honako bi irudi hauetako bakoitza:

x 2 + y 2 + z 2 + 2x – 10y + 25 = 0

x 2 + y 2 + z 2 + 2x – 10y + 25 ≤ 0

1 a) Aurkitu zer distantzia dagoen P (1, –1, –2) puntutik igaro eta π: x + 2y + 3z + 6 = 0 planoarekiko paraleloa den planotik A (1, 0, 0) puntura.

b) Aurkitu A puntuak π planoarekiko duen simetrikoa.

c) Zer angelu eratzen du A-tik eta P-tik igarotzen den zuzenak π-rekin?

2 a) Aurkitu P (5, 1, 3)-tik eta Q (3, 7, –1)-tik distantzia berera dauden puntuen leku geometrikoa.

b) Egiaztatu lortu duzun π planoa PQ zuzenkiarekiko perpendikularra dela horren erdiko puntuan.

c) π planoak A, B eta C puntuetan ebakitzen ditu koordenatu-ardatzak. Kalkulatu ABC triangeluaren azalera.

d) Kalkulatu A, B, C eta O (koordenatuen jatorria) erpinak dituen tetraedroaren bolumena.

3 Zehaztu A (–3, 1, 6) puntuak x – 1 = y z 2 3 2 1 + = + ekuazioa duen r zuzenarekiko duen simetrikoa.

86 Inekuazio-sistema honek 1 u-ko lodiera duen gomazko pilota bat adierazten du:

a) Zein da pilotaren kanpo-diametroa?

b) Idatzi diametro bera duen baina 2 u-ko lodiera duen beste pilota bat adieraziko duen sistema.

c) Zer inekuazio-sistemak adierazten du 10 u-ko diametroa eta 1 u-ko lodiera duen pilota bat?

d) Zer sistemak adierazten du c) ataleko pilotaren modukoa den beste bat, baina z = 0 planoaren gainean dagoena?

87 3D inprimagailu batek pasta berezi batekin inprimatzen du. Idatzi zer jarraibide zehaztu behar dituzun bere pantailan (inekuazio-sistemen bidez) ondorengo objektu hauetako bakoitzaren kasuan. Kontuan izan inprimatzeko darabilen oinarria z = 0 planoak adierazten duela, eta objektu bakoitza Z ardatzean zentratu behar dela. Erabiltzen dituen unitateak zentimetroak dira.

4 P (0, 1, 0) eta Q (–1, 1, 1) triangelu baten bi erpin dira, eta S hirugarren erpina r : x z 4 1 = = ) zuzenekoa da. P eta S barne hartzen dituen zuzena perpendikularra da r-rekiko

a) Zehaztu S-ren koordenatuak.

b) PQS triangeluan, aurkitu PQ aldearen gaineko altueraren luzera

5 r : x y z

=+ = =+ * eta s : xy z xz 24 0 30 –+ += += ) zuzenak izanda:

32 5 4 –m m m

a) Idatzi r eta s perpendikular ebakitzen dituen zuzenaren ekuazioa.

b) Kalkulatu r eta s arteko distantzia.

6 a) Aurkitu esfera honen zentroa eta erradioa: S : x 2 + y 2 + z 2 – 4x + 2z – 20 = 0

b) Kalkulatu 3x – 4z + 5 = 0 planoak S ebakitzean zehazten duen zirkunferentziaren erradioa.

anayaharitza.es Ariketa hauen ebazpena.

Unibertsitatera sartzeko probarako

II. multzoa: Geometria

Geometriaren atala landu duzunean, hainbat problema mota ebazteko modua ematen duten oinarrizko kontzeptu eta teknikak ikasi dituzu. Gogoratu ditzagun horietako batzuk.

Badakizu aurkitzen bi zuzenetatik igarotzen den zuzena?

Nola lortu bi bektorerekiko perpendikularra den bektore bat?

Badakizu plano bat bere bektore normalarekin lotzen?

Teknika hauekin eta beste zenbaitekin, ariketa eta problema mordoa ebatzi ahal izango dituzu.

Badakizu aurkitzen puntu batetik plano batera dagoen distantzia?

Lotzen duzu paralelogramo baten azalera biderketa bektorial baten modulualrekin?

Lotzen duzu paralelepipedo baten bolumena hiru bektoreren biderketa mistoarekin?

Ariketen eta problemen adibideak

Unibertsitatera sartzeko ebaluazio-proban hainbat zailtasun motatako ariketak eta problemak topatu ditzakezu.

Pentsatu A(2, 1, 5) eta B(3, 4, 1) puntuak ditugula. Laser-izpi bat igorri da A puntutik. Kalkulatu zein izan behar den laser-izpi hori adierazten duen zuzenaren ekuazioa, B puntuan jo dezan.

Enuntziatu honetan ulertu behar duzuna da A eta B puntuetatik igarotzen den zuzena aurkitzeko eskatzen dizutela. Hau da, A puntutik igaro eta AB bektorea duen zuzena.

Aurkitu plano baten ekuazio inplizitua, jakinda P(1, 0, 0) puntutik igarotzen dela eta barne hartzen duela zuzen hau: : rx y z 1 4 3 1 –

== +

Planoarekiko perpendikularra den bektore bat bilatu behar duzu. Nola? Planoarekiko paralelo izango diren bi bektoretatik abiatuta.

• Horietako bat da zuzenaren norabide-bektorea, v (1, –4, 3).

• Beste bat, P-tik r zuzeneko A(1, 0, –1) puntura doan bektorea.

• Etab.

Bi zuzen ditugu:

Aurkitu r eta s zuzenen arteko distantzia.

Aurkitzeko bi modu dituzu:

r-tik s-ra dagoen distantzia = P-tik π-ra dagoen distantzia:

s barne hartu eta r-rekiko paraleloa den planoa.

Paralelepipedoaren bolumena Paralelogramoaren azalera

-tik s-rako distantzia = h

Problema hauek ebazteko behar izan diren teknikak ezkerrean berrikusita ageri direnak dira.

anayaharitza.es webgunean hau aurkituko duzu:

• Geometriako oinarrizko teknikak ikasteko bide bat, arintasuna eskuratu dezagun teknika horiek ulertzeko, erabiltzeko eta aplikatzeko.

• Unibertsitatera sartzeko proben problema-bilduma bat, ebatzitakoak, proposatutakoak, laguntza eta guzti emanda, jarraibideak emanda…

Autoebaluazioa

II. multzoa : Geometria

1 Zehaztu modulua 2 duten bektore guztien artean u "(1, –1, –1) eta v "(–1, 2, 1) bektoreekiko ortogonalak direnak.

2 u "(2, 0, 0), v "(1, 0, –1) eta w " (–2, 3, 2) bektoreak izanda, kalkulatu:

a) v " eta w " bektoreek zehaztutako paralelogramoaren azalera.

b) u " eta v " bektoreek eratzen duten angelua.

c) u " , v " eta w " bektoreek eraturiko paralelepipedoaren bolumena.

3 a) Kalkulatu a "(2, 0, 0) bektorearen b " (2, 2, 0) gaineko proiekzioaren koordenatuak.

b) Aurkitu a " -ren b " gaineko proiekzioaren luzera.

4 Lortu r : xy yz 0 2 –+ = = * zuzenaren norabide-bektorea eta idatzi bere ekuazio parametrikoak

5 Lortu plano baten ekuazioa, jakinda A (0, –1, 3) eta B (2, –1, 1) muturrak dituen zuzenkiarekiko perpendikularra dela eta zuzenki horren erdigunetik igarotzen dela.

6 Kalkulatu triangelu baten azalera, jakinda bere erpinak direla 2x + y + 2z – 2 = 0 planoak koordenatu-ardatzekin dituen ebaki-puntuak.

7 Idatzi Z ardatza perpendikular ebakitzen duen eta P (1, 2, 3) puntutik igarotzen den zuzenaren ekuazioa.

8 Zuzen hauek ditugu: r : x ax y z 20 0 ––

= = * eta s : xby yz 3 3 + + = = *

a) Zehaztu a ≠ 0 eta b ≠ 0 zer baliorekin izango diren r eta s paraleloak.

b) Ba al dago a ≠ 0 eta b ≠ 0 baliorik zuzenak bat etor daitezen?

9 Zehaztu zein izan behar den k-ren balioa r eta s planokideak izateko. Idatzi, ondoren, zuzen horiek barne hartzen dituen planoaren ekuazioa:

r: x yk z 11 0 –== s : x y z

12 Zuzen hauek ditugu:

a) Aztertu bere posizio erlatiboa a-ren balioen arabera.

b) Kalkulatu zer angelu eratzen duten a = 2 kasuan.

13 Aurkitu plano baten ekuazioa, jakinda P (1, 0, –1) puntutik igarotzen dela, r : xy z 20 0 –= = * zuzenarekiko paraleloa

1 = 0 planoarekiko perpendikularra.

14 π: x + y – z = 0 planoa eta P (1, 1, –1) puntua ditugu.

Lortu:

a) π planoko Q puntua, P eta Q puntuek zehazturiko s zuzena perpendikularra izan dadin π planoarekiko.

b) s zuzeneko R puntua, kontuan izanda R-tik π-ra dagoen distantzia P-tik π-ra dagoenaren bikoitza dela.

15 Aurkitu zuzen baten ekuazioa, jakinda α: x + y + z = 3 planoan dagoela, β: x = 0 planoarekiko paraleloa dela eta P (–1, 1, 1) puntuak β-rekiko duen puntu simetrikotik igarotzen dela.

16 Zuzen hauek ditugu:

a) Zehaztu bere posizio erlatiboa.

b) Aurkitu karratu baten azalera, jakinda bi alde r-ren eta s-ren gainean dituela.

17 Ondorengo zuzena eta planoa emanda, aurkitu β-rekiko plano paralelo bat, r zuzenetik 3 unitatera dagoena:

18 Aurkitu x = –y = z zuzeneko puntu bat, r : xy z 0 3 += = *

zuzenerako distantzia 1 unitatekoa izango duena

19 Aurkitu r zuzenak π planoaren gainean duen proiekzio ortogonalaren ekuazio inplizituak.

r : (x, y, z) = (1, 2, 3) + λ(1, 3, 0) π: x – y + 2z + 5 = 0

a) Egiaztatu r eta s zuzenek elkar gurutzatzen dutela.

b) Idatzi r eta s perpendikular ebakitzen dituen zuzenaren ekuazioa.

11 Aurkitu r : x – 1 = y + 2 = z zuzeneko zer puntu diren honako bi plano hauekiko distantziakideak:

20 Aurkitu honako plano hauetatik distantzia berera dauden puntuen leku geometrikoa:

α: x – y – 5 = 0 eta β: x + y + 3 = 0

21 x 2+ y 2 + z 2 – 2x + 6y – 39 = 0 esfera izanda, aurkitu:

a) Zentroa eta erradioa.

b) P (1, –3, 7) puntuan duen plano ukitzaileari dagokion ekuazioa.

➜ anayaharitza.es Ariketa hauen ebazpena.

III. multzoa

ANALISIA

8. Funtzioen limiteak. Jarraitutasuna

9. Deribatuak

10. Deribatuen erabilerak

11. Funtzioen adierazpena

12. Primitiboen kalkulua

13. Integral mugatua

8

Funtzioen limiteak.

Jarraitutasuna

Limiteak, analisirako oinarrizkoak

Limiteen kontzeptua eta kalkulua analisirako oinarrizko tresna direlako dira, batik bat, horren interesgarriak.

Limitera igarotzeko prozesua antzinarotik erabili izan da, aritmetikako, aljebrako edota oinarrizko geometriako prozedura errazen bidez ebatzi ezin ziren problemen soluzioak lortzeko. Hasiera batean, eta mende askotan zehar, limiteen esanahia eta erabilera intuiziozkoak izan ziren huts-hutsean. Eta horrela, K.a. iv. mendean, Eudoxok zenbait eremu kurbaturen azalera hurrenez hurreneko irudi zuzenen hurbilketa gisa lortu zuen. Arkimedesek (K.a. iii. mendea) metodo hori berori erabili zuen irudi espazialen azalerak eta bolumenak kalkulatzeko.

xvii. eta xviii. mendeetako kalkulu infinitesimalak ere limiteei buruzko intuiziozko ideia izan zuen oinarri, zehaztasun gutxiko ideia. xix. mendean, Cauchyk funtzioaren, jarraitutasunaren eta, batez ere, limitearen definizio batzuk eman zituen, eta horri esker, analisi matematikoa bere aurrekoek erabili zuten baino askoz ere oinarri sendoagoetan finkatu ahal izan zuen. Weierstrassek ezarri zituen gaur egun oraindik ere erabiltzen ditugun funtzio baten jarraitutasunaren, limitearen eta deribatuaren definizioak. Berari zor diogu, neurri handi batean, analisi matematikoan horren garrantzitsuak diren formalismoa eta gaur egungo zorroztasuna barneratu izana; alegia, analisiari eraginkortasun, zorroztasuna eta sinpletasun maila altuak eman dizkioten ezaugarriak.

Weierstrass, analisi modernoaren aita

Karl Weierstrass Alemanian jaio zen, 1815ean. Aitak behartuta, Zuzenbidea ikasi zuen Bonnen, baina ez zuen inoiz titulua lortu. 24 urte zituela, Münsterreko Irakasle Eskolan sartu zen bigarren hezkuntzako irakasle gisa prestatzeko. Han hasi zitzaizkion matematikak erakargarri egiten, irakasle on baten eraginez. 1841etik aurrera, eta 14 urtez, institutuetan eskolak eman zituen eta bere kabuz lan egin zuen etengabe; baina, zailtasun ekonomikoak zituela eta, ezin izan zuen gutun-trukerik egin zientzia arloan. Hala ere, analisi matematiko modernoan eragin handiena izan zuen pertsonetako bat izan zen.

1854an Königsbergeko unibertsitateak honoris causa doktore titulua eman zion analisi matematikoan egindako lanengatik, eta 1856an matematika-irakasle izendatu zuten Berlingo Errege Eskola Politeknikoan, eta bertan lan egin zuen 1897an hil zen arte. Ikasleen artean izen handiko matematikari garrantzitsu asko izan zituen, besteak beste, Sofia Kovalevskaia ospetsua.

Karl Weierstrass (1815-1897).

Sofia Kovalevskaia: emakume zientzialari baten bide zaila Moskun jaio zen, xix. mendearen erdialdean, emakumeen bizitza etxe-eremura mugatuta zegoen garaian. Matematika arloko ezagutzekiko interes handia zuen familia batean hazi zen, eta Alemaniara joan nahi zuen ikastera. Sofia izan zen Europan unibertsitate-irakasle postua lortu zuen lehen emakumea. Baina bidea ez zen erraza izan. Hamahiru urterekin, aitak jakin gabe ezkutuan, aljebra-liburuak irakurtzen zituen. Urte batzuk geroago, geometria analitikoa eta kalkulu infinitesimala ikasi zituen. Baina bere ezagutzak eta prestakuntzak aurrera egin ahala, gero eta nabariagoak ziren emakume batek zientzia-munduan parte hartzeko zituen zailtasunak. 1869an, Heidelbergeko unibertsitatean sartzen saiatu zen, eta, ahalegin asko egin ondoren, entzule gisa onartzea lortu zuen. 1870ean, Berlinera bizitzera joatea erabaki zuen Karl Weierstrassen eskoletara joan ahal izateko. Baina unibertsitate hura are zorrotzagoa zen, eta entzule gisa parte hartzen ere ez zioten utzi. Orduan, zuzenean jarri zen harremanetan Weierstrassekin, klase partikularrak hartzeko. Weierstrass txundituta geratu zen Sofiaren talentu matematikoarekin, eta ordutik emakumearen lana babestu eta zabaldu zuen, eta bere eragin akademikoa erabili zuen doktore titulua lor zezan. Hala ere, garai hartako generozailtasunek ez zioten Europako unibertsitate batean ere lan egiten utzi, ezta Errusia jaioterrian ere. 1884an, Stockholmeko Unibertsitatean irakasle gisa onartu zuten, baina probaldi moduan, eta, beraz, ez zioten ordaintzen. 1889ra arte ez zuten ofizialki unibertsitate horretako irakasle izendatu.

Kovalevskaia bi urte geroago hil zen Stockholmen, matematika-lan garrantzitsua eta balio handiko hainbat obra utzita.

EBATZI

Sofia Kovalevskaia (1850-1891).

Funtzioen limiteen ideia grafikoa

Hasteko, lm i x " > = erako adierazpenen esanahia berrikusiko dugu, eman daitekeen kasuetako bakoitza dagokion adierazpen grafikoarekin lotuz

Limiteak x → +  ∞ denean

Limitea ez existitzea ere gerta daiteke. Ikus ditzagun bi adibide:

Limiteak x → –   ∞ denean

Pentsatu eta praktikatu

ERREPARATU

x → – ∞ denean ere gerta daiteke limiterik ez existitzea. x → + ∞ kasuan erabili ditugun adibideek balio dute kasu honetan ere, baina grafikoen orientazioa aldatuta; hau da, – ∞-ra jo dezatela eginez.

2

2 Esleitu lm i x –∞ " eta lm i x ∞ " + honako funtzio ezagun hauetako bakoitzari (marraztu horien grafikoa modu eskematikoan):

–1

2 –1

1 Deskribatu limite baten bidez honako adar hauetako bakoitza: a) b) –1

2 c) d)

2 –1

a) f (x) = x 2 b) f (x) = –x 2 c) f (x) = x 3

d) f (x) = –x 3 e) f (x) = sin x f ) f (x) = tg x

3 Irudikatu kasu hauetako bakoitzean esaten dena betetzen duen funtzio bat:

a) lm i x –∞ " f (x) = 4, lm i x ∞ " + f (x) = – ∞

b) lm i x –∞ " f (x) = 3, lm i x ∞ " + f (x) = 3

c) lm i x –∞ " f (x) = +∞ , lm i x ∞ " + f (x) = – ∞

d) lm i x –∞ " f (x) = – ∞ , lm i x ∞ " + f (x) = + ∞

Limiteak x → c denean. Alboko limiteak l c

c c lim xc –" f (x) = l lim xc –" f (x) = + ∞ lim xc –" f (x) = – ∞

Limitea c -ren ezkerretik : lim

xc –" f (x)

x-k c baino balio txikiagoak hartuz gero, c-ra hurbiltzen da

l c

c c lim xc " + f (x) = l lim xc " + f (x) = + ∞ lim xc " + f (x) = – ∞ f (x) definituta badago c-ren ezkerrera eta eskuinera, lm i xc " f (x) existitzeko, limite finituak izan behar ditu bi aldeetara eta limiteok bat etorri behar dute:

l c

() () limf xl limf xl xc xc

–= = " " + 4 Orduan, lm i xc " f (x) = l

Limitea c -ren eskuinetik : lim

xc " + f (x)

x-k c baino balio handiagoak hartuz gero, c-ra hurbiltzen da

Limitea c -n : lim xc " f (x)

x bi aldeetako edozeinetatik hurbiltzen da c-ra.

BEGIRATU

c

Kasu hauetan ez da existitzen limiterik: l c c

lm i xc " f (x) ez da existitzen lm i xc " f (x) ez da existitzen lm i xc " f (x) ez da existitzen

Pentsatu eta praktikatu

4 Deskribatu adar hauen limiteak: a) b) c)

5 Adierazi honako sei baldintzak betetzen dituen kurba bat:

lim

xc –" f (x) = + ∞ eta lim xc " + f (x) = + ∞ badira, ez dugu lm i xc " f (x) = + ∞ esaten; lm i xc " f (x) ez dela existitzen esaten dugu. Alboko limiteak finituak direnean eta bat datozenean baino ez da existitzen.

Teoria apur bat: ikas dezagun limiteak definitzen

Matematikan, urrats sendoak emateko, oinarrik behar bezala ezarrita egon behar dute. Eta unitate honen oinarria limitearen kontzeptua da. Orain arte intuiziozko ikuspegiak, interpretazio grafikoak erabili ditugu. Baina nola definitu zorrotz eta zehatz limite bat zer den?

Aurreko orrialdeetan ikusi ditugun limiteetako batzuk definituko ditugu eta zehatz aztertuko ditugu definizio horietako alderdi garrantzitsuenak. Hurrengo ikasturteetan (hau da, unibertsitatean) matematikak lantzen jarraitzen baduzu, definizio hauek finkatuko dituzu eta horietatik abiatuta limiteen propietate guztiak zorrotz ondorioztatzen ikasiko duzu.

Maila honetan, oraingoz, limiteak zehatz enuntziatzeko prozesua lantzen hasita konformatuko gara.

Nola definitu zehaztasunez lim x ∞ " + f(x) = l dela

Adierazpen horrekin esan nahi duguna da f (x) «asko hurbiltzen zaiola» l-ri x «oso handia egiten denean». Zehatzago esanda:

lm i x ∞ " + f (x) = l ⇔ f (x) guk nahi bezain hurbil egon daiteke l-tik. Horretarako nahikoa izango da x-ri nahikoa balio handiak ematea

Oraindik hobeto egiten saiatuko gara:

lm i x ∞ " + f (x) = l ⇔ ε zenbaki positibo bat emanda (arbitrarioki txikia), honako hau betetzen duen h aurki dezagun (behar bezain handia): x > h bada, orduan | f (x) – l | < ε

Ikus dezagun kasu zehatz bat lm i x ∞ "

1 510

+ = 5 dela egiaztatuko dugu:

ε > 0 hartuko dugu (eta ε oso txikia dela pentsatuko dugu). f (x)-tik 5era dagoen distantzia ε baino txikiagoa izateko, nolakoa izan behar da x?

Zenbat eta txikiagoa izan ε, orduan eta handiagoa hartu behar dugu h.

➜ Adierazi funtzioa eta kalkulatu limitea.

(*) Balio absolutua kendu dugu; izan ere, x-ren balio handietarako, x 1 15 –> 0.

Adibidez, ε = 0,001 bada → h = 0, 001 15 + 1 = 15 001.

Horrek esan nahi du «x > 15 001 bada, orduan x x 1 510 –+ milaren batera baino gutxiagora egongo dela 5etik» (frogatu kalkulagailuarekin eta eman x-ri 15 002 balioa).

Pentsatu eta praktikatu

1 lm i

x 100 320 ––= 3 dela jakinda, erabili ikasi berri duzuna h kalkulatzeko, ε-ren funtzioan.

Ondoren, kalkulatu h-ren zer baliorekin egiaztatzen den «x > h bada, oduan | f (x) – 3 | < 0,01».

Beste limite batzuen definizio zehatza

Esan dugun bezala, limiteak zehatz definitzeko prozesua azaletik landuko dugu. Baina gure mugak apur bat zabaltzeko, defini ditzagun beste limite batzuk, adibide moduan:

• x → +∞ denean funtzioak +∞-ra jotzen du lm i x ∞ " + f (x) = +∞ ⇔ f (x) guk nahi bezain handia izan daiteke. Horretarako, nahikoa dugu behar bezain handia izango den x hartzea.

Zehatzago esanda:

lm i x ∞ " + f (x) = +∞ ⇔ k zenbaki bat emanda (arbitrarioki handia), honako hau beteko duen h beste zenbaki bat aurki dezakegu (behar bezain handia izango dena):

x > h bada, orduan f (x) > k

• x → – ∞ denean funtzioak – ∞-ra jotzen du lm i x –∞ " f (x) = – ∞ ⇔ f (x) guk «nahi bezain negatiboa» egin dezakegu. Horretarako, nahikoa da x «behar bezain negatiboa» hartzea.

Zehatzago esanda:

lm i x –∞ " f (x) = – ∞ ⇔ k zenbaki bat emanda (arbitrarioki handia), honako hau betetzeko duen h beste zenbaki bat aurki dezakegu (behar bezain handia izango dena):

x < –h bada, orduan f (x) < –k

• x → c – denean funtzioak +∞-ra jotzen du lim xc –" f (x) = +∞ ⇔ x-k ezkerretik jotzen duenean c-ra, f (x)-ren limitea + ∞ da, baldin eta, x-k c baino balio txikiagoak hartu eta c-ra hurbiltzen denean f (x)-k nahi bezain balio handiak hartzen baditu

⇔ k zenbaki bat emanda, honako hau betetzen duen δ > 0 aurki dezakegu:

c – δ < x < c bada, orduan f (x) > k

• x → c denean, funtzioak l -ra jotzen du lm i xc " f (x) = l ⇔ f (x) l-tik oso hurbil egotea nahi badugu, nahikoa dugu x-ri c-tik behar bezain hurbil dauden balioak ematea

⇔ ε > 0 izanik, honako hau betetzen duen δ > 0 aurki dezakegu:

Zenbat eta handiagoa izan k, orduan eta handiago hartu behar dugu h.

Zenbat eta handiagoa izan k, orduan eta handiago hartu behar dugu h.

Zenbat eta handiagoa izan k, orduan eta txikiago hartu behar dugu δ.

Zenbat eta txikiago izan ε, orduan eta txikiago hartu behar dugu δ

2 Definitu honako limite hauek, irudi baten laguntzaz:

Limiteen eragiketa errazak

Eragiketak limite finituekin

Aztertu

Arrazoizkoena, beste eragiketarik egin gabe, honako hau egitea ematen du, ezta?:

Hori egitean, propietate hau erabili dugu:

lm i x ∞ " + [ f (x) – g (x)] = lm i x ∞ " + f (x) – lm i x ∞ " + g (x)

eta baliozkoa izango da limiteak existitzen badira eta finituak badira. Beraz, zentzuzkoa dirudi honako emaitza hauek onartzea:

lm i x " > f (x) = a existitzen bada eta finitua bada, eta lm i x " > g (x) = b existitzen bada

eta finitua bada, orduan honako erlazio hauek betetzen dira (denek balio dute x → – ∞ , x → + ∞ , x → c –, x → c + eta x → c kasuetarako):

1. lm i x " > [ f (x) + g (x)] = lm i x " > f (x) + lm i x " > g (x) = a + b

2. lm i x " > [ f (x) – g (x)] = lm i x " > f (x) – lm i x " > g (x) = a – b

3. lm i x " > [ f (x) · g (x)] = lm i x " > f (x) · lm i x " > g (x) = a · b

BEHATU

Ezkerreko emaitzetan, x → adierazpenak esan nahi du x → – ∞ , x → + ∞ , x → c –, x → c + zein x → c.

4. b ≠ 0 bada, lm i x " > () () () () lm lm i i gx fx gx fx b a x

> > H

x == "

" >

5. f (x) > 0 bada, lm i x " > [ f (x)g (x)] = () limf x () x lm gx i x " > > 9 C = a b

6. n bakoitia bada edo → lm i x " > ()fx n = () lmif xa x n n = " > n bikoitia eta f (x) ≥ 0 bada

7. α > 0, α ≠ 1 eta f (x) > 0 badira, lm i x " > [logα f (x)] = logα () lm fx i x " > 9 C = logα a

Zorrotz jokatuta, propietate horiek guztiak egiaztatu egin beharko lirateke; baina lan hori ikasturte honetarako eskatzen diren helburuetatik kanpo dagoenez, ez dugu egingo.

Pentsatu eta praktikatu

1 Aurkeztu ditugun propietate horiek guztiak oso errazak eta arrazoizkoak dira. Eta honela enuntziatu daitezke:

1. Bi funtzioren arteko batuketaren limitea funtzio horien limiteen arteko batuketa da.

Jokatu horrela 2tik 7ra bitarteko propietateekin, eta egin horietako batzuetan ageri diren murrizketei buruzko gogoeta, arrazoizkoak izan daitezen (adibidez: 4. propietatean zergatik da b ≠ 0?, 5. propietatean zergatik da f (x) > 0?, …).

Limite infinitua duten eragiketa batzuk

Ikusi berri dugun bezala, limite finituen eragiketak nola egin behar diren agerikoa izaten da. Eragiketa askotan, baina, limite infinituek parte hartzen dute. Bada, horien emaitzak ere argi ikusten dira. Adibidez:

lm i x " > f (x) = + ∞ eta lm i x " > g (x) = + ∞ badira, orduan:

lm i x " > [ f (x) + g (x)] = + ∞

Honela adierazten da: (+ ∞) + (+ ∞) = (+ ∞)

Hona hemen, limite infinituen arteko eragiketa batzuen emaitzak. Ez saiatu kasu horiek buruz ikasten. Aztertu ondo emaitza horietako bakoitza, egin proba batzuk eta jarri zenbait adibide, zeuk ebazteko. Horrela, arrazoizkoak irudituko zaizkizu eta gai izango zara gogoratzeko.

HISTORIAKO OHARRA

Irakurri Brahmagupta matematikari indiarrak () () a 0 motako adierazpen bati buruz vii.

mendean esandakoa:

«… zenbat eta txikiagoa izan zatitzailea, orduan eta handiagoa da zatidura.

Zatitzailea izugarri txikia eginez gero, zatidura izugarri handia izango da.

Baina magnitude honetakoa edo bestekoa dela esan litekeen bitartean, oraindik ez da muturreko magnitudera heldu, beti egongo baita hori baino zenbaki handiagoa. Beraz, zatitzailea minimo posiblera eramanez gero (hau da, zerora), zatidura mugagabe handituko da eta, arrazoiz, infinitua dela esan dezakegu».

Hau da, hain zuzen ere, guk iradokitzen dizugun arrazoitzeko modua («zatitzailea izugarri txikia eginez gero, zatidura izugarri handia egingo da»). Erabili kalkulagailua beharrezkoa duzunean, baina lortu ondorio argiak.

(+∞) + (+∞) = (+∞) adierazpenarekin hau esaten ari gara: +∞-ra jotzen duten bi funtzioren arteko batura, berdin dio funtzioak zein diren, infinitura jotzen duen beste funtzio bat da. Hori jakinda, zer esan dezakegu (+∞) – (+∞) eragiketaren emaitzari buruz?

Azter ditzagun zenbait adibide, edozer gauza gerta daitekeela ikusteko:

Aurreko adierazpen horiek (+

x ∞ " + [(x 2 + 5) – x 2] = 5

(*) x 3 askoz arinago hazten baita x 2 baino.

Ikusi dugunez, (+∞) – (+∞) adierazpenak, kasuaren arabera, (+∞), (– ∞) edo 5 ematen du. Hau da, bi funtziok infinitura jotzen dutela jakitea ez da nahikoa horien kendurak nora joko duen jakiteko

lm i x ∞ " + f (x) = +∞ eta lm i x ∞ " + g (x) = +∞ badira, zenbat izango da lm i x ∞ " + [ f (x) – g (x)]?

Galderari erantzuteko, kasu zehatz bakoitza sakonago aztertu behar dugu.

Indeterminazioa hau da: eragiketa batean parte hartzen duten funtzioen limiteak bakarrik jakinda, emaitzari limiterik ezarri ezin diogula onartzea. Beraz, limite horren balioa lortzera eramango gaituen ikerketa sakonagoa egin behar da

Hurrengo orrialdeetan, indeterminazio kasu ugarienak ebazteko zenbait metodo landu eta ikasiko ditugu. Garrantzitsuenak honako hauek dira:

Indeterminazio

Pentsatu eta praktikatu

→ 4 denean, honako emaitza hauek lortzen dira:

Hurrengo funtzio hauetako zein dira indeterminatuak

x → 4 denean? Kasu horietako bakoitza aztertuta, indeterminazioa badago, esan zer motatakoa den; eta ez badago, esan limitea zein den:

Infinituen konparazioa

→ +∞ bada, argi dago bai 2x-k bai x 2-k +∞-ra jotzen dutela. Horrez gain, argi dago x 2-k «askoz arinago jotzen duela» +∞-ra 2x-k baino. x 2, beraz, 2x baino goragoko ordenako infinitua dela esango dugu.

Zertarako balio du horrek? Bata bestearekin lehiatzen direnean, «irabazlea» gehien ahal duena dela jakiteko. Adibidez:

Baldin eta, x → > denean, f (x) → ±∞ eta g (x) → ±∞ badira, esaten da f (x) dela g (x) baino ordena handiagoko infinitua honako hau betetzen denean:

lm i x " > () () gx fx = ±∞ edo, bestela esanda, lm i x " > () () fx gx = 0

lm i x " > () () gx fx = l ≠ 0 bada, orduan f (x) eta g (x) dira ordena bereko infinituak.

Limiteak x → +  ∞ denean

Gogoan izan, x → +∞ denean, funtzio infinituen hiru familia handi daudela:

• Berretzaile positiboko berreketak: x3 , x , x 5 3 , …

• 1 baino berrekizun handiagoko esponentzialak: 1,5x; 2x; ex, …

• 1 baino oinarri handiagoko logaritmoak: log1,5 x; log10 x; ln x;

Erraza da ondorengo baieztapen hauek egiaztatzea:

• x-ren bi berreketa emanda, berretzaile handiena duena ordena handiagoko infinitua da: lm i x ∞ " +

• 1 baino berrekizun handiagoa duten bi funtzio esponentzial emanda, berrekizun handienekoa ordena handiagoko infinitua da:

lm i x ∞ " + ·, 1 000 15 2 x x = +∞

• 1 baino oinarri handiagoa duen edozein funtzio esponentzial edozein berreketa baino ordena handiagoko infinitua da:

lm i x ∞ " + · , x 1 000 12 x 20 = +∞

• Logaritmoek oso astiro jotzen duten infiniturantz. Edozein berreketa edozein logaritmo baino ordena handiagoko infinitua da.

• Batuketa batean zenbait batugai infinitu badaude, baturaren ordena da ordena handieneko batugaiarena: x 20 + 7 · 1,1x eta 1,1x ordena bereko infinituak dira.

Pentsatu eta praktikatu

1 Esan honako adierazpen hauetako zein diren infinituak

denean:

BEGIRATU

Definizio honetan, x → > adierazpenak esan nahi du +∞-rantz, –∞-rantz edo edozein c zenbakitarantz jotzen duela.

BESTE FUNTZIO INFINITU BATZUK

Berrekizun positiboa 1 baino txikiagoa duten esponentzialak, (–x)-ren mende.

1 baino txikiagoa den oinarri positiboa duten logaritmoak. log1/2 x = – log2 x –∞ x ∞ "

➜ Konparatu funtzioak infinituan.

➜ anayaharitza.es

Logaritmoen hazkunde-geldotasun etsigarria.

2 a) Ordenatu honako infinitu hauek txikienetik handienera:

b) Aurreko emaitzak kontuan izanda, kalkulatu:

Limiteen kalkulua x → + ∞ denean

Polinomioen arteko zatiketa

Zatiki aljebraikoen (bi polinomioren arteko zatiketa) limiteak oso modu errazean ebatziko ditugu zenbakitzailean eta izendatzailean mailarik handieneko gaiak zein diren kontuan hartuta.

f (x) = ' ' bx bx ax ax qq pp 1 1 –

–++ ++ zatikiak honela jokatzen du: b a x p – q .

• p > q bada, lm i x ∞ " + f (x) = ±∞ (limitearen zeinua a-ren eta b-ren zeinuen araberakoa izango da).

• p = q bada, lm i x ∞ " + f (x) = b a

• p < q bada, lm i x ∞ " + f (x) = 0 Adibidez:

GOGORATU

x → +∞ doanean, funtzio polinomiko batean mailarik handieneko gaiak hartzen du protagonismoa.

➜ anayaharitza.es Polinomioen arteko zatiketaren limiteak kalkulatzeko adibideak eta ariketak.

1

–2 3 + + = +∞ , izan ere, zenbakitzailearen maila izendatzailearena baino handiagoa da: zenbakitzaileak goragoko ordenako infinitua dauka izendatzaileak baino

Beste adierazpen infinitu batzuen arteko zatiketa

Aurreko erregela horrek zenbakitzailean, izendatzailean edo bietan adierazpen errodunak daudenean ere balio du. Erregela kasu horietan erabiltzean, honako hauek hartu behar ditugu kontuan:

• … ax n p + adierazpenak a p · x n/p adierazpenak bezala jokatzen du x → +∞ denean. • … ax n p + adierazpenak ez du limiterik x → +∞ denean, a negatiboa bada eta p bikoitia bada; izan ere ez dago definituta x-ren balio handietarako.

Adibidez:

Adierazpen infinituen arteko kenketa

Hiru kasu aztertuko ditugu, horietako bakoitza aurrekoa baino apur bat zailagoa

I. Begiz jota ikusten denean kenketako adierazpenak ordena desberdineko limiteak direla, zuzenean ezar diezaiekegu +∞ edo – ∞ limitea. Adibidez:

1. lm i x ∞ " + xx x xx 5 21 37 2 –– 3 2 + eo = +∞ Kenkizunaren maila 3/2 eta kentzailearen maila 1 delako.

2. lm i x ∞ " + () , x x 1 5 15 –

––x 2 4 fp = – ∞ 1 baino berrekizun handiagoa duen esponentzial bat berreketa bat baino ordena handiagoko infinitua delako

II. Eragiketa egin daitekeenean

Limitea begi hutsez ikusten ez bada (bi infinituak ordena berekoak direnean, esaterako), adierazitako kenketa egiten saiatuko gara, eta, ondoren, limitea kalkulatuko

f (x) kenkizunean, g (x) kentzailean edo bietan erro karratu bat badago, eragiketa ez dugu berehala kalkulatuko. Kasu horretan, bider eta zati f (x) + g (x) egingo dugu, eta, horrela, limitea kalkulatzeko oztopo zen erroen arteko kenketa ezabatuko

f (x) – g (x) = () () () ()]( )( ) () () () () [[ ] fx gx fx gx fx gx fx gx fx gx 22 + + =

eta praktikatu

1 Eragiketarik egin gabe, esan zein den honako adierazpen hauen limitea x → +∞ denean:

x)

2 Kalkulatu honako adierazpen hauen limitea x → +

III. Erro koadratikoak daudenean

Berreketa baten limitea

Berreketa baten limitea, kasu askotan, berrekizunaren eta berretzailearen limiteak zein diren jakinda kalkulatu daiteke. Adibidez:

1. lm i x ∞ " + (x 2 + 1)x – 3 = +∞, izan ere, (+∞)(+∞) motakoa da

2. lm i x ∞ " + x x 21 x + dn = +∞ , izan ere, (2)(+∞) motakoa da.

3. lm i x ∞ " + x x 21 x + bl = 0, izan ere, () 2 1 2 1 ∞ () (∞) = + + dn motakoa da

Baina lm i x ∞ " + f (x) = 1 eta lm i x ∞ " + g (x) = +∞ direnean, lm i x ∞ " + f (x)g (x) indeterminazio bat da, (1)(+∞) motakoa, eta kasu horiek banaka aztertu behar dira.

e zenbakiarekin erlazionaturiko berehalako limiteak

Iazko ikasturtean ikusi genuenez, e zenbakiaren definizioa n 1 1 n + dn segidaren limitea da. Beraz, hortik abiatuta, honako emaitza hauek argiak dira: lm i x ∞ " + x 1 1 x + dn = e, lm i

Horretan oinarrituta, beste limite hauek lortuko ditugu: •

i

"

1 1 x–+ dn = lm i x ∞ " + x e 1 1 x 1 1 ––+=dn> H

• lm i x ∞ " + x 1 2 1 x2 + dn = e, izan ere, 2x = y egiten badugu, lm i x ∞ " + y 1 1 y + eo geratzen da • lm i x ∞ " + x 1 1 ax + dn = lm i x ∞ " + x 1 1 x a + dn> H = e a • lm i x ∞ " + x 1 1 –axcm = e –a

• lm i x ∞ " + x 1 1 ax b + + dn = lm i x ∞ " + xx 1 1 1 1 ax b ++ ddnn = e a · 1 = e a

• lm i x ∞ " + x k 1 x + dn = lm i x ∞ " + / xk 1 1 x + dn = lm i x ∞ " + / xk 1 1 / xk k + dn> H = e k

Pentsatu eta praktikatu

3 Kalkulatu limite hauek x → +∞ denean:

a) x 1 5 1 x + dn b) x 5 5 1 x5 + dn c) x 5 5 1 x–5 + dn

d) x 1 5 1 5 + dn e) x 1 5 x + dn f ) x 1 5

g) x 5 5 x5 + dn h) x 1 1 –x5dn i)

–+ dn

➜ Aurkitu funtzio baten limitea balio jakin baterako.

EZ AHAZTU

lm x e i 1 1 x

ax b a ∞ += " +

+ cm

lm x k e i 1 x

x k ∞ += " + cm

4 Kalkulatu limite hauek x → +∞ denean:

a) x 1 1 x 32 –+ dn b) x 1 2 1 –x4dn

c) x 1 5 1 x3 + dn d) x 1 2 3 5 + dn

1 1 –

–5dn

e)

3dn f ) x 1 5 2

1 2 1

5 + dn

(1)(+∞) motako adierazpenak. Erregela praktikoa

Indeterminazio hauek e zenbakiarekin erlazionatuz ebazten dira. Batzuetan, ez dugu erlazio hori berehala ikusiko, eta, beraz, hona hemen indeterminazio hori ezabatzeko erregela praktiko bat: lm i

(1) 1 + () x 1 z erako berrekizuna jartzeko.

(2) f (x) – 1 = ()fx 1 1 1 –f (x) → 1 bada, orduan ()fx 1 1 –→ ∞

(3) Berretzailea bider eta zati f (x) – 1 egingo dugu, adierazpenak itxura hau har dezan: () x 1 1 () x z + z

(4) ϕ

orduan:

1 Kalkulatu limite hau:

• (1)(+∞) motakoa denez, aurreko erregela erabil dezakegu:

Berriro ebatziko dugu urrats guztiak emanez, «erregela praktikoa» izango ez bagenu

Pentsatu eta praktikatu

5 Ebatzi limite hauek aurreko erregela erabiliz. Gero, ebatzi ariketetako bat urrats guztiak emanez:

Limiteen kalkulua x → – ∞ denean

Limiteak x → – ∞ denean kalkulatzeko, kontuan hartuko dugu honako hau: lim x –∞ " f (x) = lim x ∞ " + f (–x)

Beraz, x-ren lekuan –x jartzean lortzen dugun adierazpenaren ∞ lm i x " + kalkulatuko dugu. Adibidez:

1. lim x –∞ " (x 2 – 5x + 3) = lim x ∞ " + [(–x)2 – 5(–x) + 3] = = lim x ∞ " + (x 2 + 5x + 3) = +∞

Ikusten duzunez, limitea kalkulatzeko nahikoa litzateke aldaketa mailarik handieneko gaian bakarrik egitea, horrek baino ez baitio eragiten azkeneko emaitzari. (Buruz ere egin daiteke, berretzailea bikoitia edo bakoitia den ikusi, eta, beraz, berretura positiboa edo negatiboa izango den kontuan hartuz).

2. lim x –∞ " (3x 3 + 2x – 1) = lim x ∞ " + [3(–x)3 + …] = lim x ∞ " + (–3x 3 + …) = – ∞

3. lim x –∞ " xx 5111 –42 + = + ∞

Maila handieneko gaia, x 4 , bikoitia delako; eta horren koefizientea, 5, positiboa

4. lim x –∞ " xx x 43 5 – 32++ = + ∞

Maila handieneko gaia, x 3 , bakoitia delako; eta horren koefizientea, – 4, negatiboa: – · – = +

5. lim x –∞ " xx57 8 32++ ez da existitzen

Errokizuna negatibo egiten delako x → – ∞ denean.

Funtzio infinituen familiak x → –∞ denean

5. epigrafean funtzio infinituen hiru familia ikusi ditugu x → + ∞ kasurako. Infinituak dira baita x → – ∞ kasurako ere? Bai, baina aldaketa batzuekin:

• Berretzaile positiboko berreketak, errotzaile bikoitiko erroetan errokizuna negatiboa ez dela zainduz x → – ∞ kasuan.

• 1 baino berrekizun txikiagoko esponentzialak.

• Logaritmoak ez daude definituta balio negatiboetarako, eta, beraz, x-k → – ∞-rantz jo dezan (–x) jarriko dugu x-ren tokian:

funtzioen limiteak zein diren berrikusteko ariketak.

Ebatzitako ariketa

1 Aurkitu adierazpen hauen limiteak x → – ∞ denean:

a) xx xx A 10 73 32 1 ––2 3 + + =

a)

Limitea zuzenean eman genezake, kontuan hartuz zenbakitzailea izendatzailea baino maila handiagokoa dela (± ∞) eta zenbakitzailea negatiboa eta izendatzailea positiboa dela

b) xx xx B 67 35 3 –32 32 + =

c) x xx C 25 52 –3 + =

b) lm i

c) Ez da existitzen

Kontuan izan 5x 3 – 2x errokizunak balio negatiboak hartzen dituela x → – ∞ denean.

d) x x x D 35 2 43 – 3 2 + + =

d)

e) x x x E 35 2 43

3

e) (+ ∞) + (–

motako indeterminazioa da. Ebazteko, kontuan hartu lehenengo batugaiaren maila 3/2 dela, eta bigarren batugaiarena, 1. Beraz, lm i

f ) xx xF 2 = ` j

g) xx xG 2 += + ` j

h) x H 1 2 3 5x +=cm

g)

1 Eragiketarik egin gabe, esan zein den honako adierazpen hauen limitea x → – ∞ denean:

2 Kalkulatu adierazpen hauen limitea x

denean:

Funtzio baten limitea puntu batean. Jarraitasuna

Ezagun ditugun emaitza batzuk gogoratu eta laburbilduko ditugu:

Puntu bateko limitea eta alboko limiteak

f (x) funtzioa c-ren ezkerrera eta eskuinera definituta dagoen funtzioa da

Alboko limiteak existitzen badira eta bat badatoz, lim xc –" f (x) = lim xc " + f (x) = l

orduan f (x)-ren limitea existitzen dela esaten dugu, eta l da: lim xc " f (x) = l

Jarraitutasuna puntu batean

f jarraitua da c puntuan, lim xc " f (x) = f (c) bada.

Hau da, f jarraitua bada c-n, hiru baldintza hauek betetzen dira:

— lim xc " f (x) existitzen da eta finitua da

— f definituta dago c puntuan. Hau da, f (c) existitzen da

— f (x)-ren limitea c puntuan bat dator f-k c-n duen balioarekin.

Beraz, funtzio batek jarraitua izateari utziko dio baldintza horietakoren bat betetzen ez badu:

I II III

ADI!

Ikusten duzunez, c puntuko limitea definitu dugunean, aipatu ere ez dugu egin funtzioak c-n zer balio duen, f (c). Hau da, c puntuko limitea definitzeko, berdin dio f ez egotea definituta c-n; edota definituta badago, berdin dio balioa zein den.

FUNTZIO ERREALEN

JARRAITUTASUNA ETA

NEURTZEAN EGITEN DIREN ERROREAK

Fenomeno errealei buruzko funtzioek kausak eta efektuak erlazionatzen dituzte sarritan.

Autoklabe bateko tenperatura eta barruko presioa erlazionatzen dituen P = f (T ) funtzioan, tenperatura kausa da, eta presioa, efektua.

f jarraitua izateak hau esan nahi du: kausan «aldakuntza txikiak» eginda, efektuan «aldakuntza txikiak» gertatzen dira.

lim

c c c x c f (x) f (c) f ez dago definiturik c-n f -k ez du limiterik c-n

Funtzio bat etena denean c puntuan, baina puntu horretan limitea existitzen denean, etena saihesgarria dela esaten dugu.

Gainerako kasuetan, etena saihestezina da. Jauzi finitu bat dagoelako gerta daiteke (alboko bi limiteak finituak dira, baina desberdinak), jauzi infinitu bat dagoelako (alboko limiteetako bat, edo biak, infinituak dira), edo alboko limiterik ez duelako. Adibidez:

IV V VI

Magnitude erreal batean hartzen ditugun neurriak hurbilduak direnez beti (sekula ez zehatzak), jarraitutasunak modua ematen digu guk nahi adina hurbiltzeko efektuaren baliora (presioa); izan ere, horretarako nahikoa izango da kausaren balioa (tenperatura) beharrezkoa den adina kontrolatzea. Funtzioan etena egongo balitz, horrek efektuetan aurreikuspen gabezia ekarriko luke, kausa neurriaren zehazgabetasunarekin lotuta baitago beti.

ETEN MOTAK

• Saihesgarria: I.a eta III.a

• Jauzi finitua: II.a eta IV.a

• Jauzi infinitua: V.a

Jauzi finitua Jauzi infinituz Ex da existitzen lim lim lim

➜  Jolas egin puntu bateko limitearekin.

Limiteen kalkulua x → c denean

Limiteak funtzioa jarraitua den puntuetan

Arrazoizkoa ematen du lim x 4 " (x + 1)2 = 52 = 25 izatea. Horrek ematen du egokiena, bai. Baina zer oinarri teorikoren arabera egiten dugu hori? Ikus dezagun: (x + 1)2 funtzioa jarraitua da Á osoan, eta, jakina, x = 4 puntuan. Beraz, funtzioak x = 4 puntuan duen limitea bat dator funtzioak x = 4 denean hartzen duen balioarekin

Orokorrean, hori gertatzen zaie oinarrizko funtzio guztiei (halakoak dira normalean erabiltzen ditugun guztiak) definituta dauden puntu guztietan

f (x) funtzioa adierazpen analitikoaren bidez emanda dagoen oinarrizko funtzio bat bada eta x = c puntuan definituta badago, orduan:

lim xc " f (x) lortzeko, besterik gabe f (c) kalkulatuko dugu

Zatika definituriko funtzioak. Limiteak eten-puntuan

Ikus dezagun nola kalkulatzen den honako funtzio honek x = c puntuan duen limitea: f (x) = (), (), fx fx xc xc < > 1 2 * , eta hor f1 (x) eta f2 (x) funtzio jarraituak dira.

f1 (x) jarraitua bada c puntuan, lim xc " f1 (x) = f1 (c) existitzen da, eta, beraz, lim xc –" f1 (x) = f1 (c).

Era berean, lm i xc " f2 (x) = f2 (c) ere existitzen da eta, beraz, lim xc " + f2 (x) = f2 (c). Ondorioz:

• f1 (c) = f2 (c) bada, lim xc " f (x) limitea existitzen da eta balioa hori da.

Kasu horretan, funtzioa x = c puntuan definituta egongo balitz (edo f1 delako x ≤ c kasuan, edo f2 delako x ≥ c kasuan), orduan f (x) jarraitua da c puntuan.

• f1 (c) ≠ f2 (c) bada, lim xc " f (x) ez da existitzen.

1 Kalkulatu lim x1 " f (x), baldin eta existitzen bada, honako hau kontuan hartuz:

(x) = ,

➜ Adierazi zatika definitutako funtzioak.

Indeterminazioak x → c denean

Limiteak kalkulatzean, kasurik zailenak (eta interesgarrienak), dakizun moduan, indeterminazio motaren bat agertzen dutenak dira. Ikus ditzagun garrantzitsuenak

• Polinomioen arteko zatiketa, () () 0 0 indeterminazioa () () lm i Qx Px xc "

• (c) ≠ 0 bada, orduan () () () () lm Qx Px Qc Pc i xc = " (ez da indeterminazioa).

• Q (c) = 0 bada, bi kasu gerta daitezke:

— P (c) = 0. Orduan zatikia sinplifikatu egin daiteke, zenbakitzailea eta izendatzailea zati x – c eginez, eta hau lortzen dugu () () () () () () () () lm i Qx Px lm Qx xc Px xc lm Qx Px ii –

xc xc xc 1 1 1 1 == "" "

— P (c) ≠ 0. Orduan limitea ± ∞ da. Limitea desberdina izan daiteke c-ren ezkerrera eta eskuinera. Hori jakiteko, kalkulagailua erabilita lortuko dugu zenbat den zatidura c-tik hurbil dauden alde bateko eta besteko x-ren balioetarako

Beharbada lagungarri izango duzu aurreko ikasturtetik ezagutzen duzun honako organigrama hau: . .= adierazpideak «-(r)en ordez jar daiteke» esan nahi du.

(Kasu honetan, 1en eskuinera – ∞ da, eta ezkerrera, + ∞).

• Beste zatiketa batzuk, () () 0 0 indeterminazioa Ikus ditzagun () () 0 0 indeterminazioa agertzen duten beste adierazpen batzuk

Indeterminazio hori ebazteko, bi erroak errotzaile komunera laburtu behar ditugu:

ZERGATIK?

existitzen. Zergatik? x → 2– denean x < 2 bada, x – 2 < 0 da; aldiz, x 2 > 0 eta (x + 3)3 > 0 dira. Beraz, x → 2– denean, errokizuna negatiboa da. Seigarren erroa ez da existitzen.

• Kenketak, (+ ∞) – (+ ∞) indeterminazioa

Mota honetako indeterminazioak ezabatzeko modurik onena eragiketa egitea (kenketa) eta lortzen dugun adierazpena aztertzea da. Adibidez:

KONTUAN IZAN

Erro koadratikoen (erro karratuak) arteko kenketak daudenean, eta (0)/(0) motako indeterminazioa agertzen denean, konjugatuarekin biderkatu eta zatitu dezakegu, indeterminazioa kentzeko, eta gero sinplifikatu.

• (1)(+ ∞) indeterminazioak

Bai 225. orrialdean erabili genuen prozesua eta bai hortik lortzen den erregela erabil ditzakegu x → c denean limiteak kalkulatzeko.

• Berrekizunak 1era jotzen duela eta berretzaileak infinitura jotzen duela egiaztatuko dugu. Beraz, (1)(+ ∞) motako indeterminazioa da. Erregela erabil dezakegu:

Limiteak kalkulatzeko ahalmen handiko tresna

Iazko ikasturtetik ezagun dugun L’Hôpitalen erregelak deribazioa erabiltzen du zatiketen limiteak lortzeko. Eta trebetasun apur batekin, beste limite batzuen kasuan ere erabil daiteke (biderketak, berreketak...).

l’hôpitalen erregela. laburpen praktikoa

lm i x " > () () gx fx motako limiteek ( > kasu horretan – ∞, + ∞ edo zenbaki bat izanik) () () 0 0 edo () () ±∞ ±∞ motako indeterminazio bat ematen badute, zenbakitzailea

eta izendatzailea deribatuz eta deribatuen arteko zatiketaren limitea kalkulatuz lor daitezke (baldin eta existitzen bada)

Batzuetan, lehenengo urrats hori eman ondoren, beste indeterminazio bat agertzen da eta, beraz, berriro egin behar da prozesua

(∞) – (∞), (1)(∞) , … motako zenbait adierazpen nahikoa erraz jar daitezke zatiketa moduan, ondoren L’Hôpitalen erregela erabili ahal

ERREGELA L'HÔPITALENA DA?

10. unitateko hasierako irakurgaia kontuan hartuz, bidezkoago litzateke erregela horri Johann Bernoulliren izena ematea.

Guillaume L'Hôpital (1661-1704)

Jarraitutasuna tarte batean

Funtzio bat Á-ko tarte batean (finitua zein infinitua) jarraitua dela esaten da tarte horretako puntu bakoitzean jarraitua bada

Normalean erabiltzen ditugun oinarrizko funtzioak jarraituak dira definituta dauden puntu guztietan. Adibidez, funtzio polinomikoak, sinu eta kosinu funtzio trigonometrikoak edo esponentzialak, guztiak dira Á osoan jarraituak; logax funtzioak (0, +∞) tartean dira jarraituak; x funtzioa [0, + ∞) tartean da jarraitua; eta abar. Dena dela, aukera daukagu puntu batean edo gehiagotan etenak diren funtzioak eraikitzeko. Adibidez:

y = () () ≤ fx fx xa xa > 1 2 *

Zatika definituta dauden funtzioek etenak dituzte lotura-puntuetan, beti ere puntu horietan alboko limiteak bat ez badatoz. Hau da, etenak dira beti, f1(a) = f2(a) kasuan izan ezik.

Honako funtzio hau etena da puntu guztietan. «Dirichleten funtzioa» du izena eta, jakina, oinarrizkotik ez du ezer.

y = D (x) = x x 0 1 ,baldineta irrazionalabada ,baldineta arrazionalabada

Funtzio baten tarte bateko jarraitutasuna aztertzeko, esandako hori guztia kontuan izan eta puntu korapilatsuetako jarraitutasuna zorrotz aztertuko dugu.

Badira zenbait teorema garrantzitsu tarte batean jarraituak diren funtzioei buruz. Bada, teoria horiek kontuan hartuta, aztertzen ari garen funtzioa jarraitua bada, baieztapen batzuk egin ditzakegu funtzio horren zenbait jokabideri buruz; baieztapen agerikoak, baina garrantzitsuak. Ikus ditzagun

Bolzanoren teorema

f (x) jarraitua bada tarte itxi batean eta muturretan zeinu desberdinetako balioak hartzen baditu, orduan tarte horretan X ardatza ebakiko du. Hau da:

f (x) jarraitua bada [a, b] tartean eta f (a)-ren zeinua ≠ f (b) -ren zeinua bada, orduan

f (c) = 0 betetzen duen c ∈ (a, b) existitzen da.

Teorema denez, egiaztatu egin beharko litzateke; baina emaitzak agerikoa ematen badu ere, egiaztapena oso zaila da, ikasturte honetan lantzeko zailegia.

Ebatzitako ariketa

1 Frogatu honako ekuazio honek

x 3 – 3x + 40 = 0

erro errealen bat duela

Hurbildu horren balioa hamarrenetara

f (x) = x 3 – 3x + 40 funtzioa hartuko dugu. Polinomikoa denez, jarraitua da. f-k hainbat puntutan zer balio hartzen duen kalkulatuko dugu, zeinu desberdineko bi aurkitzeko. Hauek aurkitu ditugu: f (– 4) = –12, f (–3) = 22.

Hau da, f jarraitua da [– 4, –3] tartean, eta f (– 4)-ren zeinua ≠ f (–3)-ren zeinua. Beraz, f (c) = 0 betetzen duen c ∈ (– 4, –3) existitzen da (Bolzanoren teorema).

c ekuazioaren erro bat da.

Hamarrenen balioekin haztamuka ibiliz, hau lortzen dugu: f (–3,8) = –3,472; f (–3,7) = 0,447. Beraz, ekuazioaren erro bat [–3,8; –3,7] tartean dagoela ziurtatu dezakegu, eta –3,7 zenbakia hamarren bat baino gutxiago hurbiltzen dela ekuazio horretako erro batera

Bolzanoren teoremaren ondorioak

Tarteko balioen teorema (Darboux)

f jarraitua bada [a, b] tartean, orduan f (a)-ren eta f (b)-ren bitarteko balio guztiak hartzen ditu.

Hau da, f (a)-ren eta f (b)-ren bitartean dagoen k zenbakia edozein dela ere, existitzen da f (s) = k betetzen duen s zenbaki bat, a < s < b izanik.

Tarteko balioen teorema Bolzanoren teoremaren berehalako ondorio bat da. Ikus dezagun beste bat:

f eta g funtzioak jarraituak badira [a, b] tartean, eta f (a) < g (a) eta f (b) > g (b) badira, orduan existitzen da f (s) = g (s) betetzen duen s ∈ (a, b) zenbaki bat.

Hau da, f eta g funtzioek (a, b) tarteko punturen batean elkar ebakitzen dute. Emaitza hori Bolzanoren teorema f – g funtzioari ezarrita lor dezakegu.

Weierstrassen teorema

f jarraitua bada [a, b] tartean, orduan maximo eta minimo absolutu bana ditu tarte horretan. Hau da, [a, b] tarteko c eta d bi zenbakiren kasuan hau betetzen da:

x ∈ [a, b] edozein dela ere, f (d ) ≤ f (x) ≤ f (c) da

Beraz, f (x)-ren balio guztiak maximoaren eta minimoaren artean daude

Ebatzitako ariketa

1 Frogatu f (x) = ln x eta g (x) = e –x funtzioen grafikoek punturen batean ebakitzen dutela elkar

Pentsatu eta praktikatu

2x 4 – 14x 2 + 14x – 1 = 0

f (1) = ln 1 = 0

g (1) = e –1 = 1/e ≈ 0,37 4 → f (1) < g (1)

f (2) = ln 2 ≈ 0,69

g (2) = e –2 ≈ 0,14 4 → f (2) > g (2)

Biak jarraituak direnez horien definizio-eremu osoan, eta, zehatzago esanda, [1, 2] tartean, 1 eta 2 bitarteko punturen batean ebakitzen dutela elkar ziurta dezakegu.

1 Bilatu ekuazio honek erroa duen lau tarte desberdin:

Bilatu – 4 eta 3 arteko tarteak. Egiaztatu f (1,5) < 0 dela, eta kontuan hartu

2 Egiaztatu e x + e –x – 1 eta e x – e –x funtzioek elkar ebakitzen dutela punturen batean

3 Arrazoitu funtzio hauetako zeinek duten maximo eta minimo absolutua kasu bakoitzean adierazitako tartean:

a) x 2 – 1, [–1, 1] tartean b) x 2, [–3, 4] tartean

c) x 1 1 –, [2, 5] tartean d) x 1 1 –, [0, 2] tartean

e) x 1 1 2 + , [–5, 10] tartean f ) e –x, [0, 1] tartean

Ebatzitako ariketak eta problemak

1. Eragiketak limiteekin

f (x) → –2, g (x) → – ∞, h (x)  → 0, u (x) → + ∞ eta v (x) → 0,4 badira

x → + ∞ denean, kalkulatu honako funtzio hauen limiteak x → + ∞ denean:

a) f (x) – g (x) b) f (x)/u (x)

c) u (x) · f (x) d) v(x)g (x)

e) u (x)/h (x)

EGIN ZUK

f, g, h, u eta v aurreko funtzio horiek izanda, kalkulatu honako funtzio hauen limiteak x → + ∞ denean:

a) v (x)u (x) b) u (x)g (x) c) g (x) · u (x)

2. Indeterminazioak

f (x) → + ∞, g (x) → – ∞, h (x) → 0 eta j (x) → 1 badira x → + ∞ denean, identifikatu indeterminazioak eta esan zein diren limiteak gainerako kasuetan.

a) lm i x ∞ " + [ f (x)/g (x)]

b) lm i x ∞ " + [g (x) · h (x)]

c) lm i x ∞ " + [ f (x)/h (x)]

d) lm i x ∞ " + [ f (x) g (x)]

e) lm i x ∞ " + [j (x) g (x)]

3. Infinituen konparazioa

Konparatu infinituen ordenak eta ezarri limitea honako adierazpen hauei:

a) lm i x ∞ " + 10xx 1 25 ak

b) lm i x ∞ " + () log x x 10 5 1 –2 3 +

c) lm i x ∞ " + ()logx 1 2 x 3 +

d) lm i x ∞ " + 2 13 –x x 5 +

EGIN ZUK

Esleitu x → + ∞ kasurako limitea honako adierazpen hauetako bakoitzari: a)

Limiteekin egindako eragiketen emaitzak erabiliko ditugu.

edo – ∞ den jakiteko, u (x) eta h (x) funtzioak zein diren jakin eta zatiduraren zeinua aztertu behar dugu x-ren oso balio handietarako

a) lm i x ∞ " + () () gx fx > H = () (∞) –∞ + Indeterminazioa da. f eta g funtzioak zein diren jakin gabe ezin dugu zatidura horren limitea jakin. Finitua edo infinitua izan daiteke.

b) lm i x ∞ " + [g (x) · h (x)] = (– ∞) · (0) Indeterminazioa da

c) lm i x ∞ " + () () hx fx > H = () () 0 +∞ = ± ∞

h funtzioa ezagutu gabe limitea + ∞ edo – ∞ den jakin ezin badugu ere, kasu hau ez da indeterminazioa, bi emaitza horietako bat baino ezin da izan eta

d) lm i x ∞ " + [ f (x) g (x)] = (+ ∞)(– ∞) = ∞ 1 + = 0

e) lm i x ∞ " + [j (x) g (x)] = (1)(– ∞) Indeterminazioa da

a)

b)

Kenkizuna kentzailea baino beheragoko mailakoa delako.

Edozein berreketa delako edozein funtzio logaritmiko baino goragoko ordenako infinitua

c)

1 baino berrekizun handiagoa duen edozein funtzio esponentzial delako edozein funtzio logaritmiko baino goragoko ordenako infinitua.

d)

1 baino berrekizun handiagoa duten bi funtzio esponentzial izanda, berrekizun handiena duena delako goragoko ordenako infinitua

4. Limiteen kalkulua

Kalkulatu honako limite hauek:

Zenbakitzailea eta izendatzailea bider

a) lim x3 " x x 6 1 3 2 –

–+ +

b) lm i x ∞ " + () ln ln x x 7 2 ln x 2 eo

c) lm i x ∞ " + e x 2 x x +

d) lim x2 " x x 2 31 /( ) x 12 –+ cm

–+

e) lm i x –∞ " ee ee –xx xx –

f) lim x1 " || x x 1 1 ––2

infinitua. Kasu honetan, berrekizun handiena izendatzailean dago. Beraz:

EGIN ZUK

Kalkulatu honako limite hauek:

a) lm i x ∞ " + x x 3 42 –x 21 – dn

b) lm i x ∞ " + (log x)1 – 3x

c) lm i x2 " x x 23 2 1 2 – +

d) lm i x4 " x 6 2 x 4 1 – + dn

e) lm i x –∞ " || x x 1 1 ––2

i x ∞ " + ee ee –xx xx –

–+

5. L'Hôpitalen erregela

Kalkulatu honako limite hauek:

a) lim x0 " () ln x x 1 11 –+ cm

b) lim x0 " sn sn i i x xx –2

c) lm i x ∞ " + (ln x)1/e x

d) lm i x ∞ " + () xarctg e 2 –x r bl =G

EGIN ZUK

Kalkulatu limite hauek:

a) lm i x 0 " () () ln cos ln cos x x 2 3

b) lm i x 0 " (cos 2x)3/x2

c) lim x 1 " ee e x 1 1 ––– x dn

6. Puntu bateko jarraitutasuna

a) Aztertu funtzio honen jarraitutasuna:

a) Funtzioa tarteka definituko dugu, balio absolutua alde batera uzteko:

+ = *

2 1 2 2 ≠– bada –

f (x) = || x x x xbada

b) Sailkatu etenak, baldin eta badaude, eta adierazi lortutako emaitzak.

EGIN ZUK

Aztertu f (x) funtzioaren jarraitutasuna eta sailkatu horren etenak.

2 + = *

f (x) = || x x x x x 1 0 0 ≠bada bada

Z [ \

] ] ] ] ]

f (x) = x x x x

2 1 2

< > + =

x x x

2 2 2

–bada –bada –bada

x < –2 denean, f (x) jarraitua da, x x 2 ere hala delako.

x > –2 denean, f (x) ez da jarraitua x = 0 puntuan, f (0) ez delako existitzen

x = –2 denean, jarraitutasuna aztertuko dugu:

limf xlim x x limf xlim x x

== = + =

2 0 2 0 xx xx

() ()

22 22

"" "" ++

b b b b Beraz, lm i x –2 " f (x) = 0.

_ ` a

f (–2) = 1 denez → lm i x –2 " f (x) ≠ f (–2) → f (x) ez da jarraitua x = –2 puntuan.

b) x = 0 puntuan jauzi infinituko eten saihestezin bat dago, lm i x 0 " f (x) = ± ∞ baita

x = –2 puntuan eten saihesgarri bat dago; izan ere, limitea existitzen da, baina ez dator bat funtzioak puntu horretan duen balioarekin

7. Parametroen mendeko funtzio jarraitua

Kalkulatu a-ren eta b-ren balioak f (x) funtzioa jarraitua izan dadin Á-n.

f (x) =

sin

EGIN ZUK

Zehaztu zein izan behar diren a-ren eta b-ren balioak f (x) jarraitua izateko.

x ≠ 0 bada, f (x) funtzioa jarraitua

8. Bolzanoren teorema

a) Aplika dakioke Bolzanoren teorema

f (x) = x 1 1 2 + funtzioari tarteren batean?

b) Egiaztatu aurreko funtzioak eta

g (x) = 2x – 1 funtzioak puntu batean gutxienez elkar ebakitzen dutela.

EGIN ZUK

Frogatu funtzio hauen grafikoak

f (x) = sin x eta g (x) = x 1

elkar ebakitzen dutela , 2 2 5 r r dn

tarteko punturen batean

9. Tarteko balioen teorema

Funtzio hau izanda

f (x) = x 3 + x – 5

frogatu f (c) = 20 betetzen duen c bat dagoela.

a) f (x) = x 1 1 2 + funtzioa jarraitua da Á osoan, izendatzailea ez baita baliogabetzen

x-ren balio batekin ere.

f (x) = x 1 1 2 + > 0 denez x ∈ Á edozein baliotarako, ezin da Bolzanoren teorema

aplikatu, f (a)-ren zeinua ≠ f (b)-ren zeinua ez delako egiaztatzen [a, b] tarte batean ere.

b) f (x) eta g (x) funtzioek elkar ebakitzen badute, orduan:

F (x) funtzioa definituko dugu: f (

F (x) jarraitua da Á osoan, izendatzailea ez baita inoiz nulu egiten.

lm i x ∞ " + F (x) = – ∞ eta lm i x –∞ " F (x) = + ∞ direnez, F (x) funtzioak zeinua aldatzen du gutxienez x ∈ Á batean, eta, beraz, Bolzanoren teoremaren arabera, F (c) = 0 betetzen duen c ∈ Á puntu bat gutxienez existituko da; eta, beraz, f (x) eta g (x) funtzioek elkar ebakiko dute c puntu batean gutxienez

f funtzio polinomikoa denez, jarraitua da Á osoan

Haztamuka joz, f (2) = 5 eta f (3) = 25 direla ikusten dugu

Tarteko balioen teoremaren arabera, f funtzioak 5 eta 25 arteko balio guztiak hartzen ditu. 20 balioa f (2) = 5 eta f (3) = 25 artean dagoenez, f (c) = 20 beteko duen c ∈ (2, 3) zenbaki bat existituko da.

Gidatutako ariketak eta problemak

Kalkulatu limite hauek:

a) lm i x ∞ " + x xx 12 35 8 –3 3 25 + + >H

b) lm i x0 " (1 + 4x 3)2/x3

c) lm i x0 + " x 1 tg x 2 cm

a) Egiaztatu (∞) (∞) motako indeterminazioa dagoela ordena bereko bi infinituren artean.

Zatiduraren limitea zenbakitzaileko eta izendatzaileko mailarik handieneko gaien koefizienteek zehazten dute.

b) (1)(∞) motako indeterminazioa da. Arrazoitu zergatik erabil daitekeen erregela praktikoa indeterminazio mota honetarako, eta lortu limitea.

c) • (∞)(0) motako indeterminazioa da. Hartu logaritmo nepertarrak eta erabili berreketa baten eta zatiketa baten logaritmoen propietateak

• Adierazi lortutako biderketa zatiketa moduan, (∞) (∞) motako indeterminazio bat lortzeko

• Erabili L’Hôpitalen erregela eta gogoratu emaitza dela bila gabiltzan limitearen logaritmo nepertarra.

Soluzioa: a) –1 b) e 8 c) 1

Kalkulatu zein izan behar den a-ren balioa hurrengo limite hau finitua izateko, eta lortu limite hori:

lm i x0 " e x a 1 1 2 ––x cm

3. Jarraitutasuna puntu batean

Honako funtzio hau izanda:

f (x) =

a) Ba al dago f (x) jarraitua izateko k-ren balioren bat?

b) Aurkitu funtzioaren limitea x → + ∞ denean eta x → – ∞ denean.

• Egiaztatu (∞) – (∞) motako indeterminazioa dagoela eta bihurtu () () 0 0 motakoa, L’Hôpitalen erregela erabili ahal izateko.

• Zehaztu zein izan behar den a-ren balioa aurrera egin ahal izateko.

• Lortu duzun a-ren balio horrekin, ezarri berriro L’Hôpitalen erregela.

Soluzioa: a = 2; lm i x 0 " e x a 1 1 2 ––x dn = 2 –1

a) Aztertu limiterik dagoen x → 0 denean, alboko limiteak lortuz

b) • Aztertu nola dagoen funtzioa definituta balio positibo «oso handietarako» eta balio negatibo «oso handietarako».

• Limiteak kalkulatzeko, kontuan izan e x -ren eta ln x-ren joera infinituan

Soluzioa:

a) Ez.

b) lm i x –∞ " f (x) = 0; lm i x ∞ " + f (x) = – ∞

Egiaztatu ekuazio honek: sin x2 = x – 1

soluzio positibo bat duela.

Arrazoitu erantzuna, soluzioa justifikatuko duen teorema edo emaitza azalduz.

• Funtzio hau hartuko dugu kontuan: F(x) = sin x2 – x + 1

• Aztertu Bolzanoren teoremaren hipotesiak betetzen dituen [0, π] tartean.

F(x) jarraitua da tarte horretan? Desberdinak dira F (0)-ren zeinua eta F (π)-rena?

• Aplikatu Bolzanoren teorema eta eskatzen dena frogatuko duzu.

Soluzioa: F(x) funtzioak Bolzanoren teoremaren hipotesiak betetzen ditu [0, π] tartean; beraz, teorema hori aplikatuz, badakigu F(c) = 0 dela c ∈ (0, π) balioren batentzat (konturatzen bazara, c > 0 da, eta horrek enuntziatuan eskatzen dena frogatzen du).

1. Limiteen kalkulua

2. Limite finitua

4. Bolzanoren teorema

Proposatutako ariketak eta problemak

Trebatzeko

Limitearen kalkulua

1 Erreparatu f (x)-ren grafikoari, eta eman honako limite hauen

6 Aurkitu funtzio hauen limiteak x → + ∞ denean eta x → – ∞ denean:

a) f (x) = x e 1 –

x 2 b) g (x) = logx xx 2 2 2 +

c) h (x) = xx32 5 –2 + d) i (x) = x 2 – x 1 –4

e)

32

5 Kalkulatu ondorengo limiteak eta adierazi grafikoki lortutako emaitzak: a) lm i

9 Lortu limite hauek: a) lm i x –∞ " () xx x 2224 +

b) lm i x –∞ " () xx 1 2 ++

10 Kalkulatu honako funtzio hauen limiteak x → + ∞ denean eta x → – ∞ doanean: a) f (x) = ,≤ , ln x x x

11 Honako hauek jakinda: lim x 2 " p (x) = + ∞ lim x 2 "

esan zein diren limite hauen balioak, kalkula daitezkeen kasuetan: a) lim x 2 " () () px sx

Proposatutako ariketak eta problemak

12 Kalkulatu limite hauek. Infinituren bat badago, kalkulatu alboko

Jarraitutasuna

18 Aztertu honako funtzio hauetako bakoitzaren jarraitutasuna. Etenak diren puntuetan, esan zein den limitea eskuinetik eta ezkerretik, eta adierazi eten mota.

c)

b)

14 Kalkulatu, eta aztertu alboko limiteak beharrezkoa denean. a) lim x 2 " x x 2 13

I) II)

2 1 0 –2

19 Aztertu funtzio hauen jarraitutasuna eta irudikatu grafikoak:

a) f (x) = ln e x x x 1 1 bada ≥bada < x ) b) g (x) = / ≥ x x x x 1 21 1 1 –bada bada < )

20 Kalkulatu zein izan behar den k-ren balioa funtzio hauek jarraituak izateko definizio-eremu osoan. Irudikatu itzazu lortutako k-ren balio horretarako:

a) f (x) = () ≥ ln xkx x x x 2 3 3 –bada bada < 2 + *

16 Aurkitu beheko limiteen balioak, hau kontuan izanda:

] ] ] ]

2 4 –2 )

b) g (x) = ≤ kx e x x 32 2 –bada bada > x

21 Kalkulatu a-ren eta b-ren balioak f (x) jarraitua izan dadin definizio-eremu osoan.

x 2 Z [ \

0 02 2 ––

3

bada bada bada << >

a) lm i x –∞ " f (x) b) lm i x 0 " f (x) c) lm i x 2 " f (x)

d) lm i x 3 " f (x) e) lm i x 4 " f (x) f) lm i x ∞ " + f (x)

17 Erabili L’Hôpitalen erregela honako limite hauek kalkulatzeko:

a) lm i x –1 " xx x 34 1 2 3 + b) lm i x 0 " () ln x ex x 3 +

c) lm i x 0 " cos sn i x x 1– d) lm i x 0 " x ab –xx

e) lm i x 0 " sn i xx arctg xx ––f ) lm i x 0 " cosx ee 1––sn i xx

g) lm i x 0 " () ln cos x x3 2 h) lm i x 0 " () ln x x 1 3 4 +

i) lm i x 0 " () cos x x 3 12 –2 2 j) lm i x 0 " sn sn i i xx xx –dn

k) lm i x 0 " cos e x 1 1 ––x l) lm i / x 2 π " secx tg x 10 8 –+

Z [ \

] ] ]

f (x) = ≤ ≤

x ax b x x x

1 2

< < 2 +

0 01 1

–bada bada bada

22 Aztertu honako funtzio hauen jarraitutasuna:

< < x 2 + + *

a) f (x) = ≤ ≥ ln

x x x 31 4

e x x

0 01 1

bada bada bada

Z [ \

] ] ]

xx sinx x

b) g (x) = ()

+ +

2 1

bada bada bada << 2 2

0 0 –π

≤ π π≤

x x x

c) h (x) = ≤ e x

x 1– 2 *

x x 1 1 1 ––bada –bada >

d) i (x) = ≠ x x x x 4 2 4 1

Z [ \

] ] ] ]

2 2 ––bada –bada 2 + =

23 Sailkatu honako funtzio hauen etenak:

a) f (x) = xx xx x 2 22 2 32 + b) g (x) = xx xx x

Ebazteko

24 Kalkulatu honako limite hauek:

a) lm i x ∞ " + xx xx 52 23 ––x 32 32 1–+ eo b) lm i x ∞ " + x x 23 25 –x 2 1 +

+ dn

2

c) lm i x 0 " cos sn i x xx 1– d) lim x 2 " x x 2 13 3 –

e) lm i x 1 " () ln x x 1 –2 f ) lm i x –∞ " x 2 e –x

g) lm i x 0 " sn i xx 11 –dn h) lm i x 0 " sn cos cos ix xx ex x 1 1 x +

25 Kalkulatu limite hauek:

a) lim (π/) x 2 –" cos x ln (tg (x)) b) lm i x 0 " x 1 tg x dn

c) lm i x 0 " (cos x + sin x)1/x d) lm i x 0 " snix 1 x 1 dn

e) lm i x ∞ " + ln x x x 1+ dn f ) lm i x 0 " (1 – sin 2x)cotg 3x

26 a) f (x) = xx kx xxx 3 1 32 32 + ++ + bada, ba al dago k-ren baliorik

lm i x 1 " f (x) existitzeko? Baiezkoa bada, aurkitu.

b) k = 0 kasurako, aurkitu lim x 1 –" f (x) eta lim x 1 " + f (x).

31 Kalkulatu zein izan behar den b-ren balioa f (x) funtzioa jarraitua izateko Á f (x) = () ≤ ln xx b x x x x

2 ++ +

32 Kalkulatu k-ren balioa honako funtzio hau jarraitua izateko x = 0 puntuan: f (x) = ≠ e x k x x 1 2 1 0 0 –––

bada bada x = *

33 Ba al dago f (x) funtzioa x = 0 puntuan jarraitua egiten duen k-ren baliorik?

f (x) =

Z [ \

] ] ] ] ]

1 0 0 0

cos sinx x k x sinx

– bada bada bada

x x x

< > 2 2 =

34 Zehaztu non diren jarraituak honako funtzio hauek:

a) f (x) = () ln x x 2 –b) g (x) = xx 6 1 3

c) h (x) = x x 2 1 –+ d) i (x) = cosx 1 1 –2

35 a) Kalkulatu zein izan behar den a-ren balioa lm i x 0 " sn i x xa x –2 finitua izateko

b) Aurkitu zein den limitea a-ren balio horretarako.

tt a a bt

t t t 35 5 100

015 15 30 30 60 –

< < +

bada bada bada *

Kalkulatu a-ren eta b-ren balioak errendimendu-funtzioa jarraitua izan dadin.

28 Badakigu f (x) = xbxx x 84 34 ––32++ funtzioa etena dela x = 2 puntuan Kalkulatu b-ren balioa eta aztertu funtzioaren jokabidea eten-puntuen inguruan.

29 f (x) = ax ax b –2 + funtzioa emanda, eta a ≠ 0 izanik, kalkulatu a-ren eta b-ren balioak funtzioa (2, 3) puntutik igarotzeko eta lm i x ∞ " + () x fx = – 4 izateko.

36 Aztertu f (x) = || x 2 1 –funtzioaren jarraitutasuna eta sailkatu etenak.

37 Aurkitu zein izango den t-ren balioa beheko funtzio hori jarraitua izateko x = 2 puntuan. Irudika ezazu t = 2 kasuan eta esan zer eten mota duen:

f (x) = || ≤ xt x x x 1 5 2 2 –bada bada > )

38 Kalkulatu beheko funtzio horien limiteak x → + ∞ denean eta x → – ∞ denean, aurretik tartetan definituz:

a) f (x) = || x x 1 + b) g (x) = | x – 3 | – | x |

c) h (x) = | 2x – 1 | + x d) i (x) = || x x 1 +

39 Aztertu beheko funtzio horren jarraitutasuna x = 0

puntuan:

a) f (x) = ≠ ln x x k x x 1 1 1 1 ––bada bada 3 = * b) g (x) = ≠ x x x x 1 1 2 1 1 ––bada bada k = *

f (x) = 2x + || x x

Zein etena mota du?

Proposatutako ariketak eta problemak

40 f funtzioa honela definituta dago:

f (x) = ≤ ln x xaxb x x 1 2 1 1 –bada bada > 2 ++

Aurkitu a-ren eta b-ren balioak funtzioa jarraitua izateko eta grafikoa koordenatuen jatorritik igarotzeko.

41 Enpresa jakin batean, akzio bakoitzaren prezioa 2 € eta 8  € bitartean dabil. Enpresa horrek burtsan duen fakturazioa akzioaren prezioaren araberakoa da, eta funtzio honek adierazten digu:

F (x) = ≤≤ ≤ Ax xBx x x 3 53 2 25 58 bada bada < 2 + ++

F (x) da enpresaren fakturazioa burtsan, milaka eurotan, eta x da akzio bakoitzaren prezioa, €-tan. Jakina da akzioaren prezioa 2 €-koa denean, fakturazioa 7 000 €-koa dela eta funtzioa jarraitua dela. Zehaztu A eta B konstanteak.

42 Gauza baten salmenta-prezioa aldatu egiten da eskatzen den ale-kopuruaren arabera, honako funtzio honek adierazten digun moduan:

C (x) = ≤ x ax x x 5 500 010 10 bada bada < > 2 +

a) Kalkulatu zein izan behar den a-ren balioa prezioa etenik gabe aldatu dadin erosten diren aleen kopurua aldatzen denean.

b) Zenbatera jotzen du ale baten prezioak ale-kopuru oso handia erostean?

43 f (x) = x xx 1 25 4 ––3 + funtzioa kontuan hartuta:

a) Aztertu funtzioaren jarraitutasuna.

b) Konturatzen bazara, f (–2) = –2/3, f (0) = 4 eta f (2) = –10 dira. Arrazoitu, informazio horretatik abiatuta, (–2, 0) tarteak funtzioaren zero bat barne hartzen duela ondorioztatu dezakegun. Eta ondorioztatu dezakegu (0, 2) tarterako?

c) Aurkitu ondoz ondoko bi zenbaki osok zehazten duten tarte jakin bat, jakinda funtzio horren zero bat gutxienez barne hartzen duela.

44 f (x) = x 3 + 3x 2 – 1 eta g (x) = 6x funtzioak emanda, justifikatu [1, 10] tartean existitzen dela bi funtzioek balio bera hartzen duten punturen bat.

45 Egiaztatu honako funtzio honek X ardatza (c, 0) punturen batean ebakitzen duela, non c ∈(–1, 1):

Galdera teorikoak

46 Honako funtzio hau daukagu:

Ikusten dugunez, f definituta dago [0, 1] tartean, eta f (0) = –1 < 0 eta f (1) = e –1 > 0 dira; baina ez da existitzen f (c) = 0 betetzen duen c ∈ (0, 1). Kontra egiten dio horrek Bolzanoren teoremari? Arrazoitu erantzuna.

47 Eman Bolzanoren teoremaren interpretazio geometriko bat, eta erabili f (x) = x 3 + x 2 eta g (x) = 3 + cos x funtzioen grafikoek punturen batean elkar ebakitzen dutela egiaztatzeko.

48 f (x) = x 2 + 1 funtzioa daukagu. Ziurta dezakegu funtzio horrek [1, 5] tarteko balio guztiak hartzen dituela? Horrela bada, enuntzia ezazu hori arrazoitzeko teorema.

49 f (x) jarraitua bada [1, 9] tartean, eta f (1) = –5 eta f (9) > 0 badira, g (x) = f (x) + 3 funtzioak [1, 9] tartean gutxienez zero bat duela ziurta dezakegu?

50 g funtzio bati buruz, badakigu jarraitua dela [0, 1] tarte itxian, eta 0 < x ≤ 1 kasuan hau dela: g (x) = x xx 2 + Zein da g (0)-ren balioa?

51 Zuzena ala okerra? Arrazoitu erantzuna.

a) Funtzio bat ez badago x = 3 puntuan definituta, lm i x 3 " f (x) = 5 izatea gerta daiteke.

b) f (x) funtzioa jarraitua bada, eta x < 3 denean f (x) < 0 bada eta x > 3 denean f (x) > 0 bada, lm i x 3 " f (x) = 5 ezinezkoa da.

c) x 5 + x + 1 = 0 ekuazioak ez du erro errealik.

d) f (x) funtzioa [a, b] tartean jarraitua dela eta f (a) = 3 eta f (b) = 5 direla jakinda, ziurta dezakegu [a, b] tarteko c-ren batekin f (c) = 7 betetzen dela.

e) sin x + 2x – 1 = 0 ekuazioak erro erreal bat du gutxienez.

f) y = tg x funtzioak ez ditu betetzen Bolzanoren teoremaren hipotesiak , 44 3 r r < F tartean.

52 Idatzi definizio bat honako adierazpen hauetako bakoitzerako, eta egin f -ren adierazpen grafiko bat :

a) lm i x –∞ " f (x) = 3 b) lm i x ∞ " + f (x) = – ∞

c) lim x 2 –" f (x) = + ∞ d) lim x 2 " + f (x) = – ∞

e) lm i x –3 " f (x) = + ∞

f ) lm i x 1 " f (x) = 4

Sakontzeko

53 Aztertu honako funtzio hauetako bakoitzaren jokabidea x → + ∞ denean:

a) f (x) = x 3 – sin x b) g (x) = cos x x 1 2 +

c) h (x) = () x x Oso d) i (x) = sn i x xx3+

* Oso (x) funtzioa x-ren atal osoa funtzioa da.

54 Kalkulatu, ahal izanez gero, zein izan behar den k-ren balioa honako funtzio hauetako bakoitza jarraitua izateko x = 0 puntuan:

a) f (x) = () ≠ cos e x k

x x 1 1 0 0 –– bada bada x 2 = *

b) g (x) = || ≠ sn i x x k

bada = * c) h (x) = tg x xsin x k

x x

0 0bada

≠bada bada 2 = *

x x

0 0

55 Aurkitu zein izan behar diren a-ren eta b-ren balioak beheko funtzio hori jarraitua izateko Á-n eta (1, –2) puntutik

igarotzeko:

AUTOEBALUAZIOA

1 Kalkulatu limite hauek:

2 a) Aztertu f (x) = xx x 3 9–2 2 + funtzioaren jarraitutasuna eta

arrazoitu zer eten mota duen.

b) Aurkitu limiteak x → + ∞ denean eta x → – ∞ denean.

c) Irudikatu a) eta b) ataletan lortutako informazioa.

funtzio

56 Erradioa 1 duen zirkunferentzia batean, x radianeko

AOP % angelua hartu dugu. Ikusten duzunez, PQ = sin x, TA  = tg x eta arku PA $ = x

PQ < PA $ < TA denez → sin x < x < tg x

Desberdintza horretatik abiatuta, frogatu lm i x 0 " sn i x x = 1 dela

57 Erabili aurreko emaitza hori honako limiteak kalkulatzeko, L’Hôpitalen erregela erabili gabe:

a) lm i x 0 " sn i x x 2 b) lm i x 0 " sn i x xx –

c) lm i x 0 " x tg x d) lm i x 0 " cos x x 1–2

58 Demagun f jarraitua dela [0, 1] tartean eta 0 < f (x) < 1 dela [0, 1] tarteko x guztiekin. Frogatu f (c) = c betetzen duen (0, 1) tarteko c bat existitzen dela.

Egin grafiko bat emaitza agerikoa izan dadin.

➜ anayaharitza.es Ariketa hauen ebazpena.

4 Zehaztu a-ren eta b-ren balioak honako funtzio hau jarraitua izan dadin x = 0 puntuan:

bada bada ] ] ] ]

x 2 =

0 0 Z [ \

5 f (x) = xx xx 3 4 4 –2 3 + + funtzioa emanda, aurkitu zein den bere definizio-eremua eta lortu zer balio eman behar zaion f (x) funtzioari x = 0 puntuan, jarraitua izan dadin puntu horretan.

7 f (x) = x + e –x funtzioa kontuan hartuta, frogatu existitzen dela c + e –c = 4 betetzen duen c zenbaki errealen bat.

Deribatuak 9

Deribatu kontzeptuaren eboluzioa

Aurkikuntza batzuk airean egoten dira garai batez. Giroa prest egoten da, helduta, eta falta izaten den bakarra da erabaki sendoa duen norbait, ideiak osotasun koherente batean hezurmamitzen ausartzea dena. Horregatik, ez da harritzekoa egoera berdinetan, aldi berean, bi edo hiru pertsona ausart agertzea. xvii. mendearen bigarren erdian, kalkulu infinitesimala bazebilen giro matematikoan, eta Newton eta Leibnizen buruetan mamitu zen, aldi berean baina bakoitzean bere alde batetik.

Asmakizun honen aitzindariek erraztu egin zuten gerora sortu ziren bi sortzaile handi horien bidea. Isaac Barrow, Newtonen maisua, izan zen aitzindari horietako bat, eta, zalantzarik gabe, eragin handia izan zuen Newtonentzat zentzu horretan. Barrowri zor zaio, esaterako, kurbekiko ukitzaileak planoan zehazteko metodo bat, deribatuaren kontzeptua ere agertzen duen gaur egungo metodoaren oso antzekoa. 1665ean, Newtonek aztergai izan zuen zer aldaketa-abiadura zuten modu jarraituan aldatzen diren magnitude batzuek: luzera, azalera, bolumena, tenperatura, etab. Urte horretan eta hurrengoan Trinity College itxi egin zen (Newtonek bertan lan egiten zuen), izurritearen ondorioz. Beraz, etxean sartu eta hilabete emankor horietan egin zituen aurkikuntza nagusiak Newtonek, besteak beste kalkulu infinitesimala.

Leibnizek aurkikuntza bera egin zuen 10 urte geroago, 1676 inguruan, baina lehena izan zen esplizituki argitaratzen 1684an. Dena dela, irakasle ona eta azalpenak ematen bikaina izanik ere, oso modu nahasian egin zuen. Horregatik, uste da iluntasun hori nahita egindakoa izan zela, inork ondoegi uler ez zezan. Horrela, batetik, argitaratzen lehena izateari eusten zion, eta, bestetik, garai hartan modan zeuden lehiaketa matematikoetan erabili eta abantaila lortzen zuen.

Baina izan zen Leibnizek idatzitakoa ulertu nahi izan zuenik. Eta batek lortu zuen, maisuki lortu ere. Hain maisuki, ezen, kalkuluari dagokionez, ez zuen ezer ikasteko ez Leibnizengandik ez Newtonengandik.

Jacob Bernoulli izan zen. Hain liluratuta geratu zen Leibnizek kalkulu infinitesimalari dagokionez emandako berritasun matematikoekin, haren defendatzaile sutsua bihurtu baitzen asmakuntzaren sortzaileari buruz Newtonekin zuen ika-mikan. Bernoulli buru-belarri aritu zen aurkikuntzari mila modu harrigarritan zukua ateratzen, hamahiru urte gazteagoa zen bere anaia Johannekin batera. Bernoulli anaiak, Basileako suitzarrak, matematikari familia handi batekoak ziren. Historian ez da egon hainbeste matematikari gailen bildu dituen familiarik: hamar bat kidek, gutxienez, matematikan eta fisikan nabarmentzea lortu zuten. Geroago, Euler, Suitzako matematikari garrantzitsuena, eurekin elkartu zen, Basileako harrotasun zientifikoa osatuz.

Basileako katedralea. Hango klaustroan dago hilobiratuta Jacob Bernoullia

Cauchy. Kalkuluaren sistematizazioa

ia mende eta erdi igaro zen Newton eta Leibniz analisi infinitesimalaren nozioak garatzen eta maneiatzen hasi zirenetik, xvii. mendearen amaieran, harik eta Cauchyk, xix. mendearen hasieran, ongi eraikitako gorputz teoriko batean sistematizatu zituen arte, gaur egun analisiaren lehen urratsetan hasteko erabiltzen dugun forma berarekin. Cauchyk kalkulu infinitesimalari egindako ekarpenik handienak bere liburuetan daude: Analisi ikastaroa (1821), Kalkulu infinitesimalari buruzko lezioak (1823), Kalkulu infinitesimala geometrian aplikatzeko lezioak (1826-28) eta Kalkulu diferentzialaren lezioak (1829). Horiekin, Cauchyk xix. mendeko matematikaren garapenean zorroztasuna ezartzeko lanari ekin zion.

Bere ekoizpen matematikoa izugarria eta askotarikoa izan zen. Cauchy salbuespen bat da matematikariaren ugalkortasun handiena gaztaroan gertatzen dela dioen erregelan: idatzi zituen 800 artikuluetatik 500 baino gehiago bere bizitzako azken 20 urteetan egindakoak dira, nahiz eta egia den bere lan sistematiko handiak 30 urte inguru zituenean idatzi zituela.

EBATZI

Funtzio deribatua

• Beheko grafikoa (berdez dagoena) goikoaren funtzio deribatua da. Hau da: g (x) = f ' (x).

• Jarraitu idazten zer arrazoitan oinarrituta duen g (x) funtzioak f (x)-ren deribatuari dagokion jokabidea.

• Beheko A, B eta C grafikoak goiko 1, 2 eta 3 grafikoen funtzio deribatuak dira, baina beste ordena batean. Azaldu zein den zeinena, eta arrazoitu.

Ikus dezagun zergatik:

— (–∞, a) tartean, f (x) gorakorra da. Beraz, horren deribatua positiboa da. Halakoa da g (x)

— f-ren deribatua a puntuan 0 da: f ' (a) = 0. Baita g (a) = 0 ere.

«Analisi ikastaroa» lanaren azala, 1821ean argitaratua

1

Funtzio baten deribatua puntu batean

y = f (x) funtzio batek bere definizio-eremuko puntu batean duen hazkundearen neurriarekin erlazionaturik dauden zenbait kontzeptu gogoratuko ditugu.

Batezbesteko aldakuntza tasa

Abzisa x0 eta x0 + h artean aldatzen denean, ordenatua f (x0)-tik f (x0 + h)-ra doa

• h da x-ren hazkundea.

• Δ f = f (x0 + h) – f (x0) da funtzioaren hazkundea [x0, x0 + h] tartean.

∆f h zatidurak tarte horretako f-ren batezbesteko hazkundea neurtzen du.

() () ∆ff xf x hh h–00 = + gehikuntza-zatidurari batezbesteko aldakuntza tasa

esaten zaio, eta neurtzen du f-k zer aldakuntza erlatibo duen x-rekiko [x0, x0 + h] tartean. Grafikoki, P0(x0, f (x0)) eta P (x0 + h, f (x0 + h)) puntuetatik igarotzen den zuzenaren malda da.

Deribatua puntu batean

Funtzioak [x0, x0 + h] tartean duen batezbesteko hazkundearen adierazpenean h-k 0rantz jo dezala eragiten badugu, aldiuneko hazkundea lortuko dugu; edo hori baino hobeto, x0 puntuko hazkundea:

h ∆ lm f i 0 h "

limiteari, existitzen bada eta finitua bada, f funtzioaren deribatua x0 puntuan esaten zaio eta honela izendatzen da f ' (x0):

f ' (x0) = () () lm fx fx i h h–0 00 h + "

f ' (x0) da f funtzioaren aldiuneko aldakuntza tasa x0 puntuan. Grafikoki, f ' (x0) da funtzioaren grafikoak x0 abzisa-puntuan duen zuzen ukitzailearen malda.

f ' (x0) existitzen bada, x0 puntuan f deribagarria dela esaten da

Ebatzitako ariketak

1 f (x) = x 2 bada, aurkitu deribatua x0 = 1 puntuan.

() () ff11 h h– + = ()11 h h–2 + = hh h 2 2 + = h + 2

f ' (1) = lm i 0 h "

() () ff11 h h– + = lm i 0 h " (h + 2) = 2

y = x 2 deribagarria da x = 1 puntuan. Bere deribatua 2 da.

Esan nahi du x = 1-en zuzen ukitzailearen malda 2 dela.

2 f (x)

aurkitu zein den deribatua

() () ff00 0 h h–h h–/ 13 + = = h–2/3

lm i 0 h " (h–2/3) = lm i 0 h " 1 h 2 3 = +∞ 1 2 –1 –2

Lortutako balioa ez da finitua, beraz, f ' (0) ez da existitzen. Kurbak x = 0 puntuan duen zuzen ukitzailea perpendikularra da X ardatzarekiko. Funtzioa ez da deribagarria puntu horretan.

= x 3 bada,

x0 = 0 puntuan.

Alboko deribatuak

f-ren ezkerreko deribatua x0 puntuan honela definitzen da:

f ' () x 0 –= lm i 0 h –"

() () fx fx h h–00 +

f-ren eskuineko deribatua x0 puntuan honela definitzen da:

f ' () x 0 + = lm i 0 h " + () () fx fx h h–00 +

Biei alboko deribatuak deitzen zaie

x0 puntuko alboko bi deribatuak bat badatoz, orduan f deribagarria da x0 puntuan.

GOGORATU

h → 0 – h-k 0ra0 baino balio txikiagoak hartuz jotzen duela esan nahi du. h → 0 + h-k 0ra0 baino balio handiagoak hartuz jotzen duela esan nahi du.

funtzio deribagarria:

x0 puntuko alboko bi deribatuak desberdinak badira, orduan funtzioaren grafikoak puntu erzduna du x0 puntuan.

BEGIRATU

Grafikoki, funtzio batek puntu batean duen deribagarritasuna lotuta dago grafikoa puntu horretan «laua» edo «suabea» izatearekin. Horrez gain, azpimarratzekoa da funtzioak ez direla deribagarriak ukitzailea bertikala den puntuetan.

puntu erzduna:

Tarte batean deribagarria den funtzioa

f deribagarria da (a, b) tarte irekian (a, b) tarteko puntu guztietan deribagarria bada.

f deribagarria da [a, b] tarte itxian (a, b) tartean ere deribagarria bada eta f ' (a +) eta f ' (b –) alboko deribatuak existitzen badira.

Oinarrizko funtzioak, normalean erabiltzen ditugunak, definituta dauden puntu guztietan deribagarriak dira, ukitzaile bertikaleko puntu batzuetan izan ezik (esaterako, aurreko orrialdean ikusi dugunez, f (x) = x 3 funtzioa x = 0 puntuan)

Pentsatu eta praktikatu

1 Lortu, urratsez urrats, honako hauen deribatuak:

a) f (x) = 4x – x2 , x = 3 puntuan

b) f (x) = x3 , x = 2 puntuan

c) f (x) = x 1 , x = 2 puntuan

d) f (x) = (x – 3)2, x = 1 puntuan

2 Aurkitu f (x) = x funtzioaren f ' (0+) alboko deribatua urratsez urrats, eta arrazoitu erantzuna.

3 Zer baldintza bete behar du f funtzio batek [1, 5) tartean deribagarria izateko?

Deribagarritasuna eta jarraitutasuna

Gerta liteke funtzio bat jarraitua izatea puntu batean, baina ez deribagarria. Hori gertatzen da puntu erzdunetan eta ukitzaile «bertikaleko» puntuetan (hau da, X ardatzarekiko perpendikular direnetan). x0

Dena dela:

x0

Funtzio bat deribagarria bada puntu batean, nahitaez jarraitua da puntu horretan.

Egiaztapena

f funtzioa x0 puntuan jarraitua dela frogatzeko, hau egiaztatu behar dugu:

lm i xx 0 " f (x) = f (x0) edo, beste era batean esanda, lm i 0 h " f (x0 + h) = f (x0)

Ikus dezagun: f (x0 + h) – f (x0) = h ·

() () fx fx h h–00 +

Berdintzaren bi ataletan limiteak hartuko ditugu h → 0 denean. f funtzioa x0

puntuan deribagarria dela kontuan hartuz, lim 0 h "

() () fx fx h h–00 + = f ' (x0); hau da:

lm i 0 h " [ f (x0 + h) – f (x0)] = lm i 0 h " h h

(h)( ) fx fx · –00 + = G = 0 · f ' (x0) = 0

lm i 0 h " [ f (x0 + h) – f (x0)] = 0 frogatu dugu, eta, beraz, lm i 0 h " f (x0 + h) = f (x0); hau da, f jarraitua da x0 puntuan

Zatika definituriko funtzio baten deribagarritasuna aztertzen

Funtzio hau dugu: f (x) = (),≤ (), fx xx fx xx > 10 20

Demagun f1 deribagarria dela (a, x0) tartean, eta f2, (x0, b ) tartean. f (x) funtzioa x0 puntuan deribagarria den aztertzeko, urrats hauek egingo ditugu:

1. Ikusi f funtzioa x0-n jarraitua den: lm i xx 0 –" f1(x) = lm i xx 0 " + f2(x) = f (x0)?

Erantzuna ezetz bada, funtzioa ez da deribagarria. Erantzuna baietz bada, aurrera.

2. Kalkulatu f ' ( x 0 – ) = lm i xx 0 –" f '1(x) eta f ' ( x 0 + ) = lm i xx 0 " + f '2(x) alboko deribatuak.

f ' ( x 0 – ) = f ' ( x 0 + ) da eta, beraz, balio finitu bat da? Baietz bada, hori da f ' (x0)-ren balioa eta f (x) funtzioa deribagarria da (a, b ) tartean.

jarraitutasuna ⇒ deribagarritasuna

deribagarritasuna ⇒ jarraitutasuna

da x0-n?

Deribagarria da x0-n?

1 Aztertu f funtzioaren deribagarritasuna x = 2 puntuan, iazko ikasturtetik ezagun dituzun funtzio polinomikoen deribazio erregelak erabiliz:

• Jarraitutasuna x = 2 puntuan:

baina

3 Kalkulatu m-ren eta n-ren balioak honako funtzio hau deribagarria izan dadin x = 1 puntuan:

•

Alboko deribatuak finituak dira eta bat datoz. Beraz, f deribagarria da x = –2 puntuan eta f ' (–2) = 1 da

• Deribagarria izateko, jarraitua izan behar da x = 1 puntuan. Horretarako, zatiak elkarrekin «lotzen» ahalegindu behar dugu; hau da, alboko limiteak berdinak izan daitezela x = 1 puntuan:

• f deribagarria izango da alboko bi deribatuak bat badatoz x = 1 puntuan:

Funtzioa deribagarria izateko x = 1 puntuan, aurreko bi baldintzak bete behar dira: mn

2, n = –1 → f deribagarria da x = 1 puntuan, baldin eta

badira. Deribatua f ' (1) = –3 da.

Pentsatu eta praktikatu

4 Aztertu beheko funtzioaren deribagarritasuna x = 3 puntuan: f (x) = ,≤ , xx x xx 33 39 3 ––> 2 *

5 Aztertu funtzio honen deribagarritasuna x = 0 puntuan:

6 Aztertu honako funtzio honen deribagarritasuna x = 0 denean: f (x) =

7 Kalkulatu m-ren eta n-ren balioak f (x) deribagarria izateko puntuan: f

Ebatzitako ariketak

Funtzio deribatua

f funtzio bat I tarte batean deribagarria bada, I tarte horretan definituta dagoen f ' funtzioa:

x ⎯→ f '(x)

f-ren funtzio deribatua dela esaten dugu.

f ' deribagarria bada, horren deribatua f '' da (f bigarrena irakurtzen da).

Eta horrela definitzen dira, hurrenez hurren, f '' , f iv , …, f n (f hirugarrena, f laugarrena, f n-garrena).

Deribatuak izendatzeko beste modu bat hau da: D f, D 2f, D 3f, …, D nf.

f ' (x) funtzio deribatua f (x)-ren adierazpenetik abiatuta lor daiteke, definizioa erabiliz:

f ' (x) = lm i 0 h " () () fx fx h h– + da deribatua x puntu aldakor batean.

Dena dela, normalean, funtzioen deribatuak «deribazio-erregela» esaten diegunak erabiliz lortzen dira. Erregela horiek modua ematen digute edozein funtzioren deribatua eroso eta azkar kalkulatzeko. Horietako asko iazko ikasturtetik dakizkigu. Hurrengo orrialdeetan, horiek eta beste batzuk landuko ditugu

IDAZKERA

Deribatuak adierazteko, erromatar goi-indizeak erabiltzen dira:

f i , f ii , f iii , f iv , …

Baina lehenengo hiruren kasuan I horrek itxura galdu du eta apostrofo bilakatu da: f ', f '', f'''

1 Funtzio hau daukagu: f (x) = 5x – x 2

a) Aurkitu f ' (x) funtzio deribatua, gehikuntza-zatiduraren limitea erabiliz.

b) Aurkitu f ' (x), iazko ikasturtetik dakizkizun deribazio-erregelak erabiliz.

c) Kalkulatu f ' (–3) eta f ' (0)-ren balioak.

d) Aurkitu x-ren zer baliorekin betetzen den f ' (x) = 3 berdintza, eta zer baliorekin den f ' (x) = 0.

e) Kalkulatu ondoz ondoko f '' (x), f ''' (x), … deribatuak.

b) Iazko ikasturtetik dakizkigun deribazio-erregelak erabiliz:

f ' (x) = 5 – 2x

f ' (x) adierazpena zein den jakiteak abantaila batzuk ditu, c) eta d) ataletan ikusiko denez.

c) f ' (x)-ren adierazpenetik abiatuta, oso azkar lor dezakegu deribatua edozein puntutan

f ' (–3) = 5 – 2 (–3) = 11

f ' (0) = 5 – 2 · 0 = 5

d) f ' (x)-tik abiatuta jakin dezakegu zer abzisarekin lortuko duen f ' (x) deribatu horrek balio jakin bat

x-ren zer baliorekin izango da f ' (x) = 3?

f ' (x) = 5 – 2

x-ren zer baliorekin izango da f ' (x) = 0? 5 – 2

e) Funtzioaren ondoz ondoko deribatuak hauek dira:

f '' (x) = –2

(1) = 3

Deribazio-erregelak

Erregela hauen guztien baliozkotasuna unitate honetako azken-aurreko atalean egiaztatzen da.

Ebatzitako ariketa

1 Kalkulatu honako funtzio hauen deribatuak:

a) f (x) = x 5

b) f (x) = x 1 4

c) f (x) = x 3 5

d) f (x) = 7x 2 3

e) f (x) = x 3 – x x 2 3 +

f) f (x) = 3x 4 – 5x 2 + 7x + 1

g) f (x) = sin (x 2 + 5x – 1)

h) f (x) = sinx

i) f (x) = sin xx51 –2 +

j) f (x) = 5 e x2 + 3x

k) f (x) = arc cos x

l) f (x) = arc tg (sin x)

m) f (x) = ln ( ln x )

n) f (x) = arc tg x

o) f (x) = (x 2 – x + sin x)4

p) f (x) = ln sn sn i i x x 1 1 –+ <F

Ebatzitako ariketa

Deribatu

Pentsatu eta praktikatu ➜

1 Erabili deribazio-erregelak honako funtzio hauetako ba-

deribatua kalkulatzeko: a)

e)

g)

i)

(x) = tg 2 x + sin 2 x j) f (x) = sn cos ix x 11 ·– +

k) f (x) = sn i arcx

l) f (x) = ()snix xx 32 2 –5 3 +

m) f (x) = snix x 1 2 ++

n) f (x) = () cosx x 3–22 3 +

Kalkulatu funtzio baten deribatua.

2 Kalkulatu honako funtzio hauen lehenengo, bigarren eta hirugarren deribatuak:

a) y = x 5

b) y = x cos x

c) y = sin 3 x + cos 2 x + x

3 Kalkulatu f ' (1), honako hau kontuan hartuz:

f (x) = · x x e x 23 3 2 5 4 3

4 Kalkulatu f ' π 6 bl , hau kontuan hartuz:

f (x) = (cos 2 3x – sin 2 3x) · sin 6x

5 Kalkulatu f ' (0), honako hau kontuan hartuz:

f (x) = ln xx arctg x 1 3 1 3 21 –2 ++ +

Funtzio baten deribatua, alderantzizkoarena jakinda

Funtzio batzuen deribatua zuzenean lortzea ez da erraza izaten: aldiz, alderantzizko edo aurkako funtzioaren deribatua jakinda, berehala lortzen da. Atal honetan, funtzio baten deribatua bere alderantzizkoaren deribatutik lortzen ikasiko dugu. Hasteko, gogoratu dezagun zer den funtzio baten alderantzizkoa.

Funtzio baten funtzio alderantzizko edo elkarrekikoa

Gogoan izan, funtzio baten y-ren balioetako bakoitza x-ren balio bakar bati badagokio, f funtzio hori injektiboa dela. f funtzio injektiboaren alderantzizko funtzio esaten diogu eta f –1 idazten dugu honako baldintza hau betetzen duen funtzioari:

f (r) = s bada, orduan f –1(s) = r

Oso garrantzitsua da honako hau kontuan izatea:

• Funtzio baten eta alderantzizkoaren grafikoak simetrikoak dira y = x zuzenarekiko.

• f funtzio baten eta horren f –1 alderantzizkoaren artean erlazio hauek betetzen dira:

x f ⎯→ f (x) f –1 ⎯→ x Hau da, f –1[ f (x)] = x

x f –1 ⎯→ f –1(x) f ⎯→ x Hau da, f [ f –1 (x)] = x

• Funtzio bat injektiboa ez bada, ezin dugu horren alderantzizkoa lortu; baina injektiboa izango den tarteetan deskonposa dezakegu eta, horrela, tarte bakoitzak bere alderantzizkoa izango du.

• y = x 2 funtzioa ez da injektiboa, baina bi funtziotan deskonposa daiteke:

(f  –1)' (x) lortzea, f '(x) jakinda

f funtzioaren deribatua zein den badakigu, eta, hortik abiatuta, f –1 alderantzizko

funtzioaren deribatua lortu nahi badugu, honela jokatu behar dugu:

— f –1 funtzioa f-ren alderantzizkoa denez, hau betetzen da: f [ f –1 (x)] = x

— Deribatuz: f ' [ f –1(x)] · ( f –1)' (x) = 1, katearen erregela erabiliz

— Askatuz: ( f –1)' (x) = [( )] ' ff x 1 –1

Adibidez:

• f (x) = x 2 , x ≥ 0, f –1(x) = x

f [ f –1(x)] = x ⇔ ( x )2 = x Deribatuz ⎯⎯⎯→ 2 x · ( x )' = 1 → ( x )' = x 2 1

• f (x) = sin x, x ∈ , 22 –rr ; D , f –1(x) = arc sin x, x ∈ [–1, 1]

f [ f –1(x)] = x ⇔ sin (arc sin x) = x Deribatuz ⎯⎯⎯→ cos (arc sin x) · (arc sin x)' = 1 →

→ (arc sin x)' = ()cossin arcx 1

Zer esan nahi du cos (arc sin x) adierazpenak? Sinua x duen angelu baten kosinua da. Hau da, badakigu sin α = x dela eta cos α kalkulatu nahi dugu. Egin dezagun: sin α = x eta sin 2 α + cos 2 α = 1 denez, cos α = snix 1122 a =

Beraz, (arc sin x)' =

(f –1)' (c) lortzea, aurretik (f –1)' (x) lortu gabe

Kalkula dezagun, adibidez, (arc sin)' 2 1 dn :

f (x) = sin x, x ∈ , 22 –rr ; D , f –1(x) = arc sin x, x ∈ [–1, 1]

f –1 2 1 dn kalkulatuko dugu: arc sin

Jakina, emaitza berera hel gaitezke ( f –1)' (x) adierazpena zein den jakinda. Ikus dezagun:

f (x) = sin x injektiboa izateko, , 22 –rr :D tartean hartuko dugu

Pentsatu eta praktikatu

1 Kalkulatu ( f –1)' (x) funtzioa f ' (x)-tik abiatuta:

a) f (x) = x 2 – 1, x ∈ [1, 3]

b) f (x) = x 3

Tarte horretan, cos x positiboa edo 0 da. Hori dela eta, cos x = snix 1– 2 askatzean + zeinuarekin baino ez gara gelditu.

(*) f ' (x) = (sin x)' = cos x

Beraz, f ' 6 r bl = cos 6 r = 2 3 .

BEGIRATU

Ez dugu ( f –1)' funtzioaren adierazpena jakin behar horren balioak kalkulatzeko.

rr bl Aurkitu ( f –1)' ( 3 ) bi modutan:

a) Lehenengo ( f –1)' (x) lortuz.

b) Zuzenean

Funtzio inplizitu baten deribatua

Funtzio batzuk ϕ(x, y) = 0 motako adierazpenen bidez ematen dira, eta adierazpen horietan oso zaila edo ezinezkoa izaten da y askatzea. Adibidez:

y 3 – 7x 2 + 5y 2x + 17 = 0

Horrelakoetan, y-ren balioak modu inplizituan ematen dira adierazpenaren bidez; baina ezin da y = f (x) motako funtzio bat modu esplizituan lortu. Funtzioaren y’ deribatua, berriz, ez da kalkulatzeko zaila. Ikus dezagun aurreko adibidearen kasuan: y 3 – 7x 2 + 5y 2x + 17 = 0 deribatzean, hau lortzen dugu: 3y 2y' – 14x + 5(2y y' x + y

F ' (X) JARRI BEHARREAN JAR DAITEKE Y' ?

Lehenengoz erabiliko dugu y’ adierazpena y = f (x) funtzioaren deribatua izendatzeko. Nomenklatura hori erabiltzean, funtzioarekin y aldagaia identifikatzen ari gara. Hori egitea zuzena da eta beti erabil daiteke, baldin eta zer esan nahi duen argi badaukagu.

Ikusten duzunez, y' deribatua x-ren eta y-ren funtzioan emanda. Beraz, deribatuak puntu batean zer balio duen kalkulatzeko, puntu horren abzisa eta ordenatua jakin behar ditugu. Adibidez, kurba (2, 1) puntutik igarotzen dela jakinda, puntu horretan zer deribatu duen lortuko dugu:

y' (2, 1) = 3102 14 25 1 –+ =

1 Aurkitu x 2 – x + tg(x + y) = 1 adierazpenaren bidez modu inplizituan emandako kurbak x = 0 abzisapuntuan duen zuzen ukitzailearen ekuazioa, honako hau kontuan har-

tuz:

y ∈ , 22 –rr bl

idatzi zein diren elipseak x = 8 abzisa-puntuetan dituen zuzen ukitzaileen ekuazioak.

Lehenengo, puntuaren ordenatua lortuko dugu. Horretarako, x-ren lekuan 0 jarri eta hau lortuko dugu, tg y = 1 → y = 4 r .

Beraz, zuzen ukitzailea 0, 4 r bl puntuan jarri behar dugu. Malda behar dugu Adierazpena deribatuko dugu: 2x – 1 + [1

x = 0, y = 4 r ordezkapenak eginez:

Baina

Deribazio logaritmikoa

Batzuetan, logaritmoak hartu eta horien propietateak erabiliz, asko errazten da funtzio baten deribatuaren kalkulua. Ikus dezagun nola honako adibide hau erabiliz:

f (x) = x x

Adierazpen hori ez da potentziala, berretzailea ez delako konstantea; ezta esponentziala ere, berrekizuna ez delako konstantea. Beraz, ez daukagu funtzio horren deribatua kalkulatzeko erregelarik. Baina logaritmoak hartzen baditugu, deribatzen dakigun funtzio bat lortuko dugu:

ln f (x) = x ln x () () · ' ln fx fx xx x

Deribatu aurretik logaritmoak hartzeko teknika horri deribazio logaritmiko esaten zaio.

Nahitaezkoa da ia teknika hori erabiltzea ϕ(x) = α(x)β(x) formako adierazpena duten funtzioak deribatzeko. Ikus dezagun:

ln ϕ(x) = β(x) ln α(x)

Deribatuz: () '( ) '( )· () () () '( ) ln x x xx x x x z z ba b a a =+ ϕ'(x) askatu eta ϕ(x)-ren lekuan adierazpena jarri behar da. Hori eginda, hau lortzen dugu:

GOGORATU

ln (A · B ) = ln A + ln B

ln B A cm = ln A – ln B

ln (A)B = B ln A

➜ anayaharitza.es

Teoria berrikusi: logaritmoen propietateak.

GOGORATU

Deribazio-teknika hau (logaritmikoa) oso lagungarria da ezagun ditugun deribazio-erregeletako batzuen baliozkotasuna frogatzeko.

b) Zuzenean deribatu badaiteke ere, kasu honetan erosoagoa izango da deribazio logaritmikoa erabiltzen badugu:

1 Aurkitu honako funtzio hauen funtzio deribatua:

Deribazio-formulak modu arrazoituan lortu

Deribazio-formulak egiaztatzeko jarraituko dugun ordena ez dator bat formula horiek aurkezteko erabili dugun ordenarekin.

Hemen jarraituko dugun segidaren arabera, emaitza batzuk hurrengoak lortzeko erabiliko ditugu eta, horrela, modua emango digu egiaztapen batzuk nabarmen sinplifikatzeko.

bi funtzioren arteko batuketaren deribatua: ϕ(x) = f (x) + g (x)

Egiaztapena egiteko, deribatuaren definizioan oinarrituko gara:

() () [( )( )] [( )( )] xx fx gx fx gx h h–h hh – zz + = ++ ++ =

= () () () () fx fx gx gx h h–h h– + + +

ϕ'(x) = lm i 0 h "

() ()xx h h–zz + =

= lm i 0 h " () () fx fx h h– + + lm i 0 h " () () gx gx h h– + =

= f ' (x) + g' (x)

funtzio konposatuaren deribatua: ϕ(x) = g [ f (x)]

() ()xx h h–zz + = (1) () () () () fx fx xx h–h–zz + + · () () fx fx h h– + =

= (2) () () [( )] [( )] () () fx fx gf xg fx fx fx h–h–h h–+ ++ =

= (3) [( )] [( )] () () gf xg fx fx fx k k –· h h– ++

Limitea h → 0 denean, k → 0 denez, hau lortzen da: lm i k 0 " [( ))][ ()] k gf xk gf x – + lm i 0 h " () () fx fx h h– + = g' [ f (x)] · f ' (x).

Hau da: ϕ' (x) = g' [ f (x)] · f ' (x)

(1) Bider eta zati f (x + h) – f (x) egingo dugu. Horretarako, pentsatu behar dugu, x-ren ingurune batean, f (x + h) ≠ f (x), eta, beraz, f (x + h) – f (x) ≠ 0.

(2) ϕ(x) adieraziko dugu g [ f (x)] eran, eta, beraz, ϕ(x + h) = g [ f (x + h)].

(3) k = f (x + h) – f (x) esango diogu, eta, beraz, f (x + h) = f (x) + k. Ikusten duzunez h → 0 bada, orduan k → 0.

logaritmo nepertar baten deribatua: ϕ(x) = ln x, x > 0

() ()xx h h–zz + = () h ln ln ln xx x x 1 h h–h · + = + dn =

= ln ln xx 1 11 h hh / 1h += +=ddnn

= // ln ln xx 1 1 1 1 hh x x x x 1 1 h h += + ddnn > H

Orain, limitea h → 0 denean hartuko dugu

x > 0 denez, orduan x h → ∞ .

Gogoan izan lm i n e 1 1 n

n ∞ += " dn dela. Kasu honetan x h da n-ren ordez.

1 1 hh h z zz = + =+ = "" dn > H

'( ) (h)( ) / ln ln xl m xx lm x e ii 1 1 h –h / x x x 00

ln e k = k ln e = k dela kontuan hartuz, hau lortzen da: ϕ ' (x) = x 1

x > 0 kasua hartu dugu, baina alboan ageri denez, x ≠ 0 denean (ln | x |)' = x 1 x ≠ 0 dela egiaztatzen da

Emaitza horrek, funtzio konposatuaren emaitzarekin batera, modua ematen du «deribazio logaritmikoaren» teknika erabiltzeko (logaritmoak hartzen dira, eta, gero, deribatu egiten da). Teknika hori probatuko dugu honako emaitza hauetan ere

funtzioen arteko biderketaren deribatua: ϕ(x) = f (x) · g (x)

Logaritmoak hartuko ditugu: ln ϕ(x) = ln f (x) + ln g (x)

Deribatu egingo dugu: () '( ) () () () () '' x x fx fx gx gx z z =+

ϕ'(x) askatuko dugu: '( )( ) () () () () () ·( ) () () () () '' '' xx fx fx gx gx fx gx fx fx gx gx

zenbaki baten eta funtzio baten arteko biderketaren deribatua:

Aurrekoaren ondorio zuzena da, k deribatua 0 duen funtzioa dela onartuz:

➜ Funtzio deribatua, ukitzailearen maldaren bidez.

BEGIRATU

ln | x | = () ln ln x x x x 0 0 –bada bada < > )

ln | x |)' = () 1 –· –= xx x

[ \

] ] ] ]

11 1 0 0

x x

bada bada < >

Beraz: (ln | x |)' = x 1 , x ≠ 0 bada y = ln (–x)

y = ln x

= ln |x |

berreketa baten deribatua: ϕ(x) = x k

Logaritmoak hartu eta deribatuz:

ln ϕ(x) = k ln x → () '( ) x x z z = k · x 1

ϕ'(x) askatuko dugu:

ϕ'(x) = k · x 1 · ϕ(x) = k · x 1 · x k → ϕ' (x) = k x k – 1

zatiketa baten deribatua: ϕ(x) = () () gx fx , g (x) ≠ 0

Biderketa baten deribatuaren eta beste honen ondorioa da:

'

() () () ' gx gx gx 1 –2 = eo

ϕ'(x) = ' () () () () () () () ' ' fx gx fx gx fx gx gx 11 2 =+ e f o p

ϕ' (x) = () () ·( )( )· () '' gx fx gx fx gx –2

edozein oinarritako logaritmoen deribatua: ϕ(x) = loga x

loga x = ln ln a x denez, (loga x)' = ln a 1 · (ln x)' → ϕ' (x) = ln a x 11

funtzio esponentzialen deribatua: ϕ(x) = e x

ln ϕ (x) = x → () '( ) x x z z = 1 → ϕ' (x) = ϕ (x) → ϕ' (x) = e x

edozein berrekizuneko funtzio esponentzialen deribatua: ϕ(x) = a x

ln ϕ (x) = x ln a → () '( ) x x z z = ln a → ϕ' (x) = a x ln a

sinu funtzioaren deribatua: ϕ(x) = sin x

GOGORATU ' ()' x xx x 11 12 2 == = cm ' () () '( ) () () ' gx gx gx gx gx 11 –22 == eo

() ()xx h h–zz + = () sniisnxx h h– + = = coss ns n 2· cos ii xx xx x 22 2 2

GOGORATU sin A – sin B = 2cos sn i AB AB 22 – +

hh –h h

2 h

h ++ + =+dn

lm sin i 0 a a " a = 1 dela kontuan izanda, limiteak h → 0 hartuz gero, berdintza hau

lortzen dugu:

ϕ' (x) = cos x · 1 = cos x

kosinu funtzioaren deribatua: ϕ(x) = cos x

ϕ (x) = cos x = sin x 2 –r bl

ϕ' (x) = cos x 2 –r bl · (–1) = –cos x 2 –r bl → ϕ' (x) = –sin x

tangente funtzioaren deribatua: ϕ(x) = tg x

ϕ' (x) = ' () () cos sn cos coscos sn sn i ii x x x xx xx –2 == dn = cos coss n cos i x xx x 1 2 22 2 + = = 1 + tg 2 x

ϕ' (x) = 1 + tg 2 x = cosx 1 2

arku sinu funtzioaren deribatua: ϕ(x) = arc sin x

ϕ (x) = arc sin x → sin ϕ (x) = x

Deribatu egingo dugu: cos ϕ (x) · ϕ' (x) = 1 → ϕ' (x) = ()cosx 1 z

Zein da sinu moduan x duen angeluaren kosinua ?

sin 2 ϕ (x) + cos 2 ϕ (x) = 1 → cos ϕ (x) = ± ()snix x 11 –± –22 z =

Beraz: ϕ' (x) = x 1 1 –2

Erroaren balio positiboa hartuko dugu, arc sin x funtzioa gorakorra dela baitakigu.

arku kosinu funtzioaren deribatua: ϕ(x) = arc cos x

ϕ (x) = arc cos x → cos ϕ (x) = x

Deribatu egingo dugu: [–sin ϕ(x)] · ϕ' (x) = 1 → ϕ' (x) = ()snix –1 z

sin 2 ϕ (x) + cos 2 ϕ (x) = 1 →

sin ϕ (x) = ± ()cosx x 11 –± –22 z = → ϕ' (x) = x 1 1 ––2

Kasu honetan, erroaren balio negatiboa hartuko dugu, arc cos x funtzioa beherakorra dela baitakigu.

arku tangente funtzioaren deribatua: ϕ(x) = arc tg x

ϕ (x) = arc tg x → tg ϕ (x) = x

Deribatuz gero: [1 + tg 2 ϕ (x)] ϕ' (x) = 1 → ϕ' (x) = () tg x 1 1 2 z + → ϕ' (x) = x 1 1 2 +

KONTUAN HARTU coscos cossin xx xx 1 22 22 = + = = cos cos cos sn i x x x x tg x 1 2 2 2 2 2 += + y = arc sen x r/2 –r/2

y = arc sin x

–1 1 y = arc cos x

r –1 1

Funtzio baten diferentziala

Funtzio batek puntu batean duen gehikuntza eta diferentziala

f funtzio batek x0 puntuan duen gehikuntza (aldagai askearen h gehikuntzari dagokiona) hau da:

Δ f (x0, h) = f (x0 + h) – f (x0) h

IDAZKERA

Df (x0 , h)

x0 x0 + h

Funtzioak x0 eta x0 + h abzisa-puntuen artean zer hazkunde duen adierazten du. f funtzio batek x0 puntuan duen diferentziala (aldagai askearen h gehikuntzari dagokiona) hau da:

d f (x0, h) = f ' (x0) · h

t h

df (x0 , h)

x0 x0 + h

t da funtzioaren grafikoak x0 abzisa-puntuan duen zuzen ukitzailea. d f (x0, h) adierazpenak t zuzenaren ordenatuak x0 eta x0 + h artean duen hazkundea ematen digu.

Diferentziala, gehikuntzaren hurbilketa moduan

Kurba batek puntu batean duen ukitzailea kurbari ondoen lotzen zaion zuzena da. Hori dela eta, esan daiteke d f (x0, h) diferentziala ∆ f (x0, h) gehikuntzaren hurbilketa ona dela x0 puntu horretan eta h-ren balio horretarako, |h| oso txikia denean

Hori guztia proposizio honen bidez laburtzen da:

(, ) ∆ lm i df x fx h h 0 0 0 h " = 1

(, )

Egiaztapena

(, )

Deribatua, diferentzialen arteko zatiketa moduan g (x) = x identitate-funtzioaren kasuan, g' (x) = 1 da, eta, beraz:

d g (x) = g' (x) · h = 1 · h = h

Hau da, dx = h. Hori kontuan izanda, hau jar dezakegu:

d f (x) = f ' (x) dx ⇒ f ' (x) = () dx df x

Deribatua diferentzialen arteko zatiketa moduan adieraz daiteke.

∆ f (x0, h) jartzen dugu, f-ren gehikuntza bai x0 puntuaren araberakoa eta bai aldagai askearen h gehikuntzaren araberakoa delako. Arrazoi beragatik, d f (x0, h) jartzen dugu.

BEGIRATU

Diferentzialak modua ematen digu f funtzio oro puntu batetik hurbil aztertzeko, funtzio lineal batetik abiatuta. Izan ere:

d f (x0, h) = f ' (x0) · h = f ' (x0) · (x – x0)

x-ren funtzio lineala da.

Ebatzitako ariketak

1 Lortu d f (x), honako hauek jakinda:

a) f (x) = x 2 – 3x + 9

b) f (x) = cos xx 2 +

2 Posizioa ekuazio honen bidez zehaztuta duen partikula bat daukagu (s zentimetrotan, t segundotan):

s (t) = 2t 4 – t 3 + t 2

Zehaztu zenbateko espazioa ibiltzen duen partikulak t = 4 unetik t = 4,01 unera.

a) Zehatz-mehatz.

b) Gutxi gorabehera.

3 Kalkulatu zenbatekoa izango den l aldeko kubo baten bolumenaren hazkundea alde bakoitza h handitzen bada.

Zehaztu emaitza hori l = 10 cm eta h = 0,02 cm direnean.

a) d f (x) = f ' (x) dx = (2x – 3)dx

b) d f (x) = cos sn i xx xx dx 2 2–2 +

a) Ibilitako espazioa lortzeko, posizio-funtzioak t = 4 s eta t = 4,01 s uneen bitartean zer gehikuntza duen kalkulatu behar dugu:

Δs = s (4,01) – s (4) = 468,73813102 – 464 = 4,73813102 cm

b) Gutxi gorabehera lortzeko, ds diferentzialetik abiatu eta t0 = 4, dt0 = h = 4,01 – 4 = = 0,01 hartuz:

d s = s' (t) · dt = (8t 3 – 3t 2 + 2t ) · dt t0 = 4 eta dt0 = 0,01 kasuan: ds = 472 · 0,01 = 4,72 cm

Ikusten dugunez, hurbilketa oso ona da.

Funtzioa: kuboaren bolumena aldearen funtzioan → V = l 3

Hazkundea:

ΔV = (l + h)3 – l 3 = (l 3 + 3l 2h + 3l h2 + h3) – l 3 = 3l 2h + 3l h2 + h3

Gutxi gorabeherako hazkundea: dV = V ' (l ) · h = 3l 2h

Interpretazio geometrikoa:

l 2h l h2

h l l 2h

1 Kalkulatu Δy, dy, Δy – dy :

h3

ΔV bigarren irudian kuboa eratuz ageri diren zazpi elementuek osatzen dute.

l 2h

l h2 l h2

dV hiru plaka karratuek osatzen dute.

ΔV – dV kenketak hiru listoiak eta kubotxoa adierazten ditu. h txikia denean, lau elementu horien bolumena ez da kontuan hartzeko modukoa

l = 10 cm, h = 0,02 cm direnean, hau lortzen dugu:

ΔV = 10,023 – 103 = 6,012 cm3, dV = 3 · 102 · 0,02 = 6 cm3

0,012 cm3-ko aldea ez da kontuan hartzeko modukoa

a) y = x 2 – x da x0 = 3, dx0 = 0,01 denean

b) y = x 1 –2 da x0 = 2, dx0 = 0,1 denean

c) y = x 3 da x0 = 125, dx0 = 1 denean

2 7 cm-ko erradioa duen brontzeko bola bati 0,2 mm-ko lodiera duen zilarrezko bainua eman diote.

Kalkulatu zenbat zilar erabili den (gutxi gorabehera, diferentzialetik abiatuta).

3 Kalkulatu 126 3 -ren hurbilketa bat urrats hauek emanda:

• Esan honela: f (x) = x 3 .

• Lortu df zein den, x0 = 125 eta dx0 = 1 direnean.

• Lortu f (126) ≈ f (125) + df (125) zein den, dx0 = 1 denean.

4 Jokatu aurreko ariketan bezala eta kalkulatu, gutxi gorabehera: a) 1,014 b) 15, 8 c) 66 3

Pentsatu eta praktikatu

Ebatzitako ariketak eta problemak

1. Deribatua definiziotik abiatuta lortzea

Aurkitu funtzio honen deribatua f (x) = x3 + definizioa erabiliz.

EGIN ZUK

Aurkitu f (x) = x 4 –2 funtzioaren deribatua, definizioa erabiliz.

2. Zatika definituriko funtzio baten deribagarritasuna

Aztertu honako funtzio honen deribagarritasuna:

• f funtzio polinomikoen bidez definituta dago (– ∞, –2), (–2, 2) eta (2, +∞) tarteetan. Beraz, f jarraitua eta deribagarria da tarte horietan.

• f jarraitua da x = –2 eta x = 2 puntuetan, izan ere: lm i x –2 " f (x) = f (–2) = 0 eta lm i x 2 " f (x) = f (2) = 0

Irudikatu f-ren eta f '-ren grafikoak.

Deribatua aztertuko dugu:

EGIN ZUK

Aztertu funtzio honen deribagarrita-

Irudikatu

f ' (x) = ≤ x x x x

2 22 2 ––bada –bada bada << > *

4 2 4

f ' (–2–) = f ' (–2+) = 4 → f deribagarria da x = –2 puntuan

f ' (2–) = – 4, f ' (2+) = 4 → f ' (2–) ≠ f ' (2+) → f ez da deribagarria x = 2 puntuan

Beraz:

f ' (x) = ≤ x x x x

2 22 2 ––bada –bada bada << > * 2

4 2 4

4 2 –2

f '

f 4 2 –2 –4

f -k puntu erzduna du x = 2 puntuan f ' ez da existitzen x = 2 puntuan

3. Parametro batek f deribagarri egiteko izan behar duen balioa zehaztea

Kalkulatu zer balio izan behar duen m parametroak f (x) funtzioa deribagarria izateko x = 1 puntuan.

•

=

bada x = 1 puntuan,

Kalkulatu zein izan behar den a-ren balioa

4. Deribagarritasuna

Aurkitu zein izan behar diren a -ren eta b-ren

Deribagarria izateko x = 1 puntuan, jarraitua izan behar da puntu horretan:

Deribagarria

(Bigarren tartean, deribazio logaritmikoa erabili dugu).

(*) eta (**) ekuazioek eraturiko sistema ebatzita, hau lortzen dugu: a

da eta deribatua hau da:

Ebatzitako ariketak eta problemak

5. Balio absolutuko funtzio baten deribatua

Aurkitu funtzio honen funtzio deribatua:

f (x) = | x – 3 | + | x |

Adierazi zer puntutan ez den deribagarria.

EGIN ZUK

Kalkulatu funtzio honen funtzio deribatua, eta irudikatu f eta f '

f (x) = | 2 – x | + | x + 1 |

Adierazi zein puntutan ez den deribagarria.

6. Deribazio-erregelak

Aurkitu funtzio hauen funtzio deribatuak:

7. (f  –1) '(x) lortzea, f '(x) jakinda

Jakintzat emango dugu funtzio honek:

f (x) = arc tg x x 1– 2

deribatu hau duela f ' (x) = x 1 1 –2 . (Ebatzitako 6. ariketan ikusi dugu).

Emaitza horretatik abiatuta, kalkulatu f (x)-ren alderantzizkoaren deribatua

EGIN ZUK

Honako hau dakigu:

f (x) = ln (ln x)2 eta f ' (x) = ln xx 2

Kalkulatu (f –1)' (x).

• Kasu honetan, (f –1)’ eta f ' deribatuen artean dagoen erlazioa erabiliko dugu:

'

• Aurrera egiteko, (f –1) (x)-ren adierazpena lortu behar dugu

8. (f  –1) '(x0) lortzea (f  –1) '(x) kalkulatu gabe

Aurreko ariketako funtzio bera hartu dugu,

f (x) = arc tg x x 1– 2 eta horren deribatua zein den badakigu:

f ' (x) = x 1 1 –2

Kalkulatu (f –1)'(0) eta (f –1)' 3 r bl , baina (f –1)'(x) alderantzizkoaren funtzio deribatua erabili gabe

Elkarrekikoa erabiliko dugu berriro kalkuluak egiten laguntzeko:

f (x) = arc tg x x 1– 2 → f –1(x) = tg x tg x

• (f –1)' (0) lortzeko, f –1(0) = tg tg 10 0 10 0 0 2 + = + = kalkulatuko dugu lehenengo.

Beraz: (f –1)' (0) = () () [] ' '

'

dugu lehenengo:

EGIN ZUK

Aurreko ariketako Egin zuk ataleko funtzioa hartuta, kalkulatu (f –1)’ (0) deribatua (f –1)’ (x) alderantzikoaren funtzio deribatua erabili gabe.

Zentzuzkoa denez, emaitza berera iritsiko gara alderantzizko funtzioaren deribatua erabilita (f –1)' (x).

Gidatutako ariketak eta problemak

1. Funtzioa deribagarri egingo duten bi parametroren balioak lortzea

Kalkulatu zein izan behar diren a eta b parametroak, beheko funtzioa deribagarria izateko x = 1 puntuan:

• Funtzioa deribagarria izateko, jarraitua izan behar da. Horretarako, a eta b parametroek zenbait baldintza bete behar dituzte. Beraz, erlazionatuko dituen ekuazio bat lortuko dugu.

• f deribagarria izateko, a eta b parametroek beste ekuazio bat ere bete behar dute.

Z [ \

] ] ] ]

x 21 –++ +

f (x) = ≤ x x a be x

xbada xbada 1 2 1 1 >

• Hori eginda, a eta b ezezagunak dituzten bi ekuazioko sistema bat lortu dugu. Ebatzi.

• Egiaztatu horrela lortu duzun funtzioa jarraitua eta deribagarria dela x = 1 puntuan

Soluzioa: a = 4 5 ; b = – 4 5

Zirkunferentzia hau izanda, x 2 + y 2 + 6x – 2y – 15 = 0

aurkitu zein puntutan izango dituen –4 3 maldako ukitzaileak. Irudikatu.

• Deribatu modu inplizituan, eta y '-ren lekuan jarri horren balioa: – 4 3

Erlazio lineal bat lortuko dugu x-ren eta y-ren artean (r zuzen baten ekuazioa).

• Aurkitu r zuzenaren eta zirkunferentziaren ebaketa. Enuntziatuan eskatzen diren puntuak lortuko ditugu

• Irudikatu.

Soluzioa: (– 6, –3), (0, 5).

(0, 5) (–6, –3)

Erabili deribazio logaritmikoa eta logaritmoen propietateak honako funtzio hauen deribatuak kalkulatzeko:

a) y = logx tg x

b) y = (x + 1) tg x

c) y = xx11 –2 4 +

a) Erabili logaritmoaren definizioa berdintza modu esponentzialean adierazteko.

Hartu logaritmoak eta erabili berreketa baten logaritmoaren propietatea y askatzeko.

Deribatu lortutako funtzio hori

b) Hartu logaritmoak bi ataletan, eta erabili aurreko ataleko propietate bera

Deribatu lortutako funtzio inplizitua, eta askatu y ' .

c) Hartu logaritmoak, aurreko ataletan bezala, eta erabili biderketa baten logaritmoaren propietatea

Adierazi erroak berreketa moduan, eta erabili logaritmoak berretzailea «jaisteko»

Deribatu aurreko atalean bezala

Soluzioa:

2. Deribazio inplizitua

3. Deribazio logaritmikoa

Trebatzeko

Deribatuaren definizioa

1 Beheko irudian funtzio baten grafikoa ageri da, y = f (x).

Deribazio-erregelak

Kalkulatu honako funtzio hauen deribatuak:

6 a) y = x x 3 3 –2 2 + b) y = x3 2 3

7 a) y = x x 1 1–/ 23 + dn b) y = x x 2 2 2 +

a) Adierazi f (–1) eta f ' (1) funtzioen balioak.

b) Adierazi, arrazoiak emanez, f deribagarria den x = –1 eta x = 0 puntuetan.

c) Esan zein diren f (x)-ren alboko deribatuen balioak x = –1, x = 0 eta x =1 puntuetan.

2 Erabili deribatuaren definizioa f ' (2) lortzeko honako kasu hauetan:

a) f (x) = x x 1 1 –+ b) f (x) = x 2 +

3 Erabili deribatuaren definizioa f ' (x) lortzeko honako kasu hauetan:

a) f (x) = x + x 1 b) f (x) = x 1 2 +

4 I) Arrazoitu bi adierazpen hauek berdinak direla: () () lm fx fx i h h–0 00 h + " = () () lm xx fx fx i ––xx 0 0 0 " = f ' (x0)

II) Idatzi honako limite hauetako bakoitzaren adierazpena (kontuan izango dugu parte hartzen duten funtzioak deribagarriak direla):

a) () () lm xa gx ga i ––xa " b) lm i 0 h " () () ff 0 h h–

c) lm i x 0 "

() () x x 22 –zz + d) lm i x 0 " () () x ff x 55–+

5 lm i 0 h " () sniisn h h–rr + limitea sinu funtzioaren deribatua

da π abzisa-puntuan; hau da, sin' (π). Beraz, limitea hau da: sin' (π) = cos (π) = –1

Kalkulatu ondorengo limiteak ere era berean; hau da, ezagun dituzun deribazio-erregelak erabiliz:

a) lm i 0 h "

42 h h– + b) lm i 0 h " ee h –22 h +

c) lm i x 3 " () x xx 3 31 1 –

+ d) lm i x 4 " x x 4 64

8 a) y = ln x x b) y = 7e –x

9 a) y = e e e e –xx xx –

–+ b) y = sin x cos x

10 a) y = snix 1 b) y = ln (x 2 + 1)

11 a) y = arc tg x 3 b) y = cos 2 (2x – π)

12 a) y = sin 2 x b) y = tg x

13 a) y = sin x 2

b) y = arc tg (x 2 + 1)

14 a) y = () x 23 –7 b) y = logx 2

15 a) y = sin 2 x 2 b) y = arc tg x 1

16 a) y = cos 5 (7x 2) b) y = 3x + 1

17 a) y = () x 53 –2 3 b) y = arc sin x 3 2

18 a) y = ln (2x – 1) b) y = tg x 2 2

19 a) y = ln (x 2 – 1) b) y = arc cos x2

20 a) y = ln x 1– b) y = (arc tg x)2

21 a) y = log3 (7x + 2) b) y = ln tg x 3 dn

22 a) y = e 4x b) y = ln ln x 1 dn

23 a) y = 2x b) y = arc sin x x 1 1 –+ dn

24 a) y = 5tg 3 (3x 2 + 1) b) y = xx +

25 a) y = tg x 2 b) y = x x 2 2 – 3 +

Proposatutako ariketak eta problemak

Deribagarritasuna eta jarraitutasuna

26 Aztertu honako funtzio hauen grafikoak eta adierazi zer puntutan diren deribagarriak: a) b) c)

Deribatzeko beste teknika batzuk

34 Kalkulatu honako funtzio hauen deribatuak, aldez aurretik logaritmoen propietateak erabiliz:

a) y = ln x x 1 1–+ b) y = ln (x tg x)2

c) y = ln x x 1 –2 2 3

d) y = ln (2x · sin 2 x)

Horietakoren bat deribagarria da Á osoan?

27 a) Egiaztatu funtzio hau jarraitua eta deribagarria dela eta aurkitu f ' (0), f ' (3) eta f ' (1): f (x) = ≥ x xx x x 31 1 1 –bada bada < 2 + )

b) Zein da horren funtzio deribatua?

c) Zer puntutan betetzen da f ' (x) = 5?

28 Egiaztatu f (x) funtzioa jarraitua dela, baina ez dela deribagarria x = 2 puntuan: f (x) = () ≥ ln x x x x 1 36 2 2 ––bada bada < )

29 Aztertu funtzio hauen jarraitutasuna eta deribagarritasuna:

35 Kalkulatu honako funtzio inplizitu hauen deribatuak:

a) x 2 + y 2 = 9 b) x 2 + y 2 – 4x – 6y = –9

c) x y 16 9 1 2 2 += d) () () x y 8 1 14 3 1 ––2 2 + =

e) x 3 + y 3 = –2xy f ) xy 2 = x 2 + y

g) x y 925 1 –2 2 = h) 4x 2 + 4y 2 + 8x + 3 = 0

i) x 2 + xy + y 2 = 0 j) yx – x 2 – y = 0

36 Erabili deribazio logaritmikoa funtzio hauek deribatzeko:

a) y = x 3x b) y = x x + 1

c) y = x e x d) y = (ln x)x + 1

e) y = sn i x x xdn f ) y = x tg x

g) y = (2x )x – 2 h) y = (x + 4)x

i) y = x x 1 x + dn j ) y = x cos x

k) y = (2x – 3)x + 1 l) y = (cos x)x

30 Aztertu honako funtzio hauen jarraitutasuna eta deribagarritasuna: a)

31 a) Kalkulatu m eta n parametroaren balioak f deribagarria

b) Zer puntutan da f ' (x) = 0?

32 Kalkulatu a eta b parametroen balioak honako funtzio hau deribagarria izateko Á osoan:

Funtzio baten diferentziala

37 Zehaztu zein den honako funtzio hauetako bakoitzerako df (x) diferentziala:

a) f (x) = x 4 – 2x 2 + 1 b) f (x) = e 2x 2 + 1

c) f (x) = ln x 4 2 d) f (x) = x 2 2 3 +

38 Aurkitu Δy, dy eta Δy – dy kasu hauetako bakoitzean:

a) y = x 2 – 3x + 1, x0 = 2 eta dx0 = 0,2 direnean

b) y = e x , x0 = 2 eta dx0 = 0,1 direnean

c) y = x 2 2 3 + , x0 = 5 eta dx0 = 0,02 direnean

d) y = xx x 25 –2 + , x0 = 1 eta dx0 = 0,1 direnean

33 Kalkulatu a-ren eta b-ren balioak f jarraitua eta deribagarria izan dadin.

39 Kalkulatu adierazpen hauen balio hurbildua diferentziala erabiliz:

a) 4, 001 1 b) , 201 1 3 c) log 10 001

Ebazteko

40 f eta g bi funtzio deribagarri dira, eta haiei buruz datu hauek dakizkigu:

f (1) = 1, f ' (1) = 2, g (1) = 3, g' (1) = 4

a) h (x) = f [(x + 1)2] funtzioa emanda, erabili katearen erregela h' (0) kalkulatzeko.

b) Kalkulatu k' (1), jakinda k (x) = () () gx fx dela.

41 f (x) = x 2 eta g (x) = 3x + 1 izanda, kalkulatu:

a) ( f ° g )' (x) b) ( g ° f )' (x)

c) ( f ° g' ) (x) d) ( f ' ° g )(x)

42 f (x) = (x + 1)2 eta g (x) = x 2 dira.

a) Kalkulatu: f ' (x 2) ( f ° g )' (x) g' [ f (x)] ( g ° f )' (x)

b) h edozein funtzio bada, aurkitu h'-ren eta h-ren funtzioan honako deribatu hauek: f [h (x)] f [x + h (x)] g [ f (x + h (x))]

43 Aztertu funtzio honen jarraitutasuna eta deribagarritasuna:

48 Esan ondorengo funtzio hauetako bakoitza deribagarria den adierazten den puntuan. Deribagarria bada, kalkulatu balioa; deribagarria ez bada, esan zenbat balio duten alboko deribatuek.

a) f (x) = ≥ x xx x x 31 3 2 2 ––bada bada < 2 + ) , x0 = 2 puntuan

b) f (x) = ≤ x x x x 1 22 1 1 ––bada bada > 2 ) , x0 = 1 puntuan

c) f (x) = | x |, x0 = 0 puntuan

d) f (x) = | x 2 – x – 6 | , x0 = –2 eta x1 = 3 puntuetan

49 Aztertu honako funtzio hauen deribatu nuluko puntuak:

a) y = () x x 3 2 + b) y = ()xx 4 16 –2

c) y = xx xx 1 1 –2 2 ++ + d) y = e x (x – 1)

e) y = x 2 e x f ) y = sin x + cos x

50 a) Irudikatu f (x) = | x + 1 | + | x – 3 | funtzioa. Grafikoa aztertuta, esan zer puntutan den deribagarria.

b) Irudikatu f ' (x).

* Kontuan izan ebatzitako 5. ariketa.

51 f (x) = x · | x | = ≥ x x x x 0 0 –bada bada < 2 2 ) funtzioa izanda:

a) Kalkulatu f ' (x). b) Kalkulatu f '' (x).

44 Aztertu beheko funtzio honen deribagarritasuna x = 0 puntuan:

Adierazi grafiko batean lortutako emaitzak.

52 Aztertu honako funtzio hauen deribagarritasuna:

a) y = | x – 2 | b) y = | x2 + 6x + 8 |

c) y = x + | x – 3 | d) y = x2 + | x|

45 Aztertu funtzio honen jarraitutasuna eta deribagarritasuna:

bada

53 Aztertu funtzio hauen jarraitutasuna eta deribagarritasuna:

a) f (x) = || x 1 1 + b) f (x) = || x x 1 –2

54 f (x) = x 2 | x | bada, aurkitu f ' , f '' eta f '''

55 Zehaztu honako funtzio hauetako bakoitzaren deribatua:

≤bada

46 Zehaztu, ahal izanez gero, a parametroaren balioa f funtzioa deribagarria izan dadin definizio-eremu osoan: f (x) = ()

47 Zehaztu g (x) = f' (x) funtzioa definituta dagoen, jarraitua den eta deribagarria den x = 1 puntuan, hau jakinda:

a) y = x 1 1 x + dn

b) y = (sin x)x

c) 4x 2 + y 2 + 4x – 12y – 6 = 0

d) xy = e x + y

e) xy = ln y

f ) x 2 – y 2 + 3xy + 5 = 0

Proposatutako ariketak eta problemak

56 Lortu beheko funtzioen deribatua bi modutan, eta egiaztatu, eragiketak eginez, emaitza bera lortzen duzula:

I) Ezagun dituzun deribazio-erregelak erabiliz.

II) Deribazio logaritmikoa erabiliz.

a) y = x x 1 2 3 + dn b) y = x x 1 1 –+

c) y = sin 3 x cos 2 x d) y = xx 1 22 3 +

57 Kalkulatu zein den honako funtzio hauetako bakoitzaren deribatuaren balioa x = 0 puntuan:

a) g (x) = e sin f (x), baldin eta f (0) = 0 eta f ' (0) = 1

b) h (x) = [sin f (x)]3, baldin eta f (0) = 4 r eta f ' (0) = 1

c) j (x) = () ln fx , baldin eta f (0) = e eta f ' (0) = 1

58 Aurkitu honako funtzio hauen n ordenako deribatua:

a) f (x) = e 2x b) f (x) = x n

59 Kalkulatu funtzio honen 50 eta 51 ordenako deribatua: y = sin x 2 r bl

60 Beheko funtzio bakoitzean, zein da adierazten den abzisapuntuan duten zuzen ukitzailearen edo ukitzaileen malda?:

a) x 2 + y 2 – 2x – 8y + 15 = 0, x = 2 puntuan

b) cos (x + y) + sin (x – y) = 0, x = 4 r puntuan

c) y = (ln x)x + 1 , x = 1 p. d) y = (arc tg x)2x , x = 1 p.

e) y x 25 81 –2 2 = 1, x = 7 p. f ) y = x ln x ` j , x = e 2 p.

g) y = sn i x x xdn , x = π p. h) x y 36 49

+ = 1, x = 5 p.

61 Frogatu f (x) = sin 2x funtzioaren ordena bikoitiko deribatu guztiak baliogabetu egiten direla koordenatuen jatorrian.

62 Kalkulatu adierazpen hauen balio hurbildua, diferentziala erabiliz:

a) 122 b) 1 370 c) log2 130

d) 260 4 e) 103 825 3 f ) 34,001

63 Aurkitu 4,012 dm-ko aldea duen kubo baten bolumena, modu hurbilduan (diferentzialen bidez).

64 Zehaztu altuera 15 dm-koa eta oinarritzat 20 dm-ko aldea duen karratua daukan ortoedro batek zenbateko bolumen gehikuntza izango duen alde bakoitzaren luzera 1 cm handituz gero. Kalkulatu zehatz eta modu hurbilduan (diferentzialak erabiliz).

Galdera teorikoak

65 Irudikatu funtzio hauetako bakoitzaren deribatuaren zirriborro bat: a) b) c)

66 Deribatu nuluko zenbat puntu izan ditzake hirugarren mailako funtzio polinomiko batek? Gerta liteke deribatu nuluko punturik ez izatea? Eta bat bakarrik izatea?

67 Arrazoitu bigarren mailako funtzio polinomiko batek ukitzaile horizontaleko puntu bat duela beti.

68 f (x) = x 3 funtzioa eta ukitzaile horizontaleko a edozein puntu ditugu. f-ren eta grafikoak (a, a 3) puntuan duen ukitzailearen arteko aldea neurtzen duen funtzioa g (x) = f (x) – f ' (a) (x – a) – f (a) da.

a) Frogatu () lim xa gx – xa " = 0 dela.

b) Frogatu f edozein funtzio bada, aurreko emaitza hori ere egiaztatzen dela. Egizu hori azalduko duen grafiko bat.

69 Zuzena ala okerra?

a) lim 0 h " () () fa fa h –h –= – f ' (a)

b) lm i 0 h " () () fa fa 2 h h– + = 2f ' (a)

c) lm i 0 h " () () fa fa 2 h h– h ++ = f ' (a)

70 f (x) = x g (x) funtzioa daukagu. g (x) jarraitua bada 0 puntuan, frogatu f (x) deribagarria dela 0 puntuan eta kalkulatu horren deribatua. (Ez pentsatu g (x) deribagarria izango dela; beharbada ez da izango).

71 Honako grafiko hauek f, g, h eta j funtzioen deribatuak

j' h'

2

a) Funtzio horietako (f, g, h eta j) zeinek dituzte ukitzaile horizontaleko puntuak?

b) Grafiko horietako zein da lehen mailako funtzio polinomiko baten funtzio deribatua?

c) Zein dagokio bigarren mailako funtzio polinomiko bati?

d) Horietakoren bat hirugarren mailako polinomikoa da?

e) Funtzioetakoren bat y = ln x izan liteke ?

Sakontzeko

72 Egiaztatu f funtzioa deribagarria dela x = 0 puntuan, eta g, ez:

75 f (x) = arc cos x da.

a) Alderantzizko funtziotik abiatuta, kalkulatu funtzio horren deribatua.

b) Lortu f ' 2 1 cm zein den, f ' (x) erabili gabe.

c) Egiaztatu b) ataleko emaitza a) atalekotik abiatuta.

73 f eta g funtzioek hau betetzen dute: f (x) = x 2 + 1 eta

g ' (x) = cos x 2 r bl eta g (0) = 4. Kalkulatu:

a) ( f ° g )' (0)

c) (g –1)' (4)

74 Funtzio hauei:

b) ( g ° f )' (0)

d) ( f –1)' (5)

76 Frogatu, deribatuaren definizioa erabiliz, honako funtzio hau deribagarria dela x = 1 puntuan, baina ez x = –1 puntuan: f (x) = (1 – x) x 1– 2

77 f funtzio polinomikoak a erro bikoitza duela diogu kasu honetan: f (x) = (x – a)2 g (x), g funtzio polinomikoa izanik.

sinh (x) = ee 2 –xx –; cosh (x) = ee 2 xx –+ ; tgh (x) = ee ee –xx xx –

–+

sinu hiperboliko, kosinu hiperboliko eta tangente hiperboliko esaten zaie.

Egiaztatu honako berdintza hauek betetzen direla:

a) cosh 2 (x) – sinh 2 (x) = 1

b) sinh (x + y ) = sinh x cosh y + cosh x sinh y

c) cosh (x + y ) = cosh x cosh y + sinh x sinh y

d) sinh' x = cosh x

e) cosh' x = sinh x

f ) tgh' x = cosh x 1 2

1 Aurkitu honako funtzio hauen funtzio deribatuak:

a) y = (2x + 2) x 1 – b) y = arc tg x x 3 3 –+

c) y = ln (sin x)2 d) y = 2 x 1 3 –

e) y = (tg x)1 – x f ) x 2 + y 2 – xy = 0

2 f (x) = | x | + | x 2 + 2x | funtzioa izanda, definitu tarteka eta lortu:

a) f ' (x) b) f '' (x)

Adierazi grafikoki f (x), f ' (x) eta f '' (x).

3 Aztertu funtzio honen jarraitutasuna eta deribagarritasuna: f (x) = ≤ xx x x x 21 1 1 1 –bada bada > 2 + + )

Badago f ' (x) = 0 den punturik? Irudikatu.

a) Frogatu f funtzioak a erro bikoitza badu, orduan: f ' (a) = 0.

b) Eta alderantziz: frogatu, a erroa f ' eta f funtzioena bada, orduan a erroa f-ren erro bikoitza dela.

78 Aurkitu honako funtzio hauen n-garren deribatua:

a) y = e ax b) y = x 1 c) y = ln (1 + x)

79 Aurkitu funtzio honen deribatua eta egiaztatu konstante

bat dela:

y = arc tg cos cos x x 1 1–+ , 0 ≤ x < π izanik

Arrazoitu tg x 2 bl -ren formula kontuan hartuz.

4 Aztertu honako funtzio honen jarraitutasuna eta deribagarritasuna x = 0 eta x = 1 puntuetan:

5 Aurkitu a eta b parametroak f (x) jarraitua izateko:

+ + + *

2 32

xa ax b x

< < 2

1 10 0

x x x

–bada –bada bada

≤

Aztertu deribagarritasuna, lortu dituzun a-ren eta b-ren balioetarako.

6 Hona hemen f funtzioaren grafikoa. Aztertu deribagarritasuna, eta esan f ' (– 4), f ' (0) eta f ' (3) existitzen diren.

anayaharitza.es Ariketa hauen ebazpena.

Deribatuen erabilerak 10

Optimizazioaren bila

Kurba batekiko ukitzailea lortzea, kurbaren puntu batean, eta higikari baten aldiuneko abiadura kalkulatzea bezalako problema historikoek deribatuaren nozioa ekarri zuten. Dena dela, optimizazio-problemak izan ziren ordura arte planteaturiko problema partikular guztiei orokortasun bat emango zien teoria bat bilatzeari aupadarik indartsuena eman ziotenak.

Zientzia, teknika, matematika bera, bai eta eguneroko bizimodua ere, optimizazio-problemaz beterik daude (maximoak eta minimoak). Gai garrantzitsu asko honela planteatzen dira: «zer da egokiena horrelako egoera batean». Greziarrek maximo eta minimoen problema asko landu zituzten; esaterako, argiak puntu batetik beste batera islapenaren bidez heltzeko egiten duen bidea (Heron, K.a. i. mendea). Kalkulu diferentziala asmatu baino lehen, problema horietako bakoitza prozedura jakin baten bitartez ebazten zen, eta ez zen inoiz beste problema batzuetara orokortzen. Gaur egun, problema horietako asko deribatuen aplikazio sinpleak dira

Idazkera on bat

Matematikako kontzeptuak sinbolikoki modu egokian adierazteko idazkera on bat edukitzea oso garrantzitsua da. Newtonek y . idatzita adierazten zuen funtzio baten deribatua, baina gaineko puntu horrek ez zuen deribatuari buruzko informaziorik ematen. Leibnizek, berriz, deribatuaren esanahia oso egoki adierazten duen dx dy , idazkera asmatu zuen.

xviii. mendearen hasieran, Britainia Handiaren eta Europaren artean eztabaida sutsua piztu zen kalkulu infinitesimalaren asmatzaileari buruz: nor izan ote zen lehenengoa,: Leibniz (kontinentekoa) edo Newton (ingelesa). Hainbeste garraztu zenez giroa, matematikari britainiarrek estu jarraitu zieten Newtonen irakaspenei xviii. mende osoan, eta batere egokia ez zen haren idazkera erabili zuten. Burugogorkeria horren ondorioz matematika britainiarrak 50 urteko atzerapena izan zuela esaten da Idazkera egokiaren maisurik handiena Euler izan zen. Hari zor diogu gaur egun erabiltzen dugun ia idazkera osoa: hark sartutakoak dira π (grekozko periferia hitzaren hasiera) eta e (ziur aski, alemanez «unitate» esan nahi duen Einheit hitzaren hasiera; e da logaritmotzat unitatea duen zenbakia). Eulerrek eman zion ospea Leibnizek deribaturako eta integralerako erabili zuen idazkerari, baita beste adierazpen egoki askori ere.

Johann Bernoulli eta L’Hôpitaleko markesa

Jakob eta Johann Bernoulli anaien aitak ustez ondo zekien seme bakoitzarentzat arlo egokiena zein zen: Jakobentzat, teologia, eta Johannentzat, medikuntza. Baina ez zuen asmatu, ez batarekin, ez bestearekin. Aitak arlo horietarantz bideratu zituen, eta bi anaiak ezarritako bideak jorratzen hasi ziren Basileako Unibertsitatean, Suitzan. Baina benetan landu nahi zuten arloa matematikarena zen, eta, beraz, aitak agindutako ikasketak amaitu ondoren, matematikaren munduan murgildu eta horretan nabarmendu ziren; izugarri nabarmendu, gainera.

1692an, Johannek kalkulu infinitesimalarekin txundituta zegoen G.F.A. L’Hôpital markes gaztea ezagutu zuen Parisera egindako bidaia batean. Topaketa horren ondorioz, markesa Bernoulliren eskolak hartzen hasi zen eta, horrez gain, kontratu bat sinatu zuten: Johannek Basileara itzuli ondoren ere soldata jasoko zuen, baina, trukean, egindako aurkikuntza guztien berri eman behar zion markesari, eta honek nahi bezala erabil zitzakeen

Johann Bernoulliren ideia eta aurkikuntzak erabiliz, L'Hôpitalek liburu bikain bat idatzi zuen 1696an: Infinitesimalen analisia. Lan horrek arrakasta izugarria izan zuen xviii. mende osoan eta haren izena betiko geratu da historian. L'Hôpitalen asmoa ez zen izan inola ere lan horretan argitaratutako emaitzen jabe egitea; kontrara, argi eta garbi aitortu zuen beti meritua Bernoullirena zela

L’Hôpitalen erregela, limiteak kalkulatzeko tresna eraginkorra eta eraginkorra, unitate honetan frogatuko dugunez, Johann Bernoulliren aurkikuntza da eta bidegabe egozten zaio markesari. L’Hôpital hil zenean, Johann Bernoullik erregela haren meritua berea zela erreklamatu zuen. Ez zion inork sinetsi. Gerora, Bernoulliren eta markesaren arteko eskutitztrukea aurkitu zenean, gauzak argitu eta egia jakiteko balio izan zuen.

EBATZI

Optimizazioa

• Pertsona bat 2 m-ko altuera duen estatua batera hurbildu da. Pertsonaren begiak eskulturaren oinen azpitik 1 m-ra daude. Zer distantziara hurbildu behar da eskultura ikusteko φ angelua maximoa izateko?

Metodo geometrikoak erabiliz egin daitekeen ebazpen eder bat dago. Azter ezazu:

A eta B puntuetatik igarotzen den eta r zuzenarekiko ukitzailea den zirkunferentzia marraztuko dugu.

Egiaztatu T ukitze-puntua

dela AB zuzenkia angelu maximopean ikusteko r zuzeneko lekua

OT zuzenkiaren luzera lortzeko, kontuan hartu behar dugu O puntuak zirkunferentziarekiko duen potentzia OA OB biderkadura adinakoa eta OT 2 adinakoa dela. Beraz:

·· OT OA OB 13 3 == =  ≈ 1,73 m

adi! Problema hau ebazteko beste bide bat φ angelua α eta β angeluekin erlazionatzea da; izan ere, bi angelu horien tangente trigonometrikoak x-ren funtzioan adieraz daitezke.

Maximo egin behar duzun

funtzio bat lortuko duzu (284. orrialdean ageri da ebazpena).

Kurba batekiko zuzen ukitzailea

Deribatuen erabilera berehalakoena da kurba batek puntu batean duen zuzen ukitzailea lortzea, iazko ikasturtetik ondo dakizunez eta aurreko unitatean erabili dugunez. Baina hain agerikoak ez diren beste batzuk ere badaude. Ikus ditzagun:

• Oinarrizko kasua: y = f (x) funtzioarekiko ukitzailea x = x0 abzisa-puntuan

• Puntuaren ordenatua: f (x0)

• Zuzenaren malda: m = f ' (x0)

Zuzen ukitzailearen ekuazioa hau da:

y = f (x0) + f ' (x0)(x – x0)

Adibidez:

Aurkitu y = x xx 3 2 –2 + funtzioak x0 = 3 puntuan duen zuzen ukitzailearen ekuazioa.

• Ordenatuaren kalkulua: f (x0) = f (3) = · 33 32

3, 2 1 dn puntutik igarotzen da.

• Malda: f ' (x) = () () () () x xx xx 3 22 32 –2 2 + + ; f '

x = 3 puntuko zuzen ukitzailearen malda hau da: y

• Funtzioa modu inplizituan dagoenean: ϕ(x, y) = 0 y (x) modu inplizituan emanda dago.

• Puntuaren koordenatuak: baliteke (x0, y0) puntuaren koordenatuak ematea, edo bestela, abzisarena bakarrik. Azken kasu horretan, ordenatua ϕ (x0, y ) = 0 ekuazioa ebatzita lortuko dugu.

• Zuzenaren malda: y ' (x, y )-ren adierazpena eta, ondorioz, y ' (x0, y0))-ren balioa lortzen da ϕ (x, y ) = 0 kasuan deribazio inplizitua eginez.

Adibidez:

Aurkitu x y 25

1 6 2 2 += kurbak x0 = 4 abzisa-puntuetan dituen ukitzaileak.

Ordenatuak

• Puntu horietan malda zein den lortzeko, modu inplizituan deribatuko dugu: ' x yy 25 2 16 2 0 += → ' y y x 25 16 – =

GOGORATU

Puntu batean funtzio baten zuzen normala puntu horretako zuzen ukitzailearen perpendikularra da.

Bere ekuazioa hau da: y = f (x0) – ´( ) fx 1 0 (x – x0)

➜ Zuzen ukitzailea edozein puntutan.

➜ Elipse baten ukitzailea.

• y = f (x) kurba batekiko ukitzailea, malda jakinda

Bila gabiltzan zuzen ukitzaileen m malda zein den badakigu, baina ez dakigu ukitze-puntuak zein diren. Puntu horietako abzisak f ' (x) = m ekuazioa ebatziz lortuko ditugu

Adibidez: Aurkitu y = sin x, x ∈ [–π, π] funtzioarekiko ukitzaileen artean x + 2y = 0 zuzenarekiko paraleloak direnak.

• Kurba batekiko ukitzailea, kanpoko puntu batetik

• P (x0, y0) puntua badakigu. T (c, f (c)) ukitze-puntua, berriz, ez.

• PT zuzenkiaren malda () xc yf c ––0 0 da, eta bat dator f ' (c)-rekin.

• Berdindu eta ekuazioa ebatziko dugu. Soluzioak ukitze-puntuen abzisak dira.

Adibidez:

Aurkitu P (2, –7) puntutik igarotzen diren y = x 2 – 5x + 3 kurbarekiko zuzen ukitzaileak.

• T ukitze-puntua kurbakoa da. Horren koordenatuak dira (c, c 2 – 5c + 3).

• PT zuzenaren malda izan behar da f funtzioak c puntuan duen deribatua:

Ukitze-puntuak T1(0, 3) eta T2(4, –1) dira

Pentsatu eta praktikatu

1 Aurkitu honako kurba hauetako bakoitzarekiko zuzen ukitzaileak, zehazturiko baldintzak kontuan hartuz:

a) y = x xx x 2 57 16 ––32 +

0, 1, 3 abzisa-puntuetan.

c) y = x xx 3 36 3 2 +

– x = 9 zuzenarekiko paraleloak.

(2, 0) puntutik igarotzen direnak.

Funtzio bat puntu batean gorakorra edo beherakorra den adierazten digun ideia grafikoa oso argia da. Baina, orain, eragiketak egiteko modua ematen digun definizio bat lortuko dugu:

f gorakorra da x0 puntuan, baldin eta x0-ren E = (x0 – a, x0 + a) eremu batek, x ∈ E, x ≠ x0 denean, hau betetzen badu: () () : () () () () xx fx fx xx fx fx xx fx fx 0

–Horrek esan nahi bada, orduan bada, orduan > >> << 0 0 00 00

Era berean, f beherakorra bada, zatidura negatiboa da.

Hazkundearen eta deribatuaren zeinuaren arteko erlazioa f (x) deribagarria eta gorakorra da x0 puntuan ⇒ f ' (x0) ≥ 0 f (x) deribagarria eta beherakorra da x0 puntuan ⇒ f ' (x0) ≤ 0

Egiaztapena

f gorakorra da x0 puntuan ⇒ () () xx fx fx 0 ––> 0 0 da x0-ren E eremu bateko x guztien kasuan

Beraz, f ' (x0) = lm i xx 0 " () () ≥ xx fx fx 0 ––0 0 ; izan ere, balio positiboak hartzen dituen

funtzio baten limitea positibedo nulua da

Era berean, f beherakorra bada x0 puntuan, f ' (x0) ≤ 0 dela egiaztatzen da.

x0 puntuko hazkunde-irizpidea f ' (x0)-ren zeinutik abiatuta

Funtzio bat adierazpen analitikotik abiatuta adierazi nahi dugunean, oso lagungarria da deribatuaren zeinutik abituta funtzioa gorakorra edo beherakorra den jakiteko modua ematen digun irizpide hau:

f ' (x0) > 0 ⇒ f gorakorra da x0 puntuan

f ' (x0) < 0 ⇒ f beherakorra da x0 puntuan

Inplikazio horien egiaztapenak 291. orrialdean ikusiko ditugu.

&

>

x x fx fx fx f f f 0 04 4 0 0 0 – GORAKORRA BEHERAKORRA GORAKORRA +

rakorrada gorakorra da

Pentsatu eta praktikatu

f '

(x0) ≤ 0

a) Non da gorakorra?

b) Non da beherakorra?

x0 – a x0 + a x – x0 f (x) – f (x0 ) x0 x f ' (x0 ) > 0 x0 f ' (x0 ) = 0 x0 0 4 funtzio gorakorrak

Ikusten duzunez, funtzio bat gorakorra izan daiteke puntu batean, puntu horretako deribatua zero izanda ere.

Funtzio baten maximo eta minimo erlatiboak

Puntu batean maximo erlatibo bat egoteak esan nahi du funtzioak, puntu horretan, inguruko puntuetan baino gehiago balio duela. Ikus dezagun eragiketei begira lagungarriagoa izango den definizioa:

f funtzioak maximo erlatibo bat du x0 abzisa-puntuan, baldin eta x0 puntuaren

E = (x0 – a, x0 + a) eremuan betetzen bada x ∈ E, x ≠ x0 izanik f (x) < f (x0) dela. Hau da, gorakorra da x0-ren ezkerrera, eta beherakorra, eskuinera. Modu berean definitzen da minimo erlatiboa.

Maximoetan eta minimoetan, deribatua 0 da

f (x) deribagarria bada x0 puntuan eta maximo edo minimo bat badu bertan, orduan f ' (x0) = 0. Hau da:

f (x) maximoa edo minimoa x0 puntuan ⇒ f ' (x0) = 0

Dena dela, gerta daiteke f ' (x0) = 0 izatea eta ez egotea ez maximorik ez minimorik x0 puntuan

maximo erlatiboa minimo erlatiboa

f deribagarria denez x0-n, hau beteko da: f ' (x0) = () ()fx''fx00 –= + ⇒ f ' (x0) = 0

Adibidea: azter ditzagun y = 3x 5 – 5x 3 funtzioaren maximoak eta minimoak.

Funtzioaren deribatua, f ' (x) = 15(x 4 – x 2) = 15(x – 1) x 2 (x + 1), baliogabetu egiten da –1, 0 eta 1en. Nola jakin puntu horietan maximorik edo minimorik dagoen?

— Azter dezagun deribatuaren zeinua eskuinera eta ezkerrera. Adibidez:

P UNTU SINGULARRAK

Ukitzaile horizontaleko puntuei, hau da, f ' (x) = 0 betetzen duten puntuei puntu singular edo puntu kritiko esaten zaie.

Puntu singular bat izan daiteke:

maximoa f gorakor izatetik beherakor izatera igarotzen da minimoa f beherakor izatetik gorakor izatera igarotzen da inflexiopuntua ez dago aldaketarik hazkundean

EGIAZTAPENAREN IDEIA

x0 puntuan maximoa badago:

x0 puntuko deribatua ezkerretik, 0 edo 0 baino handiagoa da.

— x0 puntuko deribatua eskuinetik, 0 edo 0 baino txikiagoa da.

Beraz, x0 puntuko deribatua 0 da.

Eta antzekoa gertatzen da minimoekin ere.

(, )

(, ) ' ' f f 0990 1010 beherakorra da 1enezkerrera

gorakorra da 1eneskuinera < > 4 Minimo bat dago x = 1 puntuan

Bestela, adieraz ditzagun hiru puntuak eta adar infinituak. Funtzioa deribagarria denez eta, beraz, jarraitua denez Á osoan, puntuak lotu eta funtzioak puntu bakoitzean zer jokabide duen agertuko zaigu.

Ikusten dugunez, maximo bat dago x = –1 puntuan, minimo bat x = 1 puntuan eta inflexio-puntu bat x = 0 puntuan.

1 Egiaztatu y = x 3/(x – 2)2 funtzioak bi puntu singular baino ez dituela, x = 0 eta x = 6 puntuetan. Aurkitu zer motatakoa den bi puntu singular horietako bakoitza; horretarako, deribatuaren zeinua aztertu behar duzu

2 a) Aurkitu y = –3x 4 + 4x 3 funtzioaren puntu singular guztiak (abzisa eta ordenatua). Adierazpen egokia erabiliz, esan zer motatakoa den bakoitza. b) Egin gauza bera y = x 4 + 8x 3 + 22x 2 + 24x + 9 funtzioaren kasuan

Pentsatu eta praktikatu

ez dago maximorik ez minimorik. inflexio-puntua da.

Bigarren deribatutik ateratako informazioa

Ahurtasuna, ganbiltasuna eta inflexio-puntua

Azter dezagun honako grafiko hau:

Goitik ikusita, zentzuzkoa da BC eta DE tarteak ahurrak direla esatea, eta AB eta CD tarteak ganbilak direla esatea, ezta? Kurba hori ahur izatetik ganbil izatera (edo alderantziz) pasatzen da B, C, D puntuetan: inflexio-puntuak dira

Kurbatura mota (ahurtasuna, ganbiltasuna edo inflexioa) bereizteko modurik onena da kurbak bere ukitzailearekiko duen posizioa aztertzea, ondoren egingo dugun moduan.

y = f (x) kurba dugu. Kurba horrek P puntuan duen zuzen ukitzailea marraztuko dugu, y = t (x) ekuazioduna. Orduan:

P-tik hurbil f (x) > t (x) bada, kurba ahurra da P-n

P-tik hurbil f (x) < t (x) bada, kurba ganbila da P-n

Ukitzaileak kurba P puntuan zeharkatzen badu, hau da, P-ren ezkerrera f (x) < t (x) bada, eta eskuinera f (x) > t (x) (edo alderantziz), P inflexio-puntua da.

Kurbak bigarren deribatuarekin duen erlazioa

Aztertu grafiko hau:

Erreparatu AB tarteari. Adierazita dauden lau ukitzaileek gero eta malda txikiagoa dute. Horrek adierazten digu tarte horretan f ' beherakorra dela, eta, beraz, deribatua ( f '-ren deribatua) negatiboa da. Beste horrenbeste gertatzen da CD tartean.

Eta kontrakoa gertatzen da BC eta DE tarteetan: ukitzaileen malda handitu egiten da eta, beraz, f ' gorakorra da eta f '-ren deribatua positiboa da. Orokorrean:

f funtzioak x0 puntuan bigarren deribatua badu, hau betetzen da:

f ahurra da x0-n ⇒ f ' gorakorra da x0-n ⇒ f '' (x0) ≥ 0

f ganbila da x0-n ⇒ f ' beherakorra da x0-n ⇒ f '' (x0) ≤ 0

f -k inflexio-puntu bat du x0-n ⇒ f '' (x0) = 0

grafikoaren gainean dago.

f-ren grafikoa «zeharkatzen» du.

KONTUAN HARTU

Inplikazio horiek balio dute kurbaren formatik abiatuta f '' bigarren deribatuaren joerari buruzko ondorioak ateratzeko.

Kurba mota bereizteko irizpidea

Interesatzen zaiguna kurbaren adierazpen analitikotik abiatuta haren formari buruzko informazioa lortzea denez, ikus dezagun nolakoak diren ikusi berri ditugun inplikazioen kontrakoak:

f '' (x0) > 0 ⇒ f ahurra da x0-n

f '' (x0) < 0 ⇒ f ganbila da x0-n

f '' (x0) = 0 eta f ''' (x0) ≠ 0 ⇒ f-k inflexio-puntu bat du x0-n

Maximoak eta minimoak identifikatzeko erabiltzea

f ' (x0) = 0 bada eta f '' (x0) existitzen bada, orduan:

f '' (x0) > 0 ⇒ f-k minimo erlatibo bat du x0-n

f '' (x0) < 0 ⇒ f-k maximo erlatibo bat du x0-n (Egiaztapena 291. orrialdean ikusiko dugu).

➜ Deribatu eta berdindu zerorekin.

1 Aztertu funtzio honen kurba:

f (x) = x 3 + 3x 2 .

Funtzioaren bigarren deribatua lortuko dugu:

f ' (x) = 3x 2 + 6x

f '' (x) = 6x + 6

minimoa (ahurra) maximoa (ganbila)

Bigarren deribatua zer baliok baliogabetzen duten aurkituko dugu:

f '' (x) = 0 → 6x + 6 = 0 → x = –1

f (–1) = (–1)3 + 3(–1)2 = 2

f ''' (x) = 6 ≠ 0 denez, I (–1, 2) puntua inflexio-puntu bat da.

• f '' (x) = 6x + 6 < 0 ⇔ x < –1

f ''' (x) = 6 ≠ 0 denez, I (–1, 2) puntua inflexio-puntu bat da.

• f '' (x) = 6x + 6 > 0 ⇔ x > –1

–1etik + ∞-ra, kurba ahurra da; izan ere, f '' (x) > 0

➜ anayaharitza.es

Indartzeko ariketak: bigarren deribatuaren erabilerak

Pentsatu eta praktikatu

Aztertu

2 Aztertu

Ebatzitako ariketa

1

funtzio honen kurba:

funtzio honen kurba:

Gogoan izan f (x) funtzio bat optimizatzea dela funtzio horren balio maximoa (edo minimoa) zein den lortzea eta x-ren zer baliorekin lortzen den zehaztea.

Problema mota hauek ebazten ohitzeko, honako hau egin beharko dugu:

• Adierazpen analitikoaren bidez emanda dagoen funtzio baten muturrak ahalik eta modurik eraginkorrenean aurkitzeko teknika ikasi.

• Enuntziatu baten bidez deskribatzen diren funtzioen adierazpen analitikoan trebatu.

Lehenengorako jarraibide zehatz batzuk ematen hasiko gara; eta, gero, bigarrena lantzeko adibide batzuk proposatuko ditugu

f (x) funtzioak [a, b] tartean dituen muturrak kalkulatzea

Optimizazio-problemetan, interesatzen zaiguna ez dira funtzioaren mutur erlatiboak, absolutuak baizik. Ikus ditzagun mutur horiek lortzeko erregela batzuk:

a) f (x) deribagarria bada [a, b] tartean, maximo eta minimo absolutuak daude puntu singularren eta tartearen muturrei dagozkien puntuen artean:

max max max

OPTIMIZATZEAREN GARRANTZIA

Bolumen bat, biztanleria jakin bat edo etekin batzuk maximo egitea, edota ekoizpen-kostu batzuk edo azalera bat minimo egitea funtzioen optimizazioaren adibide batzuk baino ez dira, eta ingeniariek, arkitektoek, ekonomialariek,... egunero erabiltzen dituzte.

Problema hauen zailtasunik handiena, normalean, ez da izaten adierazpen analitikoaren bidez emandako funtzioak optimizatzea, baizik eta optimizatu nahi den funtzioaren adierazpen analitikoa aurkitzea.

min min min

a b a b a b

Beraz, puntuok aurkitzeko:

• f ' (x) = 0 ekuazioa ebatziko dugu

• a eta b artean dauden x1, x2, x3, … soluzioak hautatuko ditugu

• f ((a), f (x1), f (x2), … eta f (b) kalkulatuko ditugu. Balio horiekin, maximoa eta minimoa zein diren ikusiko dugu.

b) [a, b] tarteko punturen batean funtzioa deribagarria ez bada, baina bai jarraitua, f funtzioak puntu horretan zer balio duen kalkulatuko dugu, mutur bat izan daiteke eta.

c) f ez bada jarraitua [a, b] tarteko x0 puntu batean ere, funtzioak x0 puntutik hurbil zer jokabide duen aztertuko dugu.

minimoa (ez-deribagarria)

maximoa (etenduna)

P puntua r zuzenerdian zehar lekuz aldatzen badugu, zer posiziotan lortuko dugu φ angelua maximo izatea?

1 Unitatearen bigarren orrialdean, honelako problema bat proposatu dugu:

Ebatzitako ariketak

2 Deskonposatu 36 zenbakia bi batugai positibotan, kontuan hartuz lehenengo batugaiaren eta bigarrenaren karratuaren arteko biderkadurak maximoa izan behar duela.

6 912

23636 .batugaia .batugaia: –> < 4

Honako funtzio honen balioak maximoa izan behar du:

36

deribatua non baliogabetzen den ikusiko dugu:

12 36

3 36 cm-ko aldea duten bi pieza karraturekin eskuinean ageri diren urratsak eman ditugu

Zein izan behar da ebaki dugun laukitxoaren x aldea, lortu nahi dugun kaxaren bolumena maximoa izateko?

36 ez da baliozkoa, f -ren definizio-eremutik kanpo baitago

Kasu honetan, definizio-tartea (0, 36) da; hau da, irekia da. Beraz, ez dugu aztertu behar zein den f-ren jokabidea tartearen muturretan. Dena dela, erraz egiazta dezakezunez, biderkadura 0 da; hau da, f (0) = f (36) = 0.

Beraz, balio maximoa x = 12 kasuan lortzen da, f (12) = 6 912.

Soluzioa: lehenengo batugaia 12 da, eta bigarrena, 24.

➜ anayaharitza.es

Funtzioen optimizazioari buruz

Pentsatu eta praktikatu

Kaxaren neurriak hauek dira:

x, 36 – x, 36 – x

Beraz, bolumena hau da:

V (x) = x (36 – x)2, 0 < x < 36

Hau da, optimizatu behar dugun funtzioa aurreko adibideko funtzio bera da.

Karratutxoaren aldea 12 cm-koa da.

Kasu horretan, kaxaren bolumena 6 912 cm3-koa da.

1 Aurkitu zenbaki positibo bat, jakinda bere alderantzizkoarekin hogeita bost bider batuta, baturak minimoa izan behar duela.

2 Katetoen arteko batura 10 cm duten triangelu angeluzuzen guztien artean, aurkitu azalera maximoa duenaren neurriak

3 12 m-ko perimetroa duten laukizuzen guztien artean, zeinek du diagonalik txikiena?

4 Zehaztu zer neurri izan behar dituen 6,28 litroko bolumena duen ontzi zilindriko batek ahalik eta latorri kantitate txikienarekin egiteko

Bi teorema garrantzitsu

Teorema hauek diotena oso erraza eta naturala da, eta izugarri errazten dira unitate honen hasierako ataletan enuntziatu eta erabili ditugun (baina frogatu ez ditugun) zenbait emaitzaren egiaztapenak. Gogora ditzagun horietako bi:

f ' (x0) > 0 ⇒ f gorakorra da x0 puntuan

f ' (x0) = 0 eta f '' (x0) > 0 ⇒ f -k minimo erlatibo bat du x0 puntuan

Rolleren teorema

Rolleren teoremak dio puntu erzdunik ez duen eta tarte bateko muturretan balio berdinak hartzen dituen kurba jarraitu batek nahitaez ukitzaile horizontaleko puntu bat izan behar duela

f jarraitua da [a, b] tartean eta deribagarria (a, b) tartean

f (a) = f (b) bada, existitzen da f ' (c) = 0 betetzen duen c ∈ (a, b) punturen bat. a b

Egiaztapena

hipotesia tesia

• f jarraitua da [a, b] tartean

• f deribagarria da (a, b) tartean

• f (a) = f (b)

c ∈ (a, b) punturen batek hau betetzen du:

f ' (c) = 0

f jarraitua denez [a, b] tartean, tarte horretan balio maximo bat eta balio minimo bat izango ditu (Weierstrassen teorema, 7. unitatea). Bereiz ditzagun bi kasu:

I. Maximoa eta minimoa bata a puntuan eta bestea b puntuan daude. f (a) = f (b) denez, maximoa eta minimoa bat datoz. Funtzioa konstantea da tarte osoan eta horren deribatua zero da puntu guztietan, ez punturen batean bakarrik.

II. f funtzioak maximoa edo minimoa lortzen du tarteko muturrak ez diren c puntu batean. f deribagarria denez c puntuan, f ' (c) = 0 betetzen da. (3. epigrafean egiaztatu genuena erabili dugu: f funtzioak maximo edo minimo bat badu x0 puntuan eta deribagarria bada x0 puntuan, orduan f ' (x0) = 0).

Oharrak: Zergatik exijitzen dira hipotesi hauek

• «f jarraitua da [a, b] tartean eta deribagarria (a, b) tartean» baldintza zehaztea harrigarria egingo zaigu, beharbada. Zergatik ez esan [a, b] tartean deribagarria dela, besterik gabe, eta, horrela, alboko deribatuak daudela ziurtzat eman? Bada, funtzio batzuek ukitzaile bertikala dutelako, eta, beraz, ez direlako deribagarriak muturretako batean; ondorioz, teorema honen onuretatik kanpo geratuko lirateke

Adibidez, f (x) = x 1– 2 jarraitua da [–1, 1] tartean, eta deribagarria da (–1, 1) tartean, baina ez [–1, 1] tartean. Konturatzen bazara, f (1) = f (–1) = 0 eta f ' (0) = 0.

• Eta zergatik ez zehaztu, besterik gabe, «f deribagarria izan dadila (a, b) tartean»? Bada, f funtzioa tartearen muturretan jarraitua izatea exijituko ez bagenu, alboko funtzio horren modukoak ere «pasatuko lirateke»; eta argi dagoenez ez dute tesia betetzen.

Laburbilduz: funtzioari [a, b] tartean jarraitua izateko exijitu behar zaio, eta komeni da (a, b) tartean deribagarria izatearekin konformatzea.

f (a) = f (b) da, baina ez da existitzen f ' (c) = 0 betetzen duen c ∈ (a, b) punturik, f ez delako jarraitua [a, b]-n.

1 Frogatu honako funtzio honek:

y = x 3 – 4x + 3

Rolleren teoremaren hipotesiak betetzen dituela [0, 2] tartean. Zer puntutan betetzen du tesia?

2 Rolleren teorema erabiliz, egiaztatu

x 4 – 8x 2 + k = 0 ekuazioak ezin

duela erro bat baino gehiago izan [0, 2] tartean, k-ren balioa edozein dela ere.

Funtzioa deribagarria da, eta, beraz, jarraitua Á osoan.

Horrez gainera, f (0) = f (2) = 3. Hipotesiak betetzen ditu. Beraz, tesia ere beteko du; hau da, deribatu nuluko punturen bat izango du 0 eta 2 artean.

f ' (x) = 3x 2 – 4 → 3x

Hala da, c = 3 23

Absurdora laburtuz egiaztatuko dugu: [0, 2] tartean r eta s bi erro dituela pentsatuko dugu, eta kontraesan batera helduko gara

0 ≤ r < s ≤ 2 ekuazioaren erroak r eta s badira, orduan P (x) = x 4 – 8x 2 + k ekuazioak Rolleren teoremaren hipotesiak beteko ditu [r, s] tartean; izan ere, polinomikoa denez, deribagarria da eta, beraz, jarraitua, eta horrez gain, P (r) = P (s) = 0. Tesi hau betetzen da, beraz: P' (c) = 0 egiten duen c ∈ (r, s) zenbaki bat existitzen da. Eta c ∈ (r, s) denez, orduan 0 < c < 2.

P ' (x) = 4x 3 – 16x ekuazioak hiru erro baino ez ditu: –2, 0, 2. Eta horietako bat ere ez dago (0, 2) tartean. Kontraesan batera heldu gara. Ondorioa: ekuazioak ez ditu bi erro (0, 2) tartean. (Hau da, erro bat du edo bat ere ez).

3 Kalkulatu zein izan behar diren p, m eta n , honako funtzio honek:

Rolleren teoremaren hipotesiak bete ditzan [–1, 5] tartean. Non betetzen du

5]

Adierazitako hiru ekuazioek eraturiko sistemaren soluzioa da p = 10/3, m = – 8/3, n = 9. Balio horietarako Rolleren teoremaren hipotesiak betetzen dira.

Pentsatu eta praktikatu

1 Egiaztatu f (x) = sin x funtzioak Rolleren teoremaren hipotesiak betetzen dituela [0, π] tartean. Non betetzen du tesia?

2 Kalkulatu zein izan behar den b honako funtzio honek: f (x)= x 3 – 4x + 3

Rolleren teoremaren hipotesiak bete ditzan [0, b] tartean. Non betetzen du tesia?

3 Egiaztatu funtzio honek () () ,≤ ≤≤ fx x x x x 22 52 05 1 14 –bada bada < 2 = + *

Rolleren teoremaren hipotesiak betetzen dituela [–0,5; 4] tartean. Non betetzen du tesia?

4 Rolleren teorema erabiliz, egiaztatu x 3 – 3x + k = 0 ekuazioak ezin duela erro bat baino gehiago izan [–1, 1] tartean, k-ren balioa edozein izanda ere.

Ebatzitako ariketak

Batezbesteko balioaren teorema

Batezbesteko balioaren teoremak (B.B.T.) dio A-tik B-ra doan erzdun punturik gabeko kurba jarraitu bateko bitarteko punturen batean, kurba horrekiko ukitzailea AB zuzenkiarekiko paraleloa izango dela

f jarraitua da [a, b]-n eta deribagarria (a, b)-n. Orduan, honako hau betetzen duen c ∈ (a, b) puntua existitzen da:

f ' (c) = () () ba fb fa

c b

Egiaztapena

ψ(x) funtzioa aztertuko dugu. Funtzio hori kurbaren f (x) ordenatuari A (a, f (a)) eta B (b, f (b )) puntuetatik igarotzen den r zuzenaren ordenatua kenduta lortu da. (ψ alfabeto greziarreko letra bat da, eta psi deitzen da). r zuzenaren ekuazioa hau da:

hipotesia

• f jarraitua da [a, b]-n

• f deribagarria da (a, b)-n

tesia

c ∈ (a, b) batek hau betetzen du:

Hau da:

Beraz:

y = f (a) + () () () ba fb fa xa –

––

r (x) = f (a) + () () () ba fb fa xa

ψ(x) = f (x) – r (x) = f (x) – f (a) –

––

() () () ba fb fa xa –

Funtzio horrek Rolleren teoremaren hipotesiak betetzen ditu [a, b] tartean; izan ere, [a, b] tartean jarraitua eta (a, b) tartean deribagarria izateaz gain, ψ(a) = ψ(b) betetzen du.

Ikus dezagun:

} }

f ' (c) = () () ba fb fa –

KONTUAN HARTU

–

ψ(x) = f (x) – r (x) jarraitua da [a, b]-n eta deribagarria (a, b)-n, f (x) eta r (x) ere hala direlako.

––

() () () () () () () () () () () ()

== ==

–

––

bf bf a ba fb fa ba af af a ba fb fa aa

0 0

b b b b → ψ(b) = ψ(a)

_ ` a

Beraz, ψ(x) funtzioak Rolleren teoremaren tesia betetzen du: ψ'(c) = 0 betetzen duen c ∈ (a, b) puntu bat existitzen da.

ψ'(x) = f ' (x) – () () ba fb fa –

–denez:

ψ'(c) = f ' (c) – () () ba fb fa –

–= 0

Hau da, f ' (c) = () () ba fb fa –

–betetzen duen c ∈ (a, b) existitzen da.

Ebatzitako ariketak

1 Egiaztatu y = x funtzioak betetzen dituela batezbesteko balioaren teoremaren hipotesiak [0, 9] tartean

Non betetzen du tesia?

2 Kalkulatu zein izan behar diren a eta b honako

x jarraitua da [0, 9]-n eta deribagarria (0, 9)-n. Beraz, B.B.T.-ren hipotesiak betetzen ditu. Ondorioz, tesia betetzen du. Ikus dezagun non:

B.B.T.-ren hipotesiak betetzeko [–1, 5]

jarraitua da [–1, 5] tartean eta deribagarria (–1, 5) puntuan

Beraz, B.B.T.-ren hipotesiak betetzen ditu Ikus dezagun tesia non betetzen den:

3 f (x) = mx 2 + nx + p bada, egiaztatu parabola horretako c puntuan hau gertatzen dela, f ' (c) = () () ba fb fa –

–eta hori, hain zuzen ere, a-ren eta b-ren batezbesteko aritmetikoa dela :

c = (a + b)/2

Pentsatu eta praktikatu

Tesia c = 3 2 ∈ (–1, 5) puntuan betetzen da.

() () () () a fb fa ba mb nb pmanap b –

––

–22 = ++ ++ = = () () ba mb an ba –

22 + = m (b + a) + n

f ' (c) = 2mc + n

Beraz: 2mc + n = m (b + a) + n → 2c = b + a → c = ba 2 +

5 Egiaztatu f (x) = , , x xx x x 23 10 19 4 4 –≥ < 2 + ) funtzioak batez-

besteko balioaren teoremaren hipotesiak betetzen dituela [2, 6] tartean. Zer puntutan betetzen da tesia?

6 Kalkulatu zein izan behar diren a-ren eta b-ren balioak

f a c b (a, b)-ren erdiko puntua

7 Ezarri batezbesteko balioaren teorema, ahal bada, [–2, –1] tartean honako funtzio honi:

f (x) = x 2 – 3x + 2

Kalkulatu c-ri dagokion balioa eta egiaztatu grafikoki lortutako emaitza.

f (x) = , , xx a xbx x x 20 0

≤ > 2 2 ++ + * funtzioak batezbesteko balioaren teoremaren hipotesiak betetzeko [–3, 2] tartean. Non betetzen da tesia? Egin grafikoa.

8 Egin aurreko ariketa bera funtzio honen kasuan:

g (x) = x 3 – x 2 – x + 1

Batezbesteko balioaren teoremaren erabilera teorikoak

Unitate honetan zehar hainbat propietate egiaztatu ditugu; adibidez:

«f gorakorra eta deribagarria x0 puntuan ⇒ f ' (x0) ≥ 0»

Horietan, funtzioaren propietate batzuetatik abiatuta, deribatuaren ondorioak lortu ditugu. Hala ere, egiaztatu gabe utzi ditugu era honetako beste propietate batzuk:

«f ' (x0) > 0 ⇒ f gorakorra da x0 puntuan»

Horietan, f ' (x)-ren propietateren batetik abiatuta, funtzioaren datuak lortzen dira. Batezbesteko balioaren teoremarekin, izugarri errazten dira funtzio baten f ' (x) deribatuaren propietate errazetatik abiatuta f (x) funtzioaren propietateak ondorioztatzen dituzten teorema mota horien egiaztapenak.

funtzio konstantea

Badakigu funtzio konstante baten deribatua zero dela puntu guztietan. Orain, kontrakoa frogatuko dugu: funtzio baten deribatua puntu guztietan zero bada, orduan funtzio hori konstantea da.

f jarraitua da [a, b]-n eta deribagarria (a, b)-n

f ' (x) = 0 bada (a, b) tarteko puntu guztietan, orduan f konstantea da [a, b]-n

Egiaztapena

hipotesia

• f jarraitua da [a, b]-n

• f deribagarria da (a, b)-n

• f ' (x) = 0, x ∈ (a, b) edozein dela ere

⇒

tesia f konstantea da [a, b]-n

BEGIRATU

Funtzio batzuen kasuan, puntu deribagarri guztietako deribatua 0 izan arren, funtzioa ez da konstantea.

Horrelakoa da, adibidez, zeinu (sgn) funtzioa:

f funtzioa [a, b]-n konstantea dela frogatzeko, tarteko edozein bi puntu hartu eta f-k bietan balio bera hartzen duen aztertuko dugu.

x1, x2 ∈ [a, b], x1 < x2 dira. B.B.T.-ren hipotesiak [x1, x2] tartean betetzen dira, eta, beraz: ∃ c ∈ (x1, x2), eta hau egiaztatzen du: () () xx fx fx ––21 21 = f ' (c)

Baina f ' (x) = 0 denez (a, b) tarte osoan, f ' (c) = 0. Beraz:

f (x2) – f (x1) = 0, hau da, f (x2) = f (x1)

Horrek esan nahi du funtzioak balio bera hartzen duela tarteko edozein bi puntutan, eta, beraz, konstantea dela.

puntu batean gorakorra den funtzioa

Unitate honetako 2. atalean honako hau ikusi eta egiaztatu dugu:

«f gorakorra eta deribagarria x0 puntuan ⇒ f ' (x0) ≥ 0»

Honako hau ere esan genuen: « f ' (x0) > 0 ⇒ f gorakorra da x0 puntuan».

Baina azkeneko inplikazio hori egiaztatu gabe geratu zen. Orain, batezbesteko balioaren teorema erabiliz, erraz froga dezakegu, hasierako hipotesia apur bat moldatuz.

f deribagarria da x0 inguru batean eta f ' (x0) > 0 ⇒ f gorakorra da x0 puntuan

Argi ikusten denez, ez da konstantea ez duelako hipotesia betetzen: ez da jarraitua, ez deribagarria x = 0 puntuan.

Egiaztapena

hipotesia

• f deribagarria da x0-ren ingurunean

• f ' (x0) > 0 ⇒

tesia f gorakorra da x0 puntuan

f ' (x0) > 0 bada, f ' positiboa den E = (x0 – δ, x0 + δ) ingurune bat dago.

E-ko x1 < x2 edozein bi puntu hartzen baditugu, f -k B.B.T.-ren hipotesiak betetzen ditu [x1, x2] tartean. Beraz, tesia betetzen da:

∃ c ∈ (x1, x2) non () () xx fx fx –

21 21 = f ' (c) eta, hipotesiaren arabera, f ' (c) > 0

Hortik lortzen dugu f (x2) – f (x1) > 0 dela eta, beraz, f (x2) > f (x1) dela

Funtzioa, beraz, gorakorra da (x0 – δ, x0 + δ) tartean, eta ondorioz, baita x0-n ere.

minimo erlatiboa

Unitate honetako 3. atalean hau egiaztatu dugu:

«f -k minimo bat badu x0 puntuan eta deribagarria bada, orduan f ' (x0) = 0 da»

Horrez gain, kontrako inplikazioa ez dela beti egia ere ikusi genuen. Orain dakigunarekin, aurkako proposizio horren modukoa enuntziatu eta egiaztatzeko moduan gaude:

f ' (x0) = 0 eta f '' (x0) > 0 ⇒ f -k minimo erlatibo bat du x0 puntuan

Egiaztapena

hipotesia

• f ' (x0) = 0

• f '' (x0) > 0 ⇒

tesia

f -k minimo erlatiboa du x0 puntuan

f funtzioak x0 puntuan minimo bat duela frogatzeko, ezkerrera beherakorra dela eta eskuinera gorakorra dela egiaztatuko dugu. Horretarako, funtzioaren beheratzea edota goratzea f ' deribatuaren zeinuarekin erlazionatzen duen aurreko emaitza hartuko dugu kontuan:

f '' (x0) = lm i 0 h "

() ()fx''fx h h–00 + = lm i 0 h "

(***)

(*) (**)

() ' fx h h 0 + > 0

h < 0 bada, f ' (x0 + h) < 0 ⇒ f beherakorra da x0-ren ezkerrea 1

(****)

h > 0 bada, f ' (x0 + h) > 0 ⇒ f gorakorra da x0-ren eskuinera 2

1 eta 2 kontuan hartuz, f funtzioak minimo bat du x0 puntuan

Pentsatu eta praktikatu

1 Egiaztatu f funtzioa deribagarria bada x0-ren ingurune batean eta f ' (x0) < 0 bada, f beherakorra dela x0 puntuan.

FUNTZIO BEHERAKORRA

Jakina, funtzio beherakorren kasuan pareko emaitza bat dago:

f ' (x0) < 0 ⇒ f beherakorra da x0 puntuan

GOGORATU

Modu berean, f ' (x0) = 0 eta f '' (x0) < 0 badira, orduan f funtzioak x0 puntuan maximo erlatibo bat duela egiaztatu dezakegu.

(*) Lehen hipotesiaren arabera.

(**) Bigarren hipotesiaren arabera.

(***) f ' < 0 ⇒ f beherakorra

(****) f ' > 0 ⇒ f gorakorra

2 Egiaztatu f ' (x0) = 0 eta f '' (x0) < 0 badira, orduan f funtzioak maximo erlatibo bat duela x0 puntuan.

Ebatzitako ariketak eta problemak

1. Zuzen ukitzailea eta zuzen normala

f (x) = |x| e –x funtzioa emanda, idatzi, ahal izanez gero, zuzen ukitzailearen ekuazioa eta zuzen normalarena, x = 0 denean eta x = –1 denean.

EGIN ZUK

Idatzi xy yx = 1 kurbak (1,1) puntuan dituen zuzen ukitzailearen eta zuzen normalaren ekuazioak.

Honako kurba hau izanik, f (x) = x 1 1 –aurkitu zer puntutan izango duen P (–3, 2) puntutik igarotzen den zuzen ukitzailea

EGIN ZUK

f (x) = x 2 – 2x + 4 kurba izanik, aurkitu zer puntutan izango duen koordenatuen jatorritik igarotzen den zuzen ukitzailea.

• Funtzioa tarteka definituko dugu: f (x) = ≥ xe xe x x 0 0 –bada bada < x x

–– )

Funtzio jarraitua da Á-n, izan ere, () () () limf xlim ff00 0 xx00 –== = "" + .

––+

f deribagarria da x = –1 puntuan, baina ez x = 0 puntuan; izan ere, () () '' limf xlim fx –≠11 xx00 –== "" + .

Beraz, ez dago zuzen ukitzailerik, ez zuzen normalik x = 0 puntuan.

Zuzen ukitzailea x = –1 puntuan hau da: y = f (–1) + f ' (–1)(x + 1) → y = e – 2e(x + 1)

Zuzen normala x = –1 puntuan hau da: y = f (–1) – () f 1 1 –l (x + 1) → y = e + e2 1 (x + 1)

• Ukitze-puntuaren koordenatuak hauek dira: x = a, f (a) = a 1 1

–

(

dagozkien bi ukitze-puntu daude:

3. Kurbarekiko puntu jakin batean ukitzailea den zuzena

P puntua xy = 1 funtzioaren puntua bada, frogatu OP zuzenak, kurbarekiko ukitzaileak (P-n) eta y = 0 ardatzak osatutako triangelua isoszelea dela.

EGIN ZUK

Idatzi y = x 1 kurbak (3, 1/3) koordenatuak dituen puntuan daukan zuzen ukitzailearen ekuazioa.

Egiaztatu ukitze-puntuak bi zati berdinetan erdibitzen duela koordenatuardatzen artean dagoen zuzen horretako zuzenkia

y = x 1 kurbako P edozein puntuk ,a a 1 dn koordenatuak ditu

• P puntuko ukitzailea : m = f ' (a) = –a 1 2 → y = () a a xa 11 2

• Ukitzailearen eta y = 0 ardatzaren arteko ebaki-puntua lortuko dugu: ()

• Triangeluaren aldeen luzerak kalkulatuko ditugu:

Aztertu honako funtzio hauen tarte gorakorrak eta beherakorrak, eta zehaztu maximoak eta minimoak.

a) f (x) = e x (x 2 – 3x + 1)

b) f (x) = ln xx xx x x bada bada 20 0 ≤ > 2

a) Funtzioa jarraitua da, eta deribagarria Á definizio-eremu osoan f gorakorra da f ' > 0 den tarteetan, eta beherakorra, f ' < 0 denean. Deribatu nuluko puntuak bilatuko ditugu.

> 0 denez x edozein dela ere, f ' baliogabetu egiten da baldin eta:

da (– ∞, –1) ∪ (2, +∞) tartean, eta beherakorra, (–1, 2) tartean.

b) Funtzioa jarraitua da Á osoan, baina ez da deribagarria x = 0 puntuan.

EGIN ZUK

Aztertu honako funtzio hauen tarte gorakorrak eta beherakorrak:

a) f (x) = x x 4 –2 3

b) f (x) = ln (x 2 + 4x – 5)

5. Funtzio deribatua

Deribatua nulua da x = –1 eta x = 1/e puntuetan. f '-k puntu horien ezkerretara eta eskuinetara zer zeinu hartzen duen aztertuko dugu

f gorakorra da (– ∞, –1) ∪ ,∞ e 1 + dn tartean, eta beherakorra, (–1, 0) ∪ , e 0 1 dn tartean.

Maximo bat du (–1, 1) puntuan, eta minimo bat, , ee 11 –dn puntuan

a) f (x) ez da deribagarria x = 1 puntuan f ' (1) ez da existitzen, f ' (1–) = 2 ≠ 1 = f ' (1+) baita

b) f (x) gorakorra da (– ∞, 1) ∪ (1, 2) tartean, tarte horretan f' (x) > 0 baita.

f (x) beherakorra da (2, + ∞) tartean, f ' (x) < 0 baita

f (x) funtzioak mutur bat du x = 2 puntuan, grafikoan ikusten dugunez f ' (2) = 0 baita

Goiko hori Á osoan jarraitua den f funtzio baten deribatuaren grafikoa da.

a) Azaldu, arrazoituz, f deribagarria den Á osoan.

b) Aztertu non den gorakorra eta non beherakorra f funtzioa, eta azaldu mutur erlatiborik duen.

c) Irudikatu f '' (x).

Gainera, x = 2 puntuan, f ' (x) positibotik negatibora igarotzen da eta, ondorioz, f (x) gorakorra izatetik beherakorra izatera. Beraz, ziurra da f (x)-k maximo bat duela x = 2 puntuan

c) f '' (x)-ren balioak f ' (x) eratzen duten zuzenerdien maldak dira. Grafikoa honako hau da:

4. Hazkunde-tarteak

Ebatzitako ariketak eta problemak

6. f ', f '' eta f ''' baliogabetzen diren puntuak

f (x) = 1 – (2 – x) 5 funtzioa izanda, aztertu maximorik, minimorik edo inflexio-punturik duen x = 2 puntuan.

• f ' , f '' , f ''' kalkulatuko ditugu:

f ' (x) = 5(2 – x)4 → f '' (x) = –20(2 – x)3 → f ''' (x) = 60(2 – x)2

x = 2 egitean, hau betetzen da f ' (2) = f '' (2) = f ''' (2) = 0.

• f '-ren zeinua aztertuko dugu x = 2 puntuaren ezkerrera eta eskuinera:

2 f ' > 0 f ' > 0

f hazi egiten da 2ren ezkerrera eta eskuinera → f-k ez du maximorik eta minimorik x = 2-n

EGIN ZUK

Funtzio hau daukagu:

f (x) = 3 – (x + 1)4

Aztertu maximorik, minimorik edo inflexio-punturik duen

• f ''-ren zeinua aztertuz, inflexio-puntu bat duela egiaztatuko dugu: 2 f '' < 0 f '' > 0

x = 2 puntuaren ezkerrera, funtzioa ganbila da, eta x = 2 puntuaren eskuinera, ahurra (2, 1) puntua inflexio-puntu bat da

7. Parametroak zatika definitutako funtzio batean

Funtzio hau izanda:

Zehaztu zein izan behar diren a, b eta c-ren balioak funtzioa jarraitua izateko, maximo bat edukitzeko x = –1 puntuan, eta x = –2 puntuan duen ukitzailea y = 2x zuzenarekiko paraleloa izan dadin.

EGIN ZUK

Kalkulatu b-ren eta d-ren balioak f (x) = = –x3 + bx2 + x + d funtzioak maximo erlatibo bat izan dezan (1, 4) puntuan.

8. Rolleren teorema

Funtzio hau dugu:

f (x) = (1 – x 2) sin x

Egiaztatu 0, 2 r bl tartekoa den maximo erlatibo bat duela.

• Jarraitua izateko, izan behar da: lim x 0 –" f (x) = lim x 0 " + f (x) = f (0) = c lim x 0 " + cos x x 1 0 0 –2 = dn = lim x 0 " + sn cos ix x 1 –2 = 0 → c = 0

• x = –1 puntuan maximo bat badu, izan behar da: f ' (–1) = 0; hau da, deribatua denez f ' (x) = 2ax + b → –2a + b = 0

• x = –2 puntuan duen ukitzailea paraleloa bada y = 2x zuzenarekiko, izan behar da: f ' (–2) = 2 → – 4a + b = 2

• Sistema ebatziko dugu: ab ab 20 42 ––+= += ) ; a = –1, b = –2

Eskatutako balioak hauek dira: a = –1, b = –2, c = 0.

• f jarraitua eta deribagarria da Á osoan.

•–

() () () () sn sn i i f f 01 00 0 11 11 0

•–== == 4 f-k Rolleren teoremaren hipotesiak betetzen ditu [0, 1]-en [0, 1] tartea 0, 2 r bl tartearen barruan dagoenez, ziurta dezakegu existitzen dela

c ∈ 0, 2 r bl bat, eta, bertan, f ' (c) = 0.

c puntuan maximo edo minimo bat dagoen jakiteko, bigarren deribatua erabiliko dugu:

f ' (x) = –2x sin x + (1 – x 2)cos x

f '' (x) = (x 2 – 3)sin x – 4x cos x

c ∈(0, 1) bada: c 2 – 3 < 0, sin c > 0, 4c > 0, cos c > 0 da

f '' (c) = (– · +) – (+ · +) < 0 → f funtzioak maximo bat du x = c puntuan

10 m-ko erradioa duen zirkuluerdi baten itxura daukan lorategi batean parterre laukizuzen bat jarriko dute. Parterre horren aldeetako bat diametroaren gainean egongo da, eta alde horren aurkakoak zati kurbatuan izango ditu muturrak Kalkulatu zer neurri izan behar dituen parterreak azalera maximoa izan dezan.

➜ Simulatu eremua eta lortu hura deskribatzen duen kurba.

EGIN ZUK

Zilindro itxurako depositu bat egin nahi dute latorriz, 54 cm2-ko azalera izango duena guztira. Zehaztu zer erradio izan behar duen oinarriak eta zenbatekoa izan behar den altuera zilindroaren bolumena maximoa izateko.

y P (x, y )

Koordenatuen jatorri moduan zirkunferentziaren zentroa hartuko dugu.

P (x, y) zirkunferentziako puntu bat da

Parterrearen azalera hau da S = 2xy

P puntua zirkunferentziakoa denez, hau bete behar du:

x 2 + y 2 = 100 → y = x 100 –2

Beraz, S (x) = 2x x 100 –2 maximizatu behar da

S'(x) kalkulatuko dugu: S'(x)

() x x 52 52 –ezdubalio = =

x = 52 puntuan maximo bat dago; izan ere, S'(x) > 0 da, baldin eta x < 52 bada; eta

S'(x) < 0 da, baldin eta x > 52 bada.

Parterrearen neurriak hauek izango dira: 2 10 m eta 52 m, eta azalera maximoa 100 m2 izango da.

10. Gutxieneko denboraren problema

A igerilaria hondartzatik 3 km-ra dago, egurrezko txabola baten aurrez aurre. Eta hondartza horretan bertan txabolatik

6 km-ra dagoen B punturaino joan

nahi du

3 km/h-ra igeri egiten duela eta hareatan

5 km/h-ra dabilela jakinda, esan noraino joan beharko duen igerian, ahalik eta denbora gutxien behar izateko B-ra iristeko.

Erabili

Txabolaren eta igerian lortu behar duen P puntuaren arteko distantziari x esango diogu.

Egin beharreko bidea:

AP x 9 2 =+ 3 km/h-ra eta

PB = 6 – x 5 km/h-ra

EGIN ZUK

Itsasontzi bateko oihal nagusiak

triangelu angeluzuzenaren itxura du.

Hipotenusak 6 m baditu, kalkulatu

zein izan behar diren oihalaren neurriak azalera maximoa izateko

Hau ikusten dugu:

• x < 2,25 bada, t' (x) < 0; izan ere, adibidez t ' (0) = –1/5 da.

• x > 2,25 bada, t' (x) > 0; izan ere, t ' (4) = 1/15 da.

Txabolatik 2,25 km-raino joan behar du igerian.

B-ra iristeko beharko duen denbora hau da: t = , ,

9. Azalera maximoa

Gidatutako ariketak eta problemak

1. Zuzen batekiko ukitzaile perpendikularra

Idatzi x + y – 2 = 0 zuzenarekiko perpendikularrak izan eta f (x) = 4x 3 – 2x + 1 funtzioarekiko ukitzaile diren zuzenen ekuazioak

• Zuzenaren malda m bada, bere perpendikularrarena da m –1

• Ukitze-puntuak lortzeko, ebatzi f ' (x) = m –1 ekuazioa.

• Ukitze-puntuak zein diren jakinda, eskatutako ekuazioak idatziko ditugu

Soluzioa: y = x; y = x + 2

2. Ahurtasun- eta ganbiltasun-tarteak

Esan zein diren honako funtzio honen ahurtasun- eta ganbiltasun-tarteak eta inflexio-puntuak:

f (x) = x x 1 –2 2

Kalkulatu honako funtzio honek [–1, 2] tartean dituen maximo eta minimo absolutuak:

f (x) = ln (x 2 + x + 1) – x

f (x) = x xx47 –2 + funtzioa izanda, egiaztatu f ' (c) = 4 betetzen duen c ∈ (1, 3) balio bat dagoela.

• Ebatzi f '' (x) = 0 ekuazioa

• Gogoan izan inflexio-puntu bat egoteko kurba ganbila izatetik ahurra izatera igaro behar dela, edo alderantziz.

• Kontuan izan funtzioaren definizio-eremua, f '' (x)-ren zeinua zer tartetan aztertu behar duzun erabakitzeko.

Soluzioa: Ahurra (– ∞, –1) ∪ (1, +∞) tartean, eta ganbila (–1, 1) tartean. Ez du inflexio-punturik.

• Aztertu f (x)-ren definizio-eremua eta emandako tartean jarraitua den

• Gogoan izan tarte itxi batean jarraitua den funtzio batek maximo eta minimo absolutuak tartearen muturretan lortzen dituela, edo, bestela, mutur erlatiboetan

• Lortu mutur erlatiboen abzisak. Kalkulatu f (x)-ren balioa puntu horietan, eta konparatu x = –1 eta x = 2 puntuetan dituenekin.

Soluzioa: Maximo absolutua (–1, 1) puntuan du, eta minimo absolutua, (2, ln 7 – 2) puntuan.

• Aztertu f (x)-ren definizio-eremua eta [1, 3] tartean jarraitua den.

• Aurkitu f (x)-ren deribatua, logaritmoak hartuz.

• Egiaztatu deribatua existitzen dela (1, 3) tartean. Erabili batezbesteko balioaren teorema eta lortu c.

Soluzioa: f (x) jarraitua da [1, 3] tartean eta deribagarria (1, 3) tartean. Beraz, existitzen da f ' (c) = () () ff 31 31 4 ––= betetzen duen c balio bat

f (x) = x 2 e –ax da a ≠ 0 izanik.

a) Kalkulatu zein izan behar den a-ren balioa funtzioak mutur erlatibo bat izan dezan x = 2 abzisa-puntuan.

b) Sailkatu mutur erlatiboak a = 2 den kasuan.

a) Mutur erlatiboak f ' (x) = 0 ekuazioaren soluzioen artean daude. Ekuazio horren soluzioetako bat a-ren araberakoa da. x = 2 kasuan, a-ren balioa lortuko dugu

b) Aztertu f ' (x)-ren zeinua puntu singularrek zehazten dituzten tarteetan

Soluzioa:

a) a = 1

b) Minimo erlatibo bat du (0, 0) puntuan, eta maximo erlatibo bat (1, e –2) puntuan

3. Maximo eta minimo absolutua

4. Batezbesteko balioaren teorema

5. Mutur erlatiboak

Proposatutako ariketak eta problemak

Trebatzeko

Zuzen ukitzailea

1 Idatzi kurba hauek adierazitako puntuan daukaten zuzen ukitzailearen ekuazioa:

a) y = ln (tg 2x), x =  8 r puntuan

b) y =  senx 5 , x =  6 r puntuan

c) x 2 + y 2 – 2x – 8y + 15 = 0, x = 2 puntuan

d) y = (x 2 + 1)sin x , x = 0 puntuan

2 Kurba honekiko ukitzaileen artean: y =  x x 1 2 –

aurkitu 2x + y = 0 zuzenarekiko paraleloak direnak.

3 Lortu kurba hauetako bakoitzean, abzisa ardatzarekiko paraleloa den ukitzailearen ekuazioa:

a) y = x ln x b) y = x 2 e x c) y = sin 2x

4 Aurkitu y = 2 x kurbaren grafikoko zer puntutan eratzen duen kurbarekiko ukitzaileak 60°-ko angelua X ardatzarekin. Idatzi ukitzaile horren ekuazioa.

5 a) Idatzi f (x) = x 3 – 3x 2 + 2x + 2 funtzioaren grafikoak x = 3 puntuan duen zuzen ukitzailearen ekuazioa.

b) Ba al dago lortu duzun zuzenarekiko paraleloa den f-rekiko beste zuzen ukitzailerik? Erantzuna baietz bada, aurkitu.

6 Aurkitu zein den honako kurba honekiko zuzen ukitzailea kurbaren inflexio-puntuan: y = 4x 3 – 2x 2 – 10

7 Kurba hau dugu: y = 3x 2 – 5x + 12

Aurkitu zer puntutako ukitzaileak igarotzen diren koordenatuen jatorritik.

8 Kurba hau daukagu: y =  4 1 x 2 + 4x – 4

Aurkitu, kurbako zer puntutako ukitzaileak igarotzen diren (0, –8) puntutik. Idatzi puntu horietako zuzen ukitzaileen ekuazioak.

9 Aurkitu, kurba hauetako bakoitzean, X ardatzarekiko paralelo diren ukitzaileen ekuazioak:

Maximoak eta minimoak. Inflexio-puntuak

10 Aurkitu honako funtzio hauen maximoak, minimoak eta inflexio-puntuak:

a) y = x 3 – 6x 2 + 9x b) y =  ()xx 12 38 –3

c) y = x 4 – 2x 3 d) y = x 4 + 2x 2

e) y =  x 1 1 2 + f) y = e x (x – 1)

11 Aurkitu funtzio hauen tarte gorakorrak eta beherakorrak, eta maximoak eta minimoak:

a) y =  ()xx x 2 83 –– b) y =  x x 1 1 –2 2 +

c) y =  x x 1 –2 3 d) y =  x xx 2 23 ––2

e) y =  x x 1 –2 f ) y =  ()xx 3 8 –2

12 Adierazi funtzio hauetako bakoitzaren ahurtasuna, ganbiltasuna eta inflexio-puntuak:

a) y = x 3 – 3x + 4 b) y = x 4 – 6x 2

c) y = (x – 2)4 d) y = x e x

e) y =  x x 1 2–+ f) y = ln(x + 1)

13 Aztertu honako funtzio hauek maximoak, minimoak edo inflexio-puntuak dituzten x = 1 abzisa-puntuan:

a) y = 1 + (x – 1)3 b) y = 2 + (x – 1)4

c) y = 3 – (x – 1)6 d) y = –3 + 2(x – 1)5

14 Zehaztu honako funtzio hauen maximoak eta minimoak:

a) f (x) = x +  () x 1 4 –2 b) f (x) = x ln x

c) f (x) = sin x – cos x d) f (x) = e –x2

15 Funtzio hauek izanda:

f (x) =  ≤ xx x x x 21 42 1 1 ––bada bada > 2 + )

g (x) =  ≥ xx xx x x 74 23 2 2 –bada bada < 2 2 + + *

a) Egiaztatu deribagarriak direla Á osoan.

b) Zehaztu funtzio horien tarte gorakorrak eta beherakorrak, eta maximoak eta minimoak.

16 Aztertu f (x) = x | x | funtzioaren tarte gorakorrak eta beherakorrak. Maximorik edo minimorik du?

Zehaztu ahurtasun- eta ganbiltasun-tarteak. Inflexio-punturik du?

Proposatutako ariketak eta problemak

Funtzio baten koefizienteak

17 f (x) = 1 +  x a x 6 2 + funtzioa izanda, kalkulatu a-ren balioa zein den f (x) funtzioak x = 3 abzisa-puntuan mutur erlatibo bat duela jakinda. Maximo bat da, ala minimo bat?

18 f (x) =  ax 3 +  bx funtzioari buruz badakigu (1, 1) puntutik igarotzen dela eta puntu horretan 3x + y = 0 zuzenarekiko paraleloa den ukitzaile bat duela. Aurkitu a eta b

19 Aurkitu x = 2 abzisa-puntuan mutur erlatibo bat duen eta P (1, 2) puntuan inflexio-puntu bat duen

f (x) = x 3 + ax 2 + bx + c funtzioa.

20 Kalkulatu f (x) = x 4 + ax 3 + bx 2 + cx funtzioaren a, b eta c koefizienteak, honako hau jakinda:

a) x = 0 puntuan duen ukitzailea y = x da.

b) Mutur erlatibo bat du (–1, 0) puntuan.

21 Zer balio izan behar dute a, b, c eta d koefizienteek

f (x) = ax 3 + bx 2 + cx + d funtzioak maximo erlatibo bat izateko (0, 4)-n eta minimo erlatibo bat (2, 0)-n.

22 f (x) =  x 4  +  ax 2  +  bx eta g(x) =  x –  cx 2 funtzioak (1, 0) puntutik igarotzen dira. Zehaztu zein izan behar diren a, b eta c koefizienteak, puntu horretan zuzen ukitzaile bera izan dezaten, eta kalkulatu ezazu.

23 y = ax4 + 3bx3 – 3x2 – ax funtzioa izanda, kalkulatu a eta

b koefizienteen balioak, kontuan hartuz bi inflexio-puntu dituela: x = 1 puntuan eta x = 1/2 puntuan.

24 y = x3 + ax2 + bx + c kurbak abzisa-ardatza ebakitzen du x = –1 puntuan eta inflexio-puntu bat du (2, 1) puntuan. Kalkulatu a, b eta c.

25 f (x) = x3 + ax2 + bx + c funtzioak hauek betetzen ditu: f(1) = 1, f ' (1) = 0 eta f-k ez duela mutur erlatiborik x = 1 puntuan. Kalkulatu a, b eta c

26 f (x) = x 3 + ax 2 + bx + 5 da. Aurkitu zein izan behar diren a eta b koefizienteak y = f(x) kurbak ukitzaile horizontaleko inflexio-puntu bat izan dezan x = 1 puntuan.

27 Aurkitu zein izan behar den c-ren balioa y = xc e x 2 + funtzioak puntu kritiko bakarra izan dezan.

Maximo bat da, minimo bat edo inflexio-puntu bat?

28 a) Kalkulatu zer balio izan behar duten a eta b parametroek honako funtzio hau deribagarria izateko:

f (x) =  e x x 1 0 –bada bada < x 2 ≥ xaxb x 0 ++ *

b) Aurkitu mutur erlatiboak a = –2, b = 1 kasuan.

Ebazteko

29 Aurkitu x 2  – y 2 + 2x – 6 = 0 kurbak y = 3 ordenatu-puntuetan dituen zuzen ukitzailearen eta zuzen normalaren ekuazioak.

30 (x – 3)2 + (y + 2)2 = 16 zirkunferentzia izanik, zehaztu zer puntutan izango den zuzen ukitzailea lehenengo koadranteko erdikariarekiko paralelo.

31 Kurba hau daukagu: y = arc tg x x 1 1 –+ Idatzi x – 2y + 3 = 0 zuzenarekiko paraleloa ere baden zuzen ukitzailearen ekuazioa.

32 Aurkitu x = e abzisa-puntuan y = x x/2 kurbarekiko ukitzailea izango den zuzenaren ekuazioa.

33 Aurkitu zer angelu eratzen duten f(x) eta g(x) funtzioek 2 abzisa-puntuan dituzten zuzen ukitzaileek:

f (x) = 2x – x 2 g (x) = x 2  – x – 2

34 f (x) = | x – 3|(x + 1) funtzioa izanda, aurkitu zer puntutan diren ukitzaileak y = 6x – 2 zuzenarekiko paraleloak.

35 f (x) = 4 – x 2 funtzioa emanda, hau eskatzen da:

a) Kurbako zer puntutan den ukitzailea (–1, 3) eta (2, 0) puntuak lotzen dituen kordarekiko paraleloa.

b) Zein diren (–2, 1) puntutik igaro eta kurbarekiko ukitzaileak diren zuzenak.

36 Aurkitu f (x) = x 3 + 3x 2 – 1 kurbarekiko ukitzaileen artean, malda minimoa duen zuzenaren ekuazioa.

37 y =  x 3 1 2 + kurba izanda:

a) Adierazi kurbak x puntuan daukan zuzen ukitzailearen malda ematen duen m(x) funtzioa.

b) Kalkulatu x-ren zer baliorekin lortzen den malda maximoa.

38 Aurkitu honako funtzio honen definizio-eremua eta tarte gorakorrak eta beherakorrak:

f (x) =  ln x x 1 1 –2 2 + e o

39 Aztertu funtzio honen hazkunde-tarteak, eta maximoak eta minimoak:

y = |x 2 + 2x – 3|

40 Aztertu y = |x2 – 4| funtzioak maximo eta minimo erlatibo eta absoluturik duen.

41 Aurkitu a-ren balioa, f (x) = x 2 ln a x funtzioak, a > 0 izanik, puntu singularra izateko x = e puntuan.

42 f (x) =  ≤ ln ax bx c xx x x 0 0 bada bada > 2 ++

funtzioa daukagu.

Zehaztu zein izan behar diren a, b eta c, funtzio hori jarraitua izateko, x = –1 puntuan maximo bat izateko eta x = –2 puntuko ukitzailea y = 2x zuzenarekiko paralelo izateko.

2 2 + ++

Kalkulatu m, n eta p-ren balioak f deribagarria izateko

Á osoan eta mutur erlatibo bat izateko x = 2 1 – puntuan

b) Maximo bat ala minimo bat da?

c) Aztertu beste puntu singularrik dagoen eta irudikatu funtzioa.

44 f funtzioa honela definituta dago: f (x) =  ≤ xe ab x x x 20 0 –bada bada > x–+ * .

a) Zehaztu a-ren eta b-ren balioak, f (x) funtzioa x = 0 puntuan deribagarria dela jakinda.

b) Puntu singularrik du?

45 Aurkitu y = x 2 – 1 parabolako zer puntu egongo diren

A 2, 2 1 dn puntutik gutxieneko distantziara.

46 Kalkulatu funtzio hauen mutur erlatiboak, tarte gorakor eta beherakorrak, eta ahurtasun- eta ganbiltasun-tarteak:

a) f (x) = x 2 + | x – 2 | b) f (x) = 3e –2| x |

47 Kalkulatu zer maximo eta minimo erlatibo dituen [–2, 3] tartean f (x) = ln (x 2 + 1) + (x – 3) funtzioak.

48 a) f (x) = x 4 + x 3 + x 2 – x + 1 funtzioko P (x, f (x)) puntuaren koordenatuen arteko batura h (x) dela jakinda, kalkulatu h (x)-ren mutur erlatiboak.

b) h (x)-k mutur absoluturik du?

49 P(x, y) puntua x y 25 9 2 2 + = 1 elipsean zehar dabil.

Esan P puntuak zer posiziotan izango duen (0, 0) punturainoko distantzia maximoa, baita zer puntutan izango duen distantzia minimoa.

50 x eta y bi zenbaki positiboren biderkadura 16 da. Izan daiteke x + y batura 7 baino txikiagoa? Arrazoitu.

51 Laukizuzen-itxurako lursail bat 100 m hesi metaliko erabilita itxi nahi da. Sailaren alde batean, 20 m-an hesirik ez egotea erabaki da, atea jartzeko. Kalkulatu horrela itxi daitekeen azalera maximoko lursail laukizuzenaren aldeen neurriak. Kalkulatu, horrez gain, azalera maximo horren balioa.

52 Kono-itxurako ontzi bat egin nahi dugu, 10 cm-ko sortzailea eta edukiera maximoa izango dituena. Zein izan behar da oinarriaren erradioa?

53 10 cm-ko aldea duen karratu baten gainean 50 cm2-ko alboko azalera duen zilindro bat dugu. Zein izan behar da erradioa bolumena maximoa izateko?

h

10 cm r

10 cm

54 Triangelu isoszele batek 12 cm-ko oinarria du (alde desberdina), eta 10 cm-ko altuera. Bertan laukizuzen bat inskribatu dugu, aldeetako bat triangeluaren oinarrian jarriz, eta bi erpin, alde berdinen gainean:

a) Adierazi laukizuzenaren A azalera x oinarriaren funtzioan, eta esan zein den funtzioaren definizio-eremua. b) Kalkulatu funtzio horren balio maximoa.

55 7.3 helburua. Oinarri karratua eta 80 cm3-ko edukiera duen prisma erregular baten itxurako ontzi bat egin nahi dugu. Tapa eta alboko gainazala egiteko, material jakin bat erabiliko dugu; baina oinarrirako, % 50 garestiagoa den beste bat erabili behar dugu. Kalkulatu zer neurri izan behar duen ontzi horrek prezioa ahalik eta txikiena izateko.

56 12 m-ko eta 18 m-ko altuera duten bi poste bata bestetik 30 m-ra daude. Kable bat bota nahi dugu, poste horien arteko lurzoruko puntu bat posteen muturrekin lotzeko. Non jarri behar da lurzoruko puntua kablearen luzera osoa minimoa izateko?

57 (1, 2) puntutik igarotzen diren zuzen guztien artean, aurkitu zeinek zehazten duen koordenatuen ardatzekin, lehenengo koadrantean, azalera minimoko triangelu bat.

58 Liburu bateko orrialde bakoitzak 600 cm2-ko azalera izan behar du, eta testuaren inguruan 2 cm-ko marjina utzi behar da goialdean, 3 cm-koa behealdean, eta 2 cm-koa alboetan. Kalkulatu zer dimentsio izan behar dituen orrialdeak inprimatutako azalera ahalik eta handiena izateko.

59 Laukizuzen batek erpinak (0, 0), (a, 0), (0, b) eta (a, b) puntuetan ditu, jakinda a > 0, b > 0 direla eta gainera, (a, b) puntua y = x 1 2 + 9 ekuazioa duen kurban dagoela

Baldintza horiek betetzen dituzten laukizuzen guztien artean, zehaztu azalera minimoko laukizuzena eta kalkulatu azalera minimo hori.

Proposatutako ariketak eta problemak

60 Triangelu isoszele bat daukagu, alde desberdina 12 cm-koa duena, eta altuera, 5 cm-koa. Altueraren gainean, oinarritik x distantziara dagoen A puntu bat zehaztu nahi dugu, kontuan izanda A puntu horretatik triangeluaren hiru erpinetara dauden distantzien batura minimoa dela. Aztertu irudia: A x 5 cm } 12 cm

a) Egiaztatu A puntutik triangeluaren hiru erpinetara dauden distantzien batura f (x) = 5 – x + 2 x 36 2 + adierazpenak ematen digula.

b) Kalkulatu zein izan behar den x-ren balioa distantzien batura minimoa izateko.

c) Kalkulatu kantitate minimo hori.

61 Erloju bateko orratzek 4 cm eta 6 cm dituzte. Muturrak lotuz gero, triangelu bat eratzen da.

a) Egiaztatu triangelu horren azalera A (x) = 12sin x funtzioak ematen duela, x orratzen angelua izanik.

b) Kalkulatu zein izan behar den x-ren balioa triangeluaren azalera maximoa izateko, eta kalkulatu azalera hori.

62 Partikula baten abiadura, m/s-tan, funtzio honek ematen digu: v (t ) = (t 2 + 2t)e –t , t ≥ 0 izanik.

a) [0, 3] tarteko zer unetan lortzen da abiadura maximoa?

b) Kalkulatu lm i x ∞ " + v (t ) eta interpretatu emaitza.

63 f : [1, e ] → Á daukagu, f (x) = x 1 + ln x funtzioaren bidez definituta Zehaztu f-rekiko ukitzaile diren zuzenen artean zeinek duten malda maximoa.

64 Kalkulatu 4 m-ko erradioa duen zirkunferentzia batean inskribaturik dagoen azalera maximoko triangelu isoszelearen neurriak.

66 y = x3 – 5x2 + 3x – 2 funtzioak betetzen ditu batezbesteko balioaren teoremaren hipotesiak [0, 4] tartean? Erantzuna baietz bada, esan zein den tesia betetzen duen x0

67 Funtzio hau daukagu:

f (x) =

Galdera teorikoak

65 Egiaztatu [0, 3 2 ] tartean definitutako f(x) = x3 – 18x funtzioak Rolleren teoremaren hipotesiak betetzen dituela, eta aurkitu, f ' (c) = 0 izateko, zein izan behar den c ∈ (0, 3 2 )

Z [ \

] ] ] ]

x –≤21 ≤–x x x

1 2 3 10 –

bada –≤ bada < 2

Frogatu f funtzioak betetzen dituela batezbesteko balioaren teoremaren hipotesiak [–2, 0] tartean, eta kalkulatu zer puntutan (bat baino gehiago izan daitezke) betetzen den teorema.

68 Kalkulatu daiteke a, b, c zein diren, honako funtzio honek: f (x) =  ≥ x ax bx x x 51 3 1 1 bada bada < 2 + ++ )

Rolleren teorema bete dezan [0, c] tartean?

69 f (x) = | cos x | funtzioak 1 balioa hartzen du [0, π] tartearen muturretan. Beteko du Rolleren teorema?

70 f funtzioa jarraitua eta deribagarria da, f (0) = 3 izanik. Kalkulatu zein izan behar den f (5)-en balioa, [0, 5] tartean f ' (c) = 8 betetzen duen c existitzen dela ziurtatzeko.

71 Kalkulatu zein diren a eta b, honako funtzio honek:

f (x) =  ≥ ax xx b x x 3 10 4 4 – bada bada < 2 + )

batezbesteko balioaren teoremaren hipotesiak bete ditzan [2, 6] tartean. Non betetzen du tesia?

72 f (x) = 1 – x 2/3 da.

Frogatu f(1) = f(–1) = 0 dela, baina f'(x) ez dela inoiz zero [–1, 1] tartean. Azaldu zergatik dagoen emaitza hori, itxuraz, kontraesanean Rolleren teoremak dioenarekin.

73 f funtzio baten deribatua positiboa da aldagaiaren balio guztietarako. Egon daitezke f (a) = f (b) betetzen duten a eta b bi zenbaki desberdin? Arrazoitu.

74 Kalkulatu a, b eta c, honako funtzio honek, f (x) =  ≥ xaxb cx x x 1 2 2 bada bada < 2 ++ + )

Rolleren teoremaren hipotesiak bete ditzan [0, 4] tartean. Zer puntutan betetzen da tesia?

75 Funtzio hau dugu:

f (x) =  () () ln ln xx x 31020 –x 2 ++ +

Egiaztatu f ' (a) = 0 betetzen duen a ∈ (1, 2) balio bat existitzen dela. Aipatu eta arrazoitu erabilitako emaitza teorikoak.

Zuzena ala okerra? Arrazoitu erantzuna.

a) Zuzen bat ez den funtzio batek infinitu puntutan izan dezake y = 1 zuzen ukitzailea.

b) f ' (a) = 0, f '' (a) = 0 badira, orduan f-k ezin du ez maximorik ez minimorik izan x = a puntuan.

c) 3. mailako polinomio batek minimo bat badu x = 2 puntuan, minimo hori ezin da minimo absolutua izan.

d) [0, 5] tartean jarraitua den funtzio batek ezin du maximorik izan x = 3 puntuan, puntu horretan deribagarria ez bada.

e) y = f (x) gorakorra bada x = a puntuan, orduan y = –f (x) beherakorra da x = a puntuan.

f ) f ' (a) = 0 bada, f-k maximo edo minimo bat du x = a puntuan.

g) f ' (a) = 0, f '' (a) = 0 eta f ''' (a) = –5 badira, f-k inflexiopuntu bat du x = a puntuan.

h) Honako hau f ' (x)-ren grafikoa bada, f-k minimo bat du x = –1 puntuan eta maximo bat x = 1 puntuan.

AUTOEBALUAZIOA

1 Funtzio hau izanda:

f (x) = ln cos cos x x 1 1–+ aurkitu zer puntutan den zuzen ukitzailea y = 2x – 3 zuzenarekiko paraleloa.

2 Kalkulatu funtzio honen mutur erlatiboak, tarte gorakorrak eta beherakorrak eta ahurtasun- eta ganbiltasun-tarteak:

f (x) = x | x – 2 |

3 Aztertu f (x) = e x (cos x + sin x) funtzioaren hazkundea, eta zehaztu zein diren maximoak eta minimoak x ∈ [0, 2π] tartean

4 a) Aztertu honako funtzio honen kurba:

f (x) = x 2 ln x

b) Idatzi funtzio horren inflexio-puntutik igarotzen den zuzen ukitzailearen ekuazioa.

Sakontzeko

77 Esperimentu batean, objektu beraren bost neurketa egin ditugu, eta honako emaitza hauek lortu ditugu: m1= 0,92; m2 = 0,94; m3 = 0,89; m4 = 0,90; m5 = 0,91 Neurri errealarekiko hurbilketa onena izango da erroreen karratuen arteko batura minimo egiten duen x-ren balioa. Hau da, funtzio hau:

E(x) = (x – m1)2 + (x – m2)2 + … + (x – m5)2 minimo egiten duen balioa. Kalkulatu x-ren balio hori.

78 Egiaztatu existitzen dela α ∈ (–1,3) non f ' (α) =  4 –1 den,

f (x) =  [( )] log xx x2 7 –x 22 4 3– 3 ++ izanik.

Aipatu zer emaitza teoriko erabili dituzun, eta arrazoitu horien erabilera.

79 Globo bat lurretik 200 m-ra egon eta goraka 15 m/s-ra doan unean, azpitik auto bat igarotzen da 45 km/h-ko abiaduran. Zer abiadurarekin urruntzen dira bata bestetik autoa eta globoa segundo bat geroago?

Kontuan hartu honako hauek:

— Globoa 200 + 15t m-ko altueran dago t unean.

— Autoa globoaren bertikaletik (45/3,6) · t m-ra dago. Aurkitu bien arteko distantzia, eta kalkulatu urruntze-abiadura t = 1 denean.

Ariketa hauen ebazpena.

5 Zehaztu a, b, c eta d zein izan behar diren g (x) = ax 3 + + bx 2 + cx + d funtzioak maximo erlatibo bat izan dezan (0, 4) puntuan eta minimo erlatibo bat (2, 0) puntuan.

6 Kalkulatu y = x 1 1 2 + kurbaren zer puntutan izango den zuzen ukitzailearen malda maximoa

7 9 cm-ko erradioa duen esfera batean inskribatu daitezkeen zilindro guztien artean, aurkitu bolumenik handiena duenaren altuera eta erradioa.

8 f (x) = 1 – | x | funtzioak, x ∈ [–2, 2] bada, f (–2) = f (2) berdintza egiaztatzen du.

Funtzioen adierazpena 11

Funtzio kontzeptua

xv. eta xvi. mendeetan sinbologia aljebraikoaren oinarriak ezarri ziren. Horrek matematikaren erabilera oso praktikoa ahalbidetu zuen, eta bidea ireki zuen funtzio baten aldagaiak eta ekuazio baten ezezagunak bereizteko, ezinbesteko bereizketa funtzioaren nozioa ezartzeko.

xvii. mendearen hasieran, Galileok lehen aldiz erabili zuen esperimentazio kuantitatiboa informazio-iturri gisa. Kausak eta efektuak modu funtzionalean lotzen hasi zen. Hori funtsezkoa izan zen mendeko aldagaiaren kontzeptua zehazteko.

Galileok bi aldagairen (x eta y, kausak eta efektuak) arteko erlazio matematikoei buruz egindako ikerketak funtzio kontzeptuaren aurrekari oso argia dira, eta xvii. mendean zehar itxura hartuz joan ziren.

xvii. mendeko ideia emankor eta distiratsuenetako bat funtzio kontzeptuaren eta kurba baten irudikapen grafikoaren arteko lotura ezartzea izan zen.

Diagrama kartesiarren bidezko irudikapen grafikoak funtzioak bistaratzea ahalbidetu zuen. Horrela, funtzioaren kontzeptua orokortu egin zen, eta koordenatu-ardatz batzuen gaineko grafiko bat adierazten zuen edozein zenbaki-erlaziotarako erabili zen. Baina garai hartako matematikariek formulei zegozkien grafikoak bakarrik onartzen zituzten funtzio gisa. xix. mendearen erdialdean, Dirichletek kontzeptua zabaldu zuen, eta grafikoki (edo beste era batera) emandako erlazio mota jakin batzuk ere funtzio adieran barneratu zituen, nahiz eta ez egon funtzio horiek deskribatzen zituen «formula» bat.

Limiteak eta deribatuak kalkulatzeko kontzeptuek eta prozedurek aukera ematen dute, gaur egun, formulen bidez emandako funtzioen ezaugarri garrantzitsuenak modu eroso eta eraginkorrean ikertzeko eta, ondorioz, funtzio horien irudikapen grafikoa egiteko. Kalkulagailu edo ordenagailu batekin automatikoki eta berehala lortzen da.

Dirichlet

Funtzio kontzeptuaren bere definizioak analisiaren oinarriak finkatzeko balio izan zuen. Baina Berlinen irakasle zebilen Gustav Dirichletek beste ekarpen asko ere egin zizkien matematikari eta fisikari; hala, 1855ean Gauss hil zenean, denek pentsatu zuten Dirichlet izango zela bere oinordeko duina, eta Göttingeneko katedra betetzeko deia egin zioten.

Gustav Dirichlet (1805-1859)

Funtzio bitxia eta jakintsu nahigabetua

Dirichletek, puntu batean ere jarraitua ez zen funtzioaren adibide bat jartzearren, hau definitu zuen:

D (x) = Á

bada bada x x 1 0 !

Funtzio xelebre eta bitxi horiek funtzioaren kontzeptua zehazteko diseinatu ziren. Poincare, xx. mendearen hasierako matematikari garrantzitsuentzat hartu izan dena, kexu zen «gure aurrekoen arrazoitzea okerra izan zela erakusteko asmaturiko funtzio bitxi horietaz», eta kontrajarri egiten zituen «zerbaitetarako balio zuten funtzio zintzoekin». Bi kurba interesgarri

traktrizea

X ardatzaren gainean, jatorritik 4 m-ra, bola bat dago 4 m-ko soka batekin lotuta. Pertsona bat oinez doa Y ardatzean zehar, sokaren muturra oratuta duela, eta bola arrastaka darama. Bolak egiten duen ibilbidea kurba bat da, traktize izenekoa, eta sokarekiko ukitzailea da sokaren puntuetako bakoitzean. Bere

katenaria

2,35 m-ko luzera duen kate baten bi muturrak 1,54 m-ko altuera duten eta bata bestetik 2 m-ra dauden bi zutoin sendoetara lotuz gero, kateak katenaria izeneko kurba bat eratzen du. Ardatzak egoki kokatuz gero, kurba horren ekuazioa hau da:

EBATZI

Limiteak eta deribatuak funtzio bat adierazteko

• Hartu paper koadrikulatua, marraztu koordenatu-ardatz batzuk eta irudikatu baldintza hauek betetzen dituen ahalik eta kurba sinpleena:

• Deskribatu funtzio hau ahalik eta datukantitaterik txikiena erabiliz eta aurreko ariketan egin dugun bezala:

• f deribagarria da Á osoan, x = 2 puntuan izan ezik.

Kurbak eraikitzeko oinarrizko elementuak

Funtzio baten grafikoa puntu multzo bat bada ere, funtzioak adieraztean, honezkero ondo jakingo duzun moduan, ez da egokia besterik gabe hainbat punturen koordenatuak lortzea. Bi arrazoirengatik ez da bide hori egokia:

— Denbora asko behar da

— Puntu horiek ziur aski ez dira nahikoa izango kurba nolako den egoki adierazteko; izan ere, litekeena da kurbako zatirik interesgarrienak aurkitutako puntu horien artean egotea edo aztertu dugun tartetik kanpo

Orokorrean, kurbek zenbait alderdi interesgarri izaten dituzte (puntu singularrak, adarrak, etenak,…) eta horietatik kanpo ez dute aparteko interesik izaten. Kurba bat behar bezala adierazteko, kurba bereizten duten ezaugarri horiek aurkitzen jakin behar da. Eta helburu horrekin aztertzen dira limiteak, asintotak, deribatuak,…

Unitate honetan, kurba baten ezaugarri interesgarriak zein diren jakiteko helburuarekin, eskura ditugun tresna matematiko guztiak berrikusi, sistematizatu eta ordenan jarriko ditugu, ondoren adierazpen egokia egiteko. Gogora ditzagun tresna horiek zein diren:

• Funtzioa zer eremutan aztertu erabakitzea

— Definizio-eremua. Jarraitua da? Deribagarria da?

— Simetriak (izan ere, Y ardatzarekiko edo koordenatuen jatorriarekiko simetrikoa bada, nahikoa izango da x ≥ 0 kasuan aztertzea).

— Periodikotasuna (periodikoa bada, nahikoa izango da periodo batean aztertzea).

• Adar infinituak

— x → ±∞ denean. Zer motatakoak dira?

— x → a denean. Badaude?

• Deribatuak

— Puntu singularrak: maximo eta minimo erlatiboak edo inflexio-puntuak.

• Puntu osagarriak lortzea

— Ardatzekin dituen ebaki-puntuak

— Kurbaren itxura zehazteko balio duten beste puntu batzuk Kurbaren adierazpen grafikoa egitean, ia inoiz ez ditugu elementu horiek guztiak aztertu beharko. Zerrenda hori eskulangileek tresna guztiak gordetzeko erabiltzen duten kaxaren antzekoa da. Lan bat egitean, normalean ez ditu tresna guzti-guztiak erabili beharko. Baina ona da eskura izatea, baita nola eta noiz erabiltzen diren jakitea ere Izan ditzagun, bada, prest tresna horiek guztiak, erabiltzeko moduan

Definizio-eremua

y = f (x) funtzio baten definizio-eremua (x-ren zer baliorekin existitzen den funtzioa)

Á osoa da, ezinezkoak diren eragiketak edo murrizketaren bat adierazten ez bada behintzat. Gogora ditzagun murrizketa garrantzitsuenak zein diren:

• Izendatzaileak badaude, funtzioa ez dago definituta izendatzaileak baliogabetzen diren puntuan.

• () x n { n bikoitia denean, φ (x) ≥ 0 denean soilik dago definituta.

• log φ (x) funtzioa φ (x) > 0 denean baino ez dago definituta

• arc sin φ (x) eta arc cos φ (x) funtzioak –1 ≤ φ (x) ≤ 1 denean baino ez daude definituta.

• tg φ (x) funtzioa ez dago definituta baldin eta φ (x) = k 2 r r + bada, k ∈ .

1. Adar infinituak

2. Maximoak eta minimoak: f ' (x) = 0

3. Inflexio-puntuak: f '' (x)= 0

4. Ebaki-puntuak ardatzekin: f (x) = 0 eta x = 0

➜ anayaharitza.es Funtzio ezagunak berrikusteko ariketak.

➜ Diseinatu definizio-eremuak.

1 Aurkitu honako funtzio hauen definizio-eremua:

a) y = arc sin (x + 3)

b) y = ln (3 – x 25 –2 )

a) arc sin funtzioaren balioak [–1, 1] tartekoak direnez, hau bete behar da:

–1 ≤ x + 3 ≤ 1 → –1 – 3 ≤ x ≤ 1 – 3 → – 4 ≤ x ≤ –2

y = arc sin (x + 3) funtzioaren definizio-eremua [– 4, –2] da.

b) Erro karratua atera ahal izateko, 25 – x 2 ≥ 0 izan behar da:

25 – x 2 ≥ 0

Logaritmoa hartzeko, 3 – x 25 –2 > 0 izan behar da: 3 – x 25 –2 > 0 ⇔ x 25 –2 < 3 ⇔ 25 – x 2 < 9 ⇔ –x 2 < –16 ⇔

x 2 > 16 ⇔ (x < – 4, edo, bestela, x > 4)

Bi baldintzak bete behar direnez:

Hau da, y = ln (3 – x 25 –2 ) funtzioaren

Jarraitutasuna, deribagarritasuna

Zatika lotuta modu artifizialean definitzen direnak kenduta, maila honetan erabiltzen ditugun funtzioak jarraituak dira haien definizio-eremu osoan. Deribagarriak ere badira, salbuespen batzuekin:

«Erro» funtzioek ukitzaile bertikala izan dezakete (eta, beraz, ez dira deribagarriak) errokizuna baliogabetzen den puntuetan.

Adibidez, y = x 4 –2 3 funtzioa ez da deribagarria x = –2 eta x = 2 puntuetan.

Balio absolutuak puntu erzdunak ematen ditu.

Adibidez, y = | x 2 – 4 | funtzioak puntu erzdunak ditu x = –2 eta x = 2 puntuetan

FUNTZIO JARRAITUAK ETA DERIBAGARRIAK IRUDIKATU

Tarte bateko jarraitutasunak modua ematen du funtzioari buruz dakizkigun zehaztasun guztiak (puntuak, adarrak,…) marra bakar batekin irudikatzeko

Horrez gainera, deribagarria ere bada, ez du puntu erzdunik izango.

1 Aurkitu funtzio hauen definizio-eremua, eta esan non diren jarraituak eta non deribagarriak.

2 Esan non diren jarraituak eta non deribagarriak honako funtzio hauek:

Adar infinituak puntu batean. Asintota bertikalak lm i xa " f (x) = ±∞ bada, x = a zuzena asintota bertikala da

Funtzioa ezkerretik edo eskuinetik hurbildu daiteke x = a asintotara, eta plus edo minus infiniturantz jo dezake. Ikus ditzagun kasu posibleak:

a a

ASINTOTA BERTIKALDUNAK DIRA

• () () x x z } forma hartzen duten funtzioak, ϕ(x) = 0 den puntuetan (zatikia sinplifikatuta dagoela).

a

Funtzioa asintotaren bi aldeetara definituta badago, alboko bi limiteak aztertuko ditugu:

lim xa –" f (x) eta lim xa " + f (x)

• log φ(x) funtzioak, puntu hauetan: φ(x) = 0.

• tg φ(x) funtzioak, puntu hauetan: φ(x) = π 2 + kπ, k ∈ .

Adibideak:

• y = x x 2 21 –+ funtzioak asintota bertikal bat du x = 2 puntuan ( lm i x 2 " f (x) = ±∞).

f (x) funtzioak 2ren inguruan zer zeinu duen jakiteko, x-ri 2tik hurbil dauden balioak emango dizkiogu («zertxobait txikiagoak» eta «zertxobait handiagoak»).

ezkerretik: x = 1,99 → f (x) = , , 1992 21 99 1 –·+ = – 498 (negatiboa) →

lim x 2 –" f (x) = – ∞

eskuinetik: x = 2,01 → f (x) = , ·, 2012 22 01 1 –+ = 502 (positiboa) →

lim x 2 " + f (x) = +∞

• y = x 5 1 + funtzioak asintota bertikal bat du x = –5 puntuan. Baina funtzioa asintotaren eskuinera baino ez dago definituta, eta, beraz, lim

• y = ln (x 2 – 1)

ln (x 2 – 1) → – ∞, baldin eta x 2 – 1 → 0+ Hau da, x → 1+ edo x → –1– bada:

Aurkitu asintota bertikalak eta kokatu kurbak asintotekiko:

Kontuan izan atal batzuetan zenbakitzaileak eta izendatzaileak erro komunak izan ditzaketela.

➜ Jarri asintota bertikalak.

Adar infinituak infinituan

• ∞ lm i x " + f (x) = l bada, orduan y = l zuzena asintota horizontala da x → +∞ denean.

Kurbak asintotarekiko zer posizio hartzen duen jakiteko, f (x) – l kenketaren emaitzak x-ren balio handietarako zer zeinu duen aztertu behar dugu

• ∞ lm i x " + f (x) = ±∞ , ∞ lm i x " + () x fx = m ≠ 0 eta ∞ lm i x " + [ f (x) – mx] = n badira, y = mx + n zuzena asintota zeiharra da x → +∞ denean.

Kurbak asintotarekiko zer posizio hartzen duen jakiteko, f (x) – (mx + n) kenketaren emaitzak x-ren balio handietarako zer zeinu duen aztertu behar dugu

Adi! Aurreko ikasturtetik badakizun moduan, funtzio arrazionaletan askoz errazagoa da asintota zeiharrak kokatzea (ikusi 281. orrialdea).

• ∞ lm i x " + f (x) = ±∞ bada eta asintota zeiharrik ez badago, adar parabolikoa egon daiteke, mota hauetakoren bateko adarra:

asintota zeiharra

1. mota. Gero eta hazkunde azkarragoa

Kurba gero eta azkarrago handiagotzen edo txikiagotzen da. Mota honetakoak dira funtzio polinomiko eta esponentzialen adar parabolikoak.

2. mota. Gero eta hazkunde geldoagoa.

Kurba gero eta geldoago handiagotzen edo txikiagotzen da. Mota honetakoak dira funtzio errodunak eta logaritmikoak.

x → – ∞ denean ageri diren kasuak azaldu ditugun horien modukoak dira

funtzioak asintota zeihar bat du x → +∞ denean. Aurki dezagun:

y = e x

Asintota zeiharra dago

+

Horren ekuazioa y = x – 1 da.

Kurbak asintotarekiko hartzen duen posizioa:

x = 1 000 denean, xx 2 –2 – (x – 1) adierazpenak –0,0005 balio du.

Kurba asintotaren azpitik geratzen da

adar parabolikoak

IDAZKERA

Asintotari y = mx + n esaten diogu.

= ln x y = x – 1 1

➜ anayaharitza.es

y = x2 –2x funtzioaren asintota zeiharra lortzea x → –   ∞ denean.

Laburpena: x → +∞ (*) denean egon daitezkeen adar infinituak

5 Aurkitu funtzio hauek infinituan dituzten adarrak:

a) y = 3x 5 – 20x 3 b) y = x x 1 –2 4

c) y = () x x 2 –2 3 d) y = xx 2 –2

e) y = ln (x 2 + 1) f ) y = 2x – 1

g) y = x sin x h) y = x – cos x

6 Zer adar mota dituzte funtzio hauek infinituan?

a) y = x 1 1 + b) y = x x 1 3 +

c) y = x x 1 2 + d) y = x x 1 4 +

e) y = e x x 2 f ) y = x 3 2 3 + g) y = x + x h) y = tg x

Puntu interesgarriak

ukitzaile horizontaleko puntuak (singularrak edo kritikoak)

• Ukitzaile horizontaleko puntuen abzisak f ' (x) = 0 ekuazioa ebazten dugunean lortzen ditugu

x1, x2, …, xk soluzioak aurkitu eta gero, soluzio horiei grafikoan dagozkien (x1, f (x1)), (x2, f (x2)), …, (xk, f (xk)) puntuek kurbaren gorako eta beherako tarteak zehazteko balioko digute; jakina, baldin eta f (x) funtzioa deribagarria bada puntu horiek egongo diren tarte osoan

PUNTU SINGULARRAK

Ukitzaile horizontaleko puntu guztiak (puntu singularrak) jakitea oinarri-oinarrizkoa da grafiko baten adierazpena egiteko.

Horrelako punturik ez dagoela jakitea ere oso datu garrantzitsua izaten da.

• Maximoak eta minimoak berez ageri dira kurba marraztean, adar infinituak eta deribatu nuluko puntuak lotzen ditugunean. Horrez gain, gogoan izan ukitzaile horizontaleko puntu bat maximoa edo minimoa den jakin dezakegula, bigarren deribatua erabiliz:

f ' (a) = 0 eta f '' (a) > 0 badira ⇒ (a, f (a)) puntuan minimo erlatibo bat dago f ' (a) = 0 eta f '' (a) < 0 badira ⇒ (a, f (a)) puntuan maximo erlatibo bat dagoo.

• Ukitzaile horizontaleko puntu bat maximoa edo minimoa den jakiteko beste modu bat ere badago: f ' (x)-ren zeinua ezkerretik eta eskuinetik aztertzea.

ebaki-puntuak ardatzekin

• Ebaki-puntuak X ardatzarekin: abzisak f (x) = 0 ekuazioaren soluzioak dira.

• Ebaki-puntuak Y ardatzarekin: (0, f (0)) puntua da

inflexio-puntuak

Funtzioa ahurra izatetik ganbila izatera, edo ganbila izatetik ahurra izatera igarotzen den puntuak dira. f '' (x) = 0 ekuazioaren erroetako batzuk izaten dira

beste puntu batzuk

Batzuetan, komeni da beste (a, f (a)) puntu batzuk lortzea kurbaren itxura zehazteko.

➜ Aurkitu zero deribatuaren puntuak.

Pentsatu eta praktikatu

7 Aurkitu honako funtzio hauen puntu singularrak eta inflexio-puntuak:

a) y = x 3 – 6x 2 + 9x + 5

b) y = ln (x 2 + 1)

INFLEXIO-PUNTUAK

Inflexio-puntuek kurbaren forma zehazten dute. Batzuetan, oso lagungarriak dira.

8 Aurkitu honako hauen puntu singularrak:

a) y = 3x 5 – 20x 3

c) y = () x x 2 –2 3

b) y = x x 1 –2 2

d) y = xx 2 –2

Balio absolutua funtzioen adierazpenean

Funtzio baten balio absolutua

y = | f (x) | adierazteko, y = f (x) funtzioa adieraziko dugu lehenengo, eta, gero, simetria bidez, X ardatzaren azpian dagoen kurbaren zati osoa gorantz pasatuko dugu

Adibidez, y = xx 3 1 21 –3 + adierazteko, y = xx 3 1 21 –3 + adieraziko dugu, eta, simetria bidez, X ardatzetik «gora botako dugu» behean dagoena.

eragiketak «balio absolutuekin»

Funtzio bat aztertzen dugunean, aparteko arreta jarri behar dugu zer abzisatan aldatzen duten zeinua balio absolutua duten batugai batzuek.

➜ anayaharitza.es

Teoria berrikusi: funtzio baten balio absolutua.

Funtzio polinomikoen adierazpena

y = P (x) erako funtzio polinomikoak Á osoan dira deribagarriak (eta, beraz, baita jarraituak ere).

Ez dute inolako asintota motarik. Adar parabolikoak dituzte – ∞-n eta +∞-n. Bi adar infinitu horiek eta puntu singularrak jakinda, oso zehatz adieraz daitezke. Zehatzago marraztu nahi izanez gero, ardatzekin dauden ebaki-puntuak eta inflexio-puntuak ere lor daitezke.

Simetriak izan ditzakete:

• Maila bikoitiko gaiak baino ez badituzte, Y-rekiko simetrikoak dira

Adibidez: y = 2x 4 – 3x 2 + 5

• Maila bakoitiko gaiak baino ez badituzte, koordenatuen jatorriarekiko simetrikoak dira

Adibidez: y = x 5 – 4x 3 + 2x

y = P (x) funtzio polinomiko bat adierazteko:

• Simetria motaren bat duen aztertuko dugu.

• Bi adar infinituak aurkituko ditugu: ∞ lm i x – " f (x), ∞ lm i x " + f (x)

• P' (x) = 0 ekuazioa ebatziko dugu.

Ekuazio horren soluzioak (soluziorik badago) puntu singularren abzisak dira. Hori egin ostean, ordenatuak lortuko ditugu.

• Lortu ditugun puntu guztiak elkarrekin eta adar infinituekin lotuko ditugu, baina lortutako puntu singularrak bakarrik marraztuz. Horrela, maximo eta minimo erlatiboak zein diren jakingo dugu.

• Ahal izanez gero, komeni da ardatzekin dauden ebaki-puntuak ere lortzea, adierazpena zehatzago egiteko

GOGORATU

Oso garrantzitsua da funtzio polinomikoak bereiztea eta hasieratik jakitea zer itxura izango duten.

➜

Ebatzitako ariketak

1 Adierazi honako funtzio hau:

f (x) = x 3 – 6x 2 + 9x + 5

KONTUAN HARTU

Puntu singularrak eta adar infinituak izanda, erraz ikusten da kurbak zer forma izango duen.

Adierazi funtzio polinomikoak.

➜ anayaharitza.es Funtzio polinomikoen adierazpena berrikusteko ariketak.

Simetriak: Ez da simetrikoa, ez Y ardatzarekiko, ezta koordenatuen jatorriarekiko ere.

Adar infinituak: ∞ lm i x – " f (x) = – ∞ , ∞ lm i x " + = +∞

Puntu singularrak:

f ' (x) = 3x 2 – 12x + 9

f ' (x) = 0 ⇔ x = 1, x = 3

f (1) = 9, f (3) = 5 → (1, 9), (3, 5)

Ebaki-puntuak ardatzekin:

Y ardatza (0, 5) puntuan ebakitzen du, eta X ardatza, –1 eta 0 artean; izan ere, f (–1) = –11 eta f (0) = 5

Inflexio-puntuak:

f '' (x) = 6x – 12

f '' (x) = 0 ⇔ x = 2 → (2, 7)

Datu horiekin kurba irudikatu dezakegu

(x) = 3x 5 – 20x 3

Simetriak: Ikusten dugunez, gai guztiak dira maila bakoitikoak. Beraz, simetrikoa da koordenatuen jatorriarekiko. (Gogoan izan funtzio hauei bakoiti esaten zaiela ). Adar infinituak:

3

(x) = x 4 + 8x 3 + 22x 2 + 24x + 9

Puntu singularrak (–2, 64), (0, 0) eta (2, – 64) dira. Datu horiek nahikoa dira grafikoa irudikatzeko.

Simetriak: ez da ez bikoitia, ez bakoitia. Beraz, ez da simetrikoa Y ardatzarekiko, ezta koordenatuen jatorriarekiko ere. Adar infinituak:

Puntu singularrak:

+ 24x 2 + 44x + 24. Hirugarren mailako polinomio bat denez, erroetako batzuk aurkitzeko, gai askearen (24) zatitzaileekin saiatuko gara. Gainera, koefiziente guztiak positiboak direnez, erro negatiboak baino ezin ditu izan. x = –1 probatuko

dugu:

4 24 44 24 –1 – 4 –20 –24

Erro bat x = –1 da, eta beste bi erroak 4x 2 + 20x + 24 = 0 ekuazioa ebatziz lortzen dira.

4 20 24 0 x = –2 eta x = –3 dira.

Ebaki-puntuak

Puntu singularretako bi X ardatzean daude

Kurbaren zirriborro bat egiten badugu, X ardatza ez duela puntu gehiagotan ebakitzen ikusten dugu. Y

2 Adierazi honako funtzio hau:

Adierazi funtzio hau:

Funtzio arrazionalen adierazpena

y = P (x)/Q (x) erako funtzio arrazionaletan, x zer baliorekin baliogabetzen den da kontuan hartu beharreko ezaugarri nagusia: balio horietako bakoitzean asintota bertikal bat egongo da. Funtzioa deribagarria da (eta, beraz, jarraitua) Á-ko gainerako puntu guztietan

P (x)-ren eta Q (x)-ren mailaren arabera, kurbak asintota horizontala edo asintota zeiharra izango du, edo ez du ez bata eta ez bestea izango.

Asintota horizontala edo zeiharra badu, berdina izango da x → – ∞ denean eta x → + ∞ denean.

y = f (x) = P (x)/Q (x) erako funtzio arrazional bat adierazteko:

• Simetria motaren bat duen aztertuko dugu.

• Asintota bertikalak aurkituko ditugu: abzisak Q (x) = 0 ekuazioaren soluzioak dira. Kurbak asintota horietako bakoitzarekiko zer posizio duen aztertuko dugu

• Asintota horizontala edo zeiharra duen aztertuko dugu:

P (x)-ren maila ≤ Q (x)-ren maila bada, hau aurkituko dugu:

∞ lm i x " + P (x)/Q (x) = l

y = l zuzena asintota horizontala da.

P (x)-ren maila = Q (x) + 1-ren maila bada, asintota zeihar bat dago. Asintota horren ekuazioa y = mx + n da, mx + n adierazpena P (x) : Q (x) zatiketaren emaitza izanik

(Asintota horizontala zein zeiharra egon, kurbak asintotarekiko zer posizio duen aztertuko dugu x → – ∞ denean eta x → + ∞ denean).

P (x)-ren maila > Q (x) + 1-ren maila bada, adar parabolikoak daude

• Puntu singularrak lortuko ditugu. Abzisak f ' (x) = 0 ekuazioaren soluzioak dira

• Nahi izanez gero, beste puntu batzuk ere lortu daitezke, hala nola ardatzekin dauden ebaki-puntuak, f (x) = 0 egiten duten x-ren balioak; eta (0, f (0)). Horrez gainera, baita inflexio-puntuak ere, f '' (x) = 0.

ADI!

P (x) eta Q (x) polinomioek erro berdinik ez dutela pentsatuko dugu.

f (x) = x x 1 –2 4

Funtzio arrazionaletan, asintotak zein diren eta kurbak asintota horiekiko zer posizio erlatibo duten jakinda, kurbaren forma zein den argi erakutsiko digun zirriborroa egin dezakegu.

➜ anayaharitza.es

Funtzio arrazionalen adierazpena berrikusteko ariketak.

Simetriak: f (–x) = f (x). Beraz, Y ardatzarekiko simetrikoa da

Asintota bertikalak: x 2 – 1 = 0 ⇔ x = –1, x = 1

x = 1 asintotarekiko posizioa:

Simetria bidez, x = –1 asintotarekiko duen posizioa lortuko dugu

Adar infinituak infinituan:

Ez du asintota horizontalik, ez zeiharrik; izan ere: P

1 Adierazi honako funtzio hau:

Beste funtzio mota batzuen adierazpena

Adierazi nahi dugun funtzioa ez bada polinomikoa, ez arrazionala, modu sistematikoan aztertu behar ditugu unitatearen hasieran deskribatu ditugun alderdiak. Dena dela, kontuan izango ditugu oinarrizko funtzio batzuen ezaugarriak:

• Funtzio errodunetan, definizio-eremua hartu behar dugu aintzat. Asintota eduki dezake x → + ∞ denean eta x → – ∞ denean, baina desberdinak izaten dira.

• Funtzio esponentzialek asintota horizontal bat eta I. motako adar paraboliko bat izaten dute.

• Funtzio logaritmikoek asintota bertikal bat eta oso-oso astiro hazten den adar infinitu bat (II. motako adar parabolikoa) izaten dute.

• Funtzio trigonometrikoak periodikoak izaten dira, ia beti.

1 Adierazi honako funtzio hau:

f (x) = xx 2 –2

• f (–x) = () ·( )xx xx22 –22=+ ez da f (x)-ren berdina, ezta –f (x)-ren berdina ere

Beraz, ez da simetrikoa Y ardatzarekiko, ezta koordenatuen jatorriarekiko ere

• x 2 – 2x = 0 ⇒ x = 0, edo, bestela, x = 2

x ∈ (0, 2) bada, x 2 – 2x < 0; hau da, errokizuna negatiboa da. Beraz, ez dago definituta (0, 2) tartean

Definizio-eremua: (– ∞, 0] ∪ [2, + ∞)

Kurba deribagarria da (– ∞, 0) ∪ (2, + ∞) tartean. 0 2

• Ikusi dugu (306. orrialdea) asintota zeiharrak dituela x → +∞ eta x → – ∞ denean, eta kurbak zer posizio duen asintotekiko.

Asintota zeiharrak aurkitzeko beste modu bat: () ≈( )| | xx xx xx x 22 11 11 11 –22 22 =+ ==

f (x) = xx 2 –2 funtzioa y = | x – 1 | funtziora hurbiltzen da | x |-ren balio handiekin. Gainera, «apur bat txikiagoa da», errokizunean 1 kentzen da eta

Hori honela zehazten da:

x → – ∞ denean, y = f (x) ≈ y = –x + 1

x → +∞ denean, y = f (x) ≈ y = x – 1

Kurba azpitik hurbiltzen da asintotetara

• Puntu singularrak:

f ' (x) = xx x xx x 22 22 2 1 ––––22 =

• Adierazpena:

x = 1 puntuan baliogabetzen da, baina puntu horretan funtzioa ez dago definituta. Beraz, ez du puntu singularrik.

Badakigu (0, 0) eta (2, 0) puntuetatik igarotzen dela

2 Adierazi honako funtzio hau:

(x) = ln (x 2 + 1)

• Simetrikoa da Y ardatzarekiko; izan ere, f (x) = f (–x).

• x 2 + 1 positiboa denez beti, Á osoan dago definituta eta deribagarria da. Gainera, f (x) positiboa da beti; izan ere, x 2 + 1 ≥ 1

ez du inolako asintotarik

3 Adierazi honako funtzio hau:

• sin x batugaiaren periodoa 2π da, eta sin 2x batugaiarena, π. Beraz, funtzioa periodikoa da, 2π periododuna. [0, 2π] tartean baino ez dugu aztertuko.

• Deribagarria da Á osoan (funtzio deribagarrien batura da).

• Ebaki-puntuak ardatzekin: (0, 0), (π, 0)

• Inflexio-puntuak:

ariketak

4 Adierazi honako funtzio hau:

f (x) = x e x

• Ez da simetrikoa.

• Asintota bertikala du x = 0 puntuan: lim x 0 " + f (x) = +∞ , lim x 0 –" f (x) = – ∞

• Adar infinitua x → + ∞ denean:

∞ lm i x " + f (x) = +∞ , ∞ lim x " + () x fx () x fx = +∞ . Adar paraboliko bat da. Adar infinitua x → – ∞ denean:

∞ lm i x – " f (x) = 0 balio negatiboak hartuz

• Adierazpena: y = 0 asintota horizontala da Kurba azpitik geratzen da.

• f ' (x) = () x xe e x ex 1 –– xx x 22 = f ' (x) = 0 ⇔ x = 1 f (1) = e Puntu singular bat du: (1, e).

5 Adierazi honako funtzio hau:

f (x) = (ln x) 2 y = ln x funtzioaren grafikoa ekarriko dugu gogora, oinarri moduan hartzeko.

• ln x funtzioa (0, +∞) tartean definituta dagoenez, y = (ln x)2 funtzioaren definizio-eremua D = (0, +∞) da. Eremu horretan funtzioa jarraitua da, eta, ziur aski, deribagarria ere bai.

• Adar infinituak:

y = ln x funtzioaren asintota bertikala funtzio honena ere bada. Kontua da karratura jasotzean, balio positiboak hartzen dituela: lm i x 0 " + (ln x)2 = +∞ x → +∞ denean, adar paraboliko bat du

• Puntu singularrak:

f (1) = (ln 1)2 = 0. Beraz, (1, 0) puntua ukitzaile horizontalekoa da. (ln x)2 ≥ 0 denez bere definizio-eremuan, (1, 0) puntuan minimo bat dago

• Inflexio-puntuak:

Ebatzitako ariketak eta problemak

1. Azterketatik grafikora (simetriak, asintota horizontalak, zeiharrak eta bertikalak)

Adierazi y = f (x) kasu hauetako bakoitzean:

a) I. Dom f = Á – {0} eta f deribagarria da bere definizio-eremu osoan.

II. ∞ lm i x – " f (x) = 0 +; ∞ lm i x " + f (x) = 0 –

lim x0 – " f (x) = + ∞; lim x0 " + f (x) = +∞

III. f (1) = 0;

f ' (x) = 0 ⇔ x = 2;

f (2) = –1; f '' (2) > 0

b) I. Dom f = Á – {–1, 1} eta f deribagarria da bere definizio-eremu osoan.

II. Funtzioa bikoitia da.

f (x)-ri buruzko informazioa, x ≥ 0

denean:

III. ∞ lm i x " + f (x) = + ∞; ∞ lm i x " + () x fx = 1

∞ lm i x " + [ f (x) – x] = –2–;

lim x1 –" f (x) = + ∞; lim x1 + " f (x) = – ∞

IV. f (3/4) = 0; f (3) = 0;

f ' (x) = 0 ⇔ x = 0;

f (0) = –1; f '' (0) > 0

EGIN ZUK

Adierazi y = f (x):

Dom f = Á – {–2, 2}; funtzio bakoitia.

∞ lm i x " + f (x) = – ∞; ∞ lm i x " + () x fx = –1

∞ lm i x " + [ f (x) – (–1) · x] = –1+

lim x 2 –" f (x) = + ∞; lim x 2 " + f (x) = +∞

f (3) = 0; f ' (x) = 0 ⇔ x = 0; f (0) = 0

2. Grafiko baten deskribapena

Deskribatu funtzio baten honako grafiko hau: 2 –2

a) I. Deribagarria denez definizio-eremu osoan, Á – {0}, jarraitua da eta ez du puntu erzdunik.

II. x → – ∞ denean, asintota horizontal bat dago, y = 0, eta funtzioa gainetik hurbiltzen zaio.

x = 0 puntuan asintota bertikal bat dago. Bai ezkerretara, bai eskuinetara, grafikoak + ∞-rantz jotzen du.

x → + ∞ denean, asintota horizontal bera dago, y = 0, eta funtzioa behetik hurbiltzen zaio.

III. f (1) = 0 denez, esan nahi du X ebakitzen duela

x = 1 puntuan.

f ' (x) = 0 ⇔ x = 2 baliokidetasunak adierazten du ukitzaile horizontaleko puntu bat dagoela x = 2n, eta, gainera, bakarra dela. f (2) = –1 denez, (2, –1) puntuan dago, eta f '' (2) > 0 denez, minimo bat da. Kurba marraztuko dugu.

b) I. Funtzio jarraitua da eta ez du puntu erzdunik Á – {–1, 1} eremuan.

II. Funtzioa bikoitia izateak esan nahi du simetrikoa dela Y ardatzarekiko. Hortik abiatuta, x > 0 kasurako soilik lortuko dugu informazioa, eta, gero, simetrikoa marraztuko dugu.

III. Limiteek hau erakusten dute: x → + ∞ denean, asintota zeihar bat, y = x – 2, eta kurba behetik hurbiltzen zaio; eta x = 1 puntuan, asintota bertikal bat, eta kurbak + ∞-rantz jotzen du ezkerretik eta – ∞-rantz eskuinetik.

IV. f ' (x) = 0 ⇔ x = 0 baliokidetasunak esan nahi du x = 0 dela zero deribatuko puntu bakarra. Horrez gain, f '' (0) > 0 denez, minimo erlatibo bat da. Informazio horretatik abiatuta, funtzioaren grafikoaren zirriborroa egingo dugu.

Aurrena, funtzioa x ≥ 0 denean adieraziko dugu, eta, gero, Y ardatzarekiko simetria bidez, funtzio osoa.

• Dom f = Á – {–2, 2}

• Bakoitia da. Hau da, simetrikoa da koordenatuen jatorriarekiko.

• x = –2 asintota bertikala da

• x = 2 asintota bertikala da

• f ' (x) > 0 da definizio-eremu osoan; hau da, gorakorra da, eta ez du ez maximorik, ez minimorik.

• f '' (x) = 0 ⇔ x = 0; gainera, f (0) = 0. Inflexio-puntu bat du (0, 0) puntuan.

Ebatzitako ariketak eta problemak

3. Asintota zeiharrak dituen funtzio arrazional bat adieraztea

Aztertu honako funtzio honen definizioeremua, asintotak eta puntu singularrak:

f (x) = x 42x –2

Irudikatu grafikoa

• Á – {0} eremuan definituta dago eta jarraitua da definizio-eremu osoan. Adierazpenari begiratuta, definizio-eremu osoan deribagarria dela ematen du.

• Simetria: f (–x) = () x x x x 42 42 –––2 2 = = –f (x)

Simetrikoa da koordenatuen jatorriarekiko.

• Asintota bertikala: x = 0

• Asintota zeiharra: y = –2x

Honako zatiketa hau eginez lortzen dugu:

• Puntu singularrak: asintotetatik abiatuta egin dugun kurbaren zirriborroa kontuan hartuz, ematen du ez duela ez maximorik ez minimorik. Benetan hala den ikusteko, deribatua aztertuko dugu:

EGIN ZUK

Adierazi honako funtzio hau: f (x) = () ()xx x 21 2 34

4. Adar parabolikoak dituen funtzio arrazional bat adieraztea

Aztertu honako funtzio honen definizioeremua, asintotak, tarte gorakorrak eta beherakorrak, eta maximoak eta minimoak: f (x) = () x x 31 3 +

Gero, adierazi

• Definizio-eremua: Á – {–1}. Ez du simetriarik

• Asintota bertikala: x = –1

EGIN ZUK

Aztertu funtzio honen definizioeremua, asintotak, tarte gorakor eta beherakorrak, eta maximoak eta minimoak, ondoren irudikatzeko: f (x) = () x x 1 4 –

Irudikatu funtzio honen grafikoa:

(x) = | x + 3 | + | x – 1 | – | 2x + 4 |

Aurrena, adierazi funtzio horri dagokion zatika definituriko funtzioa.

Balio

bakoitza zatika definituriko funtzio moduan adieraziko dugu:

Adierazi funtzio honen grafikoa:

= ln x x 1 3

EGIN ZUK

Adierazi beheko funtzioa, jakinda, x ≥ 0 bada, f ' (x) soilik baliogabetzen dela x = 1,98 denean:

5. Balio absolutu eta guztiko funtzioa

6. Funtzio logaritmikoa

Ebatzitako ariketak eta problemak

7. Beste funtzio batzuen azterketa eta grafikoa

a)

8. Funtzio trigonometrikoak

a) Adierazi honako funtzio hauek: y = cos 2x – cos x

a) Definizio-eremua: Á. Jarraitua eta deribagarria da. Periodikotasuna: 2

b) Adierazi honako funtzio hauek: y = snix 1 r

0 da x = 0 + kπ puntuan → maximoak: (0 + 2kπ, 0), (π + 2kπ, 2), k ∈

y'' > 0 da x = 1,32 + 2kπ eta x = 4,96 + 2kπ puntuetan →

→ minimoak: (1,32 + 2kπ; –1,12), (4,96 + 2kπ; –1,12), k

b) Definizio-eremua: Á – {k}, k ∈ . Jarraitua eta deribagarria da. Periodikotasuna: 2. Bakoitia.

• Ez ditu ardatzak ebakitzen.

• Asintota bertikalak: x = k, k ∈ izanik.

Kurbak asintotarekiko duen posizioa:

lim xk –" y = – ∞ lim xk " + y = + ∞ , k bikoitia bada

lim xk –" y = + ∞ lim xk " + y = – ∞ , k bakoitia bada

• Maximoak eta minimoak: y' = –() sn cos ix x 2 r rr = 0 → x = 1/2 + k, k ∈

Orain, y'' = sn coss n i i x xx 2 3 22 22 r rr rr + deribatuaren zeinua aztertuko dugu.

Zenbakitzailea positiboa da beti. Izendatzailea positiboa da (2k, 1 + 2k) tarterako eta negatiboa (1 + 2k, 2 + 2k) tarterako, k ∈ izanik. Beraz:

y'' > 0 da x = 1/2 + 2k puntuan → minimoak: (1/2 + 2k, 1), k ∈ .

y'' < 0 da x = 3/2 + 2k puntuan → maximoak: (3/2 + 2k, –1), k ∈

EGIN ZUK

Adierazi honako funtzio hauek:

a) y = 2sin x + cos 2x

b) y = cosx 1 r

Gidatutako ariketak eta problemak

1. Grafiko baten deskribapena

Beheko grafiko hori kontuan hartuz, deskribatu ikaskide batek grafikoa adierazi ahal izateko beharrezkoak izango diren elementuak

• Adierazi non dagoen definituta, zehaztu jarraitutasuna eta deribagarritasuna.

• Deskribatu, limite baten bidez, asintota horizontala eta kurbak zer posizio duen asintota horrekiko.

• Deskribatu, limiteen bidez, asintota bertikala eta kurbak asintotarekiko zer posizio duen ezkerretik eta eskuinetik.

• Deskribatu asintota zeiharra limiteen bidez. Horietako batean, esan kurbak zer posizio duen asintotarekiko

• Deskribatu zer baldintzaren arabera lortzen diren puntu singularrak. Adierazi maximoak eta minimoak zein diren jakiteko behar diren baldintzak

• Osatu puntu singularrei buruzko informazioa ordenatuak zehaztuz

Soluzioa: Dom f = Á – {1}; deribagarria definizio-eremu osoan

Asintota horizontala x → – ∞ denean: y = 4. Asintota bertikala: x = 1

Asintota zeiharra x → + ∞ denean: y = x – 2

Maximo erlatiboa (3, 2) puntuan. Minimo erlatiboak (–1, –1) eta (5, –2) puntuetan).

Ardatzekin dituen ebaki-puntuak: (–2, 0), (0, 0), (2, 0), (4, 0) eta (6, 0).

Balio absolutua duen funtzio logaritmiko baten adierazpena

y = || ln x x

Kalkulatu zein izan behar diren a, b, c eta d parametroak, f -ren kurbak bi mutur erlatibo izateko 1, 0) eta (0, 1) puntuetan.

Aztertu simetrikoa den. Adierazi zein Soluzioa: den definizio-eremua eta eremu osoan deribagarria den.

Aurkitu funtzioa adierazteko beharrezkoak diren elementuak: asintotak, puntu singularrak, etab.

• Funtzioaren adierazpena erabiliz, f (x) = ax3 + bx2 + cx + d, eta emandako datuak, f (0) = 1, f (1) = 0, f' (0) = 0 eta f ' (1) = 0, sistema bat eratuko dugu: 4 ezezagun eta 4 ekuazio dituen sistema.

Soluzioa:

• Ebatzi eta adierazi funtzioa. f (x) = 2x3 – 3x2 + 1

4. Funtzio arrazional parametroduna

Kalkulatu zein izan behar den k parametroaren balioa, honako funtzio honek:

f (x) = xx xk 41 2 + ++

asintota zeihar moduan y = 4x + 5 izateko.

Adierazi funtzioa.

Asintota zeiharraren ekuazioa lortzeko, egin zatiketa hau:

(4x 2 + x + 1) : (x + k)

Soluzioa: 2 10

Adierazi

1 1 (–e, –1/e) (e, 1/e)

f (x) = ax3 + bx2 + cx + d Adierazi funtzioa.

Trebatzeko

Grafiko baten deskribapena

1 Adierazi Á osoan jarraitua eta deribagarria den funtzio bat, kontuan hartuz:

lm i x " + f (x) = +∞ ∞ lm i x – " f (x) = – ∞

∞

f (2) = 1, f ' (x) ≥ 0 edozein x-tarako, f ' (2) = 0

2 y = f (x) funtzio bati buruz informazio hau dugu:

D = Á – {1, 4}

Funtzioen ezaugarriak

6 Adierazi funtzio hauen definizio-eremuak:

a) y =  xx25 –42 + b) y = 3 –  x x 1 2 +

c) y =  xx34 –2 ++ d) y =  x 321 1 –

e) y = ln (4 –  x ) f) y =  () ln x 1 9– 2

g) y =  tg x 1 h ) y =  tg x 1 1 –2

lim

x 1 –" f (x) = +∞ lim x 1 " + f (x) = – ∞

lim x 4 –" f (x) = – ∞ lim x 4 " + f (x) = +∞

lm i x ± " f (x) = 0

∞

x → +∞ bada, f (x) > 0 x → – ∞ bada, f (x) < 0

f ' (2) = 0, f (2) = –1; f ' (–1) = 0, f (–1) = –1 Adierazi.

3 Irudikatu beheko datuak ezagun dituen funtzio baten grafikoa, Á osoan jarraitua eta deribagarria dela jakinda:

∞ lm i x – " f (x) = – ∞ ∞ lm i x " + f (x) = +∞

f ' (x) = 0, baldin eta x = –2, x = 0, x = 3, x = 4 bada

f (–2) = 2; f (0) = 0; f (3) = 5; f (4) = 4

4 Adierazi funtzio hauek, bakoitzaren definizio-eremua, simetriak (baldin eta badaude), asintotak eta adar infinituak, puntu singularrak eta tarte gorakorrak eta beherakorrak zehaztuz. Egizu funtzioaren, horren deribatuaren eta zenbait limiteren balioak emanez.

7 Aztertu honako funtzio hauen simetriak:

a) y = x 2 + 1 b) y =  x x 3 –2 c) y = tg πx

d) y = e | x | e) y =  || xx x 2 –2 f ) y = 2cos x 2

8 Zehaztu funtzio hauek periodikoak diren, eta hala badira, aurkitu periodoa:

a) y = sin 3x b) y = sin 2πx

c) y = tg πx d) y = sin x + cos 2x

e) y = cos x 2 r bl  · sin x f ) y = sin (x 2 + 1)

9 Aurkitu funtzio hauen asintota bertikalak, eta esan zer posizio erlatibo duen kurba bakoitzak asintota horiekiko:

y =  x x 9 22 ––2

c)

y =  snix 1 1 –2 f ) y =  cos x 2

1

10 Aurkitu asintota horizontalak, eta esan zein den kurba bakoitzak asintotekiko duen posizio erlatiboa.

2 2

a) y =  x x 2 1 –2 + b) y =  x x 2 3 1 ––

x 1 –

c) y =  x x 2 1–2 + d) y =  e e 2 3–|| x

11 Aurkitu funtzio hauen asintota zeiharrak, eta adierazi zer posizio erlatibo duen kurba bakoitzak asintotekiko: a) y =  x xx32 –2 + b) y =  x x x 23 52 –2 + +

c) y =  (/ ) x x 12 2 –2

2 + d) y =  x 35 2 +

5 Deskribatu honako funtzio hau:

Proposatutako ariketak eta problemak

Funtzio polinomikoak

12 Aztertu eta adierazi honako funtzio hauek:

a) y = x 3 + 3x 2 b) y = x 3 – 3x 2 + 5

c) y =  x 4 2 9 –4 x 2 + 10 d) y =  xx 64 5–45

e) y = x 5 – 5x 3 f ) y = (x – 1)3 – 3x

g) y = x 4 – 4x 2 h) y = 1 – (x – 1)3

13 Aztertu honako funtzio hauen adar infinituak, tarte gorakor eta beherakorrak, maximoak, minimoak eta inflexiopuntuak. Adierazi grafiko bidez:

a) y = 3 + (2 – x)3 b) y = 2 – (x – 3)4

c) y = (x + 1)6 – 5 d) y = 3 – (1 – x)3

e) y = x (x – 1) (x + 3) f ) y = (x – 2)2 (x + 1) x 3

14 Adierazi funtzio hauek:

a) y = x 2  – x4 b) y = 3x 4 + x3 – 1

c) y = x 3  – x2 d) y = 2x 3 + 3x2 – 12x

Funtzio arrazionalak

15 Funtzio hauetan, aztertu definizio-eremua, asintotak eta kurbak asintotekiko zer posizio duten, eta lortutako emaitzetatik abiatuta, irudikatu:

Balio absolutudun funtzioak eta zatika definitutako funtzioak

18 Irudikatu funtzio hau: f (x) =  ≥ xx xx x x 22 22 0 0 –bada bada < 2 2 + + )

*

16 Irudikatu funtzio hauek, definizio-eremua, asintotak, adar infinituak eta mutur erlatiboak aztertuz:

17

Gogoan izan zatiki bat zenbakitzailea eta izendatzailea zati (x – a) eginez sinplifikatzen bada, eten saihesgarria dagoela x = a puntuan.

bada bada *

0 0 –

< 2 + +

x x 1 1 1

Aztertu tarte gorakorrak eta beherakorrak, mutur erlatiboak eta kurba.

21 Irudikatu honako funtzio hauen grafikoak eta adierazi zer puntutan diren deribagarriak:

a) y = x + | x + 2 | b) y = 2x – | x – 3 |

c) y = | x | + | x – 3 | d) y = x | x – 1 |

22 f (x) = x 2 | x – 3 | funtzioa izanda:

a) Aurkitu zer puntutan ez den deribagarria f.

b) Kalkulatu maximoak eta minimoak.

c) Adierazi grafiko bidez.

23 Adierazi grafiko batean honako funtzio hauetako bakoitza:

a) y =  || x 2 1 –b) y =  || x x 1 2 2 +

c) y =  || || x x 1 3 + + d) y = –|x 3  – x 2 + 2|

Beste funtzio mota batzuk

24 Aztertu eta adierazi honako funtzio hauek:

a) y =  x 4– 2 3 b) y =  xx –2

c) y =  xx45 –2 + d) y =  x x 1 –2 2

25 Aztertu eta adierazi honako funtzio hauek:

a) y =  e x x b) y =  ln x x

c) y = x ln x d) y = (x – 1) e x

e) y =  e x–2 f ) y = x 2 e –x

g) y =  ln x x 3 h) y = ln (x 2 – 1)

26 Aztertu eta adierazi honako funtzio hauek:

a) y = sin x + cos x b) y = 2sin x – cos 2x

c) y = cos 2x – cos 4x d) y = 3sin πx + 2

e) y = sin πx – 2 f ) y = tg πx + cos 2πx

Ebazteko

27 Aztertu funtzio hauen definizio-eremua, asintotak eta muturrak, eta informazio hori erabiliz, erlazionatu dagokion grafikoarekin:

a) y =  snix 1 b) y = x e x c) y = sin x 2

32 y = 2x + 6 zuzena honako funtzio honen asintota zeihar bat da: f (x) = xk x 21 –2 +

Aurkitu k-ren balioa eta adierazi horrela lortu duzun funtzioa.

33 f (x) = x 2 · e –ax funtzioa daukagu, a ≠ 0 izanik.

a) Kalkulatu zein izan behar den a-ren balioa funtzio horrek mutur erlatibo bat izateko x = 2 abzisa-puntuan.

b) Sailkatu mutur erlatiboak a = 2 denean.

34 f (x) =  ax +  b +  x 8 funtzioa izanda, kalkulatu zein izan behar diren a-ren eta b-ren balioak f-ren grafikoa (–2, – 6) puntutik igaro dadin, eta puntu horretan ukitzaile horizontala izan dezan. Irudikatu funtzioa a-ren eta b-ren balio horietarako.

35 Aurkitu zein izan behar diren a, b eta c-ren balioak:

f (x) =  x ax bx c 4 –2 2 ++

funtzioak asintota horizontal moduan y = –1 zuzena izateko eta minimo bat edukitzeko (0, 1) puntuan.

36 Partikula bat y = x x 1 2 –2 kurbaren grafikoan zehar mugitzen da, x > 1 kasuan

P (2, –4/3) puntuan, kurba utzi eta kurbarekiko ukitzaile den zuzenean zehar doa.

a) Aurkitu ibilbidea deskribatzen duen zatikako funtzioa.

28 Gogoan izan sinu hiperbolikoa eta kosinu hiperbolikoa honela definitzen direla: sinh x =  ee 2 –xx –cosh x =  ee 2 xx –+

Aztertu funtzio horien maximoak, minimoak eta inflexiopuntuak, eta adierazi grafiko bidez.

29 Zehaztu honako funtzio hauen asintotak:

a) y =  x x 3 1– b) y =  x xx 1 2 ++

30 Aztertu eta irudikatu honako funtzio hauetako bakoitza:

a) y =  ln x x 1 1 –2 2 + eo

b) y =  e e 1 1 –x x +

c) y =  ln x x 1 + bl d) y =  xx e 23 –|| x 2 1 –+

31 Kalkulatu zein diren a, b eta

c-ren balioak, jakinda alboko

funtzioa y =  a +  b cos c xr bl

motakoa dela.

b) Ezkerretik eskuinera mugitzen bada, aurkitu zer puntutan ebakitzen duen partikulak X ardatza.

37 Konposatu bateko nitrogeno-kontzentrazioa (%-tan) funtzio honen bidez emanda dago t ∈ [0, +∞) denboraren arabera (minututan neurtuta): N (t ) =  e12 60 t–+

a) Egiaztatu nitrogeno-kontzentrazioa hazi egiten dela denborarekin. Zer t-rekin izango da minimoa nitrogenokontzentrazioa eta zenbatekoa da kontzentrazio hori?

b) Zer baliotara jotzen du nitrogeno-kontzentrazioak denborak infinitura jotzen duenean?

38 Beheko funtzio honek adierazten digu enpresa batek t denboraren poderioz (urteetan) bildutako irabaziak (ehunka mila eurotan) zenbatekoak izan diren azken 5 urteetan:

*

2 6 2 3 03 35

bada bada 2 ! !

b) Noiz lortu zituen 500 000 €-ko irabaziak?

c) Adierazi b(t) funtzioa.

Proposatutako ariketak eta problemak

Galdera teorikoak

39 Zer esan dezakegu bi maximo eta bi minimo erlatibo dituen funtzio polinomiko bati buruz? Funtzio horretan, egon daiteke minimoetako bat maximoak baino altuago?

40 f (x) funtzio batek ezaugarri hauek ditu:

Dom f = Á – {0} eta jarraitua eta deribagarria da bere definizio-eremu osoan.

∞ lm i x – " f (x) = – ∞ ∞ lm i x " + f (x) = +∞ lim x 0 –" f (x) = +∞ lim x 0 " + f (x) = – ∞

Honako baieztapen hauetatik, esan zein diren ziurrak, zein izan litezkeen eta zein diren ezinezkoak:

a) f (x) bikoitia da.

b) f (x) bakoitia da.

c) Ez du ez maximorik ez minimorik.

d) Maximo bat eta minimo bat ditu.

e) X ardatza bi puntutan ebakitzen du.

f ) X ardatza gutxienez bi puntutan ebakitzen du.

g) Asintota bertikal bat du gutxienez.

h) Asintota bertikal bakarra du.

i) Asintota zeihar bat du.

j) Ahurra da x < 0 denean, eta ganbila, x > 0 denean.

41 Zenbat inflexio-puntu izan ditzake, gehienez, laugarren mailako funtzio polinomiko batek?

42 Egiaztatu y = || x x 1 + funtzioak bi asintota horizontal dituela.

43 y = | x 2 – 4 | kurbaren grafikoaren gainean, adierazi ahurtasun- eta ganbiltasun-tarteak. Zein dira inflexio-puntuak?

44 y = x x 1 1 –2 + ez dago definituta x = 1 eta x = –1 puntuetan; hala ere, asintota bertikal bat du. Arrazoitu

45 Zenbat asintota bertikal izan ditzake funtzio batek? Eta horizontalak?

46 Eman x = 1 puntuan minimo bat duen eta puntu horretan deribagarria ez den funtzio baten adibidea. Adierazi.

47 Eman x = 1en deribagarria den, f ' (1) = 0 duen, eta puntu horretan maximorik eta minimorik ez duen funtzio baten adibidea.

48 Irudikatu [0, 4] tartean jarraitua den funtzio bat, eta (2, 3) puntuan maximo erlatibo bat eta (3, 4) puntuan minimo erlatibo bat dituena gutxienez. Funtzio polinomikoa balitz, zer mailatakoa izan behar du gutxienez?

49 f (x) = x + e –x funtzioak asintotarik du? Asintota badu, aurkitu.

50 Zer simetria mota dute honako funtzio hauek?

Sakontzeko

54 Asintota hitza grafiko batera hurbiltzen diren zuzenak adierazteko erabili badugu ere, esanahi zabalagoa du: bi kurba asintotikoak direla esaten dugu kurbak jatorritik urruntzean horien arteko distantziak zerora jotzen duenean.

Adibidez, y =  x 2 + 1 parabola asintotikoa da y =  x x 1 –2 4

funtzioarekiko (ikusi horren grafikoa 313. orrialdean). Oso erraz egiaztatzen da hala direla, zatiketa eginez:

y =  x x x x 1 1 1 1 2 4 2 2 =+ + . Bi ekuazioen arteko x 1 1 –2

zatidurak 0ra jotzen du x → ± ∞ denean. Horrez gain, balio positiboak hartzen ditu, eta, beraz, y = f (x) funtzioaren grafikoa parabolaren gainetik dago.

Emaitza horrek funtzioa zehatzago adierazteko modua ematen du, parabolaren adierazpenean oinarrituta:

55 Aztertu kurba hauen eta horien parabola asintotikoen posizio erlatiboak. Adierazi lortutako informazioa:

parabola asintotikoa

zuzen asintotikoak

a) Aurkitu y =  x xx x 28 –32 ++ funtzioarekiko parabola asintotikoa. Zer posizio du kurbak parabola horrekiko.

b) Adierazi funtzioa datu horiek erabiliz, baita asintota bertikala eta puntu singularra ere (bakarra, x = 2 puntuan).

1 Irudikatu f funtzioaren grafikoa, honako hau jakinda:

∞ lm i x " + f (x) = +∞ , ∞ lm i x – " f (x) = –3, lm i x –3 " f (x) = – ∞ f ' (–5) = 0; f ' (0) = 0; f (–5) = 0; f (0) = 2

2 Deskribatu funtzio hauek:

3 Irudikatu Á osoan jarraitua den funtzio bat, kontuan hartuz minimo erlatibo bat duela (1, 6) puntuan eta maximo erlatibo bat (6, 2) puntuan. Polinomio bat bada, zein mailatakoa izango da, gutxienez?

56 10.5 ataleko Ebatzitako 1. ariketan, prozedura erraz bat ikusi genuen y = xx 2 –2 funtzioaren asintotak urrats hauen bidez kalkulatzeko: () || xx xx21 –≈11 –22 = Lortu beste funtzio hauen asintotak modu berean:

57 f funtzio bat periodikoa bada, g [ f (x)] ere periodikoa da, berdin dio g (x) zein den; izan ere, f funtzioa T periodoko funtzioa bada, orduan f (x + kT ) = f (x) da. Beraz: g [f (x + kT )] = g [f (x)], hau da, g ° f periodikoa da

Baina, oro har, f [g (x)] ez da periodikoa; izan ere, f [ g (x + kT )] ≠ f [g(x)] da, g(x + kT) ≠ g(x) delako.

Baieztapen horiek aintzat hartuta, adierazi honako funtzio hauetako zein diren periodikoak eta zein ez diren.

a) y = 2sin x b) y = sin2 x c) y = sin x2

d) y =  snix e) y = sin x f ) y = sin 2x

* Gogoan izan f funtzio bat T periododuna bada, orduan f(mx + n) ere periodikoa dela, eta bere periodoa T/m dela.

4 Adierazi honako funtzio hauek:

a) f (x) = |x + 3| + |x – 1| b) g (x) =  () ln x x x x x 1 1 21 1 1 ––

bada ≥bada < 2 + *

5 Adierazi funtzio hauek:

a) f (x) =  () x x 2 1 2 + + b) g (x) =  () x e 1 x

2 +

6 Kalkulatu y = ln (–x 2 + 1) funtzioak ardatzekin dituen ebakipuntuak eta puntu singularrak. Zehaztu zer tartetan den gorakorra eta zeinetan beherakorra, eta egin grafikoaren zirriborroa.

7 Aurkitu f (x) = x x 3 + funtzioaren maximoak eta minimoak. Esan asintotarik duen eta adierazi grafiko batean.

8 Aztertu funtzio hauek eta adierazi grafiko bidez:

a) 3x 4 + 4x 3 – 12x 2 b) y = sin 2x + 2cos x

AUTOEBALUAZIOA ➜ anayaharitza.es Ariketa hauen ebazpena.

Jatorrizkoen kalkulua 12

Zer da funtzio baten jatorrizkoa?

Zein da f (x)-ren deribatua? galderari 9. unitatean erantzun genion, eta maila honetan erabiltzen diren funtzio guztien kasuan aplikatu genuen. 10. eta 11. landu dugu nola erabili behar diren ikasitako prozedurak problema praktikoak ebazteko

Orain, Zein da deribatu moduan f (x) duen funtzioa? galdera jorratuko dugu. Erantzuna erraza da funtzio batzuen kasuan; zaila, beste batzuetan; eta erantzuten ezinezkoa, gehienetan. Adibidez:

• Argi dago f (x) = cos x deribatua duen funtzioa F (x) = sin x dela.

• Unitate honetan, deribatu moduan xe x duen funtzioa zein den lortzen ikasiko dugu, baita beste asko ere.

• Ezinezkoa da lortzea, ez baita existitzen, adierazpen analitiko ezagunen bidez emanda dagoen eta deribatu moduan sn i x x duen funtzio bat.

F (x) funtzio baten deribatua f (x) bada, hasierako funtzio horri f (x)-ren jatorrizkoa esaten zaio. Zertarako balio digu funtzio baten jatorrizkoa jakiteak? Hori eta arrazoitze historikoa hurrengo unitatean landuko ditugu

Matematikako jeinua

Leonhard Euler (1707-1783) matematikaren historian egon den jeinu handienetako bat izan da. Kalkulu infinitesimalari buruzko bere testuek eragin handia izan dute matematikari belaunaldi askotan. Laplacek berak, xviii. eta xix. mendeetan bizi izan zen beste jeinu batek, aholku hau ematen zien matematika arloan hasi berriei: «Irakurri Eulerren lanak. Hura da gu guztion maisu».

Euler Basilean jaio zen, Suitzan. Aita artzain kalbinista zen, eta semeak teologia ikasketak egitea nahi zuen. Baina Johann Bernoulliren lagun egin zen, eta adiskidetasun haren ondorioz matematikekin zaletu zen eta grinez landu zituen, Bernoulliren beraren tutoretzapean. Prestakuntza bikaina izan zuen: teologia, matematikak, fisika, astronomia, medikuntza eta ekialdeko hizkuntzak ikasi zituen.

Zalantzarik gabe, garai guztietako matematikaririk oparoena da. 1911n hasita editatu ziren Eulerren lan osoak, eta, guztira, 80 liburuki mardul baino gehiago osatu zituen. Liburuki horiek denetariko eremuetako ideia harrigarriz beteta daude. 33 urterekin begi bat galdu zuen, eta 60 urterekin itsu geratu zen. Hala ere, lan matematiko garrantzitsuak diktatzen jarraitu zuen, 76 urterekin hil zen arte.

Leonhard Euler (1707-1783)

Euler, talentu handi horren zergatia

Eulerren gaitasun izugarri horren hiru sekretu handiak honako hauek izan zirela esaten da:

1) Oso buru ona omen zuen, dena gogoratzeko gauza. Edadekoa zela ere gauza omen zen Virgilioren Eneida laneko liburu guztiak buruz errezitatzeko, latinez jakina. Hitzez hitz gogoratzen omen zen Akademiaren saioetako aktez, saioak egin eta handik dozenaka urtera era bai!

2) Lanean kontzentratzeko ahalmen ikaragarria omen zuen. Garai berean bizi izan zen beste matematikari batek baieztatu zuenez, «betiko geldituko diren lan handi horiek altzoan ume bat eta bizkar gainean katu bat zuela idatzi zituen»

3) Ekina eta pazientzia handikoa zen, eta, ondorioz, urteak ematen zituen problema zailenekin interesatuta, lanean, azkenean irtenbideren bat aurkitzen zuen arte.

EBATZI

Funtzio batzuen jatorrizkoak lortzea

Dakizunez, x 3-ren deribatua 3x 2 da, eta honela idazten dugu:

(x 3)' = 3x 2

• erroak ere berreketak dira

a) y xdx 2 3 / 12 b) y xdx 2 3

c) y xdx 7 d) y xdx 2 1 / –12

3x 2 dx = x 3

Hori adierazteko, 3x 2-ren jatorrizko bat x 3 dela ere esan dezakegu, eta honela idatziko dugu: y

Jatorrizkoak lortzea, beraz, deribatzearen kontrako prozesua da. Hori kontuan izanda, saiatu ondoren emandako funtzioen jatorrizkoak kalkulatzen. (Errazago egingo duzu eskura deribatuen taula bat izanez gero).

Emandako soluzioa zuzena den zalantza duzunean, egiaztatu zuk zeuk: deribatu, eta aurkitu duzun jatorrizkoa duen funtziora heldu behar duzu

• zenbakiak eta berreketa errazak

a) y 1 dx b) y 2 dx c) y 2 dx

d) y 2x dx e) y x dx f ) y 3x dx

g) y 7x dx h) y x 2 dx i) y xdx 2 1 2

• berretzaile osoko berreketak

a) y (–1)x –2 dx b) y x –2 dx c) y x dx 5 2

d) y x dx 1 3 e) y x dx 2 3 f ) y () x dx 3 5 –3

e) y x dx 2 1 f ) y xdx 5 3

• gogoan duzu (ln x)' =  x 1 dela?

a) y x dx 1 b) y x dx 5 1

c) y x dx 5 1 + d) y x dx 26 3 +

• funtzio trigonometriko batzuk

a) y cos x dx b) y 2cos x dx

c) y cosx dx 2 r + bl d) y cos 2x dx

e) y (–sin x) dx f ) y sin x dx

g) y sin (x – π) dx h) y sin 2x dx

i) y (1 + tg 2 2x) dx j) y tg 2 2x dx

• esponentzial batzuk

a) y e x – 1 dx b) y e 2x + 1 dx

Jatorrizkoak. Kalkulatzeko oinarrizko erregelak

Definizioa eta nomenklatura

F (x) funtzioa f (x)-ren jatorrizkoa da, baldin eta F ' (x) = f (x) bada. Hori honela adierazten da:

() () fx dx Fx = y

Funtzio bakoitzak infinitu jatorrizko ditu, izan ere, F (x) bada f (x)-ren jatorrizkoa (hau da, F ' (x) = f (x) bada), orduan F (x) + k ere bada, [F (x) +  k]' =  F ' (x) =  f (x) baita. Eta hori egia da k konstantea edozein dela ere. Horregatik, hau idazten da:

(( ) )fx F dx xk=+ y

()fx dx y adierazpenari f (x)-ren integral mugagabea edo, besterik gabe, integral ere esaten zaio. Horregatik, jatorrizkoen kalkuluari integralen kalkulu edo integrazio ere esaten zaio.

Propietateak

Integratzeko prozesua deribatzeko prozesuaren alderantzizkoa denez, jatorrizkoen propietate asko deribatuen propietateetatik abiatuta lortuko ditugu. Garrantzitsuenak hauek dira:

KONTUAN IZAN

F (x) da f (x)-ren jatorrizko bat: () () () () ' fx dx Fx Fx fx + == y

Hau ere f (x)-ren jatorrizkoa da: F(x) + k

k-ren balio bakoitzerako.

IKURRA

Integrazioaren ikurra Leibnizek sartu zuen. s luzatu bat da, summa hitzaren (batuketa latinez) hasierako letra. Zergatik? Hurrengo unitatean ulertuko dugu.

• y x 1 dx = y x –1 dx = ln | x | + k

Adibidez:

Integral trigonometrikoak, esponentzialak eta logaritmikoak

(337. orrialdean ondorioztatuko dugu).

EGIAZTAPENA

Egiaztatu, deribatuz eta sinplifikatuz, bi integral logaritmikoak zuzenak direla.

3. epigrafean (Zatika integratzea), urratsez urrats, emaitza hau lortzen da.

Ebatzitako ariketak

1 Kalkulatu honako integral hauek:

a) y (3 sin x + 2 cos x) dx

b) y (2 x + 3 x) dx

a) y (3 sin x + 2 cos x) dx = 3 y sin x dx + 2 y cos x dx = –3 cos x + 2 sin x + k

b)

c) y x x dx 1 1 –

–2 2

d) y x xx x dx 1 35 2 –2 32 + ++

c)

d)

e) y (3 cos x – 5 e x) dx

Berehalako integralen adierazpen konposatua

Integrazioa diferentziazioaren alderantzizko prozesu moduan

Orain arte, jatorrizkoak kalkulatzean egin duguna da integralaren ikurraren barruan deribatu ezaguna duen funtzio bat bereiztea, zuzenean edo «konponketa txiki batzuk» eginda. Hurrengo urratsa jardunbide hori zabaltzea da, katearen erregelaren bidez

Horretarako, lehenengo eta behin, erabiltzen ari garen idazkera diferentzialari zentzua emango diogu:

— Gogoan izan dF (x) = F ' (x) dx dela (9. unitatea, 264. orrialdea). Ikusten duzunez, F (x) funtzioa f (x)-ren jatorrizkoa bada, F ' (x) = f (x) da eta, beraz, dF (x) = f (x) dx:

y f (x) dx = y dF (x) = F (x) + k

— Beraz, integrazioa diferentziazioaren alderantzizko prozesua da

Katearen erregela eta jatorrizkoen kalkulua

Ekarri gogora nola erabiltzen den katearen erregela deribatuak kalkulatzeko:

ϕ(x) = g [ f (x)] bada, ϕ'(x) = g' [ f (x)] · f ' (x)

Adierazpen hori idazkera diferentzialaren bidez adieraz daiteke, honela:

d ϕ(x) = d g [ f (x)] = g' [ f (x)] · f ' (x) dx

Eta, beraz, hau egiaztatzen da:

y g' [ f (x)] · f ' (x) dx = g [ f (x)] + k

Formula horrek modua ematen digu berehalako integralen zerrenda interpretatzeko, oinarrizko funtzioak edozein funtzio motaren gainean aplikatuz:

x) dx = sin f (x) + k ·( ) ' ln af xdx a ak 1 () () fx fx =+ y

[( )] () () () () ' ' cos tg fx fx dx fx fx dx tg fx k 1 2 2 += =+ yy y ln f (x) · f ' (x) dx = f (x) ln f (x) – f (x) + k () () () ' fx fx dx arctgf xk 1 2 + =+ y () () |( )| 'lncos tg fx fx dx fx k =+ y

Adibidez, I = y cos (x 2 – 5x + 3) (2x – 5) dx integrala kalkulatzeko, kosinu funtzioak

f (x) = x 2 – 5x + 3 funtzioari eragiten diola ikusten dugu, eta horren diferentziala ondoren ageri dela

Beraz: I = sin f (x) + k = sin (x 2 – 5x + 3) + k

Ebatzitako ariketa

1 a) cos senx xdx 4 y sin4 x cos x dx

b) e x dx 2 1 x y

a) () () sn coss ncos sn ii i xx dx xx dx x k 5 44 5 == + yy

b) · e x dx I 2 1 x = 9 Ikusten duzunez, ' x x 2 1 = ` j da.

Beraz, I = ek x + .

c) ex() dx 25 –xx 5 –2 y

d) tg xdx y

e) x x dx 1 2 4 + y

c) ()ex dx ek 25 –xx xx5522 =+ y ; izan ere, (x 2 – 5x)' = 2x – 5

d) || cos sn cos sn ln cos ii tg xdx x xdx x xdx xk ––– == =+

e) () x x dx x xdx arctgx k 1 2 1 2 4 22 2 + = + =+ yy ; izan ere, (x 2)' = 2x

x 2 y

f ) e edx 1– x

g) cos x x dx 11 –2 c c m m y

h) () x xdx 57 10 –23 4 y

i) ln x x dx 31 23 1 3 + + y

– y

j) cos x x dx 31 31 –

Pentsatu eta praktikatu

x x == + yy arc sin e x + k; izan ere, (e x)' = e x g) cossin x x dx x k 11 1 –2 =+ d d n n y ; izan ere, ' x x 1 1 –2 = cm h) –() () () x xdx xx dx x kx k 57 10 57 10 4 1 57 45 7 –

x x 22 ––/ / 23 4 23 4 21 4 2 4 == += + yy i) ;( )' ln x x dx Ix x 31 23 1 3 31 23 1 1 3 · + + =+ = + y Beraz, I = ln xx xk 31 31 31 – ++ ++ j) ' x x 31 23 1 3 ––= ` j . Beraz: cos cossin x x dx x x dx xk 31 31 3 2 31 23 1 3 3 2 31 –

––– == + yy

1 a) () cosx senx dx –5 y (–sin x) dx b) () cosx senx dx –2 3 y (–sin x) dx c) esen xdx cos x y sin x dx

d) ()ex xdx32 xx 2 2 3 + + y e) · tg xx dx 2 2 9 f ) x x dx 1 3 6 2 + y

g) e e 1––x

– y dx h)

x –2

() ln xx dx 12 2 + y i)

() () xx xdx54 5 42 3 3 ++ y

Ordezkapen-metodoa

y h (x) dx erako integrala kalkulatu nahi dugu, berdintza hau bereizteko gauza izanik: h (x) = f [g (x)] · g ' (x)

Jo dezagun, gainera, y f (t ) dt = F (t ) erraz lortzen dugula

Orduan, integralean:

I = y h (x) dx = y f [g (x)] · g ' (x) dx

aldagai-aldaketa hau egin behar dugu: u = g (x) du = g ' (x) dx

Hori eginda, hau geratuko zaigu: I = y f (u) du = F (u) = F [g (x)].

Aurreko orrialdean ebatzi ditugun integral askok eskema hori zuten, eta aldagai-aldaketa egin beharra zegoela azalpenik eman gabe ikusi eta egin dugu. Dena dela, normalena izaten da ordezkapena ezin izatea buruz egin, eta zer aldaketa egin den zehaztu behar izatea. Ikus ditzagun kasu batzuk

Beste aldagai aldaketa batzuk

I = y f (x) dx integralean x = φ (t ), aldaketa egiten badugu, dx = φ'(t ) dt honetara geratzen da:

I = y f [φ (t )] φ' (t ) dt

Bada, f (x) integratzen ez badakigu, baina f [φ (t )] φ' (t ) funtzioaren integrazioa nola egiten den badakigu, orduan aldagai-aldaketa oso lagungarria izango da. Ikus ditzagun adibide batzuk.

b)

«Zatika» integratu

Biderketa baten deribatua kalkulatzeko formula hau da:

[u (x) · v (x)]' = u ' (x) · v (x) + u (x) · v ' (x)

eta idazkera diferentzialean adierazita, honela geratzen da:

d [u (x) · v (x)] = du (x) · v (x) + u (x) · dv (x)

Azkeneko batugaia askatzen badugu, honela geratzen da:

u (x) dv (x) = d [u (x) · v (x)] – v (x) du (x)

Bi ataletan integratzen badugu, hau lortzen dugu:

y u (x) dv (x) = u (x) · v (x) – y v (x) du (x)

Labur adierazita: y u dv = u · v – y v du

Formula horrek modua ematen du y u dv integrala y v du integraletik abiatuta kalkulatzeko. Erabili ahal izateko, jakin behar dugu emandako integrala y u dv formakoa dela bereizten, eta y v du integrala aurrekoa baino ebazteko errazagoa dela ikusten.

KONTUAN HARTU

Funtzio bat integratu ondoren lortzen dugun funtzio berria hasierakoa baino zailagoa izan daiteke (adibidez, polinomikoa bada). Aurkakoa gertatzen da funtzio bat deribatzen dugunean. Zatika integratzen duzunean, komeni da integratzeko errazagoak izango diren funtzioak aurkitzea.

a) x deribatzean, sinplifikatu egiten da, eta e x integratzean, ez da zailtzen. Beraz:

b) ln Ix xdx 3 = y

b) ln x-ren deribatua

1 denez, egokia izan daiteke aldaketa hauek egitea:

c) Honelako kasuetan, komeni da dv = dx hartzea:

Integral hau formula trigonometrikoak erabiliz ebatzi dugu 335. orrialdean, eta honako

Funtzio arrazionalen integrazioa

Funtzio arrazionalak bi polinomioren arteko zatiketa moduan adierazten dira: () () Qx Px .

Atal honetan, funtzio horien integrazioak ematen duen kasuistikako adibiderik garrantzitsuenak ikusiko ditugu:

• Q (x) izendatzaileak erro errealak baino ez ditu.

Q (x) izendatzailea lehen mailakoa da.

— Q (x) izendatzaileak erro erreal errazak baino ez ditu

— Q (x) izendatzaileak erro erreal anizkoitzak ditu.

• Q (x) izendatzaileak erro irudikariak ditu.

Kasu hau ez da horren ugaria eta zailagoa da. Hori dela eta, adibide erraz batzuk baino ez ditugu ikusiko, hurrengo atalean.

Landuko ditugun kasu guztietan, zenbakitzailea izendatzailea baino maila baxuagokoa dela onartuko dugu; hala ez balitz ere, zatiketa osoa eginda lortuko dugn polinomioaren batuketan, zenbakitzailea izendatzailea baino maila baxuagokoa duen zatiki bat egongo da.

P (x) Q (x)

R (x) C (x) ⇒ () () () () () Qx x Cx Qx Rx P =+

Izendatzailea lehen mailakoa da

xa A – y dx = A ln | x – a | + k denez, aldaketa txiki batzuk eginda () mx n Px dx + y mo-

tako edozein integral kalkulatzen jakingo dugu

Izendatzaileak erro erreal errazak baino ez ditu

Aurreko eredu horrek erakusten digu horrelako edozein funtzio arrazional zatikietan deskonposatzen saiatu behar dugula. Ikus dezagun nola eta noiz egin daitekeen:

y xx x dx 2 –2 +

Zatiki aljebraikoa bi zatiki sinpleren batuketa moduan jartzen saiatuko gara.

x2 + x izendatzailea bi biderkagairen biderketa eran jar daiteke: x · (x + 1). Beraz, deskonposizio hau egiten ahaleginduko gara:

xx x x A x B 2 1 –2 + =+ +

Bigarren atalean eragiketak eginez:

() xx x xx Ax Bx 2 1 1 –2 + = + ++

()

Izendatzaileak berdinak direnez, A-k eta B-k zenbakitzaileak ere berdinak izateko moduko balioak izan behar dituzte:

x – 2 = A (x + 1) + Bx → x – 2 = (A + B ) x + A

() AB A x 1 –2 coeficientede (término independiente) += = * (x-ren koefizientea) (gai askea)

A = –2, B = 3 lortzen dugu, eta, beraz:

A ETA B LORTZEA

Aztertu hurrengo berdintza honetan A-ren eta B-ren balioak lortzeko beste metodo bat:

x – 2 = A (x + 1) + Bx

x-ri –1 balioa emango diogu:

x = –1 → –3 = –B → B = 3

x-ri 0 balioa emango diogu:

x = 0 → –2 = A → A = –2

Aurreko ideia horrek, eta koefizienteak lortzeko alboan azaltzen denak, izendatzailean erro erreal errazak soilik dituen edozein funtzio arrazional deskonposatzeko modua ematen digute:

Gogoan izan P(x)-ren maila k baino txikiagoa izan behar dela. Horrela ez balitz, ezer baino lehenago zatiketa egingo dugu.

Ebatzitako ariketa

1 Kalkulatu:

Zenbakitzailea ez denez izendatzailea baino maila txikiagokoa, zatiketa egin eta honela adieraziko dugu:

Izendatzailearen erroak kalkulatu eta biderkagaietan deskonposatuko dugu:

Ebatzitako ariketa

Zatikia deskonposatuko dugu:

Lehenengo eta azkeneko zatikien izendatzaileak berdinak direnez, zenbakitzaileek ere berdinak izan behar dute

Kalkula dezagun zer balio izan behar duten A, B eta C parametroek hori horrela izateko. Horretarako, x-ri –1, –2 eta 3 balioak emango dizkiogu:

Izendatzaileak erro erreal anizkoitzak ditu Ikus dezagun kasu erraz bat:

KONTUAN HARTU

Izendatzailearen erro anizkoitza 0 da; beraz, deskonposizioa berehalakoa da.

Oso erraza izan da zatiki hori berehala integra daitezkeen hainbat zatikitan deskonposatzea, zatiketa «begiz jota» egin daiteke eta

Ikus dezagun hain erraza ez den beste kasu bat:

Zenbakitzailea (x – 2)-ren berreturak erabiliz idatzita egongo balitz, zatiki hori aurrekoa bezain erraz deskonposatuko genuke.

Beraz, berreturen bidez adierazita egongo balitz bezala jokatuko dugu:

Zenbakitzaileak

BERAZ

Egin ditugun kalkuluen arabera:

Orokorrean, zatiki aljebraiko bateko izendatzaileak k ordenako a erro anizkoitz bat badu, deskonposatzean, erroaren anizkoiztasun-ordena adina zatiki lor daitezke:

Ebatzitako ariketak

Zenbakitzaileak identifikatuz, hau lortzen dugu:

Lehenengo, izendatzailearen erroak aurkitu behar ditugu. 0, 0, 1, 1, 1 eta –1 dira

Hori kontuan izanda, deskonposizio hau egingo dugu:

Bigarren atalean eragiketak eginez, zenbakitzaileak identifikatuz eta prozesu neketsu baten ostean, hau lortzen dugu:

Beraz, integrala honela gelditzen da:

Galdera bati erantzutea falta zaigu: nola izan liteke x = –1 erroari dagokion zatikia desagertzea?

Bada, oso erraza da: erro hori zenbakitzailean ere bazegoelako

Horretaz konturatuz gero, ezer baino lehen, zenbakitzailea eta izendatzailea zati x + 1 eginez sinplifikatuko genituen. Sinplifikazioa ez dugu garaiz egin eta horrek lan handiagoa eman digu, baina bestelako arazorik ez

Izendatzaileak erro irudikariak ditu

Lehenengo kasua

ax c dx 2 + y , eta a eta c positiboak dira.

a eta c zeinu berekoak badira, ax 2 + c polinomioak ez du erro errealik.

dx

1 1 1 1 2 2 2 + = + = + = dn

Bigarren kasua

ax bx c dx 2 ++ y , ax 2 + bx + c izendatzaileak ez du erro errealik.

batzuk: • () () xx dx x dx arctgx

yy • () () xx dx x dx x dx x dx 27 16 6 1 6 1 1 6 1 6 1 1 22 22 ++

=

Mx gaia erabiliz izendatzailearen deribatuaren antzeko adierazpen

GOGORATU

Zenbakitzailea 1 baino maila handiagokoa bada, lehenengo zatiketa egin eta honetara jarriko dugu:

1 P (x) = x 4 – 3x 3 + 8x 2 + 30x – 112

Q (x) = x 3 – 7x 2 + 25x – 39

Aurkitu: () () Qx Px dx y

P-ren maila (x) ≥ Q (x)-ren maila denez, zatiketa egingo dugu.

Hau lortzen dugu:

zatidura = x + 4

hondarra = 11x 2 – 31x + 44

Integrala honela gelditzen da:

I = x xx x xx dx 4 72539 11 31 44 –32 2 ++ + +

Zatidura zatiki sinpleen batuketa moduan deskonposatu behar dugu. Horretarako, lehenengo, izendatzailearen erroak bilatuko ditugu. Hau lortzen dugu:

Pentsatu eta praktikatu

Ebatzitako ariketak eta problemak

1. Funtzio konposatuen berehalako integralak

a) () x xdx 2 35 1 ––2 y

a) Ageri den biderketa egingo dugu:

b) x dx 2 35 –3cm y

c) sec tg xx dx 2 3 2 y

d) e ee dx 32 –x xx 2 2 y

d)

e) x x dx 2 23 –+ y

f ) cos sn cos i x xx dx 2+ y

g) tg xdx 2 y

h) sn sn i i x x dx 1 1 –+ y

i) x dx 43 1 –2 y

EGIN ZUK

Kalkulatu honako integral hauek:

a) sn cos sn cos i i xx xx dx 33 33 –+ y

b) x x dx 2 3 –2 y

c) sn cos ix x dx 2 1– 2 y

honela jarriko dugu:

yy y

I = (*) () sn sn cos sn sn i i ii x x dx x xx dx 1 1 12 –2 2 2 2 + = ++ = yy = coscos sn i x dx x x dx tg xdx 2 22 2 ++ = yy y = () sn cos i tg xx xdxtgx dx 21 1 –++–22+= yy = cos cos tg x x tg xx ktgx x xk 2 1 2 2 –––1 ++ =+ +

Zenbakitzailea eta izendatzailea

bider (1 + sin x )

Ebatzitako ariketak eta problemak

2. Ordezkapen-metodoa

Ebatzi honako integral hauek ordezkapen-metodoa erabiliz:

a) cosx tg x dx 1 2 3 + y

b) x x dx 12 3 2 + y

c) edx 1 –x y

EGIN ZUK

Erabili ordezkapen-metodoa honako integral hauek ebazteko:

ln xx dx 1– y

b) x x dx 1+ y

3.

a) Kalkulatu f (x) = ln (1 + x 2) funtzioaren jatorrizko guztiak.

b) Kalkulatu f (x) = arc tg 3x funtzioaren jatorrizko guztiak.

Zatika integratzea

4.

Ebatzi: I = sn i ex dx x y

5.

EGIN ZUK

Kalkulatu:

a) I = cos xx dx 22 2 y

b) I = cos ex dx 2 x– y

Zatika integratuko dugu: sn cos ix u edxdv xdxdu xxev = = = =

→

* > y

I = () sn cos i ex ex dx –xx 1 I

cossin xu edxdv xdxdu ev –xx = = = = )

→ → → Kalkulatu: a)

I1 = cossincos ex ex dx ex I xx x += + y

Hasierako integrala agertu zaigu. (*)-ko adierazpenean I1 jarri eta I askatuko dugu:

I = e x sin x – e x cos x – I → 2I = e x sin x – e x cos x

dd

6.

b) I = y cos 4 x dx

c) I = y () ln ln ln xx x dx

EGIN ZUK

b) () ()ee e dx 11 –xx x 2 + y

c) [( )]cossxxincos xdx 2+ y

I

b) 2cos 2 x =

yy y

Zatika integratzea

Funtzio arrazionalen integrazioa

Hainbat motatako integralak

Ebatzitako ariketak eta problemak

7. Balio absolutu baten integrazioa

f (x) = x 2 – 2 funtzioa izanda, kalkulatu

|(fx)| dx y .

EGIN ZUK Kalkulatu y | x + 1| dx

8. Puntu batetik igarotzen den jatorrizkoa

Lortu funtzio honen jatorrizkoa:

(x) = e e 1 1–x x +

jakinda grafikoa (1, 1) puntutik igarotzen dela.

Integrala kalkulatzeko, aldagai-aldaketa egingo dugu:

EGIN ZUK

Lortu f (x) = e e 1 x x + funtzioaren

jatorrizkoa, jakinda grafikoa (0, 2) puntutik igarotzen dela.

Zatiki

|1 – t | + k

k lortuko dugu, kontuan izanda (1, 1) puntutik igarotzen dela:

1 – 2ln |1 – e| + k = 1 → k = 2ln (e – 1)

Hau da: I = x – 2ln |1 – ex| + 2ln (e – 1)

9. Baldintza bat betetzen duen jatorrizkoa

Zehaztu f (x) funtzioa, kontuan hartuz

honako hau:

• f '' (x) = 2

• f funtzioak x = 0 puntuan duen zuzen

ukitzailearen ekuazioa y = 3x – 5 da

EGIN ZUK

Aurkitu f (x), kontuan hartuz f (0) = 1, f ' (0) = 2 eta f '' (x) = 3x direla.

• f '' (x)-ren eta f ' (x)-ren jatorrizkoak kalkulatuko ditugu:

f ' (x) = y 2

•

Gidatutako ariketak eta problemak

1.

Kalkulatu:

a) Ix() edx 1 –22x –= y

b) I = xx x dx 3 21 –3 + y

a) Ezarri zatika integratzeko metodoa, honela deituz: u = x 2 – 1, dv = e –2x dx

Ezarri berriro zatikako integrazioa geratu den integralari.

b) () xx xx 3233 += + x 3 2 + polinomioak ez du errorik.

Deskonposatu zatiki sinpleetan eta kalkulatu integrala.

Soluzioa:

a) ex xk 2 1 2 1 ––x –22 ++cm b) () ln ln xx arctg x k 3 1 6 1 3 3 23 3 – 2 ;; ++ ++ cm

2.

Aurkitu kurba bat, kontuan hartuz kurbak edozein puntutan dituen zuzen ukitzaileen maldak f (x) = xe 2x funtzioak ematen dizkigula. Badakigu, horrez gain, kurba A (0, 2) puntutik igarotzen dela.

• Kurba batekiko zuzen ukitzailearen malda da kurbaren deribatuak ukitze-puntuan duen balioa

F ' (x) = f (x) betetzen duten F (x) funtzioak aurkitu behar dituzu; hau da, f (x)ren jatorrizkoak

• Erabili zatikako integrazioaren metodoa. Konstante baten menpekoak diren funtzioen familia bat lortuko duzu

Zehaztu konstante hori, kurba A (0, 2) puntutik igaro behar dela kontuan hartuz

Soluzioa:

F (x) = xe e 2 44 9 –xx22 +

Aurkitu Á osoan deribagarria den f (x) funtzio bat, jakinda P (–1, 3) puntutik igarotzen dela eta deribatu hau duela:

• Deribatua ezagun duen f (x) funtzio bat aurkitu behar dugu. f funtzioak definizio tarte bakoitzean dituen jatorrizkoak kalkulatuko ditugu.

• Tarte bakoitzean, jatorrizkoak izango dira emandako baldintzen bidez zehaztu behar dugun k1 eta k2 konstante baten araberakoak.

• Pasarazi f (x) emandako puntutik.

• f (x) funtzioa x = 1 puntuan deribagarria izan behar denez, puntu horretan jarraitua izan behar da.

Aurkitu f (x) = 2x – 4 funtzioaren

F (x) jatorrizko bat, kontuan izanda horren grafikoak puntu bakarrean ebakitzen duela X ardatza

• Kalkulatu f (x)-ren jatorrizkoen familia. Adierazi grafikoki k = 0 duen jatorrizkoa.

• Mugitu grafikoa gorantz, F (x) ≥ 0 izateko behar den adina, eta idatzi lekuz aldaturiko grafikoaren ekuazioa Soluzioa:

Integralen kalkulua

Zuzen ukitzaileen maldak ezagun dituen kurba

3. Funtzio deribagarria

4. Jatorrizkoen grafikoak

Proposatutako ariketak eta problemak

Trebatzeko

Integral ia berehalakoak

1 Kalkulatu honako integral hauek:

a) xx dx 2 45 7 –2 + y b) x xdx 3 y

c) x dx 27 1 + y d) () sn i xx dx – y

2 Ebatzi integral hauek:

a) ()xdx 1 22 + y b) y (x – 5)3 dx

c) xdx35 + y d) () cosx edx x + y

3 Kalkulatu:

a) x dx 2 2 3 y b) cosx dx 7 2 y

c) ()snix dx 4 – y d) () ee dx 3 xx2–+ y

4 Aurkitu integral hauek:

a) x x dx 22 2 + dn y b) () x dx 1 –3 y

5 Ebatzi honako integral

6 Aurkitu integral esponentzial hauek:

a) y e x – 4 dx b) y e –2x + 9 dx

c) y e 5x dx d) y (3x  – x 3) dx

7 Ebatzi arku tangente motako integral hauek:

a) x dx 1 2 25 2 + y b) y x dx 1 5 100 2 +

c) y x dx 33 4 2 + d) y x dx 4 2 +

e) y x dx 9 4 2 + f ) y x dx 9 2 +

g) y x dx 24 2 + h) y e e dx 1 x x 2 +

8 Adierazi zatidura Q P C Q R =+ eran eta ebatzi:

a) y x x dx 3 –2 b) y x xx dx 1 54 –2 + +

c) y x x dx 2 1 –2 + d) y x xx dx 2 22 4 2 + ++

e) y x x dx 1 –2 3 f ) y x xx x dx 2 31 –32 +

9 Aurkitu integral hauek, arku sinu motakoak direla jakinda:

a) y x dx 14 –2 b) y x dx 4– 2

c) y dx x 1 100 1 –2 d) y () ln x dx x 1– 2

10 Ebatzi integral hauek:

a) y sin x cos x dx b) y cos sn i x xdx 5

c) y x xdx 9 2 –2 d) y x xdx 5 2 +

11 Ebatzi honako integral hauek:

a) y () xx xdx21 2 b) y sn i x arcx dx 1– 2

c) y ()cossin xx dx 1 3 + d) y () ln x x dx 1 2 +

e) y () x x dx 2 2 –32 2 f ) y e e dx 1 x x +

Zatikako integrazioa

12 Erabili zatikako integrazioa honako integral hauek ebazteko:

a) y x e2x dx b) y x 2 ln x dx

c) y 3x cos x dx d) y ln (2x – 1) dx

e) y e x dx x f ) y arc cos x dx

13 Ebatzi integral hauek zatikako integrazioa birritan erabiliz:

a) y x 2 sin x dx b) y x 2 e 2x dx

c) y e x cos x dx d) y (x + 1)2 e x dx

Integral arrazionalak

14 Ebatzi:

a) y () ()xx dx ++12 b) y () () dx xx x 13 21 – + +

c) y () x dx x 4 3 + d) y ()xx dx 1 –2

15 Integral hauek ebazteko, deskonposatu zatiki sinpleetan:

a) y xx dx 6 –2 + b) y

c) y () ()xx dx 25 4 2 d) y xx

e) y xx dx 2 4 –2 +

16 Ebatzi integral hauek:

a) y xx xx dx 32 25 3 ––2 2 + + b) y xx dx 215 –16

c) y () ()xx x dx 13 24 ––2 + d) y () ()xx x dx 25 23 –+ +

e) y () ()xx dx 13 1 –2 + f ) y x x dx 4 32 –

Integralak ordezkapen bidez

17 Ezarri ordezkapen-metodoa honako integral hauek ebazteko, kasu bakoitzean adierazten den aldaketa eginez:

a) y xx dx –(egin x = t 2)

b) y xx dx 2 3 + (egin x + 2 = t 3)

c) y x xdx 1 –3 (egin x = t 6)

d) y dx e 2 2 x + (egin t = e x)

e) y dx e e 1– x x (egin e x  = t 2)

18 Ebatzi integral hauek aldagai-aldaketa bat eginez:

a) y xx dx 1 + b) y xx dx –4

c) y x x dx 1 + d) y xx dx 1 1 +

e) y xx dx 1 + f ) y x x dx 1+

Ebazteko

19 Ebatzi integral hauek:

a) y x 4 e x 5 dx b) y x sin x 2 dx

c) y x · 2–x dx d) y x 3 sin x dx

e) y ()xdx 3 5 + f ) y x x dx 26 3 ––2

g) y e 2x + 1 cos x dx h) y x 5 e –x 3 dx

20 Kalkulatu honako integral hauek:

a) y x x dx 1 2 2 + + b) y () x dx 1 1 –22

c) y xx x dx 21 2 –2 + + d) y x x dx 49 1 ––2

e) y xx x xx dx 1 27 1 –32 2 + + f ) y x x dx 28 31 –2 +

21 Ebatzi integral hauek:

a) y ln x x dx b) y cos sn i xx x dx 1–+

c) y ln xx dx 1 d) y ex e dx 1 x x + +

e) y sn i x x dx f ) y ln (x – 3) dx

g) y ln x x dx h) y ln (x 2 + 1) dx

22 Kalkulatu integral hauek:

a) y (/ ) sn i x x dx 1 2 b) y x x dx 2 2 +

c) y x arctgx dx 1 2 + d) y cos sn i x x dx 4

e) y (ln x)2 dx f ) y e x cos e x dx

g) y x dx 1 1 –2 h) y () x x dx 1 1– 2 +

23 Kalkulatu:

a) y e dx 1 1 x + b) y x x dx 9 3 –2 +

c) y ee dx 3 –xx2

e) y e ee dx 1 –x xx 2 3 +

d) y () cos sn i x tg x dx 2

f ) y x dx 1 1 +

Proposatutako ariketak eta problemak

24 Ebatzi:

a) y x x dx 1 4 –2 + b) y () x dx 12 3 2

25 Kalkulatu y () x x dx 1 2 3 +

a) Zatiki sinpleetan deskonposatuz.

b) Aldagai-aldaketa eginez.

26 Kalkulatu integral hauek:

a) y xx x x dx 33 1 5 32 2 + b) y xx x dx 25 3 ––2 2 +

c) y xx x xx dx 2 26 –32 4 + d) y () ()xx xx dx 29 2126 ––2 2 + +

27 Ebatzi integral hauek:

a) y xx dx 45 2 ++ b) y () xx xdx 23 5 2 ++ +

c) y xx x x dx 23 1 32++ + d) y xx x dx 21 –3 +

e) y x xx dx 9 38 2 2 + ++ f ) y () ()xx dx 11 22 ++

28 Aurkitu kurba-familia baten ekuazioa, jakinda kurba horiek edozein puntutan dituzten zuzen ukitzaileen malda honako funtzio honek adierazten duela:

f (x) =  x x 24 2 –+

29 y cos 3 x dx integrala ebazteko, hau egiten dugu: cos 3 x = cos x cos 2 x = cos x (1 – sin 2 x) =

= cos x – cos x sin 2 x

Ebatzi eta kalkulatu y sin 3 x dx

30 Kalkulatu integral hauek erlazio trigonometrikoak erabiliz:

a) y () sn cos ix xdx22 2 + b) y () cos coscos x xx dx 2 12 –2

c) y () sniisnxx dx 2 2 d) y () coscosxx dx 2 –2

* Laguntza: kontuan izan 1 + cos 2x = 2cos 2 x dela, eta

1 – cos 2x = 2sin 2 x dela

31 Aurkitu zein izan behar diren m-ren eta n-ren balioak

F (x) =  mx2  +  nx funtzioa f (x) = 5x + 4 funtzioaren jatorrizkoa izateko.

32 Arrazoitu F (x) = 2x3 + 3x2 – 5 eta G (x) = 2x3 + 3x2 + 9 funtzioak ba ote diren f (x) = 6x2 + 9x funtzioaren jatorrizkoak.

33 Azaldu F (x) = 12x 2 – 2 funtzio honen jatorrizkoa den: f (x) = 4x3 – 2x + 5.

34 Aurkitu (0, 3) puntutik igarotzen den f (x) =  x x 1 3 –2 funtzioaren jatorrizkoa.

35 Aurkitu F funtzioa, F ' (x) =  x 1 2 eta F (1) = 2 izan daitezen.

36 y = 4x – 6 funtzioaren jatorrizko guztien artean, zeinek hartzen du 4 balioa x = 1 kasuan?

37 Aurkitu f (x) honako hau jakinda: f '' (x) = 6x, f ' (0) = 1 eta f (2) = 5.

38 Aurkitu f (x) = x 2 sin x funtzioaren jatorrizkoen artean, x = 0 kasuan 1 balioa hartzen duena.

39 Zehaztu f (x) funtzioa, honako hau jakinda: f '' (x) = x ln x, f ' (1) = 0 eta f (e) =  e 4

40 Kalkulatu f (x) funtzio baten adierazpena, honako hauek kontuan hartuz: f ' (x) = x e –x 2 eta f (0) =  2 1 .

41 y = f (x), x > –1 funtzio bati buruz y '  =  x a 1+ deribatua duela dakigu, eta a konstante bat dela.

Zehaztu zein den funtzioa, horrez gain f (0) = 1 eta f (1) = –1 direla jakinda.

42 f : Á → Á funtzioa izanda, f (x) = ln (1 + x 2) eran definituta, aurkitu koordenatuen jatorritik igarotzen den f -ren jatorrizkoa.

43 Kalkulatu zein izan behar den a parametroaren balioa, honako funtzio honen jatorrizko bat: y (ax 2 + x cos x + 1) dx (π, –1) puntutik igarotzeko.

44 Aurkitu y e ax (x 2 + bx + c) dx integrala, a, b eta c parametroen funtzioan

45 Aurkitu f : [–1, 1] → Á funtzio deribagarria, kontuan izanda f (1) = –1 betetzen duela eta beste hau:

46 Funtzio deribagarri bati buruz, badakigu A (–1, – 4) puntutik igarotzen dela eta deribatu hau duela:

a) Idatzi f (x)-ren adierazpena.

b) Lortu f (x) funtzioak x = 2 puntuan duen zuzen ukitzailearen ekuazioa.

47 Lortu f (x) = 3x 2 – 6x funtzioaren F (x) jatorrizko bat, kontuan izanda F (x)-k minimo bat duela (2, 0) puntuan. Zehaztu F (x)-ren gainerako puntu singularrak.

48 Lortu f (x) funtzioa, f '' (x) = e x , f ' (1) = 0 eta f (0) = 1 direla jakinda.

49 Aurkitu f (x) = 2x funtzioaren F (x) jatorrizko bat, kontuan izanda F (x) ≤ 0 dela [–2, 2] tartean.

50 Lortu f (x), honako hau jakinda: f '' (x) = cos x 2 , f ' (2π) = 0 eta f (0) = 1.

51 Kalkulatu f (x) funtzioa, jakinda f '' (x) = x dela, f-ren grafikoa P (1, 1) puntutik igarotzen dela eta P puntuan dagoen ukitzailea ekuazio hau duen zuzenarekiko paraleloa

dela:

3x + 3y – 1 = 0

52 Funtzio hauek ditugu: f (x) = 12x 3 – 8x 2 + 9x – 5

g (x) = 6x 2 – 7x + 2

Aurkitu H (1) = 1 berdintza betetzen duen

H (x) = () () gx fx dx y funtzioa.

53 Kalkulatu y sn cos ix x dx 1 22

* Erabili sin 2 x + cos 2 x = 1 berdintza

54 Ebatzi:

a) y x x 19 –6 2 dx b) y xdx 81 25 –2

* a) Egin t = 3x 3. b) Egin x =  5 9 sin t.

55 Kalkulatu:

a) y | 1 – x | dx b) y (3 + | x |) dx

c) y | 2x – 1 | dx d) y x dx 2 3 4 –

e) y | x – 2 | x dx f ) y e | x | dx

56 Zehaztu ondorengo ekuazioa egiaztatuko duen f (x) funtzio bat: x 3 f ' (x) + x 2 + 2x = 3

57 f : Á → Á funtzio deribagarri bati buruz, badakigu (–1, 0) puntutik igarotzen dela eta deribatu hau duela: f ' (x) =  ≥ ex x 1 0 0 ––si si < x– ) ≥ ex x 1 0 0 ––si si < x– ) bada bada

a) Aurkitu f (x)-ren adierazpena.

b) Lortu x = 1 puntuan duen zuzen ukitzailearen ekuazioa.

58 Zehaztu f : Á → Á funtzioa, kontuan izanda bigarren deribatua konstantea eta 3 dela, eta x = 1 abzisa-puntuan duen zuzen ukitzailearen ekuazioa 5x – y – 3 = 0 dela.

59 Kalkulatu [1, e] tartean balio positiborik hartuko ez duen f (x) = 1/x funtzioaren jatorrizko bat.

60 Ebatzi honako integral hauek:

a) x x dx 2 3 + + y

b) ()xx dx 1 + y

c) xx dx 1 2 3 + ` j y d) xx dx 1 2 + y

61 a) Ondorengo integrala ebazteko, egin zenbakitzailea eta izendatzailea bider cos x , eta, gero, egin aldagai-aldaketa bat: cosx dx y

b) Erabili aurreko prozedura bera honako integral hauek ebazteko: cosx dx 3 y snix dx y

62 a eta b bi zenbaki erreal dira, edozein. Kalkulatu ondorengo integral mugagabea. Kontuan izan a = 0 edo b = 0 kasuak.

() sn cos i ab x x dx 2 + 9

63 f (x) = sin x – sin 3 x izanda, aurkitu:

a) Horren integral mugagabea.

b) , 3 1 r dn puntutik igarotzen den jatorrizkoa.

64 Kalkulatu f (x), kontuan izanda f ' (x) = 3 – 2sin x deribatuak x = π puntuan ebakitzen duela lehenengo koadrantearen erdikaria.

65 Kalkulatu hurrengo jatorrizkoa, a ≠ 1 dela onartuz: ()xa xa dx 1 –2 ++ y

66 Zehaztu f (x) funtzio bat, kontuan izanda f '' (x) = –sin x dela eta x + y – 2 – π = 0 zuzena funtzio horren grafikoarekiko ukitzailea dela x = π abzisa-puntuan.

67 Kalkulatu ||xx dx 32 – y

68 f (x) funtzio bati buruz, badakigu minimo bat duela (–1, –2) puntuan eta deribatua hau dela:

f ' (x) =

22 4

xx

xx

22 4 1 1 si si

si si > + ) bada bada

a) Idatzi f (x)-ren adierazpen analitikoa.

b) Idatzi x = 1 puntuan duen zuzen ukitzailearen ekuazioa.

Proposatutako ariketak eta problemak

Galdera teorikoak

69 Frogatu f (x) funtzioaren jatorrizkoa F (x) bada eta

C edozein zenbaki erreal bada, F (x) + C funtzioa ere f (x)-ren jatorrizko bat dela.

70 Adierazi f funtzio hauen hiruna jatorrizko :

79 Si y f (x) dx =  F (x) eta y g (x) dx =  G (x) badira, aurkitu

F (x)-ren eta G (x)-ren funtzioan:

a) y [ f (x) – g (x)] dx

b) y [( )( )] gx fx dx 2 1 –+54

c) y f (2x – 1) dx

d) y [5 – g (x)] dx

71 Integral batean t = tg x aldaketa egin dugu. Zein da dx-ren adierazpena t -ren funtzioan ?

72 Egiaztatu y cosx dx 1  = ln | sec x + tg x | + k dela.

73 Kalkulatu f (x), honako hau jakinda: y f (x) dx = ln | tg x | + k

74 y () x arctgx dx 1 2

2 + eta y () tg xtgx dx 35 + integralak

f (x)n f ' (x) dx motakoak dira? Mota horretakoak badira, identifikatu horietako bakoitzean f (x), n eta f ' (x).

75 Deribatuen kalkulua erabili gabe, frogatu honako hauek:

F (x) =  x 1 1 4 + eta G (x) =  x x 1 –4 4 + funtzio beraren bi jatorrizko direla.

76 Kalkulatu f (x) honako hau jakinda: y f (x) dx =  () || ln x x k 2 1 –2 3 + +

77 f eta g bi funtzio jarraitu eta deribagarri dira, eta bien arteko aldea konstante bat da. Ziurta dezakegu f eta g funtzioek jatorrizko bera dutela?

78 Honako hauetako zeinek adierazten dute f (x) funtzio baten grafikoa eta horren F (x) jatorrizkoetako bat?

e) y g x dx 2 3 –dn

f ) y [3f (5x – 1) – 6g (2 – 3x)] dx

g) y G ' (x) g ' (x) dx

h) y () () ' ' Fx fx dx

80 Zuzena ala okerra? Arrazoitu eta eman adibideak.

a) Funtzio logaritmiko bat funtzio arrazional baten jatorrizkoa izan daiteke.

b) y f (x) · g (x) dx =  y f (x) dx ·  y g (x) dx

c) Lehenengo mailako izendatzailea duen funtzio arrazional laburtezin baten jatorrizkoak polinomio bat eta logaritmo nepertar bat dira.

81 () cos fx xdx 9 kalkulatzeko zatikako integrazioaren metodoa erabiliz gero (f funtzio deribagarria dela kontuan hartuz), hau lortzen da:

() () coss ns iin fx xdxf xx x xdx 1 – = 9 y

Aurkitu f (x)-ren adierazpen analitikoa, (1, 2) puntutik igarotzen dela jakinda.

82 Egiaztatu funtzio hauek:

F (x) = arc tg x eta G (x) = –arc tg x 1 dn

f (x) funtzio beraren jatorrizkoak direla.

a) F eta G funtzioak berdinak dira ?

b) Horien grafikoek elkar ebakitzen dute?

Sakontzeko

83 Kalkulatu honako integral trigonometriko hauek, aldagaialdaketa eginez:

a) y sn cos ix xdx 23 b) y sn cos ix dx 32

c) y cosx dx 5 d) y cossin xx dx 33

84 Kalkulatu:

a) sn cos ix xdx 22 y b ) snix dx 6 y

* Gogoan izan: 1 + cos 2x = 2cos 2 x eta 1 – cos 2x = 2sin 2 x.

85 ab xdx –22 2 y motako integralak ebazteko, x =  sn i b a t aldagai-aldaketa erabiltzen da

Kalkulatu integral hauek:

a) xdx 100 25 –2 y b) xdx 25 64 –2 y

c)

9 Ebatzi integral hau ordezkapen-metodoaren bidez: y x x dx 1 1 + +

10 Erabili zatikako integrazioa honako hau kalkulatzeko:

a) y (x + 10)e 2x dx b) y cos (ln | x |) dx

11 f (x) funtzioari buruz honako hau dakigu:

f ' (x) =  () ,( ) x f 1 3 20 2 + =

86 Lehen ordenako ekuazio diferentziala x eta y ezezagunez gain y ' ere baduen ekuazio bat da. Ekuazio hori ebaztea da ekuazioa egiaztatuko duen y = f (x) funtzioa bilatzea: Adibidez, ebatz dezagun x y 2 + y ' = 0:

' yx y –2 = → dx dy xy–2 = → dy xy dx –2 =

Aldagaiak bereiziko ditugu: y dy xdx–2 = → () y dy xdx–2 = yy

y x k 1 2 2 =+ → y xk 2 2 –2 =

Infinitu soluzio daude. Bilatu (0, 2) puntutik igarotzen dena eta egiaztatu lortzen duzun kurbak proposaturiko ekuazioa egiaztatzen duela.

87 Ebatzi lehen ordenako ekuazio diferentzial hauek:

a) yy '  – x = 0 b) y 2 y '  – x 2 = 1 c) y' – x y = 0

d) y' x  – y = 0 e) y' e y + 1 = e x f ) x 2 y' + y 2 + 1 = 0

* Horietan guztietan, y' askatzean, bigarren atalean bi funtzioren arteko biderketa edo zatiketa lortzen da, eta horietako bakoitzak aldagai bakarra du.

12 Kalkulatu integral hauek:

13 f (x) funtzio deribagarri bati buruz, badakigu f (3) = 26 dela eta deribatu hau duela: f ' (x) =  ≤ x x x x 43 27 2 2 bada bada > + + )

Idatzi f (x)-ren adierazpena.

14 Kalkulatu y | x + 2 | dx.

15 Aurkitu kurba bat, kontuan izanda kurbak edozein puntutan izango dituen zuzen ukitzaileen malda funtzio honek

ematen digula: f (x) = cos cos x x 12 1 2 + +

Horrez gain, kurba P (π, 0) puntutik igarotzen dela ere badakigu.

16 Zehaztu f (x) funtzio bat, honako

hau jakinda:

a) Zehaztu f

b) Aurkitu (0, 1) puntutik igarotzen den f-ren jatorrizkoa zein den.

• f '' (x) = 2

• r zuzena f-rekiko ukitzailea da T puntuan.

anayaharitza.es Ariketa hauen ebazpena.

Integral mugatua 13

Integrala, deribatua baino lehen

Gaur egun deribatuaren azterketa funtzio baten integralarena baino lehenago lantzen bada ere, egiari zor, integrala deribatua baino lehenagokoa da, 18 mende lehenagokoa. Lehenengo aurrekariak Eudoxok K.a. iv. mendean konoaren eta piramidearen bolumenak kalkulatzeko erabili zuen metodo batean ditugu. Metodo hori berori Euklidesek ere jaso zuen, Elementuak bere liburuan.

Arkimedesek, K.a. iii. mendean, parabola-segmentu batek mugaturiko azalera kalkulatzeko, oso prozedura burutsua erabili zuen, Eudoxok berak erabilitakoaren eta gerora kalkulu integralean erabilitakoen oso antzekoa: ia nuluak diren «infinitu» azalera-zati batu zituen (prozesu horren azpian bazegoen limitera igarotzeko ideia, zehaztugabea baina bazegoen). Horrez gain, antzeko beste problema asko ebatzi zituen. Baina Arkimedesen metodoa ahanzturan geratu zen eta ez zuen oihartzunik izan ondorengo aurrerakuntzetan. Gai horren gainean ez zen aurrera pausorik egon harik eta Keplerrek, xvii. mendearen lehenengo erdian, kurben luzerak eta biraketa-gorputzen bolumenak lortu zituen arte. Modu serioan hasi zen bolumenen kalkulua lantzen, dirudienez, ardogileek ez zituztelako kontuak zehaztasunez egiten bere upeletan sartzen zen ardoaren bolumena neurtzean. Gaia sakon aztertu zuen eta tratatu bat argitaratu zuen: Ardo upelen bolumenen kalkulua. Lan horrek garai hartako beste matematikari batzuen motibazioari eragin zion, eta antzeko problemak ebazten hasi ziren. Baina problemak zenbat, ebazteko prozedurak ere hainbeste izaten ziren. Horrelako problemen ikuspegia bateratzeko, lehen urratsa izan zen guztiak modu berean adieraz zitezkeela ohartzea: kurba jakin baten eta X ardatzaren artean itxitako azaleraren kalkulua eginez.

Bi kontzeptuak bateratu ziren

Keplerren «Ardo-upelen bolumenen kalkulua» lanaren lehen edizioaren barruko orria, 1615ean argitaratua

Newtonen eta Leibnizen ekarpen handia (xviii. mendea), horregatik esaten baita kalkulu infinitesimalaren asmatzaileak izan zirela, problema horiek ukitzailearen problemekin lotzea izan zen:

— y = f (x) kurbak x0 puntuan duen zuzen ukitzailearen malda puntu horretan duen deribatua da: f ' (x0).

— y = f (x) kurbaren azpiko azalera f (x) deribatua duen F (x) funtziotik abiatuta lortzen da. Hau da, F funtzioa f-ren jatorrizkoa da

Kalkulu Infinitesimalaren Oinarrizko Teorema deitzen den azken erlazio horrek argi erakusten du zein garrantzitsua den aurreko unitatean funtzio batzuen jatorrizkoak lortzeko abiatu dugun bilaketa. Jatorrizko horiekin modu automatikoan lortuko ditugu «kurba baten azpiko azalerak», eta, beraz, azalerak, bolumenak… kalkulu infinitesimala erabiliz kalkulatuko ditugu

Kalkuluaren apoteosia

Deribatua eta integrala bateratzean, eragiketetarako prozedura azkarrak eta erabilgarriak lortzen dira.

Integrala, deribatuarekin batera, oso tresna indartsua bilakatu zen fisikako eta beste diziplina batzuetako kontzeptu garrantzitsuak adierazteko eta kalkulatzeko. Azaleraren eta bolumenaren ondoren, beste hainbat etorri ziren. Lana, espazio jakin bat egiten duen indarraren integral moduan; emaria, homogeneoa ez den korronte bateko aldiuneko fluxuaren integral moduan; higikari batek egindako espazioa, abiaduraren integral moduan; gorputz batek biraketa-ardatz batekiko duen inertzia, masa puntualaren eta ardatzerainoko distantziaren karratuaren arteko biderkaduraren integral moduan… Horiek guztiak integralaren erabilgarritasunaren adibide batzuk baino ez dira.

Ikaragarria da integralak matematika arloan zenbat problema eta zenbat motatakoak eman zituen

EBATZI

Bi tren

Bidaiarien tren bat, B, eta merkantzia tren bat, M, geltoki beretik irteten dira, bide beretik eta noranzko berean, bata bestearen atzetik, ia aldi berean.

Hona hemen bi higidura horiek deskribatzen dituzten denbora-abiadura grafikoak:

bidaiari-trena merkantzia-trena

a) B trena 2 orduz 120 km/h-ra doa. Noraino doa abiadura horretan?

b) 2 h eta 2 4 1 h artean, bidaiari-trenak martxa moteldu du. Zenbat kilometro egin ditu abiadura horretan?

c) M trenak 3 h-ra moteldu du abiada. Noraino joan da ordura arte?

d) Zein distantzia egiten du M trenak ordu erdian abiadura txikian?

Kalkuluak eginez, hau egiazta dezakezu:

denbora (orduetan)

Grafikoan ikusten dugunez, bidaiarien trenak abiadura gutxitu du irten eta bi ordura:

— Zer dela eta?

— Zergatik ez du gutxitu abiadura une horretan bertan beste trenak ere?

Irten eta hiru ordura, bi trenek martxa aldatu

dute: bidaiarien trena gelditu egin da minutu batzuetan, eta merkantzia-trena oso astiro joan da ordu erdiz

• Higidura horiek argi ulertzeko, kalkulu batzuk egingo ditugu:

Bi trenek 240 km egin dituzte abiadura arruntean. Leku berean moteldu dute martxa, eta horrela beste 15 km egin dituzte, eta gero bakoitzak bere abiadura normala hartu du, (hau da, M eta B trenek ez dute martxa aldi berean moteltzen, baina bai toki berean.

e) Hasierako geltokitik zer distantziatara dago bidaiarien trena gelditu den beste geltoki hori?

f) Ikusten duzunez, orain arte egindako kalkulu guztietan grafiko urdin eta gorriaren azpiko azalerak lortu ditugu. Adierazi koadernoan zer esparruren azalerak kalkulatu dituzun eta jarri zer azalera dagokion bakoitzari.

Kurba baten azpiko azalera

Azalera batzuen esanahia

Mundu errealetik ateratako hainbat funtziotan (zientifikoak, ekonomikoak…) oso garrantzitsua da grafikoaren azpiko azalera. Ikus ditzagun horietako batzuk

I. Higikari batek egindako espazioa (abiadura-denbora grafikoa)

Alboko grafiko horrek higidura bat deskribatzen du: higidura hori 5 m/s-ko abiadurarekin hasi da, gero 11 m/s-ra igo da, eta 3 m/s-ra amaitu da. Hori bai, tarteetako bakoitzeko abiadura konstantea izan da. Tarteetako bakoitzean egindako espazioa da tarte bakoitzean zehaztutako laukizuzenaren azalera

Higikariak guztira egiten duen e espazioa hiru azaleren arteko batura da:

e = 5 · 4 + 11 · 6 + 3 · 3 = 20 + 66 + 9 = 95 m

Aurreko orrialdean proposatutako ariketak («Bi tren») funtzio mota horiek garatzen ditu

II. Energia elektrikoaren kontsumoa (potentzia-denbora grafikoa)

Beheko grafikoak etxebizitza batean goizeko 7etatik gaueko 12etara uneoro zer potentzia elektriko dagoen adierazten digu.

Kurba azpiko azalera kontsumitutako energia da: potentzia × denbora = energia

Laukitxo bakoitza 100 Wh = 0,1 kWh da. 17 ordu horietan kontsumitu den energia zenbat den jakiteko, kurbaren azpian zenbat laukitxo dauden (azalera) zenbatuko dugu. Emaitza hurbildua izango da

III. Jaiotza- eta heriotza-kurbak

• Kurba berdearen azpiko azalera (jaiotza-tasa) da zenbat hazi den biztanleria jaiotzen ondorioz.

• Kurba gorriaren azpiko azalera (heriotza-indizea) da zenbat gutxitu den biztanleria heriotzen ondorioz.

• Bi kurben arteko azalera biztanleriaren gehikuntza da: positiboa, berdez, edo negatiboa, gorriz (hau da, adierazitako tarte osoan egon den gehikuntza kalkulatu nahi izanez gero, azalera berdeak batu eta gorriak kendu behar ditugu).

Enpresa bateko diru-sarrerak eta gastuak adierazten dituzten kurbek ere antzeko itxura eta interpretazioa izango dute

Ikusi ditugun funtzio horietan, kurbaren azpiko azalera oso magnitude garrantzitsua da, neurtu beharrekoa. Baina adibide batzuk baino ez dira izan. Orain, zehatzago neurtzen ikasiko dugu.

➜ anayaharitza.es

Kurba baten azpiko azaleraren grafikoa interpretatzea

Funtzio baten integral mugatua

y = f (x) funtzioaren grafikoaren eta X ardatzaren artean [a, b] tartean dagoen azalera honela izendatzen da:

f a

b y edo ()fx dx a

b y Honela irakurtzen da: f-ren a eta b arteko integrala

Kurba X ardatzaren gainetik badago ( f (x) > 0), integrala positiboa da; eta X ardatzaren azpitik badago ( f (x) < 0), integrala negatiboa da

Zergatik erabiltzen dugu funtzio baten jatorrizkoa lortzeko erabili izan dugun y ikur bera azalera bat izendatzeko?

Unitatean zehar arrazoituko dugu, eta argi ikusiko duzunez, bi kontzeptuak oso estu lotuta daude

Funtzio integragarriak

f funtzio bat [a, b] tartean integragarria dela esaten dugu, baldin eta f a

b y

integrala existitzen bada; hau da, funtzioaren grafikoak, X ardatzak eta x = a eta

x = b ardatzek mugaturiko eremuari azalera bat lotu badiezaiokegu

Baina zein dira funtzio «integragarriak»?

Argi dirudi honako funtzio hauetako bakoitzak azalera bat mugatzen duela funtzioaren grafikoaren eta X ardatzaren artean. Beraz, integragarriak izan behar dute, zalantzarik gabe.

Eta beste hau? Tira, … azalera zulotxo horietatik kanpo irteten ez dela onartzen badugu, integragarritzat har dezakegu.

Eta hau? Hiru zatietako bakoitza integragarria bada, zergatik ez onartu hirurek eratzen duten funtzioa ere integragarria dela, nahiz eta bata bestearekin lotuta egon ez? a b

Gogoan duzu Dirichleten funtzioa? 1 balio du abzisa arrazionaletan, eta 0 irrazionaletan. Ez du jarraitutasun-punturik. Argi dago ezin dugula onartu funtzio hau «integragarria» dela.

Tartearen barruan infinitu egiten diren funtzioak ere ez ditugu integragarri moduan onartuko; adibidez, y = x 1 funtzioa [–1, 1] tartean.

Hurrengo orrialdeetan, funtzio bat noiz den integragarria eta noiz ez den zehazteko irizpide bat emango dugu. Eta hori baino hobeto: normalean erabiltzen ditugun funtzioak, tarte barruan mugatuta badaude, integragarriak direla egiaztatuko dugu.

Funtzioa [a, b] tartean integragarri izateko baldintza bat

[a, b] tartean mugatuta dagoen y = f (x) funtzioa hartuko dugu (hau da, tarte horretan infinitu egiten ez dena). Prozesua sinplifikatzeko, balio ez negatiboak hartzen dituela onartuko dugu; hau da, funtzio osoa X ardatzaren gainetik dagoela, edo gehienez ere, ardatzaren gainean Hori zehaztuta, integragarria den erabakitzeko modua emango digun irizpide bat eratuko dugu.

• Azalerara txikiagora kalkulatuz hurbiltzea

Jardunbide lagungarri bat da [a, b] tartea zatitan banatzea, eta bakoitzaren azalera laukizuzenen bidez hurbiltzea, laukizuzen horien oinarria X ardatzean egonik eta altuera moduan funtzioak tarte bakoitzean hartzen duen balio minimoa izanik. [a, b] tartea n zatitan banatzen badugu (ez dute derigorrean berdinak izan behar),

a = x0 < x1 < x2 < x3 < … < xn = b eta funtzioak [xi –1, xi] tartean hartzen duen balio minimoari mi esaten badiogu, berdez marratutako azalera hau izango da:

m1 (x1 – x0) + m2 (x2 – x1) + m3 (x3 – x2) + … + mn (xn – xn – 1) = = i

n 1 = / mi (xi – xi – 1)

Azalera hori bila gabiltzan azalera (grisez) baino txikiagoa da (edo, gehienez ere, berdina). Azalerara txikiagora kalkulatuz hurbildu gara.

• Azalerara handiagora kalkulatuz hurbiltzea

Beste aukera bat gehiagora kalkulatuz hurbiltzea da. Horretarako, laukizuzen bakoitzaren altueratzat funtzioak tarte bakoitzean duen Mi balio maximoa hartuko dugu:

M1 (x1 – x0) + M2(x2 – x1) + M3(x3 – x2) + … + Mn (xn – xn – 1) =

n 1 = / Mi (xi – xi – 1) handiagora M2 M3

• Nola lortu hurbilketa hobeak

kalkulatzea

Jakina, laukizuzen finagoak hartuz gero, hau da, xi puntuak elkarrengandik hurbilago hartzen baditugu, bai txikiagora kalkulatutako azalera eta bai handiagora kalkulatutakoa gehiago hurbilduko dira eremuaren azalerara

∫

Aurreko unitatean esan bezala, ∫ ikurra s bat da, latinezko summa (batuketa) hitzaren hasierako letra. Orain, ikus dezagun integrala benetan ere infinitu azaleraren batuketa eginez lortzen dela. Estrategia hau oso antzinakoa da: badakizu Arkimedesek, azalerak eta bolumenak lortzeko, eremu bakoitza infinitu zati sinpletan deskonposatzen zuela, eta zati horiek erraz batu zitezkeela.

Kalkulu integralaren ezaugarri handiena da, unitate honetako 4. atalean ikusiko duzunez, deribatuarekin duen erlazioa. Ezaugarri horrek lotura estua sortzen du integrazioaren eta jatorrizkoen kalkuluaren artean. Eta horregatik erabiltzen da integralaren ikur bera bi prozesuetarako.

Prozesuaren sistematizazioa

x0 = a < x1 < x2 < … < xn = b puntu-bilduma bakoitzari [a, b]-ren partizio esango diogu. Eta xi – xi – 1 distantzietan handienari, partiketaren diametro deituko diogu.

[a, b]-ren P partizio bakoitzari, lehen ikusi dugun bezala, txikiagora kalkulatutako

s azalera bat eta handiagora kalkulatutako S azalera bat lotuko dizkiogu:

s = i

S = i

n 1 = / mi (xi – xi – 1)

n 1 = / Mi (xi – xi – 1)

P1, P2, P3, …, Pk … partizioen segida bat badugu, azaleren bi segida lotu beharko dizkiogu:

s1, s2, s3, …, sk … (txikiagora kalkulatutakoak)

S1, S2, S3, …, Sk … (handiagora kalkulatutakoak)

Partizioaren diametroak zerora jotzen duela pentsatuko dugu (hau da, laukizuzenen oinarriak nahi bezain txikiak egin daitezkeela)

Kenduren segida aztertuta: S1 – s

S2 – s2, S3 – s3, …, Sk – sk, … zerorantz jotzen badute,, horrek esan nahi du sk eta Sk azalerek limite berdin bat dutela, eta hori kurbaren azpiko azalera dela. Kasu horretan, funtzioa integragarria da.

Azalera negatiboak

X ardatzaren azpian dauden esparruek azalera negatiboa dutela onartzen badugu (eremuei dagozkien integralak hala dira), orduan aurreko prozesu horrek edozein funtzio motatarako balio du, f (x) ≥ 0 baldintza jarri gabe

Funtzio negatiboen kasuan ere, txikiagora kalkulatutako azalera kurbaren azpian geratzen da, eta gehiagora kalkulatutakoa, kurbaren gainean, alboko grafikoetan ikus dezakezunez

Funtzio baten integralaren ideia, edozein funtzioren kasuan, funtzio positiboen kasuan ikusi dugun bezalakoa da. Prozesu horretan, kurbaren eta X ardatzaren arteko azalera kalkulatu behar dugu, kontuan hartuta azalera positiboko esparruak eta azalera negatibokoak egoki balioesten direla. Emaitza parte hartzen duten esparruen batura aljebraikoa da: zeinu positiboa izango dute X ardatzaren gainetik daudenek, eta negatiboa, azpitik daudenek

ondorioa

Funtzio mugatu bat integragarria da [a, b] tartean, baldin eta zerorantz jotzen duen diametroa duen P1, P2, …, Pk, … edozein partizio-segidaren kasuan, txikiagora kalkulatutako sk azalerek eta handiagora kalkulatutako Sk azalerek hau betetzen badute: Sk – sk → 0.

Funtzio integragarriak bereizteko modu hau oso gogaikarria da (y = x 2 integragarria da? Izan behar du, baina ematen du oso zaila dela bide hau erabiliz frogatzea).

Dena dela, irizpide horretan oinarrituta, erabiltzeko oso erraza den ondorio berri batera helduko gara: normalean erabiltzen ditugun funtzioak integragarriak dira guztiak.

Bernhard Riemann (1826-1866) X X

txikiagora kalkulatutakoak

handiagora kalkulatutakoak

Funtzio integragarrien familia bat

Hurrengo propietate honek asko erraztuko digu bidea:

f funtzioa jarraitua eta gorakorra bada [a, b] tartean, integragarria da.

Egiaztapena

Hori egiaztatzeko, aurreko orrialdean landutako irizpidea erabili behar dugu.

P1, P2, …, Pk, … partizioen segida bat da. Horietako bat, Pk, hau da:

a = x0, x1, x2, …, xn = b

Sk – sk kendura alboan marraztuta ageri da

Jakina, honako hau betetzen da:

Sk – sk ≤ (Pk-ren diametroa) · [ f (b) – f (a)]

Pk-ren diametroa → 0 bada, orduan

Sk – sk → 0. Beraz, f integragarria da.

Modu berean egiaztatu dezakegu f jarraitua eta beherakorra bada, orduan ere integragarria dela

Orokorrean, edozein funtzio monotono (gorakor zein beherakor) integragarria da.

Propietate lagungarri eta erraza

Funtzio bat bi zatiz eratuta badago eta bi zatiak integragarriak badira, funtzioa ere integragarria da. Esan dezagun zehatzago:

f integragarria bada [a, b] eta [b, c] tarteetan, f integragarria da [a, c] tartean eta hau betetzen da:

Barra gorri eta berdeen arteko kendurak: (Mi – mi) · (xi – xi – 1) pilatu egin daitezke; izan ere, bakoitzaren goiko aldea bat dator hurrengoaren oinarriarekin.

Ondorio baliagarria

b b c =+yy y

ff f a

c a

y = x 2 funtzioa integragarria da [–2, 1] tartean? [–2, 0] tartean integragarria da, jarraitu beherakorra baita; [0, 1] tartean erebai, jarraitu gorakorra baita. Beraz, integragarria da [–2, 1] tartean

Modu berean arrazoituta, honako ondorio honetara helduko gara:

Ohiko funtzio guztiak integragarriak dira mugatuta dauden edozein tartetan.

GOGORATU

f mugatuta dago [a, b] tartean, baldin eta tarte horretan infinitu egiten ez bada.

Nola kalkulatu integralak

Badakigu f funtzioa integragarria dela [a, b] tartean. Baina nola kalkulatu f a

b y ? Ikus dezagun:

Esparruaren azalera oinarrizko geometriaren metodoak erabiliz kalkula badaiteke, metodo horiek erabiliko ditugu.

Adibidez, ()xdx 1 –2

4 y : esparrua adierazi eta trapezio bat dela ikusten dugu, 1 eta 3 oinarriak eta 2 altuera dituena. Beraz, () · f 2 13 2 4 2

4 = + = y

Integrala laukizuzenen batura erabiliz ere kalkula daiteke; hau da, () () sf cx x –* ki ii i

k 1 1 –= = / baturaren bidez, xi – 1 < ci < xi izanik; hots, ci da tarteko edozein puntu

Orduan, flims * a b k k ∞ = " + y (Metodo hau oso zaila da eta funtzio batzuetarako baino ez du balio)

(Orrialdeko honetako Ebatzitako 2. ariketa mota honetakoa da).

b y kalkulatzeko metodo indartsu eta oso eroso bat ikusiko dugu; f funtzioaren jatorrizko bat aurkitzen dakigun kasuetarako balio du

Ebatzitako

xdx 25

–

2 Aurkitu honako integral hau laukizuzenen batuketa eginez eta limitea lortuz:

xdx 2 0 1 y

Azalera = 4 1 π r 2 = 4 1 π 52 = 4 25 π ≈ 19,6 u2

lim () () sl m n nn n i 6 12 1 6 2 3 1 * n n 3 ∞ = ++ == " Beraz, xdx 3 1 2 0 1 = y 0 1 n 2 n n – 1 n n = 1 n

a) ()xdx

16

Integralaren propietateak

Ondoren landuko ditugun propietate guztiak oso zentzuzkoak dira. Ikusi berri dugun integralaren kontzeptutik abiatuta arrazoituko ditugu.

1. ()fx dx 0 a

a = y da, f edozein dela ere.

2. f (x) ≥ 0 bada eta integragarria bada [a, b] tartean, () ≥ fx dx 0 a

b y da, eta f (x)

➜ Integralaren propietateak.

≤ 0 bada [a, b] osoan, () ≤ fx dx 0 a

b y da.

3. a < b < c bada eta f integragarria bada [a, c] tartean, orduan: () () () fx dx fx dx fx dx a

b += y y y

c b c a

Gogoan izan f funtzioak zeinua aldatzen badu [a, b] tartean, f a

b y integralak X ardatzaren gainetik eta azpitik dauden azaleren (bakoitza bere zeinuarekin) arteko batura aljebraikoa emango digula. f-ren grafikoaren eta X ardatzaren artean geratzen den azalera kalkulatu nahiko bagenu, negatiboak balio absolutuan hartu beharko genituzke

Adibidez, alboan ageri den f funtzio horretan f a

b y kalkulatzen badugu, 7 – 4 + 1 = 4 azalera-unitate lortuko ditugu.

Azalera bera kalkulatzeko, f a

c y , f c

d y eta , f d b y lortu beharko ditugu, eta horien balio absolutuen arteko batura 12 da. Hori da azaleraren balioa ohiko zentzuan.

4. f jarraitua bada (a, b) tartean, eta lm i xa " + f (x) = α, lm i xb –" f (x) = β alboko limiteak existitzen badira eta finituak badira, orduan honako funtzio jarraitu hau eratuko dugu [a, b] tartean:

f1(x) = ()fx

a b * x = a bada x ∈ (a, b) bada

b 1 = : y

b a

x = b bada eta () () fx dx fx dx a

Azkeneko bi propietate horiek modua ematen digute integralaren definizioa zatikako funtzio jarraituetara ere zabaltzeko, baldin eta adar infiniturik ez badute

b y aipatzen dugunean, f funtzioa [a, b] tartean jarraitua dela onartuko dugu; edo, gehienez ere, eten-puntu batzuk dituela, baina horietan alboko limite finituak daudela.

Oraindik aurrera, ()fx dx a

b a

b a

5. () () () () fx dx gx dx fg xdx a

b += + y y y

6. () () cf xdxc fx dx a

b = y y da, c zenbakia edozein dela ere

b a

b y y

b a

7. x ∈ [a, b] kasuan f (x) ≤ g (x) bada, orduan () ≤( ) fx dx gx dx a

8. f jarraitua bada [a, b] tartean, existitzen da honako hau betetzen duen c ∈ (a, b) zenbaki bat:

b = y

() () () fx dx fc ba –a

Propietate horri kalkulu integralaren batezbesteko balioaren teorema esaten zaio.

Egiaztapena

f jarraitua bada [a, b] tartean, m balio minimoa eta M balio maximoa lortzen ditu (Weierstrassen teorema, 8. unitateko 235. orrialdea). Hau da, x ∈[a, b] edozein dela ere: m ≤ f(x) ≤ M

b y y y

b = y eta () MM ba –a

() mm ba –a

b a

b a

Aurreko 7. propietatearen arabera: ≤( )≤ mf xdxM a

b = 9 direnez, aurreko desberdintzak hau ematen du:

b y

m (b – a) ≤ () ≤( ) fx dx Mb a –a

(c ) a m

Zati b – a egingo dugu: ≤( )≤ m ba fx dx M 1 – a

b y

Horrek esan nahi du (Darbouxen teorema, 8. unitateko 235. orrialdea) honako hau betetzen duen c ∈[a, b] zenbaki bat dagoela:

b – a oinarria eta f(c) altuera duen laukizuzenaren azalera kurbaren azpiko azaleraren berdina da.

f (c) = () ba fx dx 1 – a

Beraz: ()fx dx a

b y

b y = (b – a) f (c) da c ∈[a, b ] zenbakiren baterako

b = y y

Pentsatu eta praktikatu

1 Integral hauek ditugu: ()fx dx 3 1 2 –= y eta ()fx dx 7 5 2 –= y

Zenbat balio du ()fx dx 5 1 –

– y integralak?

2 Arrazoitu desberdintza hau: () ≤| ()| fx dx fx dx a

BEGIRATU

9. propietatea integralekin kalkulu batzuk egiteko lagungarria den konbentzio bat da.

3 Arrazoitu inplikazio hauek:

a –= y

a) f bakoitia bada: ()fx dx 0 a

b) f bikoitia bada: () () fx dx fx dx 2 a a

a 0 –= y y

b yy

b a

4 Lortu kalkulu integralaren B.B.T.-n postulatzen den c puntuaren balioa f (x) = x + 3 funtziorako eta [–2, 4] tarterako

Unitate honen sarreran esan dugun moduan, integrazioak (kurba baten azpiko azalera kalkulatzea) eta deribazioak (funtzio baten aldakuntzaren neurria) erlazio estua dute. Erlazio hori ezartzen laguntzen digun bidea egingo dugu, zorroztasun eta zehaztatsunez

Azalera-funtzioa

[a, b] tartean jarraitua den f funtzio bat emanda, c ∈[a, b] edozein zenbakitarako

kalkula dezakegu f a

F (x) = f a

c y

x y , x ∈[a, b ] funtzio berria hartuko

dugu kontuan: a-ren eta x puntu aldakor baten artean dagoen f-ren azpiko azalera zatia.

Zenbat eta handiagoa izan f-ren ordenatua, orduan eta bizkorrago haziko da bere azpiko azalera (F ), eta, beraz, orduan eta handiagoa izango da F'

f negatiboa denean, azalera ere negatiboa da. Beraz, F beherakorra da eta horren deribatua negatiboa da.

Hemen intuizioz ikusi dugun f-ren eta F'-ren arteko erlazio hori zehaztuko dugu orain.

Kalkuluaren oinarrizko teorema

Isaac Newton (1643-1727)

f funtzioa [a, b] tartean jarraitua bada, F (x) = f a

x y , x ∈[a, b ], funtzioa deribagarria da eta F' (x) = f(x) egiaztatzen da

Egiaztapena

F' (x) lortzeko, hau kalkulatu behar dugu:

lm i 0 h " () () Fx Fx h h– +

Zenbakitzailea hau da:

f

F(y) = ()ft dt y ay → F' (y) = f (y)

y = φ(x), G(x) = ()ft dt () a

x { y = F [φ(x)]

G' (x) = F' [φ(x)] · φ' (x) = f [φ(x)] · φ' (x)

Beraz:

x a

x a

x h h = + + y y y

F (x + h) – F (x) = ff f –x

F (x + h) – F (x ) a x x + h

Aurreko orrialdeko 8. propietatearen arabera (kalkulu integralaren batezbesteko balioaren teorema), f jarraitua denez [x, x + h] tartean, hau betetzen duen c ∈(x, x + h) existitzen da:

x h + y = f (c) (x + h – x) = f (c) · h

f x

x h + = G y = lm i 0

h "

Ondorioa: ()ft dt () a

x { =G y ' = f [φ(x)] · φ' (x)

Beraz: ()ft dt () () x

{ 1

2

x {

>H y ' = = f [φ2(x)] · φ' 2(x) – f [φ1(x)] · φ' 1(x)

➜ anayaharitza.es

Praktika sakondu: kalkuluaren

oinarrizko teorema aplikatzea mota honetako funtzioen erabileran: A ()ft dt ) ( a

x { y

Gottfried Leibniz (1646-1716)

∫a φ(x) f (t) dt -REN DERIBATUA

Aurreko erlazio horrek azaleren kalkulua (integralak) deribazioarekin lotzen du, eta aukera teoriko eta praktiko ugarirako bidea ematen du.

x y , ikusi dugun moduan, f (x)-ren jatorrizko bat da.

f-ren grafikoaren azpiko azalera funtzioa, F (x) = f a

Horregatik, jatorrizkoak kalkulatzeari integrazio edo integralen kalkulu esaten zaio, eta f (x) funtzioaren jatorrizko bat izendatzeko ()fx dx y adierazpena erabiltzen da.

Ebatzitako ariketak

1 Kalkulatu funtzio honen deribatua: edt 1 t x 5 + y

2 Kalkulatu sinu funtzioaren ondulazio baten eta X ardatzaren artean geratzen den azalera.

Hau da, snix dx 0 π y .

➜ Integratu eta deribatu emaitza bera lortzeko.

F (x) = () edtf tdt 1 t xx 55 += yy da, f (t ) = e 1 t + jarraitua izanik.

Kalkuluaren oinarrizko teoremaren arabera: F ' (x) = f (x) = e 1 x +

F (x) = snit dt x 0y esango diogu.

Oinarrizko teoremaren arabera, F ' (x) = sin x. Beraz:

F (x) = snix dx y = – cos x + k (F sinu funtzioaren jatorrizko bat da).

F (0) = snit dt 0 0 y = 0 denez → – cos 0 + k = 0 → k = cos 0 = 1

F (x) funtzioa, beraz, F (x) = – cos x + 1.

Kalkulatu nahi dugun azalera hau da: snix dx 0 π y = F (π) = –cos π + 1 = – (–1) + 1 = 2

Bila gabiltzan azalera 2 u2 da.

Hurrengo orrialdean hori berori modu azkar eta eraginkorragoan kalkulatzeko modua ikusiko dugu.

Pentsatu eta praktikatu

1 F (x) = ()logt dt 4 x 2 0 + y funtzioa daukagu.

Kalkulatu F ' (x).

2 Kalkulatu honako integral hau: cosx dx π/ 0

2 y

Barrowren erregela

Aurreko orrialdeko bigarren ariketa ebatzian eman ditugun urratsak honako teorema honetan erabiltzen dira:

f (x) jarraitua bada [a, b] tartean eta G(x) jatorrizko bat bada, orduan:

b = y

() () fG bG a –a

Egiaztapena

F (x) = f a

x y da kurbaren azpiko azalera funtzioa.

F' (x) = f (x), kalkuluaren oinarrizko teoremaren arabera

G ' (x) = f (x), hipotesi bidez; izan ere, G (x) funtzioa f (x)-ren jatorrizko bat da.

Deribatu bera duten bi funtziok gehienez ere konstante bat dute desberdina. Beraz, F (x) = G (x) + k.

a = y denez, honela geratuko da: G (a) + k = 0; hau da, k = –G (a).

Aurreko berdintza horretan, x = a egingo dugu. F (a) = f 0 a

Beraz, azkenean honela geratuko da: F (x) = G (x) – G (a).

Eta orain, azkeneko berdintza horretan, x-ri b balioa ematen badiogu, hau lortuko dugu: () () fG bG a –a

b = y

Erregela praktikoa (Barrowren erregela) f a

b y integrala kalkulatzeko:

1. f-ren jatorrizko bat, G (x), bilatuko dugu: G (x) = ()fx y dx

2. G (b) eta G (a) kalkulatuko ditugu.

3. () () fG bG a –a

b = y egingo dugu.

x dx

IDAZKERA

Honela idatziko dugu: G (b) – G (a) = ()Gx a b8B

Isaac Barrow (1630-1677)

➜ Egiaztatu Barrowren erregela.

Azalerak integralen bidez kalkulatzea

Ikus dezagun [a, b] tartean jarraitua den y = f (x) kurba baten, X ardatzaren eta x = a, x = b zuzenen artean geratzen den azalera kalkulatzeko metodo sistematiko bat (gogoan izan 366. orrialdean aipatu genituela kalkulu mota hauek).

b 9 kalkulatzean, kasu hauetakoren baten aurrean egon gaitezke: a b + – –

Kalkulagailu batzuek tekla hau dute:

–2 2 5 + y 3 x )

x

Hemen, integralaren emaitzak ez du adierazten aurkitu behar dugun azalera. Alde positiboen eta negatiboen artean dauden konpentsazioen ondorioz gertatzen da hori.

Jokatzeko modu zuzena da zati bakoitzaren integrala bere aldetik banan-banan kalkulatzea eta, gero, horien balio absolutuen batuketa egitea.

y = f (x) kurbaren, X ardatzaren eta x = a eta x = b abzisen artean mugaturiko azalera kalkulatzeko, komeni da honako urrats hauek ematea:

I. Ebatzi f (x) = 0 ekuazioa, kurbaren eta X ardatzaren arteko ebaki-puntuak lortzeko.

II. Aukeratu aurreko ekuazioko erroen artean, a eta b artean daudenak. Pentsa dezagun erro horiek x1, x2 eta x3 direla, txikienetik handienera ordenatuta

Beraz, hau beteko da: a < x1 < x2 < x3 < b.

III. Bilatu f (x)-ren jatorrizko bat. G (x) deituko diogu.

IV. Kalkulatu G (a), G (x1), G (x2), G (x3) eta G (b).

V. G (x1) – G (a), G (x2) – G (x1), G (x3) – G (x2) eta G (b) – G (x3) bila gabiltzan azalera eratzen duten lau esparruen integralak dira.

Esparruen azalerak kantitate horien balio absolutuak dira. Bila gabiltzan azalera horien guztien arteko batura da.

Ikusten duzunez, urrats horiekin ez da beharrezkoa kurba marraztea.

Bi kurbaren artean mugatutako azalera

f eta g ondoz ondoko bi kurbak zehazten dute azalera da f – g kendura-funtzioaren eta X ardatzaren artean geratzen den azaleraren berdina.

f – g f g

) +

➜ Kalkulatu kurba baten eta X ardatzaren arteko azalera.

➜ Bi kurbaren arteko azalera.

Teoria-bitxikeriak: irudi lau ezagunen azalerak integralen bidez lortzea

1 Lortu y = x 3 – x kurbaren, X ardatzaren eta x = 0 eta x = 2 zuzenen artean mugatuta dagoen esparruaren azalera

Ondo dakizunez, ziur aski () xx dx –3 0 2 y integralak ez digu soluzio zuzena emango. Honela jokatu behar dugu:

I. Aurkitu x 3 – x = 0 ekuazioaren soluzioak. –1, 0, 1 dira.

II. Ordenatu [0, 2] tartearen muturrak eta horien artean dauden erroak: 0, 1, 2

III. Bilatu f (x)-ren jatorrizko bat:

G (x) = () () xx dx xx xx 4 2 4 1 2 –3 42 42 == y

IV. G (0) = 0, G (1) = – 4 1 , G (2) = 2

V. G (1) – G (0) = – 4 1

G (2) – G (1) = 2 – 4 1 4 9 –=dn

Bila gabiltzan azalera hau da: 4 1 4 9 4 1 4 9 4 10 2 5 –+ =+ == u2 (Grafikoa prozesua ulertzeko erabili dugu, baina ez da beharrezkoa azalera lortzeko).

2 Aurkitu zer azalera duen

y = x 4 – x + 1 eta y = x 4 – x 3 + 1

funtzioen kurbek eta x = 0, x = 2 zuzenek mugatzen duten esparruak.

Kendura-funtzioa lortuko dugu: y = (x 4 – x + 1) – (x 4 – x 3 + 1) = x 3 – x

Orain, funtzio horren, X ardatzaren eta x = 0, x = 2 zuzenen artean dagoen azalera kalkulatu behar dugu, aurreko ariketan egin dugun moduan.

Beraz, enuntziatuak eskatzen digun azalera 2 5 u2 da

1) (0, 1)

(Kasu honetan ere ez da grafikoa behar eskatutako azalera lortzeko).

Pentsatu eta praktikatu

1 Kalkulatu y = x 3 – x 2 – 6x funtzioaren eta X ardatzaren artean mugatutako azalera.

2 Aurkitu y = x 4 + x 3 eta y = x 4 + x 2 + 6x funtzioen artean dagoen azalera.

Integral inpropioak

Integrala «kurba baten azpiko azalera» dela adierazten duen kontzeptua esparru infinituen kasura eraman dezakegu, honela:

()ft dt lm i x a

x ∞ " + y limitea existitzen bada (eta finitua bada), integral inpropio esaten zaio eta honela definitzen da:

x a ∞ ∞ = " +

a

1 1 y = — x 2

➜ Integral inpropioak

1 ∞ y ez da existitzen.

1 y = x 1

f funtzioa ez badago mugatuta [a, b] tartean, f a Adibidez: lm i t dt lm t dt lm tx ii11 22 22 –x x x x x 0 1 0 1 0 1 0 == == "" " ++ + `j 8 B yy t dt t dt tx lm lm lm ii i 11 1 1 1 ∞ x x x x x 2 0 1 0 2 1 0

Pentsatu eta praktikatu

1 y = √x 1 y = — x 2

1 1

azalera = 2 azalera infinitua

0 –1y d) t dt 1 2 0 –1y

Biraketa-gorputz baten bolumena

y = f (x), x ∈ [a, b] kurbaren zati bat X ardatzaren inguruan biraraztean eratu den biraketa-gorputzaren bolumena kalkulatu nahi dugu.

Irudian gorriz dagoen zatia zilindro bat da; horren oinarriaren erradioa f (ci) da, eta altuera, (xi – xi – 1). Beraz, bolumena hau da:

π f (ci)2 (xi – xi – 1)

Gorputz osoaren bolumena () () fc xx – ii i i

n 2 1 1 –r = / da, gutxi gorabehera

Limitera igaroz, balio zehatza lortuko dugu, integral baten bidez.

y = f (x), x ∈ [a, b] kurbak X ardatzaren inguruan biraraztean eratzen duen biraketa-gorputzaren bolumena: () () fx dx fx dx a

➜ anayaharitza.es

b 22rr = yy

b a

1 Kalkulatu zer bolumen eratzen duen y = x parabolak X ardatzaren inguruan birarazten dugunean 0 eta 4 artean

➜ Biraketa-gorputz baten bolumena.

2 Ondorioztatu kono baten bolumena kalkulatzeko formula.

Teoria eta praktika sakondu: integral mugatua «kurba-arku baten luzera» eta «biraketa-gainazal baten azalera» kalkulatzeko erabiltzea

X ardatzaren inguruan birarazi behar dugun zuzenak y = r h x ekuazioa izan behar du [0, h] tartean r erradioa eta h altuera dituen kono bat eratzeko:

(kono baten bolumenaren formula)

anayaharitza.es Sakontze praktikoa: gorputz ezagunen bolumena integralen bidez lortzea.

Pentsatu eta praktikatu

1 Kalkulatu 5 cm-ko erradioa duen esfera baten bolumena, y = x 25 –2 zirkunferentzierdia X ardatzaren inguruan biraraztean eratu dela jakinda. Zer integrazio-limite hartu behar dugu?

Ebatzitako ariketak eta problemak

1. Kurba batek eta X ardatzak mugaturiko azalera

Kalkulatu y = x 3 – 5x 2 + 6x kurbaren eta X ardatzaren artean dagoen azalera.

Esparrua irudikatu gabe aurkituko dugu azalera:

• x 3 – 5x 2 + 6x = 0 ekuazioa ebatziko dugu.

Soluzioak hauek dira: x = 0, x = 2 eta x = 3 (kurbaren eta OX-ren arteko ebaki-puntuen abzisak).

• Funtzioaren jatorrizko bat kalkulatuko dugu:

• Jatorrizkoak aurreko puntuetako bakoitzean zer balio duen lortuko dugu:

G (0) = 0 G (2) = 3 8 G (3) = 4 9

• Zati bakoitzeko integrala kalkulatuko dugu:

2. Azalerak eta balio absolutuen integralak

f (x) = x 2 – 1 funtzioa emanda, kalkulatu:

a) () dx fx

b) fx() dx

c) y = f(x) kurbaren, X ardatzaren eta x = –2 eta x = 2 zuzenen artean itxitako azalera.

Funtzio bikoitia denez, hau da, f (x) = f (–x), simetrikoa da Y ardatzarekiko. Beraz, eskatutako integrala honela lor dezakegu:

b) y = | f (x)| zatikako funtzio moduan definituko dugu:

EGIN ZUK

Aurkitu f (x) = |x – 1| funtzioa duen grafikoaren, X ardatzaren eta x = –1 eta x = 2 zuzenen artean itxita dagoen azalera.

c) Eskatzen digutena bat dator aurreko atalean lortu dugunarekin. Beraz, eskaturiko azalera hau da: Azalera = 4 u2

Ebatzitako ariketak eta problemak

3. Bi kurbaren arteko azalera

Lortu zer azalera duen y = x 2 2 eta

y 2 = 2x parabolek mugatzen duten esparruak.

Adierazi esparru hori.

• Adierazi bi parabolak: y = x 2 2 , ardatz bertikalarena, eta y 2 = 2x, ardatz horizontalarena:

• Ebaki-puntuen abzisak lortuko ditugu:

EGIN ZUK

Egiaztatu y = 5 3 r x zuzenak y = sin x

funtzioaren grafikoa , 6 5 2 1 r dn puntuan ebakitzen duela

Kalkulatu bi funtzio hauen artean mugaturiko zatiaren azalera:

y = x 5 3 r eta y = sin x

4. Esparru baten azalera

Kalkulatu margoturiko esparruaren azalera, jakinda parabolaren ekuazioa y = x 2 – 1 dela, eta zuzenarena, y = 5 – x.

• Eskatu diguten azalera y = x 2 2 eta y = x2 (zati positiboa hartuko dugu) parabolen artean dagoen zatiarena da; eta hori h(x) esaten diogun kendura-funtzioaren eta X ardatzaren

EGIN ZUK

Aurkitu y = x 2 parabolaren, X ardatzaren eta y = –x + 6 zuzenaren artean itxita dagoen azalera.

• Sistema ebatzi eta A puntua lortuko dugu:

• ABC esparruaren azalera R1 eta R2 esparruen azaleren arteko batura eginda lortuko

Kalkulatu y = x, y = 2x zuzenek eta y = x 2 parabolak mugatzen duten esparru lauaren azalera.

• Zuzenak eta parabola adieraziko ditugu, esparrua zehazteko.

6. Eremu bat zati berdinetan banatzea

Bi ahizpak zati berdinetan zatitu behar duten lursail bat hartu dute herentzian.

Lursail hori y = x 2 parabolaren eta y = 1 zuzenaren artean mugatuta dagoen esparru laua da. y = a zuzen baten bidez zatitzea erabaki dute

Kalkulatu a-ren balioa

• Esparru horren azalera kalkulatuko dugu:

• Esparrua zati y = a egingo dugu.

kurbak y = a zuzenarekin dituen ebaki-puntuak ( a , a) eta (– a , a) dira.

= x 2 kurbarekin zehazten duen azalera hau da:

EGIN ZUK y = x 2 parabolak eta y = 4 zuzenak mugatzen duten esparrua azalera bereko bi zatitan banatu behar da X ardatzarekiko paraleloa den y = a zuzenaren bidez

5. Esparru baten azalera

Ebatzitako ariketak eta problemak

7. Funtzio integrala

F (x) = ()tdt 1 –x 2 1

2 y funtzioa dugu.

2 y Badakigu ()ft dt () a x { : D y ' = f [φ(x)] · φ' (x) Beraz, F' (x) = [(x 2)2 – 1] · (x2)' = [(x 2)2 – 1] · 2x = 2x 5 – 2x Muturrak zein izan daitezkeen ikusteko, F’(x) = 0 egin eta hau lortzen dugu: x1 = 0, x2 = 1, x3 = –1 F '' (x) = 10x 4 – 2 → () ,( ), () '' '' '' FF F 10 00 10 –> <> Maximo erlatibo bat dago x1 = 0 puntuan, eta bi minimo erlatibo, x2 = 1 eta x3 = –1 puntuetan. Mutur horien balioak hauek dira: F (0) = () ()tdtt dt t t 11 33 2 –22 3 0

funtzio horren muturreko 1 2 3 4 –2

F' ' (x )

Aurkitu 1 0 1 1 0 == = = G y y F (1) = ()tdt10 –2 1 1 = y ; F (–1) = ()tdt10 –2 1 1 = y Maximoa: 0, 3 2 dn ; Minimoak: (1, 0) eta (–1, 0). –1 –1 –2 1 2

8. Integrala laukizuzenen arteko baturaren limite moduan

Kalkulatu xdx 3 0 1 y , laukizuzenen arteko batura eginda eta limitera igarota.

EGIN ZUK

[0, 1] tartea luzera bereko n zatitan zatituko dugu. Partizioak honako puntu hauek izango

ditu: ,,, …, nn nn n 1 2 3 1 =

, n i n i 1 – < F tarteari dagokion laukizuzenaren

·… nn n nn nn n n 11 1 1 2 3 1 33 3 3 ++ ++ dd d b nn n l

nn i 1 3dn

) S n n 1 12 3 n 4 33 33 =+ ++ +

xdx 3 0 1 = y ∞ lim n " Sn = ∞ lim n " () n nn 4 1 4 22 + = 4 1

Kalkulatu zer bolumen eratzen duen y = x kurbak Y ardatzaren inguruan biratzen duenean, y = 0 eta y = 2 artean.

EGIN ZUK

Kalkulatu y = –x 2 + 4, –2 ≤ x ≤ 2 kurbak Y ardatzaren inguruan biratzean zer bolumen eratzen duen.

Kalkulatu C (3, 0) zentroa eta 2 erradioa duen zirkunferentzierdi batek X ardatzaren inguruan biratzen duenean eratzen duen esferaren bolumena zein den.

X ardatzaren inguruan biratzean bezala jokatu behar dugu, baina funtzioa x = g (y) eran jarrita. Honela:

Kalkulatu beheko bi funtzioetako bakoitzak X ardatzaren inguruan 1 eta + ∞ artean biratzen duenean eratzen duen esparruaren bolumena a) y = x 1

b) y = x 1

EGIN ZUK

y = x 1 2 funtzioak X ardatzaren inguruan x = 1 eta + ∞ artean biratzean eratzen duen bolumena.

• Lehenengo eta behin, (3, 0) zentroa eta 2 erradioa dituen zirkunferentziaren ekuazioa idatziko

da, a) kasuan bolumen finitu bat dago; b) kasuan, berriz, bolumen infinitu bat. a) kasuko gorputz infinituari Torricelliren tronpeta esaten zaio.

9. Bolumena (Y  ardatzaren inguruan biratzea)

11. Esparru infinitu baten bolumena (Torricelliren tronpeta)

10. Esfera baten bolumena

Gidatutako ariketak eta problemak

Kalkulatu f eta g kurben artean dagoen azalera :

f (x) = x 4 + 5x 3 – 7x 2 + 2x – 1

g (x) = x 4 + 4x 3 – 8x 2 + 4x – 1

Aurkitu ondorengo hau betetzen duen bigarren mailako P (x) polinomio bat:

P (0) = P (2) = 0

()xdx P1 0 1 = y

• Bi kurbaren arteko azalera da kendura-funtzioaren eta X ardatzaren artean dagoen azaleraren berdina.

• Lortu kendura-funtzioa, eta X ardatzarekin dituen ebaki-puntuak.

• Lortu kendura-funtzioaren jatorrizko bat.

• Kalkulatu zati bakoitzaren azalera eta egin batuketa.

Soluzioa: Azalera = 3 8 12 5 12 37 += u2

• P (0) = 0, P (2) = 0 izateak esan nahi du 0 eta 2 polinomioaren erroak direla

• Nola adierazten da a eta b erroak dituen P (x) polinomio bat?: P (x) = k(x – a)(x – b)

• Lortu bigarren mailako adierazpenaren integrala k-ren funtzioan

• Berdindu emaitza 1ekin. Ekuazio ebaztean, k-ren balioa lortuko duzu

Soluzioa: P(x) = – 2 3 x2 + 3x

Lortu integral inpropioa:

• Ikusten duzunez, f (t) = t –1/3 ez dago definituta x = 0 puntuan. Hori dela eta, integral inpropioa da.

• Aurkitu tdt / x 13 1 – y = I (x)

• Eta, ondoren, kalkulatu ()Ix lm i x 0 " + .

Soluzioa: 2 3

Aurkitu honako kurba honek: y = x 2 1 2 +

X ardatzaren inguruan biratzean eratzen duen biraketa-gorputzak zer bolumen duen x = –1 eta x = 2 zuzenen artean.

• Gogoan izan formularen bidez lor dezakegula y = f (x), x ∈[a, b] kurbak X ardatzaren inguruan biratzean eratzen duen biraketa-gorputzaren bolumena:

b 2 y

V = r ()fx dx a

2 –1

• Ezarri formula eta bila gabiltzan bolumena lortuko duzu.

Soluzioa: Bolumena = , 20

153 765u 3 r r =

1. Bi kurbaren arteko azalera

2. Baldintza batzuen bidez zehazturiko polinomio baten eraikuntza

3. Integral inpropioa: mugatu gabeko funtzio batek zehazturiko azalera

4. Bolumena (X  ardatzaren inguruko bira)

Proposatutako ariketak eta problemak

Trebatzeko

Integral mugatua

1 Kalkulatu integral hauek:

x x dx 1 2 0 2 + y b)

e 1y d) 3

– + y

Azalerak irudia ezagutuz kalkulatzea

12 Honako integral hauek kalkulatzeko, nahikoa da integralaren barruan dagoen ekuazioa zer kurba motarena den bereiztea eta geometriako oinarrizko metodoak erabiliz azalera kalkulatzea:

a) xdx2 0

4 y b) ()xdx 1 1 5 + y

dx 1

3 Aurkitu f (x) =  x 1 1 +  – 3cos (2πx) funtzioak I = [0, 2] tartean duen integral mugatuaren balioa.

4 Aurkitu: () xx dx –2 0 3 y y || xx dx –2

0 3 y

≤ ≤≤ x x x x 2 01 12 –bada bada < 2

≤≤ ≤ x x x x 1 11 13 –bada bada < 2 +

f(x), X ardatz, x = a eta x = b arteko azalera

4 –+ y

b) Aurkitu y = x 2 + x – 2 kurbak X ardatzarekin –1 eta 4 abzisen artean zehazten duen azalera.

7 Kalkulatu y = 3x2 – x + 1 kurbaren, X ardatzaren eta x = 0 eta x = 4 zuzenen artean dagoen esparruaren azalera.

8 Kalkulatu y = 3x – 2 kurbaren azpian y = 0, x = –1 eta x = 1 zuzenen artean dagoen azalera.

9 Aurkitu y = x kurbaren azpian x = 0 eta x = 4 artean dagoen azalera.

10 Kalkulatu y = (x – 1)2 (x + 1) kurbak eta y = 0, x = 1, x = 2 zuzenek zehazten duten esparruaren azalera.

11 Kalkulatu honako kurba honek: y =  x x 2 –2

eta x = 2, x = 3, y = 0 zuzenek zehazturiko esparruaren azalera.

c) x 36 –2 6 0y dx d) x 36 4 –2 0 3 y dx

* Gogoan izan a eta b ardatzerdiak dituen elipsearen azalera

A = πab dela.

13 Aurkitu honako integral hauek grafiko bidez:

4 9 C y

a) ()xdx 2 2 5 –+ y b) ()xdx 64 2 –2 0

Bi kurbaren arteko azalera

14 Aurkitu, kasu hauetako bakoitzean, ematen diren parabola-bikoteen artean dagoen azalera:

a) y = x 2 – 5 eta y = –x 2 + 5

b) y = x 2 eta y 2  = x

15 Kalkulatu honako kasu hauetako bakoitzean emandako kurben artean mugaturiko azalera:

a) y = 4 – x 2 y = 8 – 2x 2

b) y = x 2 y = 4 – x 2

c) y = x 3 – 3x 2 + 3x y = x

d) y = x (x – 1) (x – 2) y = 0

e) y = x 2 y = 1

f) y = x 2 – 2x y = –x 2 + 4x

g) y = –x 2 + 4x – 4 y = 2x – 7

16 Irudikatu zer esparru mugatzen duten kurba honek: y = x (3 – x)

eta y = 2x – 2 zuzenak, eta kalkulatu horren azalera.

17 Irudikatu zer esparru lau mugatzen duten parabola honek: y 2  – x = 1

eta (1, 0) puntutik igarotzen den y = x zuzenarekiko paraleloak. Kalkulatu esparru horren azalera.

18 Kalkulatu y = 2x – x2 funtzioak eta funtzio horrek abzisaardatza ebakitzen duen puntuetan dituen ukitzaileek mugatzen duten esparruaren azalera.

Proposatutako ariketak eta problemak

19 xy = 6 hiperbola eta x + y – 7 = 0 zuzena emanda, kalkulatu horien artean mugatutako azalera.

20 Kalkulatu zer azalera zehazten duten kurba honek, y = x 3 – 2x 2 + x eta koordenatuen jatorrian ukitzaile duen zuzenak.

21 Kalkulatu zer azalera mugatzen duen y = ln x kurbak, X ardatzarekin duen ebaki-puntuaren eta x = e abzisa-puntuaren artean.

22 Aurkitu funtzio hauen grafikoek zehazten dituzten esparruen azalerak.

a) f (x) = x 3 + x 2 g (x) = x 3 + 1

b) f (x) = x 2 g (x) = 1 – x 2 y = 2

c) f (x) = x (x – 1)(x – 4) g (x) = 0

d) f (x) = x 2 – 2x g (x) = x

e) f (x) = x 3  – x g (x) = –x 2

f ) f (x) = 2 – x 4 g (x) = x 2

Bolumena

23 Kalkulatu esparru hauetako bakoitzak X ardatzaren inguruan biratzean eraturiko bolumena:

a) f (x) =  x 1 –, x = 1 eta x = 5 artean

b) f (x) = x 2 , x = –1 eta x = 2 artean

c) f (x) = x – x 2 , x = 0 eta x = 1 artean

24 Kalkulatu zer bolumen eratzen duen beheko grafikoetako bakoitzak zehazturiko esparruak X ardatzaren inguruan biratzean:

a) f (x) =  x , g (x) = x 2 b) y 2 = 4x, x = 4

Funtzio integrala

25 Kalkulatu honako funtzio hauen deribatuak:

a) F (x) =  cost dt x 0y

b) G (x) =  ()tdt 1 x 24 3 + y

c) H (x) =  edt t x 0 –2 y

d) J (x) =  ()tdt 1 24 3 5 + y

Adi! Azkenekoa errazena da.

Ebazteko

26 Kalkulatu:

a) () d x x x 1 1 –1 3 2 + y

b) ()xdx e 10 x2 5 0 + y

27 Funtzio hau daukagu: g (x) =  ≤ ≤ ≤

2 *

x x x

x x x 2 10 3

20 02 24 –

–bada bada bada

< < <

Adierazi g funtzioa eta kalkulatu honako integral mugatu hauetako bakoitzaren balioa:

I =  ()gx dx 2 1 –y

4 y

J =  ()gx dx 1

4 –y

K =  ()gx dx 2

28 f (x) = ax 3 + bx 2 + cx + d funtzioari buruz hau dakigu: x = 1 puntuan maximo erlatibo bat du, (0, 0) puntuan inflexiopuntu bat, eta ()fx dx 4 5 0 1 = y .

Kalkulatu a, b, c eta d.

29 f (x) =  xx x 31 23 2 ++ + da. Kalkulatu f (x)-ren grafikoak, X ardatzak eta x = 0 eta x = 2 zuzenek mugatzen duten eremuaren azalera.

30 Irudikatu y =  x 1 2 , y = x, y = 8x funtzioen grafikoen artean mugaturiko esparrua, eta kalkulatu horren azalera

31 Kalkulatu f (x) = 4x eta g (x) = x 3 kurben grafikoek [0, 2] tartean mugatzen duten azalera, aurretik, tarte horretan f ≥ g dela frogatuz.

32 Kalkulatu zer azalera duen honako kurba honek: y =  x92 4 2 + abzisa-ardatzak eta kurbaren inflexio-puntuetatik igarotzen diren zuzen bertikalek eratzen duten esparruak.

33 f (x) =  x 2 eta g (x) = | 1 – x | dira:

a) Irudikatu bi grafikoak ardatz beretan eta aurkitu horien ebaki-puntuak.

b) Zehaztu bi grafikoen artean mugatutako esparruaren azalera.

34 Kalkulatu f (x) =  x x 4 4 2 + funtzioak, X ardatzak eta x = a eta x = b zuzenek mugatzen duten azalera, a eta b balioak f-ren maximoaren eta minimoaren abzisak direla jakinda.

35 Aurkitu (0, 1) eta (3, 0) puntuetatik igarotzen den bigarren mailako polinomio bat, honako hau jakinda: kurbak, Y ardatzak eta X ardatz positiboak mugatzen duten azalera 4/3 da.

36 Aurkitu ardatz bertikala duen parabola baten ekuazioa honako hau jakinda: 4ko malda duen zuzen batekiko ukitzailea da koordenatuen jatorrian, eta X ardatzarekin [0, 3]-ko oinarria eta 9ko azalera duen esparru bat mugatzen du.

37 y = x2 kurbaren eta y = bx zuzenaren arteko esparruaren azalera 2 9 dela jakinda, kalkulatu b-ren balioa.

38 Kalkulatu zein izan behar den a-ren balioa y = –x2 + ax kurbak eta X ardatzak mugatzen duten esparruaren azalera 36 izateko.

39 y = x 1 2 + funtzioa izanda, kalkulatu zein izan behar den a-ren balioa kurba horrek eta x = 0 eta x = a zuzenek mugaturiko azalera 2 izateko

40 f (x) = 2x 3 – 3x 2 + k funtzioak balio positiboak eta negatiboak hartzen dituela jakinda, aurkitu zein izan behar den k-ren balioa, kontuan hartuz X ardatzak, x = –1, x = 2 zuzenek eta f(x) kurbak mugatzen duten esparrua azalera bereko bi zatitan erdibituko duela X ardatzak.

41 y = x 2 eta y = a kurbak ditugu, 0 < a < 1 izanda. Bi kurbek abzisa positiboko (x0, y0) puntuan ebakitzen dute elkar. Kalkulatu a , kontuan izanda bi kurben artean mugaturiko azalera berdina dela x = 0 puntutik x = x0 puntura eta x = x0 puntutik x = 1 puntura.

42 y = ax 2 eta y = ax + a ekuazioak p parabola baten eta r zuzen baten ekuazioak dira, hurrenez hurren. Egiaztatu baieztapen hauek:

a) p-ren eta r-ren arteko ebaki-puntuak ez dira a-ren balioaren araberakoak.

b a-ren balioa bikoiztuz gero, p eta r arteko azalera ere bikoiztu egiten da.

43 Adierazi higikari baten posizio-funtzioa, jakinda 8 cm/s2-ko azelerazio konstantea duela, abiadura 0 dela t = 3 unean, eta 11 segundoan jatorrian dagoela.

44 Higikari bat zuzen desplazatzen da higidura uniformeki azeleratuz, 2 m/s2-ko azelerazioaz eta hasierako abiadura v0 = 1 m/s duela. Kalkulatu eta konparatu zer distantzia egiten duen t = 0 eta t = 2 bitartean eta t = 2 eta t = 3 bitartean.

45 Hartu kontuan y = ex eta y = e2x kurbek eta x = k zuzenak zehazten duten planoaren esparrua.

a) Kalkulatu zer azalera duen k = 1 denean.

b) Zehaztu zein izango den k > 0 balioa, azalera 2 izateko.

46 Kalkulatu y = x2 – 2x – 3 kurbak eta muturtzat 0 eta 1 abzisa-puntuak dituen kurbako kordak mugaturiko esparruaren azalera.

47 y = x 4 4 + kurbak, koordenatu-ardatzek eta x = 4 zuzenak S gainazala mugatzen dute. Kalkulatu S-ren azalera eta S-k X ardatzaren inguruan biratzean sortzen duen irudiaren bolumena

48 Kalkulatu x y 25 1 2 2 += elipseak OX-ren inguruan bira oso bat ematean zehazten duen gorputzaren bolumena

49 Kalkulatu zer bolumen duen koordenatu-ardatzek, y = e –x ekuazioko kurbak eta x = 3 zuzenak mugaturiko esparruak X ardatzaren inguruan biratzean eratzen duen gorputzak.

50 Kalkulatu zer bolumen lortzen dugun y =  , x 1 x = y 2 , x = 4 funtzioen grafikoek mugatzen duten esparruak X ardatzaren inguruan biratzean.

51 Kalkulatu zer bolumen eratzen duen hiperbola honek x y 4 9 1 –2 2 = x ∈[–4, 4] denean

52 Kalkulatu zer azaleratako eremua mugatzen duten X ardatzak, x = 4 zuzenak eta funtzio honen grafikoak:

(x) =  ≤ ln x e x xe ex

0 bada bada < < *

53 Aurkitu honako funtzio hauen deribatuak:

54 Integrala ebatzi gabe, adierazi non dagoen maximo edo minimo erlatiboa honako funtzio honetan: F (x) =  ()tdt 1 –x 2 0y

55 Badakigu () () ft dt xx 1 x 2 0 =+ 9 dela, Á osoan jarraitua izanik. Kalkulatu f (2).

56 F(x) =  cost dt x 2 1y da. Aurkitu funtzio horrek [0, 2π] tar-

Proposatutako ariketak eta problemak

tean izan ditzakeen muturrak.

57 Aurkitu honako funtzio hauen maximo eta minimo erlatiboak:

a) F (x) =  () ()tt dt 12 –x 22 0 + y

b) G (x) =  log t t dt x 1y

Galdera teorikoak

58 (x) funtzio integragarria da. () d gx x 4 0 3 = y eta ()gx dx 6 2 3 = y badira, zein da ()gx dx 2 0y -ren balioa?

59 Honako adierazpen hauetako zeinek ematen digu f-ren grafikoak eta abzisa-ardatzak mugatzen duten esparruaren azalera? f a b c

62 f funtzio bat positiboa bada aldagaiaren balio guztietarako, horren edozein jatorrizko funtzio gorakorra da bere puntuetako bakoitzean. Zergatik?

63 Kalkulatu funtzio honen deribatua:

bi modutan:

a) f a

c y b) f a

c) ff c a

c y

b b + y y d) ff –a

b c b + yy

60 I, II eta III grafikoak f funtzio deribagarri batena, horren f' deribatuarena eta f-ren F jatorrizko batena dira, baina ez derrigorrez ordena horretan. Identifikatu grafiko bakoitza dagokion funtzioarekin, eta arrazoitu erantzuna.

I II III

61 Badakigu f funtzio batek, abzisa-ardatzak eta x = 1 eta

x = 5 zuzenek mugatzen duten azalera 6 dela. Zenbat handiagotuko da azalera f funtzioa bi unitate eramaten badugu gorantz?

2 y

F (x) =  cost dt x 0

a) F (x) modu esplizituan lortuz, eta, gero, deribatuz.

b) Kalkuluaren oinarrizko teorema erabiliz.

64 Aurkitu funtzio hauen deribatuak:

a) F (x) =  cost dt 3 2 3 y

b) F (x) =  ()tdt13 x 2 0 + y

c) F (x) =  t x dt 1 a 1 + y

(Kontuan izan x integraletik kanpo irten daitekeela)

d) F (x) =  t x dt 1 x 1 + y

3 + y

x 3 2

e) F (x) =  ()tdt t x

65 y = x2 funtzioa izanda, aurkitu c ∈[0, 2] zer punturekin izango den azalera hau: xdx 2 0 2 y

2ko oinarria eta f(c) altuera duen laukizuzenaren azaleraren berdina.

Hau da, zer puntuk beteko duen hau: 2 f (c ) =  xdx 2 0 2 y

Zer teoremak ziurtatzen du c existitzen dela?

66 F funtzioa [0, + ∞) tartean definituta dago eta hau betetzen du:

F (x) =  () ln tdt 2 x 0 + y

Aztertu honako baieztapen hauek zuzenak ala okerrak diren:

a) F (0) = ln 2

b) F ' (x) =  x 2 1 + , x ≥ 0

c) F gorakorra da bere definizio-eremuan.

67 Egiaztatu honako desberdintza hau:

Sakontzeko

68 a) Kalkulatu 7 cm-ko eta 11 cm-ko erradioak eta 6 cm-ko altuera dituen kono-enborraren bolumena.

b) Lortu formula hau:

V =  () rrr r 3 1 h 1 2 2 2 12 r ++

r1, r2 erradioak eta h altuera dituen kono-enbor baten bolumena ematen digu.

69 a) Egiaztatu, kalkulu integrala erabiliz, x2 + y2 ≤ 9 zirkuluaren azalera 9π dela.

b) Egiaztatu, kalkulu integral erabiliz, r erradioa duen esferaren bolumena V = 3 4 π r 3 dela.

70 Kalkulatu x y 16 9 1 2 2 += elipseak mugaturiko esparruaren azalera.

71 Egiaztatu, kalkulu integrala erabiliz, x2 + 4y2 = 4 elipsearen azalera 2π dela

72 Egiaztatu a x b y 1 2 2 2

2 += elipsea biraraztean eratzen den elipsoidearen bolumena hau dela:

a) 3 4 π a b2 , baldin eta X ardatzaren inguruan biratzen badu.

b) 3 4 π a 2 b, baldin eta Y ardatzaren inguruan biratzen badu.

AUTOEBALUAZIOA

1 f (x) = x 3 + 3x 2 funtzioa izanda, kalkulatu:

a) f (x)-ren grafikoak, X ardatzak eta x = –2 eta x = 1 zuzenek mugatzen duten azalera.

b) f (x) eta g (x) = x + 3 funtzioen grafikoen artean mugatuta geratzen diren bi esparruen azalerak.

2 Kalkulatu zer azalera mugatzen duten f (x) = x 2 – 2x + 2 funtzioaren grafikoak, Y ardatzak eta f funtzioak x = 3 puntuan duen ukitzaileak.

3 Kalkulatu: ||xdx21 –0 2 y

4 Aurkitu f (x) =  () x 2 1 –2 funtzioak x ≥ 2 5 kasuan irudikatzen duen grafikoaren eta y = 1, x =  2 5 zuzenen artean geratzen den eremuaren azalera.

73 Aurkitu honako funtzio honen deribatua:

74 Aztertu honako integral inpropio hauek existitzen diren, eta hala bada, kalkula itzazu:

r 1 1 > ∞ r 1:

c) t dt 1 1 ∞

∞ 2 – + y d) edx ∞ x 0 –y

e) x dx 1 3 0 1 y f ) x dx 1 0 1 y

g) x dx 1 1 –2 0 1 y h) () u du 2 –2 2 3 y

75 f (x) =  e 1 1 x + eta g (x) =  ()ft dt x 0y bada, aurkitu: lm i x 0 " () x gx

76 Zehaztu zer balio izan behar duen a > 0 parametroak, X ardatzak eta beheko funtzio horrek mugatzen duten esparru lauaren azalera 108 izan dadin:

f (x) = a (x + 2)2 – (x + 2)3

5 Kalkulatu zer azalera mugatzen duten f (x) = e x funtzio esponentzialaren grafikoak eta x = 0 eta x = 2 abzisa-puntuak

6 F (x) =  ln tdt x 1

2 y funtzioa dugu, x ≥ 1 izanik:

a) Kalkulatu F ' (e).

b) F funtzioak inflexio-punturik du? Arrazoitu erantzuna.

7 a) Aurkitu 5 cm-ko erradioa eta 6 cm-ko altuera duen kono baten bolumena, funtzio egokia komeni den

b) Antzera jokatuz, ondorioztatu r erradioa eta a altuera duen kono baten bolumenaren formula.

lotzen dituen kurba horren kordak.

tartean integratuz.

➜ anayaharitza.es Ariketa hauen ebazpena.

Unibertsitatera sartzeko probarako

III. multzoa: Analisia

Badakizu L’Hopitalen erregela erabiltzen

() lm gx fx i erako limiteak kalkulatzeko?

Badakizu adierazpen bat prestatzen L’Hopitalen erregela ezarri ahal izateko bertan?

Menderatzen dituzu funtzioen adierazpena egiteko beharrezkoak diren teknikak?

Teknika hauekin eta beste zenbaitekin, hainbat problema ebatzi ditzakezu.

Badakizu alboko limiteak erabiltzen puntu baten jarraitutasuna eta deribagarritasuna aztertzeko?

Eta «zatika» definitutako funtzioak aztertzeko?

Menderatzen dituzu deribazio-erregelak?

Ezagutzen dituzu deribatuen erabilerak?

Gauza zara lortzeko, beharrezkoa denean, funtzio batek puntu batean duen deribatua, deribatuaren definizioa ezarrita?

Erlazionatzen dituzu jatorrizkoen kalkulua eta deribazioa?

Menderatzen duzu nahiko ondo nola lortu jatorrizkoak?

Lotzen duzu prozesu hori integrazio prozesuarekin?

Ariketen eta problemen adibideak

Unibertsitatera sartzeko ebaluazio-proban hainbat zailtasun motatako problemak topatu ditzakezu. Adibidez:

Kalkulatu b eta c, jakinda ()

Deribagarria izateko, jarraitua izan behar du,

dela x = 0 puntuan.

c izan behar da.

Limite hori kalkulatzeko L’Hopitalen erregela erabiliko dugu, eta c = 1 lortuko dugu.

Deribagarria dela ikusteko, eskuineko deribatua lortuko dugu deribatuaren definiziotik abiatuta:

Eta ezkerreko deribatuarekin berdinduta, hau lortzen dugu: b = –2 1

Pila batek sortzen duen potentzia P(t) = 25te–t2/4 adierazpenak ematen digu, t > 0 funtzionatzen duen denbora-tartea izanik.

a. Kalkulatu zer baliotarantz jotzen duen pilak sortutako potentziak, mugagabe utziz gero martxan.

b. Zehaztu pilak sortzen duen potentzia maximoa, baita zer unetan sortzen duen ere.

c. Pilak t unera arte sortutako energia, E(t), erlazionatuta dago potentziarekin, E l (t) = P(t) adierazpenaren bitartez, E(0) = 0 izanik. Kalkulatu zenbatekoa den pilak t = 0 eta t = 2 uneen artean sortu duen energia.

a. ()Pt 0 = lm i x ∞ " + berehalakoa da.

b. Maximoa lortzeko, lehenengo deribatua berdin 0 egin behar dugu: () () Pt te t 2 25 2–/ t 4 2 –2

–12 =

c. () () Et Pt dt ek–50

==

y

e 50 50 –/ t 4 –2 = Orain, oso erraza da t = 0 eta t = 2 artean sortutako energia kalkulatzea: () E e 250 50 – =

Problema hauek ebazteko behar izan diren teknikak ezkerrean berrikusita ageri direnak dira.

anayaharitza.es webgunean hau aurkituko duzu:

• Analisirako oinarrizko teknikak ikasteko bide bat, arintasuna eskuratu dezagun teknika horiek ulertzeko, erabiltzeko eta aplikatzeko.

• Unibertsitatera sartzeko proben problema-bilduma bat, ebatzitakoak, proposatutakoak, laguntza eta guzti emanda, jarraibideak emanda…

Autoebaluazioa

III. multzoa : Analisia ➜

1 Kalkulatu ondorengo limite hauek:

a) lm i x 1 " ln x x 1 1 1 ––cm b) lm i x 0 " cotg x x 1 –dn

c) lm i x 0 " () ln cos sn i x xx – d) lm i x 0 " (x + e 2x)1/x

2 a) Honako funtzio hau emanda:

f (x) = ≤ xx b ax x x 2 1 1 1 ––bada bada > 3 2 ++ *

aurkitu zein izan behar diren a eta b parametroak, funtzioa deribagarria izateko Á osoan.

b) Irudikatu.

3 Funtzio hau daukagu: f (x) = ≤ ln xe ax x x x 0 0 bada bada > x 2 + )

a) Aurkitu zein izan behar den a-ren balioa f jarraitua izateko Á-n.

b) Kalkulatu f ' (x), ahal den tarteetan.

c) Lortu ()fx dx 1 0 –y .

4 f (x) funtzioa honela definituta dago:

f (x) = ≤ cosx xaxb x x 0 0 –bada bada > 2 ++ )

eta a eta b zenbaki errealak dira.

a) Aurkitu zein izan behar den a-ren eta b-ren balioak funtzioa jarraitua eta x = 0 puntuan deribagarria izateko.

b) a-ren eta b-ren aurreko balio horien kasuan, aztertu funtzioak mutur erlatiborik duen x = 0 puntuan.

c) Kalkulatu funtzioak eta X ardatzak ,1 2 –π : D tartean zehazturiko eremuaren azalera.

5 a) Aztertu honako funtzio honen hazkundea: f (x) = 1 + 2x + 3x 2 + 4x 3

b) Egiaztatu 1 + 2x + 3x 2 + 4x 3 = 0 ekuazioak soluzio erreal bakarra duela, eta aurkitu soluzio hori barne hartzen duen 1 luzerako tarte bat.

c) Irudikatu.

6 Aztertu y = e xx23 –x 2 ekuazioa duen funtzioaren asintotak eta maximo eta minimoak. Egin adierazpen grafikoa.

7 f (x) = || x x 1 –2 funtzioa daukagu.

a) Zehaztu asintotak eta aztertu zer posizio hartzen duten kurbarekiko.

b) Kalkulatu mutur erlatiboak.

c) Adierazi grafikoki.

8 f (x) = ax ax b –2 + funtzioa daukagu, x ≠ a izanik. Kalkulatu zein izan behar den a-ren eta b-ren balioa f-ren grafikoa (2, 3) puntutik igarotzeko eta -4ko malda duen asintota zeihar bat izateko. Irudikatu funtzioa a eta b-rako lortu dituzun balioetarako.

9 f (x) = ax 3 + bx 2 + cx + d. Lortu a, b, c eta d-ren balioak, jakinda f (x) funtzioak mutur lokal bat duela x = 0 abzisa-puntuan, (1, 0) puntua inflexio-puntu bat dela, eta puntu horretan duen zuzen ukitzailearen malda –3 dela. Irudikatu.

10 O zentroa eta 10 cm-ko erradioa duen zirkunferentzia batean, AB diametroa eta diametro horrekiko perpendikularra den CD korda marraztu ditugu.

O zentrotik zer distantziatara egon behar du kordak ADC eta BCD triangeluen azaleren kendura maximoa izateko?

11 Kalkulatu a-ren eta b-ren balioak Rolleren teorema ezarri ahal izateko f (x) = ≤≤ ≤ ax bx x x x 21 02 25 bada bada < 2 + + * funtzioari [0, 5] tartean. Zer puntutan beteko da teorema?

12 f (x) = x x – 2x + 1 funtzioa izanda:

a) Frogatu badagoela α ∈ (1, 2) bat f ' (α) = 0 betetzen duena.

b) Ziurtatu dezakegu existitzen dela β ∈ (1, 3) bat f (β) = 10 betetzen duena?

c) Idatzi f -k 2 abzisa-puntuan duen ukitzailearen ekuazioa.

13 Arrazoitu f (x) = 1 + x | x | funtzioari batezbesteko balioaren teorema ezar dakiokeen [–1, 1] tartean, eta, erantzuna baietz bada, kalkulatu zer puntutan betetzen den teorema.

14 Kalkulatu: a) x x dx 41 2 + y b) xe dx 2 x3 0 1 2 y

15 a) Aurkitu bigarren mailako funtzio polinomiko bat, jakinda grafikoa (0, 0) puntutik igarotzen dela eta (1, 1) puntuan maximo bat duela.

b) Aurkitu lortu duzun kurbak eta abzisa-ardatzak zehazten duten eremu finituaren azalera.

16 Kalkulatu zein den a > 0 balioa, f (x) = –x 2 + a 2 parabolak eta abzisa-ardatzak zehaztutako eremuaren azalera bat etorri dadin f (x) funtzioak x = –a puntuan duen zuzen ukitzailearen maldarekin.

17 Kalkulatu y = x 3 – 3x kurbak eta y = x zuzenak mugatutako azalera.

18 Aurkitu zenbateko azalera duen X eta Y ardatzek eta honako funtzio honek mugaturiko eremuak:

PROBABILITATEA IV. multzoa

14. Zoria eta probabilitatea

15. Probabilitate-banaketak

Zoria eta probabilitatea 14

Probabilitatea eta zorizko jokoak

Zorizko jokoetarako zaletasuna aspaldiko kontua da: dadoak, kartak, txokoak… jokorako tresnak izan ziren. Zoriak hainbat problema-egoera sortzen zituen, eta batzuk modu gutxi gorabehera zientifikoan ebazten saiatu ziren. Problema mota horiek modu sistematikoan lantzeko lehenengo urratsak Cardanok eman zituen. 3. unitatean aipatu dugun matematikari hau jokalari sutsua izan zen, eta jokalarientzako idatzi zuen Zorizko jokoen liburua eskuliburuaren zati batean, zoria aztertu zuen. Lan hori 1663. urtean argitaratu zen, Cardano hil eta mende bat geroago; izan ere, Elizak debekatu eta jazarri egiten zituen gai horiek.

xvii. mendean, De Meré zaldunak (filosofoa, literatoa eta jokalari konpultsiboa) dado-jokoetan sortu zitzaizkion problema batzuen gainean galdetu zion bere lagun Blaise Pascali. Pascalek problema horiek aztertu, eta Pierre Fermati proposatu zizkion, gutun bidez. Bi matematikariek gutun-truke oso emankorra izan zuten, eta elkarri bidali zizkioten proposatutako problemei emandako ebazpenak, baita beste probabilitate-egoera batzuei buruzko burutazioak ere. Eskutitz horiek, Christiaan Huygensek 1657an argitaratu zituenak, probabilitatearen teoriaren sorrera ekarri zuten.

Zientzia gisa garatzea

xvii. mendearen amaieran, ausazko gertakariei buruzko ezagutzak hainbat ziren jada, eta ausazko jokoekin lotuta, proposatutako problema ugari zeuden, behar bezala ebatzita. Baina problema-mota horiek guztiak bilduko zituen ikuspegi teorikoa falta zen.

Zoria jokoaren mundutik bereizita aztertu zuen lehena Jacob Bernoulli izan zen. 1713an, Bernoulli hil ondoren, Aieruaren artea bere lana argitaratu zen. Liburu horretan, Jacobek aurreko ezagutzak bildu, sistematizatu eta probabilitatearen lehen definizio formala eman zuen.

Thomas Bayes ingelesak eta Lagrange italiarrak xviii. mendearen erdialdera arte probabilitateari buruz zeuden deiak bateratu zituzten. Bigarrenak Probabilitateen lehen teoria orokorra bildu zuen.

Pierre-Simon Laplacek, mende bat geroago, Probabilitateen teoria analitikoa argitaratu zuen. Lan horretan, 40 urte lehenagotik ordura arte lortu eta zabaldu zituen emaitza ugari bildu eta antolatu zituen. Teoria Probabilitateen teoriari inoiz egin zaion ekarpenik handiena da.

Lan horrek probabilitateen kalkulua matematikaren arlo autonomo gisa lantzen hastea ekarri zuen, eta horrek bultzada eman zion gaur egun duen garapen aparta lortzeko.

Christiaan Huygens (1629-1695).

Probabilitate modernoa. Erabilerak

xx. mendearen hasieran, probabilitatearen teoria formalizatuz joan zen, hainbat matematikariren ekarpenei esker. Horien artean, aipagarriak dira jatorri errusiarreko matematikariak. 1933an, Andrei Kolmogorovek hainbat ikuspuntu bateratu eta, multzoen teorian oinarrituta, probabilitatearen teoria axioma bihurtu zuen, zorroztasuna eta orokortasuna emanez. Probabilitate modernoak erabilera ugari ditu ekonomian, informatikan, zientzia fisikoetan, biologian (adibidez, DNA sekuentziak deszifratzeko)…

Jokoetatik jaio zen zientziak ezer gutxi du jokotik

EBATZI

Probabilitatea saiakuntzen bidez lortzea

Paperezko orri batean 3 cm × 3 cm-ko karratuak dituen koadrikula egin dugu. Paper horren gainera 2 zentimoko txanpon bat (19 mm-ko diametroa) erortzen uzten badugu, erori eta «marra ukitu» dezake, A kasuan bezala, edo «marra ukitu ez», B kasuan bezala.

Probabilitatearen kalkulu matematikoa

Aurreko problema hori modu matematikoan ebatziko dugu orain. Txanponaren posizioa horren zentroak zehazten du

G gertaeraren probabilitatea estimatuko dugu:

G = «txanponak ez du marra ukitu»

Horretarako, saiakuntza askotan egin eta maiztasun erlatiboa kalkulatu behar da.

Pentsa dezagun 30 pertsonak (ikasgela bateko neska-mutilek) 100 bider egiten duela bakoitzak saiakuntza hori (guztira 3 000 saiakuntza dira), eta G gertaera 385 bider zenbatu dugula. Maiztasun erlatiboa eta probabilitatea hauek izango dira:

fr (G) =  3 000 385  = 0,128 → P [G ] ≈ 0,13

• Estimatu zein den G-ren probabilitatea 2 zentimoko txanpon bat 100 aldiz botaz gero deskribatu dugun moduko koadrikularen gainean.

Txanponak ez dezan marra ukitu, koadrikulako zer puntutan egon behar da txanponaren zentroa? Argi eta garbi karratu txikiaren barruan geratu behar da; hau da, zentrotik marraraino dagoen distantzia txanponaren erradioa baino handiagoa izan behar da

Karratu handiaren azalera: 32 = 9 cm2

karratu txikiarena: (3 – 1,9)2 = 1,21 cm2

Probabilitatea: P [G ] =  , 9 121  = 0,134

Metodo horren bidez lortutako probabilitatea (0,134) eta saiakuntzaren bidez lortu duguna (0,13) ia-ia berdinak dira.

• Kalkulatu modu matematikoan zenbateko probabilitatea dagoen 1 cm-ko diametroa duen botoi batek «marrarik ez ukitzeko» 3 cm × 3 cm neurriko koadrikulan.

Zorizko saiakuntzak. Gertaerak

Harri bat bota eta hasierako altuera, abiadura, etab. zein diren badakigu, ziur jakingo dugu non eroriko den, zenbat denbora beharko duen erortzeko, etab. Saiakuntza determinista bat da.

Mahai baten gainera dado bat botatzen badugu, berriz, ezin dugu jakin zer aurpegi irtengo den. Emaitza zoriaren araberakoa da. Zorizko saiakuntza bat da.

Zorizko saiakuntza emaitza zoriaren araberakoa duena da.

Zorizko gertaera zoriaren arabera gertatuko dena edo ez dena da.

Eguneroko bizimodua zorizko saiakuntzaz beteta dago. Horietako asko soziologikoak dira (bidaiak, istripuak, denda handi batzuetara joango diren pertsonen kopurua...), eta banakako erabaki askoren batura badira ere, zorizko saiakuntzak izango balira bezala azter daitezke.

Lehenengo eta behin, zorizko saiakuntza errazak landuko ditugu: dadoak jaurtitzea, karta-multzo batetik karta bat ateratzea, kutxa batetik bolak ateratzea…

Lagin-espazioa

Lagin-espazioa zorizko saiakuntza batek izan ditzakeen emaitza guztien multzoari esaten zaio. Hemendik aurrera, E letrarekin izendatuko dugu

Adibidez: Dado batean, E = {1, 2, 3, 4, 5, 6}

Txanpon batean, E = {A, +}

Gertaerak

Gertaera E-ko edozein azpimultzori esaten zaio.

E-ko elementuei banakako gertaera edo oinarrizko gertaera esaten diegu; baita kasu ere

Horrez gain, ∅ gertaera hutsa edo ezinezko gertaera eta E gertaera ziurra bera ere gertaerak dira. Zorizko saiakuntza bateko gertaera guztien multzoa izendatzeko S erabiliko dugu.

E-k elementuen n kopuru finitua badu, E-ko gertaeren kopurua 2n da. Beraz, S multzoak 2n elementu izango ditu.

Adibidez: Dado batean, {1, 2}, {2, 4, 6}, {3, 5} gertaerak dira. {1}, {2}, {3}, … oinarrizko gertaerak dira.

26 = 64 gertaera daude. Zenbat eta egiaztatu zenbat gertaera dauden 0 elementukoak, 1ekoak, 2koak, 3koak…, 6koak.

Txanpon bat botatzean, 22 = 4 gertaera daude: S = {∅, {A}, {+}, {A, +}}

Pentsatu

1 Tetraedro-itxurako dado baten lau aurpegietan 1, 2, 3 eta 4 zenbakiak idatzi ditugu. Erortzen utzi eta behera begira zer aurpegi geratu den idatzi dugu.

ZORIZKO GERTAERAK

Errepide bateko zati jakin batetik egun jakin batean igaroko den autoen kopurua, zorizko gertaera da? Bai, ados egon litezkeen gidariei aldez aurretik galdetu diezaiekegula eta aurreikuspen nahiko zehatza egin. Baina pentsa zer zaila izango litzatekeen horrelako galdeketa bat egitea! Horrelakoetan, adituek gertaera zorizkotzat jotzen dute, eta aurretik egon diren pareko saiakuntzak erabiliz, nahiko zehatz aurreikusten dute zer gertatuko den.

NOIZ «JAZOTZEN DA» GERTAERA BAT

Gertaera bati dagokion zorizko saiakuntza egitean lortzen dugun emaitza gertaera horren kasuetako bat bada, gertaera hori egiaztatu edo jazo egiten dela esaten dugu. Adibidez, dado bat bota eta 5 irteten bada, besteak beste gertaera hauek jazo dira: {5}, {3, 5, 6}, {1, 5}, E.

a) Zein da lagin-espazioa?

b) Idatzi oinarrizko gertaera bat eta oinarrizkoak ez diren hiru.

Eragiketak eta erlazioak gertaerekin

A eta B bi gertaera izanda, honako egoera hauek definituko ditugu:

• Gertaeren bilketa. A ∪ B (A bil B irakurtzen da ) da A-ko kasu guztiek eta B-ko guztiek osatzen duten gertaera.

A ∪ B gertaera egiaztatzen da gertaeretako bat jazotzen denean, A edo B, edo biak jazotzen direnean.

• Gertaeren ebaketa. A ∩ B (A ebaki B irakurtzen da ) da aldi berean A-koak eta B-koak diren kasu guztiek eraturiko gertaera.

A ∩ B gertaera egiaztatzen da A eta B aldi berean jazotzen direnean.

• Gertaeren kenketa. A – B (A ken B irakurtzen da ) da B-koak ez diren A-ko kasu guztiek eratzen duten gertaera.

A – B egiaztatzen da A jazotzen denean, eta B ez.

• Gertaera osagarria. A = E – A gertaerari esaten zaio aurkako gertaera edo A-ren osagarria.

A gertaera egiaztatzen da baldin eta A egiaztatzen ez bada.

A gertaera izendatzeko A' ere erabiltzen da.

• Gertaera bateraezinak. A eta B bi gertaera bateraezinak direla esaten dugu ez dutenean kasu bat bera ere komunean. Hau da, A ∩ B = ∅ denean. Gertaera bateraezinak ezin dira aldi berean egiaztatu.

Gertaeren eragiketen propietateak

Aurreko eragiketek honako propietate hauek betetzen dituzte, besteak beste:

Banaketa A ∪ (B ∩ C ) = (A ∪ B) ∩ (A ∪ C )

A ∩ (B ∪ C ) = (A ∩ B) ∪ (A ∩ C )

Sinplifikazioa A ∪ (B ∩ A ) = A

A ∩ (B ∪ A ) = A

Osagarriarena () A = A A –

Morganen legeak 1.a = AB A , ∩ B

2.a = AB AB+,

Pentsatu eta praktikatu

2 Aztertu Morganen lehenengo legearen, = AB A , ∩ B , arrazoiketa grafikoa:

Lehenengo marrazkian, AB , urdinez dago.

Bigarrenean, A lerro bertikalen bidez adierazita dago, eta

B lerro horizontalen bidez; beraz, ebaketa egongo da biek

bat egiten duten tokian → = AB A , ∩ B

Arrazoitu grafikoki, antzera jokatuta, propietate hauek:

a) Morganen bigarren legea: = AB AB+,

b) A ∪ (B ∩ C ) = (A ∪ B) ∩ (A ∪ C )

c) A – B = A ∩ B = A – (A ∩ B)

d) (A ∪ B) – (A ∩ B)=( A ∩ B) ∪ (A ∩ B )

Maiztasuna eta probabilitatea

Gertaera baten maiztasun absolutua eta erlatiboa

Zorizko saiakuntza bat N bider egin dugu. Ekar ditzagun gogora definizio hauek.

G gertaera bat jazotzen den aldi kopuruari G-ren maiztasun absolutua edo, besterik gabe, G-ren maiztasuna esaten diogu. f (G ) idazten dugu.

G gertatzen den aldien proportzioari G-ren maiztasun erlatiboa esaten diogu

f r (G ) = () N fG

Zenbaki handien legea

Zorizko saiakuntza bat behin eta berriro egitean, gertaera jakin baten f r (G ) maiztasun erlatiboak balio desberdinak hartzen ditu aldi bakoitzean. Balio horiek aldaketa handiak izaten dituzte hasieran, baina, gero, egonkortu egiten dira apurka-apurka (gero eta gutxiago oszilatzen dute). N asko hazten denean, G-ren probabilitatea balio jakin batera hurbiltzen da, P [G ]

lm i N ∞ " f r (G ) = P [G ] zenbaki handien legea

Adibidez, dado bat bota, eta f r (3)-ren balioak lortu ditugu N = 20, 40, 60, 80, 100, 120, ... kasuetarako.

f r (3)-ren balioak 1/6 = 0,166 balioaren inguruan egonkortu dira. (Aztertu bilakaera alboko grafiko horretan).

Zergatik jotzen du egonkortzera maiztasun erlatiboak?

Dado bat behin eta berriro botatzean, jazo daiteke «3» gertaera bost aldiz jarraian irtetea? Bai, jakina; zaila da, baina gerta daiteke. Eta nola eragiten dio bolada horrek f r (3)-ri? Bada, kontuan hartu beharko da zenbat saiakuntza egin diren. Adibidez, pentsa bolada horren aurretik f r (3) = 0,16 zela:

4 «3» gertaera 5 bider ateratzeko boladarekin, f r (3) 4 ehunen handitu da

f r (3) 4 milaren handitu da

= = = = = 4 f r (3) 4 hamar milaren handitu da

Hau da, f r (3) egonkortu egiten da, izendatzailea gero eta handiagoa denez, zatidurari gero eta gutxiago eragiten diotelako zenbakitzailearen gorabeherek.

Pentsatu eta praktikatu

1 Zuzena ala okerra?

a) Ondo eginda dagoen dado batekin jolasten ari naiz, eta azken 20 jokaldietan ez dut «5» atera. Zenbaki handien legearen arabera, hurrengo botaldian «5» ateratzeko probabilitate handia daukat

➜ Lortu dado bat askotan botaz gero aurpegietako bat irteteko dagoen probabilitatearen hurbilketa bat.

b) Azkeneko 20 botaldietan «5» zenbakia ez da behin ere atera; hala ere, hurrengo botaldian «5» ateratzeko probabilitatea bolada horren aurreko bera da: 1/6 (zoriak «ez du memoriarik»)

Probabilitateen propietateak

Lagin-espazio bateko gertaera bakoitzak probabilitate bat darama lotuta. Probabilitate horiek ondoren emango ditugun propietate hauek bete behar dituzte

• Lehenengo hirurak nahitaezkoak dira; hau da, axiomak dira.

• Hurrengoak lehenengo horien ondorio moduan lortzen dira; hau da teoremak dira

AXIOMAK

Gertaera bakoitzaren probabilitatea zenbaki bat da. Axioma hauek bete behar dira:

Ax.1 G gertaera edozein dela ere, P [G ] ≥ 0

Ax.2 Bi gertaera bateraezinak badira, horien bilketaren probabilitatea probabilitateen arteko batuketa da

A ∩ B = ∅ ⇒ P [A ∪ B ] = P [A ] + P [B ]

Ax.3 Probabilitate osoa 1 da: P [E ] = 1

Funtsean, hiru propietate horiek probabilitate osoa 1 dela adierazten dute, eta modu batukorrean banatzen dela egon daitezkeen gertaeren artean. Beraz, gertaera bakoitzaren probabilitatea 0 eta 1 bitarteko zenbaki bat izango da: 0 ≤ P [G ] ≤ 1

TEOREMAK

T.1 P [ A ] = 1 – P [A ]

T.2 P [∅] = 0

T.3 A ⊂ B bada, orduan P [B ] = P [A ] + P [B – A ]

T.4 A ⊂ B bada, orduan P [A ] ≤ P [B ]

T.5 A1, A2, …, Ak, binaka bateraezinak badira, orduan: P [A1 ∪ A2 ∪ ∪ Ak ] = P [A1] + P [A2] + … + P [Ak ]

T.6 P [A ∪ B ] = P [A ] + P [B ] – P [A ∩ B ]

T.7 E lagin-espazioa finitua bada eta gertaera bat G = {x1, x2, …, xk } bada, orduan: P [G ] = P [x1] + P [x2] + … + P [xk]

Ebatzitako ariketa

1 A eta B gertaerek hau betetzen dute:

P[A] = 0,6; P[B] = 0,7; P[A ∪ B] = 0,9

P[A] = 0,6 P[B] = 0,7

P[A ∪ B] = 0,9

Kalkulatu:

P[ A ] P[ B ]

P[A ∩ B] P[ A ∪ B ]

Pentsatu eta praktikatu

Andréi Kolmogórov (1903-1987). Probabilitatearen teoriari zorroztasuna eman zion matematikari errusiarra; horretarako, sistema axiomatiko bat eraiki zuen, multzoen teorian oinarrituta.

➜ anayaharitza.es

Axiomak gertakarien maiztasun erlatiboetatik abiatuta arrazoitzea.

➜ anayaharitza.es

T.1etik T.7ra arteko teoremen egiaztapena.

• T.1 teoremaren arabera, P [ A ] = 1 – P [A ] = 1 – 0,6 = 0,4

• P [ B ] = 1 – P [B ] = 1 – 0,7 = 0,3

• T.6 teoreman P [A ∩ B ] = P [A ] + P [B ] – P [A ∪ B ] askatzen da:

P [A ∩ B ] = 0,6 + 0,7 – 0,9 = 0,4

• Kontuan hartuko dugu A ∪ B = AB + dela (Morganen 2. legea). P [ A ∪ B ] = P [ AB + ] = 1 – P [A ∩ B ] = 1 – 0,4 = 0,6

2 Probabilitate hauek dakizkigu: P [A ] = 0,4 P [B ] = 0,7 P [ A ∪ B ] = 0,8

Kalkulatu P [ AB + ], P [A ∩ B ], P [A ∪ B ].

3 Honako hau dakigu: P [M ∪ N ] = 0,6 P [M ∩ N ] = 0,1 P [ M ] = 0,7

Kalkulatu P [M ], P [N ], P [ N ], P [ M ∩ N ].

Laplaceren legea

Aurreko orrialdeko T.7 propietatearen bidez, G gertaera baten probabilitatea zein den jakinda, gertaera hori osatzen duten oinarrizko gertaeren probabilitateak kalkula ditzakegu.

Horrez gain, lagin-espazioak oinarrizko n gertaera ekiprobable baditu (denak 1/n probabilitate berekoak), orduan G-ren probabilitatea gertaera hori osatzen duten oinarrizko gertaera-kopuruaren araberakoa baino ez da izango:

P [G ] = nn n 11 1 ++ + G-k dituen elementuak adina batugai

LapL aceren Legea

E = {x1, x2, …, xn} eta P [x1] = P [x2] = … = P [xn ] badira, orduan:

P [G ] = n GG renelementukorpurua kasu posibleen kopurua renaldekokasukopurua =

Zorizko tresna batean oinarrizko gertaera (kasu) guztien probabilitatea berbera denean, tresna hori Laplacerena dela esaten da. Horrelakoak dira, adibidez, ondo egindako dadoak, txanponak, karta-multzoak

1 40 kartako multzo batean, aurkitu:

a) P[batekoa]

b) P[urrea]

c) P[irudia]

2 Karta-multzo batetik kendu egin ditugu zenbait karta. Geratu direnen artean, hona hemen karta batzuek multzotik ateratzeko zer probabilitate duten:

P[erregea] = 0,15

P[bastoia] = 0,3

P[ez errege ez bastoi] = 0,6

a) Geratu da karta-multzoan errege bastoia? Zein da karta hori ateratzeko probabilitatea?

b) Zenbat karta daude multzoan?

a) P [batekoa] = , 40 4 10 1 01 kartakop kop BATEKO=== -

b) P [urrea] = , . 40 10 4 1 025 kartakop URRE kop== = -

c) Guk normalean erabiltzen ditugun kartetan, irudiak txanka, zaldia eta erregea dira. Beraz, multzoan 12 irudi daude. Ondorioz:

P [irudia] = , 40 0 12 10 3 3 ==

a) errege gertaerari E esango diogu, eta bastoi gertaerari, B. errege bastoia gertaera E ∩ B moduan interpretatu behar dugu (eta, beraz, ematen diguten «ez errege ez bastoi» datua, R ∩ B moduan).

T.6 erabilita: P [R ∩ B ] = P [R ] + P [B ] – P [R ∪ B ] = 0,15 + 0,3 – P [R ∪ B ]

Bestalde: P [R ∪ B ] = 1 – P [ RB , ] = 1 – P [ R ∩ B ] = 1 – 0,6 = 0,4

Beraz, P [errege bastoia] = 0,15 + 0,3 – 0,4 = 0,05 = 20 1

Probabilitatea zero ez denez, errege bastoia multzoan geratu diren karten artean dago

b) Karta-multzo bat Laplaceren zorizko tresna bat da, bedin dio multzoa zenbat kartak osatzen duten; izan ere, karta guztiek ateratzeko probabilitate bera dute. Errege bastoia ateratzeko probabilitatea 1/20 bada, multzoan 20 karta daudela esan nahi du.

EGIN ZUK Egin problema bera, baina datu hauekin:

P [kopa] = 2 1 , P [batekoa] = 4 1 , P [ez kopa ez bateko] = 16 5 . Aurkitu

P [bateko kopa] eta esan zenbat karta dauden.

Pierre-Simon Laplace (1749-1827)

Ebatzitako ariketak

Noiz ezin da Laplaceren legea erabili?

Laplaceren legea oinarrizko gertaera guztiek (lagin-espazioko elementuak) probabilitate bera dutenean erabili daiteke. Baina, askotan, ez da horrelakorik gertatzen. Ikus ditzagun ohiko bi egoera

• Tresna irregularrak

Zorizko tresna batzuk irregularrak dira argi eta garbi: txarto egindako dado bat, txintxetak, txokoa. Nola kalkulatu gertaeren probabilitateak horrelakoetan?

Tresna irregularra bada, G gertaera baten probabilitatea kalkulatzeko, zenbaki handien legea erabiliko dugu. Saiakuntzen N kopuru handia egingo dugu, f (G ) maiztasuna lortuko dugu eta, hortik, fr (G ) =  () N fG maiztasun erlatiboa probabilitatearen neurri hurbildua izango da. Zenbat eta handiagoa izan N, orduan eta konfiantza handiagoa izango dugu estimazioan

Adibidez, mota bereko 100 txintxeta 10 bider erortzen uzten baditugu, 1 000 emaitza lortuko ditugu.

Demagun f ( ) = 243 eta f ( ) = 757.

Maiztasun erlatiboek probabilitateak estimatzeko balio digute:

P [ ] ≈ fr ( ) = 0,243 P [ ] ≈ fr ( ) = 0,757

Estimazioetan ziurtasun handiagoa eduki nahi izanez gero, saiakuntza gehiago egingo ditugu: 2 000, 5 000, 10 000, …

• Tresna erregularrak, ekiprobableak ez diren oinarrizko gertaerak

Ondo eginda dauden bi dado bota, eta ateratzen diren emaitzak batuko ditugu. Saiakuntza horren lagin-espazioa {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12} da. Baina saiakuntzek eta zentzuak berak argi erakusten digute baturan 2 , 7 edota 10 lortzeak ez duela probabilitate bera. Hori ikusita, saiakuntzaren deskribapena moldatu dezakegu, oinarrizko gertaera guztiak ekiprobableak izan daitezen, alboko koadroan egin dugun moduan.

Horretara, lagin-espazioak oinarrizko 36 gertaera izango ditu: (1, 1), (1, 2), …, (3, 5), …, (6, 6); eta gertaera guztiek probabilitate bera izango dute: 36 1 Deskribapen berri honetan, «batura, 2», «batura, 7», «batura, 10» emaitzak gertaera ez-oinarrizkoak dira. Horien probabilitateak erraz kalkulatuko ditugu:

1 Dado «narras» bat mila bider jaurti dugu, eta hau lortu dugu:

f (1) = 117 f (2) = 302 f (3) = 38

f (4) = 234 f (5) = 196 f (6) = 113

Estimatu aurpegi bakoitzaren probabilitatea, eta horietan oinarrituta, kalkulatu gertaera hauen probabilitateak:

bikoitia 6 baino txikiagoa {1, 2}

2 Zenbatekoa da ondo egindako bi dadoren emaitzak biderkatu eta 12 lortzeko probabilitatea? Eta 9 lortzekoa? Eta 4 lortzekoa?

3 Zenbatekoa da bi dado zuzen bota eta emaitzen arteko kendura 2 izateko probabilitatea? Eta kendura 1 izateko probabilitatea?

Pentsatu eta praktikatu

➜ Egin txintxeta jaurtiketaren simulazioa.

Probabilitate baldintzatua. Gertaera askeak

Poltsa batean, koloretako bolak ditugu, zenbakia ere ipinita. Honako hauek dira.

Zorian bola bat ateraz gero, zenbaki bikoitia izateko probabilitatea 8 4 = 2 1 da. Hori argi dago. Baina zenbakia begiratu baino lehen, bolaren kolorea zein den esaten badigute, orduan kontua aldatu egiten da:

• Bola berdea bada, bikoitia ateratzeko probabilitatea 1 3 da.

• Bola gorria bada, bikoitia ateratzeko probabilitatea 4 2 = 2 1 da.

• Eta beltza bada, ziurra da bikoitia dela. bikoitia ateratzeko probabilitatea 1 da Probabilitate horiei baldintzatu esaten diegu: «zer probabilitate dago bikoitia ateratzeko, kolorea … izatearen baldintzapean»

A eta C bi gertaera edukita, eta P[A] ≠ 0 eta P[C ] ≠ 0 direla jakinda, C -ren baldintzapeko A-ren probabilitatea deitzen da eta P [A/C ] idazten da honako hau:

P [A/C ] = [] [] PC PA C + C gertatzen den aldi guztien artean A ere gertatzen den aldien proportzioa neurtzen du.

Aurreko adierazpen horretatik ondorio hau ateratzen dugu:

P [A ∩ C ] = P [C ] · P [A/C ]

Modu berean, P [C/A ] = [] [] P P A CA +

Kalkula ditzagun aurreko adibideko probabilitateak, formula erabiliz:

Eta modu berean lortuko ditugu P [bikoitia /gorria] = 2 1 , P

Gertaera askeak

Ikusten dugunez, gorria baldintzapeko bikoitia gertaeraren probabilitatea eta baldintzarik gabeko bikoitia gertaeraren probabilitatea berdinak dira: P [bikoitia / gorria] = P [bikoitia]

Horrelakoetan, bikoitia eta gorria gertaerak askeak direla esaten dugu. Aldiz, bikoitia ez da asketa berdea eta beltza gertaerekiko.

A eta C bi gertaera askeak dira hau betetzen denean: P [A/C ] = P [A ]; edo beste era batean esanda, P [C/A ] = P [C ]

Bi gertaera askeak direnean, gertaeren ebaketaren probabilitatea gertaeren probabilitateen arteko biderketa da:

A eta C askeak dira ⇒ P [A ∩ C ] = P [A ] · P [C ]

Orain gutxira arte, automobiletako aseguruetan, emakumeei gizonei baino gutxiago kobratzen zieten. P [istripua/emakumea] < P [istripua] zelako gertatzen zen. Hau da, istripua izan eta emakumea izan gertaerak ez dira askeak. Rh+ dutenei edo ilehoriak direnei, berriz, ez zitzaien ez gehiago ez gutxiago kobratzen. Eta zentzuzkoa da; izan ere, istripua izan gertaera eta Rh+ izan gertaera edo ilehoria izan gertaera askeak dira

bikoitia eta gorria askeak dira

Bola gorrien artean dagoen bikoitien proportzioa eta bola guztien artean dagoen bikoitien proportzioa berdinak dira. «Bola gorria da» datuak ez du bikoitia lortzeko aukera aldatzen.

Probabilitate baldintzatuak kontingentzia-tauletan

Ekar ditzagun gogora kontingentzia-taulak zer diren eta ikus dezagun, adibide baten bidez, nola interpretatzen diren eta kalkulatzen diren taula horietan probabilitate baldintzatuak.

Urtebetean jarraipena egin diegu hiru markako 100 000 telefono mugikorri: punkia, pijia eta kakia. Batzuek matxuraren bat izan dute (mtx), eta beste batzuek, ez (mtx ez). Eskuineko lehenengo taulan ageri diren moduan daude banatuta.

Mota horretako taulei kontingentzia-taula esaten zaie. Multzo osoa (telefono mugikorrak) bi ezaugarriren arabera banatzen da (marka eta matxurarik izan duen).

Datuak aztertuta, bi ezaugarri horien arteko erlazioak zein diren jakingo dugu.

Kontingentzia-taulak aztertzeko, lehenengo eta behin, batura partzialekin eta batura osoarekin osatu behar dugu (bigarren taula).

Batura partzialak aztertuta, pijia markako 20 000 telefono daudela ikusten dugu, adibidez; edota 10 000 telefonok matxura izan dutela.

Matxura (mtx) izan duten 10 000 telefonoen artean zorian bat hartzen badugu, oso erraz lortuko ditugu probabilitate baldintzatuak:

P [punkia /mtx] = , 04 10 000 4 000 =

Horrek esan nahi du telefonoak matxura izan duela jakinda, punkia markakoa izateko probabilitatea 0,4 dela

Era berean, P [pijia /mtx] = , 10 000 000 0 2 2 = eta P [kakia /mtx] = 0,4.

Marka jakin bateko telefono batek matxura izateko zer probabilitate duen ere kalkula daiteke:

P [mtx/punkia] = , 0 000 4 000 0 5 08 =

P [mtx/pijia] = , 0 000 000 0 2 2 10 =

P [mtx/kakia] = , 0 000 4 000 0 3 13 =

Emaitza horiek kontuan izanda, segurtasun handieneko marka punkia dela ikusten dugu, eta segurtasun gutxienekoa, kakia.

Azkeneko probabilitate baldintzatu horiek P [mtx] = , 100 000 000 0 10 10 = probabilitate osoarekin konparatuz gero, pijia eta mtx gertaerak askeak direla ikusten dugu; punkia eta kakia, berriz, ez dira mtx gertaerarekiko askeak

Pentsatu eta praktikatu

1 Erreparatu kutxa barruan dauden bolei.

b) Kalkulatu gorria, beltza, berdea, 1 eta 2 gertaeraren probabilitatea, kutxaren konposizioari erreparatuta.

c) Egiaztatu b) puntuan lortutako probabilitateak a) puntuan lorturiko koadroaren errenkadak edo zutabeak batuz lor daitezkeela.

Br G Bl guzt.

guzt. 5

d) Kalkulatu probabilitate baldintzatu hauek: P [1/gorria], P [1/berdea], P [1/beltza], P [2/gorria], P [2/berdea], P [2/beltza], P [gorria/1], P [berdea/1].

e) Esan gorria, beltza, berdea ezaugarrietakoren bat askea den 1ekiko edo 2rekiko.

Proba konposatuak

Saiakuntza batzuetan bi etapa edo gehiago bereiz ditzakegu argi eta garbi. Proba konposatu esaten zaie. Proba konposatu horietan, gertaera konposatuen probabilitateak errazago kalkulatzen dira gertaerako osagaien probabilitateak kalkulatuz gero. Bi proba konposatu askeak dira baten emaitzak ez dionean eragiten besteari. Horrela ez bada, mendekoak dira.

• 1. adibidea. Txanpon bat eta dado bat bota ditugu. Argi dago baten emaitzak ez diola besteari eragiten. Askeak dira.

• 2. adibidea. Karta multzo batetik bi karta atera ditugu segidan. Bigarren kartaren emaitza lehenengoaren mendekoa da (adibidez, lehenengoa batekoa bada, probabilitate gutxiago dago bigarrena ere batekoa izateko). Mendekoak dira

Saiakuntza askeak

Azter dezagun goiko 1. adibidea. Kasu honetan, probabilitateen kalkulua oso erraza da, txanpona eta dadoa Laplacerenak direla jotzen badugu.

P [(A, 3)] = P [A] · P [3] = 2 1 · 1 6 = 12 1

Gertaera konposatuaren probabilitatea gertaerako osagaien probabilitateen arteko biderketa da. Adibidez:

P [(A eta bikoitia)] = P [A] · P [bikoitia] = 2 1 ·

= 1

Bi proba edo gehiago askeak direla esaten da horietako bakoitzaren emaitzak ez dienean eragiten gainerako emaitzek izan ditzaketen probabilitateei. Beraz, lehenengoari dagozkion gertaerak bigarrenari dagozkion gertaerekiko askeak dira. n proba aske edukita, proba horiei dagozkien gertaerak G1, G2, …, Gn badira hurrenez hurren, honako hau betetzen da:

P [G1 1.an eta G2 2.ean eta … eta Gn n-garrenean] = P [G1] · P [G2] · … · P [Gn ]

Zenbait kasutan probak ez dira ondoz ondo gertatzen, aldi berean baizik. Baina ahal izanez gero, komeni da denboran elkarren atzetik gertatzen direla pentsatzea.

1 Zuzena ala okerra?

a) Poltsa batean 5 bola berde eta 5 bola gorri ditugu. Lehenengo bola bat eta gero beste bat atera ditugu. Bi ateraldiak askeak dira. Beraz: P [1.a gorria eta 2.a berdea] =

= P [gorria 1.an] · P [berdea 2.ean] ,. 10 5 10 5 4 1 025 · == =

b) Bi poltsa ditugu, eta bakoitzean 5 bola berde eta 5 gorri daude. Lehenengo poltsatik bola bat eta bigarrenetik beste bola bat atera ditugu. Bi ateraldiak askeak dira. Beraz: P [1.a gorria eta 2.a berdea] =

= P [gorria 1.an] · P [berdea 2.ean] ,. 10 5 10 5 4 1 025 == =

2 Kalkulatu zer probabilitate dagoen hiru dado bota eta hiru lauko ateratzeko.

3 Kalkulatu zer probabilitate dagoen 6rik ez ateratzeko (seikorik ez) lau dado botata (seikorik ez lau bider).

4 Kalkulatu zer probabilitate dagoen seikoren bat ateratzeko lau dado botata (seikoren bat gertaera da seikorik ez gertaeraren kontrakoa).

5 Kalkulatu zenbatekoa den sei dado bota eta seikoren bat ateratzeko probabilitatea.

Txapon baten eta dado baten jaurtialdien zuhaitz-diagrama.

KONTUAN IZAN

Pentsatu eta praktikatu

Mendeko saiakuntzak

Txanpon bat eta bolaz beteriko bi kutxa ditugu. Txanpona bota eta aurpegia irteten bada, I. kutxatik bola bat aterako dugu; eta gurutzea irteten bada, II. kutxatik.

Saiakuntza konposatu hori zuhaitz-diagrama baten

babilitateak adieraziko ditugu.

Ikusten duzunez, bigarren gezietako probabilitateak baldintzatuak dira.

Adibidez, P [ /A] = 10 6 eta, beraz:

Bi saiakuntza mendekoak dira lehenengoaren emaitzak bigarrenaren gertaeraren probabilitateei eragiten dienean. Gertaera konposatuen probabilitateak honela lortzen dira:

P [G1 1.an eta G2 2.ean] = P [G1] · P [G2/G1]. Hau da:

P [G1 1.an] · P [G2 2.ean, baldin eta G1 gertatu bada 1.an]

Mendeko bi saiakuntza baino gehiago kateatzen direnean ere modu berean lortzen dira gertaera konposatuen probabilitateak. Adibidez, hiru saiakuntza daudenean:

P [G1 1.an eta G2 2.ean eta G3 3.ean] = P [G1] · P [G2/G1] · P [G3/G1 eta G2]

Pentsatu eta praktikatu

6 Zuzena ala okerra?

Poltsa batean 5 bola berde eta 5 gorri daude. Lehenengo bola bat atera dugu, eta, gero, beste bat. Bigarren ateraldia lehenengoaren emaitzaren mendekoa da. Beraz:

P [1.a eta 2.a ] = P [ 1.an] · P [ 2.ean/ 1.an] =

= 10 5 9 5 90 25 18 5 ·= =

7 Dado bat eta ondoko irudian ageri diren bi kutxak ditugu.

Dadoa bota dugu. 1 edo 2 irteten bada, I. kutxara joko dugu. 3, 4, 5 edo 6 irteten bada, II. kutxara. Dagokion kutxatik bola bat aterako dugu

a) Osatu probabilitateak zuhaitz-diagraman.

b) Aurkitu: P [{3, 4, 5, 6} eta ] P [ /1]

P [ /5]

P [2 eta ]

I. KUTXA

Probabilitate osoa

Har dezagun telefono mugikorren adibidea, probabilitate baldintzatuak kontingentzia-tauletan landu ditugunean erabilitakoa. Datuak ondo ordenatuta agertu zaizkigu taulan. Baina pentsa ez ditugula datu horiek, eta hau baino ez dakigula: marka bakoitzeko telefonoen proportzioa, P [punkia], P [pijia], P [kakia]; eta marka bakoitzeko matxuratuen proportzioa, P [mtx/punkia], P [mtx /pijia], P [mtx /kakia].

Nola lortu matxuratuta dauden telefono guztien proportzioa, P [mtx]?

P [kakia] · P [mtx/kakia] biderkadurak, matxuratuta dauden telefono guztien proportziotik, kakia markari dagozkionak emango dizkigu.

Era berean, P [punkia] · P [mtx/punkia] eta P [pijia] · P [mtx/pijia].

Beraz: P [mtx] = P [punkia] · P [mtx/punkia] + P [pijia] · P [mtx/pijia] + + P [kakia] · P [mtx/kakia]

n gertaera ditugu, A1, A2, …, An.

Binaka bateraezinak dira eta A1 ∪ A2 ∪ … ∪ An = E betetzen dute.

Orduan, G edozein gertaeraren kasuan, hau betetzen da:

P [G ] = P [A1] · P [G /A1] + P [A2] · P [G /A2] + … + P [An] · P [G /An]

Horrela deskonposatuta agertzen den P [G ] probabilitateari probabilitate oso esaten zaio.

Egiaztapena

G gertaera bateraezinetan deskonposatuko dugu:

G = (A1 ∩ G ) ∪ (A2 ∩ G ) ∪ … ∪ (An ∩ G )

Probabilitateen T.5 propietatea aplikatuko dugu:

P [G ] = P [A1 ∩ G ] + P [A2 ∩ G ] + … + P [An ∩ G ]

P [Ak ∩ G ] = P [Ak ] · P [G /Ak ] dela kontuan izanez, bila genbiltzan adierazpena lortzen dugu.

Probabilitate osoa ondoz ondoko proben kasuan

Aurreko emaitza hori oso erabilgarria da ondoz ondoko saiakuntza konposatuen kasuan batez ere. Jarraian gertatzen diren bi etaparen adibidea ikusiko dugu:

Aztertu grafikoa. A1, A2, …, An gertaerak lehenengo etapakoak dira, eta binaka bateraezinak dira. G gertaera bigarren etapakoa da. G-ra heldu daiteke A1, A2, … edo An-tik igaroz.

Zuhaitz-diagrama aztertuz, argi ikusten da zer esanahi duten, kasu honetan, honako probabilitate hauek:

P [G /Ai ]

P [Ai ∩ G ] = P [Ai ] · P [G /Ai ]

Baita P [G ] probabilitate osoak zer esan nahi duen ere.

Garbi dago, gainera, zergatik den horren lagungarria prozesu hau kasu hauetarako; izan ere, G gertaerara heltzeko modu bakarra A1, A2, …, An gertaeretako batetik igarotzea da.

[kakia] · P [mtx/kakia]

Ebatzitako ariketak

1 Dado bat botako dugu. 1 edo 2 irteten bada, I. kutxako bola bat hartuko dugu; eta 3, 4, 5 edo 6 irteten bada, II. kutxako bola bat. I II

Kalkulatu P[ ] (bola gorria izateko probabilitatea).

Prozesua zuhaitz-diagrama baten bidez deskribatuko dugu, parte hartzen duten gertaera guztien probabilitateak zehaztuz

2 Katu bat sagu bati jarraika doa. Sagua A, B edo C kaleetako batetik sar daiteke.

Orain, probabilitate osoa lortuko dugu

EGIN ZUK Aurreko ariketan, kalkulatu P [ ] eta P [ ].

Prozesua zuhaitz-diagrama

baten bidez deskribatuko

Edozein kale hartuta ere, baliteke katuak sagua harrapatzea, +, edo ez harrapatzea. Hau dakigu:

P[A-n sartu] = P[A] = 0,3

P[B] = 0,5 P[C] = 0,2

P[A-n sartu eta harrapatzea] = = P[+/A] = 0,4

P[+/B] = 0,6

P[+/C] = 0,1

Pentsatu eta praktikatu

1 Zuzena ala okerra?

[+] = 0,12 + 0,30 + 0,02 = 0,44

+

harrapau egiten du

Kalkulatu P [ ] probabilitate hori prozesu guztia jarraituz.

Lehenengo, I. kutxatik bola bat atera, eta II. kutxan sartu dugu. Gero, II. kutxatik bola bat atera dugu. I II

a) P [2.a /1.a ] = 2 1 b) P [2.a /1.a ] = 2 1

c) P [2.a /1.a ] = 1 3 d) P [1.a eta 2.a ] = 1 2 11 36 =

2 Bi kutxa ditugu: I II

Saiakuntza honetan, I. kutxatik bola bat atera, II. kutxan sartu eta bolak nahastu, eta II. kutxatik bola bat aterako dugu. Kalkulatu zer probabilitate dagoen ateratako bola kolore hauetako bakoitzekoa izateko:

a) gorria b) berdea c) beltza

«A posteriori» probabilitateak. Bayesen formula

Bi saiakuntzak osaturiko saiakuntza konposatu batean, A lehenengoari dagokion gertaera bada, eta G bigarrenari dagokion gertaera, P [A/G ] probabilitate baldintzatuaren esanahia oso interesgarria da

ADIBIDE BAT

Telefono eta matxuren beste adibide bat: Telefonoen % 80 guay markakoa da, eta % 20, puaf markakoa:

P [guay] = 0,8 P [puaf ] = 0,2 guay telefonoetan, 40tik 1 matxuratzen da; puaf telefonoetan, 10etik 4:

P [mtx/guay] =  40 1 P [mtx/puaf ] =  10 4

G gertaerara A-tik edo beste gertaera batzuetatik igaroz hel gaitezke. Azkenean G gertatu dela jakinda, zer probabilitate dago «A-tik igarota» heltzeko? P [A/G ].

Hau da, G-ra heltzeko modu guztien artean, zer proportzio pasatzen da A-tik?

Intuizioz, proportzio hori hau dela esan dezakegu:

] probabilitate oso moduan adierazten badugu, Bayesen formula lortzen da:

Zorian telefono bat hartu dugu, eta matxuratuta dago. Zer probabilitate dago guay telefonoa izateko?

Ebazteko, modu idealean banatuta dauden 100 telefonoren kasua hartuko dugu: 100 g, 80 / 120 g eta mtx, 4 p, 20 31/0 p eta mtx, 6 mtx, 10

Argi dago, beraz: zorian hartutako telefono bat matxuratuta badago, guay izateko probabilitatea 2/10 da, eta puaf izateko probabilitatea, 8/10.

Praktikan, formula bera baino lagungarriagoa da zuhaitz-diagramaren prozesuari jarraitzea:

G gertatu dela jakinda, grafikoan hau lortzen dugu:

Oroimen-plaka Thomas Bayes bizi izan zen etxean, Tunbridge Wellsen (Kent konderria, Ingalaterra).

Ebatzitako ariketak

1 Aurreko atalean ebatzi dugun problema hartuko dugu berriro, dadoarena eta bi kutxena.

Badakigu azkenean bola beltza atera dugula. Zer probabilitate dago bola hori II. kutxatik ateratakoa izateko? Hau da, P[II/ ] kalkulatu behar da.

Zuhaitz-diagrama bat erabiliko dugu P [ ] probabilitate osoa lortzeko.

2 Aurreko ataleko 2. ariketa ebatziko saguaren eta katuaren problema hartuko dugu berriro. Demagun katua saguaren atzetik ikusten dugula, eta handik gutxira katuak sagua ahoan dakarrela. Hiru bideetako zeinetan harrapatu du?

P [ ] = 60 2 + 60 8 = 60 10

P [II/ ] kalkulatzeko, P [II eta ] eta P [ ] probabilitateen arteko zatidura lortuko dugu.

P [II/ ] = [] [] / / , P P 10 60 860 10 8 08 II eta == =

Lortutako emaitza modu inozoan deskribatuko dugu: «Saiakuntza 60 aldiz egiten dugun bakoitzeko, 10 alditan bola beltza aterako dugu. Eta 10 horietatik, 2 alditan I. kutxatik aterako dugu, eta 8 alditan, II. kutxatik»

EGIN ZUK Azkenean lortzen dena bola gorria bada, zer probabilitate dago I. kutxatik ateratakoa izateko? Hau da, kalkulatu P [I/ ].

Sagua non harrapatu duen ezin dugu jakin, noski. Baina kaleetako bakoitzean harrapatzeko zer probabilitate izan duen kalkula dezakegu: P [A/+], P [B/+] edo P [C/+].

Emaitza batzuk badakizkigu, aurreko atalean kalkulatu ditugu eta:

P [C eta +] = 0,02

Eskatutako probabilitateak berehala lortuko ditugu:

Pentsatu eta praktikatu

1

Lehenago ikusi dugun guay eta puaf telefonoen kasuan, badakigu telefonoetako batek matxurarik ez duela izaten, zentzuzko denbora tarte batean. Ez dakigu zer markatakoa den, baina probabilitateak kalkula ditzakegu.

2

I. kutxatik bola bat atera eta II. kutxan sartu dugu. Bolak nahastu eta II. kutxatik bola bat atera dugu. I II

P [guay /mtx ez] = 90 76 = 0,84

P [puaf /mtx ez] = 90 14 = 0,16

90

a) Bigarren bola beltza izan dela jakinda, zer probabilitate dago lehenengoa ere beltza izateko? P [1.a /2.a ]

b) Bigarren bola gorria izan dela jakinda, zer probabilitate dago lehenengoa beltza izateko? P [1.a /2.a ]

c) Zer probabilitate dago lehenengo bola berdea izateko, bigarrena ere berdea izan bada? P [1.a /2.a ]

Zuzena ala okerra?

Ebatzitako ariketak eta problemak

1. Probabilitateen propietateak

A eta B bi gertaera ditugu, eta probabilitate hauek dakizkigu:

P[A ∪ B] = 0,55

P[ A ∪ B ] = 0,90

P[B/A] = 0,25

Hau eskatu digute:

a) Lortu P[A ∩ B], P[A], P[B] eta P[B/ A ].

b) Ondorioztatu, modu arrazoituan, A eta B askeak diren.

EGIN ZUK

a) Datu berdinak izanda, kalkulatu: P [A ∩ B ] eta P [A ∪ B ]

b) Bateraezinak dira A eta B?

2. Hiru dado jaurtitzea

Aurkitu zer probabilitate dagoen hiru dado jaurti eta batean lortutako puntuazioa beste bietan lortutako puntuazioen batura izateko.

Bi dadotan lortu daitezkeen puntuazioen batura posibleak honela biltzen dira: Guri interesatzen zaigun bakarra beste dadoko puntuazioarekin bat egitea denez, behar ditugun probabilitateak hauek dira:

P [batura = 2] = 36 1 P [batura = 3] = 36 2

P [batura = 4] = 36 3 P [batura = 5] = 36 4

P [batura = 6] = 36 5 (Ikusten duzunez, «batura = 1» ezinezkoa da).

Zuhaitz-diagrama bat egingo dugu, lehenengo dadoko puntuazioa beste bietako puntuazioen batura izateko zer probabilitate dagoen aurkitzeko:

Beraz, lehenengo dadoko puntuazioa beste bietako puntuazioen batura izateko probabilitatea hau da:

EGIN ZUK

Bi dado gorri eta berde bat jaurti gertaeran, aurkitu zer probabilitate dagoen berdean lortutako puntuazioa bi dado gorrietan lortutako puntuazioen kendura (handiena – txikiena) izateko.

Beraz, eskatutako probabilitatea hau da:

Kontuan izan behar dugu, horrez gain, gerta litekeela bigarren dadoko emaitza bat etortzea lehenengo eta hirugarren dadoetako puntuazioen baturarekin; edota hirugarren dadoko emaitza bat etortzea lehenengo eta bigarren dadoetako puntuazioen baturarekin.

1. dadoa 2.a+3.a

3. Probabilitateak diagramak erabiliz kalkulatzea

Herri bateko biztanleen % 50ek autoa dute; % 35ek, motorra; eta % 22k, autoa eta motorra.

Herriko bizilagun bat aukeratu dugu zorian. Aurkitu zer probabilitate dagoen bizilagun horrek,

a) autoa edo motorra izateko.

b) ez autorik, ez motorrik ez izateko.

c) autoa duela jakinda, motorra ere edukitzeko.

d) motorra duela jakinda, autorik ez izateko.

e) ibilgailu bietako bat bakarrik izateko.

Honako diagrama hau irudikatuko dugu, lagin-espazioa azpimultzo bateraezinetan zatituz. Adibidez, biztanleen % 50ek autoa badute, eta % 22k autoa eta motorra, orduan biztanle horien % 50 – % 22 = % 28k autoa bai, baina motorrik ez dute izango. Eta horrela jarraituz, diagrama osoa beteko dugu

autoa motorra

% 28 % 22 % 13

% 37

a) P [autoa edo motorra] = + + = 0,28 + 0,22 + 0,13 = 0,63

b) P [autoa ez eta motorra ez] = = 1 – P [autoa edo motorra] = 1 – 0,63 = 0,37

c) P [motorra /autoa] = = , , 05 022 = 0,44

d) P [autoa ez/motorra] = = , , 035 013 = 0,37

e) P [autoa bakarrik edo motorra bakarrik] = + = 0,28 + 0,13 = 0,41

4. Probabilitateak kontingentzia-tauletan

Herri bateko kultura-etxeak 300 kide ditu, eta bakoitzak jarduera batean izena emateko aukera du: saloi-dantzak (dan), mendi-irteerak (men) edo bideojokoak (bid).

Horrez gain, bi adin-tarte daude: gazteak (gaz), 26 urtetik beherakoak; eta nagusiak (nag), 26 urtetik gorakoak.

• Kideen artean 180 gazte daude, eta horietatik 15 saloi-dantzetan izena emanda daude, eta 60, mendi-irteeretan.

• Mendi-irteeretarako 100 pertsonak eman dute izena.

• Bideojokoen taldean 13 nagusi baino ez daude.

a)Egin kontingentzia-taula bat.

b) Kideetako bat hartuko dugu zorian. Aurkitu probabilitate hauek:

P[nag] P[men] P[gaz eta bid]

P[bid/gaz] P[nag/dan]

c) Egiaztatu men gertaera adinarekiko askea dela

a) Ematen dizkiguten datuekin (gorriz) kontingentzia-taula egingo dugu, eta kontuak eginez, gelditzen diren zuriuneak beteko ditugu. saloi-dantzak

b) Probabilitateak kalkulatuko ditugu:

P [nag] = 120/300 = 0,4 (120 nagusi daude.)

P [men] = 100/300 = 0,33 (100 kidek eman dute izena mendi-irteeretan.)

P [ gaz eta bid] = 105/300 = 0,35 (105 gazte daude bideojokoetan izena emanda.)

P [bid/gaz] = 105/180 = 0,58 (180 gazteetatik, 105 bideojokoetan daude.)

P [nag/dan] = 67/82 = 0,82 (Dantzetan dauden 82 kideetatik, 67 nagusiak dira.)

c) men gertaera gaz eta nag gertaeretatik askea dela ikusiko dugu.

P [ gaz/men] = 60/100 = 0,6

P [ gaz] = 180/300 = 0,6 → P [ gaz/men] = P [ gaz]

Beraz, men eta gaz askeak dira.

Modu berean egiaztatzen da P [nag/men] = P [nag].

Horrek esan nahi du adinen araberako banaketak proportzio bera duela mendi-irteeretara (men) joaten direnen artean eta kide guztien artean

EGIN ZUK Kalkulatu P [bid/nag].

Ebatzitako ariketak eta problemak

5. Baldintzapeko probabilitatea

Altzari batek 9 kutxa ditu. Kartera altzari barruan gordeta egoteko probabilitatea 1/2 da, eta, altzarian badago, 9 kutxatako edozeinetan egoteko probabilitate bera dago.

a) Zer probabilitate dago kartera bederatzigarren kutxan egoteko?

b) Lehenengo zortzi kutxak zabaldu eta kartera batean ere ez badago, zer probabilitate dago bederatzigarren kutxan egoteko?

«Lehenengo 8 kutxatakoren bat» gertaerari bestea esango diogu:

P [bai eta bestea] = = 2 1 9 8 18 8

P [bai eta 9.a] = = 2 1 918 11

a) P [9.a]

EGIN ZUK

Egin berriro problemako b) atala, baina kasu honetan kutxak 6 soilik izanda, eta aurreneko bostak irekita, batean ere ez dagoela jakinda.

6. Batuketaren jokoa

Joko batean, bi dado bota behar dira harik eta puntuazioen batura 10 edo 7 izan arte. 10 bada, irabazi egin dugu; 7 bada, galdu egin dugu. Irabazteko zer probabilitate dugu?

intuitibo egiteko, saiakuntza oso modu sinplean deskribatuko dugu: pentsatu saiakuntza 18 aldiz egin dugula; erdietan, 9, kutxatakoren batean dago, eta beste erdietan, ez dago kutxatako batean ere.

Argi dago lauki berdeko kasua 10etik 1ean gertatuko

Aztertu 2. problema ebatzian ageri den taula: bi dado jaurtitzean lor ditzakegun batura posible guztiak daude bilduta. Taulari erreparatuta, erraz ikusten da honako hau:

Zuhaitz-diagrama bat egingo dugu:

Azken-aurreko berdintzan, progresio geometriko bateko infinitu gaien batura egin dugu,

3/4:

EGIN ZUK

Egin problema bera, baina kontuan izanda batura 3 denean irabaziko dugula, eta batura 7 denean galdu.

Konturatzen bazara, bi aldiz probabilitate gehiago dago 7 ateratzeko 10 ateratzeko baino; beraz, bi aldiz probabilitate gehiago egongo da galtzeko irabazteko baino; hau da, kasuen 2/3etan galduko dugu, eta 1/3etan irabazi.

Gidatutako ariketak eta problemak

1. Probabilitateen propietateak

A eta B gertakariei buruz hau dakigu:

P[A] = 0,4

P[B] = 0,5

P[ A ∩ B ] = 0,3

Aurkitu:

a) P[A ∪ B]

b) P[A ∩ B]

a) P [A ∪ B ] eta P [ A ∩ B ], probabilitate ezaguna, elkarrekin erlazionatu ditzakegu Morganen legeetako bat erabiliz: A ∩ B = AB , Beraz, P [ A ∩ B ] = P [ AB , ] = 1 – P [A ∪ B]

b) P [A ∩ B ] kalkulatzeko, berdintza erabiliko dugu: P [A ∪ B ] = P [A ] + P [B ] – P [A ∩ B ]

Soluzioa:

a) 0,7 b) 0,2

2. Probabilitateak saiakuntza konposatuetan

Dado bat trukatuta dago: 2, 4 edo 6 ateratzeko probabilitatea bera da; 1, 3 edo 5 ateratzeko probabilitatea ere bera da; eta 2 ateratzeko probabilitatea 1 ateratzekoa baino bi aldiz handiagoa da.

Azaldu, arrazoituz, zer probabilitate dagoen dadoa birritan bota eta ateratako puntuak batuta 7 lortzeko.

3. «A posteriori» probabilitatea

Herrialde bateko biztanleen % 12k gaixotasun jakin bat dute. Gaitz hori detektatzeko proba bat dago, baina ez da fidagarria.

• Benetan gaixorik daudenen % 90ek ematen dute positibo.

• Osasuntsu daudenen % 5ek ematen dute positibo.

Zer probabilitate dago proban positibo agertu zaion pertsona bat osasuntsu egoteko?

• Enuntziatua kontuan hartuz, puntu bikoitiak lortzeko probabilitatea bakoitiak lortzekoa baino bi aldiz handiagoa da: P [1] = P [3] = P [5] = p; P [2] = 2P [1] = P [4] = = P [6] = 2p p-ren balioa lortzeko, erabili P [E ] = 1 propietatea

• «batura, 7» lortzeko, 1 eta 6, 6 eta 1, 2 eta 5, … atera behar dugu. Osatu gainerako emaitzak.

Ikusten duzunez, bikote guztietan zenbaki bakoiti bat eta zenbaki bikoiti bat daude.

• Zein da bikoteetako bakoitza ateratzeko dagoen probabilitatea?

• Zein da puntuen arteko batura 7 izateko probabilitatea?

Soluzioa: P [batura 7] = 12/81 = 0,15

Egin honelako zuhaitz-diagrama bat eta osatu kasu bakoitzari dagozkion probabilitateekin:

G: «Gaixorik»; O: «Osansuntsu»; +: «Positibo»; –: «Negatibo»

Eskatutako probabilitatea hau da: P [ [O/+] = [] [] P P Oeta + + = … Soluzioa:

konposatuak. Probabilitate osoa eta «a posteriori» probabilitatea

Bi kutxa hauek ditugu:

I. kutxa II. kutxa

I . kutxatik bola bat atera dugu zorian, eta II. kutxan sartu dugu. Gero, II. kutxatik bola bat atera dugu zorian. Kalkulatu honako probabilitate hauek:

a) P[ I.an]; b) P[ II.ean / I.an]

c) P[ I.an]: d) P[ II.ean / I.an]

e) P[ II.ean]: f) P[ II.ean]

g) P[ I.an/ II.ean]

• Osatu honako zuhaitz-diagrama hau:

• Hortik abiatuta, kalkulatu eskatzen diren probabilitate guztiak.

4. Saiakuntza

Proposatutako ariketak eta problemak

Praktikatzeko

Lagin-espazioa. Gertaerak

1 Esan zein den ondorengo zorizko saiakuntza hauetako bakoitzari dagokion lagin-espazioa:

a) Bi txanpon jaurti eta bakoitzean zer irtengo den esatea.

b) Bi txanpon jaurti eta aurpegi-kopurua idaztea.

c) Txanpon bat eta dado bat botatzea.

d) Karta-multzo batetik karta bat atera eta zer palotakoa den idaztea.

e) Pilota bat saskira jaurtitzea.

f) Pertsona bati aurten urteak asteko zer egunetan beteko dituen galdetzea.

2 40 kartako multzo batetik karta bat atera dugu. Gertaera hauek aztertuko ditugu: A, irudia; B, bastoiak, eta C, 4 baino txikiagoa.

a) Adierazi gertaera hauek A, B eta C-ren funtzioan:

• Hiruretakoren bat egin da.

• Hiruretako bat ere ez da egin.

• Hirurak egin dira.

• Baten bat ez da egin.

• A edo B egin da, baina C ez.

b) Deskribatu a) ataleko gertaeretako bakoitzari dagozkion elementuak.

3 Hiru txanpon jaurti eta bakoitzean lortzen dugun emaitza idatziko dugu, A eta +. Gertaera hauek jorratuko ditugu:

A = «Aurpegi gehiago lortzea gurutzeak baino» eta B = «Gurutze bat edo bi ateratzea». Aurkitu A ∪ B eta A ∩ B gertaerak osatzen dituzten kasu guztiak.

4 Erlazionatu diagrama bakoitza dagokion gertaerarekin.

A ∩ B

A  –  B

A ∪ B

Probabilitatearen propietateak

6 Aztertu honako multzo hauek: A B

Kalkulatu P [A ∪ B], P [ A /B], P [A / B ] eta P [A ∩ B ].

7 A eta B gertaerei buruz hau dakigu: P [A ] =  5 2 P [B ] =  3 1 P [ A ∩ B ] =  3 1

Kalkulatu P [A ∪ B] eta P [A ∩ B].

8 A eta B ondorengo hau betetzen duten bi gertaera dira: P [A ∪ B ] =  4 3 P [ B ] =  3 2 P [A ∩ B ] =  1 4

Kalkulatu P [A ], P [B] eta P [ A ∩ B ].

9 A eta B bi gertaera dira, eta P [A ] = 0,4; P [B] = 0,3 eta P [A ∩ B ] = 0,1 betetzen dute. Aurkitu, eta arrazoitu:

a) P [A ∪ B ] b) P [ A ∪ B ]

c) P [A ∩ B ] d) P [ A ∩ B ]

10 Badakigu P [A ] =  1 4 , P [B] =  2 1 eta P [A ∪ B ] =  3 2

Zehaztu A eta B gertaerak bateragarriak ala bateraezinak diren.

11 A eta B dira lagin-espazio bereko bi gertaera, eta P [A ] = 0,7; P [B] = 0,6 eta P [A ∪ B ] = 0,9 betetzen dira.

a) Arrazoitu A eta B independenteak diren ala ez diren.

b) Kalkulatu P [A / B ] eta P [B / A ].

12 A eta B bi gertaerak P [A] = 0,3; P [B] = 0,54 eta P [B/A] = 0,4 betetzen dute. Kalkulatu.

a) P [A ∪ B] b) P [A ∩ B]

13 A eta B bi gertaerak hau betetzen dute:

P [A] =  9 4 , P [B] =  2 1 eta P [A ∪ B] =  3 2

a) Aztertu A eta B independenteak diren.

b) Kalkulatu P [ A /B].

14 A eta B zorizko esperientzia bateko bi gertaera dira, eta P [A] = 0,4, P [B] = 0,6 eta P [A ∪ B] = 0,8 betetzen dute.

Kalkulatu: a) P [ A ∩ B] b) P [ AB , /A]

5 Erabili diagramen laguntza ataletako bakoitza ebazteko.

a) Adierazi A ∪ B hiru gertaera bateraezinen bilketa gisa. Hauetakoren bat erabil dezakezu: A , B , A – B, B – A,

b) A – B gertaera ondorengo hauetakoren baten berdina da; esan zeinena: A ∩ B, A ∩ B , A ∩ B, A – (A ∩ B)

15 A eta B bi gertaerak P [B] = 0,7; P [A ∩ B] = 0,3; P [A ∩ B ] = 0,2 betetzen dute. Kalkulatu.

a) P [A ∪ B] b) P [B/ A ]

16 A eta B bi gertaera ditugu. Kalkulatu P [A], jakinda

P [B] = 0,8 dela, P [A ∩ B] = 0,2 eta P [A ∪ B] dela P [A]-ren hirukoitza.

Probabilitateak saiakuntza konposatuetan

17 Lau txanpon bota ditugu. Kalkulatu zer probabilitate dagoen lortzeko:

a) Aurpegirik ez. b) Aurpegiren bat.

18 Karta-multzo batetik bi atera ditugu. Kalkulatu zer probabilitate dagoen:

a) Biak kopak izateko.

b) Bat gutxienez kopa izateko.

c) Bat kopa eta bestea ezpata izateko. Hartu kontuan bi prozesu desberdin:

I. Karta bat atera, eta berriro itzuli da multzora.

II. Bi kartak batera atera dira.

19 Karta-multzo batetik bi karta atera ditugu eta dado bat bota dugu. Zer probabilitate dago kartak txankak izateko eta dadoan lortutako zenbakia bikoitia?

Probabilitate osoa eta «a posteriori»

20 Kutxa hauetako bakoitzetik bola bat atera dugu:

Ebazteko

24 6.3 helburua. Ibai jakin bat nitratoekin kutsatuta egoteko dagoen probabilitatea 0,6 da; sulfatoekin kutsatuta egotekoa, 0,4; eta biekin kutsatuta egotekoa, 0,2. Kalkulatu zer probabilitate dagoen ibai hori:

a) Ez egoteko kutsatuta nitratoekin, jakinda sulfatoekin kutsatuta badagoela.

b) Ez egoteko kutsatuta, ez nitratoekin, ez sulfatoekin.

25 Hiri batean, herritarren % 40 ilehoria da, % 25ek begi urdinak ditu, eta % 15 ilehoria eta begi urdinekoa da. Zorian pertsona bat hartu dugu:

a) Ilehoria bada, zer probabilitate dago begi urdinekoa izateko?

b) Eta begi urdina baditu, ilehoria izateko?

c) Zer probabilitate dago ez izateko ez ilehoria, ez begi urdinekoa?

* Erabili honelako taula bat:

urdinak begi urdinak ez guzt

15 40

Zer probabilitate dago kolore berekoak izateko? Eta kolore desberdinekoak izateko?

21 Bi bonboi-kaxa daude. Lehenengoan, 7 bonboi txokolate zurizkoak dira, eta 3 txokolate beltzezkoak; eta bigarren kaxan, 3 dira txokolate zurizkoak, eta 6 txokolate beltzezkoak. Begiratu gabe bonboi bat hartu dugu lehenengo kaxatik eta bigarrenean jarri dugu. Zer probabilitate dago bigarren kaxatik bonboi bat hartu eta txokolate zurizkoa izateko?

22 Aztertu koloretako bolak dituzten kaxa hauek:

A kaxa B kaxa

Dado bat daukagu, lau aurpegitan A letra idatzita, eta bitan B letra. Dadoa bota, irten den aurpegiak adierazitako kaxa hartu, eta bola bat atera dugu zorian.

a) Zer probabilitate dago bola gorria izateko? Eta beltza izateko?

b) Atera dugun bola gorria da. Zer probabilitate dago B kaxakoa izateko?

23 A potoan 6 klip zuri eta 4 beltz daude. B potoan 5 klip zuri eta 9 beltz daude. Zorian potoetako bat hartu dugu, bi klip atera ditugu eta zuriak dira. Aurkitu zer probabilitate dagoen hartutako potoa A izateko.

26 A eta B kutxak ditugu. A kutxan 3 bola zuri eta 5 beltz daude, eta B kutxan 10 bola beltz. Bi kutxetatik bola bana hartu dugu zorian eta aldi berean, eta trukatu egin ditugu (hau da, A kutxatik ateratako bola B kutxan sartu dugu, eta B kutxatik ateratako bola A kutxan sartu dugu). Hori egin ondoren, A kutxatik bola bat ateratzen baduzu, zer probabilitate dago beltza izateko?

27 Konpainia farmazeutiko batek dermatitis atopikorako saltzen duen sendagai batek kasuen % 80an arintzen du gaixotasuna. Gaixo bati plazebo bat ematen bazaio, bat-bateko hobekuntza izateko duen probabilitatea % 10ekoa da. Ikerketa batean, gaixoen erdiak sendagaiarekin tratatu dira, eta beste erdiak, plazeboarekin.

a) Zehaztu zer probabilitate dagoen zorian hartutako gaixo batek hobekuntza izateko.

b) Ikerketa 500 gaixorekin egin bada, zenbatek gutxi gorabehera igarriko dute hobekuntza?

c) Zorian hartutako gaixo batek hobekuntza igarri badu, zer probabilitate dago sendagaiarekin tratatutakoa izateko?

28 Baso batean 50 izei, 30 altzifre eta 120 pinu daude. Beldar batek eragindako gaixotasun batek 25 izeiri, 9 altzifreri eta 48 pinuri erasan die. Kalkulatu probabilitate hauek:

a) Zorian hartutako pinu bat beldarrarekin infektatuta egoteko. Pinuen zer ehuneko egongo dira beldarrarekin infektatuta?

b) Zorian hartutako zuhaitz bat beldarrarekin infektatuta egoteko.

c) Infektatutako zuhaitzen artean bat zorian hartu eta pinua izateko.

Proposatutako ariketak eta problemak

29 Gaixotasun bat hautemateko proba azkar batean, kasuen % 2 positibo faltsuak dira (pertsonak osasuntsu daude, probak positibo eman badu ere, eta gaixotzat sailkatzen dira) eta % 1 negatibo faltsuak (pertsonak gaixo daude, probak negatibo eman badu ere, eta osasuntsutzat sailkatzen dira). Populazio batean % 4 dira gaixoak.

a) Kalkulatu zer probabilitate dagoen test batek negatibo emateko.

b) Pertsona batek positibo eman badu, zer probabilitate dago osasuntsu egoteko?

30 3.3 helburua. Kolera epidemia bat dago (K ). Sintomatako bat beherakoa da (B ), baina sintoma hori intoxikazioa (I ) jasan dutenengan ere ageri da, baita ezer larririk ez duten zenbaitzuetan ere (E ). Probabilitateak hauek dira:

P [B/K ] = 0,99 P [B/I ] = 0,5 P [B/E ] = 0,004

Ehuneko hauek eman dizkigute: populazioaren % 2k kolera du; % 0,5ek, intoxikazioa, eta gainerakoek, % 97,5ek, ez dute ezer larririk. Pertsona batek beherakoa badu, zer probabilitate du kolera izateko?

31 Leirek eta Arratek poltsa bat dute 1etik 9ra zenbakituta dauden 9 bolaz beteta. Leirek zorian bola bat atera du, zer zenbaki duen ikusi, eta poltsara itzuli du. Ondoren Arratek beste horrenbeste egin du. Atera dituzten zenbakiak batzea erabaki badute, aurkitu zer zifrak duen probabilitaterik handiena baturaren unitatea izateko.

Galdera teorikoak

33 Ziurtatu dezakegu P [{1, 2}] < P [{1, 2, 7}]?

34 Erabili diagrama bat baieztapen hauek egiaztatzeko, eta zuzenak ez diren kasuetan, jarri adibide bat:

a) A ∩ B = ∅ bada, orduan A ∩ B = B

b) A ∪ B  = E bada, orduan P [B ] = 0.

c) A eta B bateraezinak badira, orduan A eta B bateraezinak dira.

35 Ondorengo enuntziatu hau oker dago: « A eta B bateragarriak badira, orduan A eta B bateragarriak dira». Jarri A eta B-ren saiakuntza baten eta gertaera baten adibide bat, kontuan izanda A eta B bateragarriak direla, baina A eta B bateraezinak.

36 Hiru dado botaz gero, batura 9 sei modutan lortu dezakegu:

1-2-6, 1-3-5, 1-4-4, 2-2-5, 2-3-4, 3-3-3 Eta batura 10 beste sei modutan:

1-3-6, 1-4-5, 2-2-6, 2-3-5, 2-4-4, 3-3-4

Dena dela, eskarmentuak diosku errazagoa dela batura 10 lortzea batura 9 lortzea baino. Zergatik?

37 Egiaztatu honako propietate hau: P [A ∪ B ] = P [A] + P [B ] – P [A ∩ B ] A ∪ B hiru gertaera desberdinetan deskonposatuz.

Sakontzeko

38 Kutxa bat daukagu, eta barruan hiru bola zuri eta hiru beltz. Dado bat bota, eta kutxatik dadoak adierazten duen adina bola aterako ditugu. Zer probabilitate dago denak zuriak izateko?

32 Etxetresna elektrikoen marka bateko produktuen zaharkitze programatuari buruzko ikerketa batean agertu denez, mikrouhin bat garantia-aldian dagoela hondatzeko probabilitatea 0,02 da. Probabilitate hori 0,05ekoa da labe elektrikoetan, eta badakigu bi gertaerak independenteak direla. Mikrouhina garantia-aldian hondatu bada, markak bi urte gehiago luzatzen du bermea. Baina garantia luzatuta duten bezeroen % 40k ez dute gordetzen erosketaagiria luzapeneko bi urteetan.

a) Bezero batek marka horretako labe bat eta mikrouhin bat erosi ditu. Lortu zer probabilitate dagoen tresna bat gutxienez garantia-aldian hondatzeko.

b) Aurkitu zer probabilitate dagoen mikrouhin bat erosi duen norbaiti garantia-aldian hondatzeko, eta ordainagiria gordeta izateko luzapeneko bi urteetan.

39 Garazi eta Peru plater-tirora jolasten ari dira. Garazik jaurtitako 3 plateretik 1 jotzen du, eta Peruk, 2 plateretik 1. Airera plater bat jaurti, eta bi tiro-hots entzun ditugu ondoz ondo; eta probabilitate bera dago biak izateko Garaziak eginikoak, biak Peruk eginikoak, edo bana eginikoak. Kontua da ez dutela platera jo.

a) Zer probabilitate dago bi tiroak Garazik eginikoak izateko? Eta Peruk eginikoak izateko?

b) Eta tiro bana egiteko?

40 Txanpon bat behin eta berriro bota dugu. Kalkulatu zer probabilitate dagoen alde bera birritan jarraian irteteko, baldin eta saiakuntzak izan baditu:

a) 2 jaurtiketa.

b) 4 jaurtiketa.

c) n jaurtiketa, n ≥ 2.

d) Gehienez, 10 jaurtiketa.

1 Txanpon bat hiru bider botatzeari buruzko zorizko saiakuntzan, honako gertaera hauek aztertuko ditugu:

A = «Gutxienez aurpegi bat eta gurutze bat ateratzea»

B = «Gehienez aurpegi bat ateratzea»

a) Zehaztu saiakuntza horri dagokion lagin-espazioa eta A eta B gertaerak

b) Independenteak dira bi gertaerak?

2 A eta B bi gertaerak hau betetzen dute:e P [A] =  4 3 ,

P [B/A] =  1 4 eta P [A /B] =  4 3 .

a) Kalkulatu P [A ∩ B].

b) Egiaztatu A eta B gertaerak independenteak direla, baina ez bateraezinak.

c) Kalkulatu P [ A / B ].

3 Erreparatu kutxa honi:

Kopiatu honako taula hau zure koadernoan eta osatu: guztira

41 2 bola zuri, 3 gorri eta 4 beltz dituen kutxa batetik, 3 bola atera ditugu aldi berean.

Aurkitu zer probabilitate dagoen bi bola (eta bi soilik) kolore berekoak izateko.

42 3 dado bota ditugu. Zer probabilitate dago batezbesteko balioa 5 izateko? Eta 2 izateko? Eta 1?

* Kontuan izan, adibidez, 5-1-4 emaitzaren batezbesteko balioa 4 dela; 2-1-2 emaitzarena, 2; eta 4-4-4 emaitzarena, 4.

Kalkulatu:

a) P [ ], P [ ], P [ ], P [1], P [2]

b) P [ ∩ 1], P [ /1], P [1/ ]. Azaldu probabilitate horietako bakoitzaren esanahia.

c) P [ /1], P [ /1]

d) «1» gertaera independentea da , edo gertaeretakoren batekiko. Zeinekiko? Azaldu zergatik.

4 A kutxatik bola bat atera dugu zorian, eta B kutxan sartu dugu. Bolak nahasi, eta zorian bola bat atera dugu berriz ere, baina oraingo honetan B kutxatik. Kalkulatu honako probabilitate hauek:

a) P [1.a eta 2.a ], P [2.a /1.a ]

b) P [1.a eta 2.a ], P [2.a /1. a ], P [2. a ]

c) P [2.a ], P [1.a /2.a ]

5 Bidaia-agentzia batean, bezeroen % 75ek garraiobidea eskatzen dute, eta % 80k, hotel-erreserba bat. % 65ek bi gauzak eskatzen dituzte. Bezero bat zorian hartu, eta kalkulatu zer probabilitate dagoen:

a) Garraiobidea eta hotel-erreserba eskatzeko.

b) Hotel-erreserba eskatu duela jakinda, garraiobide bat ere eskatzeko.

6 Enpresa batek bi motatako ordenagailu eramangarriak egiten ditu, baina A motakoen ekoizpena bi aldiz handiagoa da B motakoena baino. Badakigu A motako ordenagailu eramangarri bat akastuna izateko probabilitatea 0,02 dela; B motakoa akastuna izateko probabilitatea, berriz, 0,06.

a) Kalkulatu zer probabilitate dagoen enpresa horrek egindako ordenagailu bat zorian hartu eta:

i) Akastuna ez izateko.

ii) A motakoa izateko, akastuna dela jakinda.

b) Gutxi gorabehera, zenbat akastun egongo dira 1 500 ordenagailuko eskari batean?

➜ anayaharitza.es Ariketa hauen ebazpena. A

Autoebaluazioa

IV. multzoa : Probabilitatea

1 Honako probabilitate hauek dakizkigu:

P [A] = 0,33 P [ A ∩ B ] = 0,41 P [ B ] = 0,62

Kalkulatu P [B ], P [A ∪ B ] eta P [A ∩ B ].

2 A eta B bi gertaera aske dira, eta badakigu P [A] = 0,3 eta P [ B ] = 0,4 direla. Kalkulatu:

a) P [A ∪ B ] b) P [ A ∩ B ] c) P [A/ B ]

3 Ikasle talde batean, % 50ek igeriketa egiten du; % 20k, saskibaloia, eta % 5ek, bi kirolak. Kalkulatu zer probabilitate dagoen zorian hartutako ikasle batek:

a) Ez egiteko, ez igeriketa, ez saskibaloia.

b) Igeriketa egiteko, jakinda saskibaloia egiten duela.

4 A B

Dadoan 1 irteten bada, bola B-tik aterako dugu. Beste puntuazioren bat irteten bada, A-tik aterako dugu. Kalkulatu:

5 Betaurrekoak edo lentillak dituzten 100 pertsonako taldea hartu, eta begien koloreari erreparatu diogu (urdina, berdea, beltza, marroia). Emaitza batzuk taula honetan bildu ditugu:

urdina berdea beltza marroia guztira

7 a) Kalkulatu zein izan behar den k, honako taula hau probabilitate-banaketa bati buruzkoa izateko:

xi 11 12 13 14 15 16

pi 0,15 0,1 0,12 0,17 k k

b) Aurkitu P [13 ≤ xi ≤ 15].

c) Kalkulatu μ eta σ parametroak.

8 B (10; 0,4) banaketa batean, kalkulatu:

a) P [x = 0], P [x = 1], P [x > 1]

b) μ eta σ parametroak.

9 Altzairuzko aleazio batean nikel-maila egiaztatzeko analisien % 8 okerrak dira. 10 analisi egin dira. Arrazoitu honako baieztapen hauek zuzenak ala okerrak diren:

a) 3 analisi edo gehiago okerrak izateko probabilitatea % 3 baino txikiagoa da.

b) Justu 3 analisi oker izateko probabilitatea % 3 baino txikiagoa da.

c) 100 analisi eginez gero, zuzen egindakoen kopurua 8 da.

10 Marka jakin bateko inprimagailu batek lehenengo matxura duen arte igaro den denborak banaketa normal bat du, batezbestekoa 1 500 ordu izanik, eta desbideratze tipikoa, 200 ordu.

Esan inprimagailu horien zer ehunekok…

a) izango duen matxura funtzionatzen 1 000 ordu egin baino lehen.

a) Osatu taula.

b) Kalkulatu P [urdina], P [betaurrekoak], P [urdina eta betaurrekoak].

c) Kalkulatu P [urdina/betaurrekoak], P [betaurrekoak/urdina].

d) Azaldu zergatik diren askeak betaurrekoak eta urdina gertaerak.

6 Ibilgailuak fabrikatzen dituen multinazional batek ibilgailuen % 40 Espainiar Estatuan egiten ditu; % 35, Frantzian, eta gainerakoa, Italian. Fabrikatzen dituen ibilgailuak hiru modelotakoak dira (Antzer, Beam eta Zelestial). Espainiar Estatuan hiru modeloen kopuru berdinak fabrikatzen ditu. Frantzian, fabrikatzen diren ibilgailuen bi heren Antzer modelokoak dira, eta gainerakoak, Beam modelokoak. Italian Beam eta Zelestial modeloak fabrikatzen dira, kopuru berdinetan.

a) Zorian ibilgailu bat hartuta, zer probabilitate dago Beam modelokoa izateko?

b) Antzer modeloko ibilgailua izanda, zer probabilitate dago Espainiar Estatuan fabrikatutakoa izateko?

b) izango duen matxura funtzionatzen 1 000 ordu egin baino lehen.

11 Pediatra bat artatzen dituen zazpi urteko haurren pisua aztertzen ari da. Haur horien pisuak banaketa normala du, batezbestekoa 26 kg eta desbideratze tipikoa 4,3 kg izanik. Haur bat hartu dugu zorian.

a) Kalkulatu zer probabilitate dagoen 25 eta 28 kg arteko pisua izan dezan.

b) Zer pisu izan behar du haurrak, gutxienez, % 20ko atalasetik gora egoteko?

12 Test erako azterketa batek ehun galdera ditu eta galdera bakoitzak lau erantzun, baina bat bakarrik da zuzena. Ikasle batek zorian erantzun du.

Kalkulatu zer probabilitate dagoen:

a) 20 galderatik gora zuzen erantzuteko.

b) 50 galderatik gora zuzen erantzuteko.

c) 50 galdera edo gehiago zuzen erantzuteko, baldin eta 40ren erantzun zuzenak badakizki.

anayaharitza.es Ariketa hauen ebazpena.

Probabilitate-banaketak 15

Banaketa normala

Probabilitate-banaketak dira banaketa estatistikoen idealizazioak, azken horietan maiztasun erlatiboak erabiltzen direnean. Maiztasun erlatiboen banaketak esperimentalak dira, eta probabilitatearenak, berriz, teorikoak. Matematikarien erronka garrantzitsuenetako bat izan da mundu errealean agertzen diren ausazko fenomenoen portaera irudikatzen duten probabilitate-banaketen ereduak eraikitzea.

Probabilitate-banaketarik garrantzitsuena normala da. Galileo (1564-1642) banaketa horretara hurbildu zen neurketa astronomikoetan egindako erroreak aztertuz. Errore horiek erabilitako tresnei edo behatzaileari egozten zizkion, baina konturatu zen erroreak simetrikoak zirela, eta askoz ere sarriago gertatzen zirela errore txikiak handiak baino. xviii. mendearen hasieran, matematikariak ohartu ziren gauza berari buruzko neurketa ugari eginda, lortutako neurri guztiak kanpai itxuran banatzen zirela, baina deskribatu eta ezagutzera eman zuen lehena De Moivre izan zen, 1733an, Hurbilketa segida gisa garatutako (a + b)n binomioaren gaien batuketara izeneko artikulu labur batean. Txanponekin eta ausazko beste tresna batzuekin esperimentatuak eginez iritsi zen ondorio horretara, baina bere aurkikuntza ahaztuta geratu zen, jokoetan soilik erabili baitzen, eta horrek ez zuen askorako eman.

Mende erdi baino gehiago itxaron behar izan zen Laplacek (1749-1827) eta Gaussek (1777-1855) berriro aurkitu zezaten, neurrietan egindako erroreen banaketa aztertzean. Horregatik deitu zitzaion «erroreen kurba». Matematikari alemaniarraren omenez, «Gaussen kanpaia» ere esaten zaio.

Adolphe Quetelet (1796-1874) matematikariak (1796-1874) aurkitu zuen zentsu, neurri eta abarren emaitza askok «errorekurbaren» ezaugarri berberak zituzten maiztasun-banaketak agertzen zituztela ustekabean. Eta kurba hori oso bestelako esparruetan aplikatzen hasi zen: demografia, osasuna, genetika, psikologia, aseguruak… Gaussek berak ere astronomiarako erabili zuen bere kalkuluetan.

Adolphe Quetelet (1796-1874)

Galtonek (1822-1911) hainbeste miresten zuen kurba normala, honako hau esan zuen: Ezerk ez du adimena liluratzen «errore-maiztasunaren legeak» berekin dakarren ordena kosmikoak bezainbeste. Grekoek haren berri izan balute, jainko baten pare gurtuko zuketen. Nahasmen basatienaren erdian ere lasaitasunez gobernatzen du.

Abraham de Moivre

Abraham de Moivre (1667-1754) frantziarra matematikari handia izan zen. Erlijio kontuengatik Londresera exiliatu zen eta han Erresuma Batuko zientzia elkarte zaharreneko kide izan zen; hots, Royal Societykoa. Newtonen laguna zen, honek izugarri miresten baitzuen Moivrek matematika arloan zuen ezagutza. Hala ere, pobre bizi izan zen, eta kontatzen dutenez, diru apur bat irabazteko, xakejokoan aritzen zen kafetegietan.

EBATZI

Galtonen makina

Aztertu eskuineko irudian ageri den tresna. Funtzionatzen jartzeko, bertikal jarri behar da eta, goiko inbututik, hainbat perdigoi bota, erortzen hasi eta beheko laukietara heltzen diren arte. Zergatik daude beteago erdiko laukiak muturretakoak baino?

Hori azaltzeko, perdigoi batek egindako bidea aztertuko dugu: ibilbide osoan 7 bidegurutze topatuko ditu, eta horietako bakoitzean, ezkerrera edo eskuinera joateko probabilitate bera izango du 2 1 cm

a) Imitatu perdigoi baten ibilbidea. Horretarako, bota txanpon bat 7 bider, bidegurutzetan honetara jokatuz: aurpegia → eskuina, gurutzea → ezkerra. Adibidez, hau lortuz gero: A A A + A + A

zein ibilbide egingo du perdigoiak? Irudikatu. Egin berriro esperientzia eta lortu beste ibilbide batzuk.

b) Saia zaitez legeren bat aurkitzen segida bakoitzean zenbat aurpegi irten diren (berdin dio txanpona botatzean zer ordenatan irteten diren) eta perdigoia zein laukitara erori den lotzeko.

c) Egin daiteke esperientzia hori 7 txanpon aldi berean botata eta lortutako aurpegien kopurua kontuan hartuta?

Saia zaitez orain azaltzen zergatik dauden perdigoi gehiago erdiko laukietan muturrekoetan baino.

Abraham de Moivre (1667-1754)

Banaketa estatistikoak

Grafikoak: barra-diagramak eta histogramak

Azter ditzagun ezkerrean ageri diren grafikoen bidez emandako bi banaketak. Aldagai kuantitatiboen (zenbakizkoak) maiztasun-banaketak dira biak.

Goikoa aldagai diskretu bati dagokio, balio bakanduak baino ezin ditu hartu eta (asmaturiko galderak 5 edo 6 izan daitezke, adibidez, baina ez tarteko balio bat). Beraz, adierazteko, testean lor daitezkeen puntuen gainean barra estuak jarri ditugu, elkarrengandik bereizita. Barra-diagrama bat da. Diagrama horretan, barra bakoitzaren altuera dagokion maiztasunarekiko proportzionala da.

Bigarren banaketan, aldagaia jarraitua da: indibiduo bakoitzak dagokion tarteko edozein puntutan dagoen balioa har dezake. Beraz, adierazpenean barrak erabili beharrean, tarte osoa hartzen duten laukizuzenak erabili ditugu. Grafiko horri histograma esaten zaio.

Histograma batean, tarteei dagozkien maiztasunak proportzionalak dira irudikatutako laukizuzenen azalerekiko. Beraz, laukizuzenen oinarriak berdinak badira, altuerak maiztasunekiko proportzionalak izango dira. Baina oinarriak zabalera desberdinekoak badira, laukizuzenen altuerak aurkitu eta kalkulatu egin beharko dira, ondoren ageri den ariketa ebatzian egin den bezala

1 Adierazi herrialde batek 2007. urtean zeukan biztanleriari dagokion honako banaketa hau.

Aldagai jarraituko (adina) banaketa bat da eta, beraz, histograma baten bidez adierazi behar dugu. Histograma batean, tarte bakoitzaren maiztasuna tarte horri dagokion laukizuzenaren azalerak ematen digu.

Kasu honetan, tarteak ez direnez guztiak luzera berekoak, laukizuzenek oinarri desberdinak dituzte. Horrek esan nahi du, altuerak kalkulatzean, kontuan izan behar dugula azalerek maiztasunekiko proportzionalak izan behar dutela. Beraz, laukizuzen bakoitzaren altuera lortzeko, azalera (dagokion maiztasuna) oinarriarekin (tartearen luzera) zatituko dugu. Horietako batzuk kalkulatuko ditugu:

1. laukizuzena. Oinarria = 5 – 0 = 5, Azalera = 1,8 → Altuera = 1,8 : 5 = 0,36

7. laukizuzena. Oinarria = 40 – 30 = 10, Azalera = 6 → Altuera = 6 : 10 = 0,60

9. laukizuzena. Oinarria = 70 – 50 = 20, Azalera = 3,6 → Altuera = 3,6 : 20 = 0,18

EGIN ZUK Aurkitu aurreko diagramako gainerako laukizuzenen altuerak.

Ebatzitako ariketa

x

eta σ parametroak kalkulatzea

Banaketa maiztasun-taula baten bidez emanda dagoenean, parametroak kalkulatzeko formulek honako itxura hau hartzen dute:

GOGORATU

Aldagaia tarteen bitartez emanda badago, xi moduan klase-marka hartuko dugu; hau da, tartearen erdiko puntua.

anayaharitza.es

Bariantzaren bi adierazpenak bat datozela ikusteko egiaztapena.

1 Kalkulatu x– eta σ, gazte-talde bateko garaierei buruzko (zentimetrotan) banaketan. Honako maiztasun-taula honen bidez emanda dago.

xi aldagaitzat tarteen klase-markak hartuko ditugu.

164,52 = 39

σ = 39 = 6,24 cm

- 178,5 4

➜ Kalkulatu banaketa estatistiko bateko batezbestekoa, bariantza eta desbideratze tipikoa.

kalkulagailuarekin:

1. Kalkulagailua modu estatistikoan prestatu behar dugu. Horretarako, sakatu → 6: Estatistika → 1:1-Aldagaia. Taula huts bat agertuko da, datuak sartzeko.

2. Kalkulagailua itzaltzean edo modu estatistikotik irtetean, datu guztiak ezabatuko dira. Behar ez ditugu datuak ezabatzeko, erabili tekla.

3. Sartu datuak taulan, datu bakoitzaren ostean = sakatuta. Era berean, sartu maiztasunak eskuineko zutabean.

4. Datuen laburpena eta parametro estatistikoen balioak lortzeko, sakatu → 3:Kalk 1-aldagaia.

1 Kalkulatu x –eta σ banaketa honetan: ikasle talde batek ikastetxetik etxeraino joateko behar izaten duen denbora. (Gogoan izan: (0, 5] tarteari 2,5 klase-marka dagokio; …).

Pentsatu eta praktikatu

Aldagai diskretuko probabilitate-banaketak

Probabilitate-banaketak dira modu enpirikoan (saiakuntzak edo behaketak eginez) lortzen diren maiztasun erlatiboko banaketen idealizazio teorikoak dira. Aldagaia diskretua denean, bai batzuk eta bai besteak barra-diagrama baten bidez adierazten dira.

ZERGATIK «MAIZTASUN ERLATIBOAK»?

Aurreko unitatean, probabilitatea eta horren propietateak definitzeko, maiztasun erlatiboak eta horien jokabidea hartu ditugu eredutzat. Beraz, probabilitate-banaketetan eredu moduan banaketa estatistikoak (maiztasun-banaketak) erabili ahal izateko, maiztasun absolutuen lekuan maiztasun erlatiboak jarri behar dira.

Aldagai diskretuko probabilitate-banaketa bat xi aldagaiaren balioetako bakoitzari pi probabilitate bat lotzea da

• pi bakoitza 0 eta 1 arteko zenbaki bat da: 0 ≤ pi ≤ 1

• pi guztien arteko batura 1 da: p1 + p2 + … + pn = ∑ pi = 1

• Barra-diagrama baten bidez adierazten da

Parametroak. Banaketa estatistikoetako parametroen antzera definitzen dira:

batezbestekoa: µ = p1 x1 + p2 x2 + … + pn xn = ∑ pi xi (batazbestekoari itxarondako balio edo itxaropen matematikoa ere esaten zaio)

bariantza: σ2 = p1(x1 – µ)2 + p2(x2 – µ)2 + … + pn(xn – µ)2 = ∑ pi (xi – µ)2

edo: σ2 = ( p1 x1 2 + p2 x2 2 + … + pn xn2) – µ2 = ∑ pi xi2 – µ2

desbideratze tipikoa: σ = ()px px ∑– µ∑ –µ BARIANTZA ii ii 22 2 ==

Aztertu bariantzaren bi formulak:

• Lehenengoan, argi eta garbi ikusten da bariantzaren esanahia: balioetako bakoitzetik batezbestekora dauden kenketa guztien karratuen batura haztatua.

• Bigarrena askoz erosoagoa da datuetatik abiatuta bariantza kalkulatzeko (aztertu hurrengo orrialdeko ariketak).

Baina, jakina, biak dira baliokideak, honako egiaztapen honekin ikusiko duzunez:

∑ pi (xi – µ)2 = ∑ pi (xi2 – 2xi µ + µ2) = ∑ pi xi2 + ∑ pi (–2xi µ) + ∑ pi µ2 =

= ∑ pi xi2 – 2µ ∑ pi xi + µ2 ∑ pi = (*)

xi P [ xi ] = pi

MATEMATIKA-HIZKUNTZA

Banaketa estatistikoak (enpirikoak) eta probabilitate-banaketak (teorikoak) erabiltzen direnean, lehenengoen parametroak izendatzeko letra latindarrak erabiltzen dira (x – edo m, s); eta bigarrenen parametroak izendatzeko, berriz, letra grekoak (µ, σ). Orain arte σ erabili izan dugu banaketa estatistikoetan desbideratze tipikoa adierazteko. Zergatik σ eta ez s ? σ kalkulagailuetan erabiltzen den letra delako.

= ∑ pi xi2 – 2µµ + µ2 · 1 =

= ∑ pi xi2 – µ2 (*) ∑ pi xi = µ ∑ pi = 1

Baina berriro diogu: aldi berean banaketa teorikoak eta banaketa enpirikoak erabiltzen ditugunean, lehenengoetarako letra grekoak erabiliko ditugu, eta bigarrenetarako, letra latindarrak.

Hurrengo probabilitate-banaketa hauetako bat bera ere ez dago ondo definituta: a) b)

1 Zuzena ala okerra?

Pentsatu eta praktikatu

Ebatzitako ariketak

1 Herri loteria batean 1 000 zenbaki daude, eta zozketa bidez, zenbaki bat aterako dute. Zenbaki horren jabeak 5 000 € irabaziko ditu. Irten den zenbakiaren aurrekoa eta hurrengoa dutenek 1 000  € eramango ditu bakoitzak. Zenbaki irabazlearen azkeneko zifra bera duten guztiek, 10  € Eta gainerakoek, ezer ez.

Nola deskribatuko dugu zenbaki bakarra erosi duen pertsona batek saria lortzeko probabilitatea?

σ

Taula bat eraiki dugu, xi sari bakoitzari saria lortzeko pi probabilitatea lotuz

Taula osatzeko, pi xi eta pi xi2 zutabeak erantsi ditugu. Horietako baturek parametroak kalkulatzeko balioko digute

batezbestekoa: µ = ∑ pi xi = 7,99 (Horrek esan nahi du loterian zenbaki bat askotan jokatuko bagenu, batezbeste 7,99  € irabaziko genituzkeela. Eta hor ez dago zenbatuta loteria kostatu zaiguna.)

desbideratze tipikoa: σ = ,, px 27 009 97 99 ∑– µ– ii 22

2 = = 164,15

xi da bi dadoren puntuazioak batzean lor daitezkeen balio posibleak; fi, berriz, balio horientzat 36 jaurtialditan «esperotako maiztasunak».

Emaitzak kalkulagailu batekin lortzeko, probabilitateak maiztasunak balira bezala sartzen ditugu. Horretarako, dagokion laukian egin dezakezu eragiketa.

1 /

Emaitzak aurreko atalean egin genuen moduan lortzen ditugu, hau da, → 3:Kalk 1-aldagaia

Pentsatu eta praktikatu

2 Kalkulatu dado bat jaurti eta ateratzen den puntuazioari dagokion probabilitate-banaketaren batezbestekoa eta desbideratze tipikoa.

3 Bi txanpon botatzen baditugu, 0, 1 edo 2 aurpegi lor ditzakegu. Kalkulatu gertakari horri dagokion probabilitate-banaketaren batezbestekoa eta desbideratze tipikoa.

4 Poltsa batean hainbat bola ditugu zenbakituta:

9 bolatan, bat zenbakia; 5 bolatan, bi, eta 6 bolatan hiru

Zorian bola bat atera eta zer zenbaki duen ikusiko dugu.

a) Zein da probabilitate-banaketa?

b) Kalkulatu batezbestekoa eta desbideratze tipikoa.

2 Aurkitu µ eta

bi dadotako puntuazioak batzean lortzen den banaketan.

Banaketa binomiala

esperientzia dikotomikoa

Zorizko esperientzia batean A gertaera nabarmentzen badugu, eta A edo horren aurkako A gertaera jazotzen den bakarrik aztertzen badugu, orduan esperientzia dikotomiko bat dela esaten dugu.

A gertaerari arrakasta esaten zaio, eta horren probabilitateari, P [A] = p.

Aurkakoaren probabilitatea P [ A ] = 1 – p = q.

Adibidez, honako hauek esperientzia dikotomikoak dira:

1. Txanpon bat botatzea: A = aurpegia, A = aurpegia ez = gurutzea

p = P [aurpegia] = 1/2 q = P [gurutzea] = 1/2

2. Dado bat bota eta 5 irteten den ikustea: A = {5}, A = «5 ez» = {1, 2, 3, 4, 6}

p = P [«5»] = 1/6 q = P [«5 ez»] = 5/6

3. Txintxeta bat botatzea: A = , A =

p = P [ ] = 0,3 (adibidez) q = P [ ] = 0,7

4. Karta-multzo batetik karta bat atera eta irudia den ikustea:

A = irudia = {txanka, zaldia , erregea} A = irudia ez = {batekoa, 2, 3, 4, 5, 6, 7}

p = P [irudia] = 0,3 q = P [irudia ez] = 0,7

banaketa binomiala

Abiapuntutzat esperientzia dikotomiko bat hartuko dugu, p arrakastaren probabilitatea izanik. Esperientzia hori n aldiz egingo dugu, eta x arrakasta-kopurua zein den aztertuko dugu (x aldagaia diskretua da, 0, 1, 2, …, n balioak hartzen baititu).

x-ren probabilitate-banaketari B (n, p) banaketa binomiala esaten zaio.

Adibidez, honako hauek banaketa binomialak dira:

1. 10 txanpon bota ditugu eta zenbat aurpegi irtengo diren jakin nahi dugu

Txanpon bat botatzea esperientzia dikotomiko bat da

Arrakasta: aurpegia → P [A ] = p = 0,5

10 txanpon botatzea txanpon bat 10 aldiz botatzearen parekoa da. Goian deskribatu dugun esperientzia dikotomikoa 10 aldiz egitea da.

Beraz, B (10; 0,5) banaketa binomiala da.

x aldagaia lortutako aurpegien kopurua da. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 eta 10 balioak har ditzake

2. Ondo egindako 6 dado bota eta zenbat «bosteko» aterako diren jakin nahi dugu.

Banaketa binomial bat da, n = 6, p = 1/6 izanik → B (6, 1/6).

3. Lurrera erortzen utzi ditugu 100 txintxeta, eta punta goraka dutela zenbat erori diren zenbatu dugu.

Txintxeta guztiak berdinak direla onartuko dugu, eta, horrela, banaketa binomiala izango da, n = 100 eta p = P [ ] izanik. P [ ] = 0,3 bada, orduan B (100; 0,3) da

4. Karta-multzo batetik karta bat atera dugu, irudia den ikusi eta berriro multzora itzuli dugu. Kartak nahastu eta beste bat atera dugu. Esperientzia hori bost aldiz egin dugu. Banaketa binomiala da: n = 5, p = 0,4 → B (5; 0,4).

OHARRA

P [ ] = 0,3 dela esaten dugunean, hau esaten ari gara: txintxeta modelo hori puntua goraka duela, batez beste, jaurtitzen dugun 10etik 3tan geldituko da.

B ( n, p ) BATEN ALDAGAIA DISKRETUA

DA

B (n, p) banaketa batean, x aldagaia arrakasten kopurua da. Esperientzia n aldiz egiten denez, x aldagaiak 0, 1, 2, 3, …, n balioak har ditzake.

Argi dago, beraz, aldagai diskretua dela.

GALTONEN MAKINA

Galtonen makina honek B (4, 1/2) banaketa binomial baten moduan jokatzen du bola bakoitzarekin.

Bolak lau bidegurutze topatzen ditu bidean, eta horietako bakoitzean alde batera edo bestera egiteko duen probabilitatea 1/2 da.

B(n, p) banaketa bateko probabilitateak kalkulatzea

40 kartako multzo batetik 5 karta itzulera eta guzti ateratzea eta ateraldi horietan guztira zenbat irudi lortu diren (x) aztertzea B (5; 0,4) banaketa binomiala da

bakoitza 5 kartako segida bat da, eta ardura duen bakarra da irudia lortu den. Ikus dezagun segida horietako batzuen probabilitatea:

ZENBAKI KONBINATORIOAK

Ekarri gogora aurreko ikasturtean landu genituen m n cm zenbaki konbinatorioak.

5 3 eo modu daude 3I eta

I ateratzeko. Beraz:

[3I ] = 5 3 eo · 0,33 · 0,72 = 0,1323

x aldagaia B (n, p) bada, k arrakasta lortzeko probabilitatea hau da:

[x = k] = n k cm p k · q n – k

Hortik, honako probabilitate-banaketa hau lortzen dugu:

x aldagaia 0 k n

P [x = k ] probabilitatea n 0 cm p0qn = qn n k cm pkqn – k n n cm pnq0 = pn

Banaketa horren parametroak hauek dira:

batezbestekoa: µ = np desbideratze tipikoa: σ = npq

1 B(8; 0,2) binomial batean, kalkulatu P[x = 0], P[x ≠ 0], P[x = 2], baita µ  eta σ parametroak ere.

B (5; 0,3) binomialaren probabilitate-banaketa eta horren adierazpen grafikoa.

KALKULAGAILUAREKIN

Zenbaki konbinatorioak kalkulagailuarekin lortzeko, teklak sakatu behar ditugu. Ikus dezagun nola: 5 3 eo → 5 3 = [VCL]

P [x = 0] = 0,88 = 0,168 («arrakastarik ez» gertaeraren probabilitatea)

P [x ≠ 0] = 1 – 0,88 = 0,832 («arrakastaren bat» gertaeraren probabilitatea)

P [x = 2] = 8 2 eo 0,22 · 0,86 = 28 · 0,04 · 0,262 = 0,294

batezbestekoa: µ = np = 8 · 0,2 = 1,6

desbideratze tipikoa: σ = , npq 128 = = 1,13

Pentsatu eta praktikatu

1 B (10; 0,4) banaketa binomial batean, aurkitu P [x = 0], P [x = 3], P [x = 5], P [x = 10] eta µ eta σ parametroen balioak.

2 7 txanpon bota ditugu. Kalkulatu 3 aurpegi, 5 aurpegi eta 6 aurpegi ateratzeko probabilitateak. Aurkitu µ-ren eta σ-ren balioak.

3 Zuzena ala okerra?

«Futbol talde batek partida batean lortuko duen emaitza irabazi edo ez irabazi izan daiteke. Beraz, esperientzia dikotomikoa da.»

Ebatzitako ariketa

➜ Kalkuluak edozein binomialetan.

Aldagai jarraituko probabilitate-banaketak

Aldagai jarraituko probabilitate-banaketak dira aldagai jarraituko banaketa estatistikoen idealizazioak. Banaketa estatistikoak modu enpirikoan lortzen dira (saiakuntzak edo behaketak eginez). Probabilitate-banaketak, berriz, banaketa teorikoak dira. Adibidez, garaierak, pisuak, denborak…, aldagai jarraituak dira.

Aldagai jarraituko probabilitate-banaketak y =  f (x) funtzio baten bidez definitzen dira. Funtzio horri probabilitate-funtzio edo dentsitate-funtzio esaten zaio, eta ondoren, horren baldintzak deskribatuko ditugu

f (x) zorizko aldagai baten dentsitate-funtzioa edo probabilitate-funtzioa izateko honako hauek bete behar dira:

— f (x) ezin da negatiboa izan: f (x) ≥ 0 izan behar da x ororako.

— y = f (x) kurba azpiko azalera 1 izan behar da.

• P [a ≤ x ≤ b ] probabilitatea lortzeko, kurba azpian [a, b ] tartean zer azalera dagoen lortuko dugu:

P [a ≤ x ≤ b ] = kurba azpiko azalera [a, b ] tartean

• Gertaera puntualen probabilitateak zero

dira:

Beraz:

P [x = a] = 0, P [x = b ] = 0, …

P [a ≤ x ≤ b ] = P [a < x < b ]

Probabilitateak y = f(x) dentsitate-funtzio batetik abiatuta kalkulatzea

Badakigu aldagai jarraituko probabilitate-banaketetan probabilitateak kalkulatzeko, y = f (x) dentsitate-funtzioak irudikatzen duen kurbaren azpiko azalerak lortu behar direla. Baina nola kalkulatu zehatz f (x) bere adierazpen analitikoaren bidez emanda dagoenean? Kasu horretan, kalkulu integrala erabiliko dugu:

P[a ≤ x ≤ b] = [Azalera f (x), y = 0, x = a, x = b artean] = ()fx dx a b y

Ikus ditzagun, jarraian, adibide batzuk.

Ebatzitako ariketak

1 Kalkulatu zein izan behar den k, funtzio hau

f (x) = , , [, ] [, ] kx x 0 15 15 g !

dentsitate-funtzioa izateko. Lortu probabilitate hau: P[2 ≤ x ≤ 3]

EGIN ZUK Kalkulatu:

a) P [2 ≤ x ≤ 5] b) P [2 ≤ x ≤ 2,5]

2 Kalkulatu m-ren balioa, honako funtzio hau

f (x) = , , [, ] [, ] mx x x 0 04 04 g !

dentsitate-funtzioa izan dadin. Aurkitu P[2 ≤ x ≤ 3].

EGIN ZUK Kalkulatu:

a) P [0 ≤ x ≤ 1]

b) P [3 ≤ x ≤ 4]

3 a) Aurkitu zein izan behar den b parametroaren balioa, honako funtzio hau:

f(x) = 1 x , 1 ≤ x ≤ b dentsitate-funtzio bat izateko.

b) Aurkitu P[1 ≤ x ≤ 2].

EGIN ZUK

Aurkitu P[0,5 ≤ x ≤ 2,5].

Pentsatu eta praktikatu

Gogoan izan kurba azpiko azalera osoa 1 izan behar dela. Kasu honetan, ez du merezi integralak erabiltzea azalera lortzeko. P [– ∞ < x < +∞] = P [1 ≤ x ≤ 5] = 4 · k = 1

Beraz, k = 1 4 . Horrela, eskatutako probabilitatea kalkula dezakegu:

Kalkula dezagun zein izan behar den m triangeluaren azalera 1 izateko. Kasu honetan ere, ez du merezi kalkulu infinitesimalera jotzea.

Triangeluaren azalera: m 2 44 = 8m. Beraz:

P [– ∞ < x < +∞] = P [0 ≤ x ≤ 4] = 8m = 1

8m = 1 → m = 1 8

Dentsitate-funtzioa y = x/8, x ∈ [0, 4] da, y = 0 hondarrean

P [2 ≤ x ≤ 3] trapezio gorriaren azalera da

P [2 ≤ x ≤ 3] = (/ /) 2 28 38 1 + = 16 5

a) Kurbaren azpiko azalera kalkulatuko dugu eta berdin 1 egingo dugu: ln ln ln ln

dx xb b

== = 8 B y (izan ere, ln 1 = 0)

Beraz, izan behar da ln b = 1 → b = e1 = e.

(x) = x 1 , 1 ≤ x ≤ e

b) Eskatutako probabilitatea kalkulatuko dugu:

1 Kalkulatu k-ren balioa f (x) = , , [, ] [, ] kx x 0 38 38 g ! * dentsitatefuntzioa izan dadin. Lortu probabilitate hauek:

a) P [4 < x < 6] b) P [2 < x ≤ 5]

c) P [x = 6] d) P [5 < x ≤ 10]

2 Kalkulatu aurreko probabilitate horiek kalkulu integrala erabilita.

3 Kalkulatu m-ren balioa f (x) = , , [, ] [, ] mx x x 0 37 37 g !

dentsitatefuntzioa izan dadin. Lortu probabilitate hauek:

a) P [3 < x < 5] b) P [5 ≤ x < 7]

c) P [4 ≤ x ≤ 6] d) P [6 ≤ x < 11]

4 Lortu aurreko probabilitate horiek kalkulu integrala eginez.

µ eta σ parametroak lortzea

Aldagai jarraituko banaketetan, f (x), a ≤ x ≤ b dentsitate funtzioak daukan papera da pi = P [xi] probabilitateak aldagai diskretuko banaketetan daukan paper bera. Aztertu paralelotasuna:

aldagai diskretua aldagai jarraitua

Aldagai diskretuetan bezala, banaketa jarraituetan bariantza honela sinplifikatu daiteke: σ2 = a b y f (x) · x 2 dx – µ2 (kalkulatzeko erosoagoa).

Lortu dezagun parametro horien balioa aurreko orrialdean ikusi ditugun hiru probabilitate-banaketetan:

= ,, 00 24 49 =

5 Egiaztatu f (x) = x 9 2 , 0 ≤ x ≤ 3 dentsitate-funtzio bat dela. Aurkitu µ eta σ parametroak.

6 Egiaztatu f (x) = x 2 2 , 1 ≤ x ≤ 2, dentsitate-funtzio bat dela. Aurkitu µ eta σ parametroak.

Banaketa normala

Aldagai jarraituko probabilitate-banaketen artean, bereziki nabarmentzekoa da banaketa normala.

Kurba normala da probabilitate jarraitua eta simetrikoa duen funtzio bat, eta horren maximoa bat dator µ batezbestekoarekin.

Kurba hori Carl Friedrich Gauss matematikari alemanak deskribatu zuen. Magnitude jakin bat behin eta berriro neurtzean egiten diren erroreak aztertuz heldu zen kurba horretara. Hona hemen kurbaren ekuazioa eta adierazpen grafikoa:

Kanpai itxura duela eta, Gaussen kanpaia esaten zaio.

Garrantzi handiko banaketa da, hainbat eta hainbat egoeratan ageri baita. Normal banatzen diren aldagai horien guztien artean, hona hemen batzuk:

• Arraza bereko indibiduoen (pertsona, animalia, landare) ezaugarri morfologikoak. Adibidez: neurriak, pisuak, luzerak, etab.

• Ezaugarri fisiologikoak. Adibidez, farmako dosi beraren edo ongarri kantitate beraren efektuak

• Ezaugarri soziologikoak. Adibidez, giza talde bereko indibiduo batzuek kontsumitzen dituzten produktuak.

• Ezaugarri fisikoak. Adibidez, itxuraz berdinak diruditen piezek hausturari dioten erresistentzia.

Eta, orokorrean, hainbat faktoreren baturatik lortzen den edozein ezaugarri.

µ batezbestekoaren eta σ desbideratze tipikoaren balio bakoitzerako, N (µ, σ) izendatzen den kurba normal bat dago

Adibidez, N (0, 4), N (10, 4) eta N (10, 2) banaketak aztertuko ditugu.

N (10, 2)

N (0, 4)

–10 0 10

N (10, 4) 20

Hiru grafiko desberdin badira ere, probabilitate-banaketa ia berdina da hiruretan. µ eta σ parametroen araberakoa baino ez da.

Ikusten dugunez, desbideratze tipiko bera duten bi kurba normal berdinak dira. Eta desbideratze tipiko desberdina badute, antzekoak dira: berdinak dira, eskalan dagoen aldea bazter utzita.

Antzekotasun horrek zer esan nahi duen hurrengo orrialdean zehaztuko dugu.

Carl Friedrich Gauss (1777-1855)

Kurba normalaren azpiko azaleraren banaketa

Banaketa normala probabilitate-banaketa bat denez, bere kurba azpiko azalera 1 da. Baina azalera hori honela dago banatuta:

Horrek esan nahi du, adibidez: zenbait pertsonaren adimen-kozienteak (A.K.) N (112, 6) banaketa jarraitzen badu, orduan:

— % 68,26ren A.K. 106 eta 118 artekoa dela.

— % 95,44ren A.K. 100 eta 124 artekoa dela.

— % 99,74ren A.K. 94 eta 130 artekoa dela.

Gehiago zehaztuz gero, honela banatzen direla esan dezakegu:

Kurba normal guztiak berdinak dira funtsean

Batezbestekoaren ezkerrera 0,5eko desbideratze tipikoa eta eskuinera 1,2koa hartu beharrean beste bi konstante hartuko bagenitu, bi kurbetan berdinak, kasu horretan ere azalerak berdinak izango lirateke.

Horrek esan nahi du, jatorrian eta eskalan egon daitezkeen desberdintasunak albo batera utzita, kurba normal guztiak berdinak direla funtsean.

Ezaugarri horrek modua ematen digu, kurba normal baten azpiko azalera zein den jakinda, beste edozein kurbaren azpian dagoen azalera jakiteko. Horretarako, beraz, kurba normal errazena erabiliko dugu: batezbestekoa 0 eta desbideratze tipikoa 1 duena.

N (0, 1) kurba normalaren azpiko azalerak, hau da, horren probabilitateak, ezagunak dira; tauletan bilduta daude eta guk ere erabiltzen ikasiko ditugu orain. Taula horiekin

N (µ, σ) edozein banaketa normaleko probabilitateak kalkulatu ahal izango ditugu

N  (0, 1) kurba normalaren azpiko azaleren taula

Geroago egin beharko ditugun aldagai-aldaketen adierazpenak errazteko, N (0, 1) banaketan, aldagaia izendatzeko z erabiltzen da. Ondoren ageri den taula horrek k-ren 0 eta 3,99 bitarteko balioen P [z ≤ k ] probabilitateak ematen dizkigu, ehunenetik ehunenera. Probabilitate horiei ϕ(k ) esaten zaie:

ϕ(k ) = P [z ≤ k ], z aldagaia N (0, 1) da

Honela topatuko dugu k-ren balioa:

Unitateak eta hamarrenak ezkerreko zutabean

Ehunenak goiko errenkadan.

Taulak ematen digun zenbakia honako honen balioa da: ϕ(k ) = P [z ≤ k ]

• Adibideak:

P [z ≤ 0,45] = ϕ(0,45) = 0,6736

P [z ≤ 1,2] = ϕ(1,20) = 0,8849

P [z ≤ 1] = ϕ(1,00) = 0,8413

Modu berean, ϕ(k ) probabilitatearen balioa zein den badakigu,  k-ren balioa lor dezakegu.

• Adibideak:

P [z ≤ k ] = ϕ(k ) = 0,7190 → k = 0,58

P [z ≤ k ] = ϕ(k ) = 0,8643 → k = 1,10

P [z ≤ k ] = ϕ(k ) = 0,5560 → k ≈ 0,14

Gogoan izan aldagai jarraituko banaketa batean probabilitate puntualak nuluak direla: P [x = k ] = 0. Beraz, P [x ≤ k ] = P [x < k ].

Pentsatu eta praktikatu

1 Aurkitu probabilitate hauek:

a) P [z ≤ 0,84]

b) P [z < 1,5]

c) P [z < 2] d) P [z < 1,87]

e) P [z < 2,35]

f) P [z ≤ 0]

g) P [z < 4] h) P [z = 1]

2 Esan zein den k-ren balioa kasu hauetako bakoitzean:

a) P [z ≤ k ] = 0,7019

c) P [z ≤ k ] = 0,5040

b) P [z < k ] = 0,8997

d) P [z < k ] = 0,7054

3 Esan zein den k-ren gutxi gorabeherako balioa kasu hauetan:

a) P [z < k ] = 0,9533

b) P [z ≤ k ] = 0,62

N  (0, 1) banaketa baten probabilitateak kalkulatzea

• k ≥ 0 bada, P [z ≤ k ] = P [z < k ] = ϕ(k ) probabilitateak zuzenean aurkituko ditugu tauletan

• P [z ≥ k ] = 1 – P [z < k ] = 1 – ϕ(k )

• Abzisa negatiboen kasuan (gogoan izan kurba simetrikoa dela).

Gainerako probabilitateak horietatik abiatuta lor daitezke, honako adibide hauetan ikusten den moduan:

= 0,9744 – 0,8413 = 0,1331

Pentsatu eta praktikatu

4 Aurkitu:

a) P [z > 1,3] b) P [z < –1,3] c) P [z > –1,3]

d) P [1,3 < z < 1,96] e) P [–1,96 < z < –1,3]

f) P [–1,3 < z < 1,96] g) P [–1,96 < z < 1,96]

➜ Aurkitu N(0, 1) banaketa baten probabilitateak.

5 Aurkitu honako probabilitate hauek, taulatik abiatuta:

a) P [–1 ≤ z ≤ 1]

c) P [–3 ≤ z ≤ 3]

e) P [0 ≤ z ≤ 1]

b) P [–2 ≤ z ≤ 2]

d) P [– 4 ≤ z ≤ 4]

f) P [0 ≤ z ≤ 4]

N  (µ,  σ) banaketa bateko probabilitateak kalkulatzea

Bi banaketa normalen probabilitateak, banaketa horiek edozein direla ere, berdin-antzean banatzen dira. Beraz, N (µ, σ) banaketa bateko probabilitateak kalkulatzeko, N (0, 1) banaketarekin erlazionatuko dugu, horretarako taulak erabiliz. Adibidez:

Azalerak, berdinak

N (0, 1) banaketarekin erlazionatzeko, tarteen muturrak beste era batera adierazi behar ditugu: batezbestekotik aldentzen diren desbideratze tipikoen kopurua zehaztu behar dugu. Eragiketa horri aldagaia tipifikatzea esaten zaio.

x aldagaia N (µ, σ) bada, P [h < x < k ] probabilitatea kalkulatzeko hau egingo dugu: P [h < x < k ] = P h z k –µ –µ << vv = G

k → k –µ v aldaketari aldagaiaren tipifikazio esaten zaio.

z aldagai tipifikatuak N (0, 1) banaketa jarraitzen du

kontuan izan: Ikusten duzunez, N (µ, σ) edozein banaketaren aldagaiari x esan diogu, eta N (0, 1) banaketaren aldagaiari, z. Horrela jokatuko dugu beti.

1 N(6, 4) batean, kalkulatu honako probabilitate hauek:

3]

6 N (173, 6)) banaketan, aurkitu probabilitate hauek:

a) P [x ≤ 173]

b) P [x ≥ 180,5]

c) P [174 ≤ x ≤ 180,5]

e) P [161 ≤

d) P [161 ≤ x ≤ 180,5]

Banaketa binomiala normalera hurbiltzen da

Atal honetan ikusiko dugunez, n-ren eta p-ren balio batzuekin, banaketa binomialek dagozkien banaketa normalen antz handia dute.

Hasteko, ikus dezagun nolakoak diren B ,n 2 1 cm banaketak n -ren balio desberdinetarako:

Probabilitatea barrek markatzen dute. Barrak biltzen dituzten lerroak normalarekin duten antzekotasuna adierazteko irudikatu ditugu. Bigarren banaketaren kasuan argia da antz hori, eta hirugarrenena, oso nabarmena.

B ,n 1 5 cm binomialen kasuan ere efektu bera ageri da (beheko grafikoan): zenbat eta handiagoa izan n, kurbek orduan eta normalaren antz handiagoa hartzen dute

Aztertu ongi. Lehenengoak (n = 5) ez du kurba normalaren antzik.

Baina hurrengoek gero eta antz handiagoa hartzen dute

Eta azkena, B (50; 0,2) binomiala, kurba normal baten berdina da ia-ia.

➜ Hurbildu binomial bat normal batera.

Orokorrean, zenbat eta handiagoa izan np biderkadura (edo nq, q < p bada), orduan eta antz handiagoa izango du B (n, p) binomialak kurba normal batekin. np eta nq biak direnean 3 baino handiagoak, hurbilketa nahiko ona da. Eta 5 baino handiagoak badira, hurbilketa ia perfektua da. Hemendik aurrera, 3 balioa hartuko dugu erreferentzia gisa informazio hori baliozkotzeko.

Jakina, hurbilketa egiteko erabilitako kurba normalak eta binomialak batezbesteko eta desbideratze tipiko berdinak dituzte; hau da:

µ = np σ = npq

GARRANTZITSUA

n · p ≥ 3 eta n · q ≥ 3 badira, orduan: B (n, p) ≈ N (np, npq )

Kidetasun horretan ez dugu ahaztu behar binomiala diskretua dela, eta normala, jarraitua. Hurrengo orrialdean, desberdintasun garrantzitsu hori landuko dugu.

Probabilitateak

binomialetik normalera igaroz kalkulatzeko erregela praktikoa

x aldagaia B (n, p) bada, eta N (np, npq ) banaketa duen x' aldagaiaren antz handia badu, x-ren probabilitateak x'-tik abiatuta lor daitezke, hau eginez: P [x = k] = P [k – 0,5 < x' < k + 0,5]

Hau da, x-ren balio puntual bakoitzari (0, 1, 2, …, k, …, n) k-n zentratzen den eta 0,5eko erradioa duen tartea dagokio x' aldagaiaren kasuan. Beraz:

P [a ≤ x < b ] = P [a – 0,5 < x' < b – 0,5]

P [a < x ≤ b ] = P [a + 0,5 < x' < b + 0,5]

P [a < x] = P [a + 0,5 < x' ]

Adibidez:

• P [3 < x < 5] = P [x = 4] = P [3,5 < x' < 4,5]

• P [3 ≤ x < 5] = P [x = 3 edo x = 4] = P [2,5 < x' < 4,5]

• P [3 ≤ x ≤ 5] = P [x = 3 edo x = 4 edo x = 5] =

Ebatzitako ariketak

KONTUAN IZAN

x aldagaia B (n,  p) bada, eta x' aldagaia

N (np,  npq ): P [x = k ] = P [k – 0,5

➜

Binomial baten probabilitatea kalkulatzea eta dagokion normalaren bidez lortutakoarekin konparatzea.

2 Makina batek egiten dituen torlojuen % 2 akastunak dira. 2 000 torlojuko multzo batean, zer probabilitate dago 50 torloju akastun baino gutxiago egoteko?

B (2 000; 0,02) binomial bat da, eta µ = np = 40 eta σ = npq = 6,26 dira. Ikusten dugunez, np = 40 > 3 da, baita nq > 3 ere. Beraz, N (40; 6,26) normalera hurbiltzen dela ziurta dezakegu

x da B (2 000; 0,02) → x' da N (40; 6,26) → z da N (0, 1)

= ϕ(1,52) = 0,9357

Eskaturiko probabilitatea 0,9357 da.

Pentsatu eta praktikatu

1 Kalkulatu honako banaketa binomial hauen probabilitateak, horietako bakoitza dagokion normalera hurbilduz.

Kontuan izan aldagai diskretu batetik jarraitu batera igarotzean egin behar den unitate erdiko doikuntza.

a) x da B (100; 0,1). Kalkulatu P [x = 10], P [x < 2] eta P [5 < x < 15].

b) x da B (1 000; 0,02). Kalkulatu P [x > 30] eta P [x < 80].

c) x da B (50; 0,9). Kalkulatu P [x > 45] eta P [x ≤ 30].

Ebatzitako ariketak eta problemak

1. Aldagai diskretuko probabilitate-banaketa

Beheko garapen lau hori duen dodekaedroa eraiki eta mahai gainera bota dugu:

a) Dodekaedroaren garapena kontuan hartuz, hau ikusten dugu:

• 5 aurpegik 1 zenbakia dute

• 4 aurpegik 2 zenbakia dute

• 2 aurpegik 3 zenbakia dute

a) Egin probabilitate-banaketen taula.

b) Aurkitu µ eta σ

EGIN ZUK

Bi dado bota eta irten den puntuaziorik altuena jasoko dugu: 3 eta 5 → 5; 4 eta 4 → 4. Kalkulatu probabilitate-banaketa horren µ eta σ.

2. Banaketa binomiala

Ugalkortasun-zentro batean, in vitro intseminazioaren saiakera bakoitzak % 30eko arrakasta du edozein bikoteren kasuan. Aste honetan 10 bikote joan dira zentrora tratamendua egitera. Bikote horietatik seme-alabak izatea zenbatek lortuko duen jakin nahi dugu.

a) Banaketa binomiala da?

b) Kalkulatu µ eta σ parametroak

c) Zer probabilitate dago bikote batek ere ez lortzeko seme-alabarik izatea? Eta zenbatekoa baten batek lortzeko?

d) Zer probabilitate dago bi bikotek baino gutxiagok edukitzeko seme-alabak?

EGIN ZUK

Aurkitu zer probabilitate dagoen tratamenduan arrakasta 2 bikotek soilik izateko , bikote guztiek izateko, eta bikoteren batek ez izateko.

• 1 aurpegik 4 zenbakia du Datu horiekin probabilitate-banaketa eraikiko dugu. Ondoren, taulan pi xi eta pi xi2 zutabeak erantsiko ditugu. Zutabe horien ∑ pi xi eta ∑ pi xi2 baturek µ eta σ parametroak kalkulatzeko balio dute.

a) B (10; 0,3) banaketa binomiala da; izan ere, hamar kasuek dute seme-alabak edukitzeko probabilitate bera: 0,3.

b) Parametroak hauek dira:

µ = np = 10 · 0,3 = 3

σ = ·, ·, , npq 10 03 07 1 449 ==

c) Formula erabiliko dugu: P [x = k] = n k cm pkq n – k

P [bikote batek ere ez du lortzen] = P [x = 0] = 10 0 eo · 0,30 · 0,710 = 0,028

«Bikoteren batek lortzen du» gertaera «bikote batek ere ez du lortzen» gertaeraren aurkakoa da: P [x > 0] = 1 – P [x = 0] = 1 – 0,028 = 0,972

d) Honako probabilitate hau kalkulatu behar da:

P [x < 2] = P [x = 0] + P [x = 1]

c) atalean ikusi dugunez, P [x = 0] = 0,028.

Falta den probabilitatea kalkulatuko dugu:

P [x = 1] = 10 1 eo · 0,31 · 0,79 = 0,121

Beraz:

P [x < 2] = 0,028 + 0,121 = 0,149

3. Dentsitate-funtzioa

a) Kalkulatu k-ren balioa f(x) dentsitate-funtzioa hau izan dadin.

EGIN ZUK

<

02 24 bada bada gainerakoan

Zehaztu zein izan behar den k -ren balioa f (x) = 0,4 + kx, dentsitate funtzioa izateko, baldin eta x ∈ [0, 4] eta 0 hondarrean. Kalkulatu P [x ≥ 3], P [x ≤ 1] eta P [1 ≤ x ≤ 3].

Dentsitate-funtzioa

1 2 3 4

Laranja koloreko eremuaren azalera k 2 22 + 2k = 4k da. Dentsitate-funtzioaren azpian dagoen azalera 1 izan behar denez, orduan: 4k = 1 → k = 1/4.

b) Lortu dugun k-ren balio horrekin, dentsitate-funtzioa adieraziko dugu.

1/4 1/2

P [x ≤ 1] esparru urdinaren azalera da, oinarria 1 eta altuera 1/4 duen triangelua:

1 2 3 4

1/4 altuera

1 0 01 –bada

gainerakoan

5. N(µ, σ) banaketa normala

Parke bateko zuhaitzen altuerak banaketa normal bat jarraitzen du, batezbestekoa 9 m eta desbideratze tipikoa 1,5 m izanik. Kalkulatu parkeko zuhaitz bat zorian hartu eta zer probabilitate dagoen:

a) 10,5 m-tik gorako altuera izateko.

b) 8,25 m-tik beherako altuera izateko.

c) Zuhaitzen zer proportziok du 8,25 m eta 10,5 m bitarteko altuera?

EGIN ZUK

Banaketa horretan bertan, aurkitu zuhaitzen zer proportziok duen 10 m eta 11 m bitarteko altuera.

x

da N

m

Ebatzitako ariketak eta problemak

Eremu jakin batean arrantzan irteten diren ontziek harrapatzen dituzten hegaluzeen kopuruak banaketa normal bat jarraitzen du, batezbestekoa 110 izanik. Badakigu arrantza-ontzi bat zorian hartuz gero, 125 hegaluze baino gehiago harrapatzeko duen probabilitatea 0,1587 dela.

a) Kalkulatu banaketa horren desbideratze tipikoa.

b) Kanpaina ona izan dela esateko, 100 hegaluze baino gehiago harrapatu behar izan dira. Ontzien zer ehunekok estimatzen da ez duela kanpaina ona izango?

c) Zenbat hegaluze arrantzatu behar ditu ontzi batek 90. pertzentilean egoteko?

EGIN ZUK

Kanpaina bikaina izan dela esateko, 130 tona baino gehiago arrantzatu behar izan badira, arrantza-ontzien zer ehunekok izango zuen kanpaina bikaina? Zenbat tona hegaluze harrapatu ditu 5 pertzentilean dagoen arrantza-ontzi batek?

Ikasgela batean 30 neska-mutil daude.

a) Zer probabilitate dago ikasleetako bat gutxienez abenduan jaiotakoa izateko?

b) Zer probabilitate dago neska-mutilen heren bat gutxienez udan jaiotakoa izateko?

a) x aldagaiak N (110, σ) banaketa jarraitzen badu, z aldagai tipifikatuak N (0, 1) jarraitzen du.

P [x > 125] = P z 125 110

0,1587 → → ϕ 15 v cm = 0,8413

Taulan begiratuta: ϕ(k) = 0,8413 bada → k = 1 15 v = 1 → σ = 15

b) P [x ≤ 100] kalkulatu, eta lortutako emaitza bider 100 egingo dugu, ehunekotan adierazteko.

P [x ≤ 100] = P

EGIN ZUK

a) Lehenengo atalean, abendua urtearen 1/12 moduan hartu dugu. Aurkitu probabilitate bera, baina abenduak urteko 365 egunetatik 31 egun dituela kontuan hartuta.

b) Zer probabilitate dago gutxienez 5 ikasle igandean jaiotakoak izateko?

F = P [z ≤ –0,67] = 1 – P [z ≤ 0,67] = = 1 – ϕ(0,67) = 1 – 0,7486 = 0,2514

15 100 110

Kanpaina ona izango ez duten ontziak % 25,14 izango dira

c) Biztanleriaren % 90 azpitik uzten duen aldagaiaren balioa kalkulatu behar dugu. Badakigu probabilitateak zer balio duen, eta k kalkulatu behar dugu

P [z ≤ k] = ϕ(k) = 0,90

Taulan 0,90etik hurbilen dagoen balioa bilatuko dugu → 0,8997 da, eta hori k = 1,28 balioari dagokio

Kasu honetan, tipifikazioaren kontrako prozesua egin behar da: balio tipifikatua zein den dakigu eta tipifikatu gabeko balioa lortu nahi dugu.

k' 110 15 – = 1,28 → k' = 15 · 1,28 + 110 = 129,2

90. pertzentilean egoteko, 130 hegaluze arrantzatu behar dira gutxienez.

a) Banaketa binomiala da: B (30, 1/12) = B (30; 0,083).

Kasu honetan ez zaigu interesatzen binomiala normal batera hurbiltzea, erraz ebazten baita binomialaren formula erabiliz. Baina ebazpenak beharko balu ere ezingo genukeen egin, np = 30 · 0,083 = 2,49 < 3 baita.

Gutxienez ikasle bat abenduan jaiotakoa izatea, hain zuzen, ikasle bat ere ez izatea abenduan jaiotakoa gertaeraren kontrakoa da. Beraz:

P [x ≥ 1] = 1 – P [x = 0] = 1 – 0,91730 = 1 – 0,074 = 0,926

b) Orain banaketa binomiala da: B (30, 1/4) = B (30; 0,25).

np = 30 · 0,25 = 7,5 > 3 denez, banaketa binomiala normalera hurbildu dezakegu. Horretarako, µ eta σ binomialean kalkulatu behar ditugu

µ = 7,5 σ = ·, ·, , 30 0250 75 237 =

x da B (30; 0,25) → x' da N (7,5; 2,37) → z da N (0, 1)

P [x ≥ 10] kalkulatzeko, oso garrantzitsua da tartearen muturrak ondo interpretatzea x'-ren kasuan, kontuan izanik x diskretua dela eta x' jarraitua dela.

6. Banaketa normala

7. Binomial bat normalera hurbiltzea

Gidatutako ariketak eta problemak

1. Probabilitate-banaketak

Karta-multzo batetik bi karta atera, eta zenbat bateko lortu ditugun idatzi dugu (0, 1 edo 2).

a) Zein da probabilitate-banaketa?

b) Kalkulatu batezbestekoa eta desbideratze tipikoa.

a) P [0 bateko], P [1 bateko] eta P [2 bateko] probabilitateak kalkulatu behar dituzu.

P [0 bateko] = P [batekoa ez 1.an] · P [batekoa ez 2.ean/batekoa ez 1.an] = …

P [2 bateko] = P [batekoa 1.an] · P [batekoa 2.ean/batekoa 1.an] = …

P [1 bateko] = 1 – [P [0 bateko] + P [2 bateko]] = …

b) µ = ∑ pi xi ; σ = px –µ ii 22 R

Soluzioa:

a)

Test erako azterketa batek 10 galdera ditu, galdera bakoitzean lau erantzun ageri dira, baina bat bakarrik da zuzena. Ikasle batek zorian erantzun badu:

a) Zer probabilitate du 4 galderari ondo erantzuteko?

b) Eta 2 galdera baino gehiagori ondo erantzuteko?

c) Kalkulatu galderaren bat txarto erantzuteko zer probabilitate dagoen.

b) µ = 0,2; σ = 0,42

Banaketa binomiala da? Zein da n-ren balioa ? Eta p-rena ?

a) Erabili P [x = k] = n k cm pkq n – k formula.

b) P [x > 2] = 1 – P [x ≤ 2] = 1 – (P [x = 0] + P [x = 1] + P [x = 2])

c) P [x ≤ 9] = 1 – P [x = 10]

Soluzioa:

a) 0,146

b) 0,474

c) 0,999999046

Herri bateko bizilagunen garaierak banaketa normal bat du, batezbestekoa 170 cm eta desbideratze tipikoa 10 cm izanik.

a) Bizilagunen zer ehunekok du 170 cm eta 185 cm bitarteko garaiera?

b) Zer garaieratatik aurrera dago biztanle altuenen % 33?

Herri horretako bizilagunen garaierari x esaten badiogu, x-k du N (170, 10) banaketa normal bat. Bertan:

a) Kalkulatu P[170 < x < 185] eta adierazi emaitza ehuneko eran.

b) α aurkitu behar da, kontuan izanda P[x > α] = 0,33; hau da: P[x < α] = 1 – 0,33 = 0,67 → bilatu normalaren taulan zer balio dagokion 0,67ko probabilitateari, eta askatu α.

Soluzioa:

a) % 43,32 b) 174,4 cm-tik aurrera.

Proba jakin batean, bi ikaslek lortutako puntuazio tipifikatuak 0,8 eta – 0,4 izan ziren, eta bere nota errealak 88 eta 64 puntu izan ziren, hurrenez hurren. Zein da batezbestekoa eta zein da azterketako puntuazioen desbideratze tipikoa?

• Adierazi 0,8 emaitza dela 88 punturen tipifikazioa: 88 –µ v

• Adierazi – 0,4 emaitza dela 64 punturen tipifikazioa.

• Ebatzi bi ekuazio eta bi ezezaguneko sistema.

Soluzioa:

µ = 72; σ = 20

2. Binomiala

3. Banaketa normala

4. Tipifikazioa

Proposatutako ariketak eta problemak

Trebatzeko

Probabilitate-banaketak

1 Osatu ondorengo probabilitate-taula hau eta kalkulatu µ eta σ parametroak:

xi 0 1 2 3

pi 0,1 0,3 0,1

2 Kutxa batean hamar bola daude 1, 1, 2, 3, 3, 3, 4, 5, 5, 10 zenbakiak idatzita. Bola bat atera eta lortu dugun zenbakia idatziko dugu. Egin probabilitate-banaketa eta kalkulatu µ eta σ

3 Egin bi dado bota eta puntuak batzean lortzen diren emaitzei dagozkien probabilitateen banaketari buruzko taula bat. Kalkulatu µ eta σ.

Banaketa binomiala

4 Hurrengo kasu hauetako bakoitzean, bereizi banaketa binomial bat eta eman n, p, q, µ eta σ parametroen balioak.

• Test erako azterketa batek 50 galdera ditu, eta galdera bakoitzak hiru erantzun, baina bat bakarra da zuzena. Zorian erantzun dugu. Zenbat galdera asmatu ditugu?

• Aurreko atalean deskribaturiko azterketa horretan, ikasle batek 20 galderaren erantzunak dakizki, eta gainerakoei zorian erantzun die. Zenbat asmatuko dituen jakin nahi dugu.

• Txanpon bat 400 bider bota dugu. Zenbat aurpegi atera ditugu?

• Soldaduren % 1 akastunak dira, eta mila aztertu ditugu. Zenbat soldadura akastun aurkituko ditugu?

5 B (9; 0,2) banaketa binomial batean, kalkulatu:

a) P [x < 3] b) P [x ≥ 7]

c) P [x ≠ 0] d) P [x ≤ 9]

Dentsitate-funtzioa

6 Arrazoitu honako hauek dentsitate-funtzioak izan daitezkeen:

a) f (x) = 0,5 + 0,5x, x ∈ [0, 2] izanik

b) f (x) = 0,5 – x, x ∈ [0, 2] izanik

c) f (x) = 1 – 0,5x, x ∈ [0, 2] izanik

7 Egiaztatu eskuinean adierazitako f (x) funtzioa

dentsitate-funtzioa dela.

Kalkulatu P [x >  2/π ].

N (0, 1) taularen erabilera

8 N (0, 1) banaketan, kalkulatu probabilitate hauek:

a) P [z = 2] b) P [z ≤ 2]

c) P [z ≥ 2] d) P [z ≤ –2]

e) P [z ≥ –2] f ) P [–2 ≤ z ≤ 2]

9 N (0, 1) banaketan, kalkulatu:

a) P [z ≤ 1,83] b) P [z ≥ 0,27]

c) P [z ≤ –0,87] d) P [z ≥ 2,5]

10 N (0, 1) banaketan, kalkulatu probabilitate hauek:

a) P [z = 1,6] b) P [–2,71 ≤ z ≤ –1,83]

c) P [1,5 ≤ z ≤ 2,5] d) P [–1,87 ≤ z ≤ 1,25]

11 Kalkulatu k kasu hauetako bakoitzean:

a) P [z < k ] = 0,8365 b) P [z > k ] = 0,8365

c) P [z < k ] = 0,1894 d) P [–k < z < k ] = 0,95

Tipifikazioa

12 Test erako azterketa batean, batezbestekoa 28 puntukoa izan da, eta desbideratze tipikoa, 10 puntukoa. Kalkulatu emaitza hauek lortu dituzten ikasleen puntuazio tipifikatuak:

a) 38 puntu b) 14 puntu

c) 45 puntu d) 10 puntu

13 Aurreko problemako azterketan ikasle baten puntuazio tipifikatua 0,8 izan bada, zenbat puntu lortu ditu? Zenbat puntu dagozkio – 0,2 balio tipifikatuari?

Probabilitateen kalkulua N (µ, σ) banaketetan

14 N (43, 10) banaketa batean, kalkulatu probabilitate hauek:

a) P [x ≥ 43]

b) P [x ≤ 30]

c) P [40 ≤ x ≤ 55] d) P [30 ≤ x ≤ 40]

15 N (151, 15) banaketa batean, kalkulatu:

a) P [x ≤ 136]

b) P [120 ≤ x ≤ 155]

c) P [x ≥ 185] d) P [140 ≤ x ≤ 160]

Binomiala → Normala

16 Dado bat mila bider botatzen badugu, zer probabilitate dago bostekoen kopurua 100 baino txikiagoa izateko?

17 Txanpon bat 400 bider bota dugu. Kalkulatu zer probabilitate dagoen lortutako aurpegien kopurua:

a) 210 baino handiagoa izateko.

b) 180 eta 220 artean egoteko.

Ebazteko

18 Aldagai aleatorio diskretu baten probabilitate-banaketa honako taula honen bidez emanda dago:

xi 0 1 2 3 4

pi 0,1 a b c 0,2

Badakigu P [x ≤ 2] = 0,7 dela, eta P [x ≥ 2] = 0,75. Aurkitu zein diren a, b eta c -ren balioak, eta kalkulatu µ eta σ.

19 Ikasle batek azterketan sartzen diren 30 gaietatik 12 ikasi ditu. Azterketan, zorian 2 gai aukeratuko dira, bata edo bestea garatzeko. Baliteke ikasleak biak ikasi izana, bat bakarrik edo bat ere ez. Egin probabilitate-banaketaren taula eta adierazi grafikoki. Aurkitu µ eta σ

20 Txanpon akastun bat daukagu, eta txanpon hori jaurtiz gero gurutzea lortzeko dagoen probabilitatea 0,4koa da. Bost aldiz jaurti dugu, eta gurutze-kopurua apuntatu dugu.

Egin probabilitate-banaketaren taula bat, adierazi grafikoki, eta kalkulatu batezbestekoa eta desbideratze tipikoa.

21 Pertsona batek mezu bat ortografia-akatsik gabe idazteko dagoen probabilitatea 0,75ekoa da. Pertsona batek egunean zehar 10 mezu idazten baditu, aurkitu zer probabilitate dagoen:

a) justu mezuen erdietan ortografia-akatsik ez egoteko.

b) 10 mezuetako batean ere ez egoteko ortografia-akatsik.

c) 8 mezutan edo gehiagotan ortografia-akatsen bat egoteko.

22 Tenis-monitore batek pilotak jaurtitzen dituen kanoi bat erosi du. Jakinda kanoiak jaurtiketen % 10 huts egiten dituela, aurkitu 20 bola jaurtiz gero zer probabilitate dagoen:

a) kanoiak justu 5 hutsegite egiteko.

b) kanoiak gehienez bi hutsegite egiteko.

23 Torlojuak fabrikatzeko prozesu batean, badakite % 2 akastunak izaten direla. Hala ere, 50 aleko kaxatan ontziratzen dituzte. Aurkitu zer probabilitate dagoen kaxa bateko torloju akastunen kopurua hau izateko:

a) Bat ere ez b) Bat c) Bi baino gehiago

24 Aurkitu zein izan behar den k-ren balioa funtzioa hau dentsitate-funtzioa izateko:

25 Kalkulatu zein izan behar den a-ren balioa honako funtzio hau dentsitate-funtzioa izateko:

1 4 bada bada gainerakoan <

Kalkulatu, horrez gain, honako probabilitate hauek: P [1 ≤ x ≤ 2], P [x ≤ 3], P [x > 2]

a 2

a

b) Kalkulatu P [x < 0,5] eta P[0,2 ≤ x ≤ 2].

c) Aurkitu µ eta σ parametroak.

28 Armada bateko konpainia batean dauden soldaduen pisuek banaketa normal bat dute, batezbestekoa 75 kg eta desbideratze tipikoa 8 kg izanik. Aurkitu zer probabilitate dagoen zorian aukeratutako soldadu batek pisu hau izateko:

a) 71 kg baino gehiago. b) 73 eta 79 kg artean.

c) 80 kg baino gutxiago. d) 85 kg baino gehiago.

29 Ebakuntza kirurgiko bat egiteko erabiltzen den denborak, ordutan, N(10, 2) banaketa normalari jarraitzen dio. Kalkulatu ebakuntza horien zer ehuneko egiten diren:

a) 6,5 eta 13 ordu bitartean.

b) 7 ordu baino gutxiagoan.

c) 9 ordu baino gehiagoan.

30 2.1 helburua. Herrialde jakin bateko pertsona helduen GMI (gorputz-masaren indizea) aldagai aleatorioak banaketa normal bat du, batezbestekoa 26 eta desbideratze tipikoa 6 izanik.

a) Zer probabilitate dago herrialde horretako pertsona helduetako bat zorian hartu eta 23 eta 30 bitarteko GMI izateko?

b) Pertsona batek 35etik gorako GMI izateak pertsona hori obesoa dela esan nahi badu, kalkulatu herrialde horretako pertsona obesoen ehunekoa.

Proposatutako ariketak eta problemak

31 Kirol-estadio baten barrualdea argiztatzeko fokuak jarriko dira. Hornitzaileak ziurtatzen duenez, fokuen bizi-iraupena aldagai normal bat da, batezbestekoa 1 500 h eta desbideratze tipikoa 200 h dituena.

a) Zer probabilitate dago zorian hartutako foku batek gutxienez 1 000 orduz emateko argia?

b) 2 000 foku erosi badira, zenbatek espero behar dugu ematea argia gutxienez 1 000 orduz?

32 Motor jakin batek irauten duena aldagai normal bat da, batezbestekoa 10 urte eta desbideratze tipikoa 2 urte dituena. Fabrikatzaileak motorrek 13 urtez ederki funtzionatzen dutela ziurtatzen du.

Motorren zer ehunekok uste behar dugu ez dutela garantia beteko?

33 Ikastetxe batean, notarik onenak dituzten ikasleen % 20k goi-mailako ikasketak egin ahal izango dituzte. Badakigu ikastetxe horretan azken notek banaketa normal bati jarraitzen diotela, batezbestekoa 5,8 izanik, eta desbideratze tipikoa, 2. Zein da ikasle batek goi-mailako ikasketak egin ahal izateko gutxienez lortu beharko duen batezbesteko nota?

34 Jende-multzo jakin baten adimen-kozienteak (A.K.) batezbestekoa 100 eta desbideratze tipikoa 10 dituen banaketa normal bati jarraitzen dio.

a) Kalkulatu multzo horren zer ehunekok duen 90 eta 110 bitarteko A.K.

b) 130etik gorako A.K. dutenak superdotatutzat jotzen direla jakinda, aurkitu jende-multzo horretako zer ehuneko har daitekeen superdotatutzat.

c) Esan digutenez, multzo horretako % 70ek balio jakin batetik beherako A.K. du. Kalkulatu balio hori.

35 Ikasgela bateko neska-mutilen garaierak N (µ, σ) banaketa du. Saioak 172 cm ditu, eta Begoñak, 167 cm; eta bere garaiera tipifikatuak 1,4 eta 0,4 dira, hurrenez hurren.

a) Zer garaiera du errealitatean Eiderrek, bere garaiera tipifikatua –1 bada?

b) Zein da Ainhizeren garaiera tipifikatua, errealitatean 165 cm dituela jakinda?

36 Lantegi batean egiten dituzten piezen batezbesteko diametroa 45 mm-koa da.

a) Zehaztu desbideratze tipikoa, jakinda pieza batek 50 mm baino diametro handiagoa izateko probabilitatea 0,0062koa dela.

b) 820 pieza aztertu baditugu, zenbatek izango dutela 39,7 eta 43,5 mm bitarteko diametroa estimatu behar dugu?

37 Espezie jakin bateko arrain batek 5 urte baino gehiago bizirauteko probabilitatea % 10ekoa da.

a) Akuario batean espezie horretako 10 arrain baditugu, aurten jaiotakoak denak, aurkitu zer probabilitate dagoen bi arrain gutxienez bizirik egoteko 5 urte barru.

b) Piszifaktoria bateko biltegi batean espezie horretako 200 arrain baditugu, denak aurten jaioak, egoera horri dagokion banaketa normalaren bidezko hurbilketa erabilita, aurkitu zer probabilitate dagoen 5 urte barru arrain horietako gutxienez 10 bizirik egoteko.

38 Test erako azterketa batek 50 galdera ditu, eta galdera bakoitzak, hiru erantzun aukeran, baina bat bakarrik da zuzena.

Azterketa gainditzeko, 25 zuzen erantzun behar dira; oso ongi ateratzeko, 35 zuzen; eta bikain ateratzeko, 45 zuzen. Zorian erantzuten baduzu, zer probabilitate dugu gainditzeko? Eta oso ongi ateratzeko? Eta bikain ateratzeko?

Erantzun galdera horiei, baina kontuan izanda ikasleak 30 galderaren erantzun zuzenak dakizkiela.

39 Minizirkuituak egiten dituen enpresa batean ziurtatu dutenez, zirkuituen % 10 akastunak dira. Lantegi horretan egin diren 300 minizirkuituen kaxa bat erosten badugu, zehaztu:

a) Zer probabilitate dagoen 27 minizirkuitu akastun baino gehiago egoteko.

b) Zer probabilitate dagoen minizirkuitu akastunen kopurua 20 eta 30 bitartekoa izateko.

40 Musika-sentsibilitateari buruzko test bateko emaitzek N (65, 18) banaketa dute.

Baremo bat egin nahi da, pertsona bakoitzari, lortu duen puntuazioarekin batera, honako komentario hauetakoren bat ezartzeko:

• Belarri gogorra.

• Musika-sentsibilitate txikia.

• Normala.

• Musika-sentsibilitate handia.

• Musikarako gaitasun ikaragarri handia.

Eta lortu nahi da baremazio-talde bakoitzean sentsibilitateproba egin zaienen kopuru hauek egotea, hurrenez hurren: %10 , % 35, % 30, % 20 eta % 5.

a) Zer puntuazioetan jarriko zenituzke taldeen arteko mugak?

b) Zer komentario ezarriko genioke 80ko puntuazio lortu duen pertsona bati? Eta 40ko puntuazioa lortu duen beste bati?

Galdera teorikoak

41 B (4; 0,25) banaketa batean, egiaztatu honako hau:

P [x = 0] + P [x = 1] + P [x = 2] + P [x = 3] + P [x = 4] = 1

42 Esan zein den honako probabilitate hauen balioa N [µ, σ] banaketa normal batean:

a) P [x ≤ µ]

b) P [x = µ]

c) P [µ – σ ≤ x ≤ µ + σ]

43 Arrazoitu honako baieztapen hauek, N(10, 2) normalari buruzkoak, zuzenak ala okerrak diren:

a) P [x ≥ 10] = 0,5

b) P [µ – 4σ ≤ x ≤ µ + 4σ] ≈ 0

c) P [µ – 4σ ≤ x ≤ µ + 4σ] ≈ 1

d) P [2 ≤ x ≤ 18] ≈ 1

44 N(10, 2) banaketa normal batean, adierazi emaitzen zer ehuneko geratuko den, gutxi gorabehera, [2, 18] tartetik kanpo.

AUTOEBALUAZIOA

1 Honako taula hau aldagai diskretuko probabilitate-banaketa bati

Sakontzeko

45 7.3 helburua. Marka jakin bateko bonbillen biziiraupenak, ordutan neurtuta, banaketa normal bati jarraitzen dio, batezbestekoa µ eta desbideratze tipikoa σ izanik. Badakigu bonbillen % 69,5ek irauten dutela 5 061,2 ordu baino gutxiago, eta bonbillen % 16,6k irauten dutela 5 116,4 ordu baino gehiago.

a) Zer probabilitate dago marka horretako bonbilla batek 5 061,2 h eta 5 116,4 h bitartean irauteko?

b) Kalkulatu banaketa normal horren batezbestekoa eta desbideratze tipikoa.

46 Edariak saltzen dituen makina bat erregulatuta dago, ematen duen likido-kantitateak banaketa normal bat izateko moduan, 200  mL-ko batezbestekoa eta 15  mL-ko desbideratze tipikoa izanik.

a) Edalontzien zer ehuneko beteko dira 224  mL baino gehiagorekin?

b) 224 mL-ko edukiera duten 6 edalontzi erabiliz gero, zer probabilitate egongo da edalontzietako baten soilik egitea likidoak gainezka?

4 Badakigu z aldagai bat N (0, 1) dela.

a) Kalkulatu honako probabilitate hauek: P [1,53 < z < 2,1] P [–1,53 < z < 2,1]

b) Aurkitu b eta k honako hau bete dadin: P [z < b ] = 0,4 P [– k < z < k ] = 0,9

a) Osatu zure koadernoan eta kalkulatu µ eta σ.

b) Zer probabilitate dago x > 7 izateko? Eta x < 7 izateko?

2 Txintxeta jakin batzuekin, honako probabilitate hauek lortu ditugu lurrera erortzen utzi ditugunean: P [ ] = 0,3 P [ ]  = 0,7 6 txintxeta utzi ditugu erortzen. Kalkulatu:

a) P [2 eta 4 ] b) P [ -rik ez]

c) P [ -ren bat] d) P [3 eta 3 ]

3 Egiaztatu y =  x 2  – 1, baldin eta 2 ≤  x ≤ 4 bada, dentsitate-funtzio bat dela. Irudikatu eta kalkulatu probabilitate hauek:

a) P [x = 3] b) P [x < 3]

c) P [x > 3,5] d) P [3 ≤ x ≤ 3,5]

5 Suhiltzaile-talde baten adimen-kozientea (A.K.) normal banatzen da, batezbestekoa 108 eta desbideratze tipikoa 3,5 izanik. Zorian hartutako suhiltzaileetako baten A.K.-ri esango diogu x. Kalkulatu:

a) P [x < 100] b) P [x > 115] c) P [100 < x < 115]

6 Ikastetxera heltzeko behar dudan denbora normal banatzen da, batezbestekoa 20 minutu izanik. Frogatuta daukat egunen % 94,5ean 28 minutu baino lehenago heltzen naizela. Urte osoan 177 egunetan joaten banaiz ikastetxera, zenbat egunetan helduko naizela ordu-laurdenean baino gutxiagoan estimatu dezaket?

7 Pertsonen % 7k jatorri genetikoa duen akats anatomiko bat dute. Enpresa batean 80 pertsonak lan egiten dute. Zer probabilitate dago akats hori duten 10 pertsona baino gehiago egoteko?

➜ anayaharitza.es Ariketa hauen ebazpena.

Unibertsitatera sartzeko probarako

IV. multzoa: Probabilitatea

Probabilitatearen atala landu duzunean, hainbat problema mota ebazteko modua ematen duten oinarrizko kontzeptu eta teknikak ikasi dituzu. Gogoratu ditzagun horietako batzuk.

Ezagutzen dituzu gertaeren propietateak eta horien probabilitateak?

Badakizu erabiltzen adierazpen grafikoa gertaeren propietateak eta probabilitateak bistaratzeko?

Teknika hauekin eta beste batzuekin, arazo asko ebatzi ditzakezu.

Badakizu erabiltzen zuhaitzdiagrama probabilitate-problemak interpretatzeko eta ebazteko?

Menderatzen duzu kurba normala nola erabili eta zer ezaugarri dituen? a b

Badakigu igarotzen N(μ, σ) banaketa duen P [a ≤ x ≤ b] probabilitatea N(0, 1) banaketan dagokion probabilitatera?

Ariketen eta problemen adibideak

Unibertsitatera sartzeko ebaluazio-proban hainbat zailtasun motatako ariketak eta problemak topatu ditzakezu.

Azoka batean, merkaturatzen diren barazkien % 70 tokikoak dira eta, gainerakoak, ez. Tokiko barazkien % 30 ekologikoak dira; tokikoak ez direnen artean, berriz, % 10 baino ez dira ekologikoak. Ausaz aukeratutako bezero batek barazki bat erosi badu, kalkulatu probabilitate hauek:

a. Erositako barazkia ekologikoa ez izateko probabilitatea.

b. Erositako barazkia tokikoa edo ekologikoa izateko probabilitatea.

a. Zuhaitz-diagrama batek datuak bistaratzeko eta horien gainean arrazoitzeko modua ematen digu.

b. P [toki edo ekol] kalkulatzeko, hau hartuko dugu kontuan: P [toki ∪ ekol] = P [toki] + P [ekol] – P [toki ∩ ekol]

Ikasle batek egiaztatu du etxetik unibertsitatera iristeko behar duen denborak banaketa normal bati jarraitzen diola, batezbestekoa 30 minutu izanik, eta desbideratze tipikoa, 5 minutu.

a. Zer probabilitate dago unibertsitatera 40 minutu baino gutxiagoan iristeko?

b. Zer probabilitate dago 20 eta 40 minutu artean iristeko?

c. Egun batean etxetik irtetean, ikasleak ikusi du justu 40 minutu falta direla eskola hasteko. Zer probabilitate dago eskolara berandu iristeko?

N(30, 5) banaketa bat da, eta probabilitate hauek kalkulatu behar ditugu:

a. P [x < 40] b. P [20 < x < 40]

c. P [x > 40]

C eta D dira ausazko esperimentu baten bi gertakari, eta P [C ] = 0,3; P [D] = 0,6 eta P [C ∪ D] = 0,8 betetzen da. Kalkulatu: a. P [C/D]

Lehenengo, P [C ∩ D] lortu behar dugu:

a. eta b. ebatziko ditugu grafikoen gainean arrazoituta:

a. Zer proportzio hartzen du C-k D-ren osotasunean?

P [C/D] = , , 0 0 6 1 6 1 =

b. Zer proportzio betetzen du C ∩ D-k C-ren osotasunean?

C ∩ D da C ∩ D multzotik kanpo dagoena, eta, beraz:

P [C ∩ D/C] = , , 03 02 3 2 =

Ariketa hau aljebraikoki ere ebatzi daiteke, probabilitatearen propietateak erabiliz.

Problema hauek ebazteko behar izan diren teknikak ezkerrean berrikusita ageri direnak dira.

anayaharitza.es webgunean hau aurkituko duzu:

• Probabilitaterako oinarrizko teknikak ikasteko bide bat, arintasuna eskuratu dezagun teknika horiek ulertzeko, erabiltzeko eta aplikatzeko.

• Unibertsitatera sartzeko proben problema-bilduma bat, ebatzitakoak, proposatutakoak, laguntza eta guzti emanda, jarraibideak emanda…

Autoebaluazioen soluzioak

1. unitatea

1 a) Sistema bateraezina da. Ez du soluziorik.

Interpretazio geometrikoa: binaka elkar ebakitzen duten hiru zuzen dira.

b) Sistema bateragarri indeterminatua da.

Bere soluzioak dira ,, 2 5 2 –3 m mm++ cm

Interpretazio geometrikoa: zuzen batean elkar ebakitzen duten bi plano dira.

2 • m = 4 bada, sistema bateragarri indeterminatua da.

Bere soluzioak dira (λ – 1, 2 – λ, λ).

• m ≠ 4 bada, sistema bateragarri determinatua da.

Bere soluzioak dira (1, 0, 2).

3 a) x, y, z dira 10 €, 20 € eta m €-ko billeteak.

2. unitatea

1 a = 3 bada, hein (A) = 2.

a ≠ 3 bada, hein (A) = 3.

2 B izan behar da 3 × 2 ordenako matrize bat.

3 A =  a c b d eo → A a b c d t = dn

A 2  =  () () abc ca d ba d bc d 2 2 + + + +

(A 2)t  =  () () abc ba d ca d bc d 2 2 + + + +

(A t )2 =  () () abc ba d ca d dbc 2 2 + + + +

4 A n  =  n 1 5 0 1 eo

x x x

mz mz 10 20 2

1 330 97 0 13 130 –

y y y

+ + + +

= = = 4

b) Bateragarri determinatua izateko, |A| ≠ 0 izan behar da.

m 10 1 1

20 1 2 1 0 – = 40 – 3m ≠ 0 baldin eta m ∈{5, 50, 100, 200}

m = 50 bada: x = 64, y = 32, z = 1

c) Kasu honetan, m = 100, eta sistemak ez du soluzio arruntik. Beraz, ezin dira egon 100 €-ko billeteak.

4 a) Ekuazioa forma honetakoa izan behar da:

a (3x – 2y + z) + b (2x – 3y + z) = k

k ≠ 5a – 4b izanik.

Hauek hartuz gero, adibidez, a = 1, b = 0, k = 1

hau lortzen dugu: 3x – 2y + z = 1.

b) Esaterako, y = 0 erantsita, sistema bateragarri determinatua da.

c) Esaterako, 5x – 5y + 2z = 1 ekuazioa erantsita, sistema bateragarri indeterminatua da.

5 a) a = 2

b) Ez dago sistema bateragarri determinatua egiten duen a-ren baliorik.

c) Soluzioak: ,, 23 2 1 mm cm

5 A =  a b b a eo

6 X =  / / 1 32 32 1 eo , Y =  0 2 2 0 –eo

7 a) A –1  =  1 2 2

––

1 2 3

1 1 1

–––

2 0 12

/ /

52 1 12

/ / /

32 12 12 fp

8 Ezin da. Errenkada bat erantsiz gero, heina gehienez ere 3 da.

5 45 54

9 ( , , , , , , , ,

3 36 35 ) · ( 2 1 3 4 )

2 18 22  = (

25 27 3 28 4 )

, ,

Familia baten asteko gastua S1 dendan 25 €-koa da; S2 dendan, 27,30 €-koa, eta S3 dendan, 28,40 €-koa.

3. unitatea

1 A ez da erregularra a = –2 kasuan.

2 a 2(a + 2)(a – 2)

3 a) a = –1, a = 5

eo

5

4 a) 5 b) 10 c) –10

5 a = 0 bada, hein (N ) = 1.

a = –3 bada, hein (N ) = 3.

a ≠ 0 bada, hein (N ) = 3.

6 a) A-k alderantzizkoa du t ≠ –1 eta t ≠ –3 badira.

7 a) a = 1 bada, sistema bateraezina da.

• a = –2 bada, hein(A) = hein (A' ) = 2 < ezezagun-kop. Sistema bateragarri indeterminatua da:

Soluzioa: x = t, y = t – 2/3, z = t – 4/3

• a ≠ 1 eta a ≠ –2 badira, hein(A) = hein(A' ) = 3, sistema bateragarri determinatua da.

98 58 18

4. unitatea

/ / /

18 38 18 ––

12 52 32

/ / /

fp

1 Matrize zabalduaren heina 3 edo 4 izan daiteke. 3 bada, sistema bateragarri determinatua da eta soluzio bakarra du. 4 bada, sistema bateraezina da, ez du soluziorik.

2 • a ≠ –2 eta a ≠ 3 badira, sistema bateragarri determinatua da.

• a = –2 bada, sistema bateraezina da.

• a = 3 bada, sistema bateragarri indeterminatua da. Kasu honetan, sistemaren soluzioak hauek dira: 5 33m ; y =  5 4m ; z = λ a = 0 bada, sistemaren soluzioa hau da: x = 1; y = –1; z = –2

3 a) • λ ≠ 1 eta λ ≠ –2 badira, sistema bateragarri determinatua da.

• λ = 1 bada, sistema bateragarri indeterminatua da.

• λ = –2 bada, sistema bateraezina da.

b) λ = 1 denean, soluzioa hau da: x = 1 – μ; y = 0; z = μ

4 Unibertsitate-graduetarako 31 beka eman ditu, lanbide heziketarako 56, eta graduondorako 28.

5 Sistema bateragarri indeterminatua da beti, k-ren balioa edozein dela ere.

Bere soluzioak (μ, –μ, 0) zuzeneko puntu guztiak dira. Zuzen batean elkar ebakitzen duten lau plano dira.

Soluzioa: ,, () x a a a a a yz a 11 1 2 21 –== + = +

b) a = 14 bada, hein (A ) = hein (A' ) = 3 = ezezagun-kop.

Sistema bateragarri determinatua da eta soluzio hau du: x = 17, y = 8, z = 6.

a ≠ 14 bada, hein (A ) = 3 ≠ hein (A' ) = 4. Sistema bateraezina da.

I. multzoa

1 a) x = 1 b) x = –2 c) x = 5/2

2 a) m = 0 bada, hein (M ) = 2. m = –1 bada, hein (M ) = 2. m ≠ 0 eta m ≠ –1 badira, hein (M ) = 3.

xy z zy xx yz xy m 13 100 10 100 10 495 ++ = ++ =+ ++ =+ * → xy z xz xy m y z 13 5 ––––++ = += = + + * m

-ren balioa edozein dela ere koefiziente-matrizearen heina 3 denez, ezezagun-kopurua adina, sistema bateragarri determinatua da.

b) Problemak soluzioa izango du ezezagunek 0 eta 9 bitarteko balio osoak hartzen badituzte. Hori m = 1 eta m = 4 kasuetan soilik gertatzen da. Azken kasu horretan, bila gabiltzan zenbakia 409 da.

b) M –1 = / / /

12 12 12–fp

–

1 0 1 –

3 x = –1, y = 2 x = 1, y = –2

5 m = –1, n = –12

6 a) Hala da, A 2 = 2 0 0 2 eo = 2I A –1 = 2 1 A

b) A 13 = 64A

7 X = // 3 6 32 1 32 3 –eo Y = 5 9 2 2 3 4 –––eo

8 a) –1/27 b) –1/3 c) 6

+= += = += =+ *

411 35 53 22

9 xy z xy yx xz zx

–––

→ →

Soluzioa: x = 1, y = 2, z = 3

10 m = 2 kasuan, infinituak dira AX = mX berdintza egiaztatzen

duten X = –2nm n m

fp

+

, λ edo μ ≠ 0, λ, μ ∈ Á matrizeak.

Autoebaluazioen soluzioak

5. unitatea

1 a) a = b = c = 0

++ ++ = = aaaa a a a a a a a a

1 1 5

2 2 6

3 3 7

4 4 8

4 4 8

b) Bai, oinarri bat eratzen dute.

c) r–5 1 u 5 4 v 5 3 w – =+

2 |u|4 = ; 6 |v |= ; (, ) uv % = 67° 47' 26''

1 5

13 a) Sistemak ez du soluziorik.

Soluzioa

2 6

3 7

b) hein (M ) = hein (M' ) = 3 = ezezagun-kop. denez, sistema bateragarri determinatua da.

14 • m ≠ 0 eta m ≠ ±1 bada, sistema bateragarri determinatua da. Soluzioa hau da:

4 8 + = 0 + 0 = 0

Interpretazio geometrikoa: binaka elkar ebakitzen duten hiru zuzen dira.

x = ()mm mm 1 22 2 –2 2 + y = ()mm mm 1 1 ––2 + z = ()mm 1 1 –

• m = 1 bada, bateraezina da.

• m = –1 bada, bateraezina da.

15 Sistema bateragarri determinatua da a ≠ 0 eta a ≠ 3 bada.

16 a) hein (A ) = hein (A' ) = 2. Sistema bateragarri indeterminatua da. Soluzioa da (λ, λ, λ).

b) Bai, ekuazio bat erantsi eta bateragarri determinatua bihurtu liteke. Eransten den ekuazioa beste biekiko linealki independentea izan behar da.

* 11 3 3 7

Adibidez: x + y + z = 1.

Ez dago modurik ekuazio bat erantsi eta bateraezin bihurtzeko, edozein ekuazio eransten dela ere, hein (A' ) = 3 baita.

u -ren v = 9 43 – gaineko proiekzio-bektorea = (4, –2, – 4)

3 a) m = 0

b) wu v # = = (–28, –21, 0)

c) ', , 5 3 5 4 0 u –= dn ; v' = (0, 0, 1); ', , 5 4 5 3 0 w ––= dn

d) Bai.

4 a) a = b 6 3 –– b) b = 3 11

5 m = 0, m = 5 –24

6 Bi soluzio daude: (, ;, ;) 75 67 55 eta (, ;, ;) 75 67 55

7 m = 3, m = –2

6. unitatea

1 a) Zuzenaren ekuazio inplizituak: r : x z 1 3 = = )

Planoaren ekuazioa: π: –x + 7y + 4z – 3 = 0

Zuzenak eta planoak elkar ebakitzen dute.

b) (1, –8/7, 3)

2 x + 3y + z – 9/2 = 0

3 π: x + 14y + 11z + 12 = 0

4 xy z x yz 10 10 – –+= = + *

92 17 0 2 2 6

5 Bi zuzenek elkar gurutzatzen dute k = 2 bada.

Zuzenek elkar ebakitzen dute (3, 1, 4) puntuan k = 5 bada.

6 m ≠ 2 bada, planoek puntu batean ebakitzen dute elkar.

= =+ = + * zuzenean elkar ebakitzen dute 1 1 5

7. unitatea

1 a) dist (A, π') = 7 4 27 u b) A' (0, –2, –3)

c) (, ) sn i sarc 35 4 2 73° r == %

2 a) π: –x + 3y – 2z – 6 = 0 planoa da.

b) n r = (–1, 3, –2)

PQ = (–2, 6, – 4) = 2(–1, 3, –2)

PQ || n r → π ⊥ PQ

PQ-ren erdiko puntua da M = (4, 4, 1) ∈ π.

π perpendikularra da zuzenkiarekiko eta bere erdigunetik igarotzen da.

c) A(– 6, 0, 0), B (0, 2, 0), C (0, 0, –3)

ABC triangeluaren azalera = 3 14 u2

d) V = 6 u3

3 A' (9, 1, 0)

4 a) S(4, 1, 1)

b) 3,54 u

5 a) t : x x y y z z 3 2 530 4 0 0 –+ ++ = =

b) dist (r, s) = 14 3 210 u

6 a) Zentroa: (2, 0, –1); erradioa = 5

b) Erradioa = 4

II. multzoa

1 ( 20,, 2 ) eta (– 20,, 2 – )

2 a) 3 2 u2

b) α = 45°

c) 6 u3

3 a) (1, 1, 0) b) 2

8 a) a = –2, b = –2 1

b) Ez.

9 k = –2

π: x – y – 2z – 2 = 0

10 a) v r = (1, 1, 1); v s = (3, 3, 1);

P (0, 0, 0) ∈ r ; Q 01,, 3 1 dn ∈ s

PQ = 01,, 3 1 dn / 1 1

3 3 1

0 1 13

1 ––≠ 0

b) t : x x y y z z 2 6 0 –1 + + = = *

11 P(1, –2, 0) Q(4, 1, 3)

12 a) a = –2 13 bada, zuzenek elkar ebakitzen dute.

a ≠ –2 13 bada, zuzenek elkar gurutzatzen dute.

b) α = 90°

13 x – 2y – 4z – 5 = 0

14 a) Q (0, 0, 0)

b) R1(2, 2, –2), R2(–2, –2, 2)

15 (x, y, z) = (1, 1, 1) + λ(0, 1, –1)

16 a) Paraleloak dira.

b) 10/3 u2

17 Bi soluzio daude:

x – 3y – z + 3 11 – 2 = 0; x – 3y – z – 3 11 – 2 = 0

18 Bi soluzio daude: (2, –2, 2) eta (4, – 4, 4).

= = = *

m m m

4 d( ,, ) 11 –1 x y z 2–

5 x – z + 1 = 0

6 Azalera = 2 3 u2

7 (x, y, z) = (1, 2, 3) + λ(1, 2, 0)

19 r : xy xz 25 0 20 ––+= = *

20 Bi planoekiko distantziakideak diren puntuak y = –4 eta x = 1 planoak dira.

21 a) Zentroa: (1, –3, 0). Erradioa: 7

b) z = 7

Autoebaluazioen soluzioak

8. unitatea

1 a) 0 b) e 1 c) 1 d) 1

2 a) f jarraitua da Á – {0, –3} tartean.

x = 0 puntuan jauzi infinituko eten bat du.

x = –3 puntuan eten saihesgarri bat du.

b)

∞ lm i x " + f (x) = –1 ∞ lm i x – " f (x) = –1

Y

c) X –3 –1 –2

3 a) f (x) etena da x = –2 puntuan, puntu horretan ez baita existitzen.

f (x) etena da x = 0 puntuan, izan ere: lm i x 0 –" f (x) = 0 ≠ lm i x 0 " + f (x) = 1

b)

∞ lm i x " + f (x) = + ∞ , ∞ lm i x – " f (x) = 1

4 a = 1, b = 1

5 Dom = Á– {0, –3}. Beraz, f (0) = 16/3 esleitu behar da.

6 Funtzioa definituko dugu: g (x) = f (x + 1) – f (x).

g funtzioa jarraitua da [0, 4] tartean, eta g(0)-ren zeinua ≠ g(4)-ren zeinua.

Bolzanoren teoremaren arabera, existitzen da c ∈ (0, 4) eta betetzen du g (c) = 0; beraz, f (c + 1) = f (c).

7 f jarraitua da Á. f (0) = 1 eta f (5) ≈ 5,007. Batezbesteko balioen teoremaren arabera, existitzen da c ∈ (0, 5) eta betetzen du f (c) = 4; beraz, c + e –c = 4.

9. unitatea

1 a) y ' = x x 1 31 ––

b) y ' = x 9 –3 2 +

c) y ' = sn cos ix x 2

d) y ' = ln 3 2 2 () / x 13 –

e) y ' = –(tg x)1 – x ln (tg x) + (1 – x)(1 + tg 2 x)(tg x)–x

f) y ' = yx yx 2 2 ––

3 Funtzioa jarraitua da Á-n eta deribagarria Á – {1} tartean. x = –1 puntuan, f ' (x) = 0.

4 Funtzioa jarraitua da x = 0 puntuan, baina ez deribagarria. Beste horrenbeste gertatzen da x = 1 puntuan.

5 a = 2; b = 2 f deribagarria da Á – {0} tartean.

6 f deribagarria da Á – {–2, 1} tartean.

f ' (–4) = 0; f ' (0) = 0; f ' (3) = –1

10. unitatea

1 , k 2 20 r r + bl

2 Minimo bat dago (1, 1) puntuan. Gorakorra da (– ∞, 1) ∪ (2, + ∞) tartean. Beherakorra da (1, 2) tartean.

Ahurra da (2, +∞+°) tartean, eta ganbila (– ∞, 2) tartean.

3 Gorakorra da 0, 2 r l ; ∪ , 2 3 2 r r d F tartean.

Beherakorra da , 22 3 r r dn tartean.

Maximo bat du , e 2 /2 r r bl puntuan.

Minimo bat du , e 2 3 –/ 32 r r dn puntuan.

4 a) f ganbila da (0, e –3/2) tartean. f ahurra da (e –3/2, +∞) tartean.

Koordenatu hauek dituen inflexio-puntu bat du:

, ee 2 3 –/ 32 3

b) y = –2 3 e –3 – 2e –3/2 (x – e –3/2)

5 a = 1, b = –3, c = 0, d = 4

6 , 3 3 4 3

7 Altuera = 6 3 cm

Erradioa = 36 cm

8 Funtzioak ez du betetzen Rolleren teoremaren hipotesia [–2, 2] tartean, ez baita deribagarria x = 0 puntuan.

Beraz, ezin dugu ziurtatu c ∈ (–2, 2) existitzen denik f ' (c) = 0 betez.

11. unitatea

2 a) Dom = Á

Asintota horizontal bat du, y = 0 ekuaziokoa, x → +∞. Adar infinitu bat du: funtzioak +∞-ra jotzen du x → –∞ denean.

Beherakorra da (–∞, 0) ∪ (2, +∞) tartean

Gorakorra da (0, 1) tartean

Maximo erlatibo bat du (2, 1) puntuan.

Minimo absolutu bat du (0, 0) puntuan.

Inflexio-puntu bat du (1, 1/2) puntuan.

b) Dom = Á – {2}

Asintota bertikal bat du x = 2 puntuan, eta asintota zeihar bat y = x puntuan.

–∞-ra jotzen du x → –∞ denean, eta +∞-ra jotzen du x → +∞ denean.

Gorakorra da bere definizio-eremu osoan. Ez du puntu singularrik.

6 Ardatzak ebakitzen ditu (0, 0) puntuan.

Maximo bat du (0, 0) puntuan.

Beherakorra da (0, 1) tartean, eta gorakorra (–1, 0) tartean.

3 Bere maila 5 izango da gutxienez.

Autoebaluazioen soluzioak

7 f (x)-k minimo bat du (–2, –2) puntuan. Ez du asintotarik.

11 a) f (x) = x x 1 2 –+

b) g (x) = x – 3ln | x + 1 | + 1

12 a) () cos arctgx k 2 1 2 –+

b) () ln xx arctg x k 2 3 46 42

12. unitatea

5 ln k 2 1 2 snix + 6 –cos (ln x) + k

7 || || ln ln xx k 10 3 3 10 7 7 –+ ++

8 arctg x k 9 1 3 –+ bl

9 () ln xx xx k 3 2 44 1 3 ++ +

10 a) ex k 22 1 1 9 x2 ++dn

b) () () coslnsinln xx xx k 2 + +

13. unitatea

1 a) Azalera = 4 21 u2

b) 4 u2 bakoitzak

2 9 u2

3 2 5 u2

4 2 1 u2 5 2 u2

6 a) F ' (e) = 4e

b) F '' (x) = 0 ⇔ x = e –1 < 1, baina ez da F-ren definizioeremukoa. Hau da, F '' ez da baliogabetzen bere definizio-eremuan. F-k ez du inflexio-punturik.

7 a) V = xdx 6 5 0 6

r dn y = 50π u3

0 2 r r = bl y

b) V = a r xdx ra 3 a

III. multzoa

b) 0

c) 0 d) e 3

2

4

b) Funtzioak maximo erlatibo bat du (0, 0) puntuan.

c) 5 3 u2

5 a) f (x) gorakorra da bere definizio-eremu osoan. b)

8 a = 4, b = –10 f (x) = x x 4 410

6 Asintota horizontala: y = 0 (+ ∞-rantz); asintota kurbaren azpitik doa.

Maximoa: , e 3 9 3 dn . Minimoa: , e 2 11 –/ 12 dn

–2

7 a) Asintota bertikala: x = 1; x → 1 bada, f (x) → + ∞.

y = ±(x + 1) asintota zeiharrak x → ±∞ denean.

b) Minimoak: (0, 0) eta (2, 4)

c)

9 a = 1 b = –3 c = 0 d = 2

10 Zentrorainoko distantzia, 50 cm.

11 a = –2 3 , b = 2 1

2 + * Rolleren teorema betetzen da c = 3/2 kasuan.

f (x) = ≤≤ xx x 02 –+ ≤ xx 2 3 2 1 21 25 bada bada <

12 a) f ' (x) = x x(1 + ln x) – 2x ln 2. Jarraitua da Á-n.

f ' (1) < 0, f ' (2) > 0. Bolzanoren teorema ezarrita, existitzen da α ∈ (1, 2) eta betetzen du f ' (α) = 0.

b) f (1) = 0, f (3) = 20. Bai, existitzen da β ∈ (1, 3) eta betetzen du f (β) = 20, izan ere 10 ∈ [0, 20].

c) y = 1 + 4(x – 2). f (x) jarraitua eta deribagarria da.

13 Batezbesteko balioaren teorema betetzen den bi puntu daude, c = 1/2 eta c = –1/2.

Autoebaluazioen soluzioak

14. unitatea

1 a) E = {(a, a, ca), (a, a, +), (a, +, a), (a, +, +), (+, a, a), (+, a, +), (+, +, a), (+, +, +)}

A = {(a, a, +), (a, + , a), (a, +, +), (+, a, a), (+, a, +), (+, +, a)}

B = {(a, +, +), (+, a, +), (+, +, a), (+, +, +)}

b) [/ ][ ]/ [] : [] [/ ][ ] PA BP AB PB PA PA BP A 8 3 8 4 4 3 8 6

+ == = = = 4 A eta B independenteak dira.

2 a) P [A ∩ B ] = 1 3 6

b) P [A ∩ B ] = P [A ] · P [B ] = 1 3 6 → A eta B independenteak dira, baina ez bateraezinak; izan ere, P [A ∩ B ] ≠ 0.

c) [/ ] PA B 4 1 =

= 0,8125 6 a) i) P [ D ] = 0,967

P [A/Ak] = 0,404 b) 50 akastun.

b) P [Bat ere ez ] = 0,1176

c) P [Baten bat ] = 0,8824

d) P [3 eta 3 ] = 0,1852

3 Dentsitate-funtzioa da, ez-negatiboa delako eta zuzenaren azpiko azalera 1 delako.

0,3125

4 a) P [1,53 < z < 2,1] = 0,0451 P [–1,53 < z < 2,1] = 0,9191

b) b = –0,25, k = 1,64

5 a) 0,0113

b) 0,0228

c) 0,9659 6 N (20, σ); P [x < 28] = 0,945

0,1587

0,1587 · 177 = 28,09

Gutxi gorabehera, 28 egunetan beharko dut ordu-laurden baino gutxiago heltzeko.

7 Probabilitatea 0,0158 da.

IV. multzoa

1 P [B ] = 0,38; P [A ∪ B ] = 0,59; P [A ∩ B ] = 0,12

2 a) 0,72

b) 0,28

c) 0,3

3 a) 0,35

b) 0,25

4 P [ /1] = 5 1 ; P [1 eta ] = 30 1 ; P [ ] = 30 16

P [ ] = 30 14 ; P [1/ ] = 16 1

P [1/ ] adierazpenak esan nahi du azkenean bola gorria irten dela eta dadoan 1 irteteko zer probabilitate dagoen jakin nahi dugula.

5 a) urdina

b) P [urdina] = 0,20 P [betaurrekoak] = 0,55

P [urdina eta betaurrekoak] = 0,11

c) P [urdina/betaurrekoak] = 0,20

P [betaurrekoak/urdina] = 0,55

d) Askeak dira, adibidez:

P [betaurrekoak/urdina] = P [betaurrekoak]

6 a) 0,375 b) 0,3636

7 a) k = 0,23

b) P [13 ≤ xi ≤ 15] = 0,52

c) μ = 13,92 eta σ = 1,73

8 a) P [x = 0] = 0,0060

P [x = 1] = 0,0403

P [x > 1] = 1 – [P [0] + P [1]] = 0,9537

b) μ = 4 eta σ = 1,55

9 a) Probabilitatea % 4,01ekoa da. Okerra.

b) Probabilitatea % 3,43koa da. Okerra.

c) Analisia eginda, 92 espero behar ditugu, ez 8.

10 a) % 0,62

11 a) 0,2718

12 a) 0,8508

b) % 98,76

b) 22,37 kg

b) 0 da gutxi gorabehera.

c) 0,9495

berdea beltza marroia guztira