Mundua helburu: Kimika 2. Batxilergoa. Lagina

Alfredo Liébana Collado

José Antonio Araque Guerrero

José M.ª Teijón Rivera

Aurkibidea Ikasturteko oinarrizko jakintzak

4 Lotura ki mi k o a

10

• Inguratzen gaituzten substantziak

• Egin erloju kimiko bat

• Aire garbia?

• Naturala hobea da?

1 Ki mi k a eta ka l k ul uak

Erreakzio kimikoak eta haien gaineko kontrola

1. Materiaren konposizioa

2. Substantzia kantitatearen unitatea: mola

3. Gasak aztertzea

4. Formula kimikoak idaztea

5. Disoluzioak. Kontzentrazioaren unitateak

6. Erreakzio kimikoen estekiometria

Kultura zientifikoa. Alkimia

Problemak ebazteko estrategiak

2 M ateria ren egitura

Isotopoak nekazaritzan eta elikaduran

1. Eredu atomikoen bilakaera

2. Argiaren izaera elektromagnetikoa

3. Espektro atomikoak

4. Teoria kuantikoaren jatorria

5. Efektu fotoelektrikoa

6. Bohrren eredu atomikoa

7. Mekanika kuantikoa

8. Orbital atomikoak. Zenbaki kuantikoak

9. Partikula subatomikoak. Unibertsoaren jatorria

Kultura zientifikoa. LHCa eta Higgs bosoia

IKTak. Efektu fotoelektrikoa aztertzea

Problemak ebazteko estrategiak

18

Nanoteknologia eta material berriak

1. Atomoak, lotura kimikoz elkarri lotuak

2. Lotura ionikoa

3. Lotura kobalentea

4. Balentzia-loturaren teoria

5. Orbital atomikoen hibridazioari buruzko teoria

6. Balentzia-geruzako elektroi bikoteen aldarapenari buruzko teoria

7. Lotura metalikoa

8. Molekularteko indarrak

9. Interes biologikoko substantzietan dauden loturak Kultura zientifikoa. Material berriak

IKTak. Geometria molekularra

Problemak ebazteko estrategiak

5 Termodin a mi k a

Termodinamika eta bolkanologia

1. Sistema termodinamikoak

42

3 S istema peri o di k o a 82

Elementu kimikoen taula periodikoa

1. Elementu kimikoen kronologia

2. Moseleyren legea

3. Atomoen konfigurazio elektronikoak

4. Egungo sistema periodikoa

5. Elementuen propietate periodikoak

6. Taula periodikoa eta erreaktibotasun kimikoa

Kultura zientifikoa. D. I. Mendeleiev

Problemak ebazteko estrategiak

2. Termodinamikaren lehenengo legea

3. Termodinamikaren lehenengo legea erreakzio kimikoei aplikatzea

4. Ekuazio termokimikoak. Erreakzio-entalpia. Diagrama entalpikoak

5. Formazio-entalpiak. Lotura-entalpiak

6. Termodinamikaren bigarren legea

7. Berezkotasun-irizpideak

8. Errekuntza-erreakzio kimikoen ondorioak gizartean eta ingurumenean

Problemak ebazteko estrategiak

Landu ikasitakoa

188

6 Z in e ti k a ki mi ko a 168

Erreakzio leherkorrak

1. Erreakzio kimiko baten abiadura

2. Abiaduraren ekuazioa

3. Talken teoria eta trantsizio-egoeraren teoria

4. Erreakzio-mekanismoa

5. Erreakzio-abiaduran eragina duten faktoreak

6. Katalisia

7. Katalisiaren erabilerak

Kultura zientifikoa. Erreakzio baten zinetika

Problemak ebazteko estrategiak

7 Oreka kimikoa

Orekak egunerokoan

1. Erreakzio kimiko itzulgarriak

2. Oreka kimikoa aztertzea

3. Oreka-konstantea adierazteko moduak

4. Erreakzio-zatidura eta erreakzioaren noranzkoa

5. Oreka, zenbait etapatan

6. Disoziazio-maila: masen legearen beste erabilera bat

7. Orekan eragina duten faktoreak: Le Châtelierren printzipioa

8. Oreka heterogeneoak: prezipitatuak eratzea

9. Prezipitatuen disolbagarritasunean eragina duten faktoreak

10. Prezipitazio zatikatua

11. Orekak egunerokoan eta naturan Kultura zientifikoa. Amoniakoaren sintesi industriala

8 Azidoak eta baseak

Azidoak eta baseak egunerokoan

1. Azidoaren eta basearen kontzeptuak

2. Azidoen eta baseen indarra

3. Azidotasuna neurtzea. pH-aren kontzeptua

4. Gatzen hidrolisia

5. Disoluzio erregulatzaileak

6. Azido-base neutralizazio-bolumetriak

7. Azidoak eta baseak industrian Kultura zientifikoa. Biografiak Problemak

202

1

Karbonotik datozen produktuak

1. Karbonoaren loturen ezaugarriak

2. Molekula organikoen irudikapena

3. Orbitalen hibridazioa

4. Isomeria

5. Talde funtzionalak eta segida homologoak

6. Nomenklatura eta formulazio organikoa

7. Hidrokarburoak

8. Konposatu oxigenatuak

9. Konposatu nitrogenatuak

10. Tiolak eta perazidoak

11. Konposatu organiko polifuntzionalak Kultura zientifikoa. Kimika organikoaren historia IKTak. Molekula organikoak. Molview

Problemak

298

Elikagaien zeregin antioxidatzailea

1. Oxidazio-erredukzio erreakzioak

2. Oxidazio-zenbakiak

3. Erredox doikuntza, ioi-elektroi metodoarekin

4. Erredox erreakzioen estekiometria

5. Gelaxka elektrokimikoak

6. Elektrodo-potentzialak eta gelaxka baten potentziala

7. Erredox erreakzioen berezkotasuna

8. Erredox balorazioak

9. Elektrolisia

10. Elektrolisi-proiektu industrialak

11. Erredox erreakzioen erabilerak eta ondorioak

Kultura zientifikoa. Erredox erreakzioak egunerokoan

IKTak. Elektrolisi-simulagailua

Problemak ebazteko estrategiak

332

Karbonoaren konposatuen erreakzioak garrantzitsuak dira

1. Erreakzio organikoak

2. Erreakzio organikoen mekanismoak

3. Erreakzio organiko motak

4. Hidrokarburoen erreakzioak

5. Deribatu halogenatuen erreakzioak

6. Alkoholen eta fenolen erreakzioak

7. Aldehidoen eta zetonen erreakzioak

8. Azido karboxilikoen erreakzioak

9. Konposatu nitrogenatuen erreakzioak

10. Interes industrialeko konposatu organikoak Kultura zientifikoa. Medikamentuen ordenagailu bidezko diseinua

Problemak ebazteko estrategiak

1 2 Po l i mero ak eta ma k romol ek ula k 36 6

Plastikoak: ingurumen-inpaktua

1. Makromolekulen eta polimeroen kontzeptuak. Propietateak

2. Polimerizazio-erreakzioak

3. Interes industrialeko polimeroak

4. Interes biologiko, biomediko eta teknologiko handiko polimeroen erabilerak

5. Naturan dauden makromolekulak eta polimeroak. Propietate biologikoak eta medikoak

6. Karbonoaren kimikaren garrantzia Kultura zientifikoa. Bioteknologia

Problemak ebazteko estrategiak

Kimika eta kalkuluak

Materialen eraldaketei Antzinarotik behatu zaie. Alabaina, eraldaketak ezin izan dira ulertu eta aplikatu, harik eta ezagutza zientifikoa behar adinakoa izan den arte.

Kimika esaten zaio materia bera eta materian gertatzen diren aldaketak aztertzen dituen zientziari. Erreakzio kimikoetan, erreaktiboen materia osatzen duten atomoak eta molekulak berrantolatu egiten dira, eta, ondorioz, substantzia berriak eratzen: produktuak. Estekiometriak aztertzen du nola doitzen den prozesu hori, eta eginkizun horretan funtsezkoa printzipio bat dago: masa konstantea da; hots, masa berbera dago erreakzioaren aurretik eta erreakzioaren ostean.

Ikuspegi kuantitatibotik begiratzen badiogu, lehengaien eta produktuen kantitateak kontrolatzen ditu kimikak, emaitzak eta aplikazioak ahalik eta errentagarrienak izan daitezen. Lehen urratsa laborategian ikerlanak egitea da, prozesu kimikoak ulertzeko aukera ematen duten prozedurak eskuratzeko. Eta, ondoren, eskala aldatu egiten da, errendimenduak hobetu, eta, azkenean, modu industrialean lan egiten hasten da.

Baina kontuan harturik, batetik, industria kimikoak duen ingurumeninpaktua, eta, bestetik, gizarteak ingurumenaren babesarekiko duen gero eta sentikortasun handiagoa, ezinbestekoa da hondakinen tratamenduak garatzea, ingurumen-inpaktua txikitzeko eta hondakinak beste helburu batzuetarako erabiltzeko.

Egin ariketa hauek taldeka:

1 Aipatu kontzeptu hauen adibide bana: nahaste homogeneo bat, nahaste heterogeneo bat, benetako disoluzio bat, koloide bat eta suspentsio bat. Esan oinarrizko zer eragiketa egin behar diren nahaste horien osagaiak bereizteko. Ondoren, ekarri gogora bi substantzia kimiko; haietako bat uretan disolbagarria izango da, eta bestea, alkoholean. Giro-tenperaturan, zer agregazio-egoeratan egongo dira? Aurreko adibideetan nahasteetako osagaiak bereizteko ikusitako oinarrizko eragiketak erabiliz, zer egingo zenukete, GJHen 6.1 eta 6.3 xedeak erdiesten laguntzeko?

2 Ikertu zer gasek eragiten duten euri azidoa, eta aipatu horietako bat. Azaldu zer ondorio kaltegarri dituen izaki bizidunentzat, bai eta nondik datorren ere. Nola lortuko zenituzkete GJHen 3.9, 6.6 eta 11.6 xedeak?

GJH KONPROMISOA

IKASKUNTZA-EGOERA

INGURATZEN GAITUZTEN SUBSTANTZIAK

Unitate honetako edukiak eta ariketak oso baliagarriak izan daitezke liburuko lehen orrialdeetako eranskinean proposatzen den proiektua egin ahal izateko.

Unitate honetan

• Erreakzio kimikoak eta haien gaineko kontrola

1. Materiaren konposizioa

2. Substantzia kantitatearen unitatea: mola

3. Gasak aztertzea

4. Formula kimikoak idaztea

5. Disoluzioak. Kontzentrazioaren unitateak

6. Erreakzio kimikoen estekiometria

• Kultura zientifikoa. Alkimia

• Problemak ebazteko estrategiak

anayaharitza.es webgunean

Motibatzeko:

• Bideoa: «Hasi baino lehen».

Lehendik dakizuna detektatzeko:

• Aurkezpena: «Zer jakin behar duzun».

Ikasteko:

• Aurkezpena: «Ikasteko».

• Simulazioak: «Isotopoak eta masa atomikoa».

«Gasak: sarrera».

«Gasen propietateak». «Kontzentrazioa».

«Molaritatea».

Ebaluatzeko:

• Amaierako autoebaluazioa.

• Ariketen soluzioak.

Eta, horrez gain, proiektuko gakoak aplikatzeko beharrezkoa den dokumentazio guztia.

Materiaren konposizioa

Natura era askotan azter daiteke. Materiaren konposizioa eta materiaren eraldaketak aztertzea erabakitzen badugu, kimikaren munduan murgiltzen gara.

Daltonek, 1803. urterako, materian elementuak eta konposatuak modu koherentean desberdintzeko aukera eman zuen, bere teoria atomikoarekin. Elementua honela definitu zuen: atomo berdinak dituen gaia, zeinak partikula material bereiziak eta suntsiezinak baitira. Elementuak desberdindu ahal izateko, haien masa eta propietate desberdinei erreparatu behar zaie.

Teoria atomikoari jarraikiz, elementuak zenbakizko erlazio errazen arabera konbinatuz lortzen dira konposatuak.

1.1. Konbinazio kimikoen legeak

Materiaren kontserbazioaren legea (Lavoisier)

Erreakzio kimikoetan, materia kantitatea ez da aintzat hartzeko moduan aldatzen, eta horrek esan nahi du erreakzioko erreaktiboen masa eta produktuen masa berdinak direla.

Proportzio finkoen legea (Proust)

Konposatu jakin batean, elementu berberak daude beti, eta proportzio berberetan.

Proportzio anizkoitzen legea (Dalton)

Elementu baten masa desberdinak eta beste elementu baten masa konstantea konbinatzen direnean, emaitza bi konposatu desberdin dira, eta haien arteko erlazioa zenbaki txiki eta osoak dira.

Elkarrekiko proportzioen edo konbinazio-pisuen legea (Richter)

Elementu jakin baten pisu berarekin konbinatzen diren elementu desberdinak haien pisu erlatiboak dira, haien artean konbinatzen direnean, edo pisu horien multiploak edo azpimultiploak.

Lege horren bitartez, elementu bakoitzerako konbinazio-pisu erlatiboak aztertu ahal izan ziren. Erreferentziatzat txikiena hartu zuten; zehazki, hidrogenoa. Hala, 1 balioa esleitu zioten hidrogenoaren konbinazio-pisuari. Aurrerago, konposatu gehien eratzen dituena oxigenoa dela ikusita, erreferentzia oxigenoa izatea erabaki zen; haren balioa 8 izatea finkatu zuten.

J. Dalton (1766-1844). Zientzialari ingelesa, teoria atomikoa definitu zuena, kimika modernoaren oinarria. Hartan, atomoak definitzen dira, eta adierazten da haien arteko konbinazioek konposatuak dakartzatela, erreakzio kimikoen bidez. Greziako Demokrito filosofoak adierazitako teoria garatu zuen.

1 H2S-aren lagin batean, 14,112 g sufre eta 0,888 g hidrogeno daude. Kaltzio sulfuroaren beste lagin batean, berriz, 2,053 g sufre eta 2,497 g kaltzio daude. Kalkulatu kaltzioaren konbinazio-pisua.

2 Bi burdina klorurotan, burdina % 34,43 eta % 44,05 da, hurrenez hurren.

Justifikatu nola betetzen duten datu horiek proportzio anizkoitzen legea.

Testuan, elementu baten pisua aipatzen da, masa atomikoa erabiliz. Liburu honetan, pisu atomikoa edo pisu molekularra erabiliko da, bakoitza dagokionean, testuinguru historiko bat jorratzen denean, orain bezala. Testuaren gainerakoan, masa atomikoa (edo masa molekularra) agertuko da beti, hori da-eta gaur egun erabiltzen den terminoa.

3 Konposatu hauek ikusirik, azaldu zer elementuk osatzen dituzten eta zer masa-proportziotan agertzen diren:

Datuak: masa atomikoa (u): K = 39; Mn = 54,9 ; N = 14; O = 16; S = 32; C = 12; H = 1

a) KMnO4 c) CH3—CH2—COOH

b) (NH4)2SO4 d) CH3—CHOH—CHO

John Dalton

Pisu atomikoa - Masa atomikoa

Ariketak

Ebatzitako ariketak

1 Oxigenoak eta sufreak hiru proportziotan bat egiten dute, eta hiru oxido eratzen dituzte. Haietan, oxigenoa % 33,33, % 50,0 eta % 60,0 da. Kalkulatu zer masa-erlaziotan batu den oxigenoa.

Ebazpena

Enuntziatuan aipatzen diren oxigenoaren ehunekoak erabilita, sufrearen ehunekoak kalkula ditzakegu, kenketa eginez, eta erlazioa bilatu:

a) ,

, , gS g O 66 67 33 33 05 - b) , gS g O 50 50 10 = c) , gS g O 40 60 15 =

Horrenbestez, zenbaki osotan, erlazioak 1, 2, 3 dira, eta oxido hauek eratuko dira: SO, SO2 eta SO3. Alegia, 3:4.

2 Fe2O3-ari HCl-a gehituta, FeCl3-a eta H2O-a lortu dira. Horiek horrela, nola egiazta daiteke Lavoisierren legea?

Ebazpena

Erreakzioa doituz, eta erreaktibo zein produktuetan ea elementu bakoitzaren atomo kopuru bera dagoen aztertuz. Baiki, erreaktibo eta produktuetan masa berbera dagoela egiazta daiteke, era horretan.

Fe OHCl FeCl HO 62 3 23 32 $ ++

Guztizko atomo kopurua erreaktiboetan eta produktuetan: Fe = 2; O = 3; H = 6; Cl = 6

1.2. Substantzia puruak. Elementuak eta konposatuak

Substantzia puru deritze konposizio uniforme eta aldaezina dutenei.

Substantzia puruak elementuak edo konposatuak izan daitezke. Adibidez, burdina, urrea, gatz arrunta (sodio kloruroa), azukrea (sakarosa) eta sufrea.

• Elementuak dira substantzia kimikoki soilagotan deskonposatu ezin diren substantzia puruak. Esate baterako, burdina, urrea eta sufrea.

• Konposatuak dira bi elementu desberdin edo gehiago konbinatuz eratzen diren substantzia puruak. Adibidez, gatz arrunta (sodio kloruroa) eta azukrea (sakarosa).

Gaur egun, 118 elementu kimiko ezagutzen dira, eta elementuen taula periodikoan jasota daude. Baina haiekin milioika konposatu desberdin eratu daitezke.

Atomoen irudikapenak

Eskuarki, atomoak eta molekulak bolak (espazio-simetriagatik) eta kolorekode jakin bat erabiliz irudikatzen dira. Bolen tamainak atomoen tamainen arteko aldea adierazten du, nahiz eta, zenbaitetan, baliteke eskalarik ez betetzea. Irudikapen batzuetan, garrantzitsuena loturak izaten dira; beste eredu batzuetan, aldiz, atomoen banaketa osoa da adierazi nahi dutena. Gaur egun, ordenagailu bidezko ereduak egiten dira, zehaztasun handihandikoak.

Eztainua (elementua), sodio kloruroa eta ura (konposatuak). Hirurak substantzia puruak dira.

bakunak. H2O CO2 Molekula kobalenteak.

1.3. Sinboloak eta formula kimikoak

Elementuen atomoak adierazteko, sinboloak erabiltzen dira. Letra bat izaten da, edo bi, zenbaitetan; normalean, latinezko erroa erabiltzen da.

Adibideak: H (hidrogenoa), He (helioa), C (karbonoa), Cl (kloroa), S (sufrea).

Formula kimikoak sinboloen konbinazio ordenatuak dira. Haietan, konposatu batean elementu bakoitzak duen gutxieneko proportzioa adierazten da, azpiindize gisa eta zenbaki osoekin. Bat denean, ez da idazten.

Adibideak: HCl, H2SO4, NaClO4, NH3

Ioien kasuan, haien karga goi-indizeekin adierazten da (Na+, SO42–). Substantzia ionikoen harira, berez molekulak ez direnez, formula-unitatea dela esaten da. Esate baterako, NaCl-a konposatu ioniko bat da, kristal bat, Na+ eta Cl– ioiz osatutakoa, proportzio berean. Ioi horiek indar elektrostatikoak elkartzen ditu, baina ez dago NaCl molekularik.

Konposatu organikoetan bereziki, ohikoa da formula enpirikoa eta formula molekularra bereiztea. Formula enpirikoak adierazten du gutxieneko zer proportziotan batzen diren konposatua osatzen duten atomoak; eta formula molekularrak, berriz, zentzu kimikoa duen formularik sinpleena. Sarritan, bi formulak berdinak izaten dira.

Adibideak: ur oxigenatua: HO (formula enpirikoa), H2O2 (formula molekularra); etanoa: CH3 (formula enpirikoa), C2H6 (formula molekularra).

Produktu organikoetan, zenbaitetan, ez da formula enpirikoa idazten, ezta formula molekularra ere, formula erdigaratua baizik, karbonoen katea eta funtzioa zehazteko. Formula garatuan, berriz, lotura guzti-guztiak ikusten dira.

• Azido propanoikoa:

Formula erdigaratua Formula garatua

Batzuetan, interesgarria da egitura-formula erabiltzea, lotura guztiak eta egitura-simetrietako batzuk adierazteko:

• Azido sulfurikoa:

• Etenoa:

Egitura-formulak

4 Aztertu konposatu kimiko hauek: MgCl2, C6H6, H2O2, NH3, CO2. Esan zein adieraz daitezkeen desberdin, formula-unitateak, formula enpirikoak, formula molekularrak eta egitura-formulak erabiliz. Azaldu zergatik.

5 Idatzi propenoaren formula enpirikoa, molekularra, erdigaratua, garatua eta egitura-formula.

6 Idatzi bentzenoaren formula enpirikoa, molekularra, erdigaratua eta egitura-formula.

Substantzia ioniko bat. Formula-unitatea

Azido sulfurikoaren eta etenoaren eredu molekularrak.

Ariketak

Substantzia kantitatearen unitatea: mola

2.1. Masa atomikoaren unitatea

Elementu baten atomo bakar baten masa adierazteko, masa atomikoaren unitate, u, deritzon unitate bat erabiltzen da. Masa atomikoa definitzeko karbono-12a erabiltzen da neurketa-patroi moduan:

u bat karbono-12 isotopoaren (12C) hamabirena da (naturan dagoen karbono guztiaren % 98,89 karbono-12 da).

Halatan, X elementu baten masa 4 u dela esaten badugu, adierazten ari gara elementu horren elementu bat masa atomikoaren unitatea baino lau bider handiagoa dela. Ildo horretan, definizio hau adieraz dezakegu:

Elementu baten masa atomiko erlatiboak (sinboloa Ar da) adierazten du zenbat bider dagoen hartan masa atomikoaren unitatea. Bi masen arteko zatidura denez, ez du dimentsiorik.

Atomo baten masaren zatirik handiena nukleoan kontzentratuta dago. Hori dela eta, elementu baten masa atomikoa eta masa-zenbakia, A, bat datoz, gutxi gorabehera. Aurreko adibidean, Ar = 4 da, eta helio elementuari dagokio (42He).

2.2. Masa atomikoa, masa molekularra eta formula-masa Naturan, elementu askok isotopo (zenbaki atomiko bereko baina masazenbaki desberdineko atomo espezie) bat baino gehiago dute, eta, beraz, elementu baten masa atomikoa adierazten denean, haren batez besteko masa atomikoa adierazten ari gara; hots, isotopo bakoitzaren masen batezbesteko haztatua.

Gogoratu

Elementu kimikoak honela adierazten dira: ZAX. Hartan:

– Zenbaki atomikoa, Z, elementu baten atomoan dagoen protoi kopurua da. Hura identifikatzeko balio du. Atomo neutroen kasuan, zenbaki hura eta elektroi kopurua berdinak dira.

– Masa-zenbakia, A, protoien eta neutroien batura da, eta atomoaren masa da, gutxi gorabehera, masa atomikoaren unitatetan.

– Elementu beraren bi isotopok zenbaki atomiko bera dute; masazenbakia desberdina da, ordea. Naturan, proportzio desberdinetan daude; ugaritasun isotopiko naturala da hori.

1. taula. Magnesioaren (24,30) eta kloroaren (35,45) masa atomiko erlatiboak.

• Substantzia molekular baten masa adierazteko (metanoarena, adibidez), masa molekularra, m (lehen, pisu molekularra), erabiltzen dugu. Zehazki, substantzia osatzen duten atomo guztien masen batura da.

• Atomoekin bezala, masa atomikoaren unitatearekin berdin jokatzen badugu, magnitude erlatibo bat izango da, eta, hortaz, unitaterik gabea: masa molekular erlatiboa, mr . Esate baterako, honela adieraz daiteke: mr (CH4) = Ar (C) + 4 · Ar (H) = 12,01 + (4 · 1,00) = 16,01

• Konposatu ionikoak indar elektrostatikoz loturiko ioiz osatuta daude, kristal-sare batean. Halakoetan, masa adierazteko formula-masa baliatzen da; hau da, formula-unitatean agertzen diren atomoen masen batura. Eta konposatu molekularrekin egiten den bezala, hor ere mr erabiltzen da. Adibidez, zesio kloruro konposatuaren formula-unitatea CsCl da, eta formula-masa erlatiboa hauxe izango da, orduan: mr (CsCl) = 132,9 + 35,45 = 168,35.

CsCl-aren formula-unitatea.

2.3. Molaren kontzeptua. Avogadroren zenbakia

Elementuen masak aztertzen ditugunean, galdera hau egin daiteke: nola finkatu zen masak neurtzeko era? Hasteko, elementurik arinena zein zen bilatu zuten, eta hidrogenoa zela ikusi zuten; eta, gero, ohartu ziren gainerako elementuekiko masa-erlazioak zenbaki osoak zirela. Orduantxe sortu zen molaren kontzeptua, masa atomikoaren unitatean zenbat atomo dauden jakin nahi izan zutenean. Modu esperimentalean, 6,022 · 1023 atomo direla frogatu zen. Kopuru horri Avogadroren zenbakia, NA, esaten zaio; eta mol bat da. Hartara, eskuarki lan egitera ohituta gauden magnitudeordenan adierazten dira multiplo horiek.

Mol esaten zaio Avogadroren zenbakian dauden oinarrizko entitateen (atomoak, molekulak, ioiak, etab.) substantzia kantitateari.

Nahiz eta mola, dozena bera bezala, unitaterik gabeko kopuru bat den, gramotan adierazten dugu askotan. Horrelakoetan, mol baten masaz (edo masa molarraz) hitz egingo dugu: M (substantzia) sinboloa erabiltzen da, eta unitate honetan adierazten: g · mol–1. Esate baterako: H-aren mol bat = 1 g; H2-aren mol bat = 2 g; H+-aren mol bat = 1 g (elektroi baten masa baztergarria da, nukleoien masa baino 1 800 bider txikiagoa baita).

Elementu batzuen molekulen mol baten masa kalkulatzeko (esate baterako, sufrearena eta fosforoarena), elementu horien ohiko egiturak aintzakotzat hartu behar ditugu; adibide horretan, S8 eta P4, hurrenez hurren. Horrek esan nahi du, elementuez ari garenean, naturan dagoen espezieari erreparatu behar diogula, eta beti ez dela atomo bakuna. Gasetan, gogoan izan behar dugu gas nobleak monoatomikoak direla (He), eta beste elementu gaseoso gehienak diatomikoak direla (Cl2); bakan batzuk poliatomikoak dira, ordea (adibidez, ozonoa, O3).

ariketak

3 Jakinik karbonoaren masa atomikoa 12 dela, karbono atomoen zer substantzia kantitate egongo da kantitate hauetan?

a) 36 g karbono.

b) 12 u karbono.

c) 12 · 1020 karbono atomo.

Ebazpena

a) g g mol 36 12 1  = 3 mol karbono atomo.

b) 12 u = C-aren 1 atomo. Beraz:

, uatC at C mol mol 12 1 6 022 10 1 0166 10 · 23 –23 ==

Ariketak

7 Ordenatu honako kantitate hauek bakoitzak duen atomo kopuruaren arabera, txikienetik handienera:

a) 1,0 g magnesio nitrato.

b) 4 mol azido klorhidriko.

c) 6,1·10 24  molekula sufre dioxido.

8 Ordenatu sufrearen kantitatea handienetik txikienera, eta esan sufre atomoen zer substantzia kantitate dagoen substantzia hauetan:

a) 256 g S8

c)

210

b) 980 g H2SO4

c) 320 g SO2

He Cl2 O3

S8 P4

S8-aren eta P4-aren espazio-irudikapena.

Helio, kloro eta ozono molekulak.

Gasak aztertzea

Gasen higidura molekularra ausazkoa da, eta erakarpen molekularreko indarrak txiki-txikiak dira. Horren eraginez, gasen molekulak ia-ia aske dabiltza. Horrenbestez, gasaren izaera kimikoa edozein dela ere, gas guztiak ekuazio errazen bidez deskriba daitezke, giroko baldintzetan edo antzeko baldintzetan daudenean.

Gasak deskribatzeko, magnitude hauek baliatzen dira: presioa, bolumena, kantitate molarra eta tenperatura. Magnitude horietako bi konstante mantentzen badira, frogatu daiteke gainerako bien arteko erlazioa lege soil erraz bat dela.

3.1.

Boyleren legeak adierazten du presioa eta bolumena alderantziz proportzionalak direla, sistemako tenperatura konstante mantentzen denean: p · V = kte.

Honela ere adieraz daiteke: p1 · V1 =  p2 · V2. Bi egoera desberdin izango lirateke 1 eta 2, tenperatura konstantean. Ekuazio beraren beste forma bat da hau: P = kte · 1 / V. Grafiko batean, koordenatu-jatorritik igarotzen den malda konstanteko zuzen bat izango litzateke.

Robert Boyle

R. Boyle kimikari ingeles bat izan zen, Irlandan sortua 1627an, eta Londresen zendua, 1691n. Aitzindari izan zen gasen legeen tratamenduan, eta, batik bat, airea aztertu zuen. The Sceptical Chymist (Kimikari eszeptikoa) lanean, alkimistengandik aldendu zen, eta oinarrizko partikulen kontzeptua proposatu zuen. Haren esanetan, oinarrizko partikulak elkarrekin hainbat proportziotan konbinatzean, ezagutzen ziren askotariko materiak eratzen zituzten. Boyle Londresko Royal Societyko kide sortzaileetako bat izan zen; munduko lehen zientzia-elkarteko kide, alegia.

Boyleren legearen simulazioa

Beheko irudian ikusten den bezala, tenperatura konstantea bada, presioa handitzean ontziko gasaren bolumena txikiagotu egiten da, hau bete ahal izateko: p  · V = konstantea. Eta alderantziz, presioa txikiagotzean (tenperatura konstantean beti), bolumena handitzen da, helburu bera erdiesteko.

Gas baten bolumena handitzea edo txikitzea, tenperatura konstantean

Tenperatura konstantea

Bolumen txikiagoa

(Presio handiagoa)

Bolumen handiagoa

(Presio txikiagoa)

Boyleren legea

Boyleren legearen grafikoak.

3.2. Charles-Gay Lussac legea

Charles-Gay Lussac legeak adierazten du nola aldatzen den gas baten bolumena tenperaturarekin, presioa konstantea denean. Prozesu horretan, proportzionaltasun hau lortzen da: V = kte · T.

Lege hori honela ere adieraz dezakegu: e. T V kt = , non R beste konstante bat den. R konstante horren balioa hau da:

R = 0,082 atm · L · mol–1 · K–1 = 8,31 mol–1 · K–1

Lege horren beste adierazpen bat hau da: T V T V 1

2 = . Bi egoera adierazten ditu, presio konstantean. Tenperatura kelvinetan (K ) adierazten da beti. Aipatzekoa da lege hori osatu egin behar izan zela geroago. Zehazki, 1848an, Kelvinek tenperaturaren zero absolutua (−273 ºC) aurkitu zuen, eta haren izena daraman eskala ere finkatu zen. Eskuineko grafikoan ikusten da balioak estrapolatu egin behar direla, zeren, tenperatura baxuetan, gasak kondentsatu eta likido-egoerara igarotzen baitira.

1 2

Orain, bolumena konstante mantentzen badugu, beste ekuazio bat lortzen da, presioa eta tenperatura erlazionatzen dituena, bolumen konstantean. Proportzionaltasuna hau da: p = kte. · T, non te n V R k= baita.

Charles-Gay Lussac legearen simulazioa

Oraingoan ikusiko dugu ezen, presioa konstantea izanik, gas baten bolumena handiagotu egiten dela hura berotzen denean. Hoztean, aitzitik, gasaren bolumenak behera egiten du.

Bolumena baldin bada konstantea, gasa berotzean, ontziari egiten dion presioak gora egiten du. Hozten denean, berriz, behera egiten du presioak.

9 Boyleren legearen ohiko aplikazio bat da forma irregularra duen ontzi baten bolumena kalkulatzea, bolumen eta presio ezaguneko gas bat ontziz aldatuz. Ontzi batean, 515 mL aire daude, 735 mmHg-an. Hutsik dagoen ontzi bati konektatu zaiola kontuan hartuta, zer bolumena du bigarren ontziak, jakinik amaieran neurtu duten presioa 432 mmHg dela?

10 Pistoi mugikorra duen zilindro baten bolumena 0,05 L da, eta, 24 ºC-an, 36,2 cm3 hartzen dituen gas batekin bete da. Gehienez ere, zer tenperaturataraino berotu daiteke zilindroa presio konstantean, pistoia ateratzea eragin gabe?

Charles-Gay Lussac legearen adierazpen grafikoa.

Ariketak

3.3. Avogadroren legea

Lege honek bolumenaren eta substantzia kantitatearen arteko erlazioa adierazten du. Amedeo Avogadrok hau ezarri zuen 1811n:

Tenperatura eta presio berean, molekula kopuru bera dago (edo atomo kopuru bera, gasa monoatomikoa bada) gas desberdinen bolumen beretan.

Horrenbestez, bi gasek elkarren artean erreakzionatzen dutenean, erlazio bolumetriko erraz bati jarraitzen diote, eta hura molekulen substantzia kantitatearekiko proportzionala, baldin eta presioa eta tenperatura konstanteak badira. V = kte. · n, non kte. = R · T / p baita.

3.4. Gas idealak eta gas errealak

Aipatu diren legeak bete egiten dira, portaera ideala duten gasetan. Gas idealetan, ulertzen da gasaren molekulek hartzen duten bolumena baztergarria dela, molekulak dauden ontziaren bolumenarekin konparatuz. Haatik, gasen portaera ez da beti horrelakoa; konplexuagoa izan daiteke. Desbideratzeak gertatzen dira gasaren molekulen arteko interakzioengatik, eta handiagoak dira, likido-egoeratik zenbat eta gertuago egon. Presioak baxuak direnean eta tenperaturak neurrizkoak, edozein gasek dihardu gas ideal baten modura; presio altu eta tenperatura baxuetan, berriz, gasak modu idealean jokatzetik urrun daude.

3.5. Gas idealen egoera-ekuazioa

Orain arte ikusitako hiru legeak konbina ditzakegu:

• Boyleren legea: te V p k = (n eta T konstanteak dira).

• Charles-Gay Lussac legea: e. V kt =· T (n eta p konstanteak dira).

• Avogadroren legea: e. V kt =· n (p eta T konstanteak dira). Hala, gas idealen egoera-ekuazioa lortzen da:

te V p n k =· T , edo honela: p · V = n · R · T

R proportzionaltasun-konstanteari gasen konstante deritzo, eta, nazioarteko SI sisteman, balio hau du: 8,31 J · mol–1 · K–1. Edo, bestela, hau: 0,082 atm · L · mol–1 · K–1.

Gas kantitatea berbera denean (moletan), hots, n1 =  n2 betetzen denean, ekuazioa honela idatz daiteke, bi egoeratarako:

11 Argi goriko bonbillek gas geldoak dituzte (nitrogenoa, esate baterako), filamentua ez erretzeko. Eman dezagun 100 W-eko bonbilla baten bolumena 130 cm3 inguru dela, eta, hartan, 3 · 10–3 mol nitrogeno daudela. Nitrogeno gasaren zer substantzia kantitate egongo litzateke 150 W-eko bonbilla baten barruan, presio- eta tenperatura-baldintzak berberak badira eta bonbillarik handienaren bolumena 185 cm3 baldin bada?

Ariketak

3.6. Gas baten bolumen molarra eta dentsitatea

Substantzia baten bolumen molar deritzo substantzia horren mol batek hartzen duen bolumenari.

Solido eta likidoetan, bolumen molarra substantzia bakoitzaren ezaugarri bereizgarri bat da. Gasetan ez, ordea. Esperimentalki, hau ikusi da:

0 °C-an (273,15 K) eta presioa 1 atm denean (p = 1 atm = 101 300 Pa), edozein gasen mol batek 22,4 L-ko bolumena hartzen du. Presio- eta tenperatura-baldintza horiek baldintza normalak (b.n.) dira.

0 ºC-an (273,15 K) eta presio estandarrean (p = 1 bar = 105 Pa), bolumen molarra 22,7 L da. Presio- eta tenperatura-baldintza horiek baldintza estandarrak (b.e.) dira.

Gogoratu behar da molekula kopuru bera dagoela beti edozein substantziaren mol batean, eta, Avogadroren legeari jarraikiz, molekula kopuru berak bolumen bera hartzen duela, baldin eta p eta T aldatzen ez badira.

Gas baten dentsitatea

Beti ez da erraza gas baten formula jakitea, eta, horregatik, ohikoa da gasak aztertzea haien dentsitatea erabiliz (d = m / V). Gasen kasuan, bolumena nabarmen aldatzen da tenperatura eta presioarekin. Hortaz, dentsitatea ere halaxe aldatzen da.

Gas idealean ekuazioa baliaturik ( Vn R T p = ), dentsitatearen eta masa molarren arteko erlazioa lortu daiteke (g · mol–1-etan), eta, hartatik abiaturik, masa molekularra (u-tan). Substantzia kantitatearen eta masa molarraren arteko erlazioa nm /M = da, eta m/ dV = betetzen da. Orduan:

Gas idealen ekuazioak gas errealetan erabiltzeagatik, lortu izan diren dentsitate-balioak desberdinak suertatu dira. Alde horiek aztertzean, espainiar zientzialari bikain batek egindako lan esperimentalak aipatu behar dira: zientzialari hura Enrique Moles y Ormella (1883-1953). Sistema esperimental konplexuak sortu zituen alde horiek neurtzeko, eta gasen masa atomikoak eta molekularrak kalkulatu zituen muga-dentsitateen metodoarekin. Hartan, dagokion gasaren eta oxigenoaren dentsitatea kalkulatzen da, erreferentzia oxigenoa izanik.

Enrique Moles nazioartean sonarik handienetakoa izan duen espainiar zientzialaria izan da (Pisu Atomikoen Nazioarteko Batzordeko idazkaria izan zen). Haren emaitza esperimentalak masa atomikoen eta masa molekularren nazioarteko tauletan txertatu ziren.

Badakigu litro batean 7,71 g daudela. Beraz:

Jakin du dentsitatea 7,71 g · L–1 dela, 36 ºC-an eta 2,88 atm-n. Kalkulatu konposatuaren masa molarra, eta, ondoren, idatzi formula molekularra.

Ebazpena

M dR T p = erabiliko dugu. Datuak idatzita, hau dugu:

Kloroa (35,45 g) eta oxigenoa (16,00 g) konbinatzeko aukerak aztertuko ditugu:

– Kloro atomo bat eta oxigeno atomo bat, ClO (51,45 g): txikiegia da.

– Beste aukera bat Cl2O (86,9 g) da, baina aukera hori ere baztertu behar da.

– Kloro atomo bat eta bi oxigeno atomo, ClO2 (67,45 g). Azken hau emaitza teorikotik hurbil dago. Horrenbestez, formula molekularra hori da.

Formula molekularra jakiteko, litro batean dagoen substantzia kantitatea kalkulatuko dugu:

Enrique Moles y Ormella

4 Kimikari batek konposatu gaseoso hori berdexka bat sintetizatu du, kloroarekin eta oxigenoarekin.

Ebatzitako ariketak

3.7. Daltonen presio partzialen legea

Daltonen presio partzialen legea honela adieraz daiteke:

Berdinak dira gas ez-erreaktiboen nahaste batek egiten duen guztizko presioa eta nahaste hori osatzen duten gasen presio partzialen batura: ppi guztizkoa = / . Adierazpen horretan, pi gas bakoitzaren presio partziala da; hau da, nahastean gas horrek egiten duen presioa.

Orduan, i gas bakoitzerako:

V nR T p i i =

Adierazpen horretan, i gasaren substantzia kantitatea da ni; V, nahastearen guztizko bolumena; eta T, nahastearen tenperatura. Eta pi presio partzialaren eta p guztizko presioaren arteko erlazioa hau da:

Ariketak

12 Ontzi baten edukiera 2,00 L da, eta, hartan, 0,36 g helio daude 25 °C-an. Eduki hori 1,00 L-eko beste ontzi batera isuri da; aldez aurretik, 0,60 g nitrogeno zeuden, tenperatura berean. Kalkulatu zer presio partzial egiten duen gas bakoitzak, eta nahastearen guztizko presioa.

13 Hidrogenoa lortu daiteke azido klorhidrikoaren eta zinkaren arteko erreakzioarekin. Gasaren 146 mL bildu dira, uretan, 20 °C-an eta 780 mmHg-ko guztizko presioan. Tenperatura berberean, ur-lurrunak 17,5 mmHg-ko presioa egiten du. Hala, kalkulatu hidrogenoaren zer masa lortu den.

5 Potasio klorato konposatu solidoa berotzean, deskonposatu egiten da, O2-a (g) askatzen du, eta hondar gisa KCl-a (s) geratzen da. Uretan, 128 mL gas bildu dira, 24 ºC-an eta 762 mmHg-ko guztizko presioan. Horiek horrela, kalkulatu oxigenoaren zer masa lortu den.

Datua: plurruna (ura, 24 ºC) = 22,40 mmHg.

Ebazpena

pp p aO HO guztizko 22 =+

,, mmHg mmHgmmHg

6 Gas naturalaren lagin batean, 8,240 mol metano, 0,421 mol etano eta 0,116 mol propano daude. Gasen guztizko presioa 1,370 atm bada, zer presio partzial izango du gas bakoitzak?

Ebazpena

Gas bakoitzaren presio partzialak, pi, kalkulatzeko, frakzio molarra jakin behar dugu: Xi = ni / nguztizkoa Beraz:

0421 0116 8777 =+ +=

Frakzio molarrak hauek izango dira:

1370 9391 286 tan me oa guzt met == = ,, , p pX atmatm1370 0480 066 tan eoaet guzt == = ,, , p pX atmatm1370 0130 018 propanoa prop guzt == =

Ebatzitako ariketak

Lurraren atmosfera gasen nahaste homogeneo bat da: % 78 N2-a da; % 21, O2-a; eta % 1 inguru, beste gas batzuk (CO2-a, Ar-a, H2O-a, etab.)

Formula kimikoak idaztea

Konposatu baten azterketa kimikoa eginez, haren konposizioa jakin daiteke, eta, hortik abiatuta, nola formula enpirikoa hala formula molekularra jakin daitezke. Eta, alderantziz, konposatu baten formula jakinik, hartan dauden elementuetako bakoitzaren kantitateak jakin ditzakegu.

4.1. Konposatu baten formula zehaztea

Orain, oso konposatu soil batzuen formula zehaztuko dugu, hidrokarburoena. Hidrokarburoak konposatu organikoak dira, karbonoz eta hidrogenoz soilik osatutakoak. Guztiz erretzen direnean, emaitza karbono dioxidoa eta ura dira beti:

Hori kontuan izanik, honela jokatuko dugu:

CH OCOH OQ nn22 22 2 $ ++ + +

1. Hidrokarburoaren kantitate ezagun bat erreko dugu erabat.

2. Errekuntzan eratu diren CO2 eta H2O kantitateak pisatuko ditugu. Horretarako, ura lehorgarri batean biltzen da, eta karbono dioxidoa bereizi eta sodio hidroxidoarekin erreakzionarazten da.

3. CO2-aren eta H2O-aren masak jakin ostean, zer C eta H kantitate dauden kalkulatzen da; errekuntza gertatu aurretik hidrokarburoan zeuden berak izango dira. Zehaztuta dugu, jada, hidrokarburoaren formula enpirikoa. Aztertu den substantzian hirugarren elementurik balego (esate baterako, oxigenoa, konposatu organiko askotan bezala), pisuen arteko kenketa eginez kalkulatuko litzateke masa.

4. Formula molekularra zehaztuko dugu. Horretarako, konposatuaren masa molekularra da, atomoen masak batuz.

Ariketak

14 Idatzi konposizio ehundar hau duen substantziaren formula enpirikoa: Fe = % 63,53, S = % 36,47.

15 Azido askorbikoan (C bitamina), masaren % 40,92 karbonoa da; % 4,58, hidrogenoa; eta % 54,50, oxigenoa. Idatzi formula enpirikoa.

Masa molekularra 176 u dela jakinda, zer formula molekular du?

16 Alizina baratxuriaren osagai bat da, hipertentsioa prebenitzeko eraginkorra, eta konposizio hau du: C, % 44,43; H, % 6,21; S, % 39,5; O, % 9,86. Kalkulatu formula enpirikoa. Zer formula molekular du alizinak, masa molekularra 162 u bada?

Hidrokarburolagina Lehorgarria (H2O-a biltzeko)

O2 soberakina irteten da CO2-a biltzea (erreakzioa NaOH-arekin) O2 korrontea

17 Esperimentu batean 2,37 g karbono erretzean, elementu hori duen oxido gaseoso baten 8,69 g sortu dira. Konposatu horren litro batek 1,98 g-ko masa du, 1 atm-eko presioan eta 273 K-eko tenperaturan. Gas idealen portaera duela jota, idatzi oxidoaren formula molekularra.

7 Konposatu organiko bat aztertuta, ikusi dugu konposizio ehundar hau duela: % 40, C-a; % 6,7, H-a; eta % 53,3, O-a. Masa molekular esperimentala 182 dela jakinik, idatzi konposatu horren formula molekularra.

Ebazpena

Lehenik, konposatuaren osagai guztien batura % 100 dela egiaztatuko dugu. Abiapuntu moduan 100 g konposatu hartuta, osagai bakoitzaren substantzia kantitatea kalkulatuko dugu:

Orduan, formula enpirikoan, erlazioa CH2O da, eta formula molekularra haren multiplo bat izango da:

Labea

Ebatzitako ariketak

Disoluzioak. Kontzentrazioaren unitateak

Disoluzioa da bi substantziaren edo gehiagoren nahaste homogeneoa, puntu guztietan propietate fisikokimikoak berdinak dituena.

Bi substantzia modu homogeneoan nahasten direnean, haietako bat bestean disolbatzen dela esaten da. Haien artean proportziorik handiena duen substantzia disolbatzailea da, eta proportzio txikiena duena, solutua.

Disoluzioa solido eta likido banak osatzen badute, solidoa solutua izango da beti, eta likidoa, disolbatzailea; azido, base eta gatzen ur-disoluzioetan, disolbatzailea beti ura dela ulertzen da.

5.1. Disolbagarritasuna

Uretan substantzia batek duen disolbagarritasuna da 100 g uretan tenperatura jakin batean disolba daitekeen substantzia kantitaterik handiena.

Disolbagarritasuna tenperaturaren mende eta disolbatzen den substantziaren izaeraren mende dago.

Aleazioak disoluziotzat jo daitezke: solido bat beste solido batean disolbatzen da (bi metal). Irudian, Pastora Imperio flamenko-dantzariaren eskultura bat ikusten da, Sevillan dagoena. Brontzezkoa da (kobre eta eztainuzko aleazioa).

Alkohola uretan disolbagarria da; olioa ez, ordea, bi substantzia horien izaera desberdina delako.

Disolbagarritasuna solutu batek disolbatzaile batean eduki dezakeen kontzentraziorik handiena dela ere esan daiteke. Gehienezko solutu kantitate hori lortzen denean, disoluzioa asea izango da. Solutua solidoa bada, prezipitatua eratzen delako ikusiko dugu disoluzioa asea dela.

5.2. Kontzentrazioaren unitateak

Kontzentrazioa erlazio bat da, solutu kantitatearen eta disoluzio kantitatearen (edo bolumenaren) artekoa; salbuespenez, solutuaren eta disolbatzailearen arteko erlazioa ere izan daiteke. Solutuaren eta disolbatzailearen molekularteko indarrak nolakoak, halakoa izango da disoluzioan disolbatzaileak hartuko duen bolumena, eta, horrenbestez, batzuetan, disoluzioaren bolumena ez da izango solutuaren eta disolbatzailearen arteko batura (masak, aldiz, beti dira). Hori dela eta, disoluzio-bolumenez jardungo dugu, ez disolbatzaile-bolumenez.

Kontzentrazioa adierazteko modurik ohikoenak hauek dira:

• Masa-ehunekoa, masa %-a: solutuaren eta disoluzioaren masen arteko erlazioa da, bider 100. Hau da, solutuaren zer masa dagoen 100 gramo disoluziotan.

masa % masa masa 100 a disoluzioaren solutuaren =

• Bolumen-ehunekoa, bolumen %-a: aurreko kasuaren ildo beretik, solutuaren eta disoluzioaren bolumenen arteko erlazioa da, bider 100. % olumen olumen 100 bolumena disoluzioarenb a solutuaren ba = -

18 Azido sulfurikoa dagoen flasko baten etiketan jartzen du disoluzioaren masa-ehunekoa % 61,54 dela, eta dentsitatea, 1,515 g · mL–1 . Kalkulatu: a) molaritatea; b) molalitatea; c) solutuaren eta disolbatzailearen frakzio molarra.

19 Al3+ eta SO42– ioien zer kontzentrazio dago 0,01 M den Al2(SO4)3 disoluzio batean?

20 Bario hidroxidoaren kontzentrazioa % 1 duen ur-disoluzioa prestatu nahi dugu, 5 L disoluzio. Idatzi argibideak.

Ariketak

• Molaritatea, M: solutuaren substantzia kantitatea eta disoluzioaren bolumena (litrotan) erlazionatzen ditu. Kontzentrazio molar ere esaten zaio erlazio horri.

solutuaren substantziakantitatea M =

disoluzioarenbolumena (L)

• Normalitatea, N: solutuaren baliokideak eta disoluzioaren bolumena (litrotan) erlazionatzen ditu.

disolu i(L) solut N z oarenbolumena uarenbaliokideak =

Unitate hori dezente erabiltzen da analisi kimiko industrialean, eta horregatik aipatu dugu hemen. Hala eta guztiz ere, IUPACek ez erabiltzea gomendatzen du, balio aldakor bat baita: zer ingurunetan erabiltzen den, balio bat edo beste bat izango du.

Baliokidea solutuaren masaren (gramotan) eta masa molar baliokidearen arteko erlazioa da. Masa molar baliokidea masa molarra zati balio aldakor bat da; balio hori erreakzio motaren arabera aldatzen da (balentzia):

Baliokideak masa molarbaliokidea(M) solutuaren masa (g) baliokidea = non masa mlarra M balentzia o baliokidea = baita.

Adibidez, azido-base erreakzioetan, balentzia izango da erreakzioan azidoak ematen edo baseak onartzen duen H+ ioi kopurua; aldiz, oxidazioerredukzio erreakzioetan, erreakzioerdian espezie batek irabazten edo galtzen duen elektroi kopurua izango da (oxidatzailea edo erreduzitzailea bada, hurrenez hurren); konplexuen erreakzio batean, espezieak konplexu bihurtzen duen estekatzaile kopurua da, etab.

Normalitatea honela ere adieraz daiteke:

L g L g lenia N MV m MV m ba tz baliokideak $ == h h h h ^h ^^ ^^

Dena den, liburu honetan ez dugu kontzentrazioaren unitate hori erabiliko.

5.3. Kontzentrazioa adierazteko beste era batzuk

Badira kontzentrazioa adierazteko beste modu batzuk, solutu kantitatearen eta disoluzio-bolumenaren arteko erlazioa erabiltzen dutenak. Hona hemen:

• Molalitatea, m: solutuaren substantzia kantitatearen eta disolbatzailearen (kilogramotan) arteko erlazioa da. Bereziki interesgarria da presio osmotikoa kalkulatu nahi denean.

disol(kg) solut m batzailearen masa

uarensubstantzia kantitatea

• Frakzio molarra, X: nahaste jakin batean «i» osagaiak duen substantzia kantitatea da, ni , guztizko substantzia kantitatearekin konparatuta (alegia, nsolutua +  ndisolbatzailea). Bateko hainbestea da, moletan. Bereziki interesgarria da disoluzioan solutu (osagai) bat baino gehiago dagoenean, edo disolbatzailea zein den solutua zein den argi ez dagoenean.

kantitatea

stantzia kantitate

Arrisku-piktogramak

Lehergaiak

Likido sukoiak

Likido erregarriak

Gas konprimatuak

Korrosiboa metaletarako. Korrosioa larruazalean

Oso toxikoa

Larruazalerako narritagarria

Arriskutsua, arnasten bada

Arriskutsua uretako ingurumenerako

2. taula. Europar Batasunean, produktu kimikoen etiketetan nahitaez agertu behar dira piktogramak (hots, arriskuikurrak), REACH Erregelamenduko (2007) azken erabakiak betez. Substantzia puruetan, etiketak nahitaezkoak dira 2010az geroztik, eta nahasteetan, 2015eko ekainaz geroztik.

Sinbologia

Zenbaitetan, kako zuzenak erabiltzen dira «zerbaiten kontzentrazioa» adierazteko. Esaterako, A espeziearen kontzentrazioa honela adieraz daiteke: cA = [A]

Disoluzioen diluzioa

Laborategietan, ohikoa da beste disoluzio batzuetatik abiatuta disoluzio diluituak prestatzea. Kontzentrazio berria prestatzeko, disoluzio kontzentratuaren bolumena kalkulatu behar da; dagokion substantzia kantitatea kontuan hartuz, disolbatzailearekin diluitzen da, disoluzioak nahi den kontzentrazioa edukitzeko (diluitua).

Hasierako disoluzioa (0. diluzioa)

8 Kalkulatu uraren eta alkohol etilikoaren frakzio molarra, aintzakotzat hartuta disoluzioa prestatu dela 50 g alkohol etiliko eta 100 g ur nahasiz.

Ebazpena

Alkohol etilikoa hau da: CH3—CH2OH. Beraz, masa molar hau du: M gmol 12 26 1161 46 –1 =+ += ^^ ^ hh h ;

Orduan, , n gmol g mol 46 50 109 alkohola –1 ==

H2O-aren kasuan, M = 18 g · mol–1 da; beraz: , n gmol g mol 18 100 555 ura 1 == -

Eta nguztizkoa = 6,64 denez, frakzio molarrak hauek dira: , , , X mol mol 664 109 0164

9 Solutuaren zer masa (gramotan) behar da, berun(II) nitratoaren 0,5 L-ko disoluzio bat prestatzeko, kontzentrazioa 1 M bada?

Ebazpena

Pb(NO3)2 berun(II) nitratoak masa molar hau du:

21 Zer masa potasio dikromato (K2Cr2O7) behar da 250 mL-ko disoluzio bat prestatzeko, kontzentrazioa 2,16 M baldin bada?

22 Sodio hidroxidoaren 0,5 M den disoluzioa lortu nahi dugu, % 70eko aberastasuna duen disoluziotik. Zenbat beharko dugu molaritate horretako hiru litro lortzeko?

23 Azido sulfuriko kontzentratu baten dentsitatea 1,81 g · mL–1 da, eta azido puruaren masa % 91 da. Kalkulatu: a) disoluzioaren molaritatea, b) normalitatea, azido-base erreakzio batean, c) molalitatea, d) zer bolumen behar den kontzentrazioa 0,5 M duen 500 cm3 disoluzio prestatzeko.

Disoluzio baten kontzentrazioaren aldakuntza; hasieran, kontzentratuago dago, eta, gero, diluituago.

24 «Arriskutsua uretako ingurumenerako» piktograma erabiliz, 6. eta 12. GJHak jorratu daitezke. Azaldu eta justifikatu helburu horien zer xederekin egon daitekeen lotuta.

25 Buru-hausgarria. Toxikotasun-arriskua aztertze aldera, garrantzitsua al da produktu kimiko baten kontzentrazioa? Edo ez du zerikusirik, eta produktu mota bakoitzaren arriskugarritasunari soilik begiratu behar zaio? Interneten, bilatu lau web-orri, erantzuna aurkitzeko. Hautatu fidagarritasunik handieneko web-orriak, eta eztabaidatu, ikaskideen aurrean aurkeztu beharreko lan batean (taldeka egin daiteke).

I. diluzioa

II. diluzioa

Gehitu ura

Gehitu ura

Irabiatu Irabiatu

Ariketak

Erreakzio kimikoen estekiometria

6.1. Ekuazio kimikoak

Erreakzio kimikoek aldaketa kimikoak adierazten dituzte: erreaktibo deritzen substantziak eraldatu egiten dira. Eta beste propietate batzuk dituzten substantzia berriak eratzen dira: produktuak, alegia.

Prozesua eta hartan parte hartzen duten substantziak ekuazio kimikoen bitartez irudikatzen dira. Esate baterako, ura eratzeko erreakzioa hau da, ura eratzen duten elementuetatik abiatuta:

HO HO 22 22 2 $ +

Erreaktiboak Produktuak

Ekuazioan, informazio gehiago ere adieraz daiteke. Adibidez, hau:

• Substantzien agregazio-egoera: parentesien artean, (s), (l), (g) edo (aq) idazten da; hots, solidoa, likidoa, gasa eta ur-disoluzioa, hurrenez hurren. Ildo horretatik, aurreko erreakzio hori honelaxe geratuko litzateke, p = 1 atm-ean eta T = 298 K-ean:

H( )O () HO () gg l 22 22 2 $ +

Erreaktiboak Produktuak

• Erreakzioaren baldintzak: katalizatzaileak erabiltzen diren edo beroa behar den adierazten da. Lehen kasuan, katalizatzailearen formula erreakzioaren geziaren gainean idazten da. Bigarrena ∆ letrarekin adierazten da.

$ HO HO O MnO 22 22 2 22 + $ CaCO CaOCO ∆ 32 + Erreaktiboak Produktuak Erreaktiboak Produktuak

• Erreakzioarekin lotutako energia: erreakzioan beroa xurgatzen den (erreakzio endotermikoa) edo beroa askatzen den (erreakzio exotermikoa) adierazten da. Horretarako, erreakzioaren ondoan, harekin lotuta dagoen entalpia idazten da, dagokion zeinuarekin. Ikusi lehengo adibidea:

H( ) 2 1 O( )H O( ) gg l 22 2 + $ ΔHº = −285,80 kJ · mol–1 (exotermikoa)

Erreaktiboak Produktuak

Aurreko adibideetan ikusi den bezala, masaren kontserbazioaren legea bete behar da erreakzio kimikoetan, eta, hortaz, baita ekuazio kimikoetan ere. Hori dela eta, ekuazioak doitu egiten dira: koefiziente estekiometriko egokiak bilatzen dira, lege hori betetzea dakartenak, eta, ahal dela, ahalik eta zenbaki oso txikienak izanik. Zehazki, elementu bakoitzaren atomo kopuru berbera izan behar du geziaren aurretik eta ondoren, eta, horrenbestez, erreaktiboen masen arteko batura eta produktuen masen arteko batura berdina izango da.

O2 2 H2

+ 2 H2O

Honela irakurtzen da: «bi hidrogeno molekulak oxigeno molekula batekin erreakzionatu dute, eta emaitza bi ur molekula dira», edo, bestela, «4 g hidrogenok 32 g oxigenorekin erreakzionatu dute, eta 36 g ur lortu dira».

Lehen atalean, 4 atomo hidrogeno eta 2 atomo oxigeno daude, eta kopuru bera bigarren atalean ere, baina beste konposatu batean.

26 Kaltzio karburoak, CaC2-ak, urarekin erreakzionatu du, eta kaltzio hidroxidoa eta azetilenoa lortu dira. Zenbat gramo CaC2 behar dira 10 L azetileno lortzeko, 5 °C eta 700 mmHg-an?

27 Kaltzio hidroxidoaren 0,5 M disoluzio baten 100 mL-k eta azido nitrikoaren 0,5 M disoluzio baten 100 mL-k erreakzionatu dute. Kalkulatu zer masa kaltzio nitrato eratzen den, gramotan.

Ariketak

Ekuazioak doituz, atomoen, molekulen edo substantzia kantitatearen erlazioak ezar daitezke, eta, gasen legeei jarraikiz, erlazio bolumetrikoa ere bai, osagaiak gasak badira eta presio- eta tenperatura-baldintzak berdinak badira:

N2

3 H2

2 NH3

Hala, hau esan daiteke: «bolumen bat nitrogenok eta hiru bolumen hidrogenok erreakzionatu dute, bi bolumen amoniako lortzeko».

6.2. Erreaktibo mugatzailea

Gerta daiteke erreakzio kimiko batean daukagun erreaktibo kantitatea ez egotea erreakzioaren ekuazioan adierazten den erlazio estekiometrikoan. Halakoetan, erreaktibo mugatzailea aurkitu behar dugu. Hau da:

Erreakzioan lehenik amaitzen den erreaktiboa, eta, agortuta dagoenean, erreakzioak jarraitzea eragozten duena.

Hasiera-hasieratik identifikatu behar da, erreaktibo horretan oinarrituta egin behar baitira erreakzioarekin lotutako zenbakizko kalkulu guztiak.

6.3. Erreakzio baten errendimendua

Erreakzio kimiko bat modu esperimentalean egiten denean, normalean ez da lortzen espero den produktu kantitate zehatza, estekiometriaren arabera lortu beharko litzatekeena.

Matematikoki kalkulatzen den kantitateak (mol, masa-unitate edo bolumenak) errendimendu teorikoa adierazten du; esperimentalki lortzen den kantitateak, berriz, benetako errendimendua adierazten du. Bi balioen arteko erlazioa ehuneko bat da, eta erreakzioaren errendimenduaren berri ematen du. Matematikoki, honela idazten da:

Benetako errendimendua 100 % ^h

= errendimendua Errendimendu teorikoa

Gogoratu

Adibideetan ikusten den moduan, masa eta mota bakoitzeko atomoak kontserbatzen dira erreakzio kimiko batean, baina ez dira kontserbatzen erreaktiboen substantzia kantitatea eta bolumenak.

10 Karbonoak eta hidrogenoak erreakzionatu eta metanoa eratu da. 72 g C eta 12 g H2 nahasi badira, erreaktiboren baten soberakina dago? Zer kantitate?

Ebazpena

Ekuazio kimiko doitua hau da: CH CH 2 24 " +

Zehatz-mehatz, erreakzioko substantziek masa molar hauek dituzte: C: 12,0 g · mol–1 eta H2: 2,0 g · mol–1. Erreaktiboen masei dagokien substantzia kantitatea kalkulatuko dugu orain.

Ekuazio doituaren arabera, mol bat C-k H2 kantitate bikoitza behar du. Horrenbestez, 6 mol C-k 12 mol H2 behar dituzte, baina ez daude hainbeste.

Hortaz, H2-a lehena amaituko da; hots, erreaktibo mugatzailea izango da, eta C-aren soberakina egongo da, 3 molek besterik ez baitute erreakzionatuko. Kantitate hau geratuko da sobera: 6 – 3 = 3 mol C.

Masa hau izango litzateke: 3 mol · 12 g · mol–1 = 36 g C.

Ebatzitako ariketak

ZIENTIFIKOA

Simulaciones sobre reacciones químicas

Filosofiaren eta alkimiaren arteko lotura

Filosofiak, alkimiak bezala, giza ezagutzaren planteamendu globala egiten du. Hala, greziar mitologian, Hermes jainko bidaiariaren mitoaren bidez, Ekialdeko eta Mendebaldeko ezagutzak uztartzea justifikatzen zen. Lehen zibilizazioek metalgintzan bilatu zuten propietate bereziko materialak lortzeko metodo bat, boterea ziurtatzeko asmoz. Baina, botereari eutsi ahal izateko, sekretupean eduki behar da haren indarra, eta hortik sortu zen alkimia, ezagutza sekretu bat, antzina-antzinakoa eta jatorri oparokoa. Eta lengoaia esoteriko eta sinboliko batekin iraun du, metalei buruzko ezagutzarekin lotuta. Arte bakartia da, eta zinez preziatua.

Bitriolo terminoaren (gerora azido sulfurikoarekin lotu zen) esanahi ezkutua metal guztiak disolbatzeko dituen aukeratik dator, eta metodo alkimistetan zirkula batez adierazten da. Zirkulu horrek eragiketa-faseak (lortzeko metodoak) biltzen ditu. Oinarrizko lau elementuak hauek dira: lurra, airea, ura eta sua. Elementu bakoitza bere eraldaketarekin lotuta dago. Alkimiari buruzko liburuetan jasotzen ziren prozedurak nahaspilatsuak eta labirintikoak ziren, nahita; hitz mitologiko eta polisemiko ugari erabiltzen zituzten, eta horrek guztiak, azkenean, sekretismoa sortzen zuen.

Alkimistek hainbat tresna baliatzen zituzten beren lanean: motrailua, materialak birrintzeko; labea, berotzeko; zenbait formatako beirazko materiala, egoera-aldaketak egiteko, substantzia baten espiritua esaten ziotena ahalik eta gehien baliatuz: lurruna. Filosofoen harria espiritua hezurmamitzearen adierazpenik behinena zen. Urrea sortzea lortzeak perfekzioa zuen xede, urreak hori irudikatzen zuelako; halaber, horrexegatik baliatzen zuten zirkulua behin eta berriz, forma geometriko moduan.

Bestalde, laborategian bi prozedura erabiltzen zituzten: bide hezea eta bide lehorra. Bide hezean, beirazko tresnak erabiltzea eta behin eta berriz egostea funtsezkoa zen; bide lehorrean, aldiz, arragoa zerabilten eta, beroa baliatuz, substantziak urtzen zituzten.

Egipto, Grezia eta Mesopotamiako antzinako zibilizazioetan, sinbolismoa apaizen esku egoten zen; horrexegatik esaten zitzaien betiereko suaren apaiz.

Baina hori baino askoz lehenago ere, gogora ekarri behar da Homo sapiensaren ezaugarri bereizgarrietako bat sua kontrolatzea izan zela; bestea, aldiz, mintzamena izan zen.

Alkimiaren sinboloetako bat bere isatsari kosk egiten dion sugea da. Materiaren eta espirituaren batasuna adierazten du sinbolo horrek, baita gorputzen transmutazio posiblea ere. Garrantzitsuena kualitatiboa da, ez kuantitatiboa. Hala, zazpi planeta alkimiko daude: Jupiter-eztainua, Saturno-beruna, Marte-burdina, Eguzkia-urrea, Artizarrakobrea, Merkurio-merkurioa eta Ilargia-zilarra.

Alkimista. David Teniers Gaztea. xvii. mendea. Pradoko Museoa, Madril.

Hennig Brandt alkimista hanburgotarrak (Alemania) fosforoa aurkitu zuen 1669 inguruan, gernu-hondar erreduzituak labean berotzen ari zenean. Haren dirdira berde argiak liluraturik, fosforo izena ipini zion (grezieraz, argieramaile).

Brandtek sekretupean gorde zuen bere aurkikuntza, eta fosforoarekin lan egin zuen aurrerantzean ere, urrea ekoizteko ahaleginean.

Alkimiaren jatorria, bilakaera eta hedatzea

Alkimiaren jatorria K.a. 1 000. urte ingurukoa da, edo, apika, Burdin Arokoa. Egipton, faraoien garaian, nabarmen garatu zuten, eta Bizantzioren esku utzi zen vi mendearen bueltan. Aurrerago, ordea, berreskuratu egin zuen islamiar munduak, eta garai horretan ere neurri handian garatu zen alkimia.

Bestalde, Ekialdean (Txinan, Pertsian eta, bereziki, Indian), drogak sailkatzen jardun zuten batez ere, osasuna zaindu eta hobetzeko. Mineralak, metalak eta gatzak identifikatzen ere aritu ziren. Txinari dagokionez, bolbora eta tinta lortu zituztela azpimarratu behar da.

Alkimia Erdi Aroko Europara heldu zen arabiar munduarekiko harremanen bitartez. Garaiko Espainia bi kultura horien arteko topalekurik garrantzitsuenetako bat izan zen. Horrez gain, judutarren presentzia handi samarra zen medikuntzan (ix-xi mendeak), eta, arlo horretan, farmakopea garatu zuten.

Orduantxe bereizi eta ordenatu ahal izan zituzten metalak egoki (eztainua, beruna, burdina, kobrea, zilarra eta urrea), haiek bereizteko sufrea eta merkurioa erabiliz.

Alkimiari eta teknikari esker, aurrerapauso handiak eman ziren prozesu kimikoetan: pigmentuak, beirak, galdaketak, ontze-lanen emaitzak, paperaren ekoizpena, konposatu farmazeutikoak eta bolbora.

Komentuetan ere alkimia garatu zen, arabiar testuen kopiak egin zituztenean mintzaira greko-latindarrean, eta haietan trebatu ziren Europako lehen zientzialariak. Besteak beste, Roger Bacon frantziskotarra eta Alberto Magno eta Tomas Akinokoa domingotarrak.

Konstantinopla erori ostean, xv  mendean, ohikoa zen alkimistak egotea Italiako hiri-estatuetako gorteetan. Era berean, gorte ingelesean egon ziren xvi  mendean, baita habsburgotarren gortean ere (Austria). Bestalde, inprenta erabiliz, Europako gainerako gorteetan zehar hedatu ziren xvii  mendean. Ondorioz, bakarkako izaera sekretu hori hausten joan zen pixkanaka.

Jarduerak

1 Zein dira alkimistek gehien-gehien erabiltzen zituzten metalak?

2 Ikertu zeri esaten zioten alkimistek bitrioloolioa. Zergatik piztu zuen hainbesteko interesa?

3 Zer elementu erabili zituzten alkimistek, metalak ez zirenak?

Dioskorides landare baten propietateak azaltzen ari zaizkio ikasle bati. De materia medica, Topkapi jauregiko liburutegia, 1229. Istanbul.

4 Laborategiko zer tresnak eta prozedurak dute jatorri alkimikoa?

5 Bilatu informazioa Umberto Ecoren Il nome della rosa (Arrosaren izena) egiteko inspirazio-iturri moduan erabili zen alkimistari buruz. Ondoren, idatzi pertsonaia horri buruzko deskribapen-testu bat.

Problemak ebazteko estrategiak

Kalkulu estekiometrikoak

1 Magnesio karbonatoak azido fosforikoarekin erreakzionatzen duenean, magnesio fosfatoa, karbono dioxidoa eta ura eratzen dira:

a) Idatzi erreakzio doitua.

b) 72 g magnesio karbonato eta 37 mL azido fosforiko (dentsitatea = 1,34 g · mL–1, eta azidoaren aberastasuna: % 50) nahastu dira.

Kalkulatu zer bolumen karbono dioxido lortu den, 23 oC-an eta 743 mmHg-ko presioan.

Datuak: masa atomikoak: C = 12 u; O = 16 u; Mg = 24 u; P = 31 u; H = 1 u.

Planteamendua eta ebazpena

1. Lehenik, enuntziatua arreta handiz irakurri behar da, konposatuak ongi identifikatu, eta, azkenik, erreakzioa doitu.

MgCO3 + H3PO4 → Mg3(PO4)2 + CO2 + H2O

3 MgCO3 + 2 H3PO4 → Mg3(PO4)2 + 3 CO2 + 3 H2O

Gogoratu ezen, doitzeko garaian, produktu edo erreaktiborik konplexuenari begiratu behar zaiola; hori izango da gainerako elementu guztiak doitzeko giltzarria. Mg-a produktu eta erreaktibo banatan dago soilik, fosfato taldea bezala. Horrenbestez, arreta haietan jarri behar da, ekuazio doitua idazteko. Karbonatoa eta fosfatoa doitu ostean, gainerakoa erraz doitu daiteke. Erreaktibo eta produktuen elementu guzti-guztiak berrikusi behar dira.

2. Masaren eta bolumenaren datuak ematen dizkigute, baina substantzia kantitateak behar ditugu (molak), doitu ahal izateko. (MMgCO3 = 84 g · mol–1 ; MH3PO4 = 84 g · mol–1)

nMgCO3 =  g g mol 72 84 1  = 0,86 mol

nH3PO4 = 1,34 g/mL · 37 mL · 0,5 ·  g mol 98 1  = 0,25 mol puru

Alegia, 37 mL azido fosforikoan, 0,25 mol azido puru daude; gainerakoa ura da. (Gogoratu substantzia kantitate puruak soilik erreakzionatzen duela).

Hurrengo galdera da ea substantzia kantitate osoak erreakzionatuko duen. Hori jakiteko, erreaktibo mugatzailea zein den bilatu behar da (erreakzioaren estekiometriari jarraituz, lehen agortzen den erreaktiboa), baita zeinen soberakina dagoen ere. Eman dezagun:

– Mugatzailea karbonatoa dela. Ekuazio kimiko doituaren arabera, hau behar dugu:

0,86 mol MgCO3 ·  molH PO molMgCO 2 3 34 3  = 0,57 mol H3PO4, baina 0,25 mol besterik ez dugu.

– Mugatzailea azido fosforikoa dela. Hau behar dugu:

0,250 mol H3PO4 ·  molH PO molMgCO 2 3 34

Kasu honetan, baditugu mol horiek. Zehazki, 0,86 ditugunez, 0,485 mol karbonato sobera egongo dira.

Hortaz, erreaktibo mugatzailea azido fosforikoa da, eta 0,375  mol MgCO3-k eta 0,250 mol H3PO4-k erreakzionatzen dute.

Orain, demagun erreakzioa eskuinera erabat desplazatuta dagoela. Edonola ere, hori logikoa da, zeren CO2-a produktu gaseosoa izango baita, eta gainontzekoak, aitzitik, ur-disoluzioan egongo dira.

3 MgCO3 + 2 H3PO4 → Mg3(PO4)2 + 3 CO2↑+ 3 H2O

Estekiometriari jarraituz, erreakzionatzen duen karbonatoaren substantzia kantitatea eta lortzen dugun karbono dioxidoarena berdinak dira. Beraz, 0,375 mol CO2 izango dira.

Galdera da zer bolumen lortzen den 23 ºC-an eta 743 mmHg-an. Orduan, gasen ekuazio orokorra erabiliko dugu (p · V = n · R · T) unitate egokiekin, eta V bakanduko:

PROBLEMAREN AZTERKETA

Ziurtatu behar dugu konposatuen formulak ongi idatzi ditugula, ekuazioa doitu dugula eta erreaktibo mugatzailea zein den ikusi dugula. Batzuetan gehiegi fidatzen gara, datuen estekiometria doitua delakoan, baina ez da beti hala izaten.

Horrez gain, aurreko ikasturteetan askotan aipatu den zerbait gogoratu behar da: kalkulu-problemak ebazten direnean kimikan, bihurketa-faktoreak erabili behar dira. Kontua da problemak ebazteko estrategia horrekin bizkorrago lan egin daitekeela urratsez urrats eginez baino. Gainera, estrategia hori lehentasunezkotzat finkatuta dago hezkuntzari buruzko legerian.

EMAITZEN EZTABAIDA

3  = 0,375 mol MgCO3

Emaitzak zuzenak direla egiaztatzeko, ebazpena berrikusi behar dugu. Zehazki, emaitza zuzena balitz bezala jokatu behar da, eta eragiketak atzekoz aurrera egin: erreakzionatu duen karbonatoaren substantzia kantitatea lortu, eta erreakzionatu ez duena batu: 0,98 atm · 9,31 L = n · 0,082 atm · L · mol–1 · K–1 · 296 K; dioxidoaren n = 0,375 mol bakandurik, erreakzioko karbonatoaren molekin bat dator. Kantitate hori gehi erreakzionatu ez duena (0,485 mol) egiten badugu, emaitza hasierako mol kopurua da (0,86 mol).

2 Azido klorhidrikoaren disoluzio baten 0,5 litro ditugu. Masa-aberastasuna % 86 da, eta dentsitatea, 1,24 g · mL–1. Kalkulatu:

a) Molaritatea.

b) Molalitatea.

c) Solutuaren frakzio molarra.

d) Azido klorhidrikoaren disoluzio horren zer bolumen behar den, 2 M den beste baten 150 mL prestatzeko.

e) Lortu den azidoaren 100 mL eta 0,5 M den azido klorhidrikoaren 0,25 L nahasiz gero, zer molaritate izango du emaitzazko disoluzioak?

Datuak: masa atomikoak: H = 1 u; Cl = 35,5 u.

Planteamendua eta ebazpena

1. Lehenik, problema arretaz irakurri behar da, eta ongi identifikatu konposatua eta ematen dizkiguten datuak. Azkenik, atal bakoitzean zer eskatzen zaigun jakin behar dugu.

a) Molaritatea =  Disoluzioarenbolumena (L) solutuaren substantziakantitatea(mol)

Kalkulua honela egingo dugu: M (HCl) = 1 + 35,5 = 36,5 g · mol–1 , mL disoluzio disoluzio 1 124  ·  gdisoluzio solutu 100 86  ·  ,g solutu molsolutu 36 5 1  ·

· Ldisoluzio mL disoluzio 1 1000  = 29,2 M

b) Molalitatea =  disolbatzailearen masa (kg) solutuaren substantziakantitatea(mol)

Problemako datuekin bat etorriz, aberastasunak adierazten du solutuaren 86 g daudela disoluzioaren 100 g-an.

Ondorioz, gainerako 14 g-ak disolbatzailearenak dira.

Beraz, disolbatzailearen 1 000 g-an (1 kg) hau dugu: gdisoluzio gsolutu 100 86  ·  ,g disoluzio molsolutu 36 5 1  ·

·  gdisolbatzaile gdisoluzio 14 100  ·  kg disolbatzaile gdisoluzio 1 100  =  , kg mol 1683

c) Solutuaren frakzio molarra bateko hainbestea da, solutuaren substantzia kantitateari (mol) begiratuta, disoluzioaren substantzia kantitate osoaren aldean (mol).

Hots, disoluzioaren 100 g-an 86 g solutu badaude:

M (HCl) =  ,g mol gHCl 36 5 86 –1  = 2,36 mol HCl.

Orain, enuntziatuan eskatzen dena kalkulatzeko behar diren datu guztiak ditugu:

Xsolutua: , , mol mol 314 236  = 0,75

Ehuneko hainbestean adierazita dagoenez, gainerakoa disolbatzailea izango da:

Xdisolbatzailea: 1 – 0,75 = 0,25

d) 2 M den disoluzio baten 150 mL prestatzeko, zenbat gramo solutu behar ditugun kalkulatuko dugu, % 86ko aberastasuna eta dentsitatea aintzakotzat harturik:

0,30 mol ·  , mol g 1 36 5  = 10,95 g

HCl puru

Hasierako disoluzioaren aberastasuna eta dentsitatea kontuan izanik, hau idatz dezakegu:

10,95 g solutu puru ·  gsolutu ghasierako disoluzio 86 100  = 12,73 g

hasierako disoluzio ·  ,g hasierakodisoluzio mL hasierakodisoluzio 124 1  =  = 10,27 mL hasierako disoluzio.

Alegia, hasierako disoluzioaren 10,27 mL beharko lirateke, eta ura gehitu harik eta 150 mL-ra heldu arte, hori delako amaieran nahi den bolumena.

e) Abiapuntua 2 M den disoluzio baten 100 mL badira, hau daukagu: L mol 1 2  ·  mL L 1000 1  · 100 mL = 0,2 mol

Beste disoluzio baten 0,25 L-rekin nahasi dugu. 0,5 M da:

, ·, L mol L 1 05 025  = 0,25 L = 0,125 mol

Guztira, 0,325 mol HCl edukiko genituzke 0,35 L disoluzioan. Hortaz: , , L mol 035 0325  = 0,93 mol/ L =  0,93 M.

PROBLEMAREN AZTERKETA

Urrats guztiak tentuz egin behar ditugu. Garrantzitsuena da argi izatea zer disoluziotatik abiatzen garen eta zer disoluzio lortu nahi dugun. Eta, azkenean, emaitza logikoa den edo ez egiaztatu behar da.

M 2 –1 2 = ^ ^h h  = 0,78 mol H2O

100– 86 gH O

HO 18 gmol

Bien batura hau da:

Disoluzioa = 2,36 mol + 0,78 mol = 3,14 mol.

Horrelako problemetan komeni da gogora ekartzea zertan diren desberdinak dentsitatearen kontzeptuak (disoluzioaren guztizko masa eta disoluzioaren guztizko bolumena erlazionatzen dira) eta kontzentrazioa adierazteko erak (gehienetan, solutuaren masa eta disoluzioaren bolumena erlazionatzen dira, molalitatean izan ezik).

Kantitateak kimikan

1 Kobaltoaren isotopo bat medikuntzan erabiltzen da, minbizia tratatzeko. Idatzi isotopo horren sinbolo nuklearra, jakinik Z = 27 dela eta 33 neutroi dituela. Halaber, aipatu elektroi eta protoi kopurua ere, eta masa-zenbakia.

2 Kalkulatu zer substantzia kantitate dagoen 67,2 L N2-an, 0 ºC-an eta 1 atm-eko presioan.

3 Laborategi batean, 45,0 cm3 bentzeno likido daude, 0,880 g · cm–3-ko dentsitatekoa. Kalkulatu:

a) Bentzenoaren masa, gramotan.

b) Bentzenoaren substantzia kantitatea.

c) Bentzeno molekulak.

d) Karbono atomoak.

4 Kalkulatu sakarosaren (C12H22O11, mahaiko azukrea) eta kaltzio nitratoaren masa-formula. Esan zenbat molekula dauden haietako bakoitzaren gramo batean.

5 Baldintza normaletan, non daude atomo gehien, etanoaren 1 L-ean, fosforoaren (P4) mol batean edo kromo(VI) sulfatoaren gramo batean?

6 Manganesoaren masa atomikoa 55 da. Zer esan nahi du horrek?

7 Kalkulatu zer substantzia kantitate dagoen bost milioi hidrogeno molekulatan.

8 Boroak bi isotopo egonkor ditu: B-10a (% 19,78) eta B-11 (% 80,22). Haien masa atomikoak 10,013 u eta 11,009 u dira, hurrenez hurren. Kalkulatu boroaren batez besteko masa atomikoa.

9 Zilar naturala osatzen duten bi isotopoen masazenbakiak 107 eta 109 dira. Ugaritasun isotopiko hau dute, zehatz-mehatz: Ag-107ak, % 56, eta Ag-109ak, % 44. Ondorioztatu zilar naturalaren batez besteko masa atomikoa.

10 Itsasoko uraren % 3,5 gatzak dira, batez beste. Uretako gatz horien % 80 NaCl-a da; % 11, MgCl2-a; % 5, MgSO4-a; eta % 4, CaSO4-a. Esan litro bat itsasoko uretan elementu bakoitzaren zenbat atomo eta konposatu bakoitzaren zenbat molekula dagoen. Itsasoko urarekin, nola erdietsiko zenuke GJHen 6.4 xedea? Eta 14.3 xedea, ura kutsatuta badago?

Gasen legeak

11 Burbuilatxo bat gorantz ari da, aintzira baten hondotik abiatuta. Aintzirako tenperatura 8 ºC da, eta

presioa, 6,4 atm. Uraren azaleran, berriz, tenperatura 25 ºC da, eta presioa, 1,0 atm. Kalkulatu burbuilak uraren azalera iristean duen bolumena (baldintza normaletan eta uraren azaleko baldintzetan), hasierako bolumena 2,1 mL bada.

12 Tenperatura- eta presio-aldaketarik ez dagoela jota, kalkulatu zer bolumen oxigeno (L) behar den 14,9 L butano guztiz erretzeko.

13 Gasez beteta dagoen globo baten bolumena 2,50 L da 1,2 atm-n eta 25 ºC-an, eta estratosferarantz doa (lurrazaletik 30 km ingurura); han, tenperatura eta presioa −23 ºC eta 3 · 10–3 atm dira, hurrenez hurren. Kalkulatu zer bolumen izango duen globoak estratosferara iristen denean.

14 Kalkulatu zenbat atomo oxigeno dauden 10 cm3 airean, tenperatura −23 ºC bada eta presioa 10–7 atm bada.

Formulak idaztea

15 Nikotina tabakoaren osagaietako bat da, eta konposizio hau du: C, % 74,07; N, % 17,28; H, % 8,65. Idatzi nikotinaren formula enpirikoa eta formula molekularra, jakinik masa molekular erlatiboa 162,2 dela.

16 Zer formula enpiriko dute konposizio hauek dituzten konposatuek?

a) C, % 40,1; H, % 6,6; eta O, % 53,3.

b) C, % 18,4 %; N, % 21,5; eta K, % 60,1.

17 Kalkulatu zer masa-konposizio duen kloroformoak (CHCl3), eta azaldu nola lortu duzun.

Disoluzioak. Kontzentrazioaren unitateak

18 Zenbat mL azido klorhidriko (masa, % 25; dentsitatea, 0,910 g · mL–1) behar dira, 0,1 M den disoluzio baten bi litro lortzeko?

19 Petrolio-findegien isurietan, kromo hexabalentearen legezko muga 0,05 mg · mL–1 da, eta berunarena, 0,1 mg · mL–1. Kalkulatu muga horiek, kontzentrazio molarretan adierazita.

20 Esan zenbat Ba(OH)2 beharko zenukeen, bario hidroxidoaren ur-disoluzio baten 3 L prestatzeko, masaren % 2 baldin bada.

21 Kalkulatu zenbat sodio karbonato dekahidratatu eta zenbat ur behar den, sodio karbonato anhidroaren disoluzio baten 12 L prestatzeko (masaren % 13,9 da), jakinda disoluzioaren dentsitatea 1,145 kg · L–1 dela. Zer molaritate du disoluzioak?

Gogoratu unitate honetako materiala zure portfoliorako aukeratu behar duzula.

22 Azido sulfurikoa dugu kontzentratuta. Haren dentsitatea 1,81 g · (cm3)–1 da, eta masaren % 91 azido purua da. Kalkulatu:

a) Molaritatea.

b) 500 cm3 disoluzio prestatzeko bolumena, kontzentrazioa 0,5 M bada.

23 Erabilgarriak al dira EBn 2007. urtean REACH

Erregelamenduaren bidez onartu ziren piktogramak, GJHen 3.9 xedea lortzeko? Arrazoitu erantzuna. Piktograma bakoitzak adierazten dituen arriskuak txikiagotuko balira, azaldu zer eragin izango lukeen airean, uretan eta lurzoruan.

a) Aipatu industriako langileei soilik eragiten dietenak. Pentsatu industriaren bat, eta erabili adibide gisa.

b) Aipatu zer arrisku nabarmen sortu litezkeen zure ohiko bizilekuan, berdin du hiri batean edo landaeremuan bizi zaren.

c) Aztertu zer piktograma agertzen diren etxea garbitzeko produktuen etiketetan, eta deskribatu zer arrisku dakartzan horiek erabiltzeak.

Kalkulu estekiometrikoak

24 Kalkulatu solutu hauen zenbat gramo behar diren, 0,100 M den disoluzio baten 2,5 · 102 mL prestatu

nahi bada:

a) Zesio ioduroa (CsI).

b) Azido sulfurikoa (H2SO4).

c) Sodio karbonatoa (Na2CO3).

d) Potasio dikromatoa (K2Cr2O7).

e) Potasio permanganatoa (KMnO4).

25 Esperimentu biokimiko batean, 3,81 g glukosa (C6H12O6) gehitu behar zaizkio erreakzio-nahaste bati. Kalkulatu glukosa-disoluzio baten zer bolumen beharko litzatekeen, mL-tan, 2,53 M dela jakinik.

26 Hidrogeno sulfuroaren bolumen jakin bat oxigenoarekin erre da, eta produktuak sufre dioxidoa eta ura izan dira:

a) Idatzi erreakzio doitua.

b) Kalkulatu zer bolumen oxigeno behar den hidrogeno sulfuroaren 20 litro erretzeko, baldintza normaletan.

27 Glukosaren (C6H12O6) errekuntza-erreakzioa gertatzen denean, karbono dioxidoa eta ura lortzen dira.

Pertsona batek 856 g glukosa kontsumitzen baditu, zenbat gramo CO2 eratuko ditu?

28 Labe garaietan egiten diren erreakzioetako batean, burdin mea burdinurtu bihurtzen da. Abiapuntua burdina(III) oxidoa eta karbono monoxidoa dira, eta produktuak, burdina eta karbono dioxidoa. Eman dezagun 1,64 · 103 kg burdina lortzen direla burdina oxidoaren 2,62 · 103 kg-ko lagin batetik. Zer purutasunehuneko izango du jatorrizko laginak?

29 Burdina(III) oxidoak eta aluminioak erreakzionatzen dutenean, aluminio oxidoa eta burdina lortzen dira. Kalkulatu zer masa burdina lortzen den, 137 g burdina(III) oxidok sobera dagoen aluminioarekin erreakzionatzen duenean.

30 Esperimentu batean, 1,50 g propano osorik erre ditugu, eta 1 030 mL karbono dioxido lortu ditugu, presioaren eta tenperaturaren baldintza normaletan neurtuta. Zer errendimendu izan du erreakzioak?

31 Titanioa lortzen da titanio(IV) kloruroak magnesio urtuarekin erreakzionatzen duenean. Saiakuntza batean, 3,54 · 107 g kloruro eta 1,13 · 107 g magnesio erreakzionarazi dira. Kalkulatu:

a) Titanioaren errendimendu teorikoa, gramotan.

b) Benetako errendimendua, 7,91 · 106 g lortu direla jakinda.

32 Eragiketa jakin batean, 7,99 g merkurio lortu dira, 10,0 g zinabrio (HgS) kaltzinatuta. Kalkulatu eragiketaren errendimendua. Erreakzio berean, sufre dioxidoa askatzen da.

33 Soda kaustikoa (sodio hidroxidoa) lortzeko sodio karbonatoa erreakzionarazten da kare hilarekin (kaltzio hidroxidoa):

a) Idatzi erreakzio doitua.

b) Zer masa sodio hidroxido (gramotan) lortu daiteke, 25 kg karbonato soberako kare hilarekin tratatzen bada?

c) Zer masa lortuko litzateke, karbonatoaren aberastasuna % 70 balitz eta prozesuak % 80ko errendimendua izango balu?

34 Disufre dikloruroa (S2Cl2) kautxuaren bulkanizazioan erabiltzen da. Prozesu horretan, kautxuaren molekulak banantzea eragozten da, kautxua luzatzen denean. Bulkanizazioa egiteko, sufrearekin (S8) berotzen da, kloro-atmosfera batean. Teorian, disufre dikloruroaren zer masa (gramotan) lortuko litzateke, 4,06 g S8 berotuko balira 6,24 g klororekin? Benetan 6,55 g disufre dikloruro lortzen badira, zer errendimendu du erreakzioak?

Materiaren egitura

ISOTOPOAK NEKAZARITZAN ETA ELIKADURAN

Gaur egun nukleo atomikoen egiturari eta propietateei buruz dakigun guztia dela eta, aukera dugu erradiazio nuklearrak erabil eta kontrolatzeko, gizakion mesedetan, gure bizi-kalitatea hobetzeko. Har dezagun, horren adibide moduan, elikagaien kontserbazioa.

Munduko biztanleriak handitzen jarraitzen du, eta gero eta beharrezkoagoa da teknika berriak bilatzea elikagaiak denbora luzez egoera onean kontserbatzeko. Horretarako, ohiko teknikak (izoztea, liofilizazioa eta ontziratzea, besteak beste) ez ezik, beste teknika batzuk ere erabiltzen dira, gaur egun; adibidez, irradiazioz esterilizatzea.

Elikagaien irradiazioak bi xede jakin ditu: elikagaiak gutxiago hondatzea bildu ondoren, eta, beraz, elikagairik ez galtzea, batetik; eta elikagaien osasunkalitatea hobetzea, bestetik. Irradiazio bidezko kontserbazioak ahalmen handia eduki dezake gosearen arazoa konpontzeko, munduan hain hedatua dagoen gosea arintzeko.

GJH KONPROMISOA

Egin ariketa hauek taldeka:

1 Hamarraldietan zehar, ahalmen handiko intsektizidak erabili izan diren arren, uzten % 20 inguru galtzen da oraindik, intsektuen izurriteek suntsitzen dituztelako. Laburki, ikertu nola erabiltzen diren erradiazio nuklearrak nekazaritzako izurriteak desagerrarazteko. Azaldu zer alde on eta zer alde txar izan ditzakeen horrek, garapen jasangarrirako 2. helburuari (GJH) dagokionez.

2 Material kirurgikoa (eskularruak, gazak, xiringak…) esterilizatzeko, kobalto-60aren iturri erradioaktiboak erabiltzen dira gaur egun. Bilatu informazioa isotopoek medikuntzan dituzten erabilerei buruz, eta azaldu hori guztia idazlan batean, IKTko tresnaren bat erabiliz. Nola laguntzen dute erabilera horiek, GJHen 3.9 xedea erdietsi ahal izateko?

Zer aurkituko duzu?

Unitate honetan

• Isotopoak nekazaritzan eta elikaduran

1. Eredu atomikoen bilakaera

2. Argiaren izaera elektromagnetikoa

3. Espektro atomikoak

4. Teoria kuantikoaren jatorria

5. Efektu fotoelektrikoa

6. Bohrren eredu atomikoa

7. Mekanika kuantikoa

8. Orbital atomikoak. Zenbaki kuantikoak

9. Partikula subatomikoak. Unibertsoaren jatorria

• Kultura zientifikoa. LHCa eta Higgs bosoia

• IKTak. Efektu fotoelektrikoa aztertzea

• Problemak ebazteko estrategiak

anayaharitza.es webgunean

Motibatzeko:

• Bideoa: «Hasi baino lehen».

Lehendik dakizuna detektatzeko:

• Aurkezpena: «Zer jakin behar duzun».

Ikasteko:

• Aurkezpena: «Ikasteko».

IKASKUNTZA-EGOERA

GURE INGURUKO SUBSTANTZIAK

Unitate honetako edukiak eta ariketak oso baliagarriak izan daitezke liburuko lehen orrialdeetako eranskinean proposatzen den proiektua egin ahal izateko.

• Simulazioak: «Rutherforden dispertsioa: Rutherforden eta Thomsonen eredu atomikoak».

«Gorputz beltzaren erradiazioa». «Efektu fotoelektrikoa».

«Barneratze mekaniko-kuantikoa eta uhin-paketea».

Ebaluatzeko:

• Amaierako autoebaluazioa.

• Ariketen soluzioak.

Eta, horrez gain, proiektuko gakoak aplikatzeko beharrezkoa den dokumentazio guztia.

Eredu atomikoen bilakaera

Fenomeno elektromagnetikoen deskribapen bateratua ematea lortu zen xix mendearen amaiera aldera. Zehazki, argia karga elektrikoen bibrazioen efektu bat dela finkatu zen, baina inork ez zekien nolako izaera zuten karga horiek.

1.1. Deskarga-hodiak

J. Plücker zientzialariak, 1858an, presio baxuaren eraginpean zeuden gasetan elektrizitatea nola eroaten zen aztertu zuen. Horretarako, beirazko hodi bat erabili zuen, barruan, mutur bakoitzean, plaka metaliko bat zuela. Plückerrek ikusi zuen ezen, plaketan elektrizitatea aplikatzean, hodi osoa argiztatzen zela; baina gasean hutsa nahikoa lortzen zenean, argia desagertu egiten zela, eta fluoreszentzia berde bat besterik ez zela geratzen, anodoan konektatutako plakaren eremutik gertu zegoen beiran. Itxura batean, katodotik igorritako izpiren batek eragiten zuen argitasun hori hodiaren barnean, elektrodo batetik besterako bidaian. Esperimentu horietan, beste gauza batez ohartu zen: argi-irudiaren posizioa alda zitekeen, anodoaren ingurura iman bat hurbilduz.

Zenbait urte geroago, J. W. Hittorf fisikariak ikusi zuen itzalak sortzen zirela argi-irudian, elektrodoen artean objektuak jarriz gero. Emaitza horrek indartu egin zuen izpien jatorri katodikoaren ideia.

Bestalde, 1876an, E. Goldstein fisikariak izpi katodiko izena jarri zien argi horiei, eta, horrez gain, frogatu zuen izpi horien propietateak ez daudela katodoaren materialen mende. Antza, horrek guztiak adierazten zuen materiak elektrikoki kargatutako partikula materialez osatuta egon behar duela.

1.2. Izpi katodikoak

Jatorria

Izpi katodikoen jatorriari buruzko lehen teorietako bat W. Crookes zientzialariak proposatu zuen. Bere esperimentuak egiteko, Crookes hodia deritzona erabili zuen: beirazko hodi bat huts bat, bi elektrodo metalikorekin (katodoa eta anodoa); goi-tentsioko iturri bat; eta gas bat (eskuarki, gas nobleak edo hidrogenoa), hodiaren barruan, presio baxuen eraginpean (100 mPa eta 100 nPa artean).

Crookesek adierazi zuen erradiazio ikusezin batek eragiten zuela katodoaren aurkako aldeko beirazko horman agertzen zen fluoreszentzia berdexka, eta erradiazio horren jatorria katodoa bera zela. Halaber, izpiak desbideratzeko gauza ere izan zen, eremu magnetiko bat aplikatuz. Hala, Crookesek berretsi ahal izan zuen izpi-sortak negatiboki kargatuta balego bezala jokatzen zuela.

Lehen esperimentuak

Gasetan zeharreko deskarga elektrikoak aztertu zituen Francis Hauskbee zientzialariak (1660-1713) 1709an, argi bat agertzen zela ikusi baitzuen beirazko ontzi bat elektrifikatzean, presio baxuko airearekin.

Michael Faraday zientzialariak (17911867) ere esperimentuak egin zituen deskarga elektrikoekin, 1838an, gas arrarifikatuetan zehar. Gas horiek erabiltzean gertatzen zen eroapen elektrikoa oso deigarria egin zitzaion, zeren, baldintza normaletan, korronte elektrikoaren eroale kaskarrak baitira gasak.

Crookes hodia, elikatze-iturri batera konektatuta.

A. Schusler zientzialariak jarraitu egin zuen aurrekoen esperimentuekin, eta metalezko plakak ipini zituen, izpi katodikoekin paraleloak izateko moduan. Ondoren, potentzial-diferentzia aplikatu zuen plaken artean, eta ikusi zuen eremu elektrikoak izpiak desbideratzen zituela karga positiboko plakarantz. Gertaera horrek agerian jarri zuen, berriz ere, izpiak karga negatiboko partikulez osaturik daudela. Geroago, 1890ean, izpien osagaien karga-masa erlazioa iritzira kalkulatu zuen.

Urte batzuk geroago, 1895ean, J. B. Perrin ohartu zen izpi katodikoek karga jalkitzen dutela elektroskopio batean. Horrenbestez, karga duten partikulak direla berretsi zuen.

Izpi katodikoen izaera

Izpi katodikoen izaera azaltzeko, bi lan-ildo hauek planteatu zituzten xix  mendean:

• Izpi katodikoak karga elektrikoa duten partikulen fluxutzat hartzea. Hori horrela bada, izpi katodikoek izaera korpuskularra izango lukete. Lanildo honen defendatzaile nagusiak Perrin, Crookes eta Thomson izan ziren.

• Izpi katodikoak uhintzat hartzea. Horrenbestez, izpi katodikoek uhinizaera izango lukete. Aukera honen defendatzaile nagusiak Hertz, Lenard eta Goldstein izan ziren.

Abiapuntu horrekin, izpi katodikoen izaerak (uhinak edo korpuskuluak diren) sortutako eztabaida ikusirik, J. J. Thomson esperimentuak egiten aritu zen 1896tik aurrera, J. Townsend eta H. Wilson zientzialariekin batera. Esperimentu horien bitartez, frogatu zuten izpi katodikoak egiatan banakako partikulak (hots, korpuskuluak) direla, eta ez uhinak hasieran uste izan zen bezala.

Thomsonen esperimentua

Thomsonek izpi katodikoen abiadura ere neurtu nahi zuen. Horretarako, izpi katodikoak eremu elektriko eta eremu magnetiko banatan zehar igaroarazi zituen. Ikusi zuen partikula horiek eragiten zituzten indar elektrikoa eta magnetikoa zuzenki proportzionalak direla kargaren eta masaren arteko erlazioarekiko (indar magnetikoa ere abiaduraren mende zegoen). Esperimentu horrekin, zehaztasun handiz neurtu ahal izan zuen partikula horien karga-masa erlazioa.

J. J. Thomson (1856-1940) Britainia Handiko fisikariak Fisikako Nobel saria jaso zuen 1906an, gasetan zehar elektrizitatea igarotzeak dituen ezaugarriei buruz egindako lanengatik. Haren seme G. P. Thomsonek (18921975) ere jaso zuen Fisikako Nobel saria 1937an, elektroiek kristaletan duten difrakzioari buruzko lanengatik eta uhin-propietateak dituztela frogatzeagatik.

Izpi kanalak edo anodo-izpiak Eugen Goldstein fisikariak (1850-1930) aurkitu zituen 1886an. Goldsteinek ikusi zuen katodo zulatu bat erabiliz Crookes hodi batean deskarga elektriko bat sorrarazten zuenean, izpi kanalek zulo horiek zeharkatzen zituztela, anodotik abiatuta eta katodoraino, eta katodoen atzealdean lumineszentzia sortzen zela.

Joseph John Thomson

Izpi kanalak

Anodoa Katodo zulatua

Izpi kanalak Pantaila fluoreszentea

Izpi katodikoen hodia, Thomsonek erabilitakoa.

Eremu magnetikoa

Katodoa

Anodoa

Pantaila fluoreszentea

J. J. Thomsonen ondorioak

Hainbat gasekin eta katodorekin esperimentatuz, J. J. Thomsonek, azkenean, izpi katodikoei buruzko ondorio hauek atera zituen:

• Izpi katodikoek ibilbide zuzena egiten zuten, argiarena baino abiadura txikiago batean. Emaitza horrek ez zion mesederik egiten izpien uhin-izaeraren hipotesia, uhin elektromagnetikoak argiaren abiaduran (c = 3 · 108 m · s–1) hedatzen baitira.

• Karga duten partikula materialez eginda zeuden, eta partikula horiek txikiak behar zuten, atomoaren tamainarekin konparatuz. Emaitza horrek izpien izaera korpuskularraren hipotesia indartzen zuen.

• Esperimentuetan lortu zuen q/m erlazioaren balioa H+ ioiari dagokiona baino mila bider handiagoa zen, gutxi gorabehera. Emaitza horrek iradokitzen zuen partikulen masa hidrogeno atomoarena baino mila bider inguru txikiagoa izango litzatekeela.

• Atomoak ezin ziren zatiezinak izan; aldiz, karga negatiboko partikulez osaturik egongo lirateke. Gainera, materia elektrikoki neutroa denez, karga negatiboko partikulak baldin bazeuden, atomoaren beste eremuren batean karga positiboa egon behar zuen.

1.3. Elektroiaren aurkikuntza

J. J. Thomsonek egindako esperimentuetan berretsi egin zen karga elektriko negatiboko partikulak daudela, eta hori ez ezik, karga-masa erlazioa zehaztu zen. Horrenbestez, esperimentu horien ondoren, Daltonek atomoari buruz finkatutako kontzeptua berrikusi behar izan zen; alegia, atomoa oinarrizko partikula zatiezina zela. Atomoaren barnean partikula txikiagoak zeudela onartu zen, eta elektroi izena jarri zitzaien. Hala, lehen partikula subatomikoa identifikatu zen: elektroia.

Robert Millikan fisikariak elektroiaren karga neurtu nahi izan zuen olio tantaren esperimentua deritzonean, 1909an. Esperimentu horretan, eremu elektriko bat erabili zuen olio tanta baten erorketa gelditzeko.

Karga hau neurtu zuen elektroirako: 1,59 · 10−19 C. Balio horren arabera, elektroiaren masa 9,11 · 10−31 kg zela finkatu zen: atomorik arinenaren, hidrogenoaren, masa baino 1 837 bider txikiagoa.

Geroago, beste bi partikula subatomiko aurkitu zituzten: protoia, 1919an; eta neutroia, 1932an.

1 Ikertu izpi kanalei buruz, eta erantzun galdera hauei:

a) Zer dira izpi kanalak?

b) Azaldu zertan diren berdinak eta desberdinak izpi kanalak eta izpi katodikoak.

2 Finkatu karga-masa erlazioa protoirako eta elektroirako, hurrenez hurren. Gero, alderatu emaitzak.

Datuak: me = 9,1 · 10−31 kg, mp = 1,67 · 10−27 kg, qe = qp = 1,6 · 10−19 C.

3 Pentsatu, gogoko izan, ikertu… Neutroiak atomoaren parte dira, baina ez zen 1932ra arte berretsi neutroiak bazirenik, James Chadwick ingeles fisikariak lortu zuen arte. Ildo horretatik, 2001az geroztik, n_TOF (Neutron Time Of Flight) instalazioa martxan dago CERNen, neutroiaren eta nukleoaren interakzioak aztertzeko, neutroien hainbat energiabaliotarako: direla meV gutxi batzuk, direla zenbait GeV. IKTak baliatuz, ikertu n_TOF instalazioan jorratzen diren lan-ildoetako batzuei buruz

Millikan fisikariak olio tantarekin egindako esperimentua.

+

Olio tantak

Goitentsioa Izpi ionizatzaileak

Elektrikoki kargatutako plakak

Atomizagailua

Ariketak

1.4. Thomsonen eredu atomikoa

Izpi katodikoei buruzko lanetan egindako hipotesiak oinarritzat hartuta, Thomson izan zen egitura atomikoaren eredu bat proposatu zuen lehen zientzialaria.

Elektroien masa txiki-txikia izanik, atomoaren ia masa osoa karga positiboan biltzen zela jo zuen, eta, horrenbestez, atomoaren bolumen osoa hartzen zuela.

Thomsonek finkatu zuen atomoa esfera trinko handi bat zela, positiboki kargatuta, eta behar beste elektroi zituela txertaturik, esferaren karga positiboa neutralizatzeko moduan.

Thomsonen eredu atomikoarekin, zenbait gertaera esperimental azaldu ahal izan ziren, modu kualitatiboan; esate baterako, marruskadura bidezko elektrizazioa eta atomoek argia igortzea.

Mahaspasa-budina ere esan zitzaion: pastelaren masa karga positiboa duen atomoaren masa izango litzateke; eta mahaspasak, berriz, esferan txertatuta dauden elektroiak.

1.5. Rutherforden eredu atomikoa

Rutherforden esperimentua

Thomsonek esperimentuak egin eta eredu atomikoa proposatu ostean, Rutherford zeelandaberritarrak, bere aldetik, atomoaren egiturari buruzko ikerlan sakonago bat egin zuen.

Rutherfordek, ikerlanetarako, alfa partikulak erabili zituen, zenbait material erradioaktibok igorritako alfa partikulak: partikula horien masa elektroiena baino 2 000 aldiz handiagoa da, gutxi gorabehera, eta, beraz, elektroiekin talka egitean ez litzateke ageriko moduan desbideratu behar.

Rutherfordek eta haren laguntzaileek beheko irudian ageri den gailu esperimentala erabili zuten. Zehazki, material erradioaktibo batek (polonioa) igorritako alfa partikulak baliatu zituzten, urrezko xafla mehe-mehe bat bonbardatzeko (platinoa eta kobrea ere erabili zituzten).

Pantaila fluoreszente mugikorra, ZnS-zkoa

Elektroiak

Elektroiak modu uniformean banatzen dira

partikulak

Berunezko

Berunezko pantaila

kutxa Iturri erradioaktiboa (Po)

A: xafla zeharkatzen duten partikula-sortak, desbideratu gabe.

B: ibilbidea desbideratzen zaien partikula-sortak.

C: partikula-sorta aldaratuak.

Rutherforden esperimentuaren muntaketa eta urrezko xaflaren xehetasunak.

Mahaspasa-budinaren

Lise Meitner

Lise Meitner (1878-1968). Austriar fisikaria, fisio nuklearra aurkitu zuen, eta laborategiko lankide zuen Otto Hahn alemaniarrak Kimikako Nobel saria jaso zuen 1944an aurkikuntza horrengatik. Emakumeen aurkikuntzek hainbatetan merezi izan duten aitorpenik izan ez dutela agerian jartzen duen adibidea da.

Lise Meitnerrek Enrico Fermi saria jaso zuen 1966an, AEBn, fisikari egindako ekarpen handiarengatik.

Haren omenez, 109. elementu kimikoaren izena meitnerio da.

eredua.

Karga positiboko eremua

Alfa partikulen igorlea berunarekin blindatutako kutxa batean jarri zuten. Kutxari zulo txiki bat egin zioten, eta hartatik alfa partikulen sorta bat atera zedin lortu zuen (berunak alfa partikula guztiak gelditzen zituen, zulotik irteten zirenak izan ezik).

Metalezko xafla bat jarri zuten sortaren ibilbidearekiko zut. Partikulen ibilbidea detektatzeko, ZnS-zko pantaila fluoreszente bat erabili zen. Hark distiratxoak egiten zituen alfa partikula batek haren kontra talka egiten zuen bakoitzean.

Ondoren, pantaila partikula-sortarekiko angelu desberdinetan kokatuz, norabide bakoitzean sakabanatzen ziren alfa partikulen kopurua zenbatu zuten.

Rutherforden esperimentuaren emaitzak eta interpretazioa

Rutherfordek, Thomsonen eredu atomikoa oinarritzat hartuta, espero zuen alfa partikulek (karga positiboa dute) desbideratu gabe zeharkatzea xafla, baina partikula batzuk desbideratzea elektroiekin topo egitean. Thomsonen ereduan, fenomeno horren azalpena hau zen: alfa partikulen tamaina askoz txikiagoa da xafla metalikoko atomoena baino.

Alabaina, Rutherfordek esperimentua egin zuenean Geiger eta Marsden fisikariekin batera, ikusi zuten alfa partikula gehienek desbideratu gabe zeharkatzen zutela xafla; zenbait partikula zertxobait desbideratzen ziren, eta beste batzuk (gutxi gorabehera, partikula bat 20 000 partikulako) angelu handiak osatuz desbideratzen ziren, edo errebotatu ere egiten zuten.

Thomsonen ereduarekin ezin zen portaera hori azaldu, eta, horregatik, Rutherfordek eredu atomiko berria proposatu zuen 1911n.

Eredu berriarekin, alfa partikulen esperimentua azaldu ahal izan zen: partikula gehienek desbideratu gabe zeharkatzen zuten xafla, atomoen karga positiboa nukleo deritzon gune txiki-txiki batean kontzentratuta zegoelako, eta partikulak nukleoarekin interakziorik gertatu gabe igaro zitezkeen.

Nukleotik gertu pasatzen ziren alfa partikula batzuk pixka bat desbideratuak ziren, eta, proportzio txiki-txiki batean, partikularen batek nukleoaren aurka talka egin, eta indar handiz aldaratzen zen.

Rutherforden ereduaren ezaugarriak

Funtsean, Rutherforden ereduaren ezaugarriak hauek dira, labur azalduta:

• Atomoaren masa gehiena eta karga positibo guztia atomoaren gune txiki-txiki batean kontzentratuta daude (gune horri nukleo izena jarri zion). Atomoaren gainerakoa espazio hutsa da.

Rutherfordi alfa partikulak angelu handiak eratuz zergatik aldaratzen ziren azaltzeko arrazoi bakarra egon zitekeela bururatu zitzaion: atomoak erdigune txiki-txiki bat eduki behar du, trinkoa eta karga positibokoa. Proposatu zuen atomoaren masaren % 99,9 baino gehiago nukleoan kontzentratuta dagoela, eta hantxe dagoela karga positiboa ere (protoiak).

Rutherford nukleoaren neurria iritzira kalkulatzeko gauza izan zen: nukleoaren erradioa neurtu eta 10−14 m balioa lortu zuen (atomoaren erradioa 10−10 m inguru da). Horrek esan nahi zuen atomoaren ia gehiena hutsik dagoela, eta atomoaren nukleoa 10 000 bider txikiagoa dela atomoa bera baino.

Ernest Rutherford

Ernest Rutherford (1871-1937) zeelandaberritar fisikari bat izan zen. Bere lehen ikerlanetan, elektromagnetismoa jorratu zuen; 1898an frogatu zuen X izpiek eta erradioaktibitateak antzeko eraginak dituztela gasetan, eta, gutxienez, bi erradioaktibitate mota daudela ikusi zuen: alfa eta beta izenak jarri zizkien. Erradioaktibitateari eta alfa partikulei buruz egindako lanak direla eta, Kimikako Nobel saria jaso zuen 1908an.

Rutherfordek, H. Geiger eta E. Marsden ikasleekin, esperimentu bat egin zuen 1909an, Thomsonen eredu atomikoa probatzeko asmoz.

Bazenekien...?

Hans Geiger (1882-1945) alemaniar fisikariak partikula erradioaktiboen presentzia detektatu eta neurtzeko kontagailua asmatu zuen.

• Karga negatiboa elektroiek daramate, eta elektroiak nukleoaren inguruan banaturik daude, orbita zirkularretan biratuz. Orbita horietan, elektroien gainean nukleoak eragiten duen indar elektrikoa indar zentripetua da, eta horrek eragiten du higidura zirkularra.

Neutroi-izpiak ia dena hautemateko

Elektroia-nukleoa interakzioa. Rutherforden eredu planetarioa.

Bi ezaugarri horiek ikusita, eta aintzakotzat hartuta nolako analogia dagoen Eguzkiaren inguruan planetek egiten duten higiduraren ereduarekin, eredu planetario izena ere erabiltzen hasi ziren zientzialariak.

Rutherforden ereduarekin ulertzen da atomoaren nukleoan protoiak daudela, eta elektroiak nukleoaren inguruan biratzen direla. Hala ere, elementuen masa atomikoen datuak ezin ziren eredu horrekin azaldu, zeren iritziz kalkulatutako masa atomikoak benetakoak baino txikiagoak baitziren. Horretaz ohartuta, Rutherfordek 1920an proposatu zuen kargarik gabeko partikulak daudela nukleoan, protoien masa berarekin; partikula horiei neutroi izena jarri zien (Chadwickek neutroiak badaudela egiaztatu zuen 1932an).

Rutherforden ereduaren mugak

Rutherforden ereduarekin, alfa partikulen sakabanatzea azaltzen zen, baina bi arazo handi zeuden:

• Rutherforden iritziz, elektroiak abiadura handian biratzen ziren nukleoaren inguruan. Maxwellen teoria elektromagnetikoari jarraituz, ordea, higitzen ari diren elektroi horiek energia igorri behar dute etengabe. Hala, elektroiaren orbitalaren erradioa gero eta txikiagoa izango litzateke: kiribil bat egin, eta nukleoarekin kolapsatuko luke azkenean.

• Rutherforden ereduarekin, ezin ziren espektro atomikoak azaldu.

Hala, 1913an, Niels Böhr Rutherforden ereduaren akatsak konpontzen saiatu zen, Planckek 1900ean proposatutako teoria kuantikoa egitura atomikoaren azterketari aplikatuz.

Böhr fenomenologikoki saiatu zen elektroien orbita batzuk soilik direla posible azaltzen. Horrek azalduko luke atomoen igorpen- eta xurgapenespektroak banda diskretu moduan agertzea.

Ariketak

4 Sufrearen zenbaki atomikoa 16 da. Kalkulatu sufrearen karga nuklearra, coulombetan.

Datua: elektroiaren karga: 1,6 · 10−19 C

Grenobleko ILL europar laborategian, munduko neutroi-iturririk bizienetako bat daukate. Neutroiak bonbardatuz, lehen xaboi magnetikoak zer mikroegitura duen finkatu ahal izan dute (oso xaboi preziatua da, itsas isuriak tratatu ostean detergentea uretatik kendu ahal izateko), bai eta zelulosazko mikrozuntzen nanoegitura ere (oso material garrantzitsua da bioerregaiak egiteko). +

Elektroia biraka dabilenez, energia askatuko luke, eta, horrenbestez, nukleoaren gainera eroriko litzateke.

5 Burdinaren karga nuklearra 4,17 · 10−18 C da. Hori hala dela jakinda, kalkulatu: a) Fe-aren zenbaki atomikoa, b) Zenbat elektroi dauden Fe atomo batean. Datua: elektroiaren karga: 1,6 · 10−19 C

Argiaren izaera elektromagnetikoa

2.1. Argiaren izaera

Argiaren izaera eztabaida zientifikoaren erdian egon da denbora luzez. Eztabaida horien jatorria argiarekin egindako zenbait esperimenturen emaitzak izan dira.

Newton (1642-1727) sinetsita zegoen argiak izaera korpuskularra zuela (hots, argia partikula-sorta bat zela). Bestalde, Huygensek (1629-1695) proposatu zuen argiak uhin-izaera zuela.

Argiak itzalak sortzeak eta itzalen mugak zehatzak izateak izaera korpuskularraren hipotesia indartzen zuen. Hori dela eta, denbora luzez, gehienek Newtonen teoria onartu zuten.

Haatik, T. Young fisikariak (1793-1829) argi-interferentziei buruz egindako esperimentuekin kontrakoa frogatu zen; hau da, argia uhin-fenomeno baten modura ulertu behar dela. Hala, uhin-izaeraren teoria garrantzia hartzen hasi zen, eta hori izan zen onartuena xx  mendearen hasierara arte.

Hiztegia

• Interferentzia deritzo espazio berean bidaiatzen ari diren bi uhinen edo gehiagoren arteko interakzioari, eta anplifikatu edo ezereztu egin daiteke, faseen arabera.

• Difrakzioa uhinak sakabanatzea da, oztopo bat aurkitzen dutenean.

Zirrikitu bikoitzaren esperimentua. 1801ean egin zuen Youngek, honela: argi-sorta batek pantaila bati erasotzea eragin zuen; emaitza banda argi-ilunen patroi bat izan zen. Hala, argiak uhin batek bezala jokatzen duela frogatu zuen.

2.2. Uhinak

Uhina bibrazio-perturbazio baten hedapena da, eta energia transmititzen da.

Uhinen ezaugarriak

Funtsean, uhin guztiek ezaugarri hauek dituzte:

• Uhin-luzera (λ): ondoz ondoko bi maximoren arteko distantzia da. Nazioarteko SI sisteman, unitatea metroa da, m.

• Anplitudea (A): uhinaren perturbazio maximoa da; alegia, uhinaren distantzia maximoa, perturbaziorik gabeko erdiko lerroarekiko. Nazioarteko SI sisteman, unitatea metroa da, m.

• Maiztasuna (f): puntu batetik denbora-unitateko igarotzen den uhin kopurua da. Nazioarteko SI sisteman, unitatea s−1 edo hertza da (Hz).

• Hedatze-abiadura (v): ingurunean zehar uhina zer abiaduratan hedatzen den adierazten du. Adierazpen honekin kalkulatzen da: v = λ · f

Hutsean zehar hedatzen den argiaren kasuan, abiadura c da, eta horren balioa, 2,997 825 · 108 m · s –1 da. Berbera da maiztasun guztietan. Beste edozein ingurunetan, argiaren hedatze-abiadura desberdina izango da maiztasun bakoitzean, eta c baino txikiagoa beti.

Anplitudea; A

Uhin-luzera; λ Gailurra

Nodoa

Hedatze-abiadura; v

Uhin baten ezaugarriak.

Harana

2.3. Maxwellen teoria elektromagnetikoa

J. C. Maxwell fisikariak (1831-1879) argiaren eredu matematiko bat garatu zuen. Argia uhin edo erradiazio elektromagnetikotzat jotzen da, eta eremu elektriko eta eremu magnetiko banaz osatua dago. Eremuak elkarzutak dira, eta hedatze-norabidearekiko zutak, orobat.

Hertz (1857-1894), bere aldetik, Maxwellen uhin elektromagnetikoak sortu eta detektatzeko gauza izan zen, eta baliozkotu egin zuen Maxwellek urte batzuk lehenago finkaturiko eredua: erradiazio elektromagnetikoa energia transmititzeko modu bat da, eta, hartan, eremu elektrikoak eta magnetikoak uhinen bidez hedatzen dira, hutsean edo beste ingurune batean zehar. Karga elektrikoa duen partikula bat azeleratuz lortzen da.

Espektro elektromagnetiko deritzo erradiazio elektromagnetikoen maiztasunen edo uhin-luzeren multzoari.

Argi ikusgaia espektro elektromagnetikoaren gune txiki-txiki bat da; gutxi gorabehera, 400 nm-tik 700 nm-ra bitarteko tartea.

1 DVD-irakurgailuetan erabiltzen den laserraren uhin-luzera 645 nm da, gutxi gorabehera.

a) Zer maiztasun du DVD-irakurgailuetan erabiltzen den laserrak?

b) Zer kolore du DVD-irakurgailuetan erabiltzen den laserrak?

Ebazpena

a) Jakinik 1 nm = 10−9 m dela, hau da uhin-luzera, nazioarteko SI sistemako

unitatetan: λ = 6,45 10−7 m.

Maiztasuna kalkulatzeko, adierazpen hau erabiliko dugu: c = λ ∙ f.

b) Balio hori eta espektro ikusgaiko maiztasunen balioak alderatuz ikusten da laserraren kolorea gorria izango dela.

Ariketak

6 Kalkulatu f, eta ordenatu txikienetik handienera:

a) 610 nm-ko argi hori bat,

b) 700 nm-ko argi gorri bat,

c) 200 nm-ko argi ultramore bat,

d) 1700 nm-ko erradiazio infragorri bat,

e) 3 nm-ko X izpiak.

Bazenekien...?

Maxwellen sintesi elektromagnetikoa mugarri bat izan zen zientziaren historian, indarrak bateratzeko ahaleginean. Hain izan zen garrantzitsua, ezen, xix   mendearen amaieran, fisikari ugarik uste izan baitzuten fisikaren legeak behar bezainbeste ulertzen zirela jada.

7 Kalkulatu zer uhin-luzera duen 1015 s–1-ko maiztasuneko argi ultramore batek. Kalkuluak egindakoan, bilatu informazioa ea nola erabil daitekeen nekazaritza jasangarrian erradiazio ultramorea. Bilaketan bildutako informazioarekin, pentsatu proiektu bat, garapen jasangarrirako 12. helburuari jarraituz aplika daitekeena.

ultramorea

Ebatzitako ariketak

Espektro atomikoak

3.1. Espektroskopia

Newtonek, 1666an, eguzki-argiaren izpi bat igaroarazi zuen beirazko prisma batean zehar, eta ikusi zuen kolore gama jarraitu bat eratuz deskonposatu zela: eguzki-espektroa da. Emaitza horren ondorioz, eguzki-argia espektro jarraitu bat zela uste izan zen.

Historia pixka bat

Gustav Kirchhoff (1824-1887) eta Robert Bunsen (1811-1899) zientzialariek batera aurkitu zituzten zesio (1860) eta rubidio (1861) elementu kimikoak, espektroskopia-lanak egiten ari ziren bitartean.

Koloretako sugarren azterketa

Bunsenek eta Kirchhoffek, xix. mendean, azterketa kimikoko metodo bat garatu zuten, koloretako sugarretan oinarrituta. Substantzia bat sugarretan sartzen denean, haren atomoetako bakoitzak interakzioa du erradiazio elektromagnetikoarekin.

Sugarra tenperatura altu-altuetara iristen denez, substantzia gas-egoerara igaroko da. Halatan, atomo isolatuak besterik ez daude, eta lortzen diren espektroak atomikoak dira, eta, beraz, etenak.

Espektro atomikoak

Kimikarientzat, hain zuzen ere, espektro atomikoak materiaren konposizioari buruzko informazio-iturririk garrantzitsuenetako bat dira. Gainera, energia kuantizatuta dagoela frogatzen dute, eztabaidarik gabe. Atomo baten egitura elektronikoak elektroien energiak deskribatzen ditu, baita elektroiak atomoaren inguruan nola antolatzen diren ere. Atomoen egitura elektronikoari buruz dakigunaren zati handi bat erradiazioaren eta materiaren arteko interakzioa aztertuz jakin zen.

Espektroa da erradiazio elektromagnetiko konplexu bat osatzen duten maiztasunen azterketaren emaitza.

Substantziek igortzen edo xurgatzen duten erradiazio elektromagnetikoa aztertzen duen zientziari espektroskopia esaten zaio. Kimikan ezinbestekoa da, elementuak identifikatzeko eta karakterizatzeko aukera ematen du eta.

Espektroak espektroskopio edo espektrografo baten bidez lortzen dira. Gailu horrekin, erradiazio konplexua haren osagairik bakunenetan deskonposa daiteke, eta horrek aukera ematen du erradiazio bakunen maiztasuna aztertzeko.

Espektroskopioa, funtsean, prisma bat da. Igorpen-iturri batetik datorren argiak prisma zeharkatzen duenean, argiaren zati bat aztergaia den laginak xurgatzen du.

Potasioaren koloretako sugarra.

3.2. Espektro motak

Bi sailkapen-irizpide hauek erabiliko ditugu espektroak sailkatzeko: Aztertu beharreko argiaren jatorria

• Igorpen-espektroa: horrelako espektroetan, aldez aurretik kitzikatu den lagin gaseoso batek igorritako erradiazioa aztertzen da.

• Xurgapen-espektroa: horrelako espektroetan, argi zuria laginetik pasarazi ondoren geratzen den erradiazioa aztertzen da. Azken batean, aztertzen dena xurgatu ez duen erradiazioa da.

Gasek igorritako erradiazioa uhin-luzeren arabera bereiz daiteke prisma bat erabiliz.

Ondoriozko espektroaren itxura

• Jarraitua: solidoen eta likidoen itxura bereizgarria da.

• Etena: egoera gaseosoan dauden laginen bereizgarria. Bi motatako espektro etenak daude: bandak (egoera gaseosoan dauden molekulen bereizgarri) eta lerroak (egoera gaseosoan dauden atomoen bereizgarri). Lerroak diren espektro atomikoetan, lerroek adierazten dute zer maiztasun dagokien atomoak igortzen edo xurgatzen dituen erradiazio bakunei.

Espektroetako lerroak elementu bakoitzaren ezaugarri bereizgarriak dira, berdin du beste substantzia batzuekin nahasita dauden edo ez.

Naturan, aurora borealak eta australak Eguzkitik datozen partikula kargatuek sorrarazten dituzte.

Sodioaren, helioaren, merkurioaren eta barioaren igorpen-espektroak.

Unibertsoa ezagutzea

Unibertsoari buruz dakigunaren zati handi bat Lurrera heltzen zaigun erradiazio elektromagnetikoaren azterketa espektroskopikoaren emaitza da. Izar baten espektroa aztertuta, haren konposizioari buruzko informazioa lortu dezakegu.

Lagin kitzikatua

Filma edo detektagailua

Uhin-luzera

Xurgapen-espektroa

Prisma

Argi zuriaren iturria

Filma edo detektagailua

Uhin-luzera

Xurgapen-espektroa Lagin xurgatzailea

Prisma

3.3. Hidrogenoaren espektro atomikoa

Hidrogenoaren espektro atomikoa guztietan soilena da. A. J. Angström espektroskopistak hidrogenoaren igorpen-espektro ikusgaiko lau lerro dirdiratsuen uhin-luzerak neurtu zituen, eta J. J. Balmer zientzialariak, 1885ean, uhin-luzeren arteko erlazioa aurkitu zuen:

1 2 1 –n 1 RH 22 = m ccmm; E

RH : Rydbergen konstantea hidrogeno atomorako = 109 677,6 cm−1

Geroago, hidrogenoaren espektro atomikoaren gune berriak aurkitu zituzten. Zehazki, ikusi zuten espektroko lerroak taldetan edo serietan agertzen direla, eta haien uhin-luzerak, λ, formula orokor baten bidez deskriba daitezkeela. J. R. Rydberg fisikariak adierazi zuen formula hori, 1889an:

11 –1 R nn H 1 2 2 2 = m eeoo= G

Adierazpen horretan, RH = 1,09678 · 107 m −1 da, eta n1 eta n2, hau betetzen duten bi zenbaki oso eta positibo: n2 > n1

Hidrogenoaren igorpen-lerroak.

xurgapen-espektroa (goian) eta igorpen-espektroa (behean).

8 Kalkulatu zer uhin-luzera eta maiztasun duten hidrogenoaren espektroko Balmerren lehen eta bigarren

Datua: RH = 1,097 · 107 m −1

9 Kalkulatu zer uhin-luzera eta maiztasun duten hidrogenoaren espektroko Lymanen lehen eta bigarren lerroek.

Datua: RH = 1,097 · 107 m −1

1.

Teoria kuantikoaren jatorria

4.1. Erradiazio termikoa. Gorputz beltza

Gorputz guztiek, tenperatura izateagatik, erradiazio elektromagnetikoa igortzen eta xurgatzen dute. Hori dela eta, erradiazio horri erradiazio termiko esaten zaio. Materia kondentsatua bada, erradiazioa uhin-luzeren espektro jarraitu batean zehar banatzen da. Uhin-luzera, igorlearen tenperaturaren mende dago, beste faktore batzuen artean. Esaterako, tenperatura baxua denean, igorpena ez da ia hautematen, baina, altua denean, objektuek distira egiten dute.

Gorputz beltzaren erradiazioari buruzko ikerlanak G. R. Kirchhoff fisikariarekin hasi ziren. Horra zer adierazi zuen:

Gorputz beltz deritze erasotzen dien argi guztia xurgatzen duten gorputzei. Ez dute argirik xurgatzen, baina zer tenperaturatan dauden, erradiazioa igortzeko gauza ere badira.

Gorputz batetik datorren erradiazioa haren erradiazioaren eta islatzen duen erradiazioaren batura da. Gorputz horren igorpena soilik aztertu nahi denean, gorputza nolabait isolatu behar da, eta hori gauza zaila da. Baina zailtasun hori desagertu egiten da gorputzak jasotzen duen erradiazio guztia xurgatzen badu.

Burdinazko barra bat berotzean, tenperatura igo ahala, kolorea aldatu egiten zaio, gorritik (uhin-luzera handia) urdineraino (uhin-luzera txikia). Gorputzen igorpen-espektroak aztertzeko, ereduzko gorputz bat baliatzen da: gorputz beltz ideala, erasotzen dion erradiazio guztia xurgatzen duen gorputza.

Gorputz beltz idealaren eredua barrunbe bat da, xurgatze-ahalmen handiko hormez osatua, horma horietako batean zulotxo bat duena. Hormek xurgatu egingo dute barrunbe horretan sartzen den edozein erradiazio, barrunbetik irteteko aukera izan aurretik. Hala, zulotik irteten den erradiazioaren jatorria barrunbearen hormak direla ziurta daiteke; alegia, gorputzaren igorpena dela.

Gorputz beltz ideal guztiek espektro bera igortzen dute tenperaturaren mende, eta ordura arte ezin zen azaldu (1900) Maxwellen teoria elektromagnetikoaren bidez.

Wienen desplazamendu-legea

Lege horretan ezartzen du ezen gorputz ideal batek igortzen duen erradiazioaren intentsitate maximoa uhin-luzerarik laburrenen gunera desplazatzen dela, tenperatura igo ahala: λmax ∙ T = 2,898 ∙ 10−3 m ∙ K

Lege hori izarren tenperatura zehazteko erabiltzen da, izarren erradiazioaren azterketa abiapuntutzat hartuta.

Modu esperimentalean lortutako kurbak (lerro jarraitua), eta gorputz beltzaren erradiazioari buruz fisika klasikoak egindako aurreikuspena (lerro etena).

Gorputz beltza.

Jeans legea

4.2. Plancken hipotesia

Max Planck alemaniar fisikariak, 1900ean, gorputz beltzaren erradiazioaren espektro-banaketa lortu zuen, baina lege klasikoetatik aldenduz. Berlingo Alemaniar Fisika Elkarteari aurkeztutako ikerlan batean, gorputz beltzaren erradiazioaren kurba esperimentalekin bat zetorren ekuazio bat ondorioztatu zuela iragarri zuen. Horretarako, Planckek jo zuen gorputz beltzaren hormetako elektroiek f maiztasun batekin oszilatzen dutela, elektroi bakoitzaren ezaugarri bereizgarria den maiztasunarekin. Oszilazioekin, elektroiek maiztasun horretako erradiazio elektromagnetikoa xurga edo igor dezakete. Formularen oinarri fisikoak lortzeko, Planckek iradoki zuen materia osatzen duten partikulek oreka-posizioen inguruan oszilatzen dutela, eta energia uhin elektromagnetiko moduan igortzen edo xurgatzen dutela.

Igorri edo xurgatu den energiak hartu ditzakeen balio bakarrak kuantu deritzon energia kantitate diskretu baten multiploak izan daitezke.

Xurga edo igor daitekeen energia honela adierazten da:

E = n · h · f

Adierazpen horretan, h oinarrizko konstante fisiko bat da, Plancken konstantea, eta haren balioa 6,626 · 10−34 J · s da; eta n, berriz, zenbaki kuantiko bat da, eta balio hauek hartu ditzake: 1, 2, 3…

Energia kuantizatuta dagoelako ideia onartzen zaila izan zen, kontraesanean baitago sistema fisiko makroskopikoetarako ordura arte lortutako emaitza guztiekin. Plancken hipotesian, errotik desberdina dena zera da, oszilatzaile baten energia kuantizatuta dagoela jotzea, eta energiak balio diskretuak besterik ezin dituela hartu; hots, ezin duela tarteko baliorik hartu. Hasieran, zientzialariei zaila egin zitzaien hipotesi kuantikoa onartzea, baita Plancki berari ere. Printzipio orokor baten modura onartu ahal izateko, beste esperimentu batzuetan frogatu beharra zegoen. Efektu fotoelektrikoari buruz Einsteinek emandako azalpena lagungarri izan zitzaion.

Ariketak

10 Rubidio atomo bat ionizatzeko, 4,2 eV-eko argi-erradiazioa behar da. Kalkulatu:

a) Erabilitako erradiazioaren maiztasuna, b) 600 nm-ko argi laranja baldin badago, argi horrekin lortu al daiteke rubidioa ionizatzea?

Datuak: h = 6,63 · 10−34 J·s, c = 3 · 108 m · s –1 , 1 eV = 1,6 · 10−19 J, 1nm = 10−9 m.

Irène J. Curie (1897-1956) Pierre eta Marie Curieren alaba izan zen, eta Kimikako Nobel saria jaso zuen 1935ean, Jean Frédéric Joliot senarrarekin batera, elementu erradioaktibo berrien sintesian egindako lanengatik.

2 Espektro ikusgaiari dagozkion erradiazioen uhinluzerak 450 nm eta 700 nm artekoak dira.

a) Kalkulatu zer energia dagokion maiztasunik handieneko erradiazio ikusgaiari.

b) Arrazoitu ea, erradiazio horrekin, litio atomoaren ionizazioa lortu daitekeen edo ez.

Datuak: e = 1,6 · 10−19 C

c = 3 · 108 m · s –1

h = 6,63 · 10−34 J · s

Litioaren lehen ionizazio-energia = 5,4 eV

1 nm = 10−9 m

Adierazpen hauek ditugu: E =  h ·  f eta cf m = . Konbinaturik, hau lortuko dugu:

b) Kontuan izanik 1 eV = 1,6 · 10−19 J dela, hona hemen zer ionizazio-energia izango den:

Ebazpena

a) Maiztasuna eta uhin-luzera magnitude alderantziz proportzionalak dira. Horrenbestez, maiztasunik handieneko uhin-luzera λ = 450 nm = 4,5 · 10−7 m da.

Energia kantitate jakin bat du lotuta 450 nm-ko erradiazioak, eta balio hau du: 4,42 · 10−19 J.

Ionizazio-energiaren balioa baino txikiagoa denez, ezingo da litio atomoa ionizatu uhin-luzera horrekin (450 nm).

Irène Joliot Curie

Ebatzitako ariketak

Efektu fotoelektrikoa

Heinrich Hertzek, 1887an, erradiazio elektromagnetikoari buruzko Maxwellen teoria egiaztatzen saiatzen ari zela, ikusi zuen gainazal metaliko bat erradiazio elektromagnetikoarekin argiztatzen zuenean, gainazal horrek elektroiak igortzen zituela. Fotoelektroi izena jarri zien elektroi horiei. Maxwellen teoriaren (argiak uhin-izaera zuela zioen teoriaren) aldeko lehen froga erabakigarria izan zen; baina, aldi berean, argiak izaera korpuskularra ere baduela erakutsiko zuten esperimentuetarako bidea zabaldu zuen.

5.1. Hertzen esperimentua

Funtsean, Hertzen esperimentuko dispositibo esperimentala elementu hauek osatzen zuten: bi plaka metaliko paralelo, huts-hodi baten barnean sartuta, eta amperemetro batera eta tentsio-iturri aldakor batera konektaturik. Katodoaren (igorlea) gainazala argiztatzen zenean, korronte elektriko txiki bat lortzen zen amperemetroan.

Hertzen esperimentuaren eskema. Esperimentuan, fisika klasikoa azaltzeko gauza ez zen hiru egoera jarri ziren agerian:

1. Elektroiak kasu honetan soilik igortzen ziren: gainazalari erasotzen zion argiaren maiztasunak f0 balioa gainditzen zuenean (atari-maiztasuna esan zitzaion) Maiztasun horretatik behera, ez zen elektroirik igortzen, nahiz eta argi-intentsitatea handitu. Teoria klasikoak zioen argiaren edozein maiztasunekin gertatu behar zuela horrek, baldin eta argi-intentsitatea behar bezain handia bada.

2. Erradiazio erasotzailearen f maiztasuna f0 atari-maiztasuna baino handiagoa bazen, igortzen zen elektroi kopurua eta erradiazio erasotzailearen intentsitatea proportzionalak ziren. Orobat, ikusten zen elektroien energia zinetiko maximoa ez zegoela argi-intentsitatearen mende, baizik eta f maiztasunaren mende soilik. Teoria klasikoari jarraikiz, energia zinetikoak handitu egin behar du intentsitatearekin.

3. Ezin izan zen sekula atzerapenik neurtu gainazal metalikoa argitzen zenetik fotoelektroiak igortzen ziren arte. Teoria klasikoaren arabera, argiaren intentsitatea ahul-ahula bazen, nolabaiteko atzerapena egon behar zuen bi gertaera horien artean.

1902an, P. Lenard efektu fotoelektrikoa behatzen ari zela, ohartu zen elektroien energia aldatu egiten zela argi erasotzailearen maiztasuna aldatzen zenean. Elektroien energia zinetikoa neurtzeko aukera ikusi zuen: izpi katodikoen hodi batean elektroiak gelditzeko behar den potentzial-diferentzia erabil daiteke horretarako. Lenarden esperimentuetan, datu kualitatiboak soilik lortu ziren, baina abiapuntu izan ziren gerora Albert Einsteinek efektu fotoelektrikoa azaldu ahal izateko.

11 Eguzki-energia elektrizitate bihur daiteke, efektu fotoelektrikoan oinarrituta dagoen teknologia bat erabiliz; hots, eguzki-energia fotovoltaikoa lortu daiteke. Luzaroan, energiarik ez edukitzeak urrutiko eta landako komunitateetan bizi direnek beharra izan dutenean osasun-laguntza lortzea eragotzi du. Orain, PNUDren (United Nations Development Programme) Solar for Health deritzon ekimenarekin, landa-eremuetako osasun-zentroetan eta kliniketan eguzki-sistemak instalatzen laguntzen zaie gobernuei. Horren bidez, orain artean arretarik izan ez duten komunitateetara heldu daiteke, eta guztientzako osasun-laguntza ziurtatu. Taldetan, bilatu proiektu horiei buruzko informazioa, eta erlazionatu garapen jasangarrirako 4. eta 11. helburuekin. Prestatu aurkezpen bat, eta azaldu han zer ondorio atera dituzuen.

Ariketak

5.2. Efektu fotoelektrikoaren azalpena

Fenomeno hori azaltzeko asmoz, Albert Einstein Plancken teoria kuantikoan oinarritu zen. Ildo horretan, 1905ean, argia energiaren kuantuz osatuta zegoela iradoki zuen (geroago, fotoi izena jarri zitzaien). Fotoien energia honela adierazten da: E = h · f. Fotoiak uhin elektromagnetikoaren energia garraiatzen duten partikulak dira.

Einsteinen emaitzak azaltzeko, eman dezagun fotoi batek gainazal metalikoko elektroi batekin talka egin duela, eta bere energia helarazi diola (eskuineko irudia). Zer gertatzen da orduan? Einsteinek efektu fotoelektrikoaren azalpen teorikoa eman zuen, ondorio hauetan laburbilduta dagoena.

Einsteinen ondorioak

1. Gainazal metalikotik elektroi bat erauzteko egin behar den lana Plancken konstantearen (h) eta atari-maiztasunaren (f0) arteko biderkadura da. Lan hori desberdina da metal bakoitzerako, eta gainazalaren egoerak ere baldintzatzen du. Honela adierazten da: W

2. Argi erasotzailearen fotoien E energia We erauzketa-lana baino handiagoa izan daiteke. Hori dela eta, sobera geratzen den energia elektroiak gainazal metalikotik erauzi ostean bereganatuko duen energia zinetikoa izango da.

Energia zinetikoa argi erasotzailearen maiztasunaren (f) eta atari-maiztasunaren (f0) mendean besterik ez dago.

3. Argi-sortaren intentsitatea handitzen denean, energia zinetikoa (Ek) ez da handiagotuko, nahiz eta fotoi gehiago heldu gainazalera, eta, beraz, elektroi gehiago erauzi.

Efotoia = We + Ek

Ekuazio hori efektu fotoelektrikoaren Einsteinen ekuazioa da.

4. Efektu fotoelektrikoa gertatzen bada, elektroiak ia-ia berehala igortzen dira. Hori horrela izatea bateragarria da argiaren ikuspegi korpuskularrarekin.

Bazenekien...?

Albert Einstein (1879-1955) historiako fisikaririk garrantzitsuenetako bat dela jotzen da, eta Fisikako Nobel saria jaso zuen 1921ean, higidura browndarrari eta efektu fotoelektrikoari buruz egindako lanengatik.

Ez zuen Nobel saria jaso fisikari egindako ekarpenik handienagatik; hots, erlatibitatearen teoriagatik.

3 Erradiazio monokromatiko baten uhin-luzera m 10 –7 m = da, eta eraso dion metalaren atari-maiztasuna, berriz, 2 · 1014 s−1. Kalkulatu lanfuntzioa eta elektroien energia zinetiko maximoa.

Ebazpena

Lehenik, lan-funtzioa kalkulatuko dugu:

10 13310

fotoelektrikoaren Einsteinen ekuazioari jarraituz:

Ariketak

12 Esperimentu batean gainazal metaliko bat 300 nm-ko uhinluzerako argi batez argiztatu dugu. Metalaren erauzketalana 2,46 eV dela jakinda, kalkulatu:

a) Metalak igortzen dituen elektroien energia zinetiko maximoa.

b) Metalari dagokion atariko uhin-luzera.

Datuak: e = 1,6 · 10−19 C, c = 3 · 108 m · s –1 , h = 6,63 · 10−34 J s

13 Erradiazio monokromatiko baten uhin-luzera 600 nm da, eta metal bati eraso dio. Haren erauzketa-lana 2 eV da. Horiek horrela, kalkulatu:

a) Efektu fotoelektrikoari dagokion atariko uhin-luzera.

b) Igorritako elektroien energia zinetiko maximoa, eV-etan.

Datuak: h = 6,63 · 10−34 J · s, c = 3 · 108 m · s –1 , e = 1,6 · 10−19 C.

Efektu fotoelektrikoa.

Bohrren eredu atomikoa

Rutherfordek nukleoa aurkitu eta atomoaren bere eredua (elektroiak nukleoaren inguruan biratzen direla dioena) proposatu bezain laster, zientzialariak eragozpenak adierazten hasi ziren:

• Fisika klasikoko teoria elektromagnetikoaren postulatuetako bati jarraituz, elektroiak, nukleoaren inguruan biratzen denean, energia erradiatu beharko luke uhin elektromagnetiko moduan, eta, beraz, energia galduko luke, eta, azkenean, nukleoaren gainera eroriko litzateke.

• Rutherforden ereduak ez zuen azaltzen espektro etenen jatorria. Niels Bohrrek, elektrodinamika klasikoak zioena alde batera utzita, beste eredu atomiko bat garatu zuen, erradiazioaren eta materiaren interakzioan energiak duen kuantizazioan oinarrituta (Planckek adierazi zuen, 1900ean, energiaren kuantizazioa).

• Adierazi zuen fisika klasikoaren postulatu bat ez zela aplikagarria; karga azeleratu batek etenik gabe erradiazioa igortzen duela dioena, hain zuzen ere. Erradiazioari buruzko Plancken legea betez, energia era kuantizatuan xurgatzen eta igortzen da.

• Hidrogeno atomoaren eta atomo hidrogenoideen (elektroi bakarrekoak) igorpen-espektroa azaldu zuen.

6.1. Bohrren postulatuak

Bohrren arrazoibidea postulatu hauetan jasota dago:

• Lehen postulatua: «Atomo batean, elektroiak nukleoaren inguruan biratzen dira, orbita zirkular geldikor jakin batzuetan, eta energia finko eta definituarekin; alegia, energia igorri eta xurgatu gabe». Orbita horiek mekanikoki egonkorrak dira, eta elektroiaren eta nukleoaren arteko interakzio elektrikoa, F e, higidura zirkularra eragiten duen indar zentripetua da, F z

Bazenekien…?

Niels Bohr (1885-1962) zientzialariak 1913ko apirilean argitara eman zuen lehen artikuluan, kuantizazioari buruzko Plancken ideiak sartu zituen, Balmerrek hidrogeno atomorako lortu zituen espektro-arau enpirikoak azaltzeko.

Adierazpen horietan, me = elektroiaren masa; 0 f  = hutserako konstante dielektrikoa; e = elektroiaren karga elektrikoa, eta K = Coulomben konstantea.

• Bigarren postulatua: «Orbitak posible izateko, elektroiaren momentu angeluarrak (L) h r 2 adierazpenaren multiplo osoa izan behar du».

L nh r 2 $ $ = mv r nh r 2 e $ $ =

Adierazpen horretan, L = elektroiaren momentu angeluarra; h = Plancken konstantea; n = zenbaki kuantikoa: 1, 2, 3…

• Hirugarren postulatua: «Atomoak energia igortzen du elektroi bat energia handiagoko orbita batetik energia txikiagoko orbita batera pasatzen denean; energia hori uhin elektromagnetiko gisa igortzen da, eta horren maiztasunak Plancken baldintza kuantikoa betetzen du»:

ΔE = Ea – Eh = h · f

Eta elektroia energia txikiagoko orbita batetik energia handiagoko batera igarotzen bada, elektroiak aldea xurgatu behar du (∆E  = h ∙ f ), erradiazio elektromagnetiko gisa, orobat.

Hala, Bohrrek espektro-lerroak azaldu zituen, Maxwellen elektromagnetismoak iragarritako erradiazio-continuumaren ordez.

Elektroiaren higidura, orbita zirkular geldikor batean.

Orbita baimenduen erradioak kalkulatzea

Lehen bi postulatuak kontuan izanik:

v bakanduko dugu eta [1] adierazpenean idatziko dugu, r bakantzeko:

Laburpena

Laburbilduz, esan daiteke elektroiak orbita zirkularretan antolatzen direla eta orbitek energia-mailak zehazten dituztela. Bohrren eredu atomikoak hidrogeno atomo baten orbita baimenduen erradioak aurreikusten ditu, bai eta elektroiaren energia eta abiadura ere orbita horietan.

Jakinik A konstante bat eta n = 1, 2, 3… direla, ikusten da erradioak ezin duela edozein balio hartu.

Elektroiaren energia kalkulatzea

Elektroiaren guztizko energia, E, haren energia potentzialaren (Ep) eta energia zinetikoaren (Ek) arteko batura da:

[1] adierazpenean, v 2 bakanduko dugu. Gero, [4] adierazpenean idatziko dugu, eta eragiketak egingo ditugu. Azkenean:

Orain, [3] adierazpeneko r-ren balioa [5] adierazpenean idatziko dugu, eragiketak egiteko:

A' konstante bat da.

Horrenbestez, Bohrren ereduaren arabera, elektroiaren guztizko energia negatiboa da, eta energia potentzialaren erdia da. Energia jakin batzuk soilik daude baimendurik, eta horiek zehazten dituen baldintza Bohrren zenbaki kuantikoa, n, da, edo zenbaki kuantiko nagusia.

Azken adierazpenak zeinu negatiboa du, eta horrek esan nahi du atomoaren energia txikiagoa dela nukleoak eta elektroiak bakoitzak bere aldetik dutena baino; hots, atomoa egonkorragoa da, osagaiak beren aldetik baino.

ΔE = E2 – E1 kalkulatzea

Bohrrek emandako hurrengo urratsa atomoa E1 energiako egoera geldikor batetik E2 energiako beste batera igarotzen denean erradiatutako energiari (∆E) erreparatzea izan zen.

Bohrren eredua betez, elektroi baten energia hau da:

Beraz, elektroia

1 orbitatik n2 orbitara igarotzen denean, hau dugu:

Hirugarren postulatuaren arabera, – EE Eh f 21 D ==  da.·Hortaz:

Igorritako energia: E3 – E1

Igorritako energia: E2 – E1

Xurgatutako energia: E2 – E1

Energia-mailen arteko trantsizio elektronikoak, Bohrren atomoan.

Badakigu f c m = dela, eta ekuazioan ordezkatuz, adierazpen hau lortuko dugu:

María Goeppert-Mayer

Ekuazio hori eta Ryderbergek hidrogeno atomoaren espektro-lerroetarako adierazitako ekuazioa berdin-berdinak dira, Z = 1 bada. Z-ren balio horretarako, k konstantea 1,0974 · 107 m −1 da. Balio hori bat dator Ryderbergek hidrogeno atomorako lortu zuen balio esperimentalarekin.

Bohrrek lortutako ekuazioak zehatz-mehatz aurreikusten ditu hidrogenoaren espektro-serieen uhin-zenbakiak (n1 eta n2-ri balioak emanez, hidrogenoaren serieen uhin-luzerak lortzen dira).

6.2. Oinarrizko energia-maila eta maila kitzikatuak

En-ren baliorik negatiboena elektroiaren energia minimoari dagokio, eta n = 1 denean lortzen da. Elektroia maila horretan dagoenean (nukleotik gertuen dagoen orbitan), egonkorragoa da, eta atomoa oinarrizko egoeran dago.

Atomoa gainerako energia-egoera posibleak (n = 2, 3…), berriz, egoera kitzikatuak dira.

Elektroiari ematen zaion energia nahikoa bada elektroia aske geratzeko (n = ∞), hidrogeno atomoa ionizatuta gelditzen da, prozesu honi jarraikiz:

HH e g E g ++ $ + ^^hh

Kasu horretan, oinarrizko egoerarekiko dagoen energia-aldea ionizazioenergia izango litzateke.

6.3. Bohrren ereduaren alde onak eta eragozpenak

Bohrren ereduan, alde on batzuek hainbat egitate justifikatzeko aukera eman zuten. Hauek dira:

• Hidrogenoaren espektro-lerroekin lotutako uhin-luzerak kalkulatzeko aukera ematen zuen.

• Atomoaren egonkortasuna justifikatzen zuen, orbita geldikorrak zeudela finkatuz.

• Halaber, orbiten erradioetarako eta energietarako balioak ondorioztatzeko aukera ematen zuen.

Baina berehala azaleratu ziren ereduaren mugak:

• Ezin ziren azaldu elektroi bat baino gehiago dituzten atomoen edo ioien espektroak (multielektronikoen espektroak).

• Ezin ziren hidrogenoaren espektroak azaldu, kanpoko eremu magnetikoak daudenean (Zeeman efektua).

Kanpoko eremu magnetiko bat aplikatzen zenean, hidrogeno atomoaren espektroko lerroetan desdoblamenduak izaten ziren.

• Elektroiaren higidura zehazteko ideia klasikoak eta ideia kuantikoak nahasten zituen.

Atomoetan elektroiek dituzten propietateak ezin ziren azaldu mekanika klasikoa baliatuz, Bohrrek egin zuen bezala.

Maria Goeppert-Mayer (1906-1972) Fisikako Nobel saria jaso zuen bigarren emakumea izan zen. 1963. urtean eman zioten, berak formulatutako atomoen geruza-ereduak, azkenean, atomoen nukleoak nola diharduen ulertzeko aukera ematen baitzuen.

14 Bohrren eredu atomikoarekin bat etorriz, hidrogeno atomoan, maila bakoitzean dagoen energia honela adierazten da: , eV E n 13 6 –2 = ^h

Kalkulatu zer balio iragartzen dituen Bohrren eredu atomikoak Balmerren seriean agertzen diren lehen hiru lerroen uhin-luzerarako.

Datua: eV 11,J 610 –19 =

15 Atomo bateko elektroi bat 5 eV-eko energia-maila batetik 3 eV-eko beste batera igaro da, eta, prozesuan, fotoi bat igorri da. Kalkulatu igorritako erradiazioaren maiztasuna eta uhin-luzera.

Datuak: c = 3 · 108 m · s –1 , e = 1,6 · 10−19 C; h = 6,63 · 10–34 J · s.

16 Kalkulatu, hidrogeno atomoan, elektroiaren erradioa eta abiadura, n = 2 orbitan (Bohrren eredu atomikoan) dagoenean. Horretarako, erabili aurreko ariketako datuak.

Ariketak

6.4. Bohr-Sommerfeld eredu atomikoa

Denboraren joanean, erabiltzen ziren espektrografoen sentikortasuna asko hobetu zenez, ikusi zen hidrogenoaren espektro-lerroetako batzuk, egiatan, bikoitzak edo hirukoitzak zirela. Era berean, ohartu ziren espektrolerroetan beste desdoblamendu batzuk agertzen zirela, dela kanpoko eremu magnetiko baten ekintzaren eraginez (Zeeman efektua), dela intentsitate handiko eremu elektriko baten eraginez (Stark efektua).

Egoera horietan, Bohrren eredua ez zen egitate esperimental berri horiek azaltzeko gauza, eta, beraz, ereduan aldaketak egin behar ziren, emaitza horiek azaldu ahal izateko.

Arnold Sommerfeld Bohrren eredua zabaltzen saiatu zen, aurrekoak baino bereizmen handiagoa zuten espektrografoekin lan egitean aurkitu zituzten espektro-lerro berriak azaltzeko. Sommerfeldek ildo horretan egindako lehen aldaketa izan zen elektroiaren orbitak eliptikoak izan zitezkeela jotzea.

Arnold J. W. Sommerfeld (18681951). Ez zuen Fisikako Nobel saria sekula jaso, baina, Municheko Unibertsitatean jardun zuen 32 urteetan, fisikari handien maisu izan zen. Haietako seik Fisikako Nobel saria jaso ere egin zuten: W. Heisenberg, W. Pauli, P. Debye, H. Bethe, L. Pauling eta I. Rabi izan ziren.

Elipse bat zehazteko, bi erradio behar dira. Hori dela eta, Sommerfeldek egindako zuzenketarekin beste bi zenbaki kuantiko sartu ziren, zeren, ordutik aurrera, orbiten forma eta orientazioa aintzakotzat hartu behar baitziren.

Horrenbestez, Bohr-Sommerfeld ereduak hiru zenbaki kuantiko berri erabiltzea zekarren, hautemandako desdoblamendu batzuk justifikatu ahal izateko. Hala eta guztiz ere, Sommerfelden eredua zabalduaren bidez ezin ziren azaldu espektroetan esperimentalki aurkitutako lerro guzti-guztiak.

4 Kalkulatu zer uhin-luzera duen hidrogeno atomoko elektroiak n = 5 mailatik n = 3 mailara jauzi egitean askatutako erradiazio elektromagnetikoak.

Datua: RH = 1,097 · 107 m –1

Ebazpena

Uhin-luzera kalkulatzeko, adierazpen hau erabiliko dugu:

Hemen, n1 = 3 eta n2 = 5 dira. Hortaz:

Beraz: , m m 1282 10 –6

Bazenekien...?

Niels Bohr daniarrak Nobel saria jaso zuen 1922an, egitura atomikoa ulertzeko egin zituen ekarpenengatik. Bohrrek 20 urte zituenean, Kopenhageko Akademisk Boldklub futbol-taldearen elastikoa jantzi izan zuen 1905eko denboraldian (Danimarkako klubik onenetakoa izan zen garai horretan). Zientzia futbola baino gehiago interesatzen zitzaionez, fulbolari-karrera laburra egin zuen.

Taldea uztea erabaki zuen, Alemaniako klub baten aurkako balentria gogoangarri baten ondoren. Bohrren taldeak jaun eta jabe ziharduen partidan, eta, aurkariek urruntze luzea egin eta gero, baloia astiro gerturatzen ari zitzaion Bohrrek zaintzen zuen ateari. Baloia aise gelditu beharrean, geldigeldi geratu zen ate erdian, zutoinetako bati begira, problema matematiko bat nola ebatzi pentsatzen ari zela, partidari inolako jaramonik egin gabe.

Arnold Johannes Wilhelm Sommerfeld

Ebatzitako ariketak

Mekanika kuantikoa

7.1. Schrödingerren eredua

Bohrren ereduak ez zuen elektroiei buruzko deskribapen egokia egiten. Horiek horrela, beste planteamendu bat bilatu behar izan zen, elektroien portaera eta energia deskribatzeko aukera ematen zuena.

1926an, Erwin Schrödinger austriar fisikariak (1897-1961), De Broglieren uhin-korpuskulu bitasuna abiapuntutzat hartuta, uhin-mekanika formulatu zuen. Uhin-mekanikaren oinarria elektroiaren uhin-izaera da. Elektroiak uhin baten modura jokatu badezake, ψ uhin-funtzio deritzon funtzio matematiko baten bidez deskribatu ahalko da. Uhin-funtzioa espazioan sistemak duen posizioaren mende dago.

Gaur egun onartuta dagoen eredu atomikoa mekanika kuantikoak proposatutakoa da: Schrödingerren eredua, hain zuzen ere.

Schrödingerren ekuazioa

Mekanika klasikoaren determinismoaren aldean, mekanika kuantikoa probabilistikoa da, eta haren formalismo matematikoa mekanika klasikoarena baino konplexuagoa da.

Uhin-mekanikan, Schrödingerren ekuazioaren soluzioak oinarri moduan erabiltzen dira, atomoa deskribatzeko:

ψ-ren adierazpenak

Schrödingerren ekuazioa honela adieraz daiteke:

edo honela: Hψ =  Eψ. Adierazpen horretan, H hamiltondar esaten zaion eragile matematiko bat da, eta E, maila baimenduetako energia.

Ekuazio hori erabiliz, sistema baten energiaren balioak kalkula daitezke.

Adierazpen horretan, m = elektroiaren masa; h = Plancken konstantea; E = elektroiaren guztizko energia; V = elektroiaren energia potentziala, posizioaren mende.

Schrödingerrena ekuazio diferentzial bat da, eta, hura ebatziz, zenbait soluzio lortzen dira. Horietako bakoitzak atomoko elektroien energia-egoera posible bat deskribatzen du.

Zenbaki kuantiko jakin batzuen balioak eta ekuazioak ezartzen dituen baldintzak jakin ahal izateko, hiru zenbaki behar dira: zenbaki kuantikoak. Aurrerago jorratuko ditugu.

Schrödingerren teoriarekin finkatuta geratu zen elektroiak ez direla orbitatan biratzen nukleoaren inguruan, Niels Bohrrek proposatu zuen bezala, baizik eta orbitaletan. Orbitalak nukleoaren inguruko espazioko guneak dira, elektroiak aurkitzeko probabilitate handia dagoen guneak.

Uhin-funtzioaren esanahia

Berez, ψ uhin-funtzioak ez du benetako esanahirik. Uhin-funtzioaren berbidura, ψ2, berriz, espazioko gune jakin batean elektroia aurkitzeko probabilitatearekin lotuta dago. Uhin-funtzioaren berbidurari elektroiaren probabilitate-dentsitate erlatibo esaten zaio.

Halatan, uler daiteke orbital bat elektroi baten uhin-funtzioa dela (ψ), eta uhin-funtzioaren berbidura (ψ2), berriz, nukleo atomikoaren inguruan elektroia aurkitzeko probabilitate handieneko gunea.

Sistema kuantiko bat ebatzita dagoela esaten da, haren ψ uhin-funtzioa ezaguna denean eta Schrödingerren ekuazioa ebazten denean.

uhin-funtzioa

ψ2 probabilitatedentsitatea

Probabilitate-dentsitatea

7.2. Uhin-korpuskulu bitasuna materiarako

Uhin-korpuskulu bitasuna argirako

Fisika klasikoaren testuinguruan, argiaren eredu korpuskularra eta uhineredua bateraezinak ziren. Fisika kuantikoaren esparruan, berriz, kontraesankorrak ziruditen bi portaerak eredu koherente batean bateratu ahal izan ziren.

Argiarekin lotutako fenomenoetan bi ereduak (korpuskularra eta uhinena) beharrezkoak zirela ondorioztatu zen. Horrek ez du esan nahi argia aldi berean bi gauzak denik, baizik eta argiaren portaera azaldu nahi dugunean, uhin-eredua erabili behar dugula zenbaitetan, eta eredu korpuskularra, beste batzuetan.

Argiaren izaera duala materiara hedatzea

De Broglieren hipotesia

Tradizioz, elektroiak partikulatzat hartu dira, eta, horrenbestez, elektroisorta bat eta uhin bat desberdinak izango lirateke.

Louis-Victor De Broglie fisikariak bereizketa hori baztertzea proposatu zuen, eta uhin-korpuskulu kontzepzioa partikula materialetara ere hedatu zuen; adibidez, elektroira. Funtsean, partikula-sorta bat eta uhin bat fenomeno bera dira; nolako esperimentua egiten den, partikula-sorta edo uhina ikusiko dugu, beraz. Hipotesi horrekin bat etorriz:

Higitzen ari den partikula orok uhin elektromagnetiko bat du lotuta, eta haren uhin-luzera honela adierazten da:

mv h Brogliem =

Adierazpen horretan, h = Plancken konstantea = 6,626 · 10−34 J · s; m = partikularen masa; v = partikularen abiadura.

Lege fisikoen elkarrekikotasuna oinarritzat hartuta, De Brogliek elektroiek uhin-izaera dutela iradoki zuen. Hartara, goiko adierazpenarekin, elektroi baten (uhin baten) λ uhin-luzera eta partikula baten p momentu lineala (m v) erlazionatu zituen. Ekuazio horri erreparatuta, kontuan izanik h zenbaki txiki-txiki bat dela, zenbat eta handiagoa izan partikularen masa, orduan eta laburragoa izango da uhin-luzera. Ostera, partikularen masa txiki-txikia bada (elektroiaren kasuan bezala), agerikoagoak dira uhin-propietateak (uhin-efektua gorputz txiki-txikietan soilik hauteman daiteke).

Argiaren izaera

Fisika modernoa sortu zenez geroztik, xvii. mendean, interpretatzea zaila izan den fenomeno bat agertu zen: argiaren izaera. Hari horretatik, Newtonen iritziz, argia korpuskuluz osatuta zegoen. Newtonek ez bezala, ordea, Huygensek uste zuen argia uhinez eginda zegoela.

2. taula. De Broglieren uhin-luzerak, partikula subatomiko batzuetarako eta, orobat, tamaina handiagoko beste objektu batzuetarako.

Elektroia uhin baten gisara

Louis-Victor De Broglie (1892-1987) xx  mendeko fisikari frantses bat izan zen, eta Fisikako Nobel saria jaso zuen 1929an, elektroiaren uhin-izaera aurkitzeagatik.

De Broglieren hipotesiaren ondorioak

• Elektroiak orbitatzen duenean, elektroiak uhin baten portaera duenez, λ uhin-luzerak orbitaren zirkunferentziarekin lotuta egon behar du.

• Elektroiak bere burua interferitzen duen uhin bat izan behar du. Uhinaren interferentzia eraikitzailea (erresonantzia) denean soilik izan daiteke egonkorra orbita elektronikoa.

Elektroiari dagokion orbitaren zirkunferentziaren luzerak De Broglieren uhin-luzeraren multiplo oso bat izan behar du. Hau da:

2 ∙ π ∙ r = n ∙ λ, eta n = 1, 2, 3…

Adierazpen horretan, zirkunferentziaren balio posibleetako batzuk baino ez dira zehazten. Era berean, elektroiaren momentu angeluarraren balio baimenduak ere deskribatzen dira.

Jakinik λ = mv h dela, eta, bestalde, 2 ∙ π ∙ r = n ∙ λ betetzen dela, konbinazioak emaitza hau du:

2 ∙ π ∙ r = n mv h $ $ ; mv r nh π 2 $$ = ; Lm vr nh π 2 $$ ==

Horrenbestez, bere bigarren postulatuan Bohrrek azaldutako kuantizaziobaldintza lortu dugu.

Clinton Davisson eta Lester Germer estatubatuar fisikariek De Broglieren hipotesia esperimentalki egiaztatu zuten 1927an, noiz eta elektroien difrakzioa ustekabean aurkitu zutenean.

Davissonen eta Germerren esperimentua

L. H. Davisson eta Germer elektroiak nola islatzen ziren aztertzen zebiltzan: huts-hodi baten barruan nikel metalikozko itu batekin talka egin ostean, nola islatzen ziren jakin nahi zuten. Halako batean, baina, hodia hondatu egin zen, eta, horregatik, oxidozko geruza bat jalki zen nikelaren gainean. Lagina salbatzeko, berriz berotu zuten, eta, orduan, gainazal kristalinoak eratu zituzten, nahi gabe. Ondoren, elektroiei behatu zietenean, harrituta ikusi zuten islatu ez ezik, elektroi-sorta difraktatu ere egiten zela (difrakzioa uhin-fenomeno bat da).

17 Bi partikulak energia zinetiko berdina dute. Kalkulatu, bi kasu hauetan:

a) Bi partikulei dagozkien De Broglieren uhinluzeren arteko erlazioa, masen arteko erlazioa

m1 = 50 m2 bada.

b) Zer erlazio dagoen abiaduren artean, De Broglieren uhin-luzeren arteko erlazioa hau baldin bada:

λ1 = 500 · λ2

18 Kalkulatu De Broglieren uhin-luzerak, eta energia zinetikoa, eV-etan adierazia: a) Elektroi batena, jakinda haren De Broglieren uhin-luzera eta 104 eV-eko energia-fotoi batek hutsean duen uhin-luzera berdinak direla; b) 80 g-ko masa duen harri batena, harria 2 m · s–1-ko abiaduran higitzen ari bada.

Datuak: h = 6,63 · 10−34 J · s, c = 3 · 108 m · s –1 , me = 9,1 · 10−31 kg, e = 1,6 · 10−19 C

Elektroien difrakzioa.

Ariketak

7.3. Heisenbergen ziurgabetasunaren printzipioa

Newtondar fisikaren arabera, neurketa batean erroreren bat egiten bada, arrazoia neurketa-tresnaren zehaztugabetasuna izango da. Hala bada, neurketa-tresna klasiko ideal bat erabiltzen denean, elektroi baten posizioa eta abiadura zehatz-mehatz lortu daitezke zirrikitu bikoitzaren esperimentuan, esate baterako. Werner Heisenbergek eta Niels Bohrrek zalantzan jarri zuten uste hori. Galdera hau jarri zegoen mahai gainean: zer neurritan zehaztu daitezke objektu kuantiko baten posizioa eta momentu lineala aldi berean?

Werner Heisenberg alemaniar fisikariak, 1927an, erantzuna eman zion galdera horri, ziurgabetasunaren printzipioa enuntziatuz. Printzipio horrek mugatu egin zuen objektu kuantiko bati buruz jakin dezakegun informazioa. Ziurgabetasunaren printzipioa honela adieraz daiteke:

Partikula baten posizioa eta higidura kantitatea ezin dira aldi berean eta zehaztasunez jakin. Posizioaren balioa zehaztasun handiz lortu bada, momentu linealaren neurketa oso zehaztugabea izango da, aldiz. Matematikoki:

Adierazpen horretan:

Δx: errorea, posizioa zehazteko garaian

Δp: errorea, momentu lineala zehazteko garaian

h: Plancken konstantea = 6,626 · 10–34 J · s

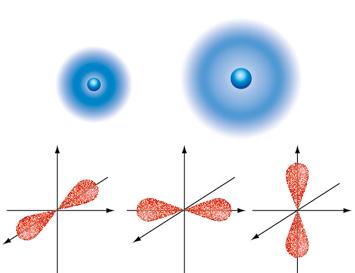
Adierazpen hori aztertuz gero, ikusten da zehaztugabetasun-maila eta Plancken konstantea erlazionatuta daudela. Horrek esan nahi du printzipio horrek partikula txiki-txikietan soilik duela eragina, partikulak h-ren balioarekin alderatzeko modukoak direnean soilik.

Ziurgabetasuna ez dago neurketa-tresnen zehaztasunarekin lotuta; aitzitik, neurtzeak ziurgabetasuna dakar berez. Maila atomikoan, magnitude fisikoen zehaztasunak funtsezko muga bat du.

Ordutik aurrera, maila atomikoari dagokionez, balio estatistikoez soilik jarduten da, eta, beraz, probabilitateez soilik.

Orbital atomikoa

Heisenbergek finkatutako zehaztugabetasun-erlazioak mekanika kuantiko

berriaren garapenaren emaitza dira. Ondoriorik nabariena da ezin dela elektroia atomoan zehatz-mehatz kokatu. Une jakin batean partikula batek dituen posizioa eta abiadura, bi-biak, ezin zehazteak ibilbidearen kontzeptua definitzea eragozten du; eta, horrenbestez, ez du zentzurik elektroiaren orbitez hitz egiteak.

Horregatik, orbitaren kontzeptuaren ordez, orbital atomikoarena sortu zen. Honela definitzen da orbital atomikoa:

Espazioko gune bat, non elektroia aurkitzeko probabilitate handia baitago (% 90etik gorakoa, hain zuzen ere).

Jarri arreta

Schrödingerren ekuazioak Heisenbergen ziurgabetasunaren printzipioa betetzen du: «ψ uhin-funtzioa ezagutzeak ez du sistemaren posizio zehatza jakiteko aukera ematen, nahiz eta berbidurak (ψ2) adierazten duen sistema espazioko gune jakin batean egoteko probabilitatea».

Heisenberg eta filosofia

Garaiko zientzia goitik behera aldatzeaz gain, W. Heisenbergen teoriek eragin handi-handia izan zuten mendebaldeko xx. mendeko pentsamendu filosofikoan.

Heisenbergen adibidea

Ziurgabetasunaren printzipioaren adibide moduan, Heisenbergek mikroskopio baten bereizmena aipatzen zuen. Demagun partikula bati beha gaudela, mikroskopioan. Argiak talka egiten du partikularen aurka, eta sakabanatu egiten da sistema optikoan. Mikroskopioaren bereizmena sistema optiko zehatz baterako mugatuta dago: erabiltzen den uhin-luzerak mugatzen du. Ezingo dugu partikula ikusi eta haren posizioa zehaztu uhinluzera hori baino distantzia laburrago batera. Horrenbestez, partikularen posizioa zehaztasun handiz finkatzeko, erabili beharreko uhin-luzerak partikula baino txikiagoa izan behar du.

Argiari ikuspegi korpuskularretik ere beha dakioke, fotoiz osatuta dagoela ulertuta. Aintzakotzat harturik fotoi baten momentua eta uhin-luzera alderantziz proportzionalak direla (mfotoia· vfotoia· = h / λfotoia), esan daiteke ezen, argiaren uhin-luzera zenbat eta txikiagoa izan, orduan eta handiagoa izango dela fotoien momentua. Halatan, uhin-luzera laburreko eta momentu lineal handiko fotoi batek mikroskopioan dagoen partikula batekin talka egiten badu, momentuaren zati bat partikulari transmitituko dio; horren ondorioz, higitu egingo da, eta ziurgabetasuna sortuko da, hain zuzen, momentu lineala jakiteko garaian (argiaren uhin-luzera zenbat eta txikiagoa, zer posizio duen hobeto jakingo dugu, baina abiaduraren balioa zehaztugabeagoa izango da).

Heisenbergen ustetan, objektu kuantiko baten x posizioaren eta p momentu linealaren balioak aldi berean jakitea ezinezkoa izateaz gain, ezinezkoa da aldi berean zehaztea objektu kuantiko baten E energiaren balio neurtua eta neurketa hori egiteko behar den denbora-tartea. Halaber, hau ere bete egin behar da:

Werner Karl Heisenberg

W. K. Heisenberg  (1901-1976)  fisikariak Fisikako Nobel saria jaso zuen 1932an. Hark adierazitako ziurgabetasunaren printzipioari jarraikiz, ezinezkoa da aldagai fisikoen hainbat pare (esate baterako, partikula baten posizioa eta momentua horietako bat da), aldi berean eta zehaztasunik handienez kalkulatzea. Heisenbergek ezarri zuen bezala, ziurgabetasun horien biderkadura ezin da sekula zero izan.

Adierazpen horretan:

ΔE: errorea, energia zehazteko garaian

Δt: errorea, denbora zehazteko garaian

h: Plancken konstantea = 6,626 · 10–34 J · s

5 Kalkulatu zer errore egin den elektroi baten posizioa neurtzean, jakinik haren abiadura v = 3,6 · 106 m · s –1 zela eta abiadura neurtzeko zehaztasuna % 1 izan dela. Ebazpena

19 Elektroi jakin baten posizioa 0,07Å-eko zehaztasunez jakin daiteke. Kalkulatu zenbat izan den ziurgabetasuna, elektroiaren abiadura neurtzean.

Orbital atomikoak. Zenbaki kuantikoak

8.1. Atomoaren eredu mekanokuantikoa. Orbital atomikoak

Mekanika kuantikoari jarraituz, alde batera utzi behar da elektroiak orbita erabat definituetan zehar dabiltzalako eredu atomikoa. Eredu mekanokuantikoan, ulertzen da elektroiaren higidura karga negatiboko hodei bat dela, nukleoaren inguruan dagoena. Hartan, elektroiak energia jakin bat du, eta hodeia trinkoagoa da elektroia aurkitzeko probabilitaterik handiena dagoen guneetan.

Elektroi-hodeiak ez ditu muga guztiz zehatzak. Hori dela eta, haren forma eta tamaina gutxi gorabehera irudikatzen dituen bolumen bat erabiltzen da, non elektroia aurkitzeko probabilitatea % 90 baino handiagoa den. Horrek orbital atomikoaren forma zehazten du.

Orbital atomiko batek energia bereizgarria du, eta dentsitate elektronikoa modu jakin batean banatuta, espazioan; horrek ematen dio, hain zuzen, orbitalari bere forma berezia.

8.2. Zenbaki kuantikoak

Schrödingerren ekuazioak soluzio infinituak ditu, eta haietako bakoitza hiru zenbaki kuantikorekin identifikatzen da. Atomoetan, elektroiak hiru dimentsioko espazioan zehar higitzen dira; hortaz, hiru zenbaki kuantikoren multzo bat behar da elektroia deskribatzeko. Hauek dira:

• Zenbaki kuantiko nagusia (n): elektroia zer energia-mailatan dagoen eta orbitala zer tamainatakoa den adierazten du. Zenbat eta handiagoa izan n, orduan eta energia handiagoa izango du elektroiak eta onduan eta urrutiago egongo da nukleotik; hots, egonkortasun txikiagoa izango du.

n zenbakiak balio oso eta positiboak soilik hartu ditzake: n = 1, 2, 3…

Atomo batean, n-ren balio bakoitzari energia-maila bat dagokio.

Energiarik txikiena n = 1 mailakoa da; egoera horri oinarrizko egoera esaten zaio. Halatan, n handitzen bada, orbitak irudikatzen dituzten hodeiak ere handitu egiten dira. Orduan, n-ren balioa handitu ahala, txikitu egiten da elektroia nukleotik gertu topatzeko probabilitatea.

Lehen maila izan ezik, gainerako maila guztiak azpimailatan banatzen dira.

• Zenbaki kuantiko sekundarioa edo momentu angeluarrarena (l): orbitek zer forma duten zehazten du, eta nolako energia-azpimailak egon daitezkeen n maila bakoitzerako. Azpimaila bateko orbital guztiek l zenbaki kuantiko bera dute, baita n zenbaki kuantiko nagusi bera ere. Zehatz-mehatz, n maila nagusi bakoitzean, n azpimaila daude.

l zenbakiak balio positiboak hartu ditzake: 0, 1, 2…, n − 1.

Orbitalen izena

Letra hauek esleitzen zaizkio l-ren balio bakoitzari (azpimaila mota):

l 0 1 2 3

Mota (azpimaila) s p d f

3. taula. Orbitalen izenak ingelesezko izenaren lehen letratik datoz: s: sharp, p: principal, d: diffuse, f: fundamental.

Azpimaila bat izendatzen denean, zenbaki kuantiko nagusia ere adierazten da. Adibidez: 2p azpimaila (n = 2, l = 1); 3d azpimaila (n = 3, l = 2), etab.

Kobrearen balentzia-orbitalak

• Zenbaki kuantiko magnetikoa (ml): zenbaki honek orbitalaren espazioorientazioa zehazten du. Espazioan zehar elektroiak egiten duen higidura orbitalaren norabidea deskribatzen du.

Magnetiko esaten zaio, espazio-orientazio hori kanpoko eremu magnetiko batekin erlazionaturik definitzen delako.

ml zenbaki kuantikoak balio hauek hartzen ditu: −l,…, 0,…, l.

Azpimaila bakoitzean zenbat orbital dauden adierazten du. Halatan, l-ren balio bakoitzerako, ml-ren (2 ∙  l + 1) balio oso daude. Hortaz, energiaazpimaila bakoitzaren barruan, (2 ∙ l + 1) orbital daude.

Horrenbestez, l = 2 bada, d motako orbitalak izango dira, eta ml-k balio hauek hartu ditzake: −2, −1, 0, 1, 2. Zehazki, egon daitezkeen bost d orbitalak dira horiek.

Hiru zenbaki kuantiko desberdinen multzo bakoitzak orbital bat definitzen du. n eta l-ren balio berak eta energia bera duten orbitalei orbital endekatu esaten zaie.

Schrödingerren ekuazioarekin ondorioztatutako zenbaki kuantikoek datu esperimental asko azaltzen dituzte, baina ezin dute azaldu zergatik duten desdoblamendua espektroko lerro batzuek, zenbaitetan.

• Spinaren zenbaki kuantiko magnetikoa (ms): atomo polielektronikoen igorpen-espektroen xehetasunak deskribatzen ditu. Zenbaki kuantiko berri horri spinaren zenbaki kuantiko magnetiko deritzo. Berez, spinaren zenbaki kuantikoak elektroiaren biraketa-noranzkoa adierazten du, bere ardatzaren inguruan biratu eta orbital baten baitan higitzen denean. Bi biraketa-noranzko besterik ez dagoenez,

ms zenbaki kuantikoak bi balio soilik hartu ditzake: –1 2 , 1 2 +

8.3. Orbital atomikoen forma eta tamaina

• s azpimaila (l =  0, ml = 0): s azpimaila batean, orbital bakarra dago. Zehazki, horrelako s orbitalek esfera-forma dute. Bestalde, s orbitalen muga-gainazalak esfera-forma du, elektroi-hodeiak esfera-forma baitu.

Orbitalaren tamaina zenbaki kuantiko nagusiaren mende dago; hala, 3s eta 2s orbital banak forma bera dute, baina lehenengoa handiagoa da bigarrena baino, eta, orobat, 2s orbital bat, 1s bat baino handiagoa (energia handiko s orbitalen muga-gainazalek diametro handiagoa dute).

ms-ren jatorria

Spinaren zenbaki kuantikoa 1925ean agertu zen: G. E. Uhlenbeck eta S. A. Goudsmit herbeheretarrek zenbaki hori zegoela postulatu zuten, Leydengo Unibertsitateko graduondoko ikasleak zirenean.

• p azpimaila (l = 1, ml = −1, 0, 1): p azpimaila bakoitzean, orientazio desberdineko hiru orbital daude: px, py , pz Forma, tamaina eta energia, aldiz, berdin-berdinak dira. Elkarren artean berdinak diren bi lobuluz eginda daude, eta ardatz batean zehar proiektatzen dira. Bi lobuluak elkartzen diren gunea bat dator nukleo atomikoarekin (bi lobuluen artean, plano nodala dago, eta nukleoa zeharkatzen du).

Chien-Shiung Wu

Chien-Shiung Wu (1912-1997). Txinan jaiotako estatubatuar fisikaria, xx. mendeko emakume zientzialari bikain izan zen. Wuren esperimentua egiteagatik da ospetsu, paritatearen kontserbazioaren lege hipotetikoarekin kontraesanean dagoen esperimentua.

Wuk Manhattan proiektuan lan egin zuen, eta, han, uranioa uranio-235 eta uranio-238 isotopoetan difusio gaseosoz bereizteko prozesuan aritu zen. AEBko Fisika Elkarteko presidente izandako lehen emakumea izan zen, 1975ean.

• d azpimaila (l = 2, ml = −2, −1, 0, 1, 2): d azpimaila bakoitzean orientazio desberdinak dituzten bost orbital daude: dz2, dx2 − y2 , dxy , dxz, dyz Berez, d orbital bakoitzean lau lobulu daude, dz2 orbitalean izan ezik.

• f azpimaila (l = 3, ml = −3, −2, −1, 0, 1, 2, 3): lobulu ugariko itxura dute. Zehatz-mehatz, zazpi f orbital mota daude.

20 Erantzun galdera hauei, eta arrazoitu erantzunak:

a) Zenbat orbital daude bigarren energia-mailan?

b) Zer gertatzen da azpimaila horietako energiarekin l zenbaki kuantiko sekundarioa handitu ahala, txikitu edo handitu egiten dira?

c) Zertan dira berdinak eta zertan desberdinak p orbitalak?

Hori guztia honela laburbil dezakegu:

• n zenbaki kuantikoko maila nagusi bakoitzean, n azpimaila daude, guztira.

• l zenbaki kuantikoko azpimaila bakoitzean, 2 ∙ l + 1 azpimaila daude, guztira.

• Orbital bakoitzean, kontrako spineko bi elektroi ere egon daitezke. Azpimaila batean, 2 · (2 ∙ l + 1) elektroi egon daitezke, gehienez.

• n zenbaki kuantikoko maila batean, n 2 orbital daude, guztira.

• n zenbaki kuantikoko maila batean, 2 · n 2 elektroi daude, guztira.

21 Erantzun galdera hauei, eta arrazoitu erantzunak:

a) Zenbat orbital daude, guztira n = 5 mailan?

b) Zenbat elektroi daude, guztira, n = 3 mailan?

c) Zenbat elektroik dituzte, gehienez, n = 4 eta l = 3 zenbaki kuantikoak?

Ariketak

8.4. Orbital atomikoen energia

Schrödingerren ekuazioa hidrogeno atomorako ebazten denean, ikusten da energia-maila bereko orbital guztiek energia-balio berbera dutela. Hots:

1s < 2s = 2p < 3s = 3p = 3d < 4s = 4p = 4d = 4f < … Energia

Atomo polielektronikoetan ez da gauza bera gertatzen. Haietan, beste faktore bat ere badago: elektroien arteko aldarapenak. Aldarapenaren ondorioz, elektroiak bata bestetik urrun egoten dira, eta ezegonkortasuna sortzen da. l zenbaki kuantiko sekundarioa zenbat eta handiagoa izan, orduan eta handiagoa da orbitalen energia. Beraz, nahiz eta hidrogeno atomoan energia n-ren mende soilik egon, atomo polielektronikoetan n-ren eta l-ren mende dago.

Orbital batek zenbat eta energia gutxiago izan, orduan eta egonkorragoa da. Elektroiek beren lekua hartzen dute orbitaletan, atomoaren energia ahal den txikiena izateko moduan.

Orbitalak betetzeko ordena zehatza esperimentu bidez finkatu zen. Honako hau da:

n + l erregela, orbital atomiko baten energiarako

Azpimailak zer ordenatan betetzen diren jakiteko, honi jarraituko diogu:

• Orbital atomikoen energia handitu egiten da n +  l batura handitu ahala. Hortaz, n +  l baturarik txikiena duen azpimaila betetzen da lehenik. Beraz, 4s azpimaila lehenago betetzen da (4 + 0 = 4) 3d azpimaila baino (3 + 2 = 5).

• Bi orbitalek n + l batura bera badute, n handieneko orbitalak izango du energia handiena. Hau da, n-rik txikiena duen orbitala beteko da lehenik. Horrenbestez, 3d lehenago beteko da (3 + 2 = 5) 4p baino (4 + 1 = 5).

Atomo jakin batean, elektroiak energia txikieneko orbitalak hartzen eta betetzen joaten dira. Horrelakoetan, oinarrizko egoeran daudela esaten da. Atomoak energia jasotzen badu, kanpo-kanpoko elektroietakoren batek energia handiagoko orbitaletara jauzi egin dezake, eta atomoa egoera kitzikatuan egongo litzateke.

8.5. Pauliren esklusio-printzipioa

Behaketa esperimentaletan oinarrituta, W. Paulik hau zehaztu zuen 1925ean:

Atomo berean ezin dira egon lau zenbaki kuantiko berdin-berdinak dituzten bi elektroi.

Ildo horretan, orbital bakoitzean gehienez bi elektroi egon daitezkeela ondorioztatzen da, kontrako spinekoak. Halaber, parekatuta egon behar dutela ere esaten da.

Pauliren esklusio-printzipioa abiapuntutzat harturik, maila batean zenbat elektroi egon daitezkeen ere jakin dezakegu. Maila jakin batean n 2 orbital egon badaitezke, 2 · n 2 elektroi besterik ezin da egon maila bakoitzean.

4 s 4 p 4 d 4 f

3s 3p 3d

2s 2p

1s

Orbital endekatuak hidrogeno atomoan.

5s 4 p 4 d

4s

3s

3p 3d

2s 2p

1s

Orbital atomikoen energia, atomo polielektronikoetan.

Neutrinoaren aurkikuntza

Wolfgang Pauli (1900-1958) suitzarrak sumoa zuen partikula neutro arin-arin bat zegoela (neutrinoa), ordura arte esperimentalki hauteman ez zena. Haren igorpena elektroiak beta desintegrazioan zuen igorpenarekin bat zetorren.

8.6. Hunden araua edo anizkoiztasunik handienaren printzipioa

1927an enuntziatu zen, eta hau dio:

Energia bereko orbitalak betetzen direnean (hiru p orbitalak, bost d orbitalak edo zazpi f orbitalak), ahal dela, elektroiak spinak paralelo dituztela banatzen dira; hots, desparekatuta.

Hunden araua elektroien arteko aldarapen-efektuarekin lotuta dago. Elektroien arteko aldarapena handiagoa da bi elektroiak orbital berean daudenean, orbital bereizitan daudenean baino. Azpimaila erdibeteek egonkortasun gehigarria izaten dute.

Notazio orbitala erabiltzen denean, orbitalak laukiz (edo marraz) irudikatzen dira, eta elektroiak, berriz, gezi bidez. Spinak paraleloak direnean, geziek noranzko berera begiratzen dute; eta spinak antiparaleloak badira, kontrako noranzkora. Adibidez:

Paramagnetismoaren erabilerak

Paramagnetismoaren erabilerarik garrantzitsuenetako bat, hain zuzen ere, elektroi-spinaren erresonantzia da (ESR). Espektroskopia-teknika bat da, eta horren bitartez, elektroi desparekatuak dituzten espezieak hauteman daitezke. Alor ugaritan erabil daiteke; besteak beste, hauek nabarmendu behar dira: erredox-prozesuak, erreakzio polimerikoak, geokronologia eta erreakzio entzimatikoak.

8.7. Diamagnetismoa eta paramagnetismoa

Substantzia bat paramagnetikoa dela esaten dugu, iman batek ahul erakartzen badu.

Paramagnetismoa momentu magnetiko iraunkorrak dituzten substantzien propietate bereizgarri bat da, eta atomo, ioi edo molekula batean elektroi desparekatuak izatearekin lotuta dago.

Hala oxigenoa eta fluorra, esate baterako, espezie paramagnetikoak dira.

22 Atomo batean, zenbaki kuantikoen multzo hauetako zein izango dira elektroi baterako ezinezkoak? (Ordena n, l, ml, ms da).

a) (4, 2, 0, 1/2), b) (3, 3, −3, −1/2), c) (2, 0, 1, 1/2), d) (4, 3, 0, 1/2), e) (3, 2, −2, −1).

23 Aztertu zenbaki kuantikoen multzo hauek:

(2, 2, 0, 1/2), (3, 1, −1, 1/2), (2, 0, 0, −1/2), (1, 0, 1, 1/2). Azaldu ea zenbaki kuantiko horiek dituzten elektroiak egon daitezkeen ala ez atomo batean. Zenbaki kuantiko posibleak diren multzoei dagokienez, adierazi zer orbitaletan egongo diren dagozkion elektroiak?

24 Idatzi elektroi bati dagokion zenbaki kuantikoen konbinazioa edo konbinazioak, orbitalak hauek baldin badira: a) 5p, b) 3d, c) 1s, d) 4f

Substantzia bat diamagnetikoa da, iman batek erakartzen ez badu (gerta daiteke zertxobait aldaratzea ere). Substantzia diamagnetikoetan, elektroi guztiak parekatuta daudenez, spin elektronikoen eraginak ezeztatu egiten dira. Berilioa eta neona, esaterako, espezie diamagnetikoak dira.

25 AOEL. Esan esaldi hauek zuzenak ala okerrak diren, eta eman arrazoiak: a) Atomo batean, n = 3 zenbaki kuantikoa duten elektroiak sei izan daitezke, gehienez; b) 2p orbital batean, elektroi bat eta sei elektroi artean egon daitezke.

Ariketak

8 Orbital atomikoak. Zenbaki kuantikoak

Partikula subatomikoak. Unibertsoaren jatorria

9.1. Partikula subatomikoak. Oinarrizko partikulak

Partikulen fisikari eta azeleragailuei esker, atomoak baino txikiagoak diren partikula asko hauteman dira gaur egun. Horren ondorioz, partikulen zoo moduko bat eratu dela esaten da. Edonola ere den, zein dira oinarrizko partikulak?

Oinarrizko partikula esango diegu barneko egiturarik ez duten partikulei, eta, horrenbestez, barnean beste partikularik ez dutenei.

Batez besteko atomoa (1Å = 10−10m) baino txikiagoak diren partikulak eta, aldi berean, oinarrizkoak ez direnak, subatomikoak dira. Esate baterako, protoia partikula subatomiko bat da; baina ez da oinarrizkoa, hiru quarkez eginda dago eta (bi up eta down bat).

Angstrom bateko distantziara, ikusten da atomoa elektroiez eta nukleoaz osatuta dagoela; 10−15 m-ko distantziara (unitate hori fermia da, 1 fm = 10−15 m), protoiak eta neutroiak ikusten dira nukleoan; eta 10−19 m-ko distantziara, quarkak bereiz daitezke, oinarrizko osagaiak baitira.

Eskuarki, partikula subatomikoak honako lau talde handi hauetan sailkatzen dira:

• Hadroiak: interakzio bortitzak izaten dituzten partikulak dira; esate baterako, protoiak eta neutroiak. Zehazki, hadroiak barioiak edo mesoiak izan daitezke.

• Leptoiak: ez dute interakzio bortitzetan parte hartzen; elektroia horrelakoa da. Oinarrizko partikulak dira.

• Kuantu interakzio-bitartekariak: esate baterako, fotoia. Oinarrizko partikulak dira.

• Quarkak: sei quark mota daude. Oinarrizko partikulak dira, eta hadronikoak.

Ezagutzen diren partikula subatomiko guztiek funtsezko propietate berri bat dute: estatistika. Propietate hori honelako sistemetan soilik adierazten da: bi partikula edo gehiagokoetan, bata bestetik oso urrun ez badaude eta berdin-berdinak badira; alegia, propietate guztiak (masa, spina, etab.) berdinak dituzten sistemetan. Partikula bakoitzaren estatistika nolakoa den, Fermiren estatistika betetzen dutenak fermioiak dira, eta Pauliren esklusio-printzipioa ere betetzen dute. Gainerako guztiak bosoiak dira, eta Boseren estatistika betetzen dute.

Atomoa ~1Å (10−10 m)

Elektroia < 10−18 m

Protoia Neutroia

Nukleoa ~ 10−14 m

Quarka ~ 10−19 m

Protoia ~1fm (10−15 m)

Pentaquarkaren aurkikuntza

Fermioiak (spin erdiosoa) Partikula materialak

Bosoiak (spin osoa) Indarpartikulak

1. familia

2. familia

3. familia

fotoia (indar elektromagnetikoa)

leptoiak aske desplaza daitezke

elektroia muoia tauoia

elektroiaren neutrinoa muoiaren neutrinoa tauoiaren neutrinoa

grabitoia (interakzio grabitatorioa)

OINARRIZKO PARTIKULAK Higgs bosoia

gluoia (interakzio bortitza)

quarkak ez dira bakarka ikusten Partikula handiagoen (hadroien) parte dira

d quarka s quarka b quarka

u quarka c quarka t quarka

W eta Z bosoiak W+, W–, Z0 (interakzio ahula)

CERNeko hadroi-talkagailuan, LHCb esperimentu batekin aditzera eman zen, 2015eko uztailaren 14an, partikula berri bat aurkitu zela: pentaquarka. Ordura arte, jakina zen quarkak ez zeudela isolaturik naturan, baizik eta bi quarkeko (mesoiak) eta hiru quarkeko (barioiak) multzotan zeudela. Alabaina, fisikariek bost quarkeko formazioak zeudela postulatzen zuten, zeinek partikula subatomiko berri bat eratu baitzezaketen: pentaquarka, hain zuzen ere

Partikula batek spin erdiosoa badu (s = 1/2, 3/2, 5/2…), fermioi batek bezala jokatzen du. Partikula batek spin osoa badu (s = 0, 1, 2…), berriz, bosoi batek bezala jokatzen du.

Paul Dirac zientzialariak, 1930ean, hipotesi hau teorikoki justifikatu zuen: m masako, s spineko eta q karga elektrikoko oinarrizko partikula bat badago, beste bat ere egongo da, lehenengoaren antipartikula deritzona, masa eta spin berdinekin eta kontrako karga elektrikoarekin: −q. Hipotesi hori modu esperimentalean berretsi zen positroia aurkitu zutenean (elektroiaren antipartikula da).

Halaber, + eta muoiak elkarren antipartikula gisa identifikatu zituzten, eta + eta − pioiak ere bai.

9.2. Masa eta karga elektrikoa

• Partikula subatomikoen lehen propietatea masa da (pausaguneko masa). Txiki-txikia izaten denez, gramoa eta kilogramoa ez diren masaunitateak erabili behar dira.

Bestalde, E = m · c2 ekuazio erlatibista kontuan hartuta, masa energiaunitatetan ere defini daiteke. Esate baterako, pausagunean dagoen elektroi baten energia 0,512 MeV da (1eV = 1,6 · 10−19 J), eta elektroiaren masa, beraz, 0,512 MeV/c2, jakinik c = 3 · 108 m · s –1 dela.

• Bigarren propietatea karga da. Partikula subatomikoen karga elektrikoen magnitudea eta elektroiarena berdinak dira, zeinu berarekin edo kontrakoarekin, edo neutroak ere izan daitezke. Quark deritzen oinarrizko partikulek zatikizko karga elektrikoak dituzte.

9.3. Partikulak, eredu estandarrarekin bat etorriz

Funtsean, esan daiteke eredu estandarra oinarrizko partikulak eta haien interakzioak identifikatzen dituen teoria bat dela. Eredu horri jarraituz, gaurdaino partikula-azeleragailuetan edo izpi kosmikoetan hauteman diren oinarrizko partikulen kopuru itzela (300 inguru) honela sailka daitezke: leptoi, hadroi eta quark multzoetan.

Zehazki, sailkapena hau da:

• Leptoiak. Haien propietateak karga elektrikoa, masa, spina, batez besteko bizitza eta zenbaki leptonikoa dira. Masaren, spinaren eta batez besteko bizitzaren balioak berdinak dira partikuletan eta antipartikuletan, baina karga elektrikoak eta zenbaki leptonikoak kontrako balioak dituzte. Kategoria honetan, honako hauek daude: elektroia, elektroiaren neutrinoa, muoia, muoiaren neutrinoa, tauoia eta tauoiaren neutrinoa.

• Hadroiak. Barioiak edo mesoiak izan daitezke. Barioirik ezagunenak protoia (hiru quarkez osatua: bi up eta down bat) eta neutroia dira (hiru quarkez osatua: bi down eta up bat). Mesoirik ezagunenak π+ eta π− pioiak dira. Oinarrizko partikula deritzen gehienak hadroiak dira, eta hiru quarkez edo hiru antiquarkez (barioiak) osatuta daude, edo quark batez eta antiquark batez (mesoiak).

• Quarkak. Sei quark ezagutzen dira: up (u), down (d), strange (s), charm (c), bottom (b) eta top (t). Quarken ezaugarri berezi bat da zatikizko karga elektrikoa dutela. Zehazki, quark mota batzuena (+2/3 e) da, eta beste batzuena, (−1/3 e).

Antimateria naturan

Naturan, antimateria oso muturreko fenomenoetan eratzen da; adibidez, neutroien izarretan, Lurra inguratzen duten Van Allenen gerrikoetan eta zulo beltzetan sortzen diren energiaagerraldietan.

Alabaina, sekula ez dira quark askeak hauteman, hadroietan konfinatuta daude beti. Hala, hadroi jakin bat osatzen duten quarken kargen batura aljebraikoa e-ren multiplo oso bat da beti. Adibidez, protoia (+2/3 e) karga duten bi quarkez eta (−1/3 e) karga duen quark batez eginda dago. Hala, protoiaren karga (2/3 + 2/3 −1/3) e da, edo, besterik gabe, e Kromodinamika kuantikoan (quarken teoria) debekatuta dago hiru quarkekoa, hiru antiquarkekoa edo quark-antiquark pare batekoa baino egitura konplexuagoa duten partikulak egotea. Hala eta guztiz ere, duela gutxi, fisikari esperimentalek bost quarkeko partikulak daudelako frogak aurkeztu dituzte. Pentaquarkak dira (lau quarkez eta antiquark batez osatuak).

9.4. Unibertsoaren jatorria

Kosmologian, Big Bangaren edo Leherketa Handiaren teoria eredu zientifiko bat da, unibertsoaren jatorria eta ondoko garapena azaltzeko helburua duena, espazio-denbora singularitate batetik abiatuta.

Big Banga da materia guztia ezerezetik sortu zen unea. Ordura arte (duela 14 000 milioi urte, gutxi gorabehera), materia oso dentsitate handiko puntu bat zen, eta une jakin batean eztanda egin zuen. Eztandaren eraginez, materia norabide guztietan hedatu zen, eta unibertsoa sortu zen (teoria horren arabera, unibertsoa abiadura bizi-bizian hedatu zen Big Bangaren osteko segundo baten trilioiren batean).

Big Bangaren teoriaren baitan, beste teoria batzuk ere badaude; besteak beste, Einsteinen erlatibitateari buruzko teoria eta oinarrizko partikulen teoria estandarra.

Egun abian diren ikerlanen helburuetako bat da jakitea ea unibertsoak hedatzen jarraituko duen edo, aitzitik, noizbait kolapsatu egingo den eta, beraz, Big Cruncha gertatuko den.

Belgikako Georges Lemaître apaizak Big Bangaren teoria iradoki zuen 20ko hamarkadan, estreinakoz. Ideia hori sinesgarritasuna irabazten joan zen denbora igaro ahala, zeren, izan ere, Hubblek galaxiei behatu baitzien gugandik urruntzen abiadura bizian, norabide guztietan, eta Robert Wilsonek, berriz, mikrouhinen erradiazio kosmikoa aurkitu baitzuen.

Big Bangaren teoriaren jatorria

CERNen egindako ALPHA esperimentuan, antihidrogeno atomoak ekoitzi eta harrapatu ahal izan ziren 2011n, hura aztertzeko behar bezainbesteko denboraz.

KULTURA ZIENTIFIKOA

LHCa ezagutzea

Gaur egun, LHCa (Large Hadron Collider) munduko partikula-azeleragailurik handiena da, eta garrantzitsuena, ikuspegi esperimentaletik. CERNen dago, Suitzako Geneva hirian. Azeleragailu horretan, partikula subatomikoek elkarrekin talka egin dezaten eragiten da, ibilbideko puntu jakin batzuetan. Puntu horietan, lau detektagailu handi daude: CMS, ATLAS, ALICE eta LHCb. Detektagailu horietan, talken ondoriozko partikulak erregistratzen dira, unibertsoa osatzen duen materiaren elementuak aztertze aldera.

LHCa eraztun moduko bat da, 26 659 metro luzekoa, eta lurpean dago, 100 metroko sakoneran. Gizakiok orain arte eraikitako gailurik konplexuenetako bat da. 9 300 iman supereroalez eginda dago, eta ezinbestekoak dira partikula sortek (gehienak protoiak dira) argiaren abiaduraren % 99,9999991n bidaiatzeko. Hala, segundoan 11 245 bider egiten dute zirkunferentzia osoa. Imanak hoztu egiten dira, −271,3 ºC-an egoteko (1,9 K inguru); tenperatura hori lortzeko, helio superfluidoa zirkularazten da eraztunaren inguruan.

LHCaren barruko presioa 10−3 atmosfera da; hau da, hutsik handieneko lekua da eguzki-sistema oso-osoan. Azeleragailuaren barnean presio hori behar da, partikulek ez dezaten gas molekulekin talka egin. Partikula-sortek huts ultrahandian bidaiatu behar dute, izarrarteko espazioko hutsean baleude bezala.

LHB detektagailua

Genevako aintzira

ATLAS detektagailua

ALICE detektagailua

Higgsen eremuarekin lotuta dagoen partikula da. Espazioan zehar hedatzen den continuum moduko bat da eremu hori, eta Higgs bosoiz osatuta dago.

Partikulen masa Higgsen eremuarekin sortzen den marruskadurak eragingo luke. Hala, eremu horrekin marruskadurarik handiena duten partikulen masa besteena baino handiagoa izango da. Partikula berri horren masa protoiarena baino 134 bider handiagoa da, eta bosoi esaten zaio.

Masarik ez Energia handia

CMS detektagailua

LHCaren eraztuna

Partikula azeleragailua

SPS

Partikulak abiadura jakin batean injektatzen dira zirkuituan, eta gero azeleratze-egituretara abiatzen dira; SPSra, adibidez. Abiadura egokia lortu dutenean, LHCrantz desbideratzen dira, eta, han, talkak eragiten dira puntu jakin batzuetan (detektagailuak dauden lekuetan), kontrako noranzkoan dabiltzan partikulen aurka. LHCan, 2010eko martxoan, partikulen arteko 7 TeV-eko talka-energia lortu zen, horrelako esperimentu batean ordura arte erregistratu izan zen handiena.

Zer da Higgs bosoia?

Higgs bosoia oinarrizko partikula mota bat da, eta haren zeregina funtsezkoa da unibertsoan masa esleitzeko mekanismoan.

Fotoia

Higgsen eremua

Masarik ez Energia handia

Elektroia

Higgs bosoia Quarka

Masaduna Energia txikia

Partikulen fisikako eredu estandarrak iragarritako partikula guztien artean, Higgs bosoia aurkitu gabeko bakarra zen, ezin baitzen zuzenean hauteman, azkar-azkar desintegratzen zelako. Partikula-azeleragailuetan sortu behar zen bosoia, eta desintegrazioaren ondoriozko partikulekin berreraiki. Haatik, dena errotik aldatu zen 2012ko uztailaren 4an: mende-erdia iraun duen bilaketaren ondoren, LHCko CMS eta ATLAS esperimentuetan Higgs bosoia aurkitu zutela aditzera eman zen (partikula hori zegoela 60ko hamarkadan postulatu zuten Peter Higgs britainiarrak eta François Englert belgikarrak).

Eredu estandarrean, oinarrizko partikulak eta haien interakzioak deskribatu ziren, baina ez zen azalpenik ematen oinarrizko partikulen masaren jatorriari buruz. Higgs bosoia aurkitu denez geroztik, galdera horri erantzun ahal izango zaio datozen urteotan.

Jarduerak

Testua irakurri eta gero:

1 Bilatu LHCko CMS eta ATLAS detektagailuei buruzko informazioa.

2 Aipatu CERNen egin diren aurkikuntzarik garrantzitsuenetako batzuk.

3 Bilatu Peter Higgsi eta François Englerti buruzko informazioa, eta aipatu zientziari egin dizkioten ekarpenik handienak.

4 Prestatu aurkezpen digital bat oinarrizko partikula horren funtsezko propietateei eta fisikan duen eraginari buruz.

LHCa eta Higgs bosoia

Efektu fotoelektrikoa H. Hertzek aurkitu zuen 1887an. Metal jakin batzuek argiztatzen direnean elektroiak igortzeari deritzo efektua. 1905ean, A. Einsteinek efektu fotoelektrikoa azaldu ahal izan zuen, Plancken hipotesian oinarriturik. Atal honetan, doako simulagailu bat baliatuko dugu efektu fotoelektrikoa aztertzeko, eta, beraz, fenomeno

horri buruzko ondorioak berresteko. Tresna horren bidez azaldu daiteke nolako eragina duten erradiazio erasotzailearen uhin-luzerak eta argiaren intentsitateak metal baten gainazaletik elektroiak erauzteko ahalmenean. Oso aplikazio erabilgarria da efektu horrekin lotuta dauden oinarrizko parametroak aztertzeko.

Lehenik, joan simulagailuaren web-orrira. http://www.varga.org/recursos-educativos/efecto-fotoelectrico/index.html

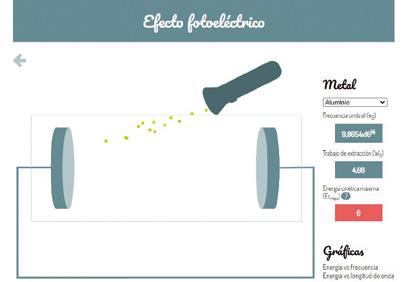
Gaztelaniaz dago, eta efektu fotoelektrikoaren azterketan giltzarri diren hainbat magnituderekin lan egiteko aukera ematen du. Halaber, energia irudikatzeko grafikoak egin daitezke, maiztasunaren edo uhin-luzeraren funtzio gisa.

Amaitzeko, simulazio osoa egin ahal izateko, argi-sortaren intentsitatea finkatu behar dugu, baita gainazal metalikotik erauzitako fotoelektroiak gelditzeko beharrezkoa den balaztatze-potentziala ere.

Erradiazio erasotzailea katodoaren gainazal metalikora bideratuko dugu, eta, gainazala hautatzeko, metalaren menu zabalgarria klikatu behar da. Simulazio horrekin, gainazal sorta handia dago aukeran (aluminioa, kobrea, kobaltoa... guztira, hogeita bi metal dira).

Metala hautatutakoan, aplikazioak berez finkatzen ditu atarimaiztasuna (f0) eta aukeratu den gainazalarekin loturik dagoen erauzketa-lana (We).

Era berean, kurtsorearekin, erradiazioaren uhin-luzera (λ) hauta dezakegu, metalari erasoko zaion erradiazioaren uhinluzera. Aldi berean, fotoi erasotzaileak zer energia duen jakiteko aukera ere ematen digu (E = h · f).

Beraz, esate baterako, eman dezagun hautatzen dugun gainazal metalikoa sodioa dela. Hartara, aplikazioak atarimaiztasuna (f0) eta erauzketa-lana (We) finkatuko ditu: 5,51 · 1014 s –1 eta 2,28 eV, hurrenez hurren.

Ondoren, gainazala argiztatzeko erradiazio erasotzailearen uhin-luzera λ = 645 nm izanik, ez dugu lortu elektroirik erauztea (erradiazioarekin lotutako energia erauzketa-lana baino txikiagoa da). Ostera, erradiazio erasotzailearen uhin-luzera λ = 400 nm bada, gainazaletik elektroiak erauztea lortuko dugu (erradiazioarekin lotutako energia erauzketa-lana baino handiagoa da).

1 Erantzun galdera hauei, ikusi dugun simulazioa erabiliz: a) Zer gertatzen da fotoelektroien energia zinetikoarekin, metal jakin bati erasotzen dion erradiazioaren maiztasuna hasierakoa halako bi denean?

b) Metal bat argi gorriarekin erradiatzean (682 nm), efektu fotoelektrikoa gertatzen da; zer gertatuko da, ordea, metal bera argi horiarekin (570 nm) erradiatzen bada?

Jarduerak

Efektu fotoelektrikoaren simulagailua

Efektu fotoelektrikoa aztertzea

Problemak ebazteko estrategiak

Erauzketa-lana eta fotoelektroien energia zinetiko maximoa kalkulatzea

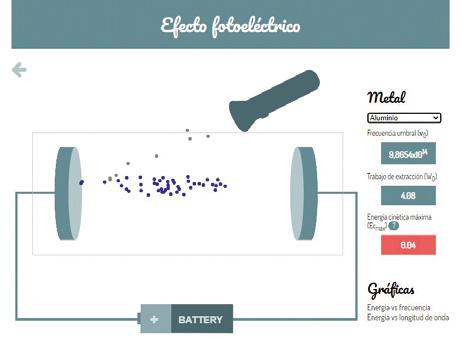
1 Siliziozko xafla bat 1,09 · 10–6 m baino gehiagoko uhin-luzera duen argi batekin argiztatzean, efektu fotoelektrikoa gelditu egiten da. Kalkulatu, arrazoiak emanez, silizioaren atari-maiztasuna, erauzketa-lana eta igorritako fotoelektroien energia zinetiko maximoa, siliziozko xafla bat 2,5 · 10–7 m-ko argi ultramorearekin argiztatzen denean.

Datuak: 6,63 · 10–34J · s , c = 3 · 108 m.s –1

Planteamendua eta ebazpena

Silizioaren atariko uhin-luzera erabilita (λ0 = 1,09 · 10–6 m), atari-maiztasuna kalkulatuko dugu:

PROBLEMAREN AZTERKETA

Fotoi baten energia erradiazioaren maiztasunaren mende dago (E= h · f). Fotoiak metalaren elektroi bati erasotzen dionean, bere energia ematen dio. Erradiazio erasotzailearen maiztasuna txikiagoa bada atari-maiztasuna baino, ez da efektu fotoelektrikoa gertatuko.

Erradiazio erasotzailearen maiztasuna handituko bagenu, igorritako fotoelektroi kopurua ez litzateke aldatuko, baina haietako bakoitzaren energia bai (elektroia bizkorrago irtengo da):

Ek = h · (f – f0)

1 –

f0 =  c 0m  =  ,· ms m 310 10910 8 6

– = 2,75 · 1014 s –1

Silizioaren atari-maiztasunaren balioa erradiazio erasotzailearen gutxieneko maiztasuna da, efektu fotoelektrikoa gertatu ahal izateko.

Atari-maiztasuna jakinda, silizioaren erauzketa-lana kalkula dezakegu, adierazpen honekin:

We = h · f0

We = 2,75 · 1014 s–1 · 6,63 · 10–34 J · s = 1,82 · 10–19 J

Orain, xafla λ = 2,5 · 10–7 m-ko uhin-luzera duen argi ultramorearekin argiztatzean igortzen diren fotoelektroien energia zinetiko maximoa kalkulatuko dugu. Horretarako, fotoi erasotzaileen energia kalkulatu behar dugu lehenik:

E = h · f  = h ·  c m  = 6,63 · 10–34 J · s  ·  ,m ms 25 10 310 7

Aldiz, erradiazio erasotzailearen intentsitatea handitzen badugu, fotoi erasotzaile gehiago egongo lirateke, eta, horrenbestez, metalak fotoelektroi gehiago igorriko lituzke, energia zinetiko maximo berarekin.

EMAITZEN EZTABAIDA

Emaitza zuzena dela egiaztatze aldera, alderantzizko bidea egin daiteke, eta, orduan, silizioaren erauzketalana eta igorritako fotoelektroien energia zinetiko maximoa erabilita, erradiazio erasotzailearen uhinluzera kalkulatu.

Problemaren garapenean, zifra esanguratsuen kopurua kontuan hartu behar da, kalkuluak ongi egiteko eta emaitza ahalik eta hurbilena izateko.

81 –

–= = 7,96 · 10–19 J

Jarraian, efektu fotoelektrikoaren oinarrizko ekuazioarekin, energia zinetiko maximoa kalkulatuko dugu:

E = We + Ek; Ek = E – We = 7,96 · 10–19 J – 1,82 · 10–19

Ek = 6,14 · 10–19 J

Ibili erne unitateekin, sistema berbera erabili behar duzu eta. Alegia, eman dezagun balio hau erabili duzula: h = 6,63 · 10–34 J · s. Kasu horretan, energia jouletan adierazi behar da, eta, maiztasuna, berriz, s–1-etan.

Efektu fotoelektrikoa gertatu ahal izateko, sorta erasotzailearen energiak handiagoa izan behar du metalaren xaflarekin lotutako erauzketa-lana baino, edo, gutxienez, horren berdina.

Hidrogeno atomoaren espektroarekin lotutako kalkuluak

2 Kalkulatu hidrogenoaren espektroko erradiazio xurgatuaren uhin-luzerarik txikiena, nm-tan.

Datuak: RH = 1,097∙ 107 m –1

Planteamendua eta ebazpena

Kasu honetan, uhin-luzerarik txikiena hidrogenoaren espektroko energia xurgaturik handienari dagokio (magnitude horiek alderantziz proportzionalak dira).

Uhin-luzerarik txikiena kalkulatzeko, J. R. Rydbergek 1889an adierazitako formula orokorra erabiliko dugu:

m 1  = RH ∙  nm 11 –22 dd d nn n

Hala, RH-ren balioa idatziko dugu, eta kontuan hartuko dugu n = 1 eta m = ∞ direla. Emaitza hau da, beraz:

m 1  = 1,097 ∙ 107 m –1  ∙  1 11 –22 3 dd c n m n

λ = 9,115 ∙ 10–8 m

Orain, uhin-luzera nm-tan adierazi behar dugu, dagozkion bihurketa-faktoreak aintzakotzat hartuta:

λ = 9,115 ∙ 10–8 m ∙  10 m nm 1 –9  = 91,15 nm

3 Aztertu zenbaki kuantikoen multzo hauek: (4,2,0,1/2), (3,3,2,-1/2), (2,0,1,1/2), (2,0,0,-1/2). Multzo horiek kontuan hartuta, erantzun galdera hauei:

a) Esan zein multzo diren posible eta zein ez, atomo batean dagoen elektroi baterako.

b) Konbinazio zuzenetan, adierazi zer orbitaletan dagoen elektroia.

c) Ordenatu energiaren arabera aurreko ataleko orbitalak, txikiena duenetik handiena duenera, eta arrazoitu erantzuna.

Planteamendua eta ebazpena

a) Ezin da inoiz gertatu l zenbaki kuantikoaren balioa eta n zenbaki kuantikoarena bat etortzea. Horrek esan nahi du (3,3,2,1/2) kasua ezin dela izan. Bestalde, ml zenbaki kuantiko magnetikoa ezin da sekula izan l zenbaki kuantiko orbitala baino handiagoa. Beraz, (2,0,1,1/2) kasua ere ezinezkoa da. Ostera, (4,2,0,1/2) eta (2,0,0,-1/2) kasuetan, zenbaki kuantikoen balioak bat datoz atomo batean dagoen elektroi batek hartu ditzakeen balioekin; hortaz, posibleak dira.

b) Zenbaki kuantikoen (4,2,0,1/2) multzoa 4d orbital bati dagokio. Bestalde, zenbaki kuantikoen (2,0,0,-1/2) multzoa 2s orbital batena da

c) Atomo polielektronikoetan, elektroi bakoitzaren energia elektroia dagoen orbitalaren tamainaren mende dago, baita n zenbaki kuantiko nagusiaren eta ml zenbaki kuantikoak dakarren orbital-formaren mende ere. Orbitalen ordena hau izango da, energia txikienetik handienera: 2s < 4d

PROBLEMAREN AZTERKETA

Atomoetan, elektroiak hiru dimentsioko espazioan higitzen dira; horren ondorioz, hiru zenbaki kuantikoko multzo bat behar da elektroia deskribatzeko. Orbital atomiko batek energia bereizgarria du; eta elektroien dentsitatea ere modu jakin batean banatzen da espazioan, eta bere forma berezia ematen dio. Hiru zenbaki kuantiko desberdineko multzo bakoitzak orbital bat zehazten du.

Atomo polielektronikoetan, elektroien arteko aldarapenek elektroiak elkarrengandik urrun egotea eragiten dute, eta ezegonkortasuna sortzen da. Orbitalen energia handitu egiten da l zenbaki kuantiko sekundarioa handitu ahala. Orbital baten energia-edukia zenbat eta txikiagoa izan, orduan eta egonkorragoa da.

EMAITZEN EZTABAIDA

Emaitzak zuzenak diren jakiteko, gogoan izan behar dugu zenbaki kuantiko bakoitzak zer balio hartu ditzakeen (bilatu unitatean, gogoratzen ez badituzu).

Orbital batek zenbat energia txikiagoa izan, orduan eta egonkorragoa da. Elektroiak lekua hartzen joaten dira orbitaletan, atomoaren energia ahalik eta txikiena izateko moduan.

4 Erantzun, eta arrazoitu erantzuna.

a) Zenbat orbital daude n = 2 energia-mailan?

b) Gehienez, zenbat elektroi egon daitezke n = 3 energia-mailan?

c) Zertan dira berdinak eta desberdinak 3px, 3py eta 3pz orbitalak?

Planteamendua eta ebazpena

a) Kalkulatuko dugu zenbat orbital dauden n = 2 mailan, aintzakotzat harturik ezen, l zenbaki kuantikoaren balio bakoitzerako, ml-ren (2 ∙ l  + 1) balio oso daudela. Horren ondorioz, energia-azpimaila bakoitzean (2 ∙ l  + 1) orbital daude.

Orduan, n = 2 denean:

n = 2 → l = 0, l = 1

• l = 1 → 2 ∙ l + 1 = 2 ∙ 1 + 1 = 3 orbital (2px, 2py; 2pz)

Hala, n = 2 mailan lau orbital egongo dira.

b) n zenbaki kuantikoko maila batean, elektroi kopuru osoa hau da: 2∙n 2

Hartara, n = 3 denean, elektroi hauek egongo dira, gehienez ere: 2 ∙ 32 = 2 ∙ 9 = 18 elektroi

c) 3px, 3py eta 3pz orbitalek zenbaki kuantiko nagusi bera dute; hots, n = 3. Tamaina berekoak dira, beraz.

Jakinik px, py eta pz direla, l zenbaki kuantiko sekundario bera ere izango dute (l =1 → p orbital). Orduan, forma ere berbera izango da denetan.

Alde bakarra orbitalen espazio-orientazioa da, zeina ml zenbaki kuantiko magnetikoak zehazten baitu (l   = 1 → ml = –1, ml = 0, ml = 1),

Hortaz:

• l = 0 → 2 l + 1 = 2 ∙ 0 + 1 = 1 orbital (2s)

Orbitaletako bakoitza koordenatu-ardatz baten norabidean kokatuta dago.

Zenbaki kuantikoak eta orbital atomikoak finkatzea

Orbital endekatuak eta Pauliren esklusio-printzipioa

Landu ikasitakoa

Eredu atomikoen bilakaera

1 Marsdenek eta Geigerrek (Rutherforden kolaboratzaileak) esperimentu bat egin zuten alfa partikulen dispertsioari buruz, metalen xafla meheetarako. Zertan zetzan esperimentua? Zein izan zen emaitzarik harrigarriena? Nola interpretatu zuen Rutherfordek?

2 Fisikan, esperimentuak egin behar dira, neurketa zehatzak egin eta, azkenean, ondorioak atera. Fisikaren bilakaeran, esperimenturik garrantzitsuenetakoa Millikanek 1909an egindakoa izan zen. Ikertu olio tantari buruz Robert Millikanek egindako esperimentuaren nondik norakoak.

3 Kontzeptu-mapa organigrama. Azaldu α, β eta γ erradiazioen ezaugarriak, eta haietako bakoitzari aurre egiteko babes mota bat. Erabili antolatzaile grafiko bat informazioa egituratzeko.

Erradiazio elektromagnetikoa. Espektro atomikoak

4 Taldetan, bilatu informazioa argiaren izaera korpuskularraren ikuspegitik azaldu daitezkeen fenomeno fisikoei buruz. Ondoren, azaldu lan batean, IKTko tresnaren bat erabiliz.

5 a) Zer da espektro bat? b) Zergatik espektro atomikoak ez dira jarraituak? Justifikatu erantzunak.

6 a) Azaldu zertan diren desberdinak igorpenespektroa eta xurgapen-espektroa. b) Bilatu bi espektro mota horien erabilerak.

7 Eguzki-sistemako beste osagai batzuk ez bezala (adibidez, planetak eta sateliteak), izarrak urrutiurruti daude espazio-ontzien helmenetik. Nola jakin dezakegu izar baten konposizio kimikoa? Bilatu horri buruzko informazioa, eta idatzi testu bat, erabiltzen diren tekniketako batzuk azaltzeko.

Plancken hipotesia. Bohrren eredua

8 Potasio gaseosoaren ionizazio-energia 418 kJ · mol–1 izanik: a) kalkulatu fotoi batek behar duen gutxieneko energia, potasio atomo bat ionizatu ahal izateko; b) kalkulatu erradiazio horrekin lotutako maiztasuna, eta esan espektro elektromagnetikoko zer gunetakoa den; c) atomo hori espektroko beste gune bateko argiarekin ioniza liteke? Zeinekin? Arrazoitu erantzuna.

9 Sodioaren igorpen-espektroan, lerro bati datu hau dagokio: λ = 5 889 Å. Kalkulatu: a) energia-aldea trantsizioa gertatzen den bi egoeren artean; b) sodioaren 2,21 gramori zer energia eman behar zaion, atomo guztiak kitzikatu daitezen aipatu den egoeran egoteko moduan.

10 Eztabaidatu ea esaldi hauek zuzenak edo okerrak diren: a) argi gorriko fotoi batek uhin-luzera handiagoa du argi urdineko fotoi batek baino; b) argi horiko fotoi batek maiztasun handiagoa du argi urdineko fotoi batek baino; c) hutsean, argi berdeko fotoi baten hedatze-abiadura txikiagoa da argi berdeko fotoi batena baino; d) argi laranjako fotoi baten energia handiagoa da argi gorriko fotoi batena baino.

11 Alderatu Rutherforden eta Bohrren eredu atomikoak. Aipatu bigarren ereduaren postulatuak.

12 Hidrogeno atomo batean, elektroiak duen energia

13,625 eV da, oinarrizko egoeran. Horiek horrela, kalkulatu hau guztia: a) hidrogenoa ionizatzeko behar den erradiazioaren maiztasuna; b) igorritako erradiazioaren uhin-luzera, nm-tan adierazita, eta maiztasuna, elektroia n = 4 mailatik n = 2 mailara igarotzen denean. Datuak: h = 6,63 · 10−34 J · s , e = 1,6 · 10−19 C, c = 3 · 108 m · s –1 .

13 Hidrogeno atomo bateko elektroiak, egoera kitzikatuan dagoela, jauzi egin du n = 3 zenbaki kuantiko nagusiko energia-maila batetik n = 1 zenbaki kuantikoko energia-mailara: a) kalkulatu igorritako erradiazioaren energia eta maiztasuna, kJ · mol–1-etan eta Hz-etan, hurrenez hurren; b) trantsizio horren energiak rubidio atomo bati eraso dio, eta erauzi den elektroia 1 670 km · s–1-ko abiaduran irten da; orduan, zenbat da rubidioaren ionizazio-energia?

Datua: NA = 6,023 · 1023 atomo · mol–1

14 Naturan, hidrogenoa ez da aske agertzen, eta, hortaz, nolabait lortu beharra dago. Zenbaitek proposatzen dute eguzki-erradiazioak erabiltzea ur molekularen O—H lotura hausteko. Halatan, justifikatu ea eguzki-erradiazioak O—H lotura hauts dezakeen, baldin eta lurrazalera heltzen den erradiazioaren maiztasuna 5 · 1014 eta 1013 s –1 artekoa bada. Ikertu zer erabilera izan ditzakeen hidrogenoak etorkizuneko erregai gisa, eta zer modutan lagundu dezakeen GJHen 7.2 eta 7.a xedeak erdiesten.

Datuak: Elotura O—H (105 Pa, 298K) = 463 kJ · mol–1, NA = 6,02 · 1023 mol–1, h = 6,63 · 10–34 J · s.

Uhin-korpuskulu bitasuna. Efektu fotoelektrikoa

15 Kalkulatu zenbateko potentzial-diferentziarekin azeleratu behar den geldirik dagoen protoi bat, jakinik, potentzial hori gainditu ostean, lotutako De Broglieren uhin-luzerak 5·10−13 m izan behar duela. Datuak: protoiaren karga = 1,6 · 10−19 C, protoiaren masa =  = 1,67 · 10−27 kg , h = 6,63 · 10−34 J · s

Gogoratu unitate honetako materiala zure portfoliorako aukeratu behar duzula.

16 Efektu fotoelektrikorako, kaltzioaren atari-maiztasuna 7,81 · 1014 s –1 da. Kalkulatu erauzketa-lana eta igorritako elektroien energia zinetiko maximoa, eV-etan adierazita, kaltzioa uhin-luzera hauetako erradiazioekin argiztatzen dela jakinda: a) 745 nm, b) 419 nm, c) 272 nm.

17 Jarrera antolatu eta haren alde egin. Efektu fotoelektrikoari buruz egindako esperimentu jakin batean, 500 nm-ko uhin-luzerako argi sorta batek metal bati eraso dio, eta metalaren lan-funtzioa (edo, bestela esanda, erauzketa-lana) 2,1 eV da. Aztertu ea esaldi hauek zuzenak edo okerrak diren: a) erauzitako elektroien De Broglieren uhin-luzerak 10−9 m baino txikiagoak izan daitezke; b) eraso zaion metalaren atari-maiztasuna 1014 s −1 baino handiagoa da.

Datuak: h = 6,63 · 10−34 J · s, c = 3 · 108 m · s–1, elektroiaren masa = 9,1 · 10−31 kg , e = 1,6 · 10−19 C.

18 De Broglieren hipotesiari jarraituz, elektroi batek uhin baten edo partikula baten modura jokatu dezake. Elektroiak λ bat badu, koloreren bat dagokio?

19 Horiaren guneko argia baliatu da, eta, ondorioz efektu fotoelektrikoa gertatu da. Hori jakinik, azaldu ea igorritako elektroien energia zinetiko maximoa aldatzen den, egoera hauetan: a) metala argi hori horrekin argiztatuz, argiaren intentsitatea bikoiztu egin da; b) metala ultramorearen guneko argiarekin argiztatu da.

20 Azal metaliko batek igorri dituen elektroien energia zinetiko maximoa 2,5 eV da, jakinda erradiazio erasotzailearen uhin-luzera 350 nm dela. Kalkulatu hau guztia: a) elektroien mol bat erauzteko lana, jouletan; b) behar den gutxieneko potentzial-diferentzia (balaztatze-potentziala), igorritako elektroiak gelditzeko. Datuak: h = 6,63 · 10−34 J · s, c = 3 · 108 m · s –1 , e = 1,6 · 10–19 C, NA = 6,02 · 1023 mol–1

21 Material metaliko baten erauzketa-lana 2,5 eV da, zehazki. Argi monokromatikoarekin argiztatu da material hori, eta igorritako elektroien abiadura maximoa 1,5 · 106 m · s–1 da. Kalkulatu honako hau: a) Argi erasotzailearen maiztasuna eta igorritako elektroiekin lotuta dagoen De Broglieren uhin-luzera; b) Zer uhin-luzerarekin argiztatu behar den material metalikoa, igorritako elektroien energia zinetiko maximoa 1,9 eV izan dadin.

Ziurgabetasunaren printzipioa. Mekanika kuantikoa. Zenbaki kuantikoak

22 Esan ea Bohrren eredu atomikoa eta Heisenbergen ziurgabetasunaren printzipioa bateragarriak diren.

23 Schrödingerren katua ospetsua da, fisika kuantikoaren ezaugarririk harrigarrietako batzuk sinbolizatzen dituelako. Bilatu Schrödingerren katuaren paradoxari buruzko informazioa, eta azaldu zure ondorioak ikaskideei, aurkezpen batean.

24 Elektroi baten abiadura 2,4 · 107 m · s –1 da, eta abiadura hori neurtzean egiten dugun errorea, % 3. Hori jakinda, esan zenbatekoa den ziurgabetasuna, elektroiaren posizioa aztertzeko garaian.

Datuak: h = 6,63 · 10−34 J · s, eta, halaber, elektroiaren masa = 9,1 · 10−31 kg.

25 Azaldu orbital atomikoen izendapen hauetatik zein ez diren posible, eta justifikatu erantzuna, labur: a) 9 s ; b) 1 p ; c) 4 d ; d) 0 s ; e) 1/2 s

26 Balio bat falta da zenbaki kuantikoen multzo honetan: n = 3, l = ¿?, ml = 2. Zein izan daiteke? Zer orbital da? Justifikatu erantzuna.

27 Justifikatu ea honako zenbaki kuantiko hauek dituzten elektroiak egon daitezkeen: a) (3, −1, 1, −1/2); b) (3, 2, 0, 1/2); c) (2, 1, 2, 1/2); d) (1, 1, 0, −1/2).

28 Aztertu zenbaki kuantikoen multzo hauek, eta azaldu ea orbital atomiko batenak izan daitezkeen. Erantzuna baietz bada, esan zer orbital den: a) n = 5, l = 2, ml = 2; b) n = 1, l = 0, ml = −1/2; c) n = 2, l = −1, ml = 1; d) n = 3, l = 1, ml =0.

29 Esan, arrazoiak emanez, zenbaki kuantikoen konbinazio hauetako zein diren zuzenak, eta, hala badagokio, n eta l balioak irudikatzen dituzten orbitalen izenak, baita elektroi horietan egon daitekeen elektroi kopurua ere: a) (2, 0, −1, 1/2); b) (3, 2, 1, −1/2); c) (2, 1, −1, −1/2); d) (1, −1, 0, 1/2); e) (4, 3, −2, −1/2).

30 Higgs bosoia 2012an aurkitzea gertaera historiko bat izan zen. Orduz geroztik, LHCak ez du partikula berririk aurkitu. CERNek Etorkizuneko Talkagailu Zirkularra (FCC) eraikitzeko proiektuari buruzko txosten bat jakitera eman zuen 2019an. Partikula berriak aurkitzeko, zergatik eraiki behar dira diametro handiagoko partikula-azeleragailuak?

31 Partikulen fisika hainbat irudi-teknikaren oinarria da; adibidez, positroien igorpen-tomografiarena (PET) edo fotoi bakarraren igorpen-tomografiarena (SPECT). Terapia batzuen oinarria ere bada; esate baterako, erradioterapiarena edo terapia hadronikoarena. Taldetan, ikertu zer diren positroien igorpentomografia (PET) eta terapia hadronikoa. Gero, jaso informazioa infografia batean, bai eta zer erlazio duen ere garapen jasangarrirako 3. helburuarekin.

© GRUPO ANAYA, S.A., 2022 - C/ Valentín Beato, 21 - 28037 Madrid.

Eskubide guztiak gordeta. Legeak lan honen edukia babestu eta espetxe-zigorrak edota isunak eta kalte-galeren ondoriozko kalte-ordainak ezartzen ditu honako hauentzat: edozein literatura-lan, artelan zein zientzia-lan, edo horren eraldaketa, interpretazioa edo gauzapena (edozein euskarritan finkatuta edo edozein eratan komunikatuta), oso-osorik edo zati batean, baimenik gabe erreproduzitu, plagiatu, banatu edo komunikatzen dutenentzat.