
MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES I BACHILLERATO
Operaciónmundo
1
LICENCIA 12 MESES INCLUYE PROYECTO DIGITAL DEMO
José Colera J., M.ª José Oliveira G., Ramón Colera C., Rosario García P., Ana Aicardo B.
Los saberes básicos del curso
0 R esoluci ón de problemas
• Análisis de algunas estrategias
Problemas para practicar
BLOQUE I. Aritmética y álgebra
1 Los n úmeros reales
1. Lenguaje matemático. Conjuntos y símbolos
2. Números reales. La recta real
3. Raíces y radicales
4. Logaritmos
5. Expresión decimal de los reales. Números aproximados
Ejercicios y problemas
Autoevaluación
2 Aritmética mercantil
1. Aumentos y disminuciones porcentuales
2. Tasas y números índices
3. Intereses bancarios
4. ¿Qué es la «tasa anual equivalente» (T.A.E.)?
5. Amortización de préstamos
6. Progresiones geométricas
7. Cálculo de anualidades o mensualidades para amortizar deudas
8. Productos financieros
Ejercicios y problemas
Autoevaluación
3 Álgebra
1. Polinomios. Factorización
2. Fracciones algebraicas
3. Resolución de ecuaciones
4. Resolución de sistemas de ecuaciones
5. Inecuaciones y sistemas de inecuaciones con una incógnita
6. Inecuaciones lineales con dos incógnitas
Ejercicios y problemas
Autoevaluación
Autoevaluación del bloque I
12
BLOQUE II. Análisis
4 Funciones I
1. Las funciones y su estudio
2. Dominio de definición
3. Funciones lineales. Interpolación
4. Funciones cuadráticas. Interpolación
5. Funciones de proporcionalidad inversa
6. Funciones raíz
7. Funciones definidas a «trozos»
8. Valor absoluto de una función
Ejercicios y problemas
Autoevaluación
5 Funciones II
1. Transformaciones elementales de funciones
2. Composición de funciones
3. Función inversa o recíproca de otra
4. Funciones exponenciales
5. Funciones logarítmicas
6. Funciones trigonométricas
Ejercicios y problemas
Autoevaluación
6 L ímites de funciones.
Continuidad y ramas
infinitas 156
1. Comportamiento de una función en el infinito
2. Cálculo de límites de funciones cuando x → +∞
3. Límite de una función cuando x → ∞
4. Cálculo de límites de funciones cuando x → ∞
5. Comportamiento de una función en un punto. Límites y continuidad
6. Cálculo de límites en un punto
7. Ramas infinitas. Asíntotas
8. Ramas infinitas en las funciones racionales
9. Ramas infinitas en las funciones trigonométricas, exponenciales y logarítmicas
Ejercicios y problemas
Autoevaluación
B reve
historia de las matemáticas 8
28
54
76
106
132
Índice
2
Derivadas
1. Medida del crecimiento de una función
2. Obtención de la derivada a partir de la expresión analítica
3. Función derivada de otra
4. Reglas para obtener las derivadas de algunas funciones
5. Tabla de derivadas
6. Utilidades de la función derivada
7. Optimización de funciones
8. Representación de funciones
Ejercicios y problemas
Autoevaluación
Autoevaluación del bloque II
BLOQUE III. Estadística, combinatoria y probabilidad
186
10 D istribuciones de probabilidad de variable discreta
1. Distribución estadística y distribución de probabilidad
2. Distribuciones de probabilidad de variable discreta
3. La distribución binomial o distribución de Bernoulli
4. Cálculo de probabilidades en una distribución binomial
5. Ajuste de un conjunto de datos a una distribución binomial
6. La distribución de Poisson
Ejercicios y problemas
Autoevaluación
8 Distribuciones bidimensionales 220
1. Distribuciones bidimensionales. Nubes de puntos
2. Correlación lineal
3. Parámetros asociados a una distribución bidimensional
4. Recta de regresión
5. Hay dos rectas de regresión
6. Tablas de contingencia
Ejercicios y problemas
Autoevaluación
9 Combinatoria y probabilidad
1. Diagrama en árbol
2. Variaciones y permutaciones (importa el orden)
3. Cuando no influye el orden. Combinaciones
4. Factoriales y números combinatorios
5. Cálculo de probabilidades
Ejercicios y problemas
Autoevaluación
Autoevaluación del bloque III
242
11 D istribuciones de probabilidad de variable continua
1. Distribuciones de probabilidad de variable continua
2. La distribución normal
3. Cálculo de probabilidades en distribuciones normales
4. La distribución binomial se aproxima a la normal
5. Ajuste de un conjunto de datos a una distribución normal
Ejercicios y problemas
Autoevaluación
Autoevaluación del bloque III
7
260
278
Anexo S olucionario de las autoevaluaciones 301 3


Funciones I 4
Primeras aproximaciones a la idea de función
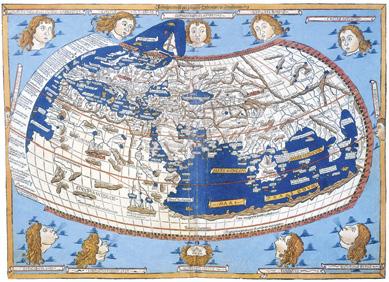
El concepto de función aparece como tal en el siglo xvii, pero el proceso hasta llegar a él fue lento y se remonta hasta la Antigüedad. En la matemática babilónica de hace 4 000 años encontramos los primeros acercamientos en forma de leyes que describen relaciones entre magnitudes, de tal manera que conociendo el valor de alguna de ellas se obtiene, inequívocamente, el valor de la otra. En el siglo ii a. C., el matemático griego Ptolomeo estudió relaciones entre variables, sin llegar a comprender el concepto de función.
Oresme (matemático francés del siglo xiv) afirmó en 1350 que las leyes de la naturaleza son relaciones de dependencia entre «dos cantidades». Fueron este tipo de relaciones las que sirvieron de origen al concepto de función. La primera idea de función es, pues, la de una fórmula que relaciona algebraicamente varias magnitudes.
Galileo, a finales del siglo xvi, utilizó por primera vez la experimentación cuantitativa como fuente de información. Empezó a medir, anotar y valorar cuantitativamente causas y efectos para establecer relaciones numéricas que describieran fenómenos naturales.
El concepto de función se generaliza
Las investigaciones de Galileo sobre las relaciones matemáticas entre dos variables (x e y, causas y efectos) son un antecedente muy claro del concepto de función, que va tomando forma a lo largo del siglo xvii. La representación gráfica mediante diagramas cartesianos (siglo xvii) permitió la visualización de las funciones. De este modo, el concepto de función se generaliza a cualquier relación numérica que responda a una gráfica sobre unos ejes coordenados.
Leibniz, en 1673, adopta la palabra función para designar estas relaciones.
Euler, entre 1748 y 1755, fue perfilando el concepto, al que dio precisión y generalidad, admitiendo que una relación entre dos variables puede ser función aunque no haya una expresión analítica que la describa. El propio Euler fue quien aportó la nomenclatura f (x) para indicar el valor de la función f asociado al número x. Se puede decir que con Euler se asienta el concepto de función.
106
Reproducción del mapamundi incluido en la obra Geographia de Ptolomeo.
Utilidad de las funciones
Las funciones se utilizan para modelizar y estudiar multitud de fenómenos sociales, naturales, científicos… Aunque algunas tienen expresiones muy complejas, es sorprendente ver la simplicidad de muchas otras.
¿Cómo se determina la cantidad de oxígeno en sangre? Entre otras, se utiliza una función cuya curva tiene forma de ese (se dice que es de forma sigmoidea).
¿Interviene alguna función en la determinación de la edad de los fósiles? Sí, una logarítmica.
Un equipo de investigadores e investigadoras de la NASA desarrolló un complejo modelo matemático destinado a predecir los eclipses de Fobos (satélite de Marte) para poder observarlos con el vehículo Curiosity desde la superficie de Marte. Entre otros datos, la predicción de dichos eclipses requiere conocer, para cualquier instante de tiempo, las coordenadas de Fobos y del Sol desde Marte. Este modelo dictamina en qué instantes la cámara situada en el mástil de Curiosity debía enfocar al Sol.
RESUELVE
Familias de funciones


Ya conoces muchas familias de funciones: sus nombres, cómo son sus expresiones analíticas y qué forma tienen sus gráficas.
Asocia cada nombre de familia con su representación gráfica y con su expresión analítica general.
1. Cuadrática 2. Raíz 3. Proporcionalidad inversa 4. Exponencial 5. Logarítmica
107
La sonda Curiosity en la superficie de Marte.
Y X Y X Y X Y Y X A B C D E Y X X Y X Y X C D E I. y = x 4 – II. y = 4x III. y = x 2 – 4x IV. y = log2 x V. y = x 3 2 –

Las funciones y su estudio
Concepto de función
En la ciencia, en la técnica, en la naturaleza, podemos identificar infinidad de funciones:
• La velocidad que lleva una partícula depende del tiempo, es función del tiempo
• La presión del agua del mar es función de la profundidad
• El tamaño con que se ve un objeto a través de una lupa es función de la distancia a la que se coloque la lupa.
• La sensación con la que se percibe un estímulo es función de la intensidad de este. En todas ellas se relacionan dos variables. Tanto en estas como en las demás funciones que manejamos habitualmente, las variables toman valores reales (es decir, se mueven en el conjunto Á de los números reales).
f es una función de Á en Á si a cada número real, x ∈Dom, le hace corresponder otro número real, f (x):
El conjunto Dom de los valores que puede tomar la variable independiente, x, se llama dominio de definición de la función.
El conjunto de los valores que toma la función se llama recorrido.
Y
= f (x)
Destaquemos que para que f (x) sea función, cada valor de x ∈ Dom debe tener asignado un único valor f (x):
f (x) es único para cada x ∈ Dom
Puesto que tanto la variable x como la función f (x) toman valores reales, estas funciones se llaman funciones reales de variable real.
Cómo vienen dadas las funciones
Las funciones nos llegan en diversos formatos:
• Mediante su gráfica
Permite que nos hagamos una idea muy clara de cómo es la función con un solo golpe de vista.
• Por su expresión analítica (fórmula)
Sintetiza algebraicamente de forma perfecta la relación entre las dos variables. Es la más precisa, pero no es fácil ver su comportamiento de un solo vistazo.
• Mediante un enunciado
Si nos viene dada por un enunciado (acompañado o no de una tabla de valores) deberemos traducirlo a una gráfica o, si fuera posible, a una expresión analítica.
La temperatura de un paciente que comienza su enfermedad hasta que vuelve a tener 37
108
1
Dom
Dom
x ⎯→ f (x
⊂ Á
⎯→ Á
)
X
y
DOMINIO
RECORRIDO
°C…
= x4 – x3 –3x
y
+1
Aspectos relevantes de una función
Analizar el comportamiento de una función dada por su gráfica es sencillo. Claro, para eso está la gráfica, para que sea fácil visualizar los vaivenes de la función.
Observamos las subidas y bajadas (crecimiento y decrecimiento), así como los máximos (puntos en donde la curva deja de subir y empieza a bajar) y mínimos. Las discontinuidades (roturas), las ramas infinitas… Todo ello es muy relevante para el análisis de la función que se está describiendo.
En los cursos anteriores nos familiarizamos con la interpretación de fenómenos físicos, biológicos, económicos… descritos mediante gráficas. Sin embargo, en este curso nos marcamos un nuevo y gran objetivo: ser capaces de representar una función a partir de su expresión analítica. Para ello, necesitamos dos importantes herramientas (límites y derivadas) que estudiaremos en las próximas unidades y que, ahora, pasamos a describir muy brevemente.
Límites
Las ramas infinitas, tanto las que se dan en puntos finitos como las que surgen cuando la función se aleja hacia la izquierda o hacia la derecha, se obtienen mediante los límites
El estudio de los límites (unidad 6) nos permitirá averiguar si existen estas ramas, dónde están localizadas y qué forma tienen. Los límites también ayudan a dilucidar si una función es o no continua en un punto o si existe algún tipo de «rotura».
Derivadas
La derivada de una función es otra función que describe la pendiente (inclinación) de la primera en cada uno de sus puntos. En la unidad 7 aprenderemos las técnicas de cálculo de derivadas.
El buen manejo de las derivadas nos permitirá averiguar los intervalos donde una función es creciente y donde es decreciente, así como a obtener sus máximos y mínimos.
PREGUNTAR A LA EXPRESIÓN ANALÍTICA
Hemos de aprender a hacerle preguntas a la expresión analítica de una función.
• ¿Eres continua?
• ¿Tienes ramas infinitas? ¿Dónde están? ¿Cómo son?
• ¿Dónde eres creciente? ¿Dónde decreciente?
• ¿Cuáles son tus máximos y mínimos?
• …
Y ser capaces de encontrar las respuestas a estas preguntas.
U 4 109
Y X
X Y crece crece decrece X Y Y X

Dominio de definición
Por qué se restringe el dominio de definición
• La función y = –5x 2 + 20x corresponde a una parábola. A cada valor real de la x le corresponde un valor de y. Su dominio de definición es todo Á
• La función a = 20t – 5t 2 indica la altura a la que se encuentra una piedra lanzada hacia arriba con una velocidad de 20 m/s. Es la misma parábola descrita en el párrafo anterior, pero ahora la función solo está definida para valores de t que hagan a ≥ 0 (la piedra se para al llegar al suelo). El dominio de esta función es [0, 4].
• La función cuya expresión analítica es y = x 7 – no está definida en x = 1, pues 17 6 = no es un número real. Solo está definida si x vale 7 o más. Su dominio de definición es [7, +∞).
El dominio de definición de una función queda restringido por alguno de los siguientes motivos:
• El enunciado o contexto real del que se ha extraído la función.
• La imposibilidad de hacer alguna operación con ciertos valores de x. Por ejemplo:
Si se anulase el denominador en una fracción algebraica.
Si apareciese un número negativo dentro de una raíz de índice par. Si un logaritmo actuara sobre un número no positivo.
• Por voluntad de quien propone la función.
Operaciones que restringen el dominio de definición
• Denominador cero
Por ejemplo, f (x) = xx x 215 1 –2 2 . Hay que excluir del dominio de definición los valores de x que anulan el denominador. Los hallamos resolviendo la ecuación x 2 – 2x – 15 = 0 → x = –3, x = 5. Por tanto: Dom f = Á – {–3, 5} = (–∞, –3) « (–3, 5) « (5, +∞)
• Raíz de índice par y radicando negativo
Por ejemplo, f (x) = x 26 + . Solo podemos hallar la raíz cuadrada para valores de x en los que 2x + 6 ≥ 0; es decir, para x ≥ –3. Por tanto: Dom f = [–3, +∞)
• Logaritmo de un número no positivo
Por ejemplo, f (x) = ln (3x – 12). Para poder hallar el logaritmo, debe ser 3x – 12 > 0; es decir, x > 4. Por tanto, el dominio de definición es: Dom f = (4, +∞)
• Varias restricciones
Cuando en la misma función confluyen más de una de estas circunstancias, hay que tener en cuenta todas ellas. Por ejemplo:
• f (x) = x 1 4 + . Para poder calcular la raíz cuadrada, el radicando, x + 4, debería ser mayor o igual que cero; pero, al estar en el denominador, no puede ser cero. Por tanto, el dominio estará formado por los valores de x tales que x + 4 > 0; es decir, x > – 4. El dominio es Dom f = (–4, +∞).
• f (x) = + x x 5 1 –. Por una parte, el denominador no puede ser cero, por lo que x = 5 no forma parte del dominio. Además, ha de ser x ≥ 0 para poder hallar la raíz cuadrada. Uniendo las dos condiciones, Dom f = [0, 5) « (5, +∞).
OBSERVACIÓN
Si no se dice otra cosa, el dominio de definición de una función es tan amplio como permita su expresión analítica.
RECUERDA
El intervalo (–3, 5) abarca todos los números comprendidos entre –3 y 5, pero no incluye a –3 ni a 5.
El intervalo [–3, +∞) abarca todos los números mayores que –3 incluyendo el –3.
➜ Ayúdate de GeoGebra para hallar el dominio de definición.
110
2 X Y 20 10 2 a = 20t – 5t 2 y = –5x 2 + 20x 4 0 a = 20t – 5t 2
Ejercicios resueltos
1 Hallar el dominio de definición de estas funciones:
a) y = + 2 x x4 x5 –+
b) y = 815
y =
2 Hallar el dominio de definición de las siguientes funciones:
a) y = x3x –2
b) y = ln (x 2 – 3x)
3 Hallar el dominio de definición de: y = 5x –x (1)logx –2
a) Hay que excluir del dominio de definición al 0, que anula el primer denominador, y al –4, que anula el segundo. Por tanto:
Dom = Á – {–4, 0} = (–∞, –4) « (–4, 0) « (0, +∞)
b) La función no está definida en los puntos en los que se anula el denominador, sin importar si el numerador se anula o no en ellos: x3 – 8x2 + 15x = 0 ⇔ (x2 – 8x + 15) · x = 0 ⇔ x = 0, x = 3, x = 5
Hay que excluir estos tres valores del dominio de definición. Por tanto:
Dom = Á – {0, 3, 5} = (–∞, 0) « (0, 3) « (3, 5) « (5, +∞)
c) El denominador no se anula en ningún punto. Por tanto, el dominio de definición es todo Á:
Dom = Á
a) Veamos para qué valores de x el radicando es mayor o igual que cero:
Tenemos: x 2 – 3x = 0 → x (x – 3) = 0 → x = 0, x = 3
Piensa y practica
La representación de la parábola nos ayuda a ver que el radicando es negativo en el intervalo (0, 3).
Por tanto, el dominio de definición es:
Dom = Á – (0, 3) = (–∞, 0] « [3, +∞)
b) La expresión sobre la que actúa el logaritmo es negativa o cero en el intervalo [0, 3].
Por tanto, el dominio de definición es:
Dom = Á – [0, 3] = (–∞, 0) « (3, +∞)
La función log debe actuar sobre valores positivos → x – 1 > 0 → x > 1
La raíz, sobre valores no negativos → 5x – x2 ≥ 0 → 0 ≤ x ≤ 5
El denominador no debe anularse → 5x – x2 ≠ 0 → x ≠ 0 y x ≠ 5 ° ¢ £ 0 < x < 5
Por tanto: Dom = (1, 5) 1 Y X 1 3
Ambas condiciones se cumplen en (1, 5).
Halla el dominio de definición de cada una de las siguientes funciones:
1 a) y = xx43 1 2 b) y = x xx43 1 –2 2 + + 2 a) y = x 39 + b) y = x 39 1 –
3
y
U 4 111
4 a)
log
– 20) b)
5 a)
xx
b)
6
a)
= xx 5 –2 b) y = xx x 5 35 ––2
y =
(5x
y = ln (x2 – 5x)
y =
x x 8 21 6 –32 + +
y = xx 6 –32
a) y = x 1 1 + – x x3 2 1 ––b) y = logx x
xx
xx –
+
76
x
32 3
c)
1 xx x3 –2 ++
x > 1 0 < x < 5 0 1 5

Funciones lineales. Interpolación
Las funciones describen fenómenos cotidianos, piscológicos, económicos… Tales funciones habitualmente se obtienen de forma experimental y, con frecuencia, responden a alguna de las grandes familias que ya conocemos de cursos anteriores.
Recordemos estas familias y algunas funciones obtenidas experimentalmente que se corresponden con ellas.
Funciones lineales
Las funciones lineales se describen con ecuaciones de primer grado y = mx + n (m, pendiente; n, ordenada en el origen), y se representan mediante rectas.
= mx + n n
La pendiente, m, es el coeficiente de la x cuando la y está despejada. Es la variación que se produce en la y cuando la x aumenta una unidad.
Si conocemos las coordenadas de dos puntos de la recta, P (x1, y1), Q (x2, y2), para hallar la pendiente, procedemos así:
–eslavariación de la –eslavariación de la 21 21 21 21
Si de una recta (función lineal) se conoce uno de sus puntos (x0, y0) y su pendiente, m, su ecuación puede ponerse así:
forma punto-pendiente de la ecuación de una recta y = m(x – x0) + y0
Ejemplo de función lineal:
La presión P (en atmósferas) en el mar y la profundidad h (en m) se relacionan con la ecuación:
P = 1 + h 10 , h > 0
A 100 m de profundidad, la presión es equivalente a que te pusieran un camión de 2 t sobre la cabeza. Imagina a 3 000 m, donde viven los peces abisales.
Ejercicio resuelto

(atm)
h
(m)
¿Sabías que la zona más profunda del mar está en la fosa de las Marianas, en el Pacífico, a 10 924 m? ¿Qué presión soportan los seres que viven allí?
Una triste noticia: cuando el sumergible Limiting Factor marcó un récord de profundidad llegando al fondo de las Marianas, encontró una bolsa de plástico y envoltorios de caramelos.
1 Escribir la ecuación de las rectas representadas en la gráfica. a c b a) Pasa por (0, 4) y (2, 5). Su pendiente es m = 5 2 20 4 1 ––= . La ordenada en el origen es 4. Su ecuación es: y = 2 1 x + 4
b) Pasa por (0, 0) y (3, 2). Su pendiente es m = 3 2 . Su ordenada en el origen es 0.
La ecuación es: y = 3 2 x
Recuerda: estas funciones lineales cuyas rectas pasan por el origen se llaman funciones de proporcionalidad.
c) Pasa por (2, 7) y por (5, 3). m = 52 37 –– = –3 4 . Ecuación: y = –3 4 (x – 2) + 7
112
Y
y
X
m = xx
xx x ––
yy yy y
3
10 50 100
PROFUNDIDAD
2 10 h P = 1 + —
> 0 10
PRESIÓN
Interpolación lineal
Si de una función conocemos solamente dos de sus puntos, es claro que nada o casi nada podremos decir de su comportamiento en otros puntos. Sin embargo, si tuviéramos motivos para suponer que entre esos dos puntos la función es lineal (al menos aproximadamente), podríamos hallar (exacta o aproximadamente) sus valores en puntos intermedios valiéndonos de la ecuación de una recta.
Una función pasa por los puntos A(x0, y0), B(x1, y1), es decir, f (x0) = y0, f (x1) = y1. Si hay razón para suponer que la función es lineal en el intervalo [x0, x1], entonces podemos hallar su valor para cualquier abscisa, x, de este intervalo a partir de la recta que pasa por A y B : si x ∈ (x0, x1), entonces f (x ) = xx yy –– 1 10 0 (x – x0) + y0
A este proceso se le llama interpolación lineal.
Si x es exterior a [x0, x1], el proceso se llama extrapolación. En la extrapolación, cuanto más alejado esté x del intervalo, menos fiable es el valor que obtenemos para f (x ).
1 Si colgamos de un muelle una pesa de 40 g, se estira hasta 12 mm. Y si colgamos una pesa de 60 g, se estira hasta 20 mm.
a) ¿Cuál sería su longitud si colgáramos una pesa de 55 g?
b) ¿Cuál sería su longitud si colgáramos una pesa de 100 g?
c) ¿Y si la pesa fuera de 5 kg?
Piensa y practica
1 Representa la siguiente función:
y = –2x + 7, x ∈ (1, 4]
a) Podemos suponer que, al menos en el intervalo [40, 60], la longitud del muelle depende linealmente del peso que le colguemos. Por tanto, podemos estimar su longitud para un peso intermedio:
8 y = (x – 40) + 12
A(40, 12)
B(60, 20)
20 – 12 = 8
20 b) Para 100 g, se obtiene f (100) = 5 2 (100 – 40) + 12 = 36 mm.
60 – 40 = 20
f (55) = 20 8 (55 – 40) + 12 = = 5 2 · 15 + 12 = 18
Para 55 g, la longitud del muelle será de 18 mm.
c) Para 5 kg = 5 000 g, f (5 000) = 5 2 (5 000 – 40) + 12 = 1 996 mm.
La extrapolación realizada en b) puede ser razonable, pues 100 g es próximo al intervalo [40, 60]. Pero en c), lo obtenido es un disparate. Para ese peso (5 000 g) el muelle se deforma o se rompe. No es válida esta extrapolación.
2 Una función lineal f cumple: f (3) = 5, f (7) = – 4, Dom f = [0, 10]. ¿Cuál es su expresión analítica? Represéntala.
3 En una universidad, en el año 2014 había 15 200 alumnos matriculados, y 18 000 en el 2019. Estima cuántos había:
a) En el año 2015. b) En el 2017. c) En el 2012.
d) ¿Cuántos cabe esperar que haya en el 2022?
e) ¿Y en el 2052?
4 El consumo de gasolina de cierto automóvil, por cada 100 km, depende de su velocidad. A 60 km/h consume 5,7 L y a 90 km/h consume 7,2 L.
a) Estima su consumo si recorre 100 km a 70 km/h.
b) ¿Cuánto consumirá a 100 km/h?
c) ¿Y a 200 km/h?
U 4 113
A(x0, y0) B(x1, y1) y 1 –y 0 x1 – x0 y1 – y0 y = (x – x0 ) + y0 x1 – x0
Ejercicio resuelto

Funciones cuadráticas. Interpolación
Las funciones cuadráticas se describen con ecuaciones de segundo grado y = ax 2 + bx + c, a ≠ 0 y se representan mediante parábolas. y = ax 2 + bx + c Y X
• Tienen sus ejes paralelos al eje Y
• Las formas de estas parábolas (que sus ramas estén hacia arriba o hacia abajo, que sean más o menos anchas…) dependen, exclusivamente, del valor de a
Si dos funciones cuadráticas tienen el mismo valor de a (el coeficiente de x 2), las parábolas correspondientes son idénticas, aunque pueden estar situadas en posiciones distintas.
Si a > 0, las ramas van hacia arriba, y si a < 0, hacia abajo.
Cuanto mayor sea |a |, más estilizada es la parábola.
• La abscisa del vértice de la parábola y = ax 2 + bx +
Ejemplos:
• La altura a (en m) a la que se encuentra un objeto que se lanza verticalmente hacia arriba con una velocidad de 50 m/s, en función del tiempo t (en s), es la siguiente: a = 50t – 5t 2, 0 ≤ t ≤ 10
a = 50t – 5t

➜ Parábolas que varían en función de sus parámetros.
DISTANCIA RECORRIDA (m)
d = 0,0074v 2 + 0,21v
• La distancia d (en m) recorrida por un coche desde que el conductor ve el peligro hasta que el coche para por completo, en función de la velocidad v (en km/h) que lleva el coche en ese instante, viene dada por esta expresión analítica: d = 0,0074v 2 + 0,21v, 0 ≤ v ≤ 100
Ejercicio resuelto
1 Representar las parábolas siguientes:
a) y = x 2 – 4x + 6
b) y = x 2 – 1
c) y = –2 1 x 2 + 2x + 5
VELOCIDAD (km/h)
d) y = 2x 2 – 8x + 4 Las abscisas de sus vértices son: a) 2, b) 0, c) 2, d) 2 Dando algunos valores en cada una, obtenemos su representación: c) d) b) a)
Piensa y practica
1 Representa estas parábolas:
a) y = x 2 – 2x + 3
e) y = (1/3)x 2 – x + 3 f) y = (1/4)x 2 + x – 2
2 Representa las funciones siguientes:
a) y = x 2 – 6x + 1, x ∈ [2, 5)
b) y = – x 2 + 3x, x ∈ [0, 4]
c) y = x 2 – 4, x ∈ (– ∞, –2) « (2, +∞)
114
c es x0 = – a
2
b
.
5 10 20 100
TIEMPO
ALTURA
2
(s)
(m)
b)
= – x 2 – 2x – 3
+ 5 d)
2 – 10
y
c) y = x 2 – 6x
y = 2x
x + 8
10 100 10 100
4
Parábola que pasa por tres puntos
Si los puntos A(x1, y1), B(x2, y2), C(x3, y3) no están alineados, entonces existe una parábola (y solo una) que pasa por A, B y C. Para determinarla, ponemos su ecuación en forma general, y = ax 2 + bx + c, y «obligamos» a que pase por cada uno de los tres puntos. Obtenemos, así, un sistema de tres ecuaciones con tres incógnitas, a, b y c. Al resolverlo, se obtienen los parámetros de la ecuación.
Ejercicio resuelto
1 Hallar la ecuación de la parábola que pasa por los puntos (2, –1), (6, –5) y (10, 7).
HAZLO TÚ
Halla la ecuación de la parábola que pasa por (0, 3), (2, –3) y (6, 9).
Expresamos la ecuación de la parábola en forma general, y = ax 2 + bx +
, y obligamos a que pase por cada uno de los puntos dados:
Resolvemos este sistema y obtenemos los coeficientes: a
La parábola buscada es y = 2 1 x 2 – 5x + 7.
Método de Newton para obtener la ecuación de una parábola
Aplicando este método, la obtención de la parábola que pasa por tres puntos, A(x1, y1), B(x2, y2), C(x3, y3), se consigue de forma más cómoda. Utiliza la siguiente expresión como ecuación de la parábola: y = p
Al imponer que pase por A, B y C, el sistema de ecuaciones obtenido es escalonado y, por tanto, más fácil de resolver.
Ejercicio resuelto
1 Hallar, por el método de Newton, la ecuación de la parábola que pasa por los puntos (2, –1), (6, –5) y (10, 7).
HAZLO TÚ
Halla, por el método de Newton, la ecuación de la parábola que pasa por (0, 3), (2, –3) y (6, 9). Comprueba que es la misma que se obtiene en el Hazlo tú anterior.
Piensa y practica
Ecuación de la parábola: y = p + m(x – 2) + n(x – 2)(x – 6)
Imponemos que pase por los tres puntos dados: (2, –1) → –1 = p + m · (2 – 2) + n · (2 – 2) · (2 – 6) → p = –1 (6, –5) → –5 = p + m · (6 – 2) + n · (6 – 2) · (6 – 6) → p + 4m = –5 →
= –1 (10, 7) → 7 = p + m · (10 – 2) + n · (10 – 2) · (10 – 6) → p + 8
Obtenemos, así, la ecuación: y = 2 1 (x – 2)(x – 6) – (x – 2) – 1
Operando y reagrupando, se obtiene la ecuación del ejercicio anterior: y = 2 1 x 2 – 5x + 7
3 Halla la ecuación de la parábola que pasa por los puntos (–1, 0), (2, 12) y (8, –72).
a) Usando su ecuación en forma general.
b) Por el método de Newton.
4 Halla los puntos de la parábola y = x 2 + 6x + 5 cuyas abscisas son 0, 3 y 5.
Obtén, por el método de Newton, la parábola que pasa por esos tres puntos y comprueba que es la misma.
U 4 115
+ m
–
n(x – x1)(x – x2)
(x
x1) +
(, ) (, ) (, ) 88 88 88 ab ca bc ab ca bc ab ca bc 21 12 24 21 65 56 6366 5 10 77 10 10 100 10 7 ·· ––·· 2 2 2 =+ ++ += =+ ++ += =+ ++ += _ ` a b b b b
c
= 2 1 , b = –5, c = 7
n = 7 → n =
m
m + 32
2 1
Interpolación parabólica
Si de una función conocemos solo tres puntos A(x1, y1), B(x2, y2) y C(x3, y3), x1 < x2 < x3, podremos hallar aproximadamente nuevos valores de la misma a partir de la parábola que pasa por ellos, y = P (x). La confianza que podemos tener en el valor estimado dependerá del tipo de función y de la situación del nuevo punto:
• Si x está en el intervalo [x1, x3], se trata de una interpolación y cabe esperar que el valor estimado sea relativamente próximo al real.
• Si x está fuera del intervalo [x1, x3], se trata de una extrapolación y la estimación será tanto más fiable cuanto más cerca esté x de alguno de los extremos del intervalo.
1 El porcentaje de paro en España en algunos años pasados fue:
año 2013 2017 2019
% 26,10 17,70 15,78
Estimar el porcentaje de paro en 2014, 2018 y 2010 mediante una interpolación (o extrapolación) parabólica.
HAZLO TÚ
El porcentaje de paro en España en algunos años fue:
año 1994 1997 2000
% 24,1 20,6 13,9
Estima el porcentaje de paro en 1998, 2001 y 2003 y compáralo con los valores reales:
año 1998 2001 2003
% 18,6 10,63 11,37

Tomamos como año cero el año 2013. En consecuencia, hemos de obtener la ecuación de la parábola que pasa por los puntos (0; 26,10), (4; 17,70), (6; 15,78). Lo haremos mediante el método de Newton.
Ecuación:
Ahora, obligamos a que pase por cada uno de los tres puntos dados: (0; 26,10) → 26,10 = p + m · 0 + n · 0 · (– 4) → p = 26,10 (4; 17,70) → 17,70 = 26,10 + m · 4 + n · 4 · 0 → m = – 2,10 (6; 15,78) → 15,78 = 26,10 – 2,10 · 6 + n · 6 · 2 → n = 0,19
La ecuación es y = P (x) = 26,10 – 2,1x + 0,19x (x – 4).
Obtenemos el valor de P en cada uno de los puntos pedidos:
2014 → x = 1 → P (1) = 26,10 – 2,1 · 1 + 0,19 · 1 · (–3) = 23,43 (Valor real: 23,67 %, bastante próximo al estimado)
2018 → x = 5 → P (5) = 26,10 – 2,1 · 5 + 0,19 · 5 · 1 = 16,55 (Valor real: 16,61 %, bastante próximo al estimado)
2010 → x = –3 → P (–3) = 26,10 – 2,1 · (–3) + 0,19 · (–3) · (–7) = 36,39 (Valor real: 19,86 %, muy alejado del estimado)
Como vemos, las estimaciones hechas por interpolación al intervalo son buenas. Al alejarnos del intervalo se obtiene un resultado poco ajustado a la realidad.
5 Meta 13.2. Una asociación ecologista tenía 12 300 miembros en el año 2015, 14 100 miembros en 2017 y 15 600 en 2020. Estima cuántos tenía:
a) En el año 2016.
b) En 2018 y en 2012.
c) ¿Cuántos cabe esperar que tenga en 2022?
Interpreta cada resultado teniendo en cuenta si es interpolación o extrapolación y cómo de alejados están los datos del intervalo de datos reales.
6 El consumo de gasolina de cierto automóvil, por cada 100 km, depende de su velocidad. A 60 km/h consume 5,7 L; a 70 km/h, 6 L y a 90 km/h consume 7,2 L. Calcula cuánto gastará por cada 100 km recorridos yendo a:
a) 80 km/h b) 100 km/h c) 200 km/h
Este enunciado es como el del ejercicio 4 del epígrafe anterior, pero enriquecido con un nuevo dato correspondiente al consumo a 70 km/h, con lo que ahora, con tres puntos, se puede efectuar una interpolación parabólica.
116
y = P (x) = p + m(x – 0) + n(x – 0)(x – 4) → y = P (x) = p + mx + nx(x – 4)
Ejercicio resuelto
Piensa y practica

Funciones de proporcionalidad inversa
Se llaman funciones de proporcionalidad inversa a aquellas cuya ecuación es y = x k , k ≠ 0 Sus gráficas son hipérbolas. Su dominio es (– ∞, 0) « (0, +∞).
Recordemos que cada hipérbola «se ciñe» a un par de rectas llamadas asíntotas. Pues bien, en las funciones de proporcionalidad inversa las asíntotas son los ejes coordenados.
También son hipérbolas las gráficas de las funciones y = cx d ax b + + .
Ejemplos:
• El aumento A producido por cierta lupa viene dado por la ecuación: A = d 4 4 –
donde d es la distancia (en cm) a la que se sitúa el objeto.
• A una jeringa de 8 cm de longitud le tapamos el orificio de salida. Al apretar el émbolo, el aire se comprime.
La relación entre la presión P (en atmósferas), y la longitud l (en cm) de la columna de aire responde a la ecuación: l = P 1 8 + , P ≥ 0
Ejercicio resuelto
1 Representar: a) y = x 6 b) y = – x 4
a) Las asíntotas son los ejes coordenados.
➜ Hipérbolas y = x k

AUMENTO
Piensa y practica 4 4 A = 4 – d
DISTANCIA (cm)
8 l = P ≥ 0 P + 1 8 LONGITUD (cm)
Algunos puntos de coordenadas enteras son: (1, 6), (2, 3), (3, 2), (6, 1), (–1, – 6), (–2, –3), (–3, –2), (– 6, –1)
b) Las asíntotas son los ejes coordenados.
Algunos puntos de coordenadas enteras son: (– 4, 1), (–2, 2), (–1, 4), (1, – 4), (2, –2), (4, –1)
PRESIÓN (atm)
1 Representa: a) y = –x 1 b) y = x 8 c) y = –x 6 d) y = x 12 e) y = –x 16
U 4 117
1
1
1 y = x 2 y = x
1
1
1 1 1 1 6 y = x 4 y = –x
5

Funciones raíz
Las funciones de ecuación y = kx , k ≠ 0
se representan mediante medias parábolas con el eje paralelo al eje X.
La función y = x 3 es continua y creciente y su dominio de definición es todo Á
Ejemplos:
• El periodo T de un péndulo (tiempo, en s, que tarda en realizar una oscilación completa) en función de su longitud l (en m). Su ecuación es: T = 2 l
¿Cuál dese ser la longitud de la cadena de un péndulo para que tarde un segundo en hacer una oscilación?
• En psicología tiene gran importancia el estudio de percepciones. Percibimos luz, olores, sonidos… La percepción (sensación) depende (es función) de los estímulos físicos que llegan por medio de los sentidos.
La fórmula que relaciona la sensación S con la intensidad I del estímulo es:
SENSACIÓN (estimada por el individuo)
ESTÍMULO FÍSICO
Esta relación entre estímulos (físicos) y sensaciones (psicológicas) se llama ley psicofísica

➜ Función raíz que varía al cambiar el valor de k

1 Representar:
Piensa y practica
1 Representa:
118
y
√
Y X
=
kx
Y X y = 3 √x
S
1 8 S
= k I 3
= k 3 √I
a) y =
–b) y = –27x 3 a) b) Y Y X X Ejercicio resuelto
a)
c)
= – x9 d) y = x9 – e) y = x–8 3
4x
y = x4 b) y = x9
y
T
T = 2 √l
l
6
Piensa y practica
2 Asocia a cada una de las siguientes gráficas una de las ecuaciones de abajo. Observa que hay más ecuaciones que gráficas.
3 Cada uno de estos enunciados se corresponde con una gráfica de entre las del ejercicio anterior. Identifícala.
1. Superficie, en centímetros cuadrados, de un círculo. Radio, en centímetros.
2. Aumento de una lupa. Distancia al objeto, en centímetros.
3. Periodo de un péndulo. Longitud, en metros.
4. Volumen de un cilindro, en centímetros cúbicos. El radio del círculo de su base mide 5 cm. Altura, en centímetros.
5. Longitud de un muelle, en decímetros. Mide 1 dm y se alarga 75 mm por cada kilo que se le cuelga.
6. Dimensiones (largo y ancho, en cm) de los rectángulos que tienen una superficie de 6 cm2.
U 4 119
X 1 1 Y K L X 1 1 Y X 1 1 Y I J X 1 1 Y X 1 Y X 1 1 Y A B 10 X X 1 1 Y Y G X 2 Y 800 H 1 X 2 1 Y E F X 1 1 Y X 1 10 Y 5 (4, 16π) 50 80 C D 1 1 100 lineales cuadráticas proporcionalidad inversa radicales L1 y = 2 3 x C1 y = x 2 – 8x + 15 PI1 y = x 1 R1 y = x 24 + L2 y = – 3 2 (x – 1) + 5 C2 y = (x + 3) (x + 5) PI2 y = x 2 2 –, x ≥ 0 R2 y = x 4 + L3 y = 25πx C3 y = x 2 , x > 0 PI3 y = x 2 R3 y = 2 x 4–L4 y = 4 3 x + 1, x ≥ 0 C4 y = πx 2 , x > 0 PI4 y = x 6 , x > 0 R4 y = x4 , x > 0

Funciones definidas «a trozos»
Las expresiones analíticas de las siguientes funciones son muy peculiares: y = xx x 1 2 2 si ≤ si > ( y =
x x x x 21 1 3 04 4 0 –si ≤ si si ≥ << 2 ++ *
Requieren de varias «fórmulas», cada una de las cuales rige el comportamiento de la función en un cierto tramo. X

➜ Dibuja una función definida a trozos.
Sus representaciones gráficas son fáciles si sabemos representar cada uno de los tramos y se presta atención a su comportamiento en los puntos de empalme.
También es sencillo obtener la expresión analítica, a partir de una gráfica formada por trozos de rectas.
Ejercicio resuelto
1 La siguiente gráfica describe la temperatura T del agua que, siendo hielo, se echa a una cazuela, se pone al fuego y se mantiene hasta que lleva un rato hirviendo.
T (° C) t (min)
15 –20 50 30 45
Obtener su expresión analítica en función del tiempo, t.
Piensa y practica
1 Representa esta función: f (x) = si si si x xx x x x 1 21 4 –2 + + *
• Primer tramo: pertenece a una recta que pasa por (0, –20) y (10, 0).
Su pendiente es: () 10 0 020 – = 10 20 = 2 (El hielo aumenta su temperatura de –20° a 0°).
Ecuación: y = 2(x – 0) – 20 → y = 2x – 20
• Segundo tramo: y = 0 (Mientras el hielo se descongela su temperatura sigue siendo 0°).
• Tercer tramo: pertenece a una recta que pasa por (20, 0) y (35, 100).
Ecuación: y = 15 100 (x – 20) → y = x 20 33 400 – (El agua sube su temperatura de 0° a 100°).
• Cuarto tramo: y = 100 (El agua hirviendo se mantiene a 100°).
Si en lugar de x e y ponemos t (tiempo) y T (temperatura), su expresión analítica es: T = f (t) = si ≤≤ si si ≤≤ si ≤ t t t t t t 220 0 3 20 3 400 100 010 10 20 20 35 35 50 ––<< < Z [ \ ] ] ] ] ]
[, ) [, ] ,) ( 30 03 37 –
2 Haz la representación gráfica de la siguiente función: g (x) = x x x x 21 1 1 1 –si si ≥ < 2 + )
3 Escribe la expresión analítica que corresponde a la siguiente gráfica: X Y 2 2
120
xx
X Y Y y = x y = 1 2 y = x – 3 y = 1 4 y = x2 + 2x + 1
∈ ∈
∈
7
Función «parte entera»
Se llama parte entera de un número x al mayor número entero menor o igual a x A partir de esto, definimos la función parte entera de x, Ent (x), que hace corresponder a cada número x su parte entera.
PRACTICA
Ent (7,5) = 7
Ent (–4) = –4
Ent (–5,3) = –6 ¡atención!
Continúa tú:
Ent (6,48) Ent (7)
Ent (–3,9) Ent (–11,3)
Ent (–8)
Función «parte decimal»
La parte decimal o mantisa de un número x es Mant (x) = x – Ent (x). Por ejemplo: Mant (7,54) = 7,54 – 7 = 0,54 Mant (–7,54) = –7,54 – (–8) = 0,46
A partir de esto, definimos la función parte decimal de x, Mant (x), que hace corresponder a cada número x su parte decimal.
PRACTICA
Mant (7,68) = 0,68
Mant (–8) = 0
Mant (–7,68) = 0,32
Continúa tú:
Mant (3,791) Mant (–6,94)
Mant (2) Mant (–4,804)
Función «valor absoluto»
Recordemos que el valor absoluto de un número a coincide con a si es positivo o nulo, o con su opuesto, si es negativo: |a| = ≥ a a a a 0 0 –si si < ( La función y = |x| se define, en consecuencia, así: y = |x| = x x x x 0 0 –si si ≥ < (
Piensa y practica
4 ¿Verdadero o falso?
a) La gráfica roja corresponde a la función y = Ent x 4 bl .
b) La gráfica verde corresponde a la función y = 5 + Ent x 4 bl . 4 8 12 5
5 Representa:
a) y = Ent (x) + 2
6 ¿Verdadero o falso?

a) La gráfica roja corresponde a y = 3Mant x 4 bl
b) La gráfica roja corresponde a y = 3Mant (4x).
c) La gráfica verde corresponde a y = 5 – Mant x 4 bl 4 8 12 5
7 Representa:
U 4 121
Ent
+ 0,5)
b) y =
(x
Mant (x) – 0,5 b) y = |Mant (x) – 0,5|
a) y =
Y
–4 –3 –2 –1 1 2 3 4 5 6 1 2 3 4 –3 –2 –1
X
–6 –5 –4 –3 –2 –1 1 2 3 4 5 6 2 –1 7 –7 1 Y X

Valor absoluto de una función
El valor absoluto de una función se define así:
Por tanto, para representar el valor absoluto de una función f (x) debemos primero representar la función f (x) y luego dejar la parte positiva como está y realizar una simetría con respecto al eje X de la parte negativa. Para ello, debemos encontrar los puntos de corte con los ejes. Veamos unos ejemplos:
Ejercicios resueltos
1 Representar la siguiente función: y = | x2 – 5 x + 4 |
2 Representar la siguiente función: y = | 2x – 4 |, x é [–1, 5]
Hallamos los puntos de corte de la función f (x) = x2 – 5x + 4 con el eje X:
3 Representar esta función:
|
Piensa y practica
1 Representa: y = | –x2 + 4x + 5|
Por tanto, entre 1 y 4 la gráfica sube sobre el eje X.
2 Representa gráficamente: y = 3 –x 2
122
f
(x) = x2 – 5x + 4 = 0 x1 = 1 x2 = 4
y = | x3 – x
y = f (x ) y = | f (x )| Y X Y X Y X Y X y = f (x ) y = | f (x )|
| f (x)| = () () () () fx fx fx fx 0 0 –si ≥ si < * y = f (x ) y = | f (x )|
8 y = f (x ) y = | f (x )| Y X Y X 1 1 1 1
Ejercicios y problemas resueltos
1. Dominio de definición
Hallar el dominio de definición de las siguientes funciones:
a) f (x) = () ln x x x 4 5 ––2 +
b) f (x) = 27xx 4 1 –2 +
HAZLO TÚ
Halla el dominio de definición de la función:
f (x) = xx56 2 +
2. Interpolación lineal
Un boing 747 consume 83 912 litros de combustible en un vuelo Madrid-Caracas (7 001 km) y 13 143 litros en un vuelo Madrid-París (1 054 km). Estimar el consumo en un vuelo Madrid-Oslo (3 044 km).
HAZLO TÚ
El porcentaje de personas que tenían acceso a Internet en España era en 2020 el 93,2 % y en 2016 el 80,56 %. Estimar el porcentaje en 2018.
3. Función cuadrática
Una feria ganadera está abierta al público entre las 10 y las 20 horas. El número de visitantes viene dado por la función:
N(t ) = –20t 2 + Bt + C donde t es la hora de visita.
Sabiendo que a las 17 h se alcanza el máximo de 1 500 visitantes, hallar B y C y representar la función.
a) La función y x x 4 –2 = no está definida en los puntos donde el denominador es nulo, que son x = 2 y x = –2. Su dominio es Á – {–2, 2}
En la función y = ln (5 – x), el logaritmo solo está definido para valores positivos. Resolvemos 5 – x > 0 → x < 5. Su dominio es (– ∞, 5).
Para que exista la función f deben cumplirse las dos condiciones.
Por tanto, Dom f = (– ∞, –2) « (–2, 2) « (2, 5).
b) La función está definida para los valores de x que cumplen 2x 2 + 7x – 4 > 0.
Resolvemos la inecuación, buscando en primer lugar las soluciones de la ecuación: 2x 2 + 7x – 4 = 0 → x = – 4; x = 1/2
Estos valores determinan los intervalos en los que hay que estudiar el signo de 2x2 + 7x – 4. (– ∞, – 4) (– 4, 1/2) (1/2, +∞)
Signo de 2x 2 + 7x – 4 + – +
Dominio de definición de f = (– ∞, – 4) « (1/2, +∞).
Análisis del problema Suponemos que el consumo en el intervalo [1 054, 7 001] depende linealmente de los kilómetros recorridos. Por tanto, podemos estimar el consumo, para un recorrido intermedio, mediante interpolación lineal.
Hallamos la ecuación de la recta que pasa por los puntos (1 054, 13 143) y (7 001, 83 912):
Pendiente: m = 7 001 1 054 8121 43 39 31 –– = 11,9
Ecuación: f (x ) = 13 143 + 11,9(x – 1 054) = 11,9x + 600,4
Para x = 3 044 → f (3 044) = 36 824. El consumo estimado para el vuelo Madrid-Oslo es de 36 824 litros.
La función N (t ) es una parábola abierta hacia abajo. Su punto más alto (17, 1 500) es el vértice.
Con la abscisa del vértice calculamos B : t = a b 2 –→ 17 = () B 220 ––→ B = 680
La parábola pasa por (17, 1 500). N (17) = 1 500 → –20 · 172 + 680 · 17 + C = 1 500 → C = – 4 280
La función es: N (t ) = –20t 2 + 680t – 4 280; 10 ≤ t ≤ 20
Para representar la función hallamos algunos puntos:
t = 10 → N (10) = 520 → (10, 520)
t = 20 → N (20) = 1 320 → (20, 1 320)
500 N.º DE VISITANTES
000
HAZLO TÚ
Representa la siguiente función: f (t ) = –t 2 + 12t – 31, 4 ≤ t ≤ 7
U 4 123
5 10 15 20 500
HORAS
1
1
Ejercicios y problemas resueltos
4. Ecuación y representación de una parábola
a) Escribir la ecuación de una parábola que tiene el vértice en el punto (1, 9) y corta al eje Y en (0, 8).
b) Representarla.
c) Determinar el dominio de definición y el recorrido.
a) Una parábola tiene por ecuación y = ax 2 + bx + c. Tenemos que hallar a, b y c.
Con la abscisa del vértice, a b 2 – , relacionamos las incógnitas a y b : 1 = a b 2
La parábola pasa por (1, 9) y (0, 8). Sustituimos estos puntos en su ecuación y obtenemos otras dos ecuaciones con a, b y c como incógnitas: (1, 9) → 9 = a ∙ 12 + b ∙ 1 + c (0, 8) → 8 = a ∙ 0 + b ∙ 0 + c
Resolvemos el sistema: ba ab c c 2 9 8 –= =+ + = 4 a = –1; b = 2; c = 8
La ecuación de la parábola es y = –x 2 + 2x + 8.
Otra forma de resolverlo: Puesto que la abscisa del vértice es 1, una forma más rápida de obtener la parábola es escribirla en la forma y = a(x – 1)2 + k y sustituir en ella los puntos (1, 9) y (0, 8).
b) Cortes con el eje X: 0 = –x 2 + 2x + 8 → x = –2, x = 4
Corta al eje X en (–2, 0) y (4, 0).
HAZLO TÚ
Escribe la ecuación de la parábola que tiene el vértice en (2, –4) y pasa por el punto (3, –3).
c) Como en todas las funciones polinómicas, su dominio es todo Á. Para determinar el recorrido, observamos que el mayor valor que alcanza la función es y = 9. Por tanto, su recorrido es (–∞, 9].
5. Representación de una función definida «a trozos» dada por un enunciado
El salario neto mensual es el que se obtiene al restar los impuestos obligatorios al salario bruto. En cierto país se aplican estos impuestos:
• 20 % de la parte del salario bruto comprendida entre 500 €, que es el salario mínimo, y 2 000 €.
• 40 % de la parte del salario bruto superior a 2 000 €
a) ¿Qué salario neto corresponde a 1 200 € de salario bruto? ¿Y a 2 500 €?
b) Escribir la función que da los impuestos según el salario bruto x, y representarla.
c) ¿Cuál debe ser, como mínimo, el salario bruto para que el neto sea superior a 2 500 €?
a) Tenemos en cuenta que los primeros 500 € no tienen impuestos.
El salario neto para 1 200 € es 1 200 – 0,2 ∙ (1 200 – 500) = 1 060 €.
El salario neto para 2 500 € es 2 500 – 0,2 ∙ 1 500 – 0,4 ∙ 500 = 2 000 €.
b) Calculamos la función que nos da los impuestos I (x) en los casos en que 500 ≤ x ≤ 2 000 y x > 2 000.
• Si 500 ≤ x ≤ 2 000:
I (x) = 0,2(x – 500) = 0,2x – 100
• Si x > 2 000:
I(x) = 0,2 ∙ 1 500 + 0,4(x – 2 000) = 0,4x – 500
800
Por tanto:
I (x) = , , ≤ x x x x 02 100 04 500 500 2000 2000 ––si ≤ si > )
(€)
c) Resolvemos la inecuación x – I (x) > 2 500: x – (0,4x – 500) > 2 500 → 0,6x > 2 000 → x > 3 333,33
El salario bruto debe ser superior a 3 333,33 €.
124
–→ –b = 2a
Y X 9 1 4 –2
500 1000
100
SALARIO BRUTO
2000 3000 500
IMPUESTOS
(€)
6. Función «parte entera»
Una tienda de ropa ofrece a su clientela la tarjeta «2MÁS», en la que ingresará 2 € para futuras compras por cada 10 € de gasto que se haga allí.
a) Representar la función que nos da la cantidad ingresada en la tarjeta según el gasto realizado.
b) Escribir su expresión analítica.
HAZLO TÚ
Representa f (x) = Ent (2x).
7. Valor absoluto de una función
Definir por intervalos las siguientes funciones y representarlas gráficamente:
a) f (x) = 4|x| – x2
b) f (x) = |x – 4| – |x|
c) f (x) = || x
HAZLO TÚ
Define por intervalos y representa.
a) f (x) = |x 2 – x – 6|
b) f (x) = x – |x |
c) f (x) = x 1
a) Por una compra inferior a 10 € no ingresan nada. Si gastamos más de 10 € y menos de 20 €, ingresan 2 €; entre 20 y 30 € nos corresponden 4 €; … 10 20 30 40 2 4 6 ingresos (€) gasto (€)
b) Es una función definida «a trozos»: f (x) = [, ) [, ) [, ) [, ) é é é é x x x x 00 10 21020 42030 63040 si si si si Z [ \ ] ] ] ] ] ]
También podemos definirla utilizando la función «parte entera»: f (x) = 2 Ent x 10 bl
a) Recordamos que la función y = |x | se define así: y = ≥ x x x x 0 0 –si si < ) 3 Por tanto:
Buscamos los vértices y los puntos de corte con los ejes de cada parábola: parábola vértice cortes con eje X
4x – x 2 (–2, 4) (0, 0) y (– 4, 0) y = 4x – x 2 (2, 4) (0, 0) y (4, 0) 2 –2 Y X 4 b)
Disponemos los cálculos en una tabla para hallar la función resultante: (–@, 0) [0, 4) [4, +@) | x – 4 | – x + 4 – x + 4 x – 4 | x | – x x x | x – 4 | – | x | 4 4 – 2x – 4 f (x) = ≤ ≤ x x x x 4 42 4 0 04 4 ––si si si < < *
c) La función está definida para todos los números reales.
Su definición es f (x) = si x x x 0 –< si ≥ x 0 * . Para x ≥ 0, la gráfica es la de la función raíz, y para x < 0, la grafica pasa por (–1 , 1); (–2, 2 ); (– 4, 2); … 2 2 –2 4 – 4 –2 Y X 4 2 4 Y X
U 4 125
f (x
= () ≥ xx xx x x xx xx x x 4 4 0 0 4 4 0 0 –si si ≥ –si si << 2 2 2 2 **44
) =
y = –
|x – 4| = si si ≥ x x x x 4 4 4 4 ––< + ) |x| =
si x x
si
x x 0 0 –≤ < )
Ejercicios y problemas guiados
1. Funciones lineales
Una empresa de alquiler de coches ofrece dos tarifas:
A: 120 km → 80 €
350 km → 137,5 €
B: 150 km → 75 €
250 km → 125 €
Analizar cuál es más ventajosa según los kilómetros que vayamos a recorrer.
2. Una función cuadrática
Los costes de producción de cierto producto (en euros) de una empresa, vienen dados por:
C(q) = 40 000 + 20q + q 2 siendo q el número de unidades producidas. El precio de venta de cada unidad es de 520 euros.
a) Expresar en función de q el beneficio de la empresa y representarlo.
b) ¿Cuántas unidades hay que producir para que el beneficio sea máximo?
Suponemos que el precio depende linealmente de los kilómetros recorridos.
• Obtén, en cada uno de los dos casos, la expresión analítica de la función que nos da el gasto según los kilómetros recorridos.
• Representa en los mismos ejes las dos funciones, eligiendo una escala adecuada.
• Halla el punto de corte de ambas funciones y observa los valores de la función a la izquierda y a la derecha de ese punto.
Solución: La opción B es más ventajosa si se recorren menos de 200 km. A partir de esta distancia, es más ventajosa la opción A.
a) • La función beneficio, B, la obtendrás restando del precio de venta de q unidades, 520q, el coste para producir esas q unidades.
• Obtendrás una función cuadrática. Represéntala.
b) Observando la representación gráfica de la función beneficio, apreciarás en qué punto alcanza su valor máximo (en el vértice, ya que es una parábola con las ramas hacia abajo).
Solución:
a) B(q) = – 40 000 + 500q – q 2
b) El beneficio máximo de 22 500 euros se obtiene produciendo 250 unidades.
3. Expresión analítica de una función
Escribir la expresión analítica de esta función f (x):
4. Producción máxima
En un huerto hay 40 manzanos. Cada uno produce 600 manzanas. Por cada árbol adicional que se plante, la producción de cada árbol se reduce en 10 manzanas. ¿Cuántos árboles se deben plantar para obtener la producción más alta posible? ¿Cuál es dicha producción?
• Para hallar la ecuación de la parábola la escribimos en forma general y = ax2 + bx + c y sustituimos en ella tres de los puntos de su gráfica. Otra opción consiste en aplicar el método de Newton utilizando la expresión y = p + m(x
x1) + n
para calcular p, m, n y con ellos la ecuación.
• Tomamos dos puntos de la recta, y escribimos su ecuación.
• Ten en cuenta que el punto (3, 1) no pertenece a la función, pero sí pertenece (3; –2,5).
Solución:
• Calcula la producción total de manzanas con 40 árboles. Al plantar 5 árboles más, ¿cuál será la producción de cada árbol?
• Escribe la función que da la producción total si se plantan x árboles más. La función obtenida es una parábola abierta hacia abajo. Su vértice corresponde al valor máximo de la función.
Solución:
La función es p (x) = –10x2 + 200x + 24 000. Se deben plantar 10 árboles más para alcanzar la máxima producción y esta será de 25 000 manzanas.
126 126
– 4 –4 –8 4 8 8 4 –8
(x – x1)(x – x
–
2)
f (x) = si si ≤ x x x x 2 1 2 25 3 3 ––> 2 + *
Ejercicios y problemas propuestos
Para practicar
Dominio de definición
1 Halla el dominio de definición de estas funciones:
a) y = () x 5 2 2 + b) y = xx x 32 3 + +
c) y = xx x 2 –2 + d) y = xx 1 2 1 + +
e) y = ()xx 2 1 2 –32 + f) y = x 2 – 4
2 Estudia el dominio de definición de estas funciones: a) y = x 25 + b) y = x 7–c) y = xx34 2 ++ d) y = xx12 +
3 Di cuál es el dominio de definición de: a) y = x 4 1 –b) y = x 1 1 2 + c) y = x 1 9– 3 2 d) y = x x 1 3 –2
4 Determina el dominio de definición de estas funciones: a) y = ln (x 2 – 4x) b) y = ln x 2 – ^ h
c) y = x 5– 3 d) y = x x 21 4– 2 +
e) y = ln x 3 1 2 + cm f) y = x x 4 1 –3 +
5 Observa las gráficas de estas funciones e indica cuál es su dominio de definición y su recorrido:
Funciones lineales y cuadráticas. Interpolación
8 Escribe las ecuaciones de las siguientes rectas y represéntalas gráficamente:
a) Pasa por P (1, –5) y Q (10, 11).
b) Pasa por (–7, 2) y su pendiente es –0,75.
c) Corta a los ejes en (3,5; 0) y (0, –5).
d) Es paralela a la recta 3x – y + 1 = 0 y pasa por el punto (–2, –3).
9 Calcula la pendiente de las rectas r, s y t y escribe su ecuación.
6 La función h(t) = 25 + 20t – 5t 2 nos da la altura a la que está una pelota lanzada hacia arriba en el instante t, hasta que vuelve al suelo. ¿Cuál es su dominio de definición?
7 La temperatura de un paciente, desde que comienza su enfermedad hasta que vuelve a tener 37 °C, ha evolucionado según la función T = – 0,1t 2 + 1,2t + 37, siendo t el número de días transcurridos desde el inicio de la enfermedad. ¿Cuál es su dominio de definición? ¿Y su recorrido?
10 Calcula, mediante interpolación o extrapolación lineal, los valores de y que faltan en cada tabla:
a) b) x 0,45 0,5 0,6 y 2 … 0,25 x 47 112 120 y 18 37 …
11 La siguiente tabla muestra los ingresos, en millones de euros, de una fábrica de cemento según el número de toneladas vendidas:
Estima, mediante interpolación parabólica, los ingresos obtenidos si se venden 2 t y 4 t.
12 Representa las siguientes funciones:
a) y = x 2 + 2x + 1 b) y = x 2 2 + 3x + 1
c) y = – x 2 + 3x – 5 d) y = x 3 2 + 3x + 6
e) y = – 4x 2 + 1 f) y = –2x 2 – 3x + 0,5
13 Halla la ecuación de la parábola que pasa por los puntos (–2, –9), (2, –5) y (4, 0).
Hazlo de dos formas distintas:
a) Utilizando la expresión y = ax 2 + bx + c
b) Por el método de Newton.
14 Halla, en cada caso, la ecuación de la parábola que pasa por los puntos dados.
a) (1, –1), (3, 3), (5, –1) b) (0, – 4), (1, –6), (3, – 4)
Halla las ordenadas de los puntos de las parábolas anteriores con abscisa x = 4 y x = –3.
127 127 U 4
a) b) 2 2 Y X 2
X 2 c) d) 2 –2 Y X 2 2 –2 Y X 2
Y
–2
2 –2
2
4 Y X r s t
4
5,2 14,8 21,2
x (toneladas) 1 3 5 y (millones de euros)
Ejercicios y problemas propuestos
Representación de funciones elementales

15 Asocia a cada gráfica su expresión analítica. a) y = –0,5x 2 + 3
16 Representa estas funciones en el intervalo indicado: a) y = 2x 2 – 4, [0, 2] b) y = –x 2 3 2 , x ≥ –1 c) y = x 1 , x < 0 d) y = x 5 330 – , [–5, 5]
17 Representa las siguientes funciones: a) y = x2 b) y = – x c) y = x 2 d) y = x– e) y = x –1 f) y = x 2
18 Halla el valor de k para que:
a) La función y = k x pase por el punto (2, 1/4).
b) La función y = kx pase por el punto (2, 2).
c) Representa las funciones obtenidas.
Funciones definidas «a trozos»
19 Asocia a cada gráfica su expresión analítica. a) y = x x
y =
20 Representa gráficamente las siguientes funciones:
21 Representa.
22 Obtén la expresión analítica de estas funciones:
Ten en cuenta el ejercicio guiado 3.
128
+ c)
= x 3 1 –2
1 –e)
2 + 5
– 1 f)
= x 1 + 2 g)
= 1 2 – x 3 h) y = – x –4 6 – 4 –2 2 4 – 4 –2 2 4 – 4 –2 2 4 Y X –2 –1 – 4 – 6 – 8 –2 –2 1 2 –3 –1 –2 Y X II I Y X 2 4 6 Y X IV III VI V Y X VIII VII 2 –2 2 4 –2 2 – 4 2 4 Y X –2 – 4 2 4 –2 – 4 –2 2 4 –2 – 4 2 4 Y X – 4 2 4 6 –2 –2 2 4 Y X
b) y = x 2
y
d) y = x 4
y = 3x
x
y
y
x x x 2 3 2 2 8 2 3 0 04 4 ––si si ≤≤ si < > Z [ \ ] ] ] ] b) y = () x x x x 2 2 0 0 ––si si ≥ < 2 + *
≥ xx x x x 42 3
2 4 4 ––si si < 2 + * d)
= x x x x x 2 3 2 2 3 4 0 04 4 4 –si si ≤≤ si < > + Z [ \ ] ] ] ] –2 2 4 Y X –2 2 4 Y X 4 6 –2 –2 Y X 2 4 6 2 4 6 2 2 4 – 4 –2 –2 2 Y X 2 4 II I IV III
c)
14
y
a)
= x x x x 2 2 2 0 04 4 ––si si ≤ si ≥ < < * b) y = x x x x 21 1 1 1 si ≤ si > + ) c)
xx x x x 2 24 2 2 ––si si ≥ < 2 * d) y = x 3 si ≤ x xx 2 2 25 3 ––si> 2 + *
y
y =
a) y = x x x x x 6 3 2 27 7 –si si ≤ si ≥ –< < 2 + * b) y = x x x x x x 1 22 1 1 11 1 ––si ≤–si –si ≥ << 2 * c)
si si ≥ < * d)
x x x x 0 0 –si si –> *
y = /x x x x 10 0
y = ≤
a) b) 2 4 4 Y X 2 4 –2 2 Y X 2 4 6 –2 *
Valor absoluto de una función
23 Representa la función y = |x – 5| y comprueba que su expresión analítica en intervalos es: y = x x x x 5 5 5 5 ––si si ≥ < + )
24 Representa las siguientes funciones y defínelas como funciones «a trozos»:
a) y = |4 – x | b) y = |3x + 6|
c) y = x 2 3 – d) y = | –x – 1|
25 Representa las siguientes funciones y defínelas por intervalos: a) y = |x 2 – 1| b) y = |x 2 – 4x |
c) y = |x 2 + 2x – 3| d) y = |x 2 – 2x + 1|
26 Define las siguientes funciones como funciones «a trozos» y represéntalas:
a) y = x 1 b) y = 1 + |x |
c) y = x x d) y = 2|x | + x
* Ten en cuenta el ejercicio resuelto 7.
27 Escribe la expresión analítica de estas gráficas como funciones «a trozos» y como valor absoluto:
30 Midiendo la temperatura a diferentes alturas, se ha observado que por cada 180 m de ascenso el termómetro baja 1 °C. Si en la base de una montaña de 800 m estamos a 10 °C, ¿cuál será la temperatura en la cima? Representa gráficamente la función altura-temperatura y busca su expresión analítica.
31 Observamos en una farmacia una tabla con los pesos de los niños menores de 9 años, según su edad: x (años) 1 3 6 9 y (kg) 10 14 20 26
Representa estos datos y utiliza el modelo de interpolación que creas más adecuado para estimar el peso de un niño a los 5 años y a los 10 años.
32 En la cocina de un restaurante, un equipo de 2 personas es capaz de preparar los pedidos para 30 comensales. Si el equipo es de 4 personas, la capacidad se eleva hasta los 50 comensales. Y si el equipo llega a 8 personas, se estorbarían unos a otros y no habría fuegos para todos, por lo que la capacidad se mantendría en 50 comensales. Estima mediante interpolación parabólica cuántos comensales podría atender un equipo de 5 personas.
33 Un opositor se enfrenta a un temario de 3 100 páginas. Sabe que si estudia 4 horas diarias es capaz de memorizar 4 páginas por día. Si dedica 8 horas, aprende 7 páginas; y si dedica 12 horas, consigue 9 páginas. Se plantea una jornada diaria de 10 horas y quiere saber el número de días que le va a suponer dar una primera vuelta al temario completo. Utiliza la interpolación parabólica para responderle.
Para resolver
28 El precio del billete de una línea de cercanías depende de los kilómetros recorridos. Por 57 km he pagado 2,85 euros, y por 168 km, 13,4 euros. Calcula el precio de un billete para una distancia de 100 km.
29 Con unos gastos en publicidad de 3 000 €, las ventas obtenidas por una empresa han sido de 28 000 €; y con 5 000 € invertidos en publicidad, las ventas han ascendido a 39 000 €.
a) Estima, mediante interpolación lineal, cuáles serían las ventas si se invirtieran 4 000 € en publicidad.
b) Si sabemos que con un gasto de 6 000 € se han obtenido unas ventas de 40 000 €, estima mediante interpolación parabólica las ventas que se obtendrían invirtiendo 4 000 € en publicidad. Utiliza el método de Newton.
34 La dosis de un fármaco comienza con 10 mg y cada día debe aumentar 2 mg hasta llegar a 20 mg. Se debe seguir 15 días con esa cantidad y a partir de entonces ir disminuyendo 4 mg cada día.
a) Representa la función que describe este enunciado y determina su expresión analítica.
b) Di cuál es su dominio y su recorrido.
35 El peso en miligramos de un embrión de una especie animal viene dado en la siguiente tabla:
tiempo (días) 3 5 8
peso (mg) 8 22 73
Halla, mediante interpolación cuadrática, el peso de un embrión de 6 días.
36 Las ganancias esperadas de una empresa en los próximos 10 años, en millones de euros, vienen dadas por la función G (t ) = –2t 2 + 20t + 5; t, en años. Representa la función y determina cuándo serán máximas las ganancias.
129 U 4
1 2 3 –1 – 2 –1 – 4 –3 –5 Y X I 1 2 –1 4 2 3 1 Y X II
Ejercicios y problemas propuestos
37 En las funciones de oferta y demanda, se llama cantidad de equilibrio al número de unidades que hay que producir para que la oferta y la demanda se igualen, o (x) = d (x). Se llama precio de equilibrio al precio con el cual se consigue esa igualdad.
a) Halla el precio y la cantidad de equilibrio de un producto cuyas funciones de oferta y demanda son o (x) = 2,5x – 100 y d (x) = 300 – 1,5x (x en euros, d y o en miles de unidades del producto).
b) Si el precio del producto es de 80 €, ¿habrá escasez o exceso del mismo? ¿Y si el precio fuese de 120 €?
c) ¿Cuál sería el precio y la cantidad de equilibrio si las funciones de oferta y demanda fuesen o (x) = 0,25x 2 – 100 y d (x) = 185 – 2x ?
38 El coste de producción de x unidades de un producto es igual a 1 4 x 2 + 35x + 25 euros y el precio de venta de una unidad es 50 – x 4 euros.
a) Escribe la función que nos da el beneficio total si se venden las x unidades producidas, y represéntala.
b) Halla el número de unidades que deben venderse para que el beneficio sea máximo.
39 En una fábrica se venden mensualmente 100 electrodomésticos a 400 euros cada uno y saben que por cada 10 euros de subida venderán 2 electrodomésticos menos.
a) ¿Cuáles serán los ingresos si suben los precios 50 euros?
b) Escribe la función que relaciona la subida de precio con los ingresos mensuales.
c) ¿Cuál debe ser la subida para que los ingresos de la fábrica sean máximos?
40 Los beneficios mensuales de una fábrica de golosinas, en miles de euros, vienen dados por f (x) = – 0,1x 2 + 2,5x – 10, cuando se venden x toneladas de producto.
a) Representa la función.
b) Calcula la cantidad mínima que se ha de vender para no tener pérdidas.
c) ¿Cuántas toneladas se han de vender para que el beneficio sea máximo? ¿Cuál es ese beneficio?
41 Para enviar un paquete desde Adelaida a París, un servicio de correo cobra 50 € por paquetes que pesen hasta 2 kg y 10 € por cada kilogramo o fracción adicional.
a) Calcula lo que cuesta enviar un paquete de 5 kg.
b) Escribe la expresión analítica del precio de enviar un paquete de x kg para x menor o igual a 8.
c) Represéntala gráficamente.
42 Tres operadores telefónicos ofrecen estas tarifas mensuales: abono 2 h coste a partir de 2 h
tarifa a 30 € 0,50 € por minuto
tarifa b 20 € 0,75 € por minuto
tarifa c 40 € 0,25 € por minuto
Analiza cuál es la tarifa más ventajosa según el tiempo que se sobrepasa las 2 h del abono.
43 Una discoteca abre a las 10 de la noche y cierra cuando se va toda la clientela. Representa la función que nos da el número de clientes, N, según el número de horas que lleva abierta, t, que es N (t ) = 80t – 10t 2
a) ¿A qué hora el número de clientes es máximo?
b) ¿A qué hora cerrará la discoteca?
44 El porcentaje de estudiantes que asisten a un curso de inglés de 10 meses de duración viene dado por la función:
P (t ) = ≤ ≤≤ at bt ct t 0 10 28 3 3 si si < 2 ++ * t, en meses
Sabemos que, inicialmente, el 100 % de los estudiantes asiste al curso; que transcurrido un mes, asiste el 60 % y que al cumplirse el tercer mes, la asistencia se reduce al 28 %. Calcula a, b, c y representa la función.
45 Las funciones I (t) = –0,5t 2 + 17t y C (t) = 0,5t 2 – t + 32, 0 ≤ t ≤ 18, representan, respectivamente, los ingresos y los costes de una empresa, en miles de euros, en función de los años transcurridos desde su comienzo y en los últimos 18 años.
a) ¿Para qué valor de t se da la igualdad C (t) = I (t)?
b) Halla la función que expresa los beneficios (ingresos menos costes) en función de t y represéntala gráficamente.
c) ¿Cuántos años después del comienzo de su actividad la empresa alcanzó el beneficio máximo? Calcula su valor.
46 Obtén la expresión analítica de las siguientes funciones:
47 Representa las siguientes funciones y defínelas como funciones «a trozos»: a) y = |2x + 5| b) y = |4 – x 2| c) y = x 2 3 3 – d) y = |– x 2 + 2x + 3|
130
c) –4 –2 –2 2 4 2 4 6 d) –4 –2 2 4 2 4 6 Y Y X X a) 2 4 6 2 4 6 8 b) –4 –2 2 4 2 4 6 Y Y X X 10
Cuestiones teóricas
48 ¿Verdadero o falso?
a) La función y = ax – no existe si a < 0.
b) Una función no puede cortar al eje Y en dos puntos.
c) La gráfica de y = mx 2 + n es una recta.
d) La parábola y = 3x 2 es más estrecha que y = x 2 .
e) El dominio de definición de la función f (x) = x 4 –3 2 es (–∞, +∞).
49 ¿Cuál es el dominio de definición y el recorrido de las siguientes funciones?
a) b) Y X –4 4 Y X 55 10 10 c) d) Y X Y X
50 ¿Cuántas soluciones puede tener cada uno de los siguientes sistemas de ecuaciones? Justifícalo con ejemplos gráficos.
a) yx yaxb 2
b) y yaxb
AUTOEVALUACIÓN
1 Halla el dominio de definición de las siguientes funciones:
a) y = x 3 – x 2 b) y = () x x 26 3 –2
c) y = x42 – d) y = xx5– 2
2 Representa las siguientes funciones:
a) f (x) = – 0,5x 2 + 2x – 2 b) f (x) = |5 + 2x |
c) f (x) = x x x x 1 3 0 0 si ≤ si –> 2 + * d) f (x) = x– –
3 Determina la expresión analítica de esta función definida en el intervalo [–6, 6]. ¿Cuál es su recorrido?
Para profundizar
51 Define por intervalos y representa.
a) y = |x + 1| + |
52 Halla el dominio de definición de estas funciones: a) y = x x 2 3 –+ b) y = x x 9 –
53 La evolución mensual del número de personas asociadas de un club, durante un año, viene dada por la función: f (x) =
a) Halla a sabiendo que se fundó con 50 personas asociadas.
b) Representa la función y di en qué mes el número de personas asociadas fue máximo y en qué mes fue mínimo.
c) Si para cubrir gastos el club necesita tener más de 47 personas asociadas, ¿en qué mes tuvo pérdidas?
54 Las tarifas de una empresa de transportes son:
• 40 € por tonelada de carga si esta es menor o igual a 20 t.
• Si la carga es mayor que 20 t, se restará, de los 40 €, tantos euros como toneladas sobrepasen las 20.
Dibuja la función ingresos de la empresa según la carga que transporte (carga máxima: 30 t) y obtén la expresión analítica.

➜ anayaeducacion.es Resoluciones de estos ejercicios.
4 Asistir a un gimnasio durante 6 meses nos cuesta 246 . Si asistimos 15 meses, el precio es 570 €. ¿Cuánto tendremos que pagar si queremos ir durante un año?
5 Ponemos al fuego un cazo con agua a 10 °C. En 5 minutos alcanza 100 °C y se mantiene así durante media hora, hasta que el agua se evapora totalmente. Representa la función que describe este fenómeno y halla su expresión analítica.
6 El precio de venta de un artículo viene dado por la expresión p = 12 – 0,01x (x = número de artículos fabricados; p = precio, en cientos de euros).
a) Si se venden 500 artículos, ¿cuáles serán los ingresos?
b) Representa la función número de artículos-ingresos
c) ¿Cuántos artículos se deben fabricar para que los ingresos sean máximos?
131 U 4
Y X 2 –2 –2 – 4 4 2
= =+ *
= =+ *
x 1 = =+ *
x
c) y yaxb
x – 3| b) y = |2x – 4| – |x – 1|
xx a xx
–si≤ ≤ si ≤ si ≤ –< < 2 2 ++ + *
x x x 6 50 20 146 06 68 812
x, en meses


Funciones II
Funciones exponenciales y logarítmicas
Ya conoces estas funciones de cursos anteriores. Como sabes, las funciones exponenciales se encuentran con muchísima frecuencia en nuestro mundo: en la naturaleza (crecimiento de poblaciones animales o vegetales), en la economía (crecimiento de un capital depositado en un banco).
Las funciones logarítmicas se utilizan para determinar la edad de los fósiles… para describir el pH (grado de acidez) de las sustancias químicas…

Amonite fosilizado.
La trigonometría: del mundo árabe a Europa
La matemática árabe, y en concreto la trigonometría, bebió de los conocimientos de Grecia y de la India. Pero sus aportaciones fueron muchas y notables. Una de ellas fue la de tomar r = 1 en la circunferencia goniométrica (en Grecia se usaba r = 60). Además, Al-Jwarizmi, nacido en Königsberg el más destacado matemático árabe, hizo las primeras tablas exactas del seno y del coseno, y tabuló por primera vez los valores de la tangente.
La matemática surgida de la cultura árabe, incluidos sus conocimientos sobre trigonometría, se extendió por Europa a partir del siglo xii. El astrónomo prusiano Johann Müller (Regiomontano), nacido en Königsberg en el siglo xv, fue el primer europeo en sistematizar y ampliar los conocimientos trigonométricos recibidos de aquella cultura.
¿Cómo fue que un prusiano se llamara Regiomontano? En aquella época el lenguaje de la ciencia era el latín y los científicos también latinizaban sus nombres. De este modo, Königsberg, montaña regia en alemán, paso a ser Regiomontanus.
Müller tradujo el Almagesto griego directamente al latín, sin partir de una traducción
árabe y escribió varios libros de trigonometría. En uno de ellos, De triangulis omnimodis (1464), hizo una exposición sistemática de los métodos de resolución de triángulos. Este libro constituye uno de los grandes hitos de la trigonometría y, debido a él, Regiomontano es considerado el padre de la trigonometría moderna.
La primera representación del seno
Gilles de Roberval, matemático francés especialmente interesado en el estudio de diversas curvas, en 1635 bosquejó por primera vez la gráfica de la mitad de un arco de la curva seno. Lo que hasta entonces era una colección de valores (tabla numérica) útil para la trigonometría, pasó a ser mirado como gráfica de una función.
Más adelante, Leibniz (1646-1716) le dio carta de naturaleza a la función seno, junto a las demás funciones trigonométricas.
5 132
Las
funciones trigonométricas hoy
A comienzos del siglo xix la trigonometría alcanzó su punto culminante con las series de Fourier, que unieron estrechamente la trigonometría al análisis, proporcionando un instrumento sin precedentes para la exploración de las vibraciones y movimientos periódicos que por todas partes aparecen en la naturaleza. El análisis armónico es la herramienta que trata de las funciones periódicas. Comenzó con el estudio de la vibración de una cuerda musical y se ha desarrollado de tal manera que con él se pueden analizar y describir todo tipo de ondas. Física, química, medicina, ingeniería, tecnología… son deudoras de esta rama de las matemáticas. Sus ingredientes básicos son las funciones trigonométricas que se estudian en esta unidad.
RESUELVE
Dos formas de visualizar la curva seno


1.ª En una hoja de papel transparente, pinta una diagonal con un rotulador rojo de trazo grueso. Enrolla la transparencia sobre el lado largo de la hoja y verás con toda nitidez la curva seno.


2.ª Enrolla una hoja de papel alrededor de una vela o alrededor del soporte de cartón de un rollo de papel higiénico o de papel de cocina. Córtalo con un cuchillo, cúter o serrucho, trazando un ángulo de 45° con su eje. Desenrolla. La curva resultante es la curva seno.



133

Transformaciones elementales de funciones
Vamos a ver cómo se transforma la gráfica de y = f (x) cuando sometemos a la función a ciertas transformaciones muy sencillas.
Traslaciones
Si k es un número positivo, entonces:
La gráfica de se obtiene trasladando la gráfica de f (x)
f (x) + k f (x) – k f (x + k)
f (x – k)
Simetrías
k unidades hacia arriba
k unidades hacia abajo
k unidades hacia la izquierda
k unidades hacia la derecha
La gráfica de es la simétrica de la gráfica de f (x) respecto al eje X –f (x)
f (–x) respecto al eje Y
Ejercicio resuelto
1 Relacionar las siguientes gráficas mediante sus ecuaciones: Y X 1 2 5 4 3
f (x ) + 5
f (x + 5) f (x – 5)
f (x )

➜ Mueve cualquier función cambiando los parámetros.
(x ) – 5
(x )
1 Es la gráfica de la función y = x
2 Se obtiene trasladando 1 6 unidades a la derecha → y = x 6 –.
3 Se obtiene trasladando 2 3 unidades hacia arriba → y = x 3 6 –+ .
4 Es la simétrica respecto al eje X de 1 → y = – x .
5 Se obtiene trasladando 4 5 unidades hacia arriba → y = – x 5 + .
Piensa y practica
1 Representa sucesivamente.
a) y = x 1 b) y = x 3 1 + c) y = –x 3 1 + d) y = –x 3 1 + + 8
2 Representa en los mismos ejes de coordenadas las siguientes funciones:
a) y = x 2 b) y = (x + 2)2 c) y = (x – 3)2 + 1 d) y = (x + 1)2 – 3
134
1
f
–
f
Y X
f
Y X
(x )
f
(–x )
Estiramientos y contracciones
Si k es un número mayor que 1, entonces:
La gráfica de se obtiene a partir de la gráfica de f (x)
estirándola en sentido vertical multiplicando por k kf (x)
k 1 f (x) contrayéndola en sentido vertical dividiendo entre k
1 Representar sucesivamente las siguientes funciones:
1 y = x 6
2 y = x5 6 –
3 y = – x5 6 –para llegar, finalmente, a la representación de:
4 y = – x5 6 4 –+
2 Representar sucesivamente:
1 y = x
2 y = 2 x
3 y = –2 x
4 y = –2 x–para llegar, finalmente, a la representación de:
5 y = –2 () x6–+
Piensa y practica
2 se obtiene desplazando 1 5 unidades a la derecha.
3 es la simétrica de 2 respecto al eje X
4 se obtiene subiendo 3 4 unidades.
2 se obtiene estirando 1 en sentido vertical multiplicando por 2.
3 es la simétrica de 2 respecto al eje X
4 es la simétrica de 3 respecto al eje Y.
5 se obtiene desplazando 4 6 unidades a la izquierda.
3 Si y = f (x) pasa por (3, 8), di un punto de: y = f (x) – 6, y = f (x + 4), y = 2 1 f (x), y = 2f (x), y = –f (x), y = f (–x), y = –2f (–x) + 3
4 Representa. a) y = –x 8 4 + – 3 b) y = 3 x 10 –+
U 5 135
Ejercicios resueltos X Y 1 2 3 4 5 X Y X Y 1 1 2 2 3 4 4 3
X Y 2f (x) f (x) f (x) 1 2

Composición de funciones
Veamos, con unos ejemplos, cómo a partir de dos funciones se obtiene otra, llamada función compuesta de ambas.
• Observa la siguiente secuencia: = 16 16 4 16 1 4 1 /x 1 =
Si ahora actuamos sobre una variable, x, obtenemos la función x 1 : xx x 1 /x 1
Pongamos nombres a las funciones utilizadas:
() xr x = () x vx 1 =
La función resultante se llama función compuesta de r y v y se designa v ° r:
r (x) = v [r (x)] 8 v ° r (16) = v [r (16)] = v ( 16 ) = v(4) = 4 1
• Otro ejemplo: f (x) = x2 – 5x; r(x) = x xx xx x55 f r 22 () () [] rf xr fx xx 5 –2 == %
r ° f (9) = r (81 – 45) = r (36) = 36 = 6
Dadas dos funciones, f y g, se llama función compuesta de f y g, y se designa por g ° f, a la función que transforma x en g [ f (x)]: x ⎯⎯→ g [ f (x)] x ⎯→ f (x) ⎯→
La expresión g ° f (x) se lee f compuesta con g. Se nombra en primer lugar la función de la derecha porque es la primera en actuar sobre la x.
En general, la función f [ g (x)] es distinta de g [ f (x)].
• Observa que, en general, no es lo mismo componer dos funciones en un sentido que en sentido contrario:
() · xxxx xx55 r f 2 =
() () () [] fr xf rx xr fx xx x 55 ·≠ – –2 == = %%
() () () ·( ) ≠ fr ff rf 99 33 53 69 6 2 == == = %%
• Sin embargo, también hay casos en los que al componer dos funciones en ambos sentidos el resultado es el mismo:
f (x) = 2x + 1 g(x) = 3x + 2
• f ° g (x) = f [g(x)] = 2(3x + 2) + 1 = (6x + 4) + 1 = 6x + 5
• g ° f (x) = g[ f (x)] = 3(2x + 1) + 2 = (6x + 3) + 2 = 6x + 5
Por tanto, en este caso, f ° g (x) = g ° f (x).
OBSERVA

➜ Composición de funciones con GeoGebra.
TEN EN CUENTA
En general, no es lo mismo f ° r (x) que r ° f (x). x f
136
v °
g
g
g [ f (x)]
° f f g
° f
x 4 8 √x 1/4 8 1/ √x 16 8 4 8 1/4 1 8 1 8 1 100 8 10 8 0,1 0,0001 8 0,01 8 100 OBSERVA x 4 2 – 5 4 8 x2 – 5x 4 8 √x2 – 5x 9 8 36 8 6 –3 8 24 8 √24 0 8 0 8 0 –0,1 8 0,51 8 √0,51
f
g g [ f (x)]
(x)
2
Ejercicios resueltos
1 Considerar las funciones:
f (x) = x 2 – x y g(x) = x1 4 +
a) Obtener la expresión analítica de: f ° g g ° f f ° f g ° g
b) Hallar f [g(1)] y g[ f (1)].
2 Dadas estas funciones:
f (x) = 1 x g(x) = x2
h(x) = x + 1
a) Indicar cómo deben componerse para obtener estas otras:
y1 = 1 x 2 y2 = x2 + 1
y3 = x2 + 2x + 1 y4 = 1 1 x+
b) Componer f{g[h(x)]}.
Piensa y practica
a) En cada caso se trata de ver la composición de dos funciones. Es bastante intuitivo.
• y1: es claro que hay que aplicar f y g, pero parece que si se hace de una forma u otra se obtiene lo mismo: f ° g (x) = f (x 2) = x 1 2 ; g ° f (x) = g xx x 11 1 2 2 ==bbll Vale tanto f ° g (x) como g ° f (x).
• y2: primero se aplica g(x) y después h(x). Es decir, h ° g(x) = h(x2) = x2 + 1.
• y3: se ha aplicado el cuadrado a x + 1, por tanto: g ° h(x) = g(x + 1) = (x + 1)2 = x2 + 2x + 1
• y4: se aplica primero h(x) y después f (x). Es decir, f ° h(x) = f (x + 1) = x 1 1 + .
b) f {g[h(x)]} = f [g(x + 1)] = f [(x + 1)2] = () x 1 1 2 +
1 Si f (x) = x 2 – 5x + 3 y g (x) = x 2 , obtén las expresiones de f [ g (x)] y g [ f (x)].
Halla f [ g (4)] y g [ f (4)].
2 Si f (x) = x y g (x) = x + 4, obtén las expresiones de f ° g, g ° f, f ° f y g ° g.
Halla el valor de estas funciones en x = 0 y x = 5.
3 Si f (x) = x 1 , g(x) = x2 + 5, halla f ° g, g ° f, f ° f y g ° g
Halla el valor de estas funciones en x = 1 y x = 2
4 Dado f (x) = x + 1, obtén en cada caso la función g(x) para que se cumpla:
a) g[f (x)] = x – 2 b) f [g(x)] = x2 + 3x – 2
c) g ° f (x) = x2 + 2x d) f ° g (x) = x
U 5 137
a) • f [ g (x)] = () () () () f xx x xx x x x 1 4 1 4 1 4 1 16 1 41 1 12 4 – ––2 22 2 + = ++ = ++ + = + cm < F ⇒ ⇒ () () fg x x x 1 12 4 –2 % = + • g [ f (x)] = () ()gx x xx xx 1 4 1 4 –2 22 = + = + ⇒ () gf x xx 1 4 –2 % = + • f [ f (x)] = f (x 2 – x) = (x 2 – x)2 – (x 2 – x) = x 4 – 2x 3 + x 2 – x 2 + x ⇒ ⇒ f ° f (x) = x 4 – 2x 3 + x • g [ g (x)] = () g x xx x x x x x 1 4 1 4 1 4 1 41 4 41 41 5 44 + = + + = + ++ = ++ + = + + < F ⇒ ⇒ () gg x x x 5 44 % = + + b) • f [ g (1)] = () 11 12 41 –2 + = 4 8 = 2; o bien, 1 g ⎯→ 1 4 1+ = 2 f ⎯→ 22 – 2 = 2 • g [ f (1)] = 11 1 4 –2 + = 4; o bien, 1 f ⎯→ 12 – 1 = 0 g ⎯→
0+
1 4
= 4

Función inversa o recíproca de otra
Vamos a componer las funciones f (x) = x 3 – 6 y f –1(x) = x 6 3 + :
x f ⎯→ x 3 – 6 f –1 ⎯→ ()xx x 66 –33 3 3 += = f –1[ f (x)] = x x f –1 ⎯→ x 6 3 + f
Vemos que f y f –1 tienen la peculiaridad de que al actuar sucesivamente sobre un número x, el número se mantiene, es decir, cada una de esas funciones deshace lo que hace la otra. Por eso se dice que f –1 es la inversa de f, o que cada una de ellas es inversa de la otra.
Observa la simetría de los puntos de una y otra función respecto a y = x : puntos de f (x): y = x 3 – 6 (–1, –7) (0, –6) (2, 2) … (a, b) puntos de f –1(x): y = x 6 3 + (–7, –1) (– 6, 0) (2, 2) (b, a)
Se llama función inversa o recíproca de f a otra función (se designa por f –1) que cumple la siguiente condición: Si f (a) = b, entonces f –1(b) = a
Como consecuencia, se dan las relaciones siguientes:
x f ⎯→ f (x) f –1 ⎯→ x ; es decir, f –1[ f (x)] = x x f –1 ⎯→ f –1(x) f ⎯→ x ; es decir, f [ f –1(x)] = x
La función inversa de f –1 es, a su vez, f. Por eso se dice, simplemente, que las funciones f y f –1 son inversas o recíprocas.
Las gráficas de dos funciones inversas son simétricas respecto a la recta y = x
Para que una función tenga inversa ha de ser inyectiva, es decir, cada valor de y ha de corresponder a un único valor de x. Si no es así, ha de descomponerse en tramos en que sea inyectiva, cada uno de los cuales tendrá su función inversa.
Por ejemplo, como y = x 2 no es inyectiva, para hallar su inversa procedemos así:
=
Piensa y practica

1 ¿Verdadero o falso?
a) La función recíproca de y = x es y = x 1 .
b) Cada una de las funciones y = x, y = x 1 es recíproca de sí misma.
c) La inversa de la función y = x 9 , x ∈ [3, 9], es y = x 9 , x ∈ [1, 3].
d) Si una función es creciente, su recíproca es decreciente.

➜ Inversa de una función.
GRÁFICAS DE FUNCIONES INVERSAS
El dominio de f coincide con el recorrido de f –1 y el recorrido de f coincide con el dominio de f –1 y = x y = f –1(x) y = f (x) X Y
2 Representa y = 2x, y = x 2 y comprueba que son inversas.

3 Comprueba que hay que descomponer y = x 2 – 1 en dos ramas para hallar sus inversas. Averigua cuáles son.
4 Comprueba que la función recíproca de y = 2x + 4 es y = 1 2 x – 2.
138
– 6 = (
x f [ f –1(
)] =
⎯→ x 6 3 3 + ` j
x + 6) – 6 =
x
x
2 () ,≥ () () ,( ) ≤ yf xx xf xx yf xx xf xx 0 0–1 2 1 1 21 22 ––" " == = == = * y = x 2 , x ≥ 0 y = √x Y X y = x 2 , x ≤ 0 y = –√x Y X
y
f (x) = x
3
Expresión analítica de la función inversa de otra
Para hallar la inversa de y = f (x), se intercambian las dos incógnitas, x = f ( y). Ahora, si se puede, se despeja la y
Por ejemplo, f (x) = 2x – 3: y = 2x – 3 → x = 2y – 3 → y = x 2 3 +
Por tanto, f –1(x) = x 2 3 +
Veamos cómo procederíamos si f (x) tuviese el dominio de definición limitado: f (x) = 2x – 3, x ∈ [–1, 4]
Para hallar su inversa, hallamos los valores que toma la función en los extremos del intervalo: f (–1) = –5, f (4) = 5.
Por tanto, f –1(x) = x 2 3 + , x ∈ [–5, 5] y = f (x ) y = f –1(x ) Y X 2 2
Veamos otro ejemplo; hallemos la inversa de la función y = f (x) = xx68 –2 + :
Para representar y = xx68 –2 + (en verde) nos apoyamos en la gráfica de y = x 2 – 6x + 8 (punteada en azul).
Como ves, y = f (x) no está definida en los valores en los cuales el radicando es negativo, es decir, en (2, 4). Por tanto, su gráfica está compuesta por dos ramas:
y = f1(x) = xx68 –2 + , x ≤ 2
y = f2(x) = xx68 –2 + , x ≥ 4
Obtenemos las expresiones analíticas de sus inversas: y = xx68 –2 + → x = yy68 –2 + → x 2 =
y 2 – 6y + (8 – x 2) = 0 → y =
x 31 ± 2 =+
Es decir:
La inversa de y = f1(x) = xx68 –2 + , x ≤ 2, es: y = f1–1(x) = 3 – x 1 2 + , x ≥ 0
La inversa de y = f2(x) = xx68 –2 + , x ≥ 4, es: y = f2–1(x) = 3 + x 1 2 + , x ≥ 0
Piensa y practica
5 Halla la expresión analítica de la función inversa de:
a) f (x) = x 2 5 –, x ∈ [3, 13]
b) g (x) = x 3 2–, x ∈ [–7, 14]
6 La función y = x 2 – 2x tiene dos ramas: una decreciente para x ≤ 1, y otra creciente para x ≥ 1.
Exprésala como dos funciones f 1(x) y f 2(x) y halla la función inversa de cada una de ellas.
U 5 139
y 2 – 6y + 8 →
()
2 6364 8 39 8
–
2 2 =+ =
→
x x
±–
±–
f 2 –1 f 1 –1 f 2 f 1 Y X 2 2 Y X 2 4 – 4 –2 6 8 2 4 6 8 y = x 2 – 6x + 8 y = √x 2 – 6x + 8 x ≥ 4 y = √x 2 – 6x + 8 x ≤ 2

Funciones exponenciales
La función exponencial de base 2: y = 2x
4 0 –4 y = 2x 5
La gráfica de la izquierda muestra la representación de la función y = 2x. Se trata de una función definida en todo Á, continua y creciente.
10 x 2 4 10 40 60 x10 1 024 1 048 576 10 000 000 000 1,049 · 1016 6,05 · 1017 2x 4 16 1 024 1,1 · 1012 1,15 · 1018 …
Crece más deprisa que cualquier función potencia. Por ejemplo, aunque la función y = x 10 al principio es mayor que y = 2x, esta «la supera» para valores suficientemente grandes de x
La función exponencial de base 1/2: y = (1/2)x
La gráfica de la función y = 2 1 xcm es simétrica, respecto del eje Y, de la de y = 2x .
La razón de esto es la siguiente:
Como consecuencia de la propiedad anterior, la función y = 2 1 xcm es también continua en todo Á, pero decreciente.
Características de las funciones exponenciales
Se llaman funciones exponenciales las que tienen por ecuación y = a x, siendo la base a un número positivo distinto de 1.
• Todas ellas son continuas en Á, y pasan por (0, 1) y (1, a).
• Si a > 1, son crecientes, tanto más cuanto mayor sea a. El crecimiento de cualquiera de ellas llega a ser muy rápido, superando incluso a cualquier función potencia. Por eso la expresión crecimiento exponencial es sinónimo de crecimiento muy rápido.
• Si 0 < a < 1, son decrecientes.
• En matemáticas superiores, la función y = e x es extraordinariamente importante. Tanto es así que cuando se habla de «la función exponencial», sin mencionar cuál es su base, se está haciendo referencia a ella.
• También son exponenciales las funciones y = a kx, pues a kx = (a k )x. Es decir, y = a kx es una función exponencial de base a k
• En las calculadoras científicas suele haber dos teclas, y , con las que se obtienen valores de las funciones y = 10 x e y = e x, respectivamente.

➜ Juega con la base de funciones exponenciales.
140
() () (/ ) yf x yf x 2 12 2 x xx 1 2 –== == = 4 f1(–x ) = f2(x ) –x x f1(–x) f1(x
)
y
4
10
1
= 2x
0 5
–4
y = ( )x 2
4
Fenómenos que se describen mediante la función exponencial La función exponencial se presenta en multitud de fenómenos de crecimiento animal, vegetal, económico, etc. En todos ellos, la variable independiente es el tiempo. Veamos algunos ejemplos:
• En un lugar aislado se introducen 1 000 moscas de una cierta especie. La población (N = n.º de moscas) varía a lo largo del tiempo t (expresado en días) según la siguiente función:
N = 1 000 · 1,02t
• Un capital de 50 000 € impuesto al 6 % anual se transforma en un capital C al cabo de t años del siguiente modo:
C = 50 000 · 1,06t
La función exponencial también sirve para describir fenómenos de decrecimiento. Por ejemplo:
• Las sustancias radiactivas se desintegran con el paso del tiempo y la cantidad de sustancia radiactiva disminuye de forma exponencial. En unas, la desintegración es rapidísima, en otras, muy lenta. Por ejemplo, una cierta cantidad de masa de una sustancia se desintegra según la ecuación:
M = m · 0,76t donde t es el tiempo y viene dado en miles de años, m es la cantidad inicial de sustancia radiactiva y M es la cantidad de sustancia radiactiva transcurrido un tiempo t .
CANTIDAD DE SUSTANCIA RADIACTIVA
Crecimiento de la población mundial
población
desde el año 10000 a. C. hasta el año 2000 d. C.
TIEMPO (miles de años)
• Si un capital de 80 000 € depositados en divisas se devalúa un 3,5 % al año, su evolución con el tiempo se describe mediante la función:
C = 80 000 · , 100 35
Piensa y practica
1 La masa de madera de un bosque aumenta en un 40 % cada 100 años. Si tomamos como unidad de masa vegetal (biomasa) la que había en el año 1800, que consideramos instante de partida, y como unidad de tiempo 100 años, la función M = 1,4t nos da la cantidad de masa vegetal, M, en un instante cualquiera, t, expresado en siglos a partir de 1800 (razona por qué).
a) Averigua cuándo habrá una masa de madera triple que en 1800 (1,4t = 3) y cuándo había la tercera parte. Observa que los dos periodos de tiempo son iguales.
b) Calcula la cantidad de madera que había en 1900, 1990, 2000, 1600 y 1550.
2 Comprueba que, en el ejemplo anterior referente a la desintegración de una cierta sustancia radiactiva, M = m · 0,76t (t expresado en miles de años), el periodo de semidesintegración (tiempo que tarda en reducirse a la mitad la sustancia radiactiva) es de, aproximadamente, 2 500 años.
Para ello, comprueba que una cantidad inicial cualquiera se reduce a la mitad al cabo de unos 2 500 años (t = 2,5).
U 5 141
1 2 3 4 5 m
100 –tcm = 80 000 · 0,965t 10 20 30 40 50 1 000 2 000 3 000 N.º DE MOSCAS DÍAS TRANSCURRIDOS
total

Funciones logarítmicas
La función inversa de y = 2x se llama función logarítmica de base 2 y se designa así: y = log2 x. Los valores que toma esta función son, obviamente, los de los logaritmos en base 2.
La gráfica de y = log2 x es simétrica respecto de la recta y = x de la gráfica de y = 2x, por ser su función inversa.
Características de las funciones logarítmicas
Se llaman funciones logarítmicas las que tienen la ecuación y = loga x, siendo a un número positivo mayor que 1.
• Todas ellas son continuas en (0, +∞) y pasan por los puntos (1, 0) y (a, 1).
• Son crecientes. Su crecimiento es muy lento, tanto más cuanto mayor sea a.
• En matemáticas superiores la función y = loge x es muy importante. Se le llama logaritmo neperiano y se designa y = ln x o y = Lx. Es la función inversa de la exponencial de base e.
• En las calculadoras científicas suele haber tres teclas, , y , con las que se obtienen valores de las funciones y = loga x (a cualquiera), y = log x e y = ln x, respectivamente.
La función logarítmica como modelo
En psicología tiene gran importancia el estudio de percepciones. El individuo percibe colores, sonidos, olores, sabores… La percepción depende (es función) de los estímulos físicos. Por ejemplo, hablemos de la iluminación (I ), que puede ser medida físicamente, y la percepción, S, que aprecia un individuo. La relación entre las dos variables viene dada por la llamada ley psicofísica o ley de Weber-Fechner:
S = C log I (C es una constante)
Para valores pequeños de I el individuo aprecia pequeños cambios. Pero cuanto mayor sea I mayores tienen que ser los cambios para que se aprecien.
Ejercicio resuelto
1 Hallar la función recíproca o inversa de y = 10 x, x ∈ [–2, 4].
10–2 = 100 1 = 0,01; 104 = 10 000

➜ Exponencial y logarítmica: funciones inversas.
Piensa y practica
1 ¿Verdadero o falso?
nota: También existen las funciones logarítmicas y = loga x, para 0 < a < 1, pero aquí no las vamos a estudiar.
S = SENSACIÓN (estimada por el individuo)
S = SENSACIÓN (estimada por el individuo)
I = ESTÍMULO FÍSICO
I = ESTÍMULO FÍSICO
La función y = 10x pasa por (–2; 0,01) y por (4, 10 000). Por tanto, su recíproca pasa por (0,01; –2) y por (10 000, 4).
Conclusión: la recíproca de y = 10x , x ∈ [–2, 4] es y = log x, x ∈ [0,01; 10 000].
La función recíproca de y = 2x , x > 0 es y = log2 x, x > 1.
2 Halla la función recíproca de: y = log2 x, x ∈ [8, 32]
142
y = 2x y=x y = log2 x 2 2 –4 10 20 –4 10 20 Y X
5

Funciones trigonométricas
Visión intuitiva
Estamos arreglando un pinchazo en una rueda de bicicleta, que tenemos situada en el borde de una mesa, tal como se ve en la fotografía.
Al girar la rueda, el punto P en el que está el pinchazo varía su altura respecto de la mesa.
La función que relaciona x con y x: longitud recorrida por el punto P al girar y: altura a la que se encuentra P respecto al nivel de la mesa tomando la longitud del radio como unidad de medida, se llama función seno: x (recorrido) sen ⎯→ y = sen x (altura)

Podemos observar que cada posición de P corresponde a un ángulo de giro, α. Si dicho ángulo lo medimos por el valor de x, diremos que está medido en radianes.
OBSERVA
A partir de la primera vuelta, los valores de la función se repiten una y otra vez. Se trata de una función periódica. Su periodo es 2π, pues esta es la distancia que recorre P al dar una vuelta completa.
U 5 143
1 2 6 7 8 9 y y y y y y y x x = π x = 2π 3 4 5 10 π π x = 2 3 x = — π 2
1 2 3 4 5 6 7 8 9 10
Así es la gráfica que obtenemos:
x α
6
P
Seno de un ángulo
Un punto P gira sobre una circunferencia de radio 1. Trazamos unos ejes coordenados, X e Y, con origen en el centro de la circunferencia.
Si α es el ángulo de giro, se llama seno de α, y se expresa sen α a la ordenada del punto P. Es la distancia de P al eje X, de modo que si el punto queda encima del eje X, la distancia es positiva (sen α > 0), y si el punto queda bajo el eje X, la distancia es negativa (sen β < 0).
El seno de un ángulo toma, pues, valores entre –1 y 1: –1 ≤ sen α ≤ 1
La circunferencia de radio unidad que utilizamos para medir los valores del seno se llama circunferencia goniométrica.
Grados y radianes
Los ángulos se miden, habitualmente, en grados. Sin embargo, para representar las funciones trigonométricas es muy útil otra unidad de medida de ángulos: el radián.
El valor de un ángulo α en radianes es igual a la longitud del arco correspondiente medido sobre la circunferencia goniométrica.
Valores del seno
Los valores del seno de un ángulo se pueden obtener con la calculadora: en grados: sen 45° 37' → 45 37 = 0,714676 en radianes: sen 1,5 rad → 1,5 = 0,997495
Observa algunos valores interesantes que dan lugar a la gráfica del margen: grados
GRADOS Y RADIANES CON CALCULADORA
En la calculadora se utilizan por defecto los grados. Para configurar la medida angular se pulsa y se selecciona 2:Unidad angular. Aparecen tres opciones para elegir:
1:Grado sexag (D)
2:Radián
3:Grado cent (G)
medida del ángulo en radianes.
La función seno
La gráfica representada en el margen es la de la función y = sen x, siendo x la medida en radianes de un ángulo del intervalo [0, 2π], es decir, entre 0° y 360°.
Si consideramos ángulos mayores que 360° (2π rad) haciendo que el punto siga girando después de la primera vuelta, y ángulos negativos cuando el ángulo gira en sentido contrario, los valores del seno se repiten. Se obtiene, así, la siguiente función, definida en todo Á, continua y periódica de periodo 2π:
FUNCIÓN PERIÓDICA
Una función es periódica si:
Es decir, si los valores de f se repiten cada vez que se avanza o se retrocede un intervalo de longitud l
144
0° 30° 45° 60° 90° 120° 135° 150° 180° 210° 225° 240° 270° 300° 315° 330° 360° radianes 0 π 6 4 π 3 π 2 π 2 3 π 4 3π 6 5π π 6 7π 5 4 π 4 3 π 3 2 π 5 3 π 7 4 π 6 11π 2π sen 0 2 1 2 2 2 3 1 2 3 2 2 2 1 0 2 –1 2 2 –2 3 ––1 2 3 –2 2 –2 –1 0
y = sen x –2π –π 1 –1 π 3π 2π 180 α° = —— α rad π 1 rad 1 rad ≈ 57° 17' 1
f
x
x
l ) = … = f (x +
∈
(
) = f (
+
kl ), k
Z
x
1 2 3 4 5 1 –1 6 π 2π 3π 2 π 2 y = sen x, x ∈[0, 2π] Y X P β α sen β sen α –1 ≤ sen α ≤ 1
:
Coseno de un ángulo
Situamos un ángulo α sobre la circunferencia goniométrica. El primer lado del ángulo es el eje X y el segundo determina un punto P. Se llama coseno de α y se designa cos α, a la abscisa de P, es decir, a su distancia al eje Y, que será positiva si está a su derecha y negativa si está a su izquierda.
El coseno de un ángulo toma valores entre –1 y 1: –1 ≤ cos α ≤ 1
Relaciones entre seno y coseno
• Puesto que cualquiera que sea el ángulo α, sen α y cos α son las coordenadas de un punto P de la circunferencia goniométrica, cuyo radio es 1, se verifica la siguiente igualdad:
(sen α)2 + (cos α)2 = 1 relación fundamental
• Si dos ángulos difieren en 90°, α y α + 90°, entonces:
sen (90° + α) = cos α
cos (90° + α) = –sen α
Valores del coseno
Los valores del coseno de un ángulo se pueden obtener con la calculadora: en grados: cos 45° 37' → 45 37 = 0,699455 en radianes: cos 1,5 rad → 1,5 = 0,070737
Observa algunos valores interesantes que dan lugar a la gráfica del margen:
x : medida del ángulo en radianes.
La función coseno
La gráfica representada en el margen es la de la función y = cos x, siendo x la medida en radianes de un ángulo del intervalo [0, 2π], es decir, entre 0° y 360°.
Si consideramos ángulos mayores que 360° (2π rad) y ángulos negativos, los valores del coseno se repiten. Se obtiene así la siguiente función definida en todo Á, continua y periódica de periodo 2π: y = cos x
RECUERDA
cos α = sen (90° + α) = sen (π/2 rad + α)
Por tanto, la gráfica de la función y = cos x = sen (π/2 + x )
es la de y = sen x desplazada π/2 a la izquierda.
U 5 145
0° 30° 45° 60° 90° 120° 135° 150° 180° 210° 225° 240° 270° 300° 315° 330° 360° radianes 0 π 6 4 π 3 π 2 π 2 3 π 4 3π 6 5π π 6 7π 5 4 π 4 3 π 3 2 π 5 3 π 7 4 π 6 11π 2π cos 1 2 3 2 2 2 1 0 2 –1 2 2 –2 3 ––1 2 3 –2 2 –2 –1 0 2 1 2 2 2 3 1
grados
–2π –π 1 –1 π 3π 2π
y
cos x,
∈[0, 2π] 1 2 3 4 5 1 –1 6 π 2π 3π 2 π 2
=
x
Y X P cos α cos β β α –1 ≤ cos α ≤ 1 cos α 90°+α α sen α cos (90° + α) sen (90° + α)
Tangente de un ángulo
En el punto U en el que la circunferencia goniométrica corta a la parte positiva del eje de las X, trazamos una recta t tangente a ella.
Situamos un ángulo sobre la circunferencia. Al prolongar el segundo lado del ángulo, o su semirrecta opuesta, corta a la recta t en un punto T. Se llama tangente del ángulo a la medida UT, que será positiva si T está por encima del eje X y negativa si está por debajo (obsérvalo en la gráfica del margen).
Los ángulos de 90° y 270° no tienen tangente, pues ni el segundo lado del ángulo ni la semirrecta opuesta cortan a la recta t.
Relaciones entre seno, coseno y tangente
Si α es un ángulo distinto de 90° y de 270°, se verifica que tg α = a a cos sen
Para probarlo, observamos que los triángulos OCS y OUT son semejantes.
Por tanto:
Si el ángulo está situado en otro cuadrante, también se cumple la igualdad, con el correspondiente signo.
Valores de la tangente
Observa algunos valores de la tangente, que dan lugar a la gráfica del margen:
NOTACIÓN
Seno, coseno y tangente de un ángulo se llaman sus razones trigonométricas
La función tangente
Procediendo de forma similar a como lo hemos hecho para las funciones sen x y cos x, se obtiene la función y = tg x. Se trata de una función definida y continua en todo Á salvo en las abscisas π 2 + k π, siendo k números enteros (las rectas y =
2 + k π son asíntotas de la función y = tg x). Es periódica de periodo π.
NOTACIÓN
Las funciones y = sen x, y = cos x, y = tg x se llaman funciones trigonométricas o funciones circulares.
146
OU UT = OC CS → a tg 1 = a a cos sen
grados 0° 30° 45° 60° 90° 120° 135° 150° 180° 210° 225° 240° 270° 300° 315° 330° 360° radianes 0 π 6 4 π 3 π 2 π 2 3 π 4 3π 6 5π π 6 7π 5 4 π 4 3 π 3 2 π 5 3 π 7 4 π 6 11π 2π tg 0 3 3 1 3 – – 3 –1 3 3 –0 3 3 1 3 – – 3 –1 3 3 –0
–2π –π 0 2π 3π π 4π y = tg x
π
270° 180° 90° A B C D U T t tg α tg γ tg β tg δ β α γ δ U O S C T sen α cos α tg α α y = tg x π 2π 0 1 2 3 4 5 6 3π 2 π 2
Ejercicios y problemas resueltos
1. Transformaciones de una función
Sus gráficas son estas:
Esta es la gráfica de la función:
f (x) = x2 – 2x – 3
Representar, a partir de ella, las funciones:
a) g (x) = f (x) + 3
b) h (x) = f (x + 2)
c) i (x) = – f (x)
d) j (x) = | f (x)|
2. Representación de hipérbolas
Representar las hipérbolas siguientes:
a) y = x x 2 35 ––
b) y = x x 1 21 + +
HAZLO TÚ
Representa la función y = x x2 3 7 ––+
3. Transformar una función
Describir las transformaciones que hemos de hacer en la gráfica de y = x 2 para representar: f (x) = x 2 – 2x – 8
HAZLO TÚ
¿Qué transformaciones hemos de hacer en la gráfica de y = x 2 para representar f (x) = x 2 – 4x + 3?
Puedes comprobarlo con su expresión analítica:
a)
+ 3
Utilizando la relación ivisor Dividendo d = cociente + divisor resto , podemos representar este tipo de funciones a partir de la hipérbola y = 1/x mediante transformaciones elementales. a) Dividimos:
Por tanto, la gráfica pedida es como la de y = x 1 desplazada 2 unidades a la derecha y 3 arriba
b) Dividimos: 2x + 1 x + 1 –2x – 2 2 –1 → x x x
La gráfica pedida es como la de y = –x 1 desplazada 2 unidades hacia arriba y 1 hacia la izquierda.
Debemos escribir f de la forma f (x) = a(x – m)2 + p. Para ello, separamos los términos en x y completamos el cuadrado de una suma o diferencia rellenando los símbolos con los números adecuados:
f (x) = x 2 – 2x + – 8 –
f (x) = (x 2 – 2x + 1) – 8 – 1
f (x) = (x – 1)2 – 9
Para representar f (x), partimos de la gráfica de y = x 2 y hacemos una traslación de 1 unidad a la derecha y 9 unidades hacia abajo.
Las coordenadas del vértice son (1, –9).
X –5
U 5 147
–4
–1 1 3
–1 4 2 a) g(x) 2 –4 –2 2 2 h(x) b) 2 2 c) i(x) –2 4 2 2 4 d) j(x)
g (x) = x 2 – 2x
x + 2) – 3 = x 2 + 2
(, ][ ,) (, ) « xx xx x x 23 23 13 13 –si si –2 2 ++ + @@ * ∈ ∈
b) h (x) = (x + 2)2 – 2(
x – 3 c) i (x) = –x 2 + 2x
d) j (x) =
3x – 5 x – 2 –3x + 6 3 1 → x x x 2 35 1 3 2 –––=+
1 21 1 2 1 –+ + =+ +
1 1 Y X 2 1 –2
Y X
Y
Ejercicios y problemas resueltos
4. Composición de funciones y función inversa
Dadas las funciones:
f (x) = 2 x+1 g (x) = 1 x 3 + h (x) = x3 – 1
hallar:
a) g ° f b) h ° f c) g ° h d) h ° g ° f e) f -1
HAZLO TÚ
Halla g ° f y f ° g, siendo:
f (x) = 3x 2 – 5 y g (x) = 2 x 1 –
Observamos que f ( ) = 2 + 1 ; g( ) = 1 3 4 + ; h( ) = 3 – 1.
a) g ° f (x) = g[ f (x)] = g(2x + 1) =
c) g
funciones
son inversas porque verifican
e) Para calcular la inversa de f, cambiamos las variables, x = 2y + 1, y tomamos logaritmos de base 2 para despejar x :
5. Reconocer funciones compuestas
Explicar cómo, a partir de las funciones f (x) = 1 + 2 x, g (x) = x1 2 + , h(x) = 1/x 2 , se pueden obtener las funciones:
a) m(x) = 12 x1 2 + +
b) n(x) = () 12 1 x2 +
c) p(x) = (/ ) x 11 4 +
HAZLO TÚ
A partir de las funciones f, g, h aquí definidas, obtén:
a) q (x ) = () 12 1 x 2 ++
b) r (x ) = x 1 1 2 +
6. Función inversa de otra
Obtener la función inversa de cada una de las funciones siguientes:
a) f (x) = x 1 3 –
b) g (x) = 3 + 2 x + 1
c) h(x) = 2 ln (x – 3)
HAZLO TÚ
Obtén la función inversa de:
a) p (x ) = 3x – 2
b) q (x ) = log2 (x + 1)
a) Observamos que m(x ) = 12 x 1 2 + + tiene que ver con f (x ) = 1 + 2x y con g (x ) = x 1 2 + , de modo que para obtener un valor cualquiera m(a) calculamos en primer lugar a 1 2 + , después elevamos 2 a ese valor y sumamos 1. Es decir, aplicamos primero g y después f :
f [ g (x)] = f ( x 1 2 + ) = 12 x 1 2 + + → m (x ) = ( f ° g ) (x )
b) En n(x ) intervienen f (x ) y h(x ). La primera que actúa sobre x es f y después h. Por tanto: h[ f (x)] = h (1 + 2x ) = () 1 12 x 2 + → n (x ) = (h ° f ) (x )
c) Para obtener p(x ), aplicamos h(x ) en primer lugar y después g (x ): g [h (x
c) r (x ) = x 4 2 + a) Para obtener la función inversa, intercambiamos las variables y despejamos la y : x = y 3 1 –→ y – 3 = x 1 → y =
b) Después de intercambiar las variables, pasamos 3 al primer miembro y tomamos logaritmos en base 2 para despejar y : x = 3 + 2 y + 1 → x – 3 = 2 y + 1 → log2 (x – 3) = y + 1 → → y = –1 +
c) Intercambiamos las variables, pasamos 2 al primer miembro y aplicamos la definición de logaritmo para despejar y :
148
)] = g x 1 2 cm = 1 + xx 1 1 1 2 2 4 += cm → p(x ) = (g ° h ) (x )
x 1 + 3 → f –1(x) = x 1 + 3
log2 (x – 3) → g –1(x ) = –1 + log2 (x – 3)
y – 3 → e x/2 + 3 =
→ →
x = 2 ln ( y – 3) → x 2 = ln ( y – 3) → e x/2 =
y
h –1(x ) = 3 + e x/2
21 x 1 3 + +
b) h ° f (x) = h[ f (x)] = h(2x + 1) = (2x + 1)3 – 1 = 23x + 3 – 1
h
x) = g
h (x)] = g(x3 – 1) = ()
=+ ++ + ^ ^^
= 2x + 1
f (x)
log2 x = log2 2y + 1 → log2 x = y + 1 → y = –1 + log2 x → f – 1(x)= –1 + log
x
°
(
[
xx 11 –3 3 += Las
g y h
( g ° h)(x) = x d) h ° g ° f (x) = hg h 22 12 11 –xx x 11 1 3 3 3 =+
h hh 7 A
=
2
7. Gráficas de funciones exponenciales y logarítmicas
A partir de estas gráficas, Y 2 2 4 6 8 X 4 6 y = 2x y = log2 x
representar:
a) y = 2 x + 1 b) y = –2 x c) y = 2 x – 2 d) y = 2 –x
e) y = log2 (x + 2) f) y = – log2 x
HAZLO TÚ
Representa:
a) y = 2x – 1 b) y = 2x + 3
c) y = log2 (x – 2) d) y = log2 (–x )
8. Función exponencial
El proceso de cicatrización de una herida sigue una ley exponencial. La superficie S de la herida al cabo de t días se puede calcular mediante la fórmula S = So e kt , donde So es la superficie inicial y k una constante.
a) Si una herida tenía una superficie inicial de 50 cm 2 y al cabo de dos días mide 24,83 cm 2, ¿cuál es el valor de k?
b) Calcular la superficie de la herida después de 8 días.
c) Representar la función.
9. Función logarítmica
La gráfica de una función logarítmica del tipo y = 1 + logb (x – a) pasa por los puntos (4, 1) y (7, 3).
a) Calcular a y b.
b) Representar la función y su inversa.
HAZLO TÚ
Halla a y b para que la gráfica de la función y = –2 + logb (x + a) pase por (1, 0) y (–1, –1).
a) Se obtiene desplazando y = 2x una unidad hacia arriba.
b) Es la simétrica de y = 2x respecto del eje X
c) Se obtiene trasladando y = 2x dos unidades hacia la derecha.
d) Es la simétrica de y = 2x respecto del eje Y. Coincide con y = (1/2)x
e) Se obtiene trasladando y = log2 x dos unidades hacia la izquierda.
f) Es la simétrica de y = log2 x respecto del eje X.
a) Conocemos S0 = 50 y un punto (2; 24,83). Sustituyendo estos valores en la fórmula
S = S0e kt podemos obtener k S = 50e kt t = 2 ⎯→ 24,83 = 50e 2k → e 2k = 0,4966 → 2
b) Para t = 8, S = 50e – 0,35 8 = 3 cm2
c) Hacemos una tabla de valores de la función S = 50 . e – 0,35t
t 1 2 4 5 8 S(t) 35,2 24,9 12,3 8,7 3
a) Pasa por (4, 1): 1 = 1 + logb (4 – a) → logb (4 – a) = 0 → b0 = 4 – a → a = 3
Pasa por (7, 3): 3 = 1 + logb (7 – 3) → 2 = logb 4 → b 2 = 4 () b b 2 2 –novale = = b) La función es y = 1 + log2 (x – 3).
Su dominio es (3, +∞). Pasa por los puntos (3,5; 0), (4, 1) y (7, 3).
La gráfica de su función inversa es simétrica respecto a la bisectriz del primer cuadrante.
Su expresión analítica es y = 3 + 2x – 1
U 5 149
Y X y = 2x + 1 2 2 4 6 4 6 a) b) c) d) e) f ) Y X y = –2x Y X y = 2x – 2 Y X y = 2–x Y X y = log2 (x + 2) X y = –log2 x 2 4 6 – 6 – 4 –2 –2 2 4 2 4 6 2 4 6 2 4 6 2 4 6 2 4 6 2 4 2 4 6 Y
ln
k =
0,4966 → k = – 0,35
1 2 3 4 5 6 7 8 5 25 50 S = 50e
t SUPERFICIE (cm2) TIEMPO (días) Y X y = 1 + (3, 7) (4, 1) (1, 4) 6 2 2 4 6 8
3)
x
–0,35
(7,
y=
Ejercicios y problemas guiados
1. Función inversa
Y 2 2 X
Esta es la gráfica de la función:
f (x) = 2 – x 2, x ≤ 0
a) Dar su dominio de definición y su recorrido.
b) Representar su función inversa.
c) Hallar la expresión analítica de f –1(x).
2. Interés compuesto
Depositamos en un banco 5 000 al 4,8 % anual con pago trimestral de intereses.
a) ¿Cuál será el capital acumulado al cabo de 3 años?
b) Escribir la función que nos dice en cuánto se transforma ese capital al cabo de t años.
3. Depreciación
Una máquina que costó 20 000 se deprecia a un ritmo del 10 % anual.
a) ¿Cuál será su valor dentro de 4 años?
b) ¿Cuántos años tienen que pasar para que su valor sea de 12 000 €?
c) Escribir la función que da el número de años que deben pasar para llegar a un valor x.
4. Función logística
La función
f (x) = (, ) 1 499 109 12 000 –x + da las ventas totales de un videojuego x días después de su lanzamiento. ¿En qué día se llegó a 6 000 juegos vendidos?
a) El dominio de definición de f está limitado. Para saber cuál es el recorrido, considera cuál es el valor máximo que puede tener f (x ).
b) Haz una tabla de valores de f (x ) e invierte las variables para obtener algunos puntos de f –1(x ). Recuerda que las funciones inversas deber ser simétricas respecto de la bisectriz del primer cuadrante.
c) Al intercambiar las variables y despejar la y, obtendrás dos funciones con distinto recorrido. Ten en cuenta que el dominio de f (x ) es el recorrido de f –1(x ).
Solución:
a) Dominio de f = (–∞, 0] b) Recorrido de f = (–∞, 2]
c) f –1(x ) = – x 2– , x ≤ 2 Y 2 2 X
• El 4,8 % anual significa un , 4 48 = 1,2 % trimestral.
• Como los periodos de capitalización son trimestrales, al final del primer año el capital se convertirá en 5 000 · , 1 100 12 4 + cm .
• Esa cantidad se multiplicará cada año por , 1 100 12 4 + cm .
Solución: a) 5 769,5 € b) f (t ) = 5 000 · (1,012)4t ≈ 5 000 · (1,049)t
a) Al cabo de un año el precio baja un 10 %. Por tanto, el valor de la máquina será 20 000 · (1 – 0,1). Repite este razonamiento para cuatro años.
b) Escribe la función, f (t ), que da el precio después de t años. Haz f (t ) = 12 000 y despeja t.
c) La función pedida es la función inversa de f (t ).
Solución: a) 13 122 € b) 5 años c) f –1(t ) = , l ll n nn x 09 20 000 –
• Observa que has de encontrar el valor de x para el que f (x) = 6 000.
• Opera la expresión hasta eliminar denominadores y hacerla lo más sencilla posible.
• Obtendrás una expresión del tipo B A = C –x. Para obtener el valor de x, toma logaritmos y utiliza la calculadora
Solución: Se llegó a los 6 000 juegos vendidos 72 días después de su lanzamiento.
150 150
Ejercicios y problemas propuestos
Para practicar
Transformaciones de una función
1 Representa f (x) = 4 – x 2 y, a partir de ella, representa las siguientes funciones: a) y = f (x) – 3 b) y = f (x + 2)
2 Esta es la gráfica de la función y = f (
Y
Representa, a partir de ella, las funciones: a) y = f (x – 1) b) y = f (x) + 2 c) y = | f (x)|
3 A partir de la gráfica de f (x) = x 1 , representa: a) g (x) = f (x) – 2 b) h(x) = f (x – 3) c) i(x) = –f (x) d) j(x) = | f (x)|
4 Representa la función f (x) = x y dibuja a partir de ella las siguientes funciones: a) g (x) = f (x + 1) b) h(x) = f (x) – 3 c) j(x) = | f (x)|
5 La expresión analítica de esta función es del tipo y = xa 1 – + b.
Observa la gráfica y di el valor de a y b. 1 1 X Y
6 La ecuación de esta gráfica es del tipo ()yx mp –2 =+
Obsérvala y di el valor de m y p 2 3 1 Y X 1 –1
7 Representa las siguientes funciones:
a) y x 1 1 –= b) y x 1 1 = + c) y x 3 –1 –= d) y x 1 2 =+
8 Representa las siguientes funciones: a) y = x 1 – b) y = – x 3 + c) y = 2 + x d) y = 1 – x
9 Dibuja la gráfica de la función ()fx xx65 –2 =+ Representa, a partir de ella, las siguientes funciones y escribe sus ecuaciones.
a) () () gx fx 2 =+ b) () () hx fx 3 – = c) () () ix fx– =
Composición de funciones
10 Dadas las funciones f (x ) = x + 3 y g (x ) = 2x 2, halla:
a) f [ g (2)] b) g [ f (– 4)] c) f [ g (x )] d) g [ f (x )]
11 Considera las funciones f (x ) = x 2 + 1 y g (x ) = x 1 . Calcula:
a) ( f ° g ) (2) b) ( g ° f ) (–3)
c) ( g ° g ) (x ) d) ( f ° g ) (x )
12 Si f (x ) = 2x + 3 y g (x ) = x 2 – 2x, obtén: a) f ° g b) g ° f c) f ° f d) g ° g
13 Dadas las funciones f (x ) = 3x + 2 y g (x ) = x , halla: a) ( f ° g ) (x ) b) ( g ° f ) (x ) c) ( g ° g ) (x )
14 Dadas las funciones f (x) = x 2 + 1 g (x) = x 2 3 –h(x) = x 3 –obtén las expresiones de: a) f ° g b) g ° f c) f ° h d) g ° h e) h ° f f) h ° g Halla, si es posible, el valor de las funciones obtenidas en x = 5 y en x = 0.
15 Dadas las funciones ()fx senx = , ()gx x 2 = , ()hx x 1 = , halla la expresión analítica de: a) g ° f b) f ° g c) f ° g ° h d) h ° g ° f
16 Con las funciones f (x ) = x 1 2 y g (x ) = x – 2, hemos obtenido por composición las funciones p (x ) = () x 2 1 –2 y q (x ) = x 1 2 – 2. Indica cuál de estas expresiones corresponde a f ° g y cuál a g ° f.
17 Explica cómo a partir de las funciones f (x) = 2x – 1 g (x) = x 2 + h(x) = x 3 1 –se pueden obtener estas otras: a) m(x) = 2 x 1 + b) n(x) = 22 x 1 –+ c) p(x) = x 3 1 2 –+ d) q(x) = 2 x x 3 4 ––e) r (x) = x 1 1 + f) s (x) = 2 1 1 –x 1 –
18 Considera estas funciones: f (x ) = x – 5 g (x ) = x h (x ) = x 2 1 +
Explica cómo, a partir de f, g y h, se pueden obtener, por composición, p, q y r : p (x ) = x 5 – ; q (x ) = x – 5; r (x ) = x 2 1 +
151 151 U 5
c)
y = | f (x)|
2 2
X
x):
Ejercicios y problemas propuestos
Función inversa de otra
19 Dada la función f (x) = x 2 31 – halla f –1(x). Representa f y f –1 y comprueba su simetría respecto de la recta y = x
20 Halla la función inversa de las siguientes funciones:
a) y = 3x – 2 b) y = x 2 3 +
c) y = x 21 + d) y = 1 + 2x e) y = 2 + log3 x f) y = 4 – x 2 , x ≥ 0
21 Representa gráficamente la función inversa en cada caso: 2 X Y 2 2 X Y 2 2 a) b) c) X Y 2
22 Comprueba si cada par de funciones son una inversa de la otra. Para ello, calcula f ° f –1 o bien f –1 ° f :
a) f (x) = x 1 2 + ; f –1(x) = x 1 2 –
b) f (x) = x 23 + ; f –1(x) = x 3 2 2 +
c) f (x) = 1 + log2 x 3 ; f –1(x) = 3 2x – 1
23 Considera la función y = x 2 + , x ∈ [–2, 7].
a) ¿Cuál es su recorrido?
b) Obtén su función inversa y determina el dominio de definición y el recorrido de esta.
24 Halla la función inversa de las siguientes funciones:
a) y = x 2 31 – b) y = x13 –3
c) y = 1 + 2x – 3 d) y = 2 + log3 (x + 1)
e) y = 1 + x 1 3 –f) y = x x 23 1 –+
Funciones exponenciales y logarítmicas
25 Representa estas funciones a partir de la gráfica de y = 2x:
a) y = 2x + 2 b) y = 2x – 3
c) y = 2x/2 d) y = 1 2 x 3 + bl
e) y = 1 – 2x f) y = 22 – x
26 Representa estas funciones a partir de la gráfica de y = log2 x :
a) y = 1 + log2 x b) y = log2 (x – 1)
c) y = 2 – log2 x d) y = log2 (–x )
27 Con ayuda de la calculadora, representa estas funciones:
a) y = 3 · 0,8x b) y = (1/2) · 1,8x c) y = ln (2x ) d) y = ln (x + 1)
28 Asocia a cada una de las siguientes expresiones la gráfica que le corresponde:
a) y = ln x b) y = 21 – x c) y = e x d) y = –log2 x e) y = –(1/2)x f) y = log2 (
29 Comprueba que las gráficas de y = 3x e y = 3 1 xcm son simétricas respecto al eje OY
30 Haz una tabla de valores de la función y = 3x. A partir de ella, representa la función y = log3 x
31 ¿Cuál es el dominio de y = log2 (2 – x )? Represéntala.
Funciones trigonométricas
32 Si un punto P recorre una circunferencia completa de radio 1, el ángulo de giro es 360º que, medido por el arco, equivale a 2π radianes. Por tanto: 360°π 2 rad = → 180°π rad = → 90° 2 π rad =
a) Expresa en radianes los siguientes ángulos 30°, 45°, 60°, 120°, 135°.
b) Expresa en grados los siguientes ángulos 5π/6, 7π/4, 4π/3, 3π/2, 7π/6.
33 Representa estas funciones: a) y = 1 + sen x b) y = –cos x
34 Representa ysen x2 = . Para ello, utiliza la calculadora seleccionando el radián como unidad angular y completa la siguiente tabla de valores en tu cuaderno: x 0 π/4 π/2 3π/4 π 5π/4 3π/2 7π/4 y 0 1 0
152
2 X Y –2 4 6 I 2 – 4 X Y – 6 2 4 X Y 4 –2 – 4 –2 2 II III 2 2 4 2 X Y –2 IV Y X Y 4 2 4 6 V VI –2 – 4 – 6 4 6 2 2 X –2 4 6
x + 3)
35 Asocia a cada una de las siguientes funciones, la gráfica que le corresponde:
a) y = cos 2x b) y = –sen x c) y = 2sen x d) y = 1 + cos x
Para resolver
36 Expresa las siguientes funciones de la forma y xa b k –=+ y describe las transformaciones que tenemos que hacer para representarla a partir de y x 1 = :
a) y x x 1 3 –= b) y x x 2 4 ––=
c) y x x 1 32 = + + d) y x x 1 1 –= +
* Mira el ejercicio resuelto 2.
37 Expresa las siguientes funciones utilizando la expresión () ya xm p –2 =+ y describe las transformaciones que tenemos que hacer para representarlas a partir de yx 2 =
a) yx x10 16 –2 =+
b) y = x2 – x + 2
* Mira el ejercicio resuelto 3.
38 Representa y halla la función inversa en cada caso. a) y = 3 + 2x – 1 b) y = 0,2 · 23 – x
c) y = 1,8 · 50,2x d) y = 1 + log2 (x + 4)
e) y = ln (3x + 2) f) y = 2,5 · e –x/2
39 La gráfica de una función exponencial y = ka x pasa por los puntos (0; 0,5) y (1; 1,7). Calcula k y a, y represéntala.
40 Los puntos (1; 1,2) y (2; 0,48) pertenecen a la gráfica de la función y = k · a x
a) Calcula k y a
b) Halla el valor de x para el cual y = 120.
41 La gráfica de la función logarítmica y = –2 + logb (x + a) corta a los ejes de coordenadas en los puntos (0, –2) y (8, 0).
a) Calcula a y b
b) ¿Para qué valor de x es y = 3?
42 La función y = a + b ln x pasa por (e, 5) y (1/e, –1).
a) Calcula a y b
b) ¿Cuál es su función inversa?
43 La función y = 9 5 (x – 32) convierte grados Fahrenheit en grados centígrados. Halla la función para convertir grados centígrados en grados Fahrenheit.
44 Un cultivo de bacterias crece según la función y = 1 + 2x/10 ( y : miles de bacterias, x : horas). ¿Cuántas había en el momento inicial? ¿Y al cabo de 10 horas? ¿Cuánto tardarán en duplicarse?
45 La función y = 80 · 2–0,4t nos da la cantidad (en gramos) de estroncio radiactivo en una muestra de agua en el instante t (en años).
a) ¿Qué cantidad habrá al cabo de 10 años?
b) ¿Cuándo la cantidad actual se habrá reducido al 50 %?
46 La concentración de un fármaco en sangre viene dada por y = 100 · (0,94)t ( y en mg, t en h).
a) Di cuál es la dosis inicial y la cantidad de ese fármaco que tiene el paciente al cabo de 3 horas.
b) Representa la función.
c) Si queremos que la concentración no baje de 60 mg, ¿al cabo de cuánto tiempo tendremos que inyectarle de nuevo?
47 La cantidad de material radiactivo que queda al cabo de t años en una muestra de 75 gramos, se puede calcular mediante la ecuación C (t) = 75(0,62)t .
a) ¿Cuántos años tienen que transcurrir para que queden 10 gramos de material radiactivo?
b) Representa la función.
153 U 5
1 –1 π 2π π –2 π – –2 3π 2 I 1 π 2π π –2 π – –2 3π 2 2 III 1 –1 π 2π π –2 π – –2 3π 2 II 1 –1 –2 π 2π π –2 π – –2 3π 2 2
IV
Ejercicios y problemas propuestos
48 Un alumno de un curso de psicología sabe que el porcentaje de conocimientos que recordará t meses después de acabar el curso se puede calcular mediante la función:
R (t) = 94 – 46,8 log (t – 1)
a) Calcula el porcentaje que recordará 6 meses después de terminar el curso.
b) Representa la función.
49 Sabemos que la presión atmosférica varía con la altura. La ecuación h (x) = 41,97(0,996)x nos da la altura de una montaña, en kilómetros, si conocemos la presión atmosférica, x, en milibares.
a) Si en la cima del Everest la presión es de 389 milibares, ¿cuál es la altura del Everest?
b) ¿Cuál será la presión en la cima de una montaña de 3 500 metros de altura?
50 Esta gráfica representa un movimiento que se repite periódicamente:
a) Represéntala en el intervalo [0, 10].
b) Calcula f (7), f (10) y f (20).
2 X Y 2 4
51 Un depósito de 10 L de agua se llena y vacía automáticamente cada 8 minutos. Cuando el depósito está vacío comienza el llenado, que tarda 2 minutos, permanece lleno 5 minutos y se vacía en 1 minuto. Este proceso se repite periódicamente.
a) Representa la función que expresa la cantidad de agua que hay en el depósito durante media hora.
b) Calcula f (12), f (16) y f (19) y comprueba que f (x + 8k) = f (x), k ∈ Z. ¿Cuál es su periodo?
52 El número de ejemplares que se venden de un libro depende del dinero que se dedica a su publicidad. La función que da esta relación es:
y = 2 + 0,5 ln (x + 1); x en miles de euros, y en miles
a) Calcula cuántos ejemplares se venden si se invierten 20 000 € en publicidad.
b) ¿Cuánto habrá que invertir para vender 5 000 libros?
53 Un capital de 10 000 € se deposita en un banco al 6 % de interés anual con pago mensual de intereses. Escribe la función que nos dice en cuánto se transforma ese capital en m meses. Calcula cuánto tarda en duplicarse el capital.
54 La población mundial ha crecido de forma exponencial desde 1650. La función P (t) = 0,5 · e0,0072t , t en años, P (t) en miles de millones, nos da una buena aproximación de la población mundial hasta 2025.
a) ¿Cuál era la población mundial en 1920?
b) Estima la población mundial en 2024.
55 El carbono 14 sirve para calcular la edad de los fósiles y otros objetos. La fórmula que se utiliza es C = C0 · e –t ln 2/5730 , donde C0 es la cantidad de carbono 14 que tenía el fósil cuando se formó y C la que tendrá dentro de t años.
a) Si en un cierto fósil C 0 = 500 g, ¿cuántos gramos de carbono 14 tendrá dentro de 2 000 años?
b) Se llama periodo de semidesintegración al tiempo necesario para que la cantidad inicial se reduzca a la mitad. Calcula el periodo de semidesintegración del carbono 14.
56 El precio de un automóvil deportivo es de 24 000 €. Sabemos que se deprecia a un ritmo de un 12 % anual.
a) ¿Qué función da el valor del coche al cabo de t años?
b) ¿Cuándo llegará a la mitad del valor inicial?
57 Invertimos 20 000 € al 4,8 % anual en una cuenta que se capitaliza semestralmente.
a) Escribe la función que nos da el dinero que tendremos en la cuenta al cabo de t años.
b) ¿Cuánto tiempo tiene que pasar para que el capital inicial aumente un 50 %?
58 El número de recetas para medicamentos emitidas por los médicos del servicio de salud de una comunidad autónoma ha crecido exponencialmente desde 2005. La función es del tipo f (t) = ke at. Calcula k y a sabiendo que en 2005 (t = 0) se emitieron 6,52 miles de recetas y en el 2008 fueron 9,84 miles. ¿En qué año se llegará a 50 miles?
59 Un estudio de la policía refleja que el número de robos en viviendas, por año, en una ciudad, decrece según una función del tipo N (t) = A – B · log (t + 2). Sabemos que en el año 2000, que es cuando se inició el estudio, el número de robos fue de 520 y en el año 2003 fueron 476.
a) Determina A y B.
b) Calcula el número de robos que se esperan en 2024.
60 Un cultivo de bacterias comienza con 100 células. Media hora después hay 435. Si sigue un crecimiento exponencial del tipo y = k e a t (t en minutos), calcula k y a y representa la función. ¿Cuánto tardará en llegar a 5 000 bacterias?
61 Una taza de café recién hecho está a 75 °C. Después de 3 minutos en una habitación a 21 °C, la temperatura del café ha descendido a 64 °C. Si la temperatura, T, del café en cada instante t viene dada por la expresión T = Ae kt + 21, calcula A y k y representa la función. ¿Cuánto tendremos que esperar para que la temperatura del café sea de 45 °C?
62 Un estudio estima que la población de un barrio va a crecer según la función y = ke 1 10 000 , t02 –+ (t, años; y, habitantes)
a) El barrio tiene, actualmente, 1 250 habitantes. Halla k.
b) Calcula cuál será la población dentro de 10 años.
154
63 Un charco circular de agua se está evaporando al sol. Al cabo de t minutos, su radio es g(t) = t 2 15 + cm.
a) Expresa el área del charco en función del tiempo.
b) ¿Cuál será el área del charco al cabo de 10 min?
c) ¿Qué relación tiene la función del apartado a) con las funciones f (r) = πr 2 y g(t) = t 2 15 + ?
64 La recta y = 20x + 1 corta a y = a x en x = 0 y x = 4.
a) Calcula a.
b) Para ese valor de a, escribe la ecuación de la recta, s, que corta a y = loga x en x = 1 y x = 81.
c) ¿Qué relación hay entre las rectas r y s?
Cuestiones teóricas
65 Dada la función y = a x, contesta:
a) ¿Puede ser negativa la y ? ¿Y la x ?
b) ¿Para qué valores de a es decreciente?
c) ¿Cuál es el punto por el que pasan todas las funciones del tipo y = loga x ?
d) ¿Para qué valores de x se verifica 0 < a x < 1 siendo a > 1? ¿Y si 0 < a < 1?
AUTOEVALUACIÓN
1 Dadas f (x) = x 1 + , g (x) = x 3 1 –, halla: a) f [ g (2)] b) g [ f (15)] c) f ° g d) g –1(x)
2 Representa la gráfica de la función inversa de y = f (x). X y = f (x) Y
3 La gráfica de una función y = a + b log 2 (x + 2) pasa por los puntos (0, 1) y (2, 0). Halla a y b y justifica si se trata de una función creciente o decreciente.
4 El precio de una furgoneta baja un 8 % cada año. Si costó 18 000 €, ¿cuánto tardará en reducirse a la mitad?
5 Un cultivo de bacterias comienza con 50 células. Dos horas después hay 162. Si ese cultivo crece de forma exponencial según una función y = ke a t (t en horas) calcula k y a ¿Cuánto tardará en llegar a 5 000 bacterias?
66 Si f (x ) = 2x y g (x ) = log2 x, ¿cuál es la función ( g ° f ) (x )?
¿Y ( f ° g) (x )?
67 Representa las funciones y = sen x, y = cos x, y = tg x.
a) ¿Cuál es su periodo?
b) Di cuál es el dominio de definición de cada una.
c) ¿Entre qué valores varían?
68 Representa las funciones ysen x 2 π – = bl cos yx 2 π =+bl ||ysen x = || cos yx =
a partir de las gráficas de ysen x = e cos yx =
69 Justifica cuál de estas funciones es la inversa de y = 3x – 2. a) y = 2 + log3 x b) y = x 2 3 + c) y = log3 (x + 2)
70 ¿Verdadero o falso? Comprueba y justifica.
a) Las gráficas de ysen x 2 π =+bl e cos yx = son iguales
b) En la función ya x = no podemos dar a x valores negativos cuando 0 < a < 1.
c) Las funciones () log yx a – = e () ln yx a – = cortan al eje X en un mismo punto.
d) Las funciones y = ln x e y = x 1 se cortan en un punto.

➜ anayaeducacion.es Resoluciones de estos ejercicios.
6 Representa y x 1 = . A partir de ella, dibuja y x x 2 25 ––= + .
7 Representa y halla la inversa en cada caso. a) y = 1,5 · 2x – 3 b) y = 2 + ln (x + 1)
8 Asocia a esta gráfica una de las siguientes expresiones y di cuál es su periodo: a) y = cos x b) y = cos 2x c) y = 2cos x
Completa estos puntos para que pertenezcan a la función y = 2 cos x : (5π/6, …), (4π/3, …), (–π/4, …).
Represéntala en el intervalo [0, 2π].
155 U 5
–1 1 π 6 π 2 π π 4 π 3 2π 3 3π 4 5π 6 5π 4 4π 3 7π 6
© GRUPO ANAYA, S.A., 2024 - C/ Valentín Beato, 21 - 28037 Madrid.
Reservados todos los derechos. El contenido de esta obra está protegido por la Ley, que establece penas de prisión y/o multas, además de las correspondientes indemnizaciones por daños y perjuicios, para quienes reprodujeren, plagiaren, distribuyeren o comunicaren públicamente, en todo o en parte, una obra literaria, artística o científica, o su transformación, interpretación o ejecución artística fijada en cualquier tipo de soporte o comunicada a través de cualquier medio, sin la preceptiva autorización.



















