MATEMÁTICAS
PRIMARIA
NÚMEROS Y MÁS NÚMEROS 1
Números de cinco y de seis cifras 12
Utilizamos la recta numérica 15
La recta del tiempo 16
Aproximaciones 17
ESTRATEGIAS DE CÁLCULO
Buscamos el número que falta en una suma 18
TALLER DE ESPACIO Y FORMA
Construcción de cuerpos geométricos 19
Los cuerpos geométricos 20
Representamos datos en tablas y gráficas 21
NOS PREPARAMOS PARA RESOLVER PROBLEMAS 23
PROBLEMAS 24
EL RETO
Buscamos todas las restas posibles 25
PRACTICAMOS 26
me pongo a prueba 28
reflexiono y aprendo 30
4
CUERPOS QUE RUEDAN
Reconocemos y representamos fracciones 80
Comparamos fracciones 81
La fracción de un número 82
TALLER DE ESPACIO Y FORMA
La circunferencia y el círculo 84
Cuerpos redondos 86
PROBLEMAS 87
Horas, minutos y segundos 88
Unidades de masa 90
ESTRATEGIAS DE CÁLCULO
Multiplicar por 5 92
PRACTICAMOS 93
EL RETO
Bandejas de frutas 95
me pongo a prueba 96
reflexiono y aprendo 98
MAPAS Y PLANOS 2
Situaciones de multiplicación 34
Tablas de multiplicar 36
Multiplicamos por una cifra 37
Situaciones de división 38
Euros y céntimos de euro 40
ESTRATEGIAS DE CÁLCULO
Sumar y restar números próximos a decenas exactas 43
Mapas e itinerarios 44
Vista desde arriba 45 PROBLEMAS 46 EL RETO
Representamos números con cubos encajables 47 PRACTICAMOS 48 me pongo a prueba 50
reflexiono y aprendo 52
EL PERÍMETRO 3
La propiedad distributiva de la multiplicación 56 Multiplicamos por dos cifras 58
TALLER DE ESPACIO Y FORMA
Desarrollos planos. El cubo 60
TALLER DE MEDIDA
Medidas de longitud 62
Perímetros iguales con formas diferentes 63
¿Qué es la media aritmética? 64
ESTRATEGIAS DE CÁLCULO
Multiplicar por números próximos a decenas exactas 66
NOS PREPARAMOS PARA RESOLVER PROBLEMAS 67
68
69
Envolviendo cajas 71 me pongo a prueba 72 reflexiono y aprendo 74
5
REDONDEAMOS
Situaciones de estimación en el cálculo 102
Dividimos por dos cifras 104
Números romanos 106
TALLER DE MEDIDA
Relación entre las superficies del triángulo y del rectángulo 108
TALLER DE ESPACIO Y FORMA
Transformamos prismas en pirámides 110
Lectura y representación de datos en intervalos 112
ESTRATEGIAS DE CÁLCULO
Dividir números acabados en cero entre 10, 100 y 1 000 113
NOS PREPARAMOS PARA RESOLVER PROBLEMAS 114
PROBLEMAS 115
PRACTICAMOS 116
EL RETO
Recortamos triángulos 117
me pongo a prueba 118
reflexiono y aprendo 120
Situación de aprendizaje / TRABAJO COOPERATIVO La gran recogida de alimentos 76
Fracciones y forma 124
Representamos fracciones en la recta y las comparamos 126
Fracciones mayores que la unidad 127
Investigamos patrones en series 128
Inventamos instrucciones 129
ESTRATEGIAS DE CÁLCULO
Encontramos números
desconocidos en sumas y restas 130
TALLER DE ESPACIO Y FORMA
Clasificación de triángulos 131
Composición y descomposición de figuras. Polígonos cóncavos y convexos 133
TALLER DE MEDIDA
Relación perímetro-superficie 134
PROBLEMAS 135
PRACTICAMOS 136
EL RETO
Hacemos caminos 137
me pongo a prueba 138
reflexiono y aprendo 140
SITUACIÓN DE APRENDIZAJE / TRABAJO COOPERATIVO
Los números en la naturaleza 142
TODO DEPENDE DEL PUNTO DE VISTA
Comparación y ordenación de números decimales 188
Situamos números decimales en la recta 190
Estimaciones en multiplicaciones ..191
Estimaciones en decimales 192
TALLER DE MEDIDA
Estimación de magnitudes usando referentes comunes 193
TALLER DE ESPACIO Y FORMA
Identificación de vistas parciales en una figura 195
Uso y análisis de datos 197 PROBLEMAS 199
ESTRATEGIAS DE CÁLCULO
Relaciones entre fracciones de 100 y de 1 000 201
PRACTICAMOS 202
EL RETO
Un sueño monstruoso 203
me pongo a prueba 204 reflexiono y aprendo 206
Situación de aprendizaje /
El
Fracciones equivalentes 146
Fracción de un número 147
Representamos números decimales 148
Comprensión de instrucciones condicionales 149
El euro y los números decimales 150
TALLER DE ESPACIO Y FORMA
Construcción y representación de cuadriláteros 152
TALLER DE MEDIDA
Construimos ángulos 154
Unidades de capacidad: litro (L) y mililitro (mL) 155
NOS PREPARAMOS PARA RESOLVER PROBLEMAS 157
PROBLEMAS 158
PRACTICAMOS 159 EL RETO
Las caras escondidas de un dado 161 me pongo a prueba 162 reflexiono y aprendo 164
Números decimales y medidas de longitud 168
Relaciones entre fracciones y decimales 170
Significado del cociente y del resto de las divisiones 172 ESTRATEGIAS DE CÁLCULO Dividir entre 4 173
TALLER DE ESPACIO Y FORMA Simetrías y giros 74 TALLER DE MEDIDA Magnitudes medibles 175 Posición de dos rectas 176 Caminos y redes
NÚMEROS Y MÁS NÚMEROS
Garachico Tajao
DE UNA DE LAS ESPECIES, HAY MUCHA DIFERENCIA ENTRE
LAS CAPTURAS QUE SE HAN HECHO EN UN PUERTO Y LAS QUE SE HAN HECHO EN OTRO.
EN EL RESTO DE ESPECIES LAS DIFERENCIAS SON MENORES.
• ¿Sabes cuántos habitantes tiene tu municipio?
• ¿Piensa por qué te ha sido útil utilizar la recta numérica hasta ahora?
• ¿En qué se parecen y se diferencian
NÚMEROS DE CINCO Y DE SEIS CIFRAS
Este verano, Paz ha conocido a algunos chicos y chicas en el camping; en total, seis. Cada uno de estos chicos y chicas ha nacido en una de estas poblaciones, con un número de habitantes diferente.
Pablo es de Puerto de la Cruz: 30 349 habitantes
Sandra es de Arrecife: 64 497 habitantes
Noa es de Zaragoza: 675 301 habitantes
Cristina es de Vic: 47 319 habitantes
Sergio es de Burgos: 175 000 habitantes
Javier es de Valencia: 805 224 habitantes
• De estas poblaciones, ¿cuál se acerca más a los 50 000 habitantes?
• ¿Cuántas cifras utilizamos para escribir la población de Puerto de la Cruz?
¿Y la de Burgos? ¿Por qué?
Fíjate en el número de habitantes de estas dos poblaciones.
POBLACIÓN DE ARRECIFE
POBLACIÓN DE ZARAGOZA
Observa el valor que tiene la cifra 6 en cada una de las poblaciones.
Arrecife 6 60 000
Zaragoza 6 600 000
EL VALOR DEL 6 ES DIFERENTE PORQUE OCUPA
LUGARES DISTINTOS. CADA CIFRA TIENE UN VALOR SEGÚN EL LUGAR QUE OCUPA.
Con números de cinco cifras podemos escribir cantidades que tienen decenas de millar. Para escribir cantidades que tienen centenas de millar, necesitamos números de seis cifras.
Buscad otras situaciones en las que utilizamos números de seis cifras.
¿CUÁL ES EL MAYOR NÚMERO DE CINCO CIFRAS QUE PODEMOS ESCRIBIR?
¿Y EL DE SEIS CIFRAS? ¿QUÉ PASA CON SUS CIFRAS?
Una unidad de millar (UM) son 1 000 unidades.
• ¿Cuántas unidades son una decena de millar (DM)? ¿Y una centena de millar (CM)?
ACTIVIDADES
1. Marcos y Rosa juegan con unas cartas de números. Tienen estas cinco cartas.
3 5 6 0 9
• Con cuatro cartas, quieren formar números comprendidos entre 9 500 y 9 600. Encuentra cuatro diferentes.
• Utilizando las cinco cartas quieren construir algunos números en los que la cifra 3 ocupe las decenas de millar. (Recuerda que no se pueden repetir cartas).
El mayor número posible
DM UM C D U
3
El más cercano a 30 600
DM UM C D U 3
El número más próximo a la población de Puerto de la Cruz
3
El menor número posible
3
Un número con 0 centenas
3
Otro número diferente
3
UTILIZAMOS LA RECTA NUMÉRICA
Fíjate en estos dos tramos de la recta numérica. La separación entre los puntos es diferente en cada tramo.
• ¿Cómo podemos saber a qué número corresponde, en cada tramo, el punto señalado con la flecha?
• Explicad la estrategia que habéis seguido para encontrarlo.
ACTIVIDADES
WRelacionar tramos de la recta numérica con otros parecidos y más sencillos ayuda a situar bien los números.
2. Sitúa estos números en el lugar correspondiente de la recta numérica.
• ¿Cuántos números hay entre punto y punto de la recta numérica?
• ¿Dónde colocarías el 1 900?
• ¿Cómo lo has pensado?
LA RECTA DEL TIEMPO
ACTIVIDADES
3. Hay muchas mujeres que han hecho contribuciones importantes al mundo de la ciencia. Sitúa, en la recta del tiempo, las fechas de nacimiento de estas mujeres.
Maryam Mirzakhani (1977).
Ganó la Medalla Fields, que es como el Premio Nobel de las matemáticas.
Rosalind Franklin (1920). Hizo la primera fotografía del ADN.
Patricia Bath (1942). Ha hecho muchas aportaciones importantes en el cuidado y en la prevención de la ceguera.
• ¿Cuál de ellas nació primero?
• ¿Nacieron todas el mismo siglo?
• ¿En qué te fijas para saber si son de siglos diferentes?
Mileva Mari´c (1875). Compartió con Albert Einstein los cálculos de la teoría de la relatividad.
MARYAM Y MILEVA NACIERON CON 100 AÑOS DE DIFERENCIA APROXIMADAMENTE.
• Lee lo que piensa la niña. ¿Tiene razón? ¿Cómo crees que ha llegado a esta conclusión?
• En la recta del tiempo, el espacio que hay entre un punto y una cruz, ¿cuántos años representa? ¿Por qué?
APROXIMACIONES
ACTIVIDADES
4. Este es el censo invernal correspondiente al año 2021 de algunas aves acuáticas del parque natural del Delta del Ebro.
Correlimos común: 37 047
Ánade real: 33 132
Focha común: 15 964
Morito común: 9 875
Flamenco: 14 906
Podemos expresar el censo de estos pájaros de manera aproximada.
• El censo aproximado de los flamencos, ¿será de 14 000 o de 15 000? ¿Por qué?
• ¿Cuál es la cantidad aproximada de fochas comunes que hay en el delta?
• Entre ánades y moritos comunes, ¿cuántos ejemplares hay aproximadamente?
¿Cómo lo has calculado?
• ¿Por qué crees que utilizamos las cantidades aproximadas? Di otras situaciones en las que utilizamos aproximaciones.
2
de cálculo
BUSCAMOS EL NÚMERO QUE FALTA EN UNA SUMA
ACTIVIDADES
5. Para encontrar el número que falta en una suma, podemos hacer una resta. Haz estas operaciones mentalmente a partir de cálculos conocidos y completa la resta que corresponde a cada suma.
6. Utiliza la calculadora para encontrar los números que faltan en estas sumas haciendo, en cada caso, la resta correspondiente.
5
CONSTRUCCIÓN DE CUERPOS GEOMÉTRICOS
Utilizando pajitas de refresco y bolas de plastilina, podemos construir cuerpos geométricos.
¿CUÁL ES EL MENOR NÚMERO DE PAJITAS
CONSTRUIR UN CUERPO GEOMÉTRICO?
Marta ha unido pajitas de refresco con bolas de plastilina, y ha construido cuerpos geométricos. Ha hecho estos.
Con 6 pajitas de refresco
Con 9 pajitas de refresco
Con 8 pajitas de refresco
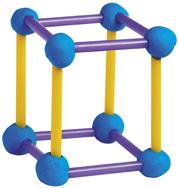
Con 12 pajitas de refresco
• Jorge dice que, con 12 pajitas de refresco también se puede construir una pirámide. ¿Sabes cuál?
• ¿Cuántas pajitas de refresco necesitamos para construir un prisma de base hexagonal?
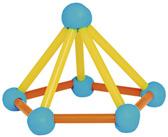
Con 10 pajitas de refresco
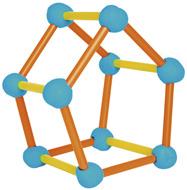
Con 15 pajitas de refresco
MEn estos geométricos,cuerpos las pajitas de refresco representan las aristas, y las bolitas de plastilina los vértices.
FORMA
LOS CUERPOS GEOMÉTRICOS
ACTIVIDADES
7. Estos niños y niñas están describiendo cuerpos geométricos diferentes. Analiza bien la información que dan y, cuando tengas claro de qué cuerpo se trata, dibújalo en el espacio correspondiente.
TIENE UNA BASE EN FORMA DE CUADRADO.
TIENE 4 CARAS LATERALES FORMADAS POR TRIÁNGULOS.
EN TOTAL, TIENE 8 ARISTAS Y 5 VÉRTICES.
TIENE DOS BASES FORMADAS POR POLÍGONOS DE 6 LADOS.
TIENE 6 CARAS LATERALES QUE SON RECTÁNGULOS.
EN TOTAL, TIENE 18 ARISTAS Y 12 VÉRTICES.
TIENE DOS BASES EN FORMA DE TRIÁNGULO.
TIENE 3 CARAS LATERALES FORMADAS POR RECTÁNGULOS.
EN TOTAL, TIENE 9 ARISTAS Y 6 VÉRTICES.
PUEDE RODAR EN TODAS LAS DIRECCIONES. NO TIENE NI VÉRTICES, NI ARISTAS, NI CARAS.
REPRESENTAMOS DATOS EN TABLAS Y GRÁFICAS
ACTIVIDADES
8. Leyre y su familia han pasado unos días de las vacaciones de verano con los abuelos en el pueblo. Algunos días han salido a buscar nidos de golondrinas para censarlos y lograr, de esta manera, que queden protegidos.
Esta tabla recoge el número de nidos que han encontrado Leyre y su abuelo.
• En la gráfica se ha representado el número de nidos que Leyre y su abuelo encontraron el viernes. Representa los que corresponden al resto de días.
Viernes Sábado Domingo Lunes Martes Días
Leyre
Abuelo
• ¿Qué día encontró más nidos Leyre?
• ¿Y su abuelo?
• El domingo, ¿cuántos nidos encontró Leyre más que su abuelo?
• ¿Cuántos nidos más tendría que haber encontrado su abuelo para llegar a los mismos nidos que encontró Leyre el domingo?
• ¿Cuántos nidos encontró, en total, el abuelo de Leyre durante los cinco días? Haz este cálculo mentalmente y explica cómo lo has hecho.
• Leyre también ha representado, en una gráfica, los lugares donde han encontrado los nidos.
• ¿Cuál es la moda con respecto a los lugares donde se encuentran los nidos de golondrinas?
• ¿Por qué crees que es así?
RSi encuentras un nido de golondrinas, no lo toques. Podría estropearse. Estos nidos están protegidos.
Buhardilla Bajo balcón En los almacenes
Estamos preparando una ruta para descubrir pequeños pueblos con encanto. Nos han pasado esta información. ¿Qué podemos hacer para conocer la distancia entre los pueblos 2 y 3? ¿Y entre los pueblos 3 y 5?
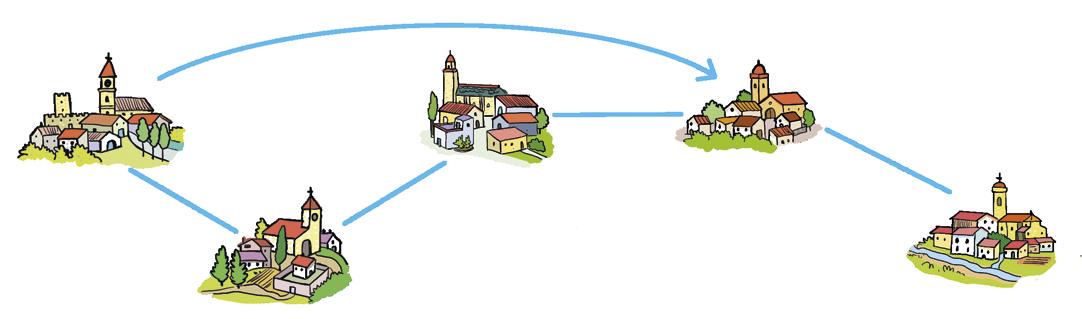
PODEMOS UTILIZAR
LAS BARRAS ADITIVAS
PARA ENCONTRAR
LAS DISTANCIAS
MÁS FÁCILMENTE.
9. Explica cómo calcularías el valor de las siguientes barras aditivas.
PREPARAMOS PARA RESOLVER
PROBLEMAS
Mirando estos itinerarios, ¿sabes decir cuántos kilómetros hay de Sira a Altavilla? ¿Y de Leris a Zuma?
SI SÉ LOS KILÓMETROS QUE HAY
DE LERIS A ALTAVILLA, Y LOS QUE HAY DE ZUMA A ALTAVILLA, PUEDO SABER LOS QUE HAY DE LERIS A ZUMA.
PRIMERO HAY QUE SABER
CUÁNTOS KILÓMETROS HACEN
CADA DÍA ENTRE EL TRAYECTO DE IDA Y EL DE VUELTA.
• La madre de Jana es comercial y 3 días a la semana hace el trayecto Tibal-Leris-Tibal. ¿Cuántos kilómetros recorre?
• El padre de Javier es repartidor. Si hace el trayecto Carmel-Altavilla-Carmel 5 días a la semana, ¿cuántos kilómetros recorre?
• ¿Quién de los dos hace más kilómetros? ¿Cuántos más?
• Juan es un campesino de Sorel y cada sábado lleva verdura al mercado de Brisa, donde tiene un puesto. ¿Cuántos kilómetros recorrerá en el mes de octubre?
BUSCAMOS TODAS LAS RESTAS POSIBLES
Con las siguientes cifras puedo hacer varias restas. 6 3 9 8
Por ejemplo, esta:
• ¿Cuántas restas diferentes podemos plantear? Confeccionad cartas de números y utilizadlas para hacer pruebas.
• ¿Qué estrategia podemos usar para no dejarnos ninguna?
10. Da los saltos indicados en las rectas para ver a qué número llegas.
• Un salto de 4, un salto de 100 y un salto de 25.
176
¿Cuánto suman todos los saltos que has dado?
• Un salto de 100, un salto de 40 y un salto de 6.
164
¿Cuánto suman todos los saltos que has dado?
11. Piensa dos combinaciones para pagar cada uno de estos objetos utilizando solo billetes y represéntalas.
12. Completa las operaciones que suman 100 y las que suman 1 000.
• ¿En qué se parecen unas parejas y otras?
13. ¿De qué número hablamos?
• Es un número de cinco cifras, cuatro de las cuales son pares y una es impar.
• La cifra que ocupa el lugar de las centenas es menor que la que ocupa el lugar de las decenas.
• La suma de las cinco cifras es un resultado de la tabla del 5.
Colorea el número.
18 434 57 643
7 325 24 220
46 212 72 468
26 485 42 680
9 461 70 003
1. Este verano muchos alumnos y alumnas de Segundo Ciclo irán a campamentos, y para que sepan qué tipo de campamento hay, se ha elaborado esta gráfica.
• ¿Qué tipo de campamento representa la moda?
• ¿Cuántos alumnos más se tendrían que haber apuntado al campamento musical para que estos representaran la moda?
• ¿Cuántos alumnos del campamento deportivo se tendrían que haber apuntado al de naturaleza para que en estos campamentos hubiera habido la misma cantidad de niños y niñas?
• En el campamento de naturaleza han estudiado cuatro tipos de mariposas. Estas son las cantidades que hay de cada tipo.
Según estos datos, ¿qué mariposa es la más numerosa? – Fíjate en lo que dice Juan: «Tan solo faltarían unas 300 mariposas para que hubiera 55 000 blanquitas de la col». ¿Es cierta esta afirmación? ¿De qué manera lo has pensado?
PAVO
Musicales De naturaleza Deportivos De idiomas Tipo de casales
• En el campamento de idiomas construyeron cabañas utilizando palos y lonas tal como hacían los indios americanos. Hicieron cabañas de dos formas diferentes.
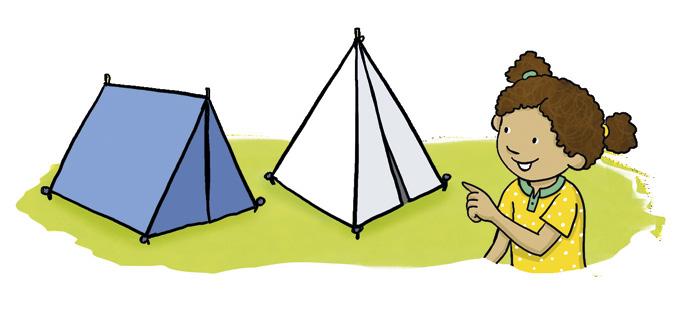
– ¿Crees que la niña tiene razón?
– Dibuja las lonas que se necesitan para hacer cada cabaña.
EN LA CABAÑA AZUL HAY MENOS LONAS EN FORMA DE TRIÁNGULO QUE EN LA BLANCA.
• En el campamento deportivo hicieron carreras de relevos según este esquema.
290 m
SALIDA LLEGADA
Laura recorrió el último tramo. Si todo el recorrido medía 870 m, ¿cuántos metros habían recorrido sus compañeros antes de que ella tomara el relevo?
• En el campamento musical han pesado varios instrumentos. Estos son los resultados obtenidos. ¿Qué aproximación propondrías tú para cada uno?
VIOLÍN VIOLA VIOLONCHELO CONTRABAJO
Peso exacto 758 gramos 747 gramos 3 283 gramos 9 991 gramos
Peso aproximado
1. Colorea la escalera de cada torre teniendo en cuenta tu progreso.
Soy capazde escribiry componer númerosde cincoy seis cifras
Necesito ayuda.
Me cuesta mucho.
A veces me equivoco.
Casi siempre.
Siempre.
Séhacer aproximaciones de números de tres cifras.
Sé encontrar el número de aristas yvérticesenlas pirámides yenlos prismas.
Siempre.
Casi siempre.
A veces me equivoco.
Me cuesta mucho.
Necesito ayuda.
Necesito ayuda.
Me cuesta mucho.
A veces me equivoco.
Casi siempre.
Siempre.
Necesito ayuda.
Me cuesta mucho.
A veces me equivoco.
Casi siempre.
Siempre.
Soy capazde relacionar tramos de recta numérica de números mayores con otros más sencillos.
Siempre.
Casi siempre.
A veces me equivoco.
Me cuesta mucho.
Necesito ayuda.
Soy capazde encontrarel número que faltaen una suma haciendo laresta correspondiente.
Necesito ayuda.
Me cuesta mucho.
A veces me equivoco.
Casi siempre.
Siempre.
Soy capazde identificarla moda enuna gráficade barras.
2. Completa.
Saber el número de lados del polígono de la base de un prisma o de una pirámide me ayuda a
Conocer la relación entre la suma y la resta me sirve para Hacer aproximaciones me sirve para .
¿Qué me ayuda a aprender?
Si, en una gráfica de barras, me fijo en la barra más alta, sé cuál es la
Podemos relacionar tramos de rectas numéricas con otros parecidos y más sencillos para
3 EL PERÍMETRO
• ¿Cómo es que 4 × 7 da el mismo resultado que 4 × 5 + 4 × 2?
• ¿Por qué al desplegar una caja de cartón, no nos queda siempre igual?
• ¿Podremos colocar las caras de cualquier manera y hacer que la caja cierre?
• ¿Cuántos centímetros son medio metro?
¿CUÁNTOS METROS DE CINTA NECESITAREMOS PARA RODEAR
TODA LA PISTA?
TENDREMOS QUE
TOMAR LA MEDIDA DE TODOS LOS LADOS.
SERÁ SUFICIENTE CON HACER 2 MEDICIONES.
LA PROPIEDAD DISTRIBUTIVA DE LA MULTIPLICACIÓN
En un parque han plantado 3 hileras de 16 árboles. Para saber cuántos árboles son, tenemos que multiplicar 3 × 16.
3 × 8 = 24
3 × 8 = 24
3 × 16 = (3 × 8) + (3 × 8) = 24 + 24 = 48
3 × 10 = 30
3 × 6 = 18
La propiedad distributiva de la multiplicación permite descomponer los factores en forma de suma y también de resta.
PUES YO HAGO 3 × 10 Y 3 × 6.
DESCOMPONER UNO DE LOS FACTORES EN DECENAS EXACTAS FACILITA LOS CÁLCULOS.
• Explica cuál es la descomposición que va mejor para calcular 7 × 23.
YO HAGO 3 × 8 DOS VECES.
ACTIVIDADES
1. Observa cómo Alex aplica la propiedad distributiva de la multiplicación y completa el cuadro.
6 × 7 = (6 × ) + (6 × )
6 × 7 = + =
PARA SABER CUÁNTO
ES 6 × 7, LO PUEDO HACER PENSANDO EN 6 × 5, MÁS 6 × 2.
2. Completa a partir de los resultados de la tabla del 5 y de la tabla del 2.
3 × 7 = (3 × ) + (3 × )
3 × 7 = + =
3. Observa cómo multiplica Emma por 8. 6 × 7 6 × 5 6 × 2
PARA RECORDAR
EL RESULTADO DE 8 × 6, PIENSO EN 4 × 6 Y HAGO EL DOBLE.
Haz lo mismo para calcular el resultado de 8 × 8.
Escribe el resultado de la tabla del 8 haciendo el doble de los resultados de la tabla del 4. 8 × 7 = (8 × ) + (8 × ) 8 × 7 = + =
4 × 3 = 12 8 × 3 = 4 × 7 = 28 8 × 7 = 4 × 4 = 16 8 × 4 = 4 × 9 = 36 8 × 9 = 4 × 6 = 24 8 × 6 = + = 6 × 7 = ?
MULTIPLICAMOS POR DOS CIFRAS
Queremos multiplicar 63 × 45.
YO LO HAGO DESCOMPONIENDO LOS NÚMEROS EN DECENAS Y UNIDADES
PORQUE ME HAGO UNA IDEA DEL RESULTADO. SEGURO QUE SERÁ MAYOR QUE 2 400.
LA DESCOMPOSICIÓN TAMBIÉN PUEDO SABER CUÁNTO ES 5 × 63 Y 40 × 63. × 60 3
• ¿De qué otras multiplicaciones podemos saber el resultado si miramos la tabla?
ACTIVIDADES
4. Calcula el resultado de estas multiplicaciones completando los resultados de la tabla. Después, calcula el resultado de las multiplicaciones que hay debajo.
Hay otra forma de multiplicar: el algoritmo tradicional. En este caso multiplicamos cifra por cifra.
CUANDO MULTIPLICO UTILIZANDO EL ALGORITMO, TENGO QUE COLOCAR BIEN LAS CIFRAS Y TENER EN CUENTA SI ME LLEVO ALGUNA.
ACTIVIDADES
5. Calcula las siguientes multiplicaciones con el algoritmo tradicional.
DESARROLLOS PLANOS. EL CUBO
ESTAS CAJAS, ¿QUÉ CUERPO GEOMÉTRICO REPRESENTAN?
¿Y ESTAS OTRAS? ¿QUÉ SON? ¡TIENEN MUCHAS CARACTERÍSTICAS IGUALES!
CUERPO GEOMÉTRICO
Tendrán formas parecidas a estas.
• ¿Qué diferencias veis entre una caja y la otra?
Buscad una caja de cada forma. Abridlas, quitad las solapas y cortad una de las aristas para que las cajas queden bien desplegadas.
Coged la caja que tiene forma de cubo. Con unas tijeras, recortad alguna de las caras, pegadla en otro lugar con cinta adhesiva y comprobad si, al doblar la figura resultante, se vuelve a formar la caja.
Id cambiando las caras de lugar e intentad doblar la caja. Buscad, entre todos, algunos desarrollos planos del cubo. Hay unos cuantos diferentes.
ACTIVIDADES
ANTES DE RECORTAR LA CARA, IMAGINO QUÉ PASARÁ CUANDO LA CAMBIE DE LUGAR Y DOBLE LA CAJA.
NUNCA M E HABRÍA
IMAGINADO QUE ESTE DESARROLLO FUERA UN CUBO AL DOBLARLO.
6. Un dado es un cubo cuyas caras tienen puntos que representan los números del 1 al 6.
• Observa estos desarrollos de un dado. Teniendo en cuenta lo que dice Marta, hay uno que no tiene los puntos bien colocados. ¿Cuál es?
LAS CARAS OPUESTAS DE UN DADO SIEMPRE SUMAN 7.
En la cara opuesta al 3 hay puntos.
En la cara opuesta al 1 hay puntos.
En la cara opuesta al 2 hay puntos.
TALLER DE ESPACIO
DE MEDIDA TALLER D e medida
MEDIDAS DE LONGITUD
Coged cinta y cortad un trozo de 1 metro de longitud.
Si la dobláis por la mitad, tendréis medio metro.
Y si la volvéis a doblar por la mitad, tendréis una cuarta parte de un metro.
Si de la cinta de 1 metro hacéis 10 partes iguales, cada una representará un decímetro.
Y, si de cada decímetro, hacéis 10 partes, tendréis los centímetros.
1 CENTÍMETRO EQUIVALE, APROXIMADAMENTE, A LA ANCHURA DE TU DEDO ÍNDICE.
• Medid varios objetos de la clase utilizando las diferentes medidas de la cinta y, también, la anchura del dedo para los centímetros. Explicad qué medidas habéis utilizado y de qué distintas formas las habéis expresado.
1 metro = 10 decímetros = 100 centímetros
0,5 metros = 1 2 metro = 5 decímetros = 50 centímetros
0,25 metros = 1 4 de metro = 2,5 decímetros = 25 centímetros
PERÍMETROS IGUALES CON FORMAS DIFERENTES
ACTIVIDADES
7. La familia Salas está de reformas. Estos son los planos de las habitaciones de Sara y de sus hermanos gemelos.
Quieren poner zócalo de madera en las habitaciones. Para saber cuántos metros de zócalo necesitarán, tendrán que medir la longitud de las diferentes paredes y sumarlas.
PARA NUESTRA HABITACIÓN,
NO HEMOS MEDIDO TODOS LOS LADOS. ¿POR QUÉ CREES
QUE LO HEMOS HECHO ASÍ? 4 m
MIDE 17 METROS. ESTA MEDIDA ES EL PERÍMETRO DE LA HABITACIÓN.
• Si cada metro de zócalo cuesta 7 euros, ¿cuánto cuesta poner el zócalo en las dos habitaciones?
TALLER DE MEDIDA TALLER DE MEDIDA
¿QUÉ ES LA MEDIA ARITMÉTICA?
Los alumnos y las alumnas de cuarto han representado números con los cubos encajables. Observa las torres que han construido cuatro niñas de la clase.
TERESA
PUEDE DAR 3 CUBOS
A NOELIA; ASÍ, TENDRÁ
6 CADA UNA.
Y MARTA
PUEDE DAR 1
A ANA; ASÍ, TAMBIÉN TENDRÁ 6
CADA UNA.
Fíjate cómo quedan las torres después de estos cambios.
Ahora, todas las torres tienen la misma altura.
La media aritmética de las alturas es 6 cubos.
QPara saber la media aritmética, todas las torres tienen que estar igualadas.
TERESA ANA MARTA NOELIA
TERESA ANA MARTA NOELIA
ACTIVIDADES
TAMBIÉN LO PODRÍAN HABER HECHO DE OTRA MANERA: DESMONTANDO LAS TORRES Y HACIENDO 4 IGUALES.
Si desmontamos las 4 torres, tendremos 24 cubos sueltos. Y, ahora, tenemos que hacer a 4 grupos iguales. Para hacer grupos iguales, utilizamos la división:
24 : 4 = 6
Para saber la media aritmética, hacemos una división.
• ¿Qué estrategia te parece más fácil?
M8. Hoy Montserrat, Pedro y Elsa han practicado tiro con arco. En esta tabla están las puntuaciones que ha obtenido cada uno de ellos en las seis tiradas que han hecho.
Esta es la representación gráfica de las seis tiradas de Montserrat.
• ¿Cuál es la media de puntos obtenidos por Montserrat en las 6 tiradas?
• ¿Cómo lo has pensado?
de cálculo
9 2 1 5 4 7 8 6 0 3
8
MULTIPLICAR POR NÚMEROS PRÓXIMOS A DECENAS EXACTAS
ACTIVIDADES
9. Completa las siguientes tablas.
3
30 90
31 90 + 3 = 93
29 90 – 3 = 87
PARA CALCULAR
41 × 20 HACEMOS 40 × 20, QUE ES MÁS FÁCIL, Y SUMAMOS 20.
+ 6 =
– 6 =
41 × 20 = (40 × 20) + 20 = 800 + 20 = 820
• Calcula el resultado de 61 × 40. ¿Qué otra multiplicación más fácil utilizarías?
CALCULAMOS 49 × 30 A PARTIR DE UN RESULTADO MÁS FÁCIL, COMO 50 × 30, Y RESTAMOS 30.
49 × 30 = (50 × 30) – 30 = 1 500 – 30 = 1 470
• Calcula el resultado de 39 × 80. ¿Qué otra multiplicación más fácil utilizarías?
HACEMOS REPRESENTACIONES
En nuestra clase de cuarto tenemos dos tabletas para cada tres alumnos. Si somos 24 alumnos, ¿cuántas tabletas tene mos?
HACER UNA REPRESENTACIÓN
ES UNA BUENA ESTRATEGIA PARA RESOLVER ALGUNOS PROBLEMAS.
Observa las representaciones que han hecho cuatro alumnos.
: 3 = 8 grupos de 3 alumnos
• Juntaos en grupos para comentar estas representaciones. ¿Qué semejanzas y diferencias observáis? ¿Qué representación haríais vosotros?
• En la clase de cuarto de otro colegio, tienen tres tabletas para cada cinco alumnos. Si son 25 alumnos, ¿cuántas tabletas tienen? ¿Tienen más tabletas o menos que en nuestra clase?
PROBLEMAS
10. En la granja del tío Bartolo hay caballos, cabras y conejos. Tiene el doble de cabras que de caballos y el triple de conejos que de caballos. Si en total tiene 60 animales, ¿cuántos tiene de cada tipo?
SÉ QUE EN LA GRANJA HAY SEIS GRUPOS
IGUALES DE ANIMALES Y EN TOTAL HAY 60; POR LO TANTO, YA SÉ CÓMO HACERLO.
Un grupo de caballos
Dos grupos de cabras
Tres grupos de conejos
• Si en vez de haber 60 animales en total hubiera 48, ¿cuántos animales tendría de cada tipo?
11. A partir de esta información, ¿cómo puedes encontrar el precio de un estuche?
¿Y el precio de un cuaderno? Explica cómo lo has pensado.
18 €
26 €
12. Completa la siguiente tabla.
13. Escribe multiplicaciones con números mayores que 1 que den los siguientes resultados.
14. ¿Qué medidas pueden tener los lados de un rectángulo si su perímetro mide 22 cm? Dibuja varias posibilidades.
PR a CTICAMOS
15. Encuentra series de 4 resultados de las tablas de multiplicar. Todas tienen que tener forma de L. Colorea cada serie de un color y escribe las multiplicaciones. Observa los ejemplos.
16. Completa la siguiente tabla.
• ¿Qué observas si comparas las tres filas?
17. Sitúa en cada etiqueta los números correspondientes.
ENVOLVIENDO CAJAS
Haced grupos. Cada grupo debe tener una caja, todas iguales, y la misma cantidad de papel de embalar.
PENSAD DE QUÉ MANERA
ENVOLVERÉIS LA CAJA PARA UTILIZAR LA MÍNIMA CANTIDAD DE PAPEL POSIBLE.
• ¿Cómo sabréis qué grupo ha gastado menos papel?
También pondremos una cinta que pasará por todas las caras de la caja y acabará con un lazo bien bonito.
Pensad qué medidas tendréis que tomar para pedir la cinta justa.
1. En nuestro colegio, cada año, para Navidad, se organiza una rifa solidaria. Durante una semana, se venden tiras de números y el último día se hace el sorteo. Este es el gráfico correspondiente a la clase de cuarto.
• ¿Cuál es la media de tiras vendidas en un día?
2. Los alumnos de 4.º han envuelto estos regalos y han colocado una cinta alrededor de cada caja, tal como puedes ver en la imagen. Las dos cajas tienen el mismo tamaño.
• ¿De qué color han necesitado más cinta?
¿Por qué?
• Para atar la caja azul, han necesitado 120 centímetros de cinta sin contar el lazo.
¿Cuánta cinta han necesitado para la caja blanca?
3. El día del concierto de villancicos, repartieron unos obsequios a los espectadores para recaudar dinero. Cada clase recaudó el mismo dinero. Las 6 clases de Educación Infantil recaudaron un total de 204 euros. Si en Primaria hay 12 clases, ¿cuántos euros recogieron en total? Berta lo ha calculado así: 204 × 2 = 408
¡Feliz Navidad!
• Explica qué ha hecho Berta para saber cuánto dinero recaudaron en Primaria.
4. Para adornar el salón de actos, utilizan cintas de 6 metros y 50 centímetros de longitud. Juan piensa que pueden cortar cintas de 7 metros y quitar medio metro de de cada trozo y Pepa dice que se tienen que cortar cintas de 6 metros y 5 decímetros. ¿Cuál de los dos tiene razón? ¿Por qué?
• Disponen de 24 metros de cinta para delimitar la zona de los puestos, que tiene que tener forma rectangular. Dibuja los tres rectángulos que se pueden hacer con los 24 metros de cinta e indica sus dimensiones. 1 m
1. Rellena el siguiente formulario.
Antes de empezar la unidad.
FECHA DE LA AUTOEVALUACIÓN
Saber para qué sirve la propiedad distributiva de la multiplicación.
Multiplicar por dos cifras.
Multiplicar por números próximos a décimas exactas.
Obtener el desarrollo plano de un cuerpo geométrico.
Saber que un cuerpo geométrico puede tener más de un desarrollo plano.
Medir una longitud de distintas formas.
Saber que puede haber objetos con el mismo perímetro y forma diferente.
Una vez acabada la unidad.
FECHA DE LA AUTOEVALUACIÓN
Saber para qué sirve la propiedad distributiva de la multiplicación.
Multiplicar por dos cifras.
Multiplicar por números próximos a décimas exactas.
Obtener el desarrollo plano de un cuerpo geométrico.
Saber que un cuerpo geométrico puede tener más de un desarrollo plano.
Medir una longitud de distintas formas.
Saber que puede haber objetos con el mismo perímetro y forma diferente.
LO SÉ Y LO
LO SÉ Y LO
2. Completa. ¿Qué me ayuda a aprender?
Si multiplico descomponiendo, me es más fácil .
Para saber qué cuerpo geométrico formará un desarrollo plano, me va bien .
La cuadrícula en las figuras me facilita .
La propiedad distributiva me es muy útil
Para poder expresar medidas de diferentes formas, me va bien .
LA GRAN RECOGIDA DE ALIMENTOS
SITUACIÓN DE APRENDIZAJE
La Federación Española de Bancos de Alimentos organiza cada año una gran recogida de alimentos básicos para las personas necesitadas. Buscad información sobre la Gran Recogida y contestad a las preguntas.
• ¿Cuándo se fundó esta entidad?
• ¿Cuáles son los alimentos básicos que se recogen?
• ¿Qué labores deben realizar los voluntarios?
Durante la campaña puedes dar alimentos o hacer un donativo a www.fesbal.org.es
Organizaos en grupos:
• Planteaos qué hay que hacer y cómo.
• Repartíos las tareas.
• Respetaos y ayudaos.
Imaginaos que participáis como voluntarios en esta campaña. Os ha tocado recoger alimentos en un supermercado y tenéis que poner todos los paquetes de harina que os den en cajas de cartón.
• Las cajas de cartón tienen forma de cubo de 0,5 metros de arista.
• Las dimensiones de un paquete de harina son las de la imagen.
15 cm 10 cm 5 cm
Pensad si conviene poner los paquetes tumbados o de pie para que quepa el máximo número en cada caja.
• ¿Cuál será vuestra propuesta? ¿Cuántos kilogramos cabrán en cada caja?
Fíjate en estas informaciones recogidas de diferentes fuentes en relación con el consumo alimentario en una gran ciudad:
Un tercio de la comida que compramos va a la basura
1 3 derrochado
2 3 aprovechados
262 471 toneladas
Se tiran 262 471 toneladas de alimentos cada año.
Cada año se derrochan 35 kg de comida por habitante. = 35 kg
Eso equivale a 112 € por persona cada año.
• ¿Qué significa que 1 3 de la comida va a la basura? ¿De qué manera pensáis que derrochamos los alimentos?
• ¿Cuántos kilogramos de alimentos se derrochan en tu provincia cada año?
• Preguntad en la cocina de vuestro colegio cuántos kilogramos de los productos indicados en la tabla compran y completadla.
EN LA SEMANA EN EL MES EN TODO UN CURSO
Pan
Patatas
Fruta
Arroz
• Si de todos estos alimentos se tirara un tercio, ¿cuántos kilogramos se tirarían a la basura en una semana? ¿Y en un mes? ¿Y en todo un curso?
• ¿Qué propondríais con el fin de evitar este despilfarro de alimentos?
© GRUPO ANAYA, S.A., 2025 - C/ Valentín Beato, 21 - 28037 Madrid. Reservados todos os dereitos. O contido desta obra está protexido pola Lei, que establece penas de prisión e/ou multas, amais das correspondentes indemnizacións por perdas e danos, para quen reproduza, plaxie, distribúa ou comunique publicamente, en todo ou en parte, unha obra literaria, artística ou científica, ou a súa transformación, interpretación ou execución artística fixada en calquera tipo de soporte ou comunicada a través de calquera medio, sen a preceptiva autorización.