MATEMÁTICAS
PRIMARIA
¿CÓMO MEDIMOS LAS COSAS? 1
Los aparatos de medida 12
El tiempo histórico: el calendario y el reloj 13
El tiempo atmosférico: la temperatura 14
Multiplicamos 16
Dividimos 18
TALLER DE ESPACIO Y FORMA
Rectas. Posiciones de las rectas 20
La recta numérica 22 EL RETO 23
¿HAY MATEMÁTICAS EN LA CALLE? 2
Probabilidad 34
TALLER DE ESPACIO Y FORMA
Tipo de ángulos 35
Medimos ángulos 35
La bisectriz 36
Fracciones 3 .................................. 8
Fracciones equivalentes 40
¿Qué números conocemos? 3
Números menores que 156
Redondeamos números decimales 57
Sumas y restas con decimales 58
Ordenamos fracciones 60
Calculamos porcentajes 62
TALLER DE ESPACIO Y FORMA La bisectriz y la mediatriz 64
y aprendo 30
¿Unidades convencionales o unidades tradicionales? 4
TALLER DE MEDIDA
Unidades de medida 78
Operaciones con decimales 80
Fracciones, porcentajes y decimales 82
Los números mixtos 84
Polígonos 86
TALLER DE ESPACIO Y FORMA
Construimos polígonos con triángulos 87
Interpretamos diagramas de
¿Qué formas observamos? 5
y aprendo 72 trabajo cooperativo.
Miramos con ojos matemáticos 74
TALLER DE ESPACIO Y FORMA Construimos cuadriláteros 102
Medimos polígonos 104
Las escalas de los planos y de los mapas 106 EL RETO 109
Gráficos de líneas 110
ESTRATEGIAS DE CÁLCULO 112 PRACTICAMOS 113
NOS PREPARAMOS PARA RESOLVER PROBLEMAS 114
PROBLEMAS 115
me pongo a prueba 116
reflexiono y aprendo 118
¿Superficie o área? 6
Operaciones con decimales 122
TALLER DE MEDIDA
Sumamos los ángulos interiores de los polígonos 124
TALLER DE ESPACIO Y FORMA
Dibujamos polígonos 126
Área y superficie 128
Buscamos regularidades 130
Composiciones geométricas.
Mosaicos ........................................ 130
EL RETO 131
ESTRATEGIAS DE CÁLCULO ........................ 132
PRACTICAMOS 133
NOS PREPARAMOS PARA RESOLVER PROBLEMAS 134 PROBLEMAS 135 me pongo a prueba 136
reflexiono y aprendo 138
trabajo cooperativo.
Miramos con ojos de acción climática 140
9
¿La calculadora resuelve todos los problemas?
Más sobre la calculadora 188
Las escaleras de las medidas 189
TALLER DE ESPACIO Y FORMA
Transformación de poliedros 190
Vistas: alzado, planta y perfil 192
Tablas de doble entrada 194
Registro de datos 196 EL RETO 197 ESTRATEGIAS DE CÁLCULO 198
7
¿Cuántas caras tiene un dado?
Proporciones y escalas 144
Recta numérica de fracciones 147
Operaciones combinadas 148
Poliedros 149
Elementos de los poliedros 150
Giros 152
EL RETO 153
Diagramas 154
ESTRATEGIAS DE CÁLCULO 156 PRACTICAMOS 157 NOS PREPARAMOS PARA RESOLVER PROBLEMAS 158 PROBLEMAS 159 me pongo a prueba 160 reflexiono y aprendo ....... 162
¿Está de moda? 8
me pongo a prueba 202 reflexiono y aprendo 204
trabajo cooperativo. Miramos con ojos sostenibles 206
La media y la moda
ESTRATEGIAS DE CÁLCULO
PRACTICAMOS
NOS PREPARAMOS PARA RESOLVER PROBLEMAS 180
y aprendo 184
¿Cómo
medimos las cosas?
• ¿Qué veis en las imágenes? ¿Qué sabríais medir?
• ¿Con qué aparato lo haríais?
• Para medir el aula, ¿podríais utilizar alguno de los aparatos de la imagen?
• ¿Necesitáis más aparatos?
• ¿Sois capaces de hacer una lista con 10 aparatos de medida?
LOS APARATOS DE MEDIDA
Los aparatos de medida nos permiten medir diferentes magnitudes físicas, como la masa, la capacidad, el tiempo, la longitud, los ángulos, la temperatura, la presión, la velocidad...
• ¿Sabríais decir con qué aparato se mide cada magnitud?
ACTIVIDADES
1. Relaciona cada aparato con la magnitud física que mide:
Masa
Tiempo
Longitud
Ángulos
Temperatura
Velocidad
Presión
Volumen
EL
TIEMPO HISTÓRICO: EL CALENDARIO Y EL RELOJ
El calendario y el reloj son aparatos que nos han permitido organizarnos y tener el control del tiempo.
W W CALENDARIO RELOJ
• ¿Por qué multiplicamos por 60 para pasar de horas a minutos?
• ¿Por qué dividimos por 24 para pasar de horas a días?
• ¿Qué operación tenemos que hacer para pasar de segundos a horas?
ACTIVIDADES
2. Relaciona los relojes que marcan la misma hora.
EL TIEMPO ATMOSFÉRICO: LA TEMPERATURA
El tiempo meteorológico hace referencia a fenómenos atmosféricos, como la temperatura, el viento, la lluvia, la humedad del aire, la radiación solar...
• ¿Conoces los aparatos que sirven para medir estos fenómenos?
• ¿Sabes qué significan los símbolos representados en el mapa? ¿Y los valores númericos que aparecen?
MI UNIDAD DE MEDIDA SON LOS GRADOS.
• ¿Qué registra este diagrama?
• ¿En qué mes hizo más frío? ¿Y más calor?
• ¿Se han registrado temperaturas bajo cero?
Máxima Mínima
El hierro
Gran Canaria
Fuerteventura
Lanzarote
Tenerife
La Palma
La Gomera
ACTIVIDADES
3. Observa, piensa y responde.
a) ¿Cuál es el termómetro con la temperatura más alta?
b) ¿Qué diferencia hay entre la temperatura más baja y la más alta?
c) Si los termómetros marcan la temperatura mínima, ¿a qué estación del año corresponde cada termómetro? Razona tu respuesta.
4. Observa este diagrama y responde.
Temperaturas en Teruel
a) ¿Qué representa el eje X? ¿Y el eje Y?
b) ¿Por qué piensas que se han recopilado estos datos?
c) ¿Qué profesionales usan estos diagramas y los datos de las temperaturas para desarrollar su trabajo?
Enero
Máxima Mínima
MULTIPLICAMOS
Yon quiere saber cuántas horas hay en un año. Para estar seguro, lo ha comprobado de cuatro maneras diferentes.
Diferentes formas de multiplicar
8 760 horas 1 3
300 60 5
20 6 000 1 200 100 4 1 200 240 20
7 200 + 1 440 + 120
1 día tiene 24 horas
365 × 24
24 = 20 + 4
365 × 20 = 7 300 Calculamos el doble de 365, que es 730, y añadimos el 0 de las decenas.
365 × 2 = 730
365 × 4
730 × 2 = 1 460
Calculamos el doble de 365 y, después, el doble de 730.
7 300 + 1 460 = 8 760 Sumamos los dos resultados.
• ¿Qué manera de multiplicar te gusta más? ¿Por qué?
ACTIVIDADES
5. ¡Se acaba de instalar un circo cerca de la escuela y eso nos hace pensar!
a) En la carpa caben 145 espectadores. Si cada uno ha pagado 12 euros por ver el espectáculo de payasos, malabaristas y artistas, ¿cuánto dinero han ganado con las entradas?
b) Una vez acabado el espectáculo, los organizadores tienen que pagar 125 euros al ayuntamiento por el alquiler del terreno y 1 000 euros a los trabajadores y las trabajadoras. ¿Cuánto dinero les queda?
c) ¿Cuánto ganarían haciendo 10 funciones? ¿Y 60?
6. Observando las figuras y las operaciones que las acompañan, ¿podrías calcular el resultado de las operaciones y completar las figuras? ¿Qué indica el resultado respecto de la figura?
7. Fíjate en el ejemplo y calcula el resultado de las otras dos multiplicaciones.
DIVIDIMOS
Lucía y sus amigos han acabado la carrera de la Olimpiada Escolar con estos tiempos:
– Hugo: 860 segundos
– Lucía: 1 000 segundos
– Alba: 1 005 segundos
– Diego: 1 269 segundos
Para expresar estos tiempos en minutos y segundos, dividimos los segundos de la clasificación entre los 60 segundos que tiene un minuto.
Observa las 4 formas de dividir y encuentra la que te vaya mejor. ¡Todas son válidas!
8 6 0 : 6 0 = 1 4 r 2 0
H¡El resto es muy importante!
YO, 16 MINUTOS Y 40 SEGUNDOS. HE TARDADO 14 MINUTOS Y 20 SEGUNDOS.
¿Quétienesignificado el resto?
HE ACABADO LA CARRERA EN 16 MINUTOS Y 45 SEGUNDOS.
YO HE TARDADO 21 MINUTOS Y 9 SEGUNDOS.
ACTIVIDADES
8. Los 45 estudiantes de 5.º vais de campamentos.
a) ¿Cuántas habitaciones de 6 personas ocuparéis?
¿Estarán todas llenas?
b) Las mesas del comedor son de 12 personas. ¿Cuántas necesitaréis?
¿Quedarán lugares vacíos?
c) Para organizar un juego tenéis que hacer 7 grupos. ¿De cuántos estudiantes serán los grupos?
9. Responde a esta pregunta utilizando dos métodos diferentes para encontrar la solución.
• ¿Cuántos libros sobran si repartes 43 libros entre 3 personas?
10. Si sabes que 342 : 7 = 48 r 6, haz los siguientes cálculos. : = 341 7 r r : = 343 7
• Explica cómo lo has resuelto.
RECTAS. POSICIONES DE LAS RECTAS
Con la regla que tienes NO puedes medir rectas
Con la regla que tienes NO puedes medir semirrectas
Con la regla que tienes SÍ puedes medir segmentos.
• ¿Te han sorprendido estas afirmaciones? ¿Cuál especialmente?
• ¿Sabrías decir cuál de las líneas dibujadas puedes medir?
Según cómo están posicionadas las rectas, hablamos de paralelas, perpendiculares o secantes
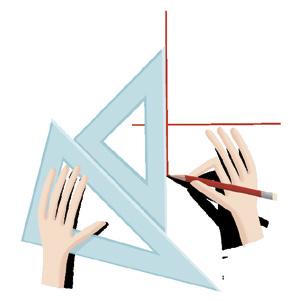
• ¿Con qué aparatos podemos medir líneas rectas?
escuadra instrumento de dibujo en forma de triángulo rectán gulo con tres ángulos dife rentes.
cartabón instrumento de dibujo en forma de triángulo rectán- gulo con dos ángulos iguales.
regla
instrumento largo, estrecho y rectangular, que sirve para trazar líneas rectas.
ACTIVIDADES
11. Aprende a dibujar una recta perpendicular a otra con escuadra y cartabón.
1.o Coloca el cartabón en la dirección en la que quieras trazar la recta y trázala.
2.o Coloca la escuadra apoyándola uno de los lados del cartabón y gira el cartabón de forma que sea otro lado el que se apoye sobre la escuadra.
12. Aprende a dibujar una recta paralela a otra con escuadra y cartabón.
1.o Coloca la escuadra sobre el papel de forma que no se mueva.
2.o Apoya un lado del cartabón en el lado más largo de la escuadra.
3.o Traza una recta en la dirección de en el lado más largo del cartabón.
4.o Desliza el cartabón hacia arriba o hacia abajo, sin mover la escuadra.
5.o Traza otra recta paralela a la recta inicial.
3.o Traza la perpendicular a la recta inicial.
DE ESPACIO
FORMA
LA RECTA NUMÉRICA
Observa el cronograma de estos inventos:
Una década = 10 años
Un siglo = 100 años
Un milenio = 1 000 años
• ¿Qué información nos da la recta numérica?
ACTIVIDADES
¡Atención con los años acabados en 00! 1800 último año del siglo xviii
• ¿Cómo se organiza la información sobre la recta?
13. La última actividad deportiva del mes ha sido una carrera.
Dibuja una flecha que una cada uno de los chicos y chicas que participan con el punto de la recta que indica la distancia recorrida.
Ha recorrido
100 metros Ya ha completado la mitad del recorrido total y 200 metros más
Solo le falta una cuarta parte del recorrido.
Está a 200 metros del final.
(Siglo vii) Molino de viento (Siglo xvi) Lápiz
(Siglo xix) Máquina de escribir
(Siglo xx) Internet
(Siglo xxi) YouTube
(Siglo xx) Ordenador (Siglo xviii) Termómetro (Siglo xv) Imprenta
(Siglo ii) Papel
(Siglo xxi) Instagram (Siglo xxi) TikTok
¡VEN AL FESTIVAL BOREAL DE LOS SILOS!
Observa los horarios de la guagua y el programa de los conciertos y responde a las preguntas.
Viernes, sábados y domingos
VIERNES 20 DE SEPTIEMBRE DE 2024
ESCENARIO LOS SILOS
MARILIA MONZÓN 18:30
LAS NINYAS DEL CORRO 20:00
ISEO Y DODOSOUND 21:30
MISS BOLIVIA 23:30
MARIA AL REVÈS 01:00
ESCENARIO CANARIAS
ANÍBAL Y LAJALADA 17:00
SURMA 19:00
NALA RAMI 20:30
ESCENARIO CONVENTO
MARIANA 17:00
YAIMA OROZCO 20:30
• Si sales de La Orotava el viernes a las 19:02, ¿a qué conciertos puedes ir?
• ¿Qué duración tiene, como máximo, el concierto de Las ninyas del corro?
¿Y el de Aníbal y Lajalada?
• Si el último autobús de vuelta sale a las 23:35, ¿puedes ir al concierto de Miss Bolivia?
SÁBADO 21 DE SEPTIEMBRE DE 2024
ESCENARIO LOS SILOS
MARALA 18:00
BOMBINO 19:30
RODRIGO CUEVAS 21:15
J NOA 23:15
FRANCISCO, EL HOMBRE 00:45
ESCENARIO CANARIAS
JULIA RODRÍGUEZ 16:00
BEWIS DE LA ROSA 17:30
RUTS Y LA ISLA MUSIC + DACTAH CHANDO + ISA IZQUIERDO 20:00
ESCENARIO CONVENTO
LOLI MOLINA 12:00
CLARA MANN 16:00
• Como muy tarde, ¿a qué hora tienes que salir el sábado de La Orotava si quieres ir al concierto de Julia Rodríguez? ¿Podrás ir también al concierto de Clara Mann?
• Dibuja en un reloj de agujas la hora del concierto de Bombino y el de Loli Molina.
de cálculo
9 2 1 5 4 7 8 6 0 3
8
MULTIPLICAMOS Y DIVIDIMOS POR NÚMEROS ACABADOS EN 0
Los avicultores de una cooperativa han hecho esta tabla para saber cuántas aves de corral tienen entre todas sus granjas.
Aves de corral N.o de granjas N.o de animales por granja N.o total de animales
Gallinas 15 30 450
Codornices 10 28 280
Ocas 23 20 460
Patos 50 30 1 500
Avestruces 30 12 360
PARA MULTIPLICAR POR UN NÚMERO ACABADO EN CERO, MULTIPLICO SIN EL CERO Y AÑADO AL RESULTADO LOS CEROS QUE
LOS FACTORES.
• ¿Has entendido la estrategia de cálculo de la multiplicación por números acabados en ceros? ¿Puedes explicarla con tus palabras?
• Poned ejemplos de multiplicaciones por números acabados en ceros y a resolvedlas entre todos.
AL DIVIDIR, ELIMINO LA MISMA CANTIDAD DE CEROS DE LOS DOS NÚMEROS Y DIVIDO EL DIVIDENDO ENTRE EL DIVISOR.
Para las Jornadas Gastronómicas de la Cocina de las Aves de Corral, los avicultores han elaborado una tabla para saber cuántos animales tienen que colocar en cada jaula.
SI QUEDAN CEROS EN EL DIVIDENDO, HAGO LA DIVISIÓN SIN
TENERLOS EN CUENTA Y, LUEGO, LOS AÑADO AL RESULTADO.
Aves de corral N.o de animales N.o. de jaulas N.o de animales
• ¿En qué filas de esta tabla se ha aplicado cada una de las estrategias de cálculo que explica la calculadora?
ACTIVIDADES
14. Relaciona con flechas las operaciones que tienen el mismo resultado. 12 × 2 000
: 5
× 60
: 5
: 5
× 32
: 5
× 16
: 10
: 10
000 × 30
: 10
× 100
: 10
15. Relaciona con flechas las operaciones que tienen el mismo resultado.
× 30
× 3
: 80
: 20
:
16. Une con el resultado correspondiente estas divisiones que dan como resultado un número decimal. ¿Qué observas? ¿Lo puedes relacionar con la estrategia de cálculo que estamos trabajando?
:
ORDENAMOS LA INFORMACIÓN:
¿QUÉ SABEMOS? ¿QUÉ QUEREMOS
SABER?
Ordenar la información facilita la tarea de resolver con éxito los problemas.
Ana y Elisa han ido a la piscina. Ana ha nadado 1 600 metros, y Elisa ha nadado la mitad de piscinas que Ana. Si la piscina es olímpica, es decir, mide 50 metros de largo, ¿cuántas piscinas ha nadado Elisa?
¿Qué sabemos?
• Que la piscina mide 50 metros.
• Que Ana ha nadado 1 600 metros nadando.
• Que Elisa ha nadado la mitad de piscinas que Ana.
¿Cómo lo averiguamos?
¿Qué queremos saber?
• Cuántas piscinas ha nadado Elisa.
• La mitad de 1 600 metros son 1 600 : 2 = 800 metros.
• Piscinas de 50 metros que hay en 800 metros: 800 : 50 = 80 : 5 = 160 : 10 = 16 : 1 = 16 piscinas
800 = 500 + 300
500 : 50 = 10
300 : 50 = 6 16 piscinas
Queríamos saber cuántas piscinas ha nadado Elisa ...ahora podemos responder: Elisa ha nadado 16 piscinas.
PROBLEMAS
17. Cada día me levanto a las 7:00, pero hoy me he levantado media hora antes que ayer. Como siempre, iré a dormir a las 22:20.
• ¿Cuántas horas habré estado despierto o despierta?
• ¿Cuántas horas dormiré?
¿Qué sabemos?
¿Qué queremos saber?
¿Cómo lo averiguamos?
• Ahora podemos responder:
18. El mayor pedido de material que ha hecho la escuela ha sido el de hojas blancas. Ha comprado 20 cajas, y en cada caja hay 5 paquetes de 500 hojas.
• ¿Cuántas hojas ha comprado? ¿Cuántas tocarán por aula si, en total, hay 12 aulas?
• ¿Cuántas hojas se han comprado por estudiante si en la escuela hay un total de 271 estudiantes?
¿Qué sabemos?
¿Cómo lo averiguamos?
• Ahora podemos responder:
¿Qué queremos saber?
1. Resuelve:
2. Identifica las casillas con el resultado correcto y píntalas.
125 : 20 = 13
45 × 20 = 900
33 : 30 = 3
100 × 100 = 1 000
462 : 10 = 4 620 87 : 40 = 23
300 × 80 = 24 000
800 : 80 = 80
3. Lee esta información sobre Fátima y fíjate en el plano.
Fátima vive en la calle Veintinueve de Abril de Las Palmas de Gran Canaria.
× 50 = 1 200
a) Escribe el nombre de una calle paralela a la suya.
b) Escribe el nombre de una calle perpendicular a la suya.
c) ¿Qué tipo de rectas forman la calle de Olof Palme y la avenida José Mesa y López?
d) ¿Qué dirías que son las líneas de los planos que indican calles; rectas, semirrectas o segmentos? Razona la respuesta.
4. Di si estas afirmaciones son ciertas (C) o falsas (F). Corrige las falsas.
a) Los aparatos de medida nos ayudan a ordenar el origen de las cosas.
b) El reloj es el instrumento de medida del tiempo.
c) Para pasar de minutos a segundos, dividimos por 60.
d) El termómetro mide la temperatura, y su unidad de medida son los números.
5. Observa estos dos diagramas y responde a las preguntas.
Temperatura corporal de los estudiantes de Ágreda (Soria)
a) ¿Los dos diagramas muestran datos de temperatura?
b) ¿Para obtener los datos y para hacer los diagramas, se ha necesitado la misma cantidad de datos en cada caso? Justifica la respuesta.
c) Si tuviéramos que hacer un informe para explicar el tiempo que hará en Ágreda, ¿tendríamos que utilizar la información de los dos diagramas?
d) ¿Qué estudiante tiene la temperatura más baja? ¿Y la más alta?
e) ¿Qué mes ha hecho más frío? ¿Y más calor?
1. ¿Qué nivel has alcanzado en esta unidad? Haz el test y lo sabrás.
1. 25 × 15
2. 96 : 32
3. 450 × 10
4. 1 600 : 20
5. Cuando dos líneas se cruzan forman... rectas paralelas. rectas secantes. siempre rectas perpendiculares.
6. Dos segmentos se pueden medir con...
7. Para resolver con éxito un problema, lo primero que tenemos que preguntarnos es...
la cinta métrica, el pie de rey, la regla y el compás. solo con la regla. con la cinta métrica y la regla.
¿Qué datos tenemos?
¿Qué operación tenemos que hacer? ¿Qué sabemos, y qué queremos saber?
8. Con el termómetro podemos medir el tiempo... atmosférico. histórico. real.
9. Para pasar de minutos a segundos hay que... mirar el reloj. × 60 : 60
10. Para pasar de horas a días hay que... × 24 mirar el calendario. : 24
• Comprueba las soluciones en la tabla del final de este libro y calcula tu puntuación.
• He conseguido puntos.
• Según la puntuación obtenida, .
• ¿Cómo te has sentido trabajando los contenidos de este tema?
2. Fíjate en que, haciendo problemas, razonando, representando, comunicando y conectando, has aprendido muchas cosas. Ahora, observa esta imagen e indica lo que eres capaz de hacer.
Observando esta imagen, me puedo inventar un problema o una actividad.
Sé contestar a esta pregunta: «¿Qué relación tiene este cuadro de Kandinski con las matemáticas que conozco?».
En esta imagen encuentro rectas paralelas, rectas secantes y rectas perpendiculares. También observo que hay figuras geométricas y segmentos de diferentes medidas.
Sé representar aspectos matemáticos en un cuadro para decorar la pared (crear un cuadro propio).
Me doy cuenta de las regularidades.
Soy capaz de relacionar esta imagen con otras situaciones de mi vida.
¿QUÉ NÚMEROS CONOCEMOS?
MANUEL UTILIZA TIKTOK
DURANTE UN 50 % DEL TIEMPO QUE TIENE EL MÓVIL EN LAS MANOS.
• De estos tres amigos, ¿quién ha estado más tiempo conectado a las redes sociales?
• ¿Quién ha estado más tiempo conectado a YouTube?
• ¿Quién ha dedicado más parte de su tiempo libre a conectarse a TikTok?
• ¿Piensas que pasamos demasiadas horas al día conectados con el móvil o con la tableta?
¿Cuántas horas habría que dedicar, diariamente, a las pantallas?
LUCÍA HA ESTADO CONECTADA A YOUTUBE
2/4 PARTES DE SU TIEMPO LIBRE.
PUES BLANCA HA ESTADO CONECTADA, A INSTAGRAM, 0,50 H DEL SUYO.
NÚMEROS MENORES QUE 1
• ¿Qué pasa cuando hacemos la unidad más pequeña?
Si lo hacemos más pequeño... o
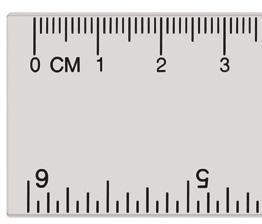
• ¿Cómo leemos cada una de las separaciones que hay del 0 al 1? ¿Y del 1 al 2?
Los números situados entre dos números enteros consecutivos son números decimales. Entre dos enteros hay infinitos números decimales.
Los números decimales...
• son números que se escriben siempre con una coma.
• ...son números comprendidos entre dos números enteros.
• ...tienen siempre la parte entera delante de la coma.
ACTIVIDADES
1. Sitúa estos números decimales sobre la recta numérica.
a) 0,3; 0,23 y 0,123 0 1
b) 0,3; 0,32 y 0,321
REDONDEAMOS NÚMEROS DECIMALES
Fíjate cómo funciona el redondeo.
Para hacer una estimación en el cálculo o en la medida, redondeamos los números.
ACTIVIDADES
6,90 €
redondeamos a 7 €
3,3 cm redondeamos a 3 cm
• Y el 3,5, ¿lo redondeamos al 3 o al 4?
2. Construye números menores que 10 utilizando todas las cifras de estas tarjetas y la coma decimal. ¡Pon la coma con buen criterio! Después, redondea a las unidades el número resultante.
J 6 9 1
SUMAS Y RESTAS CON DECIMALES
SUMAR Y RESTAR NÚMEROS DECIMALES
6 , 3 0
4
+ 0 , 2 5
1 0 , 5 5
1 2 , 5 0
0 , 8 0
+ 0 , 2 5
0 , 0 5
1 , 5 0
+ 1 2 , 0 0
1 3 , 5 5
8 , 2 5 – 4
4 , 2 5 8 , 2 5 – 0 , 8 0 7 , 4 5
ES MUY SENCILLO. SOLO TENEMOS QUE COLOCAR BIEN LA COMA.
• Observa esta operación. ¿Cuáles de los ceros tienen sentido?
• ¿Cuáles no lo tienen?
1 2 , 5 0
0 , 8 0
+ 0 , 2 5
¡ATENCIÓN!
EN LOS NÚMEROS DECIMALES, LOS CEROS A VECES NOS DESPISTAN.
0 , 0 5 Sumamos centésimas.
1 , 5 0 Sumamos décimas.
+ 1 2 , 0 0 Sumamos unidades.
1 3 , 5 5
SI EL CERO ESTÁ DETRÁS DE LA COMA PERO ENTRE OTROS NÚMEROS, TAMPOCO
LO PODEMOS TOCAR; TIENE MUCHO SENTIDO: 4,09.
EL CERO SOLO PIERDE EL SENTIDO SI ES LA ÚLTIMA
CIFRA DECIMAL: 8,70 = 8,7.
SI EL CERO ESTÁ DELANTE DE LA COMA, NO LO PODEMOS TOCAR; TIENE MUCHO SENTIDO: 0,75.
ACTIVIDADES
3. Rodea los números de la tabla que sean menores que la unidad. Después, escribe el número entero anterior y el número entero posterior de cada uno de los números de la tabla.
4. ¿Qué cartulina del bingo decimal ha resultado premiada, si los números que han salido son los siguientes?
5. Ayer, Héctor gastó 10,25 € en la comida y hoy ha gastado 1,80 € más que ayer.
¿Cuánto dinero ha gastado hoy?
ORDENAMOS FRACCIONES
Con el mismo denominador
Si comparamos dos fracciones que tienen el mismo denominador, es mayor la fracción que tiene el numerador mayor.
3 8 < 5 8
Con el mismo numerador
Si de un círculo hacemos 8 partes y del otro, 9, las partes del segundo círculo son más pequeñas. Por lo tanto, es mayor la fracción que tiene el denominador más pequeño.
5 8 > 5 9
Con distinto numerador y distinto denominador
Para comparar las fracciones 3 4 y 5 6 , las convertimos en fracciones equivalentes con el mismo denominador. ¿Como?
• Multiplicamos los denominadores entre ellos y el resultado es el nuevo denominador.
• Multiplicamos cada numerador por el valor que hemos utilizado para multiplicar el denominador correspondiente.
• Obtenemos dos fracciones con el mismo denominador y equivalentes a las iniciales. Por lo tanto; 18 24 < 20 24 ; es decir, 3 4 < 5 6
• ¿Qué fracción es mayor, 3 4 o 7 10 ?
ACTIVIDADES
6. Observa la parte pintada de cada uno de los rectángulos, escribe qué fracción representa y el símbolo <, = o > para que la relación sea cierta.
7. Pinta de formas diferentes 4 6 en los cuadrados siguientes.
CALCULAMOS PORCENTAJES
En la biblioteca de la clase hay muchos libros diferentes; en total hay 100 libros.
• De estos 100 libros, el 20 % son cómics en castellano. ¿Cuántos cómics en castellano hay?
• El 15 % de los libros de la biblioteca están en inglés. ¿Cuántos libros hay en inglés?
HAY EL MISMO NÚMERO DE LIBROS EN FRANCÉS QUE
EN INGLÉS.
• Otro 15 % de los libros están en francés.
• En la biblioteca, el 20 % de los libros son cómics, un 15 % son en inglés y otro 15 %, en francés; el resto son novelas en castellano. ¿Cuántas novelas en castellano hay en la biblioteca?
Fijaos cómo lo hacemos para escribir el resumen de la variedad de libros de la biblioteca.
100 libros = 20 cómics en castellano + 15 libros en inglés + 15 libros en francés + 50 novelas en castellano
ACTIVIDADES
8. Coge 100 cubos encajables y averigua.
• ¿Cuántos cubos son el 50 % de 100 cubos encajables?
• ¿Cuántos cubos son el 10 % de 100 cubos encajables?
• ¿Cuántos grupos del 10 % de 100 son 100 cubos encajables?
9. En una bolsa hay 100 canicas. El 20 % son de color rojo, el 30 % son de color verde y el resto son de color blanco. ¿Qué porcentaje de canicas son blancas?
10. En la puerta de una tienda hay un letrero que dice: «Rebajas».
¡Recuerda que el 25 % de descuento es la mitad de la mitad del precio! 50% DE DESCUENTO 40€ 60€
¡Recuerda que el 50 % de descuento es la mitad del precio!
QM• ¿Cuánto me costarán estos pantalones rebajados?
• ¿Cuánto me costará esta chaqueta rebajada?
25 % DE DESCUENTO
• ¿Cuánto me costará todo junto? ¿Tendré bastante con un billete de 50 €? ¿Cuánto dinero me faltará? ¿Cuánto dinero me sobrará?
LA BISECTRIZ Y LA MEDIATRIZ
ACTIVIDADES
11. ¿De qué tipo son los ángulos siguientes? Anótalo. Después, dibuja la bisectriz de cada uno: traza dos de las bisectrices con el transportador de ángulos y las otras dos con el compás.
12. Dibuja la mediatriz de cada segmento.
Recuerda que la mediatriz de un segmento es la recta perpendicular a su punto medio y que, para dibujarla, necesitas la escuadra y el cartabón.
EL MUSICAL DE BILLY ELLIOT EN EL ATENEO
¡Compra las entradas ahora mismo!
Platea
Primera planta
Segunda planta 50 € 35 € 25 €
C25 % de descuento si eres jubilado, si tienes el carné joven o si estás sin empleo. 50 % de descuento si tienes menos de 16 años.
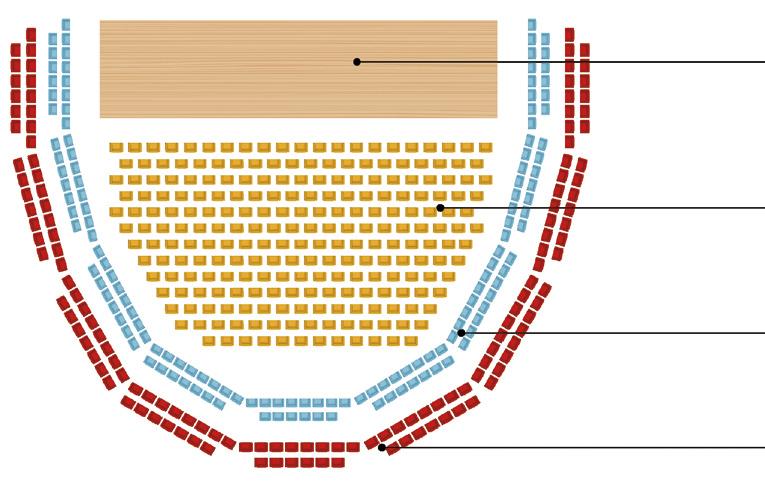
CESCENARIO
PLATEA PRIMERA PLANTA SEGUNDA PLANTA
• Si la capacidad del teatro es de 500 localidades y 234 son de platea, ¿cuántas localidades hay en la primera y la segunda planta, si las dos disponen de la misma cantidad de asientos?
• Si eres una persona jubilada, ¿cuánto te costará la entrada de platea? ¿Y la de la segunda planta?
• ¿Cuánto le costarán las tres entradas a una familia con dos adultos y un niño de 12 años si se sientan en la primera planta? ¿Y si se sientan en platea? ¿Y si se sientan en la segunda planta?
• ¿Qué fracción representa el descuento para personas que están desempleadas? ¿Y el descuento por el hecho de tener menos de 16 años?
• Si se han vendido 250 entradas, ¿qué porcentaje queda para vender?
• Y si se han vendido 400, ¿qué porcentaje representan estas ventas?
de cálculo
9 2 1 5 4
MULTIPLICAMOS Y DIVIDIMOS POR 0,5
• Si en la hucha tengo 16 monedas de 50 céntimos, ¿cuánto dinero tengo?
50 céntimos son 0,50 euros.
Por lo tanto, tenemos que multiplicar:
16 × 0,50 = 8
En la hucha tengo 8 €
LEntonces, ¿qué significa dividir entre 0,5?
Piénsalo con la ayuda de este ejemplo.
8 es la mitad de 16; por lo tanto, multiplicar un número por 0,5 da, como resultado, la mitad de este número.
Quiero repartir 16 L de agua en botellas de medio litro (0,5 L).
• ¿Cuántas botellas necesito?
1 L 0,5 L 0,5 L
ACTIVIDADES
13. Calcula.
=
×
×
=
=
¿Podríamos calcular mentalmente 15 × 0,5 sin la necesidad de utilizar la calculadora? ¿Por qué?
14. Calcula.
¿Encuentras alguna relación entre los números que has dividido y los resultados? ¿Podríamos calcular mentalmente 25 : 0,5 sin tener que utilizar la calculadora? ¿Por qué?
15. Resuelve las situaciones siguientes.
a) Tengo 14 trozos de cuerda de 0,5 metros cada uno. ¿Cuántos metros de cuerda tengo en total?
14 × 0,5 =
Respuesta:
b) He comprado 16 bolsas de pipas, a 0,50 € cada una. ¿Cuánto dinero he gastado?
Respuesta:
16. Indica qué operación hemos hecho para pasar de cada casilla a la siguiente. ¡Atención, hay alguna casilla trampa!
ESTIMAMOS RESULTADOS
La comisión de fiestas ha repartido los adornos para decorar las calles. En nuestra calle somos 12 vecinos y nos han dado 510 guirnaldas para colgar. Si las repartimos a partes iguales, ¿cuántas habrá, aproximadamente, para cada casa?
SEGURO QUE HABRÁ MENOS
DE 500 PARA CADA CASA.
HABRÁ UN CENTENAR PARA CADA CASA.
HABRÁ MENOS DE CINCUENTA PARA CADA CASA, PORQUE 500 : 10 = 50.
HABRÁ 25.
HABRÁ MÁS DE 10.
En el concurso de postres, los participantes han presentado 20 pasteles y, de cada pastel, han hecho 8 trozos. Si nos hemos comido 80 trozos, ¿qué fracción representan los pasteles que no nos hemos comido?
En el barrio hay 200 niños y niñas. Si el 75 % han participado en la fiesta de la espuma, ¿cuántos niños y niñas han participado?
PROBLEMAS
17. Responde SÍ o NO, y razona las respuestas.
a) La abuela nos ha hecho un bizcocho y dice que ha puesto 300 g de harina, 150 g de azúcar, 50 g de mantequilla, 15 g de levadura, un yogur, una piel de naranja y una piel de limón. ¡Está buenísimo! ¿Crees que, una vez horneado, el bizcocho pesará más de un kilogramo?
b) Como veo que en la cartera llevo 20 €, me compraré una libreta de 8,5 € y un paquete de bolígrafos que vale 4,30 €. Aparte de eso, ¿me quedará dinero para comprar la merienda de mi hermano y la mía, que siempre nos cuesta unos 5 €?
c) Cada día recorro el camino de casa al colegio cuatro veces. El reloj indica que camino una media de 2 km cada día. ¿Crees que la distancia de casa al colegio es aproximadamente de 1 4 de kilómetro?
d) Entre todos los grupos de 5.º hay 96 estudiantes. El 75 % tienen hermanos o hermanas en en el colegio. ¿Crees que en este curso hay menos de 25 estudiantes que no tienen hermanos o hermanas en el colegio?
1. Rodea con color verde (V) los números expresados en forma decimal, con rojo (R) los números fraccionarios, con azul (A) los números enteros y con negro (N) los porcentajes.
2. Ordena estos números y escríbelos sobre la recta numérica.
3. Calcula el resultado de estas operaciones.
a) 2 − 0,5 =
b) 44 + 0,5 =
c) 2,5 + 1,3 =
d) 7 − 0,5 =
e) 15 − 0,5 =
f ) 22,5 + 1,2 =
g) 4,2 + 7,3 = h) 3,56 − 0,65 =
4. Señala el punto exacto por el que pasará la mediatriz de los siguientes segmentos.
5. Observa el diagrama de barras y responde a las preguntas.
Actividades deportivas de los estudiantes de 5.º
a) ¿Qué representa el diagrama?
b) ¿Qué deporte es el que practican más?
¿Cuál es la diferencia con respecto al menos practicado?
Baloncesto: 25 %
Fútbol: 31 %
Balonmano: 20 %
Voleibol: 11 %
Tenis: 8 %
Ninguno: 5 estudiantes
c) ¿Qué porcentaje de estudiantes no practican ningún deporte?
d) ¿Cuántos estudiantes hay en 5.o?
e) ¿Qué deporte es practicado por 1 4 de los estudiantes?
¿Y por 4 20 ?
Baloncesto Fútbol Balonmano Voleibol Tenis Ninguno
1. Completa las tablas siguientes.
Antes de empezar la unidad...
Dibujar la mediatriz.
Identificar números decimales.
Comparar fracciones.
Redondear números decimales a enteros.
Sumar y restar números decimales.
Estimar resultados sin hacer cálculos.
Calcular un porcentaje.
Multiplicar y dividir por 0,5 mentalmente.
Al terminar la unidad...
Dibujar la mediatriz.
Identificar números decimales.
Comparar fracciones.
Redondear números decimales a enteros.
Sumar y restar números decimales.
Amar resultados sin hacer cálculos.
Calcular un porcentaje.
Multiplicar y dividir por 0,5 mentalmente.
2. Haciendo problemas, representando, comunicando y conectando has adquirido conocimientos. Ahora, fíjate en la situación siguiente y señala cuáles de estas cosas eres capaz de hacer.
1,05 kg
AObservando esta imagen, me puedo inventar una actividad.
Sé resolver un problema de porcentajes en una cuadrícula.
Sé representar números decimales de diferentes maneras:
– En la recta numérica.
– En cuadrículas.
– En diagramas circulares.
Sé encontrar regularidades.
Soy capaz de relacionar esta imagen con otras situaciones que puedo encontarme en mi vida.
MIRAMOS CON OJOS MATEMÁTICOS
SITUACIÓN DE APRENDIZAJE
Formad cuatro grupos. Tendréis que buscar información sobre un tema matemático, resolver las tareas asignadas y preparar una exposición para presentarla al resto de la clase.
Cada grupo se encargará de un tema diferente.
• Grupo 1: tipo de rectas.
• Grupo 2: tipo de ángulos.
• Grupo 3: instrumentos de medida.
• Grupo 4: simetrías.
Material para cada
grupo
• Un dispositivo para fotografiar (cámara fotográfica, teléfono móvil, tableta...).
• Un Chromebook o un ordenador.
• Material específico para la exposición: papel de embalar, cartulinas, fotografías, tijeras, papeles
Observad y pensad
Pensad en espacios, rincones y materiales del colegio que representen vuestro tema y fotografiadlos.
Poneos manos a la obra
Buscad los elementos matemáticos correspondientes, identificadlos y fotografiadlos. Todos tenéis que tener claros los conceptos y las definiciones del tema asignado.
Explicadlo
Preparad una sesión de 15 o 20 minutos para explicar todo lo que habéis encontrado en el colegio relacionado con vuestro tema.
Tenéis que presentar un producto final que puede ser un vídeo, una presentación con una aplicación como PowerPoint o Prezi, una carpeta de proyecto (lapbook)…
Tened en cuenta que la creatividad será muy valorada y apreciada por vuestro público.
PEQUEÑOS CONSEJOS
• Durante la presentación, tenéis que relacionar las imá- genes con el contenido que habéis trabajado.
• Valorad, entre todos, si el producto final lo presenta- réis también a otras clases y a vuestras familias.
• Tened claros los contenidos que queréis trabajar y consensuadlos con el profesor o la profesora.
© GRUPO ANAYA, S.A., 2025 - C/ Valentín Beato, 21 - 28037 Madrid. Reservados todos os dereitos. O contido desta obra está protexido pola Lei, que establece penas de prisión e/ou multas, amais das correspondentes indemnizacións por perdas e danos, para quen reproduza, plaxie, distribúa ou comunique publicamente, en todo ou en parte, unha obra literaria, artística ou científica, ou a súa transformación, interpretación ou execución artística fixada en calquera tipo de soporte ou comunicada a través de calquera medio, sen a preceptiva autorización.