Matemáticas 3 Andalucía. Primaria. Operación Mundo. Anayaa

Matemáticas

Claves didácticas

Recursos y materiales

Propuesta didáctica

Inclusión Evaluación

Normativa LOMLOE

Índice

Claves de Operación Mundo

Pág.

5

Competencial Comprometido

• Situaciones de aprendizaje

• Actividades competenciales

• Evaluaciones competenciales

• ODS

• Objetivo en acción

Interdisciplinar

• Interdisciplinariedad en primer ciclo

• Proyectos interdisciplinares

• Plan Lingüístico

Inclusivo

• Pautas DUA

• Lo esencial

• Recursos para la inclusión

• Herramienta de inclusión IN.ON

Metodologías activas

• Aprendizaje cooperativo

• Desarrollo del pensamiento

• Educación Emocional

• TIC

• Aprendizaje lúdico

• Evaluación

• Propuestas de secuenciación

Libros y cuadernos para el Alumnado

Propuesta didáctica

Material de aula

Pág.

Recursos y materiales para la etapa 89

Proyecto digital

Pág.

Proyecto digital

Contenidos del curso. Secuenciación de la etapa

Inclusión y atención a la diversidad Programación, propuesta didáctica y documentación del proyecto

Propuesta didáctica Inclusión Evaluación

Material impreso para el profesorado

Unidad 9

125 Pág 145 Pág. 163 Pág. 251 Pág.

Herramienta de inclusión IN.ON

Inclusión y atención a la diversidad

Pautas DUA

Lo esencial

Normativa LOMLOE

Generador de pruebas de evaluación y ejercitación

• ¿Qué es y cómo funciona?

MUESTRA MUESTRA

Unidad 9

Unidad 9

• ¿Qué es y cómo funciona?

Game Room: evaluación gamificada y digital

Competencias GYM

Evaluación inicial

• Unidad 0

MUESTRA MUESTRA

Trimestre 1

• Prueba de evaluación inicial

Evaluación por situaciones de aprendizaje

Evaluación adaptada

Evaluación competencial

Evaluación final

Instrumentos para la evaluación, autoevaluación y coevaluación

Instrumentos para evaluar la práctica docente

Normativa LOMLOE

• Estructura curricular

• Relación entre elementos del curriculo

• Glosario

Programación

• Programación didáctica

• Muestra programación. Situación de aprendizaje

Claves de Operación Mundo

Competencial

Comprometido

Interdisciplinar

Metodologías activas

Inclusivo

Competencial

Los aprendizajes del alumnado deberán orientarse a la adquisición de las habilidades y destrezas que le permitan afrontar con éxito las diferentes situaciones a las que tenga que hacer frente en su vida académica, personal, familiar y social. A largo plazo, también, en su vida laboral.

Esto exige un proyecto educativo cuya meta no será solo la de contribuir a la adquisición de contenidos o saberes por parte del alumnado, sino también la de proporcionarle todo lo necesario para que sepa aplicarlos en los diferentes contextos en los que tenga que desenvolverse.

El proyecto OPERACIÓN MUNDO aporta una gran diversidad de actividades para que el alumnado pueda responder, de manera práctica, aplicando sus capacidades, conocimientos, habilidades, destrezas y actitudes de forma integrada. Estas actividades facilitan la transferencia de los aprendizajes y su aplicación en diversos e interesantes contextos.

SITUACIONES DE APRENDIZAJE

Las situaciones de aprendizaje son una de las novedades de la nueva ley educativa (LOMLOE). Se trata de un tipo de actividad que parte de una situación problema, contextualizada y de cierta complejidad, que pone en acción los contenidos aprendidos por parte del alumnado para ser resuelta. Pone en funcionamiento, de manera integrada, todos sus saberes y competencias. Por tanto, favorece la transferencia de los aprendizajes adquiridos, para llevarlos a la práctica de manera crítica, reflexiva y transformadora.

¿Dónde está en el proyecto?

En el libro de texto del alumnado, cada unidad abre con una situación de aprendizaje, es decir, con una situación problema enmarcada en un ODS, que invitará al alumnado a que lleve a cabo

5 ¡Experimentamos con la materia y la energía!

Me gusta mucho investigar cómo funcionan mis juguetes. Por ejemplo, me he dado cuenta de que no todos funcionan igual.

Algunos tienen pilas, otros tienen una plaquita solar, a otros les tengo que dar cuerda... Qué raro, ¿no?

¡A veces los abro para ver qué piezas tienen dentro y de qué están hechas! El problema es cuando luego no sé volverlos a montar.

¿Cómo lo ves?

¿Alguna vez habéis desmontado algo para ver cómo funcionaba por dentro? ¿Qué era?

¿Vosotros también tenéis juguetes que se muevan gracias a cosas diferentes (con pilas, a cuerda...)? ¿Cómo se mueven?

¿Sabéis de qué materiales están hechos vuestros juguetes favoritos?

Para esta unidad...

Objetivo en acción

Vamos a investigar uno de nuestros juguetes favoritos para descubrir de qué está hecho y cómo funciona.

El dato

Para fabricar juguetes se usan muchos materiales. Algunos, como los plásticos y ciertos metales, son perjudiciales si se tiran al medioambiente.

ACTIVIDADES COMPETENCIALES

¡Sigue el hilo!

una reflexión final con una propuesta transformadora. Esta situación exige que el alumnado tenga que adquirir previamente los aprendizajes básicos que se plantearán a lo largo de la unidad.

Las máquinas

1

La materia ¿De qué están hechas las cosas que nos rodean?

Los cambios físicos y químicos

2

¿Puede cambiar la materia?

Los materiales 3

¿Con qué se fabrican las cosas?

La energía 4

¿Qué produce los movimientos y los cambios?

¿Qué nos ayuda a realizar trabajos?

5 Los usos de las máquinas ¿Para qué utilizamos las máquinas?

6

ACTIVIDADES COMPETENCIALES

Las actividades competenciales son actividades auténticas. Han de provocar un aprendizaje aplicado con un sentido transformador o de impacto en el ámbito social, en la comunidad educativa, en las familias o individualmente. Parten de una situación problema y no necesariamente tienen un único resultado. Han de promover el análisis, la justificación, la predicción, la argumentación, la interpretación o la revisión. Por tanto, son actividades que no solo se centran en el saber, sino también en el saber hacer y en el desarrollo de habilidades.

¿Dónde está en el proyecto?

Estarán presentes en las diferentes actividades de cada unidad. En todos los casos, el alumnado aplicará de manera práctica alguno de los aprendizajes adquiridos, para lo que necesitará llevar a cabo inferencias, conjeturas, indagaciones y reflexiones.

Experimenta para notar la energía.

1 Construye un molinillo siguiendo estos pasos:

Podrás localizar fácilmente las actividades competenciales del libro; están destacadas con fondo de color.

2 Haz este experimento:

Escribe un objeto de tu casa que necesite energía para funcionar.

compartida Elige a una persona de tu clase, repasad juntos la actividad 1 de la página anterior para saber las aficiones que más le gustan. Después, escríbele un correo electrónico en el que le des algún consejo para que cuide el medio ambiente a la vez que disfruta de su afición.

3

Si además se relacionan con la situación de aprendizaje de la unidad, verás que siguen el hilo también gráficamente.

Escribe la energía que hace que el hielo cambie de estado y se derrita.

Todo lo que ocurre en la naturaleza necesita energía.

91 noventa y una

EVALUACIONES COMPETENCIALES

Con la nueva ley educativa (LOMLOE), la evaluación ha de responder a las competencias clave que todo el alumnado debe haber adquirido y desarrollado al término de la educación básica; esto es lo que se denomina «perfiles competenciales de salida del alumnado», que se concretan en los criterios de evaluación de cada una de las áreas.

Cuando enfrentamos al alumnado a una situación real, a una situación auténtica, cuando resuelve ese problema, habrá demostrado su competencia. Un elemento clave para la inclusión y el éxito escolar.

¿Dónde está en el proyecto?

La evaluación competencial estará visible tanto en el libro de texto como en los recursos digitales para el alumnado y el profesorado. En el libro de texto, en la doble página final de cada unidad, el alumnado responderá a una serie de actividades que darán respuesta al «¿Qué he aprendido?» y «¿Cómo he aprendido?». En los recursos digitales habrá disponibles recursos que se podrán descargar para llevar a cabo evaluaciones iniciales, evaluaciones básicas y avanzadas, evaluaciones competenciales, así como un generador de pruebas.

Nombre y apellidos: EVC

Ciencias de la naturaleza 3.º

Hoy, los niños y las niñas de la clase han ido de excursión al zoo. Allí conocerán muchos de los seres vivos que habitan en nuestro planeta. Además, en el zoo que van a visitar, los animales están agrupados según los lugares o ecosistemas en los que viven. Este es el plano del zoo que muestra algunos de los diferentes medios de la Tierra y los animales que los habitan.

CENTINELAS DE PAISAJES

Fecha: Nombre y apellidos: EVC

Ciencias Sociales 3.º

1 Observa la imagen y responde a las preguntas.

1 La persona que hizo este plano se equivocó y puso un animal intruso en cada medio. Localízalo y escribe su nombre y en qué medio debería estar:

Polo norte:

Desierto: Sabana:

a) ¿Qué tipo de cambio se ha producido en ese paisaje?

b) ¿Se trata de un cambio natural o artificial?

c) ¿Qué tipo de paisaje crees que es?

d) Escribe tres elementos artificiales que veas en la imagen.

e) Escribe tres elementos naturales que veas en la imagen.

Grupo Anaya, S. A. Material imprimible autorizado.

Comprometido

De acuerdo con lo establecido en la LOMLOE, el proyecto Operación Mundo irá orientado a facilitar el desarrollo educativo de los alumnos y las alumnas, garantizando su formación integral, contribuyendo al pleno desarrollo de su personalidad y preparándoles para el ejercicio pleno de los derechos humanos, de una ciudadanía activa y democrática en la sociedad actual.

ODS

Entre los principios pedagógicos que se establecen en nuestro actual sistema educativo está el compromiso. El proyecto Operación Mundo, siguiendo las indicaciones establecidas en la LOMLOE, está claramente vinculado con los Objetivos de Desarrollo Sostenible aprobados por la ONU para la Agenda 2030. Se pretende hacer un llamamiento universal, también al ámbito educativo, para erradicar la pobreza, proteger el planeta y mejorar las vidas de las personas en todo el mundo.

Los 17 objetivos de desarrollo sostenible

¿Dónde está en el proyecto?

En el libro de texto del alumnado, cada unidad abrirá con una situación de aprendizaje, es decir, una situación problema enmarcada en un ODS, que invitará al alumnado a que lleve a cabo una reflexión final, en el «Objetivo en acción», con una

8 Actúo por el planeta

El clima de la tierra está cambiando debido a la acción del ser humano. Conocerlo, tener información sobre el estado medioambiental en el que se encuentra el planeta es vital para poder actuar. Proteger la naturaleza hoy, significa un planeta mejor para las generaciones futuras. El poder del cambio está en nuestras manos: ¿qué podemos hacer para frenar el cambio climático y sus efectos?

¿Cómo lo ves?

¿Sabes qué es el cambio climático? ¿Por qué debería importarte? ¿Estamos a

El dato

Año tras año, la temperatura del planeta sigue aumentando.

enObjetivo acción

¿Qué pequeños gestos puedes hacer tú por el clima?

Graba una noticia radiofónica.

¡ S i g u e e l h i l o

Textos periodísticos la entrevista

¿Qué puedes aprender de un niño que, como tú, quiere cambiar el mundo?

propuesta transformadora. Esta situación exige que el alumnado tenga que adquirir previamente los aprendizajes básicos que se plantearán en las siguientes páginas de la unidad. Los ODS también

Vocabulario Lectura

¿Cómo afectan tus acciones del día a día a la salud del planeta?

Utiliza palabras nuevas sobre el consumo.

Textos periodísticos: la noticia

¿Te animas a informarte e informar sobre el futuro del planeta?

Textos periodísticos la noticia

¿Por qué es importante difundir en los medios de comunicación las iniciativas medioambientales?

CONOZCO MI LENGUA El verbo. Palabras con g y j. La diéresis.

OBJETIVOS EN ACCIÓN

El objetivo en acción será la actividad que se le propondrá al alumnado para intentar dar respuesta a la situación de aprendizaje planteada al inicio de cada unidad y que se retoma en el porfolio que la cierra. Se sugerirá un posible producto final, que será el medio para provocar una reflexión transformadora.

¿Dónde está en el proyecto?

En el portfolio final de cada unidad, se planteará la actividad «Objetivo en acción», que requerirá por parte del alumnado esa reflexión final con una propuesta transformadora, dando respuesta a la situación de aprendizaje.

7 Las horas de sol

Necesitamos energía para encender las luces de casa o el ordenador. Hay energía que no daña el planeta y utiliza recursos que no se agotan, como la luz del sol con la que podrían funcionar todos los aparatos eléctricos de casa.

¿Sabías que el número de horas de sol varía de unos días a otros? Cada día amanece y anochece a una hora diferente.

Y, además, no en todos los lugares ocurre a la misma hora.

¿Cómo lo ves?

¿Por qué crees que es importante la luz del sol?

¿Cómo podemos contar las horas de sol que hay al día? Para esta unidad...

¿Cómo

PORFOLIO

OBJETIVO EN ACCIÓN ¿Qué he aprendido?

1 Ordena estas fechas de un mismo año.

OCTUBRE 26 DICIEMBRE 7 MARZO 18 MAYO 14

2 Escribe con números la fecha de hoy, de pasado mañana y la de tu cumpleaños.

3 ¿Cuántas horas está abierta la panadería el martes? ¿Y el sábado?

7 ¿Cuánto tiempo ha pasado?

Elabora una lista

Mira en la tabla a qué hora salió el sol y se puso en Almería el 23 de diciembre y el 15 de julio.

23 diciembre15 julio

4 Dibuja relojes de agujas con las horas a las que realizas estas actividades.

8 Escribe cómo se leen estas horas de dos formas distintas.

a) ¿A qué hora amaneció el 23 de diciembre? ¿A qué hora anocheció?

b) ¿A qué hora amaneció el 15 de julio? ¿A qué hora anocheció?

c) ¿Cuántas horas de sol hubo el 23 de diciembre? ¿Y el 15 de julio?

9 Rufus sale a pasear cada tarde a las 5 y cuarto. Si el paseo dura una hora y media, ¿a qué hora regresa? Dibújalo en un reloj de agujas y en un reloj digital.

10 Alba y Rocío viajan en autobús. Salen a las 10 y cuarto de la mañana y llegan a las 12 y media. ¿Cuánto ha durado el trayecto?

Nos planteamos

a) ¿Crees que es importante el número de horas de sol que tenemos? ¿Por qué?

b) Piensa y comparte en pareja. Copia y completa en tu cuaderno el esquema. Comparte tu respuesta con tu compañera o compañero.

c) ¿Cómo puedes aprovechar la luz del sol en tu día a día? En pareja, haced una lista con vuestras ideas.

Mi respuesta. La respuesta de mi compañera o compañero.

Cada uno explica por qué ha respondido eso.

¿Cuál es ahora tu respuesta?

5 Expresa en horas.

3 días 6 días 1 semana

6 ¿Qué hora marcan estos relojes?

¿Cómo he aprendido?

Copia en tu cuaderno y colorea junto a cada oración.

El semáforo. Junto a cada actividad, colorea así en tu cuaderno: si has sabido la respuesta si has necesitado ayuda si no has sabido responder

• Me alegro cuando consigo resolver un problema.

• Colaboro con mi grupo todo el tiempo.

• Me esfuerzo por hacer las actividades bien.

¿Qué cosas concretas haces para colaborar con tu grupo?

Interdisciplinar

Operación Mundo incluye actividades cuya finalidad será la de conectar los distintos saberes aprendidos en las distintas áreas.

Esta interacción entre los contenidos se ajusta a la realidad del alumnado, ya que esta realidad no se presenta en compartimentos estancos, sino como un todo.

Este enfoque interdisciplinar incrementa la efectividad del aprendizaje porque exige saber el porqué y el para qué de lo aprendido; por tanto, garantiza que el aprendizaje, más ajustado a la realidad del alumnado, sea más significativo, funcional y competencial.

APRENDIZAJES INTERDISCIPLINARES

Las situaciones de aprendizaje planteadas desde cada área y vertebradas por los Objetivos de Desarrollo Sostenible (ODS) plantean al alumnado una propuesta de contenidos desde las diferentes áreas troncales, interrelacionados entre sí, para su aplicación práctica.

Por tanto, los contenidos seleccionados están conectados entre sí a partir de las situaciones de aprendizaje, reales y auténticas, que le dan un sentido funcional y significativo para el alumnado.

¿Dónde está en el proyecto?

En las situaciones de aprendizaje planteadas desde cada área, unidad por unidad, motivadas por alguno de los Objetivos de Desarrollo Sostenible (ODS). Serán estos los que le aporten una

rubio, morena, alta, bajo...

¿Cómo lo ves?

¿Crees que todas las personas pueden hacer los mismos deportes?

Antes no existían variantes femeninas o masculinas de algunos deportes; por ejemplo, no había fútbol femenino ni gimnasia rítmica masculina.

Objetivo en acción

Haz una lista de ideas para practicar deporte en el que participen niños y niñas por igual.

lógica significativa, funcional y competencial para que el alumnado dé respuestas prácticas y transformadoras.

Además, en primero y segundo de Primaria, las unidades comparten una misma temática para la situación de aprendizaje.

Interdisciplinariedad en Operación Mundo

ODS INTERDISCIPLINARES

Educación de calidad

Salud y bienestar

Salud y bienestar

El aula como lugar acogedor y de calidad para el aprendizaje.

Bienestar personal a través del uso y disfrute del cuerpo.

Adquisición de hábitos de cuidado y aseo personal. Personas comprometidas con la salud y el bienestar.

¡Comenzamos con orden! Ordeno la clase Me divierto en el colegio

¿Qué te hace feliz? Me muevo y me oriento ¡Alegra tu cuerpo!

Un, dos, tres… me cuido otra vez Me cuido ¡A tu salud!

Ciudades y comunidades sostenibles La calidad del aire. ¡Lanzamos ideas al aire!

Respiramos aire limpio Y tú, ¿cómo vas?

Vida de ecosistemas terrestes Cuidamos los seres vivos. Los quiero y los cuido Mi mascota cumple años ¡Queremos seres vivos!

Vida de ecosistemas terrestes

Producción y consumo responsables

Protección y relación sostenible con nuestro entorno natural. Nos importa la naturaleza Veo formas en la naturaleza ¡Viva la naturaleza!

Salidas educativas y reconocimiento del entorno (turismo sostenible).

Vamos de excursión Mido distancias Protegemos el paisaje

Agua limpia y saneamiento El consumo de agua. Cada gota cuenta Uso un vaso en cada caso Agua y aire para vivir

Producción y consumo responsables

Industria, innovación e infraestructura

Ciudades y comunidades sostenibles

Modelos de producción sostenible y consumo responsable.

Infraestructura y tecnología sostenible. Aumento capacidad tecnológica.

Reducir, reciclar y reutilizar Cuento y reutilizo Reduce, recicla y reutiliza

Investigamos con energía

Calculo con mi máquina La tecnología es cosa mía

Conservación del patrimonio. ¡Salimos a escena! Un día para celebrar Aprendo del pasado

Vida submarina Protección de la hidrosfera.

¡Por un océano limpio! Es tiempo de cuidar el mar Cuido mi planeta

LENGUA MATEMÁTICAS C. DEL MEDIO

PROYECTOS INTERDISCIPLINARES

Serán experiencias de aprendizaje integradoras que permiten el desarrollo competencial del alumnado y la aplicación de los aprendizajes adquiridos. A partir de una situación de aprendizaje vinculada con los ODS, el alumnado llevará a cabo un proceso de investigación en el que consultará diferentes fuentes de información, organizará su trabajo y realizará un producto final cuya difusión tendrá un claro objetivo de acción y transformación. En definitiva, comprende procesos de: planificación, ejecución, comunicación y evaluación.

¿Dónde está en el proyecto?

Al final de cada trimestre, en el libro de texto para el alumnado, se propondrá un proyecto desde cada una de las áreas troncales, conectadas entre sí por un ODS compartido, a partir del cual el alumnado pasará por diferentes fases (Piensa, Diseña, Construye, Presenta y Comprueba) para

dar una respuesta práctica y transformadora que permita buscar soluciones y hacer aportaciones a la situación planteada. Cada proyecto tiene una clara finalidad basada en la investigación, el emprendimiento y la conexión de aprendizajes de las diferentes áreas troncales.

DESCUBRE EL PROYECTO INTERDISCIPLINAR

Naturalmente... ¡verde!:

HACEMOS NÚMEROS VERDES

¿Cómo te gustaría que fuera nuestro jardín vertical? ¡Investiga! ¡Seguro que encuentras ideas geniales!

DESCUBRE EL PROYECTO INTERDISCIPLINAR

Compromiso con las aves:

COMIDA Y BEBIDA

PROYECTOSHUELLA QUEDEJAN

1

PIENSA

PARA LAS AVES

Las aves urbanas tienen problemas para encontrar comida y bebida. ¿Podemos ayudarlas? ¡Hagamos algo!

¿Y si construimos un comederobebedero para aves?

3 CONSTRUYE

T hink

¿Son importantes los comederos-bebederos para aves? ¿Qué alimentos se ponen en ellos?

Con ayuda, buscamos en Internet algunos modelos de comederos-bebederos hechos con materiales reciclados.

setenta y ocho

2 DISEÑA

D esign

Dibujamos en un papel el comedero-bebedero que queremos construir. Señalamos en el diseño los materiales reciclados que usaremos: latas, botellas, palillos de helado, cartones… Decidimos qué alimentos poner y cómo poner el agua.

4 PRESENTA

Stage

Vamos a marcar el lugar donde irá el jardín vertical. Usad el lápiz, tizas, cuerdas… y marcad el espacio reservado. Si es una zona común, poned un cartel avisando de la próxima construcción de

4 PRESENTA

S tage

TRIMESTRE 2

Con ayuda de una persona adulta, colgamos el comedero-bebedero en el lugar escogido. Cuando las aves acudan a comer o beber, les hacemos fotos y las compartimos.

M aker

Para construir nuestro comedero-bebedero, necesitaremos ayuda.

• Fabricamos y unimos todas las piezas.

• Colocamos el alimento

COMPRUEBA 5

T est

¿Hemos aprendido algo sobre las aves?

¿Hemos ayudado a estos animales?

¿Hemos mejorado nuestro entorno?

setenta y nueve

LENGUA

PROYECTOS INTERDISCIPLINARES

MATEMÁTICAS CONOCIMIENTO DEL MEDIO

Proyecto interdisciplinar: Guía de consejos emocionantes

La lectura es el gimnasio de la El ejercicio nos hace felices ¡Dulces sueños!

Proyecto interdisciplinar: Naturalmente... ¡verde!

Hablamos del verde Hacemos números verdes Hay verdes diferentes

Proyecto interdisciplinar: Somos una cadena

Ayuda energética Sigo tu energía

Reacción en cadena. ¡En marcha!

Los proyectos trimestrales interdisciplinares fomentarán el emprendimiento, ya que el alumnado desarrollará las habilidades y la conciencia necesarias para transformar ideas creativas en acciones, lo que precisa un desarrollo de las dimensiones:

¿Dónde está en el proyecto?

Los proyectos trimestrales interdisciplinares precisarán un desarrollo de:

– La dimensión personal, en la fase llamada «Piensa», que da inicio y activa el proyecto, conlleva creatividad, imaginación, así como en la fase de «Comprueba», basada en el autoconocimiento...).

– La dimensión social, en la fase llamada «Diseña», que supone asumir responsabilidad, trabajo en equipo...

PIENSA

1 T hink

PIENSA

– La dimensión productiva, en las fases denominadas «Construye», «Presenta» y «Comprueba», ya que el alumnado deberá elaborar un producto final para su posterior difusión. Finalmente, hará una valoración del trabajo llevado a cabo para tomar conciencia de sus fortalezas individuales y grupales y de sus posibilidades de mejora.

4 PRESENTA

DESCUBRE EL PROYECTO INTERDISCIPLINAR

Somos una cadena:

SIGO TU ENERGÍA

¿Cuántas acciones en clase se te ocurren para ahorrar energía? ¡Vamos a comprobarlo!

¿Te animas a hacer una tabla con datos sobre el ahorro energético de la clase?

3

Th nk

¿En clase ahorráis energía? ¿Cómo lo hacéis? ¿Creéis que podéis mejorar? En grupo, hablad sobre cuánto sabéis de ahorro energético. Elaborad una lista con vuestras ideas.

2 DISEÑA

2 ÑA

De gn

Además de vuestras ideas sobre ahorro energético, es importante investigar para aprender más: podéis usar Internet, preguntar en casa… De todas las acciones, elegid 4 o 5 ideas. ¡Es hora de ponerse de acuerdo!

4 PRESENTA S age

Presentad vuestra investigación al resto de la clase. Podéis compartirla con otros grupos. ¡Recuerda que somos una cadena para salvar el planeta!

S tage

C ONSTRUYE Maker

C ONS RUYE

En grupo, construid un pictograma usando una imagen que represente la energía. Podéis hacer uno al inicio de la semana y volver a repetirlo días después.

COMPRUEBA 5

Te

¿Qué has aprendido en este proyecto? Investigar me parece…

COMPRUEBA 5 D esign

C ONS RUYE

3 CONSTRUYE

M aker

T est

PLAN LINGÜÍSTICO

Un Plan Lingüístico de Centro ha de tener como grandes finalidades:

1. La mejora de la expresión oral y escrita del alumnado (en la producción), que tiene como paso previo la comprensión de una situación de aprendizaje propuesta a través de una tipología textual continua o discontinua auténtica.

2. Estimular el interés y el hábito por la lectura a partir de los contenidos que se trabajen.

3. Ampliar la bibliografía de consulta o lectura con el Plan Lector del centro. Para ello, estas destrezas se aprenderán y aplicarán en las áreas lingüísticas y no lingüísticas, dándole ese tratamiento interdisciplinar a dichas destrezas.

¿Dónde está en el proyecto?

1. El alumnado tendrá disponibles organizadores visuales del Plan Lingüístico en el entorno digital, que favorecen el desarrollo de las destrezas vinculadas con la expresión, comprensión e interacción oral y escrita en las áreas lingüísticas y no lingüísticas.

La difusión de la reflexión del «Objetivo en acción» de cada unidad permite poner en práctica las destrezas comunicativas desde todas las áreas.

2. En cuanto a estimular el interés y el hábito por la lectura, el libro de texto del alumnado podrá conducir a lecturas de libros o de fragmentos a partir de dichos contenidos. Para ello, el propio libro del alumnado, la web o la propuesta didáctica serán los referentes.

SABER ESCUCHAR 1 2 3

Antes de empezar a escuchar Durante la escucha Después de escuchar

Prepárate y colócate en una posición cómoda.

1

Presta mucha atención. Recuerda lo que has escuchado.

No juegues mientras escuchas. Mira a quien habla.

No hables. 2

Piensa; ¿puedes contar o compartir lo que has esuchado? ¡Seguro que sí!

3. Respecto a la ampliación de la bibliografía de consulta o lectura, igualmente el propio libro del alumnado, el entorno digital o la propuesta didáctica serán los referentes.

HABLAR EN P ÚBLICO

1 2 3

Antes de hablar Al hablar Para finalizar 1

Piensa y elige el tema del que vas a hablar.

Antes de empezar a hablar, saluda al público.

Pide ayuda a algún familiar. No olvides mirar al público y cuidar tus gestos.

1 1 Puedes hacerlo diciendo... «Y para «Muchasterminar...»; gracias a todos y a todas...» No olvides sonreír.

Al terminar de hablar, da las gracias y haz un saludo como despedida.

No interrumpas.

Si no entiendes algo, levanta la mano para preguntar.

¿ ?

Escribe o haz un dibujo en un papel y apréndetelo de memoria.

PARA ESCRIBIR MEJOR... 1 2 3

2 Habla despacio pronunciando bien las palabras.

2

Antes de escribir, planifica Escribe un borrador Pasa a limpio

3

Ensaya en voz alta.

Piensa o imagina lo que quieres contar.

¿ ?

Puedes ensayar delante de un espejo.

En una hoja escribe un borrador con las ideas que has pensado de forma ordenada.

3 Utiliza un tono de voz adecuado: ni muy alto, ni muy bajo.

Escribe tu texto en una hoja limpia.

Escribe con buena letra.

La presentación es muy importante: no hagas tachones, ni manches el papel.

Inventa un TÍTULO

Revisa tu borrador, por si se te ha olvidado algo. ¿Qué ideas se te ocurren?

Para revisar o corregir tu borrador, puedes pedir ayuda a un adulto.

Escribe el TÍTULO

Puedes utilizar lápices de colores y hacer un dibujo.

Revisa para que no haya errores.

METODOLOGÍAS ACTIVAS

Operación Mundo cuenta con el desarrollo de destrezas vinculadas con:

• El aprendizaje cooperativo

• El desarrollo del pensamiento

• La educación emocional

• El mundo digital

• El aprendizaje lúdico

• La autoevaluación

Son destrezas que se aprenderán y aplicarán desde todas las áreas, de manera lineal y progresiva a lo largo de toda la etapa, confiriendo ese tratamiento interdisciplinar a dichas destrezas.

REPASO

Descubre a los seres vivos que mienten y escribe, en tu cuaderno, quién debería decir cada oración.

Soy herbívoro, como plantas.

Descubre el intruso que se ha colado en cada grupo y razona la respuesta:

Soy un vertebrado, tengo aletas y respiro por branquias.

Soy un artropodo y tengo patas articuladas.

En la zona de la laguna «Peleas», viven ranas, libélulas, hierbas y garzas. Completa en tu cuaderno esta cadena alimentaria con esos seres vivos.

Fíjate en la noticia siguiente:

El incendio declarado ayer en el parque El Bosquecillo ha dañado muchas hectáreas y se han perdido sus plantas y sus animales.

Los habitantes de la zona cercana al parque han leído otras noticias. Indica en tu cuaderno la que crees que es cierta.

a) Es posible recuperar el parque mediante la repoblación con árboles y llevando algunos animales al lugar.

b) Jamás se recupera el parque después de un incendio.

Asocia cada palabra con gún te inspire.

Contaminación

Residuos

Recursos naturales

Reciclaje Agricultura

Una científica de cuento sTEAM

Soy carnívoro, como otros animales.

¿Dónde está?

Para ordenar objetos es importante saber dónde están.

¿Qué pasaría si desaparecieran todas las

Maria Sybilla Merian

Maria es muy observadora, y muy curiosa.

Maria Sybilla Merian fue una naturalista, exploradora y pintora que supo unir el arte con la ciencia a través de preciosas láminas con las que dio conocer nuevas especies de insectos y plantas Escanea para escuchar el cuento completo.

Le encantan las mariposas, y se pregunta si todas proceden de orugas feas y peludas, como los gusanos de seda. La única manera de averiguarlo es observando... Durante años, estudia y dibuja las orugas, los capullos que forman y las mariposas que salen de ellos. ¡Parece una transformación mágica!

Colocar las pinturas dentro del bote nos ayuda a tener la clase ordenada.

Hemos de poner especial énfasis en garantizar la inclusión educativa, la atención personalizada al alumnado y a sus necesidades de aprendizaje, la participación y la convivencia, la prevención de dificultades de aprendizaje y la puesta en práctica de mecanismos de refuerzo, ampliación y flexibilización, alternativas metodológicas u otras medidas adecuadas tan pronto como se detecten cualquiera de estas situaciones.

Operación Mundo es un proyecto que nace comprometido con el principio de educación inclusiva y la creación de mejores condiciones de aprendizaje para todo el alumnado. Para ello, favorece la puesta en práctica de recursos destinados a conseguir una enseñanza personalizada, con una estructura flexible y con mecanismos de refuerzo y profundización.

DUA

La LOMLOE establece la necesidad de proporcionar al alumnado múltiples medios de representación, de acción y expresión y de formas de implicación en la información que se le presenta. Es decir, la aplicación de los principios del Diseño Universal para el Aprendizaje.

Es por lo que Operación Mundo está concebido para dar respuesta a estos tres principios con los diferentes elementos del proyecto:

– Múltiples formas de representación en el acceso a la información. Esto es, diversificar los canales de entrada. No todas las personas percibimos y comprendemos la información de igual manera.

– Múltiples formas de acción y expresión; esto es, diversificar los canales de salida, ofreciendo opciones para la interacción, la comunicación, actividades con diferentes niveles...

– Múltiples formas de implicación; esto es, tener en cuenta los elementos afectivos y emocionales del aprendizaje.

¿Dónde está en el proyecto?

Inclusión en Operación Mundo

para el Aprendizaje (DUA) es un conjunto de principios para de- que proporcionen a todos los estudiantes igualdad de oportu- Estos principios son los siguientes:

Proporcione múltiples formas de REPRESENTACIÓN

Proporcione múltiples formas de ACCIÓN Y EXPRESIÓN

Redes de reconocimiento El «QUÉ» del aprendizaje Redes estratégicas El «CÓMO» del aprendizaje

Proporcione opciones para percepción

Ofrezca formas de personalizar visualización de la información.

Ofrezca alternativas para la información auditiva.

Ofrezca alternativas para la información visual.

Proporcione opciones para lenguaje y los símbolos

Aclare vocabulario y símbolos.

Aclare sintaxis y estructura. Apoye la decodificación. textos, notaciones matemáticas símbolos.

Promueva la comprensión entre diferentes lenguas. Ilustre a través de múltiples medios.

Proporcione opciones para comprensión

Active o proporcione conocimientos previos.

Destaque patrones, características fundamentales, ideas principales relaciones entre ellas. el procesamiento, visualización manipulación de la información.

Maximice la transferencia generalización de la información.

Proporcione opciones para la acción física

4.1 Varíe los métodos de respuesta, navegación e interacción.

4.2 Optimice el acceso a herramienta y tecnologías de asistencia.

Proporcione opciones para la expresión y la comunicación

5.1 Use múltiples medios para la comunicación.

5.2 Use múltiples herramientas para la construcción y composición.

5.3 Desarrolle fluidez con niveles de apoyo graduados para la práctica y el desempeño.

Proporcione opciones para la función ejecutiva

6.1 Guíe el establecimiento de metas apropiadas.

6.2 Apoye la planificación y el desarrollo de estrategias.

6.3 Facilite la gestión de información y recursos.

6.4 Mejore la capacidad para monitorear el progreso.

Pautas DUA en Operación Mundo

Los diferentes elementos del Proyecto Operación Mundo están concebidos teniendo en cuen- ta los principios del Diseño Universal de Aprendizaje (DUA). En la siguiente tabla se muestra la relación entre los principios o pautas DUA y los elementos del proyecto:

OPERACIÓN MUNDO

Pautas DUA que se aplican en el proyecto MATERIAL IMPRESO ENTORNO DIGITAL Situación de aprendizaje

ODS

Imagen y contexto

¿Cómo lo ves?

• La relación directa con los ODS (retos del siglo xxi) y con la vida cotidiana del alumnado optimiza la relevancia, el valor y la autenticidad (7.2).

• La representación alternativa al texto facilita la comprensión y la conexión personal con el contexto de la Situación de aprendizaje (2.5).

• Las preguntas vinculan la Situación de aprendizaje con las experiencias y los conocimientos previos del alumnado (3.1).

El dato • Aporta información objetiva y contrastable sobre la importancia del objetivo en acción (8.1).

• Estimula la reflexión colectiva a través de una estrategia de pensamiento útil para afrontar los problemas cotidianos (9.2).

• Da acceso a información actualizada sobre los ODS al profesorado y al alumnado utilizando múltiples medios de comunicación (5.1).

• ¿Qué sé? Propone actividades interactivas trazables para la detección de ideas previas en la apertura de la unidad (3.1)

Objetivo en acción

• Fomenta la autonomía proponiendo un producto final abierto a la contextualización en el centro y a la elección del alumnado (7.1) variando los niveles de exigencia (8.2).

• Facilita la generalización y la transferencia de los aprendizajes esenciales (3.4).

• Fomenta la comunidad y la colaboración para la realización y difusión colectiva del producto final (8.3).

• Utiliza píldoras audiovisuales que presentan las situaciones de aprendizaje estimulando expectativas y creencias que aumentan la motivación (9.1) en la apertura de la unidad.

• Presenta en cada unidad información adicional de fuentes preseleccionadas en distintos formatos que proporcionan alternativas a la información auditiva (1.2) y visual (1.3) como representaciones alternativas al texto (2.5): canciones, audios o vídeos subtitulados, locuciones de la información textual, organizadores gráficos, visual thinking, etc. utilizables, además, Para dinamizar la participación.

Sigue el hilo

• Guía de forma ordenada la consecución del objetivo en acción (6.1) modelando y visibilizando el proceso (6.2) con un organizador gráfico (6.3).

• Permite reconstruir el proceso de aprendizaje de forma interactiva con el apoyo del organizador gráfico que representa el progreso hacia el objetivo en acción (3.3).

Inclusión en Operación Mundo

El Diseño Universal para el Aprendizaje (DUA) es un conjunto de principios para de- sarrollar el curriculum que proporcionen a todos los estudiantes igualdad de oportu- nidades para aprender. Estos principios son los siguientes:

Proporcione múltiples formas de MOTIVACIÓN Y COMPROMISO

Proporcione múltiples formas de REPRESENTACIÓN

Proporcione múltiples formas de ACCIÓN Y EXPRESIÓN

Los ta

Redes afectivas El «PORQUÉ» del aprendizaje

Proporcione opciones para captar el interés

7.1 Optimice las elecciones individuales y autonomía.

7.2 Optimice la relevancia, el valor y la autenticidad.

7.3 Minimice las amenazas y distracciones.

Proporcione opciones para mantener el esfuerzo y la persistencia

8.1 Resalte la relevancia de metas y objetivos.

8.2 Varíe las demandas y los recursos para optimizar los desafíos.

8.3 Promueva la colaboración y la comunicación.

8.4 Aumente la retroalimentación orientada a la maestría.

Proporcione opciones para la autorregulación

9.1 Promueva expectativas y creencias que optimicen la motivación.

9.2 Facilite habilidades y estrategias para enfrentar desafíos.

9.3 Desarrolle la autoevaluación y la reflexión.

APÉNDICES EXPERTOS

Redes de reconocimiento El «QUÉ» del aprendizaje

Proporcione opciones para la percepción

1.1 Ofrezca formas de personalizar la visualización de la información.

1.2 Ofrezca alternativas para la información auditiva.

1.3 Ofrezca alternativas para la información visual.

Proporcione opciones para el lenguaje y los símbolos

2.1 Aclare vocabulario y símbolos.

2.2 Aclare sintaxis y estructura.

2.3 Apoye la decodificación. de textos, notaciones matemáticas y símbolos.

2.4 Promueva la comprensión entre diferentes lenguas.

2.5 Ilustre a través de múltiples medios.

Proporcione opciones para la comprensión

3.1 Active o proporcione conocimientos previos.

3.2 Destaque patrones, características fundamentales, ideas principales y relaciones entre ellas.

3.3 Guíe el procesamiento, visualización y manipulación de la información.

3.4 Maximice la transferencia y la generalización de la información.

Redes estratégicas El «CÓMO» del aprendizaje

Proporcione opciones para la acción física

4.1 Varíe los métodos de respuesta, navegación e interacción.

4.2 Optimice el acceso a herramienta y tecnologías de asistencia.

Proporcione opciones para la expresión y la comunicación

5.1 Use múltiples medios para la comunicación.

5.2 Use múltiples herramientas para la construcción y composición.

5.3 Desarrolle fluidez con niveles de apoyo graduados para la práctica y el desempeño.

Proporcione opciones para la función ejecutiva

6.1 Guíe el establecimiento de metas apropiadas.

6.2 Apoye la planificación y el desarrollo de estrategias.

6.3 Facilite la gestión de información y recursos.

6.4 Mejore la capacidad para monitorear el progreso.

Decididos y motivados Ingeniosos y conocedores Estratégicos y dirigidos a la Meta

Situación de aprendizaje ODS Imagen y contexto ¿Cómo lo ves?

El dato Objetivo en acción Sigue el hilo

CAST 2018 (Center for Applied Special Technology)

LO ESENCIAL

Se orientará al profesorado sobre cuáles son los aprendizajes esenciales de cada área que posibilitarán al alumnado adquirir los perfiles de salida previstos en el desarrollo curricular de cada área.

¿Dónde está en el proyecto?

En el entorno digital se ofrecen materiales que recogen lo esencial de cada unidad de una manera muy visual.

1Ordeno la clase

Me lo aprendo en un momento

0 cero 2 dos 4 cuatro

1 uno 3 tres 5 cinco

Números Comprendo los números ¿Dónde está?

todo parte parte

Ordeno números Comparo

0 1 23 5

dentrofueradelantedetrás arriba cerca

más que menos que tantos como Nos preparamos ¿Ordenas tus cosas?

¿Dónde estás? Geografía

describe cómo es la Tierra

Paisajes

estudia

Seres vivos El tiempo Los lugares donde habitamos Relación entre seres vivos y naturaleza Cómo modificamos la naturaleza

Orientarnos

puntos cardinales el Sol nuestro cuerpo planos mapas globos terráqueos

mapamundis mapas físicos mapas políticos

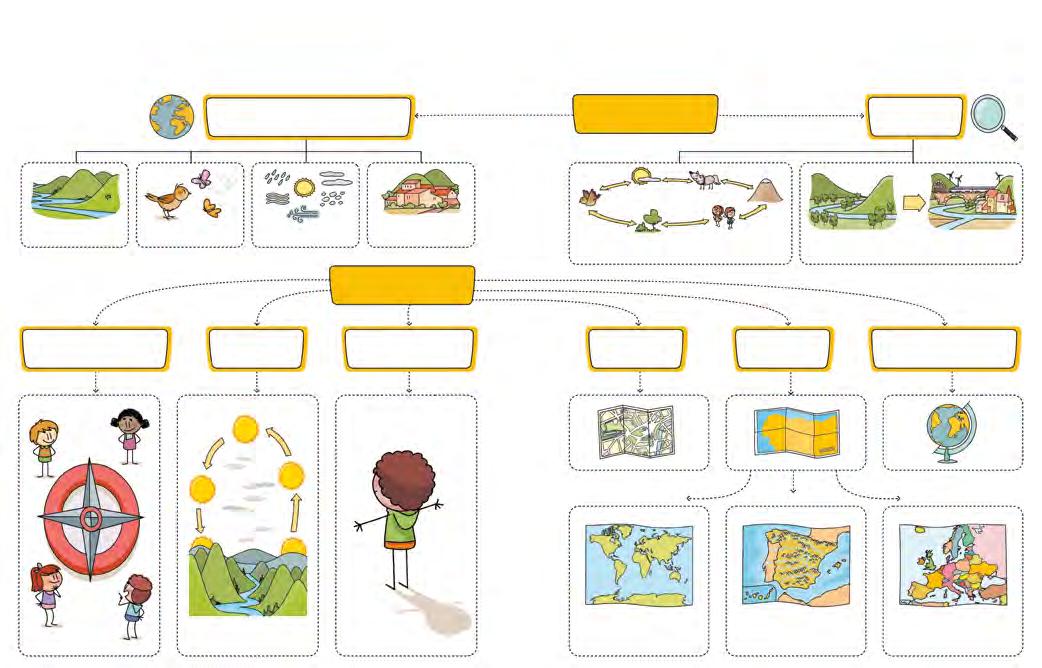
Muestran todos los continentes a la vez Muestran montañas, valles, ríos, mares y océanos

Enseñan los países que hay en los continentes

ATENCIÓN A LA DIVERSIDAD

Es necesario tener en cuenta las necesidades, características y diferentes ritmos de aprendizaje del alumnado. Los recursos de atención a la diversidad proponen actividades en las que el alumnado pondrá en práctica un amplio repertorio de procesos cognitivos, tales como identificar, analizar, reconocer, asociar, reflexionar, razonar, deducir, inducir, decidir, explicar, crear, etc., evitando centrarse, tan solo, en el desarrollo de algunos de ellos, permitiendo así un mejor ajuste a los diferentes estilos de aprendizaje.

¿Dónde está en el proyecto?

En el entorno digital podremos encontrar recursos de atención a la diversidad.

Nombre y apellidos:

1 Completa las palabras con r o con rr.

pue__os pa__ada o__eja __osal ma__ón ce__ado

2 Relaciona cada onomatopeya con el sonido que representa.

¡achís! ¡plas, plas! ¡hip! ¡crac! ¡mua! ¡ja, ja, ja!

carcajada hipo aplausos beso algo que se rompe estornudo

3 Escribe las onomatopeyas que imitan los sonidos que hacen estos animales.

4 Subraya los determinantes posesivos de estas adivinanzas y resuélvelas.

La gallina hizo una casa para meter su pollito; este rompió sus paredes cuando pudo con su pico.

B

Mi picadura es dañina, mi cuerpo, insignificante, pero el néctar que yo doy, os lo coméis al instante.

5 Completa las oraciones con numerales ordinales.

– Para llegar a mi casa coge la calle a la derecha.

HERRAMIENTA DE INCLUSIÓN IN.ON

Inclusión ANAYA Online (IN.ON) es una herramienta que pone a disposición del profesorado una gran cantidad de recursos con un objetivo principal: la enseñanza inclusiva. Favorece la integración del alumnado gracias a la enseñanza multinivel y a la atención de todas las necesidades educativas especiales.

¿Dónde está en el proyecto?

En las áreas de Lengua y Matemáticas encontraremos el acceso a esta herramienta.

Metodologías activas

Las metodologías activas son un conjunto de métodos, técnicas y estrategias que ponen al alumnado de cualquier nivel educativo en el centro del aprendizaje, fomentan el trabajo en equipo e incentivan el espíritu crítico, dejando a un lado los procesos memorísticos de repetición de los contenidos que se imparten en clase. Es una forma de trabajar que prepara al alumnado para situaciones de la vida real y para su vida profesional.

APRENDIZAJE COOPERATIVO

El aprendizaje cooperativo es el empleo didáctico de grupos reducidos en los que el alumnado trabaja de manera conjunta para maximizar su propio aprendizaje y el de los demás. Las distintas estructuras y técnicas coope rativas estarán presentes en los libros de cada una de las áreas de manera secuenciada y progresiva, a través de las actividades propias de cada unidad. Esto será, en todo caso, una sugerencia que el profesorado podrá cambiar y adaptarla a las características de su alumnado o al enfoque que quiera darse a la actividad o tarea.

¿Dónde está en el proyecto?

Habrá, al menos, una actividad en cada unidad de cada área que el alum nado tendrá la posibilidad de resolver mediante interacciones con su gru po, a través de una técnica cooperativa. Se irá progresando a lo largo de toda la etapa con técnicas cooperativas más complejas.

2 Colorea para qué usamos el aceite de oliva.

¿Quiénes intervienen para que el aceite llegue a tu casa? Escribe.

+ info sobre esta clave

Página 29

Para tomarlo en la ensalada

4

Para regar las plantas

3 Rodea la forma actual de obtener el aceite.

Para ordenar objetos es importante saber dónde están.

Para cocinar una tortilla

¡Toma nota!

«Te lo cuento en un momento» en anayaeducacion.es

Conocer los productos de tu zona te ayudará a saber a qué se dedican tus vecinos y vecinas.

33 treinta y tres

Escucha la canción «Delante de mí, en anayaeducacion.es

Metodologías

DESARROLLO DEL PENSAMIENTO

Las estrategias para el desarrollo del pensamiento son aquellas que ayudan al alumnado a aprender a pensar y a mejorar en el dominio de los conocimientos, su aplicación y su transferencia, también de forma crítica, a través de la realización de alguna de las actividades que se le plantean.

¿Dónde está en el proyecto?

Habrá, al menos, una actividad en cada unidad de cada área que el alumnado podrá resolver mediante una técnica o una llave de pensamiento. Se irá progresando a lo largo de toda la etapa con técnicas y llaves de pensamiento más complejas.

En la diferente tipología de actividades, en su enunciado, se combinan procesos cognitivos literales, de conexión y de tipo valorativo. También se utilizan técnicas de pensamiento para favorecer la reflexión que dará solución a la situación de aprendizaje en el «Objetivo en Acción».

¿Qué

Muchos juguetes son capaces de usar energía y transformarla para funcionar.

¿Qué es la energía?

¿Te has preguntado alguna vez qué es lo que hace que un coche se mueva, o que te muevas cuando caminas?

Todos estos movimientos y cambios tienen algo en común: necesitan energía para producirse.

La energía que tiene la materia es lo que le permite producir cambios.

Existen distintas formas de energía. Mira alguna de ellas.

Algunas formas o tipos de energía

¿Qué he aprendido?

Energía luminosa Energía cinética

1 Todos los años, los científicos y las científicas encuentran seres vivos que no se conocían an- tes. ¿Qué crees que hacen para clasificarlos? Elige una opción y explica por qué la has elegido.

Los combustibles

Son combustibles la madera, el carbón, el petróleo, el gas natural, los alimentos.... Liberan la energía que contienen mediante cambios químicos.

La energía se transforma

Los distintos tipos de energía se pueden transformar unos en otros. Por ejemplo, cuando enchufamos un ventilador, estamos transformando la energía eléctrica en energía cinética (movimiento de las aspas). Cuando quemamos leña, la energía química de la madera se transforma en energía térmica y luminosa, etc.

Las fuentes de energía

Las fuentes de energía son los materiales de los que obtenemos energía.

Las fuentes de energía pueden ser renovables o no renovables.

• Las fuentes renovables. Son aquellas que no se agotan, como la luz solar, el viento, la fuerza de una cascada.

1 Intuyo y deduzco Indica en cada caso qué podemos...

a) ... hacer cuando usamos la energía eléctrica.

b) ... hacer gracias a la energía luminosa.

c) ... obtener cuando quemanos leña.

Energía química

6 ¿Para qué utilizan las plantas la luz del sol?

• Las fuentes no renovables. Son aquellas que se pueden agotar, porque se gastan más deprisa de lo que se producen. Es el caso de los combustibles fósiles (carbón, petróleo, gas natural).

Las fuentes de energía y los vehículos

Vamos a reflexionar sobre los coches,

Si te fijas, puedes reconocer muchos tipos y cambios de energía a tu alrededor.

Es la que nos llega en forma de luz procedente del Sol o de fuentes artificiales como las bombillas.

a) Los comparan con otros seres vivos y los agrupan con los que son más parecidos.

Es la que tienen los objetos, sustancias y seres que se mueven, como un tren, un guepardo corriendo o el viento.

7 Observa las imágenes siguientes y trata de clasificar cada uno de los seres vivos en uno de estos grupos: Bacterias Protozoos Algas Hongos

Está en todas las sustancias y se libera cuando se produce un cambio químico. Como cuando quemamos combustibles.

b) Los sitúan en los grupos de seres vivos que tienen menos criaturas, para compensar.

c) Los colocan a ellos solos en un grupo.

d) Realizan un sorteo para elegir en qué grupo los van a clasificar.

2 Di en qué se parecen y en qué se diferencian:

a) Una planta y un alga.

b) Una bacteria y un protozoo.

3 Encuentra las cuatro palabras relacionadas con la nutrición de las plantas.

Se genera en baterías, pilas y centrales eléctricas, y llega a nuestras casas a través de cables. Se utiliza para hacer funcionar los electrodomésticos y los dispositivos electrónicos.

SNEWSHO AHDFLNS JKABETF OÑAGUAS HQISKRP

PXTTMCB OÑALUZK

4 Completa en tu cuaderno:

a) Los manzanos producen ..... vistosas y sabrosos ..... dentro de los que se en- cuentran las .....

b) Los ..... y ..... no producen ..... ni ..... .

c) Algunas plantas como los pinos produ- cen ..... poco vistosas en forma de ..... y tienen ..... en forma de aguja.

5 Construye una frase con cada grupo de palabras:

a) Sentidos, reaccionan, fijas, movimiento.

b) Oxígeno, respirar, seres vivos, fotosín- tesis, vida.

Es la que se desprende en forma de calor que pasa de un objeto caliente a otro más frío. Por ejemplo, la que emite un fogón de la cocina para calentar los alimentos.

8 Si la flor de una planta tiene un pistilo, cuatro estambres y ocho pétalos. Calcula:

a) ¿Cuántos pétalos habrá en una planta con 13 flores ?

b) ¿Cuántos estambres?

c) Si todas las flores de la planta menos una se transforman en fruto, ¿cuántos frutos encontraremos en la planta?

9 Dibuja en tu cuaderno dos ejemplos en los que las plantas reaccionen a los cambios que se producen en su entorno. Explícalos.

10 Busca información sobre tres frutos y ave- rigua cómo son sus semillas. Dibújalos en tu cuaderno.

No olvides completar tu álbum de fotos de esta unidad disponible en anayaeducacion.es

El semáforo. Junto a cada actividad, colorea así en tu cuaderno: si has sabido la respuesta si has necesitado ayuda o si no la has sabido responder

Diseñamos un póster para mostrar lo importantes que son las plantas.

1 Elige una planta en peligro de extinción que te parezca interesante. Busca infor- mación, fotos y vídeos sobre cómo es su vida. Para cada planta:

a) ¿Dónde vive?

b) ¿Qué aspecto tiene?

c) ¿Cómo se reproduce?

d) ¿Qué te parece interesante de esta especie?

e) ¿Por qué está desapareciendo?

2 Ahora que sabes mucho más sobre las plantas y en concreto sobre la espe- cie que has elegido, probablemente has cambiado de opinión sobre ellas. Aplica la técnica Antes pensaba-ahora pienso rellenando este organizador gráfico en tu cuaderno:

ALGUNAS IDEAS

Árbol baobab, venus atrapamoscas, orquídea zueco, flor cadáver, flor de jade, drago de Gran Canaria.

3 En una hoja o cartulina diseña un póster que explique cómo es la planta que has investigado y por qué está en peligro. Intenta que tenga imágenes y colores que llamen la atención, para que las personas que lo vean se den cuenta de lo interesante y valiosa que es la planta que elegiste.

Antes pensaba Ahora pienso Causas

Antes de investigar, ¿cuál era tu opinión sobre las plantas?

Después de investigar, ¿cuál es tu ahora?opinión ¿Qué te ha hecho cambiar de opinión? ¿Qué has descubierto?

¿Cómo he aprendido?

1 Al estudiar esta unidad, seguramente habrá cosas que te han resultado sencillas de aprender y otras que te han costado un poco más. Escribe en tu porfolio las tres cosas que te han resultado más difíciles y por qué.

2 Ahora que conoces un poco más a los seres vivos, di cuáles de los que has conocido en la unidad te parecen más interesantes o divertidos. Explica por qué. Di qué más te gustaría aprender sobre ellos.

Lo que más me ha costado aprender Porque.....

produce los movimientos y los cambios?

EDUCACIÓN EMOCIONAL

Aprendizaje de una serie de habilidades que contribuyen a que el alumnado, en el plano intrapersonal, identifique y reconozca las emociones, regulándolas y gestionándolas y, en el plano interpersonal, adquiera habilidades de relación con las personas y tenga experiencias de satisfacción personal.

Dimensión intrapersonal Dimensión interpersonal

Conciencia y regulación emocional

Autoconcepto y autoestima

Competencia social

Competencias para la vida y el bienestar

¿Dónde está en el proyecto?

Actividades emocionantes: figuran, de forma implícita, en las situaciones de aprendizaje propuestas al inicio de cada unidad.

Actividades emocionales: de forma explícita, se integran en el apartado «¿Cómo he aprendido?». La finalidad de esta ubicación es la de que el alumnado tome conciencia de que su estado emocional influye en su forma de apren-

+ info sobre esta clave Página 29

¿Qué he aprendido? 51 + 23 45 + 14 36 + 31 67 + 2 TVWr89a67bBCa45 `aø À HI> NOqrsu45 45p89ø. TVWr89a67 BCa45 `aø »y`aø ÃsÑÖ @A89ø.

– 1

79 78 52 – 20 58 – 6 62 – 32 79 – 5

¿Cómo he aprendido? Sé hacerlo Colorea así: Necesito ayuda No sé hacerlo DnoJK DE TUs »u<= ÑÖa45® u45> v a<=sÑÖø »p89a45r89å HIn45 jku89a89g`aa45r45 :;Þ Δ89å ΔbBC BC^_å *+a67 Δ89a45vBCa45r45 :; Δ89 23s *+d45 :; HIn45 :; TUs. ¿Q u:;@ r:; NOhi 45p45 :; HIn45 :; TU JK:; NOgjk 45r45 89a<=s »p89a45r89å n89ø *+d:; TU ~òp:; HIr89d45 89hi 89a45® *+a89gjku89å À HI> *+ >? 45r89a<=s 89a45r:; NOa<=s? Hñóa45z »u45n89å Δ6745u45v>? 89å *+d:; » 89d:; NOa<=s. ¡Upq 45 6745 45zxyå ÀJK¬ *+a89gjku89å *+d:; m89a45n:; HIr89å r:; TUs~òp89 >?n<= ÑÖa67b@A:;Þ!

Metodologías

Integra el uso de las TIC como recurso para obtener información, seleccionarla y utilizarla de acuerdo con la finalidad que persigue la actividad que sugiere su uso. Esta clave asimismo permite que el alumnado desarrolle competencias relacionadas con la planificación, la gestión y la elaboración de trabajos, la comunicación y colaboración en red y la competencia en ciudadanía digital. Las TIC favorecen también, a partir de recursos digitales de diversos tipos, desarrollar dinámicas de Flipped classroom o «clase invertida».

¿Dónde está en el proyecto?

Operación mundo incluye un proyecto digital cuyo objetivo es proporcionar recursos que fomenten el aprendizaje a través de las TIC. En las unidades, algunas de las actividades están señaladas con un icono que indica que su resolución requiere de la consulta de un recurso digital y del uso de las TIC. En el libro digital y en la web del alumnado, hay muchos más recursos digitales destinados a un uso más exhaustivo de es-

tas tecnologías para el aprendizaje, como, por ejemplo el Plan TIC-TAC. En las áreas de Matemáticas y de Conocimiento del Medio, hay actividades especialmente diseñadas para ejercitar el pensamiento computacional en varios niveles de dificultad, tanto en su concepto (pensamiento computacional desenchufado) como en su aplicación como, por ejemplo, «Aprende a usar Scratch».

APRENDE USAR SCRATCHJr

¿Para qué se utilizan los dispositivos TIC?

USAMOS LOS DISPOSITIVOS TIC Escritorio

En los dispositivos TIC podemos instalar programas informáticos o aplicaciones, también llamadas app. Las apps nos permiten realizar muchas tareas como escribir, dibujar, jugar, retocar imágenes, buscar en Internet… Están representadas en el escritorio por iconos.

ATENCIÓN. Debido a tu edad, no debes descar gar aplicaciones en el dispositivo móvil sin la su pervisión de una persona adulta de tu confianza.

Podemos utilizar los programas y las apps para hacer muchas tareas. Estas son algunas:

Icono de aplicación Textos

¿CÓMO SE MANEJA SCRATCHJr? FICHA 2

9:45 AM 100%

Nombre y apellidos:

Para manejarla hay que tocar la pantalla táctil del dispositivo y… 1 dar toques o hacer clic sobre los bloques, los botones… para selec- cionarlos.

2 tocar y arrastrar los bloques para colocarlos como si fueran un puzle. 3 tocar con dos dedos la pantalla para hacer zum; es decir, para am- pliar o disminuir la forma en la que se ve.

1 ¿Cómo explicarías el funcionamiento de ScratchJr a alguien que nun- ca lo ha utilizado, por ejemplo, tu abuelo? Cuéntalo.

2 ¿Por qué la tableta es el mejor dispositivo para manejar ScratchJr?

Elige la palabra correcta y completa la explicación.

Porque la tableta es un dispositivo fijo móvil y ScratchJr es una app.

Porque ScratchJr se maneja tocando la pantalla ratón del dispositivo y es mejor que sea grande pequeña , para sea más difícil fácil verla y tocarla.

APRENDIZAJE LÚDICO

Son aquellas actividades no tradicionales y poco habituales que ayudan al alumnado a adquirir el aprendizaje de forma lúdica y divertida, en ocasiones a través de dinámicas de gamificación. Se trata tanto de actividades que pueden realizarse sin la intervención de las TIC como de otras que requieren de estas tecnologías.

Dónde está en el proyecto ¿ ¿

En las unidades existen algunas actividades señaladas con un icono que tienen este carácter lúdico. Asimismo, en las secciones para el repaso, este se realiza a través de actividades también lúdicas en las que el alumnado jugará

aplicando su aprendizaje. Del mismo modo hay recursos digitales, como la aventura didáctica «Ultimate travellers», juegos de escape, actividades interactivas que requieren de una combinación de conocimiento y habilidad...

Salida

Proyecto

PIEZA PIEZA DE A

PIEZA PIEZA DE A

PIEZA PIEZA DE A

PIEZA PIEZA DE A

PIEZA PIEZA DE A

Erreconerre,guitarra; erreconerre,carril: rápidoruedanloscarros, rápidoelferrocarril. Tresgrandestigrestragones tragantrigo seatragantan.

PIEZA PIEZA DE A

PIEZA PIEZA DE A

PIEZA PIEZA DE A

Cuandocuentescuentos cuentacuántoscuentoscuentas, porquesinocuentas cuántoscuentoscuentas nuncasabráscuántos cuentoscuentastú.

Habíaunacaracatrepa contrescaracatrepitos. Cuandolacaracatrepatrepa, trepanlostrescaracatrepitos.

PepePecaspicapapasconunpico. ConunpicopicapapasPepePecas.

Poquitoapoquito, Paquitoempacacopitos enpocospaquetes.

MaríaChuchenasuchozatechaba, untechadorqueporallápasaba, ledijo:–Chuchena,¿tútechastuchoza,otechaslaajena?

Silabrujadesbrujaalbrujo, yelbrujodesbrujaalabruja, elbrujoquedadesbrujado, ¿cómodesbrujaelbrujoalabruja?

yjuntosjuntaronjuncos. Elcieloestáenladrillado, ¿quiénlodesenladrillará?, eldesenladrilladorquelodesenladrille, buendesenladrilladorserá.

Metodologías activas

EVALUACIÓN

Debe responder a los perfiles competenciales de salida del alumnado para esta etapa que se concretarán en los criterios de evaluación establecidos. Se llevará a cabo mediante actividades en las que el alumnado evidenciará si ha adquirido los saberes básicos y ha adquirido consciencia de sus fortalezas y debilidades en la forma de adquirirlos.

Dónde está en el proyecto ¿ ¿

Además del uso de rúbricas y de otros instrumentos para llevar a cabo procesos de autoevaluación y coevaluación, también en el libro de texto se incluye un porfolio para que el alumnado sea consciente de «qué ha aprendido» en cada unidad y «cómo lo ha aprendido», identificando sus fortalezas para consolidarlas, y sus debilidades para que se conviertan en nuevos retos en las siguientes unidades.

¿Qué

1 Busca una palabra tabú para cada uno de los eufemismos destacados. El conflicto bélico ocasionó numerosas víctimas.

2 Encuentra las palabras tabú correspondientes a los siguientes eufemismos. inodoro recluso tercera edad paciente poco agraciado invidente fallecer centro penitenciario indigente entrado en carnes

3 Sustituye el verbo consumir por otro de la lista. derretir • comer • gastar • desesperar

– La vela se ha consumido.

– La caldera consume mucho gas.

– Me consume su insistencia.

– Han consumido lo que había en el frigorífico.

4 Clasifica estas formas verbales según la conjugación a la que pertenecen: miraré, abrieron, coses, salían, lanzo, vuelan, sirvió, rellenan, he comido.

5 Sustituye los infinitivos en tu cuaderno por las formas que corresponda.

– Ayer mis amigos .... (llegar) tarde al partido.

– Si vienes, te .... (cocinar) un bizcocho.

– Las alumnas de quinto .... (ser) encantadoras. Yo jamás .... (mentir).

6 Copia y completa la tabla en tu cuaderno.

AbresCaminaré Hemos cogido

Conjugación 3.a (abrir)........

PersonaSegunda........

NúmeroSingular........

TiempoPresente........

Forma simple o compuesta Simple........

7 Escribe tres oraciones en las que el verbo encontrar esté conjugado en forma compuesta.

8 Clasifica estas palabras con g en tu cuaderno: agudo, imagen, goma, manguera, piragüista, guindilla, guepardo, gusano, galaxia, generosa, girar, antigüedad, bilingüismo, distinguido. Suave con ga, go, gu Suave con gue, gui Fuerte con ge, gi Con güe, güi

9 Completa con g o j

– Todos los ....ueves escribo un mensa....e a ....avier por correo electrónico.

– La ima....en de este televisor es ....enial.

– Me ....usta llevar la merienda a la vie....ecita.

Realiza la autoevaluación interactiva en anayaeducacion.es

DICTADO

Lee el texto para preparar el dictado.

«Todas las ciudades se parecen cuando llegas», pensó Bernal mientras miraba por la ventanilla del elegante automóvil negro que los había recogido en el aeropuerto de Sofía para llevarlos al hotel. El conductor, un amable anciano con bigote, les había indicado en un inglés bastante rudimentario que ocupasen las dos filas de asientos reservadas a los pasajeros. Bernal se había sentado con sus padres, Carmen y Mauro, en la primera fila. Detrás iban Susana y Santi, los colaboradores de Carmen en la Misión Biológica del Consejo Superior de Investigaciones Científicas en Pontevedra. Ana Alonso, Historia de una rosa, Anaya.

Noticia radiofónica: Pequeños gestos que llegan lejos

En esta unidad has comprendido cómo tus acciones de cada día pueden repercutir en la salud del planeta. También sabes ya que, para poder actuar en beneficio del medioambiente, conviene estar bien informado.

Ahora que sabes todo esto, vas a dar un paso más… Vais a crear una noticia radiofónica en la que concienciaréis a vuestra comunidad escolar sobre la importancia de adoptar hábitos respetuosos con el planeta.

1 En grupos de cuatro, inventaos una acción emprendida por alguna persona imaginaria que beneficiaría al medioambiente si todo el mundo la aplicara a su vida.

2 Completad en el cuaderno este organizador gráfico. Os ayudará a ordenar vuestras ideas.

LAS 6 W ¿Qué? ¿Quién?

Acciones cotidianas y medioambiente

¿Dónde? ¿Cuándo? ¿Por qué? ¿Cómo?

3 Redactad el guion de vuestra noticia.

4 Grabad vuestra noticia radiofónica.

5 Reunid las grabaciones de toda la clase y colgadlas en la web del colegio o difundidlas a través de la megafonía.

¿Cómo he aprendido?

1 Revisa lo estudiado en la unidad y completa en tu cuaderno.

Siento orgullo por haber…

Me enfado cuando…

Lo que más me ayuda a aprender es… El semáforo. Junto a cada actividad, colorea así en tu cuaderno: si has sabido la respuesta, si has necesitado ayuda o si no la has sabido responder.

2 Reflexiona y piensa en las cosas que se te dan mejor y en las que se te dan peor. Luego, elabora un listado de cada uno de estos aspectos.

Mis fortalezas Mis debilidades

Propuestas de secuenciación y técnicas

Más información sobre estas claves: Aprendizaje cooperativo Desarrollo del pensamiento Educación emocional

Aprendizaje cooperativo

Evaluación grupal se deben mantener y cuáles son mejorables y en qué medida sus relaciones de trabajo están siendo eficaces y contribuyen a alcanzar las tareas u objetivos que se han propuesto alcanzar.

Cabezas pensantes 1

nado sea también protagonista a la hora de detectar sus fortalezas y posibilidades de mejora para trabajar de manera cooperativa.

Grupos: 4-5 participantes

Autoría/adaptación: Variante de Varas, M.; Rodríguez, A.; García, G.; Acosta, E.; Moya, P.; Delgado, C., y Wazne, C. Cooperativa de Enseñanza José Ramón Otero: Colegio Ártica.

1. Planteada la actividad por parte del profesorado, el alumnado en pequeños grupos se van a explicar de manera mutua cómo creen que hay que realizar la actividad o reto propuesto.

2. Una vez quede claro el objetivo y los pasos a dar, efectuarán la actividad de manera individual.

3. Si surge alguna duda se volverá a repetir el procedimiento expuesto. También se volverá a repetir, si las soluciones en el mismo grupo son muy diversas.

Observación: Cada proceso de repetición hay que vivirlo como una nueva oportunidad de aprendizaje en una doble dirección continua favorecida por la interacción entre quienes conforman el grupo.

Grupos: 4-5 participantes

Autoría/adaptación: Variante de Kagan, S.

1. Es una variante de la técnica «cabezas pensantes». Tras las explicaciones entre quienes conforman el grupo y la realización de la actividad de manera individual, cada participante se enumera del 1 al 4 (si el grupo es de 4).

2. A continuación, la profesora o el profesor elige un número al azar para que quien lo tenga dé la respuesta en representación del equipo. Esta técnica requiere que, en la fase previa a la respuesta, todo el grupo tenga claro el procedimiento seguido que les ha llevado a la solución.

Claves Secundaria

Observación: La valoración que desde un punto de vista evaluativo se le realice al alumnado elegido por un número no puede afectar al resto del grupo. Se debe evitar la creación de etiquetas que condicionen la formación de futuros grupos. Por otro lado, si queremos garantizarle éxitos al alumnado, es importante que las preguntas que se le planteen sean próximas a sus posibilidades. Esto permitirá fortalecer su autoestima, ganar confianza, evitar etiquetas y contribuir a actuaciones futuras igualmente exitosas.

Grupos: 4-5 participantes

Autoría/adaptación: Variante cooperativa de la técnica lluvia de ideas o brainstorming de Faickney, A.

1. Se forman pequeños grupos y, una vez planteada la actividad, se da un tiempo para pensar en posibles ideas o respuestas de manera individual. Es importante que no se ponga el foco en la solución o resultado final, y sí en el procedimiento a seguir para llegar a esa solución.

2. A continuación, en el sentido de las agujas del reloj, se comparten las ideas o las respuestas. Han de intervenir todos los componentes del grupo según los turnos establecidos y en tiempos similares.

3. Finalizada esta fase, de manera individual se resolverá la actividad según las ideas aportadas por los demás compañeros y compañeras del grupo.

Comprobamos 4

Autoría/adaptación: Calvo, J; Mesa, R., y Quevedo, V.

Grupos: 4-5 participantes

1. Realizada la actividad de manera individual y antes de hacer una corrección en gran grupo o por parte de la profesora o el profesor, en pequeños grupos se comparten las soluciones con el fin de comprobar, corregir y argumentar e intercambiar diferentes formas de proceder.

2. Esta técnica es una gran oportunidad para que el alumnado verbalice la ruta seguida para dar respuesta a la actividad, aportando, en algunos casos, nuevas estrategias a sus compañeras y compañeros.

3. Si finalmente no quedan resueltas las posibles dudas en el grupo, la profesora o el profesor las traslada a otro equipo en la fase de puesta en común con todo el alumnado. El profesorado será en todos los casos el último recurso para dar una respuesta definitiva.

5 Interpretación compartida

Autoría/adaptación: Variante de David y Roger Johnson y Pujolàs, P.

Grupos: 4-5 participantes

1. Una vez conformados los pequeños grupos, se les propondrá la lectura de un texto o la visualiza-

APRENDIZAJECOOPERATIVO

comprobar, corregir y argumentar e intercambiar diferentes formas de proceder.

2. Esta técnica es una gran oportunidad para que el alumnado verbalice la ruta seguida para dar respuesta a la actividad, aportando, en algunos casos, nuevas estrategias a sus compañeras y compañeros.

3. Si finalmente no quedan resueltas las posibles dudas en el grupo, la profesora o el profesor las traslada a otro equipo en la fase de puesta en común con todo el alumnado. El profesorado será en todos los casos el último recurso para dar una respuesta definitiva.

5 Interpretación compartida

Autoría/adaptación: Variante de David y Roger Johnson y Pujolàs, P.

Grupos: 4-5 participantes

1. Una vez conformados los pequeños grupos, se les propondrá la lectura de un texto o la visualización de una imagen.

2. En ambos casos, el objetivo que se persigue es la comprensión mediante la presentación de textos continuos o discontinuos presentes en todas las áreas y en la vida cotidiana.

3. Posterior mente, y en el sentido de las agujas del reloj, cada alumna y cada alumno de manera individual y oralmente compartirá su interpretación de lo leído o visto para, posteriormente, resolver conjuntamente las preguntas planteadas al respecto.

Petición del oyente 6

Grupos: 4-5 participantes

Autoría/adaptación: Variante del Laboratorio de Innovación Educativa. Colegio Ártica. Cooperativa de Enseñanza José Ramón Otero.

1. En pequeños grupos, la profesora o el profesor propone una actividad en la que el alumnado, de manera individual, pensará la forma de resolverla.

2. Se abrirá un turno de palabra para que cada miembro exponga su forma de dar respuesta a la actividad. El grupo considerará la propuesta que haya despertado más interés y procederá a realizar la actividad.

Claves Secundaria

3. Con esta técnica se desarrollarán no solo habilidades necesarias para dar respuesta a la actividad, sino también aquellas otras necesarias para empatizar con el grupo y para comunicar de una manera clara y segura.

Grupos: 4-5 participantes Lápices al centro 7

Autoría/adaptación: Kagan, S.; Pujolàs, P.

1. Conformados los grupos heterogéneos, se parte de una actividad estructurada en cuatro preguntas diferentes.

2. A cada miembro del equipo se le asigna una pregunta y dejan su lápiz en el centro de la mesa.

3. Por turnos, la persona encargada de esa cuestión lee y propone una solución; el resto del grupo aporta su opinión (también por turnos, para que todos participen por igual) y se debate cómo solucionarla.

4. Cuando lo tienen claro, cogen su lápiz y resuelven la actividad (sin hablar). Si durante la resolución de la actividad a algún miembro del grupo le surge una pregunta, vuelve a dejar su lápiz en el centro para parar el ejercicio y plantear la duda al resto. De forma sucesiva, se resuelven todas las preguntas con la misma dinámica.

Grupos: 4 participantes 1-2-4 8

Autoría/adaptación: Pujolàs, P.

1. Se parte de una pregunta o cuestión común para todo el grupo.

2. Primero, de forma individual, cada alumno y alumna piensa la respuesta y la anota.

3. Después, agrupados en parejas se intercambian las respuestas, y llegan a un consenso anotando una respuesta en común.

4. Finalmente, en grupos de cuatro debaten las respuestas de las parejas y repiten la misma dinámica, llegando a una respuesta en común para todo el grupo.

Grupos: 2-4 participantes Folio giratorio 9

Autoría/adaptación: Kagan, S.; Pujolàs, P.

1. Se les proporciona un folio en blanco y un rotulador de color diferente para cada miembro del grupo.

2. Se da la pauta: una cuestión con diferentes respuestas, series, dibujos, crear historias, etc.

3. Cada miembro del grupo, por turnos, siguiendo las agujas del reloj, escribe una o varias aportacio-

3. Después, agrupados en parejas se intercambian las respuestas, y llegan a un consenso anotando una respuesta en común.

Aprendizaje cooperativo

4. Finalmente, en grupos de cuatro debaten las respuestas de las parejas y repiten la misma dinámica, llegando a una respuesta en común para todo el grupo.

Folio giratorio 9

Autoría/adaptación: Kagan, S.; Pujolàs, P.

Grupos: 2-4 participantes

1. Se les proporciona un folio en blanco y un rotulador de color diferente para cada miembro del grupo.

2. Se da la pauta: una cuestión con diferentes respuestas, series, dibujos, crear historias, etc.

3. Cada miembro del grupo, por turnos, siguiendo las agujas del reloj, escribe una o varias aportaciones (en función del número de respuestas posibles, se puede pautar para que todo el grupo participe) sin que se repitan. Cada cual tiene que escribir sus propias ideas. Mientras se van escribiendo estas aportaciones, el resto del grupo debe estar pendiente para ir debatiendo o matizando.

4. El producto final es responsabilidad de todo el grupo. Una vez que todas y todos han participado, se pone en común en el grupo-clase si se considera oportuno, con la dinamización del profesorado.

Parada de cinco minutos

Autoría/adaptación: Kagan, S.; Pujolàs, P.

Grupos: 2-4 participantes

1. Durante una exposición al grupo, el profesorado establecerá una parada de cinco minutos.

2. Se forman parejas para pensar y reflexionar sobre el contenido y formular al menos dos preguntas o dudas sobre el tema.

3. Posteriormente, se pueden unir dos parejas para conformar un grupo de 4 e intentar responderse las dudas.

4. Finalmente, por turnos, las parejas o los grupos plantean una de sus preguntas al resto de los grupos evitando preguntas repetidas. Si el alumnado de los demás grupos no resuelve la duda, será la profesora o el profesor la persona responsable de explicarla.

Observación: El tiempo se puede adaptar en función de la dificultad del tema a tratar.

Claves Secundaria

Autoría/adaptación: Pujolàs, P.

1. Se parte de la lectura de un texto o del visionado de vídeos o diapositivas.

2. Un miembro del grupo lee en voz alta un párrafo.

Grupos: 4-5 participantes

3. El siguiente (en el sentido de las agujas del reloj) tiene que explicar o resumir ese texto.

4. A continuación, el resto del grupo debe decir si están de acuerdo o no con la explicación y matizar o incluir información.

5. Después, ese segundo miembro que acaba de resumir el párrafo continúa con la lectura del siguiente, para repetir la secuencia hasta que finalice el texto.

Grupos: 4-5 participantes Grupo nominal 12

Autoría/adaptación: Delbecq y Van de Ven.

1. Se parte de una actividad o pregunta por escrito, fácil de comprender y de manera visible para todo el grupo.

2. Tras una «lluvia de ideas» individual sobre la decisión o decisiones a tomar, se ordenan por números y se escriben en el cuaderno, un folio o en tarjetas.

3. Se hace una puesta en común en el grupo, en la que una persona irá anotando esas ideas y el resto irá dando explicaciones por parte de quien la propone.

4. A continuación, se votarán las ideas.

5. La más valorada es la que más representa al grupo y tendrá mayor prioridad en el gran grupo.

Grupos: 4-5 participantes Sumamos 13

Autoría/adaptación: Calvo, J.; Mesa, R., y Quevedo, V.

1. Se propone una actividad de manera individual en la que el alumnado da una respuesta u opinión: «Creo que… porque…».

3. Se hace una puesta en común en el grupo, en la que una persona irá anotando esas ideas y el resto irá dando explicaciones por parte de quien la propone.

4. A continuación, se votarán las ideas.

5. La más valorada es la que más representa al grupo y tendrá mayor prioridad en el gran grupo.

Grupos: 4-5 participantes Sumamos

Autoría/adaptación:

Calvo, J.; Mesa, R., y Quevedo, V.

1. Se propone una actividad de manera individual en la que el alumnado da una respuesta u opinión: «Creo que… porque…».

2. Se hace una puesta en común entre quienes conforman el grupo. De manera individual, tras lo que van escuchando, anotan las respuestas u opiniones que aportan alguna novedad, completan o amplían la respuesta dada.

3. Se hace una puesta en común de todos los grupos con las respuestas enriquecidas gracias a las aportaciones de cada participante. Del mismo modo, se podrán enriquecer con las novedades aportadas desde el resto de los grupos.

4. Finalmente, cada participante podrá reformular su respuesta inicial gracias a las aportaciones incorporadas fruto de las puestas en común.

Rompecabezas 14

Autoría/adaptación:

Aronson, E.; Kagan, S.; Pujolàs, P.

Grupos: 4-5 participantes

1. Se parte de una temática que se pueda fragmentar en cuatro ámbitos o «subtemas». Estos se reparten, uno a cada miembro del grupo.

2. De forma individual se les proporcionan recursos y se da un tiempo para que cada miembro pueda profundizar en el tema.

3. Se organizan «grupos de especialistas» que han investigado el mismo subtema y se reúnen para compartir los conocimientos y profundizar.

4. Cada miembro del grupo vuelve al suyo de origen y tiene la responsabilidad de explicar al resto del grupo su parte enriquecida por las aportaciones, en el paso anterior, de las personas especialistas.

5. Para finalizar, cada grupo irá recogiendo y sintetizando todo el contenido en una cartulina o mediante una aplicación digital.

Claves Secundaria

Grupos: 4-5 participantes Folio giratorio en grupo 15

Autoría/adaptación: Variante de Kagan, S.; Pujolàs, P.

1. Con la ayuda de un folio en blanco y un bolígrafo o rotulador de color diferente al resto de los grupos, cada participante del grupo escribe la respuesta a la situación planteada: «Considero que...» de manera similar a la técnica del «folio giratorio».

2. A continuación, se comparten las propuestas entre todo el grupo y se consensúa una única respuesta que se escribe en el folio giratorio con el bolígrafo o rotulador del color elegido: «Nuestro equipo cree que...».

3. Posteriormente, en el sentido de las agujas del reloj, se pasan los folios giratorios al siguiente grupo, que con el bolígrafo o rotulador del color que ha elegido, escriben su respuesta debajo de las del grupo anterior. Así sucesivamente hasta que los folios giratorios hayan pasado por todos los grupos.

4. Una vez que el folio giratorio vuelva a cada grupo, harán una lectura de las aportaciones recibidas y darán una respuesta final consensuada: «Tras haber leído las aportaciones de los demás grupos, el nuestro considera que la respuesta a la situación planteada es...». Dichas respuestas podrán ser expuestas al resto de la clase a través de una persona por grupo que ejerza la portavocía.

Saco de dudas 16

Autoría/adaptación:

Tallón, M.ª J. a partir de Kagan, S.

Grupos: 4-5 participantes

1. Tras una temática o contenido tratado, de manera individual se escribe alguna duda que haya podido surgir.

2. En el grupo se hace una puesta en común y si alguna duda queda sin resolver pasa un «saco de dudas».

3. A continuación, y en gran grupo, la maestra o el maestro irá extrayendo una a una las dudas escritas, proponiendo que en cada grupo se debata sobre la posible respuesta.

4. Si algún grupo cree saber la respuesta, la expone a través de algún participante que ejerza la portavocía. El grupo que haya planteado la duda, escribirá la respuesta una vez haya sido validada por el resto de la clase y la maestra o el maestro.

4. Una vez que el folio giratorio vuelva a cada grupo, harán una lectura de las aportaciones recibidas y darán una respuesta final consensuada: «Tras haber leído las aportaciones de los demás grupos, el nuestro considera que la respuesta a la situación planteada es...». Dichas respuestas podrán ser expuestas al resto de la clase a través de una persona por grupo que ejerza la portavocía.

Aprendizaje cooperativo

Autoría/adaptación: Tallón, M.ª J. a partir de Kagan, S.

Grupos: 4-5 participantes

1. Tras una temática o contenido tratado, de manera individual se escribe alguna duda que haya podido surgir.

2. En el grupo se hace una puesta en común y si alguna duda queda sin resolver pasa un «saco de dudas».

3. A continuación, y en gran grupo, la maestra o el maestro irá extrayendo una a una las dudas escritas, proponiendo que en cada grupo se debata sobre la posible respuesta.

4. Si algún grupo cree saber la respuesta, la expone a través de algún participante que ejerza la portavocía. El grupo que haya planteado la duda, escribirá la respuesta una vez haya sido validada por el resto de la clase y la maestra o el maestro.

5. Si la duda queda sin resolver, será resuelta por el profesorado.

6. Una vez finalizada la técnica, es importante que se verbalicen o lean las respuestas anotadas en cada grupo para confirmar que realmente han quedado resueltas.

Grupos: 4-5 participantes Preparar la tarea 17

Autoría/adaptación: Variante del Laboratorio de Innovación Educativa del colegio Ártica a partir de David y Roger Johnson.

1. La profesora o el profesor explica la tarea que se va a realizar.

2. El grupo revisa la tarea paso a paso para asegurarse de que se ha comprendido el objetivo que se pretende. Una forma de hacerlo es repartir los pasos por cada participante. La primera alumna o el primer alumno leerá el paso asignado y tratará de explicar con sus palabras en qué consiste. Si el resto del grupo valida la explicación o se enriquece con aportaciones, se pasará el turno a la segunda persona, y así sucesivamente.

Claves Secundaria

3. Explicados los pasos y finalmente ejecutados, el grupo repasará la tarea para asegurarse de que se ha llevado a cabo de manera adecuada y de que todas y todos la han comprendido.

Cadena de preguntas 18

Autoría/adaptación: Pujolàs, P.

Grupos: 4-5 participantes

1.Cada equipo piensa y escribe una pregunta sobre el asunto tratado. No se pueden repetir preguntas.

2. El portavoz del equipo lanza la pregunta en voz alta al equipo que se encuentra al lado, siguiendo el sentido de las agujas del reloj.

3. El equipo que recibe la pregunta consensúa la respuesta y el portavoz la transmite en voz alta.

4. Se repiten los pasos hasta que el último equipo le haga la pregunta al equipo que comenzó la cadena de preguntas.

Grupos: 4-5 participantes

Autoría/adaptación: Basada en Pujolàs, P. y Kagan, S.

1. Cada equipo piensa y escribe cuatro palabras distintas sobre el asunto tratado. No puede haber palabras repetidas entre equipos.

2. De manera consensuada, cada equipo construye dos frases con cada palabra: una dentro del mismo contexto del asunto tratado y otra bajo un contexto similar.

3. Siguiendo el sentido de las agujas del reloj, el portavoz de cada equipo transmite oralmente las palabras de que dispone al equipo siguiente.

4. Siguiendo las pautas del punto 2, los equipos vuelven a construir dos frases con cada una de las palabras que ha recibido.

5. Se repite el proceso hasta que las palabras elegidas por cada equipo lleguen a todos y todas.

6. Se hace una puesta en común exponiendo y comparando las frases construidas bajo las mismas palabras.

Grupos: 4-5 participantes

APRENDIZAJECOOPERATIVO

palabras que ha recibido.

5. Se repite el proceso hasta que las palabras elegidas por cada equipo lleguen a todos y todas.

6. Se hace una puesta en común exponiendo y comparando las frases construidas bajo las mismas palabras.

Mesa redonda 20

Autoría/adaptación: Kagan, S.

Grupos: 4-5 participantes

1. De manera individual, siguiendo el sentido de las agujas del reloj, se da una respuesta como solución al problema planteado.

2. Se escuchan todas las respuestas, opiniones y argumentaciones de los miembros del equipo.

3. El equipo debate y consensúa una única respuesta que expondrá oralmente al resto de grupos mediante su portavoz.

Autoría/adaptación: Aronson, E.; Kagan, S.; Pujolàs, P.

1. De manera individual, se realiza un esquema en torno al tema tratado.

2. Por parejas, se pone en común el esquema completando mutuamente los enunciados del esquema.

3. Por equipos, se comparte y completan nuevamente los diferentes enunciados del esquema revisando la coherencia global entre todo el equipo.

4. El portavoz de cada equipo expone al resto del grupo clase el resultado y se completa dicho esquema con las aportaciones de los portavoces del resto de grupos, generando un esquema final.

Claves Secundaria

Observación: Surge como variante de las técnicas cooperativas «1-2-4» y «sumamos», en combinación con las estrategias de aprendizaje «esquema base», «mapa de conceptos», «mapa de relaciones», «línea del tiempo», etc.

Autoría/adaptación:

Calvo, J.; Mesa, R., y Quevedo, V.

1. De manera individual, se elabora un esquema en torno a un punto asignado (cada miembro del grupo trabaja sobre un punto diferente).

2. En parejas, se realiza una puesta en común donde se comparan y contrastan mutuamente los esquemas elaborados y se establecen los rasgos que los unen y que los diferencian.

3. En equipo, se comparten los esquemas nuevamente estableciendo los nuevos rasgos que los unen y los que les diferencian. Se revisa la coherencia global entre todo el equipo.

4. El portavoz de cada equipo expone al resto de grupo clase su esquema final.

Observación: Surge como variante de la técnica cooperativa anterior, «esquema a cuatro bandas». Se diferencia en que el alumnado debe analizar tantas situaciones o asuntos (que tengan que ver entre sí) como miembros tiene el equipo, en torno a una serie de rasgos o aspectos comunes que los caracterizan y otros que los diferencian.

Grupos: 4 participantes Esquema a cuatro bandas 21

Grupos: 2-4 participantes

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS

Análisis asociativo 1

Autoría/adaptación: Decroly, O.; adaptado por Escamilla, A.

Descripción: A partir de una idea central surgen interrogantes que ayudan a realizar un análisis de esta.

Acción: El profesorado formulará las interrogantes sobre el contenido que se pretende trabajar, asociadas a cuestiones espaciales, temporales, de origen y procedencia, causales, de utilidad y trabajo, y éticas, morales y sociales.

Observaciones: Se puede trabajar oralmente o por escrito con el apoyo del organizador gráfico. Es recomendable que al principio se lleve a cabo en gran grupo hasta que el alumnado aprenda el método. Las correcciones han de ser empáticas y asertivas para mantener siempre el interés y la motivación. Una vez finalizado se realizará una síntesis por parte del alumnado.

Asociaciones espaciales Ubicación, tamaño, distancia, forma ¿Dónde está? ¿Cómo es? ¿Dónde ocurre?

Asociaciones éticas, morales y sociales Costumbres, fiestas, acontecimientos, celebraciones, normas, valoración ¿Cómo, de qué manera se actúa? ¿Bajo qué normas, pautas o reglas? ¿Qué valoración le damos?

TÉCNICAS DE METACOGNICIÓN

Puede ser individual, en grupos cooperativos o en gran grupo.

Asociaciones temporales Localización en el tiempo: duración, sucesión, simultaneidad ¿Cuándo? ¿Durante cuánto tiempo? ¿Antes, después, a la vez que?

Idea central

Asociaciones de utilidad y de trabajo Consecuencias, finalidad, profesionales, útiles o herramientas ¿Para qué? ¿Qué consecuencias? ¿Quiénes? ¿Con qué?

Asociaciones de origen y de procedencia Precisión en el espacio y en el tiempo, materiales de origen, raíces de influencia ¿Desde dónde? ¿Desde cuándo? ¿Con qué? ¿Se parece? ¿Se diferencia?

Asociaciones causales Razones, causa, argumentos ¿Por qué? ¿Qué sentido?

Rueda lógica 2

Autoría/adaptación: Hernández, P., y García, L. A.; adaptado por Escamilla, A.

Descripción: Se organiza el pensamiento a partir de un contenido, identificándolo, comparándolo, relacionando causas y efectos, argumentando y valorando.

Acción: Se formula la pregunta de cada fase que servirá al alumnado para pensar y compartir su pensamiento con el resto del grupo.

Observaciones: Se puede trabajar oralmente o por escrito con el apoyo del organizador gráfico. Es recomendable que al principio se lleve a cabo en gran grupo hasta que el alumnado aprenda el método. Las correcciones han de ser empáticas y asertivas para mantener siempre el interés y la motivación. Una vez finalizado se realizará una síntesis por parte del alumnado.

Argumentar, valorar ¿Qué concluimos? ¿Qué valoramos?

Identificar ¿Qué es? ¿Cómo es? ¿Hay diferentes tipos?

Establecer relaciones causa-efecto

¿Por qué? ¿Qué repercusiones tiene?

Comparar ¿En qué se parece a...? ¿En qué es diferente de...?

Puede ser individual, en grupos cooperativos o en gran grupo.

TÉCNICAS DE PENSAMIENTO

LLAVES DE PENSAMIENTO

ORGANIZADORES GRÁFICOS

Autoría/adaptación: De Bono, E.; adaptado por Escamilla, A

Descripción: Esta técnica estimula la flexibilidad del pensamiento y nos permite analizar detalladamente las razones por las que se produce una situación, por qué reaccionamos o actuamos de un determinado modo, etc.

Acción: Para su desarrollo se formulan al alumnado una serie de interrogantes como: «¿por qué…?», «¿qué…?», «¿qué razones…?», «¿por qué debemos…?», «¿qué crees que…?», «¿a qué se debe…?», etc.

Observaciones: Se puede trabajar oralmente o por escrito con el apoyo del organizador gráfico. Una vez finalizado se realizará una síntesis por parte del alumnado. Es recomendable que al principio se lleve a cabo en gran grupo hasta que el alumnado aprenda el método. Las correcciones han de ser empáticas y asertivas para mantener siempre el interés y la motivación del alumnado.

TÉCNICAS DE METACOGNICIÓN

Puede ser individual, en grupos cooperativos. Línea de tiempo 4

Autoría/adaptación: Basada en el diagrama de Gantt, adaptada por Calvo, J.; Mesa, R., y Quevedo, V.

Descripción: Ayuda a organizar hechos, sucesos o fenómenos ocurridos durante un espacio de tiempo determinado. Se puede emplear para la comprensión y la expresión de cualquier suceso, historia o hecho real o inventado a través de una representación mental o gráfica de una serie cronológica de una forma visual.

Acción: El alumnado elaborará en su cuaderno la línea del tiempo sobre la historia, suceso o hecho que ha leído o escuchado, o bien sobre lo que quiere exponer o contar. Inicialmente debe hacerlo de una forma gráfica para posteriormente interiorizarlo y saber construir mentalmente dicha línea de tiempo, ante las distintas situaciones de vida que se le planteen.

Observaciones: Es recomendable haber mostrado algunos ejemplos previos, especialmente en los primeros cursos. Es una técnica muy útil para comprender y saber organizar el contenido de una lectura o para la invención de una historia; para organizar cualquier proceso: evolución histórica, ciclo del agua…; para explicar el procedimiento para la resolución de problemas…

Información: suceso... que se da en 1.er lugar.

Información: suceso... que se da en 2.º lugar.

Información: suceso... que se da en 3.er lugar.

Información: suceso... que se da en 5.º lugar.

Información: suceso... que se da en 7.º lugar.

Información: suceso... que se da en 4.º lugar.

Información: suceso... que se da en 6.º lugar.

Información: suceso... que se da en 8.º lugar.

Puede ser individual, en grupos cooperativos o en gran grupo.

Razón 2

Razón 1

Razón 6

Razón 3

Razón 5

Razón 4

Hecho o suceso

Desarrollo del pensamiento

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

Autoría/adaptación:

Puede realizarse en gran grupo. El alumnado expondrá sus respuestas pidiendo la palabra, respetando las opiniones de los demás y, en caso de discrepancia, argumentandosu posición.

Proyecto Spectrum: Gardner, Feldman y Krechevsky (comps.); adaptado por Escamilla, A.

Descripción: Esta técnica está dirigida a desarrollar la capacidad para contar historias, proponiendo una historia en un escenario y con unos personajes; todo ello con flexibilidad para ampliar las posibilidades del escenario, de los personajes y de los contenidos, estimulando el desarrollo de habilidades de pensamiento.

Acción: Para llevarla a cabo, el profesorado presentará la historia vinculada a la escena que representa el tablero de las historias, a través una estructura sencilla desde la que formulará diversos interrogantes:

• Planteamiento: ¿Dónde ocurrió? ¿Quiénes eran? ¿Cuándo pasó?

Escenario o personajes

• Nudo: ¿Qué ocurrió? ¿Dónde? ¿Por qué? ¿Quiénes están implicados?

• Desenlace: ¿Cómo lo solucionaron? ¿Qué pasó finalmente? Cerraremos la historia con una reflexión sobre la historia y sus posibles significados o enseñanzas.

Observaciones: Se pasará de una primera fase más dirigida en la que se motivará al alumnado para recordar el curso de la historia, a una segunda en la que se les pedirá que inventen historias guiándose con los interrogantes básicos expuestos anteriormente: planteamientonudo­desenlace.

Planteamiento ¿Dónde ocurrió? ¿Quiénes eran? ¿Cuándo pasó?

Nudo ¿Qué ocurrió? ¿Dónde? ¿Por qué?

Desenlace ¿Cómo lo solucionaron? ¿Qué pasó finalmente?

Autoría/adaptación: Visible Thinking del Proyecto Zero de Harvard; adaptado.

Descripción: Es una estrategia para activar el razonamiento y las explicaciones mediante la cual se plantea una situación, un problema o un interrogante al alumnado. Tras unos minutos de reflexión se los invita a compartir su respuesta con el compañero o la compañera que esté a su lado, con los argumentos que le llevan a ella. Es importante mantener una escucha activa.

Acción: Puede utilizarse en una gran multitud de actividades de cualquier materia como una noticia, una lectura, una obra gráfica, una canción o una obra musical, un ejercicio deportivo, un problema matemático, un suceso natural o social, etc. La pregunta del profesorado puede ser tan fácil como: ¿Qué pensáis sobre…?

Observaciones: Se puede trabajar mediante alguna técnica cooperativa.

Situación (noticia, problema matemático, proceso natural, social, lectura…).

Alumno/a «A» Respuesta y argumentación

Alumno/a «B» Respuesta y argumentación

A + B comparten sus respuestas y argumentaciones

Opción 1

Opción 2

Nueva respuesta elaborada tras escuchar la respuesta y los argumentos de otro compañero o compañera.

Opción 3

Respuesta común compartida.

Nueva respuesta elaborada tras escuchar la respuesta y los argumentos de otro compañero o compañera.

Puede ser individual, en grupos cooperativos o en un gran grupo.

Piensa y comparte en pareja

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

7

Rastreador de problemas

Autoría/adaptación: Elías, M. J.; Tobías, S. E. y Friedlander, B. S.; adaptado por Escamilla, A.

Descripción: Técnica que favorece el análisis en profundidad de situaciones de conflicto, a partir de interrogantes. Comienza por una primera fase (Atender, recordar y analizar) para el conocimiento y el análisis de los hechos y, después, pasar a una segunda fase (Valorar y proponer activamente decisiones) en la que se introducen factores emocionales, y gradualmente se pasará al juicio crítico, la valoración y la implicación activa en la toma de decisiones.

Acción: Para su desarrollo, el profesorado presenta ante el grupo­clase la situación conflictiva y, a continuación, se formularán de forma progresiva los interrogantes de las dos fases citadas.

Observaciones: Se puede trabajar oralmente o por escrito con el apoyo del organizador gráfico. Conviene que inicialmente aprendan a reflexionar y responder individualmente y que, progresivamente, las respuestas se realicen por parejas o en pequeños grupos, mediante alguna técnica cooperativa.

1. Valorar y proponer activamente decisiones

• A mí me parece que...

• Porque...

Atender, recordar y analizar

• Qué sucedió

• Dónde

• Cuándo

• Por qué

• Quiénes estaban implicados

Fase 1 ¿Qué sentí? ¿Qué sintieron los demás? ¿Actué bien? ¿Actuaron bien?

• Creo que se podría...

2. Valorar y proponer activamente decisiones

• A mí me parece que...

• Porque...

• Creo que se podría...

3. Valorar y proponer activamente decisiones

• A mí me parece que...

• Porque...

• Creo que se podría...

Autoría/adaptación: Escamilla, A.; adaptado.

Descripción: Técnica que favorece la proyección y el análisis comparativo, así como el contraste sobre la manera en que podemos situar objetos, personajes e instituciones en otras épocas y en otros lugares. Nos permitirá identificar semejanzas y diferencias entre objetos, personas y situaciones en función de coordenadas espacio­temporales.

Acción: Mediante la observación de fotografías, dibujos u objetos reales se formularán las interrogantes que se proponen en los organizadores gráficos, que permitan el análisis y el contraste para finalizar con algunos que permitan la valoración de lo que estamos analizando.

Observaciones: Se puede trabajar oralmente o por escrito con el apoyo del organizador gráfico. Conviene que inicialmente aprendan a reflexionar y responder individualmente y que, progresivamente, las respuestas se realicen por parejas o en pequeños grupos, mediante alguna técnica cooperativa.

En el pasado, hace mucho, mucho tiempo ¿Cómo eran?; ¿se parecían a los nuestros o eran diferentes?, ¿en qué?; ¿nos gustan mucho o poco?, ¿por qué?

Esta técnica es conveniente aplicarla inicialmente de forma individual y, posteriormente, en grupo cooperativo.

Viajes en el tiempo

En el presente, ahora ¿Cómo son?; ¿nos gustán mucho o poco?; ¿por qué?

Viajes en el espacio

En lugares lejanos ¿Cómo son?; ¿cuáles se parecen más o menos a los nuestros?, ¿en qué?; ¿nos gustan mucho o poco?, ¿por qué?

En el futuro, dentro de mucho tiempo ¿Cómo los imaginas?; ¿cómo crees que serán?; ¿se parecerán a los nuestros o serán diferentes?, ¿en qué?; ¿nos gustarán mucho o poco?, ¿por qué?

En lugares cercanos ¿Cómo son?; ¿cuáles se parecen más o menos a los nuestros?, ¿en qué?; ¿nos gustan mucho o poco?, ¿por qué?

Puede ser individual, en grupos cooperativos o en gran grupo.

Desarrollo del pensamiento

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

Consecuencias y resultados (CyR) 9

Autoría/adaptación: De Bono, E.; adaptado por Escamilla, A.

Descripción: Técnica que potencia la flexibilidad del pensamiento, fomenta la capacidad para reflexionar sobre las consecuencias de los actos propios o de los demás y permite reflexionar y valorar lo que ocurre en el entorno como consecuencia de los sucesos naturales.

Acción: El desarrollo de la técnica plantea tres reflexiones sobre una acción a corto y largo plazo: ¿Qué puede pasar? ¿Qué consecuencias producirá? ¿Qué resultados tendrá? Tanto para ti como para los demás. El respeto en el turno de palabra y en las reflexiones es esencial.

Observaciones: Se puede trabajar oralmente o por escrito con el apoyo del organizador gráfico. Es recomendable que al principio se lleve a cabo individualmente y progresivamente se pase a parejas o pequeños grupos mediante alguna técnica cooperativa. Es conveniente plantearla siempre como una situación muy cercana a las experiencias y a las emociones del alumnado. Las correcciones han de ser empáticas y asertivas para mantener siempre el interés y la motivación. Una vez finalizado se realizará una síntesis por parte del alumnado.

Antes pensaba..., ahora pienso... 10

CyR

Puede ser individual, en grupos cooperativos o en gran grupo.

Acción o suceso (publicar información privada en redes sociales, llevar una alimentación no equilibrada, sufrir una inundación…)

A largo plazo

¿Qué puede pasar?

¿Qué consecuencias producirá? ¿Qué resultados tendrá?

A corto plazo

¿Qué puede pasar? ¿Qué consecuencias producirá? ¿Qué resultados tendrá?

Para los demás:

Para mí Para el medio

- Los iguales: para compañeros y compañeras, amigos y amigas, hermanos y hermanas…

- Los adultos: para docentes, padres y madres, abuelos y abuelas…

Autoría/adaptación: Ritchhart, Church y Morrison. Adaptado.

Descripción: Esta estrategia ayuda al alumnado a reflexionar sobre sus pensamientos con respecto a un tema, situación o problema y a explorar cómo y por qué sus pensamientos han cambiado.

Acción: Al examinar y explicar, cómo y por qué han cambiado sus pensamientos, están desarrollando sus habilidades de razonamiento y reconocen relaciones de causa y efecto. También desarrollan habilidades metacognitivas al identificar y hablar de su propio pensamiento.

Observaciones: La utilizaremos cuando los pensamientos, opiniones o creencias iniciales del alumnado son factibles de cambio como resultado del aprendizaje producido. Pediremos al alumnado que compartan y expliquen sus cambios de pensamiento en gran grupo. Posteriormente, una vez consolidado el método, podrán hacerlo en pequeños grupos o en parejas.

Para el medio Para mí

Para los demás:

- Los iguales: para compañeros y compañeras, amigos y amigas, hermanos y hermanas…

- Los adultos: para docentes, padres y madres, abuelos y abuelas…

Inicialmente de forma individual y, posteriormente, podrán hacerlo en parejas o en pequeños grupos.

Asunto...

Antes pensaba…Ahora pienso…Causas

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

11

Autoría/adaptación: Ritchhart, Church y Morrison. Adaptado.

Descripción: Esta estrategia fomenta que el alumnado realice observaciones detalladas e interpretaciones que son fruto de pensar y sintetizar la información adquirida mediante la observación y, a partir de ahí, formularse nuevas preguntas que abren paso a nuevos campos de exploración y pensamiento, lo cual estimula la curiosidad y la investigación.

Acción: Para su desarrollo, el profesorado presentará el elemento a observar y, tras ofrecerles un tiempo de silencio para una observación detallada (2 o 3 minutos), les presentará el organizador gráfico que se propone. El respeto en el turno de palabra y en las reflexiones es esencial.

Observaciones: Es muy apropiada al comienzo de una unidad a través de un objeto, una imagen, un vídeo o un texto relacionados con el tema que se vaya a tratar, ya que permite que surjan preguntas que despertarán el interés del alumnado. Se puede trabajar oralmente o por escrito con el apoyo del organizador gráfico. Es recomendable que al principio se lleve a cabo individualmente y progresivamente se pase a parejas o pequeños grupos mediante alguna técnica cooperativa. Las correcciones han de ser empáticas y asertivas para mantener siempre el interés y la motivación. Una vez finalizado se realizará una síntesis por parte del alumnado.

Puede realizarse de forma individual, en grupo cooperativo y se compartirá el pensamiento de cada una de las fases en gran grupo.

Veo PiensoMe pregunto

Veo, pienso, me pregunto...

Desarrollo del pensamiento

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

Autoría/adaptación: Ritchhart, Church y Morrison. Adaptado.

Descripción: Esta estrategia facilita al alumnado conectar con sus conocimientos previos (qué saben o comprenden en el momento sobre un tema determinado), a desarrollar su curiosidad (qué interrogantes o dudas tengo sobre este tema) y favorece la indagación o la investigación sobre las inquietudes que tengan (qué te gustaría conocer­aprender).

Acción: Para su desarrollo, el profesorado presentará el tema o contenido sobre el que se vaya a trabajar (también una noticia, una imagen, una lectura, etc.) y se comenzarán las tres fases propuestas en el organizador gráfico.

Observaciones: Es importante que el alumnado, de forma oral, comparta sus pensamientos en cada una de las fases anteriores. Tras la fase de investigación llevada a cabo de manera cooperativa, se expondrán las conclusiones de su investigación. Las correcciones han de ser empáticas y asertivas para mantener siempre el interés y la motivación. Una vez finalizado se realizará una síntesis por parte del alumnado.

¿Qué

Autoría/adaptación: Ritchhart, Church y Morrison. Adaptado.

Descripción: Esta estrategia, aparentemente sencilla, parte de la descripción o interpretación de un objeto, imagen, lectura, suceso, etc., que tendrán que respaldar con evidencias, teniendo la posibilidad de considerar múltiples puntos de vista y diversas perspectivas sobre un tema a estudiar.

Acción: Es importante hacer visible el pensamiento que el alumnado tiene acerca de cómo funcionan las cosas, cómo surgen o por qué son como son. Igualmente hay que generar una reflexión comparada entre una creencia basada en un prejuicio o estereotipo y una certeza.

Observaciones: Puede ser utilizada para despertar las ideas previas del alumnado, para impulsarles a mayor profundidad en sus pensamientos argumentando las razones que están detrás de sus respuestas. Es importante que aprendan, simultáneamente, a exponer sus respuestas pidiendo la palabra, interviniendo cuando les corresponda, solicitando aclaraciones sobre lo que otros compañeros o compañeras han expuesto y, en caso de discrepancia, argumentando sus razones.

Puede realizarse inicialmente de forma individual. La investigación en grupo cooperativo. En gran grupo se compartirá tanto el pensamiento de cada una de las fases como el resultado de lo investigado.

Lo ideal es realizarla individualmente ante el grupo­clase

Descripción o interpretación de...

¿Qué te hace decir eso?

Justificación y evidencias

Pienso, me interesa, investigo...

Pienso Me interesa Investigo

te hace decir eso?

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

Círculo de puntos de vista 14

Autoría/adaptación: Ritchhart, Church y Morrison. Adaptado.

Descripción: Esta estrategia permite al alumnado identificar y tener en cuenta las diferentes perspectivas sobre un determinado tema u objeto de estudio que acaba de leer, observar o escuchar. Crea mayor conciencia acerca de que las personas pueden pensar diferente y fomenta la tolerancia y la empatía.

Acción: A partir de un contenido o temática, un alumno o una alumna, tras un tiempo de trabajo individual, asumirá la posición desde un punto de vista no propio, elegido de entre los planteados por el resto del grupo sobre esa temática. El resto del alumnado puede plantear sus interrogantes mediante «Una pregunta que tengo desde este punto de vista es...». Una vez finalizadas las preguntas, el profesorado podrá plantear: «¿Qué nuevas ideas tenéis sobre el tema que antes no teníais?».

Observaciones: Esta estrategia también puede llevarse a cabo mediante pequeños grupos (círculos) una vez que la dominen.

¿Qué nuevas ideas tengo sobre el tema?

Estoy pensando en... desde el punto de vista de...

Pienso que... porque...

Una pregunta que tengo desde este punto de vista es...

Autoría/adaptación: Calvo, J.; Mesa, R., y Quevedo, V.

Descripción: El alumnado aprenderá a poner ante un «espejo» dos realidades objeto de estudio y establecer una comparación a partir de sus semejanzas y diferencias de forma reflexiva y eficiente y cada vez más autónoma: animales, momentos o personajes de la historia, fenómenos naturales, obras pictóricas, eventos o figuras del deporte, lecturas, objetos, etc. La comparación parte del análisis riguroso de cada objeto de estudio y permitirá extraer conclusiones que pueden exportar a situaciones reales de su vida.

Acción: Presentadas las dos realidades: Empezaremos por las similitudes. Tras unos minutos y de manera individual, anotarán en la columna central del organizador gráfico las similitudes observadas. Posteriormente, las comentarán en grupo y llegarán a un consenso. Repetimos la dinámica y nos centraremos en las diferencias. Posteriormente, les pediremos que seleccionen las similitudes y las diferencias realmente importantes (al menos tres).

Observaciones: Las dinámicas grupales pueden pasar al gran grupo buscando como objetivo enriquecer las propuestas y llegar a una única consensuada a modo conclusión de lo que consideren más relevante. Como proceso de metacognición pueden reflexionar sobre lo que han aprendido, cómo lo han aprendido, para qué les ha servido y en qué otras ocasiones lo pueden utilizar.

Realidad «A»

Esta técnica es conveniente aplicarla inicialmente de forma individual y, posteriormente, en grupo cooperativo

Realidad «B»

Rasgos diferenciadores Similitudes Rasgos diferenciadores

Grupo­clase o grupos (círculos) poco numerosos. Solo la fase tres debe tener carácter individual.

Desarrollo del pensamiento

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS

Las 6 W 16

TÉCNICAS DE METACOGNICIÓN

Puede ser individual, en grupos cooperativos o en gran grupo.

Autoría/adaptación: Anderson y Krathwohl. Adaptado por Calvo, J.; Mesa, R., y Quevedo, V.

Descripción: Esta estrategia invita al alumnado a pensar y a comprender más profundamente sobre un hecho, asunto o tema de estudio mediante la formulación de preguntas, a modo de investigación periodística.

Acción: Se define por parte del profesorado el asunto o tema sobre el que investigar. El alumnado debe formular y responder a las preguntas atendiendo a todas o a algunas, según el contexto, de las interrogaciones planteadas en el organizador gráfico (6 W).

Observaciones: Cada pregunta debe obtener una respuesta por parte del alumnado, basada en evidencias. Pueden utilizarse estrategias cooperativas, exponiendo finalmente las conclusiones al grupo clase.

¿Quién (es)? ¿Qué? ¿Cuándo?

Inicialmente de forma individual, posteriormente, podrán hacerlo en parejas o en pequeños grupos.

Descripción: Estrategia mediante la cual se facilita al alumnado la realización de mapas conceptuales sobre un tema de estudio, suceso o lectura. Puede convertirse en una extraordinaria forma de valorar si el alumnado ha comprendido el tema u objeto de estudio.

Acción: El objetivo es crear de una forma estructurada un mapa conceptual, siguiendo estos pasos: Generar una lista de palabras o ideas del tema objeto de estudio. Clasificar las ideas o palabras teniendo en cuenta su importancia, colocando en el centro la/s más importante/s y alrededor las que tengan un carácter secundario. Conectar las ideas o palabras mediante líneas... Desarrollar el mapa conceptual con subcategorías más pequeñas.

Observaciones: Es importante que el alumnado sepa construir mapas conceptuales ya que les ayuda a organizar sus pensamientos y visualiza la forma en que las ideas se relacionan entre sí. Se sugiere que las dos primeras fases sean individuales. Finalmente, se compartirán sus mapas conceptuales con el resto del grupo clase y el método de construcción.

Autoría/adaptación: Ritchhart, R.; Church, M., y Morrison, K. Adaptado.

18

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

Razones - pones pegascontestas - sintetizas (RPPCS)

Descripción: Estrategia que permite argumentar y defender las propias ideas considerando posiciones contrarias que favorecen la reconstrucción del propio pensamiento.

Acción: Para su desarrollo, el profesorado presentará la situación sobre la que aplicar esta estrategia a partir de diversos interrogantes que se agruparán en cuatro fases de acuerdo al organizador gráfico propuesto.

Observaciones: La forma más apropiada es mediante expresión oral del alumnado, aunque también se puede plantear de forma escrita.

Autoría/adaptación: Escamilla, A. Adaptado.

Puede realizarse de forma individual, por parejas o en grupo.

Razonas

¿Por qué...? ¿Qué?

Sintetizas: En consecuencia... Entonces... Propuesta

Contestas: Sí, porque... Tenemos que pensar que...

Pones pegas: ¿Qué diría...?, No... porque... Sí, pero...

Brújula o

E - O - N -S 19

Autoría/adaptación: Ritchhart, R.; Church, M., y Morrison, K. Adaptado.

Descripción: Esta estrategia permite al alumnado considerar una idea o proposición desde diferentes puntos de vista de acuerdo con lo propuesto en el organizador gráfico. Suele utilizarse cuando el tema objeto de estudio presenta puntos de vista divergentes o cuando el alumnado tiene opiniones muy arraigadas sobre este.

Acción: El profesorado presenta la situación. Mediante el uso de cartulinas o en la pizarra, diferenciamos cuatro espacios, uno para cada punta de la brújula, y distribuiremos papeles adhesivos para que el alumnado escriba sus pensamientos. A continuación, formula los interrogantes de cada una de las puntas de la brújula: E = Entusiasmo/ Emoción: «¿Qué te entusiasma de esta idea o situación?», «¿qué aspectos positivos le encuentras?», «¿qué encuentras emocionante?». O = Obstáculo/ Pre-O-cupación: «¿Qué obstáculos o dificultades le ves a esta idea o situación?», «¿qué preocupaciones te genera?», «¿qué aspectos negativos le ves?».

N= Necesidades: «¿Qué más necesitas saber?», «¿qué información necesitas para comprender mejor este tema?». S= Sugerencias/posiciones: «¿Cuál es tu postura u opinión sobre esta idea o situación?», «¿qué sugerencias o acciones realizarías para mejorar la situación?».

Observaciones: Sobre cada uno de los puntos se dará un tiempo al alumnado para que piensen, escriban y publiquen sus ideas y se invitará al alumnado a expresar sus comentarios e ideas. La estrategia podría finalizar con al menos dos interrogantes más: «¿Qué puntos hay en común en las respuestas?», «¿qué sugerencias o acciones propuestas para mejorar la situación os parece más adecuada?», «¿por qué?».

Obstáculo/ preocupación

Esta estrategia tendrá carácter individual y se hará una puesta en común con el grupo­clase con los interrogantes finales.

Necesidades

Entusiasmo/ emociones

Sugerencias/ posiciones

puntos cardinales:

Desarrollo del pensamiento

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS

Preguntas provocadoras 20

TÉCNICAS DE METACOGNICIÓN

Esta estrategia podrá ser individual o en grupo cooperativo y se podrá llevar al grupo­clase en las dos fases finales.

Autoría/adaptación: Visible Thinking del Proyecto Zero de Harvard. Adaptado.

Descripción: Es una estrategia cuya finalidad es incentivar el pensamiento y la investigación, mediante el desarrollo de preguntas. También fomenta en el alumnado el intercambio de ideas sobre los distintos tipos de preguntas de un tema para tener una mayor visión sobre él.

Acción: A partir de las preguntas propuestas en el organizador gráfico, y en función de la temática seleccionada, el alumnado elige las que considere más provocadoras para debatir sobre ellas durante unos minutos. Se generará una reflexión final: «¿Qué nuevas ideas tienes acerca del tema, concepto u objeto, que no tenías inicialmente?».

Observaciones: Esta estrategia se puede utilizar al introducir un nuevo tema para despertar la curiosidad del alumnado o cuando se está terminando para profundizar y crear reflexiones más relevantes y de mayor interés. También de forma continua a lo largo del tema, para ayudar al grupo a hacer visible la evolución que van teniendo con el uso de la lista de preguntas.

¿Por qué?

¿Qué diferencia habría si...?

¿Cómo...?

¿Cómo sería si...?

¿Cuáles son las razones?

Supón que... ¿...?

¿Y si...?

¿Qué ocurriría si supiéramos...?

¿Cuál es el propósito de...?

¿Qué cambiaría si...?

¿Qué parecido le encuentras con...?

¿Con qué relacionarías?

Esta estrategia tendrá carácter individual y se hará una puesta en común con pequeños grupos o con el grupo­clase.

Autoría/adaptación: Ritchhart, R.; Church, M., y Morrison, K. Adaptado.

Descripción: Esta estrategia pretende facilitar la relación activa entre las nuevas informaciones que el alumnado recibe (al leer, al escuchar o al observar) con lo que ya conoce, al identificar nuevas ideas que amplían nuestro pensamiento o al cuestionarnos las ideas que tenemos ante dichas informaciones. Es decir, ayuda al alumnado a procesar de manera activa la información.

Acción: En su desarrollo podemos distinguir las siguientes fases: Relacionar­ampliar­preguntar. Al alumnado se le formularán las interrogantes propuestas en el organizador gráfico para cada fase. Se pueden plantear para ser respondidas individualmente, para que posteriormente se compartan con el grupo clase o en grupos reducidos, exponiendo las razones o pensamientos que justifican sus respuestas.

Observaciones: Es muy apropiada para trabajar al finalizar un tema o después de una lectura, un experimento, etc. Los interrogantes apropiados serían: «¿Qué conexiones se pueden establecer entre este contenido con lo que ya sabes o con lo estudiado anteriormente?», «¿qué interrogantes o desafíos han surgido a partir de la nueva información?».

Relacionar

¿Qué relaciones has establecido entre esta nueva información o experiencia y lo que ya conocías?

Ampliar

¿Qué ideas o pensamientos se han ampliado o se han hecho más profundos como resultado de la nueva información o experiencia?

Preguntar

¿Qué interrogantes o desafíos te han surgido a partir de la nueva información o experiencia?

Relacionar - ampliar - preguntar 21

22

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS

TÉCNICAS DE METACOGNICIÓN

Esta estrategia tendrá carácter individual y posteriormente se compartirá en parejas, pequeños grupos o con el grupo clase.

Autoría/adaptación: Ritchhart, R.; Church, M., y Morrison, K. Adaptado.

Descripción: Esta estrategia pretende que el alumnado, después de una lectura, una audición, algo visto o vivido, sintetice de forma metafórica y no verbal, para lo que se utilizará un color, un símbolo y una imagen.

Acción: Para ello, seguirán este procedimiento: Escoger un color. Cada alumno o alumna seleccionará un color que desde su punto de vista representa lo esencial de la información o experiencia vivida. Este color se registra y se justifica por escrito su elección. Crear un símbolo. De forma individual, cada alumno o alumna selecciona o elabora un símbolo que represente lo esencial de la información o experiencia vivida. Igualmente registran su símbolo y justifican por escrito su elección. Seleccionar o elaborar una imagen que represente la información o experiencia vivida, que también registrarán y justificarán por escrito.

Observaciones: Es conveniente que finalmente compartan sus elecciones por parejas, en grupos reducidos o con el grupo clase, exponiendo las razones o pensamientos que justifican su elección y, como consecuencia, la metáfora que han construido.

Color - símbolo - imagen (CSI)

Color Símbolo

Tema Imagen

Desarrollo del pensamiento

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS

Canal de transferencia 23

Autoría/adaptación: Ritchhart, R.; Church, M., y Morrison, K. Adaptado.

TÉCNICAS DE METACOGNICIÓN

Esta estrategia tendrá carácter individual y se hará una puesta en común con pequeños grupos o con el grupo clase.

Descripción: Esta técnica permite transferir o extrapolar aspectos de una situación concreta a otra parecida o similar. Para ello, se hace necesario conocer y comprender el asunto o tema que se está tratando y pensar en su significado para interpretar los aspectos que lo definen, explicar el modo en que dichos aspectos podrían transferirse a otros asuntos o temas y razonar la conexión establecida.

Acción: La aplicación de esta técnica requiere dividir una página en dos columnas de tal forma que se puedan observar similitudes entre dos conceptos o situaciones.

Observaciones: A su vez, esta técnica permite encontrar patrones y similitudes entre contextos que funcionan de la misma forma por lo que favorece la conexión entre conocimientos (una vez que se conoce cómo funciona un contexto, comprobamos que ese funcionamiento se replica en otro contexto, por lo que no necesitamos memorizar dos contextos diferentes, sino entender la lógica de funcionamiento de uno de ellos y saber que es aplicable al segundo contexto dado).

Asunto de partida o situación

Características del asunto de partida

Asunto similar al de partida o situación (conexiones)

Características del asunto similar

¿Qué lo causa? ¿Por qué se produce?

¿Qué causa el asunto similar? ¿Por qué se produce?

¿Cuáles son las consecuencias? ¿Cuáles son las consecuencias del asunto similar?

Resultado final o conclusiones

Resultado final o conclusiones del asunto similar

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

Diagrama en escalera 24

Autoría/adaptación: Tolman, E. Adaptado por Calvo, J.; Mesa, R., y Quevedo, V.

Descripción: El diagrama en escalera es una técnica basada en comprender situaciones, hechos, conceptos… siguiendo las fases por las cuales se procesa (se organiza y se entiende) la información que se recibe.

Esta teoría considera el aprendizaje como un proceso de concienciación a través de:

• La atención y la definición de lo que se percibe. ¿De qué trata la información que recibo?

• La búsqueda, el análisis y el pensamiento sobre lo que se ha percibido. Se trata de procesar, en sí mismo, la información recibida. Para ello, puede servir cualquiera de las múltiples técnicas que desarrollan las formas de pensamiento.

• La decisión y la respuesta. El alumno o la alumna da una o varias respuestas, lo más acertadas posible, intentando dar solución al problema o reto planteado por el profesor o profesora tras la información dada.

Esta estrategia tendrá carácter individual y se hará una puesta en común con pequeños grupos o con el grupo clase.

Acción: Se elabora un organizador gráfico que represente una escalera y se recoge, en los escalones superiores de qué trata la información recibida o cuál es la situación planteada; en los escalones intermedios, el análisis y la interpretación de la información recibida o de la situación planteada, que puedes llevar a cabo utilizando todas aquellas técnicas de pensamiento que consideres necesarias; y en los escalones inferiores, las decisiones, conclusiones o respuestas surgidas del análisis y de la interpretación realizada.

Observaciones: El análisis concreto de la información recibida o de la situación planteada puede llevarse a cabo empleando estrategias de pensamiento o técnicas de aprendizaje cooperativo que faciliten la localización y comprensión de los datos.

De qué trata la información recibida o cuál es la situación planteada

Análisis e interpretación de la información recibida o de la situación (aplicación de otras técnicas de pensamiento)

Decisiones, conclusiones o respuestas surgidas del análisis y de la interpretación realizada.

Desarrollo del pensamiento

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS

Intuyo y deduzco 25

Autoría/adaptación: Calvo, J.; Mesa, R., y Quevedo, V.

TÉCNICAS DE METACOGNICIÓN

Esta estrategia tendrá carácter individual y se hará una puesta en común con pequeños grupos o con el grupo clase.

Descripción: Esta técnica está vinculada tanto a pensamientos y respuestas repentinos como a pensamientos y respuestas más elaborados. Supone una manera de organizar el pensamiento desde diferentes grados de conciencia.

Acción: Su puesta en práctica requiere una situación base, idea o concepto sobre la cual deberemos explorar los argumentos que tenemos sobre dicha idea. Una vez realizado este ejercicio, el alumnado debe pensar en las evidencias y las consecuencias que tiene dicha situación, idea o concepto.

¿Qué genera el turismo? Más puestos de trabajo, comercio, consumo, mejora de infraestructuras, intercambio cultural, restauración y conservación de espacios, etc.

¿Qué ocurriría si dejara de haber turismo? Menos puestos de trabajo, comercio y consumo, no se mejoraría tanto en infraestructuras, no habría intercambio cultural, se restaurarían y conservarían menos los espacios, etc.

Valoración del alcance económico del turismo: Desarrolla la economía, se moviliza el capital y, en definitiva, se invierte más en la zona tanto por capital nacional como extranjero. Hechos y evidencias que lo convierten en pilar de la economía: Se incrementa el producto interior bruto y la renta per cápita, sube el número de inversores extranjeros, mejora la calidad de vida, se genera más empleo, se fomenta el consumo, etc.

El turismo como fuente de riqueza y pilar de la economía.

Observaciones: A su vez, esta técnica permite encontrar patrones y similitudes entre contextos que funcionan de la misma forma por lo que favorece la conexión entre conocimientos (una vez que se conoce cómo funciona un contexto, comprobamos que ese funcionamiento se replica en otro contexto, por lo que no necesitamos memorizar dos contextos diferentes, sino entender la lógica de funcionamiento de uno de ellos y saber que es aplicable al segundo contexto dado).

Argumentación, evidencias que sustentan la situación o el concepto.

Conjeturas y juicios sobre el alcance de la situación o el concepto.

Definición de una situación, idea o concepto.

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

Conformidad y consenso 26

Esta técnica puede llevarse a cabo entre todo el grupo­clase, en grupos reducidos o combinando ambas maneras.

Autoría/adaptación: Swartz, R. / Escamilla, A. Adaptado por Calvo, J.; Mesa, R., y Quevedo, V.

Descripción: Esta técnica posibilita llegar a acuerdos sobre un tema concreto. Permite al alumnado razonar y priorizar sus puntos de vista, contribuyendo a exponer argumentos individuales y a consensuarlos a partir de puntos de vista razonados.

Acción: Para su puesta en práctica debemos:

• Definir el tema sobre el que vamos a tratar.

• Realizar una lluvia de ideas en la que dividiremos los aspectos en los que todo el alumnado está de acuerdo y aquellos que generan discrepancias. Se recomienda en este momento de la aplicación de la técnica, motivar al alumnado para que, tras expresar una idea, la defienda y la argumente. El resultado de esta parte de la técnica será la obtención de una lista dividida en dos: ideas de conformidad e ideas de no conformidad.

• Llegar a un consenso. Para ello, aplicaremos la técnica de grupo nominal que nos permitirá jerarquizar los aspectos en función del valor o la importancia de forma colectiva.

• Definir el acuerdo final. Tras realizar los pasos anteriores, deberá ser relativamente sencillo obtener una conclusión o acuerdo final sobre el tema tratado.

Observaciones: Por su estructura y procedimiento, esta técnica de pensamiento integra en su desarrollo la «lluvia de ideas» y la técnica cooperativa «grupo nominal».

TEMA SOBRE EL QUE SE VA A TRATAR

CONFORMIDAD: LLUVIA DE IDEAS

Lista 1: Aspectos referidos al asunto tratado, sin estar repetidos y con sus argumentos correspondientes, en los que TODO el alumnado está de acuerdo.

a) …

b) …

Lista 2: Aspectos referidos al asunto tratado, sin estar repetidos y con sus argumentos correspondientes, en los que NO TODO el alumnado está de acuerdo.

a) … b) …

CONSENSO: «GRUPO NOMINAL»

Para alcanzar el consenso, haremos uso de la técnica cooperativa «grupo nominal»:

• El alumnado jerarquiza y puntúa cada aspecto dentro de su lista por separado (por un lado, los aspectos en los que hay acuerdo y, por otro lado, los aspectos en los que no hay acuerdo) del siguiente modo:

– Entre los aspectos de la lista 1 (en los que TODO el alumnado está de acuerdo), se puntúa con un 1 el aspecto que se considere más cierto o importante; con un 2, el segundo; con un 3, el tercero, y así, sucesivamente, hasta haber puntuado todos los aspectos expuestos en la lista.

– Entre los aspectos de la lista 2 (en los que NO TODO el alumnado está de acuerdo), se puntúa con un 1 el aspecto que se considere más en desacuerdo; con un 2, el segundo; con un 3, el tercero, y así, sucesivamente, hasta haber puntuado todos los aspectos expuestos en la lista.

• Acto seguido, para saber el resultado por consenso colectivo, se suman las puntuaciones de cada uno de los aspectos dentro de sus listas, siendo el que menos puntuación haya obtenido:

– Entre los aspectos de la lista 1, el mejor valorado en cuanto a certeza e importancia.

– Entre los aspectos de la lista 2, el que más en desacuerdo se está.

CONCLUSIONES Y ACUERDOS FINALES

Se hace una puesta en común en base a una conclusión y un acuerdo final sobre el asunto tratado.

Desarrollo del pensamiento

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

Las partes suman 27

Autoría/adaptación: Swartz, R. Adaptado por Calvo, J.; Mesa, R., y Quevedo, V.

Esta estrategia tendrá carácter individual y se hará una puesta en común con pequeños grupos o con el grupo clase.

Descripción: «Las partes suman» es una técnica de aprendizaje que consiste en profundizar en los distintos aspectos, componentes y factores que suman y forman un todo, permitiendo reflexionar sobre ello en cuanto a aspectos que lo definen, cómo funciona, cómo podemos mejorarlo o cómo crear algo nuevo.

Acción: Se elaborará una tabla (ver tabla A) en la que se definirá el asunto que representa el todo sobre el que se va a trabajar, se detallarán los aspectos, componentes o factores que se van a analizar de ese todo y se recogerán las cuestiones que servirán para realizar el análisis.

Observaciones: Podemos utilizar una variante simplificada de esta técnica para profundizar en las acciones que suman y forman una actitud o comportamiento colectivo, en cuyo caso se emplearía la estructura recogida en la tabla B.

TABLA A

DEFINICIÓN DEL ASUNTO QUE REPRESENTA EL TODO

¿Cuál es su función?

¿Qué ocurriría si no existiera?

¿Qué relación tiene con los demás aspectos, componentes o factores?

DEFINICIÓN DE LA ACTITUD O EL COMPORTAMIENTO COLECTIVO

¿Qué consecuencias tiene?

¿Es una acción consolidada o esporádica?

Aspecto, componente o factor 1 analizado:

Aspecto, componente o factor 2 analizado:

Aspecto, componente o factor 3 analizado:

TABLA B

Actuación-hábito 1:

Actuación-hábito 2:

Actuación-hábito 3:

¿Qué relevancia tiene respecto al todo? . . . . . . . . . . . . . . . . . .

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

Solución a cuatro 28

Autoría/adaptación: Swartz, R. Adaptado por Calvo, J.; Mesa, R., y Quevedo, V.

Esta estrategia tendrá carácter individual y se hará una puesta en común con pequeños grupos o con el grupo clase.

Descripción: Esta técnica permite pensar en posibles soluciones a un problema dado (teniendo en cuenta las propuestas generadas, sus ventajas e inconvenientes y dudas).

Acción: Para aplicar dicha técnica, partimos de la definición de una situación sobre la que haremos una lluvia de ideas referidas a posibles soluciones para dicha situación. Una vez recogidas las aportaciones de todo el alumnado, elaboraremos una tabla en la que se recojan todas las propuestas para solucionar el problema, así como las ventajas, inconvenientes y dudas de cada una de ellas.

Observaciones: Es una variante de la técnica «Las partes suman» y suele aplicarse integrada en el desarrollo de algunas técnicas cooperativas como la mesa redonda.

Esta estrategia tendrá carácter individual y se hará una puesta en común con pequeños grupos o con el grupo clase

Autoría/adaptación: Visible Thinking del Proyecto Zero de Harvard. Adaptado.

Descripción: Esta técnica ayuda al alumnado a elaborar pensamientos sólidos y críticos sujetos a valores y a reaccionar como consecuencia de ello. Se parte de la observación y el análisis de la situación, organizando el discurso y dotando de estructura y consistencia al razonamiento.

Acción: La puesta en práctica de esta técnica requiere que el alumnado organice la información en diferentes casillas o recuadros que recogerán aspectos relacionados con: afirmaciones y contexto de la situación que se defiende, motivos y causas de la situación defendida, evidencias en las que se apoya la idea defendida y valoración propia sobre la opinión o situación defendida.

Observaciones: Esta técnica puede ser utilizada en debates y en actividades que requieren contraponer opiniones.

Exposición y contextualización de la opinión o de la propuesta.

Argumentación (motivos, causas…) de la opinión o de la propuesta.

Evidencias que demuestran lo argumentado.

Evaluación de la opinión o de la propuesta mediante criterios, argumentos y evidencias propios.

Desarrollo del pensamiento

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

Discurso contradictorio 30

Autoría/adaptación: Calvo, J.; Mesa, R., y Quevedo, V.

Esta estrategia tendrá carácter individual y se hará una puesta en común con pequeños grupos o con el grupo clase.

Descripción: Esta técnica permite desarrollar el pensamiento crítico con el propósito de comprobar la calidad del argumento original e identificar las debilidades de su defensa.

Acción: El correcto desarrollo de esta técnica requiere que el alumnado elabore diferentes recuadros o casillas que deben contemplar la siguiente información: afirmación que se defiende, argumentos y motivos que van en contra de la idea defendida, evidencias que desargumentan la opinión defendida y opinión personal contra la opinión defendida.

Observaciones:Complementa a la técnica anterior y se aplica cuando queremos defender una posición en contra de la opinión del autor o autora de un discurso.

Exposición de la opinión o del planteamiento en cuestión.

Argumentación (motivos, causas…) para desarticular la opinión o la propuesta.

Evidencias que desarticulan lo argumentado.

Desarticulación de la opinión o del planteamiento mediante criterios, argumentos y evidencias propios.

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

La travesía 31

Autoría/adaptación: Calvo, J.; Mesa, R., y Quevedo, V.

Esta estrategia tendrá carácter individual y se hará una puesta en común con pequeños grupos o con el grupo clase.

Descripción: Esta técnica permite obtener de forma gráfica las conexiones que existen entre un momento previo, el actual y uno posterior al conocimiento, potenciando la predisposición a querer saber el porqué de las cosas. La finalidad de esta técnica es marcar los hitos, sugerencias o interrogantes necesarios para construir una historia o argumento, dándole orden, lógica y coherencia desde su inicio.

Acción: Sobre un dibujo o plantilla en el que se pueda intuir un camino (organizador A), el alumnado deberá situar un antes o punto de partida, un durante o evolución y un después o resultado, de tal forma que, al lado de estos momentos puedan introducirse aspectos cómo: ¿Qué sabía sobre el tema? ¿Qué dudas me surgían? Y posibles respuestas a estas dudas.

Observaciones: Una variante de esta técnica es la denominada las travesías (organizador B), que consiste en un mapa alternativo y similar a lo que ocurre en el asunto tratado en el aprendizaje, que potencia la predisposición a buscar nuevas alternativas similares y factibles a lo acontecido.

Asunto a tratar

Antes

¿Qué se sabe sobre el asunto?

Durante

Posibles respuestas a las dudas.

Dudas que surgen sobre el asunto. Motivos de las dudas.

Después

Evaluación del conocimiento que has adquirido con argumentaciones y evidencias propias.

B

Asunto a tratar

Primer tratamiento del asunto

Aspectos que definen y describen el asunto tratado.

Alternativa

Aspectos y respuestas ALTERNATIVAS al asunto tratado.

Desarrollo del pensamiento

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

Cadena

Autoría/adaptación: Decroly, O. Adaptado por Calvo, J.;Mesa, R., y Quevedo, V.

Esta estrategia tendrá carácter individual y se hará una puesta en común con pequeños grupos o con el grupo clase.

Descripción: Esta técnica se centra en orientar la atención hacia la definición del asunto para, posteriormente identificar y analizar los elementos asociados (hitos vinculados entre sí) que dan significado completo a la situación que se plantea.

Acción: Componentes de esta técnica relacionados con el asunto de aprendizaje: asunto en cuestión, causa, procedencia, tiempo­cantidad, finalidad, agentes implicados, actitud­postura.

Observaciones: Los alumnos y las alumnas transfieren los procesos de pensamiento a distintas parcelas de una misma situación mediante tres tipos de ejercicios: de atención y definición (observación cognitiva), de asociación (en el tiempo, en el espacio…) y de expresión (lectura, escritura, cálculo, dibujo…).

Asunto en cuestión

Procedencia ¿De dónde?

Agentes implicados ¿Quiénes?

Causa ¿Por qué se origina?

Tiempo-cantidad ¿Cuándo? ¿Cómo?

Finalidad ¿Para qué?

Actitud y postura ¿Cómo actuar?

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

Esta estrategia tendrá carácter individual y se hará una puesta en común con pequeños grupos o con el grupo clase.

Autoría/adaptación: Hernández, P., y García, L.A. Adaptado por Escamilla, A.

Descripción: Esta técnica es una versión de la técnica ya estudiada «Rueda lógica». Se basa en el planteamiento de interrogantes claves que fuerzan al alumnado a buscar nueva información sobre el tema de aprendizaje a partir de los conocimientos que tiene de dicho tema.

Acción: La aplicación del diagrama en cascada requiere que el alumnado se cuestione lo siguiente en relación con el tema de aprendizaje:

1. Definición: ¿Qué o cómo es?

2. Argumentación: ¿Por qué?

3. Relación causa­efecto: ¿Qué lo provoca y qué origina?

4. Similitudes y diferencias con otros contextos: ¿A qué se parece y en qué se diferencia?

5. Relevancia: ¿Cómo nos afecta?

Observaciones: Esta técnica integra un tipo de esquema para la generación de ideas, sobre la base de interrogantes claves.

Asunto

Definición del asunto ¿Qué es?

Argumentación de lo definido

¿Por qué?

Relación causa-efecto

¿Qué la provoca y qué origina?

Similitudes y diferencias con otros contextos

¿A qué se parece y en qué se diferencia?

Relevancia en nuestro contexto

¿Cómo nos afecta?

Desarrollo del pensamiento

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

Efecto y alcance 34

Autoría/adaptación: Hernández, P., y García, L.A. Adaptado por Escamilla, A.

Descripción: Versión de la técnica «Consecuencias y resultados (CyR)». Esta técnica ayuda al alumnado a sistematizar el trabajo de reflexión sobre las consecuencias de los actos y sus repercusiones a corto, medio y largo plazo en diferentes contextos.

Acción: Los elementos de esta técnica son:

1. Identificación y definición de la situación.

Esta estrategia tendrá carácter individual y se hará una puesta en común con pequeños grupos o con el grupo clase.

2. Motivos y causas.

3. Efectos y alcance de consecuencias y plazos (sobre mí, los demás, el medio, el sistema…).

Observaciones: Esta técnica tiene un enorme potencial en su funcionalidad.

Identificación y definición de la situación o el asunto

Motivos-causas

Consecuencias y plazos

• Sobre mí, los demás, el medio, el sistema...

• Alcance y plazos de sus efectos.

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

Efecto y alcance doble 35

Autoría/adaptación: De Bono, E. Adaptado por Escamilla, A.

Esta estrategia tendrá carácter individual y se hará una puesta en común con pequeños grupos o con el grupo clase.

Descripción: Esta técnica es otra versión de «Consecuencias y resultados (CyR)». Facilita que el alumnado reflexione sobre las consecuencias de los actos y sus repercusiones entre dos situaciones afines, aunque con aspectos que las diferencian.

Acción: La puesta en práctica de esta técnica requiere espacio suficiente como para que visualmente se pueda ver el resultado de la comparación de las situaciones. En relación con su contenido, el alumnado deberá reflexionar sobre motivos que se cumplen en ambas situaciones y aquellos que son diferentes. A su vez, deberá pensar en las consecuencias de una u otra situación y el efecto o alcance de su puesta en práctica.

Observaciones:Esta técnica es una variante de la técnica anterior y la complementa. También se basa en la teoría de consecuencias y resultados (CyR).

Identificación y definición de la situación o el asunto 1.

Motivos-causas de la situación o el asunto 1.

Consecuencias (comparación)

• Sobre mí, los demás, el medio, el sistema...

Identificación y definición de la situación o el asunto 2.

Motivos-causas de la situación o el asunto 2.

• Alcance y plazos de sus efectos.

Desarrollo del pensamiento

DELPENSAMIENTO

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

Decálogo de intenciones 36

Autoría/adaptación: De Bono, E. Adaptado por Escamilla, A.

Esta estrategia tendrá carácter individual y se hará una puesta en común con pequeños grupos o con el grupo clase.

Descripción: Esta técnica fomentará en el alumnado su convencimiento al cambio ayudándole a identificar cómo le afecta la situación planteada y el beneficio ante ciertas decisiones y actuaciones al respecto.

Acción:El convencimiento de llevar a cabo un cambio se fomenta mediante el siguiente proceso, representado en el organizador A:

• Una interpretación y la conclusión a la que se llega sobre un asunto.

• Una reflexión sobre cómo afecta, a nivel personal, dicho asunto.

• Una reflexión crítica sobre qué se hace o qué se podría hacer para intervenir antedicho asunto.

• Una valoración sobre por qué se debe o se debiera intervenir ante dicho asunto.

Observaciones: La técnica se podría completar añadiendo cuestiones de síntesis como las que se muestran en el organizador B.

¿Qué he identificado y percibido del asunto?

¿Qué he sacado como conclusión sobre el asunto?

¿Cómo me afecta?

¿Qué puedo hacer en relación con el asunto?

¿Por qué debería hacerlo?

Palabra que elegiría para identificar el asunto.

Frase que elegiría para expresar cómo me afecta.

Reflexión que emplearía como conclusión para mostrar mis intenciones.

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO

ORGANIZADORES GRÁFICOS

TÉCNICAS DE METACOGNICIÓN

Tony Ryan (1990, 2014), en su libro Las llaves de los pensadores: Un potente programa para enseñar a los niños a convertirse en pensadores extraordinarios, nos habla de veinte llaves para el desarrollo del pensamiento. Ryan las clasifica según la esencia de la estrategia o proceso del pensamiento en:

• Llaves que fomentan el desarrollo del pensamiento crítico. Sirven para investigar, para la organización y programación personal, para el desarrollo de planes de acción, para la reflexión…

• Llaves que fomentan el desarrollo del pensamiento creativo. Se utilizan para generar nuevas ideas, para ampliar los límites de la creatividad personal, para modificar el punto de vista…

La mayoría de las llaves hacen hincapié en el desarrollo de la innovación y el pensamiento creativo debido a que este puede crear una actitud positiva hacia el aprendizaje, ya que aumenta el vínculo emocional con este y además porque si desarrollamos nuestro potencial creativo fortalecerá nuestra capacidad para hacer frente al cambio que será una de las grandes características del siglo xxi

Estas llaves de pensadores con algunas adaptaciones a nuestro contexto son:

Brainstorming o lluvia de ideas 1

Esta llave se debe a Alex Faickney Osborn, que en su búsqueda de ideas creativas se percató de que las mejores ideas y soluciones surgían cuando el trabajo lo realizaba un grupo de personas sin estructura jerarquizada, que permitía que todas ellas pudieran exponer sus ideas de forma libre y fueran tratadas de igual manera. No olvidemos que generar muchas ideas es un ejercicio mental que beneficia al cerebro.

Es una técnica de trabajo grupal, utilizada habitualmente para la generación de nuevas y originales ideas, para resolver una situación o simplemente generar ideas útiles para un tema de estudio o situación planteada. (Se suele empezar el planteamiento por: «¿Cómo…?», o «¿Qué harías…?»).

La imagen 2

Basado en las investigaciones que indican que el desarrollo de las capacidades de visualización mejorará el aprendizaje de cualquier tema de estudio. Se planteará al alumnado que observe un dibujo o imagen, no relacionado directamente con el tema o área de estudio y se les pide que establezcan posibles conexiones.

Usos diferentes 3

Es una estrategia divertida que desarrolla el pensamiento creativo al permitir que los pensamientos vayan más allá del ámbito de lo convencional y generen otros diferentes e inusuales.

Para ello, se pedirá al alumnado que, ante cualquier objeto cotidiano (una cuchara, una caja de cartón, un lápiz, etc.), ponga la imaginación a trabajar y haga una lista de todos los posibles usos que se le ocurran.

Las variaciones 4

Sobre cualquier tema se plantean preguntas que pueden comenzar con interrogantes como:

− ¿De cuántas maneras puedes…?

Por ejemplo: «¿De cuántas maneras puedes realizar un experimento, resolver un problema, contar un proceso, resumir una información…?».

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

La pregunta 5

Mediante esta estrategia se desarrolla el pensamiento crítico en el alumnado. Una nueva variante planteada en la edición de 2014 propone pensar en la pregunta más importante para el tema o unidad de trabajo que se está estudiando, que no pueda responderse con un «sí» o un «no». Debe ser una pregunta que desafíe al alumnado a pensar profundamente y a explorar lo realmente importante del tema de estudio. Por ejemplo: «¿Por qué es tan importante el agua en nuestras vidas?», «¿Qué ocurriría si no hubiese fotosíntesis?», «¿Podrías imaginar un mundo sin números?», «¿Y sin palabras?»...

6

Las desventajas y los incovenientes

Mediante esta llave o estrategia se fomenta el pensamiento crítico haciendo reflexionar al alumnado en la multitud de objetos o actividades cotidianas que podrían mejorarse. Para ello, se elegirá un objeto, una situación o una actividad y se pedirá al alumnado que haga una lista de desventajas y proponga alternativas para mejorarlo.

Las alternativas 7

En esta llave el profesorado presentará una tarea y el alumnado realizará una lista de formas de completarla sin usar los utensilios con los que habitualmente la realizamos. Por ejemplo, busca tres formas de:

– Calcular el volumen de agua de un día de lluvia.

– Pintar una pared.

– Escribir un mensaje.

Construimos 8

Esta llave trata de fomentar el pensamiento creativo de una forma práctica y divertida. Frente a una situación problemática intenta aplicar la estrategia de «Ver­planificar­hacer­verificar» y para ello plantea que el alumnado se enfrente a distintas situaciones de construcción utilizando los materiales que tenga a su alcance. Es decir, el profesorado planteará tareas de construcción utilizando materiales limitados, disponibles y al alcance en dicho momento; por ejemplo, construir el modelo de una molécula lo más compleja posible con pan, rotuladores y palillos.

La predicción 9

Mediante las actividades que se realicen a partir de esta llave, el alumnado se enfrentará a los cambios que le depare la vida con una mente mucho más abierta, no se sentirá abrumado ante ellos y sabrá ir incorporándolos con un pensamiento crítico.

Para ello, el profesorado planteará una situación y el alumnado formulará todas las predicciones que se le ocurran. Por ejemplo:

• Cómo serán los libros dentro de 200 años…

• Cómo nos alimentaremos en el futuro…

• Cómo viajaremos dentro de…

Estas miradas al futuro se pueden plantear desde tres perspectivas:

• Posibles futuros: Proponer posibilidades increíbles, fantásticas o incluso ridículas.

• Futuros probables: Describe qué es probable que suceda en el futuro.

• Futuros preferibles: Imagina qué futuro te gustaría que ocurriera realmente.

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

¿Qué pasaría si...? 10

Esta llave es muy interesante ya que genera muchas ideas innovadoras. Puede utilizarse para introducir un tema de estudio o para reflexionar sobre él una vez estudiado. Este puede ser cercano a la realidad o intrascendente.

Para ponerla en juego, el profesorado formularía un interrogante sobre el tema u objeto: «¿Qué pasaría si…?», «¿y si…?». El alumnado respondería a esta pregunta contemplando todas sus posibilidades o consecuencias. Para responder sería interesante construir una «Rueda de Ideas». Para ello, se sitúa la idea central en el círculo de dentro y se ponen al menos cinco respuestas o consecuencias. Posteriormente, se trabaja con cada una de las cinco respuestas y se colocan tres consecuencias de cada una de ellas en círculos más pequeños. Ejemplos:

• ¿Qué pasaría si no hubiese ecosistemas?

• ¿Qué pasaría si se acabara la gasolina?

• ¿Y si pudiésemos teletransportarnos?

• ¿Qué pasaría si no hubiese dinero?

Relaciones forzosas 11

Mediante esta estrategia se fomenta el pensamiento creativo ya que ante una situación o problema el alumnado desarrollará estrategias alternativas para su solución. Para llevarlo a cabo, el alumnado debe pensar posibles soluciones a un problema considerando los objetos dispares (3 o 4) que se le proponen. Por ejemplo, construir un ábaco con un tapón de corcho, dos cartones de leche, cincuenta gominolas y un paraguas.

Los inventos 12

Esta clave potencia el pensamiento creativo y alienta al alumnado a desarrollar una invención innovadora que pueda usarse en la vida cotidiana. Lo ideal es que el alumnado previamente planifique lo que quiere realizar y comience dibujándolo y, posteriormente, intente construirlo realmente. Un desafío añadido podría consistir en que lo realizara utilizando objetos reciclados.

La inversa

Mediante esta llave se pretende ir formando en el alumnado el pensamiento, tanto crítico como creativo, ante las situaciones que se le presenten y que no siempre se deje llevar por el pensamiento previamente establecido.

Para ello, se le solicitará que elabore una lista de hechos con respecto al tema dado que no se puedan hacer o que nunca puedan ocurrir, mediante frases que empiecen por: «No se puede…» «Nunca…» «No he…».

Otra versión puede ser formular preguntas opuestas a las que podrían hacerse sobre el tema objeto de estudio. Ejemplo: «¿Cómo podemos llevar una alimentación completa y saludable?». Inversa: «¿Cómo podemos llevar una alimentación poco saludable e incompleta?».

Lo común 14

Estrategia ideal para ideas creativas y el desarrollo de conceptos inusuales. Para poner en práctica esta llave, presentaremos al alumnado dos objetos que no tengan nada en común y les pediremos mediante una lluvia de ideas que intenten buscar puntos de unión entre ellos. Por ejemplo, una flor y un libro: ambos nos traen recuerdos, ambos pueden ser un buen regalo, etc.

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

Ridículo 15

Se plantea una frase ridícula, absurda, sin sentido y se pide a los alumnos y a las alumnas que intenten hacerla realidad argumentándola y justificándola. Debemos recordar que muchas ideas excelentes se quedaron sin desarrollar debido a que se consideraron «ridículas» o que «no eran factibles», sin haberlo intentado. Por ejemplo: «En breve nos desplazaremos en coches voladores que funcionen con energía solar».

Justificación:

• Se evitaría la contaminación.

• No habría atascos.

• Se crearían edificios para poderlos aparcar.

• Existiría un nuevo modo de conducir con nuevas reglas.

• Se investigaría para mejorar su capacidad y potencia.

• Los peatones y las bicicletas podrían circular con mayor libertad por las ciudades.

Interpretamos 16

Describe tres posibles explicaciones sobre una situación poco corriente o inusual. Se pide al alumnado que piense en diferentes explicaciones o posibilidades para la existencia de esa situación. Es una actividad que fomenta el pensamiento innovador que desarrolla la capacidad de considerar una amplia gama de explicaciones o consecuencias sobre un determinado hecho o situación. Por ejemplo: Nuestra directora del centro viene todos los días con unas medias azules chillonas, ¿a qué crees que se debe?

• No tiene tiempo de comprarse medias y trae las de su hermana, que es actriz de circo.

• Lo hace como reivindicación del valor de la mujer en la sociedad.

El alfabeto 17

Con la aplicación de esta llave se intenta que el alumnado genere ideas nuevas a partir de las palabras obtenidas de una lista, de la A a la Z, que traten el tema que se está trabajando. Si el alumnado deja en blanco alguna letra en particular, simplemente se continúa y se vuelve a esa letra más adelante. En una versión más simplificada, se pide que enumere los objetos individuales de la A a la Z. Por ejemplo, si el tema es «accidentes geográficos de España», una posible lista sería:

A: Arousa: Asocia este nombre a un tipo de accidente geográfico.

B: Baleares: Escribe el nombre de las islas que componen este archipiélago. … y así sucesivamente.

La combinación 18

La creación de muchos objetos de nuestra vida cotidiana ha surgido de la combinación de dos objetos totalmente diferentes. El uso de esta llave nos ayuda a desarrollar algunos de esos nuevos productos por parte de nuestro alumnado. Para ello, colocaremos en una tabla de doble entrada algunos objetos en la parte superior y otros nombres de objetos en la parte lateral. A partir de la combinación entre ellos crearemos objetos completamente nuevos.

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

Partimos de una situación planteada que no puede ser cuestionada y se solicitan alternativas para romper el muro que nos impide alcanzarlo. Esta llave alienta a buscar cuáles son los muros de ladrillo que se interponen en el camino. No debemos dejarnos vencer por dichos muros al primer intento, sino que debemos buscar estrategias alternativas para vencerlos. Por ejemplo: Unos agricultores necesitan agua para sus cultivos, pero para llevar agua desde el río se necesitan 50 000 €. ¿Cómo podemos ayudar a conseguirlos?

Alternativas: Tras una primera lluvia de ideas, se seleccionarán aquellas que se consideren más viables. Por ejemplo:

• Escribir a las distintas instituciones, locales, provinciales, autonómicas o nacionales, contándoles el problema y solicitándoles una colaboración económica.

• Hacer una fiesta, invitando a personas conocidas para que colaboren desinteresadamente.

MAC

Es una estrategia práctica para reinventar o rediseñar objetos cotidianos. Este tipo de estrategia se usa hoy en día para crear nuevos productos para el mercado. Para ello, siguiendo el acrónimo (M: mayor, A: añadir, C: cambiar/quitar) reinventa o diseña objetos cotidianos.

La escalera de palabras es:

− Mayor/grande. (Haz una parte del objeto más grande o más importante en términos de uso).

− Añade/reinventa. (Añádele una parte extra a tu objeto).

− Cambia o quita. (Elimina una parte y/o reemplázala por otra).

El muro de ladrillos 19

Desarrollo del pensamiento

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

Un aspecto importante en el desarrollo del pensamiento del alumnado es el proceso de reflexión que debe llevar a cabo acerca de los nuevos aprendizajes que ha realizado y las relaciones existentes entre ellos, así como el nuevo vocabulario que ha aprendido y ha incorporado a su mochila de conocimiento. Además, reflexionar sobre los conocimientos adquiridos facilitará el intercambio de ideas y la conformación de significados compartidos con el resto de sus compañeros y compañeras. El conocimiento sobre el proceso del propio aprendizaje implica que el alumnado es capaz de tomar conciencia del funcionamiento de su manera de aprender y comprender por qué los resultados de una actividad puede utilizarlos en otras situaciones de su vida cotidiana. Para este proceso es conveniente utilizar «organizadores gráficos» que le ayuden a estructurar y a organizar los nuevos conocimientos. Entre ellos cabe señalar:

1. Mapas conceptuales

2. Mapas mentales

3. Diagrama jerárquico

4. Cadena de secuencias

5. Rueda de atributos

6. Esquema

7. Tablas

8. Línea del tiempo

9. Diagrama de Venn

10. Resolución de problemas y toma de decisiones

11. Diagrama causa-efecto o diagrama de Ishikawa

12. Mapa de flujo

Mapas conceptuales 1

Los mapas conceptuales son herramientas gráficas para la organización y la representación del conocimiento que nos permiten organizar y comprender ideas de manera significativa. Igualmente nos permite presentar la información de una forma gráfica en la que de un solo golpe de vista se pueda ver la estructura cognitiva del contenido objeto de aprendizaje.

De acuerdo con Novak (1988), los elementos básicos de un mapa conceptual son:

1. Los conceptos: se refieren a objetos, situaciones o hechos y suelen representarse dentro de figuras geométricas.

Los conceptos deben ser presentados de forma organizada y jerárquica, de manera que existan relaciones entre los más significativos. Todos deben partir del concepto más inclusivo que debe dar respuesta al objetivo de aprendizaje.

2. Líneas conectoras o de unión: se utilizan para unir los conceptos. Estas líneas conectoras no son suficientes para determinar la relación existente entre los conceptos y por ello suelen acompañarse de palabras de enlace que determinan la jerarquía conceptual y especifican la relación entre aquellos.

3. Las palabras de enlace: normalmente están conformadas por verbos y expresan la relación que existe entre dos o más de ellos.

4. Las proposiciones: están compuestas por la unión de uno o varios conceptos o términos que se relacionan entre sí, a través de una palabra de enlace. Estas deben formar oraciones con sentido propio y no deben necesitar otras proposiciones para tener coherencia.

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

Características de los mapas conceptuales

Para el alumnado:

1. Permiten una rápida visualización de los contenidos de aprendizaje.

2. Facilitan detectar rápidamente los conceptos clave de un tema de aprendizaje.

3. Favorecen el recuerdo y el aprendizaje de una forma organizada y jerarquizada.

4. Permiten la evaluación de lo aprendido si se parte de un mapa conceptual de lo conocido sobre el tema (conocimientos previos) y se completa con lo aprendido. El alumnado, de este modo, hace visible su aprendizaje.

5. Sirven de modelo para que el alumnado aprenda a organizar, jerarquizar o elaborar mapas conceptuales de otros temas o contenidos de aprendizaje.

Para el profesorado, le será útil en:

1. La presentación del tema.

2. Establecer las relaciones entre las ideas principales y las secundarias, favoreciendo la comprensión por parte del alumnado.

3. Facilitar al alumnado la visión global y una síntesis al final de la unidad de aprendizaje.

Estructura jerárquica de un mapa conceptual

Los mapas conceptuales organizan los conceptos de una forma jerárquica, a la que llamaremos niveles, desde un concepto más general a otros de carácter más secundario.

Además de estos niveles, con objeto de acercarnos al alumnado podemos trabajar los distintos niveles de la estructura jerárquica a través de texto, con imágenes o mediante la combinación de imágenes y texto.

Desarrollo del pensamiento

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

Tipos de mapas conceptuales:

1.1 Mapa conceptual de araña

Este tipo de mapa conceptual muestra el tema central o núcleo justo en el centro de la estructura y, alrededor de este, las ideas o conceptos de menor jerarquía. La imagen que forma se asemeja a una araña. Es muy similar a la rueda de atributos que veremos más adelante.

Concepto secundario 1

Dato 1

Dato 2

Concepto principal

Dato 1

Dato 2

Concepto secundario 4

1.2. Mapa conceptual jerárquico

Concepto secundario 2

Dato 1

Dato 2

Dato 1

Dato 2

Concepto secundario 3

Parte de un concepto principal que se situará en la parte superior. De él se desprenden en forma descendente el resto de conceptos o ideas, en función del grado de importancia o jerarquía de estos. Cuando dos conceptos tienen la misma importancia, quedarán a la misma altura. Tiene aspectos muy similares al diagrama jerárquico que veremos más adelante.

Concepto principal

palabras de enlace

Concepto secundario de primer nivel 1

Concepto secundario de primer nivel 2

palabras de enlace palabras de enlace

Concepto secundario de segundo nivel 1

Concepto secundario de segundo nivel 2

Concepto secundario de segundo nivel 3

Concepto secundario de primer nivel 3

palabras de enlace

Concepto secundario de segundo nivel 4

Concepto secundario de segundo nivel 6

Concepto secundario de segundo nivel 5

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS

Tipos de mapas conceptuales:

1.3 Mapa conceptual organigrama

TÉCNICAS DE METACOGNICIÓN

En este tipo de mapa conceptual, la información se presenta como si fuese la estructura de una organización con su jerarquía, aunque también puede ser aplicado a cualquier otro concepto. Los mapas conceptuales de organigrama según su forma pueden ser:

– Verticales (en cuyo caso son similares a los de tipo jerárquico).

Grupo

Subgrupo A

Subgrupo C Subgrupo B

Pueden ser Se clasifican por Se clasifican por

Sub Subgrupo A1

Sub Subgrupo A2

– Horizontales (en los que la jerarquía va de izquierda a derecha). Estructura

Pueden ser

– Radiales o circulares.

Sub Subgrupo C1

Sub Subgrupo C2

Sub Subgrupo C3

Subparte A1

Parte A Parte B

Se clasifican en Se clasifican en Se clasifican en

Subparte A2

Subparte B1

Subparte B2

Subparte C1

Parte C

Subparte C2

Ejemplo Ejemplo

Subsubgrupo A1

Subsubgrupo B4

Ejemplo

Grupo Sub sub grupo A2

Subgrupo

Subsub grupo B3

Ejemplo

Ejemplo

Sub sub grupo A3

Subgrupo

Subsubgrupo A4

Ejemplo

Subsub grupo B2

Subsubgrupo B1

Ejemplo

Ejemplo

Desarrollo del pensamiento

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

– Piramidales.

Tipos de mapas conceptuales:

1.4 Mapa conceptual de araña

En este tipo de mapa conceptual, la información se distribuye de tal forma que las ideas pueden ser ampliadas e incluso relacionarse entre ellas.

1.5. Mapa conceptual de paisaje

Su representación tiene como base un espacio real o ficticio en el que se muestra la información esencial organizada en torno a la imagen real o que se quiere formar y que refuerza el mensaje que se quiere transmitir.

Concepto esencial 1

Concepto esencial 3

Concepto esencial 4

Concepto esencial 2

Los mapas mentales son una forma de organizar la información, en la que el tema principal se coloca en el centro y los puntos secundarios irradian desde este añadiendo información. Esto nos posibilita aprender de una forma integrada y organizada. Son además muy útiles para almacenar datos y fomentar la creatividad y la memoria, ya que, del mismo modo que los mapas conceptuales, ayudan a ordenar y estructurar el pensamiento.

Los mapas mentales exploran todas las posibilidades creativas de un tema, desarrollan la imaginación, la asociación de ideas y la flexibilidad (podemos enriquecerlos con imágenes, colores, códigos personales, etc.), incrementando así la complejidad y el poder de la memoria (Buzan, T., y Buzan, B. 1996).

LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS ideade menor secundaria(2) Idea Idea secundaria(1) Idea Idea secundaria(4) secundaria (3 )

La definición dada por Tony Buzan es la siguiente:

«... un mapa mental consiste de una palabra o idea principal; alrededor de esta palabra, se asocian 5­10 ideas principales relacionadas con este término. De nuevo se toma cada una de estas palabras y a esa se asocian 5­10 palabras principales relacionadas con cada uno de estos términos. A cada una de estas ideas descendientes se pueden asociar tantas otras».

mentales Imagen Imagen

2 importacia importacia importacia i m tropica a i m tropica a

Imagen Imagen Imagen Imagen Imagen edaedi ronem aedi d e onem r

aedi d e onem r i dea de menor i dea de menor idea demenor

tropmi icna a imp ortancia imp ortancia importancia Imagen Imagen

TÉCNICAS DE PENSAMIENTO idea de menor idea de meno r i d ae d e ronem i d ae d e ronem

icnatropmi a tropmi icna a

Imagen Imagen Imagen Imagen Imagen Imagen

El mapa mental tiene cuatro características esenciales; a saber:

4. Las ramas forman una estructura nodal conectada.

2. Los principales temas de asunto irradian de la imagen central en forma ramificada.

3. Las ramas comprenden una imagen o una palabra clave impresa sobre una línea asociada. Los puntos de menor importancia también están representados como ramas adheridas a las ramas de nivel superior.

Aunado a estas características, los mapas mentales se pueden mejorar y enriquecer con colores, imágenes, códigos y dimensiones que les añadan interés, belleza e individualidad, fomentándose la creatividad, la memoria y la evocación de la información.

Desarrollo del pensamiento

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

Diagrama jerárquico 3

Como su nombre indica, muestra las relaciones de ordenación y subordinación entre las ideas de un campo semántico. Los datos de un mapa conceptual pueden transferirse a un diagrama jerárquico. Solo se diferenciarían en el sentido de que estos no precisan de las palabras enlace para conectarlos.

Concepto principal

Concepto secundario de primer nivel 1

CS de segundo nivel 1

CS de segundo nivel 2

Concepto secundario de primer nivel 2

Concepto secundario de primer nivel 3

CS de segundo nivel 1

CS de segundo nivel 1

CS de segundo nivel 2

CS de segundo nivel 3

Cadena de secuencias 4

La cadena de secuencias es un instrumento útil para representar cualquier serie de eventos que ocurren en un orden cronológico o para mostrar las fases de un proceso.

Hecho o fase 5

Hecho o fase 1

Hecho o fase 2

Hecho o fase 4

Hecho o fase 3

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

Rueda de atributos 5

Esta estrategia organizativa provee una representación visual del pensamiento analítico, dado que invita a profundizar en las características de un objeto determinado. Se establecerán las características o atributos principales en los rayos de la rueda sin orden de jerarquía, de forma que puedan ser leídos en cualquier dirección.

Atributo 1

Atributo 2

Atributo 5

Atributo 4

Atributo 3

Desarrollo del pensamiento

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

Esquemas 6

Un esquema es la representación simplificada de una realidad compleja. Su uso ayuda a comprender, a memorizar y a jerarquizar los elementos que la integran, engranándolos entre sí mediante vínculos conceptuales. Es una síntesis lógica y gráfica, que señala relaciones y dependencias entre ideas principales y secundarias.

Tipos de esquemas fundamentales:

6.1 Lineal:

• numeros: • letras: • con símbolos:

1. Idea principal 1

1.1 Idea secundaria 1

1.1.1 Detalle 1

1.1.2 Detalle 2

1.2 Idea secundaria 2

1.2.1 Detalle 1

2. Idea principal 2

6.2

Gráfico o de llaves

Idea principal 1

A. Idea principal A

A.a Idea secundaria a

A.a.a Detalle a

A.a.b Detalle b

A.b Idea secundaria b

B. Idea principal B

Idea secundaria 1

TEMA

– Idea principal

Idea secundaria

• Detalle

• Detalle

– Idea principal

Idea secundaria

Título

Idea principal 2

6.3 Esquema:

Título

Idea principal 1

Idea secundaria 2

Detalle 2

Idea secundaria 3 Detalle 1

Detalle 3

Idea secundaria 1

Idea secundaria 2

Detalle 2

• de flechas: • de barras:

Idea secundaria 1

Idea secundaria 2

Idea secundaria 3

Idea secundaria 1

Idea secundaria 1

Detalle 1

Detalle 2

Idea principal 2

Idea secundaria 2

Detalle 2

Detalle 3

Detalle 1 Detalle 1

Idea principal 1

Idea principal 2

Idea secundaria 2

Idea secundaria 1

Idea secundaria 2

Detalle 3

Detalle 1

Detalle 2

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

Tablas 7

Son uno de los organizadores gráficos más utilizados cuya función principal es identificar o exponer las características, diferencias o similitudes entre dos o más temas.

A veces son muy simples y, de hecho, son un esquema o cuadro sinóptico presentado en forma de tabla donde se presenta la información sobre algunos contenidos de forma jerárquica. Resulta muy visual ya que presenta globalmente los principales elementos de un determinado tema:

Tema general

Elemento principal 1 Elemento principal 2 Elemento principal 3

Detalles:

(Podría tener más niveles)

No obstante, las tablas más conocidas y utilizadas son las de doble entrada. Están formadas por un número determinado de columnas en forma vertical, en función de los elementos o temas que se desean exponer o comparar y tendrá tantas filas como características queramos presentar de cada uno de los elementos o temas.

Tema de estudio

Elemento 1Elemento 2Elemento 3Elemento 4Elemento 5Elemento 6

Característica 1

Característica 2

Característica 3

Característica…

Ejemplo:

Intención comunicativa

Muy usado en Tipo de lenguaje …

Tipo de texto

NarrativoDescriptivoExpositivoArgumentativoDialogadoPoético

Las tablas también pueden utilizarse como cuadro resumen organizando toda la información tratada en un determinado tema. Ejemplo:

Climas de España

OceánicoMediterráneoDe alta montañaSubtropical

Localización

Temperaturas

Precipitaciones

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS

Línea del tiempo 8

Son uno de los organizadores gráficos más utilizados cuya función principal es identificar o exponer las características, diferencias o similitudes entre dos o más temas.

A veces son muy simples y, de hecho, son un esquema o cuadro sinóptico presentado en forma de tabla donde se presenta la información sobre algunos contenidos de forma jerárquica. Resulta muy visual ya que presenta globalmente los principales elementos de un determinado tema:

Hecho ⊥ (suceso... que se da en 1.er lugar)

Hecho ❏ (suceso... que se da en 3.er lugar)

Hecho ✸ (suceso... que se da en 5.o lugar)

Hecho ↕ (suceso... que se da en 7.o lugar)

TÉCNICAS DE METACOGNICIÓN

Hecho ↔ (suceso... que se da en 2.o lugar)

Hecho ☛ (suceso... que se da en 4.o lugar)

Hecho # (suceso... que se da en 6.o lugar

Hecho ● (suceso... que se da en 8.o lugar)

final

Diagrama de Venn 9

Muy útil para hallar semejanzas y diferencias entre dos conceptos, ideas o informaciones. El área en que confluyen indica la existencia de un subconjunto que tiene características que son comunes a ellas; en el área restante, propia de cada figura, se ubican los elementos que pertenecen únicamente a esta. Se puede trabajar con dos o más círculos.

A B

Características exclusivas de A

Características en común de A y B

A

Características exclusivas de A

B

Características en común de A y B

Características exclusivas de B

Características en común de A, B y C

Características en común de A y C

Características exclusivas de B

Características en común de B y C

Fecha inicial Fecha

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

Resolución de problema y toma de decisiones 10

Dotar a nuestro alumnado de un pensamiento crítico y eficaz requiere de estrategias de pensamiento que le ayuden a enfrentarse a las situaciones problemáticas que se le presentan sistemáticamente y que le asistan para tomar la mejor solución posible en un contexto determinado. Conocer estas estrategias contribuirán a juzgar y evaluar situaciones desde la comprensión y el análisis de la información y los datos que se poseen, proponer diversas soluciones, valorando en cada una de ellas los aspectos positivos, negativos y secundarios o colaterales, y elegir la solución más adecuada de forma razonada.

Propuesta/Solución 1

• Aspectos positivos

• Aspectos negativos

• Efectos secundarios o colaterales

Propuesta/Solución 2

• Aspectos positivos

• Aspectos negativos

• Efectos secundarios o colaterales

Análisis de información

Situaciónproblema

Propuesta/Solución 4

• Aspectos positivos

• Aspectos negativos

• Efectos secundarios o colaterales

Propuesta/Solución 3

• Aspectos positivos

• Aspectos negativos

• Efectos secundarios o colaterales

Pasos a seguir en la resolución de un problema o toma de decisiones:

1. Identificar el problema o situación a estudiar.

2. Análisis de la información y los datos que poseemos: circunstancias, causas, personas implicadas…

3. Posibles soluciones o propuestas, analizando en cada una de ellas, sus aspectos positivos y negativos, posibles efectos secundarios o colaterales, etc.

4. Solución o decisión adoptada justificando las razones que nos han llevado a esta.

SOLUCIÓN/

Desarrollo del pensamiento

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

11

Diagrama causa-efecto o diagrama de Ishikawa

El diagrama causa­efecto es una forma de organizar y representar las diferentes teorías propuestas sobre las causas de un problema. También se conoce como «diagrama espina de pescado» por su forma similar al esqueleto de un pez. Este organizador gráfico resulta apropiado cuando el objetivo de aprendizaje busca que el alumnado piense tanto en las causas reales o potenciales de un suceso o problema como en las relaciones causales entre dos o más fenómenos.

Mediante la elaboración de diagramas causa­efecto es posible generar dinámicas de clase que favorezcan el análisis, la discusión grupal y la aplicación de conocimientos a diferentes situaciones o problemas, de manera que cada equipo de trabajo pueda ampliar su comprensión del problema, visualizar razones, motivos o factores principales y secundarios de este, identificar posibles soluciones, tomar decisiones y organizar planes de acción.

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO

Mapa de flujo 12

Este tipo de representación facilita el entendimiento de secuencias paso a paso, así como la toma de decisiones autónomas por parte del alumnado. Esta estrategia permite prever en diferentes situaciones los pasos a dar, así como sus antecedentes y sus consecuencias. Para ello, parte del planteamiento de preguntas y la observación de las consecuencias que tiene la elección de una u otra respuesta.

Para la correcta aplicación de esta técnica, se recomienda la asignación de símbolos:

ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

– RECTÁNGULO: Situación o hecho que ocurre.

– ROMBO: Contiene una pregunta que implica una toma de decisiones.

– CÍRCULO: Plantea las alternativas de respuesta de forma dicotómica.

– FLECHAS: Indican el sentido en el que se conectan los procesos descritos.

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

Rúbrica 1

Descripción: Las rúbricas permiten al alumnado tomar conciencia de los niveles de logro alcanzados tras la ejecución de sus tareas, y le pueden resultar de gran ayuda en su proceso de aprendizaje:

• Le proporcionan una visión integrada de los conocimientos y de las capacidades que deberá poner en juego para realizar las tareas y, por tanto, le ayudan a comprenderlas y a razonar cómo llevarlas a cabo.

• Le anticipan los criterios que aplicará su profesora o su profesor para evaluarle. Por ello, analizarlas y conocer esos criterios, antes de iniciar las tareas, le permitirá llevarlas a cabo teniéndolos en cuenta, y entregar sus trabajos revisados de acuerdo con ellos.

• Le servirán para reflexionar sobre cómo evoluciona su aprendizaje si se autoevalúa con la mis­

ma rúbrica cada vez que repite un determinado tipo de tarea y compara los resultados que obtiene con los que obtuvo anteriormente para así comprobar su progreso en la ejecución de esa tarea y detectar los aspectos en los que más le cuesta progresar.

Acción: Tomando como referente las categorías que definen el contexto de aplicación de lo aprendido, se recogerán en la rúbrica los descriptores observables y medibles para conocer y valorar el grado de logro de los problemas planteados.

Observaciones: También se puede emplear esta técnica para que el alumnado revise el proceso que ha guiado su aprendizaje (ejecución de su pensamiento); si se integra en ella la valoración de las técnicas con las que se ha trabajado, con la reflexión sobre para qué le han servido con relación a los logros alcanzados.

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO

Diana 2

Descripción: Es un método visual, de rápida ejecución y muy versátil, que permite conocer la opinión del alumnado sobre cualquier aspecto del proceso de enseñanza­aprendizaje (las propias actividades del proyecto, el trabajo de equipo o individual, el trabajo del profesorado…). Puede ser una herramienta muy motivadora utilizada para evaluar aspectos que sepamos que van a mejorar con el tiempo, en cuyo caso, la diana se convierte en una «aliada», en algo positivo, ya que muestra al alumnado su progreso, aquellas cosas que está aprendiendo individualmente o en equipo.

Acción: Se dibuja una diana trazando círculos concéntricos y cortándolos por radios que los dividan en porciones. Los radios representarán los aspectos de las tareas que se vayan a evaluar; y cada círculo con­

ORGANIZADORES GRÁFICOS

TÉCNICAS DE METACOGNICIÓN

céntrico de la diana, uno de los distintos niveles de calidad en los que se puede escalonar el logro de cada uno de esos aspectos. Al contrario de lo que ocurre en las dianas del juego de dardos, el círculo central es el de menor puntuación, es decir, el de menor nivel de logro, y el más externo, el de mayor puntuación o nivel de logro. Para utilizar la diana, se marca con una cruz la intersección del radio con el círculo que corresponda al nivel de logro alcanzado. Al unir los puntos correspondientes a todos los aspectos evaluados, se obtiene un polígono que aumenta de tamaño a medida que se progresa en la ejecución de esa tarea.

Observaciones: Permite comparar fácilmente los resultados en dos momentos diferentes del aprendizaje y favorece que el alumnado puede aportar y compartir su evaluación.

La escala de la diana es la misma que la de la rúbrica:

4. Siempre.

3. Habitualmente.

2. A veces.

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

Lista de verificación 3

Esta estrategia tendrá carácter individual y se hará una puesta en común con pequeños grupos o con el grupo clase.

Descripción: Esta técnica ayuda a la autoevaluación y a la autorregulación del propio aprendizaje. Sistematiza el proceso de revisión de los pasos que se han seguido, ayudando al alumnado a tomar conciencia de las técnicas con las que se ha trabajado y, por tanto, del tipo de pensamiento que ha llevado a cabo.

Acción: Los alumnos y las alumnas deberán marcar en una lista una X en la casilla que concuerde con las técnicas empleadas y puestas en marcha en un determinado tema de aprendizaje.

Observaciones: Si a esta técnica se le añaden columnas que hagan referencia a cómo nos han ayudado las técnicas aplicadas, esta lista de verificación se convertirá en una lista de verificación y reflexión.

ASUNTO O TEMA TRATADO

Estrategias empleadas

Estrategia 1

Estrategia 2

Estrategia 3

Estrategia 4

Estrategia 5

Estrategia de pensamiento Técnica cooperativa

A localizar, comprender ...

Me ha ayudado

A interpretar, analizar ... A reflexionar, valorar ...

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

Línea de avance 4

Esta estrategia tendrá carácter individual y se hará una puesta en común con pequeños grupos o con el grupo clase.

Descripción: Esta técnica facilita que el alumnado tome conciencia de su postura ante un determinado asunto, haciéndole reflexionar sobre lo que podría hacer para profundizar más en dicho asunto y cómo afrontarlo con vistas a cambiar su postura en el futuro.

Acción: Consiste en un autorregistro de lo sucedido en diferentes fases de pensamiento (mi disposición ante el tema antes, mi disposición ahora…).

Observaciones: Una variante de esta técnica introduce los conocimientos previos que tenía el alumnado sobre el tema frente a los conocimientos finales, así como los efectos de dichos aprendizajes en nuestra vida cotidiana. Dado que esta técnica resulta más completa y permite una mayor profundización, conciencia de aprendizaje y reflexión sobre él, se recomienda la utilización de esta variable cuya estructura es la siguiente.

¿Qué sabía sobre el tema?

¿Qué sé AHORA sobre el tema?

Aprendo mejor cuando…

¿Qué es lo que más me ha costado aprender?

Para qué me ha servido o me puede servir lo aprendido.

DELPENSAMIENTO

TÉCNICAS DE PENSAMIENTO LLAVES DE PENSAMIENTO ORGANIZADORES GRÁFICOS TÉCNICAS DE METACOGNICIÓN

Balance de conocimiento 5

Esta estrategia tendrá carácter individual y se hará una puesta en común con pequeños grupos o con el grupo clase.

Descripción: Esta técnica permite, mediante una sencilla tabla comparativa, que el alumnado realice una síntesis sobre lo trabajado y aprendido, tomando conciencia de los pasos seguidos para dar respuesta a las situaciones planteadas, así como la valoración de las técnicas empleadas y la reflexión sobre su utilidad.

Acción: En un organizador como en el de la imagen A, el alumnado deberá destacar los aspectos positivos de lo trabajado y los motivos, así como los aspectos negativos del tema trabajado y los motivos o argumentos que le hacen llegar a esa conclusión.

Observaciones: Una variante de esta técnica se plantea cuando pretendemos que el alumnado revise y sistematice el proceso que ha elegido como guía para la adecuada ejecución y su aprendizaje. En ese caso, se empleará un organizador como el de la imagen B.

Aspectos positivos de lo trabajado y aprendido

Aspectos negativos de lo trabajado y aprendido

Motivo:

Motivo:

Conciencia emocional

Educación emocional

1.º Primaria

2.º Primaria Activos Activos

• Identificar las emociones agradables y las desagradables.

• Identificar/reconocer las emociones básicas.

• Tomar conciencia de las emociones y compartirlas.

• Comprender las diferencias físicas y emocionales de las personas.

• Reconocer la emoción de la sorpresa.

• Reconocer la emoción del miedo y saber que todos lo podemos padecer.

• Aprendo a controlar la impulsividad (la rabia…).

• Sentir y pensar: hecho (cuando…) ➞ sentimiento (siento…) ➞ pensamiento (pienso…) ➞ consecuencia (¿qué hago?).

Regulación emocional

• Crear conciencia de la necesidad de gestionar las emociones.

• Crear el hábito de la atención plena y reforzar la comprensión.

• Practicar la relajación y conseguir sensaciones de calma.

• Recordar consignas de autocontrol.

• Aprender a sentir el silencio y encontrar momentos de calma.

• Aceptar la tristeza como una emoción más.

• Identificar emociones positivas cuando se realiza una actividad.

• Aceptar las características personales.

• Valorarnos positivamente y con mesura.

Autonomía y auoestima

• Ser conscientes de nuestros gustos y respetar los de los demás.

• Valorar las cualidades de las otras personas y ser agradecidos.

• Promover el liderazgo.

• Identificar qué sabe hacer cada uno y aprender a aceptar ayuda.

• Potenciar y valorar las conductas de ayuda.

• Aprender a valorar la convivencia con otras personas.

• Practicar la atención para escuchar y comprender lo que dicen los demás.

Competencia social

• Aprender estrategias para resolver problemas de manera satisfactoria.

• Introducir el concepto empatía.

• Aprender a identificar y a expresar las emociones.

• Identificar las emociones a partir del descubrimiento de uno mismo.

• Tomar conciencia de los momentos en que sentimos alegría y tristeza.

• Identificar y expresar la emoción del cariño.

• Reconocer, aceptar y compartir el miedo.

• Identificar la emoción de los celos y aprender a controlarla.

• Regular la rabia y la tristeza ante la burla.

• Regular el sentido del humor y aprender a no reírse de los demás.

• Sentir, valorar y buscar momentos de silencio.

• Aprender estrategias de relajación para mejorar la concentración.

• Emoción ➞ causa ➞ respuesta (¿qué respuesta? ➞ impulsiva/apropiada/adoptada) ➞ consecuencia.

• Visualizar emociones positivas en hechos imaginados reales (sacar un 10, hacer un viaje, recibir un regalo)…

• Experimentar emociones positivas en la realización de una actividad.

• Aprender a valorar la belleza interior.

• Identificar, reconocer y aceptar la propia identidad.

• Reconocer el esfuerzo como una cualidad positiva y necesaria.

• Adquirir vocabulario sobre las cualidades y las diferencias personales.

• Tomar conciencia de toda la gente que nos quiere.

• Practicar situaciones que ayuden a ponerse en el lugar del otro (empatía).

• Aprender la diferencia entre dar instrucciones y mandar.

• Saber hacer un elogio sincero y recibirlo con gratitud (asertividad).

• Potenciar los elogios y el saber decir cosas agradables a los demás (asertividad).

• Practicar la cooperación y aprender a ayudar y a dejarse ayudar.

• Aprender a definir y a valorar la amistad.

• Recordar que no estamos solos en el mundo y que hacen falta reglas de convivencia.

• Conocer las consignas para resolver conflictos.

Competencia de la vida y el bienestar

• Potenciar la imaginación.

• Sentirse parte de la familia y ser conscientes del apoyo familiar.

• Sentirse parte del colegio y ser conscientes del apoyo escolar.

• Adquirir recursos para mejorar el estado de ánimo.

• Descubrir el valor de las emociones estéticas (música, arte, literatura…) en la gestión emocional.

• Entender las emociones como un proceso variable y regulable.

• Recordar buenos momentos para mejorar el estado de ánimo.

• Valorar y fomentar los buenos momentos pasados en familia.

• Comprender la relación entre emoción, pensamiento y actuación.

Conciencia emocional

3.º Primaria 4º Primaria Activos Activos

• Renocer e identificar las emociones básicas en uno mismo y en los demás.

• Tomar conciencia de las cualidades y de los defectos propios.

• Reconocerse a uno mismo y aprender a aceptarse.

• Identificar los cambios y las dinámicas emocionales.

• Reconocer la emoción de la rabia, el estrés o la ansiedad y aprender estrategias de autocontrol.

• Tomar conciencia de los sentidos y potenciar la imaginación.

Regulación emocional

• Aprender a tener control corporal y verbal.

• Entrenar la atención para mejorar la comunicación.

• Aplicar la atención consciente con la práctica del silencio.

• Practicar el pensamiento causal y consecuencial de las emociones.

• Sentir y pensar: hecho (cuando…) ➞ sentimiento (siento…) ➞ pensamiento (pienso…) ➞ consecuencia (¿qué hago?).

• Generar emociones positivas cuando se realiza una actividad.

• Adquirir vocabulario sobre las cualidades y reflexionar sobre las diferencias.

• Potenciar las habilidades personales, aceptando la ayuda.

• Descubrir la opinión que se tiene de uno mismo y reforzar el autoconcepto.

• Diferenciar entre ser orgulloso y estar orgulloso de sí mismo.

• Reconocer e identificar las emociones básicas.

• Expresar emociones.

• Reconocer las emociones en los demás.

• Aprender a conocerse uno mismo.

• Relacionar emociones con pensamientos y acontecimientos.

• Identificar y ser conscientes de nuestros estados de ánimo y canalizarlos.

• Generar emociones positivas creativas en momentos de malestar y rabia.

• Experimentar técnicas o dinámicas de atención plena, concentración y relajación.

• Utilizar la comunicación de manera positiva para tener relaciones constructivas y mejora de la autoestima.

• Usar el elogio como forma de reconocer una actitud o un comportamiento y contribuir a mejorar la autoestima.

• Adoptar comportamientos críticos y reflexivos evitando prejuicios.

• Valorar el esfuerzo como mecanismo de aprendizaje y de crecimiento.

• Descubrir las cualidades personales y valorar la crítica positiva.

• No adoptar los comportamientos estereotipados propios de la sociedad irreflexiva y acrítica.

• Aprender a comunicarse de manera asertiva.

• Practicar el pensamiento causal y consecuencial a la hora de relacionarse con los demás y experimentar la empatía y la asertividad.

• Anticipar posibles soluciones y practicar la causa-efecto.

• Interiorizar una pauta para solucionar problemas.

• Aprender a hablar y a escuchar para relacionarnos con los otros.

• Reflexionar sobre el valor de trabajar de forma cooperativa.

• Practicar la empatía y saber ponernos en el lugar del otro.

• Practicar el diálogo para comunicarse y resolver conflictos.

Competencia de la vida y el bienestar

• Aprender a autogenerar emociones agradables (emociones estéticas).

• Descubrir que hay lugares donde nos sentimos especialmente bien.

• Aprender estrategias para serenarnos y sentir bienestar.

• Educación en valores: ciudadanía activa.

• Fluir.

• Detectar un conflicto y aprender estrategias para actuar y tomar decisiones para su resolución.

• Aplicar el autocontrol y la comunicación asertiva y empática con los demás.

• Consolidar la actitud de respeto ante uno mismo y ante quienes nos rodean.

• Asumir retos como actitud que favorece la transformación, el trabajo autónomo y la cooperación. Competencia social

• Practicar estrategias hacia la búsqueda del bienestar emocional.

• Practicar e interiorizar un lenguaje interno positivo.

• Generar vínculos afectivos y solidarios que potencien experiencias positivas.

• Fijar objetivos positivos y realistas imaginando el futuro.

• Participar en acciones que contribuyan al bienestar de la comunidad en la que se vive.

Conciencia emocional

Educación emocional

5.º Primaria

6.º Primaria Activos Activos

• Reconocer e identificar las emociones básicas en uno mismo y en los demás.

• Identificar, aceptar y nombrar las emociones en uno mismo y en los demás.

• Profundizar sobre la propia imagen y la conciencia emocional.

• Evaluar el nivel de conocimiento de uno mismo y de los otros.

• Identificar las emociones más próximas al alumnado.

• Reconocer la emoción de la rabia, el estrés, la ansiedad o la ira y constatar la necesidad del autocontrol.

Regulación emocional

• Aprender a relajarnos y a concentrarnos a través del silencio.

• Entender la necesidad de regular las emociones y conocer estrategias para hacerlo.

• Introducir estrategias para aportar calma interior.

• Practicar la relajación y la visualización.

• Autogestionar el propio bienestar emocional.

• Potenciar la responsabilidad, el esfuerzo y la satisfacción personal.

Autonomía y auoestima

• Saber valorarse uno mismo y valorar a los otros en la justa medida.

• Aprender a valorar con mesura las cualidades personales.

• Mostrar la importancia y las consecuencias positivas del esfuerzo.

• Enfrentarse con éxito a unas condiciones de vida sumamente adversas (resiliencia).

• Relacionar imágenes con emociones a partir de un proceso de empatía.

Competencia social

• Dar importancia a la for ma de decir las cosas (empatía y asertividad).

• Aprender a resolver conflictos desde la empatía y el análisis causal.

• Reflexionar sobre la capacidad de relación y comunicación con las personas.

• Introducir el concepto de comunicación no verbal.

• Conocer e integrar los diferentes estilos de comunicación.

Competencia de la vida y el bienestar

• Aprender a gestionar las emociones propias al margen de las de los otros.

• Valorar los buenos momentos y estimular su fomento.

• Comprender la relación entre emoción, pensamiento y actuación.

• Aprender a hablar de los propios problemas con los otros.

• Interiorizar y experimentar estrategias para el bienestar emocional (emociones estéticas).

• Conocer más emociones y ampliar el vocabulario emocional.

• Conocerse mejor a sí mismo utilizando un lenguaje emocional adecuado.

• Identificar emociones con estados de ánimo.

• Expresar y comprender el estado emocional interno.

• Estimular la imaginación creativa y la relajación para generar emociones positivas.

• Aceptar las emociones desagradables y aplicar habilidades de afrontamiento.

• Ser consciente de la relación entre pensamiento y emoción.

• Aprender a conocer la propia imagen de manera real.

• Alimentar la autoestima identificando y valorando las cualidades personales.

• Enfrentarse con éxito a condiciones adversas (resiliencia).

• Relacionar los éxitos alcanzados con el trabajo personal.

• Aceptar que somos diferentes y respetar la diferencia.

• Relacionar la asertividad con el diálogo, la conversación y la resolución pacífica de conflictos.

• Relacionar la empatía con el diálogo, la conversación y la resolución pacífica de conflictos.

• Practicar la asertividad y la empatía en el diálogo, la conversación y en la resolución de conflictos.

• Identificar que no hay una única realidad y que existen diversidad de puntos de vista.

• Desarrollar un comportamiento prosocial de acuerdo con los derechos humanos.

• Desarrollar un lenguaje interior que genere emociones positivas favorecedoras de un bienestar personal.

• Aprender y aplicar estrategias y rutinas de pensamiento positivo para el bienestar emocional.

• Comprender que la diversidad es un valor, potenciando la interacción activa como formas de cooperar y hacer equipo.

• Tomar decisiones, aceptar retos y superarse como bienestar emocional.

Libros del alumnado

Cuadernos del alumnado

Propuesta didáctica

Recursos y materiales etapa para la

Material de aula

Proyecto digital

Materiales para la etapa

Material para el alumnado

LIBROS

Un libro por curso con un enfoque competencial para aprender aplicando lo estudiado.

CUADERNOS

Tres cuadernos por curso. Su organización en bloques de contenidos favorece la adaptación a diferentes ritmos de aprendizaje.

3

Material para el profesorado

PROPUESTAS DIDÁCTICAS

Una para cada curso, reproducen las páginas del libro del alumnado enriqueciéndolo con actividades complementarias, claves didácticas, soluciones, material de aula, recursos digitales, etc.

3

Matemáticas

Material para el aula

Una cuidada selección de materiales por curso diseñada para aprender haciendo con actividades manipulativas, juegos y STEAM.

Bloques geométricos

Tarjetas de números

Policubos

Baraja de científicos y científicas 1 y 2

Bloques de base 10

Proyecto digital

EduDynamic es una propuesta digital que cubre todos los contenidos del curso y se adapta a cualquier plataforma y dispositivo. Ofrece un gran despliegue de recursos diseñados para facilitar las tareas del profesorado y del alumnado tales como: herramientas para la inclusión y la evaluación, vídeos, actividades interactivas trazables, esquemas, resúmenes, programaciones…

Monedas y billetes

Poemas de científicos y científicas

Cuerpos geométricos

Libro de espejos

Libros del alumnado

Libros

Los libros de Operación Mundo están organizados en doce unidades. Cada una de ellas propone una situación de aprendizaje que contextualiza la adquisición de los saberes básicos y el desarrollo de las distintas destrezas para llevar a cabo el «Objetivo en acción» que se propone al final de la unidad.

¿Cómo son?

4 Las fracciones

6 Aprendemos juntos

¿Cómo te gusta trabajar en clase?

¿En qué situaciones aprender ha sido divertido?

Para esta unidad...

7

8

2 3 6

Lo esue o in p Medios, tercios y cuartos Comparo fracciones Aprendo fracciones ¡Sigue el hilo!

1 2 3

LO RESUELVO SIN PROBLEMA

Sigo un patrón Observa esta representación de la tabla del utilizando una cua- drícula. ¿Qué patrón se ha seguido para construirla? Fíjate que el número de cuadraditos representados es el resultado de la multiplicación.

El patrón que se ha seguido es una fila de dos cuadraditos en cada paso.

1 Representa la tabla del 3 en una cuadrícula. ¿Qué patrón has seguido? ¿Te atreves a representar el resto de tablas?

Representa estas multiplicaciones en una cuadrícula. × 9

1 Hago un dibujo Clara ha comprado 12 bolígrafos. Un tercio de los bolígrafos son rojos y los otros son azules. ¿Cuántos bolígrafos hay de cada color? Como tengo que calcular de los bolígrafos, dibujo 3 partes iguales. Reparto 12 bolígrafos en estas 3 partes.

3 son rojos, hay 4 bolígrafos rojos.

3

-

por colorear

gura. ¿Tiene razón?

Problemas exprés hora son 60¿Cuántos minutos horas? Tengo 8 años y mi prima tiene el triple. ¿Cuántos años tiene mi prima?

¿Cuánto veces 100? ¿Cuántos huevos hay en dos medias docenas?

Si doblas un folio por la mitad, ¿qué fracción del folio representa cada parte?

Un cuarto de las piezas son verdes las demás son azules. ¿Cuántas piezas hay 2 Aimar tiene 14 € en su hucha. Se ha gastado un séptimo en un paquete de cromos. ¿Cuánto dinero le queda en la hucha? ¿La solución tiene sentido? Si sumamos la cantidad de bolígrafos rojos y azules, el resultado es el total de bolígrafos que ha comprado Clara. y reparte 14 monedas. Cálculo mental Ahora, hazlo tú: 53 + 44 32 + 37 81 + 81 93 + 12 37 + 52 46 + 31 25 + 64 54 13 anayaeducacion.es puedes ver cómo se hace.

4 3 cuarto de hora 15  minutos. ¿Cuántosnutos son cuatro cuartos hora?

¿Cómo funciona? Mira cómo

U4

6 5

Media hora son 30¿Cuántos minutos medias horas?

Observa la tabla y piensa qué hace la máquina con los números.

14. entra 35710 4

72 73

Si doblas un folio por la mitad dos veces, ¿qué fracción del folio representa cada parte?

figura. Indica cuál es el numerador y el denominador.

6 Dibuja tres rectángulos iguales. Colorea un medio en el primero, un tercio en el segundo y un cuarto en el tercero.

7 En el recreo, Sara ha comido un medio de su bocadillo; Miguel, un tercio y Ana, un cuarto. El resto lo dejan para la merienda. Si los bocadillos eran iguales, ¿quién se ha dejado más para merendar?

Construye un comecocos de papel

Trabajamos en equipo construimos. Cada miembro del equipo construye su comecocos. Nos ayudamos para entender las instrucciones. Solo preguntamos si nadie del equipo lo entiende.

2 3 4

2. Escribe los números sobre el comecocos plegado colorea. Abre cada pestaña del comecocos. Escribe la fracción que forman los números número menor. ¡Ya podemos empezar a jugar!

0,50,830,50,430,40,11 0,670,380,50,7810,2 0,290,670,880,50,40,33

2 Copia la figura y colorea según el código.

¿Cómo se leen estas fracciones? a) b) 5 c) 4 a) c) b) Tres cuartos d) Cinco novenos ¿Qué porción de cada pizza a) b)

Copia completa con los signos > <. a) 6 b) 8 8 Noa ha coloreado 3 5 de un dibujo, y Ángel, el resto. ¿Quién ha coloreado menos?

10 Manuel ha horneado estos bizcochos del mismo tamaño.

a) ¿Qué fracción representa una porción de cada bizcocho? b) ¿En qué bizcocho las porciones son mayores?

Junto a cada actividad, colorea si has sabido la respuesta si has necesitado ayuda si no has sabido responder

Nos planteamos a)mecocos trabajando en equipo? b) ¿Qué has aprendido jugando al comecocos? -

PROYECTOSHUELLA QUEDEJAN

¿Cómo te gustaría que fuera nuestro jardín vertical? ¡Investiga! ¡Seguro que encuentras ideas geniales!

¿Te animas a hacer un jardín vertical?

4 PRESENTA ge

3 CONSTRUYE C ONS RUYE

medio tres cuartos sextos

siete octavos 3 4 5

1 PIENSA

2 D

Antes pensaba... Ahora pienso... Causas

Tema: Aprender es divertido ? ? ?

¿Cómo he aprendido? Copia en tu cuaderno y colorea junto a cada oración. A veces me enfado porque algo no me sale. Ayudo los demás cuando no entienden algo o no consiguen terminar a tiempo. Estoy orgulloso u orgullosa de mi cuaderno y me gusta enseñarlo

¿Qué tipo de actividades no te salen a la primera?

las matemáticas la ayudaba a entender la belleza del universo. Y también vio que una matemática es como una detective que resuelve los misterios más complicados del mundo.

¿Dónde os gustaría situar el jardín vertical? ¿Dentro de clase? ¿En el exterior? ¿Necesitáis pedir permiso para ponerlo en ese lugar? Comentad estas ideas y tener en cuenta todas las opiniones.

¿Cuánto espacio necesitáis? Calculad con palmos, pies o pasos… No os olvidéis de dejar suficiente espacio para cuidar las plantas. Anotad los cálculos.

Ahora que sabéis el lugar, debéis de pensar en cómo vais a organizarlo. Si queremos cuidar nuestro entorno podemos hacerlo con materiales reciclados como palés o botellas. ¡Busca información en internet y verás qué soluciones más chulis puedes encontrar!

COMPRUEBA 5

Vamos a marcar el lugar donde irá el jardín vertical. Usad el lápiz, tizas, cuerdas… y marcad el espacio reservado. Si es una zona común, poned un cartel avisando de la próxima construcción de vuestro jardín. ¿Qué has aprendido con este proyecto? Me he dado cuenta de…

Cómo son los libros… en detalle

Situaciones de aprendizaje

Pensamiento computacional y Cálculo mental

Lo resuelvo sin problema

STEAM y Repasos lúdicos

Proyectos interdisciplinares

Material manipulativo

Las fracciones

6 Aprendemos juntos

Las matemáticas nos gustan más a unas personas que a otras.

Además, en clase a algunos parece que se les da mejor que a otros.

Muchas veces trabajamos en grupos y nos ayudamos cuando algo no nos sale o no lo entendemos.

Lo mejor es cuando hacemos juegos en los que todos podemos participar y, además, divertirnos.

¿Cómo lo ves?

¿Cómo te gusta trabajar en clase?

¿En qué situaciones aprender ha sido divertido?

El dato

Recordamos mejor lo que hemos aprendido con actividades en las que participamos de manera activa.

ODS. Las situaciones de aprendizaje están vinculadas con los Objetivos de Desarrollo Sostenible. Además, este marco ODS se aborda de manera interdisciplinar.

Para esta unidad...

enObjetivoacción

¿Podemos aprender matemáticas jugando? Construye un comecocos de papel para jugar con las fracciones.

Situaciones de aprendizaje. La unidad comienza con una situación de aprendizaje, es decir, una situación problema, que invita al alumnado a llevar a cabo una reflexión final con una propuesta transformadora.

Lo r e s u e lv o s in p r o ble m a

Saberes básicos. La situación de aprendizaje exige que el alumnado aplique las destrezas y los saberes básicos adquiridos a lo largo de la unidad.

Aprendo fracciones

Las fracciones sirven para indicar partes iguales de una unidad.

Este mural está dividido en 6 partes iguales.

3 ¿En cuáles de estas figuras se ha coloreado 2 3 ?

Porfolio.

Una parte es 1 6 Dos partes son 2 6 Tres partes son 3 6 Una fracción representa el número de partes que se toman de una unidad dividida en partes iguales.

1 ¿Cuáles de las siguientes figuras están divididas en partes iguales?

4 1-2-4 Copia estas figuras en tu cuaderno y colorea la fracción que se indica. Comparte tu respuesta con la clase.

2 3 5 6 3 4

5 Escribe el nombre de las fracciones de la actividad anterior.

6 Escribe las siguientes fracciones. Indica en cada una cuál es el numerador y el denominador. a) dos quintos c) tres séptimos b) siete décimos d) cuatro sextos

Fracción de pizza

2 Construye estas figuras con bloques geométricos. ¿Qué fracción representa un triángulo en cada figura? a) b) c)

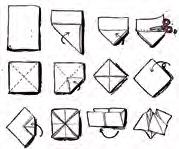
En este último apartado de la unidad, se proponen actividades que invitan al alumnado a reflexionar sobre su proceso de aprendizaje desde diferentes perspectivas.

¿Qué he aprendido?

1 Escribe la fracción que representa la parte coloreada de cada figura. Indica cuál es el numerador y el denominador.

6 Dibuja tres rectángulos iguales. Colorea un medio en el primero, un tercio en el segundo y un cuarto en el tercero.

7 En el recreo, Sara ha comido un medio de su bocadillo; Miguel, un tercio y Ana, un cuarto. El resto lo dejan para la merienda. Si los bocadillos eran iguales, ¿quién se ha dejado más para merendar?

Somos 4 personas y hemos comprado esta pizza.

• Si queremos comer 2 porciones cada uno, ¿en cuántas partes iguales la tenemos que dividir?

• ¿Qué fracción de pizza nos comeríamos cada uno?

Términos de una fracción

2 3

Numerador: número de partes que se toman de la unidad.

Denominador: número de partes iguales en que se divide la unidad.

Nombramos las fracciones

Leemos el numerador y después el denominador:

1 2 un medio

2 3 dos tercios

3 4 tres cuartos

4 5 cuatro quintos

5 6 cinco sextos

6 7 seis séptimos

7 8 siete octavos

8 9 ocho novenos

9 10 nueve décimos

Actividades competenciales. Estas actividades, cercanas al entorno del alumnado, facilitan la transferencia de los aprendizajes y su aplicación en diversos e interesantes contextos.

2 Copia la figura y colorea según el código.

8 Copia y completa con los signos > o <.

a) 2 6 ? 4 6 b) 3 8 ? 1 8

9 Noa ha coloreado 3 5 de un dibujo, y Ángel, el resto. ¿Quién ha coloreado menos?

OBJETIVO EN ACCIÓN

Construye un comecocos de papel

Trabajamos en equipo y construimos.

1. Cada miembro del equipo construye su comecocos. Nos ayudamos para entender las instrucciones. Solo preguntamos si nadie del equipo lo entiende.

2. Escribe los números sobre el comecocos plegado y colorea.

3.° Abre cada pestaña del comecocos. Escribe la fracción que forman los números en cada caso. Escribe en el numerador el número menor. ¡Ya podemos empezar a jugar!

OBJETIVO EN ACCIÓN

3 8 1 8 4 8

3 ¿Cómo se leen estas fracciones?

a) 1 3 b) 3 5 c) 4 7

4 Escribe estas fracciones en tu cuaderno.

a) Un medio c) Cuatro sextos

b) Tres cuartos d) Cinco novenos

5 ¿Qué porción de cada pizza se han comido?

a) b)

10 Manuel ha horneado estos bizcochos del mismo tamaño.

a) ¿Qué fracción representa una porción de cada bizcocho?

b) ¿En qué bizcocho las porciones son mayores?

El semáforo. Junto a cada actividad, colorea así en tu cuaderno: si has sabido la respuesta si has necesitado ayuda si no has sabido responder

Nos planteamos a) ¿Te has divertido haciendo el comecocos y trabajando en equipo?

b) ¿Qué has aprendido jugando al comecocos?

c) Antes pensaba…, ahora pienso… Copia y completa la tabla en tu cuaderno.

¿Cómo he aprendido?

Antes pensaba... Ahora pienso... Causas

Tema: Aprender es divertido ?

Copia en tu cuaderno y colorea junto a cada oración.

• A veces me enfado porque algo no me sale.

• Ayudo a los demás cuando no entienden algo o no consiguen terminar a tiempo.

• Estoy orgulloso u orgullosa de mi cuaderno y me gusta enseñarlo a todo el mundo.

¿Qué tipo de actividades no te salen a la primera?

Objetivo en acción. En el contexto de la situación de aprendizaje de la unidad, se invita al alumnado a participar en una tarea transformadora elaborando el producto final propuesto en el «Objetivo en acción».

Libros del alumnado

LO RESUELVO SIN PROBLEMA

Sigo un patrón

Observa esta representación de la tabla del 2 utilizando una cuadrícula. ¿Qué patrón se ha seguido para construirla?

Fíjate que el número de cuadraditos representados es el resultado de la multiplicación.

Problemas exprés

1

Una hora son 60 minutos. ¿Cuántos minutos son dos horas?

2

Tengo 8 años y mi prima tiene el triple. ¿Cuántos años tiene mi prima?

4 3

¿Cuánto es 9 veces 100? ¿Cuántos huevos hay en dos medias docenas?

6 5

Un cuarto de hora son 15  minutos. ¿Cuántos minutos son cuatro cuartos de hora?

¿Cómo funciona? Mira cómo pienso

Media hora son 30 minutos. ¿Cuántos minutos son dos medias horas?

El patrón que se ha seguido es añadir una fila de dos cuadraditos en cada paso.

1 Representa la tabla del 3 en una cuadrícula. ¿Qué patrón has seguido?

¿Te atreves a representar el resto de tablas?

2 Representa estas multiplicaciones en una cuadrícula. 7 × 3 8 × 5 9 × 4

Cómo son los libros… en detalle

Hago un dibujo

Clara ha comprado 12 bolígrafos. Un tercio de los bolígrafos son rojos y los otros son azules. ¿Cuántos bolígrafos hay de cada color?

1.° Como tengo que calcular 1 3 de los bolígrafos, dibujo 3 partes iguales.

2.° Reparto 12 bolígrafos en estas 3 partes. → 12 : 3 = 4

3.° Como 1 3 son rojos, hay 4 bolígrafos rojos.

4.° Calculo el número de bolígrafos azules. → 12 4 = 8 Hay 4 bolígrafos rojos y 8 azules.

1 Nuria ha hecho una construcción utilizando 16 piezas. Un cuarto de las piezas son verdes y las demás son azules. ¿Cuántas piezas hay de cada color?

¿La solución tiene sentido? Si sumamos la cantidad de bolígrafos rojos y azules, el resultado es el total de bolígrafos que ha comprado Clara. Dibuja 7 grupos y reparte 14 monedas.

El número 2 entra en la máquina convierte-números y sale el número 14. entra 35710 sale 21 35 49 70 ?

Observa la tabla y piensa qué hace la máquina con los números.

Pensamiento computacional y cálculo mental. El apartado «Mira como pienso» de cada unidad propone actividades de pensamiento computacional secuenciadas para desarrollar las bases de la capacidad analítica, la creatividad, el pensamiento crítico, la capacidad de aprender a aprender, etc.

Problemas exprés

1

¿En cuántas partes iguales dividirías un bizcocho para que 4 personas coman lo mismo?

2

Ana dice que le queda por colorear 2 5 de la figura. ¿Tiene razón?

4 3

Si doblas un folio por la mitad, ¿qué fracción del folio representa cada parte?

Si doblas un folio por la mitad dos veces, ¿qué fracción del folio representa cada parte?

Buscando patrones Mira cómo pienso

Dibuja un rectángulo. Divídelo por la mitad, una y otra vez, hasta que pue

2 Aimar tiene 14 € en su hucha. Se ha gastado un séptimo en un paquete de cromos. ¿Cuánto dinero le queda en la hucha?

ver cómo se hace.

Lo resuelvo sin problema. Un apartado específico en cada unidad para que el alumnado desarrolle las competencias matemáticas fundamentales de la resolución de problemas.

sTEAM

Adivina.

1 Piensa un número de 3 cifras

2 Capicúa 787 313

Escribe todos los capicúas de tres cifras que tengan un 5 en las decenas. 5

Réstale 153

Súmale 374

3

Súmale 400

Escribe una suma, una resta y una multiplicación cuyo resultado sea 18.

Réstale 621

4

¿Quién soy?

Escribe la letra que corresponda y sabrás a quién le gustaban los acertijos matemáticos tanto como a ti.

A M G R D O J U X B N H S E P K V Y C Ñ I T F Q L W

Z

T Novena Primera Decimoséptima

Octava Primera

5

Ordena los dorsales de menor a mayor y contesta.

Proyectos

interdisciplinares. Al final de cada trimestre se presenta un proyecto organizado en fases (Piensa, Diseña, Construye, Presenta y Comprueba); una experiencia de aprendizaje integradora que favorece el desarrollo competencial y la aplicación de los saberes básicos adquiridos.

¿Cuántos años tienen?

• Para el próximo cumpleaños de Eva necesitaremos 11 velas.

• Eva tiene el doble de años que Teo.

• Teo es un año mayor que Sara.

• Sara tiene el doble de años que Enzo.

¿Cuánto dinero tenemos?

• ¿Podemos ir al cine? • ¿Y compartir 2 de palomitas?

7 8€ 12 €

Maryam Mirzakhani

A Maryam no siempre le gustaron las matemáticas. Cuando era pequeña, la aburrían un poco, y decía que de mayor quería ser escritora. Pero un día, de golpe, empezó a ver las matemáticas de otra manera. Se dio cuenta de que aprender los secretos de las matemáticas la ayudaba a entender la belleza del universo.

Y también vio que una matemática es como una detective que resuelve los misterios más complicados del mundo.

STEAM y Repasos lúdicos. Al finalizar cada trimestre se proponen actividades con las que repasar, de forma lúdica, los saberes y las destrezas adquiridos. Incluye también el apartado STEAM, con el que el alumnado descubrirá grandes protagonistas de la ciencia leyendo y escuchando poemas que narran sus vidas.

DESCUBRE EL PROYECTO INTERDISCIPLINAR

¿Aprovechamos o desperdiciamos alimentos?:

DIME CUÁNDO

CADUCAS… Y TE DIRÉ…

¡Mira en el frigo y en la despensa, te sorprenderás!

¿Te animas a organizar una exposición de etiquetas de alimentos con fechas de caducidad y de consumo preferente?

1 Think PIENSA

Hacemos una lluvia de ideas en grupo:

¿Sabemos qué es la fecha de caducidad?

¿Y la fecha de consumo preferente?

¿Por qué unos alimentos caducan antes que otros? ¿Qué ocurre cuando un producto caduca? ¿Qué puedo hacer para que no caduquen los alimentos que he comprado?

2 DISEÑA

D esign

Si queremos reducir el desperdicio de alimentos, es importante conocer las fechas de caducidad y de consumo preferente de lo que solemos comprar. Decidimos cómo elaborar un mural con estos productos.

Fíjate en diferentes tipos de alimentos: frescos, conservas, no perecederos y congelados. Vamos a buscar etiquetas donde veamos las fechas. Traemos a clase etiquetas de distintos alimentos.

3 C ONSTRUYE Maker

ONSTRUYE

Hacemos el mural:

Organiza las etiquetas en dos grupos, según fecha de caducidad o fecha de consumo preferente.

¿De qué tipo de alimentos son según su fecha? Calcula los días que quedan para consumirlos.

PRESENTA

4 PRESENTA Stage

Hacemos una exposición sobre la importancia de conocer el etiquetado de alimentos para reducir su desperdicio. Recuerda poner ejemplos sobre caducidad y consumo preferente: qué significa, en qué tipo de alimentos se usa, cómo calcular su consumo…

PRUEBA 5

T est

Ahora entiendo cómo hacer…

1 78 79

Libros del alumnado Cómo son los libros… en detalle

Material manipulativo.

El proyecto Operación Mundo ofrece un cuidado material manipulativo para el uso individual del alumnado. Este material es muy útil para la exploración y la adquisición práctica de habilidades y destrezas.

222222333

000000001 111111122

333334444

444455555

222222333

333334444

555666666

667777777

444455555

555666666

788888888

9999999910

101010101010101010

101010101010101010

667777777

788888888

000000001 111111122 222222333 333334444 444455555

9999999910

788888888

9999999910 101010101010101010

Operación Mundo presenta tres cuadernos para cada curso de Primaria organizados en bloques de contenidos. Esta estructura hace de los cuadernos un práctico recurso inclusivo para la adaptación a diferentes ritmos de aprendizaje del alumnado.

Operaciónmundo PRIMARIA 2 Matemáticas CUADERNO 1 PRIMARIA CUADERNO 1 4 Matemáticas Operaciónmundo Operaciónmundo PRIMARIA 6 Matemáticas CUADERNO 1 Operaciónmundo PRIMARIA 3 Matemáticas CUADERNO 1 Operaciónmundo PRIMARIA 5 Matemáticas CUADERNO 1 Operaciónmundo PRIMARIA 1 Matemáticas CUADERNO 1

LOS

3. Los números de tres y cuatro cifras (III)

1 Observa las matrículas anotadas por Beatriz y colorea.

–De rojo, la matrícula en la que la cifra 6 vale 600 unidades.

–De verde, las matrículas en las que la cifra 9 vale 9 000 unidades.

–De azul, la matrícula en la que la cifra 3 vale 30 unidades.

–De amarillo, la matrícula donde la cifra 7 tiene mayor valor.

–De naranja, la matrícula en la que la cifra 4 tiene menor valor.

BC7180 BX6954

Cómo son

LOS NÚMEROS

SL8932 DF5689

4. Comparo y ordeno números

2 Lee el acertijo preparado por María y descubre las cifras que componen esa matrícula.

1.º El número es capicúa (se lee igual del derecho que del revés).

2.º La cifra de las decenas vale 20 unidades.

3.º Es mayor que 6 200 y menor que 6 300. ¿Qué número es?

CA9356 AD9143 CF

Los cuadernos están organizados en fichas de trabajo para ejercitar los saberes básicos que indica el título de cada una de ellas.

1 Observa estos cuentakilómetros y ordénalos de mayor a menor.

LOS NÚMEROS

5. Redondeo números

3 Continúa la serie sumando 5 C a cada número.

Recuerda > mayor que < menor que = igual a

1 Esta tabla representa las distancias entre varias ciudades. Observa la tabla y responde a las preguntas.

LOS NÚMEROS

¿QUÉ

1 Los números de tres y cuatro cifras (I)

2 Los números de tres y cuatro cifras (II)

3 Los números de tres y cuatro cifras (III)

2. La resta (II)

4 Comparo y ordeno números 5 Redondeo números 6 Los números ordinales

1 La suma

LA MULTIPLICACIÓN

2 Completa cada casilla sabiendo que la tira de color azul equivale a una unidad de millar.

1. La multiplicación

4 500

a) ¿Qué dos ciudades están a casi 600 km de París?

3 Escribe el signo mayor que ( > ) o menor que ( < ), según corresponda.

b) ¿Qué ciudades están a unos 300 km de París, aproximadamente?

LA SUMA

1 Resuelve las sumas y las restas y colorea para descodificar la imagen.

4 Adivina qué número corresponde en cada caso.

Distancias kilométricas entre ciudades 777Marsella Aviñón

1.º Está entre 1 500 y 1 600.

2.º La cifra de las decenas es la menor cifra impar.

3.º La cifra de las unidades es la mayor cifra par.

LA RESTA

LA MULTIPLICACIÓN

LA DIVISIÓN

2 Las propiedades de la suma (I) 3 Las propiedades de la suma (II)

1 La resta (I)

2 La resta (II)

3 La prueba de la resta

1 La multiplicación

2 Las tablas de multiplicar 3 Las propiedades de la multiplicación 4 Practico la multiplicación (I) 5 Practico la multiplicación (II)

1 La división (I)

2 La división (II)

3 Cálculo de divisiones (I) 4 Cálculo de divisiones (II) 1 Las fracciones (I)

LAS FRACCIONES

LO RESUELVO SIN PROBLEMA

Equipo de edición: María José García García, Noelia Túnez Sáez. Lecturas: Raquel Ramírez de Arellano.

Diseño y gráficos: Patricia G. Serrano, Marta Gómez, Paz Franch, Miguel Díaz-Rullo. Ilustración: José Ángel

2 Ten en cuenta la tabla de distancias kilométricas y observa la ruta desde París a Marsella. Aproxima todas las distancias a la decena, como en el ejemplo.

1 Calcula, como suma y como multiplicación, la cantidad de figuras que a) 4 + 4 + 4 c) 11 + 11

Labari, Pablo Vázquez. Maquetación: Discript Preimpresión, S.L. Corrección: Miguel Ángel Alonso. Edición gráfica: Rocío Álvarez. Fotografías: Archivo Anaya (Lacey, T; Osuna, J.), Thinkstock. Agradecimientos a las niñas: Nora Garrido y Sophia Moras.

Factores Producto

1.º Tiene cuatro cifras, todas distintas.

2.º Las tres primeras cifras son impares, suman nueve y están ordenadas de mayor a menor.

3.º Las cuatro cifras suman diecisiete.

1739 7610 7610 1739 1739 1739 7610 7610 1739 7610 7610 393 426 393 426 1534 8928 8928 8928 5910 8928 8928 5910 5910 5910 8928 5910 8928 5910 8928 2239 2239 22392239 82 50 82 50 82 51 50 851 851 1534 851 851 1534 1534 1534 1534 1534 1534 1534 1534 1534 1534 1534 1534 1534 1534 851 851 851 851 851 347 851 347 851 851 851 851 851 851 851 851 1534 1534 1534 51 51 51 51 51 51 2967 51 347 51 347 51 347 51 51 347 51 51 347 51 347 51 347 51 347 51 347 51 51 51 347 851 7780 393 426 426 2967 2967 2239 LA RESTA

Propuestas didácticas

Propuesta didáctica

La propuesta didáctica que ofrece Operación Mundo en cada uno de los cursos es un valioso instrumento para enriquecer el aprendizaje. En ellas encontrarás actividades complementarias que ofrecen alternativas para tratar la diversidad, claves didácticas, soluciones y referencias a los recursos digitales y manipulativos asociados al libro del alumnado.

¿Cómo son?

Para iniciar la unidad se ofrece un organizador gráfico que permite visualizar los saberes básicos que se trabajan.

6 Aprendemos juntos

ESQUEMA DE LA UNIDAD

Aprendo fracciones

Una fracción representa el número de partes que se toman de una unidad dividida en partes iguales.

Términos de una fracción

2 3

Numerador: número de partes que se toman de la unidad.

Denominador: número de partes iguales en que se divide la unidad.

Nombramos las fracciones Leemos el numerador y después el denominador:

1

Medios, tercios y cuartos

Si dividimos una unidad en 2 partes iguales, cada parte es un medio.

Si dividimos una unidad en 3 partes iguales, cada parte es un tercio.

2 un medio

2 3 dos tercios

3 4 tres cuartos

4 5 cuatro quintos

5 6 cinco sextos

6 7 seis séptimos

7 8 siete octavos

8 9 ocho novenos

9 10 nueve décimos

1 2 1 3

Si dividimos una unidad en 4 partes iguales, cada parte es un cuarto. 1 4

Recursos digitalesInclusión y atención a la diversidadEvaluaciónAula

RECURSOS ¿QUÉ VAMOS A APRENDER?

Página inicial

Situación de aprendizaje: Construye un comecocos de papel para jugar con las fracciones ODS 4: Educación de calidad

Aprendo fracciones

• Concepto de fracción de la unidad

• Términos de una fracción

• Nombre de las fracciones

Medios, tercios y cuartos

• Representación y lectura de las fracciones resultantes de dividir la unidad en 2, 3 o 4 partes

Comparo fracciones • Comparación de fracciones con el mismo denominador

Lo resuelvo sin problema

Estrategia heurística: Hago un dibujo Problemas exprés Cálculo mental: Suma de dos cifras con llevadas

Pensamiento computacional: Generalización

Porfolio

• ¿Qué he aprendido?

• ¿Qué he aprendido en la situación de aprendizaje?

• ¿Cómo he aprendido?

Actividades interactivas

Material de aula

Vídeo: Te lo cuento en un momento (Es 1/2, no es 1/2)

Vídeo: Te lo cuento en un momento (Es 1/4, no es 1/4)

Actividades interactivas

Actividades interactivas

Bloques geométricos

Material manipulativo descargable Tiras de fracciones

Herramientas digitales Fichas y tabla 10 Regletas Juego de sectores circulares Tiras de mecano

Murales

Vídeo: Cálculo mental (Suma de dos números de dos cifras con llevadas)

Actividades interactivas

Actividades interactivas

Fichas 1, 2 y 3 (refuerzo)

Ficha 4 (ampliación)

Lo esencial

Evaluación Evaluación adaptada Evaluación competencial

A continuación, se indican los apartados y epígrafes de la unidad del libro del alumnado, detallando los saberes básicos que se trabajan y relacionándolos con recursos del proyecto digital y material manipulativo. Para cada uno de estos últimos se indica, a través de una sencilla codificación cromática, si se trata de un recurso digital, de inclusión, evaluación o material de aula.

Se reproduce la página de apertura de la unidad y debajo se muestra la secuencia de la situación de aprendizaje propuesta en ella y cómo presentarla en el aula. Se indican también sus claves pedagógicas y los recursos digitales asociados.

4 Las fracciones

6 Aprendemos juntos

Las matemáticas nos gustan más a unas personas que a otras.

¿Cómo lo ves?

¿Cómo te gusta trabajar en clase? ¿En qué situaciones aprender ha sido divertido? Para esta unidad...

las fracciones.

Situación de aprendizaje ODS Imagen inicial

El bloqueo que se da con frecuencia en el área de matemáticas tiene, en muchas ocasiones, origen en un bloqueo emocional. Aprender jugando favorece la eliminación de estos bloqueos y es accesible para todos y todas.

Calentando motores

Objetivo 4: Educación de calidad. Se pretende poner en valor la importancia de una educación de calidad.

Recursos

PORFOLIO

1 Escribe la fracción que representa la parte coloreada de cada figura. Indica cuál es el numerador y el denominador.

Lo resuelvo sin problema Medios, tercios y cuartos Comparo fracciones

Tiene a su disposición «Las claves de Operación Mundo» en anayaeducacion.es

Claves Aprendizaje cooperativo Trabajar las preguntas de la sección ¿Cómo lo ves? en estructura cooperativa cabezas numeradas

ODS

El objetivo trabajado es la educación de calidad, desde el enfoque de aprender divirtiéndonos.

Sugerencias didácticas

• Establecer grupos de trabajo estables a lo largo de la unidad para que luego realicen el comecocos en la actividad final.

• Fomentar la participación en pequeño grupo. Se pueden establecer tiempos de intervención para la puesta en común para cada miembro del grupo.

• El ODS puede dar opción a hablar de cómo en otros lugares las niñas y los niños no pueden ir a la escuela o no tienen materiales para aprender.

¿Cómo lo ves? El dato Objetivo en acción ¡Sigue el hilo!

2 Copia la figura y colorea según el código.

A 2 B 4 6 C 3 4 D 5 8 2

b) 3 4 c)

8 a) 2 6 < 4 6 b) 3 8 > 1 8 9 Ha coloreado menos Ángel, 2 5 del dibujo.

10 a) En el primero una porción representa 1/6 del bizcocho, y en el segundo, 1/9 del bizcocho.

b) Son más grandes las proporciones del primero porque están divididas en menos partes.

a)

Se plantea el diálogo sobre las preguntas planteadas en grupo. Identificamos cómo nos gusta más trabajar y por qué. Registramos las actividades señaladas como más divertidas de manera más generalizada e identificamos por qué han sido divertidas.

3 8 8 4 8

3 ¿Cómo se leen estas fracciones?

3 b) 3 5 c) 4 7

4 Escribe estas fracciones en tu cuaderno.

a) Un medio c) Cuatro sextos b) Tres cuartos d) Cinco novenos

5 ¿Qué porción de cada pizza se han comido? a) b)

Refuerzo

1 Escribe las siguientes fracciones.

a) Un medio b) Dos quintos

c) Tres sextos

Solución: a) 1 2 b) 2 5 c) 3 6

2 Escribe el nombre de las siguientes fracciones.

a) 3 4 b) 2 8 c) 7 9

Solución:

a) tres cuartos

b) dos octavos c) siete novenos

6 Dibuja tres rectángulos iguales. Colorea un medio en el primero, un tercio en el segundo y un cuarto en el tercero.

7 En el recreo, Sara ha comido un medio de su bocadillo; Miguel, un tercio y Ana, un cuarto. El resto lo dejan para la merienda. Si los bocadillos eran iguales, ¿quién se ha dejado más para merendar?

8 Copia y completa con los signos > o <. a) 2 6 ? 4 6 b) 3 8 ? 1 8

9 Noa ha coloreado 3 5 de un dibujo, y Ángel, el resto. ¿Quién ha coloreado menos?

10 Manuel ha horneado estos bizcochos del mismo tamaño.

a) ¿Qué fracción representa una porción de cada bizcocho? b) ¿En qué bizcocho las porciones son mayores?

El semáforo. Junto a cada actividad, colorea así en tu cuaderno: si has sabido la respuesta si has necesitado ayuda si no has sabido responder

3 Mi padre ha pintado dos paredes de las cuatro que tiene la habitación, y mi madre, el resto. ¿Qué fracción ha pintado cada uno?

Solución: Cada uno ha pintado

2 4 de la habitación.

Ampliación 1 ¿Qué fracción de hora son 10 minutos?

Solución: 1 6

OBJETIVO EN ACCIÓN

Se puede aprender de manera lúdica. Participar en el proceso de aprendizaje e implicarse en la tarea de manera activa provoca mejores aprendizajes.

Pensamos en grupo situaciones donde hemos aprendido jugando, no solo en matemáticas. Identificamos cómo sabemos que lo hemos apren-

Construye un comecocos de papel

En esta unidad trabajamos con las fracciones para que nos ayude a construir el comecocos de papel. Las fracciones nos ayudan a dividir un trozo de papel en partes iguales. Comparar fracciones nos ayuda a hacer manualidades con papel.

Claves + info anayaeducacion.es Desarrollo del pensamiento Antes pensaba…, ahora pienso…

Ten en cuenta

Trabajamos en equipo y construimos.

1. Cada miembro del equipo construye su comecocos. Nos ayudamos para entender las instrucciones. Solo preguntamos si nadie del equipo lo entiende.

2. Escribe los números sobre el comecocos plegado y colorea. 3. Abre cada pestaña del comecocos. Escribe la fracción que forman los números en cada caso. Escribe en el numerador el número menor. ¡Ya podemos empezar a jugar!

• Guiar la elaboración del comecocos y revisar si se entienden todos los pasos antes de comenzar a construirlo.

• Los miembros del grupo que terminen antes, o tengan más facilidad, pueden ayudar a otros en su grupo o en otros grupos.

Nos planteamos a) ¿Te has divertido haciendo el comecocos y trabajando en equipo? b) ¿Qué has aprendido jugando al comecocos? c) Antes pensaba…, ahora pienso… Copia y completa la tabla en tu cuaderno.

¿Cómo he aprendido?

Tema: Aprender es divertido

A B C D 2 3 4 5 6 7 8 Antes pensaba... Ahora

?

Copia en tu cuaderno y colorea junto a cada oración.

¿Cómo he aprendido?

Para facilitar la metacognición Educación emocional La evaluación de ¿Cómo he aprendido? se centra en ayudar al alumnado a identificar sus emociones cuando resuelven problemas o trabajan con otros. En muchos casos identificar emociones positivas en algún tipo de tarea refuerza positivamente dicha tarea y ayuda a vencer barreras. Sugerencia didáctica:

• Dejar tiempo para la reflexión individual.

• Compartir en pareja o grupo si se alegran o no al entender un problema o si disfrutan trabajando con otros.

• Es importante reflexionar sobre el tipo de tareas o propuestas que ayudan al alumnado a mantener la atención. Se pueden dejar expuestas en el aula para retomar cuando los niveles de atención bajen.

1 2 3 4 5 6

8 b) ¿Cuántos números hay? ¿Qué fracción representa el espacio que ocupa cada número?

145 144

Junto con la reproducción de las páginas del libro del alumnado de cada apartado y epígrafe se indican recursos manipulativos y digitales asociados, se proponen actividades manipulativas, la aplicación de claves pedagógicas, sugerencias didácticas bajo el título «Ten en cuenta» y se señala el vínculo del apartado con la situación de aprendizaje de la unidad.

Material de aula

Material de aula

Operación Mundo ofrece, para cada curso, una cuidada selección de materiales de calidad diseñados para consolidar y motivar el aprendizaje a través de la manipulación, el descubrimiento y el juego.

1..°

2.° 3.°

Tarjetas de números

Tarjetas de números

Tarjetas de números

Monedas y billetes

Monedas y billetes

Formas geométricas

Bloques de base 10

Protagonistas STEAM

Protagonistas

STEAM

Poemas de científicos y científicas

Policubos

Cuerpos geométricos

Set de reglas

Baraja de científicos y científicas

Libro de espejos

Cuerpos geométricos

Protagonistas STEAM

Protagonistas

STEAM

Poemas de científicos y científicas

Policubos

Protagonistas STEAM

Protagonistas

STEAM

Policubos

Baraja de científicos y científicas

Láminas de cuentos de científicas

Hacemos una entrevista a una científica

¿Cómo es?

La tabla siguiente indica los materiales que componen la caja de material de aula de cada curso. En las páginas siguientes se presenta en más detalle los correspondientes a Protagonistas STEAM.

4.°

Tarjetas de números

Monedas y billetes

5.° 6.°

Geostick

Tiras de fracciones

Geoplanos

Cuerpos geométricos

Libro de espejos

Hypa t ia de Aleja ndría

Sectores circulares

Protagonistas STEAM

Policubos

Protagonistas

Murales de científicas

Hypatia vivió hace más de 1600 años en la ciudad egipcia de Alejandría. Su padre, Teón, era profesor en el Serapeion, un impresionante centro de estudios que albergaba la biblioteca más grande del mundo en aquella época. Hypatia pudo desarrollar su curiosidad científica en aquel ambiente de amor al saber, desde muy joven destacó como matemática astrónoma. Con el tiempo, además, se convirtió en una gran maestra. Era tan famosa que atraía a estudiantes de todos los rincones del imperio romano deseosos de asistir a sus clases y aprender de sus enseñanzas. Como matemática, Hypatia realizó importantes descubrimientos en el campo de la geometría. En su faceta de astrónoma, aplicó sus conocimientos matemáticos para explicar los movimientos de los planetas en el firmamento. También fue una gran inventora. Sus descubrimientos ayudaron a mejorar el astrolabio, un instrumento utilizado por los navegantes para fijar el rumbo de sus barcos guiándose por las estrellas. Durante toda su vida, Hypatia fue una persona muy admirada por su inteligencia sus conocimientos. Precisamente por eso, algunas personas la veían como un peligro, y terminaron con su vida. Sin embargo, sus enemigos no lograron borrar su recuerdo. Todavía hoy, su figura es considerada todo un ejemplo de tolerancia, sabiduría amor a la investigación.

Cinta métrica

Murales de científicas

Protagonistas STEAM

¿Qué es la astronomía?

Láminas de cuentos de científicas

Hacemos una entrevista a una científica

Vídeos de científicas

Tarjetas de información

Tarjetas de información

Goodalldescubrióqueloschimpancésno eranvegetarianoscomosepensaba,sino queeranomnívoros. Sudietasecomponíaprincipalmentede fruta(higosyplátanossobretodo),de brotesdepalma debambú dealgunas hojas. Peroademás,loschimpancéscomían insectos,sobretodotermitas eran capacesdecazarcríasdejabalí monos colobos, losquedevoraban

Katherine Johnson nació en 1918 en White Sulphur Spring, una localidad del sur de EE UU. Desde pequeña mostró grandes aptitudes para las Matemáticas, pero no lo tuvo fácil para desarrollar su talento. Katherine era afroamericana, y en su estado (Virginia Occidental) había leyes de segregación racial que impedían a los afroamericanos asistir a la mayoría de los centros de enseñanza. Sus padres tuvieron que mudarse de ciudad para que ella pudiese ir al instituto y más tarde la Universidad. Se graduó en Matemáticas y francés a los 18 años. Después de un breve período como profesora, empezó a trabajar para la NASA. Su increíble capacidad para realizar Los «curies» son los primeros apara- tos móviles de rayos que durante Guerra Mundial (1914) Curie inventó para ayudar a que personal médico diagnosticara a las personas heridas guerra. Este aparato era un coche con un equipo de rayos X, una sala oscura para revelado un generador (dinamo) de electricidad que funcionaba con el motor de gasolina del coche. Este impulso fue básico para que la radiología se estableciera como una técnica de diagnóstico.

Vídeos de las científicas

¿Qué son las señales de radio?

Protagonistas STEAM

¿Quieres saber más?

¿Qué te ofrece?

En la caja de material de aula

Maria Montessori

Andresa Casamayor

Enfoque competencial

Interdisciplinariedad

Florence Nightingale

Protagonistas STEAM

Protagonistas STEAM es un proyecto interdisciplinar en el que se combinan ciencia, tecnología, ingeniería, matemáticas y arte de una manera práctica y lúdica. Una propuesta de enfoque abierto diseñada para fomentar la curiosidad frente al miedo al error, que integra el arte, y la creatividad a través de

Aprender haciendo

Euclides

Gauss

Educación emocional

Gamificación

Enseñar a pensar

Leonardo Da Vinci

Maryam Mirzakhani

Clara Grima

Katherine Johnson

Hypatia de Alejandría

¿Qué te ofrece?

Para el alumnado

El alumnado dispone de recursos específicos para cada uno de los científicos y las científicas que componen el proyecto. A través de ellos y de las diferentes propuestas de gamificación, investigación, etc., descubrirán algunas figuras relevantes de la historia de la ciencia y la tecnología que servirán de inspiración tanto por sus aportaciones científicas como por su calidad humana, valores y capacidad para cooperar.

Dependiendo del curso, los recursos asociados a cada protagonista son: barajas de naipes, cuentos, láminas o pósteres, de los que se incluyen varios juegos para poder formar equipos en el aula.

Para el profesorado

El profesorado dispone de un ejemplar impreso de la propuesta didáctica específica para el desarrollo del proyecto STEAM de cada curso. En estas propuestas didácticas se incluye:

• Una ficha resumen con datos biográficos y el legado de cada uno de los protagonistas STEAM.

• Una descripción del material diseñado para el alumnado, tanto de la caja de material de aula como el digital de anayaeducacion.es

• Sugerencias para jugar y aprender con los naipes, los cuentos, los poemas, las entrevistas, los retos, los vídeos… de cada curso.

Para el alumnado

Para investigar y disfrutar descubriendo a los científicos y las científicas del proyecto STEAM; en cada curso se han diseñado recursos digitales específicos para el alumnado tales como poemas, audios, cuentos, juegos de escape o cuestionarios exprés.

Para el profesorado

El profesorado dispone de recursos diseñados para los protagonista STEAM de cada curso como son: vídeos, entrevistas interactivas, vídeoanimaciones y materiales imprimibles para trabajar con el contenido de cada proyecto.

Grupo Anaya, S.A.

© Grupo Anaya, S.A.

Sulphur Spring, una localidad del sur de EE UU. Desde pequeña mostró grandes aptitudes para las Matemáticas, pero no lo tuvo fácil para desarrollar su talento. Katherine era afroamericana, y en su es-

Protagonistas

STEAM

© Grupo Anaya, S.A.

(Virginia Occidental) había leyes de segregación racial que impedían a los afroamericanos asistir a la mayoría de los centros de enseñanza. Sus padres tuvieron que mudarse de ciudad para que ella pudiese ir al instituto y más tarde a la Universidad. Se graduó en Matemáticas y francés a los 18 años. Después de un breve período como profesora, empezó a trabajar para la NASA. Su increíble capacidad para realizar cálculos complejos hizo que muy pronto le encargasen misiones de gran importancia, como el cálculo de la trayectoria del primer viaje estadounidense tripulado al espacio, la órbita de John Glenn, el primer astronauta americano que orbitó alrededor de la Tierra, o las trayectorias de los cohetes Apolo a la Luna. Todo esto la convirtió en una de las figuras más influyentes y queridas de la NASA. En los últimos años de su carrera participó en los preparativos de una misión a Marte y recibió numerosos reconocimientos, entre ellos la medalla presidencial de la Libertad. Murió en febrero de 2020.

Protagonistas STEAM ¡Te cuentan quiénes son en primera persona!

3

De pequeña, Clara quería ser Lola. Vestir de lunares y bata de cola, salir en programas de televisión... También le gustaban otros muchos temas: comprender las cosas, plantear problemas, pensar y buscarles una solución. En el instituto, quiso ser Madonna, cantante rebelde y algo respondona. Descubrió asombrada la Filosofía que es hacer preguntas, pensar teorías, crear nuevas formas de conocimiento y entender el mundo con el pensamiento. —Quiero ser filósofa, está decidido. —Te propongo algo aún más atrevido: —le dijo un amigo que era profesor—. Hazte matemática, que es filosofía aplicada al número y a la geometría. —Atrévete, Clara, si tienes valor. Como pasa a veces con las cosas nuevas, fueron complicadas las primeras pruebas. Hace falta tiempo para ir descubriendo todos los secretos del razonamiento. Cuando los descubres, todo se ilumina. Y eres matemática, porque te fascina la extraña belleza de esas relaciones que expresan los números y las ecuaciones. Clara ha descubierto mil cosas geniales: con las matemáticas computacionales enseñó a las máquinas a ver las distancias mediante unos grafos de gran elegancia. © Anaya, A.Materialimprimibleautorizado.

EuclidesEuclides era un gran sabio un sabio de Alejandría, y, además de extraordinario, padre de la Geometría. Escribió un libro increíble, ¿y sabéis por qué lo admiro? ¿Porque tiene trece tomos? ¿Porque está hecho de papiro? ¡No es por eso! ¡No es por eso! Es por sus razonamientos y por como relaciona puntos, rectas y segmentos. El punto tiene su punto, y la recta... ¡es tan perfecta! Si lo pones todo junto ves que todo se conecta. Con Euclides descubrimos el valor de lo sencillo. ¡Aprender nunca es difícil si le coges el tranquillo!

ANDRESA CASAMAYOR Mi nombre: María Juana Rosa Andresa Casamayor de Coma. Nací Zaragoza 1720 hasta Mis primeros años: séptima de nueve hermanos y hermanas. Pertenecía a familia comerciantes aragoneses con ascendencia francesa que, mi juventud, problemas económicos lo que tuviera ponerme trabajar maestrani me casé entré ninguna institución religiosa, era lo se llevaba esa época. ¡Y tuve gran de una educación superior lo normal esa época!, hasta tenía instructor de orden de los escolapios que venía casa. mío educación, sobre todo, la didáctica de las matemáticas. Escribí manuales sobre matemáticas, concretamente sobre aritmética; más famoso que conserva Tyrocinio: Instrucción de las cuatro reglas llanas. Lo mejor de mis obras es con ellas ayudé a late comprender las matemáticas utilizarlas cotidiana. Por ejemplo, ayudé aprendices comerciantes aprender sumar, multiplicar ¿Cómoloconseguí? Supongo que mi conocimiento, razonamiento, mi experiencia como maestra mi gran capacidad de trabajo, ¡sin dejar atrás atrevimiento para pionera! Algunascuriosidades sobre mí que doynombre una calle ciudad, soy imagen un sello sacaron en honor protagonista de documental que estrenó hace poco, 2020, mismísima Biblioteca Nacional.

más, mi trabajo, logré reconocimientos insólitos una mujer iraní 105

lo dado visibilidad al papel de la en la ciencia referentes niñas que quieren dedicarse profesiones de campos STEM. ¿Cómo lo conseguí? Todavía no lo sé, está claro que la clave está, duda, en infinita imaginación creatividad, talento, conocimiento y atrevimiento para explicar desconocido. Algunas curiosidades o anécdotas mí es por desgracia, fallecí muy joven un cáncer mama; tengo muchos reconocimientos por mi trabajo, ¡hasta medalla que como un premio nobel de las matemáticas; fui hasta considerada persona interés Nature prestigiosa revista científica.

«APRENDE STEAM HACIENDO»

Clara Grima

Versátil

Adaptable a distintos enfoques y necesidades: para quienes complementan el libro en papel y para aulas plenamente digitales.

Trazable

Podrás visualizar la realización y los resultados de las actividades propuestas.

¿Cómo es Edudynamic?

Intuitivo.  Fácil de usar para ti y para tus alumnas y alumnos.

Descargable.  Permite trabajar sin cone xión a internet y descargarse en más de un dis positivo.

Multidispositivo.  Se adapta y visualiza en cualquier tipo de dispositivo (ordenador, ta bleta, smartphone...) a cualquier tamaño y reso lución de pantalla.

Sincronizable.  Los cambios que realice el usuario se sincronizan automáticamente al co nectar cualquiera de los dispositivos en los que se trabaje.

Universal. Compatible con todos los sistemas operativos, los entornos virtuales de aprendizaje (EVA) y las plataformas educativas (LMS) más utilizadas en los centros escolares.

Interactivo

Contiene diversidad de recursos como vídeos, animaciones, gamificación, actividades de autoevaluación, actividades interactivas autocorregibles… Es mucho más que una reproducción del libro en papel.

Inclusivo

Su entorno facilita la personalización del aprendizaje adaptando las tareas a las necesidades del alumnado.

Elementos multimedia de alto valor pedagógico diseñados para facilitar la adquisición de las competencias digitales.

Un proyecto digital que cubre todos los contenidos del curso y que se adapta a cualquier plataforma y dispositivo.

¿Y para el alumnado?

Para 1.° y 2.°, un libro activo que combina la versión digitalizada del libro del alumnado con los recursos desarrollados para la reproducción multimedia e interactiva de todos los contenidos del curso, gamificación, audios, vídeos...

Para el trabajo en el aula y de manera individual en casa, el libro activo se puede utilizar como complemento digital del libro impreso o como herramienta autónoma de aprendizaje.

De 3.° a 6.°, un formato especialmente diseñado para el entorno digital educativo, que utiliza todo el potencial tecnológico y es compatible con cualquier dispositivo. Se han realizado ediciones específicas de todos los contenidos teóricos y prácticos del libro de texto para obtener una versión interactiva y dinámica que incluye todo el contenido curricular del nivel, junto con una gran diversidad de recursos multimedia, vídeos, gamificación…

Recursos

Metodologías activas (técnicas y estrategias) recursos para:

• Ejercitar: vídeos, presentaciones...

• Estudiar: resúmenes, actividades interactivas...

• Aprender: Game Room, actividades lúdicas...

• Evaluar: autoevaluación, porfolio...

Inclusión y atención a la diversidad

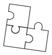
• Herramienta de Inclusión Online.

• Lo esencial.

• Atención a la diversidad: fichas de refuerzo, ampliación y multinivel.

Evaluación

• Generador de pruebas de evaluación y ejercitación.

• Evaluación inicial y unidad cero.

• Evaluación por situaciones de aprendizaje.

• Evaluación competencial.

• Evaluación adaptada.

• Evaluación final.

• Instrumentos de evaluación, autoevaluación y coevaluación.

iPad

• Instrumentos para evaluar la práctica docente.

• Competencias GYM.

3 ¿Cuál de estas figuras no representa un cuarto?

Si necesitas ayuda, «Te lo cuento en un momento» en anayaeducacion.es 4 Dibuja estas figuras en tu cuaderno. Después, colorea las fracciones que se indican.

2 3 1 4 5 Completa las oraciones en tu cuaderno con las pala- bras adecuadas. entera cuatro tercios medias

a) Dos ? tartas forman una tarta entera. b) Tres ? de tarta forman una tarta entera. c) ? cuartos de tarta forman una tarta ? 6 Observa la imagen y contesta.

a) ¿Cuántos medios forman una unidad? b) ¿Cuántos cuartos forman una unidad?

cuartos

un

Programación, propuesta didáctica y documentación del proyecto

• Las claves de Operación Mundo.

• Propuesta didáctica.

• Programaciones.

Contenidos

¿Qué vamos a aprender?

1 5 9

2 6 10

3 7 11

4 8 12

Los números Es igual, pero no es lo mismo

La suma y la resta Súmate al consumo responsable

La multiplicación. Las tablas Multiplica tu salud

Las tablas. Practico la multiplicación Cultivos que se multiplican

La división Dividir, repartir, compartir

Las fracciones Aprendemos juntos

La medida del tiempo Las horas del sol

Organización de la información De un vistazo

Unidades de longitud ¿Y tú qué mides?

Unidades de capacidad y masa Medir, pero, ¿con qué unidad?

Rectas, ángulos y planos Caminamos sin barreras

Las figuras planas Formas en la naturaleza

SITUACIÓN DE APRENDIZAJE OBJETIVO EN ACCIÓN ODS PÁG.

¿Cómo pueden los números ayudarnos a entender las diferencias entre las personas o los países? Escribe un titular para explicarlo.

¿Qué podemos hacer para consumir de manera más responsable? Elabora un cartel con tus propuestas.

¿Por qué crees que hacer deporte es bueno para tu salud y bienestar? Escribe un correo electrónico explicando tus razones.

¿Qué se cultiva en tu entorno? Realiza un anuncio publicitario en el que enseñes a otros niños y niñas qué cosas se cultivan donde vives.

REPASO TRIMESTRE 1 STEAM: Maryam Mirzakhani

¿Qué puedes hacer a diario para no desperdiciar la comida? Escribe una carta a tu familia con propuestas.

Reducción de las desigualdades

Producción y consumo responsables Salud y bienestar Fin de la pobreza

Hambre cero

¿Podemos aprender matemáticas jugando? Construye un comecocos de papel para jugar con las fracciones.

Educación de calidad

¿Cómo puedes aprovechar la luz del sol en tu día a día? Elabora una lista con las ideas.

Energía asequible y no contaminante

¿Por qué es importante comer fruta y verdura todos los días? Escribe un cuento para explicarlo.

REPASO TRIMESTRE 2 STEAM: María Andresa Casamayor

¿Por qué es importante respetar las ideas de los demás? Inventa una unidad de medida con tu cuerpo y compárala con los demás. Si compartimos nuestras ideas, ¡aprendemos juntos!

¿Qué objetos donarías tú a una web solidaria?

Dibuja un cartel publicitario para animar a los demás a donar objetos.

¿Cómo podemos eliminar las barreras arquitectónicas?

Dibuja un plano uniendo dos puntos de tu localidad y encuentra en el recorrido las barreras arquitectónicas.

¿Cómo podemos cuidar los bosques? Inventa señales con forma de figuras planas para informar sobre lo que se puede o no hacer en los bosques.

REPASO TRIMESTRE 3 STEAM: Maria Montessori

Salud y bienestar

Paz, justicia e instituciones sólidas

Producción y consumo responsables

Ciudades y comunidades sostenibles

Vida de ecosistemas terrestres

SABERES BÁSICOS LO RESUELVO SIN PROBLEMA

• Números de tres y cuatro cifras: conteo, lectura, composición, descomposición y valor de posición.

• Comparación: valor de posición y uso de la recta numérica.

• Suma por descomposición y en vertical.

• Propiedades de la suma.

• Resta por descomposición y en vertical.

• Multiplicación como suma de sumandos iguales.

• La tabla del 2. El doble.

• Las tablas del 5 y del 10.

• Las tablas del 3 y del 6.

• Las tablas del 9 y del 7.

• Multiplicación por 10, 100 y 1 000.

• Aproximación al orden que coincide con la cantidad de cifras del número.

• Números ordinales.

• Las monedas y los billetes.

• Problemas aritméticos: de cambio, de combinación y de comparación.

• Las tablas del 4 y del 8.

• Práctica de las tablas.

• Problemas aritméticos: de grupos iguales.

• Multiplicación de diferentes formas.

• Multiplicación en vertical.

• Problemas aritméticos: de grupos iguales.

• Estrategia heurística: Busco todos los casos posibles

• Cálculo mental: Sumar una cifra sin llevadas

• Pensamiento computacional: Algoritmo

• Estrategia heurística: Estimo la solución

• Cálculo mental: Restar una cifra sin llevadas

• Pensamiento computacional: Algoritmo

• Estrategia heurística: Organizo los datos en una tabla

• Cálculo mental: Sumar una cifra con llevadas

• Pensamiento computacional: Generalización

• Estrategia heurística: Sigo un patrón

• Cálculo mental: Restar una cifra con llevadas

• Pensamiento computacional: Funciones

PROYECTO INTERDISCIPLINAR · ¿Aprovechamos o desperdiciamos alimentos?: Dime cuándo caducas… y te diré…

• División como reparto: mitad, tercio, cuarto.

• División exacta e inexacta.

• División por descomposición.

• Las fracciones: concepto, nombre, términos y representación.

• Medios, tercios, cuartos.

• El calendario: año, meses.

• El día, las horas y los minutos.

• Tablas de registro de datos.

• Gráficos de barras.

• Practica de la división: propiedad del resto, prueba de la división.

• Problemas aritméticos: de reparto.

• Comparación de fracciones con igual denominador.

• Estrategia heurística: Planteo preguntas intermedias

• Cálculo mental: Sumar decenas

• Pensamiento computacional: Funciones

• Estrategia heurística: Hago un dibujo

• Cálculo mental: Sumar dos cifras sin llevadas

• Pensamiento computacional: Generalización

• Estrategia heurística: Empiezo por el final

• La lectura del reloj.

• Problemas aritméticos: de grupos iguales.

• Pictogramas.

• Gráficos de líneas.

• Cálculo mental: Sumar dos cifras con llevadas en  unidades

• Pensamiento computacional: Codificación

• Estrategia heurística: Organizo los datos en un diagrama de árbol

• Cálculo mental: Multiplicar por la unidad seguida de ceros

• Pensamiento computacional: Generalización

PROYECTO INTERDISCIPLINAR · Protegemos la vida submarina: «Recreo» al mar

• Unidades de medida: convencionales y no convencionales.

• El metro.

• El centímetro.

• Unidades de capacidad: el litro y el mililitro.

• Medio litro y cuarto de litro.

• Unidades de masa: el kilogramo y el gramo.

• Rectas secantes y paralelas. El plano.

• Los ángulos y sus elementos. Rectas perpendiculares.

• Los polígonos.

• El perímetro.

• Clases de triángulos.

• Medición con regla.

• El kilómetro.

• Problemas aritméticos: de cambio, de grupos iguales, de igualación y de comparación.

• Medio kilo y cuarto de kilo.

• Problemas aritméticos: de grupos iguales, de combinación, de comparación y de cambio.

• Clasificación según su amplitud.

• Posición y movimientos en el plano.

• Clases de cuadriláteros.

• Circunferencia y círculo.

• Estrategia heurística: Hago un esquema

• Cálculo mental: Completar decenas

• Pensamiento computacional: Funciones

• Estrategia heurística: Tanteo la solución

• Cálculo mental: Completar centenas

• Pensamiento computacional: Simulación

• Estrategia heurística: Ensayo-error

• Cálculo mental: Doble de dos cifras sin llevadas

• Pensamiento computacional: Algoritmo

• Estrategia heurística: Observo regularidades

• Cálculo mental: Mitad de cifras pares

• Pensamiento computacional: Abstracción

PROYECTO INTERDISCIPLINAR · Lo que el tiempo nos dejó: Pasos del pasado

Contenidos de la etapa

• Números del 0 al 5

1 2

1.º 2.º 3.º

• El número 10 y la decena

• Orden, descomposición

• Más que, menos que, tantos como

• Dentro-fuera, delante-detrás, arriba-abajo, cerca-lejos

• Números hasta el 9

• Conteo, orden, descomposición

• Igual o distinto

• Entre, izquierda-derecha

• Recorridos en cuadrícula

• El número 10

• Conteo, orden, descomposición

• La decena

• La suma

• Figuras planas

• Cálculo mental. Pensamiento computacional

• Estrategia de resolución de problemas

• Números hasta el 19

• Conteo, orden, descomposición

• La resta

• Comparación de longitudes

• Pesa más-menos. Cabe más-menos

• Cálculo mental. Pensamiento computacional

• Estrategia de resolución de problemas

• Números hasta el 29

• Conteo, orden, descomposición

• Mayor que y menor que

• Sumar y restar contando hacia delante y hacia atrás

• Tipos de líneas

• Cálculo mental. Pensamiento computacional

• Estrategia de resolución de problemas

• Números hasta el 39

• Conteo, orden, descomposición

• Anterior y posterior

• Sumar y restar por descomposición

• Figuras planas y sus lados

• Cálculo mental. Pensamiento computacional

• Estrategia de resolución de problemas

• Números hasta el 59

• Conteo, orden, descomposición

• Sumar en vertical

• Medir longitudes: unidades no convencionales

• Palmo-pie-paso

• Cálculo mental. Pensamiento computacional

• Estrategia de resolución de problemas

• Números hasta el 79

• Conteo, orden, descomposición

• Restar en vertical

• Comparar capacidades

• Trasvases

• Cálculo mental. Pensamiento computacional

• Estrategia de resolución de problemas

• Números hasta el 99

• Conteo, orden, descomposición

• Repaso de números y operaciones

• Pictogramas

• Gráficos de barras

• Cálculo mental. Pensamiento computacional

• Estrategia de resolución de problemas

• Los signos > y <

• Sumar tres números de una cifra

• Sumar con llevadas

• Monedas de euro

• Billetes de euro

• Cálculo mental. Pensamiento computacional

• Estrategia de resolución de problemas

• Repaso de números y operaciones

• Sumar tres números con llevadas

• Medir el tiempo

• Los días de la semana. Ayer, hoy y mañana

• El calendario

• Cálculo mental. Pensamiento computacional

• Estrategia de resolución de problemas

• Números ordinales

• Relación entre las partes y el todo

• El reloj de agujas

• El reloj digital

• Repaso de números y operaciones

• Cálculo mental. Pensamiento computacional

• Estrategia de resolución de problemas

• Repaso de números hasta el 99

• Sumas y restas

• Sumar completando al 10

• Izquierda-derecha; arriba-abajo

• Cálculo mental. Pensamiento computacional

• Estrategia de resolución de problemas

• Mayor que y menor que

• Redondear a las decenas

• La suma y sus términos

• La resta y sus términos

• Los días de la semana. El calendario

• Cálculo mental. Pensamiento computacional

• Estrategia de resolución de problemas

• El número 100

• La centena

• Números hasta el 199

• Sumas y restas de números de 3 cifras

• El reloj de agujas

• Cálculo mental. Pensamiento computacional

• Estrategia de resolución de problemas

• Números hasta el 299

• Sumas con llevadas

• El reloj de agujas y digital: La hora en punto, y media, y cuarto y menos cuarto

• Cálculo mental. Pensamiento computacional

• Estrategia de resolución de problemas

• Números hasta el 399

• Restas con llevadas

• Tipos de líneas

• Figuras simétricas

• Cálculo mental. Pensamiento computacional

• Estrategia de resolución de problemas

• Números hasta el 499

• Números hasta el 599

• Restas llevando decenas y/o centenas

• Los polígonos

• Cálculo mental. Pensamiento computacional

• Estrategia de resolución de problemas

• Números hasta el 699

• Números hasta el 799

• Propiedad conmutativa y asociativa de la suma

• Prueba de la resta

• Círculo y circunferencia. Planos y croquis

• Cálculo mental. Pensamiento computacional

• Estrategia de resolución de problemas

• Números hasta el 899

• Números hasta el 999

• Redondear a las centenas

• Pirámides y prismas

• Cuerpos redondos

• Cálculo mental. Pensamiento computacional

• Estrategia de resolución de problemas

• Números pares e impares

• La multiplicación

• Las tablas del 2, del 5 y del 10

• Gráficos de barras

• Pictogramas

• Cálculo mental. Pensamiento computacional

• Estrategia de resolución de problemas

• Números ordinales

• Las tablas del 4 y del 8

• La calculadora

• El metro y el centímetro

• Mido con la regla

• Cálculo mental. Pensamiento computacional

• Estrategia de resolución de problemas

• Las tablas de 3, del 6 y del 9

• Comparación de capacidades

• Comparación de masas

• Litro

• Kilo

• Cálculo mental. Pensamiento computacional

• Estrategia de resolución de problemas

• La tabla del 7

• Mitad de una cantidad

• Monedas de céntimo y de euro

• Billetes de euro

• Sucesos: seguro, posible e imposible

• Cálculo mental. Pensamiento computacional

• Estrategia de resolución de problemas

• Números de tres y cuatro cifras: conteo, lectura, composición, descomposición y valor de posición, comparación y ordenación

• Aproximación de números

• Números ordinales

• Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Suma por descomposición y en vertical

• Propiedades de la suma

• Resta por descomposición y en vertical

• Las monedas y los billetes

• Problemas aritméticos. Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Multiplicación como suma de sumandos iguales

• La tabla del 2. El doble

• Las tablas del 5, del 10, del 4 y del 8

• Práctica de las tablas

• Problemas aritméticos. Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Las tablas del 3, del 6, del 9 y del 7

• Multiplicación por 10, 100 y 1000

• Multiplicación de diferentes formas

• Multiplicación en vertical

• Problemas aritméticos. Estrategia heurística

• Cálculo mental. Pensamiento computacional

• División como reparto: mitad, tercio, cuarto

• División exacta e inexacta

CURSOS UNIDADES

• División por descomposición

• Propiedad del resto, prueba de la división

• Problemas aritméticos. Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Las fracciones: concepto, nombre, términos y representación

• Medios, tercios, cuartos

• Comparación de fracciones con igual denominador

• Estrategia heurística

• Cálculo mental. Pensamiento computacional

• El calendario: año, meses

• El día, las horas y los minutos

• La lectura del reloj

• Problemas aritméticos. Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Tablas de registro de datos

• Gráficos de barras

• Pictogramas

• Gráficos de líneas

• Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Unidades de medida: convencionales y no convencionales

• El metro. El centímetro. Medición con regla

• El kilómetro

• Problemas aritméticos. Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Unidades de capacidad: el litro y el mililitro

• Medio litro y cuarto de litro

• Unidades de masa: el kilogramo y el gramo

• Medio kilo y cuarto de kilo

• Problemas aritméticos. Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Rectas secantes y paralelas. El plano

• Los ángulos y sus elementos. Rectas perpendiculares. Clasificación según su amplitud

• Posición y movimientos en el plano

• Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Los polígonos

• El perímetro

• Clases de triángulos y de cuadriláteros

• Circunferencia y círculo

• Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Números de hasta seis cifras: conteo, lectura, composición, descomposición y valor de posición, comparación y ordenación

• Aproximación de números

• Estrategia heurística

• Cálculo mental. Pensamiento computacional

• La suma y sus propiedades

• La resta. La prueba de la resta

• Estimación de sumas y restas

• Sumas y restas combinadas

• Problemas aritméticos. Estrategia heurística

• Cálculo mental. Pensamiento computacional

• La multiplicación y sus términos

• Propiedades de la multiplicación

• Multiplicación por decenas, centenas y millares

• Multiplicación por varias cifras

• Problemas aritméticos. Estrategia heurística

• Cálculo mental. Pensamiento computacional

• División como reparto y como agrupación

• Prueba de la división. División por descomposición

• División entre decenas, centenas y millares

• División entre dos cifras

• Operaciones combinadas

• Problemas aritméticos. Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Nombrar fracciones. Medios, tercios y cuartos

• La fracción y la unidad

• Fracciones propias e impropias

• Comparación de fracciones

• Fracción de un número. Fracción como reparto

• Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Números decimales: lectura, escritura, valor de posición. Precios. Décimas y centésimas

• Comparación y representación de decimales

• Redondeo de números decimales

• Suma y resta de números decimales

• Problemas aritméticos. Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Unidades de medida no convencionales

• Unidades menores y mayores que el metro

• Transformación de unidades

• Expresiones complejas e incomplejas

• Problemas aritméticos. Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Unidades menores y mayores que el litro

• Unidades menores y mayores que el gramo

• Transformación de unidades

• Expresiones complejas e incomplejas

• Problemas aritméticos. Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Unidades menores y mayores que el año

• Días, horas, minutos y segundos

• El reloj de agujas y el reloj digital

• Problemas aritméticos. Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Puntos, rectas, semirrectas, segmentos

• Rectas paralelas, secantes y perpendiculares

• Ángulos: elementos, medida y clasificación

• El ángulo como giro. Simetría y traslación

• Coordenadas en el plano. Situación y movimiento

• Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Polígonos: elementos y clasificación. Perímetro

• Clasificación de triángulos y de cuadriláteros

• Área de polígonos

• Circunferencia y círculo. Cuerpos geométricos

• Prismas y pirámides. Cuerpos redondos

• Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Experiencias de azar

• Suceso seguro, posible e imposible

• Probabilidad de un suceso

• Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Números de hasta siete cifras: conteo, lectura, composición, descomposición, valor de posición, comparación y ordenación

• Aproximación de números

• Propiedades de la suma y relación con la resta

• Problemas aritméticos. Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Propiedades de la multiplicación: conmutativa, asociativa y distributiva

• Multiplicación por decenas, centenas y millares

• Operaciones combinadas

• Potencias, cuadrados y cubos

• Problemas aritméticos. Estrategia heurística

• Cálculo mental. Pensamiento computacional

• La división con divisores de dos y tres cifras

• División exacta e inexacta

• Propiedad fundamental de la división

• División por decenas, centenas y millares

• Operaciones combinadas

• Problemas aritméticos. Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Fracciones. Medios, tercios y cuartos

• Fracción y unidad. Fracciones propias e impropias

• Fracciones equivalentes. Comparación

• Suma y resta de fracciones (igual denominador)

• Fracción de una cantidad

• Problemas aritméticos. Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Décimas, centésimas y milésimas

• Números decimales: lectura, escritura y valor de posición. Precios

• Comparación de números decimales

• Aproximación de un decimal a un natural

• Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Suma, resta y multiplicación de números decimales

• Multiplicación de decimal por natural

• División de naturales con cociente decimal

• División de decimal entre natural

• División por decenas, centenas y millares

• Problemas aritméticos. Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Unidades de medida de longitud, capacidad, masa y superficie

• Transformación de unidades

• Expresiones complejas e incomplejas

• Problemas aritméticos. Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Tablas de frecuencias absolutas y relativas

• Datos cualitativos y cuantitativos

• Moda, media y rango. Gráficos de sectores

• Gráficos de barras y de líneas. Histogramas

• Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Unidades menores y mayores que el año

• Horas, minutos y segundos

• Expresiones complejas e incomplejas

• Suma y resta de datos de tiempo

• Problemas aritméticos. Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Recta, semirrecta y segmento

• Clasificación de ángulos según su amplitud y su posición. Medida de ángulos

• Clasificación de ángulos según la suma de sus amplitudes

• Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Polígonos: elementos y clasificación

• Polígonos regulares. Perímetro

• Triángulos y cuadriláteros

• Circunferencia y círculo: elementos

• Simetría, traslación y giro

• Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Medida de superficies

• Área del cuadrado y del rectángulo

• Área del triángulo

• Área del romboide y del rombo

• Estrategia heurística

• Cálculo mental. Pensamiento computacional

• El sistema de numeración decimal. Conteo

• Operaciones básicas con números naturales. Propiedades. Operaciones combinadas

• Números positivos y negativos

• Coordenadas cartesianas

• Problemas aritméticos. Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Múltiplos de un número. m.c.m.

• Divisores de un número. m.c.d.

• Criterios de divisibilidad

• Números primos y compuestos

• Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Potencia de un número natural

• Cuadrados y cubos

• Raíz cuadrada. Potencias de base 10

• Descomposición polinómica

• Unidades de información: byte, kilobyte

• Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Décimas, centésimas y milésimas

• Números: lectura, escritura y valor de posición

• Comparación, ordenación y redondeo de números decimales. Precios

• Suma, resta, multiplicación y división de números decimales

• Problemas aritméticos. Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Fracción. Fracción y unidad. Propias e impropias

• Fracción de una cantidad, equivalentes e irreducibles

• Comparación de fracciones

• Suma, resta, multiplicación y división

• Problemas aritméticos. Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Unidades de medida de longitud, capacidad, masa, superficie y volumen

• Transformación de unidades

• Expresiones complejas e incomplejas

• Problemas aritméticos. Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Magnitudes proporcionales. Reducción a la unidad

• La regla de tres. Aumentos y descuentos

• Porcentaje de una cantidad. Aumentos y descuentos

• La escala: gráfica y numérica

• Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Clasificación de ángulos (amplitud y posición)

• Medida de ángulos: grados, minutos y segundos

• Suma y resta de ángulos

• Problemas aritméticos. Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Perímetro de polígonos

• Área de paralelogramos y triángulos, de polígonos regulares y figuras compuestas

• Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Circunferencia. Círculo y figuras circulares

• Posición de puntos, rectas y circunferencias

• El número π. Longitud de la circunferencia

• Área del círculo

• Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Poliedros y cuerpos redondos

• Poliedros regulares y cuerpos de revolución

• Área y volumen de prismas, pirámides y figuras compuestas

• Estrategia heurística

• Cálculo mental. Pensamiento computacional

• Experiencias de azar

• Suceso seguro, posible e imposible

• Probabilidad de un suceso. Regla de Laplace

• Técnicas de conteo

• Estrategia heurística

• Cálculo mental. Pensamiento computacional

Recursos

Inclusión y atención a la diversidad

Proyecto digital

Evaluación

Programación, propuesta didáctica y documentación del proyecto

Recursos

Inclusión y atención a la diversidad

Evaluación

Programación, propuesta didáctica y documentación del proyecto

Recursos relacionados con las claves del proyecto

Recursos digitales ordenados tanto por situaciones de aprendizaje como por sus propósitos educativos más destacables

Herramientas digitales

Lo esencial

Pautas DUA Fichas de atención a la diversidad

Inclusión Online ANAYA (IN.ON)

Pruebas de evaluación prediseñadas

Generador de pruebas escritas de evaluación y ejercitación

Instrumentos de evaluación, autoevaluación y coevaluación

Instrumentos para evaluar la práctica docente

Las claves de Operación Mundo

Propuesta didáctica

Programaciones (versiones Word y PDF)

Recursos relacionados con las claves del proyecto

Con la información que el alumnado necesita manejar para poner en práctica las claves y las metodologías activas de Operación Mundo.

• Infografías del Plan Lingüístico y del Plan TIC-TAC.

PLAN TIC TAC

USAMOS LAS TIC

Las tecnologías de la información y la comunicación (TIC) mientas que nos ayudan a realizar muchas tareas como buscar infor mación, escribir, jugar… También sirven para comunicarse con otras personas y compartir textos e imágenes. Para utilizar las TIC necesitamos un son máquinas compuestas que utilizan energía eléctrica o electrici dad para funcionar.

¿Cuáles son los dispositivos TIC?

Herramientas digitales

Distintas herramientas para trabajar digitalmente con policubos, regletas, monedas, tangram, bloques base 10, bloques lógicos... así como una herramienta para que el profesor pueda construirse su propia ficha (numeración, sumas, restas...).

Para estudiar y ejercitar

• Resúmenes.

• Fichas fotocopiables.

• Actividades interactivas.

LO RESUELVO SIN PROBLEMA

Busco todos los casos posibles ¿De cuántas maneras distintas puedes formar una torre con estos cubos?

Para aprender

• Vídeos.

• Presentaciones.

• Audios.

Puedo formar una torre de 6 maneras distintas.

1 Diego, Claudia y Olivia echan una carrera. ¿En qué posición llegará cada uno? Escribe todas las posibilidades.

1. 2.o 3.o

DiegoClaudiaOlivia

DiegoOlivia ? Claudia ? ? ? ? ?

2 ¿Cuántos números diferentes de tres cifras puedes formar con el 1, el 2 y el 3? Encuentra todas las posibilidades.

Organizo los datos para buscar todas las posibilidades. 1. 2.o 3.o

Coloca uno de los cubos, y después, haz combinaciones con los dos restantes.

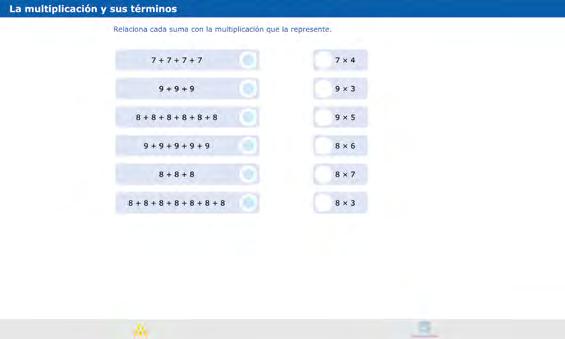
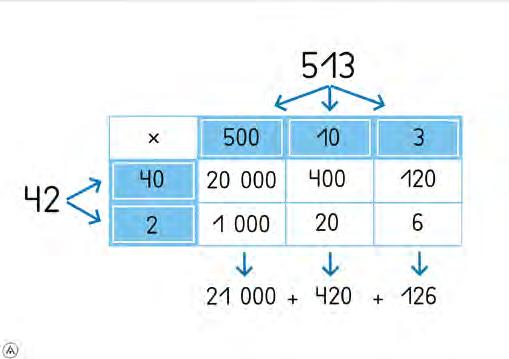
Recursos digitales ordenados tanto por situaciones de aprendizaje como por sus propósitos educativos más destacables

Para jugar

• Actividades lúdicas.

• Repasos trimestrales lúdicos.

• Game Room: Ultimate travellers. Y para seguir jugando, cuentas con recursos lúdicos en el material de aula.

Para evaluar

• Actividades y pruebas interactivas con trazabilidad, que facilitan el seguimiento del progreso del alumnado por parte del profesorado.

• Y apps recomendadas, que complementan el Plan TIC-TAC propuesto en el proyecto.

Inclusión y atención a la diversidad

Lo esencial

Recoge los aprendizajes esenciales que permitirán adquirir el perfil de salida previsto, ayudando al profesorado a adaptar el ritmo y la profundidad, haciendo uso de las metodologías activas más adecuadas en cada caso.

Inclusión y atención a la diversidad

Pautas DUA

Los diferentes elementos del Proyecto Operación Mundo están concebidos teniendo en cuenta los principios del Diseño Universal de Aprendizaje (DUA).

Pautas DUA en Operación Mundo

Los diferentes elementos del Proyecto Operación Mundo están concebidos teniendo en cuenta los principios del Diseño Universal de Aprendizaje (DUA). En la siguiente tabla se muestra la relación entre los principios o pautas DUA y los elementos del proyecto:

OPERACIÓN MUNDO Pautas DUA que se aplican en el proyecto MATERIAL IMPRESO ENTORNO DIGITAL

Situación de aprendizaje

ODS

Imagen y contexto

¿Cómo lo ves?

El dato

Objetivo en acción

• La relación directa con los ODS (retos del siglo xxi) y con la vida cotidiana del alumnado optimiza la relevancia, el valor y la autenticidad (7.2).

• La representación alternativa al texto facilita la comprensión y la conexión personal con el contexto de la Situación de aprendizaje (2.5).

• Las preguntas vinculan la Situación de aprendizaje con las experiencias y los conocimientos previos del alumnado (3.1).

• Aporta información objetiva y contrastable sobre la importancia del objetivo en acción (8.1).

• Estimula la reflexión colectiva a través de una estrategia de pensamiento útil para afrontar los problemas cotidianos (9.2).

• Fomenta la autonomía proponiendo un producto final abierto a la contextualización en el centro y a la elección del alumnado (7.1) variando los niveles de exigencia (8.2).

• Facilita la generalización y la transferencia de los aprendizajes esenciales (3.4).

• Fomenta la comunidad y la colaboración para la realización y difusión colectiva del producto final (8.3).

• Da acceso a información actualizada sobre los ODS al profesorado y al alumnado utilizando múltiples medios de comunicación (5.1).

• ¿Qué sé? Propone actividades interactivas trazables para la detección de ideas previas en la apertura de la unidad (3.1)

• Utiliza píldoras audiovisuales que presentan las situaciones de aprendizaje estimulando expectativas y creencias que aumentan la motivación (9.1) en la apertura de la unidad.

• Presenta en cada unidad información adicional de fuentes preseleccionadas en distintos formatos que proporcionan alternativas a la información auditiva (1.2) y visual (1.3) como representaciones alternativas al texto (2.5): canciones, audios o vídeos subtitulados, locuciones de la información textual, organizadores gráficos, visual thinking, etc. utilizables, además, Para dinamizar la participación.

Sigue el hilo

• Guía de forma ordenada la consecución del objetivo en acción (6.1) modelando y visibilizando el proceso (6.2) con un organizador gráfico (6.3).

• Permite reconstruir el proceso de aprendizaje de forma interactiva con el apoyo del organizador gráfico que representa el progreso hacia el objetivo en acción (3.3).

Fichas de atención a la diversidad

Permiten:

• Encontrar materiales de apoyo.

• Prestar una atención individualizada.

• Adaptar los contenidos a los diferentes ritmos de aprendizaje.

• Seleccionar y aplicar diversas estrategias metodológicas.

Inclusión Online ANAYA ( IN.ON)

Una herramienta que pone a disposición del profe sorado una gran cantidad de recursos con un ob jetivo principal: la enseñanza inclusiva. la integración del alumnado gracias a la enseñanza multinivel y a la atención de todas las necesidades educativas especiales.

I N N O INCLUSIÓN ONLINE

Evaluación

Pruebas de evaluación prediseñadas

Para evaluar conocimientos previos y el progreso en el curso:

• Evaluación inicial: unidad 0 y prueba de evaluación inicial.

• Una evaluación final.

Para cada situación de aprendizaje:

• Una evaluación.

• Una evaluación competencial.

• Una evaluación adaptada.

Para cada trimestre:

• Competencias GYM: una prueba competencial para evaluar el progreso en la adquisición del perfil de salida.

https://gev.anaya.es/geval/profesor/?YTh0bWw2ZXdjb2RlPTQ0MD...

Nombre y apellidos:

1 Completa y contesta.

son los resultados? ¿Qué propiedad se cumple?

¿Qué propiedad de la suma hemos aplicado?

2 Realiza estas operaciones:

a) 6879 8763 +375 b) 8902 –3457

3 Coloca en columna y calcula.

a) 3 594 + 9 340 + 874 = b) 70 253 – 5 784 =

4 Realiza esta resta y haz la prueba:

34935 –26967 PRUEBA

Generador de evaluaciones - Profesorado

Prueba de Matemáticas

1) Rodea las figuras que son polígonos

9:45 AM 100%

2) Dibuja un octógono. Si cada lado mide 7 cm y todos sus lados son iguales, ¿cuánto mide su perímetro?

3 Dibuja un rectángulo. Si el largo del rectángulo mide 12 cm y el ancho 3 cm, ¿cuánto mide su perímetro?

4 Dibuja un hexágono. Si cada lado mide 8 cm y todos sus lados son iguales, ¿cuánto mide su perímetro?

5 Las dimensiones de un campo de fútbol son: 100 m de largo y 55 m de ancho. ¿Cuánto mide su perímetro? Si un jugador da 5 vueltas, ¿cuántos metros recorre?

6 Escribe, V, si es verdadero y, F, si es falso.

a) Un polígono regular tiene todos sus lados iguales. _______

b) Un octógono tiene 7 lados. _______

Generador de pruebas escritas de evaluación y ejercitación

Herramienta con la que el profesorado podrá diseñar pruebas escritas de manera flexible, seleccionando, en función de sus objetivos didácticos, los aprendizajes que desea evaluar o ejercitar (parte de una unidad, una unidad completa, una situación de aprendizaje…).

c) Un triángulo tiene tres ángulos. _______

d) Un polígono tiene todos sus lados curvos, menos uno que es recto. _______

Y además...

• Fondo de instrumentos de evaluación, autoevaluación y coevaluación. Con una amplia base de rúbricas, dianas, y otros instrumentos diseñados por especialistas con el fin de proporcionar al profesorado un conjunto de herramientas con las que llevar a cabo la evaluación, la autoevaluación y la coevaluación.

• Instrumentos para evaluar la práctica docente.

Las claves de Operación Mundo

• Incluye una amplia documentación sobre las claves y las metodologías activas desarrolladas en el proyecto.

Programaciones. Con la versión en word y en pdf de:

• La programación didáctica.

• La programación por unidades.

Propuesta didáctica

• Recopila la versión en pdf de las propuestas didácticas.

Propuesta didáctica

Unidad muestra

¿Y tú qué mides?

Unidades de medida que varían

Palmo Pie

Paso

El centímetro

El centímetro es una unidad de longitud menor que el metro.

Su símbolo es cm.

Equivalencia de unidades

Un metro son 100 centímetros.

1 m = 100 cm

Dividir entre 10, 100 o 1 000

Para dividir un número entre 10, 100 o 1 000, eliminamos uno, dos o tres ceros del número.

5 0 : 1 0 = 5

5 00 : 1 00 = 5

5  000 : 1  000 = 5

El metro

El metro es la unidad principal de longitud.

Su símbolo es m. 1 m Utilizamos la cinta métrica para medir longitudes en metros.

El kilómetro

El kilómetro es una unidad de longitud mayor que el metro.

Su símbolo es km.

1 km

Equivalencia de unidades

Un kilómetro son 1 000 metros.

1 km = 1 000 m

Recursos digitalesInclusión y atención a la diversidadEvaluaciónAula

RECURSOS ¿QUÉ VAMOS A APRENDER?

Página inicial Situación de aprendizaje: Inventa una unidad de medida con tu cuerpo

ODS 16: Paz, justicia e instituciones sólidas

Unidades de medida que varían

• Concepto de unidad de medida

• Unidades de medida diversas

El metro

• Unidad de longitud

• El metro

• Suma y resta de medidas

El centímetro

• Medidas de objetos pequeños

• El centímetro

• Equivalencia entre metro y centímetro

• Suma y resta de medidas

Mido con regla

• Medida de objetos en centímetros utilizando la regla

El kilómetro

• Medida de distancias largas

• El kilómetro

• Equivalencia entre kilómetro y metro

• Medidas complejas e incomplejas

• Suma y resta de medidas

Lo resuelvo sin problema

Estrategia heurística: Hago un esquema

Problemas exprés

Cálculo mental: Completa decenas

Pensamiento computacional: Funciones

Porfolio

• ¿Qué he aprendido?

• ¿Qué he aprendido en la situación de aprendizaje?

• ¿Cómo he aprendido?

Vídeo: Te lo cuento en un momento (Medidas corporales)

Actividades interactivas

Esquema problemas aritméticos: de cambio y de grupos iguales Actividades interactivas

Esquema problemas aritméticos: de grupos iguales y de igualación Actividades interactivas

Material de aula Policubos

Actividades interactivas

Esquema problemas aritméticos: de comparación Actividades interactivas

Herramientas digitales Regletas Geoplano

Murales Otros materiales Clips Regla Cinta métrica

Vídeo: Cálculo mental (Completa decenas) Actividades interactivas

Actividades interactivas

Fichas 1, 2 y 3 (refuerzo)

Ficha 4 (ampliación)

Lo esencial

Evaluación

Evaluación adaptada Evaluación competencial

Calentando motores

9 × 8 = 72 9 × 4 = 36

9 × 5 = 45 9 × 7 = 63

9 × 9 = 81 9 × 0 = 0

9 × 1 = 9 9 × 6 = 54

9 × 2 = 18 9 × 3 = 27

Medir es comparar una cantidad con otra conocida. Puedes medir la distancia que hay de tu casa al colegio, la masa de la mochila que llevas o cuánta agua cabe en tu botella. Lo puedes hacer de diferentes maneras y ser todas correctas. Sin embargo, no es posible medir la belleza de un dibujo o el amor que sientes por tu familia.

Situación de aprendizaje ODS Imagen inicial

Se propone una reflexión sobre las cualidades que se pueden medir, esto es, magnitudes. Para ello, se toman ejemplos de la vida cotidiana cercana al alumnado. También se plantea la necesidad de una unidad de medida estandarizada para poder comparar con rigor.

Objetivo 16: Paz, justicia e instituciones sólidas.

Se trabaja el respeto a las ideas de los demás mediante el conocimiento de que, utilizando distintas unidades de medida, un objeto puede medir diferente y todo es correcto, solo que el baremo de medida es distinto.

¿Qué cosas observas en la imagen inicial?

Trabajamos la llave de pensamiento la imagen

– ¿Qué cosas ves que se pueden medir?

– ¿Qué cosas ves que no se pueden medir?

Respondemos las preguntas en grupo mediante la estrategia cooperativa asamblea de ideas relacionándolo con la actividad realizada en la imagen inicial.

Usar distintas unidades de medida y compartir el resultado ayuda a comprender que no todos pensamos igual, o vemos la realidad de la misma manera. Si respetamos las opiniones de los demás, podremos encontrar la manera de comprendernos.

Aprendizaje cooperativo

Trabajar las preguntas de la sección ¿Cómo lo ves? en estructura cooperativa asamblea de ideas

ODS

El objetivo trabajado es la paz, la justicia y las instituciones sólidas.

Sugerencias didácticas

• Establecer grupos para trabajar la doble página. Se pueden mantener para trabajar las actividades cooperativas a lo largo de la unidad.

• Fomentar la participación en grupo clase utilizando estrategias de participación, por ejemplo, usar un micro ficticio y solo habla quien tiene el micro.

• Enlazar el ODS con las instituciones sólidas en las que todos creemos (uso del sistema métrico decimal), el respeto a las ideas de los demás para evitar conflictos y cómo las instituciones o la estandarización de medidas pueden ayudar a ser más justos y vivir en paz.

Reflexionamos sobre por qué es importante respetar las diferentes ideas de todos a través de la invención de una unidad de medida que tenemos que contar a los demás.

Para diseñar la unidad de medida, ten en cuenta:

– Cuando utilizamos unidades de medida diferentes, obtenemos resultados distintos.

– Utiliza el centímetro para expresar cuánto mide una unidad de medida inventada.

– Utiliza la regla para expresar cuántos centímetros mide una cantidad de medida inventada.

Calentando motores

33 5 = 28 34 6 = 28

46 2 = 44 84 7 = 77

51 6 = 45 25 2 = 23

82 5 = 77 82 3 = 79

66 3 = 63 73 5 = 68

Recursos

Conexión con la situación de aprendizaje

El contenido del apartado ¡Toma nota! de la unidad nos ayuda a inventar una unidad de medida corporal y compartir las ideas con los demás.

Unidades de medida que varían

Las unidades de medida de longitud sirven para contar cuánto mide el largo, ancho o alto de un objeto.

Existen unidades de medida que varían según la persona o el objeto que se utilice para medir.

4 Respuesta abierta.

«Te lo cuento en un momento»

¿Cuántos palmos mide tu pareja? ¿Cómo le medirías

Se sugiere que para medir a la pareja en pasos, esta se Inventa dos unidades de medida distintas y utilízalas para medir el ancho y alto de la pizarra.

Solución: Respuesta abierta.

¿Qué ocurre si mido con unidades distintas?

1. ° Mide el ancho de tu clase con tus pies y con tus pasos.

a) ¿Cuántos pies mide la clase? ¿Y cuántos pasos?

b) ¿La clase mide más pies o más pasos? ¿Por qué crees que es así?

2. ° Ahora, tu profe tiene que medir el ancho de la clase con sus pasos.

a) ¿Cuántos pasos de tu profe mide la clase?

b) Compara tu resultado y el de tu profe en pasos. ¿Tiene sentido?

3. ° Piensa y comparte en pareja Para medir longitudes, ¿elegirías unidades que varían como el pie o el paso? Explicad vuestras respuestas al resto de la clase.

¡Toma nota!

Cuando utilizamos unidades de medida diferentes, obtenemos resultados distintos.

Refuerzo

TIC

• Vídeo: Te lo cuento en un momento (Otras unidades de medida corporales).

• Vídeo: Te lo cuento en un momento (Midiendo con las manos).

Desarrollo del pensamiento Piensa y comparte en pareja.

Ten en cuenta

• Insistir al medir que tienen que fijar dónde acaba un palmo para empezar el siguiente.

• Si usan los pasos, tienen que abrir las piernas lo mismo cada vez.

Sugerencias de las actividades

Antes de comenzar. Pedimos al alumnado que mida su mesa a palmos. Preguntamos a uno cuántos palmos medía y le decimos que está mal. A continuación, la medimos nosotros con nuestro palmo.

Iniciamos así un diálogo sobre la necesidad de llegar a una unidad de medida común. Actividad competencial. Enlazar con el Objetivo en acción de esta unidad, dado que se basa en la misma propuesta. Recordar que medir es comparar con la unidad de medida.

Solución:

a) Respuesta abierta.

b) Respuesta abierta.

c) Para poder medir longitudes, y que estas sean iguales para todos, es necesario tomar una unidad de medida que sea igual para todos. Por esta razón, el paso o pie no es la mejor unidad de medida.

1 Medir con pies o pasos depende de cada persona. ¿Conoces alguna medida de longitud que mida lo mismo para todos?

Solución:

El centímetro, el metro, el kilómetro, etc.

Ampliación

1 Recoge en una tabla de datos las medidas en pasos o palmos de tres objetos de la clase. Realiza un gráfico con esos datos.

Solución: Respuesta abierta.

Calentando motores

46 + 2 = 48 44 + 5 = 49

57 + 7 = 64 68 + 8 = 76

61 + 6 = 67 55 + 3 = 58

67 + 5 = 72 74 + 8 = 82

72 + 6 = 78 34 + 9 = 43

Recursos

Actividades interactivas

Otros materiales Cinta métrica

Secuencia

Actividades 1 y 2. Mayor o menor que un metro.

Actividad 3. Medir la clase.

Actividad 4. Estimar metros.

Actividades 5, 6 y 7. Problemas contextualizados.

El metro

Utilizamos el metro para expresar la longitud de objetos grandes o distancias pequeñas.

1 Indica si estas longitudes son mayores o menores que el metro.

a) c)

El metro es la unidad principal de longitud.

Su símbolo es m.

con la cinta métrica.

2 Lluvia de ideas Elabora una lista con longitudes que miden más de un metro y menos de un metro.

Más de 1 mMenos de 1 m

Soluciones

1 m

Utilizamos la cinta métrica para medir longitudes en metros.

3 Por parejas, medid el largo de la clase con un metro y contestad.

a) ¿Cuántos metros completos mide?

b) ¿Qué resultado han obtenido los demás?

c) ¿Crees que tendríais resultados iguales si cada uno midiese con sus pasos o sus pies? Explica por qué.

4 ¿Cuánto miden? Copia en tu cuaderno y une. El ancho del patio. 1 m

El largo de una mesa. 10 m

La altura de un monte. 1 000 m

Refuerzo

1 a) Las estatura de una alumna de 3.° es mayor que un metro.

b) La longitud de un boli es menor que un metro.

c) La altura de una mochila es menor que un metro.

2 Respuesta abierta.

3 a) Respuesta abierta.

b) Respuesta abierta.

c) Las medidas de los pasos o pies depende de la persona que tome las medidas.

4 El ancho del patio mide 10 m.

El largo de una mesa mide 1 m.

La altura de un monte mide 1 000 m.

1 Observa a tu alrededor y di objetos que miden más de un metro y menos de un metro.

Solución:

Respuesta abierta.

Ampliación

1 Utiliza una regla o un metro para saber cuánto mide tu palmo, tu pie y tu paso. Compara tus resultados con los de algún compañero o compañera. ¿Coinciden?

Solución:

Respuesta abierta.

5 Marta participa en una carrera en tres etapas: 550 m caminando, 750 m en bicicleta y 600 m corriendo. ¿Cuántos metros ha recorrido en total?

6 Un ovillo de lana tiene 340 m. Si Óscar ha utilizado 150  m, ¿cuántos metros de lana le quedan?

Resuelve paso a paso en anayaeducacion.es

7 Para adornar el pasillo del colegio, se ha dividido en 5  zonas iguales de 8 m cada una. Cada zona se ha decorado con un símbolo de la paz. ¿Cuánto mide el pasillo?

Recuerda

Para resolver un problema:

1. Comprendo el enunciado.

2. Organizo los datos.

3. Resuelvo el problema.

4. Compruebo si mi solución tiene sentido.

Desarrollo del pensamiento

Lluvia de ideas.

TIC

Resuelve paso a paso los problemas 6 y 7.

Ten en cuenta

• El metro es una unidad de medida lo suficientemente grande como para que al alumnado le cueste comprender su magnitud.

• Para medir en metros, el metro debe estar totalmente estirado.

Sugerencias de las actividades

Antes de comenzar. Pedir al alumnado que mida cuántos palmos mide un metro.

Resuelve paso a paso en anayaeducacion.es

¿Puedes medir un metro con tu cuerpo?

1. ° Utiliza una cinta métrica y mide exactamente un metro con ayuda de tu profesor o profesora.

Actividad 6. Problema de cambio: ¿Cuál es la cantidad final?

Relaciona una situación inicial y una final a través de un aumento. Se utiliza el esquema de la recta numérica.

2. ° Observa la longitud de tu palmo, paso y braza. ¿Miden más o menos de un metro?

Actividad 7. Problema de grupos iguales: ¿Cuántos en total?

Relaciona el total de elementos con los grupos y el número de elementos en cada grupo. Se utiliza el esquema grupos iguales agrupados.

3. ° ¿Qué unidad corporal se aproxima más a un metro?

Soluciones

5 550 + 750 + 600 = 1 900

Ha recorrido 1 900 m en total.

6 340 150 = 190

Le quedan 190 m de lana.

7 8 × 5 = 40

El pasillo mide 40 m.

Refuerzo

Actividad competencial. Llevar una cinta métrica para medir y comparar.

Solución: La unidad corporal que más se aproxima al metro es la braza.

1 Paqui está utilizando un cable alargador de 700 cm en su casa. Si ha necesitado 367 cm, ¿cuántos centímetros han quedado dentro del carrete?

Solución: Han quedado 333 cm dentro del carrete.

Ampliación

1 Se ha hecho una cadena a lo largo del patio para homenajear a un profesor. Si cada 2 m se ha colocado un estudiante y son 42 personas en total, ¿cuántos metros mide la cadena?

Solución: La cadena mide 84 m.

2 Se ha hecho una cadena de 84 m a lo largo del patio para homenajear a una profesora. Si han participado 42 personas, ¿qué distancia había entre cada persona?

Solución: Había 2 m entre cada persona.

Calentando motores

2 × 8 = 16 2 × 6 = 12

2 × 0 = 0 2 × 1 = 2

2 × 9 = 18 2 × 4 = 8

2 × 3 = 6 2 × 5 = 10

2 × 2 = 4 2 × 7 = 14

Recursos

Policubos

Actividades interactivas

Otros materiales

Regla

Secuencia

Actividad 1. ¿En metros o en centímetros?

Actividad 2. Paso de metros a centímetros.

Actividad 3. Paso de centímetros a metros.

Actividad 4. Conversión de forma compleja a incompleja.

Actividades 5, 6 y 7. Problemas contextualizados.

El centímetro

Utilizamos el centímetro para expresar la longitud de objetos pequeños.

1 ¿Qué unidad utilizarías para medir estos objetos: el  metro o el centímetro?

Soluciones

El centímetro es una unidad de longitud menor que el metro.

Su símbolo es cm.

Equivalencia de unidades

1 m = 100 cm

2 Copia y convierte metros en centímetros. × 100

2 m = ? cm 10 m = ? cm

5 m = ? cm 15 m = ? cm

7 m = ? cm 30 m = ? cm

Un metro son 100 centímetros.

1 m = 100 cm

100 cm = 1 m

3 Copia y convierte centímetros en metros. : 100

300 cm = ? m 1 700 cm = ? m

400 cm = ? m 2 000 cm = ? m

700 cm = ? m 5 000 cm = ? m

4 Expresa estas longitudes en centímetros.

1 m 25 cm = 100 cm + 25 cm = 125 cm

× 100

1 m 23 cm 4 m 4 cm 7 m 10 cm

2 m 45 cm 5 m 2 cm 8 m 50 cm

Refuerzo

Dividir entre 10, 100 o 1 000

Para dividir un número entre 10, 100 o 1 000, eliminamos uno, dos o tres ceros del número.

5 0 : 1 0 = 5

5 00 : 1 00 = 5

5  000 : 1  000 = 5

1 La unidad para medir el edificio es el metro; para medir el estuche y la goma, el centímetro.

2 2 m = 200 cm 10 m = 1 000 cm

5 m = 500 cm 15 m = 1 500 cm

7 m = 700 cm 30 m = 3 000 cm

3 300 cm = 3 m 1 700 cm = 17 m

400 cm = 4 m 2 000 cm = 20 m 700 cm = 7 m 5 000 cm = 50 m

4 123 cm 404 cm 710 cm 245 cm 502 cm 850 cm

1 Transforma las siguientes medidas.

1 m = … cm 2 800 cm = … m

9 m = … cm 8 000 cm = … m

Solución:

1 m = 100 cm 2 800 cm = 28 m

9 m = 900 cm 8 000 cm = 80 m

Ampliación

1 Expresa las siguientes longitudes en centímetros. 56 m 78 cm 30 m 98 cm 50 m 00 cm

m 43 cm 39 m 08 cm 78 m 50 cm

Solución:

5 Ordena los nombres de estos niños y niñas de menor a mayor altura.

Todos somos diferentes. Acéptame tal como soy.

Resuelve paso a paso los problemas 6 y 7.

Ten en cuenta

• La abreviatura de las unidades de medida (cm, m, dm...) no llevan punto.

6 La almohada de Bruno mide 5 palmos suyos. Si su palmo mide 9 cm, ¿cuánto mide su almohada?

Antes de comparar, expresa las medidas en centímetros. Eva 107 cm Julen 125 cm Olga 1 m 5 cm Fran 1 m 15 cm Kiran 1 m 20 cm ?

• Para pasar de metros a centímetros, añadimos dos ceros; y para pasar de centímetros a metros, quitamos dos ceros.

Sugerencias de las actividades

Actividad 1. ¿Cuántos metros mide una goma? ¿Y el estuche?

¿Nos sirve el metro para poder decir cuánto miden los objetos pequeños?

Actividad 6. Problema de grupos iguales: ¿Cuántos en total?

Resuelve paso a paso en anayaeducacion.es

7 Johana mide 173 cm, y su hijo Leo, 135 cm. ¿Cuántos centímetros tiene que crecer Leo para ser tan alto como su madre?

9 9 9 9 9 ? ?

173 135 ?

Resuelve paso a paso en anayaeducacion.es

Mi vida en centímetros

Con ayuda de tu familia, completa esta información en tu cuaderno.

Al nacer, medí… Ahora mido… Cuando sea mayor, mediré…

¡Toma nota!

Utiliza el centímetro para expresar cuánto mide una unidad de medida inventada.

Soluciones

5 Julen: 125 cm

Olga: 105 cm

Fran: 115 cm

Kiran: 120 cm

Eva: 107 cm

Olga < Eva < Fran < Julen < Kiran

6 9 × 5 = 45

Su almohada mide 45 cm.

7 173 135 = 38

Tiene que crecer 38 cm.

Relaciona el total de elementos con los grupos y el número de elementos en cada grupo. Se utiliza el esquema grupos iguales agrupados.

Actividad 9. Problema de igualación: ¿Cuántos faltan?

Relaciona el cardinal de dos conjuntos aumentando uno de ellos para igualarlo. Se utiliza el esquema de barras. Actividad competencial. Recordar al alumnado que escriba las cantidades en centímetros.

147

Refuerzo

1 Un palmo de Gael mide 6 cm y un palmo de Manuela mide 12 cm. Si miden una cama de 180 cm con sus palmos, ¿cuánto palmos de Manuela y cuántos de Gael medirá la cama?

Solución:

La cama medirá 15 palmos de Manuela y 30 de Gael.

Ampliación

1 Los tres montes más altos de España son el Teide con 3 718 m, el Mulhacén con 3 482 metros y el Aneto, con 3 404 metros. ¿Cuánto más alto es el Teide que el Mulhacén o el Aneto?

Solución:

El Teide es 236 m más alto que el Mulhacén y 314 m más alto que el Aneto.

Calentando motores

22 5 = 17 51 3 = 48

59 2 = 57 63 5 = 58

38 6 = 32 24 3 = 21

71 5 = 66 42 3 = 39

42 3 = 39 35 9 = 26

Recursos

Regletas

Geoplano

Actividades interactivas

Otros materiales

Regla

Secuencia

Actividad 1. ¿Cuántos centímetros?

Actividad 2. Medir con regla.

Actividad 3. Línea más larga.

Actividad 4. El camino más corto.

Actividad 5. Longitud de las regletas.

Mido con regla

Utilizamos la regla para medir longitudes pequeñas en centímetros.

1 ¿Cuántos centímetros mide cada objeto?

Soluciones

1 El sacapuntas mide 3 cm.

El clip mide 5 cm.

La goma mide 3 cm.

La chincheta mide 4 cm.

2 Naranja: 3 cm

Verde: 5 cm

Rojo: 6 cm

Azul: 4 cm

Marrón: 2 cm

3 La recta roja mide 10 cm, y la recta azul, 9,5 cm.

Por tanto, es más larga la recta roja.

2 Mide estas longitudes con la regla y anota los resultados en tu cuaderno.

Los números que aparecen en una regla indican los centímetros de longitud.

3 ¿Qué línea es la más larga? Comprueba con la regla que tu respuesta es correcta.

Empezamos a medir desde el 0.

Refuerzo

1 Dibuja en tu cuaderno rectas diferentes con ayuda de la regla.

a) Dos perpendiculares de 10 cm.

b) Dos secantes de 7 cm.

c) Dos paralelas de 5 cm.

Solución: Respuesta abierta.

Ampliación

1 Dibuja dos rectas perpendiculares en tu cuaderno, y dibuja una tercera recta que sea secante a ambas.

Solución:

4 Mide y contesta.

Aprendizaje lúdico

Nos divertimos jugando con los caminos en la actividad 4.

Ten en cuenta

• No se empieza a medir desde donde empieza la regla, sino desde el 0.

• La regla es más estrecha normalmente donde están los números. Si pintamos con tinta (rotulador, bolígrafo...), al po

a) ¿Cuál es el camino más corto?

b) ¿Y el camino más largo?

c) ¿Qué diferencia hay entre el camino más largo y el más corto en centímetros?

5 Lee y contesta.

nerla bocabajo para pintar, no se corre la tinta al quitar la regla.

Sugerencias de las actividades

Actividad 4. Podemos realizar esta actividad con un geoplano.

Para medir cada camino, no hace falta medir cada tramo. Basta saber la separación entre puntos y contar los segmentos totales. Actividad 5. Una vez sabemos cuánto mide cada regleta, las podríamos usar para medir cualquier objeto pequeño.

a) ¿Cuántos centímetros mide cada regleta?

b) ¿Qué diferencia hay entre dos regletas que están una al lado de la otra?

c) ¿Cuál es la regleta que mide 2 cm más que la regleta amarilla? ¿Cuál mide 3 cm menos que la negra?

d) ¿Qué regleta tiene la misma altura que la roja y rosa colocadas una sobre otra? Justifica tu respuesta.

Soluciones

4 a) El camino más corto es el azul. Mide 12 cm.

¡Toma nota!

Utiliza la regla para expresar cuántos centímetros mide una unidad de medida inventada.

Refuerzo

b) El camino más largo es el naranja. Mide 17 cm.

c) 17 12 = 5. La diferencia es de 5 cm.

5 a) Naranja: 10 cm Rosa: 4 cm

Azul: 9 cm Verde claro: 3 cm

Marrón: 8 cm Roja: 2 cm

Negra: 7 cm

Blanca: 1 cm

Verde: 6 cm Amarilla: 5 cm

b) La diferencia entre dos regletas consecutivas es 1 cm.

c) La regleta negra. La regleta rosa.

d) 4 + 2 = 6

La regleta verde, que mide 6 cm.

1 ¿Qué regleta obtienes si colocas una encima de otra las siguentes regletas?

a) Blanca y azul b) Rosa y verde claro

c) Negra y roja

Solución:

a) Naranjab) Negra c) Azul

Ampliación

1 ¿Cuál es el camino más corto que une dos puntos? ¿Siempre puedes ir por ese camino?

Solución:

El camino más corto que une dos puntos es la recta. En la vida cotidiana, en las calles o el camino que une ciudades no suele ser en línea recta, porque hay curvas o manzanas de edificios que lo impiden.

Calentando motores

74 + 3 = 77 34 + 9 = 43

59 + 5 = 64 58 + 4 = 62

46 + 6 = 52 36 + 7 = 43

46 + 8 = 54 18 + 5 = 23

66 + 4 = 70 28 + 7 = 35

Secuencia

Actividad 1. ¿En qué unidad?

Actividad 2. Paso de una unidad a otra.

Actividad 3. Conversión de forma compleja a incompleja.

Actividad 4. Ordenar de mayor a menor.

Actividades 5, 6, 7 y 8. Problemas contextualizados.

El kilómetro

Utilizamos el kilómetro para expresar distancias largas.

1 ¿Qué unidad utilizarías para medir estas longitudes: el metro, el centímetro o el kilómetro?

El kilómetro es una unidad de longitud mayor que el metro. Su símbolo es km. 1 km

Soluciones

2 Copia y transforma.

1 km = 1 000 m : 1 000

1 000 m = 1 km

Equivalencia de unidades

Un kilómetro son 1 000 metros. 1 km = 1 000 m

× 1 000

2 km = ? m 8 000 m = ? km

3 km = ? m 4 000 m = ? km

5 km = ? m 6 000 m = ? km

3 Expresa estas longitudes en metros. × 1 000

km 400 m = 1 000 m + 400 m = 1 400 m

150

1 La longitud del Guadalquivir se mide en kilómetros. La altura de un árbol se mide en metros.

El ancho, alto y largo de un regalo se mide en metros o centímetros.

La distancia recorrida por un avión se mide en kilómetros. El largo y ancho de una piscina se mide en metros.

El largo y ancho de un cuaderno se mide en centímetros.

2 2 km = 2 000 m 8 000 m = 8 km

3 km = 3 000 m 4 000 m = 4 km

5 km = 2 000 m 6 000 m = 6 km

3 1 200 m 6 045 m 2 007 m

2 400 m 3 050 m 4 009 m

Refuerzo

1 Transforma las siguientes medidas.

1 km = … m 2 000 m = … km

8 km = … m 9 000 m = … km

Solución:

1 km = 1 000 m 2 000 m = 2 km

8 km = 8 000 m 9 000 m = 9 km

Ampliación

1 Los tres montes más altos de España son el Teide con 3 718 m, el Mulhacén con 3 482 metros y el Aneto, con 3 404 metros. ¿Cuántos kilómetros miden aproximadamente?

Solución:

El Teide mide 4 km, aproximadamente, y el Mulhacén y el Aneto miden ambos 3 km, aproximadamente.

4 Ordena estas longitudes de mayor a menor.

a) 5 cm, 5 m, 5 km b) 10 m, 100 m, 1 km

5 En un monte hay dos rutas. La primera mide 24 km y la segunda, 13 km más que la primera. ¿Cuántos kilómetros mide la segunda ruta?

Si lo necesitas, antes de comparar, expresa las medidas en la misma unidad.

Claves

TIC

Resuelve paso a paso los problemas 5 y 6. Aprendizaje cooperativo Comprobamos.

Ten en cuenta

El kilómetro es una unidad de medida inconmensurable, inabarcable para el alumnado.

Sugerencias de las actividades

Resuelve paso a paso en anayaeducacion.es

6 El río Guadiana mide 818 km, y el Guadalquivir, 657  km. ¿Cuántos kilómetros mide el Guadalquivir menos que el Guadiana?

Guadiana Guadalquivir ?

Resuelve paso a paso en anayaeducacion.es

7 A Myriam le gusta hacer senderismo. Ha caminado 68  km en tres días. El primer día recorrió 28 km y el segundo, 21 km.

km

km

a) ¿Cuántos kilómetros recorrió los dos primeros días?

b) ¿Cuántos kilómetros caminó el tercer día?

8 Comprobamos Lupe recorre 500 m para llegar al colegio y David recorre 10 veces más.

a) ¿Cuántos kilómetros recorre David?

b) ¿Quién vive más cerca del colegio?

Soluciones

4 a) 5 km > 5 m > 5 cm b) 1 km > 100 m > 10 m

5 24 + 13 = 47. La segunda ruta mide 47 km.

6 818 657 = 161

El Guadalquivir mide 161 km menos que el Guadiana.

7 a) 28 + 21 = 49

Myriam recorrió recorrió 49 km los dos primeros días.

b) 68 49 = 19

Myriam 19 km el tercer día.

8 a) 10 × 500 = 5 000

5 000 : 1 000 = 5

David recorre 5 000 m, es decir, 5 km.

b) 500 m < 5 000 m

Lupe vive más cerca del colegio.

Refuerzo

Antes de empezar. Preguntamos por qué las señales con números cambian de uno en uno en la carretera.

A partir de aquí, partiendo de su experiencia, podemos introducir los kilómetros. Actividades 5 y 6. Problema de comparación: ¿Cuántos son, si son más?

Relaciona el cardinal de dos conjuntos comparándolos. Se utiliza el esquema de barras.

b) ¿Cuánto más cerca está Bilbao de Valencia que Sevilla?

Solución:

a) La ciudad más cercana es Zaragoza y la más lejana, Sevilla.

b) Bilbao está 64 km más cerca.

139

Calentando motores

4 × 4 = 16 4 × 3 = 12

4 × 1 = 4 4 × 8 = 32

4 × 2 = 8 4 × 6 = 24

4 × 7 = 28 4 × 0 = 0

4 × 5 = 20 4 × 9 = 36

Hago un esquema

Realizar un esquema para organizar los datos puede ayudar a comprender el problema y a encontrar una solución.

Paso 1. Comprendo el problema

Verificar si las alumnas y los alumnos entienden el enunciado describiendo la situación con sus propias palabras.

Paso 2. Organizo los datos

Realizar el esquema y comprender cómo se está realizando.

Paso 3. Resuelvo el problema

Contar el número de farolas.

Paso 4. ¿La solución tiene sentido?

Analizar si la solución tiene sentido en relación con lo que nos han pedido y verificar que se cumple lo que nos indican en los datos.

LO RESUELVO SIN PROBLEMA

Hago un esquema

En una calle de 60 m de longitud quieren colocar farolas cada 10 m. La primera farola debe estar a 5 m del comienzo de la calle. ¿Cuántas farolas colocarán?

Para averiguarlo, hacemos un dibujo.

1.° Dibujamos la calle.

2.° Marcamos 5 m desde el comienzo de la calle.

3.° Dibujamos farolas, dejando 10 m de separación entre ellas hasta llegar a los 60 m que mide la calle.

5 m10 m 10 m 15 m

10 m 10 m 10 m5 m 25 m 35 m 45 m 55 m 65 m > 60 m

Colocarán 6 farolas en la calle.

¿La solución tiene sentido? Comprobamos que la suma de todas las distancias es igual a 60  m.

1 En esta misma calle se quieren plantar árboles cada 8 m. El primer árbol debe estar a 2 m del comienzo de la calle. ¿Cuántos árboles plantarán?

2 En un cordón de 1 m de longitud queremos colocar fotografías separadas 20 cm, dejando 10 cm en cada extremo del cordón. ¿Cuántas fotografías podremos colocar?

Refuerzo

1 Queremos colocar estrellas de colores en un collar de 30 cm separadas 2 cm cada una, dejando 5 cm en cada extremo del collar. ¿Cuántas estrellas se podrán colocar?

Solución:

Se podrán colocar 11 estrellas.

Ampliación

1 Encarna tiene un cable de 8 m para hacer una guirnalda de luces. Necesita dejar libre 100 cm en cada extremo, y en la primera mitad del cable va a colocar luces cada 150 cm y en la segunda mitad, cada 100 cm. ¿Cuántas luces necesita?

Solución:

Necesita 6 luces.

Problemas exprés

1

2

Un kilómetro, ¿cuántos metros son? Un metro, ¿cuántos centímetros son?

Cálculo

TIC

Vídeo: Cálculo mental

Se explican dos formas de resolver una suma completando decenas: a través de bloques base 10 o con la estrategia que aparece en el libro.

Problemas exprés

Para medir longitudes pequeñas, ¿qué instrumento de medida utilizarías?

Ana mide 1 m. Si se pone de puntillas aumenta 7  cm. ¿Cuántos centímetros mide de puntillas?

3 5

¿Cómo funciona?

4 6

De casa al cole hay 150  m. ¿Cuántos metros recorres si vas y vuelves?

Cuando voy de mi casa a la de mis abuelos recorro 500 m, y cuando vuelvo recorro medio kilómetro. ¿Cómo es posible?

Esta máquina convierte kilómetros en metros. ¿Qué operación hace la máquina?

Salen 3 + 8 + 2 + 4 + 7 = = 10 + 10 + 4 = 24 km m

Soluciones

Problemas exprés

1 1 000 m

2 100 cm

3 Utilizaría la regla.

4 150 + 150 = 300. Recorro 300 m.

Entran En anayaeducacion.es puedes ver cómo se hace.

• Se plantean 6 problemas cortos sobre los contenidos trabajados en la unidad: unidades de medida de longitud.

• Puede ser un buen momento para en

señar a los alumnos y las alumnas a tomar datos, escribir la operación y dar la solución.

• Para poder trabajar a la vez, se pueden leer en voz alta, ellos toman datos, se les deja un tiempo para resolver de forma individual, y se corrigen.

Pensamiento computacional

Esta máquina convierte metros en centímetros. ¿Qué operación hace la máquina?

La máquina de operaciones establece una relación funcional entre dos magnitudes. En este caso, realiza la conversión de kilómetros a metros.

5 1 m 7 cm = 107 cm. De puntillas mide 107 cm.

6 Porque 500 m es medio kilómetro.

Cálculo mental

3 + 5 + 2 + 5 + 8 = 3 + 10 + 10 = 23

4 + 6 + 3 + 5 + 7 = 10 + 10 + 5 = 25

1 + 4 + 3 + 9 + 6 = 10 + 10 + 3 = 23

2 + 8 + 6 + 3 + 4 = 10 + 10 + 3 = 23

8 + 1 + 6 + 2 + 9 = 10 + 10 + 6 = 26

? ? ?

Identificar la operación que está realizando, esto es, la constante de proporcionalidad supone comprender cómo opera esta máquina.

Pensamiento computacional

La primera máquina convierte km en m multiplicando por 1 000.

Entran kilómetros 356

Salen metros 3 0005 0006 000

La segunda máquina convierte m en cm multiplicando por 100.

Entran metros 2710

Salen centímetros 200 700 1 000

centímetros m cm 141

Mira cómo pienso

Calentando motores

23 5 = 18 25 6 = 19

31 2 = 29 34 7 = 27

44 6 = 38 43 4 = 39

62 5 = 57 17 8 = 9

42 3 = 39 14 6 = 8

Recursos

Actividades interactivas

Fichas 1, 2 y 3 (refuerzo)

Ficha 4 (ampliación)

¿Q ué he aprendido?

1 Mide el ancho y el largo de tu cuaderno, utilizando como unidad de medida tu goma de borrar.

Soluciones

1 Respuesta abierta.

2 Más de un metro: la canasta de baloncesto, la puerta de entrada de la clase o del colegio, las ventanas, las estanterías de la biblioteca, etc.

Menos de un metro: regla, escuadra, cartabón, el cuaderno de matemáticas, los libros de texto, el asiento o el respaldo de las sillas, etc.

3 a) La altura de un frigorífico: 2 m

b) El largo de un camión: 10 m

c) El ancho de una piscina olímpica: 25 m

4 6 m = 600 cm 500 cm = 5 m

40 m = 4 000 cm 7 600 cm = 76 m

2 km = 2 000 m 3 000 m = 3 km

5 5 m = 500 cm 70 cm < 7 m

2 km > 200 m 3 000 m = 3 km

6 m > 6 cm 9 m < 9 km

6 40 m  3 000 m  700 m

3 000 m > 700 m > 40 m

7 4 m 50 cm = 450 cm

3 m 80 cm = 380 cm

1 m 75 cm = 175 cm

8 2 km 30 m = 2 030 m

4 km 6 m = 4 006 m

1 km 800 m = 1 800 m

9 152 84 = 68

Hay 68 m de guirnaldas de estrellas.

10

8 + 6 + 1 = 15

Zoe ha recorrido 15 km en los tres días.

2 Escribe en tu cuaderno tres objetos que midan más de un metro y otros tres que midan menos de un metro.

3 Estima la longitud de estos objetos.

a) La altura de un frigorífico.

2 m 4 m

b) El largo de un camión.

3 m 10 m

c) El ancho de una piscina olímpica.

25 m 75 m

4 Copia y completa.

6 m = ? cm 500 cm = ? m

40 m = ? cm 7 600 cm = ? m

2 km = ? m 3 000 m = ? km

5 Copia y completa con los signos >, < o =.

5 m ? 500 cm 70 cm ? 7 m

2 km ? 200 m 3 000 m ? 3 km

6 m ? 6 cm 9 m ? 9 km

6 Expresa estas longitudes en metros y ordénalas de mayor a menor.

4 000 cm 3 km 700 m

Refuerzo

1 Completa.

... m = 600 cm

... m = 4 000 cm

... km = 2 000 m

Solución:

6 m = 600 cm

40 m = 4 000 cm

2 km = 2 000 m

Ampliación

1 Estima las siguientes longitudes.

7 Expresa estas medidas en centímetros.

8 Expresa en metros estas distancias.

9 Hemos decorado un jardín con 152  m de guirnaldas, unas con banderines y otras con estrellas. Si 84 m son de banderines, ¿cuántos metros son de estrellas?

10 Zoe lleva tres días entrenando para la fiesta de la bici. El primer día recorrió 8 km; el segundo, 6 000 m; y el tercero, 1 km más que el segundo día. ¿Cuántos kilómetros ha recorrido en los tres días?

El semáforo. Junto a cada actividad, colorea así en tu cuaderno: si has sabido la respuesta si has necesitado ayuda si no has sabido responder

... cm = 5 m

... cm = 76 m

... m = 3 km

500 cm = 5 m

7 600 cm = 76 m

3 000 m = 3 km

a) El largo de tu clase. b) El ancho de tu clase. c) El alto de tu clase.

Solución:

Respuesta abierta.

OBJETIVO EN ACCIÓN

Inventa una unidad de medida

En grupo, inventad una unidad de medida de longitud.

a) Medid objetos de la clase con esta unidad y anotad los resultados.

b) Comparad vuestros resultados con los de otros grupos.

c) ¿Cuántos centímetros miden aproximadamente las unidades que habéis inventado?

Nos planteamos

Círculo de puntos de vista. Copia y completa el organizador en tu cuaderno. Comparte las respuestas en grupo.

Nuestra unidad de medida es…

Después de escuchar a todos los grupos, ¿qué nuevas ideas tenemos sobre las unidades de medida?

Pensamos que nuestra unidad de medida es buena porque…

Haz un dibujo de la historia del poema.

Los demás grupos piensan que su unidad de medida es buena porque…

En anayaeducacion.es puedes escuchar un poema en el que se cuen ta que puedes medir de diferentes maneras y ser todas correctas.

¿C ómo he aprendido?

Copia en tu cuaderno y colorea junto a cada oración.

• Cuando me he equivocado intento hacerlo bien.

• Cuando no estamos de acuerdo en el grupo intento escuchar a todos.

• Me gusta hacer actividades de matemáticas. ¿Qué actividades de la unidad te han gustado más?

¿Cómo he aprendido?

Para facilitar la metacognición

Educación emocional

La evaluación de ¿Cómo he aprendido? se centra en ayudar al alumnado a identificar sus emociones cuando resuelven problemas o trabajan con otros. En muchos casos identificar emociones positivas en algún tipo de tarea refuerza positivamente dicha tarea y ayuda a vencer barreras.

Sugerencia didáctica:

• Dejar tiempo para la reflexión individual.

• Compartir en pareja o grupo si se alegran o no al entender un problema o si disfrutan trabajando con otros.

• Es importante reflexionar sobre el tipo de tareas o propuestas que ayudan al alumnado a mantener la atención. Se pueden dejar expuestas en el aula para retomar cuando los niveles de atención bajen.

Desarrollo del pensamiento Círculo de puntos de vista.

Ten en cuenta

• Al inicio de la unidad se ha trabajado sobre el uso de medidas diversas, recordar con la clase qué medidas vimos en aquel momento.

• Sugerir diseñar nuevas unidades de medida, hacer una lluvia de ideas en cada equipo.

• En el círculo de puntos de vista es importante poner de relieve al realizarlo que todas las unidades de medida son válidas y que hay que respetar las ideas y explicaciones de los demás.

Para reforzar el aprendizaje

Para pensar más

Investiga qué unidades de medida se utilizan todavía en tu familia o en tu localidad y a cuánto equivalen en el sistema métrico. ¿Es exacta esta equivalencia? Razona tu respuesta.

Herramienta

Inclusión

de inclusión

¿Qué

es IN.ON?

Inclusión Online Anaya es una herramienta digital destinada al profesorado, cuyo objetivo es ofrecer soluciones a la atención de la diversidad de las aulas, desde los paradigmas del Diseño Universal para el Aprendizaje (DUA) y de la enseñanza multinivel, priorizando la accesibilidad sensorial y cognitiva de todo el alumnado a los contenidos.

Las actividades están diseñadas teniendo en cuenta los paisajes de aprendizaje en los que están reflejados todos los procesos cognitivos de la taxonomía de Bloom.

Damos respuesta a las diferentes capacidades intelectuales y estilos de aprendizaje.

¿Cómo es y cómo se utiliza?

Es una plataforma donde encontrarás múltiples recursos para trabajar los conceptos imprescindibles de las áreas de Lengua y Matemáticas. En ella podrás filtrar los recursos por contenidos, nivel educativo o por necesidad educativa especial para la que está pecialmente diseñada. A continuación, verás todos los tipos de recursos que encontrarás en la herramienta y una breve descripción de ellos.

Otra educación es posible.

¿Quieres ver una muestra?

Para el profesorado

TABLA DE TRES NIVELES

Permite al profesorado tener una visión general del concepto a lo largo de los tres ciclos de Primaria.

RESUMEN GENERAL

Recoge toda la información relevante que se va a tratar en las distintas etapas de la Educación Primaria.

ESQUEMA GENERAL

Presenta la información del concepto de una forma esquemática y puede servir de material de estudio en los últimos cursos.

VOCABULARIO ANTICIPADO

Define los términos más complejos con los que se va a encontrar el alumnado.

Para el alumnado

EXPLICACIÓN DEL CONCEPTO

Permite ver cómo se trabaja el concepto a lo largo de la etapa.

AUTOINSTRUCCIONES

Con procedimientos paso a paso que planifican la tarea.

ACTIVIDADES DE PRÁCTICA Y EVALUACIÓN

La enseñanza multinivel facilita al profesorado una respuesta inclusiva al alumnado, estableciendo para ello diferentes niveles de atención didáctica.

ACTIVIDADES CON PICTOGRAMAS

Versiones de todas las actividades con pictogramas destinadas al alumnado con baja capacidad lectora, alumnado TEA o con discapacidad intelectual.

La herramienta también cuenta con materiales audiovisuales que favorecen la asimilación del concepto trabajado y que propician la autonomía y la autogestión del alumnado a la hora de aprender (flipped classroom).

AUDIOTEXTOS

Explicaciones de algunos conceptos en formato audio con subtítulos.

VÍDEOS SUBTITULADOS

VÍDEOS SIGNADOS

ESQUEMAS

Verdaderos Visual Thinking que ayudan a sintetizar la información. Disponibles tanto en formato PDF como interactivo.

JUEGOS

Juegos de mesa y juegos interactivos para afianzar cada concepto de una forma lúdica.

Este proyecto ha sido elaborado por maestros y maestras que creen que otra educación es posible. Sabemos que existen tantas formas de aprender como alumnos y alumnas. Son los protagonistas de esta aventura y a ellos les debemos nuestra pasión por la enseñanza. La inclusión es el leitmotiv de nuestra herramienta, y el Diseño Universal para el Aprendizaje (DUA), el motor que nos impulsa.

Inclusión y atención a la diversidad

Nombre y apellidos: 1

1 ¿Qué unidad utilizarías para medir estas longitudes? Une con flechas.

2 Completa las siguientes igualdades.

3 Expresa las siguientes longitudes en centímetros siguiendo el ejemplo.

4 Ayer Carlos utilizó 16 m de cuerda, y hoy, 20 m. ¿Cuántos metros de cuerda ha utilizado hoy más que ayer?

16 m 20 m

? Operación:

Solución: Hoy ha utilizado m de cuerda más que ayer.

UNIDAD

9

Nombre y apellidos: 2

Matemáticas 3.º Fecha:

1 ¿Qué unidad utilizarías para medir estas longitudes: metros o centímetros?

2 Completa las siguientes igualdades.

3 m = cm

3 Expresa las siguientes longitudes en centímetros siguiendo el ejemplo.

1 m 25 cm = 100 cm + 25 cm = 125 cm

56 m 78 cm = 30 m 98 cm =

15 m 43 cm = 39 m 08 cm =

4 Carlos tiene una cuerda de 45 cm. Ayer utilizó 16 cm, y hoy, 20 cm. ¿Cuántos centímetros de cuerda ha utilizado en total? ¿Cuántos centímetros le han sobrado?

Datos: Operación:

Solución:

Ha utilizado cm de cuerda en total.

Le han sobrado cm.

Grupo Anaya, S. A. Material imprimible autorizado.

UNIDAD

9

Nombre y apellidos: 3 FICHA

Matemáticas 3.º Fecha:

1 ¿Qué unidad utilizarías para medir estas longitudes?

Para medir la longitud de una chincheta utilizaría

Para medir la profundidad de una piscina utilizaría

Para medir el lado de un cuaderno utilizaría

Para medir el largo de mi cama utilizaría

2 Completa las siguientes igualdades.

3 Expresa las siguientes longitudes en centímetros.

4 Carlos tiene una cuerda de 45 cm. Ayer utilizó 16 cm, y hoy, 20 cm. ¿Cuántos centímetros le han sobrado?

Nombre y apellidos: 4

Fecha:

Matemáticas 3.º

1 Darío, Lía, Leo, Guille y Nina han formado un equipo de baloncesto. Completa con los nombres y sus alturas.

Lía es la más alta.

Nina mide 1 m 37 cm.

Guille mide 10 cm menos que Lía.

Leo mide 5 cm menos que Nina y 8 menos que Lía. Darío mide lo mismo que Leo y usa gafas.

Utiliza este espacio para realizar tus cálculos.

Grupo Anaya, S. A. Material imprimible autorizado.

Inclusión y atención a la diversidad

Solución:

Ha utilizado 36 cm de cuerda en total.

Le han sobrado 9 cm.

Ficha 3 (Refuerzo nivel 3)

1 Para medir la longitud de una chincheta utilizaría el centímetro. Para medir la profundidad de una piscina utilizaría el metro.

Para medir el lado de un cuaderno utilizaría el centímetro.

Para medir el largo de mi cama utilizaría el metro.

Ficha 4 (Ampliación)

Inclusión en Operación Mundo

Principios del Diseño Universal para el Aprendizaje (DUA)

El Diseño Universal para el Aprendizaje (DUA) es un conjunto de principios para desarrollar el curriculum que proporcionen a todos los estudiantes igualdad de oportunidades para aprender. Estos principios son los siguientes:

Proporcione múltiples formas de MOTIVACIÓN Y COMPROMISO

Proporcione múltiples formas de REPRESENTACIÓN

Proporcione múltiples formas de ACCIÓN Y EXPRESIÓN

Redes afectivas El «PORQUÉ» del aprendizaje

Proporcione opciones para captar el interés

7.1 Optimice las elecciones individuales y autonomía.

7.2 Optimice la relevancia, el valor y la autenticidad.

7.3 Minimice las amenazas y distraciones.

Proporcione opciones para mantener el esfuerzo y la persistencia

8.1 Resalte la relevancia de metas y objetivos.

8.2 Varíe las demandas y los recursos para optimizar los desafíos.

8.3 Promueva la colaboración y la comunicación.

8.4 Aumente la retroalimentación orientada a la maestría.

Proporcione opciones para la autorregulación

9.1 Promueva expectativas y creencias que optimicen la motivación.

9.2 Facilite habilidades y estratégias para enfrentar desafíos.

9.3 Desarrolle la autoevaluación y la reflexión.

Redes de reconocimiento El «QUÉ» del aprendizaje

Proporcione opciones para la percepción

1.1 Ofrezca formas de personalizar la visualización de la información.

1.2 Ofrezca alternativas para la información auditiva.

1.3 Ofrezca alternativas para la información visual.

Proporcione opciones para el lenguaje y los símbolos

2.1 Aclare vocabulario y símbolos.

2.2 Aclare sintaxis y estructura.

2.3 Apoye la decodificación. de textos, notaciones matemáticas y símbolos.

2.4 Promueva la comprensión entre diferentes lenguas.

2.5 Ilustre a través de múltiples medios.

Proporcione opciones para la comprensión

3.1 Active o proporcione conocimientos previos.

3.2 Destaque patrones, características fundamentales, ideas principlaes y relaciones entre ellas.

3.3 Guíe el procesamiento, visualización y manipulación de la información.

3.4 Maximice la transferencia y la generalización de la información.

APÉNDICES EXPERTOS

Decididos y motivados

Redes estratégicas El «CÓMO» del aprendizaje

Proporcione opciones para la acción física

4.1 Varíe los métodos de respuesta, navegación e interacción.

4.2 Optimice el acceso a herramienta y tecnologías de asistencia.

Proporcione opciones para la expresión y la comunicación

5.1 Use múltiples medios para la comunicación.

5.2 Use múltiples herramientas para la construcción y composición.

5.3 Desarrolle fluidez con niveles de apoyo graduados para la práctica y el desempeño.

Proporcione opciones para la función ejecutiva

6.1 Guíe el establecimiento de metas apropiadas.

6.2 Apoye la planificación y el desarrollo de estratégias.

6.3 Facilite la gestión de información y recursos.

6.4 Mejore la capacidad para monitorear el progreso.

Ingeniosos y conocedores Estrátegicos y dirigidos a la Meta

Pautas DUA en Operación Mundo

Los diferentes elementos del Proyecto Operación Mundo están concebidos teniendo en cuenta los principios del Diseño Universal de Aprendizaje (DUA). En la siguiente tabla se muestra la relación entre los principios o pautas DUA y los elementos del proyecto:

OPERACIÓN MUNDO

Situación de aprendizaje

ODS

Imagen y contexto

¿Cómo lo ves?

El dato

Objetivo en acción

Pautas DUA que se aplican en el proyecto MATERIAL IMPRESO

• La relación directa con los ODS (retos del siglo xxi) y con la vida cotidiana del alumnado optimiza la relevancia, el valor y la autenticidad (7.2).

• La representación alternativa al texto facilita la comprensión y la conexión personal con el contexto de la Situación de aprendizaje (2.5).

• Las preguntas vinculan la Situación de aprendizaje con las experiencias y los conocimientos previos del alumnado (3.1).

• Aporta información objetiva y contrastable sobre la importancia del objetivo en acción (8.1).

• Estimula la reflexión colectiva a través de una estrategia de pensamiento útil para afrontar los problemas cotidianos (9.2).

• Fomenta la autonomía proponiendo un producto final abierto a la contextualización en el centro y a la elección del alumnado (7.1) variando los niveles de exigencia (8.2).

• Facilita la generalización y la transferencia de los aprendizajes esenciales (3.4).

• Fomenta la comunidad y la colaboración para la realización y difusión colectiva del producto final (8.3).

• Da acceso a información actualizada sobre los ODS al profesorado y al alumnado utilizando múltiples medios de comunicación (5.1).

• ¿Qué sé? Propone actividades interactivas trazables para la detección de ideas previas en la apertura de la unidad (3.1).

• Utiliza píldoras audiovisuales que presentan las situaciones de aprendizaje estimulando expectativas y creencias que aumentan la motivación (9.1) en la apertura de la unidad.

• Presenta en cada unidad información adicional de fuentes preseleccionadas en distintos formatos que proporcionan alternativas a la información auditiva (1.2) y visual (1.3) como representaciones alternativas al texto (2.5): canciones, audios o vídeos subtitulados, locuciones de la información textual, organizadores gráficos, visual thinking, etc. utilizables, además, Para dinamizar la participación.

Sigue el hilo

• Guía de forma ordenada la consecución del objetivo en acción (6.1) modelando y visibilizando el proceso (6.2) con un organizador gráfico (6.3).

• Permite reconstruir el proceso de aprendizaje de forma interactiva con el apoyo del organizador gráfico que representa el progreso hacia el objetivo en acción (3.3).

Pautas DUA en Operación Mundo

Secuencia didáctica

Sigue el hilo

• Aprendizajes esenciales

• Identifica el vocabulario básico (color, iconos, tipografía) de cada unidad (2.1).

• Proporciona ejemplos de buena ejecución y avisos que focalizan la atención (3.2) minimizando la inseguridad y las distracciones (7.3).

• Ofrece variedad de material manipulativo para adquirir los aprendizajes esenciales con múltiples medios (2.5) y herramientas (5.2).

• Actividades de aplicación• Proporciona definiciones claras y bien estructuradas de los conceptos (2.2) y los presenta con diversos tipos de organizadores gráficos que representan las ideas clave y sus relaciones (3.2), de manera progresiva entre los niveles de la etapa (3.3).

• Incorpora acciones de práctica y revisión sistemáticas que favorecen la generalización de los aprendizajes (3.4).

• Actividades competenciales• Incorpora actividades que permiten respuestas personales abiertas que fomentan la participación, la experimentación, la resolución de problemas y la creatividad (7.2).

• Proporciona modelos y apoyos por medio de estrategias y llaves de pensamiento que facilitan el procesamiento de la información y su transformación en conocimiento útil (3.3).

• Fomenta la interacción y la tutorización entre iguales a través de técnicas de aprendizaje cooperativo (8.3).

• Selecciona Lo esencial de cada unidad (3.2) y proporciona Para estudiar: esquemas o resúmenes (3.3) interactivos imprimibles de los saberes básicos de cada unidad que permiten la personalización en la presentación de información (1.1).

• Complementa el texto escrito a través de múltiples medios como apoyo Para exponer los saberes básicos con presentaciones o vídeos (2.5).

• Ofrece apoyo Para ejercitar los saberes básicos con actividades interactivas trazables en cada UD, utilizando herramientas y tecnologías de apoyo (4.2).

• Proporciona modelos y apoyos del proceso y pautas de comprobación de los resultados (6.1.) apoyando la planificación y el desarrollo de estrategias (6.2) y facilitando la gestión de la información y los recursos (6.3).

– Infografías Plan Lingüístico.

– Infografías TIC.

Recursos complementarios

• Clase invertida

• Proporciona métodos alternativos para que el alumnado acceda a la información e interaccione con el contenido (4.1).

• Repaso trimestral (lúdico)• Utiliza múltiples medios de comunicación como medios alternativos de expresar lo aprendido (5.1).

• Gamificación

• Atención a la diversidad

• Define competencias con niveles de apoyo graduados para la práctica y la ejecución (5.3) variando los niveles de exigencia (8.2) con actividades de refuerzo, ampliación y multinivel en cada UD.

• Proporciona alternativas para la respuesta y la navegación (4.1) por medio de vídeos y variadas herramientas tecnológicas (4.2) complementando el texto escrito a través de múltiples medios (2.5).

• Utiliza múltiples herramientas para la construcción y la composición (5.2).

• IN.ON Permite la personalización de la información adecuándola a las diversas características y necesidades educativas del alumnado (1.1) y ofreciendo alternativas a la información auditiva (1.1) y visual (1.2).

OPERACIÓN MUNDO

Evaluación

¿Qué he aprendido?

• Actividades de evaluación

Pautas DUA que se aplican en el proyecto

• Estimula la autoevaluación y la coevaluación proporcionando variedad de Instrumentos y actividades de evaluación (9.3).

• Estimula la autoevaluación y la coevaluación (9.3) con actividades interactivas no trazables con herramientas y tecnologías de apoyo (4.2).

• Aumenta la capacidad de hacer un seguimiento de los avances (6.4):

– Instrumentos y actividades interactivas trazables de heteroevaluación.

– Generador de pruebas de evaluación y ejercitación por niveles de desempeño (básico/avanzado) en los distintos momentos de la programación anual (inicial, durante el desarrollo, final) (5.3).

– Evaluación competencial.

– Competencias GYM: tablas y soluciones.

• Respuesta al objetivo en acción

• Maximiza la transferencia de los aprendizajes a nuevos contextos y situaciones (3.4).

• Porfolio digital imprimible que permite la personalización en la presentación de información (1.1) en cada UD aumentando la capacidad del alumnado para realizar un seguimiento continuo de sus avances (6.4) a través de la autoevaluación y la reflexión (9.3) y la utilización del feedback orientando una mejor ejecución (8.4).

¿Cómo he aprendido?

Proyecto interdisciplinar

• Piensa

• Diseña

• Construye

• Presenta

• Comprueba

• Estimular el logro y la mejora por medio de estrategias de autorregulación que permiten afrontar los desafíos con información relevante sobre fortalezas personales y patrones de error (9.2).

• Maximiza la transferencia de los aprendizajes a nuevos contextos y situaciones (3.4).

• Incorpora actividades que permiten respuestas personales abiertas que fomentan la participación, la experimentación, la resolución de problemas y la creatividad (7.2).

• Ofrece indicaciones y apoyo para visualizar el proceso y los resultados previstos para la consecución del producto final del proyecto (6.1).

• Fomenta la interacción y la tutorización entre iguales a través de técnicas de aprendizaje cooperativo (8.3).

Proyecto interdisciplinar

• Evidencia la relevancia de metas y objetivos relacionando los elementos curriculares vinculados con los aprendizajes esenciales (competencias específicas y criterios de evaluación) y los saberes básicos de cada UD con el perfil de salida de las competencias clave de la etapa en la PD (8.1).

• Facilita la autoevaluación y la coevaluación proporcionando instrumentos de evaluación de la práctica docente (9.3).

Medida del tiempo

9 Más rápido, más alto, más fuerte

Me lo aprendo en un momento

Unidades de tiempo

día → 24 horas

minutos → 60 segundos

quincena → 15 días

bimestre → 2 meses

cuatrimestre → 4 meses

que el año

hora → 60 minutos

semana → 7 días

mes → 28, 29, 30 o 31 días

trimestre → 3 meses

semestre → 6 meses

de tiempo mayores que el año

lustro → 5 años

década → 10 años

siglo → 100 años milenio → 1 000 años

• Expresión incompleja: una única unidad de medida.

8 418 s

• Expresión compleja: varias unidades de medida.

2 h 20 min 18 s

Nos preparamos ¿Cuántas veces controlas el tiempo en tu día a día?

¿Has participado alguna vez en una competición donde midan el tiempo?

1.° Sumamos los datos

2.° Transformamos los datos.

3.° Expresamos el resultado.

1.° Colocamos los datos.

2.° Transformamos los datos.

3.° Restamos.

Mido el tiempo

1 año tiene 365 días. Si el año es bisiesto, tiene 366 días. Cada 4 años hay un año bisiesto.

La Tierra tarda un año en dar una vuelta alrededor del Sol.

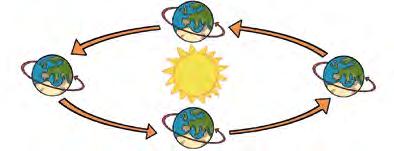
El día, la hora, los minutos y los segundos son unidades de tiempo menores que el año.

1 día tiene 24 horas.

1 hora son 60 minutos.

1 minuto son 60 segundos.

La Tierra tarda un día en dar una vuelta girando sobre sí misma.

Otras unidades menores que el año

semana: 7 días

quincena: 15 días

mes: 28, 29, 30 o 31 días

bimestre: 2 meses

Unidades mayores que el año

lustro: 5 años

década: 10 años

trimestre: 3 meses

cuatrimestre: 4 meses

semestre: 6 meses

siglo: 100 años

milenio: 1 000 años

1 Copia y completa. Haz las operaciones que necesites.

a) 2 días tienen ? horas.

b) 1 semana tiene ? horas.

c) 1 quincena son, más o menos, ? semanas.

d) ¿Cuántos bimestres, trimestres, cuatrimestres y semestres tiene un año? Explica tu respuesta.

2 Un milenio tiene 1 000 años. Un lustro tiene 5 años. ¿Cuántas veces es un milenio más largo que un lustro?

3 Copia y completa. Haz las operaciones que necesites.

a) 3 décadas son ? años.

b) 4 siglos son ? años.

c) 2 milenios son ? años.

d) 1 siglo son ? décadas.

e) 1 siglo son ? lustros.

f) 1 milenio son ? siglos.

4 ¿Cuántas veces es un siglo más largo que un lustro? ¿Y más largo que una década?

Horas, minutos y segundos

Las horas, minutos y segundos aumentan y disminuyen de 60 en 60. Forman parte del sistema sexagesimal.

1 hora = 60 minutos

La aguja de los minutos del reloj da una vuelta completa cada hora.

1 minuto = 60 segundos

La aguja de los segundos del reloj da una vuelta completa cada minuto.

Para transformar horas en minutos y en segundos, o viceversa, hacemos lo siguiente.

1 Transforma estos datos de tiempo en la unidad que se indica.

a) 2 horas =  ? minutos c) 5 minutos =  ? segundos

b) 12 horas =  ? minutos d) 30 minutos =  ? segundos

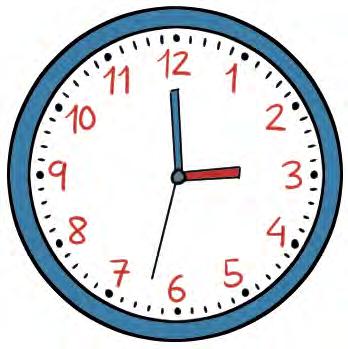
2 Transforma estos datos de tiempo en la unidad que se indica.

a) 120 minutos =  ? horas c) 240 segundos =  ? minutos

b) 600 minutos =  ? horas d) 360 segundos =  ? minutos

3 ¿Cuántos minutos son?

a) Una hora c) Dos horas y media

b) Tres cuartos de hora d) Una hora y cuarto

4 Lee y elige la respuesta correcta.

Para transformar horas en segundos…

A … multiplicamos por 60. C … multiplicamos por 3 600.

B … dividimos por 60. D … dividimos por 3 600.

HORAS MINUTOS SEGUNDOS

HORAS MINUTOS SEGUNDOS

HORAS MINUTOS SEGUNDOS

Expresiones incomplejas y complejas

Expresión incompleja: una única unidad de medida.

8 418 s

Así transformamos una expresión incompleja en compleja.

Expresión compleja: varias unidades de medida.

2 h 20 min 18 s

1 Copia y une en tu cuaderno.

Expresión incompleja Expresión compleja

2 Expresa estas cantidades de manera incompleja.

a) 3 h 16 min 32 s

b) 2 h 43 min 15 s

c) 2 h 19 min 2 s

Transforma todas las unidades en segundos, que es la unidad más pequeña.

3 Fíjate en el ejemplo y expresa estas cantidades de manera compleja: horas, minutos y segundos.

4 850 s entre 60 son 80 min y sobran 50 s. 80 min entre 60 es 1 h y sobran 20 min.

4 850 s = 1 h 20 min 50 s

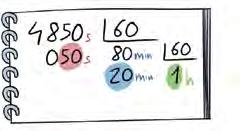
a) 695 s b) 1 025 s c) 4 035 s

4 Ordena estos datos de tiempo de menor a mayor.

Sumo y resto datos de tiempo

Suma con datos del tiempo

Si al sumar datos de tiempo los segundos superan los 60, los transformamos en minutos; si los minutos superan los 60, los transformamos en horas.

Sumamos datos de tiempo así:

1.° Sumamos los datos 2.° Transformamos los datos. 3.° Expresamos el resultado.

2 h 35 min

+ 1 h 27 min

3 h 62 min

Resta con datos del tiempo

Para poder restar datos de tiempo, preparamos la resta para tener en el minuendo datos mayores que en el sustraendo.

Restamos datos de tiempo así:

1.° Colocamos los datos. 2.° Transformamos los datos. 3.° Restamos.

4

1 Copia y suma.

a) 18 h 29 min + 4 h 45 min

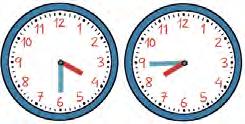
b) 29 h31 min 52 s

+ 5 h 10 min32 s

2 Copia y resta.

a) 21 h 28 min 10 h 35 min

b) 5 h 5 min29 s

1 h 4 min45 s

2

3 ¿Cuánto tiempo ha pasado en cada caso? a) b)

4 Elena entrenó durante 1 h, 25 min y 32 s. Descansó 30 min y, a continuación, siguió entrenando durante 1 h, 52 min y 34 s más. ¿Cuánto ha tardado desde que empezó a entrenar hasta que terminó?

NOS PONEMOS EN ACCIÓN

Controlamos el tiempo

Controlar el tiempo es el proceso en el que registras las horas, minutos o segundos que has pasado realizando una actividad. Este control nos permite gestionar las tareas en un determinado periodo y así optimizar mejor nuestro rendimiento. Para ello, no es necesario mirar constantemente nuestro reloj, simplemente hay que tener una buena organización. ¿Qué podemos hacer para controlar nuestro tiempo? ¿Crees que así mejorarías tu rendimiento? Investiga sobre el tema y compártelo con tus compañeras y compañeros.

Escribe en este horario semanal las actividades que realizas cada día y anota el tiempo que dedicas a ellas.

Lunes MartesMiércolesJueves ViernesSábadoDomingo ? ? ? ? ? ? ?

a) ¿Cuántos minutos dedicas a realizar actividades de ocio?

b) ¿Cuántas horas, minutos y segundos dedicas a estudiar?

c) ¿Cuántas horas dedicas a hacer algún deporte?

d) ¿Podrías organizar mejor tu tiempo? ¿Cómo podrías hacerlo?

Vas a preguntar cuánto tiempo tardan tus compañeros en llegar desde su casa al colegio. Anota todos los datos en tu libreta, completando la siguiente tabla:

Nombre Expresión complejaExpresión incompleja ? ? ? ? ? ?

Ahora calcula:

a) ¿Qué compañero tarda más?

b) ¿Qué compañero tarda menos?

c) ¿Qué diferencia de tiempo hay entre el compañero que tarda más y el que tarda menos?

d) ¿Cuánto tiempo emplea el compañero que más tarda en ir y volver?

Generador de pruebas de evaluación y ejercitación

Competencias

GYM Game Room: evaluación gamificada

Evaluación inicial

Evaluación

Evaluación adaptada

Evaluación por situaciones de aprendizaje

Evaluación competencial

Instrumentos de evaluación, autoevaluación y coevaluación

Instrumentos para evaluar la práctica docente

Generador de pruebas de evaluación y ejercitación

Es una herramienta práctica y eficaz, capaz de elaborar todas las pruebas de evaluación requeridas durante el curso. Permite obtener pruebas impresas, listas para ser distribuidas entre el alumnado.

De forma sencilla, y sin requerir conocimientos informáticos especiales, la web de Anaya le ofrece la posibilidad de realizar distintas pruebas de evaluación.

Al seleccionar la opción «Evaluación» se desplegará un menú. Una vez que haya accedido a la herramienta según se describe en el apartado anterior:

1 Aparecerá una pantalla que muestra los bloques de contenidos del curso. Al pulsar sobre ellos se despliegan concretando saberes básicos.

2 Se pueden seleccionar todos aquellos que se desee incluir en la prueba de evaluación. Al hacerlo, se van mostrando en el cuadro resumen de la derecha, pudiéndose eliminar si se considera oportuno. Una vez que se han seleccionado los contenidos deseados, solo hay que pulsar el botón Generar prueba y elegir cuántas evaluaciones diferentes se quieren generar.

3 La herramienta creará automáticamente las pruebas y las mostrará en pantalla. Solo resta imprimir, lo que puede hacerse incluyendo las soluciones.

4 Otra opción que ofrece la herramienta es Prueba personalizada. Esta opción permite previsualizar las actividades disponibles antes de seleccionarlas para generar la prueba.

¿Qué es el generador de pruebas de evaluación y ejercitación?

¿Cómo funciona?

Game Room: evaluación gamificada

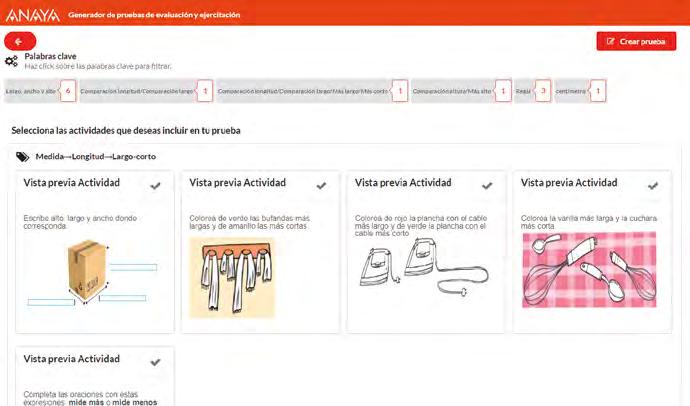
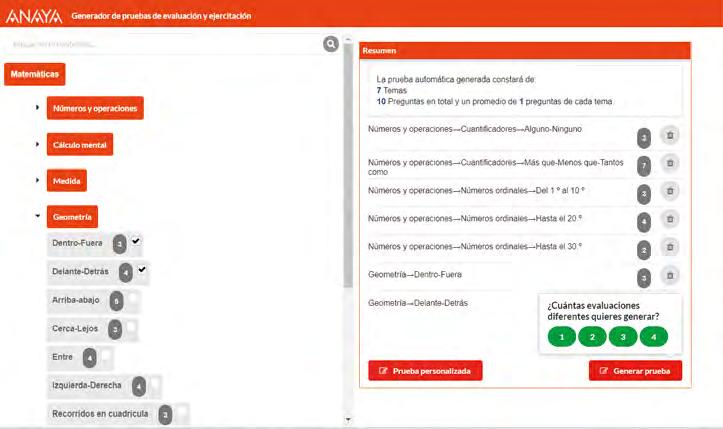
Proyecto gamificado de cada curso.

¿Qué es Game Room?

Game Room es una propuesta de evaluación trimestral gamificada y digital inspirada en los Objetivos de Desarrollo Sostenible. Su diseño, basado en storytelling, constituye una experiencia interdisciplinar lúdica y motivadora para el alumnado.

En cada escenario encontrarás un personaje que necesita tu ayuda. Presta atención para completar las misiones.

Evaluación gamificada y digital

Experiencia interdisciplinar

Utilizarás el Dolter para buscar elementos ocultos y avanzar en la historia.

¿Cómo es Ultimate Travellers?

Es un gran juego en el que el alumnado interactuará con los personajes, los escenarios, la exploración, el conflicto y la acción que se desarrolla en isla Ámbar.

DOC se comunicará contigo a través de Hermes cuando necesites una pista.

Bajo un objetivo común, el alumnado avanzará a través de escenarios personalizados, visualizando vídeos narrativos, comunicándose con los personajes, respondiendo a preguntas tipo quiz y resolviendo juegos más complejos.

Lo hará en un marco de refuerzo positivo, identificando su avance a través de la barra de progreso y recibiendo feedback del proceso.

Storytelling

Inspirado en los ODS

¿Quieres conocer más?

Arrastar objetos

Emparejar

Uso del Dolter

Adivinar palabras

Cartas iguales

Competencias GYM

¿Qué son las competencias

GYM ?

Las competencias GYM proponen un espacio de entrenamiento en el que el alumnado moviliza los aprendizajes adquiridos; son un espacio para entrenar las competencias.

Este recurso es un elemento importante para la inclusión y el éxito escolar que contribuye a desarrollar las competencias específicas del área.

Fichas para el alumnado

Matemáticas 3.º

ENCUENTRO DE JUEGOS TRADICIONALES Y POPULARES

Nombre y apellidos:

Curso:

Este año se ha celebrado el gran encuentro de juegos populares y tradicionales donde han participado alumnos de 3.º de Primaria. Los juegos que han practicado son: bolos, carrera de sacos, chapas, canicas y la cuerda. Ha sido una jornada increíble y han aprendido juegos nuevos.

1 En el juego de los bolos se ha hecho un recuento final de los puntos obtenidos. Ordena la posición en la que ha quedado cada estudiante.

de posición

2 En el juego de sacos se han organizado carreras de 5 en 5. Cada uno de los sacos lleva uno de estos números rotulado.

3 4 6 5 2

¿Cuál es el número más alto que puedes formar con los números de los sacos?

a) 64 532 b) 23 465 c) 65 432 d) 56 342

3 Al finalizar la carrera, el orden de llegada de los sacos ha formado un número. ¿Averigua cuál es?

- El número 2 ocupa la cifra de las decenas.

- La cifra de las unidades es la mitad de la cifra de las centenas.

- La cifra de las unidades de millar es el doble de la cifra de las decenas.

- El número impar que queda ocupa la cifra de las decenas de millar.

DMUM C D U 6

Para cada actividad, presenta el contenido trabajado, el proceso cognitivo y el criterio de corrección para valorar la puntuación obtenida.

Actividad 1

Contenido Números.

Proceso cognitivo Conocer y reproducir. Comprensión.

Descriptor operativo Lee, escribe y ordena, en textos numéricos y de la vida cotidiana, números naturales (hasta 10 000), interpretando el valor de la posición de cada una de sus cifras.

Máxima puntuación:

2 puntos: 7.ª- 6.ª- 3.ª- 1.ª- 5.ª- 2.ª- 4.ª

Puntuación parcial:

Escala de rendimiento

Facilita una aproximación descriptiva de la competencia del alumnado en base a la

Criterios de corrección

1 punto: Comete un error.

Ninguna puntuación:

0 puntos: Comete más de un error o se ha dejado en blanco.

Pregunta de respuesta Cerrada. Elección múltiple compleja.

Actividad 2

Contenido Números.

Proceso cognitivo Aplicar y analizar. Aplicación.

Descriptor operativo Ordena conjuntos de números de distinto tipo (naturales hasta 10 000).

Máxima puntuación:

2 puntos: Respuesta c.

Puntuación parcial:

Criterios de corrección

1 punto: Respuesta a. Ninguna puntuación:

0 puntos: Respuesta b y d o se ha dejado en blanco.

Pregunta de respuesta Cerrada. Elección múltiple.

ENCUENTRO DE JUEGOS TRADICIONALES Y POPULARES

Además de la valoración en relación con la puntuación obtenida en la prueba (0 a 19 puntos), es posible dar una aproximación descriptiva de la competencia del alumnado con respecto a su ejecución. Naturalmente, la construcción de estas escalas en las pruebas nacionales e internacionales tiene un proceso de diseño complejo y dilatado en el tiempo, que permite obtener unas descripciones del rendimiento muy afinadas y alineadas con las puntuaciones obtenidas en la prueba. En este caso, la propuesta no es más que una aproximación realizada con los descriptores operativos de cada actividad y la dificultad cognitiva en la que se sitúa cada una de ellas.

Nivel (puntuaciones esperadas) Actividades En este nivel se espera que el alumno o la alumna:

Nivel 4: Competente (16-19) 3, 4 Utilice los números para resolver problemas explicando el significado de los datos, la situación planteada, el proceso seguido y las soluciones, interpretando e intercambiando esta información en contextos de la vida cotidiana.

Nivel 3: Avanzado (8-15) 2, 6, 9, 10 Realice operaciones con los números más allá de la aplicación de algoritmos: ordene conjuntos de números de distinto tipo, calcule dobles y mitades, aproxime... En textos numéricos sencillos de la vida cotidiana, identifique e interprete datos.

Nivel 2: En desarrollo (4-7) 1, 5 Compruebe el resultado de las operaciones realizadas y, además, realice la operación de la división con números naturales utilizando los algoritmos correspondientes. Lea, escriba y ordene, en textos numéricos y de la vida cotidiana, números naturales (hasta 10 000), interpretando el valor de la posición de cada una de sus cifras.

Nivel 1: Iniciado (0-3) 7, 8

Realice operaciones de suma, resta y multiplicación con números naturales utilizando los algoritmos correspondientes. (Números naturales hasta 10 000 y multiplicación por dos cifras como máximo).

Identifique las unidades del sistema métrico decimal: longitud (km, m, cm), capacidad (L), peso (kg y g) y tiempo (año, mes, día, hora, minuto y segundo) al trabajar con las magnitudes correspondientes.

Matriz de especificaciones

Ofrece una interesante información cuantitativa sobre los procesos cognitivos asociados a las propuestas de entrenamiento.

ENCUENTRO DE JUEGOS TRADICIONALES Y POPULARES

Este año se ha celebrado el gran encuentro de juegos populares y tradicionales donde han participado alumnos de 3.º de Primaria. Los juegos que han practicado son: bolos, carrera de sacos, chapas, canicas y la cuerda. Ha sido una jornada increíble y han aprendido juegos nuevos.

1 En el juego de los bolos se ha hecho un recuento final de los puntos obtenidos. Ordena la posición en la que ha quedado cada estudiante.

2 En el juego de sacos se han organizado carreras de 5 en 5. Cada uno de los sacos lleva uno de estos números rotulado.

3 4 6 5 2

¿Cuál es el número más alto que puedes formar con los números de los sacos?

a) 64 532 b) 23 465 c) 65 432 d) 56 342

3 Al finalizar la carrera, el orden de llegada de los sacos ha formado un número. ¿Averigua cuál es?

- El número 2 ocupa la cifra de las decenas.

- La cifra de las unidades es la mitad de la cifra de las centenas.

- La cifra de las unidades de millar es el doble de la cifra de las decenas.

- El número impar que queda ocupa la cifra de las decenas de millar. DMUM

imprimible autorizado.

Matemáticas 3.º © Grupo Anaya, S. A. Material

Matemáticas 3.º

ENCUENTRO DE JUEGOS TRADICIONALES Y POPULARES

Nombre y apellidos:

4 Se han organizado 3 recorridos para el juego de las chapas con diferente dificultad. Para conseguir cada recorrido, hay que avanzar con la chapa por él y llegar hasta el final sin que se salga la chapa.

Recorrido 1 Recorrido 2 Recorrido 3 140 cm 165 cm 180 cm

En este juego han participado Daniela, Eric y Nayara, y han logrado superar las siguientes distancias:

Daniela Eric Nayara 1 m 75 cm 1 m 50 cm 1 m 62 cm

Marca con una cruz si las siguientes afirmaciones son verdaderas o falsas:

Eric logra superar el recorrido 1.

Daniela logra superar los recorridos 1 y 2.

Nayara no puede superar el recorrido 1.

Ningún niño y niña ha podido superar el recorrido 3.

5 En el juego de canicas han jugado al óvalo. Cada jugador necesita 3 canicas y tiene que disparar las canicas para ganar la de sus adversarios y apostar las suyas. Si en el juego hay 68 jugadores, ¿cuántas canicas tenemos que preparar para que puedan jugar todos?

Escribe la operación que realizas.

Solución: Necesitamos canicas en total.

© Grupo Anaya, S. A. Material imprimible autorizado.

Matemáticas 3.º

ENCUENTRO DE JUEGOS TRADICIONALES Y POPULARES

Nombre y apellidos:

6 Este año han acudido al encuentro de juegos populares y tradicionales 4 colegios en total.

Colegio Blasco Ibáñez Colegio Cervantes Colegio Mediterráneo Colegio Teide

242 estudiantes367 estudiantes275 estudiantes139 estudiantes

Aproxima a la centena el número de estudiantes de cada colegio y relaciona con flechas. ¿Qué número de alumnos y alumnas aproximadamente tiene cada colegio?

Colegio Blasco Ibáñez •

Colegio Cervantes •

Colegio Mediterráneo •

Colegio Teide •

• 100 estudiantes

• 200 estudiantes

• 300 estudiantes

• 400 estudiantes

7 ¿Cuántos estudiantes del Colegio Cervantes hay más que del Colegio Teide? Escribe la operación que realizas.

Solución: Hay estudiantes más en el Colegio Cervantes que en el Colegio Teide.

8 Fíjate en el siguiente calendario. ¿En qué semana se ha celebrado el encuentro de los juegos tradicionales y populares?

a) Del 7 al 13 de junio.

b) Del 14 al 20 de junio.

c) Del 14 al 16 de julio.

d) Del 14 al 18 de junio.

Matemáticas 3.º

ENCUENTRO DE JUEGOS TRADICIONALES Y POPULARES

Nombre y apellidos:

9 En el juego de la cuerda se ha practicado el tradicional soga-tira. Para organizar los equipos, se tienen que poner la mitad de jugadores en cada parte de la cuerda. ¿Cuántos jugadores habría en cada equipo si participan 48 niños y niñas en el juego?

Solución: Habrá jugadores en cada parte de la cuerda.

10 Al finalizar el encuentro de juegos populares y tradicionales, los participantes rellenaron una encuesta online. En el siguiente gráfico se recoge la opinión de los participantes sobre cuáles son los juegos que más han gustado. Marca con una cruz si las siguientes afirmaciones son verdaderas o falsas.

Encuesta de juegos populares y tradicionales

El juego que más ha gustado es el soga-tira.

Al menos 100 personas han votado cada juego

La carrera de sacos les gusta a más de 200 personas. Los bolos han gustado a 150 personas.

© Grupo Anaya, S. A. Material imprimible autorizado.

Matemáticas

3.º

CORRECTOR

ENCUENTRO DE JUEGOS TRADICIONALES Y POPULARES

Actividad 1

Contenido Números.

Proceso cognitivo

Descriptor operativo

Conocer y reproducir. Comprensión.

Lee, escribe y ordena, en textos numéricos y de la vida cotidiana, números naturales (hasta 10 000), interpretando el valor de la posición de cada una de sus cifras.

Máxima puntuación:

2 puntos: 7.ª- 6.ª- 3.ª- 1.ª- 5.ª- 2.ª- 4.ª

Puntuación parcial:

Criterios de corrección

1 punto: Comete un error.

Ninguna puntuación:

0 puntos: Comete más de un error o se ha dejado en blanco.

Pregunta de respuesta Cerrada. Elección múltiple compleja.

Actividad 2

Contenido Números.

Proceso cognitivo

Descriptor operativo

Aplicar y analizar. Aplicación.

Ordena conjuntos de números de distinto tipo (naturales hasta 10 000).

Máxima puntuación:

2 puntos: Respuesta c.

Puntuación parcial:

Criterios de corrección

1 punto: Respuesta a.

Ninguna puntuación:

0 puntos: Respuesta b y d o se ha dejado en blanco.

CORRECTOR

ENCUENTRO DE JUEGOS TRADICIONALES Y POPULARES

Actividad 3

Contenido Números.

Proceso cognitivo Razonar y reflexionar. Síntesis y creación.

Descriptor operativo

Utiliza los números para interpretar e intercambiar información en contextos de la vida cotidiana.

Máxima puntuación:

2 puntos: 54 623

Puntuación parcial:

Criterios de corrección

1 punto: Comete un error.

Ninguna puntuación:

0 puntos: Comete más de un error o se ha dejado en blanco.

Pregunta de respuesta Cerrada.

Actividad 4

Contenido Medida.

Proceso cognitivo Razonar y reflexionar. Juicio y valoración.

Descriptor operativo

Resuelve problemas relacionados con la medida, explicando el significado de los datos, la situación planteada, el proceso seguido y las soluciones.

Máxima puntuación:

2 puntos: V-V-F-V

Puntuación parcial:

Criterios de corrección

1 punto: Comete un error.

Ninguna puntuación:

0 puntos: Comete más de un error o se ha dejado en blanco.

Pregunta de respuesta Cerrada. Elección múltiple compleja.

CORRECTOR

ENCUENTRO DE JUEGOS TRADICIONALES Y POPULARES

Actividad 5

Contenido Números.

Proceso cognitivo Conocer y reproducir. Comprensión.

Descriptor operativo Calcula sumas, restas, multiplicaciones y divisiones, comprobando el resultado.

Máxima puntuación:

2 puntos: Plantea bien la operación, la resuelve y muestra con claridad el resultado, 204.

Puntuación parcial:

Criterios de corrección

1 punto: Plantea bien la operación, pero comete algún error de cálculo.

Ninguna puntuación:

0 puntos: No plantea bien la operación, o da el resultado correcto sin plantearla o se ha dejado en blanco.

Pregunta de respuesta Abierta.

Actividad 6

Contenido Números.

Proceso cognitivo Aplicar y analizar. Análisis.

Descriptor operativo Aproxima números naturales a las decenas, centenas y millares.

Máxima puntuación:

2 puntos: Colegio Blasco Ibáñez, 200. Colegio Cervantes, 400. Colegio Mediterráneo, 300. Colegio Teide, 100.

Criterios de corrección

Puntuación parcial:

1 punto: Comete un error (intercambio de 2 respuestas).

Ninguna puntuación:

0 puntos: Comete más de un error o se ha dejado en blanco.

Pregunta de respuesta Cerrada. Asociación.

CORRECTOR

ENCUENTRO DE JUEGOS TRADICIONALES Y POPULARES

Actividad 7

Contenido Números.

Proceso cognitivo Conocer y reproducir. Acceso e identificación.

Descriptor operativo

Realiza operaciones de suma, resta y multiplicación con números naturales utilizando los algoritmos correspondientes. (Números naturales hasta 10 000 y multiplicación por dos cifras como máximo).

Máxima puntuación:

2 puntos: Plantea bien la operación, la resuelve y muestra con claridad el resultado, 228.

Puntuación parcial:

Criterios de corrección

1 punto: Plantea bien la operación, pero comete algún error de cálculo.

Ninguna puntuación:

0 puntos: No plantea bien la operación, o da el resultado correcto sin plantearla o se ha dejado en blanco.

Pregunta de respuesta Abierta. Actividad 8

Contenido Medida.

Proceso cognitivo Conocer y reproducir. Acceso e identificación.

Descriptor operativo

Identifica las unidades del sistema métrico decimal: longitud (km, m, cm), capacidad (L), peso (kg y g) y tiempo (año, mes, día, hora, minuto y segundo) al trabajar con las magnitudes correspondientes.

Máxima puntuación:

2 puntos: Respuesta d.

Criterios de corrección

Ninguna puntuación:

0 puntos: Respuestas a, b y c o se ha dejado en blanco.

Pregunta de respuesta Cerrada. Elección múltiple.

Matemáticas 3.º

© Grupo Anaya, S. A. Material imprimible autorizado.

CORRECTOR

ENCUENTRO DE JUEGOS TRADICIONALES Y POPULARES

Actividad 9

Contenido Números.

Proceso cognitivo Aplicar y analizar. Aplicación.

Descriptor operativo Calcula dobles y mitades.

Máxima puntuación:

2 puntos: Plantea bien la operación, la resuelve y muestra con claridad el resultado, 24.

Puntuación parcial:

Criterios de corrección

1 punto: Plantea bien la operación, pero comete algún error de cálculo.

Ninguna puntuación:

0 puntos: No plantea bien la operación, o da el resultado correcto sin plantearla o se ha dejado en blanco.

Pregunta de respuesta Abierta. Actividad 10

Contenido Incertidumbre y datos.

Proceso cognitivo Aplicar y analizar. Análisis.

Descriptor operativo

Identifica e interpreta datos y mensajes de textos numéricos sencillos de la vida cotidiana (facturas, folletos, rebajas…).

Máxima puntuación:

2 puntos: Respuesta correcta: F-V-V-F

Puntuación parcial:

Criterios de corrección

1 punto: Comete un error.

Ninguna puntuación:

0 puntos: Comete más de un error o se ha dejado en blanco.

Pregunta de respuesta Cerrada. Elección múltiple compleja.

Además de la valoración en relación con la puntuación obtenida en la prueba (0 a 19 puntos), es posible dar una aproximación descriptiva de la competencia del alumnado con respecto a su ejecución. Naturalmente, la construcción de estas escalas en las pruebas nacionales e internacionales tiene un proceso de diseño complejo y dilatado en el tiempo, que permite obtener unas descripciones del rendimiento muy afinadas y alineadas con las puntuaciones obtenidas en la prueba. En este caso, la propuesta no es más que una aproximación realizada con los descriptores operativos de cada actividad y la dificultad cognitiva en la que se sitúa cada una de ellas.

En este nivel se espera que el alumno o la alumna:

Utilice los números para resolver problemas explicando el significado de los datos, la situación planteada, el proceso seguido y las soluciones, interpretando e intercambiando esta información en contextos de la vida cotidiana.

Realice operaciones con los números más allá de la aplicación de algoritmos: ordene conjuntos de números de distinto tipo, calcule dobles y mitades, aproxime... En textos numéricos sencillos de la vida cotidiana, identifique e interprete datos.

Compruebe el resultado de las operaciones realizadas y, además, realice la operación de la división con números naturales utilizando los algoritmos correspondientes. Lea, escriba y ordene, en textos numéricos y de la vida cotidiana, números naturales (hasta 10 000), interpretando el valor de la posición de cada una de sus cifras.

Realice operaciones de suma, resta y multiplicación con números naturales utilizando los algoritmos correspondientes. (Números naturales hasta 10 000 y multiplicación por dos cifras como máximo).

Identifique las unidades del sistema métrico decimal: longitud (km, m, cm), capacidad (L), peso (kg y g) y tiempo (año, mes, día, hora, minuto y segundo) al trabajar con las magnitudes correspondientes.

Actividades

Nivel (puntuaciones esperadas)

3, 4

1, 5

7, 8

Nivel 4: Competente (16-19)

Nivel 3: Avanzado (8-15)

Nivel 2: En desarrollo (4-7)

Nivel 1: Iniciado (0-3)

© Grupo Anaya, S. A. Material imprimible autorizado.

Evaluación inicial Unidad

LOS NÚMEROS

1 Colorea los siguientes números según el código.

Colorea de azul los números mayores que 50 y menores que 200.

Colorea de rojo los números menores que 420 pero mayores que 230.

Colorea de verde los números mayores que 510 y menores que 750. Colorea de naranja los números menores que 50.

2 Ordena de menor a mayor los números comprendidos entre el 500 y el 900 de la actividad anterior.

© Grupo Anaya, S. A. Material imprimible autorizado.

3 Completa la tabla escribiendo las centenas, decenas y unidades.

4 Escribe con cifras y cómo se leen los siguientes números. Un número mayor que 17 y menor que 134.

Un número menor que 572 y mayor que 490.

Un número que tenga 3 centenas, 2 decenas y más de 5 unidades.

Un número que tenga menos de 4 centenas y más de 7 decenas.

Un número menor que una decena y mayor que 8 unidades.

5 Redondea estos números.

3 Resuelve las siguientes restas.

4

5 Recuerda las tablas de multiplicar y calcula.

Nombre y apellidos: 3 FICHA UNIDAD

Fecha:

LA MEDIDA DEL TIEMPO

Matemáticas 3.º

Colorea así: Lo recuerdo con ayuda Lo recuerdo No lo recuerdo

1 ¿Qué día de la semana es hoy? Escribe también los 3 días anteriores y los 3 próximos.

Hoy es

2 Escribe los meses del año en este calendario.

© Grupo Anaya, S. A. Material imprimible autorizado.

3 ¿Cuántos días tiene…?

…el mes de enero? …el mes de abril?

…una semana? …un año?

…más el mes de noviembre que una semana?

4 Escribe las siguientes horas en los relojes.

a) Doce y media

d) Cuatro y cuarto de la mañana

:

b) Seis en punto

e) Diez menos cuarto

c) Seis y media de la tarde

f) Nueve en punto de la noche

: :

5 Alicia salió de su casa para ir a su entrenamiento de fútbol a las seis de la tarde. Tardó 15 minutos en llegar al estadio, y estuvo entrenando durante una hora y media. Después, invirtió 15 minutos en asearse, y otros 15 minutos en volver a casa. ¿A qué hora llegó a su casa?

© Grupo Anaya, S. A. Material imprimible autorizado.

Fecha:

Nombre y apellidos: 4 FICHA

Matemáticas 3.º

LA SIMETRÍA

Colorea así: Lo recuerdo con ayuda Lo recuerdo No lo recuerdo

1 Completa las simetrías.

2 Rodea los objetos que son simétricos y traza su eje de simetría.

© Grupo Anaya, S. A. Material imprimible autorizado.

Nombre y apellidos: 0

3 Mira a tu alrededor y escribe el nombre de 5 objetos simétricos y 5 asimétricos.

Simétricos Asimétricos

4 Elige uno de los objetos simétricos anteriores y dibújalo resaltando sus ejes de simetría.

© Grupo Anaya, S. A.

Material imprimible autorizado.

Nombre y apellidos: 5 FICHA UNIDAD

Fecha:

LOS POLÍGONOS Y LOS CUERPOS GEOMÉTRICOS

Matemáticas 3.º

1 Señala en las figuras: sus lados, de azul; y sus vértices, de rojo. Después, cuenta el número de lados y vértices que tienen y anótalo.

2 De las siguientes figuras, rodea la que no sea un polígono y explica por qué.

3 Escribe el nombre de estas figuras.

© Grupo Anaya, S. A. Material imprimible autorizado.

Nombre y apellidos: 0

4 ¿Cuántos triángulos hay contenidos en este pentágono?

5 Dibuja las siguientes figuras.

A. Un polígono con 3 vértices y 3 lados diferentes.

B. Un polígono con 4 lados y 4 vértices iguales.

C. 2 rectas paralelas.

D. 2 rectas perpendiculares.

E. Un polígono con 5 lados y 5 vértices (2 lados y 2 vértices tienen que ser iguales).

6 Crea una figura geométrica que esté compuesta por 2 cilindros, 1 cubo, 1 cono y 2 esferas. Una vez la tengas dibujada, ponle un nombre.

© Grupo Anaya, S. A.

Material imprimible autorizado.

Nombre y apellidos:

Fecha:

UNIDADES DE LONGITUD

Matemáticas 3.º

1 Completa las siguientes afirmaciones.

• El es la unidad de medida principal del sistema métrico internacional.

• Utilizamos el para medir longitudes pequeñas.

• Para medir distancias grandes utilizamos el

• Un metro con cm.

• Un kilómetro son m.

• 100 cm equivalen a un

2 Rodea la unidad de media más adecuada para cada situación.

• Para medir la distancia entre Madrid y Zaragoza: cm/m/km

• Queremos medir la longitud de la clase, para ello utilizaremos: cm/m/km

• Necesito medir el tamaño de mi libro de texto, tengo que utilizar: cm/m/km

• Para medir la altura de una persona: cm/m/km

• Indicar la longitud de una cuerda: cm/m/km

• Para medir la distancia que separa España de Inglaterra: cm/m/km

3 Ordena estas medidas de menor a mayor:

Grupo Anaya, S. A. Material imprimible autorizado.

Nombre y apellidos: 0 Matemáticas 3.º 6

4 ¿Cuánto miden estos objetos? Rodea las medidas correctas.

4 metros 70 metros 20 metros

40 metros 70 centímetros 2 centímetros

4 kilómetros 7 metros 2 metros

5 Inventa y resuelve un problema en el que utilices la imagen y los datos que aparecen en ella.

Enunciado:

Solución:

© Grupo Anaya, S. A. Material imprimible autorizado.

UNIDADES DE CAPACIDAD Y MASA

1 Rodea de color azul, si cabe menos de un litro, y de color verde, si en el recipiente cabe más de un litro.

2 Tenemos una jarra que tiene 1 litro de capacidad, un tazón de medio litro de capacidad y vasos de un cuarto de litro. 1L

• ¿Cuántos vasos tenemos que añadir a la jarra para llenarla?

• ¿Cuántos vasos tenemos que añadir al tazón para llenarlo?

• ¿Cuántos vasos podré llenar con la jarra llena de agua?

• Si tengo la jarra llena de agua y lleno el tazón, ¿cuántos vasos podré llenar con el agua que queda en la jarra?

Nombre y apellidos: 0

UNIDAD FICHA

Matemáticas 3.º 7

3 Escribe cuántos kilos hay en cada caso.

+++= 1kg medio kilo cuarto kilo cuarto kilo

+ +++= 1kg 1kg 1kg cuarto kilo cuarto kilo

+++= 1kg 1kg medio kilo medio kilo

= ++ medio kilo medio kilo medio kilo

4 Rodea las pesas necesarias para representar el peso de cada objeto.

4 kg y medio

2 kg y cuarto

1kg 1kg 1kg 1kg medio kilo medio kilo medio kilo cuarto kilo cuarto kilo cuarto kilo 1kg 1kg 1kg 1kg medio kilo medio kilo medio kilo cuarto kilo cuarto kilo cuarto kilo 1kg 1kg 1kg 1kg medio kilo medio kilo medio kilo cuarto kilo cuarto kilo cuarto kilo

1 kg y medio

5 Escribe el nombre de tres cosas que tengas en tu clase o en tu habitación y que pesen menos de 1 kg, y otras tres que pesen más de 1 kg.

Más de 1 kg

Menos de 1 kg

© Grupo Anaya, S. A. Material imprimible autorizado.

Nombre y apellidos: 8

Fecha:

ORGANIZACIÓN

Y PROBLEMAS

Matemáticas 3.º

Tenemos que ayudar a Jon a planificar una fiesta sorpresa para su hermana Rosa, ya que cumplirá 10 años el próximo mes. A ella le encantaría tener una fiesta temática sobre superheroínas.

1 Haz una lista de tareas que habría que hacer para organizar la fiesta de Rosa.

2 Rosa quiere invitar a muchas personas, pero su familia solo le permite 27. En la casa viven: Jon, Rosa, su padre, su madre y su abuela. Además, Rosa tiene que invitar a su tía Amelia y a sus dos primos, Fran y Juan. Jon ha pedido a su hermana que le deje invitar a 4 amigos, entre los que te encuentras tú. ¿Cuántos amigos podrá invitar Rosa a la fiesta?

Operaciones:

© Grupo Anaya, S. A. Material imprimible autorizado.

3 El día de la fiesta, Rosa termina las clases a las 17:00 horas. Tarda 15 minutos en llegar a casa y otros 15 minutos en dejar la mochila ordenada y prepararse para la fiesta. Además, calcula que necesitará una hora para organizar la fiesta. ¿A partir de qué hora podrá comenzar la fiesta?

Operaciones:

Solución:

4 Rosa ha calculado que los asistentes a la fiesta beberán 2 vasos de refresco cada uno. Los vasos de refresco son de un cuarto de litro. ¿Cuántos litros de refresco tiene que comprar?

Operaciones:

Solución:

5 La familia de Rosa le ha dicho que cuenta con un presupuesto de 55 € para organizar la fiesta. Ha pedido una tarta especial que cuesta 16 €, unas pizzas que cuestan 22 € y se ha gastado 12 € en bebidas y gusanitos. ¿Cuánto dinero le queda a Rosa para gastarse en decoración?

Operaciones:

Solución:

© Grupo Anaya, S. A. Material imprimible autorizado.

Nombre y apellidos: UNIDAD

Fecha:

METACOGNICIÓN INICIAL

Matemáticas 3.º

Colorea así: Lo recuerdo con ayuda Lo recuerdo No lo recuerdo

1 Colorea las baterías con el nivel de energía con que te encuentras en este comienzo de curso.

Ganas de comenzar el curso. Ganas de trabajar en equipo.

Ganas de aprender cosas nuevas. Ganas de ayudar a los demás.

2 Recuerda tres momentos de tu verano en el que hayas utilizado lo que aprendiste de Matemáticas en los cursos anteriores.

Grupo Anaya, S. A. Material imprimible autorizado.

Nombre y apellidos: 0

3 ¿Qué te gustaría aprender en Matemáticas que te ayudaría en tu día a día?

4 Busca tres metas que te gustaría conseguir este curso y escribe cómo podrías conseguirlas.

Meta 1:

Acción para conseguirla:

Meta 2:

Acción para conseguirla:

Meta 3:

Acción para conseguirla:

5 Para ti, ¿qué es lo mejor de trabajar en equipo?

6 ¿Qué esperas aprender de los compañeros y las compañeras de tu equipo?

7 ¿Qué talento tienes que puede ser útil para los demás?

© Grupo Anaya, S. A.

Material imprimible autorizado.

1 Respuesta abierta.

2 Enero, febrero, marzo, abril, mayo, junio, julio, agosto, septiembre, octubre, noviembre, diciembre.

3 … el mes de enero? 31 … el mes de abril? 30

… una semana? 7 … un año? 365 … más el mes de noviembre que una semana? 23

04:15

EV Matemáticas 3.º Recursos Soluciones

2

3 Respuesta abierta.

4 Respuesta abierta.

Ficha 5. LOS POLÍGONOS Y LOS CUERPOS GEOMÉTRICOS

2

• Para medir la distancia entre Madrid y Zaragoza: km

• Queremos medir la longitud de la clase, para ello utilizaremos: m

• Necesito medir el tamaño de mi libro de texto, tengo que utilizar: cm

• Para medir la altura de una persona: cm

• Indicar la longitud de una cuerda: m

• Para medir la distancia que separa España de Inglaterra: km

3 70 cm < 12 m < 150 m < 1 km

4 Coche: 4 metros

Mesa: 70 centímetros

Puerta: 2 metros

5 Respuesta abierta.

Ficha 7. UNIDADES DE CAPACIDAD Y CANTIDAD

1 Azul: vaso, cubo, jeringa

Verde: piscina, garrafa, bañera

línea poligonal abierta.

3 TriánguloCuadradoCírculoPentágono

4 Hay 35 triángulos.

5 Respuesta abierta.

6 Respuesta abierta.

Ficha 6. UNIDADES DE LONGITUD

18:30 21:00

5 18:00 18:15 19:45 20:00 20:15 Llegó a las ocho y cuarto de la tarde.

Ficha 4. LA SIMETRÍA

1 El alumnado completará las simetrías.

EV Matemáticas 3.º Recursos Soluciones

Ficha 8. ORGANIZACIÓN Y PROBLEMAS

1 Respuesta abierta.

2 Operaciones: 5 + 3 + 4 = 12

27 – 12 = 15

Solución: Podrá invitar a 15 amigos.

3 Operaciones:

17:00 17:15 17:30 18:30

Solución: La fiesta puede comenzar a partir de las

18:30 h.

4 Operaciones:

Cada persona bebe medio litro.

27 personas × medio litro 13 litros y medio

Solución: Tiene que comprar 13 litros y medio.

5 Operaciones:

55 – 16 – 22 – 12 = 5

Solución: Le sobran 5 euros para la decoración.

1 • El metro es la unidad de medida principal del sistema métrico internacional.

• Utilizamos el centímetro para medir longitudes pequeñas.

• Para medir distancias grades utilizamos el kilómetro.

• Un metro son 100 cm.

• Un kilometro son 1 000 m.

• 100 cm equivalen a un metro.

2 • 4 vasos

• 2 vasos

• 4 vasos

• 2 vasos

3 2 kg 3 kg y medio 2 kg y medio tres cuartos de kilo

4 4 kg y medio 2 kg y cuarto 1 kg y medio

1kg 1kg 1kg 1kg medio kilo medio kilo medio kilo kilo kilo kilo

1kg 1kg 1kg 1kg medio kilo kilo

1kg 1kg 1kg 1kg medio kilo medio kilo medio kilo kilo kilo kilo

5 Respuesta abierta.

Evaluac ión Evaluación inicial Prueba de evaluación

Nombre y apellidos: EI UNIDAD

1

Fecha:

1 Escribe estos números con cifras o con letras.

a) Seiscientos cuatro

b) Doscientos setenta y cinco

c) 918

d) 503

2 Copia cada número donde corresponda.

31 45 70 88

Matemáticas 3.º

PARES:

3 Ordena estos números de menor a mayor.

IMPARES:

201 99 732 58

4 Coloca y suma.

a) 265 + 473

b) 390 + 46 + 108

5 Coloca y resta.

a) 543 – 226

b) 326 – 89

6 Escribe estas sumas en forma de multiplicación.

a) 2 + 2 + 2 + 2 + 2 + 2 + 2 =

b) 5 + 5 + 5 =

© Grupo Anaya, S. A. Material imprimible autorizado.

7 Une los relojes que marcan la misma hora.

7:008:304:152:45

8 ¿Cuánto mide este lápiz? Marca.

9 km 9 m 9 cm

9 Rodea las figuras que son polígonos.

10 Elsa y Pablo juntan el dinero que tienen para comprar globos de agua.

¿Cuántos céntimos podrán gastar entre los dos?

Podrán gastar cts.

Prueba de evaluación

Evaluación por situaciones de aprendizaje

Nombre y apellidos: EV UNIDAD

9

Matemáticas 3.º Fecha:

1 Relaciona estos objetos según midan más o menos de un metro.

un peine el palo de una escoba una llave una piscina un árbol

más de un metro menos de un metro

una puerta una flauta un zapato

2 Mide con tu regla la longitud de estos objetos y completa.

a) El lápiz mide

b) La cuchara mide

3 Escribe la unidad más adecuada para medir estas longitudes.

metro kilómetro centímetro

a) Un sacapuntas.

b) La altura de un edificio.

c) Distancia entre Almería y Cádiz.

d) El ancho de una carretera.

e) El pie de un bebé.

4 ¿Cuántos metros más deben caminar estas personas para llegar a 1 km?

© Grupo Anaya, S. A. Material imprimible autorizado.

Evaluación por situaciones de aprendizaje

Nombre y apellidos: 9 Matemáticas 3.º EV UNIDAD

5 Completa.

a) 8 m = cm

b) 6 km = m

c) 8 000 m = km

d) 2 400 cm = m

6 Expresa en metros y ordena de mayor a menor.

1 km 4 m 7 000 cm 3 km 900 m

7 ¿Cuántos centímetros son?

a) 5 m 60 cm = cm

b) 2 m 7 cm = cm

8 Coloca y calcula.

a) 16 + 5 084 + 433 =

c) 10 m 10 cm = cm

d) 6 m 38 cm = cm

b) 378 : 9 =

9 Bea va todos los días en bici a comprar el pan. Si la panadería está a 500 m de su casa, ¿cuántos kilómetros recorre Bea en una semana para llevar el pan a casa?

10 Un electricista ha comprado dos rollos de cable de 100 m cada uno. Si ha utilizado 192 m, ¿cuántos centímetros le han sobrado?

100 m

100 m

© Grupo Anaya, S. A. Material imprimible autorizado.

Matemáticas 3.º Recursos Soluciones

un peine el palo de una escoba una llave una piscina un árbol

a) El lápiz mide 9 cm.

La cuchara mide 11 cm.

Evaluac ión Evaluación adaptada

Nombre y apellidos: EA UNIDAD

9

Matemáticas 3.º Fecha:

1 Relaciona estos objetos según midan más o menos de un metro.

una flauta un zapato el palo de una escoba una piscina un árbol

más de un metro menos de un metro

2 Mide con tu regla la longitud de estos objetos y completa.

a) El lápiz mide

b) La cuchara mide

3 Escribe la unidad más adecuada para medir estas longitudes.

metro kilómetro centímetro

a) La altura de un edificio.

b) Distancia entre Almería y Cádiz.

c) El ancho de una carretera.

d) El pie de un bebé.

4 ¿Cuántos metros más deben caminar estas personas para llegar a 1 km?

© Grupo Anaya, S. A. Material imprimible autorizado.

5 Completa.

a) 8 m = cm

c) 8 000 m = km

b) 6 km = m d) 2 400 cm = m

6 Expresa en metros y ordena de mayor a menor.

1 km 4 m 7 000 cm 3 km 900 m

7 ¿Cuántos centímetros son?

a) 10 m 10 cm = cm b) 6 m 38 cm = cm

8 Coloca y calcula.

a) 16 + 5 084 + 433 = b) 378 : 9 =

9 Bea va todos los días en bici a comprar el pan. Si la panadería está a 500 m de su casa, ¿cuántos kilómetros recorre Bea cada día para llevar el pan a casa? ¿Y en una semana?

10 Un electricista ha comprado dos rollos de cable de 100 m cada uno.

¿Cuántos metros de cable ha comprado en total?

Si ha utilizado 192 m, ¿cuántos centímetros le han sobrado? 100 m 100 m

Grupo Anaya, S. A. Material imprimible autorizado.

Evaluación adaptada

Matemáticas 3.º Recursos Soluciones

UNIDAD 9

1 más de un metro menos de un metro

el palo de una escoba una piscina un árbol

2 a) El lápiz mide 9 cm. b) La cuchara mide 11 cm.

una flauta un zapato

3 a) metro b) kilómetro c) metro d) centímetro

4 a) 150 m b) 700 m

5 a) 800 cm c) 8 km

6 000 m d) 24 m 6 3 000 m > 1 004 m > 900 m > 70 m 7 a) 1 010 cm b) 638 cm 8 a) 5 533 b) 42

500 m + 500 m = 1 000 m = 1 km Bea recorre 1 km cada día.

× 7 = 7 Recorre 7 km a la semana. 10 100 m + 100 m = 200 m

comprado 200 m en total.

m – 192 m = 8 m = 800 cm

han sobrado 800 cm de cable.

Evaluación competencial

UNIDAD

9

Nombre y apellidos:

Fecha:

Como cada año, los profesores de Educación Física de los colegios de Puente de la Sierra han organizado una jornada deportiva muy festiva.

Matemáticas 3.º

1 Los participantes han salido del Ayuntamiento para llegar juntos al polideportivo, donde realizarán diferentes pruebas. ¿Cuántos metros han recorrido?

2 Este año realizarán 12 pruebas deportivas. Si el año pasado realizaron la mitad, ¿cuántas pruebas hicieron entonces?

3 La prueba de natación consiste en hacer 4 largos en el menor tiempo posible. Si la piscina mide 25 m de largo, ¿cuántos metros recorrerá cada participante?

4 La exhibición de natación sincronizada recibe muchos aplausos. Comienza a las 10:45 y termina a las 11:15 horas. ¿Cuánto dura? Rodea.

A. 45 minutos B. Media hora C. Un cuarto de hora

© Grupo Anaya, S. A. Material imprimible autorizado.

5 En la prueba de salto de longitud cada participante realizará 3 intentos. Si hay 18 participantes, ¿cuántos saltos de longitud se realizarán?

6 Observa las mejores marcas de salto de longitud. Exprésalas en centímetros.

7 Al finalizar las pruebas, a todos los participantes se les entrega una medalla por el esfuerzo realizado. ¿Cuánto crees que mide la cinta de cada medalla?

8 Berta vive en Pradonuevo y participa en este evento todos los años. Ella y su familia quieren coger el camino más corto para volver desde Puente de la Sierra. ¿Seguirán la Autovía de la Sierra o pasarán por Villazul y Jaboneros?

EC Evaluación competencial

Matemáticas 3.º Recursos Soluciones

UNIDAD 9

1 300 + 180 + 275 = 755

Han recorrido 755 m.

2 12 : 2 = 6

El año pasado hicieron 6 pruebas.

3 25 × 4 = 100

Cada participante recorrerá 100 m.

4 B. Media hora

5 18 × 3 = 54

Se realizarán 54 saltos de longitud.

6 Ana 198 cm Luis 226 cm Olga 240 cm Iván 200 cm Pedro 215 cm

7 D. 80 cm

8 1006 + 4 025 + 2 086 = 7117

Recorre 7117 m si pasa por Villazul y Jaboneros.

8 km 480 m = 8 480 m Recorre 8 480 m si utiliza la Autovía de la Sierra.

Pasarán por Villazul y Jaboneros porque es el camino más corto.

Evaluac ión Evaluación final

Nombre y apellidos:

Fecha:

1 Indica cómo se leen o cómo se escriben los siguientes números.

a) 529

b) 3 804

c) seiscientos dos

d) cuatro mil doscientos cincuenta y uno

2 Ordena de mayor a menor utilizando los signos > o <.

820 80 2 087 278

Matemáticas 3.º

3 ¿Qué lugar ocupa cada pasajero para subir al avión? Completa.

4 Coloca y calcula.

a) 703 + 125 + 8 =

c) 293 × 4 =

b) 682 – 143 = d) 85 : 3 =

5 Escribe las siguientes fracciones.

a) cinco medios

b) cuatro décimos

c) tres cuartos

d) siete quintos

© Grupo Anaya, S. A. Material imprimible autorizado.

6 Colorea la fracción indicada en cada figura.

a) b)

4 6 2 3

7 Completa.

20:00

Son las Son las 7 y media. Son las 2 y cuarto.

Son las

8 Se ha realizado una encuesta sobre cuál es el medio de transporte preferido para viajar. Completa el gráfico y contesta.

15 Caravana 5

20

Avión Caravana Tren Coche

a) ¿Cuántas personas han contestado a la encuesta?

b) ¿Cuál es la moda?

9 Completa.

a) 6 m = cm

b) 4 L = mL

c) 7 000 m = km

d) 3 000 g = kg

© Grupo Anaya, S. A. Material imprimible autorizado.

Fecha:

Nombre y apellidos: EF UNIDAD 10 Dibuja.

a) Dos rectas paralelas. c) Un cuadrilátero.

b) Un ángulo recto. d) Un triángulo isósceles.

11 Cecilia compra 4 bolsas de globos para su fiesta.

a) Si cada bolsa cuesta 2 €, ¿cuánto paga en total?

Solución:

b) Si paga con un billete de 10 €, ¿cuánto le devuelven?

Solución:

c) Cada bolsa contiene 12 globos. ¿Cuántos globos ha comprado Cecilia en total?

Solución:

d) Bea y Jana ayudan a Cecilia a inflar todos los globos. Si cada una infla la misma cantidad, ¿cuántos globos ha inflado cada niña?

Solución:

Grupo Anaya, S. A. Material imprimible autorizado.

12 Lee y averigua cuántos años tiene cada uno.

– Fran tiene ocho años.

– La edad de Hugo es la mitad que la de Fran, pero el doble que la de Paula.

– Nico es el más pequeño.

– Entre los cuatro hermanos suman 15 años.

13 Pablo entrena 18 horas a la semana. Todos los días entrena el mismo número de horas y el domingo, descansa.

a) ¿Cuántas horas entrena el miércoles? ¿Y el sábado?

Solución:

b) Si hoy ha recorrido 7 8 de la ruta elegida, ¿qué fracción de la ruta le falta por recorrer? Ayúdate de un dibujo.

Solución:

14 ¿Cuántos metros de valla debemos colocar alrededor de una parcela con forma de triángulo equilátero si uno de los lados mide 25 m? Ayúdate de un dibujo.

Solución:

© Grupo Anaya, S. A. Material imprimible autorizado.

FRAN HUGO PAULA NICO

1 a) quinientos veintinueve

b) tres mil ochocientos cuatro c) 602

2 2 087 > 820 > 278 > 80

3 decimotercero - duodécimo - undécimo - décimonoveno

4 a) 836 c) 1172

b) 539 d) c = 28; r = 1

a) 5 2 c) 3 4

4 10 d) 7 5 6 a) b)

12 × 4 = 48 Ha comprado 48 globos en total.

7 Son las 5 menos cuarto.

Son las 8 de la tarde.

8 a) 30 + 15 + 5 + 20 = 70

Han contestado a la encuesta 70 personas.

b) La moda es viajar en coche.

b)

1 8

le falta por recorrer

7 8 ha recorrido

Le falta por recorrer 1 8 de la ruta.

25 m25 m 25 m

Instrumentos de evaluación, autoevaluación y coevaluación

Primaria

ANEXO DE EVALUACIÓN

La evaluación debe ir enfocada a mejorar el aprendizaje de los alumnos y de las alumnas; para ello, es necesario diversificar las herramientas y programar tiempos y espacios en el aula destinados a la evaluación de los procesos de aprendizaje.

Proponemos aquí algunos instrumentos para la evaluación de desempeños competenciales y criterios de evaluación Unas están diseñadas para el desarrollo común de competencias en todas las áreas; otras, para la evaluación de los aprendizajes concretos puestos en práctica solo en algunas de ellas.

Instrumentos de evaluación, autoevaluación y coevaluación

Para evaluar las destrezas comunicativas

1 Rúbrica para evaluar las intervenciones en clase: exposición oral.

2 Rúbrica para evaluar la comprensión oral.

3 Rúbrica para evaluar las intervenciones en clase: exposición con herramientas digitales.

4 Rúbrica para evaluar un debate.

5 Rúbrica para evaluar pruebas orales y escritas.

6 Rúbrica para evaluar la escucha activa en audiciones.

7 Rúbrica para evaluar la comprensión lectora (comprensión escrita).

8 Rúbrica para evaluar el trabajo con imágenes.

9 Rúbrica para evaluar trabajos escritos.

Instrumentos de evaluación, autoevaluación y coevaluación

%

%

%

%

%

Mejorable (14)

Con la ayuda de algún soporte (texto escrito, esquema, guion…) hace una lectura de las ideas principales ante el grupo.

Adecuado (56)

RÚBRICA PARA EVALUAR LAS INTERVENCIO NES EN CLASE: EXPOSICIÓN ORAL

Bueno (78)

Demuestra un dominio de la mayoría de las partes del tema y utiliza un vocabulario básico de este , aunque no es certero en las respuestas a las pr eguntas del grupo.

Predomina un lenguaje coloquial con algunas palabras adecuadas a las ideas, hechos o vivencias expuestas.

Sigue un cierto orden, con alguna dificultad en el control emocional aproximándose al tiempo establecido.

En general, la pronunciación y la dicción son adecuadas, aunque con una entonación o un volumen mejorables.

El dominio de la situación es intermitente y, en según qué momentos, la mirada se domina y la conversación se plantea con seguridad.

FINAL

% VALORACIÓN

Excelente (910)

Expresa sus ideas c lara y organizadamente.

Expone con buen dominio las ideas, hechos y vivencias con cl aridad, coherencia y corrección.

Exposición de ideas

Demuestra un buen dominio del tema y utiliza normalmente un vocabulario específico de este , respondiendo adecuadamente a las preguntas del grupo.

Demuestra un completo dominio del tema tratado, destacando claramente los aspectos importantes, y respondiendo adecuadamente a las preguntas del grupo.

Contenido

En general, el vocabulario utilizado se adecúa a las ideas, hechos o vivencias expuestas, así como en las intervenciones.

Utiliza un vocabulario preciso de acuerdo a las ideas, hechos o vivencias expuestas , incorporando nuevas palabras y perspectivas personales desde la escucha y las intervenciones de los demás.

Vocabulario

Sigue un orden, con interés y control emocional, y concluye correctamente y en tiempo apro ximado.

Sigue un orden lógico, con interés y control emocional, finalizando en un tiempo adecuado, aplicando normas de cortesía habituales (disculpas, agradecimientos, felicitaciones...).

Orden y gestión del tiempo

Se expresa con una pronunciación y una dicción adecuada : articulación, ritmo, entonación y volumen .

Se expresa con una pronunciación y una dicción correctas: articulación, ritmo, entonación y volumen .

Pronunciación, volumen y entonación

En general domina la situación, aunque se muestra algo más inseguro en la conversación.

Dirige la mirada a todo el grupo y participa activamente en la conversación contestando a preguntas y haciendo comentarios relacionados con el tema de la conversación.

Interacciones con el grupo

Utiliza algunos apoyos visuales a lo largo de su exposición y referencias al trabajo realizado que refuerzan el contenido.

Utiliza con soltura diversos apoyos visuales y referencias al trabajo realizado a lo largo de su exposición que refuerzan el contenido.

Recursos y apoyos

Mejorable (14)

Identifica algunas ideas con ayuda del docente o del alumnado.

Interpreta el contenido siguiendo algunas instrucciones.

Adecuado (56)

Reconoce las ideas principales y secundarias, recupera ndo la información con alguna ayuda.

Interpreta el contenido sencillo y establece algún tipo de rel ación con su ámbito cotidiano para favorecer la comprensión.

Realiza alguna valoración, reflexión, juicio propio y/o creación de manera guiada.

Realiza algunas valoraciones, reflexiones, juicios propios y/o creaciones a partir de la información.

Necesita algún tipo de ayuda mediante instrucciones o ayuda directa de alguna persona para comprender el sentido global de las situaciones orales propuestas.

Comprende la mayoría de tipologías textuales orales siguiendo algunas instrucciones orales o escritas.

Bueno (78)

PAR A EVALUAR LA COMPRENSIÓN ORAL

Capta el sentido global y reconoce las ideas principales y secundarias, recuperando la información.

Interpreta el contenido en relación con los conocimientos previos y sus propias vivencias para favorecer la comprensión.

Realiza generalmente valoraciones, reflexiones, juicios propios y/o creaciones a partir de la información, integrando ideas propias.

Excelente (910)

Capta el sentido global y reconoce las ideas principales y secundarias, recuperando la información de manera ordenada.

Comprensión literal y reproductiva

Interpreta el contenido, también implícito, en relación con los conocimientos previos y sus propias vivencias para favorecer la comprensión, mostrando interés y motivación.

Comprensión inferencial y de conexión

Realiza valoraciones, reflexiones, juicios propios y/o creaciones a partir de la información, integrando ideas propias de manera creativa.

Comprensión crítica y valorativa

Domina la mayoría de tipologías textuales orales mostrando predisposición e interés por seguir mejorando.

Domina la diversidad de tipologías textuales orales mostrando predisposición, interés y altas dosis de motivación en las respuestas.

Tipo de texto/documento

Instrumentos de evaluación, autoevaluación y coevaluación

RÚBRICA PARA EVALUAR LAS INTERVENCIONES EN CLASE: EXPOSIC IÓN CON HERRAMIENTAS DIGITALES

Mejorable (14)

La presentación la realiza con ayuda incorporando alguna propuesta propia, o bien reproduce la de algún compañero o compañera de la clase.

La presentación la realiza con ayuda incorporando alguna propuesta propia, o bien reproduce la de algún compañero o compañera de la clase.

Los recursos utilizados han sido incorporados a propuesta de otras personas o siguiendo unas instrucciones.

Adecuado (56)

La presentación recoge las ideas clave imprescindibles y más fu ndamentales mostrando un conocimiento básico de la temática.

La presentación está desarrollada a partir de una plantilla ya existente.

El uso de imágenes, vídeos u otros recursos es suficiente para ayudar a la comprensión del tema , aunque existen algunos que pueden dispersar la atención.

La presentación requiere una corrección previa para que el uso del lenguaje escrito sea el adecuado.

La presentación recoge varias faltas de ortografía y ha de incorporar algún apartado.

Siendo la carga de trabajo dispar, el grupo consigue que todas las personas participantes dominen las ideas clave o esenciales.

La carga de trabajo es dispar, recayendo el protagonismo en algunas perso nas del grupo.

Bueno (78)

La presentación cubre la temática de forma adecuada, mostrando un conocimiento adecuado sobre él.

La presentación muestra cierta creatividad sin tanto atractivo visual, predominando texto sobre imagen.

El uso de imágenes, vídeos u otros recursos es adecuado para ayudar a la comprensión del tema.

La presentación recoge alguna falta de ortografía, o bien ha de incorporar algún apartado

Excelente (910)

En l a presentación se identifican claramente las ideas clave que denotan un conocimiento profundo sobre la temática

La presentación es fácil de seguir, creativa, amena, visualmente atractiva y original , con un orden lógico y una coherencia.

Contenido e ideas clave

Formato

El uso de imágenes, vídeos u otros recursos (juegos interactivos, audios, gráficos…) es amplio y adecuado, y ayudan a la comprensión del tema.

La presentación utiliza el lenguaje escrito de manera adecuada aportando, al menos, una portada, un índice, unas conclusiones, bibliografía y agradecimientos.

La carga de trabajo está dividida equitativamente, recayendo el protagonismo en algunas personas del grupo.

La carga de trabajo está dividida equitativamente y es compartida por todos los miembros del grupo.

Recursos

Mejorable (14)

Los argumentos guardan alguna relación, aunque están construidos de oídas y sin rigor.

Demuestra un conocimiento básico que le permite participar en el debate.

Participa en el debate , aunque necesita algunas instrucciones para respetar ideas o las normas de intercambio, así como para analizar e incorporar argumentos de las compañeras y los com pañeros.

De manera frecuente hay que recordarle las normas so cio comunicativas: escucha act iva, turno de palabra.

Integra un vocabulario básico que se destaca en un guion o esquema que utiliza para sus intervenciones.

Necesita las fuentes aportadas a través de al guna persona para poder hacer el trabajo copiando literalmente.

Su volumen de voz es medi o y tiene dificultades para ser escuchado por todos en el aula.

Adecuado (56)

La defensa se construye con argumentos obvios que demuestran que no ha habido un trabajo de campo previo.

Demuestra un conocimiento básico del tema desde un punto de vista expositivo, quizá memorístico o reproductivo y sin aportaciones personales auténticas.

Escucha a sus compañer os y compañeras, mostrando dificultad en el análisis de sus argumentos.

Bueno (78)

Mantiene la defensa de su postura con argumentos variados y un dominio suficiente como para incorporar una idea no prevista.

PARA EVALUAR UN DEBATE

Excelente (910)

Mantiene la defensa de su postura con argumentos variados y un dominio que le permite ser flexible e improvisar con rigor.

Defensa de sus argumentos

Demuestra un trabajo previo evidenciado en un conocimiento del tema, aunque debe seguir avanzando en las valoraciones y juicios críticos.

Demuestra un trabajo previo evidenciado en un dominio total del tema , completamente interiorizado y reflexionado que le permite hacer buenas valoraciones.

Dominio del tema

Escucha a sus compañeros y compañeras y analiza sus argumentos.

Escucha atentamente las intervenciones de los compañeros y las compañeras y sigue las normas para el intercambio comunicativo , analizando sus argumentos, mostrando respeto y consideración por las ideas, sentimientos y emociones de los demás

Capacidad de escuchar a sus compañeros y compañeras

En varias ocasiones hay que recordarle las normas sociocomunicativas.

En alguna ocasión hay que recordarle las normas sociocomunicativas.

Aplica y tiene interiorizadas las normas socio comunicativas: escucha activa, turno de palabra, participació n respetuosa, adecuación a la intervención del interlocutor y ciertas normas de cortesía.

Respeto del uso de la palabra y de las ideas de los demás

Predomina un lenguaje coloquial con algunas palabras adecuadas a las ideas expuestas.

En general, el vocabulario utilizado se adecúa a las ideas expuestas, así como en las intervenciones.

Utiliza un vocabulario preciso de acuerdo a las ideas expuestas , incorporando nuevas palabras y perspectivas desde la escucha y las intervenciones de los demás.

Vocabulario

Se percibe que ha utilizado alguna fuente (digitales, bibliográficas, personales…) aunque no lo evidenci a.

Se evidencia alguna fuente fiable (digital, bibliográfica, personal…) dándole un toque personal, interpretando o valorando.

Se evidencia un uso variado de fuentes fiables (digitales, bibliográficas, personales…) citándolas, con interpretaciones y valoraciones.

Referencias a fuentes

No es escuchado por toda el aula cuando habla en voz alta, excepto si se siente muy seguro y aumenta su volumen de voz por unos segundos.

Su volumen de voz es adecuado y alto para ser escuchado por todos, aunque, a veces, cuando duda, baja el volumen.

Su volumen de voz es adecuado, suficientemente alto como para ser escuchado desde todas las partes del aula sin tener que gritar.

Volumen del tono de voz

RÚBRICA PARA EV ALUAR PRUEBAS ORALES Y ESCRITAS

Mejorable (14)

Necesita ayuda para respetar los elementos de presentación básicos establecidos (márgenes , ortografía, legibilidad, limpieza, orden …).

Adecuado (56)

Re speta los elementos de presentación básicos establecidos (márgenes , ortografía, legibilidad, limpieza, orden …).

Bueno (78)

Re speta casi todos los elementos de presentación establecidos (márgenes , ortografía, legibilidad , limpieza, orden …).

Excelente (910)

Re speta todos los elementos de presentación establecidos (título, márgenes , ortografía, legibilidad, limpieza, uso de imágenes y orden).

Presentación (escrita)

Consigue no tener faltas de ortografía si copia el texto.

El texto presenta más de cinco errores ortográficos. %

Las ideas principales quedan claras. %

Integra un vocabulario básico que se destaca en un guion o esquema que utiliza para la exposición.

Predomina un lenguaje coloquial con algunas palabras adecuadas a las ideas, hechos o vivencias expuestas.

%

%

Integra un conocimiento básico que se destaca en un guion o esquema que utiliza para la realización de la prueba.

Demuestra un dominio de la mayoría de las partes del tema y uti liza un vocabulario básico acorde.

%

Identifica algunas ideas con ayuda del docente o del alumnado.

Reconoce las ideas principales y secundarias, recuperando la información con alguna ayuda.

%

Interpreta el contenido siguiendo algunas instrucciones.

Interpreta el contenido y establece algún tipo de relación con su ámbito cotidiano para favorecer la compren sión.

Realiza alguna valoración, reflexión, juicio propio y/o creación de manera guiada.

% VALORACIÓN FINAL 1 Ponderación / 2 Valoración

El texto está escrito correctamente, sin errores ortográficos.

Corrección ortográfica (escrita)

Expresa sus ideas c lara y organizadamente.

Expone con buen dominio las ideas, hechos y vivencias con cl aridad, coherencia y corrección.

Expresión (oral o escrita)

En general, el vocabulario utilizado se adecúa a las ideas, hechos o vivencias expuestas, así como en las intervenciones.

Utiliza un vocabulario preciso de acuerdo a las ideas, hechos o vivencias expuestas , incorporando nuevas palabras y perspectivas personales desde la escucha e intervenciones de los demás.

Vocabulario empleado

Demuestra un buen dominio del tema y utiliza normalmente un v ocabulario específico de este.

Demuestra un completo dominio del tema tratado, destacando claramente los aspectos más importantes .

Capta el sentido global y reconoce las ideas principales y secundarias, recuperando la información.

Capta el sentido global y reconoce las ideas principales y secundarias, recuperando la información de manera ordenada.

Interpreta el contenido en relación con los conocimientos previos y sus propias vivencias para favorecer la comprensión.

Interpreta el contenido, también implícito , haciendo conjeturas y ( en relación con los conocimientos previos y sus propias vivencias para favorecer la comprensión ).

Realiza algunas valoraciones, reflexiones, juicios propios y/o creaciones a partir de la información.

Realiza generalmente valoraciones, reflexiones, juicios propios y/o creaciones a partir de la información, integrando ideas propias.

Realiza valoraciones, reflexiones, juicios propios y/o creaciones a partir de la información, integrando ideas propias de manera creativa.

Mejorable (14)

Necesita acompañamiento para centrar su atención para escuchar en silencio y destacar los detalles básicos.

Con la ayuda de alguna persona de la clase, comprende de manera sencilla el contexto en el que se ubica la audición.

Adecuado (56)

Escucha en silencio, aunque se le escapan bastantes detalles

RÚBRICA PARA EVALUAR LA ESCUCHA ACTIVA EN AUDICIONES

Bueno (78)

Respeta las normas de comportamiento en audiciones , escuchando en silencio, fijándose en la mayoría de los detalles y disfrutando de la música.

Entre varias opciones dadas, reconoce el contexto de la audición.

Reconoce los elementos esenciales como para situar la audición en su contexto.

Con la ayuda de algún documento guía o alguna persona de clase realiza comentarios descriptivos sencillos.

Realiza pequeños comentarios descriptivos sencillos, centrándose en las ideas fundamentales, con un lenguaje coloquial.

Realiza pequeños comentarios descriptivos sobre audiciones variadas con un vocabulario preciso y sencillo.

Con la ayuda de alguien de la clase, es capaz de hacer alguna aplicación en una creación colectiva o propia.

Muestra interés para aplicar en creaciones propias o aporta algunas ideas precisas.

Realiza audiciones activas que en gran medida aplica en creaciones propias o aporta algunas ideas precisas que hacen ver la conexión de la audición con los conocimientos previos.

Realiza alguna valoración, reflexión, juicio propio y/o creación de manera guiada.

Realiza algunas valoraciones, reflexiones, juicios propios y/o creaciones a partir de la audición

Realiza generalmente valoraciones, reflexiones, juicios propios y/o creaciones a partir de la audición , integrando ideas propias.

Excelente (910)

Tiene consolidadas las normas de comportamiento en audiciones , escuchando en silencio, fijándose en los detalles y disfrutando de la música.

Actitud de escucha

Sitúa la audición dentro de un contexto dando argumentos que justifican esa relación.

Contexto

Realiza comentarios de manera descriptiva sobre audiciones variadas e interpretaciones suyas , con u n vocabulario preciso y amplio.

Realiza audiciones activas que aplica en las creaciones propias o aporta ideas que hacen ver la conexión de la audición con los conocimientos previos.

Comprensión

Conexión con conocimien tos

Realiza valoraciones, reflexiones, juicios propios y/o creaciones a partir de la audición , integrando ideas propias de manera creativa.

Valoración crítica

Instrumentos de evaluación, autoevaluación y coevaluación

RÚBRICA PARA EVALUAR LA COMPRENSIÓN LECTORA (COMPRENSIÓN ESCRITA)

Mejorable (14)

Necesita ayuda para leer con una velocidad media y entonación aceptable y sin cometer errores básicos.

Identifica algunas ideas con ayuda del docente o del alumnado.

Adecuado (56)

Lee con una velocidad media y entonación aceptable, cometiendo algunos errores.

Reconoce las ideas principales y secundarias, recuperando la información con alguna ayuda.

Interpreta el contenido siguiendo algunas instrucciones.

Interpreta el contenido y establece algún tipo de relación con su ámbito cotidiano para favorecer la comprensión.

Realiza alguna valoración, reflexión, juicio propio y/o creación de manera guiada.

Realiza algunas valoraciones, reflexiones, juicios propios y/o creaciones a partir de la información.

Necesita algún tipo de ayuda mediante instrucciones o ayuda directa de alguna persona para comprender el sentido global de los textos propuestos.

Comprende la mayoría de tipologías textuales siguiendo algunas instrucciones orales o escritas.

Bueno (78)

Lee con una adecuada entonación y velocidad óptima, sin cometer errores.

Capta el sentido global y reconoce las ideas principales y secundarias, recuperando la información.

Inte rpreta el contenido en relación con los conocimientos previos y sus propias vivencias para favorecer la comprensión.

Realiza generalmente valoraciones, reflexiones, juicios propios y/o creaciones a partir de la información, integrando ideas propias.

Domina la mayoría de tipolog ías textuales mostrando predisposición e interés por seguir mejorando.

Excelente (910)

Lee con buena entonación y velocidad, respetando los signos ortográficos para facilitar y mejorar la comprensión lectora, sin cometer errores.

Fluidez lectora

Capta el sentido global y reconoce las ideas principales y secundarias, recuperando la información de manera ordenada.

Comprensión literal y reproductiva

Interpreta el contenido, también implícito (captando el doble sentido o la ironía) , en relación con los conocimientos previos y sus propias vivencias para favorecer la comprensión, mostrando interés y motivación.

Comprensión inferencial y de conexión

Realiza valoraciones, reflexiones, juicios propios y/o creaciones a pa rtir de la información, integrando ideas propias de manera creativa.

Domina la diversidad de tipologías textuales atendiendo a su finalidad (narrativo, descriptivo, expositivo…) y su f ormato (continuo, discontinuo…) mostrando predisposición, interés y altas dosis de motivación en las respuestas.

Comprensión crítica y valorativa

ALUAR EL TRABAJO CON IMÁGENES

RÚBRICA PARA EV

Mejorable (14)

Identifica algunas ideas con ayuda del docente o del alumnado.

Adecuado (56)

Reconoce la información más básica de la imagen, comprendiendo la no reconocida con alguna ayuda.

Interpreta la imagen siguiendo algunas instrucciones.

Interpreta la imagen y establece algún tipo de relación con su ámbito cotidiano para favorecer la comprensión.

Realiza alguna valoración, reflexión, juicio propio y/o creación de manera guiada.

Realiza algunas valoraciones, reflexiones, juicios propios y/o creaciones a partir de la imagen

Nece sita algún tipo de ayuda mediante instrucciones o ayuda directa de alguna persona para comprender el sentido global de las imágenes propuestas.

Comprende la mayoría de tipologías de imágenes siguiendo algunas instrucciones orales o escritas.

Bueno (78)

Capta el sentido global de la imagen , describiendo la información fundamental.

Interpreta la imagen en relación con los conocimientos previos y sus propias vivencias para favorecer la comprensión.

Realiza generalmente valoraciones, reflexiones, juicios propios y/o creaciones a partir de la imagen , integrando ideas propias.

Excelente (910)

Capta el sentido global y reconoce las ideas principales, describiendo la información obtenida de manera ordenada.

Relaciona la imagen con sus conocimientos previos y sus propias vivencias para favorecer la comprensión, mostrando interés y motivación.

Realiza valoraciones , reflexiones, juicios propios a partir de la imagen , integrando ideas propias de manera creativa.

Comprensión global

Interpretación y conexión

Reflexión y valoración

Domina la mayoría de tipologías de imágenes mostrando predisposición e interés por seguir mejorando.

Domina la diversidad de tipologías de imágenes atendiendo a su finalidad y con altas dosis de motivación en las respuestas.

Tipo de imagen

Instrumentos de evaluación, autoevaluación y coevaluación

Mejorable (14)

Necesita ayuda para respe tar los elementos de presentación básicos establecidos (título, ortografía, legibilidad, limpieza y orden), incluso con algún error.

Utiliza un v ocabul ario sencillo que, en ocasiones, guarda relación con el tema.

Utiliza los signos de puntuación con ayuda y siguiendo algunas instrucciones.

Consigue no tener faltas de ortografía si copia el texto.

Necesita algún tipo de ayuda o recurso en el que guiarse para evidenciar una estructura básica y muy sencilla (introducción, desarrollo y conclusiones).

Mediante alguna técnica de trabajo cooperativo u otra ayuda, muestra alguna evidencia relacionada con la temática del trabajo.

Adecuado (56)

Re speta los elementos de presentación básicos establecidos (título, ortografía, legibilidad, limpieza y orden).

Utiliza un v ocabulario sencillo , aunque guarda relación con el tema.

Los u tiliza ocasionalmente, pero de manera adecuada.

Bueno (78)

RÚBRICA PARA EVALUA R TRABAJOS ESCRITOS

Excelente (910)

Re speta casi todos los elementos de presentación establecidos (título, márgenes , ortografía, legibilidad, limpieza, uso de imágenes y orden).

Re speta todos los elementos de presentación establecidos (título, márgenes , ortografía, legibilidad, limpieza, uso de imágenes y orden).

Presentación

El vocabulario es algo variado, con palabras específicas del tema.

El vocabulario es rico, variado, sin repeticiones, y con palabras y expresiones específicas del tema.

Vocabulario empleado

Casi siempre los usa correctamente.

Utiliza correctamente los signos de puntuación (comas, puntos y signos de interrogación o exclamación, etc.).

Signos de puntuación

El texto presenta más de cinco errores ortográficos.

El texto está escrito con algún error ortográfico.

El t exto está escrito correctamente sin errores ortográficos.

Corrección ortográfica

%

Hay que guiarle para incluir alguna curiosidad o aportación creativa y original.

Necesita las fuentes aportadas a través de alguna persona para poder hacer el trabajo copiando literalmente.

Se evidencia una estructura básica y sencilla (introducción, desarrollo y conclusiones).

Se evidencian casi todos los apartados propios de un trabajo escrito (portada, autoría, índice, introducción, desarrollo y conclusiones) y se percibe planificación previa.

Se evidencia la estructura propia de un trabajo escrito (portada, autoría, índice, introducción, desarrollo y conclusiones) y se percibe planificación previa.

Domina las cuestiones esenciales de manera muy básica.

Demuestra un buen conocimiento del tema tratado

Demuestra un gra n conocimiento del tema tratado.

Estructura del texto

Contenido

Se percibe alguna muestra en la intención de aportar algo diferente.

Aporta alguna información curiosa.

El trabajo incluye información que llama la atención, y sorprende por su contenido y forma de presentarlo.

Originalidad y creatividad

Se percibe que ha utilizado alguna fuente (digitales, bibliográficas, personales…) aunque no lo evidencia.

Se evidencia alguna fuente fiable (digital, bibliográfica, personal…) dándole un toque personal, interpretando o valorando.

Se evidencia un uso variado de fuentes fiables (digitales, bibliográficas, personales…) citándolas, con interpretaciones y valoraciones.

Búsqueda de información

NO

SÍ

NO

SÍ

NO

SÍ

NO

SÍ

NO

SÍ

Área 5

Área 10 NO

Área 4

Área 3

9 SÍ

Área NO

Área 2

NO

SÍ

Área 8 SÍ

Área 7 NO

NO

SÍ

Área 6 SÍ

La portada del cuaderno, ¿incluye los datos acordados: área, curso y el nombre?

¿Se indica el inicio de cada tema y aparece la fecha en que se realizan las actividades o tareas? Al realizar una actividad, ¿se copia el enunciado, o al menos se indica una referencia de a qué actividad se refiere?

¿Se ha cuidado la ortografía y el uso correcto de los signos de puntuación necesarios?

¿Se han incluido correcciones y aclaraciones siempre que ha sido necesario?

Instrumentos de evaluación, autoevaluación y coevaluación

PARA LA EVALUACIÓN DEL CUADERNO DEL ALUMNADO

Mejorable (14)

La presentación del cuaderno necesita mejoras, según los acuerdos establecidos para el curso, en cuanto a limpieza, orden y claridad, en las tareas y las actividades realizadas.

Al cuaderno le faltan bastan tes actividades y tareas y es mejorable en cuanto al nivel de precisión, ilustraciones, etc.

Adecuado (56)

La presentación del cuaderno es poco adecuada a los acuerd os establecidos para el curso, en cuanto a limpieza, orden y claridad, en las tareas y actividades realizadas.

Al cuaderno l e faltan algunas actividades y tareas y es mejorable en cuanto al nivel de precisión, ilustraciones, etc.

Bueno (78)

La presentación del cuaderno descuida alguno de los acuerdos establecidos para el curso, en cuanto a limpieza, orden y claridad, en las tareas y actividades realizadas.

Excelente (910)

La presentación del cuaderno es adecuada a los acuerdos 3 establecidos para el curso, en cuanto a limpieza, orden y claridad, en las tareas y actividades realizadas.

Presentación

El cuaderno pr esenta todas las actividades y tareas, pero es mejorable en cuanto al nivel de precisión, ilustraciones, etc.

El cuaderno p resenta todas las actividades y tareas con un gran nivel de precisión, ilustraciones, etc.

Contenidos

Hay varias partes que no están ordenadas de acuerdo a las pauta s establecidas en el curso y el área. %

%

El cuaderno es mejorable, en general .

Los errores no siempre están bien corregidos y, a veces, vuelve a repetirlos.

Los errores están bien corregidos, aunque , a veces, vuelve a repetirlos.

% VALORACIÓN FINAL 1 Ponderación / 2 Valoración

Reflexiona sobre su trabajo en el cuaderno, aunque sigue pocas de las propuestas de mejora.

Reflexiona sobre su trabajo en el cuaderno y generalmente sigue propuestas de mejora.

La información está organizada de acuerdo a las pautas establecidas en el curso y el área.

Organización

Los errores están bien corregidos y no vuelve a repetirlos.

Corrección

Reflexiona sobre su trabajo en el cuaderno y sigue propuestas de mejora.

Reflexión

3 Según los acuerdos del curso/ ciclo sobre la presentación del cuaderno (márgenes, títulos, limpieza, letra, etc.).

FECHA:

REFLEXIÓN (debo/debe mejorar… porque…)

Mejorable

REGISTRO SOBRE LA EVOLUCIÓN DE LA ORTOGRAFÍA DURANTE EL CURSO

GRADO DE LOGRO

Adecuado

Bueno

Excelente

NOMBRE:

GRUPO:

Utilizo las reglas básicas de ortografía, aplicadas a las palabras de uso habitual (mayúsculas, separación de palabras, identificación de los signos de puntuación interrogación y exclamación).

1

Reconozco un repertorio de vocabulario, así como su ortografía básica sobre situaciones cotidianas y temas habituales adaptados a mi edad.

2

Utilizo con corrección las reglas generales de acentuación.

3

Realizo un uso adecuado de los signos de puntuación (punto, coma, dos puntos, guion, comillas, puntos suspensivos, paréntesis …)

4

Muestro Interés por la búsqueda de la correcta ortografía de las palabras usando diccionarios en diferentes formatos.

5

Instrumentos de evaluación, autoevaluación y coevaluación

Mejorable (14)

La letra se lee con dificultad de forma generalizada.

Adecuado (56)

Bueno (78)

Letra bastante clara, aunque presenta alguna dificultad puntual. La letra se lee con alguna dificultad y es poco clara.

RÚBRICA PARA EVALUAR TEXTOS ESCRITOS

Excelente (910)

Letra muy clara y legible. Facilita la lectura.

Texto legible

%

%

%

%

%

El texto produce una impresión general de falta de limpieza.

El texto puede mejorar en su limpieza. %

El texto produce un efecto general de limpieza.

Presenta sus textos con limpieza, con alguna enmienda esporádica. Presenta sus textos con tachones y enmiendas, aunque permiten la lectura.

Presenta sus textos con gran limpieza y sin tachones.

Limpieza

Incluye información irrelevante y falta información sustancial para el asunto tratado.

La información que aporta es relevante. Contempla casi toda la información sustancial.

La información que aporta es relevante. Posee toda la información sustancial y necesaria.

Información pertinente

Respeta el orden lógico: el progreso temático del texto presenta fallos mejorables.

El texto progresa temáticamente de forma adecuada, aunque pueda haber algún fallo.

Respeta el orden lógico: el texto progresa temáticamente de forma adecuada.

Secuencia ordenada

unidad del texto

Coherencia:

% VALORACIÓN FINAL 1 Ponderación / 2 Valoración

Se observan diversos errores en la concordancia gram atical: género, número, tiempo …

Respeta la concordancia gramatical: género, número, tiempo…con algún error.

Respeta siempre la concordancia gramatical: género, número, tiempo…

Mecanismos de cohesión léxica y gramatical

Algunas oraciones carecen de sentido completo.

L as oraciones suelen tener sentido completo.

Todas las oraciones del texto tienen sentido completo.

El empleo de los signos de puntuación p resenta algunos errores .

E l e mpleo de los signos de puntuación suele ser correcto.

Empleo correcto de todos los signos de puntuación.

Puntuación correcta

Cohesión: mecanismo que permite dar unidad al texto

En general, el léxico es adecuado al tema aunque en ocasiones emplea términos coloquiales, vulgarismos o ambos.

El léxico es adecuado al tema aunque puntualmente repita ciertos términos.

El léxico es rico y adecua do al tema que se trata.

Adecuado al tema y a la situación

% Vocabulario

Mejorable (14)

Usa los materiales y los recursos disponibles con ayuda y le cuesta ajustarse al plazo previsto.

Asume sus responsabilidades por la insistencia de los demás y le cuesta reconocer la importancia del esfuerzo individual en tareas colectivas.

Forma parte de las dinámicas establecidas por el grupo con ayuda.

Interacciona, pero necesita ayuda para mantener actitudes respetuosas hacia otros puntos de vista.

Adecuado (56)

RÚBRICA PARA EVALUAR LA PARTICIPACIÓN EN TRABAJOS COOPERATIVOS

Usa los materiales y los recursos disponibles con cierta dificultad para ajustarse al plazo previsto.

Comprende y asume sus responsabilidades, con alguna dificultad para valorar el esfuerzo individual y colectivo.

Forma parte de las dinámicas establecidas por el grupo, y realiza alguna propuesta para mejorar el aprendizaje cooperativo.

Bueno (78)

Usa los materiales y los recursos disponibles de acuerdo al procedimiento establecido por el grupo, ajustándose al plazo previsto.

Comprende y asume sus responsabilidades y las de los demás, reconociendo el esfuerzo individual en las tareas colectivas.

Excelente (910)

Realiza un uso adecuado de los materiales y los recursos disponibles de acuerdo al procedimiento establecido por el grupo, ajustándose al plazo previsto.

Planificación del trabajo

Comprende y asume sus responsabilidades y las de los demás, valorando especialmente el esfuerzo individual en tareas colectivas.

Responsabilidad

Forma parte de las dinámicas establecidas por el grupo, generando propuestas que mejoran el aprendizaje cooperativo.

Forma parte activa de las dinámicas establecidas por el grupo, generando propuestas que mejoran el aprendizaje cooperativo.

Participación

Interacciona manteniendo una actitud respetuosa hacia otros puntos de vista.

Interacciona con empatía y autocontrol, manteniendo una actitud respetuosa hacia otros puntos de vista.

Interacciona con empatía y autocontrol, manteniendo una actitud respetuosa hacia otros puntos de vista y utilizand o diferentes habilidades sociales que contribuyen a la cohesión.

Habilidades sociales

Contribuye moderadamente a la consecución de los logros en el trabajo grupal, con ayuda para responsabilizarse de su aportación e n la presentación de la tarea realizada. Contribuye algo a la consecución de los logros en el trabajo grupal, con ayuda para responsabilizarse de su aportación en la presentación de la tarea realizada.

Contribuye a la consecución de los logros en el trabajo grupal, responsabilizándose de su aportación en la presentación de la tarea realizada.

Contribuye de manera activa a la consecución de los logros en el trabajo grupal, responsabilizándose de su aportación en la presentación de la tarea realizada.

Generación y presentación del producto

Instrumentos de evaluación, autoevaluación y coevaluación

FECHA:

REFLEXIÓN (debo/debe mejorar… porque…)

Mejorable

REGISTRO PARA EVALUAR LA PARTICIPACIÓN EN TRABAJOS COOPERATIVOS

15.

GRADO DE LOGRO

Adecuado

Bueno

Excelente

NOMBRE:

GRUPO:

Ha planificado previamente la realización del trabajo asignado y ha cumplido con las actividades y tareas encomendadas.

1

Ha sido organizado en el desarrollo tanto del trabajo individual como del grupal, cumpliendo con los plazos establecidos y trabajando de forma, ordenada y limpia.

2

Ha participado en la toma de decisiones del grupo, aportando soluciones creativas y empleando material complementario.

3

Ha respetado y valorado las aportaciones de mis/sus compañeras y compañeros, motivándoles y ayudándoles en todo lo posible, y realizando críticas constructivas.

4

Ha aportado el material necesario para la realización del trabajo cooperativo.

5

Ha realizado correctamente las responsabilidades del trabajo asignado.

6

Ha realizado con esfuerzo y entrega las tareas encomendadas, i ndependientemente de los resultados.

7

Ha contribuido al buen ambiente de grupo, conociendo la importancia que esto tiene en el trabajo cooperativo.

8

Ha cumplido con los objetivos de equipo, acordados previamente.

9

10 Ha reflexionado y realizado una conclusión sobre el trabajo, elaborado de forma individual y por el grupo.

TELA DE ARAÑA PARA LA AUTOEVALUACIÓN DE LAS EMOCIONES

Sobre Conciencia emocional Identifico y expreso emociones básicas (Miedo, ira, ansiedad, tristeza, sorpresa, felicidad, humor...) positivas (alegría, amor, felicidad…) y negativas (ira, miedo, tristeza…)

Me cuesta

Avanzo

Bien

Genial

Sobre Regulación emocional Genero emociones positivas (alegría, amor, felicidad…) con aportaciones creativas en momentos de malestar Sobre competencias para la vida y el bienestar Comprendo que cooperar y hacer equipo son experiencias positivas que contribuyen a sentirme mejor y hacer sentir mejor a los demás.

Sobre autoestima y autonomía Valoro mis cualidades personales para tener relaciones constructivas y mejorar mi autoestima

Sobre competencia social Practico el diálogo y me pongo en el lugar de otras personas para hacer el bien o resolver conflictos

Instrumentos de evaluación, autoevaluación y coevaluación

He aprovechado el tiempo en el aula, realizando las actividades indicadas por el profesorado y atendiendo a sus explicaciones y a las de mis compañeros y compañeras.

He participado activamente en clase, preguntando todas las dudas que me han surgido y aportando ideas y opiniones justificadas, con criterio y respeto.

He empleado un lenguaje adecuado en todo momento, tanto verbal como no verbal, utilizando la entonación, los gestos o los movimientos de un modo apropiado y correcto.

Lee con atención cada uno de los textos que aparecen alrededor de la diana de la derecha y marca con una cruz en las intersecciones correspondientes, de acuerdo con este criterio:

1. Poco.

2. Algunas veces.

3. Generalmente.

4. Siempre. A continuación, une las cr uces; obtendrás un polígono similar al que se muestra en el ejemplo inferior. Cuanto mayor sea el área del polígono, más alta será la puntuación.

He trabajado de forma eficaz, mostrando motivación, iniciativa y creatividad en el desarrollo de las actividades y en mis aportaciones.

Mi comportamiento en el aula ha sido de respeto hacia el profesorado y hacia mis compañeros y compañeras y he contribuido a crear un buen ambi ente para la convivencia del grupo.

Ta nto al hablar como al escuchar a mis compañeros y compañeras siempre lo he hecho con interés y valorando sus aportaciones, he respetado el turno de palabra, y he aceptado comentarios y críticas constructivas.

Mejorable (14)

Reconoce y valora con ayuda sus fortalezas y debilidades personales .

Ante un hecho, situación o problema precisa de ayuda para plante ar propuestas o soluciones creativas, originales o con gran imaginación

Adecuado (56)

Reconoce y valora , aunque no siempre con objetividad sus fortalezas y debilidades personales

Ante un hecho, situación o problema plantea escasas propuestas o soluciones creativas, originales o con gran imaginación

VALORACIÓN DE LA DIMENSIÓN PERSONAL

Le cuesta abrirse a los demás tanto en el ámbito comunicativo como para trabajar de manera cooperativa

Muestra una actitud abierta, aunque no siempre, en las relaciones con los demás tanto en el ámbito comunicativo como para trabajar de manera cooperativa

Ante las decisiones adoptadas, le cuesta o precisa ayuda para aceptar y asumir las responsabilidades adquiridas .

Ante las decisiones adoptadas, acepta y asume , no siempre, las responsabilidades a dquiridas .

En las actuaciones grupales, le cuesta tomar la iniciativa, gestionar, incentivar, motivar o evaluar una actividad, tarea o proyecto.

En las actuaciones grupales, a veces, toma la iniciativa, gestiona, incentiva, motiva o evalúa una actividad , tarea o proyecto.

VALORACIÓN DE LA DIMENSIÓN SOCIAL

Ante un hecho, situación o problema propone algunas iniciativas o introduce algo novedoso con ayuda.

Ante un hecho, situación o problema , a veces, propone y gestiona iniciativas y, en ocasiones, introduce cambios o innovaciones .

Afronta los riesgos planteados y aprende de los fracasos o errores, para nuevos procesos , solo si alguien le hace reflexionar y le presta ayuda.

Afronta, con algunas dificu ltades los riesgos planteados y, en ocasiones aprende de los fracasos o errores.

Planifica, desarrolla y ejecuta, las acciones para conseguir un objetivo o un producto, solo si alguien le hace re flexionar y le presta ayuda

Planifica, desarrolla y ejecuta las acciones para conseguir un objetivo o un producto, con dificultades.

VALORACIÓN DE LA DIMENSIÓN PRODUCTIVA

Bueno (78)

Reconoce y valora sus fortalezas y debilidades personales .

EMPRENDIMIENTO

Excelente (910)

Reconoce y valora con objetividad sus fortalezas y debilidades personales.

Autoconocimiento

Ante un hecho, situación o problema plantea propuestas o soluciones creativas, originales o con gran imaginación

Ante un hecho, situación o problema plantea múltiples propuestas o soluciones crea tivas, originales o con gran imaginación.

Imaginación y creatividad

Dimensión

Muestra buena actitud en las relaciones con los demás tanto en el ámbito comunicativo como para trabajar de manera cooperativa .

Muestra una actitud generosa y abierta en las relaciones con los demás tanto en el ámbito comunicativo como para trabajar de manera cooperativa

Habilidades sociales y comunicativas

Ante las decisi ones adoptadas, acepta y asume las responsabilidades adquiridas .

Ante las decisiones adoptadas, acepta y asu me positivamente las responsabilidades adquiridas.

Responsabilidad

En las actuaciones grupales, toma la iniciativa, gestiona, incentiva, motiva o evalúa una actividad, tarea o proyecto.

En las actuaciones grupales, habitualmente suele tomar la iniciativa, gestionar, incentivar, motivar o evaluar una actividad, tarea o proyecto.

Ante un hecho, situación o problema propone o gestiona iniciativas e introduce cambios o innovaciones

Ante un hecho, situación o problema suele proponer y gestionar iniciativas e introducir cambios o innovaciones.

Afronta los riesgos planteados y aprende de los fracasos o errores, para nuevos procesos.

Aborda, desde una perspectiva proactiva, los riesgos planteados y convierte los fracaso s o errores en aprendizaje para nuevo s proceso s.

Planifica, desarrolla y ejecuta las acciones necesarias para conseguir un objetivo o un producto.

Planifica, desarrolla y ejecuta con éxito las acciones necesarias para conseguir un objetivo o un producto.

Liderazgo

Dimensión social

Iniciativa e innovación

Asunción de riesgos

Productividad

Dimensión productiva

Instrumentos de evaluación, autoevaluación y coevaluación

Mejorable (14)

Reconoce sus fortalezas y debilidades, con ayuda , para el desarrollo de las actividades y las tareas.

La confianza en sus aptitudes y habilidades a la hora de afrontar sus tareas, le paraliza o entorpece y precisa de ayuda para continuar.

Real iza las tareas por mandato o las realiza con ayuda y no suele mo stra r preocupación por mejorarlas.

Asume responsabilidades y realiza tareas individuales y grupales solo en ocasiones Actúa sin valorar las consecuencias y le cuesta asumirlas.

Cualquier listado de tareas y tiempos que realiza , es con ayuda y le cuesta conseguir su realización de forma autónoma.

Adecuado (56)

Reconoce sus fortalezas y debilidades, con alguna ayuda , para el desarrollo de las act ividades y las tareas.

Se muestra confiado en sus aptitudes y habilidades, pero dependiendo de l tipo o del contenido de estas, precisa ayuda.

Muestra interés y satisfacción por alcanzar los objetivos en un número limitado de tareas. Le cuesta analizar críticamente su trabajo y buscar estrategias para mejorarlo.

Asume responsabilidades y realiza tareas individuales y grupales de modo irregular y no siempre se ajusta a los plazos marcados.

El lis tado de tareas y tiempos que realiza no siempre es realista y, en ocasiones, necesita ayuda para su realización.

Realiza el proceso de toma de decisiones y resolución de un problema con muchas dificultades para resolverla, necesitando supervisión y ayuda casi constante.

Realiza el proceso de toma de decisiones y resolución de un problema, mostrando inseguridad y necesitando ayuda y refuerzo constante para enfrentarlo.

RÚBRICA PARA EVALUAR LA AUTONOMÍA PERSONAL

Bueno (78)

Reconoce sus fortalezas y debilidades, haciendo uso mayoritariamente de sus recursos personales para el desarrollo de las act ividad es y las tareas .

Se muestra confiado en sus aptitudes y habilidades, pero , en ocasiones , ante la dificultad necesita ayuda

Excelente (910)

Reconoce sus fortalezas y debilidades, haciendo uso de sus recursos personales para el desarrollo eficaz de las actividades y las tareas .

Autonomía y conocimiento personal

Muestra confianza en sus aptitudes y habilidades, afrontando las dificultades que surgen en el desarrollo de las actividades.

Se muestra satisfecho por el éxito obtenido en las tareas y esto motiva que la s afronte como un reto personal, pero no siempre a naliza y hace propuestas para mejorar su trabajo.

Se muestra satisfecho por el éxito obtenido en las tareas y esto motiva que las afronte como un reto personal. Analiza y hace propuestas para mejorar su trabajo.

Asume las responsabilidades individuales y en el trabajo grupal y realiza las tareas o los roles encomendados. Muestra alguna dificultad para cumplir los plazos marcados.

Asume responsabilidades, tanto en el trabajo grupal como individual, con iniciativa propia. Cumple los plazos establecidos y realiza las tareas y los roles encomendados.

Realiza un listado de tareas y tiempos de modo realista, pero no siempre gestio n a el tiempo adecuadamente

Realiza un listado de las tareas a realizar gestionando de manera eficaz los recursos y el tiempo para ejecutarlas.

I dentifica la situación problemática y las posibles soluciones y consecuencias, pero tarda demasiado tiempo en tomar la decisión para su resolución

Identifica con rapidez la situación problemática, genera diferentes soluciones y valora las consecuencias posibles de estas.

Confianza

Motivación

Responsabilidad

Toma una decisión, actúa en consecuencia. Este proceso lo realiza con determinación y rapidez.

Gestión eficaz del trabajo

Toma de decisiones/ resolución problemas

DIANA DE AUTOEVALUACIÓN DE L TRABAJO DIARIO

He realizado de un modo ordenado y completo la resolución de las tareas encomendadas.

En el trabajo en grupo he participado activamente y he aportado ideas y opiniones justificadas, con criterio y respeto .

He planificado la realización del trabajo diario y la he llevado a cabo.

Tras la corrección, he repasado los errores cometidos y, en c aso necesario, he vuelto a realizar las actividades y he añadido una reflexión sobre el trabajo realizado.

Lee con atención cada uno de los textos que aparecen alrededor de la diana de la derecha y marca con una cruz en las intersecciones correspondientes, de acuerdo con este criterio:

1. Poco.

2. Algunas veces. 3. Generalmente. 4. Siempre. A continuación, une las cruces; obtendrás un polígono similar al que se muestra en el ejemplo inferior. Cuanto mayor sea el área del polígono, más alta será la puntuación.

He corregido las actividades, siguiendo las explicaciones de mis compañeros y compañeras y las del profesor o la profesora.

Me he esforzado en la realización de las tareas y he preferido trabajar de forma autónoma, aunque no fuera capaz de completarlas, antes que terminarlas con la ayuda de un a persona adulta

He entregado las actividades en tiempo y forma, cumpliendo con los requisitos establecidos para su elaboración.

Instrumentos de evaluación, autoevaluación y coevaluación

DIANA DE AUTOEVALUACIÓN DE LA GESTIÓN Y LA ORGANIZACIÓN SEMANAL

En las tareas de clase participo activamente y trabajo de forma eficaz, realizando las actividades indicadas por el profesorado y atendiendo a sus explicaciones y a las de mis compañeros y compañeras.

He preparado, con antelación todo lo necesario el material necesario para la clase (cuadernos, estuche, agenda, libros…).

He mostrado aut onomía y responsabilidad a la hora de trabajar, tanto en el aula como en casa.

Lee con atención cada uno de los textos que aparecen alrededor de la diana de la derecha y marca con una cruz en las intersecciones correspondientes, de acuerdo con este criterio:

1. Poco.

2. Algunas veces.

3. Generalmente. 4. Siempre. A continuación, une las cruces; obtendrás un polígono similar al que se muestra en el ejemplo inferior. Cuanto mayor sea el área del polígono, más alta será la puntuación.

He tomado nota en la agenda de las actividades, los trabajos que hay que realizar y las fechas importantes (entrega de trabajos, presentaciones, etc.) y me responsabilizo de ello para que esté en el momento adecuado y lo mejor posible.

Al llegar a casa, planifico el tiempo que voy a dedicar a las tareas que debo realizar y soy responsable con ello.

En casa dedico un tiempo a la lectura de distinto tipo, como base de información, entretenimiento y reflexión.

PARA EVALUAR LA BÚSQUEDA Y EL TRATAMIENTO DE LA INFORMACIÓN

Mejorable (14)

Con ayuda, comprende la información más básica y necesaria para realizar la actividad o la investigación.

Extrae alguna información con la ayud a del docente o de otro alumno u otra alumna.

Propone alguna información gracias a la colaboración de otra persona, o reproduciendo la de una compañera o un compañero.

Realiza o lee alguna interpretación de manera guiada.

Adecuado (56)

Con ayuda, busca alguna información contrastada, adecuada a la actividad o a la investigación.

Obtiene algunos datos literales o interpretados que dan respuesta a la actividad o a la investigación, necesitando ocasionalmente la ayuda de otra persona.

La información extraída aportada es fundamentalmente literal y es expuesta de manera memorística.

Bueno (78)

Propuestas diferentes fuentes, busca y contrasta información adecuada a la actividad o a la investigación.

Obtiene bastantes datos de manera interpretada, dando respuesta a la actividad o a la investigación , ajustándose a los tiempos establecidos.

Excelente (910)

Busca información contrastada de diferentes fuentes, de manera autónoma, adecuadas a la actividad o a la investigación que se está llevando a cabo.

Búsqueda de la información

Obtiene todos los datos necesarios de manera autónoma e interpretada, para dar respuesta a la actividad o a la investigación ajustándose a los tiempos establecidos.

Obtención de la información

La información extraída aportada bastantes interpretaciones argumentadas y cita fuentes.

La información extraída es rigurosa y expuesta con soltura, aportando interpretaciones argumentadas de manera ordenada, utilizando algún recurso y citando fuentes.

Tratamiento y análisis de la información

Realiza alguna interpretació n sobre la información obtenida, aunque destacan por ser memorísticas.

Realiza bastantes valoraciones y/o emite juicio s sobre la información obtenida combinando interpretaciones espontáneas con alguna memorística.

Realiza valoraciones y/o emite juicios de manera natural y espontánea, utilizando varias fuentes, sobre la información obtenida de un modo riguroso.

Valoración de los resultados

Instrumentos de evaluación, autoevaluación y coevaluación

TABLA PARA EVALUAR LA BÚSQUEDA DE INFORMACIÓN Y FIABILIDAD DE LAS FUENTES

2. Sobre su análisis y valoración Busca la información en otras fuentes y las compara.

1. Sobre la búsqueda de información Busca la información requerida para la actividad.

8. Sobre su utilización Us a la información de manera adecuada en la situación planteada.

3. Fiabilidad Escoge la fuente más fiable.

4. Sobre la información Escribe el titular o la idea fundamental.

5. Sobre la autoría Escribe el nombre de la autora o del autor.

7. Sobre el tipo de fuente Escribe el soporte: página web, libro, prensa…

6. Sobre la fuente de información Escribe el nombre o el título de la fuen te y la fecha.

Mejorable (14)

Con ayuda o de manera guiada, colabora a formular alguna pregunta que contribuya a plantear la investigación.

Con ayuda, comprende la información más básica y necesaria para realizar la investigación.

Colabora en la investigación siguiendo alguna instrucción.

Adecuado (56)

Con ayuda o de manera guiada, propone alguna pregunta que contribuya a plantear la investigación y realiza alguna hipótesis.

Con ayuda, obtiene alguna información contrastada, adecuada a la investigación.

Bueno (78)

Propone alguna pregunta o reto que ayuda a plantear una investigación, realizando alguna hipótesis.

Excelente (910)

Propone de manera autónoma preguntas y retos que ayudan a plantear una investigación, realizando hipótesis y predicciones de manera certera.

Planificación e hipótesis

Propuestas diferentes fuentes, obtiene y contrasta información adecuada a la investigación.

Obtiene información contrastada de diferentes fuentes, de manera autónoma, adecuadas a la investigación que se está llevando a cabo.

Indagación sobre el tema

Lleva a cabo investigaciones de manera sencilla cumpliendo los objetivos básicos.

Necesita algún recordatorio para llevar a cabo la investigación usando las herramientas necesarias para su realización.

Realiza la investigación con autonomía en la ejecución de acciones y tareas, usando las herramientas necesarias para su realización.

Comprende algunas de las conclusiones a las que se han llegado con la ayuda de alguna persona de clase.

Extrae alguna conclusión sencilla, siempre con la ayuda de algún documento guía o de alguna persona .

Extrae conclusiones con un documento guía que recuerda los pasos para el análisis y el procesamiento de los datos.

Extrae conclusiones correctas, estableciendo conjeturas de manera certera.

Comunica de manera sencilla las conclusiones , oralmente o por escrito. Participa en la comunicación de alguna conclusión, siguiendo alguna instrucción.

Comunica a un buen nivel, oralmente y por escrito , las conclusi ones obtenidas.

Defiende la comunicación con argumentos sólidos y de elaboración propia de manera clara y organizada, oralmente y por escrito , utilizando un vocabulario adecuado e incluso algún soporte gráfico o digital.

Trabajo de campo

Evaluación y conclusiones

Comunicación de los resultados

Instrumentos de evaluación, autoevaluación y coevaluación

Mejorable (14)

Necesita la colaboración o la ayuda por parte del alumnado de la clase o del profesorado para seguir los pasos y llegar al prod ucto final.

Utiliza las fuentes buscadas o aportadas por parte del alumnado o el profesorado para seguir un modelo o plan de trabajo.

Adecuado (56)

Necesita que se le amplíen los plazos de finalización de la tarea.

Se ajusta a la información propuesta en el libro de texto.

Necesita algún tipo de ayuda o recurso para realizar la tarea de forma sencilla.

Se ajusta básicamente a la intención de la tarea propuest a.

Bueno (78)

RÚBRICA PARA EVALUAR TAREAS Y RETOS

Excelente (910)

Aunque se ajusta a los tiempos previstos, denota cierta desorganización en su planificación.

Demuestra orden, planificación, y se ajusta a los tiempos previstos.

Organización de la tarea en cada uno de los pasos

Se denota el uso de alguna fuente complementaria (digital, bibliográfica, personal…).

Se denota un uso variado de fuentes fiables para ampliar información (digitales, bibliográficas, personales…).

Utilización de fuentes de información

El producto se ajusta a la intención propuesta desde la tarea , aunque se le proponen algunas mejoras.

El producto se ajusta a la intención propuesta desde la tarea: presentación, funcionalidad, uso…

Elaboración del producto

Se percibe alguna muestra en la intención de aportar algo diferente. %

Hay que guiarle para incluir alguna curiosidad o aportación creativa y original.

% VALORACIÓN FINAL 1 Ponderación / 2 Valoración

Domina las cuestiones esenciales de manera muy básica.

Demuestra un buen conocimiento del tema tratado

El producto llama la atención, y sorprende por su contenido y forma de presentarlo.

Demuestra un gra n conocimiento del tema tratado al verbalizar los pasos dados y contar el producto final.

Creatividad y originalidad

Contenido

PARA EVAL UAR EL USO DE LAS TIC Y LAS TAC

Mejorable (14)

Necesita una netiqueta para aprender el uso re sponsable de los diferentes recursos TIC aplicando las normas básicas de conducta digital, evitando cualquier tipo de acoso digital.

Colabora con otra persona de la clase para aprender a usar alguna aplicación, dar los primeros pasos para guardar, compartir archivos y contenidos o proteger los dispositivos que usa.

Adecuado (56)

Aun necesitando recordar la netiqueta, empieza a tener autonomía en el uso responsable de los diferentes recursos TIC aplicando las normas básicas de conducta digital, evitando cualquier tipo de acoso digital.

Precisa la ayuda de alguna persona para usar alguna aplicación, guardar, compartir archivos y contenidos o proteger los dispositivos que usa.

Colabora con otra persona de la clase p ara aprender a dar los primeros pasos para crear su propio entorno personal de aprendizaje, elaborar sencillas producciones y citar fuentes.

Precisa la ayuda de alguna persona para crear su propio entorno personal de aprendizaje, elaborar sencillas producciones y citar fuentes.

Bueno (78)

La netiqueta está presente en el aula o en la mesa del alumnado, pero empieza a no s er imprescindible para usar de manera responsable los diferentes recursos TIC aplicando las normas básicas de conducta digital, evitando cualquier tipo de acoso digital.

Es necesario recordarle alguna instrucción para usar alguna aplicación, guardar, compartir archivos y contenidos o proteger los dispositivos que usa.

Excelente (910)

Demuestra tener interiorizado el uso re sponsable de los diferentes recursos TIC aplicando las normas básicas de conducta digital, evitando cualquier tipo de acoso digital.

Ciudadanía digital y seguridad en la Red

Usa aplicaciones, guard a de manera autónoma archivos y contenidos , y los comparte en diferentes soportes, tomando medidas básicas para proteger los dispositivos que usa.

Práctica tecnológica

Es necesario recordarle alguna instrucción para crear su propio ent orno personal de aprendizaje, elaborar sencillas producciones o citar fuentes.

Uso de las tecnologías del aprendizaje y el conocimiento Crea su propio entorno personal de aprendizaje, elaborando sencillas producciones y citando fuentes, destacando su creatividad y motivación.

Con ayuda, obtiene alguna información contrastada, adecuada a la actividad, investigación o reto que se le plantea. % VALORACIÓN FINAL 1 Ponderación / 2 Valoración

Con ayuda, accede a la información más básica y necesaria para realizar la actividad, investigación o reto que se le plantea.

Obtiene información contrastada de diferentes fuentes en la web y de manera autónoma, conociendo que no toda la información es confiable.

Uso de la información

Instrumentos de evaluación, autoevaluación y coevaluación

PARA EVALUAR LA RESOLUCIÓN DE PROBLEMAS

Mejorable (14)

Lee el enunciado identificando e interpretado, con ayuda, los datos necesarios, comprendiendo, con dificultades lo que se dice y lo que se pide.

La selección y la aplicación de la estrategia elegida no suele ser la más adecuada, y precisa ayuda continuada para ello.

Adecuado (56)

Lee el enunciado ident ificando e interpretado, en ocasiones con ayuda, los datos necesarios y localiza los elementos a resolver, comprendiendo, con alguna dificultad, lo que se dice y lo que se pide.

La selección y la aplicación de la estrategia elegida no siempre es la más adecuada, debido a una comprensi ón parcial de los conceptos matemáticos involucrados.

N o siempre a plica los cálculos de forma correcta cometiendo errores aritméticos ni algebraicos y la solución no suele ser correcta

Aplica los cálculos de forma correcta sin cometer errores aritméticos ni algebraicos, pero no siempre interpreta el resultado obtenido con la solución correcta.

Da la solución del problema, pero no comprueba si es coherente.

Bueno (78)

Lee el enunciado identificando e interpretado los datos necesarios y localiza los elementos a resolver, comprendiendo lo que se dice y lo que se pide.

La selección y la aplicación de la estrategia elegida demuestra comprensión de los conceptos matemáticos involucrados, aunque se plantea algunas dudas.

Aplica los cálculos de forma correcta sin cometer errores aritméticos ni algebraicos, pero no lo hace de forma ordenada y precisa

Excelente (910)

Lee el enunciado adecuadamente identificando e interpretado los datos necesarios y localiza los elementos a resolver, comprendiendo perfectamente lo que se dice y lo que se pide.

Lectura y comprensión del problema

La selección y la aplicación de la estrategia elegida demuestra la total comprensión de los conceptos matemáticos involucrados.

Selección y aplicación de la estrategia

Aplica los cálculos de forma correcta sin cometer errores aritméticos ni algebraicos y obtiene y presenta la solución de forma precisa.

Comprueba si la solución es coherente, sustituyendo el valor obtenido en el razonamiento inicial y viendo que es válida matemáticamente, pero no comprueba si tiene sentido en la realidad a la que el enunciado se refiere.

Comprueba si la solución es coherente, sustituyendo el valor obtenido en el razonamiento inicial y viendo que es válida, tanto matemáticamente como en la realidad a la que el enunciado se refiere.

Solución

Análisis de la solución

Mejorable (14)

Utiliza so lo estrategias aca démicas para la realización de cálculos mentales sencillos.

Utiliza el cálculo aproximado de manera comprensiva solo en ocasiones, y necesita ayuda o apoyo de lápiz y papel para obtener el resultado de la operación por esti mación.

Adecuado (56)

Utiliza casi siempre estrategias académicas para la realización de cálculos mentales.

ÚBRICA PARA LA VALORACIÓN DEL CÁLCULO MENTAL

Bueno (78)

Utiliza diferentes estrategias personales y aca démicas para la realización de cálculos mentales con las cuatro operaciones básic as.

Utiliza el cálculo aproximado de manera compresiva para obtener el resultado de la operación por estimación con ayuda o necesitando apoyo de lápiz y papel.

Utiliza el cálculo aproximado de manera compresiva para obtener el resultado de la operación por estimación de forma mental, neces itando ocasionalmente apoyo de lápiz y papel.

Realiza algunos cálculos mentales con dificultad, requiriendo ayuda siempre para lograr un resultado acertado.

Realiza cálculos mentales, logrando acertar el resultado de forma autónoma pero alguna dificultad o requiriendo ayuda.

Realiza cálculos mentales con cierta precisión en el resultado.

Aplica la operación o las operaciones que corresponden al problema mediante resolución mental, solo si estas son muy básicas y con ayuda.

Aplica la operación o las operaciones que corresponden al problema mediante resolución mental, con ayudas.

A plica la operación o las operaciones que corresponden al problema, mediante resolución mental, necesitando ayuda ocasionalmente.

Explica oralmente el proceso seguido con dificultades y la ayuda de algún recurso (pizarra o un recurso similar).

Explica oralmente el proceso seguido con alguna dificultad y la ayuda de algún recurso (pizarra o un recurso similar).

Explica oralmente el proceso seguido, pero necesita ocasionalmente la ayuda de algún recurso para apoyar su explicación.

Excelente (910)

Utiliza estrategias personales de cálculo mental (decenas y centenas exactas, redondeos de números, estimaciones del resultado por redondeo, aplicando las propiedades asociativas y conmutativas) 3

Utiliza el cálculo aproximado de manera comprensiva para obtener el resultado de la operación por estimación de forma mental.

Uso de estrategias

Realiza c álculos mentales con precisión acertando siempre el resultado.

Estimación

Resultado

Aplica la operación o las operaciones correctas que corresponden al problema, mediante resolución mental.

Resolución de problemas

Explica oralmente el proceso seguido en la realización de cálculos mentales.

Exposición oral

El equipo docente de cada curso debe establecer criterios respecto al tipo de operaciones y números (cuatro, tres, dos o una operación básica y números naturales, decimales y fracciones).

Instrumentos para evaluar la práctica docente

Primaria ANEXO DE EVALUACIÓN

Instrumentos para evaluar la práctica docente

1 Registro para la autoevaluación del profesorado: planificación

2 Registro para la autoevaluación del profesorado: motivación del alumnado.

3 Registro para la autoevaluación del profesorado: desarrollo de la metodología.

4 Registro para la autoevaluación del profesorado: seguimiento y evaluación del proceso de enseñanzaaprendizaje.

REGISTRO PARA LA AUTOEVALUACIÓN DEL PROFESORADO: PLANIFICACIÓN

4 Muy bien

3 Bien

2 Regular

1 Inadecuado

¿He tenido en cuenta los criterios de evaluaci ón ?

1 2 3 4 4

4

4 2 3

3

2

1

5 6

¿ Me he ajustado al tiempo disponible para el desarrollo de cada unidad?

4

3

2

1

¿ La planificación ha sido flexible para dar respuesta a los intereses del alumnado ?

4

3

2

1

¿ Los instrumentos de evaluación han permitido hacer el seguimiento del progreso de aprendizaje del alumnado ?

4

3

2

1

¿ He incluido instrumentos para la autoevaluación y la coevaluación del alumnado?

4

3 1

3

2

1

2 3 4 5 6

Instrumentos para evaluar la práctica docente

REGISTRO PARA LA AUTOEVALUACIÓN DEL PROFESORADO: MOTIVACIÓN DEL ALUMNADO

Para la próxima unidad ►

Para la próxima unidad ►

Para la próxima unidad ►

Para la próxima unidad ►

Para la próxima unidad ►

Para la próxima unidad ►

Para la próxima unidad ►

Para la próxima unidad ►

Para la próxima unidad ►

Para la próxima unidad ►

Para la próxima unidad ►

Para la próxima unidad ►

¿He desarrollado el reto generando la curiosidad necesaria para motivar al alumnado?

¿He relacionado los aprendizajes adquiridos con situaciones de la vida cotidiana?

¿He puesto en práctica las técnicas cooperativas propuestas en la unidad?

¿He puesto en práctica las técnicas de pensamiento propuestas en la unidad?

¿He trabajado intencionalmente el Plan Lingüístico sugerido en la unidad?

¿La educación emocional la he trabajado en la actividad sugerida?

¿Se ha trabajado de manera explícita la actividad propuesta para la cultura emprendedora?

¿Se han utilizado las tecnologías de la información y la comunicación?

¿He dado un sentido lúdico y participativo al «Organizo mi mente» y «Colecciono palabras»?

¿El «Cómo he aprendido» lo he orientado para que el alumnado se conozca mejor a sí mismo?

¿He promovido la participación y la reflexión en el alumnado?

¿Informo sobre los progresos conseguidos y las dificultades encontradas?

2 Poco

1 Nada

En próximas unidades puedo mejorar en…

4

1 3

Los aspectos que voy a considerar son…

1. ¿Favorezco la integración de los procesos cognitivos: conocer y reproducir, aplicar y analizar, razonar y reflexionar?

2. ¿Integro de manera equilibrada actividades que requieran las cuatro destrezas comunicativas: expresión y comprensión oral, expresión y comprensión escrita?

3. ¿Propongo utilizar recursos materiales complementarios al libro de texto?

4. ¿Integro el uso de las tecnologías de la información y la comunicación en las actividades y los retos propuestos?

5. ¿Contribuyo a salir del aula para relacionar los aprendizajes con situaciones reales y de la vida cotidiana?

6. ¿Incorporo el aprendizaje cooperativo como un modelo de organización y participación en el aula?

Desarrollo de la metodología

7. ¿Las actividades y los retos buscan intencionalmente ir más allá de aprendizajes academicistas, generando impacto en la vida personal y familiar del alumnado, y en la vida escolar y social?

Instrumentos para evaluar la práctica

4. REGISTRO PARA LA AUTOEVALUACIÓN DEL PROFESORADO: SEGUIMIENTO Y EVALUACIÓN DEL PROCESO DE ENSEÑANZAAPRENDIZAJE

Sobre la implicación de las familias

¿Existe una evaluación coherente con las metodologías llevadas a cabo en la unidad?

Plan de mejora ¿Qué ha quedado por hacer?

Propuestas de mejora.

Sobre la metodología de la evaluación

¿Existe una evaluación coherente con las metodologías llevadas a cabo en la unidad?

¿Los instrumentos de evaluación están consensuados con el resto de áreas del nivel educativo?

A la hora de calificar, ¿utilizo como referente los criterios de evaluación y las competencias clave?

Sobre la implicación del alumnado

¿El alumnado conoce previamente al desarrollo de cada unidad los instrumentos y los procedimientos de evaluación?

¿El alumnado realiza actividades que le permitan autoevaluarse y coevaluarse?

¿El alumnado conoce individualmente sus puntos fuertes y sabe cómo mejorar sus debilidades?

Estructura curricular

Programación didáctica

Normativa LOMLOE

Relación entre los elementos del currículo

Glosario

Muestra programación

Situación de aprendizaje

PRINCIPIOS Y FINES DE LA EDUCACIÓN (LOMLOE, ARTÍCULOS 1 Y 2)

COMPETENCIAS CLAVE (CONSEJO DE LA UE, 2018)

Logros que se espera que el alumnado haya alcanzado al finalizar la etapa y cuya consecución está vinculada a la adquisición de las competencias clave.

OBJETIVOS

8 competencias

CCL

Competencia en comunicación lingüística

CP

STEM

CD

CPSAA

CC

CE

CCEC

Competencia plurilingüe

Estructura curricular LOMLOE

Competencia matemática y competencia en ciencia, tecnología e ingeniería

Competencia digital

Competencia personal, social y de aprender a aprender

Competencia ciudadana

Competencia emprendedora

Competencia en conciencia y expresión culturales

DESCRIPTORES OPERATIVOS DE LAS COMPETENCIAS CLAVE

Orientan sobre el nivel de desempeño esperado de las competencias clave al término de cada ciclo de la etapa.

PERFIL DE SALIDA

COMPETENCIAS ESPECÍFICAS

Desempeños que el alumnado debe poder desplegar en actividades o en situaciones para lo que requiere de los saberes básicos de cada área o ámbito. Se convierte des este modo en un elemento de conexión entre las competencias clave, y los saberes básicos y los criterios de evaluación de las áreas.

ÁREAS

CRITERIOS DE EVALUACIÓN

Referentes para comprobar el nivel de desempeño de las competencias específicas que se trabajan en las actividades y situaciones de aprendizaje.

SABERES BÁSICOS

Conocimientos, destrezas y actitudes de un área o ámbito y cuyo aprendizaje es necesario para la adquisición de las competencias específicas.

ODS

Situación problema, de cierta complejidad cuya resolución creativa implique la movilización de manera integrada de los saberes básicos (conocimientos, destrezas y actitudes), a partir de la realización de distintas tareas y actividades. Favorecerán la transferencia de los aprendizajes adquiridos en la resolución de un problema de la realidad cotidiana del alumnado, en función de su progreso madurativo.

Relación entre los elementos del currículo

OBJETIVOS

COMPETENCIAS CLAVE

DESCRIPTORES OPERATIVOS

PRIMER CICLO

SEGUNDO CICLO

TERCER CICLO

COMPETENCIAS ESPECÍFICAS

CRITERIOS DE EVALUACIÓN

SABERES BÁSICOS

SITUACIONES DE APRENDIZAJE

Glosario

Son los logros que se espera que el alumnado haya alcanzado al finalizar la etapa y cuya consecución está vinculada a la adquisición de las competencias clave y de las competencias específicas.

Solo existen objetivos de etapa y no de área o ámbito.

Objetivos Competencias clave

Son los desempeños que se consideran imprescindibles para que el alumnado pueda progresar con garantías de éxito en su itinerario formativo y para afrontar los principales retos y desafíos globales y locales.

Las competencias clave son:

• Competencia en comunicación lingüística.

• Competencia plurilingüe.

• Competencia matemática y competencia en ciencia, tecnología e ingeniería.

• Competencia digital.

• Competencia personal, social y de aprender a aprender.

• Competencia ciudadana.

• Competencia emprendedora.

• Competencia en conciencia y expresión culturales.

Perfil de salida

El perfil competencial de salida del alumnado al término de la educación básica es el elemento en el que se concretan los principios y los fines del sistema educativo e identifica y define las competencias clave que se espera que los alumnos y alumnas hayan desarrollado al completar las distintas etapas. Introduce orientaciones sobre el nivel de desempeño esperado al término de la etapa de Educación Primaria.

Perfil competencial

Guía que identifica y define las competencias clave que el alumnado debe haber adquirido y desarrollado al finalizar cada ciclo de la etapa de Educación Primaria e introduce los descriptores operativos que orientan sobre el nivel de desempeño esperado al término de cada ciclo, así como de la etapa.

Descriptores operativos

Constituyen, junto con los objetivos de la etapa, el marco referencial a partir del cual se concretan las competencias específicas de cada área o ámbito. Esta vinculación entre descriptores operativos y competencias específicas facilita que de la evaluación de estas últimas pueda desprenderse el grado de adquisición de las competencias clave definidas en el perfil de salida y, por tanto, la consecución de las competencias y los objetivos previstos para la etapa.

Competencias específicas

Definen los desempeños que el alumnado debe poder desplegar en actividades o en situaciones de aprendizaje cuyo abordaje requiere de los saberes básicos de cada área o ámbito.

Las competencias específicas constituyen un elemento de conexión entre, por una parte, el perfil de salida del alumnado y, por otra, los criterios de evaluación y los saberes básicos de las áreas o ámbitos.

Funcionan a modo de objetivos competenciales de etapa.

Están formuladas con esta estructura sintáctica: qué (infinitivo) + cómo (gerundio, a través de…) + para qué (para+infinitivo).

Criterios de evaluación

Son los referentes que indican los niveles de desempeño esperados en el alumnado en las situaciones o las actividades a las que se refieren las competencias específicas de cada área en un momento determinado de su proceso de aprendizaje.

Saberes básicos

Son los conocimientos, destrezas y actitudes que constituyen los contenidos propios de un área o ámbito y cuyo aprendizaje es necesario para la adquisición de las competencias específicas. Vinculados a cada criterio de evaluación habrá unos saberes básicos mínimos.

Situaciones de aprendizaje

Hacen referencia a las situaciones y actividades que implican el despliegue por parte del alumnado de actuaciones asociadas a competencias clave y competencias específicas y que contribuyen a su adquisición y su desarrollo.

Su diseño debe suponer la transferencia de los aprendizajes adquiridos por parte del alumnado y, por ello, representan una herramienta eficaz para integrar los elementos curriculares de las distintas áreas o materias.

Con ellas se busca ofrecer al alumnado la oportunidad de conectar sus aprendizajes y aplicarlos en contextos cercanos a su vida cotidiana, favoreciendo su compromiso con su propio aprendizaje.

Educación inclusiva

La educación inclusiva se convierte en un principio fundamental con el objetivo de atender a la diversidad de las necesidades de todo el alumnado. Para ello, se deben eliminar las barreras que limitan el acceso, presencia, participación y aprendizaje de aquellos que se encuentren en situación de vulnerabilidad socioeducativa y cultural.

Diseño Universal para el Aprendizaje (DUA)

Es un enfoque basado en la flexibilización del currículo, para que sea abierto y accesible desde su diseño y facilite a todo el alumnado igualdad de oportunidades para aprender.

El DUA implica que pongamos nuestra mirada en la capacidad y no en la discapacidad, es decir, que veamos como discapacitantes los modos y los medios con los que se presenta el currículo y no a las personas, porque todos tenemos capacidades, pero de un modo diferente.

Propone tres principios fundamentales y una serie de pautas que deben presidir nuestras prácticas educativas:

• Proporcionar múltiples formas de representación.

• Proporcionar múltiples formas de acción y expresión

• Proporcionar múltiples formas de implicación

Objetivos de Desarrollo Sostenible (ODS)

La sostenibilidad es uno de los principios y fines de la LOMLOE se refiere a como dar respuesta a las necesidades actuales sin comprometer la capacidad de las generaciones futuras de satisfacer las suyas, garantizando el equilibrio entre crecimiento económico, cuidado del medioambiente y bienestar social. Es un concepto muy unido a otros como consumo responsable, salud, etc. En este sentido, la Asamblea General de la ONU adoptó la Agenda 2030 para el Desarrollo Sostenible, un plan de acción a favor de las personas, el planeta y la prosperidad, que también tiene la intención de fortalecer la paz universal y el acceso a la justicia. La Agenda plantea 17 objetivos con 169 metas de carácter integrado e indivisible que abarcan las esferas económica, social y ambiental.

Programación didáctica Educación Primaria del área y curso.

Características del entorno y evaluación inicial

Introducción

1.1. Nuevo marco normativo.

1.2. Fines de la etapa.

1.3. Principios generales.

1.4. Objetivos de la etapa.

1.5. Principios pedagógicos.

Competencias clave y perfil de salida del alumnado

2.1. Competencias clave.

2.2. Contribución del área a la adquisición de las competencias clave.

2.3. El Perfil de salida del alumnado.

2.4. Competencias clave y perfil de salida.

2.4.1. Perfil competencial del alumnado al término de cada ciclo de la etapa de Educación Primaria.

2.5. Descriptores operativos de las competencias clave en el perfil de salida.

2.6. Competencias clave y Objetivos de la Educación Primaria.

Situaciones de aprendizaje

Para cada área y curso de Educación Primaria

4.1 Introducción al área.

4.2 Competencias específicas y criterios de evaluación asociados.

4.3 Saberes básicos: Organización y secuenciación.

Principios pedagógicos y aprendizajes de carácter transversal

Metodología

6.1. Principios metodológicos.

6.2. Metodologías activas.

6.3. Orientaciones metodológicas específicas del área.

Inclusión. Atención a la diversidad y a las diferencias individuales del alumnado

7.1. Principios y pautas DUA.

7.2. Medidas organizativas y curriculares.

7.3. Materiales y recursos específicos para atender a la diversidad en el área.

Evaluación del alumnado.

8.1. Procedimiento de evaluación del alumnado.

8.2. Referentes de la evaluación.

8.3. ¿Cómo evaluar?

Evaluación del proceso de enseñanza y de la práctica docente

Materiales y recursos didácticos

Actividades complementarias y extraescolares relacionadas con el currículo

Transición y coordinación entre etapas

Programación

Muestra programación. Situación de aprendizaje

Modelo de situación de aprendizaje elaborado según esquema del Proyecto de Orden por el que se desarrolla el currículo correspondiente a la etapa de Educación Primaria en la Comunidad Autónoma de Andalucía. Este modelo podrá sufrir cambios si así lo requiere la normativa definitiva.

CURSO 3 º Primaria Matemáticas

TEMPORALIZACIÓN

8-10 sesiones

Primaria. Matemáticas 3. Situación de aprendizaje 9

SITUACIÓN DE APRENDIZAJE

1. IDENTIFICACIÓN

TÍTULO O TAREA: 9 ¿Y tú qué mides? ¿Por qué es importante respetar las ideas de los demás?

S O N D E F M A M J

2. JUSTIFICACIÓN

Esta situación de aprendizaje, presentada en el Objetivo en acción, pretende generar en el alumnado la conciencia de respetar las ideas de los demás a través de diferentes actividades, consejos y estrategias propuestas en la secuencia didáctica

La intención que se persigue con la situación de aprendizaje tiene que ver con el Objetivo de Desarrollo Sostenible (ODS) n º 16: Paz, justicia e instituciones sólidas; donde el pensamiento crítico se hace protagonista ayudando a comprender la importancia de l as matemáticas en el contexto cotidiano de medir objetos de forma diferente y correcta al mismo tiempo

La situación de aprendizaje parte de la reflexión: existen diferentes formas de medir correctamente, por lo que hay que escuchar y respetar las opiniones e ideas de los demás; pretendiendo, al final de la unidad y a través de una técnica de pensamiento, provocar una reflexión transformadora que dé respuesta al Objetivo en acción: ¿Por qué es importante respetar las ideas de los demás?

El alumnado utilizará diferentes unidades de medida y todas ellas serán correctas Esta conexión permitirá interrelacionar los elementos curriculares con actividades y tareas conectadas con la realidad, favoreciendo la transferencia de los aprendizajes

3. DESCRIPCIÓN DEL PRODUCTO FINAL

El producto final será inventar una unidad de medida con el cuerpo y compararla con los demás. Así, compartiendo sus ideas, aprenderán juntos Esta conexión ayudará al alumnado a comprender el mundo en el que vive para iniciar actuaciones que fomenten el respeto de las ideas de los demás desde una ciudadanía global comprometida, responsable y activa; lo que contribuirá a la adquisición y desarrollo de las compe tencias clave y específicas.

4. CONCRECIÓN CURRICULAR COMPETENCIAS ESPECÍFICAS

1. Interpretar situaciones de la vida cotidiana proporcionando una representación matemática de las mismas mediante conceptos , herramientas y estrategias para analizar la información más relevante.

DESCRIPTORES OPERATIVOS: STEM1, STEM2, STEM4, CD2, CPSAA5, CE1, CE3, CCEC4. CRITERIOS DE EVALUACIÓN SABERES BÁSICOS EVIDENCIAS Actividades y ejercicios

1.1.a. Reconocer de forma verbal o gráfica, problemas de la vida cotidiana, comprendiendo las preguntas planteadas a través de diferentes estrategias o herramientas, incluidas las tecnológicas, y comenzar a interpretar mensajes verbales, escritos o visuales.

MA.02.A.3.1. Estrategias de cálculo mental con números naturales y fracciones hasta el 9 999 Lo resuelvo sin problema: Cálculo mental (pág. 153).

2. Resolver situaciones problematizadas, aplicando diferentes técnicas, estrategias y formas de razonamiento, para explorar d istintas maneras de proceder, obtener soluciones y asegurar su validez desde un punto de vista formal y en relación con el contexto planteado.

DESCRIPTORES OPERATIVOS: STEM1, STEM2, CPSAA4, CPSAA5, CE3.

CRITERIOS DE EVALUACIÓN SABERES BÁSICOS EVIDENCIAS

2.1.a. Comenzar a comparar y a emplear diferentes estrategias para resolver un problema de forma pautada, implicándose en la resolución.

MA.02.A.3.5. Fases de resolución de un problema: comprensión del enunciado; elaboración de un plan de resolución; ejecución del plan siguiendo las estrategias más adecuadas; comprobación de la solución.

Actividades y ejercicios

Unidades de medida que varían (págs 142-143).

El metro (pág. 145).

El centímetro (pág. 147)

El kilómetro (pág. 151)

Lo resuelvo sin problema (págs. 152153).

¿Qué he aprendido? (pág. 154).

Producto final: Inventa una unidad de medida (pág. 155).

3. Explorar, formular y comprobar conjeturas sencillas o plantear problemas de tipo matemático en situaciones basadas en la v ida cotidiana, de forma guiada, reconociendo el valor del razonamiento y la argumentación para contrastar su validez, adquirir e integrar nuevo conocimiento.

DESCRIPTORES OPERATIVOS: CCL1, STEM1, STEM2, CD1, CD3, CD5, CE3.

Situación de aprendizaje

3.2.a. Ejemplificar problemas sobre situaciones cotidianas que se resuelven matemáticamente, comenzando a plantear preguntas y avanzando posibles conclusiones.

MA.02.A.3.6. Resolución de problemas referidos a situaciones abiertas e investigaciones matemáticas sencillas sobre números, cálculos, medidas y geometría.

Unidades de medida que varían (pág. 143).

El metro: ¿Puedes medir un metro con tu cuerpo? (pág. 145).

El centímetro: Mi vida en centímetros (pág. 147)

El kilómetro (pág. 151)

Lo resuelvo sin problema (págs. 152153).

¿Qué he aprendido? (pág. 154).

Producto final: Inventa una unidad de medida (pág. 155).

MA.02.B.1.1. Atributos mensurables de los objetos (longitud, masa, capacidad, superficie, volumen y amplitud del ángulo).

Unidades de medida que varían (pág. 142).

El metro (pág. 144).

El centímetro: Actividad 1 (pág. 147)

Mido con regla (págs. 148-149)

El kilómetro: Actividad 1 (pág. 150)

¿Qué he aprendido? (pág. 154).

4. Utilizar el pensamiento computacional, organizando datos, descomponiendo en partes, reconociendo patrones, generalizando e interpretando, modificando y creando algoritmos de forma guiada, para modelizar y automatizar situaciones de la vida cotidiana.

DESCRIPTORES OPERATIVOS: STEM1, STEM2, STEM3, CD1, CD3, CD5, CE3.

4.1.a. Comenzar a automatizar situaciones sencillas de la vida cotidiana que se realicen paso a paso o sigan una rutina, utilizando de forma pautada principios básicos del pensamiento computacional, realizando procesos simples en formato digital.

MA.02.B.2.2. Procesos de medición mediante instrumentos convencionales (regla, cinta métrica, balanzas, reloj analógico y digital).

MA.02.D.4.1. Estrategias para la interpretación y modificación de algoritmos sencillos (reglas de juegos, juegos de magia con cartas sencillos, instrucciones secuenciales, bucles, patrones repetitivos, programación por bloques, robótica educativa, etc.).

El metro (pág. 144)

Mido con regla (págs. 148-149)

Mido con regla: Actividad 4 (pág. 149) Lo resuelvo sin problema: ¿Cómo funciona? (pág. 153).

4.2.a. Iniciarse en el manejo de las herramientas adecuadas en el proceso de resolución de problemas.

MA.02.D.4.2. Utilización de medios tecnológicos en el proceso de aprendizaje para la comprensión y asimilación de contenidos matemáticos, obtención de información y realización de cálculos numéricos, resolución de problemas o investigaciones sencillas y presentación de resultados.

Unidades de medida que varían: Actividad 3 (pág. 142).

El metro: Actividad 6-7 (pág. 145).

El centímetro: Actividades 6-7 (pág. 147)

El kilómetro: Actividades 5-6 (pág. 151)

Lo resuelvo sin problema: Cálculo mental (pág. 153).

Producto final: Inventa una unidad de medida (pág. 155).

5. Reconocer y utilizar conexiones entre las diferentes ideas matemáticas, así como identificar las matemáticas implicadas en ot ras áreas o en la vida cotidiana, interrelacionando conceptos y procedimientos, para interpretar situaciones y contextos diversos.

DESCRIPTORES OPERATIVOS: STEM1, STEM3, CD3, CD5, CC4, CCEC1.

5.1.a. Comenzar a realizar conexiones entre los diferentes elementos matemáticos, aplicando conocimientos y experiencias propias, iniciando la aplicación y gestión matemática en su contexto cotidiano.

MA.02.B.2.1. Estrategias para realizar mediciones con instrumentos y unidades no convencionales (repetición de una unidad, uso de cuadrículas y materiales manipulativos) y convencionales.

MA.02.B.3.1. Estrategias de comparación y ordenación de medi das de la misma magnitud (km, m, cm, mm; kg, g; L y m L): aplicación de equivalencias entre unidades en problemas de la vida cotidiana que impliquen convertir en unidades más pequeñas.

MA.02.B.3.2. Estimación de medidas de longitud, masa y capacidad por com paración.

MA.02.B.3.3. Evaluación de resultados de mediciones y estimaciones o cálculos de medidas.

Unidades de medida que varían * (págs 142-143).

El metro * (pág. 145).

El centímetro * (págs 146-147)

Mido con regla * (págs. 148-149)

El kilómetro (págs 150-151)

Lo resuelvo sin problema (págs. 152153).

¿Qué he aprendido? (pág. 154).

Producto final: Inventa una unidad de medida (pág. 155).

*Utilizando, como ayuda, los recursos manipulativos que se detallan en la secuencia didáctica.

5.2.a. Comenzar a identificar situaciones en contextos diversos, reconociendo las conexiones entre las matemáticas y la vida cotidiana, interpretando la información gráfica de diferentes medios.

MA.02.B. 1.2. Unidades convencionales (km, m, cm, mm; kg, g; L y mL ) y no convencionales en situaciones de la vida cotidiana.

Primaria. Matemáticas 3. Situación de aprendizaje 9

7. Desarrollar destrezas personales que ayuden a identificar y gestionar emociones al enfrentarse a retos matemáticos, foment ando la confianza en las propias posibilidades, aceptando el error como parte del proceso de aprendizaje y adaptándose a las situaciones de incertidumbre, para mejorar la perseverancia, disfrutar en el aprendizaje de las matemáticas y controlar situaciones de frustración en el ensayo y error.

DESCRIPTORES OPERATIVOS: STEM5, CPSAA1, CPSAA4, CPSAA5, CE2, CE3.

7.1.a. Reconocer y comenzar a identificar las emociones propias al abordar nuevos retos matemáticos, pidiendo ayuda solo cuando sea necesario y mostrando autoconfianza y perseverancia en el control de sus emociones.

MA.02.F.1.1. Gestión emocional: estrategias de identificación y manifestación de las propias emociones ante las matemáticas. Iniciativa y tolerancia ante la frustración en el aprendizaje de las matemáticas.

MA.02.F.1.3. Espíritu de superación frente a la frustración, los retos, dificultades y errores propios del proceso de aprendizaje matemático. Autoconfianza en las propias posibilidades.

Presentación de la situación de aprendizaje (págs. 140-141).

Lo resuelvo sin problema (págs. 152153).

¿Qué he aprendido?: El semáforo (pág. 154)

Producto final: Inventa una unidad de medida (pág. 155).

7.2.a. Expresar y mostrar actitudes positivas ante nuevos retos matemáticos tales como el esfuerzo y la flexibilidad, valorando el error como una oportunidad de aprendizaje, superando la frustración y desarrollando actitudes participativas.

MA.02.F.1.2. Fomento de la autonomía y estrategias para la toma de decisiones en situaciones de resolución de problemas.

¿Cómo he aprendido? (pág. 154).

8. Desarrollar destrezas sociales, reconociendo y respetando las emociones, las experiencias de los demás y el valor de la diversidad y participando activamente en equipos de trabajo heterogéneos con roles asignados, para construir una identidad positiva como estudiante de matemáticas, fomentar el bienestar personal y crear relaciones saludables.

DESCRIPTORES OPERATIVOS: CCL5, CP3, STEM3, CPSAA1, CPSAA3, CC2, CC3.

8.1.a. Participar y comenzar a colaborar respetuosamente en el trabajo en equipo, comunicándose adecuadamente, respetando la diversidad del grupo y estableciendo relaciones saludables basadas en la igualdad y la resolución pacífica de conflictos, afianzando la au toconfianza en relaciones vividas en entornos coeducativos.

MA.02.F.2.1. Sensibilidad y respeto ante las diferencias individuales presentes en el aula: identificación y rechazo de actitudes discriminatorias.

MA.02.F.2.2. Participación activa en el trabajo en equipo, escucha activa y respeto por el trabajo de los demás.

MA.02.F.2.3. Reconocimiento y comprensión de las emociones y experiencias de los demás ante las matemáticas.

MA.02.F.2. 4 Valoración de la contribución de las matemáticas a los distintos ámbitos del conocimiento humano.

Presentación de la situación de aprendizaje (págs. 140-141).

El kilómetro: Actividad 8 (pág. 51)

Producto final: Inventa una unidad de medida (pág. 155).

8.2.a. Adoptar alguna decisión en el reparto de tareas, respetando las responsabilidades individuales asignadas y comenzando a emplear estrategias sencillas de trabajo en equipo dirigidas a la consecución de objetivos compartidos y a desarrollar una escucha activa.

MA.02.F.2. 5 Desarrollo de estrategias personales para resolver problemas, investigaciones y pequeños proyectos de trabajo.

MA.02.F.2.6. Iniciativa, participación respetuosa y colaboración activa en el trabajo cooperativo para investigar y resolver problemas.

ORIENTACIONES PARA LA COMPETENCIA ESPECÍFICA

● Competencia específica 1: Esta competencia parte de la premisa de comprender una situación problematizada como paso previo hacia su resolución. Representar o visualizar el problema ayuda siempre a su interpretación, así como a la identificación de los datos y las relaciones más relevantes. Esta comprensión no se realiza únicamente a partir de los mensajes verbales escritos, sino que incluye también los mensajes orales; los mensajes visuales a través de dibujos, imágenes o fotografías; o situaciones cotidianas o mensajes con materiales manipulativos concretos que supongan un reto. En definitiva, se pretende dotar al alumnado de herramientas que le permitan establecer una correcta representación del mundo que lo rodea. Se deberán definir contextos en la resolución de problemas para facilitar una mayor integración de las distintas experiencias y aprendizajes del alumnado, así como de las diferentes competencias, fomentando el respeto mutuo y la cooperación entre iguales, con especial atención a la igualdad de género, la inclusión y la diversidad personal y cultural. Estos contextos deberán ser variados e incluir, al menos, el personal, el escolar, el social, el científico y el humanístico. Estos contextos ofrecerán una oportunidad para incluir el planteamiento de los grandes problemas medioambientales y sociales de nuestro mundo o problemas de consumo responsable en su realidad cercana, fomentando que el alumnado participe de los mismos y se implique activamente en su futuro.

● Competencia específica 2: La resolución de problemas constituye una parte fundamental del aprendizaje de las matemáticas. Por un lado, esta competencia propone la implementación de estrategias variadas para obtener posibles soluciones: analogía, ensayo y error, resolución inversa, tanteo, descomposición en problemas más sencillos... Dicha variedad de estrategias permitirá abordar con seguridad l os retos y establecer conexiones. Las estrategias no deben centrarse únicamente en la resolución aritmética, sino que también se deberá facilitar situaciones que puedan ser resueltas a través de la manipulación de materiales, el diseño de representaciones gráficas o la a rgumentación verbal. Elegir una estrategia y revisarla durante la resolución de un problema implicará tomar decisiones, anticipar la respuesta, seguir las pautas establecidas, asumir riesgos y transformar el error en una oportunidad de aprendizaje. Por otro lado, la resolución de problemas debe entenderse como eje metodológico para la construcción del conocimiento matemático, ya que facilita nuevas conexiones entre los conocimientos del alumnado, construyendo así nuevos significados y conocimientos matemáticos. El hecho de comprobar y asegurar la validez de las soluciones supone razonar acerca del proceso seguido y evaluarlas en cuanto a su corrección matemática, fomentándose l a reflexión crítica sobre la adecuación de dichas soluciones al contexto planteado y las implicaciones que tendrían desde diversos puntos de vista (consumo responsable, salud, medioambiente, etc.).

● Competencia específica 3: Esta competencia específica propone implementar el razonamiento y el pensamiento analítico como elementos esenciales para la formulación de conjeturas o afirmaciones tanto en contextos cotidianos como en situaciones matemáticas, permitiendo al alumnado desarrollar ideas, explorar fenómenos, argumentar conclusiones y generar nuevos conocimientos. En definitiva, se trata de potenciar el análisis matemático para contribuir al desarrollo del pensamiento crítico, ya que implica analizar y profundizar en la situación o problema, explorarlo desde diferentes perspectivas, plantear las preguntas adecuadas y ordenar las ideas de forma que tengan sentido. Lograr que el alumnado detecte elementos matemáticos en el entorno que lo rodea o en situaciones de su vida cotidiana, planteándose preguntas o

Primaria. Matemáticas 3. Situación de aprendizaje 9

Situación de aprendizaje

formulando conjeturas, desarrolla una actitud activa ante el trabajo, así como una actitud proactiva ante el aprendizaje. La observación y la reflexión, el desarrollo de destrezas comunicativas a través de la expresiónde lo observado, de preguntas planteadas y del proceso de prueba llevado a cabo; contribuirá al incremento de la capacidad de razonamiento y de análisis crítico.

● Competencia específica 4: El objetivo de esta competencia específica es sentar las bases para el desarrollo del pensamiento computacional, destrezas clave en el futuro del alumnado ya queentronca directamente con la resolución de problemas y con el planteamiento de procedimientos. Requiere trabajar con la abstracción, elemento clave para identificar los aspectos más relevantes y la descomposición en tareas más simples con el fin de llegar a posibles soluciones que puedan ser ejecutadas por un sistemainformático, un humano o una combinación de ambos. Llevar el pensamiento computacional a la vida diaria supone relacionar los aspectos fundamentales de la informática con las necesidades del alumnado. Se trata de preparar al alumnado, con metodologías y estrategias guiadas, para un futuro cada vez más tecnológico, mejorando sus capacidades intelectuales y haciendo uso de abstracciones para resolver problemas complejos.

● Competencia específica 5: La conexión entre los diferentes objetos matemáticos (conceptos, procedimientos, sistemas de representación...) aporta una comprensión más profunda y duradera de los saberes adquiridos, proporcionando una visión más amplia sobre el propio conocimiento. Esta visión global e interrelacionada de los saberes será la que contribuya a la conexión con otras áreas, así como con la vida diaria del alumnado, por ejemplo, en la planificación y gestión desu propia economía personal o en la interpretación de información gráfica en diversos medios. Por un lado, comprender que lasideas matemáticas no son elementos aislados, sino que se interrelacionan entre sí, desarrollará la capacidad de comprensión del entorno y de los sucesos que en él acontecen, creando una base sólida dondeasentar nuevos aprendizajes, afrontar nuevos retos y adoptar decisiones informadas.Por otro lado, el reconocimiento de la conexión de las matemáticas con otras áreas, con la vida real o con la experiencia propia aumentará el bagaje matemático del alumnado. Es importante que el alumnado experimente con las matemáticas en diferentes contextos (personales, escolares, sociales, científicos, humanísticos y ambientales) para habituarse a identificar aspectosmatemáticos en múltiples situaciones.

● Competencia específica 7: Resolver problemas matemáticos o retos más globales en los que intervienen las matemáticas debe convertirse en al gratificante. La adquisición de destrezas emocionales dentro del aprendizaje de las matemáticas fomenta rá el bienestar del alumnado, el interés por la disciplina y la motivación por las matemáticas sin distinción de género, a lavez que desarrollará la resiliencia y una actitud proactiva ante retos matemáticos, al entender el error como unaoportunidad de aprendizaje y la variedad de emociones como una ocasión para crecer de manera personal. Para ello, esta competencia específica propone que alumnado deba identificar y gestionar sus emociones, reconocer las fuentes de estrés, mantener una actitudpositiva, ser perseverante y pensar de forma crítica y creativa. Enriquece también esta competencia el estudio de lacontribución de las matemáticas a los distintos ámbitos del conocimiento humano desde una perspectiva de género. Con todo ello, se ayudará a desarrollar una disposición ante el aprendizaje que fomente la transferencia de lo adquirido a otros ámbitos de la vida, favoreciendo el aprendizaje y el bienestar personal como parteintegral del proceso vital del individuo.

● Competencia específica 8: Con esta competencia específica se pretende que el alumnado trabaje los valores de respeto, igualdad y resolución pacífica de conflictos, al tiempo que resuelve los retos matemáticos propuestos, desarrollando destrezas decomunicación efectiva, planificación, indagación, motivación y confianza, para crear relaciones y entornos saludables de trabajo, por ejemplo, mediante la participación en equipos heterogéneos con roles asignados. Esto permitirá construir relaciones saludables, solidarias y comprometidas, afianzando la autoconfianza y normalizando situaciones de convivencia en igualdad. Así, pues, se persigue dotar al alumnado de herramientas y estrategias de comunicación efectiva y de trabajo en equipo comoun recurso necesario para el futuro ; donde trabajar la escucha activa y la comunicación asertiva, la cooperación creativa, crítica y responsable y abordar la resolución de conflictos de manera positiva, empleando unlenguaje inclusivo y no violento.

CONEXIÓN CON EL PERFIL COMPETENCIAL/PERFIL DE SALIDA

Competencias clave: CCL competencia en comunicación lingüística. CP competencia plurilingüe. STEM competencia matemática y competencia en ciencia, tecnología e ingeniería. CD competencia digital. CPSAA competencia personal, social y de aprender a aprender. CC competencia ciudadana. CE competencia emprendedora. CCEC competencia en conciencia y expresión culturales.

5.SECUENCIACIÓN DIDÁCTICA

ACTIVIDADES (TIPOS Y CONTEXTOS)

PROCESOS COGNITIVOS* RECURSOS

MOTIVACIÓN - ACTIVACIÓN - EXPLORACIÓN

Presentación de la situación de aprendizaje (págs. 140-141)

• ¿Cómo lo ves?: Se invita al alumnado a que reflexione y se exprese acerca delo que puede y no puede medir, así como las diferentes maneras de medir la longitudde un objeto

• El dato:Usar distintas unidadesde medida y compartir el resultado ayuda a comprender que no todo el mundo piensa igual ove la realidad de la misma manera. Si respetamos las opinionesde los demás, podremos encontrar la manera de comprendernos

• Presentación del Objetivo en acción (la importancia de respetar las diferentes ideas de todos a través de la invención de una unidad de medida que habrá que compartir con los demás) y los objetos matemáticos (sigue el hilo) que se abordarán durante esta situación de aprendizaje.

• Metodologías activas:

o Aprendizaje cooperativo.«Asamblea de ideas» para trabajar las preguntas de la sección ¿Cómo lo ves?

Primaria. Matemáticas 3. Situación de aprendizaje 9

1, 4, 5. Recursos de aula: • Murales.

Unidades de medida que varían (págs 142-143)

ESTRUCTURACIÓN - APLICACIÓN

• Ejercicios y actividades sobre el uso de unidades de medida diferentes que varían según la persona y/o el objeto que se utilicepara medir

• Actividad competencial titulada ¿Qué ocurre si mido con unidades distintas ?, donde se conecta con el Objetivo en acción de la unidad, dado que se basa en la misma propuesta y se demuestra que cuando utilizamosunidades de medida diferentes, obtenemos resultados distintos y todos correctos

• Metodologías activas:

o Desarrollo del pensamiento.«Piensa y comparte en pareja» para medir longitudes, ¿elegirías unidades que varían como el pie o el paso?

El metro (págs. 144-145)

• Ejerciciosy actividades donde se aborda el metro como unidad principal de longitud.

• Actividad competencial: ¿Puedes medir un metro con tu cuerpo?, donde se utiliza la cinta métrica para medir y comparar con otras unidades de medida del propio cuerpo.

• Metodologías activas:

o Desarrollo del pensamiento. «Lluvia de ideas» para elaborar una lista con longitudes que miden más de un metro y menos de un metro.

El centímetro (págs. 146-147)

• Ejercicios y actividades donde se aborda el centímetro como unidad de longitud menor que el metro y utilizado para expresar la longitud de objetos pequeños

• Actividad competencial: Mi vida en centímetros, donde investigar la estatura al nacer, en la actualidad y cuando se sea mayor.

3, 4, 5, 6. Recursos digitales:

• Actividades interactivas.

• Vídeo: Te lo cuento en un momento (Medidas corporales) Recursos de aula:

• Policubos

Recursos manipulativos:

• Clips.

2, 3, 4, 5. Recursos digitales:

• Actividades interactivas.

• Esquema problemas aritméticos: de cambio y de grupos iguales

Recursos manipulativos:

• Cinta métrica.

2, 3, 4, 5. Recursos digitales:

• Actividades interactivas.

• Esquema problemas aritméticos: de gruposiguales y de igualación

Recursos de aula:

• Policubos.

Recursos manipulativos:

• Regla

Mido con regla (págs. 148-149)

• Ejercicios y actividades donde utilizar la regla para medir longitudes pequeñas en centímetros.

• Metodologías activas:

o Aprendizaje lúdico.

El kilómetro (págs. 150-151)

• Ejercicios y actividades donde se aborda el kilómetro como unidad de longitud mayor que el metro y utilizado para expresar distancias largas.

• Metodologías activas:

o Aprendizaje cooperativo «Comprobamos» para resolver un problema.

Lo resuelvo sin problema (págs. 152-153)

• Ejercicios y actividades:

o Hacer un esquema.

o Problemas exprés.

o Cálculo mental.

• Metodologías activas:

o Pensamiento computacional.«¿Cómo funciona?» donde comprender cómo opera la máquina de operaciones que se muestra: identificar la constante de proporcionalidad

Porfolio (págs. 154-155)

Este apartado constará de tres partes:

3, 4, 5. Recursos digitales:

• Actividades interactivas.

• Regletas.

• Geoplano

2, 3, 4, 5. Recursos digitales:

• Actividades interactivas.

• Esquema problemas aritméticos: de comparación

3, 4, 5. Recursos digitales:

• Vídeo: Cálculo mental CONCLUSIÓN

2, 3, 4, 5, 6. Recursos digitales:

• Lo esencial

• ¿Qué he aprendido? Al elaborar las actividades propuestas, el alumnado tomará conciencia de todos los aprendizajes realizados en esta situación de aprendizaje y podrá comprobar sus fortalezas y debilidades, si las tuviera.

• Bajo el epígrafe de Objetivo en acción, el alumnado se encontrará co n el producto final planteado: Inventar una unidad de medida. Se implementa metodologías activas (técnica de pensamiento:Círculo de puntos de vista) que les ayudará en sus reflexiones y en la toma deconciencia dela importancia de respetar las ideas de los demás.

• ¿Cómo he aprendido? Con este proceso de metacognición se pretende que el alumnado sea capaz de hacer una reflexión personal sobre cómo se ha sentido durante el proceso de aprendizaje. Ha de analizar su aprendizaje vinculándolo a sus emociones con relación al aprendizaje mediante el uso de metodologías activas (técnica de educación emocional)

• Game room

• Actividades interactivas

• Material de aula: Policubos.

• Generador de pruebas de evaluación

• Recursos imprimibles.

Evaluación, inclusión y atención a la diversidad:

o Fichas derefuerzo

o Ficha deampliación

o Evaluación

o Evaluación adaptada

o Evaluación competencial

6.MEDIDAS DE ATENCIÓN EDUCATIVA ORDINARIA A NIVEL DE AULA MEDIDAS GENERALES

La variedad de actividades, las claves y la tarea que se proponen, se han diseñado para contribuir a que el alumnado adquiera los aprendizajes de manera progresiva adecuándonos a los diversos estilos de aprendizaje. Se proponen actividades tanto de tipo literal y reproducti vo como de carácter más competencial que incorporan procesos cognitivos más complejos asociados a inferencias, valoraciones y creac iones de productos, combinando estrategias y destrezas de pensamiento, aprendizaje cooperativo, educación emocional, cultura emprendedora y el uso de las TI C.

De igual modo disponemos de actividades complementarias de refuerzo y ampliación asociadas a la unidad para ofrecer una respuesta más adaptada el amplio abanico de los estilos de aprendizaje del alumnado. Además de todo ello, el profesorado hará referencia a medidas m ás concretas de acuerdo con las características a su grupo.

Primaria. Matemáticas 3. Situación de aprendizaje 9

*1: Conocer / 2: Comprender / 3: Aplicar / 4: Analizar / 5: Evaluar / 6: Crear (Bloom)

Situación de aprendizaje

Recursos:

• Loesencial.

• Propuesta de diversidad 1 (refuerzo).

• Propuesta de diversidad 2 (refuerzo).

• Propuesta de diversidad 3 (refuerzo).

• Propuesta de diversidad 4 (ampliación).

• Propuesta de comprensión oraly lectora

Además, de entre las medidas generales que nos permite la normativa vigente, en esta situación de aprendizaje utilizaremos (dejar solo las que correspondan):

• Agrupación de áreas en ámbitos de conocimiento.

• Apoyo en grupos ordinarios mediante un segundo profesor o profesora dentro del aula.

• Desdoblamientos de grupos en las áreas de carácter instrumental.

• Agrupamientos flexibles para la atención del alumnado en un grupo específico.

• Acción tutorial.

• Metodologías didácticas basadas en el trabajo colaborativo en grupos heterogéneos, tutoría entre iguales y a prendizaje por proyectos.

• Actuaciones de coordinación en el proceso de tránsito entre etapas

• Actuaciones de prevención y control del absentismo.

MEDIDAS ESPECÍFICAS

Como medidas específicas, de acuerdo con la normativa vigente, en esta situación de aprendizaje utilizaremos (dejar solo las que correspondan ):

• Programas de refuerzo del aprendizaje.

• Programas de profundización.

• Apoyo dentro del aula por PT, AL, personal complementario u otro personal.

• Programas específicos para el tratamiento personalizado del alumnado NEAE.

• Atención educativa al alumnado por situaciones de hospitalización o de convalecencia domiciliaria.

• Flexibilización de la escolarización para el alumnado de altas capacidades.

• Escolarización en un curso inferior al correspondiente por edad del alumnado de incorporación tardía en el sistema educativo.

• Atención específica para el alumnado que se incorpora tardíamente y presenta graves carencias en la comunicación lingüística.

• Programas de adaptación curricular:

o Adaptación curricular de acceso.

o Adaptaciones curriculares significativas.

o Adaptaciones curriculares para alumnado con altas capacidades intelectuales.

Principio 3 Proporcionar múltiples formas de implicación

Pauta 7. Proporcionar opciones para el interés

Doble página inicial:

• El Dato

• Objetivo en Acción

• ODS.

Actividades competenciales:

• ¿Qué ocurre si mido con unidades distintas?

• ¿Puedes medir un metro con tu cuerpo?

• Mi vida en centímetros

Aprendizaje cooperativo:

• «Asamblea de ideas», para la sección ¿Cómo lo ves?

• «Comprobamos», para resolver problemas

ADAPTACIONES DUA

Principio 1: Proporcionar múltiples formas de representación

Pauta 1. Proporcionar opciones para la percepción

Versión digital de la unidad. Recursos digitales de la unidad:

• Vídeos:

o Te lo cuento en un momento

o Cálculo mental

• Esquema problemas aritméticos de:

o De cambio

o De grupos iguales

o De igualación

o De comparación

Actividad «Lo resuelvo sin problema: Hago un esquema», donde se realiza un esquema para organizar los datos.

Principio 2: Proporcionar múltiples formas de Acción y Expresión

Pauta 4. Proporcionar opciones para la acción física

Recursos digitales de la unidad:

• Actividades interactivas.

• Regletas.

• Geoplano. Recursos de aula:

• Policubos. Recursosmanipulativos:

• Clips.

• Cinta métrica.

• Regla.

Aclaraciones al margen Imágenes reales en la unidad Recursos de aula: Murales.

Aprendizajes esenciales a través de actividades asociadas a múltiples procesos cognitivos:

• Expresar oralmente y/o por escrito.

• Unir

• Convertir

• Comprobar

• Transformar.

• Argumentar Recursos de aula:

• Policubos. Recursosmanipulativos:

• Clips.

• Cinta métrica.

• Regla.

Portfolio:

• ¿Qué he aprendido?

• ¿Cómo he aprendido?

• Autoevaluación interactiva

Doble página inicial: El dato Recurso digital: Lo esencial Actividades competenciales de la unidad Objetivo en Acción

Sigue el hilo Esquema de la unidad Organizadores gráficos

Primaria. Matemáticas 3. Situación de aprendizaje 9

Herramienta IN.ON

Pauta 8. Proporcionar opciones para sostener el esfuerzo y la persistencia

Pauta 2. Proporcionar opciones para el lenguaje, expresiones, matemáticas y símbolos

Pauta 5. Proporcionar opciones para la expresión y la comunicación

Pauta 9. Proporcionar opciones para la autorregulación

Pauta 3. Proporcionar opciones para la comprensión

Pauta 6. Proporcionar opciones para las funciones ejecutivas

7.VALORACIÓN DE LO APRENDIDO

PROCEDIMIENTOS DE EVALUACIÓN DEL APRENDIZAJE

CRITERIOS DE EVALUACIÓN INSTRUMENTOS DE OBSERVACIÓN RÚBRICAS

1.1.a. Reconocer de forma verbal o gráfica , problemas de la vida cotidiana, comprendiendo las preguntas planteadas a través de diferentes estrategias o herramientas, incluidas las tecnológicas, y comenzar a interpretar mensajes verbales, escritos ovisuales.

-Pruebas. -Intervenciones en clase: exposición oral.

-Cuaderno del alumnado.

-Trabajos de investigación. (Registros y/o Rúbricas)

Insuficiente (IN) Del 1 al 4 Suficiente (SU) Del 5 al 6 Bien (BI) Entre el 6 y el 7 Notable (NT) Entre el 7 y el 8 Sobresaliente (SB) Entre el 9 y el 10

Apenas reconoce, de forma verbal o gráfica, problemas de la vida cotidiana, muestra muchas dificultades para comprender las preguntas planteadas a través de diferentes estrategias o herramientas, incluidas las tec nológicas, así como para comenzar a interpretar mensajes verbales, escritos ovisuales.

Reconoce, con ayuda y/o algunas dificultades, de forma verbal o gráfica, problemas de la vida cotidiana, muestra igualmente algunas dificultades para comprender las preguntas planteadas a través de diferentes estrategias o herramientas, incluidas las tecnológicas, así como para comenzar a interpretar mensajes verbales, escritos ovisuales.

Reconoce, adecuadamente y con bastante acierto, de forma verbal o gráfica, problem as de la vida cotidiana, comprendiendo algunas preguntas planteadas a través de diferentes estrategias o herramientas, incluidas las tecnológicas, y comienza a interpretar mensajes verbales, escritos ovisuales.

Reconoce, con soltura y acierto, de forma ve rbal o gráfica, problemas de la vida cotidiana, comprendiendo las preguntas planteadas a través de diferentes estrategias o herramientas, incluidas las tecnológicas y comienza a interpretar mensajes verbales, escritos ovisuales.

Reconoce, a la perfección,de forma verbal o gráfica, problemas de la vida cotidiana, comprendiendo las preguntas planteadas a través de diferentes estrategias o herramientas, incluidas las tecnológicas, y comienza a interpretar mensajes verbales, escritos ovisuales.

2.1.a. Comenzar a comparar y a emplear diferentes estrategias para resolver un problema de forma pautada, implicándose en la resolución.

3.2.a. Ejemplificar problemas sobre situaciones cotidianas que se resuelven matemáticamente, comenzando a plantear preguntas y avanzando posibles conclusiones

-Pruebas.

-Intervenciones en clase: exposición oral.

-Cuaderno del alumnado.

-Trabajos de investigación. (Registros y/o Rúbricas)

-Pruebas.

-Intervenciones en clase: exposición oral y participación en trabajos cooperativos

-Cuaderno del alumnado.

-Trabajos de investigación.

(Registros y/o Rúbricas)

Rara vez compara empleadiferentes estrategias para resolver un problema de forma pautada implicándose en la resolución.

Comienza a comparar y emplear, con ayuda y/o algunas dificultades, diferentes estrategias para resolver un problema de forma pautada implicándose en la resolución.

Comienza a emplear, adecuadamente y con bastante acierto, diferentes estrategias para resolver un problema de forma pautada implicándose en la resolución.

Comienza a comparar y a emplear, con soltura y acierto, diferentes estrategias para resolver un problema de forma pautada, implicándose por completo en la resolución.

Comienza a comparar y a emplear, con rigor, diferentes estrategias para resolver un problema de forma pautada, implicándose en todo momento en la resolución.

No suele ejemplificar problemas sobre situaciones cotidianas que se resuelven matemáticamente ni comienza a plantear preguntas o avanzaposibles conclusiones

Ejemplifica, con ayuda y/o algunas dificultades, problemas sobre situaciones cotidianas que se resuelven matemáticamente y comienza a plantear preguntas oavanza posibles conclusiones

Ejemplifica, adecuadamente y con bastante acierto, problemas sobre situaciones cotidianas que se resuelven matemáticamente, comenzando a plantear preguntas oavanzando posibles conclusiones.

Ejemplifica, con soltura y acierto, problemas sobre situaciones cotidianas que se resuelven matemáticamente, comenzando a plantear preguntas oavanzando posibles conclusiones

Ejemplifica, ampliamente y con rigor, problemas sobre situaciones cotidianas que se resuelven matemáticamente, comenzando a plantear preguntas y avanzando posibles conclusiones.

a automatizar situaciones sencillas de la vida cotidiana que se realicen paso a paso o sigan una rutina, utilizando de forma pautada principios básicos del pensamiento computacional, realizando procesos simples en formato digital.

4.1.a.

-Pruebas.

-Intervenciones en clase: exposición oral y actitud en clase.

-Cuaderno del alumnado.

-Trabajos de investigación. (Registros y/o Rúbricas, entre ellas, para evaluar el uso de las TIC y las TAC.)

Apenas comienza a automatizar situaciones sencillas de la vida cotidiana que se realicen paso a paso o sigan una rutina ni utiliza de forma pautada principios básicos del pensamiento computacional, realizando procesos simples en formato digital

Muestra grandes dificultades para iniciarse en el

Comienza a automatizar, con ayuda y/o algunas dificultades, situaciones sencillas de la vida cotidiana que se realicen paso a paso o sigan una rutina. utilizando de forma pautada principios básicos del pensamiento computacional, realizando procesos simples en formato digital

Se inicia, con ayuda y/o algunas dificultades, en el

Comienza a automatizar, adecuadamente y con bastante acierto, situaciones sencillas de la vida cotidiana que se realicen paso a paso o sigan una rutina, utilizando de forma pautada principios básicos del pensamiento computacional realizando procesos simples en formato digital

Se inicia, adecuadamente y con bastante

Comienza a automatizar, con soltura y acierto, situaciones sencillas de la vida cotidiana que se realicen paso a paso o sigan una rutina, utilizando de forma pautada principios básicos del pensamiento computacional, iniciándose en procesos simples en formato digital.

Se inicia, con soltura y acierto, en el manejo de las

Comienza a automatizar, por completo, situaciones sencillas de la vida cotidiana que se realicen paso a paso o sigan una rutina, utilizando de forma pautada y con acierto principios básicos del pensamiento computacional, realizando procesos simples en formato digital.

Se inicia, ampliamente y con precisión, en el

Primaria. Matemáticas 3. Situación de aprendizaje 9

Comenzar

4.2.a. Iniciarse en el manejo de las herramientas

-Pruebas. -Intervenciones en clase.

adecuadas en el proceso de resolución de problemas.

5.1.a. Comenzar a realizar conexiones entre los diferentes elementos matemáticos, aplicando conocimientos y experiencias propias, iniciando la aplicación y gestión matemática en su contexto cotidiano.

-Trabajos de investigación. (Registros y/o Rúbricas para evaluar el uso de las TIC y las TAC.)

-Pruebas.

-Intervenciones en clase: exposición oral.

-Cuadernodel alumnado.

-Trabajos de investigación. (Registros y/o Rúbricas)

manejo de las herramientas en el proceso de resolución de problemas.

Muestra bastantes dificultades para comenzar a realizar conexiones entre los diferentes elementos matemáticos , le cuesta aplicar conocimientos y experiencias propias, y muestra dificultades para iniciand o la aplicación y gestión matemática en su contexto cotidiano

manejo de las herramientas en el proceso de resolución de problemas.

Comienza a realizar, con ayuda y/o algunas dificultades, conexiones entre los diferentes elementos matemáticos , con alguna dificultad aplica conocimientos y experiencias propias, iniciando la aplicación y gestión matemática en su contexto cotidiano

acierto, en el manejo de las herramientas en el proceso de resolución de problemas.

Comienza a realizar, adecuadamente y con bastante acierto, conexiones entre los diferentes elementos matemáticos, aplicando conocimientos y experiencias propias , iniciando la aplicación y gestión matemática en su contexto cotidiano

herramientas adecuadas en el proceso de resolución de problemas.

Comienza a realizar,con soltura y acierto, conexiones entre los diferentes elementos matemáticos, aplicando conocimientos y experiencias propias iniciando la aplicación y gestión matemática en su contexto cotidiano

manejo de las herramientas adecuadas en el proceso de resolución de problemas.

Comienza a realizar, a la perfección, conexiones entre los diferentes elementos matemáticos, aplicando conocimientos y experiencias propias, iniciando correctamente la aplicación y gestión matemática en su contexto cotidiano.

5.2.a. Comenzar a identificar situacio nes en contextos diversos, reconociendo las conexiones entre las matemáticas y la vida cotidiana, interpretando la información gráfica de diferentes medios.

7.1.a. Reconocer y comenzar a identificar las emociones propias al abordar nuevos retos matemáticos, pidiendo ayuda solo cuando sea necesario y mostrando autoconfianza y perseverancia en el control de sus emociones.

7.2.a. Expresar y mostrar actitudes positivas ante nuevos retos matemáticos tales como el esfuerzo y la flexibilidad, valorando el error como una oportunidad de aprendizaje, superando la frustración y desarrollando actitudes participativas.

-Pruebas.

-Intervenciones en clase: exposición oral.

-Cuadernodel alumnado.

-Trabajos de investigación. (Registros y/o Rúbricas)

Rara vez identifica situaciones en contextos diversos ni reconoce las conexiones entre las matemáticas y la vida cotidiana y muestra bastantes dificultades para interpretar la información gráfica de diferentes medios

Comienza a identificar, con ayuda y/o algunas dificultades, situaciones en contextos diversos, reconociendo las conexiones con la vida cotidiana interpretando con alguna dificultad la información gráfica de diferentes medios.

Comienza a identificar, adecuadamente y con bastante acierto, situaciones en contextos diversos, reconociendo las conexiones entre las matemáticas y la vida cotidiana interpretando la información gráfica de diferentes medios

Comienza a identificar, con soltura y acierto, situaciones en contextos diversos, reconociendo las conexiones entre las matemáticas y la vida cotidiana, interpretando la información gráfica de diferentes medios.

Comienza a identificar, sobradamente y en todo momento, situaciones en contextos diversos, reconociendo las conexiones entre las matemáticas y la vida cotidiana, interpretando con rigor la información gráfica de diferentes medios.

-Cuaderno del alumnado e intervenciones en clase (Registro, Rúbrica y/o Diana para evaluar las emociones)

Muestra bastantes dificultades para reconocery comenzar a identificar las emociones propias al abordar nuevos retos matemáticos pidiendo ayuda solo cuando sea necesario y mostrando autoconfianza y perseverancia en el control de sus emociones.

Reconoce y comienza a identificar, con ayuda y/o algunas dificultades, las emociones propias al abordar nuevos retos matemáticos, pidiendo ayuda solo cuando sea necesario y mostrando autoconfianza y perseverancia en el control de sus emociones.

Reconoce y comienza a identificar, adecuadamente y algo de soltura, las emociones propias al abordar nuevos retos matemáticos, pidiendo ayuda solo cuando sea necesario y mostrando autoconfianza y perseverancia en el control de sus emociones.

Reconoce y comienza a identificar, con soltura, las emociones propias al abordar nuevos retos matemáticos, pidiendo ayuda solo cuando sea necesario y mostrando autoconfianza y perseverancia en el control de sus emociones.

Reconoce y comienza a identificar, a la perfección, las emociones propias al abordar nuevos retos matemáticos, pidiendo ayuda solo cuando sea necesario y mostrando autoconfianza y perseverancia en el control de sus emociones.

-Intervenciones en clase (Registro, Rúbrica y/o Diana para evaluar hábitos personales, la actitud en clase y la autonomía personal)

Apenas expresa y muestra actitudes positivas ante nuevosretos matemáticos tales como el esfuerzo y la flexibilidad, valorando el error como una oportunidad de aprendizaje, superando la frustración y desarrollando actitudes participativas.

Expresa y muestra, con ayuda y/o algunas dificultades, actitudes positivas ante nuevos retos matemáticos tales como el esfuerzo y la flexibilidad, valorando el error como una oportunidad de aprendizaje, superando la frustración y desarrollando actitudes participativas.

Expresa y muestra, adecuadamente y algo de soltura, actitudes positivas ante nuevos retos matemáticos tales como el esfuerzo y la flexibilidad, valorando el error como una oportunidad de aprendizaje, superando la frustración y desarrollando actitudes participativas.

Expresa y muestra, con soltura, actitudes positivas ante nuevos r etos matemáticos tales como el esfuerzo y la flexibilidad, valorando el error como una oportunidad de aprendizaje, superando la frustración y desarrollando actitudes participativas.

Expresa y muestra, en todo momento , actitudes positivas ante nuevos retos matemáticos tales como el esfuerzo y la flexibilidad, valorando el error como una oportunidad de aprendizaje, superando la frustración y desarrollando actitudes participativas.

Primaria. Matemáticas 3. Situación de aprendizaje 9

8.1.a. Participar y comenzar a colaborar respetuosamente en el trabajo en equipo, comunicándose adecuadamente, respetando la diversidad del grupo y estableciendo relaciones saludables basadas en la igualdad y la resolución pacífica de conflictos, afianzando la autoconfianza en relaciones vividas en entornos coeducativos.

-Intervenciones en clase (Registro, Rúbrica y/o Diana para evaluar la actitud en clase y la participación en trabajos cooperativos)

Muestra grandes dificultades para participar y comenzar a colaborar respetuosamente en el trabajo en equipo, comunicándose ade cuadamente, respetando la diversidad del grupo y estableciendo relaciones saludables basadas en la igualdad y la resolución pacífica de conflictos, afianzando la autoconfianza en relaciones vividas en entornos coeducativos.

Participa y comienza, con ayuda y/o algunas dificultades, a colaborar respetuosamente en el trabajo en equipo, comunicándose adecuadamente y respetando la diversidad del grupo y estableciendo relaciones saludables basadas en la igualdad y la resolución pacífica de conflictos, afianzando la autoconfianza en relaciones vividas en entornos coeducativos

Participa y comienza, adecuadamente y con naturalidad, a colaborar respetuosamente en el trabajo en equipo, comunicándose adecuadamente y respetando la diversidad del grupo y estableciendo relaciones saludables basadas en la igualdad y la resolución pacífica de conflictos, afianzando la autoconfianza en relaciones vividas en entornos coeducativos

Participa y comienza, siempre y con naturalidad, a colaborar respetuosamente en el trabajo en equipo, comunicándose adecuadamente, respetando la diversidad del grupo y estableciendo relaciones saludables basadas en la igualdad y la resolución pacífica de conflictos, afianzando la autoconfianza en relaciones vividas en ent ornos coeducativos

Participa y comienza, siempre y con total naturalidad, a colaborar respetuosamente en el trabajo en equipo, comunicándose adecuadamente, respetando en todo momento la diversidad del grupo y estableciendo relaciones saludables basadas en la igualdad y la resolución pacífica de conflictos, afianzando la autoconfianza en relaciones vividas en entornos coeducativos.

8.2.a. Adoptar alguna decisión en el reparto de tareas, respetando las responsabilidades individuales asignadas y comenzando a emplear estrategias sencillas de trabajo en equipo dirigidas a la consecución de objetivos compartidos y a desarrollar una escucha activa.

-Intervenciones en clase (Registro, Rúbrica y/o Diana para evaluar la actitud en clase y la participación en trabajos cooperativos)

Rara vez adopta alguna decisión en el reparto de tareas, respetando las responsabilidades individuales asignadas y comenzando a emplear estrategias sencillas de trabajo en equipo dirigidas a la consecución de objetivos compartidos y a desarrollar una escucha activa.

Adopta, con ayuda y/o algunas dificultade, alguna decisión en el reparto de tareas, respetando las responsabilidades individuales asignadas y comenzando a emplear estrategias sencillas de trabajo en equipo dirigidas a la consecución de objetivos compartidos y a desarrollar una escucha activa.

Adopta, adecuadamente y con naturalidad, alguna decisión en el reparto de tareas, respetando las responsabilidades individuales asi gnadas y comenzando a emplear estrategias sencillas de trabajo en equipo dirigidas a la consecución de objetivos compartidos y a desarrollar una escucha activa.

Adopta, siempre y con naturalidad, alguna decisión en el reparto de tareas, respetando las resp onsabilidades individuales asignadas y comenzando a emplear estrategias sencillas de trabajo en equipo dirigidas a la consecución de objetivos compartidos y a desarrollar una escucha activa

EVALUACIÓN VALORACIÓN MEDIDAS DUA PARA LA DIVERSIDAD

Adopta, siempre y con total naturalidad, alguna decisión en el reparto de tareas, respetando las responsabilidades individuales asignadas y comenzando a emplear estrategias sencillas de trabajo en equipo dirigidas a la consecución de objetivos compartidos y a desarrollar una escucha activa.

Las medidas DUA para la atención a la diversidad se valorarán tras su puesta en práctica con el alumnado o el grupo clase suj eto de las mismas, valorando la efectividad de estas. Esta valoración tendrá como consecuencia el mantenimiento de las medidas adoptadas en caso de valoración positiva o la modificación o ajuste de las medidas implementadas cuando estas no hubiesen tenido la efectividad esperada.

NIVEL DESEMPEÑO COMPETENCIAL

El nivel de desempeño competencial se obtendrá a partir de la valoración de los criterios de evaluación, como referentes del grado de desempeño de las competencias específicas. Estas, nos llevan, a su vez, a una valoración del nivel de desarrollo de las competencias clave, a través de su conexión con los descriptores operativos del perfil competencial de cada uno de los ciclos.

PROCEDIMIENTOS DE EVALUACIÓN DE LA PRÁCTICA DOCENTE

Indicadores

Planificación:

• La situación de aprendizaje se ha contextualizado adecuadamente y ha sido motivado ra para el alumnado.

• Se han contemplado las competencias específicas y los criterios de evaluación adecuados a esta situación de aprendizaje.

• Se han contemplado los saberes básicos necesarios para el desarrollo de la situación de aprendizaje.

• Se ha realizado una planificación temporal con flexibilidad que ha permitido el desarrollo de la concreción curricular prevista.

• Se han establecido instrumentos de evaluación que han permitido hacer el seguimiento del progreso de aprendizaje del alumnado y comprobar en qué medida ha alcanzado las competencias y criterios de evaluación previstos.

• En el proceso de evaluación se ha posibilitado la autoevaluación del alumnado para que tome conciencia de sus fortalezas y sus ámbitos de mejora.

Instrumentos

1. Escala de valoración para la autoevaluación de la práctica docente.

2. Registro-Diana para la autoevaluación del profesorado: planificación.

3. Registro para la autoevaluación del profesorado: motivación del alumnado.

4. Registro para la autoevaluación del profesorado: desarrollo de la metodología.

5. Registro para la autoevaluación del profesorado: seguimiento y evaluación del proceso de enseñanza-aprendizaje.

6. Lista de verificación y mejora para la evaluación de las situaciones de aprendizaje.

Primaria. Matemáticas 3. Situación de aprendizaje 9

Proceso de enseñanza-aprendizaje:

• Se conectan los aprendizajes que va adquiriendo el alumnado con situaciones de vida próximas a este para que pueda extrapolar lo aprendido.

• Además del libro de texto se ponen en juego otros soportes y recursos que facilitan los aprendizajes previstos con el alumnado.

• Se ponen en juego diversidad de procesos cognitivos en la línea planteada en la taxonomía de Bloom.

• La interacción y la participación activa del alumnado en los procesos de aprendizaje y en la resolución de las situaciones de aprendizaje es una constante en el aula.

• La atención a la diversidad es un elemento que siempre es atendido en clase siguiendo los principiosy pautas DUA, así como el establecimiento de medidas generales o específicas para el alumnado que lo precisa.

• Se ha potenciado el uso de las tecnologías de la información y la comunicación.

• Se han utilizado estrategias de pensamiento y organizadores gráficos que permiten al alumnado comprender mejor los aprendizajes propuestos.

• Se ha ido informando al alumnado de sus aciertos yfortalezasy se le ha prestado la ayuda necesaria ante las dificultades encontradas.

Proceso de evaluación:

• El alumnado y sus familias conocen de antemano los procedimientos e instrumentos de evaluación que se van a utilizar.

• El alumnado dispone de actividades y herramientas que le permiten autoevaluarse y conocer sus puntos fuertes y sus ámbitos de mejora.

• La evaluación es coherente con las metodologías y las situaciones de aprendizaje propuestas.

• Se han desarrollado actividades suficientes para que el alumnado consiga los criterios de evaluación y las competencias específicas previstas.

• Los criterios de calificación están consensuados por el Equipo de ciclo, son conocidos por el alumnado y las familias y responden al grado de logro de los criterios de evaluación y las competencias específicas.

• Se han tenido en cuenta los principios y pautas DUA para el procedimiento de evaluación seguido.

• Los resultados de evaluación han sido…

Propuestas de mejora para la unidad de programación o situación de aprendizaje siguiente

Primaria. Matemáticas 3. Situación de aprendizaje 9