Muestra Física 2 Bachillerato

Índice

DE APRENDIZAJE

Desafíos que dejan huella

• Los campos ocultos

• ¿Estás en la onda?

• Qué bien me suena

U nidad inicial

10

M étodos y lenguajes de la ciencia 16

Más allá de las fórmulas matemáticas

1. Naturaleza de la ciencia

2. El método científico

3. Los lenguajes de la ciencia Estrategias de resolución de problemas

1 Campo gravitatorio 38

Física, tecnología y sociedad

1. Campo gravitatorio

2. Trabajo

3. El campo gravitatorio es conservativo

4. Potencial y energía potencial de una masa puntual

5. Campo gravitatorio de la Tierra

6. Consideraciones energéticas

7. Órbitas.

8. Limitaciones de la teoría de la gravedad de Newton

9. La teoría general de la relatividad Estrategias de resolución de problemas

2 Campo electrostático 70

Coulomb, desde París con admiración

1. Naturaleza eléctrica de la materia

2. Campo electrostático

3. Potencial eléctrico

4. Consideraciones energéticas

5. Flujo del campo eléctrico

6. Teorema de Gauss

7. Aplicaciones del teorema de Gauss

8. Campo y potencial en conductores eléctricos

9. Comparación entre el campo electrostático y el gravitatorio

Estrategias de resolución de problemas

3 Interacción magnética

De la casualidad a la Revolución Industrial

1. Fuerza magnética sobre una partícula cargada

2. Magnetismo en la tecnología

3. Fuerza magnética sobre distintos elementos de corriente

4. Creación del campo magnético

5. Ley de Ampère

6. Fuerzas entre elementos de corriente

TIC. Geogebra

Estrategias de resolución de problemas

4 Inducción magnética

Tesla, el genio que iluminó el mundo

1. Flujo del campo magnético

2. Inducción de una fuerza electromotriz

3. Dispositivos de corriente alterna

4. Autoinducción e inducción mutua

Estrategias de resolución de problemas

5 Movimiento ondulatorio

La contaminación acústica

1. Movimiento oscilatorio

2. Onda, pulso y tren de ondas

3. Ondas armónicas

4. Energía del movimiento ondulatorio

5. Ondas sonoras

TIC. Simuladores de ondas

Estrategias de resolución de problemas

6 Fenómenos ondulatorios

La energía undimotriz

1. Principios fundamentales

2. Reflexión, refracción y difracción

3. Interferencias

4. Ondas estacionarias

5. Efecto Doppler

TIC. Fenómenos ondulatorios en una cuerda. Ondas estacionarias

Estrategias de resolución de problemas

7 Ondas electromagnéticas

La contaminación lumínica

1. Síntesis electromagnética de Maxwell

134

100

2. Origen de las ondas electromagnéticas (OEM). Espectro electromagnético

3. Emisión, transmisión y detección de OEM

4. Naturaleza de la luz

5. Reflexión y refracción de la luz

6. Interferencia y difracción

7. Polarización, dispersión y esparcimiento

8. El láser y sus aplicaciones

TIC. Fenómenos ondulatorios en una cuerda. Ondas estacionarias

TIC. Óptica en la página de Walter-Fendt

Estrategias de resolución de problemas

158

186

220

Los saberes básicos del curso

8 Óptica geométrica

Óptica: una cuestión de perspectiva en la antigua

Grecia

1. Leyes de la óptica geométrica

2. Formación de imágenes mediante sistemas

ópticos

3. El mecanismo óptico de la visión humana

4. Instrumentos ópticos

TIC. Recursos TIC sobre óptica geométrica Estrategias de resolución de problemas

9

258

Energía nuclear

1. Radiactividad

2. Núcleo atómico

3. Energía de enlace nuclear

4. Reacciones nucleares y desintegraciones radiactivas naturales

5. Radiactividad artificial

6. Fisión y fusión

7. Ley de las desintegraciones radiactivas

8. Efectos biológicos y aplicaciones de las radiaciones ionizantes

290 Ciencia en tiempos de guerra

1. Sistemas inerciales. Principio de relatividad de Galileo

2. La búsqueda del éter. Experimento de Michelson-Morley

3. Postulados de la relatividad especial

4. Transformaciones de Lorentz

5. Dinámica relativista

TIC. Laboratorios virtuales para física moderna Estrategias de resolución de problemas

10 Física cuántica

Semiconductores y nuevas tecnologías

1. Radiación del cuerpo negro

2. Efecto fotoeléctrico

3. Naturaleza corpuscular de la luz

4. Modelo atómico de Bohr

5. Extensión del modelo de Bohr

6. Hipótesis de Broglie

7. Física cuántica

8. Láseres

TIC. Laboratorios virtuales para física moderna II Estrategias de resolución de problemas

320

9. Física de partículas

10. Gravitación y cosmología

TIC. Cálculo científico con gnuplot Estrategias de resolución de problemas

Ondas electromagnéticas

LA CONTAMINACIÓN LUMÍNICA

La observación de las estrellas ha sido fundamental en el desarrollo de todas las civilizaciones, así como en muchos de los avances científicos más importantes de la humanidad. Hoy, la falta de protección de nuestro cielo nocturno durante muchos años, el crecimiento sin control y el mal diseño de la luz artificial han supuesto un perjuicio en la observación de nuestros cielos.

Para dar respuesta a este problema, numerosas organizaciones promueven iniciativas para proteger la calidad de nuestros cielos, como la implantación de sistemas de iluminación inteligente que, además de evitar la contaminación lumínica, favorecen el ahorro energético y la reducción de los efectos del cambio climático en áreas protegidas como parques naturales.

En 2007 se celebró en la isla de La Palma la Conferencia Internacional Starlight sobre la Calidad del Cielo Nocturno y el Derecho a Observar las Estrellas. Organizaciones, instituciones e iniciativas participantes redactaron una declaración sobre la defensa del cielo nocturno y el derecho a la luz de las estrellas, y de ahí surgieron las Reservas Starlight, espacios naturales protegidos donde se establece un compromiso por la defensa de la calidad del cielo nocturno y el acceso a la luz de las estrellas. El Observatorio de Calar Alto, en Almería, el más grande del continente europeo, recibirá próximamente esta certificación.

COMPROMISO ODS

1 Elabora un listado de los ODS que pueden verse favorecidos por la reducción de la contaminación lumínica.

2 Folio giratorio en gran grupo. Visualiza el vídeo sobre la meta 17.7 de los ODS y propón una serie de medidas que pueden llevar a cabo los gobiernos y organismos internacionales para alcanzarla.

3 Mesa redonda. Tal como se enuncia en las metas 7.3 y 11.6 de los ODS, de aquí a 2030 se pretende duplicar la tasa mundial de mejora de eficiencia energética y reducir el impacto ambiental negativo per cápita de las ciudades. Relaciona dichas metas con las metas 9.5 y 12.8 e investiga a través de Internet qué áreas de formación (grados, másteres, cursos, etc.) habría que impulsar en tu universidad más cercana para lograr alcanzarlas en el plazo propuesto.

SITUACIÓN DE APRENDIZAJE

MI CANAL DE CIENCIA

Los contenidos y las actividades de esta unidad pueden resultar de utilidad para la realización del proyecto «¿Estás en la onda?» que se plantea en el anexo situado en las páginas iniciales del libro.

vas a descubrir?

En esta unidad

• La contaminación lumínica

1. Síntesis electromagnética de Maxwell

2. Origen de las ondas electromagnéticas (OEM). Espectro electromagnético

3. Emisión, transmisión y detección de OEM

4. Naturaleza de la luz

5. Reflexión y refracción de la luz

6. Interferencia y difracción

7. Polarización, dispersión y esparcimiento

8. El láser y sus aplicaciones

• TIC. Fenómenos ondulatorios en una cuerda. Ondas estacionarias

• TIC. Óptica en la página de Walter-Fendt

• Estrategias de resolución de problemas

En anayaeducacion.es

Para motivarte:

• Vídeo: «Antes de empezar».

Para detección previa de ideas:

• Presentación: «Qué necesitas saber».

Para estudiar:

• Simulaciones: «Interferencia de ondas»

• Presentación: «Para estudiar».

Para evaluarte:

• Autoevaluación final.

• Soluciones de las actividades numéricas. Y, además, toda la documentación necesaria para aplicar las claves del proyecto.

¿Qué

Principios fundamentales

1.1. Las ecuaciones de Maxwell

A finales del siglo xix, James Clerk Maxwell unificó las leyes de la electricidad y el magnetismo en un conjunto de ecuaciones que recogen los resultados experimentales de anteriores científicos como Coulomb, Gauss, Ampère o Faraday. Su aportación se resume en cuatro ecuaciones conocidas como ecuaciones de Maxwell, que relacionan el campo eléctrico, E " , y el campo magnético, B " , con las fuentes que los generan. Recordamos brevemente esas cuatro leyes, que se vieron al estudiar los campos eléctricos y magnéticos.

Ley de Gauss para el campo eléctrico

El flujo del campo eléctrico a través de cualquier superficie cerrada es igual a la carga neta que hay en su interior dividida por la constante dieléctrica del vacío.

E q S d 0f = " " y

De donde se deduce que:

Las fuentes escalares del campo eléctrico son las cargas.

Ley de Ampère

La circulación del campo magnético a lo largo de una línea cerrada es igual a la permeabilidad magnética del vacío, μ0, multiplicada por la intensidad de corriente que atraviesa la superficie limitada por la línea cerrada.

·· BlI d 0n = " " y

Esto significa que:

Las fuentes vectoriales del campo magnético son las corrientes eléctricas.

La ecuación anterior era válida únicamente para corrientes continuas, pero entre las placas de un condensador en un circuito de corriente alterna no hay movimiento de cargas ni, por tanto, corriente eléctrica que atraviese ninguna superficie.

Maxwell generalizó esta ley incluyendo como fuentes del campo magnético a las variaciones del flujo del campo eléctrico con el tiempo.

De este modo, a la corriente I la llamó corriente de conducción, y añadió un término a la ecuación original al que denominó corriente de desplazamiento, de modo que las variaciones del campo eléctrico se convirtieron en fuentes del campo magnético:

La ecuación anterior constituye la expresión de la ley de Ampère generalizada, según la cual:

Las fuentes vectoriales del campo magnético son las corrientes eléctricas y las variaciones del campo eléctrico.

De acuerdo con la ley de Gauss, el flujo del campo eléctrico a través de una superficie cerrada es proporcional a la carga encerrada en ella.

La superficie de la izquierda es atravesada por la corriente I; en el caso del condensador, no hay una corriente de conducción que atraviese la región entre placas.

Leyes de Gauss y Ampère

Ley de Gauss para el campo magnético

El flujo del campo magnético a través de cualquier superficie cerrada es igual a cero. Matemáticamente, se expresa como:

· BS 0 d= " " y

Podemos enunciar la ley de Gauss del campo magnético de tres formas equivalentes:

• El campo magnético no tiene fuentes escalares.

• Las líneas del campo magnético son cerradas.

• No existen los monopolos magnéticos.

Ley de Lenz-Faraday

La fuerza electromotriz inducida en un circuito es igual a la variación del flujo del campo magnético que lo atraviesa y se opone a la variación de flujo que la produce.

Ley de Gauss para el campo magnético

El flujo del campo magnético a través de una superficie cerrada es cero. Entran las mismas líneas que salen.

En esta expresión, la fuerza electromotriz inducida se entiende como el trabajo por unidad de carga que realiza el campo eléctrico inducido por las variaciones de flujo.

Otra manera de expresar esta ley es:

Las fuentes vectoriales del campo eléctrico son las variaciones del campo magnético. Así, del mismo modo que las variaciones del campo eléctrico producen campos magnéticos, las variaciones del campo magnético producen campos eléctricos.

Combinando estas ecuaciones, Maxwell obtuvo una ecuación de onda válida para los campos eléctrico y magnético, deduciendo la existencia de ondas electromagnéticas constituidas por campos eléctricos y magnéticos oscilantes. Además, dedujo que la velocidad de las ondas electromagnéticas en el vacío debía venir dada por la expresión:

c 1 00fn =

donde ε0 es la permitividad eléctrica en el vacío que aparece en la ley de Gauss (ε0 = 8,85 · 10–12 C2 · N–1 · m–2) y μ0, la permeabilidad magnética que aparece en la ley de Ampère (μ0 = 4 · π · 10–7 N · A–2). Al introducir estos valores en la ecuación, la velocidad que aparece no es otra que la velocidad de la luz en el vacío (c = 3 · 108 m · s–1), confirmándose que la luz es una onda electromagnética.

Cuando el flujo del campo magnético que atraviesa la espira varía (en este caso, aumenta), se induce una f. e. m. a lo largo de la espira que equivale al trabajo de un campo eléctrico tangente a la espira sobre las cargas.

Ejercicios

1 ¿Qué tipo de campo rodea una carga en reposo? ¿Y una carga en movimiento?

2 Dibuja las líneas de campo de un dipolo eléctrico. ¿Cuánto vale el flujo del campo eléctrico a través de una superficie cerrada que rodea al dipolo?

3 Círculo de puntos de vista. ¿Cómo cambiaría la ley de Gauss del campo magnético si se descubriese un monopolo magnético (un polo magnético aislado, sin su opuesto)?

4 Comprobamos. Demuestra que la expresión:

f " de la ley de Ampere se puede expresar en unidades de densidad de corriente eléctrica (A · m–2).

Ley de Lenz-Faraday

Origen de las ondas electromagnéticas (OEM). Espectro electromagnético

2.1. Origen de las OEM y circuitos resonantes

Hemos visto que las cargas eléctricas generan campos eléctricos, y que las cargas en movimiento, o corrientes eléctricas, generan campos magnéticos. Pero para producir campos eléctricos y magnéticos oscilantes, que son la base de las ondas electromagnéticas, necesitamos cargas aceleradas.

Una carga o conjunto de cargas acelerado es una fuente de ondas electromagnéticas.

El ejemplo más típico de generación de ondas electromagnéticas es el de una carga eléctrica que oscila con movimiento armónico simple. Esta genera a su alrededor un campo eléctrico variable cuya frecuencia coincide con la del oscilador. La variación del campo eléctrico genera a su vez un campo magnético con idéntica frecuencia. Esta perturbación se propaga a la velocidad de la luz en todas direcciones (figura inferior).

Podemos producir ondas electromagnéticas a partir de un sencillo circuito resonante o circuito LC, compuesto de un generador de corriente alterna, V; una bobina, L, y un condensador, C. Como se muestra en la secuencia de imágenes de la derecha, la energía que almacena el condensador pasa a la bobina cuando se descarga y la corriente inducida en la bobina carga de nuevo el condensador cuando disminuye la intensidad.

En su posición inicial (figura a), la corriente pasa por el condensador hasta cargarlo por completo. Una vez cargado, al cambiar el conmutador, el condensador se descarga aumentando la intensidad en la bobina (b) y produciendo una corriente inducida que se opone al aumento de la intensidad, I. Cuando el condensador se descarga completamente, la corriente en la bobina llega a su valor máximo (c).

Campo eléctrico creado por una carga oscilante.

Al disminuir la corriente en la bobina, se produce una corriente inducida en el mismo sentido que se opone a la disminución de intensidad y carga el condensador con polaridad opuesta (d). Cuando finaliza la carga, el proceso vuelve a comenzar (f, g, h) en sentido opuesto. La carga y descarga del condensador se repetirá de forma cíclica indefinidamente.

2.2. Experiencia de Hertz

En 1887, Heinrich Hertz produjo y detectó ondas electromagnéticas de radiofrecuencias a partir de circuitos oscilantes. El montaje experimental de Hertz recibe el nombre de resonador de Hertz, puesto que reproduce un fenómeno análogo a la resonancia en ondas mecánicas. Para llevar a cabo su experiencia, diseñó un generador de pulsos de alta tensión a partir de una fuente de corriente continua que conectó a dos electrodos muy próximos entre sí (antena emisora). Cuando se conectaba la fuente, las cargas viajaban entre los electrodos cambiando de sentido alternativamente como en un oscilador armónico y generando chispas que se repetían con una determinada frecuencia.

Las cargas aceleradas generaban un campo electromagnético que se propagaba hasta una antena receptora en forma de anillo abierto. Entre los extremos de la abertura, muy próximos entre sí, se inducía una corriente produciendo una secuencia de chispas con la misma frecuencia que las de la antena emisora.

Hertz, con su experimento, sentó las bases de sistemas de comunicación como la radio o la televisión. Posteriormente, demostró que las ondas electromagnéticas también obedecían a fenómenos como la refracción, la reflexión o la difracción y concluyó que la naturaleza de las ondas de radiofrecuencia era la misma que la de las ondas luminosas, diferenciándose únicamente en la frecuencia.

2.3. Fuentes de ondas electromagnéticas

En la naturaleza tenemos ejemplos de producción de OEM:

• Los núcleos atómicos emiten OEM en estados excitados y procesos de fusión nuclear.

• Los electrones que orbitan alrededor del núcleo atómico emiten radiación en forma de OEM cuando pasan de un nivel de energía superior a otro inferior.

• La materia emite OEM debido a la agitación térmica de las partículas cargadas de las que se compone. Es lo que se denomina radiación térmica.

2.4. Características de las OEM

Ecuaciones de onda

Las ondas electromagnéticas están constituidas por un campo eléctrico y otro magnético asociados que oscilan en fase (alcanzan máximos y mínimos al mismo tiempo) según la ecuación de una onda armónica unidimensional. Para una onda que se propaga en el sentido positivo del eje Y, sus ecuaciones son:

E " = E0 · k " · sen (ω · t – k · y)

B " = B0 · i " · sen (ω · t – k · y)

Doble transversalidad

Una OEM es doblemente transversal: las direcciones de oscilación del campo eléctrico y el campo magnético son perpendiculares entre sí y a la dirección de propagación de la onda. El producto vectorial del vector unitario s " , que representa la dirección de propagación de la onda, por el campo eléctrico se relaciona con el campo magnético B " y la velocidad de propagación de la onda mediante la expresión:

s " × E " = c · B "

y

Las OEM se propagan a la velocidad de la luz en dirección perpendicular a los campos eléctrico y magnético.

Resonador de Hertz

Onda electromagnética

Experimento de Hertz para la emisión de ondas electromagnéticas.

electromagnéticas (OEM).

Relación entre amplitudes

La relación entre las amplitudes del campo eléctrico, E0, y el campo magnético, B0, es igual a la velocidad de la luz, c. Matemáticamente:

E0 = c · B0

Velocidad de propagación

Las ondas electromagnéticas no necesitan un medio para propagarse. No obstante, su velocidad de propagación varía según el medio, siendo su valor en el vacío:

c = ·

1 00fn = 3 · 108 m · s –1

donde ε0 es la permitividad eléctrica en el vacío, y μ0, la permeabilidad magnética. Dado que una OEM se puede expresar como una onda unidimensional, su velocidad de propagación también responderá a la ecuación:

c = kT ~ m = = λ · f

Energía de una onda electromagnética

Una OEM transporta energía y cantidad de movimiento. A la energía media transportada por una onda por unidad de tiempo y por unidad de área perpendicular a la dirección de propagación se le denomina intensidad de la onda electromagnética y viene dada por la siguiente expresión:

electromagnético

Por otra parte, y como se verá en temas posteriores, también se puede considerar que una onda electromagnética está constituida por cuantos de energía o fotones cuya energía puede escribirse en función de la frecuencia f de la radiación o de la velocidad de propagación c y la longitud de onda, λ:

E = h · f = h · c m

donde h = 6,63 · 10–34 J · s es la constante de Planck.

2.5. El espectro electromagnético

El espectro electromagnético es el conjunto de OEM ordenadas por frecuencias (o longitud de onda) que comprende toda la radiación electromagnética conocida.

Si analizamos el espectro electromagnético en orden creciente de frecuencias, podemos dividirlo en varias zonas, representadas en la imagen inferior: ondas de radio, microondas, infrarrojo, visible, ultravioleta, rayos X y rayos gamma. Todas ellas viajan por el vacío a la velocidad de la luz y, como ya sabemos, su frecuencia, f, y su longitud de onda, λ, se relacionan mediante la expresión:

λ · f = c

donde c es la velocidad de la luz en el vacío. A continuación, describiremos cada una de estas zonas del espectro.

Ondas de radio

Son las ondas de mayor longitud de onda y menor energía y frecuencia de todo el espectro electromagnético. Su frecuencia va desde unos pocos hercios hasta los 300 MHz y, por tanto, su longitud de onda varía desde

00 n = Radio Microondas Infrarrojo Visible Ultravioleta Rayos X Rayos gamma 103 10–2 10–5 0,3 · 10–6 10–8 10–10 10–12 104 108 1012 1015 1016 1018 1020

Protozoos Moléculas Átomos Núcleo atómico

1 mm hasta 108 m. Se producen de forma natural durante la descarga de un rayo o por algunos objetos astronómicos, como púlsares y quásares. También se pueden generar de forma artificial a partir de antenas y se usan para las comunicaciones, la radiodifusión (30 kHz-30 MHz) y la emisión de señales de TV (30 MHz-300 MHz).

Microondas

Son ondas con una frecuencia entre 300 MHz y 300 GHz, lo que equivale a una longitud de onda entre 1 cm y 1 m. Las microondas de mayor frecuencia y menor longitud de onda se denominan ondas milimétricas. Las microondas se utilizan en la transmisión de señal inalámbrica a través de telefonía móvil, bluetooth y WIFI.

Su frecuencia coincide con la frecuencia de resonancia natural de las moléculas de agua; en los hornos microondas, esta característica se aprovecha para que las moléculas de agua contenidas en los alimentos absorban la radiación y vibren, elevando su temperatura.

Otra aplicación de las microondas se encuentra en los radares meteorológicos, que envían pulsos de microondas para detectar gotas de agua o partículas de hielo presentes en la atmósfera, proporcionando datos sobre la evolución de las precipitaciones.

El estudio de la banda de microondas procedente del espacio también proporciona información valiosa en astronomía. De hecho, la radiación de fondo del universo, cuyo hallazgo fue determinante para la confirmación de la teoría del bigbang, pertenece a la banda de microondas del espectro electromagnético.

Infrarrojo

Su frecuencia va de los 300 GHz a los 385 THz, y su longitud de onda varía desde 1 cm a 780 · 10–9 m (780 nm). Estas ondas electromagnéticas son emitidas por los objetos debido a su temperatura. La luz infrarroja fue descubierta por William Herschel en el siglo xviii al colocar un termómetro de mercurio en distintas zonas del espectro producido por un prisma. Herschel observó que, en la zona no iluminada junto a la franja roja del espectro, la temperatura que medía el termómetro era más alta. De ahí su nombre, por estar situado por debajo de la frecuencia roja del espectro visible.

El infrarrojo suele dividirse en tres regiones espectrales: el infrarrojo cercano, con una longitud de onda entre 1  μm y 5 μm; el infrarrojo medio, entre 5 μm y 25-40 μm, y el infrarrojo lejano, que va desde 25-40 μm a 200-350 μm. La radiación infrarroja se utiliza para detectar objetos en condiciones de oscuridad con equipos de visión nocturna y visores infrarrojos. Las cámaras termográficas nos permiten medir la temperatura superficial del cuerpo para la detección y localización de enfermedades. La radiación infrarroja transmite la señal en los mandos a distancia de los electrodomésticos y es usada en las comunicaciones con fibra óptica. También es usada por los satélites meteorológicos para obtener imágenes de la atmósfera a cualquier hora del día, aunque la superficie terrestre no se encuentre iluminada por la luz del Sol. Y en astronomía, el estudio de atmósferas de estrellas frías, planetas, cometas y nubes moleculares se hace a partir de la radiación infrarroja que emiten.

Regiones por debajo del espectro visible

Desde el radiotelescopio de Arecibo (Puerto Rico), desmantelado en 2020, se descubrieron los primeros planetas extrasolares.

Imagen de radar de un huracán. Se aprecia perfectamente su ojo. Las zonas rojas son las de mayor intensidad de precipitaciones.

Imagen de una cámara termométrica. Las zonas de diferente color corresponden a distintas temperaturas.

La radiación infrarroja es responsable del efecto invernadero en la Tierra. Los gases de efecto invernadero presentes en la atmósfera (vapor de agua, dióxido de carbono, metano, óxido de nitrógeno y ozono) absorben esta radiación y devuelven una parte hacia la superficie, lo que mantiene la temperatura media de la superficie terrestre en valores compatibles con la vida. Pero la actividad humana en el último siglo ha provocado un aumento de emisiones de estos gases, que han incrementado este efecto produciendo lo que conocemos como calentamiento global.

Visible

La radiación que pueden captar nuestros ojos recibe el nombre de luz visible. Comprende desde 780 · 10–9 m (780 nm) hasta 380 · 10–9 m (380 nm) de longitud de onda, o desde 384 · 1012 Hz hasta 789 · 1012 Hz de frecuencia. Es en el espectro visible donde podemos encontrar los distintos colores del arcoíris, subdivididos en 7, cuyas longitudes de onda corresponden, aproximadamente, a los intervalos señalados en la tabla de la derecha.

Ultravioleta

Son ondas de frecuencias comprendidas entre 7,89 · 1014 Hz y 3 · 1016 Hz, es decir, con longitudes de onda entre 380 · 10–9 m y 10 · 10–9 m (380-10 nm).

Radiación visible y de frecuencias superiores

Un arcoíris es un fenómeno que nos ofrece una muestra de todo el espectro visible.

Marcas de seguridad de un billete de cien euros, visibles únicamente bajo luz ultravioleta.

Radiografía frontal realizada en una consulta odontológica. Se distinguen los distintos tejidos de la zona.

Colimador de rayos gamma usado en radioterapia para tratar tumores cerebrales sin cirugía.

Es una radiación invisible de mayor frecuencia que la luz violeta y se subdivide en tres bandas de radiación dependiendo de su longitud de onda o de su frecuencia: la radiación UVA (320-380 nm), denominada radiación ultravioleta cercana, y las radiaciones UVB (280-320 nm) y UVC (100-208 nm), filtradas en su mayor parte por la capa de ozono de la atmósfera terrestre.

La radiación ultravioleta es responsable de la síntesis de algunas vitaminas, como la D; posee acción bactericida y es responsable de la pigmentación de la piel, aunque en dosis elevadas es nociva para los seres vivos y puede provocar quemaduras, daños en la visión y cáncer de piel. Entre sus aplicaciones se encuentran la esterilización, la espectrofotometría, las lámparas fluorescentes de «luz negra» (usadas como trampas para insectos), la autentificación de billetes y antigüedades y la detección de rastros de sustancias orgánicas en investigación forense.

Rayos X

Su frecuencia va desde los 30 · 1015 Hz hasta los 30 · 1018 Hz, y su longitud de onda, desde 10 · 10–9 m hasta 10 · 10–12 m (200-0,01 nm). Esta radiación se produce por la desaceleración o el choque contra la materia de electrones a muy alta velocidad.

Invisibles al ojo humano, los rayos X tienen un alto poder de penetración, lo que los hace útiles en el diagnóstico de enfermedades o lesiones en el esqueleto y en los tejidos blandos o para encontrar defectos en motores, tuberías, vigas, etc. También se usan para explorar mediante difracción la disposición de los átomos en redes cristalinas. Al ser una radiación ionizante, una dosis elevada es muy peligrosa.

Rayos gamma

Los rayos gamma corresponden a una frecuencia superior a 30 · 1018 Hz y longitudes de onda inferiores a 10 · 10–12 m. Se producen cuando un nucleón pasa de un estado excitado a otro de menor energía, en procesos de desintegración radiactiva o en el frenado de electrones. Se generan también en fenómenos astronómicos muy violentos como explosiones de supernovas, colisiones estelares o agujeros negros.

La radiación gamma se suele utilizar para esterilizar material médico. Además, debido su gran poder de penetración en los tejidos, se utiliza en medicina nuclear para realizar algunas pruebas de diagnóstico como la gammagrafía ósea y para erradicar determinados tipos de cáncer dirigiendo un fino haz de esta radiación hacia las células tumorales. No obstante, la radiación gamma es muy ionizante y su poder de penetración es el más elevado de todos, de modo que puede producir cambios moleculares en el ADN y es peligrosa para cualquier forma de vida.

Ejercicios resueltos

1 Una emisora de radio tiene una frecuencia de 92 MHz. Si las ondas electromagnéticas se propagan a la velocidad de la luz c = 3 · 108 m · s –1 :

a) Calcula la longitud de onda de las ondas.

b) Si el campo eléctrico emitido tiene un valor máximo de 9 · 10–3 N · C–1, ¿cuánto vale el campo magnético?

Solución

a) Como c = λ · f, podemos despejar el valor de la longitud de onda y sustituir los datos:

Ejercicios

–==

81 –

λ = , f c 92 10 310 326 ·s ·m ·s m 61

b) Como E0 = c · B0, podemos obtener a partir de esta expresión el valor máximo valor del campo magnético:

31 11 ––== =

Bc E 310 910 310 ·s ·N ·C ·T m 0 0 81

5 Ordena las siguientes ondas electromagnéticas en orden creciente de frecuencias: infrarrojo, luz verde, luz amarilla, rayos X.

6 Si el espectro visible se encuentra en el intervalo de longitudes de onda 380-780 nm, calcula a qué intervalo de frecuencias corresponde.

7 Pienso, me interesa, investigo... Encuentra algún procedimiento experimental para calcular la velocidad de la luz con un horno microondas y una barra de regaliz. Intenta realizar el experimento y analiza si el valor obtenido se aproxima al real.

8 La señal emitida por una antena de telefonía móvil tiene una frecuencia de 800 MHz. ¿Cuánto vale su longitud de onda? (c = 3 · 108 m · s–1).

9 En un determinado medio, tanto la permeabilidad magnética como la permitividad eléctrica valen el doble que en el vacío. ¿A qué velocidad se propaga la luz en ese medio?

10 Una emisora de radio emite a una frecuencia de 98,8 MHz. Sabiendo que la velocidad de la luz vale 3 · 108 m · s –1 y que μ0 = 4 · π · 10–7 N · A–2, calcula:

a) La longitud de onda emitida por la emisora.

b) El valor máximo del campo eléctrico sabiendo que, a cierta distancia, el valor máximo del campo magnético es de 2 · 10–11 T.

c) La intensidad media de la onda.

Emisión, transmisión y detección de OEM

3.1. Antenas

Una antena es un dispositivo usado para transmitir o recibir ondas electromagnéticas. La antena emisora convierte energía eléctrica en ondas electromagnéticas, y la receptora, ondas electromagnéticas en energía eléctrica. Tanto para emitir como para recibir OEM, el dispositivo más sencillo que existe es la denominada antena de dipolo (imagen lateral). Esta consiste en dos conductores metálicos, de igual longitud, conectados a una fuente de corriente alterna. La longitud de la antena debe ser la mitad de la longitud de onda correspondiente a la frecuencia de resonancia del dipolo (L = λ/2).

Cuando las cargas eléctricas comienzan a oscilar, radian un campo electromagnético cuya frecuencia coincide con la de oscilación de las cargas. A esta radiación se la denomina radiación dipolar eléctrica y su intensidad es nula a lo largo del eje de la antena y máxima en las direcciones perpendiculares. Las ondas emitidas pueden detectarse mediante una antena dipolar receptora orientada paralela al campo eléctrico o con una antena en forma de espira perpendicular al campo magnético en la que el flujo magnético induzca una corriente.

Otro tipo de antena muy utilizado hoy en día es la antena parabólica. La antena tiene la forma ideal para recibir la señal del satélite y enfocarla en un convertidor de bajo nivel de ruido (LowNoiseBlock o LNB), dispositivo que se compone de un alimentador que recibe las ondas electromagnéticas y una guía de onda que las transporta hasta una sonda donde se enfocan y convierten en una señal eléctrica.

En la gráfica superior se visualiza la emisión de ondas electromagnéticas por una antena emisora. Cada punto del 1 al 8 corresponde a un valor del voltaje en la antena emisora cuyas cargas positivas y negativas oscilan entre la parte superior e inferior de la antena. En el dibujo solo se muestran las líneas de campo eléctrico; las del campo magnético son perpendiculares a las del campo eléctrico y salen y entran en la página del libro. Al llegar a una antena, la onda hace oscilar a las cargas eléctricas de la antena del mismo modo que oscila el campo.

Emisión de OEM por una antena de dipolo

Antena yagi (izquierda), formada por tres elementos dipolo, y antena parabólica (derecha).

Para que una onda electromagnética transmita información (sonidos, imágenes, etc.), esta debe almacenarse en una onda portadora mediante modulación (como se muestra en el recuadro inferior). Esto permite que se usen para señales de radio, televisión, datos y telefonía móvil, fundamentalmente. Las frecuencias con las que trabajan las antenas se reparten en bandas destinadas a los distintos usos (tabla inferior).

Modulación de la señal

Señal original

Modulación en amplitud

Portadora sin modular

Modulación en frecuencia

La señal original es transportada por la onda portadora en forma de variaciones de amplitud (modulación de amplitud) o de variaciones de frecuencia (modulación de frecuencia).

3.2. Líneas de transmisión y guías de onda

La transmisión de información puede realizarse de forma no guiada, utilizando ondas electromagnéticas en el espacio libre, o de forma guiada, utilizando tanto señales eléctricas como ondas electromagnéticas confinadas en cables.

Líneas de transmisión

Cuando se transporta la información a través de la corriente eléctrica, la variante más simple de línea de transmisión es la línea de pares, consistente en dos hilos conductores paralelos entre sí y separados por un material no conductor. Cuando los conductores están aislados y entrelazados se llama línea de par trenzado. Otra variante es el cable coaxial, que consta de un conductor en el centro rodeado por otro en forma de malla que sirve para apantallar el ruido y evitar pérdidas.

Guías de onda

Si en vez de utilizar una corriente eléctrica se confina en un tubo una onda electromagnética cuya longitud de onda es del orden de las microondas, tenemos una guía de onda. Una guía de onda abierta en uno de sus extremos puede actuar como antena emisora.

Banda Frecuencia Usos

Baja frecuencia 30 kHz-300 kHz

Media frecuencia (MF) 300 kHz-3000 kHz

Alta frecuencia (HF) 3 MHz-30 MHz

Muy alta frecuencia (VHF) 30 MHz-300 MHz

Ultra alta frecuencia (UHF) 300 MHz-3000 MHz (3 GHz)

Radioayuda, señales horarias, radiodifusión en AM.

Radioayuda, señales horarias, radiodifusión en AM.

Radiodifusión onda corta. Radioaficionados.

Radio FM, televisión, telefonía móvil, comunicaciones aéreas, radioaficionados.

TV, comunicación por microondas, telefonía móvil, redes inalámbricas, GPS, bluetooth, radioastronomía, radioaficionados.

El cable de par trenzado (izquierda) se utiliza para la transmisión de señal de telefonía y datos; el coaxial (derecha), para televisión y transmisión de datos a larga distancia.

Súper alta frecuencia (SHF) 3 GHz-30 GHz

Comunicación por microondas, radioastronomía, redes inalámbricas, radares, comunicaciones y TV por satélite.

Existen guías de onda de diferentes materiales y sección rectangular, cuadrada, circular o elíptica. El ejemplo más frecuente es la fibra óptica, utilizada en redes de datos.

Transmisión de OEM

Líneas de pares

Guías de ondas

Naturaleza de la luz

4.1. ¿Qué es la luz?

La naturaleza de la luz ha estado sujeta a lo largo de la historia a numerosas interpretaciones. En la antigua Grecia, algunos filósofos interpretaron la luz como un fluido: para Empédocles, este era emitido por los ojos y «tocaba» los objetos, mientras que para los pitagóricos emanaba de los objetos para ser captado por nuestros ojos.

A pesar de que durante varios siglos se realizaron grandes avances en el campo de la óptica geométrica y en la construcción de instrumentos, hubo que esperar hasta el siglo xvii para que se consolidaran dos propuestas acerca de la naturaleza de la luz: una en la que la luz estaba formada por partículas y otra en la que se comportaba como una onda.

4.2. Teoría corpuscular de la luz

Isaac Newton consideraba que la luz estaba formada por diminutas partículas que salían de los cuerpos luminosos y se desplazaban en línea recta a gran velocidad. Esta teoría era consistente con la propagación rectilínea de la luz, y explicaba la formación de sombras y los fenómenos de la reflexión y de la refracción de la luz.

Para Newton, la reflexión de la luz se producía cuando las partículas que la conformaban chocaban elásticamente contra las superficies reflectantes. En la refracción, para justificar el cambio de dirección de la luz al cambiar de medio, Newton introdujo la hipótesis de que la luz, atraída por los medios más densos, viajaba más rápidamente en el agua o el vidrio que en el aire, hipótesis que con posterioridad se demostró que era falsa. No obstante, debido a que Newton era considerado una autoridad en el ámbito de la ciencia, esta teoría fue la más aceptada hasta principios del siglo xix

4.3. Teoría ondulatoria de la luz

Los padres de esta teoría fueron Christian Huygens y Robert Hooke, para los que la luz eran vibraciones que se propagaban a través de un medio elástico que llenaba el espacio y al que se llamó éter. La teoría de Huygens sobre la propagación de las ondas era capaz de explicar la reflexión y la refracción suponiendo que la luz viaja más lentamente en el vidrio y el agua que en el aire. Además, esta teoría era capaz de explicar fenómenos como la interferencia o la difracción, a los que la teoría corpuscular no había sido capaz de dar explicación. A lo largo del siglo xix, la teoría ondulatoria acabó consolidándose avalada por los experimentos sobre interferencia y difracción de Thomas Young y August Jean Fresnel, respectivamente.

4.4. Dualidad onda corpúsculo

No obstante, la teoría ondulatoria no era capaz de explicar algunas propiedades de la luz, sobre todo aquellas relacionadas con la interacción con la materia. A finales del siglo xix, Maxwell propuso que la luz es una onda electromagnética y Hertz confirmó su hipótesis con la producción y detección experimental de estas ondas. Tras el descubrimiento del efecto fotoeléctrico, consistente en la emisión de electrones por un metal cuando sobre él incide luz, se puso de manifiesto la insuficiencia del modelo ondulatorio para explicar este y otros fenómenos. Max Planck formuló la hipótesis de que la energía emitida en forma de radiación electromagnética lo hace en unidades discretas llamadas cuantos. Casi al mismo tiempo, Einstein introdujo una nueva idea: la doble naturaleza de la luz, una onda electromagnética compuesta de cuantos de energía a los que se denominó fotones. Hoy en día, la física moderna admite que la luz tiene carácter dual, y se manifiesta en su carácter corpuscular y ondulatorio dependiendo del experimento.

Izquierda: para explicar la emisión de electrones por un metal al incidir luz en él (efecto fotoeléctrico) postulamos la existencia de fotones.

Derecha: para explicar las franjas de interferencia observadas cuando la luz pasa a través de una doble rendija, hacemos uso de la luz como

Los padres de las teorías sobre la luz

Dualidad onda corpúsculo

Cristian Huygens (izquierda) e Isaac Newton (derecha), defensores de las teorías ondulatorias y corpuscular de la luz, respectivamente.

onda.

4.5. Medidas de la velocidad de la luz

Tras un amplio debate sobre la finitud de la velocidad de la luz, se realizaron algunos experimentos para poder determinar su valor. Analizaremos el de Römer y el de Fizeau:

Método de Römer

La primera evidencia de que la luz no se propagaba a velocidad infinita vino de la mano del danés Ole Christensen Römer, quien, en 1676, estudió meticulosamente las ocultaciones del satélite Ío por el planeta Júpiter, alrededor del cual orbita. A partir de sus observaciones, predijo que el suceso se produciría de nuevo pero con cierto retraso en la fecha en la que la Tierra se encontraba más alejada del planeta. Así, atribuyó este retraso a la distancia de más recorrida por la luz hasta la nueva posición de nuestro planeta. Finalmente, pudo calcular que la luz tardaba unos 11 minutos en cruzar el radio de la órbita de la Tierra alrededor del Sol, unos 150 millones de km. De este modo, se pudo asignar un valor aproximado a la velocidad de la luz de 2,4 · 108 m/s.

Método de Fizeau

Hipolite Fizeau realizó en 1849 un nuevo experimento para medir la velocidad de la luz de forma más aproximada al valor actual que el método de Römer.

Su dispositivo consistía en una rueda dentada circular de 720 dientes (el ángulo entre dos dientes era de medio grado sexagesimal). Entre los dientes de la rueda se hacía pasar una luz muy brillante que se reflejaba en un espejo situado a 8 633 metros de la rueda, para volver de nuevo hacia la rueda dentada. Con la rueda parada, se veía perfectamente el rayo de vuelta con un telescopio. Pero con la rueda en movimiento, se podía aumentar la velocidad de giro hasta que el rayo encontrase un diente en vez de un hueco y no ver así luz a través del telescopio.

Si esto ocurría, era porque la luz había tardado el mismo tiempo en hacer su viaje de ida y vuelta al telescopio (17 266 m) que la rueda en moverse de un diente al siguiente. Sabiendo que la rueda giraba a 12,6 revoluciones por segundo, se pudo obtener el tiempo que empleaba la luz en recorrer su viaje de ida y vuelta. Y dividiendo el espacio recorrido entre el tiempo empleado se obtuvo un valor para la velocidad de la luz de 313 000 km/s. Medidas más recientes de la velocidad de la luz Medidas recientes de la velocidad de la luz en el vacío sitúan su valor en 299 792 458 m/s, aunque suele aproximarse por 3 · 108 m/s. Este valor se simboliza con la letra c y es una constante universal. En 1983, la Conferencia General de Pesos y Medidas utilizó su valor para la definición del metro, la principal unidad de medida del Sistema Internacional de Unidades: un metro es la distancia que recorre la luz en el vacío en un intervalo de 1/299 792 458 s.

Ejercicios

11 Piensa y comparte en pareja. A partir de medidas más modernas realizadas a partir del experimento de Römer, se sabe que la luz invierte unos 17 minutos en atravesar el diámetro de la órbita terrestre. Calcula a partir de estos datos el valor de la velocidad de la luz en el vacío.

Dato: distancia media Tierra-Sol: 1,5 · 108 km.

12 En la Luna existen hasta 5 espejos colocados por las tripulaciones de las misiones Apolo XI, XIV y XV que reflejan la luz en la misma dirección en la que la reciben. Con ellos se descubrió que la Luna se aleja de nosotros unos 3,8 cm al año. ¿Cuál es la diferencia entre los tiempos medidos dos años consecutivos?

Dato: c = 3 · 108 m · s –1

Fuente luminosa semitransparente Rueda dentada

Si conocemos la diferencia entre las distancias Tierra-Júpiter en dos fechas diferentes, d2 – d1, y el retraso de la ocultación a la mayor de las distancias, ∆t, podemos calcular la velocidad de la luz en el vacío, c, con un simple cálculo: (d2 – d1)/∆t

Reflexión y refracción de la luz

5.1. Rayo luminoso

Para estudiar los fenómenos de reflexión y refracción de la luz, volveremos al concepto de rayo.

Un rayo es una línea imaginaria que representa la dirección en la que se propaga la energía de la onda. Su dirección es perpendicular al frente de onda. En un medio homogéneo, el rayo se propaga en línea recta.

Aunque a veces se aplica erróneamente el concepto de rayo a un haz muy fino (por ejemplo, el rayo láser), debemos tener en cuenta que un rayo no tiene entidad física, sino matemática.

5.2. Índice de refracción

Como hemos visto, la energía radiante se propaga en el vacío con una velocidad c invariable, cuyo valor es de 3 · 108 m/s. Sin embargo, esta velocidad se reduce cuando la luz se propaga en medios distintos del vacío. Para caracterizar un medio desde el punto de vista de la velocidad de propagación de la luz, se usa el índice de refracción, n, de un medio, que se define como el cociente

entre la velocidad de la luz en el vacío, c, y la velocidad de la luz en ese medio, v:

El índice de refracción es adimensional y su valor siempre es mayor que la unidad, puesto que el valor máximo de la velocidad de la luz es el que se alcanza en el vacío.

5.3.

Reflexión de la luz

La reflexión de la luz es el cambio de dirección que experimenta una onda luminosa cuando al incidir en la superficie de separación entre dos medios es devuelta al primer medio.

Si hacemos incidir un haz de rayos paralelos sobre una superficie y, tras la reflexión, los rayos siguen siendo paralelos entre sí, estamos ante una reflexión especular. Si por el contrario, los rayos se reflejan en distintas direcciones, la reflexión se denomina reflexión difusa y suele producirse cuando la luz se refleja en superficies que presentan irregularidades mayores que su longitud de onda.

Tipos de reflexión Medios homogéneos e isótropos

En medios homogéneos e isótropos como el vidrio, la velocidad de la luz es la misma en todos los puntos y en todas las direcciones, por lo que el valor de n es constante.

Si la velocidad varía de unos puntos a otros, el medio es heterogéneo, como la atmósfera terrestre, en la que el índice cambia dependiendo de factores como la densidad o la temperatura.

Si varía con la dirección de propagación estamos en un medio anisótropo, como algunos cristales. Como veremos más adelante, el índice de refracción en algunos medios depende de la longitud de onda.

Todos los rayos del haz se reflejan en la misma dirección, como la luz que incide en un espejo.

La tabla muestra el índice de refracción de algunos medios homogéneos e isótropos. A menor velocidad de la luz en el medio, mayor valor del índice.

Los rayos del haz se reflejan en todas direcciones, como la luz reflejada en el mar, que no ofrece una imagen nítida.

Dado que tanto la reflexión especular como la difusa representan casos extremos de la reflexión, la mayoría de las superficies se encuentran a medio camino y presentan ambos tipos de reflexión en mayor o menor grado. En cualquier caso, e independientemente del tipo de reflexión que se produzca, los rayos luminosos cumplen siempre las leyes de la reflexión:

• El rayo incidente, el rayo reflejado y la normal (línea perpendicular a la superficie reflectante) se encuentran en un mismo plano, llamado plano de incidencia.

• El ángulo de incidencia, t i , y el ángulo de reflexión, t i l , son iguales: t i = t i l

5.4. Refracción de la luz

Se denomina refracción de la luz al cambio de dirección que sufre un haz de luz que incide oblicuamente sobre la superficie de separación entre dos medios de diferente índice de refracción.

La refracción de la luz también obedece a dos leyes fundamentales:

• El rayo incidente, el rayo refractado y la normal se encuentran en el mismo plano, llamado plano de incidencia.

• El ángulo de incidencia, i , y el ángulo de refracción, t r, se relacionan por la siguiente expresión:

n1 · sen t i = n2 · sen t r donde n1 es el índice de refracción del primer medio, y n2, el del segundo medio; t i es el ángulo de incidencia o ángulo que forma el rayo incidente con la normal, y t r, el ángulo de refracción o ángulo que forma el rayo refractado con la normal. Esta ley, demostrada experimentalmente por W. Snell y, de forma independiente, por René Descartes, se conoce como ley de Snell.

Si llamamos v1 y v2 a las velocidades de propagación en el primer medio y en el segundo, respectivamente, las longitudes de onda en cada medio son:

Reflexión en una superficie

Sabiendo que:

y que la frecuencia no varía al cambiar de medio, podemos obtener la relación entre las longitudes de onda y los índices de ambos medios:

El rayo incidente, el reflejado y la normal están en un mismo plano, y el ángulo de incidencia es igual al ángulo de reflexión.

Refracción de un haz láser al pasar de aire a agua. Es importante notar que cuando la luz cambia de medio, la frecuencia se mantiene constante (los átomos absorben y vuelven a emitir la luz con la misma frecuencia).

ii' ii

Rayo incidente Rayo reflejado Normal Rayo incidente Normal Normal Rayo refractado Rayo refractado Rayo incidente

Refracción entre dos medios de índices n1 y n2. Si n1 < n2, el rayo se acerca a la normal. Si n1 > n2, el rayo se aleja de la normal.

Ejercicios resueltos

2 Un rayo luminoso de 4 · 1 014 Hz incide desde el aire (n = 1) hasta un bloque de vidrio (n = 1,5) bajo un ángulo de 30º respecto a la normal. Sabiendo que la velocidad de la luz en el vacío es c = 3 · 108 m · s –1 :

a) Calcula el ángulo de refracción.

b) Calcula la velocidad de propagación, la frecuencia y la longitud de onda en el interior del vidrio.

Solución

a) Para calcular el ángulo de refracción, hacemos uso de la ley de Snell:

ninr ·sen ·sen 12 = t , r 1301 5 ·sen °· sen = t , , r 15 30 033 sen sen° ==

,, r 0331927 arcsen ° == t El rayo se acerca a la normal.

b) El rayo luminoso incide desde un medio con un índice n = 1. Eso quiere decir que en aire viaja a c = 3 · 108 m · s–1. En vidrio, su velocidad será de:

nv c 2 = → , vn c 15 310·m ·s 81 –==

v 210m s 81 –=

Su frecuencia es de 4 · 1 014 Hz tanto en el vidrio como en el aire (recordemos que no cambia al cambiar de medio).

f1 = f2 = 4 · 1 014 Hz

13 Un rayo de luz incide desde un medio de índice de refracción 1,5 a otro de índice de refracción 1,2. Indica cuánto cambia la velocidad de propagación de la luz, la longitud de onda y la frecuencia.

14 Cuando incide luz desde el aire hasta un segundo medio, la longitud de onda cambia de 750 nm a 500 nm. ¿Cuánto vale el índice de refracción del segundo medio?

15 Un haz de luz incide desde el aire a un segundo medio. Si los haces reflejado y refractado forman con la normal 40º y 30º, respectivamente, deduce el índice de refracción del medio.

16 Petición del oyente. ¿Con qué ángulo debe incidir, desde el aire, un rayo luminoso para que al refractase en vidrio (n = 1,5) el ángulo de refracción sea de 30º?

La longitud de onda sí sufrirá cambios, y sus valores serán:

3 Un rayo luminoso de 500 nm de longitud de onda incide desde aire hasta agua con un ángulo de incidencia de 30º. Si el ángulo de refracción vale 22º, calcula el índice de refracción y la longitud de onda de la luz en el segundo medio.

Solución

Para calcular el índice del segundo medio, hacemos uso de la ley de Snell:

Para calcular la longitud de onda, podemos hacer uso de la expresión:

17 Preparar la tarea. Un haz de luz monocromática, de longitud de onda en el aire 6,0 · 10–7 m, incide desde el aire sobre un vidrio plano de índice 1,5 con un ángulo de incidencia de 30°. Por el otro lado del vidrio hay agua (índice 1,33). Determina:

a) El ángulo de refracción en el vidrio (entrada desde el aire) y el ángulo de salida por el agua.

b) La longitud de onda de dicho haz en el agua.

5.5. Ángulo límite y reflexión total

Cuando el índice de refracción del primer medio es mayor que el índice de refracción del segundo, el rayo refractado se aleja de la normal. A medida que el ángulo de incidencia aumenta, el rayo refractado se acerca a la superficie de separación de ambos medios.

Existe un ángulo de incidencia, llamado ángulo límite o ángulo crítico, t i L , para el que la luz refractada emerge rasante o paralela a la superficie de separación de ambos medios ( t r = 90°). Para el ángulo límite se cumplirá entonces:

n1 · sen t i L = n2 · sen 90° sen

Cuando t i > t i L , la luz no se refracta y se produce el fenómeno de reflexión total interna, en el que toda la luz incidente se refleja y es devuelta al primer medio.

La reflexión total es la base del funcionamiento de la fibra óptica, una fibra flexible y transparente de vidrio de sílice y de un grosor algo mayor que un cabello humano. Cuando entra luz en la fibra con un ángulo superior al ángulo límite, se produce reflexión total interna y la luz se propaga por el interior de la fibra sin que se produzcan pérdidas.

La fibra óptica se utiliza en haces de varias fibras para la transmisión de imágenes o información. En el campo de las telecomunicaciones, se usan transmisores ópticos para transformar señales eléctricas en señales ópticas que se envían a través de la fibra. Entre las ventajas de la fibra frente a la línea eléctrica se encuentran la menor atenuación y la ausencia de interferencias electromagnéticas, así como la mayor velocidad de transmisión de datos y ancho de banda (cantidad de información que se puede transmitir por unidad de tiempo).

En medicina se usa como instrumento de exploración y diagnóstico para iluminar y captar imágenes de órganos internos sin necesidad de utilizar la cirugía.

Cuando viajamos por carretera en verano es frecuente observar en la lejanía que el asfalto se comporta como la superficie de un espejo. De hecho, es como si la carretera estuviese mojada y el efecto desaparece en cuanto nos acercamos. Veamos cuál es la explicación física:

En verano, la temperatura del asfalto es muy elevada, por lo que el aire más próximo a la superficie es menos denso y tiene un índice de refracción menor. Imaginemos el aire cercano al asfalto dispuesto en capas de temperatura ascendente e índice de refracción descendente a medida que nos acercamos a la superficie. Cuando un rayo incide en la capa más alta, el ángulo de refracción se convierte en ángulo de incidencia para la siguiente, y así sucesivamente.

De este modo, un rayo luminoso que incida oblicuamente irá aumentando el ángulo que forma con la normal a medida que se acerque a la superficie. Cuando ese ángulo supera al ángulo límite, se produce reflexión total y el rayo es reflejado y devuelto al medio original. De este modo vemos reflejados en el suelo el cielo y algunos objetos cercanos, dando la apariencia de un charco o superficie mojada. Este tipo de fenómenos reciben el nombre popular de espejismos.

Si un rayo incide con un ángulo igual al ángulo límite, sale rasante (a), pero si el rayo supera el ángulo límite no hay luz

refractada y el rayo se refleja (b). A la derecha se observa la reflexión total interna en una guía de metacrilato.

5.6. Refracción en una lámina de vidrio

Uno de los ejemplos más habituales de refracción en vidrio es el de una lámina de caras paralelas. Para analizarlo, supondremos un rayo que incide desde el aire (n = 1) con un ángulo de incidencia t i 1 sobre una lámina de vidrio de índice nv y que se refracta con un ángulo de refracción t r1

Aplicando la ley de la refracción en la primera superficie (aire-vidrio), obtenemos:

1 · sen i 1 = nv · sen t r1

El ángulo de incidencia t i 2 en la segunda cara es igual a t r1 puesto que están delimitados por las normales a ambas superficies y por el rayo en el interior del vidrio (dos ángulos con uno de sus lados paralelos y otro en común son iguales). Aplicando la ley de la refracción en la segunda superficie de separación (vidrio-aire) obtenemos:

Como t r1 = t i 2 → nv · sen t r1 = sen t r2

Como sen t i 1 = nv · sen t r1 → sen t i 1 = sen t r2

De este modo llegamos a la conclusión de que el ángulo de incidencia en la lámina coincide con el de refracción en la segunda cara o ángulo de salida: t i 1 = t r2

A pesar de que el rayo incidente y el refractado en la lámina tienen la misma dirección, se produce un desplazamiento, d, de la trayectoria del rayo en el segundo medio. Para calcular esta desviación partimos de la relación entre la distancia AB recorrida por el rayo en el interior de la lámina y el espesor de la misma.

e = AB · cos t r1

Para hallar la distancia d, acudiremos al triángulo ABC, en el que el ángulo correspondiente al vértice A vale t i 1 –t r1 y de donde podemos obtener la relación:

d = AB · sen ( t i 1 –t r1)

Finalmente, combinando ambas expresiones podemos obtener la desviación d en función del espesor:

cos AB rr e i d sen– 1 1 1

== t t t ak

11 = t

t t ak

cos de r

irsen–1

5.7. Refracción en prismas

Un prisma óptico es un medio transparente limitado por dos superficies planas con una arista común que forman un ángulo α entre sí. Este ángulo se denomina ángulo de refringencia.

De la geometría del prisma (figura inferior derecha) observamos que el ángulo formado por las normales a ambas caras es igual al de refringencia (tiene sus dos lados perpendiculares al de refringencia original).

Del triángulo formado por las normales y el rayo en el interior se deduce que:

La desviación del rayo incidente será la suma de los ángulos de desviación del rayo en cada una de las refracciones:

Casos particulares de refracción

Refracción en un prisma Refracción en una lámina de vidrio

Un caso particular de prisma, utilizado para la fabricación de prismáticos, es el prisma de reflexión total. Este tipo de prisma aprovecha la reflexión total producida al incidir el rayo en la segunda cara con un ángulo superior al ángulo límite. En las figuras de la derecha se muestra la marcha de los rayos en estos prismas.

Ejercicios resueltos

4 Un haz de luz que se propaga por el interior de una fibra óptica (n = 1,5) incide en una de sus paredes. Si en el exterior de la fibra hay aire, con índice n = 1, ¿con qué ángulo debe incidir para que no se pierda luz por transmisión?

Solución

En primer lugar, calcularemos el ángulo límite, que es el ángulo de incidencia que corresponde a un ángulo de refracción de 90º (el rayo sale rasante): ° nin 90 vLsensen = t , i 15 190 ·sen ·sen ° L = , , i 15 1 067 sen L ==

° i 0674181 arcsen L ==

Para ángulos mayores que 41,81º no se produce refracción, sino reflexión total interna, por lo que la luz permanecerá dentro de la fibra.

5 ¿Por qué el fondo de una piscina parece que está más cerca cuando la piscina está llena de agua? Haz un esquema de la situación y justifica la respuesta.

Ejercicios

18 Calcula el índice de refracción de un medio en el que el ángulo límite al pasar al aire es de 38,2º.

19 Un rayo de luz de longitud de onda de 5,46 · 10–7 m se propaga por el aire e incide sobre el extremo de una fibra de cuarzo cuyo índice de refracción es 1,5. Determina la longitud de onda del rayo en la fibra de cuarzo y el ángulo de incidencia a partir del cual el rayo no sale al exterior.

Dato: c = 3 · 108 m · s –1

20 Un rayo de luz blanca incide sobre una de las caras de una lámina planoparalela de vidrio (n = 1,5) de 5 mm de espesor inmersa en aire. Si lo hace con un ángulo de incidencia de 40º, halla el ángulo de refracción en cada una de las caras de la lámina y el tiempo que tarda el rayo en atravesar la lámina.

Solución

Cuando la luz se refleja en el fondo de la piscina, se propaga desde el agua hasta el aire. Al ser el índice de refracción del aire menor que el del agua, el rayo se aleja de la normal.

Rayos refractados

Nuestro ojo percibe la luz refractada como si viniese en línea recta, de modo que, si dibujamos la trayectoria de dos rayos procedentes de un mismo punto del fondo, al pasar del agua al aire, los rayos refractados parecerán venir de un punto situado en un nivel superior, que es donde convergen.

21 Un rayo de luz incide sobre la primera cara de un prisma de vidrio (n = 1,5) de 60º inmerso en aire. Si el ángulo de incidencia es de 45º, calcula el ángulo de refracción en ambas caras del prisma.

22 Veo, pienso, me pregunto... En las costas de latitudes altas, en las que el agua es más fría, se produce un fenómeno óptico llamado fatamorgana, consistente en la observación de barcos y ciudades flotantes. Investiga y busca una explicación a este fenómeno.

Interferencia y difracción

6.1. Interferencia luminosa

Como hemos visto en la unidad anterior, si se combinan dos ondas armónicas de la misma frecuencia y longitud de onda pero diferente fase, la amplitud de la onda resultante depende de la diferencia de fase.

Generalmente, la diferencia de fase ∆ϕ entre dos ondas que se superponen en un punto se puede escribir en términos de la diferencia del camino ∆x recorrido por cada una de ellas desde el foco hasta el punto en el que se superponen:

∆ϕ = π 2 m · ∆x

Si en un punto, la diferencia de fase entre las dos ondas superpuestas es múltiplo entero de 2 · π o la diferencia de camino es múltiplo entero de λ, se produce interferencia constructiva: la amplitud resultante es la suma de las amplitudes y la intensidad es máxima.

Si en un punto, la diferencia de fase entre las dos ondas superpuestas es múltiplo impar de π o la diferencia de camino es múltiplo impar de λ/2, se produce interferencia destructiva: la amplitud resultante es la diferencia de las amplitudes y la intensidad es mínima.

Cuando se superponen dos haces de luz, dado que el número de ondas superpuestas es elevado, se producirán diferencias de fase distintas de unos puntos a otros que se traducirán en variaciones de intensidad luminosa a lo largo de la zona de superposición de ambas ondas, formando franjas o anillos. La energía luminosa se redistribuye al superponerse las ondas de los haces, y mientras que en algunos puntos la intensidad será nula (mínimos) en otras la intensidad será máxima por la suma de amplitudes de las ondas que se superponen (máximos).

Condiciones de interferencia

Siempre que se superponen ondas electromagnéticas se producen interacciones entre ellas, pero para que estos fenómenos sean visibles hace falta que sean permanentes y detectables, para lo que tienen que cumplirse tres condiciones fundamentales:

• Las ondas que se superponen deben tener la misma frecuencia y amplitud.

• Las ondas que se superponen tienen que tener sus campos eléctricos paralelos o que formen entre sí un ángulo muy pequeño.

• Las ondas superpuestas deben ser coherentes, es decir, que la diferencia de fase sea constante en cada punto del espacio con independencia del tiempo transcurrido.

Debido a que se deben cumplir estas condiciones, no es posible observar interferencias en cualquier situación. Dos lámparas que iluminan una misma zona no ofrecen ningún patrón de interferencia porque sus frecuencias son distintas o porque su diferencia de fase cambia a lo largo del tiempo, imposibilitando que los máximos y los mínimos sean permanentes y puedan observarse.

No obstante puede lograrse la interferencia de dos focos coherentes dividiendo el frente de onda procedente de un foco, como hizo Young con su experimento de la doble rendija.

Interferencias en una doble rendija

En este experimento se hace pasar la luz de una fuente puntual por dos rendijas separadas una distancia d. Las dos rendijas se transformarán en dos focos de luz coherente, S y S l, cuya interferencia podemos observar en un punto P de una pantalla situada a una distancia D

Interferencia de dos focos coherentes

Interferencia observada al superponer dos haces de luz coherentes. La energía luminosa se reparte en máximos y mí-

nimos de intensidad, adquiriendo la configuración de franjas (izquierda) o anillos (derecha).

Como se aprecia en la figura inferior, al estar S l más lejos de P que S, los rayos que salgan de esta fuente recorrerán una distancia ligeramente mayor que los de la fuente S l. A la diferencia entre las distancias recorridas por los dos rayos (diferencia de camino) la llamaremos ∆x Ahora, si consideramos la distancia entre rendijas despreciable frente a la distancia a la pantalla (D >> d), podremos afirmar que sen α = tg α = α y aproximar la distancia entre O y O l a D. Así pues:

• Del triángulo SS lO: sen α = α = ∆x/d

• Del triángulo OO lP: tg α = α = x/D Igualando, obtenemos para la diferencia de camino:

∆x = x · D d

Si aplicamos la condición de máximo a la diferencia de camino, obtenemos la posición de los máximos:

∆x = n · λ, con n = 0, 1, 2, 3… x · D d = n · λ → xn d D n m =

Y si aplicamos la condición de mínimo a la diferencia de camino, obtenemos la posición de los mínimos:

∆x = (2 · n + 1) · 2 m , con n = 0, 1, 2, 3…

x · D d = (2 · n + 1) · 2 m → · xn d D 21 2 n m =+ ` j

6.2. Difracción de la luz

Junto a la interferencia, la difracción es uno de los fenómenos que pone de manifiesto la naturaleza ondulatoria de la luz.

La difracción es un fenómeno ondulatorio que ocurre cuando una onda atraviesa una abertura u obstáculo del orden de su longitud de onda y se manifiesta en la observación de máximos y mínimos de intensidad.

Cuando la luz atraviesa una abertura o se encuentra con un obstáculo, todos los puntos alcanzados por la onda luminosa se comportan, basándonos en el principio de Huygens, como focos de ondas secundarias que interfieren entre sí. El tratamiento matemático de la difracción se puede hacer mediante dos aproximaciones distintas. Si la distancia del obstáculo o abertura al foco luminoso y/o a la pantalla es finita, tenemos difracción de Fresnel. Si las distancias son tan grandes como para considerar los rayos que salen de la abertura u obstáculo paralelos, tenemos difracción de Fraunhofer.

Izquierda: difracción de Fresnel en un tornillo pequeño. La sombra no tiene contornos definidos y se observan franjas de interferencia en los bordes.

Derecha: difracción de Fraunhofer de una abertura rectangular. La distribución de máximos y mínimos se extiende más allá de los bordes de la abertura y se observan figuras formadas por franjas de interferencia.

Interferencia producida por doble rendija

Interferencias producidas por una doble rendija. En la pantalla se observan máximos y mínimos distribuidos en franjas.

La intensidad de los máximos disminuye a medida que nos alejamos del máximo central (n = 0).

Difracción por una rendija

Para estudiar la difracción acudiremos al caso más sencillo, una fuente monocromática que pasa a través de una rendija de anchura d, del orden de la longitud de onda. El diagrama de intensidades sobre una pantalla lejana respecto a la anchura de la rendija nos muestra un patrón compuesto por máximos secundarios a ambos lados de un máximo central más ancho.

Si la pantalla está lo suficientemente alejada o la rendija es lo suficientemente estrecha, podemos considerar que los rayos salen de la rendija paralelos. Consideremos 3 rayos que salen con un ángulo φ de los puntos A, B y C, situados, respectivamente, en el extremo superior, en el centro y en el extremo inferior de la rendija. Tanto la distancia AB como la distancia BC valen d/2 y la diferencia de camino correspondiente a esa distancia es:

∆x = d 2 · sen φ

Si se cumple la condición (d/2) · sen φ = λ/2, o lo que es lo mismo, d · sen φ = λ, los rayos que parten de A y B interferirán en oposición de fase (interferencia destructiva) así como los rayos que parten de B y C. Por tanto, todos los pares de rayos que bajo ese mismo ángulo se encuentren a una distancia d/2 interferirán en condición de mínimo. Si aumentamos el ángulo hasta un valor φl que cumpla la condición d · sen φl = 2 · λ, interferirán en condición de mínimo todos aquellos pares de rayos distanciados entre sí d/4, ya que dividiendo entre 4 a izquierda y derecha en la igualdad obtenemos (d/4) · sen φl = λ/2.

Generalizando esta regla encontramos que la condición de mínimo viene dada por la expresión:

d · sen φ = m · λ, donde m = ±1, ±2, ±3,…

La condición no es válida para m = 0, puesto que en el centro de la distribución hay un máximo de intensidad cuya anchura corresponderá a la distancia entre los mínimos correspondientes a m = 1 y m = –1.

Normalmente, no nos interesará la distribución de mínimos más allá de m = ±2 puesto que en la figura de difracción la mayor parte de la intensidad se limita a la parte central.

Si la distancia a la pantalla es D, la posición de los mínimos en la pantalla respecto al máximo central vendrá dada por la expresión:

sen φ = m · dD xm m = → xm = m · d D m , con m = ±1, ±2,…

Difracción por una abertura circular

En el caso de una abertura circular, lo que se observa es una distribución de intensidades llamada disco de Airy, consistente en un máximo central de forma circular rodeado de anillos de intensidad menor a medida que se alejan del centro (figuras de la página siguiente).

El ángulo φ bajo el que se observa el primer mínimo de difracción desde la abertura y que determina el radio del máximo central, se relaciona con la longitud de onda, λ, y con el diámetro, D, de la abertura mediante la expresión:

sen φ = 1,22 · D m

Esta figura de difracción es de suma importancia puesto que implica que de una fuente puntual no vamos a obtener nunca una imagen puntual sino un disco cuya anchura dependerá del diámetro de la abertura.

El poder de resolución de un instrumento óptico, entendido como la capacidad para resolver o mostrar se-

A la izquierda se muestra la distribución de intensidades en la difracción por una rendija. A la derecha, las diferencias de

camino entre rayos que emergen de una rendija. Los pares de puntos A y B, y B y C, están separados entre sí d/2.

Difracción por una rendija

parados objetos que están muy juntos, está limitada por el diámetro de la abertura. El límite de resolución es la distancia mínima a la que pueden estar dos imágenes para poder visualizarse por separado. Para el caso de una abertura circular, esta distancia es aquella en la que coinciden el centro del máximo de una de las imágenes con

el primer mínimo de la otra; es decir, la distancia entre sus centros debe ser mayor que el radio angular de cada imagen. Es por ello por lo que los telescopios astronómicos usan grandes lentes o espejos en su objetivo para, además de captar más luz, aumentar su poder resolutivo al disminuir el tamaño de las figuras de difracción.

Disco de Airy

Izquierda: disco de Airy; el ángulo φ determina el radio del máximo central. Derecha: imágenes obtenidas a través de una abertura circular de dos focos puntuales muy próximos.

Ejercicios resueltos

6 Calcula la distancia entre dos máximos consecutivos (interfranja) observados en el patrón interferencial de una doble rendija de Young, si las rendijas se encuentran a 2 m de la pantalla, están separadas entre sí 1 mm y se iluminan con luz de 500 nm.

Solución

Si aplicamos la condición de máximo podemos encontrar su posición:

xm = m · 0,01 m, con n = 0, 1, 2…

Para encontrar la interfranja bastará con obtener la distancia entre dos máximos consecutivos:

i = xm+1 – xm = 0,01 m = 1 cm

7 Para averiguar la anchura de una rendija se hace incidir luz de 500 nm en ella y se observa el patrón

Ejercicios

23 Sumamos. ¿Por qué los faros de un vehículo no producen interferencias al iluminar una pared blanca?

24 ¿Qué te hace decir eso? ¿Qué ocurre con el valor de la interfranja en el patrón de interferencia de una doble rendija si aproximamos estas?

25 Investiga por qué vemos a través de nuestros ojos y de algunos instrumentos ópticos las estrellas con puntas en vez de como manchas circulares.

(a) Las imágenes están resueltas. (b) Las imágenes están próximas al límite de resolución. (c) Las imágenes están tan cerca que no están resueltas y se muestran como una sola.

de difracción sobre una pantalla situada a 5 m de la rendija. Si el máximo central (distancia entre los dos primeros mínimos) tiene 1 cm de anchura, ¿cuál es la anchura de la rendija?

Solución

Para calcular la anchura del máximo central, restamos las posiciones de los mínimos de primer orden que lo delimitan:

xmd D m m = → xd D 1 m =

xd D – –1 m =

xxd D 2 –11 –m =

Despejando d, obtenemos: , , dxxD 22 001 500105 00005 m mm m

9 –

– m == =

11

26 Calcula la posición del tercer mínimo (de orden n = 2) del experimento de doble rendija de Young cuando la rendija mide 1 mm de anchura, la pantalla se encuentra a 2 m y se ilumina con luz de longitud de onda 500 nm.

27 RPPCS. ¿A qué distancia mínima deben estar las dos imágenes obtenidas de una estrella a través de un telescopio de 20 cm de apertura (supón luz de 500 nm) para estar resueltas?

Polarización, dispersión y esparcimiento

7.1. Polarización de la luz

Como ya sabemos, la luz es una onda electromagnética transversal con sus vectores E " y B " perpendiculares entre sí y, a su vez, a la dirección de propagación.

Decimos que una onda está linealmente polarizada o planopolarizada cuando las oscilaciones del campo eléctrico (y el campo magnético asociado) mantienen una orientación constante.

Si superponemos dos ondas planopolarizadas de la misma frecuencia y dirección de propagación, cuando sus campos eléctricos sean paralelos entre sí la resultante seguirá siendo una onda planopolarizada. Pero si sus campos eléctricos son perpendiculares (figuras superiores de la derecha), dependiendo del desfase entre las dos ondas, el campo resultante podrá oscilar en un plano de dirección constante (luz polarizada plana o lineal), o un plano que cambie de dirección girando en determinado sentido (luz polarizada circular o elíptica).

Luz natural y luz polarizada

Una fuente de luz consiste en un número muy grande de átomos excitados que al desexcitarse emiten una onda planopolarizada con una orientación particular durante un corto espacio de tiempo. Al superponerse las ondas emitidas por los átomos, el haz resultante contiene campos eléctricos que vibran en todas direcciones.

En otras palabras, todas las direcciones de vibración son igualmente probables, no existiendo ninguna dirección privilegiada. Tenemos luz natural o luz polarizada al azar.

Sin embargo, si de algún modo logramos que el vector campo eléctrico tenga una dirección privilegiada de vibración, tendremos luz polarizada.

Obtención de luz polarizada

Existen varias formas de obtener luz polarizada.

• Se puede polarizar la luz por reflexión. Cuando una onda incide en la superficie de separación de dos medios bajo un ángulo, llamado ángulo de Brewster, t i B , tal que el rayo refractado y el reflejado forman entre sí 90º, la luz emerge polarizada linealmente con su campo eléctrico perpendicular al plano de incidencia.

Como t i B cumple que t i B + t r = 90° (figura inferior derecha), si aplicamos la ley de la refracción podemos obtener el valor del ángulo de Brewster:

Polarización de la luz

Polarización lineal y polarización circular Luz natural y luz polarizada

En la luz polarizada lineal (arriba), el campo de la onda resultante oscila en un plano; en la luz polarizada circular (abajo), el campo de la onda resultante gira mientras esta avanza.

Frente de onda

Frente de onda

Luz natural Luz poralizada

Al superponerse las ondas emitidas por todos los átomos, si no existe ninguna dirección privilegiada de vibración, tenemos luz natural, pero si existe alguna dirección privilegiada, tenemos luz polarizada.

Polarización por reflexión

La luz que incide sobre la superficie de separación bajo el ángulo de Brewster se refleja linealmente polarizada.

• Otra forma de obtener luz polarizada es la absorción selectiva o dicroísmo. Algunos materiales llamados láminas o filtros polarizadores, como por ejemplo los cristales de turmalina, tienen la propiedad de transmitir solamente ondas electromagnéticas con el campo eléctrico vibrando en una dirección concreta llamada eje de transmisión, y absorbiendo las ondas cuyo campo eléctrico vibra en el resto de direcciones. Al absorber parte de la radiación que incide sobre ellos, los filtros polarizadores reducen la intensidad de la luz transmitida por lo que suelen utilizarse en la fabricación de gafas de sol y filtros fotográficos. Su ventaja sobre los filtros convencionales consiste en que elimina parte de la luz polarizada por reflexión, lo que puede resultar muy útil para eliminar reflejos no deseados en determinadas superficies.

7.2. Dispersión de la luz

Mientras que la velocidad de la luz en el vacío no varía, no ocurre lo mismo en medios materiales, donde la velocidad de propagación, y por consiguiente el índice de refracción, varía con la longitud de onda. Este fenómeno recibe el nombre de dispersión cromática.

Dispersión es el fenómeno por el cual el índice de refracción de un medio material disminuye al aumentar la longitud de onda de la luz incidente en él.

Por tanto, al atravesar la luz visible un medio material, las longitudes de onda más largas sufrirán una menor desviación que las más cortas.

Dispersión en un prisma

El fenómeno de la dispersión se manifiesta de forma bastante evidente en un prisma óptico. Si dos haces de luz de longitudes de onda diferentes inciden en la primera cara de un prisma, se producirá una desviación diferente para cada una de las longitudes de onda. La diferencia de desviaciones se hará mayor cuando se produzca la refracción en la segunda cara del prisma.

Tal y como demostró Isaac Newton en el siglo xviii, si hacemos incidir luz blanca (compuesta por todos los colores del espectro visible) en un prisma, a la salida se observará la distribución de colores del espectro desde el rojo (menor desviación) hasta el violeta (mayor desviación). En la naturaleza, la dispersión de la luz se pone de manifiesto al atravesar la luz del sol las gotitas de agua dando lugar al arcoíris.

Dispersión de la luz Filtro polarizador

Filtro polarizador

Luz polarizada

Pantalla

Luz no polarizada

Cuando un haz de luz natural pasa por un filtro polarizador, la luz transmitida vibra solo en la dirección del eje principal de la lámina.

En la foto de la derecha se ha fotografiado el coche a través de un filtro polarizador, que ha eliminado algunos reflejos en la superficie.

Colores del espectro visible

Al atravesar un prisma óptico, la luz blanca se refracta sucesivamente en las caras de este y se descompone en todos los colores de los que está formada.

El arcoíris solo puede verse cuando el ángulo de la luz incidente desde el Sol a la línea de visión se sitúa entre los 40° (gotas de color violeta) y los 42° (gotas de color rojo).

40º 42º

Luz blanca

Violeta Rojo

Gota de lluvia

Rayo de sol

7.3. La luz en medios materiales: el color

Cuando la luz incide en un medio material, las oscilaciones del campo eléctrico y el campo magnético de la onda electromagnética se transmiten al medio y hacen vibrar rápidamente a los electrones.

En un medio transparente, los electrones tienen una frecuencia natural de vibración que depende de la fuerza de atracción entre ellos y sus respectivos núcleos.

Cuando incide luz de la misma frecuencia que la de los electrones del medio, estos entran en resonancia y oscilan con una gran amplitud, se producen colisiones con los átomos vecinos y se emite energía en forma de calor. Sin embargo, cuando la frecuencia de la onda es menor que la de la de resonancia, los electrones vibran con menor amplitud, se producen menos choques con los átomos vecinos y, por tanto, menos pérdidas por calor. Entonces, la energía de los electrones vibrantes se reemite en forma de luz transmitida con la misma frecuencia que la de la luz incidente.

En el caso de que el material sea opaco, la energía incidente se convierte en energía cinética aleatoria y el material se calienta pero no transmite la luz.

En el vidrio, la frecuencia de resonancia pertenece a la región ultravioleta del espectro. Es por ello por lo que el vidrio transmite la luz visible pero no deja pasar la radiación ultravioleta. Tampoco se transmite la luz infrarroja, pero en este caso porque hace vibrar tanto a los electrones como a la estructura del vidrio, disipando la energía en forma de calor.

Naturaleza del color

El color de los objetos que vemos mediante la luz que reflejan no es una propiedad intrínseca de los objetos, sino que está asociado a la luz que reciben y a la naturaleza de su superficie.

Cuando la superficie refleja toda la luz que incide sobre ella, será del mismo color de la radiación incidente: si es iluminada con luz blanca (que contiene todas las longitudes de onda) el color de la superficie será blanco, pero si es iluminada con cualquier otro color, se verá del mismo color con el que se ilumina. Cuando la superficie absorbe toda la luz que incide sobre ella se verá de color negro. Pero si una superficie refleja preferentemente una longitud de onda concreta, la veremos de ese color: vemos verde la hoja de un árbol porque absorbe todas las longitudes de onda excepto la correspondiente al color verde. Del mismo modo ocurre con la luz que transmite un filtro de color. Si el filtro es iluminado con luz blanca y transmite luz roja será porque ha absorbido todas las longitudes de onda excepto la correspondiente al color rojo. El material que absorbe la luz de distintos colores recibe el nombre de pigmento. Los átomos del pigmento absorben la luz de determinadas longitudes de onda.

La absorción de determinadas longitudes de onda en los objetos se produce gracias a los cromóforos, un conjunto de moléculas responsables de su color. Estas moléculas poseen electrones capaces de absorber la energía recibida y excitarse. Al volver a su estado fundamental, emiten radiación cuya longitud de onda dependerá de la diferencia de energía entre el estado excitado y el fundamental.

Naturaleza del color

La luz roja que incide sobre los electrones los hace vibrar. Estos reemiten la energía recibida con la misma frecuencia a los átomos vecinos, transmitiendo la luz a través del vidrio.

La luz ultravioleta hace vibrar en resonancia a los átomos y la energía se pierde en forma de calor. La luz ultravioleta no es transmitida por el vidrio.

7.4. Esparcimiento de la luz

Cuando la luz incide sobre un medio cuyas partículas tienen un tamaño mucho menor que la longitud de onda incidente, se produce un fenómeno llamado esparcimiento de Rayleigh, llamado así en honor al científico británico del siglo xix John William Strutt, también conocido como Lord Rayleigh. Aunque puede ocurrir en medios sólidos y líquidos transparentes, este fenómeno es más frecuente cuando la luz atraviesa un medio gaseoso.

La luz en la atmósfera

El esparcimiento consiste básicamente en la absorción de la radiación electromagnética recibida por las partículas del gas para ser emitida de nuevo con la misma frecuencia (y longitud de onda). Al estar las moléculas orientadas al azar, la radiación se emite en todas direcciones. Además, tal y como demostró Lord Rayleigh, la intensidad de la luz emitida es proporcional a 1/λ4, donde λ es la longitud de onda incidente. Como consecuencia, las longitudes de onda cercanas al extremo violeta del espectro visible son fuertemente esparcidas fuera del haz de luz, mientras que el rayo que atraviesa el gas tiene más intensidad para longitudes de onda situadas en el extremo rojo del espectro visible.

En el caso de nuestra atmósfera, cuando en ella incide la luz del Sol, el aire esparce de un modo más eficiente la zona del espectro de longitudes de onda más bajas (y frecuencias más altas). Esto, unido a que el espectro de la luz solar tiene un máximo de intensidad para 460 nm (luz azul) y a que nuestro ojo es más sensible al azul que al violeta, hace que percibamos el cielo de color azul.

Al haberse esparcido las longitudes de onda más cortas, la luz que llega del Sol hasta nuestros ojos carece de estas longitudes de onda. Por esta razón, cuando el Sol está alto sobre el horizonte, lo percibimos en tonos amarillos, y, al atardecer, cuando la luz del Sol atraviesa mucha más distancia y el esparcimiento es mayor, anaranjados.

Por otra parte, cuando la luz natural sufre esparcimiento, la luz esparcida está parcialmente polarizada, siendo mayor la polarización en la luz que sufre más desviación. Esto hace que la luz del cielo que se encuentra a 90º de la posición del Sol tenga máxima polarización. Aunque nuestros ojos no detectan la luz polarizada, podemos comprobarlo con el filtro polarizador de unas gafas de sol o una cámara fotográfica: la luz polarizada se oscurecerá más a través del polarizador.

En la novela del conocido autor francés Jules Verne Elrayo verde se describe un fenómeno de difícil observación que se produce bajo ciertas condiciones atmosféricas muy concretas. Cuando el Sol se pone en un horizonte muy definido, el último rayo procedente de nuestro astro rey se ve de color verde. Esto se debe a que al refractarse la luz del Sol en la atmósfera, los colores de la luz solar se separan quedando en su borde superior el violeta, azul y verde. Al sufrir el violeta y el azul esparcimiento de Rayleigh, solo el color verde llega hasta nuestros ojos.

La atmósfera marciana es mucho menos densa que la de la Tierra, por lo que el esparcimiento de Rayleigh es menor que en nuestro planeta. Además, al tener menos gravedad su atmósfera contiene numerosas partículas de polvo en suspensión. Estas partículas son de un tamaño del orden de la longitud de onda visible por lo que se produce otro tipo de dispersión llamada dispersión de Mie. Esta dispersión esparce las longitudes de onda más largas (zona roja del espectro), si bien lo hace en menor medida que la dispersión de Rayleig en la Tierra. De ahí que los cielos de Marte aparezcan rojizos y no azules en las imágenes obtenidas a través de las sondas allí enviadas.

Luz esparcida (longitudes de onda cercanas al violeta)

Luz no esparcida (resto de longitudes de onda)

Luz blanca

Cielo azul como consecuencia del esparcimiento.

El rayo verde

El cielo en Marte

El color azul del cielo en la Tierra

El láser y sus aplicaciones

8.1. Fundamento del láser

El láser es un dispositivo capaz de emitir un haz estrecho de luz coherente de una sola longitud de onda y alta intensidad. El término láser proviene del acrónimo inglés LASER (lightamplificationbystimulatedemission ofradiation; en español, luz por emisión estimulada de radiación).

Un láser, en su diseño más sencillo, está formado por un núcleo o cavidad del láser de forma alargada que puede ser una estructura cristalina (hecha, por ejemplo, de rubí) o un tubo de vidrio que contiene gas. Junto al núcleo, o rodeando a este, está el excitador, una lámpara que emite potentes destellos a modo de flash y que proporciona la energía necesaria para excitar a los electrones que se encuentran dentro del núcleo del dispositivo. El tercer componente son dos espejos paralelos, que son colocados en ambos extremos del núcleo. Uno de ellos es semirreflectante lo que permite el paso parcial de la luz y, por tanto, la salida del haz de luz del láser del dispositivo.

La lámpara del excitador es la encargada de que los electrones del material que constituye el núcleo del dispositivo suban continuamente a niveles superiores (este proceso se denomina bombeo óptico) produciendo una inversión de población y, por tanto, la emisión estimulada de fotones (ver figura inferior de la derecha). Para que el proceso no cese, se colocan los espejos que hacen regresar a la mayoría de los fotones para que la emisión estimulada continúe.

Hoy en día también se usan láseres de semiconductores, que son dispositivos semiconductores similares a un diodo LED pero que emiten luz láser.

8.2. Aplicaciones del láser

Las cortadoras láser se utilizan en la industria textil y en el ensamblaje de vehículos en la industria aeronáutica y del automóvil. En medicina, el haz de alta energía de un láser es lo suficientemente estrecho como para utilizarse en operaciones oculares y en cirugía convencional al ser instrumento de corte y cauterización simultáneamente.

Por otra parte, el láser proporciona un excelente método de medición de largas distancias. Así, el telémetro láser envía un pulso de luz láser a una superficie y mide el tiempo que tarda en volver la luz reflejada para obtener la distancia. De hecho, este método se ha utilizado para medir la distancia Tierra-Luna con precisión. Para ello, se han enviado desde observatorios situados en la Tierra potentes pulsos láser hacia reflectores que colocaron en la superficie de la Luna los astronautas de las misiones Apolo hace más de 50 años.

El láser Excitador

Núcleo o cavidad del láser Espejo reflectante Espejo semirreflectante

Emisión estimulada

Los electrones en niveles de energía excitados tienden a caer espontáneamente a niveles inferiores emitiendo radiación. Pero un fotón también puede estimular la caída de un electrón siempre que posea una energía igual a la diferencia entre los dos niveles entre los que salta el electrón. Si E1 y E2 son, respectivamente, los estados fundamental y excitado de un electrón, podemos describir el proceso de emisión estimulada:

Un electrón se encuentra en un estado excitado, E2; entonces, un fotón incidente con energía igual a la diferencia entre el nivel actual y un nivel inferior, E1, estimula una transición al nivel más bajo, produciendo un segundo fotón con la misma energía (y frecuencia) que el primero. Como al final obtenemos dos fotones, el incidente y el emitido, la luz se amplifica. E

Si un elevado número de electrones se encuentra en niveles superiores, esto se conoce como inversión de población y es el escenario ideal para que se produzca emisión estimulada de número grande de fotones.

Almacenamiento de información

Los discos compactos o CD (compactdisc), discos DVD (digitalversatiledisc, disco versátil digital) y BD (Blu-ray Disc) son unidades de disco ópticas utilizadas para el almacenamiento de la información (audio, vídeo, datos,…).

Se llaman así porque utilizan el láser tanto para la lectura como para la escritura de archivos. Su ventaja frente a los medios de almacenamiento magnéticos es su resistencia frente a los campos magnéticos y la humedad.

La estructura básica de un disco óptico consiste en un sustrato plástico de policarbonato sobre el que, mediante un láser, se realizan surcos o ranuras microscópicas, y una capa metálica reflectante (generalmente de aluminio), protegida por un recubrimiento acrílico.

El equipo de reproducción consta de un motor que hace girar el disco y un láser de semiconductor que es enfocado hacia la pista donde se encuentra la información mediante un mecanismo de seguimiento y un sistema de lentes. Al dirigir el láser a la pista, este atraviesa la capa de policarbonato, pasa por las ranuras, y se refleja en la capa metálica. Un detector interpreta la señal reflejada como «unos» o «ceros» y envía la señal al ordenador o a un conversor analógico que la interpreta o transforma.

Para conseguir discos regrabables, que permiten grabar la información sobre ellos, la capa metálica se sitúa sobre una capa fotosensible traslúcida que se vuelve opaca al ser iluminada; estas zonas se comportan, frente a la luz del lector, como las ranuras antes mencionadas. Tanto el CD como el DVD y el Blu-ray funcionan del mismo modo. La diferencia entre los tres sistemas es la longitud de onda del láser que lee la información. En un CD, el láser tiene una longitud de onda de 780 nm (rojo); en un DVD, de 650 nm (rojo), y en un BD, de 405 nm (azulvioleta). Cuanto menor es la longitud de onda, menor es el tamaño mínimo de las ranuras para poder ser leídas y menor, por tanto, la distancia entre pistas, lo que permite almacenar más información. Mientras que en un CD caben hasta 700 MB, un DVD permite almacenar 4,7 GB y un BD llega a los 25 GB de capacidad.

Holografía

La holografía es una técnica de fotografía tridimensional consistente en dividir un haz láser en dos, uno de referencia y otro que se refleja en el objeto que se quiere fotografiar. El diagrama interferencial obtenido al combinar ambos haces es registrado en una placa fotográfica. Al iluminar la placa, reconstruimos la imagen tridimensional del objeto.

Hologramas Discos ópticos

Etiqueta-cara impresa Recubrimiento protector

Capa metálica

Ranuras de datos Policarbonato

Izquierda: Perfil de una unidad de CD. En la capa de datos se almacena la información en forma de microsurcos en los que incide el láser. Derecha: La lectura de la pista de datos comienza en la parte central del disco para acabar en el borde.

Imagen holográfica. Cuando observamos un holograma, al mover el ojo respecto al plano del holograma, se observa una perspectiva del objeto análoga a la que obtendríamos mirando al objeto real.

Disposición y tamaño de los microsurcos en cada tipo de soporte. La capa de datos que lee el láser se sitúa a distinta profundidad según el soporte de almacenamiento.

Montaje para la creación de un holograma. Un solo fragmento del holograma contiene información suficiente para reproducir la imagen completa, aunque con menos resolución.

CD DVD BD

Láser

Lente Espejo

Divisor del haz

Óptica en la página de Walter-Fendt

Una página clásica de applets de física es la página alemana https://www.walter-fendt.de/html5/phes/ en la que podemos observar simulaciones sobre fenómenos físicos que ilustran diferentes campos de la física, entre ellos la óptica.

Refracción y reflexión de ondas

En este applet se nos muestran las leyes de la refracción y reflexión de la luz explicadas a través del principio de Huygens.

Aquí tenemos la opción de elegir los índices de refracción de los dos medios y el ángulo de incidencia de la onda. En una secuencia de pasos podemos observar el frente de onda, la generación de los frentes de onda secundarios, la superposición de las ondas elementales y finalmente la dirección de propagación de la luz.

Refracción y reflexión de la luz

En otro de los applets podemos elegir distintos medios con diferente índice de refracción y variar el ángulo de incidencia para obtener sus correspondientes rayos reflejado y refractado. Además, nos muestran una gráfica que representa en el eje de abscisas el ángulo de incidencia y en el de ordenadas el ángulo de refracción.

• Prueba a experimentar en ambas aplicaciones en los que el primer medio tiene mayor o menor índice de refracción que el segundo. Observa en el segundo applet en qué se diferencian las gráficas en ambos casos. ¿Son los ángulos proporcionales?

• Intenta experimentar con el ángulo límite cuando el índice de refracción es mayor en el primer medio. ¿Qué pasa con la curva en a partir del ángulo límite?

Interferencia a través de una doble rendija

El experimento de la doble rendija también tiene su simulación en esta página web. En este caso podemos modificar la longitud de onda, la separación entre las rendijas y el ángulo que subtiende el patrón de interferencia en la pantalla. Teniendo en cuenta que la ecuación correspondiente a la condición de máximo puedes intentar comprobar:

• Cómo cambia la posición de los máximos con la longitud de onda.

• Cómo cambia la anchura de los máximos al variar la distancia entre rendijas.

Principio de Huygens.

Reflexión y refracción. Ángulo límite. Experimento de la doble rendija y condiciones de máximos y mínimos.

Ondas electromagnéticas y óptica con las simulaciones PhET

Otra de las páginas en las que se pueden reproducir fenómenos relacionados con la óptica es la página de simulaciones interactivas de la Universidad de Colorado (https://phet.colorado.edu/). En el apartado «Luz y Radiación» podemos encontrar las siguientes simulaciones:

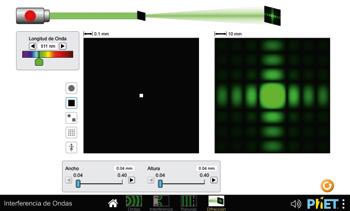
Refracción y reflexión de la luz

En esta aplicación podemos emitir un rayo o un pequeño frente de onda sobre la superficie de separación entre dos medios. Disponemos de un transportador de ángulos para medir el ángulo de incidencia y reflexión y podemos variar el índice de refracción de ambos medios.

Dentro de la misma aplicación aparece la reflexión y la transmisión de la luz a través de un prisma o de una lámina planoparalela.

• Prueba a comprobar la ley de la refracción con distintos ángulos y medios.

• Utiliza el modo de onda para visualizar los frentes de onda y el medidor de intensidad para comprobar cuánta luz se refleja y cuánta se transmite.

• Intenta aplicar la condición de reflexión total y comprueba el valor del ángulo límite.

• Intenta comprobar el fenómeno de la dispersión a través del prisma y de la esfera (análoga a una gota de agua) variando la longitud de onda de la luz o utilizando luz blanca.

Interferencia de ondas

En esta simulación podemos visualizar interferencias a través de una doble rendija y difracción de la luz a través de una abertura circular.

Observa la distribución de máximos en ambos casos cambiando las dimensiones de la abertura y la longitud de onda.

Reflexión y refracción de la luz. Frentes de onda e intensidad. Interferencia de ondas. Interferencia en doble rendija.

Reflexión y refracción de la luz. Obtención del ángulo límite variando el ángulo de incidencia.

Interferencia de ondas. Difracción a través de una abertura cuadrada.

Refracción en láminas planoparalelas

1 Un rayo de luz de 500 nm de longitud de onda incide en una lámina planoparalela de vidrio (n = 1,5) de 1 cm de espesor con un ángulo de incidencia de 30º. La parte superior de la lámina limita con alcohol (n = 1,33), y la parte inferior, con aire (n = 1). Realiza un esquema de la situación y calcula:

a) El ángulo de refracción en ambas caras.

b) Si parte de la luz se refleja en la segunda cara, ¿con qué ángulo será devuelta la luz al primer medio?

Planteamiento y resolución

a) En el esquema representamos en rojo la luz transmitida y en verde la luz reflejada.

ANÁLISIS DEL PROBLEMA

Para realizar problemas con refracciones sucesivas es importante ayudarnos de un esquema en el que aparezca el camino seguido por el rayo luminoso, teniendo en cuenta que el rayo se alejará de la normal al pasar de un índice a otro menor (vidrio-aire) y se acercará a la normal al pasar de un índice a otro mayor (aire-vidrio).

En láminas planoparalelas es importante recordar que dos ángulos con un lado paralelo y otro en común son iguales.

Aplicando la ley de la refracción en cada una de las dos caras obtenemos:

• Superficie 1: 1,33 · sen 30° = 1,5 · sen r1 t , , , r 15 13330 044 sen ·sen ° 1 == t → ,, r 0442610 arcsen ° 1 == t

Como el ángulo de refracción de la primera superficie es igual que el ángulo de incidencia en la segunda, ya podemos volver a aplicar la ley de la refracción:

• Superficie 2: ,, r 15 26 10 1 ·sen °· sen 2 = t → ,, rarcsen 0593616° 2 == t

b) Como el ángulo de reflexión de la segunda superficie es igual al de incidencia y este, a su vez, igual al ángulo de incidencia en la última superficie, la luz que se refleja en la segunda cara incide de nuevo en la primera con un ángulo de 26,10°. Si aplicamos por última vez la ley de Snell, tendremos:

, r 15

El ángulo reflejado de nuevo de la lámina al aire tiene igual valor que el ángulo de incidencia.

Esto nos permitirá reconocer ángulos idénticos como el ángulo de refracción de la primera superficie y el de incidencia en la segunda.

En cualquier ejercicio en el que un rayo luminoso se refracta de un medio a otro de índice menor habrá que tener en cuenta que a partir del ángulo límite la ley de la refracción no funciona y se produce reflexión total. De hecho, en este ejercicio, se si el ángulo de incidencia en la primera cara es mayor que 48,75° la luz no sale de la lámina. Probando con un ángulo de incidencia de 50º:

• Superficie 1:

1,33 · sen 50° = 1,5 · sen r1 t

sen r1 t = ,

,· , ° 15 13350 068 sen =

r1 t = 42,84°

• Superficie 2:

1,5 · sen 42,84° = 1 · sen r2 t

sen r2 t = 1,02 (imposible)

Lo que confirma que se produce reflexión total.

Interferencias

2 Un haz de luz compuesto por dos longitudes de onda, λ1 = 380 nm (luz violeta) y λ2 = 760 nm (luz roja), incide en dos rendijas separadas 0,5 mm. Si la pantalla se encuentra a 3 m de distancia:

a) Indica si para 380 nm hay un máximo o un mínimo en un punto de la pantalla situado a 1,026 cm del máximo central.

b) Calcula a qué distancia del máximo central se encontrará el máximo de orden 10 para cada una de las dos longitudes de onda de las que se compone el haz.

c) ¿Qué se observaría si iluminásemos la doble rendija con luz blanca?

Planteamiento y resolución

a) La posición de los máximos y los mínimos en una doble rendija viene dada por la expresión:

xnd D n m = (para los máximos)

xnd D 21 2 n m =+^h (para los mínimos)

A 1 cm del máximo central, xn = 1,026 m. Sustituyendo la distancia entre rendijas (d = 5 · 10–4 m), la distancia a la pantalla (D = 3 m) y la longitud de onda (λ1 = 380 nm) en ambas condiciones, obtenemos:

•

n = 4,5 → No la cumple

m m 7 4 ––=+^h

n = 4 → Sí la cumple

En el punto indicado hay un mínimo para 380 nm.

b) El máximo de orden 10 se podrá calcular para cada una de las longitudes de onda indicadas sustituyendo en la expresión indicada anteriormente.

• Para una longitud de onda de 380 nm:

, x 10 38010 m· 5· 10 m 3m 0, 0228 m2,28cm 10 –7 –4 == =

• Para una longitud de onda de 760 nm:

·, ·· · x 10 76010m 510m 3m 0, 0456 m4,56cm 10 7 4 ––== =

c) En el caso de iluminar la doble rendija con luz blanca observaríamos máximos y mínimos diferentes para cada longitud de onda, exceptuando el máximo central cuya posición es la misma para cualquier λ. Para los máximos no centrales se observarían máximos coloreados en forma de espectro.

ANÁLISIS DEL PROBLEMA

A la hora de realizar problemas de interferencias debemos tener en cuenta cuándo la diferencia de camino entre los rayos cumple la condición de máximo o de mínimo, y esto se hace buscando el valor de n para cada una de las condiciones y viendo si toma un valor entero.

No obstante, si al aplicar la condición de máximo (o de mínimo) el resultado es semientero, se cumplirá siempre la condición opuesta. En la siguiente gráfica se muestra la intensidad, I, frente a la distancia, x, al centro del patrón. Si aplicamos la condición de máximo, los valores n = 0, 1, 2, 3,… nos darán la posición de los máximos de distinto orden, mientras que los valores n = 0,5; 1,5; 2,5; … coincidirán con la posición de los mínimos, puesto que la diferencia de camino entre máximos y mínimos difiere en media longitud de onda.

n = 0,5 n = 1,5 n = 2,5

Evidentemente, al aplicar la condición de mínimo, sus posiciones corresponderán a valores enteros de n.

En caso de que al aplicar una de las condiciones en un punto no obtengamos valores enteros o semienteros (por ejemplo, n = 2,34), estaremos en un punto en el que la intensidad es intermedia (ni máxima ni mínima).

Trabaja con lo aprendido

OEM y espectro electromagnético

1 Ordena las siguientes ondas electromagnéticas en orden creciente de frecuencias. Indica al menos una aplicación de cada una de ellas: Rayos X, microondas, infrarrojo y ultravioleta.

2 Lápices al centro. Dadas las siguientes longitudes de onda, indica a qué franja del espectro pertenecen:

a) 4 · 10–9 m

b) 8 · 10–8 m

c) 7 · 10–7 m

3 Una antena emite ondas electromagnéticas de 106 MHz de frecuencia. Si la velocidad de la luz vale 3 · 108 m · s–1:

a) Calcula la longitud de onda emitida por la emisora.

b) Si, en un punto del espacio, el valor máximo del campo magnético es de 2 · 10–11 T, ¿cuál es el valor máximo del campo eléctrico?

4 Una onda electromagnética se propaga a 3 · 108 m · s –1 en la dirección positiva del eje Z. Si su longitud de onda es de 500 nm y el campo eléctrico oscila en el eje X con un módulo de 0,05 N/C. Escribe las ecuaciones del campo eléctrico y el campo magnético que representan esta onda.

5 Cabezas pensantes. Algunas de las señales recibidas desde la superficie de Marte por el Rover Perseverance son recogidas por el satélite Mars Reconnaissance Orbiter y reenviadas a la Tierra, recorriendo a la velocidad de la luz (3 · 108 m · s–1) una distancia aproximada de 225 millones de km. Si para ello utilizan la banda X del espectro electromagnético con una longitud de onda entre 2,5 y 3,75 cm:

a) Calcula en qué banda de frecuencias son emitidas las señales.

b) Calcula el tiempo que tarda la señal en llegar desde la órbita de Marte a la Tierra.

Naturaleza de la luz

6 Asamblea de ideas. Indica qué fenómenos de la luz pueden ser explicados a partir del modelo corpuscular y qué fenómenos pueden ser explicados a partir del modelo ondulatorio.

7 Si la distancia de la Tierra al Sol es de 1,5 · 1011 m y la velocidad de la luz en el vacío es de 3 · 108 m · s–1, ¿cuánto tarda la luz del Sol en llegar hasta nosotros?

Reflexión y refracción de la luz

8 Al penetrar un rayo de luz en un medio, su velocidad se reduce en un 25 %. Calcula el índice de refracción de ese medio.

9 Un rayo de luz amarilla de 500 nm penetra desde el vacío en un medio cuyo índice de refracción vale 2,5. Calcula su velocidad, su frecuencia y su longitud de onda en el interior de ese medio.

10 Un rayo de luz se somete a sucesivas reflexiones al pasar por un sistema de espejos perpendiculares entre sí. Dibuja la trayectoria seguida por el rayo si incide sobre el primer espejo a 45° de la normal.

11 En un medio de índice n1 = 1 se propaga un rayo luminoso de frecuencia f1 = 6 · 1014 Hz.

a) ¿Cuál es su longitud de onda?

b) ¿Cuál sería la frecuencia y la longitud de onda de la radiación si el índice de refracción del medio fuese n2 = 1,25?

12 Un rayo de luz de 700 nm incide con un ángulo de incidencia de 40° desde vidrio (n = 1,5) hasta un segundo medio en el que se propaga con un ángulo de refracción de 30°. Si c = 3 · 108 m · s –1 :

a) Calcula el índice de refracción del segundo medio.

b) Calcula la longitud de onda en el segundo medio.

Recuerda seleccionar el material de trabajo de esta unidad para tu porfolio.

13 Un rayo de luz monocromática que se propaga por el aire incide sobre un bloque de vidrio de índice 1,54, produciéndose a la vez reflexión y refracción. Si el ángulo de incidencia es de 25°, calcula el ángulo que forman el rayo reflejado y el refractado.

14 El índice de refracción de un material transparente varía desde 1,58 para la luz roja hasta 1,66 para la luz violeta. Si un rayo de luz blanca incide sobre él con un ángulo de incidencia de 30°, calcula el ángulo entre los rayos de luz roja y violeta refractados.

15 Hitos compartidos. Un rayo de luz monocromática, cuya longitud de onda es 200 nm en un medio de índice 2,5, alcanza una superficie de separación (plana) con agua (índice 1,33) incidiendo con un ángulo de 30° respecto a la normal. Dibuja un esquema del proceso descrito y calcula el ángulo de refracción y la longitud de onda de la luz refractada.

16 Interpretación compartida. Un rayo láser procedente de la parte inferior izquierda de la figura alcanza la superficie del agua (n = 4/3) que llena parcialmente la cubeta, y se observa que se refleja sin que haya ningún rayo refractado que atraviese la superficie pasando al aire que hay encima. Explica por qué se produce este fenómeno. ¿Tiene algo que ver en este fenómeno el ángulo i con el que incide el rayo de luz por debajo de la superficie?

19 Determina el ángulo límite para el fenómeno de la reflexión total entre los medios materiales aire y glicerina, cuyos índices de refracción son 1,00 y 1,47, respectivamente.

20 1-2-4. Sobre un bloque de material incide desde el aire (n = 1) un haz de luz compuesto por longitudes de onda de 400 nm (violeta) y 750 nm (rojo). Los índices de refracción del material para estas longitudes de onda son 1,66 y 1,60, respectivamente. Si, como se muestra en la figura, el ángulo de incidencia es de 60°:

a = 60 º

a) ¿Cuáles son los ángulos de refracción y las longitudes de onda en el material?

b) Determina el ángulo límite para cada longitud de onda en la frontera entre el material y el aire. Para un ángulo de incidencia de 60°, ¿escapan los rayos desde el medio hacia el aire por la frontera inferior?

17 Se lanzan tres rayos de luz desde un medio de índice de refracción 1,33 (agua) hacia otro medio de índice de refracción igual a 1 (aire). Los ángulos de estos tres rayos con la normal a la superficie de separación son: rayo A, 38°; rayo B, 49°, y rayo C, 60°. Responde justificadamente: ¿Cuál o cuáles de estos rayos se transmitirán del primer al segundo medio y cuál o cuáles no?

18 Disponemos de un cubo de vidrio de índice de refracción n = 1,45 que está inmerso en agua cuyo índice de refracción es nagua = 4/3. Un rayo monocromático incide en la cara vertical del cubo como indica la figura. ¿Cuál debe ser el ángulo de incidencia para que en la cara superior AB haya reflexión total?

21 Un buceador emite un rayo de luz, utilizando una potente linterna, que incide desde el agua hacia el fondo de la piscina que consiste en un medio transparente. Si el ángulo de incidencia es de 70° el rayo de luz se refleja, pero si el ángulo es menor se refracta.

a) Calcula el índice de refracción del segundo medio.

b) Determina el ángulo de incidencia para el cual se observa que los rayos reflejado y refractado son mutuamente perpendiculares.

22 Un rayo de luz atraviesa una lámina plana de vidrio de 3 cm de espesor de índice nv = 1,37 incidiendo con un ángulo de 30°. Al salir el rayo se ha desplazado paralelamente a sí mismo una distancia d. Si la lámina está contenida en aire, determina la distancia desplazada.

Aire

Agua

Trabaja con lo aprendido

23 Una placa de vidrio se sitúa horizontalmente sobre la superficie del agua contenida en un depósito, de forma que la parte superior de la placa está en contacto con el aire, tal como muestra la figura. Un rayo de luz incide desde el aire a la cara superior del vidrio formando un ángulo α = 60° con la vertical.

a) Calcula el ángulo de refracción del rayo de luz al pasar del vidrio al agua.

b) Deduce la expresión de la distancia (AB) de desviación del rayo de luz tras atravesar el vidrio, y calcula su valor numérico. La placa de vidrio tiene un espesor d = 20 mm.

Datos: índice de refracción del agua: 1,3; índice de refracción del aire: 1; índice de refracción del vidrio: 1,5.

25 Una capa de aceite con índice de refracción n2 flota sobre agua con índice de refracción n1 = 1,3. Un rayo de luz que se mueve hacia arriba incide en la capa de aceite desde el agua con un ángulo de incidencia θ1, como indica la figura. El rayo penetra en la capa de aceite con un ángulo de refracción de 25,68°. Tras atravesar la capa de aceite, ese rayo sale al aire con un ángulo de refracción de 40,54°. Calcula:

a) El índice de refracción n2 del aceite y el ángulo de incidencia del rayo en la interfase agua-aceite.

b) El valor mínimo del ángulo de incidencia del rayo en la interfase agua-aceite para que, tras atravesar la capa de aceite, el rayo no salga al aire debido a la reflexión total.

Aire (n3 = 1)

Aceite (n2)

Agua (n1 = 1,3)

24 Considera un vaso de agua (n3 = 1,33) en cuya superficie hay una capa de aceite (n2 = 1,45). Un rayo incide desde el aire (n1 = 1) formando un ángulo de 40° con la normal.

a) Dibuja la marcha de rayos y determina el ángulo de salida del rayo en el agua.

b) Si consideras ahora un rayo procedente del agua, determina el ángulo de incidencia mínimo en la superficie agua-aceite para que no emerja luz al aire.

26 Calcula el ángulo de salida de un rayo de luz que incide formando un ángulo de 30° con la superficie de un prisma de 50° inmerso en aire y con un índice de refracción de 1,5. ¿Con qué ángulo habrá que incidir en la primera cara para que no se transmita la luz en la segunda?

27 Piensa y comparte en pareja. En el prisma de la figura (n = 1,5) incide un haz de luz perpendicular a su superficie. Dibuja y justifica a partir de las leyes de la refracción y la reflexión la trayectoria del rayo.

Aire (n1 = 1)

Aceite (n2 = 1,45)

Agua (n3 = 1,33)

Interferencia y difracción

28 Una doble rendija de Young se ilumina con luz de 500 nm. Si un punto de la pantalla se encuentra a una distancia de 120 cm de una de las rendijas y a 119,999 cm de la otra, ¿se observará en ese punto un máximo o un mínimo?

29 Calcula la distancia entre dos máximos consecutivos en el patrón interferencial de una doble rendija situada a 2 m de la pantalla, si las rendijas están separadas 1 mm y se iluminan con luz de 500 nm.

30 Se iluminan con luz de 590 nm dos rendijas de Young separadas entre sí 2 mm. Si el patrón de interferencia se observa a 4 m de distancia, ¿cuánto medirá la separación entre las franjas observadas?

31 Calcula la anchura del máximo central del patrón de difracción de una rendija de 1 mm de anchura que es iluminada con luz de 700 nm si la pantalla se encuentra a 1,5 m de distancia de la rendija.

32 Se hace incidir luz de 780 nm en ella y se observa el patrón de difracción sobre una pantalla situada a 2 m de la rendija. Si el máximo central (distancia entre los dos primeros mínimos) tiene 1 cm de anchura, ¿cuál es la anchura de la rendija?

33 Sobre una rendija de 0,1 mm se hace incidir luz monocromática. En el patrón de difracción que se observa en una pantalla situada a 2 m de distancia de la rendija se aprecia un máximo central de 2 cm de anchura. ¿Qué longitud de onda tiene la luz incidente?

34 Folio giratorio. Si la pupila de una persona tiene un diámetro de 7 mm, ¿podrá distinguir a simple vista dos estrellas separadas 1 segundo de arco?

Polarización, dispersión y esparcimiento

35 Calcula el ángulo con el que debe incidir un haz de luz desde el aire (n = 1) hasta un vidrio (n = 1,5) para que la luz reflejada sea polarizada plana.

36 ¿Qué te hace decir eso? ¿Se puede polarizar el sonido? Justifica tu respuesta.

37 En un prisma de 20° incide un haz de luz blanca (380 nm-780 nm) perpendicularmente a su superficie. Si los índices de refracción del vidrio correspondientes al extremo rojo y violeta del espectro son, respectivamente, 1,51 y 1,53, calcula la distancia angular entre los extremos del espectro formado.

38 Pienso, me interesa, investigo... Investiga por qué los eclipses de Luna muestran durante la fase de totalidad a la Luna de una tonalidad rojiza.

39 ¿Por qué al concentrar los rayos del Sol sobre un papel, este se quema antes si es de color negro?

40 Mesa redonda. ¿Por qué el cielo en el espacio es de color negro, aunque haya luz solar?

Ciencia, tecnología y sociedad

Astrofísica y ondas electromagnéticas

Cuando la prensa se hace eco de algún descubrimiento en el campo de la astrofísica, la mayor parte de la gente lo asocia a enormes telescopios en apartados observatorios y fotografías espectaculares de planetas, nebulosas o galaxias. De lo que no siempre somos conscientes es de que gran parte de esos descubrimientos se realizan a partir de la radiación no visible que nos llega desde el espacio. Y los ejemplos son numerosos:

• El observatorio Chandra, que orbita en torno a la Tierra, observa emisiones de rayos X procedentes de agujeros negros y estrellas de neutrones.

• Satélites como el GALEX (Galaxy Evolution Explorer) nos han ofrecido imágenes en ultravioleta de regiones de formación de estrellas en la Vía Láctea.

• El IRAM (Instituto de Radioastronomía Milimétrica) estudia con su radiotelescopio de 30 metros en Sierra Nevada las microondas que llegan del gas molecular y el polvo interestelar, claves en el estudio de la formación del universo.

• El instituto SETI de búsqueda de inteligencia extraterrestre ha inaugurado recientemente un nuevo proyecto denominado BreakthroughListen. Los observatorios participantes de este proyecto, entre los que se encuentran dos de los mayores radiotelescopios del mundo, analizarán señales del espectro no visible procedentes del espacio en la búsqueda de evidencias de vida inteligente más allá de la Tierra.

Observatorio IRAM, en Pico Veleta (Sierra Nevada, Granada).