






















Fernando
Con el libro que tienes en tus manos, aprenderás Biología y Geología, Matemáticas, Física y Química, y Tecnología. Adquirirás las competencias y saberes necesarios para tu desarrollo personal, intelectual, social y emocional, siempre
En la página de inicio encontrarás tres preguntas, una por cada materia, que te permitirán descubrir qué conoces de los temas que vamos a tratar antes de comenzar.
Mira y Debate. Incluye un código QR que enlaza con un vídeo que te va a sorprender y va a despertar tu interés. Luego, podrás responder a las preguntas planteadas y debatir sobre el tema propuesto.

En esta unidad aprenderás… Aquí se enumeran los saberes que vas a adquirir al trabajar esta unidad.

Desarrolla tus competencias al realizar las actividades y resolver situaciones que pueden darse en tu entorno.
Adquiere los saberes que te presentamos en el texto y ayúdate de los ejercicios resueltos, esquemas, etc.

Recuerda y practica los saberes básicos aprendidos en la unidad. De cada materia tienes un resumen para que puedas recordar lo aprendido y actividades para practicar lo estudiado.

Explora. Realiza estas actividades de indagación siguiendo los pasos del método científico.
Reflexiona sobre el trabajo realizado y la forma de hacerlo.

Al final del trimestre, podréis llevar a cabo, entre toda la clase, un Proyecto interdisciplinar en el que pondréis en práctica distintas estrategias que habéis aprendido y, sobre todo, lo pasaréis muy bien realizando trabajo colaborativo.
Situación de aprendizaje con distintos aspectos vinculados a la unidad.

Terminarás la unidad jugando. Es El desafío: un juego de mesa para que puedas comprobar si has conseguido los saberes básicos. Entre toda la clase os podéis ayudar a conseguirlo.

INTUITIVO
Fácil de usar y diseñado para conseguir tu mejor aprendizaje.
SINCRONIZABLE
Los cambios que realices se sincronizan automáticamente al conectar cualquiera de los dispositivos con los que trabajes.
UNIVERSAL
Es compatible con los entornos virtuales de aprendizaje (EVA) y las plataformas educativas (LMS, LTI).
TRAZABLE
Integrado sobre las aulas digitales de los EVA y LMS, tu profesor puede visualizar los resultados de las actividades que has realizado.
VERSÁTIL
Utilízalo según tus necesidades: como complemento a tu libro impreso o como único material para conseguir tu aprendizaje.
MULTIDISPOSITIVO
Visualízalo en cualquier tipo de dispositivo (ordenador, tableta, smartphone…), a cualquier tamaño y resolución de pantalla. Es compatible con todos los navegadores, sistemas operativos de escritorio (Windows, Mac, Linux...) y dispositivos móviles (Android, iOS y Chromebook).
INCLUSIVO
Personaliza tu aprendizaje adaptando su funcionalidad a tus necesidades.
DESCARGABLE
Puedes trabajar sin conexión a internet y descargarlo en más de un dispositivo.


Entra y encontrarás gran variedad de digitales para que aprendas de otra manera: vídeos, animaciones, esquemas, resúmenes, etc.


Y gran cantidad de actividades interactivas con trazabilidad para que tu profesor o profesora las pueda valorar.
 Te presentamos todas las unidades de tu libro en formato web y adaptables a tus dispositivos.
Te presentamos todas las unidades de tu libro en formato web y adaptables a tus dispositivos.

¿Sabes qué tipo de mina es la de la imagen? ¿Qué impactos ambientales provoca este tipo de minería?
Si estoy en la planta 0 y bajo 2 plantas, ¿en qué planta estoy?

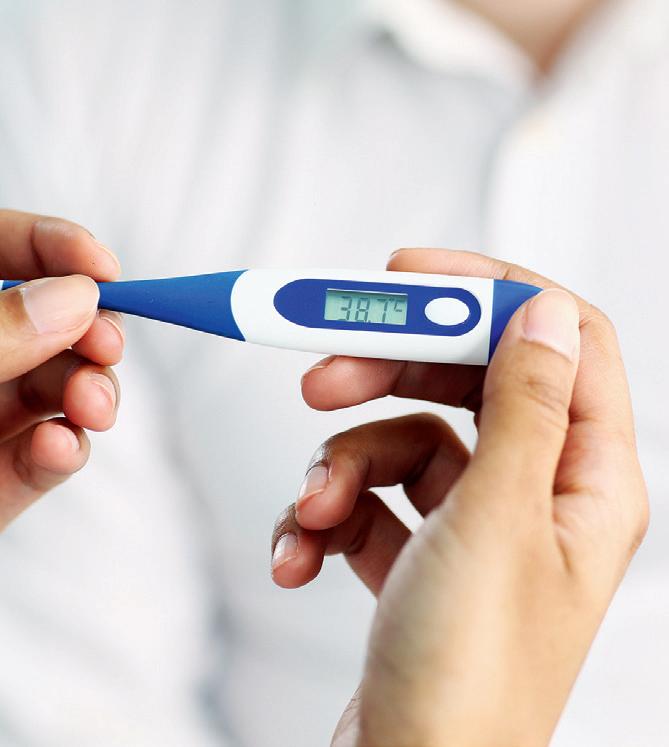
¿Cuántas cifras significativas tiene la medida de la imagen?


Mirad el vídeo sobre el sector minero y metalúrgico en Andalucía y contestad a las preguntas:
¿Cuáles son los recursos minerales más abundantes en Andalucía?
¿Has oído hablar de la Franja Pirítica Ibérica? ¿Qué minerales se extraen en esta explotación minera?
Investigad por grupos:
¿Cómo se produjo el desastre de Aznalcóllar?
¿Qué procedimientos se utilizaron para la descontaminación de los suelos?
Debate. Las explotaciones mineras a cielo abierto de las tierras raras aportan minerales que suministran metales imprescindibles para las nuevas tecnologías. Buscad información sobre el agotamiento de los recursos minerales y su uso responsable.
En esta unidad aprenderás...
Los minerales.
Números naturales. Divisibilidad. Números enteros. Magnitudes y su medida.
Los minerales son sustancias sólidas, inorgánicas, de origen natural, con composición química definida y estructura cristalina, es decir, que tienen una estructura interna ordenada.
Tienen estructura interna cristalina, pero externamente no tienen una forma definida. Es el caso del cinabrio.

Su estructura interna es cristalina y su forma externa es geométrica, con poliedros que tienen caras, vértices y aristas. Por ejemplo, la pirita. Si los cristales son gran valor se denominan gemas o piedras preciosas, como el diamante, el rubí y la esmeralda.

Los minerales se clasifican según su la naturaleza de su composición química:
• Elementos nativos. Están formados por un solo elemento, como el oro (Au) o la plata(Ag), el cobre (Cu), el azufre (S) o el diamante (C).
• Halogenuros. Son combinaciones de cloro (Cl), flúor (F), etc., con sodio (Na), potasio (K) y otros elementos, como la halita, la fluorita y la silvina.
• Sulfuros. El azufre (S) se combina con otros elementos, como la pirita, la calcopirita, el cinabrio y la galena.
• Óxidos. Están formados por combinaciones de oxígeno (O) con otros elementos, como el oligisto y la magnetita.
• Carbonatos. Son combinaciones de carbono (C) y oxígeno (O) (grupo carbonato) con otros elementos, como la calcita o la malaquita.
• Sulfatos. Están constituidos por la unión de azufre (S) y oxígeno (O) (grupo sulfato) con otros elementos, como el yeso.
• Silicatos. Son combinaciones de silicio (Si) y oxígeno (O) (grupo silicato) con otros elementos, como el talco, el cuarzo o la mica. Forman rocas y se llaman minerales petrogenéticos.
Martine Bertereau (1590-1642)
Experta en mineralogía, recibió una educación sólida en matemáticas, química, mecánica e hidráulica y, junto con su marido, Jean du Châtelet, Barón de Beausoleil, también experto en mineralogía, recorrieron Europa y varios países de América del Sur para localizar yacimientos de minerales.
Ofrecieron sus servicios al rey Luis XIII de Francia y descubrieron decenas de minas de carbón, hierro, oro, cobre, plata, rubíes, etc., sin recibir recompensa alguna.
Cuando la Baronesa de Beausoleil reclamó al cardenal Richelieu el pago por su trabajo, ella y su marido fueron acusados de brujería y encarcelados sin juicio, hasta que murieron en prisión.
Para poder distinguir a unos minerales de otros es importante que conozcas sus propiedades físicas, que dependen de su composición química y de su estructura cristalina.
Algunos minerales tienen siempre el mismo color, pero otros pueden presentar diferentes colores debido a las impurezas. Para averiguar cuál es su color verdadero, se utiliza el color de la raya.
Es el aspecto que presenta la superficie de un mineral cuando refleja la luz que recibe. Puede ser metálico, vítreo, céreo, adamantino, sedoso, etc. Si carecen de brillo se denominan mates.
Es el comportamiento del mineral cuando lo intentas romper o deformar. Puede ser:
➔ Elástico. Si vuelve a su forma original cuando finaliza la fuerza que lo deformaba (la mica).
➔ Plástico. Si se deforma de manera permanente (yeso).
➔ Frágil. Si se rompe en trozos con facilidad (galena).
➔ Dúctil. Cuando se puede estirar en hilos (cobre).
➔ Maleable. Si puede extenderse en láminas (oro y plata).
Es la rotura de un mineral en láminas (mica) (1), cubos (halita) (2) o romboedros (calcita) (3).
Es la raya que queda cuando se frota un mineral sobre una placa de porcelana blanca sin esmaltar. Su color siempre es el mismo para cada mineral y no tiene por qué coincidir con el color de su superficie.


Es la resistencia que opone el mineral a ser rayado por otro mineral o por un material afilado. Se mide con la escala de Mohs de 10 minerales ordenados de menor a mayor dureza.


2. Yeso
Minerales muy blandos (se rayan con la uña).


Minerales duros (se rayan con una lima).


Minerales blandos (se rayan con una navaja).




Minerales muy duros (rayan el vidrio).
1 ¿Cuál de estos minerales presenta exfoliación en láminas y cuál es dúctil o maleable?



2 Diseña un procedimiento para diferenciar un fragmento de un cristal de mica de uno de yeso.
Es la rotura de un mineral en fragmentos con superficies curvas, como la obsidiana (1); astillas, como el crisotilo (2) o formas irregulares.


¿Qué brillo tiene el mineral?
No metálico
¿Se exfolia en láminas?
¿Se raya con la uña?

Moscovita
Es untuoso al tacto

¿Tiene brillo vítreo?
Metálico
¿Tiene color negro, gris o amarillo?
Es de color rojizo
¿De qué color es la raya?
Rojo cereza
¿Es negro, brillante y magnético?

Magnetita
Rojo bermellón
Es verde No No No No No No
¿Produce efervescencia con los ácidos?

Malaquita

Calcita

3 ¿Sabrías deducir qué dureza tiene un mineral desconocido si has comprobado que este raya al cuarzo y es rayado por el topacio?
4 Según su tenacidad, ¿cómo son la galena, el yeso, el oro y el cobre?

Hematites

Cinabrio
Es muy pesado
Se exfolia en cubos

Galena
¿Es de color gris plomo?
Tiene color amarillo y brillo metálico

5 La galena es un mineral rico en plomo y la magnetita es un mineral rico en hierro que se comporta como un imán. Ambos son muy parecidos externamente, de color oscuro y brillo metálico. Diseña un procedimiento para diferenciar la magnetita de la galena.
Los yacimientos minerales son acumulaciones naturales de minerales. Se extraen mediante labores de minería a partir de minas subterráneas y minas a cielo abierto.
• Minerales metalíferos. Son una mezcla de metales. El mineral del que se extrae un metal es la mena, y los que le acompañan y nos son explotables son la ganga.
• Minerales no metalíferos. No son fuente de metales. Se dividen en minerales industriales (utilizados como abrasivos, fertilizantes y materiales cerámicos, y materiales de construcción.
Ejemplos de aplicaciones de los minerales

Aluminio. Su principal mena es la bauxita. Se emplea para fabricar latas (sobre todo de bebidas), pinturas o papel de aluminio.

Mercurio. Se extrae del cinabrio. Se utilizaba para fabricar pilas, plaguicidas, tubos fluorescentes, medicamentos, etc.

Plomo. Se extrae de la galena. Se aprovecha para la elaboración de pilas, baterias, pinturas y pantallas de protección radiactiva.

Da algunos minerales, como la halita, se extrae sal común que sirve para conservar v condimentar los alimentos.

Cobre. Una mena es la calcopirita. Se utiliza para fabricar cables y equipos electrónicos, tuberías de conducción de agua, etc.

De algunos minerales, como el azufre y la silvina se obtienen fertilizantes que se usan para el crecimiento de las cosechas.

Hierro. Se extrae de la magnetita Se emplea en la siderurgia para la producción acero y la fabricación de una gran variedad de productos.

La calcita y el yeso se utilizan como materiales de construcción para la fabricación de escayola o cemento.
Explotaciones mineras en Andalucía
En Andalucía, la Faja Pirítica Ibérica aporta la mayor concentración de sulfuros metálicos que existe en el mundo. Destacan los siguientes yacimientos metalíferos:
• Almonaster La Real (Huelva). Se extrae cobre, plomo y zinc.
• Riotinto (Huelva). Es una mina a cielo abierto de la que se extrae cobre, hierro, cinc, plomo y plata.
• Cobre las Cruces (Sevilla). Mina a cielo abierto de la que se obtiene cobre.
• Minas de Alquife (Granada). Se extrae principalmente hierro, siendo la mayor mina a cielo abierto de hierro de Europa.
• Minera los Frailes en Aznalcóllar (Sevilla). Se obtiene zinc, cobre y plomo.
Los números naturales se utilizan para contar. Forman un conjunto ordenado, ya que posee un primer elemento, el uno, y para cada elemento siempre hay un siguiente.
El sistema de numeración decimal está formado por las cifras {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}. Combinando estas diez cifras podemos escribir cualquier número. En el sistema de numeración decimal cada unidad que ocupa una posición equivale a 10 veces el valor de la unidad que se encuentra a su derecha.
El censo de la población andaluza, a uno de enero de 2023, es de 8 538 376 habitantes (Fuente: Instituto Nacional de Estadística). El valor de cada una de esas cifras depende de su posición:
8 5 3 8 3 7 6
Unidades de millón Centenas de millar Decenas de millar Unidades de millar Centenas Decenas Unidades
La descomposición de 8 538 376 es:
8
Un número A es divisible entre otro B si la división de A entre B es exacta; o sea, si el resto de la división es cero. En tal caso se utilizan las siguientes expresiones equivalentes:
A es un múltiplo de B ⇔ B es un divisor de A
Un número es primo si únicamente posee dos divisores distintos: él mismo y la unidad. Si un número posee más de dos divisores ese número es compuesto. El 1 no es primo.
Para saber si un número es divisible entre otro basta con efectuar la división y comprobar que el resto es cero. Pero también podemos conocer si un número es divisible entre 2, 3 o 5 sin necesidad de efectuar la división aplicando los siguientes criterios (criterios de divisibilidad):
➔ Un número es divisible entre 2 si su última cifra es par.
➔ Un número es divisible entre 3 si la suma de sus cifras es múltiplo de 3.
➔ Un número es divisible entre 5 si su última cifra es 0 o 5.
También, sin efectuar la división, sabremos que un número es divisible entre 6 si es múltiplo de 2 y 3; divisible entre 10 si es múltiplo de 2 y 5; divisible entre 15 si es múltiplo de 3 y 5; divisible entre 30 si es múltiplo de 2, 3 y 5.

Indica, sin efectuar la división cuáles de los siguientes números son divisibles entre 2, cuáles son divisibles entre 3 y cuáles son divisibles entre 5:
14, 20, 17, 22, 37, 45, 55, 59, 63, 102
Entre 2: 14, 20 y 102 porque su última cifra es par.
Entre 3: 45, 63 y 102 porque la suma de sus cifras es múltiplo de tres.
Entre 5: 20, 45 y 55 ya que acaban en 0 o en 5.
Recuerda cómo se efectúa la descomposición en factores primos:
➔ Se escribe el número que deseamos descomponer en factores primos.
➔ Colocamos a la derecha del número su menor divisor primo.
➔ El cociente de la división por el primo anterior se coloca debajo del número.
➔ Se repiten los pasos anteriores hasta que el cociente sea 1.
Realiza la descomposición factorial de 12, 18, 20 y 42.
Dos líneas de autobús salen de la misma parada. La línea A tiene una frecuencia de 4 minutos y la B de 5. A las ocho de la mañana salen los dos autobuses. ¿A qué hora volverán a coincidir saliendo de la parada?
➔ Los autobuses de la línea A saldrán a las 8:04, 8:08, 8:12, 8:16, 8:20, etc.
Los números 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44 … son múltiplos de 4
➔ Los autobuses de la línea B saldrán a las 8:05, 8:10, 8:15, 8:20, 8:25, etc.
Los números 5, 10, 15, 20, 25, 30, 35, 40, 45 … son múltiplos de 5.
Los múltiplos de un número se obtienen al multiplicar ese número por los números naturales: 1, 2, 3, 4, 5…

Entre los múltiplos de 4 y 5 aparecen 20 y 40. Así pues, 20 y 40 son múltiplos comunes. Eso significa que coincidirán saliendo de la parada a las 8:20, a las 8:40, etc.
El mínimo común múltiplo de varios números es el menor de todos los múltiplos comunes.
Se escribe: m.c.m. (4,5) = 20, y se lee: «el mínimo común múltiplo de 4 y 5 es 20».
6 Sin efectuar ninguna división, localiza cuáles de los números siguientes son múltiplos de 2, de 3, de 5 y de 6.
30, 42, 60, 70, 91, 105
7 Haz la descomposición factorial de los números 18, 105, 120, 150 y 490.
8 Halla todos los múltiplos de 4, 5 y 6 menores o iguales que 60 y, en cada uno de los siguientes casos indica cuáles son los múltiplos comunes y cuál es el mínimo común múltiplo.
a) de 4 y 5
b) de 4 y 6
c) de 5 y 6
d) de 4, 5 y 6
Se desea colocar baldosas cuadradas en una pared de 240 cm de altura y 180 cm de anchura. ¿Cuál será la longitud máxima del lado de las baldosas para que se pueda rellenar la pared sin necesidad de romper ninguna baldosa?
➔ Todos los divisores de 180 son:
1, 2, 3, 4, 5, 6, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90 y 180.
➔ Todos los divisores de 240 son:
1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 30, 40, 48, 60, 80, 120 y 240. Los divisores de un número se pueden obtener a partir de su descomposición factorial.
Los números 1, 2, 3, 4, 5, 6, 10, 12,15, 20, 30 y 60 son divisores comunes de 180 y 240. El mayor de ellos es 60. El máximo común divisor de 180 y 240 es 60: m.c.d. (180, 240) = 60.
Para cubrir la pared con baldosas de máxima longitud de lado sin necesidad de romper ninguna, el lado de cada baldosa debe medir 60 cm.
El máximo común divisor de varios números es el mayor de todos los divisores comunes.
Se escribe: m.c.d. (180, 240) = 60, y se lee: «el máximo común divisor de 180 y 240 es 60».
La descomposición en factores primos nos proporciona otro procedimiento para calcular el máximo común divisor y el mínimo común múltiplo de varios números:
➔ Mínimo común múltiplo de varios números: se realiza la descomposición factorial de todos los números y se multiplica los factores no comunes y los comunes elevados al mayor exponente.
➔ Máximo común divisor de varios números: se realiza la descomposición factorial de todos los números y se multiplican solo los factores comunes elevados al menor exponente.
Halla el mínimo común múltiplo y el máximo común divisor de los números 84 y 90.
Comenzamos efectuando la descomposición factorial de ambos números:
El mayor exponente tanto de 2 como de 3 (que son los factores comunes) es 2. Por tanto:
(84, 90)
1 260
El menor exponente tanto de 2 como de 3 (que son los factores comunes) es 1. Por tanto: m.c.d. (84, 90) = 2 · 3 = 6
Observa que m.c.m. · m.c.d. = 84 · 90. En efecto: 1 260 · 6 = 84 · 90 = 7 560
9 Calcula los diez primeros múltiplos de 45 y 60. ¿Cuántos son comunes? ¿Cuál es el mínimo común múltiplo? El m.c.m. de 45 y 60, ¿cuántas veces contiene a 45? ¿Y a 60?
10 Halla los múltiplos de 75 y 90 menores que 500. ¿Cuántos son comunes? ¿cuál es el mínimo común múltiplo? El m.c.m. calculado, ¿cuántas veces contiene a 75? ¿Y a 90?
Los números enteros son una extensión de conjunto de los números naturales que incluye a los números enteros con signo negativo y con signo positivo incluido también el cero. No hay un primer elemento, pero sí es un conjunto completamente ordenado. El valor absoluto de un entero negativo se obtiene cambiándole el signo y el de un entero positivo manteniendo su signo. Se indica colocando el número entre barras. Los enteros se representan sobre la recta numérica colocando el cero en el centro, los negativos a la izquierda y los positivos a la derecha, tanto más alejados del centro cuanto mayor sea el valor absoluto.
Suma de números enteros
➔ Si tienen el mismo signo: Se suman los números y se deja el mismo signo.
➔ Si tienen distinto signo: Se restan los números y se pone el signo del mayor.
Resta de números enteros
Para restar dos números enteros, se suma al primero el opuesto del segundo. El opuesto de un número se obtiene cambiándole el signo.
Multiplicación y división de números enteros
Para multiplicar y dividir números enteros se multiplican o dividen los números y se aplica la regla de los signos: si los números tienen el mismo signo, el resultado es positivo, pero si los números tienen distinto signo el resultado es negativo.
Jerarquía de operaciones con números enteros
También con números enteros en operaciones combinadas se sigue la prioridad establecida.
(–2)3 + (7 – (–1)) : (–4) –32 · (–2)
1.º Paréntesis de operaciones (–2)3 + 8 : (–4) –32 · (–2)
2.º Potencias –8 + 8 : (–4) –9 · (–2)
3.º Multiplicaciones y divisiones –8 + (–2) – (–18)
4.º Sumas y restas –10 + 18 = 8
11 Halla el valor absoluto, representa sobre la recta numérica y ordena de menor a mayor los números:
–2, –5, 0, +3, –6, +4, +7, +1
12 Efectúa las siguientes operaciones:
a) 3 · (–4) – 5 · (–2)
c) 13 – (2 · (–4) + 6) – 7
b) 7 : (4 + 3) + 3 – (3 – 1) d) 6 + (4 : (–2) – 5) – (–3)
13 Carmen tiene 46 años y dos hijos de 11 y 17 años. ¿Qué edad tenía Carmen el mayor tenía la edad del menor?
14 Un autobús parte de su salida. En la primera parada bajan 14 personas y suben 5, y en la segunda bajan 6 y suben 12. ¿Con cuántos salió si quedan 17 pasajeros?
15 En un depósito hay 100 litros de agua, entran 24 litros cada cuarto de hora y salen 3 cada cinco minutos. ¿Qué cantidad de agua tendrá al cabo de dos horas?

Paula se está entrenando para correr los 100 metros lisos. A la longitud se le denomina magnitud, mientras que, los metros, son la unidad de medida.
➔ Llamamos magnitudes a las propiedades de los cuerpos que se pueden medir.
➔ La cantidad de una determinada magnitud se determina utilizando una unidad de medida e identificando el número de veces que esta está contenida.
Como la elección de una unidad de medida es algo arbitrario, para evitar confusiones la comunidad científica estableció en 1960 un Sistema Internacional de Unidades, y clasificó las magnitudes en:
Magnitudes básicas
Son aquellas que se definen por sí mismas y son independientes de las demás.
Magnitudes derivadas
Son aquellas que se obtienen a partir de las magnitudes básicas.
En esta tabla se recogen las principales magnitudes básicas y derivadas con sus unidades de medida:
Magnitudes básicas
Magnitud Unidad Símbolo
Longitud Metro m
Masa Kilogramo kg
Tiempo Segundo s
Temperatura Kelvin K
Cantidad de sustancia Mol mol
Magnitudes derivadas
Magnitud Unidad Símbolo
Superficie Metro cuadrado m2
Volumen Metro cúbico m3
Densidad Kilogramo por metro cúbico kg/m3
Velocidad Metros por segundo m/s
Aceleración Metros por segundo al cuadrado m/s2
Fuerza Newton N
Para facilitar la expresión de cantidades muy grandes o pequeñas los científicos también se pusieron de acuerdo para definir una serie de múltiplos y submúltiplos:
Para pasar de una unidad a otra resultan muy útiles los factores de conversión, es decir, una fracción en la que incluimos en el numerador la unidad de medida que queremos obtener y en el denominador la unidad original:
Unidad final
Unidad original
Expresa 110 km/h en m/s:
110 km h ∙ 10 3 m 1 km ∙ 1 h 3 600 s = 30,56 m s
Para expresar magnitudes muy grandes o muy pequeñas también se emplea la notación científica, que utiliza las potencias de 10. Por ejemplo, la masa de la Luna es 73 490 000 000 000 000 000 000 kg = 7,349 ∙ 1022 kg.
Siempre se comete un pequeño error al tomar cualquier medida. Por ello, se denominan cifras significativas (c.s.) de una medida a aquellas que se pueden leer en el aparato de medida.
Las cifras significativas de una medida se determinan a partir de las siguientes reglas:
a) Todas las cifras distintas de cero de una medida son significativas. Por ejemplo, 3,46 cm tiene 3 c.s.
b) Los ceros a la derecha de la coma son significativos. Por ejemplo, 1,600 kg tiene 4 c.s.
c) Los ceros a la izquierda no se consideran significativos. Por ejemplo, 0,011 L tiene 2 c.s.
d) Los ceros al final de un número sin coma no son significativos salvo que se incluya un punto al final. Por ejemplo, 200 N tiene 1 c.s. y 200. N tiene 3 c.s.
Los datos numéricos de un experimento se recogen en tablas. Volviendo al ejemplo de Paula y los 100 m lisos, la siguiente tabla muestra la distancia recorrida en función del tiempo:
Además, representarlos en una gráfica ayuda a encontrar relaciones entre las variables. Por ejemplo, la distancia recorrida por Paula en función del tiempo podría considerarse como una relación de proporcionalidad directa entre ambas variables.
16 Utiliza factores de conversión para hacer los siguientes cambios de unidades:
a) 2 kg/m3 a g/cm3 b) 7 256 023 ns a s c) 25 km/h a m/s
17 Expresa en notación científica: a) 6 250 000 000 m b) 0,000000078 s c) 1 270 000 000 000 kg d) 0,1240000000000 L
18 Indica el número de cifras significativas: a) 6 200 kg b) 0,00560 m c) 300 N
19 Se han representado gráficamente los datos de un experimento y se ha llegado a la conclusión de que no hay una relación predecible entre las dos variables. ¿Estás de acuerdo?
➔ Los minerales son sustancias sólidas, inorgánicas, de origen natural, con composición química definida y estructura cristalina.
➔ Los minerales masivos tienen estructura interna cristalina, pero externamente no tienen forma definida.
➔ Los cristales son sólidos minerales con estructura interna cristalina y forma externa geométrica de poliedros que presentan caras, vértices y aristas.
➔ Algunos cristales de gran valor se denominan gemas o piedras preciosas, como el diamante, el rubí y la esmeralda.
➔ Los minerales se clasifican según su composición química y estructura cristalina en: elementos nativos, halogenuros, sulfuros, óxidos, carbonatados, sulfatos y silicatos.
➔ La dureza es la resistencia que oponen los minerales a ser rayados por otros minerales o por un material afilado. La escala de Mohs ordena los minerales de 1 a 10 según su dureza.
➔ La exfoliación es la rotura de un mineral en fragmentos: láminas (mica), romboedros (calcita) o cubos (halita).
➔ La fractura es la rotura de un mineral en fragmentos con superficies curvas (concoidea), astillas (fibrosa) o formas irregulares.
➔ La tenacidad es el comportamiento de un mineral cuando lo intentamos romper o deformar. Según el tipo de tenacidad, el mineral puede ser: elástico, plástico, frágil, dúctil o maleable.
➔ El brillo es el aspecto que presenta la superficie de un mineral cuando refleja la luz que recibe. Puede ser metálico, vítreo, céreo, adamantino, sedoso, etc. Si carecen de brillo se denominan mates.
➔ Los yacimientos minerales son acumulaciones naturales de minerales. Se extraen mediante labores de minería a partir de minas subterráneas y minas a cielo abierto.
➔ Los minerales metalíferos se componen de una mezcla de metales donde la mena es el mineral que se extrae y la ganga es la roca que lo acompaña, junto con otros minerales no explotables.
20 Indica el grupo al que pertenecen los siguientes minerales, desde el punto de vista de la forma externa, de su estructura cristalina y desde el punto de vista de su composición química.




21 Averigua qué tipo de fractura presenta el sílex (1).
¿Cómo favoreció esta clase de fractura la utilización de este mineral en la antigüedad y qué objetos se fabricaron con él?

22 La extracción y la manipulación de determinados minerales, como el asbesto, debe hacerse con precaución, porque pueden causar enfermedades graves a trabajadores y habitantes cercanos a las zonas de extracción y tratamiento de esos minerales.
Averiguad para qué se ha utilizado el asbesto y por qué ya no se utiliza. ¿Qué tipo de enfermedad causa este mineral? ¿Qué otras enfermedades eran comunes entre los mineros de las minas de carbón y de cinabrio?
23 Por cada tonelada de aluminio hay que extraer cuatro toneladas de bauxita. ¿Por qué es necesario el reciclaje de los residuos metálicos?
24 ¿De qué depende que un mineral sea considerado mena o ganga?
25 Según la clasificación de los minerales, ¿qué tienen en común el oro, la plata y el cobre? ¿En qué se distinguen estos de otras clases de minerales?
➔ Los números naturales:
• Sirven para contar.
• Es un conjunto ordenado.
• Está formado por el 1 y a partir de él siempre hay un siguiente.
➔ Con el sistema de numeración decimal podemos escribir cualquier número. En este sistema cada cifra es 10 veces mayor que la que está a su derecha.
➔ Los múltiplos de un número se obtienen multiplicándolo por 1, 2, 3…
➔ El mínimo común múltiplo de dos números es el menor de todos los múltiplos comunes. Se obtiene multiplicando los factores comunes y no comunes elevados al mayor exponente.
➔ El máximo común divisor de dos números es el mayor de todos los divisores comunes. Se obtiene multiplicando solo los factores comunes elevados al menor exponente.
➔ Los números enteros están formados por los números naturales con signo positivo y negativo y por el 0.
➔ El valor absoluto de un entero positivo es el propio número.
El valor absoluto de un entero negativo es su opuesto.
➔ Para sumar dos números enteros con el mismo signo, se suman sus valores y se deja el mismo signo.
➔ Para sumar dos números enteros con distinto signo, se restan sus valores y se pone el signo del mayor.
➔ El resultado de la multiplicación o de la división de números enteros es positivo si los números enteros tienen el mismo signo.
➔ El resultado de la multiplicación o de la división de números enteros es negativo si los números enteros tienen distinto signo.
➔ El orden para realizar operaciones combinadas es:
1.˚ Paréntesis.
2.˚ Multiplicaciones y divisiones.
3.˚ Sumas y restas.
26 Di, sin efectuar la división, cuáles de los siguientes números son múltiplos de 6:
9 24 51 66 80 102 444
27 Efectúa la descomposición factorial de los números:
24 30 32 98 300
28 Con los números 45 y 75:
a) Haz la descomposición factorial de cada uno de ellos.
b) Halla A = m.c.m.(45, 75).
c) Halla B = m.c.d. (45, 75).
d) Multiplica 45 · 75 y luego multiplica A · B. ¿Qué observas?
29 Tres ciclistas A, B y C están entrenado en un circuito con un ritmo regular. El ciclista A completa el circuito en 4 minutos, B en 5 minutos y C, en 6. Si los tres comienzan el circuito en el mismo punto:
a) ¿Cada cuánto tiempo coinciden en ese punto A y B?
b) ¿Cada cuánto tiempo coinciden en ese punto A y C?
c) ¿Cada cuánto tiempo coinciden en ese punto B y C?
d) ¿Cada cuánto tiempo coinciden en ese punto los tres?
30 Efectúa las siguientes operaciones:
a) (7 – 3 + 5) – (4 – 2) b) 16 – (6 – 1 – 2) + 3 · 5
c) 4 – 11 · 9 : 3 + 17 d) (–2)5 + (–3)2 – 4 · (1 – 3)
31 Un administrativo trabaja en un edificio de oficinas. Toma el ascensor desde el garaje. Sube cinco pisos para fichar. Baja dos pisos para reco ger el correo. Por fin, sube un piso más para mantener una reunión. La sala de reuniones está en el tercer piso. ¿En qué plantas están el garaje, el registro de entrada y el correo?

32 Si en un depósito vacío de 100 litros de capacidad se vierten 4 litros de agua cada 2 minutos. ¿En cuánto tiempo se llenan?
33 Este año el viaje de estudios de 4.º de la ESO lo haremos con una agencia de viajes por importe cerrado de 5 000 euros. Cada uno de los 60 alumnos pondremos 40 euros. La asociación de padres ha decidido colaborar con una donación de 1 600 euros. Para financiar el resto del dinero, vamos a representar una función de teatro a la que asistirán nuestros padres y familiares, de modo que las 200 entradas que permite el aforo del salón de actos están aseguradas. ¿Qué precio tendremos que poner a cada entrada?
➔ Las magnitudes son las propiedades de los cuerpos que se pueden medir.
➔ La cantidad de una determinada magnitud se mide indicando cuántas veces contiene una unidad de medida.
➔ Las magnitudes básicas o fundamentales son aquellas que se definen por sí mismas y son independientes de las demás.
➔ Las magnitudes derivadas son aquellas que se obtienen a partir de las magnitudes básicas.
➔ Para expresar una magnitud en distintas unidades se usan los factores de conversión.
➔ La notación científica ayuda a expresar cantidades muy grandes o muy pequeñas como potencias de 10.
➔ Las cifras significativas de una medida son aquellas que pueden leerse en el aparato de medida. Son significativas:
• Todas las cifras distintas de cero.
• Los ceros a la derecha de una coma.
• Los ceros situados entre dos cifras distintas de cero.
34 Indica cuáles de las siguientes magnitudes son básicas y cuáles derivadas.
a) Aceleración.
b) Masa.
c) Densidad.
d) Tiempo.
e) Superficie.
f) Temperatura.
35 Utiliza factores de conversión para expresar:

a) 12 250 s en h b) 13 219 m en km
c) 0,6 kg/m3 en g/cm3 d) 35 km/s en m/s
e) 0,2 m/h en m/s f) 15 cm/s en m/s
36 Expresa en notación científica:
a) 0,00025 m
c) 1 290 000 kg
e) 150 000 000 km
b) 1 700 s
d) 0,00000008 cm
f) 0,001 g
37 Indica el número de cifras significativas en las siguientes medidas:
a) 0,007 s
c) 500 cm
e) 10 150 km
b) 1 200 m
d) 1 203 km
f) 203,230 km
¿Por

En la ciudad de Acra (Ghana) se encuentra el mayor vertedero del mundo de residuos electrónicos ilegales, procedentes de los países desarrollados, en el que malviven miles de personas, entre ellos muchos niños, rebuscando componentes metálicos entre la basura y expuestos a peligrosas sustancias nocivas.
a Averiguad los nombres de los principales minerales que aportan elementos metálicos necesarios para fabricar teléfonos inteligentes.
b Buscad información sobre las ventajas de la reutilización de los metales y los principales procesos que se siguen para su reciclaje.


El coltán (columbita y tantalita) es un valioso mineral estratégico. De él se extraen el tántalo y el niobio, que tienen muchísimas de aplicaciones. El 80 % de las reservas mundiales se encuentra en África, sobre todo en la República Democrática del Congo, y es una de las razones de una guerra que, entre 1998 y 2003, acabó con la vida de más de 5 millones de seres humanos. Miles de personas trabajan en las minas de coltán; la mayor parte son niños que malviven en régimen de semiesclavitud: «Cada kilo de coltán cuesta la vida de dos niños» (Alberto Vázquez Figueroa).
Además, en Sierra Leona, Liberia y otros países africanos los conocidos como «diamantes de sangre» se extraen utilizando a personas explotadas y se comercializan ilegalmente para financiar conflictos armados.


1 Buscad información sobre el coltán. ¿Qué aplicaciones tiene? ¿Qué actividades se deberían llevar a cabo para reducir al mínimo la necesidad de importarlo?
2 Elaborad un informe sobre el tráfico ilegal de diamantes. ¿Creéis que quien compra un diamante debe solicitar al vendedor acreditación sobre la gema que va a adquirir, para certificar su origen legítimo
3 Buscad información sobre los recursos estratégicos y la «maldición de los recursos naturales». ¿Por qué para algunos países, como Noruega o Reino Unido, encontrar petróleo ha sido un privilegio del que se ha beneficiado toda la sociedad, mientras que en otros, como Rusia, Irán, Irak o Venezuela, ha resultado ser una maldición que ha empobrecido a sus ciudadanos y ha generado graves conflictos bélicos?
4 Averiguad qué mineral era estratégico en el Paleolítico ¿Y en la Edad del Bronce? ¿Por qué el wolframio era un mineral estratégico en la segunda guerra mundial?
Resolved las tareas, escribid las respuestas y las conclusiones a las que habéis llegado sobre las consecuencias de la explotación de minerales.
Presentad el trabajo en Word/Writer, PowerPoint/Impress, Prezi, Canva… e incluid animaciones, vídeos, fotografías…
1 La escala de Mohs ordena los minerales de 1 a 10 según su:
a. Dureza.
b. Tenacidad
2 Las magnitudes que se definen por sí mismas se llaman:
a. Magnitudes derivadas.
b. Magnitudes básicas.
3 En el sistema de numeración decimal, una unidad de millar equivale a:
a. 100 centenas.
b. 100 decenas.
4 Los cristales son sólidos minerales:
a. Sin forma definida.
b. Con forma externa geométrica.
10 La calcita se exfolia en:
a. Cubos.
b. Romboedros.
9 La velocidad de 36 km/h es lo mismo que:
a. 3 600 m/s.
b. 10 m/s.
8 La mica se exfolia en:
a. Hilos.
b. Láminas.
7 El comportamiento de un mineral cuando lo intentamos romper o deformar se denomina:
a. Tenacidad.
b. Exfoliación.
5 El m.c.m. de dos números es:
a. El menor de los múltiplos comunes.
b. El mayor de los múltiplos comunes.
6 Algunos cristales de gran valor se denominan:
a. Minerales masivos.
b. Gemas.
0 Se organiza la clase por parejas y cada una se identifica con un número por sorteo.
0 Empieza a preguntar la pareja 1. Esta pareja hace la primera pregunta del tablero a la pareja 2.
0 La pareja 2 debe contestar en 5 segundos.
0 Si el profesor o la profesora da por válida la respuesta, la pareja 2 gana tantos puntos (de 1 a 3) como se indiquen.
0 Ahora, la pareja 2 pregunta a la pareja 3, y así sucesivamente.
0 Gana la pareja que haya obtenido más puntos una vez hechas todas las preguntas.
Si una pareja quiere sumar más puntos, puede inventar una pregunta; con ello, suma 2 puntos, y la pareja que primero responda suma 1 punto.
11 El m.c.d. de dos números es:
a. El menor de los divisores comunes.
b. El mayor de los divisores comunes.
20 La fractura de un mineral en fragmentos con superficies curvas se denomina:
a. Fibrosa.
b. Concoidea.
12 Cuando un mineral se puede estirar en hilos se denomina:
a. Dúctil.
b. Elástico.
13 La medida de 1 cm equivale a:
a. 10 –2 m.
b. 10 –3 m.
14 El oro y la plata son minerales:
a. Frágiles.
b. Maleables.
15 El número 1 es:
a. Un número primo.
b. No es un número primo.
19 Los números naturales sirven para:
a. Contar.
b. Dividir la unidad en partes iguales.
18 Una medida de 13,60 cm tiene:
a. Tres cifras significativas.
b. Cuatro cifras significativas.
17 La prioridad en multiplicaciones y divisiones es:
a. Primero multiplicaciones y después divisiones.
b. Se efectúan de izquierda a derecha.
16 En los minerales metalíferos, el mineral que se extrae es la:
a. Mena.
b. Ganga.

¿Qué tipo de roca se utilizó para construir el Puente Nuevo de Ronda (Málaga)?
¿Qué fracción de la figura representa el bloque rojo?

¿Por qué se derrite el hielo?



Mirad el vídeo para observar cómo se forman las rocas y contestad a las siguientes preguntas:
¿Conoces alguna roca que flote en el agua?
¿Crees que el petróleo es una roca?
Investigad por grupos:
¿Qué tipo de roca forma el paisaje del Torcal de Antequera (Málaga)?
Debate. Los viajeros de una nave extraterrestre identificaron un elemento químico radiactivo formando parte de los sedimentos de una cuenca sedimentaria marina. ¿Cómo es posible que, millones de años después, lo identificaran de nuevo en una estatua de mármol de Macael (Almería)?
En esta unidad aprenderás...
Las rocas.
Fracciones. Números decimales. Fracciones y números decimales.
Los estados de la materia: cambios de estado.
Teoría cinético-molecular. Mezclas y disoluciones.
Las rocas son agregados naturales formados por uno o varios minerales que se unieron durante el mismo proceso de formación. Se pueden clasificar según dos criterios:
Composición
Homogéneas
➔ Están formadas por un único tipo de mineral.
➔ El color es uniforme, es decir, presentan solo un color en su superficie.
➔ Por ejemplo, la caliza está compuesta solo por el mineral calcita.
Textura
Heterogéneas Es la forma en la que se disponen los minerales en la roca.
➔ Son combinaciones de varios minerales.
➔ El color no es uniforme, presentan varios colores en su superficie.
➔ Por ejemplo, el granito está formado por tres minerales: cuarzo, feldespato y mica.
Granuda
A simple vista, se observan cristales de minerales de distintos colores y tamaños.
Vítrea Clástica
Carece de cristales, ya que está formada por una masa amorfa de vidrio.
Se observan fragmentos que proceden de la erosión de otras rocas.
Según su origen, las rocas se clasifican en metamórficas, sedimentarias y magmáticas.
Las rocas metamórficas se forman a cierta profundidad en la corteza terrestre, a partir de otras rocas (sedimentarias, magmáticas o metamórficas) cuando la elevada presión y temperatura a la que se encuentran sometidas modifica la composición de sus minerales. Este proceso se denomina metamorfismo.
Según su textura pueden ser:
Formadas por capas de minerales en forma de láminas o bandas paralelas. Por ejemplo, la pizarra, el gneis y el esquisto. Pizarra. Tiene un aspecto en forma de láminas u hojas, color negro azulado y sus cristales son muy pequeños y no se ven a simple vista.

1 Las fachadas de los edificios de la localidad donde vives, el suelo que pisas o algunos de los objetos que tienes en tu casa posiblemente están compuestos por muchos tipos diferentes de rocas. ¿Conoces los nombres de algunas de ellas?
No foliadas
No forman capas. Por ejemplo, el mármol y la cuarcita.


Mármol. Es una roca cristalina, no laminar, que presenta una amplia gama de colores, frecuentemente con vetas (1).
3 ¿Cómo se forman las rocas metamórficas? Busca algunos ejemplos de este tipo de rocas y describe sus características. 1
2 ¿Qué diferencia hay entre rocas homogéneas y heterogéneas? Cita algún ejemplo de cada una.
Las rocas sedentarias se forman a partir de la consolidación de sedimentos formados por partículas de distintos tamaños, transportadas por el agua, el hielo y el viento, que se depositan y sedimentan en estratos y se compactan y cementan.
Durante millones de años, el peso de los estratos de sedimentos superiores aplasta a los inferiores, que se van compactando y cementando hasta formar las rocas sedimentarias.
Según el origen de los sedimentos, las rocas se clasifican en:
Detríticas
Los sedimentos proceden de fragmentos de otras rocas.

Conglomerado. Formado por fragmentos mayores de 4 mm: si son redondeados, se denomina pudinga, y si son angulosos, brecha.

Arenisca. Compuesta por partículas menores de 2 mm, aunque observables a simple vista.
No detríticas

Arcilla. Formada por granos que solo pueden verse en el microscopio electrónico.
Los sedimentos proceden de la precipitación de sales minerales disueltas en el agua (las calizas) o de restos de seres vivos (carbón y petróleo).

Caliza. Formada por caparazones, esqueletos marinos o sustancias químicas disueltas en el agua.
4 Trabajad por parejas y fijaos en esta imagen del Caminito del Rey, en Málaga.
a) ¿Qué creéis que indican las líneas verticales de esta formación de rocas sedimentarias?
b) ¿Por qué están unas junto a otras?

Carbón. Procede de restos vegetales (antracita, hulla, lignito y turba).


Petróleo. Proviene de restos de plancton marino.
Mary Anning (1799-1847)
Las rocas sedimentarias, a diferencia de la mayoría de las rocas ígneas y metamórficas, pueden contener fósiles acumulados en sus estratos. Mary Anning fue una de las fundadoras de la paleontología y demostró que mediante los fósiles se podía estudiar la historia de los seres vivos. Descubrió los primeros esqueletos de ictiosaurios y plesiosaurios.
Las rocas magmáticas se forman cuando el magma del interior de la Tierra se enfría y solidifica.
Según donde se formen las rocas, pueden ser:
Volcánicas
Se forman cuando el magma asciende, sale a la superficie terrestre y se enfría rápidamente. Por ejemplo, el basalto, la obsidiana y la pumita.


Obsidiana. Tiene textura vítrea (vidrio volcánico). Es de color negro y se fragmenta en superficies curvas.
5 Sandra es geóloga del Departamento de Geología y Ecología de la Universidad de Málaga y quiere comprobar cuál de los dos minerales, el granito (1) o el basalto (2), es el más denso. Para evidenciarlo, pesa en una balanza dos fragmentos cúbicos de ambos minerales que ocupan el mismo volumen.
Trabajad por parejas y diseñad dos procedimientos, uno teórico y otro experimental, que permitan calcular que el volumen de los dos minerales es el mismo. Tras pesarlos, ¿cuál de los dos minerales es el más denso?


Plutónicas
Se forman cuando el magma se enfría y solidifica, lentamente, en el interior de la corteza terrestre y tienen textura granuda. Por ejemplo, el granito y el gabro.




Granito. Formado por pequeños cristales de cuarzo, mica negra (biotita) y feldespato (ortosa).
6 Explicad cómo se transforman los sedimentos en rocas sedimentarias.
7 ¿En qué tipo de rocas crees que encontrarías los cristales mejor formados, en las rocas plutónicas o en las volcánicas?
8 Macarena ha ido de excursión a Tenerife y en la llanura desértica de la Cañada de los Guancheros, al pie del volcán Teide, ha encontrado una piedra clara, porosa, de tacto áspero y muy ligera, que flota en el agua. ¿Qué roca ha recogido Macarena?

¿Qué textura tiene la roca?
Vítrea

Obsidiana
Cristales unidos entre sí
¿Produce efervescencia con los ácidos?

¿Presenta orientación laminar?

Mármol Cuarcita
¿Produce efervescencia con los ácidos?
Fragmentos de rocas
¿Es homogénea?
¿Tiene cantos redondeados?



Caliza Arenisca Pudinga
¿De qué tamaño es el grano?
El grano es fino. Se rompe en láminas

Pizarra
El grano es medio o grueso
Con bandeado Sin bandeado


Esquisto
9 Formula una hipótesis que te permita explicar cuál pudo ser el origen de los fragmentos de rocas que dieron lugar a una brecha y a una pudinga.
Claro ¿De qué color es?

Granito

Brecha
Oscuro
Grano grueso

Gabro
Grano fino

Basalto
10 ¿Qué tienen en común la pizarra, el gneis, el esquisto, el mármol y la cuarcita? ¿Y la arenisca, la pudinga, la brecha y la arcilla?
El ciclo de las rocas es el conjunto de transformaciones que sufren las rocas en el tiempo, de manera que unas rocas se modifican para convertirse en otras.
Es una transformación lenta y continua en la que intervienen dos procesos:
➔ Procesos geológicos internos. El vulcanismo genera rocas magmáticas y la orogénesis (formación de montañas) genera rocas metamórficas.
➔ Procesos geológicos externos. Destruyen las rocas de la superficie terrestre y acumulan sedimentos, que darán lugar a rocas sedimentarias.
Enfriamiento
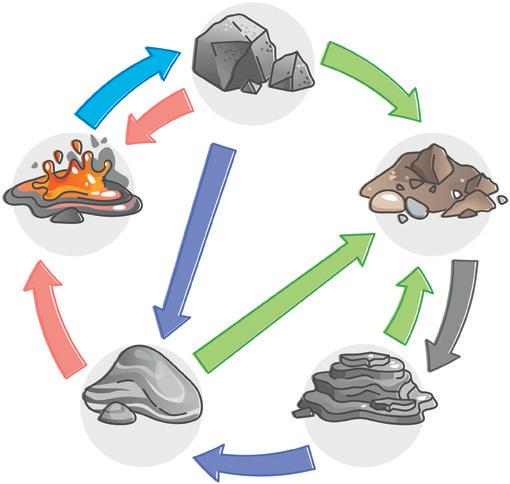
Magma
Calentamiento
Meteorización, erosión, transporte y sedimentación
Rocas ígneas
Calentamiento
Calor y presión
Meteorización, erosión, transporte y sedimentación
Sedimentos
Rocas metamórficas Rocas sedimentarias
Calor y presión
El relieve andaluz está formado por tres grandes unidades: Sierra Morena, las cordilleras béticas y la depresión del Guadalquivir.
Sierra Morena
Depresión del Guadalquivir
Sierra Morena
➔ Situada al norte de la comunidad, recorre Andalucía de este a oeste.
➔ Contiene rocas silíceas muy antiguas: granito (como el que constituye el batolito de Los Pedroches); pizarras, esquistos, cuarcita armoricana (como las de Los Órganos de Despeñaperros) y gneis.
Cordilleras Béticas
Meseta
Río Guadalquivir
➔ Se extienden de Almería a Cádiz a lo largo de la costa mediterránea y ocupan también el sur de Sevilla, Córdoba y Jaén.
➔ Constituidas por terrenos calizos (calizas, margas y mármoles), terrenos silíceos (pizarras y esquistos) y rocas volcánicas como las que afloran en la región de Cabo de Gata (Almería).
Sierra Morena
Sierra Morena. Más que una cadena montañosa, es un escalón tectónico que separa la Meseta de la Depresión del Guadalquivir.
➔ Se sitúa entre las cordilleras Béticas y Sierra Morena, donde se produce sedimentación de materiales y por la que discurre el río Guadalquivir.
➔ Los materiales del valle central, que es plano, son arcillosos; mientras que en las llanuras que lo rodean predominan suaves colinas y cerros formados por materiales calizos (calizas y margas) y arcillosos.
La extracción de rocas en Andalucía
Andalucía es una región minera histórica, con grandes recursos geológicos, siendo sus primeros yacimientos de época romana, y representa el 40 % de la producción nacional. Las rocas empleadas en la construcción y con fines ornamentales, como mármoles, yesos, calizas y travertinos, se extraen principalmente de Almería (la Sierra de Macael es famosa por su mármol blanco empleado en las columnas y la fuente del patio de los Leones de la Alhambra de Granada) y en menor medida de la sierra de Huelva. El granito se extrae de Huelva, Sevilla y Córdoba, y las pizarras principalmente de Almería y Granada.
Las rocas energéticas, como el carbón, se extraen de Córdoba y en menor cantidad de Sevilla, y los lignitos en Granada.
El vidrio, obtenido a partir de la arenisca, y la cal y el cemento, de la caliza, se utilizan en la construcción.
Las tejas, los azulejos de cerámica y los ladrillos, se obtienen de la arcilla, que son los materiales utilizados en edificios como el de la Alhambra de Granada.

Otros invertebrados
Silíceos
Calizos
Arcillosos
Volcánicos
Principales yacimientos y canteras de rocas:
1 Mármol
2 Caliza
3 Arcilla
4 Carbón
La caliza, el granito y la arenisca se emplean en la construcción de edificios y monumentos.
El mármol es una roca ornamental, utilizado para hacer edificio como el Centro Tecnológico Andaluz de la Piedra y escultura como la fuente de los leones de la Alhambra, construidos con mármol de Macael.

11 Relaciona en tu cuaderno los siguientes tipos de rocas con cada una de las unidades que conforman el relieve andaluz:
1) Materiales sedimentarios a) Sierra Morena. (arcillas y calizas).
2) Terrenos calizos, silíceos b) Cordilleras Béticas. (pizarras y esquistos) y rocas volcánicas.
3) Rocas silíceas muy c) Depresión del antiguas (granitos, cuarcitas...). Guadalquivir
La cuarcita se emplea en la construcción de edificios. La pizarra se utiliza para las cubiertas de las edificaciones, así como para el pavimento de las calles, como en los pueblos de la Alpujarra (Granada).

12 ¿Para qué se utilizan el granito, el carbón, la pizarra, el mármol y el petróleo?
13 Trabajad por parejas e investigad de qué tipos de rocas proceden los siguientes materiales de construcción: vidrio, cemento, ladrillo, hormigón, cal y tejas.
14 Un anticuario afirma que posee una estatua de la fuente de los leones de la Alhambra, pero Silvia cree que es una reproducción hecha de cuarzo blanco. Diseña un procedimiento que permita averiguar si es de mármol.
En la unidad anterior hemos revisado el conjunto de los números naturales y el conjunto de los números enteros obtenido como ampliación de los naturales.
En esta unidad vamos a repasar el conjunto de los números racionales, que se definen como cociente de números enteros. Dependiendo de la forma de expresar los racionales se denominan:
➔ Fracciones. No se efectúa el cociente.
➔ Números decimales. Se efectúa la división y se extraen los decimales.
Fracción es un cociente indicado de números enteros. El denominador de la fracción es el número de partes iguales en que se divide la unidad. El numerador indica cuántas de las partes en que se ha dividido la unidad se toman.
En la fracción 3 5 el denominador, 5, significa que hemos dividido una unidad en cinco partes iguales; el numerador, 3, significa que, de las cinco partes, hemos tomado tres.
➔ Una fracción es propia cuando el numerador es menor que el denominador. Si el numerador es mayor o igual que el denominador la fracción se denomina impropia.
Toda fracción impropia se puede descomponer en suma de un entero más una fracción propia haciendo la división entera y aplicando la regla: dividendo entre divisor es igual al cociente más resto partido por divisor:
➔ El conjunto de las fracciones, como el de números enteros es un conjunto ordenado. De dos fracciones A y B o bien A > B, o bien A < B, y si no, A y B son equivalentes.
➔ Dos fracciones son equivalentes si representan la misma cantidad. Se puede comprobar que dos fracciones son equivalentes si coinciden los productos cruzados:
3 5 y 6 10 son equivalentes porque 3 10 = 6 5
➔ Fracciones equivalentes a una fracción dada por ampliación o por simplificación: se obtienen multiplicando o dividiendo numerador y denominador por un mismo número:
➔ Una fracción es irreducible si no se puede simplificar más, es decir, cuando el numerador y el denominador son primos entre sí.
Reducir fracciones a común denominador es obtener fracciones equivalentes que tengan como denominador el mínimo común múltiplo de los denominadores. Esta tarea facilita la comparación de fracciones y también las operaciones de suma y resta de fracciones.
Ordena de menor a mayor las fracciones: 3 5 ; 3 4 ; 2 3 .
Reducimos a común denominador: m.c.m. (5, 4, 3) = 60. Después se ordenan:
3 5 ; 3 4 ; 2 3 ⇒ 36 60 ; 45 60 ; 40 60 ; ⇒ 36 60 < 40 60 < 45 60 ⇒ 3 5 < 2 3 < 3 4
Suma y resta de fracciones
Si tienen distinto denominador se reducen previamente a común denominador. Si tienen el mismo denominador, sumamos o restamos los numeradores dejando el mismo denominador.
Suma: 9 3 + 5 3 = 14 3 Resta: 5 7 –2 7 = 3 7
Multiplicación de fracciones
Multiplicamos los numeradores y los denominadores entre sí: 3 7 5 2 = 3 · 5 7 · 2 = 15 14
División de fracciones
Multiplicamos en cruz las dos fracciones:
Potencias de base fraccionaria
Elevamos numerador y denominador al exponente: U 4 3 Z3 = 43 33 = 64 27
Recuerda la jerarquía de las operaciones:
1.º Paréntesis. 2.º Potencias. 3.º Multiplicaciones y divisiones. 4.º Sumas y restas.
15 Halla tres fracciones equivalentes en cada caso:
5 3 b) 12 18 c) 25 15
16 Descompón en suma de entero más fracción propia: a) 7 4 b) 12
17 Reduce a común denominador y ordena de menor a mayor: 14 3 ; 16 5 ; 7 2
18 Haz las siguientes operaciones:
19 En una clase de 24 alumnos, 18 son chicas. ¿Qué fracción de esa clase son chicas? Simplifícala hasta hacerla irreducible.

Utilizamos los números decimales para representar cantidades no enteras. Están formados de una parte entera situada a la izquierda de la coma y otra parte decimal, a la derecha.
El número decimal 1 325,1634 se descompone en dos partes:
• Parte entera: 1 325, que tiene 1 unidad de millar, 3 centenas, 2 decenas y 5 unidades.
• Parte decimal: 0,1634, que tiene 1 décima, 6 centésimas, 3 milésimas y 4 diezmilésimas. De dos números decimales distintos es mayor el que tiene mayor su parte entera; si tienen la misma parte entera es mayor el que tiene mayor la cifra de las décimas; si estas también coinciden, se comparan las centésimas, y así sucesivamente.
También, gráficamente, si están representados dos números decimales distintos sobre la recta numérica, el menor de los dos, figura a la izquierda y el mayor a la derecha.
Representa y ordena de menor a mayor: A = 5, 2; B = 5, 0; C = 5, 5 y D = 4, 9.
Recuerda cómo se efectúan las operaciones elementales con números decimales:
Podemos clasificar los números decimales en alguno de los siguientes tipos:
➔ Exacto. Con un número finito de decimales: 3,45.
➔ Periódico puro. Su parte decimal es un grupo de cifras que se repite indefinidamente, al que se denomina periodo: 4,142857.
➔ Periódico mixto. La parte decimal, antes del periodo, tiene un grupo de cifras que no se repite, que se denomina anteperiodo: 7,457 213.
➔ No periódico. La parte decimal tiene infinitos decimales no periódicos, también conocidos como números irracionales. Por ejemplo: π = 3,14159265…
Los números racionales o fraccionarios son los que se pueden expresar como cociente de números enteros y en forma decimal. Incluyen al número decimal exacto, número decimal periódico puro y número decimal periódico mixto.
Para convertir una fracción en número decimal basta con efectuar la división y obtendremos alguno de los tres tipos que hemos indicado. Así, por ejemplo:
Recuerda cómo obtener la fracción generatriz de un número decimal:
• Si es decimal exacto, se multiplica y divide por la potencia de 10 correspondiente.
• Si es periódico: a la parte entera seguida del anteperiodo y del periodo se le resta la parte entera seguida del anteperiodo. Después, se divide entre tantos nueves como cifras tenga el periodo seguido de tantos ceros como cifras tenga el anteperiodo.
En ambos casos, la fracción obtenida se simplifica hasta que sea irreducible.

20 Realiza la descomposición de los siguientes números decimales:
21 Representa sobre la recta numérica y ordena de menor a mayor los números decimales:
22 Efectúa, sin calculadora, las siguientes operaciones con números decimales:
·
23 Expresa en forma de número decimal exacto las siguientes fracciones con ayuda de una calculadora:
13
63
612

24 Con ayuda de una calculadora, expresa en forma de número decimal periódico puro las siguientes fracciones:
25 Con ayuda de una calculadora, expresa en forma de número decimal periódico mixto las siguientes fracciones:
26 Halla la fracción generatriz de los siguientes números decimales exactos:
27 Calcula la fracción generatriz de los siguientes números decimales periódicos puros: 4,27
28 Calcula la fracción generatriz de los siguientes números decimales periódicos mixtos:
Desde la antigüedad siempre hemos querido entender la naturaleza del mundo que nos rodea. Al principio las explicaciones atendían más a razonamientos lógico-filosóficos. Es en la Edad Moderna cuando se comienza a aplicar el método científico, dando lugar al nacimiento de la física y la química como ciencias propiamente dichas. Cabe mencionar como pioneros en cada disciplina, respectivamente, a Galileo Galilei (15641642) y a Antoine Lavoisier (1743-1794).
El método científico se resume básicamente en:
➔ Observación del fenómeno en estudio con la correspondiente toma de datos y su posterior organización efectuando los cálculos oportunos.
➔ Planteamiento de hipótesis capaces de explicar los fenómenos observados.
➔ Diseño de nuevos experimentos que confirmen o refuten las hipótesis.
➔ Formulación de leyes universales que gobiernen las hipótesis confirmadas.
La Física y la Química centran su estudio en la materia y los fenómenos que la alteran. Materia es todo lo que nos rodea y que ocupa un lugar en el espacio; todo lo que podemos percibir y que de alguna manera se puede medir.
La materia está caracterizada por sus propiedades. Entre ellas podemos mencionar:
• Masa: cantidad de materia, y que se puede comparar con otras masas mediante una balanza.
• Volumen: cantidad de espacio ocupado por esa materia.
• Temperatura: estrechamente ligada al estado de agitación de las partículas que constituyen la materia.
Estas y otras propiedades de la materia son «medibles», pero ¿qué es medir?
Medir es comparar una magnitud con otra que se toma como unidad.
Medida de masa

Medida de volumen Medida de temperatura


Para la medida de las magnitudes fundamentales utilizamos el sistema internacional de unidades. En este sistema la masa se mide kilogramos, la longitud en metros, el tiempo en segundos y la temperatura en grados kelvin. Otras magnitudes derivadas, como la densidad, se obtienen a partir de las magnitudes fundamentales.
¿Qué densidad tiene la pirita, sabiendo que un fragmento de 175 g de este mineral ocupa un volumen de 35 cm3?
densidad = masa volumen = 175 35 = 5 g/cm3
La materia se presenta básicamente bajo tres formas distintas que denominamos estados de agregación:
➔ Sólido. La materia en este estado se caracteriza por mantener constante tanto la forma como el volumen.
➔ Líquido. La materia mantiene en este estado su volumen constante. Sin embargo, la forma se adapta al recipiente que la contiene.
➔ Gas. También en este estado la forma se acopla al recipiente que la contiene, pero además tiende a ocupar todo el volumen disponible del recipiente.
Los estados de agregación en los que se presenta la materia, aparte de su propia naturaleza, dependen fundamentalmente de la temperatura y, dependiendo de esta se pueden transformar de unos a otros:
sublimación
fusión
Sólido Líquido Gas
solidificación
vaporización condensación
sublimación inversa

La caloría es la cantidad de energía que hay que suministrar a un gramo de agua líquida para incrementar un grado su temperatura.
La cantidad de energía por unidad de masa necesaria para que una sustancia cambie de estado recibe el nombre de calor latente de fusión o vaporización.
El calor latente de fusión del hielo es de LF = 80 cal/g. ¿Cuánta energía se necesita para fundir 100 g de hielo a 0 ºC?
Q = m · LF = 100 80 = 8 000 cal = 8 kcal
El calor específico de una sustancia es la cantidad de energía necesaria para incrementar en un grado centígrado la temperatura de 1 gramo de sustancia sin cambiar de estado. El calor específico del agua es 1 cal/g.
¿Cuánta energía se necesita para calentar medio litro de agua desde 20 ºC hasta 40 ºC?
Q = c · m · ∆T = 1 500 (40 – 20) = 10 000 cal = 10 kcal
El punto de fusión de una sustancia es la temperatura a la que cambia de estado de sólido a líquido y el punto de ebullición es la temperatura a la que cambia de estado de líquido a gas. Esas temperaturas dependen de la presión. Para el agua, y a la presión atmosférica, esas temperaturas son de 0 ºC y 100 ºC, respectivamente.
Equivalencias entre algunas unidades:
La teoría cinético-molecular intenta justificar el comportamiento observable de la materia en cada uno de los estados de agregación. Inicialmente se aplica al comportamiento de la materia en estado gaseoso. Se plantean las siguientes hipótesis que podemos resumir en los siguientes postulados:
➔ Los gases están formados por partículas microscópicas que se mueven en línea recta en todas las direcciones y con distintas velocidades.
➔ El volumen de las partículas es insignificante frente al del recipiente que contiene el gas y prácticamente no hay fuerzas de atracción o repulsión entre partículas.
➔ Esas partículas chocan entre sí y contra las paredes del recipiente que las contiene y estos choques son perfectamente elásticos; es decir, tras los choques las partículas, aunque cambien de dirección, no alteran su rapidez porque no se pierde energía.
➔ La presión que ejerce un gas es precisamente el resultado de las colisiones de las partículas contra las paredes del recipiente y se puede efectuar una medida bien precisa.
➔ Una modificación en la temperatura del gas se traduce en una variación en la velocidad de las partículas y por tanto se refleja en un cambio de presión.
En la ilustración se muestra un gas encerrado en el interior de un recipiente cilíndrico. En la parte superior hay un émbolo o pistón que se puede accionar variando la presión o modificando el volumen.
También se puede calentar o enfriar el gas modificando su temperatura.
Tras la confirmación experimental de estas hipótesis se formulan las siguientes leyes:

➔ Ley de Boyle-Mariotte: Si se mantiene constante la temperatura de un gas el volumen del gas es inversamente proporcional a su presión:
➔ Ley de Charles: Si se mantiene constante la presión de un gas el volumen y la temperatura son directamente proporcionales:
➔ Ley de Gay-Lussac: Si se mantiene constante el volumen de un gas la presión y la temperatura son directamente proporcionales:
➔ Podemos combinar las leyes anteriores formulando la ley de gases:
En estas relaciones la presión se mide en atmósferas, el volumen en litros y la temperatura en grados kelvin.
Las conclusiones de la teoría cinético-molecular no solo justifican el comportamiento de los gases, sino que también se pueden aplicar a los estados líquido y sólido, con la idea básica de que la velocidad de las partículas, o mejor, su estado de agitación depende única y exclusivamente de la temperatura a la que se encuentran.
En los sólidos las partículas se encuentran firmemente enlazadas unas con otras, por lo que apenas pueden moverse, tan solo pueden vibrar en torno a posiciones fijas. De ahí que los sólidos tengan una forma determinada y un volumen incompresible y constante (salvo que se eleve la temperatura, en cuyo caso puede mostrar dilatación). Las partículas en este estado ni fluyen ni se difunden.


En los líquidos las fuerzas de atracción entre partículas son menores que en los sólidos. Las partículas pueden moverse libremente en el seno del líquido, pero sin perder el contacto entre ellas y sin poder escapar. Por eso los líquidos pueden adoptar la forma del recipiente que los con- tiene, pero mantienen su volumen fijo y apenas se comprimen. Las partí- culas fluyen, pero no se difunden.
En los gases las partículas se mueven libremente y al azar ya que no hay fuerzas de atracción entre ellas y están muy alejadas unas de otras salvo
quizás en eventuales choques.
Así, los gases adoptan la forma del recipiente y ocupan todo el volumen disponible: se pueden comprimir y expandir. Las partículas fluyen y se difunden.
29 Sabiendo que el calor latente de vaporización del agua es de 540 cal/g, ¿cuántas calorías se necesitan para la ebullición de 100 g de agua?
30 En un depósito cilíndrico con un pistón está encerrado un gas que ocupa un volumen de 3 litros y la presión que marca el manómetro es de 1 atmósfera. A continuación, y sin alterar la temperatura se acciona el émbolo reduciendo el volumen hasta 2 litros. ¿Qué presión marcará el manómetro?
31 En un depósito cilíndrico con un pistón está encerrado un gas que ocupa un volumen de 3 litros. La temperatura en el interior del recipiente es de 25 ºC. Suministramos calor al recipiente hasta que el gas alcanza una temperatura de 75 ºC, manteniendo la presión constante. Se observa que el gas se expande. ¿Hasta alcanzar qué volumen se habrá expandido el gas?

32 En un depósito cilíndrico con un pistón se encierra encerrado un gas comprimido a 5 atmósferas de presión ocupando un volumen de 0,25 litros. Sin alterar la temperatura, se libera el émbolo expandiéndose el gas hasta alcanzar la presión atmosférica ¿Hasta qué volumen se habrá expandido?
33 En un depósito cilíndrico con un pistón está encerrado un gas que ocupa un volumen de 3 litros. La temperatura en el interior del recipiente es de 25 ºC. Suministramos calor al recipiente hasta que el gas alcanza una temperatura de 75 ºC, manteniendo el volumen constante. Se observa que la presión aumenta. ¿Qué lectura de presión marcará el manómetro?
34 En el interior de un recipiente cilíndrico provisto de un émbolo practicable se encuentra un gas a 35 ºC de temperatura y 1,25 atmósferas de presión, siendo el volumen de 4,5 litros. Se incrementa la temperatura hasta 50 ºC y se comprime hasta que el volumen se reduce a 3 litros. ¿Cuál será la presión?
Existe una gran diversidad de sustancias en la naturaleza, que se clasifican en dos grandes grupos: sustancias puras y mezclas.
➔ Las sustancias puras son sustancias simples o compuestos químicos que:
• Tienen propiedades químicas invariables.
• Sus componentes no se pueden separar por métodos físicos.
➔ Una mezcla está compuesta de dos o más sustancias simples en proporción variable en la que:
• Su composición y propiedades son varia- bles.
• Es posible separar sus componentes por métodos físicos.
Las mezclas pueden ser heterogéneas u homogéneas.
Mezclas
Heterogéneas
Podemos observar sus componentes a simple vista o con un microscopio.
Se pueden separar sus componentes de forma sencilla.
Algunos ejemplos son el agua con aceite o la sopa con fideos.
Técnicas de separación de mezclas
Homogéneas
El tamaño de las partículas en la mezcla es tan pequeño, que no se pueden distinguir sus componentes.
Es una mezcla estable que se mantiene en el tiempo.
Algunos ejemplos son la leche, la sangre o la salsa mahonesa.
Los componentes de una mezcla se pueden separar mediante métodos físicos. La técnica de separación más adecuada dependerá del tipo de mezcla.
Mezclas heterogéneas
➔ En mezclas heterogéneas, los métodos de separación de sus componentes son:
• Filtración: para separar un componente sólido de otro líquido.
• Decantación: para separar líquidos de distinta densidad.
• Tamizado: para separar mezclas sólidas con distinto tamaño de grano.
Mezclas homogéneas
➔ En mezclas homogéneas, los métodos de separación son:
• Cristalización: un componente sólido disuelto en otro líquido precipita.
• Destilación: dos componentes líquidos se separan por tener puntos de ebullición diferentes.
Una disolución es una mezcla homogénea de dos o más sustancias puras que no reac cionan entre sí y que están en proporciones variables. Generalmente, en una disolu ción hay un componente en mayor proporción y otro u otros en proporción menor.
➔ Disolvente: es el componente que se encuentra en mayor proporción.
➔ Soluto: es el componente que se encuentra en menor proporción.
Atendiendo a la mayor o menor proporción de soluto frente al disolvente, las disolucio nes se pueden clasificar como diluidas, concentradas y saturadas.

La concentración de una disolución es la cantidad de soluto que hay presente en una determinada cantidad de disolución.
Las formas más frecuentes de expresar la concentración son:
Peso-Peso (Riqueza en peso)
masa de soluto masa de disolución · 100
Proporciona los gramos de soluto que hay en 100 g de disolución.
Peso-Volumen
masa de soluto
volumen de disolución · 100
Proporciona los gramos de soluto que hay en 100 mL de disolución.
También se calcula en gramos sobre 1 litro de disolución (g/L) y miligramos sobre litro de disolución (mg/L).
volumen de soluto volumen de disolución · 100
Proporciona la cantidad de soluto que hay en 100 unidades de volumen de disolución.
35 ¿Qué técnica utilizarías para separar las siguientes mezclas?
a) Agua y aceite.
b) Agua y alcohol.
c) Arena y grava.
d) Limaduras de hierro y sal.
Se prepara una disolución mezclando 30 g de sal con 120 mL de agua. Calcula su riqueza en peso.
masa de soluto
masa de disolución · 100
Las masas son aditivas, es decir, la masa de la disolución es la suma de las masas de soluto y disolvente. Por tanto:
30 g
30 g + 120 g 100 = 3 000 150 = 20 %
Hay disueltos 20 g de sal por cada 100 g de disolución.
A 60 mL de etanol se agrega agua hasta obte- ner un volumen de 0,30 L. Calcula la concen- tración de esta disolución como porcentaje en volumen.
% volumen volumen de soluto (mL) volumen de disolución (mL) 100 Los volúmenes de soluto y disolución deben estar expresados en las mismas unidades, tendremos en cuenta que el volumen de disolución es de 0,30 L = 300 mL. Sustituimos los datos y calculamos:
% volumen 60 mL
300 mL · 100 = 20 % Esto indica que hay disueltos 20 mL de etanol por cada 100 mL de esta disolución.

36 La concentración de una disolución salina es de 0,5 g/L. ¿Qué medida de concentración se está utilizando? ¿Cuántos gramos de sal hay en un bidón de 5 litros de esa disolución?
37 La glucosa es un azúcar que se encuentra en algunos alimentos. Calcula la concentración peso-volumen de una disolución que se preparó mezclando 65 g de glucosa con agua hasta un volumen de 300 mL de disolución.
38 Si la densidad de la disolución de del ejercicio anterior es de 1,3 kg/L, calcula la masa de la disolución y la concentración riqueza en peso.
39 Se desea preparar 500 mL de una disolución de alcohol etílico al 20 % en volumen. ¿Qué cantidad de alcohol y de agua se necesitan?
➔ Las rocas son agregados naturales formados por uno o varios minerales que se unieron durante el mismo proceso de formación.
➔ Las rocas se pueden clasificar:
• Según su composición en homogéneas o heterogéneas.
• Según su textura en granuda, vítrea o clástica.
• Según su origen em metamórficas, sedimentarias y magmáticas.
➔ Las rocas metamórficas se forman a cierta profundidad en la corteza terrestre, a partir de otras rocas cuando la elevada presión y temperatura a la que se ven sometidas modifica la composición de sus minerales. Este proceso se denomina metamorfismo.
➔ Las rocas sedimentarias se forman a partir de la consolidación de sedimentos formados por partículas de distintos tamaños, transportadas por el agua, el hielo y el viento, que se depositan y sedimentan en estratos y se compactan y cementan.
• En las rocas sedimentarias detríticas, los sedimentos proceden de fragmentos de otras rocas.
• En las rocas sedimentarias no detríticas, los sedimentos proceden de la precipitación de sales minerales disueltas en el agua (las calizas) o por restos de seres vivos (carbón y petróleo).
➔ Las rocas magmáticas o ígneas se forman cuando el magma del interior de la Tierra se enfría y solidifica.
• Las rocas volcánicas se originan cuando el magma asciende y se enfría rápidamente en el exterior de la superficie terrestre. Presentan cristales microscópicos. Por ejemplo, basalto, obsidiana y pumita.
• Las rocas plutónicas se forman cuando el magma se enfría lentamente en zonas muy profundas, Presentan cristales grandes que pueden verse a simple vista. Por ejemplo, granito y gabro.
➔ El ciclo de las rocas es el conjunto de transformaciones que sufren una roca, a lo largo del tiempo, para convertirse en otra distinta.
➔ Sierra Morena está formada por rocas silíceas.
40 Escribe en tu cuaderno cuál de las siguientes rocas es sedimentaria o magmática (volcánica o plutónica).








41 Tomando como modelo el ciclo de las rocas, indica a qué tipo de roca (sedimentaria, metamórfica o magmática) corresponde cada una de las letras:
42 Indica si son verdaderas o falsas las siguientes afirmaciones:
a) Las rocas plutónicas se forman cuando el magma se enfría rápidamente en la superficie terrestre.
b) El carbón es una roca metamórfica formada a partir de restos de vegetales.
c) La pumita es una roca plutónica.
d) La obsidiana es una roca volcánica.
e) El granito es una roca plutónica formada por cuarzo, feldespato y mica.
43 Para que se formen las rocas magmáticas, ¿ha de salir el magma necesariamente al exterior?
44 Si halláramos fósiles de un erizo de mar en lo alto de una montaña formada por rocas calizas, ¿qué podríamos decir respecto del origen de esas calizas?

➔ Una fracción es el cociente indicado de dos números enteros.
Está formada por:
• Denominador. Número de partes iguales en que se divide la unidad.
• Numerador. Número de esas partes que se toman.
➔ Si el numerador es mayor que el denominador, la fracción es propia; en caso contrario la fracción es impropia.
➔ Toda fracción impropia se puede descomponer en la suma de un número entero (cociente de la división) más una fracción propia (resto de la división partido por divisor).
➔ Dos fracciones son equivalentes si representan la misma cantidad y cumplen: a b = c d ⇔ a · d = c · b
➔ Se obtienen fracciones equivalentes a una fracción dada multiplicando (por ampliación) o dividiendo (por simplificación) sus términos por un mismo número. Si no se puede dividir, la fracción es irreducible.
➔ Operaciones con fracciones:
• Suma: a b + c d = a · d + c · b bd
• Resta: a b –c d = a d – c b bd
• Multiplicación: a b c d = a c b d
• División: a b : c d = a · d c · b
• Potencia: T a b Yn = an bn
➔ Un número decimal se obtiene dividiendo el numerador entre el denominador de una fracción.
➔ Para obtener la fracción generatriz de un número decimal:
• Si es decimal exacto, se multiplica y divide por la potencia de 10 correspondiente.
• Si es periódico: a la parte entera seguida del anteperiodo y del periodo se le resta la parte entera seguida del anteperiodo. Después, se divide entre tantos nueves como cifras tenga el periodo seguido de tantos ceros como cifras tenga el anteperiodo.
45 Halla dos fracciones equivalentes, una por simplificación y otra por ampliación:
a) 15 12 b) 21 98 c) 24 36
d) 25 15 e) 26 65 f) 39 26
46 Descompón en una suma de un número entero más una fracción propia:
a) 11 5 b) 17 3 c) 27 11
d) 31 4 e) 97 13 f) 60 17
47 Tres compañeros se reparten un trabajo de Biología. A Juan le toca realizar dos sétimos del trabajo, a Ana le corresponde 3 octavos y a Luis el resto. Ordena la cantidad de trabajo de estos compañeros de menor a mayor.
48 Efectúa las operaciones indicadas:
a) T 3 7 –2 5 Y : T 4 3 –2 7 Y
b) 3 4 · T 2 3 + 3 2 Y – T 5 6 –1 3 Y2
49 Escribe el número decimal formado por 32 unidades y 27 milésimas.
50 Efectúa sin calculadora las operaciones siguientes:
a) 73,15 + 1,25
b) 73,15 – 1,25
c) 73,15 · 1,25
d) 73,15 : 1,25
51 Expresa en forma decimal y clasifica como decimal exacto, decimal periódico puro o decimal periódico mixto e indica cuál es el anteperiodo y el periodo.
a) 143 100
b) 202 33
c) 77 30
52 Halla la fracción generatriz de los siguientes números decimales:
a) 0,142857
b) 0,3
c) 0,3127

53 Una marca blanca de arroz se vende en tres formatos A, B y C. El formato A en paquetes de 625 g cuesta 1,25 €; B en tarrinas de 200 g cuesta 0,5 € y C en cajas de 2 kg a 3,6 €. Calcula el precio por kilogramo de cada formato y ordénalos de menor a mayor.
➔ Materia es todo lo que ocupa un lugar en el espacio y podemos percibir.
➔ Los estados de agregación o fases en que se presenta la materia son sólido líquido y gas.
➔ La teoría cinético-molecular explica cómo es el comportamiento de las moléculas en estado gaseoso y, por extrapolación, también en los estados líquido y sólido.
➔ Las leyes de los gases se resumen en la fórmula:
P · V T = P’ · V’ T’
➔ La materia se presenta, desde el punto de vista químico, como sustancias puras o mezclas.
➔ Las mezclas pueden ser o bien heterogéneas o bien homogéneas (disoluciones).
➔ Disolvente y soluto son los componentes de una disolución. El disolvente es el más abundante.
➔ Las expresiones de la concentración de una disolución son:
• Peso-Peso. • Peso-Volumen.
• Volumen-Volumen.
54 ¿Cuántas calorías se necesitan para llevar 250 g de hielo desde – 5 ºC hasta 20 ºC en forma de agua? (Datos: calor específico del hielo: 0,5 cal/g; calor específico del agua: 1 cal/g; calor latente de fusión del hielo: 80 cal/g).
55 En un recipiente cilíndrico con un émbolo se encierra un gas que ocupa un volumen de 50 cm3 medidos en condiciones normales (0 ºC de temperatura y 1 atm de presión).
a) ¿Qué volumen ocupará si se comprime hasta que la presión es 1,58 atm sin alterar la temperatura?
b) ¿Qué presión se alcanzará en el interior si se eleva la temperatura hasta 25 ºC sin modificar el volumen?
c) ¿Qué volumen ocupará el gas si se eleva la temperatura hasta 25 ºC sin alterar la presión?
d) ¿Qué volumen ocupará el gas si se eleva la temperatura hasta 25 ºC y la presión aumenta hasta 1,5 atm?
56 Calcula la concentración de la disolución que se obtiene añadiendo sobre 32 g de sal común (NaCl) agua hasta completar 480 mL.
57 Se mezclan 40 g de alcohol (densidad: 0,789 g/mL) con 60 g de agua (densidad 1 g/mL). Calcula la concentración:
a) Peso-Peso.
b) Peso-Volumen (en g/L).
c) Volumen-Volumen.


El profesor Gustav von Bon quiere recrear para su alumnado el proceso de formación de un tipo de rocas y lleva a cabo este experimento:
Primer paso. Llena una botella transparente hasta la mitad con arena, grava y pequeños guijarros y rellena el resto de la botella con agua.
Segundo paso. Agita el recipiente para mezclar los materiales.
Tercer paso. Deja reposar durante algún tiempo la botella. Los materiales se habrán dispuesto tal y como puedes ver en la imagen de la derecha.
a ¿Cómo se han distribuido los materiales de distintos tamaños después de haber sido introducidos en la botella con agua?
b ¿Te recuerda a algún proceso que tenga lugar en la naturaleza ¿Sabrías decir qué tipo de rocas origina este proceso y en qué zonas de la Tierra se suelen formar?




Alba se ha propuesto estudiar las rocas en el camino que recorre desde su casa hasta el centro donde estudia en Sevilla. Durante el trayecto, se fija en las rocas con las que están hechos los bordillos, las aceras, los tejados de los edificios, las fachadas, las esculturas, los monumentos, etc.
Luego, dibuja un mapa del itinerario y, utilizando diferentes símbolos, los sitúa en él e indica el tipo de material con el que están construidos: A) Casa. B) Centro de estudios. 1) Casa antigua con tejado de pizarra. 2) Estatua de mármol, 3) Casa con la fachada de arenisca. 4) Joyería con la fachada de caliza (travertino). 5) Bordillo de la acera de basalto. 6) Obelisco de granito.
1 Buscad información sobre las rocas de vuestra ciudad utilizadas habitualmente para la construcción de edificios y monumentos y elaborad un mapa similar al realizado por Alba.
2 La geología forense emplea el análisis geológico de las partículas de tierra halladas en la suela de zapatos o en los neumáticos de los vehículos para resolver crímenes. La policía encontró en una cantera, cerca de la carretera A-349 en Macael (Almería), un camión contenedor cargado de migrantes africanos que habían sido abandonados por los traficantes de personas y estaban a punto de perecer por asfixia. Las fuerzas de seguridad se movilizaron y detuvieron a tres sospechosos. Los geólogos forenses identificaron la presencia de fragmentos de diversas rocas en las suelas de sus zapatos y en las ruedas de sus vehículos:
• El sospechoso 1 fue detenido en Los Pedroches (Córdoba), cerca de la ermita de Piedrasantas, y presentaba fragmentos de rocas graníticas.
• El sospechoso 2 fue detenido en la autovía 334, cerca de Purchena (Almería) y presentaba fragmentos de mármol blanco.
• El sospechoso 3 fue detenido en Dos Hermanas (Sevilla) y presentaba fragmentos de arcilla.
¿Qué sospechoso es más probable que sea el traficante? Si en los migrantes identificaron fragmentos de basalto, ¿por qué parte de la costa es probable que entrasen?
Resolved las tareas, escribid las respuestas y las conclusiones a las que habéis llegado sobre las rocas y el relieve de Andalucía.
Presentad el trabajo en Word/Writer, PowerPoint/Impress, Prezi, Canva… e incluid animaciones, vídeos, fotografías…
¿Qué minerales forman el granito?
¿A partir de qué tipo de roca se obtiene el vidrio?
16
¿Cómo se denomina el conglomerado defragmentos redondeados?
¿Qué número es mayor: 14,30 o 14,31? ¿Qué técnica se aplica para separar líquidos con distinta densidad?
¿En qué unidades se mide la masa en el sistema internacional?
Si aumentamos la temperatura de un ¿la presióngas,sube o baja?
¿En qué grupo de rocas se clasifica la obsidiana?
¿De qué rocas se obtienen las tejas,losazulejos decerámicaylos ladrillos?
19 19
¿Cómo se denomina el conglomerado de fragmentos angulosos?
¿Cuál es el resultado de 56,78 + 45,3?
0 El objetivo del juego es llegar a la meta habiendo sumado más puntos que los demás.
0 Se necesita un dado.
0 Situados en círculo, empieza a jugar quien saque el número más alto al tirar el dado.
0 Esta persona avanza tantas casillas como indique el dado y contesta a la pregunta que se plantea.
0 El profesor o la profesora arbitrará la partida y confirmará si la respuesta es correcta.
Si lo es, se suman los puntos correspondientes: 1 punto casilla azul y 2 puntos casilla verde.
0 Luego, pasa el dado a la persona que quede a la derecha y así sucesivamente.
0 Se toma nota en la pizarra de la casilla en la que está situado cada jugador y de los puntos que lleva acumulados.
Rubén 6 5
¿Qué tipo de roca sedimentaria es la arenisca? ¿Cuál es la parte entera del número 76,87?
¿Qué cambio se produce en la fusión?
20 20
¿Qué numero resulta de sumar 14 décimas y centésimas?342
¿Cómo se llaman los componentes de una disolución?

¿Qué rocas se forman por el enfriamiento lento del magma?
decimales¿Cuántostiene el resultado del producto 3,12 · 4,28?
9 9 11 11 10 10
¿Quéde rocatipo sedimentaria es la caliza?
¿Aquégrupo de rocas pertenece el mármol?

Si fueras un explorador espacial, ¿qué condiciones se necesitan para que los mundos que visites puedan albergar vida?
Para comprar una casa, ¿pedimos un crédito o un préstamo?

¿Qué elementos químicos conoces?



Mirad el videojuego Let’s go to Mars sobre la exploración de Marte, desarrollado por el Instituto de Astrofísica de Andalucía (IAA).
¿Dónde está la sede del IAA?
¿Cuál es el principal objetivo del IAA?
Investigad por grupos:
¿Dónde se sitúan los observatorios del IAA?
Describid tres tipos de temas que se investiguen en el IAA.
¿Qué planeta del sistema solar es candidato para la terraformación?
Debate. Entre otros, la astrobiología investiga la búsqueda de vida en otros planetas. ¿Crees que puede existir vida en otros planetas?
En esta unidad aprenderás...
El planeta Tierra
Educación financiera. La financiación.
La estructura de la materia.
¿Te has preguntado alguna vez cómo se formó la Tierra? ¿Y el sistema solar y todos los cuerpos que lo componen? Hace 5 000 millones se produjo el estallido de una supernova que liberó polvo cósmico, que enriqueció y compactó una inmensa nebulosa. La nebulosa comenzó a girar, y junto al polvo cósmico, el hielo y otras partículas, formaron pequeñas estructuras llamadas planetesimales.
Durante millones de años, los planetesimales impactaron entre ellos, dando origen a planetas, como la Tierra. El interior de esta Tierra primitiva liberaba calor, lo que le permitía estar en un estado de fusión y que su interior se diferenciara por densidades:
➔ Los elementos pesados (níquel y hierro) se hundieron al centro y formaron el núcleo.
➔ Sobre el núcleo se situaron materiales menos densos que constituyeron el manto.
➔ Los más ligeros (silicatos) ascendieron a la superficie, que poco a poco, se fue enfriando hasta formar una corteza sólida.
➔ El vapor de agua liberado por la actividad volcánica de la Tierra primitiva, junto con el agua de los cometas y meteoritos, dieron lugar al agua de la hidrosfera.
➔ Los gases liberados de las emanaciones volcánicas formaron la atmósfera primitiva, carente de oxígeno y rica en vapor de agua, amoniaco, metano y nitrógeno.
La geosfera es la parte sólida del planeta. Es una bola casi esférica formada por tres capas concéntricas de diferente composición y estado y localizadas a distintas profundidades.
Continental. Forma los continentes, tiene entre 25-90 km de espesor y contiene rocas como el granito.
Oceánica. Forma los fondos marinos, tiene entre 6-12 km de espesor y contiene rocas como el basalto.
Corteza. Capa externa, fina y menos densa, que recubre la superficie. Formada por rocas sólidas, rígidas y ligeras, con silicatos de aluminio.

Núcleo. La capa más interna, densa y con mayor temperatura. Formada por hierro y níquel. Se extiende desde los 2 900 hasta los 6 370 km de profundidad.
Externo. Fluido y móvil.
Interno. Sólido debido a la elevada presión.
Atmósfera Hidrosfera
Inferior. Más denso y con materiales completamente sólidos.
Superior. Sólido con zonas parcialmente fluidas.
Manto. Capa intermedia. Formada por rocas con silicatos de magnesio. La temperatura y presión aumentan y se extiende desde los 90 hasta los 2 900 km de profundidad.
Los astrobiólogos investigan la existencia de zonas idóneas para el nacimiento y la evolución de la vida alrededor de las estrellas. Es probable que la vida pueda surgir en cualquier planeta que tenga las mismas condiciones que la Tierra primitiva.
La Tierra se localiza en la zona de habitabilidad del Sol, es decir, una región privilegiada situada a su alrededor, ni muy cerca ni muy lejos de él, que permite temperaturas suaves para la existencia de agua en estado líquido.
La Tierra posee un tamaño determinado para que su fuerza de gravedad retenga los gases y genere una atmósfera, necesaria para la aparición y el mantenimiento de la vida.



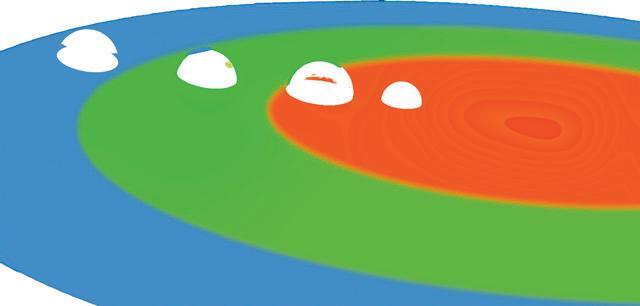

La Tierra tiene calor interno responsable de la tectónica de placas, lo que genera actividad volcánica, que aporta dióxido de carbono y es responsable del efecto invernadero que mantiene una temperatura media de unos 15 ºC, adecuada para la vida.
En 1974, el radiotelescopio de Arecibo (Puerto Rico) emitió un mensaje, mediante ondas de radio, al agrupamiento de estrellas M-13, cifrado en un código binario que daba lugar a un pictograma con datos de los seres humanos y sus conocimientos (1).
La sonda Kepler ha encontrado exoplanetas en estrellas cercanas, algunos potencialmente habitables. El instituto SETI (del inglés Search for Extra Terrestrial Intelligences) ha desarrollado proyectos para rastrear el universo en busca de señales de radio que puedan proceder de vida extraterrestre.
1 Describe las características generales de la corteza, el manto y el núcleo y de los materiales que los componen. Relaciona dichas características con su ubicación.
Aunque existen bacterias que no requieren oxígeno (anaerobias), este gas es necesario para que surjan formas pluricelulares más complejas. Para su formación es necesario que existan organismos fotosintéticos que consuman dióxido de carbono.
Inge Lehmann
Sismóloga danesa (1888-1993), estudió la velocidad de propagación de las ondas sísmicas generadas por diversos terremotos. Descubrió la existencia de un límite, la discontinuidad de Lehmann, que separa el núcleo externo líquido del núcleo interno sólido. En 1971, la Unión Geofísica Americana le concedió la máxima distinción: la Medalla William Bowie.
2 Trabajad por parejas y buscad información sobre la astrobiología. ¿Qué estudia esta disciplina? ¿Sabes cuál es el campo de estudio del científico sevillano Juan Pérez Mercader?
Juanjo ha decidido comprarse una guitarra nueva. Cuesta 300 €, así que para conseguirlo va a tener que ahorrar un poco. Piensa que lo mejor es guardar una cantidad fija al principio de cada mes de manera que, al no contar con ella, no pueda gastarla. Como no sabe qué cantidad va a poder guardar, va a escribir en una tabla los ingresos y los gastos que tiene durante este mes y así hacer una estimación. El resultado ha sido el siguiente:

Cuando termina el mes, a Juanjo le han quedado 42 €, que es la diferencia entre los ingresos y los gastos. Esta diferencia recibe el nombre de ahorro:
Ahorro = Ingresos – Gastos
Como ha sido capaz de ahorrar 42 €, decide que guardar 30 € y dejar el resto para imprevistos es una buena opción, así que todos los meses, al recibir su paga, retira esos 30 € y los guarda en una caja para no gastarlos.
Ahora sabe que, si no hay ningún contratiempo, dentro de 10 meses podrá comprarse la guitarra.
Lo que ha hecho Juanjo es un ejemplo de cómo hay que planificarse para conseguir un objetivo financiero.
Aunque los objetivos financieros pueden ser concretos, como una compra o un regalo, en general es aconsejable que el mismo ahorro se convierta en un objetivo de manera que, controlando los gastos, lleguemos a fin de mes y tengamos cierta seguridad financiera.
En nuestro día a día todos tenemos ciertas necesidades y deseos. La adquisición y utilización de los bienes y servicios para satisfacerlas recibe el nombre de

La gran oferta de bienes y servicios que tenemos a nuestra disposición hace que muchas veces confundamos nuestras necesidades o deseos y consumamos de una forma compulsiva e irracional, cayendo en el consumismo, que repercute de forma muy negativa en nuestra salud financiera y también sobre nuestro entorno.
La alternativa al consumismo es practicar un consumo inteligente. Para ello, tenemos que ser conscientes de nuestras necesidades reales y elegir aquellos productos y servicios que destaquen por su buena relación calidad-precio o por su bajo impacto en el medio ambiente.
Uno de los beneficios del consumo inteligente es el ahorro. El ahorro nos ayuda a hacer frente a imprevistos y a cubrir nuestras necesidades. Por eso, aunque no se te tenga ningún objetivo concreto, el ahorro tiene que convertirse en una prioridad. La mejor manera de priorizar el ahorro es incluirlo como un gasto fijo y que, como ha hecho Juanjo para comprar la guitarra, apartemos una cantidad todos los meses con este fin.
En general se recomienda que, como mínimo, destinemos al ahorro el 10 % de nuestros ingresos.
Ángela, la madre de Juanjo, es policía local y gana 1 800 € al mes. Teniendo en cuenta sus gastos fijos, ha decidido que va a ahorrar 190 € al mes y los va a ingresar en una cuenta que ha abierto solo con ese fin. ¿Qué porcentaje de su sueldo dedica al ahorro? ¿Cumple con las recomendaciones de ahorro?
Para calcular un porcentaje dividimos la parte entre el total y lo multiplicamos por 100. Así:
190
1 800 · 100 = 10,6 %
es superior al 10 %, por lo que cumple con las recomendaciones de ahorro.

Ahorrando 190 € al mes, al cabo de un año la madre de Juanjo ha acumulado 2 280 € en la cuenta que abrió con ese fin y, como no tiene que usarlos, ha decidido contratar un producto financiero.
Los productos financieros son instrumentos que ofrecen las entidades financieras (como los bancos) a través de los cuales se obtiene rentabilidad (intereses) de un determinado capital. En función del riesgo y del beneficio que aportan, los productos financieros pueden dividirse en dos tipos:
• Productos financieros de ahorro.
• Productos financieros de inversión.
Son productos de baja rentabilidad pero que no ponen en riesgo el capital depositado. En general, ofrecen más rentabilidad si te comprometes a no disponer del capital durante un tiempo determinado. Pero si lo que quieres es total disponibilidad, la rentabilidad es muy baja. Son productos financieros de ahorro la deuda pública, los fondos de inversión garantizados, los planes de pensiones garantizados o los depósitos.
En los depósitos, por ejemplo, la entidad te garantiza una rentabilidad igual a un porcentaje de la cantidad depositada.

Los productos garantizados, como fondos de inversióno planes de pensiones, garantizan total o parcialmente el importe de la inversión que se recupera al vencimiento, además de generar una rentabilidad que dependerá del comportamiento de una serie de valores del mercado.
El acto de abono de intereses se llama liquidación y los depósitos pueden tener liquidación al vencimiento o liquidaciones en periodos más cortos de tiempo. Vamos a ver con dos ejemplos en qué consiste cada uno de ellos.
En una determinada entidad bancaria ofrecen un depósito a un año con una rentabilidad al vencimiento del 2 %. Si Ángela deposita en él sus ahorros, ¿qué cantidad tendrá al finalizar el año?
Rentabilidad al vencimiento significa que los intereses se abonan cuando finaliza el plazo del depósito, que en este caso es un año. Como después de un año la cantidad depositada se incrementa en un 2 %, no tenemos más que calcular el correspondiente aumento porcentual:
2
Por lo que ha obtenido un beneficio de 45,6 €.
Como has visto en el ejemplo, la liquidación al vencimiento te ingresa de una sola vez todos los intereses cuando finaliza el periodo del depósito. No es así cuando los periodos son más cortos.
2,75%TAE1
2
Después de rescatar su depósito, la madre de Juanjo ha encontrado un banco en el le ofrecen una rentabilidad anual del 2,75 % a cambio de mantener su dinero durante dos años, ¿qué rentabilidad obtendrá al finalizar el plazo si los intereses se los abonan anualmente?
Si los intereses se reinvierten en el propio depósito, el aumento porcentual durante el segundo año será mayor, ya que se hará sobre los intereses generados el primer año. Para calcular el valor final de la inversión simplemente aplicamos de forma consecutiva los correspondientes aumentos porcentuales:
Lo que supone un beneficio de 129,67 €.
En estos productos el inversor asume un determinado riesgo sobre el capital a cambio de más rentabilidad. Los planes de pensiones o los fondos de inversión no garantizados, así como determinados planes de ahorro son ejemplos de estos productos. Al contratar estos productos es importante que el inversor se asesore adecuadamente y entienda los riesgos que asume.
3 Rocío ingresa todos los meses 1 400 € y gasta una media de 1 270 €. Calcula la capacidad de ahorro de Rocío y di si cumple con las recomendaciones de ahorro.
4 A Inés le han tocado 6 000 € en la lotería y, mientras decide qué hacer con ello, lo pone en un depósito a un año con un interés del 2,5 % anual. ¿Qué cantidad tendrá al finalizar el año?
5 En una entidad financiera ofrecen un depósito a tres años al 1,75 % anual. Si los intereses se r reinvierten en el depósito, ¿qué cantidad tendré después de esos tres años si invierto 5 000 €?
6 ¿Qué rentabilidad tiene un depósito que genera unos intereses de 2 000 € si inviertes 100 000 € en él?
Ángela está buscando casa en Sevilla, pero el precio de una vivienda es tan alto que no puede pagarla con sus ahorros. Lo que le pasa a Ángela es lo que nos pasa a la mayoría de las personas: ciertos bienes tienen un precio tan elevado que el dinero ahorrado no es suficiente para adquirirlos. Por suerte, las entidades financieras ponen a disposición de sus clientes productos que pueden cubrir estas necesidades de financiación.
Existen diversos productos de financiación, pero los más habituales son los préstamos y los créditos que, aunque a veces se confunden, son productos distintos.

En un préstamo, una entidad financiera entrega una cantidad a quien lo solicita (también llamado prestatario), el cual se compromete a devolverla en un plazo de tiempo determinado y abonando unos intereses que pueden ser fijos o variables. La devolución –o amortización – suele hacerse mediante cuotas periódicas.
Ángela ha encontrado por fin la casa que le gusta, pero, teniendo en cuenta lo que tiene ahorrado, todavía le faltan 100 000 €. Acude a una entidad financiera que le concede un préstamo a un interés anual del 3 %. Si devuelve el préstamo en mensualidades a lo largo de 25 años le han calculado cuotas de 474,21 € al mes. ¿Cuántos intereses habrá pagado Ángela al final de la vida del préstamo?
Al ser cuotas mensuales, al cabo de 25 años Ángela habrá pagado 25 · 12 = 300 cuotas. Como cada cuota asciende a 474,21 €, es fácil calcular que, al final de la vida del préstamo, habrá devuelto a la entidad financiera 300 · 474,21 = 142 263 €.
Los intereses pagados serán entonces la diferencia entre lo que ha devuelto y el importe de la deuda, es decir, 142 263 - 100 000 = 42 263 €.
Lo que supone un incremento de más del 42 % respecto a la deuda contraída.
En el ejemplo has visto que los intereses que se devuelven son muy altos, pero es el precio que se paga por acceder a bienes que, de otra manera, no podríamos adquirir.
En un crédito la entidad financiera pone a disposición de quien lo solicita una determinada cantidad que este puede usar en parte o en su totalidad, pagando intereses –generalmente más altos que en los préstamos– únicamente de la cantidad utilizada.
Mientras que los préstamos están más destinados a particulares, los créditos –por sus características– son más indicados para empresas.
Por otro lado, las entidades financieras hacen distinción entre préstamos hipotecarios y préstamos personales. El primero está destinado a la compra de una vivienda, es muy flexible en cuanto a los plazos de devolución y los intereses suelen ser más bajos; el segundo se destina a cualquier otro tipo de gasto, hay que devolverlo en un plazo máximo de ocho o diez años y los intereses suelen ser más altos.
7 Pedro ha pedido un préstamo de 150 000 € a un tipo de interés de 4 % para devolver en cuotas mensuales durante 20 años. Si cada cuota asciende a 908,97 €, ¿qué intereses habrá pagado al final de la vida del préstamo?
8 Eugenia me ha dicho que, al terminar de pagar su casa, en total había devuelto al banco 165 000 €. Si estuvo 30 años devolviendo el préstamo, ¿a cuánto ascendieron sus cuotas mensuales?
Teoría atómica de Dalton
En 1808 el británico John Dalton propone su modelo de estructura atómica de la materia de las sustancias puras, que se resume en estos cuatro postulados:
➔ La materia está formada por partículas pequeñas e indivisibles que llamamos átomos.
La palabra átomo procedente del griego significa «sin división». No es verdad que el átomo no se pueda dividir, pero si se divide, la sustancia en cuestión cambia de naturaleza.
➔ Los átomos de distintos elementos difie- ren fundamentalmente en la masa. Aunque no es frecuente, se pueden encontrar átomos de distintos elementos que tienen la misma masa que se deno- minan «isóbaros».
➔ Los átomos de un mismo elemento son todos iguales y tienen las mismas propie- dades, en particular la misma masa. De la mayoría de los elementos se cono- cen átomos con distinta masa que se denominan «isótopos».
➔ Las sustancias compuestas o moléculas se forman por combinación de átomos de distintos elementos. Hay moléculas obtenidas por combinación de átomos de distintos elementos, y hay moléculas formadas por unión de átomos del mismo elemento.
La teoría anterior no dice nada acerca la composición interna del átomo.
Modelo atómico de Thompson
Experimentando con los rayos catódicos, que se generan en los tubos de vacío, Thompson descubre el electrón y como este forma parte de los átomos.
En 1904, el británico Joseph John Thompson propone el modelo o imagen del átomo como una nube esférica cargada positivamente, en cuyo interior se encontraban suspendidos los electrones, como incrustados al igual que las «pasas en un pudin».
Modelo de Rutherford
En 1911, al bombardear finísimas láminas de oro con partículas alfa (núcleos de Helio) y tras observar cómo solo una ínfima parte de estas partículas eran desviadas al atravesar el metal, el neozelandés Ernest Rutherford descubrió cómo se distribuyen masa y carga en el átomo en dos zonas: núcleo y corteza.

Sus principales postulados son:
➔ La mayor parte del átomo es espacio vacío.
➔ El átomo está formado por un núcleo de reducidas dimensiones donde se concentra toda la carga positiva y casi toda la masa.
➔ En la corteza se encuentran los electrones, con carga negativa y masa insignificante.
➔ Los electrones se encuentran girando alrededor del núcleo describiendo órbitas circulares como los planetas alrededor del sol.
El átomo en la actualidad
En la actualidad el concepto de órbitas se ha sustituido por el de orbitales, que son regiones alrededor del núcleo en las que hay una alta probabilidad de encontrar algún electrón, y que adopta tamaños, formas y orientaciones específicas. La energía de cada orbital depende de esos tamaños y formas.
Las siguientes reglas establecen la configuración electrónica de los átomos:
➔ Los orbitales atómicos, dependiendo de su forma, se nombran con las letras s, p, d y f, y se antepone un número natural que indica el nivel energético del orbital.
➔ Cada orbital solo puede contener, como máximo, dos electrones.
➔ En cada nivel, solo hay un orbital s que admite 2 electrones.
➔ En niveles con orbitales p, hay 3 orbitales p que admiten 2 · 3 = 6 electrones.
➔ En niveles con orbitales d, hay 5 orbitales d que admiten 2 · 5 = 10 electrones.
➔ En niveles con orbitales f, hay 7 orbitales f que admiten 2 · 7 = 14 electrones.
En el diagrama siguiente aparecen todos los posibles orbitales en orden creciente de energía y la cantidad de electrones que pueden contener:
El número atómico de un elemento es la cantidad de protones que tiene cada átomo de ese elemento y que, en el estado fundamental, coincide con el número de electrones. Se designa con la letra Z.
El número másico de un elemento es la suma de protones y neutrones. Se designa con la letra A.
Del carbono (Z = 6) se conoce un isótopo de A = 12. Se representa: 12 6 C .
La configuración electrónica de los elementos se establece a partir del número atómico partiendo de los orbitales vacíos y añadiendo los electrones uno a uno hasta completar su número atómico.
Establece la configuración electrónica del sodio (Z = 11) y del cloro (Z = 17).
El sodio tiene 2 electrones en el primer nivel, 8 en el segundo y 1 en el tercero.
El cloro tiene 2 electrones en el primer nivel, 8 en el segundo y 7 en el tercero.
En 1869 la tabla periódica la presenta por primera vez Dimitri Mendeleiev, que dispuso los elementos conocidos entonces en orden creciente de masa atómica y los distribuyó en filas y columnas con arreglo a propiedades comunes. Posteriormente, Henry Moseley reordena los elementos en orden creciente de número atómico y de este modo encajan mejor las propiedades de los nuevos grupos que aparecen siguiendo este criterio de ordenación.
La tabla periódica actual se compone de 118 elementos que se distribuyen en:
➔ 18 Grupos: dispuestos en columnas verticales. El primer grupo está encabezado por el hidrógeno, litio, sodio... y el último, el grupo 18, por el helio, neón, argón...
➔ 7 Periodos: colocados en filas horizontales. En total son 7 periodos. El primero solo tiene 2 elementos: hidrógeno y helio.
➔ 4 Bloques:
• Bloque s: el último orbital ocupado por algún electrón es un orbital s. Está formado por los grupos 1 y 2 de la tabla periódica.
• Bloque p: el último orbital ocupado por algún electrón es un orbital p. Está formado por los grupos 13 al 18 de la tabla periódica.
• Elementos de transición o bloque d: el último orbital ocupado por algún electrón es un orbital d. Está formado por los grupos 3 al 12 de la tabla periódica.
• Tierras raras o bloque d: el último orbital ocupado por algún electrón es un orbital f. Está formado por los elementos que arrancan del tercer grupo en los periodos 6 y 7.

Además, dentro de la tabla periódica podemos agrupar los elementos en tres categorías:
➔ Metales:
• A esta categoría pertenecen todos los elementos del bloque s, los elementos de transición y los elementos más pesados del bloque p.
• Presentan brillo metálico, son buenos conductores, dúctiles, maleables, duros y con altos puntos de fusión y ebullición.
➔ No metales:
• Situados en el bloque p, son no metales los elementos más ligeros de este bloque p.
• Son aislantes frágiles, sin brillo. Salvo excepciones, no tienen altos puntos de fusión y ebullición. Son blandos.
➔ Metaloides:
• Situados en una diagonal del bloque p trazada de izquierda a derecha y de arriba abajo (que figuran en color verde).
• Su aspecto y propiedades son intermedias entre metal y no metal. Los gases nobles que forman el grupo 18 no pertenecen a ninguna de las categorías anteriores.
La tabla periódica y la distribución de los elementos en orden creciente de número atómico explica que los elementos de cada grupo tengan propiedades químicas similares, debido a que estas dependen fundamentalmente de los electrones situados en el nivel más externo. Por ejemplo, en todos los elementos del grupo 17, los electrones situados en el nivel más externo son siempre ns2 np5
9 Consulta la tabla periódica y contesta a las siguientes preguntas:
a) ¿Qué elementos forman parte del segundo periodo?
b) ¿Qué elementos forman el grupo 2?
c) Localiza, indicando el periodo y el grupo, los elementos: Magnesio (Mg), Cromo (Cr), Platino (Pt), Estaño (Sn) y Bromo (Br).
10 Copia y completa la tabla siguiente en la que figuran el número atómico (Z), el número másico (A) así como la cantidad de protones (p), electrones (e) y neutrones (n) que poseen algunos isótopos:
11 Escribe la configuración electrónica de los elementos:
a) Magnesio: Mg (Z = 12).
b) Silicio: Si (Z = 14).
c) Azufre: S (Z = 16).
d) Argón: Ar (Z = 18).
e) Calcio: Ca (Z = 20).
f) Cromo: Cr (Z = 24).
12 Localiza en la tabla periódica los elementos del ejercicio anterior indicando el grupo y el periodo al que pertenecen y en qué bloque se encuentran.
13 Busca en la tabla los siguientes elementos, indica cuál es su número atómico y señala los errores de las configuraciones electrónicas:
a) Al: 1s2 2s2 2p6 3s1 3p2
b) Fe: 1s2 2s2 2p6 3s2 3p6 4s2 3d4
c) Cl: 2s2 2s2 2p6 3s2 3p7
d) Cu: 1s2 2s2 2p6 3s2 3p6 4s2 3d9
e) Ne: 1s2 2s2 2p4
f) Ca: 1s2 2s2 2p6 3s2 3p6 4s1
➔ La Tierra y los demás cuerpos del sistema solar se formaron a partir de una inmensa nebulosa enriquecida con el polvo cósmico liberado en la explosión de supernovas cercanas.
➔ El polvo cósmico, junto con los gases, el hielo y otras partículas, dieron lugar a unas pequeñas estructuras denominadas planetesimales.
➔ La geosfera es la parte sólida del planeta. Es una bola casi esférica formada por capas concéntricas de diferente composición y estado y localizadas a distintas profundidades.
➔ La corteza es la capa externa que recubre la superficie terrestre y está formada por rocas sólidas, pero ligeras, compuestas de silicatos de aluminio:
• La corteza oceánica forma los fondos marinos, tiene entre 6-12 km de espesor y contiene rocas como el basalto.
• La corteza continental forma los contenientes, tiene entre 25-90 km de espesor y contiene rocas como el granito.
➔ El manto es la capa intermedia que se extiende desde los 90 hasta los 2 900 km de profundidad, formada por rocas densas compuestas de silicatos de magnesio.
• El manto superior es sólido con algunas zonas parcialmente fluidas.
• El manto inferior es más denso y sus materiales son completamente sólidos.
➔ El núcleo es la capa más interna, densa y con mayor temperatura, formada por hierro y níquel, que se extiende desde los 2 900 hasta los 6 370 km de profundidad.
• El núcleo externo es fluido y móvil.
• El núcleo interno es sólido.
➔ La zona de habitabilidad de una estrella es una región situada a su alrededor, ni muy cerca ni muy lejos de ella, que permite temperaturas suaves para la existencia de agua en estado líquido.
➔ La Tierra presenta calor interno responsable de la tectónica de placas, lo que genera vulcanismo, que aporta CO2 y genera un efecto invernadero que mantiene una temperatura media de unos 15 ºC, adecuada para la vida.
14 Compara las distancias a su correspondiente estrella de las zonas de habitabilidad del Sol y de una estrella llamada Gliese 581, una enana roja que posee seis planetas girando a su alrededor, llamados Gliese e, b, c, g, d y f.
a) ¿Qué es la zona de habitabilidad estelar?
b) Teniendo en cuenta que la estrella Gliese 581 es una enana roja, cuya masa es un tercio de la masa solar, ¿a qué se debe que las distancias entre las estrellas y las zonas de habitabilidad sean diferentes?
c) ¿Qué planetas del sistema solar y de la estrella Gliese 581 se sitúan en la zona de habitabilidad?
15 Esta es la imagen de un planeta que reúne una serie de condiciones para albergar vida. Escribe en tu cuaderno las respuestas correctas:

a) ¿Qué consecuencias para la existencia de vida se derivan de su actividad volcánica (A)?
b) ¿Dónde se localiza, respecto de su distancia a la estrella, y cuál debe ser su tamaño para que posea agua líquida (B) y atmósfera (C)?
c) ¿Qué organismos deben vivir en el agua para que la atmósfera posea oxígeno (D) y por qué es necesaria la presencia de este gas?
16 ¿De dónde procede el agua que dio lugar a la hidrosfera? ¿Cómo se formó la atmósfera en la Tierra primitiva?
17 Trabajad por parejas y averiguad por qué no había oxígeno en la atmósfera terrestre primitiva.
➔ El ahorro es la diferencia entre los ingresos y los gastos.
➔ El ahorro tiene que ser un objetivo financiero.
➔ El consumo inteligente tiene en cuanta nuestras necesidades reales, la relación calidad-precio y el impacto en el medio ambiente.

➔ Se recomienda que se destine al ahorro, como mínimo, el 10 % de los ingresos.
➔ Los ahorros pueden invertirse para obtener una rentabilidad.

➔ Los depósitos son productos en los que, a cambio de depositar tus ahorros y comprometerte a no tocarlos durante un determinado periodo de tiempo, se te garantiza una rentabilidad igual a un porcentaje de la cantida depositada.
➔ Los intereses de los depósitos pueden liquedarse al vencimiento o en periodos más cortos de tiempo.
➔ Para cubrir las necesidades que no podemos alcanzar con nuestrso ahorros, los bancos ofrecen productos de financiación.
➔ Los productos de financiación pueden ser préstamos o créditos.
➔ En un préstamo se recibe una cantidad que tenemos que devolver en un plazo determinado y abonando unos determinados intereses.
➔ En un crédito, la entidad financiera pone a tu disposición, durante un determinado periodo de tiempo, una cantidad que se puede usar en parte o en su totalidad.
18 Si todos los meses ingreso 70 €, gasto 50 € y ahorro el resto, ¿cumplo con las recomendaciones de ahorro?
19 Alba ahorra todos los meses el 12 % de lo que ingresa. Si al final del año ha ahorrado 240 €, ¿cuánto ingresa mensualmente?
20 Dentro de un año exactamente, Juanma queire irse de viaje con sus amigos. Calcula qué necesita ahorrar 720 €, así que decide guardar una cantidad fija todos los meses. Si ingresa mensualmente 300 €, ¿qué cantidad le queda para sus gastos mensuales?

21 Un depósito ofrece una rentabilidad del 2,15 % anual. ¿Qué rentabilidad se obtendrá al final del año si se depositan 6 500 €?
22 Mi tío me ha contado que al depositar una cierta cantidad al 1,5 % anual ha obtenido una rentabilidad de 120 €. ¿Qué cantidad depositó?
23 El banco en el que Gema tiene sus ahorros ofrece un depósito a tres años con una rentabilidad anual del 2,6 %. Si los intereses se abonan anualmente y se reinvierten en el depósito, ¿qué cantidad tendrá al final del periodo si deposita 20 000 €?
24 Mercedes quiere comprarse una casa que vale 200 000 €. Como ya tenía algunos ahorros, ha pedido un préstamo de solo las tres cuartas partes del precio. La entidad le ofrece un préstamo a un 3,75 % anual a devolver en 30 años. De esta manera deberá pagar cuotas mensuales de 694,67 €. Calcula cuánto dinero habrá devuelto al banco al finalizar la vida del préstamo.

➔ La materia está constituida por átomos que tienen:
• Un núcleo con protones y neutrones donde se acumula toda la carga positiva y casi toda la masa.
• Orbitales alrededor del núcleo que contienen electrones en distintos niveles energéticos.
➔ Número atómico (Z). Cantidad de protones presentes en el núcleo. En el átomo neutro coincide con el número de electrones.
➔ Número másico (A). Número de partículas subatómicas con masa: protones y neutrones.
➔ La configuración electrónica de un átomo es la distribución de los electrones por niveles y subniveles de energía en los distintos orbitales.
➔ La tabla periódica es la distribución de los elementos ordenados en orden creciente de número atómico. Consta de 7 filas o periodos y 18 columnas o grupos. También se distinguen cuatro bloques: s, p, d y f. Se pueden establecer, atendiendo a su reactividad, cuatro categorías: elementos metálicos, elementos no metálicos, elementos metaloides y gases nobles.
25 Escribe la configuración electrónica de los elementos:
a) Titanio (Z = 22).
b) Potasio (Z = 19).
c) Cobalto (Z = 27).
d) Bromo (Z = 35).
e) Cerio (Z = 58).
26 Localiza los elementos de la actividad anterior en la tabla periódica e indica cuál es su periodo, cuál es su grupo y a qué bloque pertenece.
27 Copia y completa la tabla siguiente en la que figuran el número atómico (Z), el número másico (A) así como la cantidad de protones (p) y neutrones (n) que poseen algunos isótopos:

¿Por qué los materiales rocosos del interior de la Tierra se distribuyen en capas?
Para averiguarlo, necesitas un vaso de precipitados de 100 cm3.
Primer paso. Introduce pequeños clavos hasta la marca de 10 cm3.
Segundo paso. Vierte 40 cm3 de agua, y añade 40 cm3 de aceite y algunos trocitos de corcho.
Tercer paso. Agítalo todo y déjalo reposar durante unos 15 minutos.
a ¿Qué observas? ¿Por qué se han distribuido las capas en ese orden? ¿Por qué crees que unas sustancias flotan y otras se hunden?
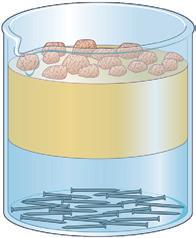
La humanidad, en ocasiones, es terca con la ciencia
No hicimos caso de las investigaciones de Aristarco de Samos (280 a. C.) y durante mucho tiempo nos creímos el ombligo del mundo, es decir, el centro del universo. Pensábamos que todo giraba a nuestro alrededor.
Pasaron muchos siglos, hasta que los cálculos matemáticos de Nicolás Copérnico nos arrebataron esta posición privilegiada. Poco después, la investigación llevada a cabo por Johannes Kepler nos desplazó a una órbita y nos «condenó» a girar eternamente alrededor del Sol. Resignados, hasta principios del siglo xx creíamos vivir en el centro de nuestra galaxia.

Pero, en los años veinte, Harlow Shapley observó, calculó y nos mandó de un plumazo a los suburbios galácticos, a la periferia de uno de sus brazos, a un punto situado a unos 30 000 años luz del centro. Desde aquí, nuestro Sol se vería como una minúscula estrella de entre los millones de pequeñas y débiles estrellas que todavía no están clasificadas.
Ni siquiera nuestra galaxia es un objeto privilegiado. Los cálculos y mediciones de Edwin Hubble nos enseñaron que la Vía Láctea es una más de entre los miles de millones de galaxias que componen el universo. Vivimos en un universo sin límites que no tiene centro. No existe ninguna posición especial ni preferente. Para nadie. Y, según la teoría del multiverso, tal vez nuestro universo, nacido de una burbuja de espuma cósmica, no sea más que otro entre un conjunto de universos distintos.
1 ¿Qué hipótesis propuso Aristarco de Samos sobre la Tierra, el sistema solar y las estrellas?
2 ¿Por qué Galileo fue condenado por el tribunal de la Inquisición? ¿Creéis que a veces la sociedad entra en conflicto con la ciencia?
3 ¿Qué le ocurrió al astrónomo y filósofo Giordano Bruno por afirmar que el Sol era una estrella más y el universo era infinito y contenía infinitos mundos habitados por animales y seres inteligentes?

Resolved las tareas, escribid las respuestas y las conclusiones a las que habéis llegado sobre sobre el sistema solar.
Presentad el trabajo en Word/Writer, PowerPoint/Impress, Prezi, Canva... e incluid animaciones, vídeos, fotografías...
La Tierra y los demás cuerpos del sistema solar se formaron por el impacto de los...
La teoría de Dalton dice que la materia está constituida por...
El núcleo está formado por...
El grupo número dieciocho de la tabla periódica está compuesto por...
Los volcanes de la Tierra primitiva, junto con los cometas y meteoritos, dieron lugar a la...
El ahorro se define como...
La región situada alrededor de una estrella que permite la existencia de agua líquida es la...
El número de protones que tiene el núcleo es...
El número de periodos de la tabla periódica es...
La atmósfera primitiva carecía de...
Se recomienda que como mínimo se ahorre...
La actividad volcánica, que aporta dióxido de carbono, genera...
La corteza oceánica contiene rocas como el...
El número de elementos en el primer periodo de la tabla periódica es...
El número de grupos de la tabla periódica es...
La discontinuidad que separa el núcleo externo del interno fue descubierta por...
La corteza continental contiene rocas como el...
Si tenemos 10 000 € al 1,5 % anual se convierten en...
La suma de protones y neutrones es...
El mensaje dirigido al agrupamiento de estrellas M-13 fue emitido por el radiotelescopio de...
0 El objetivo del juego es completar los enunciados que aparecen en las tarjetas.
0 La relación se hará asociando las tarjetas señaladas con letras con las tarjetas señaladas con números.
0 Puede llevarse a cabo por parejas.
0 En caso de que todas las parejas hayan completado bien los enunciados, ganará quien lo haya conseguido en menos tiempo.
AmpliaCió N
Cada pareja planteará la primera parte de dos enunciados nuevos en una cartulina y la segunda parte en otra cartulina. Cuando las tengáis, se mezclan unas y otras y también entrarán en el desafío.
...basalto.
...dos.
...el número másico.
...Arecibo.
...hierro y níquel.
...los gases nobles. ...siete. ...oxígeno.
...dieciocho.
...Inge Lehmann.
...hidrosfera.
...ingresos menos gastos.
...planetesimales.
...átomos.
...zona de habitabilidad.
...el número atómico.
...un 10 % de los ingresos.
...efecto invernadero. ...granito.
...10 150 €.

Los seres humanos consumimos recursos para satisfacer nuestras necesidades y, como consecuencia, impactamos en factores relacionados con la habitabilidad de la Tierra. ¿Sabías que hay estudios que estiman que, para 2050, harían falta tres planetas para obtener los recursos necesarios para mantener nuestro estilo de vida?
Uno de los problemas al que nos enfrentamos, fruto de este consumo de recursos, es a la elevada generación de residuos que provoca la erosión del medio ambiente.
Por tanto, un consumo responsable implica una buena gestión de los residuos, reduciendo en todo lo posible su liberación a la atmósfera, al agua y al suelo.
Con este proyecto vamos a intentar aportar nuestro granito de arena para consumir de manera responsable y así,
¡el impacto será muy positivo!
Vamos a formar grupos de 4 personas para llevar a cabo un proyecto en nuestro centro escolar usando materiales reciclados. Elegid un miembro del grupo para cada uno de estos roles:
Representante. Encargado de exponer el proyecto al resto de la clase. ¡Asegúrate de tener un buen trabajo que presentar!
Experto. Liderará la búsqueda de la información necesaria para desarrollar el proyecto.
Diseñador. Diseñará el póster final de vuestro proyecto.
Moderador. Coordinará al equipo y se asegurará de que todas las opiniones cuenten.
REFLEXIONAMOS Y DESARROLLAMOS UNA IDEA PASO 2
HACEMOS UNA LLUVIA DE IDEAS TAREA 1
Seguro que en vuestro centro escolar tenéis alguna zona que se podría aprovechar mejor.
¿Hay algún espacio del patio que no se usa? ¿Y si hicierais una biblioteca en esa aula que se ha quedado un poco anticuada?
¿Podríais fabricar un columpio para vuestros compañeros de infantil o primaria?
Reflexionad, debatid e identificad el espacio de vuestro centro escolar que vais a mejorar. Tened en cuenta que solo podréis usar materiales reciclados.

En esta primera fase del proyecto el papel del moderador será fundamental. Deberá asegurarse de que se expongan las ideas en orden y de que todas las opiniones sean escuchadas.
TAREA 2




Investigad cómo podéis dar un nuevo uso a aquellas cosas que parece que ya no sirven. ¿Con qué residuos podríais trabajar en vuestro proyecto?
Pensad que es posible que otras personas hayan hecho algo parecido. Buscad en internet y mirad qué materiales han empleado y qué usos les han dado.
En esta fase, el experto puede anotar todo lo que vayáis encontrando para que, una vez que tengáis información suficiente y con ayuda del moderador, decidáis qué materiales usar.
TAREA 3
En el póster deberéis mostrar el espacio que vais a cambiar, cómo va a contribuir a mejorar vuestro centro escolar y qué materiales habéis usado.
Es el turno del diseñador, y su trabajo aquí marcará la diferencia. Eso sí, el resto del equipo también tiene que aportar ideas, colaborar en todo lo que sea necesario y estar atento para que todo salga bien.
TAREA 4
COMPARTIMOS NUESTRAS IDEAS
Ahora toca confiar en vuestro representante, que tendrá que salir a presentar el proyecto lo mejor preparado posible.
Para ayudarle, pensad en qué preguntaríais vosotros si vieseis el proyecto por primera vez. Os será muy útil anticipar las preguntas que puedan surgir. Además, ¿qué podéis hacer para que el público permanezca atento? Incluid algún dato llamativo, imágenes y fotografías explicativas, esquemas, etc.

Cuando estéis preparados, presentad el proyecto al resto de la clase y prestad atención a las otras exposiciones. ¡Seguro que será un buen momento para aprender!
Al final de cada exposición, haced una ronda de preguntas y respuestas con las dudas que os hayan surgido.
NOS VALORAMOS PASO 3
¿Erais conscientes de la gran cantidad de recursos que consumimos y generamos? ¿Os habíais planteado todo lo que se puede hacer con las cosas que tiramos?
Organizad un debate de toda la clase y poned en común lo que habéis aprendido.

Como broche final, aportad alguna idea sobre otras cosas que pueden ayudarnos a llevar a cabo un consumo responsable y respetuoso con el medio ambiente.
¡Quizá sea un punto de partida para otros proyectos!
© GRUPO EDITORIAL BRUÑO, S. L., 2024 - C/ Valentín Beato, 21 - 28037 Madrid.
Reservados todos los derechos. El contenido de esta obra está protegido por la Ley, que establece penas de prisión y/o multas, además de las correspondientes indemnizaciones por daños y perjuicios, para quienes reprodujeren, plagiaren, distribuyeren o comunicaren públicamente, en todo o en parte, una obra literaria, artística o científica, o su transformación, interpretación o ejecución artística fijada en cualquier tipo de soporte o comunicada a través de cualquier medio, sin la preceptiva autorización.