En cada unidad
Un polígono regular tiene sus ángulos y lados iguales.
Estos son algunos ejemplos:
174. Escribe los nombres de estas figuras geométricas. Después rodea solo las que sean paralelogramos.

Tras la pista
54
177. Completa con los elementos indicados.
Tras la pista Centro Diámetro Cuerda Circunferencia
La circunferencia

Diámetro: segmento que une dos puntos de la circunferencia pasando por el centro de la misma.
Radio: segmento que une el centro con cualquier punto de la circunferencia. Cuerda: segmento que une dos puntos de la circunferencia. Arco: porción de una circunferencia.
Radio Arco Círculo
178. Mi amigo ha elegido una alfombra con esta forma para su habitación. ¿Cuántas unidades mide? Comprueba el resultado contando los cuadraditos.
La alfombra mide unidades.
179. Completa la tabla resumen de estos poliedros.
Tras la pista a) b)
Los poliedros son cuerpos geométricos formados por caras planas (polígonos). Sus elementos son: caras, aristas y vértices.
Son poliedros: Prismas: tienen 2 bases y sus caras laterales son paralelogramos. Pirámides: tienen 1 base y sus caras laterales son triángulos.
Tiene forma de Bases Caras laterales Vértices Aristas a b




ME PONGO A PRUEBA
Tienes unas actividades para que valores tu progreso.
Cono Cilindro Esfera
2 bases circulares y 1 superficie lateral curva



Superficie lateral curva



1 base circular y 1 superficie lateral curva



181. El nuevo depósito instalado en la depuradora permite mantener el agua limpia. Si tiene forma cilíndrica, ¿qué desarrollo corresponde al depósito?
Una de tres
175. ¿Qué nombre reciben los triángulos que aparecen marcados en estos objetos? Clasifícalos según sus lados y sus ángulos.
a) c) e) b) d) f) c) b)
a) d)
176. Calcula el perímetro de esta figura y completa.
Clasificación de los cuadriláteros Paralelogramos Los lados son paralelos dos a dos. El cuadrado y el rectángulo tienen todos los ángulos rectos, y el rombo y el romboide tienen los ángulos iguales dos a dos. No paralelogramos No tienen los lados paralelos dos a dos: trapecio y trapezoide.
Tras la pista
Clasificación de los triángulos Según sus lados Equilátero:
3 lados iguales Isósceles: 2 lados iguales Escaleno:
3 lados desiguales Según sus ángulos Rectángulo: 1 ángulo recto Acutángulo: 3 ángulos agudos Obtusángulo: ángulo obtuso 4mm

Esta figura recibe el nombre de y su perímetro mide mm.
180. Une con flechas los datos de los cuerpos redondos. Tras la pista Cuerpos redondos Son figuras geométricas formadas total o parcialmente, por superficies curvas. a) b) c)
182. El segmento que une vértices no consecutivos de un polígono se denomina: Lado Diagonal Cara
183. El paralelogramo de 4 lados y 4 ángulos iguales es un:
Cuadrado Rombo Rectángulo





184. El arco y la cuerda son elementos de: Un prisma Una pirámide Una circunferencia
185. El cuerpo geométrico cuyas caras son polígonos es un: Triángulo Cilindro Poliedro
186. El cilindro, el cono y la esfera son: Prismas Cuerpos redondos Figuras planas

Juega y aprende

PUEDES ACCEDER A ESTA APLICACIÓN Y APRENDERÁS JUGANDO
57
55
SOLUCIONES
Al final encontrarás las soluciones de las actividades.

172. Observa las formas destacadas en las imágenes y escribe si son polígonos regulares o no regulares. El perímetro (P) de un polígono regular es la suma de las longitudes de sus lados. Triángulo equilátero Cuadrado Pentágono regular Hexágono regular DOY FORMA A LO QUE ME RODEA 13 173. Completa escribiendo los nombres de los elementos de este polígono regular. Luego, dibuja todas las diagonales posibles. 3 lados 4 lados 5 lados 6 lados Ángulo Lado Vértice Las diagonales de un polígono son los segmentos que unen vértices no consecutivos. Tras la pista b) a) c) Polígono Polígono Polígono diagonal
actividades.
DE TRES
solo una opción de las 3 que aparecen. Al final del cuaderno 58 188. ¿En qué año fue incluida la cueva de Altamira en la Lista del Patrimonio Mundial de la UNESCO? 187. Completa la tabla redondeando a las unidades de millar el número de especies de seres vivos que habitan nuestro planeta. Me pongo a prueba Ordena los números de la primera columna de menor a mayor. UM anterior Número UM posterior UM más próxima 4 000 4 381 5 000 4 000 9 271 8 238 27 977 915 350 MCMLXXXV Mamíferos: 4 381 Aves: 9 271 Reptiles: 8 238 Peces: 27 977 Insectos: 915 350 64 1 CUENTO Y RECUENTO 1. a) 62 504 b) 4 CM + 7 UM + 9 C + 5 D + 1 U c) 854 090 d) 2 DM + 5 UM + 6 C + 2 D + 4 U 2. a) 5 DM = 50 000 unidades b) 000 unidades 3. a) El número menor es 01 357. Se lee: mil trescientos cincuenta siete. b) El número mayor es 75 310 Se lee: setenta y cinco mil trescientos diez c) En el menor, 7 unidades y en el mayor, 70 000 unidades. 4. a) b) 1 CM = 3 DM + 7 DM c) DM = 1 000 + 9 000 d) 1 CM = 20 000 + 80 000 5. a) 27 465 < 27 495 b) 6 CM + 5 DM > 640 000 c) 8 DM + 4 UM + 3 D > 83 999 d) 109 899 < 109 998 27 495 < 83 999 < 109 998 < 640 000 6. A = 340 000 B = 390 000 C = 450 000 D = 480 000 7. UM posterior UM más próxima 62 000 62 300 63 000 62 000 0 937 1 000 000 8. a) Hay, aproximadamente, 200 000 estrellas. b) La distancia es de 384 000 km, aproximadamente. c) 320 000, 330 000, 340 000, 350 000, 360 000, 000, 380 9. a) El coche vale, aproximadamente, 28 000 €. b) Las placas valen, aproximadamente, 4 000 €. 10. XI = 11 IX = 9 MM = 2 000 XC = 90 XL = 40 DCC = 700 11. 300 000 unidades 12. 58 701 13. 987 654 14 MCMXXV 15. 800 000 2 JUEGO CON LOS NÚMEROS 16. a) 77 804 b) 61 152 c) 45 774 17. a) 5 578 b) 56 925 c) 625 18. a) 12 325 = 10 000 + 2 000 + 300 + 20 + 5 3 152 = 3 000 + 100 + 50 + 2 + 520 = 500 + 20 10 000 + 5 000 + 900 + 90 + = 15 997 b) 36 895 =30 000 +6 000 + 800 + 90 5 – 4 570 = 4 000 + 500 + 70 30 000 + 2 000 + 300 + 20+ 5 = 32 325 19. a) 8 6 7 3 – 4 7 9 6 4 6 8 7 b) 6 4 0 3 0 –4 0 9 2 1 20. 000 + 500 = 1 500 500 + 000 = 1 500 Se cumple la propiedad conmutativa de la suma. 21. a) 135 + 40 + 52 b) 135 + 40 + 52 175 + 52 135 + 92 227 227 Los resultados de a) y b) son iguales. Se cumple la propiedad asociativa de la suma. 22. 14 24 10 12 16 20 22 8 18 23. a) 90 – (50 + 10) = 90 – 60 = 30 b) (90 – 50) + 10 = 40 + 10 = 50 Los resultados de a) b) no son iguales. 24. a) 8 954 – 5 134 = 3 820 b) 8 954 – 3 820 = 5 134 25. 2 102 + 1 307 = 3 409 4 806 – 3 409 = 1 397 El vecino del tercero ha consumido 397 L. 26. 000 – 300 = 700 La diferencia es de 700 €. 27. Sumandos total 28. Asociativa 29. Conmutativa 30. La resta 31. En primer lugar
Primero, recuerda algunos saberes de Matemáticas. La pandilla te dará pistas para que resuelvas con éxito las
UNA
Elige
+App
UNIDADES SABERES BÁSICOS ODS
➧ Órdenes de unidades del sistema de numeración de base diez hasta las unidades de sexto orden y sus equivalencias: conteo, lectura, escritura y representación; composición y descomposición según el orden de unidades y según el valor de posición de sus cifras.
➧ Comparación y ordenación de números naturales de hasta seis cifras.




➧ Estimaciones y aproximaciones. Redondeo de números naturales a las decenas, centenas y millares (unidades, decenas de millar y centenas de millar).
➧ Sistema de numeración romano. Lectura y escritura
➧ Resolución de problemas.
➧ Suma con llevadas (de hasta cinco cifras) por descomposición y en vertical de más de dos sumandos. Identificación de términos.
➧ Propiedades conmutativa y asociativa de la suma.
➧ Resta con llevadas (de hasta cinco cifras) por descomposición y en vertical. Identificación de términos.
➧ Prueba de la resta.
➧ Relaciones entre la suma y la resta.
➧ Sumas y restas combinadas. Uso del paréntesis.

➧ Resolución de problemas de adicción y sustracción.
➧ Multiplicación en vertical por números de varias cifras (2 cifras).
➧ Tablas de multiplicar.
➧ Propiedad conmutativa de la multiplicación.
➧ Propiedades asociativa y distributiva de la multiplicación.
➧ Uso de paréntesis y jerarquía de las operaciones.
➧ Multiplicación por la unidad seguida de ceros.
➧ Resolución de problemas con productos.
➧ División como reparto y como agrupamiento.
➧ Identificación de los términos de la división.
➧ División exacta y división inexacta o entera.
➧ División entera con divisor de una cifra.
➧ Divisiones con ceros intermedios o finales en el cociente.
➧ Prueba de la división. Propiedad del resto.
➧ Resolución de problemas de reparto y agrupamiento.
➧ División entera con divisor de dos cifras.
➧ Propiedad de la división exacta.
➧ División por descomposición.
➧ División por la unidad seguida de ceros.
➧ División como operación inversa a la multiplicación.
➧ Resolución de problemas de reparto y agrupamiento.
➧ Fracciones. Representación gráfica.
➧ Interpretación e identificación de los términos de una fracción.


➧ Fracción como reparto.
➧ Lectura de fracciones.
➧ Medios, tercios y cuartos.
➧ Fracción y unidad.
➧ Comparación y ordenación de fracciones con el mismo denominador.
➧ Fracción de una cantidad.
➧ Resolución de problemas con fracciones.
➧ Fracción decimal y número decimal.
➧ Número decimal. Parte entera y parte decimal: unidades, décimas y centésimas.
➧ Lectura y escritura de números decimales.
➧ Equivalencias entre órdenes de unidades. Valor de la cifra en un número.
➧ Comparación y ordenación de números decimales.
➧ Representación en la recta numérica.
➧ Redondeo de números decimales a las unidades.
➧ Suma y resta de números decimales.
➧ Resolución de problemas con números decimales.
CIUDADES Y COMUNIDADES SOSTENIBLES
12
PRODUCCIÓN Y CONSUMO RESPONSABLES
2 HAMBRE
4
Índice
11
CERO
5 IGUALDAD DE GÉNERO
1 FIN DE LA POBREZA
10 REDUCCIÓN
DE LAS DESIGUALDADES
3 SALUD Y BIENESTAR Cuento y recuento (PÁGINA 6) 1 Juego con los números (PÁGINA 10) 2 Multiplico la diversión (PÁGINA 14) 3 Me divierto agrupando (PÁGINA 18) 4 Reparto lo que tengo (PÁGINA 22) 5 Formo parte del todo (PÁGINA 26) 6 Gané por unas décimas (PÁGINA 30) 7
UNIDADES SABERES BÁSICOS ODS
➧ Experiencia aleatoria. El azar.
➧ Sucesos: suceso seguro, suceso probable y suceso imposible.
➧ Probabilidad de un suceso: casos favorables y casos posibles.
➧ Probabilidad como fracción.
➧ Resolución de problema de probabilidad. PAZ,
➧ Medida de longitudes: unidades de medida convencionales y no convencionales. El metro.
➧ Unidades menores que el metro: decímetro, centímetro y milímetro. Equivalencias entre unidades. Medición con la regla.
➧ Unidades mayores que el metro: decámetro, hectómetro y kilómetro. Equivalencias entre unidades.
➧ Expresiones complejas y expresiones incomplejas.
➧ Resolución de problemas de longitud.
➧ Unidades de capacidad menores que el litro: dL, cL y mL y sus equivalencias.

➧ Unidades de capacidad mayores que el litro: daL, hL y kL y sus equivalencias.
➧ Unidades de masa menores que el gramo: dg, cg y mg y sus equivalencias.
➧ Unidades de masa mayores que el gramo: dag, hg y kg y sus equivalencias.
➧ La tonelada.
➧ Expresiones complejas y expresiones incomplejas.
➧ Resolución de problemas de capacidad y masa.


➧ Medida del tiempo. Unidades mayores que el año: lustro, década, siglo y milenio.
➧ Sistema sexagesimal. Horas, minutos y segundos.
➧ Medición del tiempo: lectura del reloj de agujas y del digital con información sobre los períodos del día (mañana, tarde, noche; AM y PM).
➧ Resolución de problemas con unidades de tiempo.
➧ Recta, semirrecta y segmento.
➧ Rectas paralelas, rectas secantes y rectas perpendiculares.
➧ Ángulos. Identificación de sus elementos.
➧ Identificación y clasificación de los ángulos según su amplitud (rectos, agudos y obtusos).
➧ Medida de ángulos con transportador.
➧ Ángulos como giros.
➧ Traslación y simetría. Identificación y generación de figuras.
➧ Coordenadas en el plano de cuadrículas (filas y columnas). Localización, situación y movimiento de puntos en el plano de cuadrículas.
➧ Resolución de problemas.
➧ Polígonos. Clasificación según su número de lados.
➧ Identificación de los elementos de un polígono: lados, vértices y ángulos.
➧ Polígonos regulares.
➧ El perímetro.
➧ Clasificación de triángulos según sus lados y según sus ángulos.
➧ Clasificación de cuadriláteros: paralelogramos y no paralelogramos.
➧ Circunferencia y círculo.
➧ Poliedros: prismas y pirámides.
➧ Cuerpos redondos.
➧ Resolución de problemas.
Me
Soluciones (PÁGINA 63)



17
ALIANZAS PARA LOGRAR LOS OBJETIVOS
6
5
E
JUSTICIA
INSTITUCIONES SÓLIDAS 16
VIDA SUBMARINA
14
15
VIDA
DE ECOSISTEMAS TERRESTRES
ENERGÍA ASEQUIBLE Y NO CONTAMINANTE
7
¿Tendré suerte? (PÁGINA 34) 8 Soy la medida de todo (PÁGINA 38) 9 Calculo medidas (PÁGINA 42) 10 El tiempo pasa volando (PÁGINA 46) 11 Identifico las rectas y los ángulos (PÁGINA 50) 12 Doy forma a lo que me rodea (PÁGINA 54) 13
AGUA LIMPIA Y SANEAMIENTO pongo a prueba
(PÁGINA 58)
CUENTO Y RECUENTO


Los números de seis cifras están formados por seis órdenes de unidades. Se descomponen así:
1.
Se
ciento veintiséis mil cuatrocientos treinta y cinco
Valor = 30 unidades
Valor = 400 unidades
Valor = 6 000 unidades
Valor = 20 000 unidades
Valor = 100 000 unidades
2. ¿Cuántas unidades vale la cifra 5 en estos
2 596 5 C = 500 unidades
6 1
CM DM UM C D U 1 2 6 4 3 5
lee:
Completa
o descomposiciones.
con números
a) 6 DM + 2 UM + 5 C + 4 U b) 4 CM + 407 951
800 000 + 50
+ 4000 +
2 DM + 25 624 Descomposición Número
c)
000
90 d)
126 435 = 1 CM + 2 DM + 6 UM + 4 C + 3 D + 5 U 126 435 = 100 000 + 20 000 + 6 000 + 400 + 30 + 5
números? a) 50 939 b) 15 793
Valor = 5 unidades
El valor de cada cifra depende del lugar que ocupa.
3. ¿Cuál es el número mayor posible y el número menor posible que se pueden formar con estas cinco cifras?
a) El número menor es
Se lee
b) El número mayor es
Se lee .


c) ¿Cuántas unidades vale la cifra 7 en estos números?
En el menor unidades y en el mayor unidades.
4. Completa estas descomposiciones.
a) 1 DM = 4 UM + UM
b) 1 CM = 3 DM + DM
c) 1 DM = 1 000 +
d) 1 CM = 20 000 + a)
5. Compara estos números. Después, ordena los números de la columna de la derecha de menor a mayor.





b)
c)
7
27 465 27 495
6 CM + 5 DM 640 000
8 DM + 4 UM + 3 D 83 999 d) 109 899 109 998 1 DM = 10 UM = 10 000 U 1 CM = 10 DM = 100 000 U Tras la pista < < <
los signos > mayor que < menor que = igual a Tras la pista
Recuerda
6. ¿Qué número representa cada letra en la recta?

Tras la pista
Recuerda cómo aproximamos a las UM Si la cifra de las centenas es inferior a 5, redondeamos a la UM inferior:
26 436:
4 < 5 26 000
Si la cifra de las centenas es 5 o mayor que 5, redondeamos a la UM superior.
26 736:
7 > 5 27 000
7. Completa la tabla como en el ejemplo.
8. Fíjate en las fotografías y responde.
a) ¿Cuántas estrellas hay? Redondea a las CM. Hay, aproximadamente, estrellas.

b) Redondea a las UM la distancia entre la Tierra y la Luna.


La distancia es de km aproximadamente.
c) Completa la serie contando de 10 000 en 10 000.
8 D C B A
= C = B
D
UM anterior Número UM posterior UM más próxima 17 000 17 800 18 000 18 000 62 300 482 500 937
A
=
=
300 000 198 250
estrellas
384 400 km 400 000 500 000
320 000 380 000
9. Una familia quiere ser más responsable con el medio ambiente, por lo que ha decidido comprar un coche eléctrico e instalar placas solares. Redondea y estima cuánto gastará. 10. Relaciona cada número romano con su valor.
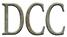
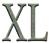
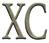





Tras la pista
Una de tres

9 11. ¿Cuántas unidades vale la cifra 3 en el número 346 204? 30 000 unidades 300 000 unidades 3 000 unidades 12. La descomposición 5 DM + 8 UM + 7 C + 1 U es igual a: 58 701 58 710 58 017 13. El número mayor es: 109 876 908 765 987 654 14. 1 925 en números romanos es: MIXV MCMXXIIIII MCMXXV 15. Redondea 798 000 a las centenas de millar: 700 000 800 000 900 000
a) El coche vale, aproximadamente, b) Las placas valen, aproximadamente, 27 650 € 700 2 000 90 11 40 9 3 875 € Sistema de numeración romano Son siete letras con estos valores: I = 1 V = 5 X = 10 L = 50 C = 100 D = 500 M = 1 000 Para sumar: VI = 5 + 1 = 6 XX = 10 + 10 = 20 Para restar: XL = 50 – 10 = 40
JUEGO CON LOS NÚMEROS
Sumamos y restamos con llevadas haciendo coincidir las cifras de los distintos órdenes de unidades de cada número.
Cómo sumamos Comenzamos por la derecha, sumando los diferentes órdenes de unidades (U, D, C, UM y DM), recordando las que nos llevamos (+1 +1 +1 +1).
1.° Restamos las U, pasando una D del minuendo a las U (12)
2.° Restamos las D, pasando una C del minuendo a las D (10)
3.° Restamos las C, pasando una UM del minuendo a las C (13)
4.° Restamos las UM, pasando una DM del minuendo a las UM (10)

5.° Restamos las DM En cada paso, recordamos las que nos llevamos (+1 +1 +1 +1).
16. Resuelve estas sumas.
17. Calcula las siguientes diferencias.
10 2
DM UM C D U Términos DM UM C D U Términos +1 +1 +1 +1 10 13 10 12 2 3 5 9 8 sumando 1 0 3 0 2 minuendo 7 4 6 sumando +1 +1 +1 +1 + 7 0 5 1 sumando 9 7 8 6 sustraendo 3 1 3 9 5 total 0 0 5 1 6 diferencia a) b) c) 5 4 6 5 8 + 2 3 1 4 6 3 2 4 7 1 9 0 5 3 + 1 9 6 2 8 3 6 5 2 5 7 4 6 + 8 5 0 3 a) b) c) 2 1 3 4 0 – 1 5 7 6 2 6 5 3 2 5 – 8 4 0 0 1 0 0 0 0 – 2 3 7 5
Cómo restamos
18. Resuelve descomponiendo como en el ejemplo.





19. Coloca en vertical estas restas y resuélvelas. Después, comprueba los resultados.
20. Un pueblo de 500 habitantes recibe 1 000 visitantes en verano. Calcula de dos formas el número total de personas que hay en verano, compara los resultados y completa.
11
Propiedad conmutativa de la suma Si se cambia el orden de los sumandos, el resultado no varía. Tras la pista 81 673 – 34 796 a) 64 030 – 23 109 b) + =
= Se cumple la propiedad de la suma.
coche, la moto
casco cuestan 29 985 €.
12
36
Ejemplo de resta 3 4 6 3 minuendo – 1 5 7 5 sustraendo 1 8 8 8 diferencia Prueba de la resta 1 5 7 5 sustraendo + 1 8 8 8 diferencia 3 4 6 3 minuendo Tras la pista 21 250 € 8 325 € 410 € 21 250 + 8 325 + 410 21 250 = 20 000 + 1 000 + 200 + 50 8 325 = 8 000 + 300 + 20 + 5 410 = 400 + 10 20 000 + 9 000 + 900 + 80 + 5 = 29 985 +
+
El
y el
a)
325 + 3 152 + 520 b)
895 – 4 570
21. Observa el número de entradas que vendió un teatro. Completa las sumas, compara los resultados y responde.
Entradas vendidas
Domingo: 135 entradas
Lunes: 40 entradas
Martes: 52 entradas

Propiedad asociativa de la suma
En una suma de varios sumandos, al agruparlos de diferente forma, el total no varía.
• ¿Cómo son los resultados de a y b? .

• Se cumple la
22. Escribe en cada casilla un número de tal manera que la suma de los números de cada fila y de cada columna sea 48.
Tras

El paréntesis indica qué operación debemos realizar en primer lugar. La colocación del paréntesis puede cambiar el resultado.
23. Resuelve las operaciones y compara los resultados.
a) 90 – (50 + 10)
b) (90 – 50) + 10
• ¿Son los resultados de a y b iguales?
24. Escribe dos restas utilizando solo los tres términos de esta suma y resuélvelas.
5 134 + 3 820 = 8 954
12
la pista
propiedad
14 10 16 22 18
de la suma.
= – =
+ =
=
52 + 52
135
135 +
a) 135 + 40 +
b)
+ 40 + 52
Tras la pista
25. Tres vecinos de un edificio han consumido en un día 4 806 L de agua en total. Si el vecino del primero ha gastado 2 102 L y el vecino del segundo, 1 307 L, ¿cuántos litros ha consumido el vecino del tercero?

El vecino del tercero ha consumido L.
26. El año pasado, el gasto medio de una familia de 4 miembros en ropa fue de 2 000 €. Este año, el gasto medio de la familia ha sido de 1 300 €. ¿Cuántos euros de diferencia hay en el gasto familiar en ropa?
La diferencia es de €.
Una de tres
27. Son términos de la suma: Sumandos y factores Sumandos y producto Sumandos y total

28. 81 + (4 + 6) y (81 + 4) + 6 representan la propiedad: Asociativa Conmutativa Ninguna
29. La operación 36 + 40 = 40 + 36 representa la propiedad: Asociativa Distributiva Conmutativa
30. Sustraendo + diferencia = minuendo es la prueba de: La resta La suma Las operaciones con paréntesis
31. Los paréntesis indican la operación que se debe hacer: En primer lugar En segundo lugar Al final

13
SOLUCIONES
1 CUENTO Y RECUENTO
1. a) 62 504
b) 4 CM + 7 UM + 9 C + 5 D + 1 U
c) 854 090
d) 2 DM + 5 UM + 6 C + 2 D + 4 U
2. a) 5 DM = 50 000 unidades
b) 5 UM = 5 000 unidades
3. a) El número menor es 01 357. Se lee: mil trescientos cincuenta y siete.
b) El número mayor es 75 310 Se lee: setenta y cinco mil trescientos diez
c) En el menor, 7 unidades y en el mayor, 70 000 unidades.
4. a) 1 DM = 4 UM + 6 UM
b) 1 CM = 3 DM + 7 DM
c) 1 DM = 1 000 + 9 000
d) 1 CM = 20 000 + 80 000
5. a) 27 465 < 27 495
b) 6 CM + 5 DM > 640 000
c) 8 DM + 4 UM + 3 D > 83 999
d) 109 899 < 109 998
27 495 < 83 999 < 109 998 < 640 000
6. A = 340 000
B = 390 000
C = 450 000
D = 480 000
7. UM anterior Número UM posterior UM más próxima
8. a) Hay, aproximadamente, 200 000 estrellas.
b) La distancia es de 384 000 km, aproximadamente.
c) 320 000, 330 000, 340 000, 350 000, 360 000, 370 000, 380 000
9. a) El coche vale, aproximadamente, 28 000 €.
b) Las placas valen, aproximadamente, 4 000 €.
10. XI = 11
IX = 9
MM = 2 000
XC = 90
XL = 40
DCC = 700
11. 300 000 unidades 12. 58 701 13. 987 654 14.
2 JUEGO CON LOS NÚMEROS
21.
135 + 40 + 52
22.
52
• Los resultados de a) y b) son iguales.
• Se cumple la propiedad asociativa de la suma.
23. a) 90 – (50 + 10) = 90 – 60 = 30
b) (90 – 50) + 10 = 40 + 10 = 50
Los resultados de a) y b) no son iguales.
24. a) 8 954 – 5 134 = 3 820
b) 8 954 – 3 820 = 5 134
25. 2 102 + 1 307 = 3 409
4 806 – 3 409 = 1 397
El vecino del tercero ha consumido 1 397 L.
26. 2 000 – 1 300 = 700
La diferencia es de 700 €.
27. Sumandos y total
28. Asociativa
29. Conmutativa
30. La resta
31. En primer lugar
64
17 000 17 800 18 000 18 000 62 000 62 300 63 000 62 000 482 000 482 500 483 000 483 000 0
1
1
937
000
000
MCMXXV
15. 800 000
16. a) 77 804 b) 61 152 c) 45 774 17. a) 5 578 b) 56 925 c) 7 625 18. a) 12 325 = 10 000 + 2 000 + 300 + 20 + 5 3 152 = 3 000 + 100 + 50 + 2 + 520 = 500 + 20 10 000 + 5 000 + 900 + 90 + 7 = 15 997
36 895 =30 000 + 6 000 + 800 + 90 + 5 – 4 570 = 4 000 + 500 + 70 30 000 + 2 000 + 300 + 20 + 5 = 32
19. a) 8 1 6 7 3 – 3 4 7 9 6 4 6 8 7 7 b) 6 4 0 3 0 – 2 3 1 0 9 4 0 9 2 1
1 000 + 500 = 1 500 500 + 1 000 = 1 500
suma.
b)
325
20.
Se cumple la propiedad conmutativa de la
a)
b)
135 + 40 + 52
175 +
135 + 92 227 227
14 24 10
16 20 22 8 18
12
199














































