МАТЕМАТИКА
Радица
МАТЕМАТИКА 7
Уџбеник
ГЛАВНИ
РЕЦЕНЗЕНТИ
Марјан Матејић, ванредни професор
Катедри за математику, Електронски факултет у Нишу
Снежана Богићевић, професор математике, ОШ „Јован Дучић”, Београд Ненад Вићентијевић, наставник математике, ОШ „Дринка Павловић”, Куршумлија
ДИЗАЈН И ГРАФИЧКА ПРИПРЕМА
DIP studio
ЛЕКТУРА И КОРЕКТУРА
Биљана Никић
ИЗДАВАЧ
Едука д.о.о. Београд
Ул. Змаја од Ноћаја бр. 10/1
Тел./факс: 011 3287 277, 3286 443, 2629 903
Сајт: http://www.eduka.rs; имејл: eduka@eduka.rs
ЗА ИЗДАВАЧА Др Бошко Влаховић, директор
ШТАМПА
ИЗДАЊЕ
ТИРАЖ
Edukapromo Предговор
Водич кроз уџбеник
рЕАЛнИ броЈЕВИ
Квадрат рационалног броја
Решавање једначине �� 2 = �� , �� ≥ 0. Квадратни корен
Ирационалан број. Скуп реалних бројева. Бројевна права
Приближна вредност реалног броја
Својства операција с реалним бројевима. Једнакост √a2 = |�� |
Функција директне пропорционалности
Продужена пропорција
пИТАгорИнА ТЕорЕМА
Питагорина теорема
Примена Питагорине теореме на
Примена Питагорине теореме на једнакокраки и једнакостранични троугао
Примена Питагорине теореме на ромб
Примена Питагорине теореме
МногоугА о
Појам и елементи многоугла. Дијагонале многоугла
Углови многоугла
Правилни многоуглови
Конструкције правилних многоуглова
Обим и површина многоугла
Ортоцентар и тежиште троугла
Неке сложеније примене ставова подударности
Неке сложеније конструкције троуглова и четвороуглова
Круг
Централни и периферијски угао
Edukapromo је
су
странице 15 cm и продају се у кутијама у којима стаје по 40 плочица. Вељко треба да
одреди колико таквих кутија треба да купи.
Решење
Површина једне плочице једнака је 15 cm ∙ 15 cm = 0,15 m ∙ 0,15 m = 0,0225 m2
Ако са �� означимо број плочица, тада
Edukapromo Edukapromo Једнакост 52 = 10 је тачна.
ДА НЕ
(Заокружи тачан одговор.)
Вредност израза −32 + (−3)2 једнака је: а) 0; б) 18; в) 9; г) −18. (Заокружи слово испред тачног одговора.)
Колико постоји рационалних бројева једнаких
а) 0; б) 1; в) 2; г) 3; д) 4 (Заокружи слово
Edukapromo
а) 9 ; −√49; √25; −√16; 0;
б) 3,1; �9 31 25 ; −√6 ,25; √1,44; 1 2 ?
4. Израчунај: а) 2√169 + 5√400; б) 4� 1 16 − 1 6 √36 + 9� 4 81 ; в) −2√0,04 + (√(−0,1)2 + 2 √25 ) ∶ (0,1)2 .
Реши једначине:
⎧ ⎫2 ⎩ ⎭ 2 15 �� − 1 = 16 25; б) − 4 25 · (3��
1,41 < √2 < 1,42 √7 = 2,6 457 5131106 459 0... √13 = 3,6 0555127
понављају?
Ако би број √2 имао коначно много децимала, онда бисмо га могли записати у облику несводљивог разломка, што није могуће, јер је ирационалан. Дакле, број √2 мора имати бесконачан децимални запис. С друге стране, особина периодичности бесконачног децималног записа важи за рационалне бројеве.
3.
4.
а) √11; б) √142 − 7 4? Помоћу интервала представи скуп реалних
а) �� > 1,3; б) �� ≤ −√3; в) �� ≥ −√
�� , таквих да
Одреди скупове:
−3)
[−3, +∞)
Број √50 је рационалан.
ДА НЕ
(Заокружи тачан одговор.)
Између којих природних бројева се налази
Edukapromo Пример 1
Пример 2
Edukapromo 1
Преведимо број 1,3333… = 1, (3) у разломак.
је 10�� − �� = 12, тј. 9�� = 12, па је �� = 12
21,2389
на:
проверавамо своје знање (5 минута)
Децимални запис разломка 1 3 је:
а) 0,3; б) 1,3; в) 0,33; г) 0, (3).
(Заокружи слово испред тачног одговора.)
Неда је број 3,75 заокруглила на једну децималу. Апсолутна грешка приликом тог
заокругљивања једнака је:
а) 0,5; б) 0,05; в) 1,05; г) 3.
(Заокружи слово испред тачног одговора.)
Марија
Пример 2 Тврђење 2
Пример 3
Пример 4
пропорЦИЈА
4 ∙ 1 800 = 7 200, Дуња: 7 ∙ 1 800 = 12 6 00, Лана: 9 ∙ 1 800 = 16 200.
Edukapromo Edukapromo пИТАгорИнА
ТЕорЕМА
Пример
Одредићемо
на основу података са Слике 1.
Решење
Пример
Одредићемо дужину странице ���� троугла
на основу података са Слике 2. Решење
Троуглови
на основу става ССУ.
подударност троуглова Слика 1 Слика 2
Нека је дат правоугли троугао
чије су катете �� и �� и хипотенуза
��. Четири троугла подударна
датом, заједно са квадратом
странице ��, чине квадрат
странице �� + �� приказан на
Слици 4.
Збир површина четири право-
угла троугла једнак је збиру
површина два правоугаоника (Слика 5). Зато су површине
фигура обојене истом бојом
једнаке.
Слика 4 Слика 5
Пример 3
Пример 4
Пример 5
Пример 6
Присетимо
Дијагонала
ДА НЕ
(Заокружи тачан одговор.)
Дужина (у cm) полупречника
природан број.
ДА НЕ
једнаке
Висина једнакостраничног
троугла зависи само од странице. Слично можемо одредити и површину једнакостраничног троугла у зависности од његове странице.
обрасци убрзавају поступке и олакшавају рад!
Висина
а) √2 cm; б) √3 cm; в) 2√3 cm; г) √
Дужина
једнака је: а) 8 cm; б)
Површина правоуглог
а) 16 cm2; б) 32 cm2; в) 8 cm2
прИМЕнА
ТрАпЕЗ
Паралелограм
Пример
5. 6.
Edukapromo Основице правоуглог трапеза су 7 cm и 4
, а висина 4 cm.
Дужи крак трапеза има дужину: а) 6 cm; б) 8 cm; в) 10 cm; г) 5 cm.
(Заокружи слово испред тачног одговора.)
Унутрашњи угао ромба је мере 6 0°, а страница ромба је 2 cm
Површина ромба једнака је: а) 2√3 cm2; б) √3 cm2; в) 4 cm2.
(Заокружи слово испред тачног одговора.)
Да ли постоји ромб чије су дијагонале 24 cm и 10 cm, а страница 12 cm?
ДА НЕ
(Заокружи тачан одговор.)
Једнакокраки трапез
трапеза једнаки 4 cm, онда је обим трапеза једнак: а) 16 cm; б) 8(1 + √2) cm; в) 8(2 + √2) cm; г) 4(4 + √2) cm (Заокружи слово испред тачног одговора.)
1
4.
���� ако је: а) ��(2, 3), ��(7 , 3); б) ��(8, −2), ��(2, −2); в) ��(2, −3), ��(2, 5).
За дате координате тачака �� и �� из претходног
задатка под б), одреди обим троугла Δ������, где је тачка �� координатни почетак.
��(2, 1) и ��(−1, 1) представљају темена квадрата у координатном
Растојање тачке �� (3, 4) од координатног
једнако је: а) 5; б) 3; в) 4;
Ако је ��(−12, 3) и ��(3, 11), онда је
једнака: а) 15; б) 17; в) 14
Edukapromo Пример 4
5 Пример 6
Пример 7
Пример 3 Пример 5 Пример 4
11 Пример 14 Пример 15 Пример 12
Edukapromo Пример 2
{−1, −2, −3, −4}
Edukapromo ��−�� и
су узајамно реципрочни. Важи ��−�� ∙ ���� = 1
а) 10−1 = 1 10 = 0,1; 10−2 = 1 102 = 0,01; 10−3 = 1 103 = 0,001; 10−4 = 1 104 = 0,0001 б) 100−1 = 1 100 = 0,01; 100−2 = 1 1002 = 0,0001; 100−3 = 1 1003 = 0,000001; 100−4 = 1 1004 = 0,00000001. в)
3.
4.
10: а) (105 ∙ 100−3) ∶ 0,016; б) (105 ∙ 100−3) ∶ 0,014; в) 10−4 ∙ 107 100−3 .
вредност
(научном) облику: а) 37 ∙ 104; б) 0,25 ∙ 108; в) 24 ∙ 10−10; г) 0,7 ∙ 10−8; д) 12,8 ∙ 10−7; ђ) 0,048 ∙ 10−14; е) 1 284 ∙ 10−13
Помоћ око 4. задатка?
Прочитај најпре Дефиницију 2, а затим пажљиво проучи Пример 5 у лекцији.
Вредност израза: 3,4 ∙ 1022 + 1,1 ∙ 1021 − 15 ∙ 1018
Вредност израза
Пример
Вредност израза 2�� 1 за �� = 1 2 једнака је: а) 0; б) 3; в) 1; г) −1; д) 5
(Заокружи слово испред тачног одговора.)
Суседне странице
правоугаоника једнак је:
(Заокружи
Задатак 1
Задатак 2
Edukapromo је �� = 3 + 1 = 4 m.
Површина нове дневне собе једнака је 16 m2. С друге стране, можемо приметити да фигуре на Сликама 1а и 1б имају једнаке површине. Дакле, важи �� (�� + 2) = �� 2 + 2 ∙ 3 + 2
Испоставља се да је �� = 4 решење наведене једначине, што можемо проверити директном заменом. Како решавати дату једначину без геометријске интерпретације?
На основу Дефиниције 1, закључујемо:
1. Сваки реалан број (константа) представља полином.
2. Променљива величина је полином.
3. Алгебарски израз у коме се
променљиву), није полином.
Пример 1
Пример 2
Пример 3
1. Сваки реалан број (константа) представља моном.
2. Променљива величина је моном.
Пример 4
Edukapromo Пример 3
Дистрибутивни
Решићемо једначину
6 �� 2 − (3�� − 4) ∙ (5+ 2�� ) = 6 .
Решење
6 �� 2 − (3�� − 4) ∙ (5+ 2�� ) = 6
6 �� 2 − (3�� ∙ 5 + 3�� ∙ 2�� − 4 ∙ 5 − 4 ∙ 2�� ) = 6
6 �� 2 − (15�� + 6 �� 2 − 20 − 8�� ) = 6
6 �� 2 − (6 �� 2 + 7 �� − 20) = 6
6 �� 2 − 6 �� 2 − 7 �� + 20 = 6
−7 �� + 20 = 6
−7 �� = 6 −20
−7 �� = −14 �� = 2 Површину обојене фигуре изразићемо полиномом у сређеном облику.
Решење �� = (5 − 2�� )(3�� + 1) − �� (�� + 7 ) = 15�� + 5 − 6 ��
Edukapromo бИноМА Пример
Edukapromo Пример 5
Пример 6
Пример 7
6 4�� 2 − 9 = 0 (8�� )2 − 32 = 0 (8�� − 3) ∙
Пример 8
Пример 9
Задатак 1
4�� 2 025 − �� 2 023 = 0
�� 2 023 ∙ (4�� 2 − 1) = 0
�� 2 023 = 0 или 4�� 2 − 1 = 0
�� = 0 или (2�� 1) ∙ (2�� + 1) = 0 �� = 0 или �� = 1 2 или �� = 1 2
(2�� + 1)2 − (�� + 1)2 = 0 ((2�� + 1) + (�� + 1)) ∙ ((2�� + 1) (�� + 1)) = 0
(3�� + 2) ∙ (2�� + 1 − �� 1) = 0 (3�� + 2) ∙ �� = 0 �� = 2 3 или �� = 0
Пример 8
Edukapromo Edukapromo Edukapromo МногоугЛА.
дИЈАгонАЛЕ
Присетимо
се састоји у томе да се два
троугла са бар једном страницом једнаке
дужине надовежу тако да имају једну
заједничку
од броја темена (страница), разликујемо многоугао
итд.
Пример
време је на
часовима математике учио о конвексним и неконвексним многоугловима, па је дошао на идеју да најпре упамти који од
континената одговарају конвексним, а који неконвексним
многоугловима. На слици је приказао приближан многоугао
који би, по његовом мишљењу, одговарао Јужној Америци.
Да ли је Вељко нацртао конвексан многоугао?
ДА НЕ
(Заокружи тачан одговор.)
Да ли постоји многоугао чији је
ДА НЕ
(Заокружи
Правилан
су свака два суседна темена на растојању једнаком �� = 3 cm.
б) Како је �� �� = �� = 4 cm, то се задатак
на конструкцију као у делу а).
в) Слично као у Примеру 1в, најпре
се конструише
Edukapromo Помоћ око 2. задатка?
Присети се како се
описане кружнице правилног шестоугла. Тада ће ти бити јасније како да решиш задатак.
МногоугЛА Edukapromo 12 cm2; б) 24 cm2; в) 36 cm2; г) 8 cm2
48 cm; б) 36 cm; в) 64 cm; г) 72 cm
Посматрајмо
тежишне
пресечну
линија троугла
Тврђење 2 (Став
Тврђење 3 (Став
Пример
Пример 3
Пример 2
Решење
Пресечна тачка дијагонала датог делтоида је тачка којом је дужа дијагонала
нормалне.
Уūу�с�во Конструисати
�� = 6 cm, �� = 5,5 cm, �� = 135°;
Edukapromo периферијског угла који
постоји бесконачно много периферијских углова
који одговарају датом луку.
Приметимо да за дату тетиву кружнице постоје
периферијски углови одређени том тетивом, такви да се њихова темена налазе са
страна тетиве.
На приказаној слици, �� и �� су периферијски
углови који одговарају
је
па су троуглови Δ������ и Δ������
Углови на
Тврђење 4 Периферијски
Одреди
дуЖИнА Пример 2
Пример 3
Пример 4
Пример 5
једнак 9 0° и да он представља 1 4 пуног угла.
Edukapromo роТАЦИЈА Пример
Edukapromo Edukapromo Edukapromo Стубичастим дијаграмом су приказани
броја ученика од добијене оцене.
а) Одредићемо укупан
оцене: 2, 3, 4, 4, 5, 1, 2, 2, 5, 5, 2, 3, 4, 5, 1, 2, 3, 4, 5, 5, 4.
1 ∙ 2 + 2 ∙ 5 + 3 ∙ 3 + 4 ∙
1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 5. Како је број података непаран, то
58 kg, 52 kg, 54 kg, 58 kg, 56 kg, 53 kg, 54 kg, 58 kg, 56 kg, 51 kg, 54 kg.
у три одељења са приближно
истим бројем ученика.
Ми ћемо се у овом задатку фокусирати
на физичке разлике међу ученицима
седмог разреда у вашој школи (пол,
боја очију и боја косе – особине које
се наслеђују преко гена).
1. на нивоу одељења;
2.
а) колико има девојчица, а колико дечака; б) колико је ученика са плавим, зеленим и браон очима; в) колико је дечака, а колико девојчица са плавим, зеленим и браон
рЕШЕЊА ЗАдАТАКА Edukapromo рЕАЛнИ броЈЕВИ
КВАдрАТ рАЦИонАЛног броЈА
Вежбамо (стр. 11)
1. а) 64; б) 81; в) 144; г) 0,04; д) 1,69; ђ) 49 9 ; е) 625; ж) 0.
2. �� = {25; 0,04; 81 4 }. Три елемента.
3. а) 8; б) −13 5 8 ; в) 729
4. а) 9; б) 4; в) 1 36
5. 0,58.
6. 961.
проверавамо своје знање (стр. 12)
1. НЕ; 2. а); 3. в); 4. в).
рЕШАВАЊЕ ЈЕднАЧИнЕ
�� 2 = �� , �� ≥ 0
Вежбамо (стр. 16)
1. 1. а) �� ∈ {−8, 8}; б) �� = 0;
в) �� ∈ {−12, 12}; г) �� ∈ {−10, 10}.
2. а) �� ∈ �− 4 7 , 4 7 �; б) �� ∈ �− 9 4 , 9 4 �;
в) �� ∈ �− 9 10 , 9 10 �; г) �� ∈ {−1,3; 1,3}.
3. a) Најмању вредност има −√49, а највећу
9;
б) Најмању вредност има −√6 ,25, а највећу �9 31 25 .
4. а) 126; б) 2; в) 49,6.
5. а) �� ∈ { 3 2 , 27 2 }; б) �� ∈ {− 3 8 , 41 24 }.
6. �� = 180.
проверавамо своје знање (стр. 17)
1. НЕ; 2. а); 3. а); 4. в).
ИрАЦИонАЛАн броЈ. СКуп рЕАЛнИХ броЈЕВА. броЈЕВнА прАВА
Вежбамо (стр. 21)
1. а) �� ∈ {−√5, √5}; б) �� ∈ {−√38, √38}; в) �� ∈ {−√17, √17}.
2. �� = {1 1 414 ; −√25; −5,666…}, �� = {√140; √0,9 ; √5,7 }.
3. а) Између 3 и 4; б) Између 11 и 12
4. а) �� ∈ (1,3; +∞); б) �� ∈ (−∞, −√3]; в) �� ∈ [−√2, √2).
5. a) ��; б) {−13}; в) �� ∈ [1, √5];
г) �� ∈ {−7, 0}.
6. а) ДА; б) НЕ.
проверавамо своје знање (стр. 22)
1. НЕ; 2. б); 3. г); 4. в).
прИбЛИЖнА ВрЕдноСТ рЕАЛног броЈА
Вежбамо (стр. 25)
1. а) 0,4; б) 0,(538461); в) 1,(4); г) 0,1(6).
2.
Број 21,2389
заокругљен на:
приближна вредност
апсолутна грешка
најближу десетицу цео број 21 0,2389 201,2389
једну децималу
две децимале
три децимале
21,20,0389
21,240,0011
21,239 0,0001
3. а) −5,415; б) −17,68.
4. а) �� < �� ; б) �� < �� .
5. Важи √0,(1) = � 1 9 = 1 3 ∈ ��
проверавамо своје знање (стр. 26)
1. г); 2. б); 3. а), в); 4. б).
СВоЈСТВА опЕрАЦИЈА С рЕАЛнИМ
броЈЕВИМА. ЈЕднАКоСТ √���� = |��|
Вежбамо (стр. 31)
1. а) 5 + √3; б) 15; в) 9 − √2; г) −12√5
2. а) 0; б) −3√6; в) 6; г) 2.
3. а) 24√3 − 19√7; б) 13√2; в) −16√3; г) −3 + 4√6 − √3.
4. 10,2.
5. �� ∈ {2, 8}
6. Вредност израза је 5 проверавамо своје знање (стр. 31)
1. НЕ; 2. б); 3. ДА; 4. а).
ФунКЦИЈА дИрЕКТнЕ
пропорЦИонАЛноСТИ
Вежбамо (стр. 34)
1. а)
2. �� = −1,2�� .
3. �� = −2,5√2.
4. а) �� > 1 3 ; б) �� < 7 4 .
5. 45°.
проверавамо своје знање (стр. 35)
1. а), в); 2. б), в), г); 3. НЕ; 4. в).
продуЖЕнА пропорЦИЈА
Вежбамо (стр. 38)
1. 140° и 40°
2. а) �� = 2,5, �� = 12,5; б) �� = 2, �� = 6.
3. 160°, 100°, 60°, 40°.
4. �� = �� = 6.
5. �� = 15, �� = 45, �� = 54.
проверавамо своје знање (стр. 38)
1. б); 2. г); 3. в); 4. в).
пИТАгорИнА ТЕорЕМА
пИТАгорИнА ТЕорЕМА
Вежбамо (стр. 44)
1. а) �� = 10 cm, �� = 24 cm, �� = 24 cm2; б) �� = 20 cm, �� = 48 cm, �� = 96 cm2; в) �� = 17 cm, �� = 40 cm, �� = 60 cm2
2. �� = 70 cm, �� = 210 cm2
3. 12 cm.
4. �� = (38 + 10√5) cm, �� = 196 cm2 .
5. �� = 36 cm, ℎ�� = 7,2 cm.
6. Површина ће се смањити за 0,84 cm2.
проверавамо своје знање (стр. 45)
1. НЕ; 2. в); 3. НЕ; 4. г).
прИМЕнА пИТАгорИнЕ ТЕорЕМЕ нА
прАВоугАонИК И КВАдрАТ
Вежбамо (стр. 48)
1. а) �� = 10 cm; б) ��= 17 cm
2. а) �� = 4√2 cm; б) �� = 1 2 √2 cm; в) �� = 2√6 cm
3. �� = 25 cm.
4. �� = 24√2 cm, �� = 72 cm2, �� = 12 cm.
5. �� �� = 5 cm.
6. �� �� = 5√2 cm.
проверавамо своје знање (стр. 49)
1. б); 2. НЕ; 3. НЕ; 4. ДА.
прИМЕнА пИТАгорИнЕ ТЕорЕМЕ нА
Вежбамо (стр. 53)
1. �� = 90 cm, �� = 300 cm2 .
2. �� = 18 cm, �� = 9√3 cm2, ℎ = 3√3 cm.
3. �� = 4(3+ √3) cm, �� = 8√3 cm2.
4. �� = 8(2+ √2) cm.
5. �� = 3 + √3 2 �� , ��= 3 + √3 2
6. �� = 120 cm2, ℎ�� = 6√10 cm.
проверавамо своје знање (стр. 54)
1. б); 2. в); 3. ДА; 4. а).
прИМЕнА пИТАгорИнЕ ТЕорЕМЕ нА
роМб И ТрАпЕЗ
Вежбамо (стр. 58)
1. а) �� = 13 cm; б) �� = 10 cm.
2. �� = 28 cm.
3. �� �� = 60 13 cm.
4. �� = 32 √3 cm2, ��1 = 8 cm, ��2 = 8√3 cm.
5. �� = 6(5+ √2) cm, �� = 45 cm2
6. а) �� = 3(5+ √3) cm, �� = 27√3 2 cm2; б) ��1 = 6 cm, ��2 = 3√7 cm.
проверавамо своје знање (стр. 59)
1. г); 2. а); 3. НЕ; 4. в).
прИМЕнА пИТАгорИнЕ ТЕорЕМЕ
у КонСТруКЦИЈАМА Вежбамо (стр. 61)
2.
3. а)
Вежбамо (стр. 64)
Edukapromo 1. а) На пример, конструиши дуж дужине √2
2
1. а) 5; б) 6; в) 8.
2. �� = 6+ 2√2 + 2√17.
3. 3√2.
4. а) �� = 12√2; б) Како је |�� �� |2 = |�� ��|2 + |�� ��|2 , то
закључујемо да је троугао Δ�� �� �� правоугли. проверавамо своје знање (стр. 64)
1. а); 2. б); 3. НЕ; 4. г).
ЦЕЛИ АЛгЕбАрСКИ
прИроднИ броЈ Вежбамо (стр. 68)
1. а) 24; б) (−8)5; в) 5,23; г) � 3 5 �6 ; д) �1 3 10 �4 ; ђ) �−2 1 2 �3 ; е) (−�� )6; ж) (2�� )3; з) (�� ��)3 .
2. а) 1; б) 10 000; в) −1 000; г) 0,0001; д) 0,00001; ђ) 1 25 ; е) − 1 32 ; ж) 9.
3. а) � 1 3 �1 ; б) � 1 3
4. а) 1 8 ; б) 8,52.
5. 0,000007.
6. 2 3
проверавамо своје знање (стр. 69)
1. б); 2. б); 3. НЕ; 4. а).
МноЖЕЊЕ И дЕЉЕЊЕ СТЕпЕнА ЈЕднАКИХ
оСноВА
Вежбамо (стр. 72)
1. а) 28; б) 72; в) �� 3; г) (−�� )14; д) (−�� )7
2. а) �� 2; б) �� 9; в) �� 2; г) �� 4
3. а) 33; б) 30.
4. 25.
5. Вредност израза је једнака 32, за
произвољан �� ∈ ��.
проверавамо своје знање (стр. 72)
1. НЕ; 2. б); 3. а); 4. ДА.
СТЕпЕн проИЗВодА , СТЕпЕн КоЛИЧнИКА
И СТЕпЕн СТЕпЕнА
Вежбамо (стр. 76)
1. а) (3 ∙ 5)2; б) (7 ∙ 11)5; в) (−2�� ∙ 3)4 .
2. а) 1; б) 1; в) −1.
3. а) 34 54 ; б) x5 75 ; в) (3�� )2 (6��)2 ; г) 133 43 ; д) m7 n7 ; ђ) (7ab)13 (3c)13
5. а) �� 5; б) 1. 6. 3�� 4 ��10
7. 31. 8. 31
9. Вредност израза је 5 2 10. 3. 11. 22 023 + 22 021 = 22 021 ∙ (22 + 1) = 22 021 ∙ 5.
Edukapromo 4. а) −32; б) 16; в) 64 25 ; г) − 125 8 .
проверавамо своје знање (стр. 77)
1. г); 2. а); 3. ДА; 4. в).
СТЕпЕн дЕКАднЕ ЈЕдИнИЦЕ ЧИЈИ ЈЕ
ИЗЛоЖИЛАЦ ЦЕо броЈ
Вежбамо (стр. 80)
1. а) 102; б) 103; в) 105; г) 10−1; д) 10−3; ђ) 10−6 .
2. а) 10−2; б) 10−18 .
3. а) 1011; б) 107; в) 109.
4. а) 3,7 ∙ 105; б) 2,5 ∙ 107; в) 2,4 ∙ 10−9; г) 7 ∙ 10−9; д) 1,28 10−6; ђ) 4,8 10−16; е) 1,284 10−10
5. 3,5085 ∙ 1022
проверавамо своје знање (стр. 81)
1. в); 2. а); 3. НЕ; 4. ДА.
АЛгЕбАрСКИ ИЗрАЗИ
Вежбамо (стр. 84)
1. 5
2. а) �� + 3; б) �� 4,8; в) 2��; г) b 7
3. а) −25; б) −81
4. 0.
5. �� = �� 2√3 48 .
6. Изрази имају једнаке вредности.
проверавамо своје знање (стр. 85)
1. а); 2. в); 3. ДА; 4. б).
поЛИноМИ
Вежбамо (стр. 89)
1. а), б), в), д), е).
2. а) 3; б) −6; в) 2 13 ; г) − 1 3 ; д) 0,8; ђ) 1; е) 1,8.
3. Слични су −5�� , 6 1 5 �� и −53�� . Такође, слични су мономи 13�� �� и 1,8�� �� Међу
сличнима су и 1 4 �� и ��
4. �� = 1 3
проверавамо своје знање (стр. 90)
1. в), г); 2. а); 3. б), г); 4. ДА.
САбИрАЊЕ поЛИноМА Вежбамо (стр. 94)
1. а) 3�� 8; б) �� 2 + �� ; в) 6�� 2 + 2�� 4. 2. а) 3�� + 1; б) 5�� + 3; в) 0,4�� �� − 0,25; г) 9�� 2 − 7�� + 1
МноЖЕЊЕ поЛИноМА
Вежбамо (стр. 98)
1. а) −20�� 2; б) 21��2; в) − 1 3 �� 3; г) 5 6 �� 3��3��2 .
2. а) 1,5�� 6; б) 195�� 7 .
3. а) 6�� −2; б) 3�� 3 − 5�� 2 − 6�� ; в) 3�� 2 − 4�� ��2 .
4. − 7,8�� 6 .
5. а) −12�� 2 + 5�� 2; б) 3�� 2; в) −��3 + 1
6. �� = 1
Edukapromo 3. а) 9�� 2 − 10�� + 1; б) 7�� 7.
4. а) 3�� 3 + 6�� 2 + 3�� 11; б) три; в) −3�� 3 − 6�� 2 − 3�� + 11; г) −17.
5. �� = −3, �� = 0,25, �� = −11,25.
проверавамо своје знање (стр. 95)
1. в); 2. а); 3. г); 4. НЕ.
7. Тражени бројеви су 15 и 17.
проверавамо своје знање (стр. 99)
1. г); 2. б), в); 3. б); 4. г).
КВАдрАТ бИноМА
Вежбамо (стр. 102)
1. а) �� 2 + 2�� + 1; б) 4�� 2 + 4�� �� + �� 2; в) 9�� 2 − 12�� + 4; г) a2 16 − 3a 2 + 9; д) 0,25�� 2 − 0,1�� �� + 0,01�� 2; ђ) �� 4 − 6�� 2��+ 9��2 .
2. −9,2.
3. �� = 5. 4. �� 2 − 34�� + 17.
5. 0.
6. �� = 2�� − 5 или �� = 5− 2��
проверавамо своје знање (стр. 103)
1. в); 2. а); 3. б); 4. ДА.
рАЗЛИКА КВАдрАТА
Вежбамо (стр. 106)
1. а) �� 2 − 12; б) 32 − �� 2;
в) �� 2 − 1,32; г) (3��)2 − �� 2 .
2. а) 1; б) −5.
3. а) 32; б) −3�� + 64; в) 40; г) 2�� 2 − �� 79.
4. −37�� 2 − 1.
5. �� = −16.
6. а) 1; б) 3√2
проверавамо своје знање (стр. 106)
1. в); 2. б); 3. в); 4. НЕ.
рАСТАВЉАЊЕ поЛИноМА нА ЧИнИоЦЕ
Вежбамо (стр. 110)
1. а) 4�� (2− 9�� ); б) 4��(�� + 3��);
в) 5��(3�� − 1); г) −5�� (4�� − 7);
д) 7�� �� (�� 3�� ); ђ) 9��2����(2 − 3����);
е) −21�� �� (2�� + 3)
2. а) 9(�� �� + �� �� + ����); б) 4(3�� 4�� + 7��);
в) 2�� (�� 2 + 4�� 2 − 6�� �� ).
3. а) (4 − �� )(4+�� ); б) (�� 0,6)(�� + 0,6);
в) (1 − ��)(1 + ��); г) ��� 1 7 � ��� + 1 7 �;
д) (1,6 − �� )(1,6 +�� ); ђ) (d − 1,1)(d + 1,1).
4. а) (1 − �� )2; б) (�� + 2)2; в) (��+ 1)2;
г) (3�� 1)2
МногоугАо
поЈАМ И ЕЛЕМЕнТИ МногоугЛА.
дИЈАгонАЛЕ МногоугЛА
Вежбамо (стр. 116)
1. а) б)
Edukapromo 5. а) (�� + ��)(3�� 2); б) (�� 1)(6�� − 5);
в) (�� ��)(�� + ��); г) ��(�� − ��)(�� + ��);
д) 4�� (2 −�� )(2 + �� );
ђ) (3�� 2�� )(3�� + 2�� )(9��2 + 4�� 2);
е) −48(�� 2 − �� + 1); ж) 2�� 2(�� 2 − 6�� �� − 12��2);
з) (5 − �� )(9 +�� ); и) −8(�� 1).
6. �� ∈ {−2, 2, 8}.
2. а) ��7 = 4; б) ��7 = 14.
3. а) осамнаестоугао; б) шестоугао.
4. 20.
5. 40.
проверавамо своје знање (стр. 117)
1. НЕ; 2. в); 3. НЕ; 4. б).
угЛоВИ МногоугЛА
Вежбамо (стр. 120)
1. а) 1 440°; б) 3 240°; в) 2 700°
2. 105°.
3. 2 880°.
4. Осмоугао.
5. Четвороугао.
6. 112°, 92°, 72°, 52°, 32°.
проверавамо своје знање (стр. 121)
1. б); 2. ДА; 3. г); 4. а).
прАВИЛнИ МногоугЛоВИ Вежбамо (стр. 128)
1. а) �� = 120°, �� = 60°, �� = 60°; б) �� = 135°, �� = 45°, �� = 45°; в) �� = 150°, �� = 30°, �� = 30°.
2. а) 36°; б) 36°; в) 35.
3. 3 960°.
4. а) �� �� = 2√3 cm, �� �� = √3 cm; б) �� �� = 3√2 cm, �� �� = 3 cm; в) �� �� = 6 cm, �� �� = 3√3 cm.
5. �� �� = 1 080°, ���� = 20.
6. 60°.
проверавамо своје знање (стр. 129)
1. НЕ; 2. ДА; 3. б); 4. ДА.
КонСТруКЦИЈЕ прАВИЛнИХ
МногоугЛоВА
Вежбамо (стр. 133)
1. Најпре конструисати кружницу датог
полупречника.
2. Важи �� �� = ��
3. Дужина дијагонале
обИМ И поВрШИнА МногоугЛА
Вежбамо (стр. 138)
1. �� = 22,5 cm
2. а) 28 cm; б) 40 cm; в) 88 cm.
3. �� = 32√3 cm, �� = 192 cm2 .
4. �� = 36 cm, �� = 54√3 cm2.
5. �� = 3(9 4√3) cm2.
Edukapromo 6. а) �� = 72√2 cm2; б) �� = 108 cm2
7. а) делтоид; б) �� = 12(1+ √2) cm; в) �� = 18(1+ √3) cm2
проверавамо своје знање (стр. 139)
1. б); 2. в); 3. б); 4. а).
орТоЦЕнТАр И ТЕЖИШТЕ ТроугЛА
Вежбамо (стр. 144)
1. а) б)
2. Све четири значајне тачке се поклапају.
3. �� �� = 12 cm
4. �� = 48 cm, �� = 96 cm2
5. 2 cm.
проверавамо своје знање (стр. 145)
1. ДА; 2. НЕ; 3. в); 4. в).
нЕКЕ СЛоЖЕнИЈЕ прИМЕнЕ СТАВоВА
подудАрноСТИ
Вежбамо (стр. 149)
1. Према ознакама са
слике важи да је
Δ���� �� ≅ Δ���� �� (став СУС),
па следи �� �� = �� ��
2. Како је �� �� = �� ��, �� �� = ����
и∡���� �� = ∡���� �� = 90°,
то важи
Δ���� �� ≅ Δ���� �� (став СУС),
па следи ���� = ����
3. Нека је �� средиште дужи �� �� , а тачка ��
произвољна тачка са симетрале те дужи.
Правоугли троуглови Δ�� ���� и Δ�� ���� су
подударни...
4. Подножја нормала из
произвољне тачке симетрале формирају подударне
правоугле троуглове...
5. Нека је �� средиште странице �� �� једнако-
страничног троугла Δ�� �� ��
и тачке �� и�� подножја
нормала из тачке �� на странице �� �� и �� ��, редом. Правоугли троуглови Δ���� �� и ΔEBS су подударни (став УСУ), па је ���� =
праве. Размотри два могућа решења.
6. Задатак се своди на конструкцију
чија је дијагонала 9 cm
7. Слично као у задатку 5. Како су углови на основици оштри, то задатак има тачно једно решење.
8. Најпре се конструише
9. Тачка �� је средиште дужи �� ��, па је
(стр. 161)
1. а) 72°; б) 140°; в) 124°; г) 230°. 2. �� = 90°, �� = 45°.
3. �� = 80°, �� = 40°.
4. а) 1 24 ; б) 1 8 ; в) 1 5 .
5. 36°, 54°, 90°.
проверавамо своје знање (стр. 162)
1. НЕ; 2. б); 3. ДА; 4. а).
обИМ КругА. дуЖИнА КруЖног ЛуКА
Вежбамо (стр. 167)
1. а) 12�� cm; б) 16�� cm; в) 2,4�� cm; г) 6√3�� cm; д) 12 5 �� cm.
2. а) 2,5 cm; б) 3 14 cm.
3. а) 2�� cm; б) 2,4�� cm.
4. 9�� (√2 − 1) cm.
5. 10 3 �� cm.
6. 54 cm.
7. а) √2�� cm; б) 20 3 �� cm; в) 4√3 3 �� cm.
проверавамо своје знање (стр. 168)
1. в); 2. а); 3. НЕ; 4. б).
поВрШИнА КругА, КруЖног ИСЕЧКА И
КруЖног прСТЕнА
Вежбамо (стр. 171)
1. а) 36�� cm2; б) 64�� cm2; в) 1,44�� cm2; г) 27�� cm2; д) 36 25 �� cm2 .
2. а) 6,25�� cm2; б) 9 196 �� cm2
3. а) 2�� cm2; б) 4 3 �� cm2 .
4. 81�� 2 cm2.
5. 9�� cm2 .
6. 338 15�� .
проверавамо своје знање (стр. 172)
1. в); 2. в); 3. ДА; 4. а).
прИМЕнА пИТАгорИнЕ ТЕорЕМЕ нА Круг Вежбамо (стр. 174)
1. 6 cm. 2. 26 cm.
3. 4√2 cm. 4. 2√3 cm.
Edukapromo 7. а) 9(�� −2)2 2 cm2; б) 18(2�� 3√3) cm2;
в) 9(4√3 + �� ) cm2 .
5. �� ��= 120 13 cm.
роТАЦИЈА
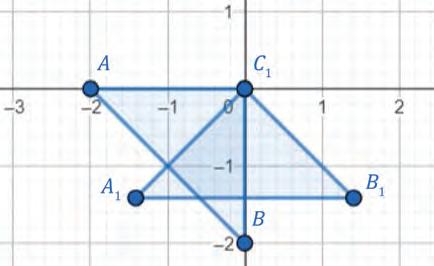
Вежбамо (стр. 178)
1. и 2. Види део у лекцији који се
ротацију тачке и дужи. 3. 4. �� 1(−√2, −√2), �� 1(√2, −√2), ��1(0, 0).
ВрСТЕ подАТАКА И ЊИХоВо
прИКАЗИВАЊЕ
Вежбамо (стр. 182)
1. а) 15 ученика; б) 4 ученика; в) 3 сата.
г) Вре ме (са ти ) 0,5 2 345
уче ни ка 42171215 д)
обрАдА подАТАКА Вежбамо (стр. 184)
1. Средња вредност је 54,9. Медијана је 54 Вредности 54 и 58 представљају мод.
Edukapromo 2. а) 70%; б) 10 ученика; медијана