A magic approach to octonionic Rosenfeld spaces

a“magic”approachtooctonionic Rosenfeldspaces 12December2022

AlessioMarrania,DanieleCorradettib,DavidChesterc , RaymondAschheimc,KleeIrwinc

a InstitutodeFísicaTeorica,DepartamentodeFísica, UniversidaddeMurcia,CampusdeEspinardo,E-30100,Spain email: alessio.marrani@um.es

b UniversidadedoAlgarve,DepartamentodeMatemática, CampusdeGambelas,8005-139Faro,Portugal email: a55944@ualg.pt

c QuantumGravityResearch, TopangaCanyonRd101S.,CaliforniaCA90290,USA email: DavidC@QuantumGravityResearch.org; Raymond@QuantumGravityResearch.org; Klee@QuantumGravityResearch.org

InhisstudyonthegeometryofLiegroups,Rosenfeldpostulatedastrictrelationbetweenall realformsofexceptionalLiegroupsandtheisometriesofprojectiveandhyperbolicspacesover the(rank-2)tensorproductofHurwitzalgebrastakenwithappropriateconjugations.Unfortunately,theprocedurecarriedoutbyRosenfeldwasnotrigorous,sincemanyofthetheorems hehadbeenusingdonotactuallyholdtrueinthecaseofalgebrasthatarenotalternativenor power-associative.Amorerigorousapproachtothedefinitionofalltheplanespresentedmore thanthirtyyearsagobyRosenfeldintermsoftheirisometrygroup,canbeconsideredwithin thetheoryofcosetmanifolds,whichweexploitinthiswork,bymakinguseofallrealforms ofMagicSquaresoforderthreeandtwooverHurwitznormeddivisionalgebrasandtheirsplit versions.Withinouranalysis,wefind7pseudo-Riemanniansymmetriccosetmanifoldswhich seeminglycannothaveanyinterpretationwithinRosenfeld’sframework.Wecarryoutasimilar analysisforRosenfeldlines,obtainingthatthereareanumberofpseudo-Riemanniansymmetric cosetswhichdonothaveanyinterpretation àlaRosenfeld

AroundthehalfoftheXXcentury,geometricinvestigationsontheoctonionicplanegaverise toafruitfulmathematicalactivity,culminatingintotheformulationof Tits-FreudenthalMagic Square [Fr65,Ti].TheMagicSquareisanarrayofLiealgebras,whoseentriesareobtained fromtwoHurwitzalgebras1 andenjoymultiplegeometricandalgebraicinterpretations[BS00, BS03,SH,Sa,El02,El04],aswellasphysicalapplications[GST,DHW,CCM].

Theentries m3(A1, A2) oftheTits-FreudenthalMagicSquarecanbedefinedequivalently [BS03]usingtheTits[Ti],Barton-Sudbery[BS03](alsocf.[Ev]),andVinberg[Vin66]constructions2 , m3(A1, A2)=

der(A1) ⊕ der(J3(A2)) + ImA1 ⊗ J3(A2); der(A1) ⊕ der(A2) + sa(3, A1 ⊗ A2); tri(A1) ⊕ tri(A2) ˙ +3(A1 ⊗ A2),

(1)

where A1 and A2 arenormedHurwitzdivisionalgebras R, C, H, O orthesplitcounterparts Cs, Hs, Os.Here, J3(A) denotestheJordanalgebraof 3 × 3 Hermitianmatricesover A and J3(A) itssubspaceoftracelesselements.Thespaceofanti-Hermitiantraceless n × n matrices over A1 ⊗ A2 isdenoted sa(n, A1 ⊗ A2).Detailsofthecommutatorsandtheisomorphisms betweentheseLiealgebrascanbefounde.g.in[BS03].Thechoiceofdivisionorsplit A1, A2 yieldsdifferentrealforms:fortheTitsconstruction,furtherpossibilitiesaregivenbyallowing theJordanalgebratobeLorentzian,denoted J2,1,asdescribedin[CCM](seeSec.2.3below); equivalently,onecanintroduceoverallsignsinthedefinitionofthecommutatorsbetweendistinct componentsintheVinbergorBarton-Sudberyconstructions,asdescribedin[ABDHN].Fora completelistingofallpossibilities3,see[CCM].Recently[WDM],Wilson,DrayandManogue gaveanewconstructionoftheLiealgebra e8 intermsof 3 × 3 matricessuchthattheLie brackethasanaturaldescriptionasmatrixcommutator;thisledtoanewinterpretationofthe Freudenthal-TitsMagicSquareofLiealgebras4,actingonthemselvesbycommutation.

WhileTitswasmoreinterestedinalgebraicaspects,Freudenthalinterpretedeveryrowofthe MagicSquareintermsofadifferentkindofgeometry,i.e.elliptic,projective,symplecticand meta-symplecticforthefirst,second,thirdandfourthrow,respectively[LM01].Thismeans that,whilethealgebrastakeninaccountwerealwaystheHurwitzalgebras R, C, H and O,all Liegroupswerearisingfromconsideringdifferenttypeoftransformationssuchasisometries, collineationsandhomographiesoftheplane[Fr65].Ontheotherhand,Rosenfeldconceived everyentryofthe 4 × 4 arrayoftheMagicSquareastheLiealgebraofthe(global)isometry groupofa“generalized”projectiveplane,latercalled Rosenfeldplane [Ro98,Ro97].Thus,while inFreudenthal’sframeworktheprojectiveplanewasalwaysthesamebut,dependingonthe consideredrowoftheMagicSquare,thekindoftransformationswaschanged;inRosenfeld’s picturethegroupoftransformationswasalwaystheisometrygroup,anddifferentLiegroups appearedconsideringdifferentplanesovertensorproductofHurwitzalgebras.

Tobemoreprecise,sincetheexceptionalLiegroupF4 istheisometrygroupoftheoctonionic projectiveplane OP 2,thenRosenfeldregardedE6 astheisometrygroupofthe bioctonionic“pro-

1EventhoughtheoriginalconstructionbyTitswasnotsymmetricinthetwoentries(cf.thethirdof(1)), thesquareturnedouttobesymmetricandwas,therefore,dubbedas“magic”.

2Theternaryalgebraapproachof[Ka]wasgeneralisedbyBarsandGünaydinin[BG]toincludesuperLie algebras.Generalizationstoaffine,hyperbolicandfurtherextensionsofLiealgebrashavebeenconsideredin [Pa].

3ConcerningtheextensionofFreudenthal-TitsMagicSquaretovarioustypesof“intermediate”algebras,the extensiontothesextonions S (between H and O)isduetoWestbury[Wes],andlaterdevelopedbyLandsberg andManivel[LM01,LM06],whereasfurtherextensiontothetritonions T (between C and H)wasdiscussedby Borstenandoneofthepresentauthorsin[BM].

4MagicSquares oforder2 ofLiegroupshavebeeninvestigatedin[DHK].Interestingly,theFreudenthal-Tits MagicSquareofLiegroupswasobservedtobenon-symmetricsince[Yo85].

jective”plane (C ⊗ O)P 2,E7 astheisometrygroupofthe quaternoctonionic“projective”plane (H ⊗ O)P 2,andE8 astheisometrygroupofthe octooctonionic“projective”plane (O ⊗ O)P 2 . DespiteRosenfeld’ssuggestiveinterpretation,itwassoonrealizedthattheplanesidentifiedby Rosenfelddidnotsatisfyprojectiveaxioms,andthisexplainsthequotesintheterm“projective”,whichwouldhavetobeintendedonlyinavaguesense.ItwastheworkofAtsuyama, followedbyLandsbergandManivel,togivearigorousdescriptionofthegeometryarisingfrom Rosenfeld’sapproach[Atsu2,LM01,AB].Indeed(unlike O R ⊗ O) C ⊗ O, H ⊗ O and O ⊗ O arenotdivisionalgebras,thuspreventingadirectprojectiveconstruction;moreover(unlike C ⊗ O),Hermitian 3 × 3 matricesover H ⊗ O or O ⊗ O donotformasimpleJordanalgebra,so theusualidentificationofpoints(lines)withtrace1(2)projectionoperatorscannotbemade [Ba].Nonetheless,theyareinfactgeometricspaces,generalisingprojectivespaces,knownas “buildings”,onwhich(thevariousrealformsof)exceptionalLiegroupsactasisometries.BuildingswhereoriginallyintroducedbyTitsinordertoprovideageometricapproachtosimpleLie groups,inparticulartheexceptionalcases,buthavesincehadfarreachingimplications;see,for instance,[Ti2,Te]andRefs.therein.

Morespecifically,Rosenfeldnoticedthat,over R,theisometrygroupoftheoctonionicprojectiveplanewasthecompactformofF4,i.e.F4( 52),whiletheother,non-compactrealforms, i.e.thesplitformF4(4) andF4( 20),wereobtainedasisometrygroupsofthe split-octonionic projectiveplane OsP 2 andofthe octonionichyperbolicplane OH 2 [CMCAb,CMCAa],respectively.Thence,heproceededinrelatingallrealformsofexceptionalLiegroupswithprojective andhyperbolicplanesovertensorialproductsofHurwitzalgebras[Ro97,Ro98].

Despitebeingveryinsightful,tothebestofourknowledgeRosenfeld’sapproachwasnever formulatedinasystematicway,andalargepartoftheveryRosenfeldplaneswereneverreally rigorouslydefined.Inthepresentinvestigation,wegiveasystematicandexplicitdefinition ofalloctonionic5 “Rosenfeldplanes”ascosetmanifolds,byexploitingallrealformsofMagic Squaresoforder3overHurwitzalgebrasandtheirsplitversions,thusallpossiblerealforms ofFreudenthal-TitsMagicSquare.Indoingso,wewillalsofindatotalof10cosetmanifolds, namely7“planes”and3“lines”,whosedefinitionisstraightforwardaccordingtoourprocedure, butthatapparentlydonothaveanyinterpretationaccordingtoRosenfeld’sapproach.

Theplanofthepaperisasfollows.InSec.2wewillresumeallthealgebraicmachinery usedinthispaper,i.e.Hurwitzalgebras,theirtrialityandderivationsymmetries,Euclidean andLorentziancubicJordanalgebras,MagicSquaresoforder3and2,etc.InSec.3wewill thenpresentthe“magic”formulæwhichwewilluseinordertodefinetheoctonionicRosenfeld planesinSec.4;then,wewilldothesameforoctonionicRosenfledlinesinSecs.5and6.Some finalremarksandanoutlookaregiveninSec.7.

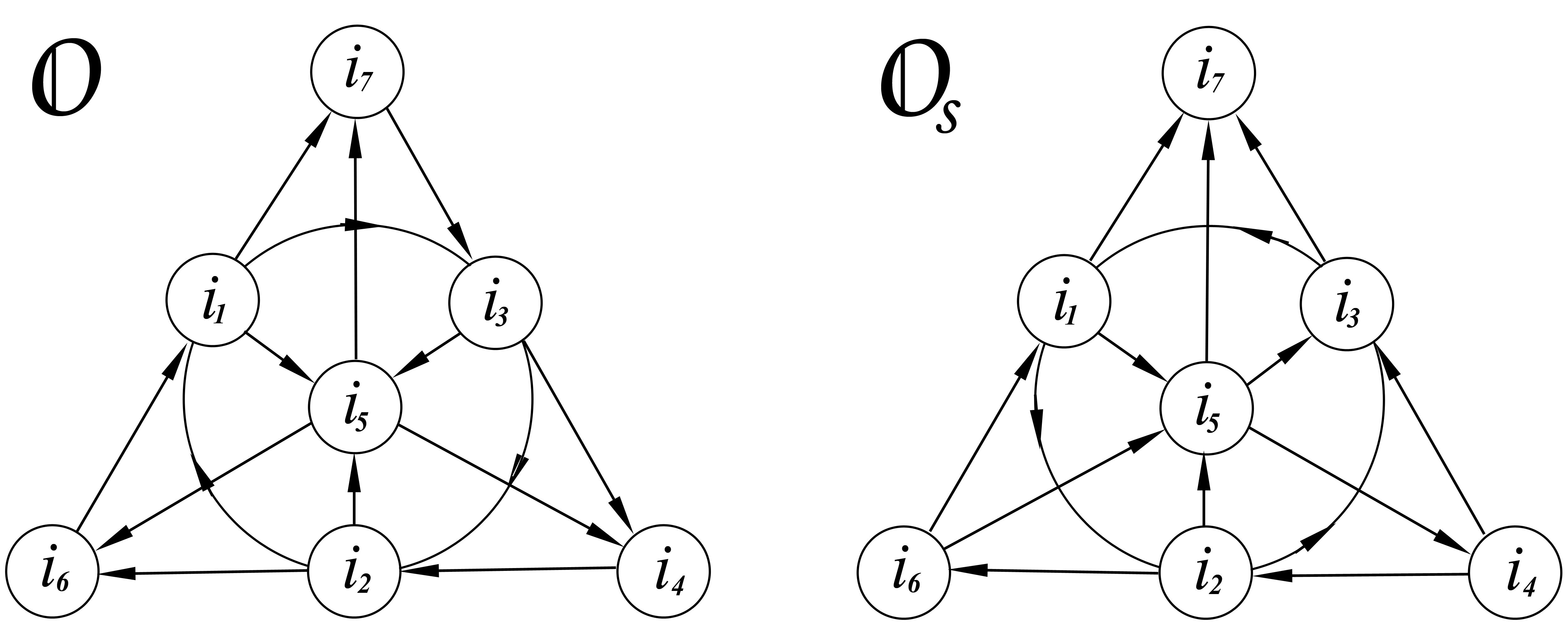
Figure1:Multiplicationruleofoctonions O (left)andofsplit-octonions Os (right)asreal vectorspace R8 inthebasis {i0 =1, i1,..., i7}.Inthecaseoftheoctonionsi2 0 =1 andi2 k = 1 for k =1 7,whileinthecaseofsplit-octonionsi2 k =+1,for k =1, 2, 3 andi2 k = 1 for k =1, 2, 3

N (x) bedefinedas

N (x):= 7 k=0 (xkik)2 , (3) anditspolarisationas x,y := N (x + y) N (x) N (y) Thenthe realpart of x is R (x):= x, 1 and x :=2 x, 1 − x. Wethenhavethat N (x)= xx, x,y = xy + yx,andthat N (xy)= N (x) N (y) , (4)

or,inotherwords,thatoctonionsarea compositionalgebra withrespecttotheNorm N defined by(3).

Wenowdefineasthealgebraof quaternions H asthesubalgebraof O generatedbythe elements {i0 =1, i1, i2, i3} andthealgebraof complexnumbers C asthesubalgebraof O generated bytheelements {i0 =1, i1}.

Thus,the split-octonions Os canbedefinedastheonlyunital,non-associative,normed algebrawith R8 decompositionof x ∈ Os givenby(2)where,again, {i0 =1, i1,..., i7} isabasis of R8,butthemultiplicationrulesareencodedinadifferentvariantoftheFanoplane,given bytherightsideofFig.1,alongwithi2 k =1 for k =1,..., 3 andi2 k = 1 for k =4, 5, 6, 7 Normandconjugationaredefinedasintheoctonioniccaseand,asforthedivisionoctonions, weobtainthatsplitoctonionsarea compositionalgebra withrespecttotheNorm N defined by(3).Wethendefinethealgebraof split-quaternions Hs asthesubalgebraof Os generatedby {i0 =1, i1, i4, i5} andthe split-complex (or hypercomplex ) numbers Cs asthesubalgebraof Os generatedby {i0 =1, i4}.

2.2Trialitiesandderivations

Let A beanalgebraandEnd (A) theassociativealgebraofitslinearendomorphisms.Then,the trialityalgebra tri (A) istheLiesubalgebraof so (A) ⊕ so (A) ⊕ so (A) definedas

tri (A):= (A,B,C) ∈ End (A)⊕3 : A (xy)= B (x) y + xC (y) , ∀x,y ∈ A , (5)

wheretheLiebracketarethoseinheritedasasubalgebra.Derivationsareaspecialcaseof trialitiesoftheform (A,A,A) andthereforetheyagainformaLiealgebra,definedas

der (A):= {A ∈ End (A): A (xy)= A (x) y + xA (y) , ∀x,y ∈ A} , (6)

R C H O

tri (A) Ø u (1) ⊕ u (1) so (3) ⊕ so (3) ⊕ so (3) so (8) tri (As) Ø so (1, 1) ⊕ so (1, 1) sl2 (R) ⊕ sl2 (R) ⊕ sl2 (R) so (4, 4) der (A) Ø Ø so (3) g2( 14) der (As) Ø Ø sl2 (R) g2(2) A (A) Ø u1 su2 Ø A (As) Ø so1,1 sl2 (R) Ø

Table1:TrialityandderivationalgebrasofHurwitzalgebras.Moreoverwealsoaddedthe algebra A (A):= tri (A) so (A) , thatwillbeusedinSec.3.2inthedefinitionoftheRosenfeld planes.

wherethebracketisgivenbythecommutator.Inthecaseof A = C, H, O weintended so (A) as so (2), so (4) and so (8) respectively;while,fortheirsplitcompanions,weintended so (As) as so (1, 1), so (2, 2) and so (4, 4).TrialityandderivationLiealgebrasoverHurwitzalgebrasare summarizedinTable1.

2.3EuclideanandLorentziansimplerank-3Jordanalgebras

Let A beacompositionalgebraand Hn (A) bethesetofHermitian n × n matriceswithelements in A suchthat

X † := X t = X, (7)

wheretheconjugationistheonepertainingto A itself.When6 n =2 or 3,wedefinethesimple, rank-n EuclideanJordanalgebra Jn (A) asthecommutativealgebraover Hn (A) withthe Jordan product ◦ definedbytheanticommutator

X ◦ Y := 1 2 (XY + YX)=: {X,Y } , ∀X,Y ∈ Hn (A) , (8)

wherejuxtapositiondenotesthestandard’rows-by-columns’matrixproduct.Moreover,we define Jn (A) asthesubspaceoftheJordanalgebraorthogonaltotheidentity I (namely,the subspaceoftracelessmatricesin Jn (A)),endowedwiththeproductinherited7 from Jn (A) (see e.g.[BS03,p.8]).Inparticular,for n =3 thesimple,rank-3 EuclideanJordanalgebra J3 (A) haselements X :=   ax1 x2 x1 bx3 x2 x3 c   ∈ J3 (A) , (9) where x1,x2,x3 ∈ A and a,b,c ∈ R TheHermiticitycondition(7)canbegeneralizedbyinsertingapseudo-Euclideanmetric:

Correspondingly,onedefinesthesimple,rank-n pseudo-EuclideanJordanalgebra Jn p,p (A) Jp,n p (A).Inparticular,bysetting n =3,thesimple,rank-3 LorentzianJordanalgebra 6Excluding A = O and Os,onecanactuallyconsider any n ∈ N 7Notethat Jn (A) isnotclosedundertherestrictionofthe Jordanproduct ◦ of Jn (A) to Jn (A) itself.However, onecandeform ◦ intothe Michel-Radicatiproduct ∗,definedas X ∗ Y := X ◦ Y Tr(X ◦Y ) n I ∀X,Y ∈ Jn (A), underwhich Jn (A) isclosed[MR70,MR73].

J2,1 (A) J1,2 (A),whoseelementsreadas

X :=   ax1 x2 x1 bx3 x2 x3 c   ∈ J1,2 (A) , (12) where x1,x2,x3 ∈ A and a,b,c ∈ R.

2.4RealformsoftheFreudenthal-TitsMagicSquare

Asanticipatedin(1),given A1 and A2 twocompositionalgebras,thecorrespondingentryof Tits-FreudenthalMagicSquare m3 (A1, A2) isaLiealgebrathatcanberealizedin atleast three different,butequivalentways,onwhichwewillnowbrieflycomment(withouttheexplicit definitionoftheLiebrackets,thatcanbefounde.g.in[BS03]).

1.Titsconstruction[Ti]isgivenbythefirstlineofther.h.s.of(1): m3 (A1, A2):= der(A1) ⊕ der(J3(A2)) + ImA1 ⊗ J3(A2), (13) thusinvolvingthederivationLiealgebraof A1 andthederivationLiealgebraofthesimple, rank-3 EuclideanJordanalgebra J3 (A2) over A2.Titsconstruction,despitebeingnot manifestlysymmetricundertheexchange A1 ↔ A2,isthemostgeneralofthethree constructionspresentedhere,sinceitholdsforanyalternativealgebras A1 and A2,as longasitispossibletodefineaJordanalgebraover A2 itself.Asmentionedabove,Tits constructioncanbegeneralizedto J2,1(A2),thusyielding8 m1,2 (A1, A2)

2.AmoresymmetricapproachwaspursuedbyVinberg[Vin66],whoobtainedtheformula givenbythesecondlineofther.h.s.of(1),

m3 (A1, A2)= der(A1) ⊕ der(A2) + sa(3, A1 ⊗ A2) (14)

Thisformulaismanifestlysymmetricundertheexchange A1 ↔ A2,butitonlyholdsif A1 and A2 arebothcompositionalgebras;itinvolvesonlythederivationLiealgebrasof A and B,aswellasthe 3 × 3 antisymmetricmatricesover A1 ⊗ A2.Asmentionedabove,a suitabledeformationof(14)ispossible,inordertogiveriseto m1,2 (A1, A2)

3.Anothersymmetricformulaundertheexchange A1 ↔ A2 wasobtainedbyBartonand Sudbery[BS03](alsocf.[Ev]),anditisgivenbythethirdlineofther.h.s.of(1), m3 (A1, A2)= tri(A1) ⊕ tri(A2) +3(A1 ⊗ A2), (15)

involvingthetrialityalgebras tri (A1) and tri (A2),togetherwiththreecopiesofthetensor product A1 ⊗ A2.Again,asmentionedabove,asuitabledeformationof(15)ispossible,in ordertogiveriseto m1,2 (A1, A2)

Other,differentversionsoftheconstructionofFreudenthal-TitsMagicSquarehavebeendevelopedbySantanderandHerranz[SH,Sa],Atsuyama[Ats,Atsu2]andElduque[El04,El02,El18], allinvolvingcompositionalgebras(eventhoughElduque’sconstructioninvolves flexible compositionalgebrasinsteadof alternative compositionalgebras[El18]).

8Since J2,1 (A2 ) J1,2 (A2 ),itholdsthat m2,1 (A1 , A2 ) m1,2 (A1 , A2 )

2.5MagicSquareoforder2

InspiredbytheworksofFreudenthalandTits,BartonandSudbery[BS03]alsoconsidereda differentMagicSquare,basedon 2 × 2 matrices,anddefinedbythefollowingformula:

m2 (A1, A2):= so (A1) ⊕ der (J2 (A2)) ⊕ (A1 ⊗ J2 (A2)) , (16)

whichalsoenjoysa“Vinberg-like”equivalentversionas

m2 (A1, A2)= so (A1) ⊕ so (A2) ⊕ sa2 (A1 ⊗ A2) , (17)

thatwasmorerecentelyusedatLiegrouplevelin[DHK].Formula(16)canbegeneralizedto involvesimple,rank-2 Lorentzian Jordanalgebras J1,1 (A2) (seeSec.2.3),thusobtainingthe LorentzianversionoftheMagicSquareoforder2,

m1,1 (A1, A2):= so (A1) ⊕ der (J1,1 (A2)) ⊕ A1 ⊗ J1,1 (A2) , (18)

whichwewillexplicitlyevaluateinthetreatmentbelow(forthefirsttimeinliterature,tothe bestofourknowledge).

2.6OctonionicentriesofMagicSquaresoforder2and3

Inordertorigorouslydefineallpossibleoctonionic “Rosenfeldplanes” and “Rosenfeldlines” over R (i.e.allpossiblerealformsthereof),weneedtoisolatealloctonionicandsplit-octonionic entriesofallrealformsoftheFreudenthal-TitsMagicSquare(order3)[CCM,BM,ABDHN, BS03]andoftheMagicSquareoforder2[BS03],i.e.weneedtoconsidertheentries mα (A1, A2) inwhich atleastone of A1 and A2 is O or Os,forallpossiblerealforms,namelyfor α =3 (Euclideanorder3), 1, 2 (Lorentzianorder3), 2 (Euclideanorder2)and 1, 1 (Lorentzianorder 2).

TheoctonionicentriesoftheEuclideanMagicSquaresoforder3 m3 (i.e.,ofallEuclidean realformsofFreudenthal-TitsMagicSquare)are

A m3 (A, O) m3 (As, O) m3 (Os, A) m3 (As, Os)

R f4( 52) f4( 52) f4(4) f4(4)

C e6( 78) e6( 26) e6(2) e6(6) H e7( 133) e7( 25) e7( 5) e7(7)

O e8( 248) e8( 24) e8( 24) e8(8)

Theentriesofthetableabovecompriseallrealformsof e8 and e7,andmostofthereal formsof e6 and f4.Themissingrealforms f4( 20) and e6( 14) canberecoveredastheoctonionic entriesoftheLorentzianMagicSquaresoforder3 m2,1 (i.e.,ofallLorentzianrealformsof Freudenthal-TitsMagicSquare),givenby

A m1,2 (A, O) m1,2 (As, O) m1,2 (Os, A) m1,2 (As, Os)

R f4( 20) f4( 20) f4(4) f4(4)

C e6( 14) e6( 26) e6(2) e6(6) H e7( 5) e7( 25) e7( 5) e7(7)

O e8(8) e8( 24) e8( 24) e8(8)

Ontheotherhand,theoctonionicentriesoftheEuclideanMagicSquaresoforder2 m2 are9

9Theexplicitformof m2 (As, Bs) is,asfarasweknow,notpresentinthecurrentliterature.Wewillpresent adetailedtreatmentelsewhere,andhereweconfineourselvestoreportitsoctonioniccolumnonly.

A m2 (A, O) m2 (As, O) m2 (Os, A) m2 (As, Os)

R so (9) so (9) so (5, 4) so (5, 4)

C so (10) so (9, 1) so (6, 4) so (5, 5)

H so (12) so (10, 2) so (8, 4) so (6, 6)

O so (16) so (12, 4) so (12, 4) so (8, 8)

Finally,theoctonionicentriesoftheLorentzianMagicSquaresoforder2 m1,1 aregivenby10

A m1,1 (A, O) m1,1 (As, O) m1,1 (Os, A) m1,1 (As, Os)

R so (8, 1) so (8, 1) so (5, 4) so (5, 4)

C so (8, 2) so (9, 1) so (6, 4) so (5, 5)

H so (8, 4) so (10, 2) so (8, 4) so (6, 6)

O so (8, 8) so (12, 4) so (12, 4) so (8, 8)

3“Magic”formulæforRosenfeldplanes

InhisstudyofthegeometryofLiegroups[Ro97],Rosenfelddefinedits“projective”planes (A ⊗ B) P 2 asthecompletionofsomeaffineplanesobtainedasnon-associativemodulesoverthe tensoralgebra A ⊗ B.HethenarguedtheformofthematricescomposingthelineartransformationsassociatedwiththeLiealgebraofthecollineationsthatpreservedthepolarity,i.e.the isometriesoftheplane.ThisapproachallowedhimtorelateallrealformsofexceptionalLie groups[Ro93,Ro98]withisometriesofsuitable“projective”hyperbolicspaces.Asmentioned above,unfortunatelytheprocedurecarriedoutbyRosenfeldwasnotrigorous,sincemanyof theoremsusedin[Ro97]donotextendtothecaseofalgebrasthatarenotalternativenorof composition,asitisinthecaseofmanyalgebraslistedinTable2.

WepresenthereageneralandrigorouswaytodefinethespacesconsideredbyRosenfeld,in termsoftheirisometryandisotropygroups,namelyusingthetheoryofcosetmanifolds.

3.1Cosetmanifolds

Sinceour“magic”formulædefineallRosenfeldplanesascosetmanifolds,itisworthbriefly reviewingthem,andtheirrelationtohomogenousspaces.An homogeneousspace isamanifold onwhichaLiegroupactstransitively,i.e.amanifoldonwhichisdefinedanaction ρg from G × M in M suchthat ρe (m)= m for e theidentityin G and m ∈ M andforwhich,given any m,n ∈ M itexistsaanotnecessarelyunique g ∈ G suchthat ρg (m)= n.Withinthis framework,the isotropygroup Isotm (G) isthesetformedbytheelementsof G thatfixthe point m ∈ M undertheactionof G,i.e.

Isotm (G)= {g ∈ G : ρg (m)= m} (19)

Since,bydefinitionofgroupaction,wehavethat ρe (m)= m and ρgh (m)= ρg (ρh (m)),then K = Isotm (G) isaclosedsubgroupof G and,moreoverthenaturalmapfromthequotientspace G/K in M givenby gK → gm isadiffeomorphism(see[Ar]andRefs.therein).

GivenaLiegroup G andaclosedsubgroup K<G,thenthecosetspace G/K = {gK : g ∈ G} isendowedwithanaturalmanifoldstructureinheritedby G andis,therefore,calleda coset manifold.Noticethattheactionof G onthecosetmanifold G/K,givenbythetranslation τg definedas

τg (m)= gm, (20)

10TheLorentzianmagicsquareofordertwoyieldtothreealgebras,i.e. so (8, 1), so (8, 2) and so (8, 4) which arenotcoveredinothermagicsquares.Theexplicitformsof m1,1 (A, B), m1,1 (As, B) and m1,1 (As, Bs) are,as farasweknow,notpresentinthecurrentliterature.Wewillpresentadetailedtreatmentelsewhere,andhere weconfineourselvestoreporttheiroctonionicrowsandcolumnsonly.

Algebra Comm. Ass. Alter. Flex. Pow.Ass.

C ⊗ C Yes Yes Yes Yes Yes

C ⊗ H No Yes Yes Yes Yes

H ⊗ H No Yes Yes Yes Yes

C ⊗ O No No Yes Yes Yes H ⊗ O No No No No No

O ⊗ O No No No No No

Table2:Propertiesofthealgebra A ⊗ B where A, B areHurwitzalgebras.Asfortheproperty analgebra A issaidtobe commutative if xy = yx forevery x,y ∈ X;itisdefinedas associative ifsatisfies x (yz)=(xy) z; alternative if x (yx)=(xy) x; flexible if x (yy)=(xy) y and,finally, power-associative if x (xx)=(xx) x

forevery g ∈ G and m ∈ G/K,is transitive,i.e.forevery m,n ∈ G/K itexistsa(notnecessarily unique) g ∈ G suchthat n = gm,andthusthecosetmanifold G/K isanhomogenousspace.On theotherhand,sincemultiplegroupscanacttransitivelyonthesamemanifoldwithdifferent isotropygroups,thenanhomogeneousspacecanberealisedinmultiplewayasacosetmanifold. Moreover,acloselooktothedefinitionsshowsthattheisotropygroupIsotm (G/K) isexactly theclosedsubgroup K 11 Ingeneral,the holonomysubgroup andtheisotropysubgrouphave thesameidentity-connectedcomponent;so,ifoneassumesthat G/K issimply-connected,they areequal(seee.g.[Be,He]andRefs.therein).

Moreover,let G beaLiegroupand K aclosedandconnectedsubgroupof G,denotingwith g and k theirrespectiveLiealgebras,thenthecosetmanifold G/K is reductive ifthereexistsa subspace m suchthat g = k ⊕ m and [k, k] ⊂ k, [k, m] ⊂ m, (21)

whileifinadditionto(21)wealsohave [m, m] ⊂ k, (22)

thenthespaceis symmetric.AllRosenfeldplanesaresymmetriccosetmanifolds.

Itisalsoworthnotingthatforanycosetmanifold G/K thestructureconstantsoftheLie algebra g oftheLiegroup G definecompletelythestructureconstantsofthemanifold,thusthe invariantmetrics,andallthemetric-dependenttensors,suchasthecurvaturetensor,theRicci tensor,etc.Indeed,let {E1,...,En} beabasisfor g insuchawaythat {E1,...,Em} areabasis for k,whichwewillalsocall {K1,...,Km} forreadibilityreasons,and {Em+1,...,En} abasis for m thatwewillalsodenoteas {Mm+1,...,Mn}.Thenconsiderthestructureconstantsofthe algebra g,i.e. [Ej ,Ek]= n i=1 C i jkEi, (23) forevery j,k ∈{1,...,n}.Conditionsforreductivityin(21)arethentranslatedin

Kj ,Mk]= n i=m+1

i jkMi for j ∈{1,...,m} ,k ∈{m +1,...,n} , (24)

11Inparticular,theoriginof G/K is,bydefinition,thepointatwhichthe K-invarianceisimmediatelymanifest.

while,ontheotherhand,from [Mj ,Mk]= m i=1 C i jkKi+ n i=m+1 C i jkMi, (25)

1 λ2 1 8 C a edC e bc 1 8λ C a beC e cd C a ecC e bd 1 2λ2

m i=1 C a biC i cd, (26)

wededucethatif C i jk =0 forall i,j,k ∈{m +1,...,n},wehavealsoasymmetricspace.From thestructureconstants C i jk,allgeometricalinvariantsofthecosetmanifoldcanbeobtained (see[FF17]foralltechnicaldetails)suchastheRiemanntensoroverthecosetmanifold G/K whichisgivenby Ra bcd = n e=m+1

andthat,incaseofsymmetricspaces,i.e.when C i jk =0 for i,j,k ∈{m +1,...,n},reduces drasticallyto Ra bcd = 1 2λ2

m i=1 C a biC i cd, (27)

forevery a,b,c,d ∈{m +1,...,n} Infact,whatisrelevantforourpurposesisthattheLiegroup G,whichactsasisometry group,anditsclosedsubgroup K,whichactsasisotropygroup,definecompletelyallthemetric propertiesandgeometricinvariantsoftheRosenfeldplanes.Ontheotherhand,insteadof workingonLiegroups G and K,i.e.withtheisometrygroupandtheisotropygrouprespectively, inthefollowingsectionswewillworkwiththeirrespectiveLiealgebras g and k,inordertorecover theappropriate G and K andthusdefinetheRosenfeldplane.

3.2“Magic”formulæ

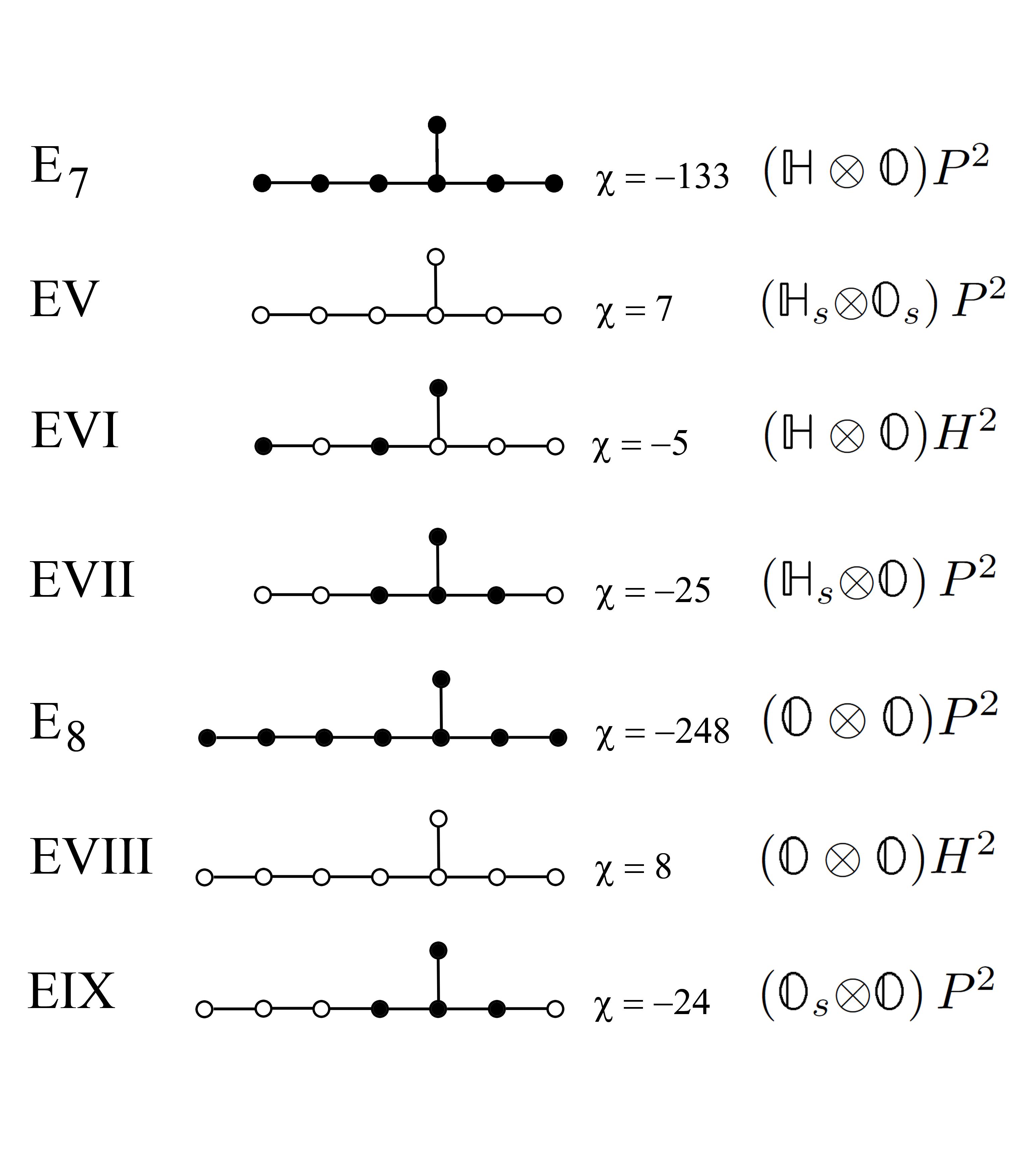
Asseenintheprevioussection,thegeometryofacosetmanifoldisfullydeterminedbythe (global)isotropyLiegroup G andbyits(local)subgroupgivenbytheisotropyLiegroup K WenowcharacterizetheRosenfeld“projective”planesbyspecifyingtherealformoftheLie groupsthatwillactasisometryandisotropygroups,whiletheLiebrackets-andthereforethe metricalpropertiesofthespace-arethosearisingfromTitsconstruction.Itishereworthnoting thattheclassificationoftherealformsofsimpleLiegroupsmakesuseofthe character χ,defined asthedifferenceofthecardinalityofnon-compactandcompactgenerators,i.e. χ :=#nc #c; consequently,Rosenfeldplaneswillhaveacorresponding χ

Let A and B betwoHurwitzalgebras,intheirdivisionorsplitversions.Moreover,letthe Liegroup A (A) besuchthatitsLiealgebraisLie(A (A)) ≡ A(A):= tri (A) so (A),cfr.Table1. Moreover,let Mα (A, B) betheLiegroupwithLiealgebragivenbythe (A, B)-entryoftheMagic Square mα (A, B),namely12 Lie(Mα (A, B))= mα (A, B).Inordertocharacterize“projective” RosenfeldplanesovertensorproductsofHurwitzalgebrasintermsofcosetmanifoldswith isometry(resp.isotropy)LiegroupswhoseLiealgebrasareentriesofrealformsoftheMagic Squareoforder3(resp.2),wenowintroducethefollowingthreedifferentclassesoflocally symmetric,(pseudo-)Riemanniancosetmanifolds,thatwenameas Rosenfeldplanes :

1.The projectiveRosenfeldplane (A ⊗ B) P 2 M3 (A, B) M2 (A, B) ⊗A (A) ⊗A (B) . (28)

12Forthepseudo-orthogonalLiealgebras,wewillgenerallyconsiderthespincoveringofthecorrespondingLie group.

2.The hyperbolicRosenfeldplane

(A ⊗ B) H 2 M1,2 (A, B) M2 (A, B) ⊗A (A) ⊗A (B) . (29)

3.The pseudo-Rosenfeldplane

(A ⊗ B) H 2 M1,2 (A, B) M1,1 (A, B) ⊗A (A) ⊗A (B) (30)

Eqs.(28),(29)and(30)arenamed “magic”formulæ,sincetheycharacterizetheRosenfeld planesashomogeneous(symmetric)manifolds,withisometry(resp.isotropy)groupswhose LiealgebrasaregivenbytheentriesofsomerealformsoftheMagicSquareoforder3(resp. 2),withfurtherisotropyfactorsgivenbytheLiegroups A associatedtothealgebras A and B definingthetensorproductassociatedtotheclassofRosenfeldplaneunderconsideration.As previouslynoticed,theterm“projective”and“hyperbolic”areheretobeintendedinavague sensesincenoneoftheoctonionicRosenfeldplaneswithdimensiongreaterthan16satisfyaxioms ofprojectiveorhyperbolicgeometry.Nevertheless,thoseadjectivesarenotarbitrarysincethe notionofsuchprojectiveplanescanbemadepreciseasin[Atsu2,AB]anditthenagreeswith theabovedefinitions.

4 Octonionic Rosenfeldplanes

Wenowconsiderthe“magic”formulæ(28)-(30)inthecases13 inwhich A and/or B is O or Os :thiswillallowustorigorouslyintroducethe octonionicRosenfeldplanes,whichallshare thefactthattheirisometrygroupisarealformofanexceptionalLiegroupofF-orE-type; however,itishereworthanticipatingthatafewrealformsofRosenfeldplaneswithexceptional isometrygroupscannotbecharacterizedinthisway.

4.1 O R ⊗ O

Thesimplestcaseconcernsthetensorproduct R ⊗ O,whichisnothingbut O :infact,this wastheoriginalobservationbyRosenfeldthatstarteditall,yieldingtotheusualoctonionic projective,split-octonionicandhyperbolicplane,i.e. OP 2 , OH 2 and OsP 2,respectively.Within theframeworkintroducedabove,thestartingpointisgivenbythe Cayley-Moufangplane over C,namelybythe octonionicprojectiveplane over C,i.e.bythelocallysymmetriccosetmanifold havingasisometrygroupthecomplexformofF4,andasisotropygroupSpin (9, C),i.e. OP 2 C FC 4 Spin (9, C)

(31)

Inthiscosetspaceformulation,thetangentspaceof OP 2 C canbeidentifiedwiththe 16CdimensionalspinorrepresentationspaceoftheisotropygroupSpin (9, C) Then,byspecifyingtheformulæ(28),(29)and(30)for A = R and B = O or Os,weobtain all realforms14 of(31)asRosenfeldplanesover R ⊗ O O orover R ⊗ Os Os;theyare summarizedbythefollowing15 Table[CMCAb]:

13Asmentionedabove,thisrestrictiondoesnotimplyanylossofgenerality,asfarastheother,non-octonionic Rosenfeldplanescanbeobtainedassuitablesub-manifoldsoftheoctonionicRosenfeldplanes.

14Byrealformsof OP 2 C ,weheremeanthecosetswithisometrygroupsgivenby all real(compactandnoncompact)formsof F4 ,andwithisotropygroupgivenbyall(compactandnon-compact)realformsofSpin(9) whicharesubgroupsofthecorrespondingrealformof F4

15Recallthat A(R)= A(O)= A(Os)= ∅

Plane Isometry Isotropy #nc #c χ

OP 2 F4( 52) Spin (9) 0 16 16

OH 2 F4( 20) Spin (9) 16 0 16

OH 2 F4( 20) Spin (8, 1) 8 8 0

OsP 2 F4(4) Spin (5, 4) 8 8 0 alongwith

OsP 2 OsH 2 OsH 2 . (32)

4.2 C ⊗ O

Inthebioctonioniccase,i.e.for C ⊗ O,thestartingpointisgivenbythe bioctonionicprojective plane over C,i.e.bythelocallysymmetriccosetmanifoldhavingasisometrygroupthecomplex formof E6,andasisotropygroupSpin(10, C) ⊗U1,i.e.

(C ⊗ O) P 2 C EC 6 Spin (10, C) ⊗ (U1)C , (33)

whichisaKählermanifold,andhasbeenrecentlytreatedin[CMCAa].Inthiscase,the tangentspaceofthecosetmanifold(33)isthe 16C,+ ⊕ 16C, representationoftheisotropy groupSpin (10, C) ⊗ U1

Then,byspecifyingtheformulæ(28),(29)and(30)for A = C or Cs and B = O or Os,weobtainallrealforms16 of(33)whichcanbeexpressedasRosenfeldplanesover C(or Cs)⊗O(or Os); theyaresummarizedbythefollowing17 Table:

Plane Isometry Isotropy #nc #c χ

(C ⊗ O)P 2 E6( 78) Spin (10) ⊗ U1 0 32 32 (C ⊗ O)H 2 E6( 14) Spin (10) ⊗ U1 32 0 32 (C ⊗ O)H 2 E6( 14) Spin (8, 2) ⊗ U1 16 16 0 (C ⊗ Os) P 2 E6(2) Spin (6, 4) ⊗ U1 16 16 0 (Cs⊗O) P 2 E6( 26) Spin (9, 1) ⊗ SO (1, 1) 16 16 0 (Cs⊗Os) P 2 E6(6) Spin (5, 5) ⊗ SO (1, 1) 16 16 0 alongwith

(C ⊗ Os) P 2 (C ⊗ Os) H 2 (C ⊗ Os) H 2 , (34) (Cs⊗O) P 2 (Cs⊗O) H 2 (Cs⊗O) H 2 , (35) (Cs⊗Os) P 2 (Cs⊗Os) H 2 (Cs⊗Os) H 2 , (36)

expressingthefactthatprojective,hyperbolicandpseudoRosenfeldplanesinvolving Cs and/or Os areallisomorphic.

ThefirstfourmanifoldsoftheaboveTable,havingaU1 factorintheisotropygroup,are Kählermanifolds,whereasthelasttwo,havingaSO(1, 1) factorintheisotropygroup,are pseudo-Kählermanifolds.

16Byrealformsof (C ⊗ O) P 2 C ,weheremeanthecosetswithisometrygroupsgivenby all real(compact andnon-compact)formsof E6 ,andwithisotropygroupgivenbyall(compactandnon-compact)realformsof Spin(10, C) ⊗ (U1 )C whicharesubgroupsofthecorrespondingrealformof E6

17Recallthat A(C)= u1 ,and A(Cs)= so1,1

Finally,andmoreimportantly,therearetworealformsof(33),namelythelocallysymmetric, pseudo-RiemanniancosetKählermanifolds

X32,I := E6(2) SO∗(10) ⊗ U1 , #nc =20, #c =12 ⇒ χ =8; (37)

X32,II := E6( 14) SO∗(10) ⊗ U1 , #nc =12, #c =20 ⇒ χ = 8, (38)

whoseisotropyLiegrouphasthecorrespondingLiealgebrawhichisnotanentryofanyreal formoftheMagicSquareoforder2.

Inotherwords,sincetheLiealgebra so∗(10) doesnotoccurinanyrealformoftheMagic Squareoforder2(seeSecs.2.5and2.6),thesymmetricKählermanifolds(37)and(38)cannot becharacterizedasRosenfeldplanesover C(or Cs)⊗O(or Os).

4.3 H ⊗ O

Inthequaternoctonioniccase,i.e.for H ⊗ O,thestartingpointisgivenbythe quaternoctonionic “projective”plane over C,i.e.bythelocallysymmetriccosetmanifoldhavingasisometrygroup thecomplexformof E7,andasisotropygroupSpin(12, C) ⊗ SL (2, C),i.e.

(H ⊗ O) P 2 C EC 7 Spin (12, C) ⊗ SL (2, C) , (39) whichisaquaternionicKählermanifold,andwhosetangentspaceisgivenbythe 32( ) , 2 C representation18 oftheisotropygroupSpin (12, C) ⊗ SL (2, C)

Then,byspecifyingtheformulæ(28),(29)and(30)for A = H or Hs and B = O or Os,weobtainallrealforms19 of(39)whichcanbeexpressedasRosenfeldplanesover H(or Hs)⊗O(or Os); theyaresummarizedbythefollowing20 Table:

Plane Isometry Isotropy #nc #c χ

(H ⊗ O)P 2 E7( 133) Spin (12) ⊗ SU (2) 0 64 64 (H ⊗ O)H 2 E7( 5) Spin (12) ⊗ SU (2) 64 0 64 (H ⊗ O)H 2 E7( 5) Spin (8, 4) ⊗ SU (2) 32 32 0 (Hs⊗O) P 2 E7( 25) Spin (10, 2) ⊗ SL (2, R) 32 32 0 (Hs⊗Os) P 2 E7(7) Spin (6, 6) ⊗ SL (2, R) 32 32 0 alongwith

(H ⊗ O)H 2 (H ⊗ Os) P 2 (H ⊗ Os) H 2 (H⊗Os) H 2 , (40) (Hs⊗O) P 2 ∼ = (Hs⊗O) H 2 ∼ = (Hs⊗O) H 2 , (41) (Hs⊗Os) P 2 ∼ = (Hs⊗Os) H 2 ∼ = (Hs⊗Os) H 2 (42)

Theplanesthatdonotinvolvesplitalgebras,namelytheoneshavingaSU(2) factorinthe isotropygroup,arequaternionicKählermanifolds,whereasalltheonesinvolvingsplitalgebras, namelytheoneshavingaSL(2, R) factorintheistropygroup,arepara-quaternionicKähler manifolds.

18Forthepossibleprimingofthesemispinor 32 ofSpin(12),seee.g.[Min].

19Byrealformsof (H ⊗ O) P 2 C ,weheremeanthecosetswithisometrygroupsgivenby all real(compact andnon-compact)formsof E7 ,andwithisotropygroupgivenbyall(compactandnon-compact)realformsof Spin(12, C) ⊗ SL2 (C) whicharesubgroupsofthecorrespondingrealformof E7

20Recallthat A(H)= su2 ,and A(Hs)= sl2 (R)

Again,therearethreerealformsof(39),namelythelocallysymmetric,pseudo-Riemannian (para-)quaternioniccosetmanifolds

X64,I := E7(7)

SO∗ (12) ⊗ SU (2) , #nc =40, #c =24 ⇒ χ =16; (43)

X64,II := E7( 5) SO∗ (12) ⊗ SL (2, R) , #nc =32, #c =32 ⇒ χ =0; (44)

X64,III := E7( 25)

SO∗ (12) ⊗ SU (2) , #nc =24, #c =40 ⇒ χ = 16, (45)

whoseisotropyLiegroup-uptothefactorSU(2) orSL(2, R)-hasthecorrespondingLiealgebra whichisnotanentryofanyrealformoftheMagicSquareoforder2.

Inotherwords,sincetheLiealgebra so∗(12) doesnotoccurinanyrealformoftheMagic Squareoforder2(seeSecs.2.5and2.6),thesymmetric(para-)quaternionicKählermanifolds (43)-(45)cannotbecharacterizedasRosenfeldplanesover H(or Hs)⊗O(or Os).Itshouldhowever benoticedthattheisotropygroupof(43)-(45)admitsaninterpretationintermsofrealforms oftheMagicSquareoforder3,namely

X64,I M3 (Hs, Os) M3 (Hs, H) ⊗A(H) , (46)

X64,II M3 (H, Os) M3 (H, Hs) ⊗A(Hs) , (47)

X64,III M3 (Hs, O) M3 (Hs, H) ⊗A(H) , (48)

butstillthe rationale (ifany)ofsuchformulæismissing,anditissurelynottheoneunderlying the“magic”formulæ(28)-(30).

4.4 O ⊗ O

Intheoctooctonioniccase,i.e.for O ⊗ O,thestartingpointisgivenbythe octoooctonionic “projective”plane over C,i.e.bythelocallysymmetriccosetmanifoldhavingasisometrygroup thecomplexformofE8,andasisotropygroupSpin(16, C),i.e. (O ⊗ O) P 2 C EC 8 Spin (16, C) , (49)

whosetangentspaceisgivenbythe 128( ) C representation21 ofSpin (16, C) Then,byspecifyingtheformulæ(28),(29)and(30)for A = O or Os and B = O or Os,weobtainallrealforms22 of(49)whichcanbeexpressedasRosenfeldplanesover O(or Os)⊗O(or Os); theyaresummarizedbythefollowingTable:

Plane

Isometry

Isotropy #nc #c χ (O ⊗ O)P 2 E8( 248) Spin (16) 0 128 128 (O ⊗ O)H 2 E8(8) Spin (16) 128 0 128 (O ⊗ O)H 2 E8(8) Spin (8, 8) 64 64 0 (Os⊗O) P 2 E8( 24) Spin (12, 4) 64 64 0

21Again,forthepossibleprimingofthesemispinor 128 ofSpin(16),seee.g.[Min].

22Byrealformsof (O ⊗ O) P 2 C ,weheremeanthecosetswithisometrygroupsgivenby all real(compact andnon-compact)formsof E8 ,andwithisotropygroupgivenbyall(compactandnon-compact)realformsof Spin(16, C) whicharesubgroupsofthecorrespondingrealformof E8

alongwith

(O ⊗ O)H 2 (Os⊗Os) P 2 (Os⊗Os) H 2 (Os⊗Os) H 2 , (50)

(O ⊗ Os) P 2 (O ⊗ Os) H 2 (O⊗Os) H 2 (51)

Again,therearetworealformsof(49),namelythelocallysymmetric,pseudo-Riemannian cosetmanifolds

X128,I := E8(8) SO∗ (16) , #nc =72, #c =56 ⇒ χ =16; (52)

X128,II := E8( 24) SO∗ (16) , #nc =56, #c =72 ⇒ χ = 16, (53)

whoseisotropyLiegrouphasthecorrespondingLiealgebrawhichisnotanentryofanyreal formoftheMagicSquareoforder2.

Inotherwords,sincetheLiealgebra so∗(16) doesnotoccurinanyrealformoftheMagic Squareoforder2(seeSecs.2.5and2.6),thesymmetricmanifolds(52)-(53)cannotseemingly becharacterizedasRosenfeldplanesover O(or Os)⊗O(or Os).Itshouldhoweverbenoticedthat theisotropygroupSO∗(16) of(52)-(53)admitsaninterpretationintermsoftheMagicSquare oforder4,namely

X128,I M3 (Os, Os) M4 (H, Hs) ; (54) X128,II M3 (O, Os) M4 (H, Hs) , (55)

butstillthe rationale (ifany)ofsuchformulæismissing,anditissurelynottheoneunderlying the“magic”formulæ(28)-(30).

5“Magic”formulæforRosenfeldlines

LetSpin(A) thespincoveringLiegroupwhoseLiealgebraisLie(Spin (A))= so (A),namely theLiealgebrawhichpreservesthenormoftheHurwitzalgebra A.Inordertocharacterize “projective”RosenfeldlinesovertensorproductsofHurwitzalgebrasintermsofcosetmanifolds withisometryandisotropyLiegroupswhoseLiealgebrasrespectivelyareentriesofrealformsof theMagicSquareoforder2andnorm-preservingLiealgebrasoftheinvolvedHurwitzalgebras, wenowintroduceavariationof(28)and(29),givingrisetothefollowingtwodifferentclasses oflocallysymmetric,(pseudo-)Riemanniancosetmanifolds,thatwenameas Rosenfeldlines :

1.The“projective”Rosenfeldline

(A ⊗ B) P 1 M2 (A, B) Spin (A) ⊗ Spin (B) (56)

2.The hyperbolicRosenfeldline

(A ⊗ B) H 2 M1,1 (A, B) Spin (A) ⊗ Spin (B) (57)

Eqs.(56)and(57)arenamed “magic”formulæ,sincetheycharacterizethe Rosenfeldlines as homogeneous(symmetric)manifolds,withisometryandisotropyLiegroupsrespectivelygiven bytheentriesofsomerealformsoftheMagicSquareoforder2andbynorm-preservingLie algebrasoftheinvolvedHurwitzalgebras.

Figure2: Cartanclassification,Satakediagram,character χ ofexceptionalLiegroupsF4 and E6 andrelatedoctonionicprojectiveorhyperbolicRosenfeldplaneofwhichtheyareisometry group.

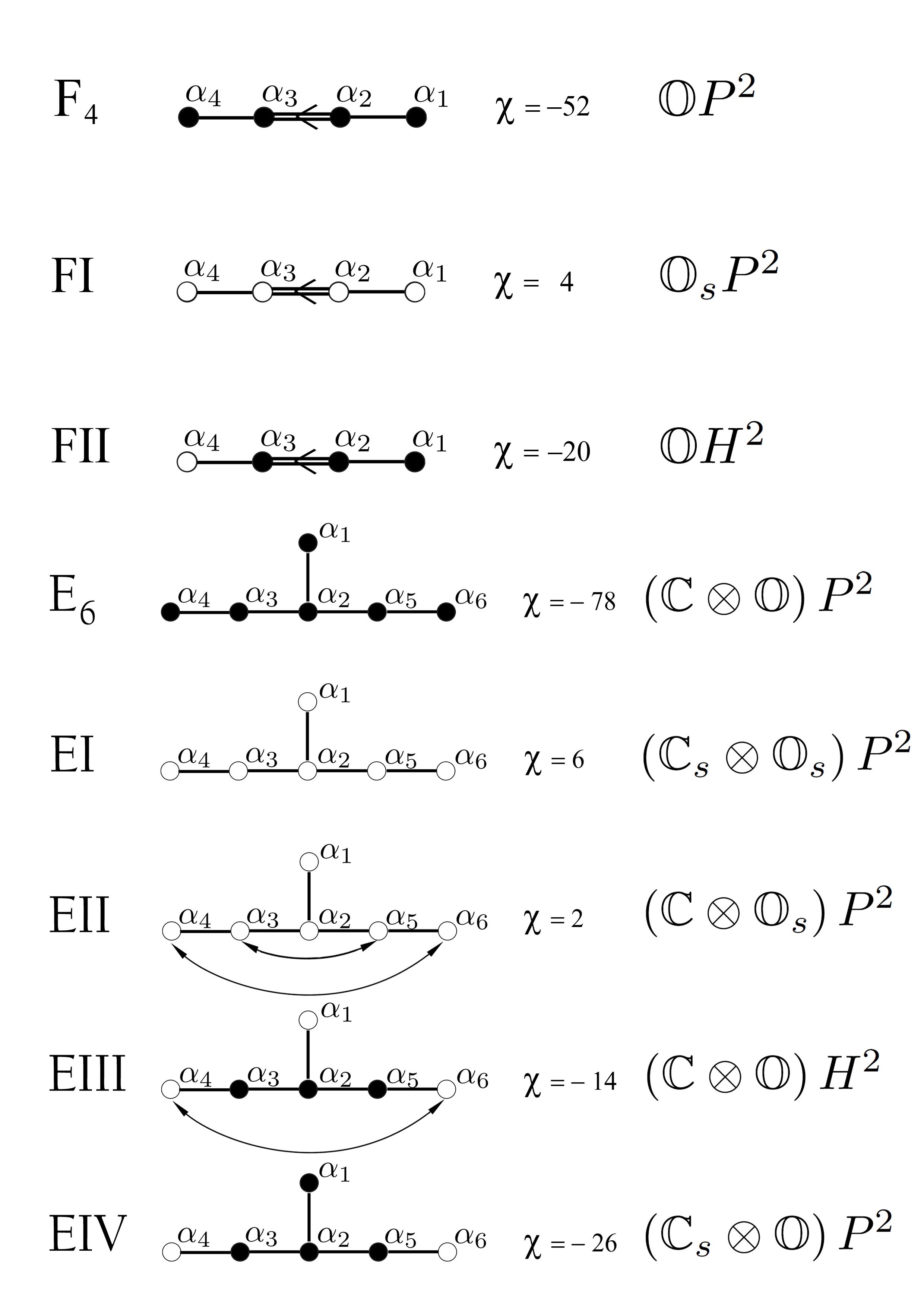
Figure3: Cartanclassification,Satakediagram,character χ ofexceptionalLiegroupsE7 and E8 andrelatedoctonionicprojectiveorhyperbolicRosenfeldplaneofwhichtheyareisometry group.

Octonionic Rosenfeldlines

Wenowconsiderthe“magic”formulæ(56)-(57)inthecases23 inwhich A and/or B is O or Os : thiswillallowustorigorouslyintroducethe octonionicRosenfeldlines;however,again,itishere worthanticipatingthatafewrealformsofoctonionicRosenfeldlinescannotbecharacterized inthisway.

6.1 O R ⊗ O

Withintheframeworkintroducedabove,thestartingpointisgivenbythe octonionicprojective line over C,whichisnothingbutthe8-sphere S8 C over C,i.e.thelocallysymmetriccoset manifoldhavingasisometrygroupSpin(9, C) andasisotropygroupSpin (9, C) :

OP 1 C Spin (9, C) Spin (8, C) . (58)

Inthiscosetspaceformulation,thetangentspaceof OP 1 C canbeidentifiedwiththe 8(v,s,c),C representationofSpin (8, C) where d4-triality[Por]allowstoequivalentlychoose v, s,or c. Then,byspecifyingtheformulæ(56)and(57)for A = R and B = O or Os,weobtainallreal forms24 of(58)whichcanbeexpressedasRosenfeldlinesover R ⊗ O O orover R ⊗ Os Os; theyaresummarizedbythefollowingTable:

Plane Isometry Isotropy #nc #c χ

OP 1 Spin (9) Spin (8) 0 8 8 OH 1 Spin (8, 1) Spin (8) 8 0 8 OsP 1 Spin (5, 4) Spin (4, 4) 4 4 0

alongwith OsH 1 OsP 1 Itshouldthenberemarkedthattheoctonionicline OP 1 canbeidentifiedwiththe8-sphere S8 ≡ S8 R over R,thehyperbolicline OH 1 withthe8-hyperboloid H 8 andthesplit-octonionicline OsP 1 withtheKleinian8-hyperboloid H 4,4 (forsomeapplicationstophysicsandtonon-compact versionsofHopfmaps,seee.g.[Ha]).

Therealformsof OP 1 C (58)havethegeneralstructures

Spin (p, 9 p) Spin (p, 8 p) structure I

or Spin (p, 9 p) Spin (p 1, 9 p) structure II

, (59) with p =0, 1,..., 9,whichgetsexchangedunder p ↔ 9 p OP 1 , OH 1 and OsP 1 OsH 1 respectivelycorrespondtostructure I with p =0, 8, 4 (or structure II with p =9, 1, 5).

Allotherrealformsof OP 1 C (58)cannotbecharacterizedasRosenfeldlinesover O (or Os).

6.2 C ⊗ O

Inthebioctonioniccase,i.e.for C ⊗ O,thestartingpointisgivenbythe bioctonionicprojective line over C,i.e.bythelocallysymmetriccosetmanifoldhavingasisometrygroupSpin (10, C) withSpin (8, C) ⊗U(1) asisotropygroup: (C ⊗ O) P 1 C Spin (10, C) Spin (8, C) ⊗ (U (1))C (60)

23Alsointhiscase,thisrestrictiondoesnotimplyanylossofgenerality,asfarastheother,non-octonionic Rosenfeldlinescanbeobtainedassuitablesub-manifoldsoftheoctonionicRosenfeldlines.

24Byrealformsof OP 1 C ,weheremeanthecosetswithisometrygroupsgivenby all real(compactandnoncompact)formsofSpin(9, C),andwithisotropygroupgivenbyall(compactandnon-compact)realformsof Spin(8, C) whicharesubgroupsofthecorrespondingrealformofSpin(9, C)

Inthiscosetspaceformulation,thetangentspaceof (C ⊗ O) P 1 C canbeidentifiedwiththe 8(v,s,c),C+ ⊕ 8(v,s,c),C representationofSpin (8, C) ⊗ (U (1))C,where,asabove, d4-triality[Por] allowstoequivalentlychoose v, s,or c.

Then,byspecifyingtheformulæ(56)and(57)for A = C or Cs and B = O or Os,weobtain allrealforms25 of(60)whichcanbeexpressedasRosenfeldlinesover C(or Cs)⊗O(or Os);they aresummarizedbythefollowingTable:

Plane Isometry Isotropy #nc #c χ

(C ⊗ O) P 1 Spin (10) Spin (8) ⊗ U (1) 0 16 16 (C ⊗ O) H 1 Spin (8, 2) Spin (8) ⊗ U (1) 16 0 16 (C ⊗ Os) P 1 Spin (6, 4) Spin (4, 4) ⊗ U (1) 8 8 0 (Cs ⊗ O) P 1 Spin (9, 1) Spin (8) ⊗ SO (1, 1) 8 8 0 (Cs ⊗ Os) P 1 Spin (5, 5) Spin (4, 4) ⊗ SO (1, 1) 8 8 0 alongwith

(C ⊗ Os) P 1 (C ⊗ Os) H 1 ; (61) (Cs⊗O) P 1 (Cs⊗O) H 1 ; (62) (Cs⊗Os) P 1 (Cs⊗Os) H 1 (63)

Therealformsof (C ⊗ O) P 1 C (60)havethegeneralstructures

Spin (p, 10 p; C) Spin (p, 8 p; C) ⊗ U1 structure I

or Spin (p, 10 p; C) Spin (p 2, 10 p; C) ⊗ U1 structure II

Spin (p, 10 p; C) Spin (p 1, 9 p; C) ⊗ SO (1, 1) structure III

, (64)

, (65)

Y16 := SO∗ (10) SO∗ (8) ⊗ U (1) SO∗ (10) Spin (6, 2) ⊗ U (1) , (66)

with p =0, 1,..., 10,suchthatstructures I and II getexchanged(whilestructure III isinvariant)under p ↔ 10 p. Theplanes (C ⊗ O) P 1 , (C ⊗ O) H 1 , (C ⊗ Os) P 1 respectivelycorrespondtostructure I with p =0, 8, 6 (orstructure II with p =10, 2, 4),whereas (Cs⊗O) P 1 and (Cs⊗Os) P 1 respectively correspondtostructure III with p =9 (or p =1)and p =5.Allotherrealformsof (C ⊗ O) P 1 C (60),andinparticular(66),cannotbecharacterizedasRosenfeldlinesover C(or Cs)⊗O(or Os).

6.3 H ⊗ O

Inthequateroctonioniccase,i.e.for H ⊗ O,thestartingpointisgivenbythe quateroctonionic projectiveline over C,i.e.bythelocallysymmetriccosetmanifoldhavingasisometrygroup Spin (12, C) withSpin (8, C) ⊗Spin(4, C) asisotropygroup: (H ⊗ O) P 1 C Spin (12, C) Spin (8, C) ⊗ Spin (4, C) . (67)

25Byrealformsof (C ⊗ O) P 1 C ,weheremeanthecosetswithisometrygroupsgivenby all real(compactand non-compact)formsofSpin(10, C),andwithisotropygroupgivenbyall(compactandnon-compact)realforms ofSpin(8, C) ⊗ (U (1))C whicharesubgroupsofthecorrespondingrealformofSpin(10, C)

Inthiscosetspaceformulation,thetangentspaceof (H ⊗ O) P 1 C canbeidentifiedwiththe 8(v,s,c), 2, 2 representationofSpin(8, C) ⊗Spin(4, C),whereweusedSpin(4, C) SL(2, C) ⊗SL(2, C) and,asabove, d4-triality[Por]allowstoequivalentlychoose v, s,or c. Then,byspecifyingtheformulæ(56)and(57)for A = H or Hs and B = O or Os,weobtain allrealforms26 of(67)whichcanbeexpressedasRosenfeldlinesover H(or Hs)⊗O(or Os);they aresummarizedbythefollowingTable:

Plane Isometry Isotropy #nc #c χ

(H ⊗ O) P 1 Spin (12) Spin (8) ⊗ SU (2) ⊗ SU (2) 0 32 32 (H ⊗ O) H 1 Spin (8, 4) Spin (8) ⊗ SU (2) ⊗ SU (2) 32 0 32 (H ⊗ Os) P 1 Spin (8, 4) Spin (4, 4) ⊗ SU (2) ⊗ SU (2) 16 16 0 (Hs ⊗ O) P 1 Spin (10, 2) Spin (8) ⊗ SL (2, R) ⊗ SL (2, R) 16 16 0 (Hs ⊗ Os) P 1 Spin (6, 6) Spin (4, 4) ⊗ SL (2, R) ⊗ SL (2, R) 16 16 0 alongwith

(H ⊗ Os) P 1 (H ⊗ Os) H 1 ; (68) (Hs⊗O) P 1 (Hs⊗O) H 1 ; (69) (Hs⊗Os) P 1 (Hs⊗Os) H 1 (70) Therealformsof (H ⊗ O) P 1 C (67)havethegeneralstructures

Spin (p, 12 p; C) Spin (p, 8 p; C) ⊗ SU (2)⊗2 structure I

or Spin (p, 12 p; C) Spin (p 4, 12 p; C) ⊗ SU (2)⊗2 1 structure II

Spin (p, 12 p; C) Spin (p 1, 9 p; C) ⊗ SL(2, C)R structure III

Spin (p, 12 p; C) Spin (p 2, 10 p; C) ⊗ SL(2, R)⊗2 structure V

, (71)

or Spin (p, 12 p; C) Spin (p 3, 11 p; C) ⊗ SL(2, C)R structure IV

, (72)

, (73)

Y32 := SO∗ (12) SO∗ (8) ⊗ SO∗ (4) SO∗ (12) Spin (6, 2) ⊗ SU (2) ⊗ SL (2, R) , (74) with p =0, 1,..., 12,suchthatstructures I and II (andstructures III and IV )getexchanged (whilestructure V isinvariant)under p ↔ 12 p (H ⊗ O) P 1 , (H ⊗ O) H 1 and (H ⊗ Os) P 1 respectivelycorrespondtostructure I with p =0, 8, 4 (orstructure II with p =12, 4, 8),whereas (Hs⊗O) P 1 and (Hs⊗Os) P 1 respectively correspondtostructure V with p =2 (or p =10)and p =6. Allotherrealformsof (H ⊗ O) P 1 C (67),andinparticular(74),cannotbecharacterizedas Rosenfeldlinesover H(or Hs)⊗O(or Os).

6.4 O ⊗ O

Intheoctooctonioniccase,i.e.for O ⊗ O,thestartingpointisgivenbythe octooctonionic projectiveline over C,i.e.bythelocallysymmetriccosetmanifoldhavingasisometrygroup Spin (16, C) withSpin (8, C) ⊗Spin(8, C) asisotropygroup: (O ⊗ O) P 1 C Spin (12, C) Spin (8, C) ⊗ Spin (8, C)

(75)

26Byrealformsof (H ⊗ O) P 1 C ,weheremeanthecosetswithisometrygroupsgivenby all real(compactand non-compact)formsofSpin(12, C),andwithisotropygroupgivenbyall(compactandnon-compact)realforms ofSpin(8, C) ⊗Spin(4, C) whicharesubgroupsofthecorrespondingrealformofSpin(12, C)

Inthiscosetspaceformulation,thetangentspaceof (O ⊗ O) P 1 C canbeidentifiedwiththe 8(v,s,c), 8(v,s,c) representationofSpin(8, C) ⊗Spin(8, C),where,asabove, d4-triality[Por]allowstoequivalentlychoose v, s,or c (inallpossiblepairsforthetwoSpin(8, C) factorsofthe isotropygroup).

Then,byspecifyingtheformulæ(56)and(57)for A = O or Os and B = O or Os,weobtain allrealforms27 of(75)whichcanbeexpressedasRosenfeldlinesover O(or Os)⊗O(or Os);they aresummarizedbythefollowingTable:

Plane Isometry Isotropy #nc #c χ

(O ⊗ O) P 1 Spin (16) Spin (8) ⊗ Spin (8) 0 64 64 (O ⊗ O) H 1 Spin (8, 8) Spin (8) ⊗ Spin (8) 64 0 64 (O ⊗ Os) P 1 Spin (12, 4) Spin (8) ⊗ Spin (4, 4) 32 32 0 (Os ⊗ Os) P 1 Spin (8, 8) Spin (4, 4) ⊗ Spin (4, 4) 32 32 0 alongwith

(O ⊗ Os) P 1 (O ⊗ Os) H 1 , (76) (Os⊗Os) P 1 (Os⊗Os) H 1 (77)

Therealformsof (O ⊗ O) P 1 C (75)havethegeneralstructures

Spin (p, 16 p; C) Spin (p, 8 p; C) ⊗ Spin (8, C) structure I

or Spin (p, 16 p; C) Spin (p 8, 16 p; C) ⊗ Spin (8, C) structure II

Spin (p, 16 p; C) Spin (p 1, 9 p; C) ⊗ Spin (1, 7; C) structure III

Spin (p, 16 p; C) Spin (p 2, 10 p; C) ⊗ Spin (2, 6; C) structure V

Spin (p, 16 p; C) Spin (p 3, 11 p; C) ⊗ Spin (3, 5; C) structure VII

Spin (p, 16 p; C) Spin (p 4, 12 p; C) ⊗ Spin (4, 4; C) structure IX

or

, (78)

Spin (p, 16 p; C) Spin (p 7, 15 p; C) ⊗ Spin (1, 7; C) structure IV

, (79)

or Spin (p, 16 p; C) Spin (p 6, 14 p; C) ⊗ Spin (2, 6; C) structure VI

or Spin (p, 16 p; C) Spin (p 5, 13 p; C) ⊗ Spin (3, 5; C) structure VIII

, (80)

, (81)

, (82) Y64 := SO∗ (16) SO∗ (8) ⊗ SO∗ (8) SO∗ (16) Spin (6, 2) ⊗ Spin (6, 2) , (83) with p =0, 1,..., 16,suchthatstructures I and II, III and IV , V and VI, VII and VIII get exchanged(whilestructure IX isinvariant)under p ↔ 16 p Theplanes (O ⊗ O) P 1 , (O ⊗ O) H 1 and (O ⊗ Os) P 1 respectivelycorrespondtostructure I with p =0, 8, 4 (orstructure II with p =16, 8, 12),whereas (Os⊗Os) P 1 correspondsto structure IX with p =8.Allotherrealformsof (O ⊗ O) P 1 C (75),andinparticular(83),cannot becharacterizedasRosenfeldlinesover O(or Os)⊗O(or Os).

27Byrealformsof (O ⊗ O) P 1 C ,weheremeanthecosetswithisometrygroupsgivenby all real(compactand non-compact)formsofSpin(16, C),andwithisotropygroupgivenbyall(compactandnon-compact)realforms ofSpin(8, C) ⊗Spin(8, C) whicharesubgroupsofthecorrespondingrealformofSpin(16, C)

Inthiswork,inordertoprovidearigorouscharacterizationofRosenfeld“projective”spacesover (rank-2)tensorproductsof(divisionorsplit)Hurwitzalgebras,wehaveintroducedsome“magic” formulæ(28)-(30)(forplanes)and(56)-(57)(forlines),whichallowedustocharacterizemany Rosenfeldspacesassymmetric(pseudo-)Riemanniancosets,whoseisometryandisotropygroups haveLiealgebraswhichareentriesofrealformsoftheorder-3(Freudenthal-Tits[Ti,Fr65]) MagicSquare,oroftheorder-2(Barton-Sudbery[BS03])MagicSquare.

For“projective”planes,theapplicationofthe“magic”formulæ(28)-(30)tothecasein whichatleastoneofthetwoHurwitzalgebrasintheassociatedtensorproductisgivenbythe octonions O orbythesplitoctonions Os,allowsustoretrieveall(compactandnon-compact) realformsofthecorresponding octonionic Rosenfeldplanes, except foralimitednumbersof pseudo-Riemanniansymmetriccosets,named X32,I , X32,II , X64,I , X64,II ,X64,III , X128,I and X128,II ,andrespectivelygivenby(37),(38),(43),(44),(45),(52)and(53).Allsuchcosets shareacommonproperty:uptosomepossiblerank-1Liegroupfactor,theirisotropygroup isgivenbythenon-compactLiegroupSO∗ (N ) for N =10, 12, 16.Thefactthatsuchspaces arenotencompassedbyour“magic”formulæ(28)-(30)isultimatelyduetothefactthatthe correspondingLiealgebra so∗(N ) doesnotoccurinanyrealformoftheMagicSquareoforder 2(exceptforthecase N =8,forwhichitholdsthespecialisomorphism so∗(8) so(6, 2)).

For“projective”lines,theapplicationofthe“magic”formulæ(56)-(57)tothecaseinwhichat leastoneofthetwoHurwitzalgebrasintheassociatedtensorproductisgivenbytheoctonions O orbythesplitoctonions Os,allowsustoretrievesome(compactandnon-compact)real formsofthecorresponding octonionic Rosenfeldlines, butstillanumberofotherrealformsof Rosenfeldlinesisleftout.Again,therearespaces,suchas Y16,Y32 and Y64 (respectivelygiven by(66),(74)and(83))thathavetheirisometryandisotropygroupscontainingfactorsSO∗(M ) for M =4, 8, 10, 12, 16;buttherearealsootherpseudo-Riemannianspacesleftout,givenby (59),(64)-(65),(71)-(73)and(78)-(82).

Thefactthatsomepseudo-Riemanniansymmetricspacesarenotcoveredbytheclassification yieldedbythe“magic”formulæ(28)-(30)and(56)-(57),whicharerelatedtotheentriesofthe MagicSquaresoforder2and3,meansthat notall realformsofRosenfeldspacescanberealized as“projective”linesorplanesover(rank2)tensorproductsof(divisionorsplit)Hurwitzalgebras. IfonestillbelievethatRosenfeld’sapproachwasrightafterall,onemightwanttoextendour “magic”formulætoinvolvenotonly unital,alternative compositionalgebras,i.e.(divisionor split)Hurwitzalgebras,butalsootheralgebraswhicharenotunitaloralternative.Extensive workonMagicSquaresoverflexiblecompositionalgebrashasbeendonebyElduque(seee.g. [El04,El02]),whereasageometricalframeworkforthesealgebrashasbeenrecentlydiscussed in[CZ22]and[CMZ22].

Therefore,afterall,Rosenfeldmightstillberight....wehopetoreportonthisinforthcoming investigations.

Acknowledgments

TheworkofD.CorradettiissupportedbyagrantoftheQuantumGravityResearchInstitute. TheworkofAMissupportedbya“MariaZambrano”distinguishedresearcherfellowshipat theUniversityofMurcia,ES,financedbytheEuropeanUnionwithintheNextGenerationEU program.

References

[Ar]ArvanitoyeorgosA., AnIntroductiontoLieGroupsandtheGeometryofHomogeneousSpaces,AmericamMathematicalSociety,2003.

[AB]AtiyahM.,BerndtJ., Projectiveplanes,Severivarietiesandspheres,Surveysin DifferentialGeometryVolume 8 (2003),1-27.

[Ats]AtsuyamaK., AnotherconstructionofrealsimpleLiealgebras,KodaiMath.J., Tome 6 (1983)no.1,122-133.

[Atsu2]AtsuyamaK., Projectivespacesinawidersense.II, KodaiMath.J. 20(1):41-52 (1997).

[ABDHN]AnastasiouA.,BorstenL.,DuffM.J.,HughesL.J.,NagyS., Amagicpyramidof supergravities,JHEP 04 (2014)178, arXiv:1312.6523[hep-th]

[ABHN]AnastasiouA.,BorstenL.,HughesM.J.,NagyS., GlobalsymmetriesofYangMillssquaredinvariousdimensions,JHEP 01 (2016)148, arXiv:1502.05359 [hep-th]

[ABDHN14]AnastasiouA.,BorstenL.,DuffM.J.,HughesM.J.,NagyS., SuperYang-Mills, divisionalgebrasandtriality,J.HighEn.Phys. 1408 (2014)080, arXiv:1309.0546 [hep-th].

[Ba]BaezJ.C., Theoctonions,Bull.Am.Math.Soc. 39 (2002)145-205,erratumin: Bull.Am.Math.Soc. 42 (2005)213, math/0105155[math.RA]

[BD]BentzL.,DrayT., SubalgebrasoftheSplitOctonions,Adv.Appl.CliffordAlgebras 28 (2018)2,40.

[Be]BesseA.L.: “EinsteinManifolds”,ClassicsinMathematics,Springer,BerlinHeidelberg(1987).

[BG]BarsI.,GünaydinM., ConstructionofLieAlgebrasandLieSuperalgebrasFrom TernaryAlgebras,J.Math.Phys. 20 (1979)1977.

[BM]BorstenL.,MarraniA., AKindofMagic,Class.Quant.Grav. 34 (2017)23, 235014, arXiv:1707.02072[hep-th]

[Br00]BryantR.L., Pseudo-RiemannianmetricswithparallelspinorfieldsandvanishingRiccitensor,in: “Globalanalysisandharmonicanalysis” (Marseille-Luminy, 1999),vol. 4 ofSemin.Congr.,pp.53–94.Soc.Math.France,Paris(2000).

[Br99]BryantR.L., Remarksonspinorsinlowdimension,unpublishednotes,1999.

[BS00]BartonC.H.,SudberyA., MagicSquaresofLieAlgebras, math/0001083 [math.RA].

[BS03]BartonC.H.,SudberyA., MagicsquaresandmatrixmodelsofLiealgebras,Adv. Math. 180 (2)(2003)596-647, math/0203010[math.RA]

[CCM]CacciatoriS.L.,CerchiaiB.L.,MarraniA., SquaringtheMagic,Adv.Theor. Math.Phys. 19 (2015)923-954, arXiv:1208.6153[math-ph]

[Car]CartanE., Latheoriedesgroupescontinusetlageometrie,extendedtranslationof apaperbyG.FanoforEncycl.Sci.Math.,Œuvrescompletes III,(1915),17271861.

[Ca19]CastroPerelmanC., RCHO-valuedgravityasagrandunifiedfieldtheory,Adv. Appl.CliffordAlgebras 29 (2019)no.1,22.

[Ca19b]CastroPerelmanC., On CHO-valuedgravity,sedenions,hermitianmatrixgeometry andnonsymmetricKaluza-Kleintheory,Adv.Appl.CliffordAlgebras 29 (2019) no.3,58.

[CFG]CecottiS.,FerraraS.,GirardelloL., GeometryofTypeIISuperstringsandthe ModuliofSuperconformalFieldTheories,Int.J.Mod.Phys. A4 (1989)2475.

[Con37]ConwayA., Quaterniontreatmentofrelativisticwaveequation,Proc.R.Soc.Lond. Ser.A,Math.Phys.Sci.,162(909)(1937).

[CMCAb]CorradettiD.,MarraniA.,ChesterD.,AschheimR., OctonionicPlanesand RealFormsof G2, F4 and E6,Proc.Geom.Int.Quant. 23 (2022)39-57, arXiv:2203.02671[math.RA]

[CMCAa]CorradettiD.,MarraniA.,ChesterD.,AschheimR., ConjugationMatters.BioctonionicVeroneseVectorsandCayley-RosenfeldPlanes,Int.J.Geom.Meth.Mod. Phys. 19 (2022)09,2250142, arXiv:2202.02050[math-ph].

[CZ22]CorradettiD.,ZucconiF., AGeometricalInterpretationofOkuboSpinGroup,J. Geom.Phys. 182 (2022)104641, arXiv:2202.10356[math.RA].

[CMZ22]CorradettiD.,MarraniA.,ZucconiF., DeformationoftheOkubicAlbertalgebraanditsrelationtotheOkubicaffineandprojectiveplanes, arXiv:2208.03967 [math.RA].

[Di]Dixon,G.M.:“Divisionalgebras:Octonions,quaternions,complexnumbersand thealgebraicdesignofphysics”,KluwerAcademicPublishers(1994).

[DHK]DrayT.,HuertaJ.,KincaidJ., TheMagicSquareofLieGroups:The2 ×2Case, Lett.Math.Phys. 104 (2014)11,1445-1468, arXiv:2009.00390[math.RA]

[DHW]DasguptaK.,HussinV.,WissanjiA., QuaternionicKählerManifolds,ConstrainedInstantonsandtheMagicSquare.I,Nucl.Phys. B793 (2008)34-82, arXiv0:708.1023[hep-th]

[El18]ElduqueA., Compositionalgebras;in:“AlgebraandApplicationsI:NonassociativeAlgebrasandCategories”,Chap.2,pp.27-57(A.Makhloufed.), Sciences-Mathematics,ISTE-Wiley,London(2021).

[El02]ElduqueA., Themagicsquareandsymmetriccompositions,RevistaMat. Iberoamericana 20 (2004),no.2,475-491.

[El04]ElduqueA., AnewlookatFreudenthal’smagicsquare,in:“NonAssociativeAlgebraandItsApplications”,(L.Sabinin,L.Sbitneva,I.P.Shestakov,eds.),Lecture NotesinPureandAppliedMathematics,vol. 246,pp.149-165,Chapmanand Hall,BocaRaton(2006).

[Ev]EvansJ.M., TrialitiesandExceptionalLieAlgebras:DeconstructingtheMagic Square, arXiv:0910.1828[hep-th].

[FF17]FréP.,FedotovA., GroupsandManifolds:LecturesforPhysicistswithExamples inMathematica, DeGruyter,Boston(2017),pp.323-350.

[Fr63]FreudenthalH., BeziehungenderE7undE8zurOktavenebene.X,XI, Indagationes Mathematicæ 25 (1963),457-471,472-487.

[Fr65]FreudenthalH., Liegroupsinthefoundationsofgeometry, AdvancesinMathematics,volume 1,(1965),145-190.

[Fu14]FureyC., Generations:threeprints,incolour, JHEP 10 (2014)046, arXiv:1405.4601[hep-th].

[Fu15]FureyC., StandardModelphysicsfromanalgebra? PhDthesis,Universityof Waterloo,2015, arXiv:1611.09182[hep-th]

[Fu18]FureyC., Threegenerations,twounbrokengaugesymmetries,andone eight-dimensionalalgebra,Phys.Lett. B785 (2018)84-89, arXiv:1910.08395 [hep-th]

[FH22]FureyN.,HughesM., OnegenerationofstandardmodelWeylrepresentationsasa singlecopyof R ⊗ C ⊗ H ⊗ O,Phys.Lett. B827 (2022)136959, arXiv:2209.13016 [hep-ph].

[Gr]GresnigtN., Sedenions,theCliffordalgebra Cl(8),andthreefermiongenerations, PoSEPS-HEP2019(2020)615.

[GG73]GünaydinM.,GürseyF., Quarkstructureandtheoctonions, J.Math.Phys. 14 (11)(1973).

[Gun76]GünaydinM., OctonionicHilbertspaces,thePoincarégroupand SU (3 ),J.Math. Phys. 17 (1976)1875.

[GSS]GünaydinM.,SamtlebenH.,SezginE., OntheMagicalSupergravitiesinSixDimensions,Nucl.Phys. B848 (2011)62-89, arXiv:1012.1818[hep-th].

[GST]GünaydinM.,SierraG.,TownsendP.K., ExceptionalSupergravityTheoriesand theMagicSquare,Phys.Lett. B133 (1983)72-76.

[Ha]HasebeK., TheSplit-AlgebrasandNon-compactHopfMaps,J.Math.Phys. 51 (2010)053524, arXiv:0905.2792[math-ph]

[He]HelgasonS.: “DifferentialGeometry,LieGroups,andSymmetricSpaces”,GraduateStudiesinMathematics 34,AMS(2001).

[Hur]HurwitzA., UberdieCompositionderquadratischenFormenvonbeliebigvielen Variabeln,Nachr.Ges.Wiss.Gottingen,309-316(1898).

[Ja]JacobsonN.:“StructureandRepresentationsofJordanAlgebras”,American MathematicalSocietyProvidence,RI(1968).

[JVW]JordanP.,vonNeumann,J.,Wigner,E, Onanalgebraicgeneralizationofthe quantummechanicalformalism,Ann.Math. 35,29–64(1934).

[Ka]I.L.Kantor, ModelsofexceptionalLiealgebras,SovietMath.Dokl,vol. 14,254258(1973).

[Kr11]KrasnovK., Spin (11 , 3 ),particlesandoctonions,J.Math.Phys. 63 (2022)3, 031701, arXiv:2104.01786[hep-th].

[KT]KugoT.,TownsendP.K., SupersymmetryandtheDivisionAlgebras,Nucl.Phys. B221 (1983)357-380.

[LM01]LandsbergJ.,ManivelL., TheProjectiveGeometryofFreudenthal’sMagicSquare, J.ofAlgebra 239 2(2001)477-512, math/9908039[math.AG]

[LM06]LandsbergJ.,ManivelL., Thesextonionsand e7 1 2 ,AdvancesinMathematics 201 (2006)no.1,143-179, math/0402157[math.RT]

[LG72]LorenteM.,GruberB., ClassificationofSemisimpleSubalgebrasofSimpleLie Algebras,J.Math.Phys. 13 10(1972)1639-1663.

[MD]ManogueC.A.,DrayT., Octonions,E6,andparticlephysics, J.Phys.Conf.Ser., 254 (2010)012005, arXiv:0911.2253[math.RA]

[Ma]MasiN., AnexceptionalG(2)extensionoftheStandardModelfromthecorrespondencewithCayley–Dicksonalgebrasautomorphismgroups,Sci.Rep. 11,22528 (2021), arXiv:2111.11849[hep-ph].

[McCr]McCrimmonK.:“ATasteofJordanAlgebras”,Springer-Verlag,NewYork(2004).

[Min]MinchenkoA.N., TheSemisimpleAlgebrasofExceptionalLieAlgebras,Trans. MoscowMath.Soc. 67 (2006)225-259.

[MNY]MkrtchyanR.,NersessianA.,YeghikyanV., HopfmapsandWigner’slittlegroups, Mod.Phys.Lett. A26 (2011)1393-1405, arXiv:1008.2589[hep-th]

[MR70]MichelL.,RadicatiL., PropertiesoftheBreakingofHadronicInternalSymmetry, Ann.ofPhys 66 (1971)758-783.

[MR73]MichelL.,RadicatiL., Thegeometryoftheoctet,Ann.Inst.HenriPoincare 18 (1973)185.

[N8]BorstenL.,DahanayakeD.,DuffM.J.,FerraraS.,MarraniA.,RubensW., ObservationsonIntegralandContinuousU-dualityOrbitsin N = 8 Supergravity,Class. Quant.Grav. 27 (2010)185003, arXiv:1002.4223[hep-th].

[OV]OnishchikA.L.,VinbergE.B.:“ LieGroupsandLieAlgebrasIII”, Springer, Berlin(1991).

[Pa]PalmkvistJ., AgeneralizationoftheKantor-Koecher-Titsconstruction,J.General. LieTheor.Appl. 2 (2008)226, arXiv:1308.3761[math.RA].

[Por]PorteousI.: “Cliffordalgebrasandtheclassicalgroups”,CambridgeStudiesin AdvancedMathematics 50,CambridgeUniversityPress(1995).

[Ro93]RosenfeldB.A., SpaceswithExceptionalFundamentalGroups,Publicationsde l’InstitutMathématique,nouvellesérietome 54 (68),97-119(1993).

[Ro97]RosenfeldB.A.:“GeometryofLieGroups”, Kluwer(1997).

[Ro98]RosenfeldB.A., GeometryofPlanesoverNonassociativeAlgebras, ActaAppl. Math. 50 (1998)103-110.

[Sa]SantanderM., AperspectiveontheMagicSquareandthe’specialunitary’realizationsofsimpleLiealgebras,Int.J.Geom.Meth.Mod.Phys. 10 08(2013)1360002, arXiv:2208.14702[math-ph]

[Si87]SierraG., AnapplicationtothetheoriesofJordanalgebrasandFreudenthaltriple systemstoparticlesandstrings,Class.Quant.Grav. 4 (1987)227.

[SH]SantanderM.,HerranzF., ‘Cayley-Klein’schemesforrealLiealgebrasandFreudhentalmagicsquares, in: “Group21.PhysicalApplicationsandMathematicalAspectsofGeometry,GroupsandAlgebras,Vol.I”,Eds:H.D.Doebner,P.Nattermann,W.Scherer,(WorldScientific,Singapore),1997,pp.151-156.

[SO]BorstenL.,DuffM.J.,FerraraS.,MarraniA.,RubensW., SmallOrbits,Phys. Rev. D85 (2012)086002, arXiv:1108.0424[hep-th].

[Sud]SudberyA., Divisionalgebras,(pseudo)orthogonalgroupsandspinors,J.Phys. A17,vol.5,939(1984).

[Te]TentK.(ed.): “Titsbuildingsandthemodeltheoryofgroups”,vol. 291 ofLondon MathematicalSocietyLectureNoteSeries,CambridgeUniversityPress(2002).

[Ti]TitsJ., Algébresalternatives,algébresdeJordanetalgébresdeLieexceptionnelles, IndagationesMathematicæ 28 (1966)223–237.

[Ti2]TitsJ.:“BuildingsofsphericaltypeandfiniteBN-pairs”,vol. 386 ofLecture NotesinMathematics,Springer,Berlin-Heidelberg(1974).

[To18]TodorovI.,Dubois-VioletteM., DeducingthesymmetryoftheStandardModel fromtheautomorphismandstructuregroupsoftheexceptionalJordanalgebra, Int.J.Mod.Phys. A33 (20)(2018)1850118, arXiv:1806.09450[hep-th]

[Vin66]VinbergE.B., AconstructionofexceptionalsimpleLiegroups,Tr.Semin.Vektorn. Tensorn.Anal. 13 (1966)no.7-9.

[Wes]WestburyB.W., Sextonionsandthemagicsquare,JournaloftheLondonMathematicalSociety 73 (2006)no.2,455–474, math/0411428[math.RA]

[WDM]WilsonR.A.,DrayT.,ManogueC.A., Anoctonionicconstructionof E8 andthe Liealgebramagicsquare, arXiv:2204.04996[math.GR].

[Yo85]YokotaI., Non-symmetryofFreudenthal’smagicsquare,J.Fac.Sci.ShinshuUniv. Vol. 20(1),13(1985).

[Yo09]YokotaI., ExceptionalLieGroups, arXiv:0902.0431[math.DG]