Algebraic Morphology of DNA–RNA Transcription and Regulation

Algebraic Morphology of DNA--RNA Transcription and Regulation

Preprint · December 2022 DOI: 10.20944/preprints202212.0256.v1

SEE PROFILE

SEE PROFILE

All content following this page was uploaded by Michel Planat on 14 December 2022. The user has requested enhancement of the downloaded file.

Michel Planat Institut FEMTO-ST (Besançon) and Quantum Gravity Research (Los Angeles USA)

CITATIONS

Marcelo M. Amaral Quantum Gravity Research 62 PUBLICATIONS 234 CITATIONS

Klee Irwin Quantum Gravity Research 81 PUBLICATIONS 389 CITATIONS

Article

AlgebraicmorphologyofDNA–RNAtranscriptionand regulation

MichelPlanat 1,*,† ,MarceloM.Amaral 2,† andKleeIrwin 2

1 InstitutFEMTO-STCNRSUMR6174,UniversitédeBourgogne-Franche-Comté,F-25044Besançon,France

2 QuantumGravityResearch,LosAngeles,CA90290,USA;marcelo@quantumgravityresearch.org(M.M.A.); klee@quantumgravityresearch.org(K.I.)

* Correspondence:michel.planat@femto-st.fr

†Theseauthorscontributedequallytothiswork.

Abstract: Transcriptionfactors(TFs)andmicroRNAs(miRNAs)areco-actorsingenome-scale 1 decodingandregulatorynetworks,oftentargetingcommongenes.Inthispaper,wedescribe 2 thealgebraicgeometryofbothTFsandmiRNAsthankstogrouptheory.InTFs,thegeneratorof 3 thegroupisaDNA-bindingdomainwhile,inmiRNAs,thegeneratoristheseedofthesequence. 4 Forsuchagenerated(infinite)group π,wecomputethe SL(2, C) charactervariety,where SL(2, C) 5 issimultaneouslya‘space-time’(aLorentzgroup)anda‘quantum’(aspin)group.Anoteworthy 6 resultofourapproachistorecognizethatoptimalregulationoccurswhen π lookslikeafreegroup 7 Fr (r = 1 to 3)inthecardinalitysequenceofitssubgroups,aresultobtainedinourpreviouspapers. 8 Anonfreegroupstructurefeaturesapotentialdisease.Asecondnoteworthyresultisaboutthe 9 structureoftheGroebnerbasis G ofthevariety.Asurfacewithsimplesingularities(likethewell 10 knownCayleycubic)within G isasignatureofapotentialdiseaseevenwhen G lookslikeafree 11 group Fr initsstructureofsubgroups.Ourmethodsapplytogroupswithageneratingsequence 12 madeoftwotofourdistinctDNA/RNAbasesin {A, T/U, G, C}.SeveralhumanTFsandmiRNAs 13 areinvestigatedindetailthankstoourapproach. 14

Keywords: Transcriptionfactors;micro-RNAs;diseases;finitelygeneratedgroup; SL(2, C) character 15 variety,algebraicsurfaces 16

Citation: Planat,M.;Amaral,M.M.; Irwin,K.Algebraicmorphologyof DNA–RNAtranscriptionand regulation. Int.J.Mol.Sci. 2022, 1,0. https://doi.org/

Received: Accepted: Published:

Publisher’sNote: MDPIstaysneutral withregardtojurisdictionalclaimsin publishedmapsandinstitutionalaffiliations.

Copyright: © 2022bytheauthors. Submittedto Int.J.Mol.Sci. for possibleopenaccesspublication underthetermsandconditions oftheCreativeCommonsAttribution(CCBY)license(https:// creativecommons.org/licenses/by/ 4.0/).

0.Introduction

17

Recently,wewroteapaperaboutacommonalgebrapossiblyrulingthebeautyand 18 structureinpoems,musicandproteins[1].Wefoundthatfreegroupsgovernthestructure 19 ofsuchdisparatetopicswherealanguageemergesfrompurerandomness.Wecoined 20 theconceptof‘syntacticalfreedom’forqualifyingthisoccurrenceofsymbolsorganized 21 accordingtoaperiodicity[2,3].Accordingtoourview,theescapeto‘syntacticalfreedom’ 22 meansalackofbeautyandthesignatureofapotentialdiseaseatthegenomescale.The 23 secondarystructuresinthesequenceofproteinsorvirusesare,mostofthetime,organized 24 accordingtotherulesoffreegroupsand,otherwisetheymaybeawitnessofapotential 25 aberranttopology.Onefavoritedecompositionofthesecondarystructureofproteinsisin 26 termof α-helices, β-sheetsandcoils[4]butthisdecompositionandtheresultingsyntaxis 27 modeldependent[1]. 28

ApartfromthecanonicaldoublehelixB-DNAwenowknowthatthereexistsa 29 diversityofnon-canonicalcoding/decodingsequencesorganizedinstructuressuchas 30 Z-DNA(oftenencounteredintranscriptionfactors),G-quadruplex(intelomeres)andother 31 typesthataresingle-stranded,two-strandedormultistranded[5].RNAisusuallyasingle- 32 strandedmoleculeinashortchainofnucleotides,asisthecaseforamessengerRNA 33 (mRNA)ora(non-coding)microRNA(miRNA). 34

Inourapproach,theinvestigatedsequencesdefineafinitelygeneratedgroup f p 35 whosestructureofsubgroupsiscloseorawayfromafreegroup Fr ofrank r,where r + 1 is 36

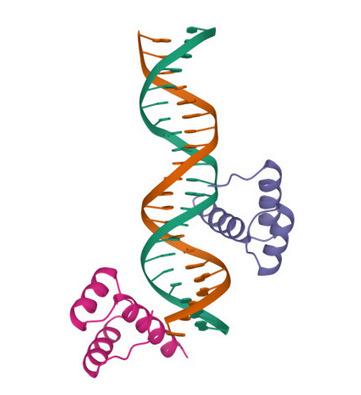
Figure1. Left:theNanogtranscriptionfactor(PDB9ANT).Right:thepre-miR-155secondary structure[10].

thenumberofdistinctaminoacidsinthesequence(orthenumberofdistinctsecondary 37 structuresconsideredintheproteinchain).Recently,wealsointroducedconceptsfor 38 representingthegroups f p overtheLiegroup SL(2, C).The SL(2, C) charactervariety 39 of f p anditsGroebnerbasisaretopologicalingredients,theyfeaturealgebraicgeometric 40 propertiesofthegroup f p underquestion[6,7].ForthedefinitionoftheGroebnerbasisof 41 anidealcontainingmultivariatepolynomialrings,thereadermayconsultReference[8]. 42 Inthispaper,wewillfocusupontranscriptionfactorsandmiRNAs,bothserveat 43 properlydecodingandregulatingthegenesandtheiraction,eitherindependentlyof 44 eachotherortogetherbytargetingcommongenes[9].Figure 1 (Left)isapictureofthe 45 pluripotenttranscriptionfactorNanog.Figure 1 (Right)isanexampleofapre-miRNA 46 associatedtoadisease[10].Bothwillbeinvestigatedindetailinthispaper. 47

InSection 1,wedescribethemathematicalmethodsandthesoftwareneededfor 48 describingthealgebraicsurfacesrelevanttoDNA/RNAsequences.Thisincludesthe 49 definitionofinfinitegroupsunderquestion,ofthefreegroups Fr ofrank r = 1 to 3 50 correspondingto 2-to 4-basesequencesandthecalculationof SL(2, C) representationof 51 suchgroups.AspecialcareisneededtocomputeaGroebnerbasisofthecharactervariety. 52

Section 2 isadiscussionaboutthetypeofsingularsurfacesencounteredinthisresearch. 53 Theyplayanimprtantroleinourviewofapotentialdisease. 54

InSection 3,themethodsareappliedtorepresentativeexamplesofsequencestaken 55 fromtranscriptionfactorsandmicroRNAswhosegroupiscloseorawayfromafreegroup, 56 andwhoseGroebnerbasisofthevarietycontainssimplesingularities.Figures 2 to 6 feature 57 themaintopologicalingredientsresultingfromthisresearch. 58

1.MaterialsandMethods

59

1.1.Finitelygeneratedgroups,freegroupsandtheirconjugacyclasses 60

Afreegroup Fr on r generators(ofrank r)consistsofalldistinctwordsthatcanbe 61 builtfrom r letterswheretwowordsaredifferentunlesstheirequalityfollowsfromthe 62 groupaxioms.Thenumberofconjugacyclassesof Fr ofagivenindex d isknownandis 63 agoodsignatureoftheisomorphism,orthecloseness,ofagroup π to Fr [3,11].Inthe 64 following,thecardinalitystructureofconjugacyclassesofindex d in Fr iscalledthecard 65 seqof Fr,andweneedthecasesfrom r = 1 to 3 tocorrespondtothenumberofdistinct 66 basesinaDNA/RNAsequence.Thecardseqof Fr isinTable 1 forthe 3 sequencesof 67 interestinthecontextofDNA/RNA. 68

Table1. Numberofconjugacyclassesofsubgroupsofindex d infreegroupofrank r = 1 to 3.The lastcolumnistheindexofthesequenceintheon-lineencyclopediaofintegersequences[12].

r cardseq sequencecode

1 [1,1,1,1,1,1,1,1,1, ] A000012

2 [1,3,7,26,97,624,4163,34470,314493, ] A057005 3 [1,7,41,604,13753,504243,24824785,1598346352, ··· ] A057006

Next,givenafinitelygeneratedgroup fp witharelation(rel)givenbythesequence 69 motif,weareinterestedinthecardinalitysequence(cardseq)ofitsconjugacyclasses. 70 Often,theDNA/RNAmotifinthesequenceunderinvestigationisclosetothatofa 71 freegroup Fr,with r + 1 beingthenumberofdistinctbasesinvolvedinthemotif.But 72 thefinitelygeneratedgroup f p = ⟨x1, x2|rel(x1, x2)⟩,or f p = ⟨x1, x2, x3|rel(x1, x2, x3)⟩,or 73 f p = ⟨x1, x2, x3, x4|rel(x1, x2, x3, x4)⟩ (wherethe xi aretakeninthefourbasesA,T/U,G,C 74 andrelisthemotif)maynotbethefreegroup F1 = ⟨x1, x2|x1 x2⟩,or F2 = ⟨x1, x2, x3|x1 x2 x3⟩, 75 or F3 = ⟨x1, x2, x3, x4|x1 x2 x3 x4⟩.Theclosenessof f p to Fr canbecheckedbyitssignaturein 76 thefiniterangeofindicesofthecardseq. 77

1.2.TheSL(2, C) charactervarietyofafinitelygeneratedgroupandaGroebnerbasis 78

Let f p beafinitelygeneratedgroup,wedescribetherepresentationsof f p inthe 79 (doublecoverofthe)Lorentzgroup SL(2, C),thegroupof (2 × 2) matriceswithcomplex 80 entriesanddeterminant 1.Thegroup SL(2, C) maybeseensimultaneouslyasa‘space-time’ 81 (aLorentzgroup)anda‘quantum’(aspin)group. 82

Suchagroupcontainsrepresentationsasdegreesoffreedomforallquantumfields 83 andisthegaugegroupforEinstein-CartantheorywhichcontainstheEinstein-Hilbert 84 actionandEinstein’sfieldequations[13].TheHolstactionusedinloopquantumgravity 85 hasquantumgravitystatesgivenintermsof SL(2, C) representations[14]. 86

Representationsof f p in SL(2, C) arehomomorphisms ρ : f p → SL(2, C) withchar- 87 acter κρ (g)= tr(ρ(g)), g ∈ f p.Thesetofcharactersallowstodefineanalgebraicsetby 88 takingthequotientofthesetofrepresentations ρ bythegroup SL(2, C),whichactsby 89 conjugationonrepresentations[15,16]. 90

Fortheeffectivecalculationsofthecharactervariety,wemakeuseofasoftwareon 91 Sage[17].WealsoneedMagma[18]forthecalculationofaGroebnerbasis,atleastfor 3- 92 and4-basesequences. 93

Following[19],inthissection,wedescribethespecialcaseofrepresentationsforthe 96

1,1)

Letustaketheexampleofthepuncturedtorus T1,1 whosefundamentalgroup,that wedenote π,isthefreegroup F2 = ⟨a, b|∅⟩ ontwogenerators a and b.Theboundary

componentof T1,1 isasinglelooparoundthepunctureexpressedbythecommutator [a, b]= abAB with A = a 1 and B = b 1.Weintroducethetraces

x = tr(ρ(a)), y = tr(ρ(b)), z = tr(ρ(ab)).

Thetraceofthecommutatoristhesurface[15,19]

tr([a, b])= κ2(x, y, z)= x2 + y2 + z2 xyz 2.

Anothernoticeablesurfaceisobtainedfromthecharactervarietyattachedtothe fundamentalgroupoftheHopflink L2a1 thatlinkstwounknottedcurves.FortheHopf link,thefundamentalgroupis

π(S3 \ L2a1)= ⟨a, b|[a, b]⟩ = Z2 , andthecorrespondingcharactervarietyistheCayleycubic[6] κ4(x, y, z)= x2 + y2 + z2 xyz 4.

Surfaces κ2 and κ4 havebeenobtainedfromtwodifferentmathematicalconcepts,from topologicalandalgebraicconceptsindimension 2,respectively.Torelatethemonemakes useoftheDehn-Nielsen-Baertheoremappliedtotheoncepuncturedtorus[20].According tothistheorem,forasurfaceofgenus g ≥ 1,wehave

Mod±(Sg ) ∼ = Out(π(Sg )),

wherethemappingclassgroup Mod(S) denotesthegroupofisotopyclassesoforientation- 99 preservingdiffeomorphismsof S (thatrestricttotheidentityontheboundary ∂S if ∂S = ∅), 100 theextendedmappingclassgroup Mod±(S) denotesthegroupofisotopyclassesofall 101 homeomorphismsof S (includingtheorientation-reversingones)and Out(π) Thisleadsto 102 the(topological)actionofMod± onthepuncturedtorusasfollows 103

Mod±(S1,1)= Out(F2)= GL(2, Z).(1)

Theautomorphismgroup Aut(F2) actsbycompositionontherepresentations ρ andinducesanactionoftheextendedmappingclassgroup Mod± onthecharactervarietyby polynomialdiffeomorphismsofthesurface κd definedby[19] f (4) H (x, y, z)= κd (x, y, z)= xyz x2 y2 z2 + d.(2)

TheCayleysurface κ4(x, y, z) possesses 4 simplesingularities.Wealreadyshowed 104 thatitplaysaroleinthecontextofZ-DNAconformationsoftranscriptionfactors[7,Tables 105 2and5].Seealsothesection 3 belowandnotablyFigures 3 (Left)and 6 (Left). 106

Thesurface κ3(x, y, z) lieswithinthecharactervarietyforthefundamentalgroupof 107 thelinkL6a1[21].WeshowbelowthatthissurfacealsoliesinthegenericGroebnerbasis 108 obtainedfor4-basesequences,seeFigure 6 (Right)below. 109

1.3.2.Three-basesequences

110

Ourmainobjectinthissectionisthefourpuncturedsphereforwhichthefundamental 111 groupisthefreegroup F3 ofrank 3 whosecharactervarietygeneralizestheFrickecubic 112 surface(2)tothehypersurface Va,b,c,d (C) in C7 113 Wefollowtheworkofreferences[15,19,22]. 114

Let S4,2 bethequadruply-puncturedsphere.Thefundamentalgroupfor S4,2 canbeex- 115 pressedintermsoftheboundarycomponents A, B, C, D as π(S4,2)= ⟨A, B, C, D|ABCD⟩ ∼ = 116 F3. 117

Arepresentation π → SL(2, C) isaquadruple

α = ρ(A), β = ρ(B) γ = ρ(C), δ = ρ(D) ∈ SL(2, C) where αβγδ = I

Letusassociatetheseventraces 118

a = tr(ρ(α)), b = tr(ρ(β)), c = tr(ρ(γ)), d = tr(ρ(δ)) x = tr(ρ(αβ)), y = tr(ρ(βγ)), z = tr(ρ(γα)),

where a, b, c, d areboundarytracesand x, y, z aretracesofelements AB, BC, CA represent- 119 ingsimpleloopson S4,2. 120 Thecharactervarietyfor S4,2 satisfiestheequation[15,Section5.2],[19,Section2.1],[22, Section3B],[23,Eq.1.9]or[24,Eq.(39)]

Va,b,c,d (x, y, z)= x2 + y2 + z2 + xyz θ1 x θ2y θ3z θ4 = 0(3) with θ1 = ab + cd, θ2 = ad + bc, θ3 = ac + bd and θ4 = 4 a2 b2 c2 d2 abcd 121 The 4-puncturedsphere,whosefundamentalgroupisthefreegroup F3 withgenerator 122 theproductofthe 4 letters,isagenerictopology.Itisstraightforwardtocheckthatthe 123 Groebnerbasisfor F3 contains(amongothersurfacesanddependingonthechoiceof 124 parameters)asinglecopyofthegenericsurfaces κ4(x, y, z), κ3(x, y, z) and V1,1,1,1(x, y, z)= 125 xyz + x2 + y2 + z2 2x 2y 2z + 1,asurfacewealsodenote f (3A1) (x, y, z) becauseit 126 contains3simplesingularitiesoftype A1 asshowninFigures 2 and 6 (Right). 127

ThereareothersurfacesencounteredinourstudyoftheGroebnerbasisfortranscrip- 128 tionfactorsandmiRNAswhenthegeneratedgroupiscloseorawayfromthefreegroup 129 F2 (for3-basesequences)orthefreegroup F3 (for 4 basesequences).Thesesurfacesare 130 describedinSection 3 131

1.3.3.Four-basesequences

132

TheredoesnotexistahugedifferenceinthestructureofaGroebnerbasisofthe 133 charactervarietyinthecaseofa 4-basesequencecomparedtothecaseofa 3-basis 134 sequence.Onedifferenceisthatonehastomanagea 14-dimensionalhypersurface 135 Va,b,c,d,e, f ,g,h (x, y, z, u, v, w) in C14 (insteadofa 7-dimensionaloneasintheprevioussub- 136 section).Ingeneral,aftertheappropriatechoiceofthe 8 parameters a, b, c, d, e, f , g, h,the 137 GroebnerbasiscontainsmorethanonecopyofthegenericGroebnerbasis,asshownin 138 Table 4.Eachcopy S ofarelevantsurfacemaybeoftheform S(x, y, z), S(x, u, v), S(y, u, w) 139 or S(z, v, w) 140

2.Discussion

141

Givenanordinaryprojectivesurface S intheprojectivespace P3 overanumberfield, 142 if S isbirationallyequivalenttoarationalsurface,thesoftwareMagma[18]determinesthe 143 maptosucharationalsurfaceandreturnsitstypewithinfivecategories.Thereturned 144 typeof S is P2 fortheprojectiveplane,aquadricsurface(foradegree 2 surfacein P3),a 145 rationalruledsurface,aconicbundleoradegree p DelPezzosurfacewhere1 ≤ p ≤ 9. 146

Afurtherclassificationmaybeobtainedfor S in P3 if S hasatmostpointsingularities. 147 Magmacomputesthetypeof S (orrather,thetypeofthenon-singularprojectivesurfaces 148 initsbirationalequivalenceclass)accordingtotheclassificationofKodairaandEnriques 149 [25].ThefirstreturnedvalueistheKodairadimensionof S,whichis ∞, 0, 1 or 2.The 150 secondreturnedvaluefurtherspecifiesthetypewithintheKodairadimension ∞ or 0 151 cases(andisirrelevantintheothertwocases). 152

Kodairadimension ∞ correspondstobirationallyruledsurfaces.Thesecondreturn 153 inthiscaseistheirregularity q ≥ 0 of S.So S isbirationallyequivalenttoaruledsurface 154 overasmoothcurveofgenus q andisarationalsurfaceifandonlyif q iszero. 155

Kodairadimension 0 correspondstosurfaceswhicharebirationallyequivalenttoa K3 156 surface,anEnriquessurface,atorusorabi-ellipticsurface. 157

EverysurfaceofKodairadimension 1 isanellipticsurface(oraquasi-ellipticsurface 158 incharacteristics 2 or 3),buttheconverseisnottrue:anellipticsurfacecanhaveKodaira 159 dimension ∞,0or1. 160

SurfacesofKodairadimension2arealgebraicsurfacesofgeneraltype. 161

Oneimportantattributeofasurfaceisitsdegreeofsingularity.Mostsurfaces S 162 ofinterestbelowarealmostnotsingularinthesensethattheyhaveatworstsimple 163 singularities.Thetypeandthenumberofsimplesingularitiesaredenotedinanexponent 164 suchas S(lA1) forlsingularitiesoftype A1.Thenotation A1 referstothetypeofaCoxeter 165 rootsystem.Noothertypesofsingularsurfacesareencounteredinourpaper.Allsuch 166 surfacearedegree 3 delPezzosurfaces.FortheCayleycubic f (4) (x, y, z),theexponent (4) 167 means (4A1).Ofcoursetherearenonsingularsurfacesinthecharactervarietyforsome 168 sequences,correspondingtotheothertypes.Butwedonotdiscusstheminthispaper. 169

ThereareadditionalfacilitiesofferedbyMagmaforstudyingasingularscheme.A 170 schemeinMagmaisanygeometricobjectdefinedbythevanishingofpolynomialsin 171 aprojectivespace.Analgebraicsurfaceisascheme.Iftheschemeissingular,onecan 172 calculateitssingularsubscheme,itsdegreeanditssupport,thatareimportantsignatures 173 ofthescheme.Mostofthetime,intheexamplesofthispaper,forasingularsurface S(lA1) , 174 thedegreeis l andthesupportcontains l simplesingularpoints.Otherwise,weadda 175 lowerindexto S(lA1) toqualifytheindexandthesupportofthesingularsubscheme.The 176 notation S(lA1) m,{} meansthatthereare l singularitiesoftype A1,thatthedegreeofthesingular 177 subschemeis m andthatthesupportistheemptyset. 178

Bytheway,transcriptionfactorsandmicroRNAsseemtohavesmoothrulesunderlyingthesingularitiesoftheirsequences.Thiscontrastswithsomesequencesencounteredin anothercontext.In[7],wefoundtwocasesoftwo-basesequenceswhosecorresponding Groebnerbasiscontainsthesurfaces

f H (x, y, z)= z4 2xyz (+z3)+ 2x2 + 2y2 3z2( 4z) 4.(4)

Aplotofoneofthemin[7,Figure3(Right)]showsthattheylooklikeageneralization 179 f H (x, y, z) oftheCayleycubic f (4) H (x, y, z).Thesesurfacesareconicbundlesinthefamilyof 180 K3 surfaces.Incontrastto f (4) H (x, y, z),accordingtoMagma,theresolutionofsuchsingular 181 surfaces f H (x, y, z) leadstomanynonisolatedsingularities(onecannotdesingularisethe 182 surfacesbyblowup). 183

Tosummarizetheimportantissuesbelow,anoticeableresultofourapproachisto 184 recognizethatoptimalregulationoccurswhenthegroupunderlyingthesequencelooks 185 likeafreegroup Fr (r = 1 to 3)inthecardinalitysequenceofitssubgroups,aresultobtained 186 inourpreviouspapers.Anonfreegroupstructurefeaturesapotentialdisease.Asecond 187 noticeableresultisaboutthestructureoftheGroebnerbasisofthevariety.Asurfacewith 188 simplesingularities(likethewellknownCayleycubic)withintheGroebnerbasisisa 189 signatureofapotentialdiseaseevenwhenthegeneratedgrouplookslikeafreegroup Fr 190 initsstructureofsubgroups.Ourmethodsapplytogroupswithageneratingsequence 191 madeoftwotofourdistinctDNA/RNAbasesin {A, T/U, G, C}.SeveralhumanTFsand 192 miRNAsareinvestigatedindetailthankstoourapproach. 193

3.Results

194

Inthissection,weapplythe SL(2, C) representationtheorytogroupsgeneratedby 195 DNA/RNAsequencesoccurringintranscriptionfactorsandmicroRNAs.Bothplaya 196 leadingroleinthedecodingofthegenomeandingenome-scaleregulatorynetworks. 197 Two-lettertranscriptionfactors(TFs)whosestructureiscloseorawayfromthefreegroup 198 F1 werealreadyinvestigatedin[7,Table2].TheoccurrenceoftheCayleycubic κ4(x, y, z) 199 intheGroebnerbasisofthecharactervarietywasfoundtobeasignatureintheformer 200 case.Inthiscasethissurfaceseemstopossessaregulatoryactionthatmaybelostinthe 201

lattercase.In[7,Table3],thepotentialdiseasesassociatedtoanon-freegroupstructureare 202 mentioned.Inthepresentsection,oneexploresinTable 2 thecaseofa 3-lettersequenceof 203 aTFandinTable 3 thecaseof 3-lettersequenceofamiRNA.Thecaseof 4-lettersequence 204 ofamiRNAissummarizedinTable 4.Theroleofsurfaceswithsimplesingularitiesinthe 205 Groebnerbasisisemphasized. 206

3.1.AlgebraicmorphologyofthetranscriptionfactorPrdm1

207

ThetranscriptionalrepressorPRdomaincontaining1(Prdm1),alsoknownasB- 208 lymphocyte-inducedmaturationprotein-1(Blimp1),isessentialfornormaldevelopment 209 andimmunity[26].Itisofazincfingertype.TheconsensussequenceACTTTCcorresponds 210 tothecodeMA0508.2in[27]. 211

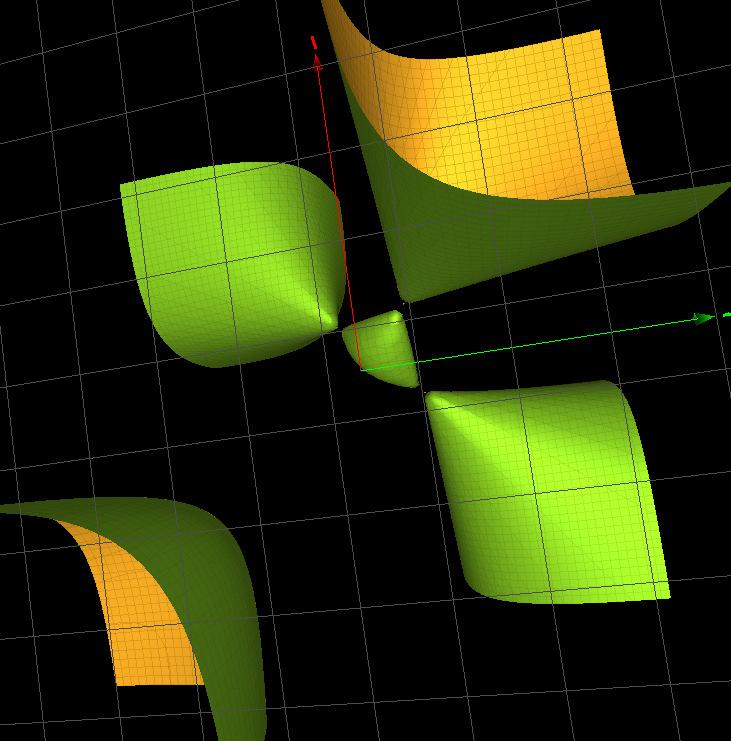
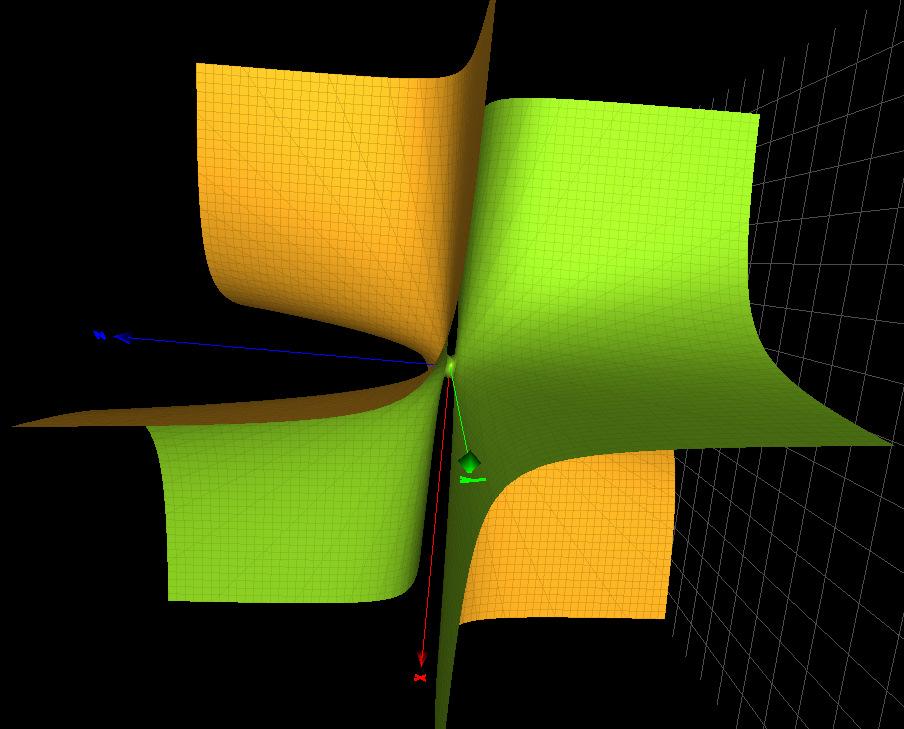
Figure2. TheFrickesurface V1,1,1,1(x, y, z)= f (3A1 ) a (x, y, z) (withthreesimplesingularitiesoftype A1).

Thecharactervariety

212

Theidealforthecharactervariety fPrdm1(a, b, c, d)(x, y, z) forafewvaluesofthe 213 parametersis 214

fPrdm1(0,0,0,0)= κ 4(x, y, z)(yz + x + 2), fPrdm1(0,1,1,0)= yκ 2(x, y, z)(x 1),

fPrdm1(0,1,0,0)= zκ 3(x, y, z)(z2 + 1)(yz + x + 1)(yz + x + 2), fPrdm1(1,1,1,1)= f (3A1) a (x, y, z)(y + 1)(y + z 1), where κ 2(x, y, z), κ 3(x, y, z) areFrickesurfaces[21]and f (3A1) a (x, y, z)= xyz + x2 + 215 y2 + z2 2x 2y 2z + 1 isthesurfacedrawninFigure 2.Thesubscript 3A1

bundleofthe K3 type S2 := z4 + 2yz3 + x2 6yz 2x 8 whosesingularsubschemeis 224 nonzerodimensionalandofdegree1. 225

ThesetwosurfacesarenonstandardinourcontextofTFsandmiRNAs. 226

3.2.AlgebraicmorphologyofhomeodomainsforNanogandXvent 227

Thepluripotencyinembryonicstemcellsandtheirregulationischaracterizedbythe 228 expressionofseveraltranscriptionfactors[28,29].Amongthem,thetranscriptionfactor 229 Nanogispresentintheembryonicstagesoflifeofseveralvertebratespecies.Nanogbinds 230 topromoterelementsofhundredsoftargetgenesasaregulatoryelement.Ithasaconserved 231 DNA-bindinghomeodomainwithconsensussequenceTAATGG.Theclosesthomolog 232 ofNanogisthe(nonmammalia)Xenopus,aXventtranscriptionfactorwithconsensus 233 sequenceCTAATT[29].Inthissubsection,weinvestigatethealgebraicmorphologyofboth 234 transcriptionfactorsNanogandXventthankstotheirconsensussequences. 235

Table2. Afew(three-base)transcriptionfactorswhosegroupstructureisawayfromafreegroup orwhoseGroebnerbasisofthe SL(2, C) charactervarietycontainsa(possiblyalmost)singular surface.ThesymbolgeneisfortheidentificationofthetranscriptionfactorintheJaspardatabase [27],motifisfortheconsensussequenceofthetranscriptionfactor,cardseqisforthecardinality sequenceofconjugacyclassesofsubgroupsofthegroupwhosemotifisthegenerator,singisforthe identificationofasingularsurfacewithintheGroebnerbasis,thelastcolumnnisforareferencepaper andthecorrespondingdisease.Thegroup F2 isthefreegroupofranktwo.Thecardseqfor π2 is [1, 3, 10, 51, 164,1230,7829,59835,491145 ],closetothecardseqofthegroup ⟨x, y, z|(x, (y, z))= z⟩. Thelatergroupisfoundasgoverningthestructureofmanytranscriptionfactorsandisassociatedto thelinkfoundin[7,Figure2].Thecardseqfor π3 is [7,14,89,264,1987,11086,93086 ].Thesurface f (A1 ) b (x, y, z)= x2 + y2 6z2 + 4xyz (notdefinedinthetext)ispartofthecharactervarietyforthe genesPitx1,OTX1,...

gene motif cardseq singref&disease Prdm1 ACTTTC F2 S1, S2(x, y, z) [27],MA0508.2 lupus,rheumatoidarthritis POU6F1 TAATGAG π2 nosing.,MA1549.1 lungadenocarcinoma ELK4 CTTCCGG . nosing,Fricke .,MA0076.2 gastriccancer OTX2 GGATTA π3 nosing .,[MA0712.2,MA0883.1] medulloblastomas N-box TTCCGG nosing,Fricke [30] drugsensitivity Pitx1,OTX1, TAATCC. f (4) H , f (A1 ) b (x, y, z) [27],[MA0682.1,MA0711.1] autism,epilepsy, Nanog TAATGG f (4) H , f (A1 ) a (x, y, z) [28] cancercells Xvent CTAATT F2 f (2A1 ) 4,{} , f (A2 ) (x, y, z) [29]

TheGroebnerbasisforXvent fNanog(0,0,0,0) takestheform 236 fNanog(0,0,0,0)= f (4) H (x, y, z) f (A1) a (x, y, z) where f (4) H (x, y, z) istheCayleycubic(withits 4 simplesingularities)and f (A1) a (x, y, z)= 237 x2 + y2 z2 + xyz (asurfacewithasinglesimplesingularityoftype A1)asshowninFigure 238 3 (Right).Theforgottenfactorsarefactorsforplanesortrivialsmoothsurfaces. 239 TheGroebnerbasisforXvent fXvent(1,1,1,1) takestheform 240 fXvent(1,1,1,1)= f (3A1) b (x, y, z) ···

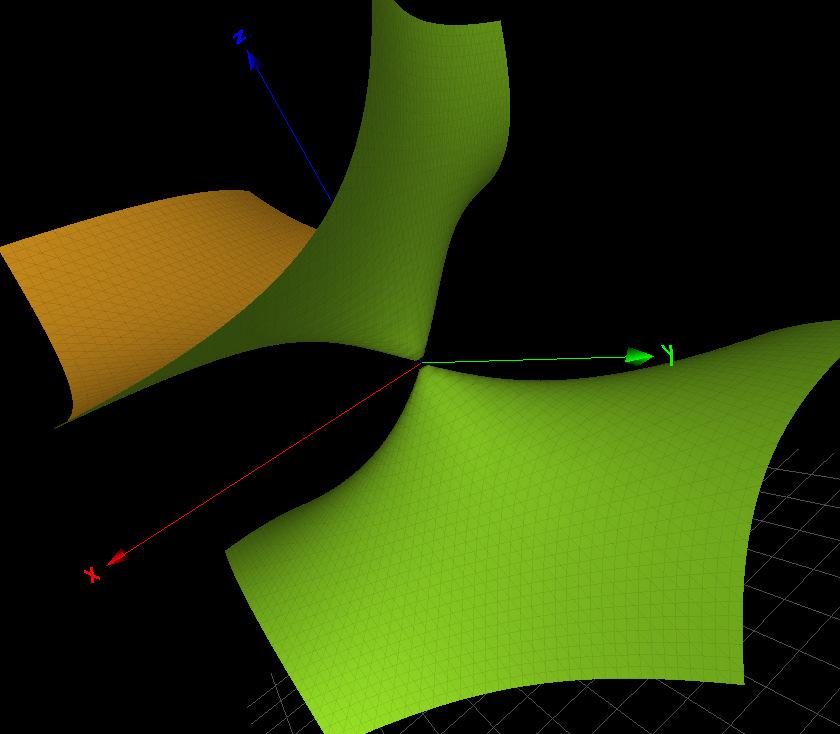
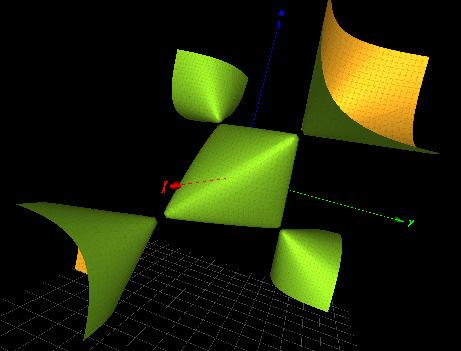
Figure3. Left:theCayleycubic κ4(x, y, z).Right:thesurface f (A1 ) a (x, y, z) where f (3A1) b (x, y, z)= x2 + y2 + xyz xy z 1 (asurfacewiththreesimplesingularity 241 oftype A1).Themissingtermdoesnotcontainsurfaceswithsingularities.Thecharacter 242 variety fXvent(0,0,0,0) containsthecubicsurface f (2A1) 4,{} (x, y, z)= 2z3 + x2z + 2xyz + 243 2y2 z2 6z (withtwosimplesingularitiesoftype A1)andotherfactorsforplanesor 244 trivialsmoothsurfaces.Bothsurfaces f (3A1) b (x, y, z) and f (2A1) 4,{} (x, y, z) arepicturedinFigure 245 4 246 Figure4. Left:thecubicsurface f (2A1 ) 4,{} (x, y, z).Right:thecubicsurface f (3A1 ) b (x, y, z) Table 2 listsafewselectedtranscriptionfactors,theircardseqandthecorresponding 247 singularsurfaces,ifanyAsannounced,intheselectedtranscriptionfactors,thereexistsa 248 correlationbetweenthelackof‘syntacticalfreedom’,orthepresenceofasingularsurface 249 inthecharactervariety,withanidentifieddisease. 250

3.3.AlgebraicmorphologyofmicroRNAs 251

MicroRNAs(miRNAs)playafundamentalroleintheexpressionandregulationof 252 genesbytargetingspecificmessengerRNAs(mRNAs)fordegradationortranslational 253 repression.ThemiRNAsareapproximately22ntlongsingle-strandedRNAmolecules. 254 ThegenesencodingmiRNAsaremuchlongerthantheprocessedmaturemiRNAmolecule. 255 ManymiRNAsareknowntoresideinintronsoftheirpre-mRNAhostgenesandsharetheir 256 regulatoryelements,primarytranscript,andhaveasimilarexpressionprofile.MicroRNAs 257 aretranscribedbyRNApolymeraseIIaslargeRNAprecursorscalledpri-miRNAs.Thepre- 258 miRNAsareaproximately70-nucleotidesinlengthandarefoldedintoimperfectstem-loop 259 structures,seeFigure 1 (Right)foranexample. 260

EachmiRNAissynthesizedasamiRNAduplexcomprisingtwostrands(-5pand-3p). 261 However,onlyoneofthetwostrandsbecomesactiveandisselectivelyincorporatedinto 262

theRNA-inducedsilencingcomplexinaprocessknownasmiRNAstrandselection[31,32]. 263 FordetailsaboutthemirRNAsequencesweusetheMirdatabase[33,34]. 264

PlantmiRNAsusuallyhavenear-perfectpairingwiththeirmRNAtargetssothat 265 generepressionproceedsthroughcleavageofthetargettranscripts.Incontrast,animal 266 miRNAsareabletorecognizetheirtargetmRNAsbyusingasfewas 6 to 8 nucleotides 267 (theseedregion)whichisnotenoughpairingforleadingtocleavageofthetargetmRNAs. 268 AgivenmiRNAmayhavehundredsofdifferentmRNAtargets,andagiventargetmight 269 beregulatedbymultiplemiRNAs. 270

DisregulationofmiRNAsmayleadtoadiseaselikecancer.AkeymicroRNAknown 271 asanoncommir(involvedinimmunityandcancer)ismir-155. 272

Specificallythe-3pstrandismir-155-3p.Figure 5 (top)illustratesthecomplementary 273 base-pairingbetweenmiR-155-3pandthehumanIRAK3(interleukin-1receptor-associated 274 kinase3)mRNA[10,Figure4]andtherelevantseedsequenceUCCUAC.Thecardseqfor 275 thissequenceisthetwo-letterfreefroup F2 andtheGroebnerbasisforthecorresponding 276 charactervarietycontainsthesurface f (A1) b (x, y, z)= x2 + y2 6z2 + 4xyz thathasasingle 277 simplesingularityasshownatthebottomofFigure 5.Ifoneretainsthefullseedsequence 278 isUCCUAC(A)thenthecardseqpassestothatofthefreegroup F2 tothegroup π2 andthe 279 singularsurfaceislost.Thisisacasewherethe‘bandwidth’oftheseediscriticalinthe 280 (dis)regulationofthemiRNA.TheseresultsaretranscribedinTable 3 281

Figure5. Up:Complementarybase-pairingbetweenmiR-155-3pandthehumanIrak3(interleukin-1 receptor-associatedkinase3)mRNA[10,Figure5].Therequisite‘seedsequence’base-pairingis denotedbythebolddashes.Down:thesurface f (A1 ) b (x, y, z)= x2 + y2 6z2 + 4xyz

Forthecaseof-5pstrandmir-155-3p,theseedsequenceUUAAUGCUAcontains 282 fourdistinctletters.ThiscaseissimilartogenericGroebnerbasesobtainedfromfour 283 letterseeds.Dependingonthechoicesofparameters a, b, c, d, e, f , g, h,theGroebnerbasis 284 containstheCayleycubic f (4) H (x, y, z),theFrickesurface κ3(x, y, z) (thatisrelatedtothe 285 linkL6a1[21,Figure2]),thesurface f (3A1) a (x, y, z) showninFigure 2 andothersurfaces.In 286 thisgenericcase,thesurfaceisfoundwith(atmost) 4 copieswhereeachcopyisattached 287 toadistinctpunctureofthe4-punctured4-sphere S4,2. 288 Intable 3,thisgenericcaseisdenoted 4 × generic (or 3 × generic formir-133-5p). 289 TheseresultsaretranscribedinTable 4. 290

AsmalllistofhumamiRNAsisinvestigatedinTables 3 and 4 correspondingto 3-letter 291 and 4-letterseeds.theprefix‘hsa’isforthehumanspecie.Likefortranscriptionfactors 292

Table3. Afewhuman(prefix‘hsa’)microRNAswhosegroupstructureisawayfromafreegroupor whoseGroebnerbasisofthe SL(2, C) charactervarietycontainsasingularsurface.Thesymbolmiris fortheidentificationintheMirdatabase[34],seedisfortheseedofthemiRNA,cardseqisforthe cardinalitysequenceofconjugacyclassesofsubgroupsofthegroupwhoseseedisthegenerator,sing istheidentificationofasingularsurfacewithintheGroebnerbasis,thelastcolumnnisforareference paperandthecorrespondingdisease[31].Thecardseqfor π1 and π′ 1 aregivenin[3,Table5].The cardseqfor π′ 2 is [1,3,7,34,139,931,5208,43867 ··· ].Forhsa-mir-124-1-3p,oneencounterstheFricke surface f (A1 ) 2,{} = xyz + x2 + y2 + z2 2y inthecharactervariety.

mirseedcardseqsingref&disease hsa-mir-193b-5pGGGGUU π1 nosing[31,34] GGGGUUU π′ 1 nosinglungcancer hsa-mir-155-3pUCCUAC F2 f (A1) b (x, y, z) [31,32,34] UCCUACA π2 nosingmultiplesclerosis hsa-mir-193a-5pGGGUCUU F2 f (A1) b (x, y, z) [31,34] breastcancer hsa-mir-223-5pGUGUAUU... hsa-mir-133-3pUUGGUC F2 f (3A1) b (x, y, z) [31,34] UUGGUCC π′ 2 nosingatrialfibrillation hsa-mir-124-3pAAGGCA F2 f (3A1) b , f (A1) 2,{} [34,35]

AAGGCAC.nosingAlzheimer’sdisease Table4. TheoppositestrandofthemicroRNAconsideredinTable 3.Theseedsequenceismade of 4 distinctbasesandthecorrespondingcardseqisthefreegroup F3 ofrank 3.TheGroebner basiscontains 4 copiesofthegenericcollectionofsurfaces κ4(x, y, z), f (3A1 ) (x, y, z), κ3(x, y, z),etc,as showninFigure 6,exceptforthe-5pstrandofmir-133wherethereareonly 3 copiesofthegeneric surfaces.

mirseedcardseqsingref&disease hsa-mir-193b-3pACUGGCC F3 4× generic[31,34] hsa-mir-155-5pUUAAUGCUA..[31,32,34] hsa-mir-193a-3pACUGGCC..[31,34] hsa-mir-223-3pGUCAGUU... hsa-mir-124-5pGUGUUCA... hsa-mir-133-5pGCUGGUA.3× generic.[34,35]

inTable 2,thelackof‘syntacticalfreedom’,ortheoccurrenceofasingularsurfaceinthe 293 charactervariety,issymptomaticofadisease. 294

4.Conclusion

295

Wefoundinthisworkthatasignatureofadiseasemaybegivenintermsofthe 296 groupstructureofaDNA/RNAsequenceandtherelatedcharactervarietyrepresenting 297 thegroup.TheDNAmotifofatranscriptionfactor,ortheseedofamicroRNA,defines 298 thegeneratorofagroup π.Assoonas π isawayfromafreegroup Fr (with r + 1 the 299 numberofdistinctbasesinthesequence)orthe SL(2, C) charactervariety G of π contains 300 singularsurfaceswithisolatedsingularities,apotentialdiseaseisonsight.Onewouldlike 301 tobemorepredictiveinidentifyingthepotentialdiseasewithpeculiargroupsorsingular 302 surfaces. 303

Firstofall,mostofthetime,thesurfacesencounteredinthecontextofTFsandmiRNAs 304 aredegree 3 delPezzo,incontrasttosurfacesobtainedfromotherDNAsequences,as 305 inEquation 4.Butthedegree 3 delPezzofamilyisveryrich.Forinstance,thesingular 306 surface f (A1) b = x2 + y2 6z2 + 4xyz (seeFigure 5)ispartofthecharactervarietyofTF 307

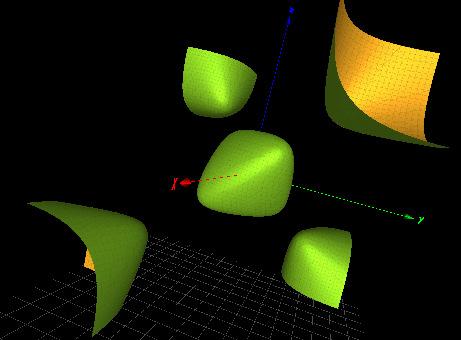
Figure6. Up:Complementarybase-pairingbetweenmiR-155-5pandthehumanSpi1(spleenfocus formingvirusproviralintegrationoncogene)[10,Figure4].Therequisite‘seedsequence’base-pairing isdenotedbythebolddashes.Down(fromlefttoright):thesurfaces f (4) H = κ4(x, y, z), f (3A1 ) (x, y, z) and κ3(x, y, z),fourcopiesofthemarecontainedwithintheGroebnerbasisforthecharactervariety.

Pitx1(seeTable 2)andofmiRNAs155-3pand193a-5p(inTable 3).Then,thesingular 308 surface f (A1) 2,{} = x2 + y2 + z2 + xyz 2y ispartofthecharactervarietyofmirRNA133-3p. 309

Bothsurfaceshaveasimplesingularpointoftype A1 butdistinctsingularsubschemes(see 310 Section 2 forthenotation). 311

Anexceptiontothedegree 3 delPezzorulewasfoundininvestigatingthecharacter 312 varietyforthePrdm1transcriptionfactorinsubsection 3.1 313

Dothesefeaturesandotheronestobedescribedlatermayhelpforthediagnosticofa 314 potentialdisease?Thereisroomformuchworkinthefuturealongtheselines. 315 AuthorContributions: “Conceptualization,M.P.;methodology,M.PandM.A.;software,M.P.;vali- 316 dation,M.A.andK.I.;formalanalysis,M.P.;investigation,M.A.;resources,K.I.;datacuration,M.P.; 317 writing—originaldraftpreparation,M.P.;writing—reviewandediting,M.P.andM.A.;visualization, 318 M.A.;supervision,M.P.;projectadministration,K.I.;fundingacquisition,K.I.Allauthorshaveread 319 andagreedtothepublishedversionofthemanuscript”. 320

330 andgenomedecoding. Curr.IssuesMol.Biol. 2022, 44,1417–1433. 331

4. Dang,Y.;Gao,J.;Wang,J.;Heffernan,R.;Hanson,J.;Paliwal,K.;Zhou,Y.Sixty-fiveyearsofthelongmarchinproteinsecondary 332 structureprediction:Thefinalstrech? Brief.Bioinform. 2018, 19,482–494. 333

5. Bansal,A.;Kaushik,S.;Kukreti,S.Non-canonicalDNAstructures:Diversityanddiseaseassociation. Front.Genet. 2022, 13,959258. 334 https://doi.org/10.3389/fgene.2022.959258. 335

VersionDecember13,2022submittedto Int.J.Mol.Sci. 13of13

6. Planat,M.;Aschheim,R.;Amaral,M.M.;FangF.;Chester,D.;IrwinK.Charactervarietiesandalgebraicsurfacesforthetopology 336 ofquantumcomputing. Symmetry 2022,14,915. 337

7. Planat,M.;Amaral,M.M.;FangF.;Chester,D.;Aschheim,R.;Irwin,K.DNAsequenceandstructureundertheprismofgroup 338 theoryandalgebraicsurfaces. Int.J.Mol.Sci. 2022, 23,13290. 339

8. Gröbnerbasis.Availableonline:https://en.wikipedia.org/wiki/Gröbner_basis(accessedon1August2022). 340

9. Martinez,N.J.;Walhout,A.J.M.TheinterplaybetweentranscriptionfactorsandmicroRNAsingenome-scaleregulatorynetworks. 341 Bioessays 2009, 31,435–445. 342

10. miR-155.Availableonline:https://en.wikipedia.org/wiki/MiR-155(accessedon18November2022). 343

11. Kwak,J.H.;Nedela,R.Graphsandtheircoverings. Lect.NotesSer. 2007, 17,118. 344 12. TheOn-LineEncyclopediaofIntegerSequences.Availableonline:https://oeis.org/book.html(accessedon1November2022). 345 13. Hehl,F.W.;vonderHeyde,P.;Kerlick,G.D.;Nester,J.M.,Generalrelativitywithspinandtorsion:Foundationsandprospects. Rev. 346 Mod.Phys. 1976, 48 (3),393-416. 347

14. Rovelli,C.,Vidotto,F.:CovariantLoopQuantumGravity.CambridgeUniversityPress1edition,(2014). 348 15. Goldman,W.M.TracecoordinatesonFrickespacesofsomesimplehyperbolicsurfaces.In HandbookofTeichmüllertheory,Eur. 349 Math.Soc.,Zürich, 2009, 13,611-684. 350

16. Ashley,C.;BurelleJ.P.;Lawton,S.Rank1charactervarietiesoffinitelypresentedgroups, Geom.Dedicata 2018, 192,1–19. 351

17. Pythoncodetocomputecharactervarieties.Availableonline:http://math.gmu.edu/slawton3/Main.sagews(accessedon1May 352 2021). 353

18. Bosma,W.;Cannon,J.J.;Fieker,C.;Steel,A.(eds). HandbookofMagmafunctions,Edition2.23;UniversityofSydney:Sydney, 354 Australia,2017;5914pp(accessedon1January2019). 355

19. Cantat,S.BersandHénon,PainlevéandSchrödinger. 2009, DukeMath.J.149,411–460. 356

20. Farb,B.;Margalit,D. Aprimeronmappingclassgroups;PrincetonUniversityPress:Princeton,NewJersey,USA,2012. 357

21. Planat,M.;Chester,D.;Amaral,M.;IrwinK.Fricketopologicalqubits. Quant.Rep. 2022, 4,523-532. 358

22. Benedetto,R.L.;GoldmanW.M.Thetopologyoftherelativecharactervarietiesofaquadruply-puncturedsphere. Experiment. 359 Math. 1999, 8,85–103. 360

23. Iwasaki,K.Anarea-preservingactionofthemodulargrouponcubicsurfacesandthePainlevéVI. Comm.Math.Phys. 2003, 242, 361 185-219. 362

24. Inaba,M.;Iwasaki,K.;Saito,M.H.DynamicsofthesixthPainlevéequation. arXiv 2005,arXiv:math.AG/0501007 363

25. EnriquesKodairaclassification,availableonline:https://en.wikipedia.org/wiki/Enriques-Kodaira_classification 364

26. Doody,G.M.;Care,M.A.;Burgoyne,N.J.;Bradford,J.R.;Bota,M.;Bonifer,C.;Westhead,D.R..Anextendedsetof 365 PRDM1/BLIMP1targetgeneslinksbindingmotiftypetodynamicrepressionooze,R.M. Nucl.AcidsRes. 2010, 38 5336–5350. 366

27. Sandelin,A.;Alkema,W;Engström,P;Wasserman,WW;Lenhard,B,JASPAR:anopen-accessdatabaseforeukaryotictranscription 367 factorbindingprofiles. NucleicAcidsResearch 2004, 32,D91–D94;softwareavailableathttps://jaspar.genereg.net/(accessedon1 368 November2022). 369

28. Jauch,R.CrystaltructureandDNAindingofthehomeodomainofthestemcelltranscriptionfactorNanog. J.Mol.Biol. 2008, 376, 370 758–770. 371 29. Schuff,M;SiegelD.;Philipp,M.Bunsschu,K.;Heymann,N.;Donow,C.;Knöchel,W.CharacterizationofDaniorerioNanogand 372 FunctionalComparisontoXenopusVents. StemcellsandDevt. 2012, 21,1225–1238. 373 30. Schaeffer,L.N.;Huchet-Dymanus,M.;ChangeuxJ.P.ImplicationofamultisubunitEts-relatedtranscriptionfactorinsynaptic 374 expressionofthenicotinicacetylcholinereceptor. EMBOJ. 1998, 17,3078–3090. 375 31. Medley,C.M.;PanzadeG.;Zinovyeva,A.Y.MicroRNAstranselection,:unwindingtherules. WIREsRNA 2021, 12,e1627. 376 32. Dawson,O.;Piccinini,A.M.miR-155-3p:processingby-productorrisingstarinimmunityandcancer? OpenBiol. 2022, 12,220070. 377 33. Kozomara,A.;Birgaonu,M.;Griffiths-Jones,S.miRBase:frommicroRNAsequencestofunction. Nucl.AcidsRes. 2019, 47, 378 D155–D162. 379 34. miRBase:themicroRNAdatabase.Availableonline:https://www.mirbase.org/(accessedon1November2022). 380 35. Kou,X.;Chen,D.;Chen,N.TheregulationofmicroRNAsinAlzheimer’sdisease. Front.Neurol. 2020, 11,288. 381