Knowsys TSI Math Sample

TSI 2.0

Math

By: Sheila Griffith, PhD, MBA

Kevin Griffith, MA, MDiv

Overview of TSI Math

1. The TSI Assessment (TSIA 2) launched in January 2021.

2. The Math College Readiness Classification (CRC) Test has ________ multiple choice questions.

• You cannot use your own calculator.

• A pop-up calculator will appear for use on ________________ questions.

• It’s best to prepare to take the entire test _____________________ a calculator.

3. The TSIA 2 Math CRC tests 4 content areas:

• Elementary Algebra and Functions = _____% (_____ out of 20 questions)

1. Linear equations, inequalities, and systems

2. Algebraic expressions and equations

3. Word problems and applications

• Intermediate Algebra and Functions = _____% (_____ out of 20 questions)

This content area tests expressions, equations, & functions dealing with

1. Quadratics and other polynomials

2. Powers, roots, and radicals

3. Rational and exponential numbers

• Geometry and Measurements = _____% (_____ out of 20 questions)

1. Plane geometry

2. Transformations and symmetry

3. Linear, area, and three-dimensional measurements

• Data Analysis, Statistics, and Probability = _____% (_____ out of 20 questions)

1. Interpreting categorical and quantitative data

2. Statistical measures (average, median, mode, and range)

3. Probabilistic reasoning (= probabilities)

1. College Readiness Cut Score: _____________________ on the Math CRC OR Math CRC Below ______________ PLUS a Math Diagnostic Test score of ________

2. Timing: The TSI is ________________________, so you can take your time & enjoy it!

3. The TSI Assessment (TSIA) is a Computer Adaptive Test (CAT).

• The CAT adapts to your performance, selecting questions based on how you answer.

• You start the test with an average score and an average-level question.

• Here’s how the test responds to your performance: Get this question . . . The next question is . . . Your score . . . Right Wrong

4. How should taking a CAT affect your test-taking strategy?

• Questions at the beginning of the test count ________________ than those at the end.

• At the beginning of the test, the computer makes ____________________ adjustments to try to hone in on your skill level.

• After every question, the computer is better able to calculate your score.

1. Your goal is to set your score as ___________________ as possible.

2. Spend all the ___________________ you need on all the questions.

3. Don’t ___________________ through the first questions.

4. Double and even triple check to make sure you are setting your score as high as possible.

5. Avoid ________________________ mistakes (they will tank your score).

• Don’t let the CAT psych you out!

1. ___________________ say, “This is an easier question. I must have missed the last one.” That sets you up to miss the current question.

2. Don’t ___________________ on past questions.

3. Focus on the ___________________ question.

4. Think of each new question as an opportunity to ______________ your score.

Lesson

2

Translating Word Problems into Math

In the prior lesson we saw that solving single-variable equations is straightforward and doable. However, most of the math we encounter in life doesn’t come to us in the format, “If 3x - 7 = 15, what is the value of x?” Most math we encounter will actually be in the form of word problems.

1. The key to word problems is correctly translating from English to math.

2. To translate correctly, we need to know the key words used in word problems and what math symbols or processes they represent.

3. Fortunately, you’re probably very familiar with these key words and their math translations.

Category Examples Math

Equals (=)

is was has costs

Addition (+)

sum of combine more than older than farther than greater than

difference less than fewer than younger than

Mark is 5 years old.

4 burgers and 2 orders of fries costs $18.00

The sum of Caleb’s and Andrew’s hourly wages is $25. Noah has 6 more DVDs than Tom has.

Rashid is 2 years older than Vaneet. Will drove 3 miles farther than Vince. The cost of the regular movie ticket is $2.50 greater than the cost of the matinee ticket.

Subtraction (-)

The difference between my new salary and my old salary is $45,000.

The first call cost two dollars less than the second call. The old prison holds three hundred fewer inmates than the new prison.

Allan is four years younger than his brother Alex.

Multiplication (x)

of by Ten percent of the students applied for the business program. Only half of the applicants were admitted to the program. Ratios (/)

for per

For every 5 students who apply, 3 get accepted. The speed limit in the school zone is 20 miles per hour.

S = 3

m = 5 Sally has 3 CDs, and Malachi has 4.

M = 4

Task: Write a linear equation to represent each situation.

1. My first test grade was 5 points less than my second test grade. What was the sum of my two test grades?

5. Thomas has read four times as many books as Samuel. How many books have the two boys read?

2. Sarah’s salary is three times that of Mary. What is the sum of their salaries?

6. Amanda has 5 more pairs of shoes than Becky does. Together, how many pairs of shoes do the two girls have?

3. Mark has three times as much money as Victor. How much money do the two boys have together?

7. The central library owns three times as many books as the downtown library.

4. Frank is three years younger than twice Susan’s age.

What is the sum of their ages?

Together, how many books do the two libraries own?

8. Carla is three inches shorter than Darlene. Together, how tall are the two girls?

Exercises: Translate and solve the word problems below. Show your work.

1. Abby had p pairs of shoes. She kept 7 pairs of shoes and divided the remaining shoes into 3 equal batches to donate to a local charity. If each charity received 5 pairs of shoes, how many pairs of shoes did Abby have originally?

4. Prior to her birthday, Adelle owned x DVDs. At her birthday party, she received an additional 6 DVDs plus cash. She then used the cash to double the number of DVDs in her collection. In terms of x, how many DVDs did Adelle own after her purchase?

2. James baked a batch of cookies. He ate 2 cookies and then divided the remaining cookies equally into 12 plastic baggies. If each baggie contained 5 cookies, how many cookies did James bake?

5. John cut a piece of string x inches long. He cut a second piece of string 20% longer than the first. The length of shorter piece of string is what percent of the length of the longer piece of string?

3. Last year company X sold s sockets. This year, the company sold 50 more than three times the number of sockets sold last year. Next year, the company expects to sell twice the number of sockets as it sold this year. In terms of s, how many sockets does company X plan to sell?

6. The width of a particular rectangle is x meters. If the length is 30% greater than the width, what is the area of the rectangle, in square meters, in terms of x?

7. If n is the least of three consecutive integers, which of the follow expressions represents the sum of the three integers?

A. 3n

B. n + 3

C. 3n + 3

D. 3n + 6

8. If n is the middle of three consecutive odd integers, which of the follow expressions represents the sum of the three integers?

A. 3n

B. n + 3

C. 3n + 3

D. 3n + 6

9. If n is the largest of three consecutive even integers, which of the follow expressions represents the average of the three integers?

A. n - 2

B. n - 1

C. n

D. n + 2

10. The long distance company charges 20 cents per minute for all long distance calls. How much will a 15 minute call cost?

11. A computer repair technician charges a flat rate of $75 plus an hourly charge of $110. How much will it cost to repair a computer if the job takes 3 hours?

12. An amusement park charges $35 for adults and $15 for children. How much will the park charge for 2 adults and 3 children?

13. A National Park charges $5.00 per car plus an extra $1.50 per passenger. How much will the Park charge if there are 5 passengers in the car?

14. A typist charges 3 cents per word plus 50 cents per image. How much would the typist charge to type a document with 500 words and four images?

15. The charge for cell phone minutes is $0.40 per minute. A text message costs $0.05 per message. If Charles makes 3 hours worth of calls and sends 30 text messages, how much will his bill be?

16. The cost of internet service is given by the function C(m) = 5.25 + .05m, where m is the number of minutes of internet service used. How much would 3 hours of internet service cost?

A. $5.40

B. $9.00

19. Mike’s Lawn Service charges a flat fee of $60 plus an additional $20 per hour, or part thereof, for yard work. Mark’s Lawn Service charges a flat fee of $40 plus $25 per hour, or part thereof. For how many hours of yard work would the charge be the same, regardless of which company you selected?

C. $11.25

D. $14.25

17. Mike’s Lawn Service charges a flat fee of $60 plus an additional $20 per hour, or part thereof, for yard work. What function represents the scenario?

A. 60 + 20h

B. (60 + 20)h

C. 60h + 20

D. 80h

18. Mike’s Lawn Service charges a flat fee of $60 plus an additional $20 per hour, or part thereof, for yard work. If Mike worked from 1 to 4:30, how much would he charge?

A. $120

B. $140

C. $160

D. $180

A. 3

B. 4

C. 5

D. 6

20. There are 2x - 5 seats in each row of bleachers. If there are a total of 50x - 125 seats in the bleachers, how many rows are in the bleachers?

A. 48x - 130

B. 48x - 130

C. 25x

D. 25

SAMPLECOPY

21. There are 4x - 7 raisins in each box of raisins. If there are 32x - 56 raisins in a multi-pack of raisins, how many boxes are in the multi-pack?

A. 28x - 63

B. 28x - 49

C. 8x

Lesson 12

Factoring Quadratic Equations

• The Standard Form for a Quadratic Equation is

• Facts about quadratic equations:

1. The highest power attached to a variable in a Quadratic Equation is

2. The equation must be in the Standard Form:

3. The graph of a Quadratic Equation will be in the shape of a

4. The parent function of a Quadratic Equation is:

Example 1: 5x2 + 3x - 18 = 0

Highest Power = Type = Parent =

Highest Power = Type = Parent =

Solutions of a Quadratic Equation

• The values of x that are ________________________ in a quadratic equation are called its ______________________ or ______________________ or ______________________.

• To find the solutions of a quadratic equation:

1. Set the equation equal to ________________________________.

2. Use the Distribution Rules to factor out the _______________ common factor (GCF).

3. Use FOIL to factor what's left:

4. Set the factors equal to __________________ and solve.

Number of distinct real solutions?

Number of distinct real solutions?

GCF: Factors: Solutions:

Example 5:

5a2 – 45 = 0

_________________________ _________________________

GCF: Factors: Solutions:

Example 7: 18a2 + 30a – 12 = 0

_________________________ __________________________

Number of distinct real solutions?

Example 6:

8a2 – 4a – 12 = 0

GCF: Factors: Solutions:

_________________________ __________________________

GCF:

Factors: Solutions:

Number of distinct real solutions?

Number of distinct real solutions? _________________________ __________________________

21x2 + 81x – 12 = 0

Example 8: SAMPLECOPY info@myknowsys.com

Number of distinct real solutions?

Exercises: Provide the information requested to solve each Quadratic Equation by factoring using Reverse FOIL.

1. x2 + 5x + 6 = 0

GCF:

Factors: Solution:

Number of distinct real solutions?

2. x2 – 9x + 20 = 0

GCF:

Factors:

Solution:

Number of distinct real solutions?

4. x2 + 9x = 0

GCF:

Factors: Solution:

3. x2 + 4x – 21 = 0

GCF:

Factors:

Solution:

Number of distinct real solutions?

Number of distinct real solutions?

5. x2 – 25 = 0

GCF:

Factors: Solution:

Number of distinct real solutions?

6. x2 + 6x – 16 = 0

GCF:

SAMPLECOPY

Factors:

Solution:

7. 2x2 + x – 3 = 0

GCF:

Factors: Solution:

10. 2x2 – 11x – 6 = 0

GCF:

Factors:

Solution:

Number of distinct real solutions?

8. 3x2 + 10x – 8 = 0

GCF:

Factors: Solution:

Number of distinct real solutions?

9. 5x2 + 34x – 7 = 0

GCF:

Factors: Solution:

Number of distinct real solutions?

Number of distinct real solutions?

11. 2x2 – 5x – 3 = 0

GCF:

Factors:

Solution:

SAMPLECOPY

Number of distinct real solutions?

12. x2 – x – 2 = 0

GCF:

Factors:

Solution:

13. Which of the following equations has both 0 and -2 as solutions?

A. 3x2 + 6x = 0

B. x2 - x - 6 = 0

C. x2 - 2x = 0

D. x2 = 4

14. Which of the following equations has both 0 and 7 2 as solutions?

A. x2 - 9x - 14 = 0

B. 2x2 - 14x = 0

C. 2x2 + 7x = 0

D. 2x2 – 7x = 0

15. For which values of x does 2x2 – 5x = 3?

A. -3 and 1 2

B. 3 and 1 2

C. -2 and 5

D. 2 and -5

17. For which values of x does x2 = -11x?

A. -11 and 11

B. 0 and -11

C. 0 and 11

D. 0, -11, and 11

18. For which values of x does 2x2 + 27 = -21x?

A. -9 and 0

B. -9 and 3 2

C. 3 2 and 3 2

D. 0 and 3 2

19. Simon throws a ball into the air from the top of a building. After t seconds, the height of the ball above the ground is f feet, where f = t2 - 3t. After how many seconds does the ball hit the ground?

A. 0 seconds

B. 2 seconds

SAMPLECOPY

C. 3 seconds

16. For which values of x does 2x2 + 15x = -25?

A. -5 and 5

B. -5 and 5 2

C. -5 and 5 2

D. 0 and 5

20. Tyron throws a ball into the air from the top of a building. After t seconds, the height of the ball above the ground is f feet, where f = -t2 - 8t + 99. After how many seconds does the ball hit the ground?

A. 4.24 seconds

B. 6.72 seconds

C. 9.80 seconds

D. 14.72 seconds

21. Miranda tosses a sphere into the air from the top of a building. After t seconds, the height of the sphere above the ground is f feet, where f = -t2 - 8t + 80. After how many seconds does the ball hit the ground?

A. 5.80 seconds

B. 7.85 seconds

C. 10.00 seconds

D. 13.80 seconds

22. A bride tosses her bouquet from the top of a platform. After t seconds, the height of the bouquet above the ground is f feet, where f = -t2 - 16t + 61. After how many seconds will the bouquet hit the ground if no one catches it?

A. 2.42 seconds

B. 3.18 seconds

C. 6.61 seconds

D. 19.18 seconds

23. A man climbs a tree to recover a shoe that has gotten stuck in the branches. He tosses the shoe from one of the branches. After t seconds, the height of the shoe above the ground is f feet, where f = -3t2 - 30t + 171. After how many seconds will the shoe hit the ground?

A. 1.90 seconds

B. 2.09 seconds

C. 4.06 seconds

D. 14.06 seconds

24. A construction worker drops a hammer while working on the roof of a house. After t seconds, the height of the hammer above the ground is f feet, where f = -6t2 - 12t + 330. After how many seconds will the hammer hit the ground?

A. 2.50 seconds

B. 4.58 seconds

C. 6.48 seconds

D. 8.48 seconds

25. A construction worker drops a hammer while working on the construction of a multi-story building. If, after 12.2 seconds the hammer hits the ground, which of the following equations can be used to calculate the height of the hammer in feet, f, after t seconds?

A. f = -t2 - 18t + 38

B. f = -t2 + 20t - 2

C. f = -t2 + 4t + 59

D. f = -t2 + 4t + 100

26. The manager of a certain game store determines that in order to sell x games, the price, P, per game should be P(x) = 160 - x dollars. The cost, C, the store pays for the games can be calculated using the function C(x) = 3600 + 40x dollars. If the store’s revenue from selling x games is R(x) = x * P(x), for what value of x will the store’s cost equal its revenue?

A. 23

B. 60

C. 84

D. 90

27. For a certain band fundraiser, the cost, C, of the items to be sold is C(x) = 8200 + 40x dollars. The sales price, P, of each item, x, is P(x) = 280 - x dollars. The band’s revenue from selling x items is R(x) = x * P(x). For what value of x will the band earn $6,200 more than its costs?

A. 34

B. 120

C. 232

D. 463

28. How many real solutions does the =+−6314xx equation have?

A. None

B. One

C. Two

D. More than two

30. For which of the following values of x is the function =− 2 ()9 fxx NOT defined as a real number? A. -3 B. -1 C. 2 D. 4

31. For which of the following values of x is the function =− 2 ()24 fxx NOT defined as a real number? A. -12

29. How many real solutions does the equation =++ 314305 xx have?

A. None

B. One

C. Two

D. More than two

32. For which of the following values of x is the function =− 2 ()25fxx NOT defined as a real number?

33. The quadratic equation y = ax2 + bx + c is graphed in the xy-coordinate grid above. The equation ax2 + bx + c has

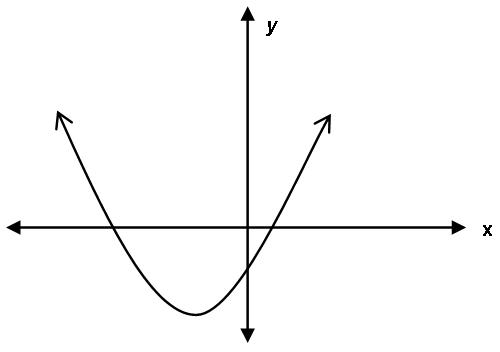
35. The quadratic equation y = ax2 + bx + c is graphed in the xy-coordinate grid above. The equation ax2 + bx + c has

A. No real or complex roots

B. Exactly one real root

C. Two real roots

D. One real root and one complex root

A. No real or complex roots

B. Exactly one real root

C. Two real roots

D. One real root and one complex root

34. The quadratic equation y = ax2 + bx + c is graphed in the xy-coordinate grid above. The equation ax2 + bx + c has

36. The quadratic equation y = ax2 + bx + c is graphed in the xy-coordinate grid above. The equation ax2 + bx + c has

A. No real or complex roots

B. Exactly one real root

C. Two real roots

D. Two complex roots

E.

A. Exactly one real root

B. Two real roots

C. Two complex roots

D. One real root and one complex root

37. In the xy-plane, what is the y-intercept of the graph of the equation

y = (x - 7)(x + 8)?

A. -56

B. -7

C. 1

D. 8

38. In the xy-plane, what is the y-intercept of the graph of the equation

y = 2(x - 7)(x + 8)?

A. -112

B. -56

C. 2

D. 56

39. In the xy-plane, what is the y-intercept of the graph of the equation

y = 3(x - 1)(x + 2)?

A. 6

B. 3

C. -2

D. -6

40. In the xy-plane, what is the y-intercept of the graph of the equation

y = 1 2 (x - 4)(x + 8)?

A. -32

B. -16

C. 2

D. 32

41. The formula for the volume of a right circular cylinder is V = πr2h. If r = x + 3 and h = 4x, what is the volume of the cylinder in terms of x?

A. 4�x3 + 36�x

B. 4�x3 + 10�x2 + 13�x

C. 4�x3 + 12�x2 + 36�x

D. 4�x3 + 24�x2 + 36�x

42. The formula for the volume of a right circular cylinder is V = πr2h. If r = 3x and h = 5 - x, what is the volume of the cylinder in terms of x?

A. 8�x2 + 3�x3

B. 15�x2 - 3�x3

C. 45�x2 - 9�x3

D. 45�x3 - 9�x2

Lesson 18 Interpreting Data

• In these problems, you have to read and understand what’s given.

• The data may be presented in paragraph form or in chart form.

• There are 3 scenarios in these problems:

1. Prove you _____________________________________ what’s written.

2. ______________________________________________ what’s written.

3. Make __________________________________ based on what’s written.

• The key is ____________________________________________________.

• As long as you pay attention to what they give you and work carefully, you can handle these problems.

Let’s learn some methods that always work.

Scenario 1: Understand what's written Example

Step 1: What's Rohlfs' record?

Step 2: What does "exceed" mean?

Was Rohlfs faster or slower?

Step 3: Write an ___________________:

Step 4: Solve:

1. Whose air-speed record did Rohlfs exceed by exactly 36.4 mph?

Step 5: Answer:

Scenario 1: Understand what's written

Example 1: Early Air-Speed Records

Scenario 2: Apply what's written

Example 2:

In a particular county in Texas, consumers pay tax, t, based on the amount of dollars they spend, d, based on the formula: t = 0.085d. If a consumer purchases one shirt for $25 and two pair of jeans that cost $30 each, approximately how much tax will be due?

A. $4.68

B. $7.23

2. Whose air-speed record approximately doubled Leblanc’s?

Step 1: What's Leblanc’s record?

C. $1.70

D. $8.42

Step 1: Find d:

Step 2: What does "double" mean?

Step 2: Use the ____________________:

Step 3: Think! Estimate! Round! (If there’s no calculator available)

Method 1:

Step 3: Write an ___________________:

• Think .085 is less than __________.

• 10% would be _________________.

Step 4: Solve:

Step 5: Answer:

• We need _______________than that.

• Pick _________________________.

Method 2:

A. Think $85 x .08 is ______________.

B. Think: That's a little ____________

C. Pick _________________________.

Example 3:

In a particular county in Texas, consumers pay tax, t, based on the amount of dollars they spend, d, based on the formula: t = 0.085d. If a consumer purchases 2 items for $10 and 1 item for $20, approximately how much tax will be due?

Scenario 3: Make predictions based on what's written

Example 4:

The value of a certain item in 1990 was $0.10. The table below shows its value from 1990 to 1996.

A. $2.55

B. $4.25

C. $3.40

D. $1.70 Step 1: Find d: Step 2: Use the ____________________:

Year Value

1990 $.10

1991 $.20

1992 $.30

1993 $.40

1994 $.50

1995 $.60

1996 $.70

Based on the information in the table, what is a reasonable prediction for the value of the item in 2000?

Step 1: Identify the _________________.

Step 3: Think! Estimate! Round!

Method 1:

• Think .085 is less than __________.

• 10% would be _________________.

SAMPLECOPY

• We need ______________than that.

• Pick _________________________.

Method 2:

• Think $40 x .08 is ______________.

• Think: That's a little ____________

• Pick _________________________.

Step 2: Apply the ___________________ carefully.

1997 = 1998 = 1999 =

2000 =

Step 3: Answer:

Exercises:

1. The value of a certain stock has fluctuated over the years, as shown in the chart below, which gives the value on January 1 of each year.

Year Value 2000 $10.50

2001 $13.73

2002 $8.64

2003 $14.59

2004 $15.99

2005 $17.23

2006 $17.01

The value in 2005 exceeds the value in which year by $3.50?

3. The value of a certain stock has fluctuated over the years, as shown in the chart below, which gives the value on January 1 of each year.

Year Value 2000 $10.50

2001 $13.73

2002 $8.64

2003 $14.59

2004 $15.99

2005 $17.23

2006 $17.01

The value in 2004 is approximately 50% greater than the value in what year?

2. To calculate the selling price, p, of items in his shop, Chase takes the original cost, c, of the item and applies the following formula:

p = 1.25c

Chase sells 2 items that cost $15 each and 1 item that costs $30. What was the selling price for the items?

4. For babysitting, Zoey gets paid $4.00 an hour plus a base fee of $20. She uses the formula below to calculate t, her total earnings based on h, the number of hours she babysits.

t = 20 + 4h

If Zoey babysits one Saturday for 4 hours 15 minutes, how much will she earn?

5. The value of a certain stock has fluctuated over the years, as shown in the chart below, which gives the value on January 1 of each year.

Year Value

2000 $10.50

2001 $13.73

7. The value of a certain item has increased since it was first released to the public in 1990 at a price of $100.

Year Value

1990 $100.00

1991 $110.00

1992 $121.00

2002 $8.64

2003 $14.59

2004 $15.99

2005 $17.23

2006 $17.01

The value of the stock in 1985 was 12.5% of the value in 2002. What was the value of the stock in 1985?

6. Kyle earns $8 an hour + a flat-rate commission on sales. He uses the following formula to calculate what his gross wages, w, will be based on the number of hours, h, that he works and the value of his sales, s.

w = 8h + .05s

If Kyle works 6 hours and sells $380 worth of merchandise, how much will he earn?

1993 $133.10

1994 $146.40

1995 $161.05

Based on the table, which of the following is a reasonable prediction for the price of the item in 1997?

8. The cost of Isabel’s monthly telephone service, c, can be found using the formula c = 25 + .06m + .05t, where m represents the number of minutes of phone calls she makes and t represents the number of text messages she sends. If Isabel makes 160 minutes worth of calls and sends 150 text messages, how much will her monthly service cost? SAMPLECOPY

9. The graph below shows the average salary for employees with a masters degree after a certain number of years in the workforce.

10. Josiah works at a call center and gets paid a flat hourly rate of $10 per hour plus a per call rate of $0.30 per call for each call he makes where he actually talks to a potential customer for at least 15 seconds. His gross wage, w, is calculated based on the equation below, where c is the number of calls that meet the requirement and h is the number of hours worked:

w = 0.30c + 10h

If Josiah works 6 hours 45 minutes and makes 400 calls that meet the requirements, how much will he earn?

If an employee with a masters degree is paid $90,000, what is the most likely length of time the employee has been in the workforce?

A. Between 5 and 10 years

B. Between 10 and 15 years

C. Between 15 and 20 years

D. Between 20 and 25 years

11. The value of a certain stock has fluctuated over the years, as shown in the chart below, which gives the value on January 1 of each year.

Year Value

2000 $10.50

2001 $13.73

2002 $8.64

2003 $14.59

2004 $15.99

2005 $17.23

2006 $17.01

The value of the stock in 2011 is predicted to be around $32.00. This value is approximately 100% greater than the value in what year?

12. The graph below shows the average salary for employees with a masters degree after a certain number of years in the workforce.

14. The value of a certain item in 1880 was $2.05. Its value from 1880 to 1885 is included in the table below.

If an employee with a masters degree has worked 8 years, her approximate salary should be --

A. Between $25,000 and $30,000

B. Between $30,000 and $35,000

C. Between $35,000 and $40,000

D. Between $45,000 and $50,000

13. The fare, f, of a taxi ride is based on the equation f = $2.25 + $1.25m, where m is the number of miles or part thereof driven. If a patron travels 48 miles, how much will the fare be?

Based on the table, which of the following is a reasonable prediction for the price of the item in 1890?