https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html


































































































































https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
1) 13 145 + 7435 (Красилівка) = 20580 чол

2) 203 912 + 825 137 (Одеса) = = 1 029 049 чол

3) 78 117 – 13 256 (Прилуки) = 64 861 чол 4) 974 002 – 725 189 (Рівне) = 248 813 чол


5) 313 · 42 (Баштанка) = 13 146 чол 6) 833 · 281 (Кременчук) = 234 073 чол


7) 64 246 : 13 (Рудки) = 4 942 чол 8) 1 536 470 : 106 (Судак) = 14 495 чол

2. Обчисліть:


1) 137 125 + 321 117 = 458 242 2) 429 113 – 253 087 = 176 026


3) 429 · 17 = 7 293 4) 91 575 : 45 = 2 035



3.
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html

1) 297 + (495 + 703) = (297 + 703) + 495 = 1000 + 495 = 1 495
2) 329 + 1 075 + 1925 + 671 = (329 + 671) + (1 075 + 1925) = 1000 + 3000 = 4 000
3) 250 · 49 · 4 = (250 · 4) · 49 = 1000 · 49 = 49 000
4) 125 · 37 · 8 · 2 = (125 · 8) · (37 · 2) = 1000 · 74 = 74 000
4.
1) (724 + 913) + 276 = (724 + 276) + 913 = 1000 + 913 = 1913
2) 2715 + 256 + 1285 + 744 = (2715 + 1285) + (256 + 744) = 4000 + 1000 = 5000
3) 500 · 73 · 20 = (500 · 20) · 73 = 10 000 · 73 = 730 000
4) 25 · 13 · 400 · 7 = (25 · 400) · (13 · 7) = 10 000 · 91 = 910 000
5. Запишіть усі дільники числа:
1) 16: 1, 2, 4, 8, 16;
2) 38: 1, 2, 19, 38;
3) 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.
6. Запишіть усі
1) 25: 1, 5, 25;
числа:
2) 36: 1, 2, 3, 4, 6, 9, 12, 18, 36;
3) 78: 1, 2, 3, 6, 13, 26, 39, 78.
7. Розкладіть на прості множники число:


=
·



1) 19 і 3;
19 = 19 · 1; 3 = 3 · 1;
НСД = 1;
НСК = 3 · 1 · 19 = 57
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
2) 36 і 48;
36 = 2 · 2 · 3 · 3 = 22 · 32;
48 = 2 · 2 · 2 · 2 · 3 = 24 · 3;
НСД = 12;
НСК = 24 · 32 = 144


3) 17 і 51; 17 = 17 · 1;
51 = 3 · 17;
НСД = 17;
НСК = 3 17 1 = 51
1) 7 і 12;
7 = 1 · 7;
12 = 2 · 2 · 3 = 22 · 3
НСД = 1;
НСК = 22 · 3 · 1 · 7 = 84
2) 39 і 52;
39 = 3 · 13;
52 = 2 · 2 · 13 = 22 · 13
НСД = 13;
НСК = 22 · 3 · 13 =156
3) 54 і 18;
54 = 2 · 3 · 3 · 3 = 2 · 33
18 = 2 3 3 = 2 32
НСД = 18;
НСК = 2 · 33 = 54
4) 12; 16 і 20;
12 = 2 2 3 = 22 3
16 = 2 · 2 · 2 · 2 = 24
20 = 2 · 2 · 5 = 22 · 5
НСД = 4;
НСК = 24 · 3 · 5 = 240
4) 10; 15 і 25;
10 = 2 · 5
15 = 3 · 5
25 = 5 · 5
НСД = 5;
НСК = 5 · 5 · 2 · 3 = 150




https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
1) 7293² = 53 187 849
2) 4007³ - 129² = 64 336 588 343 – 16 641 = 64 336 571 702
3) 125³ + 138³ - 45² = 1 953 125 + 2 628 072 – 2 025 = 4 581 197 – 2 2025 = 4 579 172
15. Знайдіть найменше
Найменше – 10 086
Найбільше – 99 999
16. Знайдіть найменше і
Найменше – 1 014
Найбільше – 9 984
17. (Усно.) Обчисліть:
1) 4 + 2,7 = 6,7
2) 1,8 + 3,2 = 5
3) 4,5 – 1,2 = 3,3
4) 7,2 – 4,5 = 2,7
18. Виконайте дію:
1) 4,92 + 5,713 = 10,633
2) 12,38 – 4,113 = 8,267
3) 3,5 · 2,14 = 7,49
4) 2,6² = 6,76
19. Виконайте дію:
1) 5,731 + 9,28 = 15,011
2) 17,52 – 9,293 = 8,227
3) 7,6 · 4,15 = 31,54
4) 3,2² = 10,24
20.

39.
5) 10 · 5,2 = 52
6) 4,3 · 0,01 = 0,43
7) 3,6 : 3 = 1,2
8) 2,8 : 0,1 = 28
5) 5,9 · 4,03 = 23,777
6) 41,04 : 12 = 3,42
7) 8,55 : 2,5 = 3,42
8) 0,7³ = 0,343
5) 2,05 · 4,7 = 9,635
6) 31,2 : 15 = 2,08
7) 8,82 : 2,8 = 3,15
8) 0,6³ = 0,216
2,8 (С); 2,81 (Л); 2,89 (І); 2,9 (П); 3,14 (К); 3,4 (А).
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
22. Округліть числа:
1) До десятих:
7,25 = 7,3 3,739 = 3,7 8,03 = 8,0 9,05 = 9,1
2) До сотих: 5,713 = 5,71 9,8999 = 9,90 4,115 = 4,12 8,718 = 8,72
3) До одиниць: 7,389 = 7 4,5 = 5 9,93 = 10 7,38 = 7
4) До десятків: 135,72 = 140 431,431 = 430
23. Округліть числа: 1) До десятих: 17,38 = 17,4 49,55 = 49,6 4,06 = 4,1 7,02 = 7,0
2) До сотих:
= 13,55 29,341 = 29,34
3)
= 10,00
3,713 = 4 14,52 = 15 7,111 = 7 24. Знайдіть значення виразу:
1) 2,9 · (7,32 + 0,08 : 0,125) – 4,2 · 0,25 + 7,35 = 2,9 · (7,32 + 0,64) – 1,05 + 7,35 = 2,9 · 7,96 – 1,05 + 7,35 = 23,084 – 1,05 + 7,35 = 29,384
2) (7,85 + 4,2²) : 5 – 0,9³ : 3 = (7,85 + 17,64) : 5 – 0,729 : 3 = 25,49 : 5 – 0,243 = 5,098 – 0,243 = 4,855
25. Знайдіть значення виразу:
1) 45,2 · 0,75 – (9,34 + 0,06 : 0,25) · 2,8 – 4,05 = 33,9 – (9,34 + 0,24) · 2,8 – 4,05 = 33,9 – 9,58 · 2,8 – 4,05 = 33,9 – 26,824 – 4,05 = 3,026
2) (8,93 – 2,6²) : 4 + 0,6³ : 2 = (8,93 – 6,76) : 4 + 0,216 : 2 = 2,17 : 4 + 0,108 = 0,5425 + 0,108 = 0,6505
26. Запишіть три десяткові дроби, кожний з яких:
1) більший за 4,8 і менший від 4,9: 4,8 < 4,81 < 4,85 < 4,88 < 4,9
2) менший від 0,43 і більший за 0,41: 0,41 < 0,42 < 0,421 < 0,425 < 0,43
27. Запишіть три десяткові дроби, кожний з яких: 1) менший від 9,6 і більший за 9,4: 9,4 < 9,45 < 9,5 < 9,55 < 9,6
2) більший за 4,83 і менший від 4,84: 4,83 < 4,831 < 4,832 < 4,833 < 4,84 28. (Усно.) Обчисліть:

1) зниження ціни на 10%; 26%:
150 – (150 · 0,10) = 150 – 15 = 135 (грн)
150 – (150 · 0,26) = 150 – 39 = 111 (грн)
2) підвищення ціни на 8%; 20%:
150 + (150 · 0,08) = 150 + 12 = 162 (грн)
150 + (150 · 0,20) = 150 + 30 = 180 (грн) 34.
1) підвищення ціни на 15%; 9%:
200 + (200 · 0,15) = 200 + 30 = 230 (грн)
200 + (200 · 0,09) = 200 + 18 = 218 (грн)
х + 0,4 = 7 15

2) зниження ціни на 4%; 30%: 200 – (200 · 0,04) = 200 – 8 = 192 (грн)
1)
2) 910 – 364 = 546 (км) – залишилося подолати автомобілю
Відповідь: 546 км.
38. Придбавши книжку за 90 грн, Оля витратила 30% грошей, які мала. Скільки грошей
у дівчинки?
1) Нехай сума грошей, яку

9 кг сушених?
1) Нехай маса
0,18х
х = 9 0
х · (1 + 0,20) = х ·1,20
х · (1 – 0,15) = х · 1,20 · 0,85
х · 1,20 · 0,85 = х · 1,02
Таким чином, кінцева ціна становить 102%
2) (1,02 – 1) · 100% = 0,02 · 100% = 2%


1) 28
5 + 2 = 7 –
28
7 = 4 –
5 · 4 = 20 – перша частина.
2 · 4 = 8 – друга частина.
Перевірка: 20 + 8 = 28.
52. Поділіть число:
5 : 2
2) 36
1 + 3 + 5 = 9 –
1 · 4 = 4 – перша частина.
3 · 4 = 12 – друга частина.
5 · 4 = 20 – третя частина.
Перевірка: 4 + 12 + 20 = 36.
1 : 3 : 5
1) 48 на ді частини у відношенні 1 : 3
1 + 3 = 4 – загальна кількість частин.
48 4 = 12 – значення однієї частини.
1 · 12 = 12 – перша частина.
3 · 12 = 36 – перша частина.
Перевірка: 12 + 36 = 48.
53. Розв’яжіть рівняння:
1) 2х 7
4 = 5 8
8(2х – 7) = 20
16х – 56 = 20
16х = 20 + 56
16х = 76
х = 19 4
54. Розв’яжіть рівняння: 1) 2х+3 5 = 7 10
10(2х + 3) = 35
20х + 30 = 35
20х = 35 – 30
20х = 5
х = 1

2) 50 на три частини у відношенні 2 : 5 : 3 2 + 5 + 3 = 10 – загальна кількість частин.
50 10 = 5 – значення однієї частини.
2 · 5 = 10 – перша частина. 5 · 5 = 25 – друга частина.
3 · 5 = 15 – третя частина.
Перевірка: 10 + 25 + 15 = 50.
+ 1) = 7(3 – 4х)
42х + 14 = 21 – 28х 42х + 28х = 21 – 14
70х = 7
х = 1 10
12(2х – 1)= 4(5 – 4х) 24 – 12 = 20 – 16х
24х + 16х = 20 + 12 40х = 32
2) 84 грн:
84 80 80 ∙ 100% = 4 80 ∙ 100% = 0,05 ∙ 100% = 5%
Відповідь: ціна товару
57. До 180 г 10-
1) 180 · 0,10 = 18 (г) – маса солі.
2) 180 + 70 = 250 (г) – нова маса розчину.
3) 18 250 ∙ 100% = 0,072 ∙ 100% = 7,2% -
Відповідь: 7,2%.
58.
1) 250 · 0,40 = 100 (г) – маса олова.
2) 250 + 150 = 400 (г) – нова маса сплаву.
3) 100 + 150 = 250 (г) – загальна маса олова.
4) 250 400 ∙ 100% = 0,625 ∙ 100% = 62,5% - відсотковий вміст олова.
Відповідь: 62,5%.
59. Обчисліть:
1) -8 + (-9) = -8 – 9 = -17
2) -13,6 + (-7,9) = -13,6 – 7,9 = -21,5
3) 29 + (-11) = 29 – 11 = 18
4) -37 + 4,5 = -(37 – 4,5) = -32,5
5) -8 – 5 = -(8 + 5) = -13
6) -9 – (-4) = -9 + 4 = -5
60. Виконайте дії:
1) -6 + (-10) = -6 – 10 = -16
2) -4,9 + (-5,7) = -4,9 – 5,7 = -10,6
3) -38 + 12 = -(38 – 12) = -26
4) 7,2 + (-5) = 7,2 – 5 = 2,2
5) -4 – (-3) = -4 + 3 = -1 6) -9 – 11 = -(9 + 11) = -20
7) 7 – (-3) = 7 + 3 = 10
8) 4 – 9,1 = -(9,1 – 4) = -5,1
9) 2,9 · (-10) = -(2,9 · 10) = -29
10) -4 · (-4,5) = 4 · 4,5 = 18
11) -4,2 : (-4) = 4,2 : 4 = 1,05
12) 8 : (-0,01) = -(8 : 0,01) = -800
7) 0 – (-9) = 9
8) 5 – 10,2 = -(10,2 – 5) = -5,2
9) -5,1 · (-0,1) = 5,1 · 0,1 = 0,51
10) -6 · 2,5 = -(6 · 2,5) = -15
11) -7,2 : 10 = -(7,2 : 10) = -0,72 12) -7,5 : (-5) = 7,5 : 5 = 1,5 61. Виконайте дії:
1) 6 7 + � 4 21� = 6 7 4 21 = 22 21 = 1 1
2) 4 7 12 + 5 1 6 = 55 12 + 31 6 = 7 12 3) 12 41 1 =

1) -2,7 і 4,1: -2, -1, 0, 1, 2, 3, 4.
2) -102,5 і -97,9: -102, -101, -100, -99, -98.
3) 5 1 3 і 2 11 : -5, -4, -3, -2, -1, 0.
1) 1 2 3 і 4,7: -1, 0, 1, 2, 3, 4.
2) -85,3 і -78,4: -85, -84, -83, -82, -81, -80, -79.
3) 4 11 і 3 2 5 : 0, 1, 2, 3.
точки: А(-2; 4), М(0; -3), К(5; 1), D(4; 0), L(6; -2); N(2; -3).


точки: В(2; -5), С(-2; 0), Т(4; 2), Е(0; 3), Q(-4; -1), P(-5; 2).

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
68.
1) 7p – 2m + 6p + 2m = (7p + 6p) + (-2m+ 2m) = 13p + 0 = 13p
2) -14b + 3,9 – 7,2 + 18,5b = (-14b + 18,5b) + (3,9 – 7,2) = 4,5b – 3,3 = 4,5b – 3,3
3) 5х – 8у + 5 – 4х + у = (5x – 4x) + (-8y + y) + 5 = x – 7y + 5
4) 2,5а – 2,9b + 3a + 3,7b – 5,5a = (2,5a + 3a – 5,5a) + (-2,9b + 3,7b) = 0a + 0,8b = 0,8b
69. Розкрийте дужки і зведіть подібні доданки:
1) -5(2а – 3) + 3(4а – 5) = -5 · 2а + (-5) · (-3) + 3 · 4а + 3 · (-5) = -10 + 15 + 12а – 15 = (-10а + 12а) + (15 – 15) = 2а + 0 = 2а
2) 2(a – 3m) – 7(2a + m) = 2 · a + 2 · (-3m) – 7 · 2a – 7 · m = 2a – 6m –
– 7m = (2a – 14a) + (-6m – 7m) = -12a – 13m 3) (2y – 3) · (-3) + 2(4y – 1) = (2у · (-3)) + (-3) · (-3) + 2 · 4у + 2 · (-1) = -6у + 9 + 8у – 2 = (6у + 8у) + (9 – 2) = 2у + 7
4) 2,4(2x – 3) – 4,8(x – 5) = 2,4 · 2х + 2,4 · (-3) –
(4,8х – 4,8х) + (-7,2 + 24) = 0 + 16,8 = 16,8 70. Розкрийте
1) -4(3а – 2) + 6(2а – 1) = -4 · 3а + (-4) · (-2) + 6 · 2а + 6 (-1) = -12а + 8 + 12а – 6 = (-12а + 12а) + (8 – 6) = 0а + 2 = 2 2) 5(b – 3c) – 3(4b + c) = 5b – 15c – 12b – 3c = -7b – 18c 3) (7x – 2) · (-4) + 2(4 – 3y) = (7х · (-4)) + (-2) · (-4) + 2 · 4 + 2 · (-3у) = -28х + 8 + 8 – 6у =28х + 8 + 8 – 6у = -28х + 16 – 6у
4) 2,6(3а – 5) – 7,8(а – 10) = 2,6 · 3а + 2,6 · (-5) – 7,8 · а – 7,8 · (-
= (7,8а – 7,8а) + (-13 + 78) = 0а + 65 = 65
71. Розв’яжіть рівняння:
1) 0,5(2х – 3) + 2,6 = 0,2(4 + 2х)
х – 1,5 + 2,6 = 0,8 + 0,4х
х + 1,1 = 0,8 + 0,4х
х – 0,4х = 0,8 – 1,1
0,6х = -0,3
х = -0,5
72. Розв’яжіть рівняння:
1) 0,5(3 – х) + 1,4 = -0,3(2х – 2)
1,5 – 0,5х + 1,4 = -0,6х + 0,6
2,9 – 0,5х = -0,6х + 0,6 -0,5х + 0,6х = 0,6 – 2,9
0,1х = -2,3
х = -23

-7х – 5х = 28 – 12 -
=
–
–
+
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
5(2,6а + 3,4b) – 2(6a – 2,5b) = 13a + 17b – 12a + 5b = a +
10b – 2b – 4x = 8b – 4x
х – 2b = -5
x = -5 + 2b
8b – 4(-5 + 2b) = 8b – 4(-5) – 4(2b) = 8b + 20 – 8b = 20
Відповідь: 20.
81. Знайдіть значення виразу 15a – (3a + 4m), якщо m – 3a = -3.
15a – (3a + 4m) = 15a – 3a – 4m = 12a – 4m
m – 3a = -3
m = -3 + 3a
12a – 4(-3 + 3a) = 12a – 4(-3) – 4(3a) = 12a + 12 – 12a = 12

Відповідь: 12.
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
82. Чи є число -2 коренем рівняння:
1) х + 5 = 7 – ні, оскільки:
-2 + 5 = 7
3 ≠ 7
2) х · 4 = -8 – так, оскільки:
-2 · 4 = -8
83. Знайдіть корінь рівняння:
1) х – 3 = 8
х = 8 + 3
4) -10 : х = -5 – ні, оскільки: -10 : (-2) = -5 5 ≠ -5
-8 = -8 3) х – 3 = -5 – так, оскільки: -2 – 3 = -5 -5 = -5
х = 11 2) 7 + х = 3 х = 3 – 7 х = -4 3) -4х = -20 -4х : (-4) = -20 : (-4) х = 5 4) х : 3 = -7 х = -7 · 3
х = -21
1) 4х – 12 > 0
Це нерівність,
2) 3х + 7 Це
3) 4х – 2 = 10
Це рівняння, оскільки
4) (14 – 10) · 2 = 8
Це також рівняння,

1.6. Доведіть, що
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
із
1,2 та -1,2
х² = 1,44. (1,2)² = 1,44
1,2 · 1,2 = 1,44 (-1,2)² = 1,44 (-1,2) · (-1,2) = 1,44
1.7. Чи є рівносильними рівняння:
1) х + 2 = 5 і х : 3 = 1 – так, оскільки: 2) х – 3 = 7 і 2х = 18 – ні, оскільки: х + 2 = 5
х = 5 – 2
х = 3 х : 3 = 1
х = 3 · 1
х = 3
1.8. Чи є рівносильними рівняння:
х – 3 = 7 х = 7 + 3
х = 10 2х = 18
х = 18 : 2
х = 9
1) х – 2 = 3 і 2х = 10 – так, оскільки: 2) х + 3 = 7 і х : 2 = 3 – ні, оскільки:
х – 2 = 3
х = 3 + 2
х = 5
1.9. Доведіть, що:
2х = 10
х = 10 : 2
х = 5
1) коренем рівняння 2(х – 3) = 2х – 6 є
будь-яке число:
2(х – 3) = 2х – 6
2х – 6 = 2х – 6
Це рівняння є тотожністю, яке вірне для
х + 3 = 7
х = 7 – 3
х = 4
х : 2 = 3 х = 3 · 2 х = 6
будь-якого значення х. Таким чином, коренем цього рівняння є будь-яке число. 2) рівняння у – 7 = у не має коренів: у – 7 = у у – у – 7 = у – у -7 = 0 Це явно хибне твердження.
1.10. Доведіть, що:
1) коренем рівняння 3(2 – с) = 6 – 3с є
будь-яке число:
3(2 – 1) = 6 – 3с
6 – 3с = 6 – 3с
Це рівняння є тотожністю, яке вірне для
будь-якого значення с. Таким чином, коренем цього рівняння є будь-яке число с.
значення у, яке б
задовольняло. Отже, рівняння не
коренів.
2) рівняння х = х + 8 не має коренів: х = х + 8 х – х = х + 8 – х 0 = 8 Це явно хибне твердження. Тому рівняння
Отже, рівняння не має коренів.
1.11. Складіть рівняння, що має: 1) єдиний корінь – число -2: Щоб створити рівняння, яке має єдиний корінь x = −2, можна скористатися рівнянням
лінійного типу: x + 2 = 0
Якщо x = −2, то підставивши це значення у рівняння, ми отримаємо: −2 + 2 = 0
Це правильне рівняння, що має єдиний
2) два корені – числа 5 і -5:

1)
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
4(х – 2) = 19 і 4х – 8 = 19 є
2х – 3 = 3х + 5 і 2х
3)
4)
2) Рівняння 3х + 7 = 4х – 8 і 3х – 4х = -8 – 7 є рівносильними, оскільки
3) Рівняння 9(х + 2) = 18 і х + 2 = 2 є
1.14.
1) х + 2 = 2 – х
х + х + 2 = 2
2х + 2 = 2
2х = 0
х = 0
Це рівняння має єдиний розв’язок х = 0.
3) х + 1 = -1 + х
х – х = -1 – 1
0 ≠ -2
Розв’язків немає.
5) 0 · (х – 1) = 3
0 = 3
Це явно хибне твердження. Таким чином, це рівняння не має жодного розв’язку.
7) 0 : х = 0
0 = 0
Це тотожність,

2) х + 3 = 3 + х х – х + 3 = 3
3 = 3
Це тотожність, яка вірна для будь-якого х. Таким чином, це рівняння має безліч розв’язків.
4) 0 · х = 0
0 = 0
Це тотожність, яка вірна для будь-якого х. Таким чином, це рівняння має безліч розв’язків.
6) 5(х – 1) = 5х – 5
5х – 5 = 5х – 5
Це тотожність, яка вірна для будь-якого х. Таким чином, це рівняння
розв’язків.
8) 2(х – 3) = 2х – 7
2х – 6 = 2х – 7 2х – 2х – 6 = -7 -6
Початкові витрати:
Придбання лічильника: 1500 грн
Встановлення та облік: 500 грн
Загальні початкові витрати: 1500 грн + 500 грн = 2000 грн
на електроенергію:
для населення: 2,64 грн за 1 кВт ·год

1.18.
1) 5у + 11 = 5 – 3у
5у + 3у = 5 – 11
8у = -6
у = 3 4
3) -2m – 13 = -3m + 5
-2m + 3m = 5 + 13
2) 6х – 13 = 2х + 7 6х – 2х = 7 + 13 4х = 20
х = 5
m = 18 4) -1 – 4х = 17х – 8 -1 + 8 = 17х + 4х 7 = 21х х = 7 21 = 1 3
1.19. Розв’яжіть рівняння:
1) -3х = -21 -3х : (-3) = -21 : (-3)
х = 7 2) -2х = 40 -2х : (-2) = 40 : (-2) х = -20
3) 0,2х = -5
0,2х : 0,2 = -5 : 0,2
х = -25 4) 50х = -5
1.20. Яку остачу при діленні
13 + 2000?
1001 = 7 · 11 · 13.
Тому
і 13.
Остача залежить від другого
2.1. (Усно.)
1) 15х = 0 – лінійне
2)
3) х² = 2х – нелінійне
2.2. (Усно.)
2.3.

2.4. (Усно.) Розв’яжіть
1) -2х = -12
2.7.
8х = -72
= -9
2.8.
1) 7х + 14 = 0
7х = -14

х = -2 2) 0,3х – 21 = 0,5х – 23 0,3х – 0,5х = -23 + 21 -0,2х = -2 х = 10 3) 4х + 3 = 6х – 13 4х – 6х = -13 – 3 -2х = -16 х = 8
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
4) 5х + (3х – 7) = 9
5х + 3х – 7 = 9
8х – 7 = 9
8х = 9 + 7
8х = 16
х = 2
2.9. Розв’яжіть рівняння:
1) 2х – 10 = 0
2х = 10
х = 5
4) 12 – (5х + 10) = -3
12 – 5х – 10 = -3
2 – 5х = -3
-5х = -3 – 2
-5х = -5 х = 1
5) 47 = 10 – (9х + 2)
47 = 10 – 9х – 2
47 = 8 – 9х
9х = 8 – 47 9х = -39 х = 13 3 = 4 1 3
2) 1,4х – 12 = 0,9х + 4 1,4х – 0,9х = 4 + 12
6) (3х + 2) – (8х + 6) = 14 3х + 2 – 8х – 6 = 14 -5х – 4 = 14 -5х = 14 + 4 -5х = 18 х = 18 5 = 3 3 5
0,5х = 16 х = 32 3) 3х + 14 = 5х + 16 3х – 5х = 16 – 14 -2х = 2 х = -1
5) 6 – (8х + 11) = -1
6 – 8х – 11 = -1 -5 – 8х = -1 -8х = -1 + 5 -8х = 4 х = -0,5 6) (3х – 4) – (6 – 4х) = 4 3х – 4 – 6 + 4х = 4
2.10. Яке з рівнянь рівносильне рівнянню 5х – 10:
5х – 10 → х = 2
1) х + 3 = 5 х = 2 - рівносильне
2) 5 – х = 7 -
7х – 10 = 4
7х = 4 + 10
7х = 14 х = 2
3) х + 2 = х + 1 2 = 1 -
4) х – 7 = -5 х = 2 - рівносильне 5) х = 8 – 3х 4х = 8 х = 2 - рівносильне 6) 4х – 7 = 4х -7 = 0 -
2.11. Чи є рівняння рівносильними?
1) 4х – x = 17 і 3х = 17 - рівносильні
3x = 17 3х = 17
х = 17 3 х = 17 3
3) 2х = -12 і х + 6 = 0 - рівносильні
2х = -12 х + 6 = 0
х = -6 х = -6
2.12. Для якого значення х значення
1) 3х + 7 дорівнює -2
3х + 7 = -2
3х = -2 – 7
3х = -9
х = -3
2.13. Для якого значення у:
1) значення виразу 5у – 13 дорівнює -3
5у – 13 = -3
5у = -3 + 13
5у = 10

2) 5х – 9 = 3х і 6х = 21 - нерівносильні 5х – 9 = 3х 6х = 21 2х = 9 х = 21 6 = 7 2
4) 12х = 0 і 15х = 15 - нерівносильні 12х = 0 15х = 15 х = 0 х = 1
2) 4(х + 1) дорівнює значенню виразу 5х – 9
4(х + 1) = 5х – 9 4х + 4 = 5х – 9 4 = 5х – 4х – 9 4 = х – 9 х = 13
у = 2 2)
3(у – 2) = 13у – 8
3у – 6 = 13у – 8 -6 + 8 = 10у – 3у
2 = 10у
у = 2 10 = 1 5
3(у – 2) і 13у – 8
2.14. Розв’яжіть
1) х+1 3 = 5
х +1 = 15
х = 15 – 1
х = 14
3) х 3 + х 5 = 8
5х + 3х = 120
2) 2х 7 5 = −1
2х – 7 = 5
2х = 5 + 7
2х = 12 х = 6
8х = 120 х = 15 4) х 4 х 5 = 1 5х – 4х = 20 х = 20
2.15. Знайдіть корінь рівняння: 1) х 2 4 = 1 х – 2 = 4 х = 4 + 2 х = 6 2) 3х+2 5 = 4 3х + 2 = 20 3х = 20 – 2 3х = 18 х = 6
3) х 3 х 4 = 1 4х – 3х = 12
= 12
2.16. Складіть
1) число -2 х + 2 = 0
2.17. Складіть лінійне рівняння:
2.18. Складіть лінійне рівняння, коренем якого є:
1) число -8
х + 8 = 0 або 2х +16 = 0
2.19. Знайдіть корінь рівняння:
1) (4х – 2) + (5х – 4) = 9 – (5 – 11х)
4х – 2 + 5х – 4 = 9 – 5 + 11х
9х – 6 = 4 + 11х
9х – 11х = 4 + 6
-2х = 10
х = -5
3) 3(4х – 5) – 10(2х – 1) = 33
12х – 15 – 20х + 10 = 33
-8х – 5 = 33
-8х = 33 + 5
-8х = 38
х = 19 4 = 4 3 4

+ 2х = 60
= 60
= 12
2) будь-яке число 0 ⋅ х = 0 або 0 = 0
2) (7 – 8х) – (9 – 12х) + (5х + 4) = -16
7 – 8х – 9 + 12х + 5х + 4 = -16
2 + 9х = -16
9х = -16 – 2
9х = -18
х = -2
4) 9(3(х + 1) – 2х) = 7(х + 1)
9(3х + 3 – 2х) = 7х + 7
9(х + 3) = 7х + 7
9х + 27 = 7х + 7
9х – 7х = 7 – 27
2х = -20
х = -10
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
2.20. Розв’яжіть рівняння:
1) (9х – 4) + (15x – 5) = 18 – (25 – 22х)
9х – 4 + 15х – 5 = 18 – 25 + 22х
24х – 9 = -7 + 22х
24х – 22х = -7 + 9
2х = 2
х = 1
3) 7(х – 1) – 3(2х + 1) = -х – 15
7х – 7 – 6х – 3 = -х – 15
х – 10 = -х – 15
х + х = -15 + 10
2х = -5
х = -2,5
2.21.
2х+13 3 = 6х 1 4
4(2х + 13) = 3(6х – 1)
8х + 52 = 18х – 3
8х – 18х = -3 – 52 -10х = -55
х = 5,5
5,5 + 10,5 + 1788 = 16 + 1788 = 1804
2.23. Розв’яжіть
1) 2х + а = х + а
2x = x
2x – x = 0 x = 0 2) b + x = c – x x + x = c – b 2x = c – b ���� = 1 2 (с ���� )
2) (10х + 6) – (9 – 9х) + (8 – 11х) = -19
10х + 6 – 9 + 9х + 8 – 11х = -19
8х + 5 = 19
8х = -19 – 5
8х = -24
х = -3
4) 5(4(х – 1) – 3х) = 9х
5(4х – 4 – 3х) = 9х
5(х – 4) = 9х
5х – 20 = 9х
5х – 9х = 20 -4х = 20
х = -5

3(3у – 9) = 5(у + 3) 9у – 27 = 5у + 15
9у – 5у = 15 + 27
4у = 42 у = 10,5
3) 6x + 2m = x – 8m 6x – x = -8m – 2b 5x = -10m x = -2m
4) 9a + x = 3b – 2x x + 2x = 3b – 9a 3x = 3b – 9a x = b – 3a
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
2.24. Розв’яжіть рівняння, де х = змінна:
1) 7x + m = 2x + m
7x = 2x
7x – 2x = 0
5x = 0
x = 0
2) a + x = 2m – x
x + x = 2m – a
2x = 2m – a ���� =
2.25. Чи є рівносильними рівняння:
1) 2х – 4 = 2 і 5(х – 3) + 1 = 3х – 8 - рівносильні
2х – 4 = 2
2х = 2 + 4
2х = 6
х = 3
3) 3x + b = 9b – x
3x + x = 9b – b
4x = 8b
x = 2b
4) 5p + 2x = 10a – 3x
2x + 3x = 10a – 5p
5x = 10a – 5p
x = 2a – p
5(х – 3) + 1 = 3х – 8
5х – 15 + 1 = 3х – 8
5х – 14 = 3х – 8
5х – 3х = -8 + 14
2х = 6 х = 3
2) 5х + 3 = 8 і 7(х – 2) + 20 = 4х + 3 - нерівносильні
5х + 3 = 8
5х = 8 – 3
5х = 5
х = 1
3) 5х = 0 і 0 ⋅ х = 5 - нерівносильні
5х = 0
5х : 5 = 0 : 5
х = 0
7(х – 2) + 20 = 4х + 3
7х – 14 + 20 = 4х + 3
7х + 6 = 4х + 3
7х – 4х = 3 – 6
3х = -3
х = -1
0 ⋅ х = 5 0 = 5
Розв’язку немає
4) 7х + 1 = 7х + 2 і 5(х + 1) = 5х + 5 - нерівносильні
7х + 1 = 7х + 2
1 = 2
Розв’язку немає
5) 0 : х = 7 і 0 ⋅ х = 7 - рівносильні
0 : х = 7
0 = 7
Розв’язку немає
5(х + 1) = 5х + 5
5х + 5 = 5х + 5
х – будь-яке число
0 ⋅ х = 7 0 = 7
Розв’язку немає
6) 3(х – 2) = 3х – 6 і 2(х + 7) = 2(х + 1) + 12 - рівносильні
3(х – 2) = 3х – 6
3х – 6 = 3х – 6
х – будь-яке число

2(х + 7) = 2(х + 1) + 12
2х + 14 = 2х + 2 + 12
14 = 2 + 12
14 = 14
х – будь-яке число
1) 5у + 7
виразу у + 5
5у + 7 = 3(у + 5)
5у + 7 = 3у + 5
5у + 7 – 3у = 15
2у + 7 = 15
2у = 8
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
у = 4 2) 2у – 4
2.27. Для якого
1) 7х + 8
виразу х + 7
7х + 8 = 2(х + 7)
7х + 8 = 2х + 14
2х + 8 – 2х = 14
5х + 8 = 14
3 – 7у
2у – 4 = 3 – 7у + 7,4
2у – 4 = 10,4 – 7у
2у + 7у – 4 = 10,4
9у – 4 = 10,4
9у = 14,4
у = 1,6
5х = 6 х = 6 5 2) 5х – 8
2.28.
7(2х – 8) = 5(7х – 8) – 15х
14х – 56 = 35х – 40 – 15х
14х – 56 = 20х – 40
14х – 20х = 56 – 40 -6х = 16
х = 16 : (-6)
х = 8 3
Рівносильним буде рівняння 3х + 8 = 0
3х + 8 = 0
3х = -8
х = 8 3
2.29. Розв’яжіть рівняння: 1) ǀхǀ + 3 = 7
ǀхǀ = 7 – 3
ǀхǀ = 4
х = 4 або х = -4
4) ǀх + 5ǀ = 0
х + 5 = 0

виразу х + 2
5х – 8 = (х + 2) – 17,2
5х – 8 = х + 2 – 17,2
5х – 8 = х – 15,2
4х – 8 = -15,2
4х = -15,2 + 8 4х = -7,2 х = -1,8
2) ǀхǀ - 2 = -9
ǀхǀ = -9 + 2
ǀхǀ = -7 Розв’язку немає
х = -5 5) ǀ7 - хǀ = 1
7) ǀ2х + 1ǀ = 7
2х + 1 = 7 або 2х + 1 = -7
х = 3 або х = -4
7 – х = 1 або 7 – х = -1
х = 6 або х = 8
8) 2(ǀхǀ - 3) = ǀхǀ
2 ⋅ ǀхǀ - 6 = ǀхǀ
2 ⋅ ǀхǀ - ǀхǀ = 6
ǀхǀ = 6
х = 6 або х = -6
3) 2ǀхǀ - 6 = 0
2 ⋅ ǀхǀ = 6 ǀхǀ = 3 х = 3 або х = -3
6) ǀх + 12ǀ = -3
Розв’язку немає
9) 1 2 ǀх 1ǀ + 3 = 5
ǀх – 1ǀ + 6 = 10
ǀх – 1ǀ = 10 – 6
ǀх – 1ǀ = 4
х – 1 = 4 або х – 1 = -4
х = 5 або х = -3
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
2.30. Розв’яжіть
1) ǀхǀ - 5 = 4
ǀхǀ = 4 + 5
ǀхǀ = 9 х = 9 або х = -9 2) ǀхǀ + 1 = -2
= -2 – 1
4) ǀ2х - 1ǀ = 0
2х – 1 = 0
2х = 1
х = 0,5 5) ǀ2х - 7ǀ = 3 2х – 7 = 3 або 2х – 7 = -3 х = 5
3) 1 2 ǀхǀ − 4 = 0
- 8 = 0
= 8 х = 8 або х = -8
ǀхǀ - ǀхǀ = 12
⋅ ǀхǀ = 12
= 4
= 4 або х = -4
2.31. Для якого
2а ⋅ 4 = 16 → 8а = 16 → а = 16 8 = 2
2) 3х = а має корінь, що дорівнює 4 7
3 ⋅ 4 7 = а → 12 7 = а
4
3) 5(а + 1)х = 40 має корінь, що дорівнює -1
5(а + 1)(-1) = 40 → -5(а + 1) = 40 → -5а – 5 = 40 → -5а = 45 → а = 45 5 = -9
2.32. Для якого значення b коренем рівняння:
1) 3bx = -24 є число -4
3b ⋅ (-4) = -24
12b = 24 → b = 2
2.33. Розв’яжіть рівняння:
1) 4х + 7 = 3(х – 2) + х
4х + 7 = 3х – 6 + х
4х + 7 = 4х – 6
7 = -6
Розв’язку немає
2.34. Знайдіть корінь рівняння:
1) 3(х – 2) + 4х = 7(х – 1) + 1
3х – 6 + 4х = 7х – 7 + 1
7х – 6 = 7х – 6
х – будь-яке число
2.35. Розв’яжіть рівняння:
1) 3х 1 2 + 6х+3 11 = 10
11(3х – 1) + 2(6х + 3) = 220
33х – 11 + 12х + 6 = 220
45х – 5 = 220
45х = 220 + 5
45х = 225
х = 5

2) (2b – 5)x = 45 є число 3 (2b – 5) ⋅ 3 = 45 → 6b – 15 = 45 6b = 45 + 15 → 6b = 60 → b = 10
2) 2х + 5 = 2(х – 4) + 13
2х + 5 = 2х – 8 + 13
5 = -8 + 13
5 = 5 х – будь-яке число
2) 2(х + 1) + 4х = 6(х + 3)
2х + 2 + 4х = 6х + 18
6х + 2 = 6х + 18 2 = 18 Розв’язку немає
2) 8х 3 7 3х+1 10 = 2
10(8х – 3) – 7(3х + 1) = 140
80х – 30 – 21х – 7 = 140
59х – 37 = 140
59х = 140 + 37
59х = 177
х = 3
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
3) х 10 + 2х 5 = 7х 15 1 6
3х + 12х = 14х – 5
15х = 14х – 5
15х – 14х = 5
х = -5
5) 2х 3 5 1 х 4 + 5х+1 20 = 9х+3 10
4(2х – 3) – 5(1 – х) + 5х + 1 = 2(9х + 3)
8х – 12 – 5 + 5х + 5х + 1 = 18х + 6
18х – 16 = 18 + 6 -16 = 6
Розв’язку немає
2.36. Знайдіть корінь рівняння:
1) 2х+1 3 + х+7 2 = 5
2(2х + 1) + 3(х + 7) = 30
4х + 2 + 3х + 21 = 30
7х + 23 = 30
7х = 30 – 23
7х = 7
х = 1
3) х 3 + 2х 9 = 5х 6 1 18
6х + 4х = 15х – 1
10х = 15х – 1
10х – 15х = -1
-5х = -1
х = 0,2
2.37.
1) 4х – 3 = 5 і 3х + b = 17
4х – 3 = 5
4х = 8
х = 2
3 ⋅ 2 + b = 17
3(1 + 2х) – 2(3х + 2) = 5х + 4 3 + 6х – 6х – 4 = 5х + 4 -1 = 5х + 4 -5х = 4 + 1 -5х = 5 х = -1
12 9х – 15 – 8 + 4х + 2х + 5 = 15х – 18 15х – 18 = 15х – 18 х = 0
2(5х – 6) – 3(х – 5) = 24 10х – 12 – 3х + 15 = 24
7х + 3 = 24
7х = 24 – 3
7х = 21 х = 3
3х+1 5 2+х 2 = х 8 10 2(3х + 1) – 5(2 + х) = х – 8
6х + 2 – 10 – 5х = х – 8
х – 8 = х – 8
х – будь-яке число
6 + b = 17 b = 11 2) х + b = 9 і 2х – b = х 2x – x = b x = b b + b = 9 2b = 9 b = 4,5
2.38.
1) 2х – 3 = 7 і а – 3х = 9
2х – 3 = 7
2х = 10
х = 5
а – 3 ⋅ 5 = 9
а – 15 = 9

а = 24 2) х + а = 7 і 3х – а = 2х
3х – 2х = а
х = а
а + а = 7
2а = 7
а = 3,5
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
2.39.
х = 4
дільником числа 4.
Дільниками числа 4 є: 4, 2, 1, -1, -2, -4.
Таким чином, цілі значення m,
m = 1, 2, 4, -1, -2, -4.
2.40. Знайдіть усі цілі значення b, для
того, щоб корінь рівняння bx = -6
від’ємне, дає додатне число.
Дільники числа -6: -1, -2, -3, -6.
Таким чином
b = -1, -2, -3, -6.
2.41. Для якого значення
1) (а – 1)х = 5
bx = -6 є
Рівняння (а – 1)х = 5 не матиме розв’язків, якщо (а – 1) = 0, оскільки
ліворуч буде нуль, а праворуч 5, що неможливо:
а – 1 = 0
а = 1
Отже, при а = 1 рівняння не має коренів.
2) (а + 3)х = а – 2
Рівняння (а + 3)х = а – 2 не матиме розв’язків, якщо а + 3 = 0, оскільки в цьому випадку
ліворуч буде нуль, а праворуч а – 2, що не дорівнює нулю (окрім випадку а = 2,
розглядаємо умову а + 3 = 0):
а + 3 = 0
а = -3
Отже, при а = -3 рівняння

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
Рівняння (b + 1)х = 6
b + 1 = 0 b = -1
Отже, при b = -1 рівняння не має коренів.
2) (b – 3)х = b
Розглянемо випадок, коли b – 3 = 0. Тоді: b – 3 = 0 b = 3
У цьому випадку рівняння стає:
0х = 3
Це рівняння не має розв’язків, оскільки 0 не може дорівнювати 3. Таким чином, при b = 3
рівняння не має коренів.
3) (b + 1)х = b + 1
Розглянемо два випадки для цього рівняння: 1. Якщо b + 1 не дорівнює 0, то ми можемо поділити обидві сторони рівняння на b + 1:
х = 1
2. Якщо b + 1 = 0, тобто b = -1, то рівняння перетворюється на 0х = 0, що є тотожною рівністю і має нескінченну кількість розв’язків.
Отже, це рівняння завжди має розв’язки для всіх значень b, крім випадку b = -1, де існує нескінченна кількість розв’язків.
2.43. Для якого значення m будь-яке число є
рівняння: 1) (m – 1)х = 1 – m
Розглянемо випадок, коли рівняння стає тотожністю, тобто ліворуч і праворуч
будуть однакові вирази, незалежно від x.
Для цього:
(m – 1)x = 1 – m (m – 1)x = −(m – 1)
Можемо винести m−1 як спільний множник: (m – 1)(x + 1) = 0
Щоб це рівняння було тотожним, m – 1 повинно дорівнювати нулю:
m – 1 = 0 m = 1
При m = 1 рівняння стає 0 ⋅ x = 0, що є тотожністю, і будь-яке x є коренем рівняння. 2) m(m + 2)х = (m + 2)
Аналогічно, щоб будь-яке x було коренем рівняння, потрібно, щоб
виразу праворуч. m(m + 2)x = (m + 2)
Можемо винести m + 2 як спільний
(m + 2)(mx − 1) = 0

(m – 3)x = 5
2.44.
1) (а + 2)х = 2 + а
Розглянемо випадок, коли рівняння стає тотожністю, тобто ліворуч і праворуч
будуть однакові вирази, незалежно від х.
(a + 2)x = 2 + a
(a + 2)x = a + 2
Можемо винести a + 2 як спільний множник:
(a + 2)(x − 1) = 0
Щоб це рівняння було тотожністю, a + 2 повинно дорівнювати нулю:
a + 2 = 0
a = −2
При a = −2 рівняння стає 0 ⋅ x = 0, що є тотожністю, і будь-яке х є коренем рівняння. Отже,
при a = −2 рівняння має безліч коренів.
2) (а – 3)х = 9
Щоб рівняння (a – 3)x = 9 мало безліч
(a – 3)x = 9 Для того, щоб
a(a – 4)x = 4 – a
того,
це рівняння було тотожністю, необхідно, щоб a(a–4)=0 і
і праворуч були однакові вирази. Винесемо спільний множник: (a(a–4))(x+1)=0
Щоб це рівняння було тотожністю, a(a–4) повинно дорівнювати нулю: a(a–4)=0
Це відбувається, коли a=0 або a=4.
Якщо a = 0, то рівняння стає 0 ⋅ x = 4, що неможливо.
Якщо a = 4, то рівняння стає 0 ⋅ x = 0, що є тотожністю, і

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
2.46. Розв’яжіть рівняння:
1) ǀхǀ + 4х = 15
х + 4х = 15, х ≥ 0 або -х + 4х = 15, х < 0
х = 3, х ≥ 0 або х = 5, х < 0
х = 3 2) ǀ7хǀ - х = 24 7х – х = 24, х ≥ 0 або 7(-х) – х = 24, х < 0 х = 4, х ≥ 0 або х = -3, х < 0 х = 4 або х = -3
2.47. Знайдіть значення виразу:
1) 4а + 12b + 8а, якщо а = -13; b = 13.
4 ⋅ (-13) + 12 ⋅ 13 + 8 ⋅ (-13) = -52 + 156 – 104 = 0
2) (3х
2.48. Знайдіть число, якщо: 1) 15% його
300 : 0,15 = 2000
2) 11% його дорівнюються 28,16 28,16 : 0,11 = 256
2.49. Зведіть подібні доданки: 1) 7х – 2у + 3х +
3) -
+
4) 5 1 2 р − 2 5 6 а + 7 1 2 р + 4 1
2.50. Розкрийте дужки і спростіть
1) а – (а – (2а – 8)) = a – (a – 2a + 8) = a – (-a + 8) = a + a – 8 = 2a - 8
2) 5m – ((n – m) + 3n) = 5m – (n – m + 3n) = 5m – (4n – m) = 5m – 4n + m = 6m – 4n
3) 15a – (2a – (3a – (a + 1))) = 15a – (2a – (3a – a – 1))) = 15a – (2a – (2a – 1)) = 15a – (2a – 2a + 1) = 15a - 1
4) b – (b – ((b – a) – 2a)) = b – (b – (b – a – 2a)) = b – (b – (b – 3a)) = b – (b – b + 3a) = b – 3a
2.51. Добова

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
x + (х – 6) = 62
2х – 6 = 62
2х = 68
х = 68 : 2
х = 34 (тюльпанів) - на
х – 6 = 34 – 6 = 28 (тюльпанів) - на
2.55. Відомо, що х + у = 13. Для яких
найбільшого значення?
Щоб знайти найбільше значення
рівнянню x + y = 13, спробуємо
дорівнює 13):
При a = 1: y = 13 – 1 = 12, тоді xy = 1 ⋅ 12 = 12
При a = 2: y = 13 – 2 = 11, тоді xy = 2 ⋅ 11 = 22
При a = 3: y = 13 – 3 = 10, тоді xy = 3 ⋅ 10 = 30
При a = 4: y = 13 – 4 = 9, тоді xy = 4 ⋅ 9 = 36
При a = 5: y = 13 – 5 = 8, тоді xy = 5 ⋅ 8 = 40
При a = 6: y = 13 – 6 = 7, тоді xy = 6 ⋅ 7 = 42
При a = 7: y = 13 – 7 = 6, тоді xy = 7 ⋅ 6 = 42
При a = 8: y = 13 – 8 = 5, тоді xy = 8 ⋅ 5 = 40
При a = 9: y = 13 – 9 = 4, тоді xy = 9 ⋅ 4 = 36
При a = 10: y = 13 – 10 = 3, тоді xy = 10 ⋅ 3 = 30
При a = 11: y = 13 – 11 = 2, тоді xy = 11 ⋅ 2 = 22
При a = 12: y = 13 – 12 = 1, тоді xy = 12 ⋅ 1 = 12
Отже, максимальне значення xy досягається при a = 6 або a = 7, коли xy = 42.
Отже, для натуральних значень x і y, які задовольняють x + y = 13, максимальне значення виразу xy дорівнює 42 і досягається при x = 6 і y = 7 або навпаки.

3.5.
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
3.6.
3.7.
3.8.
течії, тобто 24 − x км/год.
3.9. Загадали
матимемо 12. Яке число загадали?
Нехай загадане число буде x.
Складемо рівняння на основі умови:
х 7 9 = 12
Помножимо обидві частини рівняння
x – 7 = 108
Додамо 7 до обох частин рівняння: x = 115
Отже, загадане число дорівнює 115. 3.10. Знайдіть
Нехай це число буде х. Тоді половина цього числа
2x
2x

2x
маму на 25 років?
Нехай вік мами дорівнює x років.
Тоді
Згідно з умовою, сумарний
x + (x + 25) = 99
2x + 25 = 99
2x = 74
x = 37
Отже, вік мами дорівнює 37 років,
два числа дорівнюють 5x і 7x,
цих чисел
7x = 7 ⋅ 20 = 140
ці числа 100 і 140. 3.16.
− 4x = 36
3x = 36 х = 36 3 = 12

7x = 7 ⋅ 12 = 84
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
x + (x + 1) + (x + 1) = 20
x + x + 1 + x + 1 = 20
3x =

x + 3 = x +
x + 3 = 1,05x
3 = 0,05x
х = 3
0,05 = 60 Отже,
x + 3 = 60 + 3 = 63 Таким
0,05x
1,05x = 11760
х = 11760
1
х = 11200
= v в. +
2v в. + 54 = 5v в.
54 = 3v в.

v в. = 54 : 3 = 18
a = l + 3
4a = 5l
Тепер підставимо a = l + 3 у рівняння 4a = 5l:
4(l + 3) = 5l
4l + 12 = 5l
12 = l
Знайдемо масу ящика з апельсинами: a = l + 3 = 12 + 3 = 15
Отже, маса
2b + 4 =
2b = 14

b = 14 : 2 = 7
Тепер
a = b + 4 = 7 + 4 =
оповідань.
Протягом
2x = x + 24
2x – x = 24
Таким чином,
2x = 2 ⋅ 24 = 48
Отже,
За умовою, після цього
3x – 18 = x
3x – x = 18
2x = 18
x = 9
Таким чином, Оля мала x=9 гривень спочатку.
3x

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
(x + 12) + 31 = x + 43 За умовою, загальна
x + (x + 12) + (x + 43) = 430
x + x + 12 + x + 43 = 430
3x + 55 = 430
3x = 375
x = 125
Отже, кількість подарованих наборів «Добре» дорівнює 125.
Кількість наборів «Солодко»:
x + 12 = 125 + 12 = 137
Кількість наборів «Смачно»: x + 43 = 125 + 43 = 168
Отже, було подаровано 125
«Смачно».
3.29. Одна сторона
Периметр
x + (x + 9) + 2x = 105
x + x + 9 + 2x = 105
4x + 9 = 105
4x = 96
x = 24
Отже, довжина першої сторони трикутника
Друга сторона дорівнює:
x + 9 = 24 + 9 = 33 см
Третя
2x = 2 ⋅ 24 = 48
3.30.
x + 2x + (x − 3) = 68 x + 2x + x – 3 = 68
4x – 3 = 68
4x = 71 х = 17,75

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
y = (x − 5) – 3 = x − 8 За умовою,
x + y + (x − 5) = 90
x + (x − 8) + (x − 5) = 90
x + x – 8 + x – 5 = 90
3x – 13 = 90
3x = 103
х = 34,33
Оскільки
38 + x = 3(10 + x)
38 + x = 30 + 3x
38 = 30 + 2x
8 = 2x
x = 4
3x – 12 = x + 12
3x – x – 12 = 12
2x – 12 = 12
2x = 24
x = 12
Отже,
3x = 3

х 24 = 1 4 (х + 24)
4(x − 24) = x + 24
4x – 96 = x + 24
4x – x – 96 = 24
3x – 96 = 24
3x = 120
x = 40 Отже,
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
х 8 = 1 2 (х + 8)
2(x − 8) = x + 8
2x – 16 = x + 8
2x – x – 16 = 8
x – 16 = 8
x = 24
Отже,
18x + 17y = 440
y = 25 − x
18x + 17(25 − x) = 440
18x + 425 − 17x = 440
x + 425 = 440
x = 15
y = 25 – x = 25 – 15 = 10

x + y = 12
Загальна
55x + 62,5y = 697,5 y = 12 − x
55x + 62,5(12 − x) = 697,5
55x + 750 − 62,5x = 697,5
−7,5x + 750 = 697,5
−7,5x = 697,5 − 750
−7,5x = −52,5
х = 7
Знайдемо y
першого
y = 12 – x = 12 – 7 =
Отже,
того, є ще три жінки: 3 Всі учні разом становлять:


https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
(v + 2) ⋅ 2,5 = (v − 2) ⋅ 3,6 − 7,6
2,5v + 5 = 3,6v − 7,2 − 7,6
2,5v + 5 = 3,6v − 14,8
5 + 14,8 = 3,6v − 2,5v
19,8 = 1,1v v = 18
Отже,
3.43.
Позначимо швидкість течії річки через u км/год.
Власна швидкість катера v = 16 км/год.
Відстань за течією = (v + u) ⋅ 1,6
Відстань проти течії = (v − u) ⋅ 2,5
Відомо, що відстань, подолана проти течії, на 6,2
течією:
(v − u) ⋅ 2,5 = (v + u) ⋅ 1,6 + 6,2 (16 − u) ⋅2,5 = (16 + u) ⋅ 1,6 + 6,2
40 − 2,5u = 25,6 + 1,6u + 6,2
40 − 2,5u = 31,8 + 1,6u
40 − 31,8 = 2,5u + 1,6u
8,2 = 4,1u u = 2
Отже,
12t + 45(t − 3) = 235,5
12t + 45t – 135 = 235,5
57t – 135 = 235,5
57t = 370,5
t = 6,5

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
Відстань,
14 (t + 2) + 4t = 73
14t + 28 + 4t =73
18t + 28 = 73
18t = 45 t = 2,5
Отже,
Відстань пішохода = 4 ⋅ 2,5 = 10 км
Отже, пішохід
виходу.
3.46.
x = y – 5
Перший
х = 1 3
Перший
x + z = 2y
x + 3x = 2y
4x = 2y
y = 2x
x = 2x − 5x
-х = -5
х = 5
у = 2х = 2 ⋅ 5 = 10
z = 3х = 3 ⋅ 5 = 15
2) 3х = у – 3 і х = 1 2 ���� маємо: z = 2х
3) Підставимо

х + z = 2,1у:
+ 2х = 2,1у
3.48.
4)

5) 0 : х = 13
6) 3(х + 1) = 3х
3.51. Знайдіть усі
1) додатний корінь Нехай x > 0. Тоді рівняння виглядає так: ax = −8
Щоб це рівняння мало додатний корінь x,
пояснюється тим, що для від'ємного a і додатного x, добуток ax буде від'ємним,
Отже, для додатного кореня x: a < 0
2) від’ємний корінь Нехай x < 0.

8:
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
якого рівняння є число 8?
А. х : 4 = 3
8 : 4 = 2
Це рівняння не підходить, оскільки 2 ≠ 3.
Б. х – 9 = 1
8 – 9 = −1
Це рівняння не підходить, оскільки −1 ≠ 1.
В. х + 7 = 15
8 + 7 = 15
Це рівняння підходить, оскільки 15 = 15.
Г. 2х = 10
2 ⋅ 8 = 16
Це рівняння не підходить, оскільки 16 ≠ 10.
2. Яке з рівнянь є лінійним?
А. 4х² = 5
Це рівняння є квадратним, оскільки ступінь змінної x дорівнює 2.
Б. х + 7 = х² Це
В. 3х + х² = 0
Це рівняння є квадратним, оскільки воно
Г. 2х = 0 Це рівняння є
3. Яке з рівнянь не має коренів?
А. 7х = 0
Це
Б. 0х = 7
Жодне значення x не
коренів.
В. 0х = 0
Будь-яке
коренів.
Г. 7х = 7

12 Б 16
буде 3x.
Разом книжок на обох полицях:
x + 3x = 4x
Відомо, що разом 48 книжок:
4x = 48
х = 12
Кількість книжок на більшій полиці: 3x = 3 ⋅ 12 = 36
Отже, кількість книжок на більшій полиці 36.
7. Укажіть рівняння, коренем якого є будь-яке число.
А. 12х = -8
Рівняння має один корінь
Б. 2(х – 1) = 2х
Це рівняння не має розв'язків.
В. 2(х – 1) = 2х – 2
Рівняння є ідентичним для будь-якого x.
Г. 2х = 2х – 2
Це рівняння не має розв'язків.
8. Знайдіть корінь рівняння х+2 5 + х 2 10 = 1 2 .
2(х + 2) + х – 2 = 5
2х + 4 + х – 2 = 5
3х + 2 = 5
3х = 5 – 2
3х = 3
х = 1
А. 0 Б. 1 В.
якщо рівняння
Розв'язок першого рівняння:
2x – 5 = 7
2x = 12 x = 6
Розв'язок
2x – 5 = −7
2x = −2 x = −1

0,8x = 2 7y x + y = 76
Вирішимо
у = 7 0,8х 2 у = 2,8х
Підставимо це
х + 2,8 = 76
3,8х = 76
х = 20
Знайдемо у:
у = 76 – х
у = 76 – 20
у = 56
Перевіряємо умову: 0,8 ⋅ 20 = 16
2 7 ⋅ 56 = 16
Оскільки
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
задачі (1-3) та відповідями до них (А-Г).
Питання:
1. Скільки яблук у першому кошику? х = 14
2. Скільки яблук у другому кошику? х + 6 = 14 + 6 = 20
3. Скільки яблук у третьому кошику? 2х = 2 ⋅ 14 = 28
Відповіді:
А. 28 ябл.
Б. 20 ябл.
В. 16 ябл.
Г. 14 ябл.
1 – Г, 2 – Б, 3 – А Завдання для перевірки
4 + 7 = 11 (не корінь)
2) 3х = 12
3 ⋅ 4 = 12 (корінь)
2.

1) -3х = 5 – 1 корінь
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
2) 0х = 7 – не має коренів
4. Розв’яжіть рівняння:
1) -4х = 12
-4х : (-4) = 12 : (-4)
х = -3
2) 0,2х – 1,2 = 0
0,2х = 1,2
х = 6
5. Чи рівносильні рівняння: 3х – 2 = х + 8 і 2(х – 3) = х – 1?
1) 3x – 2 = x + 8
3x – x – 2 = 8
2x = 10 x = 5 2) 2(x − 3) = x − 1 2x – 6 = x – 1 2x – x – 6 = −1 x = 5 Обидва
x + 2x = 78
3х = 78
х = 26
2x = 2 ⋅ 26 = 52
Отже, у
1) 2х+1 5 + 3х 2 4 = 2
4(2х + 1) + 5(3х – 2) = 40
8х + 4 + 15х – 10 = 40
23х – 6 = 40
23х = 40 + 6
23х = 46
х = 2
2) 5х – (х + 5) = 4(х – 2)
5х – х – 5 = 4х – 8
4х – 5 = 4х – 8 -5 = -8 Розв’язку немає

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
що відстань
d1 = d2 + 9,8
(v + 2) ⋅ 3,5 = (v − 2) ⋅ 4,2 + 9,8
3,5v + 7 = 4,2v − 8,4 + 9,8
3,5v + 7 = 4,2v + 1,4
7 = 0,7v + 1,4
5,6 = 0,7v v = 8
Отже, власна швидкість човна дорівнює 8 км/год. Додаткові завдання
9. Розв’яжіть рівняння ǀ4х - 3ǀ = 5.
4х – 3 = 5 4х – 3 = -5 х = 2 х = -0,5
10. Знайдіть усі цілі значення а, для яких корінь
-6, 6, -3, 3, -2, 2, -1, 1.
11.
38 км − 8 км = 30 км від села.
Обчислимо час, за який велосипедистка
наздожене пішохода. Тоді:
Пішохід за цей час
яка залишилась до зустрічі):
4t + 16t = 30
20t = 30
t = 1,5 год
Отже, велосипедистка їхала 1,5 години
+ 3 = -2 ≠ 2
2) 2 – х = 7 – так
2 – (-5) = 2 + 5 = 7 = 7
3) х : 5 = 1 – ні -5 : 5 = -1 ≠ 1

2(2 − 2)(2 + 3) = 2 ⋅ 0 ⋅ 5 = 0
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
Отже, число 2 є коренем рівняння.
2) Підставимо x = −3:
−3(−3 − 2)(−3 + 3) = −3 ⋅ (−5) ⋅ 0 = 0
Отже, число -3 є коренем рівняння.
3) Підставимо x=0:
0(0 − 2)(0 + 3) = 0 ⋅ (−2) ⋅ 3 = 0
Отже, число 0 є коренем рівняння.
Таким чином, кожне з чисел 2, -3 і 0 є коренем рівняння x(x − 2)(x + 3) = 0.
3. З’ясуйте, чи є рівносильними рівняння:
1) ǀхǀ = 2 і х(х + 2) = 0
ǀхǀ = 2
х = 2 або х = -2
х(х + 2) = 0
х = 0 або х = -2
Множини розв'язків не збігаються,
2) ǀхǀ = 4 і х² = 16
ǀхǀ = 4
х = 4 або х = -4
х² = 16
х = 4 або х = -4
розв'язків
4. Чи є правильним

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
5) 4,7х – 2 = 4,5х + 3
4,7х – 4,5х = 3 + 2
0,2х = 5
х = 25
6) 2х – 3 – (3х – 2) = -8
2х – 3 – 3х + 2 = -8
-х – 1 = -8 -х = -8 + 1
-х = -7
х = 7
7. Знайдіть корінь рівняння:
1) 10(2х – 7) – 5(4х – 2) = -60
20х – 70 – 20х + 10 = -60 -60 = -60
Розв’язку немає
3) 3х+1 7 + 2х+1 5 = 2
5(3х + 1) + 7(2х + 1) = 70
15х + 5 + 14х + 7 = 70
29х + 12 = 70
29х = 70 – 12
29х = 58
х = 2
8. Для якого значення а: 1) рівняння ах = 8 не має коренів Для рівняння ax = 8
нулю. Тобто:
Якщо a ≠ 0, то рівняння має єдиний
Якщо a = 0, то рівняння стає 0 ⋅ x = 8, що
може дорівнювати 8.
Отже, рівняння ax = 8 не має коренів, якщо
2) 3(5х – 4) – (15х – 2) = 9 15х – 12 – 15х + 2 = 9 -10 = 9 Розв’язку немає

2(2х + 1) – (7 – х) = 3(5х – 3)
4х + 2 – 7 + х = 15х – 9
5х – 5 = 15х – 9
5х – 15х = -9 + 5 -10х = -4 х = 2 5 = 0,4
щоб рівняння (a + 3)x = a + 3 мало будь-яке число як корінь,
кількість автівок.
Позначимо кількість відремонтованих
Нехай ширина прямокутника дорівнює х
: 2) = 18 см. Складаємо рівняння:
х + 2х = 18
3х = 18
х = 6 (см) – ширина прямокутника;
2 ⋅ 6 = 12 (см) – довжина прямокутника;
6 ⋅ 12 = 72 (см²) – площа прямокутника.
Відповідь:6 см, 12 см, 72 см².
12. За 7 олівців
7х + 3(х + 4,95) = 50,85
7х + 3х + 14,85 = 50,85
10х = 36
х = 3,6

4,5(14 + х) = 6(14 – х)
63 + 4,5х = 84 – 6х
4,5х + 6х = 84 – 63
10,5х = 21
х = 2
Отже, швидкість
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
2,5х = 2(х + 15)
2,5х = 2х + 30
2,5х – 2х = 30
0,5х = 30
х = 60
Отже, початкова
(60 – х) вареників,
Складаємо рівняння:
60 – х = 2(60 – 3х)
60 – х = 120 – 6х –х + 6х = 120 – 60
5х = 60
х = 12 (в.) – було на I тарілці;
60 – 12 = 48 (в.) – залишилося на I тарілціі;
3 ⋅ 12 = 36 (в.) – було на II тарілці;
60 – 36 = 24 (в.) – залишилося на II тарілціі.
Відповідь: 48 вареників і 24 вареники. Відповідь:48 вареників, 24 вареники.
17. Для преміювання

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
11 000x – 12 000x = −6000 – 2000
−1000x = −8000
x = 8 – кількість
y = 11 000 ⋅ 8 + 2000
y = 88 000 + 2000
y = 90
що залишилися
95 − 7x
Через x днів кількість лимонів, що залишилися
60 − 6x
За умовою задачі, у
другій:
95 − 7x = 2(60 − 6x)
95 − 7x = 120 − 12x
95 + 5x = 120
5x =25 x = 5 (дн.)
Відповідь:через
Позначимо
розчину як y.
Загальна маса розчину: x + y = 180
Маса добрива в розчинах: 0,15x + 0,05y = 0,075 ⋅ 180
0,15x + 0,05y = 13,5
y = 180 – x
0,15x + 0,05(180 − x) = 13,5
0,15x + 9 – 0,05x = 13,5
0,1x = 4,5
x = 45 (г)
y = 180 – 45 y = 135 (г)
Відповідь: взяли 45 грамів 15-

4.1.
2) Прямій
4)
4.2.


4.4. 1) CA, CD, CM, CN –
2) BD і DC, DK і
4.5. 1) На рисунку зображені промені – NM, NP, NK, NF.
2) Серед променів, зображених на
променів – NM і NK. 4.6.

4.7.

Можливі назви проведеної прямої – MN, MF, NF, FN, FM, NM.
Пряму можна ще назвати: BD, DB, BC, DC.
4.8. 1) Так, прямі m і CB перетинаються.
2) Прямій m належать точки A i L.
3) Прямій ВС належать точки С, В і Q.
4) Ані прямій m, ані прямій ВС не належать точки К і D. 4.9.


1) DP, DF, DE, EP, EF, PF.
2) Всього утворилося шість прямих.
3) Прямі розбивають площину на 16 частин.

4.11.


1)
Точки
Точки
4.12. (800 + 600) · 2 = 2800 (м) = 2,8 (км) – периметр парку; 1) 2,8 : 14 = 0,2 (год) = 60 · 0,2 = 15 (хв.) – витрачає на пробіжку Вадим; 2) 2800 : 50 = 56 (м/хв) – швидкість батьків Вадима.
Відповідь: 1) 15 хв, 2) 56 м/хв.
4.13.

4.14.
1) відрізки з кінцем у точці М: АМ, BM, NM; 2) відрізки з кінцем у точці N: BN, AN, MN; 3) відрізки з кінцем у точці А: MA, BA, NA; 4) відрізки з кінцем у точці В: AB, MB, NB.

4.15. Найменша загальна кількість
62 – 50 = 12 мм Відрізок AB < CD на 12 мм.
Відстань між двома точками
5.1. На рисунку зображені відрізки: АВ, АК, ВК, ВМ. АК = 38 мм, МВ = 12 мм.
5.2. На рисунку зображені відрізки: РС, PD, CD, PT. PC = 9 мм, PD = 31 мм, PT = 27 мм.
5.3. CD = 40 мм

5.4. АВ = 7 см 2 мм, MN = 6 см 3 мм. AB > MN, оскільки з двох відрізків більшим вважають той, довжина якого більша.


https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
5.5. KL = 5 см 9 мм, FP = 6 см 8 мм. FP > KL,

5.6. Оскільки
1) АВ = АС + СВ = 5 см + 2 см = 7 см.
маємо:
2) АВ = АС + ВС. Звідси ВС = АВ – АС = 12 дм – 9 дм = 3 дм.
5.7. 1) PQ = PK + KQ = 3 дм + 7 дм = 10 дм.
2) PQ = PK + KQ. Звідси PK = PQ – KQ = 8 см – 6 см = 2 см.
5.8. 1) Точки К, L і M лежать на одній прямій, оскільки KM = KL + LM, KM = 8 см + 3 см = 11 см. Точка L лежить між точками К і M.
2) Точки К, L і М не лежать на одній прямій, оскільки найбільша відстань
дорівнює сумі двох інших відстаней: LM = 9 см ≠ KL + KM = 5 + 8 = 13 (см).
5.9.
+
= 7 см + 3 см = 10 см.
5.10.
5.12.
= CD + BC. Оскільки АВ = CD, маємо BD = AB + BC, тому AC = BD.
5.13. Згідно з основною властивістю вимірювання
АС =
+ ВС, BD = CD + BC. Оскільки АС = BD, маємо AB + BC = CD + BC. Звідси AB = CD.
5.14. Згідно з основною властивістю вимірювання
AB = AC + CB, звідси CB = AB – AC = 40 см – 25 см = 15 см; AB = AD + BD, звідси AD = AB – BD = 40 см – 32 см = 8 см; AB = AD + CD + CB, звідси CD = AB – AD – CB = 40 см – 15 см – 8 см = 17 см.
Відповідь: 17 см.
5.15. За
CD = MC + MN + ND = 40 см + 50 см + 16 см = 106 см.
106 см.

5.16. Задача
CD = CM + MD = 5,2 см + 4,9 см = 10,1 см.

см – 4,9 см = 0,3 см.
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html

Відповідь: 10,1 см; 0,3 см.
5.17. Задача має два розв’язки.
І випадок.
AN = AM + MN = 7,2 см + 2,5 см = 9,7 см.
ІІ випадок.

AN = AM – MN = 7,2 см – 2,5 см = 4,7 см.
5.18. 1) AC втричі менший від BC:
Нехай AC = x, тоді BC = 3x.
Відрізок AB складається з AC і BC:
AC + BC = AB
x + 3x = 14 дм
4x = 14 дм
x = 3,5 дм – АС.
BC = 3 ⋅ 3,5 дм = 10,5 дм
2) AC більший за BC на 1,8 дм:
Нехай AC = y + 1,8, тоді BC = y.
Відрізок AB складається з AC і BC:
AC + BC = AB
(y + 1,8) + y = 14 дм
2y + 1,8 = 14 дм
2y = 14 дм – 1,8 дм
2y = 12,2 дм
y = 6,1 дм – ВС.
AC = 6,1 дм + 1,8 дм = 7,9 дм
3) AC : BC = 3 : 2:
Нехай AC = 3z, а BC = 2z.
Відрізок AB складається з AC і BC:
AC + BC = AB
3z + 2z = 14 дм
5z = 14 дм
z = 2,8 дм – АВ.
AC = 3 ⋅ 2,8 дм = 8,4 дм
BC = 2 ⋅ 2,8 дм = 5,6 дм
Тепер

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
10,5 дм 8,4 дм 7,9 дм 6,1 дм 5,6 дм 3,5 дм Х А Р К І В
Перша столиця України - Харків.
5.19. 1) CM більший за DM на 0,6 см:
Нехай DM = x, тоді CM = x + 0,6.
Відрізок CD складається з CM і DM:
CM + DM = CD
(x + 0,6) + x = 8,4 см
2x + 0,6 = 8,4 см
2x = 8,4 см – 0,6 см
2x = 7,8 см
x = 3,9 см – DM.
CM = 3,9 см + 0,6 см = 4,5 см
2) CM : DM = 1 : 3:
Нехай CM = y, а DM = 3y.
Відрізок CD складається з CM і DM:
CM + DM = CD
y + 3y = 8,4 см
4y = 8,4 см
y = 2,1 см – СМ.
DM = 3 ⋅ 2,1 см = 6,3 см
Тепер
СМ більший за DM на 0,6 см
2,1 см 3,9 см 4,5 см 6,3 см С Т У С
Прізвище українського
5.20. 1)
S = πr²
де r - радіус круга,
π - математична константа.
Для r = 200 м:
S = π ⋅ (200 м)²
S = 3,14 ⋅ 40000 м²
S = 125600 м²
2) Довжина мотузка,
круга:
C = 2πr
де r - радіус круга.
Для r = 200 м:
C = 2π ⋅ 200 м
C = 2 ⋅ 3,14 ⋅ 200 м
C = 1256 м
Відповідь: 125600 м²; 1256 м.
5.21. 1) 52° - гострий
2) 180° - розгорнутий

3) 129° - тупий
4) 90° -
5) 2° - гострий кут (менше 90°)
6) 173° - тупий кут (більше 90°, але
5.22.

4) 110°

5.23.




2) L
кута, LB і LK – сторони кута BLK.
6.3. З даних кутів гострі кути: ∠А = 39°, ∠Q = 79°, ∠Р = 1°3, ∠К = 89°30; прямий кут:
= 90°; тупі кути: ∠С = 91°, ∠D = 170°, ∠F = 173°12; розгорнутий кут: ∠М = 180°.
6.4. З
кути: ∠L = 12°, ∠М = 89°; прямий
∠А = 90°; тупі кути: ∠К = 121°, ∠N = 93°12; розгорнутий кут: ∠Е = 180°.
6.5. На
другому малюнку промінь OK є бісектрисою.
OK не є бісектрисою.
6.6. 1) На малюнку зображені кути: АВС, ABD, DBC.
2) ∠АВС = 130°, ∠DBC = 70°.
3) ∠ABD = ∠ABC - ∠DBC = 130° - 70° = 60°.
6.7 ∠АМК = 45°, ∠PLF = 90°, ∠BNC = 100°.





6.10. BD – бісектриса кута АВС. ∠ABD = 70°, ∠DBC = 70°.

6.11. BD – бісектриса кута АВС. ∠АBD = 25°, ∠DBC = 25°.

6.12. 1) 7°13´ + 12°49´ = (7° + 12°) + (13´ + 49´) = 19° + 62´ = 19°+ 1°12´ = 20°12´
2) 52°17´ - 45°27´ = 51°77´ - 45°27´ = 6°50´
6.13. 1) 4° = 4 ⋅ 60´ = 240´
2°15´ = 2 ⋅ 60´ + 15´= 120´+ 15´ = 135´
2) 5´ = 5 ⋅ 60´´= 300´´
2° = 2 ⋅ 60´ ⋅ 60´´ = 7200´´
1°3´ = 60 ⋅ 60´´ + 3 ⋅ 60´´ = 3780´´


Оскільки
6.15

- ∠АРС = 108° - 68° = 40°.
6.16.

Оскільки градусна
6.17 1) 180°; 2) 90°; 3) 30°; 4) 120°.
6.18. 1) 90°; 2) 180°; 3) 150°; 4) 60°. 6.19.

= 2 3
=

= 2 3 ∙ 60° = 40°
= 60° - 40° = 20°

Згідно з умовою задачі ∠ВАК = 60% ∠МАВ. Отже, ∠ВАК = 70° ⋅ 0,6 = 42°.
∠МАК = ∠МАВ + ∠ВАК = 70° + 42° = 112°.
Відповідь:112°. 6.21.

Нехай АОС – заданий кут. ОМ – продовження сторони ОА за вершину О.
ОК – бісектриса кута АОС. ∠АОМ – розгорнутий, ∠АОМ = 180°.
∠КОМ = 142°, ∠АОМ = ∠АОК + ∠КОМ.
Отже, ∠АОК = 180° - 142° = 38°.
Оскільки ОК – бісектриса кута
Тоді ∠АОС = ∠АОК + ∠КОС =
Відповідь:76°. 6.22.


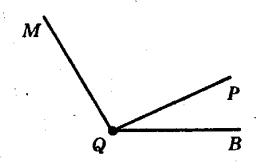
1. Нехай ∠PQB = х, тоді ∠MQP = 4х. Градусна
кутів, на які він розбивається променем, що
∠MQB = ∠MQP + ∠PQB. Складемо рівняння:
4х + х = 120°
5х = 120°
х = 24°
Отже, ∠PQB = 24°, ∠MQP = 24° ⋅ 4 = 96°.
2. Якщо ∠PQB : ∠MQP = 3 : 2, то
∠PQB = 3х, ∠MQP = 2х, тоді
3х + 2х = 120;
5х = 120°
х = 24°
Отже, ∠PQB = 3 ⋅ 24° = 72°, ∠MQP = 2 ⋅ 24° = 48°.
3. Якщо ∠PQB на 20° > ∠MQP, то
∠MQP = х, ∠PQB = х + 20°
За властивістю кутів:
х + х + 20 = 120
2х = 100
х = 50
Отже, ∠MQP = 50°, ∠PQB = 50° + 20° = 70°.
Відповідь:КРАВЧУК. 6.24.

1. Нехай ∠САN = х, тоді ∠МАС = х + 14. Оскільки ∠MAN = ∠МАС + ∠СAN (згідно з основною властивістю вимірювання кутів), то маємо:
х + х + 14 = 84
2х = 84 – 14
2х = 70
х = 35
Отже, ∠САN = 35°, ∠МАС = 35° + 14° = 49°.
2. Якщо ∠МАС у 3р. < ∠САN, то
∠МАС = х; ∠САN = 3х
За властивістю кутів:
х + 3х = 84
4х = 84

х = 21
Отже, ∠МАС = 21°; ∠САN = 21 · 3 = 63°
Відповідь:ВАРШАВА.
6.25.

Оскільки ∠АОВ = ∠АОК + ∠КОВ, то ∠КОВ = ∠АОВ - ∠АОК = 180° - 140° = 40°.
Оскільки ∠BOL = ∠LOK + ∠KOB, то ∠LOK = ∠BOL - ∠KOB = 100° - 40° = 60°.
Відповідь:60°.
6.26.

Оскільки ∠COD = ∠COM + ∠MOD, то ∠СОМ = ∠COD - ∠MOD = 90° - 80° = 10°
∠CON = ∠COM + ∠MON
∠MON = ∠CON - ∠COM = 70° - 10° = 60°.
Відповідь:60°.
6.27 28 м 50 см = 28,5 м
1) S = 28,5 ⋅ 16 = 456 (м2) – площа теплиці.
2) 456 ⋅ 30 = 13680 (кг) – кількість огірків.
3) 13680 ⋅ 18 = 246240 (грн) – виторг.
Відповідь:родина збере 13680 кг огірків; виторг від продажу огірків становитиме
246240 грн.
6.28

Відповідь:Кравчук.

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
8.1. На
8.2. 1) Ні, два
2) Так, оскільки 90° + 90° = 180°.
3) Так, суміжні кути можуть дорівнювати 166° і 14°, оскільки 166° + 14° = 180°.
4) Ні, суміжні кути не можуть дорівнювати 23° і 156°, оскільки 23° + 156° = 179°, а сума суміжних кутів дорівнює 180°.
8.3. 1) Так, оскільки 13° + 167° = 180°.
2) Ні, оскільки 5° + 165° = 170°, а сума суміжних кутів дорівнює 180°.
3) Ні, оскільки 11° + 179° = 190°, 190° не дорівнює 180°.
4) Так, оскільки 91° + 89° = 180°.
8.4. 1) Позначемо невідомий кут х.
180°, то маємо: 15° + х = 180°
х = 180° - 15°
х = 165°
2) Позначимо
113° + х = 180°
х = 180° - 113°
х = 67°
Відповідь: 165°; 67°.
8.5. 1) Позначемо
127° + х = 180°
х = 180° - 127°
х = 53°
2)
39° + х = 180°
х = 180° - 39°
х = 141°
Відповідь: 53°; 141°.
8.6.
KON = ∠KOM - ∠NOM = 180° - 50° = 130° Відповідь: 130°

8.7.
+ ∠
180°.
= 180°
+ 115° = 180°
= 180° - 115° = 65° Відповідь: 65°.


8.8. Нехай ∠BOD – даний кут,
∠BPD, ∠BOC = 72°, ∠COD = 15°.
∠BOD = ∠BOC + ∠COD = 72° + 15° = 87°
∠AOB суміжний з кутом BOD. Оскільки
∠BOD + ∠AOB = 180°
∠AOB = 180° - ∠BOD = 180° - 87° = 93°
Відповідь: 93°.

8.9. МК – бісектриса кута М, ∠KML = 36°, ∠LMK = ∠KMN, оскільки
два різних кути.
∠LMK = ∠KMN = 36°
∠LMN = ∠LMK + ∠KMN (згідно з основною
∠LMN = 36° + 36° = 72°. ∠BML суміжний
LMN.
дорівнює 180°, то ∠BML + ∠LMN = 180°, звідси:
∠BML = 180° - ∠LMN = 180° - 72° = 108°. Відповідь: 108°.

8.10. Спільна



https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
8.14. 1) Нехай ∠АОВ = х, тоді ∠СОА = х + 18°, маємо:
х + х + 18° = 180°
2х = 162°
х = 81° - ∠АОВ
∠СОА = 81° + 18° = 99°
2) Нехай ∠АОВ = х, тоді ВОС = 3 7 х, маємо:
х + 3 7 х = 180°
10
7 х = 180°
х = 180 ∶ 10 7
х = 126° - ∠АОВ
ВОС = 3 7 ∙ 126° = 54°
Відповідь: 1) 81° і 99°; 2) 126° і 54°.
8.15. 1) Нехай ∠АОВ = х, тоді ∠СОА = 3х, маємо:
х + 3х = 180°
4х = 180°
х = 45° - ∠АОВ.
∠СОА = 3 ⋅ 45° = 135°
2) х + 0,25х = 180
1,25х = 180
х = 180 : 1,25
х = 144°
180° - 144° = 36°
Відповідь: 1) 45° і 135°; 2) 144° і 36°.
8.16. ∠РМК = 140° може бути
= 2х,
LNS = 5х, тоді за теоремою про суміжні
ОМР + РМК = 180°
2х + 140 = 180
2х = 40
х = 20°
М = 2 ⋅ 20 = 40°
N = 5 ⋅ 20 = 100°
Відповідь: 40° і 100°.
8.17.
= 180° -
4х = 100°
х = 25°
∠В = 3 ⋅ 25° = 75°
100° і 75°.
8.18.

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html

8.19. Оскільки ∠АОВ : ∠KQM = 1 : 2, то нехай ∠АОВ = х, ∠KQM = 2х, тоді: ∠ВОС = 180° - х, ∠MQL = 180° - 2х. За умовою ∠BOC : ∠MQL = 7 : 5, тому:
180°−х
180°−2х = 7 5
5(180° - х) = 7(180° - 2х)
900° - 5х = 1260° - 14х
9х = 360°
х = 40° - ∠АОВ.
∠KMQ = 2 ⋅ 40° = 80°.
Відповідь: 40° і 80°.
8.20. Нехай ∠АОВ = х, ∠KQM = х + 20°, тоді: ∠ВОС = 180° - х, ∠MQL = 180° - (х + 20°).
Оскільки ∠АОВ < ∠KQM, то ∠ВОС > ∠MQL. За умовою ∠MQL: ∠BOC = 5 : 6, тому:
160°−х
180°−х = 5 6
960° - 6х = 900° - 5х
х = 60° - ∠АОВ.
∠KMQ = 60° + 20° = 80°.
Відповідь: 60° і 80°.
8.21. Нехай один із
1
випадок:
х = 2(х – (180° - х))
х = 2(2х - 180°)
х = 4х – 360°
3х = 360°
х = 120°
Суміжний з ним кут - 60°.
2 випадок:
180° - х = 2(х - 180° - х))
180° - х = 2(2х - 180°)
180° - х = 4х - 360°
5х = 540°
х = 108°
Суміжний з ним кут - 180° - 108° = 72°. Відповідь: 120° і 60° або 108° і 72°.
8.22.

8.23. Відстань
2,7 + 3,6 = 6,3 (см), або 3,6 – 2,7 = 0,9 (см).
Відповідь: 1) ні; 2) так; 3) ні; 4) ні; 5) так; 6) ні.
8.24. S кільці = S великого
– S
����

= �������� 2 −�������� 2 = ���� (���� 2 −���� 2 )
S
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
= 3,14 ⋅ (15² - 10²) = 3,14 ⋅ (225 – 100) = 3,14 ⋅ 125 = 392,5 (м²)
Відповідь: 392,5 м².
8.25. 1) КУТ; 2) ПРЯМА; 3) ЕВКЛІД; 4) ГЕОМЕТРІЯ. §9.
9.1. ∠АМР і ∠TMF; ∠AMF і ∠РМТ.
9.2. Ні, немає.
9.3. 1) За
вертикальний до кута 15°, дорівнює 15°.
2) За властивістю вертикальних кутів –
рівні. Отже, кут, вертикальний до кута 129°, дорівнює 129°.
9.4. 1) За властивістю
дорівнює 42°.
2) За властивістю вертикальні кути рівні.
139°.
9.5. Пари вертикальних кутів – це: ∠ВРС і ∠KPL, ∠APB i ∠LPM,
APC i
KPM,
APK i ∠CPM, ∠BPK i ∠LPC, ∠APL i ∠MPB.
9.6. При перетині двох прямих утворилося чотири кути. Нехай ∠КРN = 40°, тоді ∠LMP = 40°, бо за властивістю вертикальні кути рівні.

Тоді за властивістю суміжних кутів ∠KPL + ∠LPM = 180°, звідси ∠KPL = 180° - ∠LPM; ∠KPL = 180° - 40° = 140°. ∠KPL і ∠NPM – вертикальні. За властивістю вертикальні кути
рівні, отже, ∠NPM = 140°.
Відповідь: 40°; 140°; 140°.
9.7. ∠AML та ∠РМВ – вертикальні кути. ∠РМВ = ∠AML = 120°.
∠AML та ∠LMB – суміжні, отже, їх сума дорівнює 180°. ∠AML + ∠LMB = 180°, звідси ∠LMB = 180° - ∠AML; ∠LMB = 180° - 120° = 60°.
∠AMP та ∠LMB – вертикальні. ∠АМР = ∠LMB = 60°.
Відповідь: 60°; 120°; 60°.
9.8. Ні, кут між прямими – менший з кутів,
- 130° = 50°.
9.9. За означенням кутом
9.10.

9.11.

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
та ∠MON – суміжні,
= 180° -
MON = 180° - 110° = 70°. ∠NOL = ∠MOK = 70°.

Відповідь: 70°; 70°; 110°.
9.12. Оскільки OD доповняльний
DOP, ∠DOA та ∠РОВ –
Отже, ∠DOP = ∠AOB = 30°.
∠DOA + ∠AOB = 180°, ∠DOA + 30° = 180°, ∠DOA = 150°.

Відповідь: 30°; 150°; 150°. 9.13. 1)
х + х = 180°
2х = 180°
х = 90°
Відповідь: всі кути по
Сума двох будь-яких
9.14. 1) При перетині
суміжних. Оскільки сума суміжних
16°, то ці кути – вертикальні.
Один з кутів дорівнює 16° : 2 = 8°, а суміжний
2) Оскільки три з чотирьох кутів рівні, то
2х = 180°
= 90°
+ х +
2х = 162°
х = 81°

POB = ∠DOA = 150°.
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
х + 81° = 81° + 18° = 99°
2) ∠1 + ∠2 + ∠3 = 293°; отже, ∠3 = 293° - 180° = 113°.
Тоді ∠2 = 180° - 113° = 67° - кут між прямими.
3) х + 4 5 х = 180
1,8х = 180
х = 180 : 1,8
х = 100°
180° - 100° = 80°
Відповідь: 1) 81°; 2) 67°; 3) 100°.
9.16. 1) Два кути, які утворилися
суміжні,
вертикальні. Оскільки вертикальні кути рівні, то кути, про які йде мова у задачі, - суміжні.
Нехай ∠1 = х, тоді ∠2 = 2х, тоді:
х + 2х = 180°
3х = 180°
х = 60° - кут між прямими.
2) х + 0,2х = 180
1,2х = 180
х = 180 : 1,2
х = 150°
180° - 150° = 30°
Відповідь: 1) 60°; 2) 30°.
9.17. ∠АМК = ∠СМР (як вертикальні)
∠СМР = 180° - (∠ВМС + ∠LMP) = 180° - (20° + 60°) = 100°, отже ∠АМК = 100°
Відповідь: 100°.
9.18. ∠АМВ = ∠LMP (як вертикальні)
∠LMP = 180° - (∠KML + ∠CMP) = 180° - (25° + 105°) = 50°, отже ∠АМВ = 50°.
Відповідь: 50°.
9.19. ∠4 = ∠1 (як вертикальні)
∠1 + ∠2 + ∠3 = ∠4 + ∠2 + ∠3 = 180°

Відповідь: 180°.
9.20. Нехай ∠СОВ і ∠AOD – вертикальні, OL –
AOD. Доведемо, що ∠KOL = 180°. Оскільки ∠СОВ = ∠AOD, то ∠BOL =
рівних кутів.
∠KOL = ∠AOK + ∠AOC + ∠COL


https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
9.22. 1) Ні; 2) так; 3) ні; 4) ні; 5) так; 6) ні.
9.23. S вікна = 2 ⋅ 1,8 = 3,6 (м²)
3S вікон = 3,6 ⋅ 3 = 10,8 (м²)
S підлоги = довжина ⋅ ширину
35% від 14 = 14 ⋅ 0,35 = 4,9 (м)
S підлоги = 14 ⋅ 4,9 = 68,6 (м²)
����з вікон
���� підлоги = 10,8 68,6 ≈ 0,16 <0,2
Відповідь: норми дотримано.
9.24. 1) Маємо один квадрат 3 х 3, чотири квадрати – 2 х 2 та дев’ять
Всього 1 + 4 + 9 = 14 квадратів. 2)

1. Як прямій а, так і прямій b належить точка М.
Правильна відповідь – В)
2.
3.
– А) ∠М = 129°.

Отже, правильна відповідь – Б) 70°.



https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
180°, маємо:
х + 2х = 180°
3х = 180°
х = 60°
2х = 120°
Отже, правильна відповідь – Г) 120°.
10. Приавльна відповідь – В) 10.

11. ∠AON = ∠MON - ∠MOA = 180° - 120° = 60°
∠MOB = ∠MON - ∠NOB = 180° - 110° = 70°
∠BOA = ∠MON - ∠AON - ∠MOB = 180° - 60° - 70° = 50°

Отже, правильна відповідь – А) 50°.
12. Нехай градусна міра одного
- 180° - х, з другим - 180° - 2х, тоді:
180° - х – (180° - 2х) = 70°
180° - х - 180° + 2х = 70°
х = 70°
2х = 140°
Отже, правильна відповідь – Г) 140°.
13. AM — 30 см (Г)
MN — 20 см (А)
NB — 24 см (Б)
1. В ∈ а, D ∈ а, М ∉ а, С ∉ а.
2. 1) ∠А = 92° - тупий
2) ∠В = 180° - розгорнутий
3) ∠С = 90° - прямий
4) ∠D = 31° - гострий
3. ∠BAD і ∠KAN, ∠BAK i ∠DAN – вертикальні.
4. MN = CM + CN, звідски CM = MN – CN = 7,2 см – 3,4 см = 3,8 см.

Відповідь: 3,8 см.
5. ∠АОВ = 70°, ОС –



Відповідь: 48°.
7. AN = AB – BN = 30 – 16 = 14 (см)
MB = AB – AM = 30 – 20 = 10 (см)
MN = AB – (AN + MB) = 30 – (14 + 10) = 30 – 24 = 6 (см)

Відповідь: 6 см.
8.
180°, маємо:
х + х + 12° = 180°
2х = 168°
х = 84°
Отже, один з кутів дорівнює

Відповідь: 84°, 96°.

= АК + КВ = 9,3 + 3,7 = 13 (см)



Відповідь: 156°.
11. Нехай один з кутів х, тоді другий – 3х. Кут, суміжний з першим кутом - 180° - х, з другим - 180° - 3х. Градусні міри цих кутів відносяться, як 7 : 3, тоді:
180°−х
180°−3х = 7 3
3(180° - х) = 7(180° - 3х)
540 – 3х = 1260 – 21х
18х = 720°
х = 40°
Отже, один
40°, 120°.







АВ = 3 см 3 мм; ВС = 2 см; АС= 4 см.

DE = 2 см 5 мм; DF = 5 СМ; EF = 2 см 5 мм.

7. KL = 6 см 8 мм; КР = 43 мм = 4 см 3 мм.
KL = KP + PL (за основною
PL = KL – KP = 6 см 8 мм – 4 см 3 мм = 2 см 5 мм.
Відповідь:2 см 5 мм.
8. MN = MA + AN; MN = MB + BN
9. 1) Відрізок




Якщо АВ = 20 см, то АС = СВ = АВ 2 = 10 см
AD = 1 2 �������� = 1 2 ∙ 10 =5 (см)
АВ = AD + DB, звідси DB = AB – AD = 20 – 5 = 15 (см)
2) Якщо ВС = 12 дм, то АВ = 12 ⋅ 2 = 24 (дм)
АС = ВС = 12 дм
AD = 1 2 �������� = 1 2 ∙ 12 =6 (дм)
DB = AB – AD = 24 – 6 = 18 (дм) 11

CN = CD – DN = 15 – 11 = 4 (см)
NM = CM – CN = 12 – 4 = 8 (см)
Відповідь:8 см.
12. 1 випадок

АК = КР = АР

;

CD = а, L – середина



18.
2) За 12 годин годинна стрілка обертається на 360°. Отже, за 1

OL – бісектриса, ∠КОВ = 60°, ОТЖЕ ∠LOK = 1 2 ∠K�������� = 1 2 ∙ 60° = 30°.

OL – бісектриса кута КОВ, отже, ∠КОВ = 2∠LOB = 2 ⋅ 37° = 74°
ОК -бісектриса кута АОВ, отже, ∠АОВ = 2∠КОВ – 2 ⋅ 74° = 148°
стрілка повертається на 360° : 12 = 30°, тому за 1 хв стрілка повернеться на 30° : 60 = 0,5° = 30´, за 6 хв – на 30´ ⋅ 6 = 180´ = 3°, за 40 хв – на 30´ ⋅ 40 = 1200´ = 20°. 19. ОК – бісектриса, ∠АОВ = 120°, отже, ∠АОК = ∠КОВ = 120° : 2 = 60°.
20. 1) ∠АОЕ = ∠АОВ + ∠ВОС + ∠COD + ∠DOE (згідно з основною властивістю вимірювання кутів).
Оскільки ∠АОВ = ∠ВОС, ∠COD = ∠DOE, то ∠АОЕ = 2(∠ВОС + ∠COD) = 2∠BOD
∠BOD = ∠AOE : 2 = 140° : 2 = 70°.
2) ∠BOD = ∠AOB + ∠DOE, оскільки ∠BOD = ∠BOC + ∠COD і ∠AOB = ∠BOC, ∠COD = ∠DOE. Отже, ∠АОЕ = 2∠BOD = 2 ⋅ 73° = 146°
Відповідь:1) 70°; 2) 146°. 21.

Введемо
∠АОВ = ∠АОМ + ∠МОВ. Складемо рівняння:
3х + 4х = 168
7х = 168
х = 24
Отже, ∠АОМ = 3 ⋅ 24° = 72°, ∠МОВ = 4 ⋅ 24° = 96°.
= 3х, ∠МОВ =4х.

Відповідь:72° і 96°.
10.1. (Усно.)

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
10.8. Знайдіть значення виразу:
1) 5x – 3, якщо x = 1,8; х = 2 1 5;
5 ⋅ 1,8 – 3 = 9 – 3 = 6
5 ⋅ 2 1 5 – 3 = 5 ⋅ 11 5 – 3 = 11 – 3 = 8 2) a² + 3a, якщо a = –1; a = 0,8. (–1)² + 3 ⋅ (–1) = 1 – 3 = –2 0,8² + 3 ⋅ 0,8 = 0,64 + 2,4 = 3,04
10.9. Знайдіть значення виразу: 1) Якщо m = –1,3; n = 2 1 2;, тоді 5m + 2n = 5 ⋅ (–1,3) + 2 ⋅ 2 1 2 =
1,5
2) Якщо a = 1,5; b = 3,2; c = –1,4, тоді a(2b – c) = 1,5(2 ⋅ 3,2 – (–1,4)) = 1,5(6,4 – (–1,4)) = 1,5 ⋅ 7,8 = 11,7
10.10. Знайдіть значення виразу:
1) Якщо b = –2, тоді b² – 4b = (–2)² – 4 ⋅ (–2) = 4 + 8 = 12
Якщо b = 0,5, тоді b² – 4b = 0,5² – 4 ⋅ 0,5 = 0,25 – 2 = –1,75
2) Якщо x = 5; y = –3, тоді x² – y² = 5² – (–3)² = 25 – 9 = 16
Якщо x = 0,1; y = 0,2, тоді x² – y² = 0,1² – 0,2² = 0,01 – 0,04 = –0,03
10.11. Запишіть у вигляді виразу:
1) сума чисел b і c; b + c 2) добуток чисел 5m і n3; 5m ⋅ n3

10.15. Порівняйте
1) a + b < a ⋅ b
Якщо
10.16.
8x + 4y
⋅ b
10.17. (Усно.) Нехай
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
прямокутника
3) 2a; сума довжин прямокутника
4) ���� ���� . У скільки разів більша довжина
1)
2)
3)
Вираз: 45а + 15b + 10c
Якщо a = 6; b = 2; c = 3, тоді
якщо х = 8; у = 5; z = 20.
Вираз: 50х + 100у + 200z Якщо x = 8; y = 5; z = 20, тоді 50х +
4000 = 4900 (коп.) = 49 (грн)
Відповідь: 49 грн.
10.21. Спростіть вираз

10.22.
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
5 1 7 ���� 2,6���� + 1 6 7 ���� + 1,6���� = 7а – b Якщо a = 225, b = –40, тоді 7а – b = 7 ⋅ 225 – (–40) = 1575 + 40
академія». 10.23. Складіть формулу натурального числа, яке: 1) кратне числу 9; 2) при ділення на 5 дає в остачі 1.
1)
d² – (d – a)(d – b); 10.27. Обчисліть:
1) 13² = 13 ⋅ 13 = 169 2)

1) 14000 + 8000 ⋅ 2 + 10000 = 40000 (грн) – щомісячна
2) 40000 ⋅ 0,015 = 600 (грн) – щомісячний
3) 700 + 300 ⋅ 2 + 400 = 1700 (грн) – щомісячний
4) (1700 + 600) ⋅ 12 = 27600 (грн) –
Відповідь: 27600 грн.
10.31. Спростіть вираз:
1) За ⋅ 7 = 21а
3) –6,2а ⋅ 5b = –31ab 2) 2b ⋅ (–0,1) = –0,2b 4) –0,2с ⋅ (–0,5d) = 0,1cd
10.32. Розкрийте дужки:
1) 4(b + 1) = 4b + 4 4) –10(7 + а) = –70 – 10a 2) 3(m – 2) = 3m – 6 5) 5(–1,4 + k) = –7 + 5k 3) –7(с – 5) = –7c + 35 6) (t – 2,5) ⋅ (–8) = –8t + 20
10.33. Чи існує таке значення
1)
2)
3)
4)

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
3) 5x + y = y + 5x; Так,
4) b + b
5) 2(x – 3) = 2x – 6; Так,
6) 2a ⋅ b
11.3. (Усно.) Чи є тотожністю рівність:
1) 2x + 3y ≠ 6xy; Ні 2) 5a – 1 = –1 + 5a; Так 3) 9(a – b) ≠ 9a – 5b. Ні
11.4. Розкрийте дужки:
1) 2(m – 1) = 2m – 2 3) –(a – 5) = –a + 5 2) 9(3x + 2) = 27x + 18 4) –(–7 + 2m) = 7 – 2m
11.5. Розкрийте дужки:
1) –(m – 2) = –m + 2 2) 4(a + 1) = 4a + 4 3) 7(1 – 3p) = 7 – 21p 4) –(–3a + 5) = 3a – 5
11.6. Зведіть подібні доданки: 1) 2a – a = a 3) –3b – 2b = –5b 2) –5p + 7p = 2p 4) c – 8c = –7c
11.7. Назвіть
⋅ а = –8,4а
3) 0,2x ⋅ (–3у) = 0,2 ⋅ (–3) ⋅ х ⋅ у = –0,6ху 4) 1 1 3 ���� ∙ ( 3����) = 4 3 ∙ ( 3) ∙ ���� ∙ ���� = 4��������
11.10. (Усно.) Спростіть вираз:
1) 2x – 9 + 5x = 7x – 9
3) –2x ⋅ 3 = –6x 2) 7а – 3b + 2а + 3b = 9a 4) –4а ⋅ (–2b) = 8ab
11.11. Зведіть подібні доданки:
1) 5b – 8а + 4b – а = (5b + 4b) – (8a + a) = 9b – 9a
2) 17 – 2p + 3p + 19 = (–2p + 3p) + (17 + 19) = p + 36
3) 1,8а + 1,9b + 2,8а – 2,9b = (1,8a + 2,8a) + (1,9b – 2,9b) = 4,6a – b
4) 5 – 7c + 1,9p + 6,9c – 1,7p = 5 – (7c – 6,9c) + (1,9p – 1,7p) = 5 – 0,1c + 0,2p
11.12.
1) 4(5x – 7) + 3x + 13 = 20x – 28 + 3x + 13 = 23x – 15
2) 2(7 – 9а) – (4 – 18а) = 14 – 18a – 4 + 18a = 10
3) 3(2p – 7) – 2(p – 3) = 6p – 21 – 2p + 6 = 4p – 15
4) –(3m – 5) + 2(3m – 7) = –3m + 5 + 6m – 14 = 3m – 9
11.13.
1) 3(8а – 4) + 6а = 24a – 12 + 6a = 30a – 12
2) 7p – 2(3p – 1) = 7p – 6p + 2 = p + 2
3) 2(3x – 8) – 5(2x + 7) = 6x – 16 – 10x – 35 = –4x – 51

4) 3(5m – 7) – (15m – 2) = 15m – 21 – 15m + 2 = –19
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
1) 0,6x + 0,4(x – 20) = 0,6x + 0,4x – 8 = x – 8
Якщо x = 2,4, тоді x – 8 = 2,4 – 8 = –5,6
2) 1,3(2а – 1) – 16,4 = 2,6а – 1,3 – 16,4 = 2,6а – 17,7
Якщо а = 10, тоді 2,6а – 17,7 = 2,6 ⋅ 10 – 17,7 = 26 – 17,7 = 8,3
3) 1,2(m – 5) – 1,8(10 – m) = 1,2m – 6 – 18 + 1,8m = 3m – 24
Якщо m = –3,7, тоді 3m – 24 = 3 ⋅ (–3,7) – 24 = –11,1 – 24 = –35,1
4) 2x – 3(x + у) + 4у = 2х – 3х – 3у + 4у = –х + у
Якщо x = –1, у = 1,тоді –х + у = –(–1) + 1 = 1 + 1 = 2
11.15. Спростіть вираз і знайдіть його значення:
1) 0,7x + 0,3(x – 4) = 0,7х + 0,3х – 1,2 = х – 1,2
Якщо x = –0,7, тоді х – 1,2 = –0,7 – 1,2 = –1,9
2) 1,7(у – 11) – 16,3 = 1,7у – 18,7 – 16,3 = 1,7у – 35
Якщо у = 20, тоді 1,7у – 35 = 1,7 ⋅ 20 – 35 = 34 – 35 = –1
3) 0,6(2а – 14) – 0,4(5а – 1) = 1,2а – 8,4 – 2а + 0,4 = –0,8а – 8
Якщо а = –1, тоді –0,8а – 8 = –0,8 ⋅ (–1) – 8 = 0,8 – 8 = –7,2
4) 5(m – n) – 4m + 7n = 5m – 5n – 4m + 7n = m + 2n
Якщо m = 1,8; n = –0,9, тоді m + 2n = 1,8 + 2 ⋅ (–0,9) = 1,8 – 1,8 = 0
11.16. Доведіть тотожність:
1) –(2x – у) = у – 2x; –(2x – у) = –2х + у = у – 2х
2) 2(x – 1) – 2x = –2; 2(x – 1) – 2x = 2х – 2 – 2х = –2
3) 2(x – 3) + 3(x + 2) = 5x; 2(x – 3) + 3(x + 2) = 2х – 6 + 3х + 6 = 5x
4) c – 2 = 5(c + 2) – 4(c + 3). 5(c + 2) – 4(c + 3) = 5с + 10 – 4с – 12 = с – 2
11.17. Доведіть тотожність:
1) –(m – 3n) = 3n – m; –(m – 3n) = –m + 3n = 3n – m
2) 7(2 – p) + 7p = 14; 7(2 – p) + 7p = 14 – 7р + 7р = 14
3) 5a = 3(a – 4) + 2(a + 6); 3(a – 4) + 2(a + 6) = 3а – 12 + 2а + 12 = 5а 4) 4(m – 3) + 3(m + 3) = 7m – 3. 4(m – 3) + 3(m + 3) = 4m – 12 + 3m + 9 = 7m – 3
11.18. Довжина
3а + 4 см.
прямокутника. (х + (х + 3)) ⋅ 2 = (2х + 3) ⋅ 2 = 4х + 6 Відповідь: 4х + 6 см. 11.20.
1) х – (x – (2x – 3)) = х – (х – 2х + 3) = х – (–х + 3) = х + х – 3 = 2х – 3
2) 5m – ((n – m) + 3n) = 5m – (n – m + 3n) = 5m – n + m – 3n = 6m –4n
3) 4p – (3p – (2p – (p + 1))) = 4p – (3p – (2p – p – 1)) = 4p – (3p – (p – 1)) = 4p – (3p – p + 1) = 4p – (2p + 1) = 4p – 2p – 1 = 2p – 1
4) 5x – (2x – ((y – x) – 2y)) = 5x – (2x – ((y – x – 2y)) = 5x – (2x – (–y – x) = 5x – (2x + y + x)) = 5x – (3x + y) = 5x – 3x – y = 2x – y

1) a – (a – (3a – 1)) = a – (a – 3a + 1) = a – (–2a + 1) = a + 2a – 1 = 3a –
3) 5y – (6y – (7y – (8y – 1))) = 5y – (6y –
1) = 5y – 7y + 1 = –2y + 1 4)
11.22. Доведіть тотожність:
1) 10x – (–(5x + 20)) = 5(3x + 4);
10x – (–(5x + 20)) = 10x – (–5x – 20)) = 10x + 5x + 20 = 15x + 20 = 5(3x + 4)
2) –(–3p)–(–(8 – 5p)) = 2(4 – p); –(–3p)–(–(8 – 5p)) = 3p –(–8 + 5p) = 3p + 8 – 5p = 8 – 2p = 2(4 – p)
3) 3(a – b – c) + 5(a – b) + 3c = 8(a – b).
3(a – b – c) + 5(a – b) + 3c = 3a – 3b – 3c + 5a – 5b + 3c = = 3a – 3b – 3c + 5a – 5b + 3c = 8a – 8b = 8(a – b)
11.23. Доведіть тотожність:
1) 12a – (–(8a – 16)) = –4(4 – 5a); 12a – (–(8a – 16)) = 12a – (–8a + 16)) = 12a + 8a – 16 = 20a – 16 = –16 + 20a = = –4(4 – 5a)
2) 4(x + y – t) + 5(x – t) – 4y = 9(x – t).
4(x + y – t) + 5(x – t) – 4y = = 4x + 4y – 4t + 5x – 5t – 4y = 9x – 9t = 9(x – t) 11.24. Доведіть, що значення
1,8(m – 2) + 1,4(2 – m) + 0,2(1,7 – 2m) = 1,8m – 3,6 + 2,8 – 1,4m + 0,34 – 0,4m = –0,46 11.25. Доведіть,
тому самому числу. a – (a – (5a + 2)) – 5(a – 8) = a – (a – 5a –
парні числа: 2n; 2n + 2; 2n + 4,
2n + 2n + 2 + 2n + 4 = 6n + 6 = 6(n + 1),
11.27. Доведіть, що якщо n –
на 6
–2(2,5n – 7) + 2 1 3(3n – 6) = –5n + 14 + 7n – 14 = 2n, а 2n – парне число.
11.28. Сплав
15% = 0,15
1,6 ⋅ 0,15 = 0,24 (кг) – міді у сплаві.
0,24 кг. 11.29. Скільки
1) квадрата; 20² = 400; 20 400 ⋅ 100% = 0,05 ⋅ 100% = 5%

2) куба?
203 =
2(х – 12) + 3х = 56
2х – 24 + 3х = 56
5х = 80
х = 80 : 5
х = 16
Відповідь:
2x + 1 1 3 x = 200
2x + 4 3 x = 200 (6 3 + 4 3)x = 200 10 3 x = 200
х = 200 : 10 3
х = 200 ⋅ 3 10
x = 60 (км/хв) – швидкість;
60 ⋅ 2 = 120 (км) – довжина дороги туди;
60 ⋅ 1 1 3 = 60 ⋅ 4 3 = 80 (км) – довжина
Відповідь: 120 км і 80 км.
11.32. Обчисліть значення квадрата або куба:
1) (3,1)² = 3,1 ⋅ 3,1 = 9,61
2) (–5)3 = –5 ⋅ (–5) ⋅ (–5) = –125
3) ( 1 7)2 = 1 7 ∙ � 1 7� = 1 49
4) 0,13 = 0,1 ⋅ 0,1 ⋅ 0,1 = 0,001 5) �12�3 = 1 2 ∙ 1 2 ∙ 1 2 = 1 8 6) � 5
8) (1 1 2)2 = 1 1 2 ∙ 1 1 2 = 3 2 ∙ 3 2 = 9 4 11.33. Обчисліть:

1) (–1)2 + (–2)3 – 82 = 1 + (–8) – 64 = 1 – 8 – 64 = –71
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
2) (33 – (–4)2) ⋅ 7 = (27 – 16) ⋅ 7 = 11 ⋅ 7 = 77
12.2. Запишіть
1) 0,5 ⋅ 0,5 = 0,5²
2) (–7 ) ⋅ (–7 ) ⋅ (–7) = (–7)3
3) 1 8 ∙ 1 8 ∙ 1 8 ∙ 1 8 ∙
12.3. Подайте добуток
6) xy ⋅ xy = (xy)² 7) p ⋅ p ⋅ p ... ⋅ p (18 множників) = p18 8) (m – p)(m – p)(m – p) = (m – p)3
1) 0, 8 ⋅ 0, 8 ⋅ 0,8 = 0,83 2) –2 ⋅ (–2) ⋅ (–2) ⋅ (–2) = (–2)4 3) m ⋅ m ⋅ m ⋅ m ⋅ m = m5 4) (с + 3)(c + 3) = (c + 3)² 5) 1 9 ∙ 1 9 ∙
12.4. Запишіть

6) a ⋅ a ⋅ a ... ⋅ a (12 множників) = a12
6) (–
7) � 1 2

1)
2)
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
12.17. Обчисліть:
1) 0,5 ⋅ 40² = 0,5 ⋅ 1600 = 800
2) 30 0,33 = 30 ∶ 0,027 = 30 ∶ 27 1000 = 30 ∙ 1000 27 = 10000 9 =
3) 5 ∙ �15�3 = 5 ∙ 1 125 = 1 25
4) � 7 8�2 ∙ 16 = 49 64 ∙ 16 = 49 4 = 12,25
5) (12 ∶ 6 7)2 = �12 ∙ 7 6�2 = 142 = 196
6) �−3 ∙ 2 9�4 = �− 2 3�4 = 16 81
7) 6² – (–6)3 = 36 + 216 = 252
8) (1,7 – 1,9)4 = (–0,2)4 = 0,0016
9) (–2,5 + 8,5)² = 6² = 36
12.18. Чи є правильними рівності:
1) 3² + 4² = 5²; Так. 3² + 4² = 9 + 16 = 25, а 5² = 25, 25 = 25
2) 4² + 5² = 53; Ні. 4² + 5² = 16 + 25 = 41, a 6² = 36, 41 ≠ 36
3) 23 + 33 = 53; Ні. 23 + 33 = 8 + 27 = 35, а 53 = 125, 35 ≠ 125
4) 26 + 62 = 102; Так. 26 + 62 = 64 + 36 = 100, а 102 = 100, 100 = 100
5) 13 + 23 + 33 = 62; Так. 13 + 23 + 33 = 1 + 8 + 27 = 36, а 62 = 36, 36 = 36
6) (–5)² + (–12)² = (–13)²; Так. (–5)² + (–12)² = 25 + 144 = 169, а (–13)² = 169, 169 = 169
12.19. Подайте числа:
числа у вигляді квадрата; 0 = 0²; 4 = 2²; 0,16 = 0,4²; 9 25 = �35�2 ; 169 = 13²; 1 24 25 = 49 25 = �75�2 2) Подайте числа у вигляді куба. 64 = 43; –27 = (–3)3; 0 = 03; 1 = 13; − 1 8 = �− 1 2�3 ; 1
12.20. Подайте числа: 1)
числа у
степеня з основою 5; 5 = 51; 125 = 53; 625 = 54
2) Подайте числа у вигляді степеня з основою 10. 100 = 102; 10 000 = 104; 10 = 101 12.21. Подайте: 1) Подайте у вигляді квадрата
числа; 8 = 23; 81 = 92; –125 = (–5)3; –64 = (–4)3; 0,16 = 0,42; 0,001 =
; 1 11 25 = 36 25 = �65�2
2) Подайте у вигляді степеня з основою 2; 2 = 21; 4 = 22; 8 = 23; 256 = 28
3) Подайте у вигляді степеня з
–3. 81 = (–3)4; –27 = (–3)3; –3 = (–3)1
12.22. Обчисліть:
1) сума квадратів чисел 0,6 і –0,7; 0,62 + (–0,7)2 = 0,36 + 0,49 = 0,85
2) квадрат суми чисел 5,7 і –6,3; (5,7 + (–6,3))2 = (–0,6)2 = 0,36 3) різниця кубів чисел 2,3 і 2,2; 2,33 – 2,23 = 12,167 – 10,648 = 1,519 4) куб суми чисел 8,2 і 1,8. (8,2 + 1,8)3 = 103 = 1000

2)
2)2 + (–2)3 = –2 + 4 + (–8) = –6
3) Якщо x = 1 3, тоді (15x)4 = (15 ⋅ 1 3)4 = 54 = 625
Якщо х = –1 5, тоді (15x)4 = (15 ⋅ (–1 5))4 = 34 = 81
4) Якщо a = –6; b = –8, тоді a² – b² = (–6)² – (–8)² = 36 – 64 = –28
12.24. Знайдіть значення виразу:
1) Якщо a = 2, тоді 0,01 ⋅ a4 = 0,01 ⋅ 24 = 0,01 ⋅ 16 = 0,16
Якщо а = –5, тоді 0,01 ⋅ a4 = 0,01 ⋅ (–5)4 = 0,01 ⋅ 625 = 6,25
Якщо а = 10, тоді 0,01 ⋅ a4 = 0,01 ⋅ 104 = 0,01 ⋅ 10000 = 100
2) Якщо c = 0,2, тоді 5c² – 4 = 5 ⋅ 0,2² – 4 = 5 ⋅ 0,04 – 4 = 0,2 – 4 = 3,8
Якщо с = –0,1, тоді 5c² – 4 = 5 ⋅ (–0,1)² – 4 = 5 ⋅ 0,01 – 4 = 0,05 – 4 = –3,95
Якщо c = 0, тоді 5c² – 4 = 5 ⋅ 0² – 4 = 0 – 4 = –4
3) Якщо m = –4, n = –1, тоді (m + n)3 = (–4 + (
4) Якщо x = 1, тоді 4x2 – x3 = 4 ⋅ 12 – 13 =
12.25. Не виконуючи обчислень, порівняйте: 1) –24 < (–2)4 2) (–7)3
12.26. Порівняйте значення виразів: 1) якщо x = 5; –3; 0, тоді –x2 і (–x)2: –52 < (–5)2 –(–3)2 < (–(–3))2 –02 = (–0)2
–(–2)3 > (–(–2))3 –03 = (–0)3 –33 = (–3)3
12.27. Замініть «зірочку» знаком >, <, ≤, ≥ так, щоб нерівність
яких значень змінних:
1) a² ≥ 0
4) –р² – 1 < 0
7) x² + y² + 5 > 0
12.28.
1) a² + 1;
2) –b² ≤ 0
5) (a – 3)² ≥ 0 8) (m – n)² + 1 > 0
3) m² + 3 > 0
6) a² + b² > 0 9) –(р + 9)² ≤ 0
+ 1 = 1.
2) 3 + (m – 3)²;

(m – 3)² = 0, m
1) 48 : 4 = 12 (р.)
2)
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
на 4, тобто: N = 4 ⋅ k для деякого цілого числа k, то:
100 ⋅ q + r = 4 ⋅ k.

13.1. (Усно.)
1) a3 ⋅ a5 = a15; Ні 4) b6 : b2 = b4; Так
13.2. (Усно.)
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
2) a2 ⋅ a8 = a10; Так 5) (a5)7 = a35; Так
3) b20 : b4 = b5; Так 6) (a3)4 = a7? Ні
13.7.
1) (a4)5 = a20 2) (с7)2 = c14
13.13.
1) (–7)3 ⋅ (–7)4 ⋅ (–7) = (–7)8
3) bbbb9 = b12
5) 147 ⋅ 145 ⋅ 149 = 1421 2) аа5а11 =
13.14.
1) 123 ⋅ 129 ⋅ 12 = 1213 3) (a + b)3(a + b)5 = (a + b)8
13.15.
2 і 3 (див. № 307
1) 23 ⋅ 24 = 27 = 128
3) 3 ⋅ 33 ⋅ 34 = 38 = 6561 2) 36 : 3 = 35 = 243 4) 29 : 23 = 26 = 64
13.16. Виконайте
1) (xy)9 = x9y9
3) (0,1а)3 = 0,001a3
5) (–2а)5 = –32a5
7) (–4ab)3 = –64a3b3 2) (abc)7 = a7b7c7 4) (2xy)4 = 16x4y4 6) (–0,3а)2 = 0.09a2 8) (–2 3 ⋅ axz)4 = 16 81 ⋅ a4x4z4
13.17.
1) (ab)5 = a5b5
4) (–3 4 ac)4 = (–3 4)4a4c4

2) (2p)4 = 8p4 5) (–0,1m)3 = –0,001m3
3) (–5ax)3 = –125a3x3 6) (–0,07mx)2 = 0,027m2x2
13.22. Спростіть
1) а7 ⋅ а9 : а3 = a16 : a3 = a13 2) b9 : b5 : b3 = b4 : b3 = b 3) m12 : m7 ⋅ m = m5 ⋅ m = m6 4) p10 : p9 ⋅ p3 = p ⋅ p3 = p4
13.23. Запишіть
1) (а3)4 ⋅ а8 = a12 ⋅ a8 = a20
2) ((а7)2)3 = (a14)3 = a42
13.24.
3) (b³)2 : b4 = b6 : b4 = b2 4) (а4)5 ⋅ (а7)2 = a20 ⋅ a14 = a34
1) (b3)4 ⋅ b7 = b12 ⋅ b7 = b19 2) ((х4)5)6 = (x20)6 = x120 3) (с3)8 : с10 = c24 : c10 = c14 4) (m3)5 ⋅ (m2)7 = m15 ⋅ m14 = m29
13.25.
ab: 1) а5b5 = (ab)5 2) а3b3 = (ab)3
1) а4Ь4 = (ab)4
3) 0,001а3b3 = (0,1ab)3
5) –32а5b5 = (–2ab)5
7) 1 27 х3у3 = (1 3 ⋅ x ⋅ y)3
13.28.
1) 35 ⋅ 32 = 35+х; правильно для x = 2
2) 27 ⋅ 28 = 21+х;
–64 125 p3q3 = (–4 5 ⋅ p ⋅ q)3
для x = 14 3) 4х ⋅ 45 = 48; правильно для x = 3 4) 98 : 9х = 95. правильно для x = 3 13.29. Знайдіть
1) 1,89 : 1,8 = 1,89–х; правильно якщо x = 1
2) 19х : 197 = 199; правильно якщо x = 16
3) 412 : 4х = 47. правильно якщо x = 5

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
1) p7 : p4 = p3 2) p14 : p5 = p9 3) p9 : p5 ⋅ p3 = p7 4) p15 : p9 ⋅ p4 = p10
1)
2; 87 = (23)7 = 221; (163)5 = (24)3)5) = 260
2) Подайте вираз у
степеня з
5. 253 = (52)3 = 56; 6257 = (54)7 = 528
13.33. Подайте вираз: 1) Подайте
97 = (32)7) = 314; (813)5 = ((34)3)5 = 360
2) Подайте
1004 = (102)4 = 108; 10009 = (103)9 = 1027 13.34.
1) 256 : 25 = 28 : 25 = 23 = 8
2) 243 : 34 ⋅ 9 = 35 : 34 ⋅ 9 = 35 : 34 ⋅ 32 = 3 ⋅ 32
3)
4)
1) x5xn = x5+n
2) x8 : xn = x8–n, n < 8
3) xn : (x8 ⋅ x9) = xn : x17 = xn–17, n > 17 4) x2n : xn ⋅ x3n+1 = xn ⋅ x3n+1 = x4n+1
5) ((xn)3)5 = x15n
6) (–x4)2n = x8n
13.36. Знайдіть значення виразу:
1) 53 ⋅ 23 = (5 ⋅ 2)3 = 103 = 1000
2) (1 4)2 ⋅ 202 = (1 4 ⋅ 20)2 = 52 = 25
3) 0,213 ⋅ 513 = (0,2 ⋅ 5)13 = 113 = 1
4) (1,5)7 ⋅ (1 1 3)7 = (1,5 ⋅ 4 3)7 = (15 10 ⋅ 4 3)7 = 27 = 128
5) 0,57 ⋅ 28 = (0,5 ⋅ 2)7 ⋅ 2 = 17 ⋅ 2 = 2
6) (1 1 2)6 ⋅ (2 3)8 = (3 2 ⋅ 2 3)6 ⋅ (2 3)2 =
13.37. Обчисліть:
0,257 ⋅
(
3) (1 1 8)9 ⋅ (8 9)10 = (9 8 ⋅ 8 9)9 ⋅ 8 9 = 8
4) 1,57 ⋅ (2 3)9 = (15
1) 95 37 = (32 )5 37 = 310
2)

3)
13.42. Спростіть вираз:
1) 5,2 ⋅ 6а = 31,2a
2) –4,5b ⋅ 8 = –36b
3) –5x ⋅ (
1) а + b – с = 5 – (–2) = 5 + 2 = 7 2) а – 2с + b = (a + b) – 2c = 5 – 2 ⋅ (–2) = 5 + 4 = 9 3) ����+����+���� ���� = 5 2 2 = 3 2 = 3 2 = 1,5 4) с(а + b – 4с) = (–2)(5 – 4 ⋅ (–2)) = –2

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
1) 4000 – 4000 ⋅ (0,18 + 0,015) = 4000 –
2) 3220 : 2 = 1610 (грн)
3) 1610 : 100 = 16,1 (кв.)
Найбільша кількість троянд в
Відповідь: 15 троянд. 13.47.
1) 5с коефіцієнт буквеного
2)
3) 0,17kb
4) –1 3 ⋅
5)
6)
2) x1 + х2 = х3 + x4 + х5, причому, якщо припустити, наприклад,
числа різні, тому таке розбиття неможливе.
Отже, таке
лише одним способом. §14. Одночлен. Стандартний вигляд
14.1. (Усно.)
Одночлени: 1) 4,5a²b; 2) -0,45mpc; 4) p · (-0,2); 5) a²am; 8) c¹² · c³; 10) -m; 11) -4,9; 12) 0. Не є одночленами: 3) a² - 9; 6) (2 3p + 7)m; 7) x - y; 9) 5(m + p)⁷.
14.2. (Усно.) Назвіть одночлени
Одночленами стандартного вигляду є: 1) 5xy - коефіцієнт 5; 4) -a⁷b³ - коефіцієнт -1; 6) -2xyt - коефіцієнт -2; 7) x⁹c⁷ - коефіцієнт 1; 8) 17 - коефіцієнт 17;

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
1) 5a · 3b; 2) -7x²y; 4) x · xy · 7; 6) -m²; 8) -145; 10) p¹⁸; 12) -xytm. Одночлени, що
2) -7x²y; 6) -m²; 8) -145; 10) p¹⁸; 12) -xytm. 14.4. Зведіть
1) 7a²a³ · a = 7a⁶; коефіцієнт 7, степінь 6; 2) 8 · a · 0,1m · 2p = 1,6amp; коефіцієнт 1,6, степінь 3; 3) 5t · (-4at) = -20at²; коефіцієнт -20, степінь 3; 4) -12 3m⁴ · 12m²p = -20m⁶p; коефіцієнт -20, степінь 7;
5) -5a² · 0,2am⁷ · (-10m) = 10a³m⁸; коефіцієнт 10, степінь 11; 6) t³ · (-p)⁷ · t = -p⁷t⁴; коефіцієнт -1, степінь 11.
14.5. Зведіть одночлен до стандартного вигляду, укажіть його коефіцієнт і степінь:
1) -7m²b · 8mb² = -56m³b³; коефіцієнт: -56, степінь: 6
2) 5m · 2a · (-3b) = -30abm; коефіцієнт: -30, степінь: 3
3) -7a · (-5a²) = 35a³; коефіцієнт: 35, степінь: 3
4) -2,2a² · 25 44a³p =5 4a⁵p; коефіцієнт:5 4, степінь: 6
5) -a · (-0,2a²p) · (-0,3p⁴) = -0,06a³p⁵; коефіцієнт: -0,06, степінь: 8
6) c⁵ · (-a) · (-c⁴a) · a⁷ = c⁹a⁹; коефіцієнт: 1, степінь: 18
14.6. Знайдіть значення одночлена:
1) Якщо a = 4, то 3,5a² = 3,5 · 4² = 3,5 · 16 = 56;
якщо a = 0,1, то 3,5a² = 3,5 · 0,1² = 3,5 · 0,01 = 0,035;
2) Якщо m = 0, то -4m³ = 0;
якщо m = -1, то -4m³ = -4 · (-1)³ = 4;
3) Якщо x = 1,4, y = -5, то 10xy = 10 · 1,4 · (-5) = -70;
4) Якщо a = 5, c = -2, то -0,01a²c = -0,01 · 5² · (-2) = 0,5.
14.7. Обчисліть значення одночлена:
1) 1,6a². Якщо a = -5, то 1,6 · (-5)² = 1,6 · 25 = 40;
якщо a = 0, то 1,6 · 0² = 0;
якщо a = -1, то 1,6 · (-1)² = 1,6;
2) 5b²c. Якщо b = 0,2, c = 0,1, то 5 · (0,2)² · 0,1 = 5 · 0,04 · 0,1 = 0,02; якщо b = -0,4, c = 2, то 5 · (-0,4)² · 2 = 5 · 0,16 · 2 = 1,6.
14.8. Заповніть таблицю
4a2 25 16 9 4
4 9 16 25 -2a2 -12,5 -8 -4,5 -2 -
14.9. Знайдіть:
1) значення x, для
-0,8x
0; 1; -1; 12; -0,8x = 0 x = 0 : (-0,8) x = 0 -0,8x = 1 x = 1 : (-0,8) x = -1,25 -0,8x = -1 x = -1 : (-0,8) x = 1,25 -0,8x = 12 x = 12 : (-0,8) x = -15
2) значення a і b, для яких значення одночлена 15ab дорівнює 10; -60; 0. 15ab = 10
ab = 10 15 ab = 2 3
Наприклад:

а = 2; b = 1 3
15ab = -60 ab = -60 : 15 ab = -4
Наприклад: а = 2; b = -2 15ab = 0 ab = 0 : 15
ab = 0
Наприклад: а = 7; b = 0
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
14.10. Знайдіть:
1)
-0,6a = 0
a = 0 : (-0,6)
a = 0 -0,6a = -3
2)
12xy = 15
xy = 15 12
xy = 5 4
Наприклад:
x = 5; y = 1 4
14.11. (Усно.)
a = -3 : (-0,6)
a = 5 -0,6a = 12
a = 12 : (-0,6)
a = -20 -0,6a = -300 a = -300 : (-0,6)
a = 500
12xy = -120
xy = -120 : 12
xy = -10
Наприклад: x = 5; y = -2
12xy = 0
xy = 0 : 12
xy = 0
Наприклад: x = 0; y = 4
1) Одночлен 7m2 для будь-яких
Ні, оскільки при m = 0 → 7m2 = 0;
2) Одночлен 1 16p4 для будь-яких значень p
Так, оскільки p4 > 0 при будь якому значенні p;
3) Одночлен −12a2 для будь-яких значень a
Ні, оскільки при a = 0 → −12a2 = 0;
4) Одночлен 8b3 для
Ні, оскільки при b = 0 → 8b3 = 0.
14.12. Знайдіть об'єм прямокутного паралелепіпеда, висота якого дорівнює x см, ширина у 3 рази більша за висоту, а довжина у 2 рази більша за ширину.
V = abc, де a довжина, b ширина, c висота. x см висота, 3x см ширина, довжина 2 · 3x = 6x. Отже, об'єм паралелепіпеда V = x · 3x · 6x = 18x³ (см³).
14.13. Ширина прямокутника дорівнює b дм, а довжина втричі більша
ширину. Знайдіть площу прямокутника. S = a · b. Ширина b дм, довжина 3b дм. S = b · 3b = 3b² (дм²).
14.14. Розкрийте дужки та спростіть вираз: 1) 3(12x − 5) + 4x = 36x − 15 + 4x = 40x − 15; 2) 7(a − 1) − 7a + 13 = 7a − 7 − 7a + 13 = 6; 3) 4,2(x − y) + 3,5(x + y) = 4,2x − 4,2y + 3,5x + 3,5y = 7,7x − 0,7y; 4) 12 − 5(1 − x) − 5x = 12 − 5 + 5x − 5x = 7.
14.15. Серед виразів 3(y – x); –3(x – y); –3x – 3y, –3x + 3y
виразу 3y – 3x. 3y − 3x = 3(y − x); 3y − 3x = -3(х − у).
14.16. Подружжя, Леонід
1) 4 · 4 = 16%
2) 100 000 · 0,16 = 16 000
3) 100
4) 17 000 – 16 000 = 1000 (грн).

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
14.17. Спростіть
1) -4a · (-0,5b) = 2ab; 2) 10c · 0,1d = cd; 3) 0,25y · (-40x) = -10yx; 4) 4c · (-2a) · (-3b) = 24cab. 14.18.
1) 9 · 1 = 9 (цифр) -
від 1 до 9);
2) 90 · 2 = 180 (цифр) - використав для нумерації сторінок двоцифровими
від 10 до 99);
3) 9 + 180 + х · 3 = 1890 (цифр) – використав всього цифр; 4) х = (1890 – 180 – 9) : 3 = 567 (сторінок) – з трицифровими числами.
5) 9 + 90 + 567 = 666 (сторінок)
Відповідь: у книжці 666 сторінок.
15.1. (Усно.) Перемножте одночлени:
1) 3x ∙ 5y = 15xy; 2) –a ∙ 2b =
Виконайте
8a ∙ (–
степеня.
) = –0,7m8n5; 6) –0,2m7p9 ∙ (–4m4p) = 0,8m11p10; 7) –0,6ab2c3 ∙ 0,5a3bc7 = –0,3a4b
15.3. Знайдіть добуток одночленів: 1) 20a ∙ (–0,5b) = –10ab; 2) –a2 ∙ (–3a7b) = 3a9b;
3) 5b ∙ (–1 5 b3) ∙ 2c = –2b4c; 4) 3 5xy3 ∙
5) 3 5 ab2 ∙ (–5 6 a3) ∙ 2b7 =
15.4. Перемножте одночлени: 1) –13x2y ∙ 12ху3 = –156х3у4; 2) 0,8mn8 ∙ 50m2n = 40m3n9; 3) –1 5 ab2 ∙ 15a2p ∙ (–1 3pb4) = 1
4) 20xy2 ∙ (–0,1)х2у ∙ 0,2х2y2 = 0,4х5y5 .
15.5.

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
15.8. Піднесіть до квадрата
1) (3а)2 = 9а2; 2) (2b2)2 = 4b4; 3) (–4a3b7)2 = 16a6b14; 4) (–0,1p9a4)2 = 0,01p18a8; 5) (–1 5 m5)2 = 1 25 m10; 6) (6 7p6m8)2 = 36 49p12m16 .
15.9. Піднесіть до куба одночлен: 1) (2р)3 = 8p3; 2) (7m5)3 = 343m15; 3) (–3a3b2)3 = –27а9b6; 4) (–0,1а7b2)3 = –0,001а21b6; 5) (1 4p6)3 = 1 64p18; 6) (–2 5 mn4)3 = –8 125 m3n12 .
15.10. Виконайте піднесення до степеня: 1) (–хy3)3= –х3y9; 2) (–7a2bc3)2 = 49а4b2c6; 3) (p3m4q5)4 = p12m16q20; 4) (–2a2b)4 = 16a8b4; 5) (1 6p2c5)3 = 1 216р6c15; 6) (–c5m10a3)5 = –c25m50a15
15.11. Подайте у
стандартного
1) (–5х)2 = 25x2; 2) (1 2p4)3 = 1 8р12; 3) (–0,2a2b3)4 = 0,0016а8b12; 4) (–ab7c5)6 = а6b42с30; 5) (–10a11b)5 = –100000a55b5; 6) (а8с10)7 = а56с70 .
15.12. Подайте вираз: 1)
1 9 x6 = (1 3 x3)2; 0,25m6p10 = (0,5m3p5)2; 121а18b2c4 = (11а9bс2)2;
15.13. Який одночлен
одночлена: 0,001а9 = (0,1а3)3; –125р3b12 = (–5pb4)3; 8 27 c6m15a21 = (2 3 c2m5a7)3 .
рівність була правильною: 1) (2m3)2 = 4m6; 2) (0,6р4q5)2 = 0,36p8q10; 3) (–2с3)3 = –8с9; 4) (10c2m4)3 = 1000c6m12; 5) (2аb2)4 = 16a4b8; 6) (с3p9)5 = с15p45 .
15.14. Який одночлен стандартного
одержати правильну рівність: 1) 3m5n11 ∙ 4m2n = 12m7n12; 2) 5а2b ∙ 1 5 ab6= a3b7; 3) –12mp ∙ (–2m2р) =

1) (8аb3)2 ∙ (0,5а3b)3 = 64а2b6 ∙ 0,125а9b3 = 8а11b9;
2) (3 4 m2n8)3 ∙ (–4m7)2 = 27 64 m6n24 ∙ 16m14 = 27 4 m20n24 = 63 4 m20n24; 3) –(–m2n3)4 ∙ (7m3n)2 = –m8n12 ∙ 49m6n2 = –49m14n14; 4) (–0,2х3с7)5 ∙ (10xc3)5 = (–0,2х3с7 ∙ 10xc3)5 = (–2х4с10)5 = –32х20с50.
15.20. Спростіть вираз: 1) (10m2n)2 ∙ (3mn2)3 = 100m4n2 ∙ 27m3n6 = 2700m7n8;
2) (–1 2 ab3)3 ∙ (4а5)2 = –1 8 a3b9 ∙ 16a10 = –2a13b9;
3) –(3a6m2)3 ∙ (–a2m)4 = –(27a18m6)(a8m4) = –27a26m10; 4) (–5ху6)4 ∙ (0,2x6y)4 = 625x4y24 ∙ 0,0016x24y4 = x28y28 .
15.21. Подайте
у
яких
: 1) 8a2b2 = –4ab2 ∙ (–2a); 2) –1 5 ab4 = –4ab2 ∙ 1 20b2;
3) –7,8a3b5 = –4ab2 ∙ 1,95a2b3; 4) 11 8 a3b2 = 9 8 a3b2 = –4ab2 ∙ (–9 32 a2).
15.22.
: 1) 12m2n2 = 3mn2 ∙ 4m;
–
∙ (–1 12)n3; 3) –6,9m7n8 = 3mn2 ∙ (–2,3m6n6); 4) 11 5 m8n2 = 6 5 m8n2 = 3mn2 ∙ 5 15 m7.
15.23. Запишіть
1) (–0,2an+5bn+2) ∙ (0,5n–2bn+3) = (–0,2 ∙ 0,5)(an+5an–2)(bn+2bn+3) = –0,1a2n+3b2n+5; 2) (2a2nb5)3 ∙ (–3а3b3n)2 = 8a6nb15 ∙ 9a6b6n = 72а6n+6b6n+15; 3) (a2b3)n ∙ (a2nb)3 ∙ (a2b3n)5 = a2nb3na6nb3a10b15n = a8n+10b18n+3; 4) (x2n–1y3n+1)2 ∙ (х3n–1y2n+1)3 = x4n–2y6n+2x9n–3y6n+3 = х13n–5y12n+5 . 15.24. Відомо, що 3ab2 = 7. Знайдіть значення виразу:
1) ab2 = 1 3 ∙ 3ab2. Якщо 3аb2 = 7, то 1 3 ∙ 3аb2 = 1 3 ∙ 7 = 21 3;
2) 5ab2 = 5 3 ∙ 3аb2. Якщо 3аb2 = 7, то 5 3
; 3) –9а2b4 = –3аb2 ∙ 3аb2. Якщо 3аb2 = 7, то –3ab2 ∙ 3аb2 = –
7 = –49; 4) 27a3b6 = (3ab2)3. Якщо 3аb2 = 7, то (3аb2)3 = 73 =
15.25. Відомо, що 5xy2 = 9.
1) хy2 = 5ху2 ∙ 1 5. Якщо 5xy2 = 9, то 5xy2 ∙
3) –25х2y4 = –(5ху2)2. Якщо 5xy2 = 9, то –(5хy2)2 = –92 = –81; 4) 125х3y6 = (5ху2)3

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
3х + 2y = 3 ∙ 20 + 2 ∙ 22 = 60 + 44 = 104 (шк.). Відповідь: 3х + 2у; 104 школярі.
15.27. Замініть
(b
2) (m2)
1) 1000 : 4 = 250 (родин) – мають автомобіль;
2) 1000 ∙ 0,05 = 50 (родин) – мають два автомобіля;
3) 50 ∙ 2 + 250 = 350 (шт.) – всього автомобілів;
4) 350 ∙ 10 = 3500 (кг) – гумового пилу.
Відповідь: 3500 кг.
15.30. Накресліть прямокутник ABCD

утворилися. ВА ⊥ ВС, BA ⊥ AD, CD ⊥ BC, CD ⊥AD 15.31. Видатні українці


вираз 1 – (a – 3)2? Найбільшого начення вираз набуватиме при (a – 3)2 = 0, тобто 1. А. 1☺ Б. -1 В. -3 Г. -8
із
2300, 3200, 7100, 2550 2300 = (23)100 = 8100; 3200 = (32)100 = 9100; 7100; 2550 = (52)50 = 5100; 5 < 7 < 8 < 9. А. 2300 Б. 3200☺ В. 7100 Г. 2550
Якщо 2ху2 = –5, то 8х2у4 = 2 ∙ (–5)2 = 50. А. 25 Б. -50 В. 50☺ Г. 100
1. 29 : 64 = 29 : 26 = 29 – 6 = 23 = 8 (В) 2. 1,54 ∙ �1 1 3�4 = �1 1 2�4 ∙ �1 1 3�4 = �3 2 ∙ 4 3�4 = (2)4 = 16 (Г)
3. 84 25 4 8 = (23 )4 25 (22 )8 = 212 25 216 = 217 216 = 2 (А)
1 – В, 2 – Г, 3 – А.

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
1) 3b + 4b і 7b; - так, оскільки 3b + 4b = 7b
2) a + a + a і a3; - ні, оскільки a + a + a = 3а ≠ a3
3) m + 2a і 2a + m; - так, оскільки m + 2a = 2a + m
4) 3(x – 2) і 3x – 2? - ні, оскільки 3(x – 2) = 3х – 6 ≠ 3x – 2
2. Подайте у вигляді степеня добуток: 1) 4 · 4 · 4 = 43; 2) –3 · (–3) · (–3) · (–3) · (–3) = (–3)5.
3. Виконайте дії: 1) x5x4 = x5+4 = x9; 2) x7 : x2 = x7–2 = x5. 4.
виразу: 1) 0,4 · (–5)4 = 0,4 · 625 = 250; 2) 25 – 43 + (–1)5 = 32 – 64 – 1 = -33.
)4
1) 0,2a2b
8. Доведіть тотожність: 2(a + b – c) + 3(a – c) – 2b = 5(a – c) 2(a + b – c) + 3(a – c) – 2b = 2a + 2b – 2c + 3a – 3c – 2b = 5a – 5c = 5(a – c).
9. Порівняйте вирази:
1) 512 і 256; 256 = (52)6 = 512, отже 512 = 256
2) 230 і 320. 230 = (23)10 = 810; 320 = (32)10 = 910; 8 < 9, тому 810 < 910. Отже 230 < 320
10. Доведіть, що сума трьох
переше
х + 2, а ще наступне
3(х + 2) – ділиться на 3. 11. Якого
0, якщо m = 0, тоді
m4 – 12
2) вираз (a + 2)8 ≥ 0
якщо a = -2,
12. Відомо, що 4m2n = 9.
1) 12m2n = 3 · 4m2n = 3 · 9 = 27; 2) 4m4n2 = 1 4 · 16m4n2 = 1 4 · (4m2n)2 = 1 4 · 92 = 81 4 =

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
: 10х + у;
2) двоцифрове число, у якому 5 десятків і a одиниць: 50 + а;
3) трицифрове число, у якому a сотень, b десятків і c одиниць: 100а + 10b + c; 4)
число, у якому m сотень, n десятків і 6 одиниць: 100m + 10n + 6.
4. Відомо, що x - y = 2 і p = 3. Знайдіть значення виразу:
1) x + p – y = (x - y) + p = 2 + 3 = 5;
2) x - y + 5p = 2 + 5 ⋅ 3 = 17;
3) (y - x)p = -(x - y) ⋅ p = -2 ⋅ 3 = -6;
4) 3(���� ����) ����+4(���� ���� ) = 3(���� ����) 4(���� ����
5) 7x - 7y – p = 7(x - y) – p = 7 ⋅ 2 – 3 = 14 – 3 = 11;
6 ���� 4 5(���� ���� )
5. Спростіть вираз:
1) 2 + 3a – 5 = 3a – 3; 2) 0,4m + m = 1,4m;
3) 3p - 2p + 5 = p + 5; 4) -(m - 3) = -m + 3.
6. Розкрийте дужки та зведіть
1) 7(5x + 8) - 12x = 35x + 56 - 12x = 23x + 56; 2) 9m + 3(15 - 4m) = 9m + 45 - 12m = -3m + 45; 3) 6(x + 1) - 6x - 9 = 6x + 6 - 6x - 9 = -3; 4) 12x - 2(3x - 5) = 12x - 6x + 10 = 6x + 10; 5) -(2x + 1) - 3(2x - 5) = -2x - 1 - 6x + 15 = -8x + 14; 6) 5(x - 2) - 4(2x - 3) = 5x - 10 - 8x + 12 = -3x + 2.
7. Доведіть тотожність:
1) 18(a - 2) = 12a - (20 - (6a - 16)); 18(a - 2) = 18a - 36; 12a - (20 - 6a + 16) = 12a - 20 + 6a - 16 = 18a - 36; 2) 2(x - y + t) - 3(x + y - t) - 5(t - y) = -x; 2x - 2y + 2t - 3x - 3y + 3t - 5t + 5y = -x.
8. Доведіть,
n, n + 1, n + 2
числа; n + (n + 1) + (n + 2) = 3n + 3 = 3(n + 1) ділиться на 3. 9.
1) |a + 5| = a + 5;
2) |m² + 1| = m² + 1; так
3) |m - n| = |n - m|; так

4) |a| + |b| = |a + b|?
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
1) 0,3 · 0,3 · 0,3 = 0,33;
2) -2 · (-2) · (-2) · (-2) = (-2)4; 3) aa = а2; 4) ����
1) m³ = m · m · m;
2) 17⁴ = 17 · 17 · 17 · 17; 3) (p + 2)² = (p + 2)(p + 2); 4) (���� 9 )⁵ = ���� 9 · ���� 9 ·
9 · ���� 9 · ���� 9 .
11. Обчисліть:
1) 2⁶ = 2 · 2 · 2 · 2 · 2 · 2 = 64; 2) (0,2)³ = 0,2 · 0,2 · 0,2 = 0,008;
3) (1 8)² =1 8 · (1 8) = 1 64;
4) (-11 6)³ =7 6 · (7 6) · (7 6) = 343 216;
5) -(-2)³ = -(-2) · (-2) · (-2) = -(-8) = 8;
6) - (1 4)² = -(1 4) · (1 4) =1 16;
7) -(-0,1)² = -(-0,1) · (-0,1) = -0,01;
8) -(-1)²⁷ = -(-1 · (-1) · … · (-1)) = -1 · (-1) = 1. (27 разів)
12. Не виконуючи обчислень, порівняйте з
1) (-1,7)¹⁵ · (-2,7)² < 0;
2) (-2,3)³ · (-5,89) > 0;
3) -3,7² · (-2,8)⁴ < 0;
4) -(-2,6)⁸ · (-5,7)⁵ > 0
13. Знайдіть останню цифру числа:
1) 2015¹³; остання цифра 5
2) 5011⁷; остання цифра 1
3) 1006¹⁷; остання цифра 6
4) 15⁹ + 16⁸ + 101¹⁷. остання цифра 2, оскільки 5 + 6 + 1 = 12
14. Чи є число:
1) 10¹⁷ + 5 кратним числу 3; так, тому що сума цифр 6 ділиться на 3 2) 10²⁹ + 7 кратним числу 9? Ні, тому що сума цифр 8
= b10; 2) a³a = a4;
9⁸ · 9⁷ = 915; 4) p¹⁰ : p³ = p7; 5) 19⁸ : 19⁶ = 192; 6) 7¹⁵ : 7¹⁴ = 7; 7) (a³)⁴ = a12; 8) (2⁵)³ = 215. 16. Обчисліть:
1) 3⁸ : 3⁷ = 3; 2) 2⁵ · 2¹² : 2¹⁵ = 217 : 215 = 22 = 4; 3) 104 ∙109 1010 = 1013 1010 = 103 = 1000; 4) 85 ∙810 811 83 = 815 815 = 81 = 8. 17. Знайдіть
1) (4⁷)ˣ = 4²¹;

7x = 21 x = 3 2) (3²)⁶ = 3³ˣ; 2x = 12 x = 6
3) (((1 7)ˣ)³)⁴ = (1 7)²⁴. 12x = 24 x = 2
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
1) 8⁴ⁿ; (84)n – остання цифра 6; 2) 7⁴ⁿ⁺¹; 7⁴ⁿ · 7
1) -a²c; 2) 7a · 2b · 4; 3) 17; 4) aaba; 5) 6(1 2 x1 3y); 6) p + 1; 7) -p²; 8) c⁹ - c²?
Одночлени: 1) -a²c; 2) 7a · 2b · 4; 3) 17; 4) aaba; 7) -p²;
У стандартному вигляді: 1) -a²c; 3) 17; 7) -p². 21. Зведіть одночлен
1)1 2 a²b · 2ab⁷ = -a3b8; коефіцієнт -1, степінь 11
2) 3m · (-2m²) · 5m⁷ = -30m10; коефіцієнт -30, степінь 10
3) -7ap² · 0,1a²p⁹ = -0.7a3p11; коефіцієнт -0,7, степінь 14
4) 11 8 m² · 8 9 mc² = m3c2; коефіцієнт 1, степінь 5
5) -a · (-b) · (-c) · (-5d) = 5abcd; коефіцієнт 5, степінь 4
6) p⁹ · (-2a²) · (-5p⁷) · a⁸ = 10a10p16 . коефіцієнт 10, степінь 26 22. Складіть два різних
a і b так, щоб: 1) степінь кожного з них дорівнював 7, а коефіцієнт
-8; 2) степінь
1) 1. -2ab · 4a · b5 = -8a2b5; 2. -a4b · 8ab = -8a5b2; 2) 1. -a2 · (-17b) = 17a2b; 2. 34a · (1 2b2) = 17ab2 До §15 23. Знайдіть
1) 3m ⋅ 2n = 6mn; 2) -4p ⋅ 2a = -8pa; 3) 8m² ⋅ 3n = 24m²n; 4) -2a³ ⋅ (-b⁷) = 2a³b⁷.
24. Подайте вираз у вигляді одночлена стандартного вигляду: 1) -2,5m² · (-4m³p) = 10m5p; 2) 12p²m · (5 5p³m⁷) = -10p5m8;
3) 0,6m⁷a⁹ · 10m²a⁷ · 1 2 m³ = 3m12a16; 4) (-mn⁷)³ = m3n21; 5) (-2a⁵b⁷)² = 4a10b14; 6) (m³p⁷a⁹)⁵ = m15p35a45 .
25. Знайдіть одночлен A, якщо: 1) A · 14m²n = 42m⁴n²; A = 3m2n; 2) 3p²q⁷ · A = -21p³q⁷. A = -7p.
26. Виконайте множення одночленів 0,4m · 10mn² та
якщо m = -2, n = 0,5. 0,4m · 10mn² = 4m3n. Якщо m = -2, n = 0,5, то 4 · (-2)3 · 0,5 = -16. 27.
1) 49m⁸n¹² = (7m4n6)2; 2) –25a⁴b⁸ - ні; 3) –0,2m⁴n² · (–5m²n⁴) = m6n6 = (m3n3)2; 4) – (–3a⁴)³ · 3a¹² = 27a12 · 3a12 = 81a24 = (9a12)2.




16.5.



https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
16.8.

16.9.

16.10. 1)
2)
16.11. 1) Дві прямі перпендикулярні, якщо вони перетинаються під прямим кутом.
∠МОА = ∠МОК - ∠АОК = 122° - 31° = 91°. Отже, прямі АВ і MN не перпендикулярні.
2)
МОВ = ∠MOL + ∠LOB = 59° + 31° = 90°.
1.
2. Відрізок може бути частиною перпендикуляра,
геометричному сенсі, оскільки перпендикуляр має
(прямою),
чином, правильніше сказати, що перпендикуляр
прямим кутом. Відрізок, який є частиною цієї прямої, також буде перпендикулярним до даної прямої, але це вже похідне поняття.
16.13. 1. 1) ∠CON = ∠COB - ∠NOB = 90° - 25° = 65°
2) ∠MOD = ∠CON = 65° (як вертикальні)
2. 1) ∠MOD = ∠MOB - ∠DOB = 150° - 90° = 60°
2) ∠CON = ∠MOD = 60° (як вертикальні)
Відповідь:1) 65°; 2) 60°.
16.14. 1. 1) ∠FOL = ∠NOF - ∠NOL = 140° - 90° = 50°
2) ∠KOP = ∠FOL = 50° (як вертикальні)
2. 1) ∠MOF = ∠PON = 37° (як вертикальні)
2) ∠KOF = ∠KOM + ∠MOF = 90° + 37° = 127°
Відповідь: 1) 50°; 2) 127°.
16.15. Промінь СВ – спільна
АВС + ∠СВМ = 90° + 90° = 180°. Отже, ці


суміжних кутів х + х = 180°, 2х = 180°, х = 90°. Отже,

16.17. 1) ∠BON = 180° - (∠AOE + ∠EON) = 180° - (20° + 110°) = 50°
2) ∠CON = ∠COB + ∠BON = 90° + 50° = 140°
Відповідь: 140°.
16.18. 1) ∠BON = ∠CON - ∠COB = 135° - 90° = 45°
2) ∠EOD = 180° - (∠AOE + ∠BON) = 180° - (25° + 45°) = 110°
Відповідь: 110°.
16.19. 1) Позначимо ∠AOB = ∠COD = x; ∠BOC = ∠DOE = y. Оскільки ∠АОВ + ∠BOC + ∠COD + ∠DOE = 180°, то 2х + 2у = 180°; 2(х + у) = 180°; х + у = 90°.
2) ∠АОС = ∠АОВ + ∠ВОС = х + у = 90°, тому ОС ⊥АЕ.
3) ∠BOD = ∠BOC + ∠COD = х + у = 90°, тому ВО ⊥ OD.
Задачу доведено.

16.20.


https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html

16.22. 1) MK = MN + NK = 3,2 + 4,1 = 7,3 (см)
2) MN = MK – NK = 7,8 – 2,5 = 5,3 (см)

16.23. Нехай один із суміжних кутів х, тоді другий х + 36°. Оскільки сума суміжних кутів
дорівнює 180°, маємо: х + х + 36° = 180°; 2х = 144°; х = 72°.
Отже, один із кутів дорівнює 72°, другий - 180° - 72° = 108°.
Відповідь: 72°; 108°.
16.24. Знайдемо S1 рулону шпалер: 50 см = 0,5 м
S1 рулону = 0,5 ⋅ 10 = 5 (м²)
Обчислимо S стін:
S стін розміром 4,5 х 2,5: 4,5 ⋅ 2,5 = 11,25 (м²)
Таких стін у кімнаті дві: 2S = 11,25 ⋅ 2 = 22,5 (м²)
S стіни розміром 3 х 2,5: 3 ⋅ 2,5 = 7,5 (м²)
Таких стін дві: 2S = 7,5 ⋅ 2 = 15 (м²)
Загальна площа стін 22,5 + 15 = 37,5 (м²)
S стін – S дверей і вікон S = 37,5 – 3,5 = 34 (м²) – площа для поклейки шпалер.
1) Знайдемо кількість рулонів: 34 : 5 = 6,8
Отже, необхідно купити 7 рулонів шпалер
2) Обчислимо кількість коробок
7 : 4 = 1,75
Отже, необхідно придбати 2 коробки клею
3) Обчислимо вартість шпалер: 7 ⋅ 240 = 1680 (грн)
Вартість клею: 85 ⋅ 2 = 170 грн
1) 7 рулонів; 2) 2
16.25. АВ ∥ СD; BC ∥ AD

16.26.

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
17.1. 1) а ∥ m; 2) CD ∥ PK.
17.2. На мал. 8.5: а ∥ b; на мал. 8.8: k ∥ с.
17.3. m ∥ a; b ∥ n.
17.4.

2) Взагалі можна

17.6.

17.7.


17.9. 1)



2) Побудова аналогічна
17.11.




17.15. 1)

2) АВ = 2,6 см; АС = 2,1 см; ВС = 1,7 см
АС + ВС = 2,1 + 1,7 = 3,8 (см)
3) АВ < АС + ВС 17.16. Нехай ∠AOD = х, тоді ∠BOD = 0,25х. ∠AOD і ∠BOD – суміжні, ∠AOD + ∠BOD = 180°, x + 0,25х = 180°; 1,25х = 180°; х = 144°. Отже, ∠AOD = 144°, ∠BOD = 36°. Оскільки
кутом між прямими є менший із кутів, які утворились при перетині двох прямих, то ∠BOD = 36° - кут між прямими.
Відповідь: 36°

17.17. Примітка: 50 см = 0,5 м.
S плитки = 0,5 ⋅ 0,5 = 0,25 (м²)
S майданчика = 3,5 ⋅ 6,5 = 22,75 (м²)
22,75 : 0,25 = 91 (шт.) – кількість плиток.
91 ⋅ 52 = 4732 (грн) – вартість плитки.
Вартість додаткових матеріалів:
35% від 4732
4732 ⋅ 0,35 = 1656,2 (грн)
4732 + 1656,2 = 6388 грн 20 коп – всього
Відповідь: 6388 грн 20 коп.
17.18. Площа вказаного квадрата є 2017² клітинок. Але число







внутрішні односторонні відповідні кути внутрішні різносторонні
18.3.
Внутрішні односторонні кути: ∠ANM і ∠BMN, ∠CNM i ∠DMN;
Внутрішні різносторонні кути: ∠ANM і ∠DMN; ∠CNM i ∠BMN;
Відповідні кути: ∠ANK і ∠BMN; ∠KNC і ∠NMD; ∠ANM і ∠BML; ∠CNM і ∠DML.
18.4.
Внутрішні односторонні кути: ∠PCM і ∠DMC; ∠FCM і ∠LMC;
Внутрішні різносторонні кути: ∠PCM і ∠LMC; ∠FCM і ∠DMC;
Відповідні кути: ∠PCB і ∠DMC; ∠BCF і ∠CML; ∠PCM і ∠DMK; ∠FCM і ∠LMK.
18.5. Так, оскільки дві прямі, перпендикулярні
18.6.





https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html



18.8. Позначимо кути цифрами
∠2 = 70° (як вертикальний кут до ∠4).
∠1 = 180° – 70° = 110° (як суміжний кут до ∠4).
∠3 = 110° (як вертикальний кут до ∠1).
∠5 = 120° (як вертикальний кут до ∠8).
∠6 = 180° – 120° = 60° (як суміжний кут до ∠8).
∠7 = ∠6 = 60° (як вертикальний кут до ∠6).


18.10.


∠4 = ∠1 = 50° (як вертикальний кут до ∠1).
∠2 = 180° – 50° = 130° (як суміжний кут до ∠1). ∠3 = ∠2 = 130° (як вертикальний кут до ∠2). ∠7 = ∠6 = 130° (як вертикальний кут до ∠6). ∠5 = 180° – 130° = 50° (як
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
18.11.
∠1 + ∠2 = 118° + 62° = 180°; тому а ∥ b.
∠2 ≠ ∠3, тому прямі b і с — не паралельні.
∠1 + ∠3 = 118° + 63° = 181°; тому прямі
18.12.
∠1 + ∠2 = 121° + 60° = 181°; тому прямі а і b —
∠2 = ∠3, тому прямі b ∥ с.
∠1 + ∠3 = 121° + 60° = 181°; тому прямі
18.13.

18.14.

18.15.

18.16.

18.17.


1)
2)
3)
1) ∠MNP = 125°.
2)

18.19.

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
За умовою ∠1 = ∠2. Позначимо кут 3 — вертикальний із кутом 2. ∠3 = ∠2. Тому ∠1 = ∠3. Відповідні кути рівні, тому m ∥ n, що й треба було довести.
За умовою ∠4 + ∠5 = 190°. 1) ∠2 = ∠4 (як вертикальні), ∠7 = ∠5 (аналогічно). Отже, ∠2 + ∠7 = ∠4 + ∠5 = 190°. 2) ∠1 = 180° – ∠4 (за властивістю суміжних кутів); ∠8 = 180° – ∠5 (аналогічно).
Тому ∠1 + ∠8 = 180° – ∠4 + 180° – ∠5 = = 360° – (∠4 + ∠5) = 360° – 190° = 170°.
3) ∠3 = 180° – ∠4 (за властивістю суміжних кутів);
∠6 = 180° – ∠5 (аналогічно);
∠3 + ∠6 = 180° – ∠4 + 180° – ∠5 = 360° – (∠4 + ∠5) = 360° – 190° = 170°.
Відповідь: 1) 190°; 2) 170°; 3) 170°.
18.20. За умовою ∠3 + ∠6 = 160°. 1) ∠2 = 180° – ∠3 (за властивістю суміжних кутів), ∠7 = 180° – ∠6 (аналогічно).

Тому ∠2 + ∠7 = 180° – ∠3 + 180° – ∠6 = = 360° – (∠3 + ∠6) = 360° – 160° = 200°. 2) ∠1 = ∠3 (як вертикальні), ∠8 = ∠6 (аналогічно). ∠1 + ∠8 = ∠3 + ∠6 = 160°.
3) ∠4 = 180° – ∠3 (за властивістю суміжних кутів), (аналогічно).
Тому ∠4 + ∠5 = 180° – ∠3 + 180° – ∠6 = 360° – (∠3 + ∠6) = 360° – 160° = 200°.
Відповідь: 1) 200°; 2) 160°; 3) 200°.
18.21.

18.22.
Розглянемо 2 випадки:
∠ABC і ∠BCD – внутрішні односторонні кути.
∠ABC + ∠BCD = 70° + 100° = 170°.
Прямі АВ і CD не можуть бути паралельними, оскільки у паралельних прямих сума внутрішніх односторонніх кутів дорівнює 180° (наслідок 2).
Відповідь: ні.


https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
1-й випадок. ∠MNP і ∠NPK -
Отже, MN і PK не паралельні.
2-й випадок. ∠MNP і ∠NPK -
Оскільки ∠NMP + ∠NPK = 60° + 120° = 180°, то MN ∥ PK.
Відповідь: так. 18.23.

Відповідь: ні.
18.24.
1-й випадок. Прямі а і с паралельні, оскільки відповідні кути при перетині прямих а і с з прямою b, рівні. 2-й випадок. Прямі а і с перетинаються.

1-й випадок. Прямі а і b паралельні.
2-й випадок. Прямі а і b перетинаються.
Відповідь: ні.
18.25.


MF – бісектриса кута KMN, то ∠KMN = 2 ∙ ∠FMK; KF – бісектриса кута MKP, то ∠MKP = 2 ∙ ∠MKF. За умовою ∠MKF + ∠FMK = 90°.
Маємо ∠MKP + ∠KMN = 2 ∙ ∠MKF + 2 ∙ ∠FMK = = 2(∠MKF + ∠FMK) = 2 ∙ 90° = 180°.
Кути MKP і KMN – внутрішні односторонні, утворені при перетині прямих MN і KP січною MK.
Оскільки ∠MKP + ∠KMN = 180°, то MN ∥ KP.

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
18.27.

18.28.

18.29.
1) ∠АВС = 70°.
2) m ⊥ BA, n ⊥ BC.
3) Кут між прямими m i n дорівнює 70°.
∠АОB = ∠BOC = 130°.
∠АОC = ∠AOD + ∠DOC, ∠AOD + ∠АОB = 180° (як суміжні кути).
Звідси ∠AOD = 180° – ∠АОB = 180° – 130° = 50°.
∠DOC + ∠BOC = 180° (як суміжні кути).
∠DOC = 180° – ∠BOC = 180° – 130° = 50°.
∠АОC = ∠AOD + ∠DOC = 50° + 50° = 100°.
Відповідь: 100°.
Радіус Землі становить приблизно 6378 км.
Довжина окружності Землі на рівні екватора: C=2πR
де R — радіус Землі. Визначимо ефективні радіуси для
Радіус на рівні ноги: Rноги = R = R.
різницю в довжині шляху: ΔC=2π × 0,0016 км ≈ 0,01005 км ≈ 10,05 м.
верхівка голови Сергія пройшла б на 10,05 метрів більше, ніж кінець його ноги, якби він пройшов земну кулю по її екватору. 18.30.


Відповідь: так (див. малюнок).
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
19.1.
1) Кути 5 і 4 – рівні; кути 2 і 7 – рівні.
2) Кути 1 і 3 – рівні.
3) ∠1 + ∠4 = 180° 19.2.
1) Кути 1 і 8 – рівні; кути 6 і 3 – рівні.
2) Кути 2 і 4 – рівні.
3) ∠2 + ∠3 = 180° 19.3.
1) ∠1 = 110° (як відповідний даному куту).
2) ∠2 = 180° – 110° = 70° (оскільки кут 110° і ∠2 – внутрішні різносторонні кути).
3) ∠3 = ∠1 = 110° (як вертикальні)
19.4.
Відомо, що m ∥ n, тоді:
1) ∠1 = 60° (як відповідний даному куту).
2) ∠2 = 180° – 60° = 120° (оскільки кут 60° і ∠2 – внутрішні різносторонні кути).
3) ∠3 = ∠1 = 60° (як вертикальні)
19.5.

19.6.

19.7.

Нехай ∠1 = 140°.
∠3 = ∠1 = 140° (як вертикальні кути).
∠5 = ∠1 = 140° (як відповідні кути).
∠7 = ∠1 = 140° (як вертикальні кути).
∠1 + ∠2 = 180° (як суміжні кути). Звідси
∠2 = 180° – ∠1 = 180° – 140° = 40°.
∠4 = ∠2 = 40° (як вертикальні кути).
∠8 = ∠4 = 40° (як відповідні кути).
∠6 = ∠8 = 40° (як вертикальні кути).
Нехай ∠2 = 50°.
∠4 = ∠2 = 50° (як вертикальні кути).
∠4 = ∠8 = 50° (як відповідні кути).
∠6 = ∠8 = 50° (як вертикальні кути).
∠1 + ∠2 = 180° (як суміжні кути). Звідси
∠1 = 180° – ∠2 = 180° – 50° = 130°.
∠3 = ∠1 = 130° (як вертикальні кути).
∠5 = ∠1 = 130° (як відповідні кути).
∠7 = ∠5 = 130° (як вертикальні кути).

19.9.





1) Нехай ∠2 = х, тоді
∠1 = х + 16°. Маємо:
х + х + 16° = 180°
2х = 164°
х = 82°
Отже, ∠2 = 82°; ∠1 = 82° + 16° = 98°.
2) Нехай ∠2 = х, тоді
∠1 = 3х. Маємо:
х + 3х = 180°
4х = 180°
х = = 45°
Отже, ∠2 = 45°; ∠1 = 3 ∙ 45° = 135°.
Відповідь: 1) 82° і 96°; 2) 45° і 135°; 3) 75° і 105°.
19.16.

1) Нехай ∠1 = х, тоді
∠2 = 4х. Маємо:
х + 4х = 180°
5х = 180°
х = 36°
Отже, ∠1 = 36°;
∠2 = 4 ∙ 36° = 144°.
2) Нехай ∠1 = х, тоді
∠2 = х + 8°. Маємо:
х + х + 8° = 180°
2х = 172°
х= 86°
Отже, ∠1 = 86°;
∠1 = 86° + 8° = 94°.
Відповідь: 1) 36° і 144°; 2) 86° і 94°; 3) 100° і 80°.
19.17.


3) Нехай ∠2 = 5х, тоді
∠1 = 7х. Маємо:
5х + 7х = 180°
12х = 180°
х = 15°
Отже, ∠2 = 5 ∙ 15° = 75°; ∠1 = 7 ∙ 15° = 105°.
3) Нехай ∠2 = 5х, тоді
∠1 = 4х. Маємо:
5х + 4х = 180°
9х = 180°
х = 20°
Отже, ∠2 = 5 ∙ 20° = 100°; ∠1 = 4 ∙ 20° = 80°.
∠1 = ∠3 = 120° (як вертикальні кути).
∠4 = ∠1 = 120° (як відповідні кути). Отже, a ∥ b
∠2 і ∠6 — відповідні, ∠2 = ∠6 = 110°.
∠5 і ∠2 — суміжні.
x + ∠2 = 180°
x + 110° = 180°
x = 180° – 110°
x = 70°
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html


Відповідь: 1) 70°; 2) 65°; 3) 129°. 19.18.
∠1 і ∠2 суміжні кути. ∠1 + ∠2 = 180°, ∠2 = 180° –
∠1, ∠2 = 180° – 55° = 125°.
∠2 = ∠3 = 125° (як відповідні кути). Отже, a ∥ b
з ознакою паралельності прямих. ∠4 і ∠5 — внутрішні різносторонні кути при паралельних прямих a і b і січній d.
∠4 = ∠5 = 65°.

∠1 + ∠2 = 48° + 132° = 180°. Оскільки ці кути внутрішні односторонні і
a і b
180°, то
(наслідок 2).
Розглянемо паралельні прямі a і b і січну d.
∠3 і ∠4 — внутрішні односторонні кути при паралельних прямих a і b і січній d.
∠3 + ∠4 = 180°
∠4 = 180° – ∠3
∠4 = 180° – 51°
∠4 = 129°.



∠3 = ∠4 = 80° (як вертикальні кути).
∠1 = ∠3 (як відповідні кути).
Отже, a ∥ b згідно з ознакою паралельності
прямих.
Розглянемо a ∥ b і січну d.
∠2 = ∠5 як відповідні кути.
Отже, x = 50°.
∠4 + ∠5 = 130° + 50° = 180°. Оскільки ці кути внутрішні односторонні та їхня сума дорівнює 180°, то згідно з наслідком 2 прямі a і b паралельні. Розглянемо a ∥ b і січну d.
∠1 = ∠2 = 70° (як вертикальні кути).
∠2 і ∠3 — внутрішні односторонні кути, отже,
∠2 + ∠3 = 180°.
∠3 =

7 + ∠6 + ∠2 = 120°.
вертикальні, ∠2 і ∠6 — як відповідні), то
дорівнює 40°. ∠2 = 40°, ∠6 = 40°, ∠7 = 40°.
∠3 = ∠2 = 40° (як вертикальні кути).
∠1 + ∠2 = 180° (як суміжні кути).
Звідси ∠1 = 180° – 40° = 140°.
∠4 = ∠1 = 140° (як вертикальні кути).
∠5 = ∠1 = 140° (як відповідні кути).
∠8 = ∠5 = 140° (як вертикальні кути).
Відповідь: чотири кути по 40°, чотири кути по 140°. 19.21.

Відповідь: чотири
19.22.

Відповідь: 130°.
19.23.

Оскільки сума чотирьох кутів, утворених при перетині двох паралельних прямих січною, дорівнює 128°, то це дві
пари відповідних гострих кутів.
∠1 + ∠5 + ∠3 + ∠7 = 128°. Оскільки ці кути рівні, то кожен з них дорівнює 32°. ∠1 = ∠5 = ∠3 = ∠7 = 32°.
∠1 + ∠2 = 180° (як суміжні кути).
∠2 = 180° – ∠1 = 180° – 32° = 148°.
∠4 = ∠2 = 148° (як вертикальні кути).
∠6 = ∠2 = 148° (як відповідні кути).
∠8 = ∠6 = 148° (як вертикальні кути).
148°.
Через т. М проведемо пряму паралельні CD. KM ∥ CD, KM ∥ AB. Тоді ∠CMA = ∠CMK + ∠AMK.
Розглянемо AB ∥ KM і січну AM.
∠AMK = ∠MAB = 50° (як внутрішні різносторонні кути).
Розглянемо CD ∥ KM і січну CM.
∠CMK = ∠DCM = 80° (як внутрішні різносторонні кути).
Отже, ∠CMA = 80° + 50° = 130°.

Відповідь: 100°.
MN. KF ∥ MN, KF ∥ PL.
Тоді ∠MKP = ∠MKF + ∠PKF.
Розглянемо MN ∥ KF і січну MK. ∠MKF + ∠KMN = 180° (як внутрішні односторонні кути). ∠MKF = 180° – ∠KMN = 180° – 120° = 60°.
Розглянемо PL ∥ KF і січну KP. ∠PKF + ∠KPL = 180° (як внутрішні односторонні кути). ∠PKF = 180° – ∠KPL = 180° – 140° = 40°.
Отже, ∠MKP = 60° + 40° = 100°.
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
19.24.

19.25.

19.26.

19.27.

AB = 16 см.
1) BC = x см, AC = x + 2, x + x + 2 = 16; 2x = 14; x = 7.
Отже, BC = 7, AC = 7 + 2 = 9.
Оскільки a ∥ b, то ∠KBA = ∠BAL (як внутрішні різносторонні). Оскільки BC і AD —
то ∠CBA = ∠DAB (як половини рівних кутів).
цих
Розглянемо прямі BC і AD та січну AB. ∠CBA і ∠DAB — внутрішні різносторонні рівні, отже, BC ∥ DA.
Отже, бісектриси двох внутрішніх різносторонніх кутів при паралельних прямих і січній паралельні.
Оскільки a ∥ b, то ∠MAK = ∠ABL (як відповідні кути).
Оскільки AC і BD — бісектриси цих кутів, то ∠ABD = ∠MAC (як половини рівних кутів). Розглянемо прямі AC і BD і січну MN: ∠MAC і ∠ABD — відповідні кути і рівні. Отже, AC ∥ BD.
Отже, бісектриси двох
2) BC = x см, AC = 3x см, x + 3x = 16; 4x = 16; x = 4.
Отже, BC = 4 см, AC = 3 · 4 = 12 см.
4 см 6 см 7 см 9 см 10 см 12 см
Відповідь: Франко.
19.28.
1) 20 · 20 = 400 (м2) –
2) 400 : 40 = 10 (г) – потрібно
3) Нехай AC = 5x, BC = 3x. 5x + 3x = 16; 8x = 16; x = 2.
Отже, BC = 3 · 2 = 6 см, AC = 5 · 2 = 10 см.

3) 10 · 90 = 900 (грн) Відповідь:
19.29.
1) 7а – 6b – 2а + b = 5a – 5b; 2) –11х + 10у – 3x – 2у = –14x + 8y; 3) 10,3m – 12,9t + 6,7m = 17m – 12,9t; 4) 3c + d + Зс – d = 6c. 19.30.
Розв’язання подано на малюнку.


Відповідь: Г. 2.

Відповідь: Б.

Відповідь: Г. внутрішні різносторонні. 4.

Відповідь: А.
6.

– 35° = 145°.
В. 145°.
7. 1) ∠CON = ∠MOD (як вертикальні); ∠CON = 20°. 2) ∠AON = ∠CON + ∠COA = 20° + 90° = 110°. Відповідь: В. 110°.


∠1 + ∠4 = (180° – ∠2 ) + (180° – ∠3) = 360° – (∠2 + ∠3) = = 360° – 175° = 185°.
Відповідь: Б. 185°.
9.

Відповідь: А. 80°.
10.

Відповідь: В. 90°.
11.
∠2 = ∠3 = 70° (як вертикальні кути).
∠1 = ∠2 = 70° (як відповідні кути). Отже, a ∥ b згідно з ознакою паралельності прямих. Розглянемо a ∥ b і січну d. Кути 100° і x — внутрішні
односторонні кути, отже, їхня сума дорівнює 180°.
Тоді 100° + x = 180°; x = 80°.
1) Позначимо ∠AOC = ∠BOD = х; ∠COK = ∠DOK = у.
Тоді 2x + 2y = 180°
2(х + у) = 180°
х + у = 90° 2) ∠AOK = х + у = 90°.

Відповідь: Б. 110°.
12.

Через т. P проведемо пряму PK ∥ BA. Тоді
∠BPD = ∠BPK + ∠DPK.
Розглянемо BA ∥ PK і січну BP. ∠PBA + ∠BPK = 180° (як внутрішні односторонні кути).
∠BPK = 180° - ∠PBA = 180° - 100° = 80°.
Розглянемо PK ∥ DC і січну PD. ∠DPK + ∠CDP = 180° (як внутрішні односторонні кути).
∠DPK = 180° - ∠CDP = 180° - 150° = 30°.
Отже, ∠BPD = 80° + 30° = 110°.
AOC, цей кут
AOC = ∠AOK + ∠KOC = 2∠KOC
AOK та

KOC.










1) 1 і 2 - внутрішні різносторонні кути; 2) 1 і 3 - внутрішні односторонні кути; 3) 1 і 4 - відповідні кути.
1) ∠KOM = ∠KOA + ∠AOM= 70° + 19° = 89°; прямі KL і MN – не перпендикулярні. 2) ∠KON= ∠KOB – ∠NOB = 111° – 21° = 90°; прямі KL і MN – перпендикулярні.
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html

Нехай ∠1 = 78°, тоді ∠3 = ∠1 = 78° (як вертикальні
= ∠1 = 78° (як відповідні кути), ∠7 = ∠5 = 78° (як вертикальні кути).
∠1 + ∠2 = 180° (як суміжні кути),
∠2 = 180° – ∠1 = 180° – 78° = 102°.
∠4 = ∠2 = 102° (як вертикальні кути).
∠6 = ∠2 = 102° (як відповідні кути).
∠8 = ∠6 = 102° (як вертикальні кути).
Відповідь: чотири кути по 78°, чотири кути по 102°.
7.

Відповідь: 52°.
8.
Оскільки AB ⊥ CD, то ∠AOC = 90°. ∠AOK = ∠AOC – ∠KOC, ∠KOC = ∠DOL = 38° (як вертикальні кути).
Отже, ∠AOK = 90° – 38° = 52°.

Відповідь: 50°. 9.

Відповідь: 110°. 10.


a і b паралельні.
a ∥ b і січну c. ∠5 = ∠3 = 130° (як внутрішні різносторонні кути).
∠5 + ∠4 = 180° (як суміжні кути).
∠4 = 180° – ∠5 = 180° – 130° = 50°.
Проведемо пряму PR ∥ DC, тоді ∠BKD = ∠BKP + ∠DKP. Розглянемо BA ∥ PR і січну BK. ∠BKP = ∠KBA = 40° (як внутрішні різносторонні кути).
Розглянемо KR ∥ DC і січну KD. ∠DKP = ∠KDC = 70° (як внутрішні різносторонні кути).
Отже, ∠BKD = 40° + 70° = 110°.





https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
∠LOB = ∠BOC − ∠COL = 90° − ∠COL.
Оскільки ∠KOC = ∠COL, то ∠AOK = ∠LOB.
∠AOL = ∠AOC + ∠COL = 90° + ∠COL.
∠KOB = ∠COB + ∠KOC = 90° + ∠KOC.
Оскільки ∠KOC = ∠COL, то ∠AOL = ∠KOB.
2) ∠KOB = 90° + ∠KOC, ∠AOK = 90° − ∠KOC.
Отже, ∠AOK < ∠KOB.
6.

1) Так, ∠AOC = ∠COB = 45°
2) Так, ∠AOB = ∠COB = (360° – 90°) : 2 = 135°.
7.



Оскільки 90° = 15 ∙ 6°, то
шаблона.
Нехай BL бісектриса кута ABC. ∠ABC = 2∠LBC, BM бісектриса кута CBD: ∠CBD = 2∠CBM. Оскільки
бісектриси перпендикулярні, то ∠LBC + ∠CBM = 90°.
Знайдемо ∠ABD = ∠ABC + ∠CBD = 2∠LBC + 2∠CBM = 2(∠LBC + ∠CBM) = 2 × 90° = 180°. Отже, кут ABD розгорнутий, точки A, B, D
















18.
∠1 = 180° - 130° = 50° (як суміжний з кутом 130°).
∠2 = ∠1 = 50° (як внутрішні різносторонні кути).
∠3 = 130° (як внутрішній різносторонній з кутом 130°).
∠4 = ∠3 = 130° (як вертикальні кути).
19.
Згідно з властивістю паралельних
одна одній.
Оскільки a ∥ b і b ∥ c, то a ∥ c. Оскільки a ∥ c і c ∥ d, то a ∥ d. 20.

Відповідь: 100°, 80°.
21.
= 0,8x.
x + 0,8x = 180°; 1,8x = 180°; x = 100°. Отже, ∠6 = 100°, ∠3 = 0,8 × 100° = 80°.
Розглянемо a ∥ b і січну d. ∠2 = ∠1 = 100° — як відповідні кути. ∠3 + ∠1 = 180° — як
суміжні кути. ∠3 = 180° - ∠1 = 180° - 100° = 80°.
Розглянемо d ∥ c і січну a: ∠4 = ∠3 = 80° — як внутрішні різносторонні кути. Відповідь: 100°, 80°, 80°.
22. Нехай паралельні прямі AB і CD перетинає пряма BD; ∠ABD і ∠CDB — внутрішні односторонні кути; ∠ABD = 72°, тоді ∠CBD = 180° - ∠ABD, ∠CDB = 180° - 72° = 108°; BO — бісектриса ∠ABD, DO — бісектриса ∠CDB, тоді ∠ABO = 1 2 ∠ABD = 1 2 ⋅ 72° = 36°; ∠CDO = 1 2 ∠CDB = 1 2 ⋅ 108° = 54°.

через точку O пряму OM ∥ CD, тоді OM ∥ AB. ∠BOM = ∠ABO = 36°; ∠DOM = ∠CDO = 54°. ∠BOD —
∠BOD = ∠BOM + ∠DOM; ∠BOD = 36° + 54° = 90°.
90°. 23.


MNF + ∠FNB.
CM: ∠CMP = ∠DCM = 50° —
∠PMN = ∠CMN - ∠CMP = 80° - 50° = 30°.
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
Розглянемо MP ∥ NF і січну MN: ∠MNF = ∠PMN = 30°
Розглянемо NF ∥ AB і січну NB: ∠FNB + ∠ABN = 180° як внутрішні
∠FNB = 180° - 140° = 40°. Отже, ∠MNB = 30° + 40° = 70°. Відповідь: 70°.
1 2t; так 7) 4,9; так 8) (m - 2c)²; так 9) а���� ���� ; ні
d²; так
4) x(x - y); так 5) -41 7; так 6) (x + 5)(x - 5); так
7) c⁷ - 1; так 8) (a + b)²; так 9) с���� 5 ; так
20.3. Назвіть члени многочлена: 1) 4x²y, -7xy², 5, 3xy; 2) -a³, 4a², -9a, 3.
20.4. Складіть многочлен з одночленів: 1) 5m² - 2m + 3; 2) 7ab - 2a² + b²; 3) 4p + 2q³; 4) -c² - 3mc + m³ + 7.
20.5. Складіть многочлен з одночленів: 1) 5m - 5n; 2) m³ - 2m² + mn; 3) -x³ - 2y² + xy + 4.
20.6.
1) 5m² + m³ + 1; так, степінь 3 2) 7x² + 2x + 3x²; ні
3) 2 + a + a²b + 3; ні 4) c²c + c⁵ - 8; ні
5) 3x²x + 2xx² + x; ні 6) p² - 19. Так, степінь 2
20.7. Зведіть подібні члени многочлена:
1) 7x - 15xy - 8xy = 7x - 23xy;
2) 8ab - 5ab + 4b² = 3ab + 4b²;
3) 9a⁴ - 5a + 7a² - 5a⁴ + 5a = 4a² + 7a²;
4) 18a⁴b - 9a⁴b - 7ba⁴ = 9a⁴b - 7ba⁴;
5) 4b³ + b² - 15 - 7b² + b³ - b + 18 = 5b³ - 6b² - b + 3;
6) 9xy² - x³ - 5xy² + 3x²y - 4xy² + 2x³ = 3x²y + x³.
20.8. Зведіть подібні члени
1) a³ - 2a³ + 3a³ = 4a³ - 2a³ = 2a³;
2) -x⁴ + 2x³ - 3x⁴ + 5x² - 3x² = -4x⁴ + 2x³ + 2x²;
3) 7 + 3m⁶ - 2m³ - 5m⁶ + 2m⁶ - m⁵ - 7 = -m⁵ - 2m³;
4) 9xy³ + 6x²y² - x³y + x²y² - 9xy³ = 7x²y² - x³y.
20.9. (Усно.)
1) a³ + 3a² + 1;

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
2) a²a² - 8; так, оскільки a²a² - 8 = a⁴ - 8
3) a⁴ - 4a³ - a⁴; ні, оскільки a⁴ - 4a³ - a⁴ = - 4a³
4) aa³ + 2; так, оскільки aa³ + 2 = a⁴ + 2.
20.10.
1) m³ + m⁴ - m²; ні, оскільки тут
2) 12 + mm⁴; так, оскільки 12 + mm⁴ = 12 + m⁵
3) mm + mm² + m²m²; ні, оскільки mm + mm² + m²m² = m² + m³ + m⁴, немає
4) m⁵ - 3 - m⁵; ні, оскільки m⁵ - 3 - m⁵ = -3, тут
20.11. Зведіть многочлен до стандартного вигляду та
1) x²y + xyy = x²y + xy², (3 степінь);
2) 2a · a² · 3b + a · 5c = 2a³ · 3b + 5ac = 6a³b + 5ac, (4 степінь);
3) 7x · 5y² - 4y · 7x² = 35xy² - 28yx², (3 степінь);
4) 3a · 4a · (-5a) - a³ · (-8b) = -60a³ + 8a³b, (4 степінь).
20.12. Подайте многочлен у стандартному
1) 3x · x² + 2x · 5y² = 3х3 + 10ху2, (3 степінь);
2) 5a · b²a + 3b · 2ab² = 5a2b2 + 6ab3, (4 степінь);
3) -5mn³m + 4mmm = -5m2n3 + 4m3, (5 степінь);
4) 5p · 3p · (-p) - p⁴qp = -15p3 – p5q, (6 степінь).
20.13. Перепишіть
1) 7x - 5x³ + x⁴ - 9x² + 1 = x⁴ - 5x³ - 9x² + 7x + 1;
2) 8y³ - 5 + 7y⁶ - 9y⁴ + y² = 7y⁶ - 9y⁴ + 8y³ + y² - 5.
20.14. Перепишіть
степеня
та визначте його степінь:
степенів змінної: 1) 3m² - 3m + m³ - 8 = -8 - 3m + 3m² + m³; 2) 7a² - 9a⁵ + 4a³ + 5 - a⁴ = 5 + 7a² + 4a³ - a⁴ - 9a⁵.
20.15. Знайдіть значення:
1) Двочлена 3x² - 1, якщо x = -1; 2;
якщо x = -1, то 3x² - 1 = 3 ⋅ (-1)² - 1 = 3 - 1 = 2; якщо x = 2, то 3x² - 1 = 3 ⋅ 2² - 1 = 12 - 1 = 11; 2) Тричлена 5m + 9n² - 1, якщо m = -2, n = 1 3 .
якщо m = -2, n = 1 3, то 5 ⋅ (-2) + 9 ⋅ (1 3)² - 1 = -10 + 1 - 1 = -10.
20.16. Обчисліть значення многочлена:
1) 64x³ - x² + 1, якщо x = 1 4; 64x³ - x² + 1 = 64 ⋅ (1 4)³ - (1 4)² + 1 = 11 16 + 1 = 21 16 = 115 16; 2) 4mn - 3m + 2n - 4mn, якщо m = 4, n = -3. 4mn - 3m + 2n - 4mn = -3m + 2n = -3 ⋅ 4 + 2 ⋅ (-3) = -12 - 6 = -18.
20.17. Обчисліть значення многочлена: 1) 9p² - p³, якщо p = 1 3; 9p² - p³ = 9 ⋅ (1 3)² - (1 3)³ = 9 ⋅ 1 91 27 = 11 27 = 26 27 . 2) 2xy - 4x + 3y + 4x, якщо
x² + 5 > 0.

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
2) 3ху2 ∙ 4x3у + 5х3у ∙ 2у ∙ (–х) – 10х3y3 ∙ 1 2 х – 7ху ∙ (–3хy3) = = 12х4y3 – 10х4y2 – 5х4y3 + 21х2y4 = 7х4y3 – 10х4y2 + 21х2y4, (7 степінь).
20.20. Зведіть
степінь:
1) 3a²b³ - ab³ - a³a - a²b² · b + 0,5ab · 2b² + 4ab · 0,5ab² = 3a2b3 – ab3 – а4
2) 7x · 2y³ - 5x · 3xy · (-x) + 1 2y · (-14xy) - 3yx · 4y² = 14xy3 + 15х3у – 7xy2 – 12ху3 = = 2хy3 + 15х3y – 7хy2 (4
8 = 747,75 + 1 4 = 747,75 + 0,25 = 748 (км).
значень. a² + b² + 1 > 0, оскільки a² ≥ 0; b² ≥ 0; 1 > 0. 20.23. Замість «зірочки» замініть
степеня:
1) x³ + 3x² + ∗ - 2 = x³ + 3x² + x⁴ - 2;
2) m⁶ - 4m⁴ + mn + ∗ = m⁶ - 4m⁴ + mn + (-m⁶);
3) a³b - 3a⁴b³ + 3a² + ∗ = a³b - 3a⁴b³ + 3a² + 3a⁴b³;
4) pq³ - p²q² + p²q³ + ∗ - p³q = pq³ - p²q² + p²q³ + (-p²q³) - p³q.
20.24. Замість
1) 3x - 12 + 5x + 15 - 9x + ∗ = –x + 3 + * = – x + 3 + x = 3;
2) 5xy² - y³ + 7y² + 7y²x - 5 + ∗ = 12ху2 – y3 +7y2 – 5 + * = 12xy2 – y3 + 7y2 – 5 – 12хy2 = = –y3 + 7y2 – 5. 20.25.
5x³ + 2x² - x + 7.
змінну x на одночлен:
1) 5m3 + 2m2 – m + 7;
2) 5(–х)3 + 2(–х)2 – (–х) + 7 = –5х3 + 2x2 + х + 7;
3) 5(2а)3 + 2(2а)2 – 2а + 7 =
4) 5(3b2)3 + 2(3b2)2 – 3b2 + 7 = 5 ∙ 27b6 + 2 ∙ 9b4 – 3b2 + 7 = 135b6 +18b4 – 3b2 + 7.
20.26. Дано многочлен 3a³ - 5a² +
1) 3х3 – 5х2 + х – 8; 2) 3(–а)3 – 5(–а)2 + (–а) – 8 = –3a3 – 5а2 – а – 8; 3) 3(2b)3 – 5(2b)2 + 2b – 8 = 3 ∙ 8b3 – 5
4b2 + 2b – 8 = 24b3 – 20b2 + 2b – 8; 4) 3(3с2)3 – 5(3с2)2 + 3с2 – 8 =
1) a⁴ + 3a² + 5 > 0;
3) -p² - 7 < 0;
4) -m² - m²n² - n² - 9 < 0;
6) x⁸ + y⁶ + c⁴ + 1 > 0.

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
20.28.
1) х + 5 + (2х – 7) = х + 5 + 2 х – 7 = 3х –2;
2) 2у – 1 – (3у – 8) = 2у – 7 – 3у + 8 = –у + 1; 3) 7 – (2x + 9) + (3х – 11 ) = 7 – 2x – 9 + 3x – 11 = x – 13.
20.29. Складіть числовий
1) сума квадратів чисел 3,1 і -2,7; 3,12 + (–2,7)2 = 9,61 + 7,29 = 16,9;
2) квадрат різниці чисел -3,8 і -3,7; ((–3,8 –(–3,7))2 = (–0,1)2 = 0,01;
3) куб суми чисел 1,52 і -1,5. ((1,52 + (–1,5))3 = 0,023 = 0,000008.
20.30. Замініть пропуски степенем
1) x³ · ( ... )² = x¹³; ⇒ x3 ∙ (х5)2 = x13;
2) ( ... )³ · x⁷ = x¹⁹. ⇒ (х4)3 ∙ x1 =x19.
20.31. Життєва математика: 1)
грн/кВт ∙ год.
1250 ∙ 8 = 10000 (грн) – у жовтні; 1500 ∙ 8 = 12000 (грн) – у
20.32.
1) d – (d – 1) = d – d + 1 = 1;
2) –(а + 10) + а = –a – 10 + a = –10;
3) р + (–р + а) = p – p + a = a; 4) (t + 4) – (t – 5) = t + 4 – t + 5 = 9;
5) –(10 – х) + (–х + 7) = –10 + x – x + 7 = –3; 6) –(b – 5 + а) – (2 – b) = –b + 5 – a – 2 + b = 3 – a.
20.33.

63;
147
252 < 4���� 252 < 154 252;



4n = 148, 149, 150, 151, 152, 153. n = 148 : 4 = 37; 150 : 4 = 37,5; 152 : 4 = 38. Відповідь: n = 37, 38.
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
21.1. (Усно.)
1) а + (b – 5) = а + b – 5; 2) у + (3 – m + t) = y + 3 – m + t; 3) x – (p – 1) = x – p + 1; 4) c – (–b2 + 1) = c + b2 – 1.
21.2. Знайдіть суму многочленів: 1) (2x2 + 3x3 –1) + (5x3 + 3x2 + 7) = 2x2 + 3x3 – 1 + 5x3 + 3х2 + 7 = 8х3 + 5x2 + 6; 2) (а3 + 3a2 + 1) + (2a2 – 5) + (6 – 5a2) = а3 + 3a2 + 1 + 2a2 – 5 + 6 – 5a2 = a3 + 2.
21.3. Знайдіть суму многочленів: 1) (3m3 + 5m2 – 7) + (2m3 + 6) = 3m3 + 5m2 – 7 + 2m3 + 6 = 5m3 + 5m2 – 1; 2) (b2 + 3b – 1) + (2b – 3b2) + (2b2 + 7) = b2 + 3b – 1 + 2b – 3b2 + 2b2 + 7 = 5b + 6.
21.4. Знайдіть різницю многочленів:
1) (4p3 + 7p2 – р) – (2p2 +р) = 4p3 + 7p2 – р – 2p2 – р = 4p3 + 5p2 – 2р;
2) (m2 + 2m – 1) – (m3 + 2m – 1) = m2 + 2m – 1 – m3 – 2m + 1 = –m3 + m2.
21.5. Знайдіть різницю многочленів: 1) (2a3 – 3a2 + 7) – (а3 – 5a2 – 8) = 2a3 – 3a2 + 7 – а3 + 5a2 + 8 = а3 + 2а2 + 15; 2) (с4 + с3 – 2) – (с3 + 2с2 – 2) = с4 + c3 – 2 – с3 – 2c2 + 2 = с4 – 2с2.
21.6. Знайдіть суму і різницю виразів:
1) (х + y) + (х – y)= х + y + х – y = 2х; (х + у) – (х – у) = х + у – х + у = 2у;
2) (х – у) + (–x + у) = х – у – х + у = 0; (х – у) – (–x + у) = х – у + х – у = 2х – 2у;
3) (–х – у) + (у – х) = –х – у + у – х = –2х; (–x – у) – (у – х) = – х – у – у + х = –2у; 4) (х – у) + (у – х) = х – у + у – х = 0; (х – у) – (у – х) – х – у – у + х = 2х – 2у.
21.7. Знайдіть суму і різницю виразів:
1) (2а + b) + (2а – b) = 2а + b + 2а – b = 4а; (2а + b) – (2a – b) = 2a + b – 2a + b = 2b;
2) (2а – b) + (–2а + b) = 2а – b – 2а + b = 0; (2а – b) – (–2а + b) = 2а – b + 2а – b = 4а – 2b;
3) (–2а – b) + (2а + b) = –2а – b + 2а + b = 0; (–2а – b) – (2а + b) = –2а – b – 2а – b = –4а – 2b;
4) (2а – b) + (b – 2а) = 2a – b + b – 2a = 0; (2а – b) – (b – 2а) = 2а – b – b + 2а = 4а – 2b.
21.8. Знайдіть
вигляду:
1) (3x2 – 2х+ 1) + (3х2 – 4) = 3х2 – 2х+ 1 + 3x2 – 4 = 6х2 – 2х – 3; (3х2 – 2х + 1) – (3x2 – 4) = 3х2 – 2х + 1 – 3x2 + 4 = –2х + 5;
2) (2х + 1) + (–3х2 – 2х – 1) = 2х + 1 – 3х2 – 2х – 1 = –3х2; (2х + 1) – (–3х2 – 2х – 1) = 2х + 1 + 3х2 + 2х + 1 = 3х2 + 4х + 2;
3) (а + 5b) + (3а – 5b) = а + 5b + 3а – 5b = 4а; (а + 5b) – (3а – 5b) = а + 5b – 3а + 5b = –2а + 10b;
4) (m2 – 2mn – n2) + (m2 + n2) = m2 – 2mn – n2 + m2 + n2 = 2m2 – 2mn; (m2 – 2mn – n2) – (m2 + n2) = m2 – 2mn – n
.
1) (5y2 + 2y – 10) + (3y2 – у + 7) = 5y2 + 2у – 10 + 3у2 – у + 7 = 8y + у – 3; (5y2 + 2у – 10) – (3у2 – у + 7) = 5y2 + 2y – 10 – 3у2 + у – 7 = 2у2 + 3у – 17; 2) (5m3 – m + 3) + (4m2 + m – 4) = 5m3 – m + 3 + 4m2 + m – 4 = 5m3 + 4m2 – 1; (5m3 – m + 3) – (4m2 + m – 4) = 5m3 – m + 3 – 4m2 – m + 4 = 5m3 – 4m2 – 2m + 7; 3) (5р2 – 2pq – 7q2) + (3р2 + 2pq + 5q5) = 5p2 – 2pq – 7q2 + 3р2 + 2pq + 5q2) = 8p2 – 2q2; (5р2 – 2pq – 7q2) – (3р2 + 2pq + 5q5) = 5p2 – 2pq – 7q2 – 3р2 – 2pq – – 5q2 = 2p2 – 4pq – 12q2.

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
21.10. Спростіть
1) (1 + 2p) + (p2 – p) = 1 + 2p + p2 – p = p2 + p + 1;
2) (5a2 + a3) – (–a + 5a2) = 5a2 + a3 + a – 5a2 = a3 + a; 3) (x2 – 5x) + (5x – 13) = x2 – 5x + 5x – 13 = x2 – 13;
4) (3b3 – 5b2) – (5 + 3b3 – 2b2) = 3b3 – 5b2 – 5 – 3b3 + 2b2 = –3b2 – 5.
21.11. Перетворіть на многочлен стандартного
1) (5ab2 – 12ab – 7a2b) – (15ab + 8a2b) = 5ab2 – 12ab – 7a2b – 15ab – 8a2b = = 5ab2 – 27ab – 15a2b;
2) (3 5 a3b2 –3 4ab2) – (–5 8 b2a –7 10 b2a3) = 3 5 a3b2 –3 4 ab2 + 5 8 ab2 + 7 10 a3b2 = = 6 10 a3b2 + 7 10 a3b2 –6 8 ab2 + 5 8 ab2 = 13 10 a3b2 –1 8 ab2 = 1 3 10 a3b2 –1 8ab2;
3) (x + y – z) – (–2х + 3y – z) – (–5y + 4z + x) = x + y – z + 2x – 3y + z + 5y – 4z – x = = 2x + 3у – 4z;
4) (2m – 3n) – (4m – 3mn + 3m2) – (5mn – 5n2 – 3n) = = 2m – 3n – 4m + 3nn – 3m2 – 5mn + 5n2 + 3n = – 3m2 + 5n2 – 2m – 2mn.
21.12. Спростіть вираз:
1) (15x2 – 3xу) – (12х2 – 5ху + у2) = 15х2 – 3xy – 12x2 + 5xy – y2 = 3х2 + 2ху – y2;
2) (5а2b – 12аb + 14аb2) – (–5ab + 14аb2 – 7a2b) = = 5a2b – 12ab + 14ab2 + 5ab – 14аb2 + 7a2b = 12а2b – 7аb;
3) (m + n – 2р) – (–2m + р – 3n) – (4n + 3m – 4р) = = m + n – 2р + 2m – р + 3n – 4n – 3m + 4р = р.
21.13. Розв’яжіть рівняння:
1) 5х + 2x2 – (2x2 – 10) = 25;
5х + 2х2 – 2х2 + 10 = 25;
5х = 25 – 10;
5х = 15;
х = 3
21.14. Розв’яжіть рівняння:
1) 5х2 + 7х – (2х + 5х2 – 8) = 8;
5х2 + 7х – 2х – 5х2 + 8 = 8;
7х – 2х = 8 – 8;
5х = 0;
х = 0
21.15. Подайте
1) ха + b – m – xb = (ха – xb) + (m – m);
2) 5 – x3 – (2х + 7 – х3) = –8;
5 – х3 – 2х – 7 + х3 = –8; –2х = –8 + 2; –2х = –6; х = 3
2) 2 – 3х3 – (5х – 3х3) = –13;
2 – 3х3 – 5x + 3х3 = –13;
2 – 5х = –13;
–5х = –15;
х = 3
2) ха2 – 17а + 5х + 10b = (ха2 + 5х) + ( –17а + 10b).
21.16. Запишіть многочлен 5х2 – 9х3 + 7x – х4 –
розв’язки задачі.
1) 5х2 – 9х3 + 7x – х4 – 1 = (5х2 – 9х3) + (7х – х4 – 1).
2) 5х2 – 9х3 + 7х – х4 – 1 = (5х2 – х4) + (–9х3 + 7x – 1).
21.17. Для якого значення х: 1) значення різниці одночлена 5х і
многочлена 7x + 5х2 – 18;
5х – (3х – 5х2 + 12) = 7х + 5х2 – 18;
5х – 3х + 5х2 – 12 = 7х + 5х2 – 18;
3х – 5х2 + 12

2х + 5х2 – 7х – 5х2 = –18 + 12; –5х = –6; х = 1,2.
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
многочлена 5х2 + Зх3 + 14?
(5х3 + 3х2 – х) – (2x3 – 2х2 + х) = 5х2 + 3х3 + 14;
5х3 + 3х2 – х – 2х3 + 2х2 – х = 5х2 + 3х3 + 14;
3х3 + 5х2 – 2х = 5х2 + 3х3 + 14;
3х3 + 5х2 – 2х – 5х2 – 3х3 = 14; –2х = 14; х = –7.
21.18. Для якого значення змінної у:
1) сума многочленів 2у3 – 3у + у2 та 5у – 2у3 – у2 + 7 дорівнює 19: (2y3 – 3у + у2) + (5у – 2у3 – у2 + 7) = 19; 2y3 – 3у + у2 + 5у – 2у3 – у2 + 7 = 19; 2у + 7 = 19; 2у = 12; у = 6.
2) різниця
5у2 – 7y i тричлена 2у2 – 8у + 9
3у2 – 3у: (5y2 – 7у) – (2у2– 8y + 9) = 3y2 – 3у; 5у2 – 7у – 2у2 + 8у – 9 = 3у2 – 3у; 3y2 + у – 3y2 + 3у = 9; 4у = 9; у = 2,25.
21.19.
у,
1) –уа + ух + х – у – а + 1 = (–уа + ух – у) – (–х + а – 1); 2) –р2 + у2 + 2р – 7y – 1 = (у2 – 7у) – (р2 – 2р + 1).
21.20. Який
одержати тотожність:
1) –(–4р + q) = 4p – q; 2) –(–4m2 + р2 – 5) = 4m2 – р2 + 5; 3) (7m2 – 2m2n + 2mn2) + 2m2n – 5mn2 = 7n2 – 3nm2;
4) 7a2b + 9a3 + (a2b – 9a3) = 8a2b;
5) 3 + 2a2 – 5a + (7a2 – 15 + 5a) = 9a2 – 12; 6) (9x2 – 4xy + 5) – (4x2 – 2xy) = 5 + 5x2 – 2xy. 21.21. Знайдіть многочлен стандартного
1) –M = 5a – b2 + 7; M = –(5a – b2 + 7) = –5a + b2 – 7;
2) M + (3a2 – 2ab) = 5a2 + 3ab – b2; M = (5a2 + 3ab – b2) – (3a2 – 2ab);
M = 5a2 + 3ab – b2 – 3a2 + 2ab; M = 2a2 + 5ab – b2;
3) M – (3mn – 4n2) = m2 – 4mn + n2; M = (m2 – 4mn + n2) + (3mn – 4n2);
4) (7a2 – b2 – 9ba) – M = 0; M = 7a2 – b2 – 9ba. 21.22.
M = m2 – 4mn + n2 + 3mn – 4n2;
M = m2 – mn – 3n2;

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
2) за третю годину: (x + 3) + 3 = (x + 6) км;
3)
три
x + (x + 3) + (x + 6) = (3x + 9) км; 4)
час руху: (3x + 9) + (x + 6 + 3) = (4x + 18) км. 21.23.
3)
a + (a – 2) = 2a – 2 (м);
4) за останніх три дні: за четвертий день бригада викопала (а – 4) – 2 = (а – 6) (м);
п’ятий день (а – 6) – 2 = (а – 8) (м).
Тоді за останні три дні бригада викопала (a – 4) + (а – 6) + (а – 8) = (3а – 18) (м).
21.24. Доведіть тотожність: 1) (х – у) + (у – р) – (х – р) = х – у + y – p – х + p = 0; 2) (а2 + b2 – с2) – (b2– a2 – c2) – (а2 – b2) = a2 + b2 – c2 – b2 + a2 + с2 – a2 + b2 = а2 + b2.
21.25. Доведіть тотожність: (а3 + а2 – а) + (2а2 – 5а + 3а3) – (4а3 – 6а + 2а2) = = а3 + a2 – a + 2a2 – 5а + 3а3 – 4а3 + 6а – 2a2 = а2.
21.26. Доведіть, що
-
11n) є кратним числу 4. (15 – 7n) – (7 – 11n) = 15 – 7n – 7 + 11n = 4n + 8 = 4(n + 2)
(1 8 a2b + 3 5ab) – ( 7 10 ab –3 4ba2) – (
= 1 8 a2b + 6 10 ab –7 10 ab + 6 8 a2b –7 8 a2b + 1 10 ab + 2 = 2. 21.29.
(7х5 – 4х4 + x3 – 8) – (3х5 – 4х4 + 4х3) – (4х5 – 3х3 + 7) = = 7х5 – 4x4 + х3 – 8 – 3х5 + 4х4 – 4х3 – 4х5 + 3х3 – 7 = –15. 21.30. Знайдіть
виразу: 1) (b2 + 3b – 8) – (7b2 –5b + 7) + (5b2 – 8b + 10) = = b2 + 3b – 8 – 7b2 + 5b – 7 + 5b2 – 8b + 10 = –b2 – 5. Якщо b = –2 , то –b2 – 5 = (–2)2 –5 = – 4 – 5 = – 9; 2) 17x2 – (3х2 – 2ху + 3у2) – (14х2 + Зху – 4у2) = = 17x2 – Зх2 + 2ху – 3у2 – 14х2 – Зху + 4у2 = –ху + у2. Якщо х = –0,1 , у = 10, то –ху + у2 = –(–0,1) ⋅ 10 + 102 = 101.

+
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
21.31. Знайдіть
1) (m2 – 2m – 8 ) – (0,1m2 – 5m + 9) + (4m – 0,9m2 + 5) = = m2 – 2m – 8 – 0,1m2 + 5m – 9 + 4m – 0,9m2 + 5 = 7m – 12.
Якщо m = 1 7, то 7m – 12 = 7 ⋅ 1 7 – 12 = –11; 2) 7a2 – (3ab – 2а2) + (4ab – 9а2) = 7a2 – 3ab + 2а2 + 4ab – 9а2 = ab.
Якщо а = –1 8, b = –32, то ab = –1 8 ⋅ (–32) = 4.
21.32. Подайте многочлен Зm2n – 5mn + 4n2 – 9n – 7 у
так, щоб усі члени
3m2n – 5mn + 4n2 – 9n – 7 = (3m2n + 4n2) – (5mn + 9n + 7).
21.33. Нехай а = 7m2 + 5mn – n2, b = –6m2 + 2mn + Зn2, с = m2 – 2n2. Підставте ці многочлени
а, b, с у
1) Якщо а = 7m2 + 5mn – n2, b = – 6m2 + 2mn + 3n2, с = m2 – 2n2 то
а + b + c = 7m2 + 5mn – n2 – 6m2 + 2nm + 3n2 + m2 – 2n2 = 2m2 + 7mn;
2) Якщо = 7m2 + 5mn – n2, b = –6m2 + 2mn + 3n2, с = m2 – 2n2 то а – b – с = 7m2 + 5mn – n2 – (– 6m2 + 2mn + 3n2) – (m2 – 2n2) = = 7m2 + 5mn – n2 + 6m2 – 2mn – 3n2 – m2 + 2n2 = 12m2 + 3mn – 2n2.
0,3x4 + x3 – 0,7x2 – 9
1) ������������ = 100 ⋅ x + 10 ⋅ y + z = 100x + 10y + z; 2) ������������ = –100 ⋅ z + 10 ⋅ у + х = 100z + 10у + х; 3) ������������ + �������� = (100x + 10y + z) + (10z + у) = 100x + 11y + 11z; 4) ������������ – �������� = (100у + 10x + z) – (10y + x) = 100y + 10x + z – 10y – х = 90у + 9х + z. 21.38. Обчисліть
виразу: (0,018 + 0,982) : (4 ⋅ 0,5 – 0,2) = 1 : (2 – 0,2) = 1 : 1,8 = 1 : 18 10 = 1 ⋅ 10 18 = 5 9 .
1) –8х ⋅ 1,5у = –12ху.

рідині складає 2 літри на день?
2 ⋅ 0,15 = 0,3 л = 300 мл.
Відповідь: 300 мл.
21.42. Розкрийте дужки:
1) –0,6d(–5b + 4р – 0,3х) = 3db – 2,4dp + 0,18dx;
2) 10(0,9х – 2,3у + 0,1z) = 9x – 23y + z;
3) (–0,3а + 5b – 2с) ⋅ (–20) = 6a – 100b + 40c;
4) (–1 6 n + 1 2 m – 11 3x) ⋅ 12 = –12 6 n + 12 2 m –4 12
21.43. Знайдіть цифри
число
����2 = 12, 32, 52, 72 і 92. Щоб число
ділилася на 9:
9 + а + 6 + b + 2 = (17 + а + b) : 9.
Якщо b = 1, то маємо: 17 + а + 1 = 18 + а; а = 0, а = 9; шукані числа 90612, 99612; якщо b = 3, то маємо: 17 + а + 3 = 20 + а; а = 7; шукане число 97632;
якщо b = 5, то маємо: 17 + а + 5 = 22 + а; а = 5; шукане число 95652;
якщо b = 7, то маємо: 17 + а + 7 = 24 + а; а = 3; шукане число 93672; якщо b = 9, то маємо: 17 + а + 9 = 26 + а; а = 1; шукане число 91692.
Відповідь: 90612, 91692, 93672, 95652, 97632, 99612. § 22. Множення одночлена на многочлен
22.1. Виконайте множення: 1) х(а – 3) = ха – 3х; 2) –р(х + у) = –pх – ру; 3) m(a – b + 2) = ma – mb + 2m; 4) –y(x – 3 + p) = –yx + 3y – yp.
22.2. Виконайте множення:
1) a(b – 2) = ab – 2а; 2) m(а + с) = mа + mс; 3) р(а – b – 3) = pa – pb – 3р; 4) –b(a – с + 3) = –bа + bс – Зb.
22.3. Виконайте множення одночлена на многочлен:
1) 7a2(3 – а) = 7a2 ∙ 3 – 7а2
= 21а2 – 7а3; 2) –5x2(x3 + 4х) = 5х2 ∙ x3 + (–5х2) ∙ 4х = –5х5 – 20х3; 3)

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
2) –а2b(ab2 – b2 + а2) = – а2b ∙ ab2 + (–a2b) (–b2) + (–а2b) ∙ а2 = – а3b3 + a2b3 – а4b; 3) (2mn – 3m2 – 5n2) ∙ (–4m2) = 2mn ∙ (–4m2) – 3m2 ∙ (–4m2) – 5n2 ∙ (–4m2) = = –8m3n + 12m4 + 20m2n2; 4) (–2х2у +3хy – x2) ∙ xy2 = –2х2у ∙ ху2 + 3ху ∙ xy2 – x2 ∙ xy2 = –2x3у3 + 3x2y3 – x3у2; 5) (2,8a2b – 3,7a3b – 0,8b) ∙ 10аb2 = 2,8a2b ∙ 10ab2 – 3,7a3b ∙ 10ab2 – 0,8b ∙ 10ab2 = = 28a3b3 – 37а4b3 – 8ab3;
6) –1,8a2b6(5a2b – 1,5a – 2b3) = –1,8a2b6 ∙ 5a2b + (–1,8а2b6 ) ∙ (–1,5а) + (–1,8а2b6) ∙ (–2b3) = = –9а4b7 + 2,7a3b6 + 3,6a2b9 .
22.5. Подайте добуток у вигляді многочлена:
1) 4a(а2 – 2а + 3) = 4a3 – 8а2 + 12а;
2) –3b2(4b3 – 2b2 + 3b – 8) = –12b5 + 6b4 – 9b3 + 24b2;
3) (3х2 – 4х + 12) ∙ (–0,1х3) = –0,3х5 + 0,4х4 – 1,2х3;
4) (р2 – 9р3 + 7p – 1) ∙ 3p4 = 3р6 – 27р7 + 21р5 – 3р4;
5) 7ab(2a2b – 3аb2 – 3а3)= 14а3b2 – 21а2b3 – 21а4b; 6) –6m2n(m2n – 3mn2 – 4n3) = –6m4n2 + 18m3n3 + 24m2n4 ;
7) (9a2b – 8ab3 – а2b2) ∙ (–3а2b3) = –27a4b4 + 24a3b6 + 3a4b5; 8) (p2q3 – 2pq4 + 3р3) ∙ 5p3q2 = 5p5q5 – 10p4q6 + 15p6q2.
22.6. Виконайте множення:
1) 1 7 a2b (1,4a2 – 2,1b3) =
2) –2 3 x2y3 ∙ (1,2y5
3) (11
4)
22.7. Виконайте множення:
2) –2 5 ab3(1,5ab –5 6b2) = –2 5 ab3 ∙ 15 10 ab – (–2 5)ab3 ∙ 5 6 b2 = –
3) (11 2 x2y –9 10xy4)
4) (1,5a –4 7b) ∙ (–1 14 a2b5) = 15 10a
22.8. Подайте у вигляді многочлена:
1) 5(x – 3) – 2(х– 3) = 5x – 15 – 2х + 6 = 3х – 9; 2) 5(7а – 1) – 7(5а + 3) = 35а – 5 – 35а – 21 = –26;
3) 2b(b – 3) – 5b(b + 7) = 2b2 – 6b – 5b2 – 35b = –3b2 – 41b; 4) 7у2(3у – 2) + 4у2(у + 5) = 21у3 – 14у2 + 4у3 + 20у2 =25у3 + 6у2.
22.9. Спростіть вираз:
1) 5(3 – 2а) + 7(3а – 1) = 15 – 10а + 21а – 7 = 11а + 8;
2) 3(2х – 8) – 3(2х – 5) = 6x – 24 – 6х + 15 = –9;
3) 3m(m – 2) – 5m(7 – m) = 3m2 – 6m – 35m + 5m2 = 8m2 – 41m;
4) 2а2(3а – 5) + 4а2(а + 3) = 6а3 – 10а2 + 4а3 +12а2 = 10а3+ 2а12.
22.10. Перетворіть вираз на многочлен:
.
1) 5m(m – n) + 3n(n – m) = 5m2 – 5mmn + 3n2 – 3mn = 5mn2 + 3n2 – 8mn;
2) 2а(2b – 3а) – 3а(5b – 7а) = 4аb – 6а2 – 15аb + 21а2 = 15а2 – 11аb;
3) а(3а2 – 2b) – b(5а2 – 2а) = 3а3 – 2аb – 5а2b + 2аb = 3а3 – 5а2b; 4) 0,2mn(m2 – n2 + 3) – 0,5m(nm2 – n3) = 0,2m3n – 0,2mn3 + 0,6mn – 0,5m3n + 0,5mn3 = = –0,3m3n + 0,3mn3 + 0,6mn.

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
22.11. Виконайте дії:
1) 3а(а – b) + 5b(а + b) = 3а2 – 3аb + 5ab + 5b2 = 3а2 + 2аb + 5b2;
2) 3y(x – y) + y(2у – 3х) = 3ху – 3y2 + 2у2 – 3ху = –у2; 3) p(р2 – 2а) – a(a2 – 2р) = р3 – 2ар – а3 + 2ар = р3 – а3;
4) 3ху(х2 – у2 + 7) – 5xy(y2 + х2) = 3х3y – 3xy3 + 21xy – 5ху3 – 5х3у = –2х3у – 8хy3 + 21хy.
22.12. Розв’яжіть рівняння:
1) 6 + 2(5х + 4) = 24
6 + 10x+ 8 = 24
10х = 24 – 6 – 8
10x = 10 x = 1 2) 3(5х – 1) = 4(4х – 8)
3) 7 – 4(у – 1) = (3у – 2)(–2)
7 – 4у + 4 = –6y + 4
–4у + 6у = 4 – 7 – 4
2у = –7
15х – 3 = 16х – 32
15х – 16х = –32 + 3 –х = –29 х = 29
y = –3,5 4) 3 (у – 2) – 5(у + 7) = –7(у – 1)
22.13. Розв’яжіть рівняння:
1) 5(2x – 1) = 3 (4x + 5)
10x – 5 = 12x + 15
10x – 12x = 15 + 5
–2x = 20
x = –10
22.14. Знайдіть корінь рівняння:
1) x(x – 3) – 9 = 12 + x2
x2 – 3x – 9 = 12 + x2
x2 – 3x – x2 = 12 + 9 –3х = 21
x = –7
22.15. Знайдіть корінь рівняння:
1) 7 – x(x – 2) = 5 – x2
7 – x2 + 2x = 5 – x2
–x2 + 2x + x2= 5 – 7
2x = –2
x = –1
22.16. Запишіть
3y – 6 – 5у – 35 = –7y + 7 –2у + 7y = 7 + 6 + 35
5y = 48
у = 9,6
2) 9 – 5(y + 2) = (7у – 5) ∙ (–3)
9 – 5y – 10 = – 21y + 15
–5y + 21y = 15 – 9 + 10
16у = 16 у = 1
2) 3x – 2x2 = 2x(5 – x) + 14 3x – 2x2 = 10x– 2x2 + 14
3x – 2x2 – 10x + 2x2 = 14 –7x = 14
x = –2
2) 3x(x – 5) = 3x2 – 5x + 20 3x2 – 15x = 3x2 – 5x + 20 3x2 – 15x – 3x2 + 5x = 20 –10x = 20
x = –2
1) (a + b) ∙ m = am + bm; 2) –n ∙ (x – у) = –nx + ny; 3) x2 ∙ (a – b + c) = ax2 – bx2 + cx2; 4) –аb ∙ (c – n + p) = –abc + abn – abp; 5) y2 ∙ (x2 – xy) = x2y2 – xy3; 6) (p – 1) ∙ pq2 = p2q2 – pq2
22.17. Доведіть, що
-
а(3а + 1) – a2(a + 2) + (a3 – a2) – (a + 1) = 3а2 + a – a3 – 2a2 + a3 – a2 – a – 1 = –1.

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
22.20. Перетворіть
1) –7a5b(2b4 + ab5 – 3a2b6 + a3b7) = –14a5b5 – 7a6b6 + 21a7b7 – 7a8b8; 2) (3x3 + 5x2 – 2a – 3a2)xay = 3x4ay + 5x3ay – 2xa2y – 3a3xy; 3) –4pm3 (m4 – 2p3m + 7p6m7 + 11p7m3) = –4pm7 + 8p4m4 – 28p7m10 – 44p8m6; 4) (–1 2 a2b9 + 1 6 ab7 –1 3 a3b6) ∙ (–12a3b7) = 6a5b16 – 2a4b14 + 4a6b13
22.21.
2a2(a – 5) – a(–6a + 2a2 + 3a3) – 4 =
5(m2 – 3m + 1) – 3m(m – 5) = 5m2 – 15m + 5 – 3m2 + 15m = 2m2 + 5
1) 3а(5а2 – 3аb + ab2 – b2) ∙ b = 3аb(5а2 – 3аb + аb
22.24. Спростіть
1) 4a – 2(5a – 1) + (8a – 2) = 4a – 10a + 2 + 8a – 2 = 2a.
Якщо a = –3,5, то 2а = 2 ∙ (–3,5) = –7; 2) 10(2 – 3x) + 12x – 9(x + 1) = 20 – 30x + 12x – 9x – 9 = –27x + 11
Якщо x = –1 27,то –27x + 11 = –27 ∙ (–1 27) + 11 = 1 + 11 = 12; 3) а(3а – 4b) – b(3b – 4а) = 3а2 – 4ab – 3b2 + 4аb = 3а2 – 3b2.
Якщо a = –5, b = 5, то 3a2 – 3b2 = 3 ∙ (–5)2 – 3 ∙ 52 = 0; 4) 3ху(5х2 – у2) – 5ху(3х2 – у2) = 15х3у – 3ху3 – 15x3у + 5xy3 = 2xy3 .
Якщо х = 1 8 , у = –2 , то 2xy3 = 2 ∙ 1 8 ∙ (–2)3 = –2. –7 + 12 + 0 + (–2) = 12 – 9 = 3 (рази).
22.25. Спростіть вираз і знайдіть його значення:
1) 7а(2а – 0,1) – 0,1а(10а – 7) = 14а2 – 0,7а – а2 + 0,7а = 13а2
Якщо а = 1 13, то 13а2 = 13 ∙ ( 1 13)2 = 1 13
2) 4х(2х – 5у) – 2у(4у – 10x) = 8x2 – 20ху – 8у2 + 20xy = 8x2 – 8y2
Якщо х = –15, y = 15, то 8x2 – 8у2 = 8 ∙ (–15)2 – 8 ∙ 152 = 8 ∙ 152 – 8 ∙ 152 = 0
22.26. Розв’яжіть рівняння:
1) 5x 9 4 + 5x 7 4 = 1
5х – 9 + 5х – 7 = 4
10х = 4 + 9 + 7
10x = 20
х = 2 2) 3x 1 14 –x 7 = – 2 3х – 1 – 2х = –28 3х – 2x = –28 + 1 х = –27
3) x 6 3 + 2x + 3 3 = 2x
х – 6 + 2х + 3 = 6х
3х – 6х = 6 – 3 –3х = 3

х = –1 4) 2 x 5 –x 15 = 1 3 6 – 3х – х = 5 –3х – х = 5 – 6 –4х = –1 х = 1 4
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
5) 2х(1 – 3х) + 5х(3 – х) = 17х – 11х2 2х – 6х2 + 15х – 5х2 = 17х – 11х2 –11х2 + 17х – 17х – 11х2 = 0
0 = 0
х – будь яке число.
22.27. Розв’яжіть рівняння:
1) 7x 3 6 –5x + 1 2 = 0
6) (7х3 + 2х2 – 4х – 5) – (6х3 – х2 + 2х) = = 3х2 – (6х – х3)
7х3 + 2х2 – 4х – 5 – 6х3 + х2 – 2х = 3х2 – 6х – х3 х3 + 3х2 – 6х – 5 – 3х2 + 6х + х3 = 0 –5 ≠ 0. Не має розв’язків.
7х – 3 – 15х – 3 = 0 –8х = 6 х = –3 4 2) x 3 5 –x 4 = 1 4х – 12 – 5х = 20 –х = 20 + 12 х = –32
3) 4x + 1 6 –10x + 1 6 = x
4х + 1 + 10x + 1 = 6х
14х – 6х = –1 – 1
8х = –2
х = –1 4
5) 3х(2 + х) – 4(1 – х2) = 7х2 + 6х
6х + 3х2 – 4 + 4х2 = 7х2 + 6х
7х2 – 7х2 + 6х – 6х = 4
0 ≠ 4. Не має розв’язків.
22.28. Для якого значення змінної: 1) значення виразу 2(3у + 1) у 4 рази
2(3у + 1) = 4(3у – 2)
6у + 2= 12у – 8
6y – 12y = –8 – 2 –
6у = –10
y = 5 3 = 12 3 2) добуток
і 2х+1
3x ∙ (2х + 1) = х(4х – 1) + 2(х2 – 3)
6х2 + 3х = 4х2 – х + 2x2 – 6
6x2 – 4x2 – 2х2 + 3х + х = –6
4х = –6 x = –1,5

4) x + 2 15 = 1 3 –x 5
х + 2 = 5 – 3х х + 3х = 5 – 2 4х = 3 х = 3 4
6) (х2 + 4х – 8) – (7х – 2х2 – 5) = 3х2 – (3х + 3) х2 + 4х – 8 – 7х + 2х2 + 5 = 3х2 – 3х – 3 3х2 – 3х – 3х2 + 3х = –3 + 3 0 = 0. х – будь яке число.
3у – 2;
– 3)?
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
80х – 50х – 50х = 80 – 200 – 200
20х = 320
х = 16 Отже,
Нехай
(х + 3250) коп.
8х + 4(х + 1750) + (х + 3250) = 26500
8х + 4х + 7000 + х + 3250 = 26500
13х = 16250
х = 1250
Олівець
блокнот 1250 + 3250 = 4500 (коп.) = 45
Відповідь: 12 грн 50 коп., 30 грн,
+ 6)
Складемо рівняння:
6,5х + 5,4(х + 6) = 175,2
65х + 54х + 324 = 1752
119х= 1428
х = 12
Отже,
(х + 2) км/год, а проти течії (х – 2) км/год. За течією човен подолав (х + 2) ∙ 3,5 = (3,5х + 7) (км), а проти течії (х – 2) ∙ 2,5 = (2,5х – 5) (км).
Складемо рівняння:
3,5х + 7 = 2,5х – 5 + 30
3,5х – 2,5х = – 5 + 30 – 7 х = 18
Відповідь: 18 км/год.
22.33. Якими
1) 5ax2 ∙ (х + 7) = 5ax3 + 35ах2; 2) (9а2 + 6а2) ∙ 3а = 27а3 + 18а3; 3) (m2 – 4mc2) ∙ 3mс2 = 3m3c2 – 12m2c4; 4) (5 – 7у) ∙ х2y3 = 5х2y3 – 7х2y4 .
22.34. Які одночлени треба
1) 3a2(3a3 – 4) = 9а5 – 12а2; 2) (1+ 2ab) ∙ 5ab2 = 5ab2 + 10а2b3; 3) (2m – 2m2а) ∙ 7m = 14m2 – 14m3а; 4) (7x2а – 9ха2) ∙ 2ха4 = 14х3а5 – 18x2a6.

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
22.35. Спростіть вираз (n – натуральне число): 1) xn+3(xn+4 – x) – x2n+7 = x2n+7 – хn+4 – х2n+7 = –хn+4; 2) yn(yn+2 – yn – y2) – y2(y2n – yn) = y2n+2 – y2n – y2+n – y2n+2 + y2+n = –y2n; 3) zn(z2 – 1) – z2(zn + 2) – 2(zn – z2) = zn+2 – zn – zn+2 – 2z2 – 2zn + 2z2 = –3zn.
22.36. У яких координатних чвертях розташовуються точки A(4; –8), B(–5; –7), С(1; 17), D(–9; 8)?
Точка A(4; –8) знаходиться у четвертій чверті, B(–5; –7) у третій, С(1; 17) у першій, a D(–9; 8) у другій.
22.37. Спростіть: 1) (–3а2b3)2 ∙ (1 3ab2)3 = 9a4b6 ∙ 1 27 a3b6 = 1 3 a7b12; 2) (0,1mn7)2 ∙ (–10m2n3)3 = 0,01m2
22.38. Використовуючи
1)
tС = (95 – 32) : 1,8 = 35
22.40. Винесіть за
спільний множник: 1) 7а – 7b = 7(a – b); 2) –2у – 2х = –2(y + x); 3) 9n + 9m = 9(n + m); 4) bx + by = b(x + y); 5) 3m – mх = m(3 – x); 6) 7t + 7 = 7(t + 1); 7) 5ар + 5рb = 5p(a + b); 8) 4ах– 4bx = 4x(a – b).
22.41. Відомо, що
7.

23.3. Винесіть за
1) 5а + 5c = 5(а + c);
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
2) 7x – 7u = 7(x – u);
3) аp – аb = а(p – b); 4) mx + yx = х(m + y).
23.4. Винесіть за дужки спільний множник:
1) 2u – 2p = 2(u – p); 2) 7x + 7y = 7(x + y);
3) аt + bt = t(а + b); 4) ma – mc = m(a – c).
23.5. Чи правильно виконано розкладання на множники:
1) 7a + 7 = 7a, ні; 2) 5m − 5 = 5(m − 5), ні; 3) 2a − 2 = 2(a − 1), так; 4) 7xy − 14x = 7x(y − 2), так; 5) 5mn + 5n = 5m(n + 3), ні; 6) 7ab + 8cb = 15b(a + c), ні.
23.6. Запишіть суму у вигляді добутку:
1) 3а + 12b = 3(а + 4b); 2) –6а – 9х = –3(2а + 3х);
3) 17a + 17 = 17(а + 1); 4) –ab – а = –а(b + 1);
5) 14а – 21х = 7(2а– 3х); 6) 8b – 8 = 8(b – 1).
23.7. Розкладіть на множники:
1) 4m – 16а = 4(m – 4а); 2) –12m + 18а = 6(–2m + 3а);
3) 14m – 14 = 14(m – 1); 4) –хb – b = –b(х + 1);
5) 8р + 8 = 8(р + 1); 6) 20b – 30с = 10(2b – 3с).
23.8. Розкладіть на множники:
1) 5ab + 5xb = 5b(а + х); 2) 2ху – 8у = 2у(х – 4);
3) –5ab + 5а = 5а (–b + 1); 4) 7а + 21ау = 7а(1 + 3у);
5) 9х2 – 27х = 9х(х – 3); 6) За – 9а2 = 3а(1 – 3а); 7) m2 – mа = m(m – а); 8) 12ах – 4а2 = 4а(3х – а);
9) –18хy + 24у2 = 6у(–3х + 4у); 10) a2b – ab2 = ab(a – b); 11) рm – р2m = рm(1 – р); 12) –х2у2 – ху = –ху(ху + 1).
23.9. Винесіть за дужки спільний множник:
1) 7ах – 7bх = 7х(а – b); 2) 3аb + 9а = 3а(b + 3);
3) 6хm – 8хn = 2х(3m – 4n); 4) 15ху + 5х = 5х(3у + 1);
5) 9m2 – 18m = 9m(m – 2); 6) 15m – 30m2 = 15m(1 – 2m); 7) 9ху + 6х2 = 3х(3y + 2х); 8) а2b – ab = ab(a – 1); 9) –p2q – pq2 = –pq(p + q).
23.10. Розкладіть на множники:
1) х3 – х2 = х2 (х – 1); 2) а4 + а2 = а2(а2 + 1); 3) m3 – m5 = m3(1 – m2); 4) а3 + а7 = а3(1 + а4); 5) 3b2 – 9b3 = 3b2(1 – 3b); 6) 7а3 + 6а = а(7а2 + 6);
7) 4y2 + 12y4 = 4y2 (1 + 3y2); 8) 5m5 + 15m2 = 5m2(m3 +3); 9) –16а4 – 20а = –4а(4а3 + 5).
23.11. Розкладіть на множники:
1) m4 – m2 = m2(m2 – 1); 2) а4 + а5 = а4(1 + а);
3) 6а – 12а3 = 6а(1 – 2а2); 4) 18р3 – 12р2 = 6р2(3р – 2); 5) 14b3 + 7b4 = 7b3(2 + b); 6) –25m3 – 20m = –5m(5m2 + 4).
23.12. Запишіть суму 6х2у + 15х у
0,5, у = 5.
6х2у + 15x = 3х(2ху + 5). Якщо х = –0,5, у = 5, то 3х(2ху + 5 ) = 3 ∙ (–0,5) ∙ (2 ∙ (–0,5) ∙ 5 + 5)) = –1,5 ∙ 0 = 0.
23.13. Запишіть
12а2b – 8a = 4a(3ab – 2). Якщо а = 2, b = 1 3, то 4a(3ab – 2) = 4 ∙ 2 ∙ (3 ∙ 2 ∙ 1 3 – 2) = 8 ∙ 0 = 0.

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
23.14. Винесіть за дужки спільний множник:
1) а4 + a3 – а2 = a2(a2 + а – 1); 2) m9 – m2 + m7 = m2(m7 – 1 + m5);
3) b6 + b5 – b9 = b5(b +1 – b4); 4) –y7 – у12 – у3 = –y3(y4 + y9 + 1).
23.15. Подайте у вигляді добутку:
1) р7 + р3 – р4 = р3(р4 + 1 – р); 2) а10 – а5 + a8 = a5(a5 – 1 + а3); 3) b7 – b5 – b2 = b2(b5 – b3 – 1); 4) –m8 – m2 – m4 = –m2(m6 + 1 + m2).
23.16. Обчисліть зручним способом:
1) 132 ∙ 27 + 132 ∙ 73 = 132(27 + 73) = 132 ∙ 100 = 13200;
2) 119 ∙ 37 – 19 ∙ 37 = 37(119 – 19) = 37 ∙ 100 = 3700.
23.17. Розв’яжіть рівняння: 1) х2 – 2х = 0
х(х – 2) = 0
х = 0 або х – 2 =0
х = 0 або х = 2
23.18. Знайдіть корені рівняння:
1) х2 + 3х = 0
х(х + 3)= 0
х = 0 або х + 3 = 0
х = 0 або х = –3
23.19. Розкладіть многочлен на множники:
2) х2 + 4х = 0
х(х + 4) = 0
х = 0 або х + 4 = 0
х = 0 або х = –4
2) х2 – 7x = 0
х(х – 7) = 0
х = 0 або х – 7 = 0 х = 0 або х = 7
1) 4a3 + 2а2 – 8а = 2а(2а2 + a – 4); 2) 9b3 – 3b2 – 27b5 = 3b2(3b – 1 – 9b3);
3) 16m2 – 24m6 – 32m3 = 8m2(2 – 3m4 – 4m); 4) –5b3 – 20b2 – 25b5 = –5b2(b + 4 + 5b3).
23.20. Винесіть за
1) 5с8 – 5с7 + 10c4 = 5с4(с4 – c3 + 2);
2) 9m4 + 27m3 – 81m = 9m(m3 + 3m2 – 9);
3) 8p7 – 4р5 + 10p3 = 2р3(4р4 – 2р2 + 5); 4) 21b – 28b4 – 14b3 = 7b(3 – 4b3 – 2b2).
23.21. Винесіть за
1) 7m4 – 21m2n2 + 14m3 = 7m2(m2 – 3n2 + 2m);
2) 12a2b – 18ab2 + 30ab3 = 6ab(2a – 3b + 5b2);
3) 8x2y2 – 4х3у5 + 12х4y3 = 4х2у2(2 – ху3 + 3х2у); 4) –5p4q2 – 10p2q4 + 15р3q3 = 5p2q2(–p2 – 2q2 + 3pq).
23.22. Розкладіть многочлен на множники:
1) 12a – 6a2х2 – 9a3 = 3a(4 – 2aх2 – 3а2); 2) 12b2у – 18b3 – 30b4у = 6b2(2у – 3b – 5b2у);
3) 16bx2 – 8b2x3 + 24b3х = 86х(2х – bх2 + 3b2); 4) 60m4n3 – 45m2n4 + 30m3n5 = 15m2n3(4m2 – 3n + 2mn2).
23.23. Обчисліть зручним способом:
1) 843 ∙ 743 – 7432 = 743(843 – 743) = 743 ∙ 100 = 74300; 2) 11032 – 1103 ∙ 100 – 1103 ∙ 3 = 1103(1103 – 100 – 3) = 1103 ∙ 1000 = 1 103 000.
23.24. Знайдіть значення виразу:
1) 4,23a – a2 = a(4,23 – а).
Якщо a = 5,23, то a(4,23 – a) = 5,23(4,23 – 5,23) = 5,23 ∙ (–1) = –5,23; 2) х2у + x3 = x2(у + х). Якщо х = 2,51, у = –2,51 то х2(у + х) = = 2,512(–2,51 + 2,51) = 0; 3) am5 – m6 = m5(a – m). Якщо m = –1 , а = –5 , то m5(a – m) = = (–1)5(–5 +1) = 4; 4) –ху – x2 = –х(у + х). Якщо х = 2,7, у = 7,3, то –х(у +х) = –2,7(7,3 + 2,7) = –27.
23.25. Знайдіть значення виразу:
1) 9,11a + a2 = a(9,11 + a).

Якщо a = –10,11, то a(9,11 + a) = –10,11(9,11 – 10,11) = –10,11 ∙ (–1) = 10,11; 2) 5ax2 + 5a2x = 5ax(x + a). Якщо a = 2 5, x = 3 5, то 5ax(x + a) =
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
23.26. Розкладіть
1) 2р(х – у) + q(x – у) = (х – у)(2р + q); 2) а(х + у) – (х + у) = (х + у)(а – 1);
3) (a – 7) – b(a – 7) = (a – 7) (1 – b);
4) 5(а + 1) + (а + 1)2 = (a + 1)(1 + a + 1) = (a + 1)(а + 2);
5) (х + 2)2 – х(х + 2) = (х + 2)(х + 2 – х) = 2(х + 2);
6) –5m(m – 2) + 4(m – 2)2 = (m – 2)(–5m + 4(m – 2)) = (m – 2)(–5m + 4m – 8) = = (m – 2)(–m – 8).
23.27. Подайте вираз у вигляді добутку:
1) a(x – у) + b(у – х) = а(х –у) – b(x – у) = (х – у)(а – b);
2) р(b – 5) – n(5 – b) = р(b – 5) + n(b – 5) = (b – 5)(р + n);
3) 7х(2b – 3) + 5у(3 – 2b) = 7х(2b – 3) – 5у(2b – 3) = (2b – 3)(7х – 5y);
4) (х – у)2 – а(у – х) = (х – у)2 + а(х – у) = (х – у)(х – у + а);
5) 5(x – 3)2 – (3 – х) = 5(х – 3)2 + (х – 3) = (х – 3)(5(х – 3) + 1) = (х – 3)(5х – 15 + 1) = = (х – 3)(5х – 14);
6) (а + 1)(2b – 3) – (а + 3)(3 – 2b) = (а + 1)(2b – 3) + (а + 3)(2b – 3) = = (2b – 3) ∙ (а + 1 + a + 3) = (2b – 3)(2а + 4).
23.28. Розкладіть на множники:
1) 3х(b – 2) + у(b – 2) = (b – 2)(3х + у); 2) (m2 – 3) – х(m2 – 3) = (m2 – 3)(1 – х);
3) а(b – 9) + с(9 – b) = а(b – 9) – с(b – 9) = (b – 9)(а – с);
4) 7(а + 2) + (а + 2)2 = (а + 2)(7 + а + 2) = (а + 2)(а + 9);
5) (с – m)2 – 5(m – с) = (с – m)2 + 5(с – m) = (с – m)(с – m + 5);
6) –(х + 2у) – 5(х + 2y)2 = (х + 2у)(–1 – 5(х + 2у)) = (х + 2у)(–1 – 5х – 10y).
23.29. Знайдіть корені рівняння:
1) 4х2 – х = 0
х(4х – 1) = 0
х = 0 або 4х – 1 = 0
7х(х + 4) = 0
х = 0 або х = 1 4 2) 7х2 + 28х = 0
3) 1 9 х2 + х = 0
х2 + 9х = 0
х(х + 9) = 0
х = 0 або х + 9 = 0
7х = 0 або х + 4 = 0
х = 0 або х = –4
х = 0 або х = –9 4) 2 11 х2 –3 11 х = 0
х( 2 11 х –3 11) = 0
х = 0 або 2 11 х –3 11 = 0
х = 0 або 2 11 х = 3 11
х = 0 або х = 3 11 : 2 11
х = 0 або х = 1,5
23.30. Розв’яжіть рівняння:
1) 12х2 + х = 0
х(12х + 1) = 0
х = 0 або 12х + 1 = 0
х = 0 або х = –1 12
3) 1 14 x2 – x = 0
x( 1 14 x – 1) = 0
х = 0 або 1 14 х – 1 = 0
х = 0 або 1 14 х = 1

2) 0,2х2 – 2х = 0
х(0,2х – 2) = 0
х = 0 або 0,2х – 2 = 0
х = 0 або х = 10
х = 0 або х = 14 4) 11 3 x2 + 2 3 x = 0 x(11 3 x + 2 3) = 0
х = 0 або 11 3 х + 2 3 = 0
х = 0 або 4 3 х = –2 3
х = 0 або х = –1 2
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
23.31. Розв’яжіть рівняння:
1) x(3x + 2) – 5(3х + 2) = 0
(3х + 2)(х – 5) = 0
3х + 2 = 0 або х – 5 = 0
3х = –2 або х = 5
х = –2 3 або х = 5
23.32. Розв’яжіть рівняння:
1) х(4х + 5) – 7(4х + 5) = 0
(4х + 5)(х – 7) = 0
4х + 5 = 0 або х – 7 = 0
4х = –5 або х = 7
х = –11 4 або х = 7
2) 2х(х – 2) – 5(2 – х) = 0
2х(х – 2) + 5(х – 2) = 0
(х – 2)(2х + 5) = 0
х – 2 = 0 або 2х + 5 = 0
х = 2 або х = –2,5
2) 7(х – 3) – 2х(3 – х) = 0
7(х – 3) + 2х(х – 3) = 0
(х – 3)(7 + 2х) = 0
х – 3 = 0 або 7 + 2х = 0
х = 3 або х = –3,5
23.33. Доведіть, що значення виразу: 1) 173 + 172 кратне числу 18; 173 + 172 = 172(17 + 1) = 172 ∙ 18 кратне 18; 2) 914 – 816 кратне числу 80. 914 – 816 = 914 – (92)6 = 914 – 912 = 912(92 – 1) = 912 ∙ 80 кратне 80.
23.34. Доведіть, що значення виразу: 1) 399 – 398 ділиться на 38; 399 – 398 = 39(39 – 1) = 39 ∙ 38 кратне 38; 2) 495 – 78 ділиться на 48. 495 – 78 = (72)5 – 78 = 710 – 78 = 78(72 – 1) = 78 ∙ 48 кратне 48.
23.35. Винесіть за дужки спільний множник:
1) (5m – 10)2 = (5(m – 2))2 = 52(m – 2)2 = 25(m – 2)2; 2) (18a + 27b)2 = (9(2а + 3b))2 = 92(2а + 3b)2 = 81(2а + 3b)2.
23.36. Знайдіть корені рівняння:
1) х(х – 3) = 7х – 21
х(х – 3) – 7(х – 3) = 0
(х – 3)(х – 7) = 0
х – 3 = 0 або х – 7 = 0
х = 3 або х = 7
23.37. Розв’яжіть рівняння:
1) х(х – 2) = 4х – 8
х(х – 2) – 4(х – 2) = 0
(х – 2)(х – 4) = 0
х – 2 = 0 або х – 4 = 0
х = 2 або х = 4
2) 2х(х – 5) = 20 – 4х
2х(х – 5) + 4(х – 5) = 0
(х – 5)(2х + 4) = 0
х – 5 = 0 або 2х + 4 = 0
х = 5 або х = –2
2) 3х(х – 4) = 28 – 7х
3х (х – 4) – 28 + 7х = 0
3х(х – 4) + 7(х – 4) = 0
(3х + 7)(х – 4) = 0
3х + 7 = 0 або х – 4 = 0
х = –21 3 або х = 4
23.38. Доведіть, що число: 1) 104 + 53 ділиться на 9; 104 + 53 = (5 ∙ 2)4 + 53 = 54 24 + 53 = 53(5 ∙ 24 + 1) = 53 ∙ 81 кратне 9;
2) 415 – 414 + 413 ділиться на 13; 415 – 414 + 413 = 413(42 – 4 + 1) = 413 ∙ 13 кратне 13; 3) 273 – З7 + 93 ділиться на 25; 273 – 37 + 93 = (33)3 – 37 + (32)3 = 39 – 37 + 36 = 36(33 – 3 + 1) = 36 ∙ 25 кратне 25;

4) 213 + 143 – 73
на 34. 213 + 143 – 73 = (7 ∙ 3)3 + (7 ∙ 2)3
1) –3х2 + 7x2 – 4x2 + 3х2 = 3х2. Якщо х = 0,1, то 3х2 = 3 ∙ 0,12 = 0,03; 2) 8m + 5n – 7m + 15n = m + 20n. Якщо m = 7, n = –1, то m + 20n = 7
23.40.
на тотожність:
1) 2m2 – 4mn + n2 + (m2 – 5mn – 6n2) = 3m2 – 9mn – 5n2; 2) 7x2 – 10y2 – ху – (8x2 – 2ху – 13y2) = –x2 + 3у2 + ху.
23.41.
прямокутника зменшити на 5 см, то
і ширину прямокутника.
Нехай ширина прямокутника дорівнює
Складемо рівняння:
х(3х – 5) + 40 = 3х ∙ х
3х2 – 5х + 40 = 3х2
3х2 – 5x – 3х2 = –40 – 5х = –40; х = 8
Початкова довжина прямокутника
Відповідь: 8 см; 24 см.
23.42. Ширина
1)
2) 16 : 0,8 = 20 (с) –
23.43. Відомо, що а < b < с. Чи можуть одночасно виконуватися нерівності |а| > |с| і |b| < c? Можуть одночасно виконуватись, наприклад: а = –2, b = 0, с = 1.
Тоді –2 < 0 < 1 і |–2| > |0|; |0| < |1|. § 24. Множення многочлена на многочлен
24.1. (Усно.) Знайдіть добуток: 1) (x + y)(a + t) = xa + xt + ya + yt; 2) (a – 2)(b + 1) = ab + a – 2b – 2; 3) (7 – p)(b – c) = 7b – 7c – pb + pc; 4) (1 – m)(2 – d) = 2 – d – 2m + md.
24.2. Виконайте множення: 1) (а – b)(х + m) = ах + am – bx – bm; 2) (с + n)(a + y) = сa + сy + na + ny; 3) (p – t)(c – у) = pc – pу – tc + ty; 4) (а + 3)(b – 2) = ab – 2а + 3b – 6.
24.3. Перемножте дужки:
1) (с – 7)(x + 1) = cx + с – 7x – 7; 2) (a + b)(p + y) = ap + ay + bp + by;
3) (b + 2)(y – 4) = by – 4b + 2y – 8; 4) (c – b)(а – x) = ca – cx – bа + bx.
24.4. Спростіть вираз:
1) (а + 3)(а + 2) = а2 + 2а + 3а + 6 = а2 + 5a + 6;
2) (у – 2)(у + 4)= у2 + 4у – 2у – 8 = у2 + 2у – 8;
3) (2 – р)(р + 1) = 2p + 2 – р2 – р = –p2 + p + 2;
4) (b – 5)(2b + 1) = 2b2 + b – 10b – 5 = 2b2 – 9b – 5;
5) (3а – 4)(2а + 1) = 6a2 + 3а – 8а – 4 = 6а2 – 5а – 4;
6) (5y – 3)(1 – 2у) = 5у – 10y2 – 3 + 6у = –10y2 + 11y – 3.

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
24.5. Спростіть вираз:
1) (у + 2)(у – 3) = у2 – 3у + 2у – 6 = у2 – у – 6;
2) (а – 3)(а – 2) = а2 – 2а – 3а + 6 = а2 – 5а + 6;
3) (4 – р)(р + 3) = 4р + 12 – р2 – 3р = –р2 + р + 12;
4) (5а – 2)(а + 3) = 5а2 + 15а – 2а – 6 = 5а2 + 13а – 6;
5) (4b – 3)(2b – 1) = 8b2 – 4b – 6b + 3 = 8b2 – 10b + 3;
6) (7m – 2)(1 + 2m) = 7m + 14m2 – 2 – 4m = 14m2 + 3m – 2.
24.6. Подайте вираз
1) (2 + 4х)(2у – 1) = 4у – 2 + 8xy – 4х;
2) (х2 + а)(х – a2) = x3 – а2х2 + ах – а3;
3) (4р – 2m)(3р + 5m) = 12p2 + 20mр – 6mр – 10m2 = 12p2 + 14mp – 10m2;
4) (2х2 – 1)(3х + 1) = 6х3 + 2x2 – 3х – 1;
5) (7х2 – 4х)(3х – 2) = 21х3 – 14х2 – 12х2 + 8х = 21х3 – 26х2 + 8x;
6) (b – 2)(3b3 – 4b2) = 3b4 – 4b3 – 6b3 + 8b2 = 3b4 – 10b3 + 8b2;
7) (m2 – 2m)(3m – 7m2) = 3m3 – 7m4 – 6m2 + 14m3 = –7m4 + 17m3 – 6m2;
8) (n3 – 2n2)(n + 7) = n4 + 7n3 – 2n3 – 14n2 = n4 + 5n3 – 14n2.
24.7. Спростіть вираз:
1) (3m2 − 2p)(m2 + p) = 3m4 + 3m2р – m2р – р2 – 3m4 + 2m2р – р2;
2) (5a2 + b)(b2 − 4a2) = 5a2b2 – 20а4 + b3 – 4a2b;
3) (12a2 − 3)(5a − 7a2) = 60а3 – 84а4 – 15а + 21а2; 4) (2a3 − 3a2)(a + 5) = 2а4 + 10а3 – 3а3 – 15а2 = 2а4 + 7а3 – 15а2.
24.8. Виконайте множення:
1) (m – n)(а + b – 1) = mа + mb – m – nа – nb + n;
2) (3 – а)(р + 5 – m) = 3р + 15 – 3m – ар – 5a + am;
3) (а + х – 3)(n + 2) = an + 2а + хn + 2х – 3n – 6;
4) (c – d – 7)(х + у) = cx – су – dx – dy – 7x – 7y.
24.9. Перетворіть вираз на многочлен:
1) (а + b)(m – 2 + р) = am – 2а + ар + bm – 2b + bр;
2) (5 – х)(m – n – р) = 5m – 5n – 5р – хm + хn + хр;
3) (х + у – 2)(а – m)= ха – хm + уа – уm – 2а + 2m;
4) (р + q + 3)(–а – х) = –ра – рх – qa – qx – 3а – 3х.
24.10. Виконайте дії:
1) (2x + 7)(2x − 4) + 28 = 4x2 – 8x + 14x – 28 + 28 = 4x2 + 6x; 2) 5m2 + (3 − 5m)(m + 2) = 5m2 + 3m + 6 – 5m2 – 10m = –7m + 6;
3) (a + 7)(a − 2) − a(a + 5) = а2 – 2а + 7a – 14 – а2 – 5а = –14; 4) (2b + 1)(3b − 1) − (6b2 − 1) = 6b2 – 2b + 3b – 1 – 6b2 + 1 = b.
24.11. Спростіть вираз:
1) (2p − 1)(3p + 5) − 6p2 = 6р2 + 10p – 3р – 5 – 6р2 = 7p – 5; 2) 12 + (3m − 2)(5m + 6) = 12 + 15m2 + 18m – 10m – 12 = 15m2 + 8m;
3) (m + 3)(m − 5) − m(m − 2) = m2 – 5m + 3m – 15 – m2 + 2m = –15; 4) (3a − 2)(4a + 1) − (12a2 − 2) = 12а2 + 3а – 8а – 2 – 12а2 + 2 = –5а.
24.12.
1) (2a − 3)(3a + 5) − 6a2, якщо a = 13,5; (2а – 3)(3а + 5) – 6а2 = 6а2 + 10а – 9а – 15 – 6а2 = а – 15 = 13,5 – 15 = –1,5; 2) (5x − 1)(1 − 2x) − 7x, якщо x = −2. (5x – 1)(1 – 2x) – 7x = 5х – 10x2 – 1 + 2х – 7x = –10x2 – 1 = –10 ∙ (–2)2 – 1 = –41.
24.13. Спростіть

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
1) (7x + 3)(2x − 1) − 14x2, якщо x = −8; (7х + 3)(2х – 1) – 14x2 = 14х2 – 7x + 6x – 3 – 14x2 = –x – 3 = –(–8) – 3 = 5;
2) (2a + 4)(1 − 3a) + 10a, якщо a = −1. (2а + 4)(1 – 3а) + 10а = 2а – 6а2 + 4 – 12а + 10а = –6а2 + 4 = –6 ∙ (–1)2 + 4 = –6 + 4 = –2.
24.14. Виконайте дії:
1) x(x − 5) + (x + 4)(x + 2) = x2 − 5x + x2 + 2x + 4x + 8 = 2x2 + x + 8.
2) (m + 3)(m − 4) − m(m − 1) + 5 = m2 − 4m + 3m − 12 − m2 + m + 5 = −7;
3) (a + 3) ∙ a − (a + 1) + (4 − a)(4 + a) = a2 + 3a − a − 1 + 16 − a2 = 2a + 15; 4) (y + 2)(y − 3) − 2y(1 − y) = y2 − 3y + 2y − 6 − 2y + 2y2 = 3y2 − 3y − 6.
24.15. Спростіть вираз:
1) (5x − 1)(4x + 7) − 4x(5x − 8) = 20x2 + 35x − 4x − 7 − 20x2 + 32x = 33x − 7;
2) (a + 3)(a − 2) − a(a + 9) + 6 = a2 − 2a + 3a − 6 − a2 − 9a + 6 = −8a;
3) 2x(3x − 1) + (x − 9)(5x − 6) = 6x2 − 2x + 5x2 − 6x − 45x + 54 = 11x2 − 53x + 54;
4) (2x + 3)(5x − 4) − 2x(x − 3) − 13(x − 1) = 10x2 − 8x + 15x − 12 − 2x2 + 6x − 13x + 13 = = 8x2 + 1.
24.16. Розв’яжіть рівняння:
1) (x − 1)(x + 2) − x2 = −8; x2 + 2x − x − 2 − x2 = −8; 2x − x = −8 + 2; x = −6.
Відповідь: −6.
24.17. Розв’яжіть рівняння:
1) (x + 3)(2x − 1) − 2x2 = 7; 2x2 − x + 6x − 3 − 2x2 = 7; 5x = 10; x = 10 : 5; x = 2.
Відповідь: 2.
24.18. Перетворіть
2) (3x + 1)(5 − 2x) + 6x2 = 5; 15x − 6x2 + 5 − 2x + 6x2 = 5; 13x = 5 − 5; 13x = 0; x = 0.
Відповідь: 0.
2) 10x2 + (5x − 1)(4 − 2x) = −4; 10x2 + 20x − 10x2 − 4 + 2x = −4; 22x = 0; x = 0.
Відповідь: 0.
1) (a2 + ab − b2)(a − b) = a3 − a2b + a2b − ab2 − ab2 + b3 = a3 − 2ab2 + b3; 2) (x2 − xy − y2)(x + y) = x3 + x2y − x2y − xy2 − xy2 − y3 = x3 − 2xy2 − y3; 3) (m − n)(−m2 − 3mn + n2) = −m3 − 3m2n + mn2 + m2n + 3mn2 − n3 = = −m3 + 2m2n + 4mn2 − n3;
4) (p − 2)(p2 + 3p − 4) = p3 + 3p2 − 4p − 2p2 − 6p + 8 = p3 + p2 − 10p + 8;
5) (9 − 4m − m2)(m − 2) = 9m − 18 − 4m2 + 8m − m3 + 2m2 = −m3 − 2m2 + 17m − 18; 6) (y2 − 3y − 7)(4y − 2) = 4y3 − 2y2 − 12y2 + 6y − 28y + 14 = 4y3 − 14y2 − 22y + 14. 24.19. Виконайте множення та
1) (a + b)(−a2 + ab − b2) = −a3 + a2b − ab2 − a2b + ab2 − b3 = −a3 − b3;
2) (x − y)(−x2 − xy + y2) = −x3 − x2y + xy2 + x2y + xy2 − y3 = −x3 + 2xy2 − y3
3) (7a2 + a − 1)(a + 1) = 7a3 + 7a2 + a2 + a − a − 1 = 7a3 + 8a2 − 1; 4) (2m2 − 3m − 2)(m + 5) = 2m3 + 10m2 − 3m2 − 15m − 2m − 10 = 2m3 + 7m2 − 17m − 10.
24.20. Перетворіть на многочлен
1) (3m + 2n)(9m2 − 6mn + 4n2) = 27m3 − 18m2n + 12mn2 + 18m2n − 12mn2 + 8n3 = = 27m3 + 8n3;
2) (4x2 + 10xy + 25y2)(2x − 5y) = 8x3 − 20x2y + 20x2y − 50xy2 + 50xy2 − 125y3 = 8x3 − 125y3;
3) (−x2 + 3xa − a2)(x + 2a) = −x3 − 2ax2 + 3ax2 + 6a2x – a2x − 2a3 = −x3 + ax2 + 5a2x − 2a3;
4) (3m − x)(5mx − m2 + x2) = 15m2x − 3m3 + 3mx2 − 5mx2 + m2x − x3 = = −3m3 + 16m2x − 2mx2 − x3 .

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
24.21.
1) (3x − y)(9x2 + 3xy + y2) = 27x3 + 9x2y + 3xy2 − 9x2y − 3xy2 − y3 = 27x3 − y3;
2) (9a2 − 2ab − b2)(3a + 2b) = 27a3 + 18a2b − 6a2b − 4ab2 − 3ab2 − 2b3 = = 27a3 + 12a2b − 7ab2 − 2b3 .
24.22. Виконайте дії:
1) 9m2 − (3m − 2)(3m + 7) = 9m2 − (9m2 + 21m − 6m − 14) = = 9m2 − 9m2 − 21m + 6m + 14 = −15m + 14; 2) 18y − (3y + 1)(6y + 4) = 18y − (18y2 + 12y + 6y + 4) = 18y − 18y2 − 18y − 4 = −18y2 − 4; 3) (a + 4)a − (a + 2)(a − 2) = a2 + 4a − a2 + 4 = 4a + 4;
4) (b + 7)(b + 1) − (b + 8)(b − 1) = b2 + b + 7b + 7 − (b2 − b + 8b − 8) = = b2 + 8b + 7 − b2 − 7b + 8 = b + 15.
24.23. Спростіть вираз:
1) 8x − (x + 5)(x + 3) = 8x − (x2 + 3x + 5x + 15) = 8x − x2 − 8x − 15 = −x2 − 15;
2) a(a + 8) − (a + 2)(a − 5) = a2 + 8a − (a2 − 5a + 2a − 10) = a2 + 8a − a2 + 3a + 10 = 11a + 10; 3) 12x2 + 5 − (4x + 7)(3x − 1) = 12x2 + 5 − (12x2 − 4x + 21x − 7) = = 12x2 + 5 − 12x2 + 4x − 21x + 7 = −17x + 12;
4) (x + 1)(x − 5) − (x + 3)(x − 7) = x2 − 5x + x − 5 − (x2 − 7x + 3x − 21) = = x2 − 4x − 5 − x2 + 4x + 21 = 16.
24.24. Перетворіть на многочлен
1) a2(a − 2)(a + 5) = a2(a2 + 5a − 2a − 10) = a4 + 5a3 − 2a3 − 10a2 = a4 + 3a3 − 10a2; 2) −5m2(m − 1)(2 − m) = −5m2(2m − m2 − 2 + m) = −15m3 + 5m4 + 10m2; 3) −4x3(2x − 3)(x − x2) = −4x3(2x2 − 2x3 − 3x + 3x2) = −20x5 + 8x6 + 12x4; 4) 0,2b2(5b + 10)(b2 − 2) = 0,2b2(5b3 − 10b + 10b2 − 20) = b5 − 2b3 + 2b4 − 4b2.
24.25. Розкрийте дужки і спростіть одержаний вираз:
1) m2(m − 4)(m + 2) = m2(m2 + 2m − 4m − 8) = m4 − 2m3 − 8m2; 2) −a2(2a − 3)(3a + 7) = −a2(6a2 + 14a − 9a − 21) = −6a4 − 5a3 + 21a2; 3) −5b3(2b + b2)(b − 1) = −5b3(b2 + 2b)(b − 1) = −5b3(b3 − b2 + 2b2 − 2b) = −5b6 − 5b5 + 10b4; 4) 0,5x2(2x − 6)(x2 + x) = 0,5x2(2x3 + 2x2 − 6x2 − 6x) = 0,5x2(2x3 − 4x2 − 6x) = x5 − 2x4 − 3x3 .
24.26. Доведіть тотожність:
1) (m − 3)(m + 7) − 10 = (m + 8)(m − 4) + 1; (m − 3)(m + 7) − 10 = (m2 + 7m − 3m − 21) − 10 = m2 + 4m − 21 − 10 = m2 + 4m – 31 (m + 8)(m − 4) + 1 = (m2 − 4m + 8m − 32) + 1 = m2 + 4m − 32 + 1 = m2 + 4m − 31 2) (2x − 1)(3x + 5) + 9x = (3x − 1)(2x + 5) + 3x. (2x − 1)(3x + 5) + 9x = (6x2 + 10x − 3x − 5) + 9x = 6x2 + 7x − 5 + 9x = 6x2 + 16x – 5 (3x − 1)(2x + 5) + 3x = (6x2 + 15x − 2x − 5) + 3x = 6x2 + 13x − 5 + 3x = 6x2 + 16x − 5 24.27. Доведіть, що для кожного значення змінної a: 1) значення виразу (a − 8)(a + 3) − (a − 7)(a + 2) дорівнює −10; (a − 8)(a + 3) − (a − 7)(a + 2) = (a2 + 3a − 8a − 24) − (a2 + 2a − 7a − 14) = = (a2 − 5a − 24) − (a2 − 5a − 14) = a2 − 5a − 24 − a2 + 5a + 14 = −10.
2) значення виразу (a2 − 2)(a2 + 5) − (a2 − 4)(a2 + 4) − 3a2 дорівнює 6. (a2 − 2)(a2 + 5) − (a2 − 4)(a2 + 4) − 3a2 = (a4 + 5a2 − 2a2 − 10) − (a4 − 16) − 3a2 = = (a4 + 3a2 − 10) − (a4 − 16) − 3a2 = a4 + 3a2 − 10 − a4 + 16 − 3a2 = 6.
24.28.
1) (m − 7)(m + 1) − (m + 2)(m − 8) = m2 + m − 7m − 7 − m2 + 8m − 2m + 16 = 9; 2) a2(a2 − 1) − (a2 − 2)(a2 + 3) + 2a2 = a4 − a2 − a4 − 3a2 + 2a2 + 6 + 2a2 = 6.
24.29.
-якого
(a + 7)(a − 3) − 4(a − 8) є
числом. (a + 7)(a − 3) − 4(a − 8) = a2 − 3a + 7a − 21 − 4a + 32 = a2 + 11 −

число.
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
24.30. Запишіть
1) (x − y)2 = x2 − 2xy + y2; 2) (p + 2a)2 = p2 + 4ap + 4a2; 3) (4x − 3y)2 = 16x2 − 24xy + 9y2; 4) (7a + 2b)2 = 49a2 + 28ab + 4b2.
24.31. Перетворіть
1) (2a − 3b)2 = 4a2 − 12ab + 9b2; 2) (4x + 5y)2 = 16x2 + 40xy + 25y2
24.32. Спростіть вираз і обчисліть його значення: 1) (2x2 − x)(3x2 + x) − (x2 + x)(6x2 − 2x), якщо x = −2; (2x2 − x)(3x2 + x) − (x2 + x)(6x2 − 2x) = 6x4 + 2x3 − 3x3 − x2 − 6x4 + 2x3 − 6x2 + 2x2 = = −5x3 + x2 = −5 ∙ (−2)3 + (−2)2 = 40 + 4 = 44.
2) (a + 2b)(a2 − 2ab + 4b2) − 8b3, якщо a = 3, b = −2015. (a + 2b)(a2 − 2ab + 4b2) − 8b3 = a3 − 2a2b + 4ab2 + 2a2b − 4ab2 + 8b3 − 8b3 = a3 = 33 = 27.
24.33. Спростіть вираз і знайдіть його значення:
1) (x − 9)(x + 9) − (x − 3)(x + 27), якщо x = 11 8; (x − 9)(x + 9) − (x − 3)(x + 27) = x2 − 81 − x2 − 27x + 3x + 81 = −24x = −24 · 11 8 = = −24 · 9 8 = −27.
2) 8a3 − (2a − 3b)(4a2 + 6ab + 9b2), якщо a = −7 8, b = 1 3 . 8a3 − (2a − 3b)(4a2 + 6ab + 9b2) = 8a3 − (8a3 + 12a2b + 18ab2 − 12a2b − 18ab2 − 27b3) = = 8a3 − 8a3 + 27b3 = 27b3 = 27 · (1 3)3 = 27 · 1 27 = 1.
24.34. Знайдіть корені рівняння:
1) 4x − (x + 2)(x − 3) = (5 − x)(x + 3);
4x − (x2 − 3x + 2x − 6) = 5x + 15 − x2 − 3x; 4x − x2 + x + 6 = 5x + 15 − x2 − 3x;
5x − 2x = 15 − 6;
3x = 9;
x = 3.
Відповідь: 3.
24.35. Розв’яжіть рівняння:
1) x(2x − 5) − x2 = 2 − (x − 1)(2 − x);
2x2 − 5x − x2 = 2 − (2x − x2 − 2 + x);
x2 − 5x = 2 − 2x + x2 + 2 − x;
−5x + 2x + x = 2 + 2;
−2x = 4; x = −2.
Відповідь: −2.
24.36.
2) 2x(x + 1) − (x + 2)(x − 3) = x2 + 7; 2x2 + 2x − (x2 − 3x + 2x − 6) = x2 + 7; 2x2 + 2x − x2 + x + 6 = x2 + 7;
3x = 7 − 6;
3x = 1;
x = 1 3 .
Відповідь: 1 3 .
2) 2x2 − (x + 1)(x + 19) = (x + 3)(x − 2) + 8; 2x2 − (x2 + 19x + x + 19) = (x2 − 2x + 3x − 6) + 8; 2x2 − x2 − 20x − 19 = x2 + x − 6 + 8;
−20x − x = 19 − 6 + 8;
−21x = 21; x = −1.
Відповідь: −1.
стала тотожністю: 1) (x − 1)(* + 3) = x2 + * − * ⇒ (x − 1)(x + 3) = x2 + 3x − x − 3 = x2 + 2x − 3; 2) (y + 2)(y − *) = * + y − * ⇒ (y + 2)(y − 1) = y2 + 2y − y − 2 = y2 + y − 2.
24.37. Доведіть, що
1) (n + 2)(n + 3) − n(n − 1) є
-якого натурального
числу 6; (n + 2)(n + 3) − n(n − 1) = n2 + 3n + 2n + 6 − n2 + n = 6n + 6 = 6(n + 1) кратно 6; 2) (n − 5)(n + 8) + (n + 1)(2n − 5) + 46
1. (n − 5)(n + 8) + (n + 1)(2n − 5) + 46 = n2 + 8n − 5n − 40 + 2n2 − 5n − 5 + 2n + 46 = 3n2 + 1
1.

n; n + 1; n + 2 три
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
n2 + 44 = (n + 1)(n + 2);
n2 + 44 = n2 + 2n + n + 2; 3n = 42; n = 14.
Відповідь: 14, 15, 16.
24.39. Дано два добутки 27 · 18 і 12 ·
(27 − 2) · (18 − 2) = (12 − 2) · (42 − 2); 400 =
24.40. Дано
22 · 15 і 27 · 12.
(22 + 3) · (15 + 3) = (27 + 3) · (12 + 3); 450 = 450,
24.41. Виконайте множення: 1) (a2 − 2a + 1)(a2 + 3a − 7) = a4 + 3a3 − 7a2 − 2a
+
+ 3a −
= = a4 + a3 − 12a2 + 17a − 7; 2) (7 − 2b + 3b2)(2b2 − 2b − 1) = 14b2 − 14b − 7 −
3 +
+ 2b +
− 6b3 − 3b2 = = 6b4 − 10b3 + 15b2 − 12b − 7.
24.42. Виконайте множення: 1) (x2 − x − 1)(x2 + 3x + 5) = x4 + 3x3 + 5x2 − x3 − 3x2 – 5x − x2 − 3x − 5 = = x4 + 2x3 + x2 − 8x − 5. 2) (7 − a − 2a2)(a2 + 3a − 1) = 7a2 + 21a − 7 − a3 − 3a2 + a − 2a4 − 6a3 + 2a2 = = −2a4 − 7a3 + 6a2 + 22a − 7.
24.43. Знайдіть чотири послідовних цілих числа,
більший за
n; n + 1; n + 2; n + 3
(n + 2)(n + 3) − 78 = n(n + 1);
n2 + 3n + 2n + 6 − 78 = n2 + n; 3n + 2n − n = −6 + 78; 4n = 72; n = 18.
Відповідь: 18; 19; 20; 21. 24.44. Знайдіть чотири послідовних натуральних
на 102 менший
n; n + 1; n + 2; n + 3 послідовні цілі числа; n(n + 1) + 102 = (n + 2)(n + 3); n2 + n + 102 = n2 + 3n + 2n + 6; −4n = −96; n = 24.
Відповідь: 24; 25; 26; 27.
24.45. Перетворіть вираз на многочлен стандартного
1) (a + 2)(a − 1)(a + 3) = (a2 − a + 2a − 2)(a + 3) = (a2 + a − 2)(a + 3) = = a3 + 3a2 + a2 + 3a − 2a − 6 = a3 + 4a2 + a − 6; 2) (a − 4)(a − 7)(a + 1) = (a2 − 7a − 4a + 28)(a + 1) = (a2 − 11a + 28)(a + 1) = = a3 + a2 − 11a2 − 11a + 28a + 28 = a3 − 10a2 + 17a + 28.
24.46. Виконайте множення: 1) (x + 1)(x4 − x3 + x2 − x + 1) = x5 − x4 + x3 − x2 + x + x4 − x3 + x2 − x + 1 = x5 + 1; 2) (b − 1)(b4 + b3 + b2 + b + 1) = b5 + b4 + b3 + b2 + b − b4 − b3 − b2 − b − 1 = b5 − 1.

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
ширину цього прямокутника. x довжина прямокутника; (30 − x) ширина прямокутника; x(30 − x)
довжина прямокутника;
площа прямокутника; (x + 1)
30 − x − 3 = (27 − x) ширина прямокутника; (x + 1)(27 − x)
площа прямокутника.
x(30 − x) − 45 = (x + 1)(27 − x);
30x − x2 − 45 = −x2 + 27x + 27 − x; 30x − 26x = −x2 + 27 + 45 + x2; 4x = 72; x = 18.
18 см
довжина; 12 см ширина.
Відповідь: 18 см; 12 см.
24.48. Швидкість автомобіля
Рівняння:
70x = 50(x + 2);
70x = 50x + 100;
20x = 100; x = 5.
Відстань від села до міста: 70 · 5 = 350 км.
Відповідь: 350 км.
24.49. Знайдіть додатнє число,
1) збільшується в 4 рази;
Нехай шукане число дорівнює
x. Складемо рівняння:
x2 = 4x;
x2 − 4x = 0;
x(x − 4) = 0;
x = 0 або x − 4 = 0;
x = 0 або x = 4.
Додатнє число 4.
Відповідь: 4.

2) зменшується
5a2 = a; 5a2 − a = 0; a(5a − 1) = 0; a = 0 або 5a − 1 = 0; a = 0
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
x + 2 = 5 7 (3x − 2);
7x + 14 = 15x − 10; 7x − 15x = −10 − 14; −8x = −24; x = 3.
У
каністрі 3 л, а в першій 9 л. Відповідь: у 1-й – 9 л, у 2-й – 3 л.
24.51.
1) (5x2 − 8b + a) − (b2 − 5x + 1) − (2b − x2 + 7x) = 5x2 − 8b + a − b2 +
= (6x2 − 2x) − (b2 + 10b − a + 1). 2) (8mx2 + 7mn2 − p) − (x2 + mx2 + 2p) − 17x = 8mx2 + 7mn2 − p −
= (7mx2 − x2 − 17x) − (−7mn2 + 3p).
24.52.
(3 – a)(4 + b) + (3 + a)(5 + b) – 6b = 12 + 3b – 4a – ab + 15 + 3b + 5a + ab – 6b = = a + 27 = 1 125 + 27 = 27 1 125 .
25.1. У многочлені ca − 2c + 5a − 10
спільним множником 2. ca − 2c + 5a – 10 = (ca + 5a) – (2c + 10) = а(c + 5) – 2(c + 5) а(c + 5) – група зі спільним множником a; 2(c + 5) – група
спільним множником 2.
25.2. Закінчіть розкладання многочлена на множники: xy + yt − 2x − 2t = (xy + 2x) + (yt − 2t) = x(y − 2) + t(y − 2) = (y − 2)(x + t).
25.3. Закінчіть розкладання многочлена на множники: ab − cd − ad + cb = (ab − ad) + (cb − cd) = a(b − d) + c(b − d) = (b – d)(a + c).
25.4. Подайте вираз у вигляді
1) a(b + c) + 3b + 3c = a(b + c) + 3(b + c) = (b + c)(a + 3);
2) p(x − y) + 7x − 7y = p(x − y) + 7(x − y) = (x − y)(p + 7);
3) m(t − 5) + t − 5 = (t − 5)(m + 1);
4) b(m − c) + c − m = (m − c)(b − 1).
25.5. Розкладіть на множники:
1) c(x − y) + 3x − 3y = c(x − y) + 3(x − y) = (x − y)(c + 3);
2) a(c + m) + 9c + 9m = a(c + m) + 9(c + m) = (c + m)(a + 9);
3) x(c + 5) + c + 5 = (c + 5)(x + 1);

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
4) y(p − 3) + 3 − p = y(p − 3) − (p − 3) = (p − 3)(y − 1).
25.6. Розкладіть
1) ax + ay + 6x + 6y = a(x + y) + 6(x + y) = (x + y)(a + 6);
2) 5m − 5n + pm − pn = 5(m − n) + p(m − n) = (m − n)(5 + p);
3) 9p + mn + 9n + mp = 9(p + n) + m(p + n) = (p + n)(9 + m);
4) ab + ac − b − c = a(b + c) − (b + c) = (b + c)(a − 1);
5) 1 − by − yb = (1 − y) + (b − by) = (1 − y) + b(1 − y) = (1 − y)(1 + b);
6) ma + 2a − 2m − 4 = a(m + 2) − 2(m + 2) = (m + 2)(a − 2).
25.7. Подайте у вигляді добутку многочленів:
1) ab + 5a + bm + 5m = a(b + 5) + m(b + 5) = (b + 5)(a + m); 2) mp − b + bp − m = m(p − 1) + b(p − 1) = (p − 1)(m + b); 3) am − b + m − ab = m(a + 1) − b(a + 1) = (a + 1)(m − b); 4) cm − 3dm + cp − 3dp = m(c − 3d) + p(c − 3d) = (c − 3d)(m + p).
25.8. Запишіть
ab − ac + 2b − 2c у
якщо a = −1; b = 5,7; c = 6,7. ab − ac + 2b − 2c = a(b − c) + 2(b − c) = (b − c)(a + 2) = (5,7 − 6,7) · (−1 + 2) = −1 · 1 = −1.
25.9. Запишіть вираз 5x − 5y + xt − yt у
x = 7,2; y = 6,2; t = −4,5. 5x − 5y + xt − yt = 5(x − y) + t(x − y) = (x − y)(5 + t) = (7,2 − 6,2) ⋅ (5 − 4,5) = 1 ⋅ 0,5 = 0,5.
25.10. Подайте
1) a3 + a2 + a + 1 = a2(a + 1) + (a + 1) = (a + 1)(a2 + 1);
2) b5 − b3 − b2 + 1 = b2(b2 − 1) − (b2 − 1) = (b2 − 1)(b2 − 1).
3) c4 + 3c3 − c − 3 = c3(c + 3) − (c + 3) = (c + 3)(c3 − 1);
4) a6 − 5a4 − 3a2 + 15 = a4(a2 − 5) − 3(a2 − 5) = (a2 − 5)(a4 − 3);
5) m2 − mn − 8m + 8n = (m2 − mn) + (−8m + 8n) = m(m − n) − 8(m − n) = (m − n)(m − 8);
6) ab − 9b + b2 − 9a = (ab − 9a) + (b2 − 9b) = a(b − 9) + b(b − 9) = (b − 9)(a + b);
7) 7t − ta + 7a − t2 = (7t − t2) + (7a − ta) = t(7 − t) + a(7 − t) = (7 − t)(t + a);
8) xy − ty − y2 + xt = xy + xt + (−ty − y2) = x(y + t) − y(t + y) = (y + t)(x − y).
25.11. Розкладіть многочлен на множники:
1) x2 + bx − b2y − bxy = (x2 + bx) + (−b2y − bxy) = x(x + b) − by(b + x) = (x + b)(x − by);
2) a2b + c2 − abc − ac = (a2b − abc) + (c2 − ac) = ab(a − c) + c(c − a) = (a − c)(ab − c);
3) 7a3m + 14a2 − 6bm − 3am2b = 7a2(am + 2) − 3bm(2 + am) = (am + 2)(7a2 − 3bm);
4) 21x + 8tm3 − 24m2 − 7xtm = (21x − 7xtm) + (8tm2 − 24m2) = 7x(3 − tm) + 8m2(tm − 3) = = (7x − 8m2)(3 − tm).
25.12. Подайте многочлен у вигляді добутку:
1) b2 + xb − x2y − xby = b2 + xb + (−x2y − xby) = b(b + x) − xy(x + b) = (b + x)(b − xy);
2) m2 + 7m − bm − 7b = m(m + 7) − b(m + 7) = (m + 7)(m − b); 3) 4a − ax + 4x − x2 = a(4 − x) + x(4 − x) = (4 − x)(a + x); 4) ma − mb − m2 + ab = (ma − m2) + (−mb + ab) = m(a − m) + b(a − m) = (a − m)(m + b).
25.13. Обчисліть
1) 157 ⋅ 37 + 29 ⋅

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
= (1,4 + 5,17) ⋅ (5 ⋅ 1,4 − 7) = 0.
2) 3a3 − 2b3 − 6a2b2 + ab, якщо a = 1 3; b = 2 3 .
3a3 − 2b3 − 6a2b2 + ab = 3a2(a − 2b2) + b(a − 2b2) = (a − 2b2)(3a2 + b) = = (1 3 − 2 ⋅ 4 9) ⋅ (3 ⋅ 1 9 + 2 3) = (1 3 − 8 9) ⋅ 1 = −5 9 .
25.15. Знайдіть значення виразу, попередньо розклавши
1) 27x3 + x2 + 27x + 1, якщо x = − 1 27;
27x3 + x2 + 27x + 1 = 27x(x2 + 1) + (x2 + 1) = (x2 + 1)(27x + 1) = = ((− 1 27)2 + 1)(27 ⋅ ( 1 27) + 1) = 0.
2) 5p + px2 − p2x − 5x, якщо p = 2,5; x = 2,4. 5p + px2 − p2x − 5x = 5(p − x) − px(p − x) = (p − x)(5 − px) = = (2,5 − 2,4) ⋅ (5 − 2,4 ⋅ 2,5) = 0,1 ⋅ (5 − 6) = 0,1 ⋅ (−1) = −0,1.
25.16. Запишіть вираз у вигляді добутку:
1) 45x3y4 − 9x5y3 − 15x2y2 + 3x4y = (45x3y4 − 15x2y2) + (−9x5y3 + 3x4y) = = 15x2y2(3xy2 − 1) − 3x4y(3xy2 − 1) = (3xy2 − 1)(15x2y2 − 3x4y) = 3x2y(5y − x2)(3xy2 − 1). 2) 2,1mn2 − 2,8mp2 − 2,7n3 + 3,6np2 = 0,7m(3n2 − 4p2) − 0,9n(3n2 − 4p2) = = (3n2 − 4p2)(0,7m − 0,9n).
25.17. Розкладіть на множники:
1) 8m2c − 6m2x − 16cx3 + 12x4 = 8x(m2 − 2x3) − 6x(m2 − 2x3) = (m2 − 2x3)(8c − 6x); 2) 1,2xy3 + 1,6x3y2 − 2x7y − 1,5x5y2 = 0,3xy2(4y − 5x4) + 0,4x3y(4y − 5x4) = = (4y − 5x4)(0,3xy2 + 0,4x3y) = xy(4y − 5x4)(0,3y + 0,4x2).
25.18. Розв’яжіть рівняння:
1) x2 − 5x + 40 = 8x;
x2 − 5x + 40 − 8x = 0;
x(x − 5) − 8(x − 5) = 0;
(x − 5)(x − 8) = 0;
x − 5 = 0; x = 5 або
x − 8 = 0; x = 8.
Відповідь: 5; 8.
25.19. Розв’яжіть рівняння:
1) x2 + 7x − 7 = x;
x2 + 7x − 7 − x = 0;
x(x + 7) − (x − 1) = 0;
(x + 7)(x − 1) = 0;
x + 7 = 0; x = −7 або x − 1 = 0; x = 1.
Відповідь: −7; 1.
25.20. Розкладіть на множники:
2) 5y3 + 2y2 + 5y + 2 = 0.
y2(5y + 2) + (5y + 2) = 0;
(5y + 2)(y2 + 1) = 0; 5y + 2 = 0, y2 + 1 > 0;
5y = −2; y = −2 5 .
Відповідь: 2 5 .
2) 7y3 + y2 + 7y + 1 = 0.
y2(7y + 1) + (7y + 1) = 0; (7y + 1)(y2 + 1) = 0; 7y + 1 = 0, y2 + 1 > 0; 7y = −1; y = −1 7 .
Відповідь: 1 7 .
1) at2 − ap + t3 − tp − bt2 + bp = (at2 − ap) + (t3 − tp) + (−bt2 + bp) = = a(t2 − p) + t(t2 − p) − b(t2 − p) = (t2 − p)(a + t − b); 2) ax2 + ay2 − mx2 − my2 + m − a = (ax2 − mx2) + (ay2 − my2) + (m − a) = = x2(a − m) + y2(a − m) + (a − m) = (a − m)(x2 + y2 − 1);
3) mb − m + 7 − 7b − 7m2 + m3 = (m3 − 7m2) + (mb − 7b) + (−m + 7) = = m2(m − 7) + b(m − 7) + (m − 7) = (m − 7)(m2 + b − 1); 4) 6ax + 3ay − az − 6bx − 3by + bz = (6ax − 6bx) + (3ay − 3by) + (bz − az) = = 6x(a − b) + 3y(a − b) − z(a − b) = (a − b)(6x + 3y − z).

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
25.21. Розкладіть на множники:
1) a2b + a + ab2 + b + 9ab + 9 = (a2b + a) + (ab2 + b) + (9ab + 9) = = a(ab + 1) + b(ab + 1) + 9(ab + 1) = (ab + 1)(a + b + 9); 2) 8ax + 4bx − 4x + 10am + 5bm − 5m = (8ax + 4bx − 4x) + (10am + 5bm − 5m) = = 4x(2a + b − 1) + 5m(2a + b − 1) = (4x + 5m)(2a + b − 1).
25.22. Розкладіть на множники тричлен:
1) x2 + 5x + 4 = (x2 + 4x) + (x + 4) = x(x + 4) + (x + 4) = (x + 4)(x + 1); 2) x2 − 5x + 4 = (x2 − 4x) + (4 − x) = x(x − 4) − (x − 4) = (x − 4)(x − 1);
3) x2 + x − 6 = x2 − 2x + 3x − 6 = x(x − 2) + 3(x − 2) = (x − 2)(x + 3);
4) a2 + 4ab + 3b2 = a2 + 3ab + ab + 3b2 = a(a + 3b) + b(a + 3b) = (a + 3b)(a + b).
25.23. Розкладіть на множники:
1) x2 − 6x + 5 = x2 − x − 5x + 5 = x(x − 1) − 5(x − 1) = (x − 1)(x − 5);
2) x2 − x − 6 = x2 − 2x + 3x − 6 = x(x − 2) + 3(x − 2) = (x − 2)(x + 3);
3) x2 + 2x − 15 = (x2 + 5x) + (−3x − 15) = x(x + 5) − 3(x + 5) = (x + 5)(x − 3); 4) a2 + 5ab + 6b2 = (a2 + 3ab) + (2ab + 6b2) = a(a + 3b) + 2b(a + 3b) = (a + 3b)(a + 2b).
25.24. Спростіть вираз і знайдіть його значення:
1) 0,8(a − 5) − 0,6(2 − a), якщо a = −5;
0,8(a − 5) − 0,6(2 − a) = 0,8a − 4 − 1,2 + 0,6a = 1,4a − 5,2 = 1,4 ⋅ (−5) − 5,2 = = −7 − 5,2 = −12,2.
2) 4 7(7x − 14y) − 2 9(18x − 27y), якщо x = 2024, y = −1 2 . 4 7 (7x − 14y) − 2 9(18x − 27y) = 4x − 8y − 4x + 6y = −2y = −2 ⋅ (−1 2) = 1.
25.25. Знайдіть корінь рівняння:
1) 6x(x − 1) − 2x(3x − 5) = −8; 6x2 − 6x − 6x2 + 10x = −8; 10x − 6x = −8; 4x = −8; x = −2.
Відповідь: −2.
25.26.


2) 5(2 − x2) − 4x(x − 1) = 3x(1 − 3x); 10 − 5x2 − 4x2 + 4x = 3x − 9x2; 4x − 3x = −10; x = −10.
Відповідь: −10.
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
x5 + y5 = 336? 336 = 33 ∙ 335 = 32 ∙ 335 + 1 ∙ 335 = 25 ∙ 335 + 335 = 665 + 335. Отже, такими натуральними числами можуть бути, наприклад, числа х = 66, у = 33.
ДОМАШНЯ САМОСТІЙНА РОБОТА №5
1. Укажіть вираз, що не є многочленом. Вираз ���� ���� 5 не є многочленом.
А. ���� ���� ����; Б. x2 − 2x + 7; В. −b – 19; Г. 6c2.
2. k(n − m) = ...
k(n − m) = kn – km.
А. kn – m; Б. n – km; В. kn + km; Г. kn – km.
3. 4c + 8 = ...
4c + 8 = 4(c + 2).
А. 2(c + 4); Б. 4(c + 2); В. 8(c + 1); Г. 4(c − 2)
4. Якому з многочленів дорівнює вираз (x − 5)(x + 2)?
(x − 5)(x + 2) = x2 – 5x +2x – 10 = x2 – 3x – 10.
А. x2 + 3x – 10; Б. x2 − 3x – 10; В. x2 + 3x + 10; Г. x2 − 3x – 3.
5. Подайте вираз (3m2 − m) + (4m2 − 5) − (7m2 + 3) у вигляді
вигляду. (3m2 − m) + (4m2 − 5) − (7m2 + 3) = 3m2 – m + 4m2 – 5 – 7m2 – 3 = –m – 8
А. 14m2 − m – 2; Б. −m – 2; В. −m – 8; Г. 8 – m.
6. Розкладіть вираз am − an − 2m + 2n на множники. am − an − 2m + 2n = a(m – n) – 2(m – n) = (m – n)(a – 2).
А. (m − n)(a − 2); Б. (m − n)(a + 2);
В. (m + n)(a − 2); Г. (m − a)(n − 2).
7. Для якого значення x значення різниці
дорівнює значенню многочлена 3x + 4x2 − 4?
8x − (3x + 4x2 + 2) = 3x + 4x2 − 4; 8x − 3x − 4x2 − 2 = 3x + 4x2 − 4; 5x + 4x2 − 2 − 3x − 4x2 + 4 = 0; 2x + 2 = 0; 2x = −2; x = −1.
8x і
3x − 4x2 + 2
А. 2; Б. 1; В. −1; Г. 0. 8. Обчисліть 297 · 397 − 3972 найзручнішим способом. 297 · 397 − 3972 = 397(297 – 397) = 397 · (–100) = –39700.
А. 39 700; Б. −39 700; В. −29 700; Г. 29 700
9. Знайдіть значення виразу (x − 5)(x + 2) − (x − 7)(x + 4), якщо x = 10,2. (x − 5)(x + 2) − (x − 7)(x + 4) = x2 − 5x + 2x − 10 − (x2 − 7x + 4x − 28) = x2 − 3x − 10 − x2 + 3x + 28 = 18.
А. 18,2; Б. 18; В. 28,2; Г. 7,8.
10. Розв’яжіть рівняння x2 + 7x = 2(x + 7). x2 + 7x = 2(x + 7);

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
x(x + 7) − 2(x + 7) = 0; (x − 2)(x + 7) = 0; x − 2 = 0 або x + 7 = 0; x = 2 або x = −7.
А. −7; 2; Б. −7; В. 2; Г. −2; 7
x + 6.
Складемо рівняння:
x(x + 4) + 44 = (x + 2)(x + 6); x2 + 4x + 44 = x2 + 2x + 6x + 12; 4x = 32; x = 8.
Тоді найбільше
дорівнює 8 + 6 = 14.
А. 10; Б. 6; В. 18; Г. 14. 13. Установіть відповідність між виразами (1–3)
дорівнюють (А–Г).
Вираз:
1) (3x3 + x2 − 2x) − (2x3 − 4x2 − 2x + 6)
2) 2x2(3x − 5) − 5x(x2 − 3x)
3) (x2 + 6x)(x − 1)
Многочлени:
А. x3 + 5x2
Б. x3 + 5x2 − 6
В. x3 + 5x2 − 6x
Г. x3 + 5x − 6
1) (3x3 + x2 − 2x) − (2x3 − 4x2 − 2x + 6) = 3x3 + x2 − 2x − 2x
2) 2x2(3x − 5) − 5x(x2 − 3x) = 6x3 − 10x2 − 5x3 + 15x2 = x3 + 5x2.
3) (x2 + 6x)(x − 1) = x3 − x2 + 6x2 − 6x = x3 + 5x2 − 6x.
Відповідь: 1 – Б; 2 – А; 3 – В.
ДО §§ 20-25
1. Виконайте множення: 1) m(a − b + 3) = ma – mb + 3b; 2) −p(x + y − 4) = –px – py + 4p.
2. Винесіть за дужки спільний множник: 1) 7a − 7b = 7(a – b); 2) xm + ym = m(x + y).
3. Виконайте множення: 1) (a + 2)(x − 3) = ax + 2x – 3a – 6; 2) (b − 5)(c − m) = bc – 5c – bm + 5m. 4.
1) (2x2 − x) + (3x − 5) − (x2 − 5) = 2x2 – x + 3x – 5 – x2 + 5 = x2 + 2x; 2) −2xy(x2 − 3xy + y2) = –2x3y + 6x2y2 – 2xy3 .
5. Розкладіть многочлен на множники: 1) 9a2 − 12ab = 3a(3a – 4b); 2) 7x − 7y + ax – ay = 7(x – y) + a(x – y) = (7 + a)(x – y).

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
6. Спростіть вираз (x + 5)(x − 2) − x(x + 3). (x + 5)(x – 2) – x(x + 3) = x2 + 5x – 2x – 10 – x2 – 3x = –10.
7. Розв’яжіть рівняння (2x + 3)(3x − 7) = x(6x − 3) − 17. (2x + 3)(3x − 7) = x(6x − 3) – 17
6x2 – 14x + 9x – 21 = 6x2 – 3x – 17 –14x + 9x + 3x = –17 + 21 –2x = 4 x = –2
8. Розкладіть многочлен на множники: 1) 9m3 − 3m4 − 27m8 = 3m3(3 – m – 9m5); 2) m2 + 2n − 2m – mn = m(m – n) – 2(m – n) = (m – 2)(m – n).
9. Знайдіть чотири
від добутку двох більших.
Нехай найменше із заданих чисел x, тоді наступні x + 1, x + 2, x + 3.
Складемо рівняння:
x(x + 1) + 90 = (x + 2)(x + 3);
x2 + x + 90 = x2 + 2x + 3x + 6;
2x + 3x − x = 90 − 6; 4x = 84; x = 21.
Тоді наступними числами є 21 + 1 = 22, 21 + 2 = 23, 21 + 3 = 24.
Відповідь: 21, 22, 23, 24.
10. Доведіть, що сума п’яти послідовних натуральних чисел ділиться на 5.
Нехай найменше із заданих чисел x, тоді наступні x + 1, x + 2, x + 3, x + 4.
Знайдемо суму цих п’яти чисел: x + (x + 1) + (x + 2) + (x + 3) + (x + 4) = 5x + 10 = 5(x + 2) ділиться на 5.
11. Розв’яжіть рівняння x2 − 5x = 4x − 20.
x2 − 5x = 4x − 20; x2 − 5x − 4x + 20 = 0; x(x − 5) − 4(x − 5) = 0; (x − 4)(x − 5) = 0; x − 4 = 0 або x − 5 = 0; x = 4 або x = 5.
12. Перетворіть вираз на многочлен стандартного
1) (x2 − 2x + 5)(x2 + 3x − 1) = x4 + 3x3 − x2 − 2x3 − 6x2 + 2x + 5x2 + 15x − 5 = = x4 + x3 − 2x2 + 17x − 5;
2) (a + 3)(a − 5)(a − 1) = (a2 + 3a − 5a − 15)(a − 1) = (a2 − 2a − 15)(a − 1) = = a3 − a2 − 2a2 + 2a − 15a + 15 = a3 − 3a2 − 13a + 15.
теми 5
1.
1) 5a2 + 4b,
2) −a2 + ab + m,
степінь; 3) 5c3 − 8, третя степінь; 4) 3mn2 + 4mn − 5m2n − 7, третя степінь.
2.
1) 8a2b − 7ab2 + 5a2b + 4b2a = 13a2b − 3a2b;
2) 5mn − 2mn − 8 − 3mn = −8;
3) 7m3 + m2 − 8 – m8 + 3m2 = 6m8 + 4m2 − 8;
4) 2x2y − 7xy2 − 5xy + 3yx2 + 7y2x = 5x2y − 5xy.

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
1 4 ab(−8ab2) + 8a2(−1,5ab) + 20ab(−0,1ab2) + a2ab + 2a · 6a2b і
якщо a = 5; b = − 1 25 .
1 4 ab(−8ab2) + 8a2 ·(−1,5ab) + 20ab(−0,1ab2) + a2ab + 2a · 6a2b =
2a2b3 − 12a3b − 2a2b3 + a3b + 12a3b = a3b.
Якщо a = 5, b = − 1 25, то a3b = 53 ·(− 1 25) = 125(− 1 25) = −5.
4. Чи існують такі натуральні значення змінної a, для
2a2 + 6a + 7 є парним числом?
2a2 + 6a + 7, натуральних значень змінної a, при яких значення многочлена є
числом, не існує: 2a2 парне; 6a парне; 7 непарне. До §21
5. Спростіть вирази:
1) (3m + 5n) + (9m − 7n) − (−2n + 5m) = 3m + 5n + 9m − 7n + 2n − 5m = 7m;
2) (12ab − b2) − (5ab + b2) + (ab + 2b2) = 12ab − b2 − 5ab − b2 + ab + 2b2 = 8ab;
3) (3x2 + 2x) + (2x2 − 3x − 4) − (17 − x2) = 3x2 + 2x + 2x2 − 3x − 4 − 17 + x2 = 6x2 − x − 21;
4) (m − n + p) + (m − p) − (m − n − p) = m − n + p + m − p − m + n + p = m + p.
6. 1) Подайте многочлен 4x3 − 4x2 + 5x − 7 у вигляді суми
4x3 − 4x2 + 5x − 7 = (4x3 − 4x2) + (5x − 7); 2) Подайте многочлен x3 − 5x + 7x2 − 9 у вигляді
і тричлена. x3 − 5x + 7x2 − 9 = x3 – (5x − 7x2 + 9).
7. Який многочлен у сумі з многочленом 2x2 − 3x + 7 дає: 1) 2x2 − 3x + 7 + (−2x2 + 3x − 7) = 0; 2) 2x2 − 3x + 7 + (−2x2 + 3x − 2) = 5; 3) 2x2 − 3x + 7 + (−2x2 − 6) = −3x + 1; 4) 2x2 − 3x + 7 + (−x2 − 2x) = x2 − 5x + 7.
8. Доведіть, що сума двох послідовних
цілих чисел ділиться на 4. 2n − 1 і 2n + 1 − послідовні непарні цілі числа; 2n − 1 + 2n + 1 = 4n − ділиться на 4.
9. Спростіть вираз 5xy − 8x2y − (3xy − (41 4 xy2 + 8x2y) − 2,75xy2)
і знайдіть його значення, якщо x = −1; y = 3. 5xy − 8x2y − (3xy − (41 4 xy2 + 8x2y) − 2,75xy2) = 5xy − 8x2y − (3xy – 41 4 xy2 − 8x2y − 2,75xy2) = 5xy − 8x2y − 3xy + 41 4 xy2 + 8x2y + 23 4 xy2 = 2xy + 7xy2.
Якщо x = −1, y = 3, то... 2(−1) · 3 + 7(−1) · 32 = −6 − 63 = −69.
Відповідь: −69
10. Виконайте множення:
1) a(b + 7) = ab2 + 7a; 2) c(2 − x) = 2c − cx; 3) −a(m − 3) = −am + 3a; 4) −b(a − x + y) = −ab + bx − by.
11. Перетворіть добуток на многочлен:
1) 2ax(a2 − 3ax) = 2a3x − 6a2x2; 2) −3mp(2m3 − 5mp) = −6m4p + 15m2p2; 3) 4ab2(a2 − 2ab − b2) = 4a3b2 − 8a2b3 − 4ab4; 4) (4m3 − 2mn2 − n2) · mn2 = 4m4n2 − 2m2n4 + mn4; 5) (−0,1x3y + 0,2x2y − y2) − (5x2y) = 0,5x5y2 – x4y2 + 5x2y3; 6) −10n3x(5nx2 − 2n2x + x5) = −50n4x3 + 20n5x2 − 10n3x6 .

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
1) 2x(x + y) − y(2x − y) − y(y + 1) = 2x2 + 2xy − 2xy + y2 – y2 – y = 2x2 − y.
Якщо x = −5, y = −10, то 2(−5)2 − (−10) = 2 · 25 + 10 = 60. 2) m2(m2 − 5m + 1) − 2m(m3 − 4m2 + m) + m4 – 3m2 + 2 = = m4 − 5m3 + m2 − 2m4 + 8m3 − 2m2 + m4 − 3m2 + 2 = −m2 + 2.
Якщо m = −3, то − (−3)2 + 2 = −9 + 2 = −7.
13. Для якого значення
значення виразу 3(4x2 − 5)?
2x(6x − 5) + 5 = 3(4x2 − 5); 12x2 − 10x + 5 = 12x2 − 15; −10x = − 15 −5; −10x = −20; x = −20 : (−10); x = 2.
Відповідь: 2.
2x(6x − 5) на 5 менше
4 9 (x + x + 3) = 4 9 (2x + 3) ц
Рівняння:
x + (x + 3) + 4 9 (2x + 3) = 65;
9x + 9x + 27 + 8x + 12 = 65 × 9; 26x = 546; x = 546 : 26; x = 21.
За другий день продали 21 ц, за перший 24 ц,
4
9 (2 · 21 + 3) = 4 9 · 45 = 20 (ц) овочів.
Відповідь: 21 ц; 24 ц; 20 ц.
16. Розв’яжіть рівняння:
1 3x 2 4 + 2 x 4 3 = x – 2 | ∙ 12; 3(1 3x 2 ) + 4(2 x 4 ) = 12x – 24;
З – 4,5х + 8 – х = 12x – 24; –4,5х – х – 12x = –24 – 3 – 8; –17,5x = –35; x = 2.
Відповідь: 2. До §23
17. Винесіть за дужки спільний множник:
1) 5x − 5y = 5(x − y); 2) 7m + 7n = 7(m + n);

3) ap + ac = a(p + c); 4) bm − bk = b(m − k).
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
18. Розкладіть на
1) 7ax − 7bx = 7x(a − b); 2) 8a + 24ac = 8a(1 + 3c);
3) 18p − 24p2 = 6p(3 − 4p); 4) 5m3 − 10m2 = 5m2(m − 2);
5) −15a2 − 20a3 = −5a2(3 + 4a); 6) a7 − a2 + a5 = a2(a5 − 1 + a3).
19. Подайте
1) 6xy − 12x2y + 15x2y = 3xy(2 − 4x + 5);
2) 7mn5 + 28m2n3 − 7m3n2 = 7mn2(n3 + 4mn − 7m2); 3) a(x − 2) + 3b(x − 2) – 2(2 – x) = (x − 2)(a + 3b + 2); 4) 8(m − 1)2 − n(1 − m) = 8(m − 1)2 + n(m − 1) = (m − 1)2 · (8 + n).
20. Розв’яжіть рівняння:
1) x|x − 3| − 5|x − 3| = 0; |x − 3|(x − 5) = 0; |x − 3| = 0; x = 3; x − 5 = 0; x = 5;
Відповідь: 3; 5.
21.
2) |x| · |x − 2| − 7|x − 2| = 0; |x − 2|(|x| − 7) = 0; |x − 2| = 0; x – 2 = 0; x = 2; |x| − 7 = 0; |x| = 7; x = 7 або x = −7.
Відповідь: 2; 7; −7.
x2
виразу: 1) 2x2 − 6x − 26 = 2(x2 − 3x − 13). Якщо x2 – 3х – 13 = –1, то 2(х2 – 3
– 13) = 2(–1) = –2; 2) х2(х2 – 3х – 13) – 3х(х2 – 3х – 13) = (х2 – 3
+ 31 = 3(х2 – 3х – 13) + 31.
Якщо x2 – 3х – 13 = –1, то 3(х2 – 3х – 13) + 31 = 3(–1)
– 3x – 13) + 101).
Якщо x2 – 3х – 13 = –1, то 1 12(5(х2 – 3х – 13) + 101) = 1 12(5(–1) + 101) = 96 12 = 8.
До §24
22. Виконайте множення:
1) (m − p)(a + x) = ma + mx − ap − px; 2) (2 + t)(a − 3) = 2a − 6 + ta − 3t; 3) (a + b)(2 + c) = 2a + ac + 2b + bc; 4) (a − 2)(b − 3) = ab − 3a − 2b + 6. 23. Подайте у вигляді многочлена:
1) (2m − 3p)(3m + 2p) = 6m2 + 4pm − 9pm − 6p2 = 6m2 − 5pm − 6p2; 2) (2a2 + b)(3b − 5a2) = 6a2b − 10a4 + 3b2 − 5a2b; 3) (7x2 − 2x)(3x + 1) = 21x3 + 7x2 − 6x2 − 2x = 21x3 + x2 − 2x; 4) (5a3 − 4a2)(9a2 + 8a) = 45a5 + 40a4 − 36a4 − 32a3 = 45a5 + 4a4 − 32a3; 5) (3a2 + 5ab)(3b − 4a) = 9a2b − 12a3 + 15ab2 − 20a2b = −11a2b + 15ab2 − 12a3;
6) (mn − n2)(4n3 + 2n2m) = 4mn4 + 2n3m2 − 4n5 − 2n4m = 2mn4 + 2n3m2 − 4n5
24. Спростіть вираз:
1) (a − 8)(2a − 2) − (a + 9)(a − 3) = 2a2 − 2a − 16a + 16 − (a2 − 3a + 9a − 27) = = 2a2 − 18a + 16 − a2 − 6a + 27 = a2 − 24a + 43; 2) (x − y)(x + 3) − (x + y)(x − 3) = x2 + 3x − xy − 3y − (x2 − 3x + xy − 3y) = = x2 + 3x − xy − 3y − x2 + 3x − xy + 3y = 6x − 2xy; 3) (3a − 5)(5a + 3b) − (5a − 3b)(3a + 5b) = 15a2 + 9ab − 25ab − 15b2 − (15a2 + 25ab − 9ab − 15b2) = 15a2 − 16ab − 15b2 − 15a2 + 16ab − 15b2 = −30b2; 4) (a3 + 4m)(a2 − 4m) − (a2 + 4m)(a3 − 4m) = a5 − 4a3m + 4ma2 − 16m2 − (a5 − 4a2m + 4ma3 − 16m2) = a5 − 4a3m + 4ma2 − 16m2 − a5 + 4a2m − 4a3m + 16m2 = −8a3m + 8ma2.

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
25. Розв’яжіть рівняння:
1) (3x − 1)(2x + 6) − (2x − 2)(3x + 1) = −24;
6x2 + 18x − 2x − 6 − (6x2 + 2x − 6x − 2) = −24; 6x2 + 16x − 6 − 6x2 + 4x + 2 = −24.
16x + 4x = −24 + 6 − 2; 20x = −20; x = −20 : 20; x = −1.
Відповідь: −1.
2) (3x + 9)(x − 5) − (x − 7)(3x − 1) = 12 + 8x; 3x2 − 15x + 9x − 45 − (3x2 − x − 21x + 7) = 12 + 8x; 3x2 − 15x + 9x − 45 − 3x2 + x + 21x + 7 = 12 + 8x; −6x + 22x − 8x = 12 + 45 + 7; 8x = 64; x = 64 : 8; x = 8.
Відповідь: 8.
26. Доведіть, що значення виразу 2(10x − 5)(x + 0,6) + (4x2 − 1)(2x − 5) − (2x − 1)(4x2 + 2x + 1) не
від значення змінної. 2(10x − 5)(x + 0,6) + (4x2 − 1)(2x − 5) − (2x − 1)(4x2 + 2x + 1) = = 2(10x2 + 6x − 5x − 3) + 8x3 − 20x2 − 2x + 5 − 8x3 + 1 = = 20x2 + 2x – 6 − 20x2 − 2x + 6 = 0
27. Доведіть, що (x + 1)(y + 1) − (x − 1)(y − 1) = 8, якщо x + y = 4. (x + 1)(y + 1) − (x − 1)(y − 1) = xy + x + y + 1 − (xy − x − y + 1) = = xy + x + y + 1 − xy + x + y − 1 = 2x + 2y = 2(x + y) = 2 · 4 = 8. 28. Два
x(x + 10) · 25(см3) об'єм води у першому акваріуму. (x + 10) см ширина другого акваріуму; (x + 30) см довжина другого акваріуму; (x + 30)(x + 10) · 25(см3) об'єм води у другому акваріуму.
37,5 л = 37,5 дм3 = 37 500 см3 .
Рівняння: x(x + 10) · 25 + 37 500 = (x + 30)(x + 10) · 25; 25x2 + 250x + 37 500 = (x2 + 10x + 30x + 300) · 25; 250x − 1000x = 7 500 − 37 500; 750x = 30 000; x = 30 000 : 750; x = 40.
Довжина: 50 см. Ширина: 40 см.
Відповідь: 40 см; 50 см. До §25 29. Закінчіть розкладання
ab − 7b + 3a − 21 = (ab − 7b) + (3a − 21) = b(a − 7) + 3(a − 7) = (a − 7)(b + 3).

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
30. Розкладіть на множники:
1) m(a − b) + 3a − 3b = m(a − b) + 3(a − b) = (a − b)(m + 3);
2) a(b + c) + b + c = (b + c)(a + 1);
3) 3a – 3c + xa – xc = 3(a – c) + x(a – c);
4) ab – ac – 4b + 4c = a(b – c) – 4(b – c) = (b – c)(a – 4).
31. Подайте многочлен у вигляді добутку:
1) 12x2c – 8x2y − 9xy3 + 6y4 = 4x2(3c − 2y) − 3y3(3c − 2y) = (3c − 2y)(4x2 − 3y3); 2) 1,6mn2 − 2,4mp2 – n3 + 1,5np2 = 0,8m(2n2 − 3p2) − 0,5n(2n2 − 3p2) = = (2n2 − 3p2)(0,8m − 0,5n).
32. Розв’яжіть рівняння x2 + 5x − 6 = 0, застосувавши розкладання многочлена на
множники. x2 + 5x − 6 = 0; x2 + 2x + 3x − 6 = x2 – x + 6x − 6 = x(x − 1) + 6(x − 1) = (x − 1)(x + 6).
ТЕМА 6.
26.1. P△MKL = MK + KL + LM = 2 + 3 + 4 = 9 (см).

26.2.

26.3.
Вершини трикутника: P, K, L. Сторони трикутника: PK, KL, LP.
Кути трикутника: ∠KPL, ∠PKL, ∠KLP.

26.4.

Сторони трикутника: AM, MN, NA. Кути трикутника: ∠MAN, ∠AMN, ∠MNA.

25 мм = 2,5 см; 0,4 дм = 4 см. P = 2,5 + 3,2 + 4 = 9,7 (см). Відповідь: 9,7 см.


https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
26.6.
29 мм = 2,9 см; 0,3 дм = 3 см.
P = 4,3 + 2,9 + 3 = 10,2 (см).
Відповідь: 10,2 см.
26.7.

26.8.

26.9.
AB = 2,8 см; BC = 1,5 см; AC = 3 см. P = 2,8 + 1,5 + 3 = 7,3 см.
Відповідь: 7,3 см.
PL = 5,3 см; PK = 3,2 см; KL = 2,9 см. P = 5,3 + 3,2 + 2,9 = 11,4 см.
Відповідь: 11,4 см.
Нехай довжина найменшої сторони трикутника дорівнює x см, тоді довжина другої 3x см, а третьої (x + 7) см. Оскільки периметр трикутника дорівнює 32 см, маємо
рівняння:
x + 3x + (x + 7) = 32; 5x + 7 = 32; 5x = 25; x = 5 (см).
Отже, довжина однієї сторони 5 см, другої 5 × 3 = 15 см, третьої 5 + 7 = 12 см. Відповідь: 5 см, 15 см, 12 см.
26.10.
Нехай довжина однієї
трикутника
x дм, тоді довжина другої (x − 2)
дм, третьої 1,5x дм. Оскільки периметр трикутника дорівнює 40 дм, маємо рівняння: x + (x − 2) + 1,5x = 40; 3,5x − 2 = 40; 3,5x = 42; x = 12 (дм).
Отже, довжина однієї сторони трикутника
12 дм, другої 12 − 2 = 10 дм, третьої 12 × 1,5 = 18 дм.
Відповідь: 12 дм, 10 дм, 18 дм. 26.11. Побудуємо ∠A = 60°

26.12.

26.13.

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
3x + 4x + 6x = 52; 13x = 52; x = 4.
Отже, одна із сторін трикутника дорівнює 3 × 4 = 12 см, друга 4 × 4 = 16 см,
третя 6 × 4 = 24 см.
Відповідь: 12 см, 16 см, 24 см.
26.14.
Нехай одна із сторін трикутника дорівнює 2x, друга 3x, третя 4x. Оскільки P△ = 72,
маємо рівняння: 2x + 3x + 4x = 72; 9x = 72; x = 8.
Отже, одна із сторін трикутника дорівнює 2 × 8 = 16 (см), друга 3 × 8 = 24 (см), третя 4 × 8 = 32 (см).
Відповідь: 16 см, 24 см, 32 см. 26.15.

26.16.

26.17.
△MNK, △MKN, △NKM, △NMK, △KNM, △KMN.
AB + BC = 11 см, BC + AC = 14 см, AC + AB = 13 см.
AB + BC + BC + AC + AC + AB = 11 + 14 + 13; 2(AB + BC + AC) = 38;
AB + BC + AC = 38 : 2 = 19 (см).
Відповідь: 19 см.

26.18.

∠ABC = 78°, BD бісектриса кута ABC.
∠ABD = ∠DBC = 39°. BE допоміжний промінь
сторони BC кута ABC.
∠EBA суміжний до ∠ABC, ∠EBA = 180° - 78° = 102°.
∠EBD = ∠EBA + ∠ABD = 102° + 39° = 141°.
Відповідь: 141°. 26.19.
1) 3 га ⋅ 18 млн м3 = 54 (млн м3) 2) 2 км2 18 млн м3 = 200 га 18 млн м3 = 3600 (млн м3) 26.20.


https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html

1) AB = 2,5 см, CD = 2,8 см.
Отже, AB ≠ CD.
2)

27.2.
∠M = 55°, ∠K = 55°.
Отже, ∠M = ∠K.

1) MN = 3 см, PK = 3 см.
Отже, MN = PK.
2)

27.3.
∠A = 60°, ∠B = 50°.
Отже, ∠A ≠ ∠B.
1) Так, оскільки 1,7 см = 17 мм, то АК = MF.
2) Ні, оскільки градусні міри кутів різні.
27.4.

27.5.

27.6.

27.7.

1) ∠A = ∠M; 2) ∠B = ∠P; 3) ∠C = ∠L.
1) MP = DC; 2) PT = CK; 3) MT = DK.
1) △AKM = △LPT; 2) △MAK = △TLP.

1) △ABC = △PFK; 2) △CAB = △KPF.
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
27.8.

27.9.

27.10.
1) Ні, наприклад, трикутники із сторонами 4, 2, 3 і 1,
вони не рівні, оскільки відповідні сторони не рівні.
2) Ні, оскільки у рівних трикутників рівні
27.11.
△ABC = △CBA, тоді AB = CB, BC = BA, AC = CA.
Отже, у △ABC рівні сторони AB і BC.
27.12.
Оскільки △MNK = △MKN, то ∠M = ∠M, ∠N = ∠K, ∠K = ∠N.
Отже, у трикутника MNK ∠N = ∠K.
27.13.
Оскільки △ABC = △BCA, то AB = BC, BC = CA, AC = BA.
Отже, AB = BC = CA. △ABC рівносторонній.
P△ABC = 3 × AB = 3 × 7 = 21 (см).
Відповідь: 21 см.
27.14.
Оскільки △ABC = △KLP, то їхні відповідні сторони рівні.
KL = AB = 6 см, BC = LP = 8 см, KP = AC = 10 см.
Оскільки △PMT = △DCF, то їхні відповідні кути рівні. ∠D = ∠P = 41°, ∠M = ∠C = 92°, ∠F = ∠T = 47°.
рівні периметри,
периметри.
Оскільки △PKL = △KLP, то PK = KL, KL = LP, LP = KP. Отже, PK = KL = LP.
P△PKL = 27 см, P△DKL = 3PK, 27 = 3PK, PK = 9 см.
Відповідь: 9 см.
27.15.
Вісім точок, що розташовані
112 : 7 = 16 см.
16 см. 27.16.

30°, 60°, 90°.

COD = 2x, ∠COA = 3x. ∠DOB + ∠COD + ∠COA = 180°, x + 2x + 3x = 180°; 6x = 180°, x = 30°. Отже, ∠DOB = 30°, ∠COD = 2 × 30° = 60°, ∠COA = 3 × 30° = 90°.
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
27.17.
1. 1) V = 20 0,5 2,5 = 25 (м3) – об’єм кладки
2) 25 ⋅ 400 = 10000 (шт) – кількість цеглин
3) 25 ⋅ 20% = 25 ⋅ 0,2 = 5 (м3) – об’єм розчину
2. 1) 10000 ⋅ 4,2 = 42000 (грн) – вартість цегли
2) 5 ⋅ 1520 = 7600 (грн) – вартість розчину
3) 42000 + 7600 = 49600 (грн) –
27.18.






28.5.

28.6.
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
За умовою AB = BC. Оскільки BK ⊥ AC, то ∠ABK = ∠CBK = 90°, KB спільна сторона. Отже, ΔABK = ΔCBK за двома сторонами і

28.7.

28.8.
Оскільки PL ⊥ MN, то ∠PKM = ∠LKN = 90°.
За умовою MK = KN, ∠M = ∠N.
Отже, ΔMKP = ΔNKL за стороною
кутами.
За умовою KB = KC, ∠ABK = ∠DCK. ∠AKB = ∠DKC – як вертикальні кути. Отже, ΔABK = ΔDCK за стороною і

28.9.

28.10.

За умовою AB = CD, ∠ABC = ∠BCD. CB спільна сторона. Отже, ΔABC = ΔDCB за двома сторонами і
ними.
Оскільки ОС бісектриса кута AOB, то ∠AOC = ∠NOC. За умовою ∠OCM = ∠OCN, OC спільна сторона. Отже,

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html

28.12.

28.13.

28.14.
Розглянемо ΔBOC і ΔDOA: OC = OA, OB = OD, ∠BOC = ∠DOA, як вертикальні кути. Отже, ΔBOC = ΔDOA за двома сторонами і кутом між ними. Отже, BC = AD, оскільки у рівних трикутників відповідні сторони рівні. Розглянемо ΔBOA і ΔDOC: AO = OC, OB = OD, ∠BOA = ∠DOC як вертикальні кути. Отже, ΔBOA = ΔDOC за двома сторонами і кутом між ними. Отже, AB = CD, оскільки у рівних трикутників відповідні сторони рівні.
За умовою AB = CD, ∠BAC = ∠DCA. AC спільна сторона. Отже, ΔABC = ΔCDA за двома сторонами і кутом між ними.
За умовою ∠LMK = ∠PKM і ∠LKM = ∠PMK. MK спільна сторона. Отже, ΔMKL = ΔKMP за стороною і прилеглими кутами.

28.15.

28.16.

28.17.


Оскільки за умовою ΔABC = ΔA1B1C1, то у них
сторони і
рівні. Отже, AC1 = AC, ∠C1 = ∠C. Тоді ΔALC = ΔA1L1C1 за стороною і двома прилеглими кутами.
Оскільки за умовою ΔABC = ΔA1B1C1, то у
Отже, AB = A1B1, ∠BAM =
18.

28.19.

28.20.

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
ΔABK = ΔCBL, то
рівні. Отже, ∠A = ∠C, AB = CB, AK = CL. AL = AK + KL, CK = CL + KL, отже, KL спільний відрізок
для AL і CK, AL = CK. Тоді ΔABL = ΔCBK за двома сторонами і
Оскільки ΔAKC = ΔALC, то у них відповідні сторони і кути рівні. Отже, KC = LC, ∠KCA = ∠LCA. Оскільки ∠KCA = ∠LCA, то рівні і суміжні з ними кути ∠KCB = ∠LCB. CB спільна сторона трикутників ВКС і BLC. Отже, ΔBKC = ΔBLC за двома сторонами і кутом між ними.
Оскільки AB бісектриса кута A, то ∠MAB = ∠NAB, AB спільна сторона трикутників AMB і ANB. Отже, ΔAMB = ΔANB за стороною і прилеглими кутами. У рівних трикутників відповідні сторони рівні. Отже, AM = AN. Розглянемо ΔAMP і ΔANP. AP спільна сторона.
ΔAMP = ΔANP за двома сторонами і кутом між ними (∠MAP = ∠NAP, AM = AN).
рівних трикутників відповідні кути рівні, отже, ∠MPA = ∠NPA.
Оскільки ці кути суміжні і рівні, то маємо ∠MPA + ∠NPA = 180°; ∠MPA = ∠NPA = 90°.
Тож MN ⊥ AB.
28.21.
1) 12 см + 4 дм = 1,2 дм + 4 дм = 5,2 дм друга сторона трикутника.
2) 4 дм : 2 = 2 дм третя сторона трикутника.
3) PΔ = 4 + 5,2 + 2 = 11,2 (дм).
Відповідь: 11,2 дм. 28.22. Якщо ці три кути 1, 3, 5, то ∠1 + ∠3 + ∠5 = 270°;

28.23.
a ⊥ c, b ⊥ c. Якщо ці три кути 1, 2, 3, тоді ∠1 + ∠2 = 180° (як суміжні), звідси ∠3 = 90°. Отже, і інші
1) 3,5 ⋅ 6 = 21 (м2) – площа підлоги
2) 0,07 ⋅ 0,4 = 0,028 (м2) –
3) 21 : 0,028 = 750 (шт) Відповідь: потрібно 750 дощечок.
28.24.
РΔ = 6 + 6 + 8 = 20 (см).
Відповідь: 20 см.
28.25.
Можна скласти
101 × 50.
1 × 1 і 1 × 100; 1 × 2 і 1 × 99; ...; 1 × 50 і 1 × 51.




29.5.
= 3 × AB = 3 × 12 = 36 (см).


29.6.
= P : 3 = 18 : 3 = 6 (см).

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html

Відповідь: 19 см.
29.8.
тоді основа AC = 7 - 2 = 5 (см). P = 7 + 7 + 5 = 19 (см).
У рівнобедреному трикутнику
сторони рівні,
кожна з
дорівнює 8 + 4 = 12 (см).
Тоді периметр PΔ = 8 + 12 + 12 = 32 (см).
Відповідь: 32 см.
29.9.
Ні, не може, оскільки, у рівнобедреного трикутника кути при основа рівні (теорема 1).
29.10.

29.11.

29.12.

29.13.

29.14.
Нехай в ΔABC: AC основа, AB = BC = 7 см. PΔABC = 20 см.
Отже, маємо P = AB + BC + AC. 20 = 7 + 7 + AC, AC = 20 - 14 = 6 (см).
Відповідь: 6 см.
Нехай в ΔAMN: AM = AN = 7 дм (як бічні сторони). PΔAMN = 18 дм.
Отже, AM + AN + MN = 18; 7 + 7 + MN = 18; MN = 18 - 14 = 4 (дм).
Відповідь: 4 дм.
Нехай в ΔACD: CD = 12 дм, PΔACD = 30 дм.
PΔACD = AC + AD + CD, 30 = AC + AD + 12, 30 = 2AC + 12 (оскільки AC = AD), 2AC = 18, AC = 9 (дм).
Відповідь: 9 дм.
Нехай в ΔABC: AB = BC, AC = 5 см, PΔABC = 17 см.
PΔABC = AB + BC + AC, 17 = AB + BC + 5, 17 = 2AB + 5 (оскільки AB = BC), 2AB = 12, AB = 6 (см).
Відповідь: 6 см.

За умовою ΔABC рівнобедрений, отже, AC = CB і ∠CAB = ∠CBA (за властивістю кутів рівнобедреного трикутника).
∠KAC і ∠CAB суміжні, ∠KAC + ∠CAB = 180°, ∠KAC = 180° - ∠CAB.
∠MBC і ∠CBA суміжні, ∠MBC + ∠CBA = 180°, ∠MBC = 180° - ∠CBA. Оскільки ∠CAB = ∠CBA, то і ∠KAC = ∠MBC. 29.15. За умовою ΔKLM рівнобедрений


рівнобедреного трикутника ∠MKL = ∠MLK. ∠MLK = ∠PLN як вертикальні кути. Оскільки ∠MLK = ∠MKL, то ∠PLN = ∠MKL.
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
29.16. 1)
2)
29.17.

29.18.

29.19.

Нехай ΔABC рівнобедрений, AB = BC, PΔABC = 14 см.
AB + BC = 14 - 6 = 8 (см), AB = BC = 8 : 2 = 4 (см).
AC = PΔABC - (AB + BC) = 14 - 8 = 6 (см).
Відповідь: 4 см, 4 см, 6 см.
Нехай ΔABC рівнобедрений, AB = BC, P = 44 см.
Позначимо основу AC = x, тоді AB = x + 4, BC = x + 4.
Складемо рівняння: (x + 4) + (x + 4) + x = 44; 3x + 8 = 44; 3x = 36; x = 12.
Отже, AC = 12 см, AB = BC = 12 + 4 = 16 (см).
Відповідь: 12 см, 16 см, 16 см.
Нехай ΔABC рівнобедрений, AB = BC, P = 35 дм.
Позначимо основу AC = x, тоді AB = BC = 2x.
Складемо рівняння: x + 2x + 2x = 35; 5x = 35; x = 7.
Отже, AC = 7 дм, AB = BC = 7 × 2 = 14 (дм).
Відповідь: 7 дм, 14 дм, 14 дм. 29.20.

29.21.

Оскільки ΔABC рівнобедрений (AB = BC) з основою AC, то ∠BAC = ∠BCA (за властивістю кутів рівнобедреного трикутника).
Розглянемо ΔCKA і ΔALC: AC спільна, KA = LC (за умовою),
∠KAC = ∠LCA.
Отже, ΔCKA = ΔALC (за двома сторонами і кутом між ними).
Отже, AL = KC (як відповідні сторони).
Нехай ΔABC рівнобедрений, AB = BC, ∠KCA = ∠LAC.
Розглянемо ΔAOC.
Оскільки ∠KCA = ∠LAC, то за теоремою 2 ΔAOC рівнобедрений.
Звідси OA = OC.
Розглянемо ΔKOA і ΔLOC. ∠KAO = ∠BAC - ∠LAC, ∠LCO = ∠BCA∠KCA.
Оскільки ∠BAC = ∠BCA і ∠KCA = ∠LAC, то ∠KAO = ∠LCO.
∠KOA = ∠LOC як вертикальні.
Отже, ΔKOA = ΔLOC за стороною і прилеглими кутами. Звідси AK = CL. 29.22.


Розглянемо ΔLCM і ΔMAK. CM = AK (за умовою), LC = LB + BC, MA = MC + AC, отже, LC = MA, оскільки MC = CB за умовою, BC = AC як сторони рівностороннього ΔABC.
∠LCM = ∠MAK як кути, суміжні з рівними кутами. ΔLCM = ΔMAK за двома сторонами і кутом між ними.
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
Звідси LM = KM.
Аналогічно з рівності ∠MAK та ∠KBL отримаємо KM = KL. Маємо LM = KM = KL.
Отже, ΔKLM рівносторонній.
29.23.

29.24.
За умовою AB = BC = AC, AP = BK = LC, тоді PB = AB - AP, KC = BC – BK, AL = AC - LC, PB = KC = AL. Оскільки ΔABC рівносторонній, то ∠A = ∠B = ∠C. ΔPBK = ΔKCL = ΔLAP за двома сторонами і кутом між ними. Отже, PK = KL = LP, то ΔPKL рівносторонній.
Припустимо, що обидва суміжні кути більші за 90°, або один з кутів більший за 90°,
другий дорівнює 90°. Тоді їх сума буде більшою за 180°, а це суперечить означенню суміжних кутів. 29.25.

29.26.
Оскільки ΔAOB і ΔCOD рівні, то рівні їхні відповідні
тобто ВО = OD, ∠ABO = ∠CDO. Розглянемо ΔKBO і ΔLDO. ∠KOB = ∠LOD як вертикальні кути. ΔKBO = ΔLDO за стороною і прилеглими кутами. Отже, KO = OL, KB = DL.

Нехай довжина відрізка AK = x см, тоді BK = (48 - x) см. За умовою 5AK = 7BK, отже маємо рівняння: 5x = 7(48 - x); 5x = 336 - 7x; 12x = 336; x = 28.
Отже, AK = 28 см, BK = 48 - 28 = 20 (см).
Відповідь: 28 см, 20 см.
29.27.
1) 100 ⋅ 12 ⋅ 10 = 12000 (м3) – повітря очищає одне дерево; 2) 200 ⋅ 12000 = 2 400 000 (м3) – повітря очистять 200 каштанів за рік.
Відповідь: 2 400 000 м3 повітря.
29.28.
1) Конус, сукно; 2) сектор, корсет. § 30. Медіана, бісектриса і висота трикутника. Властивість бісектриси рівнобедреного трикутника
30.1.


висота трикутника ABC.

трикутника ABC.

ABC.
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html

30.3.

30.4.

30.5.

30.6.

30.7.

1) AT висота трикутника ABC.
2) AN медіана трикутника ABC.
3) AP
трикутника ABC.
Оскільки AK
то ∠ВКА = ∠CKA = 90°.
Оскільки AK бісектриса, то ∠BAK = ∠CAK = 35°. Отже, ∠BAC = ∠BAK + ∠CAK = 35° + 35° = 70°.
Оскільки AK медіана, то BK = KC = �������� 2 = 12 2 = 6 (см).
AL, BN, CK – медіани ΔABC.

PL, CP, AM – бісектриси ΔABC.

30.9.

30.10.

30.11.
AE, BF, CD – висоти ΔABC.
то: ∠CAK = ∠BAK, ∠ACK = ∠ABK, ∠AKC = ∠AKB, AC = AB, CK = KB.

30.12.
то: ∠EDP = ∠EFP, ∠DEP = ∠

30.13.

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html

1) сумістяться половини кута з якого виходить бісектриса
30.15.

30.16.

30.17.

2) сумістяться частини основи
Нехай в ΔABC BD бісектриса і висота.
∠ABD = ∠CBD, ∠BDA = ∠BDC, BD спільна сторона ΔABD і ΔCBD.
Отже, ΔABD = ΔCBD за стороною і прилеглими кутами. Оскільки у рівних трикутників відповідні сторони рівні, то AB = CB. Отже, ΔABC рівнобедрений.
Нехай в ΔABC BD медіана і висота.
∠BDA = ∠BDC = 90°, AD = DC, BD спільна сторона ΔABD і ΔCBD.
Отже, ΔABD = ΔCBD за двома сторонами і кутом між ними. Оскільки у рівних трикутників відповідні сторони рівні, то AB = CB. Отже, ΔABC рівнобедрений.

30.18.

30.19.

ΔABC = ΔA1B1C1, отже, A1C1 = AC, ∠B1C1A1 = ∠BCA (як відповідні сторони і кути рівних трикутників).
AD бісектриса ΔABC, ∠BAD = ∠DAC. A1D1 бісектриса ΔA1B1C1, ∠B1A1D1 = ∠D1A1C1. Отже, ∠DAC = ∠D1A1C1. ΔADC = ΔA1D1C1 за стороною і прилеглими кутами.
Нехай в ΔABC AB = BC, BF = FC = 1 2BC, BD = DA = 1 2AB, отже, AD = FC.
ΔADC = ΔCFA (оскільки AC спільна, ∠DAC = ∠FCA як кути при основі рівнобедреного трикутника, AD = FC як половини рівних сторін AB і BC). З рівності трикутників маємо: DC = FA.

Нехай в ΔABC AB = BC, ∠BAC = ∠BCA, AF і CD бісектриси, тобто ∠FAC = ∠FAB = 1 2 ∠BAC, ∠DCA = ∠DCB = 1 2 ∠BCA, отже, ∠FAC = ∠DCA, ΔADC = ΔCFA (оскільки AC спільна, ∠FAC = ∠DCA, ∠DAC = ∠FCA). З рівності трикутників маємо: AF = CD.
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
30.20.

30.21.

30.22.
Нехай в ΔABC AB = BC, BD ⊥ AC, BD = 10 см, PΔABC = 40 см.
PΔABC = AB + AD + BD, AB + AD = P - BD = 40 - 10 = 30 (см).
AB = BC - за умовою, AD = DC - оскільки BD є медіаною.
AB + AD = BC + DC, тоді PΔABC = AB + AD + BC + DC = 30 + 30 = 60 (см).
Відповідь: 60 см.
Нехай в ΔABC CB = CA, BK = KA, PΔABC = 16 см, PΔACK = 12 см. PΔACK = CA + AK + KC, PΔABC = CA + AB + BC = CA + AK + KB + BC = 2(CA + KA) = 16 (см). CA + AK = 8 см, KC = PΔACK - (CA + AK) = 12 - 8 = 4 (см).
Відповідь: 4 см.

Нехай в ΔABC CN – медіана і бісектриса. Продовжимо
медіану CN так, щоб NK = CN. Проведемо відрізки КА і
Розглянемо ΔCNB і ΔKNA. CN = KN (за побудовою), NB = NA (за умовою). ∠ANK = ∠BNC (як вертикальні), отже, ΔCNB = ΔKNA за двома сторонами і кутом між ними.
У рівних трикутників рівні відповідні кути і сторони, тож ∠NCB = ∠NKA, CB = KA.
Аналогічно з рівності трикутників CAN і KBN отримаємо ∠CAN = ∠BKN, AC = BK.
Розглянемо ΔCAN і ΔKBС. Вони рівнобедрені. AK = CA, CB = BK.
Отже, отримали AC = CB = AK = KB. У ΔABC дві сторони
30.23.

30.24.

30.25.


170° ≠ 180°.
Отже, сума внутрішніх односторонніх кутів не дорівнює 180°. Кути ∠6 і ∠7 теж не можуть дорівнювати відповідно 140° і 30°, бо вони суміжні.
Нехай ΔABC рівносторонній, PΔABC = 12 см. ΔACD рівнобедрений.
AD = CD, PΔACD = 18 см. AB = BC = AC (як сторони рівностороннього трикутника).
AC = P : 3 = 12 : 3 = 4 (см).
P = AC + AD + CD, AD + CD = P - AC = 18 - 4 = 14 (см).
Отже, AD = CD = 7 см.
Відповідь: 7 см.
Нехай ΔABC рівнобедрений, AB = BC, P = 69 см.
Позначимо довжину AB = x см, тоді AC = 0,3x см.
Складемо рівняння: x + x + 0,3x = 69; 2,3x = 69; x = 30.
Отже, AB = BC = 30 см, AC = 30 × 0,3 = 9 (см).
Відповідь: 30 см, 30 см, 9 см.
кімнати (паралелепіпеда).
1) 2 ∙ (9,4 + 6,5) = 31,8 (м) – периметр кімнати (основи);
2) 31,8 ∙ 3,2 = 101,76 (м2) – площа стін
3) 101,76 ∙ 0,09 = 9,1584 (м2) – площа
4) 101,76 – 9,1584 = 92,6016 (м2) – площа стін без вікон і дверей;
5) 2 ∙ 9,4 ∙ 6,5 + 92,6016 = 214,8016 (м2) – площа всієї кімнати, яку потрібно пофарбувати;
6) 25 ∙ 214,8016 = 5370,04 ≈ 5370 грн.
Відповідь: за фарбування тренажерного залу потрібно сплатити 5370 грн. 30.27.
125 л = 125 дм³. Олесь придбав акваріум розмірами 15 дм × 5 дм × 5 дм.
Якщо Олесь наповнив акваріум,
31.1.

31.2.

31.3.

31.4.

ΔABC = ΔCDA за третьою ознакою рівності трикутників.
У трикутників ACD і ABD AC = BD, CD = BD за умовою, AD спільна сторона, отже, ΔACD = ΔABD за третьою ознакою рівності трикутників.

MK = ML, KN = NL за умовою, MN спільна сторона ΔMKN і ΔMLN. Отже, ΔMKN = ΔMLN за трьома сторонами. У рівних трикутників відповідні кути рівні, тому ∠K = ∠L.
31.5.

31.6.

13.7.
PK = ML, PM = KL за
трикутники: ΔABK і ΔCBK.
AB = BC, AK = KC за умовою, BK спільна сторона ΔABK і ΔCBK. Отже, ці трикутники рівні за третьою ознакою рівності трикутників. У рівних трикутників відповідні кути рівні, тому ∠ABK = ∠CBK. Отже, BK бісектриса кута ABC.

31.8.

31.9.

З'єднуємо т. М і т. L. Отримаємо два трикутники: ΔMPL і ΔMKL. MP = MK, PL = LK за умовою, ML спільна сторона ΔMPL і
ΔMKL.
ΔMPL = ΔMKL за третьою ознакою рівності трикутників. У рівних трикутників відповідні кути рівні, тому ∠PML = ∠KML. Отже, ML бісектриса кута PMK.
AB = CD, AC = BD за умовою, DA спільна сторона ΔCDA і ΔBAD. ΔCDA = ΔBAD за третьою ознакою рівності трикутників. У рівних трикутників відповідні кути рівні, тому ∠BDA = ∠CAD. Ці кути є кутами ΔDAO, тоді за ознакою рівнобедреного трикутника ΔDAC рівнобедрений.
AO = OB, CO = OD за умовою. ∠DOB = ∠COA як вертикальні кути. Отже, ΔDOB = ΔCOA за першою
рівності трикутників. У рівних трикутників відповідні сторони рівні, тому DB = CA. DA = DO + OA, CB = CO + OB, DA = CB, оскільки DO = CO, OA = OB. AB спільна сторона ΔABC і ΔBAD. Отже, ΔABC = ΔBAD за третьою
31.10. У рівних трикутників відповідні сторони рівні, тобто якщо AB ≠ MN, BC ≠ NP, AC ≠ MP, то ΔABC ≠ ΔMNP.


https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
31.11.

31.12.

Ні, оскільки може бути AB = 6 см і MN = MP = 6 см; BC = AC = 8 см і NP = 8 см. Тому ΔABC може бути не рівний трикутнику MNP.
ΔACK = ΔABK за третьою ознакою рівності трикутників (оскільки AB = AC, BK = KC за умовою, AK спільна сторона). ∠CAK = ∠BAK, оскільки у рівних трикутників відповідні кути рівні. Отже, AN бісектриса трикутника ABC. У рівнобедреному трикутнику бісектриса, проведена до основи, є висотою, тобто AN ⊥ CB. Оскільки K ∈ AN, то AK ⊥ CB.
31.13. ΔDPN = ΔDPM за третьою ознакою рівності трикутників. Звідси виходить, що ∠MDP = ∠NDP, отже DK – бісектриса ΔDMN. Оскільки у рівнобедреного трикутника бісектриса, що проведена до основи є також висотою і медіаною, то MK = KN.

31.14.

31.15.
Треба кут 10° відкласти послідовно 9 разів (10 ⋅ 9 = 90°).

Оскільки 4∠BAK = 5∠KAC, то = ∠BAK ∠KAC = 5 4 . Позначимо ∠BAK = 5х, тоді ∠KAC = 4х. Складемо рівняння: 5х + 4х = 126°; 9x = 126°; х = 14°. Отримаємо: ∠BAK = 5 ∙ 14° = 70°; ∠KAC = 4 ∙ 14° = 56°. Відповідь: ∠ВАК = 70°; ∠КАС = 56°.
31.16.

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
конструкції, щоб зробити їх
31.17.
1) (x + 3)(x + 3) = x2 + 3x + 3x + 9 = x2 + 6x + 9; 2) (y − 2)(y − 2) = y2 – 2y – 2y + 4 = y2 – 4y + 4;
3) (7 − m)(7 − m) = m2 – 7m – 7m + 49 = m2 – 14m + 49; 4) (5 + a)(5 + a) = a2 + 5a + 5a + 25 = a2 + 10a + 25. 31.18.

1.
P = 4 + 7+ 10 = 21 (см).
Відповідь: Б) 21 см.
2.
Відповідь: Б) ∠T.
3.
Відповідь: Б) ∆ABC = ∆A1B1C1 (за другою ознакою).
4. (17 – 5 ) : 2 = 6 (см).
Відповідь: Г) 6 см.
5.

6.
№ 6 (§§ 26–31)
∠KOL = ∠MON (як вертикальні), тому ∆KOL = ∆MON (за першою ознакою).
Відповідь: В) ∆KOL = ∆MON.
Оскільки ∠A = ∠B, то ∆ABC рівнобедрений
і висотою.
Відповідь: В) CL.
7.

AB.

медіана CL є також
Нехай AB = х см, тоді AC = 2х см і BC = (х + 2) см.
За умовою х + 2х + х + 2 = 22; 4х = 22 – 2;
4х = 20;
х = 5 (см).
Тому BC = 5 + 2 = 7 (см); AC = 2 ∙ 5 = 10 (см).
Відповідь: Г) 10 см.


10.
Оскільки ∆KLM = ∆MLK, то KL = ML і ∠K = ∠M.
Відповідь: А) 17 см.
Оскільки у ∆ABC AB = BC, то BK є не тільки висотою, а й медіаною і бісектрисою. Отже, хибним є твердження, що ∠ABC = ∠BKA, оскільки кут ABC гострий, а кут BKA прямий. Відповідь: A) ∠ABC = ∠BKA.
Оскільки ∆ABC = ∆BCA, то ∠A = ∠B і ∠B = ∠C, тобто ∠A = ∠B = ∠C.
Тому ∆ABC рівносторонній і BC = CA = AB = 5 см.
Відповідь: Г) BC = 5 см; CA = 5 см. 11.

12.

Оскільки CK бісектриса рівнобедреного трикутник, що проведена до основи, то CK є також і медіаною. Отже, AK = KB. За умовою AC = CB.
P∆ABC = AC + AB + CB = 2АС + 2AK = 2(AC + AK). Тому AC + AK = 36 2 = 18 (см).
P∆AСК = AC + AK + CK. Тому CK = 30 – 18 = 12 (см).
Відповідь: Г) 12 см.
BM = MC, тому ∠MBC = ∠MCB.
Оскільки AB = AC; BM = MC (за умовою) і AM – спільна сторона трикутників ABM і ACM. Тому ∆ABM= ∆ACM (за третьою ознакою).
Маємо ∠BAM = ∠САМ; ∠BMA = ∠CMA і ∠MBA = ∠MCA.
Твердження ∠MBA > ∠MCA хибне.
Відповідь: Б) ∠MBA > ∠MCA. 13.


1) Нехай х – АС; АВ – х – 2; ВС –3 2(х – 2).
х + х – 2 + 3 2(х – 2) = 37; 2х – 2 + 1,5х – 3 = 37; 3,5х – 5 = 37; 3,5х = 42; х = 12 (см) – АС. 2) 12 – 2 = 10 (см) – АВ. 3) 37 – (12 + 10) = 37 – 22 = 15 (см) – ВС.
1. АВ – А. 10 см; 2. ВС – В. 15 см; 3. СА – Б. 12 см.
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html

Вершини: М; N і K; Сторони: MN; NK і MK; Кути трикутника: ∠M; ∠N; ∠K.


4.




Оскільки ∆ABC = ∆KMF, то KM = AB = 5 см, MF = BC = 4 см, AC = KF = 7 см.
5. LK – спільна сторона трикутників MKL і NKL. Також

6.
умовою відомо, що MK = KN; ∠LKM = ∠LKN. Тому ∆MKL = ∆NKL (за першою ознакою).
1) 12 + 3 = 15 (см) бічна сторона трикутника; 2) P = 2 ∙ 15 + 12 = 42 (см).
Відповідь: 42 см.
7.

8.

1) AC = BD; DC = AD; CD спільна сторона трикутників ACD і BDC. Тому ∆ACD = ∆BDC (за третьою ознакою).
2) Звідси отримаємо, що ∠BCD = ∠ADC, що й треба було довести.

Нехай AB = х см, тоді BC = 2х см і AC = (х + 3) см. Складемо рівняння: x + 2x + x + 3 = 23; 4х = 23 – 3; 4х = 20; х = 5.
Отже, AB = 5 см; BC = 2 ∙ 5 = 10 (см); AC = 5 + 3 = 8 (см).
Відповідь: 5 см; 10 см; 8 см.
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html

10.

11.
1) MP = 8 дм; P∆МКР = KM + KP + PM; P∆МКР = 24 (дм), тому KM + KP= 24 – 8 = 16 (дм).
2) Оскільки ∆KML рівнобедрений з основою KL, тo KM = ML.
3) MP – медіана ∆KML, тому KP = PL.
4) P∆KML = KM + ML + KL = 2KM + 2KP = 2(KM + KP) = = 2 ∙ 16 = 32 (дм).
Відповідь: 32 дм.
1) Оскільки ∆ANB = ∆AMB, то AN = AM і ∠NAB = ∠MAB.
2) AC спільна сторона трикутників ANC і AMC.
∆ANC = ∆AMC (за першою ознакою).
3) Звідси отримаємо, що NC = MC, що й треба було довести.

За умовою 3х – х = 10; 2х = 10; х = 5 (см).
P∆MКL = 3 ∙ 5 = 15 (см).
Відповідь: 15 см.
1.

2.
Оскільки ∆MKL = ∆KLM, то ∠M = ∠K і ∠K = ∠L. Тому ∠M = ∠K = ∠L. Тобто трикутник MKL рівносторонній.
Позначимо MK = KL = ML = х (см).
Тоді P∆MКL = 3х.
Вправи для повторення теми 6 До §26
Вершини: K, L, P. Сторони: KL, LP, PK. Кути: ∠K, ∠L, ∠P.
Нехай 18 + 6 = 24 (см) друга сторона трикутника, 24 : 2 = 12 (см) третя сторона. PΔ = 18 + 24 + 12 = 54 (см).
Відповідь: 54 см.
3. Відкладемо відрізок ML = 5 см. Від т. М відкладемо кут M = 40°, від т. L відкладемо кут L =

із сторін трикутника
х см, тоді
2х см,
0,8 × 2х = 1,6х. Отже, маємо рівняння: х + 2х + 1,6х = 46; 4,6х = 46; x = 10.
одна сторона трикутника дорівнює 10 см, друга 2 × 10 см = 20 см, третя 1,6 × 10 = 16 см. Відповідь: 10 см, 20 см, 16 см.

https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html
5.
AB + AC + AC + CB = 12 + 15, AB + CB + 2AC = 27.
Оскільки AB + BC = 13 см, маємо: 13 + 2AC = 27; 2AC = 27 - 13 = 14, AC = 7 (см).
AB = 12 - AC = 12 - 7 = 5 (см), CB = 15 - 7 = 8 (см).
Відповідь: 7 см, 5 см, 8 см. До §27
6. 1) Сторони рівного трикутника дорівнюють 3 см, 7 см і 8 см.
2) Кути рівного трикутника дорівнюють 40°, 60°, 80°.
7.
Так, бо вони рівні.
8.
Ні, оскільки у рівних трикутників
9.


∆ABC = ∆ACB, AB = 7 см, BC = 4 см.
AC = AB = 7 см.
PΔABC = 7 + 4 + 7 = 18 (см).
Відповідь: 18 см.
До §28




Мал. 1. AB спільна сторона трикутників ACB і ADB. Вони рівні за
рівності трикутників (AC = AD, AB спільна, ∠CAB = ∠DAB).
Мал. 2. MN спільна сторона трикутників MKN і NPM. ∆MKN = ∆NPM за другою ознакою рівності трикутників (MN спільна сторона, ∠KMN
DO = OB за умовою, ∠AOD = ∠COB за доведенням).

AX = AC, тому що ∆CAB = ∆XAB
трикутників (AB спільна сторона, ∠XAB = ∠CAB, ∠XBA = ∠CBA), а у рівних трикутників
15. ∠BCD = ∠DFE як суміжні кути рівних кутів. DC – спільний відрізок сторін AC і FD. AC = AD + DC, FD = CF + DC, AC = FD.

16.

Отже, ∆ABC = ∆DEF
першою ознакою (BC = EF, AC = FD, ∠BCD = ∠DFC).
1) ∆ABE = ∆ADC за другою ознакою (AB = AC за умовою, ∠A спільний, ∠ABE = ∠ADC = 90°, оскільки DC ⊥ AE, BE ⊥ AD). Із рівності трикутників маємо: AD = AE. Тоді BD = AD - AB, CE = AE – AC. Оскільки AB = AC за умовою, AD = AE за доведенням, то BD = CE.
2) ∆BOD = ∆COE за стороною і двома прилеглими кутами (BD = CE за доведеним в п. 1), ∠OBD = ∠OCE = 90°, ∠BDO = ∠CEO як кути рівних трикутників ACD і ABE. З рівності трикутників маємо BO = CO. ∆ABO = ∆ACO (за двома сторонами і кутом між ними: AB = AC - за умовою, BO = CO за доведенням, ∠ABO = ∠ACO). Із рівності цих трикутників маємо ∠BAO = ∠CAO, отже, AO бісектриса



20.
= ∆ADC (за першою
AB = AD за умовою, ∠BAC = ∠CAD за умовою, AC спільна сторона).
рівності цих трикутників
BC = CD. Отже, ∆BCD рівнобедрений.

21.

22.

23.
ΔKLM – рівнобедрений, KL = LM, тоді ∠K = ∠M. ΔK1L1M1 - рівнобедрений K1L1 = L1M1, тоді ∠K1 = ∠M1.
Оскільки ∠K = ∠K1, то ∠M = ∠M1. Отже, ΔKLM = ΔK1L1M1 за другою ознакою рівності трикутників.
Нехай у рівнобедреного ΔMNL MN = NL, ML = 3x см, тоді MN = NL = 4x.
За умовою задачі маємо 3x + 4x + 4x = 88; 11x = 88; x = 8.
Отже, ML = 3 × 8 = 24 (см), MN = NL = 4 × 8 = 32 (см).
Відповідь: 24 см, 32 см, 32 см.
ΔABC - рівнобедрений, AC = CB, тоді ∠CAB = ∠CBA.
ΔABD - рівнобедрений, AD = DB, тоді ∠DAB = ∠DBA.
∠CAD = ∠CAB + ∠DAB, ∠CBD = ∠CBA + ∠DBA, ∠CAD = ∠CBD. ΔACD = ΔBCD за першою ознакою трикутників (AC = CB, AD = DB - за умовою, ∠CAD = ∠CBD).
До §30
1) Відрізок, що сполучає вершину із серединою протилежної сторони, називається медіаною трикутника.
2) Перпендикуляр, проведений з його вершини до прямої, що є протилежною стороною, називається висотою трикутника.
3) Відрізок бісектриси кута трикутника,


https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html

26.
∠NMK = ∠NKL - як кути при
∠MNK = ∠LNK - оскільки NK є бісектрисою, проведеною до основи.
∠NKM = ∠NKL = 90°, оскільки NK є висотою.
NM = NL - як сторони рівнобедреного трикутника.
MK = KL - оскільки NK - медіана рівнобедреного трикутника.


28.

29.


Нехай ΔABC = ΔA1B1C1, AM - медіана ΔABC (CM = MB),
A1M1 - медіана ΔA1B1C1 (C1M1 = M1B1).
Розглянемо ΔABM і ΔA1B1M1: AB = A1B1 - як відповідні сторони рівних трикутників, ∠B = ∠B1як відповідні кути рівних трикутників. MB = M1B1 - як половини рівних сторін. Отже, ΔABM = ΔA1B1M1 за першою ознакою рівності трикутників.
Оскільки ΔABC - рівнобедрений, то AB = BC. Оскільки BD – висота, то BD є бісектрисою, отже, ∠ABD = ∠CBD. ΔABO = ΔCBO за першою ознакою рівності трикутників (AB = BC, BO – спільна, ∠ABO = ∠CBO). Із рівності цих трикутників випливає, що AO = CO.
Оскільки ∠ABD = ∠ADB, то ΔABD - рівнобедрений згідно з ознакою рівнобедреного трикутника, тоді AB = AD.
Оскільки ∠DBC = ∠CDB, то ΔBCD - рівнобедрений згідно з
ознакою рівнобедреного трикутника, тоді CB = CD. ΔABC = ΔADC за двома сторонами і кутом між ними (AB = AD, BC = DC - за доведенням, ∠B = ∠D - як сума рівних кутів).
Із рівності цих трикутників маємо ∠BCA = ∠DCA. Оскільки пряма AC містить бісектрису кута C рівнобедреного трикутника BCD, то пряма AC містить висоту ΔBCD. Отже, AC⊥BD.
ΔAMK = ΔBMK (за першою ознакою рівності трикутників: AM = BMза умовою, MK - спільна сторона, ∠BMK = ∠AMK = 90° - за умовою).
Отже, BK = AK.
PΔABC = AB + BC + AC = AB + BK + KC + AC = AB + AK + KC + AC = a + PΔAMK = a + b.
AC = PΔABC = (AB + BC) = a + b − (2a) = a − b.
Відповідь: a − b; a + b.
https://shkola.in.ua/3099-hdz-matematyka-7-klas-ister.html

ΔABC = ΔCDA за третьою
оскільки AB = CD, BC = AD - за умовою, AC - спільна сторона.
31. Оскільки у рівностороннього трикутника усі сторони рівні, три сторони
трикутника дорівнюють трьом сторонам другого трикутника. Отже, ці рівносторонні трикутники рівні за третьою ознакою рівності трикутників.
32.

Нехай у трикутників △ABC і △A1B1C1: AB = A1B1, AC = A1C1, BM = B1M1, де BM і B1M1 - медіани.
Доведемо, що △ABC = △A1B1C1.
ΔABM = ΔA1B1M1 - за трьома сторонами, оскільки AB = A1B1 - за умовою, BM = B1M1 - за умовою, AM = A1M1 - як половини рівних сторін. Із рівності трикутників маємо ∠A = ∠A1. Тоді △ABC = △A1B1C1 - за першою ознакою рівності трикутників, оскільки AB = A1B1 - за умовою, AC = A1C1 - за умовою, ∠A = ∠A1 - за доведенням.

