A mathematical approach to settling

COMING TO AN AGREEMENT: A MATHEMATICAL APPROACH TO SETTLING DISPUTES

BERNARD O‘BRIEN

INTRODUCTION

Since the early 1960s there has emerged amongst both academic lawyers and economists an ever-growing interest in the study of law and economics. This has now become such an amorphous and diverse field of academic interest that there are encyclopedias on law and economics. It has also become an intellectual discipline in its own right. So much so that it has readily spread across that great divide between the common law and the civil law traditions. Whilst much of the scholarship in this area is essentially of theoretical interest only with no immediately foreseeable practical applications there are some areas where that is not quite true. One of those areas is what I would call “Settlement Theory”. This is a formal theory about the way litigants and their legal advisers settle disputes.

What is sought to be developed in this endeavour is what is called a formal system. A formal system is a system of logic built on axioms or assumptions from which theorems or conclusions are derived by the application of a rigorous process of reasoning. Whilst this can be very mathematical, it doesn’t always need to be and in fact there are some outstanding examples which are devoid altogether of both numbers and mathematical symbols. A famous example of which is Ronald Coase’s article on “The Problem of Social Cost”. For this work and others he was awarded the Nobel Prize in 1991. That article contains no equations at all but makes copious reference to some 19th century English cases in actions in nuisance. From that article is derived the now famous Coase Theorem, one formulation of which states: and there are sufficiently low transaction costs, bargaining will lead to a Pareto efficient outcome regardless of the initial allocation of property”

Essentially the same methodology is adopted when analysing how the parties to a dispute would arrive at a settlement. In the first instance the analysis shows that there is what is called the basic model. Whilst this model represents a very good place to start, however, its effectiveness in terms of modelling the real world is limited by the assumptions upon which it relies. Initially the model proceeds as an application of Decision Theory but it quickly becomes an analysis in Games Theory.

Settlements in both criminal and civil matters are so pervasive that if a matter goes to trial that is seen as a failure. Why did the settlement process fail to resolve the dispute? That is a question which would be posed by those responsible for the administration of the court caseload, it is not the first question a practitioner would ask. A practitioner would ask what can this analysis tell me about how I can get the best result for my client? This paper will look at this area of study principally from that point of view. In doing so I will put to one side settlements in crime and personal injuries and focus exclusively on commercial litigation.

THE BASIC MODEL

As we all know the overwhelming majority of cases settle before a trial is concluded. The question is how is the decision to settle arrived at? There is a branch of mathematics which is formally known as decision theory which analyses decisions which involve risk. The mathematics involved in decision theory is quite simple and straight-forward. It can best be explained by taking, as an example, a simple piece of litigation. P sues D for breach of contract and is seeking $100,000 in damages. We will assume that from the commencement of the action to judgment solicitor/client costs will be $40,000 and taxed costs will be $30,000. We will also assume, again for the sake of simplicity, that solicitor/client costs and taxed costs will be the same for both P and D.

It is far from certain that P will win, however we can derive an estimate of P’s chances of success. Let us assume that P’s chances of success are 60%, we can now analyse the nature of the decision which P faces by the use of the following diagram.

FIGURE 1:

If P wins, he will get $100,000 in damages, he will have paid $40,000 in solicitor/client costs and will be paid in taxed costs $30,000. That information is set out at the top diagram. Therefore, if he wins, he will be paid a total of $90,000 and he has a 60% chance of that happening which is therefore 0.6 x 90,000 = 54,000. If he loses, he will have paid $40,000 and will have to pay a further $30,000 in taxed costs, which gives a total of $70,000, which has a 40% probability of occurring, thus 0.4 x -70,000 = -28,000.

The expected value of the litigation to P is the sum of those two products namely $54,000 +(-28,000) = 26,000. If we now undertake the same analysis in relation to D then we obtain the following diagram:

FIGURE 2:

Undertaking exactly the same approach for D, as we did in respect of P, results in a very different outcome. Instead of it being an expected value for D of $-26,000, we have an expected value for D of -$106,000. Whilst the use of actual numbers is useful it is more revealing to examine the problem algebraically. Let: Vp be the expected value of the litigation to P; Vd be the expected value of the litigation to D; J be the judgment sum (in the example $100,000); S be solicitor/client costs (e.g. $40,000); C be the taxed costs (e.g. $30,000); p is the probability of P winning; and (1 – p) is the probability of D winning. The expected value of the litigation to P is: Ep = p(J + C - S) + [(1 – p)( - C - S)] Ep = pJ + pC – pS - C – S + pC + pS Ep = pJ + 2pC – C – S = $26,000

Equation 1

The expected value of the litigation to D is: Ed = p(- J - C - S) + [(1 – p)(C - S)] Ed = - pJ - pC – pS + C – S - pC + pS Ed = C – S – pJ – 2pC = - $106,000

Equation 2

If we add both Equations 1 and 2 together in order to arrive at the joint expected value of the litigation then that net amount is -2S, namely double the parties’ individual solicitor/client costs. Ed + Ep = -2S

And

Equation 3

(Ed + S) + (Ep +S) = 0

Equation 4

Thus, from the collective perspective of the parties, the litigation is a negative sum game with the only winners being the lawyers. Obviously once litigation is viewed in this light the most sensible course for the parties to take is to resolve the dispute and bring the litigation to an end. For the purposes of this analysis I will assume that both parties are risk neutral, that is they are neither gamblers nor unusually timid little souls. Whilst they are prepared to take a risk, they will only take risks when sensible and prudent.

Equations 1 and 2 set out the expected value of the litigation to P and D respectively. That is to say that if the matter goes to trial then P has an expectation which is valued at $26,000 and similarly D has an expectation of being out of pocket to the tune of $106,000. Thus, if D was offered a settlement by paying any amount greater than $106,000 then he would refuse, assuming that he was both rational and risk neutral. Similarly, P would refuse any offer which was less than $26,000 for the same reason. In each case the offer would fall short of the respective parties’ expected value of the litigation. Therefore, if this matter is going to settle the settlement offers will have to come within the difference between the expected value of the litigation to both P and D. In other words, the only settlement offers which will resolve the dispute are those that come within the -2S range or in the case of this illustration $80,000, that is from $26,000 to $106,000. This range is sometimes called the Settlement Range and sometimes called the Surplus. For the purposes of this paper I will adopt the term Surplus. In short, any offer greater than D paying P $26,000 and not more than D paying P $106,000 is better for both parties than if they went to trial. If they were to settle for say $66,000 then P gives up a claim worth $26,000 and gets an additional $40,000. Whereas D escapes a potential liability of $106,000 and incurs a cost of $66,000, thus, in theory, saving $40,000. Note that that $40,000 each is the equivalent of the saving which each party makes by settling and therefore not having to pay their respective lawyers. An “all in” settlement of $66,000 satisfies Equation 4 above. Indeed, it is the only amount which will satisfy Equation 4.

One may well object to the fact that this dual saving of $40,000 each is somewhat illusory in that it rests entirely on a speculative scenario as to what would happen if the matter did not settle and instead went to trial. The expected value of the litigation if it went to trial is necessarily hypothetical. Obviously if P is offered $26,001 in settlement, she would not be persuaded that by accepting such an offer she would be better off by a dollar than if she were to go to trial. Similarly, an offer of $105,999 made to D would not persuade him that this constituted an improvement in his position. However, the midpoint between these two expected values will ordinarily maximise the likelihood that both parties are better off by settling at that midpoint than if they went to trial.

STRATEGIES IN HOW TO DIVIDE THE SURPLUS

The Surplus could in theory be divided in a variety of different ways. However, there is a certain intuitive appeal in simply splitting it down the middle, it is certainly the most equitable division, but it is ultimately a matter of negotiations between the parties and there is no guarantee that the concepts of fairness will drive those negotiations. One would have thought that the parties’ respective attitudes to risk would potentially play a critical role. Thus, if one party was risk averse and the other was either a risk taker or was risk neutral then that would shift the point of division in favour of the latter. In addition to attitudes to risk there is also the assessment of risk. Up to now I have assumed that the parties agree on the measurement of risk, namely that P has a 60% chance of success and conversely D’s prospects of success are 40%. If the parties disagreed on the extent of the risk which each were exposed to then that would add another dimension to the difficulty in arriving at a compromise.

In Table 1 below I have set out the variation in what is a fair settlement given different assessments of the risk:

TABLE 1:

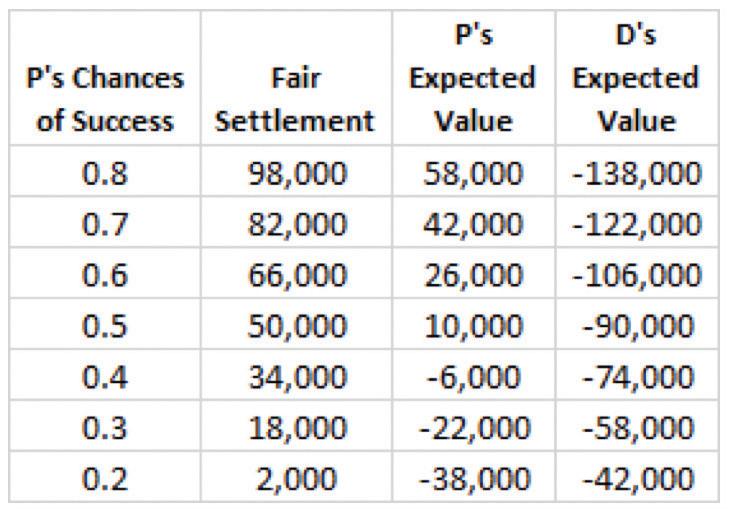
Thus, if P put her chances at 70% a fair settlement to her would be $82,000, whereas if D’s estimate of P’s chances of success was say 50% then he would assess a fair settlement at $50,000. This of course assumes that both parties are not only fair but are also risk neutral. If, however, they are both risk takers and also refuse to be fair, that is refuse to split the Surplus down the middle, then if they were also both optimistic about their chances of success they would end up “hopelessly apart”. Thus, ideally for a matter to settle both parties have to be realistic, risk neutral and fair, unless of course optimism is matched by pessimism, risk taking is matched by risk aversion and feelings of over-entitlement are matched by feelings of being undeserving. We could describe this combination as a hawk-dove confrontation in which the hawk will always be significantly better off than the dove and, as a consequence, every litigator will be a hawk and hence the game will be transformed into a hawk against hawk contest in which relatively few matters will settle. For that reason, a perpetuation of hawk against hawk contests would not be sustainable. Of course, if one’s opponent is a dove then it would obviously profit the other party to play the role of a hawk. However, assuming both parties are represented by experienced litigators one would not expect that there would be that many hawk-dove contests. A hawk against hawk contest is the best combination if one wants to prolong the dispute and maximise the costs arising out of it. A hawk against hawk contest takes a bad situation and only makes it worse.

It needs to be remembered that litigation is a negative sum game. Given that it is a negative sum game the best one can do, all else being equal, is to get out of it sooner rather than later. Consequently, a hawk is not an ideal litigator any more than is a dove. The obvious choice is therefore something in between in which the parties search for common ground. I will call this the owl strategy. The owl begins by first determining what is at stake, namely undertakes an assessment of damages and costs and the respective parties’ chances of success. In order to undertake those evaluations both the lawyers and the parties need to familiarise themselves with the case which usually takes time and money. In addition, usually the parties have to move on from a relentless desire to see justice being done to a more pragmatic appreciation of the costs and the risks which litigation invariably entail. In short, the parties will typically need to arrive at least at a point of indifference between wanting the case to go on and wanting the case to settle. All of which takes both time and money. If, having arrived at that point of indifference, the parties share a common assessment of costs, damages and their respective chances of success then the matter ought to be ripe for settlement. The most likely point of settlement is the one that is perceived by both parties as being fair, namely one which splits the Surplus down the middle. A settlement which both parties, with some equanimity, can walk away from. The “all in figure” is therefore arrived at by simply adding S to both P and D’s expected value of the litigation and if one adds those two sums together one arrives at zero, which is Equation 4.

Thus, what began as a negative sum game becomes a zero sum game and by moving from a negative sum game to a zero sum game both parties are better off. Such an outcome is fine if both parties will, in the end, want to cooperate and settle upon an objectively fair division. However, what if one of the parties had no interest in being fair and all that he wanted was to take as large a share of the Surplus as he can get. How would he do that? One possibility is that he could play the role of the proposer in what is called the Ultimatum Game.

In an ultimatum game there are two players, a proposer and a responder. The proposer is given, for want of a better word, an endowment of some description. Let us say $100. The proposer must share the endowment with the responder however the proposer gets to determine the allocation of the shares. So, for example, the proposer may offer $1 to the responder and retain $99 for himself, or he may offer to split the pie with the responder evenly, a 50:50 split or somewhere in between. However, that is not the end of the matter, before any division of the endowment can take place the responder must accept the proposer’s offer. If she rejects the offer then neither party gets anything. There is no opportunity for the responder to reject the proposed offer and to come back with a counter-offer. Likewise, the proposer cannot put a second offer if the first is rejected. Either the responder accepts the offer and goes away with something in her pocket or rejects the offer and both parties walk away empty handed. It is a take it or leave it situation.

This game has been studied in an experimental setting, typically employing university students as subjects, around the world for decades. A meta-analysis of the published literature shows that typically the proposer offers on average a 60:40 split in favour of the proposer and around 16% of offers are rejected.

Obviously such an outcome does not sit comfortably with the assumption of homo economicus namely that in their economic dealings with others people are essentially rational self-maximisers of their utilities. That is a fundamental axiom of neo-classical economics. However, all is not lost. When the proposer was given $100, he was actually given that sum of money and it was to be shared between himself and the responder, as per an agreed split. Otherwise it was forfeited if there was no agreed split. Carrying out this experiment using university students in advanced industrial economies imposed a practical limit on the size of the endowment. If the amount of the endowment was not $100 but rather $1million would an offer of a 1% share (i.e. $10,000) be so readily rejected? Given the limits on the availability of research funds it was decided to conduct the experiments using villagers drawn from 8 rural villages in India where the endowments ranged from 20 rupees to 20,000 rupees (1.6 hours of work to 1,600 hours of work).

Thus there was a sufficient variation in the size of the pie in order to see what impact its size had on the rejection rate.