Family Law Case Notes

As the size of the stake increased there was an exponential decay in the rejection rate. It went from 40% when the size of the pie was around the equivalent of one hour of work to zero when the amount involved reached the equivalent of 100 hours of work.

Hence when the stakes are low there is a lot of enthusiasm for fairness and cooperation, however as the stakes increase naked self-interest becomes the horse to beat.

In litigation, so far as the parties are concerned, the stakes are nearly always very high. However, as is superficially obvious, negotiations to resolve a litigious dispute is not an ultimatum game. The parties are not assigned roles, such as proposer and responder, and negotiations are not confined to a single round which concludes with a take it or leave it offer. Nonetheless, one or both the parties can attempt to turn negotiations into an ultimatum game. A party who plays the role of a hawk would: • Always plays hard ball, • at every opportunity treat the other side’s case with contempt, • issue orders as to the procedural steps which the other party must take, as if he was a Master of the Court, • never miss an opportunity to be bloody-minded, and unpredictable.

If the other side is a dove then the hawk, by doing the above, is able to define the nature of the game and to assume the role of the proposer. When the hawk makes a proposal, he states emphatically that this is his client’s first and only offer and thus he attempts to define the negotiations as an ultimatum game in which he, without as it were a "by your leave", has assumed the role of the proposer and conversely this leaves the dove as a responder in a high stakes ultimatum game. If the offer is significantly better than that party’s expected value of the litigation, even though the offer gives the lion’s share of the Surplus to the hawk, the dove will, if persuaded that this is an ultimatum game, feel that she has no choice but to take the offer. However, once one realises that this is not an ultimatum game and there is no reason why any offer made by either party will be final, there is therefore no reason why the hawk would not come back with a better offer if the first offer was rejected, so long as any subsequent offer left the hawk better off than if he went to trial.

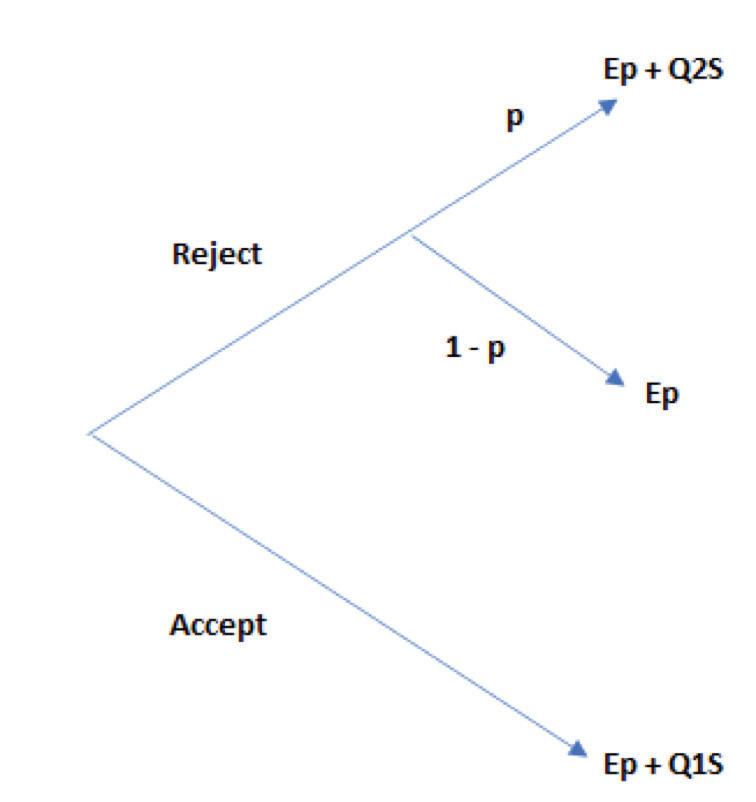
Let us suppose in the first round of negotiations D offers as an “all in” settlement Ep + Q1S where Q1is equal to 0.2. In other words, he offers an 80:20 split in his favour. It is an offer which is not so small that it can be dismissed with contempt and if P is a dove then P would be under a lot pressure to accept, even though it is palpably an unfair offer.

FIGURE 3:

Figure 3 sets out P’s options. She can either accept the offer the value of which is Ep + Q1S or reject the offer in the hope or expectation that a better offer is sitting in the wings, namely p(Ep + Q2S) + Ep(1 – p), p is the probability that a further offer will be made and Q2 is P’s proposed share of the Surplus. Thus, P’s point of indifference (i.e. the point where P’s expected value of acceptance is equal to P’s expected value of rejection) is: p(Ep + Q2S) + Ep(1 – p) = Ep + Q1S

or

pEp + pQ2S + Ep – pEp = Ep + Q1S

Equation 5

From the above it follows that p = Q1/Q2 at the point of indifference. Thus if P, for example, is hoping that D will come back with an offer of a 50:50 split then if P estimates that the probability of D making such an offer is 40% or less then the expected value of rejecting D’s original offer is no better than the actual value of accepting that offer. In which case, it may be thought, that P should accept the original offer unless P is a risk-taker or wants to stand on her pride. Nevertheless, there is more to the analysis than just that. As one can see D’s offer puts P in something of a pickle, however if P rejects D’s original offer and makes a counter-offer of a 50:50 split that would put him in a pickle as well. He is now the one facing a take it or leave it offer. The position which P presents to D is that either he accepts P’s offer or they will see each other in court. D is thus faced with four choices: • Insist on an 80:20 split and if necessary, go to trial, • Make a further offer of a 70:30 split, • Make a further offer of a 60:40 split, or • Accept a 50:50 split.

Of those four choices in reality there are only two that feasible. If D proposes either a 70:30 split or a 60:40 split he is signaling to P that his previous take it or leave it was just a bluff and that would only encourage P to hold out for a 50:50 split. Therefore, D’s choices in reality are either to accept P’s offer or to insist on an 80:20 split. In fact, D’s decision-tree will look essentially the same as was P’s in Figure 3. See Figure 4 below:

FIGURE 4:

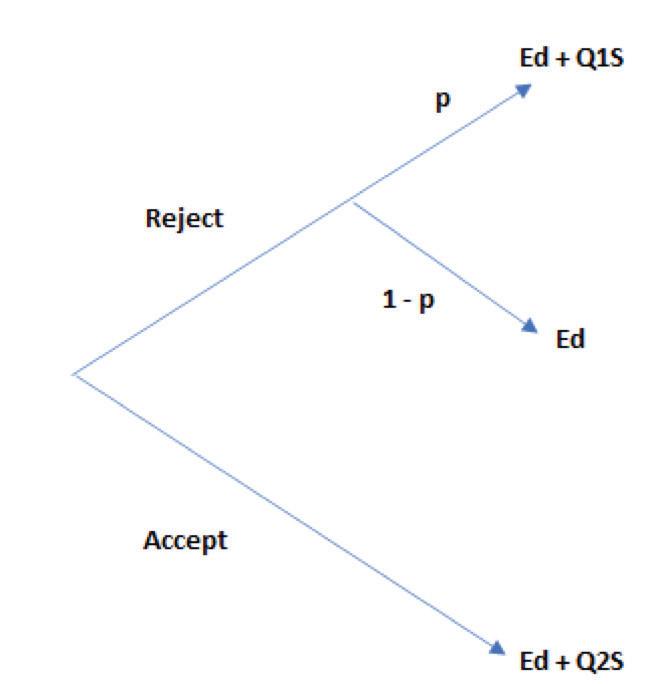
At D’s point of indifference, the following equation holds: p(Ed + Q1S) + Ed(1 – p) = Ed + Q2S

Equation 6

From which it follows that p = Q2/ Q1. It will be recalled that Q2 equals 50% and Q1 equals 80% therefore p = 0.625.