

This book belongs to
LEVEL D
Lighthouse Math
Program Directors
Mrs. Zehava Kraitenberg M.S. Curriculum Advisor Elementary School Principal
Jane Chamberlain Master of Education Curriculum and Instruction
CURRICULUM
Credits
Curriculum Writers
Jane Chamberlain Middle School Math Instructor
M.Ed. in Curriculum and Instruction
Susannah Maria Malarkey 4th Grade Instructor
M.A. in Teaching K-8
Karen Williams
5th Grade Teacher
Affiliate Faculty
Ed.D. - Curriculum and Instruction
Karen Legreid Math Interventionist K-5
M.A. in Curriculum and Instruction
Mizuho Shiomi
3rd Grade Instructor
M.A. of Arts in Education K-8
Review Team
Zehava Kraitenberg M.S. Curriculum Advisor
Elementary School Principal
Jane Chamberlain
Middle School Math Instructor
M.Ed in Curriculum and Instruction
Layout & Design
Akiva Leitner Project Manager Kevanyc.com
Joy Aragones
4th Grade Instructor
M.A. in Education Technology
Chelsea Ruocco
6th Grade Instructor
M.A. in Childhood Education 1-6
Kelly Boehme
1st Grade Instructor
M.Ed. in Elementary Education K-6
Jennifer Ramos-Martinez Curriculum Specialist
M.A. in Curriculum and Instruction
Rebecca Kay-Lewis
5th Grade Instructor
M.Ed. in Elementary Education K-6, 5-8 Math
Sarah Thorman 2nd/3rd Grade Instructor
B.S. Liberal Arts and Sciences (Psychology) Post-Baccalaureate Teacher Certification (Grades K-6)
Kelly Christensen 6th-7th Grade Math Teacher
M. Ed in Administration and Leadership (K-12)
Lydia Masao 4th Grade Math Instructor
M. Sc. in Child Development and Education
M. Ed. In Elementary Education, pre K-6
Allison Paul Education Consultant Middle School Math Instructor
M.Ed. in Secondary Mathematics & Educational Leadership
Michele Grega
Data and Assessment Coach
M.Ed in Elementary Education K-6
M.Ed. in Curriculum and Instruction
M.Ed. in Administration and Leadership (K-12)
Glory Sterling High School English Teacher
M.Ed. in Curriculum and Instruction
Rebekah Jorgensen Middle/High School Math Teacher
M. Ed. Learning & Technology
Esther Aboud
Curriculum Consultant
M.Ed. in Special Education
Fraydel Sharf Content Director and Editor
Miriam Shulamis Eisemann Content Editor
Luke Bote K-12 Instructor
M.Ed. in Leadership
Mirko Zunic/Chris Dunn Layout Directors
©Copyright 2021 Lighthouse Curriculum Inc. All rights reserved.
Molly Fernholz K-6 Instructor B.A. in Education
Francine S. Foote 5th and 6th Grade Instructor
M.A. in Instruction and Curriculum
Yehuda Gartenhaus M.A. Elementary School Principal
Mechel Weizer Curriculum Advisor Elementary School Principal
Issac Flores Illustration Director
Distributed by Leren Curriculum Inc. T: 718-834-1231 E: lerenec@gmail.com
Lighthouse Math level D • ISBN 978-1-955773-03-4
No part of this publication may be reproduced, stored in a retrieval system, stored in a database and/or published in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, without the prior written permission of the publisher. To obtain permission to use portions of material from this publication, please contact Lighthouse Curriculum.
Content developed in collaboration with The Reimagined Classroom
Contact Lighthouse Curriculum: By calling: 718.285.7100, or emailing: info@lighthousecurriculum.com For more information visit www.lighthousecurriculum.com

Introduction and overview of skills at the beginning of each chapter
Color coded pages - easy to find tabs at the top and bottom of the Lesson Page and Exercise Page
Daily review at the beginning of every lesson to provide review of previous skills
Vocabulary at the bottom of the page with important terms and definitions
Learn and Connect introduces the lesson with real life situations, illustrations and helpful hints
Apply provides problems for the teacher and the students to practice together
Practice is a full page of exercises for students to practice the skills and concepts they have learned
Tabs on the top of each page allow you to find chapters and lessons easily
Call outs and Hints help remind students of important steps and give them clues
Clear, worked out examples
Challenge problem solving or challenges to extend and enrich student learning
Review for every chapter
Assessment provided for every chapter
Hi, my name is Flash!
to the Lighthouse Math Curriculum!
is a list of items that will help as you navigate through the book!

A better way to teach
Dear Educator,
Welcome to the Lighthouse Math Curriculum!
What makes our curriculum so unique? Lighthouse Math uses a scaffolded approach to learning and mastering math skills. When provided with a solid foundation, students can retain more information and prepare for the next level of skills.
Instead of separate workbooks and textbooks, students have everything they need built into one place: a soft covered book containing 14 chapters, comprised of 8 lessons per chapter, with each lesson containing review, new skills, and practice. All lessons include step by step instructions for clarity, giving all teachersneophyte as well as seasoned - the tools for success.
The books are custom illustrated, providing a vibrant learning experience. They are formatted in a way that each grade level can be completed successfully by the culmination of the school year. Lighthouse Math gives teachers the tools they need to teach and gives students everything they need to learn.
We, at Lighthouse CurriculumTM, are committed to providing support and guidance to our educators. We look forward to hearing from you and are available to answer any questions you may have.
Sincerely,
Lighthouse Curriculum Team
Lighthouse Curriculum. Copying strictly prohibited.
Chapter 2-7 Word Problems
A box has a total of 100 buttons. Six of them are black. If a tailor can use any button color except black, how many buttons are there that could be used?
The letter b stands for the number of buttons that can be used. Which equation could be used to solve the problem?
100 − 6 = b 100 + 6 = b
The number of usable buttons is less than the number of total buttons in the box, so is correct.

Circle the correct equation that matches the story problem and solve. Explain your answer using pictures and/or numbers.
75 − 62 = c 1.
There are 62 cups in a restaurant cupboard. If the restaurant is full, it can seat 75 people. How many more cups does the restaurant need if every seat is full?
75 + 62 = c
An unfinished block tower is 35 inches tall. One more block is placed on top. The new block is 5 inches tall. How tall is the tower? 35 + 5 = t 35 − 5 = t 2.
56,000 − 5,978 = g 3.
A truck is carrying 56,000 pounds of goods. At its first stop, 5,978 pounds of goods are unloaded. How much is on the truck now?
56,000 + 5,978 = g
Lighthouse Math
Chapter 7 Fraction Concepts
Chapter 10 Geometry
Chapter 11 Measurement
Chapter 12 Measurement and Geometry
Chapter 13 Data
Review 1
In Review 1, we will review
Addition, Subtraction, Multiplication, Division
Students will review number sense skills related to the four operations and practice facts to gain fluency.
• Round and estimate
• Relate addition and subtraction
• Addition and subtraction with regrouping
• Represent and solve multiplication and division facts
• Relate multiplication and division
We can round numbers to estimate sums and differences.
We can use properties of operations to find missing addends or factors.
We can add and subtract using regrouping. We can use multiple strategies to multiply and divide.
Learn and Connect
Let’s review rounding!
Step 1: Underline the place value you want to round.
Step 2: Circle the number to the right.
Step 3: If the circled number is 4 or less, round down. If the circled number is 5 or more, round up.
Let’s practice rounding 119 to the nearest tens. What we are trying to figure out is if 119 is closer to 110 or 120. Fill in the missing numbers on the number line. Make a point on 119.
Let’s use the steps above to check our answer.
1) Find the rounding place value and underline it. 1 1 9
2) Circle the number to the right.
3) If the circled number is 4 or less, round down. If the circled number is 5 or more, round up. The circled number is 5 or more, so we round up 120.
119 is closer to 120. 119 rounded to the nearest ten is .
Fill in the numbers on the number line and mark the target number with an x. Then, check your answer.
Round each number. Complete the number line with the two benchmark numbers and the target number.
282 to the nearest ten:
456 to the nearest hundred:
Estimate. Round each number to same place value. Solve.
The first bus had 85 passengers. The second bus had 273 passengers. About how many passengers were there altogether?
Use the table to solve.
On a hot sunny day, the ice cream parlor sold 123 scoops of vanilla and 372 of chocolate ice cream. About how many scoops of ice cream did they sell in all?
Michael is traveling from New York to Anchorage. He wants to decide if he should fly direct there or if he should stop in Seattle. About how long would each trip be?
Let's estimate each trip to the highest place value.
About how long is the direct trip from New York to Anchorage? miles
About how long is it from New York to Seattle? miles
About how long is it from Seattle to Anchorage? miles
About how long is the combined trip? miles
Which trip is shorter?
Estimate each number to the highest place value and solve.
6. 2,793 people went to the carnival on Monday, and 4,251 people went to the carnival on Tuesday. About how many people went all together?
7. One grain silo can hold 6,489 pounds of grain, and a smaller grain silo can hold 3,219 pounds of grain. About how many pounds can they hold altogether?
Review 1-2 Addition and Subtraction Properties, Missing Addends
Daily Review Add or subtract to solve.
Learn and Connect
Addition Properties
Commutative Property
You can add in any order.
5 + 7 = 12 7 + 5 = 12
Associative Property
You can group any two addends, but add the numbers in parentheses first.
(3 + 2) + 4 = 9
3 + (2 + 4) = 9
Zero Property
Adding zero does not change the value.
0 + 8 = 8 7 + 0 = 7
Subtraction
Properties
Subtraction Property of Equality
Subtracting the number from itself always equals zero. 8 − 8 = 0 3 − 3 = 0
Inverse Operation
Addition and subtraction are related, and we can find a subtraction answer by adding digits. 9 − 3 = 6 5 − 2 = 3 6 + 3 = 9 3 + 2 = 5
Zero Property
Subtracting zero does not change the value.
2 − 0 = 2 4 − 0 = 4

Paul is saving to buy a new skateboard. He currently has $8, and they are on sale for $15. How much more does Paul need to save to buy the skateboard?
Remember that addends are the numbers being added in an addition problem. We can use a letter, such as n, or an empty square to show the missing addend: 8 + n = 15 or 8 + = 15. How can we find the missing addend? Which property listed above can help us? Inverse operation.
Apply
Identify the property used in each example.
15 − 8 = , the missing addend in the first equation is 7. Paul needs to save $7 more to buy the skateboard. 8 + 3 = 11 11 − 3 = 8 (4 + 1) + 5 = 10 4 + (1 + 5) = 10 6 − 6 = 0
Vocabulary
Property - pattern (or rule) in addition and subtraction that is helpful in quickly answering problems
Addend - a value that is added with another value in an addition problem
Identify the property used in each example.
Write the subtraction problem that solves for the missing addend, n.
Solve for the missing addend, n.
Solve for the missing addend or sum.
Write the number sentences used to solve each problem and identify the properties used to check your answers. Challenge
21. Henry wanted to bring cupcakes to his class. There are 17 students and 1 teacher. If he had 9 cupcakes packed, how many more does he need to bring to have a cupcake for everyone?
22. Eric went fishing with his father in the afternoon. He caught 11 fish, and his father caught 13 fish. When they got home, they cleaned 6 fish for dinner. How many more fish still need to be cleaned?
Robert was working on his reading goal. He read 75 pages yesterday and 29 pages today. How many more pages did he read yesterday than today?

Solve each addition problem.
+
12. At a sticker store, there were 987 flower stickers and 307 tree stickers. How many stickers were in the store?
13. Each of Farmer Ben’s 1,638 lambs are either black or white. There are 67 white ones. How many of Farmer Ben’s lambs are black?
Review 1-4 Multi-Digit Addition and Subtraction,
Daily Review Solve for the missing value, n.
Learn and Connect
Never get a subtraction problem wrong again!
Use your addition skills to help you check your subtraction (especially when the problems are tricky)!

Solve each subtraction problem and check your answer by using addition.
Solve each subtraction problem and check your answer by using addition.
Solve each problem. Draw a line to the matching inverse operation.
529 + 259 = 745 + 639 = 527 + 957 =
259 + 380 = 547 + 612 = 744 + 612 = 1,384 − 639 = 639 − 259 = 788 − 259 = 1,484 − 527 = 1,356 − 612 = 1,159 − 547 =
Solve each word problem.
7. An airplane traveled 456 miles one way to its destination. How many total miles will it travel once it returns back home?
9. So far, an orchard has sold a combined total of 948 pounds of fresh and frozen fruit this season. If they sold 567 pounds of frozen fruit, how many pounds of fresh fruit has been sold so far?
8. Mr. Levine’s car broke down. He used $785 from his savings to repair it. After that, he had $850 left in his savings account. How much money did Mr. Levine have saved before his car broke down?
10. There were 343 people who visited an amusement park before 9am. A second group of 480 people visited the park around noon. Another group of 855 people came to the park around 3 o’clock. How many people visited the park altogether?
Challenge
11. Jonah read 56 pages yesterday and 145 pages today. If his book has 700 pages, how many more pages does he have to read to finish the book?
Daily Review Solve these addition problems.
Learn and Connect
David is planting a garden with his family. He gets to plant his own small part of the garden and chooses to plant carrots. If David plants three rows of five carrots each, how many carrots will he plant altogether?
Let’s review our multiplication strategies:
Multiplication Strategies
Equal groups
Repeated addition
5 + 5 + 5 = 15
Count all the objects: 15
Add 5 three times Skip counting
5, 10, 15
Count
Apply
Take hops of 5 three times
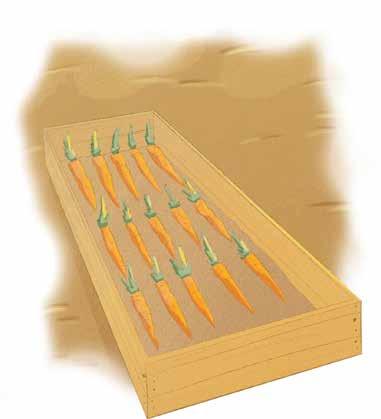
Write the number sentence that represents each problem.
Vocabulary
Factor - any one or two numbers multiplied together to give a product
Product - the answer to a multiplication problem
Write the number sentence that represents each problem.
Solve the equations by writing the missing factor or product.
Draw an array, then solve.
Draw an array that represents 4 � 9 and solve.
Solve the problem.
Draw an array that represents 3 � 4 and solve.
Draw an array that represents 8 � 3 and solve.
A clothing store can hang 5 winter coats on each rack. The store has 15 coats for sale. How many racks should the store use? Show two different ways to solve.
John bought 4 boxes of donuts. How many donuts were in each box if there were 20 donuts in all? Write the equation and solve.
16. 19. 20. 17. 18.
Review 1-6 Multiplication Fact Review
Daily Review
Write the first five multiples of each number.
Learn and Connect
It is strawberry season, and the Stark family is making strawberry jam. They fill each jar and pack the jars in boxes that hold 4 jars each. If they were able to pack 4 boxes full of jars, how many jars of jam did they make?
First, look at the illustration and write out the multiples of 4: , , ,
The Stark family made jars of jam.
Apply
Complete the table.

Write two different multiplication equations that describe the array.
Fill in each missing number to complete the equations.
Complete each fact triangle and the two multiplication equations represented.
Use the chart to answer the questions.
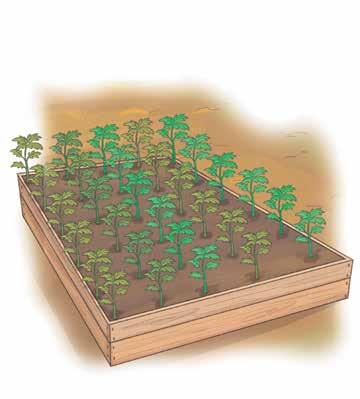
Larry is helping in the community garden. He is working to figure out the total yield for 6 rows of carrots.
How many carrots will 3 rows yield?
What pattern do you notice in this table?
Complete the rest of the table.
How many carrots will 6 rows yield?
Review 1-7 Represent and Solve Division
David’s fourth grade class wants to play tug of war. There are 32 students in his class, and they need to split into 4 equal teams. How many students should be on each team?
How many students are in the class?
How many teams do they need to make?
Divide by to find the amount on each team.
Learn and Connect Apply
Draw a picture to help you solve. Solve for quotient.
Use a related multiplication fact to help you solve!
There are students on each team.
Vocabulary
Dividend - the amount being broken into groups
Divisor - the amount of groups being made
Quotient - the answer to a division problem
Use the dots to help you divide. Divide.
Solve each problem.
24. Larry paid $72.00 for 9 balls for his club. How much did each ball cost?
25. 42 people showed up to play ball. Seven equal teams were made. How many people were on each team?
Review 1-8 Relating Multiplicaton and Division
Caleb was planting flowers in his garden. He planted 7 rows of flowers with the same number of flowers in each row. He planted 35 total flowers. How many flowers did Caleb plant in each row?
Division and multiplication are related!

Caleb planted 5 flowers in each row.
Learn and Connect Apply
Write 2 multiplication equations and 2 division equations for each group of numbers.
1. 3, 9, 27
Complete each fact family.
2. 8, 32, 4
3. 36, 6, 6
Vocabulary Inverse - having an opposite relationship
family - a group of math facts or equations created using the same set of numbers
Solve each multiplication and divison problem.
Complete each fact family.
Review 2
In Review 2, we will review
Word Problems and Fractions
Students will gain fluency in solving word problems and deepen their understanding of fractions. This will prepare them for more advanced problem solving and decimal work in level D.
• Divide with single-digit divisors
• Problem solve
• Find perimeter and area
• Write and model fractions
• Find equivalent fractions
• Compare and order fractions
We can use arrays to show division and multiplication to check our work.
We can solve one-step word problems with all four operations.
We can find the perimeter of any shape and the area of a rectangle.
We can visualize and write fractions.
We can find equivalent fractions with a model and multiplication or division.
We can compare and order fractions using number lines and models.
Learn and Connect
Josh and Noah are packing 48 cookies. Cookies at Hillside Bakery are sold in half dozen quantities. If six cookies fit in a box, how many boxes of cookies will Josh and Noah fill?
How many cookies do they need to pack?
How many cookies go in each box?
Use the picture to solve 48 ÷ 6 =
Josh and Noah will need to pack boxes of cookies.

Josh and Noah can check their answer by multiplying their quotient by the divisor .
Apply
Complete the chart below.
Vocabulary
Quotient - the answer to a division problem
Divisor - a number by which another number is to be divided
Dividend - the number being divided
Draw an array and write the multiplication fact that relates to each division problem.
Divide to solve. Write the related multiplication fact below each division equation.
Solve each problem.
22. Kevin has 48 books he wants to place on six shelves equally. How many can he put on each shelf?
23. Justin paid $63 for 7 sandwiches. Each sandwich cost the same amount. How much did he pay for each sandwich?
24. Mrs. Smith has 54 pencils she wants to distribute equally among 9 students. How many pencils will each student get?
25. Pat has 21 lollipops and wants to put 3 into each party bag for his birthday. How many party bags will he be able to make?
Solve each division problem.
Learn and Connect
Mannie is buying equipment. He sees a skateboard on the shelf and wants to make sure he has enough money to buy it. He currently has $25 worth of equipment. If he buys the skateboard, how much money will he spend altogether?
To solve this problem, use the CUBES strategy below.

Circle the numbers in the problem above.
C Circle the numbers
U Underline the question
B Box the key words
E Eliminate what you don't need
S Does your answer make sense?
Complete the chart below.
Mannie has a $50 bill. He wants to buy $40 worth of equipment. How much money will he have left after he has paid?
Underline the question and write it below:
Box the key words. What operation are you going to use to solve this problem?
Addition Subtraction Multiplication Division
Eliminate what you don’t need and solve your problem.
25 + 15 =
S Does your answer make sense? Does it make sense that the sports equipment that Mannie has would cost $40?
Circle the numbers in the problem.
Underline the question.
Box the key words. What operation are you going to use to solve this problem?
Addition Subtraction Multiplication Division
Eliminate what you don’t need and solve your problem.
S Does your answer make sense?
Solve using the CUBES strategy.
There are 48 students in the fourth grade. If they are divided into teams of 6, how many students will be in each team?
Circle the numbers in the problem.
Underline the question.
Box the key words and write the operation.
Timothy has 127 toy cars, and Eli has 118. How many toy cars do they have combined?
Circle the numbers in the problem.
Underline the question.
Box the key words and write the operation.
Lisa's mom made 148 cookies for a bake sale. If she sold 96 cookies, how many cookies does she have left?
Circle the numbers in the problem.
Underline the question.
Box the key words and write the operation.
Eliminate what you don’t need.
Eliminate what you don’t need.
Eliminate what you don’t need.
Solve. Solve. Solve.
Does your answer make sense?
Solve the following problems.
There are 10 crayons in each box and 9 boxes on the shelf. How many crayons are there on the shelf?
Does your answer make sense?
Does your answer make sense?
Steven has 81 candies to share with his friends. If he wants each of his 9 friends to get the same amount, how many pieces of candy will each one receive?
Nick started the year with a pack of 24 pencils. He has 9 left. How many pencils has he used? Larry has 16 stickers, Leo has 34 stickers, and Sam has 27 stickers. How many stickers do they have altogether?
Solve each division problem.
Learn and Connect
George and his brother, Hank, were looking at old pictures together. They decide to build a 4" x 6" wooden frame to put around a picture of their grandfather. They need a long strip of wood to cut up to make the frame. They can either buy a 15 inch strip of wood or a 25 inch strip. Which one should they buy so they will have enough wood for the frame?
To find the correct length of wood to make a frame, you need to find the perimeter of the picture.
What is the name of this polygon (shape)?
How many sides are on the polygon?
List the lengths of each side.
Add each side of this shape together.
George and Hank will need inches of wood.
So they should buy the wood that is inches long.
Apply
Identify the polygon and find the perimeter.


Polygon
Identify the polygon and find the perimeter.
Polygon Name:
Perimeter:
Polygon Name:
Perimeter:
Solve each problem.
5. 6. Joseph wanted to build a fence around his garden. If his garden is a square with a side of 4 yards, how much fencing will Joseph need?
Polygon Name:
Perimeter:
What would be the length of each side of a regular octagon if the total perimeter is 64 feet?
Polygon Name:
Perimeter:
Larry is putting wood trim around his window. The window is a rectangle that is 7 feet wide and 4 feet high. How much trim will Larry need?
Label the length of the sides on the octagon.
7.
Daily Review
Name the polygon.
Learn and Connect
Marc and Eric were helping their dad put new tiles in their bathroom. Each tile was 1 foot by 1 foot. Use the diagram of the bathroom to find how many tiles are needed in all.
The total space inside an object is called the area. To find the total amount of area in this space, we need to find how many square units are inside the shape.
Bathroom Diagram


The bathroom is feet long. The bathroom is feet wide. There are 3 ways to find the area.
Counting Squares: square feet
Repeated Addition: 8 + 8 + 8 + 8 = or 4 + 4 + 4 + 4 + 4 +4 + 4 + 4 =
Marc and Eric will need square feet of tile for the bathroom.
Apply
Find the area of the shapes below.
Length: 4 units
Width: 4 units
Area Equation (Add):
4 + 4 + 4 + 4 =
Area:
Length: 5 units
Width: 4 units
Area Equation (Add): Area: Length:
Area Equation (Multiply): 6 × 3 =
Multiplication: 8 × = 32 square feet or 4 × = 32 square feet
Find the area of the shapes below.
Draw lines for the length and width. Then find the area of the shapes.
Use the grid below to draw rectangles with the target area. Label the length and width of the rectangles you draw. Area:
Area: 12 sq. units
Length:
Width:
Using the grid, draw two rectangles that have the SAME area, but a DIFFERENT perimeter.
Rectangle 1
Rectangle 1
Area: 20 sq. units
Length:
Width:
Daniel is at the Littleville Model Train Museum. He notices a trains made up of two colors. If Daniel wanted to recreate this exact train at home, what fraction of the train would need to be red?
Fractions represent part of a whole figure.
The train is made of equal parts. We describe the parts using numerators and denominators.
Numerator (part of the whole) Denominator (the number of parts in a whole)
You can write it as a fractional part 1 5 .
You can say it in words as one fifth.
You can create a picture.

Complete the chart to represent each fraction.
Vocabulary
- the part of the whole
- the amount of parts in the whole
Write a fraction to show what part of each figure is blue.
Complete the chart to represent each fraction.
Use this set to answer the questions.
What fraction represents what part of the set are triangles?
What fraction represents what part of the set are circles?
What fraction represents what part of the set are squares?
Daily Review
Find the perimeter and area of the polygons.
Learn and Connect
Anthony was feeding 5 sea lions. He had already fed 2 of the sea lions. What fraction shows how many more sea lions Anthony still needs to feed?
Fractions tell us how many equal parts of a whole we have.
Cross out two of the sea lions because they have been fed. Circle the remaining sea lions. How many sea lions or parts do you have circled?
How many sea lions were in total?
Anthony still has to feed of the sea lions.


We can show this same value with a picture (set), fractions bars, and unit fractions.
Apply
Complete the chart to show the value of each fraction as a set, a part of a whole, and unit fractions.
Write the fraction that is represented in each picture.
Complete the chart to show the value of each fraction as a set, a part of a whole, and unit fractions.
Solve each problem.
8. Jack was cleaning out his toy chest. He noticed that out of his 10 toy cars, 8 were red. What fraction represents this value? Draw a set to represent your fraction.
Challenge
Joshua ate 3 5 of a pumpkin pie, and Tom ate 3 7 of an apple pie.
Who ate more pie?
Use the fraction bars to help find your answer.
Danny and John were helping to put away the equipment after recess. Danny put away 3 7 of the basketballs, John put away the rest. What fraction did John put away?
Can you use another fraction representation to prove your answer?
9. Joshua Tom
7.
4. 5.
6.
Review 2-7 Equivalent Fractions
Daily Review Write the word form of each fraction:
Learn and Connect Apply
We can check to see if fractions are equivalent by multiplying the top and bottom by the same amount or by dividing them by the same amount. Circle all of the fractions that are
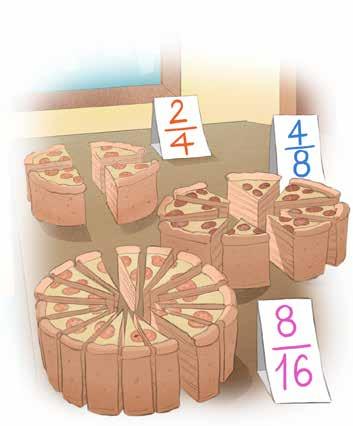
Vocabulary
Equivalent
-
with different numbers above the line (numerators) and below the line (denominators) that equal the same amount
Draw a line to match the equivalent fractions.
Complete the equivalent fractions.
Color in the bars to make an equivalent fraction.
Daily Review
Solve each problem.
Learn and Connect
Noah and Owen are building a bookshelf. They each have a board the same length. Noah cuts 2 3 of his board. Owen cuts 3 4 of his board. Which piece is longer? We need to compare 2 3 to 3 4 . The number line helps to show the boards. One way to compare the fractions is to divide the number line to match the denominator and then find the fraction on the line.

You can also use models to represent these fractions and check your comparison.
Start by drawing two rectangles that are the same size. Shade 3 4 of the top rectangle and 2 3 of the bottom one. Compare the areas that are modeled. 3 4 has more area shaded. Therefore, 3 4 is greater than or less than 2 3 .
Place the missing fractions on the number line.
Shade the fractions. Put the fractions in order from least to greatest.
Place the fractions on the number line.
Shade in the fraction bars to match the fractions and compare. Circle the greater fraction.
Compare the fractions using the following symbols: <, >, or =.
Circle the group that is in order from least to greatest. Then, put the other groups in the correct order from least to greatest.
Solve the story problem.
19. Owen cut another board at 5 6 ft, and Noah cut a different board at 5 8 ft. Which board was cut longer? How do you know this?
Chapter 1
In Chapter 1, we review and learn about
Place Value, Rounding, Patterns with Rules
Place Value Skills are important for understanding how to compose and decompose numbers, round, compare numbers, and do operations with numbers.
• Place value to the millions
• Place value with expanded form
• Patterns in place value
• Comparing and ordering whole numbers
• Rounding whole numbers
• Number patterns
We can name place values up to the millions. We can write numbers in different forms.
We can use place value to help us compare and order numbers.
We can round numbers to the indicated place value.
We can analyze patterns.
Chapter 1-1 Place Value to The Millions
1. ...with a 7 in the ones place.
2. ...with a 9 in the thousands place.
This portrait of the Earth and the moon was taken from over 4 million miles away. We can use place value to write larger numbers. Look at the following number in the place value chart.
4 is in the millions place
2 is in the hundred thousands place
8 is in the ten thousands place
3 is in the thousands place
1 is in the hundreds place
9 is in the tens place
3 is in the ones place
Learn and Connect Apply 4, 2 8 3, 1 9 3
The written form of this number is: four million, two hundred eighty-three thousand, one hundred ninety-three

Write the place value of the orange digit.
1. 5,392,391 2. 3,203,293 3. 9,876,003 4. 1,487,942
Write these numbers in standard form.
5. Six million, eight hundred seventy-five thousand, nine hundred nineteen
Vocabulary
One Million - a 1 with 6 zeros; 1,000,000 Daily Review Write a number…
6. Two million, four hundred thirty-two thousand, five hundred eighty-six
Place Value - the position of a digit in a number determines its value
Identify the place value of the orange digit.
5,362,323 5. 9,675,888
7,246,212 6. 4 56,087
8,234,614
Write each number in standard form.
9. Eight hundred sixty-six thousand, three hundred twenty-one
10. Twenty-one million, three hundred eighty-five thousand, two hundred twenty
Write the value of each number.
What is the value of 3?
What is the value of 6?
What is the value of 4?
What is the value of 3?
What is the value of 7?
What is the value of 5?
What is the value of 4? 11. 3,751,428 12. 8,132,967 13. 7,561,234 4. 3,512,462 8. 7,019,550
What is the value of 1?
What is the value of 2?
Find the mystery number.
14. I have 6 digits, and my leading digit is 4. I have a 9 in my tens place and a 2 in my thousands place. I have a 2 in my hundreds place, and my ten thousands place is five larger than my hundreds place. My ones digit is a 5. What number am I? Am I EVEN or ODD?
Chapter 1-2 Place Value - Expanded Form
Daily Review Name the place value of the underlined digit.
How are the two 9s in the price of the motorcycle different?
The form of a number that shows the value of each digit is called expanded form.
9,492
The value of 9 is
The value of 4 is
The value of 9 is
The value of 2 is
You write the expanded form: 9,000+400+90+2
One 9 has a value of 9,000 and one 9 has a value of 90.
Learn and Connect Apply
Write the value of each digit in each number.

Fill in the missing values to write each number in expanded form.
Vocabulary
Write the value of each digit in each number.
Write the standard form of each digit. Hint: Every place needs a value; you can't just skip over it. Use a zero to show when a value is missing. For example, 300 + 2 = 302.
5. 600 + 30 + 2
8. 500,000 + 60,000 + 4,000 + 900 + 50 + 7
Write each number in expanded form.
905
Solve each problem.
15. There were 16,932 pieces of mail delivered yesterday by the postal service. What is this number written in expanded form?
5,603
8,956
16. What is the difference between the 9 in 964 and the 9 in 109?
Chapter 1-3 Patterns in Place Value
Daily Review Write the expanded form.
60,190
576,003
Learn and Connect
3,568
Three thousand, five hundred sixty-eight
What place is the 8 in?
Value:
What place is the 3 in? place
Value: .
Apply
Write the number and the word.
Write the answer in standard form and then written form. 30 thirty
3 × 10 =
30 × 10 =
300 × 10 =
Write the number in expanded form.
7. 5,389 =
× 10 = 35,680
What place is the 8 in now? .
Value: What place is the 3 in now? place
Value: 30,000
3,000 × 10 =
30,000 × 10 =
300,000 × 10 =
=
Vocabulary
Written form - the form of a number that uses words to express a number: Three hundred fifty two
Expanded form - a way to express the value of each digit of a number: 300 + 50 + 2
Standard form - the form of a number written with digits: 352
Write the answer in standard form and then written form.
Example: 40 × 10 = 400, four hundred
3 × 10 = , 80 × 10 = , 200 × 10 = , 6 × 10 = ,
× 10 = ,
× 10 = ,
Write the equation that matches the underlined number.
Example: 8,244,256 → 5 × 10 = 50
Write the place value of 4 in each number.
Example: 8,247,256 → Ten thousands
3,245,293 → 8,495,384 → 1,268,485 → 6,235,493 → 2,4 53,623 → 8,534,293 → 24 3,293 → 4,294,849 → 7,2 34,392 → 4,294,849 →
Write the written form.
Example: 3,875,110 - Three million, eight hundred seventy-five thousand, one hundred ten
Write the standard form.
Example: one million, three hundred sixty-one thousand, seventy-five = 1,361,075
4,560,090five million, one hundred thirty-two thousand, two hundred twelvesix million, seven hundred twenty-two thousand, five hundred sixnine million, six hundred sixty-five thousand, nine hundred ninety-nine3,576,0032,085,604 -
Chapter 1-4 Comparing and Ordering Whole Numbers
What city, Portland or Albuquerque, has the greater population?
What is Portland’s population?
What is Albuquerque’s population?
To compare, look at the highest place value: 645,291 619,374
If they are the same, continue to smaller place values: 64 5,291 619,374
You say 645,291 is greater than 619,374. You write 645,291 > 619,374.
Learn and Connect Apply
Remember: The symbols < and > open to the greater number. For example: 3 < 10 and 10 > 3.
Compare the following place values using <, >, = .
1. Tens Thousands
3. Ten Thousands Millions
Compare the following numbers using <, >, = .
2. Hundreds Ones
4. Ten Thousands Ten Thousands
Fill in the missing numbers to order the following numbers from least to greatest.
Vocabulary
Compare - to choose a value that is greater, less, or equal to the original value Order - to arrange values from greatest to least or least to greatest Daily Review Identify the place value of the underlined digit.
Solve each problem.
1. If 23,456 books are in the Lewistown library, and 23,546 books are in the Emmitsburg library, which library has the greater number of books?
2. At an animal show on July 8, 167,893 fans were in attendance. On July 9, 176,893 fans were in attendance. Which animal show had fewer fans?
3. The Mississippi River is 2,318 miles long. The Missouri River is 2,341 miles long. Which river is longer?
4. If the fifth grade had 145 students, and the fourth grade had 154 students, which grade had more students?
Use the chart to answer questions 5-7.
Order the number of products produced in each factory from least to greatest.
Least Greatest
Underline the factory that produces the most products a day.
Circle the factory that produces the least amount of products a day.
8.
What is the tallest famous structure?
What is the shortest famous structure?
Put the structures in order from shortest to tallest.
Chapter 1-5 Rounding Whole Numbers
Learn and Connect
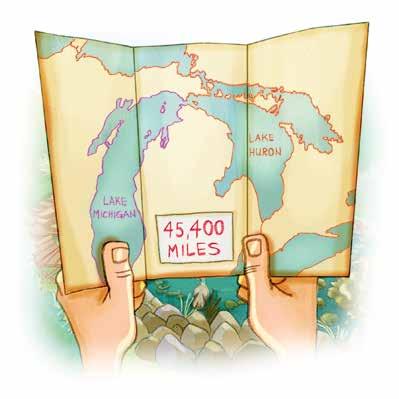
The largest lake in the United States is the combined waters of Lake Michigan and Lake Huron. About how large is Lake Michigan-Huron?
How large is Lake Michigan-Huron?
We can round this number to the ten thousands, thousands, and hundreds place. This will tell us about how large the lake is.
To round a number:
• Mark the place you are rounding.
• Look to the right of that digit.
• If the digit is 0, 1, 2, 3, or 4, keep the digit you marked the same.
• If the digit is 5, 6, 7, 8, or 9, add one to the marked digit.
45,400 rounded to the nearest ten thousand is: Lake Michigan-Huron is about miles.
Hint:
The digits to the right of the rounded place value all become 0s.
Vocabulary
Round each number to the nearest millions place.
Round each number to the nearest hundred thousands place.
Round each number to the nearest ten thousands place.
962,835
Round each number to the nearest thousands place.
1. 1,698,308 7. 5,789,354 13. 69,327 19. 74,592 4. 7,934,885 10. 632,988 16. 6,735,893 22. 56,932
Complete the table below.
Chapter 1-6 Place Value Word Problems
Daily Review Identify the place value of the underlined digit.
Learn and Connect
Rose is organizing a fantastic pizza party for her friends. She wants to order special pizzas with a unique twist. The number of toppings on each pizza is determined by the place value of a digit in a mystery number.
• The digit in the ten thousands place is 4.
• The digit in the thousands place is 3 more than the digit in the ten thousands place.
• The digit in the hundreds place is double the digit in the ten thousands place.
• The digit in the tens place is 1 less than the digit in the hundreds place.
• The digit in the ones place is 2 less than the digit in tens place.
What is the mystery number? ,

This number has a 5 in the ten thousands place. There are 4 more thousands than ten thousands and the same number of hundreds as thousands. If there are 3 fewer tens than hundreds, and there's a 7 in the ones place, what is the mystery number?
Vocabulary
Place value - the position of a digit in a number determines its value
Standard form - the form of a number that uses digits to express it
Written form - the form of a number that uses words to express it
What number has 9 thousands, 3 fewer hundreds than thousands, 2 fewer tens than hundreds, and 2 fewer ones than tens?
Read the clues. Write the answers in standard form.
What number has 5 ten thousands, 2 more thousands than ten thousands, the same number of hundreds as thousands, 3 fewer tens than hundreds, and 1 more ones than ten thousands?
What number has 3 thousands, 2 more hundreds than thousands, the same number of tens as hundreds, and 1 less ones than tens?
What number has 4 ten thousands, 3 more thousands than ten thousands, the same number of hundreds as thousands, 2 fewer tens than hundreds, and 1 more ones than ten thousands?
What number has 8 hundred thousands, 2 less ten thousands than hundred thousands, 3 more thousands than ten thousands, the same number of hundreds as thousands, 2 less tens than hundreds, and 1 more ones than tens?
Use the space below to write your own place value word problem for a partner to solve.
Sam is solving a place value word problem. Explain what his mistake is and what the correct answer should be. Sam's answer = 35,367.
What 5-digit number has 3 ten thousands, 2 more thousands than ten thousands, 1 fewer hundreds than thousands, 2 more tens than hundreds, and 1 more ones than tens?
Chapter 1-7 Number Patterns
Daily Review Rewrite the equation vertically and then solve.
25 + 9 + 17 + 10 = 2. 12,345 + 7,308 = 3. 95,304 − 27,546 =
Look at the steps and find the pattern. How many dots are in the fourth step?
Look at the steps and find the pattern. How many dots are in the twelfth step?
Step 1
Learn and Connect Apply 1.
These are increasing and decreasing number patterns. Fill in the missing number(s) in the sequence. In this pattern, the numbers are increasing, or getting bigger.
Step 2
Step 3
Look at the steps and find the pattern. How many dots are in the eighth step? Write an equation to show how you solved for the answer.
2
2, 4, 7, 11, 16,
Solve by identifying the rule.
6, 21, 36, 51, 66, 81
Rule:
Complete the table using the rule.
Rule: add 4
Solve each problem.
Mr. Anderson was setting up chairs for the school assembly. He realized that there were 3 chairs in the first row, 5 chairs in the second row, 9 chairs in the third row, and 15 chairs in the fourth row. If the pattern continues, how many chairs will be in the sixth row?
Challenge
Rule: subtract 3
Aaron loves to read. He is trying to double the amount of time he reads each month. In January he read for 25 minutes. How many minutes will he read in June? Write the number pattern and solve.
Look at the shape pattern. Jack says that the ninth step will have 100 dots. Is he correct? Explain your answer.
Step 1
Step 2
Step 3
Chapter 1-8 Review
Daily Review Compare each set of numbers using <, >, =.
The Green family is shopping for a new car. Look at the price of cars in the table to the right.
What would be the most expensive car they could buy?
What would be the least expensive car they could buy?
Round the price of the Nissan Maxima to the nearest thousands place.
Order the cars from least to greatest. ; ; ; ;
Learn and Connect Apply
Complete the table.
Write the place value of the digit in blue.
Compare the following numbers using <, >, and =.
Write the answer in standard form.
13. What number has 2 ten thousands, 1 more thousands than ten thousands, the same number of hundreds as thousands, 1 fewer tens than hundreds, and 3 more ones than ten thousands?
14. What number has 1 thousands, 8 more hundreds than thousands, the same number of tens as hundreds, and 4 less ones than tens?
Round each number to the largest place value.
8,930
984
Solve each problem.
21. Timothy was looking at buying a new bike. The bike costs $186. He has $155. How much more money does he need to buy a new bike?
903,678
22. Emma loves to read. She is trying to double the amount of minutes she reads each week. Last week she read for 7 minutes. How many minutes will she read after four weeks? Write the number pattern and solve.
Chapter 2
In Chapter 2, we will expand on
Addition and Subtraction with Large Numbers
We will apply our knowledge of addition and subtraction and work with larger numbers.
• Estimate sums and differences
• Addition and subtraction to the millions place
• Input and output tables with addition and subtraction
• Finding missing digits
• Solving word problems
We can quickly estimate sums and differences by rounding to any place value.
We can add and subtract large numbers, including subtracting across zeros.
We can write rules and find missing values in input and output tables.
We can use the relationship between addition and subtraction to find missing digits in addition and subtraction problems.
We can write equations and solve addition and subtraction word problems.
Daily Review Fill in the missing numbers in the number patterns.
Learn and Connect
Kennedy is looking at two lawn mowers to buy. He can’t decide between the blue or red lawn mower. When we estimate, we make a good guess instead of finding the exact answer. About how much more money would he pay for the blue lawn mower than the red lawn mower?
To solve, we have to round each price. Then, we should subtract the estimated price of the red lawn mower from the blue lawn mower.
Therefore, Kennedy would pay about $ more for the blue lawn mower.
Apply

Estimate by rounding to the nearest hundred. Rewrite the equations horizontally and solve.
Estimate by rounding to the nearest thousand. Rewrite the equations horizontally and solve.
Estimate by rounding to the nearest thousand. Rewrite the equations vertically and solve.
Estimate by rounding to the nearest ten thousand. Rewrite the equations vertically and solve.
Estimate to the largest place value and solve.
Solve each problem.
10. Sheldon picked 456 apples, and Dennis picked 312 apples from the apple tree. About how many apples did they pick together? Round to the nearest hundred.
11. Anthony's school sold 672 boxes of chocolate for a fundraiser this year. He sold 157 boxes. About how many boxes were sold by the rest of the students? Round to the nearest ten.
12. There are three baby elephants at the zoo. One weighs 242 pounds, one weighs 226 pounds, and one weighs 246 pounds. Which is the better estimate of the total weight: 600 or 900 pounds? Explain your answer.
13. Two neighboring cities have a population of 43,637 and 57,694 . Which is the better estimate of the total population: 80,000 or 100,000? Explain your answer.
Chapter 2-2 Addition to the Millions Place
Compare the following numbers using the symbols: <, >, or =.
The school library has fiction books, nonfiction books, and comic books. What is the total amount of books in the library?
To solve, we have to add all of the amounts. Start by lining up the digits by their place value. Then, add the numbers starting with the smallest place value to the right.
9 8 2, 8 9 2 9 7 8, 2 8 1 + 2 8, 9 7 2
Therefore, the school library has books.


+ 95,216 Add.
658,306 + 132,001 932,697 + 226,811
Rewrite vertically, then add.
Use the chart below to solve the problems.
19. What is the distance around Mars and Jupiter combined?
20. What is the distance around Mars and Neptune?
21. What is the combined distance around Mars, Saturn, and Neptune?
22. Would it take longer to fly a rocket around Jupiter or to get around Saturn and Neptune combined?
There are two large cities on each side of a river. One city has a population of 425,637, and the other has a population of 745,891. What is the total population of the two cities?
273,036 983,567 + 783,911 10.
Chapter 2-3 Subtraction Across Zeros
Learn and Connect
Aaron bought a box that contained 1,000 paper plates. If he used 786 for a picnic, how many plates are left?
Justin drove his car 6,024 miles in 2020. So far in 2021, he has only driven 381 miles. How many more miles does he have to drive to match his 2020 mileage?
Expert Tip: When you are subtracting by many zeros, you can regroup each zero OR you can follow this simple trick.
213 (just subtract 1) (now add back the one) = 214 No regrouping necessary!
-
Apply
Subtract.
Rewrite vertically, and then subtract.
Find the difference. Check your answer by using addition.
Subtract.
Rewrite vertically and find the difference.
Rewrite vertically and subtract. Check your solution by using addition.
Solve each problem.
20. A bunch of roses cost $3.76. If you give the clerk $5, how much change will you receive?
Challenge
21. There were 400 apples picked at the orchard on Friday. On Sunday, 243 apples were picked. What is the difference in apples picked between the two days?
22. Two brothers spent a month gathering loose coins into a jar. When they counted the coins, they had exactly 500 cents. They poured some of the money onto the table and counted it. If there was 376 cents on the table, how much was still in the jar? Bonus: Write it using dollars and cents or $.
782,182 + 263,821 = 2. 782,082 + 89,291 =
Learn and Connect
A company called You-Pick-It allows people to pick tulips for a fee. On the first day it was open, 24,928 tulips were picked. How many tulips are left in the field?
To solve, we have to subtract the tulips removed from the total amount of tulips in the field. Start by lining up the digits by their place value. Then, subtract the numbers starting with the smallest place value to the right.
2 4 0, 2 7 2 � 2 4, 9 2 8
Therefore, the field has tulips left.
Apply
Subtract.
Rewrite vertically and find the difference.
Subtract, then check using addition.
892,108 + 27,192 =

Subtract and check with addition.
Subtract.
Solve each problem.
13. If rockets need a speed of 25,000 miles per hour to break through Earth’s atmosphere, how much faster does a rocket going 18,975 miles per hour need to go to break through?
14. In 1967, the fastest rocket could go 4,520 miles per hour. Today, the Solar Probe can go 153,454 miles per hour. What is the difference between these two speeds?
Solve. Show your work. Use the expert tip (from the previous lesson) of subtracting 1 and then adding one back to subtract without borrowing.
Chapter 2-5 Input and Output Tables with Addition and Subtraction
1. 396 + 201 = 2. 9,211 − 4,709 = 3. 9,787 + 2,111 = 4. 12,165 − 3,376 =
Learn and Connect
Look at the input and output tables. All of the rows in a table have the same addition or subtraction rule. What numbers complete the tables?
In the first table, 2 + 6 = 8 and 5 + 6 = 11.
The rule is add 6. 6 + 6 = 12 and 10 + 6 = 16.
In the second table, 30 − 15 = 15 and 35 − 15 = 20. The rule is subtract 15. 50 − 15 = 35 and 100 − 15 = 85.
Write the rule, then fill in the missing numbers.
Write the rule, then fill in the missing numbers. Fill in the missing numbers.
These tables use two rules. Write the rules and fill in the missing numbers.
Daily Review Solve each problem.
Learn and Connect
We have to use our addition and subtraction skills to crack the code! Are you able to find the missing digits to complete these equations?
Start in the ones column:
7 + 5 = 12. The missing digit must be a 7.
3 5 + 1 5 8 2
In the tens column, we carry the 1.
1 + 5 + ? = 8
6 + ? = 8 ? = 2
Last, in the hundreds column, add 3 + 1. The missing digit must be a 4.

Apply
Solve for the missing digits.
Can you crack the code?
Solve each problem to find the missing digits. As you find the missing digits, cross them off the control panel. The remaining four digits will open the safe!
Solve each problem.
7. 567 customers go grocery shopping on Monday, and 432 customers go grocery shopping on Tuesday. How many customers went grocery shopping on those two days combined?
9. Stephen has earned $156 doing jobs around the house. He was given $65 dollars for his birthday. How much money does he have saved?
8. Michael read 134 pages last week and 243 pages this week. How many pages has he read in total?
10. Susan had 384 napkins in her collection. If she received 84 more napkins from her grandmother, how many does she have now?
Learn and Connect
A box has a total of 100 buttons. Six of them are black. If a tailor can use any button color except black, how many buttons are there that could be used?
The letter b stands for the number of buttons that can be used. Which equation could be used to solve the problem?
100 − 6 = b
100 + 6 = b
The number of usable buttons is less than the number of total buttons in the box, so is correct.
Apply

Circle the correct equation that matches the story problem and solve. Explain your answer using pictures and/or numbers.
1.
There are 62 cups in a restaurant cupboard. If the restaurant is full, it can seat 75 people. How many more cups does the restaurant need if every seat is full?
75 + 62 = c
75 − 62 = c
An unfinished block tower is 35 inches tall. One more block is placed on top. The new block is 5 inches tall. How tall is the tower?
35 + 5 = t
35 − 5 = t
A truck is carrying 56,000 pounds of goods. At its first stop, 5,978 pounds of goods are unloaded. How much is on the truck now?
56,000 + 5,978 = g
56,000 − 5,978 = g
Choose the correct equation that matches the story problem and solve. Explain your answer.
There are 42 flowers in a garden. Of these flowers, 21 are purple or blue. The rest are white. How many white flowers are there?
42 + 21 = f 42 − 21 = f
A national park had 912,687 visitors in the first 11 months of the year. In December, 75,823 people visited. How many visitors in total visited the park during the year?
912,687 + 75,823 = v
Write an equation using a variable that matches the story problem and solve.
A library has an inventory of 47,823 books. Funding is approved to buy 3,278 more books. How many books will the library have altogether?
Solve each problem.
45,429 square meters of parking lot needs to be paved. So far, 37,920 square meters have been paved. How much is left to be paved?
A town received 37 inches of rain in one month. There were 24 inches of rainfall in each of the next two months. What is the total amount of rainfall?
Challenge
A magic square has the same sum for every row, column, and diagonal. Use your addition and subtraction skills to find the magic sum. Then complete the Magic Square.
Hint: Find 3 numbers in a row.
− 75,823 = v
An artist is using square tiles to create a mosaic. The mosaic needs 54,978 tiles. Currently the artist has 48,389 tiles. How many more tiles are needed?
A tree is 89 feet tall. Lightning strikes the top of the tree, causing 23 feet to fall off. How tall is the tree now?
A bus is carrying 48 people. At one stop, 6 people get off and 2 more get on. How many people are on the bus now?
The magic number is 10 7 6 4
Daily Review Find the missing digits to solve the addition and subtraction equations.
The Green family is shopping for a new car. Look at the price of cars in the table to the right.
About how much more is the Jeep than the Hyundai Kai?
The Jeep is about more than the Hyundai Kai.
Estimate the difference between the most expensive and least expensive cars.
About how much would it cost to buy the two least expensive cars?
Learn and Connect Apply
Hint: Is it an estimate or an exact answer? Look for keywords like “about”.
Write an equation that matches the word problem and solve.
On Monday, the town of Cityville used 6,398 gallons of water. On Tuesday, the town used 5,934 gallons. How many more gallons were used on Monday?
1. The Jones family bought a house for $436,800 and a car for $34,500. How much did they spend in all?
A student read 1,304 pages in one month. In the second month, the student read 986 pages. How many more pages were read the first month?
Accord $27,049
Kai $28,222
Maxima $30,913
$40,698
Rewrite vertically and solve for the sums or differences.
+ 27,109 = 5,845 + 5,990 − 4,125 =
+ 925,830 =
+ 30,978 − 25,998 =
Write the rules and find the missing numbers in the input-output tables.
Solve each problem.
8. Timothy was looking at buying a new bike. The bike costs $186. He has $155. How much more money does he need to buy a new bike?
9. Sam has 389 business cards in his collection. Leo has 456 business cards in his collection. If Sam gives 145 cards to Leo, how many cards does Leo have now?
Challenge
Solve the following problems.
10. Four trucks are carrying goods to a grocery store. One truck is carrying 53,987 pounds, a second truck is carrying 26,948 pounds, a third truck is carrying 72,851 pounds, and the last truck is carrying 58,928 pounds. How many pounds of food are they carrying in all?
11. An office building has 352 workers. At 2:00 in the afternoon, 144 leave the building and 253 enter the building. How many workers are in the building now?
Chapter 3
In Chapter 3, we will learn about
Multiples, Factors, and Multiplying by a Single Digit
The concepts in this chapter build foundational skills that are used for multi-digit multiplication, estimation, and long division.
• Find multiples and factors
• Identify prime and composite numbers
• Multiply by multiples of 10
• Multiply a multi-digit number by a single digit
We can use skip counting, repeated addition, or multiplication to find multiples of a number. We can list the factors of a number and determine if it is prime or composite.
We can multiply a number by a multiple of 10 or multiply two multiples of 10.
We can use models, partial products, and/or the standard algorithm to multiply a multi-digit number by a single digit.
Chapter 3-1 Multiples
Eddie was planting tomato plants in his garden. If he plants 5 tomato plants in each row, how many rows would it take to get to 30 plants?
We can use multiples of 5 to solve this problem.
1 row - 5 plants
3 rows - plants
5 rows - plants 2 rows - plants 4 rows - plants 6 rows - plants
It would take rows to get to 30 plants.
Learn and Connect Apply
5, 10, 15, 20, 25, and 30 are some of the multiples of 5. We can use skip counting or multiplication to find the multiples of a number.
Skip count by the indicated number. Circle the check mark if the numbers are multiples of the number you were skip counting by. Write the next six multiples for each number.
By 5: 15,
Vocabulary
Multiple - the product of a number when it is multiplied by other numbers
Skip counting - a method of counting forward by numbers other than 1. (For example: 3, 6, 9, 12, 15...)
Write the next six multiples for each number.
Skip count by the indicated number.
7. By 2: 22, , , , , , 6. By 6: 48, , , , , ,
8. By 3: 12, , , , , ,
By 9: 72, , , , , ,
10. By 8: 32, , , , , ,
11. Name two multiples of 8 between 60 and 75.
12. Name two multiples of 6 between 40 and 50.
13. I am a multiple of 7. I am between 30 and 50. I am 2 more than a multiple of 10. What number am I? and and
9.
Solve.
Challenge
Chapter 3-2 Finding Factors and Multiples
Learn and Connect Apply
3 rows of 4 dots 3 × 4 = 12 2 rows of 6 dots 2 × 6 = 12
rows of 1 dot 12 � 1 = 12 Solve
We can line up the dots into equal rows to find all of the factors of 12. Get out some counters and try it yourself.
Factors of 12: 1, 2, 3, 4, 6, 12
Numbers that can be multiplied to equal 12.
• Smaller than 12
• 6 factors
Multiples of 12: 12, 24, 48, 120…
Numbers you get when you multiply 12 by a different number.
• Bigger than 12
• Unlimited multiples
Did you know that every number has the factors 1 and itself?
For each number on the left, check off all of its factors 1 - 10 by adding a check mark ( ).
Vocabulary
Factors - the numbers we multiply together to get a new amount: 5 × 3 = 15, 5 and 3 are factors
Circle the numbers that are factors of 30.
Write down all factors of each number.
Which multiplication facts helped you find the factors of 30? (These are called factor pairs.)
Use the hundreds chart to answer questions 5-7.
Cross out all the factors of 32 with an “X”. List the multiplication facts that helped you find the factors.
Use a colored pencil to color in all the multiples of 7.
Use a different colored pencil to color in all the multiples of 11.
8. Guess the number. I am a factor of 64 and a multiple of 4.
9. Circle the numbers that are factors of both 8 and 20.
Solve. Challenge
Chapter 3-3 Prime and Composite Numbers
How many arrays can you make with 9 counters?
What are the equations that represent the arrays?
Now, remove 2 counters and make arrays with 7 counters.
How many arrays can you make, and what are the equations that represent the arrays?
When a number has only one way to make an array, it is called a prime number. Prime numbers have only two factors, 1 and the number itself. When a number has more than one way to make an array, it is called a composite number. Composite numbers have more than 2 factors. Which number above is prime and which is composite? is composite, and is prime.
Learn and Connect Apply
List all the factors of each number. On the hundreds chart, color the number yellow if it’s prime and blue if it’s composite.
For each number, draw arrays and list all the factors. Then circle whether the number is prime or composite.
Solve.
Aaron completed a math problem incorrectly. Solve the problem correctly, using arrays and words to explain your answer.
Aaron's answers
Factors of 36: 36 and 72
Multiples of 36: 1, 2, 3, 6, 12, 36
Arrays that make 36: 1 × 36
Prime or composite: prime
Explain what Aaron did incorrectly:
Your answers
The number 48 has ten factors. Can you list them all?
This hundreds chart shows all the prime numbers. Use the hundreds chart to answer questions 6-11.
Color all the multiples of 2 pink.
Color all the multiples of 3 green.
Color all the multiples of 5 blue.
Color all the multiples of 7 purple.
Color all the multiples of 11 yellow.
What are some patterns that you noticed?
Chapter 3-4 Multiplying by Multiples of 10
Learn and Connect
David is measuring his pumpkin vines. There are some that measure 3 meters long. He is trying to grow the longest vines for the state fair, but he must submit his measurements in centimeters.
If there are 100 centimeters in a meter, David must multiply 3 � .
Look at these patterns of multiplication to find the answer.
3 � 1 = 3
3 � 10 = 30 3 � 100 = 300 3 � 1,000 = 3,000
There are centimeters in 3 meters.
Apply
Daily Review Find the missing factor. 5 � 1 = 5 � 10 = 5 � 100 =

Complete the pattern for multiplying by powers of 10.
� 1,000 =
� 10,000 =
Use the patterns of multiplication to solve each problem.
Use the patterns of multiplication to solve each problem.
Complete the pattern for multiplying by powers of 10.
Solve each problem.
20. The Brokaws have been flying for 8 hours. If the plane was moving at a rate of 600 miles per hour, how many miles have they flown?
21. Students have 30 spelling words to study each week. If school lasts for 40 weeks, how many words will they have studied altogether?
Solve the problem.
There are 20,000 plants in one farmer's field. If this farmer has 5 different fields with the same number of plants, how many plants can the farmer raise each summer?
The students in Mr. Riser’s fourth grade class are practicing their multiplication facts. They take one-minute tests to help them practice for their three-minute test. Their goal is to reach 100 facts in 3 minutes. If Timothy is working at the same pace, how many facts can he currently do in 3 minutes?
We want to know the number of math facts Timothy can do in minutes.
Timothy can currently complete problems in 1 minute.
To find the number of problems in 3 minutes, we multiply by
Learn and Connect Apply
Create your own model of the multiplication equations by drawing base-10 blocks.
Multiply.
Rewrite vertically, and then multiply.
Solve using repeated addition and multiplication.
21. A parking garage has 4 levels. There are 311 parking spots on each level. How many parking spots are there in all?
Learn and Connect
David’s family decided to plant corn this year. They planted 5 rows with 25 corn plants in each row. How can David find the total number of corn plants?
We have to multiply 25 � 5. We can solve this using partial products.
Step 1
Decompose the larger factor into expanded form:
Step 2
Multiply the factors in each place and list their products:
25 and 100 are the partial products.

Step 3
Add the partial products:
David’s family has corn plants.
Apply
Write a multiplication equation that matches the blocks. Then solve using partial products.
Vocabulary
Write a multiplication equation that matches the blocks. Then solve using partial products.
Equation:
Solve the following problems using the partial products strategy.
Solve each problem.
6. Danny is volunteering at the local aquarium. He is helping order new fish food. The food is only ordered every 4 weeks, and he needs to make sure all the fish have enough food. How many cups of food does Danny need to order to make sure that each type of fish has enough?
7. Harry usually bikes 216 miles a week going to and from work. At this rate, how many miles will he bike after 4 weeks?
8. There are 9 students in the poetry club. Last year, each student wrote 304 poems. How many poems did the students in the club write in all?
Chapter 3-7 Multiplication Practice
Learn and Connect
Charlie, Joseph, and Philip are all brothers. They are looking at their weekly schedules and calculating how much time they spend on homework in a month so they can plan their schedules and time with their friends. How much time does Joseph spend on homework in a month?
How many minutes does Joseph spend on homework in a week?
There are weeks in a month.
Solve each problem.
6. Dennis bought 2 bags of candy. There were 213 pieces of candy in each bag. How many pieces of candy did Dennis buy?
7. A city has 3 parking spots on each block. How many parking spots are there on 120 blocks?
Solve each problem.
16. There is a small jar with 423 jelly beans on the table. A large jar holds 2 times as many jelly beans. How many jelly beans does the large jar hold?
18. A restaurant purchased 2 boxes of ketchup packets. There were 342 packets per box. How many ketchup packets in total did the restaurant purchase?
17. A school building has 5 lecture halls. There are 110 seats in each lecture hall. How many seats are there in all?
20. Kim sells homemade pizza sauce. If she uses 9 tomatoes to make one jar of sauce, how many tomatoes does she need to make 115 jars?
19. A candy factory makes 212 pieces of candy each day. How many pieces of candy will the factory make in 2 days?
21. If Eric solves 7 crossword puzzles every week, how many puzzles will he solve in 112 weeks?
Learn and Connect
David has learned a lot about farming this season. He is thinking about what to plant for next season. He is thinking about buying 36 bean plants but isn’t quite sure how to arrange them in arrays. What are all of the possible ways David can arrange 36 bean plants?
David plans on tripling the number of bean plants for the next year. How many bean plants will he have?
If David’s family decides to triple the garden again in two years from now, how many bean plants will he have to care for in total? Write a multiplication equation and solve it using partial products.

Solve each problem using partial products.
Answer the questions.
1. Write the next six multiples of 12.
2. Skip count by 9:
3. List the factors of 30 and circle the factors that are prime. Factors of 30
Complete the patterns for multiplying by powers of 10.
Solve using partial products or the standard algorithm.
Solve each problem.
11. Rose wants to buy chocolates for her family. Each box has 28 pieces. She buys 6 boxes. How many pieces of chocolate will she have in total?
Challenge
13. Solve using partial products.
14. Find the missing digits. 12, 9,
12. Fred is helping clean up books in the library. Each bookshelf holds 42 books. If there are 9 empty shelves, how many books can Fred put on the shelves?
Chapter 4
In Chapter 4, we will extend our multiplication skills to
Multiplying Two-Digit Numbers
These skills are important to expand our skills in multiplication and problem solving.
• Multiply two-digit numbers by two-digit numbers
• Estimate products
• Problem solve
• Identify patterns that follow rules
We can understand three different strategies for solving double-digit multiplication problems.
We can accurately and efficiently multiply double-digit numbers.
We can estimate products of double-digit numbers. We can identify and solve word problems that require multiplication.
We can find patterns within and between two sequences.
Chapter 4-1 Multi-Digit Multiplication
Daily Review
Learn and Connect Apply
Mickey is organizing a canned food drive. He is hoping to collect 55 cans a week for 12 weeks. How many cans is he hoping to collect?
Let’s break it down into groups

Multiply.
Mickey is hoping to collect 660 cans.
Solve the equation. Use commas in your answers.
Solve the story problems. Show your work.
5. Marc is planning to build a rectangular garden. The length of the garden is 35 feet, and the width is 28 feet. What is the total area of Marc's garden?
6. Helen is making gift bags for a party. She wants to give away 56 bags, and each bag contains 11 small toys. How many small toys does Helen need in total for all the gift bags?
Pretend that you are the teacher! You are correcting papers. You see the following problem and answer:
233 × 19 = 2,330
Check the student work. Is the answer correct? Why or why not? Show your work and write a sentence to explain your reasoning.
Student work
Chapter 4-2 Estimating while Multiplying
Daily Review Round each number to the highest place value.
The Ridge Creek Bike Race is 24 miles along the edge of Ridge Creek that runs through the town. About how many yards is that?
How many miles is the race?
How many yards are in each mile?
To estimate, round each number to the highest place value and multiply.
24 = 1,760 =
20 × 2,000 =
The Ridge Creek Bike Race is about yards long.
Learn and Connect Apply

Round the numbers to the nearest ten and then multiply.
Vocabulary
Estimate - to give a general idea of what the value or amount is
Round each number to the highest place value.
Circle the best estimate without solving for the correct answer and then write why you selected the answer.
11. There are about 17 crayons in each box, and there are about 29 boxes. About how many crayons are there in total?
A. 600 crayons
B. 450 crayons
12. The mail room at school mails about 48 letters a day. There are about 19 days left of school. About how many more letters will get mailed before school ends?
A. 1,000 letters
B. 675 letters
Round to the highest place value and then solve.
Round the numbers to the highest place value and then solve. Write a number story that matches this equation.
Chapter 4-3 Multiplying Two-Digit Numbers using an Area Model
Learn and Connect
Lisa was working after school to help Mrs. Jenkins plan the kindergarten celebration. Each kindergartener was going to get 52 macaroni pieces to make a necklace. If there were 36 students in kindergarten, how many macaroni pieces in total would they need?
How many pieces does each student need?
How many students are there? .
Use an area model to multiply by .
The 36 is separated by place value to and .
The 52 is separated by place value to and .
Multiply and find the product for each box, then add the products together.
Lisa needs pieces of macaroni for the kindergarten celebration.
Apply
Use the area model to solve the equation.
Vocabulary
Area model - a rectangular model used to solve multiplication equations where the factors define the length and width of the rectangle
Solve the equations using the area model method.
Solve each problem.
11. It takes Jordan 45 minutes to sew each blanket. He needs to sew 25 blankets in total. How many minutes will he spend sewing in total?
12. Manny swims 35 laps in the pool every week. There are 52 weeks in a year. How many laps will Manny swim in a year?
Solve the equation using the area model method.
Learn and Connect
A local farm has a fresh egg stand by the road. They sell their eggs in cartons containing one dozen and a dozen and a half eggs. How many eggs did they sell in dozen cartons on Monday?
How many eggs are in a dozen?
How many cartons of a dozen eggs were sold?
Use partial products to multiply by .
Apply
Use the partial product method to solve these equations.
Vocabulary
Partial
Egg Cartons Sold on Monday
Dozen 42
Dozen and a Half 28
Find the partial products to solve.
Solve each problem.
11. David ran 21 laps around the track, Each lap took him 14 minutes. How many minutes did David spend running?
13. Fred reads 30 pages every day. How many pages will Fred read in 18 days?
12. Farmer Pat gives all the cows 12 cups of extra feed to eat each week. There are 16 cows on the farm. How many cups of extra feed do the cows eat in a week?
Use the partial product method to solve the 3-digit equation.
14. Ryan plants 12 pepper seeds in each hole. There are 25 holes. How many seeds will Ryan use in total?
Chapter 4-5 Two-Digit Multiplication Practice
Daily Review Use multiplication strategies to find the product.
Learn and Connect
David and his family are planning to make strawberry shortcake, which means they need strawberries. They go to a local strawberry patch to pick their own. The strawberry patch has 12 rows of 26 strawberry bushes. How many bushes does the strawberry patch have in total? Use the standard algorithm, area model, or partial products method to solve.
Multiply the ones place. Multiply the tens place. Add the products together.
Apply

Fill in the missing steps of the following problems using the standard algorithm.
Complete each of the steps of the area model method.
Vocabulary
Product - the answer to a multiplication problem
Area model - a rectangular model used to solve multiplication equations where the factors define the length and width of the rectangle
Multiply using the standard algorithm.
Complete the following problems using the strategy of your choice.
Solve each problem.
15. Jonathan was organizing his toy cars. He put them in five rows of 15. How many toy cars did he have altogether?
Challenge
16. A local toy store was grouping marbles into bags. They placed 25 marbles in each bag and made 37 bags. How many marbles in total did they use?
17. The parking garage can hold 5 rows of 15 cars on each level. If there are 7 levels in the parking garage, how many cars can park in the garage?
Chapter 4-6 Problem Solving with Multiplication
A dump truck can hold 2,674 pounds of dirt. If the truck takes 8 trips to the garden center, how many pounds of dirt can it move?
How many pounds can the dump truck hold? .
How many trips does it take?
Do you add, subtract, or multiply?
Solve. 2,674 � 8 = pounds of dirt.
Learn and Connect Apply

Solve. Underline the words that let you know to multiply.
1. Timothy studies for 60 minutes a day, every day, for the month of July. After 31 days, how many minutes has Timothy studied?
3. Frank charges $16 for a haircut. Today, Frank gave 18 haircuts. How much money did he make?
2. Harry picks 28 lemons off every tree in his lemon farm. There are 30 trees on the farm. How many lemons does Harry pick?
4. Mr. Bates orders 24 pencils for each classroom in our school. There are 21 classrooms. How many pencils are ordered in total?
Solve the 2-digit multiplication equations.
Solve. Underline the words that let you know to estimate.
6. Sal makes 60 oatmeal cookies and 50 sugar cookies in a day. About how many cookies does he make in a day? About how many cookies would he make in a week?
7. Ken practices reading for 80 minutes a week. Estimate how many minutes of reading Ken will have completed after 12 weeks.
8. Ned is making goodie bags for Martin’s birthday. He puts about 12 pieces of candy in each bag. There are 25 bags to fill. Approximately how much candy does Ned need?
Use the space below to create your own word problem using estimation for a partner to solve.
9.
Solution:
How much gold did Captain Jack find?
10. Captain Jack finds hidden treasure buried in a cave. He decides he is going to share the treasure with his shipmates, and everyone will get an equal share of gold. After giving all 15 people aboard 18 bars of gold, he is left with 130 bars of gold for himself. How much gold did Captain Jack find in total? Show your work.
Solve for the difference.
Learn and Connect
Sequences are shapes or numbers in a certain order. We can find the rules for two sequences, then find the rule that relates the sequences to each other.
The arrow shows that to change from sequence 1 to sequence 2, we multiply by . This is the relating rule.
These are the rules for the numbers in each sequence.
We can use the relating rule to find missing terms of greater values in the sequence. Which terms should be in the missing spaces in the table?
Anne wants to make identical beaded necklaces for her friends. Each necklace will have 6 red beads and 12 purple beads. If Anne needs to make 14 necklaces, how many red and purple beads will she need to purchase? Fill in the table of values to solve for the number of beads for each necklace.
A customer ordered 38 cakes from Jack’s Bakery. Each cake requires 2 eggs and 8 teaspoons of vanilla. How many teaspoons of vanilla and eggs will the bakery need to use to complete the order? Identify the patterns and relating rules. Then, fill in the missing terms in the sequences to solve.
Jack’s Bakery is getting more and more orders for cherry pies. The bakers made 4 cherry pies in January, 12 in February, 36 in March, and 108 in April. If this pattern continues, how many cherry pies will the bakery make in May? Fill in the rule. 4, 12, 36,
Identify the pattern and solve for the missing terms. Show your work.
Daily Review
Written Form:
Expanded Form:
Write 568,431 in written and expanded form.
Learn and Connect
Emma is making bracelets for her friends. She needs 32 beads for each bracelet, and she needs to make 12 bracelets. How many beads does she need to make the bracelets? Use the space below to solve the problem using standard algorithm or area model.
Multiply the ones place. Multiply the tens place. Add the products together.
Apply
Solve the equations using your strategy of choice and show your work.
Round to the highest place value and then solve.
1. 52 × 11 = × =
Solve and explain.
4. David was practicing his multiplication skills to improve his grade in math. When he timed himself yesterday, he completed 31 equations per minute.
He estimated that he could complete 148 problems in 8 minutes. Is that about right? Why or why not? Be sure to explain your answer.
5. Estimate the product. Round the first factor to the nearest ten, and then multiply.
27 × 7 =
The product is approximately . Create a word problem that matches this equation.
6. What is the rule for this input/output table? Circle the correct rule and explain your reasoning using words and equations.
Solve each problem.
7. It takes Robert 36 minutes to bake a tray of cookies. He needs to bake 12 trays of cookies in total. How many minutes will he spend baking cookies in total?
8. Sarah has a rectangular garden that is 27 meters long and 36 meters wide. She wants to find the total area of the garden. How many square meters is the garden?
Chapter 5
In Chapter 5, we will be introduced to
Long Division
Students will use models and mental math to gain proficiency in solving division problems.
• Problem solve
• Estimate quotients
• Interpret remainders
• Use divisibility rules
• Divide with long division
• Use error analysis for multiplication and division
We can solve multi-step word problems that use multiple operations.
We can list the factors of a number and determine if it is prime or composite.
We can find compatible numbers and use them to estimate quotients.
We can use divisibility rules to list the numbers a number is divisible by.
We can use long division to divide.
We can find errors in multiplication and division problems.
Chapter 5-1 Multiplication and Division Word Problems
Find the rule of each in/out table.
Five friends went food shopping. They bought 2 bags of oranges, 2 bags of bananas, 3 bags of plums, and 1 bag of apples. They split the bill evenly between them. How much did they each pay?
They bought bags of oranges that cost .
They bought bags of bananas that cost .
They bought bags of plums that cost .
They bought bag of apples that cost . ×
Altogether, the bill was split between the friends.
Learn and Connect Apply
÷ = Each boy paid .
Read and solve. Write the equations you used to solve.
Solomon bought 3 packs of pencils that cost $4 each. Then he bought 2 bags of markers that cost $25 each. Finally, he bought 5 scissors for $10 each. How much money did he spend?
Vocabulary
George baked 2 trays of sugar cookies and 3 trays of oatmeal cookies. Each tray holds 10 cookies. He is going to make goody bags for his class. Each goody bag holds 5 cookies. How many goody bags did George make?
Complete each fact family.
Read and solve. Write the equations you used to solve and show your work.
Three friends went shopping for pet supplies. They bought 2 bags of puppy food that cost $5 each. Then, they bought 2 boxes of fish food that cost $8 each. Finally, they bought 1 bag of cat food that cost $4. How much money did they spend? If they split the bill evenly, how much will they each pay?
Morris has 99 feet of fabric. He needs 9 feet of fabric to make an art project. How many art projects can he create using the fabric?
Marc has 12 roses, 8 daffodils, 9 daisies, 14 lilies, and 7 sunflowers. He needs 10 flowers to make 1 bouquet. How many bouquets can he make?
The entire 4th grade at Williams Elementary are going to the zoo. There are 68 4th graders. Each ticket costs $12. How much money will it cost for the all of the 4th graders to go to the zoo?
A pack of 100 pencils costs $15. George bought 20 packs. How much money did he spend?
George wants to know how many pencils he will have. 20 × 100 = p. Find p.
Henry builds miniature toy trucks. He needs 18 wheels for each truck. He wants to build 48 trucks. 48 × 18 = p. Find what p represents.
Jake made 24 sandwiches. He is packing 2 sandwiches in each lunch bag. How many lunch bags can he pack?
Chapter 5-2 Using Compatible Numbers to Estimate
Learn and Connect
Samuel, Alan, Jeffrey, and Tom are in a book club at school. It has been four months so far, and they want to know about how many books they are each reading a month.
To estimate quotients in division problems, it is helpful to find compatible numbers. Compatible numbers are numbers that are multiples of the divisor.
What are we dividing these numbers by?
List the multiples of 4:
Apply
Vocabulary Estimate - a close, but not exact answer
Estimate. List the multiples of the divisor and write the equation you used to estimate.
Estimate. Circle if your answer will be greater than or less than the actual answer.
Solve. Write the equation you used to solve for the answer.
In 3 months, Kane read 91 books from the library. About how many books does he check out from the library per month? How do you know?
There are 98 students taking the train. Each car holds 8 students. Solomon thinks they will use 10 cars. Aaron thinks they will use 12 cars. Who has the better estimate? Why?
Solve and draw a picture to support your answer.
Mr. Ross needs to buy boxes of pencils for his students' end of the year test. Each box has 25 pencils. He wants each student to get 5 pencils. He has 9 students. Should he buy 2 or 4 boxes? Why?
Chapter 5-3 What is a Remainder?
Learn and Connect
Sometimes, when we divide, we are left with some left over. We call this the remainder.
Look at 24 cookies divided evenly among 5 plates.
Remainder
How many cookies are there? Dividend
How many plates are there?
How many leftover cookies are there?
Divisor
Remainder
We write an “R” to show a remainder: 24 ÷ 5 = 4 R4
Interpreting the Remainder
Drop It!
Ignore the remainder and use the quotients as your answer.
Use when question asks for FULL or WHOLE items.
Add It!
Add one more to the quotient.
Use when you cannot leave anyone or anything.
Use It!
Use the remainder for your answer.
Use when question asks how many or left over or left out.
Share it!
Share the remainder as a fraction or decimal.
Use with food, money, or items easily split in real life.
Use the picture to solve. Circle what to do with the remainder: drop, use, or add.
Timothy has 23 cereal boxes to place onto shelves. If each shelf holds 6 cereal boxes, how many shelves will he need to place all the boxes?
Vocabulary
Jim is planting rows of roses in his garden. He wants to place 5 rose bushes in each row. If he has 18 rose bushes, how many complete rows will he have?
Remainder - the amount left over after you divide a divisor that does not go into a dividend evenly
Solve. Draw a picture that matches the problem. Circle whether you should drop the remainder, use the remainder, or add one to the quotient.
A chicken farmer collected 39 eggs from his hens. He packs the eggs in containers that hold 6 eggs. How many containers can he completely fill?
Jill's mother gave her $35 to buy as many $4 bags of flour as possible. She told her she could keep any money left over. How much money will Jill get to keep after buying the bags of flour?
George sells lemonade for $5 a cup. He needs to earn $48 to buy a baseball bat. How many cups of lemonade does he need to sell?
An apple farmer picked 59 apples. He sells them in boxes of 8 and saves the rest for his son. How many apples does he save?
Sam has 39 photos to put in an album. Each page holds 4 photos. How many pages will he use if he places all of the photos in the album?
Use mental math to solve.
Chad bought 57 chocolates. He needs 5 chocolates for each treat bag. How many treat bags can he make?
Chapter 5-4 Divisibility Rules
Learn and Connect
Thomas has 30 pieces of candy that he wants to share with his friends. He is not sure how many friends he can give candy to if he gives them all the same amount. Will it work for Thomas to share his candy with 2 friends? How about 3, 5, 6, 9, or 10 friends?
We can use the rules in the table below to find out which numbers can be equally divided into 30 with no remainder.
2 A number is divisible by 2 if the last digit is 0, 2, 4, 6, or 8. 30 is divisible by 2 because the ones digit is .
3 A number is divisible by 3 if the sum of its digits is divisible by 3. 30 is divisible by 3 because 3 + 0 = , and is divisible by 3.
5 A number is divisible by 5 if the ones digit is 0 or 5. 30 is divisible by 5 because the ones digit is .
6 A number is divisible by 6 if it is divisible by both 2 and 3. 30 is divisible by 6 because it is divisible by and .
9 A number is divisible by 9 if the sum of its digits is divisible by 9. 30 is not divisible by 9 because 3 + 0 = , and is not divisible by 9.
10 A number is divisible by 10 if the ones digit is 0. 30 is divisible by 10 because the ones digit is .
Thomas can divide 30 pieces of candy equally among , , , , and friends. He shouldn't share his candy with friends because he won't be able to give them equal amounts.
List which numbers, 2, 3, 5, 6, 9, or 10, the given number is divisible by.
List which numbers, 2, 3, 5, 6, 9, or 10, the given number is divisible by.
Solve each problem.
21. There are 50 members in the marching band. Can they line up in 2, 3, 5, 6, 9, or 10 equal rows? List all the possibilities.
Challenge
23. The number of students in a fourth grade class is only divisible by 5 (and 1) but not any other number. There are more than 10 students in the class. How many students are in the class?
22. Jeff has 36 books. He wants to place them on shelves in equal numbers. Can he place them on 2, 3, 5, 6, 9, or 10 shelves? List all the possiblities.
24. Barry’s uniform number is a 2-digit number divisible by 2, 3, 5, 6, 9, and 10. What is Barry’s uniform number?
Chapter 5-5 Introduction to Long Division
We are going to use long division to solve 85 ÷ 5.
Rewrite the problem.
÷ 5 = 1) Multiply (5 x 1 = 5)
Subtract (8 - 5 = 3)
Bring down the next digit (5)
(35 ÷ 5 = 7)
Multiply (5 x 7 = 35)
Subtract (35 - 35 = 0)

Each time you subtract, make sure the answer is less than the divisor. In this problem, it should be less than 5. If your remainder is larger than the divisor, you have more equal groups to make, so keep on dividing!
There are 96 students in fourth grade with the same amount of students in each class. There are 3 classes. How many students are in each class?
A baker divides cookies into groups of 6. If there are 78 baked goods, how many groups does he have?
Danny had to solve 75 ÷ 3 = x. Danny thinks x = 24. Look at his work below. What did Danny do wrong? What is x?
36 ÷ 2 = x. Eli thinks x = 17. He is wrong. Look at his work below. What did Eli do wrong? What is x?
Chapter 5-6 Long Division Practice without Remainders
Learn and Connect
Mr. Stewart is stocking apples at the supermarket. He has 72 apples to place in 6 rows. How many apples can he put in each row?
We want to know how many apples Mr. Stewart can place in each row.
There are apples in all. There are rows.
To find how many apples will be in each row, we divide by .
Divide the tens. Divide the ones.
Multiply (1 x 6)
Subtract (7 - 6)
Bring down the next digit
Apply Daily Review Use the Divisibility Rules to list 1-digit divisors for each number.
Divide. Show your work.

Look to see if the divisor can divide into the tens place. Then, regroup the tens with the ones.
Divide. Show your work.
Rewrite each problem, and then divide.
Solve each problem.
There are 98 rooms in a building. There are 7 floors. How many rooms are there on each floor?
Challenge
Aaron bought 2 bags of cookies to make snack packs with. Each bag has 24 cookies. Each snack pack gets 3 cookies. How many snack packs will Aaron make? Explain how you found your answer.
Rick picked 88 oranges and divided them into 4 equal bags. How many oranges did Rick put into each bag?
Look at the long division work David did below. What mistake did he make? What’s the correct answer?
Chapter 5-7 Multiplication and Division Error Analysis
Review Solve. Use a separate piece of paper to show your work.
Learn and Connect
Joshua’s teacher asked him to solve 39 × 48. He used the area model below to solve. His final product of 792 was wrong. What was his mistake?
Fill out the checklist to help you find his error.
39 separated by place value is and .
48 separated by place value is and .
The product of 40 × 30 =
The product of 40 × 9 =
The product of 8 × 30 =
The product of 8 × 9 =

What was his error?
All of the products added together equal .
What is the correct answer?
Josh was doing a division problem. He did the first two steps but felt that he was doing something wrong because in this step, he could divide the divisor more than 10 times! How can you help him fix his work? Here is his work:
Read and solve.
Compare the partial products models. Circle the letter of the correct model. What was wrong with the other model?
For each problem, write the error, the correct answer, and a strategy to prevent the same error.
Bob used partial products to solve 17 × 32 in the model below. His final product is not correct.
Chapter 5-8 Review
Learn and Connect
Mr. Jameson needed to pack up cupcakes and cookies for a local bake sale. He had 10 cupcakes and 12 cookies. He wanted to know how he could best package his cookies and cupcakes so he did not have any left out of the box.
Complete the table to the right.
What box type will give him no leftover cupcakes or cookies?
Boxes of 4 2 boxes, 2 left
Boxes of 5
Apply
Read and solve. Write the equations you used to solve.
An apartment building has 111 apartments. The basement has 3 apartments. The other 9 floors have the same number of apartments. How many apartments are on each of the 9 floors?
John baked 27 yellow cupcakes, 32 chocolate cupcakes, and 15 lemon cupcakes. He is packing snack bags for his class. Each snack bag holds 2 cupcakes. How many snack bags can he make?
84 students are going on a field trip to a farm. The students will be taking a hayride in a wagon. Each wagon holds 8 people. Should the school order 9 or 11 wagons? Why?
Eddie has 26 glasses. Each of his cabinet shelves holds 7 glasses. How many shelves will he use to store all of his glasses? Why?
Estimate.
Use divisibility rules to find divisors that are 2-9 to solve each problem.
There are 48 plants. How many equal rows can the plants be placed in?
If there are 45 cans, how many shelves can they be equally placed on?
Choose the correct model. Explain why the other model was wrong.
Divide. Use mental math and related multiplication facts to solve.
Solve the problems.
Manny’s soccer uniform number is between 70 and 79 and is divisible by 2 and 3 but not by 5, 9, or 10. Which number does Manny wear?
Charlie has 30 cookies. He wants to split them equally among 4 boxes. How many will go in each box? How many will he have left over?
Chapter 6
In Chapter 6, we will expand on
Long Division with Remainders
Students will continue to build fluency in long division as they practice with larger numbers and remainders.
• Divide multiples of 10
• Estimate quotients
• Use long division with remainders
• Use multiplication to check division
We can use patterns of division to divide multiples of 10. We can use compatible numbers to estimate quotients.
We can use long division to divide up to four-digit dividends and find quotients with and without remainders.
We can use multiplication to check division.
Chapter 6-1 Patterns of Division: Dividing by Multiples of 10
Learn and Connect
Hector was creating an art project. He had 150 inches of yarn. He needed to cut the yarn into 30 equal pieces. How long will each piece be?
150 ÷ 30 =
150 ÷ 30 =
15 ÷ 3 =
Each piece will be inches long.


Divide. 72 ÷ 8 =
Vocabulary
Multiples - the products you get when you multiply by a certain number. In this case, multiples of 10 are the products you get when you multiply a number by 10: 15 × 10 = 150, and 3 × 10 = 30.
Divide.
10. Hector completed the pattern below and made a mistake.
÷ 9 =
÷ = 3
mistake?
11. Hector has 630 inches of yarn. He is going to cut them into 9-inch pieces. He wants to cut 100 pieces. Does Hector have enough yarn to cut 100 pieces? Why or why not?
Solve.
Learn and Connect
Hannah baked 56 cookies to share with her friends. She has 6 friends. About how many cookies will each friend get?
Let’s estimate to find out about how many cookies each friend will get.
She has friends to share them with.
Hannah has cookies.
The closest multiples of 6 are 54 and 60.
54 ÷ 6 = 60 ÷ 6 =
Which is the better estimate?
Each friend will get about cookies.
Apply

Circle the better estimate. Write the equation you used to solve for the answer.
Rick has $75 to buy books. Each book costs about $9. About how many books can Rick buy?
A) 11 B) 8
Paul has 68 floor mats that he uses to build reading nooks. Each reading nook uses 5 mats. About how many reading nooks can Paul build?
A) 14 B) 8
Helen has 89 forks she needs to pack into boxes. Each box holds 7 forks. About how many boxes does Helen need?
A) 12 B) 20
There are 95 students going to the cafeteria. Only 8 students can sit at a table. About how many tables should the cafeteria manager order?
A) 20 B) 12
Kayla needs 78 placemats. The placemats are sold in packs of 4. About how many packs does she need to buy?
A) 20 B) 18
Circle the better estimate. Write the equation you used to solve for the answer. Solve the problem.
The art teacher needs 90 crayons for the class art project. Each box holds 8 crayons. About how many boxes will be needed?
A) 9 B) 11
There are 64 fourth graders going on a field trip. Each car holds 5 kids. About how many cars will they need?
A) 11 B) 13
The school secretary has $45 to buy pens. A pack of pens costs $8. About how many packs can she buy?
A) 5 B) 8
There are 58 oranges that need to be packed into bags. Each bag holds 6 oranges. About how many bags will be used?
A) 10 B) 7
Moses has 82 books. He is building a bookshelf to store all of his books. Each shelf can hold 7 books. About many shelves does Moses need in his bookcase?
A) 12 B) 18
Deborah has $100 to buy packs of cupcakes. Each pack costs $9. Deborah thinks she has enough money to buy 12 packs. Is her estimate reasonable? Why or why not?
Harry and Abe have $130 to spend on puzzle packs. Each puzzle pack costs $9. Harry estimates they can buy 12 puzzle packs. Abe estimates they can buy 15 puzzle packs. Who has the better estimate? Why?
Chapter 6-3 Long Division with Remainders
Learn and Connect
Jack was working to organize the 201 jars at a local supermarket. There was space for 6 jars on each self.
How many jars are there in total?
We can find the remainder to know how many jars will be on the last shelf. How many jars go on each shelf?
Use long division to help you solve.
When there are no more numbers to bring down, you can find the remainder.
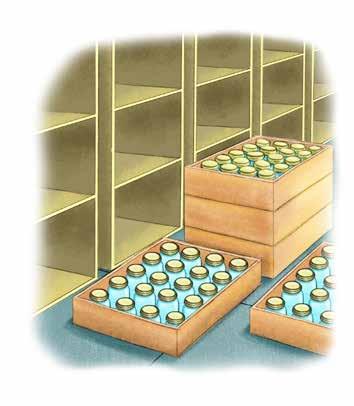
35 shelves are completely filled. jar/s will be on the 36th shelf.
Divide.
Solve each problem.
Jake has 89 photos. He can place 4 photos on each page of his photo album. How many pages will Jake use in his photo album?
Will Jake fill all of the pages he uses? Why or why not? pages
Leo ordered 12 boxes to pack his paint brushes. He has 57 paint brushes. Each box holds 5 paint brushes. Did Leo order enough boxes?
If Leo has enough boxes, will all of his boxes have 5 paintbrushes? Why or why not?
The students in Ben’s grade go on a boat ride for a class trip. Each boat can carry 7 students. There are 96 students. They need x amount of boats to carry all of the students. Find x and explain why that number is needed.
There are 89 cases of water. Each pallet holds 6 cases. Jake needs to order x amount of pallets to store all the cases. Find x and explain why that number is needed.
and 3-Digit Dividends
Daily Review Name the place value of the digit underlined in each number.
Learn and Connect
Dennis and his brother Arnold are going to paddle their boat across the pond at their grandfather’s farm. How many yards across is the pond?
How many feet is the pond? feet
How many feet are in 1 yard? feet
Divide by to find the number of yards.
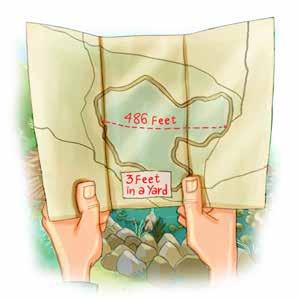
Apply Divide.
Vocabulary
List the numbers 2, 3, 5, or 9 that each given number is divisible by. Refer to lesson 5-4 to review the rules of divisibility.
Solve each problem.
16. It takes Robert 120 minutes to bake 5 cakes. Each cake takes the same amount of time. How much time does each cake take to bake?
18. Farmer Stan has 136 tomato plants. He plans to plant the same amount of plants in 8 rows. How many plants should go in each row to make them all the same?
17. 42 people showed up to play ball. Seven equal teams were made. How many people were on each team?
19. Donald separates 116 books equally on 4 shelves in the library. How many books belong on each of the 4 shelves?
Challenge
Divide.
Learn and Connect
The stocker has 7,748 cans of soup to put on the supermarket shelves. The cans are arranged in 6 even rows. How many cans will be in each row? How many cans will be left over?
There are cans of soup.
The cans will be arranged in rows.
To find out how many cans are in each row, divide by . The remainder is the number of cans left over.
Divide the thousands.
Divide (7 ÷ 6)
Multiply (1 × 6)
Subtract (7 − 6)
Bring down the next digit.
Divide the hundreds.
Divide (17 ÷ 6)
Multiply (2 × 6)
Subtract (17 − 12) Bring down the next digit.
Divide the tens.
Divide (54 ÷ 6)
Multiply (9 × 6)

Divide the ones.
Divide (8 ÷ 6)
Multiply (1 × 6)
Subtract (8 − 6) We are left with the remainder.
There will be cans in each row with cans leftover. Apply Solve.
Solve.
Solve each problem.
Jack made 2,309 donuts. He sells them in boxes of 8. How many full boxes did he make? How many more donuts does he need to make to fill another box?
Solomon’s orchard ships 8,946 apples to 8 grocery stores per week. The apples are sent in bags that hold 9 apples. How many bags does he use per week?
Fred needs to order boxes to pack his basil plants. He has 6,598 basil plants. Each box holds 5 plants. All of the plants must be packed in a box. How many boxes does Fred need to order? Will all of the boxes have 5 plants? Why or why not?
David solved the following division problem: 8,664 ÷ 5 = 1,731 R9. Is David correct? Why or why not?
Daily Review
Fill in the blanks to complete the pattern.
Learn and Connect
At the race, the cars do 4 laps around the track. At the end of the race, they have traveled 424 feet. How many feet do they travel in each lap?
We want to know how many feet the cars travel in lap.
We know the cars travel feet in laps.
To find the number of feet traveled in 1 lap, we divide by .
Divide the hundreds.
Divide the tens. Since 4 cannot go into 2, we write a 0 in the tens place.
Be sure to put the 0 here. If you leave it out, your answer will be 16. That is VERY different from 106!
Bring down the ones. Divide the ones.
The cars travel feet per lap.
Apply
Divide. Show your work.
Divide. Show your work.
Solve each problem.
13. Aaron has 314 water bottles that he wants to pack in bags. He is putting 3 bottles in each bag. How many bags does he pack? How many water bottles are left over?
15. Michael has 437 flowers. He is going to place them in 4 arrangements. How many flowers will go into each arrangement?
Challenge
Solve for the correct answer. Name
17. Rick solved 630 ÷ 6 as shown on the right. His answer is 15. Explain what Rick did wrong.
14. 320 students signed up for the annual Uno competition. Each game table seats 6 students. How many tables do they need to seat everyone?
Will all the tables be full? Why or why not?
16. Fred read the same amount of books each month for 5 months. He read 545 books in total. How many books did Fred read each month?
What is the correct answer?
Daily Review Round each number to the highest place value.
Learn and Connect
Jack had to split 275 jelly beans into 6 different bags. He found that he had 45 jelly beans in each bag with five left over. He wants to make sure he is correct, but how can he do that without going back to count every single jelly bean?
Jack can multiply to check his work.
First: Write Jack’s division problem.
275 ÷ 6 = 45 R5
Multiply the quotient by the divisor .

Now add the remainder, 5, to the product you found above + 5 =
Divide. Check your work by multiplying. Apply
Divide. Then multiply to check your work.
Divide. Use multiplication to check your work. Remember to add back any remainders.
Use mental math to solve the problems below.
Describe the pattern in problems 7 - 10. What mental math strategy did you use to solve them?
Daily Review Estimate the quotient of 28 ÷ 5 =
Learn and Connect
Paul is picking apples and storing them in bushels. He has picked 765 apples. He has 5 bushels to fill. How many apples are in each bushel?
Paul has apples.
He puts them in bushels.
Divide the hundreds.
Bring down the tens. Divide the tens.
Bring down the ones. Divide the ones.

Estimate. List the multiples of the divisor and write the equation you used to estimate.
÷
Divide. Check your work using multiplication.
There are 347 fourth graders in the local elementary school. During their fall field trip, the students went on a helicopter ride. Each helicopter holds 4 students. How many helicopters will they need?
Why?
Emma and Hannah both solved 2,604 ÷ 8. Emma’s quotient was 325 R3. Hannah’s quotient was 325 R4. Without using division, how can you check to see who has the correct quotient?
Whose quotient was correct?
Challenge
What was Jack’s mistake? What is the correct quotient? Solve.
Jack made a mistake when he was solving 347 ÷ 6. Below is his work.
Chapter 7
In Chapter 7, we will explore
Fraction Concepts
Understanding concepts about fractions has a lot of practical application in real-world situations and higher level operations with fractions.
• Find prime factors
• Generate equivalent fractions
• Simplify fractions
• Compare and order fractions
• Convert between improper fractions and mixed numbers
We can use factor trees and factor ladders to find the prime factors of a number.
We can use models, multiplication, or division to generate and represent equivalent fractions. We can use a common factor to simplify fractions. We can compare and order fractions. We can write, represent, and convert between improper fractions and mixed numbers.
Chapter 7-1 Factor Trees
Daily Review List 2 or 3 ways to make each number using multiplication.
To find the prime factors of 18, think about the whole numbers you can multiply to get 18. First list two numbers to multiply to get 18. Start with 6 × 3. Since 6 is not a prime number, find the factors of 6 next. We add the next branch with those factors. Once all of the factors are prime, the factor tree is complete. We can list these factors in a factor tree:

The equation lists the prime factorization of that number: 18 = 2 × 3 × 3
We can also use a factor ladder. Start by dividing the number by its smallest prime factor:
Continue dividing by the smallest prime factor:
The ladder is complete when the last remaining factor is prime 18 = 2 × 3 × 3
Learn and Connect Apply
Create factor trees or factor ladders and write the prime factors as an equation.
Vocabulary
Factors - numbers we multiply together to get a new number: 2 x 4 = 8. The factors of 8 are 2 and 4.
Prime number - a number that has only two factors, 1 and itself
Prime factorization - finding the prime numbers that multiply together to get the original number
Circle the prime numbers.
Use a factor tree to find the factors. Write the prime factors as an equation.
Use a factor ladder to find the factors. Write the prime factors as an equation.
Circle the correct prime factorization of 24.
Challenge
Solve each problem.
9. Create a factor tree and a factor ladder for the number 112 and write the equation.
10. Find a number that is less than 60 and has a prime factorization with 5 factors. There is more than one answer.
Chapter 7-2 Equivalent Fractions
Daily Review Determine if the number is prime or composite.
Alice is baking using her mother’s recipe. She noticed that she needs 1 2 cup of sugar. However, she only has a 1 8 cup measuring cup. How many 1 8 cup scoops should she use to equal a 1 2 cup?
To solve, we need to find an equivalent fraction to 1 2 that has a denominator of 8.
An equivalent fraction is a fraction that is equal to another fraction. To make an equivalent fraction, you have to divide or multiply the numerator and the denominator by the same number.
First, consider: 2 × 4 = 8. Then, multiply the numerator by the same number.

Therefore, 1 2 is equivalent to . This means that Alice needs to add scoops of sugar with the 1 8 measuring cup.
Learn and Connect Apply
For each fraction below, write an equivalent fraction and represent the new fraction in the fraction circle.
Fill in the boxes to make an equivalent fraction.
Write two equivalent fractions that can represent the shaded part of the figure.
Divide and color in the bars to make two equivalent fractions. Then, write the equivalent fractions on the line.
Solve the problem.
9. One lap around a certain track is 1 16 of a mile. After running 12 laps, what fraction of a mile have you run? Color in the fraction bar. Then write two equivalent fractions.
11. Samuel then decides to add a book that weighs 1 2 a pound to the seesaw. How many 1 12 pound weights should he add to the other side to balance the seesaw? Solve.
10. Samuel put a book that weighs 5 6 of a pound on one end of a seesaw. How many 1 12 pound weights should he put on the other end to balance the seesaw?
Daily Review Complete the equivalent fraction.
Learn and Connect
Ben made a cheesecake for his family on Monday. He cut the cake into 16 equal pieces. By Friday, his family had eaten all but 4 pieces of the cheesecake. What fraction of the cheesecake remains?
To solve, we need to create a fraction by making the numerator the number of cheesecake pieces that remain and the denominator being the total number of pieces that made up the entire cheesecake.
Remaining pieces
Total pieces
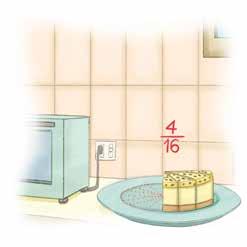
To write this number in simplest form, we need to find a common factor for both the numerator and the denominator. Then, we divide both numbers by that factor.
Factors of numerator: , ,
Factors of denominator: , , , ,
There is of the cheesecake remaining.
Apply
Simplify each fraction.
Simplify each fraction and represent both fractions in the fraction model.
Simplify each fraction.
Simplify each fraction and draw a visual representation to match the simplest fraction.
Solve the problem.
Kayla is trying to balance weights on a scale. She only has weights in 1 8 s and 1 16 s. What are two ways that she can balance the scale?
Challenge
Solve each problem.
11. Steven is running a 24-mile race. He has already run 10 miles. How much of the race has he completed? Express your answer as a simplified fraction.
12. Nathan has been working on a worksheet with 20 problems for 2 days. He has finished 12 of the problems. How much of the worksheet has he completed? Express your answer as a simplified fraction.
Chapter 7-4 Comparing and Ordering Fractions
Daily Review Find a common multiple for each pair of numbers.
1. A common multiple of 4 and 6 is
Learn and Connect
2. A common multiple of 15 and 22 is
3. A common multiple of 3 and 25 is
Mr. Williams gave three students each a card with a fraction written on it. He asked the students to stand in order from greatest to least. What is the order they should stand in?
Since the fractions have different denominators, they are cut into different sized pieces. This makes it difficult to compare them. One way to compare the fractions is to use benchmark numbers. Benchmark numbers tell us how close the fractions are to 0, 1 2 , or 1.
The denominator in the fraction tells us how many pieces we need to make 1 whole. Determine how many pieces we need to make 1 whole and half for each fraction.
1

Then, determine if the numerator is closer to 0, 1 2 , or 1 whole. Notice that 5 8 is closer to 1 2 because 5 is closer to 4 than 8. Since 1 is closer to zero than 6, 1 12 is closer to zero, and 9 10 is closer to one whole. Therefore, student C should be first in line, followed by student A, and then student B.
Apply
Use benchmark numbers to determine if the fraction is closer to 0, 1 2 , or 1.
Compare fractions by shading the figures or plotting the number line. Use the following symbols: < , > , = .
Use benchmark numbers to determine if the fraction is closer to 0, 1 2 , or 1.
Compare fractions by shading the figures or plotting the number line. Use the following symbols: < , > , = .
Challenge
Place the following fractions on the number line in order from least to greatest.
Chapter 7-5 Decomposing Fractions
Daily Review Circle the group that is in order from least to greatest. Then, put the other groups in the correct order from least to greatest.
Learn and Connect
Emma has 6 8 of a pizza left and wants to share it with a few friends. However, she’s not sure how many friends will eat pizza, so she wants to be ready with all the possibilities.
Emma needs to decompose or break down the fraction 6 8 into smaller parts. Think about how many fractions with the same denominator can be added together to give us 6 8 .
6 8 = 3 8 + 3 8 If Emma has two friends eating pizza, each person will get 3 8 .
What if Emma has three friends who want pizza? What are three fractions that can be added to make 6 8 ? What other ways can you decompose 6
Apply
Decompose each fraction below in two different ways and show each combination in the fraction bar.
Use benchmark numbers to determine if the fraction is closer to 0, 1 2 , or 1.
Compare fractions by shading the figures or plotting the number line. Use the following symbols: <, >, =.
Add each fraction to a number line and compare.
Decompose the fractions.
Solve the problem.
Tim wrote this equation, but it is not correct. How can he correctly decompose 5 8 into 3 fractions and show it using fraction bars? There is more than one correct answer.
Tim’s Equation: 5 8 = 5 8 + 0 8 + 1 8
How many different ways can you decompose 8 9 ? Write the equations and pick one of the ways to show visually in fraction circles.
Chapter 7-6 Improper Fractions
Daily Review Color in the bars to make equivalent fractions. Then write the equivalent fraction on the line.
Learn and Connect
We know that in a fraction, the numerator shows us how many parts are being used, and the denominator shows us how many parts make up the whole. What happens when the numerator is larger than the denominator?
This is known as an improper fraction. When we have an improper fraction, it means we have at least one whole plus a part.
Lets see what 5 3 of a circle looks like.
Apply
Label each part in the fraction circle. Write the number of wholes and the fraction left. Then, write the improper fraction.
To show 5 3 of a circle, we need two whole circles divided into 1 3 pieces. We shade in 5 of those parts. Wholes: Fraction:
Vocabulary
Improper Fraction - a fraction that has a numerator equal to or larger than the denominator
Write the improper fraction that matches the fraction circles in each row.
Show the improper fractions on the fraction bars.
Solve each problem.
8. The bakery cuts their cakes into fourths and sells them by the slice. If you want 2 whole cakes and 1 extra slice, how many slices do you need to buy?
Draw a picture to explain.
9. A school brought some cases of water bottles on trip. Each case comes with 12 water bottles. After the trip, there were 31 water bottles left. Write how many cases of water bottles are left as an improper fraction. Draw a picture to explain.
Challenge
Solve the story problem.
10. Donna ordered 4 pizzas for her family, which were cut into 8 slices each. There were 2 slices left over after dinner. How much pizza did Donna’s family eat? Show the amount as an improper fraction.
Chapter 7-7 Mixed Numbers
A mixed number has both a whole number and a fraction part. Mixed numbers show a whole of something and a part of another whole being used. We can switch between improper fractions and mixed numbers without changing the value.
To change an improper fraction to a mixed number, we can divide.
Learn and Connect Apply Daily Review
• Divide the numerator by the denominator
• The quotient becomes the whole number
• The remainder becomes the numerator of the fraction, with the same denominator as the improper fraction
To change a mixed number to an improper fraction, we can use the MAD method. M - Multiply A - Add D - Denominator
Vocabulary
Decompose the fractions in two different ways.
Change these improper fractions to mixed numbers.
Solve the story problem.
Sara is putting away blocks on the shelves. She has 20 blocks, and each shelf holds 6 blocks. How many shelves will she fill? Write the answer as a mixed number.
Solve the story problem.
Lisa was baking, and the recipe called for 3 1 2 cups of flour. She wants to use her 1 2 measuring cup to measure the flour. How many 1 2 cups of flour will Lisa need? Write the answer as an improper fraction and a mixed number. Draw a visual to show your work.
Solve the story problem.
12.
Joshua is making cookies for his class. He has to make two batches so everyone can have one. In the first batch, he adds 1 1 4 cups of chocolate chips. In the second batch, he adds 16 12 cups of chocolate chips. Are the amounts of chocolate chips in both batches equal? Show each batch visually and explain your answer.
Daily Review
Learn and Connect
Timothy is looking at the whiteboard in school. He says the shaded fraction represented is 1 3 2 . Andrew say it represents 7 3 . Who is correct?
What is the improper fraction of 1 3 2 ?
What is the mixed number of 7 3 ?
Who is correct?
Apply
Determine if the fractions are closer to 0, 1 2 or 1. Write the whole and half for each fraction. 1.

Complete the chart with the picture form, written form, and fractional form of each fraction.
Convert the mixed numbers and improper fractions. Draw an image to represent the fraction.
Vocabulary
Create factor trees or factor ladders and write the prime factors as an equation.
Simplify the fractions.
Shade and compare the fractions by using >, <, =.
Add each fraction to a number line and compare.
Danny is trying to decompose the fraction 5 11 in two different ways. Correct his work and show the combinations in the fraction bar. There is more than one correct answer.
Mrs. Williams accidentally dropped a few fraction cards. Help her put these cards back in order from least to greatest before class starts.
Sara has 11 classmates. Each of them gave her 1 4 of their chocolate bar. How many chocolate bars does Sara have in total? Write the number as an improper fraction and a mixed number.
If Sara wants to give away 3 4 of a chocolate bar to 3 friends, how many pieces would each friend get so that they all get an equal amount?
Chapter 8
In Chapter 8, we will learn how to
Add, Subtract, and Multiply Fractions
Many measurement problems, such as with cooking, length, and time, involve fractions.
• Add and subtract fractions with like denominators
• Add and subtract mixed numbers with like denominators
• Problem solve with fractions
• Multiply fractions by a whole number
We can add and subtract fractions and mixed numbers with like denominators.
We can use models and number lines to multiply a fraction by a whole number.
We can solve word problems with addition, subtraction, and multiplication of fractions.
Chapter 8-1 Adding and Subtracting Fractions with Like Denominators
Learn and Connect
Mr. Smith had 9 12 of a carton of eggs left in the refrigerator. He used 4 12 to make egg salad. What fraction of Mr. Smith’s eggs were left in the refrigerator?

Starting fraction:
Fraction to subtract:
We can use a number line:

We can also subtract the numerators of fractions with the same denominators. Put the difference over the same denominator.
9 12 � 4 12 = (9 � 4) 12 = 5 12 Mr. Smith has of a dozen eggs left.
Apply
Use the fraction models to write the equations and solve. Then, reduce the fractions.
Vocabulary
Numerator - top number in a fraction; shows how many parts
Denominator - bottom number in a fraction; shows how many parts make up the whole
Difference - answer to a subtraction problem
Add the fractions using the number lines. Reduce the fractions to their simplest terms.
Add or subtract the fractions. Then, reduce them to their simplest terms.
Solve. Reduce the fractions to their simplest terms.
Marc is cooking. He used 2 8 of a cup of chopped onions when he first started cooking. When he was almost done, he added 4 8 more of a cup of chopped onions. How many cups of onions did he use in his dish?
Nick runs 1 mile every week. On Monday, he ran 2 6 of a mile. On Tuesday, he ran 3 6 of a mile. How far did he run on Wednesday to reach his goal of running 1 mile?
Mr. Levine’s stamp collection is made up of liberty stamps and flag stamps. 2 5 of his collection is liberty stamps. How much of his collection is made of flag stamps?
Jack needs to walk 8 10 of a mile to get to school. He has already walked 3 10 of a mile. How much farther does he need to walk to get to school?
Andrew ate 1 8 of the pizza. Paul ate 3 8 of the pizza. How much of the pizza did they eat altogether?
There is 7 8 of the pie left. James ate 2 8 of it for lunch. How much pie is left now?
Chapter 8-2 Adding Mixed Numbers
Daily Review Add or Subtract. Reduce the fractions to their lowest terms.
Learn and Connect
Charlie works at the pizza parlor on the weekends. He worked 1 2 2 hours on Friday and 1 2 3 hours on Sunday. How many hours did he work altogether?
Hours worked: Friday: Sunday: + = ?
Add
Then add the whole numbers. Combine the whole numbers and the fractions to simplify the answer.
Charlie worked hours over the weekend.

Use the fraction models to write the equations and solve. Reduce to their
Vocabulary
Mixed number - a whole number with a fractional part
Use the number line to solve each equation. Reduce the fractions to their simplest terms.
Create a model or number line to add the mixed numbers. Reduce the fractions to their simplest terms.
Hint: 3 3 = 1 whole
Solve. Show your work by drawing models or number lines to support your solutions.
Eddie grows sunflowers. 2 3 5 acres of his field is made up of yellow sunflowers. 1 2 5 acres of his field is made up of orange sunflowers. How many acres of his field are used for growing sunflowers?
Leo and Steven are going on a trip. Leo’s suitcase weighs 4 4 8 kgs. Steven’s suitcase weighs 5 2 8 kgs. What is the total weight of their suitcases?
Chapter 8-3 Subtracting Mixed Numbers
Daily Review Reduce the fractions to their simplest terms.
Learn and Connect
Mike is a house painter. He has 8 4 8 gallons of paint. He used 6 2 8 gallons of paint. How much paint does Mike have left?
Which operation will we use to find how many gallons are left?
Subtract the fractions.
Subtract the whole numbers.
Reduce the fraction.
Apply

Mike has gallons left.
Use the fraction models to write the equations and solve. Reduce the fractions to their simplest terms.
Use the number line to solve each equation. Reduce the fractions to their simplest terms.
2. Create a model or number line to subtract the mixed numbers. Reduce the fractions to their simplest terms.
Solve. Show your work by drawing models or number lines to support your solutions.
Mannie bought 8 5 6 pounds of fruit. He used 5 3 6 pounds of the fruit to make a fruit salad for the fourth grade class picnic. Then, he used 2 1 6 pounds of fruit to make fruit cups for snack time. How many pounds of fruit does he have left? 9.
Victor has 12 7 8 gallons of gas in his car. He drove to work and used 5 3 8 gallons of gas. How much gas does he have left?
Solve. Write the strategy you used.
Chapter 8-4 Fraction Story Problems with Addition and Subtraction
Daily Review Compare each set of fractions using <, >, or =.
Learn and Connect
David collected 2 4 8 pounds of fruit for his class. He also received a donation of 1 6 8 pounds of fruit. How many pounds of fruit will he have for his class?
This fraction is made up of BOTH a mixed number AND an improper fraction. Change the improper fraction to a mixed number and add again.
Can you reduce this fraction? YES!

Apply
Use the fraction models to solve. Reduce fractions to their simplest terms.
1. 2.
A family is eating pizza for dinner. Six large pizzas are cut into 8 slices each. On Monday night they ate 2 7 8 . On Tuesday they eat 2 3 8 .
David will have pounds of fruit. Adam's father drove him 3 4 6 miles from his house to school. He decided to walk the rest of the way, which was 1 5 6 miles. What is the distance from Adam’s house to school?
How much of the pizza did they eat?
Draw the rest of the models.
How many slices do they have left over?
Solve. Show your work with fraction models and/or equations. Reduce the fractions to their simplest terms.
James has 7 10 pounds of apples. Peter has 6 10 pounds of apples, and Sam has 8 10 pounds of apples. How many pounds of apples do they have altogether?
David is building a model of a skyscraper. He has 4 1 8 pounds of clay. He needs 8 7 8 pounds of clay. How much more clay does he need?
Solomon can’t work more than 19 8 10 hours per week. On Monday, he worked 6 hours. On Tuesday, he worked 5 4 10 hours. On Wednesday, he worked 4 3 10 hours. How many hours can he work on Thursday without going over 19 8 10 hours?
The cows on the farm eat cow feed 4 times per day. At 8:00 am, they eat 4 12 of a ton of feed. At 12:00 pm, they eat 6 12 of a ton of feed. At 4:00 pm, they eat 7 12 of a ton of feed. At 8:00 pm, they eat 9 12 of a ton of feed. How much feed do they eat per day?
Eddie spent 4 1 4 hours reading on Monday. On Wednesday, he spent 3 3 4 hours reading. How many hours did he spend reading altogether?
John runs 2 7 8 miles every week. On Tuesday, he ran 7 8 of a mile. He ran 6 8 of a mile on Wednesday. How many more miles does he have left to run to meet his weekly goal?
Kane needs to order tiles. He has 1 9 10 square feet of tiles already. He needs 2 7 10 to complete the project. He can order 2 sizes of packages. Circle the size he should order.
Ben poured 5 12 gallons of paint into an empty container. Charlie poured 2 12 gallons of paint into the same container. Howard also poured 3 12 gallons of paint into the container. How much paint is in the container? Why is your choice the better estimate? 4 10 9 10
Daily Review Reduce each fraction to its simplest term.
Learn and Connect
David bikes 3 8 of a mile to and from school. How far does he bike to school in two days? How far does he bike in three days? The word ‘of ’ in the word problem is a key word that tells us to multiply. We can write the distance David rides in two days as 2 × 3 8 of mile.
When we multiply fractions by a whole number, we can create fraction models to help us.
2 × 3 8 or 2 groups of 3 8 looks like this: 1 8
How many are shaded altogether? Shade the models to show 3 × 3 8 . Simplify your answer by converting your improper fraction to a mixed number. Written as a mixed number =
Divide 9 by 8.
The answer is 1 R1.
Create a fraction. The remainder becomes the numerator. The denominator is the same as the improper fraction.
Draw models to help you solve. Simplify the products. Write improper fractions as mixed numbers.
Draw a model to represent each equation. Solve the equations. Change all improper fractions to mixed numbers and simplify.
Match the model with the correct equation.
Challenge
Solve the story problem. Draw models to help you solve. Simplify your answer by changing the improper fraction to a mixed number.
Fred had 3 buckets of water that were 3 4 full, and Gary had 2 buckets of water that were 7 8 full. Who had more water?
Daily Review Add or subtract. Reduce fractions to their simplest forms.
Learn and Connect
We can use a number line to find 3 × 3 8 .
When we multiply 3 × 3 8 , we are adding 3 groups of 3 8 . This is repeated addition.
Start at 0 and make 3 8 sized jumps. We land on 9 8 .
How many parts are between each arrow?
Change 9 8 to a mixed number =
Use the number line to solve 5 × 3 4 = ? and simplify your final product. How many parts are between all 3 arrows? 3 × 3 8 =
A) How many parts are between each arrow?
C) Change your improper fraction to a mixed number =
Apply
B) How many parts are between all 5 arrows? D) 5 × 3 4 =
Use the number line to solve. Simplify the products.
Solve. Create a number line for each equation. Simplify the products.
Fill in the blanks to complete the equations. Use the number line to help you solve.
× 8 ×
Solve by drawing a number line. Simplify your answers.
Fred had 6 pounds of cashews. He gave away 1 3 of his cashews to his brother. How many pounds of cashews did he give away?
Challenge
Eddie ate 5 6 of a cup of popcorn. Jamie ate 7 times more popcorn. How many cups of popcorn did Jamie eat?
Solve by drawing a number line. Simplify your answer.
11. Aaron ran 8 miles on Monday. On Tuesday, he ran 1 2 of the amount of miles he ran on Monday. How many miles did he run on Tuesday? How many miles did he run altogether?
Learn and Connect
Solomon is filling 2 buckets with the apples he is picking. He puts 3 8 of a pound of apples in each bucket. How many pounds of apples has he picked?
Step 1: Rewrite the whole number as a fraction over 1
Step 2: Multiply the fractions straight across


Step 3: Simplify!
Between what two whole numbers does your answer lie? 0 and 1 or 1 and 2? Why? Because each bucket is less than half full.
We solved 2 × 3 8 = . Now, let’s use the steps to solve 3 × 4 7 .
Step 1: Rewrite × = ?
Step 2: Multiply:
Apply
Read and use the steps to solve.
1. 2. Leo is making a mural. He uses 3 5 of a sheet of metal on each part. He is making 5 parts. How many sheets of metal will Leo use?
Step 3: Simplify =
Eli spends 7 hours doing homework. Eitan spends 1 4 of that time completing his homework. How much time does Eitan spend doing his homework?
5 × 3 5 = ? 7 × 1 4 = ? Rewrite: Rewrite:
Solve. Use the “rewrite, multiply, and simplify” strategy.
Read, solve, and simplify. Write all improper fractions as mixed numbers.
Charlie owns a bakery. He sells 6 times as many donuts as he does cupcakes. Today, he sold 5 8 of a tray of cupcakes. How many trays of donuts did he sell?
Solomon feeds each of his kittens 2 3 of a cup of cat food every day. He has 8 kittens. How many cups of cat food does he feed his kittens per day?
Between what two whole numbers does your answer lie?
Yesterday, David read for 6 hours. Paul reads 1 2 as many hours as David did. How many hours did Paul spend reading yesterday?
Between what two whole numbers does your answer lie?
Howard is making fruit mix for his friends. He uses 1 3 of a cup of apples in each fruit mix. He has 9 friends. How many cups of apples does he use?
Mr. Levine gave Ben 1 3 4 yards of cloth. Ben bought 4 4 yards more of cloth. Mr. Levine gave Robert 11 4 yards of cloth. Comparing the amounts of cloth, does Ben have more cloth than Robert? Why or why not?
Daily Review Reduce the fractions to their simplest terms.
Learn and Connect
Three boys were doing their homework after school. The boys wanted to know who had the largest fraction.
Charlie added 5 8 + 2 8 .
Sam added 1 6 + 2 6 .
Peter added 6 12 + 3 12 .
Help the boys find out who has the largest fraction. Don’t forget to simplify when you can!
Add the fractions:

Put the fractions in order from least to greatest: Plot the simplified fractions on the number line below.
Who has the largest fraction?
Add or subtract to solve. Reduce the fractions to their simplest terms.
Add or subtract to solve. Reduce the fractions to their simplest terms.
Multiply. Reduce the fractions to their simplest terms.
Read, write the equation that matches the story, and solve. Reduce the fractions to their simplest terms.
Peter has 4 5 of a pound of strawberries. James has 3 5 of a pound of strawberries. Robert has 2 2 5 pounds of strawberries. How many pounds of strawberries do they have altogether?
Kane studied for 4 3 4 hours. Solomon studied for 2 1 4 hours. How many more hours did Kane study than Solomon?
Richard sold 8 flower arrangements on Monday. On Wednesday, he sold 1 2 as many flower arrangements. How many arrangements did he sell on Wednesday?
Challenge
Paul owns a 6-acre farm. 2 5 of the farm is used to grow corn. 3 5 of the farm is used to grow okra. How many acres has he used?
17. Harry put 1 4 cup of candy into the jar. He needs 8 times more candy to fill the jar. How many more cups of candy does he need to fill the jar?
Write the equation that matches the problem and solve.
Which model matches the solution?
What equation does the other model represent?
In Chapter 9, we will be introduced to
Decimals
Decimals are another way to write fractions and can be a helpful way of showing exact amounts.
• Understand decimals
• Name the place value of decimals
• Add fractions with denominators of 10 and 100
• Compare and order decimals
• Locate decimals and fractions on a number line
We can show decimals with models and number lines.
We can write parts of a whole as a decimal, as a fraction, and in word form.
We can find equivalent denominators to add fractions with denominators of 10 and 100.
We can use place value to compare and order decimals.
Chapter 9-1 Introduction to Decimals
Daily Review
Compare each fraction with <, >, or =.
Learn and Connect
Decimals are another way to write fractions with denominators of 10 or 100.
Fractions with denominators of 10:
Number of tenths
Number of tenths
Fractions with denominators of 100:
Number of hundredths
Number of hundredths
Number of wholes
6 10
1 1.6
Number of wholes
Decimal point
45 100
Number of wholes
0.45
Decimal point
Dennis took two tests today. He did not have enough time to finish either test. Write the amount of questions Dennis finished with words, fractions, and decimals.
Math Quiz:
Dennis finished 9 out of 10 questions.
Fraction: of the questions
Word Form: nine tenths of the questions
Decimal: 0.9 of the questions
Apply
Complete the table.
We read decimals and fractions the same way. For example, 45 100 and 0.45 are both read as forty-five hundredths.
Science Test: Dennis finished 93 out of 100 questions.
Fraction: of the questions
Word Form: hundredths of the questions
Decimal: 0.93 of the questions
Write each number as a fraction and a decimal. Match to the correct letter on the number line.
Seven hundredths
Fraction: Decimal: Letter on the number line:
Three tenths
Fraction: Decimal: Letter on the number line:
Sixteen hundredths
Fraction: Decimal: Letter on the number line:
Identify the missing fraction or decimal. Shade in the value shown by each number.
Write the total value in dollars as a fraction and a decimal.
13. What is the total value represented in problems 10 - 12 written as a fraction and a decimal?
Chapter 9-2 Place Value with Decimals
Learn and Connect Daily Review
With a 4 in the tens place.
With a 6 in the hundreds place.
724.124
This number is read as seven hundred twenty-four AND one hundred twenty-four thousandths.
Use the word AND to separate the values after the decimal point.
7 is in the hundreds place
2 is in the tens place 4 is in the ones place
Say “AND” at the decimal point.
1 is in the tenths place (0.1) 2 is in the hundredths place (0.12) 4 is in the thousandths place (0.124)
Vocabulary
Decimal
Identify the digit in each place.
4,556.123
tens place: ones place: tenths place: hundredths place: thousandths place:
Write the value of each digit.
6,354.245
tens place: thousands place: ones place: hundreds place: tenths place: hundredths place: thousandths place:
Write each decimal in word form. Example:
of the 8:
Write a decimal for each number.
Chapter 9-3 Adding Fractions with Denominators of 10 and 100
Daily Review
Compare each set of fractions using <, >, or =.
Learn and Connect
Eli and and his brother Josh found some spare change in their room. Eli found 3 dimes, and Josh found 30 pennies. How much of a dollar did each boy find? Who has more money? How much money do they have altogether?
How many dimes are in a dollar?
Write a fraction to show how many dollars 1 dime is worth.
How many pennies are in a dollar?
Write a fraction to show how many dollars 1 penny is worth.
Eli found 3 dimes, or 3 10 of a dollar. Josh found 30 pennies, or 30 100 of a dollar.
We can solve in two ways.
When we add fractions, they must have the same denominator!
We can see that Eli and Josh have an equal amount of money. Eli’s 3 sections are equal to Josh’s 30 sections, 3 10 = 30 100 . They have 60 100 or 6 10 of a dollar altogether.
Write an equivalent fraction with a denominator of 100.
Use the model to find the missing number.
Write an equivalent fraction with a denominator of 10 and 100.
Write an equivalent fraction to solve.
Draw a line to match the model to the correct equation.
Solve and make a visual model to represent each problem.
11. 12. There are two worms in the park. One is 53
cm long, and the other is 6 10 cm long. What is the total length of both worms?
A plant in the greenhouse grew 97
in one day, 9 10 cm the next day, and 4 10 cm the third day. What’s the total amount the plant grew in three days?
Chapter 9-4 Decimal Practice: Tenths and Hundredths
Daily Review
Write the place value of the underlined digit.
Learn and Connect
Look at the images on the right to see what happens to the place value when we divide a digit by ten.
What is the place value of 1?
What is the place value of 0.1?
What happened when we divided by 10?
When we divide a digit by 10, it becomes one place value smaller.
What is 0.01 ÷ 10? Ones Place Tenths Place
Apply
Circle the place value that correctly identifies the place value of the quotients.
Color in the amount shown.
Vocabulary
Solve.
Mickey planted 100 flowers in his garden. 34 flowers have started to bloom. Write the amount of flowers that have started to bloom as a fraction, a decimal, and in written form.
When all the flowers in Mickey’s garden bloom, there are 57 red flowers, and the rest are white. Write the amount of red flowers as a fraction, a decimal, and in written form.
Draw an X over the fraction or decimal in each row that doesn’t fit. Match to the correct picture. Color in the amount shown.
4 100 0.4 four hundredths 0.4 ÷ 10
Use the hundreds flat to explain how 0.60 = 0.6.
Create a visual model to show the equation 0.6 + 0.5 = 1.1
Chapter 9-5 Comparing Decimals
Name the place value of the underlined digit in each number.
Learn and Connect
When comparing decimals, start with the whole numbers and work your way down to the right.
5.63 and 7.39 7.39 > 5.63 because 7 wholes is greater than 5 wholes.
0.08 and 0.06 0.08 > 0.06 because 8 hundredths is greater than 6 hundredths.

and
because 2.4 are the same, but the digits in the hundredths place are different, and 8 is greater than 5.
Apply
Compare the two decimals and complete the statement using >, < , or =.
1. 5.35 5.87
4. Howard and Danny went fishing. Howard’s fish weighs 8.72 pounds. Danny’s fish weighs 8.27 pounds. Whose fish weighs more? How do you know? 5. Shade in the two models and compare.
Vocabulary
Decimal point - a point (small dot) used to separate the whole number part from the fractional part of a number
Compare each set of decimals using <, >, or =.
Order each decimal group from least to greatest.
9.3 6.89; 6.98; 6.90 0.57; 0.75; 0.05 11.05; 11.45; 11.04 6.51; 6.5; 6.05
Select one of the problems from 1-8 above and draw a visual model to represent your answer.
Fill in the amount shown.
Solve each problem.
Henry is measuring earthworms he digs up in his backyard. The first worm he found was 3.96 inches long. The second worm he found was 2.99 inches long. Which worm is longer?
Challenge
Amy and Kayla each went through an obstacle course at the park. Amy took 56.55 seconds, and Kayla took 56 1 2 seconds. Who completed the obstacle course in less time?
John is planning a hike with his friends. He wants to do the longest route. Which route should he choose?
Stone Creek: 2.66 miles
River Bank: 2.64 miles
Flat Rock: 2.24 miles
Draw a visual model that explains why 5.06 is less than 5.6.
Chapter 9-6 Locating Decimals and Fractions on a Number Line
Compare the decimals using <, >, or =.
Learn and Connect
Sarah has 0.3 feet of blue ribbon and 0.17 feet of red ribbon. Help her plot the lengths of ribbon on the number lines.
Step 1: Find two wholes that the decimals are between.
Both 0.3 and 0.17 are
Step 2: Make a number line that shows all the tenths between those two wholes.
Step 3: Find two tenths that the decimal is between.
Step 4: Make a number line that shows all the hundredths between those two tenths.
Circle 0.3 and 0.17 on the number lines. Which ribbon is bigger? How do you know?
Plot the fractions on the number line.
Rewrite the fractions as decimals and plot them on the number line.
Identify the points.
Change the improper fractions to mixed numbers and plot them on the number line.
Measure each of the ribbons to the nearest tenth cm using the number line.
Learn and Connect
Donna is trying to put the following decimals in order from smallest to largest: 1.01, 0.14, 1.41 Let’s follow the steps to help Donna.
Step 1: Write the numbers by lining up the decimal points vertically. Use a place value chart to help.
Step 2: Start on the left with the largest place value and compare numbers. The smallest value here will be the smallest number between the different numbers you are comparing.
Step 3: Look at the remaining numbers. If all the whole numbers are the same, go to the next place value to the right of the decimal point, the tenths place.
Step 4: Keep moving right one place value at a time until you have compared all digits. Rewrite the numbers in order.
Let’s plot these numbers on a number line to double check: Smallest to largest , , Plot the following fractions on the number line below.
0.14 The digit in the ones place is 0.0, which is smaller than 1, so this decimal, 0.14, is the smallest of the three.
The digits in the tenths place are 0 and 4. 0 tenths is smaller than 4 tenths.
is the next number in order.
Put the decimals in order from smallest to largest. Then, plot them on a number line.
Order each decimal group from smallest to largest.
0.24, 2.42, 0.42
0.3, 0.03, 3.00
Order each decimal group from largest to smallest.
0.01, 1.05, 0.15
8.97, 4.06, 9.15
0.07, 0.77, 0.7 0.7, 0.49, 0.74
0.55, 5.0, 0.45 0.08, 8.88, 0.88
Circle the answer that has the numbers in order from smallest to largest.
9.1, 8.55, 8.9, 8.89
Explain how you found your answer for problem 9 and plot the decimals on the number line below.
Solve.
Ben has three boxes of different sizes to hold his piles of marbles by weight. He must put the lightest pile in the smallest box and the heaviest in the largest box. The piles weigh 2.165, 2.156, and 1.256 pounds. Which pile goes in which box?
Order these decimals from largest to smallest and draw a picture to explain: 80.479, 800.479, 8.047, 0.847, 4.479 9.1, 8.9, 8.55, 8.89 8.9, 8.89, 9.1, 8.55 8.55, 8.9, 8.89, 9.1 8.55, 8.89, 8.9, 9.1
Daily Review
Write the digit found in each place for 734.57
ones tenths tens hundredths
Learn and Connect
At a local fishing contest last week, the goal was to catch the largest fish.
Order the fish from the smallest to the largest.
Plot each of the weights on the number line.
Apply
Shade in the correct amount to show each decimal.
Write a decimal for each number.
Write each decimal in word form.
Identify the place value that is underlined in each number.
Compare each set of decimals using <, >, or =.
Show both fractions on the grid and write an equivalent fraction to solve.
Write the answer to problem 9 as a decimal and in word form.
Write the following numbers on the number line and write their fraction or decimal equivalents.
0.3 = 21.32, 31.23, 20.11
Order each decimal group from smallest to largest.
Two friends went to the store. Tim has 3 quarters, 4 dimes, 2 nickels, and 4 pennies. Abe has 5 quarters, 1 dime, 3 nickels, and 12 pennies.
How much money does each boy have?
Which boy has more money to spend at the store?
Chapter 10
In Chapter 10, we will learn about
Geometry
Geometry is important because the world is made up of different lines, angles, and shapes.
• Identify points, lines, line segments, and rays
• Label angles
• Measure and draw angles
• Solve for the unknown angle
• Identify perpendicular, parallel, and intersecting lines
• Classify triangles and quadrilaterals
We can draw and label points, lines, line segments, and rays.
We can find the angle of a fraction of a circle and identify it as acute, right, or obtuse.
We can use a protractor to measure and draw angles.
We can add or subtract to solve for an unknown angle.
We can identify if lines are parallel, perpendicular, or intersecting.
We can classify different types of triangles and quadrilaterals according to the measure of their sides and angles.
Chapter 10-1 Points, Lines, Line Segments, and
Learn and Connect
Line
Line Segment
Ray
A straight path that extends indefinitely in both directions
Part of a line that has two endpoints
Part of a line that has one endpoint and the other side extends indefinitely
• Locations on a map
• Bullet points for a list
• The equator
• Timelines
• Part of a ruler
• A city block
• Light coming out from a flashlight
• Laser beam
Draw and label the figure. Write the geometric term that matches what you draw.
Use the figure below to answer the questions.
Name all the points that lie on AC:
Name any three line segments:
Name any endpoints on a line in the figure:
Name a ray in the figure:
Write the geometric term for each figure.
5. Name any two lines:
Name five different line segments in each line.
Chapter 10-2 Types of Angles
15)1,260
Learn and Connect
An angle is the space between two straight lines when they meet at a common point. Angles are measured in degrees (°) of a circle.
An angle that creates a square corner is a right angle. A right angle measures 90°. In the example below, it is written as <XYZ.
An angle that has a measure less than 90° is called an acute angle. In the example below, it is written <ABC.
An angle that has a measure greater than 90° is called an obtuse angle. In the example below, it is written as <JKL.
The vertex is the point in which the two rays meet. Circle the letter that represents the vertex in each angle above.
Angles can be seen in our everyday lives. One way we use angles is to help us build streets and cities.
Take a look at this community map. Can you spot the different types of angles used to build the neighborhood?
Write the name of the figure.
Identify each angle as acute, obtuse, or right.
3. Acute angle <JKL 4. Obtuse angle <XYZ 5. Right angle <LMN 6. Obtuse angle <QRS
For each shape, count the number of obtuse (O), acute (A), and right (R) angles.
Draw and label the figure. Challenge
Rationalize whether each statement is true or false.
16. A square only has right angles.
A square has four vertices (vertex).
18. A parallelogram always has three acute angles.
Daily Review
Write acute, obtuse, or right to tell which type of angle is shown.
Learn and Connect
Angles are measured in degrees. A circle is 360 degrees. One degree in a circle is equal to 1 360 .
In this image, the circle is split into four parts. The number line below also shows 360 split into four equal parts. What similarities do you notice?
Don’t forget! Whatever you do to the denominator, you must also do to the numerator!
The highlighted portion of the clock is 1 4 of the entire clock or circle. What angle do the minute and hour hand make on the clock? A right angle. Since all the way around the circle is 360 degrees, to find how many degrees is 1 4 of the circle, write 1 4 as a fraction with the denominator 360.
To solve for the number of degrees within a circle:
Step 1: Divide 360 by the denominator. 360 ÷ 4 = degrees
Step 2: Multiply the quotient by the numerator.
Step 3: Check to see if your answer matches the type of angle you see (acute, obtuse, or right).
Find the measure of the angles.
How many degrees would you turn the oven dial to set the oven to Med- high?
If you start facing north (N) and then you turn to your right until you are facing southeast (SE), how many degrees did you turn?
How many degrees does the hour hand of the clock turn between 7:00am and 10:00am?
Hint: First, find the fraction. There are 12 numbers on the clock. How many twelfths does the hand move? (Can you reduce the fraction?)
Chapter 10-4 Measuring and Drawing Angles
Daily Review
Parallel lines
Sketch an example of each of the vocabulary terms.
A ray
Intersecting lines
An angle is formed when two lines meet at a shared point. We measure angles in degrees, which is represented by the symbol “ ° ” next to a number.

Obtuse angle: More than 90°
To measure an angle, you can use a tool called a protractor.
Learn and Connect Apply

Right angle: Equal to 90°
The sum of all of the angles of a triangle is equal to 180 degrees.

Acute angle: Less than 90°
Line up the bottom of the protractor to one of the lines related to the angle you are trying to measure. The number that the opposite line points to tells you the degree of the angle.
Identify the type of angle and its measurement.
Use your protractor to find the type and measurement of the angle.
Vocabulary
Identify the type of angle and its measurement.
Type of Angle:
Measurement:
Type of Angle:
Measurement:
Type of Angle:
Measurement:
Type of Angle:
Measurement:
Type of Angle:
Measurement:
Type of Angle:
Measurement:
Use your protractor to find the type and measurement of each angle.
Type of Angle:
Measurement:
Type of Angle:
Measurement:
Type of Angle:
Measurement:
Type of Angle:
Measurement:
Type of Angle:
Measurement:
Type of Angle:
Measurement:
Daily Review
1. 6
Factors:
Write the factors and first four multiples for each number.
Multiples:
Learn and Connect
2. 8
Factors:
Multiples:
Morris is moving into a new house. He tilted his couch 110 degrees off the ground to fit through a doorway, but it did not fit. After he took a few measurements, he realized he needed to lift it a total of 155 degrees to fit through.
Which equation will tell us the measure of the additional angle, a, that Morris needs to lift his couch to reach 155 off the ground?
A) 155 + 90 = a B) 180 − 110 = a
C) 155 − 110 = a D) 155 + 110 = a
The figure to the right helps us visualize the angle of the couch. In order to find the missing angle, a, we need to subtract.
155 − 110 = a a = degrees

We can use the inverse operation, addition, to check our work.
a + 110 = 155 + 110 = 155
Apply
Label the figure below and write the equation that will help you find the missing angle. Then, solve for the missing angle.
1. A crocodile wants to eat a duck. He can open his mouth at an angle of 25 degrees. In order for the duck to fit in his mouth, he needs to open it up to 65 degrees. What is the additional angle that the crocodile needs to open his mouth for the duck to fit?
Solve for the missing angle.
What is the value of d?
What is the measure of z? Hint: y is a right angle.
What is the measure of y?
Two angles join to form a 120° angle. The first angle measures 60°. What is the measure of the second angle?
Two angles that have the same measurement join to form a right angle. What do both angles measure to be?
Three angles join to form a 150° angle. The first angle measures 45°. The second angle measures 80°. What is the measure of the third angle?
Three angles join to form a 166° angle. The first angle measures 90°. What are two different possibilities that the other two angles might measure to?
Choose the best estimate for the measurement of the angles below.
Challenge
Which equation will tell us the measure of x?
Choose one answer:
Solve for x:
Which type of angle is x? How do you know?
Daily Review
Determine if the angle is acute, obtuse, or right.
A line is a straight path that goes on in either direction indefinitely. There are different types of lines, such as parallel lines, perpendicular lines, and intersecting lines.
Parallel Lines Lines that never touch
Everyday Examples:
• Train tracks
Learn and Connect Apply

Perpendicular Lines
Lines that cross and make right angles

Everyday Examples:
• Window panes
Intersecting Lines
Lines that cross but do not make right angles
Everyday Examples:
• Scissors

Label each pair of lines as parallel, perpendicular, or intersecting. Draw each type of
Intersecting Lines
Parallel Lines
Perpendicular Lines
Circle the statement(s) that appears to be true.
A) KL is parallel to MN.
B) KL is perpendicular to OP.
C) KL is parallel to OP.
D) KL intersects MN and OP.
A) WX is perpendicular to YZ.
B) WX intersects YZ.
C) UV is parallel to YZ.
D) UV is perpendicular to WX.
Write three true statements about the figures below.
A) PQ is parallel to TU.
B) RS is parallel to TU.
C) PQ is parallel to RS.
D) RS intersects PQ.
Draw a picture that includes: 1 set of parallel lines, 2 sets of perpendicular lines, 3 intersecting lines. Label each part.
For each shape, count the number of obtuse (O), acute (A), and right (R) angles.
Learn and Connect
An art teacher asked her students to create an animal out of quadrilaterals. One student created a penguin. How many quadrilaterals did the student use to create the image? A quadrilateral is a 2-dimensional, 4 sided figure that is closed. The shapes below are all quadrilaterals:
Some quadrilaterals have special names that can be identified by their unique characteristics.

Trapezoid
One pair of opposite sides is parallel.
Rhombus
Opposite sides are parallel, all sides are equal; similar to a tilted square.
Square
Opposite sides are parallel; all sides are equal, and all angles are right angles.
Rectangle
Opposite sides are equal and parallel; all angles are right angles.
Parallelogram
Opposite sides are equal and parallel; opposite angles are equal.
Triangles come in many different sizes. You can distinguish the type of triangle by its angles and the length of its sides.
Equilateral triangle
All three angle measurements are equal. All three sides lengths are equal.
Circle all the quadrilaterals below.
Circle all the parallelograms below. 1. 2.
Isoscelas triangle
Two angle measurements are equal. Two sides lengths are equal.
Scalene triangle
None of the angle measurement or side lengths are equal.
Classify each of the shapes in the table below. Look at row 1 for an example.
Label the triangles below as scalene, isosceles, or equilateral based on their sides or angles.
Rationalize whether each statement is true or false.
15. A square is always a rectangle.
16. A square is always a rhombus.
17. A parallelogram is always a rectangle.
Learn and Connect Apply Daily Review
Sketch two examples of each of the vocabulary words below.
1. Parallelogram 2. Quadrilateral 3. Trapezoid
Use the map to help you answer the following:
Name two roads that are not perpendicular.
Algebra Ave and Geometry Street are roads.
Subtraction Street and Geometry Street are roads.
Algebra Avenue and Polygon Place are roads.
Name a road that Algebra Avenue is perpendicular to.
Which roads intersect with Mathematics Way?
Name a road that is parallel to Bar Graph Boulevard.
Write two true statements about 1st street.
Solve for the missing angle. Identify the missing angle as acute, obtuse, or right.
What is the value of w? What is the value of s?
Two angles join to form a 115 degree angle. The first angle is a right angle. What is the measure of the second angle?
Identify the angle measurement and type of angle (acute, obtuse, right).
Type of Angle:
Measurement: Type
Identify if the triangle is equilateral, isosceles, or scalene.
Type of Triangle: Type of
Draw a line to match the quadrilateral with its definition.
It has opposite sides that are parallel and equal in length
It has four right angles and two sets of sides equal in length
It has four sides all equal in length and four right angles
It has four sides equal in length and two sets of parallel lines
It is a quadrilateral with exactly one pair of parallel sides
This angle cuts out 1 2 of the circle. Find the measure of the angle.
This angle cuts out 1 9 of the circle. Find the measure of the angle.
So, the measure of the angle is = =
So, the measure of the angle is
Chapter 11
In Chapter 11, we will learn about
Measurement
Understanding the U.S. customary measurement system is important for accurately describing the size of objects or liquids.
• Estimate and convert length
• Find area and perimeter
• Estimate and convert weight
• Estimate and convert liquid capacity
We can understand the relative sizes of measurements in the U.S. customary measurement system. We can convert between different units of measurement. We can compare measurements and solve word problems with measurement.
Chapter 11-1 U.S. Customary Measurement: Length
Daily Review
Classify the triangles by side.
Learn and Connect
We can measure length using a ruler, a yardstick, or a tape measure. There are two measurement systems that we use to measure length: Customary and Metric. In the United States, most of our measurements are in Customary Units.
Match each object to the tool you would use to measure it.

Tape measures can be different lengths. They can be anywhere from 5-50 feet long.
Anthony needs to cut a board that is 9 feet in length; however, his tape measure only has inches listed. How many inches are in 9 feet? Complete the table to find the answer.
There are inches in 9 feet. Anthony needs to measure inches.
Apply Check the best estimate for the length of each object.
Vocabulary
Inch - a unit of measurement that is equal to 2.54 centimeter, 1 12 of a foot, or 1 36 of a yard
Foot - a unit of measurement that is equal to 1 3 of a yard, 30.48 centimeters, or 12 inches
Yard - a unit of measurement that is equal to 3 feet or 36 inches
Match the item with the unit of measurement best used.
garden shed
domino
inches
Complete the conversion tables. Circle the larger measurement.
Ned and Sam saw a six-foot long snake at the zoo. How long is the snake in yards?
Fill in the table with items that would be best measured in inches, feet, yards, or miles.
Tom has to cut a piece of wood that is six inches. What fraction of a foot is that?
Chapter 11-2 Converting and Estimating Length
Fill in the conversions below.
Learn and Connect
Chad is building a garden box. Each side is 35 inches, so he will need 140 inches of lumber. The lumber yard only sells boards by the foot. About how many feet of wood will Chad need to build his garden box?
First, we need to know that inches are in a foot.
Divide when converting from a smaller unit (in) to a larger unit (ft).
Multiply when converting from a larger unit (ft) to a smaller unit (in).
Chad is converting inches to feet. Should he multiply or divide?
140 inches ÷ 12 = or feet and inches.
About how many feet of board will Chad need? feet of board.
Apply
Convert each of measurements below. Check off if you will multiply or divide.
Estimate the best answer for each conversion.
Vocabulary
Inch - a unit of measurement that is equal to 2.54 centimeter, 1 12 of a foot, or 1 36 of a yard
Foot - a unit of measurement that is equal to 1 3 of a yard, 30.48 centimeters, or 12 inches
Yard - a unit of measurement that is equal to 3 feet or 36 inches Daily Review
When you estimate, round to the nearest whole number.
Convert each measurement. Circle the operation you used.
= The
Circle the best estimate.
of a window
The distance around a backyard
The length of a crayon
The width of a bookshelf
The length of a school bus
Convert.
Estimate the best answer for each conversion. 12 inches = 1 foot
Who is the tallest? Show your work.
Chapter 11-3 Area and Perimeter
Daily Review
Round each number to the highest place value.
Sunnyside Elementary is building a new playground. They are planning to create a fenced area with a play area inside.
Look at the map to find the area and perimeter of this new play area.
Perimeter - Add all the sides together to find the amount of fencing needed. P = l + l + w + w
15 + 27 + 15 + 27 = feet
Area - Multiply the length and width together to find the amount of space for playing. A = l × w
15 � 27 = ft2
Learn and Connect Apply

Find the perimeters (length + length + width + width). Write the equation you used.
Find the areas (length × width). Write the equations you used.
Find the area and perimeter of each shape.
Solve each problem.
Circle the figure that has a greater perimeter.
A bedroom door is 3 ft wide and 8 ft tall. What is its area?
Each side of a square painting is 3 ft. long. A frame shop charges $3.00 per foot for a frame. How much would it cost to buy a frame for the painting?
The materials to build Fred’s backyard deck cost $88.00 per square meter. The deck is 8 meters wide and 12 meters long. How much will it cost to build his deck?
A rectangular concrete patio has an area of 70 square meters. Its perimeter is 34 meters. What are the dimensions of the patio?
Find the area and perimeter of each of these rectangles. What do you notice? Can you draw a similar example?
Learn and Connect
We measure weight, or how heavy an object is, in ounces, pounds, and tons. To weigh an object, we use a scale. Ounces measure very light objects, and tons measure very heavy objects!
Fill in tons, pounds, or ounces to label the most accurate unit to measure weight for each object.
Jake has a large stack of books he wants to store on a shelf. The shelf can hold 6 pounds total. He weighs the books on his scale, and they measure 80 ounces. Can the shelf hold his books? Complete the conversion table to help solve the problem.
80 ounces = pounds. That means that the shelf CAN / CANNOT hold the books.
Draw a line from the object to the scale that would measure them.
Use the pictures to help convert pounds to ounces.
Circle the best unit to measure each object.
Fill in the blanks with an object you would measure with each unit.
Convert the measurements. Use the conversion table to help.
96 ounces = pounds
Solve. Use the conversion table to help you. A feather Ounces:
1 pound = ounces 32 ounces = pounds 64 ounces = pounds
At the Bronx Zoo, a baby chimpanzee was born weighing 80 ounces. How many pounds did it weigh at birth?
The zookeeper at the Bronx Zoo weighed Max the manatee, and he weighed one ton. How much does he weigh in pounds?
Hint:
Numerator = number of ounces
Denominator = 16 (The number of total ounces in a pound)
Complete the conversion tables to help you place each tile on the number line.
Chapter 11-5 Converting and Estimating Weight
Daily Review
Learn and Connect
Arnold wanted to enter one of his pumpkins in the county fair. He needed to pick his largest pumpkin. His dad picked up one pumpkin and weighed it at 160 ounces. His largest pumpkin so far is 11 pounds. Is this pumpkin lighter or heavier than 11 pounds?
First, we need to know that ounces are in a pound.
Divide when converting from a smaller unit (oz) to a larger unit (lbs). Multiply when converting from a larger unit (lbs) to a smaller unit (oz).

Arnold is converting ounces to pounds. Should he multiply or divide?
160 ounces ÷ 16 = How many pounds is Arnold's pumpkin? pounds.
Arnold's pumpkin (IS/IS NOT) larger than his 11 pound pumpkin.
Apply
Convert each of measurements below. Check off if you will multiply or divide.
pounds = 16 ounces
pounds = ounces
Estimate the best answer for each measurement.
× 16 = A baby kitten A dump truck full of rocks
Vocabulary
Convert using multiplication or division. Circle the operation you used.
8,000 lbs = T
Complete the conversion table.
Compare the measurements using <, >, or =. Use the conversion tables or multiplication/ division to help you.
8,000 = 2
Anthony wanted to enter the largest pumpkin in the county fair. Which pumpkin should Anthony enter? Use the conversion tables. Show your work.
Hint: The first two you solved in the Learn and Connect Section
The weights of Anthony's pumpkins
1) 11 pounds
2) 160 ounces
3) 10 pounds, 12 ounces
4) 11 1 4 pounds
5) 174 ounces
6) 10 1 2 pounds
Chapter 11-6 U.S. Customary Measurement: Liquid Capacity
Daily Review
96 feet = yards
Learn and Connect
Draw a line to the most accurate unit of measurement.
72 inches = yards
5 yards = inches
Eddie has a bottle that holds 1 quart of juice. How could he represent 1 quart using smaller units of liquid capacity? Use the diagram above to help you.

Apply
Use the diagram to write equivalent units.
Vocabulary
Ounce - a unit of measurement for liquids that is equal to 1 16 of a pint
Cup - a unit of measurement for liquids that is equal to 8 fluid ounces
Pint - a unit of measurement for liquids that is equal to 16 ounces or half a quart
Quart - a unit of measurement for liquids that is equal to two pints or a quarter of a gallon
Gallon - a unit of measurement for liquids that is equal to four quarts or eight pints
Circle the best estimate for the unit
Use the pictures to complete the conversions.
Complete the conversion table.
Convert using the conversion table or the liquid capacity diagram.
Aaron just bought a gallon of milk, and it has a crack. Milk is starting to leak out. He needs to transfer it to another container, but he doesn’t have any other gallon jugs. Circle the containers he could use to hold his gallon of milk.
Chapter 11-7 Converting and Estimating Liquid Capacity
Daily Review
Convert the measurements.
Learn and Connect
Leo and Nick are helping their grandfather harvest honey. They both have different jars and are working to gather the honey together.
Leo fills 3 pints and 4 cups. Nick fills 2 quarts and 2 cups.
Who filled more? First, we need to have all of the measurements in the same unit. It is easiest to convert to the smallest unit. What is the smallest unit they used?
Divide when converting from a smaller unit (c) to a larger unit (pt).
Leo is converting pints to cups. Should he divide or multiply?
(pints) × (cups in a pint) = cups
Now, add for the total number of cups.
cups + cups = 10 cups for Leo
Multiply when converting from a larger unit (qt) to a smaller unit (c).
Nick is converting quarts to cups. Should he divide or multiply?
(quarts) × 2 (pints in a quart) × (cups in a pint) = cups
Now, add for the total number of cups .
cups + cups = 10 cups for Nick
Leo has collected cups of honey, and Nick has collected cups of honey.
Apply
Convert. Circle which method to use, multiply or divide.
1 gallon = 16 cups 5 gallons = cups Multiply or Divide
× 16 =
or Divide
Convert using multiplication or division. Circle the operation you used.
Fill in the missing labels.
Compare the measurements using <, >, or =. Use the diagram or multiplication/division to help you.
Examine the diagram above for liquid conversions. It looks similar to fractions. You can represent quarts, pints, cups, and fluid ounces as fractional parts of a gallon. Write each unit as a fraction and then use your best estimate to place each unit on the number line below. Quarts = Pints = Cups = Fluid Ounce =
The amount of units you have (1)
The total amount in a gallon
Daily Review
Complete the conversions.
Learn and Connect
Andrew and Dennis brought drinks down the hill to the picnic area. Together, they brought down 1 gallon of lemonade, 6 quarts of water, and 8 juice boxes that held 8 fluid ounces.
How much liquid in total did they bring down the hill?
How many quarts are in a gallon? Circle those quarts to show they make a gallon. Is it possible to make a gallon with the other units? How many cups makes up a quart? . Put a box around each quart you can make with the juice boxes.
How many quarts do we have now? Is it enough to make a gallon?
Andrew and Dennis brought down total gallons.
If a gallon of liquid weighs about 8 pounds, and their table holds 320 ounces, will their table hold all the drinks?
Complete the reference charts.
Use the pictures to help solve each problem.
Solve each problem by converting the measurements.
Paul ran 10 yards. How many feet did he run?
Ann has 3 quarts of lemonade. How many pints does she have?
The table is 60 inches long. How many feet is that?
A bus weighs about 20,000 pounds. How many tons is that?
Richard needs 2 cups of tea. How many fluid ounces is that?
Jack’s book bag weighs 6 pounds. How many ounces is that?
Challenge
12. A different cutting board also has an area of 80 square inches but a different perimeter. What are two possibilities of the dimensions and perimeter of the cutting board? 13.
The perimeter of a rectangular cutting board is 36 inches. The area is 80 square inches. What are the dimensions of the cutting board?
inches by inches
Chapter 12
In Chapter 12, we will expand on
Measurement and Geometry
The metric measurement system is an easy system to use and is used all over the world.
• Estimate and convert length
• Estimate and convert weight
• Estimate and convert liquid capacity
• Estimate and convert time
• Find elapsed time
• Find lines of symmetry
• Problem solve
We can understand the relative sizes of measurements in the metric measurement system.
We can convert between different units of measurement, including time.
We can compare measurements and solve word problems with measurement.
We can find the elapsed time from two analog clocks or a word problem.
We can find and count lines of symmetry. We can solve measurement word problems with whole numbers and fractions.
Chapter 12-1 The Metric System: Length
Daily Review
Solve the problems.
Learn and Connect
The metric system is a system of measurement that uses units based on ten. The meter is the base unit for metric length and is made up of 100 centimeters. Here are some examples to show each unit of metric length.
The tip of a sharp pencil is about 1 millimeter in length.
A door is about 1 meter in length. There are 100 centimeters in 1 meter.
Apply
Which unit would you use to measure?
Length of a pencil
Distance to your friend’s house
Convert the measurements.
How many meters is 500 centimeters?
Hint: 500 ÷ 100 = ?
Circle the better estimate.
A staple is about 1 centimeter in length. There are 10 millimeters in 1 centimeter.
A long road bridge could be about 1 kilometer in length. There are 1,000 meters in 1 kilometer.
How many millimeters are in 3 centimeters?
Hint: 10 x 3 = ?
Thickness of a credit card
How many meters are in 8 kilometers?
Hint: 8 x 1,000 = ?
Match each item with the best estimate of its length.
Length of a glue stick Distance from home to school Length of a sailboat Length of a fly
Fill in the tables to convert the measurements.
Use <, >, or = to compare the measurements.
Challenge
Solve the story problem.
Aaron measured his pencil and said that it was 12 centimeters long. Jacob measured his pencil and said that it was 120 millimeters long. Whose pencil is longer? How do you know?
Chapter 12-2 The Metric System: Weight
Daily Review
Solve the problems.
Learn and Connect
We can measure the weight of items in the metric units kilograms, grams, and milligrams
There are 1,000 grams in a kilogram and 1,000 milligrams in a gram.
If the potatoes on the scale weigh 3 kilograms, how many grams do they weigh?
Hint: 3 × 1,000 = ?
If one small potato weighs 85,000 milligrams, how many grams does it weigh?
Hint: 85,000 ÷ 1,000 = ?
Apply
Circle the better estimate.
Circle the greatest measurement.

Fill in the tables to convert the measurements.
Match each item with the best estimate of its weight.
20 milligrams A classroom chair 20 kilograms Travel-sized tube of toothpaste 20 grams A fly
Fill in the tables to convert the measurements.
Use <, >, or = to compare the measurements.
3,150 milligrams 3 kilograms
1,500 milligrams 1 gram
5,000 kilograms 5,000 grams
3,000 milligrams 70 grams 4 grams 4,000 milligrams 7 kilograms 6,500 grams 2,000 milligrams 2 grams 4,000 milligrams 4 kilograms
Challenge
Solve the story problem. The weight limit on the food scale is 5 kilograms. Could you weigh 3,250 grams of nuts on the scale? How do you know? 12.
Chapter 12-3 The Metric System: Capacity
Daily Review
Solve the problems.
Learn and Connect
Capacity is how much liquid a container can hold. The metric units of capacity that we will use are liters and milliliters.
A mason jar and a large can of tomatoes each hold about 1 liter.
A 1 4 tsp holds about 1 milliliter.
There are 1,000 milliliters in a liter.
How many milliliters are in 2 liters? 5 liters?
How many milliliters is 4 liters? 8 liters?
How many liters is 3,000 milliliters? 7,000 milliliters?
Apply
Which unit would you use to measure each? Circle liters or milliliters.
To convert from milliliters to liters, multiply by 1,000. To convert from liters to milliliters, divide by 1,000.
Circle the better estimate.
Fill in the table to convert the measurements.
Which unit would you use to measure each? Circle liters or milliliters.
Fill in the table to convert the measurements.
Use <, >, or = to compare the measurements.
4,250 milliliters 4 liters
1,750 milliliters 2 liters
700 milliliters 0.7 liters
Solve the problem.
Chad and Leo each poured some water into their measuring cups. Chad had 1,800 milliliters in his cup. Leo had 2 liters in his cup. Who had more water? How do you know?
Challenge
Solve the story problem.
Moses has 3 containers of milk in his fridge, one with 4 liters, one with 3,000 milliliters, and one with 5 liters. Which container has the most milk in it? How many liters of milk does he have in all?
Learn and Connect
The flight from New York to Virginia will take 2 hours and 36 minutes. How many minutes will it take to arrive in Virginia?
1 hour = minutes
2 hours = minutes
120 minutes + 36 minutes = minutes

The trip will take minutes.
Hint: You need to multiply!
Solve the conversions. Show your work.
2 days = minutes
9 hours = minutes
Solve the word problems. Show your work.
Leo practiced playing the piano for four days. He practiced for a total of two hours and 20 minutes. He played the same amount of time every day. How many minutes a day did he practice?
Challenge
Solve the story problem.
It took a carpenter a week and two days to complete a woodworking project. He only worked for six hours each day. He charges 50 dollars per hour. How much should he bill his client?
288 hours = days
Eric’s birthday is January 15. He is 12 years old. He thinks that when he turns 13, he will have been alive for 4,745 days. Is he correct? 1 2 minute = seconds 4 years = days
Find the mystery time. I am less than one week. I am between two and five days. I am three times as many as 1,674 minutes.
I am days, hours, and minutes
Learn and Connect Daily Review
Find the equivalent amount of time.
1. 840 hours = weeks 2. 18 weeks = days 3. 4 days = minutes
When we solve for the elapsed time, we are finding the amount of time that passes between one time and another time.
What is the time on Clock A?
What is the time on Clock B?
How much time has elapsed between Clocks A and B?
Today, we will use a number line as a strategy to help us solve the elapsed time between Clock A and Clock B.
1. Put the start time on the number line.
Apply
2. Hop forward using the largest unit of time that you can until you reach the end time. (1 hour, 1 2 hour, 10 min, 5 min, 1 min.)
3. Add the amount of time you jumped forward.
Solve for the elapsed time between Clocks A and B. Create a number line to solve.
What is the time on Clock A?
What is the time on Clock B?
How much time has elapsed between Clock A and B?
Solve for the elapsed time between Clocks A and B. Create a number line to solve.
What is the time on Clock A?
What is the time on Clock B?
How much time has elapsed between Clocks A and B?
B
Solve.
Sam starts from home at 6:30 a.m. to get to school by 7:25 a.m when school starts. School is eight hours long. What time will school be over?
A train arrived at 11:30 a.m. in the morning after a 120-minute journey from its last stop. When did it leave its last stop?
Who started the earliest?
Max 1 hour 56 minutes 7:15
David 2 hours 5 minutes 7:45
Robert 8:30 9:27
Ben 1 hour 12 minutes 7:15
Challenge
Four boys tracked the time they spent on homework. Fill in the missing times. Answer the questions. Solve the riddle.
I am between 7:30 and 1:50.
I am more than 20 minutes past the hour.
My number of minutes is a multiple of 4.
My number of hours is a factor of 24. I am 3 hours and 56 minutes earlier than 4:28.
Which clock am I?
Who spent the shortest amount of time on homework?
Convert the measurements.
1. 4 liters = milliliters 2. 2.5 liters = milliliters 3. 6,000 milliliters = liters
Learn and Connect
A line of symmetry is a line that divides a shape or object into two identical parts. If you were to fold the shape on the line, it would match up perfectly.
Some shapes have multiple lines of symmetry. How many lines of symmetry can you find?
Apply
Is the line a line of symmetry? Circle Yes or No.
Write how many lines of symmetry each shape has. Draw the lines of symmetry.
Is the line a line of symmetry? Circle Yes or No.
Write how many lines of symmetry each shape has. Draw the lines of symmetry.
Challenge
Draw and label a rectangle that is 4 cm tall and 8 cm long. Then draw all the lines of symmetry on your rectangle.
The lines of symmetry cut your rectangle into how many smaller rectangles?
The smaller rectangles are each: cm tall and cm long.
Daily Review
Change the mixed numbers to improper fractions.
Learn and Connect
The Andersons' yard is 6 meters wide by 9 meters long. Their neighbor’s yard is 2 3 the width and 2 3 the length of their yard. How many centimeters wide and long is their neighbor’s yard?
Step 1
Find 2 3 of 6m
6 1 × 2 3 = 12 3 or 4m
Find 2 3 of 9m
9 1 × 2 3 = 18 3 or 6m
Step 2
Convert Meters to Centimeters 4m × 100 = cm
6m × 100 = cm
The neighbor’s yard is cm wide and cm long.
Apply
Solve the word problems.
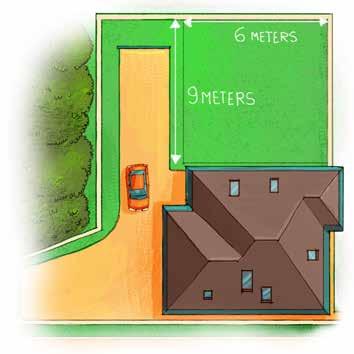
Hint: Use the table below to help you convert metric measurements.
Metric Length 1 meter = 100 cm 1 cm = 10 millimeters
Metric Weight 1 gram = 1,000 milligrams 1 kilogram = 1,000 grams
Metric Capacity 1 liter = 1,000 milliliters
We can get the same answer if we convert the measurements before or after solving, but sometimes it is easier to do it in a specific order.
1. 2. Robert practices playing the piano for an hour a day on Mondays, Wednesdays, and Fridays. How many minutes does Robert play the piano in 2 weeks?
Dennis has 3 liters of juice in a large jug. If he divides the juice equally among 6 cups, how many milliliters of juice are in each cup?
Step 1
How many hours of piano a week? 2 weeks?
Step 2
Convert to minutes:
Step 1
Convert liters to milliliters:
Step 2
Divide by 6: 3,000 ÷ 6 =
Solve the word problems. Show your work.
Ben’s water bottle is 24 centimeters tall. David’s water bottle is 3 4 as tall as Ben’s. How many millimeters tall is David’s water bottle?
Steven had a wooden board that had a length of 1 meter and 20 centimeters. He cut the board into 4 equal pieces. How long was each piece?
Answer: millimeters
A bag of potatoes weighs 6 kilograms. A bag of grapes weighs 1 4 of the weight of the bag of potatoes. How many grams does the bag of grapes weigh?
Answer: centimeters
There are 4 containers of milk in the refrigerator that hold 2 liters of milk each. How many milliliters of milk are in the refrigerator?
Answer: grams
There are 28 days in February. It took 1 2 of the month for the tomato plant to sprout. How many minutes did it take for the plant to sprout?
Answer: millimeters
Jack has 810 milliliters of water and 575 milliliters of sports drink. Max has 2 liters of water. Who has more to drink?
Answer: minutes
Answer: has more to drink.
Mike and Eric kept track of how long they jogged last week and this week. Mike jogged for 1 1 3 hours last week and 1 3 4 hours this week. Eric jogged for 200 total minutes. Who jogged longer? Show your work.
Answer: jogged longer
Learn and Connect
Which unit would you use to measure how much milk to feed a newborn baby?
Which unit would you use to measure the length of the school building?
Which unit would you use to measure how much your friend weighs?
Which unit would you use to measure the thickness of a credit card?
Which unit would you use to measure the weight of a 1 4 tsp of salt?
Fill in the tables to convert the measurements.
Use <, >, or = to compare.
4,250 grams 5 kilograms
1,500 milliliters 1.5 liters
50 kilometers 5,000 meters
Solve the word problems. Show your work.
Justin gets on the school bus at 6:45 am. He is on the bus for 1 hour and 35 minutes. He arrives at school exactly as the first bell is ringing. What time does the first bell ring?
Tim spends 5 hours on homework each week? Steven spends 1 4 of the time that Tim spends on homework. How many minutes does Steven do homework each week?
The first bell rings at
A 6-year-old boy is 1.1 meters tall. His 2-year-old brother is 0.7 meters tall. How many centimeters taller is the 6-year-old than his brother?
Henry’s bucket holds 5 liters. Donald’s bucket holds 3 4 as much as Henry’s. How many milliliters does Donald’s bucket hold? 1 day 1,440 minutes 7 centimeters 68 millimeters 1 week 150 hours
minutes
Chapter 13
In Chapter 13, we will work with
Data
We will learn how to organize and graph information we collect about the world.
• Create and interpret bar graphs, picture graphs, and tally graphs
• Create and interpret frequency charts
• Create and interpret dot plots with and without fractions
• Create and interpret line and double-line graphs
We can understand the relationship between bar graphs, picture graphs, tally graphs, and frequency charts.
We can use a dot plot to understand data and create a dot plot from a frequency chart.
We can create dot plots with fractions.
We can draw a line graph and double-line graph given a frequency chart.
Chapter 13-1 Bar Graphs, Picture Graphs, and Tally Charts
Learn and Connect
Today, Sam, the mailman, delivered mail to five streets in my neighborhood. The picture graph, bar graph, and tally chart below show how many pieces of mail were delivered to each street.
Apply
Use the picture graph to make a tally chart and answer the questions.
Vocabulary
= Mail = 1 stamp
1. How many stamps were sold on Wednesday? 2. How many stamps were sold during the week in total?
3. On what day of the week were the most stamps sold?
Picture Graph - a graph that shows data on a chart using pictures or symbols to represent the data collected Bar Graph - a graph that shows data with rectangular bars that are the height or length of the number value they represent Tally Chart - a chart that has vertical dashes that represent one occurrence of information. For every five occurrences, a diagonal line is drawn through the four vertical lines
Look at the data in the graphs below. Answer the questions that follow.
1. Hours it takes to deliver mail
2. Number of boxes received per week
Week 1
Week 2
Week 3 Week 4
Week 5
Week 6
A) Which mailman delivered mail the fastest?
B) How many hours did it take mailman 4 to deliver mail?
C) What was the average of all five mailmen's delivery times?
A) In which week were the most boxes received?
B) How many boxes arrived in week 6?
C) How many boxes were received in total for all six weeks?
Make a picture graph, tally chart, or bar graph to show the information on each chart. Use a different type of graph for each question.
3. Stamps bought per hour 4. Monthly delivery totals
Chapter 13-2 Interpret Frequency Charts
Daily Review Find the areas and perimeters of the following shapes.
Learn and Connect
We can show the eye colors of students in our class on a picture graph and frequency chart. Both of these display the same information or data.
= 1 student
How many students have green eyes?
How many students are there in all?
Title - the main idea of the table
Picture Graph Frequency Chart
Categories - the type of data that the table shows Apply
Frequency means how often something happens.
How many students do not have blue eyes?
How many more students have brown eyes than green eyes?
Fill in the missing frequencies in the tables. Answer the questions.
Number of boxes of candy sold each day
Amount of time students spend reading
On how many days were 4 boxes of candy sold?
How many students spent 15 minutes reading?
Fill in the missing tally marks to match the frequencies given. Answer the questions.
How many roses were there?
Which flower appeared the least?
How many more daisies than lilies were there?
What was the total number of flowers?
Fill in the missing tally marks to match the frequencies given. Answer the questions.
What was the most common way to get to school?
What was the least common way to get to school?
How many students use transportation with wheels to get to school?
How many more students take the bus than use any other way to get to school?
Circle the best title. Explain.
A) Favorite Types of Music for Adults
B) Instruments Played in a Band C) Toy Store Gifts
D) Favorite Subjects in School
The fifth-grade students were asked to help the teachers determine which activities to include during Field Day this year. The results are shown in the table to the left.
Which activity received exactly half the number of votes as the Egg & Spoon Race?
make
Chapter 13-3 Create and Interpret Frequency Charts
How many more students are right-handed than left-handed?
Learn and Connect
How many students are there in all?
Henry took a poll in his class about everyone’s favorite jelly bean flavor. The results were as follows: cherry, cherry, lime, orange, lemon, orange, cherry, cherry, lime, orange, lemon, cherry, lemon.
Make a frequency chart to display the data.
Step 1: Set up the chart. Write the titles and label the columns.
Hint: there should be three columns, one for the category, one for the tallies, and one for the frequency.
Step 2: Add in the categories. In this case, flavors of jelly beans.
Step 3: Tally each category/flavor using a tally mark for each response.
Step 4: Count the number of tallies to find the frequency.

20 coin flips: heads, heads, heads, tails, heads, tails, tails, heads, tails, tails, heads, heads, tails, tails, heads, tails, heads, heads, tails, heads
20 spinner results: red, red, blue, blue, green, red, blue, yellow, green, yellow, blue, green, red, yellow, yellow, blue, green, red, red, blue
Use the data to answer the questions.
Ages of students in a high school band: 14, 18, 15, 16, 17, 18, 16, 15, 17, 15, 16, 17, 14, 16, 18, 14, 15, 17, 15, 18, 16, 17, 14, 15, 16, 18, 14, 17, 18, 15
Complete the frequency table.
How many students are over 15?
How many students are under 15?
How many students are there in the band?
Colors of T-shirts in a drawer: green, green, black, black, black, black, green, blue, green, white, white, black, white, blue, green, white, black, blue
Complete the frequency table.
How many T-shirts are in the drawer?
What is the most common T-shirt color?
How many T-shirts are not black or white?
Ice cream survey data.
Vanilla, chocolate, vanilla, mint, chocolate, vanilla, mint, vanilla, mint, chocolate, vanilla, vanilla, chocolate, mint, mint, vanilla, vanilla, chocolate, chocolate What was the least common flavor?
Create a frequency table to show the data. How many more people got the most common flavor than the least common flavor?
Daily Review
Convert the following times into hours and minutes.
Learn and Connect
There were 18 families playing at the park. We can show the number of children in each family in the park on a frequency chart or a dot plot.
chart
The number line shows the number of children. Each dot represents 1 family with that many children. There are 5 families that each have 1 child.
The most common number of children per family is .
A flower shop collected data on what customers ordered. Use the dot plot to match the questions to the answers.
What information or data does the graph show?
What does each dot represent?
What does the number line show?
The number of flowers per bouquet
One bouquet of flowers Apply
How many flowers per bouquet each customer ordered
Answer the questions using the given dot plot.
An after-school program collected information about their students. The graph shows the ages of the students enrolled in the program.
How many students in the group are 8 years old?
How many more 11-year-olds are there than 8-year-olds?
Which ages have equal numbers of students?
How many students are there in all?
How many more 9-year olds are there than 11 year-olds?
A company surveyed its employees and asked, on average, how many minutes it takes them to commute to work in the morning. The results are shown on the dot plot below.
(minutes) Employee Commuting Time Survey Results
Commute to
How many people said it takes them an hour or more to commute to work?
How many people were surveyed?
Did more people say it takes them less than a half hour or more than a half hour to get to work?
What is the difference between the number of people who travel less than a half hour and the number of people who travel more than a half hour?
Write two statements that are true about the data shown in the dot plot above.
Use the dot plot to fill in the frequency table.
# of people
Daily Review Answer the questions about the frequency chart.
How many more people liked grapes than blueberries?
What was the least popular fruit?
How many people responded to the fruit preference survey?
Learn and Connect
A gardener collected data on her flowers as they grew. She recorded the heights of 30 flowers at the end of spring. She wants to create a dot plot to organize her data. Let’s walk through the steps to create the dot plot.
Heights of flowers in inches: 13, 13, 12, 12, 12, 12, 13, 11, 14, 12, 11, 14, 12, 13, 10, 12, 15, 11, 13, 14, 13, 13, 12, 11, 15, 12, 13, 15, 14, 10
Step 1: Use the smallest number, the minimum, and largest number, the maximum, of heights to create your number line.
Step 2: Add the dots to your graph. The dots represent the number of flowers for each height. Each dot represents the same amount.
Apply
Step 3: Finally, add a title to the graph and a label under the number line.
Fill in the missing dots, then add a title and a label.
Create a dot plot from the data.
Students in Mrs. Levine’s class were surveyed about the number of books they read each week. Make a dot plot that shows the results. Use the checklist to help you.
When creating your dot plot graph, make sure you include:
This data shows the student grades on a recent math test. Show the results on a dot plot.
70, 70,70, 75, 75, 80, 80, 80, 80, 80, 80, 80, 80 , 80, 80, 80, 90, 90, 90, 90, 90, 90, 90, 90, 90, 100, 100, 100
Use the data shown below to complete the frequency table and dot plot.
Ages of children at a park: 6, 7, 8, 6, 5, 7, 8, 10, 5, 6, 8, 7, 5, 10, 6, 12
Daily Review
Determine the time elapsed in each problem.
1. A lunch period starts at 11:45 and ends at 12:10.
2. A factory shift starts at 8:40 and ends at 4:15.
3. A family gets to a park at 2:37 and leaves at 4:23.
Learn and Connect
Eric wants to make a project out of his leftover scrap wood. In order to know how many pieces of wood he has and their lengths, he makes a dot plot. The lengths in inches of the leftover wood are:
1, 3, 3 1 2 , 2, 1 1 2 , 2, 4, 4, 1 2 , 1 2 , 2, 2, 3, 2 1 2
Put the numbers in order to find the minimum and maximum on Eric's number line.

If Eric skip counts by halves, he can show all the different lengths of wood on the number line.
s
Length of Wood (inches)
Use the dot plots to answer the questions.
Robert recorded the amount of pies that each person ate during the pie-eating contest. The results are: 2 3 4 , 3, 3 1 2 , 3 1 2 , 3 3 4 , 4, 4, 4 1 4 , 4 1 4 , 4 1 2
Write the minimum: 2. Write the maximum:
Which fraction does the dot plot use to skip count by?
Fill in the missing dots on the dot plot.
Contest
Number of pies
A tailor cut strips of fabric into various lengths in inches for a project. The lengths were as follows: 3 1 8 , 3, 3 3 8 , 3, 3 1 2 , 3 5 8 , 3 5 8 , 3 1 2
Write the minimum: 6. Write the maximum:
Which fraction does the dot plot use to skip count by? Fill in the missing numbers on the number line.
of Fabric (inches)
Create a dot plot for the data. Answer the questions.
The class was doing a donut taste testing. Each donut was cut into thirds so that students could taste multiple kinds. After the tasting was done, the teacher counted the donuts of the remaining flavors. The totals were as follows: 1 1 3 , 1, 1 3 , 1 2 3 , 2 3 , 1, 1, 2 3 , 1
What was the most common amount leftover?
How many flavors had 2 3 leftover?
How many total donut flavors were there?
In science class, the students were monitoring the lengths of caterpillars and got the following lengths: 1 4 , 1 4 , 1, 1 2 , 3 4 , 3 4 , 1, 1 4 , 3 4 , 1, 1 4 , 1 4 , 1 2 , 3 4
What was the most common length of a caterpillar?
What is the difference between the longest and shortest caterpillars?
If all the caterpillars were lined up in a line, how long would the line be?
Make a dot plot for the data, then answer the question.
George tested the battery life of 23 batteries and got the following results: 2 lasted 6 1 2 hours, 4 lasted 7 hours, 6 lasted 7 1 2 hours, 7 lasted 8 hours, 3 lasted 8 1 2 hours, and 1 lasted 9 hours.
How would the dot plot change if George tested 4 more batteries that have a lifespan of 7 1 4 hours?
Chapter 13-7 Interpret Line Graphs
Daily Review
In a recent poll of students' favorite lunches, it was found that 25 chose hotdogs, 8 chose pizza, 7 chose burgers, 6 chose sandwiches, and 4 chose salads.
1. What did half the students say was their favorite school lunch?
2. How many students voted in total?
3. How many students voted for pizza?
Learn and Connect
Farmers at Marble Hill have been measuring the growth of their sunflowers for the past five months. Look at the line graph to see how much they have grown. Then, answer the questions.
A) What month did the sunflowers grow the most in comparison to the previous month?
B) What is the range in growth?
C) How many inches did the sunflowers grow from May to July?
Apply
Use the line graph to answer questions 1-3.
How many inches of rain fell from March to August?
What month had the least amount of rain?
What was the average rainfall for all 6 months?
Vocabulary
Line Graph - a set of data that shows how something changes over time
Double Line Graph - a line graph that compares two things in the same scale and on the same graph
Growth of the Sunflowers in Inches
Look at the tables below. Create line graphs using the information in the tables.
Hint: Inches go on the y-axis, and days go on the x-axis.
Hint: Number of plants goes on the y-axis, and days of the week go on the x-axis.
Make a double line graph. Label the line to show the fruit it represents. Then, draw a second line to represent the other fruit.
Daily Review
Write tally marks to represent the following numbers.
Learn and Connect
Mrs. Brown’s class was cleaning out their desks. They decided to record how many of each supply they have in their desks. Use the table to make a bar graph and a frequency table.
School Supplies Students Have In Their Desks
Rulers 8
Pencils 12
Notebooks 15
Erasers 6
Sharpeners 4
Tally Number of Students
Total number of supplies
Write true or false by each statement: There are more notebooks in the students’ desks than all the other supplies combined.
The number of pencils is the same as the number of rulers and sharpeners combined.
Apply
Make a dot plot using the frequency table.
Fred went to the post office to mail packages to his family members. He weighed each package to make sure he added enough stamps to them.
for Family Members
When creating your dot plot graph, make sure you include:
Look at the charts below. Answer the following questions.
The frequency chart below shows the results from a survey given to students about what they prefer on the lunch menu at school.
A) What is the most frequent amount of minutes it takes for someone to walk to school?
B) How many students can walk to school in less than 9 minutes?
C) How many people walk for more than 10 minutes?
A) How many more students prefer pizza over salad?
B) Which two lunch choices combined received as many votes as pizza?
Create a line graph using the information in the table about the pounds of bananas sold at a grocery store over the span of several months.
A) How many students in grade 2 bring lunch?
B) How many students bring lunch in grades 1-5?
C) What grade has the least amount of students bringing lunch?
1.
Chapter 14
In Chapter 14, we will conclude with
Level D Review
This chapter includes all concepts covered in this book.
• Understand place value with large numbers and decimals
• Use all four operations with multi-digit numbers
• Add, subtract, and multiply fractions
• Compare, order, and find decimals on a number line
• Identify and solve for unknown angles
• Problem solve
We can identify place value from millions to hundredths. We can use all four operations to solve problems with multi-digit numbers.
We can add, subtract, and multiply fractions and mixed numbers and simplify our answers.
We can understand the size of decimals.
We can describe an angle as acute, obtuse, or right, measure angles, and find a missing angle.
We can solve multi-step word problems with all four operations.
Chapter 14-1 Place Value Review
Daily Review
Estimate the sums and difference: round to the nearest tens.
Learn and Connect
6,584,791 (six million, five hundred eighty-four thousand, seven hundred ninety-one)
6 is in the millions place (6,000,000)
5 is in the hundred thousands place (500,000)
8 is in the ten thousands place (80,000)
4 is in the thousands place (4,000)
7 is in the hundreds place (700)
9 is in the tens place (90)
1 is in the ones place (1)
6,584,791.032 DECIMALS!
0 is in the tenths place (0.00)
3 is in the hundredths place(0.03)
2 is in the thousandths place (0.032)
Apply
Write the digit in each place.
1. What number is in the millions place?
3. What number is in the hundred thousands place?
5. What number is in the ten thousands place?
7. What number is in the thousands place?
9. What number is in the hundreds place?
Vocabulary
MILLIONSHUNDREDTHOUSANDSTENTHOUSANDSTHOUSANDS
9,374,293. 473
2. What number is in the tens place?
4. What number is in the ones place?
6. What number is in the tenths place?
8. What number is in the hundredths place?
10. What number is in the thousandths place?
Decimal - the part of a number that shows a value smaller than 1 whole
Write the number in each place.
8,456,293. 839
1. What number is in the millions place?
3. What number is in the hundred thousands place?
5. What number is in the ten thousands place?
7. What number is in the thousands place?
9. What number is in the hundreds place?
Write the value of the number.
2. What number is in the tens place?
4. What number is in the ones place?
6. What number is in the tenths place?
8. What number is in the hundredths place?
10. What number is in the thousandths place?
Example: What is the value of the yellow 1? .01
6,235,247.218 428. 694
11. What is the value of the number 2?
12. What is the value of the yellow 4?
13. What is the value of the yellow 9?
61,234. 468
14. What is the value of the black 6?
15. What is the value of the number 1?
16. What is the value of the yellow 4?
17. What is the value of the yellow 6?
Write the mystery number.
18. What number has 8 ten thousands, 3 fewer thousands than ten thousands, 3 more hundreds than thousands, 6 fewer tens than hundreds and 6 fewer ones than ten thousands?
19. What number has 4 ten thousands, the same number of thousands as ten thousands, 4 more hundreds than thousands, 1 more ten than ten thousands and 3 fewer ones than tens? , ,
Chapter 14-2 Addition and Subtraction Review
Solve each problem and use addition to check your answers.
Learn and Connect
Moses and Arnold were thinking about where they wanted to go on vacation this year. Last year, their family went all the way to Charlotte, North Carolina. This year, they are hoping to go to Orlando, Florida. How much farther is the trip to Orlando?
How far is it to Charlotte? miles
How far is it to Orlando? miles
Will you add or subtract to find the difference?
Apply Daily Review
Hint: Remember to align the place values before subtracting.

Estimate each sum or difference and then solve for the exact answer.
There are 2,347 gallons of water in the swimming pool. Tom adds 5,995 gallons to the pool. How many gallons of water are in the pool?
In year 1, a factory built 91,395 model airplanes. In year 2, the factory built 154,637 model airplanes. In year 3, they only built 57,099 model airplanes. How many total model airplanes did the factory build?
There are 1,789 buildings in the town of Andersonville. If the planning committee wants to build 10 more buildings each year, how many buildings will they have in five years?
Isaac is saving his allowance to earn money for a new bike. The bike costs $175. If he earns $20 each week, how long will it take him to earn enough for the bike?
Chapter 14-3 Multi-Digit Multiplication Review
Learn and Connect Daily Review Use the patterns of multiplication to solve each problem.
The Williams School is planning an event for all its students and needs to buy supplies. Each box has a different amount of supplies. How many of each item will they have if they buy 12 boxes of each?
Will they have enough supplies for 500 students? If not, what will need more of?
Rewrite vertically, and then multiply.
There are 225 paperclips in each box. If you have 5 boxes, how many paperclips in total do you have?
An airplane can hold 343 passengers. How many passengers could 11 airplanes hold?
A jewelry company ordered 48 boxes of beads. They also ordered 30 boxes of clasps. Each box has 75 beads in it. How many beads did the company in total?
14. Judy has 175 blue popsicle sticks. She has 12 times as many green popsicle sticks as blue ones. She also has 14 times as many yellow popsicle sticks as blue ones. How many popsicle sticks does Judy have in all?
Anna’s printer can print 275 pages every 15 minutes. How many pages can it print in an hour? How many pages can it print in a day?
Chapter 14-4 Long Division Review
Daily Review
Multiply. Write the related division fact.
There is a sale at the local book store. Charlie can buy a set of 8 books for $248. There is another set of 5 books for $225. Which set has a better price per book?
To find the price of each book in the set of 8, divide by 8.
Solve below.
÷ = $
To find the price of each book in the set of 5, divide by . Solve below.
÷ = $
The set of is a better deal.
Learn and Connect Apply
Solve.

Use compatible numbers to estimate each division problem.
÷ 8 = about 5,400 ÷ 90 =
÷ 5 = about 6,400 ÷ 800 =
÷ 4 = about
Use the patterns of division to solve each problem.
÷ 100 =
Use mental math and divisibility rules to decide whether each quotient will have a remainder. Circle the correct choice and explain using divisibility rules to support your answer.
287 ÷ 3 = ? Remainder No Remainder
Explanation: Explanation:
3,981 ÷ 6 = ? Remainder No Remainder
4,345 ÷ 5 = ? Remainder No Remainder 429 ÷ 4 = ? Remainder No Remainder
Explanation: Explanation:
Solve.
Solomon owns a bakery. He wants to place newspaper ads about his bread. He has $360. Each ad costs $5. How many ads can he pay for?
Michael helped his grandfather box up 252 books to donate to four local libraries. If he put an equal amount in each box, how many books did he donate to each library?
Solve. Circle whether you should drop, use, or add the remainder.
849 students are going camping. They are taking boats to the lakeside. Each boat carries 9 people. How many boats do they need to order?
Charlie has 6,346 bottles of juice. He puts them in 6-packs. How many 6-packs did he make?
Leo’s bakery baked 2,579 cookies for the school bake sale. He sells the cookies in bags of 8. He gives any extra cookies to his brother. How many cookies will his brother get?
How many bags of cookies did he make to sell? Drop Use Add Drop Use Add Drop Use Add
Daily Review Complete the equivalent fractions.
Eric’s walk to school is 4 10 miles. Eric walked home from school and made a couple of stops on the way. Look at the map to compare how far he walked today compared to his usual route. Use <, >, or =.
How far was each section of Eric’s walk?
Add 3 10 + 4 10 + 1 10 =
Compare the total to his normal route.
Learn and Connect Apply
Write the multiplication equation and solve.
Joshua sold 2 pitchers of lemonade on Monday. On Tuesday, he sold 1 1 2 times as much as on Monday. How much lemonade did Joshua sell on Tuesday? 2.
Solve and shade in the fraction circles to represent the equation.
There are 18 grapes in the bowl. 1 3 of them are red. How many of the grapes are red? 3 × 1 2 =
Complete each equivalent fraction.
Compare the fractions below using <, >, or =.
Change the improper fractions to mixed numbers.
Add or subtract. Then simplify if necessary.
Solve each problem.
There are 12 cars in the parking lot. 1 3 of them are silver and the remaining are black.
How many cars are silver?
How many are black?
Challenge
There were 25 people waiting at the bus stop. It began to rain. 1 5 of the people took out their umbrellas just in time. How many people took out umbrellas?
Mrs. Miller drives 9 1 2 miles each way to get to school and home every day. In the mornings, she likes to stop at a coffee shop that is halfway to school.
A) How far is the coffee shop from her home?
B) How many miles does she drive in a day?
C) How many miles does she drive in a school week (Monday - Friday)?
Daily Review
Write the following fractions as decimals.
Learn and Connect
Mr. Becker is a mailman. He has 2 packages to deliver today. One package weighs 4.78 pounds, and the other weighs 4.87 pounds. His boss said that both weighed the same. Is this correct?
To solve, compare the two numbers, 4.78 and 4.87. Remember to line up the numbers by the decimal point first.
Start on the left, with the whole number. Since both numbers have the same whole, 4, we move to the right of the decimal point.
4. 7 8 4. 8 7

We can double check by plotting both numbers on a number line. Since both numbers have a whole of 4, the number line can be from 4 to 5. Can you find 4.78 and 4.87 on the number line?
4.87 > 4.78, Mr. Becker’s boss was not correct. 4.87 weighs more than 4.78. The packages are not the same weight. Look at the numbers in the tenths place.
Apply
Compare the decimals using <, >, or =.
Find and circle 0.4 and 0.7 on the number line. Which number is closer to 0.0?
Identify the place value of the underlined number.
Write each number in its word form.
Color in the correct decimal amount.
Order each group from smallest to largest.
Create a number line and plot the following decimals. Hint: Divide the number line into fourths and space the numbers apart equally.
Mr. Monroe’s fourth-grade class raised $5,355.25 for a charity, and Mr. William’s class raised $5,335.52 for the same charity. Who raised more money?
Explain how you know.
If these numbers are plotted on a number line, where would the number line have to start and end? Challenge
The flower plant grew 9.85 cm on Monday, 0.99 cm on Tuesday, 7.1 cm on Wednesday, and 0.03 cm on Thursday. Which day had the most growth for the plant?
16. 13.
17.
Chapter 14-7 Angles Review
Daily Review Compare the decimals. Write <, >, or =.
Learn and Connect
Let’s Review Angles!
Find the missing angle.
ADB = 180° and ADC = 79°
CDB = 180° − 79°
CDB =
Apply
Angles in a circle. How many degrees does the minute hand move from 9:00 to 9:25? Hint: Each number on the clock is 1 12 of the clock. A full circle is 360°.
5 12 = ? 360 = °
Identify the type of angle and its measurement.
Solve for the missing angle.
Choose the best estimate for the measurement of the angles below.
Identify the type of angle and its measurement.
Type of Angle:
Measurement:
Solve for the missing angle.
Solve the word problems.
How many degrees would you turn the oven dial to set the oven to warm?
Type of Angle:
Measurement:
Type of Angle:
Measurement:
Three angles that all have the same measurement join to form a right angle. What degree is each angle?
If you start facing north, and then you turn to your right until you are facing west, how many degrees did you turn?
Challenge
10. Imagine you are standing in the middle of a clock. You start facing 12, and then you turn to your right (clockwise) until you are facing 9. Then, you turn back to your left (counterclockwise) 120 degrees.
What number are you facing on the clock now?
How many degrees are you from 12 o’clock if turning clockwise?
Hint: Clockwise numbers go higher 1, 2, 3, 4… and counterclockwise numbers go
Chapter 14-8 Multi-Step Problem Solving with All Operations
Daily Review Name each quadrilateral.
Learn and Connect
Herman Elementary is having a car wash. There are 240 students who will help wash cars. If each of them helps wash 4 cars, how many cars were washed in all?
cars
Out of the 240 students, 1 6 of them were fourthgrade students. How many were fourth graders?
fourth graders
If the remaining students were equally divided between kindergarten and third grade, how many students would be in each grade?
students
Apply
Solve each problem.
1. 3.
Addition Subtraction
sum
In all
total
and
plus
join
altogether
perimeter
together
times
twice
area
in all
each
per
product
multiple
equal groups
When they say... They mean...
remain
less than
are not
difference
minus
left over
how many more
take away
multiplied by half
separate
split
divisor
same
quotient
cut up
dividend
divided by
On the chart, circle the words in the problem that help us know which operation to use.
At School A, 32 students walk to school. At School B, there are 6 times as many walkers as there are at School A. School C has half the amount of students walking to school than School B. How many students are walkers at School C?
Twelve children are going to the park. 6 of them brought 4 lollipops each to share with everyone. How many lollipops can each child have?
Larry is bringing treats to school to celebrate the last day. There are 26 students in the class. He bought 3 boxes of granola bars with 8 in each box. How many more granola bars does he need?
Daniel played three games and scored a total of 1,096 points. In his first game, he scored 326 points. In his last game, he scored 418 points. How many points did he score in his second game?
You have two buttons. One measures 6 13 millimeter in length. The other one measures 4 13 millimeter in length. What is the difference in length between the two buttons?
Each bookshelf weighs 60 pounds. The truck has a weight limit of 1,000 pounds. How many bookshelves will fit in the truck at one time? How many shelves are remaining if there are 20 to move?
A puppet show on Tuesday had 11,267 people in attendance. What is the attendance rounded to the nearest ten thousand?
Mike’s parents are recarpeting their living room. The room measures 11 feet by 16 feet. How many square feet of carpet do they need to cover the area of the living room?
The kitchen needs 695 potatoes. Potatoes come in bags of 9. How many bags should the kitchen buy?
In the picture graph to the right, how many more students chose peanut butter cookies than animal crackers as their favorite cookie?
Rick needs 4 6 cup of oil for a recipe. He has 1 3 in the cup already. How much more oil should Rick add?
each = 2 students
Number of students
Kelly is making jewelry for her family. Necklaces need 18 inches of wire, and bracelets need 8 inches of wire. She has 200 inches of wire. How many necklaces and bracelets can Kelly make?
Mr. Miller works about 11 hours a day, 5 days a week, for 48 weeks a year. He estimates that he works approximately 2,500 hours a year. Is his estimate higher or lower than the actual amount of hours?
Cookie
Peanut butter
Chocolate chip
Oatmeal
Animal cracker
Favorite Cookie
Line
Line up the place values.
DOUBLE DIGIT SUBTRACTION (NO BORROWING)
Line up the place values.
DIGIT SUBTRACTION WITH BORROWING
Line up the place values. Subtract the ones. There are not enough ones. Borrow a ten.
WITH MANY DIGITS
Line up the place values.
There will not be enough ones to subtract. Regroup.
Subtract the tens.
Subtract from right to left.
SUBTRACTING FRACTIONS (SAME DENOMINATORS)
Subtract the numerators. Write the denominator.
Draw an array. Repeated Addition. Skip count. 1. Draw 3 rows of 4 2. Count Add 3 4s together. Skip count by 4s for 3 numbers.
MULTIPLYING 2 DIGITS BY 1 DIGIT
Rewrite vertically.
Multiply the ones. Regroup extra ones as tens.
Multiply the tens. Add the number you regrouped.
MULTIPLYING 2 DIGITS BY 2 DIGITS
Multiply the ones. Add a 0. Erase any numbers you carried.
MULTIPLYING FRACTIONS BY A WHOLE NUMBER
Write the whole number as fraction. 3 1 × 5 6
Multiply the numerators. 3 1 × 5 6 = 15
Multiply the denominators.
SINGLE DIGIT DIVISION
1. Draw 12
Draw an array. Skip count. Use a multiplication fact.
2. Circle groups of 3
3. Count the number of groups.
Count by 3s. Count how many numbers you say until you get to 12.
Fractions
EQUIVALENT FRACTIONS
Draw a model.
1. Draw 2 3
2. Show 6ths.
3. How many are colored?
Multiply or divide by 1. 2 3 = 4 6
When the numerator and denominator are the same the fraction equals 1.
SIMPLIFY FRACTIONS
List factors of the numerator and denominator.
3: 1, 3 6: 1, 2, 3, 6
CONVERTING IMPROPER FRACTIONS TO MIXED NUMBERS
Circle the biggest factor they have in common.
3: 1, 3 6: 1, 2, 3, 6
simplest form: 1 2
Divide the numerator and denominator by the greatest common factor.
Divide the numerator by the denominator. Write the remainder as fraction. The denominator is the number you divided by.
CONVERTING MIXED NUMBERS TO IMPROPER FRACTIONS
Multiply the denominator by the whole number. 2 2 3 3 × 2 = 6
Add the numerator to that number.
Write an improper fraction. The sum is the numerator. Keep the denominator. 8 3
Underline the place you are rounding to.
Look to the digit on the right. To round up, add 1 to the underlined digit. All digits to right of the underline turn into 0s. ROUNDING
If it is 4 or less round down. If it is 5 or more round up.
CONVERTING FRACTIONS TO DECIMALS
Find an equivalent fraction with a denominator of 10, 100, or 1,000.
When we round down, we leave the underlined digit and turn all digits to it's right into 0s
Write a decimal. Use the denominator to help with place value. 3 4 as a decimal: 0.75
PERIMETER
Add all the side lengths together.
Label with the correct unit of measurement. Perimeter of : 19 in
AREA OF A RECTANGLE
Multiply the length times the width.
Area of : 8 cm2 4 × 2 = 8 8 cm2
Label with the correct unit of measurement squared.
Acute angle an angle that measures less than 90° C
Addend any number added to another number R1.2, R1.4
Angle a figure formed by two rays or lines that share a common endpoint
10.5, 14.7 Area the measurement inside a flat object (length × width)
Area model a rectangular model used to solve multiplication equations where the factors define the length and the width of the rectangle
Bar graph a bar graph that shows data with rectangular bars that are the height or length of the number value they represent
Benchmark numbers numbers that are used as reference points to compare other numbers
Common denominator when two or more fractions have the same denominator
Commutative property of multiplication changing the order of the factors does not change the product R1.6
Compare to choose a value that is greater than, less than, or equal to the original value
Compatible numbers numbers that are multiples of the divisor 5.2
Composite number a number that has more than two factors 3.3, 3.8
Convert to change a value or expression from one form to another
Cup a unit of measurement for liquids that is equal to 8 fluid ounces
Data a set of values that is gathered to show information
Decimal the part of a number that shows a value smaller than 1 whole
Decimal point a point (small dot) used to separate the whole number from the fractional part of a number 9.1, 9.5, 9.7, 9.8, 14.6
Decompose to break down into smaller parts 7.5, 7.8
Degrees the measure for angles - 360 degrees in one full rotation 10.3, 14.7
Denominator the bottom number in a fraction that represents the parts in the whole
R2.5, R2.6, R2.8, 7.2, 7.3, 7.8, 8.1, 8.5, 8.6
Difference the answer to a subtraction problem R1.3, R1.4, 2.3, 2.6, 2.8, 8.1, 14.2
Digit a single symbol (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) used to make numbers 2.2, 2.4, 2.8
Dividend the amount that is being divided; located before the ÷ or inside the 8)16
R1.7, R2.1, 5.3, 5.5, 5.6, 5.8, 6.4, 6.6, 6.7, 6.8, 14.4
Divisible capable of being divided evenly with no remainder 5.4, 5.8
Division breaking a number into equal groups 5.1
Divisor the number you're dividing by; the number in each group or the number of equal groups; located after the ÷ or outside the
R1.7, R2.1, 5.3, 5.5, 5.6, 5.8, 6.6, 6.7, 6.8, 14.4
Dot Plot a graph that shows data as marks above a number line, showing each value’s frequency 1 2 3 4 13.4, 13.5, 13.6, 13.8
Double line graph a line graph that compares two things in the same scale and on the same graph 13.7, 13.8
Elapsed Time the amount of time that passes between one time and another time 12.5, 12.8
Expanded form a way to express the value of each digit of a number 5,000 + 600 + 3
Fact family a group of math facts created with the same numbers. For example 3, 4, 12
Factor any one or more numbers multiplied together to give a product
R1.8, 5.8
R1.5, R1.6, 3.2, 3.4, 3.8, 4.1, 7.1, 7.3, 7.8, 14.3
Foot unit of measurement that is equal to 12 inches or 1 3 of yard 11.1, 11.2, 11.8
Frequency the number of times an event or a value occurs 13.2, 13.8
Frequency Table a data display that shows how often a category appears in a set of data 13.2
Gallon a unit of measurement for liquids that is equal to four quarts or eight pints
11.6, 11.7, 11.8
Equation a statement that two mathematical expressions are equal 2.6, 2.7, 2.8
Equilateral triangle all three angle measurements are equal and all three sides lengths are equal 10.7, 10.8
Equivalent fractions two fractions that have different numerators and denominators but are equal in value R2.7, 7.2, 7.3, 7.8, 9.2, 9.3
Estimate a close, but not exact answer 4.2, 4.6, 4.8, 5.2, 6.2, 6.8, 8.4
Estimation a close, but not exact answer; an educated guess of the approximate calculation 2.1, 2.8
Gram a metric unit of weight that is equal to 1,000 milligrams 12.2, 12.7, 12.8
Hundredths the decimal place value showing a whole separated into a hundred equal pieces
Improper fraction a fraction where the numerator is greater than the denominator
5 3
Inch unit of measurement that is equal to 1 12 of a foot
9.4, 9.8, 14.6
7.6, 7.8, 8.2, 8.3, 8.4, 8.7, 8.8, 14.5
11.1, 11.2, 11.8
Input the starting number for the rule in an inputoutput table 2.5, 2.8
Intersecting lines lines that will cross but do not make right angles 10.6, 10.8
Inverse multiplication and division are inverse operations; addition and subtraction are inverse operations; they can be used to check calculations R1.8, 5.8
Isosceles triangle two angle measurements are equal. Two sides are equal 10.7, 10.8
Kilogram a metric unit of weight that is equal to 1,000 grams 12.1, 12.2, 12.7, 12.8
Kilometer a metric unit of length that is equal to 1,000 meters 12.8
Line a straight path of points that has no beginning or end 10.1, 10.2, 10.6, 10.8
Line graph a set of data that shows how some things change over time. Line graphs are good to use when small changes happen frequently in the data. The x-axis shows the 13.7, 13.8
Line of Symmetry a line that divides a shape into 2 identical parts 12.6, 12.8
Line segment a portion of a line that has two endpoints 10.1, 10.2, 10.8 Liter
a metric unit of length that is equal to 100 centimeters
Milligram a metric unit of weight that is one onethousandth of a gram
Milliliter a metric unit of capacity that is one onethousandth of a liter
Millimeter a metric unit of length that is one tenth of a centimeter
Minimum the lowest data point
Minuend the number other numbers are subtracted from R1.4
Mixed number a whole number with a fraction part 1 4 3
Multiple/s the product or products of a number when it is multiplied by other numbers 3.1, 3.8, 5.2, 6.1, 7.1, 7.8
Multiplication the process of combining equal groups R1.5, 3.5, 3.6, 3.7, 3.8, 4.6, 5.1
Number line a straight line used to represent and compare numbers 0 1 2 3 4 5 9.6
Numerator the top number in a fraction that represents the part of the whole
Obtuse angle an angle that measures more than 90°
R2.5, R2.6, 7.2, 7.3, 7.8, 8.1, 8.5, 8.6
10.2, 10.4, 14.7
One Million a 1 with 6 zeros; 1,000,000 1.1
Operations the process used to arrive at a mathematical solution. (addition, subtraction, multiplication, division)
R2.2
Order to arrange values from greatest to least or least to greatest 1.4, 1.8, 8.4
(Fluid) Ounce a unit of measurement for liquids that is equal to 1 16 of a pint 11.6, 11.7, 11.8
Ounce a unit of weight that equals 1 16 of a pound (oz) 11.4, 11.5
Output the result after the rule is applied to the input 2.5, 2.8
Parallel lines lines that never touch 10.6, 10.8
Partial product the products you get when you multiply one digit of a multi-digit number by one digit of the other where each digit maintains its place value in order 4.4
Patterns things that repeat in a logical way 1.7, 3.4, 3.8
Perimeter the measurement around an object
R2.3, 10.8, 11.3, 11.8
Perpendicular lines lines that will cross to make right angles 10.6, 10.8
Picture graph a picture graph shows data on a chart using pictures or symbols that represent the data that was collected
Grade 1
Grade 2
Grade 3
Grade 4 1 = 5 lunches 13.1, 13.8
Pint a unit of measurement for liquids that is equal to 16 ounces or half a quart 11.6, 11.7, 11.8
Place Value the position of a digit in a number determines its value 1.1,
Point a position in space or on a line 10.1, 10.8
Polygon a closed shape with straight sides (triangle, square, rectangle, hexagon, etc.)
Pound a unit of weight that equals 16 ounces (lb)
11.4, 11.5
Prime number a number that has only two factors, 1 and itself 3.3, 3.8, 7.1, 7.8
Product the answer to a multiplication problem 25 × 5 = 125 R1.5, R1.6, 3.4, 3.6, 3.8, 4.1, 4.5, 4.8, 5.7, 14.3
Property a pattern (or rule) in addition and subtraction that is helpful in quickly answering problems R1.2
Quadrilateral a 2-dimensional, 4-sided figure that is closed 10.7, 10.8
Quart a unit of measurement for liquids that is equal to two pints or a quarter of a gallon 11.6, 11.7, 11.8
Quotient the answer to a division problem; the number in each group or the number of equal groups; located after the = or on top of the
R1.7, R2.1, 5.3, 5.5, 5.6, 5.7, 5.8, 6.6, 6.7, 6.8, 14.4
Ray portion of a line that has one endpoint and extends forever in one direction 10.1, 10.2, 10.8
Regroup the process of making groups of tens R1.3, 2.3, 2.8
Regrouping rearranging numbers into groups by place value to make it easier to carry out operations 2.2, 2.4
Remainder the amount left over after you divide a divisor that does not go into a dividend evenly 5.3, 5.5, 5.8, 6.3, 6.5
Right angle an angle that measures 90°
Rounding a type of estimation that follows certain rules to find close estimates based on place value R1.1, 1.5, 1.8, 2.1, 2.8, 6.2
Scalene triangle none of the angle measurements or side lengths are equal
10.8
Sequence shapes or numbers in a certain order 1.7, 4.7
Simplest form a fraction where the numerator and denominator have a common factor of 1 7.3, 7.8, 8.7, 8.8
Skip counting a method of counting forward by numbers other than 1 (For example: 3, 6, 9, 12, 15...) R1.6, 3.1, 3.8
Standard form the form of a number that uses digits to express that number 198,304 1.6, 1.8
Subtrahend the number subtracted from the minuend R1.4
Sum the answer to an addition problem R1.3, R1.4, 14.2
Tally chart a chart that has vertical dashes that represent one occurrence of information. For every 5 occurrences, a diagonal line is written through the four
Street 1
Street 2
Street 3
Street 4
Street 5 13.1, 13.8
Tenths the decimal place value showing a whole separated into ten equal pieces
Term each number in the pattern
Ton a unit of weight that equals 2,000 pounds (T) 11.4, 11.5
Variable a letter or symbol that stands for an unknown quantity 2.7, 2.8, 10.8
Vertex a point where two or more lines, curves, or edges meet or intersect
10.2, 10.4, 14.7
Written form the form of a number that uses words to express a number 1.3, 1.8
Yard a unit of measurement that is equal to 3 feet or 36 inches
www.lighthousecurriculum.com
