LHM - Level E

This book belongs to

LEVEL E

Lighthouse Math

Program Directors

Mrs. Zehava Kraitenberg M.S. Curriculum Advisor Elementary School Principal

Jane Chamberlain Master of Education Curriculum and Instruction

CURRICULUM

Credits

Curriculum Writers

Jane Chamberlain Middle School Math Instructor

M.Ed. in Curriculum and Instruction

Susannah Maria Malarkey 4th Grade Instructor

M.A. in Teaching K-8

Karen Williams

5th Grade Teacher

Affiliate Faculty

Ed.D. - Curriculum and Instruction

Karen Legreid Math Interventionist K-5

M.A. in Curriculum and Instruction

Mizuho Shiomi

3rd Grade Instructor

M.A. of Arts in Education K-8

Review Team

Zehava Kraitenberg M.S. Curriculum Advisor Elementary School Principal

Jane Chamberlain Middle School Math Instructor

M.Ed in Curriculum and Instruction

Layout & Design

Akiva Leitner Project Manager Kevanyc.com

Joy Aragones

4th Grade Instructor

M.A. in Education Technology

Chelsea Ruocco

6th Grade Instructor

M.A. in Childhood Education 1-6

Kelly Boehme

1st Grade Instructor

M.Ed. in Elementary Education K-6

Jennifer Ramos-Martinez Curriculum Specialist

M.A. in Curriculum and Instruction

Rebecca Kay-Lewis

5th Grade Instructor

M.Ed. in Elementary Education K-6, 5-8 Math

Sarah Thorman 2nd/3rd Grade Instructor

B.S. Liberal Arts and Sciences (Psychology)

Post-Baccalaureate Teacher Certification (Grades K-6)

Kelly Christensen 6th-7th Grade Math Teacher

M. Ed in Administration and Leadership (K-12)

Lydia Masao 4th Grade Math Instructor

M. Sc. in Child Development and Education

M. Ed. In Elementary Education, pre K-6

Allison Paul Education Consultant Middle School Math Instructor

M.Ed. in Secondary Mathematics & Educational Leadership

Michele Grega

Data and Assessment Coach

M.Ed in Elementary Education K-6

M.Ed. in Curriculum and Instruction

M.Ed. in Administration and Leadership (K-12)

Glory Sterling High School English Teacher

M.Ed. in Curriculum and Instruction

Rebekah Jorgensen

Middle/High School Math Teacher

M. Ed. Learning & Technology

Esther Aboud

Curriculum Consultant

M.Ed. in Special Education

Fraydel Sharf Content Director and Editor

Miriam Shulamis Eisemann Content Editor

Luke Bote K-12 Instructor

M.Ed. in Leadership

Mirko Zunic/Chris Dunn Layout Directors

©Copyright 2021 Lighthouse Curriculum Inc. All rights reserved.

Molly Fernholz K-6 Instructor

B.A. in Education

Francine S. Foote 5th and 6th Grade Instructor

M.A. in Instruction and Curriculum

Yehuda Gartenhaus M.A. Elementary School Principal

Mechel Weizer Curriculum Advisor Elementary School Principal

Issac Flores Illustration Director

Distributed by Leren Curriculum Inc. T: 718-834-1231 E: lerenec@gmail.com

Lighthouse Math level E • ISBN 978-1-955773-04-1

No part of this publication may be reproduced, stored in a retrieval system, stored in a database and/or published in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, without the prior written permission of the publisher. To obtain permission to use portions of material from this publication, please contact Lighthouse Curriculum.

Content developed in collaboration with The Reimagined Classroom

Contact Lighthouse Curriculum: By calling: 718.285.7100, or emailing: info@lighthousecurriculum.com For more information visit www.lighthousecurriculum.com

Introduction and overview of skills at the beginning of each chapter

Color coded pages - easy to find tabs at the top and bottom of the Lesson Page and Exercise Page

Daily review at the beginning of every lesson to provide review of previous skills

Vocabulary at the bottom of the page with important terms and definitions

Learn and Connect introduces the lesson with real life situations, illustrations and helpful hints

Apply provides problems for the teacher and the students to practice together

Practice is a full page of exercises for students to practice the skills and concepts they have learned

Tabs on the top of each page allow you to find chapters and lessons easily

Call outs and Hints help remind students of important steps and give them clues

Clear, worked out examples

Challenge problem solving or challenges to extend and enrich student learning

Review for every chapter

Assessment provided for every chapter

Hi, my name is Flash!

to the Lighthouse Math Curriculum!

is a list of items that will help as you navigate through the book!

A better way to teach

Dear Educator,

Welcome to the Lighthouse Math Curriculum!

What makes our curriculum so unique? Lighthouse Math uses a scaffolded approach to learning and mastering math skills. When provided with a solid foundation, students can retain more information and prepare for the next level of skills.

Instead of separate workbooks and textbooks, students have everything they need built into one place: a soft covered book containing 14 chapters, comprised of 8 lessons per chapter, with each lesson containing review, new skills, and practice. All lessons include step by step instructions for clarity, giving all teachersneophyte as well as seasoned - the tools for success.

The books are custom illustrated, providing a vibrant learning experience. They are formatted in a way that each grade level can be completed successfully by the culmination of the school year. Lighthouse Math gives teachers the tools they need to teach and gives students everything they need to learn.

We, at Lighthouse CurriculumTM, are committed to providing support and guidance to our educators. We look forward to hearing from you and are available to answer any questions you may have.

Sincerely,

Lighthouse Curriculum Team

Chapter 8-2 Multiplying Fractions

Jamie had 2 3 of a pound of blueberries. He let his friend Caleb eat 1 4 of the blueberries. How many pounds of blueberries did Caleb eat?

To solve, we must multiply the pounds of blueberries by the amount of blueberries eaten.

A model like the one below can help us multiply the fractions.

You can also solve by multiplying using the standard algorithm. First, multiply the numerators and denominators. Then, simplify. Therefore, Caleb ate 1 6 pounds of blueberries.

Learn and Connect Apply Daily Review Solve, reducing each answer to its simplest form.

Multiply using models or the standard algorithm. Simplify your answers.

Lighthouse Math

Chapter 7

Fractions

Chapter 8

Chapter 10 Geometry

Chapter 11

Chapter 13 Coordinate Planes and Graphing

Review 1

In Review 1, we will review

Place Value and the Four Operations

In Level E, students will practice working with large numbers, gain fluency in addition, subtraction, multiplication, and division, and solve word problems to prepare for higher-level math skills.

• Place value

• Addition and subtraction with large numbers

• Double-digit multiplication

• Long division

We can understand the value of digits based on their place value, including decimals.

We can add and subtract any large number. We can fluently multiply a number by a single or double digit.

We can use long division to solve division problems with two or three-digit dividends.

We can use the four operations to solve word problems.

2,486 + 3,458 =

3,488 − 1,485 =

6,584,791 (six million, five hundred eighty-four thousand, seven hundred ninety-one)

6 is in the millions place (6,000,000)

5 is in the hundred thousands place (500,000)

8 is in the ten thousands place (80,000)

4 is in the thousands place (4,000)

7 is in the hundreds place (700)

9 is in the tens place (90)

1 is in the ones place (1)

6,584,791.032 DECIMALS!

0 is in the tenths place (0.00)

3 is in the hundredths place(0.03)

2 is in the thousandths place (0.032) 1. 545 + 674 =

Learn and Connect Apply

Write the digit in each place value. 9,374,293. 473

1. What number is in the millions place?

3. What number is in the hundred thousands place?

5. What number is in the ten thousands place?

7. What number is in the thousands place?

9. What number is in the hundreds place?

Vocabulary

2. What number is in the tens place?

4. What number is in the ones place?

6. What number is in the tenths place?

8. What number is in the hundredths place?

10. What number is in the thousandths place?

Decimal - the part of a number that shows a value smaller than 1 whole

Write the digit in each place value.

8,456,293. 839

1. What number is in the millions place?

3. What number is in the hundred thousands place?

5. What number is in the ten thousands place?

7. What number is in the thousands place?

9. What number is in the hundreds place?

Write the value of the numbers.

Example:

6,235,247. 218 428. 694

11. What is the value of the number 2?

12. What is the value of the yellow 4?

13. What is the value of the yellow 9?

18. What number has 8 ten thousands, 3 fewer thousands than ten thousands, 3 more hundreds than thousands, 6 fewer tens than hundreds, and 6 fewer ones than ten thousands?

2. What number is in the tens place?

4. What number is in the ones place?

6. What number is in the tenths place?

8. What number is in the hundredths place?

10. What number is in the thousandths place?

What is the value of the yellow 1? .01

61,234. 468

14. What is the value of the black 6?

15. What is the value of the number 1?

16. What is the value of the yellow 4?

17. What is the value of the yellow 6?

19. What number has 4 ten thousands, the same number of thousands as ten thousands, 4 more hundreds than thousands, 1 more ten than ten thousands, and 3 fewer ones than tens? , ,

Review 1-2 Adding and Subtracting Multi-Digit Numbers

Review Write the value of the underlined digit in each number. 1. 67,985 = 2. 980,642 = 3.

= 4.

=

A basketball arcade hoop showed a high score of 25,928 points. James scored 1,784 points less than the high score. What was James' score?

To solve, first subtract the digits in the ones place: 8 – 4 = 4

2 5 9 2 8 – 1 7 8 4 4

Then, subtract the digits in the hundreds place: 8 – 7 = 1

Learn and Connect Apply

Next, regroup and subtract the digits in the tens place: 12 – 8 = 4

Next, subtract the digits in the thousands place: 5 – 1 = 4

Last, subtract the digits in the ten thousands place: 2 – 0 = 2

Now, use the inverse operation of addition to check your work. 24,144 + 1,784 = 25,928

Therefore, James scored 24,144 points.

Find the difference. Add to check your answers.

–

Estimate the answers by rounding to the greatest common place value.

Read each problem, then solve. Write the equation for each.

Max has $5,121 to go school shopping. He spends $3,648. How much money does he have left over?

There are 2,376 fish of different species in the aquarium. The aquarist has ordered 3,856 more fish for a new exhibit. How many fish will the aquarium now have?

A small town currently has 9,799 houses. The town has decided to build 8,212 more houses. How many houses will the town have when all the buildings are done?

Victor’s restaurant served 3,287 people in January. In February, the restaurant served 4,128 people. How many more people ate at the restaurant in February?

This week, Justin made 3,901 chocolate chip cookies. He also made 1,637 oatmeal cookies. How many cookies did he make this week?

Moses and Frank were traveling for summer break. They traveled 2,321 miles to England. Then, they traveled 4,589 to Italy. How much farther is Italy than England?

Tim works at a book store. This week, he shelved 3,128 fiction books and 1,278 nonfiction books. How many books did he shelve this week?

A car dealership needs to sell 2,753 cars by the end of the year. So far, they have sold 2,182 cars. How many cars do they still have to sell?

Review 1-3 Subtracting Across Zeros

1,253 – 118 = 2. 2,523 – 391 = 3. 2,554 – 1,654 = 4. 8,164 – 3,254 =

Learn and Connect

Mike’s vegetable stand has 400 fruits and vegetables to sell at the farmers market. By the end of the day, Mike sold 287 fruits and vegetables. How many fruits and vegetables does Mike have left to sell?

To solve, first subtract the digits in the ones place. However, there are not enough tens to regroup a ten.

Instead, regroup using “40” instead of 0. Remove 1 ten to make 10 ones and 39 tens remaining.

Therefore, there are 113 more fruits and vegetables left.

Apply

Subtract.

Then, subtract the remaining tens and hundreds.

Solve.

Estimate each difference by rounding to the nearest hundred. Circle the better estimate. Then, solve for the exact difference.

405 – 299 =

Solve.

Leo is painting a mural 900 feet long. He has already painted 689 feet. How many more feet does he have left to finish?

Ben’s farm sold 9,008 pounds of apples this year. He sold 992 pounds less last year than he did this year. How many pounds of apples did he sell last year?

Aaron’s old school had 299 classrooms. His new school has 409 classrooms. How many more classrooms does his new school have? 8,012 people visited the museum this week. 2,999 of them were adults, and the rest were children. How many children visited the museum this week?

Chad and Jack’s teacher had them solve 9,000 − 8,988 = ?

Jack’s answer was 12. Chad’s answer was 112. Who had the correct difference? Why was the other difference incorrect?

How could each of them check to see if their answer was correct without subtracting again?

Andrew has a bakery that sells cookies. It takes 2 cups of flour to make a dozen cookies. How many cups of flour will he need to make 5 dozen cookies?

To solve, you can find the first five multiples of 2 or multiply 2 × 5.

Therefore, Andrew will need 10 cups of flour to make 5 dozen cookies.

Learn and Connect Apply

Properties of Multiplication

Commutative Property

The order in which you multiply does not affect the product. 3 × 2 = 6 2 × 3 = 6

Identity Property

If a factor is 1, the product is the same as the other factor. 4

Write the next five multiples.

Associative Property

The order of the factors does not affect the product. 3 × (4 × 2) = 24 (3 × 4 ) × 2 =24

Zero Property If a factor is zero, the product is zero.

Vocabulary

Factors - numbers that can be multiplied together to make a new number Product - the result of two or more numbers when multiplied together

Write the next 8 multiples.

Find the missing factor or product for each number sentence.

Fill in the multiplication wheels.

Solve, showing your work.

Joshua’s wagon can carry 12 boxes in 1 load. Ken’s wagon can hold 8 boxes per load. If Joshua makes 4 trips with a full wagonload, how many boxes can he transport? If Ken needs to move the same number of boxes, how many trips does he need to make?

Cirle the correct answer.

Rachel was playing a math game with her friends. For every correct answer, she got 5 points. In the first round, Rachel got 7 questions correct. In the second round, Rachel got 4 questions correct. How many points did Rachel get in all?

25. Mike is packing some cupcakes into boxes. He has 8 boxes. He wants to figure out how many cupcakes he needs to put into each box. He currently has 40 cupcakes. Which of the following multiplication number sentences can be used to solve Mike's problem? Fill in the missing factor.

Daily Review Compare the numbers using <, >, or =.

You can multiply two-digit numbers in two different ways. Consider the following problem:

Multiplying using area models and partial products:

Write the expanded form of each of the factors on opposite ends of the large box. Then, multiply the digits that are on opposite ends of each smaller box to fill in the missing answers.

Multiplying using the standard algorithm:

When using the standard algorithm, you will regroup the tens and ones as you move along.

Learn and Connect Apply

Round to the highest place value to estimate. Then, solve for the exact product using partial products. Show your work.

85 × 78

Solve using the standard algorithm.

14. 15. Three classes of fifth-grade students are purchasing tickets to see a play as a class trip. There are 24 children in each class and 16 adults attending the play. How much money will the total bill be to purchase the tickets?

If they decide to purchase the large group tickets instead, how much money will they save?

Review 1-6 Multiplication and Division Fact Families

Daily Review Find the missing factors.

Learn and Connect

Fact families are sets of three numbers that are related. You can use different operations to show the relationship between the numbers.

For example, let's look at this fact family: 12, 3, and 4

You can make two multiplication and two division number sentences: 3 × 4 = 12

Properties of Division

Identity Property

If we divide a number by 1, the quotient is the number itself.

÷ 4 = 3

÷ 3 = 4 4 × 3 = 12

You can use your understanding of fact families to solve division problems by thinking of the fact family and inserting the missing number.

For example, to solve 6 ÷ 3, you can think of it as 3 × = 6. Since you know that 3 × 2 = 6, you know that 6 ÷ 3 = 2.

Apply

If we divide a number by itself, the answer is 1

Zero Property

0 divided by a number gives zero as the quotient.

Zero cannot be divided by any number. 4 ÷ 0 = No answer

Solve. Write the related multiplication fact below each equation.

Vocabulary

Dividend - a number being divided by another number

Divisor - a number by which another number is divided

Quotient - the answer to a division problem

Use your understanding of fact families to find the quotients.

Complete each fact family.

Solve. Then, write the equation.

Dennis has 132 crayons. He places them in boxes of 12. Five are yellow, and the rest are red. How many boxes did he make?

Jack bakes 9 donuts on a baking sheet. He used 7 sheets. How many donuts did he bake?

Arnold drank 4 glasses of water. Each glass holds 8 ounces. How many ounces did he drink?

Write an equation for each. Then, solve.

Richard runs 5 miles every day. If in a week he runs 280 minutes, how long does it take him to run one mile?

Eddie has 56 feet of cloth. He needs 7 feet of cloth to make a costume. How many costumes can he make?

Richard keeps the same pace but starts running 7 miles every day. How many days does he need to run each week to still spend 280 minutes a week running?

Learn and Connect

Mr. James has $379 to buy packs of juice boxes for his after school program. How much money will he have remaining after buying as many juice box packs as possible?

To solve, divide 379 dollars by 3 dollars. First, divide the hundreds.

You can only make 1 group of 3 with 3. 3 ÷ 3 = 1

Then, bring down the tens and divide again.

You can make 2 groups of 3 with 7.

7 ÷ 3 = 2

Then, bring down the ones and divide again.

You can make 6 groups of 3 with 19. 19 ÷ 3 = 6

Mr. James will have $1 left over after buying 126 juice packs.

Find each quotient and write the remainder on the line next to each R.

Eli needs 62 plastic plates for a party. He found some packs of plates at the store that have 5 plates in each pack. How many packs does he need to buy to have enough plates? Explain your answer.

Nan collected 38 shells on the beach. She wants to make bracelets using 4 shells per bracelet. How many shells will she have left if she makes as many full bracelets as possible?

Victor is making keychains. He has a string that is 84 inches long. If each keychain needs 9 inches, how many inches of leftover string will he have once he has made all of his keychains?

Danny is making fruit baskets. He has 39 strawberries to put into baskets. Each basket needs 7 strawberries. He wants to make as many full baskets as he can; then he can eat the remaining strawberries. How many strawberries will Danny be able to eat?

In the kindergarten class, there are 389 crayons. The students need to separate an equal amount of crayons into 6 containers. How many crayons will go into each container? How many crayons will be left over?

Jack has 378 toy building blocks. He wants to separate them into 5 groups and give the remaining pieces to his brother. How many toy building blocks will his brother get?

with Zeros in the Dividend and Quotient

Daily Review Find the quotient and remainder in each of the following problems.

How to decide where to start:

When dividing, start in the highest place value. However, if the digit in the dividend is smaller than the divisor, move to the next place value.

In this problem, the 7 in the tens is bigger than 3. Therefore, you can make 2 groups of 3 using 7.

In this problem, the 2 in the tens is smaller than 3. Therefore, you CANNOT make any groups of 3. Instead, place a zero in the quotient and move to the next place value. Now, you are dividing 26 into 8 groups of 3.

If there is a zero in the dividend, treat it the same as any other number. Bring it down and make new groups. You can make 3 groups of 3 with 10.

Learn and Connect Apply

Solve.

However, if you cannot make any groups, place a zero in the quotient and bring down the next place value. Now, you can make 2 groups of 3 with 6.

Find each quotient and write the remainder on the line next to each R.

2)169

2)711

13.

15. Charlie and Sam both solved 549 ÷ 5. Charlie wrote 549 ÷ 5 = 109 R 5. Sam wrote 549 ÷ 5 = 109 R 4. Without using division, find who has the correct quotient. How did you know?

Kane bakes 405 cookies, and Eddie bakes 410 cookies. They are going to sell them in boxes of 5. How many boxes will they use?

Challenge

16. Look at Mannie’s work below. What did he do wrong? What is the correct quotient?

14. The second, third, and fourth-grade students are seeing a play for a field trip. There are 112 second-graders, 120 third-graders, and 109 fourth-graders. Each row seats 8 people. How many rows will they need to seat everyone? − 28 16

Circle the equation that will help you solve. Then, find the solution.

17. Harry is ordering vans for a field trip for the fifth and sixth-graders. There are 4 fifth-grade classes with 22 kids in each class. There are 98 sixth-graders. Each van can hold 9 students. How many vans does Harry need to order?

A) Step 1: 22 × 4 = 88

Step 2: 88 + 98 = 186

Step 3: 186 ÷ 5 = ?

Harry needs to order vans.

B) Step 1: 22 × 9 = 198

Step 2: 198 + 98 = 296

Step 3: 296 ÷ 4 = ?

C) Step 1: 22 × 4 = 88

Step 2: 88 + 98 = 186

Step 3: 186 ÷ 9 = ?

Review 2

In Review 2, we will review

Fraction, Decimals, and Geometry

Students will deepen their understanding of fractions and decimals, which will prepare them for using operations with fractions and decimals in Level E.

• Find area and perimeter

• Define geometry vocabulary

• Find equivalent fractions

• Simplify fractions

• Compare, order, and locate fractions on a number line

• Add and subtract fractions with like denominators

• Place value with decimals

• Compare, order, and locate decimals on a number line

We can find the perimeter of any shape and the area of a rectangle.

We can draw geometric figures and name them.

We can use a model, multiplication, or division to find equivalent fractions.

We can use a common factor to simplify fractions. We can compare fractions with models, number lines, or benchmark fractions.

We can write fractions as decimals and write the word form of decimals.

We can compare decimals by using a model or place value.

Find the perimeters of the figures.

There is a pool in Steven’s backyard. He counted the tiles around the pool and drew a diagram. If each tile is 1 foot long, what are the area and perimeter of Steven’s pool?

Area is a term used to define the space occupied by a flat shape or the surface of an object. The area of a figure is the number of unit squares that cover the surface of a closed figure. We measure area in square units: yd², ft2, or in². To find the area of the rectangular pool, multiply the length by the width.

Learn and Connect Apply

The area of Steven’s pool is . Perimeter is the distance around a shape. To find the perimeter, add all of the sides together. What is the perimeter of the pool?

Find the area and perimeter of each figure. Label with the correct units.

Find the areas. A rectangle with a width of 12 yd and a length of 31 yd.

Vocabulary

A rectangle with a width of 5 ft and a length of 521. A square with side lengths of 32 in.

Find the perimeter of each figure.

Use the perimeters to find the missing sides. Then write the name of each shape.

Perimeter: 48 in

Sides: 12 in, 15 in, 7 in, 8 in Missing side: This shape has 5 sides. It is a

Perimeter: 148 ft

Sides: 25 ft, 56 ft, 42 ft

Missing side: This shape has 4 sides. It is a

Draw a picture to help solve each problem.

Perimeter: 100 ft

Sides: 43 ft, 21 ft, 12 ft, 17 ft, 5 ft

Missing side: This shape has 6 sides. It is a

If a park is 340 feet by 120 feet, how much fence will be needed to enclose it?

10. 9.

8. The school is painting a new mural with a blue border. The wall is 10 feet tall by 15 feet wide. How many feet is the border?

11. How much grass will be needed to cover the park if it is 340 feet by 120 feet?

A kitchen is 14 feet by 8 feet, and it needs a new baseboard. If the baseboard goes around the edge of the room, how much is needed?

12. The kitchen needs flooring. How many square feet of tile is needed to cover the kitchen floor if it is 14 feet by 8 feet?

13. The school is painting a new mural, and the wall is 10 feet tall by 15 feet wide. They need to prep the wall with 2 coats of white paint. How many ft2 will be painted?

Name the shapes shown.

Learn and Connect

Types of lines

point - an exact location

line segment - part of a line that has two endpoints

line - a straight path that goes on forever in both directions

ray - a line with a single endpoint that goes on and on in one direction

Line relationships

intersecting - lines that cross but don’t make a right angle

perpendicular - lines that intersect and create a 900 angle

parallel - lines that continue on indefinitely, are equidistant, and never touch

Types of angles

right - measures exactly 900

acute - measures less than 900

obtuse - measures more than 900

Name each figure.

Draw and label each figure.

Line AB intersecting line CD Acute

Review 2-3 Equivalent Fractions

Daily Review Determine if each number is prime or composite.

Learn and Connect

Alice is baking using her mother’s recipe. She noticed that she needs 1 2 cup of sugar. However, she only has a 1 8 cup measuring cup. How many 1 8 cup scoops should she use to equal a 1 2 cup?

To solve, we need to find an equivalent fraction to 1 2 that has a denominator of 8.

An equivalent fraction is a fraction that is equal to another fraction. To make an equivalent fraction, divide or multiply the numerator and the denominator by the same number.

First, consider: 2 × = 8

Then, multiply the numerator by the same number.

Therefore, 1 2 is equivalent to . This means that Alice needs to add scoops of sugar with the 1 8 measuring cup.

Apply

Write two equivalent fractions that can represent the shaded part of each figure.

Fill in the boxes to make an equivalent fraction.

Write two equivalent fractions that can represent the shaded part of each figure.

Challenge

16. One lap around a certain track is 1 16 of a mile. After running 12 laps, what fraction of a mile have you run? Write two equivalent fractions.

17. Samuel put a book that weighs 5 6 of a pound on one end of a seesaw. How many 1 12 pound weights should he put on the other end to balance the seesaw?

Review 2-4 Simplifying Fractions

Ben made a cheesecake for his family on Monday. He cut the cake into 16 equal pieces. By Friday, his family had eaten a lot of the cheesecake. What fraction of the cheesecake remains?

To solve, we need to create a fraction by making the numerator the number of cheesecake pieces that remain and the denominator the total number of pieces that made up the entire cheesecake.

Remaining pieces

Total pieces

Factors of numerator:

Learn and Connect Apply

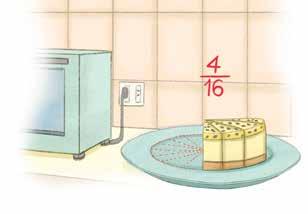
To write this number in simplest form, we need to find a factor that both the numerator and denominator can be divided by without a remainder. List the factors for each number and circle the factors they have in common. Divide the numerator and denominator by the largest factor they have in common.

Therefore, there is of the cheesecake remaining.

Simplify each fraction using the given models. Write in the factors each numerator and denominator will be divided by to reach the simplest terms.

Divide the numerator and denominator by: 2

Vocabulary

Divide the numerator and denominator by:

Divide the numerator and denominator by:

Divide the numerator and denominator by:

List factors of the numerators and denominators. Circle the common factors.

Is each fraction in its simplest form? If no, simplify it.

Simplify each fraction and complete the fraction circles to show each fraction in its simplest form.

13. True or false: 8 12 simplified to its lowest term is

Create a visual model explaining your answer.

14. Steven is running a 24-mile race. He has already run 10 miles. How much of the race has he completed? Express your answer as a simplified fraction.

15. Nathan is working on a worksheet that is 20 problems long. He has finished 12 of the problems. How much of the worksheet has he completed? Express your answer as a simplified fraction.

Solve.

Daily Review Write two equivalent fractions for each fraction below.

Learn and Connect

Paul and Josh are painting their rooms. Paul has painted 5 6 of his wall, and Josh has painted 4 10 of his wall. Who has painted more of their wall?

Use a model:

Shade in 4 10 on the top model and 5 6 on the bottom model. Circle the larger fraction.

Use benchmark fractions:

Benchmark fractions tell us how close the fractions are to 0, 1 2 , or 1.

The numerator (4) is closer to half (5) than one (10) or zero (0). 4 10 is closest to 1 2 . 5 6 is closest to . Since 5 6 is closer to a larger benchmark fraction, it is larger. painted more than John.

Apply

Determine if the fraction is closer to 0, 1 2 , or 1.

The denominator tells us how many pieces we need to make 1 whole. The numerator tells us how close we are to 0, 1 2 , or 1.

Compare the fractions by shading in the figures or plotting on the number line. Use <, >, or =.

Determine if each fraction is closer to 0, 1 2 , or 1.

Compare the fractions by shading in the figures or plotting on the number line. Use <, >, or =.

Create a dot plot. Then, answer the questions.

In a science class, a group of 8 students was measuring their bean sprouts in inches. Their results were:

Create a dot plot to show the results.

What was the most common length for the bean sprouts?

What was the least common length for the bean sprouts?

Daily Review Determine if each fraction is closer to 0, 1 2 , or 1.

Learn and Connect

There are some ducks in a pond. After an hour, 4 12 of the ducks flew away. Thirty minutes later, another 3 12 of the original ducks flew away.

A) About what fraction of the ducks flew away over the past hour and a half?

Solve for the exact fraction: 4 12 + 3 12 =

Round to the nearest benchmark fraction: About of the ducks flew away.

B) About what fraction of the original ducks are left in the pond?

Solve for the exact fraction: 12 12 − 7 12 =

Round to the nearest benchmark fraction: About or the ducks are left.

Estimate whether the fractions are closer to 0, 1 2 , or 1. Then, place them on the number line.

Solve, simplifying answers if necessary.

Solve and represent your answer in the fraction circles.

Eli brings 1 2 8 pizza to a pizza party, and Jamie brings 1 7 8 of a pizza. How much pizza combined did the two boys bring? Amy and Kelly are training for a relay race. Amy can run 3 10 of the race. Kelly can run 7 10 of the race. How much more of the race can Kelly run than Amy?

Your neighbor came to borrow flour. You have 4 5 8 cups of flour. The neighbor borrowed 2 3 8 cups. How many cups of flour do you have left?

A runner is running a course that is 9 13 16 miles long. The runner has already run 3 3 16 miles. How many miles are left before the runner reaches the end of the course?

Daily Review Name the place value of the underlined digits.

A scientist is carefully measuring the amount of liquid for an experiment. He needs 32.079 milliliters in the beaker to ensure the experiment works correctly. If we were to estimate to the nearest whole number, that would be 32 milliliters.

We can use a place value chart to understand how to read decimals and know each number’s value.

When saying a decimal number, the decimal point is said as the word “and.” We end saying each number with the last place value name.

What place is the 0 in?

What place is the 7 in?

Learn and Connect Apply

Write each as a decimal.

twenty-three and six tenths

Write the word form for each.

Vocabulary

Tenths - one place to the right of the decimal point

Hundredths - two places to the right of the decimal point

This number is said as: thirty-two and seven hundredths

seven thousand two hundred eighteen and nine hundredths

5.

6.

7. 54.75

8. 993.42

Write each decimal.

Thirteen and three

Write each decimal number in word form.

Two hundred and three tenths

Read each problem, then solve.

In Mr. Larson’s fifth-grade glass, students were put into groups to create a model parachute. Students were given time to work on and test the dropping speed of their parachutes. The table shows the final results of each group’s parachute drop speed from the top of the school to the ground.

Put the speeds in order from fastest to slowest.

Which group had the parachute that fell the slowest?

Which group’s parachute does the model represent?

Mr. Herman drove 100 miles. He had to stop after 57 miles to get gas. What decimal represents the part of the whole trip that Mr. Herman drove before he stopped for gas?

Challenge

Round each to the nearest whole number.

In a survey of 100 people, 78 said that they like chocolate ice cream. What decimal represents the number of people who did not like chocolate ice cream?

Review 2-8 Comparing and Ordering Decimals

Learn and

Connect Daily Review Write the following fractions as decimals.

A few friends are racing in the park. Tim, Josh, Nick, and Sam all ran the times shown in the table. Let’s put those times in order from least to greatest.

1) Line up the decimal points.

2) Compare each number starting from the largest place value, and move to the right one place at a time.

Add a 0 in the hundredths place to make 60.4 = 60.40. Then, compare to the other decimals.

We can double check by plotting the numbers on a number line. Where should the number line start and end? Least , , , Greatest

Vocabulary

Compare the decimals using <, >, or =.

Shade in the two models and compare using <, >, or =.

Color in the correct decimal amounts and order the three decimals in 7-9 from largest to smallest.

Largest to smallest

Order each group from smallest to largest.

6.35, 6.57, 6.4

Create a number line and plot the following decimals.

Hint: Divide the number line into fourths and space the numbers apart equally.

Rick can recite a poem in 45.45 seconds. Paul can recite the same poem in 45.54 seconds, and Jeffrey can recite it in 44.55 seconds.

Who recites the poem the fastest?

Who recites it the slowest?

Mickey is measuring earthworms he finds in his backyard, The first one is 5.05 cm, the second is 5.15 cm, and the third is 5.51 cm. Put these lengths in order from largest to smallest.

Chapter 1

In Chapter 1, we will learn about

Place Value, Multiplication, and Exponents

Large numbers can be used to describe enormous quantities such as of money, weight, or distance.

• Place value to billions

• Compare and order whole numbers

• Write whole numbers in expanded form and expanded notation

• Estimate products

• Multiply two-digit numbers by three-digit numbers

• Multiply with zeros

• Evaluate exponents with powers of 10

We can label the place value of whole numbers up to the billions place.

We can use place value to compare and order whole numbers and write them in expanded form.

We can use rounding to estimate products of whole numbers.

We can use area models, partial products, and the standard algorithm to multiply two-digit numbers by three-digit numbers.

We can understand, write, and evaluate exponents with powers of 10.

Chapter 1-1 Place Value to the Billions

Circle the digit in the hundred thousands place in each number.

Learn and Connect

As of 2019, the Earth had a population of about 7 billion people. A billion is a very large number. In fact, to make 1 billion, you would need 1,000 millions! Look at the place value chart below to see how the number 7 billion is written in standard form.

Remember, the position of a digit in a number determines its value. For example, the 7 in 7,000,000,000 represents 7 billion.

Apply

For each of the following numbers, write the place value of the digit in red.

The following numbers are written in word form. Write the standard form of each number.

5. Nine billion, two hundred million, six thousand, forty-two

6. Twenty-five billion, three hundred ten million, five

The following numbers are written in standard form. Write the word form of each number.

7. 7,209,000,120

8. 28,000,302,124

Vocabulary

Digit - a single numeral (0, 1, 2, 3, 4, 5, 6, 7, 8, or 9) that makes up larger numbers

Standard Form - a number written in digits 0-9; Example: 9,154

Word Form - a number written using words; Example: Nine thousand, one hundred fifty-four

Write the place value of each blue digit.

1. 3,408,789,234

3. 13,285,375,392

5. 243,108,483,009

7. 9,482,908

9. 9,001,904,234

Write the standard form of each number.

2. 5,281,008

4. 12,341,098,091

6. 2,004,908,210

8. 7,912,342,067

10. 214,240,000,001

11. One billion, twenty-five million, three hundred

12. Twelve billion, sixteen million, four hundred fifteen thousand, seven

13. Eight million, two hundred sixteen thousand, four hundred seven

14. Twenty-one billion, six hundred thousand, four hundred eighty-two

15. Six thousand, three hundred seventy

Write the word form of each number.

16. 2,408,082,001

17. 18,000,019,021

18. 4,208,072,002

19. 3,000,408

Solve.

20. Timothy wrote the number two hundred thirty-seven billion, five million, six hundred fifteen thousand, twelve in different color markers on a poster board. The digit in the ten billions place is red, and the digit in the ten millions place is blue.

What is the digit in red? What is the digit in blue?

Chapter 1-2 Expanded Notation and Expanded Form of Whole Numbers

Review Write the place value and standard form of the bolded digit in each number.

Learn and Connect

Expanded form and expanded notation are both ways of writing numbers to represent their values. You can identify the value of a digit by looking at its place or location within the number.

For example, in $432, the digit 4 represents 4 hundreds, 400, or 4 × 100. The digit 3 represents 3 tens, 30, or 3 × 10, and the digit 2 represents 2 ones, 2, or 2 × 1.

Therefore, the number 432 written in expanded form is 400 + 30 + 2 = 432. In expanded notation, it would be written as (4 × 100) + (3 × 10) + (2 × 1).

Apply

five billion, two hundred million, thirty-two thousand, five hundred nine 5,000,000,000 + 200,000,000 + 30,000 + 2,000 + 500 + 9 = 5,200,032,509 780,103

+

=

(3 x 1,000,000,000) + (2 x 10,000,000) + (3 x 1,000,000) + (7 x 100,000) + (9 x 10,000) + (8 x 1,000) + (7 x 1)

Order the standard form numbers used in the chart from least to greatest:

Circle the correct answer to the following questions.

1. When written in expanded form, which number will include (8 × 1,000,000,000)?

A) 27,894,294,567

B) 7,198,902,362

C) 198,932,362

D) 28,962,344,107

2. Circle the correct expanded form for the number 756,098,004.

A) 700,000,000 + 50,000,000 + 6,000,000 + 90,000 + 8,000 + 4 = 756,098,004

B) 700,000 + 50,000 + 6,000 + 90,000 + 8,000 + 4 = 756,098,004

Compare the following numbers using the symbols >, < or =.

3. 129,936,782 127,998,681

6. 8,094,700 7,908,001

9. (2 × 1,000,000) + (3 × 100,000) + (7 × 10,000) + (9 × 1,000) + (1 × 100) + (2 × 10) + (3 × 1) (2 × 1,000,000) + (3 × 100,000) + (7 × 10,000) + (4 × 1,000) + (9 × 100) + (9 × 10) + (9 × 1) 4. 13,936,782 7,428,981 7. 191,936,762 180,094,631 5. 9,936,782 107,998,681 8. 2,936,782 19,094,664

Write the following numbers in order.

8,659,564,271 9,865,234 200,865,895 1,028,655,754 205,695,125 799,989,785 98,250,368 7,895,002,986 10. 11.

Solve.

12. Four local schools conducted a fundraiser to raise money for a charity. The school that collected the most money was awarded a special field trip for the whole school. The second place school won a new chapter book for each student.

Which school won first place?

Which school won second place?

Write the expanded form for the amount of money of the school that came in last place.

Chapter 1-3 Estimating Products

At the airport, 56 airplanes leave every hour. About how many airplanes leave the airport after 12 hours?

5 6 6 0

1 2 1 0

Then, estimate the product. First, multiply the nonzero digits.

Round to the highest place value.

6 0 × 1 0

6 0 0

Learn and Connect Apply

Look at the number in the ones place. If it is 5 or higher, round the number in the tens place up one. If the number is 4 or less in the ones place, keep the number the same in the tens place.

6 × 1 = 6 The factors include 2 zeros.

The product should include the same number of zeros that are included in the factors. Therefore, about 600 planes leave the airport after 12 hours.

8,000 × 20 = 160,000 8 × 2 16 = 1. 10 × 4 =

Here is another example:

Underline the digits you are multiplying and circle the zeros in these multiplication problems.

8,000 × 20 = 160,000 How many zeros are on either side of the equation?

500,000 × 500 = 250,000,000 How many zeros are on either side of the equation?

Round the numbers to the highest place value and multiply.

432 × 48 523 × 99 89 × 72 × = × = × =

Underline the zeros in these multiplication problems. Then, solve for the missing products.

2,000 × 30 = 60,000

How many zeros?

90,000 × 4,000 =

How many zeros?

Round, then estimate the products.

× 89 = ??

× 28 = ??

× 76 = ??

Round, then estimate the products.

300,000 × 700 = 210,000,000

How many zeros?

8,000 × 700 =

How many zeros?

Challenge

Select the more reasonable estimate. Show your work.

A school ordered 9 boxes of paper. There were 895 sheets of paper per box. About how many sheets of paper did the school order?

Kelly purchased 65 packages of paper napkins for an event. There were 63 napkins in each package. About how many napkins did Kelly buy?

Solve using the standard algorithm.

45 × 19 2. 34 × 32

Learn and Connect

19 × 18

You can multiply three-digit numbers in two different ways. Consider the following problem:

623 × 41

Multiplying using area models:

Write the expanded form of each of the factors on opposite ends of the large box. Then, multiply the digits that are on opposite ends of each smaller box to fill in the missing answers.

Multiplying using the standard algorithm:

When using the standard algorithm, group the tens and ones as you move along.

623 × 41 3

Start by multiplying the ones of both factors: 1 × 3 = 3

623 × 41 23

Next, multiply the tens of the first factor by the ones of the second: 1 × 20 = 20

Next, multiply the hundreds of the first factor by the ones of the second: 1 × 600 = 600 623 × 41 623

25,543

Next, repeat using the tens of the second factor. 40 × 3 = 120

Solve using area models.

324 × 23 =

Solve using area models.

Solve using area models or the standard algorithm.

1. 125 × 32 = 2. 763 × 21 =

3. 734 × 19 = 4. 652 × 42 =

5. 762 × 24 =

716 × 64 =

7. 138 × 38 =

273 × 18 =

Chapter 1-5 Multiplying 2-Digit by 3-Digit Numbers

Daily Review

Multiply each number by the number in the center. Write the products in the outer ring.

Learn and Connect

Each student in Mr. Johnson’s class brought a pack of paper to donate to the class. If Mr. Johnson has 27 students, how many pieces of paper does he have for the class?

To solve, multiply 27 × 152. Start by multiplying the ones of both factors:

7 × 2 = 14

Next, multiply the tens of the first factor by the ones of the second factor. Then, add the additional tens:

7 × 5 = 35 + 1 = 36

Then, multiply the hundreds of the first factor by the ones of the second factor. Then, add the additional hundreds:

7 × 1 = 7 + 3 =10

Mr. Johnson has 4,104 pieces of paper for the class.

Apply

Practice multiplying 683 × 24 using three different strategies.

Add a zero underneath. Then, repeat using the tens of the second factor:

Don't forget to put a 0 in the ones place.

Solve using the standard algorithm.

Solve using area model, partial products, or the standard algorithm.

Order the products from questions 12, 13, and 14 from greatest to least:

Read each problem, then solve.

Each night, Steven reads his book for 45 minutes. How many total minutes will he have spent reading after 365 days?

An airplane carries 454 people per trip. If each flight is full, how many people will the airplane have carried after 32 trips?

Fill in the missing digits.

17. A grocery store gets an egg shipment every Tuesday. 427 egg cartons are delivered with a dozen eggs in each carton. Each carton is sold for $4. If all of the eggs are sold each week, how much money will be made in 6 months?

Chapter 1-6 Multiplying with Zeros

Solve using the standard algorithm.

Learn and Connect

A local store put all bikes on sale for the same price for one day only. If they sold 32 bikes that day, how much money did they make in total?

To solve, multiply 32 × 208. Start by multiplying the ones of both factors: 2 × 8 = 16

Next, multiply the tens of the first factor by the ones of the second factor. Then, add the additional tens:

× 0 = 0 + 1 = 1

The store made $6,656 from the sale of the bikes.

Then, multiply the hundreds of the first factor by the ones of the second factor:

Repeat using the tens of the second factor:

Solve using the standard algorithm.

× 22

× 31

×

Solve using area models.

Read each problem, then solve.

A factory makes 203 rubber ducks every hour. How many rubber ducks will the factory make in 24 hours?

A test was given to 42 people. Each test had 110 questions. How many questions need to be graded?

Mike's weekly income is $560. He will work 4 weeks every month. How much will he make in a year?

Challenge

Jamie makes $16 per hour mowing lawns. If he works for 105 hours this month, how much money will he earn?

Tom and Fred each worked 306 hours in the month of June. Tom earned $23 per hour, and Fred earned $28 per hour. How much more money did Fred make than Tom?

Chapter 1-7 Exponents - Powers of 10

Learn and Connect

Powers represent the repeated multiplication of a factor. The base number is the digit that is multiplied by itself. The smaller number is called an exponent and tells us how many times to multiply the base number.

exponent base power

We read this as “ten to the ninth power”.

What patterns do you see in the chart?

Let’s multiply 5 by 102.

5 × 102 = 500

Now, multiply 5 × 103.

Can you multiply 5 by 107?

Apply

Write the powers of 10 in standard form. Then write the expression underneath. Use the chart above to help you.

Multiplication shows repeated addition, while exponents show repeated multiplication.

Multiply by the powers of 10. Hint: When multiplying by to a power of 10, your answer will have the same amount of zeros as the exponent.

Write the numbers as powers of 10 and then in standard form.

10 × 10 × 10 × 10 = = 4 × 10 = 40,000

Fill in the missing exponents.

Multiply by the powers of 10.

102 × 8 =

× 5 =

Read each problem, then solve.

Explain how you used patterns to solve question 9.

Three companies are investing large amounts of money into retirement plans. Company A invests 106, Company B invests 104, and Company C invests 10 times as much money as company B. How much money did each company invest?

B

C

Select all the expressions that have a value less than 1,000,000.

A) 109 B) 104

C) 107 D) 105

E) 108

15.

The distance between Earth and the moon is approximately 2 × 106 miles. Evaluate this expression.

A) 2,000 miles B) 20,000 miles

C) 200,000 miles D) 2,000,000 miles

E) 20,000,000 miles

16. Mickey learned about exponents with powers of 10. He now wants to try solving other types of exponent problems. He decides to write his own exponent problem and solve. Look at his work and find what he did wrong. 17.

A billionaire has 300 billion dollars. Write how much money he has as multiplication by a power of 10.

Mickey's work 2 3 = 6

Write the place value and standard form of the bolded digit in each number.

Learn and Connect

Complete the chart.

Four hundred nine million, nine thousand, nine hundred ninety-nine (4 × 100,000,000) + (9 × 1,000,000) + (9 × 1,000) + (9 × 100) + (9 × 10) + (9 × 1)

1,389,043 1,000,000 + 300,000 + 80,000 + 9,000 + 40 + 3 = 1,389,043

Apply

Compare. Fill the circle in using <, >, or =.

89,136,743,971 89,037,943,172

Seventy-nine million, sixty thousand, nine hundred seventy-two 904,142 906,102 19,762 110,094 1. 3. 5.

497,174,386 99,164,487 (7 × 1,000,000) + (8 × 100,000) + (9 × 10,000) + (9 × 1,000) + (2 × 100) + (2 × 10) + (3 × 1)

(7 × 10,000,000) + (9 × 1,000,000) + (6 × 10,000) + (9 × 100) + (7 × 10) + (2 × 1) Three hundred million, forty-nine thousand, twenty- three 300,049,023 (7 × 1,000,000) + (8 × 100,000) + (9 × 10,000) + (7 × 1,000) + (2 × 10) + (3 × 1)

Solve using standard algorithm or partial products.

Round to the highest place value to estimate, then solve for the exact product.

Solve using area models.

34 × 22 = +

Multiply by powers of 10. Fill in the missing products or factors.

9 × 103 =

Solve the problems. Show your work.

A factory makes 672 cardboard boxes per day. How many boxes will they make in the month of October? Hint: There are 31 days in October.

A truck driver drove 486 miles every day for 62 days. He is required to stop for a 30-minute break each day. How many miles did he drive in all?

Estimate the solution to each word problem. Then, solve for the exact answer.

Abe is a part of a club that gets badges for participation. Abe has 23 badges. Every boy in the club has the same amount of badges as he does. If there are 17 boys in Abe's club, about how many total badges do they have?

A zookeeper says he puts 693 lbs of food in the lion enclosure per day. There are 6 lions in the cage. About how much food do the lions eat in two weeks?

Chapter 2

In Chapter 2, we will delve into

Order of Operations and Division

Learning how to interpret a remainder or divide by a two-digit number helps increase division number sense.

• Use order of operations

• Multiply and divide multiples of 10

• Estimate quotients

• Interpret quotients

• Divide by two digits

We can use PEMDAS to solve multi-step problems.

We can use patterns to multiply and divide multiples of 10, 100, 1,000….

We can find compatible numbers to estimate quotients. We can decide whether to round, drop, use, or split the remainder in a division word problem.

We can see how many times the divisor goes into the dividend to divide a number by two digits.

Chapter 2-1 Order of Operations

Learn and Connect

Mr. Chase wrote the equation on the board. He asked two students to solve it any way they would like. John and David got different answers. Follow the steps that John and David used to find their answers.

John added 2 + 6 first. Then, he multiplied the answer times 5. What was John’s answer?

David multiplied 6 times 5 first. Then, he added 2 to the answer. What was David’s answer?

The order of operations is a set of rules that tells you the order in which operations must be solved. You can use a strategy called PEMDAS to help you remember the order of operations.

First, solve for all the operations that are in parentheses or brackets, if there are any.

Next, solve the exponents, if there are any included.

Then, solve all the multiplication and division from left to right.

Lastly, solve all the addition and subtraction from left to right.

Based on the order of operations, was John or David correct? Explain.

Use the visual to follow the order of operations and solve each equation.

Solve using the order of operations. Mark off the steps on the checklist as you solve.

(14 − 12) + 9 − 1 (9 + 36) − 23 + 37

P (parentheses)

E (exponents)

MD (multiply, divide L to R)

AS (add, subtract L to R)

P (parentheses)

E (exponents)

MD (multiply, divide L to R)

AS (add, subtract L to R)

− 3 + (40 − 31)

P (parentheses)

E (exponents)

MD (multiply, divide L to R)

AS (add, subtract L to R)

P (parentheses)

E (exponents)

MD (multiply, divide L to R)

AS (add, subtract L to R)

P (parentheses)

E (exponents)

MD (multiply, divide L to R)

AS (add, subtract L to R)

P (parentheses)

E (exponents)

MD (multiply, divide L to R)

AS (add, subtract L to R)

Circle the correct expression to help you solve each number story, then solve.

Kane ran 2 miles Monday, 3 miles Tuesday, and 4 miles Wednesday. He runs this same amount of miles for 8 weeks. How many miles did he run?

David baked 24 cookies. Then, he baked 56 more cookies. He wants to give the same amount of cookies to each of the 4 fifth-grade classes. How many cookies will each class get?

Challenge

Place parentheses in the equation below to make the answer equal 4. Which equation has the greatest answer?

Place parentheses in the equation below to make the answer equal 1,351.

Chapter 2-2 Patterns of Division and Multiplication

Daily Review Complete the number sentence.

Learn and Connect

Multiply with zero

Step 1: Multiply basic fact 3 × 2

Step 2: Count the zeros and add them to the product!

Divide with zero

Step 1: Divide basic fact 9 ÷ 3.

Step 2: Add back the zeros.

If there are 0s in the dividend and divisor, first cross off the same number of 0s. Then divide.

Multiply. Keep track of the zeros in the factors so that they match the number of zeros in the products.

6 × 100 =

Divide. Keep track of the zeros in the dividends and divisors.

=

Use what you know about patterns of zeros in division and multiplication to complete the table.

Read each problem, then solve.

Danny is buying potato salad for the school picnic. He bought 50 pounds of potato salad. Each pound is $12. How much money did he spend?

Richard shipped 14,000 cards last year. He shipped them in boxes that held 70 cards. How many boxes did he use last year?

Leo and Max both solved 490,000 ÷ 7,000 = ? Leo’s quotient was 7. Max’s quotient was 70.

Who was correct? What do you think the mistake was with the other quotient?

Chapter 2-3 Estimating with Compatible Numbers

Daily Review Round each number to the highest place value.

Learn and Connect

Mr. Anderson asked two of his students to quickly estimate a solution for the division problem. Compare how they solved the problem.

Sam

I listed multiples of 8 and then multiplied each of them by 10 to get a three-digit number close to 637.

8, 16, 24, 32, 40, 48, 56, 64, 72, 80 80, 160, 240, 320, 400, 480, 560, 640, 720, 800

640 is the closest to and a compatible number for 637.

640 ÷ 8 = 80 Estimated quotient: 80

Compatible numbers are called “friendly numbers” because they make it easy to divide without using paper and pencil.

Mark I looked at the first two digits of 637 and turned the other digits into 0s. Then, I used a multiplication fact that would give me a close answer.

630: I know that 63 is close to 64 and that 8 × 8 = 64.

That means that 8 × 80 = 640 and that 640 is a compatible number for 637.

640 ÷ 8 = 80 Estimated quotient: 80

Will Sam and Mark’s estimates be greater or less than the actual answer? Explain.

Write the matching letter for each problem with its compatible estimate. Apply

Problem

Compatible Estimate

Complete the table.

Circle the better compatible number. Write the estimated equation and explain why the compatible number you chose is better.

Abe has 869 tiles. He packs them in boxes of 10. About how many boxes does he need?

Read each problem, then solve.

Bob made 98 sandwiches for the school fundraiser. He puts 2 sandwiches in each lunch. About how many lunches will he have?

Circle pairs of numbers whose quotient is 10.

Challenge

Jeffrey and Mannie had to make an estimate of what the quotient would be for 598 ÷ 6 = ? Both of them used a multiple of the divisor 6 to make their estimate.

Jeffrey’s estimated equation was 540 ÷ 6 = 90, so his estimated quotient was 90. Mannie’s estimated equation was 600 ÷ 6 = 100, so his estimated quotient was 100. Who had the better estimate? Why?

Learn and Connect

Mr. Herman had 68 ounces of grape juice. He wants to pours 8 ounces into each glass.

1) About how many glasses did he use?

2) How many left over ounces of grape juice does he have?

3) How many glasses did he fill with 8 ounces?

4) How many ounces will each cup have if he splits the leftovers and adds them?

Take the quotient and add one more or round up.

Use when everything or everyone has to fit and you can’t leave any out!

Use the remainder (and not the quotient) as your answer.

Use when the question asks how much is left over or partially filled.

Solve the Problem

Ignore the remainder and use the quotient as your answer.

Use when the question asks for FULL or WHOLE items.

Include the remainder in your answer as a fraction or decimal.

Use with food, money, or measurements that are easy to split in real life.

What does the remainder represent in this problem?

What should you do with the remainder? What is the answer?

Solve. Use the chart from the Learn and Connect to help you.

Solomon has $279 to buy candy bars. Each candy bar costs $4. He buys as many candy bars as he can with the money. How many candy bars does he buy?

Estimate using compatible numbers.

Solve for the exact answer.

What does the remainder represent?

What do you with the remainder?

What is the answer?

Abe has 3,199 toy wheels to build model trucks. Each truck has 8 wheels. He gives the leftover wheels to his brother. How many wheels will he have left over?

Estimate using compatible numbers.

Solve for the exact answer.

What does the remainder represent?

What do you with the remainder?

What is the answer?

Richard needs 537 pencils. The pencils are sold in boxes of 9. How many boxes of pencils does he need to buy?

Estimate using compatible numbers.

Solve for the exact answer.

What does the remainder represent?

What do you with the remainder?

What is the answer?

Mr. Levine has 6 kids. He divides $429 evenly between the kids. How much money does each child get?

Hint: Divide $3 left over between the 6 kids.

Estimate using compatible numbers.

Solve for the exact answer.

What does the remainder represent?

What do you with the remainder?

What is the answer?

Daily Review

Estimate the quotient using compatible numbers.

Learn and Connect

Joshua made 74 donuts. He packs them in boxes of 12. How many boxes will he use? How many donuts will he have left over?

Let’s solve 74 ÷ 12 = ?

A strategy we can use is to see how many groups of 12 are in 74. Let’s multiply the divisor by the following number of groups:

5: 12 × 5 =

6: 12 × 6 =

7: 12 × 7 =

Which number of groups is close to 74 without going over?

We know that is our quotient because groups of 12 is closest to the total of 74 donuts without going over it. How many donuts are left over?

Let's count up to 74 to find our remainder. + = 74 Our remainder is .

74 ÷ 12 = Joshua will use boxes and have donuts left over.

Apply

Step 1: Circle the multiplication fact whose product will bring you closest to the dividend without going over.

Step 2: Add up to find the remainder. Step 3: Write the quotient and remainder.

68 ÷ 22 = 79 ÷ 15 = 97 ÷ 18 =

2: 2 × 22 =

3: 3 × 22 =

4: 4 × 22 =

5: 5 × 15 =

6: 6 × 15 =

7: 7 × 15 =

+ = 68

+ = 79

8: 8 × 18 =

6: 6 × 18 =

5: 5 × 18 =

Remainder: + = 97

Find the remainder for each of the following.

48 ÷ 15 = 3 R

Step 1:

Answer the following questions.

Does 20 go into 79 four times? How did you know?

Does 16 go into 70 six times? How did you know?

Does 15 go into 93 five times? How did you know?

Is there enough left over to make another group of 15?

Does 45 go into 98 two times? How did you know?

Is there enough left over to make another group of 45?

Andrew had a string that was 96 inches long. He cut it into pieces that were each 18 inches. How many 18 inch lengths of string was he able to cut? How much string was left over?

Learn and Connect

We are going to use the standard algorithm to solve 78 ÷ 17. 4 R 10

How many 17s go into 78? 17 × 3 = 17 × 4 =

When the remainder is less than the divisor, there are no more equal groups to make.

Let’s use multiplication to check if our quotient is correct for 78 ÷ 17 = 4 R 10.

Multiply the divisor (17) by the quotient (4).

Add the remainder to the product. Your final answer should equal the dividend. 17

Steps For Division

Divide (How many 17s in 78?)

Multiply (4 x 17 =68)

Subtract (78 - 68 = 10)

Bring Down (There is nothing to bring down.)

We add the remainder because it’s the part of the dividend that was not enough for an equal group.

Multiplication is the inverse of division.

Use the standard algorithm to solve. Use the checklist to remind you of the steps. Use multiplication to check your answer. Apply

Solve. Check your work using multiplication in the space provided.

Solve. Write the equations and check your work.

Richard has 87 crayons. He sells them in boxes of 12. How many boxes will he fill? How many more crayons does Richard need to fill another box?

Mr. Ross’s class has 99 tulip bulbs to plant in the school garden. He wants to plant 16 bulbs per row. His class is assigned 7 rows. How many rows can they fill?

Eitan has $90 to buy picnic baskets. Each basket costs $13. Sandwiches cost $5. What is the maximum amount of baskets he can buy? How many sandwiches can he buy with the leftover money?

Mannie has 94 tickets for the school fair. The game he plays costs 14 tickets. The snack packs he likes cost 10 tickets. What is the maximum amount of times he can play the game? How many snack packs can he buy with the leftover tickets?

David made 65 cookies and 24 donuts. He has 10 boxes. The boxes he uses can either fit 13 cookies or 12 donuts. How many boxes of cookies will he fill? After filling boxes with cookies and donuts, how many boxes does he have left?

9. Challenge

Daily Review Circle the better estimated equation to solve.

3,199 ÷ 71

3,000 ÷ 60

3,200 ÷ 80

Learn and Connect

Mr. Levine needs 3,239 donuts for the school’s end of the year celebration. Kane’s Donut Shop sells donuts in boxes of 12. How many boxes does Mr. Levine need to order?

Let’s use the standard algorithm to solve 3,239 ÷ 12. What should you do with the remainder in this problem? Why?

How many boxes should Mr. Levine order?

Use the standard algorithm to solve. Use the checklist to remind you of the steps. Use multiplication to check your answer. Apply

Solve. Check your answers with multiplication, showing your work.

Check your work

Check your work

Solve and interpret the remainders by circling round, use, drop, or split. Explain your choices.

Moses has 812 photos he puts into a photo album. Each page holds 24 photos. How many photos are on the last page?

There are 2,377 students at the elementary school. The students are taking a flight to visit Washington, D.C. Each plane holds 84 people. How many planes do they need?

B) How much more money do they need to buy ticket for all the students? 7. Challenge

David’s school has $8,235 to buy tickets for a field trip to the zoo. Each ticket costs $25. There are 330 students that will attend the trip.

A) How many tickets can they buy?

Learn and Connect

Solve. Use multiplication to check your answer.

Mr. Smith needs 1,605 napkins for his restaurant. Each box has 32 napkins. How many boxes will he need to buy to have enough for his restaurant?

What should he do with remainder?

Solve using compatible numbers to estimate the quotients.

Solve. Use multiplication to check your answers.

Solve using compatible numbers to estimate the quotients.

1. 447 ÷ 15 = ÷ =

109 ÷ 50 = ÷ =

Solve. Use multiplication to check your answers.

18. Steven is playing a game with his brother. Each time one of them shoots the basketball into the hoop, they get 24 points. So far, Steven has gotten 360 points. How many times has Steven shot the basketball into the hoop?

19. A store is selling lamps for $32 each. One person purchased $1,312 worth of lamps. About how many lamps did they buy?

Solve.

Chapter 3

In Chapter 3, we will learn about

Decimal Place Value

Decimal numbers are important because they can describe a situation more accurately than whole numbers.

• Place value of decimals to thousandths

• Write decimals in expanded form

• Write mixed numbers as decimals

• Identify decimals

• Compare and order decimals

• Round decimals

• Problem solve

We can write the place value of digits up to the thousandths place.

We can write decimals in decimal and fractional expanded form.

We can write a decimal from a model or mixed number.

We can use place value to compare and order decimals.

We can round decimals to a given place value.

We can solve word problems with decimals.

Chapter 3-1 Place Value of Decimals to the Thousandths

Write the place value of the bolded digit in each number.

In a place value chart, numbers to the left represent amounts greater than a whole. The farther left you move, the bigger the number gets. Numbers to the right represent amounts less than one whole. The amounts get increasingly smaller as you move to the right of the decimal.

Each grid below represents one whole. Each whole is cut into different sized parts: 10, 100, 1,000. The shaded part in each grid represents an amount that is less than one whole.

Learn and Connect Apply

Shade each model to represent the decimal.

Wholes (More than 1) Decimals (Less than 1)

Complete the chart by identifying the decimals shown in the models.

Color the models to represent the decimal numbers. Then, compare using the symbols: <, >, or

Chapter 3-2 Expanded Form of Decimals to the Thousandths

Write the fraction form and word form of each number.

Write the value of each separate piece of the model on the line below it.

The model above shows 3.45 in expanded form. The expanded form of a number shows the value of each individual digit. In this case, there are three ones, four tenths, and five hundredths.

Learn and Connect Apply Daily Review

Write the value of the blue digit in each number.

Write the expanded form of each number in decimal form.

Write the expanded form of each number in fraction form.

Form Fraction Form

Write the value of the blue digit in each number.

Write the expanded form for each number. Expand with decimals and fractions.

Write the standard form of each number. 200 + 3 + 0.4 +

+ 0.4 + 0.07

Challenge

Write the expanded form of each number.

3,421,235.92

2,034,123,456.008

2,123,532.209

7,234,213.081

Write the fraction form and word form of each number.

The weight of the can of soup is represented as a mixed number in decimal form. In fraction form, the number would be written as:

When reading mixed numbers, start with the largest place value to the left. The decimal point is read as “and” followed by the value of the last digit. Therefore, this number is read as: eight and five hundredths. The model below represents this amount using hundredths. There are 8 fully shaded boxes to represent 8 wholes. The final box represents 5 100 or 0.05.

Learn and Connect Apply

Complete the chart by identifying the decimals shown in the models.

Challenge

Draw a line to the decimal that matches each fraction.

3.

4.

Chapter 3-4 Using Models to Represent Decimals

Daily Review

Write the expanded form of each number.

Learn and Connect

When we use base ten blocks to represent whole numbers, the unit cube equals 1 whole.

We can rename 1 whole in different ways. Lets see what happens when we rename the other blocks as 1 whole.

When the tens rod is 1 whole:

When the hundreds flat is one whole:

When the thousands cube is one whole:

Write each decimal in its fraction and word forms. Then draw it on the model.

Use the chart to fill in the different ways to

Use the block on the left to find the

as an example.

Daily Review

Write the numbers in decimal expanded form.

Learn and Connect

Leo and Andy bought some fruit at the grocery store. Leo bought apples, and Andy bought oranges. When they got home, they placed their fruit on a scale. The oranges weighed 14.20 lb, and the apples weighed 14.2 lb. Leo stated that his fruit weighed more than Andy’s fruit. Is this true? Explain.

To solve, shade in the decimal that represents the weight of each of the boy's fruit.

Andy’s Oranges Leo’s Apples

Notice that the shaded part of the whole in both models is equal. This is because 2 tenths and 20 hundredths are the same amount cut into different size pieces.

• To make comparing decimals easier, stack the decimals on top of each other. (Make sure to line up the decimals,)

• Then, compare starting with the largest place value to the left.

• If the numbers are equal, move to the next number. If a digit is missing, add in a zero.

Does Leo's fruit weigh more than Andy's fruit? No, they both weigh the same amount.

Apply

Compare the numbers using: <, >, or =.

Write the numbers in order from greatest to least.

Shade in the models to represent the decimal numbers and compare usin: <, >, or =.

Use the following symbols to compare the numbers: >, <, or =.

Write the numbers in order.

Read the problem, then solve. 0.8 0.08

28. Donald, Eric, and Mark raced each other to the end of the block. Donald took 1.08 minutes, Eric took 1.2 minutes, and Mark took 1.007 minutes to get to the end of the block. Who won the race?

29. Create the largest number possible using each of the following digits once: 3, 4, 7, 8. Your number must include three digits after the decimal.

Chapter 3-6 Rounding Decimals

Daily Review

Compare the decimals using: <, >, or =.

Learn and Connect

Peter's father took him to the gas station to put gas in his car. Peter noticed that the machine told his father how many gallons of gas went into the car and how much it cost per gallon.

How much did Peter's father pay for gas, rounded to the nearest whole?

How many gallons of gas did Peter's father put in his car, rounded to the nearest hundredths?

How much was the price per gallon, rounded to the nearest tenths?

To round decimal numbers, you first need to identify the digit in the place value you are rounding to.

Nearest whole: 18.10

Nearest hundredths: 6.387

Nearest tenth: 2.834

Apply

Then, determine if the number directly to the right is less than or greater than five. 0, 1, 2, 3, 4 keep the same 5, 6, 7, 8, 9 round up 1 18 6.39 2.8

Nearest whole: 18.10

Nearest hundredths: 6.387

Nearest tenth: 2.834

Round the following decimals to the nearest whole number.

Round the following decimals to the nearest tenths.

Round the following decimals to the nearest hundredths.

Round the following decimals to the nearest whole numbers.

Round the following decimals to the nearest tenths.

Round the following decimals to the nearest hundredths.

Challenge

Circle the correct answer.

49. Which numbers would equal the same amount when rounded to the nearest hundredths?

A. 3.478 & 3.472

B. 4.562 & 4.559

C. 5.753 & 5.763

D. 3.128 & 3.118

50. Which number equals the same amount when rounded to the nearest tenth and nearest hundredth?

A. 7.238

B. 8.702

C. 9.421

D. 4.210

Chapter 3-7 Decimal Applications and Problem Solving

Daily Review

Round the following decimals to the nearest hundredths.

Learn and Connect

Eitan and Marc decide to make cookies for their school’s bake sale. They compare two recipes. Help Eitan and Marc decide which recipe to use by comparing the amount of ingredients in fractions and decimals.

Recipe 1

Write each amount as a fraction.

Recipe 2

Write each amount as a decimal.

When Eitan and Marc check their kitchen for ingredients, they find the following:

2.459 cups flour, 0.54 cup butter, and 0.6 cup sugar. Help them decide which recipe to use by comparing or ordering the quantities of each ingredient. Use <,>, or = to compare the amounts.

Flour - 2.459 2.35;

Butter - 0.54 0.45; Sugar - 0.6 0.5;

Which recipe can they use and why?

They have enough flour for They have enough butter for They have enough sugar for

Anna is comparing two recipes for bread. The one for white bread asks for 0.4 teaspoons of salt, and the one for wheat bread asks for 3 10 teaspoon of salt. Which recipe requires less salt?

Judy is helping Anna with baking bread. She notices that the white bread recipe asks for 3 4 cup flour, and the wheat bread recipe asks for 0.75 cup flour. They have 9 10 cup of flour. Which recipe should they follow?

Write in the decimal and put the boxes in order from the smallest to largest value shaded.

Victor went to the store with $90 and wanted to buy three items. One cost $49.95, another cost $19.95, and the last cost $31.95. Estimate if Victor has enough money by rounding each amount to the nearest dollar. 105.456 50.501 6.012 5,142.003

A school used 612 of the 1,000 pages printed for distribution. Write a decimal for the number of pages used.

In a school of 1,000 people, there are 680 students, 200 teachers, 25 administrators, and 95 volunteers. Write each value as a decimal and place them in order from smallest to largest.

Jamie is watching 4 bean plants grow and is tracking their heights. By the end of the week, plant 1 grew 5.051 cm, plant 2 grew 5.15 cm, plant 3 grew 5.55 cm, and plant 4 grew 5.015 cm.

Which plant grew the fastest?

Which plant grew the slowest?

Compare using <, >, or =.

Learn and Connect

Complete the chart using the prices of each item.

A big store is having a sale. Some boys are walking around the store and looking at the prices of the items. Color the model to represent each decimal number.

Crayon

Identify the value of the digit in blue. Then, write the number in both word and expanded form.

Use the number line to answer the questions. 5.237 15.236

Expanded form:

Word Form:

Digit Value: Digit Value:

Expanded form: Word Form:

Which letter best represents the location of 1.10?

Which letter best represents the location of 0.74?

Order the decimals from greatest to least.

2.3, 2.34, 2.03, 2, 2.58

46.37, 46.8, 46.2, 46.9, 46.34 5, 5.23, 5.51, 5.02, 5.74 14.78, 46.1, 25.5, 14.8, 32.32

Round the decimals to the place value indicated.

Use the block on the left to find the decimal value of the set of blocks on the right.

Chapter 4

In Chapter 4, we will delve into

Addition and Subtraction of Decimals

Decimals are used in everyday life, especially with money.

• Add decimals

• Subtract decimals

• Check subtraction with addition

• Find missing addends and continue patterns

• Problem solve

We can use models and place value to add and subtract decimals.

We can use inverse operations to check our work.

We can find a rule for a pattern and use it to find missing numbers.

We can solve decimal word problems with money.

Chapter 4-1 Adding Decimals using Models

Daily Review

Round to the underlined digit.

Learn and Connect

Add 0.6 + 0.13 with models.

Add 0.6 + 0.13 with the standard algorithm.

Color in the grids and write the answers.

Add using the standard algorithm.

Add using the models and the standard algorithm.

Chapter 4-2 Adding Decimals

Daily Review

Round each number to the place value indicated. Tenths: 3.821 1.

Steven is riding his bike along a trail made of three smaller trails. He found a map that said how many miles each smaller bike trail is. If he takes all three bike trails in one direction, how many miles will he have traveled in total?

To solve, you have to add the miles of all three trails. When adding decimal numbers, it is important to line up the place values. Include zeros to the right of the decimal as placeholders for numbers that do not include those digits. 6 . 2 4

Learn and Connect Apply

Add as usual, starting with the number on the right. Remember to include the decimal in the same location that it is in, between the ones and tenths.

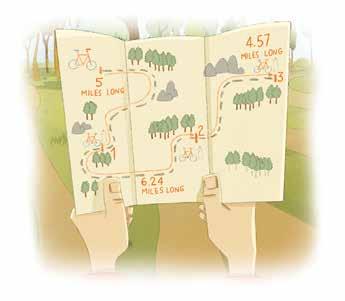
Therefore, Steven will travel a total miles.

Add by coloring in the models. Start by coloring in the first number, then follow with the additional numbers.

Add. Hint: Add in zeros to the right of the decimal point to fill in missing place value spots.

Add by stacking the numbers on top of each other and lining up the place values.

+ 9.9 = 1.

1 + 22.21 + 41.3 = 4.9 + 9.04 =

Add by coloring in the models. Start by coloring in the first number, then follow with the additional numbers.

0.03 + 0.17 + 0.61 =

+ 0.37 =

Circle the number in each box that completes the sentence.

+

+

=

Read each problem, then solve.

Victor and his friend went bike riding. First, they rode 7.7 kilometers (km) to the park. From there, they rode 2.06 km to another friend’s house. Then, they rode 3.4 km to an ice cream shop. How many km did Victor ride?

Challenge

0.4 and have a sum of 3.3. and have a sum of 333.81. 2.1 and have a sum of 4.41.

and have a sum of 265.43.

11. How many km did Victor and his friend ride combined?

Circle two numbers from the box to complete the sentence. Fill in the missing decimals in the table.

Chapter 4-3 Subtracting Decimals using Models

Daily Review

Learn and Connect

Early in the growing season, Daniel’s tallest bean plant is 3.25 inches tall, and his shortest bean plant is 1.72 inches tall. How much taller is the tallest bean plant than the shortest? Find the difference by modeling. Below is 3.25.

Cross out 1.72.

Now try using the standard algorithm!

Count. What’s left?

The tallest plant is inches taller.

Apply

Fill in the grid. Cross out the amount to subtract. Write the answer.

Subtract using the standard algorithm.

Subtract by coloring in the models. Start by coloring in the minuends, then cross out the subtrahends.

− 0.2 =

−

Subtract using the standard algorithm.

−

William wants to walk across the frozen pond. For safety, he cannot walk on the pond unless the ice is at least 4 inches thick. On Monday, the ice was 7.24 inches thick. It melted 1.28 inches on Tuesday and another 2.4 inches on Wednesday. Was the ice still thick enough to walk on? How thick was it?

Richard bought a large box of cereal to share with his siblings. By the end of the week, they had eaten a total of 12.35 oz of cereal. How many ounces of cereal do they have left?

To solve, we have to subtract the amount eaten from the total weight of the cereal. When subtracting decimal numbers, it is important to line up the place values. Include zeros to the right of the decimal as placeholders for numbers that do not include those digits.

1 8 . 0 0

1 2 . 3 5 5 . 6 5

7 9 10 Then, subtract normally. Remember to include the decimal in the same location that it is in, between the ones and tenths.

Therefore, there are oz of cereal left over.

Learn and Connect Apply

Subtract by coloring in the models. Start by coloring in the minuends, then cross out the subtrahends. (Tip: minuend − subtrahend = difference)

Subtract by stacking the numbers on top of each other and lining up the place values. Example: 0.65 � 0.14 = 0.51

Subtract by stacking the numbers on top of each other and lining up the place values.

Find the mistake, solve correctly, and explain the error using words. 14 � 3.2 =

Kane and Tim went to the doctor recently. The doctor said Kane was 4.01 feet tall, and Tim was 5.71 feet tall. They both grew about 0.8 inches in the last three months. What is the difference in their height?

Fill in the missing numbers to complete the patterns. Show your work. Solve.

Eric spends about $500 a month on groceries. He spent $131.56 on groceries the first week and $56.91 the next week. How much more money did he spend on groceries the first week than the next week?

Solve.

Explain the error.

Chapter 4-5 Checking Decimal Subtraction with Addition

Daily Review

Subtract.

Learn and Connect

How many more ounces are in the larger bag of chips?

We can subtract to find the difference.

Is this correct? How can we check?

Use addition to check. Do the difference, (2.53), and the subtrahend (2.78) add up to equal the minuend (5.25)?

Try again! And check!

No! This answer is incorrect because it should equal the minuend, 5.25.

Apply

Subtract. Then check with addition.

The big bag is more oz than the small bag.

Solve. Then, check subtraction with addition.

Victor has the flu. His temperature when he woke up was 99.8°. Later that afternoon, it was 101.4°. How many degrees had his temperature risen?

Vocabulary

Difference - the answer to a subtraction problem

Minuend - the number that you start with in a subtraction equation

Subtrahend - the number that is being taken away in a subtraction equation

Solve. Then, check with addition.

Solve. Then, check subtraction with addition.

A small box of cereal has 12.6 oz. A large box of cereal has 18 oz. The children ate 4.55 oz of the small box. How many ounces of cereal are left in the small box?

The tomato plant was 4.86 inches tall after 1 week and 8.25 inches tall after 2 weeks. How much did the plant grow between week 1 and week 2?

Jack and Howard spent 1.5 hours building towers. Jack built a tower that was 8.35 centimeters tall. Howard built a tower that was 13.1 centimeters tall. How much taller was Howard’s tower than Jack’s?

Kayla went to the store at 3 o’clock. She had $10.50 in her pocket. She bought a candy bar for $4.99. How much money does she have left?

Write your own word problem involving subtraction of decimal numbers on the lines below. Then, trade with a partner. Solve each other’s word problems and check your answers with addition.

Chapter 4-6 Missing Addends and Patterns with Decimals

3, 6, 9, 12, 1. 75, 70, 65, 60, 2. 1, 3, 5, 7, 3. 2, 4, 8, 16, 32, 4.

Learn and Connect

What pattern do you see on the desk?

What is the rule that the pattern follows?

What is the next number in the pattern?

We can use subtraction to find a missing addend:

Identify the rules and fill in the missing numbers in the sequences.

Fill in the missing numbers in Input/Output tables. Write the rules.

Find the missing addends.

Last week it rained on Tuesday, Wednesday, and Thursday. On Tuesday, it rained 1.82 inches, and on Wednesday, it rained 0.98 inches. The total rainfall last week was 3.5 inches. How much did it rain on Thursday?

Chapter 4-7 Money Applications and Word Problems

Estimate the sums by rounding each number to the highest place value.

and

Daniel has saved $4.25 to buy a turtle. He just received $11.50 from his aunt. How much money does he have now?

Line up the place values.

forget to line up the decimal points!

Daniel has saved.

Hint: Don’t forget to add the decimal and money sign when you are finished adding. Add. Solve.

Rewrite vertically. Then, solve.

Solve. Show your work on a separate piece of paper.

The money pictured below is Danny’s. How much money is pictured?

The money pictured below is Eli’s. How much money is pictured?

A) Danny needs to purchase a book for $12.99. How much money will he be left with after his purchase?

B) Danny unexpectedly finds an old wallet in his house that has some money in it, which is pictured below. How much money did he find?

C) After purchasing the book and finding the additional money in his wallet, how much money does Danny have now?

The table below shows the prices of several items at the store.

George had $5.00 when he went to the store. If he bought one cup, what is the most expensive item he can buy with the money he has left?

A) Eli owes his friend $27.50 but also needs to purchase 2 train tickets for $9.99 each. How much money will the tickets and repaying his friend cost in total?

B) Does he have enough money to repay his friend and buy the train tickets?

Yes or No

C) How much money will he have left after repaying his friend and purchasing the train tickets?

D) Will he have enough left over for another train ticket?

Yes or No

You purchased one of each of the fruits below.

If you paid with a 20 dollar bill, how much change would you receive?

Daily Review Fill in the missing numbers.

3.2, 3.4, 3.6, 3.8, 1. 7.5, 8, 8.5, 9, 2. 1, 1.05, 1.1, 1.15, 3.

Learn

and Connect

Mrs. Davis is making a pumpkin pie. She buys this pumpkin. She removes the peel, stem, and seeds and weighs them. They weigh 2.08 lbs. How much pumpkin does she have left to use for her pie?

Subtract: 8.24 − 2.08 =

One pie recipe calls for 2.25 lbs of pumpkin, and another calls for 1.8 lbs of pumpkin. If she makes both recipes, how much pumpkin does she need?

+ 1.8 =

Apply

Fill in the missing 0s. Then, solve. Fill in the missing 0s. Color in the models to add or subtract. Then, solve.

Use models to solve.

Fill in the missing 0s. Then, solve.

Solve. Then, check with addition.

Fill in the missing numbers in the sequences.

Use subtraction to find the missing addends.

Solve.

Andrew wants a new coat that costs $89.99. He has $50.31 in his bank account. His grandfather gives him $30, and he finds $8.90 on his dresser. How much money does he have now?

Can he buy the coat yet?

If yes, how much money will he have leftover? If no, how much more does he need?

Chapter 5

In Chapter 5, we will learn about

Multiplying Decimals

We will begin to recognize the role of the decimal point in multiplication and use estimation to see if our answers are reasonable.

• Estimate decimal products

• Multiply decimals by whole numbers and decimals

• Multiply decimals by 10, 100, or 1,000

• Find area and perimeter with decimals

We can use rounding or compatible numbers to estimate decimal products.

We can use models and an algorithm to multiply decimals.

We can use patterns of 10 to move the decimal point over when multiplying by 10, 100, or 1,000. We can find area and perimeter with decimals.

Chapter 5-1 Estimating Decimal Products

Daily Review

Estimate the sum of each problem by rounding to the nearest whole.

Learn and Connect

Charlie and his three friends want to ride the ferris wheel. About how much money would they need to pay for all four of them to ride?

To solve, you must estimate and multiply the cost of the ferris wheel ride times the amount of people who want to ride.

Estimate using rounding:

Round to the nearest whole number.

Estimate using compatible numbers:

Choose numbers that would make it easier to multiply.

Therefore, they would need approximately $7.00 for all of them to ride the ferris wheel.

Apply

Round to estimate.

Estimate each product using rounding.

Estimate each product using compatible numbers.

Read each problem, then estimate to solve.

On Monday and Wednesday, Joshua went driving to visit his family. He drove 58 miles per hour to see them. He drove for 4.75 hours each way. About how many miles did he travel each way?

The pumpkin patch has 235 pumpkins on sale. Each pumpkin costs $4.89. Mark bought 19 pumpkins, and David bought 25 pumpkins. About how much money did Mark spend?

David and Eli are reading the same book. Eli read 1 chapter in 7.32 minutes. David read 1 chapter in 8.03 minutes. Eli read 4 chapters, and David read 6 chapters. About how much time did it take David to read if all the chapters are the same length?

Challenge

Grapes cost $2.27 per pound, bananas cost $1.45 per pound, and apples cost $2.09 per pound. Leo bought 4.8 pounds of grapes and 2.1 pounds of apples. About how much money did Leo pay for the grapes?

Daniel tried estimating the following products. Circle his errors and write the correct solution on the line.

11. 3.05 � 14.2

Estimate: 30 � 15 Solution: 450

Correct solution:

8.74 � 18

Estimate: 9 � 20 Solution: 18

Correct

� 16

Estimate: 5 � 20 Solution: 100

Correct solution:

Chapter 5-2 Multiplying Decimals using Models

Learn and Connect

Let’s use an area model to solve 0.5 × 0.2. What does 0.5 × 0.2 mean? It means 5 10 of 2 10 .

Step 1: Show 2 tenths (0.2) on the base ten block.

Show the one factor vertically on the model.

Step 2: Show 5 tenths (0.5) going across on the base ten block.

Show the other factor horizontally on the model. The Product Apply

Step 3: Look for the place where they overlap. This is the product of 0.5 × 0.2 or 0.5 of 0.2 = 0.10.

Match the letter of the multiplication sentence to the correct model.

Use the models to help you solve.

Find the missing value in each equation. Use the model to help you.

Draw a model for each equation and solve.

Daily Review

Estimate each product by rounding to the nearest whole.

A bakery is selling cupcakes. A customer wants to buy 4 of the cupcakes. What will be the customer’s bill?

To solve, you must multiply the number of cupcakes by the cost of each cupcake.

To multiply with decimals:

Step 1: Set up the multiplication problem by putting the number with the most digits at the top.

Step 2: Solve the multiplication problem as you would do normally.

Step 3: Then, count the number of digits after the decimal in each factor. Put the same number of digits behind the decimal in the product.

Learn and Connect Apply

Solve.

Two digits after decimal +

Zero digits after decimal =

Two digits after decimal

Therefore, the customer’s bill will be $10.32.

Digits after decimal:

Digits after decimal:

Digits after decimal:

Digits after decimal:

Digits after decimal:

Digits after decimal:

Write a multiplication expression to represent each scenario. Then, solve.

11. Apples are $1.23 per pound. How much will 5 pounds cost?

12. Shirts are $5.98 each. How much will 8 shirts cost?

14. Water fills a pool with 12.5 gallons a minute. How many gallons will there be after 3 minutes?

15. Tickets for the play are $25.85. How much will 6 tickets cost?

13. Gas is $3.21 per gallon. The gas tank holds 9 gallons. How much will it cost to fill it?

16. A recipe calls for 3.75 cups of flour. You make 4 batches. How much flour will you use?

17. Bananas are $0.86 each. How much will 8 bananas cost?

18. Cereal is $3.57 a box. How much will 9 boxes cost?

Challenge

20.

What is the total of your shopping trip if you purchase:

• 2 watermelons for $2.75 each

• 6 packs of strawberries for $4.32 each

• 3 pounds of kiwi for $3.18 per pound

19. Average points per game is 12.3. How many points will be scored in 7 games?

Daily Review Solve.

Learn and Connect

The library is selling boxes of old used books for $5.25.

Mrs. Becker buys 12 boxes for her classroom.

How much does Mrs. Becker spend on the books?

Step 1: Set up the problem by putting the number with the most digits on top.

Step 2: Solve the multiplication problem as you would normally do.

Step 3: Count the number of digits after the decimal point in each factor. Put the same number of digits after the decimal in the product.

Digits after decimal: + Digits after decimal: = Digits after decimal: Apply

Solve.

Digits after decimal: +

Digits after decimal =

Digits after decimal

Read each problem, then solve.

11. Play tickets cost $20.35 each. If 26 students buy tickets, what is the total cost?

12. The cake recipe uses 1.5 cups of sugar. The baker makes 15 cakes. How many cups of sugar are used?

14. Dad drives an average of 67.8 miles per hour on the highway. How far can Dad drive in 24 hours of total driving?

15. Macaroni costs $2.58 per box. How much will 12 boxes cost?

13. Soup is $1.38 per can. How much will 14 cans cost?

16. Gas costs $3.42 per gallon. The truck’s gas tank holds 22 gallons. How much does it cost to fill the tank?

Challenge

17. At the takeout store on Tuesday, they sold 32 burgers, 28 orders of fries, and 46 sodas. How much money did the store bring in Tuesday night?

Chapter 5-5 Multiplying Decimals by Decimals

Learn and Connect

Skyler mows lawns. He had some customers call to have their lawns mowed after school. By Monday night, Skyler had spent 5.5 hours mowing lawns. How much money did Skyler make?

To solve, you must multiply the number of hours Skyler worked by his hourly wage.

Step 1: Set up the multiplication problem by putting the number with the most digits at the top.

Step 2: Solve the multiplication problem as you would do normally.

Step 3: Then, count the number of digits after the decimal in each factor. Put the same number of digits behind the decimal in the product.

Solve.

Write a multiplication expression for each scenario. Then, solve. Round to the nearest hundredths for dollar amounts.

13. Apples are $1.83 per pound. How much will 2.5 pounds cost?

14. Peppers cost $0.76 per pound. How much will 3.2 pounds cost?

15. Gas is $2.86 per gallon. The gas tank holds 7.6 gallons. How much will it cost to fill it?

16. When it rains, a pond fills with 12.5 gallons a minute. How many gallons will it fill up after 5.5 minutes?

17. The temperature drops 0.75 degrees per hour. How much will it drop after 10 hours?

18. A recipe calls for 1.75 cups of sugar, and you make 2.5 batches. How much sugar will you use?

19. Lemons are $2.67 per pound. How much will 5.3 pounds cost?

20. Ribbon is $1.77 a yard. How much will 22.5 yards cost?

21. Average points per game is 11.2. How many points will be scored in 6.5 games?

Three friends fill up their cars with gas at different stations. Determine the amount each person spent.

22. Henry 12.5 gallons at $2.86 per gallon

23. Larry 10.8 gallons at $2.96 per gallon

24. Mickey 15.2 gallons at $2.53 per gallon

Learn and Connect

Dennis works at a party store. His boss gave him an order form that shows how many balloon packs he needs to order in each color. Each balloon pack costs $3.22. Find the total price the store will need to pay for each color.

To solve, you must multiply the amount of balloons needed by the cost of each balloon pack.

When multiplying decimals by 10s, 100s, or 1,000s, you can use this trick to solve quickly.

First, multiply the nonzero numbers and include the same amount of zeros at the end of the factor to the end of the product.

Green Balloons: 3.22 � 10 = 3.220 = $32.20

Red Balloons: 3.22 � 100 = 3.2200 = $322.00

Blue Balloons: 3.22 � 1,000 = 3.22000 = $3,220.00

Then, shift the decimal to the right the same number of places as the power of ten. Count the number of zeros in the ten factor. That's how many places the decimal moves.

Apply

Look at the decimal number sentences in 1-9. What pattern do you see?

Calculate the price for the different quantities of each item.

Leo swims 4.8 miles every day. How many miles does he swim in 10 days? Use mental math to solve, and explain how you got your answer.

Mr. Levine wrote 62.89 x 100 = ? on the board. Moses wrote 628.9 as the product. Kane wrote 6,289 as the product. Who has the correct answer, Moses or Kane? Why was the other answer wrong?

What pattern do you notice? Use it to complete the table.

Learn and Connect

To find the area and perimeter of this rectangle, we need to add and multiply decimals.

Perimeter = Sum of all side lengths

Bring the decimal straight down.

Add zeros as placeholders.

Remember: In a rectangle, opposite side lengths are equal!

Remember to label the units “squared” for area!

Digits after decimal: + Digits after decimal: = Digits after decimal:

Apply

Find the perimeter and the area of each figure.

Solve the word problems.

The playground has a rectangular fence around it that is 15.85 yards long by 9.6 yards wide. What is the perimeter of the fence around the playground?

What is the area inside the fence around the playground?

Find the perimeter and area of each figure.

Read each problem, then solve.

Dad wants to build a fence around the back yard. The yard is 8.2 meters by 6.85 meters. How many meters of fencing will Dad need to fence the whole back yard?

Emma is painting a wall in her bedroom yellow. The wall measures 13.2 feet long by 8.5 feet tall. How many square feet is Emma going to paint?

A piece of printer paper is 8.5 inches by 11 inches. What are the perimeter and area of a piece of printer paper?

Challenge

The Madison family is getting new carpet for the baby’s room. The room measures 9.7 ft by 12.1 feet. How many square feet of carpet do they need?

The perimeter of this rectangle is 14.8cm. What is the missing side length?

What is the area of the rectangle?

× 100 =

Learn and Connect

Bill’s Burger Palace sells burgers and other items. Richard wants to place an order:

3 regular burgers

3 small fries

What will be the total Richard will pay before taxes?

To solve, we need to multiply the number of burgers times the cost of each burger. Next, we need to multiply the number of small fries times the cost of the small fries.

3 × 5 = $15 3 × 1.35 = $4.05

Then, we need to add the total cost.

Therefore, Richard will pay before taxes.

Apply

Use Bill’s Burger Palace Menu to answer the questions below.

1. Mickey bought 12 of the same item from Bill’s Burger Palace. His total before taxes was $60. Which item did Mickey buy 12 of?

2. Chad wants to buy 15 large fries. What would be the total cost of the large fries before taxes?

3. David ordered 2 regular burgers and 2 medium fries. Eli ordered 5 large fries and 1 regular burger. Whose order cost more before taxes? How much more?

4. Kane bought 10 of the same item, and it cost $17.50 before taxes. Solomon bought 10 of the same item, and it cost $21.30 before taxes. What did each of them order?

Solve.

Use the order of operations to solve.

Solve and use estimation to check each answer.

Solve.

Solve. Show your work each model.

Write the equation that matches each model.

Chapter 6

In Chapter 6, we will expand on

Multiplying and Dividing Decimals

We can use multiplication and division of decimals to find the price of a unit item or the price when we buy a few of the same item.

• Estimate decimal quotients

• Multiply decimals by whole numbers and decimals

• Multiply and divide money

• Use multiplication to check division with decimals

• Problem solve with decimals

We can use compatible numbers to estimate decimal quotients.

We can use models and an algorithm to divide decimals by whole numbers and decimals.

We can use what we know about decimals to multiply and divide money.

We can check our work by using inverse operations. We can solve word problems with decimals using all four operations.

Chapter 6-1 Estimating Decimal Quotients

Learn and Connect

Leo and Aaron worked together at the school bake sale to sell cupcakes. Together, they earned $22.80. If they plan on splitting the profit evenly, about how much will each boy earn?

What equation would Leo and Aaron use to solve for the exact answer? Are Leo and Aaron looking for the exact answer or an estimate?

When finding the estimates for division, first find compatible numbers by listing the multiples of the divisor.

2 2, 4, 6, 8, , , , , , , ,

What multiple of our divisor (2) is closest to the total of 22.80?

We use these compatible numbers to create an estimate: 22 ÷ 2 =

This means that Leo and Aaron will both take home about dollars.

Apply

List the multiples of the divisors. Use the compatible numbers to circle the closest estimates.

Vocabulary

Compatible numbers - pairs of numbers that are easy to add, subtract, multiply, or divide in your head

Divisor - a number by which another number is to be divided; the number of equal groups the dividend is divided into in a division equation

Dividend - a number to be divided by another number; the number a division equation starts with

Quotient - the answer to a division problem

Use compatible numbers. Circle the best estimate.

For problem 2, explain why your estimate is the closest estimate for that problem.

Rewrite each equation to show the best estimate for each problem below.

Read each problem, then solve.

Marvin would like to split 6.5 brownies between 3 people. About how many brownies will each person get?

Challenge

Max received $33.75 for his birthday. He is going to split it to save half and spend half. About how much money will he have to spend?

Sam says that 7.5 ÷ 3 is about 2. Tom says 7.5 ÷ 3 is about 3. Who is right? Prove your answer using pictures or a number line.

Chapter 6-2 Dividing Decimals using Models

Learn and Connect

After the fifth-grade celebration, there were 1.6 pans of brownies remaining. Mrs. Herman would like to divide the brownies evenly among the 4 fifth-grade classes. How many brownies will each class receive?

Look at the model. It shows the 1.6 pans of brownies that remain.

We have a total of tenths. We can divide these 16 tenths into 4 equal groups, using a quick picture. Draw a line to represent each tenth, and then divide the 16 tenths into groups of 4.

How many groups did you make? Circle the 4 groups of 0.4 in the original model.

Our model shows that 1.6 ÷ 4 = We can check our division by using multiplication 0.4 × 4 =

Mrs. Herman will give each class pans of brownies.

Apply

Use a model to help you divide. Then, use multiplication to check.

Hint: Remember that you can break up a tenth into hundredths to help divide evenly.

Draw a model to help you divide, then use multiplication to check.

Read each problem, then solve.

Eric had 3.2 sheets of poster board. If he wanted to split his poster to make 4 smaller posters the same size, how much would he use for each smaller poster?

Use a model to find your answer.

Draw a model for 1.2 ÷ 4 =

How is it related to this model of 1.2 ÷ 0.3 = 4?

William bought 6 of the same size metal cubes. All together, they weighed 1.26 pounds. How much did each cube weigh?

Chapter 6-3 Dividing Decimals by Whole Numbers (no

Learn and Connect

A store is selling a bundle of toy cars. Each bundle includes 5 toy cars. The store wants to sell the toy cars separately. If each toy car is worth the same amount, how much would one toy car sell for?

To solve, we need to divide the price of the bundle by 5 toy cars.

When dividing decimals, set up the division problem. Divide the same way you would divide whole numbers. Then, place a decimal in the quotient by moving your decimal point directly above the decimal in the dividend.

Apply

Divide.

Find the quotients.

Write a division expression to help you solve.

11. If 8 shirts cost $148.80, how much is each shirt?

14. The total bill was $54.80, and 8 pizzas were ordered. How much was each pizza?

12. If 3 pounds of celery costs $2.34, how much is it per pound?

13. If 123.2 gallons of grass seed will be used on 14 acres, how many gallons will be used for each acre?

17. A pack of 4 yogurt costs $5.32. How much is each yogurt?

15. A dozen bagels cost $13.44. How much is each bagel?

18. If 28.4 pounds of flour is divided into 8 containers, how much is in each container?

16. If 36 students are in class, and they collected $892.80, how much did each student collect, assuming they each collected the same amount?

19. A 12-pack of juice is $4.92. How much is each juice box?

Fill in the missing digits to make this division true. Challenge

20.

Chapter 6-4 Dividing Decimals by Decimals (no remainders)

Learn and Connect

Mike is a house painter. He uses 2.3 gallons of paint to paint one room. If he has a total of 34.96 gallons of paint, how many rooms can he paint?

To solve, we need to divide the total amount of paint he has by the number of gallons it takes to paint one room.

When dividing decimals, set up the division problem. Move both decimal points until the divisor is a whole number.

2.3)34.96

Then, move up the decimal point to be used in the quotient.

23)349 . 6

We always move the decimal point over the same number of times in the dividend as in the divisor.

Therefore, Mike can paint rooms using the paint he has.

Apply

Find the quotients. Remember to move the decimals so the divisors are whole numbers.

Write division expressions to help you solve.

11. A 1.7 lb package of salmon costs $20.91. How much is it per pound?

12. The temperature rose 12.8 degrees in 3.2 hours. How much did it rise each hour?

14. You have 18.5 yards of fabric, and you cut it into 5 equal pieces. How long is each piece?

15. A bag of flour weighs 5.25 pounds, and there are 15 cups. How much does each cup weigh?

13. If 8.8 pounds of apples cost $19.80, how much are they per pound?

17. A 12-pound bag of potatoes cost $6.60. How much is it per pound?

Challenge

Try to solve mentally.

18. There are 8.25 inches of snow after 2.5 hours of snowing. How much did it snow each hour if it fell at a steady rate?

16. A plant is 19.2 inches tall after growing for 3.2 weeks. How much did it grow per week if it grew the same amount every week?

19. 8.4 ounces of vanilla costs $52.92. How much is each ounce?

Learn and Connect

The farm stand sells each carton of one dozen eggs for $3.24. On Sunday, they sold 28 cartons of eggs. How much money did they make on Sunday?

When combining groups of items, you multiply. Complete the multiplication.

3.24 × 28 Hint: Don’t forget to add back in the decimal and dollar sign when you finish multiplying.

The farm stand made on Sunday.

Now, find how much money the farm stand makes per egg.

When breaking apart a group, you divide. Complete the division.

Each egg costs at the farm stand.

Apply Solve.

are 12 eggs in a dozen.

Decide which operation to use to answer each question. Solve.

A pack of 12 juice boxes costs $9.00.

How much does each juice box cost?

How much would it cost for 5 packs?

A box of 7 granola bars costs costs $8.75.

How much does each granola bar cost?

How much would it cost for 3 boxes?

A basket of 19 apples costs $5.70.

How much does each apple cost?

How much do 15 baskets cost?

A container of 30 cookies costs $4.50.

How much does each cookie cost?

How much would 8 containers cost?

Chapter 6-6 Using Multiplication to Check Division

Learn and Connect

Mannie and Jack were walking home from school and passed by the circus that was set up for tomorrow. They read the sign.

Mannie pulled a $5.00 bill from his pocket and yelled, “Only $4.50 a ticket!”

“No,” said Jack, “It is $8.75 a ticket.”

Which boy is correct?

When checking the answer for a division problem, we can use the inverse (or opposite) operation. That means we can multiply.

The sign says that 4 tickets will cost $35.00. That means we need to multiply each boy's guess by , to see which one gives us the total of $35.00.

Mannie said it was $4.50 a ticket. Solve the multiplication problem to see if Mannie was correct.

Jack said it was $8.75 a ticket. Solve the multiplication problem to see if Jack was correct.

is correct; each ticket will cost .

Apply

Use multiplication to check each division problem. Put a check if the answer is right, and circle it if the answer is wrong.

Vocabulary

Use the number cards to create your own division problems. Solve the division problems, and switch with a partner. Check each other’s answers using multiplication.

Solve. Then, check your answers using multiplication.

Read each problem, then solve.

Arnold paid $12.75 for 3 dozen eggs. He thinks he paid $3.25 for each dozen. Is he right?

Challenge

Peter bought a case of juice for $9.00. If there are 12 juice boxes in the case, how much did each juice box cost? Check your answer with multiplication.

Rick needs to buy 24 juice boxes for a party this Sunday.

He can buy them individually for $0.75. He can buy them in a box of 6 for $3.00. He can buy them in a box of 12 for $4.80. He can buy them in a box of 24 for $12.00.

What packaging is the cheapest price for Rick? How much per juice box will he end up spending?

Chapter 6-7 Problem Solving with Decimals

Learn and Connect

Charlie and his father went to a fruit stand. They bought 5 oranges and 12 apples. How much money did they spend at the fruit stand all together?

How much was each orange?

Solve the multiplication. How much was each apple? How many oranges did they buy? How many apples did they buy?

Charlie and his dad spent on oranges and on apples. What operation do we use to find out how much they spent all together?

Solve the addition. + =

Charlie and his dad spent at the fruit stand.

Apply

Solve each problem below using addition, subtraction, multiplication, or division.

Steven was at the aquarium. He spent $35.50 on his admissions ticket, $12.75 for lunch, and $15.85 for a special dolphin show. About how much did he spend at the aquarium? (Round to the nearest 10.)

David has $56.78 in his savings, and his brother Tim has $82.43 in his savings. What is the difference in their savings?

Justin needed to buy 3 quarts of milk. If each quart of milk is $1.78, how much will he spend in total?

Jeffrey saw that a box of 8 erasers was $2.80. How much does each eraser cost?

Circle the expression that will help solve each problem correctly.

Jake earns $9.00 an hour at work. How much does he earn in 12 hours?

Muffins are sold by the dozen. If each dozen costs $4.99, how much would 36 muffins cost?

Steven has $4.56, Leo has $15.75, and Chad has $11.34. How much more does Chad have than Steven?

If a pack of 3 toy cars costs $3.96, how much does each toy car cost?

Solve each problem below using addition, subtraction, multiplication, or division.

About how much change does Joshua get from a 5-dollar bill if he buys a candy bar for $1.75?

Frank bought a bottle of water for $2.99 and a slice of pizza for $5.75. How much money did he spend all together?

It costs $0.65 for one taffy at the local grocery store. How much does it cost for Rick to buy 6 taffies?

It costs $16.52 for a newspaper to be delivered for a month. What is the weekly cost to have the newspaper delivered? (use 4 weeks = 1 month)

If a box of bakery cookies costs $6.00, and there are 10 cookies in the box, how much does it cost per cookie?

Challenge

A shopkeeper bought a blender for $15.25 and sold it for $32.50. What was the profit?

The local bakery makes 56 trays of cookies each day to sell. Each tray holds 15 cookies. The cookies are then boxed in packages of 12. How many packages of 12 cookies does the bakery make each day?

If they sell each package of cookies for $3.75, how much money will they make?

Learn and Connect

Arnold and Nick are working together to solve math problems. They have to create a model of 0.84 ÷ 4.

They drew two very different looking models. Who is correct?

First, solve the division problem and check it with multiplication.

Analyze Arnold’s Model

How many total units are shown?

How many groups are shown? How many units are in each group?

models are correct.

Analyze Nick’s Model

How many total units are shown? How many groups are shown? How many units are in each group?

Apply

Circle the best estimate for each problem and then solve for the exact answer.

Solve, then check with multiplication.

Draw a model to help you divide, then use multiplication to check.

Solve.

How much does each juice box cost?

How much would it cost for 8 packs?

How much does each yogurt pouch cost?

How much would it cost for 2 boxes?

How much do 4 packages of cupcakes cost?

How much does each cupcake cost?

Chapter 7

In Chapter 7, we will practice

Addition and Subtraction with Fractions

This chapter involves fractions that have different denominators since many fractions we need to work with in the real world do not have the same denominator.

• Compare, order, and locate fractions on a number line

• Estimate sums and differences with mixed numbers

• Add and subtract fractions with unlike denominators

• Add and subtract mixed numbers with unlike denominators

• Problem solve

We can find equivalent fractions in order to compare them. We can use benchmark numbers to estimate sums and differences of mixed numbers.

We can find a common multiple to make equivalent fractions or mixed numbers so we can add or subtract them. We can solve word problems with addition and subtraction of fractions and mixed numbers.

Chapter 7-1 Comparing, Ordering, and Locating Fractions on a Number Line

Daily Review Turn each improper fraction into a mixed number.

Learn and Connect

Paul and Josh are painting their rooms. Paul has painted 2 3 of his wall, and Josh has painted 3 5 of his wall. Who has painted more of their wall?

To solve, we have to compare 2 3 and 3 5 to see which is the larger number. First, we need to find equivalent fractions for each number so they both have the same denominator.

List the multiples for each denominator and find the first one they have in common. Then, rewrite your fractions with a common denominator.

Last, compare the fractions by finding the fraction with the larger numerator.

Therefore, has painted more of his wall. We can check our work by plotting both fractions on a number line. Both fractions are less than 1 whole, so the number line is from 0 to 1, or 15 15 .

Rewrite each set of fractions with a common denominator. Then, compare using >, <, or =.

Rewrite these fractions with a common denominator and plot them on the number line.

Rewrite each set of fractions with a common denominator. Then, compare using >, <, or =.

Write true or false next to each comparison. Write equivalents fractions and fill in the models to show your work.

Rewrite each fraction with a common denominator. Then, order them from smallest to largest.

Select three fractions from this page and show their order from smallest to largest on a visual model (fraction circles, fraction bars, number lines).

Hint: Select fractions with the same denominator or write equivalent fractions to have the same denominator.

Solve and create a visual model to show your answer.

11. John and Sam are both working on their math homework. John’s worksheet has 10 problems, and he has finished 6 of them. Sam’s worksheet has 15 problems, and he has finished 8 of them. Who has finished the larger fraction of problems on his worksheet?

12. Charlie and Jack are riding their bikes to school. Charlie lives 5 miles away and has already biked 3 miles. Jack lives 7 miles away and has already biked 5 miles. Which boy has the smaller fraction left to bike to school?

Chapter 7-2 Estimating Sums and Differences with Mixed Numbers

Daily Review

Compare each fraction set below using <, >, or =.

Learn and Connect

Jack bought some fruit at the grocery store. He made a chart of the weights of each type of fruit he bought. If Jack combined the red and green grapes, about how many ounces of grapes would he have?

To solve, you must estimate the weight of the red grapes and the green grapes and then add. To estimate mixed numbers, we can use benchmark numbers. Use the closest whole number as a benchmark.

Add the wholes to get an estimated total.

Therefore, Jack has about 12 oz of grapes in total.

Apply

Use the visual fraction models to estimate to the closest whole number. Then, solve.

Estimate to the closest whole numbers, rewrite the equations, and solve.

Circle the answer that is more reasonable for each equation based on benchmark whole numbers.

Look back at the estimate you circled for #1, and explain why your estimate is the more reasonable answer.

Estimate using benchmark numbers to find the solutions.

Read each problem, then solve.

The palm tree by Larry’s house grew 2 1 8 inches last month. This month, it grew 1 8 9 inches. About how much did the tree grow over the past two months?

Peter poured 4 3 9 cups of milk into a bowl to make biscuits. The bowl tipped, and 2 7 9 of the milk spilled onto the floor. About how much milk does Peter have left?

Jake is trying to finish putting up the molding in one room of his house. He needs 3 1 4 feet of molding on one wall and 2 3 8 ft. of molding for a second wall.

He has 5 feet of molding. Does he have enough to finish the walls?

Draw a fraction model in the space provided to justify your answer. Use words to explain your thinking.

Chapter 7-3 Adding Fractions with Unlike Denominators

Daily Review

Solve, reducing these fractions to simplest form.

Learn and Connect

Peter is making a special mixture of nuts. He places 3 4 cup of almonds and 3 5 cup of peanuts into a bowl. How many total cups of nuts does he have in the bowl? How can we solve 3 4 + 3 5 ?

We need to find equivalent fractions for 3 4 and 3 5 that will have the same or like denominators.

Step 1: Find a common multiple of both denominators.

Step 2: Create equivalent fractions. Use the common multiple as the new denominator.

Fractions with different denominators can’t be added or subtracted because the denominators represent different size pieces.

4, 8, 12, 16, 20, 24, 28 5, 10, 15, 20, 25, 30

Step 4: Simplify. There is 1 group of 20 in 27 with 7 left over.

Step 3: Add the fractions with like denominators.

Therefore, Peter had 1 and 7 20 cups of mixed nuts.

Apply

Solve and reduce the fractions to simplest form. If the answers are improper fractions, turn them into mixed numbers.

Solve, reducing the fractions to simplest form. If the answers are improper fractions, turn them into mixed numbers.

Read the problem, then solve.

10. Frank filled two water bottles of the same size. Water bottle A was filled 3 8 of the way. Water bottle B was filled 2 16 of the way. How much more full was water bottle A than water bottle B?

Circle the correct answer. Challenge 11. Which fraction when added to 3 4 will equal 1 whole?

Which fraction when subtracted from 12 10 will equal 1 whole?

Chapter 7-4 Adding Mixed Numbers with Unlike Denominators

Daily Review

Solve, simplifying answers if necessary.

Learn and Connect

Elijah is making a floral arrangement. He originally cut 1 3 4 in. off the stem of each flower. He realized that the flowers were still too tall, so he cut off another 1 2 6 inches. How many total inches did Elijah cut off the stems?

To solve, you must add the lengths of both pieces that Elijah cut off the stems. However, numbers with different denominators cannot be added or subtracted as is because the denominators represent different size pieces. Therefore, you must use equivalent fractions.

First, find a common multiple for each denominator.

4, 8, 12, 16

6, 12, 18, 24

Then, create equivalent fractions by multiplying the numerators by the same factor.

Finally, add the numerators. Then, add the wholes and simplify if necessary.

Apply

Solve, simplifying answers if necessary.

Elijah cut inches off the stem.

Solve, simplifying answers if necessary.

Match each problem to the correct sum.

Solve and simplify if necessary.

11.

A flag is raised 2 2 5 feet from the ground up a flagpole. Then, it is raised another 4 1 4 feet. How many feet up the pole is the flag?

12. Samuel started a new book and read 3 1 2 chapters. After dinner, he read another 2 2 3 chapters. How many chapters has he read in total?

Chapter 7-5 Subtracting Fractions with Unlike Denominators

Daily Review

Solve, simplifying answers if necessary.

Learn and Connect

Micah and Noah are making milkshakes. Micah used a 2 3 cup ice cream scooper to get his ice cream. Noah used a 3 4 cup ice cream scooper to get his ice cream. How much more ice cream did Noah use than Micah?

To solve, we have to subtract the amount of ice cream Micah is using from the amount of ice cream Noah is using.

First, find a common multiple for each denominator.

3, 6, 9, 12, 15

4, 8, 12, 16

Then, create equivalent fractions by multiplying the numerators by the same factor.

Therefore, Noah used 1 12 cup more ice cream than Micah.

Finally, subtract the numerators and simplify if necessary.

simplifying answers if necessary.

Solve, simplifying answers if necessary.

Match each problem to the correct sum.

Solve, simplifying if necessary.

A share of 3 4 of a pie is divided up and given to the guests. There is

11. 12. Before class today, you had used 1 6 of the pages in your notebook. After taking notes in class, you had used a total of 2 9 of the pages in your notebook. What fraction of the pages of your notebook were used by today’s notes?

Daily Review

Solve, simplifying answers if necessary.

Learn and Connect

Oliver and his brother were racing toy cars. Oliver’s car traveled 5 8 ft less than his brother’s. If Oliver’s brother’s car traveled the entire length of their backyard swimming pool, how far did Oliver’s car travel?

To solve, we need to subtract 5 8 from the total length Oliver’s brother’s car traveled.

Numbers with different denominators cannot be added or subtracted because the denominators represent different size pieces. Therefore, you must use equivalent fractions.

First, create equivalent fractions for each number by finding a common multiple for each denominator.

3, 6, 9, 12, 15, 18, 21, 24 8,16, 24, 32, 40, 48, 56

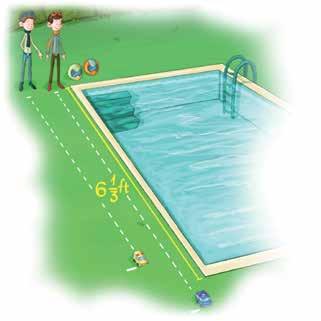
Notice you cannot subtract the numerators because 8 is smaller than 15. Therefore, you have to borrow a whole in fraction form.

Therefore, Oliver’s toy car traveled ft.

Solve, simplifying answers if necessary.

Solve, simplifying answers if necessary.

Match each problem to the correct sum.

11. 12. A cook is bringing a pot filled with 4 1 6 pints of water to a boil. After heating the water, there are 3 9 10 pints of water left in the pot. How many pints of the water were lost to steam?

A student is making a project using fabric. The student has 9 3 4 feet of fabric. After using 6 7 8 feet of the fabric, how many feet of fabric are left?

Chapter 7-7 Problem Solving with Adding and Subtracting Mixed Numbers

Daily Review

Estimate the solutions using benchmark numbers.

Learn and Connect

Fred studied 8 10 of an hour on Monday. On Tuesday, he studied 4 5 of an hour. How many total hours did Fred study on Monday and Tuesday combined?

To solve word problems, use the following strategy:

» Read and Understand

Read the problem and consider what is being asked.

In this problem, we need to find the total. This means we need to combine the hours Fred spent studying on Monday and Tuesday.

»» Plan

Make a plan to solve the problem.

We know that we need to add in order to combine the fractions. However, the fractions have different denominators. This means we will need to change the fractions so they have the same denominators.

»»» Solve

Work out the problem and check that your answer is reasonable by estimating the answer.

1 3 5 is reasonable because it is close to our estimated answer of 2.

1. Dennis read his book 3 4 hours on Monday, 2 3 hours on Tuesday, and 1 hour on Wednesday. How many total hours did Dennis read his book?

Solve using the problem solving strategy. Reduce all fractions to simplest forms and mixed numbers.

» Read and Understand

Read the problem and consider what is being asked.

»» Plan

Make a plan to solve the problem.

»»» Solve

Work out the problem and check that your answer is reasonable by estimating the answer.

2. James is making a bookmark out of a piece of cardboard. The bookmark needs to be 5 2 3 in. long. The cardboard is 7 2 14 in. long. How many inches of cardboard will James have left over once the bookmark is cut out?

1. Anthony and his brother decided to go strawberry picking. Anthony picked 3 3 4 oz. of strawberries, and his brother picked 2 4 16 oz. of strawberries. How many more oz. of strawberries did Anthony pick than his brother?

3. Justin wants to mix all of the chopped fruits he has together in a bowl. He has 2 3 cups of mangoes and 4 5 cups of strawberries. How many total cups of fruit will he have in the bowl?

4. Richard likes to run at least a mile each day. On Monday, Richard ran 2 7 8 of a mile. On Tuesday, he ran 3 16 more miles than on Monday. How many miles did Richard run on Tuesday?

5. Larry needs 5 3 4 cups of flour to make a recipe. He only has 4 1 3 cups. How many more cups of flour does he need in order to have enough for the recipe?

Solve.

6. On Monday, Harry biked 3 2 15 miles. On Tuesday, he biked a park trail that was 3 5 of a mile long and then took another bike trail that was 1 1 3 miles long. How many more miles did he bike on Monday than on Tuesday?

Daily Review Solve, simplifying answers when necessary.

Learn and Connect

Students are in the science lab conducting experiments. They are all given the same amount of mystery colored liquids in separate beakers.

If the students combine all of the red and clear liquid into a beaker, how many ounces of liquid will be in the beaker?

To solve, we have to add the red and clear liquids together and then simplify.

First, create equivalent fractions by finding a common multiple for each denominator.

7, 14, 21, 28,35,42,49,56 8, 16, 24, 32,40,48,56,64

Apply

Then, add the numerators and the whole numbers, keeping the denominators the same. 9 38 56 = 9 19 28

�2 Simplify the fraction.

Therefore, the total ounces of liquid in the beaker is 9 19 28 oz.

Use the chart above to answer the following questions.

One student poured out 3 4 oz of the green liquid. About how many ounces of the green liquid remain? Is your estimate a little over or a little under the actual answer?

If the students combined the blue and the green liquids, about how many ounces of liquid would they have in total? Use the number lines to help you.

How much more clear liquid is there than blue liquid?

The science teacher added an additional 3 8 oz. of liquid to the blue liquid. How many ounces of blue liquid are there now?

Solve each problem using the chart below.

How much farther does Leo walk than Ricky?

How many miles do Ricky and John walk to school combined?

Who walks farther to school: Just Leo alone or John and Frank together? How much more do they walk compared to the other(s)? Is John’s answer reasonable? Use visual models to justify your response.

Chapter 8

In Chapter 8, we will learn about

Multiplying Fractions

Multiplying fractions comes up often in real life, especially in statements that use the word “of.”

• Multiply fractions and wholes

• Multiply fractions and fractions

• Multiply fractions and mixed numbers

• Use factoring to multiply fractions

• Understand size when multiplying fractions

• Problem solve

We can use models and the standard algorithm to multiply fractions by fractions, wholes, or mixed numbers.

We can use factoring to get a simplified product. We can accurately predict if the product will be greater or less than each factor and one.

We can solve word problems with multiplication of fractions.

Chapter 8-1 Multiplying Fractions and Whole Numbers

Daily Review Change the improper fractions into mixed numbers. Simplify your answers.

Learn and Connect

Scott baked some cupcakes. He wants to figure out how many cups of frosting he will need to make to frost all of the cupcakes. Each cupcake uses 1 8 of a cup of frosting. How many cups of frosting does Scott need to make?

To solve, we must multiply 15 cupcakes by the amount of frosting each cupcake needs.

A numberline like the one below can help us multiply the fractions. Since each cupcake uses 1 8 cup of frosting, each whole on the numberline is cut into 8 pieces.

We can also multiply by using the standard algorithm. First, turn the whole number into a fraction by placing the whole over 1.

Then, multiply the numerators and denominators.

Therefore, Scott must make 1 7 8 cups of frosting.

Apply

Since the answer is an improper fraction, we must turn into a mixed number.

Multiply using the number lines or the standard algorithm. Simplify your answers.

Solve. Simplify your answers, writing them as mixed numbers if possible.

Challenge

Use the ad to help solve the problems below.

31. What is the sale price of a pair of pants that are regularly $32?

32. How much will John save if he buys a pair of shoes that are $26 full price?

33. A pair of shoes are $42, and a shirt is $18. How much will John save if these are bought on sale?

Chapter 8-2 Multiplying Fractions

Daily Review Solve, reducing each answer to its simplest form.

Learn and Connect

Jamie had 2 3 of a pound of blueberries. He let his friend Caleb eat 1 4 of the blueberries. How many pounds of blueberries did Caleb eat?

To solve, we must multiply the pounds of blueberries by the amount of blueberries eaten.

A model like the one below can help us multiply the fractions.

You can also solve by multiplying using the standard algorithm. First, multiply the numerators and denominators. Then, simplify.

Therefore, Caleb ate 1 6 pounds of blueberries.

Apply

Multiply using models or the standard algorithm. Simplify your answers.

Solve, writing answers in their simplest forms.

Solve, simplifying answers if necessary.

30. Leo is painting his room. He paints 3 4 of the walls green and plans to decorate 1 3 of the green walls with black dots. What fraction of the walls will have black dots?

31. Justin is cutting a recipe in half. If the original recipe calls for 3 4 cup of sugar, how much sugar will the new recipe need?

Chapter 8-3 Multiplying Fractions and Mixed Numbers

Daily Review Solve, reducing answers to their simplest forms.

Learn and Connect

Leo is making a recipe. He pours 3 4 of a cup of canola oil into his measuring cup. The recipe requires him to use 2 1 2 times as many cups of water as canola oil. How many cups of water will he need?

To solve, we must multiply the amount of canola oil by 2 1 2 .

To multiply, we must turn the mixed number into an improper fraction.

Then, multiply the numerators and denominators.

Last, change the improper fraction back to a mixed number and simplify if necessary.

Therefore, Leo needs 1 7 8 cups of water.

Apply

Solve, simplifying your answers.

Solve, simplifying your answers.

Solve each problem. Simplify if necessary.

30. Harry is trying to find the area of a garden plot. The length of the garden is 8 1 2 ft, and the width is 4 ft. What is the total area of the plot?

31. A painter used 3 3 4 gallons of paint for the trim around a house. He used 3 1 2 times that amount for the walls of the house. How much paint did he use for the walls?

Chapter 8-4 Multiplying Fractions with Factoring

Daily Review Solve each problem and simplify.

Learn and Connect

A local bakery made cupcakes and cookies on Monday. 3 8 of the orders were for cupcakes. Of the cupcakes, 4 9 of them were vanilla cupcakes. What fraction of the baking on Monday was for vanilla cupcakes?

To find out the fraction part of an item, we multiply. We know this because the word of in 4 9 of them were vanilla cupcakes means multiply.

Instead of reducing the fraction at the end of the problem, we can use factoring before we multiply. Then, the product will already be simplified.

1) Divide diagonal numerators and denominators by the same number.

2) Multiply the new numerators and denominators. of the baking was for vanilla cupcakes.

Solve by factoring.

What is 2 3 of 24?

What is 8 9 of 63?

What is 1 5 of 10 12 ? What is 3 12 of 4 6 ?

What is 3 7 of 28?

What is 5 7 of 1 15 ?

What is 1 4 of 8 12 ?

Solve, simplifying your answers.

What is 3 5 of 45?

What is 6 11 of 22 36 ?

Read each problem, then solve.

A field is 1 4 of a mile long. If a student walks 8 10 of that field, how many miles did he walk?

Last year, a farmer was able to sell 5 6 of the apples harvested from a tree. If he picked 72 apples, how many did he sell?

David is creating keychains to sell at the farmer’s market. He makes 32 keychains and sells 3 4 of them. Of the key chains that he sold, 1 2 were red. How many red key chains did David sell?

Daily Review Solve, simplifying your answers.

Learn and Connect

William was making cookies for a party. He knows there will be many people there, so he needs to triple the recipe. If the recipe calls for 2 3 cups of brown sugar, how much brown sugar will William need for triple the recipe?

We know that William needs cups of sugar per batch.

He will be making times the recipe.

What equation will help us solve this problem?

Look at your equation and circle the answer that is true.

William will need MORE/LESS than 2 3 cups of brown sugar for 3 batches.

William will need MORE/LESS than 3 cups of brown sugar total if there is 2 3 in each batch.

William will need cups of brown sugar, which is more than and less than .

Apply

Shade in the models to represent each multiplication equation and answer the questions.

Will your answer be more or less than 3 8 ?

Will your answer be more or less than 2?

Will your answer be more or less than 1 2 ?

Will your answer be more or less than 5?

Will your answer be more or less than 2 3 ?

Will your answer be more or less than 4?

Create models to represent each multiplication equation and answer the questions.

Will your answer be more or less than 1 5 ?

Will your answer be more or less than 5?

Will your answer be more or less than 2 7 ?

Will your answer be more or less than 4?

Will your answer be more or less than 5 6 ?

Will your answer be more or less than 2?

Analyze each equation. Then, circle MORE or LESS to answer each question.

Write your own multiplication story problem.

Look at the model on the right. Write a story problem that could be solved using this model. Then, write an equation that would solve it.

9. The Burj Khalifa in Dubai is about 1 3 4 times as tall as the Willis Tower in Chicago. The Shanghai World Finance Center in China is about 4 5 as tall as the Willis Tower.

A) Which of these buildings is the tallest? Which is the shortest? Explain.

B) Draw a picture or model to illustrate.

Learn and Connect

Bill walked 1 2 of a 1 4 mile path around a local lake. He said he walked less than 1 4 of a mile, but his friend Danny said that he must have walked more because when you multiply fractions, the product is always larger than at least one of the factors, and the smallest factor is 1 4 .

Study the model and solve: 1 2 of 1 4 = Is Danny correct in his thinking that the product is always bigger than one factor?

Use Danny's model and the model below to write two true rules about multiplying fractions.

When multiplying two fractions, if one factor is GREATER than one whole, the answer will be than the smallest fraction factor.

When multiplying two fractions, if both factors are LESS than one whole, the answer will be than the smallest fraction factor.

Apply

Shade in the models to represent each multiplication equation and answer the questions.

Will your answer be more or less than 1 2 ?

Will your answer be more or less than 1 3 ?

Will your answer be more or less than 3 4 ?

Will your answer be more or less than 1 1 4 ?

Will your answer be more or less than 2 3 ?

Will your answer be more or less than 1 4 ?

Create models to represent each multiplication equation and answer the questions.

Will your answer be more or less than 3 4 ?

Will your answer be more or less than 1 6 ?

Will your answer be more or less than 1 3 ?

Will your answer be more or less than 1 4 ?

Will your answer be more or less than 1 2 ?

Will your answer be more or less than 1 5 6 ?

Analyze each equation. Then, circle MORE or LESS to answer each question.

Write your own multiplication story problem.

Look at the model. Write a story problem that could be solved using this model. Then write an equation that would solve it.

9. 10. Marc is remodeling his bathroom. He plans to cover the bathroom floor with tiles that are 1 square foot. His bathroom is 5 1 2 feet wide by 4 1 4 feet long. How many tiles will he need to cover the floor?

In the grid, each big square represents one tile. Draw a rectangle on the grid to show the measurements of Marc's bathroom.

Learn and Connect

The fifth-grade students are selling cakes. Each cake costs $12.00. However, you can also buy a part of the cake for that fraction of the price. The Miller family buys 1 2 of a lemon cake for $6.00. Then, Mrs. Ross comes and sees the 1 2 of lemon cake left. She buys 3 4 of the remaining cake to take home. What portion of the whole cake is Mrs. Ross buying, and how much will it cost her?

If Mrs. Ross is taking 3 4 of the piece left, is she taking more or less than 1 2 ?

What equation would help us find out the portion of cake Mrs. Ross is buying?

Mrs. Ross is buying of the cake.

Circle the equation that represents how much the cake will cost Mrs. Ross. Then, solve.

Mrs. Ross will pay dollars or $ .50.

Apply

Create a model to solve each problem.

Abe walked 1 3 mile every day for a week. How many miles did he walk in total?

Choose the equation that would help answer the problem. Then, solve. 1. 3.

Kane is preparing a recipe that calls for 2 3 cup of milk per serving. How much milk does he need to prepare 2 1 4 servings?

There was 1 2 of a pizza left in the refrigerator. Mickey ate 1 4 of it. How much pizza did Mickey eat?

At a local animal shelter, 3 4 of the animals are cats. Of the animals that are cats, 1 8 are kittens. How many of the total animals at the shelter are kittens?

There are 24 hours in a day, and scientists say we should sleep for 3 8 of them. How many hours should we be sleeping?

It takes 3 8 pint of milk to make a large chocolate milkshake. The medium shake takes 1 2 that amount. How much milk does it take to make a medium milkshake?

After a party, there was 2 3 of a pizza left over. If Marc gives away 3 8 of the pizza, how much did he give away?

Match each problem to the equation that will help answer it. Then, solve just those equations. Read each problem, then solve.

Joshua read 2 3 of a book on Tuesday. He read 3 8 of that amount on Wednesday. Did he read more or less on Wednesday than he did on Tuesday?

Sarah and her two friends are sharing pizza equally. They all want to get 2 3 of the pizza. How much pizza do they need to order so they can all have the same amount?

Howard is having 30 people come to his party. He needs to adjust the recipe below to make enough cupcakes for everyone. Rewrite the recipe to make sure that it serves 30.

Serving Size Hint: 30 ÷ 12 =

A geologist had two rocks on the scale with a combined weight of 2 1 2 pounds. If Rock A was 1 3 of the total weight, how much did Rock A weigh?

Peter has a garden that is 5 1 4 yards long. If he has a sprinkler that covers 3 5 the length of his garden, how many yards does the sprinkler cover?

Cupcake Recipe: Serves 12

Butter: 1 2 cup

Sugar: 1 1 4 cup

Vanilla: 1 teaspoon

Eggs: 2

Flour: 1 2 3 cup

Baking Powder: 1 4 teaspoon

Milk: 3 4 cup

Cupcake Recipe: Serves 30

Butter: cup

Sugar: cup

Vanilla: teaspoon

Eggs:

Flour: cup

Baking Powder: teaspoon

Milk: cup

Learn and Connect

There are two design proposals for a new rectangular park in town.

Design One: 1 3 of the park will be a play area, and 2 3 of the park will have a large grassy area. 2 5 of the grassy area will be made into a ball playing field.

Design Two: 1 2 of the park will be a play area, and 1 2 will be a grass area. 1 4 of the grassy area will be made into a ball playing field.

Which design will have a bigger ball playing field? Draw a diagram that can be used to support your answer and model the sizes of both ball playing fields.

Park Design One

Park Design Two

will have a larger ball playing field that covers of the area.

Create models to represent each multiplication equation and answer the questions.

Analyze each equation. Then, circle MORE or LESS to answer each question.

Read each problem, then solve.

16. Kane grew 15 pounds of tomatoes in his garden. He sold 4 5 of his tomatoes at the farmers' market. How many pounds did he keep for himself?

Challenge

There are three boys standing together. Dennis was 1 1 2 times as tall as Chad and 3 4 as tall as Victor. Label the boys in the picture and explain your reasoning.

Mike picked 2 5 6 pounds of strawberries. His friend Nick picked 1 3 as many. How many pounds did Nick pick?

15.

17.

In Chapter 9, we will expand on

Dividing Fractions

Dividing fractions helps us figure out how much we get when we share a portion of a fraction.

• Write fractions as division equations

• Find reciprocals of fractions

• Divide whole numbers and fractions

• Use patterns that follow rules

• Use the order of operations with fractions

• Problem solve

• Estimate products and quotients with fractions

We can rewrite fractions as division problems and solve them.

We can flip the numerator and denominator to find the reciprocal of a fraction. We can multiply by the reciprocal to divide fractions. We can fill in an input/output table using a rule and find missing values in patterns with fractions. We can use the order of operations to solve problems with fractions.

We can solve word problems with division of fractions. We can use compatible numbers to estimate products and quotients with fractions.

Chapter 9-1 Fractions as Division Equations

Daily Review

Multiply the fractions by factoring. Simplify if necessary.

Learn and Connect

While Max and Paul were in math class, their teacher asked them to write 8 divided by 4 on the board. They both wrote the problem in different ways. Which boy is correct? Both boys are correct because each answer is 2.

each fraction in column 1 with an equivalent division problem in column 2.

Complete the table.

Write each mixed number as a division problem.

Find the error and correct it.

Mike was given the fraction 5 8 . He had to write it as a division problem and then as a decimal. Find his error and correct it.

Correct Way Mike's Answer

Chapter 9-2 Reciprocals of Fractions

Daily Review Solve, simplifying if necessary.

Learn and Connect

Solve the four problems below.

Notice that each of the problems results in 1 as an answer. What do you notice about the fractions being multiplied? How are they similar? How are they different?

The factors are reciprocals of each other.

To find the reciprocal of a fraction, we switch the numerator and the denominator.

Fraction Reciprocal Check

To find the reciprocal of a mixed number or whole number, first rewrite it as an improper fraction.

Write the reciprocals.

Write the missing factors.

Draw a line to each missing fraction that completes the expression.

32. Explain what a reciprocal is and how we can check if a number is the reciprocal of another number.

33. What is the reciprocal of 12? Write your answer below and explain using what you know about reciprocals.

Chapter 9-3 Dividing Whole Numbers and Fractions

Daily Review Solve, reducing to the simplest forms.

Learn and Connect

Jake has four pieces of paper. He want to divide each paper into sixths. How many total pieces of paper will Jake have after dividing the papers?

To solve 4 ÷ 1 6 , you can use a model like the one below. Each large rectangle represents one piece of paper. Each of the four pieces of paper is divided into 1 6 pieces. Now, there are a total of 24 pieces. This means that 4 papers divided by 1 6 = 24 pieces.

You can also use the standard algorithm to solve.

First, create a multiplication problem by using the reciprocal of the second fraction.

Next, turn the whole into a fraction by placing a 1 as the denominator. Then, multiply the numerators and denominators.

Therefore, Jake will have 24 pieces of paper.

Apply

Solve, simplifying the answers.

Since the answer has a 1 as the denominator, we know it is a whole number.

Solve, simplifying if necessary.

31. Max has 6 cakes. He wants to cut each cake into 1 8 slices. How many slices will he have after he cuts all of the cakes?

32. Steven has 2 3 of a package of cookies that he wants to divide into 3 separate containers. What fraction of the cookies will go into each container?

Daily Review Solve, simplifying your answers.

Learn and Connect

Input/Output tables work with many different patterns, including fractions. Let’s use the following rule to fill in our table:

Rule: Multiply by 3 4

Step 1: Change the whole number to a fraction with denominator 1

Step 2: Multiply numerator by numerator

Step 3: Multiply denominator by denominator

Step 4: Simplify if necessary

Here is a new pattern. Which numbers are missing?

To find the pattern, make an observation about what is happening from one number to the next.

Use the rules to complete the tables. Write the rules. Solve.

The tomato plant was 1 1 4 inches tall after week 1, 2 inches tall after week 2, 2 3 4 inches tall after week 3, and 3 1 2 inches tall after week 4. How much did the plant grow every week? The bean plant grew 5 6 inch each week for 4 weeks. If it started out 2 1 6 inches tall, how tall is it now?

Challenge

When he was 8, Ben was 48 1 4 inches tall. He grew 2 3 8 inches each year. How tall was he when he was 12?

Daily Review Fill in the missing numbers.

Learn and Connect

Use the correct order of operations. Which is correct?

First solve the numerator, then solve the denominator, then divide. Imagine there are parentheses around the numerator and around the denominator.

Circle which equation is correct in each pair.

David solved the problem below incorrectly:

2 3 × 5 2 − 5 3 ÷ 2 =

Explain David’s mistake.

What is the correct answer to the problem?

Chapter 9-6 Problem Solving with Division

Daily Review Solve using the correct order of operations.

Learn and Connect

How much chocolate will each person get if 3 people share 1 2 lb of chocolate equally?

We can draw a model to solve. Circle a square of chocolate and draw an arrow to each person to show how to share it equally with 3 people. Write fraction of the total chocolate each piece represents.

We can write an equation to solve.

Apply

Solve each problem. Draw a model and write an equation to represent the problem.

1. 2. A serving of raisins is 1 3 cup. The box contains 2 cups of raisins. How many servings are in the box?

The teacher has 3 boxes of crackers for snack. There are 24 students in the class. What fraction of the box of crackers can each student have?

Solve each problem. Draw a model and write an equation to represent the problem.

2. There is 1 3 of a pan of brownies left on the counter. If Rachel wants to divide the brownies between 5 people, how much of the pan does each person get?

The box holds 3 cups of pasta. If a serving size is 1 4 cup, how many servings are in the box?

Solve.

A container of yogurt is 4 cups. If a serving size is 2 3 of a cup, how many servings are in the container?

There are 5 packages of cookies to share among 15 children. What fraction of a package does each child get?

The bag holds 3 1 2 cups of chips. How many cups of chips does each person get if 5 people share the chips?

A bucket holds 8 gallons. If Larry used a cup that holds 1 6 of a gallon to fill the bucket, how many cups will he pour into the bucket?

5 6 of the bag of flour is left. If Mom bakes 10 batches of cookies with the flour, how much of the bag does each batch use?

A bag of potting soils holds 13 3 4 cups of soil. The science teacher divides the soil among 25 smaller containers. How many cups are in each small container?

A bag of sugar holds 11 1 4 cups. If each cake uses 1 1 2 cups of sugar, how many cakes can be made with 1 bag of sugar? How much sugar will be left over?

Chapter 9-7 Estimating Products and Quotients with Fractions

Daily Review Solve, reducing to simplest terms.

Learn and Connect

Paul is making snack packs. He has the ingredients listed in a chart.

If Paul wants to make 2 5 6 of the recipe, about how many cups of peanuts will he need?

To estimate, we can use benchmark numbers.

Therefore, Paul needs about 4

cups of peanuts.

Estimate the answers using benchmark numbers.

Estimate each product using benchmark numbers. Show your work.

Estimate each quotient using benchmark numbers. Show your work.

11. 22. Steven has 9 1 2 pounds of potatoes. He uses 3 7 of the potatoes for dinner. He says that he used about 2 pounds of potatoes. Is this reasonable? Explain.

Robert has a board that is 7 5 6 feet long. He needs to cut it into pieces that are 1 6 7 feet long. He thinks he will be able to cut about 4 pieces. Is this reasonable? Explain.

Challenge

Solve using estimation. Simplify if necessary.

23. John is replacing some broken steps on the porch. If each step is 2 7 16 feet in length, approximately how many feet of lumber will he need to replace 3 steps?

24. Each row of the garden is 16 1 8 ft in length. The squash plants need to be planted 1 3 4 ft apart. Approximately how many squash can be planted in a row?

Daily Review

Simplify each fraction.

Learn and Connect

Marc and Peter are playing with blocks. They build a tower that is 18 1 5 inches tall with 7 red blocks. How tall is each red block?

To solve, we need to divide the height of the tower by the height of each block.

1) First, turn the mixed numbers into improper fractions.

× 18 + 1 = 91 5

Then, set up the division problem.

2) Then, multiply by the reciprocal of the second fraction. Reduce using factoring.

Each red block is 2 3 5 inches tall.

3) Last, write the improper fraction as a mixed number.

Solve.

Use the rules to fill in the tables.

Solve using the order of operations.

Solve. Simplify if necessary.

Arnold has 4 2 3 cakes that he wants to split among 24 of his friends. How much cake will each friend get to eat?

The custodian has to paint 8 1 3 walls in the school. If he spreads the work out over 5 days, how much does he have to paint each day?

Sam has a board to make a stair railing. It is 9 1 5 ft long. If he cuts it into 6 equal pieces, how long will each piece be?

At the deli, 8 people ate 13 3 5 sandwiches. If each person ate the same amount, how much did each person eat?

Chapter 10

In Chapter 10, we will explore

Geometry

The world is composed of three-dimensional shapes that are each composed of two-dimensional shapes.

• Classify polygons, triangles, and quadrilaterals

• Classify 2-D figures in a hierarchy

• Find area and perimeter with fractional side lengths

• Classify solid figures

We can name 2-D figures and describe them by their side lengths and angles.

We can classify a shape in more than one category.

We can solve word problems with area and perimeter with and without fractions.

We can name 3-D figures and describe them based on the number of faces, edges, and vertices.

Daily Review

Write the reciprocals.

Learn and Connect

Polygons are closed figures made up of line segments or sides. The corner points of a polygon are the vertices (or a vertex, in singular).

Regular polygons - all angles are equal in measure and all sides are equal in length

Irregular polygons - angles are not equal in measure and sides are not equal in length

Name the two irregular polygons in the chart on the right. and

Name the regular polygons in the chart on the right.

Apply

Name each polygon. Write regular or irregular.

Name each polygon. Write regular or irregular.

Complete the chart.

Number of sides

Number of vertices

Drawing

Polygon triangle quadrilateral pentagon hexagon

Chapter 10-2 Classifying Triangles

Daily Review

Name each polygon.

Learn and Connect

A triangle is a three-sided polygon. It always has three sides and three angles, but that doesn’t mean every triangle looks the same! You can classify or distinguish the type of triangle by its angles and by the length of its sides.

Based on Sides

We draw the same number of lines on congruent sides to show they are equal in measurement.

Based on Angles

We draw the same number of curves on congruent angles to show they are equal in measurement.

Apply

Scalene Triangle No sides equal

Triangle Two sides equal

Equilateral Triangle All sides equal

Triangle All angles acute (<90°)

Identify the type of triangle based on its sides and angles. Based on sides: Based on angles:

Isosceles

Acute

Obtuse Triangle One obtuse angle (>90°)

Right Triangle One right angle (90°)

Label the triangles below based on their sides as scalene, isosceles, or equilateral.

Match each triangle to the correct description.

Two sides are equal length Two equal angles

No equal sides No equal angles

All sides are equal length All angles are equal size (60°)

One right angle

One right angle Two equal sides Two equal angles (45°)

Chapter 10-3 Classifying Quadrilaterals

Daily Review

Find the perimeters or areas for the rectangle dimensions given.

Learn

Connect 1. l = 2 in, w = 6 in A = 2. l = 5 ft, w = 9 ft P = 3. l = 2.2 cm, w = 4 cm A = 4. l = 18 m, w = 3 m P =

and

Parallelogram - opposite sides are parallel, 2 sets of sides are different in length

Types of Quadrilaterals * shapes with 4 sides and 4 angles *

Rectangle - a parallelogram with 4 right angles

Square - a rectangle with all sides equal length

The sum of the angles in a quadrilateral equals 360°.

Apply

Rhombus - opposite sides are parallel, 4 sides are equal in length

Trapezoid - a quadrilateral with exactly one pair of parallel sides

Write the name of each type of quadrilateral and the number of pairs of parallel sides it has.

parallel sides parallel sides parallel sides

Write the letter of each polygon that fits each description.

Have equal sides Are quadrilaterals

Have 2 sets of parallel sides

Have only 1 set of parallel sides

Write the name of each type of quadrilateral and the number of pairs of parallel sides it has. Fill in the chart.

Figure How many right angles?

How many pairs of sides have equal length?

How many pairs of parallel sides?

Circle the words(s) that describe(s)

Square Rectangle Rhombus

Parallelogram

Trapezoid Quadrilateral Square Rectangle

Rhombus

Parallelogram Trapezoid Quadrilateral Square Rectangle Rhombus

Parallelogram Trapezoid Quadrilateral Square Rectangle Rhombus

Parallelogram Trapezoid Quadrilateral Square Rectangle Rhombus

Parallelogram Trapezoid Quadrilateral

Chapter 10-4 Classifying 2-D Figures in a Hierarchy

Daily Review

Write the number of pairs of parallel sides.

Learn and Connect

Some 2-D shapes fit into more than one category because of the attributes, or characteristics, they share.

How do you know which triangles are right triangles?

How do you know which polygons are triangles?

Apply

Draw a line from each shape to the category it fits in. Some shapes will fit in more than one category.

Hierarchy of Quadrilaterals

Quadrilateral

Trapezoid

Square

Parallelogram

Rhombus Rectangle

Kite

Polygon

Polygons

Right triangles Triangles

Parallelogram

Rectangle

Rhombus

Square

Trapezoid

Quadrilateral:

Kite:

Trapezoid:

Parallelogram:

Rhombus:

Rectangle:

Square:

A quadrilateral containing two pairs of parallel sides

A quadrilateral containing four right angles

A quadrilateral containing four equal-length sides

A quadrilateral with four right angles and equal-length sides

A quadrilateral with one pair of parallel sides

I am a quadrilateral with only 1 pair of parallel sides. I am a polygon with 8 sides. All of my sides are the same length.

Sketch two examples of each of the figures below. 1. Parallelogram 2. Quadrilateral 3. Trapezoid

Learn and Connect

Solid figures are three-dimensional figures. This means they have a length, width, and height. Some solid figures are named by the face of their base, while others have unique names.

3-D figures are made up of edges, faces, and vertices. A surface can be flat (face) or curved. An edge is the part where two surfaces meet, and a vertex is where two or more edges meet at a point.

Can you find 2 solid figures that do not have any vertices?

Name the solid figures and then determine how many vertices, edges, and faces they have. Name of figure:

Name the solid figures.

Name of figure: Name of figure: Name of figure: Name of figure:

Name the solid figures and then determine how many vertices, edges, and faces they have.

Name of figure:

Vertices:

Edges: Faces:

Compare the figures.

Name of figure: Vertices: Edges: Faces:

Which figure has the most vertices?

Name of figure: Vertices:

Edges: Faces:

Name of figure: Vertices: Edges: Faces:

Which figure has fewer faces?

Which figure has fewer edges?

Which figure has the most faces?

Daily Review

Identify the irregular polygons.

Learn and Connect

Mrs. Williams needs a fence built around her flowers to keep animals out. How much fencing will she need to purchase to enclose her garden?

Should Mrs. Williams find the PERIMETER or AREA?

P = 27.3 + 27.3 + 13.1 + 13.1 =

Mrs. Williams needs to purchase feet of fencing.

Each foot of fencing costs $2.75. About how much will the fencing cost?

Now solve for the exact amount. Your estimate should not be too far off from the exact amount.

• Round $2.75 to the nearest dollar amount.

• Round 80.8 ft to the nearest whole number.

• Then, multiply.

A wall needs to be repainted. The wall is 17 ft wide by 8.25 ft high.

A) Draw and label the wall using the given dimensions.

B) Find the area to see how many square feet of paint will be needed.

C) The paint store is sold out of gallons and quarts, so the homeowner will need to purchase pints of paint. A pint of paint only covers 65 square feet. How many pints will he need to buy?

D) One pint of paint costs $24.40. How much will it cost to paint the wall?

Solve, showing your work.

Chad wants to install a fence around his backyard, which measures 26.45 yards by 14 yards. Fencing costs $12 per yard. How much will Chad spend on fencing for his backyard?

Eddie walks around a lake on a nice sunny day. The rectangular path around the lake is 2.25 miles by 1.6 miles. If he walks around the lake twice, how far will he walk?

Rachel is painting two walls in her bedroom pink. Each wall is 14 ft long and 8.75 ft high. If one gallon of paint covers 250 square feet, will one can be enough?

Explain why or why not.

Find the length of each missing side, x.

Mr. Davis wants to tile his kitchen floor. If the floor is 12.46 ft long and 9.3 ft wide, how many one-square-foot tiles will he need to cover the floor?

Donna bought a large picture frame with 24 x 30 inch dimensions. She plans to put as many 4 x 6 in photos of her grandchild as she can in the frame. How many pictures can she fit without trimming any of the photos? Show your work.

Chapter 10-7 Area with Fractional Side Lengths

Daily Review

Find the areas of the rectangles described.

Learn and Connect

A poster on the wall is 2 3 yd by 3 5 yd. What is the area of the poster?

You can find the area of the rectangular poster with fractional side lengths by tiling. We use the unit fractions for the side lengths.

When you combine the fractions into one rectangle, divide one side of a rectangle into 3 equal parts to show thirds and the other side into 5 equal parts to show fifths.

Then, shade in 2 3 and 3 5 . The overlapping or purple portion is the area.

There are total squares. are overlapping.

The area of a 2 3 yd by 3 5 yd poster is .

Find the areas.

Shade in to find the areas. Then, multiply the side lengths to find the areas. Simplify if possible.

Tile and shade in to find the areas. Then, multiply the side lengths to find the areas. Simplify if possible.

Tile and shade in to find the areas. Then, multiply the side lengths to find the areas. Simplify if possible.

Grandma is using fabric scraps to make a quilt. She has a piece of fabric that is 8 9 of a meter by 3 4 of a meter. How many square meters is the fabric scrap?

The section of the garden with broccoli plants is 1 4 yard by 6 7 yard. How many square yards do the broccoli plants take up?

The cold air return vent on the wall is 1 2 3 feet by 1 1 4 feet. How much wall space does the vent take up?

Challenge

A pipe leaked and got some ceiling tile in the classroom wet. The section of ceiling tile that needs to be replaced is 4 5 of a meter by 7 8 of a meter. How many square meters of ceiling tile need to be replaced?

The kitchen backsplash is getting new tile. The backsplash is 1 7 8 ft by 4 2 5 feet. How many square feet of tile are needed for the backsplash?

The store only sells ceiling tile measured in square centimeters. How many square centimeters of ceiling tile are needed?

Hint: 1m = 100 cm

Daily Review Solve, simplifying answers when possible.

Learn and Connect

Name each figure shown.

Label the triangles as scalene, isosceles, or equilateral.

Name each quadrilateral and write how many pairs of parallel sides it has.

Tile and shade in to find the areas. Then, multiply the side lengths to find the areas. Simplify if possible.

=

14. Challenge A piece of construction paper is 3 7 yd by 2 3 yd. How many pieces of construction paper will it take to cover a bulletin board that is 2 yds by 4 yds?

Chapter 11

In Chapter 11, we will learn about

Volume and Data

Volume helps us understand how much space is inside different shapes.

• Find volume

• Use volume to find a missing side

• Find volume of composite figures

• Find elapsed time

• Create and interpret line plots

We can use cubes and side lengths to find the volume of a rectangular prism.

We can find the length of a missing side when we are given the volume.

We can divide composite figures into two smaller prisms to find the total volume.

We can use a number line or subtraction to find elapsed time.

We can create and interpret a dot plot with whole numbers and fractions given a list or frequency chart.

Chapter 11-1 Measuring Volume with Cubes

Daily Review Find the areas of the rectangles below.

Area is the space that a two-dimensional object occupies. Volume is similar, but it is the space that a three-dimensional object occupies.

To find area, we find the total number of units by multiplying the number of units in the length by the number of units in the width.

Dimensions:

Length (l) = Width (w) =

Area: 5 units × 3 units =

Learn and Connect Apply

To find volume, we find the total number of square units in one layer, and then multiply that by the number of layers.

of one layer:

Review the example and then find the volumes of the rectangular prisms.

Example:

Area of base = 3 × 2 = 6u2

Multiply by the layers = 4

6 × 4 = 24 u3 = 6 = 6 = 6 = 6

Find the volumes.

Determine if the work is correct. If there is a mistake, correct it.

Chapter 11-2 Finding Volume

Daily Review Write 2 things you know about area and two things about volume.

Learn and Connect

Rick is building a new garden bed, and he needs to figure out how much dirt is needed to fill it. To find out how much dirt will fit inside the rectangular garden bed, he needs to find the volume.

Here is the flowerbed represented using unit cubes.

How many unit cubes is the length?

How many unit cubes is the width?

How many unit cubes is the height?

To find the volume, we multiply length × width × height.

Units for volume are cubed because you are multiplying 3 numbers together.

Apply

Find the length, width, and height of the rectangular prisms. Write the volumes using the correct labels.

Find the length, width, and height of the rectangular prisms. Write the volumes using the correct labels.

Use the measurements to find the volume of each rectangular prism.

Write an equation. Then, find the volumes for the following scenarios.

A gift box is 18in long, 7in wide, and 3in tall. How much space is inside the gift box?

A cabinet is 2.5 feet tall by, 1 foot deep, and 3 feet wide. How much space is there?

Help Morris determine which box is the best buy, the lowest cost per cubic inch.

Box 1: 6in × 5in × 10in Cost: $6.00 Volume:

Cost per cubic inch:

Box 3: 8in × 10in × 3in Cost: $3.60 Volume: Cost per cubic inch: Length: Width: Height: Volume:

Box 2: 5in × 5in × 8in Cost: $5.00 Volume: Cost per cubic inch:

Chapter 11-3 Using Volume to Find a Missing Side

Learn and Connect

This prism has a volume of 60 in3. How can we find the missing side length if we know the volume?

1. Volume = length × width × height = × ×

2. Multiply the side lengths = ×

3. Find the missing side length by dividing the volume by the number found in step 2.

60 ÷ =

4. The missing side length, x, is .

Apply

If the volume of prism is 60 in3,

Find the missing side lengths of the rectangular prisms below. Show your work.

If the volume of prism is 160 cm3

If the volume of prism is 240 m3

If the volume of prism is 189 in3

If the volume of the cube is 8 in3, each side of this cube is

Fill in the missing side lengths. Write the units.

Find the missing side lengths for each scenario.

A storage bin has a capacity (volume) of 45 cubic feet. You know it has a base of 3 ft by 5 ft, but you are not sure about the height. What is the height?

A cereal box says it holds 176 in3 of cereal. If the height is 11 in, and the length is 8 in, what is the width of the box?

A pool holds 350 cubic feet of water. How deep is it if it’s 7 ft long and 10 ft wide?

A locker is 10 in wide and 36 in tall. How deep is the locker if its volume is 2,880 in3.

Challenge

A textbook has a volume of 240 in3. If the width is 8 in, and height is 10 in, what is the length?

Find the missing side lengths in the scenarios below.

A carton of juice has a base that is 6 in by 6 in. How tall is the carton if the volume is 360 in3?

A big locker is above a small locker. They are both 0.5 m wide and 0.6 m deep.

1) The volume of the big locker is 0.36 m3. What is the height?

2) The small locker is half of the height of the big locker. What is the height?

3) What is the total volume of the lockers?

Chapter 11-4 Volume of More than One Prism

Review Fill in the missing side lengths. Then match to the correct prism.

Learn and Connect

Sometimes, we have a figure that is made up of multiple figures. We can break up the figure into smaller figures. Then, we can find the volume of each and add to find the total.

Find the total volumes, using the red lines to help you determine the two shapes.

Find each volume by separating the figure into two rectangular prisms.

Prism 1:

L = W = H =

Prism 2:

L = W = H =

Prism 1:

L = W = H = Prism 2: L = W = H = Prism 1: L = W = H =

Prism 1: L = W = H =

Find the volume of this figure.

Daily Review Write the time shown on the clocks.

Rick started studying at 11:45 A.M. He checked the time when he was finished and then went to have a snack. How long did Rick study before going to get a snack?

To solve, we must determine the elapsed time, or the hours and minutes that have passed between one time and another.

Remember, 1 hour = 60 minutes.

You can make a number line to help you find elapsed time.

Learn and Connect Apply

Time

You can convert to hours and minutes and subtract to find the time elapsed.

Start by finding how many minutes it takes to get to 12pm.

Then, add the remaining time. Regroup minutes to hours if necessary.

Determine the elapsed time using a number line.

Determine the elapsed time.

Use the train schedule below to determine the length of the trips.

Morning: Stop A – Stop E

Morning: Stop C – Stop H

Afternoon: Stop G – Stop D

Morning: Stop B – Stop F

Afternoon: Stop E – Stop A

If you live near Stop C and work near Stop F, how much time do you spend commuting each day?

Challenge

Stop A 5:19 AM 6:25 PM Stop B 5:31 AM 6:14 PM Stop C 5:46 AM 5:56 PM Stop D 5:58 AM 5:40PM Stop E 6:12 AM 5:26 PM Stop F 6:34 AM 4:55 PM Stop G 6:47 AM 4:40 PM Stop H 7:16 AM 4:25 PM

Determine the elapsed time. Be sure to pay attention to the days!

Monday at 3:12 pm to Tuesday at 8:00 am Sunday at 11:55 am to Monday at 3:07 pm Sunday at 8:20 am to Wednesday at 10:40 am

Daily Review Find the elapsed times.

Learn and Connect

Mike and Victor visit the aquarium everyday to see the dolphin. For the past 30 days, the boys recorded how many times the dolphin swam right up to the glass. They want to create a dot plot to organize their data. Let’s walk through the steps to create a dot plot.

Dolphin sightings

13, 13, 12, 12, 12, 12, 15, 11, 14, 12, 11, 14, 12, 13, 10, 12, 15, 11, 13, 14, 13, 13, 12, 11, 15, 14, 13, 15, 14, 10 8:45 am to 9:30 pm 3:17 am to 8:22 pm 4:18 am to 1:15 pm

Dolphin Sightings

Use the smallest number, the minimum, and largest number, the maximum, of dolphin sightings to create your number line.

1 2 3

Add the dots to your graph. The dots represent the number of times the dolphin swam by the glass. There is one dot for each day.

Number of Dolphin Sightings

Finally, add a title to the graph and label under the number line.

Create a dot plot. Then, answer the questions.

Moses planted tomato plants in his garden. When it came time to harvest, he kept track of the number of tomatoes he got from each plant. He recorded the results in the frequency table below. Fill in the tallies and create a dot plot.

When creating your dot plot graph, make sure you include:

(dots)

What is the most common number of tomatoes that Moses got off the plant?

How many plants did he harvest tomatoes from?

How many tomatoes did he harvest?

Mr. Davis recorded the test grades from the chapter test on multiplying fractions. The test scores were: 91, 98, 90, 99, 92 ,94, 94, 94, 98, 99, 92, 91, 94, 92, 97. Make a dot plot to display this data. Then, use the dot plot to answer the questions.

What was the most common test score on the multiplying fractions test?

What is the difference between the highest test score and the lowest test score?

How many students took the test?

If another student took the test, predict what their test score might be according to the data. Justify your answer.

Chapter 11-7 Creating Dot Plots using Fractions of a Unit

Daily Review Find the total amount of storage in the two storage containers.

Learn and Connect

A farmer has just harvested a bunch of bushels of apples. He weighed each bushel to the closest quarter of a pound. In order to keep track of his inventory, he makes a dot plot. The weights in pounds of the bushels of apples are:

Put the numbers in order to find the minimum and maximum.

If the farmer skip counts by fourths, he can show all the different weights of bushels on the number line.

Apply

Use the dot plots to answer the questions.

of Apples

Chad recorded the amount of donuts that each person ate during the donut eating contest. The results are: 2 3 4 , 3, 3 1 2 , 3

Donut Eating Contest

1. Write the minimum:

2. Write the maximum:

3. What fraction is used to skip count by?

4. Fill in the dots on the dot plot.

A woodworker cut planks of wood into various lengths in inches for a project. The lengths were as follows:

5. Write the minimum:

6. Write the maximum:

7. What fraction is used to skip count by?

8. Fill in the missing numbers on the number line.

Number of Donuts Length of Wood (inches)

Planks of Wood

Create dot plots for the data. Then, answer the questions.

The class took a survey on how long each student reads each night in hours. The totals were as follows: 3 4 , 3

,

1. What was the most common reading time?

2. How many students read for 1 1 2 hours?

3. What is the difference between the maximum and the minimum?

4. How many students were surveyed?

In science class, the students were monitoring how far snails moved in inches per minute, and got the following lengths: 1, 1 4 , 1 4 , 3 4 , 0, 1, 1 4 , 0, 1 4 , 1, 1 4

5. How far did most snails move in 1 minute?

6. What is the difference between the longest and shortest distances?

Use the dot plot to answer the questions.

8. 9. How many cups of flour will Steven need to make all the dessert recipes?

Explain how you solved problem 8.

7. If all the snails’ distances were added together, how far would they go? Amount of Flour (cups)

Flour needed for 26 different dessert recipes

Daily Review Find the elapsed times.

Learn and Connect

Volume = area of base × height V = 21 × 3 V = u3

A running club records how far its members ran this week.

Fill in the missing frequencies in the frequency chart.

Draw dots in the dot plot.

Which distance(s) were the most frequent?

How many people ran 11km?

Apply

Complete the frequency chart and dot plot. Then, answer the questions.

A community center asks its members how many children are in their family.

Results: 0, 6, 1, 1, 0, 1, 2, 4, 3, 0, 2, 2 1, 4, 1, 3, 2, 1, 4

Which number of children was the least frequent?

How many families have 4 kids?

How many more families have 2 kids than 6 kids?

Find the volumes of the figures or word problems below. Check your units!

Find the volume of a box with measures: 8 in × 6 in × 12 in.

How much dirt fits in a planter box that is a cube with sides of 2 ft?

How much water fits in a pool that is 6 meters × 10 meters and is 2 meters deep?

The volume of a rectangular prism is 42 ft3. If the length is 3 ft and height is 7 ft, what is the width?

A cereal box has a volume of 288 in3. What is the height if the area of the base is 24 in2?

You are building a wooden chest. The length is 6 ft, and width is 4 ft. If the volume is 72 ft3, what is the height?

A rectangular prism has a rectangular hole punched out of the middle. Find the volume of the prism after the hole has been removed. Hint: If we take away a part of the prism, what operation will we use?

Chapter 12

In Chapter 12, we will delve into

Measurement

The customary system of measurement is the most commonly used system in the U.S., while the metric system is easier to use and is used all over the world.

• Convert length

• Convert weight

• Convert capacity

• Problem solve

We can convert between units of length, weight, and capacity within the U.S. customary system.

We can move the decimal point over to convert between units of length, weight, and capacity within the metric system.

We can solve problems with conversions in everyday life.

Chapter 12-1 Converting Length (U.S. Customary)

Daily Review Convert the measurements.

Jessie has a window that is 3 feet and 8 inches wide. He wants to buy blinds that will fit in the window. He found some blinds that were 84 inches wide. How much wider are the blinds than the window?

To solve, we first have to determine the width of the window in inches. Because we are moving from larger to smaller units, we will be multiplying.

3 ft × 12 inches = 36 in + 8 in = 44 in

Next, we have to subtract the total width of the window from the width of the blinds.

84 in – 44 in = 40 in

The blinds are 40 inches too wide.

Learn and Connect Apply

Remember:

• When converting from greater to lesser units, multiply.

• When converting from lesser to greater units, divide.

Customary Units of Length

1 yard (yd) = 3 feet (ft) 1 foot (ft) = 12 inches (in)

1 mile (mi) = 1,760 yards (yd)

mile (mi) = 5,280 feet (ft)

Determine the length of each object. Convert the lengths.

Use the chart on the previous page to help convert the lengths.

Solve.

13. Henry ran 2 miles. How many yards is that?

16. If 21 yards of fabric were purchased, how many feet is that?

14. If it is half a mile to the market, how many feet is it?

15. How far in miles did Simon run if he ran 4,400 yards?

17. If the rug is 8 feet � 5 feet, what are the measurements in inches?

19. If there are 20 feet of ribbon, and you cut it into 8 inch sections, how many will you get?

20. Each block is 22 yards, and there are still 3 blocks to walk. How many feet is that?

18. There are 180 inches of rope. How many yards is that?

Complete the table. Round to the nearest whole number.

21. How many feet are 1.5 miles?

Chapter 12-2 Converting Length (Metric System)

Daily Review Convert the customary measurements.

1. 6ft = yds 2. 3ft = inches 3. 2yds = inches 4. 3 miles = yds

Learn and Connect

The most commonly used metric units of length are kilometers (km), meter (m), centimeters (cm), and millimeters (mm).

To convert between metric units of length, move the decimal point the direction and number of places shown below.

Multiply, divide, or move the decimal point to convert. 2 meters = millimeters

(2 × 103 = ?)

Apply

Multiply, divide, or move the decimal point to convert.

Hint: The number you multiply or divide by has the same number of zeros as places you move the decimal point.

Ben walked 0.3 kilometers 3 days this week. How many meters did he walk this week?

David has 20 blocks that are each 8 millimeters tall. Can he build a tower that is 32 centimeters tall?

Multiply, divide, or move the decimal point to convert. Use the chart above to help you.

Aaron’s garden hose was 6 meters long. He connected a new hose to it that measured 475 centimeters. Then, he shortened his hose by rolling 1 meter of it up. How many meters long is the hose now?

Nick rode his bike a total of 66 kilometers this week. He rode the same distance on each of 4 days. How many meters did he ride each day?

Larry is building a wheelchair ramp. Each board is 30 centimeters wide. If he needs 24 boards to build the whole ramp, how many meters long is the finished ramp? There were 100 meters of yarn in the package. 24 students each used 50 cm of yarn for a project. How many meters of yarn are left?

Each piece of Sam’s toy train track is 120 mm long. He puts pieces together to make a 3-meter long track. How many pieces is the track?

Jake ran 1.6 km on Monday, 1.9 km on Wednesday, and 1.7 km on Friday? How many meters did he run this week?

William has 40 boards that are each 18 centimeters wide. Can he build a deck that is 5 meters wide?

If yes, how many extra centimeters does he have?

If no, how many more centimeters does he need?

Chapter 12-3 Converting Weight (U.S. Customary)

Learn and Connect

At the Lakeway Zoo, a baby koala was born weighing 160 ounces. How many pounds did it weigh at birth?

The zookeepers at the zoo weighed Alex the hippo, and he weighed 2 tons. How much did he weigh in pounds?

At the zoo, it costs $1 for 8 ounces of popcorn. How much will it cost to buy 2 pounds of popcorn?

The horse trailer at the zoo can carry up to 10,000 pounds of weight. How many tons can it carry?

23. The rhinos at the zoo eat 80 ounces of food for 3 meals every day. How many pounds do they eat a day?

24. The zoo has 4 trucks that carry animals. The trucks each weigh 4,000 pounds. What is the total weight of all 4 trucks in tons?

Chapter 12-4 Converting Weight (Metric System)

Daily Review Convert the measurements.

1. 5 tons = pounds 2. 64 ounces = pounds 3. 7 pounds = ounces

Learn and Connect

To measure metric weight, we will use kilograms (kg), grams (g), and milligrams (mg).

To convert between metric units of weight, move the decimal point the direction and number of places shown below.

0.475 kilograms = 475 grams

0.475 × 103 = 475 or 0.475 = 475 grams

Apply

A crayon weighs 9 grams. How many milligrams does the crayon weigh? 9 × 103 = or 9. . =

Multiply, divide, or move the decimal point to convert.

Metric Weight Conversions

1 gram (g) = 1,000 milligrams (mg)

1 kilogram = (kg) 1,000 grams (g)

Reminder: We weigh people and larger items in kilograms, small items like crayons in grams, and tiny items like salt or sugar grains in milligrams.

A 10-year-old boy weighs 35 kilograms How many milligrams does the boy weigh?

35 × 106 = or

35. . =

The cookie recipe calls for 200 grams of flour. The baker wants to triple the recipe. He has 0.75 kilograms of flour. Does he have enough?

Richard weighs 30 kg. His baby sister weighs 3,600 grams. How much more does Richard weigh than his sister in kg?

Multiply, divide, or move the decimal point to convert. Use the chart above to help you.

A tablespoon of flour weighs 8 mg. How many tablespoons of flour are in a 2.4 kg bag of flour?

Each marker weighs 13,610 mg. If there are 4 markers in a box, how many grams does the box of markers weigh?

The weight limit on the elevator is 500 kg. If 4 people ride on the elevator who all weigh the same amount, what is the maximum number of grams they can each weigh?

There were 340 grams of baking soda in the box. 30 students each used 800 mg for an experiment. How many grams are left in the box?

Rick is making a large cake. He mixed 420 grams of sugar, 560 grams of flour, 20 grams of baking powder, and 40 grams of salt. How many kilograms do all of the dry ingredients weigh?

Rachel’s baby sister gained 850 grams in her first month, 800 grams in the second month, and 810 grams in the third month. How many total kg had she gained by the time she was 3 months old?

Debra has 3 partial bags of flour. The first weighs 700 grams, the second one weighs 1,400 grams, and the third one weighs 2,100 grams. Can she combine them all in a container that holds 3 kg of flour?

If yes, how many more grams could she fit in the container? If no, how many extra grams does she have?

Chapter 12-5 Converting Capacity (U.S. Customary)

Daily Review Find the elapsed time.

Learn and Connect

Tom has a gallon of milk. He wants to pour the milk into large glasses that can each hold 1 pt. How many glasses will he be able to fill with the gallon of milk?

To solve, we have to determine the capacity of the milk gallon in pints.

Capacity is the measurement of how much a container can hold. We know that the milk container holds 1 gallon, but we have to convert this into pints.

Since there is no direct conversion from gallons to pints in the chart, we can solve by first finding how many quarts are in a gallon. Then, we must determine how many pints are in those quarts. We are moving from large measurements to smaller ones. Therefore, we must multiply.

Tom can fill glasses.

Apply

Convert the measurements.

Remember:

• When converting from greater to lesser units, multiply.

• When converting from lesser to greater units, divide.

1 gallon � 4 = quarts quarts � 2 = pints

Use the chart on the previous page to help convert the liquid measurements.

1. 3 gal = qt

Use conversion table to solve the problems below.

13. There are 2 1 2 pints of paint left. How many oz is that?

16. 100 cups of water are poured into gallon jugs. How many jugs are needed?

14. If 3 gallons of milk need to be split into cups, how many cups are needed?

15. If 12 pints of juice will be poured into quart containers, how many are needed?

17. You mix 3 quarts of red paint, 1 quart of purple, and 4 quarts of blue. How many gallons will this make?

18. The recipe calls for 6 cups of broth, and they come in pint-size containers. How many do you need?

19. If 96 oz of sports drink are left after the game, how many cups can you make to give out?

20. Each T-shirt needs 4 oz of dye. How many shirts can be dyed with 1 quart?

21. Each plant needs 2 cups of water. There are 10 plants. How many quarts are needed to water them all?

Complete the table.

22. Challenge

Chapter 12-6 Converting Capacity (Metric System)

Daily Review Convert the liquid measurements.

1. 12 quarts = gallons 2. 4 quarts = pints 3. 3 cups = pints

Learn and Connect

To measure metric capacity, we will use kiloliters (kL), liters (L), and milliliters (mL).

To convert between metric units of capacity, move the decimal point the direction and number of places shown below.

75 liters = kiloliters

75 ÷ 103 = 0.075 or

. 75 liters = 0.075 kiloliters

There are 3 liters in the juice bottle. How many milliliters are there?

3 × 103 = Or 3. . =

The cake recipe calls for 150 mL of oil. The bakery sells 48 cakes this week. How many liters of oil did they use this week?

20 × 106 = Or 20. . = Metric Capacity Conversions

Reminder: We measure liquids like water in a swimming pool in kiloliters, the amount of liquid in a large bucket in liters, and the amount of liquid in a small cup or dropper in milliliters.

A small backyard pool has 20 kiloliters of water. How many milliliters does it have?

The gardener uses 12.6 kL of water to water her garden each week. How many liters of water does she use in 4 weeks?

Multiply, divide, or move the decimal point to convert. Use the chart above to help you.

There were 3.8 liters of vinegar in a jug. Thirty-two students each used 110 mL for an experiment. How many liters are left in the jug?

The hot sauce sampler has 6 sauces. Each sauce is 240 mL. How many liters of sauce are there total in the sampler?

The water park has 3 water slides that each slide into their own pool. The 3 pools are the same size. If the total amount of water in the pools is 126 kL, how many liters are in each pool?

The disaster relief volunteers gave out 24,550 liters of water in the morning and 32,685 liters of water in the afternoon. How many kL of water did they give out that day?

Donald takes 5 mL of allergy medicine twice a day. He takes the medicine every day for a year (365 days). How many liters of medicine does he take in a year?

Ruth poured 2,890 mL of water into a bucket. Then, she added 1,540 mL of cleaning fluid. She used 1 liter of the mixture to clean the floor. How many liters of the liquid are left?

Two fire trucks arrive at the scene of a fire. Each truck is carrying 1,890 liters of water. It will take 4 kiloliters of water to put out the fire. Is there enough water?

If yes, how many extra liters of water are there? If no, how many more liters of water are needed?

Chapter 12-7 Conversions in Everyday Life

Daily Review Solve the conversions.

1. 120 milliliters = liters 2. 7 kiloliters = liters 3. 33.2 liters = milliliters

Learn and Connect

We need to know how to convert between many different units to solve problems in everyday life!

The Davis family has a leaky faucet. When the faucet is turned off, it drips 5 mL of water every minute. How many liters of water drip out of the Davis’ faucet in a whole day if it is turned off?

We need to convert milliliters to liters and minutes to days.

Step 1: How many minutes are in 1 day?

60 min/hour × 24 hours/ day = 1,440 min

Step 2: How many mL drip in 1 day?

5 mL/min × 1,440 min/day = 7,200 mL

Step 3: Convert milliliters to liters.

7,200 mL = liters

Apply

Remember: Move the decimal point 3 places to the left, or divide by 1,000!

Multiply, divide, or move the decimal point to convert.

1. 2. The cake recipe calls for 200 grams of flour.

A 2.4 kg bag of flour costs $3.60. How many cents does the flour for 1 cake cost?

1: $3.60 = cents

2: 2.4 kg = grams

3: How many cakes can you make with 1 bag of flour?

2,400 ÷ 200 =

4: How many cents for each cake?

360 ÷ 12 =

- length grams - weight liters - capacity

The railroad workers repair 9 meters of track each hour, and they work 8 hours each day. How many days will it take them to finish 27 kilometers of track?

1: 27 km = m

2: How many meters do they repair per day? 9 meters/hour × 8 hours/day =

3: How many days to repair the whole track?

27,000m ÷ 72m =

The cookie recipe calls for 8 mL of vanilla extract. A 0.64 liter bottle of vanilla costs $32. How many cents does the vanilla for 1 batch of cookies cost?

Step 1: $32 = cents Step 2: 0.64 L = mL

Step 3: How many batches can you make with 1 bottle of vanilla? 640 ÷ 8 =

Step 4: How many cents for each batch? 3,200 ÷ 80 =

Mrs. Anderson is knitting a scarf. The scarf uses 360 meters of yarn total. If she uses 40 cm of yarn per minute, how many hours will it take her to knit the scarf?

Justin used 950 mL of broth in the soup he made on Monday. The soup was so good that he made it again on Wednesday and again on Sunday. How many liters of broth did he use?

The Ross family has set a goal of of spending a total of 1,000 hours outside this year. If they spend 170 minutes outside each day, will they meet their goal?

Ben is a baker. He uses 3,000 grams of flour each day. A 24 kg bag of flour costs $42. How much does the flour for 1 day cost?

Mrs. Mills’ class is making an art project with yarn. One package has 110 meters of yarn in it. Each of her 24 students uses 5 cm of yarn per minute. If they work on the project 1 hour each day for 10 days, how many packages of yarn will they need?

The Carter family is filling their new pool with water. The pool is 1 meter deep. They have used 1,500 liters of water and have only filled the pool 2 cm. How many kL of water will it take to fill the whole pool?

If it costs $4 for a 2-liter bottle of soda, how many cents does each 250 mL serving cost?

The zoo buys about 25,550 kg of meat each year to feed the animals. If there are 350 meat-eating animals at the zoo, what is the average number of grams each animal eats per day ?

Learn and Connect

We can measure many items using U.S. customary units or metric units.

convert to a smaller unit, move the decimal point to the right (or multiply).

convert to a larger unit, move decimal point to the left (or divide)

Convert the customary units.

Convert the metric units. Solve.

John’s grandfather bought 3 yd 14 inches of fabric. How many inches of fabric did he buy?

Bob long jumped 12 ft 10 inches. Isaac long jumped 14 ft 2 inches. How many more feet and inches did Isaac jump than Bob?

The baker uses 7,000 grams of sugar each day. A 28 kg bag of sugar costs $52. How much does the sugar for 1 day cost?

A baby blue whale is born 20 feet long and weighs 5 tons. How many pounds is the baby blue whale at birth?

The car took 3 quarts and 1 pint of oil. The truck needed 6 quarts and 1 pint of oil. How much oil is needed for both the car and the truck? If you have 3 gallons of oil, is there enough for both the car and the truck? Why or why not?

Mrs. Smith’s class is making an art project with strips of construction paper. They can get 20 meters of strips from one package of construction paper. If each of her 22 students uses 300 cm for their project, how many packages does she need?

Chapter 13

In

Chapter 13, we will explore

Coordinate Planes and Graphing

A coordinate plane can be used to describe a specific place in a space. It can also be used to show patterns.

• Define lines, points, and planes

• Find and plot points on a coordinate plane

• Graph points in a line to represent real-world scenarios

• Generate patterns

• Problem solve with dot plots

We can draw different types of lines and points.

We can write the coordinates for a point on a coordinate plane and use an ordered pair to plot a point on a coordinate plane.

We can interpret a coordinate plane with points that represent a real-world situation.

We can generate a pattern to find ordered pairs and graph them on the coordinate plane.

We can interpret and problem solve with dot plots.

Daily Review

Convert between units. Remember: 1 yd = 3 ft and 1 ft = 12 inches.

Learn and Connect

Plane geometry is about flat shapes that can be drawn on a piece of paper like lines, circles, and triangles. A plane is a two-dimensional surface. This means that it does not have height, only length and width that extends indefinitely in all directions.

Read the definitions of each of the plane geometry below and draw a line to the image that best represents the description.

Point

A point is undefined. It is just a dot on the page with no size or shape, just position.

Line segments

A line segment is a portion of a line that has two endpoints.

Ray

A ray is a portion of a line which has one endpoint and extends forever in one direction.

Line

A line is a straight path of points that has no beginning or end.

Parallel lines

Parallel lines are lines that never touch.

Perpendicular lines

Perpendicular lines will cross to make right angles.

Intersecting lines

Intersecting lines will cross but do not make right angles.

Write the name of each figure. Draw a picture. Use words to explain how draw it.

Determine if the statements are true or false. If false, correct the sentence so it is true.

Intersecting lines always cross at a 90 degree angle.

A line segment is a portion of a line with dots showing the ends. A line extends in both directions forever. A ray extends forever in both directions.

Parallel lines always intersect one time.

Chapter 13-2 Introduction to Coordinate Planes

Daily Review

Plot the numbers on the number lines.

Learn and Connect

A coordinate plane has two intersecting number lines, one horizontal and one vertical, that create a grid.

Graph the point (2, 3)

Step 1: Start at the origin (0, 0).

Step 2: The x-coordinate tells us to move 2 right.

Step 3: The y-coordinate tells us to move 3 up.

Step 4: Draw a dot on that location.

Coordinate Point

- coordinate (x, y) shows the

Origin (0, 0): Center point where axes meet

Apply

Plot the points below on the coordinate plane. Write the letter by the point.

1. Point Right Up

(1, 3)

(8, 4)

(2, 7)

(7, 10)

(4,6)

1. 0, 2, 6, 9 2. 1, 3, 4, 7

Use the coordinate plane to answer the questions.

Find each point on the coordinate plane. Write the letter of each point.

Find each point on the coordinate plane. Write the coordinates of each letter.

Plot each point on the coordinate plane. Write the letter of each point.

A friend of yours missed class today. Explain to them the steps to plot the points below.

Horizontal axis

Vertical axis (0,0) middle of the graph (x,y) tells the location of a point

Learn and Connect

Below is a treasure map with locations and items that need to be collected. Write the coordinates of the locations and identify which item will be collected at each location.

Remember: coordinate points are (x, y) where the x tells us how far to go right, and the y tell us how far to go up.

If you walk from the castle to the windmill to the tree, what shape will your path make?

What item will create a square with the windmill, lighthouse, and fruit tree?

Apply

Determine what shape is created with the coordinates. Plot a point and connect it to the next point. When you get to the last point, connect it to the first.

Determine what shape is created with the coordinates. Plot a point and connect it to the next point. When you get to the last point, connect it to the first. Color in each shape.

(2,16) (10,16) (10,19) (2,19)

(12, 0) (18,0) (17,2) (13,2)

(16,13) (16,16) (19,16) (19,13)

(1,0) (3,1) (5,0) (4,2) (6,3) (4,3) (3,5) (2,3) (0,3) (2,2)

blue: (13,14) (10,14) (9,12) (10,10) (13,10) (14,12)

(7,5) (8,9) (18,9) (17,5)

(4,8) (2,9) (4,10) (6,9)

Graph the points below. What shape is created?

(1, 11) (1, 14) (5, 11) (1,3) (1,5) (3,5) (3,6) (5,4) (3,2) (3,3)

Recreate the same shape, but instead of starting at (1,3), start at (4,5). Draw the shape and write the coordinates.

Red:

Blue:

Pink:

Dark

Purple:

Gray:

Yellow:

Orange:

10. (4,5)

Learn and Connect Daily Review

Find each point on the graph. Write each color.

John left his house at 7 a.m. for a bike ride. He recorded how many miles he traveled after each hour in the graph below. Use it to answer the questions below.

Bike Trip

The -axis tells us the time of day.

The -axis tells us the distance in km.

Find the point (9,14). This point means that at 9 a.m., John traveled 14 km total.

John stopped for an hour to have a snack and take pictures. When did he stop? How do you know? Hint: Find two hours that have the same distance.

How long did John ride his bike? How tall is the meerkat at 8 months?

John’s

Use the table to complete the graph and answer the follow-up questions.

a) What does the point (3,60) mean?

b) If you read for 2.5 hours, how many pages would be read?

a) What does the point (3,6) mean?

b) Which month had the most and least classes?

a) What does the point (2019, 7) mean?

b) How many total students joined grade 2 in the years 2017 - 2020?

Daily Review

Complete each table given the rule.

Learn and Connect

Anthony is preparing for a carnival this afternoon. He makes one batch of popcorn and knows that each batch has enough popcorn for 6 large bags of popcorn. He also knows that he sells 3 more bags of popcorn (p) than sodas (s), p = s + 3. Complete the tables and answer the questions.

p = s + 3 Plug the values you know into the equation. p = popcorn; s = soda If you have 2 sodas, P = (2) + 3 P = 5

If Anthony sold 48 bags of popcorn, how many batches did he have to make?

If Anthony sold 53 sodas, how many bags of popcorn did he sell?

Complete each table given the rules.

Read each scenario and complete the table. Choose any number to input for the last row. Then, explain what the chosen quantities mean given the context.

Each dime you find means you have 10 cents. If d = dimes and t = total, then t = 10d.

The extra credit question is 3 points. If s = score, and f = final score then f = s + 3

A dentist sees 7 patients every day. If p = patients and d = days, then p = 7d

In a board game, the player who makes the last move gets 2 points. If p = points and t = total, then t = p + 2

Each week you save $8. If w = weeks and s = savings, then s = 8w.

Your brother always has 2 more crayons than you. If b = brother's and c = yours, then b = c + 2.

Challenge

Create your own scenario given each equation. Complete the table and explain one point.

Chapter 13-6 Forming Ordered Pairs to Create Graphs

Daily Review

Complete each table given the equation.

Learn and Connect

Let’s think back to the carnival problem from the last lesson. We know that one batch of popcorn makes 6 large bags of popcorn. Use the table to create ordered pairs and graph these points to represent the relationship.

Pairs (x, y)

If p = batches of popcorn and b = amount of bags, then p = 6b.

Batches of Popcorn Apply

Complete each table and use the coordinates to create a graph. Be sure to label your graphs!

1. 2. The extra credit question is 5 points. If s = score, and f = final score, then f = s + 5.

Each dime you find means you have 10 cents. If d = dimes, and t = total, then t = 10d.

Use the story to complete each table, find the coordinates, and create a graph.

Bob always buys 5 more vegetables than fruits when he grocery shops.

f = fruit bought and v = veggies bought.

Equation: f + 5 = v

Each sandwich costs $3. s = sandwiches purchased and t = the total spent. Equation: t=3s

The museum requires 1 chaperone for every 15 students on the field trip.

c = chaperones and s = students.

Equation:

Chapter 13-7 Problem Solving with Dot Plots

Daily Review

Create a dot plot for the data set.

Number of states students have visited: 6, 3, 4, 3, 5, 7, 4, 6, 5, 3, 4, 4, 5, 1, 0, 3, 2, 2, 1, 1

Learn and Connect

The weather the past week has been rainy. Look at the weather report and create a dot plot to represent the rainfall each day.

What was the total rainfall across the 5 days?

How much more rain fell on the most rainy day than the least?

How many times as great is the amount of rain on the most rainy day than the least rainy?

Apply

Use the dot plot to answer the following questions.

The orange dots on the plot show the volume of paint, measured in pints, left in 4 different cans.

How much more paint is in the most full can when compared to the least full can?

What is the total volume of paint remaining?

If we split the remaining paint equally across the 4 cans, how much would be in each can?

Two more cans were found with 3 1 2 and 5 1 2 pints. Add dots to the dot plot for these cans.

Use the dot plot to answer the following questions.

The plot shows the amount of time, in seconds, it took 5 hamsters to navigate a maze.

a) How much faster did the fastest hamster complete the maze compared to the slowest?

b) What was the total time it took all 5 hamsters to complete the maze?

c) If a sixth hamster was 1 2 a second slower than the fastest hamster, what was its time?

The plot shows the weight of 9 parrots, measured in kilograms.

a) How much heavier is the heaviest parrot compared to the lightest parrot?

b) Is it more likely for a parrot to weigh 4 10kg or 8 10 kg? How do you know?

The plot shows the amount in ounces of salt used for each recipe.

Challenge

a) How much total salt was needed for all 4 recipes?

b) How much more salt is needed in the recipe with the most salt compared to the recipe with the least?

Create a question to ask 5 classmates. Then, use that information to create a dot plot.

a) Choose your question.

b) Ask students & record your data below.

c) Create a dot plot: create a title, determine your intervals, plot your data.

Daily Review

Draw an image for each term below.

Learn and Connect

Plot the points on the coordinate plane. Write the letter by the point.

Write the coordinates of the points for each letter.

B (2, 3)

C (8, 2)

D (4, 6)

E (8, 9)

F (0,7)

Apply

Determine what shape is created with the coordinates. Plot a point and connect it to the next point. When you get to the last point, connect it to the first. Label each shape with the problem number.

(11,4) (10,6) (7,6) (2,11) (4,13) (2,15) (0,13) (7,0) (12,0) (13,2) (8,2) (9,12) (10,10) (13,10) (14,12) (13,14) (10,14)

Use each story to complete the table, find the coordinates, and create a graph.

Moses always buys 3 more shirts than pants when he goes shopping. When he shops, p = pants bought and s = shirts bought.

Each pie costs $4. p = pies purchased and t = the total spent.

The science center requires 1 chaperone for every 12 students on the field trip. c = chaperones and s = students.

Use the dot plot to answer the questions.

The data represent how long orchestra students practice in hours each week.

How much more does the student who practices the most practice compared to the one who practices the least?

Time (hours)

What is the total time students practice?

If the student who practiced the least practiced for 1 2 an hour more, how long did they practice?

Chapter 14

In Chapter 14, we will conclude with

Review

This chapter includes all concepts covered in this book.

• Understand place value with decimals

• Add and subtract decimals

• Use the order of operations with decimals and whole numbers

• Add and subtract fractions

• Multiply fractions and mixed numbers

• Divide fractions

• Solve for volume

• Use coordinate planes

We can write decimals in expanded notation and order numbers.

We can use place value to add and subtract decimals. We can use the order of operations to solve multistep problems with fractions, decimals, and whole numbers. We can find equivalent fractions to add and subtract fractions.

We can multiply fractions and mixed numbers with models and an algorithm. We can multiply by the reciprocal to divide fractions. We can find the volume or a missing side given the dimensions of a rectangular prism. We can find and plot points on a coordinate plane.

Chapter 14-1 Place Value Review

Daily Review

Identify the place value and value of each underlined digit.

Learn and Connect

Complete the chart by filling in the word form for each place value.

Write the word form of this number.

Apply

Write the expanded form for each number.

Compare using <, >, or =.

Vocabulary

Place value - the value of each digit of a number

Standard form - a number written in digits 0 -9

Word form - a number written using words

Expanded notation - a way to write a number that represents it as the sum of each of its digits multiplied by their place value

Decimal - a way to show a number less than one whole that is based on the number ten and uses a decimal point

Complete the chart by identifying the number shown in each model.

Write the numbers from the chart above in order from smallest to largest.

Hint:

Chapter 14-2 Addition and Subtraction with Decimals Review

Review Round each decimal to the underlined digit.

Christopher and Brian are trying to decide what to order at Sam's Pizza Parlor. Their mom gave them $25 to spend. They each want to get a cookie, a drink, and to share a pizza. Do they have enough money?

The easiest way to answer the question is to estimate the cost to the nearest dollar, add up the items, and see if they have enough money.

2 drinks

2 cookies 1 pizza

Learn and Connect Apply

Remember to line up the decimal points when adding or subtracting.

About how much will they be spending? Do they have enough money?

Round to the nearest whole numbers and estimate the sums or differences.

Rewrite, round to the nearest whole number, and estimate.

Circle the better estimate for the sum or difference of each problem. Explain how you made your estimate.

10.63 - 1.7

A) 9 B) 10

Read and solve for the estimated amount. Then, solve for the exact solution.

When Richard weighed his puppy on Monday, he was 7.88 lbs. He weighed him again after one month, and he was 11.52 lbs. About how many pounds did his puppy gain?

Solomon bought 8.75 lbs of fruit salad. He gave 3.75 lbs of salad to Mr. Levine and 2.5 lbs of salad to Kane. About how many pounds does he have left?

Justin ran 40 yards in 5.2 seconds. Morris ran 40 yards in 6.75 seconds. Dennis ran the fastest, 40 yards in 4.1 seconds. About how many seconds faster was Dennis than Morris? About how many seconds faster was Dennis than Justin?

Chad’s father gave him $25 to spend at a carnival. He bought 2 buckets of popcorn for $4.75 each, 2 drinks for $3.50 each, and a box of candy for $2.25. About how much change does he get back?

Mr. Miller asked Chad and Justin to estimate the answer for 39.78 + 29.58 + 15.02.

Chad’s estimated equation was: 40 + 30 + 16 = 86. Justin’s estimated equation was: 40 + 30 + 15 = 85.

Who had the better estimate? Why?

What was the exact answer?

Chapter 14-3 Order of Operations Review

Learn and Connect

Use the correct order of operations. Which is correct?

Circle which equation is correct in each pair.

Circle which sign makes the statement true.

Circle which equation is correct in each pair.

Put parenthesses in the correct place to make the expression true.

Match the statement to the sign that makes it true.

Solve.

Eddie solved the problem below incorrectly:

Explain Eddie’s mistake. What is the correct answer to the problem?

Learn and Connect Daily Review

Solve, simplifying answers if necessary.

A gardener measured the height of the trees growing in his yard. He made the chart below to keep track of how tall each tree was.

What is the difference between the height of the tallest tree and the shortest tree?

To solve, we need to subtract the height of the shortest tree from the height of the tallest tree.

Multiples of tallest tree denominator:

Multiples of shortest tree denominator: Tallest tree Shortest tree

Therefore, the difference between the tallest and shortest tree is ft.

Apply

Use the chart above to answer the questions. Simplify your answers if necessary.

A month later, the gardener noticed that the papaya tree grew 1 3 4 ft. How tall is the papaya tree now?

Two months later, the oak tree was a total height of 6 3 4 ft tall. How much did it grow in two months?

The gardener bought a new mango tree that was 7 8 9 ft tall. How much taller is the new mango tree than the old one?

Papaya Tree

Mango Tree

Estimate the solution to each problem to the nearest half or whole. Solve, simplifying answers if necessary.

17.

18. A student is coloring in shapes for a math project. The student colored 6 1 15 shapes yesterday and 10 3 10 shapes today. How many shapes did the student color? A recipe calls for 5 3 4 cups of flour. A baker has 2 5 12 cups of flour. How many more cups of flour does the baker need to complete the recipe? Simplify your answer if necessary.

Daily Review Simplify the fractions.

Learn and Connect

Justin bought a box of donuts, and it was 3 4 filled with donuts. If he ate 2 3 of the donuts, how much of the total box did Justin eat?

To solve, first multiply the numerators, followed by the denominators Then, simplify.

The Donut Shop sold 2 4 8 times as many strawberry donut boxes as chocolate donut boxes. If they sold 2 2 10 boxes of chocolate donuts, how many boxes of strawberry donuts did they sell? To solve, multiply the number of chocolate donut boxes sold, , by .

1) To multiply, we must turn the mixed numbers into improper fractions.

2) Then, factor to reduce the fractions.

3) Next, multiply the numerators and denominators.

4) Last, change the improper fraction back to a mixed number and simplify if necessary.

Therefore, the store sold 5 1 2 boxes of strawberry donuts.

Solve.

1. What is 1 3 of 24? 2. What is 3 5 of 5 8 ? 3. What is 4 6 of 30?

Solve and use the grid to show the two fractions. Solve.

A student lives 3 4 of a mile from school. He has walked 3 7 of the way to school. What fraction of a mile has he walked?

An oak tree is 11 1 9 feet tall. A pine tree is 2 1 40 times as tall as the oak tree. How tall is the pine tree?

A teacher has 5 8 of a package of paper. The teacher uses 2 5 of the paper for an assignment. What fraction of the package of the paper was used for the assignment?

The art teacher has 10 2 7 feet of ribbon for the next project. The project needs 2 3 8 times as much ribbon for the whole class to be able to participate. What is the total length of ribbon the teacher needs for the project?

Ricky is doing a science experiment. To do the experiment, he needs 3 2 5 ounces of baking soda. If he wants to use 1 2 3 of the amount, how many ounces of baking soda should he use?

There was 5 8 of a pie left in the fridge. Daniel ate 1 4 of the leftover pie. How much of a pie did he have?

Chapter 14-6 Division with Fractions Review

Daily Review

Simplify each fraction.

Learn and Connect

Henry has 4 2 3 boxes of cookies to pass out to his 8 friends. What portion will each of his friends get?

Write the problem.

Change the mixed number to an improper fraction and the whole number to a fraction.

Multiply by the reciprocal of the second fraction.

Use factoring to simplify before multiplying.

Apply Fill in the table.

Each friend will get of a package of cookies.

Solve, simplifying if necessary.

Use the rule to fill in each table.

add 1 4

Solve using the order of operations.

Solve, simplifying if necessary.

Danny has 5 2 3 pies that he wants to split among 34 of his friends. How much pie will each friend get to eat?

Nick has to paint 6 1 4 walls in his house. If he spreads the work out over 5 days, how much does he have to paint each day?

Justin has a slab of marble to make a countertop. It is 8 3 4 ft long. If he cuts it into 7 equal pieces, how long will each piece be?

At the pizza eating contest, 8 people ate 12 2 5 pizzas. If each contestant ate the same amount, how much did each person eat?

Daily Review Define the variables in the two volume formulas.

Learn and Connect

Volume = Area of base × height

V = 21 × 3 V = u3

V = l × w × h

V = 7 × 3 × 3 V = u3 or Apply

Find the volume of each rectangular prism using both formulas.

V = Area of base × height

V = l × w × h

V = Area of base × height

V = l × w × h

V = Area of base × height

V = l × w × h

V = Area of base × height

V = l × w × h

Find the volumes of the rectangular prisms below. Check your units!

1. V = l × w × h

2. V = A × h

Complete the table.

Find the volume of a box with measures:

5 in × 5 in × 12 in.

How much dirt fits in a planter box that is a cube with sides of 4 ft.?

How much water fits in a pool that is 8 meters × 12 meters and is 3 meters deep?

The volume of a rectangular prism is 48 ft3. If the length is 3 ft and height is 8 ft, what is the width?

Find each volume.

A cereal box has a volume of 420 in3. What is the height if the area of the base is 30 in?

You are building a wooden cabinet. The length is 4 ft, and the width is 1 ft. If the volume is 24 ft3, what is the height?

Daily Review

Explain how to plot the points or write the coordinate it is describing.

Learn and Connect

Plot the points on the coordinate plane. Write the letter by the point.

Write the coordinates of the points for each letter.

Apply

Determine what shape is created with the coordinates. Plot a point and connect it to the next point. When you get to the last point, connect it to the first. Label each shape with the problem number.

(4,9) (7,9) (9,7)

(4,2) (2,4) (0,2)

Use each story to complete the table, find the coordinates, and create a graph.

Bob always volunteers at the food bank 2 more times than the library each month.

f =

and

Each loaf of bread costs $5.

b = bread purchased and t = the total spent

The museum requires 1 chaperone for every 20 students on the field trip.

c =

and s

Use the graph to create a list of coordinates, a table, and a story.

Line up the place

Add the ones. Add the tens. Add the hundreds. Add the thousands.

Add the numerators. Write the denominator.

Find a common multiple of the denominators. Write equivalent fractions with same denominators. Add the numerators. Write the denominator.

3: 3, 6, 9, 12, 15, 18, 21 2: 2, 4, 6, 8, 10, 12, 14

Line up the decimals. Add from right to left. Move the decimal down.

WITH MANY DIGITS

Line up the place values.

There will not be enough ones to subtract. Regroup.

Subtract from right to left.

Subtract the numerators. Write the denominator.

Find a common multiple of the denominators.

3: 3, 6, 9, 12, 15, 18, 21 2: 2, 4, 6, 8, 10, 12, 14

Line up the decimals.

Write equivalent fractions with same denominators.

Subtract the numerators. Write the denominator.

Subtract from right to left. Move the decimal down.

Rewrite vertically.

Multiply the ones. Regroup extra ones as tens.

Multiply the tens. Add the number you regrouped.

MULTIPLYING FRACTIONS BY A WHOLE NUMBER

Write the whole number as fraction.

Multiply the numerators.

Multiply the denominators. Simplify.

Multiply the numerators

Multiply the denominators Simplify.

Rewrite. Divide. Multiply. Subtract. Bring Down. Repeat.

Write the reciprocal of the second

Rewrite as multiplication of the reciprocal.

For division with decimals, see the decimals page.

Multiply the numerators. Multiply the denominators.

1. Draw 2 3 .

2. Show 6ths.

3. How many are colored?

Draw a model.

SIMPLIFY FRACTIONS

List factors of the numerator and denominator.

3: 1, 3 6: 1, 2, 3, 6

CONVERTING MIXED NUMBERS TO IMPROPER FRACTIONS

Multiply or divide by 1. 2 3 = 4 6

Circle the largest factor they have in common. 3: 1, 3 6: 1, 2, 3, 6

When the numerator and denominator are the same, the fraction equals 1.

Divide the numerator and denominator by the greatest common factor.

Divide the numerator by the denominator. Write the remainder as a fraction. The denominator is the number you divided by.

CONVERTING IMPROPER FRACTIONS TO MIXED NUMBERS

Multiply the denominator by the whole number. 1 2 3 3 × 1 = 3 Add the numerator to that number.

Write an improper fraction. The sum is the numerator. Keep the denominator. 5 3

Decimals

CONVERTING FRACTIONS TO DECIMALS

Find an equivalent fraction with a denominator of 10, 100, or 1,000.

Underline the place you are rounding to

Look at the digit on the right.

Write a decimal. Use the denominator to help with place value.

If it is 4 or less, round down. If it is 5 or more, round up.

DIVIDING DECIMALS

DIVIDING DECIMALS BY DECIMALS

Move the same number of decimal places in the divisor and dividend so the divisor is a whole number.

To round down, leave the underlined digit. All digits to right of the underline turn into 0s.

PERIMETER

Add all the side lengths together.

Label with the correct unit of measurement.

AREA OF A RECTANGLE

Multiply the length times the width

Label with the correct unit of measurement squared.

Multiply the length times the width times the height.

Label with the correct unit of measurement cubed.

3 dimensions length, width, and height 10.5, 10.8

Acute measures less than 90° R2.2

Addend the numbers being added together in an addition equation 4.6, 4.8

Area the number of square units that cover a shape 4 cm 9 cm R2.1, 5.7, 10.6, 10.7, 10.8

Area model of multiplication a visual representation of the partial products method of multiplication R1.5, 1.6, 1.8

Associative property in multiplication, when three or more numbers are multiplied, they can be grouped in any order, and the product will be the same R1.4

Attributes the characteristics of an object that allow you to group it with other similar objects 10.4, 10.8

Base number the digit that is multiplied by itself in a number with an exponent 1.7, 1.8

Benchmark Numbers numbers that are used as reference points to compare other numbers

R2.5, 7.2, 9.7

Capacity how much can be held in a container; liquid capacity or volume 12.5

Centimeter a metric unit of length equal to 10 millimeters 12.2, 12.7, 12.8

Commutative property the order you multiply does not affect the product R1.4

Compatible numbers pairs of numbers that are easy to add, subtract, multiply or divide in your head

Convert to change forms or units 11.5, 11.8

Coordinate plane a plane with two perpendicular axes 3

2.3, 2.8, 6.1, 6.8

Congruent equal in measurement 10.2, 10.8

Coordinate point (x,y) ordered pair of numbers that define a specific point on a coordinate plane

13.2, 13.3, 13.8, 14.8

13.6, 13.2, 13.3, 13.4, 13.8, 14.8

Decagon a polygon with ten sides 10.1, 10.8

Decimal a way to show a number less than one that is based on the number ten and uses a decimal point

R1.1, R2.8, 3.1, 3.3, 3.4, 3.5, 3.6, 3.7, 3.8, 4.2, 4.4, 4.8, 5.1, 5.2, 5.3, 5.4, 5.5, 5.6, 5.7, 5.8, 6.3, 6.4, 14.1

Decimal point a point (small dot, like a period) used to separate the whole number part from the fractional part of a number 4.7, 5.4

Denominator the bottom part of a fraction that represents the total parts in which the whole was divided 5 3

R2.3, R2.4, R2.6, 7.1, 7.3, 7.4, 7.5, 7.6, 8.1, 8.2, 8.4, 8.8, 9.1, 9.2, 9.4, 9.8, 14.4, 14.5, 14.6

Difference the answer to a subtraction problem R1.3, 4.5, 6.7

Digit a single symbol (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) used to make numbers 1.1, 1.8

Divide to split a number into equal groups 2.5

Dividend a number to be divided by another number; the number you start with in a division equation

R1.6, R1.7, R1.8, 2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 6.1, 6.2, 6.4, 6.8, 9.1, 9.8, 14.6

Division the act of dividing 2.5

Divisor a number by which another number is to be divided; the number of equal groups you divide the dividend into in a division equation

R1.6, R1.7, R1.8, 2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 6.1, 6.2, 6.4, 6.8, 9.1, 9.8, 14.6

Dot Plot a graph that shows data as marks above a number line, showing each value’s frequency 11.6, 11.7, 11.8, 13.7

Elapsed time how much time has passed between two given times 11.5, 11.8

Equal (=) having the same value R2.8

Equation a number sentence that has two equal sides separated by an equal sign 2.1

Equilateral triangle all three angle measurements are equal, and all three side lengths are equal 10.2, 10.8

Equivalent fraction if two fractions are equivalent, it means they are equal even if they have different numerators and denominators 2 6 = 1 3

Estimate to find a close enough answer when the exact answer is not needed

24 × 78 = 20 × 80

R2.3, R2.4

Expanded notation a way to write numbers that represents it as the sum of each of its digits multiplied by their place value 1.2, 1.8, 14.1

Exponent a small number written to the upper right of a number that shows the number of times it is multiplied by itself 1.7, 1.8, 2.1

Expression a math phrase with no equal sign

Factoring to simplify an expression before multiplying by factoring out common factors in the numerator and denominator

1 4 × 7 8 = 7 32 8.4, 8.8

Factors numbers that, when multiplied together, equal a product

R1.5, 1.3, 1.8, 2.3, 2.8, 5.1

Estimation a close, but not exact answer; an educated guess of the approximate calculation 14.2

Expanded form a way to write numbers that show the value of each individual digit; a number written by the sum of its place values

R1.5, 1.2, 1.4, 1.8, 3.2, 3.8

Foot linear measurement unit; there are 12 inches in 1 foot (ft)

Gram a metric unit of weight equal to 1,000 milligrams

Greater than (>) a sign used to compare number values

R1.5, 1.3, 1.4, 1.5, 1.6, 1.8, 2.2, 5.2, 5.8, 8.5, 8.6, 8.7, 8.8

Greatest the largest value of a set of numbers R2.8

Heptagon a polygon with seven sides 10.1, 10.8

Hexagon a polygon with six sides 10.1, 10.8

Hierarchy a way to classify something based on properties that become more specific as you move down 10.4, 10.8

Hundredth a decimal place that is 1 100 of a whole of 1 part of a hundred; 0.01

R2.7, 4.1, 4.3

Identity property of division if we divide a number by 1, the quotient is the number itself R1.6

Identity property of multiplication if a factor is 1, the product is the same as the other factor; when multiplied by one, a number keeps its identity R1.4

Improper fraction a fraction in which the numerator is larger than the denominator 14.5

Inch linear measurement unit; there are 12 inches in 1 foot (in) 12.1

Intersecting lines lines that will cross but do not make right angles R2.2, 13.1

Inverse operations using the opposite operation to find an answer; the opposite operation that can be used to check your work 6.6

Irregular polygons angles are not equal in measure and sides are not equal in length 10.1, 10.8

Isosceles triangle two angle measurements are equal and two sides are equal

Kilogram a metric unit of weight equal to 1,000 grams

Kiloliter a metric unit of capacity equal to 1,000 liters

Kilometer a metric unit of length equal to 1,000 meters

Least the lowest value of a set of numbers R2.8

Less than (<) a sign used to compare number values R2.8

Line a straight path that goes on forever in both directions 13.1, R2.2

Line segment a portion of a line that has two endpoints 13.1, R2.2

a metric unit of length equal to 100 centimeters

Milligram a metric unit of weight equal to 1 1,000 of a gram

Milliliter a metric unit of capacity equal to 1 1,000 of a liter

Millimeter a metric unit of length equal to 1 10 of a centimeter

Minimum the lowest data point 11.6, 11.7, 11.8

Minuend the number that you start with in a subtraction equation 4.4, 4.5

Mixed number a whole number and a fraction 7.2, 7.7, 7.8, 8.3, 14.5

Multiples skip counting from a number (count by starting with the number that you’re counting by) R1.4

Nonagon a polygon with nine sides 10.1, 10.8

Number pattern a set of numbers that follows a rule 13.5

Numerator the top part of a fraction that represents parts of a whole R2.3, R2.4, R2.6, 7.1, 7.3, 7.4, 7.5, 7.6, 8.1, 8.2, 8.4, 8.8, 9.1, 9.2, 9.4, 9.8, 14.4, 14.5, 14.6

Obtuse measures more than 90° R2.2

Octagon a polygon with eight sides 10.1, 10.8

Order of Operations a set of rules that tells you the order in which operations must be solved 2.1, 9.5, 14.3

Origin (0,0) the center point of a coordinate plane 13.2, 13.3, 13.8, 14.8

Ounces a unit of weight that equals 1 16 of a pound 12.3

Parallel lines lines that never touch

R2.2, 13.1

Product the answer to a multiplication equation

Parallelogram opposite sides are parallel, 2 sets of sides are equal in length 10.3, 10.8

PEMDAS a way to remember the order of operations; Parentheses Exponents Multiply Divide Add Subtract 2.1, 9.5, 14.3

Pentagon a polygon with five sides 10.1, 10.8

Perimeter the distance around the outside path of a shape or object; the sum of all the sides

R2.1, 5.7, 10.6, 10.8

Perpendicular lines lines that will cross to make right angles R2.2, 13.1

Place value the position of a digit in a number determines its value; the value of each digit depending on where it is in a number

Point an exact location

R2.7, 1.1, 1.8, 14.1, 14.2

R2.2, 13.1

Pound a unit of weight that equals 16 ounces 12.3

Power the number of times a number is used as a factor in a multiplication problem 1.7, 1.8

R1.5, 1.3, 1.4, 1.5, 1.6, 1.8, 2.2, 5.1, 5.2, 5.3, 5.5, 5.6, 5.8, 6.5, 6.7, 6.8, 8.5, 8.6, 8.7, 8.8, 9.7

Quadrilateral a polygon with four sides 10.1, 10.8

Quotient the answer to a division equation problem R1.6, R1.7, R1.8, 2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 6.1, 6.2, 6.3, 6.4, 6.5, 6.7, 6.8, 9.7

Ray a line with a single endpoint that goes on and on in one direction

R2.2, 13.1

Reciprocal the inverse of a number value; the “flip” of the numerator and denominator 9.2, 9.3, 9.6, 9.8, 14.6

Rectangle a parallelogram with four right angles 10.3, 10.8

Regrouping the process of making groups of tens R1.2

Regular polygons all angles are equal in measure, and all sides are equal in length 10.1, 10.8

Remainder the number left over after making equal groups; portion of the dividend that is left over after division

R1.7, R1.8, 2.4, 2.5, 2.6, 2.7, 2.8

Rhombus opposite sides are parallel, four sides are equal in length 10.3, 10.8

Right measures exactly 90° R2.2

Round find a close but easier to work with number to a given number R1.5, 1.3, 1.8

Rounding making a number simpler but keeping its value close to what it was 14.2

Scalene triangle none of the angle measurements or side lengths are equal 10.2, 10.8

Simplest form a fraction where the numerator and denominator have 1 as the largest factor they have in common

Solid figures three-dimensional figures

10.8

Triangle a polygon with three sides 10.1, 10.8

Vertices (vertex) corner points of a polygon 10.1, 10.8

Volume the space a three-dimensional object occupies, units are cubed 11.1, 11.2, 11.3, 11.4, 11.8, 14.7

Square a rectangle with all sides equal length 10.3, 10.8

Standard algorithm a method of multiplying larger numbers vertically by carrying the regrouped numbers to the next place value 1.5, 1.6, 1.8

Standard form a number written in digits 0-9 (example: 342) 1.1, 1.2, 1.8, 14.1

Subtrahend the number that is being taken away in a subtraction equation R1.3, 4.4, 4.5

Sum the answer to an addition problem 6.7

Tenth a decimal place that is 1 10 of a whole or 10 parts of a hundred. Written 0.1 R2.7, 4.1, 4.3

Ton a unit of weight that equals 2,000 pounds 12.3

Trapezoid a quadrilateral with exactly one pair of parallel sides 10.3, 10.8

Word form a number written using words (example: three hundred forty-two) R2.7, 1.1, 1.2, 1.8, 14.1

X-axis horizontal axis of a coordinate plane x y

13.3, 13.8, 14.8

Y- axis vertical axis of a coordinate plane 13.2, 13.3, 13.8, 14.8

Yard linear measurement unit; there are 3 feet in 1 yard (yd) 12.1

Zero property 0 divided by a number gives zero as the quotient R1.4, R1.6

www.lighthousecurriculum.com