

TheNLCSJejuJournalof PureandAppliedMathematics Volume3,Issue1 MathematicsSociety MathematicsPublicationCCA March2023
Credits
Firstofall,wewouldliketoexpressoursinceregratitudetothefollowingcontributorstoVolume3Issue1 ofNLCSJejuAnnualJournalofMathematics.
TheMathematics Society
Chair
AarenJoonseokKang(12)
Co-Chair
JamesDaewoongKang(12)
PublicityOfficer
TerryTaehoonKim(11)
Secretary
EmmaChaeeunChung(11)
Members
JooyoungKim(12)
AlvinSehunJeong(12)
JeanKim(11)
JuneKim(11)
SophieJisuLee(11)
AidenHyunminPark(10)
AlbertJinyongShin(10)
DerekYejunYoo(10)
JamesJiminLee(10)
SangyoonLee(10)
DanielTaehyeonJun(10)
JungseoPark(9)
LinkTeachers
MrWilliamHebbron MsDuyguBulut
TheMathematics PublicationCCA
ProgramLeader AarenJoonseokKang(12) JamesDaewoongKang(12)
Writers AidenHyunminPark(10) JungseoPark(9)
LinkTeacher MsDugyuBulut
LATEXEditors&Managers
AarenJoonseokKang(12)
JooHyunKim(12)
TaeheeKim(12)
EmmaChaeeunChung(11)
VictoriaSeoyunJu(12)
DanielSoohyukChang(12)
Also,wewouldliketothankthefollowingcontributorsthatarenotpartofthemathematicssocieties,but haveassistedusinvariousways.
MarketingDepartment forhelpinguswiththeprintingandpublicizingourjournal. MrTamlyn forcoordinatingsocietiesinourschool.
© CopyrightbytheNLCSJejuJournalofPureandAppliedMathematics
FormattingbyAarenJoonseokKang
EditedbyJPAMEditingTeam
3
Editor’sNote
IamveryexcitedtoannounceourfirstissueoftheNLCSJournalofPure andAppliedMathematics(JPAM)ofthe2022-23academicyear.Thisyear, itwasevidentthattalentedmathematiciansinourschoolhavedevotedtheir besteffortsandprecioustimetoproduceaqualityarticle.Allthecontributorshaveresearchedaboutaspecificdisciplineinmathematicstheyaremost interestedinandhaveputintheirutmosteffortinvariouswaysbysolving problems,programming,anddraftingtheirarticles.Itisdoubtlessthatthe academicrigourofthisjournalisatahighlevelregardlessofthefieldand thecomplexityofthetopic.
ThisversionoftheJPAMprovidesvaluableinsightintomathematicsin twodifferentsections:PuremathematicsandAppliedmathematics.Pure mathematicsinvolvesthediscussionoftheoreticalandmethodologicalaspectsofmathematicsinvariousmathematicalideasandproofs,divingfurtherintothebeautyofthepurenessinmathematics.Ontheotherhand, Appliedmathematicsapproachesmathematicsinaninterdisciplinaryaspect displayinghowthebeautyofmathematicsisappliedindisciplinessuchas computerscience,physics,socialsciences,andsportssciences.
Asthechiefeditorofthisjournal,Ienjoyedreadingandeditingevery singlepieceofarticleinthisjournal.MymanythankstothefellowJPAM editorsintheteam-JooHyunKim,VictoriaJu,EmmaChung,Daniel Chang,andTaeheeKim-whohavehelpedspeeduptheprocesstremendously.Itwasthefirstyeartohaverecruitedaformalteamofeditors,but wehaveworkedveryefficientlyasateamtoproduceahighqualityjournal intermsofformatandlayout.Also,anotherlargethankstoHyeminLyoo, ourdesignerofthecoverpageofthisissue,fordesigningamathematical,yet artisticcoverpage.
Onafinalnote,IwouldliketoexpressmygratitudetoallthecontributorsandreaderswhoareinterestedinourpublicationsofNLCSJejuJournal ofPureandAppliedMathematics.
AarenJoonseokKang-ChairoftheMathematicsSociety,Leader oftheJPAMEditingTeam
Contents PureMathematics 6 1MathematicalProofandParadox EmmaChaeeunChung(Y11) 7 2Goldbach’sConjecture TerryTaehoonKim(Y11) 11 3GeometricalInterpretationofComplexNumbers JooyoungKim(Y12) 14 4TheValidityofConsideringtheSignificanceofanImaginaryNumber inRelationtoReality AidenHyunminPark(Y10) 16 5ThePainter’sParadox AlbertJinyongShin(Y10) 29 6ThePowerTowerFunction JamesJiminLim(Y10) 32 7ConicSectionasLociofPoints SophieJisuLee(Y11) 36 8InscribedRectangleProblem:Topology DerekYejunYoo(Y10) 39 AppliedMathematics 42 9FindingtheOptimalPolicytoExploretheGridWorldusingDynamic ProgrammingandQ-learninginReinforcementLearning AarenJoonseokKang(Y12) 42 10EstimationoftheChangingVelocityDuringRocketLaunchUsing Euler’sMethod JamesDaewoongKang(Y12) 51 11BifurcationDiagram AlvinSehunJeong(Y12) 54 12TicTacToe:WinningStrategyoftheGame JuneKim(Y11) 57 13ProbabilityAppliedtoSocialSciences JeanKim(Y11) 59 5
14EquationofCircleandGPS JungseoPark(Y9) 61 15OpticalIllusions SangyoonLee(Y10) 64 16ApplicationsofGraphTheory DanielTaehyeonJun(Y10) 67 6
MathematicalProofandParadox
EmmaChaeeunChung
Year11Noro
SecretaryofMathematicsSociety
MemberoftheJPAMEditingTeam
Email:cechung25@pupils.nlcsjeju.kr
Editor
EmmaChaeeunChung ∗
RecommendedYearLevel:KS4andabove
Keywords:Proof,Paradox,ProofbyContradiction, ProofbyInduction
1Introduction
“IfonlyIhadtheTheorems!ThenIshouldfind theproofseasilyenough”,saidBernhardRiemann,the renownedGermanmathematician.Indeedmathematical‘proof’maynotbedifficulttowrite-thatis,fallacies thatareoftentimesdeceivingbecausetheyinitiallyseem derivedfromobviouslogic.Inthispaper,methodsof appropriatemathematicalproofwillbediscussed,along withcommonmathematicalerrors.
2Definitions
Proofplaysacentralroleindeveloping,establishing andcommunicatingmathematicalknowledge.Amathematicalproofisdefinedasan‘inferentialargument’ thatlogicallyguaranteestheconclusion,constructedby originalassumptionscalledaxoims.Asfirstprinciples, orunprovablerulesthatareacceptedastrue,axioms serveasastartingpointforreasoning.
Belowisanexampleofalogicalaxiom-Axiomof Equality-inwhichastatementisusedtodeduceother logicallyvalidformulas:
x = x (1)
Anon-logicalaxiom,ontheotherhand,aretheoryspecificassumptions.Inotherwords,theyshouldbe tetheredtotheapplicationbeforeusingtheminproofs. (Rocha,2019).
∗ MemberofJPAMEditingTeam
‘QED’,theinitialismoftheLatinphrase,‘quoderat demonstrandum(thusithasbeendemonstrated)’ora Halmostombstone(❚)isoftenwrittenattheendofa proof.Theyannouncetheendoftheproof,actingas avisualcueandremindsthereaderofthepreposition thatwasproven,especiallyusefulinextensivenested proofs(Weisstein,n.d.).
3TypesofMathematicalProof
3.1ProofbyContradiction
ProofbyContradictionestablishesthevalidityofa statementbyshowingthatassumingthestatementto befalseleadstocontradiction.Proofbycontradictionis alsoknownas‘indirectproof’,inwhichthealternatives ofastatementisdeniedandtheoriginalstatementis impliedvialogicaldeductions.Followingisaproofby contradictionthat √2 isanirrationalnumber.
(i)Suppose √2 isarationalnumberexpressedas a b whereaandbarenon-zerointegerswithnocommon factor.
(ii)b√2 =a,2b2 = a2 a2 iseven,whichimpliesthatamustalsobeeven.Let a=2c,wherecisaninteger.Substitute2cinto2b2 = a2 andweget2b2 =4c2 .Dividingbothsidesby2yields b2 =2c2 ,implyingthatbisdivisibleby2.
(iii)aandbarebotheven,with2astheircommon factor.Thiscontradictsthepreviousstatementthata andbsharenocommonfactors.
(iv)Assuming √2 tobearationalnumberleadstoa contradiction,thereforetheoppositemustbetrue. √2 isanirrationalnumber.
However,itistobenotedthatinsomemathematicalcircles,directprovingmethodsarepreferredover proofbycontradiction.Mathematicalconstructivists mayconsidersomecasesofproofbycontradictionin-
7
validbecausetheprovingstatementsareindependentof axiomsandtheproofsarelowinfecundityasthereare nointermediaryconclusions(Korner,2011).
4ProofbyMathematicalInduction
Mathematicalinductionisamethodusedtoprove athatastatementistrueforallnaturalnumbers.
ProofbyInductionconsistsoftwosteps:firsta‘base case’isprovesthestatementtrueinasinglecase, usuallywhenn=1.Thesecondstepistheinduction stepwhichprovesthatifthestatementistrueforn=k, itisalsotrueforn=k+1(Pierce,2017).Belowproves thatallpositiveintegersintheform2n-1areodd.Let P(n)represent‘2n-1isodd’.
(i)Forn=1,2n-1=1and1isodd.P(1)istrue.
(ii)Foranyn,if2n-1isodd,(2n-1)+2mustalsobe odd,becauseadding2toanoddnumbergivesanodd number.
(2n-1)+2=2n+1=2(n+1)-1 P(n)impliesP(n+1).
Thus2n-1isoddforallpositiveintegers n(zimmer.csufresno.edu,n.d.).
FirstraisedbyGeorgePólyain1954,the‘Horse Paradox’isawell-knownexampleofaflaweduseof mathematicalinduction.TheHorseParadoxstates that‘allhorsesarethesamecolour’,asillustrated below:
(i)Thebasecaseisonehorse.Withonlyonehorse, obviouslyallhorsesinthisgrouparethesamecolour.
(ii)AssumethatNhorsesarealwaysthesamecolour. ConsiderN+1horses:ifthelasthorseisexcluded, theremainingNhorseswillbethesamecoloursince Nhorsesarethesamecolour.Byexcludingthefirst horse,theotherNhorseswillbethesamecolourby thesamereasoning.
ThebasecaseprovedthestatementtrueforN=1.The inductivestepproveditvalidforN=2,3,andsoon. Thusinanygroupofhorses,allhorsesmustbethe samecolour.
TheHorseParadoxdoesn’tcontainanycontradictions,butargumentsthemselvesareincorrect.TheinductivestepiserroneousgoingfromN=1toN=2becausethefirstandlasthorsehavenohorsesincommon andmaybeindifferentcolours(Benjamin,2019).
4.1ProofbyContraposition
InProofbyContraposition,theconclusion‘ifA, thenB’isinferredbyproving‘ifnotB,thennotA’.The twostatementsarelogicallyequivalentbecausethey arecontrapositives;astatementisformedbynegating bothtermsandreversingthedirectionofinference. Proofbycontrapositionisoneofthetwotypesof
indirectproofalongwithproofbycontradiction.
Afamouscaseofproofbycontrapositionisthe provingofthestatement:‘If x2 iseven,xiseven.’
(i)Thecontrapositiveofthestatementis:‘Ifxisnot even,then x2 isnoteven’.
(ii)Thelatterstatementcanbeproven.Ifxisnoteven, i.e.,odd,then x2 isalsooddbecausetheproductoftwo oddnumbersisodd.
(iii)Thereforetheoriginalstatementistrue. If x2 iseven,xiseven.
5VisualProof
Visualproofisavisualdemonstrationofapreposition.Utilisingcomputergraphicscouldbeaneffective meansofshowingverity,hencevisualproofissometimesreferredtoas‘proofwithoutwords’.
Provingtheformulafortheareaofacircleisoftendemonstratedbytheimageabove.Whenacircle isdividedintoinfinitelysmallsectorsandplacedalternatelyforminganalmost-rectangle,thelengthishalf theperimeter(= π r)andthewidthistheradius.
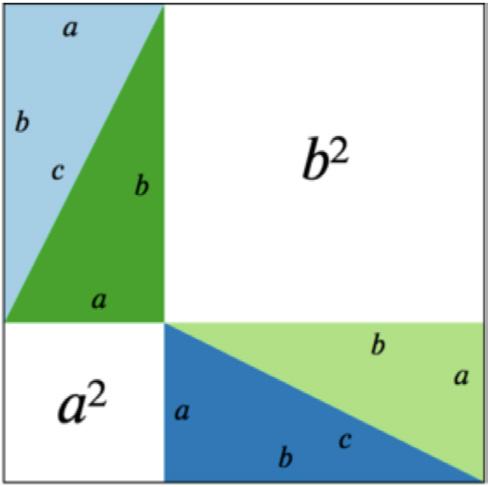
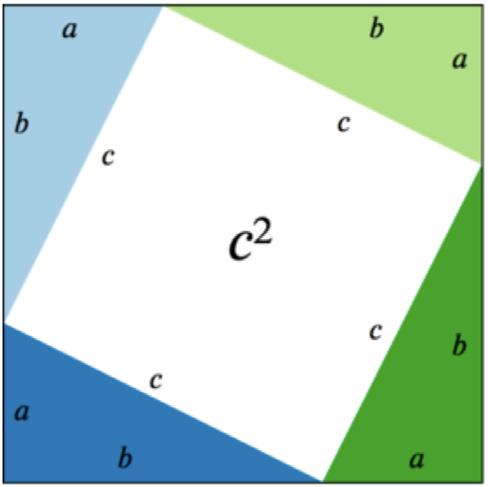
TheimageaboveprovesthePythagoreantheorem. Theareaoftheoutersquareis (a + b)2 andthesumof thetriangles’areagives(2ab). (a + b)2 -(2ab)gives a2 + b2 ,whichisequaltothesubtractionofthetriangles fromtheoutersquareyieldingthewhiteinnersquare; c2
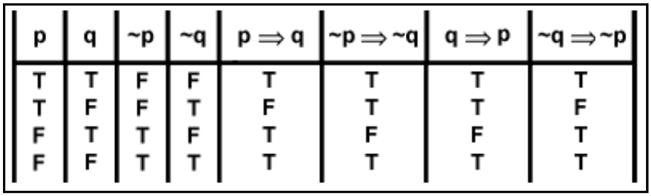
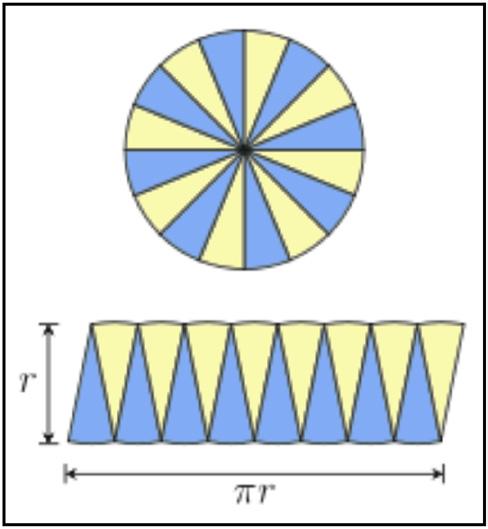 Fig.1:LogicStatements:TruthTable
Fig.2:Areaofacircle
Fig.1:LogicStatements:TruthTable
Fig.2:Areaofacircle
8
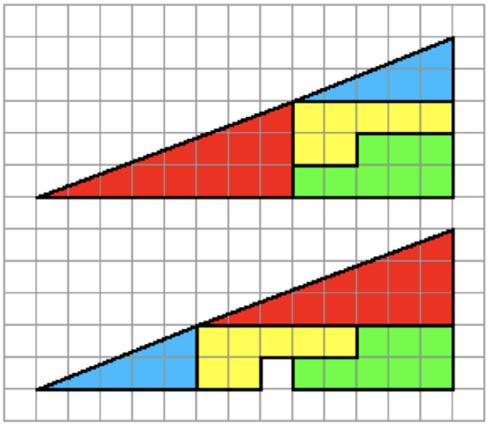
Alternately,thePythagoreantheoremcanbe provenbyrearrangingthetrianglesasbelow,showing twosquaresofarea a2 and b2 ,equaltotheprevious c2
Ontheotherhand,visualproofisnotaformal methodofmathematicalproof.Illusionsareeasily created,perplexingtheviewers.
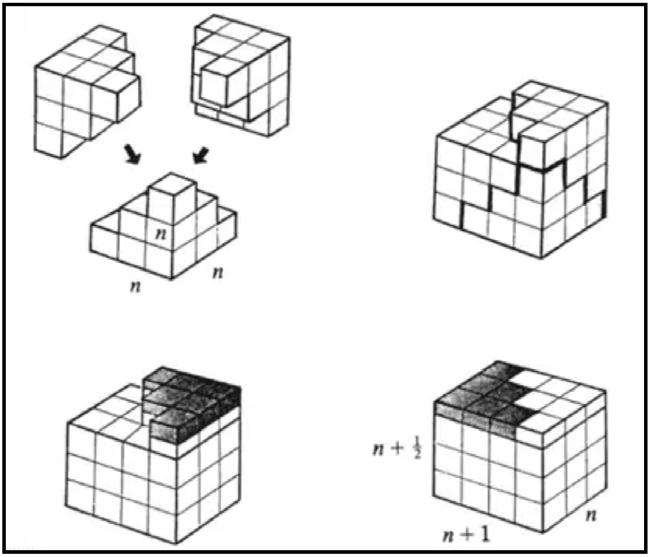
Thefollowingvisualproofprovesthatthesum ofnsquaresis 1 3 n(n+1)(n+ 1 2 ).Threeblockspieces representingthesumofnsquaresmergetocreatea cuboidwithsidesn,n+1,andn+ 1 2
Thesetwotrianglesappeartobeconsistingof identicalsmallerpieces,althoughthesecondtriangle hasamissingblock.Thefirsttriangle’shypotenuse slightlycurvesoutwardsandthesecondcurvesinwards, resultingintheinaccuracy.
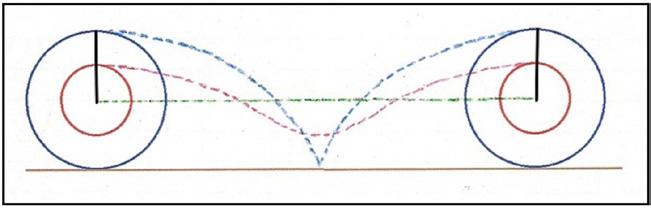
TheAristotle’sWheelParadoxisanotherdeceptive caseofvisualproof.Awheelisdepictedastwocircles tangentialtothesurface/ground.Thesmallerinner circleisfixedtothelargeroutercircleandhasthesame center.Assumingthelargercirclerollswithoutslipping foronefullrevolution,thedistancestravelledbyeach circleisequaltothelargercircle’scircumference, therebycreatingaparadox.
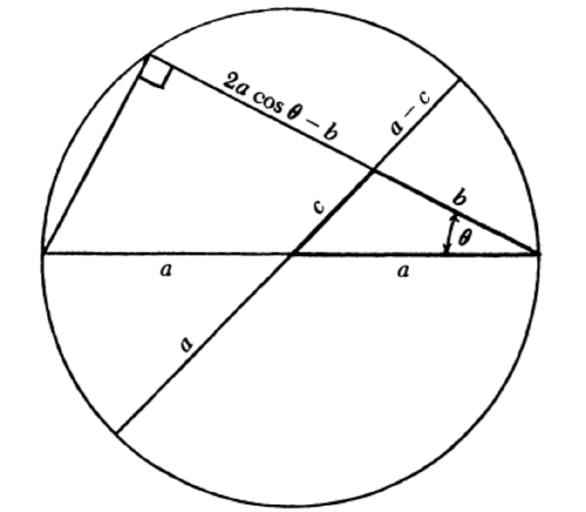
Thelawofcosinescanalsobeprovenwithvisual proof.Intheimagebelow,(2acosθ -b)b=(a-c)(c+a) andrearrangingthisequationresultsin c2 = a2 + b2
Galileoanalysedtheproblembysubstitutingthe circleswithhexagons.Considerrollingthehexagon, andonemaynoticetheinnerhexagon’slittle‘skips’of spacewitheachrevolutionoftheouterhexagon.Since acirclecanbemadeincreasingthenumberofsidesofa polygon,these‘skips’areinfinitelysmallandinfinitely
Fig.3:ProvingthePythagoreanTheorem(1)
Fig.4:ProvingthePythagoreanTheorem(2)
Fig.5:SumofNsquares
-2abcosθ (Doyle,2014).
Fig.6:LawofCosines
Fig.7:Anillusioninvisualproof
9
Fig.8:Aristotle’sWheelParadox many(orunquanitfiable)inacircularwheel.

https://www.zmescience.com/other/featurepost/10-beautiful-visual-mathematical-proofselegance-and-simplicity/.
5. Rocha,H.(2019).Mathematicalproof: frommathematicstoschoolmathematics. PhilosophicalTransactionsoftheRoyalSocietyA:Mathematical,PhysicalandEngineeringSciences,377(2140),p.20180045. doi:https://doi.org/10.1098/rsta.2018.0045.
6. Weisstein,E.W.(n.d.).Axiom.[online]mathworld.wolfram.com.Availableat: https://mathworld.wolfram.com/Axiom.html.
7. zimmer.csufresno.edu.(n.d.).MathematicalInduction.[online]Availableat: http://zimmer.csufresno.edu/larryc/proofs/proofs.mathinduction.html.
Drawingapoint’stravelpathduringtherevolution corroboratestheerrorintheoriginalstatement.As seenbelow,thepointonthesmallerinnercircletravels ashorterpathwaythanthepointonthelargerouter circle,thereforethedistancetravelledisnotequivalent tothesmallercircle’scircumference(Puiu,2016).
6Bibliography
1. Doyle,T.(2014).ProofsWithoutWords andBeyond-PWWsandMathematicalProof|MathematicalAssociationof America.[online]www.maa.org.Available at:https://www.maa.org/press/periodicals/ convergence/proofs-without-words-and-beyondpwws-and-mathematical-proof.
2. Korner,K.(2011).AnIntroductiontoProofby Contradiction.[online]nrich.maths.org.Available at:https://nrich.maths.org/4717.
3. Pierce,R.(2017).MathematicalInduction.[online]Mathsisfun.com.Availableat: https://www.mathsisfun.com/algebra/mathematicalinduction.html.
4. Puiu,T.(2016).10BeautifulVisualMathematicalProofs:EleganceandSimplicity.[online]ZMEScience.Availableat:
Fig.9:Substitutingcircleswithhexagons
Fig.10:Drawingapoint’stravelpath
10
Goldbach’sConjecture
TerryTaehoonKim Year11Mulchat
PublicityOfficeroftheMathematicsSociety
Email:th3kim25@pupils.nlcsjeju.kr
Editor JooHyunKim∗
RecommendedYearLevel:KS4,KS5
Keywords:NumberTheory,OldestConjuncture, Unproved,PrimeNumber
1Introduction
Goldbach’sconjecture,suggestedbyrenownedGermanmathematician,ChristianGoldbach,isregardedas oneofthemostcomplextheoremsinmodernmathematics.TheGoldbachconjecturestatesthat“everyeven naturalnumbergreaterthan2isthesumoftwoprime numbers ”.Consideringtherelativelyshortlengthofthis conjecture,onecanbemisguidedthatitisrelatively straightforwardintermsoftheequationandproving. However,this“simpleconjecture”remainsamystery despitetheprodigiousadvancementsinmodernmathematicssinceitsemergencein1742.Thestudiesbelow willmainlyfocusonthefactorwhichmakesthisconjectureinexplicablefor250years.
2TheConjecture
“Everyevennaturalnumbergreaterthan2isthe sumoftwoprimenumbers.”
3ResearchAim
(a) AnalysisoftheConjecture
(b) ApproachestotheConjecture
(c) Analysisontheapproaches
(d) CurrentProgress
(e) RelatedProblems
4Analysis-Conjecture
Theconjecturestates, “Everyevennaturalnumbergreaterthan2isthesum oftwoprimenumbers.”
Thisstatementmeansthatanyevennumbergreater thantwoiscomposedofthesumoftwoprimenumbers.
Figure1(Fig.1)showsthegeometricalapplicationofthisconjecture.
∗ MemberofJPAMEditingTeam
Fig.1
11
5ApproachestotheConjecture
5.1ComputationalApproach
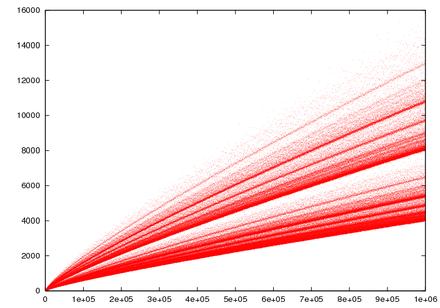
Oneapproachtothisconjectureissimplysubstitutingeveryprimenumberforthesumofevennumbers. Withtheadventofcomputers,manymorevaluesof n havebeenchecked;T.OliveiraeSilvaranadistributed computersearchthatdemonstratedtheconjecturefor n ≤ 4 × 1018 asof2013.Onerecordfromthissearchis that3325581707333960528isthesmallestnumberthat cannotbewrittenasasumoftwoprimeswhereoneis smallerthan9781.
5.2HeuristicApproach
Theprimenumbertheoremstatesthatrandomly selectedinteger m wouldhaveroughly 1 ln(m) chanceof beingprime.Hence,since n inthisconjecturerefersto anevenintegerbetween3and n 2 ,theprobabilityofboth mm n beingaprimenumberwouldbe 1 ln(m)ln(m n) Thetotalnumberofmethodstoexpressalargeeven integerasthesumoftwooddprimenumberswouldbe:
6In-depthAnalysis
In-depth,however,thisheuristicapproachisrather inaccurate.Thefollowingmethoddoesnotputcorrelationsbetweenthelikelihoodof m and n m being prime.Thiscouldresultinvariousconsequences.For instance,ifweconsider m asodd,then n m would alsobeodd,andif m iseven,then n m iseven,a non-trivialrelationbecause(besides2)onlyoddnumberscanbeprime.Exploringthisstyleofanalysisin depth,HardyandLittlewoodin1923conjecturedthat foranyfixed c ≥ 2,thenumberofrepresentationsofa largeinteger n asthesumof c primes:
Thequantitywouldincreasetoinfinityas n increaseseverylargeevenintegerhasnotjustonerepresentationasthesumoftwoprimesbutinfactvery manysuchrepresentations.
Shouldbeasymptoticallyequalto:
wheretheproductisoverallprimes p and γc,p (n) is thenumberofsolutionstotheequation n = q1 + + qc ( mod p) inmodulararithmetics,subjecttotheconstraints q1 , ,qc =0(mod p) Thisformulahasbeen provedtobevalidbyVinogradovonrangeof c =2.In laterissue,theformulaabovesimplifiesto0when n is oddandto:
When n iseven,where 2 isthetwinprimesconstant:
7Goldbach’sWeakConjecture
Goldbach’s“weak”conjecturestatesamore moderatetermforGoldbach’sconjecture.Theweak conjecturestates: 12
Fig.2:PossibilityCalculationbyprogram
2 n m=3 1 ln(m)ln(n m) ≈ n 2(ln(x = n)2 (1)
n is: ln(n) ≪ √n (2)
Duetothefactthat
n = p1 + + pc (3)
p1 ≤···≤ pc (4)
With:
( p pγc,p (n) (p 1)c ) 2≤x1 ≤···≤xc :x1 + +xc =n dx1 ··· dxc 1 ln(x1 ) ln(xc ) (5)
2 2 ( p|n;p≤3 p 1 p 2 ) n 2 dx ln2 (x) ≈ 2 2 ( p|n;p≤3 ) n ln2 (6)
2 := pprime (p≤3) (1 1 (p 1)2 ) ≈ 0 660
(7)
“Everyoddnumbergreaterthan5canbeexpressedas thesumofthreeprimes.(Aprimemaybeusedmore thanonceinthesamesum.)”
Thisconjectureiscalled"weak"becauseitdependson itsvalidityontheGoldbach’sstrongconjecture(Ifthe strongconjectureistruethenthiswouldalsobetrue). Forifeveryevennumbergreaterthan4isthesumof twooddprimes,adding3toeachevennumbergreater thanfourwillproducetheoddnumbersgreaterthan7 (andsevenitselfisequalto 2+2+3).Thisisproven byHaraldHelfgottin2019throughthemajorand minorarcestimates,whichweresufficientenoughto provetheGoldbach’sweakconjecture.Unfortunately, theexplanationofthemajorandminorarcisexcessive intermsoflength,whichwouldmakeitunavailablefor thisstudytoexplorefurther.
8Goldbach’sComet
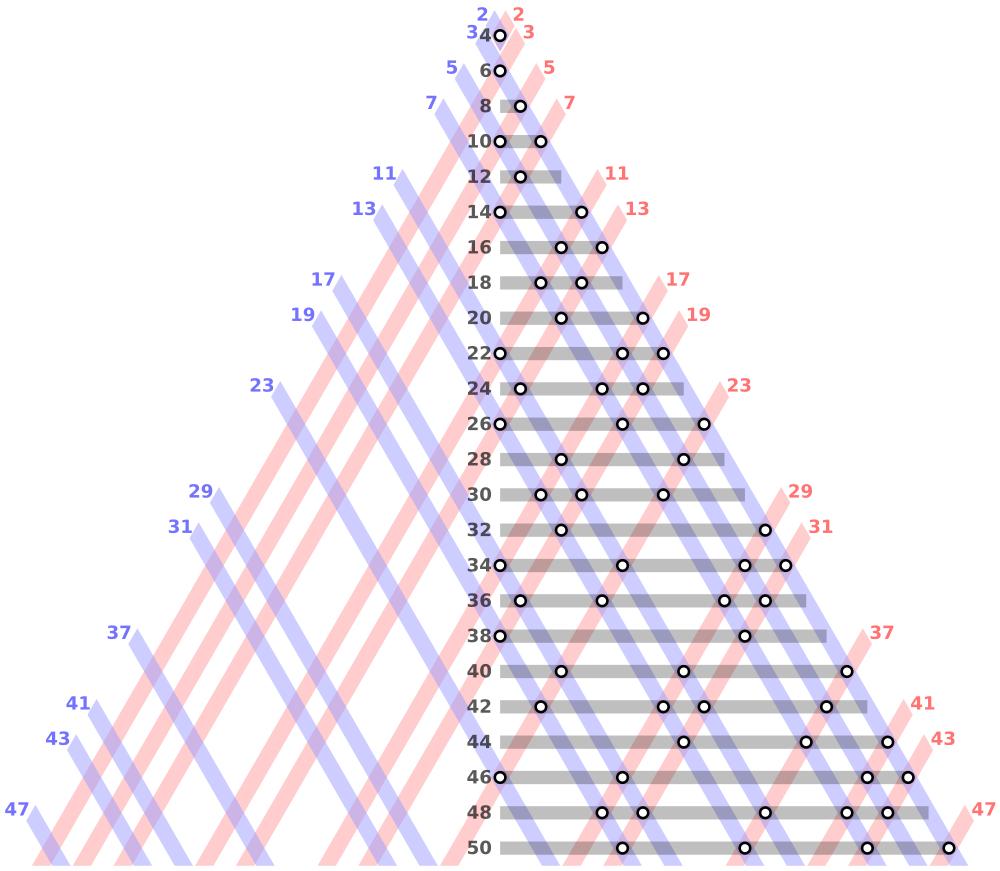
OneofthemostwellknowninfluencesofGoldbach’sconjecturewouldbeGoldbach’sfunction,also knownasGoldbach’scometduetoitsdistinctshape. Itassociatestoeachevenintegerthenumberofwaysit canbedecomposedintoasumoftwoprimes.
Thecoloringofpointsintheaboveimageisbased onthevalueof E 2 mod3 withredpointscorrespondingto 0mod3,bluepointscorrespondingto 1mod3 andgreenpointscorrespondingto 2mod3.Moreover, thegraphalsosuggeststhatthetightupperandlower boundsonthenumberofrepresentationsofaneven numberasthesumoftwoprimes,andalsothatthe numberoftheserepresentationsheavilydependonthe valuemodulo3ofthenumber.
 Fig.3:Goldbach’sComet
Fig.3:Goldbach’sComet
13
GeometricalInterpretationofComplexNumbers
JooyoungKim
Year12Halla
MemberofMathematicsSociety
Email:jy2kim24@pupils.nlcsjeju.kr
Editors
VictoriaSeoyunJu∗
RecommendedYearLevel:KS5andabove
Keywords:ComplexAnalysis,ComplexNumbers, Cauchy-RiemannEquation,HolomorphicFunction
InthefieldofcomplexanalysistheCauchyRiemannequationsfortwopartialdifferentialequationswhosesatisfactionareaconditiononwhether ornotacomplexfunctionisholomorphic.Itsname comesfromtwomathematiciansAugustinCauchyand BernhardRiemann.Acomplexfunctionisconsidered holomorphicwhenitisdifferentiableateverypoint. Thiscanonlybethecaseifandonlyifthethe functionsatisfiestheCauchy-Riemannequationsas wellasanothercondition:if f (z )= u(x,y )+ iv (x,y ), thenuandvmustberealdifferentiable.Thisstems fromthedefinitionofaholomorphicfunction:A function f (z ): C → C issaidtobeholomorphic inanopenset A ⊂ C ifitisdifferentiableateach pointoftheset A.Inthisentry,IwillbegivingabasicguidetotheproofoftheCauchy-Riemannequations.
Akeythemehereistheseparationofrealandimaginarypartsofthecomplexfunction.Wewilldothisby usingvariousprinciplesofmultivariablecalculus.
Proof
Considerthefunction f (z ): C → C,z ∈ C Bythefirstprinciple
f ′ (z )=lim h→ 0( f (z + h) f (z ) h )
Wecandothisbythinkingof h asapoint (a,b) andthe originas (0, 0)
Thus:
f ′ (x + iy )=lim h→0( f (x + iy + h) f (x + iy ) h )
⇒ f ′ (x + iy )
=lim (a,b)→(0,0)( f (x + iy + a + bi) f (x + iy ) a + bi )
(2)
Thislimitisonlytakingintoconsiderationthe casewhereboth a and b areapproachingzero.Inthe idealcasewewouldwanttoconsidertwolimitsfor easeofsimplification: a → 0 and b =0,and a =0 and b → 0,whichwouldyielduspartialderivatives.While thetwolimitsexpressedabovearenotthesameas (a,b) → (0, 0) aseachasaservererestriction,butifthe derivativefor f (z ) existstheneachofthetwolimits wouldbeequaltolimit (a,b) → (0, 0).Howeverforthis tohappen,wemustbeabletoexpress f (z ) intermsof realnumbers.
⇒ f ′ (x + iy )
=lim h→ 0( f (x + iy + h) f (x + iy ) h ) (1)
Thoughthelimitisfor h → 0,wecancontinuewith furtherseparatingtherealandimaginarypartsof f (z )
∗
Consideranewfunction F : R2 → C where F (x,y )= f (x + iy ).Thisnewfunctionallowsus toconsider f (z ) intermsofrealvariablewhileclearly distingushingitfromthefunctionofasinglecomplex variable f (z ).
Backtotheequationwecannowwrite f ′ (z ) in thetermsoftworealvariablesthus:
MemberofJPAMEditingTeam
f
F
a
14
′ (x + iy )=lim (a,b)→(0,0)(
(x + a,y + b) f (x + y )
+ bi ) (3)
Bythesetwoequations,wecanseethatif f (z ) iscomplexdifferentiablethen:
Byequatingtherealandimaginarypartsofthis equality,wegettwoequationsthatrelateboththepartialderivativesofrealandimaginarypartsof f (z ):
Itisimportanttonotethat ∂ notationisnotthesame as d,astheformerisapartialderivative,whichisthe functionoftwoormorevariableswithrespecttoone variable,theother(s)beingtreatedasconstants.In ourcase, a and b areourtwovariables,andineach caseoneortheeitherweresettoequal0.
Wecancontinueseparatingtherealandimaginary partsofthefunction, f ,byfurtherdefiningbyreal functions:
u : R2 → R,v : R2 → RF (x,y )= u(x,y )+ iv (x,y )
Whilethismightseemconfusingatfirst,itis importanttounderstandthatacomplexfunctionhas4 componentstoconsider:therealpartsoftheinputand output,andthesamefortheimaginaryparts.This hastheinterestingeffectofmakingcomplexfunctions technicallyrequiring4dimensionstoproperlygraph. Whatfunctionsuandvdohereisbypullingoutthe realandimaginaryoutputsof F (x,y ).Anotherwayof puttingisthat u and v aretherealandimaginaryparts ofthecomplexfunctionofasinglecomplexvariable, with u(x,y ) beingtherealvalueof f (z ) and iv (x,y ) beingthesamefortheimaginarypart.
Bydefining F intermsof u and v wecanturnthe rewritetheequation
Puttingtheseequationsintowords
Theequationontheleftsaysthatthechangein realoutput(∂u)bytherealpartof f isequaltothe changeoftheimaginaryoutputbythechangeinthe imaginarypartof f
Thesecondequationchangeinrealoutputby changeintheimaginarypartof f isnegativeofthe changeinimaginaryoutputbuthechangeinrealpart of f
Asstatedbefore,afunctionisholomorphicwhen theCuachy-Riemannequationsandanotherproperty issatisfied,whichisthattherealandimaginaryparts of f (z ),functions u and v ,arereal-differentiable.
Example
Considerthat f (z )= z 2 isdifferentiableatanypoint z = x + iy inthecomplexplane:
Ifwedefine u(x,y ) and v (x,y ) astherealandimaginarypartsof f (z ),then:
andtheirpartialderivativesare
Since u and v arerealdifferentiableandtheirpartial derivativessatisfytheCuachy-Riemannequations,we cansaythat f (z ) isaholomorphicfunction.
)=lim a→0,b=0
F
a
=lim a→0
F
a
= ∂F ∂x
x,y
a=0,b→0
a
=lim b→0( F
x,y
bi
= 1 i ∂F ∂y
and: f ′ (x + iy
(
(x + a,y + b) f (x + y )
+ bi )
(
(x + a,y ) f (x + y )
)
(
) (4) f ′ (x + iy )=lim
( F (x + a,y + b) f (x + y )
+ bi )
(
+ b) f (x + y )
)
(x,y ) (5) (6)
∂x
∂F
= 1 i · ∂F ∂y (7)
∂x
∂u ∂x + i ∂v ∂x = 1 i ( ∂u ∂y + i ∂v ∂y )= 1 i ∂u ∂y + ∂v ∂y (8)
∂F
= 1 i ∂F ∂y as:
∂u ∂x = ∂v ∂y (9) 1 i · ∂u ∂y = i · ∂v ∂x ⇒ ∂u ∂y = ∂v ∂x (10)
f (z )=(x + iy )2 = x 2 y 2 +2ixy (11)
u(x,y )= x 2 y 2 (12) v (x,y )=2
xy (13)
∂u ∂x =2x; ∂u ∂y = 2y ; ∂v ∂x =2y ; ∂v ∂y =2x (14)
15
TheValidityofConsideringtheSignificanceofan ImaginaryNumberinRelationtoReality
AidenHyunminPark Year10Sarah
MemberoftheMathematicsSociety Email:hmpark26@pupils.nlcsjeju.kr
Editor
AarenJoonseokKang ∗ VictoriaSeoyunJu †
RecommendedYearLevel:KS4
Keywords:ImaginaryNumbers,ComplexNumbers
1Introduction
1.1Whatdomathstandfor
Considerasimplequestion.“Whatisthemostbasicreasonforusdoingmath?”Tosomepeople,itisbecausemathhelpsthemtounderstandtheworldbetter andtosomeothers,mathcouldbejustahasslefortheir grades.However,thefundamentalmeaningofmathematicsissomethingtodowithquantity.Inotherwords, dealingwiththingsintherealworld.Startingfromsimplycountingthingswithfingers,mathematicsbasically allowedhumanstoperformsomuchstuff,suchasmeasuringlandscapes,derivingnumerouslawsandformulas fromasingleright-angledtriangle,andevendeducing theinstantaneousspeedbetweenveryshortperiods.In thisway,animaginarynumberwhichdoesn’texistin thefirstplace,seemsobscureandextraneoustolearn inregardstothebasicmeaningofmathematics.To giveananswertothisobscurity,itmightbehelpfulto discussabitmoreaboutthenumbersthemselves.
1.2Evolutionofnumbers
Behindtheaspectofmathematicscurrentlystandingasoneofthebasicsubjects,mathematicsencounterednumerousaltercationsandsupplementationsover time,startingfromprimitiveagestomoderndays.Likelyinthefuturetoo.-Humansstartedmathematics
∗ ChairoftheMathematicsSociety,LeaderofJPAMEditing Team
† MemberofJPAMEditingTeam
bymerelycountingthings;however,ascivilizationadvanced,itsconcepts,calculationsandapplicationsbecamesimultaneouslymoresophisticatedandcomplex. Theearlyhistoryofmathisextremelymurkytotell theclearorigin.Inotherwords,nobodycantellexactlywhenhumanbeingsbeganusingnumbersorsimplycountingstuff.Althoughtheoriginhasconsigned tooblivion,historianssuspectthatthepeoplebackthen wouldhavebeenunabletodothingsmorethansimply countingstuff.Ifweweretodrawanumberlinewith theinterpretationofnumbersatthattime,thenumber linewouldbeascalar;onlyallowedtomovetowards theright-Thisisbecausesincethenegativenumber wasn’tpresentbackthen,theonlywaynumberscould befurtheredfromthezeroisbyincreasing.
1.3Fractions

ThetrendstayedthesameuntilEgyptians(ancient egypt1740B.C.)cameupwiththefirstinnovation about4000yearsago,theconceptoffractions.
Althoughnowadays,theegyptianfractionsareno longercurrentandhavebeensupersededwithdecimal notationsandvulgarfractions(theformoffractionused nowadays),themeaningofitsusage,whichledusto anotherlevelofmathshouldbefocusedprimarily.
1.4Zeroandnegativenumbers
Thenextinnovativestepofmathematics,followed byfractions,wastheallowanceofzeroandnegative
Fig.1:Theprimitiveconceptofnumbers
16
numbers.Unlikethesedayswhereuseofnegativenumbersandzerohasbecomevirtuallynecessaryinmath, thesetwoconceptswereoccasionallymetupwithskepticismamongpeoplebackthen.Overall,earliercultures seemedtoprohibittheuseofzeroandnumberssmaller asanumber.Amongvariousreasonsbehind,itturns outthattheprimaryfactorwhichdeterminedtheacceptabilityofthesenumbersbackthenwas“Howpeople viewedtheconnectionbetweenmathematicsandreality.”(WelchLabs,2015)Mainly,itisthesubtletyofconsideringthevoidandsomethingevenlessthanemptyas numberswhichhaspreventedtheuseofzeroandnegativenumbers.Clearly,itwasnotbecausepeopleinthe pastwerelessintelligenttoperceivetheabstractconcept,but,theconceptsthemselveswerefartoosubtle tobeimplementedasnumbers.Tonameafew,ancient culturesliketheAncientEgypt(1740B.C),Babylonians(300B.C),andOlmecs(400B.C)haveseemedto admittheconceptofvoidastheplaceholderofnumber lines,however,stilltheuseofzeroandnegativenumberswerefollowedbyaskepticism.-Itisambiguous totelltheexactoriginofzero:Somehistoriansclaim thatitwasfirstintroducedbyBrahmaguptatheIndian mathematician,whereastheclaimthatitwasfirstused byMesopotamia(around3B.C.E)isoftenbroughtup too.-AroundB.C200,negativenumberswerefinally imposedaspropernumbersbyChina.Manyhistorians expecttheChinesetohaveusednegativenumbersfor recordingdebts.
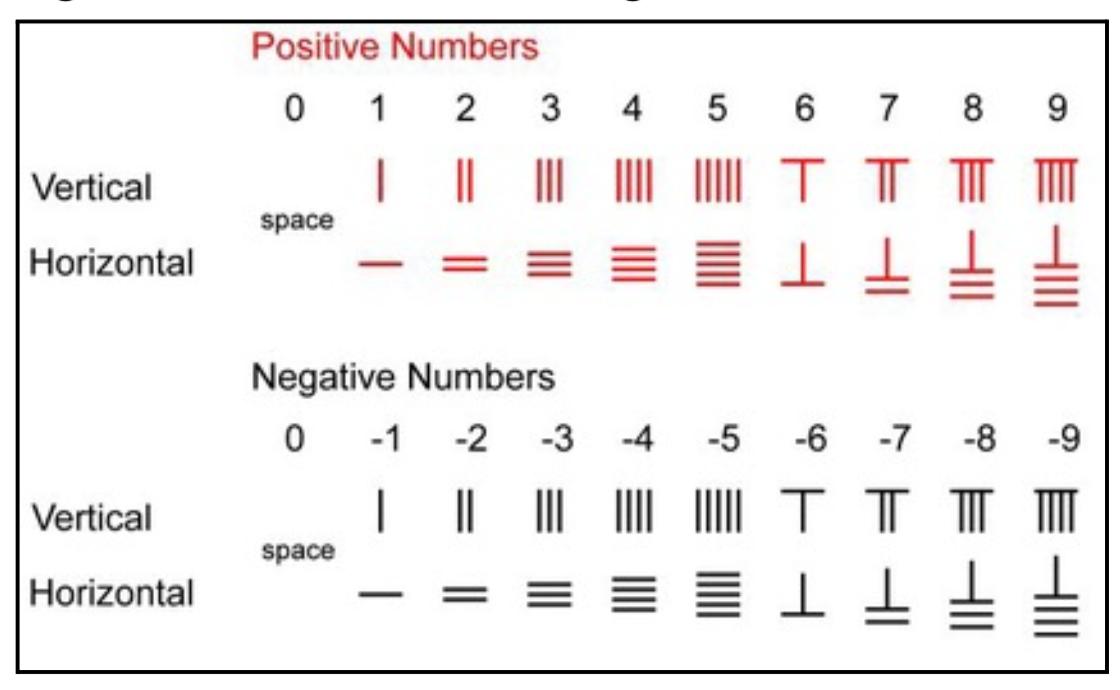
StartingfromancientChina,countriesaroundthe worldstartedtoacknowledgetheconceptofnegative numbersandzeroinrelationtotheirpuredefinitionin mathdespitetheirmeaningsbeingsubtleinnature.
1.5Subtletyofnegativenumbers
Itisconceivablethatthischapterseemstrivialto some.Itlookslikethewholediscussionhasseguedinto thelonghistoryofmathwhilethemainfocusisimaginarynumbers.However,notonlythehistoryofimaginarynumbershasalottodowithpeople’sperception ofnumbersjustspoken,butweshouldalsofocusonthe factthatwearetakingnegativenumbersforgranted whilsttheyarestillsubtletermstorelatewithreal-
Fig.3:TheancientChina’snegativenumbers
itylikeimaginarynumbers.Althoughtheyareused forquantifyingobjectssuchasthebasementfloorsand debts,thoseobjectsarestilltechnicallycountedwith positivenumberswhereweconsiderthemasnegative sincetheyareoppositefromthestandard.Generally, negativenumbersarealsonotpresentinnaturewhere westillconsiderthemasnumbersforgranted.Asamatteroffact,theallowanceofnegativenumbersandzero hashittedwithbigchangestothenumbergrid.The acceptance0andnegativenumbersallowedthenumberlinebeingavector,meaningthatnumberswereno longermerelyincreasingbutalsodecreasingtoinfinity fromthen.Infact,thewayhowimaginarynumbersare consideredsignificantintermsofmathisveryanalogous tothewayhowthenegativenumberswere.Inspiteof thembeingsubtleintermsofthenature,themeanings theyinheremademathtobeconsistentwithitslaw.
2HistoryofImaginaryNumbers
2.1Avoidingnegativenumbers
Thisisnowthepointwherethingsspokenarefinallyembeddingwiththeimaginarynumbers.AlthoughculturesstartedtoacknowledgenegativenumbersaspropernumbersinancientChina,theoccasional appearanceoftheminequationsandformulaswerestill largelyignoredandavoidedevenuntilthe16thcentury, andthistrendhaseventuallyledtothediscoveryof imaginarynumbers.Generally,mathematiciansatthat time(Europe,16thcentury)tendedtoavoidanysort ofequations,havingthelikelihoodofnegativenumbers gettinginvolved.Inparticular,consideraquadratic equation,seencommonlyinclass:
Ofcoarse,asexpected,wehave2solutionswhere x=3couldbetheoneAndx=-5couldbetheother. However,unlikethesedayswhereequationslikethis arenosuchproblem,mathematiciansinthe16thcenturyweresoaversetonegativenumberssincenegative
Fig.2:TheEgyptianunitfractions
x 2 2x 15=0 (1)
17
Fig.4:ExamplesofKhayyam’sdepressedcubic
numbersclearlydidn’tmakeanysensewithreality.In thisway,mathematiciansmanipulatedandalteredpolynomialequationstobekeptinapreferableformwhere anypresenceofnegativenumberswaseliminated.Thus, quadraticequationsandanyotherpolynomialwithadegreeofevennumbersweretotallyavoided,sinceingeneral,theyinevitablyhavenegativenumbersinvolved.
2.2Depressedcubics
Thesameapproachwasdonetocubicequations, wherethepersianmathematician,OmarKhayyamidentifieddifferentformsofcubicequationsknownasthe “depressedcubic”:
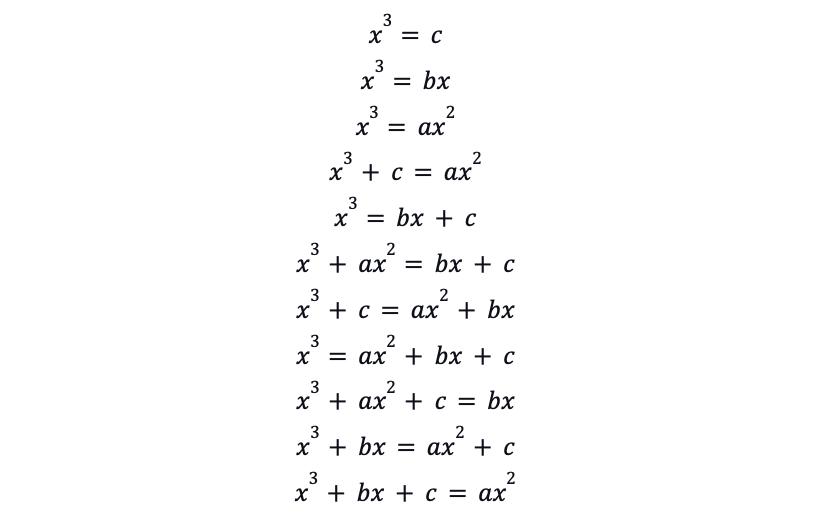
Asdemonstratedinfigure4,depressedcubicisa formofcubicequationwhereanynegativecoefficients andthetermofx2areabsentforthesakeofeliminatingnegativenumbers.-Anypolynomialofdegree nissaidtobedepressedifthetermof(n-1)ismissing.-Infact,cubicfunctionsandimaginarynumbers, twoconceptswhichseemmutuallyrelationless,share agreatconnection-“Complexnumbersarosefromthe needtosolvecubicequations,andnot(asitiscommonly believed)quadraticequations.”(AShortHistoryOf ComplexNumbers,2006)-.Thejourneyofimaginary numbersstartedfromanItalianmathematician,ScipionedelFerro(professoroftheuniversityofbologna).-It isoftenknownthatthefrenchscholar,ReneDescartes hasinventedtheimaginarynumber,howeveritistechnicallynottruesincetherewerealreadyothermathematicianspredatedtheconceptbutDescartesonlyhad formallydefinedthetermas“imaginarynumber”.
Inthe11thcenturywhenKhayyamidentifiedthose depressedcubics,thoseequationswerecomposedpreciselyandcleverlyenough,howeveritwasanotherissue formathematiciansatthattimetosolvethem.Atlast, bythetimearound1510,about5centurieslater,Del Ferrodiscoveredamethodsolvingdepressedcubicsin suchaconvenientandreliablemanner.Byperformingseveralcalculations,hecameupwithhiscompletely originalformulawhichmadehimabletosolveanydepressedcubicbysimplyplugginginvaluesintothefor-

mula.-Youcouldthinkofitlikeaquadraticformulafor cubicequations.-Sincethisisaverysignificanttopicin regardstothehistoryofimaginarynumbers,wewould talkaboutitfurther,startingwiththederivation.
ordertodeducetheformula,wesimplystartwith adepressedcubic:
Sincetheformulashouldworkforanycircumstance, wecansetthepremisethat3uv+c=0.Inthisway,
Fig.5:ScipionedelFerro
x 3 + cx = d (2) Let x = u + v ,thentheequationcouldbewritten as: (u + v )3 + c(u + v )= d u 3 +3uv 2 +3u 2 v + v 3 + c(u + v )= d u 3 +3uv (u + v )+ v 3 + c(u + v )= d u 3 + v 3 +(u + v )(3uv + c)= d (3)
u 3 + v 3 = d (4) and v = c 3u (5) Aswewritevintermsofu: u 3 c 3u = d u 3 [u 3 +( c 3u )3 d]=0u 3 u 6 du3 c3 27 =0 (6) 18
Considertheequationisquadraticandsubstitute valuesintothequadraticformula:
Inthisway,DelFerrodeducedtheultimatesolution totheconundrumwhichbotheredmathematiciansfor centuries.However,surprisingly,thissolutionwasnever revealedtothepublicevenafterDelFerro’sdeath.The reasonwhyDelFerroharboredhisinnovativesolution hastodowiththecustomamongmathematiciansin the1500s.Amathematicianwouldoftenchallengeanothermathematicianfortheirpositionwhichcouldbe saidasmathduels.Thiswasdonebyeachparticipant submittingaseriesofmathproblemstotheopponent andsimplytheonewhogotmoresolvingscorrectseized thetriumph.-wheretheloserwasoftencondemnedto
humiliation-.SinceDelFerrowastheonlyonewhohad thesolutiontothosedepressedcubics,hekeptitsecret toguaranteehisjobsecurity.Aftertwodecades(1526), whileonhisdeathbed,DelFerrofinallyhandeddown thesecretmethodtohisstudent,AntonioMariaFior. AfterDelFerro’sdeath,Fiorwasconceivedofhismathematicalprowessasheknewtheformula.Hewasboastfulandthoughthewouldbeinvincibleinmathduelsso thathechallengedawaymoreskilledmathematicianat thattime,NiccoloFontanaTartaglia.
OnFebruary12,1535,FiorchallengedTartaglia andtheygave30problemstoeachother,allofwhich weredepressedcubics.Surprisingly,eventhoughFior knewtheformula,hestruggledtosolveevenasingle questionwhereasTartagliacompletedsolvinginless than2hoursandprocessedtocompletelydominate Fior.Evenfurther,Tartagliafoundtheformulasolving depressedcubicshimselfashesuspectedFiorwasgiven downasecretmethodfromsomeothergreatmathematiciansincehehadtheboastfulnessbutdidn’tseem tobecapableoffindinghisown.Aftertheduelwhere Tartagliahadalsobecomeawareoftheformula,healso kepttheformulasecrettothepublicjustlikeDelFerro didforthesamereason.

Afterall,Tartagliabecamerenownedforhisvictory andmathematiciansreveredhimandstrivedtolearnthe know-howofsolvingdepressedcubics.WhileTartaglia kepthimselfspeechless,oneItalianpolymath,named GerolamoCardano-knownasoneofthemostinfluentialmathematiciansduringRenaissance-wasparticularlydesperatetolearnthemethod.
CardanopersistentlysentletterstoTartaglia,sometimessoundingflattery,butsometimesalsothreatening. Atlast,March25,1539,-inMilan-Tartagliarevealed hismethodtoCardonosecretlyunderasolemnoathfor Cardanotomaintainthesecrecythusnotpublishingit andtoonlywritethemethodinacypher.
Bygoingthroughfurthercalculations,Cardano
a 2 da c3 27 =0 (7)
Letanothernewvariablea=u3.Aswerewritethe equationintermsofa:
x = b ± √b2 4ac 2a ⇒ a = d ± d2 4 c3 27 2 = d 2 ± d2 4 +4 c3 27 4 = u 3 ∴ u = 3 d 2 ± d2 4 + c3 27 (8) Asweknowthat v 3 = d u3 ,Wecanwrite v in termsof u: v 3 = d [ d 2 ± d2 4 +4 c3 27 4 ] = d 2 ∓ d2 4 +4 c3 27 4 (9) ∴ v = 3 d 2 ∓ d2 4 + c3 27 (10) Ultimatelytofindanexpressionof x
x = u + v : x = 3 d 2 ± d2 4 + c3 27 + 3 d 2 ∓ d2 4 + c3 27 (11)
,whereweconsider
wouldbeourfinalequation.
Fig.6:NiccolòFontanaTartaglia
19
foundawaytoturnanyformofcubicequationintoa depressedcubicandthussolveinTartaglia’sway.The followingshowsthemethod:
Considerastandardcubicequationinaform: y = ax 3 + bx2 + cx + d (12)
Tofindtherootsof x,thiscouldbeturnedas:
ax 3 + bx2 + cx + d (13)
Atthispoint,substituteanothervariable, z to x where
Inthisway,theequationwillbewrittenas:
add b 3a to x sincetheinitialpremisewasthat x b 3a Cardanowasdelightedbythefactthatfinallytheissue thathadstumpedmathematiciansovercenturieswas solvedandhadthedesiretopublishthesecretmethod. Simply,whatcountedthemosttoaforward-looking physicianwasthecreditthatwouldhavebeengiven byrevealingthetruth.Alsoasforbeingacontemporaryphysician,hewasn’tinvolvedinthosemathduels inthefirstplace,sohehadnoreasontomaintainthe secrecy.Thatbeingsaid,theonlythingthatstopped himfromdoingsowastheoathhesworetoTartaglia. SincehesworenottopublishTartaglia’smethod,he wasobligatedtokeepthesecret,whichonlyhappened until1543.In1543,CardanotravelledtoBolognawith hisstudent,Ferrariandmetanothermathematician, HannibalNave.
(14)
HannibalNavewasason-in-lawofDelFerroand healsotookoverDelFerro’sstatusintheuniversity ofBologna.HehadthenotebookpassedbyDelFerro whichDelFerrokepttherecordsofhisdiscoverywhile hewasalive.HestillkeptthenotebookbythetimeCardanotraveledtoBolognatoseehimandCardanogotto knowthatTartaglia’smethodwasalreadypredatedby anothermathematicianashesawDelFerro’snotebook. Inthisway,theoathCardanosworetoTartaglianotto publishthemethodwasnolongervalidasTartagliawas notthefirsttosolvethedepressedcubic.Thatbeing so,in1545,Cardanopublishedabook,ArsMagna,in whichhecoveredabunchoftopicsandconceptsinalgebra-whichhappenedtobemainlyaboutthedepressed cubic-.ThefollowingisfromtheArsMagna:

Inthisway,theformoftheequationcanbefurther solvedbyTartaglia’sformulaandthenwecouldsimply
ScipioneFerroofBologna,almostthirtyyearsago, discoveredthesolutionofthecubeandofthingsequalin number[thatis,theequationx3+px=q,wherepand qarepositivenumbers],areallybeautifulandadmirable accomplishment.Indistinctionthisdiscoverysurpassess allmortalingenuityandallhumansubtlety.Itistruly agiftfromheaven,althoughatthesametimeaproofof thepowerofreason,andsoillustriousthatwhoeverattainsitmaybelievehimselfcapableofsolvinganyprob-
Fig.7:GerolamoCardano
0=
z = x b 3a
⇒ az 3 + bz 2 + cz + d
⇒ a(x b 3a )3 + b(x b 3a )2 + c(x b 3a )+ d =0 ⇒ ax 3 2bx2 3 + b2 x 9 bx2 3 + 2b2 x 3 2 27a + bx2 ⇒− 2b2 x 3a + b3 9a2 + cx bc 3a + d =0 ⇒ ax 3 + b2 x 9 + 2b2 x 3 2 27a 2b2 x 3a + b3 9a2 + cx bc 3a + d =0 ⇒ ax 3 +(c b2 3a )x +(d + 2bx3 27a2 bc 3a =0
=0
Fig.8:MilantoBologna
20
lem.InemulationofhimNiccolòTartagliaofBrescia, afriendofours,inordernottobeconqueredwhenhe enteredintocompetitionwithadiscipleofFerro,AntinioMariaFiore,cameuponthesamesolution,and revealedittomebecauseofmymanyentreatiestohim.

3ComplexNumbers
3.1Whyiscomplexnumberexpressedas a + bi?
However,therewasonlyoneproblemCardanofaced withDelFerro’smethod.
Considerthecase:
x 3 =15x +4 (15)
Thisproblemcouldbesolvedeasilyusinghighschoolmathematics,wheretheansweris x =4.However,aswepluginthevaluesintoDelFerro’sformula, somethingverystrangehappens.
Magna,thenheaddedthequotethatitis“subtleasit isuseless”.Todiscussthisobscurity,wehavetoclarify thethingswehaveobservedsofar:
1. Thegivenequation,x3=15x+4hasx=4asthe solution.
2. However,thedepressedcubicformulaseemstobe brokenaswepluginthevaluesfromtheequation.
3. Thus,wecansuspectthatalthoughtheequation seemstonotmakeanysense,somehow,thereisthe correlation.
Totellthetruth,thishashappenedneitherbecause Cardano’sformulawaswronginthefirstplace,norbecausetherewasamistakewhilederivingtheequation, butinfact,theequationwejustderivedactuallydenotesthevalueof4.
Toprovethis:
First,wehavetosubstitutevaluesassymbolsfrom theequationsothatthingscouldbemoremanageable.
Theformulahasslightlychangedascbecamenegative.
4= a + bi + a bi andastheterm bi wouldbecancelledout,weareleftwiththevalueof 4=2a,a =2
Asanidenticalequation,thevalueof a3 3ab2 shoulddenote2whichisatermthatdoesn’tinvolve anegativeterminasquareroot,andbythesamelogic, thevalueof 3a2 b b3 shoulddenote11.(Bothremoved negativeroots).
Aswealreadyknowthata=2, a3 3ab2 =2 could bewrittenas 83 6b2 =2,whichmakes b = ±1
Linkingthistoourfirstexpression,
Andinthisway,thislastwithoursupposedanswer 4.
Asshown,anequationwitharealnumberasthe solutionhasbrokendownintoanexpressionwithcomplexnumbers.Infact,CardanoavoidedthecaseinArs
I’mawaresomeindividualsarefacingdifficultiesat presentbutthissharesthesamelogicthatmakesyou abletowriteacomplexnumberinaform:a+bi.Apparently,thisisonlyasimplesubstitutionofnumbers whereweseparatedtermsthatinvolvenegativeroots fromthosewhichdon’t.Justlikewecanrewritethe expression: x +3x +4+1 5 into 4x,wejusthavesimplifiedtheexpression.
Fig.9:ArsMagna-Thegreatart
x = 3 d 2 ± d2 4 + c3 27 + 3 d 2 ∓ d2 4 + c3 27 (16)
x = 3 4 2 ± 42 4 153 27 + 3 4 2 ∓ 42 4 153 27 = 3 2+ √ 121+ 3 4 2 √ 121 (17)
x = 3 2+ √ 121+ 3 4 2 √ 121 3 2+ √ 121= a + bi 3 2 √ 121= a bi (18)
2+ √121= a 3 3ab2 +3a 2 bi b3 i (19)
3 2+ √ 121+ 3 4 2 √ 121=(2+ i)+(2 i) (20)
21
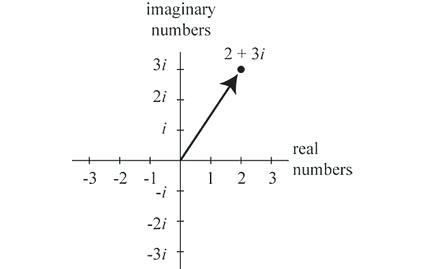
3.2ComplexPlanes
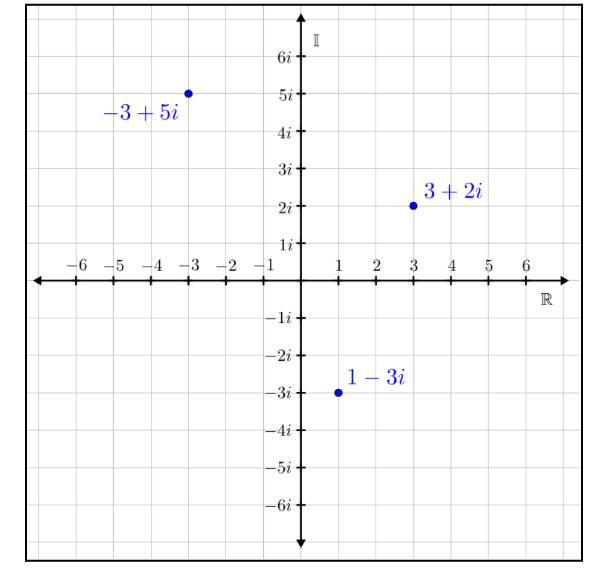
However,somethingreallymakesthisform, a + bi, verydifferentfromanyothersimplificationofexpressionisthatthisentireformitselfdenotesavaluefrom amoresophisticateddimension.Unlikeanyrealnumberwhichitsvaluecanbemerelyexpressedasasingle numberwithoutusinganycalculationsignssuchas+or -,acomplexnumbershouldinvolveatleasttwoterms, thefirsttermwhichdenotesthevalueoftherealnumber,thesecondtermwhichdenotesthevalueofthe imaginarynumber.Inthisway,thesetwoincompatible terms,realnumberandimaginarynumbersrequiretwo dimensionsinordertorepresentitstruevalue.
Whenthinkingofacomplexplane,itiseasytostart withanimageofacartesianplane.However,thenoticeabledifferencebetweenanormalgridandacomplex planeisthatonecomplexplanedenotesthevalueofone complexnumberwhereasapointplottedinanormal griddenotesacoordinate,apairoftworealnumbers todetermineaposition.Thegeneralideatoseparate imaginarynumbersfromtherealnumberswasoriginally devisedbyanItalianmathematician,RafaelBombelli.
RafaelBombelliwasacontemporarymathematicianwiththoseaforementionedmathematicians,andhe wasalsotheactualfigurewhosolvedthebrokenDel Ferro’sformulawhichCardanostruggledwith.

Basicallytheideabehindthesubstitution:
wasbasedonhisinterpretationthatanegativenumberinsideasquarerootwasanunprecedentedconcept,
therebytherehadtobedistinctionsbetweenrealnumbersandimaginarynumbers,thuslettingatodenote therealvalueand b todenotethevalueofanimaginary number.-Inthiscase,theactualvalueof b isareal number,butithappenstodenotethevalueofimaginary termssinceitismultipliedwith i,intheform:a+bi.In acomplexplane,thevalueof a isplottedinthehorizontalaxiswhichcalledthe“real-axis”,denotingthevalue ofrealnumberinacomplexnumberandthevalueof b isplottedintheverticalaxiswhichiscalled“imaginaryaxis”,denotingthevalueofanimaginarynumber inacomplexnumber.Inthisway,therepresentation ofacomplexnumberonacomplexplaneresemblescoordinatesonacartesianplane.However,asmentioned beforethisshouldnotbeconfusedthatthepointona complexplaneisnotacoordinateofapairofnumbers, butthisrepresentsavalueofasinglecomplexnumber. Alsoasyoucansee,anynumberinvolvinganimaginaryterminitsvaluecan’tbeplottedonthehorizontal plane.Thisisbecauseintheform a + bi,theonlyway acomplexnumbercouldbelieonthehorizontalaxisis whenthevalueofimaginarynumber, b is0.However, asthenumbersinvolveimaginarytermsinitsvalue, b getstohaveavalueother0,thusmakingthenumber tolieuponorbelowtherealaxis.Infact,thecomplex planecouldbesaidasanupgradeversiontotheinitial numbergridwheretheseconddimensionofimaginary numberhasbeenadded,thusbecomingatwodimensionednumberfromapointonastraightline.Inthis way,youcouldalsoconcludethateveryrealnumberis writteninaform a +0i,sothatonlythevalueofadeterminesanumber’spositionontherealaxis.Justlike inacartesiangrid,eachaxisstartsfrom0andincreases by1asitgoesupandby-1asitgoesdowntheaxis. Itcouldbesaidthatthecomplexplaneistheultimate weaponofmathwhichtheplaneitselfcouldrepresent everynumberhumanshaveinventedsofar,andsurpris-
Fig.10:Thecomplexplane
3 2+ √ 121= a + bi 3 2 √ 121= a bi (21)
Fig.11:RafaelBombelli
22
inglycomplexnumbersseemstobetheultimatelyfinalcategoryofnumberswhereanynewkindofnumber can’tbemadeanymore.Supposemultiplying,square rooting,ordividingacomplexnumber.Althoughits valuecouldbeabitmessy,stillthenumberisdefined asacomplexnumber.
3.3Euler’sidentityandthespiral
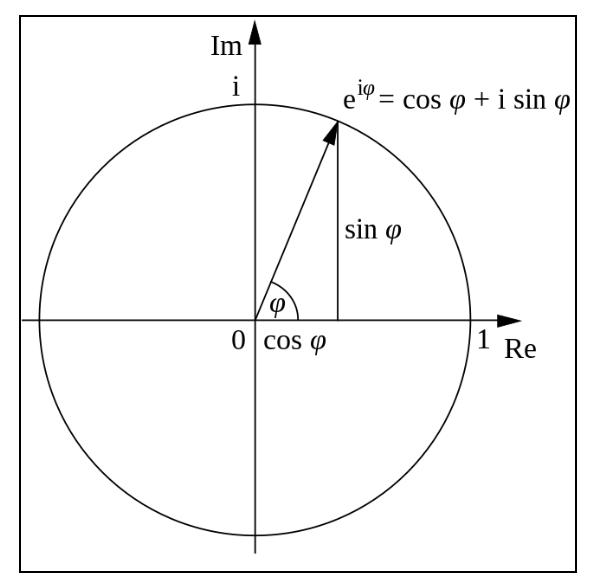
Consideraunitcircledrawnonacomplexplane whereitsradiusis1,thusaright-angletriangledrawn withinthecirclehasahypotenuseof1.Inthisway,the pointontheunitcirclewhichhappenstobeoneofthe
verticesofthetrianglewouldalsobe1.Inthisway, letting ϕ tobetheanglethatacomplexnumberhas fromtheorigin,thiscouldbewrittenas cos ϕ + i sin ϕ Thisisbecauseinthissituation,thehorizontalheight oftherightangletriangleisdenotingthevalueofthe imaginarytermofacomplexnumber.Rememberthis istechnicallynotagraph-thefollowingcanbealso writtenas: ϕ asanabbreviation.Inthisway,thiscould beconsideredasafunctionwheretheformis: f (ϕ)= cos ϕ + i sin ϕ anditshouldbealsonoticedthatthisform isaformfurtheredfromtheinitialform: a + bi.By consideringthefollowingasafunction,wecananalyze thefeatureofthisfunction:
Firstly,bymultiplyingthefunction f (a) and f (b):
f (a) f (b)=(cos a + i sin a)(cos b + i sin b) (22)
Whichbysimplificationturnsouttobe:
cos a(cos b + i sin b)+ i sin a(cos b + i sin b)
=cos a cos b + i cos a sin b + i sin a cos b sin a sin b (23)
Howeverasthetrigonometricidentitysuggest,
cos a cos b sin a sin b =cos(a + b) (24)
Andalso i cos a sin b + i sin a cos b canbewrittenas i(cos a sin b +sin a cos b).Andinthesameway,thiscould bewrittenas i(sin a + b)
Bytrigonometryidentitiesandthusthewholeexpressioncanbewrittenas:
cos(a + b) i sin(a + b) (25)
Thisalsocorrespondstothevalueof f (a + b).In thiswaythefirstfeatureofthisfunctionisthat:
f (a + b)= f (a) f (b) (26)
Tofindthesecondfeatureofthisfunction,wesimplysquarethefunctionandget:
f (x)2 =(cos x + i sin x)2
=cos 2 x +2i cos x sin x sin2 x
=cos(2x)+2i cos x sin x
=cos(2x)+ i sin(2x) (27)
Thusthesecondfeatureisthat:
f (2x)= f (x)2 (28)
Fig.12:ComplexPlane2
Fig.13:TheComplexPlane3
23
Thethirdfeatureofthefunctioncouldbefoundby takingthereciprocal:
1 f (x) = 1 f (x) f ( x) f ( x) = f ( x) f (x) f ( x) (29)
Byinvokingthefirstfeatureofthisformulawhere f (a + b)= f (a) f (b).Thiscanwrittenas f ( x) f (x x) .However,sincethevalueof f (x x)=1 -as cos0+ i sin0=1, where i sin0=1, 1 f (x) = f ( x) becomestrue.
Lastly,wewoulddifferentiatethefunction:
f ′ (x)=( sin x + i cos x) (30)
Andinthisway, f ′ (x)= if (x).Thatsaid,amathematiciannamedEulerfoundaparticularsingularity whichthewholefeatureofthefunctionisveryanalogouswiththerulesofhisconstant, e,wherethefunctionhadthealmostsamefeaturewithanotherfunction, f (x)= ex Tocomparethis,thefunctionwediscovered hadarule:
f (a + b)= f (a) f (b)
f (2x)= f (x)2
1 f (x) = f ( x)
f ′ (x)= if (x)
Whilethefunction f (x)= ex hassimilaridentities: e( a + b)= ea e b
Alsotoreiterate, ϕ standsfortheangleofacomplex numberfromtheoriginandrstandsforthedistancea complexnumberisfurtheredfromtheorigin.
Inthisway, ex and (x) showedverysimilartrait wheretheonlydifferencewasthatwhendifferentiated, (ex )′ didn’tcorrespondtothevalue.ThuswhatEuler divisionwasthatbyslightlychangingtheformto ei x thefunctiontotallyworkedthesameas (x) wherestill otherrulesworkedthesame.Thisisbecause (ei x)′ = iex ,thusmakingthefunctionfollowthefeatureof (x) perfectly.
Theultimatebottomlineisthatwhenthecomplex number’sdistancefromtheoriginequalsto1,itsvalue canberepresentedas cos ϕ + i sin ϕ orinanotherway around: eiϕ .However,sincenoteverycomplexnumberhasadistancefromtheoriginas1,wemultiply thedistancebetweentheorigin, r infrontoftheboth functions,thusthefinalderivationis:
z = reiϕ orr cos ϕ + ri sin ϕ (33)
Byusingtheform z = reiϕ ,thisallowstheperformanceofmuchmoresophisticatedcalculationssuchas thevalueof 2i ,ii oreven i √i.First,weshouldbasically knowtherulesofthecomplexplane.Althoughitseems likeacomplexnumberisplacedatsomekindofrandompositionontheplaneaswemultiplyordividesome numbers,thatactuallydoesn’tturnouttobethecase. Firstofall,forthemultiplicationrules,anyrealnumberdoesn’tgetawayfromtherealaxis,anyimaginary ismultipliedandviceversa,anypureimaginarynumberdoesn’tmoveawayfromtheimaginaryaxisunlessa complexnumberinvolvingarealtermisn’tmultiplied.
Justlikethediagramabove,arealnumberlieson therealaxis,thusitcan’tincludeanyimaginaryterm unlessitismultipliedbyanothercomplexnumber.In thisway,therealnumberrotatesexactly180degrees clockwise(whennegativenumbersaremultiplied)or keepsinthesameanglewhenthesametypeofnumberismultiplied.
Inthisway,theruleofmultiplicationofcomplex numbersisthatwhentwocomplexnumbersaremulti-
(31)
e
2 1
1 d dx
(32)
2x =(ex )
ex =(ex )
(ex )= ex
Fig.14:ComplexPlane4
Fig.15:ComplexPlane5
24
plied:
1. Theanglesoftwocomplexnumbersfromtheorigin areaddedtogether.
2. Theeachdistanceoftwocomplexnumbersfromthe originaremultiplied.
Forexample,consideracase 5 (1+2i).Inthis case,5hasadistance r ,and r =5.Also,theangleof 5fromtheoriginequals0or2sincethenumberstays onthepositivesideoftherealaxis.Thus,thiscouldbe writtenas reiθ =5 ei 0 =5,wherewearebacktothe initialvalue,provingthatthisisnotthewrongmethod todenoteacomplexnumber.
Ontheotherhand,thedistanceof(1+2i)from theorigincanbecalculatedeasilyusingthePythagoras theorem, adjacent2 + height2 = hypotenuse2 ,wheredistance, d = √12 +22 = √5 andthe angleθ =arctan( 2 1 )= 1 1rad
Thevalue 5 · (1+2i)=5+10i hasadistanceof √52 +102 = √1025=11 18.Andhasanangleof arctan( 2 1 )=1 1rad.Ascouldbeseen,thedistance, 11.18isactuallythevaluewhichthedistanceof5from theorigin,5multipliedby √5,thedistanceof 1+2i fromtheoriginandtheangle,11.18radisaresultof theadditionofanglesoftwocomplexnumbers,0and
11.18.Inthisway,whenacomplexnumber, z1 = reiθ is multipliedbyanothercomplexnumber, z2 = veiϕ ,the valuecanbewrittenas: rv (ei (θ + ϕ)).Thisisthesame reasonthatmakesthecycleofmultiplicationof i which:
Althoughthisisacommonsensethatnoone doubts,byapplyingtheterminologywehaveacquired, thiscouldbeexplainedbecauseihasadistanceof1from theoriginanditsangleis90degreesfromtheorigin.In thisway,thedistancegetsmultipliedbutsinceitis1, itremainsthesamebut,thedegreesgetsincreasedby 90degreesasitkeepsgettingmultiplied,thusthefirst 90degreesrotationlastwith i,thesecondwith-1,the thirdwith i andreturningbacktotherealaxisandso on.Inthisway,letusputourselvesintosomeridiculous casessuchas 2i .Intuitively,thismeanswearemultiplying2,itimes,howeverthisdefinitioniswaytoosubtle togothroughourcalculation.Instead,letusturnthis intoafrom:reiϕ .Firstly,astheruleoflogarithms,2 canbewrittenas eln2 .Sincewearefindingthevalue of 2i ,thisequalstothevalueof (2ln2 )i .Thus,weare leftwiththesolution, ei ln2 ,valuewhichitsdistanceis 1furtheredfromtheoriginandtheangle, ln2 fromthe origin.
Thenhowabout ii ?Toquicklygothrough:
Inthisway,wegettoknowthatanimaginarynumbertothepowerofanimaginarynumberissurprisinglycorrespondingtoarealnumber,furtherproving thatimaginarynumbersandrealnumbersarenotentirelyseparatetermsbuttheyshowcorrelationunder thealgebrawhichcalculationsinvolvingcomplexnumberscanalsoresultwithrealnumbersasthesolution. Inaddition,thereasonwhythesolutionderivedfrom theequationinvolvingimaginarynumbersisvalidis becausealthoughimaginaryandcomplexnumbersare subtletermsinnature,theystillfollowthewholerules ofmathjustlikerealnumbersdo,thustheirvaluesare consideredequallyinthealgebra.
Lastly,solvingfor i √i:
Fig.16:ComplexPlane6
Fig.17:ComplexPlane7
i1 = i i2 = 1 i3 = i i4 =1 (34)
i = e i π 2 ii =(e i π 2 )i = e π 2 ≈ 0 20787 (35)
i √i =(i) 1 i =(e i π 2 ) 1 i =(e i i π 2 )= e π 2 (36)
25
Alsointhiscase,theequationmerelyinvolvingacomplexnumberhasarealnumberasitssolution.
3.4TheFundamentalTheoremofalgebra& Themissingpuzzlepieces
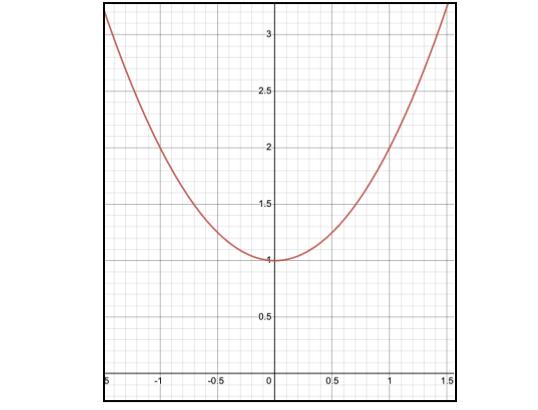
Thebottomlineofthisjournalshouldbespoken withoneparticularterminvoked,thefundamentalTheoremofAlgebra.Thegeneralideaofthistheorem,conceivedbyCarlFriedrichGauss(1799),statesthatevery polynomialequationofdegree n,mustcomeupwith nsolutions/rootsintotal.Thefundamentaltheorem ofalgebrastandsasthebasicfoundationwhichmost studyofAlgebraisbuilton.Anyequations,polynomials,functionsarefollowingthetheoremandthisisthe theoremthatstatesalinearequationhasasingleroot andthequadraticequationhastwo.Supposeacase y = x2 +1.Thisisakindoffunctioninwhichitsvertex liesuponthex-axiswithaconcaveup,thushavingno intersectionstothex-axis.
Thisisbecauseinorderforafunctiontohavea x-intercept,thevalueofymustbe0,thusmakingthe equationtobewrittenas x2 +1=0.Asexpected,there isn’tanypossiblerealnumberthatcanbethesolution ofthisequationsinceeveryrealnumbermusthavea positivevaluewhenit’ssquared.Thatsaid,thisisthe primarypartinwhichusingimaginarynumbersiscrucial.Sincetherootoftheequationisiand-i,imaginary termsarenecessaryinordertoconservethefundamentaltheoremofalgebra,sincewecan’tonlyallowthose equationswithsolutionsofrealnumberstofollowthe rule.
3.5Howtofindeverycomplexrootsofanequation
Asthefundamentaltheoremofalgebrastates,any polynomialshouldhavethesamenumberofrootswith itsdegree;however,Isuspecttheschoolhasonlytaught thewaystofindtherealsolutionsanddon’tconsider thoselateralcomplexroots.However,thiscouldbea hugemistakeinthegreatmeaningofalgebrasinceas wesawpreviously,complexnumbersworkandfollowthe
sameruleinmathandtheyarenotnecessarilyalways remainingcomplexnumberssincetheycanbecomereal numbersthroughadditionalcalculationsandmostimportantly,thefundamentaltheoremofalgebrashouldbe conserved.Usingthis,amethodexistsinwhichdervies all n rootsfromanequationapplyingtheconceptswe havelearned.Firstly,considerasituationwhere x4 = i Sofar,thewaythattheequationabovecanbeexpress intermsofxis x = 4 √i.
However,althoughthisistrue,sincetheequation hasadegreeof4,thereshouldbe3moresolutionsto thisandalsowedon’tknowtheactualvalueof 4 √i, expressedinaform:eiϕ
Tostartwiththegeneralpremise,weknowthat thereare4possiblesolutions,thusthereshouldbe4 complexsolutionsintotalthatcouldbelyingonthe complexplane.Inthisway,wecanconcludethateach solutionhasadifferenceof24inanglewiththeprevious root.ThiscouldbeprovenbyfurtheringDeMoivre’s rule,firstlettingntobethedegreeoftheequation, andtobetheangleofthefirstrootoftheequation,it couldbesaidthat n(θ )= ϕ sinceasthedegreeofthe equationis n.Thedistanceissquaredntimesandthe sameangleisaddedntimes.Thisisthesamewith n(θ + 360 n + + 360 n )= ϕ
Sinceanangleaddedwith360degreesequalsitself. Inthisway,theanglewillrotatebythevalue 360 n as wegodownthenumbersthatcanbetherootandthe distancewouldremainallthesameforthoserootswhich wouldbe n √d,where d isthedistanceofthenumber whichhastheseroots.Therotationgoesaroundthe wholecomplexplaneanditwillcomebacktoitsoriginal startingpoint,whichisthefirstroot.Thismeansthat therootshaveadifferenceof 360 n intheiranglesand allofthembecomewhenaddedntimes.Thiscould happenforinfinitybuttheresulthasonlynanglesin totalthattheywouldlastwithwhichisthesamereason whythecycleof i repeats.
Toconsiderthecurrentsituation n(θ )= ϕ where ϕ =90 and n =4.Inthisway,thismeansthat 4(θ )=90, andthisconcludesthatthefirstrootoftheequationis x = ei π 8 .Subsequently,weknowthat 4( π 8 + 360 4 + + 360 4 )=90,theangleofthenextrootwouldbe π 8 + 360 4 whichis112.5degrees,thenextwouldbe202.5andthe nextwouldbe292.5andthenextis382.5whichisthe sameanglewiththefirstangle,22.5( π 8 inrad).Thus the4solutionswouldbe x = e0 392i or e196 3i or e3 53i or e5 1i
Onceyouhavefoundtheangle,youcaneasilylook attheunitcirclediagramandguessthevalueofthe rootintheform: a + bi aswealreadyknowthevalueof thoserootsintheform: eiϕ
3.6RootsofUnity
Forthelastbutnotleasttopictocover,thereare rootsofunity.Byapplyingtheconceptswe’velearned we’llbeabletoprovetwomorerulesthatcouldbe
Fig.18:FunctionwithNoRoots
26
foundincomplexnumbers.First,wecanknowhow togetthemultipleofeveryrootofanumberbygoingthroughasimpleproof.First,considertheprevious casewhere x4 = i.Ultimately,therootsoftheequationwere x = e0 392i or e196 3i or e3 53i or e5 1i andthe sumoftheangleswere 22 5+112 5+202 5+292 5=630, whichequatesto270degrees.Inthisway,thevalueof themultipleofeveryrootis-isinceacomplexnumber with270degreesrotatedand1furtheredfromtheoriginis i whereasthenumberwhichhastheserootsis i.Wecanprovethisbyunderstandinghowthecalculationisdonewhilewearemultiplyingtheroots.First, lettingthefirstrootofacomplexnumberis eiθ where itis ei π 8 inthiscase.Assaidbefore,eachrootshasa differenceof 1 2 π ,sothatthenextrootcanbeusedthat itis ei π 8 · ei π 2 = ei( π 8 + 2π 4 ) .Thiswouldbe e πi 8 · e 2πi 4 · e 2πi 4 andsoon.Thatsaid,thechangeinanglescanbeconsideredasageometricprogressionandtheprogression ofrootis w,w e 2π n ,w e 2π n e 2π n .Wherewisthefirst rootofthecomplexnumber e ϕi n .Intermsoftheangles ontheotherhand,itisanarithmeticsequencesinceas e 2πi n ismultipliedeachtimetoacomplexnumber,the anglesareadded.Thusitis θ,θ + 2π n ,θ + 2π n + 2π n
Weknowthatsinceallthedistancesoftheseroots arethesametheyhavethesamenumbertheyarelasting withwhentheyaremultipliedntimes.Inthisway, themultipleoftheirdistancewouldcorrespondtothe complexnumberthathastheserootsbuttheonlything thatmightchangeistheangleitisawayfromtheorigin. Byturningthisintoasumofanarithmeticprogression formula,Wecansaythat:
2πi n .Thisisbecausethedistanceof1fromtheorigin is1,thusthedistanceofrootsallequalto1sincethey shouldremainthesameeventhoughtheyaresquared ntimesandtheangleis0,butthisalsomeans360. Youcanalsostarttheprogressionwith e θi n ,ifyoulike butthismaymakethecasemorecomplicatedsince youarestartingthesequencefromthenthterm,since w n =1.However,unlikeothergeometricsequences,this sequencerevolvesforeversincetheprogressionwould eventuallycomebacktotheinitialtermasitwillrotate thewholecomplexplane.Inthisway,youmaystart with1,butforthesakeofsimpleexplanation,Istarted theprogressionwith e 2πi n .Butstill,thisworksthesame regardlessofthetermoftheprogressionyouarestarting with.
Thisway, w = e 2πi n ,theprogressionofrootsis w,w e 2π n ,w e 2π n e 2π n andrepeat.Inthisway, w = e 2πi n ,sincetherearenrootsintotalandtheirangles arehavingadifferenceof 2π n andtheprogressioncanbe changedas w,w 2 ,w 3 , ,w n 1 ,w n
Byusingthesumofgeometricsequenceformula, sum = w (w n 1) w 1 .Inconclusion,nomatterwhatvaluew takes,thewholeexpressionbecomes0,thusthesumof rootsof w ,where w n =1 is0.
4Conclusion
Overall,wehavegonethroughthehistoryofimaginarynumbersandthebasicrulesofthecomplexplane. Apparently,thefundamentaltheoremofalgebramakes theusageofimaginarynumbersessentialeventhough theirexistencemaynotmakesenseinreality.Imaginarynumbersarenecessarytomakeanyequationto haveasolutionwhichcan’tbedonebyusingonlyreal numbers.
Asaresult,wenowknowthatthemultipleofroots ofacomplexnumberwillbecomethesamewiththat complexnumberwhenthedegreeisoddnumbersince whenn=oddnumber,thewholevalueoftheexpressionwouldbe ϕ + π ∗ evennumber ,makingthenumber tobethesameas360degreesrotationequalstothe samepoint.Ontheotherhand,whenthedegreen= evennumber,thevalueofmultiplesofrootswouldbe theconjugateofthecomplexnumbersinceitmakesthe pointtoberotated180,makingittheconjugate.This isthereasonwhyweareleftwith-iasthemultipleof rootsofxwhere x4 = i
Lastly,wewillproveasimpleruleofacomplex numberwithrootsofunity.Consideracomplexnumber w and w n =1.Surprisingly,thesumofrootsofwequals 0.Toprovewhythisishappening.
First,considertheprogressionoftheanglesofroots likewehavedonebefore.Theprogressionstartswith
Alsousingimaginarynumbersisnotakindofwordplay,butsometimesevenanequationwithasolution whichhappenstobearealnumberinvolvesimaginary numbersinitssolvingjustlikethespecialcaseinDel Ferro’sformula.Eventhoughtheexpressionseemed virtuallymeaningless,wecouldderivethesolutionby goingthroughthecalculationwhileseparatingimaginarynumbersfromrealnumbers,andinthisway,it couldbesaidthatusingimaginarynumberswasacrucialpartinthesituation.Imaginarynumbersareconsideredsignificantbecauseeventhoughthevaluethey denotedoesn’tmakesense,theirexistenceistheonly waytoconservethelawofmath,-literallyanybasiclaw suchasthemultiplication,subtractionandespecially thefundamentaltheoremofalgebra.Imaginarynumbersstillfollowtherulesofmathandinthisway,the ruleofmathdoesn’thaveanyparadoxorerror.Thus makingmathanunerringsubject.-Inaddition,calculationsinvolvingimaginarynumbersdon’talwaysend upinasubtleandmeaninglessnumberbutimaginary numbersaresometimesconsideredcrucialintermsof derivingareal-numbersolution.
Sumofangles = n( ϕ n +(n 1) 2π n ) 2 = ϕ +(n 1)2π ) 2 = ϕ + π (n 1) (37)
27
1. NegativeNumbers. (n.d.). https://nrich.math.org/5747
2. OpenCourseWare,M.(2017,July 5).Necessityofcomplexnumbers [Video].YouTube.https://www.youtube.com/ watch?v=f079K1f2WQkfeature=youtu.be
3. 3Blue1Brown.(2017,May2).What’sso specialaboutEuler’snumbere?|Chapter5,Essenceofcalculus.YouTube. https://www.youtube.com/watch?v=m2MIpDrF7Es
4. Veritasium.(2021,November1).HowImaginaryNumbersWereInvented.YouTube. https://www.youtube.com/watch?v=cUzklzVXJwo
5. WelchLabs.(2015b,August28).ImaginaryNumbersAreReal[Part1:Introduction].YouTube. https://www.youtube.com/watch?v=T647CGsuOVU
6. WelchLabs.(2015b,September4).
ImaginaryNumbersAreReal[Part 2:ALittleHistory].YouTube. https://www.youtube.com/watch?v=2HrSG0fdxLY
7. WelchLabs.(2015b,September11).
ImaginaryNumbersAreReal[Part 3:Cardan’sProblem].YouTube.
https://www.youtube.com/watch?v=N9QOLr fcKNcfeature=youtu.be
8. WelchLabs.(2016,September3).
ImaginaryNumbersAreReal[Part 13:RiemannSurfaces].YouTube. https://www.youtube.com/watch?v=4MmSZrAlq Kcfeature=youtu.be
9. WelchLabs.(2015c,September18).
ImaginaryNumbersAreReal[Part 4:Bombelli’sSolution].YouTube. https://www.youtube.com/watch?v=DThAoT3 q2V4feature=youtu.be
10. WelchLabs.(2015d,September25).
ImaginaryNumbersAreReal[Part 5:NumbersareTwoDimensional]. YouTube.https://www.youtube.com/watch?v =65wYmy8Pf-Yfeature=youtu.be
11. WelchLabs.(2015d,October2).
ImaginaryNumbersAreReal[Part 6:TheComplexPlane].YouTube. https://www.youtube.com/watch?v=z5IG_6_zP Dofeature=youtu.be
12. WelchLabs.(2015f,October9).ImaginaryNumbersAreReal[Part7: ComplexMultiplication]. YouTube. https://www.youtube.com/watch?v=YHv R8siIiD0feature=youtu.be
13. Dunham,W.(1990).Journeythroughgenius:The greattheoremsofmathematics.NewYork.–https://ve42.co/Dunham90
14. Merino,O.(2006).Ashorthistoryofcomplexnumbers.UniversityofRhodeIsland.–https://ve42.co/Merino2006
15. ScipionedelFerro.(n.d.).math
5bibliography
History. https://mathhistory.standrews.ac.uk/Biographies/Ferro/ 28
ThePainter’sParadox
AlbertJinyongShin Year10Noro
MemberofMathematicsSociety
Email:jyshin26@pupils.nlcsjeju.kr
Editor
JooHyunKim∗
RecommendedYearLevel:KS4andabove
Keywords:Integration,Volume,SurfaceArea,Limit, Infinity,Paradox
Gabriel’sHornParadox,orthePainter’sParadox isnamedafterGabriel,anangelintheChristianBible, whoblowsthehorn.Inmathematics,itreferstothe 3-dimensionalshapeofahornmadefromafull 360◦ revolutionofthegraphof y = 1 x ,where x> 1.The actualparadoxisthattheinnersurface,orthesurface area,isinfinite,andhenceaninfiniteamountofpaint shouldbeneededtopaintalloftheinnersurfaces., butthevolumeofthehornisactuallyfinite,sothe horncouldbepaintedbypouringpaintthenemptying it-aninfiniteamountofpaintisneededtopaintthe sameareathatcouldbepaintedwithafiniteamount ofpaint.Simply,itsaysthatthesurfaceareaisinfinite whilethevolumeisfinite.
3SurfaceArea
Theareaofthetotalsurfaceofanobject.
4Limit
Avaluetowardwhichanexpressionconvergesas oneormorevariablesapproachacertainvalue.
5Infinity
Aconcepttodescribesomethingbiggerthanany naturalorfinitenumber-somethingwithoutaspecific valueorlimit.
6Paradox
Anideawheretwoviewsmakesenseseparatelybut don’tmakesenseatthesametime.
Tounderstandthis,therearefewterminologiesto knowandunderstand:
1Integration
Awayofgettingareaunderagraphandbasedon splittingtheareaunderthegraphintoinfinitelysmall rectangles.
2Volume
Theamountofspacethereisina3-dimensional shape.
∗ MemberofJPAMEditingTeam
Firstly,howdoweknowthesurfaceareaisinfinite, whilethevolumeisfinite?Ifwethinkaboutit,integrationistheprocessofsplittingthegraphintoinfinitely smallrectangles.Inthiscase,asitisa3-dimensional horn,itissplitintoinfinitelysmallcylinders.Theheight ofthecylinderis dx.Lettheradiusbe r .Thenthearea ofthecylinderbecomes:
A = πr 2 dx (1)
Thistendstoinfinity.Hence,wegettheintegral: ∞ 1 πr 2 dx (2)
Thehornisalsosymmetricalwhenviewinga2dimensionalview,wherethetoppartis:
29
y = 1 x (3)
Andthebottompartis: y = 1 x (4)
Thismakestheshapesymmetricalalongthe x-axis; hence,thedistancefromthe x-axistothegraphis y , or 1 x ,whichisequaltotheradiusofthehorn.Ifwe substitutethisvalueintotheintegral,weget: ∞
π ( 1 x )2 dx (5)
Wecouldgetthevolumeusingthis. π ,sinceit isaconstant,couldbepulledforwardsinfrontofthe integral.Moreover,itisquitecomplicatedtoworkwith aninfiniteintegral,sowelet ∞ be c.Thenwegetthe expression:
π c 1 ( 1 x )2 dx (6)
Ifwesolvethisintegral,weget:
π 1 x

c 1 (7)
Butcisinfinite,soweshouldputalimitaroundit toget:
However,wemustassumethatthecylinderisnot perfectlyround,andisslightlyslanted.Ifwelayit out,itlookslikeapartofacirclesegment,likeapizza crust,orFigure1(Fig.1).
Let’ssaythattheinnercurveis A,andthestraight edges B .Wecouldmergethetwoendswithlengths B togethertoformapartofaslantedcone.Whenwe shrink B ,wecouldmakeitintoaderivative;let’ssay thatthisis ds.Weshouldn’tuse x becausethistime, B isnothorizontal;itisslanted. A wouldnowbecome thecircumference,asnowthetwo B sidesarejoined. Togetthecircumference,wesaythattheformulais 2πr ,butforthereasonsexplainedearlier,theradius isagain y ,or 1 x ,Togetthesurfacearea,weagainuse integrationtoget: ∞ 1 2π 1 x ds (9)
(8)
Weshouldnowconvert ds into dx.Thiscanbe expressedasaright-angletriangle;thehypotenuseis theslanted ds,thehorizontalsideis dx,andthevertical sideis dy .UsingPythagoras’Theorem,weget:
Hence,thevolumeisequalto π ,whichisaconstant andthereforefinite.
Wecouldalsofindtheinnersurfaceareaina similarway.Thesurfaceareaalsoworksbyslicing thehornintoverysmallcylinderwithheightof dx
ds2 = dx2 + dy 2 ds = dx2 + dy 2 = 1+( dy dx )2 (10)
Weknowthat:
1
π
= π
c
=
=
=
lim c→∞ ( 1 c ( 1 1 ))
lim
→∞ ( 1 c +1)
π (0+1)
π 1
π
Fig.1:Source:Youtube-NumberPhile
30
Althoughthismightseemcomplex,itisquiteeasy tounderstand.Weknowthat x ∈ [1, ∞].Ifweplugin anyvalue, 1+ 1 x4 willalwaysbebiggerthan1,as x4 alwayshasapositivevalue(evenexponent),and 1+ a, where a ∈ R+ ,willalwaysbebiggerthan1; √b,where b> 1,isalwaysgreaterthan1.Therefore, 1+ 1 x4 is alwaysgreaterthan1forallvaluesof x greaterthan1. Wecannowsolvethis.Thesurfaceareais:
Thenwecansolvethistoget:
Ifwegobacktotheparadoxitself,nowwecan saythat ∞ unitsofpaintisneededtopaintthesame areawhere π unitsofpaintcouldalsopaint;otherwise, itissaying π = ∞,whichisobviouslynottrue,which istheparadox.
y = 1 x = x 1 (11) Therefore: dy dx = x 2 = 1 x2 (12) Hence: ds = 1+( 1 x2 )2 (13)
∞ 1 2π 1 x 1+( 1 x2 )2 dx (14)
Theexpressionfortheinnersurfaceareais:
2π c 1 1 x 1+( 1 x2 )2 dx (15) Where c = ∞ Weknowthat
lim c→∞ c 1 1 x dx =lim c→∞ ln(x) c 1 =ln(∞) ln(1) = ∞ (16)
2π c 1 1 x · 1+( 1 x2
dx isinfinite
1+( 1 x2 )2 isalwaysgreaterthan1.
Therefore,
)2
31
ThePowerTowerFunction
JamesJiminLim Year10Mulchat
MemberoftheMathematicsSociety
Email:jmlim26@pupils.nlcsjeju.kr
Editor JooHyunKim∗
RecommendedYearLevel:KS5
Keywords:LambertWFunction,Derivative,Integral, Tetration,ConvergenceandDivergence
1Introduction
Thepowertowerfunction,alsoknownastheinfinitetowerfunction,isconsideredoneofthemostcomplexfunctions.ThemathematicianLeonardEuler,the fatherofmanydifferentmathematicaldiscoveries,also statedinhisownpaperthat"nomanclearlyknows aboutthepowertower,"denotingthecomplexityofthe function.
2Representation
2.1Generalexpression
Thepowertowerfunctionisusuallyexpressedas:
f (x)= xx (1)
However,toexpressitmorealgebraically,itcanbe furthersimplified.Sincethereareinfinitelymanypowersof x,wecanexpressthisas:
y = xy (2)
Thismethodismorepreferredwhensolvingmathematicalquestionsandconjectures,howeverisnotthe mostelegantmethodtoexpressthefunctionitself.
2.2AlternateMethod:LambertWFunction
2.2.1LambertWfunction
TheLambertWfunctionisoneofthespecialfunctionsandisalsoknownastheomegafunctionorthe productlogarithm.Itwasdiscoveredandnamedafter aFrenchmathematiciannamedJohannHeinrichLambertandwasfirstintroducedinhisarticle"Lambert’s TranscendentalEquation"in1758.Thisspecialfunctionisoftenusedwhensolvingequationsinwhichthe unknownvariableisbothinsideandoutsideofanexponentialoralogarithmicfunction.TheLambertW functioncanbenotedas:
TheLambertWfunctionalsohasauniqueproperty where:
Whichcanbefurtherappliedindifferentbranches ofalgebraandcalculus.
2.2.2UsingtheLambertWFunction
Fromthegeneralexpressionofthepowertower functionabove,thenaturallogofbothsideswilllook as:
) (5)
Throughmultiplesteps,theequationcanbeturned intothefollowing: 32
∗ MemberofJPAMEditingTeam
W (x)= f 1 (x),f (x)= xex (3)
W (x)e W (x) = x
(4)
ln(y )= y ln(x
1 y ln(y )= ln(x)
1 y ln( 1 y )= ln(x)
ln( 1 y )eln( 1 y ) = ln(x)
(6)
usedinsimpleproblemsolvingorfindingspeed(in kinematics),butarealsocreativelyusedinotherparts ofmathematicssuchaspredictingfluctuationsinstock marketsetc.
Thederivativeofthepowertowerfunctioncanbe rathereasilycalculated.Fromthegeneralexpression ofthepowertowerfunction,puttingthenaturallogon bothsidesleadto:
Fromthisstage,theimplementationoftheLambert Wfunctionwillsimplifythisequationinto:
ln( 1 y )= W ( ln(x))
1 y = e W ( ln(x)) (7)
Beforeanymoremanipulationofthecurrentequation,thepropertyoftheLambertWfunctioncanbe slightlymodifiedinto:
W (x)e W (x)= x
e W (x) = x W (x) (8)
Then,theequationfinallyresultsinto:
1 y = ln(x)
W ( ln(x))
y = W ( ln(x)) ln(x) (9)
AlthoughtheutilisationoftheLambertWfunction makesthefunctionmoreelegant,therearelimitations ofthisformula.Thebiggestlimitationisthatthisformulaforcesthepowertowerfunctiontoconvergewith anycomplexvaluesof x,whichisnottrue.Thevalues of y onlyconvergesintheinterval[e e , e 1 e ]intheinitial powertowerfunctionandoutsidethisdomain,thefunctiondiverges.Therefore,inordertousethemodified formulawiththeLambertWfunction,itisnecessaryto maketheassumptionthattheinfinitetetration(power) of x convergestoavalue,orthevalueof x isinthe interval[e e , e 1 e ].
3Calculus
3.1Derivative
Thedefinitionofderivativevariesindifferent branchesofmathematics,butincalculusthederivative ofafunctionistherateofchangeofanunknown variablewithrespecttoanotherunknownvariable. Inpuremathematics,derivativesoffunctionsare
Usingimplicitdifferentiation,amethodofdifferentiationwhenitisnecessarytodifferentiatebothsides treatingeachvariableasawholefunction,theequation becomes:
3.2Integral
3.2.1Integration
Comparedtothederivative,theintegralofthe powertowerfunctionisnearlyimpossibletobemanuallycalculatedbyhandduetothedifficultyinthe integration.However,itcanbepartlyderivedusingthe LambertWFunction,thoughitstilltakesnumerous stepsbeforehand.
3.2.2Integraloftheinverse
Theintegraloftheinverseofafunctionexistsand thewayitisderivedisasthefollowing:
Substitutingthisintotheoriginalequationbecomes:
y = xy ln(y )=ln(xy ) ln(y )= y ln(x) (10)
1 y dy =ln(x)dy + y x dx xdy = xy ln(x)dy + y 2 dx (x xy ln(x))dy = y 2 dx dy dx = y 2 x xy ln(x) (11)
f 1 (x) dx (12) Let u = f 1 (x) x = f (u) dx = f ′ (u)du (13)
uf ′ (u) du (14) 33
Usingintegrationbypartsthisisexpandedas:
uf (u) f (u) du = xf 1 (x) F (u) = xf 1 (x) F (f 1 (x))+ C
3.2.3IntegralofLambertWFunction
(15)
Usingtheproductruleandletting u = 1 ln(x) and dv = W ( ln(x)),theintegralofthepowertowerfunctionis:
Theformulaoftheintegraloftheinversecanbe usedtocalculatetheintegraloftheLambertWFunction.However,astheinitialgoalistocalculatethe integralofthepowertowerfunction,itisrequiredto calculatetheintegralof W ( ln(x)) ratherthan W (x) Thecalculationisasthefollowing:
f 1 ( ln(x))= W ( ln(x))
f ( ln(x))= ln(x)e ln(x)
AstheintegraloftheLambertWFunctionisalreadycalculated,iftheexpressionissubstituted,itbecomes:
f ( ln(x))= ln(x) x
(16) Let u = ln(x) du = 1 x dx (17)
Goingbacktotheintegralof ln(x) x
Substitutingthisbackintotheoriginalequationwill finallygivetheintegral:
Usingtheformulafortheintegraloftheinverse,the integraloftheLambertWFunctionis:
xW ( ln(x))+ ln2 (W ( ln(x)) 2 (19)
3.2.4CalculatingtheIntegral
Tocalculatetheintegralofthepowertowerfunction,theproductrulemustbeused.Theproductrule isasthefollowing:
= uv vdv (20)
Asmentionedabove,sincethisintegralusesthe LambertWFunction,thisintegralisonlyvalidinthe domain[e e ,e 1 e ]
4PowerTowerFunctionandtheComplex Plane
4.1ComplexPlane
Thecomplexplane,alsoknownastheArgand planeoftheGaussplane,isaplanetorepresent plottingofcomplexnumbers.Thecomplexnumbers thatareplottedusuallycomeintheformof z = x + yi, where x and y arethehorizontalandverticalaxis respectively.However,dependingoncircumstances, thepointscouldbeplottedas z = reiθ ,where θ isthe anglebetweenthelinethatconnectsthepointandthe originandthehorizontalaxisand r isthelengthofthe line.
ln(
x = udu = u2 2 = ln2
x
2
x)
(
)
(18)
udv
1
ln(x) W ( ln(x)) ( W ( ln(x)))u ′ (21)
1 ln(x) (x(W ( ln x)))+ ln2 (x) 2 ) (x(W ( ln(x))+ ln2 (x) 2 )u ′ (22)
u = 1 ln(x) u = ln 1 (x) du = ln 2 (x) x dx du = 1 x ln2 (x) dx (23)
Thederivativeofuisasthefollowing:
1 ln(x) (x(W ( ln(x)))+ ln2 (x) 2 ) (x(W ( ln(x))+ ln2 (x) 2 ) 1 x ln2 (x) dx (24)
34
Themaindifferencebetweenthecomplexplane andthecartesianplaneisthatinthecomplexplane, the y axisisimaginaryinsteadofreal,whichenables ustoplotcomplexnumbers.
Themainreasonfortheuseofthecomplexplane istogeometricallyrepresenttheconvergenceandthe divergenceofafunction.Inthecomplexplane,xcoordinateswithyvaluesthatconvergeinthecartesian planeareplottedasablackandvaluesthatdivergeare plottedaswhitedots.Thisway,differentfunctionsshow differentinterestingshapesinthecomplexplane.
4.2PowerTowerFunctioninthecomplex planeandthefractalshape
Thepowertowerfunctioninthecomplexplanehas averycomplexandaninfinitefractalshape.
Fractalisdefinedasamathematicalshapewhere thepatterninfinitelycontinuesforever.Nomathematicianhasfoundoutthereasonbehindthefractalshape ofthepowertowerfunctioninthecomplexplane, howeveritisassumedtoberelatedtotheinfinite tetrationof x.
5Bibliography
1. Peter,L.(2013).ThePowerTowerFunction[online]https://thatsmaths.files.wordpress.com/2013/ 01/powertowerlambert.pdf
2. Steve,C.(2018). TheMost FunDerivativeofxˆxˆxˆx... https://www.youtube.com/watch?v=i_l1lz26C2M
3. Mathoma.(2016).CoolMath:TheLambertWFunctionAndInfiniteTetration https://www.youtube.com/watch?v=TNeJyVzDU20
4. Steve,C.(2021).LambertWFunction https://www.youtube.com/watch?v=Qb7JITsbyKs
5. CueMath.ArgandPlane-Definition, Formulas,Properties,PolarForm... https://www.cuemath.com/geometry/argandplane/
6. PeterL.TheFractalBoundaryofthePower TowerFunctionhttps://maths.ucd.ie/plynch/Publications/PowerTower.pdf
u ′
Fig.1
AsseeninFigure1(Fig.1),thecomplexnumbers areplottedasdotsandthevectorcanberepresented asarrows.
Fig.2
35
ConicSectionasLociofPoints
SophieJisuLee
Year11Mulchat
MemberoftheMathematicsSociety
Email:jisulee25@pupils.nlcsjeju.kr
Editor EmmaChaeeunChung ∗
RecommendedYearLevel:KS4andabove
Keywords:ConicSection,Eccentricity,Ellipse, Parabola,Hyperbola
1Introduction
Conicsectionisoneoftheconceptsofgeometry.It demonstrateshowdifferentfiguresareformedbyonly usingtwoobjects,aconeandaflatplane.Itseemslikea simplemethod,butitisacomplexideatounderstand theprocess.Howiseachfiguredefinedasaspecific shape?
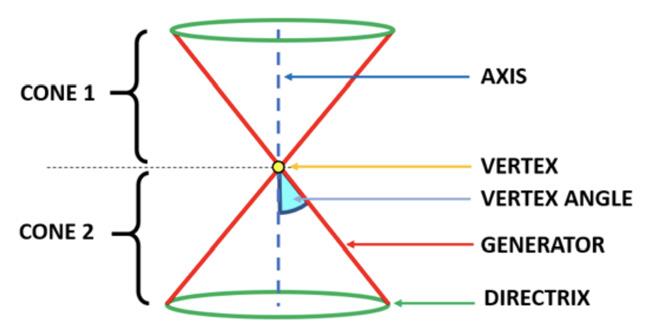
2Cone
Coneisathree-dimensionalshapewithaflatcircularbasecalleddirectrixandapointededgecalledthe vertex.
foundbytheformula θ 2 whilethethetaisequaltothe givenangle.
3ConicSection
Conicsectionisafigureformedbytheintersection ofaflatplaneandacone.Thereisacircle,ellipse, parabolaandhyperbolaforthetypesofaconicsections. Theformedshapesdependontheangleoftheflatplane intersectingthecone.
4DandelinSphere
ADandelinsphereisasphereinsidethatistangent toacone.Itislocatedperpendiculartotheconeaxis, andtheaxisdividesthethetaintotwo.Thissphere isalsocalleda‘focalsphere’becauseofthename‘focus’ofitspointsthattouchtheplane.Insomecases, twoDandelinspheresareneededinoneconetoforma particularfigure,ahyperbola.Thisideacanprovehow theshapesareformedinaconethroughclearimages showingthelocusofpoints,furtherexplainedinlater sections.
5Eccentricity
Inafocus-directrixproperty,thetheoremproven byDandelinspheresstatesabouttheconstantineach conicsectioniscalledeccentricity.
Fig.1:
Thediagramaboveshowsthefigureoftwocones reverselyattachedattheirvertex.Thegeneratorsare thelinespassingthroughthevertexatavertexangle fromacone.Thevertexangleistheanglebetweenthe verticalconeaxisandthegeneratorofacone.Itcanbe
Eccentricityisanon-negativerealnumberedvalue inaconicsection.Itistheratioofthedistancefrom anypointtothefocusdividedbythedistancefromthat pointtothevertex,expressedin [e = c a ].
Aseccentricityisaconstant,itcandistinguishthe shapeofaconicsection.Itisduetothedifferentdistancesandanglesthateachshaperequirestobeformed. Thiscanbeinferredfromtheequation e = c a above,as thevalueofewillvarybyvaluecanda.Thus,thereis arangeofeccentricityforeachconicsectionthatdefines
∗ MemberofJPAMEditingTeam
36
itsshape.Thiswillbeintroducedinthesectionswhere eachconicsectionisexplained.
6Ellipse
Anellipseisformedundertheconditionwhere 0<e<1.Thefigurecanbeprovedthatitisanellipse throughitsproperty.PointP.isthelocusofthepoint. F1.andF2indicatesthefocalpointsoftheintersectioncurveC.ThesefocilieonthecurveCandarerespectivelylocatedonthefirstandtheseconddandelion sphere.
Inordertoprovetheconicsectionasacircle,only onefocuspointisrequired.Similartotheellipse,assumethatthisfocuspointismovingaroundthecircumferenceoftheconicsection.Asthepointwherethe verticalaxisandtheintersectionpointmeetsisthecentreoftheconicsection,thedistancebetweenthefocus pointandthecentrewillremainconstantasthefocus moves.Thisisthepropertyofacirclethatanypointon acircumferenceisalwaysequidistantfromthecentre,as mentionedabove.
8Parabola
Aparabolaisasymmetricalcurvewhereanypoint isatanequaldistancefromafixedpoint,focus.Itis formedwhentheplaneintersectstheconeinparallelto thegeneratorline.
Theeccentricityshouldbe1.Aparabolahasthis specificvaluefortheeccentricityratherthanarange becauseitcanbeformedintheonlycasewhereitsgradientisequaltotheslantofthegeneratorline.This meansthatthedistancefromanypointtothefocus andthedistancefromthatpointtothevertexmustbe thesame.
AssumethatthepointPmovesaroundthealong thecurveC.ThedistancesbetweenthepointPand eachF1,F2varydependingonthelocationofP.The importantfactorofthiscaseisthesumofthedistance fromPtoF1andPtoF2,whichcanbewritteninthe expression:
S = d(P,F 1)+ d(P,F 2) (1)
Thesumwillremainthesame.Thisistheproperty andalsothedefinitionofanellipse,wherethesumof thelocusofapointfromthetwofocalpointsisthe constant.
7Circle
Acircleisafigureofallpointsequidistantfromone point.Acurveneedstointersecttheconeinparallelto thebase,perpendiculartothedirectrix.
Theeccentricityis0foracircleduetothesame locationofthecentreofacircleanditsfocus.Using theexpression e = c a ,eresultsin0regardlessofthe valueofaandthevalueofcis0.
Toprovethattheintersectionisaparabola,aflat planeperpendiculartotheconeabovethesphereandan additionaltwocirclesparalleltothisplaneareneeded. TheplaneEwillbetheplaneinwhichitsgradientis equaltotheslantofthecone.
ThegeneratorlinegistangenttopointMonthe sphereandstartstorotatearoundthecircle.Theplane K,paralleltothebaseofthecone,intersectsthesphere throughthecirclethatpointsMandAlieon.
WhenlinegmeetstheintersectionplaneE,pointP istheintersectionpointofplaneE,linegandthecircle closesttothecone.AsthepointsFandMareboth tangentstothesphere,PFisequaltoPMaccordingto two-tangenttheorem.PointNliesonplaneEandplane K,formingaperpendicularlinetopointP.Thisinforms thatNPandABisthesamelengthastheyareinthe
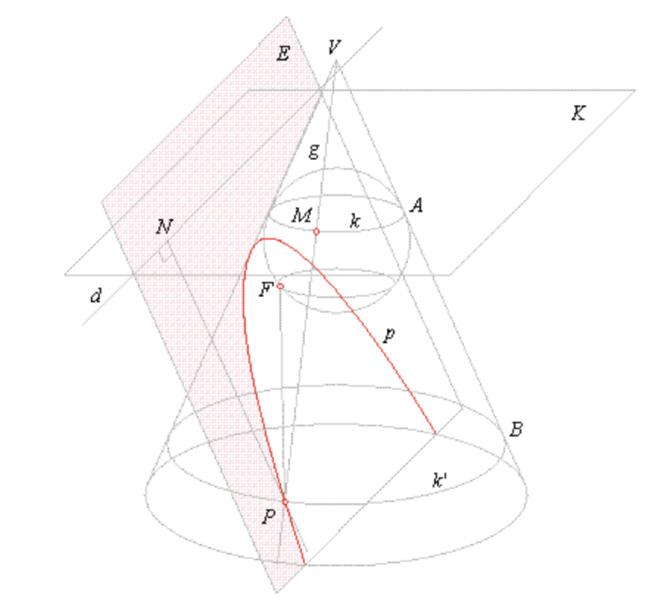
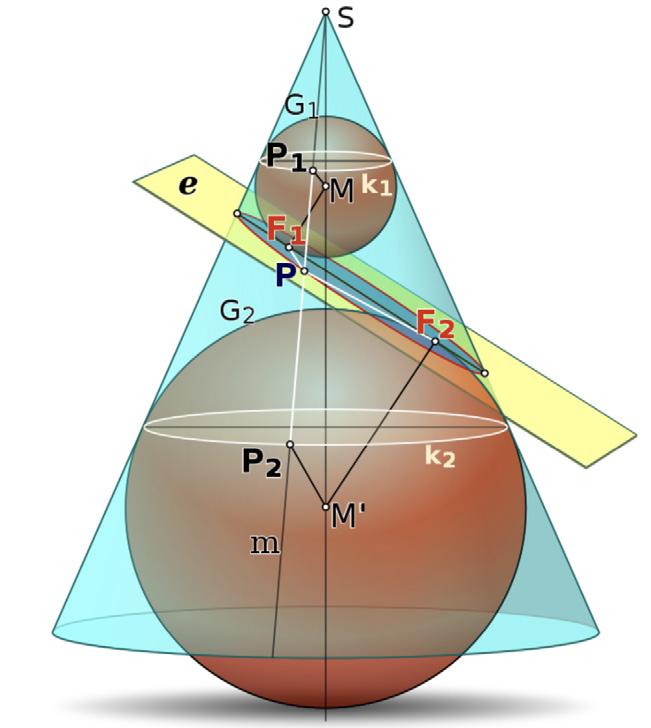 Fig.2:
Fig.3:
Fig.2:
Fig.3:
37
samegradientwithpointNandA,andpointPandB eachlieatthesameheight.ABequalsMP.Thus,it isNP==PM=BA.Thisisinterpretedthatthedistance fromthemovingpointPtothefixedpointFandthe linedwillalwaysbethesame,matchingthedefinition ofaparabola.
9Hyperbola
Ahyperbolaisatwo-branchedopeninfinitecurve symmetricalongitsconjugateaxis.Itisformedwhen theplaneintersectsbothnappesofadoublecone.
Itcanalsobedefinedasthelocusofapointmoving inwhichtheratioofthedistancefromthefocustothe distancefromthedirectrixisaconstantgreaterthan one.Thismeansitseccentricityshouldbegreaterthan 1,expressedine>1.
tothepointP.Thentwoequationscanbewritten:
PM = PF 1
PN = PF 2
ThepointP,MandNlieonthegeneratorlineg, whichmeansthatMN=PM-PN.Also,asonlythepoint PismovingwhileF1andF2areatthefixedpositions,it isdeducedthatPF1-PF2isconstant.Thelocusofpoint PontheintersectioncurvehfromthefixedpointsF1 andF2isconstant,thereforethecurveisahyperbola.
10Bibliography
1. https://mathimages.swarthmore.edu/index.php/ConicSectionCircles
2. https://mathimages.swarthmore.edu/index.php/DandelinSpheres-TheoryTwo-Theorems
3. https://www.ucl.ac.uk/rmhajc0/cone.pdf
4. https://mathimages.swarthmore.edu/index.php/ConicSectionCircles
5. https://byjus.com/maths/eccentricity/
6. https://mathimages.swarthmore.edu/index.php/DandelinSpheres-TheoryTwo-Theorems
7. http://www.nabla.hr/PC-ConicsProperties2.htm
Todemonstrateahyperbola,adoubleconeandtwo spheresineachnappearerequired.TheflatplaneE verticallyintersectsatasmalleranglethantheangleof thegeneratorlinetogoacrossbothnappesofthecone. Thehyperbolahisthelineofintersectionoftheplane Eandthecone.
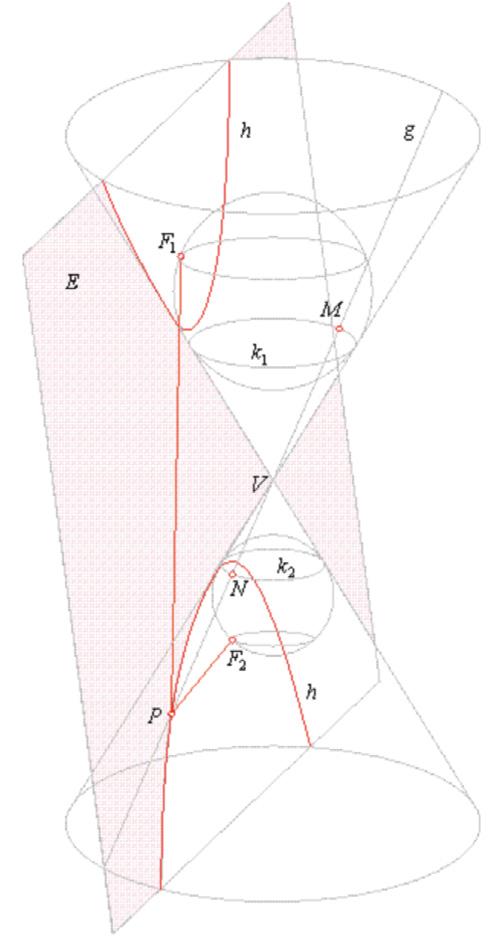
IttouchesthetwospheresatthepointsF1and F2.Insideeachtwosphere,therearethecirclesk1 andk2touchingthecone.ThepointsMandNlieson eachcirclek1andk2,andthegeneratorlinegintersects acrossthesepoints.
AsthelinegrotatesaroundtheconeatthevertexV,thePmovesalongthehyperbolah.Theline segmentsPF1andPMarethetangentsfromtheupper sphere,PF2andPNthetangentsfromthelowersphere
Fig.4:
38
https://mathimages.swarthmore.edu/index.php/Dandelinhttps://mathimages.swarthmore.edu/index.php/Dandelin-
InscribedRectangleProblem:Topology
DerekYejunYoo Year10Noro
MemberoftheMathematicsSociety
Email:yjyoo26@pupils.nlcsjeju.kr
Editor EmmaChaeeunChung ∗
RecommendedYearLevel:KS4andabove
Keywords:Topology,InscribedRectangle,Mobius Strip
1Introduction
Oneofthemostcommonstatementsrelatedto Topology;topologistsviewacoffeemugandadoughnut tobethesame.Butthesestatementsalwaysleavea question:howisthisrelatedtomaths?Asanexample oftopologybeingusedtosolveamathsproblem,The “inscribedrectangleproblem”iselegantlysolvedby understandingthepropertiesoftheconcept.
fourverticesthatwillcreateanyformofasquare?This probleminvolvesunderstandingtopologyatahigher level,sinceitisaquestionthathasbeenyetanswered.
2Theinscribedrectangletask Toshowtheessenceoftopologyinvolvedinthis question,asolutionwouldbefurtherexploredfora weakerversionoftheproblem.Asaninitialapproach totheproof,wehavetounderstandthefeaturesofa rectangle;thetwodiagonalsegmentswouldalwaysbe equalinlengthpassingthrougheachother’smidpoint.
Theinscribedrectangleproblemoriginatedfrom along-lastingproblem;Theinscribedsquareproblem, alsoknownastheToeplitz’conjecture:WouldaJordan curve(figure.1)-planesimpleclosedcurve-alwayshave
Beingthekeytotheproblem,Infigure.2,ifwecan guaranteethatsegments(A,C)and(B,D)sharetheir midpointFanddistance,thequadrilateralwouldbe provedarectangle.Hence,atthispoint,arectangle canbeevaluatedbythreepoints:twodescribingthe distancebetweenthepoints,andonedescribingthemidpoint.
3Dataintothe3Dplane
Theinformationcanbesimplifiedwiththefunction f(A,B)=x,y,z.Pointsxandywouldcoordinatethe segmentontheinitialcurve,butthezvaluewouldhave
Fig.1:
∗ MemberofJPAMEditingTeam
Fig.2:
39
xandyvalueatthemidpointandazvalueofthelength ofthesegment.Then,thismeansiftwosetsofvalues haveasharedzvalue,itshouldsimultaneouslysharethe midpointandlength:ultimately,aprovenrectangle.
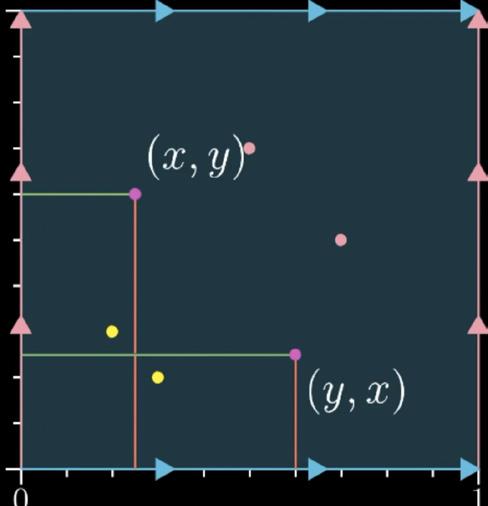
4OrderedorUnorderedpairs?
Ifweassumethatwearecuttingthecurveatone point,andstraighteningit.Thetwopointsmakingup asegmentwouldlieonastraightlinerepresentingthe curve.Figure.3wouldbeshownasfigure.4.
thiscasethereciprocalrepresentationjustshowsthe samesegment,wehavetorepresentthesepointsasan unorderedpaironfigure.5.
Then,extendingthisrepresentationintoa2dimensionalplane,eachpointwouldrepresentingavalueof anaxis(figure.5)

Inthisrepresentation,wecanfindalineofsymmetrythatjustreflectstwopointsprovidingthesame information.So,thefollowingisrequired.
However,nowthereisadistinctionbetweenanorderedpair,andanunorderedpair.Anorderedpairdescribes(a,b)and(b,a)tobeseparatepoints;whereas, unorderedpairssaytheopposite.Consideringthatin
Theplaneisfoldedinhalf,dissolvingtwosame pointstoone.However,toproperlyrepresentthe points,thebluearrowshavetobeconnectedtogether, seemingimpossible.
 Fig.3:
Fig.4:
Fig.5:
Fig.6:
Fig.7:
Fig.3:
Fig.4:
Fig.5:
Fig.6:
Fig.7:
40
Fig.8:
Alternatively,theplaneiscuttedinhalf,imposing arathereasierway:yellowarrowsshouldbetogether inthesamedirection,andsameforthebluearrows.
tothe3D-plane,itmeansthatatleasttwounordered pairsofpointscorrespondstothesameoutputofthe zvalue:provingourpremisethatiftherearetwodistinctsegmentsoutputtingthesamezvalue,itcreatesa rectangle.
6RequiredImprovements
Theprocesswascorrect,howeverthefinalstepof consolidatingthestripintothe3D-planehasbeenmore “seemingtrue”thanproved.Furthermore,inadifferent circumstanceknownasthe“SudaneseMobiusBand”, Dr.BlainLawsonhasproventhatitispossibletoarrangetheMobiusstripinawaythattheedgesdon’t passeachother.However,theprocessexplainedinthis writingstillhasspacetoremainsolid.Thepractical proofthatDr.Lawsonprovidedthesurfaceofthestrip togobothunderandabovethecurveformedbythe edge,whichisnotsoinourcase.
Theorientationoftheplanenowallowstheblue arrowstounify,followedbyflippingoneoftheedgesto connectwiththeotheryellowarrow.
4.1TheMöbiusStrip
Surprisingly,theshapeappearstoshowdirectcongruencewiththeMobiusstrip(!!).Evidently,theplane thatrepresentsallpointsonacurvehappenstobea Mobiusstrip.
5Proof
Now,bringingbackthe3Dplanepreviouslyexplained,thereisahighcorrelationbetweentheMobius stripandthegraph.Sincethestripisadirectrepresentationofthecurveonthexy-plane,theMobius stripiscapableofreplacingtheprimitivecurve;Inthe Mobiusstrip,theedgesarerepresentingasinglepoint, notasegment.Sodoesthexy-plane.Hence,wewould havetomanipulatethesizeandshapeofthestrip(In thisprocess,thevaluesareneverdistortedsinceitis justchangingthescalefactorsofthevalues).Inthis process,thenatureoftheMobiusstripdoesnotallow thisharmonisingsteptohappenwithouttheedgespassingeachother.SincetheMobiusstripvisualisespoints onthecurve,ifthestiphastointersectitselftofitin
 Fig.9:
Fig.10:
Fig.9:
Fig.10:
41
FindingtheOptimalPolicytoExploretheGrid WorldusingDynamicProgrammingand Q-learninginReinforcementLearning
AarenJoonseokKang
Year12Halla
ChairoftheMathematicsSociety
LeaderoftheJPAMEditingTeam
Email:jskang24@pupils.nlcsjeju.kr
Editor
AarenJoonseokKang∗
RecommendedYearLevel:KS5andAbove
Keywords:ReinforcementLearning,DynamicProgramming,Q-learning,Grid-World,OptimalValue Function
1Introduction
1.1MachineLearning
Therearenumeroustasksthatcomputersarecapableofandarefasterinthanhumans.Thisisthe mainreasonforcreatingnumerousmachinesandsystemswithartificialintelligence(AI)embedded.Althoughanartificialintelligencethatperformssimple tasksseemseasytocreate,thereareheavybehind-thescenescalculationsconcurrentlyprocessed.
Themachineswithartificialintelligencethatare mostseeninoureverydaylivesarebasedonatrainingprocessnamedmachinelearning.Machinelearning canbefurtherbranchedintothreedifferentparadigms oflearning:supervisedlearning,unsupervisedlearning, andreinforcementlearning.Supervisedlearningand unsupervisedlearningarebasedonpre-givendata,while reinforcementlearningistraininganAIbasedontrial anderror.Thispaperwillparticularlyfocusonreinforcementlearningonagridworldenvironmentthatis designedincustom.
1.2ReinforcementLearning
Onekeyconcepttoreinforcementlearningisthat theagent,theAIitself,willlearnhowtoproducethe bestoutputinthegivenenvironmentbyexploringthe
∗ ChairofMathematicsSociety,LeaderofJPAMEditingTeam
environmentthroughtrialanderror.Itwillexploreaimingtomaximisethenumericalrewardthatisgivento theagentineachaction.Theultimategoaloftheagent istomaximisetheaccumulatednumericalrewardatthe endofoneepisodeoronetrial.
Thispaperaimstoimplementbothsimulationsof dynamicprogrammingandQ-learninginacustomised basicgridworldenvironmenttocomparetheprocessof training.
2Keywords&BackgroundKnowledge
2.1ReinforcementLearningKeywords
Itisessentialtounderstandthebasicconceptsand keywordsofreinforcementlearningasitissignificantin understandingthelargerconceptsthataregoingtobe mentionedinthispaper:
1. Agent -Agentisthecomputerwhichinteractswith theenvironmentthroughobservingandtakingactions.Itsultimategoalistomaximisethereward inasingleepisodebyfindingaseriesofoptimal actions.
2. Environment -Theagentinteractswiththeenvironmentthroughaseriesofactions,statechanges, andtherewarditreceives.Theinteractionisdisplayedinthefigure1:Thekeywordsstate,reward, andactionsdisplayedinthediagramarefurtherdefinedbelow.
3. State -Stateisasetofinformationwhichdefines thecurrentsituationoftheagent.Theinformationinthestatecanbetransformedwhentheagent takesanactionintheenvironment.Thestatein timestep t isdefinedas St
4. EndCondition -Theendconditionisthecon42
Fig.1:Agent-EnvironmentInteraction ditioninwhichtheepisodewillterminate.The agent’saimistoreachthisstatewiththemaximised reward.
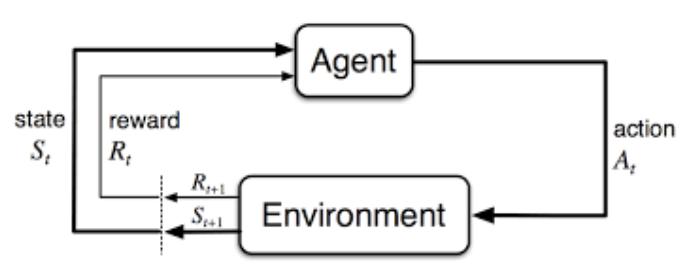
5. Action -Actionisthedecisionmadebytheagent dependingontheenvironment.Eachactionwill changethestateoftheenvironmentandtheaction takenattimestep t isdefinedas At
6. Reward -Rewardisanumericalvalueinwhichthe agentaimstomaximiseattheendoftheepisode. Rewardisawardedtotheagentforeveryaction thattheagenttakes.Similartostatesandactions, therewardattimestep t isdefinedtobe Rt .The rewardfunctioncanbemodelledintermsofthe currentstateandactionusingtheconditionalprobability:
2.2GridWorld
Itisalsoakeysteptodefinetheenvironmentin whichtheagentwillinteractthroughoutthispaper. Therearegoingtobetwodifferentgridenvironments whichtheagentisgoingtobeinteractingwith.
Agridenvironmentingeneralisasimpleenvironmentwhichisformedofatwodimensionalplane.Each gridisnumberedwiththetuple (x,y ) andtheagentcan movealongthegridinthefourdifferentcompassdirectionsineachtimestep.Unlessthereareotherspecific rules,theagentwillbeabletomovealongasinglegrid inasingletimestep.
Thefirstgridinwhichtheagentwillreactwithisa fourbyfourgridinwhichtheendconditionisdefinedto beatthecoordinates (0, 0) and (3, 3) whicharethetop leftandthebottomrightcorner.Everyothercoordinate ofthegridwillreturnthenumericalrewardof 1.The gridwilllooklikethefollowing:
7. DiscountFactor -Discountfactorisusedtocalculatetheprojectedrewardaswellasthereward receivedineachaction.Asthesignificanceofthe actionwilldecreaseasitisdoneinthefurtherpast orfuture,thediscountfactorisusedtoweigheach action’sreward.Thediscountfactorisdefinedas γ whichisintheinterval[0,1]asitismultipliedtothe actionsthataredoneinthepastinanexponential sense.Forexample,theweightedrewardforthe actiontakenntimestepsagowouldbe γ n Rt n where n ≤ t
8. ExpectedReturn-Expectedreturnisthesumof theprojectedrewardbasedontheactionsthatthe agentchoosesinthecurrentstate.Itissignificant whentheagentisdecidingforanactionasitsgoal istomaximisetherewardatthefinalstate.The expectedreturnGtattimestep t ismodelledas:
Thesecondgridworldwouldbearectangulargrid withthesizethreebyfour.Theendstatewillbeatthe twocoordinates (0, 3) and (1, 3),yetthetwocoordinates willhavedifferentrewardsof +1 and 1 respectively. Thestartingcoordinatewillbe (2, 0) asseeninthediagram,aswellashavingagridwhichtheagentcannot enterat (1, 1)

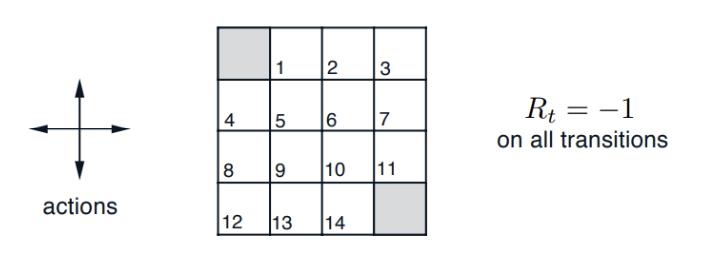
9. Policy-Policyistheactionthattheagentformulatestofollowthroughtheepisode.Inorderforthe agenttomaximisetherewarditreceives,itwould havetofindanoptimalpolicywhichisdefinedto havetherewardthatisequalorlargertoallthe otherpolicies.Thepolicyisnotatedwith π andis modelledasaconditionalprobability:
MarkovDecisionProcessisanessentialconceptunderlyingreinforcementlearningasitisalargepartof definingtheenvironment.TheMarkovdecisionprocess willonlybeimpliedwhentheenvironmentisfullyobservablewithanadditionalpropertythat“thefutureis independentofthepastgiventhepresent”.Thisspecific propertycanbemodelledasanequationofaspecific
Ra s = E[Rt+1 |St = s,At = a] (1)
Gt = Rt+1 + γRt+2 + ··· = ∞ k =0 γ k Rt+k +1 (2)
π (a|s)= P [At = a|St = s] (3)
Fig.2:GridWorld1
Fig.3:GridWorld2
2.3MarkovDecisionProcess(MDP)
43
inwhichtheexpressionimpliesthatthecurrentstate containsalltheinformationofthecurrentstatestraversedbytheagent.
Themarkovdecisionprocessinreinforcementlearningisdefinedasthetuple (S,A,P,R,γ ) where S isthe finitesetofstates, A isthefinitesetofactions, P beingthestatetransitionprobabilitymatrix, R beingthe rewardfunction,anddefinedasthediscountfactor.
2.4ValueFunctionsandBellmanExpectation Equations
DerivedfromtheMDP,therearetwovaluefunctionsdefinedinreinforcementlearningfortheagentto basethelearningfrombothvaluefunctionsreturnsthe expectedreturn.
Thestate-valuefunctionistheexpectedreturn whengiventhestatethattimestep t whichis St followingpolicy π .Thefunctionismodelledasafunction v whereittakestheparameter s:
Thus,byutilisingthetreediagrambelow,thevalue function vπ canbeexpressedintermsof qπ (s,a) tofind theBellmanExpectationEquationfor vπ :
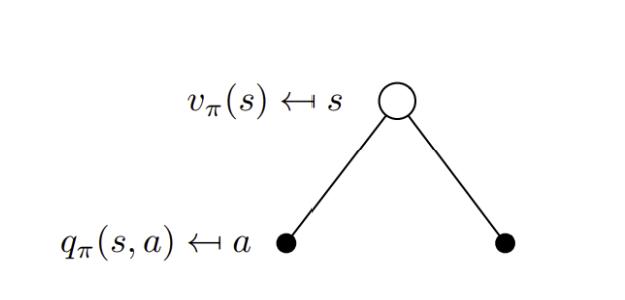
Thesecondvaluefunctionistheaction-valuefunctioninwhichisexpressedastheformoftheexpected returnfromstate s takingaction a,followingpolicy π Thisismodelledasthefunction q whereittakes s and a asthetwoparameters:
Usingasimilartreediagram,buttransformedin orderfortheaction-valuefunction qπ tobetheroot nodeofthetree(Figure4),theBellmanExpectation Equationfor qπ canbeexpressedas:
BothvaluefunctionscanbeexpandedtobeexpressedastheBellmanExpectationEquationwhich showstherelationshipbetweenthestate-valuefunction andtheaction-valuefunction.
Inordertogettotheequationswhichareexpressed intermsof vπ and qπ ,thetwofunctions vπ and qπ have tobedecomposedtopossessrecursiveproperties:
Thesevaluefunctionsaresignificantintheprocess oftrainingtheagentusingQ-learningasitisQ-learning isbasedontheactionvaluefunctioninordertofindthe bestactionsateachstate.
3ExploringusingDynamicProgramming
Inthissection,thegridworldwillbeexploredusing dynamicprogramming(DP).DynamicProgrammingis ageneraltechniqueofsolvingtheproblemusingtwo differentcharacteristics:optimalsubstructureandoverlappingsub-problems.
Thesimilarprocesscanbedonefor qπ whichderives thenew qπ (s,a) topossessarecursiveproperty: q
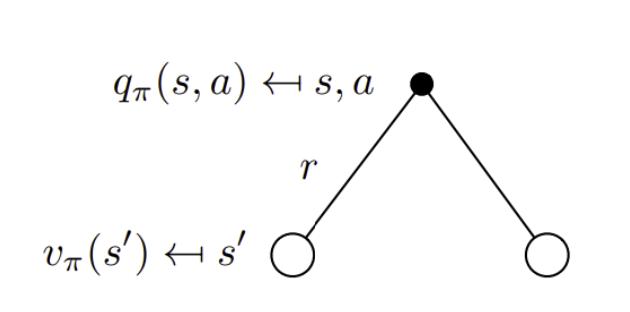
3.1DPSimulation
SimulatingDPinreinforcementlearninginvolves twomainsteps:iterativepolicyevaluationandpolicyimprovement.DynamicProgrammingisoneofthe
stateatatimestep t: P [St+1 |St ]= P [St+1 |S1 , ,St ] (4)
vπ (s)= E[Gt |St = s] (5)
qπ (s,a)= Eπ [Gt |St
s,At
=
= a] (6)
π (s)= Eπ [ ∞ k =0 γ k Rt+k =1 |St = s] = Eπ [Rt+1 + γvπ (St+1 |St = s
v
] (7)
π
s,a)= Eπ
Rt
π
S
t
s,At = a]
(
[
+1 + γq
(
t+1 ,A
+1 )|St =
(8)
vπ (s)= a∈A π (a|s)qπ (s,a) (9)
Fig.4:TreeDiagramfrom vπ
qπ (s,a)= Ra s + γ s′ ∈S P a ss′ vπ (s ′ ) (10)
Fig.5:TreeDiagramfrom qπ
44
trainingprocessestofind*whichistheoptimalpolicy inthegivenenvironment.
3.1.1PolicyEvaluation
Iterativepolicyevaluationistheprocessoffinding vπ byiterativelyapplyingtheBellmanExpectationbackup.WhenapplyingtheBellmanExpectation backupfornumerousiterations,thevaluefunctionwill convergetoacertainvaluefunction vπ
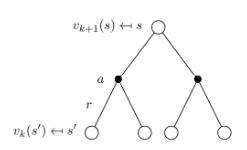
Theprocessmainlyusessynchronousbackupin whichtheprogramupdatesthevaluefunction vk +1 from thepreviousvaluefunction vk .Thisvaluefunctionis calculatedforallpossiblestates s′ ∈ S foreveryiteration.Thevaluefunctionforstate s′ - vk +1 (s) -will beupdatedfromthevaluefunctionofstate s′ fromthe previousiteration- vk (s′ )
Usingthediagram,theprocessoftheevaluation willlooklikethefollowingtreediagram:
considered.Then,wecanimprovethepolicygreedily usingthe argmax functioninwhichactsforallactions which a ∈ A:
Inanequationtoexpressthenewvaluefunction v
3.1.2PolicyIteration&Improvement
Toimprovethepolicy π ,thereneedstwomainsteps init:evaluatingthepolicy π andimprovingthepolicy π greedily.While vπ (s) canbefoundin3.1.1usingpolicy evaluation,thisvaluefunctionofthepolicyneedstobe evaluated,whichultimatelyevaluatespolicy π :
Then,thisfunctionwillimprovethevaluefromall state s ∈ S overthenewpolicy π ′ whichcanbeexpressed astheequation:
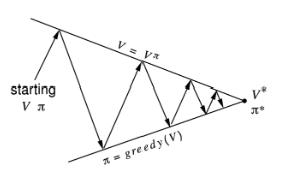
Then,actinggreedily,anewpolicy π ′ canbecreatedinreturnofthevaluefunction vπ .Repeatingthis stepagainnumerously,itisguaranteedtoconvergeto π ∗,whichistheoptimalpolicy.Thisiterationcanbe describedusingfigure7:
Toprovethattheiteratingthestepsofevaluating thepolicyandactinggreedilytoimprovethepolicyconvergesthe π ∗,adeterministicpolicy a = π (s) hastobe
improvingthenewvaluefunction v
π (s) fromtheold valuefunction vπ (s).Thiscanbeexplainedthrough theexpansionoftheequation q (s,π ′ (s)),inwhichis guaranteedtohavevalueswhicharegreaterorequalto thevaluefunction vπ (s):
s]
≤ Eπ ′ [Rt+1 + γRt+2 + γ 2 qπ (St+2 ,π ′ (St+2 ))|St = s]
≤ Eπ ′ [Rt+1 + γRt+2 + )|St = s]= vπ ′ (s) (15)
Then,whentheimprovementstops,theactionvaluefunctionofthecurrentdeterministicpolicy π will be:
qπ (s,π ′ (s))=max a∈A qπ (s,a)
= qπ (s,π (s))
= vπ (s) (16)
Thus,theBellmanoptimalityequation vπ (s)= max a∈A qπ (s,a) issatisfiedwhichmakestheequation vπ (s)= v∗ (s) true.
Fig.6:PolicyEvaluationof vk +1 (s)
+1 (s): vk +1 (s)= a∈A π (a|s)(Ra s + γ s′ ∈S P a ss′ vk (s ′ ) (11)
k
vπ (s)= E[Rt+1 + γRt+2 + ···|St = s]
(12)
Fig.7:PolicyImprovementof vπ
π ′ (s)=argmax a∈A qπ
s,a
(
) (13)
qπ (s,a)=max a∈A qπ (s,a) ≥ qπ (s,π (s)) = vπ (s) (14)
vπ (s) ≤ qπ (s,π ′ (s))= Eπ ′ [Rt+1 + γvπ (St+1 )|St = s] ≤ Eπ ′ [Rt+1 + γqπ (St+1 ,π ′ (St+1 ))|St =
′
45
3.2DynamicProgrammingSimulationonGrid World
Inthissection,applyingtheprinciplesofDynamic Programming,willbeperformedongrid1mentioned previouslyinsection2.2willbeused:

Asstatedinthefigureabove,therearefouractions -north,south,east,andwest,andeachtransitionhas thereward Rt of 1
Additionally,eachofthefouractionswillhavea uniformrandompolicy:
Then,afteroneiteration- v1 (s) -thevalueofeach gridwillchangeto-1exceptthetwoendstatesasthe valuefunctionwillmodelthevaluefunctionafterone moveofthemodelfromthespecificgrid.Thus,each gridwillbecalculatedwiththevaluesofthefoursurroundinggridsweightedequallyasthegridhasauniformrandompolicy.Thefigures11and12displaythe changedvaluefunctionandthepolicy.
Thesimulationwillendintwoendstatesatthe squares (0, 0) and (3, 3) inthefourbyfourgrid.
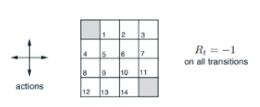
ThesimulationhasbeencreatedusingPythonand thefullcodeisattachedinAppendixA.
Toexplainthecodebriefly,thefunction“policyEvaluation”withtheparameter“grid”willcalculatethe newpolicy π ′ (s) fromthepreviousvaluefunction vπ (s) Additionally,thenumberofiterationsisdeterminedby thevariable“ITERATIONNUM”statedatthetopof thecodeinthe“Variables”section.
3.3Results
Theoutputsofthecodeisprogrammedtohavetwo partsforeveryiteration:thevaluefunction vk forthe randompolicyandthegreedypolicywithrespectto vk
Fortrial0,thestartingstate,thevaluefunction v0 hasbeeninitialisedtoall0asitisthestartingstate theandthegreedypolicy π (s) hasbeeninitialisedto randompolicyasthevaluesofallgridareequal.
Figure9and10representsthevaluefunction v0 and greedypolicy π (s)
Thesameprocesswillbeiteratedinfinitelyconverg-
Fig.8:GridWorldforDynamicProgramming
π (n|·)= π (e|·)= π (s|·)= π (w |·)=0 25 (17)
Fig.9: v0 (s) ofthegridworld
Fig.10: π (s) accordingto v0 (s)
Fig.11: v1 (s) ofthegridworld
Fig.12: π (s) accordingto v1 (s)
ingto vπ (s) whichisdisplayedinfigure13and14.
46
Fig.13: vπ (s) ofthegridworld
Fig.14: π (s) accordingto vπ (s)
Thispolicy π (s) startstoconvergetofromwhen k =3 inthisparticulargridworldwhichisveryearly. However,thismayvaryindifferentgridsandenvironmentsdependingonthecomplexity.
Additionally,thisgridworlddidnotneedaseparate stepofpolicyimprovementanditerationasthepolicy v( s) convergedto vπ∗ (s) automaticallyafterthesteps ofpolicyevaluation.
4ExploringusingQ-Learning
4.1Q-Learning
4.1.1BellmanEquation
Q-learningisthemostbasicalgorithmintherealm ofreinforcementlearningasitisanapplicationofa simplegreedyalgorithm-analgorithmwhichchooses thebestactionineverystate.However,itmightnotbe abletoeasilyidentifyhowtoapplythegreedyaspectin a2-dimensional,orevena3-dimensionalenvironment.
Thisisthroughusingaq-valuefunction-action valuefunction q (s,a) -andthebellmanequation.
TheQ-valuefunctionisupdatedusingtheBellman equationlikethefollowing:
functiondoesnothavetohaveadefinitivevalueasthe recursivepropertywillmakethefunctionconvergetoa specificvalue.
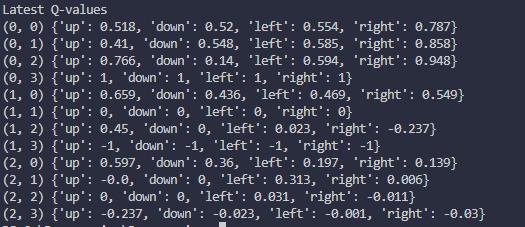
4.1.2 ϵ-GreedyAlgorithm
Sofar,Q-learningwasconsideredtobeagreedyalgorithmwhichalwaystakestheactionsbyprioritising theexpectedrewardusingtherecursivecharacteristicof theequation.However,thissometimesdoesnotguaranteeconvergencetoanoptimalpolicybecausetherecan becasesinwhichtheactionwhichisinitiallychosenby theagentisnotthebestaction.Thus,thiswillresult inanexploitationratherthananexplorationinwhich theagentdoesnotknowtheexactrewardsoftheother actions.
Tosolvethisproblem,thereisatechniquecalled “ϵ-greedy”whichencouragesexplorationoftheagent byacertainprobability.Theepsilonvalue(ϵ)isavalue intherange [0, 1] whichtakesagreedyactionwitha probability p =1 ϵ andexploresrandomlyusingthe probability p = ϵ.Thus,whenassumingthattheagent explorestheenvironmentnumerouslymanytimes,the agentwouldconvergetotheoptimalpolicy π∗ bya higherchancethanonlytakingthegreedyactions.
4.2Q-LearningSimulation&Results
ToimplementtheQ-learningalgorithmingrid world2inFigure3(Section2.2),theBellmanupdate hastobeimplementedintheprogram.Thespecificline ofprogramusedisthefollowing:
reward = curQVal + self.learningRate
∗ (self.discFactor ∗ reward curQVal ) (19)
Thefunctioniscomposedoftwodifferentparts:the immediaterewardandthemaximumexpectedreward. r (s,a) istheawardinwhichisgiventotheagentwhen theagentexecutestheactionaatstates.Ontheother hand, q (s′ ,a) istherewardthatisexpectedfromthe nextstatewhichis s′ .Applyingthe max a function, whichtakesaction a astheparametertofindthebest actioninwhichreturnsthemostreward.Thediscount factor γ ismultipliedtotheresultofthe max a function astheexpectedrewardhastobeweightedinorderto balancewiththeimmediaterewardbeingreceived.
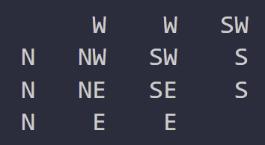
ThisBellmanequationisveryusefulintwodifferent ways.ThefirstwayisiftheMarkovianenvironmentis applicabletothereinforcementlearningenvironment, theexpectedrewardfromthefarfuturewillbeableto betakenintoaccountusingtherecursivecharacteristic oftheequation.ThesecondwayisthattheQ-value
Toexplainthegridenvironmentimplementedinthe programfurther,whiletheenvironment’sstateshave beenconsistentwiththediagram,therehasbeenan stochastic,randomisedvariable,aspectaddedtotheenvironmentinwhichtheagentmaybeforcedtomoveto anotherdirectionby20%chanceeachmoveotherthan theintendedaction.
Afterrunning100episodes(simulations)ofthisgrid environment,theQ-valuesateachstatewascalculated tobethefollowing:
q (s,a)= r (s,a)+ γ max a q (s ′ ,a
) (18)
47
Fig.15:Q-LearningResults
Thisshowsthattheagentwillconvergetotheoptimalrouteofthisgridworld.Thus,thesimulation displayshowQ-learningoperatesandshowshowtheQtableofvaluesofeachgridiscalculated.Forthespecific code,refertoAppendixB-Q-learningAlgorithmCode.
AnextensiontothebasicQ-learningalgorithmis theDeepQ-learningalgorithm,whichaddsaDeep learningaspectintothealgorithm.Q-learninghasa highlimitationontheproblemsitcanbeappliedtobecauseofthealgorithmdependsonthecomplexityofthe problem.Iftherearenumerouscasestobeconsidered, eachstateoftheenvironmentwouldnotbeabletocalculatefortheQ-value,whichispivotalintheQ-learning algorithm.
Thus,tosolvethisproblem,atechniquefromdeep learningisaddedtothealgorithm:theneuralnetwork. Theneuralnetworkenablesthealgorithmtoestimate theQ-valueexponentiallyfasterthantheprogramcalculatingitstepbystep.Thisisbecausetheneural networkestimatesthevaluethroughthehiddenlayers inthemiddlewhichisoptimisedtooperateinanextremelyquickmanner.However,althoughtheapproximationmethodchanges,thenatureofthealgorithmremainsequal,thushavingthename“DeepQ-learning” althoughbeingcalledasavariationwiththenamessuch asapproximatingfunctionorapproximator.
FortheneuralnetworktocalculatetheQ-valuesof theenvironment,itneedsa“CostFunction”.Wehave tousetheapproximatorfunctionwhichisexpressedas thefollowingadding θ whichistheweightofthenode intheneuralnetwork:
q (s,a; θ ) (20)
ApplyingthistocalculatetheCostfunction,the costfunctionwouldbemodelledasthefollowing:
5Conclusion&FurtherStudies
Overall,inthispaper,explorationofthetwokey fundamentalaspectsofreinforcementlearninghasbeen reviewedusingthesimplegridworldtofindtheoptimal policyusingbothofthemethods.Itcanbeseenthat eachofthealgorithmsshowsitslimitationwhenthe environmentbecomescomplexasitishardtocalculate allthevaluesofeachstate.
Thesetwofundamentalconceptshavebuiltup thebranchof“Model-freealgorithms”inreinforcement learning.Now,thereareseveralmorecomplexways inwhichanenvironmentcanbeexploredsuchasthe DDPGalgorithmorthePPOalgorithm;bothalgorithmsalsoinvolveadeeplearningaspecttooptimise theprocess.
Theareaof“reinforcementlearning”isdrawing moreandmoreattentioninrecentyearsasthereare successfulproductscreatedusingreinforcementlearning suchasAlphaGoandAIsplayingfamousvideogames. Althoughdivingdeepintothearearequiresmoredeep knowledge,understandingthebasicsofreinforcement learningcanprovideagoodinsightintohowtrial-anderrorprocessisimplementedtoanaivecomputer.
6Bibliography
1. R.SuttonandA.Barto,1998,Reinforcement Learning:AnIntroduction[online]Availableat: http://www.incompleteideas.net /book/RLbook2020.pdf
2. DavidSilver,2015,Lecture2:Markov DecisionProcess[online]Available at: https://www.davidsilver.uk/wpcontent/uploads/2020/03/MDP.pdf
3. DavidSilver,2015,Lecture3:Planning ByDynamicProgramming[online]Availableat:https://www.davidsilver.uk/wpcontent/uploads/2020/03/DP.pdf
4. JeremyZhang,2019,ImplementGrid WorldwithQ-Learning[online]Availableat: https://towardsdatascience.com/implement-gridworld-with-q-learning-51151747b455
5. JeremyZhang,2019,gridWorld_Q.py,Availableat: https://github.com/MJeremy2017/reinforcementlearning-implementation /blob/master/GridWorld/gridWorld_Q.py
ThisisextremelysimilartotheMeanSquaredError (MSE)asQ-learningiscalculatedinasimilarwaytoa calculationoftheMSE. MSE
Usingthischaracteristic,themodifiedQ-valuefunction q (s,a; θ ) iscalledaQ-target.
6. ,2018, (Q-learning,ReinforcementLearning)[online]Availableat: https://bluediary8.tistory.com/18
7. Jeina,2019,DeepQNetworks,10[online]Availableat:https://jeinalog.tistory.com/20
ADynamicProgrammingCode
4.3DeepQ-LearningNetwork(DQN)
=[q
s,a
theta)
s,a) + γ max a q (s ′ ,a
θ
C
(
;
(r (
;
))]2 (21)
= 1 n n 1 (yi y ′ i )
2 (22)
1 import numpyasnp
48
2 3 #Variablesthatcanbechanged 4 ROWS=4
BQ-LearningAlgorithmCode
5 COLS=4 6 END_STATE1=(0,0) 7 END_STATE2=(3,3) 8 9 GRID=[[0 for inrange (COLS)] for in → range (ROWS)] 10 MOVE=[[1,0],[-1,0],[0,1],[0,-1]] 11 MOVEMAP={0: ' S ' ,1: ' N ' ,2: ' E ' ,3: → ' W ' } 12 13 ITERATIONNUM=100 14 15 #Thepolicy\piusedisrandomiterative → policywhere\pi(e|.)=\pi(w|.)=\pi(s → |.)=\pi(n|.)=0.25 16 17 def policyEvaluation(grid): 18 newGrid=[[grid[x][y] for x inrange ( → COLS)] for y inrange (ROWS)] 19 for x inrange (ROWS): 20 for y inrange (COLS): 21 if (x,y)==END_STATE1 or (x,y) → ==END_STATE2: 22 newGrid[x][y]=0 23 else : 24 tmp=0 25 for z inrange (4): 26 if x+MOVE[z][0]<0 → or y+MOVE[z][1]<0 or x+MOVE[z][0] → ==ROWS or y+MOVE[z][1]==COLS:tmp+= → (grid[x][y]-1)*0.25 27 else :tmp+=(grid[x+ → MOVE[z][0]][y+MOVE[z][1]]-1)*0.25 28 newGrid[x][y]=tmp 29 return newGrid 30 31 for x inrange (ITERATIONNUM): 32 for y inrange (ROWS): 33 for z inrange (COLS): 34 print ("%6.2f"%(GRID[y][z]), → end="") 35 print () 36 print () 37 for y inrange (ROWS): 38 for z inrange (COLS): 39 if (y,z)==END_STATE1 or (y,z) → ==END_STATE2: 40 print ("%4s"%(""),end=" → ") 41 continue 42 tmp=[] 43 ans="" 44 for a inrange (4): 45 if y+MOVE[a][0]<0 or z → +MOVE[a][1]<0 or y+MOVE[a][0]== → ROWS or z+MOVE[a][1]==COLS:tmp. → append(GRID[y][z]) 46 else :tmp.append(GRID[y+ → MOVE[a][0]][z+MOVE[a][1]]) 47 maximum= max (tmp) 48 for a inrange (4): 49 if maximum==tmp[a]:ans → +=MOVEMAP[a] 50 print ("%4s"%(ans),end="") 51 print () 52 print () 53 GRID=policyEvaluation(GRID)
1 import numpyasnp 2 3 #Variablestoalter 4 ROWS=3 5 COLS=4 6 WIN_STATE=(0,3) 7 LOSE_STATE=(1,3) 8 START=(2,0) 9 LEARNINGRATE=0.25 10 EXPLORATIONRATE=0.25 11 DISCOUNTFACTOR=0.95 12 13 class State: 14 def __init__(self,state=START): 15 self.grid=np.zeros([ROWS,COLS]) 16 self.grid[1,1]=-1 17 self.state=state 18 self.isEnd=False 19 20 def checkEnd(self): 21 if (self.state==WIN_STATE or self → .state==LOSE_STATE): 22 self.isEnd=True 23 24 def chooseAction(self,action): 25 if (action=="up"): 26 return np.random.choice([ ' up ' , ' → left ' , ' right ' ],p=[0.8,0.1,0.1]) 27 if (action=="down"): 28 return np.random.chocie([ ' down ' → , ' left ' , ' right ' ],p=[0.8,0.1,0.1]) 29 if (action=="left"): 30 return np.random.choice([ ' left ' → , ' up ' , ' down ' ],p=[0.8,0.1,0.1]) 31 if (action=="right"): 32 return np.random.chocie([ ' right → ' , ' up ' , ' down ' ],p=[0.8,0.1,0.1]) 33 34 def nextPos(self,action): 35 if action=="up": 36 nextState=(self.state[0]-1, → self.state[1]) 37 elif action=="down": 38 nextState=(self.state[0]+1, → self.state[1]) 39 elif action=="left": 40 nextState=(self.state[0], → self.state[1]-1) 41 elif action=="right": 42 nextState=(self.state[0], → self.state[1]+1) 43 if (nextState[0]>=0 and nextState → [0]<=2) and (nextState[1]>=0 and → nextState[1]<=3) and (nextState!= → (1,1)): 44 return nextState 45 return self.state 46 47 def giveReward(self): 48 if self.state==WIN_STATE: 49 return 1 50 elif self.state==LOSE_STATE: 51 return -1 52 else : 53 return 0 54 55 class Agent: 56 def __init__(self): 49
57 self.states=[] 58 self.actions=["up","down","left → ","right"] 59 self.State=State() 60 self.isEnd=self.State.isEnd 61 self.learningRate=LEARNINGRATE 62 self.expRate=EXPLORATIONRATE 63 self.discFactor=DISCOUNTFACTOR 64 self.QVals={} 65 for x inrange (ROWS): 66 for y inrange (COLS): 67 self.QVals[(x,y)]={} 68 for i in self.actions: 69 self.QVals[(x,y)][i]= → 0 70 71 def choice(self): 72 maxNextReward=0 73 action="" 74 if (np.random.uniform(0,1)<=self. → expRate): 75 action=np.random.choice(self. → actions) 76 else : 77 for a in self.actions: 78 curPos=self.State.state 79 nextReward=self.QVals[ → curPos][a] 80 if nextReward>= → maxNextReward: 81 action=a 82 maxNextReward= → nextReward 83 return action 84 85 def takeAction(self,action): 86 position=self.State.nextPos( → action) 87 return State(state=position) 88 89 def reset(self): 90 self.states=[] 91 self.State=State() 92 self.isEnd=self.State.isEnd 93 94 def play(self,rounds=10): 95 cnt=rounds 96 while cnt: 97 if self.State.isEnd: 98 reward=self.State. → giveReward() 99 for x in self.actions: 100 self.QVals[self.State. → state][x]=reward 101 print ("EndReward:", str ( → reward)) 102 for s inreversed (self. → states): 103 curQVal=self.QVals[s → [0]][s[1]] 104 reward=curQVal+self → .learningRate*(self.discFactor*reward → -curQVal) 105 self.QVals[s[0]][s[1]] → = round (reward,3) 106 self.reset() 107 cnt-=1 108 else : 109 action=self.choice() 110 self.states.append([(self. → State.state),action]) 111 print ("CurPosition{} → action{}". format (self.State.state, → action)) 112 self.State=self. → takeAction(action) 113 self.State.checkEnd() 114 print ("NextStates:",self. → State.state) 115 print (" → ___________________________________") 116 self.isEnd=self.State. → isEnd 117 118 agent=Agent() 119 print ("InitialQ-values") 120 print (agent.QVals) 121 agent.play(100) 122 print ("LatestQ-values") 123 for x in agent.QVals: 124 print (x,agent.QVals[x]) 50
EstimationoftheChangingVelocityDuring RocketLaunchUsingEuler’sMethod
JamesDaewoongKang Year12Halla
Co-ChairoftheMathematicsSociety Email:dwkang24@pupils.nlcsjeju.kr
Editor
AarenJoonseokKang∗ JooHyunKim†
RecommendedYearLevel:KS5andAbove
Keywords:ResultantForce,Euler’sMethod
1Introduction
1.1ModellingthePathofRocketMotion
Inthisinvestigation,rocketmotionduringliftoff willbeanalysedmathematically.Theliftoffofarocket isacrucialphaseinitsjourneytowardsspace,its motiondeterminedbyacomplexinterplayofvarious physicalfactorssuchasthrust,weight,dragand gravitationalforces.
Inordertoaccuratelyunderstandandpredictthe motionofarocketduringliftoff,itisnecessarytoapplymathematicalmodelsandequationstoanalysethe differentcomponentsoftheseforces.Thispaperdelves intothemathematicsbehindrocketmotionduringliftoff andexplorestherelationshipsbetweenthevariousphysicalfactorsthatdetermineitsbehaviourusingcalculus andtheEuler’smethodforestimation.
2Calculations
2.1ForcesActingonaRocket
Onarocket,therearefourforcesthatareinaction: weight,thrust,drag,andlift-asseeninthediagram below.Specificallyduringrocketlaunch,liftforcesare ignored,asthrustandliftforcesarebothindirections paralleltotherocketmotion.(TomBenson, Four forcesonaRocket )
Letthethrust,drag,andweightforcesbe T(t), D(t) and W(t),giventhatthesevalueschangeover time.Similarly,somevariablesthatareinvolvedinthe equationchangeovertime-massandvelocity-and thereforetheyaredenotedas m(t) and v(t).Theequationsfor T(t) and D(t) canbefoundontheNASA website:
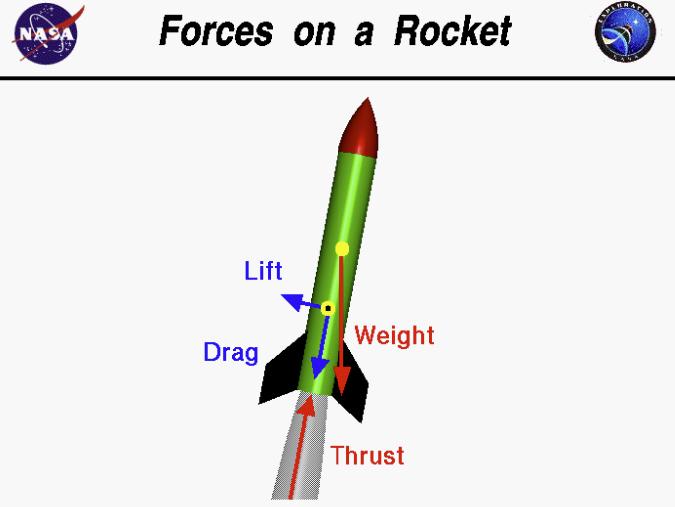
∗ ChairofMathematicsSociety,LeaderofJPAMEditingTeam † MemberofJPAMEditingTeam
Fig.1
T (t)= dm dt ve +(Pe P0 )Ae (1) D (t)= 1 2 Cd pv (t)2 A (2) Notethatthefuelflowrate, dm dt ,isaconstant, 51
Ve standsforexhaustgasvelocity, Cd standsfordrag coefficient, p forpressure, v (t) forvelocity,and A for thecrosssectionalareaofarocketincontactwiththe atmosphere.(TomBenson, Thedragequation )(Nancy Hall, RocketThrustequation )
Thethrustequationisoftensimplified:
3Euler’sMethod
Ifwearegivenvaluesforthefollowing,itispossible toestimatethevelocityusingEuler’smethod.
Assumethat k = dm dt =300kgs 1 , Cd =0 75, A = 10m2 , p =1 0kgm 1 , g =9 81ms 2 , Ve =5000ms 1 , m(0)=2600000kg , v (9177)=0ms 1
Theequationforweight,W(t),isgivenas:
2.2ResultantForce
Theresultantforceactingontherocketiscalculated by T (t) W (t) D (t) inrocketmotion.Inamoregeneralcontext,theresultantforceistherateofchangeof momentum.Therefore,thefollowingdifferentialequationissetasfollows:
Then, dv (t) dt = 3 75 2600000 300t v 2 (t) + 300 2600000 300t v (t) 1500000 2600000 300t 9 81
(10)
Notethatwhen t =9177, v (t)=0,fromtheassumptionsmadeabove.Thisvalueisobtainedbygraphing theequationitself-becausethepointmustbeonthe curve.However,ifrealvaluesareobtainedandused therewillbenoproblemswiththeequation.

Euler’smethodapproximatesthesolutiontoadifferentialequationatdiscretepointsintime,anditworks byusingthetangentlineateachpointtoestimatethe valueofthesolutionatthenexttimestep.Therefore, itisassumingaconstantrateofchangeof v (t),andthe accuracyincreaseswithasmallersteplength.Here,for simplicity,thesteplength, δx,issetas100.
Let xn bethe nth valueof t, yn bethe nth valueof v (t), mn bethe nth valueof dv (t) dt ,and yn bethe nth changein v (t).
Thevelocityoftherocketateachtimeintervalcan betabulatedasfollows.
Substitutethisintotheoriginalequation:
δyn iscalculatedusing mn δx,as mn = δy δx
4Conclusion
Asthegradientvaluesaredecreasing,thevaluesin thetableareanoverestimate.Euler’smethodissimple toimplementandprovidesagoodapproximationofthe solutionforsmallstepsizes,butitmaynotbeveryaccurateforlargerstepsizesorformorecomplexODEs.
T (t)= dm dt Ve (3)
W (t)= m(t) g (4)
ΣF = T (t) W (t) D (t) = d dt [m(t) v (t)] (5) dm dt ve m(t) g [ 1 2 Cd pv (t)2 A] = dm(t) dt v (t)+ dv (t) dt m(t) (6) dv (t) dt = 1 m(t) dm dt ve g 1 2m(t) Cd pv (t)2 A (7)
t
t 0 dm dt dt = t 0 kdt ∴ m(t)= kt + m(0) (8)
Assumethat dm dt = k ,asfuelislost.Integrate bothsideswithrespectto
:
dv (t) dt = Cd pA 2(m(0) kt) v 2 (t)+ k m(0) kt v (t) k ve m(0) kt g (9)
52
Therearemoreaccurateandefficientnumericalmethodsavailable,suchasRunge-Kuttamethods,thatcan beusedtosolveODEs.However,inthesecircumstances wheresecondorderdifferentialequationsareinvolved, estimationmethodssuchasslopefieldsorisoclinesmay beuseful-asdemonstratedinthisstudy.
5Bibliography
1. TomBensonFourforcesona Rocket(nodate).NASA.Available at: https://www.grc.nasa.gov/www/k12/rocket/rktfor.html(Accessed:February11, 2023).
2. TomBensonThedragequation.(nodate).NASA. Availableat:https://www.grc.nasa.gov/www/k12/rocket/drageq.html(Accessed:February11,2023).NancyHallRocketThrust equation(nodate).NASA.Available at: https://www.grc.nasa.gov/www/k12/airplane/rockth.html(Accessed:February 11,2023).
53
BifurcationDiagram
AlvinSehunJeong
Year12Jeoji
MemberoftheMathematicsSociety
Email:shjeong24@pupils.nlcsjeju.kr
Editor
TaeheeKim ∗
RecommendedYearLevel:KS4,KS5
Keywords:BifurcationDiagram,DrippingFaucet, MandelbrotSet
1Introduction
WrittenbyRobertM.May,thearticle“Simple mathematicalmodelswithverycomplicateddynamics” waspublishedin1976.Thepaperinitiatedadebate abouthowsuchunpredictablechaoscanbecommenced fromasimple,intuitiveequation.Theequationwas designedtoimitatethepopulationofanorganismina controlledenvironment.Itshowsthechangeofthepopulationratio-aportionofthepopulationthataspecies occupiesintheecosystem-whichisintherangebetween0and1.Apopulation(ratio)ofaspeciesinyear nis xn andthenextyearis x[ n +1].Theequationis
xn+1 = λxn (1 xn ) (1)
wherelambdaisaconstantand xn isbetween0and 1. λxn representsthe‘reproduction’ofaspecies.Let (λ -1)astheaveragenumberofoffspringthatananimalproduces,then λ willrepresentthenumberofthe animalmultipliedayearlateronlyifnoneofthemdied. However,everylivingorganismdies.Sotheequation needsa‘death’termwhichdecreasesthepopulationof thespeciesovertime.(1- xn )worksasthedeathterm intheequation.Inaclosedenvironmentofrealnature, limitedresourcesworkasaregulatoroftheoverpopulatedspecies.Forinstance,overpopulation(high xn value)willleadtothelackoffood,consequentlydecreasingthepopulationoftheanimal.
Inthecaseof λ between0and1,theyfound xn convergesto0.Youmaythinkofaninferiorspeciesof rabbitswhicharesexuallydisabled.Intherealecosystem,thespecieswilldisappearbytheprocessofnatural selection.When1< λ <3,thedeathterm,(1- xn ),starts tointervene.Thepopulationinitiallyincreasesgeometricallybythereproductiontermbutasoverpopulation occurs,thepopulationdecreasesrapidlybythedeath term.Afterseveralrepetitionsofincreaseanddecrease ofthepopulation,thepopulationseemstosettledown toastaticvalueasthereproductionrateandthedeath rateattainequilibrium.
Thisistheextentinwhichecologistsareinterested, butwiththeiruncontrollabledesire,mathematicians wantedtofindhowtheresultoftheequationchanges when λ islargerthan3.Theydidwhattheydobestat; theygraphedit.
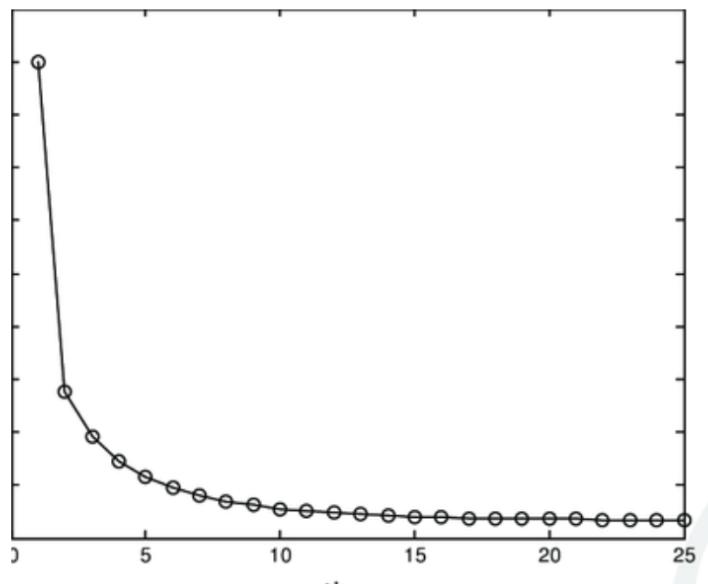 ∗ MemberofJPAMEditingTeam
Fig.1: λ <1
∗ MemberofJPAMEditingTeam
Fig.1: λ <1
54
Whattheyfoundisthatthegraphbifurcates-a fancywordforsayingthatthegraphisbranchinginto two-atrandompoints.Thismeansintheregionof valueL1,thepopulationofrabbitsoscillatesbetween twovaluesthan4valuesinregionL2then8inregion L3,andsoon.
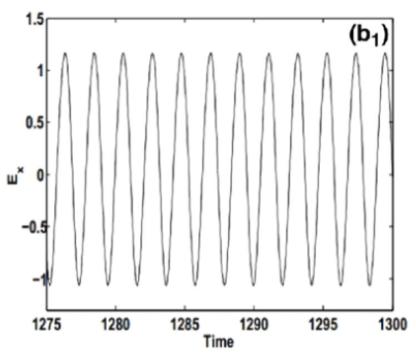
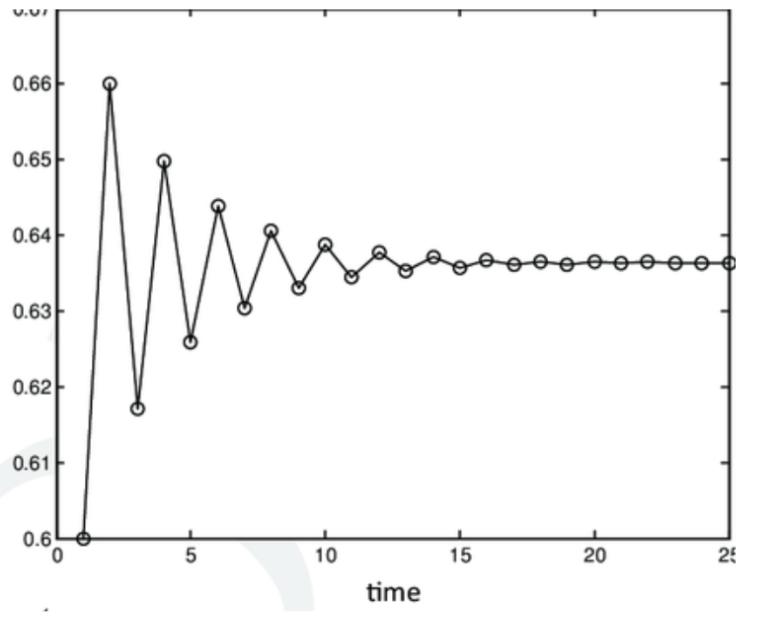
Mathematicianscouldnotfindthereasonforthe constantthusthevalueleftasthefundamentalconstant ofmaths,alongwithpi,e,and √2.Graphsthatfollow thesameruleandhavesimilarmathematicalstructures arecalledbifurcationdiagrams.Eventhoughyoumight notbefamiliarwiththeconcept.However,itmight existinyourbathroomrightnowaswell.
Ifafaucetisnotwellclosed,waterdropletsfall withaconstantperiodlikedab,dab,dab,dab.However, ifthewaterflowincreases,theperiodincreasesby2as wellsoitdropslikedadab,dab,dadab,dab.Lateritbecomeschaoticandimpossibletofindtheperiod.dadaddadadb,daddadab,dadab,dadadadb,da....Thisincreaseofperiodcreatesthebifurcationdiagram.
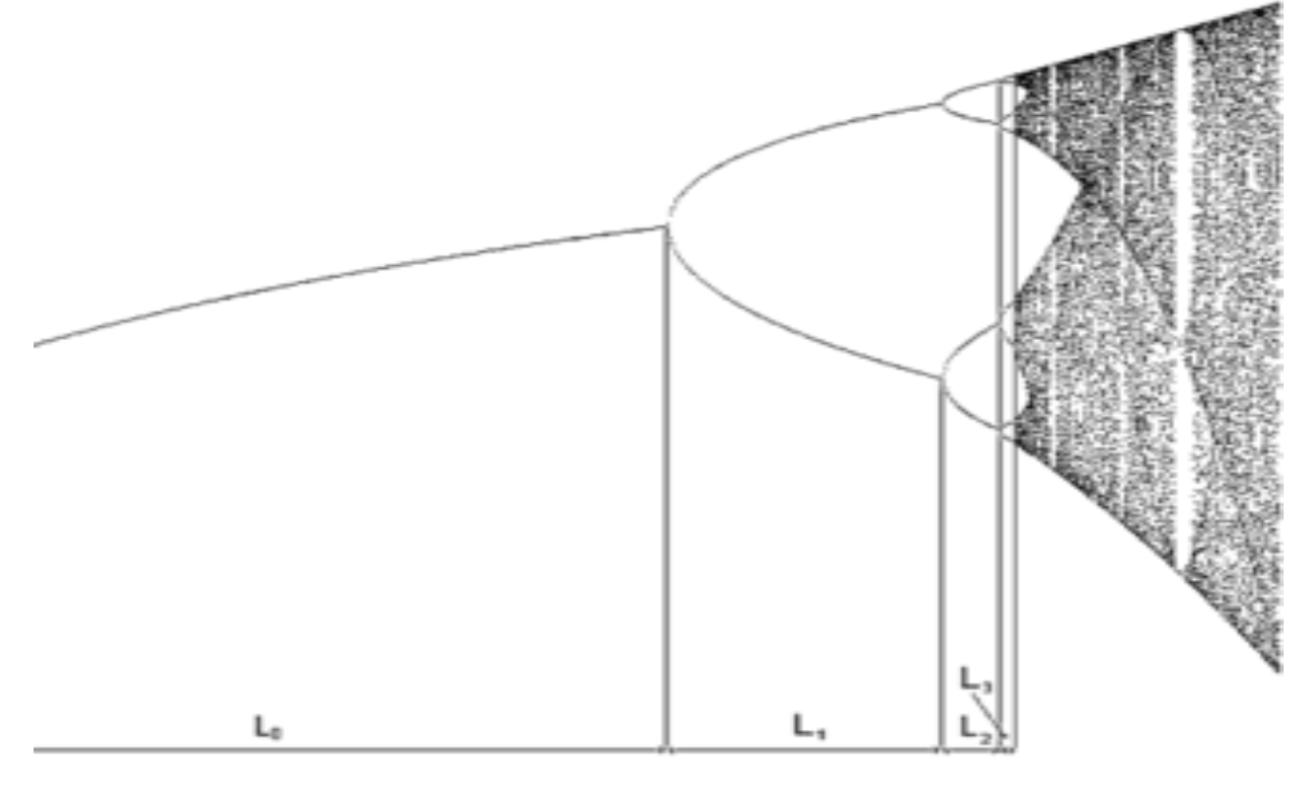
Itwaschaotic,andseemedtohavenorulesat all.However,amathematicianwhosenameisMichael Feigenbaumfoundaverysimpleyetextraordinaryrule.
Twodimensionalversionofamandelbrotsetiswell known.Howeveritsthreedimensionalversionismuch different.
Fig.2:1< λ <3
Fig.3:.
Fig.4:period2
(y-axisisthepopulationofrabbitsandx-axisisthe time)
Fig.5:period4
Fig.6:period8
Fig.7:period18
L1 L2 = L2 L3 = L3 L4 =4.669... (2)
Theratiobetweenthetwogapsbetweenthreeconsecutivebifurcationsisalways4.669...
2Drippingfaucet
3Mandelbrotset
55
Thisshowsthatthemandelbrotsetisanotherway torepresentthebifurcationdiagramwherethelessdivergentpartofthegraphisrepresentedasflatareas.

 Fig.8:.
Fig.9:.
Fig.8:.
Fig.9:.
56
TicTacToe:WinningStrategyoftheGame
JuneKim
Year11Jeoji
MemberoftheMathematicsSociety
Email:jukim25@pupils.nlcsjeju.kr
Editor EmmaChaeeunChung ∗
RecommendedYearLevel:KS3,KS4
Keywords:TicTacToe,WinningCondition
1Introduction
TicTacToeisaclassicgameoftwoplayerstaking turnsandmarkingthespaceswithXorOinagrid. Despiteitbeingsimple,ithasamathematicalstrategy thatensuresaplayerawinoradraw.Thestrategy canbeexplainedintwosections:whenplayingfirst andwhenplayingsecond.
Players:
1. Player1=X(playingfirst)
2. Player2=O(playingsecond)
TicTacToeGrid:
2Whenplayingfirst(X)
2.1Player1startsfromthecorners
i)Player2doesn’tmarkatthecentrenextturn Startingfromthecornersistheeasiesttogetmany guaranteedwins.Theonlyplacethesecondplayercan winistoputatthecentre.Inalltheothercases,player 1getsthewin.
Forexample,whenplayer1marksXat(1),the secondplayermarksOat(2),andplayer1marksX at(7),thesecondplayerwouldhavetomarkat(4)to preventplayer1fromwinningwiththerow1-4-7.This allowsplayer1tomarkatthecentre,whichguarantees theplayerawinastheplayerwouldbeabletoputat both(3)and(9)tomaketherow3-5-7and1-5-9.
Guaranteedwinswhenplayer1startsfrom thecornersandplayer2doesn’tmarkatthecenter afterplayer1aretotalofseven,includingtheoneabove.
Fig.1:
1. Side:(2),(4),(6),(8)
2. Corner:(1),(3),(7),(9)
3. Centre:(5)
Notethatduetothesymmetryoftheboard,the boardcanberotatedinanydirection,andtheoutcome wouldstillbethesame.
Notethat“awinisguaranteed”whencompleting tworowsispossibleinoneturn.
∗ MemberofJPAMEditingTeam
ii)Player2marksatthecentrenextturn Markingatsymmetryiscriticalinthiscase.Forexample,withXat(1)andOat(5),player1mustmarkat (9),whichispositionedsymmetricalto(1).Forguaranteedwins,player2mustmarkatcorners,(3)or(7),as thiswouldallowplayer1tomarkat(4)or(8)tomake therows1-4-7and7-8-9togetawin.
However,thisdoesn’tmeanthatonlymarkingat thesymmetryguaranteesawinforplayer1inthiscase. Whenplayer1breaksthesymmetryandmarksat(6), withXat(1)andOat(5),player1mustmarkat(3)or (7)forawin,asthisguaranteewinswithpossiblerows 1-2-3and3-6-9or1-4-7and7-8-9.
2.2Startingfromthesides(forexample,(4)) i)Player2marksat(1)
Inthiscase,thepositionofthesecondXthatguaranteesthehighestchanceofwinningisat(3),asitis thepositionofsymmetrytoO.Whenplayer1marks Xat(3),player1willwinwhenplayer2marksat 57
(2),(7)and(9),whichgivesplayer1threechancesof winning.Forexample,withXpositionedat(3)and(4) andOat(1),whenplayer2marksOat(9)player1 wouldmarkXatthecentreinturntopreventplayer2 fromwinning,player1willgetaguaranteedwin,with possiblerowsof3-5-7and4-5-6.
ii)Player2marksat(2)
Inthiscase,player1mustmarkat(1)or(5)for guaranteedwins,asthepositionstouchthefirstX, allowingmorechancesforthefirstplayertomakea row.Forexample,withXat(4)andOat(2),when player1marksat(1),player2wouldhavetomarkat (7)topreventrow1-4-7.Thenplayer1wouldbeable tomakerows1-5-9and4-5-6andwin.
iii)Player2marksat(3)
Inthiscase,player1wouldhavetomarkat(9),a positionofsymmetrytoO,foraguaranteedwin.With Xat(4)and(9),andOat(6),player1willwinwhen player2marksat(2),(5),(6),(7),and(8),givingfive chancesofwinning.Forexample,whenplayer2marks at(5),player1willmarkat(7),topreventplayer 2fromwinningwithrow3-5-7,whichgivesplayer1 possiblewinswithrows1-4-7and7-8-9.
iv)Player2marksat(6)
Inthiscase,player1wouldhavetomarkat(9),which isasymmetricalpositionto(6).Thisgivesfourchances ofwinningforplayer1,asitguaranteeswinsforplayer 1whenplayer2marksat(2),(3),(5),(8).
v)Player2marksatthecentre(5)
Winninggetsharderinthiscase.Twocasesthatguaranteewins:markingat(2)andmarkingat(3).
2.3Startingfromthecentre
(i)Player2markingatoneofthesides
Inthiscase,markingatanyoneofthecornersguaranteesplayer1awin.Forexample,withXatthecentere andOat(2),player2mustmarkatoneofthecorners, suchas(1).Thentheplayer2willmarkat(9)to preventplayer1fromwinningwiththerow1-5-9.The nextturnplayer1markingat(4)guaranteesplayer 1awin,withtwopossiblerowstomake:1-4-7and4-5-6.
(ii)Player2markingatoneofthecorners
Inthiscase,player1shouldbackintothediagonally oppositecorner.Forexample,withXatthecentreand Oat(1),player1mustplaceatthediagonallyopposite corner(9).Thisguaranteesseveralchancesofwinning; whenplayer2inturnmarksat(2),(4),(6),or(8), player1wins.Forexample,withXatthecentreand (9)andOat(1),whenplayer2marksat(2),player1 willmarkat(3)topreventplayer2fromwinningwith therow1-2-3.Thisthenguaranteesplayer1awin,with twopossiblerows:3-5-7and3-6-9.
3Whenplayingsecond(X)
3.1Player1startingfromthecorners
Asmentionedbefore,wheneverOisplacedona side,Xisguaranteedawin,meaningthatforallstarts, thefirstOshouldneverbeplacedonside.Player2 markingatthecentreisthebestwaynottoallowplayer 1fromwinningeasy.
3.2Player1startingfromthesides
Inthiscase,thereisachanceofwinning,butwinningonX’sside-startismoreluckthanlogic.Asanalyzedin1.2,therearetoomanychancesofplayer1 winning,nomatterwhereplayer2marks.
3.3Player1startingfromthecorner
FromX’scentre-starttherearenopossibleOwins, asinbothcaseswhereplayer2marksatanyofthesides andwhereplayer2marksatanyofthecornersplayer 1hasawaytowin.
4Conclusion
Inconclusion,simplysaying,whenstartingfirst, puttingXinanycornerguaranteesplayer1asimplest winaslongasyouropponentdoesn’tputtheirfirst‘O’ inthecentrebox.
Whenstartingsecond,itmaytakemoreworktowin thegame.Ifplayer1takesthecentre,player2should placeOatthecorner.Ifplayer1takesthecorner,player 2shouldplaceOatthecentre.Thiswillmakeadraw inbothcases.Inthiscaseofplayer1markingatthe centeroratthecorner,winningisalmostonlypossible ifamistakeismadebyplayer2.
But,ifplayer1startsonaside,player2canwin. Inthiscase,player2mustmarkOinthecentretowin. Thisistheonlycaseplayer2canwin.Otherwise,player 2maydraworlose.
5Bibliography
1. Aycock,R.(2002).HowtoWinat Tic-Tac-Toe.[online]Availableat: https://www.cs.jhu.edu/jorgev/cs106/ttt.pdf.
2. Cappiello,E.(2020).HowtoWinTicTac-Toe:TheStrategiesYouNeedtoMaster.[online]Reader’sDigest.Available at:https://www.rd.com/article/how-to-win-tictac-toe/.
58
ProbabilityAppliedtoSocialSciences
JeanKim
Year11Jeoji
MemberofMathematicsSociety
Email:jnkim25@pupils.nlcsjeju.kr
Editor AarenJoonseokKang∗
RecommendedYearLevel:KS3andKS4
Keywords:GameTheory,SocialSciences
1WhatisProbability
Probabilityisdefinedasthelikelihoodofsomething happeningorbeingthecase.
P (x)= NumberoffavourableoutcomestoA Totalnumberofpossibleoutcomes (1)
2GameTheory
Gametheoryisabranchofappliedmathematics thatprovidestoolsforanalysinginterdependentsituations.Accordingtothistheory,eachsideconsidersthe other’spossibledecisionsandusesthemtoformulate strategiesforhimorherself.Thepurposeofthis‘game’ istofindthebestdecisionfortheplayers,andtheresultsmaydifferregardingtheirfindings.
Gametheoryhaswideapplications,especiallywhen players’choicesaffecteachother’spossibleoutcomes. Therearetwokeywordsingametheorythatneedsto bedefined:
1. Game:Asetofcircumstancesinwhichtheresult dependontheactionsofdecision-makers(moreor equalto2)
2. Players:Strategicdecision-makerswithinthecontextofthegame
3CooperativeandNon-CooperativeGames
Therearevariousgametheories,mostcommonly cooperativeandnon-cooperative.Cooperativegame
theoryisabouthowcooperativegroupsactwhenthe payoffisknown,morelikelyagamebetweenagroup ofplayersratherthanbetweenindividuals.Itquestions howgroupsareformed,andpayoffsareallocatedamong players.
Ontheotherhand,thenon-cooperativegametheorydealswithhowindividualsdealwitheachother toachievetheirowngoals.Themostcommonnoncooperativegamehappenstobethestrategicgame, wheretheavailablestrategiesandtheoutcomesresult inalreadyknownresults.Themostwell-knownand simpleexampleofareal-worldnon-cooperativegameis Rock-Paper-Scissorsandprisoner’sdilemma,whichwill appearlaterinthisarticle.
Zero-sumandnon-zero-sumgamesarealsogame theories.Whenthereisaconflictamongmultiple groupswantingthesameoutcome,itisoftenazerosumgame.Thereisalwaysaloserinthiskindofgame, astherearewinners.Alternatively,italsomeansthat thebenefitreceivedequalsthebenefitlost.Mostsports gamescanbeknownaszero-sumgamesasthereare bothwinnersandlosers.
Contrarytozero-sumgames,inanon-zero-sum game,winnerscanbeloserssimultaneously.Abusiness partnershipthatismutuallybeneficialandfostersvalue forbothentities.Insteadofcompetingandattempting towin,inthiscase,bothpartiesbenefit.
5Volunteer’sDilemma
Volunteer’sdilemmaiswhensomeonehastoundertakeachoreorajobforthecommongood.The worstpossibleoutcomehappenswhentherearenovolunteers.Areal-lifeexamplecanbewhentheelectricity ofthewholeapartmentfails.Peoplelivinginthesame apartmentknowthattheelectricitycompanywillfixthe
∗ ChairofMathematicsSociety,LeaderofJPAMEditingTeam
4ZeroSumandNon-zeroSumGames
59
problemifsomeonecallstonotifythematsomecost. Ifatleastonepersoncallsthecompany,everyonecan benefitfromit.However,ifnoonevolunteers,theworst possibleoutcomeisobtainedforallparticipants.
Forexample,ifIliveinafourstoryapartmentwith twohousesineachstory.Considerineachhousethere isatleastonepersonstayinginthehousewhenthe electricityfails.Theminimumprobabilityofatleastone personotherthanmecallingtheelectricitycompanyis 7 8 .Therefore,inthiscasethereisahigherprobability thatsomeoneelsewillcallthecompanyeventhoughI donothing.Ontheotherhand,ifIamawarethatonly twopeoplearecurrentlystayingathome.Thenthe probabilityofanotherpersonintheapartmentcalling thecompanyisonly 1 2 ,whichmakesmemorelikelyto callthecompany.
6Prisoner’sDilemma
Oneofthemostfamousexamplesofgametheoryis theprisoner’sdilemma.
Forexample,twocriminalsarearrestedforcommittingacrime.However,prosecutorsdonothaveappropriateevidencetoconvictthem.Togainaconfession, officialsoftenseparatetheprisonersandquestionthem indifferentareas,providingprisonerswithnomeansof communication.Therearetwooptionsfortheprisoners,toconfessornot.However,thisleadstodifferent consequences.
Forexample,
1. Ifbothconfess,theywilleachreceiveafive-year prisonsentence;
2. IfPrisoner1confesses,butPrisoner2doesnot, Prisoner1willnotgotojail,butPrisoner2will getaten-yearsentenceorviceversa.
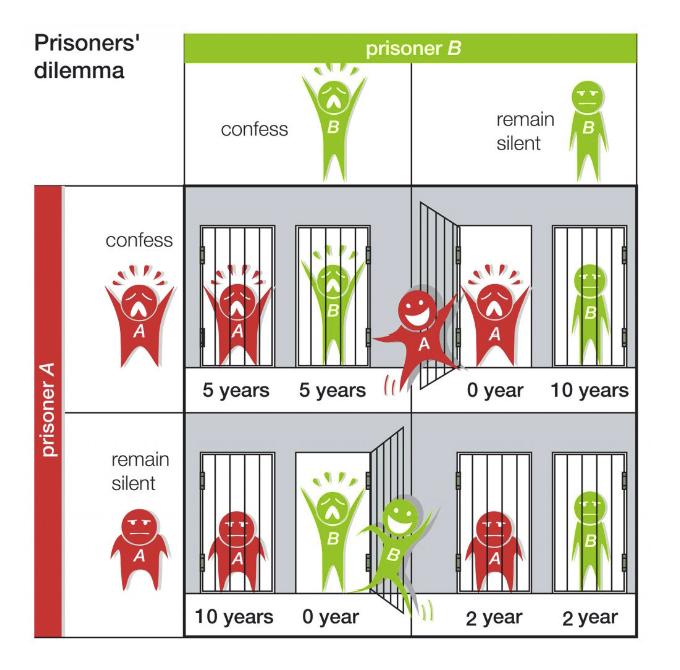
3. Ifneitherconfesses,eachwillservetwoyearsin prison.
bothprisonersdonotconfess.However,asbothprisonersareunawareoftheother’sstrategy,theprobability ishelpfulforthemtopredictwhatothersmightdo.In thiscase,thenumberoffavourableoutcomestoAis1, butthetotalnumberofpossibleoutcomesis3.Therefore,theopponent’sprobabilityofstayingsilentisonly 13.Thislackofcertaintythattheotheronewillnotremainsilentcausestheprisonertoconfess,whichmakes itmorelikelyforbothprisonerstoserveinprisonfor fiveyears.
Assuch,gametheoryiscloselyrelatedtoourlives. Thistheoryisfrequentlyusednotonlyintheprisoner’s dilemmabutalsoinareassuchasbusinessandeconomics.
Asbusinessesrequiremanystrategicchoicesthat affecttheireconomicgain,theymayfacemanydilemmaswhendecidingwhethertodevelopnewproducts, stopproducingoldones,orusemarketingstrategies.
7RepeatedOligopolyGames
Unliketheprisoner’sdilemmawhichisonlyplayed bytwoplayerswitheachgivenapayoffmatrix,only beingabletomakeonechoice,andthegameendsafter thefirstroundofchoices,therealworldoligopolyhas asmanyplayers.
Asoligopolygamesmayhavemorethantwoplayers,theyarefarmorecomplex.However,itdoesnot changeitsbasicstructure.Thefactthattheverygames arerepeatedintroducesnewstrategicconsiderations. Playersmustconsiderhowtheirchoicesmightaffect theirfuture,nottherivals.
8Bibliography
1. britannica.com.2022.GameTheory-Britannica.[online]Availableat: <https://www.britannica.com/science/gametheory>
2. hal.scence.2019.Probabilityandsocialscience. [online]Availableat:<https://hal.science/hal02065664/document>
3. investopedia.com.2022.GameTheory-Investopedia[online]Availableat: <https://www.investopedia.com/ terms/g/gametheory.asp>
4. innovationmanagement.se2020.IntroductiontoGameTheory[online]Availableat: <https://innovationmanagement.se/2020/11/06/ introduction-to-game-theory/>
Fig.1:Prisoner’sDilemma
Themostfavourablestrategyischoice3,where
60
EquationofCircleandGPS
JungseoPark
Year9Geomun
MemberoftheMathematicsSociety
Email:js2park27@pupils.nlcsjeju.kr
Editor
TaeheeKim ∗
RecommendedYearLevel:KS4,KS5
Keywords:Equationofacircle,GPS
1Introduction
Nowadays,GPSisusedinvariousplaces.GPStechnologyisusedintrafficaccidentnotificationdevices, vehiclenavigationsystems,vehicleenforcementdevices, anddatacollectiondevicesforroadusagefeescollection.
2GPS
GPS,ortheGlobalPositioningSystem,isaglobal navigationsatellitesystemthatprovideslocation,velocityandtimesynchronization.
2.1GPSprinciple
AGPSreceiverreceivessignalstransmittedfrom threeormoreGPSsatellitestodeterminethepositions ofthesatellitesandthereceiver.Bymeasuringthetime differencebetweenthesignaltransmittedfromthesatelliteandthesignalreceivedbythereceiver,thedistance betweenthesatelliteandthereceivercanbeobtained. Inthiscase,thetransmittedsignalcontainsinformation aboutthepositionofthesatellite.Inmostcases,the locationisdeterminedusingthreesatellitestoreduce theerror.
3Equationofacircle
Thestandardequationofacircleisgivenby:
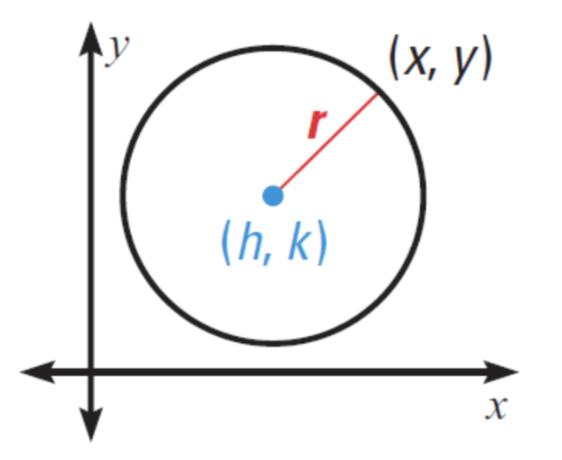
(x h)2 +(y k )2 = r 2 (1) ∗ MemberofJPAMEditingTeam
Fig.1:.
Where(h,k)isthecoordinatesofthecentreofthe circleandristheradius.
61
Fig.2:.
4TheusesofcircleofequationinGPS
Nowthisisthemethodtofindthelocationbyusing theequationofthecircle.Tounderstandeasily,itwill findthelocationofArchimedeswhoisrandomlylocated onEarth.
First,thesatellitesendsradiowavestodetermine thedistancetoArchimedes.Atthistime,Archimedes liesonacirclewhoseradiusistheknowndistance.However,onecirclecannotdeterminetheexactlocation,so othersatellitesareusedtomeasurethedistance.
Second,measurethedistancefromanothersatellite towhereArchimedesis.Thistimeasecondcircleis createdandArchimedesisalsopositionedonthesecond circle.
Amongthecorrectionsofthetwocircles,thelower intersectionpointtouchingtheearthisArchimedes’sposition.Nowconnectthecircletothecoordinateplane. Thisconfirmsthatthegpsmeasurementprincipleis linkedtotheequationproblemofacircle.
ThemidpointofcircleAis(-3,0)andthemidpoint ofcircleBis(0,3).Therefore,theradiusofcircleAis 2kmandtheradiusofcircleBis4km.Now,ifeach circleisexpressedasanequation, A :(x +3)2 + y 2 =4 (2) B : x 2 +(y 3)2 =16 (3)
Fig.3:.
Fig.4:.
62
Fig.5:.

63
Fig.6:.
OpticalIllusions
SangyoonLee
Year10Jeoji
MemberoftheMathematicsSociety

Email:sy2lee26@pupils.nlcsjeju.kr
Editor
DanielSoohyukChang∗
RecommendedYearLevel:KS3,KS4
Keywords:OpticalIllusion
1Introduction
mostfamousopticalillusions,asshownin Figure1.This trianglecannotexistintherealworld.Exceptforthis triangle,therearemanyopticalillusionsexisting.
2Howdoesopticalillusionwork
Fig.1:PenroseTriangle

Inthedictionary,opticalillusionmeanssomething thatdeceivestheeyebyappearingtobeotherthanit is.Thesedays,manyopticalillusionsaremadebymany famousartists.PenroseTriangleisoneoftheworld’s
∗ MemberofJPAMEditingTeam
Fig.2:Exampleofbrainfillingtheinformationwhich isnotreal
Iwillexplainthisinaverysimpleway.Whenwe seeorfeelthingsandgatherimagesfromthesenses,it sendstheinformationtothebrain.Inthisway,they domorethanjustgatherthedata.Whenthereis incompleteinformation,ourbrainfillsthisgapwithour ownperception.Whenourbraincreatesanimagethat isnotthere,theopticalillusionoccurs.Forexamplein Figure2,therearefoursectorswithanangleof270° However,inourbrains,theyfindthemissinggapinthe image.Assaidatthetop,whenourbrainfindsthegap, theytrytofillthegapwithperception.Theconclusion
64
ofthiscreatingimageismakingawhitesquare.Our brainmakesawhitesquareandseemslikeitisonthe topoffourcircles.Thisishowtheopticalillusionworks.

calillusionartistsintheworld.HeisaHungarianFrenchartistwhoobtainedtheentrancequalificationto theBudapestUniversityMedicalFacultytobecomea doctorbutgaveitupandwenttoDesignSchool.He wasgreatlyinfluencedbytheworkofMoholyNagyand wasinfluencedbytheworkofMalevich,Mondrian,and Kandinsky.Hisgrid-likepaintingsandsculpturesare hismostfamousworks.
thatthecoloroftheshoeispinkwithwhitehighlights. Somescientistssaythatthisdependsonwhichbrained personyouare.Ontheotherhand,theysayitdepends onlighting,background,andanythingrelated.

4Conclusion
Byresearchinghowopticalillusionworks,examples ofopticalillusions,andfamousopticalillusionartists,I wasabletounderstandopticalillusions.Also,bystudyinghowopticalillusionworks,Ihavelearnedthatthere

 3Examplesofopticalillusionandfamous artists
Fig.3:Coloroftheshoe
Figure3 isoneofthefamousphotosshowingoptical illusion.Inthisphoto,peoplecanbedividedintotwo groups.Onegroupofpeoplesaysthecoloroftheshoe isgraywithtealhighlights.Andtheothergroupsays
Fig.4:VictorVasarely(1906-1997)
VictorVasarelyisoneofthemostfamousopti-
Fig.5:VictorVasarely’s‘Zebra’
Fig.6:VictorVasarely’s‘KepleGestalt’
Figure5 and Figure5 aretwofamousartworksby VictorVasarelythatshowopticalillusions.In Figure 5,heexpressesthezebrawithopticalillusion,andin Figure5,hemadeanopticalillusionwithasquareand thedifferenceofcolorofeachsquare.
3Examplesofopticalillusionandfamous artists
Fig.3:Coloroftheshoe
Figure3 isoneofthefamousphotosshowingoptical illusion.Inthisphoto,peoplecanbedividedintotwo groups.Onegroupofpeoplesaysthecoloroftheshoe isgraywithtealhighlights.Andtheothergroupsays
Fig.4:VictorVasarely(1906-1997)
VictorVasarelyisoneofthemostfamousopti-
Fig.5:VictorVasarely’s‘Zebra’
Fig.6:VictorVasarely’s‘KepleGestalt’
Figure5 and Figure5 aretwofamousartworksby VictorVasarelythatshowopticalillusions.In Figure 5,heexpressesthezebrawithopticalillusion,andin Figure5,hemadeanopticalillusionwithasquareand thedifferenceofcolorofeachsquare.
65
aremanydifferenttypesofopticalillusionsandtheprinciplesofopticalillusionsarealldifferent.Itmightbe betterifIstudymoreaboutmakingdifferenttypesof opticalillusions.
5Bibliography
1. Britannica‘illusion’
https://www.britannica.com/topic/illusion
2. NationalGeographic‘Unravelingopticalillusions withmaths’
https://www.nationalgeographic.com/science/article/partnercontent-when-circles-are-finally-squared
3. QueenslandBrainInstitute‘Howdoesanoptical illusionwork’
https://qbi.uq.edu.au/blog/2019/10/how-doesoptical-illusion-work
4. AmericanMuseumofNaturalHistory‘Optical IllusionsandHowTheyWork’
https://www.amnh.org/explore/ology/brain/opticalillusions-and-how-they-work/filling-in
5. Health‘IsThisShoePinkorGray—andCanYour AnswerReallyTellYouAnythingAboutYour Brain?’
https://www.health.com/mind-body/sneakeroptical-illusion
6. PanArt‘VictorVasarely’
https://pan-art-connections.com/content/vasarely/
66
ApplicationsofGraphTheory
DanielTaehyeonJun Year10Geomun
MemberofMathematicsSociety
Email:thjun26@pupils.nlcsjeju.kr
Editor AarenJoonseokKang∗ DanielSoohyukChang†
RecommendedYearLevel:KS4andabove
Keywords:GraphTheory,Dijkstra’sAlgorithm, Floyd-WarshallAlgorithm
1Introduction
LeonhardEulerintroducedgraphtheoryinthepaperSevenBridgesofKönigsbergin1736.Thefundamentalofthispaperwastodeviseawalkthrough thecityofKönigsberg-crossingeachofthebridgesin PregelRiveronlyonce.Interestingly,Eulerprovedthat theproblemhadnosolutioninitiallybecausetheroute choiceandlandmasswereirrelevant.Therefore,he hadtoreformulatetheprobleminmoreabstractterms, namely"edge"and"vertex",whichlaidthefoundation ofgraphtheory.Graphtheoryisaboutpracticaluse. Mostofthedataweuseoncomputersheavilyrelieson graphtheory.Forinstance,thelinkstructureofawebsiteisrepresentedbythedirectgraphinwhichvertices representthewebpages,andedgesrepresentthelink fromonepagetoanother.Moreover,incomputerscience,graphtheoryisusedinchemistryandphysicsto studymoleculesandhowtheyinteract.
Thispaperwillgoin-depthaboutvariousterminologiesingraphtheoryandhowthedifferenttypesof algorithmsworkaswellastheapplicationsinreallife.
2Terminology
Inunderstandinggraphtheory,preciseknowledge ofeachkeyterminologyisveryimportant.
1. Graph -Agraphisanorderedpairwhichcanbe representedas G =(V,E ) where G standsforgraph,
∗ ChairofMathematicsSociety,LeaderofJPAMEditingTeam
† MemberofMathematicsSociety
V isasetofverticesand E isasetofedges.
2. WeightedGraph -Ifagraphhasanumberassociatedwitheachedge,itiscalledaweightedgraph. Ifnot,itiscalledanunweightedgraph.(Referto Fig.3)
3. DirectedGraph -Ifagraphhasadirectionassociatedwitheachedgeinsteadofanumber,itis calledadirectedgraph.(RefertoFig.5)
4. Walk -Awalkisaroutethroughagraphalongthe edgesfromonevertextothenext
5. Path -Apathisawalkinwhichnovertexisvisited morethanonce.
6. Trail -Atrailisawalkinwhichnoedgeisvisited morethanonce.
7. Cycle -Acycleisawalkinwhichtheendvertex isthesameasthestartvertexandnoothervertex isvisitedmorethanonce.
8. Degree -Adegreeisthenumberofedgesincident tothevertex.
9. AdjacencyMatrix -A nxn matrixwhichrepresentstheweightofthegraphforeverypossible route.Forexample,iftheweightoftheedgelinkingthevertices C and D is 5,thecorresponding values, aCD and aDC willbelabelled 5.Ifitwas adirectededgefrom C to D ,thematrixvaluefor aCD wouldbe 5 but aDC doesnothaveavalue.
10. DistanceTable -Atableformofadjacencymatrix thatshowstheweightorthedistanceoftheshortest route.(RefertoFig.1)
11. RouteTable -Atablethatshowstheshortest routefromeverysinglepossiblerouteusingthealphabetofthevertex.(RefertoFig.4)
Inordertocalculatetheshortestroutefromthe startvertextothedestinationvertex,Dijkstra’salgorithm,Bellman-FordalgorithmandFloydalgorithmare themostsuitable.ThedifferencebetweenthethreealgorithmsisthatDijkstra’salgorithmcanonlybeused
67
ingraphswithpositiveweightmeaningpositiveedges whereastheBellman-FordalgorithmandFloydalgorithmcanhandlebothpositiveandnegativeweights oftheedges.So,whatisthepointofusingDijkstra’salgorithm?TheadvantageofDijkstra’salgorithm overtheBellman-FordalgorithmandFloydalgorithm isthatittakeslesstimetocalculatetheshortestdistance.ThedifferencebetweentheFloydalgorithmand Dijkstra’salgorithm,excludingthatonecanhandlenegativeweightandtheothercannot,isthatDijkstra’salgorithmonlycalculatestheshortestroutewhereasthe Floydalgorithmcalculatesallofthepossibleroutesand comparesthedistancetofindtheshortestroute.This allowstheFloydalgorithmtobeusedinplaceswhere Dijkstra’salgorithmcannotbeused.
3Dijkstra’sAlgorithm
3.1Definition
Dijkstra’salgorithmcanbeappliedtoanytype ofgraphwithpositiveweightincludingdirectededges, suchasaroutewithone-waystreets.
Thefirststepistocreateaboxlikethefigurebelow foreachvertex.Inthetopleftspace,writedownthe vertex,inthespacetotheright,writedowntheorder oflabellingandinthespacefarright,rightdownthe finalvalue.Inthespacebelowisfortheworkingspace incalculatingtheorderoflabellingandfinallabel.
Repeatthesestepsuntilthedestinationvertexreceivesitsfinallabel.
Findtheshortestpathbytrackingbackfromthe destinationvertextothestartvertex.Includeanedge AB ontherouteif B isalreadyontherouteandthis becomes:
finallabelB finallabelA = weightofedgeAB (2)
Byusinganexampleofthefollowingfigurebelow, wewillcalculatetheshortestpathfromvertex S to vertex T
Followingthesteps,thefirstthingtodoistosubstitutethevectorswithboxesandfillthevertexcellwith thecorrespondingvertexalphabet.Thenextstepisto assign 0 inthefinallabelboxofvertex S and 1 inthe orderoflabellingboxsincethequestionisrequiringus tofindtheshortestpathfrom S to T
Wethenfindtheweightofeveryvertexthatisdirectlyconnectedtovertex S whichinthiscasearevertex
A,vertex B andvertex C .Comparetheweightofthe threeverticesandassign 2 intheorderoflabellingbox ofthevertexwiththesmallestweightandtheweightin thefinallabelbox.Forourexample,thisbecomes:
Thesecondstepistoassign0forthefinallabelof thefirstvertex.
Thethirdstepistorecordaworkingvalueatevery vertex, Y ,thatisdirectlyconnectedtothevertexthat hasjustreceiveditsfinallabel, X :
finallabelatX + weightofedgeXY (1)
Fromeveryworkingvaluefound,selectthesmallest workingvalueandassignittothefinallabel.

Thisprocessisrepeated.Fromvertex A,calculate thefinallabelofthedirectlyconnectedverticesexcludingvertex S .Inthisstage,wealreadyhavethevalue forvertex B whichis 12 butsincetheweightfromvertex A tovertex B is 3,thenewworkingvalue, 11,by adding 8 and 3 replacestheworkingvalue.Comparing thefinallabelofvertex B andvertex D , 11 and 21 respectively,wecanconcludethatproceedingtovertex B istheshorterroutethanproceedingtovertex D .The productofvertex B becomes:
Aftergoingthroughthisrepetitiveprocedureuntil wereachthedestination,vertex T ,thefinalstepisto tracebacktheroutefromthedestination.Thisisnot thesamewiththeorderoflabellingandwehaveto matchtheweightandthefinallabel.RefertoAppendix B forthefinallabelofeachvertex.
Fig.1:Exampleofadistancetable
Fig.2:BoxinDijkstra’salgorithmreplacingeachvertex
68
Bymatchingtheweightandthefinallabel,select thevertexwhichmatchesitsfinallabelandthevalue offinallabelofvertex T -weightlinkingthevertexwith vertex T .Inthisexample,therearethreeoptions,vertex F ,vertex G andvertex H .Vertex F andvertex G cannotbethenextvertexsincethetwovaluesdonot match.Thisleaveswithvertex H ,whichbecomesthe nextvertex.Repeatthisprocessuntilwereachbackto thestartvertex.Therecanbemultipleroutesforthe shortestdistanceandinthiscase,therearetwopossibleroutes. SCEHT and SABDGEHT .Eitherofthem arecorrect.
route,includingnegativeweightedgedgraph.Thefirst stepistodrawadistancetablethatmatchesthegraph. Wherethereisnodirectedroute,whetherduetobeing adirectededgeorhavingnopath,theinfinitysymbol ()isusedtorepresenttheweight.Afterdrawingthe distancetable,drawaroutetablewhicheveryinitial onewouldlooklikethefollowing:
Sincegraphtheoryisaboutalgorithms,asmentionedpreviously,itisalsorelatedtocomputerscience. ForanexamplePythoncodeofDijkstra’salgorithm, refertoAppendixC.
3.2ApplicationoftheDijkstra’salgorithm
Thepurposeofthenavigatingsystemistofindthe shortestorthefastestrouteonecantakefromastarting pointtothedestinationpoint.Theprogramsetsthedeterminedstartinglocationasthestartingvertexandthe stoppinglocationasthedestinationvertex.Eachstreet betweenthestartingpointandthestoppingpointwill berepresentedbyedgesandtheotherpossibledestinationsarerepresentedbyvertices.Theprogramrunsthe algorithmandfindstheshortestpossibleroutesomeone cantakebyfollowingthemechanismaforementioned. Also,navigationmustbeabletodeterminetheshortest drivingtimesaccordingtotheupdatingreal-timedata. Usingtheexampleabove,assumethattheweightofthe graphisthetimetakenfortheedge.Iftheweightof theedgefromvertex H tovertex T waschangedfrom 5 to 13,thefinalvaluewouldalsochangefrom 31 to 32.Thismeansthatthetotaltimetakenfrom S to T hasincreasedbyoneminuteandalsotheshortestroute wouldhavechanged.Theoriginalshortestroutewas SCEHT from SABDGT or SABDFGT
4Floydalgorithm 4.1Definition
Asintroducedseveraltimesbefore,Floydalgorithm isusedtofindtheshortestrouteamongsteverypossible
Ifthetwotablesareready,shadethefirstrowand columnofthedistancetable.Ineachoftheunshaded positions,comparethesumoftheshadedvaluesthatare inthesamerowandcolumnoftheselectedunshaded position.Ifthesumissmallerthanthevalueassignedin theunshadedposition,replacethevaluewiththesum andifthesumisgreater,leaveitasitis.
Intheroutetable,replacethealphabetwith[A]for anyvaluesthathavebeenreplacedfromtheprevious step.Thisistheendofthefirstiteration.
Theseconditerationstartsbyshadingthesecond rowandcolumnofthedistancetable.Oncemore,comparethesumoftheshadedvaluesforeveryunshaded positionandifthevalueissmaller,replaceandifnot, donot.Intheseconditeration,replacethealphabet with[B]foranyvaluesthathavebeenreplacedduring theseconditerationonly.
Repeatthethirdandfourthiterationjustlikethe previoustwobutinstead,shadethethirdrowandcolumnforthethirditerationandreplacethecorrespondingvalueintheroutetablewith[C]andshadethefourth rowandcolumnforthefourthiterationandreplacethe correspondingvalueintheroutetablewith[D].
Finally,supposethattheshortestroutewewantto findisfromvertexAtovertexC.Findthevaluefrom thedistancetablewiththestartingvertexontherow andthedestinationvertexonthecolumn.Thisvalue representstheshortestdistancefromvertexAtovertex C.Inordertofindtheroute,findthealphabetwith thesamemethod.IfthealphabetisB,thisissuggestingthattheshortestroutefromvertexAtovertexC requirestopassthroughvertexB.
UsingFig.5asanexample,wewillnowinvestigate howtocalculatetheshortestdistancebetweenavertex toanotheraswellastheroutebyusingFloydalgorithm.
Thefirstthingtodoistocreateadistancetable andaroutetable.Thedistancetablewilllooklikethe
Fig.3:Exampleofaweightedgraph
Fig.4:Exampleofaroutetable
69
onebelow:
Andtheroutetablewillalwaysbeliketheonein Fig.4.
Forthefirstiteration,thenextstepistoshadethe firstrowandcolumnlikethefollowing:
Afterthefirstiterationisover,starttheseconditeration.Usingthetablewiththeupdatedvalues,shade thesecondrowandcolumn.
Replaceanyvaluethatislargerthanthesumofthe twosuitablevalues,onefromarowandacolumn.After replacing,thedistancetableandroutetableshouldlook likethis:
Repeattheprocesswedidinthefirstiteration.Replacingallofthevaluesthataresmallerthantheoriginalvaluewegetanupdatedtablethatlookslike:
Nowforthethirditeration,shadethethirdrow andcolumnandafterfollowingtheprocess,thetables become:
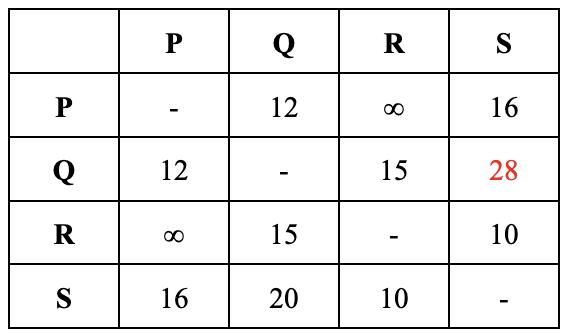
70
IfweseethepositionRowQ,ColumnSfromthe distancetable,wecanseethatavaluethathasbeen replacedinthepreviousiterationhasalowervaluein thethirditeration.Inthiscase,replacethevalueonce morelikethetableabove.
Afterthefourthiteration,wegetthefinaldistance androutetablewhichisshownunderneath.
5Conclusion
Thispapercoveredtwotypesofalgorithmsoutof manyalgorithmsingraphtheory.Thebeautyofthis theoryisthatitisnotonlylimitedtomathematics,but alsoseveralothersubjectsthatseemtohavenorelationshipwithmathematics.Theimportanceofgraphtheorycannotbestressedenoughasitisthebasicprincipleinnavigatingsystemsbutalsoincomputing,search engines,linguisticmodellinginstructureoflanguage, epidemiology,socialmediaandsomuchmoreothersystemsthatweencountereveryday.Letusnotforgethow graphtheoryimpactsourlivesandunderrateitsquality.
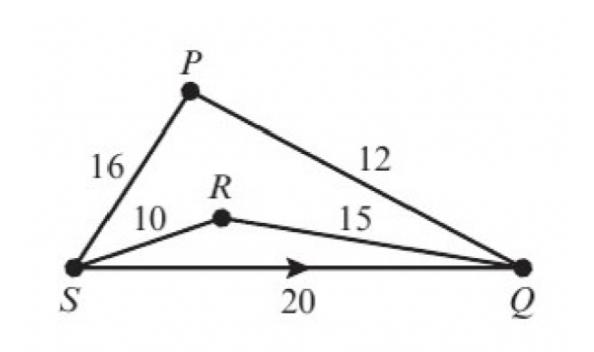
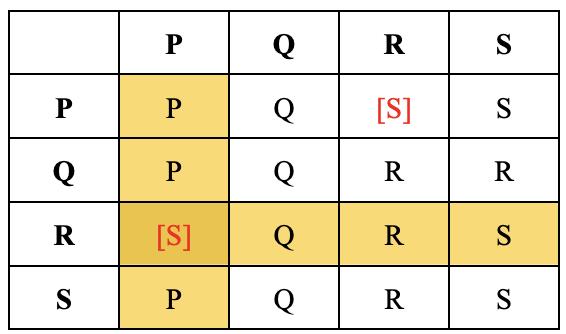
Assumingthatwewanttofindtheshortestpath anddistancefromvertexRtovertexP,weshade inRowRandColumnPonboththefinaldistance androutetable.Whatwecaninterpretfromthe distancetableisthatthecellthatisoverlappedbythe twoshadedregionsistheshortestdistancefromthe designatedstartinganddestinationvertex.Forthe routetable,theoverlappingcellmustbetravelled.In thiscase,vertexSisthevalueintheoverlappingcell andtherefore,theshortestroutemusttravelthrough vertexS.
 Fig.5:Exampleofadirectedgraph
Fig.5:Exampleofadirectedgraph
71
1stIteration-Distancetable
2ndIteration-Routetable
3rdIteration-Distancetable
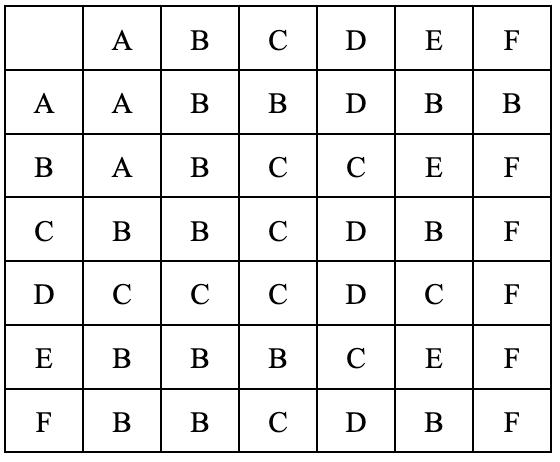
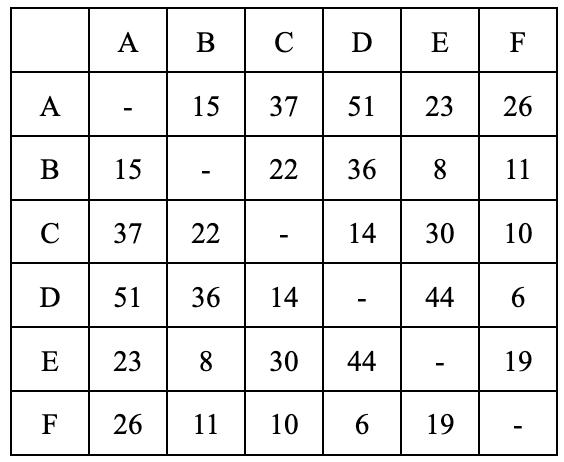
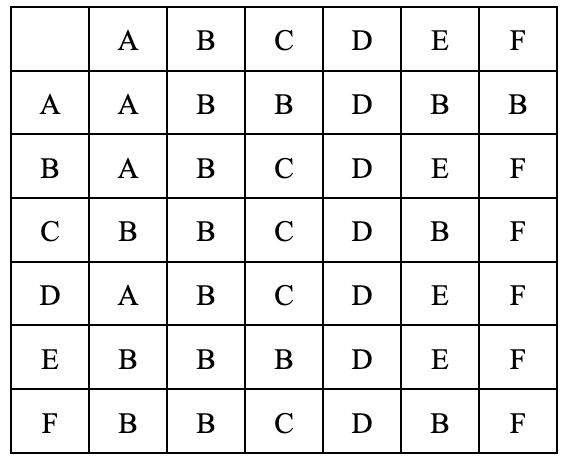
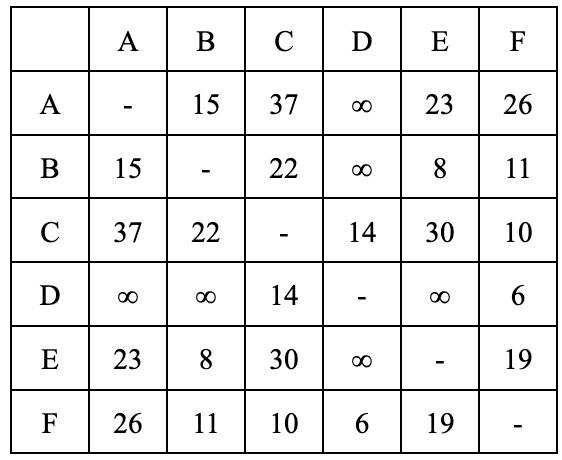
1stIteration-Routetable
2ndIteration-Distancetable
3rdIteration-Routetable
4thIteration-Distancetable
6AppendixA
72
4thIteration-Routetable
5thIteration-Distancetable
6thIteration-Routetable
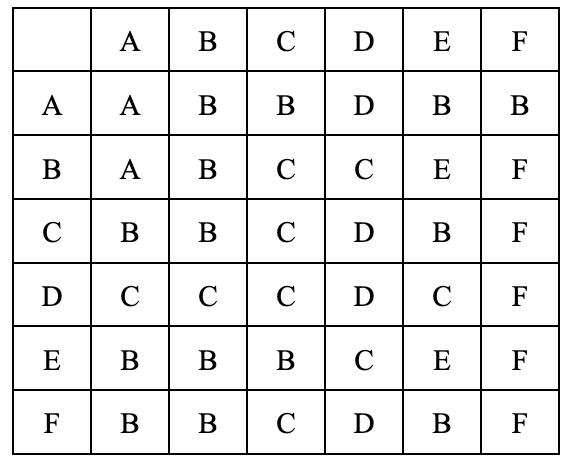
7AppendixB
5thIteration-Routetable
6thIteration-Distancetable
73
import sys
class Graph( object ): def __init__(self,nodes,init_graph): self.nodes=nodes self.graph=self.construct_graph(nodes ,init_graph)
def construct_graph(self,nodes,init_graph ):
graph={} for node in nodes: graph[node]={}
graph.update(init_graph)
for node,edges in graph.items(): for adjacent_node,value in edges. items(): if graph[adjacent_node].get( node,False)==False: graph[adjacent_node][node] =value
return graph
def get_nodes(self): return self.nodes
def get_outgoing_edges(self,node): connections=[] for out_node in self.nodes:
if self.graph[node].get(out_node, False)!=False: connections.append(out_node)
return connections
def value(self,node1,node2): "Returns␣the␣value␣of␣an␣edge␣between␣ two␣nodes."
return self.graph[node1][node2]
def dijkstra_algorithm(graph,start_node): unvisited_nodes= list (graph.get_nodes())
shortest_path={}
previous_nodes={}
max_value=sys.maxsize for node in unvisited_nodes:
shortest_path[node]=max_value
shortest_path[start_node]=0
while unvisited_nodes:
current_min_node=None for node in unvisited_nodes:
if current_min_node==None: current_min_node=node elif shortest_path[node]< shortest_path[current_min_node
]:
current_min_node=node neighbors=graph.get_outgoing_edges( current_min_node) for neighbor in neighbors:
tentative_value=shortest_path[ current_min_node]+graph.value (current_min_node,neighbor)
if tentative_value<shortest_path[ neighbor]: shortest_path[neighbor]= tentative_value previous_nodes[neighbor]= current_min_node
unvisited_nodes.remove(current_min_node ) return previous_nodes,shortest_path
def print_result(previous_nodes,shortest_path, start_node,target_node):
path=[] node=target_node
while node!=start_node: path.append(node) node=previous_nodes[node]
path.append(start_node)
print ("We␣found␣the␣following␣best␣path␣ with␣a␣value␣of␣{}.". format ( shortest_path[target_node])) print ("␣ >␣".join( reversed (path)))
nodes=["Reykjavik","Oslo","Moscow","London ","Rome","Berlin","Belgrade","Athens", "Vaduz","Seoul","Toronto","Warsaw"]
init_graph={}
for node in nodes: init_graph[node]={}
starting_city= input ("Enter␣the␣initial␣ location:␣")
destination_city= input ("Enter␣the␣final␣ location:␣")
init_graph["Reykjavik"]["Oslo"]=5 init_graph["Reykjavik"]["London"]=4 init_graph["Oslo"]["Berlin"]=1 init_graph["Oslo"]["Moscow"]=3 init_graph["Moscow"]["Belgrade"]=5 init_graph["Moscow"]["Athens"]=4 init_graph["Athens"]["Belgrade"]=1 init_graph["Rome"]["Berlin"]=2 init_graph["Rome"]["Athens"]=2 init_graph["Vaduz"]["Warsaw"]=2 init_graph["Vaduz"]["London"]=2 init_graph["Warsaw"]["Athens"]=5 init_graph["Seoul"]["Toronto"]=20 init_graph["Toronto"]["Reykjavik"]=8 graph=Graph(nodes,init_graph) previous_nodes,shortest_path= dijkstra_algorithm(graph=graph,start_node= starting_city)
print_result(previous_nodes,shortest_path, start_node=starting_city,target_node= destination_city)
8AppendixC
74




 Fig.1:LogicStatements:TruthTable
Fig.2:Areaofacircle
Fig.1:LogicStatements:TruthTable
Fig.2:Areaofacircle











 Fig.3:Goldbach’sComet
Fig.3:Goldbach’sComet






















 Fig.2:
Fig.3:
Fig.2:
Fig.3:








 Fig.3:
Fig.4:
Fig.5:
Fig.6:
Fig.7:
Fig.3:
Fig.4:
Fig.5:
Fig.6:
Fig.7:

 Fig.9:
Fig.10:
Fig.9:
Fig.10:
















 ∗ MemberofJPAMEditingTeam
Fig.1: λ <1
∗ MemberofJPAMEditingTeam
Fig.1: λ <1







 Fig.8:.
Fig.9:.
Fig.8:.
Fig.9:.













 3Examplesofopticalillusionandfamous artists
Fig.3:Coloroftheshoe
Figure3 isoneofthefamousphotosshowingoptical illusion.Inthisphoto,peoplecanbedividedintotwo groups.Onegroupofpeoplesaysthecoloroftheshoe isgraywithtealhighlights.Andtheothergroupsays
Fig.4:VictorVasarely(1906-1997)
VictorVasarelyisoneofthemostfamousopti-
Fig.5:VictorVasarely’s‘Zebra’
Fig.6:VictorVasarely’s‘KepleGestalt’
Figure5 and Figure5 aretwofamousartworksby VictorVasarelythatshowopticalillusions.In Figure 5,heexpressesthezebrawithopticalillusion,andin Figure5,hemadeanopticalillusionwithasquareand thedifferenceofcolorofeachsquare.
3Examplesofopticalillusionandfamous artists
Fig.3:Coloroftheshoe
Figure3 isoneofthefamousphotosshowingoptical illusion.Inthisphoto,peoplecanbedividedintotwo groups.Onegroupofpeoplesaysthecoloroftheshoe isgraywithtealhighlights.Andtheothergroupsays
Fig.4:VictorVasarely(1906-1997)
VictorVasarelyisoneofthemostfamousopti-
Fig.5:VictorVasarely’s‘Zebra’
Fig.6:VictorVasarely’s‘KepleGestalt’
Figure5 and Figure5 aretwofamousartworksby VictorVasarelythatshowopticalillusions.In Figure 5,heexpressesthezebrawithopticalillusion,andin Figure5,hemadeanopticalillusionwithasquareand thedifferenceofcolorofeachsquare.

















 Fig.5:Exampleofadirectedgraph
Fig.5:Exampleofadirectedgraph













