Maths Plus NSW Assessment Book 5 Full Digital Sample

Name: Class Name:

Oxford University Press is a department of the University of Oxford. It furthers the University’s objective of excellence in research, scholarship, and education by publishing worldwide. Oxford is a registered trademark of Oxford University Press in the UK and in certain other countries.

Published in Australia by Oxford University Press

Level 8, 737 Bourke Street, Docklands, Victoria 3008, Australia.

© Harry O’Brien and Greg Purcell 2023

The moral rights of the authors have been asserted.

First published 2023

All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, without the prior permission in writing of Oxford University Press, or as expressly permitted by law, by licence, or under terms agreed with the reprographics rights organisation. Enquiries concerning reproduction outside the scope of the above should be sent to the Rights Department, Oxford University Press, at the address above.

You must not circulate this work in any other form and you must impose this same condition on any acquirer.

ISBN 9780190338213

Reproduction and communication for educational purposes

The Australian Copyright Act 1968 (the Act) allows educational institutions that are covered by remuneration arrangements with Copyright Agency to reproduce and communicate certain material for educational purposes. For more information, see copyright.com.au.

Edited by Fiona Olney-Fraser

Cover illustration by Wesley Valenzuela

Typeset by Newgen KnowledgeWorks Pvt. Ltd., Chennai, India

Illustrated by Gareth Conway, Gregory Baldwin and Daniel Rieley

Proofread by Cara Torrance

Printed in China by Golden Cup Printing Co Ltd

Oxford University Press Australia & New Zealand is committed to sourcing paper responsibly.

Acknowledgements

NSW Mathematics K–6 Syllabus © NSW Education Standards Authority for and on behalf of the Crown in right of the State of New South Wales, 2023. NESA does not endorse model answers prepared by the Publisher and takes no responsibility for errors in the reproduction of the Material supplied by NESA.

Acknowledgement of Country

Oxford University Press acknowledges the Traditional Owners of the many lands on which we create and share our learning resources. We acknowledge the Traditional Owners as the original storytellers, teachers and students of this land we call Australia. We pay our respects to Elders, past and present, for the ways in which they have enabled the teachings of their rich cultures and knowledge systems to be shared for millennia.

Printer FSC logo

Message to teachers

Maths Plus Assessment Book Year 5 is an easy-to-use book for both students and teachers. It provides students and teachers with an assessment book that should easily fit into the whole-school maths assessment policy of most schools. The book is designed to diagnostically assess students at Year 5 level. Each assessment page is a snapshot of work that addresses the specific outcomes from the NESA Syllabus. The book provides students with a variety of opportunities to demonstrate their skills, knowledge and understanding of key concepts in Number, Algebra, Measurement, Space, Statistics and Probability. The pages in this book can assist with:

• assessing understanding of specific knowledge required by the NESA Syllabus

• diagnosing students’ knowledge to assist with future scaffolding of work

• providing evidence for A–E reporting

• providing meaningful work samples of students’ work and understanding. Supported by discussion, observation, hands-on experiences and teachers’ own observations, these assessment pages can become a useful component in assisting teachers to accurately assess their students.

Answers for the assessment tasks and a Student Book–Assessment Book correlation chart can be found online on the Maths Plus Teacher Dashboard.

Harry O’Brien, Greg Purcell

Write these numbers in numerals.

1 Two hundred and thirty-seven

2 Two thousand, seven hundred and twelve

3 Five thousand, four hundred and sixty-two

4 Thirty-five thousand, three hundred and sixty-five

5 Two hundred and twenty-seven thousand, six hundred and ninety-four

State the place value of each bold digit.

Order these numbers from smallest to largest.

Expand the following numbers. The first one has been done for you.

Describe the shaded section of the hundredths grids as two-place decimals.

Give the place value of each bold digit.

5 9.325

6 1.468

7 9.921

8 3.713

Recently, Year 5 students visited the Sports Laboratory, where they participated in a series of tests that measured their levels of fitness, flexibility and skill. The first group had their mass and height measured.

13 Write the students’ names on the ladder in order of height, from shortest to tallest.

14 Write the students’ names on the scales in order of mass, from lightest to heaviest.

Decide whether these statements are true (T) or false (F).

Place these fractions in order from smallest to largest.

The largest fractions are closest to 1.

13 Explain why 1 2 is larger than 1 8 .

14 Colour 1 2 of the circle blue.

15 Colour 1 10 of the circle red.

16 Colour 1 5 of the circle green.

17 What fraction of the circle has not been coloured: 1 5 or 1 10 ?

Use the models to help add the fractions.

Add the fractions, which have a sum greater than 1. Show how your answer can be shown as a whole number and a fraction. The first one is done for you.

Subtract the fraction from 1 whole.

12 How many tenths does Alina have now if she was given 9 10 of a chocolate bar, but gave 3 10 to Jade?

13

How many fifths of the pentagon puzzles does Ryder have if he has 4 5 of the red one and 3 5 of the green one?

Addition and subtraction strategies

Bridge to a decade to calculate the totals. 1

Think

Split the numbers into hundreds, tens and ones in order to add or subtract these numbers.

Use bridging to add these amounts. The first one is done for you.

80

5 + 4 9

Equals 789

Use the constant difference to complete these subtractions.

7 10 785 – 352 = 11 489 – 267 = 12 597 – 352 = estimate MP_NSW_AB5_38213_TXT_PPS_NG.indb 6 23-Aug-23 12:38:10

8 DRAFT

Use the halve and halve again strategy to divide by 4.

1 112 ÷ 4 =

2 128 ÷ 4 =

3 144 ÷ 4 =

Use the halve, halve and halve again strategy to divide by 8.

4 240 ÷ 8 =

5 320 ÷ 8 =

6 280 ÷ 8 =

Supply the missing quotient, including the remainder, in the number sentences, which describe how the arrays have been divided. The first one has been started for you.

Answer these division facts with remainders. 11

Write your answer with a fractional remainder.

If the divisor is a composite number, it can be broken into factors to make division easier. Use factors of the divisor to find these quotients. The first one has been started.

26 How many 5 kg packets of nails are in the crate if the total mass of the contents is 720 kg?

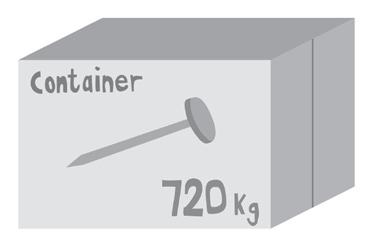
27 How many 9 kg packets of nails could fit in the crate?

28 How many 4 kg packets of nails could fit in the crate?

Mentally calculate the answers to these questions. 1

3 × 4 = 12

So: 3 × 4 tens = 12 tens (120)

3 × 40 = 120

32 × 4 =

Think:

Calculate the answers to these multiplications.

Use the area model to find these products. The first one has been started for you.

Use the distributive property of multiplication to find these products. The first one has been done for you.

Make an estimate of what you think the answer should be.

Example: 8 x 395

Think: 8 x 400 = 3200

8 x 395 should be about 3200.

Rules for order of operations

Always do the work in the grouping symbols (brackets) first. (3 x 6) x 7 = 126

Do the operations with division and multiplication from left to right. 3 x 8 ÷ 2 = 12

Do operations with addition and subtraction from left to right. 5 + 8 – 6 = 7

Do multiplication and division before addition and subtraction. 6 + 8 x 3 = 30

Follow the order of operations rules to complete these number sentences.

1 6 x 4 ÷ 3 =

2 12 + 24 ÷ 3 =

3 105 – 5 x 8 =

4 (20 + 20) ÷ 4 =

5 5 x 10 ÷ 5 + 4 =

6 5 + 4 x 8 =

7 (5 + 4) x 8 =

8 36 ÷ 9 x 2 =

9 36 ÷ (9 x 2) =

10 50 x 10 ÷ 2 =

Do work inside the brackets first.

Create number sentences that will help solve the problems below.

11 How much did Zac earn if he worked for 3 hours @ $40 per hour and 2 hours @ $50 per hour?

DRAFT

13 How much washing powder is left in the 1 kilogram pack if 5 scoops of 25 grams were used to wash the uniforms?

12 How far did Hanika swim in the 50 metre pool if she did 6 laps of freestyle and 4 laps of backstroke?

14 Eve’s holiday house is 250 km away. How far does she still have to go if she has driven for 2 hours @ 80 km/h?

15 Complete the number cross.

Constructs and completes number sentences involving multiplicative relations, applying the order of operations to calculations MA3-MR-02

Name the school building or field found at these coordinates.

Remember, the first number refers to a point on the x-axis and the second number refers to a point on the y-axis

Use the map below to help answer the following questions.

Plot the coordinates (1,6), (2,5), (4,5), (8,4), (10,2), (9,1), (7,1), (3,1), (3,2), (2,2) and (2,3), then join them to see the route the post van takes.

8 Which street did the route finish in?

9 What are the coordinates for the intersection of Bent Rd and Porters Rd?

10 What are the coordinates for the intersection of Porters Rd and Dobe Place?

If you know that all the sides of a 2D shape are equal in length, the perimeter can be found by multiplying the length of one side by the number of sides.

10 Draw a line to match each distance to a sporting site.

using decimal

1 In which shape above are all the angles acute angles?

2 In which shape above are all the angles obtuse angles?

3 In which shape above are all the angles right angles?

Measure these angles using a protractor.

Use the base line to construct the angles using a protractor. 8 9

Investigates and classifies two-dimensional shapes, including triangles and quadrilaterals based on their properties MA3-2DS-01

Draw a line to match each quadrilateral to its description.

1 2 y y

x x

Parallelogram

• Opposite sides are parallel

• Opposite sides are of equal length

3

4

Trapezium

• One pair of parallel sides

Rectangle

• 4 right angles

• Two sets of parallel lines of equal length

Rhombus

• Opposite angles are equal

• 4 equal sides

• Two sets of parallel lines

Measure and record the angles on the triangles. Name each type of triangle.

equilateral isosceles right angle scalene

5 6 7 8

9 Construct an equilateral triangle with sides of 40 mm. Measure and label all three angles.

10 Construct and label an isosceles triangle with two sides the same length and two angles the same size.

Triangles, quadrilaterals and symmetry

Polygons are shapes with three or more straight sides.

1 Which shapes below are polygons?____________________________________

2 Which shapes above are also quadrilaterals? ________________

3 Draw diagonals on the rectangle.

4 Draw all lines of symmetry on the square.

5 Circle all the shapes below that have rotational symmetry.

6 Draw a line to match each right-angled triangle to a name.

D Scalene triangle Isosceles triangle

Isosceles and scalene triangles can also be right-angled triangles. Equilateral triangles cannot be right angled.

Investigates and classifies two-dimensional shapes, including triangles and quadrilaterals based on their properties MA3-2DS-01

A netball court is 30 metres long and 15 metres wide.

The court is divided into three equal sections.

11 Calculate the area of the whole court and the area of the centre third.

Whole court Centre third

Selects and uses the appropriate unit to

areas, including areas of rectangles MA3-2DS-02

3D objects

Draw a line to match each object to its net. Write the name of the object below each one. 1 2 3 4

Draw a line to match the objects to their descriptions given in the table below.

Visualises, sketches and constructs three-dimensional objects, including prisms and pyramids, making connections to two-dimensional representations MA3-3DS-01

Use cubic centimetre blocks to construct shapes like these. Estimate, then measure and record each shape’s volume.

4 How many millilitres of water are in the beaker?

5 How many millilitres would need to be added to fill the beaker to 500 mL?

6 How many full 500 mL beakers would be needed to fill a 3 L jug?

Fact: One millilitre of water has a mass of 1 gram and a volume of 1 cubic centimetre. This means that for every cubic centimetre block that is added to a jug of water, the water level will rise by 1 mL.

At the moment, the measuring glass is filled to the 30 mL mark.

Colour the mark on the measuring glass to show how much water would be displaced if a 20 cm3 block was placed inside the measuring glass.

Complete this millilitres/litres conversion chart.

The scales below show pieces of fruit being balanced by blocks and a 1 kg weight.

1 How many blocks were needed to balance the apple?

2 How many apples were needed to balance the 1 kg mass?

3 How many blocks would it take to balance a 1 kg mass?

4 How many apples would it take to balance a 750 g rockmelon?

5 What is the mass of one block?

Convert the measurements below from grams to kilograms. Use decimal notation to record the kilogram measurements.

Convert the measurements below from tonnes to kilograms.

Remember! 1 litre of water has a mass of 1 kilogram.

The truck below can carry only 1 tonne. How many of each type of container filled with water would equal 1 tonne? 22 23 24 25

On each clock, show the 24-hour time given, then write the times in 12-hour digital form.

Use the timetable above to answer true or false to the following statements.

5 A trip from Bennett to Miller takes 42 minutes.

6 The buses run at 40-minute intervals.

7 A trip from Shell to Francis takes 53 minutes.

8 The 1338 bus from Frost arrives at Miller at 1359

9 The 1322 bus from Bennett arrives at Francis at 2:09 pm.

10 The bus that leaves Shell at 1:15 pm arrives at Harris at 1359.

Use am and pm notation to record the time each person finished work.

Finishing time

11 Noah started at 9 am and worked for 8 hours.

12 Indira worked for 9 hours, having started at 7 am.

13 Ruby started at 9:30 pm and worked for 7 1 2 hours.

14 Giada started at 10:30 pm and worked for 8 1 2 hours.

A phone conference will start in Sydney at 5:15 pm on 3 June. Show the starting times for the conference in Perth, Adelaide and Hobart in 24-hour time.

Cawarra Bus Service

Madison has made a column graph to show how she spends her weekly wages. Answer true (T) or false (F).

1 Madison saves $60 per week.

2 The total amount she spends on rent, food and her car is $150.

3 She spends about $15 per week on clothes.

4 She spends twice as much on sport as she does on clothes.

5 Her total wage is $255.

6 According to the temperature graph on the left, at what time was the highest temperature?

DRAFT

10 When was the lowest temperature shown on the graph?

7 What was the rise in temperature between 8 am and 10 am?

8 What was the fall in temperature between 4 pm and 7 pm?

9 At what times of the day was the temperature 20°C?

11 Estimate the temperature at these times:

• 9:30 am

• 12:30 pm

• 10:30 am

• 4:30 pm

= 2 people

12 How many members are in the 14–17 year age group?

13 How many members are over 21 years?

14 How many members are under 10 years old?

15 How many members belong to the club?__________

16 Which age group represents 1 4 of the total membership? ___________

The six faces of a die used when playing board games are shown here. Each number has a 1 in 6 chance of being thrown.

Use the fractions 1 6 ,

,

,

1 A 6 is thrown first go.

6 and 6 6 to describe the likelihood of these outcomes.

2 A 2 is thrown first go.

3 An odd number is thrown first go.

4 An even number is thrown first go.

5 A number greater than 3 is thrown first go.

6 A number greater than 4 is thrown first go.

True or false

7 The total of all the fractions that describe the probability of throwing a number on the dice is 1. _______

Lucky colour wheel

8 What fraction describes the probability of the spinner landing on one of the sectors of the spinner?

Pink Pink Blue Blue

Pink Pink Pink Gold

9 What fraction would best describe the probability of the spinner landing on the pink sectors of the spinner?

10 Which colour has the best probability of being the winning colour?

11 Which colour has the least chance of being the winning colour?

Words such as impossible, unlikely, 50/50, likely and certain are often used by people when discussing the probability of an outcome occurring.

12 Draw a line to match each word to a place on the number line.

DRAFT

DRAFT

ASSESSMENT BOOK PRACTISE, MASTER, ASSESS

Maths Plus NESA Syllabus / Australian Curriculum Edition, Year K to 6 is a whole-school program based on the NSW Education Standards Authority Mathematics K–6 Syllabus for the Australian Curriculum.

Maths Plus follows a graded and spiralling approach, allowing teachers to revisit concepts throughout the year. It provides students with opportunities to sequentially develop, practise and master their skills and knowledge in the content strands of the Australian Curriculum: Mathematics:

• Number

• Measurement

• Statistics

• Algebra

• Space

• Probability

The Assessment Books feature post-tests to assess the concepts and skills developed in the Student Books and Mentals and Homework Books. Answers can be found online on the Maths Plus Teacher Dashboard.

www.oxfordowl.com.au

Oxford Owl is the home for Oxford Primary professional resources.

Printer DRAFT

logo