Maths Plus NSW Student Book 5 Full Digital Sample

The Maths Plus NSW Syllabus/Australian Curriculum series, Year K to Year 6, is based on the NSW Education Standards Authority 2023 Mathematics K–6 Syllabus for the Australian Curriculum Mathematics (ACARA). Each book after Year K builds upon prior knowledge and works towards an understanding of the achievement standards for the relevant year level and beyond. Maths Plus provides students with opportunities to sequentially develop their skills and knowledge in the strands of the Australian Curriculum Mathematics: Number, Algebra, Measurement, Space, Statistics and Probability

Series components

Student Books

Work towards achieving the relevant outcomes by developing skills and competency in understanding mathematical structures, fluency, reasoning and problem solving.

Mentals and Homework Books

Provide concise, essential revision and consolidation activities that correspond with the concepts and units of work presented in the Student Books.

Assessment Books

Include short post-tests with a simple marking system to assess students’ skills and understanding of the concepts in the Student Books.

Student Book features

• All pages are colour coded.

Number and Algebra

and Space

Statistics and Probability

• Australian Curriculum Mathematics content descriptions, proficiency strand references and general capabilities appear on each page.

• The Dictionary (Years 2 to 6) features clear and simple explanations of mathematical terms and language.

Diagnostic term reviews

• Diagnostic term reviews (Years 1 to 6) assist in pinpointing students’ strengths and weaknesses, allowing intervention and re-teaching opportunities where required.

• The Find a topic page allows teachers the freedom to address particular topics and student needs as appropriate, providing essential revision and consolidation opportunities.

Teacher Book and Teacher Dashboard

Provide access to a wealth of resources and support material:

• curricula and planning documents

• interactive teaching tools

• potential difficulties videos

• learning activities

• support and extension activities

• reflection

• blackline masters and investigation pages

• links to Advanced Primary Maths (Years 3 to 6)

• assessment tests

• answers for student resources

www.oxfordowl.com.au

Oxford Owl is the home for Oxford Primary professional resources.

NSW Syllabus Outcomes

MA3-RN-01

Applies an understanding of place value and the role of zero to represent the properties of numbers

MA3-RN-02

Compares and orders decimals up to 3 decimal places

MA3-RN-03

Determines percentages of quantities, and finds equivalent fractions and decimals for benchmark percentage values

MA3-AR-01

Selects and applies appropriate strategies to solve addition and subtraction problems

MA3-MR-01

Selects and applies appropriate strategies to solve multiplication and division problems

MA3-MR-02

Constructs and completes number sentences involving multiplicative relations, applying the order of operations to calculations

MA3-RQF-01

Compares and orders fractions with denominators of 2, 3, 4, 5, 6, 8 and 10

MA3-RQF-02

Determines

MA3-GM-01

of measures and quantities

Locates and describes points on a coordinate plane

MA3-GM-02

MEASUREMENT AND SPACE

Selects and uses the appropriate unit and device to measure lengths and distances including perimeters

MA3-GM-03

Measures and constructs angles, and identifies the relationships between angles on a straight line and angles at a point

MA3-2DS-01

Investigates and classifies two-dimensional shapes, including triangles and quadrilaterals, based on their properties

MA3-2DS-02

Selects and uses the appropriate unit to calculate areas, including areas of rectangles

MA3-2DS-03

Combines, splits and rearranges shapes to determine the area of parallelograms and triangles

MA3-3DS-01

Visualises, sketches and constructs three-dimensional objects, including prisms and pyramids, making connections to two-dimensional representations

MA3-3DS-02

Selects and uses the appropriate unit to estimate, measure and calculate volumes and capacities

MA3-NSM-01

Selects and uses the appropriate unit and device to measure the masses of objects

MA3-NSM-02

Measures and compares duration, using 12- and 24-hour time and am and pm notation

MA3-DATA-01

Constructs graphs using many-to-one scales

MA3-DATA-02

Interprets data displays, including timelines and line graphs

MA3-CHAN-01

Conducts chance experiments and quantifies the probability

MAO-WM-01 Working mathematically

STATISTICS AND PROBABILITY

Develops understanding and fluency in mathematics through exploring and connecting mathematical concepts, choosing and applying mathematical techniques to solve problems, and communicating their thinking and reasoning coherently and clearly

STATISTICS AND PROBABILITY

MA3-DATA-01

MA3-DATA-02

MA3-CHAN-01

MAO-WM-01 Working mathematically

The 4 facts associated with this array are:

4 × 3 = 12

3 × 4 = 12

12 ÷ 3 = 4

12 ÷ 4 = 3

Write 4 facts you can derive from each array. 1

Associative and commutative laws

The commutative law of multiplication tells us that two factors of a multiplication number sentence can be multiplied in reverse and it will not change the answer.

3 × 4 has the same result as 4 × 3.

The associative law states that it does not matter in which order factors are multiplied. 3 × 2 × 4 has the same result as 4 × 2 × 3.

Complete these pairs of number sentences. 2

Write some division number sentences to find out if division is commutative. 3

Addition and subtraction strategies

Last year, the following strategies were taught. Use them to solve the questions on this page.

Use the split strategy to add and subtract these numbers.

Bridge to a decade to calculate the answers.

Estimate an answer to each of the additions and subtractions by rounding each number. The first one is done for you.

Solve these problems using your mental arithmetic skills.

a Jim has 54 m of timber in one pile and 38 m of timber in another. How much timber does he have altogether?

b Sarah had $73 in her bank account but spent $48 on clothes. How much money does she have left in her bank account?

Recognising angles

An angle is the amount of turn between two arms. Angles can be measured and named according to the size of their opening. This common angle is called a right angle.

It is equal to a 1 4 turn of the hands on a clock face.

Angles are classified according to the amount of turn between two arms.

Right angle

Obtuse angle

Acute angle

Straight angle

Reflex angle

Square corner; 90°

Larger than a right angle; greater than 90°

Smaller than a right angle; less than 90°

Can be made from two right angles; 180°

Label the angles either right angle, obtuse, acute, reflex or straight.

Larger than a straight angle; greater than 180°

A B

C

Identify which shape is being described.

a I have four right angles.

b I have one obtuse angle, one acute angle and two right angles.

c I have three acute angles.

d I have three right angles and two obtuse angles.

e I have six obtuse angles.

D E

Find two acute angles and two obtuse angles in your classroom.

Longer distances are measured in kilometres. There are 1000 metres in 1 kilometre. Trundle wheels are often used to measure long distances because each revolution equals 1 metre.

How many times would a trundle wheel click when measuring 1 kilometre?

Measuring 1 kilometre

You will need a trundle wheel and about 11 traffic cones. With your teacher, select an area that you think is about 1 kilometre long. Mark your starting point with a traffic cone and begin walking in a straight line, counting the clicks of the trundle wheel as you go. At the count of every 100 metres, place a cone until you have covered 1000 metres.

Mark out a 1 kilometre cross-country course

11 12 13

In your school, mark out a cross-country course that is about 1 kilometre. You may need to write some distances in chalk on the ground or mark distances with markers. It can zigzag or go around buildings a number of times.

Use a stopwatch to record how long it takes your group members to run your course.

Use the map of New South Wales and the distances from Sydney to calculate the distances between these places.

10 × 100 m equals 1 km.

Use a street directory or online map to help you name locations about 1 2 a km from school, about 1 km from school and about 2 km from school.

Learning to trade in an addition sum

PROCESS Hund Tens Ones

Add 9 ones plus 3 ones equals 12 ones. Exchange 10 ones for 1 ten. Record 2 in the ones column.

Add 1 hundred plus 1 hundred equals 2 hundreds. Add 1 ten plus 3 tens plus 1 ten equals 5 tens. Trade the 10 ones for a ten.

Complete each addition algorithm.

Solve the problems.

a At Kingsland primary school there are 248 girls on the school roll and 249 boys. How many children attend the school?

b Ms Green, the garden shop owner, banked $389 on Monday and $456 on Tuesday. What was her total banking for the two days?

Selects and applies appropriate strategies to solve addition and subtraction problems PROBLEM SOLVING, COMMUNICATING L N CCT MP_NSW_SB5_38343_TXT_PPS_NG.indb 6 30-Aug-23 08:58:37 DRAFT

2 3

Thirds and sixths 2

The numerator shows us how many parts out of the whole (the fractional part).

The denominator shows us how many parts are in the whole.

What fraction of each shape is shaded? The first one has been done for you.

Label the fractions on the number lines.

Which fraction is larger:

?

A polygon is a shape made up of three or more straight sides.

Give a clear description of each shape by recording its properties.

A parallelogram is a four-sided shape with two pairs of parallel sides. Opposite sides and angles are equal. A square and a rectangle are examples of a parallelogram.

Circle the parallelogram.

and classifies two-dimensional shapes, including triangles and quadrilaterals, based on their properties

Bank

Calculating area 2

Martha wanted to know what the area of her bank card was, so she divided it exactly into square centimetres and counted them up.

a Find a quicker way for finding the area using the square centimetres Martha drew on the card.

b Explain what it is.

Apply the formula ‘Area = length × width’ to find the area of these shapes. 11

12

Calculate the areas of this ticket.

a What is the area of the smaller section of the ticket? cm2

b What is the area of the larger section of the ticket? cm2

MP_NSW_SB5_38343_TXT_PPS_NG.indb 9 30-Aug-23 08:58:37 DRAFT

Subtract 1 hundred from 2 hundreds to give 1 hundred.

1 ten

Trade a ten for 10 ones.

9 ones from 3 ones can’t be done. Trade a ten from the tens column to the ones column to make 13 ones.

4 tens becomes 3 tens. 9 ones from 13 ones equals 4 ones.

Complete these subtractions without trading.

2 Complete these subtractions with trading in the ones.

Complete these subtractions with trading in the tens.

Crack this secret code by matching shapes with their numbers.

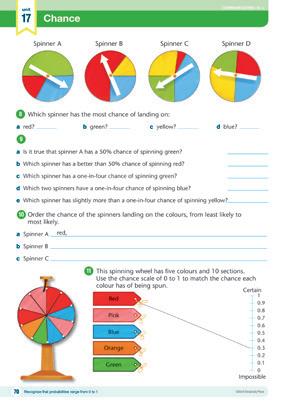
Probability using fractions 3

Fractions can be used to describe chance. For example, the chance of a dice landing on 6 is one out of 6, or 1 6 .

Write the fraction to describe the chance of a dice:

a landing on a five

b landing on a one

c landing on an even number

d landing on a number less than five

8 9

Write the fraction to describe the chance of these spinners landing on blue.

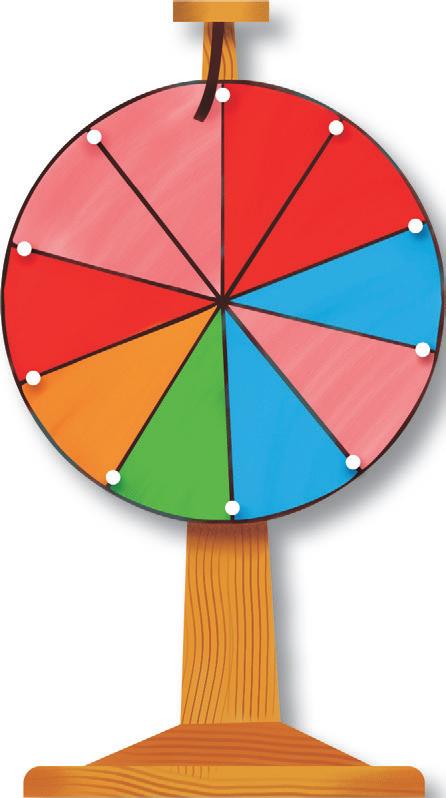
b c

Lena put 20 different-coloured marbles in a bag. Write true or false to answer the questions about marbles being drawn from the bag first go.

a The chance of blue being drawn is 4 20 .

b The chance of red being drawn is 5 20 .

c The chance of green being drawn is 3 20 .

d The chance of yellow being drawn is 5 20

e The chance of purple being drawn is 1 20 .

f The chance of orange being drawn is 5 20

10 11

Make up a bag of different-coloured marbles or counters yourself and write the chances, as fractions, of drawing a colour from the bag.

Which objects above are most suitable for packing or stacking?

Explain why.

A base unit for measuring volume is the cubic centimetre. It can be shown by a cube measuring 1 cm long, 1 cm wide and 1 cm high. A centicube or MAB one are good examples of a cubic centimetre (cm3).

Use centicubes or MAB ones to build each prism, then record the volume of each.

Challenge!

Daya has constructed a shape that has a volume of 24 cm3. Construct a shape of your own that has the same volume, then sketch it in the box.

Addition and subtraction strategies

Last year the following strategies were taught. Use them to answer the questions on this page.

Use your knowledge of number facts to extend these additions and subtractions.

2 Use the jump strategy to add and subtract these numbers.

Add the numbers mentally using the compensation strategy.

Subtract the numbers mentally using the compensation strategy.

Use the strategies above to write addition and subtraction number sentences that have an answer of 54.

Reading numbers

When we read numbers, we read them in groups of hundreds, tens and ones. The following chart best illustrates this concept.

Write these numbers in numerals. The first one is done for you.

a Two hundred and sixteen thousand, four hundred and twenty-six.

b Three hundred and twenty-one thousand, two hundred and sixteen.

c Four hundred and thirty-five thousand, five hundred and sixty.

d One million, five hundred and eighteen thousand, six hundred and twenty.

e Twelve million, two hundred and seventy thousand, four hundred and eighty.

f Twenty-eight million, three hundred and seventy-eight thousand, nine hundred and ninety-nine.

The table below shows the areas of each state and territory of Australia.

a List the states and territories in order of their areas. ACT,

b Which state has an area closest to 1 000 000 km2?

c Which state has an area closest to 3 000 000 km2?

d Which states are more than double the area of NSW?

e Which state is more than double the area of SA?

f Which state is closest to the area of NSW?

Coordinates are used to locate position on a number plane. The order of the numbers is very important.

The first number is the reading on the x axis

The second number is the reading on the y axis

The number plane, on the left, shows the point (3,2).

8

Plot the coordinates, then connect them to make a polygon.

a Plot these points: (2,1), (1,3), (3,5), (5,3) and (4,1).

b Join (2,1) to (1,3).

c Join (1,3) to (3,5).

d Join (3,5) to (5,3).

e Join (5,3) to (4,1).

f Join (4,1) to (2,1).

What shape did you make?

Remember! Read the horizontal before the vertical, e.g. (9,3) Port Macquarie

Find the closest coordinate for each place.

Estimate the mass of each object in grams, then measure them using standard masses.

Object Estimate Mass

a Pencil case

b Textbook

c Basketball

11 12

This cardboard box can hold a mass of 3 kg. How many of each item could be packed into a box of this type?

250 g 750 g 150 g 50 g 2 3 0 +

+ =

-

% C / 4 5 6 7 8 9 a b c d

Masses can be recorded using decimal notation. 300 g = 0.3 kg 250 g = 0.25 kg 258 g = 0.258 kg

13

Write the masses as decimals.

a 500 g = kg

b 250 g = kg

c 275 g = kg

d 376 g = kg

e 459 g = kg

f 674 g = kg

g 1 kg and 632 g = kg

h 1 kg and 347 g = kg

i 1 kg and 250 g = kg

j 2 kg and 374 g = kg

k 2 kg and 500 g = kg

l 3 kg and 200 g = kg

Draw a line from each object to the most suitable measuring device. 14

d e a b Dictionary Dictionary

5.25 kg

c

Kitchen scales

Bathroom scales

Weighbridge

Electronic scale

BUTTER 250 g MP_NSW_SB5_38343_TXT_PPS_NG.indb 17 30-Aug-23 08:58:43 DRAFT

d

5

Complete the multiplication facts using your knowledge of place value.

Use your knowledge of place value to multiply by tens. For example, 50 × 60 equals 5 tens × 6 tens which equals 30 hundreds (3000).

a 20 × 50 =

b

c 40 × 40 =

d

Mentally calculate the products of these multiplications.

The product is the result of multiplying.

Use mental computation skills to solve the problems.

a Mary bought 6 games. How much did she spend?

b Thomas bought 3 watches. How much did he spend?

c Sarah bought 5 T-shirts. How much did she spend?

d How much would 5 books cost?

e How much would 4 dresses cost?

If you had $150 to spend on the above items, how might you spend it? 5

Problem solving 5

Discuss with a friend what strategies you would use to solve these problems. Solve them, then check your solutions with other groups in the class.

Problem Strategies Answer

a A farmer planted 78 trees in 6 paddocks. If the trees were shared equally, how many trees would there be in each paddock?

b A teacher shared 96 counters among 6 students. How many did each student receive?

c Mabel bought 5 tins of beans for 79c per tin and a can of dog food for 96c. How much did she spend on her purchases?

d Samuel saved $35 per week for 9 weeks from his weekly wages. How much did he save altogether?

e Huan planted 100 flowers but only 1 4 of them sprouted. How many flowers sprouted?

f A bicycle wheel has a circumference of 2 m. How many times will it need to turn to cover a distance of 528 m?

g The cake stall collected $296 at the fete. If $20 was spent hiring a tent and $70 was spent on ingredients, what was the cake stall profit?

h The cost of a camp was $40 per student plus $15 each for the bus. How much money did the teacher collect from 30 students?

Think about the strategies you used to solve question 6g, then write another method you could use in the future to solve a problem like it.

Baked Beans

Chance experiments 5

Dice-rolling experiment

a If you rolled two dice and totalled the scores, what do you think would be the most common score?

b Roll two dice 40 times, recording the total of each roll in the table below.

c Which total was most frequent?

d Which total was least frequent?

Use the data in the table above to order the scores from least to most.

Do you think 7 would usually have more responses than 12?

Explain why.

Mr Carson put 30 of his favourite-coloured round lollies in a bag.

a How many of each lolly are there? R Y G O

b Which is the most likely colour to be drawn out of the bag?

c How would you describe the chance of red being drawn out of the bag?

d Which is the least likely colour to be drawn out of the bag?

e Is it more likely that an orange lolly would be drawn than a green one?

f Is it more likely that a yellow lolly would be drawn than a green one?

Naming prisms and pyramids

Prisms have two bases that are the same shape and size. All other faces on a prism are rectangular. Prisms are named from the shape of their bases.

Pentagonal prism

Draw a line to join each object to its name.

Pyramids have only one base, with all other faces being triangles. The triangular faces meet at a common apex. Pyramids are named from the shape of their base.

rectangular prism

rectangular pyramid

square pyramid

triangular pyramid cube

hexagonal prism

triangular prism

pentagonal prism

pentagonal pyramid

octagonal prism

hexagonal pyramid

octagonal pyramid

Visualises, sketches and constructs three-dimensional objects, including prisms and pyramids, making connections to two-dimensional representations

apex

Pentagonal pyramid

Another way of recording division is by using the division symbol. ÷ The quotient is the result of a division.

Find the quotients of these divisions.

means

= 4

An example of division that leaves a remainder: Tina wanted to share 26 icy-pole sticks among 5 people. She knows that it will not work out equally and that there must be a remainder.

Solve these divisions that have remainders. The first one is done for you.

DRAFT

There are 72 students in Year 5 who need to be transported to the Sports Carnival. How many trips would each vehicle below make if it was the only vehicle available to transport the students? (Working paper may be needed.)

trips

trips

3 passengers

4 passengers c trips

5 passengers 12 passengers

trips

How many trips would the whole fleet of vehicles need to make if they transported the students together? trips

Continue

Write a rule for each number pattern, then use it to predict the next two terms in the pattern.

You must look closely at the previous terms in the pattern.

Continue to make the pattern of square numbers and record the numbers. 4 9 16

Look for a rule or a pattern in the square numbers, then extend the table to the twelfth square number.

Square numbers 4 9 16

A column graph is a graph that uses columns to record the frequency of events. For example, in this survey six people selected C.

Ashton threw a set of three dice forty times and recorded the totals on a column graph. Use his graph to answer the questions.

a Which score occurred most frequently?

b What was the frequency of the second most frequent score?

c Which scores occurred 2 times?

d Which scores did not appear at all in this sample?

e Explain why the scores 10, 11 and 12 account for 50% of the results.

Class 5G were given a Quick Quiz about Australia. Madeleine and Grace recorded the scores on this column graph.

9 10

Answer true or false to these statements.

a 13 correct answers was the most common score.

b Most scores were between 11 and 16.

c 8 was a score apart from the main cluster.

d 30 people participated in the quiz.

am and pm time

am is an abbreviation for ante meridiem which means “before midday”. pm is an abbreviation for post meridiem which means “after midday”.

Write a digital label for each clock using “am and pm” notation.

Calculate the

Solve these problems.

a A soldier commenced duty at 1:30 pm. She finished 8 hours later. When did she finish work?

b Jim started work at 6:30 am and finished at 4:30 pm. How long did he work if he had an hour off for lunch?

c The lamb started cooking at 3 pm. We ate it 2 hours 15 minutes later. When did we have dinner?

If I go to bed at 9 pm and wake up 12 hours later, it will be 9 am.

7 Two digits multiplied by 1 digit/area model

How to solve 35 × 4

The area model partitions 35 into its place values of 30 and 5. It creates two separate equations: 30 × 4 and 5 × 4.

Solve these multiplications using the area models.

3 × 5 = 15 ones

Write 5 in the ones column and trade 10 ones for 1 ten, and write the 1 in the tens column.

3 × 3 tens equals 9 tens plus 1 ten which equals 10 tens. Write the 0 in the tens column and the 1 in the hundreds.

Solve each multiplication using the shortened form.

Solve these problems.

a The pilot usually completes 29 flights each month. How many flights will she complete in 9 months?

b How many thumb tacks are there if there are 7 packs with 52 thumb tacks in each pack?

Equivalent fractions

Equivalent fractions

Use the fraction grid to write an equivalent fraction for each fraction given below. The first one is done for you.

Use the greater than, less than or equals symbols to make each number sentence true.

Draw a line to place these fractions on the number line.

7 Protractors

Answer these questions about the protractor.

a Complete the degrees on the protractor. You’ll need to look closely at a protractor to do this.

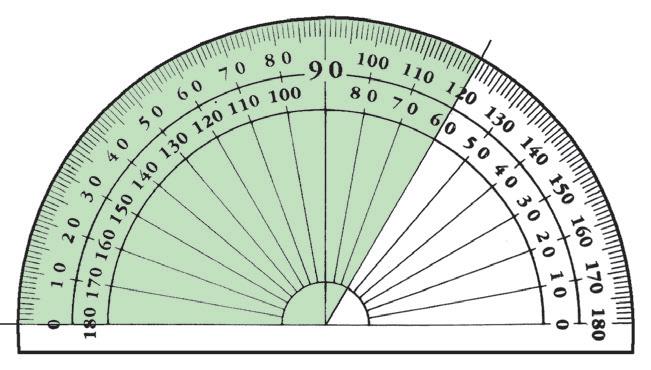
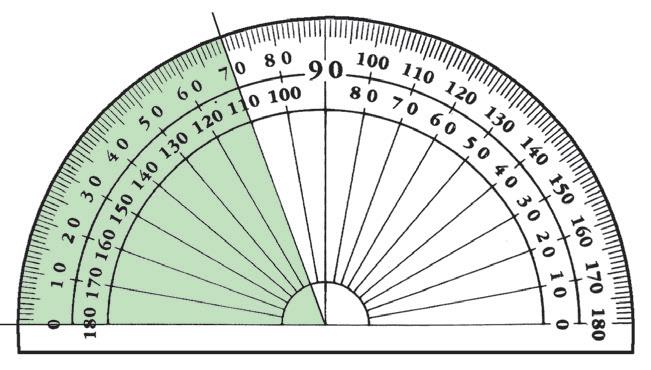
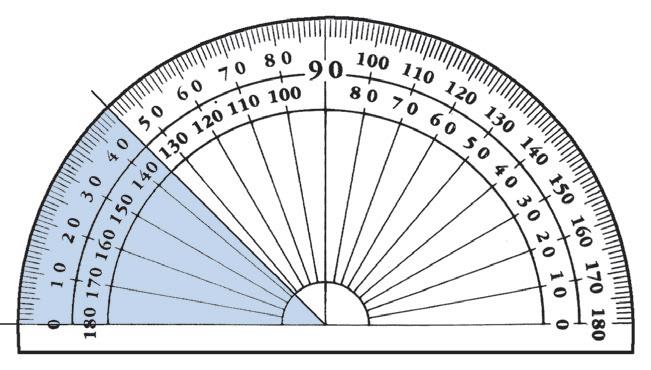
b Why do you think the numbers go both ways?

Name each angle and then write its size in degrees.

To measure these angles, place the base-line of a protractor along the lower arm of the angle, and place the centre point of the protractor on the vertex of the angle.

To convert metres to kilometres, divide by 1000. A metre is one thousandth of a kilometre.

Use a calculator to convert the metres to kilometres. Your calculator will express some measurements as decimals. The first one is done for you.

To change metres to kilometres, I divide by 1000.

Which distance above is closest to 3 km?

To convert kilometres to metres, multiply by 1000.

Convert these measurements from kilometres into metres without the use of a calculator. Then use a calculator to check.

To change kilometres into metres, I multiply by 1000.

Calculate the distances between towns in metres, then convert the metres into kilometres.

Kilometres

Name a journey longer than 13 km. 14

to

Learning to trade in an addition sum

5 thousands plus 3 thousands plus 1 thousand equals 9 thousands.

Add 9 hundreds to 4 hundreds = 13 hundreds. Exchange 10 hundreds for 1 thousand. Record the 3 in the hundreds column.

Complete these additions without trading.

Complete these additions with trading in the ones.

9 ones plus 3 ones equals 12 ones. Exchange 10 ones for 1 ten. Record 2 in the ones column. DRAFT

Estimate an answer to each addition before completing them.

On a scrap of paper, check your answers to question 3 by using an inverse operation, e.g. subtraction to check addition.

can be checked by

Mark did this question and got it wrong. Explain what he did wrong.

Missing numbers

Solve each number sentence by finding the missing numbers.

Given the value of the triangle in each group, find the value of all the other shapes. Write their values on them, then complete the number sentences.

Solve these equations expressed in words.

a Seventeen oranges plus 8 oranges minus 6 oranges = oranges

b Twenty dollars plus $27 plus $30 = $

c Nine dollars times 6 plus $16 = $

d Thirty-five books shared among five children = books

9

Challenge! Use the numbers 4, 5 and 6 in each equation to obtain the answer.

Create and solve a long equation of your own. 10

Drawing objects

Prisms step 1 Prisms step 2 Pyramids step 1 Pyramids step 2

Trace the bases of the objects first before joining their vertices.

a b c

DRAFT

d e f

Put dotted lines in the following drawings to show the hidden detail (faces, edges and vertices). The first one has been done for you.

a b c d

Study the objects, then use a ruler and a pencil to draw them. Always draw lightly first, then firmly later, so trial-and-error mistakes don’t show.

a b c d

Visualises, sketches and constructs three-dimensional objects, including prisms and pyramids, making connections to two-dimensional representations

The number of cars that used a major city car park during one week were recorded, then the information was graphed on a picture graph to analyse the results.

a On which days was the car park used the most?

b How many cars used the car park on Thursday?

c How many cars were in the car park on Tuesday?

d If the owners of the car park couldn’t afford to open on 7 days, which day could they close?

e How many more cars were in the car park on Wednesday than on Sunday?

f How many cars used the car park in the week?

Name another scale that could be used for this data.

Cars in car park

Design a picture graph to display the data presented in the column graph.

Key: = books

Which book graph did you prefer? Why? 17

We can use rounding to the nearest 10 or 100 to estimate division, e.g. 492 ÷ 5: 492 is almost 500, so the answer is about 100. (500 ÷ 5 = 100)

Round to 10 or 100 to estimate a quotient to each division.

To solve 48 ÷ 8, think 8 × = 48.

Use a multiplication fact to solve the divisions.

Use the halve and halve again strategy to divide by 4.

Use the halve, halve again and halve again strategy to divide by 8.

=

Create your own number sentences. The first one is done as an example.

A mixed numeral is a number that consists of a whole number and a fraction, e.g. 112 , 234 , 512

Improper fractions can be changed to mixed numerals, e.g. 5 4 = 114 .

Write an improper fraction and a mixed numeral to describe each set of shapes.

Gina labelled her number line using mixed numerals and improper fractions.

Use Gina’s number line to write an improper fraction for each mixed numeral.

Use the number line to write a mixed numeral for each improper fraction.

Classifying three-dimensional objects 9

Faces are the surfaces that make up a 3D object. A cube has six faces.

An edge is where two faces meet or intersect. Edges can be straight or curved.

A vertex is where two or more lines meet to form an angle or a corner. The plural of vertex is vertices.

Use the words “face”, “edge” or “vertex” to label each set of arrows.

Give a clear description of each 3D object by recording its properties. Remember pyramids are named from their bases. Object Name Faces Edges Vertices

A triangular pyramid has 4 faces, 6 edges and 4 vertices.

Visualises, sketches and constructs three-dimensional objects, including prisms and pyramids, making connections to two-dimensional representations

What is the most common vowel?

a Choose any paragraph from something you can read and make a tally of the number of times each vowel appears in that paragraph. Stop when one vowel reaches 30.

Vowel Tally Frequency

b Which vowel occurred the least?

c Which vowel occurred the most?

d How many words did not contain a vowel?

e Construct a column graph of the data you have collected.

Making a column graph

a Construct a column graph to record the number of people attending Dr Know’s surgery for sports injuries. The number of patients is recorded in the table below.

You will need to work out a scale for the vertical axis of the graph before you can start.

Month Dec Jan Feb Mar Apr

Patients 14 16 24 28 30

b Which month was the worst for sports injuries?

c Which month had the least number of sports injuries recorded?

Use the array to write 2 multiplication and 2 division facts.

Answer these questions.

d Draw a line to match the mixed numerals to the improper fractions of the same value.

i 496 children belong to the softball club. If 324 are girls, how many are boys? boys

PART

a Make the largest number you can from the digits: 7, 2, 5, 6, 3.

b Write the number for six million, two hundred and seventy-six thousand, three hundred and thirty-seven.

c Arrange the following numbers in order of size, from the smallest to the largest. 167 412 17 412 716 241 7241

PART

Complete the sequences.

a 27 30 33 36

b 147 152 157 162 c

Use the words “acute”, “obtuse” and “right” to name the angles.

Draw a line to match each shape to its name.

Draw a rectangle with an area of 8 cm2.

pentagon hexagon octagon rhombus

Answer these questions.

a How many edges does this object have?

b How many vertices does it have?

c How many faces does it have?

d Name this object.

Calculate the volume of each object made from 1 cm cubes.

a How many books were read in March?

b How many books were read in May?

Learning to trade in a subtraction

2 thousands from 5 thousands equals 3 thousands.

4 hundreds from 2 hundreds can’t be done, so trade a thousand from the thousands column to make 12 hundreds. 6 thousands becomes 5 thousands. 4 hundreds from 12 hundreds equals 8 hundreds.

Complete

Complete

PROCESS

4 ones from 3 ones can’t be done. Trade a ten from the tens column to the ones column to make 13 ones. 5 tens becomes 4 tens. 4 ones from 13 ones equals 9 ones.

Subtract 2 tens from 4 tens equals 2 tens.

From Sydney

Calculate the distances between:

683 km

869 km ALBURY 553 km KALGOORLIE 3440 km

PERTH 3967 km

BROKEN HILL 1140 km

Prime and composite numbers

Prime numbers are numbers that have only themselves and 1 as factors, e.g. 2, 3, 5 and 7 are prime numbers but 4, 8 and 9 are not. Composite numbers are numbers with more than two factors, e.g. 24 has factors of 1, 2, 3, 4, 6, 8, 12 and 24.

Write all the factors of these numbers, then write whether they are prime or composite.

b 7

c 9

23 d 11

Write prime or composite after each number.

a 5

b 20

c 19

d 24

6

29

42

31

60

Explain why you agree or disagree with these statements.

DRAFT

a All odd numbers are prime numbers.

b There are more composite numbers than prime numbers.

7

Square and oblong numbers

9 is a “square” number.

Write the numbers under 101 that are both square and oblong.

Prime numbers have only themselves and 1 as factors.

8 is an “oblong” number.

Measure then calculate the perimeter of each shape in millimetres.

Explain how you could use a shortcut to find the perimeters of these shapes.

Warm colours

Cool colours

Impossible Unlikely Even chance Likely Certain

All the coloured cubes were put into a box. Use the cubes and the words above to describe the chance of pulling a particular colour or colour set from the box and returning it.

How would you describe the chance of drawing a:

a red cube from the box?

b yellow cube from the box?

c warm-coloured cube from the box?

d cool-coloured cube from the box?

e blue or orange cube from the box?

f pink cube from the box?

g blue, orange, red, green or yellow cube from the box?

12 13 14 15

Are you more likely to pull a blue cube than an orange cube?

Are you more likely to pull a blue cube than a green cube?

Look carefully at the spinner and answer the questions with the chance words below.

Impossible Unlikely Even chance Likely Certain

a The chance of spinning grey.

b The chance of spinning orange.

c The chance of spinning blue.

d The chance of spinning yellow.

e The chance of spinning blue or yellow.

f The chance of spinning purple.

g The chance of spinning grey, yellow, orange or blue.

h The chance of spinning the side containing orange, grey and yellow.

Rick had 77 stamps to share among his five children. This is what he did.

77 shared among 5 Share out the tens, with each person getting 1 ten.

Trade the 2 tens left for 20 ones. Now share the 27 ones among 5.

Division and multiplication are connected.

Solve these problems and discuss with your classmates what you might do with any remainder.

a Jon had 27 football cards to share among himself and another two boys. How many cards did each child receive?

c Fatima had a bag of 34 lollies which she shared among herself and 3 other friends. How many did each child get?

b There were 42 stickers to be shared among 8 children. How many did each child receive?

d Zoe scored 28 home runs in 7 softball matches. What was her average score of home runs per match?

Describe the shaded section of the hundredths grid as a two-place decimal. The first one is done for you. Ones Tenths Hundredths

Place these decimals in ascending order.

4.35, 2.50, 8.22, 4.45

Use a decimal point to separate whole metres from fractions of a metre. The first one is done for you.

The six people in the following group were measured and their heights recorded.

a Who was the tallest person?

b Who was the shortest person?

c Who is 2 cm taller than Scott?

d Explain why 1.90 m is taller than 1.09 m.

Round the decimals to one decimal place, e.g. 3.19 is 3.2.

a

Partitioning numbers

Expand

b

c

11

37 623 expands to 30 000 + 7000 + 600 + 20 + 3.

Write the number that is equal to:

a 3 tens

b 30 tens

c 20 tens

d 70 tens

e 2 hundreds

f 50 hundreds

g 70 hundreds

h 3 thousands

i 8 thousands

j 30 thousands

k 7 tens of thousands

l 2767 ones

12

How many tens are there in:

a 372?

b 2374?

d 29 637

Use the formula length × width = area to calculate the area of each shape in square centimetres.

Use the formula length × width = area to create two rectangles, each with an area of 24 cm2.

Kate drew this 12 cm2 shape and told her friend that all shapes with a 12 cm2 area have a perimeter of 16 cm. Draw two more shapes of 12 cm2 to find out if Kate is right.

Are area and perimeter related?

5-digit addition with trading 12

Estimate an answer first and write it in the box, then complete these additions with trading in the tens and ones.

Use the map to calculate the distances travelled.

a return journey that is between 450 km and 600 km.

From one destination on the map to another, calculate a return journey that is between 1100 km and 1300 km.

Rounding money

In Australia, we do not have 1c and 2c coins. This means that prices are rounded to the nearest 5c or 10c. Prices ending in 3 or 4 are rounded up to the nearest 5c. Prices ending in 6 or 7 are rounded down to the nearest 5c. Prices ending in 8 or 9 are rounded up to the nearest 10c. Prices ending in 1 or 2 are rounded down to the nearest 10c.

Here are the prices of items being sold at various shops.

Rounding down Rounding up

11c to 10c 13c to 15c

12c to 10c 14c to 15c

16c to 15c 18c to 20c

17c to 15c 19c to 20c

Write the rounded cost of each item to the nearest 5c.

a flour $ b butter $ c mayo $

d milk $ e chocolate milk $ f honey $

Complete the grid to calculate the cost.

DRAFT

When we buy groups of items, it is only the total at the end that is rounded.

Total price Rounded price

a flour and a jar of mayo

b butter and a litre of milk

c a jar of honey and a chocolate milk

d a jar of mayo and a jar of honey

e flour, butter and a jar of mayo

f butter, a litre of milk and a jar of mayo

g two jars of mayo and two jars of honey

7 8 9

Calculate the change from $10 after buying the items below.

Total price Rounded price Change

a flour and a litre of milk

b a jar of honey and a litre of milk

c a jar of mayo and a jar of honey

d three jars of mayo

10

An average Australian car uses 12 litres of petrol for every 100 km travelled.

a Complete the table to show how far the car could travel on the litres supplied.

Litres 6 12 18 24 30 36 42

Kilometres 50 100 150

b Record this information on the line graph.

c How far did the car travel on 24 L of petrol?

d How far did the car travel on 36 L of petrol?

e How far would the car travel on 9 L of petrol?

f How many litres would the car use for a 250 km trip?

g How many litres would the car use for a 350 km trip?

h How many litres would the car use for a 400 km trip?

11

Drawing a line graph

DRAFT

Jane’s athletic coach made a table of the distance she walked in 6 minutes.

Minutes 1 2 3 4 5 6

Metres 200 400 600 800 1000 1200

a Create a line graph to represent this data. You will need to work out a scale for the vertical axis before you start.

b If Jane walked for 10 minutes, how far would she walk?

Kilometres 6 5 4 3 2 1 0 Minutes Jane’s walk Metres

Constructs graphs using many-to-one scales Interprets data displays, including timelines and line graphs

MP_NSW_SB5_38343_TXT_PPS_NG.indb 50 30-Aug-23 08:59:00

Sarah, John and Alisha built three rectangular prisms out of centicubes. In groups of three, make the three prisms. Complete the grid for length, width and height. Record the volume for each prism by counting the centicubes.

What did you notice about your results?

Use centicubes to make models with these dimensions. Record the number of cubes used in the tally column of the grid, then record the volume of each model.

Did any prisms have the same volume?

If you multiplied the length, width and height of the prisms above, what would you find?

Three digits multiplied by one digit 13

5 × 3 = 15 ones

Write 5 in the ones column and trade the 10 ones for 1 ten, then write the 1 at the top of the tens column.

3 × 4 tens = 12 tens plus the 1 traded ten equals 13 tens.

Write 3 in the tens column and trade the 10 tens for 1 hundred, then place a 1 at the top of the hundreds column.

3 × 2 hundreds = 6 hundreds plus the 1 traded hundred equals 7 hundreds.

Write 7 in the hundreds column.

Solve each multiplication using the shortened form.

Problems to solve

a The Earth takes about 365 days to orbit the Sun. How many days would it take to complete 5 orbits?

b A plane flew at 505 km per hour on a 4-hour flight. How far was the flight?

c How much soft drink did Hans drink if he drank all 3 of his 375 mL cans?

3

What numbers could 124 be multiplied by to give an answer of between 600 and 1000?

Kola Kola Kola

Constructing number sentences

Celebrity heads

Read the number sentences and carry out the operations to find the missing numbers.

a If you multiply me by 2 and add 4, the answer is 10.

b If you halve me and halve me again, the answer is 6.

c If you add 2 and multiply by 4, the answer is 36.

Write a number sentence to solve the problems. The first one is done for you.

a Double the number and add 6 to get 14.

b Multiply the number by 3 and subtract 7 to get 5.

c Subtract 5 from the number and add 8 to get 10.

d Divide the number by 5 and add 3 to get 7.

e Multiply the number by 4 and divide by 3 to give 8.

f Add 5 to the number and multiply by 7 to get 56.

g Subtract 15 from the number and divide by 5 to get 3.

h Add 3 to the number, take away 5 and multiply by 9 to get 63.

Think of a secret number and write some clues so that a friend can work out your secret number. 7

Constructing shapes

Follow the instructions to draw a rectangle.

a Place a protractor exactly on the line AB, with the centre point exactly on the end of the line where A is.

b Put a pencil dot at 90 ° , then draw a faint line from A to the dot.

c Repeat exactly for the B end of the line.

d Measure 4 cm on each vertical line you have drawn and put a dot.

e Join the dots to form a rectangle.

Now construct a congruent copy of the square below by following the same procedure as above. All the angles and sides are given on the shape.

Measure the smaller angle, then deduct it from 360 ° to find the reflex angles. (You can also use a 360 ° protractor.)

Measures and constructs angles, and identifies the relationships between angles on a straight line and angles at a point

A day has 24 hours. Time can be expressed in 12-hour am/pm form or 24-hour time. Note that when writing 24-hour time, neither punctuation nor a space is used; e.g. 0745 hours = 7:45 am, 2318 hours = 11:18 pm.

Convert these from 12-hour “am and pm” time to 24-hour time. The first is done for you.

Complete this grid showing time expressed in analog, digital and 24-hour forms.

Read the program guide then answer the questions to set the TV to record using 24-hour time.

a Jim set his TV to record Channel 6 at 0900 for one hour. What show did he record?

b Maria wanted to record Home and Away Complete the information she would need.

c Mohammed set his TV to record Channel 6 at 1600 for one hour. What show did he record?

d Sylvester wanted to record Water Snakes so he set his TV for Channel 6 at 1830 for one hour. Was he successful?

e Ronald wanted to record Sportstime. Complete the information he would need.

Time

One mental strategy used in subtraction is to take away the thousands first, then the hundreds, followed by the tens and the ones.

6657 − 3843 6657 − 3843...3657 − 843...2857 − 43...2817 − 3 = 2814

Subtract the thousands

Subtract the tens

Subtract the hundreds

Subtract the ones

Use mental strategies to solve these subtractions, then use a calculator to check your answers.

a 9598 8172

b 7898 3576

c 8438 6847

d 3347 2634

e 8265 3733

Another strategy is the constant difference strategy. You simply adjust both numbers to make the subtraction easier.

5012 – 2996 becomes 5016 – 3000 = 2016.

4 is added to both sides.

Use the constant difference strategy to solve the following.

a 6821 – 396 =

b 7842 – 492 =

c 6821 – 2990 =

d 7643 – 2988 =

e 8624 – 3994 =

2 3

Use addition to solve subtractions.

a 8085 – 3996 =

b 6004 – 4985 =

c 7006 – 3996 =

d 8016 – 5986 =

e 9107 – 6989 =

f 6010 – 2992 =

6004 – 3996 becomes 6008 – 4000.

5008 – 3985

Think

3985 + = 5008

3985 + 15 = 4000

4000 + 1008 = 5008

Answer 15 + 1008 = 1023

Number patterns and rules

Follow the rules in order to complete the number patterns.

Create two number patterns and above each one write its rule. Each pattern should involve one or two operations.

Selects and applies appropriate strategies to solve addition and subtraction problems Selects and applies appropriate strategies to solve multiplication and division problems

Describing objects

Draw lines to match each piece of information with a skeletal model and a prism name.

Name Information

Skeletal model

Cube

Rectangular prism

Triangular prism

I have 8 vertices and 12 edges. Each one of my 6 faces is a square.

I have 6 rectangular faces, 12 edges and 8 vertices. A shoe box is a good example of me.

I have 9 edges and 6 vertices. I have 5 faces of which 2 are triangular and 3 are rectangular.

Hexagonal prism

I have 5 rectangular sides, 10 vertices and 15 edges. My other 2 faces are pentagons.

Pentagonal prism

Answer these questions.

I have 12 vertices and 18 edges. Two of my 8 faces are hexagonal while the others are rectangular.

a Name the shapes needed to make a hexagonal prism.

b List the number and shape of the identical faces needed to make a hexagonal prism. (For example, 2 × hexagonal faces . . .)

c How many pairs of parallel faces are there on a hexagonal prism?

d Name the shapes needed to make a pentagonal pyramid.

e List the number and shape of the identical faces needed to make a pentagonal pyramid.

f How many pairs of parallel faces are there on a pentagonal pyramid?

Visualises, sketches and constructs three-dimensional objects, including prisms and pyramids, making connections to two-dimensional representations

10 Measure the length of each side to calculate the perimeter of each shape.

9 P = cm

Estimate and then measure the perimeter of each triangle, in centimetres.

11

Use the dot paper to make two staircase shapes, one with a perimeter of 12 cm and another with a perimeter of 16 cm.

a 12 cm perimeter

b 16 cm perimeter

State the perimeters of these gardens.

a Stauros made a rectangular garden with sides 7 m and 3 m. m

b Jenny made a triangular garden bed with sides measuring 4 m, 3 m and 5 m. m

MP_NSW_SB5_38343_TXT_PPS_NG.indb 59 30-Aug-23 08:59:04

15 Expanding numbers

Write the numbers.

a Twenty-six thousand, two hundred and thirty-seven

b Forty-two thousand, seven hundred and thirteen

c Sixty-seven thousand, three hundred and sixty

d Thirty-five thousand and nine

e Fifty thousand, two hundred and four

State the place value of each bold digit.

Expand the following numbers. The first one is done for you.

Numbers to 1 billion

What is the missing expansion in these large numbers?

Fractions on a number line

Draw lines to match the fractions to their position on the number lines.

Related fractions can be located on the same number line, e.g.

can be located on a number line divided into quarters.

Draw lines to match the related fractions to their position on the number lines.

Databases are used to store and organise data. Mailing lists, inventories and large amounts of data, such as historical records, can be kept on databases.

Gillian Walters wants to create a phone list of all her friends. She also wants to list their birth dates to remind her when to buy birthday presents. To do this she will make five fields on her database: given name, family name, date of birth, suburb and phone number.

Gillian needs to enter three more people, whose details she has scribbled on a scrap of paper, to complete her database. Enter the data on the database above for her.

Complete these lists of information from the database. The first one is done for you.

Square metres

The formula for area is Area = Length × Width

15

Use the formula A = L × W to calculate the area of these billboards by the highway.

Lunar Planet

FOREVER COOL!

DRAFT

Outer Space Fun!

Calculate the area of these shapes in square metres if they are drawn so that 1 cm represents 1 metre.

Solve these problems.

a Alison’s room is 4 metres long and 3 metres wide. How much will it cost to carpet her room if carpet is $20 a square metre?

b What would be the perimeter and area of a court 30 metres long and 15 metres wide?

There are many ways of doing division. Here is one method. Share out the hundreds with each paddock getting 1 hundred.

Trade the 1 hundred left over for 10 tens. Now share the 12 tens. Each paddock gets 4 tens.

Share out the 6 ones, with each paddock getting 2 ones.

426 sheep shared among 3 paddocks?

Complete these division algorithms.

On a piece of note paper, check your answers to question 1 by using an inverse operation. You can use multiplication to check division.

Complete the divisions with trading.

Division can be done mentally by dividing the hundreds, then tens, then ones.

2464 ÷ 4 = 24 hundreds

4 = 15

Therefore, 2464 ÷ 4 = 616.

Solve these divisions mentally. You may need a piece of note paper.

Factors are whole numbers that can be multiplied with another number to make a new number. For example, the factors of 16 are:

1, 2, 4, 8 and 16. (2 × 8 = 16 4 × 4 = 16 16 × 1 = 16)

Answer true or false.

a 3 is a factor of 6

b 7 is a factor of 15

c 5 is a factor of 20

Use division to find the missing factor.

d 4 is a factor of 13

e 10 is a factor of 50

f 6 is a factor of 18

Write all the factors of the following numbers. Remember that the number itself and 1 are also factors. a 20

b 12

c 18

d 25

e 49

f 64

8

Work backwards to find three numbers that multiply together to produce the number in the box.

a 60 = × ×

b 100 = × ×

c 140 = × ×

All multiples of 10 always have 2, 5 and 10 as some of their factors.

Drawing angles with a protractor

Name each angle and then write its size in degrees. Remember that protractors can be read from both ends.

Use a protractor to measure and name each angle.

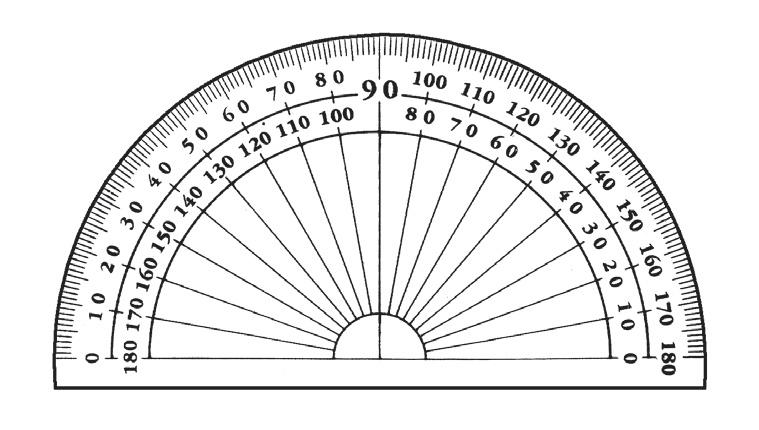
Use the starting lines below to draw the angles.

a An acute angle of 40

A right angle

An obtuse angle of 110°

b An acute angle of 60°

An obtuse angle of 130°

An acute angle of 45°

Measures and constructs angles, and identifies the relationships between angles on a straight line and angles

Symmetry/rotational symmetry

What is line symmetry?

A shape has line symmetry if both of its parts match when it is folded along a line.

How many lines of symmetry does each polygon have? a b c d e

A diagonal is a line connecting the opposite vertices of a polygon. A square has two diagonals.

Draw the diagonals on the quadrilaterals below.

Which quadrilaterals above have diagonals as lines of symmetry?

What is rotational symmetry?

A shape has rotational symmetry if, after the shape is turned around its centre point, it matches the original shape more than once through a full turn.

Colour all the shapes that have rotational symmetry. You may need to trace the shapes and pin them to discover the answers. a b c d e f g h

5-digit addition

Complete these additions.

Flying distances between cities

DRAFT

2

Calculate the length of each journey (working paper may be needed).

a Hobart to Sydney via Melbourne km

b Cairns to Melbourne via Brisbane and Sydney km

c Perth to Brisbane via Sydney km

d Alice Springs to Melbourne via Darwin and Sydney km

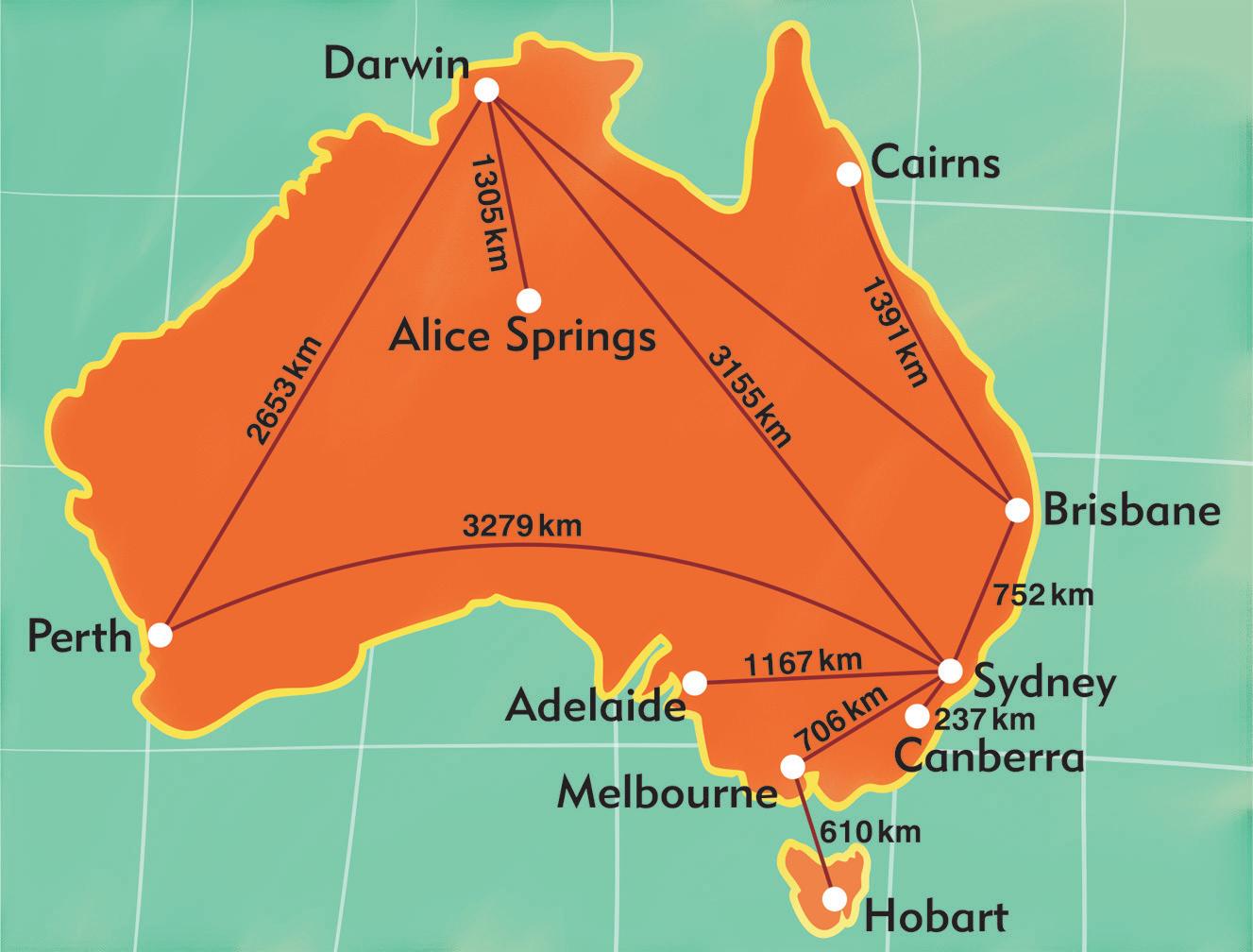
e Adelaide to Cairns via Sydney and Brisbane km

f Cairns to Hobart via Brisbane, Sydney and Melbourne km

Adding and subtracting fractions 17

Draw arcs on the number lines to add or subtract the fractions.

Use the number line below to help you with the questions.

Which spinner has the most chance of landing on:

a red? b green?

c yellow? d blue?

a Is it true that spinner A has a 50% chance of spinning green?

b Which spinner has a better than 50% chance of spinning red?

c Which spinner has a one-in-four chance of spinning green?

d Which two spinners have a one-in-four chance of spinning blue?

e Which spinner has slightly more than a one-in-four chance of spinning yellow?

Combinations of Scissors Paper Rock

scissors paper rock

scissors paper paper paper rock paper

scissors scissors paper scissors rock scissors

scissors rock paper rock rock rock

Rules of the game: Rock beats scissors, scissors beats paper and paper beats rock. If you both have the same result, nobody wins. Repeat the turn.

Conduct this chance experiment to see if Scissors Paper Rock is a fair game. Play the game 20 times with a classmate and record the results using tally marks.

I win

Classmate wins

5 6

Spinner A Spinner B Spinner D Spinner C

Top, front and side views

3D objects can be represented by drawings of their views from the top, front and side.

Find objects like these, then draw the top, front and side view of each.

a b c d

top top top top front front front front side side side side

DRAFT

Draw the top, front and side views of each object.

Top view Front view Side view a b c

Visualises, sketches and constructs three-dimensional objects, including prisms and pyramids, making connections to two-dimensional representations

5-digit subtraction

Complete these subtractions with trading in the hundreds.

Complete these subtractions with trading in the hundreds, tens and ones, then check them with a calculator.

Round to estimate an answer, then solve the problem. Estimate Answer

a The school dance received $2856 in ticket money. How much profit was made if $976 was spent on expenses?

b The Town Hall has room for 5070 people. How many more people can fit in if there are 3667 already in the Town Hall?

c 6537 eggs were taken from the farms to the packaging factory. How many were broken if 6238 were placed into cartons?

d Eve has paid a deposit of $972 for the car she wants to buy. How much does she owe if the car is $9720?

Rules for order of operations

• Always do the work in the grouping symbols (brackets) first. (3

• Do operations with division and multiplication from left to right.

with addition and subtraction from left to right.

and division before addition and

Do the

first.

Do multiplication and division before addition and subtraction.

Write your own operations and answers in the space below. 9

Study the line graph carefully before attempting the questions. 10

The vertical axis tells us the temperatures and the horizontal axis tells us the times.

a What was the temperature at 1:00 pm?

b What was the temperature at 4:00 pm?

c What was the temperature at 10:00 am?

d Estimate the temperature at 9:30 am?

11

A hose uses 2 L of water every 10 seconds.

e Estimate the temperature at 7:30 am.

f What was the difference in temperature between 1:00 pm and 4:00 pm?

g Did the temperature remain the same between 11:00 am and 1:00 pm?

a Use this information to complete the table, then record the information on a line graph.

C

C

b How many litres of water were used in 70 seconds?

c How many litres of water were used in 85 seconds?

d How long would it take the hose to use 40 L?

When we record millilitres as a decimal, we record them as a fraction of a litre. 400 mL = 0.4 L 370 mL = 0.37 L 495 mL = 0.495 L

Record the capacity of the items in millilitres then as a decimal.

1 litre and 700 millilitres equals 1.7 L. litres millilitres

c Honey

d Choc milk

e Kola

Record the total capacity of the combined items in litres and millilitres then as a decimal.

c Milk and cup

d Cordial and choc milk

e Cordial and milk

f Cordial and glass

Convert these litre measurements to millilitres.

Give the place value of each bold number.

of the following numbers.

Draw a line to the scale of 0 to 1 to show the chance of the spinner landing on red.

a Draw a square with a perimeter of 20 cm on the 1 cm grid paper.

Does

a It was warmest at

b The coolest temperature shown is

3-digit mental and written division

Share out the hundreds, with each school getting 1. One hundred is left over.

Trade the 1 hundred left over for 10 tens. Now share the 17 tens. Each school gets 4.

Trade the 1 ten left over for 10 ones. Now share out the 13 ones. Each school gets 3. That leaves a remainder of 1.

Complete these divisions.

Using place value

You can use your knowledge of multiples and place value to help you solve larger divisions. 492 ÷ 4 can be broken into its place value components.

4 492

= Think

Answer

Draw sketches on a separate piece of paper or use place value materials to solve the divisions.

573 paint brushes were shared among 4 schools

Ordering decimals

Draw lines to match the decimals to their position on the number lines.

Ordinal data is categorical data and not specifically numerical. It can be sorted into groups or categories. For example, a child might be asked to rate a new toy from 1 to 10.

The 20 students in Ms LaHood’s karate class all went to the cinema to watch a new movie. They rated the movie from 1 to 5, with 5 being the highest rating.

Ordinal data is data that can be put in order.

Make a tally of the ratings of Ms LaHood’s class.

Answer the questions.

a How many students gave the movie the highest rating?

b How many students gave it the lowest rating?

c Did more children rate it 3 than 4?

d How many children rated it 2?

e Is it fair to say that most students thought the movie was a reasonable movie?

Use your computer to make a column graph of the ratings like the one below on the right. Use computer software, such as word processing software or spreadsheet software, to make your graph. You may have to fill in a table that looks like the one below to make your graph.

1 tonne = 1000 kilograms. The tonne is used to measure large masses such as cars. The symbol for tonne is t.

Explain some situations when it would be more convenient to measure mass in tonnes rather than in kilograms.

Place the following in order of mass, from lightest to heaviest.

Name

Mass

Complete these problems.

a What is the difference in mass between a cruise ship and a submarine?

DRAFT

b What is the total mass of all three ships?

Choose the appropriate mass unit to measure the mass of the following. Write g, kg or t for your answers.

a a matchbox e an elephant i a glue stick

b a dog f a ruler j a desk

c a pencil g a ship k a whale

d a person h a pony l a building

How many kilograms are in each of these masses?

A television set would be measured in kilograms.

3 3 4 t equals 3750 kg.

Cruise ship 4788 t

Frigate 3921 t

Submarine 2456 t

Kim has written estimates for the questions in the table below. Use your estimation skills, such as rounding to the nearest ten, to write your own estimates and decide whether Kim's estimates are reasonable or unreasonable.

Question Kim’s estimate My estimate Reasonable

a 39 + 43 80

b 149 + 52 250

c 212 + 68 380

d 331 + 71 400

e 309 + 78 500

f 1111 + 83 1900

g 2127 + 43 2170

Calculate the cost of a return trip to London for a family of four people.

d

e Which is the most expensive travel agent?

f Which is the most economical travel agent?

PROBLEM SOLVING

Sequences of fractions

Draw arcs on the number lines to continue the sequences, then record them in the tables below.

Use the number line below to help you continue the sequences.

Design problems

Mr Snodgrass is thinking about buying a one-bedroom city apartment. He has been given this plan and a scale to work from. Use the scale to help Mr Snodgrass work out the sizes of his rooms.

Lauren has a new bedroom and some new furniture. Use the scale and follow the instructions to draw a plan view of her room as you would like it. (Plan views are views from above.)

a Use the scale to draw the boundary of the room first.

b Place her bed in an appropriate position.

c Put her new desk against a wall.

d Put her mat on the floor.

e Put her shelves against a wall.

Scale: 2 cm = 1 m

Quadrilaterals are shapes that have 4 straight sides. There are many types of quadrilaterals and some have special names.

S R RH

A square is a quadrilateral that has 4 equal sides and 4 right angles.

A rectangle is a quadrilateral that has 2 pairs of equal sides and 4 right angles.

A rhombus is a quadrilateral that has 4 equal sides and the opposite angles are equal.

T P Q

A trapezium is a quadrilateral with one set of parallel sides.

A parallelogram is any quadrilateral with 2 sets of parallel sides.

4-sided shapes with no special name are given the family name of quadrilaterals.

8

9 10 11 4 m

Use the letters in the shapes above to identify the shapes below. For example, rectangle = R.

Is a triangle a quadrilateral? _________

Do all quadrilaterals have parallel sides? __________________

MP_NSW_SB5_38343_TXT_PPS_NG.indb 85 30-Aug-23 08:59:14

The distributive law can be used as a mental strategy to solve multiplications.

Use mental and written strategies to complete these multiplications.

You can also use an area model to calculate larger multiplications.

Solve these multiplications.

Solve the questions below using any strategy you wish.

Selects and applies appropriate strategies to solve multiplication and division problems Constructs and completes number sentences involving multiplicative relations, applying the order of operations to calculations

Order the decimals from least to greatest.

Use a decimal point to separate whole metres from thousandths of a metre. The first one has been done for you.

Write each

Round each to the nearest whole number, e.g. 7.896 = 8.

A parallelogram is any shape with 4 straight sides. It must have 2 sets of parallel sides. Its opposite angles are equal.

Colour the shapes below that are parallelograms.

Draw parallelograms to fit the descriptions.

a I am a parallelogram that b I am a parallelogram that c I am a parallelogram that has 4 right angles and has 2 pairs of sides that are has 2 pairs of sides that are 4 equal sides. equal and 4 right angles. equal and no right angle.

Explain why this shape is not a parallelogram.

Is it possible for a triangle to be a parallelogram?

Is it possible for a parallelogram shape to tessellate?

What is the size of angle x on the parallelogram?

The faces of which objects are all parallelograms?

Which object contains an equilateral triangle?

Refer to the bus timetable and write how long each section of the trip takes.

a Brisbane–Toowoomba

b Moree–Dubbo

c Peak Hill–Forbes

d Griffith–Deniliquin

e Deniliquin–Bendigo

f Bendigo–Tullamarine

g Tullamarine–Melbourne

Answer these questions.

a How long is the rest stop at Dubbo?

b How long is the rest stop at Griffith?

c How long is the rest stop at Bendigo?

d How long is the entire trip from Brisbane to Melbourne?

DRAFT

Prepare a timetable for the events in your day.

5-digit subtraction

As part of Paula’s job at the mail centre she needs to know the population of the major towns in NSW and the differences in size between them. Help her calculate the difference in population between these towns.

Adding and subtracting fractions

Colour each fraction addition in a different colour to find the answer. The first one is done for you.

Complete these addition sentences.

Complete these operations.

Find pairs of fractions that could be added or subtracted to give the answer 9 10 .

Three primary schools each raised the same amount of money at their fetes.

School

Greenway Primary School

Answer these questions.

a Which activity raised the most money at Hill Top Primary School?

b Which activity raised the most money at Greenway Primary School?

c Which activity raised the most money at Binga Primary School?

d Which activity raised the least amount at Binga Primary School?

e Which activity raised the least amount at Hill Top Primary School?

f Which activity raised the least amount at Greenway Primary School?

g Were pony rides the least successful at all schools?

h Which two activities raised the most money at all schools?

i Which was more successful at Greenway, craft or pony rides?

j Which was more successful at Binga, craft or pony rides?

k Which was less successful at Hill Top, craft or cakes?

l If $300 was raised at Hill Top’s auction, is it reasonable to say that the raffle raised about $350?

d

Constructing objects 22

Draw a line to match each object to its set of views.

Top Front Side

front view

Construct the objects from their views then sketch them in the space provided. Useful materials may be centicubes, Base 10 ones or blocks.

DRAFT

top front side

top front side

top front side

Visualises, sketches and constructs three-dimensional objects, including prisms and pyramids, making connections to two-dimensional representations

How much would the Internet Cafe pay for 5 new computers at $2325 each?

1 Complete the multiplications.

Round the larger numbers to the nearest thousand to estimate the product.

a 3988 × 7 ≈

b 2895 × 6 ≈

c 1991 × 5 ≈

d 4887 × 3 ≈

e 5011 × 4 ≈

Solve these problems using any strategy you wish.

a How many kilometres would a pilot travel if she completed 6 trips of 2410 km?

b Kim reckons there are 1952 thumb tacks in the pack. How many would there be in 5 packs?

Subtracting fractions from wholes

Fractions can be subtracted from whole numbers, e.g. Tom had a chocolate bar and gave away 1 3 of

Use the diagrams to help you subtract the fractions from one whole.

Fractions can be subtracted from more than one whole number, for example, Alexis had 2 pizzas and gave away 1 4 of one.

Subtract the fractions of pizza.

Use the number lines to solve the subtractions.

Tree diagrams are used to display all possible outcomes from a simple chance experiment.

Aliya wanted to order a new sports car. Her choices were as follows:

7 8

Convertible or hard top Automatic or manual V6 engine or 4-cylinder

Red or black

Complete the tree diagram to find all possible combinations of sports car.

Convertible

Automatic V6 4-cylinder V6 4-cylinder

Red Black

DRAFT

Cora made her daughter a sandwich. Her choices were cheese or salad, on white or brown bread, with or without margarine.

Draw a tree diagram to display all possible combinations of the sandwich.

cheese salad

Letters can also be used in coordinates.

Name the streets found at these coordinate points.

Give one set of coordinate points for each location.

Division by ten/estimation

575 nails were shared among 10 carpenters.

Divide 57 tens by 10. Each carpenter gets 5.

Trade the 7 tens for 70 ones. Now share the 75 ones. Each carpenter gets 7. That leaves a remainder of 5.

5 7 10 5 775 r5

Estimate an answer to each division by rounding the larger number. Check if the answer supplied is reasonable or unreasonable. The first one is done for you.

Find the averages.

a John has 7 cards, Ava 6, Leanne 5, Toula 7 and Leo 30. What is the average number of cards per child?

b Linh scored 17 runs, 6 runs, 10 runs and 11 runs in 4 innings. What was her average?

c Sam is 127 cm high, Jilly 140 cm, Tom 153 cm, Soula 133 cm and Tim 147 cm. What is the average height of the group?

Averages are found by totalling the scores, then dividing by the number of scores.

Fractions can name part of a group.

1 3 of 6 girls = 2 girls

Find the fraction of each group.

Use the array to find these fractions of the group of 48. a 1 3 of 48 =

Solve these problems.

a There were 3 dozen cakes on a tray until Jana tripped on a loose tile and spilt 1 4 of them. How many did she spill?

b Jackson had 60 cents to spend. How much was the ice cream he bought if it was equal to 1 3 of his money?

c If 1 10 of the 100 seats in the restaurant were reserved for Kai’s birthday party, how many were reserved for Kai’s party?

d Our family had 45 raffle tickets to sell. How many did Aunty Donna buy if she bought 1 5 of them?

Keira ate 1 3 of a cake, and Abdul ate 1 2 of a cake. If Keira ate more than Abdul, explain how this is possible.

Measuring angles in triangles

Measure the angles in these triangles.

a Equilateral triangle

b Scalene triangle Angle A

c Isosceles triangle d Right-angled triangle

What can you say about the size of the angles in an equilateral triangle?

What can you say about the size of the angles in a scalene triangle?

Follow the directions to draw an isosceles triangle using compasses.

a Set your compasses to 7 cm.

b Place the point of the compasses at A on the line drawn for you, then draw an arc softly.

c Place the point of the compasses at B on the line, then draw an arc softly until it crosses the first arc you drew.

d Join the ends of the line to the point where the arcs cross.

Time zones/24-hour time

Study the map that shows Australia’s three time zones.

Key White: Eastern standard Yellow: Central standard Green: Western standard

Central standard time is 1 2 an hour behind Eastern standard time.

Western standard time is 2 hours behind Eastern standard time.

Complete the time zone tables using 24-hour time.

Complete the clocks to show the time in each location.

In summer in NSW we have daylight saving. This has the effect of making the days seem longer, with more daylight hours in the evenings.

In addition to NSW, the ACT, Victoria, Tasmania, South Australia and Western Australia also have daylight saving. This means that clocks are moved forward one hour on the first Sunday in October and moved back again on the last Sunday in April the following year. Complete the clocks to show the times in the other capital cities compared to Sydney during daylight saving.

Alice Springs

BRISBANE

CANBERRA SYDNEY PERTH ADELAIDE MELBOURNE HOBART

Calculator problems

Fred’s Fruit and Veg Barn

Use a calculator to calculate these purchases.

a Charlotte bought 3 kg of bananas, 2 kg of strawberries and 6 pears. How much did she spend? $

b Hudson bought 5 pears, 4 pumpkins and 7 kg of oranges. How much did he spend? $

c Mr Nguyen bought 17 pears and 15 kg of strawberries for his catering business. How much did he spend? $

d Kelly bought 4 kg of bananas, 3 kg of oranges, 2 pears and 7 pumpkins. How much change did she receive from $50? $

Write and solve two problems using the shopping items above.

Draw a line to match each number sequence with its correct problem, then solve the problems.

a Twenty-seven children attended the movies. If it cost them $6.50 each, what was the total amount charged by the theatre?

b Lily bought six books at $7 each, three books at $9 each and seven books at $5 each. How much did she spend?

c Sarah bought 1 4 of a box of 24 apples. If she paid 60c for each apple, how much did she spend?

d Xavier bought five tins of dog food at 90c each and a magazine at $5.60. How much did he spend?

e Matilda planted 6 rows of 8 flowers. 1 4 of them died. How many flowers died?

Complete these charts which involve multiplication by 10, 100 and 1000.

Estimate the following by rounding the first number to the nearest 10 or 100 before multiplying them.

Step 1: Write the 0 because you are multiplying by a ten.

Step 2: Multiply by 4 using the shortened method.

Complete these multiplications.

Adding fractions greater than 1 whole

Add or subtract these fractions. The first one is done for you.

Subtracting fractions with like denominators is easy.

Converting improper fractions to mixed numerals

When adding fractions we often obtain an answer that is greater than one. In such cases the answer is first given as an improper fraction then converted to a mixed numeral by dividing its numerator by its denominator.

EXAMPLE 7 10 + 7 10 = 14 10 = 1 4 10

Add the fractions, then convert the improper fraction answer to a mixed numeral. The number line may help you.

Add the fractions to get an improper fraction, then convert it to a mixed numeral. The first one is done for you.

+

The pizza shop

a Tom ate 5 8 of a pizza and Zac ate 7 8 of a pizza.

How much pizza did they eat?

b Amal ate 5 8 of a pizza, Nullah ate 5 8 and Sam ate 6 8 .

How much pizza did they eat?

c Allegra ate 7 8 of a pizza, Fatima 5 8 , Ahmad 7 8 and Nara 4 8

What was the total amount of pizza they ate?

Gross and net mass

Builders use different types of screws to join different types of materials. Some common materials are chipboard, used to make laundry cupboards, plasterboard for bedroom walls, metal for roofs and steel for factory walls. The length and mass of these screws are recorded on this chart.

Screws For chipboard For plasterboard For metal For steel

Length 20 mm 40 mm 32 mm 50 mm

Mass 8 grams 6 grams 8 grams 12 grams

Use the information in the table above to calculate the mass of these packets of screws.

a 100 chipboard screws g e 25 steel screws g

b 100 plasterboard screws g f 150 metal screws g

c 200 metal screws g g 1000 chipboard screws g

d 100 steel screws g h 500 plasterboard screws g

Gross mass is the total mass. Net mass is the mass of the contents only. For example, some fruits bought at the fruit shop may have a net mass of 1800 g but have a gross mass of 1995 g because the cardboard box they are packaged in has a mass of 195 g.

Solve the problems to find the gross mass.

DRAFT

a The cereal has a net mass of 250 g but the cardboard box that it is packaged in has a mass of 70 g. What is the gross mass of the cereal?

b A bar of soap has a mass of 120 g. What would be the gross mass of 5 bars of soap in a cardboard box with a mass of 55 g?

c A golf ball has a mass of 45 g. The box that they come in has a mass of 40 g. What is the gross mass of 8 golf balls packed in one box?

d A pencil has a mass of 5 g. What would be the gross mass of a box of twelve pencils if the box has a mass of 18 g?

e A set of 36 pencils with a net mass of 5 g each is sold in a metal case. The case has a mass of 400 g. What is the gross mass of the pencil set?

f Peta bought 20 small apples in a cardboard box. What would the gross mass of the box of apples be if the apples averaged 200 g each and the box had a mass of 400 g?

Top Cereal

EaglesGolfBalls

26

Two digits multiplied by two digits

37 by 25.

Each carton of tomato soup has 32 cans in it. How many cans of soup are held on this pallet? 2

State the place value of each bold digit.

Decimal place value

Decimal place value

Write the number before and after each decimal.

To convert fractions to decimals, divide the numerator by the denominator. Calculators can help. For

Use a calculator to convert each fraction into a decimal, some will include whole numbers.

The six people in the following group were measured and their heights recorded.

a Who is the tallest person?

b Who is the shortest person?

c Who is 1 mm taller than Scott?

d Whose height is between Catherine and Kimberly’s?

Making objects and nets 26

Make copies of these 3D objects using straws and plasticine or other construction materials. (For example, matches, toothpicks, playdough or commercial materials.)

help make objects rigid.

Make a copy of these objects by making their nets on light card and folding them to make the objects. All dimensions are given.

Mr Knox the jeweller wants to make a new box in which to sell his jewellery. He has drawn the box but can’t draw the net. Design a net for Mr Knox’s box on the 5 mm grid paper. It has been started for you.

A recent newspaper article said that children spend too much time playing games on their tablets. Stella told her teacher that the article was not correct and that children do other things on the tablet besides play games.

a Write some questions you could use in a survey to find out what other things children may do on a tablet, and to find out if Stella is correct.

(i)

(ii)

(iii)

b Who should you interview for this survey?

c Make your own prediction about how children use tablets.

Games are only a small part of what kids can do on tablets.

how children use tablets.

Conduct your survey and record your data in the

Below is a set of rulers. Colour a section of each ruler to match the label.

one half

one quarter

one fifth

one eighth

one tenth

As you completed colouring each ruler, what did you notice about the fraction you coloured each time?

What effect does increasing the denominator have?

4 Solve the problems. Problem Answer

a Khan had forty-eight sheep but sold a quarter of them at the market. How many sheep did he sell?

b Sam had a stamp collection of 45 stamps. If she gave away one fifth of them, how many did she give away?

c Diya’s class has twenty-four children. If one eighth of the class has long hair, how many children have long hair?

d Yindi cooked one hundred cakes to sell at the fete. If she accidentally dropped one tenth of them, how many did she have left?

4 Grandad decided to share 36 of his old football cards with his four grandchildren. Tom received 1 4 of the set, Millie received 1 3 and Jessica received 1 6 . George received what was left.

a How many did Tom receive?

b How many did Millie receive?

c How many did Jessica receive?

d How many did George receive?

QUESTION: ANSWER:

How do you find the average?

Averages are found by totalling the scores then dividing by the number of scores.

4 Find the averages of these numbers.

a 4, 5, 6, 7, 8 30

b 8, 10, 12, 14, 16

c 7, 9, 13, 11, 5

d 18, 6, 9, 15, 12

e 30, 10, 15, 25

f 40, 36, 32

g 12, 15, 18, 21, 24, 27, 30

Find the averages.

a What was the average time taken to run a race if Ryan took 11 seconds, Brooke took 9 seconds, Conrad took 10 seconds and Marcel 14 seconds?

b Four types of gifts were for sale at the Mother’s Day stall, for $4, $6, $10 and $12. What was the average price of the gifts?

c There are five children in the Wong family. Work out the average age of the children if they are 15, 13, 13, 9 and 5.

d The temperature in our classroom at 10:00 am, Monday to Friday, last week, was 21°C, 22°C, 23°C, 20°C and 24°C. Work out the average daily temperature for that week.

e What was the average amount of time Maya spent on her homework last week if her times were 10 minutes, 50 minutes, 20 minutes, 40 minutes and 30 minutes?

Write as many groups of numbers as you can that have an average of 10.

27 Cubic centimetres and millilitres

A small unit for measuring capacity is the millilitre 1000 mL = 1 L

Estimate and measure the capacity of each of these small vessels in millilitres (mL). (You may need a medicine glass and a 1 mL eye dropper.)

a tablespoon

b tea cup

c screwcap

d mug

Estimate: Estimate: Estimate: Estimate:

Capacity: Capacity: Capacity: Capacity:

Does 1 cubic centimetre displace one millilitre of water? Conduct this experiment to see.

Use a measuring glass filled to 30 mL to measure the water displaced by cubic centimetres (centicubes). Colour the new water levels on each measuring glass below.

d Did you notice any relationship between the cubic centimetres and the water displaced by them?

e What is it?

How many centicubes (cm3) would be needed to displace 100 mL?

Which measurement in the advertisements is easier to understand?

49 950 square metre farm for sale.

Large areas of land can be measured in hectares.

1 hectare = 10 000 m2

Two soccer fields with a large space between them are about 1 hectare. The symbol for hectare is ha. A square metre can be any shape, and so can a hectare.

50 hectare farm for sale.

Is your school less than a hectare, about a hectare or more than a hectare?

a Use suitable measuring instruments to mark a hectare within your school.

b Place markers at the corners so that it is roughly the shape of a rectangle or square.

c Use a calculator to make your calculations.

m × m = m2

d Tick the correct box.

My school is about one hectare.

My school is less than one hectare.

My school is more than one hectare.

Circle the pictures that represent areas of one hectare or more. (Pictures are not drawn to scale.)

Find the answers.

m Mr Brown planted 381 seeds in 3 boxes. How many seeds were in each box? seeds PART

Record the value of the bold digits.

Find the answers. a

Add these fractions. g

Add the fractions to get an improper fraction, then convert it to a mixed numeral.

Write each decimal as a fraction. a 0.765 =

Round each decimal to the nearest whole number. e 8.7

Continue the number patterns.

3

Colour the new water level on the measuring glass to show how many millilitres of water would be displaced if a model with a volume of 10 cm3 was put in the measuring glass.

Write how many kilograms in each of these.

a 1 t = kg c 1.25 t = kg

b 1.5 t = kg d 2.75 t = kg

a If you caught the bus at 1255 hours from Boogie St, when would you arrive at Lion St?

b If you caught the bus at 1107 hours from Rap St, when would you arrive at Rock St?

40 children were surveyed about their favourite takeaway food.

a About how many liked hamburgers?

b Do

pies than like chips?

When we talk about large amounts of money, we often put the letter K after the amount. The K stands for thousands, e.g. $36K = $36 000.

Write these amounts in full.

Write an estimate for the total cost of each purchase in the coloured box before calculating the exact amount. Each estimate must be in complete thousands and use the K.

a How much for 6 bracelets? b How much for 5 cars? c How much for 7 diamond rings? d How much for 8 laptops?

Complete these algorithms.

Supply the missing numbers to complete the additions.

Calculate the total cost for the purchase of the vehicles described below.

SUV Purple hatch Mini-bus Red hatch

Vehicles purchased Working

a Goode Real Estate bought the mini-bus and the SUV to transport their customers to look at houses for sale.

b Pete’s Pizza bought the purple hatch and the red hatch cars because they thought customers wanted their pizzas delivered in new cars.

c Ocean Tours bought the SUV and the mini-bus to take tourists on trips, and the purple hatch for the office manager.

d Helen’s Hire Cars bought the SUV, the purple hatch and the red hatch because they are the most popular cars that people hire.

Savings spreadsheet

Complete this spreadsheet. The C column has the calculations listed and has been widened to allow for your answers.

8

Add these items to the Bombers spreadsheet.

a Item 8. On 28 September the club bought helmets for $250.00.

b Item 9. On 11 November the club bought trophies for $178.00.

c Item 10. On 12 November the club spent $40.00 on oranges.

d Item 11. On 15 November the club spent $55.50 on stationery.

Complete the map.

a Use the marks on the map to draw vertical and horizontal lines to make a coordinate grid.

b Complete the labelling of the coordinates.

c Draw a shade area by joining the coordinate points (3,3), (7,3) and (3,7).

d Draw the school hall by joining the coordinates (12,5), (12,6), (11,6), (11,7), (12,7), (12,8), (16,8) and (16,5).

e Draw in the toilets by joining the coordinates (12,1), (12,2), (16,2) and (16,1).

f Find a place for the canteen, draw it on the map and list its coordinate points.

g Draw any object you like on the map and give its coordinate points.

What can be found at these coordinate points?

a (2,2)

b (8,9)

Give a set of coordinate points for:

a Class 5S

9 10 11 12

b The office

c (1,5) d (4,4)

9 If the school’s office is 9 m long, make up a suitable scale for the map.

Scale: 1 cm =

Adding and subtracting decimals 29

Remember, always keep the decimal points in a vertical, straight line.

Add or subtract the decimals.

Complete the balance column, which shows the amount Sally has banked this year.

Calculate the shortest distance between:

Calculate the cost of the individual items in the boxes. You will need a calculator.

You may need a calculator for this exercise.

a Cost of a pair of socks?

c Cost of a soccer book?

b Cost of a stapler?

d Cost of a pencil set?

The Good Fit Shoe Shop recently ordered several shoes for its store. Complete the ‘Cost’ column on the order form.

You may need a calculator for this exercise.

DRAFT

The

Play the ‘Zero in Five’ game. You have a maximum of five moves to turn the numbers into zero. You can only use one digit at a time (digits 1–9). You can use any operation. One has been done for you.

$89 Bootz $78 Sportz $65 Ozees $59 Sprintz

Finding all possible combinations

A witness remembers seeing a car speed away from a bank robbery. She remembers the two letters that were on the car’s number plate (TR), and the three numbers (1 2 3), but not the order they were in.

a Predict how many possible number plates can be made from the combinations of the three numbers.

b Write in the box all possible combinations of the three numbers. It has been started for you.

TR-132

Shaking hands

At the end of a doubles tennis match, each player shook hands with every other player. How many handshakes took place?

Complete the tree diagram to show all the possible combinations when the spinner is spun three times.

Draw a line to match each object to its net.

A box is displayed and another identical box has been pulled apart to show the net.

a Colour the top view on the net yellow.

b Colour the front view on the net red.

c Colour the side view on the net blue (be careful). Top

Mr Singh makes cube puzzles for children. Study the net to answer the questions.

a If B was the base, what letter would be on the top?

b If A was the front face, what letter would be on the back face?

Mr Singh’s cube

c What letter do you think is on the opposite side to E?

Visualises, sketches and constructs three-dimensional objects, including prisms and pyramids, making connections to two-dimensional representations

6-digit subtraction 30

Complete these subtractions.

Solve these problems.

a Jaya had an amount of $4773 in the bank but spent $2765 at the travel agency. How much does she have left?

b Tony left Sydney on a trip to the USA of 11 920 km. How far does he still need to travel if he has already covered 6577 km?

c Tina’s new car cost $27 834. If she was given a trade-in for her old car of $12 477, how much more money does she need?

d There were 18 654 spectators at the football match. If 11 076 of them were adults, how many were children?

Complete the spreadsheet for the Dolphins Soccer Club. It has been started for you.

Spreadsheets organise and calculate data.

Factors are whole numbers that are multiplied with another number to make a new number, e.g. the factors of 20 are 1, 2, 4, 5, 10 and 20.

4

List all the factors of these numbers.

a 24 f 36

b 15 g 42

c 21 h 45

d 25 i 32

e 28 j 51

Knowing the factors of a number may help when multiplying, e.g. 25 × 12 = . 25 × 12 becomes 25 × 3 = 75 then 75 × 4 = 300, so 25 × 12 = 300.

3 × 4 factors

Break the multiplier into factors to help complete these multiplications.

Strategy

a 12 × 15 12 × 15 becomes 12 × 3 = then × 5 =

b 15 × 12 15 × 12 becomes 15 × = then × =

c 14 × 18 14 × 18 becomes 14 × = then × =

d 17 × 16 17 × 16 becomes 17 × = then × =

e 25 × 20 25 × 20 becomes 25 × = then × =

Answer

There are 48 people at a party. List four ways they could be evenly seated at tables.

Choosing length units 30

Shade the boxes with the suggested colours to select the most appropriate unit of length to measure each of the following.

a The length of a sultana packet

b The length of a calculator

c The thickness of a mobile phone

d The length of a grasshopper

e The length of a pool

f The width of your home

g The length of a fingernail

h The length of the Hume Highway

Choose an appropriate measuring device from the ones given to measure each of the following.

a The length of a pencil

b The length of a room

c The circumference of a bin

d The length of the playground

e The circumference of a bottle

f The perimeter of a large curved garden

g The distance between two towns

h The perimeter of a book

i The perimeter of your school

Convert these measurements to the length unit given.

Use the 5 mm dot paper to design:

30 Triangles

A triangle is a 3-sided shape with 3 angles. The total of all angles is always 180°. There are 4 main types of triangles: equilateral, isosceles, scalene and right-angle triangles.

Study the 4 types of triangles given, then answer the questions.

Equilateral triangle

Scalene triangle

a Which triangle has all sides of equal length?

b Which triangle has two sides of equal length?

c Which triangle contains a right angle?

d Which triangle has all angles the same size?

Isosceles triangle

Right-angle triangle

Make a right-angle triangle by enlarging the one below on the expanded dot paper.

Use the dot paper to show how a scalene triangle can also be a right-angle triangle.

Sketch some isosceles triangles.

Juan and Sammy are in charge of organising the school formal. Juan doesn’t want to compromise on the food, drinks and venue. Sammy wants to dance all night so the main thing that she wants is great entertainment.

The principal told them that they must come up with the best budget available for under $30.00 per student. Each budget must include bus hire, venue, meals, drinks and entertainment.

Create a budget for Juan and Sammy for the school formal.

DRAFT

What is the best value you can get when buying soap? Why?

What is the best value you can get when purchasing juice? Why?

5

Use multiplication to check these divisions. Use the box to tick the correct answers and write the correct answer for those that you think are incorrect.

Use an inverse operation, such as multiplication, to check these statements. Answer by stating true or false.

a 50 ÷ 10 must be more than 3

b 60 ÷ 5 is less than 15

c 100 ÷ 4 is greater than 20

d 80 ÷ 4 must be more than 25

e 100 ÷ 5 is less than 15

f 160 ÷ 4 is more than 50

g 200 ÷ 5 is more than 30

h 250 ÷ 5 is more than 45

i 500 ÷ 3 is more than 120

j 800 ÷ 5 is less than 120

k 1000 ÷ 5 is more than 250

l 900 ÷ 6 is more than 130

m 1500 ÷ 5 is more than 30

n 2000 ÷ 4 must be more than 50

o 2400 ÷ 6 must be more than 50

Check the answers to these division questions using multiplication. The first one is done for you.

Estimate an answer to each problem by rounding the larger number.

a 58 sheep were shared among 3 paddocks. Estimate how many sheep per paddock.

b $789 was shared among 4 people. Estimate each person’s share. $

c 309 books were shared among 10 shelves. Estimate the number of books per shelf.

d $3987 was shared among 8 people. Estimate each person’s share. $

Area of a triangle 31

The area of a triangle can be found by drawing a rectangle around it. The area of the triangle is half the area of the rectangle. Rectangle 8 cm2. Triangle 4 cm2

Calculate the area of the triangles below.

Enclose the triangles in rectangles, then calculate their areas.

130

Investigates and classifies two-dimensional shapes, including triangles and quadrilaterals, based on their properties Combines, splits and rearranges shapes to determine the area of parallelograms and triangles

10 11

Square kilometres

31

Areas of land larger than a hectare can be measured in square kilometres (km2), e.g. 100 ha equals 1 km2, or a square 1000 m × 1000 m = 1 km2.

List the states and territories in order of size (largest first) and then use a calculator to work out the total area of Australia.

12

Use the scale to mark an area of 1 km2 on the street directory page.

Scale 1 cm = 200 m

DRAFT

Source: Gregory’s 1998 Street Directory, 62nd edition, page 317. Copyright © Universal Press Ltd 1998. Reproduced with permission.

Would you use square metres (m2), hectares (ha) or square kilometres (km2) to measure these areas?

a cricket oval d Wollongong

b tennis court e golf course

c Royal National Park

f soccer field

g Old McDonald’s Farm

h your school

MP_NSW_SB5_38343_TXT_PPS_NG.indb 131 30-Aug-23 08:59:37

Multiplication methods

Mentally calculate the answers to these multiplications.

Complete these multiplications using any method you choose.

Multiply these numbers by a multiple of 10.

Multiply these numbers.

Solve these mentally by multiplying the hundreds, tens and ones separately, then adding them.

Rounding for estimation

Round each number to the nearest 100. Remember numbers ending in 50 are rounded up.

=

Round each number to the nearest 1000. Remember numbers ending in 500 are rounded up.

Round each number to the nearest 1 000 000. Remember numbers ending in 500 000 are rounded up.

DRAFT

Over the year, Bill ordered the following items from his supplier. Estimate how much he spent by rounding each item to the nearest $100.

a Two tennis racquets and a set of headphones. $

b Four phones and a tennis racquet. $

c A table and a guitar. $

d A guitar and four sets of headphones. $

e Three tennis racquets and a table. $

f Two guitars and two phones. $

List three different ways you could spend between $1600 and $1700.

9 Stopwatches are used to accurately measure periods of time. Minutes Seconds Hundredths of a second

11

That is, 5 minutes 28 seconds and 64 100 of a second. Use a stopwatch to record how long it takes to perform these activities. Before performing the activity, make an estimate of the time it will take.

a Wash your hands

b Pack your bag

c Write your name

d Read a page

e Count to 100

f Walk 10 metres

g Walk to the canteen

h Do 10 push-ups

12

9 Estimating intervals

Try to judge how long an interval of time lasts. When you think the time is up, call out “stop” to your partner who has been timing you with a stopwatch or a watch with a second hand function. Next, record the reading on the stopwatch and see how close your estimation is.

Time Stopwatch reading

a 10 seconds

b 20 seconds

c 30 seconds

d 40 seconds

e 1 minute

9 Choose a time unit from the box to measure the length of time taken to: seconds hours months minutes days years

13

a play a soccer game

b put a belt on

c attend a school camp

d sneeze

e write a short paragraph

f build a house

It took me 6 seconds to tie my shoelace.

Put a cross on the following locations.

a Chadwick Cr (D,5) g Evans St (L,9)

b Ferngrove Rd (D,1) h Hamilton Rd (E,8)

c Thorney Rd (F,5) i Gurney Cr (A,7)

d The Boulevarde (M,3)

e Throsby St (N,8)

f Lombard St (K,6)

Use the legend to answer the questions.

a Is there a church near (M,8)?

b Is there a toilet facility near (J,3)?

c Is there a school near (A,1)?

d Is Thorney Road a main road?

e How many parking stations are on the map?

Write a clear set of directions to describe how to get from Greenvale St (F,7) to Delamere St (O,1).

Draw a path to show how to get from Edward Pl (C,1) to Hubert St (P,4).

Use the scale to calculate the approximate length of these streets to the nearest 100 m.

a Thorney Rd (F,5)

b Margaret St (K,4)

c Linda St (K,7)

d Eliza St (O,9)

Scale 1 cm = 200 m

Study the mobile phone data and answer the questions.

a Do all the prepaid plans above cost the same to buy?

b Do you think that some will be better than others? Jack uses his phone a lot. He sends 300 text messages a month and makes 50 phone calls that average 1 minute in length.

c Calculate usage costs of each credit plan above for Jack. You may need a calculator. Flag fall costs for 50 phone calls Costs

phone calls

Answer the questions.

a Which company offers the best deal for Jack?

b Are some deals much worse after you calculate the costs?

c Was the Dodgy deal really dodgy?

d Did all the companies entice you with their advertising slogans?

e Can you trust the advertising of all the companies?

f Was it worthwhile to calculate the best deal?

g What is the difference in usage costs between the best and worst deal?

4

Introducing basic percentages

A percentage is another way of recording a fraction with a denominator of 100 (out of 100). A percentage sign, %, is used to display percentages. For example, 25 100 can be written as 25%.

Fill in the missing cells on the equivalence tables.

DRAFT

An easy way to find a percentage is to think about its equivalent fraction. 10% of 50 think 1 10 of 50 = 5.

Find the percentages of these amounts.

a 10% of $10

b 10% of $30

c 20% of $10

d 20% of $40

e 10% of $100

f 25% of $40

g 25% of $60

h 30% of $50

i 40% of $60

j 75% of $40

30% of $20

30% of $30

Think 10% (1/10) of $30 = $3

Think 10% (1/10) of $30 = $3

30% is 3 times that amount = $9.

30% is 3 times that amount = $9.

Determines percentages of quantities, and finds equivalent fractions and decimals for benchmark percentage values

Design three survey questions to improve your school canteen. You could consider such things as days it is open and types of food.

c Survey some children, then report on their responses to your questions.

Write a statement about a possible improvement the canteen could make, according to your survey.

Do you think that you surveyed enough students to make a fair sampling of students in your school? Why?

Does the oldest person run the fastest?

a Order 8 students in your class from youngest to oldest.

b Number them from 1 to 8, then record their dates of birth (D.O.B.) and sprinting times over 50 m in the table below.

c Did the oldest person run the fastest?

Enlarging two-dimensional shapes

This 2 cm × 2 cm square has an area of 4 cm2.

a How big do you think the area of the square would be if you doubled its dimensions (length of sides)?

b Test your answer by drawing a square with sides of 4 cm on the grid.

c How many times larger was the area of the square with doubled dimensions?

d Enlarge the rectangle by doubling its dimensions to see if the area of the rectangle is also enlarged by the same amount.

e Having done this for both the square and the rectangle, write a brief rule for what happens to the area of a two-dimensional shape when its dimensions are doubled.

Reducing two-dimensional shapes

a Reduce the shape by halving its dimensions. A starting point has been given.

b Did the area of the smaller shape halve?

c What happened to the area of the smaller shape?

Create two shapes. The first shape must have an area of 16 cm2 and the second must have an area of 32 cm2.

A simple percentage can be viewed as a fraction with a denominator of 100. A percentage sign, %, is used to display percentages.

20 100 is the same as 2 10 and can be written as 20%.

Shade the given percentages of the 100 pieces of candy in the jar. Hint, shade them in rows starting from the top of the jar.

a 10% or 1 10 of the candy is red.

b 20% or 2 10 of the candy is green.

c 30% or 3 10 of the candy is orange.

d 40% or 4 10 of the candy is blue.

Circle the correct percentages of the battery chargers.

Lollies

Convert 10% to a fraction to calculate the discount and then the cost.

Example:

10% of $20 = 1 10 of $20 = $2

6

Division with fractional remainders

Remainders can be written as a common fraction. Simply place the remainder over the divisor to form a fractional remainder.

Calculate the answers to the following divisions. Write any remainders as fractions.

5

Calculate the average distance between railway stops over 728 km:

a If the train stopped at 4 stations.

b If the train stopped at 8 stations.

DRAFT

You need to think about your remainder when answering question 6. If you divide 17 sheep into 4 paddocks, the answer could be 4 r 1, not 1 4 of a sheep!

Solve these problems, choosing the best way to write the remainders.

a Josh shared 256 sheep evenly into 7 paddocks. How many sheep were in each paddock?

b Shari had 657 marbles that she shared evenly among herself and her four friends. How many marbles did each friend receive?

c Rami bought 260 small chocolate bars to share among himself and his 7 friends. How many chocolate bars did each child receive?

d Teresa had a roll of ribbon measuring 185 m. She had to cut the ribbon into 4 equal lengths. How long was each piece of ribbon?

Cross-sections 34

In the space provided, draw the cross-section of each object. All objects are cut parallel to their bases. You may need to model some of these objects from soft substances to discover the shape of the cross-section. Prisms cut parallel to their base have uniform cross-sections.

What objects could these shapes be the cross-sections of? Note: You can have more than one answer.

When you do a number of cross-sections of a prism, parallel to its base, are the cross-sections always the same size?

When you do a number of cross-sections of a pyramid, parallel to its base, are the cross-sections always the same size?

A dot plot is a number line that uses dots to record the frequency of events. For example, in this survey, six people selected C.

Mr Chambers took the pulse rates of 60 Year 5 students after recess and recorded them.

Create a dot plot graph of the collected data.

Use the data above to answer whether the questions are true or false.

a More children had a pulse rate of 64 than 67.

b Fewer children had a pulse rate of 67 than 71.

c More children had a pulse rate of 80 than 79.

d Fewer children had a pulse rate of 85 than 88.

e More children had a pulse rate of 80 than any other.

f More children had a pulse rate of 78 than 83.

g Fewer children had a pulse rate of 82 than 77.

Equivalent number sentences

An equation is a number sentence that contains an equals sign, e.g. 100 ÷ 5 = 10 × 2.

Balance these equations by supplying the missing number.

a 51 ÷ = 25 8 f 365 ÷ 5 = 7

b 48 + = 99 16 g 48 ÷ 8 = ÷ 20

c 14 × = 35 × 2 h 75 × 5 = + 80

d 959 = 910 ÷ 1 i 102 + 52 = × 5

e 320 ÷ = 64 48 j 21 9 = ÷ 12

The solutions to these equations are in the cloud. Use the “guess and check” method to solve them. 3 6 7 8 9 10 35 50 72 86

a 16 × 3 = 2 f 8 + × 7 = 50

b 95 = 14 + 9 g ( + 3) × 4 = 40

c 63 ÷ 7 = 81 ÷ h 54 6 × = 6

d + 53 = 8 × 11 i 100 ÷ + 10 = 20

e 64 21 = ÷ 2 j 3 × 3 × = 30 3

Order of operations: × and ÷ before + and – .

Apply the order of operations to complete the equations below.

a 3 + 7 + 6 x 3 =

b 3 + (7 + 6) x 3 =

c 7 x 3 x 4 – 52 =

d (3 + 7) x 3 – 5 x 3 =

e 7 x 5 + 19 – 3 x 6 =

f 100 – 7 x 5 + 15 =

25 – 8 = 17 51 ÷ 3 = 17

My guess for ‘c’ is 9, but I’ll check.

g (8 + 6) x 10 – 100 – 30 =

h 25 x 5 + 90 – 150 =

Create equations that will help you solve these problems. 4

a How much did Daniel pay for his surfboard if he paid $90 per month for two years?

b A hamburger costs $2.95. With sauce it costs 5c extra. How much for 6 with sauce and one without sauce?

c How much did Alexa actually receive if she worked 5 days at $40 per day, but one quarter of the amount was taken out in taxes?

d How much medicine is left in the 150 mL bottle if Erica took 4 doses of 25 mL?

35 GST and budgets

GST is a Goods and Services Tax. That means we pay an extra percentage or fraction of the cost of the goods or services being provided, as a tax. For example, you might pay an extra 10% ( 1 10 ) of the cost of a T-shirt as GST. If a tradesperson provides you with a service, you will pay an extra 10% to them.

COST $20

The seller or provider of the goods or services collects Plus GST $ 2 the GST and sends it to the government.

Total cost $22

Calculate the GST and then the total price for these items. Divide by 10 to find 10% or 1 10 of the cost.

Henry earns $678.00 per week but has many commitments and needs to budget.

a Total all the weekly expenses to calculate how much Henry spends. (You may need a calculator.)

b Does Henry spend more than he earns?

c How could Henry trim his spending to balance his earnings with his spending?

d What is the difference between what he earns and what he spends?

e If the extra money he spends is put on a credit card, would this be a good idea? Why?

Recognising metric units

Units of length prefixes and their meanings

deca ten kilo one thousand centi one hundredth

hecto one hundred deci one tenth milli one thousandth

Use the prefixes above to describe these lengths (e.g. decimetre = 1 10 of a metre).

a decametre b hectometre

d centimetre e millimetre

c kilometre

f decimetre

Grams g, kilograms kg, tonnes t, litres L, millilitres mL, cubic centimetres cm3, cubic metres  m3, square metres m2, square centimetres cm2, millimetres mm, centimetres cm, decimetre  dm, metre m, decametre dam, hectometre hm, kilometre km

Choose the correct measuring unit to measure the items. You may need to write two abbreviations in some cases. For example, the length of a long jump might be m and cm

Items Unit/s

a The length of a pencil.

b The length of an ant.

c The length of a car.

d The capacity of a small cup.

e The capacity of a barrel of water.

f The volume of a matchbox.

g The volume of a cubby house.

h The mass of a ruler.

i The length of first base from home plate.

j The mass of a bag of oranges.

k The mass of an elephant.

l The area of a postage stamp.

m The area of a park.

n The area of a handball court.

9

Solve the problems.

a The length of a rope was 3 dam and 4 m long. How many metres in total is that?

b The length of a matchbox is 5 cm and 3 mm long. How many millimetres is that?

c The length of a spear is 2 m and 23 mm long. How many millimetres is that?

d The length of a road is 4 dam and 7 m long. How many metres is that?

Timelines 35

Timelines are used to place events in a sequence.

Make your own personal timeline. Start by writing the year you were born. Make sure to include important events in your life.

CE means ‘Common Era’. BCE means ‘Before the Common Era’.

Draw a line to match each event to a place on the timeline.

Answer these questions.

a How many years between the Battle of Hastings and Columbus’s voyage

b How many years between the first Olympics and the completion of the Great Wall of China?

c How many years between the first Olympics and the Battle of Hastings?

d How many years between the completion of the Great Wall of China and the Federation of Australia?

e How many years between the Federation of Australia and the year you were born?

f Put a cross on the timeline to estimate 1250 ce.

g Tick the timeline where you think 250 bce would be.

h Put an O on the timeline to mark the Sydney Olympics in 2000.

PART

Round each number to the nearest 10 and nearest 100.

Number Round to 10 Round to 100

a 91

b 229

c 1356

d 1497

e 2986

Make an estimate of each addition by rounding each number to the nearest 100.

f 397 + 207 ≈

g 896 + 787 ≈

h 1679 + 623 ≈

i 2071 + 1641 ≈

List all factors for these numbers.

a 18

b 27

PART

Solve the following.

Find the highest common factor of these numbers.

c 18 and 42

d 27 and 45

PART

Write

Calculate these percentages.

a 10% of 40

b 25% of 60

c 50% of 80

d 10% of 100

e 10% of $500

f 25% of $80

a Enlarge this shape by doubling its dimensions (sides).

Write the letter found at each grid reference to discover the secret word.

b How many times larger is the shape’s area?

Name the objects these nets form.

acute angle

An angle less than 90°

acute angle

addend

Any number that is added to obtain the sum or total.

3 + 7 + 8 = 18

(addends) (sum)

average

The total of a series of numbers divided by the amount of numbers in the group.

Average of 3, 5, 7, 9:

• add 3 + 5 + 7 + 9 = 24

• divide 24 by the number of scores

24 ÷ 4 = 6

The average is 6.

axis

A line that divides a shape symmetrically in half.

adjacent

Next to; adjacent sides of a triangle have a common vertex.

X

Y Z

XY and YZ are adjacent because they have a common vertex, Y.

algebra

Where letters or symbols are substituted for numbers in a number sentence.

3 × b = 15 (b = 5)

Lines of reference for a graph.

algorithm

The calculation procedure for setting out a mathematical problem in a certain way.

324 874 364 + 207 23 × 30

Celsius A scale for measuring temperature.

ice begins to melt

boiling point of water

human body temperature

circumference

The distance around a circle.

am

Abbreviation from the Latin words ante meridiem (before noon). Any time from midnight to noon.

apex apex

The highest point of a solid (3D) object from its base.

associative property

When using addition and multiplication, it doesn’t matter how the numbers are grouped. The answers will always remain the same.

5 × 4 × 2 = 40 3 + 6 + 7 = 16 and and 5 × 2 × 4 = 40 7 + 3 + 6 = 16

column graph

A graph where vertical columns or horizontal bars are used to represent data.

CIRCUMFERENCE

commutative law

Numbers can be added or multiplied in any order. 5 + 6 is equal to 6 + 5

× 7 is equal to 7 × 5

complementary angles

Two angles whose sum is 90

composite number

A number that has more than two factors.

Example: 10 has four factors – 1, 2, 5 and 10.

congruent

Two shapes or objects that are identical in all ways.

coordinate point

congruent circles

Coordinates locate points or positions on a grid using ordered pairs. The horizontal position is given before the vertical position. Example: The circle is located at (C,3).

dot plot

A graph that uses scale to represent data. Each value is recorded as a dot.

edge

The intersection of two faces.

elapsed time (duration)

The time taken to do something. For example, the time it takes to prepare a meal is elapsed time.

cross-section

The shape of the face made by slicing through a solid. Example:

cubic metre (m3)

A metre cube has a volume equal to one cubic metre.

denominator

1 m

cross-section

equilateral triangle

A triangle that has three equal sides and three equal angles.

equivalent fraction

Fractions that have the same value.

1 m

1 m

The bottom number of a fraction that tells how many equal parts in the whole.

1 ➔ numerator

4 ➔ denominator

diameter

A straight line touching both sides of a circle which passes through the centre point.

divided bar graph

diameter

A graph that shows how a total is divided into parts.

Science Art Maths

face

70

100 = 7 10

The surfaces of a three-dimensional (solid) object.

face

face face

factor

Any whole number that can be multiplied with another to make a given number.

Factors of 12: 12, 6, 4, 3, 2, and 1

factor tree

A diagram that displays factors of a number.

36

6 × 6

3 × 2 × 3 × 2

frequency

In a collection of data, the frequency of a category is the number of occurrences for that category.

Animal Frequency Sheep

Horses Cows Dogs

The frequency of the horses in the table is 7.

greater than ( > )

Symbol used to show that one number has a value greater than the other number.

27 > 15

improper fraction

A fraction where the numerator is greater than the denominator. Improper fractions have a value greater than one whole.

5 ➔ numerator

isosceles triangle

A triangle that has two sides of equal length and two angles the same size.

3 ➔ denominator x x

kilogram (kg)

A mass unit.

1 kg = 1000 grams

grid references

Grid references locate positions on a map or grid. The horizontal position is given before the vertical position, e.g. the circle is located at (C,3).

kilolitre (kL)

A capacity unit.

1 kL = 1000 litres

kilometre (km)

A length unit.

1 km = 1000 metres

less than ( < )

Symbol used to show that one number has a value less than the other number.

gross mass

The total mass of any item, including its packaging.

hectare (ha)

A unit of area.

1 ha = 10 000 m2

hexagon

A 2D shape with six straight sides. regular hexagon irregular hexagon horizontal

A straight line at right angles to the vertical and parallel to the horizon.

vertical line

horizontal line

line graph

240 < 420

Information represented on a graph by joining plotted points with a line.

mean

The centre of a set. It is found by adding all the values in the data sample, then dividing the total by the number of values in the set. It is often called ‘the average’.

8 is the mean for the scores:

6, 8, 6, 9, 10 and 9

6 + 8 + 6 + 9 + 10 + 9 6 = 8

metre (m)

The basic SI unit of length.

1 metre = 1000 mm

1 metre = 100 cm

millilitre (mL)

A measurement of capacity.

1000 mL = 1 litre

millimetre (mm)

A measurement of length.

1 mm = 1 thousandth of a metre

10 mm = 1 centimetre 1 mm

order of rotational symmetry

The number of times a shape matches the original as it completes one full rotation.

1 000 000 1000 × 1000 = 1 000 000 or 10 × 100 000 = 1 000 000

mixed numeral

A number that consists of a whole number and a fractional part.

Example: 4 1 2

Order of rotation of 4

Any shape that still looks the same when it is turned around a fixed point has rotational symmetry.

outcome

The result of a mathematical investigation. For example, when three coins are tossed there are 8 possible outcomes.

multiple

The result of multiplying a given number by any other number is a multiple of that given number. Multiples of 3 are: 3, 6, 9, 12, 15, 18, etc.

negative numbers

Numbers that have a value less than zero. A minus sign is placed in front of a number to identify it as negative.

Example: The temperature was 5°C.

net

A flat shape which can be folded to make a 3D object.

Net of a triangular prism

net mass

The mass of any item without its packaging.

numerator

The top number of a fraction, telling us how many parts there are out of the whole.

3 ➔ numerator

4 ➔ denominator

obtuse angle

An angle larger than 90° but less than 180° .

per cent (%)

A fraction of 100.

87% means 87 out of 100

i.e. 87 100 = 87% = 0.87

perimeter

The distance around the outside of a shape. 3 m 5 m 4 m

Perimeter = 3 m + 4 m + 5 m

Perimeter = 12 m

perpendicular lines Lines which meet at right angles.

pie sector graph

A circular graph whose parts look like portions of a pie. plan

Tennis Hockey

Softball

Bowls Netball

A diagram from above, showing the position of objects. Also known as the top view of a 3D object.

radius

A straight line extending from the centre of a circle to the circumference.

ray

pm

Abbreviation for the Latin words post meridiem which means after midday.

polygon

A 2D shape with three or more angles and straight sides.

hexagon pentagon

prime number

A number that is divisible only by itself and 1.

Examples: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29

probability

The likelihood or chance of an event happening. The range of probability is from zero to one.

quadrilateral

A 2D shape with four straight sides.

Examples:

radius

A line that has a starting point but does not end.

rectangle

A four-sided figure with four right angles and two pairs of parallel sides.

rectangular prism

A 3D object which consists of six rectangular faces.

reflective symmetry

A mirror image of a shape.

reflex angle

An angle between 180° and 360°

Example: 330°

revolution

A full turn of 360°

rhombus

A four-sided shape with four equal sides. Opposite angles are equal and it has two sets of parallel lines.

Roman numerals

Number system devised by the ancient Romans.

Examples:

I = 1 D = 500

V = 5 M = 1000

X = 10

L = 50 XCV = 95

C = 100 MMX = 2010

rotation

The turning of an object through a fixed point.

scalene triangle

A triangle with sides of different lengths and angles of different sizes.

sequence

An order of numbers or objects arranged according to a rule or pattern.

Example: Number 1 2 3 4

$ $5 $10 $15 $20

square centimetre (cm2) A unit for measuring area.

supplementary angles

Two angles that have a total of 180

surface area

The total area of all faces of a 3D object.

square number

The product of a number multiplied by itself.

Examples:

A rectangular prism has six faces. tally marks

Groups of marks used to keep count. Every fifth mark usually crosses the four before it. = 17

three-dimensional (3D)

Solid objects have three dimensions: height, length and width (breadth). height length width (breadth)

timeline

A line which represents a span of time.

2003 Born 2008 School 2013 2018 2023 Work High school

tonne

A unit for measuring mass. 1 tonne = 1000 kilograms

translate (slide)

The sliding of a shape into a new position.

slide

trapezium

A four-sided figure that has two parallel sides and two that are not parallel.

triangular numbers

Numbers that can be arranged as a triangular pattern.

triangular prism

A prism with two congruent triangles as bases, 3 rectangular faces, 9 edges and 6 vertices.

triangular pyramid (tetrahedron)

3D object with 4 triangular faces, 6 edges and 4 vertices.

turn

To rotate a shape around a point.

twelve-hour time

Analog clocks break the day into two lots of 12 hours: am (midnight–midday) pm (midday–midnight).

twenty-four-hour time

Time divided into 24-hour intervals, so as to distinguish between am and pm.

two-dimensional (2D)

Plane shapes have only two dimensions: length and width (breadth).

width (breadth)

unit fraction

length

Fractions with a numerator of 1.

Examples: 1 2 , 1 3 , 1 4 , 1 5 , 1 10

vertex

The point where two or more lines meet to form an angle.

vertical

vertex

DRAFT

Vertical lines are at right angles to the horizontal.

vertices

Plural of vertex. A triangle has 3 vertices.

vertical line

horizontal line

vertices

A rectangular prism has 8 vertices.

volume

The amount of space an object occupies.

Formula:

Volume = length × width × height 2 m 3 m

2 m

Volume = 3 m × 2 m × 2 m = 12 m3

whole numbers

The counting numbers from one to infinity. 1, 2, 3, 4, ➔ infinity

f 1000 m 1200 t 1400

g 700 n 200 u 1400

7 a 92 m b $25

8 a Right angle e Obtuse angle

b Acute angle f Obtuse angle

c Right angle g Reflex angle

d Reflex angle h Straight angle

9 A B C D

a I have four right angles. B

b I have one obtuse angle, one acute angle and two right angles.

c I have three acute angles. E

d I have three right angles and two obtuse angles D

e I have six obtuse angles. A

10 Hands on.

11 1000 clicks

12–13 Hands on.

14 a 433 km c 396 km e 378 km

b 368 km d 245 km

15 Hands on.

161

f 21 m 179 t 330

g 128 n 176 u 393

3 a 63 e 69 i 369

b 64 f 91 j 283

c 75 g 68 k 194

d 96 h 79 l 572

4 a 36 e 34 i 159

b 33 f 14 j 228

c 47 g 27 k 138

d 24 h 35 l 225

5 Hands on.

6 a 216 426 d 1 518 620

b 321 216 e 12 270 480

c 435 560 f 28 378 999

7 a ACT, Tas, Vic, NSW, SA, NT, Qld, WA

b SA c WA d Qld, WA e WA f SA

Answers

13 a 0.5 kg e 0.459 kg i 1.25 kg

b 0.25 kg f 0.674 kg j 2.374 kg

c 0.275 kg g 1.632 kg k 2.5 kg

d 0.376 kg h 1.347 kg l 3.2 kg

14 a Kitchen or electronic scales

b Kitchen or electronic scales

c Displacement tank

d Weighbridge

e Bathroom scales

UNIT

1 a 90 d 180 g 210 j 400

b 120 e 240 h 320 k 540

c 200 f 300 i 280 l 490

2 a 1000 f 2400 k 2800

b 1200 g 3000 l 4900

c 1600 h 2500 m 3500

d 1500 i 2100 n 6400

e 2000 j 3600 o 5600

3 a 120 d 91 g 111 j 204

b 115 e 98 h 238 k 114

c 160 f 132 i 216 l 215

4 a $180 c $200 e $184

b $180 d $130

5 Hands on.

6 a 13 c $4.91 e 25 g $206

b 16 d $315 f 264 h $1650

7–9 Hands on.

10–11 Discussion. Six combinations give 7 but only one combination gives 12.

12 a R 15 Y 8 G 5 O 2 d Orange

b Red e No

c Hands on (fair, 50/50, f Yes even)

13

rectangular prism rectangular pyramid square pyramid

pyramid cube

hexagonal prism triangular prism pentagonal prism

pentagonal pyramid

octagonal prism

hexagonal pyramid octagonal pyramid

b 0.77 d 0.66 f 0.99

6 Possible solution: Sydney to Grafton and return (1220 km).

7

8

9

UNIT

1 a 1426 c 1591 e 4532

b 4322 d 713

2 a 6425 c 3831 e 4630

b 7350 d 4655

3 a 4089 c 3010 e 2118

b 1019 d 2030 f 3018

4 a 12, 17, 22, 27, 32, 37, 42

b 25, 28, 31, 34, 37, 40, 43

c 28, 27, 26, 25, 24, 23, 22

d 35, 39, 43, 47, 51, 55, 59

e 25, 28, 31, 34, 37, 40, 43

f 39, 33, 27, 21, 15, 9, 3

5 Hands on.

6 a Subtract 8 c Add 9

b Subtract 14 d Multiply by 5

7 Cube Rectangular prism Triangular prism

8

16

7 a 1, 2, 4, 5, 10, 20 b 1, 2, 3, 4, 6, 12

c 1, 2, 3, 6, 9, 18

d 1, 5, 25

e 1, 7, 49

f 1, 2, 4, 8, 16, 32, 64

8 Hands on.

9 a acute, 50° c obtuse, 135°

b acute, 70°

10

a acute, 50° e acute, 40°

b right angle, 90° f right angle, 90°

c acute 45° g acute, 60°

d obtuse, 130° h reflex, 270°

11 Hands on.

9.919, 89.423

3.567, 13.561, 13.651

21.524, 52.421, 215.246

3.378, 3.387

3.549, 35.49

6.306, 6.630

11

$73.05

2

4 a 30, 300, 3000

b 50, 500, 5000

c 60, 600, 6000

d 70, 700, 7000

e 90, 900, 9000

f 100, 1000, 10 000

g 180, 1800, 18 000

h 250, 2500, 25 000

i 310, 3100, 31 000

j 440, 4400, 44 000

k 560, 5600, 56 000

7800,

UNIT

1 a 575 f 999 k 2679

b 1224 g 2520 l 1512

c 1125 h 2184 m 2494

d 1260 i 756 n 2331

e 1334 j 1365 o 3216

2 864 cans

3 a hundredths g ones

b hundredths h tens

c ones i ones

d hundredths j thousandths

e tenths k ones

f hundredths l hundreds

12 50 hectare farm for sale.

13 Hands on.

14 Hands on. (a zoo and d shopping mall would normally be larger than a hectare.)

DIAGNOSTIC REVIEW

The

DRAFT

12, 24

b 1, 3, 5, 15

c 1, 3, 7, 21

d 1, 5, 25

e 1, 2, 4, 7, 14, 28

f 1, 2, 3, 4, 6, 9, 12, 18, 36

g 1, 2, 3, 6, 7, 17, 21, 42

h 1, 3, 5, 9, 15, 45

i 1, 2, 4, 8, 16, 32

j 1, 3, 17, 51

5 Hands on. Possible solutions:

a 12 × 3 = 36 then 36 × 5 = 180

b 15 × 4 = 60 then 60 × 3 = 180

c 14 × 9 = 126 then 126 × 2 = 252

d 17 × 8 = 136 then 136 × 2 = 272

e 25 × 4 = 100 then 100 × 5 = 500

6 Hands on. Some examples:

48 × 1, 24 × 2, 16 × 3, 12 × 4, 8 × 6

7 a cm c mm e m g mm

b cm d cm f m h km

8 a 30 cm ruler

b 1 m ruler

c tape measure

d 1 m trundle wheel

e tape measure

f 1 m trundle wheel

g odometer

h 30 cm ruler

i 1 m trundle wheel

9 a 50 mm f 800 cm k 2 km

b 260 mm

g 900 cm l 6 km

c 370 mm h 550 cm m 4 km

d 3 cm i 2 m n 6000 m

e 6 cm j 7 m o 850 cm

10 Hands on.

11 a equilateral triangle

b isosceles triangle

c right-angle triangle

d equilateral triangle

12-14 Hands on.

1 Hands on.

2 Discussion Single = 65c each

5 pack = 50c each

10 pack = 60c each

3 Discussion 250 mL = 50c per 250

UNIT

7 a ten metres

b one hundred metres

c one thousand metres

d one hundredth of a metre e one thousandth of a metre f one tenth of a metre

DIAGNOSTIC REVIEW