Creative

How to draw a spiral - Golden Ratio

By ML Barber, London volunteer

If you’re looking for a fun and easy activity to pass the time while you enjoy the sunshine, why not learn how to draw a spiral? Whether it’s drawing, painting, knitting or colouring, getting creative and unleashing your inner artist is a great form of self-care to help manage day-to-day stresses.

In Renaissance art, the golden ratio was widely used, because it was pleasing to the eye. This is no coincidence. Examples include: da Vinci’s Vitruvian Man, The Last Supper, Mona Lisa. Other artists include Botticelli and Michelangelo.

The golden ratio appears naturally in the world of nature and science, the spiral in a sunflower, the spiral in a galaxy, generally any spiral originates from the golden ratio.

The Italian Mathematician, Fibonacci, developed a sequence when looking at the population growth of rabbits in an ideal situation. This started with 1,1 with any number in the sequence being obtained by adding the previous two. So, the sequence is 1,1,2,3,5,8,13 etc

This sequence can also be used to find the golden ratio, by dividing one number in the sequence by the previous one. The further into the sequence you are, the closer the number gets to the golden ratio.

Follow the process below to construct an approximate spiral, by applying the above sequence

1. Take a piece of squared paper and draw a one by one square. On the top, draw another one by one square. You now have a two by one rectangle.

2. Now against the left-hand longer side, draw a two by two square, you now have a three by two rectangle.

3. Now draw a three by three square against the bottom to obtain a five by three rectangle.

5.You are now back to drawing a square on the top. But now it will be an eight by eight square, obtaining a thirteen by eight rectangle.

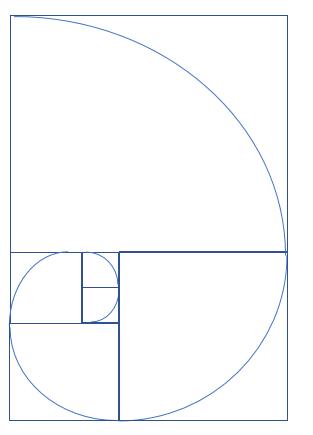
This process can be continued until you run out of space!

You can draw an approximate spiral, starting at the bottom left-hand corner of the original square, draw a quarter circle to the opposite corner (which coincides with the bottom right hand corner of the second square). Draw a quarter circle from here to the opposite corner of the second square (which coincides with the top right-hand corner of the third square (two by two). Continue this process.

If you want to investigate the mathematical value of the ratio, for each rectangle divide the longer side by the shorter side (Use a calculator if needed).

The length of the longest side of the next rectangle is simply found by adding together the length and breadth of the current rectangle. The shorter side of the next rectangle is equal to the longer side of the current one.

If you were to continue this process indefinitely, then the larger your rectangle, the closer that the ratio will get to the golden ratio.

For the better mathematicians, see if you can form a quadratic equation and solve it to find the exact value.