The Power of Doodling: Impossible Symmetries and Diffraction Patterns; Roger Penrose Michelle Paolicelli

engineering methods modify the genetic makeup and sequences of microorganisms.10

Specifi ed Microbial Therapeutic Against Cancer

Regardless of their species, all microbial anti-cancer mechanisms can be classifi ed into three categories: direct antitumor mechanism, vasculature destruction, and immune activation. Related treatments can also be enhanced by genetic engineering.

Direct Antitumor Mechanisms

Microbes can eliminate tumor tissues by infecting and killing host cells through virulent mechanisms that often lead to cell lysis, the breaking of cell membranes. Some microbes infect tumor cells internally, while many others attack extracellularly. For instance, toxin-bearing microbes produce peptides and virulent elements that can damage tumor tissues and suppress vital functions like immune systems, which is more effective than chemotherapy, as the latter targets all tissues and can cause fatal side effects.11 Microbes can be engineered to transform molecules with little pharmacological activity into toxins or active chemotherapy reactants within target tissues.12 Notably, microbes can also embed radioisotopes-coupled antibodies into their membranes to deliver lethal radiation to tumors.13

Attacks on Vascular Structures

Many scholarships have demonstrated that cancerous tumors rely on vasculature, namely blood vessels, to provide oxygen and nutrients for their high metabolism.14 Current chemotherapies, although effective at inhibiting the growth of new blood vessels, are impotent against treating existing vessels that support tumor growths. However, through genetic expressions that allow the development of specifi c pathway-binding protein structures, microbes can not only suppress tissue growth with higher success rate than traditional treatments but also trigger apoptosis (programmed cell death) in malignant and blood vessel cells.15,16,17 The destruction of harmful vasculature would facilitate immune cells’ targeting on cancer cells and support therapeutic bacterial infections. Tumors have developed mechanisms that allow them to inhibit and suppress immune cells within tumors.18 However, through both genetic engineered and intrinsic properties, microbes emerge as a useful tool to activate immune systems and attract immune cells. For instance, through infecting tumors, microbes can trigger infl ammatory responses of the host’s innate immune system to destroy both cancerous tissues and related vasculatures.19 Specifi cally, microbes can be engineered to produce cytokine proteins to attract immune cells like macrophages (cells that can fi lter through tumor membranes, infuse therapeutic microbes, and trigger antitumor infl ammations)20 and neutrophils (white blood cell that can stimulate non-specifi c infl ammation).21 Additionally, microbial vaccines can deliver tumortargeting antigens like tumor necrosis factor alpha (TNF-�) to activate adaptive immune responses independent of tumor’s infection status, which allow the implementation of multifaceted attacks.22 Eventually, by inducing immune memory, microbes could help to establish a surveillance system that identifi es and removes metastatic cells before they create further dysregulation.23

Concerns

One risk of applying microbe-based therapeutics is induced septic shock—a body-wide bacterial infection. When a microbial vaccine activates immune systems, some bacterias might be lysed during the release process of macrophages and excrete toxins that can lead to fatal septic shock. Thus, it is essential for future treatments to minimize that risk. A potential solution is to engineer phage to delete genes corresponding to lysing. Another concern surrounds immune system clearance, which can rapidly clear therapeutic phages and signifi cantly reduce their effi cacy. One potential solution is couple directed evolution that can increase phages’ lifetime with genetic engineering that boosts their immunity against the hosts’ immune system.24 REFERENCES

THE POWER OF DOODLING:

IMPOSSIBLE SYMMETRIES AND DIFFRACTION PATTERNS

The mark of a great scientist is someone who is constantly questioning. Questioning the world around them, the way things work, and why things are the way they are. But beyond this, a scientist with the potential to pioneer will question established truths. The things that others take for granted and believe to be unequivocally true. Many people exhibit a passion for science, but what sets pioneers of science apart is their hunger to explore a subject further than anyone else before them. Sometimes their discoveries may not be the most fl ashy or exciting, but their impacts are more profound than anyone could have imagined. Roger Penrose did just that, opening the door to the discovery of an entirely new form of matter, and it all started with a handful of shapes.

Penrose, a contemporary of Stephen Hawking, is a British mathematician and relativist. His work on black holes earned him the 2020 Nobel Prize for Physics. Alongside Hawking, Penrose proved that

Written By Michelle Paolicelli Designed By Saraswati Sridhar

all matter within a black hole reduces to a point of infi nite density and zero volume, also known as a singularity. In addition to this, Penrose created a way to model the effects of a black hole upon an object as it approaches a black hole. Although Penrose’s achievements in Physics are extraordinary on their own, his love for mathematics and doodling led to perhaps his most interesting contribution to science in the fi eld of crystallography. 1

In crystallography, tiling is defi ned as the fi lling of all space with a repeating geometric pattern, called a motif, without gaps or overlaps. As a general rule, only motifs that result in global 1, 2, 3, 4, and 6-fold rotational symmetry are able to do this. This was a widely accepted truth. However, Roger Penrose discovered a way to tile while creating 5-fold symmetry using a motif of only four shapes. This was revolutionary as it was thought to be impossible. Shortly after this initial discovery, two other types of Penrose tiling were discovered using different motifs. As Penrose tiling was further explored, scientists soon realized that infi nite variations of Penrose tiling exist in which a pattern with fi ve-fold rotational symmetry fi lled all space.2 This redefi ned an absolute truth within crystallography, and Penrose tiling has been found to naturally occur in quasicrystals and used in architecture and art.

What makes Penrose tiling so revolutionary is that its novelty goes beyond its forbidden 5-fold symmetry. Other scientists studied Penrose tiling at length, coming up with their own variations, identifying new patterns and features, and translating the 2D pattern to a 3D representation of matter.3 Apioneer himself, Penrose’s work inspired others to push further and search for greater meaning in Penrose tiling.

One person of note who extended the meaning of Penrose tiling was Robert Ammann. Ammann’s contribution to Penrose tiling is unique in that he was an amateur mathematician. He did not complete a college degree but rather spent his time developing

his genius and a knack for pattern recognition. He was fi rst introduced to Penrose tiling through Martin Gardner’s Mathematical Games column in Scientifi c American. Ammann discovered his own aperiodic sets of tiles, some more simplistic than the kite and dart version Penrose himself proposed. He also developed a way to help form new tilings by placing lines on a plane in a semi-regular pattern. These lines are known as Ammann bars and show that all edges of an aperiodic tiling connect via straight lines. More intriguing is that the spacing of these lines follows Fibonnacci’s sequence, also known as the golden ratio.1 As an amateur mathematician, but surely a genius, Ammann’s contributions to crystallography and the understanding of Penrose tiling are not to be overlooked.

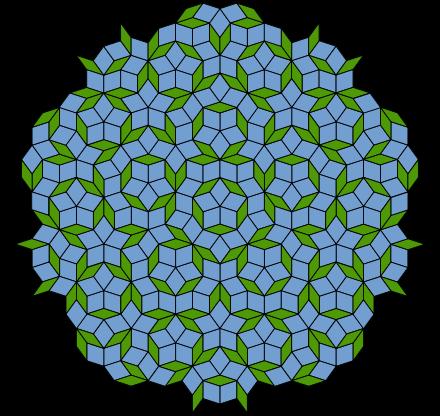
Another great scientifi c discovery that was enabled by Penrose tiling was the idea of quasicrystals. Quasicrystals are just what their name sounds like–crystal-like. The classic defi nition of a crystal is an ordered, periodic structure with predictable makeup. Quasicrystals modify this description as they are ordered structures, but they are aperiodic in nature. This means that although a quasicrystal pattern can fi ll all space, it lacks the translational symmetry of traditional, periodic crystals. In addition, crystals follow the symmetry restrictions of 2, 3, 4, and 6-fold symmetry while quasicrystals possess the forbidden symmetrys.3 It is this connection to Penrose tiling that led from one discovery to the other.

Prior to the publishing of Penrose tiling, it was widely accepted in the fi eld of crystallography that the symmetry rules were not broken under any circumstances. With this understanding came the acceptance of the idea that 2, 3, 4, and 6-fold symmetries were the only to occur in nature.4 However, Penrose tiling cast doubt upon this tenet of crystallography and scientists began to look deeper. Prior to the introduction of Penrose tiling, diffraction patterns of many different crystals had been made. Most often, they followed the established rules of symmetry. However, when they did not, scientists found some other explanation for the appearance of other symmetries. One explanation was that the crystals were twinning, or overlapping, causing the diffraction pattern to appear to possess a forbidden symmetry. In some instances, this was the case, but in others the blind trust in established theories led to a missed opportunity for discovery.1

Paul Steinhardt, formerly of the University of Pennsylvania, refused to accept the notion that quasi crystals did not exist in nature. His work with Penrose tiling led him to the theory of naturally occuring forbidden symmetries and after years he fi nally discovered icosahedrite as the fi rst known naturally occurring quasicrystal.1 This discovery was a culmination of Steinhardt’s entire career of work and was enabled entirely by his tendency to question and discover things on his own.

Today, quasicrystals are better understood. From two-dimensional Penrose tiling to threedimensional diffraction patterns observed in nature, quasicrystals are the result of the collaboration of manypioneering minds. Applications of quasicrystals include serving as steel-hardening agents, non-stick pan coatings, solar absorbers, and biomedical uses among others.5

Penrose’s legacy stretches forward decades and reaches back generations to explain previously mysterious phenomena and behaviors. His original tiling patterns have formed the basis of other scientists’ careers as they work to uncover all their hidden meanings, all because he liked to doodle.