PORTAFOLIO ESTRUCTURAS I

Docente: Iván Raúl Izquierdo Casafranca Sección 624

Facultad de Ingeniería y Arquitectura Carrera de Arquitectura Área de Construcción y Estructuras Ciclo 2022 2

CONTENIDOS

01

EJERCICIO 1

CG 01, CG 08, CG 10 04

02 PRÁCTICA CALIFICADA 1

CG 01, CG 08, CG 10 08

03 PRÁCTICA CALIFICADA 2

CG 01, CG 08, CG 10 14

04 EJERCICIO 2

CG-01, CG-08, CG-10 20

05 EJERCICIO 3

CG 01, CG 08, CG 10 24

06 PRÁCTICA CALIFICADA 3

CG 01, CG 08, CG 10 28

07 EJERCICIO 4

CG 01, CG 08, CG 10 34

EC1-1

EJERCICIO 1

TEMA

Momentos: Teorema de Varignon

RESULTADO

3/3

DESCRIPCIÓN

Se realizó un ejercicio de momentos en tres dimensiones, para el cual fue necesario aplicar el Teorema de Varignon Se empezó descomponiendo cada fuerza en sus componentes i, i, k, para luego calcular los momentos según sus puntos de origen, a partir de los cuales se llega a un momento total

REFLEXIÓN

Este ejercicio me permitió repasar para la PC1 y me fue de mucha ayuda, pues considero que trabajar en tres dimensiones le agrega un grado de dificultad al ejercicio, pero tras desarrollarlo en parejas puede comprender el proceso a seguir, dándome seguridad para la prueba. Lo más importante fue reconocer correctamente los signos de cada fuerza en función de la dirección de los ejes de coordenadas.

VALORACIÓN

Dificultad

Dedicación

Entendimiento

MOMENTO

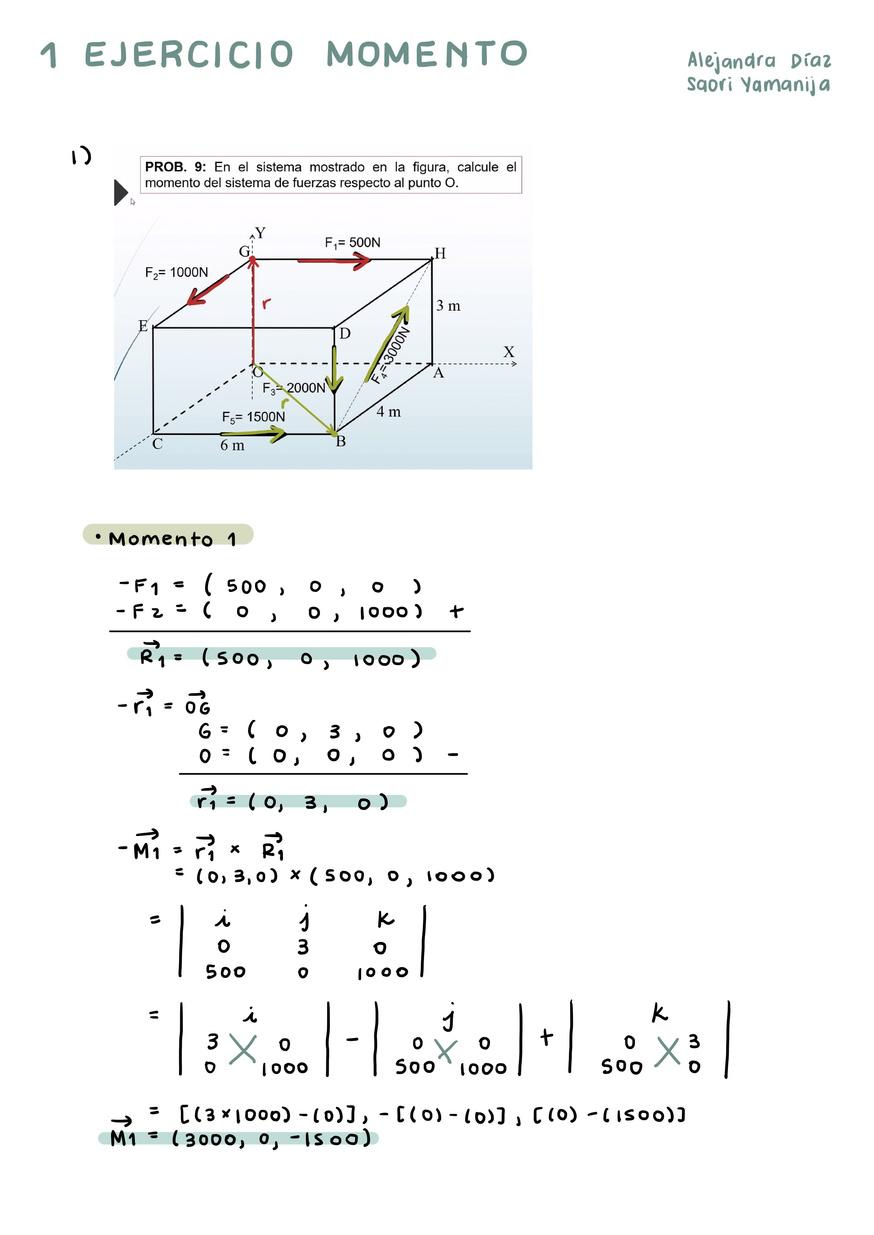
En el sistema mostrado en la figura, calcule el momento del sistema de fuerzas respecto al punto O

TEORÍA

1) Momento de una fuerza: La medida de cómo una fuerza hace girar un cuerpo respecto a un punto determinado.

2) Teorema de Varignon: Para resolver el momento en tres dimensiones, teniendo fuerzas concurrentes se aplica el Teorema de Varignon. Según este, el momento de una fuerza respecto a un punto dado es igual a la suma de los momentos de sus componentes respecto al punto.

En este caso contamos con dos fuerzas concurrente sobre el punto G y tres fuerzas concurrentes sobre el punto B Se transforman las fuerzas en sus formas vectoriales Respecto a cada punto, se halla la resultante de la suma de fuerzas concurrentes La resultante se multiplica por el vector posición Se halla la resultante de los dos momentos

EC1-2

PRÁCTICA CALIFICADA 1

TEMAS

Resultante de sistema de fuerzas Centro de gravedad

Momento: Teorema de Varignon y Vector Unitario

RESULTADO 20/20

DESCRIPCIÓN

Esta práctica contiene 4 ejercicios sobre los temas realizados en las primeras 3 semanas. Para poder resolverlo se utilizaron las herramientas aprendidas en clase y conocimientos previos sobre operaciones vectoriales.

REFLEXIÓN

Esta primera prueba me permitió recordar una serie de temas que ya conocía, sobre operaciones con vectores y los teoremas y estrategias a utilizar para halla una resolución eficiente. Así, tras practicar con todos los ejercicios resueltos en clase logré obtener un resultado satisfactorio que demuestra una buena compresión de los temas

VALORACIÓN

Dificultad

Dedicación

Entendimiento

CALIFICAD

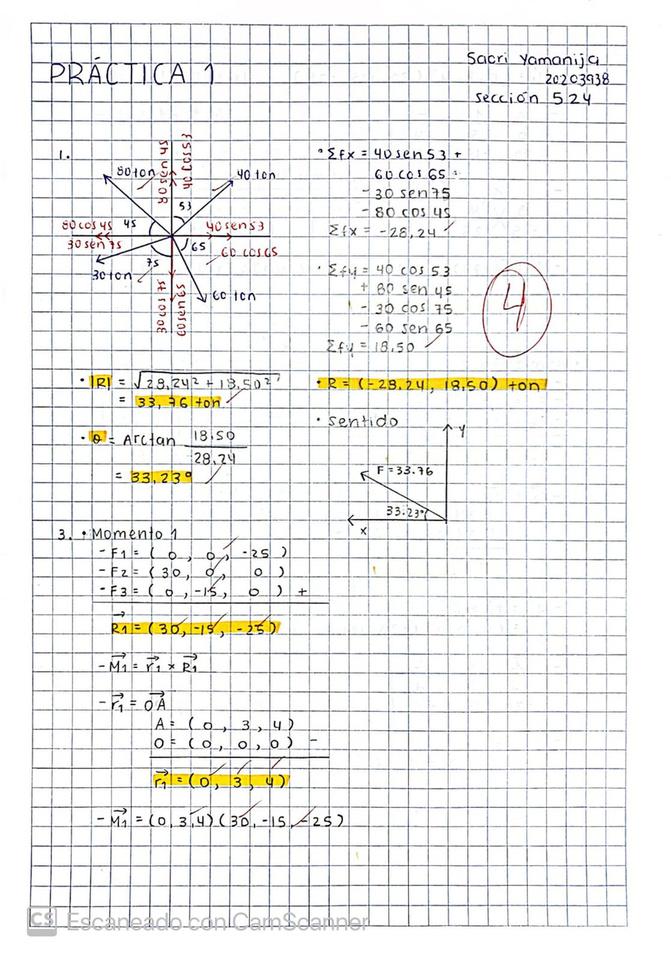
1) Calcule la resultante del siguiente sistema de fuerzas aplicadas a un punto. Indicar magnitud, dirección y sentido

2) Determine la ubicación del centro de gravedad del área mostrada, tomando como referencia los ejes X e Y indicados. Llene en la tabla adjunta los valores correspondientes

TEORÍA

1) Centroide: Punto que define el centro geométrico de un objeto

2) Hallar el centro de gravedad

Dividir la figura

Hallar el área de cada figura

Definir el centro de gravedad e indicar sus coordenadas en x, y Multiplicar las coordenadas por el área de cada figura y dividirlo entre el área Estas coordenadas representan el centro de gravedad de la figura completa

3) En el sistema mostrado, calcule el momento de las fuerzas respecto al punto O. Cotas en metros

TEORÍA

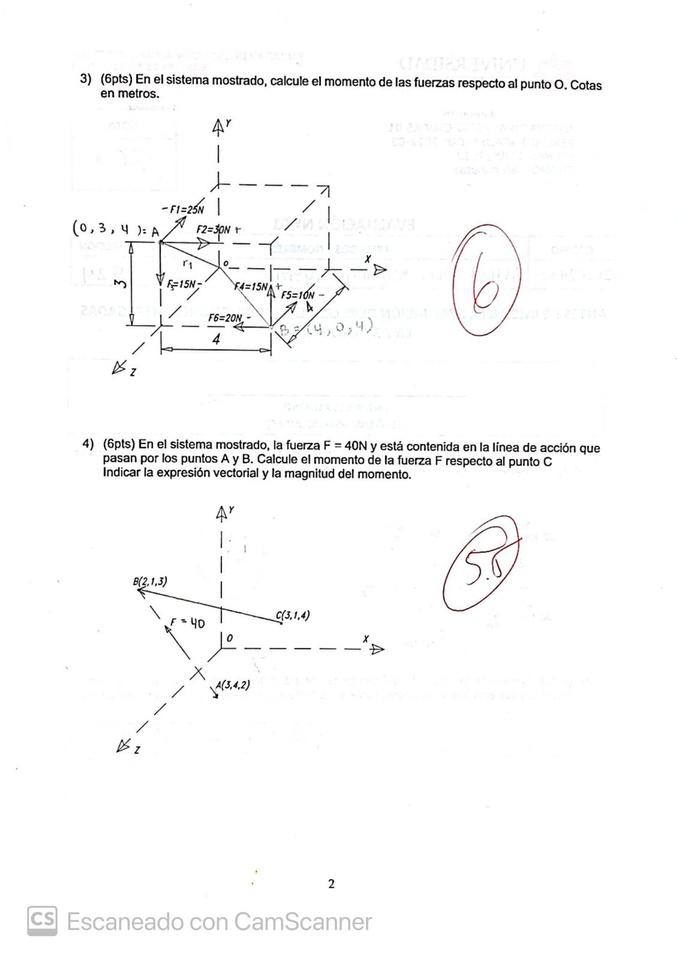
1) Teorema de Varignon: Para resolver el momento en tres dimensiones, teniendo fuerzas concurrentes. se aplica el Teorema de Varignon.

Según este, el momento de una fuerza respecto a un punto dado es igual a la suma de los momentos de sus componentes respecto al punto

4) En el sistema mostrado, la fuerza F=40N y está contenida en la línea de acción que pasa por los puntos A y B Calcule el momento de la fuerza F respecto al punto C Indicar la expresión vectorial y la magnitud del momento

5.5/6

TEORÍA

1) Vector Unitario: Vector equivalente a 1 en una recta determinada.

Debido a que nos enfrentamos a un sistema de fuerzas, en donde tres se encuentran en su forma vectorial y una en su forma escalar, es importante encontrar el vector unitario de la línea que contiene F para poder transformarla en su forma vectorial.

A partir de ello, es posible trabajar con las fuerzas para halla el momento

Error: Durante la multiplicación vectorial tuve una confusión respecto a los signos que influyó únicamente en el resultado final, mientras que el resto del proceso estuvo correcto

EC1-3

PRÁCTICA CALIFICADA 2

TEMAS

Centro de gravedad

Equilibrio: Sistema de fuerzas y vigas RESULTADO 19/20

DESCRIPCIÓN

Esta práctica contiene 4 ejercicios sobre los temas realizados en las semanas 4 6. Para poder resolverlo se utilizaron las herramientas aprendidas en clase respecto al centro de gravedad y equilibrio

REFLEXIÓN

En esta práctica utilicé los conocimientos adquiridos en el contenido del primer examen, como base para la resolución de los ejercicios, así como estrategias recogidas en clase sobre el equilibrio Comprendí la importancia de resolver correctamente el DCL para poder obtener resultados acertados Sin embargo, en esta oportunidad, los nervios me jugaron en contra provocando que ocasiones errores simples.

VALORACIÓN

Dificultad

Dedicación

Entendimiento

PRÁCTICA CALIFICADA 1

1) Determine la ubicación del centro de gravedad del área mostrada, tomando como referencia los ejes x e y indicados. Llene en la tabla los valores correspondiente.

Error: Al trasladar el resultado de la calculadora, omití un decimal

TEORÍA

1) Centroide: Punto que define el centro geométrico de un objeto

2) Hallar el centro de gravedad

Dividir la figura Hallar el área de cada figura Definir el centro de gravedad e indicar sus coordenadas en x, y Multiplicar las coordenadas por el área de cada figura y dividirlo entre el área Estas coordenadas representan el centro de gravedad de la figura completa

2) Hallar la fuerza F necesaria para mantener a la siguiente partícula en equilibrio

TEORÍA

1) Teorema de Varignon: Para res fuerzas concurrentes se aplica el T una fuerza respecto a un punto d componentes respecto al punto

2) Proceso: Se halla el vector unitario para transformar las fuerzas en sus formas vectoriales A partir de ello, se calcula la resultante igualando las ecuaciones a 0, determinar que la partícula se halla en equilibrio y encontrara las incognitas.

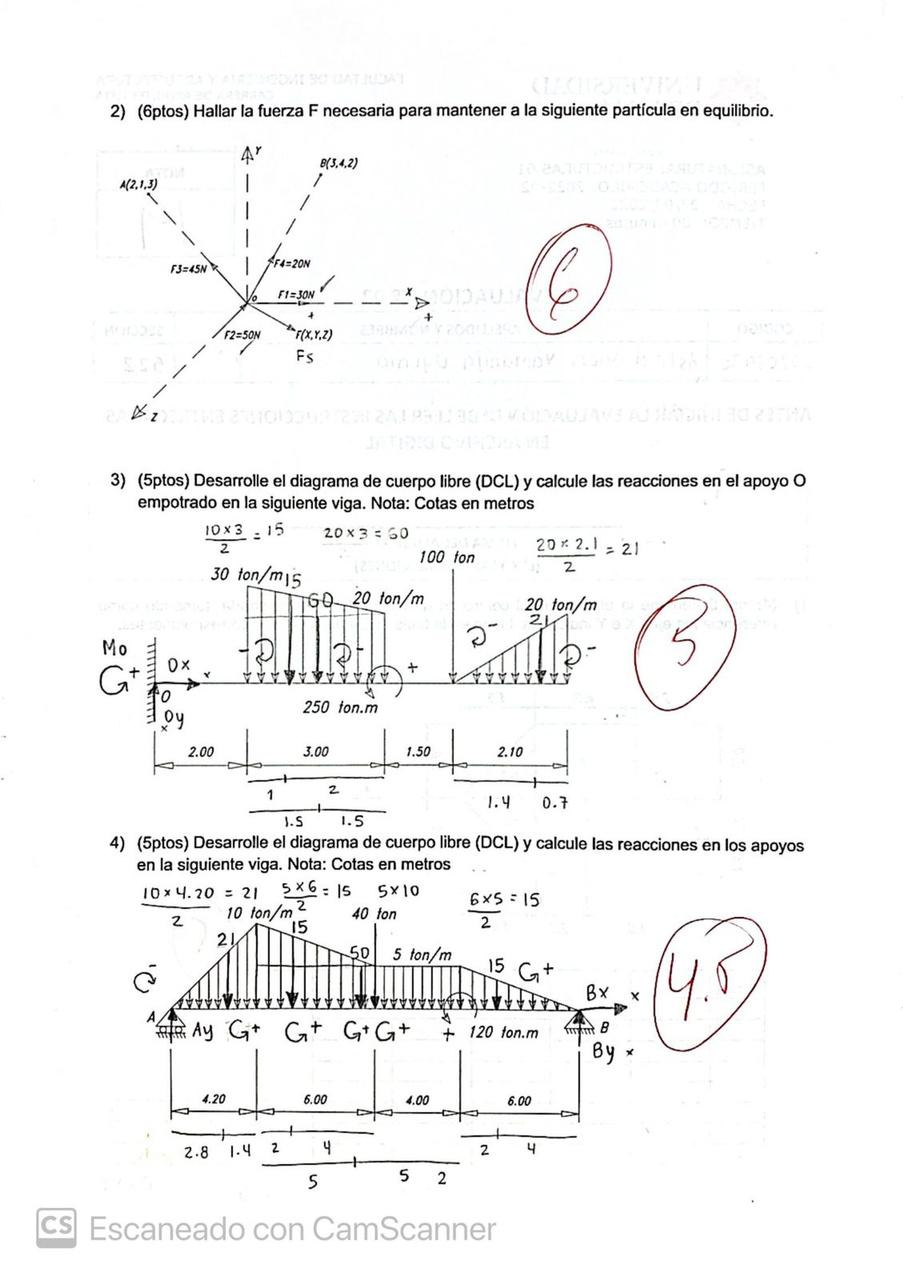
3) Desarrolle el diagrama de cuerpo libre y calcule las reacciones en el apoyo O empotrado en la siguiente viga. Cotas en metros

1) Equilibrio: Estado en que se encuentra una partícula en reposo, aceleración = 0

2) Sistemas de apoyo: Trabajamos con cuatro tipos de apoyo para una viga: simple, móvil, empotrado y cable, para los cuales aparecen una reacciones específicas

3) Proceso

Completar DCL con reacciones, transformando cargas distribuidas en puntuales equivalente y descomponiendo fuerzas diagonales Igualar las sumatorias en x, y e de momentos a 0

4.5/5

EC1-4

EJERCICIO 2

TEMA Equilibrio

RESULTADO

3/3

DESCRIPCIÓN

Se realizó un ejercicio sobre el equilibrio de una viga con apoyos móvil y simple, la cual cuenta con cargas distribuidas aplicadas sobre esta.

REFLEXIÓN

Este ejercicio me ayudó a repasar para la PC2, contando con cargas distribuidas no uniformes, las cuales me resultan más complejas de resolver Fui importante prestar mucha atención para no cometer errores a la hora de desarrollar el DCL, definiendo las reacciones y puntuales equivalentes, pero también las distancias en las que se ubican estas fuerzas. Tuve mayor dificultad desarrollando el equilibrio de momentos, pues en ocasiones olvidaba multiplicar la distancia con la fuerza.

VALORACIÓN

Dificultad

Dedicación

Entendimiento

EQUILIBRIO

Desarrolle el diagrama de cuerpo libre y calcule las reacciones en los apoyos en la siguiente viga. Cotas en metros

TEORÍA

) Equilibrio: Estado en que se encuentra una partícula en reposo, aceleración = 0

2) Sistemas de apoyo: Trabajamos con cuatro tipos de apoyo para una viga: simple, móvil, empotrado y cable, para los cuales aparecen una reacciones específicas

3) Proceso

Completar DCL con reacciones, transformando cargas distribuidas en puntuales equivalente y descomponiendo fuerzas diagonales Cuando se tienen cargas cargas distribuidas no uniformes, estas se deben descomponer en figuras para hallar la puntual equivalente Igualar las sumatorias en x, y e de momentos a 0

TEMA Marcos o Armazones

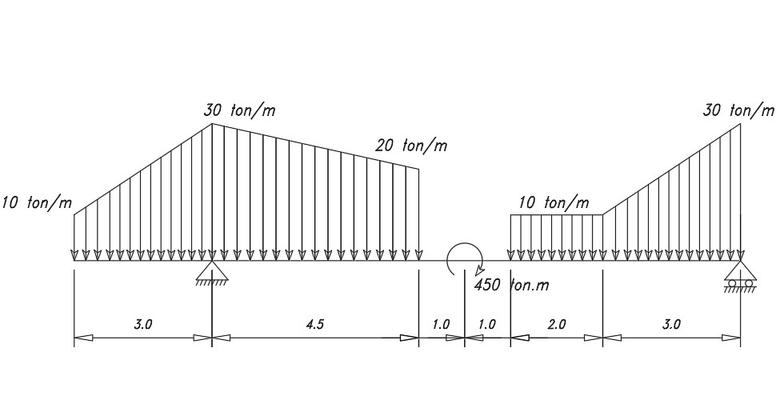
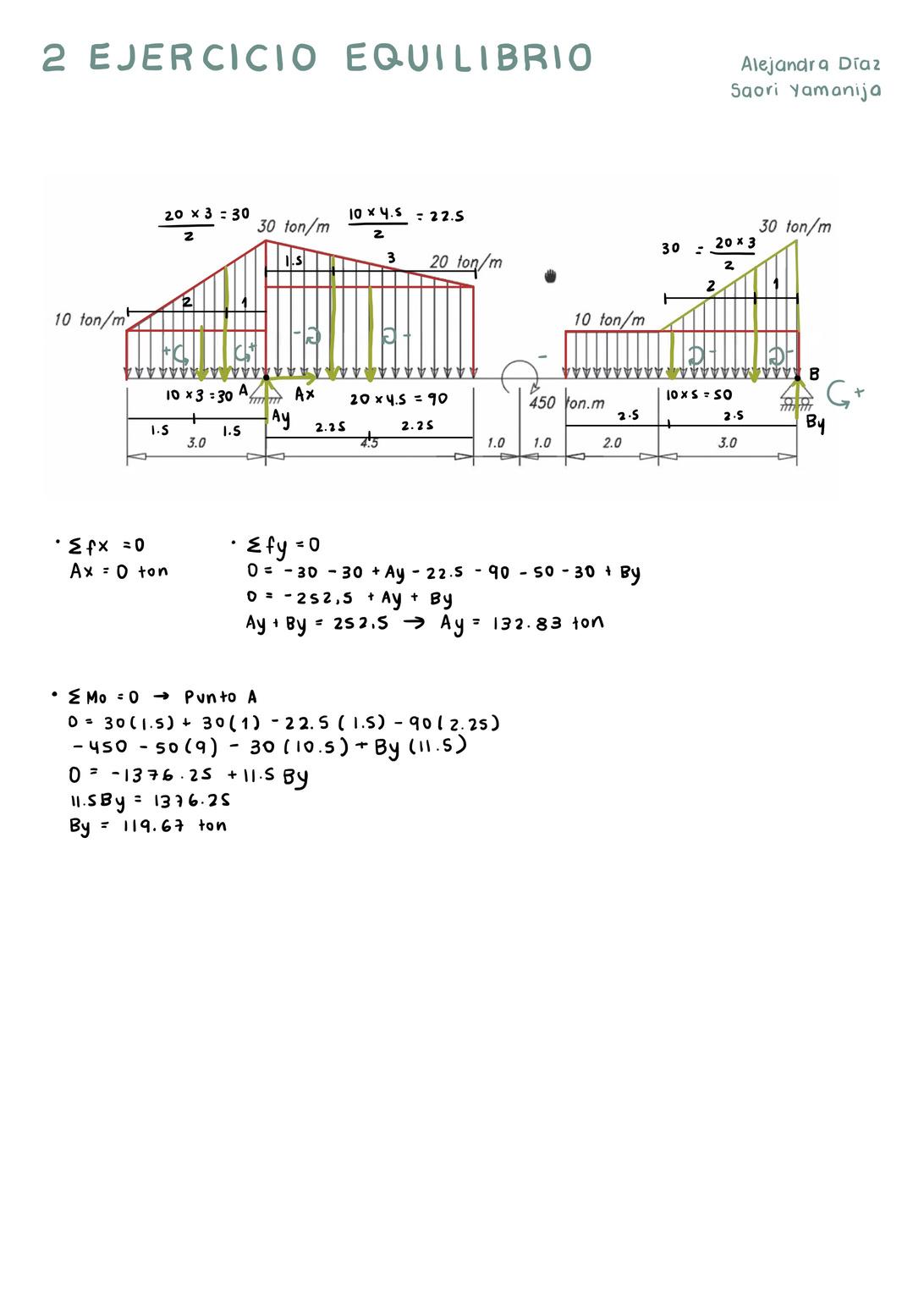
RESULTADO

3/3

DESCRIPCIÓN

Se realizaron dos ejercicios sobre marcos y armazones para ganar un punto extra en la PC2.

REFLEXIÓN

Estos ejercicios me sirvieron para practicar para la PC3, con problemas muy similares a los que podría enfrentar Este tema le agrega un grado mayor de dificultad al de equilibrio, así como mayor tiempo de solución. Asimismo, el tema de marcos o armazones me resulta muy interesante pues empezamos a tratar estructuras más complejas, compuestas por más de un elemento y que genera nuevas situaciones sobre la misma, que se deben considerar dentro del diseño arquitectónico.

VALORACIÓN

MARCOS

1) Determine las reacciones en los apoyos A y C y las fuerzas internas en el pasador ubicado en B

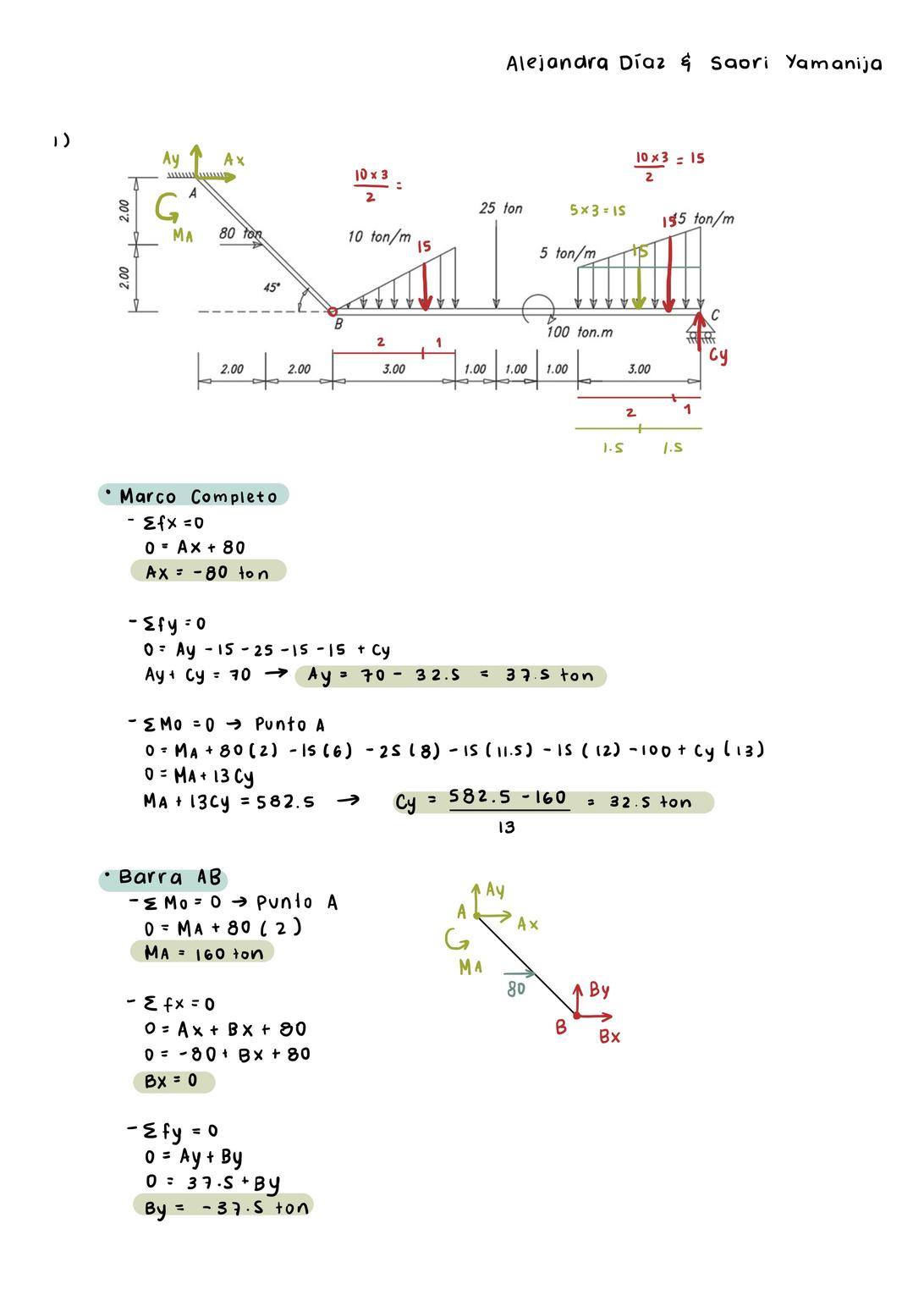
1) Determine las reacciones en los apoyos A y C y las fuerzas internas en el pasador ubicado en B

EC2-2

PRÁCTICA CALIFICADA 3

TEMAS

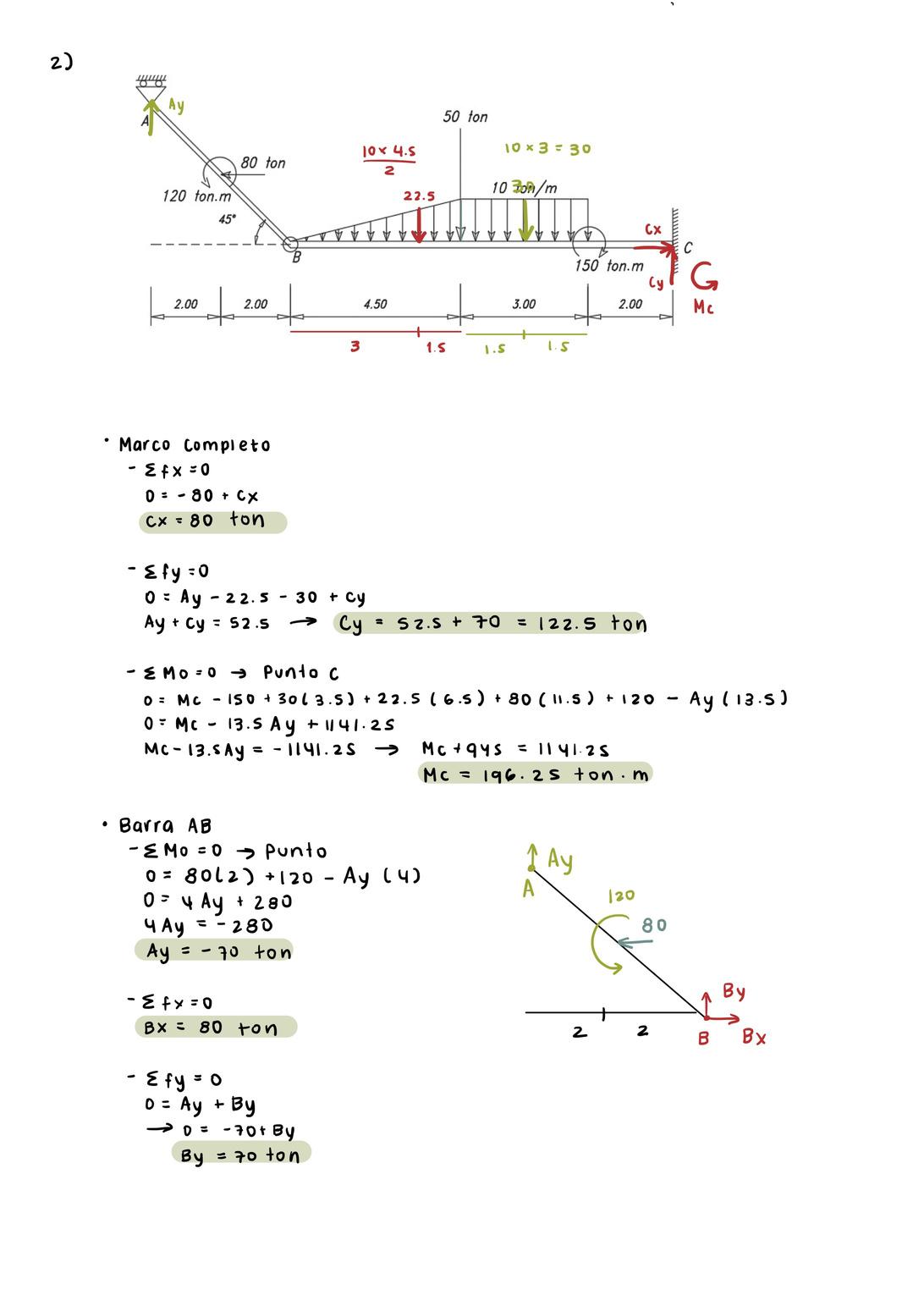
Marcos o Armazones

Fuerzas Internas

RESULTADO 20/20

DESCRIPCIÓN

Esta práctica contiene 3 ejercicios centrados en el tema de marcos o armazones y fuerzas internas.

REFLEXIÓN

En esta prueba, los procesos requerían de un dominio del tema de equilibrio, por lo que practiqué mucho para evitar cometer errores. Asimismo, en vista de que se debía de realizar el proceso de equilibrio dos veces para encontrar las incognitas, tuve que manejar mi tiempo eficientemente. Los temas trabajados me parecieron muy interesantes, pues empezamos a tratar barras dentro de sistemas y situaciones más complejas, como en la realidad

VALORACIÓN

Dificultad

Dedicación

Entendimiento

CALIFICADA 3

1) El marco mostrado está formado por dos barras conectadas por un pin en B y sujeta a las cargas que se indicas. Desarrolle el diagrama de cuerpo libre y calcule las reacciones en los apoyos A y C y en el pin en B

TEORÍA

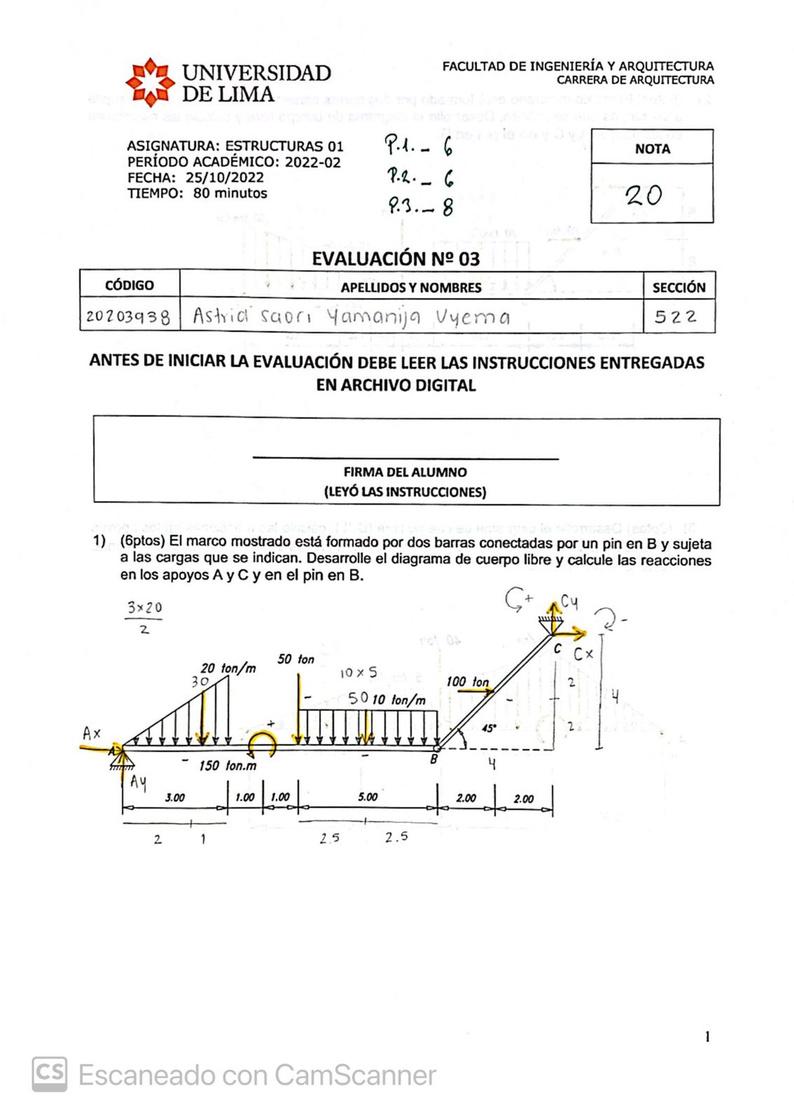
1) Marcos o Armazones: Estructuras compuestas por más de un miembro, conectados mediante pasadores

2) Proceso

Realizar DCL del marco completo Resolver el equilibrio del marco completo Separar las partes Realizar el DCL de cada parte, considerando las reacciones que aparecen sobre el pasador Resolver el equilibrio de cada parte

2) El marco mostrado está formado por dos barras conectadas por un pin en B y sujeta a las cargas que se indican. Desarrolle el diagrama de cuerpo libre y calcule las reacciones en los apoyos A y C y en el pin B

6/6

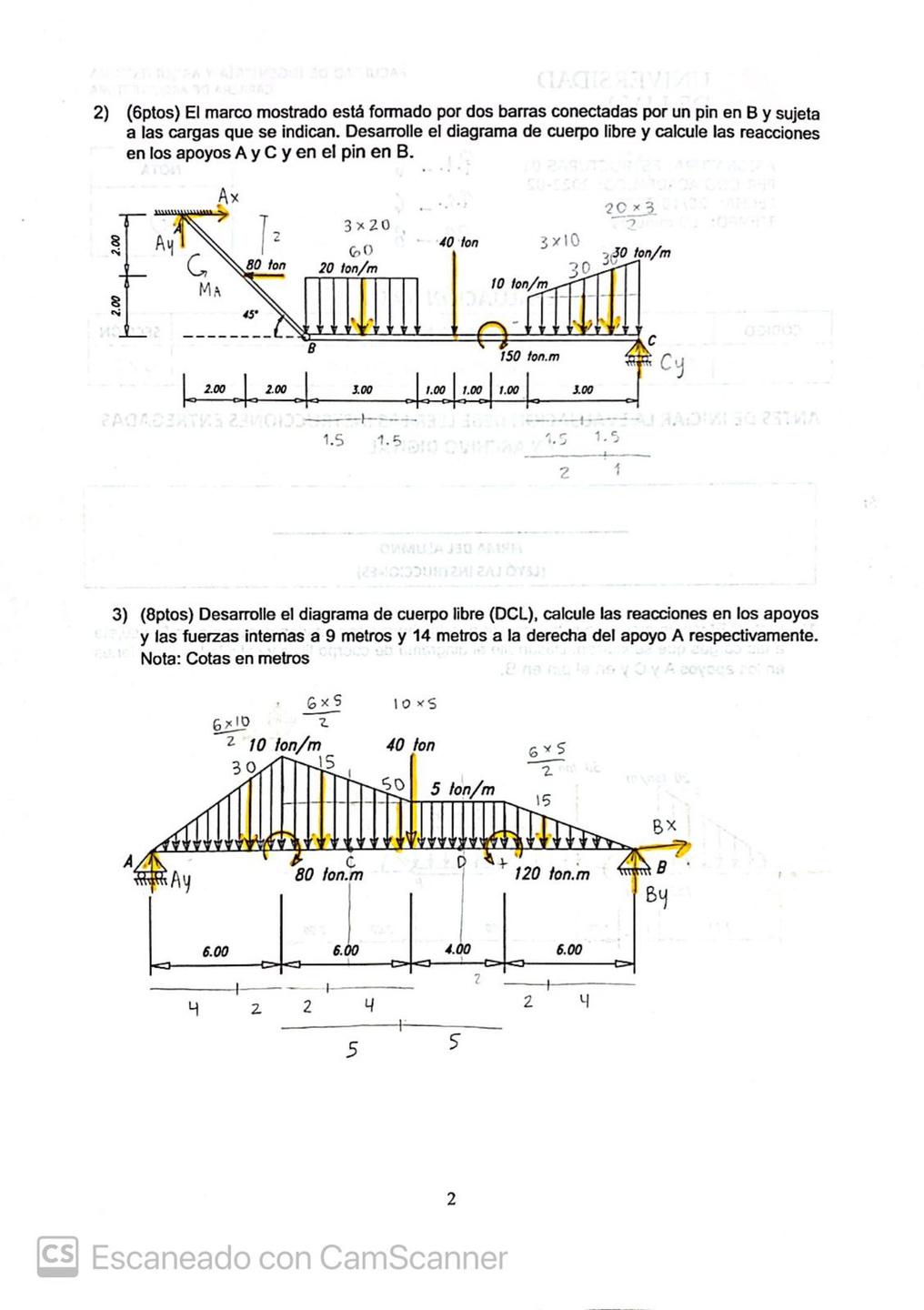
3) Desarrolle el diagrama de cuerpo libre (DCL), calcule las reacciones en los apoyos y las fuerzas internas a 9 metros y 14 metros a la derecha del apoyo A respectivamente. Cotas en metros

8/8

TEORÍA

V: Cortante

N: Axial M: Momento

EC2-3

EJERCICIO 4

TEMA

Diagrama de Fuerza Cortante y Momento Flector

DESCRIPCIÓN

Se realizaron los diagramas de fuerza cortante y momento flector de una viga con fuerzas puntuales aplicadas en su longitud. Se inició con el método de áreas para tener una idea general de los diagramas y luego se aplicó el proceso por ecuaciones para obtener un gráfico preciso

REFLEXIÓN

Este ejercicio me ayudó a practicarlos pasos requeridos para desarrollar ambos tipos de diagrama, debido a que, al ser un proceso largo y que incluye varios de los temas antes revisados, había posibilidad de confundirme en algún aspecto. Asimismo, pude reconocer las tendencias de la naturaleza de las líneas del diagrama según el tipo de carga aplicada y ecuación

VALORACIÓN

Dificultad

Dedicación

Entendimiento

DIAGRAMAS FC & MF

TEORÍA

1) Diagrama de Fuerza Cortante y Momento Flector: Permiten conocer el comportamiento de la fuerza cortante y el momento flector a lo largo de una viga

2) Sistema de Ecuaciones: Proceso

En el caso de una viga simplemente apoyada con varias cargas puntuales, resuelva por ecuaciones y áreas Desarrollar el equilibrio de la viga para definir reacciones en los apoyos Definir tramos Desarrollar el equilibrio de cada tramo, considerando que al cortar una viga se genera una fuerza cortante negativo (V) y un momento flector positivo (M) Desarrollar los diagramas sustituyendo los valores límite de cada tramo en las ecuaciones y uniendo los puntos generados

REFLEXIÓN

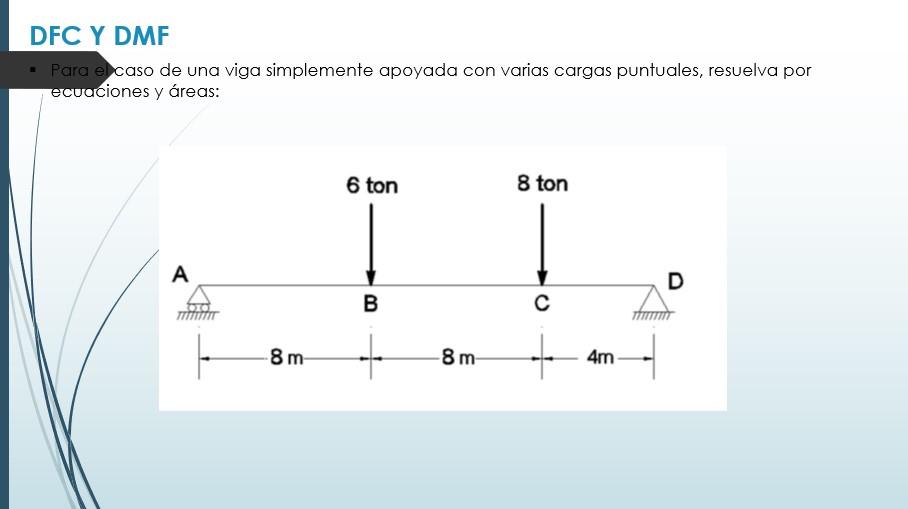
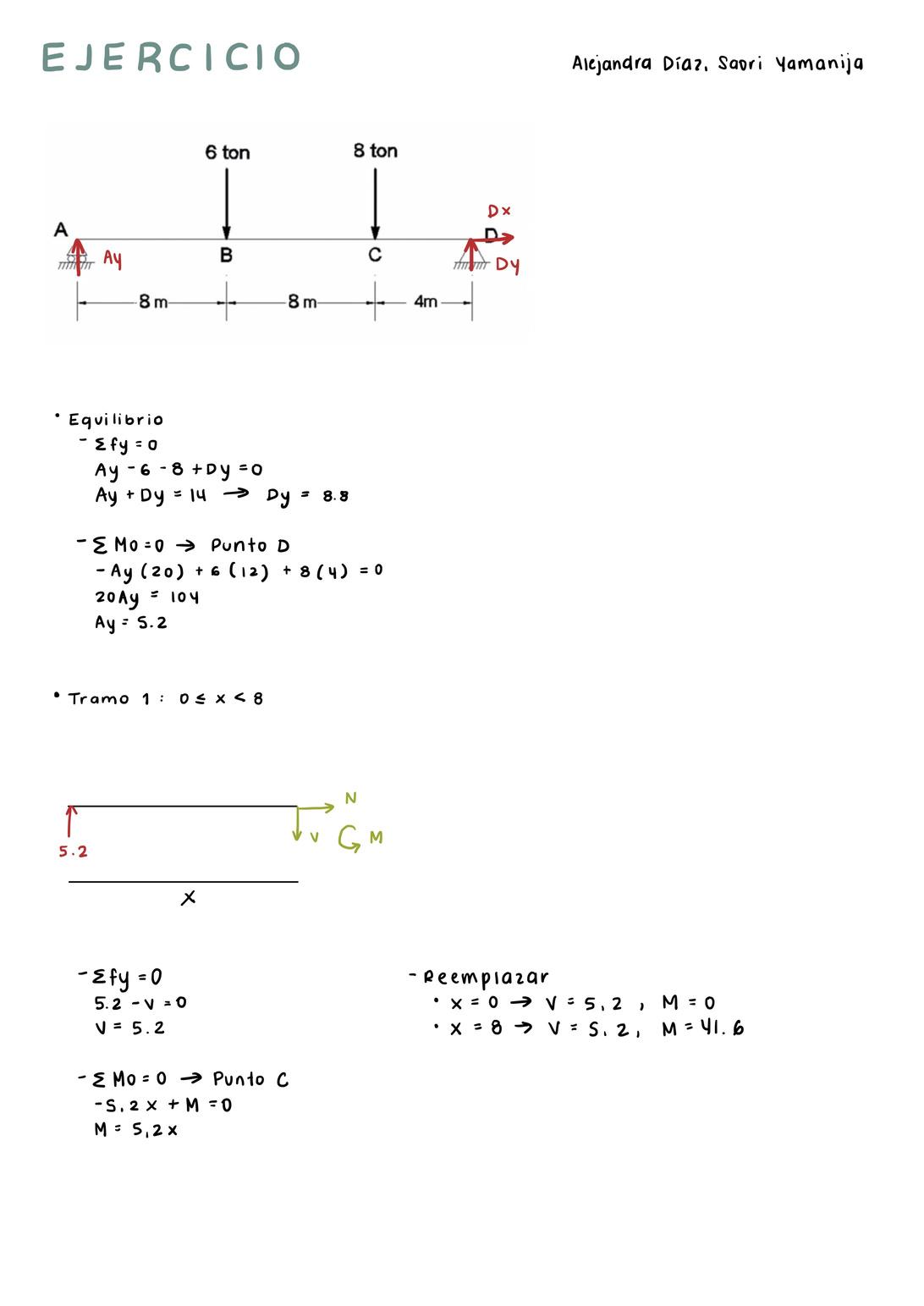
Culminando el curso de Estructuras I, considero que he sido capaz de dominar una serie de cálculos estructurales básicos, que me brindan una mirada más amplia y precisa sobre las bases estructurales de la arquitectura

Fue muy interesante desarrollar tantos temas que puedo asociar a elementos físicos, como el equilibrio en las vigas y estructuras más complejas. Asimismo, el curso me brindó herramientas para desarrollar un ojo crítico en el análisis arquitectónico, considerando la variable estructural, la cual poco a poco podré ir implementando con mayor certeza en el diseño proyectual

Finalmente, considero que los conocimientos adquiridos serán muy importantes para desarrollar los siguientes cursos de Estructuras, pero también, más adelante en la vida profesional, pues he logrado generar una base sólida en el tema estructural, que me acompañará el resto de la carrera.