7

АЛГЕБРА

Проєкт

НАТАЛІЯ

підручника

ЛАРИСА

АЛГЕБРА 7

Підручник

rnk.com.ua/106123

видавництва

Контрольна робота № 1 (діагностична), с . . 14

робота № 2, с . . 61

Самостійнаробота№1

Домашнєзавдання

Домашнєзавдання

§

Домашнєзавдання

§ 5. Одночлени . . Множення одночленів

Піднесення одночлена до степеня

Домашнєзавдання

Підсумовуємо вивчене в § 1–5

Контрольна робота № 2

§ 6. Многочлени . . Степінь многочлена

та віднімання многочленів

Самостійнаробота№4

Домашнєзавдання

§ 7. Множення одночлена на многочлен

Множення многочленів

Самостійнаробота№5

Домашнєзавдання

Проєкт майбутнього

робота № 3, с . . 92

робота № 4, с . .128

Теми навчальних

1, с . . 15

«MATH FOR LIFE »

с . . 22, 30, 38, 48, 57, 70, 78, 88, 100, 108, 116, 125

с . . 17, 30, 34, 51, 76, 84, 85, 86, 93, 96, 104

с . . 21, 35, 49, 56, 65, 68, 77, 87, 98, 107, 115, 119

с . 21, 26, 37, 44, 56, 68, 77, 84, 86, 99, 105, 116, 124

с . . 20, 38

с . 23, 29, 36, 50, 58, 71, 80, 90, 101, 110, 117, 126

TO BE SMART

с . . 23, 31, 39, 50, 59, 71, 80, 90, 101, 108, 117, 126

§ 9. Формули скороченого множення . .

Квадрат двочлена .

Домашнєзавдання

§ 10. Формули скороченого множення . .

Різниця квадратів

Самостійнаробота№7

Домашнєзавдання

§ 11. Формули скороченого множення . .

Сума та різниця кубів

Домашнєзавдання

§ 12. Розкладання многочленів на множники

із застосуванням декількох способів

Самостійнаробота№8

майбутнього підручника

140, 154, 164

141, 150

§ 17.

Домашнєзавдання

Рівняння з двома змінними та

Лінійне рівняння з двома змінними

та його графік .

Самостійнаробота№12

Домашнєзавдання .

Підсумовуємо вивчене в § 16–17

Контрольна робота № 5

§ 18. Системи двох лінійних

до розділу 3, с . . 171

«MATH FOR LIFE »

с . . 183, 195, 207, 217, 224,

с . . 17 3 , 174, 176, 189, 205, 214,

Домашнєзавдання

Самостійнаробота№14

Домашнєзавдання

с . . 174, 175, 180, 103, 224

с . . 181, 194, 195, 223, 237,

. 202

с . . 186, 198, 218,

TO BE SMART

с . 1 85, 1 98, 2 18, 2 26, 2 35, 249

Проєкт майбутнього підручника видавництва

потім множення і ділен­

ня зліва направо по порядку, а потім — додавання й відніман­

ня зліва направо по порядку.

Зведення

подібних доданків

Щоб звести подібні доданки, треба додати їх коефіцієнти

і знайдений результат помножити на спільну буквену частину.

підручника

Додавання й віднімання

звичайних дробів

y При додаванні (відніманні)

дро бів з одн аковими зна ­

менниками до чисельника першого дробу додають чисельник другого дробу (від чисельника першого дробу віднімають чисельник другого дробу) і залишають той самий знаменник.

y При додаванні (відніманні) дробів з різними знаменниками спочатку їх зводять до спільного знаменника, а потім застосовують правило додавання (віднімання) дробів з однаковими займеннниками)

y Щ об д одати ( відняти) д ва мiшаних числа, треба окремо додати (відняти) їх

1 Знайдіть значення виразу:

1) 95 54 + () ; 5) 12 47 ,,63 + () ; 2) 3070 3 + () ⋅ ; 6) 26 73 ,,36 + () ⋅ ; 3) 82 3210() : ; 7) 101 6868 47 () ,: ,, ; 4) 64 14 5 () : ; 8) 1001 3434 82 () ⋅ ,: ,, .

Проєкт

2 Обчисліть у найзручніший спосіб:

1) 4376 37 ⋅+ ; 5) 43 587435 86 ,, ; 2) 8412 41 ⋅+ ; 6) 51 974519 73 ,, ; 3) 93 52 93 42 ⋅− ⋅ ; 7) 14 23 14 23 518⋅+ ⋅ ; 4) 65 36 65 26 ⋅− ⋅ ; 8) 26 37 26 37 15 22 ⋅+ ⋅ .

3 Спростіть вираз: 1) 44xx ; 5) 47 yy ; 2) 1818mm ; 6) 58aa ; 3) 54bb + ; 7) 44 54 pp ; 4) 12 6 cc + ; 8) 27 67 nn .

4

майб

рівняння: 1) x −= 37 0 ; 5) 1412 6 xx−= ; 2) x += 55 0 ; 6) 1615 9 xx−= ; 3) 250 x = ; 7) 2320 1717 xx−+ = ; 4) 360 x = ; 8) 39341111 xx−+ = .

5 Обчисліть: 1) 2 3 1 3 + ; 4) 19 13 6 13 ; 7) 30

утнього

7 Виконайте множення:

1) 2 1 2 ⋅ ; 3) 16 16 4 5 ⋅ ; 5) 4 2 7 7 12 ⋅ ; 7) 0 19 4 15 ⋅ ; 2) 1 3 3 ⋅ ; 4) 5 6 18 18 ⋅ ; 6) 8 3 1875 ⋅ , ; 8) 12 17 0 25 ⋅ .

8 Виконайте ділення:

1) 3 8 3 8 : ; 3) 5 1 2 : ; 5) 1 5 6: ; 7) 9 14 :,45; 2) 5 7 5 7 : ; 4) 4 1 3 : ; 6) 1 7 2: ; 8) 1 2 13 5 13 : .

9 Обчисліть:

1) 40:,1; 4) 72 01 ,: , ; 7) 47 20 01 ,: , ; 2) 60:,1; 5) 0050 1 ,: , ; 8) 25 12 001 ,: , . 3) 53 01 ,: , ; 6) 0 006 01 ,: , ;

підручника

10 Визначте: 1) 4 % від числа 100; 5) 50 % від числа 140; 2) 3 % від числа 100; 6) 50 % від числа 250; 3) 10 % від числа 60; 7) 25 % від числа 80; 4) 10 % від числа 90; 8) 20 % від числа 65.

11

Знайдіть число, 1) 10 % якого дорівнюють 15; 2) 10 % якого дорівнюють 21; 3) 50 % якого дорівнюють 60; 4) 50 % якого дорівнюють 90; 5) 25 % якого дорівнюють 40; 6) 20 % якого дорівнюють 100; 7) 30 % якого дорівнюють 300; 8) 40 % якого дорівнюють 500.

12 Пам’ять роботизованого

Проєкт майбутнього

ною його дробу, треба цю величину спочатку поділити на

дану величину поділити на цей дріб

підручника

Знаходження дробу від числа

Щоб знайти дрiб вiд числа, треба число помножити на цей дрiб.

Проєкт

Властивості пропорції

Добуток крайніх членів пропорції дорівнює добутку її середніх членів: a b c d adbc =⇒ =

Модуль числа

y Якщо a 0 , то aa = y Якщо a < 0 , то aa =−

1) ab::25 = ; 3) 47::ab = ; 5) b a = 9 2 ; 7) b a 8 3 = ; 2) ab :: 31 = ; 4) 14 :: ab = ; 6) a b = 4 5 ; 8) 1 7 b a = .

Обчисліть:

майбутнього

22 Розв’яжіть рівняння:

1) −=327 x ; 4) −=540 x ; 7) −⋅ =− 5 17 10 17 x ;

2) 210 x =− ; 5) 9116 xx−= ; 8) =− 4 19

23 Розкрийте дужки:

x . 3) −=436 x ; 6) 131615 xx−= ;

1) 21⋅+() x ; 4) x () ⋅ 64 ; 7) −⋅ ()27 3 ab ; 2) 34⋅+() x ; 5) 73() ab ; 8) ()38 5 ba .

3) x () ⋅ 25 ; 6) 84⋅−() ba ;

24 Знайдіть

1) 41 a + , якщо a = 5 ; 5) a 10 4 , якщо a =−70 ; 2) 27 a , якщо a

підручника видавництва

Проєкт

майбутнього

1

2

підручника

3

5

Проєкт майбутнього

і

На скільки відсотків швидкість руху одного велосипеда більша за

Алгебраїчні

основ, неможливо розв’язати жодної практичної задачі. Опанувавши цей розділ, ви навчитеся:

y спілкуватися універсальною мовою алгебри; y скорочувати запис великих чисел, зокрема об’ємів інформації чи космічних відстаней y перетворювати складне завдання на декілька простіших і знаходити їхні розв’язки

4x + 2y Проєкт майбутнього підручника видавництва

y розв’язувати задачі в загальному вигляді

y правильно ставити завдання для комп’ютерного опрацювання

способом

y розвивати інтуїцію, використовувати нестандартні підходи для розв’язування завдань

(variable expressions)

(rational expression)

(value of expression)

Виконайте завдання

1. Запишіть за умовою задачі числовий вираз, використовуючи свій номер телефону.

2. Чому дорівнює значення отриманого числового виразу?

3. Перевірте, чи правильно записані в наведеному буквеному виразі всі дії, що ви виконували?

ab ⋅+ () ⋅+ ⋅− () 80 1250 2250 2:

4. Назвіть порядок виконання дій.

Проєкт

1. Введіть перші три цифри номера свого телефону

без коду оператора: *** **** a

2. Помножте це число на 80. a 80

5. Додайте двічі до отриманого добутку число, що складається з чотирьох останніх цифр вашого номера телефону: *** **** b

ab ⋅+ () ⋅+ 80 1250 2

6. Відніміть від отриманої суми 250.

7. Поділіть отриману різницю на 2.

ab ⋅+ () ⋅+ 80 1250 2250

ab ⋅+ () ⋅+ ⋅− 80 1250 2250

5. Які значення мають букви a і

3. Додайте до отриманого добутку 1. a ⋅+ 80 1

4. Помножте отриману суму на 250. a ⋅+ () ⋅ 80 1250

ab ⋅+ () ⋅+ ⋅− () 80 1250 2250 2:

ab ⋅+ () ⋅+ ⋅− () 80 1250 2250

8. Запишіть відповідь. *** **** ab Здивувались?

ГОЛОВНА ІДЕЯ

рази зі змінними.

В алгебраїчних виразах НЕ використовують знаки «=», «<», «>».

Невідомі числа, які можуть набувати різних значень, у ви-

разах зі змінними позначають буквами. Ці букви називають змінними. Вирази зі змінними можуть містити одну, дві, три й більше змінних.

Наприклад: 512m ; an ()3 ; 52 52 acb() + .

одназміннадвізміннітризмінні Числові вирази

1 Числові вирази — це записи, що утворюють із чисел за допомогою знаків арифметичних дій та дужок.

Наприклад: 58,,01 + ; 712 3 () ; 12 5 π+ .

Зверніть увагу! π≈ 31 4, — число.

2 Числовим виразом вважають також будьяке число.

Наприклад: 25; –17; 0,48; π — числові вирази.

3 Значення числового виразу — це число, яке отримують у результаті виконання всіх арифметичних дій

1 Вирази зі змінними — це записи, що складають із букв (змінних) і чисел за допомо-

Наприклад: 320ab + ; ab + ()2 .

2 Виразом зі змінною вважають також саму змінну.

Наприклад: x; y; a; d вирази зі

3

1) підставити замість змінних відповідні числові значення; 2) виконати всі арифметичні дії.

Значення а 10,10

Вираз: 32 a + 32 1 ⋅+ 32 01 ⋅+

151515 83 242424 0 ⋅− ==

1. 17 a ; 5b

2. 99 ⋅=bb ; mnpmnp =

3. 15 1151⋅+() =+() aa ; 21 21 + () () =+() ()abab

1.

2.

3.

ЧИ ВІДОМО ВАМ?

Французький філософ і математик Рене Декарт (1596–1650) запропонував позначати в записах відомі числа (коефіцієнти, параметри) першими буквами алфавіту: a , b , c ,

а невідомі (змінні) останні­

ми буквами алфавіту x, y, z.

підручника видавництва

Це виявилось не дуже зруч­

ним, оскільки знак множення

зі змінною x: xy × .

тому в алгебрі знак

заміняють точкою або, у деяких випадках, зовсім не записують. У всьому винен Декарт

Проєкт майбутнього

ПРИКЛАД 1

Знайдіть значення числового виразу 11 01 327101 8 2 +⋅() ,: :, .

Розв’язання

11 01 327101 8 2 +⋅ −= ( ) ,: :, Виконаємо дії в дужках.

=+ () = 11 01 27 10 18 32 ,: :, Знайдемо значення степеня.

=+ () = 11 18 01,:92710 :, Виконаємо множення й ділення зліва направо.

=+ () = 11 18 09,,27 :, Знайдемо різницю в дужках.

=+ = () 11 1818 ,: , Виконаємо ділення.

== +−() 11 1 Знайдемо суму.

= 10 ....................................... Отримали значення виразу.

Відповідь: 10.

ТРЕНУЄМОСЯ 1

Знайдіть значення числового виразу: 1) 34 20 7 () : ; 5) 111 3154 245 : −⋅ () ⋅+ ; 2) 18 66 + () : ; 6) 1244 13 25 28 : () ; 3) 45 90 59 + ():: ; 7) 10 02 56 04 17 39 2 ⋅+ ( ) ,, :, :, ; 4) 31 80 45() ⋅

РОЗМИНКА 2 Прочитайте вираз різними способами: 1) cd ; 2) 10a ; 3) 2ad ; 4) bc : .

ПРИКЛАД 2

Прочитайте

ви

будете вивчати програму

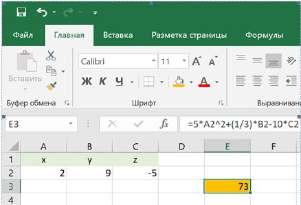
Microsoft E xcel , з а д опомогою якої з легкістю зможете

обчислювати значення виразів зі змінними за різних значень змінних.

Наприклад, о бчислити з на ­

чення виразу 510 2 1 3 xyz +− ,

якщо x = 2, y = 9 , z =−5 .

Для цього треба:

1) ввести в комірки A2, B2, C2

значення x, y і z відповідно;

2) ввести в комірку Е3 формулу для обчислення значення

підручника

виразу:

y виділити комірку Е3, натис­

нути =;

y ввести 5*, клацнути на ко ­

мірку A2 (значення змін ­

ної x), ввести ^2 (піднесення

до степеня 2),

y натиснути +(1/3)*, клацну­

ти на комірку B2 (значення

змінної y);

y ввести – 10*, к лацнути н а

комірку C2 (значення змін­

ної z).

У комірці Е3 маємо формулу =5*A2^2+(1/3)*B2–10*C2.

Відповідь: 73.

Проєкт майбутнього

5) добуток суми й різниці чисел a і b; 6) частка суми й різниці чисел a і b. РОЗМИНКА 3

1) 3 + a , якщо a = 7; 4) c :4 , якщо c = 24 ; 2) a 6 , якщо a = 4 ; 5) xy , якщо x = 20 , y = 15; 3) 2b, якщо b =−5; 6) mn + , якщо m =−12, n = 8 .

видавництва

ПРИКЛАД 3

Знайдіть значення алгебраїчного виразу,

3 , y =−10: 1) 62 x () ; 2) 62xy .

Розв’язання

Підставляємо числові

відповідь. 1) Якщо x =−3 , то 62 x () = 62 3 () ==⋅ () =− 65 30 ; 2) якщо x =−3 , y =−10 , то 62xy = 62 3 10 () () = =− += 18 20 2 .

Відповідь: 1) –30; 2) 2.

ТРЕНУЄМОСЯ 3

виразу: 1) 21 x , якщо x = 5 ; 3) 10 4 x (), якщо x =−1; 2) 34 x + , якщо x = 2 ; 4) 61() x , якщо x =−3 ; 5) 10 6

1.1

1) 10 24 04 02 ,: ,, ; 3) 10 24 04 02 (),: ,, ; 2) 10 24 04 02 () () ,: ,, ; 4) 10 24 04 02 () ,: ,, .

1.2

1) 52 x + ; 3) 6 ()xy : ; 5) xy + () 2 ; 2) xy + 2 ; 4) 52 x + () ; 6) 6 xy : .

1.3

1) сума добутку чисел 8,2 і –10 та числа 42; 2) добуток різниці чисел 3,6 і 10,4 та числа

4) добуток суми чисел 5,3 і 4,7 на їх

1.4 З’ясуйте, чи має

Проєкт майб

на якій відстані

MATH FOR LIFE

Для заварювання чорного

чаю середньої міцності за ­

звичай використовують таке

правило:

у розігрітий чайник насипають

чай із розрахунку стільки чай­

них ложок чаю, скільки чашок

води міститься в чайнику; до­

датково насипають ще одну

чайну ложку чаю на весь

чайник. Щоб

за 1 год

Дорослий10020

Дитина5010

майбутнього підручника

Проєкт

видавництва

1.10

1) Складіть вираз, за яким можна

2)

1.13

1.14

4)

1.15

1) 45 x , якщо x = 3 ;

2) 72() x , якщо x =−4 ;

3) 95xy , якщо x = 6 , y =−7;

4) 01,,05yx , якщо x =−8 , y

1.16

1.17

1.18

# BE SMART

1

2

3

підручника

змінних, що входять до неї.

Прикладами тотожностей є рівності, що виражають властивості (закони) дій над числами: переставні та сполучні властивості додавання та множення, розподільна властивість.

РОЗМИНКА 1

1 Установіть відповідність між формулами (1–5), якими записані властивості арифметичних дій, і тотожностями (А–Д).

1 aa bb +=+ А 47 24 74 2 xyxy + () =⋅ +⋅

2 aa bb⋅= ⋅ Б xyyx +=+ 33

3 aabbcc + () += ++()

(identical expressions) рівні

(equivalent expressions) тотожність (identity)

доведення тотожностей (proof of identity)

aa += 0 , aa+−() = 0 , a ⋅=00 , aa ⋅= 1

ПЕРЕРВА НА ЛОГІКУ

Існує відомий алгебраїчний со­

фізм «Усі числа дорівнюють

одне одному».

Доведемо, що 56 = .

Запишемо тотожність: 3510 4542 1254 +− =+ .

Винесемо за дужки спільні

множники:

5 72 97 29 6 +− () =+().

Поділимо обидві частини тотожності на спільний множник:

5 72 9 72 9 72 9 72 9 6 +− +− +− +− ( ) ( ) = ( ) ( )

Отже, 5 6 = .

Знайдіть помилку в діях.

Проєкт майбутнього підручника видавництва

ПРИГАДАЙТЕ!

Доданки, що мають однакову буквену частину, називають подібними доданками. У виразі aabb−+211 7 : 17211 aabb++ + () ()

Коефіцієнти

Подібні доданки

1) 10 3 ab + і 310ba + ; 4) 23 0 cd + () і 23cd + ; 2) 53cd і −+35dc ; 5) 27 n () і 27 n ; 3) 32xy і 23yx ; 6) 520 b + () і 5 100 b +

1) 87 15 +− ; 8) 39 12 aaa +− ; 2) 91111 −+ ; 9) 14 67 14 aaaa −+ ; 3) xx + 3 ; 10) 17 99 18 aaaa −+ ; 4) 52xx + ; 11) abaab +− +− 35 13 3 ; 5) 64yy ; 12) 6114 17 ababa −+ ; 6) 79yy ; 13) ++ 16 75 52012 abaab ; 7) 56 11 aaa +− ; 14) +− −+ 815123 414 ababb . aa =⋅ 1

(переставна і сполучна властивості); =+ = () −+ () 17 211 ab додати їхні коефіцієнти (розподільна властивість); =+ 6 9 ab ....................... результат помножити на спільну буквену частину. РОЗМИНКА 2

1) xyx ++23 ; 2) 22 2 abab ++ ; 3) 51 5 + cc .

Пригадайте вивчене раніше: при розкритті

користуємось такими правилами.

Якщо перед дужками стоїть знак «+», то, розкриваючи дужки, ЗНАК кожного доданка НЕ ЗМІНЮЄМО.

Наприклад:

32 45 32 45 abcdabcd +− + () =+ +− + () = =+ −+ 32 45 abcd

Знаки не змінюються

РОЗМИНКА 3

Якщо перед дужками стоїть знак «–» , то, розкриваючи дужки, ЗНАК кожного доданка ЗМІНЮЄМО НА ПРОТИЛЕЖНИЙ.

Наприклад: 32 45 32 45 abcdabcd + () =− +− + () = =− +− 32 45 abcd

Знаки змінюються на протилежні: «+» на «–», «–» на «+»

1 Розкрийте дужки у виразі: 1) xy+−(); 3) −+ ()ab ; 5) xyz +−() (); 2) xy(); 4) ()ab ; 6) () +−()abc .

2 Розкрийте дужки у виразі:

1) 21 a + () ; 3) −+() 31 b ; 5) + () 6 ab ; 2) 53() x ; 4) ()42 y ; 6) () 10 mn .

ПРИКЛАД 1

Розкрийте дужки і зведіть подібні доданки у виразі 82 10 4204 aa + () () , .

Розв’язання:

8 21 20 4 04 aa + () () = , ................... Розкриємо дужки.

=⋅ +⋅ −⋅−⋅ () = 8821 20 4 0404 aa ,, Виконаємо множення. =+ −+ = 16 16 88 aa , Зведемо

= 17 a ........................................... Записуємо відповідь.

Відповідь: 17 a .

підручника видавництва

ТРЕНУЄМОСЯ 1

Розкрийте дужки і

1) 34 3 () + aa ; 5) 75 40 55610 aa() ++() , ; 2) 45 4 aa + () ; 6) 53 60 2 15010 aa() +−() , ; 3) 92 13 6 bb + () ; 7) 84 114 3 7 56 3 pp()

4) 12 31 49 bb() ; 8) 46 118

+−() =− () =+ bb bb

aaa bcbc + () + = 45 44 54 20 xxx ()++=⋅ =+ aaa bcbc() =

44 54 20 xxx() =⋅ =−

Ліва частина тотожності

Права частина тотожності

AB → або BA →

ACB →←

AB−= 0

ЗВЕРНІТЬ УВАГУ!

підручника

Для доведення тотожностей слід вибирати найбільш раціональний спосіб.

22 314bcb + () −+ = ...................

+ 23 4 14 bb c

чи є

рівність: 1) xxx +=34 ; 3) 14 86 aaa −= ; 5) 98 bbb () = ; 2) 85 3 xxx =+ ; 4) 57 2 aaa −= ; 6) () =− 87 bbb .

ПРИКЛАД 2 Доведіть тотожність:

1) 10 713152 3 aabbba −+() += + ;

2) 22 3143 27 2 bcbcbcb + () −+ =− () +− + () .

Розв’язання: 1) Тотожне перетворення лівої частини тотожності у

10 15 713 ab ab −+ = + () =+ = 10 15 713 ab ab .............. Розкрили дужки. == −+ + 10 73 1315 2 aaabbb Звели подібні доданки. 32 23 abba +=+ Тотожність доведено.

2)

+ 23 4 14 bbc .........................................

Проєкт майбутнього

ПРИГАДАЙТЕ!

abcabc −+() =−

abcabc () =− + abcabc () =+ +

1) 51 27 1 bbb −+ =− ; 4) 18 4131314 aaa () =+ ; 2) 42 8122bbb −+ =− ; 5) 23 37 82015 aabbab −+() −= ; 3) 15 5111110 aaa () =+ ; 6) 31 9113020 aabbab −+() −= ; 7) () ++ =+() 53 417162 20 4 mmm ; 8) 42 124183 64 432cccc + () =−() .

ПРАКТИКУМ

2.1 Запишіть вираз, тотожно рівний заданому:

1) 25 1715 7 abab +− ; 4) 351211 mkmk +− ;

2) 24 16 41 abab −+ + ; 5) 2924 8125 621 abba ++ + , ;

3) bcbc +− + 42 221 ; 6) 15 2199 14 8601 ,,xyxy +− +− + .

2.2 Розкрийте дужки і спростіть вираз:

1) abab + () +−() ; 3) xyxy() −+(); 5) abca + (); 2) abab + () () ; 4) xyyx + () (); 6) abca +− () .

2.3 Спростіть вираз і знайдіть його значення:

1) 62 25 15 aa−+() + , якщо a = 40 ;

2) 89 449bb −+() + , якщо b = 20;

3) 07 30 64 2 ,,xx() −+(), якщо x =−30 ;

4) 01 43 0054 8 ,, () −+()xx , якщо x =−5 .

2.4 З’ясуйте, чи є тотожними вирази:

1) 52xxy −+() і 32xy ; 3) 03 10 , () ab і 30 03 ab , ;

2) 412xyy() + і 84yx ; 4) () 02 12 , ab і 24,,02ba ; 5) + () () 301615 2 cdcd і d ; 6) 23 66 2 abab() () і 12a .

2.5 Доведіть

1) 46 1814 2143 14 aabaab +−() −= ;

2) 53 27 34 2148 19 babaab −+() −= −+ ; 3) 23 2116 xxyxyx =− + () ++ () ; 4) yxxyyxy =− () ++ () 22 33 2 .

2.6 Доведіть, що

a і b: 1) 10 48 55 11 413 aababa +−() () + ; 2) −+ () () −+ 35 12 2105 72aababa .

2.7

1) 2ababab −= .

22 22 2 ababababaabbab() () =− −+

MATH FOR LIFE

2.10 Зведіть подібні доданки:

1) aaa +−78 ; 3) abaab +− +− 716187 ; 2) 15 56 15 aaaa −+ ; 4) 20 28 14 917 ababab +− .

2.11 Розкрийте

2.12 Доведіть тотожність:

.

1) 53 15 () + aa ; 3) 64 50 47510 aa() ++() , ; 2) 10 21 45 bb + () −⋅ ; 4) 85 112 7 6 48 7 bb()

1) 43 59 3 bbb −+ =− ; 3) 27 78 12 2020 aabbab −+() −= ; 2) 16 815158 aaa () =+ ; 4) 30 61119368 aabbab () () += + .

2.13 З’ясуйте, чи є наведений вираз

abc +− .

підручника

1) acb −+ ; 3) −+ + cba ; 5) acb(); 2) cab ; 4) bca ; 6) bac().

2.14

1) 4 7 3 5 28 75 ,,14 abba + () 

, якщо a =−10 , b = 120;

2) () +−() 70 45 18 9 4 9 ,,baba , якщо

2) Знайдіть значення цих виразів, якщо a = 245 м, b = 190 м.

2.16 За умовою завдання 9 на с. 30 (див. Math for life):

1) Складіть вираз для обчислення витрат (у г. о.) для підготовки до навчання: однієї школи, яка налічує m кабінетів; n таких шкіл.

2)

# BE SMART

1) 1 секунду; 4) 4 секунди; 2) 2 секунди; 5) 5 секунд; 3) 3 секунди; 6)

ГОЛОВНА ІДЕЯ

Означення. Степенем числа a з натуральним показником n, більшим за 1, називають добуток n множників, кожний із яких дорівнює a. aaaa n n =⋅ ... множників , n ∈ N, n > 1

Степенем числа a з показником, що дорівнює 1, називають саме ’ число а. aa 1 =

Обчислення значення степеня числа — це

підручника

Основа степеня — множник, що повторюється

Проєкт

Показник степеня — число, що показує кількість множників

дія, яку називають піднесенням до степеня. 3 33333 243 5

5 = = множників

Степінь числа

Значення степеня

Основа степеня

Показник степеня Алгебраїчний

Степінь числа a

підручника

РОЗМИНКА 2

1 Обчисліть:

1) 02; 2) 13; 3) () 1 2 ; 4) () 1 3 ; 5) 11 4 4+−() ; 6) 11 5 5+−() .

2 Не виконуючи обчислень, порівняйте

1) 17 ; 2) () 1 6; 3) () 6 8 ; 4) () 4 5 ; 5) 712 ; 6) () 8 7 . ПРИКЛАД 1 Обчисліть значення виразу:

1) 03 10 32 , ; 3) 12 3 4

2) 03 100 4 , ⋅ () ; 4) () () 51032

Проєкт

2) 03 100 4 , () === 30 4 810 000

3)

4) () () = 51032 == 125100 –225

5)

майбутнього

1.

2. Піднесення до степеня.

3. Множення й ділення (зліва направо).

4. Додавання й віднімання (зліва направо).

ПРИКЛАД 2

Знайдіть значення виразу 53 2 3 xx() , якщо x =−2 .

53 2 3 xx() = ..........

= () () = 532223

Підставимо значення x =−2 .

Виконаємо дію в дужках. =−() () = 52 5 23

Обчислимо: () = 24 2 ; () =− 5125 3 . =⋅ () = 5 4125 .........

Проєкт

Виконаємо множення, розкриємо дужки. == + 20 125 145

Відповідь: 145.

ТРЕНУЄМОСЯ 2

Отримали значення виразу.

Знайдіть значення виразу: 1) x 2 12 + , якщо x = 6; 5) xx 2 3 3 ++() , якщо x =−7 ; 2) x 2 11 + , якщо x = 7 ; 6) xx + () + 5 3 2 , якщо x =−8 ; 3) 28 2 2 x , якщо x = 3; 7) 29 13 23() ()xx ,

3.1 Знайдіть значення виразу:

1) 23 4 33 3 +− ; 3) 25 10 8 2 3 + () ; 5) 25 24 1012 3 52 ,, () ⋅+ ; 2) 56 7 22 2 +− ; 4) 111519 2 3() ; 6)

3.2 Запишіть добуток у вигляді степеня:

1) 10101010 ; 3) () () ()101010

2) 01010101 ,,,, ⋅⋅⋅ ; 4) () ⋅−() ⋅⋅ ()010101 7 ,,

3.3 Запишіть у вигляді степеня з основою 10:

1) кількість сантиметрів в 1 м; 2) кількість метрів в 1 км;

3) кількість квадратних метрів в 1 квадратному кілометрі.

3.4 Подайте задані числа у вигляді степеня із зазначеною

основою:

1) 2; 4; 8; 16; 32; 64 з основою 2;

2) –5; 25; –125; 625; –3125 з основою –5; 3) –10; 100; –1000; 10 000; –100 000 з основою –10; 4) 0,1; 0,01; 0,001, 0,0001; 0,000 01 з основою 0,1;

5) 1 4 ; 1 16 ; 1 64 ; 1 256 з основою 1 4 ; 6) 1 9 ; 1 27 ; 1 81 ; 1 243 з основою 1 3 .

3.5 Обчисліть: 1) 1076 + ; 2) 11 4 9+−() ; 3) 10 1 1310 14 −+ () ; 4) 10 1 811 17 −+ () .

3.6 Знайдіть значення виразу: 1) 12 2 x , якщо x =−0;11 ; 3) 25 4 c , якщо c =−21 ; ; 2) 24 3 y () , якщо y =− 1 12 3 8 ; ; 4) c + () 5 4 , якщо c =−55 ; ; 5) ab23 , якщо

підручника

Обчислимо

Отримаємо: 7 2401 4

Перевіримо себе за допомогою калькулятора: xy 7 4 = 7 4 = 7 4 =7 2401 4 =

Вво­

димо

число

Натискаємо

кнопку

степеня

Вводимо показник степеня

Спробуйте самостійно ро ­

зібратися, як знайти степінь числа 10.

MATH FOR LIFE

3.8

3.9

Проєкт

3.10

майбутнього

3.15

Проєкт

# BE SMART

3.18

3.20

3.21

підручника

Розробки однієї з перших у Європі електронно ­ обчис ­

лювальних машин Малої електронно ­ обчислювальної

машини (МЕОМ) проводились із 1948 року в Київському Інституті електротехніки під керівництвом академіка Сергія

Олексійовича Лебедєва.

Розв’язання перших матема­

тичних з адач з а д опомогою МЕОМ, зокрема піднесення

до степеня, відбулося 4 січня 1951 року.

Проєкт майб

утнього

степенів

Пояснення:aaaaaaaa 2 2 4 4 6 =⋅ ⋅ ⋅⋅⋅

== + aa 2 4 6

Доведення:aaaaaamaaaaa mm n nn =⋅ = + ......

1 Подайте у вигляді степеня

1) 5525 ; 3) () () 3344 ; 5) aa 29 ; 7) cc 6 ; 2) 02029 ,, ; 4) 77 7 42 ; 6) bb55 ; 8) ddd 15 2 .

2 Подайте вираз a 10 у

1) a 3 ; 2) a 8 ; 3) a 5 ; 4) a 9 ; 5) a 1 .

3

1) 2243 ; 2) 3332 ; 3)

Риска дробу знак ділення 3 7 37 = :

підручника

Наприклад:

bbbb 9966 3 : == cccccc 10101011 9 ::== = ddddd 11 11 1010 1 : == =

777777 55 2 : ==

9999 99 88 8 11 7 ::== = 1010101010 6655 1 : == = ЗВЕРНІТЬ

a a m m n an = , mn > , a ≠ 0

aaaa mmnnkk :: =

підручника

1) b 2 ; 2) b 3 ; 3) b 4 ; 4) b 6 ; 5) b 8 ; 6) b12 .

ПРИКЛАД 1

Запишіть у

1) 246 , якщо a = 2 ; 2) 734323 , якщо a = 7 .

Розв’язання: 1) 2 46 ⋅==⋅ () = 2 22 6 =⋅ = 22 1 2 6 == + 22113 12 ; 2) 7 343

1) 213 ; 2) 711 . ТРЕНУЄМОСЯ 1

Запишіть у

Проєкт майбутнього

16 25 ⋅ , якщо a = 2 ; 7) 6216 3 2 4 ()

a = 6 ; 4) 749 4 , якщо

підручника

1) піднесення степеня

степеня: aamm n n () = ;

2) множення степенів: aaa mmnn = + ;

3) ділення степенів: aaammnn : = ;

4) ділення степенів: a a m m n an = .

Проєкт майбутнього

() () ()

будь-яких чисел a і b та довільного натурального

aabbnnn() =⋅

Пояснення

Проєкт майб

4.1

1) 22 2 512 ⋅= ; 3) 55 513 ⋅= ; 5) 77 20 6 14 : = ; 2) 12 99618⋅= ; 4) 33 3 16 11 : = ; 6) 44 4 9 : = .

4.2 Запишіть у

1) a 4 ; 2) b 6 ; 3) c 8 ; 4) 410 ; 5) 712 ; 6) 1030 .

4.3

:

33

4.4

1) () () 1167

4.5

1) () () 7763 і () 7 8 ; 3) () 1 4 і () () 2234 ; 2) () () 5537 і () 5 11 ; 4) () 1 5 і ()

Проєкт майбутнього підручника

m > n; aamm n n () = , aamm n n = () aabbnnn() =⋅ , aabb nnn ⋅= () aa bb nn

ab

4.16

4.17

1

Завдання 4.18, → Розминки 1–3 4.19

Завдання 4.20 → Практикум, 4.5

Завдання 4.21 → Приклад 1

Завдання 4.22 → Приклад 2

Завдання 4.23 → Приклад 3

Завдання 4.24 → Приклад 4

Завдання 4.25 → Актуальна задача

ПРАКТИЧНЕ

майбутнього підручника видавництва

# BE SMART

Учені з’ясували, що: y головний мозок людини містить близько 91010

Проєкт

1.

2. Запишіть вираз

3.

формулу площі круга Sr =π 2 , запишіть вираз для обчислення

( πx 2 ; 12 2 πx .)

Проєкт майб

4. Яка площа частини аркуша, що не використовується? 48 12 22 xx

2 5 4 ab , xy 23 2 5 4

7 a ; 1 3 3 mn , оскільки містять у своєму записі лише один числовий множник ,

відмінний від нуля, записаний на першому місці, і степені з різними основами.

НЕ Є одночленами стандартного вигляду

12 3 2 bc — містить два числові множники;

xxx ⋅⋅ ()23 25 — числовий

множник не стоїть на першому місці, інші множники — степені з однією основою.

15 23 xyzabab33 1 =⋅

коефіцієнти

−=mnkmnk 45 45 1 100

Проєкт

і піднесення їх до степеня.

При множенні одночленів

і сполучну

abba = , abcabcabc () = () = ;

y властивість множення степенів з однаковими основами aaanmnm = + .

Алгоритм множення одночленів

1. Знайти добуток коефіцієнтів.

2. Знайти добуток змінних.

3. Записати добуток

множників. Для піднесення одночлена до степеня застосовують властивість піднесення добутку

1. Піднести до цього степеня кожний множник

2.

Результатом

РОЗМИНКА 2

1 Виконайте множення: 1) 34xx ⋅ ; 3) 2332 ab ⋅ ; 5) 7553 cdcd ⋅ ; 2) 4523 yy() ; 4) 52 4 ab ; 6) cdcd 76 3 8 () .

2

коефіцієнт k: 1) 17 2 xy ; 3) 41023 5 abba ; 5) 22 24 5 ababm ; 2)8,05bc ; 4) 25 8 44 xyxy () ; 6) xyxyz 84 4 11 () .

3

до степеня: 1) a 2 3() ; 3) 2 4 3 a () ; 5) ab 8 5() ; 7) ab410 6() ; 2) a 5 2() ; 4) 3 7 2 a () ; 6) ab 6 4() ; 8) ab92 3() .

125 15 18ab

3 4 12 2 xxx

aaa

n n m = () = ()

ababnnn = ()

abcannbcnn = ()

Проєкт

2)

1) x 6 ; 3) xy 24 12 ; 5) 564824 xy

: 245

abcabcabc () = () =

128 1215ab .

......() () = 128 1215ab

64 86 2 ab = () ... 27 612 3 ab = () ...

1) 20a; 3) 500 2 xy ; 5) 02 33 , ab ; 7) 005 37 , xy ; 2) –30b; 4) 400 2 xy ; 6) 03 55

8 64

; 2) 32 43ab ; 3) 8 43ab ; 4) 32 64ab .

27 612ab ? 1)

5.15

5.16

1) 64 93 xy ; 3) 125 10 6 xy ; 2) 27 1218 xy ; 4) xy 27 15 .

першої коробки удвічі,

а ширина — утричі більші за

висоту. Нарисуйте цю короб­

ку. Запишіть вираз для обчис­

лення її об’єму.

Об’єм другої коробки удві ­

чі більший за об’єм першої,

а висоти обох коробок одна­

кові. Якою може бути друга

коробка? Нарисуйте можливі

варіанти.

1

Проєкт

майб

2

# BE SMART

1

Алгебраїчними виразами називають

числові вирази та вирази зі змінними.

Алгебраїчні вирази, які містять лише дії додавання, віднімання, множення, піднесення до степеня й ділення, називають раціональними виразами.

Проєкт майб

2

Тотожними, або тотожно рівними, називаються вирази, відповідні значення яких рівні при будь-яких значеннях змінних, що входять

3

Цілі вирази — числа, змінні, степені та їхні добутки називають одночленами.

1

2

3

Гарбузи

3 2 x Буряки xy Морква 2xy

Перець

2 2 x

Проєкт

1.

2.

3.

(Спосіб 1: 322223 2 xxyxyxxxy ++ ++ + ; спосіб 2: 6xxy + () .)

3222 xyxx ++ ; спосіб 2: 3xxy + ().)

4. На скільки площа, запланована для

x 2

множення одночленів і піднесення одночлена до степеня з

1

1) xyxyx 2332 ++ ; 3) 2 34 abcd : ; 5) abab 2 (); 2) xyxyy 42 2 23 ; 4) −+ 3 74abcd ; 6) abab + () 4 . 2

многочлени

1) 7 3 a ; 3) 54 32 43 22 xxyxy −+ ; 5) 10; 2) 94 2 +−bc ; 4) cd22 ; 6) –х.

y визначаємо подібні члени;

y групуємо подібні члени; y додаємо коефіцієнти; y множимо результат на спільну буквену частину.

1. Подібні члени зручно підкреслювати різними рисками: xxxx xyxy 2233 2 3 3 2 ++ ++ + .

2. Не можна додавати доданки, які не є подібними!

x 2 + y 7 + z 4 + x 2 + z 4 = 2 2 x + 2 4 z + y 7 ПРИГАДАЙТЕ!

1) 23 abab +− ; 2) abab 22 33 1 +− ; 3) abcabcabc 2255 −+ + .

1) 4 22 xx ; 3) 32xyxy ; 5) 6533 xyxy ; 2) xx 33 5 ; 4) −+ 7 22 xyxy ; 6) 5644xyxy .

Проєкт майбутнього

1) xyxyxy 44 2 −+ + ; 3)

Проєкт майб

ПРИКЛАД 2

213 43 3 2 abab aabba−+ += ⋅ ⋅−()

= () +− + () = 23 121322 abababab

Зведіть многочлен 24 33 13 2 abaabbaab +⋅ () + до стандартного вигляду та визначте його степінь.

Запишемо всі члени у стандартному вигляді.

=− +=213 12 3 2 2 abab abab ......................

Визначаємо подібні члени.

Групуємо подібні члени, зводимо подібні члени. =+abab 2 . Визначаємо степінь кожного члена.

ЗВЕРНІТЬ УВАГУ!

Многочлени можна додавати й віднімати у стовпчик. Додавання многочленів

підручника

1. Записати перший многочлен.

2. Записати під ним другий многочлен так, щоб подібні ч лени було р озміщено один під одним.

3. Виконати додавання подіб­

них членів.

Наприклад:

Проєкт майбутнього

11 2 += 21 3 += ...................... Маємо: найбільший зі степенів дорівнює 3.

Відповідь: −+abab 2 — многочлен 3-го степеня.

ТРЕНУЄМОСЯ 2

Визначте степінь многочлена: 1) 75abab +⋅ (); 5) 16 38 76 2 abaabbaab +⋅ () ; 2) 62abba +⋅ () ; 6) 14 54 98 2 abaabbaab −⋅ +⋅ () ; 3) 25 8 abaab ⋅+ ; 7) 12 82 13 4 1 3 2 abba

⋅− ⋅+ ⋅−() ; 4) 37 15 abbab ⋅+ ; 8) 20 63 11 5 1 4 2 abbabbaab ⋅− ⋅+ ⋅−() .

Додавання та віднімання многочленів

Сума та різниця будь­яких многочленів є многочленом. Алгоритм додавання многочленів

+−+=3247 24 22 mmnn

=+ +− + () = () () 32 47 24 22 mmnn

=+ mn 2 3 2

ТРЕНУЄМОСЯ 3

Знайдіть суму многочленів:

1) 15 2n і 215 n ; 5) 12 33 2 mn−+ і 32 1 2 nm−+ ;

2) 314 n і 14 3n ; 6) 4107 2 nm−+ і 10 32 2 mn ;

3) nn 2 64+− і nn 2 63−+ ; 7) mmnn 22 64 23 −+ і 52 22520mnnm +;

4) 87 2 nn−+ і nn 2 75 ; 8) 85 22925mnnm + і 4106 15 22 mmnn−+ .

Алгоритм віднімання многочленів

1. Записати різницю многочленів: ............ () () .

2. Розкрити дужки.

3. Визначити подібні члени утвореного многочлена.

4. Звести подібні члени.

5. Записати у відповідь многочлен стандартного вигляду.

РОЗМИНКА 4

підручника

Розкрийте дужки:

1) −+() 5 n ; 3) () n 2 4 ; 5) () n 3 7 ; 7) () nn 3 29 ; 2) −+() n 2 ; 4) () 6 2 n ; 6) () 8 3 n ; 8) () 54 3 nn .

ПРИКЛАД 4

Знайдіть різницю многочленів 34 5 2 ab+− і 25 5 2 ab () .

Розв’язання 34 52 55 22 abab +− () () = Записуємо різницю многочленів.

=+ −= −+ + 34 52 55 22 abab Розкриваємо дужки, змінюємо . . . . . . . . . . . . . . . . . . . . . . . . . . знаки на протилежні.

=− += ++ 324555 22 aabb Визначаємо подібні доданки.

=+ +−() = () + () 32 45 55 22 aabb ... Групуємо подібні доданки.

=+ab 2 9 Зводимо подібні доданки.

Відповідь: ab 2 9 + .

ТРЕНУЄМОСЯ 4

Спростіть вираз:

Проєкт майбутнього

1) 67 57xx +− + () ; 5) xyyx −+ () + ()8112 1511 ; 2) 73 63xx +− + () ; 6) 17 94 39xyyx() (); 3) 81 1 xx + () () ; 7) xyxy 22 6203 518 () ();

4) 53 23xx + () () ; 8) 23 24 58 21 22 xyxy() ().

() = + xyxy

() = + xyxy

УВАГУ! Віднімання многочленів у стовпчик

22 53 32 . A – B =

6.1

1) 2a і 4 3 a ; 2) xy , –5 і 4

1) 42 1 52 35 yyyy ++ , якщо y = 1; 2) 23 42 4 −+ ++ xxxx , якщо x =−1 ; 3) 24 32 2 abaabab ++ , якщо a = 3 , b =−1 . 4) aabaab33 41 24 −+ −+ , якщо a = 2 , b =−1. 6.3

його степінь:

1) 22 45 10 22 22 xxyxxy −+ +− ; 2) 83 59 6 33 33 xxyxxy+− −+ ;

3) ⋅−() +⋅ () 25 25 1 44 abababab ; 4) abababab 52 52 84 2 −⋅ () ⋅+ −+ ⋅−().

6.4 Запишіть по два приклади многочленів: 1) першого степеня; 4) четвертого степеня; 2) другого степеня; 5) п’ятого степеня; 3) третього степеня; 6) нульового степеня.

6.5 Знайдіть суму та різницю многочленів: 1) 510 2 xx + і 411 2 x ; 3) 82 4 3 aa−+ і 35 7 3 aa++ ; 2) y 3 4 і 52 3 yy + ; 4) 63 2 2 bb+− і 87 9 2 bb−+ ; 5) 02 10 06 3 ,,abab +− і −+ 12 0408 3 abab ,, ; 6) 05 81 1 4 ,, xxyy−+ і 09 25 12 4 ,,yxxy −+ .

6.6 Визначте, який многочлен потрібно вписати замість

тотожність: 1) 39,.33410 .. xxxx +− () =+ ; 2) xyxy 55 02 11 () =− ... , ; 3) 02 13 23 20 33 ,, ... aabaab +− + () =+ + ; 4) ... ,, , () +− += +− 72 29 8100 110 44 aabaab .

54 12 35 74 2 abababab

6.8 Розв’яжіть рівняння:

1) 25 38 83 xx() ++() = ; 2) 84 46 90 xx + () () = ; 3) 42 75 100 22 2 xxxxx() ++() =− ; 4) xxxxx 33 61580 + () () =+ .

6.9

1) 62 36 1 33 aaaa() + () + , якщо a = 5 ; 2) 12 62 6 2 9 4 7 3 7 2 9 45 54 xxxx +−

+− 

+ , якщо x =−1 .

6.10

ного вигляду: 1) 53xaxa −+ () () ; 3) 18 26 32 22 22 xaxaxxax −+ () ( ) ; 2) 82xaxa −+ () () ; 4) 15 38 73 22 22 xaxaxxax −+ () ( ) ; 5) 97 56 43 22 22 22 xaaxxaax −+ −+() ( ) ; 6) 11 84 32 6 22 22 22 xaaxxaax −+ −+() ( ) .

6.11

1) ab ; 2) abba + ; 3) abccba + ; 4) abcd .

6.12 Доведіть, що

1) xxxx 6767 52 5 100 + () + () +

2) () + ()xxxx 43 38 22 7 100

6.13

1) abab 224242 0 −+ −= ;

2) abab 224242 4 −+ −= ; 3) abab 224242 4 −+ −= .

6.14

Проєкт майбутнього підручника

MATH FOR LIFE

6.15

6.16

Проєкт

РОБОТА № 4 У завданнях 1–5 виберіть одну правильну

відповідь.

1 Який із наведених виразів є многочленом? АБ В Г

32 2 xx : () 24 3 xy + () 2 3 xyy + 2xyxy : +

2 Зведіть подібні члени многочлена −+ + 32 44 mnmn .

5 Визначте пери-

трикутника, зображеного на рисунку. АБ В Г 8x 53 x + 66 x + 63 x +

6 Установіть

3 Запишіть многочлен 45 5 abb () + у стандартному вигляді.

В Г −+ 20 5 abb 4a −+abb 5 4a

4 Укажіть степінь

6.17 Укажіть вирази, які є многочленами, та

їхні члени: 1) 9 32 abc ; 3) 222 32 aaa +− ; 5) a b a −+212 ; 2) xxy() ; 4) 42 1 4 xx : () ; 6) x x 2 2 23 .

6.18 Класифікуйте многочлен за

степінь: 1) xyy 23 6 4 + ; 3) 43 6 24 xxyy−+ ; 5) 9 10 x ; 2) ab + 16 ; 4) −+ + 3232 2 aabb ; 6) abc 32 .

6.19 Зведіть

чення, якщо x =−10 : 1) 44 4 22 xxx +− ; 3) 40 5305 9 22 xxxx−−++ ; 2) 36 6 22 xxxx +− ; 4) 30 55 7 22 1 2 xxxx +− +− , .

6.20

його степінь:

1) 53abab +⋅ (); 3) 15 27 86 2 abaabbaab +⋅ () ; 2) 29 12 abaab ⋅+ ; 4) 20 94 13

6.21

1) 92 x + і 82 x + ; 5) xy412 і yx812 ; 2) 11 3n і 311 n ; 6) 6149 2 nm−+ і 14 37 2 mn ; 3) 67 2 x + і

Проєкт майбутнього

# BE SMART

3, 4

Многочлен, або поліном; одночлен, або моном; двочлен, або біном; тричлен, або трином. Порівняйте

підручника

y Починаючи з 2004 року, серед дорослих і

проводяться Чемпіонати світу з усної лічби (Mental Calculation

World Cup).

y Щороку понад 30 000 осіб беруть участь у змаганнях «Прангліміне» з усної лічби, які проходять у країнах Балтії, у Словені ї та Україні.

y За допомогою онлайн­тренажера «Прангліміне Міксіке» ви можете провести тренування та взяти участь у цих змаганнях.

Проєкт

майбутнього

12 і 18, 23 і 27, 307 і 303, 906 і 904?

1) 33 3 44 312aaa + () =⋅ +⋅ =+ 33 3 44 312aaa() =⋅ +⋅

=

28 6 2 xxxx + +⋅ () +⋅ = .

підручника

Розкрийте

1) 91 + () x ; 3) xx 3 () ; 5) −+() 5xxy ; 7) xx 2 7 () ; 2) 52 y (); 4) yy() 4 ; 6) () 9yyx ; 8) yy

30 52 5 23 xxx , +− () . Розв’язання: 3 05 25 2 3 xxx , +− () =

=⋅ +⋅+⋅ () = 33 3 05 25 22 2 31 xxx xx ,

+⋅+⋅ () = ++ 30 53 23 5 22 2 31 , xxx

aaa bcbc ()++ =

aaa bcbc() =

aaaa bcdbcd ++ () =+ +

abab =+ ()

aaa bcbc() = ,

aaa bcbc ()++ = ,

aaann11 ⋅= +

Проєкт майбутнього

: 52 5 2 aabbbaAB () −+() =− ,

де Aaab =−() 5 2 , Bbba =+() 25 ......

. . різниці A–B.

Aababaab aaa = () =⋅ ⋅= 55 5 55 22 3 ; Спрощуємо вирази А

Bbababab bbb = () =⋅ ⋅= + ++25 25 25 2 .. та В окремо. ABaabbab=−() + () = 553225 Знаходимо різницю

. . AB . =− =− 52 52 55 10 32 32 abab ababab Зводимо подібні члени.

Відповідь: 510232 aabb .

ТРЕНУЄМОСЯ 2

Спростіть вираз: 1) aaba 33 2 + () ; 5) 63 4 2 aabbba () −+() ; 2) aaba 22 2 + () ; 6) 47 3 2 aabbba () −+() ; 3) aabab () ++()55 1 ; 7) 24 43 2722aaabbbab () () + ; 4) aabab () ++()44 1 ; 8) 56 32 10 8 22aaabbbab () () + .

3

1) 20 x = ; 2) −=321 x ; 3) x +=210 ; 4) x −=717 .

ПРИКЛАД 3

Розв’яжіть рівняння 21 35 26 2 xxxxx () +− + () =− .

Розв’язання: 2 15 26 3 2 xxxx x () +− + () =− Розкриємо дужки.

22 15 26 33 2 xxxxx xx ⋅− ⋅+ ⋅−() +⋅ =−

222231526 2 xxxxx +=

23215 26 222 xxx xx −+−+ =

13 26 x = ; x = 2

Відповідь: 2.

ТРЕНУЄМОСЯ 3

Розв’яжіть рівняння:

підручника

доданок зі

частину

1) 31 24 0 xx + () +−() = ; 5) 56 31 3 2 xxxx + () +−() = ; 2) 41 32 0 xx + () +−() = ; 6) 63 41 4 2 xxxx + () +−() = ; 3) 24 272 2 xxx + () −= ; 7) 23 52 24 3 2 xxxxx () +− + () =− ; 4) 71 784 2 xxx () += ; 8) 35 46 63 2 xxxxx () +− + () =− .

Правило множення многочленів Щоб помножити

члена і додати знайдені добутки.

Розглянемо різні способи множення многочленів.

ПРИКЛАД 4 Виконайте множення многочленів, застосувавши розподільну властивість множення: xx + () + ()32 .

xxxxx + () + () + () + () =+ = 33 22 2 Двічі застосуємо

=⋅ +⋅ +⋅+⋅ = xxxx22 33 ........... розподільну властивість. = +++ = xxx 2 23 6 xx 2 5 6 ++ Зводимо подібні члени.

Відповідь: xx 2 56++ .

ТРЕНУЄМОСЯ 4

Виконайте множення:

Проєкт майбутнього

79 45 xx −= + 75 49 xx−= +

1) xx + () + ()31 ; 4) xx() ()25 ; 7) () ()xx 83 2 ; 2) xx + () + ()21 ; 5) 21 1 xx + () () ; 8) () ()xx 71 4 .

3) xx() ()34 ; 6) 31 2 xx + () ();

ДОСЛІДЖУЄМО! Порівняйте степінь добутку

многочленів і степені многочленів­множників у Прикла­

дах 4, 5.

З’ясуйте, чи є правильним

висновок: степінь добутку

многочленів дорівнює сумі степенів многочленів-множників. Застосовуйте цей висновок для самоконтролю!

підручника

Проєкт

5

Виконайте множення: 1) xx + () + ()14 2 ; 4) 37 2 () + ()xx ; 7) 29 6 3 xx() () ; 2) xx + () + ()

65 2 () +

; 6)

27 2

; ПРИКЛАД 6 Виконайте множення многочленів табличним способом (спосібкоробки): 35 73xx + () (). Розв’язання:

1. Будуємо таблицю, що містить 2 рядки і 2 стовпчики (таблицю 2×2).

2. Записуємо члени двочленів уздовж сторін таблиці (перший — ліворуч, другий — зверху).

3. Кожний член першого многочлена множимо на кожний член другого многочлена.

4. Результати множення записуємо у відповідні

таблиці.

5. Записуємо суму всіх добутків.

6. Зводимо подібні члени, записуємо відповідь.

видавництва

майбутнього

7.1 Перетворіть добуток у многочлен:

7.2

1) 34 8 2 xxx−+ () ; 4) 53 11 xyxy −+ () ;

2) 25 9 2 xxx+− () ; 5) −+ () ()412332 xyxy ;

3) 43 610xyxy() ; 6) 37 15 2 23 xyxy() () .

Доведіть тотожність:

1) aaaaaa 42 24 22 −+ () +−() = ;

2) aaaaaa 95 59 22 +− () +−() = ;

3) babbbab −+ () +−() = 4104 10 ;

4) 29 18 22 23aaabbabaa −+ () +−() =− .

7.3 Подайте у вигляді

підручника

1) aababa 71 34 2 22 −+ () +−() ;

Проєкт

2) 42 52 66 33 bbabab +− () +− + () ;

3) 24 43 2722aaabbbab () () + ;

4) 56 32 10 8 22aaabbbab () () + .

7.4 Спростіть вираз і

1) 12 54 ,,02 aaa () ; 3)

2) 25 23 ,,25 aaa () ; 4)

7.5 Розв’яжіть рівняння:

1) 29 75 32 xxxx + () += + () ;

2) xxxx 34 34 56 + () =+() + ;

3) 24 25 23 22 xxxxxx + () −= () + ;

4) xxxxxxx 22 23 36 21 () += + () ;

5) 40 53 53 23 2 xxxxx + () −= () + , ;

6) 21 51 4 23 2 xxxxx , () += () + .

7.6 Розкрийте дужки:

+−() .

1) 21 xyxy() ++ () ; 4) 46 2 xyxy + () ();

2) 32 xyyx + () −+ () ; 5) 32 15 4 2 xyxy() () ;

3) xyxy + () () 54 2 ; 6) 25 13 6 2 xyyx() ().

2322 aabb−+ 4ab −+2322 3 ababb

8147 32 23 aababb −+ × +

8124 32 2 aabab −+

1) cccc + () −+() + () 72 5 дорівнює –10; 2) cccc() + () −+() 39 6 дорівнює –27.

рівняння: 1) xxx + () + () −= 31 0 2 ; 4) xxx + () () = 42 2 ; 2) xxx + () + () −= 12 0 2 ; 5) xxx() () = 52 12 2 ; 3) xxx() + () = 46 2 ; 6) 32 43 2 xxx() () = .

1) xxx + () + () + () 31 9 ; 4) xxx() + () () 25 3 ;

xxx + () + () + () 12 8 ; 5) xyxy + () () + () 32 1 ; 3) xxx() + () () 14 7 ; 6) 24 3 xyxy + () () + ().

MATH FOR LIFE

2)

7.11

в x разів фотографію розміром 10 см на 15 см і розмістити

7.14

1

вираз aabab 3 () + .

В Г

план паркової зони, що має форму прямокутника. Визначте

Завдання 7.15 → Приклад 1

Завдання 7.16 → Приклад 2

Завдання 7.17 → Приклад 3

Завдання 7.18 → Практикум, 7.4

Завдання 7.19 → Приклад 4

Завдання 7.20 → Приклади 5, 6

Завдання 7.21 → Практикум, 7.8

Завдання 7.22 → Math for life, 7.12

ПРАКТИЧНЕ ЗАВДАННЯ

см З аркуша паперу потрібно

30 см

зробити коробку висотою a, довжиною b і шириною c.

1) Запишіть вираз, за яким можна обчислити об’єм коробки Vabc =⋅ (a змінна). Подайте його у стандартному вигляді.

2) Знайдіть об’єми коробки для двох різних значень a і порівняйте результати.

# BE SMART

Проєкт майбутнього підручника

IQ

Опанувати прості методи, які дозволяють блискавично ви

видавництва

многочленів: 1) xx + () + ()41 ; 4) xx() ()27 ; 7) () ()xx 92 4 ; 2) xx + () + ()25 ; 5) 41 2 xx + () () ; 8) () ()xx 61 5 . 3) xx() ()56 ; 6) 51 3 xx + () ();

1) xx + () + ()32 2 ; 4) 37 6 3 xx() (); 7) 45 32 xyxy + () + (); 2) 58 2 () + ()xx ; 5) 31 21xx() + () ; 8) 78 25 xyxy() (). 3) () ()19 2 xx ; 6) 23 61xx() ();

1) xxx + () + () −= 41 0 2 ; 3) xxx() () = 32 42 2 ; 2) xxx() + () = 64 2 ; 4) 52 13 5 xxxx() () =−().

1. Пряма задача 2. Обернена задача

Для перевезення морозива замовили контейнер, висота, ширина і довжина якого дорівнюють x см, x + () 2 см і x + () 5 см відповідно.

Якийоб’ємморозиваможнаперевезтивконтейнерітакихрозмірів?Відповідьзапишітьувигляді многочлена.

Розв’язаннязадачі1

Для перевезення морозива, об’єм якого становить xxx 32710 ++ () см3, треба

замовити контейнер.

Якимимаютьбутидовжинаіширинаконтейнера,якщойоговисота дорівнюєxcм?

Множимо одночлен і многочлени. Vxxxx xxxxxx xxx

Відповідь:Vxxx =+ + 32710 (см3).

Розв’язаннязадачі2

Розкладаємо многочлен на множники. Розглянемо

Для розкладання многочленів на множники застосовують:

y розкладання числа на прості множники;

y правило знаходження найбільшого спільного дільника (НСД);

y винесення спільного множника за дужки; y зведення подібних членів;

y властивості додавання, множення, степенів.

підручника

ПРИГАДАЙТЕ!

Розкладання числа на прості множники 105 5 21 3 7 7    1 105 35 7 =⋅ ⋅

Знаходження найбільшого

спільного дільника

1) Розкладаємо числа на

прості множники.

2) Знаходимо спільні множники.

3) Знаходимо НСД добу-

ток спільних множників.

60 2325 = ⋅⋅⋅ ; 42 7 23=⋅ ⋅ ;

54 33 23 = ;

НСД 60 42 54 6 23 ,, () =⋅ = .

ЗВЕРНІТЬ УВАГУ! y Спільний числовий множ ­

— це найбільший спіль­

дільник (НСД) коефіці­

Проєкт

винесення спільного множника за дужки застосовують до многочленів, які МАЮТЬ спільний множник для

членів многочлена.

Для знаходження спільногомножника треба:

1. Розкласти кожний член многочлена на множники.

2. Визначити спільні множники.

3. Записати добуток

видавництва"

змінних)

найменшим показником степеня.

Наприклад, знайдемо спільні множники одночленів: 1) 12 3 x і 42 2 x ; 2) 12 22ab , 30 3 ab і 42 3

1. Розкладаємо на множники

майб

2. Визначаємо спільні множники

3. Записуємо добуток 1) 12 2 23 3 xx xx = ⋅⋅ ⋅⋅⋅ 42 7 23 2 xxx = ⋅⋅⋅

⋅⋅⋅⋅ 30 5 12 3 3 abaaab

⋅⋅⋅ 42 7 12 3 3 abbb

утнього

1.

2.

3.

2. 26 2 13 xyxy=⋅ 12 2 6 2 xyxyy =⋅ −=

3.

ПРИКЛАД 1

1) 8102 24 5 32 aaaaaaa −+ =− + () 8102 24 5 32 aaaaaaa −+ =− + () ;

2) += () 12 93 39 33 22 ababababab += + () 12 93 39 3 33 22 abababababab .

Розкладіть на множники двочлен 2443 2 abab .

Розв’язання:

2 2 4 ababbbb =⋅ Розкладаємо

4 2 2 32 ababb aa =⋅ .. член многочлена.

22 2 ⋅⋅ ⋅= abbab

24 22 2 43 2 2222ababababba −= ⋅−

24 22 2 43 2 2222abababba −= ⋅− ⋅=

=−() 2 2 2 22abba

Відповідь: 24 22 43 22 22abababba −= () .

ТРЕНУЄМОСЯ 1

на множники многочлен: 1) aa 2 ; 3) aab 43 + ; 5) 7 42 2 abab ; 7) 12 4 42 4 abab + ; 2) aa + 3 ; 4) aab 42 ; 6) abab 34 25 11 + ; 8) 510 52 24abab . Спільний

РОЗМИНКА 2

1) 41 21xx + () ++() ; 3) xxyyx 52 5 () (). 2) 42 33 2 xyyyx + () −+() ;

ПЕРЕРВА

АЛГЕБРА 96 57 3 abc

БРАУНІ 72 94 3 abc

БРА ?

32 32 32 32 xbxbx() () += ()

() () +−().

32 23 () = xx . =− = () () () 32 2323 23xxx bb

23 x . = () = () = () () 23233323 xxbbb ...

abba −= ()

ДОСЛІДЖУЄМО!

1. Чи зможете ви розв’язати рівняння xxx 3 28 0 = ?

2. Знайдіть добуток xxx () + ()42 .

3. Чи зможете ви розв’язати рівняння xxx () + () = 42 0 ?

Застосуйте правило рівності добутку нулю. xxx () + () = 4 2 0

x = 0 або x = 4 0 або x + = 2 0

x = 0 x = 4 x = 2

Відповідь: –2; 0; 4. aaabcbc += + () aaaa bcdbcd ++ =+ + ()

Проєкт

. =−() () = 23 1 33 xb ........................ Визначаємо спільний =−() () 3 23 1 xb .

3 і виносимо

за

Відповідь: 32 31 xb() ().

2

1) axx + () ++()13 1 ; 5) axx 2 34 10 43 + () −+() ; 2) xaa + () ++()24 2 ; 6) 12 65 56 3 + () −+()axa ; 3) 64 4 axa() () ; 7) yxyxyyx () () +−() 42 48 4 ; 4) 85 5 xax() () ; 8) xxyxyyx 69 62 6 () () +−() . Розв’язування рівнянь

ПРИКЛАД 3

Розв’яжіть рівняння 28 0 2 xx−= . Розв’язання: 28 0 2 xx−=

22 40 xx x ⋅− ⋅=

2 4 0 xx⋅= ()

2 0 x = або x = 4 0

Відповідь: 0; 4.

ТРЕНУЄМОСЯ 3 Розв’яжіть рівняння:

за дужки 2x .

МАЮТЬ спільного

способом групування

1. Групуємо члени многочлена так, щоб доданки кожної групи мали спільний множник

2. У кожній групі виносимо за

одночлена.

3. У кожній групі виносимо за дужки спільний

підручника видавництва

многочлена. Спосіб 1

Проєкт майбутнього

aaaaaa xyxyxyxyxyxyxy bbbbbb ++ += + () ++() =+() ++() =+() + ()

xxxxxx yyyyyy++ += + () ++() =+() ++() =+() + ()

ПЕРЕРВА НА ЛОГІКУ

У виразі 34 7 aa−+ розставте дужки так, щоб отримати вираз:

1) −+921 a ;

2) 31728 2 aa .

Розгляньте запис многочленів у таблиці та знайдіть закономірність.

у

25 615 2 xyyxy +− −=

= 2255 33xx yyyy ..

=⋅() +⋅() = 22 3355xxyyyy

=−() +−() = 2 33 5 xyy y ......

25 615 2 xyyxy +− .

=+() ()yxy 3 25 Виносимо за дужки спільний

y () 3 . Відповідь: yxy() + ()32 5 .

4

у вигляді

1) xxx 2 62 6 () +−() ; 5) 33010 22 xxyy −+ ; 2) xxx 2 94 9 + () −+(); 6) yxyx 22 1212 −+ ; 3) xyxyx −+ () 2 5 ; 7) 38 212 2 xyxyx −+ ; 4) xyyxy ++ + () 2 4 ; 8) 4153 20 2 xyyyx +− .

8.1 Винесіть спільний множник за дужки:

1) 23 5 32 xxx ++ ; 4) 4128 42 xxx +− ;

2) 47 3 532 xxx ; 5) 14 21 63 26 xxx ;

3) 36 12 64 2 xxx −+ ; 6) −+ 27 18 45 510 xxx .

8.2 Розкладіть многочлен на множники: 1) 7332 abab + ; 3) 12 4 33 5 abab ; 5) 69 15 22 ababab −+ ; 2) 9523abab ; 4) 21863 4 abab + ; 6) 4208 32 abbaab +− .

8.3 Які вирази треба вписати в порожні комірки, щоб отримати правильну рівність?

1) 1035 27 42 2 abbab −= () ;

2) 8204 6 axaxax −= () ;

підручника

3) 22 11 2 42 22 xyyxy += () ;

4) 361243 32 yxyxy −= () .

8.4 Розкладіть на множники вираз:

1) 10 3203xxx () +−(); 4) yyyy 34 63 4 () +−();

2) 16 4324xxx + () ++() ; 5) xyxxyx() + () () () 34 37 ;

3) 32 12 1 yxyx + () −+() ; 6) 31 4 xxyxyx() + () −+() + () .

8.5 Знайдіть спільний множник виразів і винесіть

1) axbx () +−()55 ; 4) 42 32 () ()yby ; 2) cydy () ()77 ; 5) cxyyx 27 72 () +−() ; 3) 21 31 axx () +−() ; 6) 43 34 xyyx() () .

8.6 Подайте степінь у вигляді добутку й розкладіть

на множники: 1) 2 2 abab + () ++() ; 4) 54 2 cddcd + () −+() ; 2) cdcd + () −+() 2 3 ; 5) abbab + () −+() 32 ;

3) 32 2 abaab + () ++() ; 6) abaab() +−() 32 .

8.7 Розв’яжіть рівняння: 1) xx() () = 57 0 ; 3) xx60() = ; 5) 28 39 0 xx() + () = ; 2) yy + () + () = 41 0; 4) 70 + () = yy ; 6) 15 3102 0 () + () = yy .

8.8 Розв’яжіть рівняння: 1) 32 30 20 xxx + () −+() = ; 4) 64 24 40 xxx () +−() = ; 2) 75 14 50 xxx () () = ; 5) xxx +− + () = 10 2100 ; 3) 43 12 30xxx () +−() = ; 6) 26 60 xxx () +− = .

abba() =− () () =− += ababba ababab + () =+() + () 2

ababab() =−() () 2

ababab + () =+() + () 32 ababab() =−() () 32

ВАМ?

Ви навчилися розкладати мно­

гочлени на множники й розв’я­

зувати рівняння за допомогою цього способу. Отже, вам ста­

не в нагоді наслідок з основної

теореми алгебри: многочлен n ­ го степеня має n коренів. Ця тема була об’єктом ви ­

вчення багатьох математиків, зокрема А . Ж ирара, Р . Д екарта, К. Маклорена, Л. Ейлера, Ж. Д’Аламбера, К. Гаусса тощо.

Дізнайтеся, хто першим надав повне доведення вказаного твердження.

підручника

1) aaa 3244 16 ++ + ; 4) 10 45 2 aybyab + ; 2) aabab 2 33 + ; 5) 73 73 aybyaxbx + ; 3) 12 62 axbxayby −+ ; 6) 58 85 axbyaybx + .

1) 42 21 22 xyxyyy −+ () ; 4) 111132 xxyxy+− ; 2) xxxx 32 3 43 43 () +− ; 5) 35 610 2 xxyxy+− ; 3) 1010 2 xyyxy +− ; 6) 27 621 2 xyyxy +− .

Проєкт

1) 88 2 xyyxy −+ , якщо x = 01 , , y = 02 , ; 2) xxyxy 2 32 6

x = 3, y =−10 .

Номінації,

кількість учасників / учасниць:

y діти віком 5–7 років 24a;

y діти віком 7–13 років 72b;

y підлітки віком 14–16 ро ­

ків 32c;

y молодь віком 17–18 ро ­

2)

Ряди y

ків — 16d. 60y 55х x ?

видавництва"Ранок"

3)

1) xxx 2 75 35 0 −+ −= ; 4) xxx 231616 0

MATH FOR LIFE

майбутнього

8.15

на

многочлен: 1) 23 42 6 22 2 xyxxyyxyy −+ ++ ; 2) 62 39 22 2 xxyyxyxxy ++ .

8.16

1–4.

1) 44 14 14 44 44 4 2 2 nnnn nnnnn+= += ⋅+ ⋅= + () () ;

2) aaaaaa aaa a nnnnnnn

8.17 Доведіть, що значення виразу: 1) 171754 + ділиться націло на 18; 2) 25 5 713 ділиться націло на 20.

1–5

1 Перетворіть вираз cc 5 + .

В Г c 6 cc 5 1 + () ccc 4 + () cc 4 1 + ()

2 Запишіть у вигляді добутку вираз xyy () +−()43 4 . АБ В Г 34 xy() yx() + ()43 yx() ()43 xy() + ()43

3 Розкладіть многочлен 26 2 aab + на множники.

В Г aab + () 6 23ab + () 23aab + () 21 3 2 ab + ()

4 Розкладіть на множники многочлен aaa 2 17 517 () () .

№ 6

АБ В Г 517 aa() ()417aaa () + () 17 5 aa() () 17 5 5 У першому містечку m будиночків, кожен із яких розрахований на a місць. У другому містечку n будиночків, кожен із яких розрахований на a місць.

Завдання 8.18 → Розминка 1

Завдання 8.19 → Приклад 1

Завдання 8.20 → Приклад 2

Завдання 8.21 → Приклад 3

Завдання 8.22 → Приклад 4

Завдання 8.23 → Приклад 5

Завдання 8.24 → Актуальна задача

Завдання 8.25 → Math for life, 8.13

ПРАКТИЧНЕ ЗАВДАННЯ

Вам треба створити з ква ­

дратних мотивів прямокутне

полотно площею 24 2 y см2

підручника

За підказкою намалюйте мож­

ливі схеми розміщення моти­

вів. Визначте загальну довжину швів у кожному випадку. Sx = 12 2 x 12x 6x 2x 3x 4x

# BE SMART

IQ

Розкладання многочленів на

множники використовується в цифровому шифруванні інформації.

Щоб обмінюватися секретами з друзями, ви можете кожній букві присвоїти певний

Проєкт майбутнього

1) axx + () ++()32 3 ; 4) yxyyx () () 65 6 ; 2) 75 5 axa() () ; 5) xxyxyyx 57 53 5 () () +−(); 3) axx 3 19 13 91 () () ; 6) xyyxayx 26 62 2 −+ () −+() .

1) xx 2 40−= ; 3) 4100 2 xx−= ; 5) 12 55 0 2 xx() +−() = ; 2) xx 2 0 +=

1) xxx 2 73 7 () +−() ; 4) xxx 2 10 660 −+ ; 2) xyyxy −+ () 2 8 ; 5) 5204 22 xxyy −+ ; 3) yyy 2 55 + ; 6) 58 410

1 Ви дізналися про многочлени.

Многочленом

називають суму кількох одночленів.

многочлен, усі члени якого є одночле- нами стандартного вигляду, серед яких

членів.

Доданки, із яких складається многочлен, називають членами многочлена. одночлен вважають окремим випадком многочлена.

Проєкт

многочлена стандартного вигляду — найбільший зі степенів одночленів, із

2 Ви дізналися, що многочлени можна додавати й віднімати, множити на одночлен та на многочлен, підносити до степеня, та познайомилися з алго-ритмами та правилами виконання цих дій.

Сума та різниця будь-яких многочленів є многочленом.

У результаті множення одночлена на многочлен або многочлена на многочлен отримуємо многочлен.

3 Ви навчилися розкладати многочлени на множники двома способами.

майбутнього

1 Розкладіть на множники вираз abab 2 2 + .

АБ В Г

abb + () 2 bab + () 2 aba + () 2 ab 2 2 + ()

2 Виконайте множення: xx() + ()45 .

В Г x 2 20 xx 2 20 xx 2 20 +− x 2 20

3

4 Виконайте множення: aa 26 2( ) .

Проєкт майб

В Г 2 212 aa 2 28 aa 2 8 a 2 12 a

5

1)

2)

суми ab + ()2

ab ()2 ababab ++ + () = ()() 2 ababab() = ()() 2

abba + () + () =+ = ++ 22

abba () () =+ = 22

=+ + ab ab 22 2 =+ab ab 22 2

квадрат першого виразу

підручника

квадрат суми

(binomial) квадрат суми (square of a sum) квадрат різниці (square of a difference) ПРИГАДАЙТЕ!

квадрат другого виразу

abaabb()++=+ 2 22 2

подвоєний

Наприклад: xxxxx ()++=⋅ ⋅+ =+ + 55 5 21025 2 22 2 .

квадрат першого виразу

квадрат другого виразу

abaabb () =+ 2 22 2

квадрат різниці

Наприклад:

подвоєний добуток першого виразу на другий

77 7 24914 2 22 2 () =⋅ ⋅+ =− + yyyyy . За допомогою формул квадрата двочлена

формулу квадрата різниці: aaabbb() =− + 2 22 2

тричлен: abab + () ≠+ 2 22 ; abab() ≠− 2 22 .

2

Застосовуємо формулу квадрата суми aaabbb + () =+ + 2 22 2 і формули aabbnnn() = , aamm n n () = .

1) () =+()abab22 ; 2) baab() = () 22

Доведення:

1) () =+() () = () + () =+()abababab 2 2 22 2 1 =+() () = () + () =+()abababab 2 22 2 1 ;

bbaaaabbab =+ =+ = () 22 22 2 22 .

підручника

Проєкт

2) babbaaaabbab () =+ =+ = () 2 22 22 2 22

12 + 22 + 32 + 42 = ?

давніх­давен відома форму­

для обчислення суми послі­

чисел: 12 3 1 2 +++ += ( ) + ... n nn .

: 21822 xy + .

3

майбутнього

1) xx() () 141422 ; 5) 42 32 22 xyyx() () ; 2) 151522 () ()xx ; 6) 53 43 22

;

ПРИКЛАД 4

Відповідь

ТРЕНУЄМОСЯ 4

Перетворіть

1) xaxa 22 2 −+ ; 5) mmnn 22 10 25 −+ ; 2) bbyy 22 2 ++ ; 6) mmnn 22 816++ ; 3) mmnn 22 22 4 +⋅ + ; 7) 361222 4 mmnn−+ ; 4) mmnn 22 23 9 + ; 8) 49 14 23 6 mmnn++ .

РОЗМИНКА 5

Розв’яжіть рівняння: 1) x −=80; 2) x () = 11 0 2 ; 3) x + () = 16 0 2 ; 4) 2180 2 x + () = .

ПРИКЛАД 5

Розв’яжіть рівняння 4129 0 2 xx−+ = , використовуючи формулу квадрата двочлена.

Розв’язання: 4129 0 2 xx−+ =

2220 33 2 2 xx() −⋅ ⋅+ = ....

2 3 0 2 x () = Якщо a 2 0 = , то a = 0.

23 0 x −= ; 23 x = ; x = 15 , .

xx 2 1236 0 ++ = ;

Обміняйтесь записами. Перевірте правильність виконання завдання за допомогою формули квадрата суми.

() =+()abab22 baab() = () 22

Проєкт майбутнього

1) 24 2 2 xyxyy + () =+ + ; 2) xyxxy () =− + 36 2 2 ; 3) 63616 2 22 aaabb() =− + ; 4) 52 4 2 2 ababb + () =+ + ; 5) 01 10 2 22 , xyxy + () =+ + ; 6) 10 02 2 22 xyxy() =− + , . 9.4 Спростіть вираз: 1) 4242 16 xyxyxy + () + () ; 2) 5353 30 xyxyxy() () + ; 3) () +−() + () 25 34 4 2 xyxyxy ; 4) () +−() + () 32 45 5 2 xyxyxy ; 5) 27 42 2 xyxyyx + () −+() () ; 6) 34 34 2 xyxyxy() + () () . 9.5 Спростіть

значення: 1) xx + () 60 120 2 , якщо x = 4 ; 2) xx() + 50100 2 , якщо x = 3; 3) xyxy + () () 22 , якщо x = 3, y = 1 3 ; 4) xyxy() −+() 22 , якщо x = 7 , y = 1 7 ; 5) xyxyx() +−()510 2 , якщо x = 11, y =−1; 6) 36 2 xyyxy() +−(), якщо x =−1 , y = 12 .

1) 1012 ; 3) 992 ; 5) 522 , ; 2) 2012; 4) 492 ; 6) 982 , .

1) 68 2682 4 2 +⋅ ⋅+ ; 4) 75 2755 25 2 −⋅ ⋅+ ;

підручника

2) 37 2373 9 2 +⋅ ⋅+ ; 5) 99 2991 2 +⋅ + ; 3) 54 2546 36 2 −⋅ ⋅+ ; 6) 2012 2011 2 −⋅ + . 9.9 Подайте

1) aa 2 816 ; 4) −+3612 1 2 dd ;

2) bb 2 21; 5) 30 25 9 22abab ; 3) −+9124 2 cc ; 6) + 49 114 2 cc .

9.10 Спростіть вираз:

1) 47 74 49 2 () () + aaa ; 4) () () + aaa 99 18 ; 2) 65 56 36 2 aaa() () + ; 5)

3) () + () + 88 16 aaa ; 6)

9.11

1) aa 2 1450++

4) −+aa 2 18 85

1) 23 40 2 2 xx() −= ; 4) xxx + () () = 42 0 2 ;

MATH FOR LIFE

9.20 Перетворіть у тричлен квадрат двочлена: 1) 3 2 + () x ; 2) 2 2 xy () ; 3) 35 2 xy + () ; 4)

9.21 Піднесіть вираз до квадрата: 1) 1 3 2 + () n ; 2) mn 26 2() ; 3) 5 34 2 nm + () ; 4) 1 2 57 2 8 nm

9.21 →

2

.

9.22 Спростіть вираз: 1) xx() () 121222 ; 3) 64 54 22 xyyx() () ; 2) () −+()77 27 2 xx ; 4) 36 64 6 22 2 xyxyyx() +−() () .

9.23

1) 512 ; 2) 10012 ; 3) 1992 ; 4) 9992 ; 5) 10,12 ; 6) 992 , .

9.24 Перетворіть у квадрат

9.25

1) −+xxyy 42 24 2 ; 3) −+ 25 30 9 12 63 6 xxyy ; 2) xxyy 636924 ; 4) 91 16 87 14 1 2 1 16 xxyy .

Проєкт майб

9.26 Розв’яжіть рівняння: 1) xx 2 21 0 ++ = ; 3) xx 2 10 25 0 ++ = ; 2) xx 2 69 0 −+ = ; 4) 16 24 90 2 xx−+ = .

9.27 Загадайте число. Піднесіть його до квадрата. Відніміть від результату

одиницю. Запишіть число, квадрат якого дорівнює отриманій

9.28

IQ

() +−() () 11 2 22 ,

1.

чисел дорів­

квадрату певного числа:

12 3 2 += ; 13 3 5 2 ++ = ; 13 54 7 2 ++ += .

Із кожної такої тотожності

можна отримати різницю ква­

дратів:

21 3 22 −= ;

32 5 22 −= ; 43 7 22 −= ; 54 11 22 −= .

Піфагор припустив, що кожне

непарне число 21 n + () , крім одиниці, є різницею квадратів: nnn + () −= + 1 21 2 2 .

Спробуйте довести тотожність Піфагора.

Проєкт

2.

3.

5.

РОЗМИНКА 1

Перетворіть наведені вирази за формулою ababab() + () =− 22 :

1) xyxy() + () ; 3) cc() + ()55 ; 5) aa() + ()11 ;

2) mnmn + () (); 4) 44() + ()dd ; 6) bb + () ()22 .

ПРИКЛАД 1

Перетворіть у многочлен добуток:

1) 0202 ,,xyxy() + (); 2) 53 35 yxxy + () () .

Розв’язання:

1) 020202 004 2 22 2 ,, , , xxxyyyxy() + () = () −= ;

2) 55 55 5 33 33 3 925 22 22 yyyyy xxxxxxy + () () =+() () = () () =− .

Відповідь: 1) 004 22 , xy ; 2) 92522 xy .

ТРЕНУЄМОСЯ 1

Перетворіть у многочлен добуток:

1) 33xyxy() + (); 5) 56 56 xyxy + () ();

2) xyxy() + ()22 ; 6) 73 73 xyxy + () () ;

3) xyxy () + ()0101 ,, ; 7) 80 60 68 yxxy + () (),, ;

4) 0404 ,,xyxy() + () ; 8) 03 99 ,,03 yxxy + () ().

Проєкт майбутнього підручника

aaabbb() + () =−

aaabbb() + () =− 22 aaabbb + () () =− 22 aaa bbb + () () =− 22

aaabbb() + () =− 22 a2 b2 bb aa +=+ a2 b2

ПРИКЛАД 2

Перетворіть добуток 43 43xyxy() + () () () у

ab + abab22

44 4 33 3 16 8 9 2 2 22 xyxyxyxxyy () + () () () =

1) aaa() + () =+ 11 1 2 ; 2) xxx() + () =− 55 25 ; 3) 0101 02 2 ,, , () + () =− aaa ; 4) xxx + () () =− 0202 004 2 ,, , .

Застосовуємо формули aaabbb() + () =− 22 ; abaabb () =− + 2 22 2

1.

2. Виконайте обчислення,

ТРЕНУЄМОСЯ 2 Перетворіть у

1) 10 3103yy() + (); 5) 25 25ynyn() () () + (); 2) 20 1201yy + () () ; 6) 34 34ynyn + () + () + () (); 3) ynyn + () () + () + () 44 ; 7) 73 73 () () +−() ()ynyn ; 4) ynyn() + () () () 55 ; 8) 65 65 ++() () −+() ()ynyn .

Проєкт

3

майб

многочлена

утнього

aaabbb22 −= () + () . РОЗМИНКА 2

1 Розкладіть на множники за формулою ababab 22 −= () + ():

4

Проєкт майбутнього підручника видавництва

10.1

1) xyxy 22() + () ; 4) xyxy 5533() + () ;

2) xyxy() + ()33 ; 5) 45 45 65 65 xyxy + () () ; 3) 2244 xyxy() + () ; 6) 76 76 77 77 xyxy + () () . 10.2

рівність:

1) 3737 9 2 ababa() + () =− ;

2) 7575 25 2 ababb() + () =− ;

Проєкт

3) 01 03 01 009 2 ,, ,, abab() + () =− ; 4)

10.4 Обчисліть значення виразу:

1) 90 36 90 36362 () + () + ; 4) 246 354542⋅+ ;

2) 80248024242 + () () + ; 5) 1752 25 0252 ,, , ⋅+ ;

3) 157 243432⋅+ ; 6) 0861 14 0142 ,, , ⋅+ .

10.5 Спростіть вираз:

1) mm() + () + 33 32 ; 4) mmm + () () ++() 22 2 2 ; 2) mm() + () + 44 42 ; 5) () () ()mmm 66 6 2 ;

3) mmm + () () ++() 55 5 2 ; 6) () () ()mmm 77 7 2 .

10.6 Спростіть вираз: 1) xxx() + () + () 11 1 2 ; 4) 44 16 22 xyxyxy + () () + () ;

1) 78 9 ; 2) 19 2021⋅⋅ ; 3) 99 100101⋅⋅ .

=− + ()abab ; aa bb +=+ ; () =− abba . Наприклад: () () =+() () =− xxxx xx 5 555 55 () () =+() () =− + () () =− xxxx xx 5 555 55 () () =+() ()

2) xxx() + () + () 22 4 2 ; 5) xyxyyx 22 24 33 9 () + () + () ;

3) xyxyxy + () () + () 55 25 22 ; 6) 22 4 33 62 xyxyyx() + () + () .

10.7 Розв’яжіть рівняння:

1) 7171 49 2 xxxx() + () += ; 3) 4545 1516 4 xxxx() + () −= + () ; 2) 38 83 64 2 + () () += xxxx ; 4) 69 6295 66 5 xxxx () −= () + () .

# BE SMART

У 1643 р. французький мате­

матик П’єр Ферма запропо­

нував алгоритм факторизаці ї (розкладання на множники)

непарного цілого числа n .

Цей метод дозволяє знайти цілі числа x і y, які задоволь­

няють тотожність xyn 22 −= ,

тобто nxyxy =−() + () .

Зараз алгоритми факториза­

ції застосовуються для шиф­

рування даних (криптографі ї

та криптоаналізу).

r x + 1 x + 1

Проєкт майб

MATH FOR LIFE

1

В Г xp 22 xp 22 + xxpp 22 2 −+ xxpp 22 2 ++

2 Перетворіть у квадрат двочлена вираз qqnn 22 2 ++ . АБ В Г qn + ()2 qn ()2 qn ()2 qn 22 +

3 Перетворіть многочлен 16 2 n у добуток. А Б ВГ 88() + ()nn 44() + ()nn 4 2() n 8 2() n

4 Перетворіть добуток abab() + ()55 у многочлен.

АБ В Г ab22 25 + ab22 10 + ab22 10 ab22 25

5 Усередині квадратного ігрового залу розташований лабіринт (див. рисунок). Визначте

Завдання 10.17 → Приклад 1

Завдання 10.18 → Практикум, 10.1

Завдання 10.19 → Приклад 2

Завдання 10.20 → Приклад 3

Завдання 10.21 → Практикум, 10.5

Завдання 10.22 → Приклад 4

Завдання 10.23 → Приклад 5

Завдання 10.24 → Приклад 6

Завдання 10.25 → Актуальна задача

Завдання 10.26 → Math for life, 10.14

ПРАКТИЧНЕ ЗАВДАННЯ

1. Виріжте з паперу квадрат зі стороною a (a число на

підручника

ваш вибір).

2. Із цього квадрата виріжте квадрат зі стороною b, де ba < (див. рисунок).

3. Розріжте отриману фігуру по діагоналі.

4. Складіть фігури А і Б , як показано на рисунках.

5. Запишіть вирази, за якими можна знайти площу зафарбованої фігури АБ + () на обох рисунках.

а – b

а – b

Б ba а – b

1) 44xyxy() + (); 3) 25 25 xyxy + () () ; 2) xyxy () + ()0303 ,, ; 4) 70 10 17 yxxy + () (),, .

Проєкт

1) xyxy 33() + (); 3) xx yy55 44

; 2) 3322 xyxy() + () ; 4) xx yy

1) 10 1101yy() + () ; 3) 35 35ynyn() + () () (); 2) ynyn + () () + () + () 33 ; 4) 84 84 () () +−() ()

видавництва"

майб

1) n + ()1212 2 2 ; 3) n + ()13100 2 ; 2) n ()525 2 ; 4) 51 4 2 n () .

1) x 2 25 0 −= ; 3) 53 43 0 2 2 x () −= ; 2)

утнього

ПРОЄКТ

За проєктом, поданим на рисунку, планується побудувати

секцій, можна обчислити

Спосіб 1: Vab =+33 . Спосіб 2: VVVV =+ + III III .

1. Запишіть вирази для знаходження об’ємів кожної сек-

як суми об’ємів трьох секцій.

2. Перетворіть вираз для знаходження

добуток.

Розв’язання:

1. Vaaab I =⋅ () ; Vabab II =⋅ () ; Vbbab III =⋅ ⋅+() .

2. Vababbbaabaabab =+ =⋅ ⋅ () +⋅ ⋅ () +⋅ ⋅ () = + 33

= ()() + () = ++ aababab b 2 Групуємо доданки, виносимо спільний множник aab

= ()() + () = + abaabb 2 Виносимо спільний множник= ()() + () = + abaabb 2 за дужки. = () −+ () + abaabb 22 Спрощуємо вираз. Ми отримали

Проєкт майбутнього

Квадрат суми: abaabb + () =+ + 2 22 2 .

Неповний квадрат суми: abaabb + () ++ ≠ 2 22 .

Квадрат різниці: abaabb () =− + 2 22 2 .

Неповний квадрат різниці: abaabb () −+ ≠ 2 22

підручника

ЗНАЙДІТЬ ПОМИЛКУ

1) xyxxyyxy () ++ () =+ 22 33 ;

2) xxxx + () ++ () =+ 44 16 64 23 ;

3) pqppqqpq + () −+ () =+ 22 33 2 ;

4) aaaa() ++ () =− 3623927 ;

5) aaaa + () −+ () =+ 55 25 5 23 .

Проєкт майбутнього

1

22 2 2 2 xyxxyy +

6) 56 25 3036 22 xyxxyy () ++ (); 7) 025502210010

8) 100 20 220410

1.

aaaa bb33 2 += + ()

b bb + () 2

Проєкт майбутнього

aabb33 −= ()

aabb 22 ++ ()

ababaabb 33 22 += + () −+ () ababaabb 33 22 −= () ++ ()

11.1 Запишіть у вигляді многочлена добуток:

1) xxx 24 2 33 9 () ++ () ; 3) yxyyxx 7147 2 () ++ () ;

2) 24 2 33 6 + () −+ ()xxx ; 4) yxyyxx + () −+ ()52 510 ;

5) 03 10 0093 100 32 63 24 ,,xyxxyy + () −+ () ;

6) 20 02 4004 004 46 84 612 yxyyxx() ++ (),, .

11.2 Які

треба

рівність?

−+

1) abaabbab +

2) 1 5 1 25 1 5 22 33 abaabbab

++

=− ;

3) 82 64 16 8 512 22 3 xyxxyyx () ++ () =− ;

4) 36 91836216 22 3 xyxxyyy + () −+ () =− ;

5) 02 0040 02 0010 001 22 3 ,, ,, , aaabbb() ++ () =− ;

6) + () −+ () =− 07 0090 21 0490 027 22 3 ,, ,, , baabba .

11.3 Спростіть вираз:

1) 24 2 23 + () −+ () mmmm ; 3) 3323913 () ++ () ++mmmm ;

2) mmmm() ++ () 1123 ; 4) mmmm + () −+ ()4164 14 23 .

11.4 Спростіть вираз та знайдіть його значення:

1) 1212 442221 () ++ () +−()mmmmm , якщо m = 9;

2) 31 93 19 13 22 mmmmm + () −+ () −+(), якщо m = 8;

3) 47 16 2849 232 22 mmmmmm() ++ () +−() , якщо m =−10;

4) 56 25 30361218 5 22 () ++ () +−() mmmmmm , якщо m =−2 .

11.5 Розв’яжіть рівняння:

1) xxxxx () ++ () () = 0202 0044 0 22 ,, , ;

2) xxxxx 30 30 09 03 0 22 + () −+() −+ () = ,, , ;

3) xxxxx 22 11 1 () =−() ++ ();

4) xxxxx() ++ () =+() 44 16 1 22 .

скульптур. x + 1 x + 1 Проєкт

MATH FOR LIFE

1) 33 3 2 2 xyxxyy + () () −⋅ + () ;

2) xyxxyy () ++ ()44 16 22 ;

3) 57 25 35 49 22 xyxxyy + () −+ () ;

4) 00422210010 1 5 , xxyyxy++ () 

.

11.13 Спростіть вираз:

1) 39 3 23 + () −+ () mmmm ;

2) 4164 26 23 () ++ () ++mmmm .

11.14 Спростіть

1) 21 12 42 14 22 mmmmm() ++ () +−() , якщо m = 7 ;

2) 64 36 24 1616 4 22 () ++ () +−() mmmmmm , якщо m =−5 .

1) xy 3 3 7 () ; 3) 1 8 33 xy ; 2) 216 33 xy + ; 4) 0027 125 33 , xy + .

11.16 Обчисліть: 1) 34 21 3434 2121 33 22 +⋅ + ; 3) 814525 9533 ++ ; 2) 16 34 224 14 33 22 14 + −+ ; 4) 10

Проєкт майбутнього підручника

ДОСЛІДЖУЄМО! Проаналізуйте розв’язан

способи розкладання многочлена на

множники, які були використані для розв’язування рівняння.

ЧИ ВІДОМО ВАМ?

Розміри акваріума, у якому житимуть черепахи, залежать від розмірів і кількості цих черепах. Для однієї черепахи потрібен акваріум, об’єм якого

дорівнює:

y 50 л для маленької, зав­

довжки 3–10 см;

y 50–80 л — для середньої, завдовжки 11–16 см;

y 80–150 л для великої, зав­

довжки 17–25 см. x x 1 x + 9

видавництва

Vxxx = () () + 1 9

xxx () + () = 1 9 72 ......................

рівняння.

Проєкт майбутнього підручника

xxx 3289 72 +− = Розкрили дужки, звели

подібні доданки.

xxx 3289 0 72 +− = Перенесли 72 у ліву частину

xxx 3289 72 0 + () −+() =

. . . рівняння, змінили знак.

Згрупували доданки.

xxx 2 88 0 9 + () −+() = ................. Винесли за дужки спільні

xx + () () = 8 9 0 2

xxx + () ()() = −+ 80 33

. множникиx 2 і 9.

Винесли за дужки спільний

. . . множникx + () 8 .

Застосували формулурізниці

. квадратів.

x +=80 або x −=30 або x +=30 .... Розв’язуємо рівняння.

x =−8 x = 3 x =−3 Розміри не можуть бути

ГОЛОВНА ІДЕЯ

Розкладання многочленів на множники різними способами

Для розкладання многочленів на множники ви

совували:

y винесення спільного множника за дужки;

y групування;

y формули скороченого множення.

(removing a common factor)

розкладання

(factorization)

спосіб групування (grouping method)

Ви знаєте, що, залежно від кількості членів многочлена, зазвичай використовують такі способи розкладання його на множники.

Кількість членів мно­

гочлена

Способи розкладання на множники

Два Використання формул:

y різниці квадратів;

y суми кубів;

y різниці кубів

Три Використання формул:

y квадрата суми;

y квадрата різниці

Декілька y Винесення спільного множника за дужки.

Проєкт майб

Формули, приклади

ababab 22 −= () + ()

ababaabb 33 22 += + () −+ () ababaabb 33 22 −= () ++ ()

aabbab22 2 2 ++ =+() aabbab22 2 2 −+ =−()

ababababab ab 24 33 32 2 +− =+() ababababab ab 24 33 32 2 +− =+()

y Групування

квадрат суми (square of a sum)

квадрат різниці (square of a difference)

різниця квадратів (difference of two squares)

сума кубів (sum of two cubes)

різниця кубів (difference of two cubes)

aaaa xyxyxyxyxy bbbb ++ += + () ++() =+() + ()

aaaa xyxyxyxyxy bbbb ++ += + () ++() =+() + () aaaa xyxyxyxyxy bbbb ++ += + () ++() =+() + ()

Під час розкладання многочленів на множники в окремих випадках доводиться застосовувати декількаспособів. РОЗМИНКА 1

1 Винесіть спільний множник за дужки: 1) 22ax ; 3) abbc ; 5) xx 3 ; 7) 2632 xx + ; 2) 33yn + ; 4) xnxm + ; 6) xx 4 4 + ; 8) 121646 xx .

1) x 2 36 ; 3) 163622 xy ; 5) xy 44 ;

2) 25 2 y ; 4) 009922 , xy ; 6) xx 86 .

1) Винесення спільного множника за дужки.

2) Застосування формули різниці квадратів: ababab 22 −= () + () .

Стратегія

1) Винесення спільного множника за дужки.

2) Застосування формули квадрата різниці: aabbab22 2 2 −+ =−() .

ПРИКЛАД 3

у

94 4 22−+xxyy .

Розв’язання:

94 4 22−+ −= xxyy

=− () = −+ 9 44 22 xxyy

Згрупуємо доданки, винесемо

«мінус» за дужки.

1) Групування доданків.

2) Винесення знака «–» за дужки

Застосуємо формулу квадрата .

=− = () 9 2 2 xy =− = () 3 2 2 2 xy

=−() + () = () ()3322 xyxy

= () +− () + 32 32 xyxy

Записуємо вираз як різницю

квадратів, застосовуємо формулу.

Розкриваємо дужки,

Відповідь: 32 32 −+ () +− () xyxy .

ТРЕНУЄМОСЯ 3

Запишіть у

Проєкт

4 Обчисліть значення виразу

3) Застосування формули квадрата двочлена: aabbab22 2 2 −+ =−() ; aabbab22 2 2 ++ =+() .

4) Застосування

5)

Стратегія

1) Винесення спільного множника за дужки.

2) Застосування формули квадрата різниці aabbab22 2 2 −+ =−() .

3) Застосування формули різниці квадратів ababab 22 −= () + ().

4) Застосування правила рівності добутку нулю: abc = 0 , якщо a = 0 або b = 0, або c = 0 .

Проєкт майбутнього підручника

корені: x1 0 = , x2 2 = , x3 2=− . 2) Запис ±2 дає можливість об’єднати корені x2 2 = і x3 2=−

50 4 2 2 xx() =

1.

2.

3.

4.

5.

Наприклад:

aabbab

ПРИКЛАД 6

Виділіть

на множники.

Розв’язання:

майб

1) Виділення квадрата двочлена.

2)

3) Застосування формули різниці квадратів ababab 22 −= () + (). Стратегія

4) Спрощення виразу (обчислення).

вираз: 1) aa 53 ; 3) aa 10 8 36 ; 5) 98 2 52 aab ; 2) aa 57 ; 4) 25 79 aa ; 6) 45 5 43abb .

1) yxyxx 2 32 33 () +−() +−() , якщо x = 203 , y =−09 , ; 2) xyxyy 2 21 6219 21 + () −+() ++(), якщо x = 32 , , y = 39; 3) yxyxx 2 58 51680 () +−() +− , якщо x = 1005 , y =−43 , ; 4) yxyxx 2 3103 25 75 + () −+() ++ , якщо x = 9997 , y = 54 , .

1) xxy + () −+() 12 22 ; 4) xbbxx + () + () 15 44 2 22 ; 2) 13 22() −+()xxy ; 5) mmmnn + () −+ 86 9 2 22 ; 3) xxxaa() −+ + ()94 4 2 22 ; 6) mnnmm () 10 96 2 22 .

xxyxy 2 25 10 −+ ; 4)

на множники: 1) aaa + () −+() 55 2 ; 3) aaa −+ ()77 2 ; 5) 41 4 2 +−()aaa ; 2) 88 2 () () aaa ; 4) aaa −+ ()33 2 ; 6) 18 29 2 +−()aaa .

MATH FOR LIFE

12.9

12.10

вали влаштувати басейн, а

газон (див. рисунок).

1) Запишіть вираз, за яким можна

а) усієї ділянки; б) басейну; в) газону. Якщо можна, спростіть отримані вирази.

2) Визначте, скільки квадратних

треба замовити, якщо a = 15 м.

1

Завдання 12.11 → Приклад 1

Завдання 12.12 → Приклад 2

Завдання 12.13 → Приклад 3

Завдання 12.14 → Приклад 4

Завдання 12.15 → Приклад 5

Завдання 12.16 → Приклад 6

Завдання 12.17 → Актуальна задача

Завдання 12.18 → Math for life, 12.9

ПРАКТИЧНЕ

Многочлен

Розкладання многочлена на множники

Способи

# BE SMART

Перша наукова публікація всесвітньо відомого українського математика Георгія Вороного,

підручника видавництва

розкладанню мно­

на множники, вийшла

коли авторові було

16 років!

сьогодні в комп’ютерній

геометричному моделюванні,

Проєкт майбутнього

1

2

ababaabb 33 22 += + () −+ ( ) ,

Проєкт

ababaabb 33 22 −= () ++ ( ) .

y

формул скороченого множення.

aabbab22 2 2 ++ =+() , aabbab22 2 2 −+ =−() .

ababaabb 33 22 += + () −+ ( ) , ababaabb 33 22 −= () ++ ( ) .

ababab 22 −= () + ()

1

2

підручника

3

4

5

Проєкт майбутнього

2

що функ-

— це залежність однієї величини від іншої, інакше кажучи, відображення взаємозв’язку між двома величинами. Усе, що

нас оточує, пов’язане одне з одним. Отже, ми живемо у світі функцій. Наприклад, функцією є залежність маси немовляти

від віку, залежність температури повітря від часу, залежність суми, сплаченої за спожиту воду, від витраченого об’єму води тощо.

Проєкт майбутнього підручника видавництва"Ранок"

Опанувавши цей розділ, ви навчитеся: y встановлювати зв’язки, яким підпорядковуються реальні процеси; y визначати найкращий спосіб задання функції; y отримувати інформацію за графіками реальних процесів; y прогнозувати перебіг процесів, які описуються лінійними функціями

підручника

Проєкт

Велика панда є символом Всесвітнього фонду дикої

природи (WWF).

Маса великої панди становить від 100 до 150 кілограмів. Понад 12 год на добу панда зайнята харчуванням. Маса їжі, яку вона споживає щодня, дорівнює приблизно 12–15 % маси самої панди. Маса новонародженої панди складає лише 1 800 маси

3. Чи можна визначити кількість їжі для панди на 7 днів за допомогою поданої таблиці?

4. Нехай y кількість бамбука (у кг), що з’їдає панда за x днів. Виразіть y через x запишіть відповідну рівність.

5. Необхідно обчислити кількість їжі для панди на 10 днів. Як це зробити зручніше?

(function)

незалежна змінна (independent variable)

залежна змінна (dependent variable)

6. Який спосіб подання інформації, на Вашу думку, найбільш наочний ?

Розв’язуючи Актуальну задачу, ми отримали формулу yx = 30 , яка виражає залежність маси y їжі для панди від кількості днів х. Змінюючи значення змінної х, ми отримуватимемо нові значення змінної у.

Зауважимо, що кожному значенню змінної х

відповідати єдине значення

Проєкт майб

записують так: yfx = () або yx() . Для функції yfx = () незалежна

мент, залежна змінна y це функція. Правило f, що задає функцію, зазвичай подають у вигляді формули, наприклад: fxx () =− 3 або yx=− 3, fxx () = 2 або yx = 2 . Найчастіше аргумент позначають через x ,

fx() .

залежність (relation)

правило (rule)

таблиця (table)

упорядковані пари (ordered pairs)

діаграма відображення (mapping diagram)

Значення функції

yfx = ()

Функціональна залежність y від x

СЛІД ЗНАТИ! Функція Називають: x аргумент; y — залежна змінна / функція; Записують: yfx = () функціональна залежність y від x. Читають: «y дорівнює f від x».

1)

підручника

1.

2.

3.

4. Переконайтеся, що вами зроблено правильний висновок.

5.

1)

a за формулою: Va = 3

2) Залежність значення F температури за шкалою Фаренгейта від

значення C температури за шкалою Цельсія розраховується за формулою:

2) Сума, яку належить сплатити

за холодну воду y (у грн) залежить

від кількості спожитої води x (у м3)

і розраховується за формулою (дані

для Києва на січень 2024 р.):

Проєкт

FC=+ 18 32 ,

начення функції Аргумент yx=+303843919 ,,

Якщо функцію задано аналітично , то

поданими

аргумента можна знайти значенняфункції, підставивши відповідні значення у формулу, якою задано функцію.

Табличний спосіб — це спосіб задання функції

помогою таблиці, яка містить

ної x (аргумента) і відповідні їм значення залежної змінної y (функції).

Табличний спосіб

експериментальних даних у прикладних науках, інженерії, статистиці тощо. У випадку заданняфункціїзадопомогоютаблиці певним значенням аргумента вжепоставленіувідповідність

змінної відповідають два значення залежної змінної, 6 і 7, отже, залежність не є функцією.

6)

95 ; () , 97 ; () , 95 ; ()

Значенню 9

незалежної змінної відповідають три значення залежної змінної, 5, 7 і 9, отже, залежність не є функцією.

8)

Залежністьміжкористувачамиінтернетута їхнімиелектроннимиадресами:деякікористувачі маютьбільшніжодну адресуелектронноїпошти. Окремим значенням

досягнень.

ПРИКЛАД 2

Функцію задано аналітично: yx=−47 .

1) Знайдіть значення функції, якщо x =−24 ; .

2) Знайдіть значення аргумента, для яких значення

функції дорівнюють 1; 5.

Розв’язання:

Щоб знайти значення функції, треба підставити у формулу значення

знайти значення аргумента , треба

у формулу значення функції

підручника

функції.

1) yx = 5 . Знайдіть y, якщо x = –4; 10. Знайдіть x, якщо y = 45; 100.

2) yx =− 15 2 . Знайдіть y, якщо x = –1; 3.

Знайдіть x, якщо y = –3; 21.

3) yx =−43 .

Знайдіть y, якщо x = 0; 8.

Знайдіть x, якщо y = –7; 17.

4) yx=+71 . Знайдіть y, якщо x = –2; 5.

Знайдіть x, якщо y = –20; 15.

3

yx =− 2 ,

1) Складіть

2

1) fxx () =+ 4 . x 5–1 fx() 4–6

() =

таблицею:

1) назвіть значення функції, які відповідають значенням аргумента x = 02 3 ;; ;

2) назвіть значення аргумента, при яких значення функції дорівнюють 4; 8; 12;

3) запишіть відповідні значення аргумента й функції у вигляді впорядкованих пар чисел та побудуйте на

координатній площині точки, координатами яких є ці пари чисел.

3 Складіть таблицю значень функції fxx () =−25, якщо аргумент задано в межах від –2 до 6 включно із

4)

Розв’язання:

1) За даними таблиці: якщо x = 2, то y = 6000 .

2) За даними таблиці:

якщо y = 12000 , то x = 4 .

3) Знаходимо залежність yx() , дослідивши закономірність зміни витрат пального із часом.

польоту лайнера x (год) 1234

Витрати

пального y (л) 30006000900012 000

1 → 3000, 2 → 6000, 3 → 9000, 4 → 12 000, x → 3000x. Отже, yx = 3000

4) Підставляємо у формулу значення аргумента і знаходимо значення функції. x = 5 → y =⋅ 3000 5; y = 15000

5) Підставляємо у формулу .

функції і знаходимо

аргумента. y = 18000 → 3000 18000 x = ; x = 6 Відповідь: 1) 6000 л; 2) за 4 год; 3) yx = 3000 ; 4) 15 000 л; 5) за 6 год.

1 У таблиці наведено дані щодо віку й

Вік x (роки) 23367

Маса y (кг) 220350380670810

1) Яка маса крокодила віком 6 років?

2) Яка маса крокодилів віком 3 роки?

3) Запишіть відповідні значення аргумента й функції у вигляді впорядкованих пар чисел xy ; () .

4) Чи є подана залежність y від x функцією?

2 У таблиці наведено дані щодо витрат рейсовим автобусом пального протягом подорожі.

Відстань, яку долає автобус х (км) 1234 Витрати пального у (л) 0,30,60,91,2

1) Скільки літрів пального витратив автобус, проїхавши 3 км?

2) Яку відстань може подолати автобус, витративши 0,6 л пального?

3) Спираючись на дані таблиці, виразіть у через х . Вважайте, що витрати пального постійні протягом подорожі.

4) Визначте за формулою, скільки літрів пального витратить автобус на 10 км шляху.

5) Визначте за формулою, яку відстань може подолати автобус, витративши 4,5 л пального.

3 Під час ходьби людина витрачає 2 ккал за хвилину.

1) Складіть таблицю значень x і y, якщо x визначено в межах від 1 до 5 хв включно із кроком 1 хв.

2) Задайте формулою залежність (функцію) кількості y витрачених кілокалорій від часу x (у хв).

3) Визначте, скільки хвилин треба йти, щоб «спалити» 300 ккал.

4 Ціна оренди автомобіля за 1 добу складає 25 г. о.,

1) Задайте формулою

залежність є функцією.

Злата

Олег

Макар Танці Шахи

Аліса

підручника

13.1 У

1) yx=+34; 4) nk=+21;

2) stt =− + 2 2 ; 5) pa = 4 ;

Проєкт

3) Sa = 2 ; 6) Lr = 2π .

13.2 Чи є

1) Кожному

2) Залежність вартості

3) Залежність

4) Кожному

5) Залежність

ПРИГАДАЙТЕ!

1 км = 1000 м

1 кг = 1000 г

1 год = 60 хв

1 хв = 60 с

1 год = 3600 с

ПРАЦЮЄМО В ПАРАХ

Складіть відповідність між вашими друзями й подругами та їхніми захопленнями. Обміняйтеся записами. Визначте, чи є відповідність функцією.

Юля Сашко Іван Музика Ігри Читання Спорт ?

видавництва"Ранок"

13.3

1)

2) y

майб

x

5) y с через x хв; 3) y кг через x г; 6) y м/с через x км/год.

13.4

13.5

утнього

13.6

13.7 Робот-прибиральник за 10 хв прибирає 5 столиків у кафе.

1) Скільки столиків прибере цей робот за 6 хв?

2) Запишіть формулу, що виражає залежність кількості g прибраних столиків від часу t (у хв).

3) Знайдіть значення t, при якому g = 12 .

13.8 У ботанічному саду висадили рідкісне дерево заввишки 1,5 м. Упродовж першого року воно виросло на 0,2 м, а кожного наступного року його висота збільшувалась на 0,3 м.

Проєкт

1) Знайдіть залежність висоти y дерева від x — кількість років з моменту його посадки. Запишіть відповідну формулу та спростіть її.

2) Визначте, якою буде висота дерева через: 2 роки, 5 років, 10 років після посадки.

13.9 Функцію y задано певною формулою. Складіть таблицю значень функції для значень аргумента x =−2; –1; 0; 1; 2, якщо: 1) yx = ; 3) yx=+ 1; 5) yx=− 2 ; 2) yx =− ; 4) yx =− 3 ; 6) yx =− 4 .

13.10 У таблиці записано

і у для певної функції. Відновіть формулу, якою задана ця функція. Вважайте,

12 3

підручника

ВАМ?

Про лікувальні властивості термальних вод було відомо ще за часів Римської імперії. Сьогодні вони застосо-

вуються для лікування серцево-судинних та нервових

захворювань, а також захворювань опорно-рухового

апарату та органів дихання.

MATH FOR LIFE

13.11

Завдання 13.14 → Приклад 1

Завдання 13.15 → Приклад 2

Завдання 13.16 → Приклад 3

Завдання 13.17 → Приклад 3

Завдання 13.18 → Приклад 3

Завдання 13.19 → Приклад 4

Завдання 13.20 → Приклад 4

Завдання 13.21 → Приклад 4

Завдання 13.22 → Інтелектуальний фітнес, 13.10

Проєкт майбутнього

1) Якою

2) Якою була

видавництва"

3) Через

С. Упродовж дня температура води щогодини підвищувалася на 2 °С.

1) Запишіть формулу, що виражає залежність температури води від часу t, рахуючи від 7:00.

2) Якою була температура води в момент часу t = 04 , ; 1; 2; 3,5 год, рахуючи від 7:00?

13.15

1)

13.16

мулою.

1) fxx () =+ 3. x 2–4 fx() 9–5

2) fxx () = 4 . x 0–20 fx() 3–6 3) fxx () =− 18 5 . x 1 5 –4

12345 Кількість (квт·год), x Вартість (грн), y

IQ

# BE SMART

Катерина Пожарська, нау­

кова співробітниця відділу теорії функцій Інституту математики Національної

Наук України, здобула міжнародну премію з математики «Joseph F. Traub InformationBased Complexity Young Researcher Award 2023». Ця премія щороку

2)

Проєкт

3)

1) x 23452) x –5 –4 –3 –2 y 10152025 y 9753 x 1234 y 2468

5)

Проєкт

графіки й визначте:

1) якою була найвища температура протягом 9 год;

2) яким був курс долара у 2015 році;

3)

4) чи можна сказати, що наведені

(function graph)

значення аргумента (value of argument)

значення функції (value of function)

ДОСЛІДЖУЄМО!

Розгляньте

чи є фігура графіком функції, застосовують тест

зможете знайти вертикальну пряму, що перетинає фігуру

Проєкт

(формулою), і навпаки, за даним значенням функції знаходити значення аргумента.

значення функції та аргумента можна знайти також у випадку, коли функція задана графічно (тобто за допомогою графіка).

2

1) значення

аргумента, якщо задано значення функції. Розв’язання:

1) За значенням аргумента x = 5 знайдіть значення функції у

2) За значенням функції y = 3 знайдіть значення аргумента

1. На осі Ox позначаємо точку з абсцисою 5.

2.

графіком функції.

3. З одержаної точки перетину

пряму, паралельну осі Ox, до перетину

віссю Oy.

4. Ордината цієї точки є шуканим

y = 2 .

5. Відповідь: якщо x = 5, то y = 2 . Алгоритм

1. На осі Oy позначаємо точку, ордината якої дорівнює 3.

2.

Проєкт

незалежної змінної ставиться у відповідність єдине

значення залежної змінної. Незалежну змінну називають аргументом, а залежну — значенням функції

або функцією від цього

аргумента.

ПЕРЕРВА

Знайдіть відповідність між

Проєкт

майб

значень: 15 x . ПРИГАДАЙТЕ! Функція — це залежність однієї змінної від іншої, при якій кожному значенню

Відповідь. Область визначення: –2; 0; 1; 3.

0; 2; 3; 4

ком відповідні значення аргумента і функції, як

визначення: 44 x .

ПРИКЛАД 3

За графіком функції, поданим на рисунку, знайдіть:

1) область визначення функції;

2) область значень функції; 3) координати точок перетину графіка функції з осями координат.

Розв’язання:

1) Графік функції побудований для всіх значень

аргумента x таких, що 47 x , отже, областю визначення Dy() і буде вказаний

відрізок — від –4 до 7, включаючи числа –4 і 7.

2) Функція набуває значень, які не менші від –2 . . . . . . і не більші за 5, тобто 25 x , отже,

областю значень Ey() і буде вказаний відрізок — від –2 до 5, включаючи числа –2 і 5.

3) Точки перетину графіка з віссю Ox мають

координати x;0 (); точка перетину графіка з віссю Oy має координати 0; y () () 3 0; ; () 1 0; ; 6 0; () — точки перетину з віссю Ox; 0 3 ; () — точка

Відповідь: 1) Dy() : 47 x ; 2) Ey() : 25 x ; 3) ; () 30 ; ; () 10 ; ; 60 () ; ; () 30 .

ТРЕНУЄМОСЯ 3

Функції 1–8 задані

Проєкт

1)

2) Протягом якого часу (у год) Богдан

3) Скільки часу (у год) витратив

4) На якій відстані (у км) від

5) Через який час (у год)

лонтерського

Богдана від будинку. Абсциси (час t) точок О та А дорівнюють 0 та 1 відповідно. Отже, хлопець був у дорозі 10 1 −= (год).

2) Перебування Богдана у волонтерському

центрі позначено на графіку ланкою АВ, оскільки у той час, як хлопець

Відповідь: 1) 1 год; 2) 3 год; 3) 1,5 год; 4) 10 км; 5) через 0,5 год.

ТРЕНУЄМОСЯ 2

Марія вийшла зі школи (точка А) й поїхала додому (точка F). На рисунку зображено графік руху дівчини: s — відстань (у м) між Марією та її будинком, t — час (у хв), протягом якого їхала дівчина. По дорозі Марія зустрілася й поспілкувалася із двома подругами (ланки ВС та DЕ).

1) Скільки часу (у хв) тривала вся подорож

2) Яку загальну відстань (у м) проїхала дівчина?

3) Яку відстань (у м) проїхала

4) Скільки часу (у хв) Марія спілкувалася

5) З першою

6)

ЗВЕРНІТЬ УВАГУ!

Знаходимо координати точок перетину графіка функції:

� З віссю Ox точка

з координатами (x; 0)

y підставляємо у форму-

лу значення y = 0;

y знаходимо значення x.

� З ві ссю Oy то чка

з координатами (0; y)

y підставляємо у форму-

лу значення x = 0;

y знаходимо значення y.

14.2

1) A () 31 ; , B () 11 ; , C 31 ; () ;

2) A () 13 ; , B 01 ; (), C 21 ; () ;

3) A () 21 ; , B 12 ; () , C 20 ; ();

4) A () 20 ; , B () 12 ; , C 20 ; ();

5) A () 41 ; , B () 12 ; , C 12 ; () ;

ПРАЦЮЄМО В ПАРАХ

Чи є подана залежність функцією?

Поясніть одне одному свою думку. Задайте цю функцію різними способами. Обміняйтеся записами. Хто запропонував більше способів?

Виграє той, хто напише більшу кількість способів.

Проєкт майбутнього підручника

0 x y 1 1

6) A () 21 ; , B 21 ; () , C 41 ; (). Використовуючи побудований графік, укажіть: а) область визначення функції;

існують.

14.3 Не виконуючи побудови графіка функції,

1) yx =+ 36 3 ; 3) yx =+ 8 ; 5) y x =− 4 3; 2) yx=+218 ; 4) yx =− 7 ; 6) y x =+ 5 2.

14.4

1) Область визначення

цієї функції.

2) Область визначення

2.

3.

1

2

підручника

22 x 25 x

3 За графіком 1 визначте область значень

14.9 Чи є фігури 1–3 графіками функцій?

14.10

підручника

x = 1 ; 3; y ? y =−2 ;

14.11 За

функції; б) область значень функції; в) координати

функції.

1) Скільки часу (у хв) тривала прогулянка?

2) На яку найбільшу відстань (у м) відійшла

від свого будинку?

3)

зупинки?

4) Скільки часу (у хв) тривала перша зупинка?

5)

6)

Проєкт

1. Скільки води було в резервуарі в початковий момент

часу x = () 0 ?

2. Скільки води залишилося в резервуарі через 10 год

після початку поливу x = () 10 ?

3. Через скільки годин після початку поливу вода в ре-

зервуарі закінчилася?

Розв’язання

1. Підставимо у формулу yx =−4008 значення x = 0 .

Отримаємо: y =−4008 0; y 0400() = м3.

2. Підставимо у формулу yx =−4008 значення x = 10 .

Отримаємо: y =−4008 10 ; y 10320() = м3.

3. Запишемо твердження «вода в резервуарі закінчилася» математичною мовою: у = 0 . Підставимо у формулу yx =−4008 значення у = 0 . Отримаємо: 0 4008=− х , звідки x = 50. Це значення x можна визначити й за графіком.

Коефіцієнт

при змінній, кутовий

Аргумент

Коефіцієнт, вільний член yxkb=+

коефіцієнт

підручника

Проєкт

ПРИГАДАЙТЕ!

y Щоб знайти значення

функції, треба підстави -

ти у формулу значення

аргумента й виконати

обчислення.

y

Щоб знайти значення аргумента, треба підставити у

формулу значення функції і розв’язати рів -

няння відносно аргумента.

y Щоб перевірити, чи належить точка графіку функції , її координати треба підставити у формулу, якою задана функція. Якщо в результаті

отримують правильну рівність, то ця точка належить графіку.

1) Знайдіть значення функції, якщо

мента дорівнює

майбутнього

ТРЕНУЄМОСЯ 1

Для заданої формулою

та дорівнює 0; 3; б) знайдіть значення аргумента, для якого

функції дорівнює –1; 0; в) з’ясуйте, чи належить точка B графіку функції.

1) yx=+ 1, B 23 ; () ; 5) yx=−26 , B 14 ; () ;

2) yx=− 2, B 53 ; () ; 6) yx =− 10 5 , B 410 ;–() ;

3) y x = 4 , B 14 ; (); 7) yx =−90 , B 10 1 ;–();

4) y x =− 3 , B 31 ; () ; 8) yx =+80 , B () 56 ; .

Побудуємо графік лінійної функції, наприклад yx =− + 1,05 . Складемо таблицю

x –10123 y 1,510,50–0,5 1 1 y x 0

ЗНАТИ! y Ox II III I IV

4.

5. Проаналізуйте рис. 4 і доповніть твердження: y якщо b > 0 , то

Проєкт

6. Порівняйте

майб

— пряма, що

через точку з координатами 0; b ()

Графік — пряма, що проходить через початок координат 00 ; () Графік — пряма, паралельна осі Ox, яка проходить через точку з координатами 0; b () Графік

ПРИКЛАД 2

підручника

та проводимо через

графіком функції.

ТРЕНУЄМОСЯ 2

Побудуйте графік функції: 1)

3

ПРАЦЮЄМО В ПАРАХ

Запишіть кілька прикладів лі­

нійної функції. Обміняйтесь

записами із сусідом або сусідкою по парті. Чи є серед

прикладів пряма пропорцій­

ність?

3

1) yx−=30; 3) 40 yx+= ; 5) xy−=22 ; 7) 25 4 xy+= ; 2) yx+=20; 4) 50 yx−= ; 6) xy+=33; 8) 34 6 xy−= .

ПРИКЛАД 4

ykx

25 , проходить через точку A () 24;,5 . Розв’язання: ykx =− 25 , , ........ A () 2 45 ; , 45 2 25 , , =⋅ () k Підставляємо у формулу, якою задана функція, координати точки A.

її координати мають перетворити формулу в правильну

1) yxb =+ , A 14 ; (); 5) ykx = , A () 0;52 ; 2) yxb =+ , A () 23 ; ; 6) ykx = , A 24 4; () ; 3) yxb =+ , A

15.2

yyx = () ,

1) yx=+ 11; 3) yx=−460; 5) y x =−8 2 ; 2) yx =− 14 ; 4) yx =+ 70 5 ; 6) y x =− 3 6 .

x є прямою пропорційністю, а її графік проходить через точку B 0;21 () ;

2) функціональна залежність змінної y від змінної x є прямою пропорційністю, а її графік проходить через точку B () 12 3; ;

3) її графік проходить через точку C () 43 ; паралельно осі абсцис;

Проєкт

4) її графік проходить через точку C 21 ; () паралельно осі абсцис.

15.4 У яких координатних чвертях розташовані графіки функцій?

1) yx = 5 ; 4) yx = 8 ; 7) yx=+ 1 ;

2) yx =−8 ; 5) yx =−15 , ; 8) yx=−23 .

3) y = 2 ; 6) y =−4 ;

15.5 Не виконуючи побудови графіків функцій, визначте, чи є серед наведених функцій такі, графіки яких паралельні. Якщо є, укажіть

1) yx=+72; 4) yx=−45; 7) y = 0 ; 2) yx =− + 72 ; 5) yx =−45 ; 8) yx=−54 .

3) y = 8 ; 6) yx=−74;

1) y = 2 , yx =− ; 4) y x =− 3 , yx=+27 ;

2) y =−1, yx = ; 5) yx=− 2, yx =−36;

3) y x = 2 , yx =− + 25; 6) yx =− 2 , yx=− 1 4 3 .

завданнях 1–5 виберіть одну правильну відповідь.

1 Укажіть лінійну функцію.

2 Визначте значення функції y x = 5 , якщо значення аргумента дорівнює 20.

Проєкт

41525100

3 Визначте значення аргумента, для якого значення функції yx =−92 дорівнює 1.

АБВГ –554–4

4 Укажіть точку, яка належить графіку

функції y x =− 3 2.

A () 13 ; B 31 ; () C 02 ; () D 60 ; ()

5 Залежність ціни попкорну y (у г. о.)

MATH FOR LIFE

15.7

15.8

1) Яку

2) Скільки

3) Яку

1)

1. В одній системі координат будуємо графіки функцій, заданих формулами (див. Приклад 2). Обидві функції лінійні, тому одержуємо дві прямі. Досліджуючи рисунок, робимо висновок: побудовані прямі паралельні.

2. Визначаємо кутові коефіцієнти

3. Порівнюємо кутові

Завдання 15.10 → Приклад 1

Завдання 15.11 → Приклад 2

Завдання 15.12 → Приклад 3

Завдання 15.13 → Приклад 4

Завдання 15.14 → Math for life, 15.7

Завдання 15.15 → Math for life, 15.8

ПРАКТИЧНЕ ЗАВДАННЯ

Прислів’я можуть бути ма-

тематичними «портретами»

функцій.

Ось прислів’я, що можуть «проілюструвати» властивості прямої пропорційності.

y Хто багато читає, той багато знає.

y Багато снігу — багато хліба.

Пригадайте ще кілька схожих прислів’їв.

підручника видавництва"

Проєкт

1 Ви познайомилися з особливою

ністю — функцією.

Функція — це залежність однієї змінної від іншої, при якій кожному значенню незалежної змінної ставиться у відповідність єдине значення залежної змінної.

Незалежну змінну називають аргументом, а залежну — значенням функції, або функцією від цього аргумента.

2 Ви дізналися про те, як можна задавати функцію.

Усі значення, яких може набувати незалежна змінна (аргумент), утворюють область визначення функції, її позначають D(y). Усі значення, яких може набувати залежна змінна (функція), утворюють область значень функції, її позначають E(y). Виділяють

3 Ви навчилися будувати графік функції та використовувати його під час виконання завдань.

Графіком функції називають фігуру, що складається з усіх точок координатної площини, абсциси яких дорівнюють значенням аргумента, а ординати відповідним значенням функції.

4 Ви познайомилися з окремим видом функції — лінійною функцією,

підручника видавництва

Проєкт майбутнього

КОНТРОЛЬНА РОБОТА № 5

У завданнях 1–6 виберіть одну правильну відповідь.

1 Функцію задано формулою yx=+ 4. Знайдіть значення функції, якщо x =−2. АБВГ 026–2

2 Знайдіть значення аргумента, для якого значення функції yx=−27 дорівнює 3. АБВГ

1

3 Знайдіть область визначення функції, графік якої

рисунку. 1 1 y x 0

21 x 22 x 34 x 14 x

4 Знайдіть

функцією yx

2 , де x 0.

1) Який об’єм розчину залишиться у флаконі через 6 хв після початку процедури?

2) Через який час після початку процедури флакон із розчином спорожніє?

21 y 22 y 34 y 13 y 5

3 ЛІНІЙНІ РІВНЯННЯ.

Лінійні рівняння та їх системи використовуються для розв’язування задач, пов’язаних із фізикою, хімією, технікою тощо.

Вони широко застосовуються в економіці, зокрема для моделювання та вирішення

проблем, пов’язаних з оптимізацією виробництва, управлінням фінансами та аналізом економічних явищ. Опанувавши цей розділ, ви навчитеся: y встановлювати зв’язки, яким підпорядковуються реальні процеси;

y створювати схеми реальних об’єктів; y описувати реальні ситуації математичною мовою, тобто будувати математичні моделі задач;

y «читати» інформацію, подану в графічному вигляді; y зводити розв’язування системи кількох лінійних рівнянь до розв’язування лише одного рівняння.

(linear equations)

(solve an equation)

рівняння (solution of equation) модуль (absolute value)

(mathematical simulation)

Проєкт

x −=713; x −=++71377 ; x = 20

Коефіцієнт

при

змінній

Коефіцієнт, вільний член

axb =

Змінна

ДОСЛІДЖУЄМО!

Проаналізуйте розв’язан­

ня лінійних рівнянь 1–4.

Скільки коренів мають ці рівняння? Зробіть висновки

щодо того, як значення ко­

ефіцієнтів a і b впливають

на кількість коренів ліній­

ного рівняння. Порівняйте свої висновки зі схемою. ПРАЦЮЄМО В ПАРАХ

1) 420 x = ; x = 20 4 ; x = 5. Рівняння має один корінь 2) 70 x = ; x =

Скільки коренів має рівняння?

1) 416 x = ;

2) 33 5 () = x ;

3) xx −=42 ;

4) 33 0 xx−= .

Обміняйтеся записами. Перевірте одне одного.

4) 00 x = ; 00 = — рівність

Звели подібні доданки. Аналізуємо

Записали відповідь

Відповідь: 1) коренів (розв’язків) немає; 2) x — будь-яке число.

ТРЕНУЄМОСЯ 1

Розв’яжіть рівняння: 1) 7112 9 xx −= + ; 5) 12 3171339 () =−xx ; 2) 13 4104−=xx ; 6) 31 5211984 () =+xx ; 3) 61 56xxx() −= ; 7) 94 24 93 xxxx() −= () + ; 4) 82 3165 () += xxx ; 8) 63 15 49 17 xxxx () =−() + ;

2

рівняння

ПРИГАДАЙТЕ!

Якщо a bd c = ( b ≠ 0 , d ≠ 0), то adbc ⋅= ДОСЛІДЖУЄМО!

Складіть алгоритм розв’я­

рівнянь, що зво­

до лінійних рівнянь з однією змінною, пронумерувавши кроки в правильному порядку.

підручника

Проєкт

28 66 54 48 () += −+()xxx . . . 16 54 8 12 64 −+ =−xxx 16 46 64 = xx −+ =− 64 46 16 xx Зведемо рівняння до лінійного, використовуючи властивості рівнянь. = 2 30 x x =−() 302: x =−15 Розв’яжемо утворене лінійне рівняння. Відповідь:x =−15 (інший запис: –15). ТРЕНУЄМОСЯ 2 Розв’яжіть рівняння:

— у праву, змінюючи знаки доданків, які переносимо, на протилежні.

КРОК

з модулем можна звести до

рівнянь. Кількість розв’язків (коренів) рівняння xa = залежить від значення a. a > 0 a = 0 a < 0

Два розв’язки xa = або xa = Один розв’язок x = 0 Розв’язків немає

Наприклад:Наприклад:Наприклад: 1) x = 11; x = 11 або x =−11 2) x = 0; x = 0 3) x =−10 .

РОЗМИНКА 3

1 Скільки коренів має рівняння: 1) x = 3 ; 2) x = 0; 3) x =−5; 4) −= x 8 ?

Проєкт

2 Скориставшись означенням модуля числа, запишіть лінійні рівняння, до яких

з модулем: 1) x −=45 ; 2) 33 −= x ; 3) 70 −= x ; 4) 24 x = .

ПРИКЛАД 3

Розв’яжіть рівняння 43 7 −= x .

Розв’язання: 43 7 −= x . За означенням модуля: 43 7 −= x або 43 7 −= x .

майб

Розв’яжемо кожне з отриманих рівнянь: −=34 7 x ; −=33 x ; x =−() 33 : ; x =−1 −=34 7 x ;

311 x ; x =−() () 113: ; x = 11 3 x = 3 2 3

Відповідь: x =−1; x = 3 2 3 .

ТРЕНУЄМОСЯ 3

рівняння: 1) x −=40; 4) 315 x = ; 7) 14 31 −= x

5,7

1

1. Проаналізувати умову задачі (основні

2. Створити математичну

3. Скласти рівняння

4. Розв’язати отримане рівняння.

5.

6. Записати відповідь.

ПРИКЛАД 4 Сума трьох чисел дорівнює 135. Знайдіть найменше із цих чисел, якщо друге число на 3 більше, ніж перше,

третє в 4 рази більше, ніж сума першого та

1) x Позначаємо перше число . . . . . . . . . . . . . . . . . . . . . . . . змінною.

2)І число x 135 Складаємо схему ІІ числона 3 більше, ніж

ІІІ числоу 4 рази більше, ніж

3) І — x . . . . . . . . . Записуємо зв’язки між

ІІ — x + () 3 135 .. числами математичною

ІІІ — 43 ⋅+ + () xx ...... мовою.

4) xxxx ++() +⋅ ++ () = 34 3 135 Складаємо рівняння.

5) xxx ++ ++() = 34 23 135 ... Розв’язуємо рівняння

23 812 135 xx ++ +=

1015135 x +=

10120 x = x = 12

6)Найменшим числом

є значення виразу x (див. схему), тобто 12.

Відповідь: 12.

ПРИКЛАД 5 Катер пройшов за течією

Аналізуємо отриманий результат

15 хв, а назад повернувся за 1 год 45 хв.

1) Вибір і позначення невідомої.

2)

3)

4) Складання рівняння.

5) Розв’язування

6)

Стратегія

1) Складання таблиці.

2) Складання рівняння.

3) Розв’язування рівняння.

4) Аналіз результату.

підручника

ЗНАЙДІТЬ ПОМИЛКУ

515 x = ; 50 15 0 x ⋅= ⋅ ; 00 = .

Корінь рівняння — будь­яке число або коренів немає.

ПРАЦЮЄМО В ПАРАХ

Складіть лінійні рівняння, коренями яких є числа: 1) 5; 2) –7; 3) –0,5; 4) 1 7 .

Обміняйтесь записами. Перевірте, чи правильно складені рівняння.

Проєкт майбутнього

1)

2)

3)

4)

5)

6)

задачі складіть рівняння для визначення x.

1) Число x помножили на 5, отримали 120.

2) У результаті зменшення числа x на 20 отримали 50.

3) Перше додатне число дорівнює x, а друге у 3 рази менше. Сума цих чисел дорівнює 48.

4) Перше додатне число дорівнює x, а друге на 18 більше. Сума цих чисел дорівнює 46.

5) Відстань 88 км велосипедист долає за 8 год, рухаючись зі швидкістю x км/год.

Проєкт

6) Відстань 150 км автомобіль

16.7

43 75 37xx + () =+() .

1

abaabb + () =+ + 2 22 2

abaabb () =− + 2 22 2

abacabc += + ()

Проєкт

16.12

рівняння:

1) 2340 x −= ; 4) x = 23 1;

2) = 3720 x ; 5) 61 60 x −+ = ;

3) x +− = 14 6 ; 6) 23 26 0 () +− = xx .

16.13 При якому

1) 31416 x −= і 24xb −= ;

2) 19 561+= x і 4208xb += ;

3) 83xb −= і 43xb += ; 4) 65xb −= і 12 7 xb += ;

5) 25 2 xbb() =− і xbb += + 55 1; 6) 31 3 xbb + () =+ і xbb −= 2 ?

MATH FOR LIFE

Задачі

16.14 Хлопчик, перебуваючи

16.15

16.16

20030 300 20 += + xx

Проєкт

42 3036xx() =

Ромашка500,5400

М’ята400,4

підручника

число. 1) 4141 xx −= ; 3) 1 9 8 9 xxx += ; 2) 37 21 3 () =− xx ; 4) 320 4 0255 x xx + += + , . 16.26 Розв’яжіть рівняння: 1) 23 25 x += ; 4) 14 8151254 () =−xx ; 2) 23 9329−=xx ; 5) 11 55 11 5 xxxx() −= () + ; 3) 71 67xxx() −= ; 6) 3159 25 xxxx () =−() .

16.27 Розв’яжіть рівняння: 1) 41 3 22 3 3 xx −+ = ; 3) 34

Після виконання фізичних

вправ частота пульсу лю ­

дини не повинна перевищу­

вати певного значення, яке

обчислюють за допомогою

виразу 08 220 , () x , де x

вік людини в роках.

1) Максимальний пульс людини після виконання фі­

підручника

зичних вправ дорівнює

164. Знайдіть її вік.

2) Обчисліть максимальну

частоту пульсу для вашого віку, віку членів вашої родини чи знайомих.

3) Порахуйте частоту свого

пульсу після фізичного навантаження на уроці фізкультури і порівняйте її з максимальним зна ­

ченням пульсу для вашого віку.

16.29 Розв’яжіть рівняння: 1) =− 58 27 4 xx ; 3) () =− 56 322xx ; 2) =− 11 67 xxxx ; 4) () =− 410 1 5 xx .

16.30 При якому значенні x значення виразу: 1) 213 x дорівнює 47; 2) 312 x + дорівнює 72; 3) 25 x + () дорівнює значенню виразу 325 x ; 4) 31 x () дорівнює значенню виразу 437 x + ; 5) 10 4 x у три рази

Проєкт

виразу 218 x + ; 6) 517 x + на 35

361 x + ?

Розв’яжіть рівняння: 1) x −=60; 2) 324 x = ; 3) x +− = 7130; 4) 32 21 −= x .

ЗВЕРНІТЬ УВАГУ!

Позначте кількість камер відеоспостереження, встановлених у другому районі міста, через x.

11 42 , xx=+

видавництва"

16.32 Триває побудова містечка

16.33

коробок. Мала

коробка розрахована на 5 кг вантажу, а велика — на 10 кг.

1. Складіть рівняння за умовою задачі.

2. Визначте, скільки потрібно великих коробок, якщо

надали 38 малих коробок.

3. Знайдіть необхідну кількість малих коробок, якщо

надали 20 великих коробок.

4. З’ясуйте, чи можна упакувати

допомоги в 60 малих і 24 великих

(solution of the equation)

(graph of an equation with two variables)

xyc

54 10 x +=

+=92 2 xy () = 31 3 xy() +−() = 23 4 22

ЗВЕРНІТЬ УВАГУ!

рівняння зазви­

підручника видавництва

, а на другому —

xy+=212 можна

записати так: x = 2 і y = 5

або 25 ; () .

Проєкт майбутнього

1) xy+=25 ; 4) 39 0 xyy+= ; 2) −+ = 41 xy ; 5) 03 0 xy+= ; 3) 57 0 2 xy−= ; 6) 60 10 xy+= .

xy 32 4 xy+=

2 –1 32 4 2 1 ⋅+ ⋅= () 44 =

1 0 32 4 1 0 ⋅+ ⋅= 34 ≠

правильна. Пара чисел 21 ; () розв’язком рівняння

не є правильною. Пара чисел 10 ; () не є розв’язком рівняння

Відповідь: пара чисел 21 ; () є розв’язком даного рівняння, а пара чисел 10 ; () — ні.

ТРЕНУЄМОСЯ 1

Визначте, чи є пара чисел розв’язком заданого рівняння:

1) 12 ; () , 24 xy+= ; 4) 03 ; () , 52 15 xy−= ; 2) 31 ; () , xy+=25 ; 5) 41 ; () , 05 79 , xy−= ; 3) () 50 ; , 43 15 xy−= ; 6) () 15 ; , 80 27xy−= , .

Рівняння Розв’язки рівняння, xy ; ()

Проєкт

xy−= 0 55 ; () () 22 ; 00 ; () ? ?

xy+=25 31 ; () () 55 ; ?? ? Означення.

1) 57 214xx −= + ; 52 14 7 xx+= + ; 721 x = ; x = 3.

2) 34 44 33xx + () =+() ; 12121212 xx += + ; 12121212 xx−= ; 00 = .

ТРЕНУЄМОСЯ 2

1–4

1) xy+=35 , якщо y = 0 ; 3) 25 9 xy−= , якщо y = 1; 2) 49 xy+= , якщо x = 0 ; 4) −+ = 72 1 xy , якщо x = 1.

5–8

та виконайте перевірку.

5) 10 330xy−= ; 7) = 21352 xy ; 6) −+ = 42040 xy ; 8) = 17 468xy . ПРИКЛАД 3

рівняння. Розв’язання: 6 24xy−=

24 6 yx

частину рівняння доданок 6x, змінюємо знак. = 24 6 22 y x yx=−32

обидві частини рівняння на –2.

1. Обираємо три значення змінної x.

2. Знаходимо відповідні значення змінної y.

Властивості рівнянь

1. У будь­якій частині рів­

2. Будь­який член рівняння

3. Записуємо пари чисел xy ; () .

Відповідь: 24 ; (), 0;41 () , () 0;62 .

5)

6) −+ = 63 12 xy ; 8) = 43 15 xy .

графік рівняння.

Означення. Графік рівняння

це фігура, що складається з усіх точок координатної площини, координати яких є розв’язками даного рівняння.

Якщо точка належить

динати задовольняють це рівняння

рівняння в правильну числову рівність.

Розглянемо, як побудувати графік лінійного рівняння

двома зминними. Для цього можна:

1) виразити змінну у через змінну х,

2) скласти таблицю

3) побудувати на координатній площині графік рівняння, використавши дані таблиці.

Ураховуючи, що лінійне рівняння з двома змінними можна

якої є пряма, можна скласти таблицю відповідних значень

1.

1) Складаємо таблицю розв’язків рівняння, для яких x = 0 або y = 0

2) Записуємо координати точок, через які проходить пряма.

3) Позначаємо знайдені точки на координатній площині та проводимо через них пряму. Ця пряма й буде шуканим графіком рівняння 23 6 xy−= .

4) Перевіряємо, чи належить

точка A () 3 4 ; графіку заданого рівняння, підставивши її

координати в це рівняння

замість змінних х та у.

5) Позначаємо на координатній

площині дві будь-які точки, які не належать графіку заданого рівняння.

Записуємо їх координати.

Утворена рівність є правильною, тому точка A () 34 ; належить графіку рівняння.

Наприклад, точки B () 24 ; і C 52 ; ().

Оскільки точки В і С не належать графіку, то пари чисел, що відповідають координатам точок, не є розв’язками рівняння.

Відповідь: точка ; A 213 () належить графіку заданого рівняння.

змінними axbyc += в окремих випадках: 1) a = 0, b ≠ 0 , c ≠ 0 ; 2) a ≠ 0 , b = 0 , c ≠ 0 . 1) a = 0, b ≠ 0 , c ≠ 0 2) a ≠ 0 , b = 0 , c ≠ 0

byc = , y c b = axc = , x c a =

Графік — пряма, паралельна осі Ох

Графік — пряма, паралельна осі Оy

Наприклад:

02 6 xy+= y = 3

Графік рівняння:

y проходить через точку з координатами 03 ; ()

y паралельно осі Ох

ПРИКЛАД 5

Графік рівняння: y проходить через точку з координатами () 20 ; y паралельно осі Оy

Побудуйте графік рівняння: 1) 48 0 y += ; 2) 62 36 yxy + () =+ .

Розв’язання:

ПРИГАДАЙТЕ!

1. Як розкривати дужки.

2. Як зводити подібні доданки.

ЗНАЙДІТЬ ПОМИЛКУ

Дівчинка вважає, що пара

чисел () 21 ; є розв’яз ­

ком рівняння 25 1 xy−= ,

а хлопчик каже, що ні. Хто

з них правий?

Дівчинка

25 1 xy−= ; 22 51 1 ⋅−() −⋅ () = ; −+ = 45 1 ; 11 =

Хлопчик

25 1 xy−= ; 21 52 1 ⋅−() −⋅ () = −+ = 2101 81 ≠

Проєкт

ПЕРЕРВА НА ЛОГІКУ

У фермера є курки і поросята. Всього в них 20 лап.

Скільки курок і скільки поросят може бути у фермера?

2y 4x

видавництва"Ранок"

1) 46 xy−= ; 4) 8216 xy+= ; 2) yx−=38; 5) 54 18 0 xy−−=

: 1) yx=− 12 4 ; 3) 05 64 , yx−= ; 2) 2128 yx−= ; 4) yx =+() 41 3 .

1) Ay 1; () , 50 xy

32 15 xy−= .

Проєкт

1) xy = 20 ; 4) 54 4 yxy −+() = ; 2) xy+− = 10 ; 5) 22 12 xyyx() ++() = ; 3) 34 3 xyy() += ; 6) 55 30 xyxy + () () = .

17.10 Установіть відповідність

MATH FOR LIFE

ВАМ?

Художники, які створюють

мульфільми, займаються

різними справами залежно

від масштабу фільму. Якщо

фільм маленький, то один

художник може виконати всі технологічні завдання.

Великі проєкти вимагають

командної роботи, де кож­

ний художник спеціалізується на певній операції.

Сьогодні процес створення

мультфільмів суттєво полегшують сучасні комп’ютерні

програми.

Відповідь: при a = 8. 1) 52xya −= , M () 11 ; ; 2) −+ = 38xya , M () 23 ; ; 3) 23 1 xy−= , Ma;1 () ;

8.

1 Укажіть лінійне рівняння з двома змінними.

2 Укажіть рівняння з двома змінними, розв’язком якого є пара чисел 13 ; () . АБВГ 53 xy−= xy+=58 58 xy

3

03 ; () 50 ; () () 50 ; 03 ; ()

4 Виразіть у рівнянні −+ = 62 xy змінну y через

5

було x хлопців та y дівчат. Кожному хлопцю було видано

1) 14 ; (), xy+=29;

2) 05 ; () , 34 20 xy−= ;

3) () 14 ; , 90 511xy−= , ;

4) () 84 ; , = x y 4 626.

графік рівняння 81 84 xxy() =− .

1)

Допоможіть волонтерам Один волонтер витрачає на пакування гуманітарної

допомоги в малу та велику коробки 3 хв та 5 хв відпо­

відно. Скільки волонтерів

можуть спакувати 60 ма ­

лих та 24 великі коробки за

30 хвилин?

# BE SMART

Тип рівнянь із цілими кое­

фіцієнтами, у яких невідо­

мі змінні можуть набувати

тільки цілих значень, но ­

сить ім’я «діофантові рів ­

няння» — на честь грець­

кого математика Діофанта

Александрійського (при ­

близно III ст. н. е.).

Діофантові рівняння впер­

ше докладно досліджувалися у збірнику задач Діофанта «Арифметика», що

3)

Проєкт майб

x 01 –1 y x 01 –1 y

3) 62 8 xy−= ; 4) = 53 18 xy .

1) xy+= 1, A 10 ; (); 3) 28 xy−= , A 51

1) x = 2; 3) 48 0 x −= ;

2) y +=30 ; 4) 53 53xyx += ().

1 Ви пригадали, що таке рівняння та його розв’язок,

2

підручника

що ті рівняння, які ви розв’язували раніше, мають

Рівняння виду ax = b , де x — змінна, a і b— деякі числа, називають лінійним рівнянням з однією змінною. Числа a і b— коефіцієнти рівняння.

Математична модель — це опис реальної ситуації математичною мовою, тоб- то мовою математичних понять, формул, рівнянь тощо.

Проєкт майб

Лінійне рівняння з однією змінною може мати один корінь, немати коренів або

безліч коренів.

Алгоритм розв’язування

1.

2. Створити математичну

3. Розв’язати отримане рівняння.

4. Проаналізувати отримані результати

5. Записати відповідь.

3

4

Лінійним рівнянням із двома змінними називають рівняння виду ax + by = c, де x і y —

змінні, a , b і c — деякі числа. Числа a, b і c називають коефіцієнтами рівняння, a ≠ 0 , b ≠ 0.

Розв’язком рівняння з двома змінними називають пару значень змінних (пару чисел), яка перетворює це рівняння в правильну рівність (задовольняє рівняння).

1

2

3

4

Бонусне завдання При якому значенні a рівняння axxa −= + 84 не має коренів? Проєкт

Побудуйте графік рівняння 42 xy−= .

чи належить точка A () 16 ; графіку цього рівняння.

10 Побудуйте графік рівняння 99 27 xyy + () =+ .

Проєкт

позначено графіками рівнянь xy−=21 і yx+=212, по-

будованими в прямокутній системі координат.

1. Визначте координати точки перетину цих автомагістралей.

2. Графік якого рівняння позначає автомагістраль, що проходить через населений пункт, розташований у точці з координатами 31 ; () ?

3. Архітектурна пам’ятка розташована в точці з координатами 26 ; () . Яка з автомагістралей проходить найближче до цієї пам’ятки? Укажіть відповідне рівняння.

Математичною моделлю Актуальної задачі є не одне, а два лінійних рівняння з двома змінними. Причому,точка перетину графіків цих рівнянь (5; 2) визначає пару чисел, що є розв’язком обох рівнянь одночасно.

такому випадку кажуть, що рівняння утворюють систему,

КЛІК

Пропонуємо скористатись

онлайн ­ калькулятором

Desmos, який можна використовувати для побудови

графіків функцій та рівнянь, дослідження функцій, розв’язування систем

рівнянь графічним спо ­

собом тощо. Працюючи

з онлайн ­ калькулятором

Desmos, пам’ятайте:

y у лівій частині панелі роз­

ташовано поле для вве ­

дення даних, у правій частині — область побудов;

y сервіс дозволяє будувати

декілька графіків в одній координатній площині;

y вводити символи можна з клавіатури комп’ютера або вбудованої клавіатури, встановивши англій ­

ську мову введення. Якщо хочете дізнатися більше, зверніться до електронного додатку.

Проєкт майб

Відповідь: пара чисел 16 6; () є розв’язком

— ні.

ТРЕНУЄМОСЯ 1 З’ясуйте, чи є вказана пара чисел

рівнянь.

1) 10 ; (), x xy −= += { 10 1 , ; 5) 43 ; () ,

2) 03 ; () , y

3) 14 ; (), 28 3 y xy

4) 31 ; () , 39 4 x xy = −+ =− { , ; 8) () 34 ; , −+ = −= { 52 7 39 xy xy , .

1. Побудувати в одній системі

2. Знайти координати точки перетину графіків.

3. Перевірити, чи є знайдена пара чисел розв’язком системи рівнянь.

4. Записати відповідь.

1) yx=+21 і yx =− + 36 ;

2) yx=+21 і

1) Виражаємо в кожному рівнянні

підручника

Розв’язання:

2) Складаємо таблицю відповідних значень х та у для двох точок, що належать графіку

3) Проводимо прямі через точки з координатами: y 01 ; () , 25 ; () та y 06 ; (), 22 ; ()

4) Знаходимо координати точки .......... перетину графіків рівнянь.

5) Перевіряємо чи є пара чисел 1 2 ; () ... розв’язком заданої системи рівнянь.

6) Робимо висновок.

Проєкт майбутнього

підручника

залежитьвідвзаємногорозміщенняцихпрямих.

Розглянемо випадки, коли системи лінійних рівнянь із двома змінними

ПРИКЛАД 3

Визначте графічним способом кількість розв’язків

1) 22 xy+= 24 xy+= yx =− + 22 yx =−

2. Проводимо прямі через точки з

y 02 ; (), 10 ; () та 04 ; () , 20 ; ()

3.

Побудовані прямі паралельні, отже, задана система рівнянь не має розв’язків

Кількість розв’язків системи лінійних рівнянь із двома

змінними можна визначати не лише графічним, але й

аналітичним шляхом . Ця

кількість залежить від відношення коефіцієнтів рівнянь, що складають систему.

Дізнайтеся про це більше з електронного додатка до підручника ЗНАЙДІТЬ ПОМИЛКУ

рів ­

Проєкт

02 ; (), 10 ; () та 02 ; (), 10 ; ()

18.2 Виконайте завдання за рисунком, на якому зображені графіки чотирьох рівнянь.

1) Визначте кількість спільних точок прямих, заданих рівняннями:

а) xy−=21 і xy+=21 ; б) xy−=21 і 24 10 xy−= ; в) xy−=25 і 24 10 xy−= .

2) Запишіть систему рівнянь, яка: а) має єдиний розв’язок 10 ; () ; б) не має жодного розв’язку; в) має безліч розв’язків.

18.3 Розв’яжіть графічним способом систему рівнянь: 1)

18.4 Визначте кількість розв’язків

Проєкт

18.5

1 Укажіть систему лінійних рівнянь із двома змінними.

2 Укажіть пару чисел, яка є розв’язком

системи рівнянь y xy −= += { 30 5 , . АБВГ 53 ; () 13 ; () 23 ; () 32 ; ()

3 На рисунку подано графічне розв’язання системи лінійних рівнянь

4

18.7

Система лінійних рівнянь має безліч розв’язків. Користуючись рисунком, на якому точками зображено два розв’язки системи:

1) знайдіть ще два розв’язки цієї системи;

2) з’ясуйте, чи є пара чисел 11 ; () розв’язком системи.

18.8 Система лінійних рівнянь має безліч розв’язків. Користуючись рисунком, на якому точками зображено два розв’язки системи:

1) знайдіть ще два розв’язки цієї системи; 2) з’ясуйте, чи є пара чисел () 43 ; розв’язком системи.

18.9 Чи існує таке значення a, за якого:

1) система рівнянь yx yax =− = { 3, має безліч розв’язків?

Якщо так, то знайдіть його;

2) система рівнянь yx yax = = { 2, не має розв’язків?

Проєкт майб

1) () 20 ; , x xy += += { 20 2 , ; 3) 31 ; () , xy

1) y yx = =− { 2 3 , ; 3)

Слово коефіцієнт походить

від латинських co — спіль­

но, разом і efficients — той, що виробляє і позначає

в математиці сталий або ві­

домий множник при іншій, зазвичай невідомій величи­

ні. Але це не єдиний зміст

цього терміну. Інше значен­

ня — відносна величина, що

визначає певну властивість.

Тобто поняття коефіцієнт

пов’язане з порівнянням.

Коефіцієнти зустрічаються

в різних сферах життя:

y коефіцієнт активності ре­

човини в хімії;

y коефіцієнт корисної дії

у фізиці;

y коефіцієнт зайнятості населення в соціології;

y коефіцієнт ануїтету в еко­

номіці;

y дихальний коефіцієнт у ме­

дицині;

y коефіцієнт інтелекту IQ

тощо.

8 xy+= xy+=24

рівнянь xy−=21 і 111456 xy+= , побудованими

1. Запишемо систему рівнянь за умовою задачі: xy xy −= += { 21 111456 , .

2. Розв’яжемо цю систему рівнянь графічним способом.

1) Будуємо в одній системі координат графіки двох рівнянь xy−=21 і 11 1456xy+= .

2) Знаходимо координати точки перетину цих графіків: Axy ; () .

Поміркуйте й дайте відповіді на запитання.

y Чи вдалося вам знайти координати точки A?

y Якщо вдалося, чи впевнені ви, що

(to express variable)

1.

2.

3.

4.

5.

6. Записати відповідь.

ТРЕНУЄМОСЯ 1 Розв’яжіть систему рівнянь:

1) yx+= 8 ; 3) xy+=35; 5) 2xy =− ; 7) yx−=34; 2) xy−= 9 ; 4) 21 yx−= ; 6) −= 5xy ; 8) 47 xy−= .

ПРИКЛАД 2

Виразіть

34 815 xx+− =−

y Вибрати будь­яку змінну з першого рівняння системи;

y вибрати будь­яку змінну з другого рівняння системи;

y вибрати будь­яку змінну з простішого рівняння

системи;

y в ибрати з будь ­ я кого рівняння системи ту змінну, коефіцієнт при якій дорівнює 1 або –1.

ПРИГАДАЙТЕ

Властивості рівнянь

y Якщо до обох частин рівняння додати (відняти)

одне й те саме число;

y якщо в рівнянні пере ­

нести доданок з однієї

частини рівняння в іншу, змінивши його знак на протилежний;

y якщо обидві частини рівняння помножити (поділити) на одне й те саме відмінне від нуля число, то отримаємо рівняння, яке має такі самі корені, що й дане.

підручника видавництва

Проєкт майб

Відповідь: 25 1 ,; () .

і зведення подібних

рівнянь.

xy xy += += { 39 25 , ; 1) xy =−93

2) 93 39 () +=yy

93 39 −+ = yy

99 =

СЛІД ЗНАТИ! Якщо точки A 1 5 ; () і B 3 7 ; () належать графі­

функції ykxb=+ , то, підставивши координати

k і b: 5 7 1 3 =⋅ + =⋅ + { kb kb , .

Проєкт

якщо: 1) A 12 ; () , B 52 ; () ; 4) A 31 ; () ; B () 15 ; ; 2) A 01 ; () ; B 31 ; () ; 5) A 15 ; () ; B () 1;21 ; 3) A 71 ; () ; B () 39 ; ; 6) A () 22 ; ; B1;11() .

# BE SMART

Найдавніший у світі опис роз­

в’язування систем лінійних рівнянь, про який нам відо­

мо, міститься у китайській бамбуковій книзі Chu Chang

Suan Shu (Чу Чанг Суань Шу). Її вік становить приблизно 2000 років. IQ

ПРАКТИЧНЕ ЗАВДАННЯ

1. Позначте вагу ананаса, груші, яблука та дині змін­

підручника

ними a, b, c, d відповідно.

2. Складіть рівняння за першими трьома рисунками.

3. Скористайтеся методом підстановки й визначте кількість яблук на чет ­

вертому рисунку.

Проєкт майбутнього

золотої корони 704 г, об’єм — 46 см3. Скільки грамів срібла у складі корони, якщо густина золота близько 19 г/см 3, а

срібла — 10,5 г/см3?

Розв’язання.

1. Складемо таблицю за умовою задачі.

складових (см3)

2. Складемо систему

3. Розв’яжемо систему

корони (см3)

Згідно з легендою, цар Сиракуз Гієрон II мав одержа­

ти корону із чистого золота,

але в нього виникла підозра, що майстер додав до

золота срібло. Славнозвіс­

ний Архімед довів, що цар

правий, визначивши густину

матеріалу корони. Масу

підручника

корони він знав, а об’єм

знайшов завдяки своїй спостережливості. Приймаючи ванну, Архімед зрозумів, що будь­яке тіло, занурене у воду, витісняє об’єм води, що дорівнює об’єму тіла.

3) Розв’яжемо отримане рівняння: −= 85 170 , y ; y = 20 .

4) Знайдемо масу срібла у сплаві: 10 5105 20210 ,, y =⋅ = (г).

Відповідь: 210 г срібла.

Поміркуйте й дайте відповіді на запитання.

Проєкт

y Чи зручно було б вам розв’язувати цю систему рівнянь графічним способом? Чому?

y Чи раціонально було б застосовувати спосіб

змінної? Чому?

y Як ви вважаєте, чому перше рівняння системи помножували на –19?

28 90 9 x x x y y y + =− =− { + += , ;

99 x =−

x = 1

Розв’язуємо отримане рівняння. 71 1 ⋅+ =− () y

видавництва

ТРЕНУЄМОСЯ 1

Розв’яжіть систему рівнянь:

1)

3)

РОЗМИНКА 1

системи, щоб отримати два рівняння з протилежними коефіцієнтами при одній зі змінних.

рівнянь, розмістивши подібні доданки (доданки з однаковими змінними) один під одним. xy xy −= −= {

почленно

Проєкт

майб

1)

1. Записати систему рівнянь, розмістивши

одним.

підручника

протилежними числами.

Проєкт

2. Домножити (за потреби) одне чи обидва рівняння системи на таке число, щоб коефіцієнти

3. Додати почленно отримані рівняння.

4. Розв’язати отримане рівняння

5. Підставити знайдений корінь рівняння

заданої системи

6. Перевірити, чи є

7. Записати відповідь.

ПРАКТИКУМ 20.1

розв’язувати

систему рівнянь?

Проєкт

1) 32 3 xy−= , xy+=51, −+ = xy 2 ; 2) xy−= 2, xy+=25 , 45 7 xy+= ; 3) 54 6 xy−= , xy+=46 , 35 xy−= ; 4) 72 13 xy−= , = xy514, xy+=38; 5) 30 58xy−= , , 311 xy+= , =− 45 22 xy ; 6) 92 8 xy+= , 05 29 , xy+= , −+ = 47 43 xy .

MATH FOR LIFE

ЗНАЮ, ВМІЮ, МОЖУ

У завданнях 1–5 виберіть одну правильну відповідь.

1 З рівняння 78 ху+= виразіть змінну у через змінну х. АБВГ

ух =−87 ух =+87 ух =− + 87 ух =−87

2 Використовуючи метод підстановки для системи рівнянь x xy = += { 3 12 , , ви -

значте значення y. АБВГ у = 9 у = 6 у = 15 у = 4

3 Якщо до системи рівнянь xу xy −= += { 310 53 8 ,

застосувати метод додавання, то отримаємо рівняння…

АБВГ 618 у = 62 у = 618 x = 62 x =

4 Визначте розв’язок системи рівнянь xy xy −= += { 1 24 , методом підстановки. Чому дорівнює значення

# BE SMART

Якщо алгебра стане вашою улюбленою дисципліною, ви навчитеся розв’язувати системи лінійних алгебраїчних рівнянь різними методами, зокрема:

y Матричним методом y Методом Гаусса

y Методом Гаусса Жордана

y Методом Крамера y LU-розкладанням

y Методом ітерації тощо

Проєкт майбутнього

Проєкт

територіях України необхідно придбати 12 одиниць техніки — броньованих автомобілів та роботів-саперів, на загальну суму 30 млн. г. о. Один броньований автомобіль коштує 3,2 млн. г. о., а один робот-сапер — 2 млн. г. о.

Скільки броньованих автомобілів та скільки роботів-саперів можна придбати, виконавши зазначені умови?

Розв’язання

1

Аналізуємо умову задачі

Основнівеличини: кількість броньованих автомобілів,

кількість роботів-саперів, загальна кількість одиниць тех-

ніки, загальна вартість техніки, ціна броньованого автомобіля, ціна робота-сапера.

Аналізвзаємозв’язківміжвеличинами : нехай х —

кількість броньованих автомобілів, у — кількість роботів-

саперів. Тоді вартість усіх броньованих автомобілів становить 32 , x млн. г. о., а всіх роботів-саперів — 2y млн.

(mathematical model of a problem

(system of linear equation with two variables)

спосіб (graphical method)

підстановки (substitution method) спосіб додавання (method of addition)

(linear combinations method)

ПРИГАДАЙТЕ!

Математичне моделювання — це процес побудови й вивчення математичних

моделей, тобто процес розв’язування деякої не ­

математичної задачі чи

проблеми математичними

методами.

Математична модель —

це опис реальної ситуації

математичною мовою, тобто мовою математич­

них понять, формул, рів ­

нянь тощо.

умови задачі

модель задачі

3

2. Створити

3. Розв’язати отриману систему

4.

5.

Задачі геометричного

ПРИКЛАД 1

Маскувальна сітка має форму прямокутника (див. рисунок), периметр якого дорівнює 28 м. Якщо ширину

прямокутника збільшити на 6 м, а а довжину зменшити на 2 м, то площа цієї сітки збільшиться на 24 м2. Визначте

початкові довжини сторін прямокутника.

Розв’язання:

1 Аналізуємо умову задачі

Основнівеличини: довжини сторін, периметр і площа

прямокутника.

Аналізвзаємозв’язківміжвеличинами: нехай х м —

ширина прямокутника, у м — довжина. Тоді після зміни

довжин сторін вони дорівнюватимуть x + () 6 м і y () 2 м.

2 Створюємо математичну модель задачі: складаємо си-

Прямокутник

Початкові значення (м)

Початковий периметр (м)

Початкова площа (м2)

Змінені значення (м)

площа (м2)

Ширина х 2 xy + () xy x + 6 xy + () ()62 Довжина уy 2

За умовою задачі складаємо два рівняння. Початковий периметр прямокутника дорівнює 28 м, тому 228 xy + () = . Площа сітки збільшиться на 24 м 2, тому xxyy + () () −= 62 24 . Обидва рівняння мають виконува-

228 62 24 x xx y yy + () = + () () −=    , .

3 Розв’язуємо отриману систему

маса 10 %-г о розчину, у г

Систему рівнянь

становки, або способом додавання. У результаті отримаємо x = 40 , y = 10.

4 Аналізуємо отримані результати з огляду на умову задачі, знаходимо решту шуканих величин, записуємо відповідь

Шукані числа мають бути додатними, отже, знайдені числа задовольняють умову задачі.

Отже, фармацевтка має взяти 40 г 10%-го розчину

лимонної кислоти і 10 г 15%-го розчину.

Відповідь: 40 г, 10 г.

Задачі економічного змісту

ПРИКЛАД 3

За оренду двох велосипедів і двох шоломів

1800 грн. Після того як оренда велосипеда подорожчала

на 50 %, а оренда шолома подешевшала на 10 %, за оренду

одного велосипеда й одного шолома заплатили 1290

1) одного велосипеда й одного шолома до зміни цін (у грн.).

2) одного велосипеда після

Розв’язання:

1 Аналізуємо умову

3

21800 xy + () = і 15 09 1290 ,,xy+=

21800 15 09 1290 x x y y + () = +=

21800 15 09 1290 x x y y + () = +=

, ,,

Розв’язання:

1 Аналізуємо умову задачі

Основнівеличини: швидкості руху обох випробувачів, співвідношення між цими швидкостями, час руху.

Аналізвзаємозв’язківміжвеличинами: уже задано, що х м/с і у м/с — швидкості руху першого і другого випробувачів відповідно. Відстань, яку подолав кожний випробувач, знаходимо як добуток швидкості на час руху.

2 Створюємо математичну модель задачі: складаємо систему рівнянь В умові задачі наведено два твердження щодо руху

випробувачів. Урахуємо їх окремо.

ВипробувачШвидкість

Проєкт

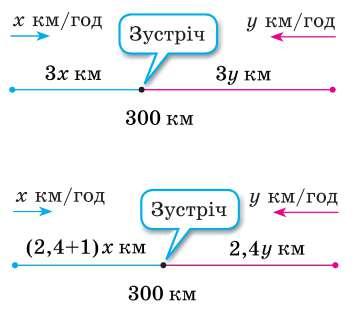
33 300 34 24 300 x x y y += += { , ,, ; x x y y += += { 100 17121500 , .

Систему рівнянь доцільно розв’язати способом підстановки. У результаті отримаємо x = 60 , y = 40 .

4

Аналізуємо отримані результати з огляду на умову задачі, записуємо відповідь

Шукані числа мають бути додатними, отже, знайдені числа задовольняють умову задачі. Отже, швидкість автоколони з Рівного 60 км/год, із Кам’янця-Подільского — 40 км/год.

Відповідь: 60 км/год, 40 км/год.

ПРАКТИКУМ

21.1 Периметр рівнобедреного трикутника дорівнює 144 см. Визначте довжини його сторін, якщо бічна сторона трикутника в 4 рази більша за його основу.

21.2 Перша трав’яна суміш містить 25 % м’яти, а друга — лише 5 %. Скільки грамів кожної суміші потрібно взяти, щоб отримати 80 г трав’яного чаю, що містить 10 % м’яти?

21.3 Два 3D-принтери за день мали разом надрукувати 42 корпуси для ліхтариків. Коли перший 3D-принтер виконав половину свого завдання, а

— третину свого, виявилося, що перший 3D-принтер надрукував на 1 корпус більше,

мав надрукувати кожний 3D-принтер за день?

21.4 У двох каністрах

ністри перелили в другу, пального

21.5

# BE SMART

У завданнях 1–5 виберіть одну правильну відповідь.

1 На першому рівні комп’ютерної гри треба перемогти n монстрів, а на другому рівні — на 10 монстрів більше.

Скільки монстрів треба перемогти на другому рівні цієї гри? Укажіть правильний вираз.

АБВГ

n 10 n + 10 n ⋅ 10 n :10

Проєкт

2 На виставці скульптур італійські митці представили m робіт, а українські — на 20 % менше. Скільки робіт

представили українські митці? Укажіть правильний вираз.

АБВГ m + 20 m 20 12 , m 08 , m

3 Яку відстань долає скат за 20 хв, рухаючись зі швидкістю 6 км/год?

АБВГ 1 км1,2 км2 км3

4

5

(1–3) та правильною відповіддю на нього (А–Г). 1 2 3 За скільки годин один

7

3D-принтер надрукує 48 ваз?

Скільки ваз надрукують два

3D-принтери за 1 годину?

Скільки ваз надрукує один

3D-принтер за 3 години?

Земельна ділянка для проведення змагань пластунів має форму прямокут-

ника (див. рисунок), периметр якого дорівнює 50 м. Якщо ширину прямокутника збільшити на 1 м, а довжину зменшити на 2 м, то площа цієї ділянки зменшиться на 37 м2. Розв’яжіть задачу, склавши систему рівнянь.

21.7

і

якою

21.8 Два

на

безпілотники

з пунктів А і В, відстань між якими дорівнює 50 км. Якщо безпілотники рухатимуться назустріч один одному, то зустрінуться через 15 хв, а якщо в одному напрямі так, що більш швидкий опиниться позаду, то він наздожене того, що рухається повільніше, через 1 год 15 хв. Із якими швидкостями рухаються безпілотники?

21.9 Середнє арифметичне двох чисел дорівнює 52. Визначте ці

21.10

21.11

ЧИ ВІДОМО ВАМ?

Українські діти не тільки ві­

рять у перемогу, але й до­

помогають її наблизити.

Малята й підлітки продають

поробки та застосовують

свої таланти, щоб зібрати

кошти на потреби українських захисників.

1 Ви познайомилися з новим математичним поняттям системою рівнянь.

рівнянь — це

у

кілька рівнянь об’єднані фігурною дужкою. Сутність системи рівнянь: розв’язок (множина розв’язків) системи одночасно є розв’язком усіх її рівнянь.

Розв’язати систему двох лі- нійних рівнянь із двома змінни- ми означає знайти всі її розв’яз- ки або довести, що їх немає.

Розв’язком системи рівнянь із двома змінними називають

2 Ви дізналися про способи розв’язування систем лінійних рівнянь із двома змінними.

Способи розв’язування

систем

двома змінними:

y графічний спосіб;

y спосіб підстановки;

y спосіб додавання.

3 Ви дізналися, що системи лінійних рівнянь із двома змінними також можуть бути математичними моделями прикладних задач.

підручника видавництва"Ранок"

Проєкт майбутнього

пару значень змінних, які задовольняють кожне з рівнянь, тобто перетворюють їх у правильну рівність.

1 Укажіть пару чисел, яка є розв’язком

системи рівнянь xy xy −= += { 1 9 , .

0;91 () 10 9; () 45 ; () 54 ; ()

2 Застосуйте спосіб підстановки для роз-

в’язування системи рівнянь y xy =− += { 2 7 , .

Укажіть одержане значення х.

Проєкт

АБВГ x =−9 x = 9 x = 5 x =−5

3 Укажіть рівняння, одержане в ході розв’язування системи рівнянь xy xy −= += { 91 59 59 , способом додавання.

АБВГ 458 y = 660 y = 458 x = 660 x

6

майбутнього

7

8

9 Зранку киянин протягом 30 хв їхав на електросамокаті, а потів 10 хв ішов пішки, усього подолавши 9800 м. Увечері він 5 хв ішов пішки, а потім 40 хв їхав на електросамокаті й подолав разом 12 400 м. Вважайте, що швидкість руху киянина на електросамокаті дорівнює x м/хв, а пішки — y м/хв.

1) Складіть систему рівнянь за умовою задачі.

2) Визначте x та y.

1 Знайдіть значення алгебраїчного виразу:

1) 23 x + , якщо x = 1; 5) xy 4 , якщо x =−3, y = 5; 2) 32 x , якщо x = 2; 6) 6xy , якщо x = 8 , y =−2 ; 3) x 3 5 , якщо x = 9; 7) 05 4 , y x , якщо x =−100, y =−4; 4) x 2 7 + , якщо x = 6; 8) y x 5 02 , , якщо x =−10, y =−20.

2 Для дослідження ефективності реклами визначають рейтинг кліків СТR (клікабельність), який обчислюють за формулою CTR k n =⋅ 100 %, де n число показів певного оголошення, k число кліків на це оголошення.

1) Визначте СТR, якщо: а) n = 30, k = 6; б) n = 74 , k = 37 . 2*) З’ясуйте,

1) 55 1 aa+−(); 5) 05 14 83 4 , aa() () ; 2) 62 6 + ()aa ; 6) 01 1350 13 6 ,, () () aa ; 3) 43 2 24 2 a a + () ; 7) 5 11 22 11 04 25 12 5 aa() (),, ; 4) 90 15 27 3 a a +−() ; 8) 3 8 16 40 2307 5 () () aa ,, .

Проєкт

а) третьої хвилини; б) п’ятої хвилини; в) сьомої хвилини; г) m-ї хвилини? 2*)

1) Відтворіть

а) 7 2 xy і 1 7 46 xy ; в) 10xy , 4 22 xy і 0125 33 , xy . б) 02 10 5 , xy і 5 510 xy ; 2*) Поміркуйте, чи

результат бути виразом: а) m 2025 ; в) 1000 4 3 mn () ; б) 216; г) 04 23 57 3 , mn () . 11 Спростіть вираз: 1) 34 39xx + ; 5) 62 14 23xyxy −+ () + (); 2) 5114 11 + xx ; 6) xyxy +− () + () 94 1 ;

3) 8178 3 xx +− () ; 7) 3117 95 22 xyxy() −+ () ;

4) 15101210() xx ; 8) 5146 3 22 xyxy −+ () +− () .

(х і у натуральні числа).

1) Скільки всього сомів та вугрів мешкає у двох водоймах? (Запишіть вираз та спростіть його.)

2) На скільки більше сомів та вугрів разом мешкає у водоймі В, ніж у водоймі А? (Запишіть вираз та спростіть його.)

3) За якого значення х кількість сомів у водоймі В на 450 рибин перевищуватиме кількість сомів у водоймі А?

4*) У скільки разів кількість сомів у

1) 36 4 2 xxx−+ () ; 5) xx 2 310 + () () ;

2) 47 1 2 xxx() ; 6) xx() + () 14 5 2 ;

3) 611() ()xx ; 7) xxx() +− () 12 2 ;

4) xx + () ()912 ; 8) xxx() −+ ()23 1 2 .

aaa mnm n n m = () = ()

ababnnn = ()

abcannbcnn = ()

2x 3y 5x 6y

«Mitsubishi» «Hyundai»

ЧИ ВІДОМО ВАМ?

«Mitsu bishi» з японської перекладається як «Три ромби»

ПРИГАДАЙТЕ!

1. Винесення спільного множника за дужки.

2. Групування.

3. Використання формул скороченого множення

3x

ПРИГАДАЙТЕ!

aabbab abab 22 2 2 ++ =+() = =+() + () aabbab abab 22 2 2 −+ =−() = =−() ()

1) кількість автомобілів корпорацій «Mitsubishi» на стоянці;

Проєкт майбутнього

2) кількість автомобілів корпорацій «Hyundai» на стоянці;

3) загальну кількість автомобілів на стоянці.

4*) Значення x, за якого кількість автомобілів корпорацій «Hyundai» на стоянці дорівнюватиме 600. 15 Розкладіть на

1) aa 5 3 + ; 5) 58 8 aba + () −+() ;

2) 5 2 aa ; 6) abb () +−()32 3 ; 3) 4 2 abab ; 7) aabab 32 44 −+ ; 4) abab + 3 2 ; 8) ababb3233 ++ + .

16 На рисунку

розставлені рядами, як

на схемі, загальна кількість

1) Визначте кількість рядів. 2) За якого значення x кількість

1) 2 2 xy + () ; 5) xy 52 2 + () ; 2) xy + () 3 2 ; 6) xy 73 2 + () ; 3) x 3 2 7 () ; 7) 40 5 10 6 2 xy () , ; 4) 6 4 2 () y ; 8) 02 10 98 2 , xy () .

1) 32 3 22 +⋅ ⋅+xx ; 5) yy 2

1) Скільки бійців стояло в кожному ряду під час тренування?

2) За якого значення х кількість рядів дорівнює 11? 3*) Початок тренування зафільмували з дрона. Яка геометрична фігура (круг, трикутник, квадрат) найточніше описує розташування військових на початку тренування?

20 Розкладіть на множники:

1) 6 2 2 mn() ; 4) 64 25 22 mn ; 7) 036 28 , mn ; 2) mn 2 2 4 () ; 5) n m 2 2 4 121 ; 8) mn 10 2 016 , . 3) 814922 mn ; 6) 144 2 2 9 n m ;

21 На рисунку зображено схему патріотичної нашивки. У центральному квадраті зі стороною 3 см буде розміщено стилізований Герб України. За межами центрального квадрата, усередині більшого квадрата зі стороною х см, буде розміщено патріотичні написи.

1) Яка площа на майбутній вишивці виділена для патріотичних написів?

2*) За якого значення х площа, виділена для патріотичних написів, дорівнюватиме 16 см2? 22 Розкладіть на множники:

1) 11 3 3 ab() ; 4) ab33 27 + ; 7) 0 001 33 1 27 , ab + ;

2) ab 3 3 12 () ; 5) 15 64 33 3 ⋅−ab ; 8) 1 8 33 0216 ab + , .

Проєкт майбутнього

3) 8 33ab + ; 6) 1251633 3 ab −⋅ ;

52 25 10 4 22 xyxxyy () ++ () .

3 x 3 x

Архітектурна пам’ятка Харк ова Д ержпром, а бо Будинок Державної промисловості, побудований у 1925–1928 рр, став першим на той час 13-поверховим хмарочосом. Будівля має унікальну конструкцію, саме для її створення була розроблена технологія індустріального залізобетону.

підручника

СЛІД ЗНАТИ!

Основні способи задання функції:

y аналітичний

y табличний

y описовий

y графічний

1) Скільки відеоматеріалів

2) Задайте формулою

Проєкт майбутнього

кількості N

жених відеоматеріалів від часу t (у хв).

3) Знайдіть значення t, при якому N = 2400 .

1) Залежність M від n така, що кожному натуральному числу n ставиться у відповідність число М, яке втричі більше за n.

2) Залежність у від х така,

3) Залежність

2) Функцію задано аналітично, формулою

yxx =+ + 2 10 25 . Знайдіть:

а) значення функції, якщо x = 1;

б) значення аргумента, для якого значення функції дорівнює 0.

3) Функцію задано таблицею. Знайдіть:

а) значення функції, якщо x = 2;

б) аргумента, для якого значення функції дорівнює 7.

29 За графіком, поданим на рисунку, знайдіть:

1) значення функції, якщо x = 1;

2) значення аргумента, якому відповідає значення

функції y =−2 ;

підручника

3) область визначення функції; 4) область значень функції.

30 На рисунку зображено графік функціональної залежності заряду y акумуляторної батареї мобільного телефону від часу заряджання x.

1) Яким був заряд акумуляторної батареї, коли телефон поставили заряджатися x = () 0 ?

2) Яким був заряд акумуляторної

3) Через який час (у хв) після підключення до джерела живлення заряд

4) Через який час (у хв)

100 %?

31 Функція задана формулою ykxb=+ , її

проходить через точку A. Знайдіть значення невідомого коефіцієнта, якщо:

1) yxb =+ , A () 25 ; ; 5) ykx = , A 0;63 ();

2) yxb =+ , A () 19 ; ; 6) ykx = , A 10 40 ; () ;

3) yxb =+ , A 05 12 ,; () ; 7) ykx =+ 73 , , A 5177 ;, ();

4) yxb =+ , 19;,02 () ; 8) ykx =− 95 , , A 4295 ;, () .

1) 31980 x −= ; 5) 45 320xxx() −=

2) 22331 x += ; 6) 38 9246 () += + xxx ; 3) 3311 22 11 −=xx ; 7) 14 35 319 () =−

Проєкт

; 4) 153015 45 xx −= ; 8) 33 5252184 () =+

СЛІД ЗНАТИ!

Чи є пара чисел розв’язком системи рівнянь?

y Якщо пара чисел задовольняє обидва рівняння системи, то вона є р озв’язком с истеми рівнянь.

y Якщо пара чисел не задо вольняє хо ча б од не з рівнянь, то вона не є розв’язком системи рівнянь

теми рівнянь: 1) yx y =− = { 2 1 , ; 4) yx yx = −= { 3 39 0 , ; 7) 51 10 22 xy xy −= −+ =− { , ; 2) yx y =+ =− { 3 1 , ; 5) xy xy −= −= { 0 55 5 , ;

# BE SMART

2

3

Проєкт майбутнього

а кожен другокурсник 3, причому всього було виконано 180

АБВГ 23 180 xy+= 32 180 xy+= 5180 xy = 5180 += xy

7 Розв’яжіть рівняння 9182 0 2 xxx −+ −= , розклавши його ліву частину на

ники.

8 Побудуйте графік рівняння 28 xy+= . Перевірте, чи належить точка A 32 ; () цьому графіку.

9 Розв’яжіть систему рівнянь 71022 25 2 xy xy += += { , .

10 За о ренду 4 п ікапів і 4 м опедів з а добу заплатили 440 г. о. Після того як оренда пікапа подешевшала на 10 %, а оренда мопеда подорожчала на 20 % від попередньої

Повторення матеріалу, що вивчався у 5–6 класах

1. 1) 400; 2) 300; 3) 5; 4) 10; 5) 60; 6) 180; 7) 470; 8) 8200. 2. 1) 370; 2) 410; 3) 930; 4) 650; 5) 43,5; 6) 51,9; 7) 14; 8) 26. 3. 1) 0; 2) 0; 3) 9b ; 4) 18c ; 5) 46 y ; 6) 57a ; 7) 10 p ; 8) 40n . 4. 1) 37; 2) –55; 3) 25; 4) 20; 5) 3; 6) 9;

7) 0; 8) 0. 5. 1) 1; 2) 1; 3) 1; 4) 1; 5) 1 4 ; 6) 1 6 ;

7) 31 51 ; 8) 24 67 . 6. 1) 3 1 2 ; 2) 4 1 3 ; 3) 7 4 5 ; 4) 6 5 6 ; 5) 7 24 ; 6) 17 21 ; 7) 3 1 14 ; 8) 7 5 6 . 7. 1) 1; 2) 1;

3) 4 5 ; 4) 5 6 ; 5) 2 1 2 ; 6) 5; 7) 0; 8) 0. 8. 1) 1; 2) 1;

3) 10; 4) 12; 5) 1 30 ; 6) 1 14 ; 7) 1 7 ; 8) 3. 9. 1) 40;

2) 60; 3) 53; 4) 72; 5) 0,5; 6) 0,06; 7) 4720; 8) 2512. 10. 1) 4; 2) 3; 3) 6; 4) 9; 5) 70; 6) 125; 7) 20; 8) 13. 11. 1) 150; 2) 210; 3) 120; 4) 180; 5) 160; 6) 500; 7) 1000; 8) 1250. 12. На 25 %.

13. На 60 %. 14. На 20 %. 15. На 40 %.

16. 1) 6; 2) 10; 3) 80; 4) 32; 5) 18; 6) 27; 7) 250; 8) 490. 17. 100, 45, 95. 18. 50, 84, 46.

19. 1) a b = 2 5 ; 2) a b = 3 ; 3) a b = 4 7 ; 4) a b = 4 ;

5) a b = 2 9 ; 6) a b = 4 5 ; 7) a b = 24 ; 8) a b = 7 . 20. 1) 2;

2) 0; 3) 14; 4) 17; 5) 9; 6) 12; 7) 4,5; 8) 5,25. 21. 1) –30; 2) –50; 3) 5; 4) –5; 5) –24; 6) –3; 7) 4; 8) 50. 22. 1) –9; 2) –5; 3) 9; 4) 8; 5) 3; 6) 5; 7) 2; 8) 3. 23. 1) 22 x + ; 2) 12 3 + x ; 3) 510 x ; 4) 424 x ; 5) 21 7 ab ; 6) 832ba ; 7) −+ 14 6 ab ; 8) −+ 24 15 ba . 24. 1) 21; 2) 1; 3) –9; 4) –12; 5) –20; 6) –20; 7) 1; 8) 1. 25. 1) 12,4 > –34,1; 2) –5 < 0; 3) 72 9 24 3 = ; 4) 16 8 12 4 < ;

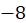
РОЗДІЛ 1 § 1

Проєкт майбутнього

1.1. 1) 0,2; 2) 3,8; 3) 1,7; 4) –0,2. 1.3. 1) –40; 2) 68; 3) –10; 4) 6. 1.4. 1) Не має; 2) має; 3) не має. 1.5. 1 – В, 2 – Е, 3 – Д, 4 – Б, 5 – А, 6 – г. 1.6. 1) 15; 2) 20; 3) 13; 4) 6; 5) ; 6) 18. 1.7. а) 4 км; б) 10 км; в) x :3 км. 1.9. а) 6; б) 11; в) x + 1. 1.10. 1) а) 100 2503⋅+ ⋅ ; б) 4202 10 3 ⋅+ ⋅ () ; в) t 20 2103⋅+ ⋅ (); 2) а) 350 грн; б) 280 грн; в) 70t грн. 1.11. 1) 513 a + () ; при a = 7 , a = 10 , a =−3; 2) 25 a + ; при a = 3 , a = 7 , a =−1. 1.12. 2) 440; 3) 333 300. 1.13. 1) 17; 2) 9; 3) –30; 4) 1,6. 1.14. 1) ab () 4 ; 32; 2) ab + () 2 ; –4; 3) abab 22 2 +− ; 4; 4) ab + () 2 5 ; –1. 1.15. 1) 7; 2) 42; 3) 89; 4) 1. 1.16. 1) 10; 2) 16. 1.17. а) 1720 м; б) 3440 м; в) 6880 м. 1.19. а) 10050ab + ; б) 42010ab + () ; в) tab 20 10 + () . § 2

2.1. 1) 1010ab + ; 2) 2525ab + ; 3) 21cb ; 4) 34mk + ; 5) 5011 52ab++ , ; 6) 30 41 8 xy .

2.2. 1) 2a ; 2) 2b ; 3) 2y ; 4) 2x ; 5) −+bc ; 6) 2abc +− . 2.3. 1) 150; 2) 120; 3) 10,5; 4) 2,5. 2.4. 1) Так; 2) ні; 3) ні; 4) так; 5) так; 6) так.

2.7. 2) xx +− + () = 22 0 ; 3) () +− = xyxyx 2 .

2.8. 1) 23ab + ; abc ++ 3 ; 82ab + ; 2) 142 м; 90 м; 268 м. 2.9. 1) 10 90 12 20 3 300 1200 ⋅+ ⋅+ ⋅+ ⋅ ; 2) 3109012203 300 1200 ⋅+ ⋅+ ⋅+ ⋅ () ; 3) n 10 90 12 20 3 300 1200 ⋅+ ⋅+ ⋅+ () .

2.10. 1) 0; 2) a; 3) 3a; 4) 35ab . 2.11. 1) 15; 2) 10; 3) 28a; 4) 26b. 2.13. 1) Так; 2) ні; 3) так; 4) ні; 5) так; 6) ні. 2.14. 1) 34; 2) 855. 2.15. 1) 52ab + , 33ab + ; 2) 190 м, 1305 м.

2.16. 1) m 10 90 12 20 3 300 1200 ⋅+ ⋅+ ⋅+ ⋅ () ; mn 10 90 12 20 3 300 1200 ⋅+ ⋅+ ⋅+ ⋅ () ; 2) 1 344 000 г. о.

5) −< 2 3 2 5 ; 6) −> 7 4 7 2 ; 7) –3,602 > –3,612; 8) –0,138 > –0,831. 26. Через 2 год. 27. Через 3 год.

§ 3

3.1. 1) –29; 2) 12; 3) 713; 4) 185; 5) 244; 6) 2,375. 3.2. 1) 10 4 ; 2) 014 , ; 3) () 10 10 ;

4) () 01 7 , . 3.3. 1) 102 ; 2) 103 ; 3) 106 . 3.5. 1) 1; 2) 0; 3) 1; 4) –1. 3.6. 1) 12; 1200; 2) 1 72 ; 81 64 ;

3) 9; 24; 4) 0; 10000; 5) 10; 6) 3 16 . 3.8. 25 106 , .

3.9. 232 5 = ; 210 . 3.10. n 2 ; 6 2 n ; 10 2 n . 3.12. 1) 1; 2) 2; 3) 8. 3.14. 1) 16; 4; 1; 125; 2) 49; 1; –27; –1; 3) 1 25 ; 27 64 ; 1 36 ; 8 125 ; 4) 0,64; 0,81; –0,08; –0,000 01. 3.15. 1) –10; 2) –64; 3) –41;

4) 49 16 . 3.17. 1) 38; 2) 50; 3) 73; 4) 51. 3.18. 1) 1; 2) –2; 3) 0; 4) –2. 3.19. 1) 3443 > ; 2) 4236 = ;

3) 5335 < ; 4) 6932 > ; 5) 119, 617 , 618 ; 6) () 7 13 , 015 , () 7 14 ; 7) () 3 2 , () 2 8 , 23 . 3.21. 1) 9; 27; 81; 3n ; 2) 3 1 m n . 3.22. 1) –10; 2) –22; 3) –3. § 4

4.1. 1) 7; 2) 9; 3) 12; 4) 5; 5) 7; 6) 10. 4.3. 1) 0,5; 2) 9; 3) 25; 4) 1; 5) 64; 6) 216.

4.6. 1) 1 9 ; 2) 7 1 9 ; 3) 2 1 4 ; 4) 5 1 3 ; 5) 024 , ; 6) () 025 3 , . 4.7. 1) a 8 ; 2) a 9 ; 3) b 21 ; 4) b 20 ; 5) c; 6) 1. 4.8. 1) 25; 2) 64; 3) 343; 4) 3; 5) 9; 6) 228 .

4.9. 1) a 6 ; 2) b12 ; 3) c 20 ; 4) d 25 ; 5) a 16 ; 6) b 6 ; 7) c 12 ; 8) d 35 . 4.13. 1) 4; 2) 2; 3) 2; 4) 5;

5) 6,9; 6) 10 1 3 . 4.16. 2) 1; 3) 1. 4.19. 1) –128;

2) 729; 3) () 01 7 , ; 4) 10 000; 5) 16; 6) –10;

7) 256; 8) () 01 3 , . 4.22. 1) 8; 2) 1; 3) 3; 4) 5. 4.23. 1) x 2 ; 2) x; 3) x 3 ; 3) x 4 . 4.24. 1) 1; 2) 27; 3) 1; 4) 0,2. § 5

5.2. 1) 10 23 xy ; 2) 48 42 xy ; 3) 10000 42ab ;

4) 20 26 xy ; 5) 80 34 6 abc ; 6) 60 79ab . 5.3. 1) 9 55ab ; 2) 27 22ab ; 3) 3 6 ab ; 4) 9 86ab ; 5) b; 6) –1.

5.11. 1) 64 15 x ; 2) 025 12 , x ; 3) xy 49 7 ; 4) xy 2424 .

5.15. 1) nk; 4nk; 2) 500 000 г. о.; 2 000 000

г. о. 5.18. 2) 3 43 2 ba() () ; 3) 9 3 2 bab () () ;

4) abab 46 3 2 5 () ⋅ () ; 5) 10 4 32 57 2 abab() ⋅ () .

5.21. 1) 10 5 a ; –10; 2) 1 4 4 a ; 1 4 ; 3) 28 510ab ; –28; 4) ab1112 ; 1. 5.23. 1) 512 36 a ; 2) 64 51 a ;

3) 64 81 22 a ; 4) 1 13 36 26 8 ab . 5.25. 1) а) x 9 2 () ; б) x 6 3 () ; 2) а) xy 63 2 () ; б) xy 42 3 () ; 3) а) 1000 21 15 2 xy () ; б) 100 1410 3 xy () ; 4) а) 8 33 24 2 xy () ; б) 4 22 16 3 xy () . 5.26. 1) 36 9 xy ; 2) xy 15 7 ;

3) 90 1333 xy ; 4) 70 2122 xy . 5.28. 1) abab 52 4 2 6 () () ; 2) 53 98 46 2 abab() ⋅ () . § 6

6.10. 1) 2x; 2) 6x; 3) 16 6 22 xa ; 4) 9822 xa ; 5) 45 2 xax + ; 6) 94 2 xax + . 6.16. 1) а) 3mn ; б) 6mn ; в) 9mn ; 2)1800 дерев; 3) 240 кг.

6.19. 1) 4x ; –40; 2) 2 2 x ; 200; 3) 10 9 x + ; –91; 4) −+27 2 x ; –193. 6.20. 1) 2ab ; 2; 2) 6aba + ; 2; 3) 720 2 abab ; 3; 4) 943 2 abab ; 3. § 7

7.1. 1) 31224 32 xxx −+ ; 2) 21018 32 xxx +− ; 3) 12 222440 xyxyxy ;4) −+51555 22 xyxyxy ; 5) 12 3233642 xyxyxy −+ ; 6) −+ + 61430 33 43 xyxyxy .

7.4. 1) 34; 2) 40; 3) 6; 4) 6. 7.5. 5) –1; 6) 2.

7.61) 22 22 xxyyxy+− +− ;2) −+ ++ + 32 62 22 xxyyxy ; 3) xxyyxyxy 32 2 55 420 +− ; 4) ++ yxyxxyxy 32 2 44 24 6 ; 5) −+ +− +− 1510 8123 2 32 2 xxyyxyxy ; 6) 15 612302 5 32 2 yxyxxyxy ++ .

7.8. 1) 3 4 ; 2) 2 3 ; 3) 12; 4) 4; 5) 5 11 ; 6) 4 7 . 7.9. 1) xxx 321339 27 ++ + ;

2) xxx 32 11 26 16 ++ + ; 3) xxx3242528 + ; 4) xx 3 1930−+ ; 5) xyxyxyxyxy 223622 26 ++ −+ ; 6) 26 45 24 12 22 22 xyxyxyxyxy ++ .

7.10. 1) xx510 (); 510 2 xx ; 2) 1800 см2. 7.11. 1) а) 1050 x + () см, 15x см; б) 151050 xx + () см2; 2) 22 500 см2; 3) 225 г. о. 7.12. 99, 100, 101 років. 7.15. 1) 22 8 2 xx++ ;

2) 5305 32 xxx −+ ; 3) 63 30 54 2 xxx +− ;

4) xxxx 54 2 73 6 −+ . 7.16. 1) ab ; 2) a 2 3 + ;

3) 79 5 32 aabb ; 4) 3722 ab . 7.17. 1) –13; 2) –2; 3) 4; 4) 34. 7.19. 1) xx 2 54++ ; 2) xx 2 710++ ;

3) xx 2 1130−+ ; 4) xx 2 914−+ ; 5) 49 2 2 xx ;

6) 5163 2 xx ;7) 43418 2 xx+− ;8) 5296 2 xx+− .

7.20. 1) xxx 3232 6 ++ + ; 2) −+ −+xxx 3258 40;

3) ++xxx 32 99 ; 4) −+ +− 37 18 42 43 xxx ; 5) 61 2 xx+− ; 6) −+ + 1216 3 2 xx ;

7) 12 23 10 22 xxyy++ ; 8) 1451 40 22 xxyy−+ .

7.21. 1) 4 5 ; 2) –12; 3) 6 5 ; 4) 1 3 . § 8

8.1. 1) xxx 23 5 2 ++ ();

2) xxx 2347 3 () ; 3) 32 4 24 2 xxx−+ () ;

4) 43 2 3 xxx+− () ; 5) −+ + ()72 39 5 xxx ;

6) + ()93 2549xxx . 8.2. 1) abab 73 2 + () ;

2) abba9522 () ; 3) 4332 2 abab() ;

4) 29 33 3 abab + () ; 5) 32 35abba−+ () ;

6) 45 2 2 abab+− () . 8.4. 1) 10 32xx() + () ;

2) 16 41 2 xx + () + () ; 3) 22 1 yx + () ;

4) 73 4 yy() ; 5) xyx() ()32 3 ; 6) xyx + () () 25 .

2) ax() ()57 ;3) 19 13 3 () + ()xa ;4) xyy() + ()65 ; 5) 510 xyx() () ; 6) 26 2 yxxya −+ () () .

8.21. 1) 0; 4; 2) –1; 0; 3) 0; 2,5; 4) 1 3 ; 0; 5) –7; 5;

6) 2 3 ; 7. 8.22. 1) xx() + ()73 ; 2) xyy() + () 8 ;

3) yy() + ()51 ;4) xx + () ()610 ;5) 54 2 () + ()yx ;

Проєкт майб

8.6. 1) abab + () ++ () 2 ; 2) cdcd + () +− () 3 ;

3) abab + () + () 53 ; 4) cdcd + () + () 5 ;

5) aab + () 2 ; 6) abab() () 2 2 . 8.8. 1) –2; 10;

2) 2; 5; 3) –3; 3; 4) –4; 4; 5) –10; 0,5; 6) –0,5;

6. 8.10. 1) yyxy 21 2 () + () ; 2) xxx 2 43 1 () + () ;

3) yxy() + ()110 ; 4) xyx 2 11 1 + () () ;

5) 35 2 xyx + () () ; 6) yxy() + ()32 7 . 8.13. 1) 8;

2) 39 42 abcd +++ ; 3) 90. 8.14. 1) 5 учасників; 2) 11x; 12y; 3) 1112xy + ; 91.

8.15. 1) xyxyy + () +− ()22 3 . 8.16. 3) 31 3 2nn() ;

2) 21 2 24nn++ + () . 8.18. 1) 5y ; 2) 2x ; 3) 3 4 xy ;

4) 18xy ; 5) x; 6) y 2 . 8.19. 1) 33 ba() ; 2) 42ab + ();

3) aa 1 () ; 4) aab 22 + (); 5) abba 24 13 () ;

6) 62 32 22abab + () . 8.20. 1) xa + () + ()32 ;

6) yxy() ()25 4 . 8.23. 1) aa + () () 13 4 ; 2) aa + () ()72 ; 3) aa() ()51 . 8.24. 56 x () м. 8.25. 1) 6 м; 2) жовтого 25, синього 21, білого 22. 8.26. 1) bbnn42 1 + (); 2) bb n + ()13 1 . § 9

9.5. 1) x 2 3600 + ; 3616; 2) x 2 2500; –2491; 3) 4xy ; 4; 4) 4xy , –4; 5) 25 2 y ; 25; 6) 9 2 x ; 9.

9.7. 1) xy 22 2 + () ; 2) xy 33 2 () ; 3) 2 32 2 xy () ; 4) xy 23 2 2 + () ; 5) 5334 2 xy + () ; 6) 3526 2 xy () ; 7) 6 49 2 1 5 xy

; 8) 4 75 2 1 3 xy +

. 9.10. 1) 5616 a ;

2) 60 25 a ; 3) a 2 64 ; 4) a 2 81 + ; 5) aa 2 + ; 6) aa 2 04 + , . 9.15. 3123 72 432 2 2 xxx + () =+ + .

9.16. 1) 34 x + () см; 2) 912 x + () см. 9.20. 1) xx 2 69++ ; 2) 4422 xxyy−+ ; 3) 9302522 xxyy++ ; 4) 16 4 22 1 4 xxyy−+ .

9.21. 1) nn6321 ++ ; 2) mmnn 42 612 2 −+ ; 3) 25 10 63 48 nnmm ++ ;4) 1 16 10 57 14 464 nnmm −+ .

9.22. 1) 0; 2) x 2 ; 3) 16 8 22 xxyy−+ ; 4) 24xy . 9.24. 1) xb + () 2 ; 2) mn () 4 2 ; 3) mn + () 6 2 ; 4) 3 3 2 mn () . 9.25. 1) () xy 22 2 ; 2) −+() xy 32 2 3 ; 3) () 5363 2 xy ; 4) −+       3 87 2 1 4 xy . 9.26. 1) –1; 2) 3; 3) –5; 4) 3 4 . 9.28. 1) 25 y () см; 2) 25 2 y ()

см2. 9.29. 1) x () =− 51 2 , коренів немає; 2) x + () =− 72 2 , коренів немає.

10.1. 1) xy 42 ; 2) xy 26 ; 3) 4 28 xy ; 4) xy 10 2 9 ; 5) 16 25 1210 xy ; 6) 49 36 1414 xy .

10.2. 1) 1 4 1 9 22ab ; 2) 4 81 9 25 22cd ;

3) x y 14 2 36 ; 4) x y 2 12 49 . 10.5. 1) m 2 ;

2) m 2 ; 3) 210 2 mm + ; 4) 24 2 mm + ; 5) 1272 m ; 6) 14 2 2 mm . 10.12. 1) –40; 2; 2) –6; 40; 3) –9; 7; 4) –8; 10. 10.13.50 років. 10.14. 1) ππ rr + () 2 2 2 ;

2) 41 π r + (); 3) 20 62 8 π≈ , м2; 4) 63. 2) 49 28 nm . 8. x =−4 або x = 5 . 10.16. 2) –1; 1; 3) –5; 5. 10.17. 1) 16 22 xy ; 2) xy 22 009 , ; 3) 42522 xy ; 4) 0014922 , xy . 10.18. 1) xy 62 ;

2) 9 24 xy ; 3) x y 10 2 16 ; 4) x y 8 12 25 009 , .

10.10. 1) 100 1 2 y ; 2) yynn 2229 ++ ;

3) 96 25 22 yynn−+ ; 4) 64 816 22−+yynn .

10.20. 1) 9999; 2) 9775; 3) 80,99;

4) 99 9 25 . 10.21. 1) m 2 ; 2) 26 2 mm + ;

3) 10 2 2 mm ; 4) 432 m . 10.22. 1) xtxt() + ()1414 ;

2) 77xtxt() + () ; 3) xx tt22 55

+ 

4) 2 9 2 9 6677 xtxt

;

. 10.23. 1) nn + () 24 ;

2) nn() 10 ; 3) nn + () + ()323 ; 4) 53 51nn() + () .

10.24. 1) –5; 5; 2) –0,3; 0,3; 3) –8; 9,2; 4) –2,5; 3,5. 10.25. 1) –1; 1; 2) –3; 3; 3) –2; 2. § 11

11.3. 1) 8; 2) –1; 3) 40; 4) 50.

11.4. 1) 14m ; –35; 2) 19m ; –71; 3) −+3432 2 m ; –143;

підручника видавництва

3) 0; 4) 0. 11.12. 1) 27 33 xy + ; 2) xy 33 64 ; 3) 12534333 xy + ; 4) 1 125 33 1000 xy . 11.13. 1) 27;

2) 90. 11.14. 1) −+12m ; 13; 2) 21616 2 m ;

–184. 11.15. 1) xyxxyy () ++ ()77 49 22 ; 2) 636622 xyxxyy + () −+ () ;

Проєкт майбутнього

4) 12560 2 m ; –115. 11.7. 1) aaa + () −+ ()36 21 2 ; 2) 69 3 2 () −+ ()bbb ; 3) 21 24 2 xxx() −+ () ;

4) 23 636 2 yyy + () ++ () ; 5) xxxyy 22 1575−+ () ;

6) −+ + () yxxyy 1081822 . 11.8. 1) а) x 3 ;

б) x + () 1 3 ; в) xxxxx 3 3 32 12 33 1 ++() =+ ++ ;

2) xxxx + () −= ++ 13 31 3 32 . 11.10. 2) 0;

++

3) 1 2 1 4 1 2 22 xyxxyy

; 4) 03 50 09 15 25 22 ,, , xyxxyy + () −+ () . 11.16. 1) 13; 2) 30; 3) 0,25; 4) 76. 11.17. 1) mx 3 ; 2) mx + () 1 3 ; 3) 23 3 32 mxmxmxm ++ + . § 12

12.1. 1) aaa 3 11() + () ; 2) aaa 5 11() + () ; 3) aaa 8 66() + () ; 4) aaa 7 55() + () ; 5) 27 7 22 aabab () + () ; 6) 53 3 22 babab () + ().

12.2. 1) xy() + ()31 2 ; 2; 2) yx + () () 21 3 2 ; 2,4; 3) xy() + ()54 2 ; 90; 4) xy + () ()35 2 ; 1600.

12.3.1) 12 212 () ++ () yxy ;2) 13 213() + ()xyy ; 3) () −+ () 92 29 2 axa ; 4) 2152 15 2 xbb +− () + () ; 5) 83 28 3 + () +− () nmn ;6)() −+ () 10 32 10 3 nmn .

12.4. 1) xyx() + ()25 ; 2) xyx() + ()34 ; 3) xxxy() + () + () 22 ; 4) xxxy() + () () 33 ; 5) yxyxxy() + () ++ () 2 ;6) xyxyxy() + () −+ () 3 .

12.5. 1) aaa + () () + () 51 1 ; 2) 81 1 () () + ()aaa ; 3) aaa() () + () 71 1 ; 4) aaa() () + () 31 1 ; 5) aaa() () + () 12 2 ; 6) aaa() () + () 23 3 .

12.8. 2) bbbb 22 22 22 −+ () ++ () ; 3) cccc 42 42 48 48 −+ () ++ () . 12.9. ba() + ()75 2 ;

–20. 12.10. 1) а) 4 2 + () a ; б) aaa + () () =− 22 4 2 ; в) 42 24 5 2 + () −+() () =+() aaaa ; 2) 80 м2.

12.11. 1) 31 1 xx() + (); 2) 34 4 () + ()xx ;

3) 21 71 7 2 xxx () + () ; 4) 07 23 23 37 7 , xxx () + () .

12.12. 1) xx() 1 2 ; 2) 35 2 xx + () ; 3) −+() 72 1 2 xx ; 4) () 02 51 3 2 , xx .12.13.1) 4040 −+ () +− () xyxy ; 2) 72 72 () ++ () xyxy ;3) 93 93 −+ () +− () xyxy ;

++ 

4) 0202 1 2 1 2 ,, 



 xyxy .12.14. 1) 1;

2) 5; 3) 2; 4) 0,5. 12.15. 1) x1 0 = , x2 1=− ; 2) x = 0, x =±6 ; 3) x = 0, x =±2; 4) x = 0, x =±3. 12.16. 1) xx() + ()53 ; 2) xx + () ()521 ;

3) xx() ()35 ; 4) xx + () ()57 ; 5) xx() + ()28 ; 6) 32 34xx() + () . 12.17. 1 м, 2 м, 6 м; 80 черепах. 12.18. ba + () ()46 2 ; 120. РОЗДІЛ 2 § 13

13.2. 1) Так; 2) так; 3) так; 4) так; 5) ні.

13.6. sn =+ 75,,015 . 13.7. 1) 3; 2) gt = 1 2 ;

3) 24 хв. 13.8. 1) yx=+ 03,,14 ; 2) 2 м, 2,9 м, 4,4 м. 13.10. 1) yx = 2 ; 2) yx=− 5; 3) yx=−31; 4) yx =− + 21. 13.12. 1) 2 °С; 2) 32 °С; 3) через 11 хв. 13.13. 1) yt=+225. 13.14. 1) Так; 2) ні; 3) так; 4) так. 13.17. 1) 3; 4; 8 людей; 2) yx=+ 2 . 13.19. 1) 6; 2) 4; 3) yx = 2 ; 4) 12; 5) 20. § 14

14.1. 1) 66 x ; 44 y ; () 40 ; , 00 ; () , 50 ; () ; 2) 45 x ; 41 y ; 30 ; () , 04 ; () ; 3) 44 x ; 31 y ; 20 ; () , 01 ; () ; 4) 12 x ; 33 y ; 05 0 ,; () , 01 ; () .

14.3. 1) () 12 0; , 6;03 (); 2) () 90 ; , 8;01 () ; 3) () 80 ; , 08 ; () ; 4) 70 ; () , 07 ; () ; 5) 12 0; () , 03 ; () ; 6) () 10 0; , 02 ; () . 14.4. 1) –3; –1; 3; 5; 2) –15; –7; 1; 9. 14.7. Порожній

басейн наповнюють водою, а потім знов спорожнюють. 14.8. 1) 400 м; 300 м; 2) 9 хв; 3) 600 м, 3 хв. 14.9. 1) Так; 2) так; 3) ні. 14.10. 1) а) y =−1 , y = 1 ; б) x = 0, x = 4; 2) а) y = 1 , y =−2 ; б) x = 4, x =−4 ; 3) а) y = 0 , y =−2 ; б) x =−6 або x = 4; x =−4 або x = 2 ; 4) а) y =−2 , y = 4 ; б) x =−5; x =−2 або x = 6 . 14.11. 1) а) –4; –2; 1; 4; б) 3; 2) а) 41 x ; б) 14 y ; в) () 30 ; , 03 ; () ; 3) а) 25 x ; б) 23 x ; в) () 10 ; ; 40 ; () ; 02 ; () ; 4) а) 55 x ; б) 33 y ; в) () 40 ; , 40 ; () , 01 ; () . 14.12. 1) 60 хв; 2) на 700 м; 3) 400 м; 4) 10 хв; 5) друга, на 5 хв; 6) 700 м. 14.13. 1) 3; 9; 21; 33; 2) 3; 7; 15; 23. 14.15. yx=−22. § 15

15.1. 1) yy03() < () ; 2) yy05() < () ; 3) yy () > ()36 ; 4) yy () > ()62 ; 5) yy () > ()10 ; 6) yy () < ()20 . 15.2. 1) 1;01 (), () 11 0; ; 2) 4;01 () , 14 0; () ; 3)0;06() , 15 0; () ; 4) 0;07 () , () 14 0; ; 5) 08 ; () , () 16 0; ; 6) 06 ; () , () 18 .

15.3. 1) yx = 5 ; 2) y x =− 4 ; 3) y = 3; 4) y =−1 .

15.4. 1) І, ІІІ; 2) II, IV; 3) I, II; 4) I, III; 5) II, IV; 6) III, IV; 7) I, II, III; 8) I, III, IV. 15.5. 1 і 6; 3 і 7. 15.6. 1) () 22 ; ; 2) 11 ; () ; 3) 21 ; () ; 4) () 31 ; ; 5) () 13 ; ; 6) 42 ; () . 15.7. 1) 662 г.

о.; 2) 21 г. о. 15.8. 1) 100м; 2) 2 хв; 3) 200 м; 4) 50 м/хв. 15.9. Прямі перетинаються.

15.10. 1) а) 3; 5; б) –6; –3; в) так; 2) а) 0; –1 ; б) 6; 0; в) ні; 3) а) 6; –2; б) 2,25; 1,5; в) так; 4) а) 7; 7,4 ; б) –50; –35; в) ні. 15.12. 1) yx =−3 ; 2) y x =− 5 ; 3) y x = 4 4 ;4) y x =− 3 5 4 5 .

15.13. 1) b = 7 ; 2) b = 1475 , ; 3) k =−6 ; 4) k =−11 . 15.14. 1) 436 г. о.; 2) 54 г. о. 15.15. 1) 300 м; 2) 3 хв; 3) 400 м; 4) 100 м/хв.

РОЗДІЛ 3 § 16

16.3. 1) x =−8 1 3 ; 2) x = 26 2 3 ; 3) x =−360; 4) x = 140; 5) x = 16 ; 6) x =−50 . 16.4. 1) x = 26; 2) x = 12 ; 3) x =−8 ; 4) x =− 8 3 ; 5) x = 2 3 7 ; 6) x = 1 7 . 16.5. 1) y =−9 ; 2) y = 1 ; 3) y = 18; 4) y = 15; 5) y = 13; 6) y = 6 . 16.6. 1) 5120 x = ; 2) x −= 20 50 ; 3) x x += 3 48; 4) xx++() = 18 46; 5) 888 x = ; 6) 100150 x = . 16.7. 1) x = 18 ; 2) x =−14 ; 3) x = 5,82 ; 4) x = 3 1 3 ; 5) x = 24 , ; 6) x = 22 . 16.8. 1) x =−06 , ; 2) x = 04 , ; 3) x = 12 13 ; 4) x =−12 ; 5) x = 17 2 3 ; 6) x = 5 3 4 . 16.9. 1) x1 15=− , ; x2 6 = ; 2) x1 7=− ; x2 25 = , ; 3) x1 65=− , ; x2 0 = ; x3 9 = ; 4) x1 8=− ; x2 0 = ; x3 75 = , ; 5) x1 64=− , ; x2 5=− ; x3 5 = ; 6) x1 7=− ; x2 7 = ; x3 81 = , . 16.10. 1) x1 9=− ; x2 4=− ; 2) x1 8 = ; x2 11 = ; 3) x1 1 = ; x2 7 = ; 4) x1 2=− ;

x2 5 = ; 5) x1 3=− ; x2 8 = ; 6) x1 4 = ; x2 19 = .

16.11. 1) xa =−2 ; 2) xa=+43 ; 3) xa=+53; 4) xa =−636 ; 5) xa =−55 ; 6) xa=+510 .

16.12. 1) x1 17=− ; x2 17 = ; 2) x1 34=− ;

x2 34 = ; 3) x1 11=− ; x2 9 = ; 4) x1 2=− ;

x2 0 = ; x3 4 = ; x4 6 = ; 5) коренів немає; 6) x довільне число. 16.13. 1) b = 16 ; 2) b =−55 , ;

3) b = 9 ; 4) b =−17 ; 5) таких b не існує; 6) таких b не існує. 16.14. Через 20 с. 16.15. Через 12 хв. 16.16. Через 0,6 год. 16.17. Через

0,25 год = 15 хв. 16.18. 1) 10 атракціонів; 2) вистачить. 16.19. 33 замовлення. 16.20. 16 завдань. 16.21. 124 пари. 16.22. 100 г. 16.23. 300 г. 16.26. 1) x = 11; 2) коренів немає; 3) x довільне число; 4) x =−20 ; 5) x довільне число; 6) коренів немає. 16.27. 1) x = 23; 2) x =−11; 3) x =−28 ; 4) коренів немає. 16.28. 1) x =−6 ; 2) x = 0; 3) x = 288 ; 4) x =−24 . 16.29. 1) x = 19 ; 2) x = 0; 3) x =−65 , ; 4) x = 1 2 3 . 16.30. 1) 30; 2) 20; 3) 35; 4) –40; 5) 14,5; 6) 39,5. 16.31. 1) xx1266 =− = , ;

2) xx1288 =− = , ; 3) xx 12 20 6 =− = , ; 4) xx12912 =− = , . 16.32. 12 480+= x ;

x = 17 . 16.33. Через 2,4 хв. 16.34. Через 0,5 год. 16.35. 462 та 420 камер. 16.36. 300 г. § 17

17.3. a) 1) xy=+ 12; 2) xy =− + 10 ; 3) xy=+520 ; 4) xy =− + 6,05 ; 5) xy =− + 4 3 8 ; 6) xy=+ 2 5 2 ; б) 1) yx=− 12 ; 2) yx =− 10 ; 3) yx=−4,02 ; 4) yx =− + 26 ; 5) yx =− + 3 4 6 ; 6) yx=− 5 2 5 . 17.4. 1) yx=−46 ;

2) yx=+38 ; 3) yx=−37 ; 4) yx =−84 ; 5) yx=−1254,,5; 6) yx =−04,,22 . 17.5. 1), 4). 17.6. 1) y =−5 ; 2) x = 6 ; 3) x = 7 ; 4) y = 2; 5) y =−17 ; 6) x = 1. 17.7. 1) 10 0; () , 04 ; () ; 2) 60 ; () , 4;01 () ; 3) 20 ; () ,6;01() ; 4) 20 ; () , 0;06() ; 5) () 80 ; , 06 ; () ; 6) () 50 ; , 08 ; () .

2) графіком рівняння є вісь ординат. 17.17. 1) –3; 2) 30; 3) 2. 17.18. 1) Так; 2) ні; 3) так; 4) так. 17.19. 1) 80 ; () ; 2) 17 ; () . 17.20. 1) yx =−83 ; 2) yx =+ 5 . 17.21. 1) Так; 2) так; 3) ні; 4) так. 17.23. 45 60 390 xy+= . 17.24. 23 170 xy+= , обидві пари. 17.25. 1) y = 6 ; 2) x =−3. § 18

підручника видавництва

18.1. 1) a =−2, b = 4 ; 2) a = 9 , b = 5; 3) a = 2 , b = 6 ; 4) a = 20 , b =−14 ; 5) a = 17 , b =−15; 6) a = 1, b = 22 . 18.2. 1) а) одна; б) жодної; в) безліч; 2) а) xy xy −= += { 21 21 , ; б) 24 10 25 xy xy −= −= { , ; в) xy xy −= −= { 21 25 , . 18.3. 1) () 22 ; ; 2) 33 ; () ; 3) () 12 ; ; 4) () 12 ; ; 5) 31 ; () ; 6) 13 ; (). 18.4. 1) Один, 10 ; () ; 2) безліч; 3) жодного; 4) жодного; 5) безліч; 6) безліч. 18.5. 2) 13 ; () ; 3) yx+= 4 . 18.6. 2) Траєкторії не перетинаються. 18.7. 1) Наприклад, 64 ; () , 02 ; () ; 2) так. 18.8. 1) Наприклад, () 10 ; , 12 ; (); 2) так. 18.9. 1) Так, a =−3; 2) ні. 18.10. 1) Так; 2) так; 3) ні; 4) так.

18.11. 1) 52 ; (); 2) () 22 ; ; 3) () 23 ; ; 4) () 13 ; ; 5) 32 ; () ; 6) 42 ; () . 18.12. 1) Один; 2) безліч; 3) жодного; 4) безліч; 5) жодного, 6) безліч. 18.13. 1) Ні; 2) так, a ≠ 3 . 18.14. 2) 12 ; () ; 3) yx−=20 . 18.15. 2) Траєкторії не перетинаються; 3) yx−= 1 . 18.16. 1) а) жодної;

б) безліч; в) одна; 2) а) xy xy += −= { 23 23 8 , ;

б) xy xy += += { 24 23 , ; 3) xy xy += += { 24 24 8 , . § 19

19.1. 1) () 0;21 ; 2) () 14 2; ; 3) 13 ; () ; 4) 11 ; () ; 5) 03 ; () ;

17.10. 1–А, 2–Д, 3–Б. 17.11. 35 235 xy+= . 17.12. 76 142 xy+= ; 1012 ; (). 17.13. 1) 70 ; () ; 2) 0;01 () . 17.14. 1) xy+=50 ; 2) xy+=20 . 17.15. 1) y = 4 ; 2) y =−3 ; 3) x = 2 ; 4) x =−5. 17.16. 1) Графіком рівняння є вісь абсцис;

6) 20 ; () . 19.2. 1) 76 ; () ; 2) 87 ; () ; 3) 51 ; () ; 4) 42 ; () ; 5) 61 ; () ; 6) () 12 ; . 19.3. 1) () 27 ; ; 2) () 11 ; ; 3) 13 ; (); 4) 14 ; () ; 5) 81 ; () ;

6) 91 ; () . 19.4. 1) 64 ; () ; 2) 5;61 () ; 3) 75 ; (); 4) 41 ; () ; 5) () 40 ; ; 6) 01 ; () . 19.5. 1) 12 1; () ;

2) 33 ; () ; 3) () 58 ; ; 4) () 86 ; ; 5) 52 ; (); 6) 16 ; () .

19.6. 1) y = 2; 2) y =−1 ; 3) yx=− 6 ; 4) yx =− + 4; 5) yx =− + 27 ; 6) yx =−38 . 19.7. 1) a = 5; 2) a =−17 ; 3) a = 3 ; 4) a =−4; 5) такого

значення a не існує; 6) такого значення

a не існує. 19.8. 1) x = 2 , y = 1 ,

z =−1 ; 2) x = 1, y =−4 , z = 2 ; 3) x = 3 , y =−2 ,

z = 1 . 19.9. xy xy += += { 65 54 285 , ; x = 25, y = 40 . 19.10.

x = 120, y = 240. 19.11. 1) 45 ; () ; 2) 77 ; () ;

3) 4;82 (); 4) 99 47 ; () ; 5) 0;41 () ; 6) () 26 ; . 19.12. 1) 51 ; () ; 2) 24 ; () ; 3) 81 ; () ;

4) 05 ; () ; 5) 10 8; () ; 6) () 59 ; . 19.13. 1) 8;31 () ; 2) () 20 10 ; ; 3) 27 18 ; () . 19.14. 1) yx=+27; 2) yx=− 6 ; 3) yx=+31 ; 4) yE =−52 . 19.15.

xy xy += += { 32 20 15565 , ; x = 17 , y = 15. 19.16. x = 86 , y = 258. 19.17. 32 1 ;; () . § 20

20.1. 1) 10 3; () ; 2) () 0;41 ;

3) 10 5; (); 4) 56 ; () . 20.2. 1) 16 ; () ; 2) () 10 4; ; 3) 86 ; () ; 4)2;71() ; 5) () 5;81 ; 6) () 69 ; .

20.3. 1) 21 ; () ; 2) 12 ; () ; 3) () 31 ; ; 4) () 13 ; ;

5) 11 ; () ; 6) 11 ; () . 20.4. 1) Не перетинаються;

2) не перетинаються; 3) перетинаються

в точці 21 ; () ; 4) перетинаються в точці 13 ; (); 5) перетинаються в точці

32 ; () ; 6) перетинаються в точці () 25 ; .

20.5. 1) yx=+ 3 ; 2) yx =− + 2 ; 3) yx =− + 3,05 ;

4) yx=− 1 3 2 . 20.6. 43 180 34 170 xy xy += += { , ; x = 30, y = 20 .

20.7. x = 20, y = 12. 20.8. 1) 41 ; () ; 2) 35 ; (); 3) () 42 ; ; 4) () 16 ; ; 5) 46 ; () ; 6) 32 ; () .

20.9. 1) 21 ; (); 2) () 31 ; ; 3) 14 ; () ; 4) () 16 ; ; 5) 23 ; () , 6) 84 ; () . 20.10. 1) 40 ; () ; 2) 11 ; () ; 3) () 12 ; ; 4) 23 ; () ; 5) 53 ; () ,

6) 05 5 ,; () . 20.11. 1) yx =− 2 ; 2) yx=− 3; 3) yx=+24 ; 4) yx =− 3,05 . 20.12. x = 380 , y = 420 . 20.13. x = 6 , y = 2.

§ 21

21.1. 16 см, 64 см та 64 см. 21.2. 20 г і 60 г. 21.3. Перший 18 шт, другий 24 шт.

21.4. У першій 18 л, у другій 54 л. 21.5. Перший 56 тис. г. о., другий 87 тис. г. о.

21.6. 180 кг і 210 кг. 21.7. 20 км/год, 10 км/год. 21.8. 120 км/год і 80 км/год. 21.9. 13 і 91. 21.10. 54. 21.11. Ціна пари балістичних окулярів 250 г. о., ціна пари тактичних рукавичок 400 г. о. 21.12. 0,7 м; 1 м. 21.13. 30 г 12%-го сплаву і 50 г 24%-го сплаву. 21.14. 1) 260 г. о.; 2) 216 г. о. 21.15. Швидкість квадроциклістки 36 км/год, велосипедиста 12 км/год. 21.16. Швидкість Олени 18 км/год, Миколи 12 км/год. 21.17. Ціна бронепластини 1200 г. о., ціна штурмового рюкзака 600 г. о. 21.18. 4800 грн, 3850 грн.

Повторення матеріалу, що вивчався в 7 класі

1. 1) 5; 2) 4; 3) –2; 4) 10; 5) –23; 6) 50; 7) 23; 8) –2. 2. 1) а) 20 %; б) 50 %; 2) kn > .

3. 1) 5; 2) 12; 3) 8; 4) 14; 5) 4a; 6) a; 7) 0; 8) 0.

4. 1) а) 3a ; б) 4b ; в) 34ab + ; 2*) не достатньо.

5. 1) –63; 2) 24; 3) –24; 4) –54; 5) 9; 6) 1; 7) 0,0025; 8) 0,0001. 6. 1) а) 8 Гб; б) 32 Гб; в) 128 Гб; г) 2m Гб; 2) так, настане.

7. 1) 4; 2) 9; 3) 1; 4) 1; 5) 4; 6) 25; 7) 0,5; 8) 27.

8. 1) 76 1010 , ⋅ ; 2) В; 3) 5; 4) неправильно.

9. 1) 36 8 a ; 2) 30 10 a ; 3) 5 20 a ; 4) 2 16 a ; 5) 2 23 a ; 6) 10 14 a ; 7) 8 620ab ; 8) 3 23 12ab . 10. 1) а) xy 18 21 ; б) xy 4545 ; в) 125 1818 xy ; 2) а) так, б) так, в) ні, г) ні. 11. 1) 5; 2) 1; 3) 20; 4) 3; 5) 22 x ; 6) 10 5 y ; 7) 42 12 2 xy ; 8) 67 17 2 xy−+ .

12. 1) 79xy + ; 2) на 33xy + ; 3) x = 150; 4*) у

2,5 разу; 5*) на 100 %. 13. 1) 31812 32 xxx −+ ; 2) 4284 32 xxx ; 3) −+xx 2 17 66; 4) −+ + xx 2 3 108 ; 5) xxx 32 10 330 −+ ; 6) xxx 32 14 570 −+ ; 7) xx 3 32−+ ; 8) xxx 3257 2 −+ . 14. 1) 210 2 xx + ; 2) 6 2 x ; 3) 810 2 xx + ; 4*) 10. 15. 1) aa 4 3 + () ; 2) aa 5 () ;

3) aba41 () ; 4) abb 13 + () ; 5) ab + () ()85 ; 6)

ba() + ()32 ; 7) aba() + () 2 4 ; 8) abb + () + ()31 2 .

16. 1) 10 4 x + ; 2) 7. 17. 1) 4422 xxyy++ ;

2) xxyy 22 69++ ; 3) xx 63 14 49 −+ ;

4) 3612 48−+yy ; 5) xxyy 10 52 4 2 ++ ;

6) xxyy 14 73 6 2 ++ ; 7) 16 40 25 20 10 612 xxyy −+ , ;

8) 0044 100 18 98 16 , xxyy −+ .

18. 1) 3 2 + () x ; 2) x () 1 2 ; 3) mn () 2 ;

4) pq + () 2 ; 5) y () 6 2 ; 6) 7 2 + () y ; 7) 52 2 a + () ;

8) 410 2 a () . 19. 1) 25 x + ; 2) 3; 3*) квадрат.

20. 1) 66mnmn() + () ;

2) mnmn() + ()44 ; 3) 97 97 mnmn() + () ;

+

4) 85 85 mnmn() + () ; 5) nn mm 22 1111 

+

6) 1212 33 nn mm

;

;7) 060644 ,,mnmn() + ();

8) mnmn 550404() + (),, . 21. 1) x 2 9 см;

2*) 5 см. 22. 1) 111211122 abaabb () ++ () ;

підручника

2) abaabb () ++ () 121214422 ;

3) 24 2 22abaabb + () −+ () ;

4) abaabb + () −+ ()33 9 22 ; 5)

15 4 225 60 16 22abaabb () ++ () ;

6) 516258025622 abaabb () ++ () ;

7) 01 001 1 3 1 30 1 9 22 ,,abaabb +

−+

8) 1 2 1 4 060303622abaabb +

;

Проєкт майбутнього

23. 2y м. 24. 1) –1; 1; 2) –1; 1; 3) 0; –4; 4; 4) 0; –5; 5; 5) 0; –2; 6) 0; –3; 7) 0; –2; 2; 8) 0; –1; 1. 25. Vx=− 3 343. 26. 1) 12; 36; 2) Nt = 12 ; 3) 200. 27. 1) Mn = 3 ; 2) yx=− 8 ; 3) Tt=+ 300 . 28. 1) а) –7; б) 5; 2) а) 36; б) – 5; 3) а) –3; б) –3. 29. 1) 2; 2) –4; 3) 52 x ; 4) 44 y . 30. 1) 20 %; 2) 30 %; 3) 40 хв; 4) 120 хв = 2 год. 31. 1) b = 7 ; 2) b = 10 ; 3) b = 11 ; 4) b =−18 ; 5) k = 5 ; 6) k = 4; 7) k =−5 ; 8) k =−5 . 32. 1) 33; 2) 4; 3) коренів немає; 4) коренів немає; 5) x довільне число; 6) x довільне число; 7) –15; 8) 14. 33. 1170 звернень. 34. 1) Належить; 2) належить; 3) належить; 4) належить; 5) не належить; 6) належить; 7) належить; 8) не належить. 35. 1) Один розв’язок; 2) один розв’язок; 3) безліч розв’язків; 4) безліч розв’язків; 5) жодного розв’язку; 6) жодного розв’язку; 7) безліч розв’язків; 8) жодного розв’язку.

36. 1) 2429 ; (), 2) () 2;41 ; 3) 51 ; () ; 4) () 23 ; ;

5) 12 ; () ; 6) 13 ; () ; 7) 22 ; () ; 8) 11 ; () . 37. 1) 57 ; (),

2) 83 ; () ; 3) 15 ; () ; 4) 31 ; () ; 5) 62 ; () ; 6) 71 ; () ;

7) () 0;11 ; 8) 41 ; () . 38. xy xy += += { 200 03 01 24 , ,, ;

x = 20, y = 180 . 39. 81010 6060 30 xxy xy += =+ { , ; x = 10 , y = 18.

Аналітичний спосіб задання функції 133

Аргумент 131

Вираз алгебраїчний 17

зі змінною (буквений) 17

раціональний 18

цілий раціональний 18

числовий 17

Вирази тотожні 25

Властивості степеня 41–43, 45–46

Виділення квадрата двочлена 123

Віднімання многочленів 67

Властивості рівнянь 173

Графік лінійного рівняння з двома

змінними 191

Проєкт

рівняння з двома змінними 191 функції 147

Графічний спосіб задання функції 148

розв’язування системи лінійних

рівнянь із двома змінними 203

Доведення тотожностей 28

Додавання многочленів 66

Значення функції (функція) 131

Змінна 17

Кутовий коефіцієнт 160

Лінійна функція 160

Лінійне рівняння з двома змінними 188 з однією змінною 174

Математична модель 178, 228

Математичне моделювання 228

Многочлен 62

стандартного вигляду 65

майбутнього підручника видавництва

Множення многочленів 75

одночлена на многочлен 73

одночленів 53

Область визначення функції 150

значень функції 150

Одночлен 52

стандартного вигляду 52

спосіб задання функції 134

Піднесення одночлена до степеня 53

Подібні члени многочлена 63 Пряма пропорційність 162

Рівняння 173

з модулем 177 Розв’язок рівняння 173 з двома змінними 188

системи рівнянь із двома змінними 202 Розв’язування текстових задач за допомогою лінійних рівнянь з однією змінною 178 системи лінійних рівнянь із двома змінними 228

Розкладання многочлена на множники 82, 85 за допомогою формул скороченого множення 96, 104, 113, 119 Розкриття дужок 27

Система лінійних рівнянь із двома

змінними 201

Спосіб винесення спільного множника за дужки 82

групування 85

додавання розв’язування системи

лінійних рівнянь із двома змінними 223

підстановки розв’язування системи

лінійних рівнянь із двома змінними 212

Способи задання функції 132–134, 148 розв’язування систем лінійних рівнянь із

двома змінними 203, 212, 223

Степінь 33

многочлена стандартного вигляду 65

одночлена 52

Табличний спосіб задання функції 133

Тотожне перетворення виразу 26

Тотожність 25

Точки перетину графіка з осями

координат 149

Формули квадрата двочлена 92 різниці квадратів 104

скороченого множення 94, 104, 112 суми та різниці кубів 113

Функція 131

АЛГЕБРА 7

Підручник

видавництва