OPTIMISING GLULAM STRUCTURES
COMPUTING TIMBER BIFURCATION SYSTEMS FOR FUNICULAR TYPOLOGIES

SVENJA SIEVER
UNIT PG 14
MARCH THESIS 2021/2022
ACKNOWLEDGEMENTS
Thesis Tutor
Tim Lucas (Price and Myers / Bartlett)
Module Coordinators
Oliver Wilton (Bartlett)
Robin Wilson (Bartlett)
Stephannie Fell Contreras (Bartlett)
PG 14 Tutors
Dirk Krolikowski (DKFS / Bartlett)
Jakub Klaska (ZHA / Bartlett)
Structural Engineers
Damian Eley (Expidition Engineering)
Florian Gauss (Knippershelbig)
Advice and Support
Fellow PG14 students
(Special thanks to Chenru Sung, Vegard Elseth, Kacper Pach)
OPTIMISING GLULAM STRUCTURES
ABSTRACT
Wood performs best along the grain, making bending timber more resource-efficient, durable and structurally effective than cutting it. Therefore, this design thesis will investigate glulam construction and the opportunities for resource-efficient building through parallel-to grain bending. It proposes a computational workflow for projecting an optimised glulam bifurcation system onto free-form funicular structures for optimal force transmission. This workflow includes particle-spring form-finding and structure system generation through computer-aided design (CAD) tools.
The thesis is divided into 3 Sections: Glulam History and Development, Computational Experiments and Design Studio Project Synthesis.
Section 1 delineates the evolution and milestones of composite timber construction through the investigation of historical case studies. The current digital shift towards CAD enables file-to-factory workflows and the associated opportunities for mass customisation.
Section 2 focuses on digital experiments and fabrication and executes the established workflow for glulam projection onto funicular shapes, starting from perimeter definition to wood species selection.
Section 3 focuses on applying the learning outcomes to the studio design project.
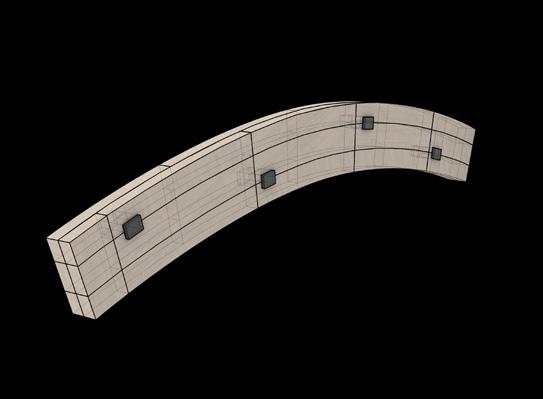
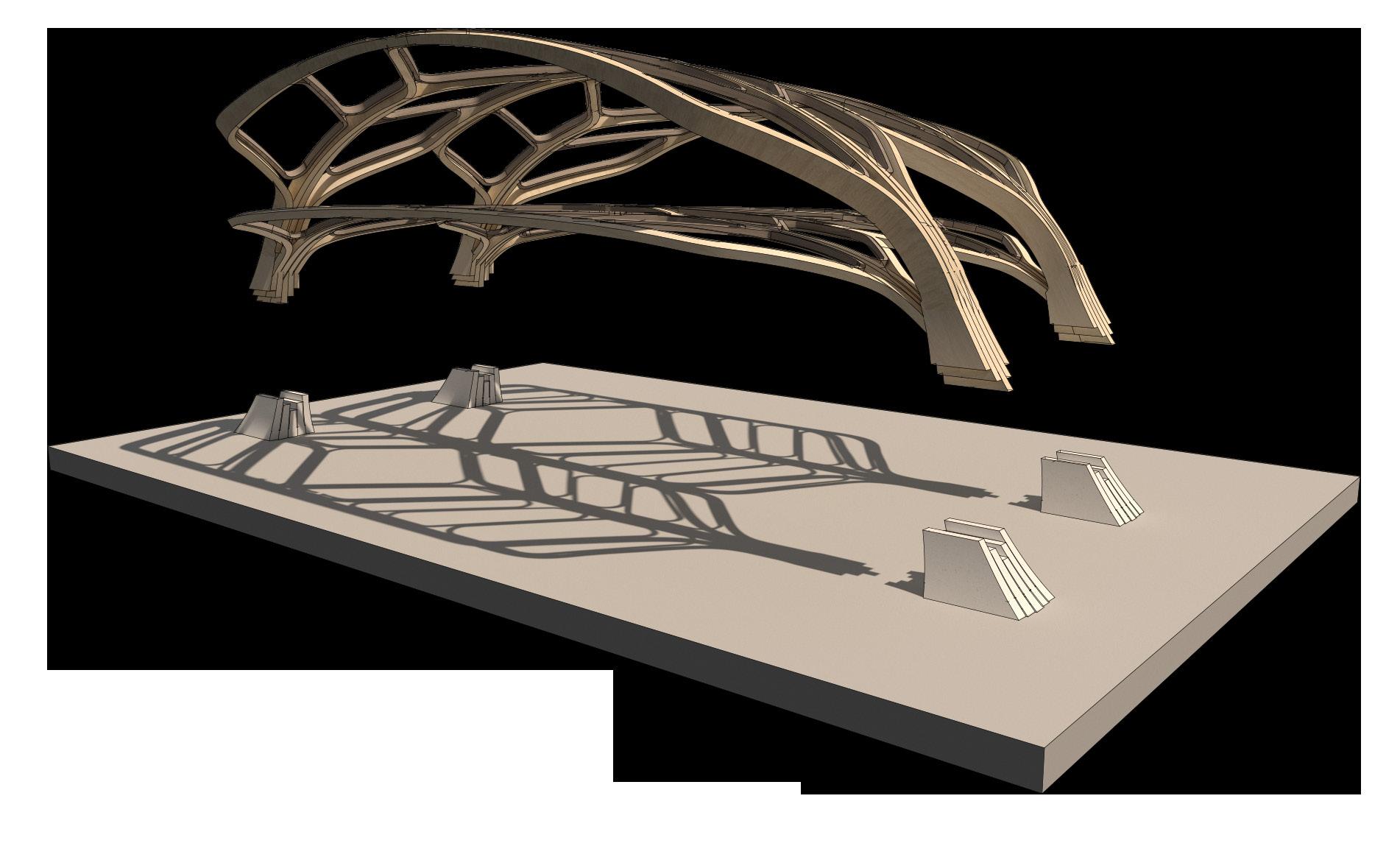
Fig. 1a, b Title Page (Title Page, Left) Bifurcated glulam structure projected onto continuous surface
Glulam History and Development

01
1.2.2 Bolt-Laminated Timber: Armand-Rose Emy

The industrial revolution in the nineteenth century brought about profound changes in society and technology. Large industrial buildings were in high demand, and roof structures had to span greater distances. Machine-driven saws and mass-produced nails and bolts were developed, significantly lowering costs and making truss assembly easier. New technologies for timber composites were investigated in order to compete with steel. This development resulted in the invention of laminated timber (Toussant, 2007).
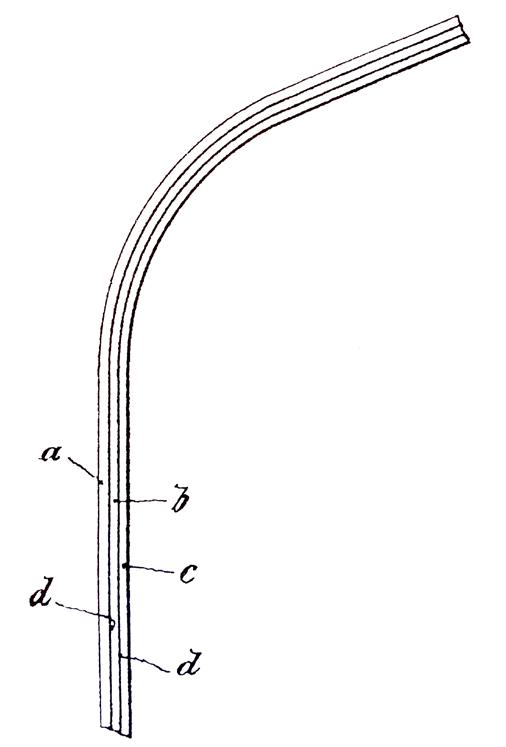
Convinced of the advantages of De l’Orme’s method, French Colonel Armand-Rose Emy (1771-1851) was one of the first engineers who used laminated timber instead of short pieces of wood, which he illustrates in his publication Description d’un nouveau system d’arcs (Müller, 2000).


The fundamental difference between the Emy method (Fig. 1.6), which was invented around 1830, and Philibert de L’Orme’s system is that Emy’s invention uses stacked laminations that are glued together and bent, whereas De L’Orme uses vertical laminations (Jeska and Pascha, 2014).
The various layers were joined using clamping bolts and collars to increase friction between the laminations and transfer forces between the layers (Müller, 2000). The Emy approach aligned the timber with the arch’s ideal stress line, reducing the need for additional outside edge cutting to suit the curvature (Svilans, 2020).


However, as the splice connections were neither glued nor interlocked, bending and shear loads caused the laminations to be displaced relative to one another. This, along with the low stiffness of the Emy composite members, resulted in deflections under changing load patterns (Müller, 2000, p. 15).


14 1 Glulam History and Development
Fig. 1.5 Composite Beam Evolution (Bottom) Chronology of proposals marking the evolution of beam reconstruction
Fig. 1.6 De L’Orme System Detail (Opposite) Multiple curved planks, fixed together with bolts and metal straps
Leonardo Da Vinci 16th Century
Phillibert de L‘Orme 16th Century (1567)
Armand-Rose Emy 19th Century (1837)
Fausto Veranzio 16th Century
Guiseppe Del Rosso 18th Century
Pierre Henri Migneron 19th Century
Karl Friedrich Otto Hetzer 20th Century (1906)
Carl Friedrich Wiebeking 19th Century (1817)


15 1 Glulam History and Development
1 Steel collar
2 Timber connection element to roof structure
1 2 3 4
3 Steel clamping bolts
1.2.3 Glued-Laminated Timber: Karl Friedrich Otto Hetzer
Tests on the first glulam beams were carried out in Karl Friedrich Otto Hetzer’s (1846-1911) firm after 1900 (Müller, 2000). Between 1891 and 1910, Hetzer obtained several patents for a series of improvements aimed at optimising the use of wood in structural elements such as beams and trusses (Svilans, 2020).
The bending diagram of a simply supported beam was mapped by patent number 125895 (Fig. 1.7), which led to a pair of profiled web components attached between a straight top flange and a curved bottom flange. This was the first time the crosssection of a laminated timber beam was optimised, with the cross-section changing in response to the load (Svilans, 2021).
Patent number 163144 (Fig. 1.10) depicts a spruce beam sawn longitudinally to form a parabola and filled with a pine plank glued into place under pressure. By that, Hetzer tackles the issue of cross-section optimisation and connection via adhesive application (Müller, 2000)
However, the Hetzer beam failed on the underside due to breaking wood fibres, and the saw cut along the length remained a costly manufacturing procedure (Müller, 2000).
The 1906 patent 197773 (Fig. 1.8) replaced mechanical fasteners with adhesives and was designed as a composite component for roof posts and rafters (Svilans, 2020). This patent was a significant turning point in modern glued laminated timber construction since it offered an efficient method for producing curving structures in timber without wastage (Jeska and Pascha, 2014).
Before glueing, individual wood laminations were bent to the desired shape. Hetzer carried the Emy composite member to its logical conclusion, allowing the structure to be closely matched to the ideal pressure line while achieving the highest possible bending strength, thus saving material.
Wooden planks could now be bent and attached to others; the shape was cemented once the adhesive cured. Introducing prestress into the wood fibres increased the structural response (Jeska and Pascha, 2014).
Hetzer’s patents were licensed to other international producers, resulting in the worldwide glulam construction endorsement (Müller, 2000).
Fig. 1.7 Hetzer Patent 125895: Load-Optimised Composite Beam
(Bottom Left) Web element with straight top flange and curved bottom flange
Fig. 1.8 Hetzer Patent 197773: Glued-laminated Timber Beam (Bottom Right) Curved timber member serving as both column and rafter
Fig. 1.9 Hetzer Patent 125895: Composite I-Beam
(Opposite Top Left) Composite beam with harder heartwood in the at the edges and softer sapwood in the middle to match the stresses
Fig. 1.10 Hetzer Patent 163144: Parabolic Composite Beam

(Opposite Top Right) Composite beam sawn lengthwise to form parabola and complement
Fig. 1.11 Case Study: Doecker Gymnasium Wuppertal 1911
(Opposite Bottom) The dismantable “Doecker system building” inspired by Hetzer’s patents has a supporting structure made of three-hinged laminated timber arches
16 1 Glulam History and Development
Heartwood (compression-resistant)



Sap wood
Heartwood (tension-resistant)
17 1 Glulam History and Development 1 2
1 Bent glued-laminated I-beam 2 Barrel vault louver ceiling 3 Purlin roof system
Solid wood girder (spruce)
40mm pine panel infill along moment path
3
compression tension compression tension
1.3 The Digital Shift
Computer-Aided Design (CAD)
File-to-Factory
Nowadays, digital tools have permeated all aspects of the designto-production process (Svilans, 2020).
New building construction logic such as the “digital chain,” “design for manufacture and assembly (DfMA),” and “file-tofactory” processes have resulted from the convergence of digital design and digital production, supported by computationallydriven parametric and procedural modelling paradigms (Larsen and Schindler, 2008, p. 399). These workflows refer to a method that involves the direct transfer of data from a 3D modelling programme to a CNC (Computer Numerically Controlled) machine. This process aims to fully utilise digital tools, particularly BIM, which can provide a smooth transition from design to manufacture (Robinson, 2019).
Prefabrication
Prefabrication provides more control, flexibility, and customisation. Buildings can be prototyped and tested before being assembled by moving construction from the site to a controlled environment (Svilans, 2020). This facilitates experimentation and iterative prototyping by experts.
Case Study: Savill Building, 2006
As demonstrated by the Savill Building, varying elements are a distinguishing feature of free-form timber constructions, made possible only through the digitalisation of the design process (Svilans, 2020). The perimeter is drawn on a plan using arcs formed by two intersecting circles (Fig. 1.12). A sine curve generates the roof’s centre line with variable amplitude. The cross-section is drawn as a series of parabolic arcs across the centre line. The surface is then covered with a grid generated by a programme that defines the “shape as z = f(x, y) with a damped cosine wave in the x-direction and upside down parabolas in the y-direction” (Harris and Roynon, 2008).
The architects and engineers worked together to fine-tune and settle on a shape that met aesthetic and functional needs (Fig. 1.13). Once the form-finding model was agreed on, it was imported into a structural analysis model. The Robot 3D programme helped determine load concentrations (Fig. 1.14) The model was then sent to the fabricator to detail the structural elements (Harris and Roynon, 2008).


18 1 Glulam History and Development
Fig. 1.12 Savill Building Workflow: Digital Perimetre Definition (Top) The perimetre is set out using the arcs of two intersecting circles
Fig. 1.13 Form-Finding and Analysis Model (Middle) Once form-finding is concluded, the model is imported into a structural analysis model
Digital Form-Finding
Definition (Pre-)fabrication
Structural Analysis (Robot 3D)
Perimeter
1.4 Understanding Timber Characteristics
1.4.1 Grain Direction and Strength Factors
There are three perpendicular principal orientation axes: longitudinal, radial, and tangential. The ability of wood to withstand weights is affected by several elements, including the kind, direction and duration of loading, defects, moisture, and temperature (Green, 2001).


Defects
Strength-reducing properties can dramatically diminish tensile and compression strength in structural timber (Harte, 2009). Therefore, the given values only apply to clear, straight-grained wood samples.
Moisture and Temperature
Water held in the cell wall is bound water, whereas water held in the free gaps is called free water (Svilans, 2021). The moisture content at which all free water has been eliminated is known as the fibre saturation point (FSP). Changes in FSP moisture content cause the wood to swell or shrink (Fig. 1.18). Softwoods have an equilibrium moisture content of about 12% in a typical indoor climate with a temperature of 20°C and relative humidity of 65%.
Duration of Load
Because wood is a time-based visco-elastic material, bending it for an extended time keeps part of the bent shapes even after eliminating the forces. This is known as creep (Svilans, 2021).

Elastic Properties
The elastic qualities of wood are created under mild stress and are entirely recoverable once the forces are eliminated. The elastic constants and elastic constant ratios vary depending on the species, moisture content, and temperature at which they are tested (Green, 2001).
20 1 Glulam History and Development
Fig. 1.16 The Three Primary Axes of Wood (Top) Three principal axes of wood with respect to grain direction and growth rings
Fig. 1.17 Timber Cuts (Middle) Plain-sawn, rift-sawn and quarter-sawn timber logs are subjected differently to shrinkage
Tangential
Bow Twist Cup Spring Fibredirection
Fig. 1.18 Distortion of wood due to shrinkage and swelling (Bottom) Depending on shape and the location of the cut, the lumber warpes differently
Longitudinal Radial Plain-Sawn Rift-Sawn Quarter-sawn
Mechanical Properties
Plastic deformation or failure occurs when the timber is “loaded to higher stress levels beyond the elastic range” (Green, 2001, p. 9732).

• Compressive strength indicates how much load a wood species will support parallel to the grain.
• Bending strength shows the forces wood can withstand perpendicular to the grain (Engler, 2007).



• Shear strength is characterised by three types of failure: shear parallel to the grain, shear perpendicular to the grain and rolling shear (Harte, 2009).
• Flexural strength illustrates the compression in the top half of a bent timber beam and tension in the bottom half.


Grain Direction
Wood cells are formed of lignin-bound long, strong cellulose fibres. As a result, splitting a board along the grain is significantly easier than breaking it across the grain (Engler, 2007). Therefore, wood can be ten times stronger than across the grain (Fig. 1.19) (Svilans, 2021).

Parallel-to-grain Properties
From a structural standpoint, the parallel-to-grain direction is the strongest and stiffest. Softwood tensile strength parallel to grain typically ranges between 70 and 140 MPa (bending strength). The compression strength is typically 30–60 MPa. These values are often greater for hardwoods (Harte, 2009, p. 710).

Perpendicular-to-grain Properties
The equivalent parallel-to-grain properties are much lower than the perpendicular-to-grain values. Tensile strength in the radial and tangential directions can be as low as 5–8 per cent and 3–5 per cent of the values in the grain direction, respectively. Compressive strengths perpendicular to grain are around 10–20% of parallel-tograin values (Harte, 2009, pp. 710-711).
21 1 Glulam History and Development
Fig. 1.19 Hankinson’s Equasion
(Top) Relationship between wood grain orientation and the compressive/tensile strength of wood
Fig. 1.20 Timber Load Behaviour Parallel and Perpendicular to Grain
0 45 90 Angle relative to grain Strength σ α = σ0 σ90 σ0 sin2 α +σ90 cos2α Tension Compression Bending Parallel to grain Perpendicular to grain
to grain Perpendicular to grain
(Bottom) Mechanical Properties: Tension, Compression, Shear and Bending
Parallel
Shear
Strength
Sliding Kinking Rolling Flexual
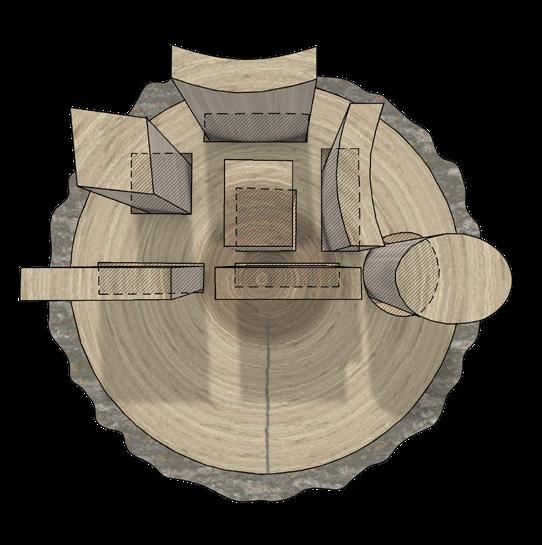
1.4.2 Glulam Blank Types and Lamella Assembly
Straight glulam blank
Straight glulams are the easiest blanks to fabricate. Straight glulams are typically constructed by vertically stacking dimensioned lumber to produce the appropriate depth (Svilans, 2020, pp. 95-96).

Single-curved glulam blank
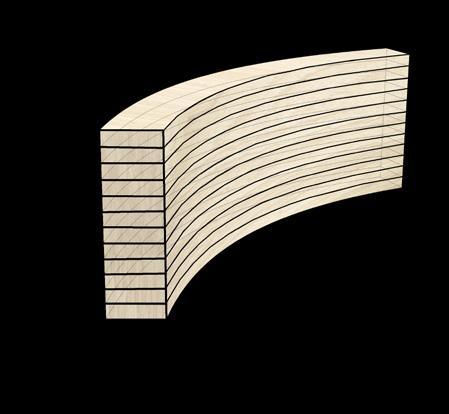
Single-curved glulams are curved in-plane. The timber boards are arranged so that their shortest dimension faces the curvature direction. Single-curved glulam production is more complex than straight glulam production due to the usage of a curved press (Svilans, 2020).
Double-curved glulam blank
The degree of curvature in out-of-plane glulams influences the lamellae’ width and thickness. The beam is constructed using a multi-axis glulam press; it is first created as a single-curved blank before being cut into parallel slices. In a subsequent production step, it is twisted out of plane (Svilans, 2020) (Fig. 1.21)
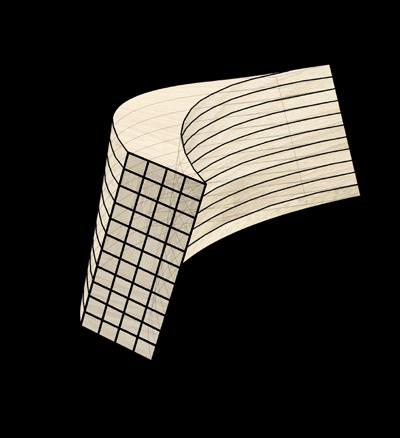
Lamella Assembly
Thinner wood elements can be bent with less force. Therefore, the thinner the lamellae, the more a glulam beam can be bent (Fig. 1.22). Using more layers of lamellae increases the amount of glue surface.
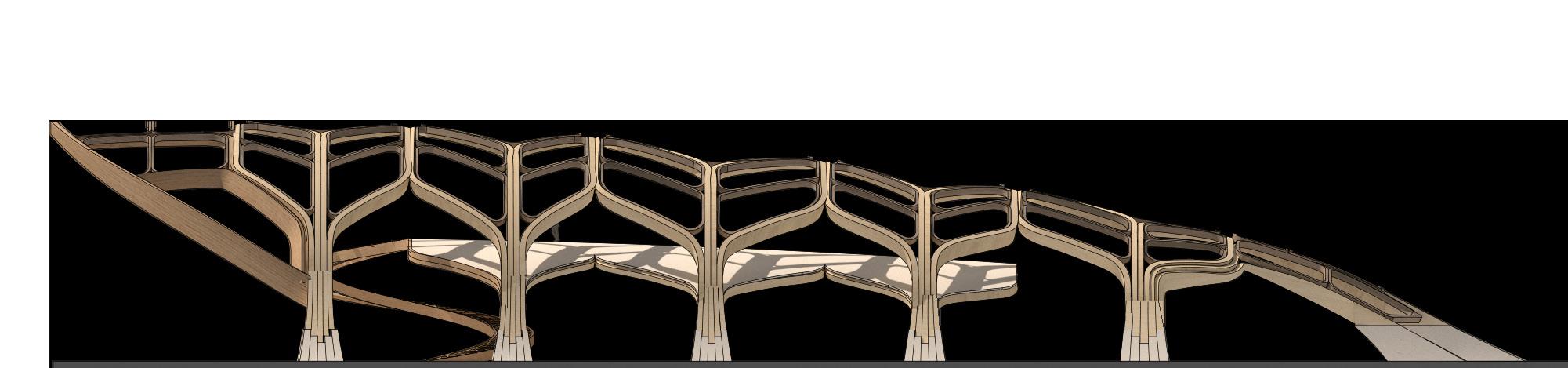
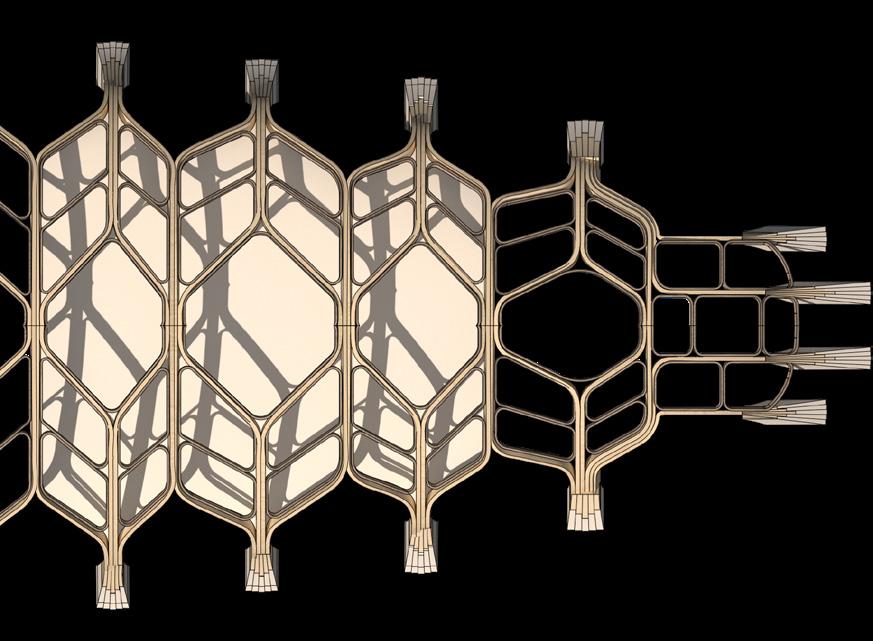
This thesis will focus on finding a bifurcation system for shell structures that minimises the application of double-curved elements, as the fabrication is complex and expensive. This will be further investigated with an example model in Section 2.

22 1 Glulam History and Development
Fig. 1.21 Types of Glulam Blanks (Bottom Left) Glulam beams can be bent in one or two directions
Fig. 1.22 Lamella Assembly According to Bending Magnitude (Bottom Right) Bending direction and bending degree have an influence on lamella assembly. Generally speaking: The smaller the bend raduis, the thinner the slices get Glulam Beam Straight Glulam Freeform Glulam Single Curved Glulam Double Curved Glulam
Timber Beam Single-Curved Double-Curved Low Curvature High Curvature
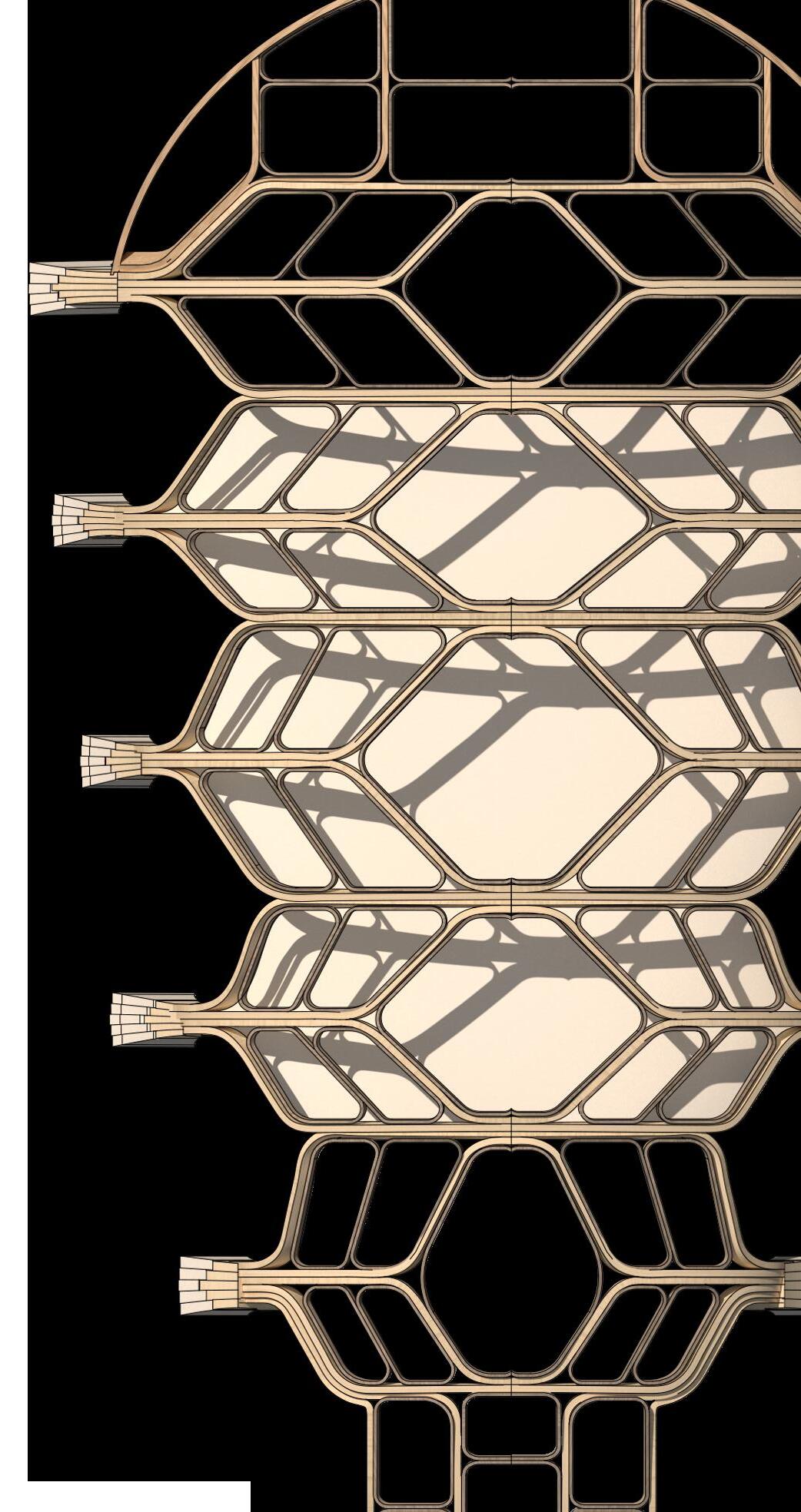

29 2 Digital Workflow 02 Digital Workflow
2.2.2 Inverted Catenary Framing - Case Studies
Since this thesis focuses on projecting glulam bifurcation systems onto shells, the behaviour of the chords inside the system is critical, as they will reflect the respective glulam beam structure in later tests.
As Isler’s cloth simulation is more applicable for thin concrete shells, this subsection examines two case studies that exclusively used hanging chain form-finding methods to generate skeletal structures.

Woodchip Barn - Catenary Arch Framing
The structure of the woodchip barn in Hooke Park (Fig. 2.6) was created by ‘shuffling’ between available component geometries and using an equilibrium method to align elements optimally. This process is conceived in which natural tree junctions can be reconfigured into architectural structures without needing complex connection hardware. The concept was investigated during the design and erection of the barn by Design & Make students in late 2015 (Menges, 2017). After discussions with the engineering team, the structural form was established to have the necessary invertedcatenary shape for a compression structure and a crosssectional geometry that could support the dimensions and angles of the sourced tree forks (Self, 2017).
Magazzini Generali - Inverted Arch Framing
Inspired by his bridge designs, Robert Maillart (18721940) envisioned the primary frame of the Magazzini Generali warehouse as a narrow inverted arch connected to a rigid ribbed slab using slender vertical links (Fig. 2.7). The idea evolved from the deck-stiffened arch bridge concept: the inverted arch is a concrete prism in tension rather than a curved slab in compression (Billington, 1997). Maillart’s analysis methods were primarily based on graphical computations (Fig. 2.6) The architect was familiar with Gaudí’s designs through visits to his Barcelona office and, therefore, applied his knowledge about funicular structures to the Chiasso project.
32 2 Digital Workflow
Fig. 2.6 Case Study: Woodchip Barn Hooke Park, AA Design+Make, 2016 (Top) Selection of naturally grown bifurcated tree branches, which are structurally composed so the grain direction follows the ideal line of pressure
GSEducationalVersion 25.0m 20.0m A=19.0+8.8=27.8t 3.8t 7.2t 5.1t M=6.0t 5.6t 5.7t 5.2t +37t +10t -43t -43t -43t -43t +37t +37t +38t -11t -34t -40t 6.2t 1.2t Bar forces Dead loads and snow loads 4.2m 4.2m 2.5m 2.5m 1 Roof slab 2 Eave beam 3 Inverted arch 4 Vertical columns 5 Inward curving columns 6 Stiffening flange 1 3 4 2 6 5 -47t 9F09 9G15 11B09 11B16 11B25 12A03 12B10 12B13 11A12 11B03 11B06 8C11 9B04 8A14 8C05 8C14 8D02 8D03 8A20 8A12 11A12 11B03 11B06 11B09 11B16 11B25 12A03 12B10 12B13 8A12 8A14 8A20 8C05 8C11 8C14 8D02 8D03 9B04 9F09 9G15 9F09 9G15 11B09 11B16 11B25 12A03 12B10 12B13 11A12 11B03 11B06 8C11 9B04 8A14 8C05 8C14 8D02 8D03 8A20 8A12
Fig. 2.7 Case Study: Magazzini Generali Chiasso, Robert Maillart, 1925 (Bottom) The structural form of the arching truss has the inverted-catenary forn for a compression structure and a cross-sectional geometry accommodating the sources tree forks
2.4 Digital Workflow Establishment
Perimeter Definition
Funicular Form-Finding
Gridshell
Workflow Objectives
The suggested workflow proposes learning by discovery through the support of computational tools (Fig. 2.10). The architect can directly view the spectrum of structural responses while exploring various forms, which fosters unusual solutions adapted to the design objectives and encourages an exploratory approach.
However, the design goal is not solely driven by ideal structural shapes. Structural and dimensional analyses are also included. The proposed workflow allows for the iterative back and forth between design decisions and structural response. Variable degrees of optimisation enables the architect to be less efficient, facilitating the incorporation of non-funicular slabs and circulation. The structural system can then be adapted accordingly.
Therefore, the workflow includes form-finding through funicular surfaces, which can be manipulated according to design needs. Different bifurcation systems are projected onto the surface and structurally tested, catering to varying load conditions. The system with the best overall structural and aesthetic performance for each iteration is selected and developed further.
35 2 Digital Workflow
Fig. 2.10 Digital Workflow Proposal
This diagram illustrates the design approach with the support of digital tools
Site
Generation
Species Selection According to Span and Bending Magnitude
Testing
Bifurcation Rationalisation
Optimisation Slab Integration
Jig Development
Shell Analysis Wood
Single-Layer Iterative
Multi-Layer L-System
Cross-Section
Adjustable
Prefabrication
2.5 Computational Funicular Form-Finding
2.5.1 Perimeter Definition
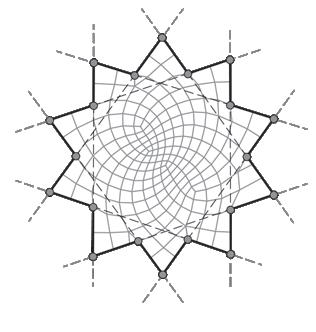
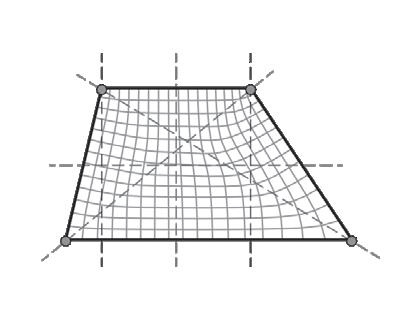
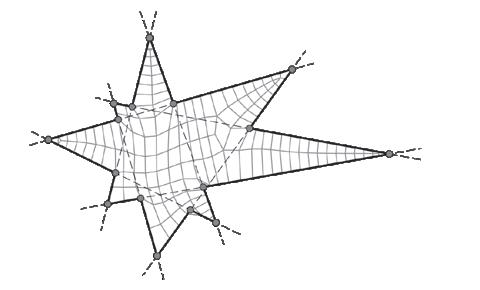
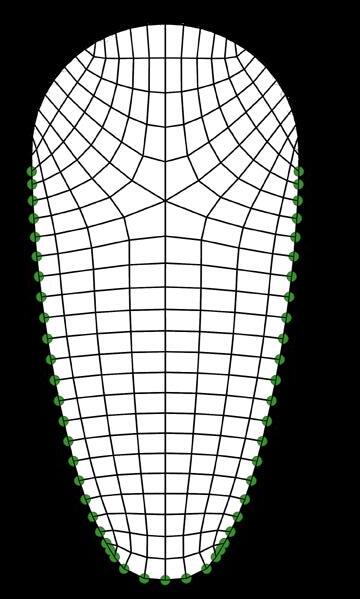
The boundary definition is a purely aesthetic choice. It is entirely up to the designer to determine the perimeter according to their specifications and restrictions. A Conoid Shell structure is used to demonstrate the workflow for demonstration purposes. The Conoid Shell is a simplified model of the design studio project, which will be examined in detail in Section 3.

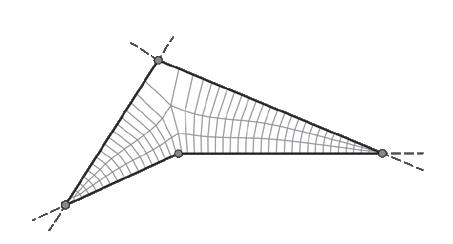

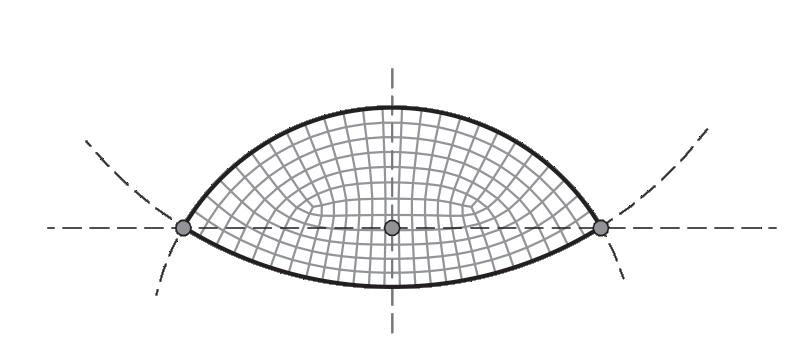
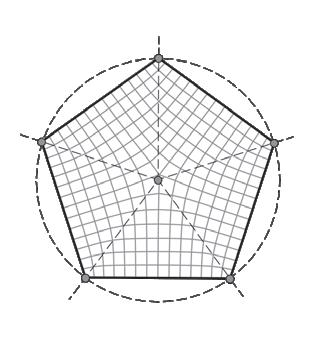
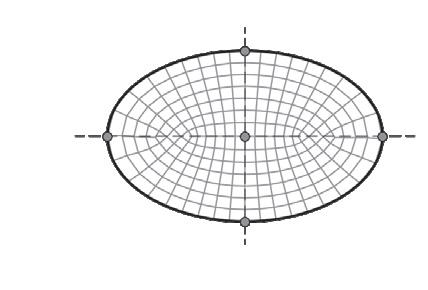
Like the Savill Building case study, the perimeter is defined by two intersecting ellipses that characterise the Conoid Shell’s footprint.
A surface is generated from the boundary curve and subdivided to start the live physics simulation (Fig. 2.12)
For this proceidure, RhinoVAULT 2.0 is used instead of Kangaroo 2, as it provides an intuitive funicular form-finding method independent from additional modelling tools such as Grasshopper. Features, such as mesh subdivisions, reciprocal diagrams and a few analysis options, are integrated into the plugin, simplifying the design process.

36 2 Digital Workflow
Circular Area/Ellipses GSEducationalVersion GSEducationalVersion GSEducationalVersion Two intersecting ellipses Boundary Definition Symmetrical Y-Axis Meshing Star
Quadliteral Circular
Perimeter Generation Examples
Polygon
Intersections Poligon
Fig. 2.11 Basic and Complex Shape Boundaries (Top) Selection of basic and complex boundary condition examples
Fig. 2.12 Project Perimeter (Bottom) Boundary condition generation adapted to the project
2.5.2 Pattern Generation (RhinoVAULT 2.0)
Pattern Vertical Equilibrium
Pattern From Surface (QuadMesh)

Pattern From Features (QuadMesh)
As mentioned in the workflow objectives, form-finding will be done with funicular surfaces on which bifurcation systems will be projected.
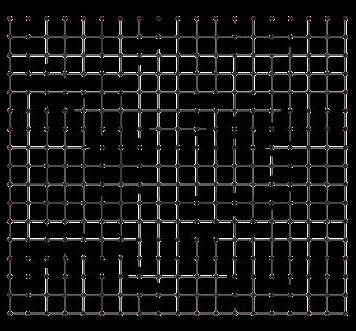
To run the simulation, the example surface needs to be subdivided first. Mesh Patterns in RV2 can be generated from surfaces or lines (Fig. 2.13). A Pattern describes the topology of the FormDiagram. It comprises a series of vertices linked together by lines or edges. RV2 has several tools for modifying and refining a Pattern’s geometry (Block Research Group, 2022).
Pattern From Triangulation (TriMesh)
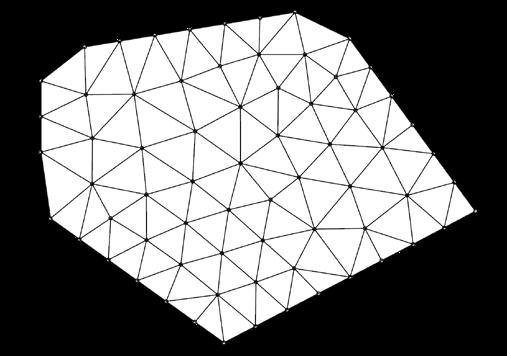

Pattern From Skeleton (QuadMesh)
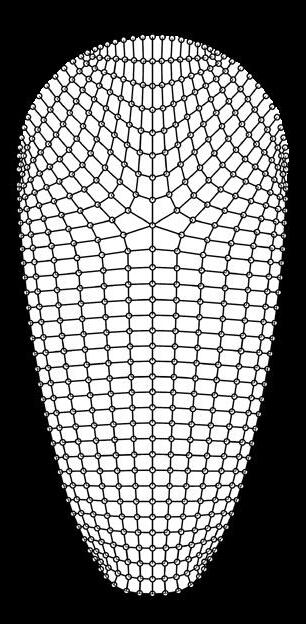
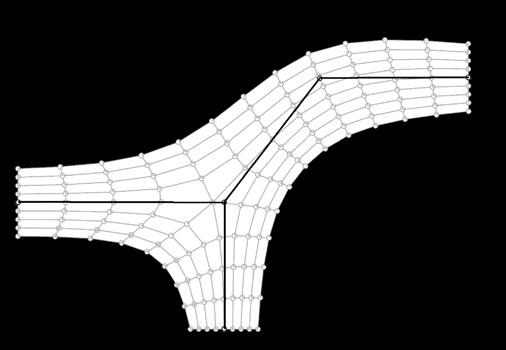
The unstructured TriMesh is simple to generate, and it comes in handy when the boundary conditions are very irregular. Triangulation quickly generates a pattern that helps to dive into form-finding immediately. However, TriMeshes are not suitable for complex schemes. In contrast, a structured QuadMap is more accurate for complex simulation, as often domains need to be partitioned. It is capable of producing better outcomes at higherorder schemes while maintaining numerical stability and accuracy.

The PatternFromFeatures attribute in RV2 is the most applicable to the Conoid Shell project, as the QuadMesh adapts well to the perimeter and boundary conditions (Fig. 2.14)


37 2 Digital Workflow
Fig. 2.13 RhinoVAULT2.0 Meshing options (Top) (1) Mesh from Surface, (2) Mesh from Triangulation, (3) Mesh from Features, (4) Mesh from Skeleton
CreatePattern --> FromFeatures CreateFormDiagram Pattern Vertical Equilibrium Pattern From Features (QuadMesh)
Fig. 2.14 Project Meshing (Bottom) QuadMesh pattern generated through Mesh from Features
2.5.3 Support Definition
Boundary
Supports
After the generation of the Pattern, further information is added, such as the identification of support vertices and refinement of the geometry of the unsupported boundaries. Refinement includes the Sag option, which relaxes the Pattern.

In the drop-down menu, select Define Boundary Conditions > Define Boundary Conditions > Identify Supports
RV2 includes four support selection options: AllBoundaryVerticies, ByContinuousEdges, Corners, Manual (Fig. 2.15)
The Conoid Shell Project has a cantilever, and therefore, ByContinuousEdges is used for anchor point selection. Once the edge is set, all the vertices along that boundary from corner to corner will be automatically selected (Fig. 2.16)




Boundary conditions --> Select ByContinuousEdges

38 2 Digital Workflow
Vertical Equilibrium --> ThrustObject Define Sag Vertical Equilibrium --> ThrustObject
conditions --> Select AllBoundaryVerticies Boundary conditions --> Select Corners/Manual
Vertical Equilibrium --> ThrustObject
Boundary conditions --> Select ByContinuousEdges
Fig. 2.15 Anchor Point Definition Options (RhinoVAULT 2.0) (Top) All boundaries, continuous edges, corners
Fig. 2.16 Project Supports (Bottom) All continuous edges serve as supports, with exception of the cantilever
1 2 3
Vertical Equilibrium --> ThrustObject
Cantilever
2.6 Conoid Shell Analysis
Pipe Diagram (RhinoVAULT2)
Several features facilitate analysis and enhance 3D visualisation in the ThursutObject Settings
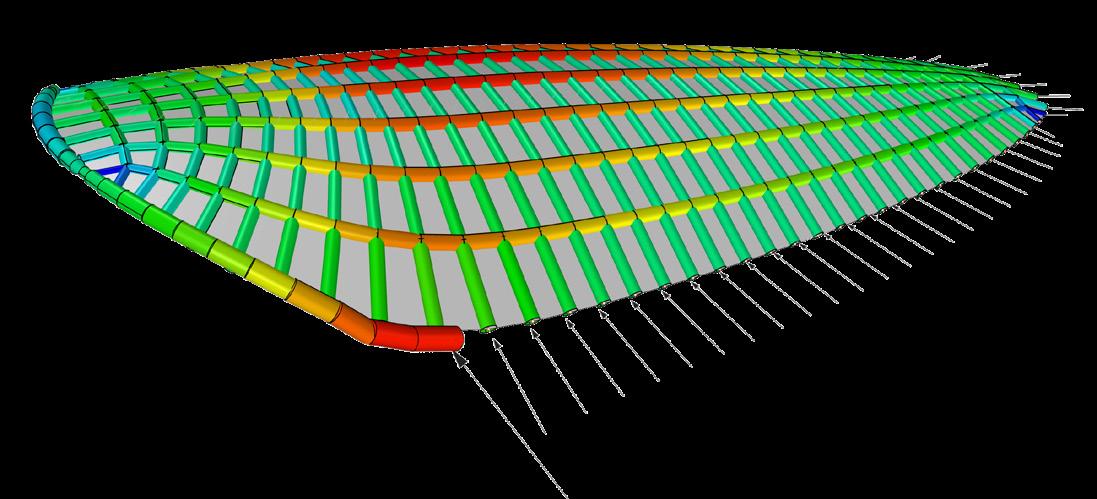
When the ShowColourAnalysis function is enabled, a colour scheme depicts the magnitude of forces in proportion to the model size. With Display Pipes, the boundaries of the ThrustDiagram can be displayed with pipes, the diameters of which are proportionate to the internal forces (Fig. 2.24). The pipe diameter can be adjusted according to the scale of the form diagram. The force-dependent pipe network visualises the force distribution and can help to determine the material distribution of the glulam beam cross-sections in later steps.

Using Karamba for Accurate Shell Analysis
Since precise analysis options are limited in RV2, stresses are also assessed with the help of the structural engineering programme Karamba3D. Karamba accurately analyses spatial trusses, frames, and shells, and it is fully integrated into the Grasshopper and Rhino design environments (Karamba 3D, 2022). The workflow of setting up the model for Karamba analysis is similar to RV2, in which the shell surface, load and anchor points are defined. The results are displayed in the ShellView mode.
It is crucial to recognise that Karamba3D is not a formfinding device but rather a tool to analyse and optimise an already established design idea.
Utilisation and Stress Lines (Karamba3D)
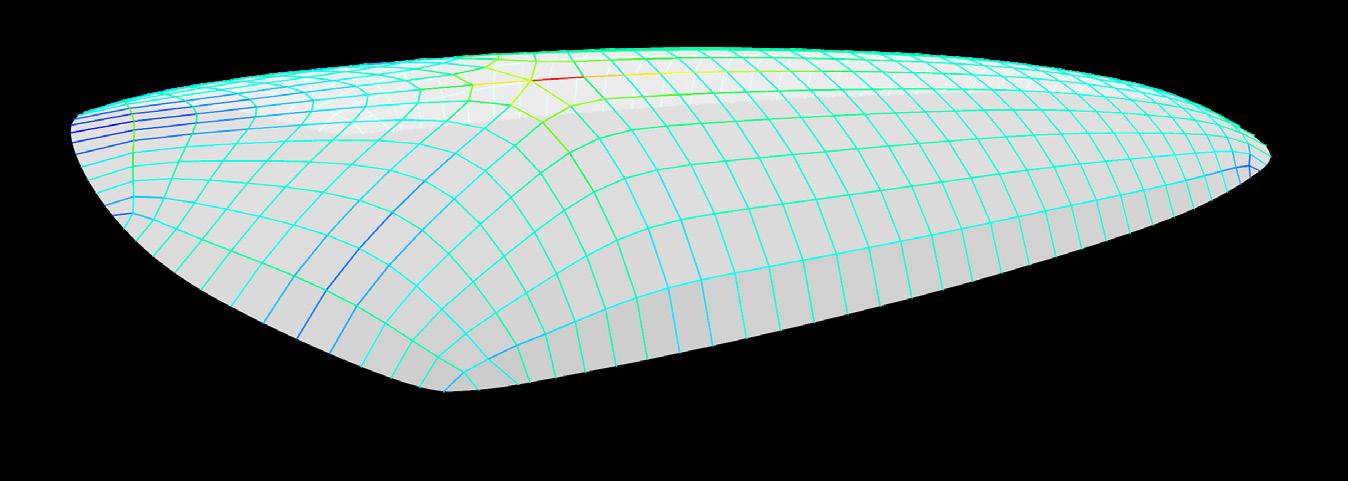
The Utilization displays the axial force causing either tension or compression. The Conoid Shell example shows that the structure experiences compression around the shell’s vertex and the cantilever edges and tension around the supported perimeter (Fig. 2.25a). Internal force trajectories are indicated by principal Stress Lines, which are pairs of orthogonal curves. Subsequently, the curves idealise material continuity paths and represent the best topology for every structure, given a set of boundary conditions (Kam-Ming, 2015). The stress-line analysis provides a direct and geometrically provocative approach to optimisation, synthesising design and structural goals (Fig. 2.25b)

42 2 Digital Workflow
Fig. 2.24 Pipe Diagram (RhinoVAULT 2.0) (Top) Pipe material distribution of form diagram proportional to model size
Utilisation Stress Trajectory Less Material More Material Pipe Diagram: Material Distribution RV2Settings --> Thrustobject --> Pipes ShellView --> Render Settings: Utilization Reactions LineResultsOnShells --> Render Settings: PrincStress Tension Compression
Fig. 2.25a,b Stress Analysis (Karamba3D) (Bottom) Tension and compression visualised through utilisation (a) and principle stress lines (b)
2.7.3 Branching Typology (Lindenmayer-System)
The Lindenmayer-System
Aristid Lindenmayer (1925–1989) presented the L-System mathematical formalism in 1968 as a framework for an axiomatic theory of biological development. Two significant fields are first, the production of fractals and secondly, the accurate modelling of plants. The concept of rewriting is vital to L-Systems. Rewriting, in general, is a method of defining complicated objects by replacing elements of a simple beginning object with a collection of rewriting rules or productions (Fig. 2.28) (Prusinkiewicz and Lindenmayer, 1990). Branching denotes a diverging fork in organic, tree-like structures. In his work, Lindenmayer proposed using strings with brackets to express graph-theoretic trees (Fig. 2.29). The goal was to use the L-System’s framework to properly characterise branching structures found in nature (Ochoa, 1998).
Based on this system, a Grasshopper script is developed that mimics branching in nature within a designated Region (A1). Next, one or multiple Start Points are defined (A2). To start the branching process through “Shortest Walk” path-finding, random Seed Points are generated through 2D Population (A3). However, Seed Points are oriented along the rationalised stress lines and supporting perimeter for the Conoid Shell project, shown in Fig. 2.31. The branches’ Shortest Walk (A5) is specified through Proximity Definition (A4): The fewer the points, the straighter the branch paths will be. Lastly, the Nurbs Curves indicate the smoothness of the overall bifurcation system. Fig. 30 explains the Grasshopper script and the related graphical breakdown of the Lindenmayer-System.
c
F
F →FF-[-F+F+F]+ [+F-F-F]
Figure1.24:Examplesofplant-likestructuresgeneratedbybracketedOLsystems.L-systems(a),(b)and(c)areedge-rewriting,while(d),(e)and (f)arenode-rewriting.
44 2 Digital Workflow
GSEducationalVersion Initial Curve Curve from Previous Recursion Vector Lengthprevious(Percentageof curve length) 1. Recursion 2. Recursion 1. Production Rules 2. Production Rules Applied Twice 3. Production Rules Applied thgree Times + Angle - Angle 1.6.Branchingstructures 25 a n=5,δ =25 7◦ F F →F[+F]F[-F]F b n=5,δ =20◦ F F →F[+F]F[-F][F] c n=4,δ =22 5◦ F F →FF-[-F+F+F]+ [+F-F-F] d n=7,δ =20◦ X X →F[+X]F[-X]+X F →FF e n=7,δ =25 7◦ X X →F[+X][-X]FX F →FF f n=5,δ =22 5◦ X X→F-[[X]+X]+F[+FX]-X F→FF
1.6.Branchingstructures 25 a n=5,δ =25 7◦ F F →F[+F]F[-F]F b n=5,δ =20◦ F F →F[+F]F[-F][F]
◦
n=4,δ =22 5
d n=7,δ =20◦ X X →F[+X]F[-X]+X e n=7,δ =25 7◦ X X →F[+X][-X]FX f n=5,δ =22 5◦ X X→F-[[X]+X]+F[+FX]-X 1.6.Branchingstructures 25
n=5,δ =25 7◦ F F →F[+F]F[-F]F b n=5,δ =20◦ F F →F[+F]F[-F][F] c n=4,δ =22 5◦ F F →FF-[-F+F+F]+ [+F-F-F] d n=7,δ =20◦ X e n=7,δ =25 7◦ X f n=5,δ =22 5◦ X
a
Fig. 2.28 Basic L-System Production Rules and Results After Two and Three Generations (Top) L-Systems have a set of production rules, which are repeated through a few recursions or generations
Fig. 2.29 Plant-Like Structures Generated by Bracketed 0L-Systems (Bottom) L-systems (a), (b) and (c) are edge-rewriting, while (d), (e) and (f) are node-rewriting
the Lindenmayer Branching System (Grasshopper)
L-System mimics biological branching and enables efficient directional deforming (“shortest walk”), which helps to save material







45 2 Digital Workflow
Parameters A1 A2 A5 A3 A6 A4 B1 B2 C1 C2 Region definition Proximity definition Start point Shortest Walk Seed points Nurbs Curve Seed Point Count: 10 | 70 | 250 Number of starting points: 1 | 2 | 3 Number of closest points: 50 | 25 | 5 Curve degree: 1 | 2 | 10 10 2D Branching Grasshopper Setup GSEducationalVersion Group Start Points X Size Y Size Count Seed Degree Seed Points Grow P X Y R R L R N S P P P C P i D L i W A B L P G R+ L T RC P L W S D L C L C1 A2/B2 A1 A3/B1 A5 A4 A5 A6/C2 P t C L D V D P C D C Rectangle Pop 2 D CP Item Ln Prox ShortWalk Disc Nurbs Su bCrv Grasshopper Script 3
Fig. 2.30 Breakdown of
The
Branching Variations
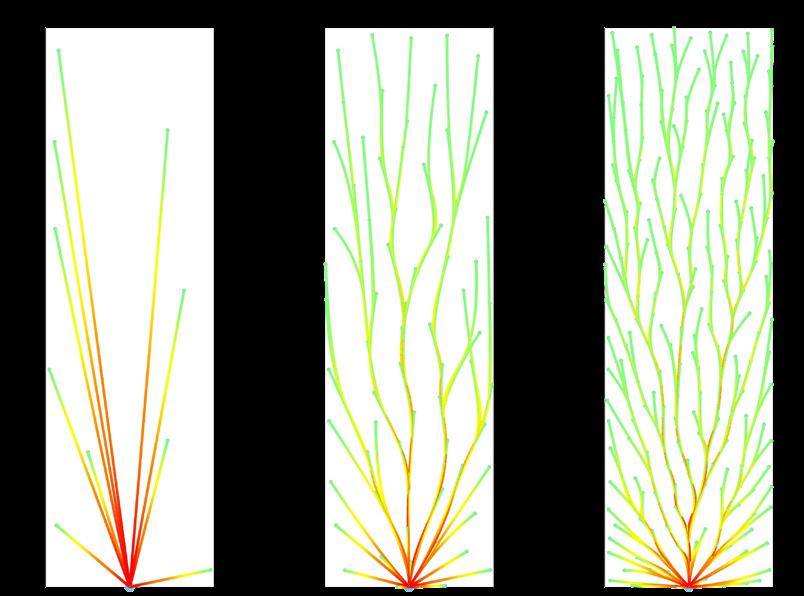
The following three variations will investigate the rationalised L-System bifurcation adapted to the Conoid Shell perimeter and projected onto its surface. Seed Points of all three variations are placed onto the shell’s stress lines, as shown in Fig. 2.25b. Iteration 3a has a single Start Point placed at the end opposite the cantilever (Fig. 2.31a). Iterations 3b and c have multiple Start Points located at the perimeter (Fig. 2.31b) and along the Y-axis vertex (Fig. 2.31c)
Iteration 3a: Single Starting Point
This iteration showcases the L-System bifurcation system with a single starting point at the end opposite the cantilever (Fig. 2.32). Even though the branching follows seed points arranged along the stress lines, the material distribution does not make sense from a structural point of view. As the volume of material is highest at the Start Point, the branches thin out towards the rest of the perimeter, especially at the cantilever, where more material is required. This issue is also reflected in the displacement diagram, where deformation is exceptionally high where axial compression forces are located. To solve this issue, Start Points need to be placed more logical in force flow.





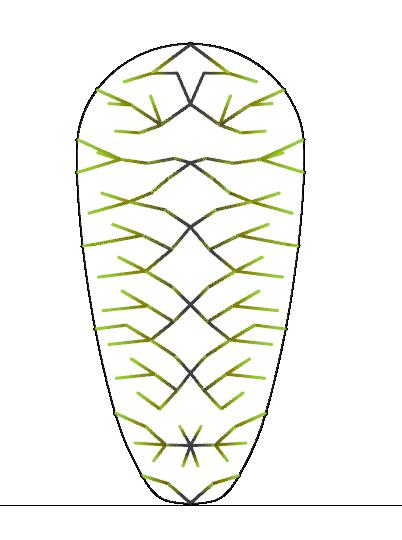
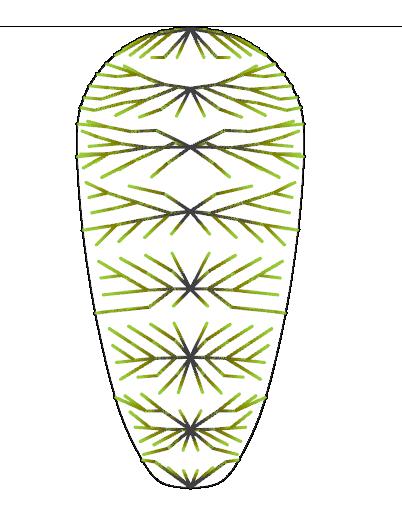
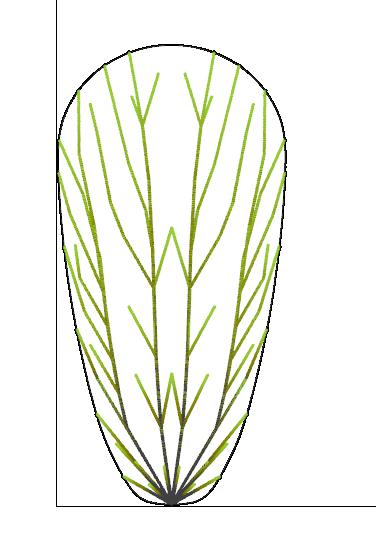

46 2 Digital Workflow
Fig. 2.31a, b, c Branching Variations Using the Lindenmayer-System (3a, 3b, 3c) (Top) Differentiating locations of starting point(s) create different branching pattern outputs
Fig. 2.32 Variation 3a - Rationalised (Bottom) Application of tension members to overhang
Iteration 3a | Start point: Bottom
Iteration 3b | Start points: Perimeter
Axonometry Beam depth: 200mm Full length: 22.0m Widest span: 11.0m Tension Compression Utilisation Displacement Low High
Iteration 3c | Start points: Y-Axis Vertex
Iteration 3b: Perimeter Starting Points
A system change through relocation of Starting Points can avoid dominant displacements caused by inappropriate material distribution. Therefore, this iteration showcases the L-System bifurcation system with multiple starting points at the perimeter (Fig. 2.33)
Structurally, this branching network works better than iteration 3a, as the support members are the thickest and most dense where the forces flow together. There is minor displacement in the cantilever area that can be addressed through cross-section optimisation (see Section 2.8).



For the most part, gridshells are confined to roof or pavilion structures. Required slab and circulation systems function as separate, independent entities.


However, this branching strategy offers the opportunity to integrate slabs by separating glulam splices near the Starting Points at the perimeter. Using that technique, slab systems can be spatially integrated as part of a continuous structure.
Iteration 3c: Y-Axis Vertex Starting Points
This iteration showcases the L-System bifurcation system with multiple starting points at the Y-axis vertex (Fig. 2.34)
The structural logic of this branching strategy is similar to iteration 3b. Nonetheless, less timber is used while achieving similar displacement output, making this variation more material-efficient. It also responds better to lateral forces as all splices are interconnected.
Due to the horizontal alignment of the branching “trees”, most of the blanks are single-curved. Only the splices shifting away from the x-axis experience slight double curvature. Nevertheless, these diagonal splices help to brace the system.

Analogous to 3b, slabs and circulation can be integrated into the branching network. However, it is essential to mention that the slabs will be non-funicular and be exposed to dead and live loads. For that reason, crosssections need to be adapted accordingly.
Due to the improved properties, further investigations will be conducted using variation 3c.
47 2 Digital Workflow
2.33 Variation 3b - Rationalised (Top)
2.34 Variation 3c - Rationalised (Bottom)
Axonometry Beam depth: 200mm Full length: 22.0m Widest span: 11.0m Tension Compression Utilisation Displacement Low High Axonometry Beam depth: 200mm Full length: 22.0m Widest span: 11.0m Tension Compression Utilisation Displacement Low High
Fig.
Holes/openings, tension members, creases Fig.
Application of tension members to overhang
2.8 Cross-Section Optimisation
2.8.1 Main Members
Define Elements (Beams)
Define Cross-Sections --> Depth: 300-600mm
Define Supports
Define Loads --> Meshload Const
Define Material --> Timber
OptimizeCrossSections
Material Distribution (RhinoVAULT 2.0)
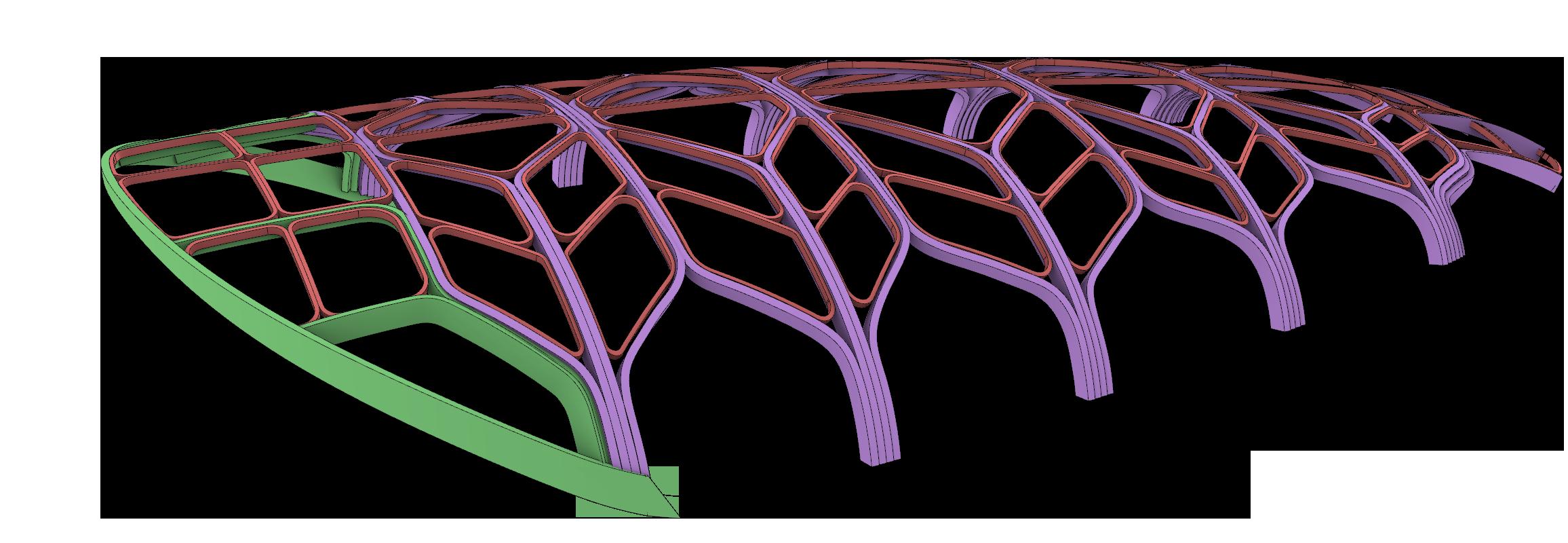
To analyse material distribution, a Pipe Diagram is generated in RV2, as demonstrated on the shell structure in Section 2.6. For this simulation, a Pattern is created with the FromLines command in the RV2 drop-down menu. The lines represent an abstracted version of iteration 3c’s branching network. As expected from the displacement and utilisation diagrams, more material is needed around the cantilever. With the widest span of 11.0m, the Conoid Shell’s largest cross-section will have a depth of 450mm, while the smallest cross-section will have a depth of 200mm (Fig. 2.35)
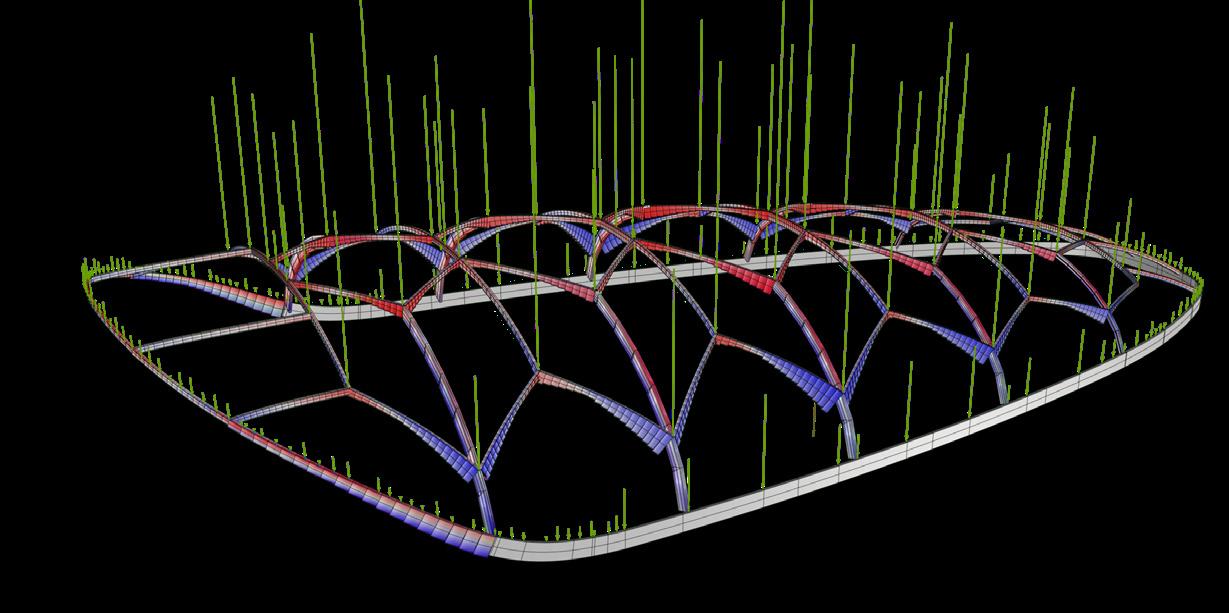

Cross-Section Optimisation (Karamba3D)
Karamba 3D’s Optimize Cross-Section component automatically picks the best cross-sections for beams and shells. It considers the cross-load-bearing section’s capacity and, if desired, restricts the structure’s maximum deflection (Karamba, 2022). The OptiCroSec component calculates each element’s cross-section to ensure that its load-bearing capability is adequate for all load cases (Fig. 2.36). Karamba3D uses the following procedure to do this:
1. Define Elements: Using the abstracted branching network, section forces at nSample points along all lines are determined. The stiffness of the members, i.e. crosssection and materials, influences the section forces in statically indeterminate structures.
2. Define Cross-Sections: The beam depth range is set from 300-600mm so that depth variations lie within the 200-450mm determined via the Pipe Diagram in RV2.
3. Define Supports: The points where the branching line network converges with the perimeter are selected.
4. Define Loads: The type of load is set to MeshLoad Const - the input will be the Conoid Shell surface.
5. Define Material: The defined material is wood. An advantage of using Karamba 3D’s Cross-Section Optimizer alongside RV2’s Pipe Diagram is the possibility of visual demonstration of the varying crosssections of a beam. High curve subdivision allows for the determination of many section forces, leading to a smooth output demonstration.
48 2 Digital Workflow
Ø 200mm Ø250mm Ø300mm Ø350mm Ø400mm Ø450mm CreatePattern --> FromLines RV2Settings --> Thrustobject --> Pipes
Fig. 2.35 Material Distribution RhinoVault 2.0
(Top) Differentiating locations of starting point(s) create different branching pattern outputs
Fig. 2.36 Cross-Section Optimisation Karamba3D
Loads Tension Compression
(Bottom) Application of tension members to overhang
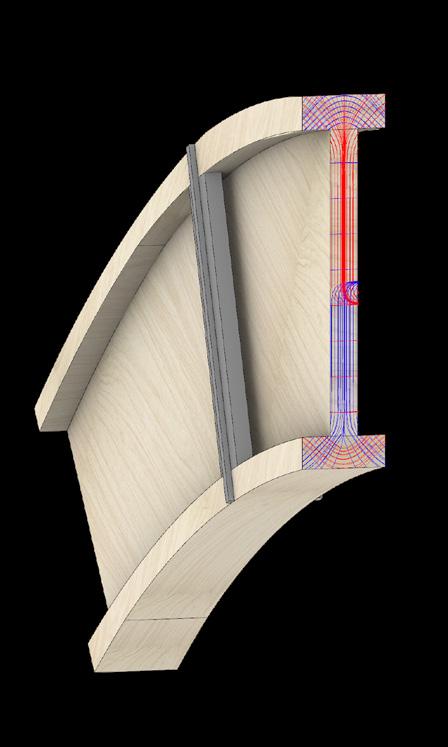
2.8.2 Secondary Members (Lateral Stiffening)
Primary and Secondary Members
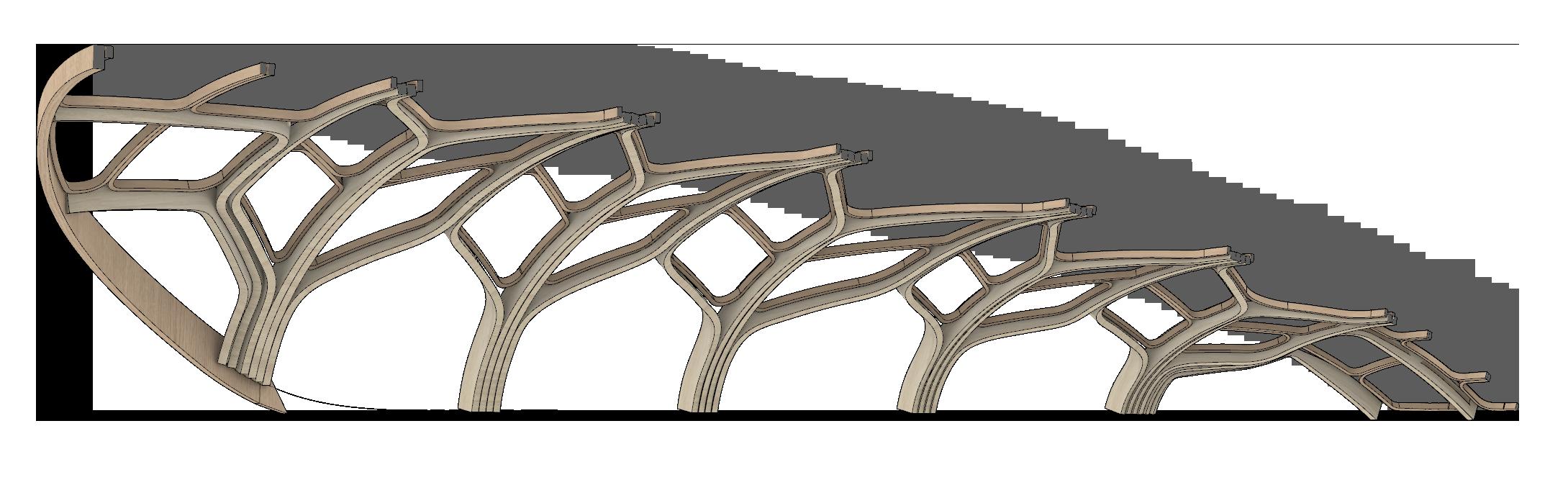
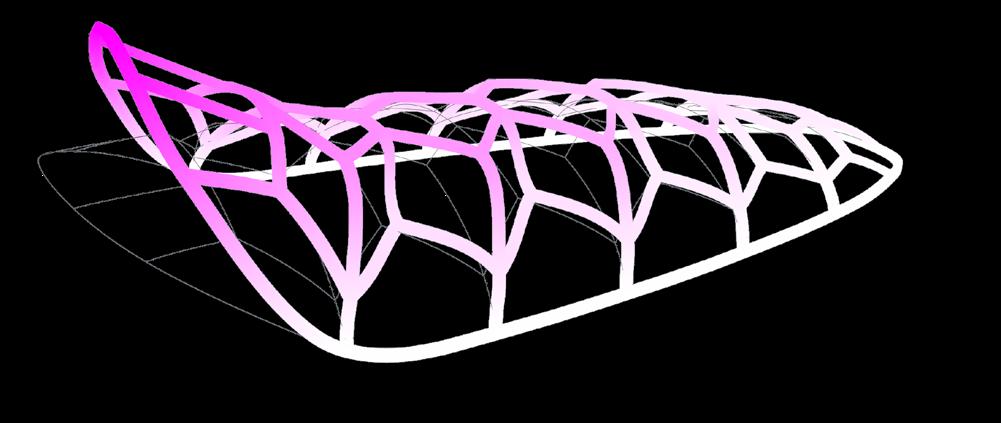
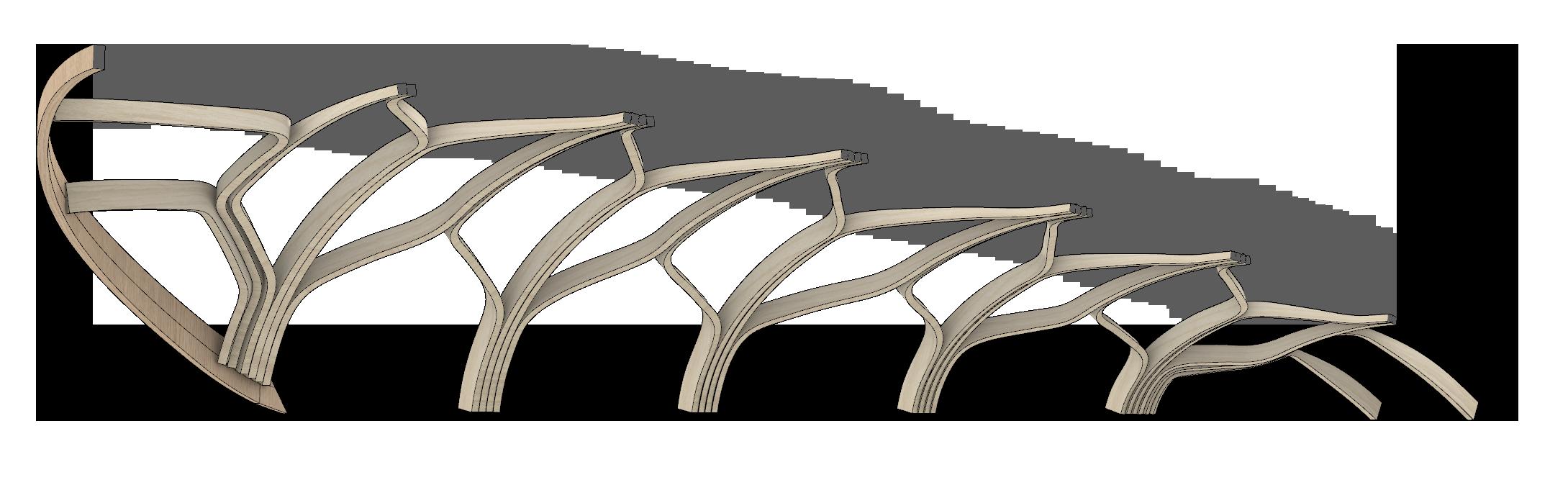
The results from cross-section optimisation are implemented onto the branching system to achieve uniformly distributed loads in the structure (Fig. 2.37). Secondary, lateral stiffening elements can help to further stabilise the structure (Fig. 2.38), as demonstrated in the deformation analysis.

49 2 Digital Workflow
Fig. 2.37 Main Member Material Distribution (Top) Differentiating locations of starting point(s) create different branching pattern outputs
Fig. 2.38 Added Secondary Strcture for Lateral Support (Bottom) Model deflects less in X-direction after the addtion of lateral stiffening
150mm 450mm 250mm 350mm Deformation: 100 100mm Deformation: 100


51 2 Digital Workflow Bending Magnitude Wood Species Selection Final Timber Roof Structure 1 150.00° 2 45.00° 3 153.00° 2 1 3
Cantilever: Pollmeier Beech
Lateral Bracing: Pollmeier Beech Spruce: Binderholz Spruce
Fig. 2.40 Bending Magnitude (Top) The secondary structure has the highest bending magnitude, requiring beech LVL for implementation
Fig. 2.41 Wood Species Selection (Middle) Pollmeier beech and Binderholz spruce
Fig. 2.42 Final Timber Roof Structure (Bottom) Rendered axo
2.11 Ground Connection

Foundation and Structural Wood Protection
An essential aim of the design is to make the structure as longlasting as possible. Structural wood protection is a precaution to increase wood’s lifespan and make the building more ecological. The wood moisture content should be held below 20% to prevent fungal infestation. Timber preservation is given through avoidance of direct ground contact. The foundation height of the project is >30cm, protecting the wood from splash water and contact with damp subsoil (Fig. 2.46). With that, chemical wood preservatives can be omitted. A roof overhang, which protrudes at least 30cm over the wooden structure, also protects the underlying timber (See Section 3)
Architecturally, the transition from wood to concrete can also be elegantly accentuated. Based on examples of Japanese timber joinery, a finger tenon joint with notches following the stepped glulam splices can help connect the two materials (Fig. 2.47) The notches offer an almost rigid composite action between timber and concrete and provide continuous load transmission without additional steel fasteners such as screws or dowels (Müller and Frangi, 2021).
54 2 Digital Workflow
Fig. 2.46 Ground Connection Investigation (Top) Foundation serving as wood protection structure (Design Studio Drawing)
Fig. 2.47 Conoid Shell Project Ground Connection (Bottom) Stepped Tenon joint created through stepping of glulam splices
Final Outcome
The use of different timber species takes advantage of the static properties of the distinct species and visually highlights the structural hierarchy. The implemented foundation system helps protect the timber from moisture and contributes to the structure’s longevity (Fig. 2.48, 2.49a, b, c)
This concludes the Conoid shell digital workflow demonstration. Further investigation with the application of the workflow onto more complex shells is illustrated in Section 3

Fire safety
Fire safety needs to be carefully considered with long-span structures like this example. In a fire, timber structures with a broad cross-section remain highly stable. Glulam has a modest penetration rate of 0.5–1 mm per minute (Fig. 2.50). The charcoal layer that accumulates on the surface of the glulam acts as insulation in the first instance and can slow down the rate of burn (Swedish Wood, 2021).

56 2 Digital Workflow
Fig. 2.48 Final Sectional Perspective (Top) Conoid shell branching with integrated slab, circulation and structural timber protection (foundation system)
Fig. 2.49a, b, c Final Elevations (Middle) Side, top, and back view
2.12 Final Outcome
Fig. 2.50 Glulam Fire Penetration Rate (Bottom Right) Glulam beam after 30 minutes of burning (centre) and after 60 minutes of burning (right) in a four-side fire attack
Top Side
There are three standard methods to reduce the flaring attributes of wood:


1. Construction requiring a fire resistance of 30, 60, and 90mins can be achieved through appropriate dimensioning according to the fire penetration rate.

2. Water-borne synthetic chemicals are impregnated into the wood during impregnation treatment. Many synthetic compounds have fire-retarding qualities; however, only a few are regarded as generally feasible due to cost or other considerations.
3. Coatings on wood surfaces are another method for altering the flame characteristics of wood (e.g., intumescent paints). It functions as a thin-film coating that significantly improves fire resistance.
57 2 Digital Workflow Back
-This page is intentionally left blank-
61
Studio Project Synthesis

03
3.2 Project Description
The project site is located on the Theresienwiese in Munich, where the Oktoberfest takes place (Fig. 3.2). It was chosen due to its lack of usage, while the Oktoberfest does not occur. The site is effectively operated for only 53 days a year and is unusable during the temporary infrastructure’s assembly months. Even though there were debates on building onto the site, nothing has been implemented so far, as the festival has sentimental value to the locals.
Therefore, the project idea is to build a permanent structure that facilitates indoor and outdoor spaces for the Oktoberfest while providing a structure for other activities during the off-season, including other festivals and exhibitions. With this measure, value can be added to the deserted space.
In search of the building typology, the Olympic Park, designed by Frei Otto and Günther Behnisch, serves as a role model for creating an urban park as it successfully synthesises the city and landscape (Fig. 3.3). The case study also embodies the Munich sentiment of praising both the established and the innovative.
Timber construction is a traditional and widespread building method in Bavaria and has regained popularity in recent years due to its sustainability - especially in larger-scale projects. The new festival space structure aims to exploit the characteristics of glued-laminated timber to create an advanced structural system through the computational approach presented in Section 2. The project’s footprint provides the perimeter for particle-spring formfinding.
64 3 Studio Project Synthesis
0 250 500 THERESIENWIESE LINDWURMSTRASSE
Bavaria Statue and Hall of Fame
Fig. 3.2 Site Plan: Theresienwiese Munich The building footprint serves as the perimeter for shell generation
Munich

65 3 Studio Project Synthesis
Fig. 3.3 Case Study: Olympic Park Munich, Frei Otto, Günther Behnisch, 1972 Creating an urban park: The building as part of the landscape
3.3 Perimeter and Shell Form-Finding
The idea behind the global form is to create a canyon-like condition where the buildings seem carved out of the site. The terrain steps down towards a central plaza. The advantage of this urban strategy is the seamless integration of the landscape and the possibility of creating multi-level stories without severely impacting the existing urban fabric. The sections show that the cascading landscape allows for the terracing of the slabs to evenly distribute direct sunlight on all floors (Fig. 3.5a)
The diagrams in Fig. 3.4 illustrate the global form design genesis. Using the building footprints as perimeters, the funicular roofs are quickly generated with Kangaroo 2 to get a general overview of the roof height and rough shape. Since Kangaroo has no builtin analysis tools, RV2 is used to determine and alter the shell in further design stages.

Before starting analysis, the funicular shape can be modified for aesthetic, programmatic or site-specific purposes. As demonstrated in Section 2.8, these changes can be compensated through cross-section adaption.
Since the Conoid Shell example examined in Section 2 resembles the studio project, the same procedure is used to create and analyse openings and overhangs. Free boundaries are created to avoid edge relaxation in these areas. Therefore, the cantilever edges of the Force Diagram are flipped from compression to tension with the FlipEdge command in the ModifyForceDiagram settings.





After force analysis, the branching system is generated using the L-System script with Seed Points placed onto the shell’s stress lines. The output is then rationalised (Fig. 3.5b), and doublecurved elements are avoided as much as possible. Non-funicular elements such as slabs and circulation are integrated into the structure.
Finally, a clay shingle roof is implemented to protect the timber structure and impose a sense of scale. The tiling system formalises the large surface areas and allows for greenery to grow in defined areas so that the structure can become part of the landscape (Fig. 3.5c)
66 3 Studio Project Synthesis
1
3
5 Greenery Transition - Ground
Building Footprints
Roof generation (Kangaroo 2, RhinoVault 2.0)
2 4
Outdoor Circulation/Plazas Interconnections
6 Greenery Transition - Buildings
Fig. 3.4 Global Shape Funicular roof generated through RhinoVault 2.0 and Kangaroo



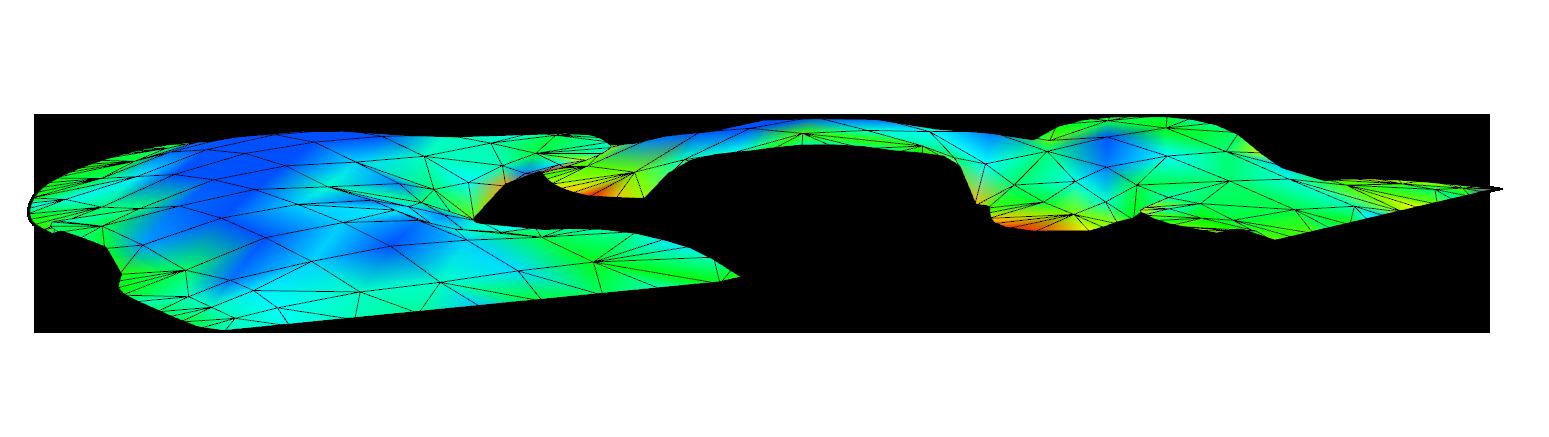
67 3 Studio Project Synthesis
Fig. 3.5 Full Site Sections
Less Forces More Forces
Ground terracing, RV2 analysis and glulam structure, roof tiling and landscape integration
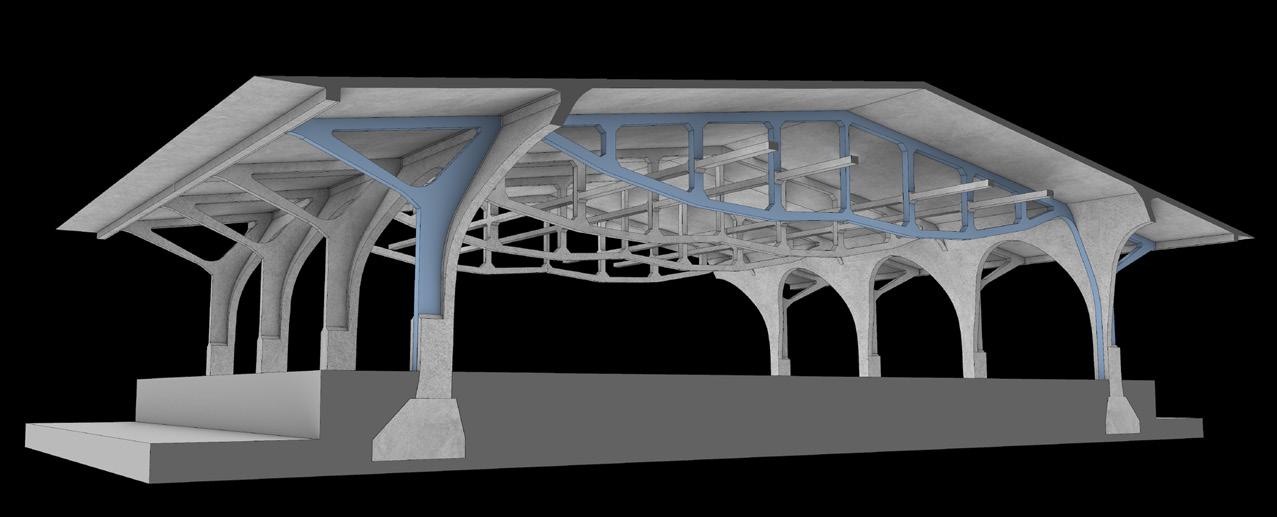
3.4 Branching Application
Similar to the demonstration in Section 2.6, the Utilisation analysis in Karamba shows that the structure experiences compression around the shell’s vertex and the cantilever edges and tension around the supported perimeter, especially in the segments connecting the buildings.

Fig. 3.6 depicts the Karamba shell analysis and the rough structural outline responding to it. Cross-sections have more depth in the overhangs and connecting areas around the perimeter. The glulam beams gradually get more slender towards the shell’s vertex as forces decrease.
Fig. 3.7 illustrates the structural branching system in a more detailed fragment (with consideration of lateral bracing). Slab beams are thicker as they are non-funicular and exposed to live loads. The foundation is a tenon joint with notches following the stepped glulam splices, allowing continuous load transmission. Foundation concrete height is kept at >30cm for structural wood protection. Overhangs and clay roof tiles also protect the timber substructure.

68 3 Studio Project Synthesis
Tension Compression
Fig. 3.6 Branching System Using the L-System (Simplified) Karamba Analysis (Principle Stress and Stress Lines)
Tiling
Roof Substructure

Integrated Slab System (non-funicular)
Roof/Enclosure System
Assembled Model


69 3 Studio Project Synthesis
Fig. 3.7 Branching System Using the L-System (Detailed) Structural build-up of a fragment
Opened tiles
Tiling
1 Heat-reflecting clay tiles (white) 50mm
2 Substructure tiling system
3 Steel fixing rod Ø 20mm
Intensive green roof Vegetation
4 Growing substrate 200mm
5 Filter layer5mm
6 Drainage layer 60mm
7 Root barrier 5mm
8 Protection mat 10mm
9 PVC waterproof membrane 1mm
10 Expanded Polystyrene insulation (EPS) 140mm
11 Vapour control layer 1mm
12 Timber cladding 20mm
Closed tiles
Roof structure

13 Pollmeier® Baubuche GL75 beech LVL beam (secondary) 200x60mm
14 Spruce glulam beam (primary) 600x120mm
Skylight
15 Triple-glazed laminated glass (LG) 10mm
16 Aluminium window frame
Roof Structure (no vegetation)
17 Timber battens 20mm
18 Pollmeier® Baubuche GL75 beech LVL beam (secondary) 200x60mm
19 Spruce glulam beam (primary) 400x120mm
70 3 Studio Project Synthesis GSEducationalVersion GSEducationalVersion 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
Fig. 3.8 Roof Structure Detail
(Top) Intensive green roof allows the building to become part of the landscape
Fig. 3.9 Sectional Perspective
(Bottom) Interior lighting is established through rotated shingle openings
3.5 Details
3.6 Final Views
The next series of building fragments show the project’s relation to the street, surrounding buildings, and the green plaza. Timber and slate shingles are very popular in Bavaria; therefore, the project possesses a contemporary heat-reflecting clay tile covering. The parametric rotation system opens wherever the envelope touches the ground to let the grass grow between the tiles. Daylight comes in through the openings in the centre of the roof.


71 3 Studio Project Synthesis
Fig. 3.10 Relationship Interior-Exterior Greenery grows on the roof where it dips down; the wood paneling in the interior radiates warmth
-This page is intentionally left blank-
72


72 3 Studio Project Synthesis
Fig. 3.11 Plaza Relationship
(Top) The plaza works similar to a Volksgarten (people’s garden), where people enjoy the perks of an urban park (e.g., outside dining, Biergarten)
Fig. 3.12 Street Relationship
(Bottom) The building also reacts to the surrounding streets and Gründerzeit building context


73 3 Studio Project Synthesis
Thesis Conclusion
The core of the thesis consisted of establishing a digital workflow in projecting bifurcation systems onto funicular shells while simultaneously allowing architectural exploration. Next to the primary research done through computational experimentation, it was beneficial to gather knowledge about glulam structures through case study examination and literature review.
In the start, it was advantageous to investigate the characteristics and capabilities of timber, the importance of grain direction and the subtle variations of different timber species, which helped to exploit the strengths of the material in design.
Different computational tools helped modify and adapt funicular shapes to accommodate specific site conditions and user needs. Thanks to the link to parametric systems such as Grasshopper, this was made possible. Nonetheless, the investigation showed that the programmes cannot substitute the design process and should be used as analysis tools only.
An advantage of the final branching system selected in Section 2 was the possibility of slab and circulation integration, the provision of lateral bracing and the opportunity for effective material distribution through glulam splice separation. The outcome is a structure with outstanding properties linked to the material, including performance consistency, longevity and fire resistance. As demonstrated in Section 3, this system can also be applied to other shell structures. Different timber species and cross-sections adapted to the analysis make the design structural and materialefficient and establish an aesthetic hierarchy.
However, production costs due to mass-customisation procedures and high prices should not be underestimated. Even though double-curvature is minimised as much as possible, it is not entirely unavoidable, primarily when diagonal branches orient away from the x- or y-axis. Therefore, these elements will always be slightly curved in two directions - and as mentioned in Section 1, producing double-curved glulam blanks is time-consuming and expensive.
Glulam is also made by glueing numerous splices together and then finger-jointing them to other components. When substandard wood is used in the manufacturing of a timber block, the entire block can deteriorate.
The thesis research has shown that industrial timber can achieve amazing things, especially with the support of digital form-finding and analysis tools. As these are in constant development, it is exciting to see what else can be accomplished in the future.
76 Thesis Conclusion
Bibliography
Books
Adriaenssens, S. et al. (2014). Shell Structures for Architecture: Form Finding and Optimization. London: Routledge.
Billington, D. P. (1997). Robert Maillert. Builder, Designer, and Artist. Cambridge: Cambridge University Press.
Jeska, S., Pascha K. S. (2014). Emergent Timber Technologies: Materials, Structures, Engineering, Projects. Edited by: Rainer Hascher. Basel/Berlin/ Boston: Birkhäuser.
Menges, A. (2017). Advancing wood architecture: a computational approach. Edited by: Tobias Schwinn and Oliver David Krieg. London: Routledge
Müller, C. (2000). Laminated Timber Construction. Basel/Berlin/Boston: Birkhäuser.
Lennartz, M. W., Jacob-Freitag, S. (2015). New Architecture in Wood. Basel: Birkhäuser.
Published Thesis
Kam-Ming, M. T. (2015). Principal stress line computation for discrete topology design. Master of Engineering Thesis. Massachusetts Institute of Technology. Available at: https://dspace.mit.edu/handle/1721.1/99630 (Accessed: 04 April 2022).
Rippmann, M. (2016). Funicular Shell Design. PhD Thesis. ETH Zurich. Available at: https://block.arch.ethz.ch/brg/files/Final_PhD_ rippmann-2_1468394847.pdf (Accessed: 03 March 2022).
Robinson, M. (2019). File-to-Factory: Transferring design intent to manufacture. M. Arch. (Professional) Thesis. Victoria University of Wellington. Available at: https://openaccess.wgtn.ac.nz/articles/thesis/ File-to-Factory_Transferring_Design_Intent_to_Manufacture/17148746
(Accessed: 26 February 2022).
Svilans, T. (2021). Integrated material practice in free-form timber structures. PhD Thesis. The Royal Danish Academy of Fine Arts, Schools of Architecture, Design and Conversation. Available at: https://discovery. ucl.ac.uk/id/eprint/10121947/1/Svilans%20-%202020%20-%20 Integrated%20material%20practice%20in%20free-form%20timber%20 structures.pdf (Accessed: 13 February 2022).
Toussant, M. H. (2007). A Design Tool for Timber Gridshells. MSc Thesis. TU Delft. Available at: https://homepage.tudelft.nl/p3r3s/MSc_projects/ reportToussaint.pdf (Accessed: 13 February 2022).
Book Chapters
Green, D. W. (2001). ‘Wood: Strength and Stiffness’ in Bushow, K. H. J., Flemings, M. C., Kramer, E. J., Veyssière, P., Cahn, R. W., Ilschner, B. and Mahajan, S. (eds.) Encyclopedia of Materials: Science and Technology. Amsterdam/New York: Elsevier, pp. 9732-9736.
Harte, A. (2009). ‘Timber engineering: an introduction’ in Forde, M. (ed.) ICE manual Construction Materials: Volume I/II: Fundamentals and Theory; Concrete; Asphalts inroad construction; Masonry. Institution of Civil Engineers, pp. 707-715.
Self, M. and Vercruysse, E. (2017). ‘Infinite Variations, Radical Strategies’, in Menges, A. et al. (ed.) Fabricate. London: UCL Press, pp. 30-35.
Prusinkiewicz, P. and Lindenmayer, A. (1990). ‘Graphical modeling using L-systems’, in Prusinkiewicz, P. and Lindenmayer, A. (eds.) The Algorithmic Beauty of Plants. New York: Springer, pp. 1-50.
Websites
Baerwald Research (2021). No-nails structural wood – Shigeru Ban’s Tamedia office building. Available at: http://www.baerwaldresearch. com/no-nails-structural-wood-shigeru-bans-tamedia-office-building/ (Accessed: 06 March 2022).
BAM Construct UK (2022). German Gymnasium, London. Available at: https://www.bam.co.uk/how-we-do-it/case-study/german-gymnasiumlondon (Accessed: 09. April 2022).
Binderholz (2022). Produkte. Available at: https://www.binderholz.com/ produkte/brettschichtholz/ (Accessed: 14. April 2022).
Block Research Group (2022). Workflow+UI, Tutorial. Available at: https:// blockresearchgroup.gitbook.io/rv2/quick-start/workflow (Accessed: 04 April 2022).
Buckland Timber (2021). Glulam Timber Species. Available at: https://www.bucklandtimber.co.uk/timber-species/#:~:text=The%20 sapwood%20has%20a%20thickness,density%20and%20good%20 strength%20properties (Accessed: 28 Feburary 2022).
Clearloop (2021). Gate vs Grave: What’s the Best Way to Measure Your Carbon Footprint? Available at: https://clearloop.us/2021/03/24/cradleto-gate-vs-cradle-to-grave/#:~:text=Cradle%2Dto%2Dgate%20refers%20 to,composted%2C%20avoiding%20the%20landfill%20altogether (Accessed 15 April 2022).
Debney, P. (2015). Why It’s Good to be a Lightweight. Available at: https:// www.structuremag.org/?p=8043 (Accessed 24 April 2022).
79
Bibliography
Engler, N. (2007). The Way Wood Works. Available at: https://www. popularwoodworking.com/article/the_way_wood_works/ (Accessed: 13 February 2022).
HDP Construction (2021). Disadvantage of Glulam Timber. Available at: https://www.hpdconsult.com/what-is-glulam-beam/ (Accessed: 24. April 2022).
Koru Architects (2022). 3 reasons sustainable timber is the best construction material. Available at: https://www.koruarchitects.co.uk/ choose-sustainable-timber/#:~:text=Sustainable%20timber%20has%20 (Accessedthe%20lowest,processing%20compared%20to%20other%20 materials (Accessed: 15 April 2022).
Ochoa, G. (1998). An Introduction to Lindenmayer Systems. Available at: http://www1.biologie.uni-hamburg.de/b-online/e28_3/lsys.html (Accessed: 09 April 2022).
PEFC (2022). Standards and Guides. Available at: https://pefc.org/ standards-implementation/standards-and-guides#:~:text=PEFC%20 chain%20of%20custody%20establishes,health%2C%20safety%20 and%20labour%20issues (Accessed: 15 April 2022).
Pfeiffer (2022). Brettschichtholz. Available at: https://www.pfeifergroup. com/de/produkte/holzbau/brettschichtholz/das-produkt/ (Accessed 15 April 2022).
Pollmeier (2022). Über Baubuche. Available at: https://www.pollmeier. com/de/produkte/ueber-baubuche#gref (Accessed: 05 March 2022).
Karamba3D (2022). Parametric Engineering. Available at: https://www. karamba3d.com/ (Accessed: 04 April 2022).
Knippershelbig (2013). Wilhelma Elephant World. Available at: https:// www.knippershelbig.com/en/projects/wilhelma-elephant-world (Accessed: 05 March 2022).
Spring, M. (2006). Bespoke Savill style. Available at: https://www.building. co.uk/buildings/bespoke-savill-style/3069742.article (Accessed 09. April 2022).
Swedish Wood (2022). Manufacturers & manufacture. Available at: https://www.swedishwood.com/building-with-wood/about-glulam/ manufacturers-manufacture/ (Accessed 14. April 2022).
Swedish Wood (2022). Technical Properties. Available at: https://www. swedishwood.com/building-with-wood/about-glulam/choosing_glulam/ technical_properties/ (Accessed 15. April 2022).
Timber Online (2022). The biggest glulam producers. Available at: https:// www.timber-online.net/blog/biggest-glulam-producers.html (Accessed 14. April 2022).
Trada (2022). Bishop Edward King Chapel, Cuddesdon, Oxfordshire. Available at: https://www.trada.co.uk/case-studies/bishop-edward-kingchapel-cuddesdon-oxfordshire/ (Accessed 24. April 2022).
Wood Awards (2017). Savill Building. Available at: https://woodawards. com/portfolio/savill-building/ (Accessed: 09 April 2022).
Articles
Bergqvist, S. (2020). ‘240 metres of precision’, Wood Magazine, (Summer issue), pp. 14-17.
Scott, R. (2014). ‘Timber Case Study: Bishop Edward King Chapel’, In Touch with Timber, (March), pp. 22-29.
Conference Papers
A. Kalama, D. Tzoni, and I. Symeonidou (2020). ‘Kerf Bending: A Generalogy of Cutting Patterns for Single and Double Curvature.’ 7th International Conference on Geometry and Graphics. Faculty of Mechanical Engineering Belgrade, 18-21 Septenber. Thessaly: University of Thessaly, pp. 1-16.
Harris, R. and Roynon, J. (2008). ‘The Savill Garden Gridshell design and construction.’ 10th World Conference of Timber Engineering. Miyazaki, Japan, 02-05 June. Bath: University of Bath, pp. 1-3.
Kilian, A. (2004). ‘Linking Hanging Chain Models to Fabrication’. Proceedings of the 23rd Annual Conference of the ACADIA. Waterloo/ Buffalo/Nottingham. 8-14 November, pp. 1-17.
Pellis, D. and Pottman, H. (2020). ‘Geometry and Statics of Optimal Freeform Gridshells’. 14. Fachtagung Baustatik – Baupraxis. University of Stuttgart. 23-24 March 2020, pp. 1-8.
Rippmann M. and Block P. (2013) ‘Funicular Shell Design Exploration’. Proceedings of the 33rd Annual Conference of the ACADIA. Waterloo/ Buffalo/Nottingham. 24-26 October, pp. 1-19.
Journals
Kilian, A. and Ochsendorf, J. (2005). ‘Particle-Spring Systems For Structural Form Finding’, Journal of the International Association for Shell and Spatial Structures, 46(147), pp. 77-84.
Larsen, K. E. and Schindler, C. (2008). ‘From Concept to Reality: Digital Systems in Architectural Design and Fabrication’, International Journal of Architectural Computing, 4(6), pp. 397-413. doi: 10.1260/147807708787523312.
Müller, K. and Frangi, A. (2021). ‘Micro-notches as a novel connection system for timberconcrete composite slabs’, Engineering Structures, 245, pp. 1-10. doi: 10.3929/ethz-b-000474874.
Olsson, A., Briggert, A. and Oscarsson, J. (2019). ‘Increased yield of finger jointed structural timber by accounting for grain orientation utilizing the tracheid effect’, European Journal of Wood and Wood Products. 77, pp. 1063–1077. doi: 10.1007/s00107-019-01465-0.
Rippmann M., Lachauer L. and Block P. (2012). ‘RhinoVAULT - Interactive Vault Design’, International Journal of Space Structures, 27(4), pp. 219230. doi: 10.1260/0266-3511.27.4.219.
80
Bibliography
List of Figures
82 List of Figures
1. Glulam: History and Development
Fig. 1 Title Page
a, b Drawing by author, design studio drawing
Fig. 1.0 Glulam Spiral Staircase
Drawing by author, design studio drawing
Fig. 1.1 Section 1 Title Page
Drawing by author
Fig. 1.2 “Why timber bends, breaks and remains stiff, and how it can be made rigid”, 1726 Müller, 2000, p.8
Fig. 1.3 Composite beam in Amsterdam City Hall 1648-1645 Müller, 2000, p. 9
Fig. 1.4 De L’Orme System
Drawing by author
Fig. 1.5 Composite Beam Evolution https://www.archweb.com/en/design/page/Laminated-wood/ (11.04.2022), redrawn by author
Fig. 1.6 De L’Orme System Detail
Drawing by author
Fig. 1.7 Hetzer Patent 125895: Load-Optimised Composite Beam Müller, 2000, p. 23
Fig. 1.8 Hetzer Patent 197773: Glued-laminated Timber Beam Müller, 2000, p. 25
Fig. 1.9 Hetzer Patent 125895: Composite I-Beam
Drawing by author
Fig. 1.10 Hetzer Patent 163144: Parabolic Composite Beam
Drawing by author
Fig. 1.11 Case Study: Doecker Gymnasium Wuppertal 1911
Drawing by author
Fig. 1.12 Savill Building Workflow: Digital Perimetre Definition Harris and Roynon, 2008, p.3, redrawn by author
Fig. 1.13 Form-Finding and Analysis Model Harris and Roynon, 2008, p.3
Fig. 1.14 Structural Analysis of the Savill Building Elastic Gridshell Harris and Roynon, 2008, p.4
Fig. 1.15 Case Study: Savill Building Surrey, Glenn Howells Architects, 2006
Adriaenssens, S. et al., 2014, p. 88
Fig. 1.16 The Three Primary Axes of Wood Green, 2021, p. 9732, redrawn by author
Fig. 1.17 Timber Cuts
Drawing by author
Fig. 1.18 Distortion of wood due to shrinkage and swelling Svilans, 2021, p.75, redrawn by author
Fig. 1.19 Hankinson’s Equasion Svilans, 2021, p.71, redrawn by author
Fig. 1.20 Timber Load Behaviour Parallel and Perpendicular to Grain https://slideplayer.com/slide/5043121/ (15.03.2022), redrawn by author
Fig. 1.21 Types of Glulam Blanks Svilans, 2020, p. 94, redrawn by author
Fig. 1.22 Lamella Assembly According to Bending Magnitude Drawing by author
Fig. 1.23 Glulam Profiles Drawing by author
Fig. 1.24 Case Study: Tamedia Office Building Zurich, Shigeru Ban Architects, 2013 https://www.archdaily.com/478633/tamedia-office-buildingshigeru-ban-architects/53042af5e8e44ee8ac0000cc-tamediaoffice-building-shigeru-ban-architects-detail-1 (19.03.2022), redrawn by author
Fig. 1.25 Finger Joint Drawing by author
Fig. 1.26 Case Study: Deal Pier Café Kent, Niall Mclaughlin Architects, Price & Myers, 2008 Drawing by author
Fig. 1.27 Threaded Rod Connection Scott, 2014, p. 27, redrawn by author
Fig. 1.28 Glulam Interception
Drawing by author
Fig. 1.29 Case Study: Bishop Edward King Chapel Cuddeson, Niall Mclaughlin Architects, Price & Myers, 2013
Drawing by author
Fig. 1.30 Case Study: German Gymansium London, Edward A. Gruning, 1864 Drawing by author
Fig. 1.31 Case Study: Swatch Headquarters Biel, Shigeru Ban Architects, 2019 Drawing by author
Fig. 1.32 Case Study: Savill Building Surrey, Glenn Howells Architects, 2006
Drawing by author
Fig. 1.33 Case Study: Elephant Enclosure Stuttgart, Herrmann + Bosch Architekten, MKK-Architekten, Knippershelbig, exp. 2025 Knippershelbig, https://www.knippershelbig.com/en/projects/ wilhelma-elephant-world (11.04.2022), redrawn by author
2. Abstraction: Computational Experiments
Fig. 2.1 Section 2 Title Page
Drawing by author
Fig. 2.2 Robert Hooke: Hanging Chain Adriaenssens, 2014, p. 8
Fig. 2.3 Antoni Gaudí: Chain Network https://cooksipgo.com/gaudi-la-pedrera-barcelona-spain/ (15.03.2022)
Fig. 2.4 Heinz Isler: Hanging Cloth: https://parametricsemiology.wordpress.com/2014/01/11/ grp05final-presentation/ (15.03.2022)
Fig. 2.5 Shell Categories
Drawing by author
Fig. 2.6 Case Study: Woodchip Barn Hooke Park, AA Design+Make, 2016 Menges, 2017, p. 151
Fig. 2.7 Case Study: Magazzini Generali Chiasso, Robert Maillart, 1925
https://www.atlasofplaces.com/architecture/lagerhaus-dermagazzini-generali/ (25.04.2022), redrawn by author
83
List of Figures List of Figures
Fig. 2.8 Catenary Model Guidance
Drawing by author
Fig. 2.9 Catenary Model Testing
Drawing by author
Fig. 2.10 Digital Workflow Proposal
Diagram by author
Fig. 2.11 Basic and Complex Shape Boundaries
Drawing by author
Fig. 2.12 Project Perimeter
Drawing by author
Fig. 2.13 RhinoVAULT 2.0 Meshing options
Drawing by author
Fig. 2.14 Project Meshing
Drawing by author
Fig. 2.15 Anchor Point Definition Options (RhinoVAULT 2.0)
Drawing by author
Fig. 2.16 Project Supports
Drawing by author
Fig. 2.17 Multihalle Mannheim, Carlfried Mutschler, Joachim Langner, Frei Otto, 1975
https://www.marlowes.de/frei-ottos-multihalle-in-gefahr/ (04.04.2022)
Fig. 2.18 Holes and Openings
Drawing by author
Fig. 2.19
Fig. 2.20
Tension Members
Drawing by author
Crease
Drawing by author
Fig. 2.21 Form Diagram
Drawing by author
Fig. 2.22
Force Diagram
Drawing by author
Fig. 2.23 Thrust Network
Drawing by author
Fig. 2.24 Pipe Diagram (RhinoVAULT 2.0)
Drawing by author
Fig. 2.25 Stress Analysis (Karamba3D)
a, b
Drawing by author
Fig. 2.26 Pattern adpated to Stress Lines
Drawing by author
Fig. 2.27 Pattern adapted to Form Diagram (QuadMesh)
Drawing by author
Fig. 2.28
Basic L-System Production Rules and Results After Two and Three Generations
https://generativelandscapes.wordpress.com/2014/10/07/ fractal-trees-basic-l-system-example-9-4/ (09.04.2922), redrawn by author
Fig. 2.32 Variation 3a - Rationalised
Drawing by author
Fig. 2.33 Variation 3b - Rationalised
Drawing by author
Fig. 2.34 Variation 3c - Rationalised
Drawing by author
Fig. 2.35 Material Distribution RhinoVault 2.0
Drawing by author
Fig. 2.36 Cross-Section Optimisation Karamba3D
Drawing by author
Fig. 2.37 Main Member Material Distribution
Drawing by author
Fig. 2.38 Added Secondary Strcture for Lateral Support
Drawing by author
Fig. 2.39 Most Popular Timber Species Used For Glulam Construction and Their Characteristics https://www.bucklandtimber.co.uk/timberspecies/#:~:text=The%20sapwood%20has%20a%20 thickness,density%20and%20good%20strength%20properties (03.04.2022), redrawn by author
Fig. 2.40 Bending Magnitude
Drawing by author
Fig. 2.41 Wood Species Selection
Drawing by author
Fig. 2.42 Final Timber Roof Structure
Drawing by author
Fig. 2.43 Integrated Slab
Drawing by author
Fig. 2.44 Non-Funicular Slab and Circulation Integration
Drawing by author
Fig. 2.45 Integrated Spiral Staircase
Drawing by author, design studio drawing
Fig. 2.46 Ground Connection Investigation
Drawing by author
Fig. 2.47 Conoid Shell Project Ground Connection
Drawing by author
Fig. 2.48 Final Sectional Perspective
Drawing by author
Fig. 2.49 Final Elevations a, b, c Drawing by author
Fig. 2.50 Top Ten Biggest Glulam Producers in Central Europe https://www.timber-online.net/blog/biggest-glulam-producers. html (14.04.2022), redrawn by author
Fig. 2.51 Glulam Fire Penetration Rate
https://www.swedishwood.com/building-with-wood/aboutglulam/choosing_glulam/technical_properties/ (15.04.2022)
Fig. 2.52 Transport via Train
Fig. 2.29
Plant-Like Structures Generated by Bracketed 0L-Systems
Prusinkiewicz and Lindenmayer, 1990, p. 25
Fig. 2.30 Breakdown of the Lindenmayer System (Grasshopper)
Drawing by author
Fig. 2.31 Branching Variations Using the Lindenmayer-System (3a, a, b, c 3b, 3c)
Drawing by author
https://www.meinbezirk.at/schwaz/c-lokales/binderholzverlagerung-auf-die-schiene-ist-eine-erfolgsmodell_a4716539 (14.04.2022)
Fig. 2.53 Cradle-to-Gate Glulam Life Cycle https://m.facebook.com/GlulamSolutionsLimited/photos/a.10 3312798085095/284423853307321/?type=3 (14.04.2022), redrawn by author
List of Figures
84
List of Figures
3. Synthesis: Design Studio Project
Fig. 3.1 Section 3 Title Page
Drawing by author
Fig. 3.2 Site Plan: Theresienwiese Munich
Drawing by author
Fig. 3.3 Case Study: Olympic Park Munich, Frei Otto, Günther Behnisch, 1972
https://www.istockphoto.com/photo/munich-olympic-park-insummer-germany-gm1174718346-326817845 (23.04.2022)
Fig. 3.4
Global Shape
Drawing by author, design studio drawing
Fig. 3.5 Full Site Sections
a, b, c Drawings by author, design studio drawing
Fig. 3.6 Branching System Using the L-System (Simplified)
Drawing by author, design studio drawing
Fig. 3.7
Fig. 3.8
Fig. 3.9
Branching System Using the L-System (Detailed)
Drawing by author, design studio drawing
Roof Structure Detail
Drawing by author, design studio drawing
Sectional Perspective
Drawing by author, design studio drawing
Fig. 3.10 Relationship Interior-Exterior
Drawing by author, design studio drawing
Fig. 3.11 Plaza Relationship
Drawing by author, design studio drawing
Fig. 3.12 Street Relationship
Drawing by author, design studio drawing
Fig. 3.13 Continuous Surface with Projected Branching System
Drawing by author, design studio drawing
85
of
List
Figures
List of Figures









































































































































