








Knowledge of Statistics is the sine qua non in today’s data-driven digital world. From business and economics to the natural and social sciences, the ability to collect, analyze, and interpret data is a crucial skill. The discipline of statistics equips students with the tools necessary to extract meaningful insights from data, make informed decisions, and critically evaluate the world around them. This book is designed to introduce undergraduate students to the core concepts and applications of statistics in a systematic and comprehensive manner.
Statistics is not just about numbers; it is about understanding variability, uncertainty, and making inferences. While this book emphasizes the practical applications of statistical techniques, it ensures that the underlying theoretical foundations are thoroughly explained. The aim is to strike a balance between theory and application empowering students to confidently apply statistical methods to real-world problems.
Although many excellent textbooks on statistics are available, this book adopts a student-centric approach, specifically designed for undergraduate learners. The content is presented in clear, easy-to-understand language, ensuring that even students without a background in mathematics or statistics at the Senior Secondary level can easily grasp the fundamental statistical concepts. For undergraduate students, this book offers acute insights into the cardinal concepts that govern the use of statistical methods in the data-driven universe.
The key features of this book include:
Student-Centric Design: Aligned with the B.Com. (Hons.) and B.Com. syllabi under the new UGCF-NEP 2020 Framework of the University of Delhi, as well as other central universities in India and abroad.
Solved Examples: Each chapter is enriched with a variety of solved examples to illustrate key statistical concepts and techniques.
Practice Problems: At the end of each chapter, students will find a range of exercises, including conceptual questions, numerical problems, and data analysis tasks, to test their understanding.
Formula Summaries: A concise summary of formulas at the end of each chapter for quick reference.
Excel-Based Exercises : To help students gain practical experience, the book includes exercises and demonstrations using Excel, a widely used tool in statistical analysis.
Each chapter begins with a clear outline of the topics covered, allowing students to focus on key learning objectives. The structure of the book aligns with the typical undergraduate curriculum, ensuring it fits within the prescribed teaching hours and course weightage. The chapters are sequenced to facilitate a smooth progression from basic to advanced topics. This book is an essential ingredient in the repertoire of every undergraduate student aiming to understand the subject thoroughly and perform well in examinations.

By the end of this chapter, you will be able to understand:
Introduction
Measures of central tendency, dispersion and symmetry
Data analysis toolpak
Use of Pivot Tables in descriptive statistics
Probability and probability distributions
Computation of probability
Computation of probability for binomial distributions
Computation of probability for poisson distributions
Computation of probability for normal distributions
Correlation and regression analysis
Simple correlation analysis
Simple regression analysis
Time series analysis
Index Numbers
Questions for practice
Key Excel Functions
A spreadsheet is an application used to organize, analyze, and visualize data in tabular form. It consists of a grid of rows and columns where each cell can hold data or formulas. They are used in various fields for tasks ranging from simple calculations to complex data analysis. Some of the popular spreadsheets include MS Excel, Google Sheets, Apple Numbers, LibreOffice Calc, Zoho Sheets, Smartsheet, Airtable, Quip, etc. Excel sheets can
be utilized for a wide range of applications in business and commerce including accounting, tax, linear programming, investment and statistical analysis. A basic understanding of fundamental Excel commands like formulas and functions. It also offers various statistical functions and includes the Data Analysis ToolPak, which provides advanced statistical tools. Worksheets also contain charts necessary for comprehensive analysis. In business statistics, spreadsheets can be used to enable users to perform a wide range of statistical calculations and analyses. This chapter will cover fundamental formulas and functions in spreadsheets, providing a foundation for using this powerful tool effectively.
The following sections will explore core concepts in business statistics that can be explored through practical applications using spreadsheets.
Before exploring the statistical functions available in Spreadsheet, we may generate data and then the various statistical measures are calculated to understand and interpret the data so generated. The data may be generated using the Excel function of RANDBETWEEN.
The RANDBETWEEN function returns a random integer number between the specified numbers. A new random integer number is returned every time the worksheet is calculated. Its syntax is RANDBETWEEN (bottom, top) where the bottom argument is the smallest integer and the top argument is the largest integer RANDBETWEEN will return. Since a new random integer number is returned every time the worksheet is calculated, we will copy the random numbers, paste them separately as VALUES, and then use these fixed numbers to calculate the Excel functions. The relevant Excel Functions used to compute the various measures of central tendency are explained below.
1. Arithmetic Mean: Mean is the average of the given numbers and is calculated by dividing the sum of given numbers by the total of numbers. The AVERAGE function returns the average (arithmetic mean) of the arguments. Its syntax is AVERAGE(number1, [number2], ... or range containing observations)
2. Median: It is the middle value in a dataset. The MEDIAN function returns the median of the given numbers. The median is the number in the middle of a set of numbers. Its syntax is MEDIAN(number1, [number2], ... or range containing observations).
3. Mode: It is the value that appears most frequently in a dataset. Excel Functions used to compute mode include MODE function, MODE.MULT function and MODE. SNGL function.
MODE function returns the most frequently occurring, or repetitive, value in an array or range of data. Its syntax is MODE(number1, [number2],... or range of observations)
MODE.MULT function is an array function that returns a vertical array of the most frequently occurring, or repetitive values in an array or range of data. For horizontal arrays, TRANSPOSE (MODE.MULT(number1, number2,...)) is used. It returns more than one result if the data has multiple modes. Its syntax is:
MODE.MULT (number1,[number2],...or range of observations)
MODE.SNGL function returns the most frequently occurring, or repetitive, value in an array or range of data. Its syntax is MODE.SNGL (number1,[number2], ... or range containing observations)
It may be noted that if the data set contains no duplicate data points, these functions return the #N/A error value.
4. Quartile: Quartiles are statistical values that divide a set of data into four equal parts. The QUARTILE function returns the quartile of a data set. Its Syntax is QUARTILE (array,quart) and its arguments are array which is an array or cell range of numeric values for which we want to determine the quartile value and quart which indicates which value to return.
0
1
2
3
4
Minimum value
First quartile (25th percentile)
Median value (50th percentile)
Third quartile (75th percentile)
Maximum value
If the array argument is empty, QUARTILE returns the #NUM! error value. If quart is not an integer, it is truncated. If quart < 0 or if quart > 4, QUARTILE returns the #NUM! error value. MIN, MEDIAN, and MAX return the same value as QUARTILE when quart is equal to 0 (zero), 2, and 4, respectively.
5. Percentile: The PERCENTILE function returns the kth percentile of values in a range. Its syntax is PERCENTILE(array, k) where the array argument is the array or range of data that defines relative standing and argument k is for the percentile value in the range 0 to 1, inclusive. Thus, for calculating P40 or the 40th percentile, the value for k is 40/100 or 0.4.
We also have two new functions for calculating percentiles in Excel viz., the PERCENTILE.EXC function returns the kth percentile of values in a range, where k is in the range 0 to 1, exclusive. The PERCENTILE.INC function returns the kth percentile of values in a range, where k is in the range 0 to 1, inclusive.
6. Decile: There is no Decile function in Excel to compute deciles, however, we can use the PERCENTILE function to compute it. For computing the nth decile, in the argument k, we should type n/10.
7. Standard Deviation: The standard deviation is a measure of how widely values are dispersed from the average value (the mean). STDEV.P function calculates standard deviation based on the entire population given as arguments. STDEV.P uses the following formula: ( ) 2 XX N ∑− . Its syntax is STDEV.P(number1, [number2],... or range of observations). STDEV.P assumes that its arguments are the entire population. If data represents a sample of the population, the standard deviation is computed using the STDEV Function. For large sample sizes, STDEV.S and STDEV.P return approximately equal values.
STDEV.S function estimates standard deviation based on a sample using the formula: ( ) 2 1 XX N ∑− . Its syntax is STDEV.S(number1, [number2],... or range of observations).
8. Variance: It is the square of the standard deviations. Excel has two functions for Variance, viz., VAR.P and VAR.S. The VAR.P function calculates variance based on the entire population. VAR.P uses the following formula: ( ) 2 XX N ∑− . Its syntax is VAR.P(number1, [number2],... or range of observations). VAR.S function estimates variance based on a sample using the formula: ( ) 2 1 XX N ∑− . Its syntax is VAR.S(number1, [number2],... or range of observations).
9. Kurtosis: Kurtosis characterizes the relative peakedness or flatness of a distribution compared with the normal distribution. Positive kurtosis indicates a relatively peaked distribution. Negative kurtosis indicates a relatively flat distribution. The KURT function returns the kurtosis of a data set. Its Syntax is KURT(number1, [number2], ... or range of observations).
10. Skewness: The SKEW function returns the skewness of a distribution. Skewness characterizes the degree of asymmetry of a distribution around its mean. Positive skewness indicates a distribution with an asymmetric tail extending toward more positive values. Negative skewness indicates a distribution with an asymmetric tail extending toward more negative values. Its Syntax is SKEW(number1, [number2], ...,or range of observations)
11. Minimum: The MIN function returns the smallest number in a set of values. Its syntax is MIN(number1, [number2], ... or range of observations).
12. Maximum: The MAX function returns the largest value in a set of values. Its Syntax is MAX(number1, [number2], ... or range of observations).
13. Range: Range is a measure of dispersion that determines the difference between the highest and the lowest values in a dataset. It is calculated as MAX(number1, [number2], ... or range of observations) – MIN(number1, [number2], ... or range of observations).
14. Count: The COUNT function counts the number of cells that contain numbers, and counts numbers within the list of arguments. It is used to determine the number of entries in a number field that is in a range or array of numbers. Its syntax is COUNT(value1, [value2], ... or range of observations). For example, to count the numbers in the range A1:A100, the formula is = COUNT(A1:A100).
15. Largest Number: The LARGE function returns the kth largest value in a data set. It can be used to select a value based on its relative standing, that is to return the highest, second-highest, third-highest value, etc. Its Syntax is LARGE(array, k) with arguments: Array i.e., the array or range of data for the kth largest value is to be determined, and k i.e. the position (from the largest) in the array or cell range of data to return. For example, if n is the number of data points in a range, then LARGE(array, 1) returns the largest value, and LARGE(array, n) returns the smallest
value. If the array is empty, LARGE returns the #NUM! error value. If k ≤ 0 or if k is greater than the number of data points, LARGE returns the #NUM! error value.
16.Smallest Number: The SMALL function returns the kth smallest value in a data set. It is used to return values with a particular relative standing in a data set. Its Syntax is SMALL(array, k), where Array is the array or range of numerical data for which the kth smallest value is to be determined and k is the position (from the smallest) in the array or range of data to return. For example, if n is the number of data points in the array, SMALL(array, 1) equals the smallest value, and SMALL(array, n) equals the largest value. If the array is empty, SMALL returns the #NUM! error value. If k ≤ 0 or if k exceeds the number of data points, SMALL returns the #NUM! error value.
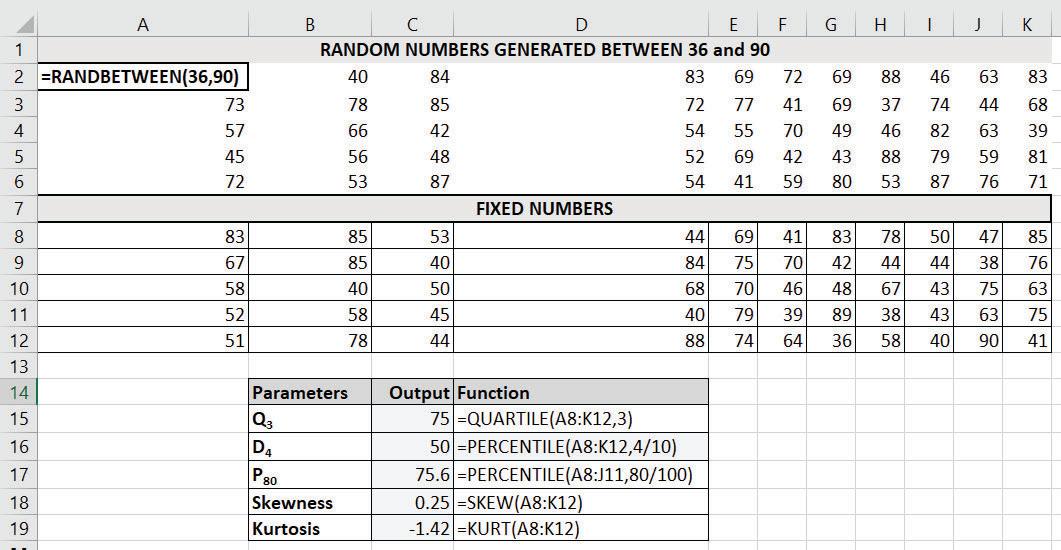
Example 13.1: Generate 40 numbers randomly between 36 to 90 and calculate Q3, P80, Kurtosis and Skewness.
Solution:
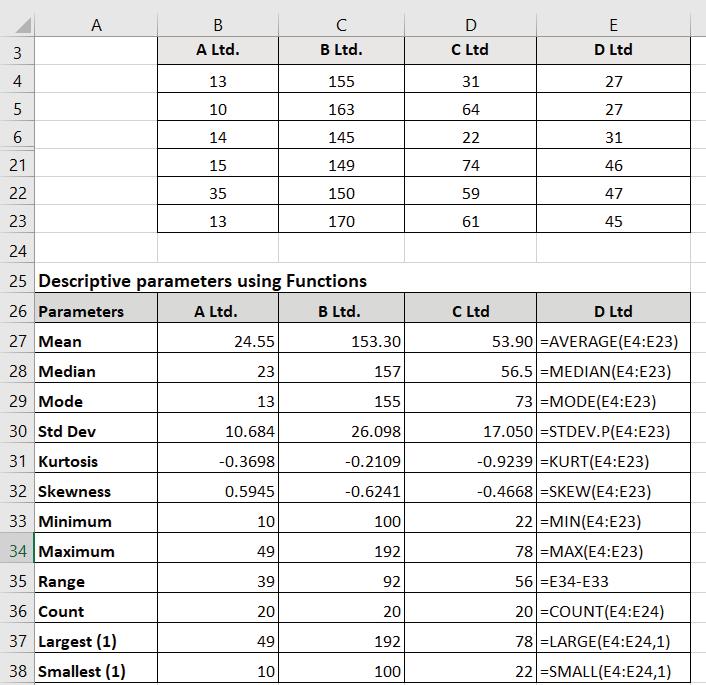
Example 13.2: You are given the following data about the share prices of four companies during Jan 2025. Compute various measures of descriptive statistics using excel functions.
Example 13.3: For the following data, check whether Mean, Median, Mode, Variance and Standard Deviation are independent of change of origin or not:
Solution:


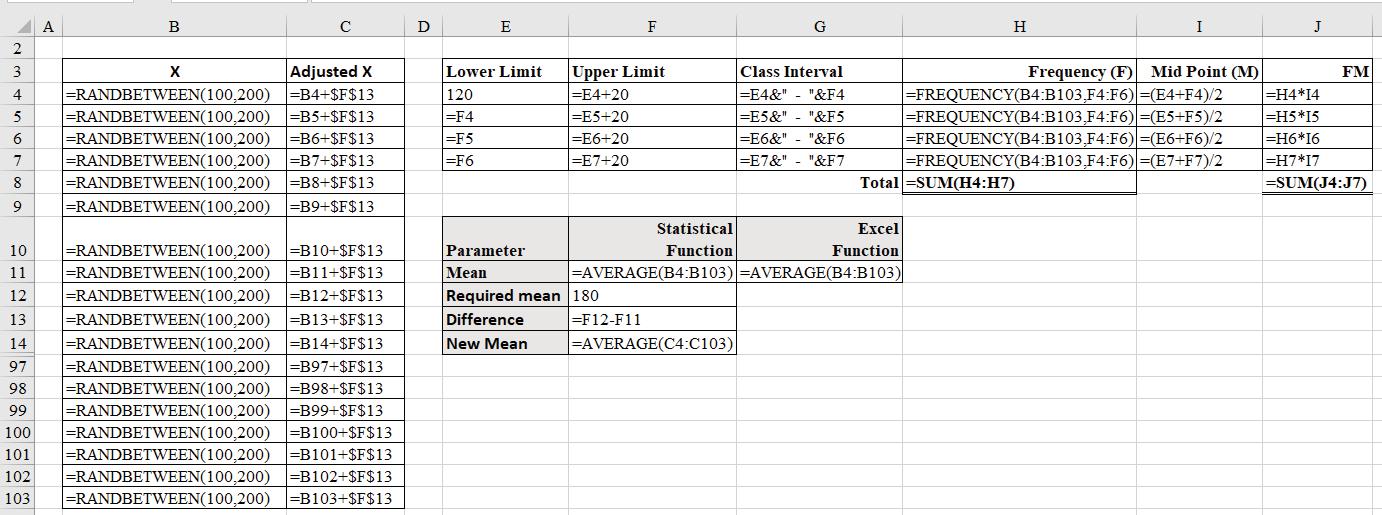
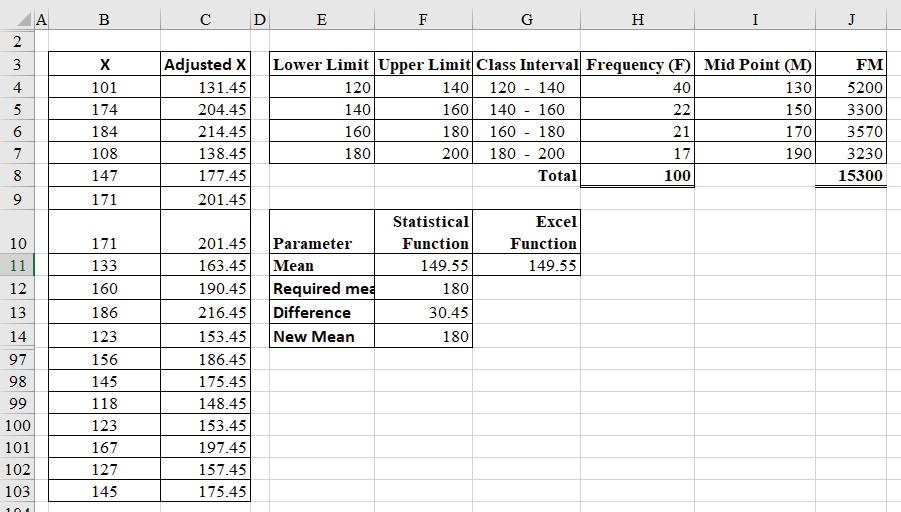
Example 13.4: Generate 100 random numbers between 120 and 200 and create frequency distribution using appropriate class intervals. Adjust the original values such that the mean of the adjusted observations becomes 180.
Solution:
Formulas used:
OUTPUT SHEET:
Example 13.5: Calculate mean using Excel in-built function and statistical formula, central moments for the following data. Also, verify that the second moment is equal to variance.
X 235781011236789
Solution:
Formula used:

OUTPUT SHEET:

The Data Analysis ToolPak is an Excel add-in that can be used for calculating statistical measures such as descriptive statistics, correlation, regression, etc. automatically without using the Excel functions or formulas.
To install the Data Analysis ToolPak on Windows, select the File tab: then Options; then select Add-ins: and under Manage click “Go”. Then Excel Add-ins: check data analysis tool pack ok. The Analysis ToolPak will be installed and it can be located by clicking the Data tab.

The functions available in this ToolPak are:
Anova: Single Factor
Covariance
Fourier Analysis
Rank and Percents
t-Test: Two-Sample Assuming Equal Variances
Correlation
t-Test: Paired Two Sample for Means
Exponential Smoothing
F-Test Two-Sample for Variance
Anova: Two-Factor with Replication
Descriptive Statistics
Histogram
Regression
t-Test: Two-Sample Assuming Unequal Variances
Random Number Generation
Anova: Two-Factor Without Replication
Z-Test: Two-Samples for Mean
Sampling Moving Average
Example 13.6: Generate 50 random numbers between 1000 to 1500. Compute descriptive statistical measures using data analysis toolpak in Excel.
Solution:
Firstly, we generate 50 random numbers either in a column from A2 to A51 or in a row using the function = RANDBETWEEN(1000, 1500). Copy the data and paste it as Values in Cells B2:B51 and name it X. The steps used to compute descriptive statistics using the data analysis tool pack are as follows.
Step 1: Click Data Analysis from the Data tab, then select Descriptive Statistics and click ok.
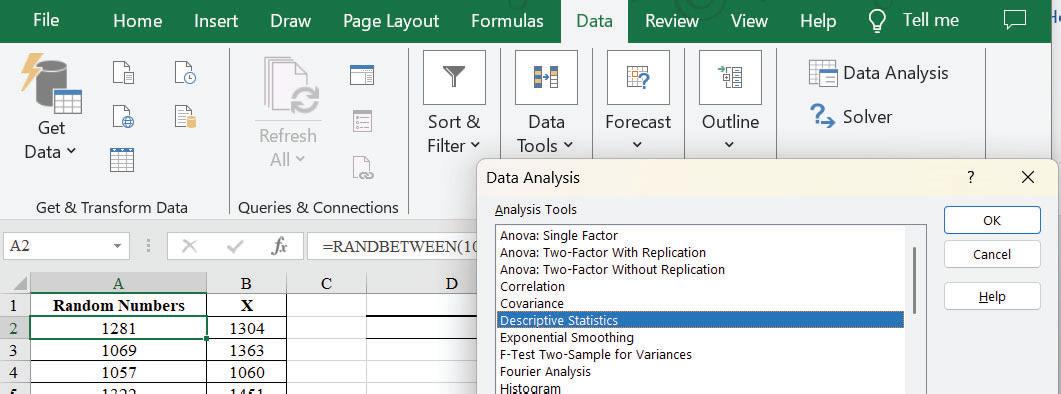
Step 2: The following pop up Window appears:
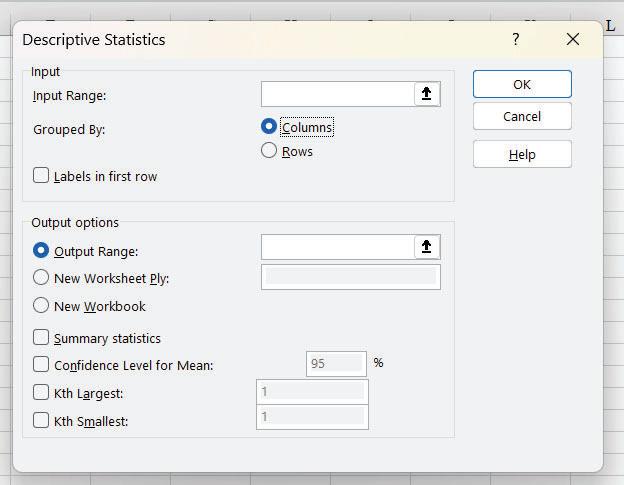
In Input Range: Select the data from B1:B51, Grouped By: Columns (because we have generated data in a column), check the checkbox for Labels in the first row as we have selected the column heading in the input range. In Output options, select Output Range and Cell D1, check the checkbox for Summary Statistics, kth Largest 1 and kth Smallest 1 as shown in the figure below and click ok.

AUTHOR : GURMEET KAUR, SOUMYA SHARMA, RACHAN SAREEN
PUBLISHER : TAXMANN
DATE OF PUBLICATION : JANUARY 2025
EDITION : 2025 EDITION
ISBN NO : 9789364550758
NO. OF PAGES : 788
BINDING TYPE : PAPERBACK

Business Statistics is a comprehensive, student-centric textbook meticulously aligned with the UGCF-NEP 2020 framework. It aims to cultivate theoretical knowledge and practical data-analysis skills, ensuring learners can confidently apply statistics in modern business and economic contexts. Building upon fundamental principles, this text bridges the gap between theory and application by illustrating how probability, distributions, correlation, and regression can inform critical decision-making. It uses examples, solved problems, and Excel-based exercises to solidify learning, making even complex statistical concepts accessible to students from diverse academic backgrounds.
This book will be helpful for undergraduate students, teachers & practitioners, and general readers.
The Present Publication is the 1st Edition, authored by Dr Gurmeet Kaur, Soumya Sharma, and Dr Rachan Sareen, with the following noteworthy features:
• [Student-Centric Design]
o Clear & Accessible Language to ensure all learners can easily grasp statistical concepts
o Systematic Pedagogy that transitions from foundational principles to advanced topics
o Alignment with UGCF-NEP 2020, providing seamless integration with contemporary course requirements
• [Balanced Theory & Application]
o Thorough Explanations of statistical methods, discussing both the how and the why
o Examples interwoven throughout, showcasing practical business applications
• [Rich Pedagogical Tools]
o Solved Examples in every chapter, illustrating formula applications and interpretations
o Practice Problems & Exercises that encourage hands-on problem-solving
o Formula Summaries offering quick revision aids
o Excel-Based Exercises to cultivate crucial digital proficiency for the modern workplace
• [Comprehensive Content Coverage]
o Descriptive Statistics (Central Tendency, Dispersion, Skewness, Kurtosis, Moments)
o Probability & Probability Distributions (including Binomial, Poisson, Normal)
o Correlation & Regression Analysis (correlation vs. causation, regression lines, coefficients)
o Time Series Analysis (components, trend analysis, linear & parabolic fitting)
o Index Numbers (construction, uses, CPI, SENSEX, NIFTY)
o Business Statistics Using Spreadsheet (hands-on Excel-based applications)
• [Supplementary Support]
o Previous Years’ University Exam Questions to understand exam formats and expectations
o Step-by-step solutions to break down complex problems into manageable parts
o Project Work & Small Research Tasks fostering independent exploration and practical application