
https://editorial.konradlorenz.edu.co/paskin-matematico.html
e-mail: paskin@konradlorenz.edu.co
Editor
John A. Arredondo
Fundación Universitaria Konrad Lorenz alexander.arredondo@konradlorenz.edu.co


https://editorial.konradlorenz.edu.co/paskin-matematico.html
e-mail: paskin@konradlorenz.edu.co
Editor
John A. Arredondo
Fundación Universitaria Konrad Lorenz alexander.arredondo@konradlorenz.edu.co
Ruth Alejandra Torres Julián Jiménez Cárdenas Fundación Universitaria Konrad Lorenz Universidad de los Andes rutha.torresr@konradlorenz.edu.co jo.jimenezc1@uniandes.edu.co
Camilo Ramírez Maluendas Andrés Mauricio Rivera Universidad Nacional de Colombia Pontificia Universidad Javeriana Sede Manizales Sede Cali camramirezma@unal.edu.co amrivera@javerianacali.edu.co
Leidy Catherinne Sánchez Jesús Muciño
Fundación Cardio Infantil Centro de Ciencias Matemáticas UNAM-Morelia lcascanio@lacardio.org amrivera@javerianacali.edu.co
Esta publicación puede ser difundida y reproducida con fines académicos y científicospor todos aquellos que tengan a bien hacer un correcto uso de su contenido.
ISSN 2665-2471
Fundación Universitaria Konrad Lorenz: Tel: (57 1) 347 23 11, Carrera 9 Bis No. 62- 43 Bogotá –Colombia, email: info@konradlorenz.edu. Carácter académico: Institución Universitaria. Personería Jurídica por Resolución 18537 del 4 de noviembre de 1981 del Ministerio de Educación Nacional. Institución de Educación Superior sujeta a inspección y vigilancia por el Ministerio de Educación Nacional (Art. 2.5.3.2.10.2, Decreto 1075 de 2015).
DairoAndr´esSierraZamora * dairoa.sierraz@konradlorenz.edu.co
Enelpresenteart´ıculosepresentaunestudiodeladin´amicadelp´endulodobleyapartirdeestesistemaseintroduce elconceptodecaosensistemasdin´amicosdeterministas.La estrategiaempleadainiciaconladeducci´ondelasecuaciones demovimiento,paralocualseempleaelenfoqueusadoenla mec ´ anicaanal´ıticamedianteelplanteamientodellagrangiano delsistema,yapartirdeestesededucensusecuacionesde movimientousandolasecuacionesde Euler-Lagrange.Para comprenderc´omoabordarelproblemamedianteestametodolog´ıaseusacomoejemploelp´endulosimpleyposteriormenteseaplicalaestrategiaalp´endulodoble.Finalmente,se introducelanoci´ondecaosmedianteelestudionum´ericode ladin´amicadelasecuacionesdemovimientoparaelp´endulo dobleysusmapasdePoincar´e.
Elestudiodelcaosenlossistemasdin´amicosseoriginaen elsiglo XIX conHenriPoincar´e,mientrasestudiabaelproblemadelostrescuerpos.Unsistemadin´amicoesunsistemaque evolucionaeneltiempo.Unejemplodeestoeselmovimiento delaTierraalrededordelSol,oc´omocambiaciertapoblaci´on deconejoseneltiempo. ´ Estossondosdelosejemplosm´as conocidosenlaliteratura,dehecho,tambi´ensonejemplosde sistemadin´amicocontinuoysistemadin´amicodiscreto,respectivamente.Laprimerasituaci´oncorrespondeaunsistema din´amicocontinuoendondelaposici´ondelaTierrasepuedemodelarmedianteunafunci´onquedependedeltiempo.La segundasituaci´oncorrespondeaunsistemadin´amicodiscretoenlacualpodemospensarquelapoblaci´ondeconejoseste a ˜ noes xt yladelsiguientea˜noser´a xt+1;ladiferenciaentre ´ estoseseldominiopermitidoparalavariableindependiente t.Enelprimeroesclaroque t ∈ R yenelsegundoseconsideraque t ∈ N.Deacuerdoa[SSaRLD13]podemosdefinir formalmenteunsistemadin´amicodelasiguienteforma.
Definici´on1.1. Un sistemadin´amicocontinuo en Rn esuna funci´oncontinuamentediferenciable φ : R × Rn → Rn llamadaflujo,donde φ (t, X)= φt (X) satisfacelassiguientespropiedades:
φ0 : Rn → Rn eslafunci´onidentidad: φ0(X0)= X0
*Estudiantedematem´aticasFundaci´onUniversitariaKonradLorenz.

Elobjetivocentralenlossistemasdin´amicosesencontrar cuandoesposiblelafunci´on φ (t, X),sinembargo,estonoes posibleentodosloscasos,paraelcasodelp´endulosimplees sencillodeterminarestafunci´onperoparaelcasodelp´endulodoblenoesposibleobtenerestafunci´on.Porestaraz´onen elestudiodelossistemasdin´amicosexistenestrategiascualitativasquepermitenobtenerinformaci´onsobreelcomportamientodelsistemadin´amico;talescomolosretratosdefase, elestudiodelaestabilidadenlospuntosdeequilibrioolos diagramasdePoincar´e.
Acontinuaci´onsepresentar´aelestudiodelp´endulodoble pormediodelosmapasdePoincar´e.ElmapeodePoincar´e esunafunci´ondefinidaenunsubespaciodemenordimensi´onllamadosecci´ondePoincar´e[Nol15].Acontinuaci´onse representalasecci´ondePoincar´eparaunflujoentresdimensionesenelcualnotamosqueesdedosdimensiones.
MedianteelmapeodePoincar´eesposibleestudiardeformacualitativalaevoluci´ondeunsistemadin´amiconolineal comoloeselp´endulodoble.Alfinalizarelestudiodelp´endulodoblesepresentar´analgunasseccionesdePoincar´epara ciertosvaloresdeenerg´ıa,yas´ıpoderestudiarladin´amicade estesistema.
1. 2. φt ◦ φs = φt+s paracadat, s ∈ R Figura1: Secci´ondePoincar´eparaunflujo3D,lastrayectoriaspuedenpasarporencimaopordebajodecadaunodelos puntosmostradosanteriormente.Elp´endulosimpleop´endulomatem´aticoesunodelossistemasdin´amicosm´assencillosdeestudiar.Talessusimplicidadqueencursoselementalesdef´ısicaselograobtenerinformaci´onimportantedelsistemaparaoscilacionespequenas, esdecir,dondesinθ ≈ θ;comoqueelper´ıododeoscilaci´on (tiempoquetardaencompletarunciclocompletodeiday vuelta)esdirectamenteproporcionalalalongituddelp´enduloyest´adadopor T = 2π ℓ/g.Estehechoesmuyimportanteporquealleercondetalleestaexpresi´onnotamosqueel periododeoscilaci´on T esindependientedelaamplitud θ y delamasa m,afirmacionesquechocanconelsentidocom´un, puesparecesensatopensarquesielp´endulosedejacaerdesdeunaamplitud θ1 > θ2 elperiododeoscilaci´on T1 > T2 ver figura(2).Sinembargo,estonoesciertocomosepuedecomprobarexperimentalmente.Adem´as,elperiododeoscilaci´on esindependientedelamasa,esdecir,noimportasilamasa suspendidade ´ esteesgrandeopequenasuperiododeoscilaci´oneselmismo;estoesrealmenteespectaculardeverificar. Paraellosugieroallectorverlasiguienteclasemagistraldel profesorWalterLewinendondeestoshechosseverificande unamanerasorprendente[LW11].
qα quedeterminanlaposici´ondelapart´ıculademasa mα y lasvelocidadesasociadas˙ qα .Ellagrangianodeunsistemade part´ıculascarecedesignificadof´ısico,peroesdegranutilidad matem´aticaporquenospermiterelacionarlaenerg´ıacin´etica Kα ylaenerg´ıapotencial Uα delsistemaencadainstante.El lagrangianoparaunsistemade n part´ıculasest´adefinidopor
Enestesentidoellagrangianoesunafunci´ontalque
Portanto,paraelplanteamientodellagrangianodelp´endulosimpleesimportanteencontrarlaenerg´ıacin´eticayla energ ´ ıapotencialparaunsistemadiscretodepart´ıculas.
Energ´ıacin´etica:
Laenerg´ıacin´eticaesunacantidadescalarqueparauna masapuntualest´adadapor Kα = 1 2 mα r2 α . mα representala masadelapart´ıcula α y˙ rα lavelocidadasociadaaesta.De acuerdoalsistemadecoordenadasplanteadoenlafigura(2) elvectorposici´onest´adadopor
r = ℓ(sinθ ˆ ı cosθ ˆ j), ysuderivadaconrespectoaltiempoes
˙ r = ℓ ˙ θ (cosθ ˆ ı + sinθ ˆ j), conlocualpodemosmostrarquelaenerg´ıacin´eticapara lapart´ıcula m est´adadapor
K = 1 2 mℓ2θ 2 (2)
Energ´ıapotencial:
Paraelestudiodeladin´amicadeestesistemaf´ısico emplearemoselenfoquedadoporlamec´anicaanal´ıticao mec ´ anicadeLagrange,esdecirdondelaevoluci´ontemporaldelsistemasepuedeobtenerapartirdec´omosecambiala energ ´ ıacin´eticaylaenerg´ıapotencialdelsistema.Posteriora elloesposibleobtenerlasecuacionesdemovimientomediantelasecuacionesdeEuler-Lagrangeyas´ıtenerlaevoluci´on temporaldelsistema,elotroenfoquequesepuedeutilizaren estecasoeseldadotradicionalmenteporlasegundaleyde Newton,estudiandolasfuerzasqueact´uansobreelsistema, paraas ´ ıdeterminarsucomportamientoenfunci´ondeltiempo,sinembargo,esta ´ ultimaestrategianoesrecomendable cuandoelsistemaescomplejocomoloeselp´endulodoble.
Lagrangianodeunsistema:
Ellagrangiano L paraunsistemadepart´ıculasesunafunci´onescalarquedependedelascoordenadasgeneralizadas
Sedenominaenerg´ıadeconfiguraci´onosimplemente energ ´ ıapotencial,aaquellaquedependedelaposici´ondel objetorespectoaunpuntodereferencia,yest´adefinidaporla expresi´on U(r)= ⃗ F · d⃗ r.Antesdedeterminarlosvalores deenerg´ıapotencial,esnecesarioestableceralgunospuntos dereferencia,yas´ıdeterminarcomoest´adadalaenerg´ıapotencialparaestesistema(verfigura2).
U = 0,enlarecta y = 0denuestrosistemadereferencia.
U esm ´ ınimacuando θ = 0,esdecircuandoelp´endulo est´aenlaposici´onm´asbajadelaconfiguraci´onmostrada enlafigura(2).
U esm ´ aximacuando θ = π,esdecircuandoelsistema seencuentraenlaposici´onm´asaltaenrelaci´onalpunto dereferencia.
Observaremosentoncesqueelvalordelaenerg´ıapotencialdepender´adelavariable θ comovariabledemovimiento, peroadem´astambi´endelalongitud ℓ,constantedurantetodo elmovimiento.Luego,dadoqueelelementodel´ıneaencoordenadasrectangulareses d ⃗ l = dx ˆ ı + dy ˆ j laenerg´ıapotencial decadapart´ıculaest´adadapor
U = mgℓ cosθ (3)
Previamentedeterminamoslaenerg´ıacin´eticaylaenerg´ıa potencialdelapart´ıcula,porloquedeacuerdoalaecuaci´on (1)tenemosqueellagrangianoparaestesistemaes
L (θ , θ )= 1 2 mℓ2θ 2 + mgℓ cosθ (4)
Conociendoellagrangianodeunsistemadepart´ıculaspodemosdeducirlasecuacionesdemovimientoparapoderdeterminarlaevoluci´ontemporaldelsistema.Lasecuacionesde movimientolaspodemosobtenerapartirdelasecuacionesde
Sobreelestudiodeunsistemadin´amicousualmentenos debemosplantearunconjuntodepreguntasquenospermitir´anhacerunadescripci´ondelsistemaaestudiar,comopor ejemplo¿Cu´alessonlospuntosdeequilibriodeestesistema? Esdecir,aquellospuntosenloscualeselsistemapermanecer´a completamenteinvarianteeneltiempo.¿Qu´etipodecomportamientotieneelsistemadin´amicoeneltiempo?Estapuede serunadelaspreguntasm´asinteresantes,yaqueenelestudiodelossistemasdin´amicosapartirdeltrabajohechopor Lorenzen1881paraelproblemadelostrescuerpos[Lyn18], sabemosquealgunossistemasdin´amicossevuelvenca´oticos eneltiempo;sinembargoestenoeselcasodelp´endulosimple,comosepuedeobservarenlagr´aficasdelafigura(2) estossistemasbajoausenciadefricci´onsonmuyestablesy sucomportamientoesperi´odicoeneltiempo.
Esteconjuntodeecuacionesdiferencialesjueganunpapel an ´ alogoaldelasegundaleydeNewton.Conellaspodemos deducirc´omosecomportaelsistemaeneltiempo,esdecir, cu ´ alser´asuposici´onysuvelocidadencadainstantedetiempo despu´esdeunvalor t = t0.Alaplicarestasecuacionesobtenemos
Lasoluci´ondelasecuacionesdiferencialesdelp´endulo simplesonmuyconocidasdentrodelaliteraturadelaf´ısica matem´atica.Sinembargo,laintenci´ondeestasecci´onesmostrarelenfoqueempleadoenlamec´anicadeLagrangeparala deducci´ondelasecuacionesdemovimientodelp´endulosimple.Notemosquelasecuacionesdiferencialesobtenidasen lasecuaciones(7)y(6)sonexactamentelasmismasquelas quesepuedenencontraraplicandolasegundaleydeNewton. Acontinuaci´onsepresentaunasimulaci´onhechaenPython medianteintegraci´onnum´ericaparaunp´endulosimplecon par ´ ametros ℓ = 1 0 m y g = 9 8 m/s2,luegosepresentala soluci´onnum´ericadelaposici´onangular θ ylavelocidadangular ω paraelsistemamostradoenlafigura(3).
La ´ ultimadeestasecuacionesesunaecuaci´ondiferencial nolinealdesegundoordenmuyconocidaenlaliteraturadela f´ısica-matem´atica,ysesueledenotarcon ω2 = g ℓ porlocual tomalaforma
(7)
Adem´as,esmuyusualquedentrodelaliteraturaserealice unalinealizaci´ondeestaecuaci´ontomandolaformadeuna ecuaciondiferencialordinarialinealdesegundoorden;donde sesuelenhaceraproximacionesdeprimerordenmediantela
Elobjetivoalpresentarestasecci´onesmostrarlametodolog´ıaqueseemplear´aparaladeducci´ondelasecuaciones demovimientoparaelp´endulodobleenlasiguientesecci´on. Notemosqueenestecasoelenfoquedelamec´anicadeLagrangeresultamuchom´assencilloquetratardeabordarel
problemamediantelaaplicaci´ondelasegundaleydeNewton.Finalmente,unadelasestrategiascualitativasparaelestudiodelossistemasdin´amicoseseldiagramadefaseque, seg ´ un[Nol15]sedefinecomouncasoespecialdeespacios deestadosparasistemasHamiltonianosoLagrangianoscompuestosde2N dimensionespara N coordenadasgeneralizadas independientes.
consistir´aenencontrarunconjuntodeecuacionesdiferencialesquepermitandescribirsuevoluci´ontemporaleneltiempo.Enotrapalabras,encontrary“solucionar”unconjuntode ecuacionesdiferencialesquenospermitanconocersuvelocidadysuposici´onencadainstantedetiempo.Sinembargo, notaremosqueenestecaso,hallarlasecuacionesdiferencialesquedescribenelmovimientoesunpocom´aslaboriosoque lovistoenlasecci´onanterior.
(a) Posici´onangular. (b) Velocidadangular.
Figura4: Soluci´onnum´ericaparaelp´endulosimplemediante laecuaci´on(7)ylascondicionesdadasenlafigura(3).
Enlafigura(5)podemosnotarquetenemospuntosde equilibrioen ( π, 0), (0, 0) y (π, 0) enestecasoparaelmarco dereferenciaplanteado,elprimerpuntodeequilibrioresulta serexactamenteeltercerpunto;porlatrayectoriassepuede notarquesonpuntosrepulsoresoinestables,loquequieredecirquecercadeestospuntoselsistemaesaltamentesusceptibleacambios,comoesdeesperardesdeelpuntodevista f´ısico.Porotraparte,tenemosqueelpuntode (0, 0) esun atractorestableyvemosquelastrayectoriasalrededordeeste puntosonc´ıclicas,ysepuedeninterpretarcomolasoscilacionesperi´odicasparavaloresde θ peque ˜ nos.Elhechoquesea unatractornosdicequecercaaestepuntoelsistematender´a aestarenequilibrio.

Elp´endulodobleesunsistemacompuestodedosp´endulosacopladosdelongitudes l1, l2 ydemasas m1, m2 comose ilustraenlafigura(6).Cadaunadelasmasasformaun ´ angulo respectoalaverticalde ϕ1 y ϕ2,respectivamente.Aplicaremoslaestrategiausadaenlasecci´onanteriorparaelcasodel p ´ endulosimpleparahallarsusecuacionesdemovimiento,es decir,hallaremoslaenerg´ıacin´eticaylaenerg´ıapotencialde cadamasayconellodeterminaremosel lagrangiano delsistemaparafinalmenteaplicarlaecuacionesdeEuler-Lagrange.
Energ´ıaCin´etica:
Enestecasolaposici´ondecadapart´ıculadeacuerdoala figura(6)est´adadapor
( π, 0), (0, 0) y (π, 0)
Acontinuaci´onaplicaremosunenfoquesimilaralusadoen lasecci´onanteriorparaelestudiodeladin´amicadelp´endulo doble.Estudiarycomprenderladin´amicadelp´endulodoble
Detalformaquelaenerg´ıacin´eticapara m1 y m2,respectivamentees K1 y K2,conlocualtenemosque
Observaremosquelosvaloresdelaenerg´ıapotencialdepender´andelasvariables ϕ1 y ϕ2 comovariablesdemovimiento,peroadem´astambi´endelaslongitudes l1 y l2 constantesdurantetodoelmovimiento.Dadoqueelelementodel´ınea encoordenadasrectangulareses d ⃗ l = dx ˆ ı+dy ˆ j laenerg´ıapotencialdecadapart´ıculaest´adadapor
Conlasecuaciones(11)y(12)podemosdescribirla din´amicadelp´endulodoble.Notemosprimeroalgointeresante:sienlaecuaci´on(11)hacemos m2 = 0y l2 = 0tenemosla ecuaci´ondelp´endulosimple(7),porlocualpodemosconsiderarqueestemodeloesunaampliaci´ondelmostradoenlafigura(2).Porotrolado,hemosobtenidounsistemadeecuacionesdiferencialesnolinealesdesegundogrado,paraelcualno tenemosherramientasmatem´aticasparaencontrarsusoluci´on deformaanal´ıtica.Sinembargo,disponemosdeherramientas computacionalesparacomprenderunpocoladin´amicadeestesistema.Acontinuaci´onsepresentanalgunassimulaciones hechasenPythonmediantelaintegraci´onnum´ericadeestas expresiones.
Previamentehallamoslaenerg´ıacin´eticaylaenerg´ıapotencialparacadapart´ıcula,ahorapodemosdeterminarellagrangianomediantelaecuaci´on(1);teniendoencuentaqueen estecasodebemoscontemplarlosvaloresdelaenerg´ıacin´eticaylapotencialobtenidosenlasecuaciones(8)y(9)respectivamente.Demodoqueellagrangiano
Enlasimulaci´onpresentadaenlafigura(7)sepuedeobservarquebajociertascondicionesiniciales(valorespeque˜nos de ϕ1, ϕ2, ω1 y ω2)ladin´amicadelp´endulodoblees cuasiperi´odica,esdecir, ´ estepresentauncomportamientorepetitivo eneltiempobajolaausenciadefricci´on,enrelaci´onalas posicionesangularesyvelocidadesangulareslascualesson similaresauninstanteprevio.Estadin´amicaesmuchom´as evidenteenlasgr´aficas(8)y(9),enlascualessepresentasu evoluci´onenunintervalodetiempode12s,dondeobservamosquetantolaposici´onangularylavelocidadangularde ambasmasasescuasiperi´odicaeneltiempo.
Comonotamosenlaanteriorexpresi´on,ellagrangianode estesistemaesmuchom´ascomplejoqueelpresentadoenla ecuaci´on(4),loquepermiteintuirqueladin´amicadelp´endulodobleesmuchom´aselaboradaqueladelp´endulosimple. Ahoraconociendoellagrangianodeunsistemadepart´ıculaspodemosdeducirlasecuacionesdemovimientoparaas´ ı poderdeterminarlaevoluci´ontemporaldelsistema.Enestecaso,dadaslasecuacionesdeEuler-Lagrange(5)podemos encontrarlaecuaci´ondemovimientoparacadapart´ıcula
Enlafigura(10)serepresentaeldiagramadefaseparael sistema,queresultasermuyimportanteparaelestudiocualitativodelaevoluci´ondelsistema,debidoaqueenestecasono esposibleconocerlasoluci´onanal´ıticadelasecuacionesde
movimientoobtenidas.Acontinuaci´onseseleccionar´anciertosvaloresparalascondicionesiniciales,dondeladin´amica delp´endulodobleescompletamenteca´oticaenelsentidoque laposici´onangularde m2 noesperi´odicaypredecirlaesuna tareacompleja;esusualenlaliteraturallamaraestetipode sistemasquepresentanun caosdeterminista
Paraelp´endulodobletenemosquelospuntosdeequilibriodelsistemaest´andadosdelaforma (ϕ1, ϕ2, ω1, ω2) son (0, 0, 0, 0), (π, 0, 0, 0), (0, π, 0, 0) y (π, π, 0, 0),convieneenestecasoclasificarqu´etipodepuntoscr´ıticossondeformasimilaralohechoenelcasodelp´endulosimple.Desdeelpunto devistaf´ısicoesclaroqueelpunto (0, 0, 0, 0) esunpuntoestablecomoesdeesperarbajoelsentidof´ısicodelproblema yquelospuntos (π, 0, 0, 0), (0, π, 0, 0) y (π, π, 0, 0) sonpuntoscr´ıticosinestables,loscualessonmuysusceptiblesporla acci´ondelagravedad.

Seg´un[Nol15]lossistemasca´oticosposeensensibilidad exponencialalasvariacionesdelascondicionesinicialeses decir,queunmismosistemapuedetenerunaevoluci´onenel tiempomuydiferentebajopequenoscambiosenlascondiciones.Enlasfiguras(11),(12)y(13)sepresentaestehecho medianteunaseriedesimulacioneshechasenPythonatrav´es delaintegraci´onnum´ericadesusecuacionesdemovimiento. Seobservar´aqueefectivamenteesunsistemaca´otico.
diantelasecuaciones(12)y(11),conpar´ametros g = 9 8 m/s2 y l1 = l2 = 1 m.
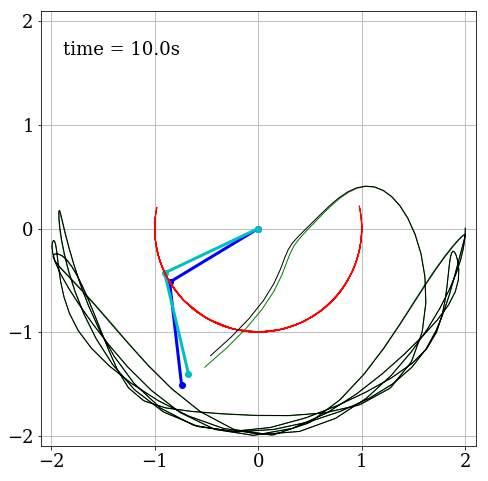
Enlafigura(12)serepresentalasimulaci´ondedosp´endulosdeformasimult´aneaconcondicionesinicialesmuycercanas,conelfindeobservarlasensibilidadquetieneladin´amicadelsistemafrenteapequenoscambiosdelascondiciones iniciales.Sepuedeobservarquelaevoluci´ondelsistemaes similarlosprimeros10segundos,peroapartirdeestemomentoelcomportamientodelp´enduloazulesmuydiferente alp´endulocyan.Estehechosehacemuchom´asevidenteenla
figura(13),enlacualsemuestrac´omohanevolucionadoambosp´endulospasados22segundos.Latrayectoriadelamasa m2 paraelp´endulodecolorazulsemuestradecolorverdey latrayectoriadelamasa m2 paraelp´endulodecolorcyanse muestradecolornegro,enestepuntoseobservaqueaunque lascondicionesinicialesdeambosp´endulossonmuycercanasentres´ı, ´ estostienenunaevoluci´ontemporalmuydiferenteconlocualpodemosverificarelcomportamientoca´oticode estesistemadin´amico.
previamente.
Cuadro1: Condicionesinicialesdelassimulacionesmostradasenlasfiguras(12)y(13).
Figura12: Representaci´ondedosp´endulosdeformasimult´aneapasados10 s.Par´ametros g = 9 8 m/s2 y l1 = l2 = 1 m paraambosp´endulos.
Medianteintegraci´onnum´ericadelasecuaciones(11)y (12)podemosestudiarcondetalleelcomportamientodeeste sistema,enlafigura(14)seobservalaevoluci´ontemporalde laposici´onangularparaelp´enduloazulconcondicionesinicialesdadasenelcuadro(1).Enestagr´aficaseobservaque laposici´onangularde m2 escompletamenteerr´aticaynocorrespondeaunmovimientoperi´odico.Tambi´enpodemosevidenciarlasensibilidaddelsistemaalascondicionesiniciales dadasenelcuadro(1)enlafigura(15)enlacualsepuedever queelcomportamientodelaposici´onangularpara m2 esmuy similarlosdiezprimerossegundos,peroquedespu´esdeeste instantelaevoluci´ondelsistemaesmuydiferente.Lacuales unacaracter´ısticaesencialdelcaosdeterministamencionado
Figura14: Posici´onangular vs. tiempoparaelp´endulodoble. Sepuedeevidenciarelcomportamientoerr´aticopara ϕ2

Figura15: comparaci´ondelaevoluci´ontemporaldelaposici´onangularpara m2.Sepuedeevidenciarelcomportamiento ca ´ oticopara ϕ2 ylasensibilidadalascondicionesiniciales.
Lasecci´ondePoincar´eesunaherramientamuy ´ utilparael estudiodelossistemasdin´amicos. ´ Estasseccionesnospermitenestudiardeformacualitativalaevoluci´ondeunasistema din´amicocomplejousualmentenolineal,ydeterminarsi ´ este poseeuncomportamientocuasiperi´odicooca´otico.Poincar´e usolaideadeunasecci´on(Secci´ondePoincar´e)demenor dimensi´onalflujo φ (t) ytransversalaeste,demodoque,el flujooriginaldelsistemacortaestasecci´onenalgunospuntos x1, x2,... comosepuedeobservarellafigura(1).Porejemplo sielsistemadin´amicomodeladoeselp´endulomostradoenla primerasecci´on,debidoaquesucomportamientoesperi´odicoeneltiempolarepresentaci´ondelasecci´ondePoincar´e ser ´ ıaunpuntoyaqueel φ (t) cortar´ıalasecci´onsiempreen elmismopunto.Sinembargoensistemasnolinealescomoel casodelp´endulodoblelasecci´ondePoincar´eesm´asinteresante.Acontinuaci´onsepresentanalgunosmapasdePoincar´e paraelp´endulodobleparadistintosvaloresdeenerg´ıa.
Enlasanterioresfigurasseobservaqueparavaloresbajos delaenerg´ıadelsistemaelp´endulodobletieneuncomportamientocuasiperi´odico,locualsepuedeevidenciarenlafigura (16)enlasregionesovaladas.Cuandolaenerg´ıadelsistema aumentaseobservaquelospuntosenlasecci´ondePoincar´e lainterceptandeformadispersalocualcaracterizaelcomportamientoca´oticolocualseobservaenlafigura(18).
E = 0
completamenteelcaosdelsistema.
Comovemoselestudiodeladin´amicadelp´endulopor mediodelasseccionesdePoincar´epermiteelan´alisisdecualitativodeunsistemadin´amico,ydeterminarsi ´ esteposeeun comportamientoca´otico.Unaventajadeestudiarestesistema medianteestaestrategiaesqueunpuntodelflujo φ (t) est´a encuatrodimensiones,conayudadelasecci´ondePoincar´e podemoshacerestarepresentaci´onenunadimensi´onmenor yproyectarlaenelplanocomosehizoenlas ´ ultimasfiguras.
[Lyn18] S.Lynch, DynamicalSystemswithApplicationsusingPython, SpringerInternationalPublishing,2018.
[Nol15] D.D.Nolte, IntroductiontoModernDynamics:Chaos,Networks,SpaceandTime,OxfordUniversityPress,2015.
[LLaEML94] L.D.LandauandE.M.Lifshitz, Mec´anica:Cursodef´ısica teorica: Cursodefısicateorica,1994.
[SML70] S.M.Lee, Thedouble-simplependulumproblem,American JournalofPhysics 38 (1970),536-537.
[SSaRLD13] StephenSmaleandRobertL.Devaney, DifferentialEquations, DynamicalSystems,andanIntroductiontoChaos,ThirdEdition,AcademicPress,2013.
[LW11] LewinW., Fortheloveofphysics,2011. https://www. youtube.com/watch?v=sJG-rXBbmCc
Acercadelautor:Dairoactualmenteesestudiantedeoctavosemestredematem´aticasenlaFundaci´onUniversitaria KonradLorenz,tieneunaformaci´onpreviaenlicenciaturaen f´ısicadelaUniversidadPedag´ogicaNacional.Entresusinteresesseencuentranlasecuacionesdiferencialesylossistemasdin´amicos.Ensutiempolibrelegustadisfrutardebuena m ´ usicayesperaalg´und´ıaaprenderatocarbater´ıa.
GonzaloMedina* gmedinaar@unal.edu.co
Esteart´ıculoest´adedicadoalcl´asicoProblemadelosCuatroSubespacios,queconsisteenobtenerlaclasificaci´oncompleta,salvoisomorfismo,decuatrosubespaciosvectoriales deunespaciovectorialdedimensi´onfinitasobreuncampo. Nuestroobjetivoesdescribirelproblemaenuncontextom´as generalquepermiteexhibiryexaminaralgunasdelascaracter´ısticasquelohaceninteresante.
Elc´elebreProblemadelosCuatroSubespacios,como yadijimos,consisteenclasificar,salvoisomorfismo,los 4-sistemasdesubespaciosvectorialesdeunespaciovectorialdedimensi´onfinitasobreuncampo k.Elproblemafue planteadoeinicialmenteresueltoporGelfandyPonomarev, en[GP70],parauncampoalgebraicamentecerrado.Demaneraindependienteyutilizandom´etodosdiferentes,Nazarova,en[Naz67,Naz75],resolvi´otambi´enelproblema,caside manerasimult´aneaaGelfandyPonomarev,peroahoraparauncampoarbitrario.Dehecho,talcomosedemostr´oen [Naz75,p´ags765-770],Nazarovaresolvi´oen[Naz67]unproblemamatricialqueesequivalentealproblemadeloscuatro subespacios.
Posteriormente,Brennerdiootrasoluci´on,primeroparcial en[Bre67]endondeconsider´oelcasoahoradenominadono regular,yposteriormenteen[Bre74a]modific´oyextendi´olos resultadosdeGelfandyPonomarevalcasodeuncampoarbitrariooinclusoaldeunanillodedivisi´onnoconmutativo.
Brennerfuequienprimerodescribi´ocompletamentelosanillosdeendomorfismosasociadosenlosdosart´ıculosmencionados.
En[MZ04],MedinayZavadskijpresentaronunasoluci´on muchom´ascortaydecar´acterelementalparaelproblemasobreuncampoarbitrario,quedehechoesv´alidasobreanillos dedivisi´onarbitrariosyenlaquetambi´ensedescribenlos anillosdeendomorfismosasociados.
Forbregd,en[For08](tesisdemaestr´ıadirigidapor Smalø),presentaunasoluci´onparacamposalgebraicamente cerradoshaciendousodelateor´ıadeAuslander-Reiten.
LasdemostracionesoriginalesdeGelfandyPonomarev ydeNazarova,as´ıcomolascorrespondientesvariantesde BrennerydeForbregd,sonlargasym´asbiencomplejas;la
*DepartamentodeMatem´aticayEstad´ıstica,UniversidadNacionaldeColombia,SedeManizales
soluci´ondadaporMedinayZavadskijescortayrequieretan soloherramientasde ´ algebralineal,formascan´onicasyde teor´ıadeanillos.
Nuestrointer´esenesteart´ıculoespresentaralgunasdelas caracter´ısticasquehaceninteresanteelproblemadeloscuatro subespacios.Laestructuradelart´ıculoeslasiguiente:comenzamospresentando,enlasecci´on2,lasdefinicionesynotacionesinicialesnecesarias;enlasecci´on3mostramosc´omo seresuelveelproblemaprincipalparaloscasosiniciales(en losquelasoluci´onesrelativamentesencilla)yexaminamos loscasosqueactualmentesonintratables;finalmente,enla secci´on4nosocupamosdelcasoespecialquecorrespondeal cl´asicoproblemadeloscuatrosubespacios.
Elautoragradecealrevisorporsusvaliososy ´ utilescomentariosysugerencias.
Vamosaconsiderarelproblemam´asgeneraldeobtenerla clasificaci´oncompleta,salvoisomorfismo,deunn´umerofinitocualquieradesubespaciosvectorialesdeunespaciovectorialdedimensi´onfinitasobreuncampo.Demaneraprecisa, dadouncampo k,paracadaenteropositivofijo r,unsistema de r-subespaciossobre k esunacolecci´on
U =(U0,U1,...,Ur), endonde U0 esunespaciovectorialdedimensi´onfinitasobre k ycada Ui,para i ∈{1,..., r},esunsubespaciovectorial de U0.La dimensi´on del r-sistema U =(U0,U1,...,Ur) esel vectordimU =(d0, d1,..., dr) ∈ Zr+1 talque,paratodo i ∈ {0,..., r},setieneque di = dimUi.
Dadosdossistemasde r-subespacios U =(U0,U1,...,Ur) y V =(V0,V1,...,Vr),su sumadirecta eselsistema U ⊕ V dado,demaneranatural,por
U ⊕V =(U0 ⊕V0,U1 ⊕V1,...,Ur ⊕Vr).
Paraunenteropositivo l yunsistema U de r-subespacios, definimos
U l = U, para l = 1. U l 1 ⊕U, para l ≥ 2.
Un morfismo A entredossistemasde r-subespacios U = (U0,U1,...,Ur) y V =(V0,V1,...,Vr) esunatransformaci´on k-lineal A :U0 → V0 talque A (Ui) ⊆ Vi,paratodo i ∈{1,..., r}.Dossistemasde r-subespacios U =

(U0,U1,...,Ur) y V =(V0,V1,...,Vr) son isomorfos,locual denotamos U V ,siexisteunisomorfismo k-lineal A :U0 →
V0 talque A (Ui)= Vi,paratodo i ∈{1,..., r}.
Unsistemade r-subespacios U es indescomponible sicada vezquesetenga U = V ⊕W ,parasistemasde r-subespacios
V y W ,necesariamente V = 0o W = 0.Aqu´ı,0eselsistema nulode r-subespacios:0 =(0, 0,..., 0).Unsistemasedenomina descomponible sinoesindescomponible.
Paraunsistemade r-subespacios U =(U0,U1,...,Ur) sobreuncampo k,su sistemadual eselsistemade r-subespacios
U
∗ =(U ∗ 0 ,U ∗ 1 ,...,U ∗ r ) sobre k dadopor
U ∗ 0 = Homk(U0, k)
= {A :U0 → k | A esfuncional k-lineal},
U ∗ i = U ⊥ i
= {B ∈ U ∗ 0 | B(Ui)= 0}, paratodo i ∈{1,..., r}.
Dadounmorfismo C :U → V entredossistemasde r-subespacios,su morfismodual C ∗:V ∗ → U ∗ est´adefinido por
C ∗(A )= AC , paratodo A ∈ V ∗
Nota. Yaque U0 esdedimensi´onfinitasobre k,tenemos un k-isomorfismolinealHomk(U0, k) U0;enparticular, dimU ∗ 0 = dimU0.Adem´as,secumple,paratodo i ∈{1,..., r}, quedimU ∗ i = dimU0 dimUi = codimUi
Tomandocomoobjetoslossistemasde r-subespaciosycomomorfismoslosmorfismosentresistemasde r-subespacios, tenemos,paracadanaturalpositivofijo r,lacategor´ıa (Sr, k) desistemasde r-subespaciossobreelcampo k.Estacategor´ıa esdeKrull-Schmidt:esaditiva,todosistemade r-subespacios oesindescomponibleosedescomponeenunasumadirectadesistemasde r-subespaciosindescomponiblesyestadescomposici´ones ´ unicasalvoisomorfismoylosanillos deendomorfismosasociadosalossistemasindescomponiblessonanilloslocales(unademostraci´onpuedeconsultarse en[Med20,p´ags.25-29]).Paraunenteropositivofijo r yun campodado k,denotamosInd(Sr, k) aunconjuntocompleto derepresentantesdelasclasesdeisomorfismodesistemasde r-subespaciosindescomponiblessobreelcampo k
Acadasistemade r-subespacios U =(U0,U1,...,Ur) le podemosasociarsu anillodeendomorfismos EndU dadopor elconjunto
EndU = {A | A esmorfismode U en U }, conlaestructuradeanilloobtenidaalconsiderarlasumay composici´onusualesdetransformaciones k-lineales.Claramente,EndU esunsubanillodelanilloEndk(U0) delosendomorfismos k-linealesde U0.
Elproblemacentralesentonceselobtener,paracadaenteropositivo r fijoyuncampo k,ladescripci´ondeInd(Sr, k), as ´ ıcomodeloscorrespondientesanillosdeendomorfismos.
Yaqueestamosconsiderandoespaciosvectorialesdedimensi´onfinita,tenemoslaposibilidaddeasignarlesbasesy detrabajarconlasmatricesasociadas,talcomoveremosa continuaci´on.
Una presentaci´onmatricial deunsistemade r-subespacios
U =(U0,U1,...,Ur) esunamatrizcon r franjasverticales
MU = M1 Mr
endonde,paracada i ∈{1,..., r},lascolumnasdelafranja Mi correspondenalascoordenadas(conrespectoaunabasefija para U0)deunsistemaminimaldegeneradoresdelespacio Ui.Dospresentacionesmatriciales MU , MV son equivalentes siunadeellaspuedetransformarseenlaotramediantelaaplicaci´ondeunn´umerofinitodelassiguientes transformaciones admitidas:
(a) Transformacioneselementalesconfilasdetodalamatriz.
(b) Transformacioneselementalesconcolumnasdentrode cadafranjavertical Mi
N´otesequelastransformacionesadmitidasdetipo(a)correspondenacambiosdebasepara U0 ylastransformacionesadmitidasdetipo(b)correspondenacambiosdebasedelos subespacios Ui locualnosllevaalsiguienteresultado:
Proposici´on2.1. Dossistemasder-subespaciosUyVson isomorfossiysolosidoscualesquieradesuspresentaciones matricialesMU yMV sonequivalentes.
Siconsideramosdospresentacionesmatriciales
A = A1 ··· Ar y B = B1 ··· Br
correspondientesadossistemasde r-subespacios U y V ,respectivamente,apartirdelasdefinicionestenemosqueuna presentaci´onmatricialpara U ⊕V est´adadaporlamatriz
A ⊕ B = A1 0 Ar 0 0 B1 0 Br
Teniendoencuentalaproposici´on2.1,resolverelproblema central,esdecir,clasificarlossistemasde r-subespaciosindescomponiblesequivalearesolverun problemamatricial;es decir,resolverelproblemafundamentalequivaleahallarformascan ´ onicasparalaspresentacionesmatricialesutilizando lastransformacionesadmitidas.Enlaproposici´on3.4daremosunejemplodeestosproblemasmatriciales.
Nota. Porsupuesto,elproblemacentralpuedeversecomo unsubproblemadelateor´ıaderepresentacionesdeconjuntos parcialmenteordenadosordinarios(sinestructuraadicional) finitosyaquecorrespondeprecisamenteaobtenerlaclasificaci´ondelasrepresentacionesindescomponiblessobreun campodado k paraunaanticadenacon r elementos.Enesteart´ıculo,sinembargo,noasumimosfamiliaridadconesta teor´ıayutilizamosotroenfoque.Loslectoresinteresadosenel enfoquedesdelateor´ıaderepresentacionesdeconjuntosparcialmenteordenados,puedenconsultar,porejemplo[Arn00] o[Med20].
Hacemosahoraunaobservaci´onsimplede ´ algebralineal quenosser ´ a ´ util:
Lema2.2. CualquiermatrizrectangularNpuedellevarse,utilizandolastransformacionesadmitidas,alaformasiguiente(quedenominaremosformaest´andar):
ytambi´en β =(1 A )(δ )= δ A (δ ),paraalg´un δ ∈ Ui.
Deaqu´ı,usandoelque A 2 = A ,obtenemos
β = A (γ)= A 2(γ)= A (A (γ))
= A (δ A (δ ))= A (δ ) A 2(δ )
= A (δ ) A (δ )= 0.
endondeIn eslamatrizidentidaddeordenn(estenesprecisamenteelrangodeN)ylosbloques 0 representanmatricesnulas;algunosbloquesdelaformaest´andarpuedenser vac ´ ıos.
Demostraci´on. Inicialmenteutilizamostransformacionesadmitidasdetipo(a),talcomosehaceenelprocesodereducci´ondeGauss-Jordan,paraobtenerlamatriz R enformaescalonadareducidaasociadaa N yfinalmente,aplicandotransformacionesadmitidasdetipo(b),anulamoscualquierposible elementononuloaladerechadelosunosprincipalesde R y luegopermutamosapropiadamentelascolumnashastaobtenerunamatrizenlaformaest´andar.
Decimosqueunsistemade r-subespacios U = (U0,U1,...,Ur) es trivial sidimU0 = 1o,equivalentemente,si U0 es(isomorfoa) k
Lema2.3. SeaUunsistematrivialder-subespacios.Entonces,Uesindescomponibley EndU k.
Demostraci´on. Esclaroquesi U0 k,entoncesnecesariamente U esindescomponible,pues U = V ⊕W condimU0 = 1 implicaqueobiendimV0 = 1ydimW0 = 0obiendimV0 = 0 ydimW0 = 1.Porotrolado,lamultiplicaci´onporescalarinduceunainyecci´on k → EndU.Adem´as,EndU ⊆ EndU0 = Endk k;conesto,EndU k.
Elsiguienteresultadomuestraquelosanillosdeendomorfismospermitenobtenerinformaci´onsobrelossistemasalos queest´anasociados:
Lema2.4. SeaUunsistemader-subespaciossobreuncampok.Entonces,Uesindescomponiblesiysolosi 0 y 1 sonlos ´ unicosidempotentesdelanillo EndU.
Demostraci´on. Si U =(U0,U1,...,Ur) esunsistemade r-subespaciossobreuncampo k y A ∈ EndU esunidempotente,veamosque U = A (U) ⊕ (1 A )(U);atalefecto, vamosaprobarque,paratodo i ∈{0, 1,..., r ¸},setieneque
Ui = A (Ui) ⊕ (1 A )(Ui):si α ∈ Ui,entonces
α = A (α)+(α A (α))
= A (α)+(1 A )(α)
quemuestraque Ui = A (Ui)+(1 A )(Ui).Paraverquela sumaesdirecta,nosfaltaverquelaintersecci´ondelossumandosestrivial:supongamosentoncesque β ∈ A (Ui) ∩ (1
A )(Ui).Tenemosentoncesque β = A (γ),paraalg´un γ ∈ Ui
Porlotanto,si A esunidempotenteenEndU y U esindescomponible,necesariamente A (U)= 0o (1 A )(U)= 0;esdecir, A = 0o A = 1sonlos ´ unicosidempotentesde EndU.Rec´ıprocamente,supongamosque U = V ⊕W ,endonde U,V sonsistemasnonulosde r-subespacios;elmorfismo B:U → U definidopor
B(υ, ω)=(υ, 0),paratodo (υ, ω) ∈ V ⊕W , esentoncesunidempotentedeEndU distintode0yde1 pueseln´ucleode B esunsubespaciopropionotrivialde U (kerB W ).
Unpequenoejemploparailustraralgunasdelasideasexpuestashastaelmomento:
Ejemplo2.5. Dadouncampok,consideremoslossistemas de 3-subespaciossiguientes: U =(k, k, 0, k) yV =(k, 0, 0, k)
Porellema2.3,sabemosqueUyVsonindescomponiblesy que EndU kytambi´en EndV k.Escogiendobasesapropiadas,tenemoslaspresentacionesmatricialesMU yMV :
SiU =(k,U1,...,Ur) esunsistematrivialdesubespaciossobreelcampok,entoncessusistemadualU ∗ = (U ∗ 0 ,U ∗ 1 ,...,U ∗ r ) es(isomorfoa) (k,W1,...,Wr),endonde, paratodoi ∈{1,..., r},setieneque
Wi = k, siUi = 0 0, siUi = k. ,
Enparticular,paralosdossistemasde 3-subespaciosdados alcomienzodeesteejemplo
U =(k, k, 0, k) yV =(k, 0, 0, k), setienequesusdualesson(isomorfosa)
U ∗ (k, 0, k, 0) yV ∗ (k, k, k, 0)
ylascorrespondientesdimensionesest´andadaspor dimU =(1, 1, 0, 1), dimV =(1, 0, 0, 1), dimU ∗ =(1, 0, 1, 0), dimV ∗ =(1, 1, 1, 0)
Despu´esdelospreliminaresanteriores,vamosinicialmenteaexaminarelproblemacentralparaloscasos r ∈{1, 2, 3} enlastresproposicionessiguientes;comoveremos,enestoscasoselproblemadeclasificaci´ondelossistemasde r-subespaciosindescomponiblesesrelativamentesencillo:
Proposici´on3.1. Dadouncampoarbitrariok,tenemosque Ind(S1, k)= {(k, 0), (k, k)} y,enamboscasos,losanillosde endomorfismosasociadossontriviales.
Demostraci´on. Si U =(U0,U1) esunsistemaarbitrariode1subespacio,entonces,paraalg´uncomplemento X de U1 en U0 setieneque
U =(U0,U1)
=(U1 ⊕ X,U1)
=(X, 0) ⊕ (U1,U1)
(km , 0) ⊕ (kn , kn)
=(k, 0)m ⊕ (k, k)n ,
endonde X km y U1 kn,paraalgunosenterosnonegativos m y n.Deaqu´ıseobtienenlossumandosindescomponiblesdelresultadoyellema2.3garantizaquelosanillosde endomorfismossontriviales.
Nota. Elprocedimientoparallevarcualquiermatrizasuformaest´andar,descritoenellema2.2,correspondealasoluci´ondelproblemamatricialasociadoalossistemasde1subespaciosobreuncampo k;dehecho,laformaest´andarno esotracosaqueunasumadirectaderepresentacionesmatricialesde1-sistemasindescomponiblesdelaforma (k, k) y (k, 0)
Proposici´on3.2. Dadouncampoarbitrariok, Ind(S2, k)= {(k, 0, 0), (k, k, 0), (k, 0, k), (k, k, k)}
yloscuatroanillosdeendomorfismosasociadossontriviales.
Demostraci´on. Consideremos U =(U0,U1,U2) unsistema arbitrariode2-subespaciossobre k ysea W = U1 ∩ U2;entonces U1 = W ⊕ X y U2 = W ⊕Y ,paraalgunossubespacios complementarios X,Y yadem´as U1 +U2 = W ⊕X ⊕Y .Yaque U0 =(U1 +U2) ⊕ Z paraalg´uncomplemento Z,tenemosque
U =(W,W,W ) ⊕ (X, X, 0) ⊕ (Y, 0,Y ) ⊕ (Z, 0, 0) (km , km , km) ⊕
dedondeobtenemoslossumandosindescomponiblesanunciados.Nuevamenteellema2.3garantizaquelosanillosde endomorfismossontriviales.
Conlaayudadelsiguienteresultadoauxiliar,enlaproposici´on3.4obtendremoslaclasificaci´oncompletadelossistemasde3-subespaciosindescomponibles,ydesusanillosde
endomorfismosasociados.Enlapruebadelaproposici´onharemosusodelaspresentacionesmatriciales;unasoluci´onen usandoellenguajedelosespaciosvectorialespuedeconsultarseen[Arn00,Ejemplo1.1.5,p´ags.4–7]
Lema3.3. Paralossistemasde 3-subespacios
(U0,U1,U2,U3) conlasrelacionesadicionalesU1 ⊆ U3 yU2 ⊆ U3 setienequetodoslosobjetosindescomponibles vienendados,salvoisomorfismo,porloselementosdel conjunto
} ytodoslosanillosdeendomorfismosasociadossontriviales. Demostraci´on. Consideremos U =(U0,U1,U2,U3) unsistemade3-subespaciossobre k conlasrelacionesadicionales
V,V,V,V ) ⊕ (W,W, 0,W ) ⊕ (X, 0, X, X) ⊕ (Y, 0, 0,Y ) ⊕ (Z, 0, 0, 0),
dedondeobtenemoslossumandosindescomponiblesanunciados.Yaquetodoslosobjetosindescomponiblessontriviales,ellema2.3garantizaquesusanillosdeendomorfismos tambi´enloson.
Proposici´on3.4. Dadouncampoarbitrariok,
endondeUes(isomorfoa)elsistemade 3-subespaciosdado delamanerasiguiente:
ylosnueveanillosdeendomorfismosasociadossontriviales. Demostraci´on. Consideremosunapresentaci´onmatricial
M = M1 M2 M3
deunsistemade3-subespacios U =(U0,U1,U2,U3).Inicialmente,aplicandotransformacionesadmitidas,llevamosla franja M1 alaformaest´andar(verellema2.2),obteniendoas´ ı unamatrizdelaformasiguiente(loscoloressonutilizados ´ unicamentecomogu´ıaduranteelprocesodereducci´on): 0
M1 M2 M3
Lafranjahorizontalinferiordeestamatrizcorrespondeaciertapresentaci´onmatricialdeunsistemade2-subespaciosya
queaplicarenestafranjatransformacionesadmitidasdetipo(a)noalteralosbloquesnuloscorrespondientesa M1 y, porotrolado,setienentransformacionesadmitidasindependientesdetipo(b)paralosbloques C y D quedejaninvariante elbloque M1;utilizandoelresultadodelaproposici´on3.2,en losbloques C D colocamosbloquescorrespondientesa sumandosdelossistemasindescomponiblesde2-subespacios (k, k, 0), (k, 0, k), (k, k, k) y (k, 0, 0) yutilizamosadicionesde filasparaanularen A yen B loselementosporencimade losbloques I de (k, k, 0), (k, 0, k) ydeunodelosbloques I de (k, k, k),paraobtenerlasiguientematriz(deahoraenadelante,losbloquesquenoaparezcanmarcadosenlasmatrices representanbloquesnulos):
obtenemos,finalmente,lasiguientematriz:
Analizandoahoracu´alestransformacionesadmitidasnocambianlosbloques I nilosbloquesnulosdelamatrizanterior, resultaque,apartedelasadicionesobviasdecolumnasde Q acolumnasde R,tenemosahoratambi´enadicionesdecolumnasde P acolumnasde R (estasadicionesest´anindicadaspor lasflechascurvasenlamatrizanterior):enefecto,cualquier columnade P puedeadicionarsealbloquenulojustoaladerechade P;alrestaurarloscerosdeestebloqueadicionamos filasdelbloque I asociadoa (k, k, k),peroentoncestambi´en sedebenrealizarlasmismasadicionesdelotrobloque I de (k, k, k) albloque R.Porlotanto,losbloques P Q R correspondenaunapresentaci´onmatricialdeciertosistemade3-subespacios U =(U0,U1,U2U3) conrelacionesadicionales U1 ⊆ U3 y U2 ⊆ U3.Graciasallema3.3,sabemos quelosindescomponiblesdeestesistemaconrelacionesson (k, k, 0, k), (k, 0, k, k), (k, 0, 0, k), (k, k, k, k) y (k, 0, 0, 0);colocamosentonces,enlugardelosbloques P Q R bloques I correspondientesasumandosdelosanterioressistemasy
Conesto,tenemosquelossistemasde3-subespaciosindescomponiblesson (k, k, k, 0) (obtenidodelaprimera,deabajohaciaarriba,franjahorizontaldelamatriz), (k, k, 0, k) (obtenidodelasegundafranjahorizontaldelamatriz), (k, k, k, k) (obtenidodelacuartafranjahorizontaldelamatriz), (k, k, 0, 0) (obtenidodelaquintafranjahorizontaldela matriz), (k, 0, k, 0) (obtenidodelasextays´eptimafranjashorizontalesdelamatriz), (k, 0, 0, k) (obtenidodelaoctavay novenafranjashorizontalesdelamatriz), (k, 0, k, k) (obtenido delad´ecimafranjahorizontaldelamatriz), (k, 0, 0, 0) (obtenidodela ´ ultimafranjahorizontaldelamatriz)yelsistema notrivialconpresentaci´onmatricial
(2) obtenidodelatercerayund´ecimafranjashorizontalesdela matriz.
Graciasallema2.3,tenemosquelosanillosdeendomorfismosasociadosalosocho3-sistemastrivialesdesubespacios sontambi´entriviales;paraterminarlademostraci´on,examinemoselanillodeendomorfismosdelsistemaindescomponiblenotrivial:lapresentaci´onmatricialdadaen(2)correspondealsistemade3-subespacios U =(U0,U1,U2,U3),endonde
U0 = k ⊕ k, U2 = 0 ⊕ k, U1 = k ⊕ 0, U3 = {(x, x) | x ∈ k}
Sihacemos ε1 =(1, 0) y ε2 =(0, 1),tenemosquelosconjuntos {ε1, ε2}, {ε1}, {ε2} y {ε1 + ε2} sonbasesparalos subespacios U0, U1, U2 y U3,respectivamente.Ahorabien,si
A :U → U esunendomorfismode U,lacondici´on A (U1) ⊆
U1 implicaque A (ε1)= aε1,paraalg´un a ∈ k;lacondici´on
A (U2) ⊆ U2 implicaque A (ε2)= bε2,paraalg´un b ∈ k yla condici´on A (U3) ⊆ U3 implicaque A (ε1 + ε2)= c(ε1 + ε2), paraalg´un c ∈ k,peroentonces
cε1 + cε2 = c(ε1 + ε2)
= A (ε1 + ε2)
= A (ε1)+ A (ε2)
= aε1 + bε2,
conloque a = b = c;esdecir, A esmultiplicaci´onporun escalaryestonosllevaaqueEndU k (teniendoencuenta ellema2.4,estotambi´enreafirmaelqueestesistemade3subespaciosesindescomponible).
Valelapenanotarquetodoslosindescomponiblesparalos sistemasde1y2subespaciossontriviales,perocuandopasamosalossistemasde3-subespaciosyaapareceunindescomponiblenotrivial.Entodosloscasos,sinembargo,setiene quedimU0 ≤ 2ytodoslosanillosdeendomorfismosasociadossontriviales.Comovamosaver,cuandoconsideramos lossistemasde r-subespaciospara r ≥ 4lasituaci´oncambia dram´aticamente:elconjuntoInd(Sr, k) resultainfinito,para todo r ≥ 4;adem´as,aparecensistemasindescomponiblesen losquedimU0 puedesertangrandecomosequieraytambi´en aparecenanillosdeendomorfismosnotriviales.Primero,un lemaauxiliar:
Lema3.5. Paraenterospositivosrys,conr ≤ s,setieneuna inyecci´on ι:Ind(Sr, k) → Ind(Ss, k)
Demostraci´on. Para U =(U0,U1,...,Ur) ∈ Ind(Sr, k),definamos ι(U)= U =(U 0,U 1,...,U s) haciendo
U 0 = U0 y,para r ∈{1,..., s},
U i = Ui, si i ∈{1,..., r}. 0, si i ∈{r + 1,..., s}
Esinmediato,apartirdeladefinici´ondada,que ι esunainyecci´onyque ι(U) esindescomponiblesi U loes.
Proposici´on3.6. Parar ≥ 4,elconjunto Ind(Sr, k) esinfinito.
Demostraci´on. Dadouncampo k,consideremoselsistema de4-subespacios U =(U0,U1,...,U4) talque,paracadaentero n ≥ 0,el k-espaciovectorial U0 es kn+1 ⊕ kn+1 dedimensi´on2n + 2conbase {ε1,..., ε2n+2} y,para i ∈{1,..., 4},los subespacios Ui est´andadosdelasiguientemanera: U
+2} , U4 = {ε2 + εn+2,..., εn+1 + ε2n+1}
Si A ∈ EndU,debetenerseque A (Ui) ⊆ Ui,paratodo i ∈{1,..., 4},yestonoslleva,despu´esdeunan´alisissobreel efectode A sobrelosgeneradoresdelosespacios Ui,aque A essimplementemultiplicaci´onporunelementofijode k Tenemosas´ıqueEndU k y,enparticular,los ´ unicosidempotentesdeEndU son0y1;usandoellema2.4,concluimos que U esindescomponible,paratodo n ≥ 0.Tenemosas´ıque Ind(S4, k) esunconjuntoinfinitoyellema3.5nospermiteentoncesconcluirqueInd(Sr, k) estambi´enunconjunto infinito,paratodo r ≥ 5.
Vamosahoraaexaminarlasituaci´onparalossistemasde r-subespaciospara r ≥ 5;comoveremos,enestoscasosel problemaesmuyinteresanteperosurgeunadificultadinsalvable:
Proposici´on3.7. Parar ≥ 5,elproblemadeclasificaci´onde lossistemasindescomponiblesder-subespaciosesunproblemadetiposalvaje.
Demostraci´on. Teniendoencuentaellema3.5,bastaprobar elresultadopara r = 5:dadouncampo k,consideremosel sistemade5-subespacios
,...,U5) dadopor:
endonde E esunespaciovectorialdedimensi´onfinita n sobre k y A1, A2 sontransformaciones k-linealesde E en E.Seleccionandobasesapropiadaspara U0 yparacadaunodelos subespacios Ui,obtenemospara U unapresentaci´onmatricial MU quetieneelaspectosiguiente: M
endonde A1 y A2 sonlasmatricesdelosoperadores A1 y A2, respectivamente.
Supongamosahoraqueaplicamosunatransformaci´onadmitida T sobrecolumnasdelafranjaverticalquecontienea A1;estaoperaci´oncambia A1 porciertamatriz B1 ymodificaelbloque In queest´aporencimade A1;pararestaurarel bloqueidentidaddebemosaplicarahoralaoperaci´oninversa T 1 sobrefilasdelaprimerafranjahorizontal;estocorrige elbloqueidentidadanteriorperomodificaotrostresbloques identidad.Eneldiagramadelafigura1seilustralasecuenciadetransformacionesadmitidasquedebenaplicarsepara restaurarlosbloquesidentidadoriginales:cadatransformaci´onadmitidaserepresentamedianteunaflechahorizontal, siessobrefilas,overtical,siessobrecolumnas;unbloque identidadencolorrojoindica,quealaplicarlaoperaci´oncorrespondiente,esebloquesufremodificaciones.
As´ıpues,despu´esderecomponerlosbloquesidentidad,tenemosqueaplicarlatransformaci´on T sobrelascolumnasde A1 implicaaplicaresamismaoperaci´onsobrelasmismascolumnasde A2 ytambi´enaplicarlatransformaci´oninversa T 1 sobrefilastantode A1 comode A2;demaneracompletamentean´alogapuedeversequealgosimilarsucedesiseaplica inicialmenteunatransformaci´onadmitidasobrelascolumnas de A2.Teniendoencuentaqueaplicartransformacionesadmitidassobrecolumnas(sobrefilas,respectivamente)equivaleamultiplicaci´onaderecha(aizquierda,respectivamente) porunamatrizinvertible,elan´alisisanteriornosmuestraque lasmatrices A1 y A2 seest´antransformando,demanerasimult´anea,pormultiplicaci´onaderechaporciertamatrizinvertible P ypormultiplicaci´onaizquierdaprecisamentepor lamatrizinversa P 1 .
As´ıpues,elsistemade5-subespaciosconsideradocorrespondealproblemadelareducci´onsimult´anea,porsemejanza, deunpardematricescuadradasdelmismoorden:
Figura1: sucesi´ondetransformacionesqueilustranelproblemadelareducci´onsimult´aneadeunpardematricesporsemejanzacomocasoespecialdeunsistemade5-subespacios.
endonde P esunamatrizinvertibledelmismoordenque A1 y A2,Esteproblema,queest´aasociadoalcarcaj
as ´ ıqueespr ´ acticamenteimposiblepensarenobtenerunaclasificaci´oncompletadelossistemasindescomponiblespara r ≥ 5.
Nota. Aunquehemospedidoqueelentero r seapositivo,de hecho,podemosdartambi´enlaclasificaci´ondelossistemas de0-subespacios:enestecaso,lossistemastienenlaforma (U0),endonde U0 unespaciovectorialdedimensi´onfinita sobreuncampo k yesinmediatoque,salvoisomorfismo, (k) esel ´ unicoobjetoindescomponibleyquesuanillodeendomorfismosestrivial.
Enestasecci´onvamosacentrarnosexclusivamenteenel casodelossistemasde4-subespacios.Estecasoesespecialmenteinteresanteporvariasrazones:porunlado,noespara nadasencillo(adiferenciadeloscasospara r ∈{1, 2, 3})y, porotrolado,aunquesabemosyaqueenInd(S4, k) hayinfinitossistemasindescomponibles(verlaproposici´on3.6),a diferenciadeloquesucedepara r ≥ 5,losinfinitossistemas enInd(S4, k) puedenserdescritoscompletamenteas´ıcomo susanillosdeendomorfismos.Adicionalmente,elproblema deloscuatrosubespacioscontiene,comocasosparticulares, variosproblemascl´asicoseimportantes,talcomoejemplificamosenlasubsecci´onsiguiente.
Nota. Ent´erminosprecisos,mientrasqueelproblemadela clasificaci´ondeInd(Sr, k),para r ≥ 5,esunproblemadetipo salvaje,elproblemaparaInd(S4, k) esdetipomanso.Intuitivamente,elqueunproblemadeclasificaci´ondeobjetossea salvajesignificaquenoadmitesoluci´oncompletayqueel problemaseamansosignificaque,aunqueinvolucrainfinitos objetos,estospuedenserclasificadoscompletamente.Lasdefinicionesprecisasdemansedumbreysalvajismo,as´ıcomo algunosdelosresultadoscl´asicosalrespectopuedenconsultarseen[Dro80].
4.1.Elproblemadeloscuatrosubespacios.
Antesdeexaminarelproblemaysusoluci´on,mencionemosunpardecuestionescl´asicasde ´ algebralinealqueaparecencomocasosespecialesdelproblemadelaclasificaci´onde lossistemasde4-subespacios:
1. Sea A :E → E unatransformaci´onlinealsobreun kespaciovectorial E dedimensi´onfinitasobre k.Consideremoslacu´adrupla U =(U0,U1,...,U4),endonde
Elqueelproblemadelaclasificaci´ondelossistemasde rsubespaciospara r ≥ 5seaunproblemadetiposalvajesignificaque,para r ≥ 5,elconjuntoInd(Sr, k) contieneunacopia detodoslos R-m ´ odulosindescomponiblesfinitodimensionalesparacada k´ algebra R dedimensi´onfinita[Arn00,Bre74b],
taci´onmatricialsiguiente:
endonde n = dimE y A eslamatrizcuadradadeorden n asociadaaloperadorlineal A .Alhacerelan´alisisde lastransformacionesadmitidasquesepuedenaplicarsin alterarlosbloquesidentidadynulosenlapresentaci´on matricialanterior,resultaqueelbloque A sereducepor semejanza:
A → P 1AP,
endonde P esunamatrizinvertibledeorden n.Esteproblemaesprecisamenteelproblemadelbucle
cuyassolucionessonlasformascan´onicas:porejemplo, ladeJordan,introducidaen1870en[Jor70],ylaracional odeFrobenius.
2. Sean E y F unparde k-espaciosvectorialesdedimensi´onfinitasobre k yconsideremosdostransformaciones k-lineales A1:E → F y A2:E → F.Tenemoslacu´adruplaasociada U =(U0,U1,...,U4),endonde
U0 = E ⊕ FU3 = {(α, A1(α)) | α ∈ E},
U1 = E ⊕ 0, U4 = {(α, A2(α)) | α ∈ E}.
U2 = 0 ⊕ F,
Despu´esdeescogerbasesapropiadasparalosespacios, resultaquea U lecorrespondeunapresentaci´onmatricial quetienelaformasiguiente:
In 0 In In 0 Im A1 A2 ,
endonde n = dimE, m = dimF y A1, A2 sonlasmatricesdetamano m × n asociadasalastransformaciones A1, A2,respectivamente.Analizandoahoracu´alesdelas transformacionesadmitidassepuedenaplicardejando invarianteslosbloquesidentidadynulosenlapresentaci´onmatricialanterior,resultaqueelpardematrices cuadradas A1 y A2 sereduceporequivalencia:
(A1, A2) → (PA1Q, PA2Q), endonde P y Q sonmatricesinvertiblesdeorden m y n, respectivamente.Esteproblemaeselproblemadelhaz deKronecker: A1 A2
queWeierstrassresolvi´oinicialmenteparaelcasoregularen[Wei68]y,posteriormente,Kroneckerextendi´oal casosingular(noregular)en[Kro90].Unasoluci´onm´as reciente,conunaextensi´onaloscasossemilinealypseudolinealpuedeconsultarseen[Zav07,Zav08]
Nota. Dehecho,elproblemadeloscuatrosubespacioscontiene,comocasosespeciales,muchosotrosproblemascl´asicoseimportantesde ´ algebralineal;elautorest´apreparando unart´ıculoenelqueseincluyeunestudiodetalladodeesta situaci´on.
Dadouncampo k,lossistemasde4-subespaciossobre k sedenominantambi´encu´adruplas(desubespacios)sobre k Elproblemadeloscuatrosubespaciosnoesotracosaque elproblemadeobtenerlaclasificaci´oncompleta,salvoisomorfismo,detodaslascu´adruplasindescomponiblessobreun campo k.
A4.2.Clasificaci´ondelascu´adruplasindescomponiblesydesusanillosdeendomorfismos.
Enlapresentaci´ondelaclasificaci´oncompletadelas cu ´ adruplasindescomponiblesydelosanillosdeendomorfismoscorrespondientesseguimoslasideasde[MZ04];all´ ı puedeconsultarseunademostraci´ondelosdosteoremassiguientes:
Teorema4.1. Todaslascu´adruplasindescomponiblesU = (U0,U1,...,U4) sobreuncampoarbitrariokest´andadas,salvoisomorfismo,salvodualidadysalvopermutacionesdelos subespaciosU1,...,U4,porlascu´adruplasindescomponibles delosseistipos 0, I,...,Vpresentadosenformamatricialen loscuadrosdelafigura2.
Teorema4.2. SeaUunacu´adruplaindescomponiblesobre uncampoarbitrariok,seand0 = dimU0 y E = EndUelanillo deendomorfismosdeU.Entonces,setienelosiguiente:
(a) SiUesregulardetipo 0 cond0 = 2n (n 1),entonces E k[t]/(ps(t)),endondeps(t) eselpolinomiominimal delac´eluladeFrobeniusindescomponibleXdeordenn (mostradaenlafigura2)conp(t) m ´ onicoirreducibley diferentedetydet 1 (claramenten = s deg p(t)).
(b) SiUesregulardetipoIcond0 = 2n (n 1),entonces E k[t]/(tn).
(c) SiUesregulardetipoIIcond0 = 2n + 1 (n 0),entonces E k[t]/(tn+1)
(d) SiUesnoregular,entonces E k.
4.3.Cuadrodelascu´adruplasindescomponibles.
Enestasecci´onexplicamoslasnotaciones,lasconvencionesytodalainformaci´oncontenidaenloscuadrosdelafigura2enquesemuestrantodaslascu´adruplasindescomponibles,salvoisomorfismoypermutacionesdelossubespacios.
Siunamatrizidentidad Ik est´aequipadaconunaflechade laforma ←, →, ↑ o ↓,estoindicaquedebemosagregara Ik unacolumnaofiladecerosalaizquierda,aladerecha,encimaoabajo,respectivamente.
Fn(ps(t)) denotalac´eluladeFrobenius(tambi´enconocidacomolac´eluladelaformacan´onicaracional)deorden n quetienecomopolinomiominimal ps(t),endonde p(t) es m ´ onicoeirreducible.Enotraspalabras, Fn(ps(t)) eslamatriz acompanantede ps(t) (enparticular, n = s deg p(t)).
Denotamos J+ n (0) (Jn (0))elbloquedeJordandeorden n convalorpropio0yentradas1enladiagonalqueest´apor encima(pordebajo)deladiagonalprincipal.
Cadatipodecu´adruplaindescomponiblevieneacompa ˜ nadoconun ´ utildiagramacaracter´ısticoformadoporcuatrov´ertices(querepresentanlossubespacios U1,...,U4)junto cons ´ ımbolosadicionalesdelaforma
otambi´en
Estoss´ımbolossignificanquelossubespacioscorrespondientes Ui y Uj satisfacenlarelaci´ondim(Ui ∩ Uj)= 1o codim(Ui +Uj)= 1,respectivamente.Encasodeausenciade estes´ımbolo, Ui ∩ Uj = 0o Ui + Uj = U0,respectivamente. Losdiagramastambi´enincluyenlascoordenadasdelvector dimensi´on d = dimU
Enelcuadroincluimostambi´enlosvalores
delaformacuadr´aticadeTits f enelvectordedimensi´on d = dimU.Asimismo,damosparacadatiposucorrespondiente anillodeendomorfismos E = EndU
Parauntipo T denotamos T ∗ eltipodual(formadoporlas cu ´ adruplasduales U ∗ endonde U esdetipo T ).
EnlasmatricesdetiposVyV∗ la ´ ultimafranjahorizontal es ´ unicamentedeunafila.
Nota. (a) Delaconstrucci´onusadaen[MZ04],sesigueque todaslascu´adruplaslistadasenelcuadroson,dehecho, indescomponiblesymutuamentenoisomorfas.Adem´as, cadacu´adrupla U deunodelostiposII,...,V(odelos tiposduales)est´adeterminadademaneraun´ıvoca,salvo isomorfismo,porsuvectordedimensi´on d = dimU (que esunara ´ ızdelaforma f enelsentidoque f (d)= 1).
Cadacu´adrupladetipo0oIest´adeterminadaporel par (d, p(t)) o (d,t) respectivamente(endonde p(t) y t sonlospolinomiosmencionadosantesyelvectorde dimensi´on d esunara ´ ızimaginariade f enelsentido que f (d)= 0).
(b) Sitomamos p(t)= t o p(t)= t 1eneltipo0,obtenemoseltipoI.Lascu´adruplasdetipoIdadaspormatrices con J+ n (0) y Jn (0),sonisomorfas.
(c) Sisustituimos J+ n (0) por Jn (0) enlaformadetipoV,debemossimult´aneamentesustituir (0 01) por (10 0) enlas ´ ultimasfilasdelasfranjas M3, M4 (las ´ ultimasfilas
en M1, M2 sonfilasnulas).Correspondientemente,enla formaV∗ podemosinvertirladirecci´ondetodaslasflechas,ysimult´aneamentesustituir (0 ... 01) por (10 ... 0) enla ´ ultimafiladecadafranja Mi, i ∈{1,..., 4}
[Arn00] D.M.Arnold, Abeliangroupsandrepresentationsoffinitepartially orderedsets,Vol.2,CMSBooksinMathematics,Canada,2000.
[Bre67] S.Brenner, Endomorphismalgebrasofvectorspaceswithdistinguishedsetsofsubspaces,J.Algebra 6 (1967),100–114.
[Bre74a] , Onfoursubspacesofavectorspace,J.Algebra 29 (1974), 587–599.
[Bre74b] , Decompositionpropertiesofsomesmalldiagramsofmodules,1974.
[Dro80] Ju.A.Drozd, Tameandwildmatrixproblems, inRepresentation TheoryII(VlastimilDlabandGabriel,ed.),Springer,Berlin,Heidelberg,1980.
[For08] T.A.Forbregd, The4SubspaceProblem: Advisor:SverreSmalø, Master’sThesis,NorwegianUniversityofScienceandTechnology, 2008., t.ly/28hz
[Jor70] C.Jordan, Trait´edessubstitutionsetdes ´ equationsalg´ebriques, Paris,1870.
[GP70] I.M.GelfandandV.A.Ponomarev, Problemsoflinearalgebraand classificationofquadruplesofsubspacesinafinitedimensional vectorspace,Colloq.Math.Soc.JanosBolyai,Hilbertspaceoperators,1970,pp.163–237.
[Kro90] L.Kronecker, AlgebraischeReduktionderScharenbilinearerFormen,Sitzungsber.Akad.Berlin(1890),763–776.
[Med20] G.Medina, Introducci´onalateor´ıaderepresentacionesdeconjuntosparcialmenteordinarios,Notasdeclase,Departamentode Matematicas,2020.
[MZ04] G.MedinaandA.G.Zavadskij, Thefoursubspaceproblem:Anelementarysolution,LinearAlgebraanditsApplications 392 (2004), 11-23.
[Naz67] L.A.Nazarova, Representationsofatetrad,Izv.Akad.Nauk.SSSR 31 (1967),1361–1377.Traducci´onalingl´esenMath.USSRIzv.1, 1967.
[Naz75] , Partiallyorderedsetsofinfinitetype,Izv.Akad.Nauk. SSSR 39 (1975),963–991.Traducci´onalingl´esenMath.USSR Izv.9,1975.
[Wei68] K.Weierstrass, ZurTheoriederquadratischenundbilinearenformen,Monatsber.Akad.Wiss.(1868),311–338.
[Zav07] A.G.Zavadskij, OntheKroneckerProblemandrelatedproblems ofLinearAlgebra,LinearAlgebraanditsApplications 425 (2007), no.1,26–62,DOIhttps://doi.org/10.1016/j.laa.2007.03.011.
[Zav08] , Amatrixproblemoveracentralquadraticskewfieldextension,LinearAlgebraanditsApplications 428 (2008),393–399.
Acercadelautor:desde1999GonzaloesprofesordelDepartamentodeMatem´aticasyEstad´ısticadelaUniversidad NacionaldeColombia;su ´ areadetrabajoeslateor´ıaderepresentacionesdeestructurasalgebraicas.Amantedel ´ algebra,delatipograf´ıaydelahistoriayepistemolog´ıadelas matem´aticasas´ıcomoapasionadoporlam´usicadeBach,las novelasdeHeinrichB¨ollyloscubosdeRubik.
DanielEstebanGalvisSandoval * daniele.galviss@konradlorenz.edu.co
El ´ algebralineal,aunqueseestudiaaprofundidadenmatem´aticasof´ısica,amenudoparecetanabstractaquenose conoceclaramentesugradodeaplicaci´on.Enesteart´ıculo, sever ´ aquelosconceptosclavecomotransformacioneslinealesyproductosinternos,llevar´anaentenderlal´ogicadela computaci´oncu´antica,unparadigmaconunacomplejaestructurainform´aticaquepretendeevolucionarlatecnolog´ıa, yelfuturo.Poreso,seintroduceelespaciovectorialdelos cuaterniones,yseinterpretacomorotaci´ondevectoresenla esferaderadio1,queseasociaenciertaformaconlaesfera deBloch.Esta ´ ultima,entendidacomolarepresentaci´onde estadosdeunsistemaf´ısicoyenparticular,delosqubits,que sonlosvectoresdelespaciodeHilbertcuyosestadosvienen dadosporunconjuntodetransformacioneslinealesocompuertascu´anticas.Adicionalmente,sepresentar´aunpequeno c ´ odigoenPythonconlaideaderepresentarlarotaci´ondevectoresenlaesferaderadio1delespaciodeloscuaterniones. Por ´ ultimo,yconelfindeaplicarestasrotaciones,seexplica brevementeelalgoritmodeShorparafactorizaci´ondeenteros positivosysuusoenlacriptograf´ıacu´antica.
Desdequeelmatem´aticoingl´esAlanTuringdisen´oelprimerprototipodeordenadorcl´asicoparadescifrarelc´odigo secretodelaarmadaNazidurantelasegundaGuerraMundial,elsistemacomputacionalhaidomoderniz´andose,donde cadavezm´as,losordenadorestienenmejorescaracter´ısticas dedise˜no,memoria,velocidad,entreotras,todasbajoelmismosistemadiscretocuyam´ınimaunidaddeinformaci´onesel bit 1 deunosyceros.Estosd´ıgitosrepresentandosestados: Encendidooapagado,ciertoofalso,siono[Lop16a].Dentro delacircuiter´ıaelectr´onicadeunsistemadecomputadora,estosvaloressignificanpresenciaoausenciadevoltaje.Unbit eslam´ınimaunidaddeinformaci´on,puesapartirdeellosse construyecantidadesm´asgrandesdeinformaci´on.As´ı,ocho bitsconformanunocteto,tambi´enllamadobyte[Lop16b],de modoque,comolascomputadorasest´andise˜nadasparatrabajarconbytes,ycadaespaciodeloctetotienedosposibles

*Estudiantedematem´aticas,Fundaci´onUniversitariaKonradLorenz,Bogot´a-Colombia.
1Lapalabrabitrepresentaunaabreviaci´ondebinarydigit(d´ıgitobinaria) [Lop16a]
estados1o0,entoncesexisten28 combinacionesposibles, osea256valoresdiferentesyseusanparamedirelalmacenamientodememoriadeundato.Sidigitamosunp´arrafo completotendremosunaseriedebytesquepuedentenerun tama˜nodeunkilobyte(103 bytes)ounmegabyte(106 bytes)etc.,yenfraccionesdesegundo,elordenadoryasabelo queseleest´aescribiendo.Perocuandoeltama˜nodelasinstruccionesalordenadorexcedesucapacidad,puedellegara hacerqueestesedemore.Estosucedemuchoenmatem´aticas cuandosemodelaporordenadorproblemasquerequierenuna enormecantidaddec´alculos.Puesbien,comolacomputadoracl´asicaelaboraestasinstruccionesdeformaserial,esdecir deformasecuencial,pasoapaso,unatrasotradeformaindependiente,entoncesseabrumalamemoriaporelconsumode recursos.
Apartirdeestadificultad,hasalidoalaluz,laideade construirunordenadorquerealiceoperacionesdemanerasimult´anea.Enela˜no2000,EnmanuelKnill,RaymondLaflamme,RudyMartinezyChing-HuaTsengdelMITlograrondesarrollaruncomputadorcu´anticode7Qubits[CC20] UnQubit,eslaabreviaci´ondeQuantumbit,yrepresentala unidadm´ınimayb´asicadeprocesamientodeinformaci´onde uncomputadorcu´anticoyacomparaci´ondelbit,estepuede estarenestado0,1oenunacombinaci´onlinealdeambos. M´asadelante,definiremosformalmenteelqubitysutransformaci´onenelespaciodeHilbert.Elfindeesto,esreflejar laimportanciadelosestadosquepuedetomarunqubiten unaoperaci´ondada.Conlosbitsconvencionales,siten´ıamos unregistrodetresbits,hab´ıaochovaloresposibles,yelregistros´olopod´ıatomarunodeesosvalores.Encambio,si tenemosunvectordetresqubits,lapart´ıculapuedetomar ochovaloresdistintosalavezgraciasaloquesedenominalasuperposici´oncu´antica.Deestemodo,unvectordetres qubitscomputar´ıauntotaldeochooperacionesenparalelo. Parahacerseunaideadelgranavancequeestosupone,un computadorcu´anticode30qubitsequivaldr´ıaaunprocesador convencionalde10teraflops(millonesdemillonesdeoperacionesencomaflotanteporsegundo),esdecir,unacantidad abrumadoradeoperaciones,quenoescomparableconlacapacidaddeunprocesadorconvencionaldehoyd´ıa,yaque actualmentelascomputadorastrabajanenelordendegigaflops(milesdemillonesdeoperacionesencomaflotantepor segundo)[CC20].Enesteart´ıculo,sever´alaformadeoperar delosqubitsmediantetransformacioneslinealesenunespaciodeHilbert,yc´omodesdelaperspectivadelasrotaciones
enelespaciodecuaterniones,sepuedeinterpretarlasmismas querealizaenunespaciotridimensionaldeHilbert.Enlasiguientesecci´onsegeneralizaunainterpretaci´ongrossomodo delaf´ısicacu´antica,yc´omoestoserelacionaconelobjeto deestudiodeesteescritoquesonlasrotacionesdeunvectorenunespaciocomplejo,posteriormenteseintroducenlos cuaterniones,yluegolosespaciosdeHilbert.Finalmente,se presentaunaaplicaci´onencriptograf´ıamedianteelcasode factorizaci´onconelalgoritmodeShor.
Deacuerdocon[Haw10]ensulibro ElGranDise˜no,el universonotieneunaexistencia ´ unicasinoquecadaposible versi´ondeluniversoexistesimult´aneamenteenloquesedenominalasuperposici´oncu´antica;yconestaextranaintroducci´on,nospreguntamos,¿aqui´enseloocurri´ohablardealgo comoesto?,¿porqu´esehabladeunanuevaf´ısicadelmundo subat´omico?,¿qu´etienequeverestoconlacomputaci´on?y ¿porqu ´ enosinteresaparaelestudioderotaciones?
Bueno,hayqueremontarseacomienzosdelsigloXX, cuandoelproblemadesaberenqu´edirecci´onoqu´epatr´on segu ´ ıalaemisi´ondeluzdeuncuerpocaliente,erairresoluble. MaxPlanck,descubri´olaleydelaradiaci´onelectromagn´eticaemitidaporuncuerpoaciertatemperaturaydiosoluci´ona esteproblemapasandoaserconsideradocomoelpadredela f´ısicacu´antica[An´o19].Enestetrabajo,intent´oexplicarque laluzsecomportabanosolocomoondasinocomocorriente depart´ıculas,queloselectronessonsimult´aneamentepart´ıculasyondas,yadem´as,queloselectronesocupabandiferentes puntosdesu ´ orbitademanerasimult´aneasaltandodeunaa otra,siendoimposibledeconocerconprecisi´onsutrayectoriayllevandoapensarqueeraunacuesti´ondelazardela naturaleza.
Seg´un[An´o20],eltrabajodePlanckcondujoaqueAlbert Einsteinrealizarasutrabajodelefectofotoel´ectrico,basado enlaideadelcomportamientodelaluznocomoondacontinuasinocomochorrodepart´ıculasdenominadascuantosde luzofotones.En1925,WernerHeisenbergdesarroll´olamatem´aticadelamec´anicacu´anticausando ´ algebradematrices, lesigui´oelfamosof´ısicoaustriacoErwinSchrodingerque formul´oen1927lafunci´ondeondayquecondujoalfamosoexperimentodelgatoqueseencuentravivoymuertoala vezdebidoalaspropiedadescu´anticasdelamateriaypropiamentedeloselectrones.Este ´ ultimoexperimento,juntocon elexperimentodeladoblerendija(quetratabadeexplicarel comportamientoenformadeondadeloselectronescuando interactuabaconuncristaldeniquel)llevadoacaboen1927 porClintonDavissonyLesterGermer[Haw10]llevaronala cienciaaotraescalayapensarqueesecomportamientode ondadelosfotonesyelectronespod´ıanexplicarelentrelazamientocu´antico.Estomotiv´oalf´ısicoRichardFeynmana estudiarelexperimentodeladoblerendijayaconcluirqueno setratabadeunaposici´onindeterminadadelapart´ıculasino queellatomabatodosloscaminosposiblesalavez,yellodependedecu´antasrendijasocompuertasseencuentrenabier-
tasendichoinstante,esdecir,quesiunarendijaseencuentra abierta,entoncestodaslaspart´ıculaspasaranporall´ıyhar´an una ´ unicahistoria,mientrasquesihaym´asrendijasabiertas, entoncesellaspasaranportodasalmismotiempoyhar´anhistoriasalternativas.Seanadequeelmatem´aticoyf´ısicoPaul Dirac,introdujoelprocesodeunificaci´ondelateor´ıadela mec ´ anicacu´anticaconlateor´ıadelarelatividadespecialyen 1932elmatem´aticoH¨engaroJohnVonNeumannformul´ola matem´aticaparalamec´anicacu´anticamediantelosespacios deHilbert,yporestaraz´on,usamosnotaci´ondeDiracenlas siguientessecciones.
Unavezsabemosdequ´etrataestaf´ısica,esimportantecuestionarseporqu´eestotuvograntrascendenciaenla computaci´ondelsigloXXI,puesbien,lasideasdeentrelazamientocu´anticoyn´umerodeposiblesposicionesdeuna part´ıculaserelacionanconeltama˜nodelasoperacionesque realizaunordenadorylosrecursosconlosquedispone.Por lotanto,sienlaf´ısicacu´anticaunapart´ıculaquevadelpunto A aunpunto B pasandopordiferentesrendijastomando todosloscaminosposiblessimult´aneamente,enlacomputaci´oncu´antica,lasoperacionesdeunalgoritmoserealizan deformasimult´aneaynoserestringeados ´ unicosestados deoperaci´on(0,1)sinoquepuedentenermultituddeestadosintermedioscomoresultadodelasuperposici´ondeestos dosestados[Her10],esdecir,sepermitelaevaluaci´ondetodoslosposiblesestadosalmismotiempo(algoqueseconoce comoparalelismocu´antico)ysetraduceenunadisminuci´on detiempoyrecursosparaelprocesamientodeunaoperaci´on [Cai10].Porestaraz´on,consideramosquemedianteelestudiodecuaternionesyel ´ algebralineal,queeselcaballito debatallaparaentenderestacomputaci´on,podr´ıamosintentarexplicarsufuncionamientoapartirdesimplesrotaciones enunespaciotridimensionalcomplejo.
WilliamRowanHamilton,unmatem´aticonacidoenDublinen1805,sepregunt´oporlaformadetrasladarlanoci´on geom ´ etricadelosn´umeroscomplejosdelplanoadimensiones superiores,enparticular,alaterceradimensi´on.Lociertoes quenopudo,perocuandolointent´oconcuatrodimensiones lefueposible.Deacuerdocon[Rod12]Hamiltonseencontrabapaseandoconsuesposaun16deOctubrede1843por elcanalRealdeDublin,cuandoderepentelelleg´ounaideaa sucabeza,comosifueseuntipodealucinaci´onyparaqueno seleolvidase,escribi´olaidentidad i2 = j2 = k2 = ijk = 1 enunapiedradelpuentedeBroom,donde i, j, k ∈ C,esdecir,formanunespaciotridimensionalcomplejo,ylacuarta dimensi´onladenot´oconunacomponentereal a,porlotanto, denomin´oa q comocuaterni´onsi q = a + bi + cj + dk donde a, b, c, d ∈ R
Trasestedescubrimiento,elestudiodelascienciasevolucion´o,enparticular,enaplicaciones ´ algebrasdeLieomatricesdePauli,oinclusoeninform´atica,conlasrotacionesen elespaciotridimensionalusadaenlarob´oticaeinteligencia artificial.
Algebraicamenteelconjuntodeloscomplejosformauna estructuradecuerpoconciertaspropiedadesyqueser´ande granutilidadenelconjuntodeloscuaterniones.Ahorabien, uncuaterni´on,comobienyasedijo,esunn´umeroounobjeto decuatrodimensionesdelaforma:
q = a + bi + cj + dk, (1) donde i, j, k ∈ C y a, b, c, d ∈ R,oseaquesi a = b = c = d = 0setieneelcuaterni´onnulo,osi a = 0y b = c = d = 0 entoncessetieneunobjetoenelespaciotridimensionalcomplejo.As´ı,podr´ıamosseguird´andoledistintasformasalcuaterni´onyusarlocomobienconvenga.Acontinuaci´on,sedan unasdefinicionesindispensablesparaabordarpropiedadesde loscuaterniones,estasdefinicionessebasanenlaspropiedadesdelosn´umeroscomplejos.
Definici´on4.1. Dadoelcuaterni´onq = a + bi + cj + dk,su cuaterni´onconjugadoes q = a bi cj dk [Fav08]
Definici´on4.2. Dadoelcuaterni´onq = a + bi + cj + dk,su cuaterni´onopuestoes q = a bi cj dk [Fav08]
Definici´on4.3. Dadoelcuaterni´onq = a + bi + cj + dk,se definesunormacomo |q|= √a2 + b2 + c3 + d2,adem´as,qse puedenormalizarmediantelasiguienteoperaci´on:q′ = q |q| dondeq′ esqnormalizado [Fav08].
Definici´on4.4. Dadoelcuaterni´onq = a + bi + cj + dk,se dicequeqesunitariosisunormaesigualauno [Fav08]
Definici´on4.5. Dadoelcuaterni´onq = a + bi + cj + dk,su inversoesq 1 = q |q|2 [Fav08]
Elconjuntoquecontienealoscuaternionessedenota H, con H = {q : q = a + bi + cj + dk, i, j, k ∈ C ∧ a, b, c, d ∈ R}
Deformaan´alogaalosn´umeroscomplejos,sedefinela sumadelosn´umeroscuaterniones:
Dados q = a1 + b1i + c1j + d1k, p = a2 + b2i + c2j + d2k,se definelasumadecuaternionescomo:
q + p =(a1 + a2)+(b1 + b2)i +(c1 + c2)j +(d1 + d2)k, donde (a1 + a2), (b1 + b2), (c1 + c2), (d1 + d2) ∈ R
Debidoalaspropiedadesdelosn´umeroscomplejosylos n ´ umerosreales,sepuedeverf´acilmentequeloscuaterniones cumplenlaasociatividadyconmutatividad,adem´as,porladefinici´on4.2,existeelneutroaditivoycuandotodaslascomponentesrealessoncero,seaseguralaexistenciadelneutro aditivo,oseaque (H, +) esungrupoabeliano.
Larestadecuaternionessehacedeformaan´alogayse puedeprobarf´acilmente.As´ıtambi´en,podemospensarenla sumadeuncuaterni´onconsuconjugado:
q + q =(a + a)+(b b)i +(c c)j +(d d)k = 2a.
Porsuparte,elproductodecuaternionesesunpocodiferentealamultiplicaci´ondecomplejospuestoquesedebetenerencuentalaidentidadarribadescrita i2 = j2 = k2 = ijk =
Conestoenmente,sedefineelproductodecuaterniones as
[Fav08].Dehecho,esteresultadoesmuycomplejo, yaqueusalaspropiedadesde2,porloquetieneunamejor visualizaci´ondelasiguientemanera:
Cuadro1:Multiplicaci´ondecuaterniones. realizandolosproductosdefinidos:
Cuadro2:Multiplicaci´ondecuaterniones.
yorganizandoporcolumnasyport´erminossemejantesse tiene:
Cuadro3:Multiplicaci´ondecuaterniones.
Esdecir,tomandoporcolumnasyfactorizandotenemos que
guienteteorema:
Teorema4.1. Seaq = t + xi + yj + zk ∈ H,entonceslamatriz asociadaL(q) es:
Elteoremaanteriornosdicequeexisteunamatrizasociada paracualquiercuaterni´onyesonoesm´asqueloquevimosen lastrestablasanteriores,soloqueall´ıorganizamosporcolumnasysumamost´erminossemejantes.Dehecho,estaformaes ´ utilcuandolosproductossonmuchom´ascomplejos.Adem´as,
deestaformatambi´enpuedeprobarsequeelproductodecuaternionesesasociativo.
Porotraparte,nospodemosdarcuentaf´acilmente,quedadalaidentidad1ylosproductos2,laconmutatividaddecuaternionesnosecumpleysepuedeprobardelamismaforma. Ahorabien,igualqueconlasuma,podemosmirarqu´epasa conelproductodeuncuaterni´onconsuconjugado,estoes:
q · q = a 2 + b2 + c 3 + d2 (4)
Esteresultadoser´amuyimportantepuestoquedeaqu´ısurgelaideadelarotaci´ontridimensionaldepuntosrespectoa unvector.
As´ıtambi´en,otrapropiedadquevaleresaltareselconjugadodelproductodedoscuaterniones:
q p = p q.
Sintetizandounpoco,loscuaternionessonunconjuntocon ciertaspropiedadesparalasumayparalamultiplicaci´onescalar.Dehecho,teniendoencuentaquesatisfacetodaslaspropiedadesparalasumaycasitodasparalamultiplicaci´onescalaraexcepci´ondelaconmutatividad,podr´ıamosdecirque loscuaterniones (H, +, ) formanunaestructuraalgebraicade anillonoabelianoyconelementoneutro.Ahorabien,observemosquesigeneralizamosesteanillo,nosdamoscuentaque loscuaternionessonunespaciovectorialde R′4 quenorepresentaelmismo Rn sinoquelodenotamos R′ considerando quelaprimeracomponenteesrealylasotrastressoncomplejas.Sepuedeprobarqueesteconjuntoesunespaciovectorial peculiarprobandocadaunodelos10axiomasdeespaciovectorial;sinembargonolohacemosporquenoeselobjetivode esteescrito.Detodasformas,esteresultadoesdemasiadoimportanteporquecomoveremosm´asadelante,nosservir´apara interpretarunvectorbidimensionaldeHilbertenesteespacio,pararealizaroperacionessobreestevectorenunaesfera deradiouno.Porahora,nosayudabastantetenerlaideaclara delaformadeunvectoren H
Hastaaqu´ıhemosvistotansololaspropiedadesdeestos conjuntos;sinembargosonsuficientes,as´ıque,sinm´asque decir,vamosacomenzarconunodelosresultadosclavede esteart´ıculo:
Consideremosporejemploquecualquierpunto P(x, y, z) delespaciotridimensionalconocidopuedeserrepresentado comouncuaterni´oncuyaparterealescero: P(x, y, z) → P =

0 + xi + yj + zk.As´ı,si P =(1, 2, 3) → P =(i + 2j + 3k).Ahora,consideremosotropunto S =(x1, y1, z1),represent´emoslo comocuaterni´onyluegonormalic´emoslo.Deestaforma,podemosimaginarnosalcuaterni´on S comolaesferaderadio 1enelespaciotridimensional,donde (x, y, z) sonlascomponentesdelosejes.Porlotanto,estaesferalapodemosrotar ytodoslospuntosdelespacioconella,pero¿c´omo?Consideremosahoraun ´ angulo θ ydejemosqueelvectorunitario S seaelejederotaci´on,esdecir,elvectorreferenciarespecto dequienserealizalarotaci´ondelespacioenun ´ angulo θ dado.Entonces,estaoperaci´onderotaci´onsepuederepresentar comouncuaterni´on q:
q =(s, v), (5)
donde s = cos θ 2 y v = S sin θ 2 [Mar16].
Elpunto P′ finaldespu´esdelarotaci´onseobtienederealizarlasiguienteoperaci´on:
P′ = q P q (6)
Enesencia,necesitamosunpunto,unvectorunitarioque act´uacomoelejedereferenciadelarotaci´onyun ´ angulode rotaci´on.Veamoslasiguienteilustraci´on:
Comosepuedeobservar,elvectorreferenteoejederotaci´ones n ytodoslospuntosdelplanooriginal xy (azul)rota un ´ angulo β haciaelplanorojo.Ahorabien,recordandoque estamostrabajandoconelpunto P yelvectornormalizado q y suconjugado,notemosquesielvectorunitario q lotomamos respectodealg´uneje,esdecir,respectoa x, y o z,elc´alculo sehacedemasiadosencillo.Porejemplo,siqueremosrotar elespaciorespectoaleje z,entoncestenemosquecalcular P′ = q · P · q,queequivalea:
· sin θ 2 )
Contodo,nosiempresequiereunarotaci´onrespectoauno delosejessinoqueenlamayor´ıadeloscasos,lasrotaciones sonsobredistintosvectoresreferenciadelespacio,yeneste, hayinfinitos.Adem´as,unodelosmayoresproblemasser´ıa elhechoderotacionessucesivassobredistintosejes.Esclaro queparaellohar´ıamosunamatrizconcuantoscuaterniones consideremosnecesariosparahacerlasrotacionesdelespacionecesarias,perohaciendoestatareacondistintosejesdel espacio,elresultadofinaloposici´onfinaldecadapuntono podr´ıaserresultadodeunn´umeromayoraunodevectores referenciasobreelqueserot´oelespacio.Estodacabidaal siguienteteoremapropuestoporLeonhardEulerantesdeque Hamiltondescubrieraloscuaterniones:
Teorema4.2. SiResunamatrizquerepresentaunarotaci´on en R3,entoncesRtieneunvectorpropion ∈ R3 talqueRn = n,estoes,nesunvectorpropioconvalorpropio1 [An´o10].
Esteteoremaloquenosdiceesque,contodaseguridad, cualquierrotaci´onporuncierto ´ anguloenelespaciotridimensionaldejafijaunal´ınearecta,queeselejederotaci´on, oseaquedadaunasecuenciaderotacionessobredistintos ejes,existeunarotaci´onquegeneralizatodalasecuenciade rotaciones,yesta,asuveztieneasociadaunasolamatrizde rotaci´onsobreunejedereferenciaoejederotaci´on.
Yavimosqueunvectorcualquieraenelespaciosepuedeexpresarcomocuaterni´on,yeste,normalizado,esunaesferaderadio1quesepuederotar.As´ıpues,podemosusar lageometr´ıaanal´ıticaparadeducirunaexpresi´onsumamente importanteyeslasiguiente:
Consideremoselplano R2 convector v decoordenadas (vx, vy) quesequiererotar θ gradosensentidoantihorario hastaelvector w decoordenadas wx, wy.
Digamosquelanormadelvector v = r,as ´ ı, |v|= |w|= r,la coordenadaen x destino wx = r cosθ + α = r [cosα cosθ sinα sinθ ]= r cosα cosθ r sinα sinθ,pero vx = r cosα y vy = r sinα,oseaquereescribiendosetiene: wx = vx cosθ vy sinθ.An´alogamente,lacoordenadaen y destino wy = vx sinθ + vy sinθ
Siexpresamosestoenformamatricial:
wx wy = cosθ sinθ sinθ cosθ vx vy
Extrapolaresteresultadoa R3 noescomplicado,paraempezar,podr´ıamostomarlasiguientematrizcuyoejederotaci´oneseleje z,entoncessetendr´ıa:
Ahora,si q =(s1, γv2) con s1 = cos θ 2 y γ = sin θ 2 sepuede llegarademostrarquedadoelpunto P quesequiererotar,6 esequivalente.
ElresultadodeRodriguesnosdapasoabuscarunvector caracter´ısticoquepodamosrotarynosarrojealg´unresultado interesante.Enlasiguientesecci´on,introducimoslosespacios deHilbert,yaquelasrotacionesdevectoresquenosinteresa, serealizanenunaesferaderadio1cuyosvaloresposibles representanlosestadosdeunqubit.
Definici´on5.1. SeanV,Wdosespaciosvectorialesdedimensi´onfinita,Funcampoyf : V → Wunafunci´on,diremosque fesunatransformaci´onlinealdeVenWsisecumple:
f (x + y)= f (x)+ f (y) ∀x, y ∈ V.
f (αx)= α f (x)∀x ∈ V, α ∈ F.
Loanterioreslomismoque f (αx +αy)= α f (x)+α f (y). Ahora,sabemosqueelproductointernoesunafunci´onlineal quevadelespaciovectorialalcamposobreelquesedefine dichoespaciovectorial.
Definici´on5.2. SeaVunespaciovectorialdedimensi´onfinitay R elcamposobreelquesedefineV.Elproductointernoo productoescalardefinidosobreVesunaaplicaci´onofunci´on f : VxV → R,denotado < u, v > quesatisfacelassiguientes propiedadesparatodou, v, w ∈ Vytodoescalar α ∈ R:
Paraentenderlarelaci´onentreelresultadoanterioryla rotaci´onusandocuaterniones,esnecesarioasociarlasrotacionestridimensionalesalaf´ormuladeRodr´ıgues[An´o10] enhonoralmatem´aticoOlindeRodrigues, 2 queconsisteen rotarunvector v alrededordeotrounitario n ycuyascoordenadasseobtienende vcosα +(nxv) sinα +n(n·v)(1 cosα), donde (nxv) eselproductocruzdevectoresy (n·v) elproductopuntodeambosvectores.As´ı,concuaterniones,sedefinen doscuaternionesentrelaspartesimaginariasdedoscuaterniones q =(s1, v1), p =(s2, v2):Elproductopuntoyelproducto cruz (v1xv2) y (v1 v2).Luego,setienequeelproductode cuaternioneses:
2Aquienseleatribuyentrabajosmemorablespreviosaldescubrimiento deHamiltondeloscuaterniones.
Esdecir,elproductointernoentredosvectoresdelespaciodevuelveunn´umerodelcampodelosreales.Adem´as, sepuededemostrarf´acilmentequelapropiedad3de5.2es linealenlasegundacomponentecomoenlaprimeracomponente.Esdecir,aplicando5.1 < u, αv + αw >= α < u, v > +α < u, w >.Lomismoconlaprimeracomponente.As´ı,se dicequeelproductointernoesunaformabilinealsim´etricay definidapositivaporlasanteriorespropiedades;sinembargo, ¿qu ´ esucedeconestaformacuandosetienenvectoresdeun cuerpocomplejo?
Supongamosunvector u =(1, 0, i) ∈ C3 yprobemosla cuartapropiedadde5.2.As´ı, (1, 0, i) (1, 0, i)= 0,oseaque nosecumplelapropiedaddeque u = 0.Porlotanto,sedebe hacerunapequenamodificaci´on.Sihacemosquelapropiedad sea < u∗, u >,esdecir,elcomplejoconjugadoporelvector, entoncespodemosobservarlosiguiente: (1, 0, i) · (1, 0, i)=
2 = 0.Ahora,lapropiedadsim´etricanosecumpleynecesitamosque < u, v >=< v, u > ∗,oseaalcomplejoconjugado,yahorasedicequecumplelapropiedadherm´ıtica. Por ´ ultimo,ynomenosimportante,sepuedeprobarquebajolascondicionesimpuestasenestep´arrafo,ahora,lacondici´ondebilinealidadnosecumplir´ıasinosoloparalasegundacomponente,mientrasqueparalaprimera,losescalaressaldr´ıancomplejosconjugadosdelasiguienteforma:
.Porconsiguiente,tenemoslasiguientedefinici´on:
Definici´on5.3. SeaVunespaciovectorialdedimensi´onfinitasobreelcuerpo K,elproductointernooproductoescalar definidosobreVesunaaplicaci´onofunci´onf : VxV → K, denotado < u, v > quesatisfacelassiguientespropiedades paratodou, v, w
Definici´on5.9. Llamamosbraaunvectordelaforma:
Esdecir,losketssonvectorescolumnaylosbrassonvectoresfiladondecadaunadesusentradaseselcomplejoconjugadodeunn´umerocualquieradelcampodeloscomplejos. Ahora,dijimosanteriormentequeunqubitpodr´ıaserexpresadocomounacombinaci´onlinealdelosvectoresdelabase de H .Enestecaso,definimoscomovectoresdelabasefundamentaldelacomputaci´oncu´anticaalosvectores |0⟩ y |1⟩, queennotaci´onconvencional:
As´ı,cualquiervectordelespaciodosdimensionaldeHilbertpuedesergeneradoporelketceroyelketuno,enparticular,elqubit |ψ⟩ = α |0⟩ + β |1⟩ con α, β ∈ C
Conlabasefundamental,podemosverqu´esucedeconel productointernodelasmismasyquesenotadelasiguiente manera:Sellamabraketa ⟨ψ|ψ⟩.Enparticular,teniendoen cuentalamultiplicaci´ondematrices:
Delaanteriordefinici´onsesigueque:
Definici´on5.4. Unespaciopre-Hilbertianoesunespacio vectorialsobre K conproductointernoynormadocon ||v||=
< v, v > [AD15]
Definici´on5.5. UnespaciovectorialVescompletoparala norma,s ´ ıys ´ olositodasucesi´ondecauchy3 convergeconesa norma [AD15].
Deloanterior,tenemoslasiguientedefinici´on:
Definici´on5.6. UnespaciodeHilbert H esunespaciopreHilbertianocuyanormaescompleta [AD15]
UnavezhemosintroducidoelespaciodeHilbert,definimosformalmenteelqubit:
Definici´on5.7. Unqubitobitcu´anticoesunvectornormalizadodelespaciodeHilbert C2 [AD15]
As´ı,vemoscomonoshavenidodebienintroducirpreviamentelosn´umeroscomplejosyelproductointernosobre ellos.Ahorabien,yamaneradesintaxis ´ unicamente,definiremoslanotaci´ondeDiracqueseempleaenlamec´anica cu ´ anticaparavectores:
Definici´on5.8. Llamamosketaunvetordelaforma:
Hastaaqu´ı,definirunqubitnecesit´odelaintroducci´onde unespaciovectorialperfecto,peroahora,queremosoperar con ´ el,yclaro,paraqueunacomputadorainterpreteunqubit, debeexistirunaoperaci´ondenominadamedici´on,yasuvez, unoperadorqueact´uesobreelqubitparacolapsarlo,esdecir, paraquelolleveaotrabasedelmismoespacioocambiede estado.Estamedici´ontieneuncomportamientopeculiarsiguiendolasleyesdelaf´ısicacu´antica.Esporesoqueacontinuaci´onpresentamostrespostuladosdelamec´anicacu´antica queservir´anparadefinirelcomportamientodeunqubit.
1. Estadodelespacio: Nosdicequeacadasistemaf´ısico aislado,seasociaunespaciodeHilbertqueeselespaciodeestadosdelsistema.Hayquetenerencuenta,que enelplanocomplejo,losvectoresnorepresentanposicionessinoestados,oseaquecadaejedelplanooespaciocomplejoexplicanunestadodelacosaovector. Elsistemaf´ısicoest´acompletamentedescritoporelestadodesusvectores,yladimensi´ondelespaciodepende delosgradosdelibertaddelapropiedadf´ısica,esdecir, eln´umerodeposiblesvaloresquepuedetomarelobjeto dentrodelsistema.
Estepostuladoimplicaqueunacombinaci´onlinealdeun vectorgeneraotrovectordelmismoespacio,yestoseconoce comoelprincipiodesuperposici´on.
2. Evoluci´oncu´antica: Nosdicequeelestadodeunsistemaeneltiempo t2 deacuerdoalestadoeneltiempo t1 est´adadopor |
Oseaqueelestadodeunsistemasealteraconlaaplicaci´onde unoperador U quesedefinir´acomounatransformaci´onlineal sobreelvectorenelespacio H .As´ı,aplicandounoperador deestosaunqubit,encontraremoselestadodeesteyser´a equivalenteacorrerunprogramaenunacomputadora.
3. Medidacu´antica Nosdicequetodoslosresultadosde unexperimentosongeneradosdeacuerdoaciertadistribuci´onprobabil´ıstica.Adem´as,antesdelamedici´on elestadocu´anticodeunsistemaesdiferentealestado cu ´ anticodelobjetodespu´esdelamedici´on.
Deltercerpostuladoseextraequelamedici´onesunprocesoprobabil´ıstico,losestadospreypostmedici´onnoson iguales,ymedirunsistemaequivaleaproyectarelvectorsobrelasbasesdelespaciodeHilbertsobreelqueemana.
As´ıpues,almedirunqubit,nosreferimosalaevaluaci´on probabil´ısticadelestadopreypost.Esporesoqueparala preparaci´ondeunqubit,sedebenelegiradecuadamentelos escalares α, β detalmaneraque |α|2+|β |2 = 1,yestasmedicioneslaspodemosconseguirmedianteoperadoresob´asicamente,transformacioneslinealesenelmismoespaciode Hilbert.Acontinuaci´on,veremosqueestastransformaciones est´andefinidasporciertascompuertasdenominadasoperadores.
Alastransformacioneslinealesselesconocecomooperadoresocomopuertascu´anticas,quesignificanunamultiplicaci´ondeunamatrizporlosvectoresdelabasedelqubity poderencontrarlosdiferentesestados.Estamatriz,generalmenteesunitaria,esdecir,unamatrizcuyainversaesigual asuconjugadatranspuesta.Sihacemosunaanalog´ıadeuna compuertacu´anticaconunacompuertal´ogicadelacomputaci´oncl´asica,laspuertasl´ogicasAND,ORyNOTseaplican aunbitdetalformaquesielestadodeestees0yseaplicaNOTentoncesseobtiene1;sinembargo,alaplicaruna compuertacu´anticasobreunqubitnoseobtieneunresultado discretoyenterosinoprobabilidadesdeobtenerunodelos dosestadosyporendemultituddeestadosintermedioscomo resultadodelasuperposici´ondeestos.As´ı,podemosempezar apensarenunconjuntodematricesquenosvanapermitir obtenerm´asresultadosdeuneventof´ısico,enparticular,nos interesamosenbuscarcompuertascu´anticasdefinidascomo operadoressobrequbits.Peroantesdeello,esimportanteenterarnosdelassiguientesdefiniciones.
Definici´on5.10. UnOperador ˆ Ade Cn esunamatrizcuadradadedimensi´onnconentradascomplejas [AD15]
Definici´on5.11. Eladjuntodeunoperador ˆ Asenota ˆ A† conocidocomoAdaggerysignificaeloperadortranspuestoconjugadode ˆ A[1007AD15].
Eloperador ˆ A† loquehaceestransformarunbra,mientras queeloperador ˆ A inducesobreunketas´ı:
Definici´on5.12. Sea ˆ Aunoperadorlinealtalque ˆ A : H → H , ˆ A,entonces |ψ⟩ → |ψ⟩′ .
Estadefinici´onesmuyimportanteporqueestamosdiciendoqueexisteunatransformaci´onlinealenelespacio n dimensional deHilbertquellevaunketaotroketdel mismoespaciomedianteunoperadorlineal.As´ı,unqubitse transformaycomoresultadodeestatransformaci´onlineal,se obtieneotroqubitdediferenteestado.
Enteor´ıadelacomputaci´oncu´antica,sehandefinidounas compuertasmuyespecialescomoeloperadordeHadamard, queesunacompuertal´ogicasobrelaquesecimientanmuchos circuitoscu´anticos.Lasiguientedefinici´on,ayudaaentender esteoperador.
Definici´on5.13. AlosoperadoresdelaformaP = |φ
| se lesllamaproyectores 4 [AD15]
Deacuerdocon7,8,esclaroqueunproyectordevuelve unamatrizadiferenciadelproductointernodeambosque devolv´ıaunn´umerodelcampocomplejo.Porello,unarepresentaci´onmatricial
Ahorabien,conbaseenloanteriorpodemosobtenerque (
como evidentementesepodr´ıaprobarhaciendoelproductodela mismamatriz.Lomismosuceder´aconeloperadordaggersi
toser´aimportanteparaminimizareln´umerodeoperaciones enunacompuertacu´anticaym´asa´un,paraelc´alculodeprobabilidades.
4Selamanproyectoresporqueproyectanortogonalmenteunket |ψ⟩ cualquierasobreelket
Definici´on5.14. SedefinecomoeloperadordeHadamarda
Hadamard.Seapues |ψ⟩ = ˆ H |0⟩,vemosqueestequbitest´a definidosobrelabasecomputacional B = {|0⟩ , |1⟩}.Adem´as, comoviveenelespaciodosdimensionaldeHilbert,tienedos eventosposibles,asaber {0, 1}
necesitamossaberc´omosecomportaeloperadorparacada estadoposible.As´ı,nosinteresa
Teniendoencuentaelresultadoobtenido,nosdamoscuenta queunqubittendr´ıaunestadointermediodadoporlacompuertacu´anticadeHadamard,puestoqueelresultadoinvolucratantoalketcerocomoalketuno,ybastar´ıanom´ascon multiplicarlamatrizobtenidaconcualquierotroketoqubit.
Recordemosquehemosencontradoc´omoeslaformade operarunqubit.As´ıpues,paradescribiromedircualquier sistemacu´anticoserequieredefinirelsistemaquedeseamosanalizar(enestecasounqubitenunespaciodosdimensionaldeHilbert),tenerencuentalosposiblesresultadosquepuedetomarelsistema(estostambi´envienendadosporladimensi´ondelespacio),tenerunabaseortonormal
H n},unconjuntodeoperadoresdemedici´on
ˆ A dadosporlaproyecci´ondecadapardevectoresdelabase, yunadistribuci´onprobabil´ısticaenfunci´ondelosexperimentossobreelsistema.Paraeste ´ ultimorequisito,sabemosque elestadopreypostmedici´onsondistintos.Porlotanto,se tienelasiguientedefinici´on:
Definici´on5.15. Deacuerdocon [VM13],sedicequeunsistemarepresentadoporunket |ψ⟩ evolucionaalsistema |φ⟩, cuandoserealizaunadelassiguientesoperaciones:
1 Sepremultiplicaporunacompuertacu´antica ˆ A: |φ⟩ =
2 Seaplicaunoperadordemedici´on ˆ M: |φ⟩ =
Esdecir,laprobabilidaddeobtenerelketceroesdel50%. Lomismosuceder´asirepetimoselprocedimientoparaelestadouno.Estolopodemoscorroborarsiusamosunasimulaci´on delacomputadoracu´anticadeIBM.Acontinuaci´on,veremos unaaplicaci´onsimuladasobreunqubitusandolacompuerta deHadamard:
Figura2: Aplicaci´ondelacompuertadeHadamardenelsimuladorcu´anticodeIBM.
Vemosquetantoparaelket0comoelket1,laprobabilidaddeestarensuperposici´onenunaoperaci´onesdel50%. Veamosahoraqu´esucedesicambiamosdebaseyvolvemos aaplicarlacompuertadeHadamardsobre |ψ⟩ :
Sea B2 = {|+⟩ , | ⟩} labasedelespacio H 2,conocidacomolabasediagonaldonde:
tendr´ıamoslasiguienteoperaci´on:
† ˆ M |ψ⟩ esunestadoquenoseconoce,mas s ´ ısuprobabilidad.As´ıpues,buscamoslaprobabilidaddeobtenerunestadodelqubitusandolacompuertacu´anticadeHadamard.
Comovimospreviamente, 1 √2 |0⟩ + 1 √2 |1⟩ eselestadode unqubitluegodemultiplicarloporlamatrizuoperadorde

Esdecir,elqubitnoreflejaposibilidadalgunadetomar elestado + cuandoseleaplicalacompuertadeHadamard
.Siloreplicamosenelsimulador,vemosqueconfirma
unaprobabilidaddel100%delqubitenfunci´ondelabase escogida.
Acontinuaci´on,vemosalgunasotrascompuertasquese puedenemplearparalaconstrucci´ondecircuitosoalgoritmos cu ´ anticos:
X,Y, oZ.Elefectoquecausansobrelosestadosb´asicosdel qubitdescritosanteriormentesepuedenobservaracontinuaci´on:
As´ı,hemosobservadolaescenciadelascompuertas cu ´ anticassobreunqubit.Pero,¿c´omoseest´anviendoestas probabilidadesgr´aficamente?Bueno,elturnoesdelaesfera deradio1,esamismaquerotauncuaterni´onenelespaciotridimensional.Resultaquesinosfijamosbien,elsimuladorejecutaunacompuertasobreunvectorquerotaenunaesferade radiouno.Estevectornoesm´asqueunqubit,cuyasrotacionesrepresentanunestadomasnounaposici´on,enmec´anica cu ´ antica,seusalaesferadeBloch,comounarepresentaci´on geom ´ etricadelosestadosdelsistema.Lainterpretaci´onque sesigueesquecuandoelvectoroqubitseencuentraenelnortedelaesfera,elqubittienevalor |0⟩,ycuandoseencuentra enelpolosurdelaesfera,suvalores |1⟩ [MP19].
Losextremosdeleje Z representanlosestadosdelabase (enestecasolabasecomputacional).Deestaforma,setrabaja rotandoelvectoratrav´esdelespaciotridimensional.Antes deproponer,resaltamosquesepuederepresentarcualquier estadoopuntoenlaesferadeBlochcomounacombinaci´on linealde |0⟩ , |1⟩ as ´ ı: |ψ⟩ = cos θ 2 |0⟩ + sin θ 2 eiφ |1⟩. Ahorabien,deacuerdocon[MP19]lastransformaciones enlaesferadeBlochsepuedendividirentresgrupos:Puertas dePauli,PuertadeHadamardyPuertasdefase.
Definici´on5.16. LaspuertasdePaulisonaquellasqueaplicanaunqubitungiroo ´ anglode π conrespectoalosejes X,Y, Z.Dependiendodelejerecibenelnombredepuertas
Definici´on5.17. Laspuertasdefasesongirossobreeleje Z.Estaspuertasnomodificanelvalorfinaldelqubit,peros´ ı afectanafuturasoperacionessobreelmismo.DentrodeestegruposeencuentranlaspuertasSySt,quecorresponden aungirode ´ angulo π 2 yde π 2 respectivamente.Tambi´ense encuentranlaspuertasTyTt,querealizanungirode ´ angulode π 4 y π 4 respectivamente.acontinuaci´onseobservasu efectosobreelqubit:

Figura7: Efectodelatransformaci´onconPuertasdefase.
Hemosllegadoaverqueelestadodeunqubitsecomporta deacuerdoconlatransformaci´onocompuertaqueseutilice sobre ´ el.Nuestraintuici´onnosllevaapensarquepodemos llevarestevectoralespaciodeloscuaternionesymirarqu´e pasaall´ısiserotarespectoaleje Z einterpretarcadapunto comounestadodelsistema.
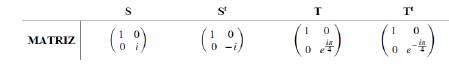
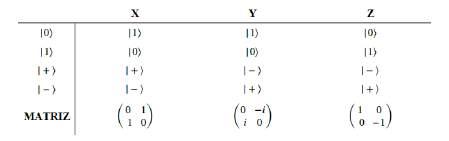

Paramigrarelqubit,debemosllevarelvectordosdimensionalalabasecuaterni´onica,poresointroducimoslasiguientedefinici´on:
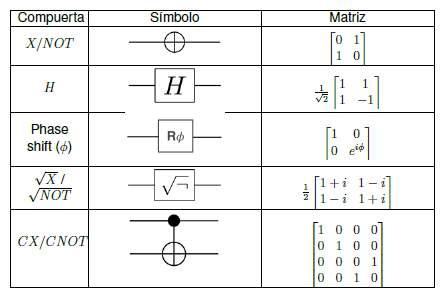
Definici´on6.1. ElproductotensorialdedosmatricesPyQ sedefinecomolamatriz [AD15]:
1 import matplotlib.pyplotasplt
2 import pandasaspd
3 from mpl_toolkits.mplot3d import axes3d
4 import matplotlib.cmascm
5 import numpyasnp
Acontinuaci´ondefinimoselvector V quequeremosrotar enunarrayquecontendr´asuscoordenadas.
1 # Coordenadas del vector unitario
Adicionalmentetengamosencuentalassiguientesdefiniciones:
Definici´on6.2. [AD15] SeanB1 = {v1, v2,..., vn} unabase delespaciovectorialVyB2 = {w1, w2,..., wm} unabasedel espaciovectorialW.Elproductotensorialentredichasbases sedefinecomo:
Esdecir,elproductotensorialentreespaciosvectorialesse definecomoelespaciogeneradoporelproductotensorialde todoslosvectoresdeunabasedelprimeroconlosvectoresde unabasedelsegundo.
Definici´on6.3. SeanB1 unabasedelespaciovectorialV, yB2 unabasedelespaciovectorialW,entonces:V ⊗ W = span(B1, B2) [AD15]
Conformeloanterior,podemosrealizarelsiguienteejercicioyprobarqu´esuceder´ıasilosvectoresdelabasecomputacionalquegeneranunqubiten C2 lesaplicamoselproducto
2 V=np.array([(0,0,0),(1/sqrt(2),1/sqrt(2),0)])
3 4 Ax=[] # Lista de primeras componentes
5 By=[] # Lista de segundas componentes
6 Cz=[] # Lista de terceras componentes
laslistasvac´ıas Ax, By,Cz seusar ´ anacontinuaci´onparaalmacenarlasnuevascoordenadasrotadas,esdecir,lascoordenadasqueresultanalmultiplicarelvectorporlamatrizde rotaci´on.Acontinuaci´on,definimoslafunci´onquellamamos imp quecontienelamatrizderotaci´ondelosvectoresiniciales:
1 # Funcion que rota las coordenadas del vector V en
2 # funcion del ngulo theta
3 def imp(theta):
4 # Matriz de Rotacin
5 R=np.array([[np.cos(theta),np.sin(theta), 0.],
6 [-np.sin(theta),np.cos(theta),0.],
7 [0.,0.,1.]])
8 for row in V:
9 output=(R.dot(row)) # Multiplicacion de la
10 # matriz por el punto respectivo
11 x,y,z=output[0],output[1],output[2]
12 # Coordenadas transformadas
13 Ax.append(x) # Se guardan las coordenadas
14 By.append(y)
15 Cz.append(z)
16 return Ax,By,Cz
Claramenteelespaciogeneradodadoporelproductotensorialde C2 es C4.Dejemosque C4 = {l, i, j, k} sealabase, yque l = 0.Porlotanto,elqubitdelespaciodeHilbert,de algunamanerapuedeserinterpretadoenelespaciodeloscuaternionescuando l = 0.
Deacuerdoconlovistopreviamentecuandopresentamos loscuaterniones,vimosqueeraposiblerotarvectoreseneste espaciosobreunaesferaderadiouno,yconformevimosen 4.1supimosc´omohacerlosobreeleje z.As´ıpues,podr´ıamos simularunadelascompuertascu´anticasenesteespacio.Por ejemplo,vamosasimularunacompuertadePauli.Deacuerdo con5.16,elqubitrota ´ angulosde π eneleje X, Y o Z.Veamos elsiguientec´odigoenpythonquereplicaunarotaci´onrespectoaleje Z deunvector,esdecir,unarotaci´ondelmismoen eleje Y .Comovamosaverdiferentesrotaciones,dejaremos acontinuaci´onexplicadoelc´odigoqueusamosparaello:
Importamoslibrerias:
5
Lamatriz R trabajaenfunci´ondel ´ anguloquesereciba comopar ´ ametroyelbucletienelafinalidaddemultiplicar cadavector.Enelsiguientecicloleindicamosalafunci´on imp quequeremosquelatransformaci´onsehagadepoloa polosobreeleje x y
1 fig=plt.figure()
2 for i in range (1,10):
3 ax=plt.gca() # gca = obtiene los ejes actuales
4 A,B,C=imp((np.pi)*i) # rotamos un ngulo Pi
6 ax=fig.add_subplot(111,projection= ’ 3 d ’ )
7 ax.scatter3D(Ax,By,Cz,c=Cz,cmap= ’ Set1 ’ )
8 plt.show()
Tenerencuentaqueas´ısereiteren n rotaciones,siempre veremoscomosemuestraacontinuaci´on:
Caberesaltarquelosvectoresest´annormalizados.En elcasoparticular,tenemosunvectorconcoordenadas 1 √
Mirandoelsimulador:
Elmismovectorusandopuertasdiferentessepuederotar sucesivamente:
Laraz´ondeestasrotacionessejustificaenlab´usquedade laprobabilidaddeobtenerunodelosestadosdelqubit.Es claroqueas´ıdesimplenoseconsigueesto,porelcontrario, surgecomounproblema;sinembargo,eslaformacomose interpretar´ıaunqubityclaro,ahoranosinteresasaberporqu´e lasprobabilidadessontanimportantespararesolverproblemasyporqu ´ eestosuponequeunam´aquinahar´ıamillones deoperacionesm´asqueunam´aquinadeturingconvencional. Hastaaqu´ı,nosemocionahablardecuaternionesyqubits,peroveamosqueunadelasm´asgrandesaplicacionesdelasrotacionesdeunvectorenestaesferaradicaenlacriptograf´ıa.

Deantemano,debemosempezarapensarqueunbitesun estadoquelodefineelpasoonodeelectricidadporuncabledeuntransistordeuncomputador.Cuandoseejecutaun algoritmo,elpasodeelectricidadact´uamedianteuncircuito electr´onicool´ogicobajociertascompuertasyquepermiten lainteracci´onconelordenador.Oseaquesisequiereevaluar unafunci´oncon10valores,setendr´ıaquehaceruncircuito dondepaselafunci´onygenereunresultadoparacadavalor deformaindependienteyserial.Ahora,siloquisi´eramoshacerenparalelo,necesitar´ıamosporcadavalorunafunci´on,un circuito,odiferentesordenadoresyesosignificar´ıaineficienciaentiempoyrecursos.Conestoenmente,laimportancia delasuperposici´ondeestadosdelacomputaci´oncu´anticaes quesecontemplalatotalidaddeestadosposiblesentreceroy uno,yenestamismafunci´onseevaluar´ıanlos10valoresde formasimult´anea.Lointeresanteesquecuandoseeval´uauna funci´on,estaessometidaaunsistemadeprobabilidadesque dependedelcolapsodelafunci´ondeondayporlotantohay unosestadosquesevuelvenm´asprobablesqueotros.
Aniveldealgoritmos,hayproblemasquecuestandemasiadoresolverloscomoelhechodefactorizarunn´umero.Enrespuestaaesto,yaldesarrollodeteor´ıacu´antica
computacionaldelas ´ ultimasdosd´ecadas,PeterShor,unmatem´aticoestadounidenseyactualmenteprofesordelMIT, 5 disen´ounalgoritmopensandoenlaeficienciacomputacional deunam´aquinadeTuringcomparadaconladeunam´aquina cu ´ antica.Estealgoritmocimientasupotenciaendeterminarel per ´ ıododeunafunci´onmedianteelusodeteor´ıaden´umeros. Aunquesuestudiopresentaungradodecomplejidadrelativamentealto,esmuyinteresanteanalizarelnuevoenfoque quelamec´anicacu´anticaofreceparasolucionarelproblema defactorizaci´on.[Cai10]Antesdeexplicarbrevementeeste algoritmo,debemostenerencuentaqueenlateor´ıacu´antica computacional,setienenporahoratresclasesdealgoritmos:
Algoritmosbasadosenlatransformadacu´anticadeFourier.

Algoritmosdeb´usqueda.(Ejemplo:AlgoritmodeGrover)
Algoritmosdesimulaci´ondeexperimentosf´ısicos
Delaclasificaci´onanterior,elalgoritmodeShorsebasa enlatransformadacu´anticadeFourier,yestoesb´asicamente porquealtenersetantasoperaciones,aplicarlatransformada ayudaaeliminarruido,esdecir,reprocesos.Enesteejemplo simpledeaplicaci´on,nonoscentraremosenindagarelfuncionamientoexactodelatransformadaenuncircuitocu´antico sinosimplementeexplicarporqu´elasrotacionesylasprobabilidadessonunaventajaenlacomputaci´oncu´anticarespecto alacl´asica.
Ent´erminossimples,elalgoritmodeShorbuscafactorizar unn ´ umeronatural.Esdecir,dado n ∈ N,queremosencontrar p, q primos ∈ N talque p q = n.Esteinter´essurgeporque muchossistemasdeencriptaci´ontrabajanconn´umerosmuy grandesproductodedosom´asprimosqueseconviertenen lasclavesdeencriptaci´onydesencriptaci´on.As´ı,silogramos factorizarestosenteros,tendr´ıamoslaposibilidadderomper estossistemasytendr´ıamosunagranoportunidaddehacernosconelcontroldelsistemaecon´omicomundial,losbancos, sistemasdeseguridadohastadelmercadodelascriptomonedas;sinembargo,estonoestanf´acilpuestoqueyahayteor´ıa cu ´ anticadesarrolladaparaevitarestassituaciones.
5MassachusettsInstituteofTechnology.

Acontinuaci´on,introducimosalgunosteoremasnecesarios paralacomprensi´ondelalgoritmo:
Teorema7.1. Seann, n + 1 dosenterospositivos,entonces mcd(n, n + 1)= 1.
Estoesgraciasalaspropiedadesdeladivisibilidad,yaque si a, b, c ∈ Z y c|a ∧ c|b → c|ax + by, x, y ∈ Z.Enparticular,si x = 1, y = 1entonces c|(n + 1) n yestoesposiblesi c = 1.
Teorema7.2. Sean > 1 ∈ N,entonces ∀n,nposeeuna ´ unica factorizaci´on(salvoelorden)enn´umerosprimos,esdecir
∃m ∈ N talquen = p1 p2 pm = ∏m i=1 pi conpi primoy 1 ≤ i ≤ myp1 ≤ p2 ≤ ≤ pm
Teorema7.3. Dadon ∈ N,x ≡n ysiys´olosin|x y.
Teorema7.4. Dadosn, m, r ∈ Z,m > 0 entoncesm
≡n ri.M´asa´un,mi+1 ≡n m · ri
Esdecir,quetodon´umeroescongruenteconsuresiduo m ´ odulo n.Deaqu´ısededucequesiexiste r j = 0,entonces
ri = 0 ∀i > j.Oseaquecuandounrestoseacero,apartir deall´ı,todoslosrestospotencialesenadelanteser´ancero. Deigualmanera,apartirdelprimerrestoqueserepita,toda lasecuenciaderesiduospreviossereproduceenigualorden infinitamente.
Conloanterioressuficienteparaentenderelalgoritmo. Ahorabien,¿qu´epretendeShor?,bueno,enprimerlugar,introduceelconceptodelara´ızcuadradanotrivialm´odulo n Esdecir,si x ∈ N,entonces x esunara ´ ızcuadradanotrivial m ´ odulo n si x2 ≡n 1y x ∈ [2, n 2).Paraentenderelporqu´e deesteintervalo,podemoshacerusode7.3delasiguiente forma:
Si x2 ≡n 1,entonces x2 1 ≡n 0,deaqu´ısetieneque
(x + 1)(x 1)= kn yaque n|x2 1.As´ı,por7.1ni (x + 1) ni (x 1) puedenser n 1ni n.Porlotanto,2 ≤ x < n 2. Elalgoritmosuponequeencontrarlara´ızcuadradanotrivialm´odulo n equivaleaencontrarlosn´umerosprimos p, q talesquefactorizan n.Supongamosahoraquelosfactores (n + 1), (n 1) poseenlossiguientesfactores:
P = {pi ∈ N : pi|(x + 1)}
P = {qi ∈ N : qi|(x 1)}
Sededuceque p, q pertenecena P, Q respectivamentey noexistelaposibilidaddeque p, q est´enenelmismofactoryasea (x + 1) o (x 1).Deestaforma, mcd((x + 1), n)= p, mcd((x 1), n)= q.Porlotanto,siencontramos x ycalculandoelm´aximocom´undivisorcomoacabamosdesenalar, habremosencontrado p, q yeln´umeroquedar´ıafactorizado. Perobien,¿c´omoencontrar x?Bueno,paraellorecordamos queintroducimoselteorema7.4.Us´emosloenelsiguiente ejemploparaentenderlo:
Supongamosquequeremosencontrarelorden r m ´ odulo n. Siendo m = 11, n = 7.Buscamosquelafunci´on f (i)= 11 mod(7)seaperi ´ odica
Comoelunovuelveyserepite,searmaunbucleinfinito yhemosencontradoelper´ıodouordendelafunci´on f ,en estecasoes3.Muybien,ahorapodr´ıamospensarencoger unn ´ umeroalazarentre2y n 2,construimoslafunci´ony calculamoselper´ıodoesperandoqueelper´ıodoseaenalg´un momento2talycomolodefineShorparaelc´alculodela ra ´ ızcuadradanotrivialm´odulo nx2 ≡n 1.Paraestecaso,hemosvistoquenuestroper´ıodouordenfue3,porlotantono tuvimossuertedeencontrar2yestecasononosservir´ıaparadescomponerunn´umero.Pero¿qu´epasasibuscamosel per ´ ıodode f (i)= 3imod(7)?
Bueno,replicandoelanteriorejercicionosdar´ıamoscuentaqueelper´ıodoes6yno2;sinembargo,siestoloexpresamoscomo (34)2 ≡7 1claramentehabremosencontradola ra ´ ızbuscadaquees34 yelproblemasereducir´ıaasimplementeencontrar x talesquesuper´ıodoseaunn´umeropar.Por loanterior,Shordefineelsiguienteteorema:
Teorema7.5. Dadounn´umeroaleatoriox ∈ [2, n 2),la probabilidaddequextengaper´ıodoparesmayora 0, 5
Veamosahoras´ı,c´omodescomponer15enfactoresde n ´ umerosprimos.Puestoque n = 15,entoncesporelteorema deShor,escogemosunn´umeroalazar x ∈ (2, 13).Escogemos 4ybuscamoselper´ıodo:
i = 0, 40 ≡1 51.
i = 1, 41 ≡1 54.
i = 2, 42 ≡1 51.
As´ı,lara´ızcuadradanotrivialm´odulo n ser ´ ıa4.Ahora, calculamos mcd((4 + 1), 15) y mcd((4 1), 15),dandocomo resultados5y3respectivamente.
Enestepunto,claramentetodoestealgoritmosepuedehacerenunordenadorcl´asico;sinembargo,cuandoeln´umero esmuygrande,probarcada x alazarentre2y n 2esuna tareatit´anicaymuydif´ıcilderesolverentiempopolinomial, osea,deber´ıatomarcadaelementodelintervalo,calcularsus potencias,verificarsusresiduos,yesosehar´ıaenformaserialparafinalmentecompararlos.Elalgoritmosedisen´opara computarloenunordenadorcu´antico,porqueestosignifica quesiponemosunvalor x quetengaper´ıodoparyotroque seaimpar,entonceselsistemavaacolapsarhaciael x que tengaprobabilidadm´asaltadeserper´ıodopar.Adem´as,esteprocesodetomaruna x,evaluarlaenunacantidadfinitade n ´ umeros,evaluarsuspotenciasyresiduos,serealizamediante latransformadacu´anticadeFourierusandolosprincipiosde superposici´onyparalelismo.Finalmente,encuantoatiempo polinomialserefiere,encomputaci´oncl´asica,solohacerel pasodelatransformadadeFouriertoma n2n pasospara2n datos,mientrasqueencomputaci´oncu´anticatansolotoma n2 pasos.Oseaquepasamosdeuncostoexponencialapolinomial,haciendoqueproblemasqueantessesolucionabanen siglos,enunfuturosepuedanresolverenminutos.
Elconjuntodeloscuaternioneseselconjuntodelosdenominadoshipercomplejosquerepresentaunespaciovecto-
rialabstractobajolaoperaci´onsumausualdecomplejosy multiplicaci´onescalardefinidasenlaidentidaddescubierta porHamilton.Abstraerelmovimientodevectoresunitarios alrededordeunejeenelespaciotridimensionalnosllev´oa presentarlosespaciospreHilbertianosyposteriormentelos espaciosdeHilbert,queporsuscaracter´ısticasmatem´aticas, sonmuyricossobretodoparatrabajarconvectoresquerepresentanestadosdeunsistemaf´ısico.Encontramosquelas operacionesrealizadassobreunqubitqueeslam´ınimaunidad deinformaci´ondeuncomputadorcu´antico,representatodala l´ogicaquehoypodemosasociarconlal´ogicadelascompuertasdigitalesdelacomputaci´ontradicional.Estasoperaciones asuvezserepresentangr´aficamentemedianteunaesferade radio1cuyovectordedimensi´ondosrotasobreunplanoasoci´andoleacadaposiblepuntodelmismounaprobabilidadde ocurrencia.Finalmente,vimosquerotarestevectortieneaplicacionessignificativasenlacriptograf´ıa,porqueesas´ıcomo sedeterminaelper´ıododelafunci´onolara´ızcuadradano trivialm´odulo n medianteelusodelalgoritmodeShor.
AlprofesorJohnAlexanderArredondo,porladin´amica implementadaenlaclasede ´ algebralinealincentivandolainvestigaci´on.Adem´as,porsudisposici´onysusvaliososcomentariosencadarevisi´onparahacerposibleestapublicaci´on.
[Rod12] VRodriguez, Sobreloscuaterniones, ´ algebrasdeLie,ymatricesdePauli.Teor´ıab´asicayaplicacionesf´ısicas.,Universidadde Oviedo,2012.
[Bae11] JBaez, Octonionesyteor´ıadecuerdas,Investigaci´onyCiencia, 2011.
[Mar16] AMarkelov, UsodeCuaternionesparaRepresentarRotaciones, Anonimo,2016.
[An´o19] An´onimo, MaxPlanck,elpadredelateorıacuanticaqueintento convenceraHitlerdequepermitieratrabajaraloscientıficos judıos,BBCnews,2019.
[An´o20] , Ellargocaminoparaentenderlaf´ısicacu´antica,OpenMindBBVA,2020.
[Pas19] JPastor, Elcuaterni´onest´am´asvivoquenunca:as´ıescomola NASAylosvideojuegoslousanm´asdeunsiglodespu´esdesu descubrimiento,Xataca,2019.
[Her10] CHernando, Algoritmodefactorizaci´onparauncomputador cu ´ antico,Edvcatiophysicorvmqvononascendam,2010.
[Fav08] AFavieri, Introducci´onalosCuaterniones,EditorialdelaUniversidadTecnol´ogicaNacional–U.T.N.-ArgentinaedUTecNe, Haedo,Argentina,2008.
[Haw10] SandMlodinowHawkingL, ElgranDiseno,BantamBooks,NuevaYork,EEUU,2010.
[Cai10] HCaicedo, Algoritmodefactorizaci´onparauncomputador cu ´ antico,UnidadProfesional“AdolfoL´opezMateos”,Zacatenco, Delegaci´onGustavoA.Madero,2010.
[Ano10] Anonimo, RotacionesyCuaternios,UnidadProfesional“Adolfo LopezMateos”,Zacatenco,DelegacionGustavoA.Madero,2010.
[Lop16a] ELopategui, Historiadelascomputadoras,2016.
[Lop16b] , Manejodelainformaci´onyusodelacomputadora., 2016.
[CC20] CarlosCoy, Implementaci´ondeCircuitosCu´anticosyPropuesta ExperimentalParaCompuertasCuanticas,UniversidaddelValle, 2020.
[AD15] AlejandroDiaz, Introduccionalacomputacioncuantica,UniversidaddeRosario,2015.
[VM13] VicenteMoret, PrincipiosFundamentalesdelaComputacion Cuantica.,UniversidaddelaCoruna,2013.
[MP19] MariaPrieto, AlgoritmosCuanticosparalaResoluciondelProblemadeSatisfacibilidadBooleana.,UniversidadAut´onomade Madrid,2019.
Acercadelautor:DanielEstebanGalvisSandovalesestudiantedemaestriaeninteligenciaartificialybigdatadela universidaddeValencia.Legustalamusicaska,blues,reggae.Esunapasionadoporlaprogramaci´on,laschaquetasde cuero,lasteor´ıasdevidaextraterrestre,quiereaprenderatocarelpianoyaprepararcocteles.
Laevoluci´ondelosmercadosfinancieros,generadaentre otrascosasporlaaparici´ondeinstrumentos derivados1,evidenci´olanecesidaddeformalizarlas finanzas empleandoconceptosyteor´ıasmatem´aticasimportantes,comoelc´alculoy laprobabilidad.Dichasinergiatuvodosconsecuenciasdirectas:laprimera,facilit´oencontrarexpresionesquepermitieran valorar dichosinstrumentosy estimar elriesgoquesuponemantenerinversionesenellos;lasegunda,dot´oalasinstitucionesreguladorasdeherramientasparaestablecerm´ınimosdecapital,conelprop´ositodequelasempresasemisorasdedichosinstrumentospudieranresponderanteeventuales p ´ erdidas.
Enesesentido,sehanconstruidomedidasderiesgofinanciero,entrelasquesedestacanel ValorenRiesgo o VaR y el ValorenRiesgoCondicional o CVaR,lascualespermiten cuantificar,estableciendounniveldeconfianzayunhorizontetemporal,laexposici´onalriesgodemercado.Sinembargo, comoencualquierteor´ıaecon´omicayfinanciera,esnecesarioestablecersupuestosquefacilitenrepresentarunsituaci´on realenlenguajematem´atico.Enesesentido,enelpresente art´ıculoseexponenlasmedidasantesmencionadasylascondicionesquesedebencumplirparaquesean coherentes;asimismo,sepresentandosexpresionesan´aliticas,unaparael VaR yotraparael CVaR,quefacilitanaterrizarlosc´alculosa losrendimientosdiariosdelaacci´ondeEcopetrolentreel01 deenerode2018yel18demarzode2022.
Acontinuaci´onsepresentaunadefinici´onderiesgoylos tiposderiesgoquecomponenelconjuntode riesgosfinancieros,conelfindeintroducirallectorenlosconceptosfundamentales.Asimismo,seexponeformalmenteelconcepto de medidaderiesgo ylosatributosquedebetenerparaser coherente.
*EstudiantedeMatem´aticas,UniversidadSergioArboleda.
1Sonaquellosinstrumentosfinancieroscuyovalordependedeotroactivo quesedenomina subyacente.Algunosejemplosdesubyacentesson:acciones,bonos,commodities,entreotros.
Elriesgo,seg´unlaRealAcademiaEspanola,sedefinecomola“contingenciaoproximidaddeundano”[RAE19].Por otraparte,en[Kni21]sediferenciaelriesgodelaincertidumbre,debidoaquealriesgoselepuedeasociarunaprobabilidadperoalaincertidumbreno.Conbaseenloanterior,el riesgopuededefinirsecomolaprobabilidaddequeocurraun eventodanino;enel ´ ambitofinanciero,dichodanoseentiende comola p ´ erdida devalordeunactivo2
Enesesentido,en[AB10]seexponequeexistendiferentes fuentesderiesgo,locualsederivadelhechodequediferentes variables,tantointernas(porejemplo:laestrategiadeventas) comoexternas(porejemplo:lainflaci´on),puedenafectarnegativamenteelvalordeunaentidadodeunainversi´on.Dentro delconjuntoderiesgos,existentresquecomponenelriesgo financiero 3:
Riesgodemercado: hacereferenciaalap´erdidadevalordeunactivocomoconsecuenciadelasfluctuaciones quepuedenexperimentarlospreciosdemercado.
Riesgodeliquidez: hacereferenciaalriesgoquesupone realizartransaccionesenunmercadoconliquidezbaja (bajovolumendetransacciones).
Riesgodecr´edito: hacereferenciaalriesgoquesederivadelimpagototaloparcialporpartedeundeudor.
Teniendoencuentaloanterior,elpresenteart´ıculosecentraen medir laexposici´onal riesgodemercado,esdecir,la p ´ erdidam´aximadevalorquepuedeexperimentarunactivoen unhorizontedetiempo,debidoafluctuacionesensusprecios demercado.
Lossistemasdeadministraci´onderiesgodemercado4,en general,secomponendecuatroetapas:identificaci´on,medici´on,controlymonitoreo.Dichasetapassiguenunproceso
2Algunosejemplosdeactivosson:acciones,bonos,derivados,CDT, cuentasporcobrar,entreotros.
3Paramayordetalleconsultar[AB10].
4Paraelcasocolombiano,consultarelcap´ıtuloXXIdelaCircularExterna 100de1995delaSuperintendenciaFinancieradeColombia.

secuencial,esdecir,nosepuedemediralgoquepreviamente nohasidoidentificado,as´ıcomotampocosepuedecontrolar algoquenohasidomedido,porlocualcadaetapaconstituye unpilarfundamentaldentrodelproceso.
Paracomprenderlaimportanciademediradecuadamenteelriesgo,supongaqueunacompan´ıamidesuexposici´onal riesgodemercadoen$100yqueocurrealgunodelossiguientesescenarios:primero,elriesgosematerializaylacompa˜n´ıa pierde$150;segundo,elriesgosematerializaylacompa˜n´ıa pierde$35.Enelprimerescenariolacompa˜n´ıanocontaba conlosrecursosparaatenderlap´erdida,porlocualafect´o surentabilidadm´asall´adelopronosticadoycomprometi´osu estabilidadfinancieraenelcortoplazo;enelsegundoescenario,lacompan´ıainmoviliz´ounacantidadconsiderablede recursosqueexcedieronlap´erdidareal,locualgener´opara lacompan´ıauncostodeoportunidad,yaquelos$65queinmoviliz´odem´asloshubiesepodidoinvertirparaobteneruna rentabilidadadicional.
Delejemploanteriorseconcluyequelamedici´ondelriesgoquehizolacompan´ıafueerr´onea,yaqueenelprimerescenariolasubestim´oyenelsegundoescenariolasobreestim´o considerablemente.Enesesentido,esimportantemediradecuadamenteelriesgoyparaellosedebenemplearmedidas coherentes deriesgo.
Formalmente,unamedidaderiesgoes elresultadodeun mapeosobreunavariablealeatoriaX,definidasobreunespaciodeprobabilidadfijo (Ω, F , Pθ ),donde θ esunvector depar´ametrosasociadosconladistribuci´ondeX,quetiene comoresultado ρ = A → R,donde A = {X|X : Ω → R} representaelconjuntoderetornosposiblesdeunportafolioo unactivo [Gar15].Noobstante,dichamedidadebecumplir cuatroaxiomasparaser coherente[ADEH99]:
Homogeneidadpositiva: ρ (λ u)= λρ (u)
Esteaxiomagarantizaquesiseincrementaen λ laposici´onenunactivo,entonceselriesgoaumentaproporcionalmenteen λ
Monotonicidad: u ≤ v implica ρ (u) ≤ ρ (v) Esteaxiomagarantizaquesecumplaelprincipio riesgo/rentabilidad,esdecir,unamayorrentabilidadimplicaun mayorriesgo.
Invarianteentraslaci´on: ρ (u + a)= ρ (u)+ a Esteaxiomagarantizaquealadicionaralaposici´onuna cantidadinicialsegura a elriesgosedisminuyeendicho montoadicional.
Subaditividad: ρ (u + v) ≤ ρ (u)+ ρ (v)
Esteaxiomaestablecequeelriesgodelportafolionoaumenteporlacomposici´ondelportafolio.Enotraspalabras,seesperaqueconlainclusi´ondeactivosenel portafolioelrisgodisminuyao,alosumo,permanezca constante.
Graciasaloscuatroaxiomasenunciados,segarantizaquelas medicionesdelriesgoseancoherentes,locualpermitecontrolarlosdeunamaneraadecuadayresponsable.Esimportante
resaltarqueelser coherente noessin´onimode exacta,porlo cual,enlamayor´ıadeloscasos,existir´andesviacionesentre lasp´erdidasquesematerializanylamedidaderiesgoobtenida,esdecir,lamedidaderiesgoesuna estimaci´on,yporlo tanto,elobjetivodequeunamedidaderiesgoseacoherente esaproximardichaestimaci´on,enlamedidadeloposible,a larealidad.Conbaseenloanterior,acontinuaci´onsepresentandosmedidasderiesgodemercado:el ValueatRisk - VaR ,lacuals´oloes coherente bajociertasdistribucionesdeprobabilidad;yel ConditionalValueatRisk - CVaR,lacualse calculaapartirdel VaR yesunamedida coherente deriesgo.
Elvalorenriesgoo VaR (porlasinicialesdelt´ermino Value atRisk)esunamedidaderiesgoampliamenteutilizadaporlos participantesdelmercadofinanciero,bienseaninversionistas, emisores,entidadesreguladoras,entreotros.Lapopularidad deestamedidasedebeaqueintentaresumirelriesgototal deunactivo,ounacarteradeactivos,enunasolacifra,lo cualresulta ´ utilparalatomadedecisionesyaque,enesencia, dacuentadelap´erdidam´aximaquepodr´ıaexperimentarun activo,ounacarteradeactivos,enunhorizontedetiempoy unniveldeconfianzaestablecidos.
Formalmente, elvalorenriesgodeXalniveldeconfianza 1 qdenotadopor VaRX 1 q,sedefinecomoelpeorvalordel activo(oportafolio),enunper´ıododetiempodado[t,T],para unintervalodeconfianzadel (1 q)100% (ver [Ven06]).Es decir:
Pθ ( VaRX 1 q ≤ X)= 1 q y Pθ (X ≤−VaRX 1 q)= q.
Dadoloanterior,esposibledefinirel VaR medianteel supremo5 oel ´ ınfimo6 delossiguientesconjuntos:
Demaneraequivalente:
Dadoqueelconjuntodereferenciaes R,el ´ ınfimo yel supremo existendebidoaquelosconjuntosen(1)y(2)no sonvac ´ ıosyest´anacotados7
5Lamenordelascotassuperiores.
6Lamayordelascotasinferiores.
7Alrespectoconsultar[Rud76]-axiomadelsupremo.
Amaneraderesumen,laFigura3.1permitevergr´aficamentetantolaexpresi´on(1)comola(2)as´ı:laregi´onno sombreadacorrespondealconjuntodetodoslos x talque laprobabilidaddequelavariablealeatoria X tomeunvalormenoroigualque x,esmenoroigualque q,esdecir, {x ∈ R|Pθ (X ≤ x) ≤ q}.Ahoranotequecualquiervalorala derechadel VaRX 1 q (incluy´endolo),esunacotasuperiorde dichoconjunto,porlocual,altomarlam´aspeque˜nadeellas obtenemoslaexpresi´on(1).
Porotraparte,laregi´onsombreadacorrespondealconjuntodetodoslos x talquelaprobabilidaddequelavariable aleatoria X tomeunvalormayoroigualque x,esmenoro igualque1 q,esdecir, {x ∈ R|Pθ (X > x) ≤ 1 q}.Ahoranotequecualquiervaloralaizquierdadel VaRX 1 q (incluy´endolo),esunacotainferiordedichoconjunto,porlo cual,altomarlam´asgrandedeellasobtenemoslaexpresi´on (2).
Unavezdefinidoel VaR,esimportantetener expresiones quefacilitensuc´alculo.Enesesentido,existentresenfoques paraello:param´etrico,hist´oricoyMonteCarlo.Paraelpresenteart´ıculoseemplear´aunenfoqueparam´etricoysesupondr´aquelosrendimientosfinancierossiguenunadistribuci´onnormaldeprobabilidad.
Comoseinfieredeloexpuestoanteriormente,elvaloren riesgoesaquelvalorquedivideelconjuntoderendimientosdeunactivoendos: {x ∈ R|Pθ (X ≤ x) ≤ q} y {x ∈
R|Pθ (X > x) ≤ 1 q}.Porlotanto,el VaRX 1 q representaun cuantil deladistribuci´onderendimientosfinancieros.Deesta manera,ypartiendodelafunci´ondedistribuci´onacumulada (cdf) deunadistribuci´onnormaldeprobabilidad,seobtiene lasiguienteexpresi´onparael VaR normal:
Enefecto,sitomamosla cdf deunadistribuci´onnormal: FX (x)=
Si FX (xq)= q,entonces:
donde Φ( ) esla cdf deunadistribuci´onnormalest´andar. Despejando xq,sellegaa:
Laexpresi´on(5)correspondeal VaRq(X).Amaneradeejemplo,secalcular´ael VaR paralosrendimientosdiarios (rt ) de laacci´ondeEcopetrolentreel1deenerode2018yel18 demarzode2022.Paraelc´alculodedichosrendimientosse emple´olasiguienteexpresi´on: rt = pt pt 1 pt 1 . (6)
Donde pt correspondealpreciodecierredeunactivo financieroenelmomento t y pt 1 alpreciodecierreen elmomentoinmediatamenteanterior t 1.Parafacilitarla obtenci´onyeltratamientodelosdatos,seemplearonRy Python,siguiendolossiguientespasos:
Paso1a:importaci´ondelospaquetesen R. install.packages(‘‘quantmod’’) library(‘‘quantmod’’)
Paso1b:importaci´ondelospaquetesen Python. importnumpyasnp importpandasaspd importpandas datareader frompandas datareaderimportdataaswb frompylabimport * importscipy.statsasst
Paso2a:obtenci´ondelosdatosde Yahoofinance con R getSymbols(‘‘EC’’,from=‘‘2018−01−1’’)
Paso2b:obtenci´ondelosdatosde Yahoofinance con Python
precio Ecopetrol= wb.DataReader(’EC’, data source=’yahoo’, start=’01−01−2018’, end=’18−03−2022’)
Paso3:seasignanlosdatosalobjeto Ecopetrol yseeliminandatosfaltantesen R.
Ecopetrol=Ad(EC)
Ecopetrol=na.omit(Ecopetrol)
Paso4:secreaunafunci´onquecalculalosretornosdiarios en R.
retornos aritmeticos=function(datos) \{ return(datos/lag(datos,k=1)−1) }

Paso5a:secalculanlosretornosdiariosen R.
Rendimientos=na.omit(retornos aritmeti cos(Ecopetrol))
Paso5b:secalculanlosretornosdiariosen Python
retorno Ecopetrol=((precio Ecopetrol[’Adj Close’]/precio Ecopetrol[’Adj Close’].shift(1))−1).dropna()
Paso6a:segraficanlosrendimientosfinancierosdeEcopetrolen R.
plot(Rendimientos,main=”Rendimientos Ecopetrol”,col=’blue’)
Paso6b:segraficanlosrendimientosfinancierosdeEcopetrolen Python.
precio Ecopetrol[’retorno Ecopetrol’].plot (figsize=(9,6.5),color=”deepskyblue” ,label=’Retornodiario’)
plt.legend(loc=’lowerright’)
plt.grid(color=’grey’, linestyle=’dotted’, linewidth=0.6)
plt.title(’RetornosdiariosEcopetrol’)
Enestepasoesimportantenotarquelosrendimientosfinancierospresentanexcesodecurtosis(colaspesadas).Al compararladistribuci´onemp´ıricaconladistribuci´onnormal, seevidenciaquelagr´aficaverdenoseajustaalagr´aficaazul, locualpermiteinferirquelosrendimientosfinancierosnosiguenunadistribuci´onnormaldeprobabilidad.Porotraparte, esimportantenotarquelospuntosdecolormoradoenlaFigura3reflejanlaconcentraci´ondelosdatos(rendimientos), enesesentido,lospuntosaisladosrepresentanrendimientos extremos(gananciasop´erdidas)quepordefinici´on,el VaR notieneencuentaensutotalidad.
Paso7:secreaunafunci´onquegr´aficaelhistogramade losretornos,lafunci´ondedensidademp´ırica(naturaldelos datos)ylafunci´ondedensidadnormalen R
Paso8:serealizalagr´aficaQ-Qploten R.
qqnorm(Rendimientos)
qqline(Rendimientos,col=”red”)
ApartirdelaFigura4,sedemuestrandoshechosimportantes:quelosrendimientosfinancierosnosiguenunadistribuci´onnormaldeprobabilidadyquedichosdatostienencolas pesadas.Caberesaltarqueexistendatosquenoest´ansobrela l´ınearoja,locualindicaquesondatosextremosquenosiguen unadistribuci´onnormal.
Caberesaltarqueunadelascaracter´ısticasdeladistribuci´onnormalesqueessim´etrica,locualimplicaque lafrecuenciadeloseventoscentralesesmayoraladelos eventosextremos.Alrespecto,sehademostradoqueel comportamientodelosrendimientosdeactivosenmercados financierosnoesnormal,evidenciandolaexistenciadecolas pesadasyasimetr´ıasnegativas[CB12].Laexistenciadeasimetr´ıasnegativasimplicalaexistenciadealtasprobabilidades dequeocurran p ´ erdidasexcesivasoextremas [Her13].Porlo tanto,sedebenempleardistribucionesdecolaspesadas,con elfindeconformarportafolios ´ optimosquetenganencuenta losposibleseventosextremos[HdV07].
Paso9a:c ´ alculodel VaR paraEcopetrolen R.
VaR Ecopetrol=mean(Rendimientos)+ sd(Rendimientos) * qnorm(0.95)
VaR Ecopetrol *100
Paso9b:c ´ alculodel VaR paraEcopetrolen Python
VaR normal=(retorno Ecopetrol.mean +retorno Ecopetrol.std() * st.norm.ppf(0.95))
VaR normal *100
Estec´alculopermiteconcluirqueel VaR paraEcopetroles de4 82%,esdecir,conel95%deconfianzaseconcluyeque lam´aximap´erdidaquepodr´ıaexperimentarlaacci´ondeEcopetrolesde4 82%.Sinembargo,conel5%designificancia seconcluyequelam´ınimap´erdidaquepodr´ıaexperimentar dichaacci´onser´ıade4.82%.Enestepasoesnaturalqueel lectorsepregunte:¿qu´esucedeconlosvaloresquepuedetomarlavariablealeatoria(rendimientos)queexcedenel VaR?.
Larespuestaalapreguntaplanteadaesqueel VaR noda cuentadelriesgoqueloexcede,esdecir,noledaimportancia alcomportamientodelavariablealeatoriaenlascolasdela distribuci´on.Asimismo,caberesaltarqueel VaR escoherente enelcasoenquelosrendimientosfinancierossiguenunadistribuci´onel´ıpticadeprobabilidad(porejemplo:lanormalola t-Student),enotrocasoel VaR noessubaditivoyporlotanto dejadesercoherente(ver[ADEH99]).
Debidoaestasdebilidadesquepresentael VaR,en[AT02] seproponeunamedidaderiesgoquelassuperay,porlotanto,escoherente,lacualdenominanExpectedShortfall(ES)o ValorenRiesgoCondicional(CVaR).
El ES,tambi´enconocidocomo“ValorenRiesgoCondicional”(CVaR),“P´erdidaEsperadaenlaCola”(ETL,porsus siglaseningl´es“ExpectedTailLoss”)o“ValorMedioen Riesgo”(AVaR,porsussiglaseningl´es“AverageValueat Risk”)[Jim14].Sonmedidasquebuscantenerencuentalas p ´ erdidasqueest´anm´asall´adel VaR.Formalmente,en[Jim14] sedefineel ES como:
Esdecir,el CVaR secalculacomoelvaloresperadodelosrendimientosquesonmayoresqueel VaRX 1 q o,demaneraequivalente,menoresqueel VaRX 1 q.Parahallarunaexpresi´on param ´ etricadel CVaR,sesigueelsiguienteprocedimiento.
Empleandoladefinici´onde CVaR,laexpresi´on(5)yla funci´ondedensidaddeprobabilidad(pdf )deunadistribuci´on normal,seobtiene:
donde ϕ(·) denotala pdf deunanormalest´andar8.Continuandoconelejemplodelaacci´ondeEcopetrol,el CVaR al95%deconfianzasecalculaapartirdelaexpresi´on(9),as´ı:
Paso10a:c ´ alculodel CVaR paraEcopetrolen R.
distribuci´onnormalest´andar.
CVaR Ecopetrol=mean(Rendimientos)+ sd(Rendimientos)
*pnorm(0.95) * (1/(1−0.95))CVaR Ecopetrol *100
Paso10b:c ´ alculodel CVaR paraEcopetrolen Python.
CVaR normal=(retorno Ecopetrol.mean()+ ((retorno Ecopetrol.std())/(1−0.95)) * st.norm.pdf(st.norm.ppf(0.95)))
CVaR normal
Unavezcomputadoel CVaR seconcluyeque,con95% deconfianza,lap´erdidaesperadaquepodr´ıaexperimentarla acci´ondeEcopetrolesde6 04%.Esimportantenotarqueel
CVaR ≥ VaR,debidoaqueel CVaR tieneencuentap´erdidas queexcedenal VaR,porlocualesdeesperarsequeel promedio aumente.Loanteriortieneimplicacionesimportantes, tantoparalosinversionistascomoparalosreguladores,debidoaquepermiteestablecercoberturasalriesgodemercado adecuadasquegenerenconfianzaenlasociedad;establecer coberturasbasadasenestimacionesincorrectasponeenriesgoalasorganizacionesquelasemplean,yaquepuedenestablecercoberturasqueseaninsuficientesalahoradeatender unap ´ erdidaexcesiva.
Tantoel VaR comoel CVaR representanmedidasderiesgo,aunquelaprimera,comoseindic´oanteriormente,noes coherenteylasegundas´ı.Elefectodelacoherenciadelas medidasderiesgo,ajuiciodelautor,seevidenciaenelnivelde ajuste quetienelainformaci´onhist´oricaconbaseenla cualsecalcularon.Enotraspalabras,qu´etantainformaci´on est´ateniendoencuentalamedidade VaR o CVaR deltotalde rendimientosfinancieroshist´oricos.
Paraestimardicho ajuste seproponeunametodolog´ıa gr ´ afca yotra cuantitativa,lascualessepresentanacontinuaci´on:
Unavezrealizadoelc´alculodel VaR yel CVaR parala acci´ondeEcopetrolseprocedeagraficarlos,juntoconlos rendimientosfinancierosdelaacci´on,talcomoseevidencia enlaFigura5:
El VaR (colorrojo)yel CVaR (colorverde)segraficancomol´ıneasrectas,conelfindeobservarsilosrendimientos financierosdiarios(colorazul)losexceden.Enesesentido, cadad´ıaenquelarectarojaesintersecadaporlagr´aficaazul seprodujounap´erdidaqueexcedi´oofueigualal VaR.Del mismomodo,cadad´ıaenquelarectapunteadaverdeesintersecadaporlagr´aficaazulseprodujounap´erdidaqueexcedi´o ofueigualal CVaR
Porlotanto,gr´aficamenteseapreciaquelamedida CVaR presentamejorajustequeel VaR debidoaquelagr´aficaazul intersecam´asalagr´aficarojaquealapunteadaverde,esdecir,hubomenosp´erdidasqueexcedieronel CVaR encomparaci´onconel VaR,debidoaqueel CVaR capturaensuc´alculo elpromediodelosdatosqueexcedenal VaR.
Deloanteriorsedesprendeinmediatamentequeel CVaR permiterealizarunacoberturaadecuadadelriesgodemercado.
5.2.M´etodocuantitativoodelporcentajede ajuste.
Estem´etodo9 intuitivobuscaestablecerunporcentajede ajuste delasiguientemanera:
%ajuste = 1
Excepciones
Totalobservaciones ∗ 100%
Enesesentido,sebuscaqueelporcentajedeefectividadsea mayoroiguala95%,yaqueestefueelniveldeconfianza queseestableci´o.Pararealizardichoc´alculo,seproponendos algoritmosenPython,unoparael VaR yotroparael CVaR, respectivamente,loscualessepresentanacontinuaci´on:
Paso11:c ´ alculodelporcentajedeajuste VaR paraEcopetrolen Python
9Caberesaltarqueelm´etodoqueaqu´ısepresentanoconstituyeunametodolog´ıade backtesting
excepciones VaR=0 foriinprecio
Ecopetrol[’retorno Ecopetrol’]:
ifi < VaR normal: excepciones VaR+=1
ajuste VaR=(1−(excepciones VaR/ len(precio Ecopetrol[’retorno Ecopetrol’]))) * 100
ajuste VaR
Paso12:c ´ alculodelporcentajedeajuste CVaR paraEcopetrolen Python
excepciones CVaR=0 foriinprecio
Ecopetrol[’retorno Ecopetrol’]:
ifi < CVaR normal: excepciones CVaR+=1
ajuste CVaR=(1−(excepciones CVaR/ len(precio Ecopetrol[’retorno Ecopetrol’]))) * 100
ajuste CVaR
Unavezejecutadoslosalgoritmosdelospasos11y12se llegaqueelajustedel VaR y CVaR esde96 5%y98 4%,respectivamente.Locualindicaqueel CVaR seajustamejorala informaci´onhist´oricafacilitandorealizarunagesti´onadecuadadelriesgo.
Deldesarrolloanteriorsedestacancuatroconclusiones:
1. Lasseriesfinancieras,comoladelosrendimientosdiariosdeEcopetrol,presentanexcesodecurtosis,porlo cualsuponerquesedistribuyennormalmenteconstituye unerrorqueconllevaalasubestimaci´ondelriesgode mercado.
2. El VaR,comomedidaderiesgonocoherente,subestima laexposici´onalriesgodemercadopordosrazones:en primerlugarnotieneencuentalasp´erdidasqueloexceden,esdecir,noledaimportanciaalosdatosquese ubicanenlacoladeladistribuci´on;ensegundolugar,el VaR est´aconstruidoparafuncionaradecuadamentebajo distribucionesel´ıpticas(entreellaslanormal),sinembargo,lasseriesfinancieras,engeneral,nosiguendicha distribuci´on.
3. El CVaR,comomedidacoherentederiesgo,permite cuantificardemaneraadecuadalaexposici´onalriesgode mercadoalpromediarlasp´erdidasqueexcedenel VaR. Enestesentido,logracapturarlosdatosquesealojanen lacoladeladistribuci´on,loscualesrepresentanp´erdidas extremasquepodr´ıasufrirelactivoencuesti´on.
4. Elc´alculoylaprobabilidadcobranespecialimportancia enelmundofinanciero,yaquepermitendotarlodecierto gradodeformalidadlocualgeneramayorconfianzaen
losinversionistas,reguladoresydem´asparticipantesde losmercados.
AlosprofesoresOscarMart´ınezySergioCarrillo,quienes meense ˜ naronlapotenciadelaintegraci´on.AlprofesorJohn Arredondoporsudisposici´onydireccionamiento.AMafe, porsermimotivaci´on.
[RAE19] RAE, Definici´onderiesgo,2019.
[Kni21] F.Knight, Risk,UncertaintyandProfit,HoughtonMifflinCo, Boston,MA,1921.
[AB10] J.AlonsoandL.Berggrun, Introducci´onalan´alisisderiesgo financiero,2nded.,UniversidadIcesi,Bogot´a,D.C.,2010.
[ADEH99] P.Artzner,F.Delbaen,J.Eber,andD.Heath, CoherentMeasures ofRisk,MathematicalFinance 9 (1999),no.3,203-228.
[Gar15] J.Garc´ıa, Medidasderiesgocoherentesysuaplicaci´onsobrela asignaci´onestrat´egicadeactivosbajoelesquemaRiskParity: casoreservasinternacionalesdepetroleo.,UniversidadEAFIT, 2015.
[Ven06] F.Venegas, Riesgosfinancierosyecon´omicos:productosderivadosydecisionesecon´omicasbajoincertidumbre,2nded.,CengageLearning,2006.
[Rud76] W.Rudin, PrinciplesofMathematicalAnalysis,Internationalseriesinpureandappliedmathematics,McGraw-Hill,1976.
[AT02] C.AcerbiandD.Tasche, Onthecoherenceofexpectedshortfall, JournalofBanking&Finance 26 (2002),no.7,1487-1503.
[Jim14] J.Jimenez, Distribucionesdeprobabilidadalternativasparala gestionderiesgoenmercadosfinancieros,UniversidaddeValencia,Valencia,Espana,2014.
[CB12] MConstantinoandCBrebbia, ComputationalFinanceandits Applications,WITPress,2012.
[Her13] LHerrera, AcercadelaTeorıadelosvaloresextremosysuaplicabiliddalaestimaciondelriesgofinanciero,AnuariodelaFacultaddeCienciasEcon´omicasdelRosario 9 (2013),31-57.
[HdV07] NHyungandCdeVries, Portfolioselectionwithheavytails, JournalofEmpiricalFinance 14 (2007),no.3,383-400.
Acercadelautor:MarcoesunestudiantedesextosemestredeMatem´aticasdelaUniversidadSergioArboleda.Entre loscamposdelamatem´atica,encuentraespecialinter´esenla teor´ıadelamedida,laprobabilidad,elc´alculoysurelaci´on conelmundofinanciero.Practicaciclomontanismoconregularidadyesperaalg´und´ıaensenarmatem´aticasyfinanzas cuantitativasaniveluniversitario.
Su mirada, como las estepas de nuestra patria, en las que de nina yo jugaba justo antes del inicio del otono: reverdecida, profunda, y serena, me tom ´ o por sorpresa; m ´ as que el tibio clima de la ciudad a mitad del verano de 1967, la impresionante arquitectura medieval, la fastuosidad del complejo que ser ´ ıa mi hogar por los pr ´ oximos anos, o la estricta pesquisa que nos practicaban a quienes all´ ı entr ´ abamos, cada vez que lo hac´ıamos; fue su penetrante mirada lo que m ´ as desconcierto me produjo en mi primer d´ıa en Praga. Son hombres como Vuk Baranov los que, sin propon ´ erselo, causan una intensa impresi ´ on en quienes con ´ el se cruzan; no fue su garbo de diplom ´ atico, sus facciones escrupulosamente definidas, su lenguaje corporal masculino ni su estilo sutil y distante, no, no era eso, es que era en cada aspecto, en cada gesto, hasta en el m ´ as balad´ı: enteramente ´ el, enteramente Vuk Baranov

Ten´ıa muchas expectativas por mi nombramiento como cript ´ ologa adscrita al Ministerio de Relaciones Exteriores de la URSS, y asignada al Departamento de Comunicaciones de la Embajada Sovi ´ etica en Checoslovaquia Mi deber era garantizar una parte de la seguridad en la transmisi ´ on de los mensajes entre el Kremlin y el destacamento consular al que ahora pertenec´ıa, el alcance espec ´ ıfico de mi servicio: hacer in ´ util -mediante cifrado algor´ıtmico- cualquier mensaje que cayera en poder de un tercero distinto al destinatario previsto, sobre todo al haber sido entrenada en la Uni ´ on Sovi ´ etica, antes del inicio de mi viaje, para repeler el programa anglosaj ´ on de descifrado Venona.
Siempre quise sumar al prop ´ osito de alcanzar las formas de organizaci ´ on m ´ as avanzadas para la humanidad, como matem ´ atica pens ´ e que entender la progresi ´ on de la sociedad a trav ´ es de una ciencia objetiva ser ´ ıa un aporte valioso, por esto, el estudio de los Sistemas Din ´ amicos -y su eventual aplicaci ´ on a los Sistemas Sociales- capt ´ o mi atenci ´ on durante buena parte de mi vida acad ´ emica.
Un sistema din ´ amico con determinada estabilidad estructural es propenso a contener regiones inestables que provocan cambios sustanciales, cualitativos: singularidades. En la teor´ıa de cat ´ astrofes las singularidades poseen propiedades como la discontinuidad, la divergencia y la no reversibilidad, es decir que, aunque las transformaciones en el estado del sistema obedezcan ´ unicamente a determinadas variaciones, al invertirse ´ estas, no necesariamente retorna el sistema a su estado inicial Las cat ´ astrofes en la teor´ıa son eventos en los que se da un cambio disruptivo que generalmente no se deshace de ma-
nera trivial, su estudio involucra los conceptos de estabilidad y bifurcaciones, y es ´ util -entre otras cosas- para identificar las condiciones en las que el sistema presenta diferentes estados, a ´ un sin que las ecuaciones se encuentren completamente resueltas


Me dediqu ´ e al estudio de la Teor´ıa de Cat ´ astrofes al terminar la carrera en ciencias fisicomatem ´ aticas en la Universidad Estatal Lom ´ onosov de Mosc ´ u, tema que, luego de concluir la C ´ atedra de Investigaci ´ on en Sistemas Din ´ amicos, ser ´ ıa medular en mi Candidatura en Ciencias.

Replante ´ e la materia de mi Candidatura al recibir el consejo de uno de mis profesores, quien not ´ o en m ´ ı habilidades sobresalientes para la criptolog´ıa, esto por mi destacada participaci ´ on en un concurso que, realmente, era una prueba de aptitud que por encargo del Politbur ´ o, la Academia de Ciencias realiz ´ o para identificar funcionarios capaces para el servicio al pueblo socialista; la criptolog´ıa era una materia ´ util en las condiciones pol´ıticas del momento y que me permitir´ıa el honor de servir con eficiencia al socialismo, la instancia m ´ as evolucionada de la sociedad.
En mi primer desayuno en el restaurante de la embajada, el d´ıa siguiente a mi arribo, Vuk Baranov se dirigi ´ o a mi mesa, saludando a quienes nos encontr ´ abamos en medio de una conversaci ´ on marcada por los rituales propios de una bienvenida entre compatriotas, incursion ´ o sutilmente en la pl ´ atica, en el tercer comentario ya puso el ritmo de la conversaci ´ on, capt ´ o la atenci ´ on de los m ´ as activos part´ıcipes de la charla, les devolvi ´ o a ellos el protagonismo en el discurso y, antes de darme cuenta, ya hab´ıa dos conversaciones distintas, una en la que participaban los dem ´ as comensales, y otra en la que apenas est ´ abamos ´ el y yo; como una fiera en cacer ´ ıa pero con la elegancia propia de la esgrima, me apart ´ o de la manada Supo de m ´ ı y supe de ´ el, de su cargo como Agregado Cultural, su marcado sentido de compromiso pol´ıtico por el que se negaba a aprender un idioma distinto a los oficiales en los pa ´ ıses del Pacto de Varsovia (a parte de su ruso natal), su mala condici ´ on f´ısica por sus problemas respiratorios cong ´ enitos, su incapacidad con los n ´ umeros, pero sobre todo pude notar su aguda sensibilidad art´ıstica, manifiesta en la forma en que cualquier comentario -por superficial que fuera- le serv ´ ıa para citar referencias en la literatura, la arquitectura, la pintura, la m ´ usica y el cine sovi ´ eticos, a trav ´ es de sus labios tuve una perspectiva m ´ as profunda de Dostoyevski, Tr´ıfonov, Rudnev, Vladimirski, Musorgsky y Eisenstein, entre muchos otros; lo
que fue una constante: conversar con ´ el acerca de cualquier cosa, por banal que fuera, era un paseo por la arquitectura bizantina, el modernismo, el realismo socialista, el constructivismo y en general, por la cultura del y para el nuevo hombre
Inevitablemente, antes de que finalizara el ano 1967, ya estaba profundamente enamorada de Vuk, pasaba m ´ as tiempo en los aposentos que se le hab´ıan asignado a ´ el al interior de la Embajada que en los que a m ´ ı me correspond´ıan; el limitado alcance de las competencias de Vuk lo hac´ıan un candidato poco interesante para las misiones en otros pa ´ ıses diferentes a Checoslovaquia, por lo que pasamos ese primer semestre mucho tiempo juntos.
Modelar matem ´ aticamente eventos sociales no es una tarea sencilla (y si se es riguroso, puede ser imposible), pero se puede partir de axiomas elementales y de f ´ acil aceptaci ´ on de la sociolog´ıa y de la psicolog´ıa de masas, as ´ ı como de simplificaciones y generalizaciones que no eviten la caracterizaci ´ on de los matices relevantes del sistema
A pesar de que Anton´ın Novotn ´ y como Primer Secretario del Partido Comunista de Checoslovaquia (en la pr ´ actica, su Presidente), inici ´ o el proceso de desestalinizaci ´ on encabezado por el Secretario General del Partido Comunista de la Uni ´ on Sovi ´ etica: Nikita Jruschov desde 1956, hab´ıa desde que llegu ´ e a Praga -en 1967- una fuerte oposici ´ on a tales reformas, principalmente por la lentitud de las mismas y por el impacto econ ´ omico que hab´ıan generado; en los informes de inteligencia, la KGB afirmaba que tales efectos hab´ıan sido magnificados por elementos instigadores al interior de la sociedad Checoslovaca, y con mayor ah´ınco, en los colectivos de los estudiantes El Secretario General del Partido Comunista de la Uni ´ on Sovi ´ etica de la ´ epoca, Leonid Br ´ ezhnev hab´ıa sido informado de tal situaci ´ on y promovi ´ o un cambio en el liderazgo del pa ´ ıs y el desarrollo de reformas para que fueran m ´ as agudas y aceleradas
Alexander Dub ˇ cek fue nombrado el nuevo Secretario General del Partido Comunista de Checoslovaquia en enero de 1968 y desarroll ´ o los principios de una apertura que podr´ıan darle m ´ as estabilidad al sistema comunista, de alguna manera un modelo que formul ´ e para el sistema socialista parec ´ ıa llegar a esa conclusi ´ on al ubicar el estado actual del sistema m ´ as lejos del vecindario de la singularidad (la cat ´ astrofe) que bajo el mando de Novotn ´ y, seguramente empleando razonamientos muy distintos, Br ´ ezhnev llegaba a las mismas conclusiones y apoyaba los cambios
El modelo que formul ´ e mostraba una alta inestabilidad del sistema en general, de todo el bloque oriental en el caso en que se dieran dos eventos: que los movimientos por los derechos civiles en occidente perdieran fuerza de contrapeso en sus sistemas de gobierno capitalista, y a la vez, se desataran represiones violentas masivas en los pa ´ ıses del Pacto de Varsovia, sobre todo en la periferia, como el caso de Checoslovaquia; estas conclusiones las guard ´ e en mi habitaci ´ on y con justificada paranoia, las encript ´ e empleando elementos matem ´ aticos y gramaticales anglo germ ´ anicos, hasta que d´ıas despu ´ es sorprend´ ı a Vuk hurgando en mi archivo, cuando le encontr ´ e le mir ´ e de forma at ´ onita, me mostr ´ o de inmediato que intentaba,
de manera inocente, esconder entre mis papeles de consulta cotidiana (en los que me ve ´ ıa invertir horas casi a diario), un extrano cristal de centro oscuro, era una hermosa piedra que hab´ıa conseguido Vuk y que me entregaba para mostrarme sus nuevos intereses; desconoc´ıa su afici ´ on por la mineralog´ıa y su habilidad para ingresar ese elemento extrano a la Embajada (¿c ´ omo lo hizo?), aunque nada era sorprendente en el genio de Vuk
La total ignorancia de Vuk de las m ´ as elementales matem ´ aticas, as ´ ı como de las lenguas anglosajonas, me tranquilizaron con respecto a que hubiera visto algunos de los muy agudos resultados de mi modelizaci ´ on, de la propensi ´ on a singularidades del sistema socialista, sin embargo, evit ´ e volver a hacer registro de mis investigaciones y realic ´ e un esfuerzo por guardar en mi memoria los nuevos resultados, al menos hasta que pudiera mostrar una teor´ıa s ´ olida a mis superiores
El Primer Alto Directorio de la KGB (encargado de las operaciones en el extranjero y del contraespionaje) nos sorprendi ´ o al otro d´ıa, fuimos interrogados por aparte a causa del ingreso del extrano mineral a la Embajada por parte de Vuk, nuestras versiones fueron registradas, comparadas, el cristal fue analizado, se concluy ´ o que hab´ıa sido un obsequio sin trascendencia para la seguridad de la Embajada, y todo no pas ´ o de ser un evento si se quiere, anecd ´ otico, del que preferimos no hablar de nuevo; Vuk se ofreci ´ o para deshacerse de la roca y as ´ ı olvidarnos eventualmente del tema.
En mis investigaciones ampli ´ e el alcance del sistema din ´ amico analizado en un segundo sistema: el comunista –capitalista, llegu ´ e a la conclusi ´ on de que la desestabilizaci ´ on de uno de los dos reg ´ ımenes en el estado actual de las cosas, conllevar´ıa a una singularidad, la cat ´ astrofe se dar´ıa por el uso desmedido de las fuerzas de una de las partes; una interpretaci ´ on del modelo podr´ıa ser que la discontinuidad del sistema, la variaci ´ on divergente del estado del mismo y la no reversibilidad podr´ıa darse por el uso del arsenal nuclear por la parte que se viera gravemente desestabilizada, y la respuesta de la otra parte.
Para mi terror, empez ´ o a darse antes de terminado el primer semestre de 1968, una de las dos condiciones que, en el primer modelo, causar ´ ıan la singularidad en el sistema comunista: la p ´ erdida del contrapeso que al sistema capitalista daba el movimiento por los derechos civiles: los asesinatos de Martin Luther King Jr y de Robert Kennedy en Estados Unidos, y los preparativos para las represiones de los movimientos del 68 en Estados Unidos, Francia y Espana
La segunda condici ´ on estaba a punto de darse, y seg ´ un el modelo, con ella la desestabilizaci ´ on del sistema comunista, lo que, en ese momento de la historia, podr´ıa causar el uso de fuerzas incontenibles en busca de mantener el estatus quo. Br ´ ezhnev y Dub ˇ cek hab´ıan sido desinformados y se agudizaban las tensiones entre ellos, se hab´ıa notificado a la Embajada de forma secreta que entre el 20 al 21 de agosto arribar´ıa a Praga una enorme cantidad de fuerza militar del Pacto de Varsovia, para contener el descontento popular, ¿ocurrir´ıa una masacre de la poblaci ´ on civil, provocada por fuerzas oscuras? ¿era acertado el modelo al advertir que esto causar ´ ıa la deses-
tabilizaci ´ on del modelo comunista? ¿era acertado el segundo modelo al predecir que la desestabilizaci ´ on ser ´ ıa general y que ocurrir´ıa la cat ´ astrofe del uso de las fuerzas a disposici ´ on de las dos superpotencias?
Jam ´ as hab´ıa visto a Vuk respirar con dificultad como esa manana del s ´ abado 17 de agosto, a pesar de sus antecedentes de asma, estos no le imped´ıan un desempeno vigoroso en las actividades f´ısicas, pero esa manana se desmay ´ o justo al abrirme la puerta de su habitaci ´ on, de inmediato ped´ ı auxilio y le pusimos en manos de un m ´ edico de la Embajada, que en principio encontr ´ o sus v ´ ıas respiratorias inflamadas, ¿algo le habr´ıa causado alergia?, no sab´ıa qu ´ e, pero antes de devolverle a su habitaci ´ on decid´ ı abrir las ventanas y cortinas para que se ventilara.
Al hacerlo toqu ´ e sin querer su escritorio y un sistema mec ´ anico cambi ´ o la disposici ´ on de las gavetas, cerrando violentamente una de ellas en el proceso, la cual conten´ıa un dispositivo que pude ver unos segundos antes de que se retrajera al interior del mueble, mir ´ e hacia el piso por un momento, luego me recompuse y en ese instante lleg ´ o Vuk, esforz ´ andose por respirar con tranquilidad, pero con la mitad de la camisa a ´ un por fuera del pantal ´ on, le pregunt ´ e como segu ´ ıa y le ayud ´ e a recostarse, le coment ´ e que hab´ıa escuchado a un mueble estremecerse y me explic ´ o que era un dispositivo normal en los escritorios de funcionarios de su rango, para el resguardo de documentos clave, le not ´ e verme a los ojos m ´ as que de costumbre, me tom ´ o las munecas para recostarse, buscaba tal vez una dilataci ´ on de mis pupilas o un incremento de mi ritmo cardiaco que revelara un comportamiento anormal de mi parte, jam ´ as sabr ´ e si lo encontr ´ o
Casi no quisiera haberlo visto, casi que quisiera haber perdido la capacidad de asociaci ´ on de conceptos, pero un vistazo de apenas segundos bast ´ o para formular una hip ´ otesis terriblemente coherente con los hechos
Por mi formaci ´ on en el Ministerio de Comunicaciones pude reconocer un muy compacto transmisor de onda corta, fabricado artesanalmente, seguramente aqu ´ ı mismo, para burlar los controles de acceso a la Embajada, empleaba casi en su totalidad materiales de uso cotidiano con excepci ´ on de una extrana piedra, del mismo tipo que el cristal oscuro que me obsequi ´ o, que estaba puesta en un tubo adyacente al comunicador, lo que deber´ıa ser el filtro de gu ´ ıa de onda, y el mineral: octaedrita, un tipo de ´ oxido de titanio que, calibrado con total precisi ´ on, causa la resonancia de las ondas de inter ´ es y difracci ´ on de las que no lo son, el posicionamiento requiere de conocimientos muy s ´ olidos de ingenier´ıa y matem ´ aticas y su inhalaci ´ on puede causar la inflamaci ´ on de las v ´ ıas respiratorias. La octaedrita en forma de cristales obscuros y grandes corresponde a vetas muy espec ´ ıficas de Noruega, un pa ´ ıs que no pertenece al Pacto de Varsovia, las marcas de posicionamiento se encontraban dispuestas en fracciones, no en d ´ ecimas (como en el sistema internacional), era un aparato de comunicaciones construido con t ´ ecnicas estadounidenses y un material clave de occidente, era un artefacto de contraespionaje
Vuk claramente sab´ıa m ´ as de lo que dec´ıa conocer, ¿qu ´ e
tanto conoc ´ ıa de mi hip ´ otesis de la desestabilizaci ´ on del bloque oriental?, ¿particip ´ o en el desarrollo de los hechos motiv ´ andolos o informado al enemigo para que lo hiciera?, ¿faltaba el paso final de la masacre a la poblaci ´ on civil en Praga?, ¿colaboraba con las facciones radicales que podr´ıan motivar una confrontaci ´ on?
Una cat ´ astrofe u otra, denunciar a Vuk Baranov, el traidor al que amaba, el desertor quien, sin duda alguna, tambi ´ en me hab´ıa entregado su coraz ´ on; o arriesgar la ocurrencia -si los modelos eran acertados- de la singularidad en el estable sistema comunismo - capitalismo, pasando por la masacre en Praga que marcar ´ ıa ese punto discontinuo, divergente e irreversible, que abrir´ıa la puerta a las dos superpotencias para que pudieran actuar sin autocensura, usando todas sus capacidades de ataque.
S ´ e que Vuk me am ´ o tan intensamente como yo a ´ el, pero en el estable sistema de nuestras vidas juntos, la cat ´ astrofe: discontinua, divergente e irreversible, se daba por estar en este momento hist ´ orico, por nuestras convicciones contrarias, por pertenecer a bandos distintos, esa ser ´ ıa la devastadora singularidad que marcar ´ ıa nuestras vidas
Sal´ ı de la habitaci ´ on de Vuk y al terminar el pasillo y girar, de inmediato ingres ´ e a un apartamiento distinto al m ´ ıo y frente a la mirada sorprendida del camarada responsable de las traducciones oficiales -quien era el ocupante de la habitaci ´ onllam ´ e a la operadora de la Embajada, notifiqu ´ e mi hallazgo y en segundos un grupo de 10 oficiales del KGB ingres ´ o a la habitaci ´ on de Vuk derribando la puerta; lo encontramos sentado en su escritorio, a sus pies el dispositivo de comunicaciones hecho pedazos, en sus manos una copa de brandi y en sus labios un puro; el comandante del grupo le pidi ´ o a Vuk que se abstuviera de usar el diente, y que podr´ıan conversar en favor de la patria ¿Ten´ıa Vuk una capsula de cianuro en su diente?, ¿era entonces un esp ´ ıa sovi ´ etico?, ¿transmit´ıa mensajes tambi ´ en a occidente y era entonces un agente doble?
Luego de mirarme a los ojos, nuevamente, de la misma forma que ese primer d´ıa, escuchamos un sutil sonido de algo quebr ´ andose; los oficiales se abalanzaron hacia ´ el y lo sacaron de la habitaci ´ on intentando hacerle escupir; fui interrogada por varios d´ıas y luego de contar todo lo que sab´ıa y todo acerca de mi modelo, la ocupaci ´ on de la ciudad se realiz ´ o por parte de las fuerzas del Pacto de Varsovia, con un balance que, aunque tr ´ agico, no alcanz ´ o a ser ni siquiera una fracci ´ on de lo que pudo haber sido, ni de lo que fueron las represiones que en ese mismo ano se dieron en occidente, sobre todo la ocurrida m ´ as tarde en Tlatelolco, en las vecindades y bajo la influencia de la contraparte. Fui reasignada a Mosc ´ u y se me prohibi ´ o hablar del tema.
En 1975 encontr ´ e un obituario en el diario Pravda con la fotograf´ıa de Vuk Baranov en el que se anunciaba la muerte por causas naturales de un tal Vlad´ımir Aleks ´ androvich Pozner, en Mosc ´ u, ¿habr´ıa sobrevivido Vuk? ¿realmente era Vuk Baranov?, ¿el obituario buscaba legalizar las acciones de inteligencia de la KGB de hac´ıa siete anos? Como iba yo a saberlo, si durante mi tiempo de servicio me present ´ e como Brana Sokolova, el que tampoco era mi nombre
Dayron Fabi ´ an Achury-Calder ´ on dayronf.achuryc@konradlorenz.edu.co
Acerca del autor: Fabi ´ an Achury-Calder ´ on es ingeniero de la Universidad Distrital Francisco Jos ´ e de Caldas y matem ´ atico de la Fundaci ´ on Universitaria Konrad Lorenz Se ha interesado por estudiar la interacci ´ on de las matem ´ aticas con otras ciencias Es Auxiliar de la Justicia y de manera indepen-
diente asesora compa ˜ n ´ ıas en asuntos financieros y de direcci ´ on estrat ´ egica. Le apasionan la ´ opera, el ballet y las ciencias sociales. Sus pasatiempos favoritos son la lectura y la colecci ´ on de registros de radio internacional Disfruta recorrer museos cuando viaja y admite que se conmueve con facilidad Alg ´ un d´ıa espera aprender a tocar piano
UnaturistavisitaBogot´aconelobjetivodeconocerelcentrodelaciudad.Despu´esdeleereninternetsobrelaciudad, cre ´ olasiguientelistadelugaresquequer´ıaconocer,eincluy´o eltiempoquedeseabapermanecerencadauno:
LaPlazadeBol´ıvar(45minutos).
ElMuseodelOro(6horas).
LaterrazadelaTorreColpatria(30minutos).
LaplazadelaPerseverancia(2horas).
Laexposici´ondelMuseoBotero(6horas).
LaBibliotecaLuis ´ AngelArango(7horas).
ElcerrodeMonserrate(5horas).
ElMuseoNacional(6horas).
ElMuseodeArteModerno(150minutos).
Laturistasehospedar´aenelHotelTequendama,ubicado enlaCarrera10#26-21.Estandoah´ı,planeainiciarsurecorridoaloslugaresdeinter´esalas8:00a.m.Despu´es,almorzar ´ atodoslosd´ıasentrelas12:00yla1:00p.m.,continuar´a surecorridoyregresar´aalhotelm´aximoalas5:00p.m.Dado quelaturistarealizar´atodoslosrecorridoscaminando,consideraremosquesedesplazar´aaunavelocidadconstantede4.5 km/hora.
Conelobjetivodeconocertodoslugaresenelmenortiempoposible,¿qu´elugaresdeber´aconocercadad´ıayenqu´e orden?
Pararesolverelproblematengaencuentalasiguienteinformaci´on:
•Elobjetivoconsisteendisenaruncronogramadetallado queminimic´elom´asposibleeltiempoquelaturistaest´apor fueradelhotel.
•Paralosrecorridospodr´autilizarcualquiercaminoentrelacarrerad´ecima(sobrelaqueest´aubicadoelhotel)yla carrerasegundaeste(sobrelaqueest´aubicadalaentradaal cerrodeMonserrate),as´ıcomoentrelascalles31(sobrela queest´aubicadalaPlazadelaPerseverancia)ylacalle11 (sobrelaqueest´aubicadaeliniciodelaPlazadeBol´ıvar).
•Utilicelaaplicaci´onGoogleMapsparadise˜narelmapa quelaturistautilizar´a.
•Nosedebenconsiderartiemposdedesplazamientoparaalmorzarnibuscarrestaurantes,yaquelaturistaalmorzar´a siempreenalgunadelasatraccionestur´ısticas.Almorzarse puedehacerantes,duranteodespu´esdeunavisita.Encualquiercaso,esahoradealmuerzonosedebeincluircomoel tiempodevisitaaunsitio.
•Laturistapuederegresaralhotelencualquiermomento deld´ıa,peronuncadespu´esdelas5pm.Poreso,elcronogramadetalladodesuvisitadebetambi´enconsiderarlostiempos quetomanlosdesplazamientos.
•Lostiemposdecadadesplazamientosedebenredondear hac´ıaabajo.Porejemplo,siirdelpuntoAalpuntoBtoma3 minutosy45segundos,entoncesseconsideraqueeltiempo deldesplazamientoesde3minutos.
•Cadalugardebevisitarseenunsolod´ıaydemaneracontinua.Porejemplo,silavisitaalsitioAesde5horas,laturista nopuedepasar3horasund´ıayluego2horasotrod´ıa.Elalmuerzo,sinembargo,puedeinterrumpirlavisitayesel ´ unico casoenelcuallavisitaaunsitionoescontinua.
BasesdelConcurso:

Elegibilidad:
Estudiantesmenoresde18anos,decualquiernacionalidad ypertenecientesauncolegiocolombiano.
Duraci´on:
Elconcursofinalizaunanodespu´esdelapublicaci´ondel Pask´ınquepresentaelproblema,ohastaquehayaunapersonaganadora.
DocumentoSoluci´on:
Lasoluci´ondebepresentarsedemaneraindividualenun documentoformal,escritoenespanol,enelqueseexplique demaneradetalladalasoluci´onalproblemaplanteado.
Laprimerap´aginadeldocumentodebecontenerporlomenoslossiguientescuatroelementos:
(1)Elnombrecompletodelapersonaparticipante.
(2)Elcursodelapersonaparticipante.
(3)Laedaddelapersonaparticipante.
(4)Elnombrecompletodelcolegiodelapersona.
(5)Municipioociudadderesidencia.
(6)Telefonoycorreoelectr´onicodecontacto. Elcuerpodeldocumento,quesigueaestaprimerap´agina, puedetenercualquierextensi´onparainformarsobrelasoluci´on.
Losylasparticipantespuedenusarlibros,blogs,computadores,internet,programascomputacionales,peronopuedenconsultarointeractuarconningunaotrapersonadurante lasoluci´on.Ningunacontribuci´onpuedeserhechaporotra personaquenosealapersonaqueenv´ıalasoluci´on.
Aunquelosproblemasestar´andestinadosaunan´alisis te´orico,losparticipantespuedenrealizarexperimentosrelevantesypresentarlosdatosresultantesensutrabajosilodesean.
Encasodequeseutilicen,cadasoluci´ondebeincluiruna listadetodaslasreferencias.
Lassolucionespuedenusaralgoritmosyherramientas computacionalesexistentes(queincluyennosoloherramientasdisponiblesgratuitamente,sinotambi´enherramientasdentrodesistemascomoMatlaboMathematica),siemprequese mencionenycitencorrectamenteylosm´etodosseexpliquen claramenteenlasoluci´ondelproblema.Cualquierprograma decomputadoraescrito,siseescribi´ouno,debeincluirsecomounap ´ endicedelasoluci´on.Sinembargo,todoslosalgoritmos,m´etodosyresultadosdebenexplicarseeneltexto principaldeldocumentopararecibirconsideraci´ondurantela evaluaci´on.
Lassolucionesenviadaspuedenincluirecuaciones,gr´aficos,figurasytablas.Cadasoluci´ondebeincluircomom´ınimo:
(1)Unacortaintroducci´ondelproblematalcomolointerpret´olapersonaparticipante.
(2)Unaexplicaci´ondetodaslassuposicionesyaproximacionesrealizadas.
(3)Justificaci´ondetodoeltrabajorealizado.
(4)Unabrevediscusi´ondelasfortalezasydebilidadesdel enfoqueadoptado.
Lassolucionespuedenenviarsecomoarchivos.pdf,.odf, .docodocx.Cadaparticipantedebeenviarsusoluci´onpor correoelectr´onicoapaskin@konradlorenz.edu.coylosdocumentosdebenrecibirseantesdequefinaliceelconcurso.Si lasoluci´onnoserecibeporcorreoelectr´onicoduranteladuraci´ondelconcurso,lasoluci´onnoser´aconsiderada.Eldocumentocompletodebeincluirsecomounarchivoadjuntoal correoelectr´onico.Noenv´ıeunenlacealdocumentoenun servicioenlanubecomoGoogleDocs,Dropbox,etc.Una vezrecibidalasoluci´onselenotificar´alarecepci´onenunplazomenoracincod´ıash´abiles.SiUd.norecibeconfirmaci´on, comun ´ ıqueseconeleditordelarevista.
Resultados:
Todasoluci´onrecibidaseir´aevaluandoenordendellegadahastalafinalizaci´ondelconcurso.Cuandounasoluci´onsea correcta,laoelparticipanteser´ainvitadaoinvitadoaexponer yjustificardemaneraverbalsusoluci´ondemaneraremota sincr´onicautilizandoalgunaplataformavirtualcomoTeams, ZoomoGoogleMeets.
Premiaci´on:
-Laprimerasoluci´oncorrectaser´apublicadaenunasiguienteedici´ondelPask´ın.Ser´aunaversi´onsimplificadade lasoluci´onrealizadaencolaboraci´onconelcomit´eeditorial, queincluir´aunacortarese˜nadelapersonaganadora.
-Certificado.Cadapersonaqueparticipeypresenteuna soluci´oncorrectarecibir´auncertificado.Elcertificadoseenviar´aporcorreoelectr´onicoaladirecci´onutilizadaparael env ´ ıodelasoluci´on.Esperevariassemanasdespu´esdeenviar susoluci´onpararecibirsucertificado.
-Lapersonaqueenvi´elaprimerasoluci´oncorrectarecibir´a unbonovirtualderegaloporunvalorde 300.000COP (trescientosmilpesoscolombianos).Lapersonaganadorapuede escogerelestablecimientocomercialquedesee,siemprey cuandoofrezcabonoselectr´onicosyelcomit´eeditorialpueda adquirirlos.
El Paskín Matemático es una producción del Programa de Matemáticas de la Fundación Universitaria Konrad Lorenz. Está abierto a todos y todas. Si tienes interés en escribir un artículo con cualquier tipo de contenido matemático, reseñar a un personaje, comentar un problema o tienes comentarios sobre nuestra publicación, envía un mensaje a paskin@konradlorenz.edu.co
El Programa de Matemáticas de la Fundación Universitaria Konrad Lorenz fue creado en 1998. Conoce más acerca de nuestro programa en nuestra página institucional
http://www.konradlorenz.edu.co/es/aspirantes/carrerasuniversitarias/carrera-de-matematicas/presentacion.html
Bogotá, Colombia. 2023

Contenido
• DairoAndr´esSierra
SeccionesdePoincare:delatandoelcaosenelp´endulodoble..................1
• GonzaloMedina
Sobreelproblemadeloscuatrosubespacios...........................................9
• DanielEstebanGalvis
Delacuartadimensi´onyespaciosperfectos,arotarunespaciotridimensional.............................................................................................19
• MarcoBlancoAriza
Siquieroinvertir¿c´omomedebocubrir?Unaaproximaci´onalasmedidascoherentesderiesgoenRyPython.................................................32
• DayronFabianAchurry
MateKuento..........................................................................................39
• JohnA.ArredondoyAlejandroC´ardenas
Pask´ınChallenge..................................................................................43
Laesenciadelasmatem´aticasresideensulibertad.