Portada
Col·lecció
INFORMÁTICA GRÁFICA
2ª EDICIÓN
José Ribelles Ángeles López
Departamento De Lenguajes y sistemas informáticos
Codi d’assignatura: Informática Gráfica (VJ1221)
Crèdits
Edita: Publicacions de la Universitat Jaume I. Servei de Comunicació i Publicacions Campus del Riu Sec. Edifici Rectorat i Serveis Centrals. 12071 Castelló de la Plana http://www.tenda.uji.es e-mail: publicacions@uji.es
Colección Sapientia 151 www.sapientia.uji.es
Primera edición, 2015 Segunda edición, 2019
ISBN: 978-84-17429-87-4

DOI: http://dx.doi.org/10.6035/Sapientia151
Publicacions de la Universitat Jaume I es miembro de la une, lo que garantiza la difusión y comercialización de sus publicaciones a nivel nacional e internacional. www.une.es.

Atribución-CompartirIgual 4.0 Internacional (CC BY-SA 4.0) https://creativecommons.org/licenses/by-sa/4.0
Este libro, de contenido científico, ha estado evaluado por personas expertas externas a la Universitat Jaume I, mediante el método denominado revisión por iguales, doble ciego.
Índicedefiguras
1.1.EjemplodeescenatridimensionaldibujadaconWebGL......21
1.2.Ejemplosdeobjetosdibujadosmediante shaders .........22
1.3.ResultadoconéxitodeltestdesoportedeWebGLenunnavegador (http://get.webgl.org)...................23
1.4.Resultadodelapágina http://webglreport.org queproporcionainformaciónsobrealgunaspropiedadesrelativasalsoportedeWebGL2.0enelnavegador..................25
1.5.ElprimertriánguloconWebGL..................30
1.6.Secuenciabásicadeoperacionesdel pipeline deWebGL.....31
2.1.Alaizquierda,objetorepresentadomediantecuadriláterosyala derecha,objetorepresentadomediantetriángulos.........35
2.2.Representaciónpoligonaldeunacopayresultadodesuvisualización36
2.3.Ejemplosdemallaspoligonales,deizquierdaaderecha, Bunny, Armadillo y Dragon (modeloscortesíadel StanfordComputerGraphicsLaboratory)..........................37
2.4.Esquemadealmacenamientodeunamallapoligonalmediantela estructuradecarasindependientes.................38
2.5.Esquemadealmacenamientodeunamallapoligonalmediantela estructuradevérticescompartidos.................38
laizquierdasepuedenobervarlospolígonosutilizadospararepresentarla...............................42
3.2.Enlaimagendelaizquierdaserepresentadeperfilunpolígono ysunormal n.Enlaimagendeladerechasemuestraelmismo polígonotrasaplicarunatransformacióndeescaladonouniforme S(2, 1).Siseaplicaestatransformaciónalanormal n,seobtiene p comovectornormalenlugarde m,queeslanormalcorrecta..58
3.3.Lanuevabaseformadaporlosvectores d, e y f setransformapara coincidirconlosejesdecoordenadas................61
3.4.Escenamodeladaapartirdelaprimitivageométricacubo.....65
3.5.Ejemplodeunagrúadeobramodeladaconcubosytransformacionesgeométricas...........................66
3.6.Tanquemodeladoapartirdediferentesprimitivasgeométricas..66
3.7.Relojmodeladoapartirdeprimitivasgeométricasbásicas.....66
3.8.Otrosejemplosdejuegosdebloquesdemaderacoloreados....67
4.1.Parámetrosparaubicaryorientarunacámara: p,posicióndela cámara; UP ,vectordeinclinación; i,puntodeinterés.......70
p en laimagendelaizquierdasetransformaparaquedarcomoseobservaenlaimagendeladerecha.Dichatransformaciónseaplicaal objetodetalmaneraqueloqueseobservasealomismoenambas situaciones..............................70
proyecciónparalela.........................71
decoordenadas...........................72
viewports.Laescena eslamismaenlastresáreas,sinembargo,latransformacióndela cámaraesdistintaparacadaárea...................74
visibilidady(b)conelproblemadelavisibilidadresuelto.....75
viewports enlosqueseespecifica
viewport)coincidennoseproduciráningúntipodedeformaciónenla
derecortado.............................78
4.13.Encoloramarillo,lastareasprincipalesqueserealizanenlaetapa correspondientealprocesadodelfragmentodondeseindicaqueel testdeprofundidadserealizaconposterioridadalaejecucióndel shader defragmentosydemaneraopcional............79
5.1.EjemplodelascomponentesdelmodelodeiluminacióndePhong: (a)Luzambiente;(b)Reflexióndifusa;(c)Reflexiónespecular..82
5.2.EjemploobtenidoutilizandoelmodelodeiluminacióndePhong.82
5.3.Ejemplosdeiluminación:(a)Sololuzambiente;(b)Luzambiente yreflexióndifusa; (c)Luzambiente,reflexióndifusayreflexiónespecular......83
5.4.Vectoresinvolucradosenelcálculodelareflexióndifusa.....84
5.5.Vectoresinvolucradosenelcálculodelareflexiónespecular...85
5.6.Ejemplosdeiluminacióncondiferentesvaloresde α paraelcálculodelareflexiónespecular.....................85
5.7.Vectoresinvolucradosenelcálculodelareflexiónespecularconel vectorintermedio..........................86
5.8.Ejemplodeescenasinatenuación(izquierda)yconatenuaciónde laluz(derecha)...........................86
5.9.Ejemplosdemateriales,deizquierdaaderechaydearribaaabajo: Oro,Cobre,Plata,Obsidiana,Jade,Rubí,Bronce,Turquesa....88
nalyaladerecha,conlafuenteconvertidaenfoco........89
raudyPhong............................97
carasparaunacorrectavisualización................98
toonShading condiferentesvaloresdela variable levels
shader deniebla........101
, 1]
da)yrepeticiónnormalcomoladelafigura6.7(imagendelade-
(izquierda)ysolofiltrobili-
http:
reflectionmapping
hautilizadoparasimularqueeltoroestáreflejandosuentorno..118
6.17.Ejemplode refractionmapping
reflectionmapping enWebGL...121
refraction y reflectionmapping en WebGL.Elíndicederefracciónes,deizquierdaaderecha,de0,95 y0,99................................122
6.20.Objetostexturadosconlatécnicade bumpmapping.Lamodificacióndelanormalproducequeaparentementelasuperficietenga bultos................................123
6.22.Ejemplosdeaplicacióndelatécnica alphamapping ........124
alphamaps sobreelmismo
caso,elvalordevueltoporlafuncióndetexturaseutilizaparadeterminarsihayqueeliminarundeterminadofragmento......127
izquierdaelobjetoesdibujadosintextura,enelcentroseleha aplicadounatextura2D,yaladerechasehacombinadolatextura
shader
shader
shader
delcírculo..............................133
8.1.Tresejemplosdetransparenciacon,deizquierdaaderecha, alfa
ordeneneldibujadodelosobjetostransparentes..........141
8.3.Losplanostransparentesdelaizquierdasehanpintadoutilizando lafunción gl.ONE mientrasqueenlosdeladerechasehautilizado gl.ONE_MINUS_SRC_ALPHA
8.4.Ejemplodeobjetotransparentecon,deizquierdaaderecha, alfa= 0 3, 0 5 y 0 7,pintadoutilizandoelcódigorecogidoenellistado8.2.143
8.5.Ejemplodeobjetoreflejadoenunasuperficieplana........144
8.6.Aldibujarlaescenasimétricaesposibleobservarlafueradelos límitesdelobjetoreflejante(izquierda).El buffer deplantillase puedeutilizarpararesolverelproblema(derecha).........145
8.7.Escenaenlaqueelsuelohacedeobjetoespejo..........145
8.8.Enesteejemplo,lamismaescenaseinterpretademaneradistinta dependiendodesiseañadeonolasombra.............147
8.9.Ejemplode stiching producidoporsercoplanareselsueloyelobjetosombra.............................148
8.10.Elobjetosombrasuperaloslímitesdelasuperficiesobrelaquerecae148
shadowmapping.Alaizquierdaseobservaelmapade profunidadobtenidodesdelafuentedeluz;aladerechasemuestra laescenaconsussombras......................150
Gráfica
lera,quesehacemássuaveenlaimagendeladerecha......164
supersampling
MSAA (izquierda)ynoapli-
dedeteccióndebordesenlaparteizquierdadelaimagen.....171
Warping deunaimagen:imagenoriginalenlaizquierda,malla modificadaenlaimagendelcentroyresultadoenlaimagendela
edición)
Índicedelistados
1.1.Ejemplodecreacióndeuncanvascon
1.2.Código JAVASCRIPT paraobteneruncontextoWebGL2.0....27
1.3.CódigoqueutilizaórdenesdeWebGL...............27
1.4.Compilaciónyenlazadodeun shader
1.5.Ejemplobásicode shader devérticesy shader defragmentos...30
2.1.Estructuracorrespondientealarepresentacióndecarasindependientes................................37
2.2.Estructuracorrespondientealarepresentacióndevérticescompar-
2.3.ModelodeuncubodefinidocontriángulosdispuestoparaserutilizadoconWebGL.........................43
2.4.Códigomínimoquesecorrespondeconlaestructurabásicadeun programaqueutilizaWebGL(disponibleen c02/dibuja.js)....47
2.5.Código HTML queincluyeuncanvasylosdos shaders básicos (disponibleen c02/dibuja.html)...................49
2.6.Ejemplodevariable uniform enel shader defragmentos.....50
uniform myColor
2.8.Ejemplodemodelocondosatributosporvértice:posiciónycolor51
shader condosatributosporvértice:posiciónycolor.52
triángulosindependientes......................63
Shader devérticesqueoperacadavérticeconlamatrizdetransformacióndelmodelo........................64
z-buffer
devérticesparatransformarlaposicióndecadavértice..76
Shader pararealizarunsombreadodeGouraud..........92
Shader
malenel shader apartirdelamatrizmodelo-vista........94
shader quecontendránelmaterial...........................95
setShaderMaterial recibeunmaterialcomoparámetro einicializalasvariablesdel shader correspondientes.Enlafunción drawScene seestableceunvalordematerialantesdedibujarelobjeto95
shader quecontendránlosvaloresdelafuentedeluz.................96
setShaderLight inicializalasvariablesdel shader correspondientes............................96
5.13.Iluminaciónenambascaras,modificaciónenel shader defragmentos98
shader defragmentos99
Shader deniebla..........................100
6.1.Cambiosnecesariosparaqueun shader utiliceunatextura2D..107
shader defragmentosparautilizarvariastexturas2D108
sampler2D
shader para reflectionmapping
shader para refractionmapping
shader para skybox
Shader para skybox y reflectionmapping
Shader
Shader
Shader
José
Prefacio
Elobjetivodeestelibroesproporcionarunmaterialteóricoyprácticopara apoyarladocencia,tantopresencial,desarrolladaenclasesdeteoríaoenlaboratorio,comonopresencial,proporcionandoalestudianteunmaterialquefaciliteel estudiodelamateria,deunnivelycontenidoadecuado para la asignatura Infor mática Gráfica del grado en Diseño y Desarrollo de Videojuegos de la Universitat Jaume I.Estelibropretendeserelcomplementoidealalasexplicacionesqueel profesorimpartaensusclases,nosusustituto,ydelcualelalumnodeberámejorar elcontenidoconsusanotaciones.
Informática Gráfica segunda edición es un libro que renueva la obra publicada en el año 2015 de título Informática Gráfica, número 107 de la colección Sapientia. Por una parte, se ha pasado a utilizar WebGL 2.0 cuya especificación apareció a principios del 2017, mucho más moderna que la versión 1.0, la cual está basada en una especificación de hace más de diez años. Por otra parte, se han realizado mejo ras en todos los capítulos incluyendo cambios en prácticamente todas sus seccio nes, nuevas figuras, más ejemplos y ejercicios, y una nueva sección de cuestiones al final de cada capítulo.
El contenido del libro se puede dividir en tres bloques. El primer bloque lo formarían los primeros cuatro capítulos en los que se introduce la programación moderna de gráficos por computador a través de la interfaz de programación de hardware gráfico WebGL 2.0, el modelado y visualizado de modelos poligonales, el uso de transformaciones geométricas, transformaciones de cámara y proyec ción, y el problema de la visibilidad. El segundo bloque se centra principalmente en introducir técnicas para mejorar la calidad visual de la imagen sintética y lo formarían los capítulos 5 a 7. En este bloque se incluye, por ejemplo, el modelo de iluminación de Phong, modelos de sombreado, diversas técnicas para la aplicación de texturas e implementación de texturas procedurales básicas. El tercer y último bloque del libro lo forman los capítulos 8 a 10 que principalmente presentan técni cas avanzadas de realismo visual, como transparencia, espejos y sombras, métodos relacionados con el desarrollo de aplicaciones gráficas como, por ejemplo, meca nismos de interacción y animación con shaders, y métodos de procesamiento de imagen como la corrección gamma o filtros de convolución.
Informática
Recursosenlínea
Sehacreadoelsitioweb http://cphoto.uji.es/grafica2 como apoyoaestematerial,dondeellectorpuededescargarlosprogramasdeejemplo queseincluyenenlosdiferentescapítulos.
José Ribelles y Ángeles López
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
IntroducciónaWebGL
)paragenerar imágenesporordenadorenpáginasweb.Permitedesarrollaraplicacionesinteractivasqueproducenimágenesencolordealtacalidadformadasporobjetostridimensionales(véasefigura1.1).Además,WebGLsolorequieredeunnavegador quelosoporte,porloqueesindependientetantodelsistemaoperativocomodel sistemagráficodeventanas.Enestecapítuloseintroducelaprogramacióncon WebGLatravésdeunpequeñoprogramaysepresentaellenguaje GLSL parala programaciónde shaders

1.1.Antecedentes
OpenGLsepresentóen1992.SupredecesorfueIrisGL,un API diseñadoysoportadoporlaempresaSiliconGraphics.Desdeentonces,laOpenGLArchitecture ReviewBoard(ARB)conducelaevolucióndeOpenGL,controlandolaespecificaciónylostestsdeconformidad.
Ensusorígenes,OpenGLsebasóenun pipeline configurabledefuncionamientofijo.Elusuariopodíaespecificaralgunosparámetros,peroelfuncionamientoy elordendeprocesamientoerasiempreelmismo.Conelpasodeltiempo,losfabricantesde hardware gráficonecesitarondotarlademayorfuncionalidadquela inicialmenteconcebida.Así,secreóunmecanismoparadefinirextensionesque, porunlado,permitíaalosfabricantesproporcionar hardware gráficoconmayores posibilidades,almismotiempoqueofrecíanlacapacidaddenorealizarsiempreel mismo pipeline defuncionalidadfija.

Enelaño2004apareceOpenGL2.0,elcualincluiríaelOpenGLShadingLanguage, GLSL 1.1,eibaapermitiralosprogramadoreslaposibilidaddeescribir uncódigoquefueseejecutadoporelprocesadorgráfico.Paraentonces,lasprincipalesempresasfabricantesde hardware gráficoyaofrecíanprocesadoresgráficos programables.Aestosprogramasselesdenominó shaders ypermitieronincrementarlasprestacionesyelrendimientodelossistemasgráficosdemaneraespectacular,algenerarademásunaampliagamadeefectos:iluminaciónmásrealista, fenómenosnaturales,texturasprocedurales,procesamientodeimágenes,efectos deanimación,etc.(véasefigura1.2).



Figura1.2:Ejemplosdeobjetosdibujadosmediante shaders


Dosañosmástarde,elconsorcio ARB pasóaserpartedelgrupoKhronos. 1 Entresusmiembrosactivos,promotoresycontribuidoresseencuentranempresas deprestigiointernacionalcomo AMD, Apple, arm, Epic Games, Google, Huawei, Qualcomm, Nvidia, Intel, Nokia, etc.Esenelaño2008cuandoOpenGL,conla aparicióndeOpenGL3.0y GLSL 1.3,adoptaelmodelodeobsolescencia,aunque
1http://www.khronos.org/
José Ribelles y Ángeles López
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
manteniendocompatibilidadconlasversionesanteriores.Sinembargo,enelaño 2009,conlasverionesdeOpenGL3.1y GLSL 1.4,escuandoprobablementese realizaelcambiomássignificativo;el pipeline defuncionalidadfijaysusfunciones asociadassoneliminadas,aunquedisponiblesaúnatravésdeextensionesqueestán soportadasporlamayorpartedelasimplementaciones.
OpenGL ES 1.0 aparece en el 2003. Se trata de la primera versión de OpenGL para sistemas empotrados incluyendo teléfonos móviles, tabletas, consolas, vehícu los, etc. Se basó en la especificación inicial de OpenGL. La versión 2.0 creada a partir de la especificación de OpenGL 2.0 aparece en el 2007, eliminando parte de la funcionalidad fija y permitiendo la programación con shaders. Esta versión, so portada en sistemas Android desde la versión 2 e IOS desde la versión 5, es la base para la especificación de WebGL 1.0 que aparece en el 2011 y que en la actualidad está ampliamente soportada por los navegadores Safari, Chrome, Firefox, Opera e Internet Explorer, entre otros. Derivada de OpenGL 3.3, la primera especificación de OpenGL ES 3.0 se hace pública en el 2013 y está soportada en sistemas Android desde la versión 4.3 e IOS desde su versión 7. A su vez, esta nueva versión es la base para la especificación de WebGL 2.0 que ve finalmente la luz en el año 2017.
1.2.PruebadeWebGL

AveriguarsisedisponedesoporteparaWebGLesmuysimple.Abreunnavegadoryaccedeacualquieradelasmuchaspáginasqueinformandesielnavegador soportaonoWebGL.Porejemplo,lapágina http://get.webgl.org esuna deellas.Sifunciona,semostraráunapáginacon el dibujo deuncuboenalambre dandovueltassobresímismocomoelqueapareceenlafigura1.3.
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
Ejercicios
1.1 CompruebaladisponibilidaddeWebGLenlosdiferentesnavegadoresquetengas instaladosentuequipo.Sitienesvariossistemasoperativosrepitelaspruebasencadauno deellos.Sitienesdispositivosmóviles,teléfonosotabletasatualcance,pruebatambiénel soporteconlosdiferentesnavegadores.Despuésdelasdistintaspruebas:
¿CuálestuopiniónrespectoalestadodesoportedeWebGLenlosdiferentesnavegadores?
¿Creesqueessuficienteoqueporcontratendremosqueesperaraúnmásaque aparezcannuevasversionesdelosnavegadores?
¿PiensasqueloquedesarrollesenWebGLvasaatenerqueprobarloencadanavegadorysistemaconelfindecomprobar,nosolosufuncionamiento,sinotambién siseobtieneonoelmismoresultado?
1.2 Accedealasiguienteweb: http://webglreport.com/.Obtendrásunapáginaconuncontenidosimilaralquesemuestraenlafigura1.4.Aunque algunas caracte rísticasteresultenincomprensibles,tratadecontestaralassiguientespreguntas: ¿CuáleslaversióndeWebGLquesoportatunavegador?
¿Cuántos bits se utilizan en el framebuffer para codificar el color de un píxel?
1.3 Sirealizasunabúsquedaeninternetencontrarásbastantespáginasqueofrecen unaseleccióndeejemplosy donde también los desarrolladores pueden colgar sus propios trabajos. Algunos ejemplos
1.3.Elmínimoprograma
Incluir una aplicación WebGL en una página web requiere de dos pasos pre vios: crear un canvas y obtener un contexto WebGL. Como ya sabes, HTML es un lenguaje estandard que se utiliza para el desarrollo de páginas y aplicaciones web.
incluye entre sus nuevos elementos el denominado canvas. Se trata de un elemento
versión
que establece el área de la página web donde se visualizará la aplicación WebGL. El listado 1.1 muestra el código HTML que crea un canvas de tamaño 800 × 600.
Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151

Ejercicios
1.4 Examinaellistado1.1,utilizauneditorparaescribirloyguárdaloconelnombre canvas.html.Ahoraábreloconelnavegadorquehayasseleccionadoparatrabajar.Pruebaa cambiaralgunosdelosparámetroscomoeltamaño,eltipodeborde,osucolor.Realmente, queelmarcoseavisiblenoesnecesario,perodemomentofacilitaverclaramentecuáles eláreadedibujoestablecida.
Listado1.1:Ejemplodecreacióndeuncanvascon HTML5 <!DOCTYPEhtml> <html> <head> <metacharset="utf 8"> <title>Canvas</title> <styletype="text/css"> canvas{border:1pxsolidblack;} </style> </head> <body> <canvasid="myCanvas"width="800"height="600"> ElNavegadornosoportaHTML5 </canvas> </body> </html>
TambiéneselpropiocanvaselquenosvaaproporcionaruncontextoWebGL, objeto JAVASCRIPT atravésdelcualseaccedeatodalafuncionalidad.Siempre crearemosprimeroelcanvasyentoncesobtendremoselcontextoWebGL.Observa elcódigodellistado1.2quetratadeobteneruncontextoWebGL2.0einformade sudisponibilidad.
Ejercicios
1.5 Examinaellistado1.2,utilizauneditorparaescribirloyguárdalocomo contexto.js.Ahorarecupera canvas.html yañadeel script justoantesdecerrarelcuerpodela páginaweb (etiqueta </body>):
<scriptsrc=”contexto.js” ></script>
Guárdalo y refresca la página en el navegador. Comprueba el resultado, ¿tienes soporte para WebGL 2.0?
Observa ahoralanuevafunción initWebGL dellistado1.3.Estafunciónespecificauncolordeborrado,ocolordefondo,utilizandoelmétodo clearColor, yordenaqueborreelcontenidodelcanvasconlaorden clear yelparámetro
José Ribelles y Ángeles López
ISBN: 978-84-17429-87-4
Informática Gráfica (2ª edición)
DOI: http://dx.doi.org/10.6035/Sapientia151
COLOR_BUFFER_BIT.AmbasinstruccionessonyaórdenesdeWebGL.Cabeseñalarqueaunqueesteprogramacontienelamínimaexpresióndecódigoqueutiliza WebGL,laestructurahabitualdeunprogramaqueutiliceWebGLsecorresponde conelquesemuestramásadelanteenellistado2.4.
Listado1.2:Código JAVASCRIPT paraobteneruncontextoWebGL2.0 functiongetWebGLContext(){ varcanvas=document.getElementById("myCanvas"); try{ return canvas.getContext("webgl2"); } catch(e){ } return null; } functioninitWebGL(){ vargl=getWebGLContext(); if (!gl){ alert("WebGL2.0noestádisponible"); } else { alert("WebGL2.0disponible"); } } initWebGL();
Listado1.3:CódigoqueutilizaórdenesdeWebGL functioninitWebGL(){ vargl=getWebGLContext(); if (!gl){ alert("WebGL2.0noestádisponible"); return ; }
//especificaenRGBAelcolordefondo(4valoresentre0y1) gl.clearColor(1.0,0.0,0.0,1.0);
//rellenaelbufferdecolorutilizandoelcolor //especificadoconlaordenclearColor gl.clear(gl.COLOR_BUFFER_BIT);
José Ribelles y Ángeles López
978-84-17429-87-4
Informática Gráfica (2ª edición) DOI: http://dx.doi.org/10.6035/Sapientia151
Ejercicios
1.6 Ejecutaelprograma c01/minimoPrograma.html queimplementalafunción initWebGL dellistado1.3.ConsultaenlaguíadeprogramacióndeWebGLlasórdenes clear y clearColor ycontestaalassiguientescuestiones:
¿Quéhasdecambiarparaqueelcolordefondoseaamarillo?
¿Quéocurresiintercambiaselordende clear y clearColor?¿Porqué?
1.4.Elprimertriángulo
El listado 1.4 muestra la nueva función initShader cuyo objetivo es compilar y enlazar un shader. Pero, ¿qué es un shader? Un shader no es más que un programa que se ejecuta en la GPU. En la actualidad, una GPU puede llegar a contener hasta cinco tipos de procesadores: de vértices, de control de teselación, de evaluación de teselación, de geometría y de fragmentos; por lo que también decimos que hay cinco tipos de shaders, uno por cada tipo de procesador. Sin embargo, WebGL 2.0 solo soporta dos tipos de shaders, el de vértices y el de fragmentos, de modo que únicamente podremos escribir shaders de vértices y shaders de fragmentos.
Un shader, antes de poder ser ejecutado en una GPU, debe ser compilado y enlazado. El compilador está integrado en el propio driver de OpenGL instalado en tu máquina (ordenador, teléfono, tableta, etc.). Esto implica que la aplicación en tiempo de ejecución será quien envíe el código fuente del shader al driver para que sea compilado y enlazado, creando un ejecutable que puede ser instalado en la GPU Tres son los pasos a realizar:
1.Crearycompilarlosobjetos shader.
2.Crearunprogramayañadirlelosobjetoscompilados.
3.Enlazarelprogramacreandounejecutable.
Ejercicios
1.7 Ellistado1.4muestraunejemplodetodoelproceso.Observadetenidamente lafunción initShader eidentificaenelcódigocadaunadelastresetapas.Consultala especificacióndeWebGLparaconocermásafondocadaunadelasórdenesqueaparecen enelejemplo. Señalar que para que el programa ejecutable sea instalado en los proce sadores correspondientes, es necesario indicarlo con la orden glUseProgram, que como parámetro debe recibir el identificador del programa que se desea utilizar. La carga de un ejecutable siempre supone el desalojo del que hubiera con anterioridad.
1.8 Editaelfichero c01/miPrimerTrianguloConWebGL.js.Observacómoquedaincluidalafunción initShader dentrodelaaplicaciónyenquémomentoselellamadesdela función initWebGL
José Ribelles y Ángeles López
Informática Gráfica (2ª edición)
DOI: http://dx.doi.org/10.6035/Sapientia151
Listado1.4:Compilaciónyenlazadodeun shader functioninitShader(){
//paso1
varvertexShader=gl.createShader(gl.VERTEX_SHADER); gl.shaderSource(vertexShader, document.getElementById(’myVertexShader’).text); gl.compileShader(vertexShader);
varfragmentShader=gl.createShader(gl.FRAGMENT_SHADER); gl.shaderSource(fragmentShader, document.getElementById(’myFragmentShader’).text); gl.compileShader(fragmentShader);
//paso2
program=gl.createProgram(); gl.attachShader(program,vertexShader); gl.attachShader(program,fragmentShader);
//paso3 gl.linkProgram(program); gl.useProgram(program);
program.vertexPositionAttribute=gl.getAttribLocation( program,"VertexPosition"); gl.enableVertexAttribArray(program.vertexPositionAttribute); }
Ellistado1.5muestraunejemplode shader,elmássimpleposible.Los scripts identificadoscomo myVertexShader y myFragmentShader contienenloscódigos fuentedel shader devérticesydel shader defragmentosrespectivamente.Estos scripts sedebenincluirenelfichero HTML.
Cuandodesdelaaplicaciónseordenedibujarunmodelopoligonal,cadavértice producirálaejecucióndel shader devértices,elcualasuvezproducecomosalidalaposicióndelvérticequesealmacenaenlavariablepredefinida gl_Position. Elresultadodeprocesarcadavérticeatraviesael pipeline,losvérticesseagrupan dependiendodeltipodeprimitivaadibujar,yenlaetapadeconversiónal raster laposicióndelvértice(ytambiéndesusatributosenelcasodehaberlos)es interpolada,generandolosfragmentosyproduciendo,cadaunodeellos,laejecucióndel shader defragmentos.Elpropósitodeesteúltimo shader esdeterminar elcolordefinitivodelfragmento.Siguiendoconelejemplo,todoslosfragmentos sonpuestosacolorverde(especificadoenformato RGBA)utilizandolavariable fragmentColor
Ejercicios
1.9 Cargaenelnavegadorelfichero c01/miPrimerTrianguloConWebGL.html ycompruebaqueobtienesunasalidasimilaralaquesemuestraenlafigura1.5.
José Ribelles y Ángeles López
978-84-17429-87-4
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
Listado1.5:Ejemplobásicode shader devérticesy shader defragmentos
<scriptid="myVertexShader" type="x shader/x vertex">#version300es
//Shaderdevértices
//Declaracióndelatributoposición invec3 VertexPosition;
void main(){
//seasignalaposicióndelvérticea //lavariablepredefinidagl_Position gl_Position= vec4 (VertexPosition,1.0);
}
</script>
<scriptid="myFragmentShader" type="x shader/x fragment">#version300es
//Shaderdefragmentos precisionmediump float ; outvec4 fragmentColor; void main(){
//seasignaelcolorverdeacadafragmento fragmentColor= vec4 (0.0,1.0,0.0,1.0);

}
</script>
José Ribelles y Ángeles López ISBN: 978-84-17429-87-4
Informática Gráfica (2ª edición) DOI: http://dx.doi.org/10.6035/Sapientia151
Figura1.5:ElprimertriánguloconWebGL1.4.1.El pipeline
Elfuncionamientobásicodel pipeline serepresentaeneldiagramasimplificadoquesemuestraenlafigura1.6.Lasetapasdeprocesadodelvérticeydel fragmentosonprogramables,yeselprogramadorelresponsabledeescribirlos shaders quesehandeejecutarencadaunadeellas.

Figura1.6:Secuenciabásicadeoperacionesdel pipeline deWebGL
Elprocesadordevérticesaceptavérticescomoentrada,losprocesautilizando el shaderdevértices yenvíaelresultadoalaetapadenominada«procesadodela primitiva».Enestaetapa,losvérticessereagrupandependiendodequéprimitivageométricaseestáprocesando(punto,líneaotriángulo).Tambiénserealizan otrasoperacionesquedemomentosevanaomitir.Laprimitivapasaporunaetapa de«conversiónal raster»,quebásicamenteconsisteengenerarpequeñostrozos denominadosfragmentosquetodosjuntoscubrenlasuperficiedelaprimitiva.
Elprocesadordefragmentosdeterminaelcolordefinitivodecadafragmento utilizandoel shaderdefragmentos.Elresultadoseenvíaal framebuffer nosin antesatravesaralgunasetapasquedemomentotambiénseomitenporcuestiónde claridad.
1.4.2.GLSL
Ellenguaje GLSL formapartedeWebGLypermitealprogramadorescribirel códigoquedeseaejecutarenlosprocesadoresprogramablesdela GPU WebGL 2.0 utiliza la versión 3.0 ES de GLSL Por este motivo los shaders comienzan con la directiva #version 300 es (véase listado 1.5).
GLSL esunlenguajedealtonivel,parecidoalC,aunquetambiéntomaprestadasalgunascaracterísticasdelC++.Susintaxissebasaenel ANSI C.Constantes, identificadores,operadores,expresionesysentenciassonbásicamentelasmismas queenC.Elcontroldeflujoconbucles,lasentenciascondicionales if-then-else y lasllamadasafuncionessonidénticasalC.Pero GLSL tambiénañadecaracterísticasnodisponiblesenC,entreotrassedestacanlassiguientes:
Tiposvector:vec2,vec3,vec4
Tiposmatriz:mat2,mat3,mat4
José Ribelles y Ángeles López
Informática Gráfica (2ª edición)
DOI: http://dx.doi.org/10.6035/Sapientia151
Tipos sampler paraelaccesoatexturas:sampler2D,samplerCube
Tiposparacomunicarseentre shaders yconlaaplicación: in, out, uniform
Accesoacomponentesdeunvectormediante:.xyzw.rgba.stpq
Operacionesvector-matriz,porejemplo: vec4 a = b ∗ c,siendo b detipo vec4 y c detipo mat4
VariablespredefinidasquealmacenanestadosdeWebGL
GLSL tambiéndisponedefuncionespropiascomo,porejemplo,trigonométricas(sin, cos, tan,etc.),exponenciales(pow, exp, sqrt,etc.),comunes(abs, floor, mod,etc.),geométricas(length, cross, normalize,etc.),matriciales(transpose, inverse,etc.)yoperacionesrelacionalesconvectores(equal, lessThan, any,etc). Consultalaespecificacióndellenguajeparaconocerellistadocompleto.También haycaracterísticasdelCquenoestánsoportadasenOpenGL,comoeselusode punteros,delostipos: byte, char, short, longint ylaconversiónimplícitadetipos estámuylimitada.DelC++, GLSL copialasobrecargayelconceptodeconstructor.
Por último indicar que en GLSL hay que establecer la precisión numérica de las variables mediante el uso de uno de estos tres calificadores: lowp, mediump, highp Estos calificadores se pueden utilizar tanto en la declaración de la variable como de forma general para todas las variables de un determinado tipo. Este último caso se realiza mediante la sentencia: precisioncalificador_de_precisióntipo;
Por ejemplo, en el listado 1.5 se ha utilizado el calificador mediump para las varia bles de tipo float Sin embargo, en su lugar se podría haber utilizado el calificador de precisión directamente en la declaración de la correspondiente variable: outmediumpvec4fragmentColor;
En el shader de vértices todos los tipos tienen una precisión establecida por defec to. En el shader de fragmentos ocurre lo mismo a excepción del tipo float, para el que es necesario que el programador lo especifique en el propio shader Consulta la especificación del lenguaje para conocer el calificador establecido por defecto para cada tipo así como la precisión numérica asociada a cada calificador.
Ejercicios
1.10 Modificaelcolorderellenodeltriángulodelejercicioanteriorporotroquetu elijas.Recuerdaqueelcolordecadafragmentoseestableceenel shader defragmentos cuyocódigofuenteestáenelfichero HTML
1.11 Aunqueaúnnosehatratadoeldibujadodegeometría,pruebaamodificarlas coordenadasdelosvérticesdeltriángulodefinidoenlavariable exampleTriangle. Porejemplo,tratadeobtenereltriángulosimétricorespectoaunejehorizontal.Prueba tambiénaespecificarcoordenadasdemagnitudmayorqueuno,einclusoautilizarvalores distintosdeceroenlacomponenteZ.Haztodaslaspruebasqueseteocurran,eslamejor maneradeaprender.
José Ribelles y Ángeles López
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
CUESTIONES
1.1 ¿Quéesuncanvas?
1.2 ¿QuéesuncontextoWebGL?
1.3 ¿CreasprimeroelcanvasyapartirdeéluncontextoWebGLoalrevés?
1.4 ¿EnquélenguajesecodificalaobtencióndeuncontextoWebGL, HTML oJavaScript?
1.5 ¿Quéelementode HTML tepermitecargarunficheroquecontengacódigoescrito enJavaScript?
1.6 ExplicaparaquésirvelafuncióndeWebGL clearColor.¿Cómosecomplementaconlafunción clear?¿Aquéhacereferencia COLOR_BUFFER_BIT?
1.7 ¿Quéesun shader?
1.8 ¿Quétiposde shaders tienesdisponiblesenWebGL2.0?
1.9 ¿Quéesunfragmento?¿Enquetipode shader seestableceelcolordefinitivode unfragmento?
1.10 ¿Quévariablehadealmacenarelcolordefinitivodeunfragmento?
1.11 ¿Quévariablehadealmacenarlascoordenadasdefinitivasresultadodeprocesar unvértice?
1.12 Enel pipeline deWebGL,¿quéserealizaantes,elprocesadodelvérticeoeldel fragmento?
1.13 ¿Enquélenguajeyversiónseescribeun shader paraWebGL2.0?
1.14 ¿Paraquésirvelaorden useProgram?
José Ribelles y Ángeles López ISBN: 978-84-17429-87-4
Informática Gráfica (2ª edición) DOI: http://dx.doi.org/10.6035/Sapientia151
Modeladopoligonal

deserutilizadoporunsistemagráficoparaservisualizado.Hablamosdemodelo poligonalcuandoseutilizanpolígonosparadescribirlo.Engeneral,eltriángulo eslaprimitivamásutilizada,aunquetambiénelcuadriláteroseempleaenalgunas ocasiones(véasefigura2.1).

Ribelles
El hardware gráficoactualsecaracterizaporsuvelocidadalahoradepintar polígonos.Losfabricantesanunciandesdehaceañostasasdedibujadodevarios millonesdepolígonosporsegundo.Poresto,elusodemodelospoligonalesparavisualizarmodelos3Denaplicacionesinteractivasesprácticamenteunaobligación. Porcontra,losmodelospoligonalesrepresentanlassuperficiescurvasdemanera aproximada,comosepuedeobservarenlafigura2.1.Sinembargo,haymétodos quepermitenvisualizarunmodelopoligonaldemodoqueesteseavisualmente exacto.Porejemplo,lafigura2.2muestralarepresentaciónpoligonaldelmodelo deunacopa en la quesepuedeobservarqueelhechodequelasuperficiecurvase representemedianteunconjuntodepolígonosplanosnoimpidequelaobservemos comosideunasuperficiecurvasetratara.
2.1.Representación
Normalmentelosmodelospoligonalesrepresentanobjetosdondearistasyvérticessecompartenentrediferentespolígonos.Aestetipodemodelosselesdenominamallaspoligonales.Lafigura2.3muestravariosejemplos(modeloscortesía del StanfordComputerGraphicsLaboratory 1).Alahoradedefinirunaestructuraparalarepresentacióndemallaspoligonalesesimportantetenerencuentaesta característicaparatratardereducirelespaciodealmacenamiento,elconsumode anchodebandayeltiempodedibujado. La tabla 2.1 muestra los datos de cada uno de los modelos de la figura 2.3.
Bunny Armadillo Dragon
#Vértices 35.947 172.974 435.545

#Triángulos 69.451 345.944 871.306
Tabla2.1:Datosdelosmodelos

, Armadillo y Dragon
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
Figura2.3:Ejemplosdemallaspoligonales,deizquierdaaderecha, Bunny, Armadillo y Dragon (modeloscortesíadel StanfordComputerGraphicsLaboratory)




2.1.1.Carasindependientes
Estetipoderepresentaciónsecaracterizaporalmacenarcadatriángulode maneraindependiente,comosiestosnocompartieraninformaciónalguna.Suestructuradedatos(véaselistado2.1)secorresponderíaconunaúnicalistadetriángulos,dondeparacadatriángulosealmacenanlascoordenadasdecadaunodesus vértices,talycomosemuestraenlafigura2.4.
Listado2.1:Estructuracorrespondientealarepresentacióndecarasindependientes struct triángulo{ vector3coordenadas[3]; }Triángulos[nTriángulos];
2.1.2.Vérticescompartidos
Enestecasoseseparalainformacióndelosvérticesyladelostriángulosen doslistas(véaselistado2.2).Deestamanera,cadavérticecompartidosealmacena unaúnicavezycadatriánguloserepresentamediantetresíndicesalalistade vértices(véasefigura2.5).
La tabla 2.2 muestra que el uso de la estructura de vértices compartidos reduce a aproximadamente la mitad el coste de almacenamiendo que conlleva utilizar la estructura de caras independientes.
José Ribelles y Ángeles López
978-84-17429-87-4
Informática Gráfica (2ª edición)

http://dx.doi.org/10.6035/Sapientia151

(x5,y5,z5)(x4,y4,z4)(x3,y3,z3)
F3
F0
F1 F2
(x0,y0,z0) (x1,y1,z1) (x2,y2,z2)
Triángulos[]={{x0,y0,z0,x1,y1,z1,x3,y3,z3}, {x1,y1,z1,x4,y4,z4,x3,y3,z3}, {x1,y1,z1,x2,y2,z2,x4,y4,z4}, {x2,y2,z2,x5,y5,z5,x4,y4,z4}}
Figura2.4:Esquemadealmacenamientodeunamallapoligonalmediantelaestructuradecaras independientes
(x5,y5,z5)(x4,y4,z4)(x3,y3,z3)
F0
F1 F2
Listado2.2:Estructuracorrespondientealarepresentacióndevérticescompartidos struct vértice{ float coordenadas[3]; }Vértices[nVértices]; struct triángulo{ unsignedint índices[3]; }Triángulos[nTriángulos]; (x0,y0,z0) (x1,y1,z1) (x2,y2,z2)
Vértices[]={{x0,y0,z0}, {x1,y1,z1}, {x2,y2,z2}, {x3,y3,z3}, {x4,y4,z4}, {x5,y5,z5}}
F3 Triángulos[]={{0,1,3}, {1,4,3}, {1,2,4}, {2,5,4}}
Figura2.5:Esquemadealmacenamientodeunamallapoligonalmediantelaestructuradevértices compartidos
José Ribelles y Ángeles López ISBN: 978-84-17429-87-4
Informática Gráfica (2ª edición) DOI: http://dx.doi.org/10.6035/Sapientia151
Bunny Armadillo Dragon
Carasindependientes 2.500.236 12.453.984 31.367.016
Vérticescompartidos 1.264.776 6.227.016 15.682.212
Tabla2.2:Costesdealmacenamientoen bytes delosmodelos Bunny, Armadillo y Dragon asumiendoqueunrealdesimpleprecisiónounenteroson4 bytes
Ejercicios

2.1 Compruebaqueloscostesdealmacenamientosegúneltipodeestructurautilizada quesemuestranenlatabla2.2soncorrectosdadoslosdatosdelatabla2.1.
2.2 Obténycomparaloscostesdealmacenamientoen bytes deuntetraedroutilizando losdostiposderepresentación.Asumequealmacenarunacoordenadaouníndicecuesta 4 bytes.
2.1.3.Tirasyabanicosdetriángulos
Estostiposderepresentacióntratandeaumentarlasprestacionesdelsistema gráficocreandogruposdetriángulosquecompartenvértices.
Enelcasodeungrupodetipotiradetriángulos,losprimerostresvérticesdefinenelprimertriángulo.Cadanuevovérticedefineunnuevotriánguloutilizando esevérticeylosdosúltimosdeltriánguloanterior(véasefigura2.6derecha).
Enelcasodeungrupodetipoabanicodetriángulos,suprimervérticerepresentaaunvérticecomúnatodoslostriángulosdelmismogrupo. De nuevo, los tres primeros vértices definen el primer triángulo, pero después cada nuevo vérti ce produce que se elimine el segundo vértice del triángulo anterior y se agrege el nuevo (véase figura 2.6 izquierda).
También es posible utilizar tiras de triángulos generalizadas que permiten, por ejemplo, representar mediante una sola tira la malla de la figura 2.7. Esto se con sigue repitiendo vértices que producen a su vez triángulos degenerados (triángulos donde dos de sus vértices son el mismo).
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
AbanicoTriángulos[]={1,0,3,4,5,2}
v2
TiraTriángulos[]={0,3,1,4,2,4,5,6}
Figura2.7:Representacióndelamallamedianteunatiradetriángulosgeneralizada
La tabla 2.3 muestra para el modelo Bunny que el uso de la tira de triángulos en conjunto con la estructura de vértices compartidos reduce a aproximadamente un tercio el coste de almacenamiendo comparado con utilizar triángulos y la es tructura de caras independientes. Estos datos se han obtenido utilizando una única tira de triángulos que representa toda la malla y está compuesta por 102.997 índi ces. La tabla también muestra que, en este ejemplo, el uso de tiras de triángulos ha producido un incremento del 50% en el número de imágenes por segundo (Fps) independientemente del tipo de estructura utilizada.
Ejercicios
2.3 Obténlarepresentacióndeuntetraedromedianteunaúnicatiradetriángulos, ¿consigueshacerlosinutilizartriángulosdegenerados?Obténelcostedealmacenamiento utilizandolaestructuradevérticescompartidos,¿hasreducidoelcostealutilizarlatirade triángulosenlugardetriángulos?
José Ribelles y Ángeles López
Informática Gráfica (2ª edición)
DOI: http://dx.doi.org/10.6035/Sapientia151
2.4 Obténlarepresentacióndelasiguientemallamedianteunaúnicatiradetriángulos ycontesta,¿cuántostriángulosdegeneradoshasintroducido?
Primitiva Estructura Bytes Fps
Triángulo

Carasindependientes 2.500.236 20 Vérticescompartidos 1.264.776 20 Tiradetriángulos Carasindependientes 1.235.964 30 Vérticescompartidos 843.352 30
Tabla2.3:Costesdealmacenamientoen bytes ytasasdeimágenesporsegundo(Fps,delinglés framespersecond)delmodelo Bunny utilizandodiferentesestructurasyprimitivas
2.2.Lanormal
Unmodelopoligonal,ademásdevérticesycaras,suelealmacenarotrainformaciónamododeatributoscomoelcolor,lanormalolascoordenadasdetextura. Estosatributossonnecesariosparamejorarelrealismovisual.Porejemplo,en lafigura2.8semuestraelresultadodelavisualizacióndelmodelopoligonalde unateteraobtenidograciasaque,ademásdelageometría,sehaproporcionadola normaldelasuperficieparacadavértice.
Lanormalesunvectorperpendicularalasuperficieenunpunto.Silasuperficieesplana,lanormaleslamismaparatodoslospuntosdelasuperficie.Paraun triánguloesfácilobtenerlarealizandoelproductovectorialdedosdelosvectores directoresdesusaristas.Yaqueelproductovectorialnoesconmutativo,esmuy importanteestablecercómosevaarealizarelcálculoytambiénquelosvértices queformanlascarasseespecifiquensiempreenelmismoorden,paraasíobtener todaslasnormalesdemaneraconsistente.
y
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
José
Figura2.8:Visualizacióndelmodelopoligonaldeunatetera.Enlaimagendelaizquierdasepueden obervarlospolígonosutilizadospararepresentarla
Ejercicios

2.5 Averiguacómosabersitodaslascarasdeunamalladetriángulosestándefinidas enelmismoorden(horariooantihorario),ycómoarreglarloenelcasodeencontrarcaras definidasensentidosdistintos.
2.6 Averiguacómosabersiunamalladetriángulosescerradaosi,porcontra,presenta algúnagujerocomo,porejemplo,ocurreenlacopadelafigura2.2.
2.7 Observalasiguientedescripciónpoligonaldeunobjeto.Laslíneasquecomienzan por v secorrespondenconlosvérticeseindicansuscoordenadas.Elprimerosereferencia conelnúmero1ylosdemásseenumerandeformaconsecutiva.Laslíneasquecomienzan por f secorrespondenconlascaraseindicanquéverticesloforman. v000 v001 v101 v100 v010 v011 v111 v110 f132 f143 f125 f265 f326 f367 f347 f487 f418 f158
Dibújaloenpapel,¿quéobjetorepresenta?
¿Estántodassuscarasdefinidasenelmismoorden?
¿Enquésentidoestándefinidas,horariooantihorario?
López
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151

Obténlastirasdetriángulosquerepresentanelobjeto,¿puedesconseguirloconsolo unatira?
Calculalanormalparacadavértice,¿quéproblemaencuentras?
2.3.MallasyWebGL
Habitualmentesesueleasociarelconceptodevérticeconlascoordenadasque definenlaposicióndeunpuntoenelespacio.EnWebGL,elconceptodevérticeesmásgeneral,entendiéndosecomounaagrupacióndedatosalosquese denominanatributos. Por ejemplo, la posición y la normal son dos de los atri butos más comunes de un vértice. En cuanto al tipo de los atributos, estos pue den ser reales, enteros, vectores, etc. Y respecto al número máximo de atribu tos que un vértice puede tener en WebGL 2.0, se puede consultar con la orden gl.getParameter(gl.MAX_VERTEX_ATTRIBS) que habitualmente retor na 16 (que es el valor mínimo establecido por el estándar).
WebGLnoproporcionamecanismosparadescribiromodelarobjetosgeométricoscomplejos,sinoqueproporcionamecanismosparaespecificarcómodichos objetosdebenserdibujados.Esresponsabilidaddelprogramadordefinirlasestructurasdedatosadecuadasparaalmacenarladescripcióndelobjeto.Sinembargo, comoWebGLrequierequelainformaciónquevayaavisualizarsesedispongaen vectores,lohabitualesutilizartambiénvectoresparaalmacenarlosvértices(sus atributos)yutilizaríndicesadichosvectoresparadefinirlasprimitivasgeométricas (véaselistado2.3).
Listado2.3:ModelodeuncubodefinidocontriángulosdispuestoparaserutilizadoconWebGL varexampleCube={
"vertices":[ 0.5, 0.5,0.5, 0.5, 0.5,0.5, 0.5,0.5,0.5, 0.5,0.5,0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5,0.5, 0.5, 0.5,0.5, 0.5],
"indices":[0,1,2,0,2,3, 1,5,6,1,6,2, 3,2,6,3,6,7, 5,4,7,5,7,6, 4,0,3,4,3,7, 4,5,1,4,1,0]
2.3.1.Preparaciónydibujado
Enprimerlugar,elmodelopoligonalsehadealmacenaren bufferobjects.Un bufferobject noesmásqueunaporcióndememoriareservadadinámicamentey controladaporelpropioprocesadorgráfico.Siguiendoconelejemplodellistado 2.3senecesitandos buffers,unoparaelvectordevérticesyotroparaeldeíndices. Despuéshayqueasignaracada buffer susdatoscorrespondientes.Ellistado2.4 recogeestasoperacionesenlafunción initBuffers,examínaloyacudealaespecificacióndellenguajeparaconocermásdetallesdelasfuncionesutilizadas.
Ellistado2.5muestraelcódigo HTML queincluyedos scripts,unoparacada tipode shader,eldevérticesyeldefragmentos.Observaqueenel shader de vérticessedefineunúnicoatributodeposiciónparacadavértice (utilizando la pa labra clave in).Elsegundopasoconsisteenobtenerlosíndicesdelasvariables del shader querepresentanlosatributosdelosvértices(quedemomentoessolola posición)yhabilitarelvectorcorrespondiente.Estasoperacionessemuestranenel listado2.4ysehanincluidoalfinaldelafunción initShaders,queeslaencargada decompilar,enlazarycrearunejecutabledel shader
Una vezqueelmodeloyaseencuentraalmacenadoenlamemoriacontrolada porla GPU,el shader yaestácompiladoyenlazado,ylosíndicesdelosatributos delosvérticesyasehanobtenido,soloquedaelúltimopaso:suvisualización. Primero,hayqueindicarlos buffers quecontienenlosvérticesylosíndicescorrespondientesalmodeloquesevaavisualizar.Tambiénhayqueespecificarcómose encuentrandispuestoscadaunodelosatributosdelosvérticesenel buffer correspondiente.Despuésyasepuedeordenareldibujado,indicandotipodeprimitiva ynúmerodeelementos.Losvérticesseprocesarándemaneraindependiente,pero siempreenelordenenelquesonenviadosalprocesadorgráfico.Estasoperaciones semuestranenellistado2.4,enlafunción draw.Denuevo,acudealaespecificacióndellenguajeparaconocermásdetallesdelasórdenesutilizadas.
2.3.2.Tiposdeprimitivasgeométricas
LasprimitivasbásicasdedibujoenWebGLsonelpunto,elsegmentodelínea yeltriángulo.Cadaprimitivasedefineespecificandosusrespectivosvértices,y estasseagrupanasuvezparadefinirobjetosdemayorcomplejidad.EnWebGL, laprimitivageométricaseutilizaparaespecificarcómohandeseragrupadoslos vérticestrasseroperadosenelprocesadordevérticesyasípoderservisualizada.
Sonlassiguientes:
Dibujodepuntos:
• Secuenciaotiradesegmentos:gl.LINE_STRIP
• Secuenciacerradadesegmentos:gl.LINE_LOOP
Triángulos:
• Triángulosindependientes:gl.TRIANGLES
• Tiradetriángulos:gl.TRIANGLE_STRIP
• Abanicodetriángulos:gl.TRIANGLE_FAN
Ejercicios
2.8 ¿Cuántostriánguloscreesquesepintaríanconlasiguienteorden?(tenencuenta quealtratarsedeunatirapuedenhabertriángulosdegenerados)
gl.drawElements(gl.TRIANGLE_STRIP,30,gl.UNSIGNED_SHORT,12)
2.9 Abreconelnavegadorelarchivo c02/dibuja.html,queincluyeelcódigodellistado 2.5,ycargaasuveza c02/dibuja.js,quecontieneelcódigodellistado2.4.¿Quéobjetose muestra?
2.10 Sustituyeelmodelodeltriánguloen dibuja.js porelmodelodelpentágonoque semuestraacotinuación:
varexamplePentagon={
"vertices":[0.0,0.9,0.0, 0.95,0.2,0.0, 0.6, 0.9,0.0, 0.6, 0.9,0.0, 0.95,0.2,0.0], "indices":[0,1,2,3,4]
};
Ahoradibújaloutilizandopuntosprimeroydespuéslíneas:
Puntos: gl.drawElements(gl.POINTS,5,gl.UNSIGNED_SHORT,0);.Si noerescapazdedistinguirlospuntosañadeenlafunción main del shader devértices: gl_PointSize=5.0;
Líneas: gl.drawElements(gl.LINE_LOOP,5,gl.UNSIGNED_SHORT,0);
2.11 Realiza las modificaciones necesarias para pintar el pentágono del ejercicio an terior como triángulos independientes. De esta manera pasarás a verlo relleno (en lugar de solo sus aristas). Piensa primero y haz los cambios después, y recuerda que
1. Aunque los vértices son los mismos, tendrás que modificar el vector de índices para ahora especficar los triángulos.
2. Los valores de los parámetros de la orden drawElements van a cambiar.
José Ribelles y Ángeles López
ISBN: 978-84-17429-87-4
Informática Gráfica (2ª edición)
DOI: http://dx.doi.org/10.6035/Sapientia151
2.12 Continúautilizandolosmismosvérticesdelmodelodelpentágonoyrealiza lasmodificacionesnecesariasparaobtenerunaestrellacomoladelafigura2.9.Prueba tambiénacambiarelgrosordeltrazomediantelaorden gl.lineWidth(5.0) justo antesdeordenareldibujadodelageometría (esto no funciona en Windows).
Figura2.9:Estrelladibujadaapartirdelosvérticesdeunpentágono


2.13 Utilizaahoraladescripcióndelosvérticesquefiguraacontinuación.Creauna funciónquesellame drawGeometryLines yqueutilizandodichosvérticesdibujelaestrella conlíneasdemaneraqueseobtengaelresultadodelafigura2.10(imagendelaizquierda). Creaotrafunciónquesellame drawGeometryTriangles yquedibujelaestrellamediante triángulosindependientesdemaneraqueseobtengaelresultadoquesemuestraenlafigura 2.10(imagendeladerecha).

"vertices":[0.0,0.9,0.0, 0.95,0.2,0.0, 0.6, 0.9,0.0, 0.6, 0.9,0.0, 0.95,0.2,0.0, 0.0, 0.48,0.0, 0.37, 0.22,0.0, 0.23,0.2,0.0, 0.23,0.2,0.0, 0.37, 0.22,0.0],
Figura2.10:Estrelladibujadaconlíneas(izquierda)ycontriángulos(derecha)
Informática
Listado2.4:Códigomínimoquesecorrespondeconlaestructurabásicadeunprogramaqueutiliza WebGL(disponibleen c02/dibuja.js) vargl,program; varexampleTriangle={
"vertices":[ 0.7, 0.7,0.0, 0.7, 0.7,0.0, 0.0,0.7,0.0], "indices":[0,1,2]
};
functiongetWebGLContext(){
varcanvas=document.getElementById("myCanvas"); try{ return canvas.getContext("webgl2"); } catch(e){ } return null; } functioninitShaders(){
varvertexShader=gl.createShader(gl.VERTEX_SHADER); gl.shaderSource(vertexShader, document.getElementById("myVertexShader").text); gl.compileShader(vertexShader);
varfragmentShader=gl.createShader(gl.FRAGMENT_SHADER); gl.shaderSource(fragmentShader, document.getElementById("myFragmentShader").text); gl.compileShader(fragmentShader);
program=gl.createProgram(); gl.attachShader(program,vertexShader); gl.attachShader(program,fragmentShader); gl.linkProgram(program); gl.useProgram(program);
//Obtenerlareferenciadelatributoposición program.vertexPositionAttribute= gl.getAttribLocation(program,"VertexPosition");
//Habilitarelatributoposición gl.enableVertexAttribArray(program.vertexPositionAttribute);
José Ribelles y Ángeles López
Informática Gráfica (2ª edición) DOI: http://dx.doi.org/10.6035/Sapientia151
functioninitBuffers(model){
//Bufferdevértices
model.idBufferVertices=gl.createBuffer(); gl.bindBuffer(gl.ARRAY_BUFFER,model.idBufferVertices); gl.bufferData(gl.ARRAY_BUFFER, newFloat32Array(model.vertices),gl.STATIC_DRAW);
//Bufferdeíndices
model.idBufferIndices=gl.createBuffer(); gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER,model.idBufferIndices); gl.bufferData(gl.ELEMENT_ARRAY_BUFFER, newUint16Array(model.indices),gl.STATIC_DRAW); }
functioninitRendering(){ gl.clearColor(0.15,0.15,0.15,1.0); }
functiondraw(model){
gl.bindBuffer(gl.ARRAY_BUFFER,model.idBufferVertices); gl.vertexAttribPointer(program.vertexPositionAttribute,3, gl.FLOAT,false,0,0);
gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER,model.idBufferIndices); gl.drawElements(gl.TRIANGLES,3,gl.UNSIGNED_SHORT,0); }
functiondrawScene(){ gl.clear(gl.COLOR_BUFFER_BIT); draw(exampleTriangle); } functioninitWebGL(){ gl=getWebGLContext(); if (!gl){ alert("WebGL2.0noestádisponible"); return ; }
initShaders(); initBuffers(exampleTriangle); initRendering(); requestAnimationFrame(drawScene);
} initWebGL();
José Ribelles y Ángeles López
Informática Gráfica (2ª edición) DOI: http://dx.doi.org/10.6035/Sapientia151
Listado2.5:Código HTML queincluyeuncanvasylosdos shaders básicos(disponibleen c02/dibuja.html) <!DOCTYPEhtml> <html>
<head> <metacharset="utf 8"> <title>Dibuja</title> <styletype="text/css"> canvas{border:1pxsolidblack;} </style>
<scriptid="myVertexShader" type="x shader/x vertex">#version300es invec3 VertexPosition; void main(){ gl_Position= vec4 (VertexPosition,1.0);
}
</script>
<scriptid="myFragmentShader" type="x shader/x fragment">#version300es precisionmediump float ; outvec4 fragmentColor; void main(){ fragmentColor= vec4 (0.0,1.0,0.0,1.0);
}
</script> </head> <body>
<canvasid="myCanvas"width="600"height="600"> ElNavegadornosoportaHTML5 </canvas>
<scriptsrc="dibuja.js"></script> </body> </html>
José Ribelles y Ángeles López ISBN: 978-84-17429-87-4
Informática Gráfica (2ª edición) DOI: http://dx.doi.org/10.6035/Sapientia151
2.3.3.Variables uniform
Imaginaque,porejemplo, quieres que el color de la estrella de los ejercicios an teriores no sea fijo sino que pueda cambiarse de forma dinámica. Paraconseguirlo esnecesarioqueelcolorquefiguraenel shader defragmentosseaunavariable, talycomosemuestraenellistado2.6.
Listado2.6:Ejemplodevariable uniform enel shader defragmentos
#version300es
precisionmediump float ; uniformvec4 myColor; outvec4 fragmentColor;
void main(){
fragmentColor=myColor;
}
Lavariable myColor esdetipo uniform porquesuvalorseráconstantepara todoslosfragmentosquerecibaprocedentesdeprocesarlaestrella,perosepuede hacerqueseadiferenteparacadaestrellacambiandosuvalorantesde ordenar su dibujado.Observaelfragmentodecódigodellistado2.7.Esaslíneassonlas encargadasdeobtenerelíndicedelavariable myColor enel shader ydeespecificar suvalor.Mientrasquelaprimeralíneasoloesnecesarioejecutarlaunavez,la segundahabráqueutilizarlacadavezquesenecesiteasignarunnuevovalora lavariable myColor.Así,laprimeralíneasepodríaañadiralfinaldelafunción initShaders,mientrasquelasegundalíneahabráqueañadirlajustoantesdeordenar eldibujadodelmodelo.
Listado2.7:Obtienelareferenciayestableceelvalordelavariable uniform myColor varidMyColor=gl.getUniformLocation(program,"myColor"); gl.uniform4f(idMyColor,1.0,0.0,1.0,1.0);
Ejercicios
2.14 Dibujadosestrellas de colores distintos,unaparapintarelinteriorylaotrapara pintarelborde(véasefigura2.11).Elijecoloresquecontrastenentresí.Tenencuenta tambiénqueelordendedibujadoesimportante,piensaquéestrelladeberíasdibujaren primerlugar.Nota:puedesdefinirdosvectoresdeíndices,cadaunoconunnombredistinto, ycrearun buffer adicionalenlafunción initBuffers
José Ribelles y Ángeles López
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
Figura2.11:Ejemplodedosestrellas:unaaportaelcolorinteriorylaotraelcolordelborde
2.3.4.Variables out
Hasta el momento, cada vértice consta de un único atributo: su posición. Ahora se va a añadir un segundo atributo, por ejemplo, un valor de color para cada vértice. En primer lugar hay que ampliar la información de cada vértice para contener su valor de color. El listado 2.8 muestra el modelo de un triángulo tras añadir las cua tro componentes de color (RGBA) a cada vértice. También es necesario habilitar los dos atributos correspondientes, tal y como se muestra en el listado 2.9. Estúdialo y contesta a esta pregunta, ¿dónde colocarías este código en el listado 2.4?
Listado2.8:Ejemplodemodelocondosatributosporvértice:posiciónycolor varexampleTriangle={

"vertices":[ 0.7, 0.7,0.0,1.0,0.0,0.0,1.0, //rojo 0.7, 0.7,0.0,0.0,1.0,0.0,1.0, //verde 0.0,0.7,0.0,0.0,0.0,1.0,1.0], //azul "indices":[0,1,2]
};
Listado2.9:Localizaciónyhabilitacióndelosdosatributos:posiciónycolor program.vertexPositionAttribute= gl.getAttribLocation(program,"VertexPosition"); gl.enableVertexAttribArray(program.vertexPositionAttribute); program.vertexColorAttribute= gl.getAttribLocation(program,"VertexColor"); gl.enableVertexAttribArray(program.vertexColorAttribute);
José Ribelles y
López
Informática Gráfica (2ª edición) DOI: http://dx.doi.org/10.6035/Sapientia151
Listado2.10:Ejemplode shader condosatributosporvértice:posiciónycolor
# version300es //Shaderdevértices
invec3 VertexPosition; invec4 VertexColor; outvec4 colorOut;
void main(){
colorOut=VertexColor; gl_Position= vec4 (VertexPosition,1.0); }
# version300es //Shaderdefragmentos precisionmediump float ;
invec4 colorOut; outvec4 fragmentColor;

void main(){
fragmentColor=colorOut; }
Los cambios correspondientes al shader se recogen en el listado 2.10. Observa que ahora están declarados en el shader de vértices los dos atributos de tipo in, VertexPosition y VertexColor Por otra parte, la variable colorOut, en el shader de vértices, se ha declarado como variable de salida mediante la pala bra clave out A la variable colorOut simplemente se le asigna el valor de color por vértice representado con el atributo VertexColor Las variables declaradas como variables de salida en el shader de vértices deben estar declaradas con el mismo nombre en el shader de fragmentos como variables de entrada (utilizando la palabra clave in) y serán interpoladas linealmente en el proceso de rasteriza ción. También la variable fragmentColor es de tipo out y contiene el color de salida del shader de fragmentos. La figura 2.12 muestra el resultado.
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
Porúltimo,hayquemodificarlafuncióndedibujo.Observalanuevafunción enellistado2.11querecogeloscambiosnecesarios.Prestaatenciónalosdos últimosparámetrosdelasdosllamadasa gl.vertexAttribPointer.Consultaladocumentaciónparaentenderelporquédeesosvalores.
Listado2.11:Dibujodeunmodelocondosatributosporvértice functiondraw(model){
gl.bindBuffer(gl.ARRAY_BUFFER,model.idBufferVertices);
gl.vertexAttribPointer(program.vertexPositionAttribute,3, gl.FLOAT,false,7 ∗ 4,0);
gl.vertexAttribPointer(program.vertexColorAttribute,4, gl.FLOAT,false,7 ∗ 4,3 ∗ 4);
gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER,model.idBufferIndices); gl.drawElements(gl.TRIANGLES,3,gl.UNSIGNED_SHORT,0); }
Ejercicios
2.15 ¿Cuál es el número mínimo de buffers que necesitas en WebGL para almace nar un modelo poligonal que utiliza la representación de vértices compartidos si para cada vértice almacenas los atributos de posición y normal?
2.16 Observalaimagendelafigura2.13,¿quécoloressehanasignadoalosvértices? Edita c02/interpola.js,queyaincluyelosfragmentosdecódigoquesehanexplicadoen estasección,ymodificalosvaloresdecolorparaobteneresemismoresultado.Cargaenel navegador c02/interpola.html paracomprobarsihasacertado.
Figura2.13:Observaeltriánguloycontesta,¿quécolorsehaasignadoacadavértice?

2.17 Simodificaselprograma interpola paraquesemuestreunaestrellaconcolor amarilloenlascincopuntasycolorazulenelrestodevértices,¿quéresultadocreesquese obtendrá?Hazloscambiosoportunosycompruebasielresultadocoincideconelesperado. Pruebatambiénacambiarloscoloresdelosvérticesdelaspuntas,ydelosotrostambién, conloscoloresquetúelijas,experimenta,yobténunacombinaciónqueseadetuagrado.
José Ribelles y Ángeles López
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
CUESTIONES
2.1 Algunosconceptosrelacionadosconlosmodelospoligonalesson:teselado,triangularización,simplificaciónyoptimización.Averiguaelsignificadodedichosconceptos. Ponalgúnejemplodonderesulteinteresanteaplicarcadaunodeellos.
2.2 ¿Porquéesimportantehacerquetodaslascarasdeunamallapoligonalestén orientadasdelamismaforma?
2.3 ¿Porquéesimportantesabersiunmodelopoligonalescerrado(quenopresenta agujeros)?
2.4 ¿Quéesunatiradetriángulos?
2.5 Supónquetienesdostirasdetriángulosdondecadatirarepresentauntrozodiferentedelasuperficiedeunmodelo,ynohayvérticesencomúnentreambastiras.La primeratiraestáformadaporlasiguientesecuenciadeíndices:10,11,12,13y14.Y lasegundatirapor:20,21,22y23.Sideseasunirambastirasparatenerunaúnicatira detriángulos,uniendoelfinaldelaprimeratiraconeliniciodelasegunda,determinala secuenciacompletadeíndices: 10, 11, 12, 13, 14,..., 20, 21, 22, 23.
2.6 ¿Quéesun bufferobject?
2.7 ¿Cuántos bufferobjects necesitascomomínimoparaalmacenarunmodelopoligonal?¿Porqué?
2.8 ¿Quésignificaelsegundoparámetrodelaorden drawElements sielprimero es gl.LINES?
2.9 Paraelmodelodeunhexágono,¿quévaloreseladecuadoparaelsegundoparámetrodelaorden drawElements paraloscasosenlosqueelprimerosea gl.LINES, gl.LINE_STRIP y gl.LINE_LOOP?
2.10 ¿Quésignificaqueunavariablesea uniform?
2.11 ¿Quésignificaqueunavariableseadetipo in enel shader devértices?¿Puede haberunavariabledetipo in enel shader defragmentos?
2.12 Sitienesunavariable uniform paraespecificarelcolordedibujodelmodelode unaestrella,enelcasodequererdibujarvariasestrellasperotodasellasdelmismocolor, ¿esnecesariollamara gl.uniform antesdeordenarcadadibujado?
2.13 Siañadesunnuevoatributoporvértice,¿cómoespecificaslosvaloresparaeste nuevoatributoenelmodelo?
2.14 ¿Quéesunavariabledetipo out cuandoestaapareceenel shader devértices? ¿Yquésignificacuandoapareceenel shader defragmentos?¿Creesqueesposibleque hayamásdeunavariabledetipo out enel shader devértices?¿Yeneldefragmentos?
2.15 ¿Esposibleestablecerelvalordeunavariabledetipo out como,porejemplo,se haceconlasvariables uniform?
2.16 Sitienesvariosatributosporvértice,¿cómoobtieneslosdosúltimosparámetros delaorden vertexAttribPointer?
José Ribelles y Ángeles López
978-84-17429-87-4
Informática Gráfica (2ª edición)
DOI: http://dx.doi.org/10.6035/Sapientia151
Transformacionesgeométricas


sistemadecoordenadasconocidocomosistemadecoordenadasdelmundo.Este cambiodesistemadecoordenadasesnecesarioyserealizamediantetransformacionesgeométricas.Lafigura3.1muestraalgunosejemplosdeobjetosobtenidos mediantelaaplicacióndetransformacionesaprimitivasgeométricassimplescomo

Latransformacióndetraslaciónconsisteendesplazarelpunto
Latransformacióndeescaladoconsisteenmultiplicarelpunto
Ejercicios
Latransformaciónderotacióngiraunpuntounángulo
Unagranventajadelusodelastransformacionesgeométricasensuformamatricialconcoordenadashomogéneasesquesepuedenconcatenar.Deestamanera, unasolamatrizpuederepresentartodaunasecuenciadematricesdetransformación.
Cuandoserealizalaconcatenacióndetransformaciones,esmuyimportante operarlasecuenciadetransformacionesenelordencorrecto,yaqueelproducto dematricesnoposeelapropiedadconmutativa.
Porejemplo,piensaenunaesferaconradiounaunidadcentradaenelorigende coordenadasyenlasdossiguientesmatricesdetransformación T y S: T (5, 0, 0) desplazalacomponente x cincounidades; S(5, 5, 5) escalalastrescomponentes conunfactordecinco.Ahora,dibujaenelpapelcómoquedaríalaesferadespués deaplicarlelamatrizdetransformación
silasmatricessemultiplicandelasdos
(2ª edición)
formasposibles,esdecir, M = T S y M = S T .Comoverás,losresultadosson bastantediferentes.
Porotraparte,elproductodematricessíqueposeelapropiedadasociativa. Estosepuedeaprovecharparareducirelnúmerodeoperaciones,aumentandoasí laeficiencia.
3.3.Matrizdetransformacióndelanormal
Lamatrizdetransformacióndelmodeloesconsistenteparageometríaypara vectorestangentesalasuperficie.Sinembargo,dichamatriznosiempreesválida paralosvectoresnormalesalasuperficie.Enconcreto,estoocurrecuandoseutilizantransformacionesdeescaladonouniforme(véasefigura3.2).Enestecaso,la matrizdetransformacióndelanormal N eslatraspuestadelainversadelamatriz detransformacióndelmodelo:
N =(M 1)T (3.9)
Además,comolanormalesunvectorylatraslaciónnoleafecta(yelescalado ylarotaciónsontransformacionesafines),solohayque tomarlos 3 × 3 componentessuperiorizquierdade M
Antes de la transformación Después de la transformación Y
Y X1
1
X
1n p m 2 Figura3.2:Enlaimagendelaizquierdaserepresentadeperfilunpolígonoysunormal n.Enla imagendeladerechasemuestraelmismopolígonotrasaplicarunatransformacióndeescaladono uniforme S(2, 1).Siseaplicaestatransformaciónalanormal n,seobtiene p comovectornormal enlugarde m,queeslanormalcorrecta
Señalarporúltimoque,despuésdeaplicarlatransformación,yúnicamenteen elcasodeincluirescalado,laslongitudesdelasnormalesnosepreservan,porlo queesnecesarionormalizarlas.Comoestaoperaciónescaracomputacionalmente, ¿seteocurrealgunamaneradeevitarla?
José Ribelles y Ángeles López
Informática Gráfica (2ª edición)
DOI: http://dx.doi.org/10.6035/Sapientia151
José
Ejercicios
Enlossiguientesejercicioseleje X eseldecolorrojo,el Y eseldecolorverdeyel Z eseldecolorazul.
3.2 Comienzaconuncubodeladounocentradoenelorigendecoordenadas,taly comosemuestraenlafigura(a).Usadoscubosmáscomoesteyobténelmodeloquese muestraenlafigura(b),dondecadanuevocubotieneunalongituddelladolamitaddela delcuboanterior.Detallalastransformacionesutilizadas.

3.3 Determinalastransformacionesquesitúanelconoquesemuestraenlafigura(c) (radiodelabaseyalturadevalor1)enlaposiciónquesemuestraenlafigura(d)(radio delabasedevalor1yalturadevalor3).Tenencuentaelpuntodereferencia P señalado conunaflecha,demaneraquequedeubicadotalycomoseobservaenlafigura.
Informática Gráfica (2ª edición)


http://dx.doi.org/10.6035/Sapientia151

3.4 Comienzaconunaesferaderadiounocentradaenelorigendecoordenadas.La figura(e)muestralaesferaescaladaconfactoresdeescala
=0 5 y sz =3.Obtén lastransformacionesquesituanalaesferatalycomosemuestraenlafigura(
),dondeun puntofinalestáenelorigenyelotroenlarecta
3.5 Observalaposicióninicialdelobjetoenlafiguradelaizquierda.Esteobjetolo vasautilizardosvecesparacrearelbrazoarticuladoquesemuestraenlafiguradela derecha.Determinalastransformacionesquehasdeaplicarle.Laposiciónfinaldelbrazo hadedependerdelosángulos alfa
Informática Gráfica (2ª edición)



http://dx.doi.org/10.6035/Sapientia151

Sean d y φ elvectorunitariodelejedegiroyelángulodegiro,respectivamente. Pararealizarlarotaciónhayquecalcularenprimerlugarunabaseortogonalque contenga d.Laideaeshaceruncambiodebaseentrelabasequeformanlosejes decoordenadasylanuevabase,haciendocoincidirelvector d con,porejemplo, eleje X,paraentoncesrotar φ gradosalrededorde X yfinalmentedeshacerel cambiodebase.
Lamatrizquerepresentaelcambiodebaseesesta:
donde e esunvectorunitarionormala d,y f eselproductovectorialdelosotros dosvectores f = d × e.Estamatrizdejaalvector d eneleje X,alvector e eneleje Y yalvector f eneleje Z (véasefigura3.3).Elvector e sepuede obtenerdelasiguientemanera:partiendodelvector d,hazcerosucomponente demenormagnitud(elmáspequeñoenvalorabsoluto),intercambialosotrosdos componentes,niegaunodeellosynormalízalo.
Figura3.3:Lanuevabaseformadaporlosvectores d, e y f setransformaparacoincidirconlosejes decoordenadas
Así,teniendoencuentaque R esortogonal,esdecir,quesuinversacoincide conlatraspuesta,lamatrizderotaciónfinales:
3.5.Labiblioteca GLMATRIX
Comoayudaalaprogramación,labiblioteca GLMATRIX proporcionafuncionestantoparalaconstruccióndelasmatricesdetransformacióncomoparaoperar conellas.Enconcreto,lassiguientesfuncionespermitenconstruir,respectivamente,lasmatricesdetraslación,escaladoygiroalrededordeunejearbitrarioquepasa porelorigen:
José Ribelles y Ángeles López
978-84-17429-87-4
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
mat4.fromTranslation (out, v)
mat4.fromScaling (out, v)
mat4.fromRotation (out, rad, axis)
Ejercicios
3.6 Accedealapáginaweb glmatrix.net.Vealadocumentacióny,porejemplo,buscaelmétodo fromTranslation delaclase mat4.Lapropiaayudatepermite accederalcódigofuentedelalibrería.Vealcódigodelmétodo fromTranslation y compruebacómoconstruyelarespectivamatrizdetransformación.
Porejemplo,lamatrizdetransformación M queescalaunobjetoaldoblede sutamañoydespuéslotrasladaendireccióndeleje X untotaldediezunidades, seobtendríadelasiguienteforma:
varM= mat4 .create(); varT= mat4 .create(); varS= mat4 .create(); mat4 .fromTranslation(T,[10,0,0]); mat4 .fromScaling(S,[2,2,2]); mat4 .multiply (M,T,S);
Ejercicios
3.7 ¿Quétransformaciónproducessienelejemploanterior,envezde mat4.multiply(M,T,S),apareciese mat4.multiply(M,S,T)?
Si M es la matriz de transformación del modelo, para obtener la matriz de transformación de la normal, N , utilizando GLMATRIX se puede hacer, por ejem plo, lo siguiente:
varN= mat3 .create(); mat3 .fromMat4(N,M); mat3 .invert(N,N); mat3 .transpose(N,N);
GLMATRIX también porporciona la función normalFromMat4(N, M) que realiza exactamente las mismas operaciones que las del listado anterior.
José Ribelles y Ángeles López
978-84-17429-87-4
Informática Gráfica (2ª edición)
DOI: http://dx.doi.org/10.6035/Sapientia151
3.6.TransformacionesenWebGL
WebGLnoproporcionamodelosdeprimitivasgeométricas3D.Porlotanto, yenprimerlugar,esnecesarioobtenerunadescripcióngeométricadeprimitivas básicascomoelcubo,laesfera,elcono,etc.Porejemplo,ellistado2.3(delcapítulo anterior)muestraelfragmentodecódigoquedefineuncubodelado1centrado enelorigendecoordenadas,consuscarasparalelasalosplanosdereferencia XY,XZeYZ.Observaqueestemodeloconstadedosvectores,unocontienelas coordenadasdelosvérticesyelotrocontienelosíndicesalvectordevértices quedetresentresdescribenlostriángulos.Elíndicedelprimervérticees0.De momentoseutilizanmodelosquesoloconstandegeometría,esdecir,nocontienen otrosatributos(normal,color,etc.),porloquevamosavisualizarlosenalambre, esdecir,sololasaristas(véaselistado3.1).
Listado3.1:Visualizaciónenalambredeunmodelopoligonaldefinidocontriángulosindependientes functiondraw(model){
gl.bindBuffer(gl.ARRAY_BUFFER,model.idBufferVertices); gl.vertexAttribPointer(vertexPositionAttribute,3, gl.FLOAT,false,0,0);
gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER,model.idBufferIndices); for (vari=0;i<model.indices.length;i+=3) gl.drawElements(gl.LINE_LOOP,3,gl.UNSIGNED_SHORT,i ∗ 2);
}
Observaahoralanuevafunción drawScene() enellistado3.2. Esta función incluye ahora los tres pasos necesarios para dibujar un modelo que requiere de una matriz de transformación:
1. Se obtiene la matriz de transformación del modelo, modelMatrix, que en este caso se trata de un escalado a la mitad de su tamaño.
2. Se establece el valor de la matriz de transformación en el shader de vértices.
3. Se ordena el dibujado del modelo. Será entonces cuando cada vértice del mo delo se multiplique por la matriz de transformación especificada en el paso anterior.
El listado 3.2 también muestra comentadas las líneas que permiten obtener la matriz de la normal a partir de la matriz de transformación. Esta matriz también es enviada al shader de vértices para que sea operada con el atributo correspondiente.
En el shader de vértices se incluye la operación que multiplica cada vértice por su correspondiente matriz de transformación (véase listado 3.3).Observaque laslíneascomentadascorrespondenalcódigoqueharíafaltaenelcasodeque, además,sesuministraraelatributodelanormalparacadavértice.
José Ribelles y Ángeles López
Informática Gráfica (2ª edición)
DOI: http://dx.doi.org/10.6035/Sapientia151
Listado3.2:Ejemplodelospasosnecesariosparadibujarunobjetotransformado functiondrawScene(){
gl.clear(gl.COLOR_BUFFER_BIT);
//1.calculalamatrizdetransformación varmodelMatrix= mat4 .create(); mat4 .fromScaling(modelMatrix,[0.5,0.5,0.5]);
//2.establecelamatrizmodelMatrixenelshaderdevértices gl.uniformMatrix4fv(program.modelMatrixIndex,false, modelMatrix);
//paralamatrizdelanormal: //varnormalMatrix=mat3.create(); //mat3.normalFromMat4(normalMatrix,modelMatrix); //gl.uniformMatrix3fv(program.normalMatrixIndex,false, normalMatrix);
//3.dibujalaprimitiva draw(exampleCube);
}
Listado3.3: Shader devérticesqueoperacadavérticeconlamatrizdetransformacióndelmodelo # version300es uniformmat4 M; //matrizdetransformacióndelmodelo //uniformmat3N;//matrizdetransformacióndelanormal
invec3 VertexPosition; //invec3VertexNormal; //outvec3VertexNormalT;
void main(){
//VertexNormalT=normalize(N ∗ VertexNormal); gl_Position=M ∗ vec4 (VertexPosition,1.0);
}
José Ribelles y Ángeles López ISBN: 978-84-17429-87-4
Informática Gráfica (2ª edición) DOI: http://dx.doi.org/10.6035/Sapientia151
Ejercicios
3.8 Edita c03/transforma.html y c03/transforma.js.Compruebaquesehanincluido todosloscambiosexplicadosenestasección.Observatambién common/primitivasG.js, queincluyelosmodelosdealgunasprimitivasgeométricassimples.Echaunvistazoala descripcióndelosmodelos.Pruebaavisualizarlasdiferentesprimitivas.
3.9 Se dispone del modelo de un cubo definido con su centro en el origen de coordena das, lado 1, y sus aristas paralelas a los ejes de coordenadas. Dado el siguiente fragmento de código en el que se especifican una serie de transformaciones geométricas, dibuja una vista frontal XY (no hace falta que dibujes la Z) de cómo quedan los dos cubos que se ordena dibujar teniendo en cuenta dichas transformaciones (asume que la funcion drawCubo() produce el dibujado del modelo del cubo).

varS= mat4 .create();
varT1= mat4 .create();
varT2= mat4 .create(); varM= mat4 .create();
mat4 .fromScaling(S,[1,2,1]); mat4 .fromTranslation(T1,[0,0.5,0]); ma4.multiply(M,S,T1); gl.uniformMatrix4fv(program.modelMatrixIndex,false,M); drawCubo();

mat4 .fromTranslation(T2,[1,0,0]); ma4.multiply(M,M,T2); gl.uniformMatrix4fv(program.modelMatrixIndex,false,M); drawCubo();
3.10 Observalaescenaquesemuestraenlafigura3.4.Creaunaescenaqueproduzca lamismasalidautilizandoúnicamentelaprimitivacubo.Enprimerlugar,piensasobreel papelquétransformacionesnecesitasaplicarysolodespuésprocedeconlaescrituradel código.Elcubocentraltienedelado 0 1,ylosqueestánasuladotienenlamismabase perounaalturaquevaincrementándoseen 0 1 amedidaquesealejandelcentral.Usaun bucleparapintarlostrececubos. Nota: ambasimágenesmuestranlamismaescena,pero enlaimagendeladerechasehagiradolaescenaparaapreciarmejorquesonobjetos3D.
Figura3.4:Escenamodeladaapartirdelaprimitivageométricacubo
3.11 Modelalatípicagrúadeobracuyoesquemasemuestraenlafigura3.5utilizando comoúnicaprimitivacubosdelado1centradosenelorigendecoordenadas.Lacargaes delado 1,elcontrapesoesdelado 1 4,ytantoelpiecomoelbrazotienen 10 delongitud.
José Ribelles y Ángeles López
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
Incluyelastransformacionesquegiranlagrúasobresupie,quedesplazanlacargaalo largodelbrazo,yquelevantanydesciendenlacarga.
Figura3.5:Ejemplodeunagrúadeobramodeladaconcubosytransformacionesgeométricas
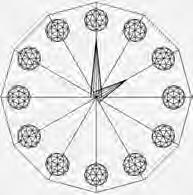
3.12 En este ejercicio vas a hacer un tanque. En la figura 3.6 puedes observar lo que has de conseguir. Los cilindros de las ruedas tienen una altura de 0 8 y un radio de 0 1 Tapa los cilindros por ambos lados. El cuerpo del tanque es un cubo escalado para ocupar lo mismo que las ruedas, y una altura de 0.2 La torreta del cañón es un cilindro de radio 0 2 y altura 0 8 Observa dónde está situada y haz coincidir la tuya en la misma posición. Tápala también. Por último, añade el cañón, que es un cilindro de longitud 0 8 y radio 0 03
Figura3.6:Tanquemodeladoapartirdediferentesprimitivasgeométricas



3.13 Crea un reloj como el de la figura 3.7. No te doy dimensiones, elígelas tú. Imítalo en la medida de lo posible. Sí que te pido que marque las dos en punto.
Figura3.7:Relojmodeladoapartirdeprimitivasgeométricasbásicas
José Ribelles y Ángeles López
Informática Gráfica (2ª edición) DOI: http://dx.doi.org/10.6035/Sapientia151
3.14 Indica la secuencia de transformaciones que debes aplicar a un cubo centrado en el origen de coordenadas (y sus lados paralelos a los ejes de coordenadas) para que gire 30 grados alrededor de su diagonal (del ( 1, 1, 1) al (1,1,1)). Solo puedes usar giros alrededor de los ejes de coordenadas.

3.15 Internetesunafuentedeinspiraciónexcepcional,utilízalaparabuscarejemplos quetesirvandemuestraypracticarconelusodelastransformacionesgeométricas.Fíjate enlosqueaparecenenlafigura3.8.

Figura3.8:Otrosejemplosdejuegosdebloquesdemaderacoloreados
CUESTIONES
3.1 ¿Quéeslamatrizdetransformacióndelmodelo?
3.2 ¿Dóndeoperaslamatrizdetransformacióndelmodeloconcadaunodesusvértices?
3.3 ¿Porquéenel shader sedeclaralamatrizdetransformacióndelmodelodetipo uniform?
3.4 ¿Enquétipode shader,vérticesofragmentos,utilizaslamatrizdetransformación delmodelo?
3.5 ¿Quéeslamatrizdetransformacióndelanormal?¿Dóndeoperascadanormal consumatrizdetransformación?
3.6 ¿Porquélastransformacionesdetraslaciónsepuedenomitirenelprocesode cálculodelamatrizdetransformacióndelanormal?
3.7 Dadaunamatrizdetransformaciónquealoperarlaconunmodeloproducesu simétrico,¿quéleocurrenalasnormalessilasoperamosconesamismamatriz?¿produce lasnormalescorrectas?
3.8 ¿Quéhaceexactamentelafunción create delalibrería GLMATRIX?
3.9 Sitienestrestransformacionesrepresentadascadaunadeellasporlasmatrices mA, mB y mC,¿cómodebesoperarlasmatricesparaobtenerlamatrizdetransformación delmodelocuandolaprimeratransformaciónquedeseasaplicares mB,después mA y porúltimo mC?
3.10 DadouncilindrocuyabaseestásobreelplanoZ=0ysuejeenel+Z,radiouno yalturauno,obténlamatrizdetransformación, T ,queaplicadasobredichocilindrolo llevaaquesuejecoincidaconladiagonalpositiva X = Y,Z =0 teniendoencuentaque elpuntocentrodelabasequeresidíaenelorigendecoordenadaspermaneceenlamisma posicióndespuésdesutransformación.
José Ribelles y Ángeles López
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151

José
3.11 Imaginaquenecesitasvisualizarunmodelopoligonalcreadoporuntercero.Del modelotienessudescripcióngeométrica(vértices,normales,índices,etc.).Pordesgracia, altratardevisualizarloconWebGLsinaplicarleningúntipodetransformacióngeométrica obtienesuncanvasvacío.Indicaquétransformacionesaplicaríassobreelmodeloafinde conseguirvisualizarlodemaneraqueesteaparezcacompletodentrodelcanvasyalmismo tiemposedibujelomásgrandeposible.Indicatambiéncómoobtendríaslosvaloresque necesitaspararealizardichastransformaciones.
Informática Gráfica (2ª edición)
DOI: http://dx.doi.org/10.6035/Sapientia151
Viendoen3D
Índice
fías,ennuestromundovirtualtambiénesnecesariodefinirunmodelodecámara quepermitaobtenervistas2Ddenuestromundo3D.Elprocesoporelquelacámarasintéticaobtieneunafotografíaseimplementacomounasecuenciadetres
Transformacióndelacámara:ubicalacámaravirtualenelorigendelsistema decoordenadasorientadademaneraconveniente.
Transformacióndeproyección:determinacuántodelmundo3Desvisible. Aesteespaciolimitadoseledenomina volumendelavista ytransformael contenidodeestevolumenalvolumencanónicodelavista.
Transformaciónaláreadedibujo:elcontenidodelvolumencanónicodela vistasetransformaparaubicarloenelespaciodelaventanadestinadoa mostrarelresultadodelavista2D.
4.1.Transformacióndelacámara
Laposicióndeunacámara (el lugar desde el que se va a tomar la fotografía), seestableceespecificandounpunto p delespacio3D.Unavezposicionada,lacámaraseorientademaneraquesuobjetivoquedeapuntandoaunpuntoespecífico
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
delaescena.Aestepunto i seleconoceconelnombrede puntodeinterés.En general,losfotográfosutilizanlacámaraparahacerfotosapaisadasuorientadas envertical,aunquetampocoresultaextrañoverfotografíastomadasconotrasinclinaciones.Estainclinaciónseestablecemedianteelvector UP denominado vector deinclinación.Conestostresdatosquedaperfectamenteposicionadayorientada lacámara,talycomosemuestraenlafigura4.1.

$!"# %
Figura4.1:Parámetrosparaubicaryorientarunacámara: p,posicióndelacámara; UP ,vectorde inclinación; i,puntodeinterés


Algunasdelasoperacionesquelossistemasgráficosrealizanrequierenque lacámaraestésituadaenelorigendecoordenadas,apuntandoenladireccióndel eje Z negativoycoincidiendoelvectordeinclinaciónconeleje Y positivo.Por estarazón,esnecesarioaplicarunatransformaciónalmundo3Ddemaneraque, desdelaposiciónyorientaciónrequeridasporelsistemagráfico,seobservelo mismoquedesdedondeelusuarioestableciósucámara(véasefigura4.2).Aesta transformaciónseledenomina transformacióndelacámara
p

F

S U
Z
Y Y -Z
F S
U XX
Figura4.2:Transformacióndelacámara.Lacámarasituadaenelpunto p enlaimagendelaizquierdasetransformaparaquedarcomoseobservaenlaimagendeladerecha.Dichatransformaciónse aplicaalobjetodetalmaneraqueloqueseobservasealomismoenambassituaciones
Si F eselvectornormalizadoquedesdelaposicióndelacámaraapuntaal puntodeinterés, UP eselvectordeinclinaciónnormalizado, S = F × UP y U = S × F ,entonceselresultadodelasiguienteoperacióncrealamatrizde
José Ribelles y Ángeles López
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
4.2.Transformacióndeproyección
Elvolumendelavistadeterminalapartedelmundo3Dquepuedeservista porelobservador.Laformaydimensióndeestevolumendependedeltipode proyección:
Proyecciónperspectiva.Essimilaracomofuncionanuestravistayseutiliza paragenerarimágenesmásfielesalarealidadenaplicacionescomovideojuegos,simulacioneso,engeneral,lamayorpartedeaplicacionesgráficas.


Proyecciónparalela.Eslautilizadaprincipalmenteeningenieríaoarquitectura.Secaracterizaporpreservarlongitudesyángulos.
Lafigura4.3muestraunejemplodeuncubodibujadoconambostiposde vistas.
4.2.1.Proyecciónparalela
Estetipodeproyecciónsecaracterizaporquelosrayosdeproyecciónsonparalelosentresíeintersectandeformaperpendicularconelplanodeproyección.El volumendelavistatieneformadecaja,lacual,sealineaconlosejesdecoordenadastalycomosemuestraenlafigura4.4,dondetambiénsehanindicadolos nombresdelosseisparámetrosquedefinendichovolumen.
Informática Gráfica (2ª edición)
Engeneral,lossistemasgráficostrasladanyescalanesacajademaneraquela conviertenenuncubocentradoenelorigendecoordenadas.Aestecuboseledenomina volumencanónicodelavista (véasefigura4.5)yalascoordenadaseneste volumen coordenadasnormalizadasdeldispositivo.Lamatrizdetransformación correspondienteparauncubodelado2eslasiguiente:
4.2.2.Proyecciónperspectiva
Estetipodeproyecciónsecaracterizaporquelosrayosdeproyecciónparten todosellosdesdelaposicióndelobservador.Elvolumendelavistatieneforma depirámidetruncada,quequedadefinidamediantecuatroparámetros:losplanos cercaylejos(losmismosqueenlaproyecciónparalela),elángulo θ enladirección Y ylarelacióndeaspectodelabasedelapirámide ancho/alto.Enlafigura4.6 sedetallanestosparámetros.
cerca
lejos
Figura4.6:Esquemadelvolumendelavistadeunaproyecciónperspectiva
Engeneral,lossistemasgráficosconviertenesevolumenconformadepirámideenelvolumencanónicodelavista.Lamatrizdetransformacióncorrespondiente parauncubodelado2eslasiguiente:
Ejercicios
4.1 Elresultadodeunaproyecciónperspectivadepende,entreotrascosas,deladistanciadelacámaraalaescena.Esdecir,elresultadodelaproyeccióncambiasilacámara seacercaosealejadelaescena.Sinembargo,siseutilizaproyecciónparalelasuresultadoesindependientededichadistancia.Sideseasutilizarproyecciónparalelayalmismo tiemposimularelefectodeque,porejemplo,alacercarlacámaraalaescenalaproyección aumente,¿cómoloharías?
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
4.3.Transformaciónaláreadedibujo

Eláreadedibujo,tambiénconocidaporsutérminoeninglés viewport,esla partedelaventanadelaaplicacióndondesemuestralavista2D. Por ejemplo, la figura 4.7 muestra un canvas con tres áreas de dibujo donde para cada una de ellas se muestra la misma escena pero vista desde una posición y orientación di ferentes.Latransformaciónal viewport consisteenmoverelresultadodelaproyecciónadichaárea.Seasumequelageometríaavisualizarresideenelvolumen canónicodelavista,esdecir,secumplequelascoordenadasdetodoslospuntos (x,y,z
.Entonces,si
deláreadedibujoenpíxeles,y
delaesquinainferiorizquierdadeláreadedibujo,paracualquierpuntoqueresida enelvolumencanónicodelavista,suscoordenadasdeventanaseobtienenconla
4.4.Eliminacióndepartesocultas
(a) (b)

Figura4.8:Ejemplodeescenavisualizada:(a)sinresolverelproblemadelavisibilidady(b)conel problemadelavisibilidadresuelto
Elalgoritmo z-buffer secaracterizaporsusimplicidad.Paracadapíxeldela primitivaqueseestádibujando,suvalordeprofundidad(sucoordenada z)secomparaconelvaloralmacenadoenun buffer denominado bufferdeprofundidad.Si laprofundidaddelaprimitivaparadichopíxelesmenorqueelvaloralmacenado enel buffer paraesemismopíxel,tantoel buffer decolorcomoeldeprofundidad seactualizanconlosvaloresdelanuevaprimitiva,siendoeliminadoencualquier otrocaso.
Elalgoritmosemuestraenellistado4.1.Enestealgoritmonoimportaelorden enquesepintenlasprimitivas,perosíesmuyimportantequeel buffer deprofundidadseinicialicesiemprealvalordeprofundidadmáximaantesdepintarlaprimera primitiva.
Listado4.1:Algoritmodel z-buffer if (pixel.z<bufferProfundidad(x,y).z){
bufferProfundidad(x,y).z=pixel.z; bufferColor(x,y).color=pixel.color;

4.5.Viendoen3DconWebGL
Hastaahora,enlosejerciciosrealizadosenloscapítulosanteriores,sehaconseguidovisualizarmodelossintenerquerealizarnilatransformacióndelacámara niestableceruntipodeproyección.Estoocurreporquelaescenaavisualizarseha definidodemaneraquequedasedentrodelvolumencanónicodelavista.Deesta
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
formaseobtieneunaproyecciónparaleladelcontenidodelvolumenobservandola escenaendireccióndeleje Z
Enestecapítulosehavistocómoconstruirlamatrizdetransformacióndela cámaraparapoderobservarlaescenadesdecualquierpuntodevista,ylamatrizde proyecciónparapoderelegirentrevistaparalelayvistaperspectiva.EnWebGLes responsabilidaddelprogramadorcalcularestasmatricesyoperarlasconcadauno delosvérticesdelmodelo.
Habitualmente,lamatrizdelacámaraseoperaconladetransformacióndel modelo,creandolatransformaciónconocidaconelnombrede modelo-vista.Esta matrizyladeproyección se suministran al procesador de vértices, donde cada vértice v debe ser multiplicado por ambas matrices. Si MC es la matriz de trans formación de la cámara, MM es la matriz de transformación del modelo, y MMV es la matriz modelo vista, es decir MMV = MC · MM , el nuevo vértice v se obtiene como resultado de la siguiente operación: v = MProy · MMV · v; donde MProy será MPar o MPer.Ellistado4.2recogeestasoperaciones.
Listado4.2: Shader devérticesparatransformarlaposicióndecadavértice # version300es
uniformmat4 projectionMatrix; //perspectivaoparalela uniformmat4 modelViewMatrix; //cameraMatrix ∗ modelMatrix invec3 VertexPosition;
void main(){
gl_Position=projectionMatrix ∗ modelViewMatrix ∗ vec4 (VertexPosition,1.0);
}
Lalibrería GLMATRIX proporcionadiversasfuncionesparaconstruirlasmatricesvistasenestecapítulo.Así,lafunción mat4.lookAt construyelamatrizdetransformacióndelacámara(ecuación4.1),apartirdelaposicióndelacámara p,el puntodeinterés i yelvectordeinclinación UP Además, las funciones mat4.ortho y mat4.perspective construyen las matrices que transforman el volumen de la vista de una proyección paralela y perspectiva, respectivamente, al volumen canónico de la vista.Sonestas:
mat4.lookAt(out,p,i,UP)
mat4.ortho(out,izquierda,derecha,abajo,arriba, cerca,lejos)
mat4.perspective(out, θ,ancho/alto,cerca,lejos)
José Ribelles y Ángeles López ISBN: 978-84-17429-87-4
Informática Gráfica (2ª edición)
DOI: http://dx.doi.org/10.6035/Sapientia151
Traselprocesamientodelosvértices,estossereagrupandependiendodeltipo deprimitivaqueseestédibujando.Estoocurreenlaetapadeprocesadodela primitiva(véasefigura4.9).Acontinuaciónserealizalaoperaciónconocidaconel nombrede divisiónperspectiva,queconsisteenquecadavérticeseadivididopor supropia w (lacuartacoordenadadelvértice). Esto es necesario, ya que el resul tado de la proyección perspectiva puede hacer que la coordenada w del vértice sea distinta de 1.
Figura4.9:Encoloramarillo,lastareasprincipalesqueserealizanenlaetapacorrespondienteal procesadodelaprimitiva
Latransformaciónaláreadedibujoserealizaacontinuación,aúnenlamisma etapa.Elprogramadorsolodebeespecificarlaubicacióndel viewport enelcanvas mediantelaorden gl.viewport,indicandolaesquinainferiorizquierda,elanchoy elaltoencoordenadasdeventana:
gl.viewport(x, y, ancho, alto)
La figura 4.10 muestra el origen y tamaño de cada una de las tres áreas de di bujo del ejemplo de la figura 4.7 teniendo en cuenta que el canvas es de 800 × 600 píxeles.
Además, la llamada a la función gl.viewport debe realizarse cada vez que se produzca un cambio en el tamaño del canvas con el fin de mantener el tamaño del viewport actualizado. Es muy importante que la relación de aspecto del viewport sea igual a la relación de aspecto utilizada al definir el volumen de la vista para no deformar el resultado de la proyección (véase figura 4.11).
Laúltimatareadentrodelaetapadeprocesadodelaprimitivaeslaoperación derecortado,queconsisteeneliminarloselementosquequedanfueradeloslímites establecidosporelvolumendelavista.Siunaprimitivaintersectaconelvolumen delavista,serecortademaneraqueporel pipeline únicamentecontinúenlostrozos quehanquedadodentrodelvolumendelavista. Por ejemplo, la figura 4.12 mues tra un cono en el que su vértice queda fuera del volumen de la vista produciendo el efecto de cono truncado.
José Ribelles y Ángeles López
978-84-17429-87-4
Informática Gráfica (2ª edición)
DOI: http://dx.doi.org/10.6035/Sapientia151

Figura4.10:Ejemplodetresáreasdedibujoo viewports enlosqueseespecificaparacadaunode ellossuorigenytamaño
Figura4.11:Silaproporcióndelvolumendelavistaydeláreadedibujo(viewport)coincidenno seproduciráningúntipodedeformaciónenlaescenavisualizada


Figura4.12:Elvérticedelconoenlaimagendeladerechaquedafueradelvolumendelavistayse puedeapreciarelresultadodelaoperaciónderecortado
José Ribelles y Ángeles López
978-84-17429-87-4
Informática Gráfica (2ª edición) DOI: http://dx.doi.org/10.6035/Sapientia151


Respectoalaeliminacióndepartesocultas,WebGLimplementaelalgoritmo del z-buffer yla GPU compruebalaprofundidaddecadafragmentodeformafijaenlaetapadeprocesadodelfragmento,perodespuésdeejecutarel shader de fragmentos(véasefigura4.13).Aestacomprobaciónseledenominatestdeprofundidad. Aunque esta operación está implementada en la GPU, el programador aún debe realizar dos tareas:
1. Habilitar la operación del test de profundidad (ya que por defecto no se rea liza):

gl.enable(gl.DEPTH_TEST);
2.Inicializarel buffer alaprofundidadmáximaantesdecomenzaradibujar: gl.clear(... | gl.DEPTH_BUFFER_BIT);
Figura4.13:Encoloramarillo,lastareasprincipalesqueserealizanenlaetapacorrespondienteal procesadodelfragmentodondeseindicaqueeltestdeprofundidadserealizaconposterioridadala ejecucióndel shader defragmentosydemaneraopcional
Ejercicios
4.2 Cargalapágina c04/mueveLaCamara.html.Compruebaquesehaañadidouna cámarainteractivaquepuedesmodificarutilizandoelratónylatecla shift.Editaelfichero c04/mueveLaCamara.js yestudialafunción getCameraMatrix,quedevuelvelamatrizde transformacióndelacámara,¿cuáleselpuntodeinterésestablecido?Estudiatambiénla función setProjection,¿quétipodeproyecciónseutiliza?,¿quécambiosharíasparautilizar elotrotipodeproyecciónvistoenestecapítulo?
4.3 Amplíalasolucióndelejercicioanteriorparaquesepuedacambiardeproyección paralelaaperspectiva,yviceversa,yquesinmodificarlamatrizdetransformacióndela cámarasesigaobservandoelmodelocompleto.
4.4 Parte, por ejemplo, del modelo del tanque que ya hiciste en el capítulo anterior y modifícalo para que en el canvas se muestren cuatro áreas de dibujo. Utiliza proyección
José Ribelles y Ángeles López
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
paralela en las cuatro áreas pero haz que en tres de ellas la dirección de la vista coincida con uno de los ejes de coordenadas y que la cuarta sea en dirección (1,1,1). En todas ellas el modelo debe observarse en su totalidad.
4.5 Amplíalasolucióndelejercicio4.4paraqueserealicelaeliminacióndelaspartes ocultas.Paraobservarlomejor,utilizauncolordiferenteparacadaprimitivaydibújalas comotriángulos,nocomolíneas.
CUESTIONES
4.1 ¿Quéeslamatrizdetransformacióndeproyección?¿ydequétiposconoces?
4.2 ¿Quésignificacadaunodelosparámetrosdelafunción perspective?Dibújaloenpapel.
4.3 ¿Quéfuncióndelalibrería glMatrix utilizarássiquierestrabajarconproyección paralela?
4.4 ¿Quéfuncióndelalibrería glMatrix tepermiteobtenerfácilmentelamatrizde transformacióndelacámara?
4.5 ¿Quédosmatricesseoperanhabitualmenteentreellasparacrearlamatriz modelo-vista?
4.6 Enel shader devértices,¿enquéordendebesoperarcadavérticeconlasmatrices deproyección,cámaraymodelo?
4.7 Sielusuariomodificademanerainteractivalaposicióndelacámara,estáclaro queparaobtenerlanuevavistadebesobtenerlanuevamatrizdetransformacióndela cámarapero,¿tesiguevaliendolamatrizdetransformacióndeproyecciónqueyateníaso porelcontrariotambiéndebesobtenerla?
4.8 Coneltestdeprofundidadhabilitado,describequéocurresialdibujarnoinicializasalamáximaprofundidadel buffer correspondiente.
4.9 Ordenademaneratemporal(primerolaquesehaceantes)lassiguientestareas queserealizanenel pipeline delsistemagráfico:transformaciónaláreadedibujo,test deprofundidad,transformacióndelacámara,divisiónperspectivayasignacióndecoloral fragmento.
4.10 Explicaelproblemaqueaparececuandolarazóndeaspectodefinidaenelmodelo decámaraesdiferentedelarelacióndeaspectodeláreadedibujo.Ponalgúnejemploque loilustre.Explicaquétransformacionesestáninvolucradaseneseproceso.Explicatambién cómoresolveríasesteproblema.
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
Modelosdeiluminacióny sombreado
5.1.ModelodeiluminacióndePhong

ElmodelodeiluminacióndePhongtieneencuentalostresaspectossiguientes: Luzambiente:luzqueproporcionailuminaciónuniformealolargodela escena(véasefigura5.1(a)).
Reflexióndifusa:luzreflejadaporlasuperficieentodaslasdirecciones(véasefigura5.1(b)).
Reflexiónespecular:luzreflejadaporlasuperficieenunasoladireccióno enunrangodeángulosmuycercanoalángulodereflexiónperfecta(véase figura5.1(c)).
(a) (b) (c)
Figura5.1:EjemplodelascomponentesdelmodelodeiluminacióndePhong:(a)Luzambiente;(b) Reflexióndifusa;(c)Reflexiónespecular


Y la combinación de estos tres aspectos produce el resultado que se muestra en la figura 5.2.

5.1.1.Luzambiente
El modelo de Phong establece que la luz ambiente en una escena es constante. Esto produce que la iluminación que se observa en cualquier punto de la superficie de un objeto debida a la luz ambiente sea siempre la misma. Sin embargo, los dife rentes objetos de la escena pueden estar construidos de diferentes materiales y cada material puede reflejar en mayor o menor medida la luz ambiente. El modelo de Phong modela este efecto con el coeficiente ka, 0 ≤ ka ≤ 1, que será característico de cada material.
Si La es la luz ambiente, la iluminación ambiente Ia que se observa en un pun to de la escena depende tanto de dicha luz como del material del objeto y se calcula de la siguiente manera:
Ia = kaLa (5.1)


Lafigura5.3(a)muestraunejemploenelqueelmodelodeiluminaciónúnicamenteincluyeluzambiente.
Figura5.3:Ejemplosdeiluminación:(a)Sololuzambiente;(b)Luzambienteyreflexióndifusa;
5.1.2.Reflexióndifusa
Lareflexióndifusaescaracterísticadesuperficiesrugosas,mates,sinbrillo. El modelo de Phong establece que para modelar este tipo de reflexión se utilice la ley de Lambert. Así, la iluminación observada en un punto de la superficie de un objeto depende del ángulo θ, 0 ≤ θ ≤ 90, entre la dirección a la fuente de luz L y la normal N de la superficie en dicho punto (véase figura 5.4). De manera similar a la luz ambiente, el modelo de Phong también tiene en cuenta que el material del objeto influye en la cantidad de luz reflejada y propone utilizar el coeficiente kd, 0 ≤ kd ≤ 1, que también será propio del material.
Dada una fuente de luz, si L y N son vectores unitarios y Ld es la cantidad de luz producida por dicha fuente, la iluminación observada en un punto de la super
José Ribelles y
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151

ficie de un objeto debido a la reflexión difusa, Id, se obtiene mediante la siguiente ecuación:
Lafigura5.3(b)muestraunejemploenelqueelmodelodeiluminaciónincluye luzambienteyreflexióndifusa.
Figura5.4:Vectoresinvolucradosenelcálculodelareflexióndifusa
5.1.3.Reflexiónespecular
Estetipodereflexiónespropiadesuperficiesbrillantes,pulidas,yesresponsabledelosbrillosquesuelenobservarseenesostiposdesuperficies. Su principal característica es que este tipo de reflexión depende de la posición del observador. También ocurre que el color del brillo suele ser diferente del color de la superficie del objeto y más bien parecido al color de la luz cuya fuente es responsable del brillo.
El modelo de Phong establece que la luz que llega al observador depende del ángulo Φ entre el vector de reflexión perfecta R y el vector de dirección al observador V (véase figura 5.5). De manera similar a las otras dos componentes, el modelo de Phong también tiene en cuenta que el material del objeto influye en la cantidad de luz especular reflejada y utiliza el coeficiente ks, 0 ≤ ks ≤ 1, que será propio del material. Además, propone modelar el tamaño del brillo, α, como expo nente del producto escalar de los vectores R y V y que al igual que la kd dependa del material del objeto.
Dada una fuente de luz, si R y V son vectores unitarios y Ls es la cantidad de luz producida por dicha fuente, la iluminación observada en un punto de la superfi cie de un objeto debido a la reflexión especular, Is, se obtiene mediante la siguiente ecuación:

seobtienedelasiguientemanera:
Señalar que GLSL
:
función
que implementa el cálculo del
I eselvectorincidente,esdecir,
Figura5.5:Vectoresinvolucradosenelcálculodelareflexiónespecular




Lafigura5.3(c)muestraunejemploenelqueelmodelodeiluminaciónincluye luzambiente,reflexióndifusayreflexiónespecular.
Respectoalvalorde α,unvaloriguala1modelaunbrillogrande,mientras quevaloresmuchomayores,porejemplo,entre100y500,modelanbrillosmás pequeños,propiosdemateriales,porejemplo,metálicos.Lafigura5.6muestra variosejemplosobtenidoscondistintosvaloresde
Figura5.6:Ejemplosdeiluminacióncondiferentesvaloresde
paraelcálculodelareflexión especular
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
Elvectorintermedio



El uso de la función reflect es caro. En su lugar, se propone a modo de optimización utilizar el vector intermedio, H Este vector se calcula como la suma de los vectores L y V (véase figura 5.7). En el modelo de Phong, la reflexión espe cular se calcula ahora a partir del producto escalar entre el vector intermedio y la normal de la siguiente forma:
5.1.4.Atenuación
Paratenerencuentalaatenuaciónquesufrelaluzalviajardesdesufuentede origenhastalasuperficiedelobjetosituadoaunadistancia d (véase figura 5.8),el modelodePhongestableceutilizarlasiguienteecuacióndondeloscoeficientes a, b y c sonconstantescaracterísticasdelafuentedeluz:
5.1.5.Materiales
ElmodelodeiluminacióndePhongtieneencuentalaspropiedadesdelmaterialdelobjetoalcalcularlailuminaciónyasíproporcionarmayorrealismo.En concretosoncuatro:ambiente ka,difusa kd,especular ks ybrillo α.Latabla5.1 muestraunalistadematerialesconlosvaloresdeejemploparaestasconstantes. Y la figura 5.9 muestra algunos resultados de su aplicación.
Esmeralda ”ka ” :[0.022,0.17,0.02]
”kd ” :[0.08,0.61,0.08]
”ks ” :[0.63,0.73,0.63]
”α” :[0.6]
Obsidiana ”ka ” :[0.05,0.05,0.07]
”kd ” :[0.18,0.17,0.23]
”ks ” :[0.33,0.33,0.35]
”α”:[0.30]
Rubí ”ka ” :[0.18,0.01,0.01]
”kd ” :[0.61,0.04,0.04]
”ks ” :[0.73,0.63,0.63]
”α”:[0.60]
Bronce ”ka ” :[0.21,0.13,0.05]
”kd ” :[0.71,0.43,0.18]
”ks ” :[0.39,0.27,0.17]
”α”:[0.20]
Oro ”ka ” :[0.25,0.20,0.07]
”kd ” :[0.75,0.61,0.23]
”ks ” :[0.63,0.56,0.37]
”α”:[0.40]
Plástico ”ka ” :[0.0,0.0,0.0]
”kd ” :[0.55,0.55,0.55]
”ks ” :[0.70,0.70,0.70]
”α”:[0.25]
Jade ”ka ” :[0.14,0.22,0.16]
”kd ” :[0.54,0.89,0.63]
”ks ” :[0.32,0.32,0.32]
”α” :[0.10]
Perla ”ka ” :[0.25,0.21,0.21]
”kd ” :[1.0,0.83,0.83]
”ks ” :[0.30,0.30,0.30]
”α”:[0.09]
Turquesa
Cobre
”ka ” :[0.10,0.19,0.17]
”kd ” :[0.39,0.74,0.69]
”ks ” :[0.29,0.31,0.31]
”α”:[0.10]
”ka ” :[0.19,0.07,0.02]
”kd ” :[0.71,0.27,0.08]
”ks ” :[0.26,0.14,0.09]
”α”:[0.10]
Plata ”ka ” :[0.20,0.20,0.20]
”kd ” :[0.51,0.51,0.51]
”ks ” :[0.51,0.51,0.51]
”α”:[0.40]
Goma ”ka ” :[0.05,0.05,0.05]
”kd ” :[0.50,0.50,0.50]
”ks ” :[0.70,0.70,0.70]
”α”:[0.08]
Tabla5.1:EjemplosdepropiedadesdealgunosmaterialesparaelmodelodePhong
5.1.6.ElmodelodePhong
Apartirdelasecuaciones5.1,5.2,5.3y5.6sedefineelmodelodeiluminación
Figura5.9:Ejemplosdemateriales,deizquierdaaderechaydearribaaabajo:Oro,Cobre,Plata, Obsidiana,Jade,Rubí,Bronce,Turquesa.
Listado5.1:FunciónqueimplementaparaunafuentedeluzelmodelodeiluminacióndePhongsin incluirelfactordeatenuación
struct LightData{ vec3 Position; //Posiciónencoordenadasdelojo vec3 La; //Ambiente vec3 Ld; //Difusa vec3 Ls; //Especular }; uniform LightDataLight;
struct MaterialData{ vec3 Ka; //Ambiente vec3 Kd; //Difusa vec3 Ks; //Especular float alpha; //Brilloespecular }; uniform MaterialDataMaterial; //N,LyVseasumennormalizados
vec3 phong( vec3 N, vec3 L, vec3 V){
vec3 ambient=Material.Ka
Light.La; vec3 diffuse= vec3 (0.0); vec3 specular= vec3 (0.0); float NdotL=dot(N,L);

(NdotL>0.0){
float
Informática
http://dx.doi.org/10.6035/Sapientia151
Ejercicios
5.1 Si deseas incorporar el factor de atenuación en la función del listado 5.1, ¿en qué estructura habría que incluir los parámetros a, b y c?
5.2 Indica los cambios que realizarías en la función del listado 5.1 para implementar la optimización que propone el método del vector intermedio.
5.2.Tiposdefuentesdeluz
Engeneral,siempresehanconsideradodostiposdefuentesdeluzdependiendo desuposición:
Posicional:lafuenteemiteluzentodaslasdireccionesdesdeunpuntodado, muyparecidoacomoiluminaunabombilla,porejemplo.
Direccional:lafuenteestáubicadaenelinfinito,todoslosrayosdeluzson paralelosyviajanenlamismadirección.Enestecasoelvector L enel modelodeiluminacióndePhongesconstante.

Enocasionessedesearestringirlosefectosdeunafuentedeluzposicionala unárealimitadadelaescena,talycomoharía,porejemplo,unalinterna.Aeste tipodefuenteposicionalseledenominafoco(véasefigura5.10).
Figura5.10:Ejemplodeescenailuminada:alaizquierda,conunaluzposicionalyaladerecha,con lafuenteconvertidaenfoco

Adiferenciadeunaluzposicional,unfocovienedado,ademásdeporsuposición,porladirección S yelángulo δ quedeterminanlaformadelcono,talycomo semuestraenlafigura5.11.Unfragmentoesiluminadoporelfocosolosiestá dentrodelconodeluz.Estoseaveriguacalculandoelánguloentreelvector L yel vector S.Sielresultadoesmayorqueelángulo δ esqueesefragmentoestáfuera delcono,siendo,enconsecuencia,afectadoúnicamenteporlaluzambiente.
Además,sepuedeconsiderarquelaintensidaddelaluzdecaeamedidaque losrayosseseparandelejedelcono.Estaatenuaciónsecalculamedianteelcoseno delánguloentrelosvectores L y S elevadoaunexponente.Cuantomayorseaeste exponente,mayorserálaconcentracióndeluzalrededordelejedelcono(véase
José Ribelles y Ángeles López
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
Figura5.11:Parámetroscaracterísticosdeunfocodeluz figura5.10,imagendeladerecha).Finalmente,elfactordeatenuacióncalculado seincorporaalmodelodeiluminacióndePhong,multiplicandoelfactordeatenuaciónqueyaexistía.Ellistado5.2muestraelnuevo shader queimplementael focodeluz(laestructura LightData muestrasololoscamposnuevos).
Listado5.2: Shader paracalcularlailuminaciónconunfocodeluz struct LightData{ //Solofiguranloscamposnuevos
vec3 Direction; //Direccióndelaluzencoordenadasdelojo float Exponent; //Atenuación float Cutoff; //Ángulodecorteengrados } uniform LightDataLight;
vec3 phong( vec3 N, vec3 L, vec3 V){
vec3 ambient=Material.Ka ∗ Light.La; vec3 diffuse= vec3 (0.0); vec3 specular= vec3 (0.0); float NdotL=dot(N,L); float spotFactor=1.0; if (NdotL>0.0){
vec3 S=normalize(Light.Position ec); float angle=acos(dot( S,Light.Direction)); float cutoff=radians(clamp(Light.Cutoff,0.0,90.0));
if (angle<cutoff){ spotFactor=pow(dot( S,Light.Direction),Light.Exponent);

vec3 R=reflect( L,N); float RdotV_n=pow(max(0.0,dot(R,V)),Material.alpha); diffuse=NdotL
(Light.Ld
(Light.Ls
Material.Ks);
Material.Kd); specular=RdotV_n
Informática Gráfica (2ª edición) DOI: http://dx.doi.org/10.6035/Sapientia151
5.3.Modelosdesombreado






Unmodelodeiluminacióndeterminaelcolordelasuperficieenunpunto.Un modelodesombreadoutilizaunmodelodeiluminaciónyespecificacuándousarlo. Dadosunpolígonoyunmodelodeiluminación,haytresmétodosparadeterminar elcolordecadafragmento:
Plano:elmodelodeiluminaciónseaplicaunasolavezysuresultadose aplicaatodalasuperficiedelpolígono.Estemétodorequierelanormalde cadapolígono. Un ejemplo del resultado obtenido se muestra en la figura 5.12(a). Para obtener este tipo de sombreado en WebGL 2.0 hay que utilizar el calificador flat con la variable que almacene el color (tanto en el shader de vértices como en el de fragmentos) para evitar que precisamente se realice la interpolación del color por fragmento.
Gouraud:elmodelodeiluminaciónseaplicaencadavérticedelpolígono ylosresultadosseinterpolansobresusuperficie.Estemétodorequierela normalencadaunodelosvérticesdelpolígono.Unejemplodelresultado obtenidosemuestraenlafigura5.12(b).Ellistado5.3muestrael shader correspondienteaestemodelodesombreado.
Phong:elmodelodeiluminaciónseaplicaparacadafragmento.Estemétodo requierelanormalenelfragmento,quesepuedeobtenerporinterpolación delasnormalesdelosvértices.Unejemplodelresultadoobtenidosemuestra enlafigura5.12(c).Ellistado5.4muestrael shader correspondienteaeste modelodesombreado.
Listado5.3: Shader pararealizarunsombreadodeGouraud
# version300es //Shaderdevértices uniformmat4 projectionMatrix; uniformmat4 modelViewMatrix; uniformmat3 normalMatrix;
invec3 VertexPosition; invec3 VertexNormal; outvec3 colorOut; //...aquívaelcódigodellistado5.1ó5.2
void main(){
vec3 N =normalize(normalMatrix ∗ VertexNormal); vec4 ecPosition=modelViewMatrix ∗ vec4 (VertexPosition,1.0); vec3 ec= vec3 (ecPosition); vec3 L =normalize(Light.Position ec); vec3 V=normalize( ec);
colorOut=phong(N,L,V); gl_Position=projectionMatrix ∗ ecPosition; }
# version300es //Shaderdefragmentos precisionmediump float ; invec3 colorOut; outvec4 fragmentColor; void main(){ fragmentColor= vec4 (colorOut,1); }
Listado5.4: Shader pararealizarunsombreadodePhong
# version300es //Shaderdevértices uniformmat4 projectionMatrix,modelViewMatrix; uniformmat3 normalMatrix; invec3 VertexPosition; invec3 VertexNormal; outvec3 N,ec;
void main(){
N =normalize(normalMatrix ∗ VertexNormal); vec4 ecPosition=modelViewMatrix ∗ vec4 (VertexPosition,1.0); ec= vec3 (ecPosition); gl_Position=projectionMatrix ∗ ecPosition; }
José Ribelles y Ángeles López ISBN: 978-84-17429-87-4
Informática Gráfica (2ª edición) DOI: http://dx.doi.org/10.6035/Sapientia151
# version300es //Shaderdefragmentos precisionmediump float ;
//...aquívaelcódigodellistado5.1ó5.2
invec3 N,ec; outvec4 fragmentColor;
void main(){
vec3 n=normalize(N); vec3 L=normalize(Light.Position ec); vec3 V=normalize( ec); fragmentColor= vec4 (phong(n,L,V),1.0); }
Para poder aplicar el modelo de iluminación de Phong, es necesario que se proporcionen las normales para cada vértice. Por ejemplo, el listado 5.5 define el modelo de un cubo donde para cada vértice se proporcionan la posición y la nor mal. Observa que en el modelo del cubo, la normal de un vértice es diferente según la cara que lo utilice. Por este motivo, la descripción del cubo ha pasado de 8 a 24 vértices.
Listado5.5:Modelodeuncuboconlanormaldefinidaparacadavértice varexampleCube={
"vertices":[ 0.5, 0.5,0.5,0.0,0.0,1.0, 0.5, 0.5,0.5,0.0,0.0,1.0, 0.5,0.5,0.5,0.0,0.0,1.0, 0.5,0.5,0.5,0.0,0.0,1.0, 0.5, 0.5,0.5,1.0,0.0,0.0, 0.5, 0.5, 0.5,1.0,0.0,0.0, 0.5,0.5, 0.5,1.0,0.0,0.0, 0.5,0.5,0.5,1.0,0.0,0.0, 0.5, 0.5, 0.5,0.0,0.0, 1.0, 0.5, 0.5, 0.5,0.0,0.0, 1.0, 0.5,0.5, 0.5,0.0,0.0, 1.0, 0.5,0.5, 0.5,0.0,0.0, 1.0, 0.5, 0.5, 0.5, 1.0,0.0,0.0, 0.5, 0.5,0.5, 1.0,0.0,0.0, 0.5,0.5,0.5, 1.0,0.0,0.0, 0.5,0.5, 0.5, 1.0,0.0,0.0, 0.5,0.5,0.5,0.0,1.0,0.0, 0.5,0.5,0.5,0.0,1.0,0.0, 0.5,0.5, 0.5,0.0,1.0,0.0, 0.5,0.5, 0.5,0.0,1.0,0.0,
0.5, 0.5, 0.5,0.0, 1.0,0.0, 0.5, 0.5, 0.5,0.0, 1.0,0.0, 0.5, 0.5,0.5,0.0, 1.0,0.0, 0.5, 0.5,0.5,0.0, 1.0,0.0],
"indices":[0,1,2,0,2,3,4,5,6,4,6,7, 8,9,10,8,10,11,12,13,14,12,14,15, 16,17,18,16,18,19,20,21,22,20,22,23]
};
Lafunción initShaders esunbuensitiodondeobtenerlareferenciaalnuevo atributoyhabilitarlo,asícomoparaobtenerlareferenciaalamatrizdetransformacióndelanormal(véaselistado5.6).
Listado5.6:Obtencióndereferenciasparaelusodelasnormales program.vertexNormalAttribute= gl.getAttribLocation(program,"VertexNormal"); program.normalMatrixIndex= gl.getUniformLocation(program,"normalMatrix"); gl.enableVertexAttribArray(program.vertexNormalAttribute);
Porsupuesto,lamatrizdelanormalespropiadecadamodelo,yaquesecalculaapartirdelamatrizmodelo-vistayseobtiene,comoseexplicóenelcapítulo3, mediantelatraspuestadesuinversa.Comoestaoperaciónhayquerealizarlapara cadamodelo,esconvenientecrearunafunciónespecíficayllamarlaantesdeordenarsudibujadoparaobtenerasílamatrizdelanormaldel shader,talycomose muestraenellistado5.7.
Listado5.7:Funcionesparaelcálculoylainicializacióndelamatrizdelanormalenel shader a partirdelamatrizmodelo-vista functiongetNormalMatrix(modelViewMatrix){
varnormalMatrix= mat3 .create();
mat3 .normalFromMat4(normalMatrix,modelViewMatrix); return normalMatrix;
} functionsetShaderNormalMatrix(normalMatrix){ gl.uniformMatrix3fv(program.normalMatrixIndex,false, normalMatrix);
}
Porúltimo,alahoradedibujarelmodelo,hayqueespecificarcómoseencuentraalmacenadodichoatributoenelvectordevértices(véaselistado5.8).
José Ribelles y Ángeles López
Informática Gráfica (2ª edición) DOI: http://dx.doi.org/10.6035/Sapientia151
José
}
Listado5.8:Nuevafuncióndedibujoqueincluyedosatributos:posiciónynormal functiondrawSolid(model){
gl.bindBuffer(gl.ARRAY_BUFFER,model.idBufferVertices); gl.vertexAttribPointer(program.vertexPositionAttribute,3, gl.FLOAT,false,2
4,0); gl.vertexAttribPointer(program.vertexNormalAttribute,3, gl.FLOAT,false,2
gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER, model.idBufferIndices); gl.drawElements(gl.TRIANGLES,model.indices.length, gl.UNSIGNED_SHORT,0);
5.4.2.Materiales
Paraespecificarunmaterialesnecesario,enprimerlugar,obtenerlasreferenciasdelasvariablesquevanacontenerelvalordelmaterialenel shader.Examina ellistado5.1pararecordarlas.Ellistado5.9muestraelcódigocorrespondientea estepaso.Unbuensitioparacolocarloseríaenlafunción initShaders.
Listado5.9:Obtencióndelasreferenciasalasvariablesdel shader quecontendránelmaterial program.KaIndex=gl.getUniformLocation(program,"Material.Ka"); program.KdIndex=gl.getUniformLocation(program,"Material.Kd"); program.KsIndex=gl.getUniformLocation(program,"Material.Ks"); program.alphaIndex=gl.getUniformLocation(program, "Material.alpha");
Ensegundolugar,hayqueespecificarelmaterialparacadamodelojustoantes deordenarsudibujado.Paraesto,esbuenaideadefinirunafunciónqueinicialice lasvariablesdel shader correspondientesalmaterial. El listado 5.10 muestra un ejemplo del material Silver, una función para asignar valores de material a las variables del shader así como un ejemplo de cómo dibujar un cubo con dicho material.
Listado5.10:Lafunción setShaderMaterial recibeunmaterialcomoparámetroeinicializalasvariablesdel shader correspondientes.Enlafunción drawScene seestableceunvalordematerialantes dedibujarelobjeto
"mat_ambient":[0.19225,0.19225,0.19225],
"mat_diffuse":[0.50754,0.50754,0.50754],
"mat_specular":[0.50827,0.50827,0.50827], "alpha":[51.2]
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
functionsetShaderMaterial(material){
gl.uniform3fv(program.KaIndex,material.mat_ambient); gl.uniform3fv(program.KdIndex,material.mat_diffuse); gl.uniform3fv(program.KsIndex,material.mat_specular); gl.uniform1f(program.alphaIndex,material.alpha);
} functiondrawScene(){ //estableceunmaterialydibujauncubo setShaderMaterial(Silver); drawSolid(exampleCube);
} 5.4.3.Fuentedeluz
Respectoalafuentedeluz,porunapartehayqueobtenerlasreferenciasalas variablesdel shader (véaselistado5.11)quedefinenlosparámetrosdelafuente deluz,yquedemanerasimilaralmaterialpodemoscolocarenlafunción initShaders.Porotraparte,hayqueinicializarlasvariablesdel shader antesdeordenarel dibujadodelprimerobjetodelaescena.Esinteresanteagruparlainicializaciónen unasolafunción(véaselistado5.12).
Listado5.11:Obtencióndelasreferenciasalasvariablesdel shader quecontendránlosvaloresde lafuentedeluz program.LaIndex=gl.getUniformLocation(program,"Light.La"); program.LdIndex=gl.getUniformLocation(program,"Light.Ld"); program.LsIndex=gl.getUniformLocation(program,"Light.Ls"); program.PositionIndex=gl.getUniformLocation(program, "Light.Position");
Listado5.12:Lafunción setShaderLight inicializalasvariablesdel shader correspondientes functionsetShaderLight(){
gl.uniform3f(program.LaIndex, 1.0,1.0,1.0); gl.uniform3f(program.LdIndex, 1.0,1.0,1.0); gl.uniform3f(program.LsIndex, 1.0,1.0,1.0); gl.uniform3f(program.PositionIndex,10.0,10.0,0.0);
}
Ejercicios
5.3 Ejecutaelprograma c05/phongConSombreadoGouraud.html,queimplementael modelodeiluminacióndePhongyelmodelodesombreadodeGouraud.Comoresultadoobtendrásimágenessimilaresalasdelafigura5.13(b).Examinael shader ycomprueba
José Ribelles y Ángeles López
Informática Gráfica (2ª edición) DOI: http://dx.doi.org/10.6035/Sapientia151
quelosfragmentosdecódigocomentadosenestasecciónseincluyenen c05/iluminacion.js Compruebatambiéncómoelfichero c05/primitivasGN.js contienelasnormalesdecada vérticeparacadaunadelasprimitivasdefinidas.









5.4 ImplementaelmodelodesombreadodePhongapartirdelmismoprogramadel ejercicioanterior.Lafigura5.13(c)muestratresejemplosderesultadosobtenidosutilizandoestemodelodesombreado.
5.5 A partir del programa c05/phongConSombreadoGouraud.html realiza los cambios necesarios para implementar el modelo de sombreado plano. La figura 5.13(a) muestra algunos resultados obtenidos utilizando
modelo
sombreado.
5.5.Iluminaciónporambascaras
Cuandolaescenaincorporamodelosabiertos,esposibleobservarlospolígonos queseencuentranenlapartetraseradelosobjetos,como,porejemplo,ocurreen lacopadelafigura5.14.Paraunacorrectavisualizaciónesnecesarioutilizarla normalcontrariaenlospolígonosqueformanpartedelacaratrasera.Estoesuna operaciónmuysencillaenWebGLysemuestraenellistado5.13.
Listado5.13:Iluminaciónenambascaras,modificaciónenel shader defragmentos if (gl_FrontFacing)
fragmentColor= vec4 (phong(n,L,V),1.0); else fragmentColor= vec4 (phong( n,L,V),1.0);

Figura5.14:Ejemplodemodeloenelquehayqueaplicariluminaciónenambascarasparauna correctavisualización
Ejercicios
5.6 Implementa un shader que te permita sombrear objetos por ambas caras. Esto es muy útil en el caso de que los objetos sean abiertos como, por ejemplo, ocurre con las pri mitivas del cilindro, el cono o el plano. El listado 5.13 muestra el código necesario. Decide tú mismo dónde ponerlo (quizá debas también eliminar alguna línea en tu shader actual). Recuerda que solo verás diferencias si alguna de las primitivas de la escena es abierta.

5.7 Tratar las dos caras de los polígonos te permitiría utilizar un tipo de material di ferente para cada cara. Por ejemplo, material oro para las caras delanteras y material plata para las traseras. Comenta las modificaciones que tendrías que hacer al shader del listado 5.1 para conseguirlo.
5.6.Sombreadocómic
Elobjetivoessimularelsombreadotípicoencómics.Esteefectoseconsigue
enellistado5.14realizaestaoperaciónparacadafragmento.Lavariable levels determinaelnúmeromáximodecoloresdistintos(véasefigura5.15).
Listado5.14:Iluminaciónenambascaras,modificaciónenel shader defragmentos vec3 toonShading( vec3 N, vec3 L){
vec3 ambient=Material.Ka ∗ Light.La; float NdotL=max(0.0,dot(N,L)); float levels=3.0; float scaleFactor=1.0/levels;
vec3 diffuse=ceil(NdotL
levels)
scaleFactor
(Light.Ld ∗ Material.Kd);
return (ambient+diffuse);
} void main(){
vec3 n=normalize(N); vec3 L=normalize(Light.Position ec);
fragmentColor= vec4 (toonShading(n,L),1.0);



}
Figura5.15:Resultadodelafunción
José Ribelles y Ángeles López ISBN: 978-84-17429-87-4
Informática Gráfica (2ª edición) DOI: http://dx.doi.org/10.6035/Sapientia151
Ejercicios
5.8 Añadelafunción toonShading atu shader defragmentosyhazquesellameaesta enlugardealafunción phong.Observaquelacomponenteespecularsehaeliminadode laecuación,porloquelafunción toonShading solonecesitalosvectores N y L.
5.9 Para complementar el shader de sombreado cómic, sería muy interesante reforzar también los bordes del objeto dibujado utilizando el color negro. Dirígete a la bibliografía y encuentra técnicas que te permitan conseguir este segundo efecto utilizando shaders
5.7.Niebla
Elefectodenieblaseconsiguemezclandoelcolordecadafragmentoconel colordelaniebla.Amayordistanciadeunfragmentorespectoalacámara,mayor pesotieneelcolordelanieblayalcontrario,amenordistancia,mayorpesotiene elcolordelfragmento.
Enprimerlugarhayqueobtenerelcolordelfragmentoydespués,amodo deposproceso,semezclaconelcolordelaniebladependiendodeladistanciaa lacámara.Paraimplementaresteefectosedefinentresvariables:distanciamínima,distanciamáximaycolordelaniebla.Así,dadounfragmento,tenemostres posibilidades:
Sielfragmentoestáaunadistanciamenorqueladistanciamínima,noseve afectadoporlaniebla,elcolordefinitivoeselcolordelfragmento.
Sielfragmentoestáaunadistanciamayorquelamáxima,elcolordefinitivo eselcolordelaniebla(esimportantequeelcolordefondocoincidaconel delaniebla).
Sielfragmentoestáaunadistanciaentrelamínimaylamáxima,sucolor definitivodependedelcolordelfragmentoydeldelaniebla.Estavariación puedeserlinealconladistancia,perosueleproducirmuchomejorresultado utilizarunafunciónexponencial.
Ellistado5.15muestralaestructura FogData yelcálculodelvalordenieblade maneralinealy,concomentarios,demaneraexponencial.Lafigura5.16muestra algunosresultados.
FogData{
maxDist;
minDist;
FogDataFog;
Informática Gráfica (2ª edición)
void main(){
Fog.minDist=10.0;
Fog.maxDist=20.0;
Fog.color= vec3 (0.15,0.15,0.15);
vec3 n=normalize(N);
vec3 L=normalize(Light.Position ec); vec3 V=normalize( ec);
float dist=abs(ec.z);



//lineal
loatfogFactor=(Fog.maxDist dist)/ (Fog.maxDist Fog.minDist);
//exponencial
//floatfogFactor=exp( pow(dist,2.0));
fogFactor=clamp(fogFactor,0.0,1.0);
vec3 phongColor=phong(n,L,V);
vec3 myColor=mix(Fog.color,phongColor,fogFactor);
fragmentColor= vec4 (myColor,1.0);
Ejercicios
5.10 Implementa
de niebla
color de cada fragmento con
color
la distancia
fragmento a la cámara (es importante que
color
de la niebla). Utiliza el código del listado 5.15.
5.11 Busca la diferencia visual que produce la variación
gustado
la niebla si se calcula de manera lineal
CUESTIONES
5.1 ¿Enqué shader sedeclaraelatributodelanormal,vérticesofragmentos?¿Por qué?
5.2 Respectoalamatrizdetransformacióndelanormal,¿cuáldelastransformacionesbásicasqueconocesnuncaestáincluidaendichamatriz:traslación,girooescalado?
5.3 ¿Porquélamatrizdetransformacióndelanormalsesueleobtenerapartirdela matrizmodelo-vistaynoúnicamenteapartirdelamatrizdetransformacióndelmodelo?
5.4 ¿Quécreesquepasaríaconunanormalenelcasodequelamatrizdetransformacióndelmodelocontuvieseunaoperacióndeescaladoenelqueunodesusfactoresde escalaestuvieseacero?
5.5 Hemosorganizadolosatributosdeunvérticedetalformaqueenprimerlugar figuralaposiciónydespuéslanormal.¿Creesquepodríamoshacerloalrevés,esdecir, primerolanormalydespuéslaposición?
5.6 ¿Quérepresentala Kd paraelobjeto?¿Yla Ks ?¿Podríasconseguirqueunaluz blancailumineunaesferablancayqueelbrilloobservadoseapreciedecolorazúl?
5.7 ¿AquécomponentesdelmodelodelmodelodeiluminacióndePhongafectael factordeatenuacióndelaluz?,¿cómoloaplicaríasenlafunción phong?
5.8 ¿Quéeslavariable ec queapareceenel shader devérticesquerealizaunsombreadodeGouraud?¿YelvectorV?¿Sabríasdibujarunbocetodondesemuestreloque ambasvariablesrepresentan?
5.9 Imaginaquelafuentedeluzestácolocadaenunpuntofijodelaescena(como unalámpara,porejemplo),yquelavariable Lp contienedichaposición,¿quétendríasque hacerparaobtenerlacorrectaposicióndelaluzquetepermiteseguirutilizandoel shader dellistado5.3?
5.10 Explicalasdiferencias,ventajaseinconvenientes,quehayentrelostresmétodos desombreado:Plano,GouraudyPhong.
5.11 EnlaimplementacióndelmodelodesombreadodePhong,¿enqué shader se calculaelvector V ?
5.12 SiutilizaselmodelodeiluminacióndePhongconunafuentedeluzdireccional, ¿esciertoquealserelvector L constanteparatodalaescenatambiénloseráelvectorde reflexión R?
5.13 EnelmodelodeiluminacióndePhong,¿quésignificaqueelproductoescalar entrelosvectores N y L seanegativo?
5.14 Si M eslamatrizmodelo, C esladelacámara, P ladeproyección, vp esel atributodeposicióndelvértice,y Lp eslaposicióndelafuentedeluz,escribeelfragmento decódigodeun shader quecalculalosvectores L y V parautilizarlosenelmodelode iluminacióndePhong.Asume vp y Lp detipo vec3.
5.15 EnelmodelodeiluminacióndePhong,explicacómosemodelalareflexiónespecularpropiadesuperficiesbrillantesomuypulidas.Escribeelcódigo GLSL quepermite calcularlaparaunvérticedelcualconocessuposiciónynormal,ytambiénconocesla posicióndelafuentedeluz.
5.16 SegúnelmodelodeiluminacióndePhong,¿quéinformaciónnecesitasparapoder calcularelcolordeunpuntodebidoalareflexióndifusa?Escribelaexpresiónquete
permiteobtenerloparaunafuentedeluzposicional.¿Quédiferenciashaysilafuentede luzfuesedireccional?
5.17 EnlaimplementacióndelmodelodesombreadodeGouraud,¿quéinformación hadeinterpolarla GPU?
5.18 TuescenasecomponeúnicamentedeuncuadradoyutilizaselmodelodeiluminacióndePhong.Comparaestasdosposiblessituaciones:a)utilizarunafuentedeluz posicionalysombreadoplano;b)utilizarunafuentedeluzdireccionalysombreadode Gouraud.¿Creesqueenamboscasosseobtendráunefectodesombreadosimilarosipor elcontrariohabrádiferenciasevidentes?
5.19 ExplicaladiferenciaentrelosconceptosmodelodeiluminacióndePhongymodelodesombreadodePhong.
5.20 Dadounaluzdetipofoco,¿quévectoresycómoseutilizanparasabersiun fragmentoestádentrodelconodeluz?
5.21 ¿Quétipodesombreado(Plano,GouraudoPhong)seríamásconvenienteutilizar enelcasodequetuescenamostraraobjetosdesuperficieplanaydematerialespecular (comounmesademármolmuypulida,porejemplo)?
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
Texturas
Ahora, el objetivo
mejorar un poco más dicho realismo visual mediante el uso de texturas, es decir, imágenes que a modo de mapas de color se utilizarán
calcular el color definiti vo de los píxeles(observalasfiguras6.1 y 6.2).Elusodetexturasparaincrementar elrealismovisualesmuyfrecuente,porloqueelnúmerodetécnicasenlaliteratura estambiénmuyelevado.Enconcreto,enestecapítulosevanarevisartécnicasque resultanespecialmenteidóneasparagráficosentiemporeal.
6.1.Coordenadasdetextura
de textura
textura sobre la superficie
necesarias
ejemplo,
cómo se ha de pegar
figura
muestra cómo
Ribelles y
una misma textura se ha aplicado sobre el mismo modelo produciendo resultados distintos. La diferencia reside únicamente en las coordenadas de textura que se han utilizado.
Las coordenadas de textura se suministran como un nuevo atributo del vértice, aunque lo más habitual es que sea en el procesador de fragmentos donde se accede a la textura por lo que será necesario que la GPU las interpole y así obtenerlas para cada fragmento. El rango de coordenadas válido en el espacio de la textura es [0, 1], siendo este rango independiente del tamaño en píxeles de la textura (véanse figura 6.4).

El listado 6.1 muestra los cambios necesarios. El shader de vértices recibe el nuevo atributo que contiene las coordenadas de textura y las asigna a una variable de tipo out para que cada fragmento reciba sus coordenadas de textura interpoladas.


López

Informática Gráfica (2ª edición)





http://dx.doi.org/10.6035/Sapientia151

Figura6.4:Enelespaciodelatextura,elrangodecoordenadasválidoes [0, 1].Enelespaciodel objeto,cadafragmentorecibelascoordenadasdetexturainterpoladas

El shader de fragmentos utiliza la función texture para,apartirdelascoordenadasy unatextura,obtenerunvalordecolor.Latexturaestádeclaradadetipo sampler2D, queeseltipoque GLSL estableceparaunatextura2D.Lafigura6.5muestrados resultadosdelaaplicacióndetextura.
Listado6.1:Cambiosnecesariosparaqueun shader utiliceunatextura2D
//Shaderdevértices
invec2 VertexTexcoords; //nuevoatributo outvec2 texCoords;
void main(){
//seasignanlascoordenadasdetexturadelvértice
//alavariabletexCoords texCoords=VertexTexcoords;
}
//Shaderdefragmentos
uniform sampler2DmyTexture; //latextura invec2 texCoords; //coordsdetexturainterpoladas
void main(){
//accesoalatexturaparaobtenerunvalordecolorRGBA fragmentColor=texture(myTexture,texCoords);
}
Por supuesto, desde el shader de fragmentos es posible acceder a diferentes tex turas y realizar cualquier combinación con los valores obtenidos para determinar el color definitivo. La figura 6.6 muestra un ejemplo donde se han combinado dos texturas y el listado 6.2 muestra los cambios necesarios en el shader de fragmentos
107
José Ribelles y Ángeles López
ISBN: 978-84-17429-87-4
Informática Gráfica (2ª edición)
DOI: http://dx.doi.org/10.6035/Sapientia151
sehaobtenidoapartirdelatexturaydelmodelodeiluminacióndePhong
acceder a varias texturas (el shader de vértices no cambia). Observa, por ejem plo, que se utilizan las mismas coordenadas de textura para acceder a las diferentes texturas. Observa también que se ha utilizado la operación de multiplicación para combinar los colores obtenidos de cada textura, pero se podría haber usado cual quier otra operación.


6.1.1.Repeticióndelatextura
Enelcasodeproporcionarvaloresmayoresque1enlascoordenadasdetextura,esposiblegobernarelresultadodelavisualizaciónutilizandolafunción gl.texParameter.Tressonlosmodosposibles,ypuedencombinarseconvalores distintosencadadirección S y T (véanse ejes en la figura 6.4).Sonestos:
Repitelatextura(véasefigura6.7)
• gl.texParameteri(gl.TEXTURE_2D, gl.TEXTURE_WRAP_[S|T],gl.REPEAT);
Extiendeelbordedelatextura(véasefigura6.8)
• gl.texParameteri(gl.TEXTURE_2D, gl.TEXTURE_WRAP_[S|T],gl.CLAMP_TO_EDGE);


Repitelatexturademanerasimétrica(véasefigura6.9)
• gl.texParameteri(gl.TEXTURE_2D, gl.TEXTURE_WRAP_[S|T],gl.MIRRORED_REPEAT);
Informática

Figura6.9:Repeticióndelatexturademanerasimétrica(imagendelaizquierda)yrepeticiónnormal comoladelafigura6.7(imagendeladerecha)

Ejercicios
6.1 Viendolaimagenizquierdadelafigura6.8,¿cuálescreesquesonlascoordenadas detexturaquesehanespecificadoparacadaunodelosvérticesdelpolígono?,¿yenelcaso delaimagenizquierdadelafigura6.9?


6.2 Determinalascoordenadasdetexturadecadaunodelosvérticesqueseencuentrannumeradosenlasiguientefigurademaneraquetrasaplicarlatexturadecespedse obtieneelsiguienteresultado.
6.3 Determinalascoordenadasdetexturadecadaunodelosvérticesqueseencuentrannumeradosenlasiguientefigura.Paraaveriguarlas,tenencuentaelresultadoque tambiénsemuestraenlafigura.Enestecaso,elanchoyaltodeltrozodetexturautilizado sondeuncuartodelanchoyaltototaldelatexturarespectivamente.

6.4
Determinalascoordenadasdetexturadelossiguientesvértices(enumeradoscomo a,b,c,d,e,f,g,h,i,j,k,l)demaneraquelatexturaquedecomosemuestraenlasiguiente figura.

6.5
Trabajandoconcoordenadasdetexturamayoresqueunoysiseextiendeelcolor delbordedelatextura,¿enquécoordenadasdetexturaseconvertiránlascoordenadas (0.7, 2.3)?
6.6 Trabajandoconcoordenadasdetexturamayoresaunoysiserepitelatextura,¿en quécoordenadasdetexturasetransformanlascoordenadas (3 5, 2 7)?¿ysilascoordenadasson (0 1, 7 7)?
6.7 Utilizandolatexturaquesemuestraenlasiguientefigurayaplicandoelmodo derepeticiónbasadoenespejodeOpenGL(MIRRORED_REPEAT),dibujacomoquedaría latexturasobrecadaunodelossiguientesobjetosteniendoencuentalascoordenadasde texturaqueseespecificanparacadaunodeellos.
6.8 Siparaunfragmentosuscoordenadasdetexturason (1 3, 0 7),obténlasrespectivascoordenadasdetexturaenelespaciodelatexturaparacadaunodelosmétodosde repeticiónsoportadosenWebGL.
6.2.Leyendotéxeles
Untéxelesunpíxeldelatextura.EnlosorígenesdeOpenGL,elaccesoalos téxelesdeunatexturasoloeraposiblerealizarlodesdeel shader defragmentos. Sinembargo,losprocesadoresgráficosque aparecieron en el2008eliminabanesa limitaciónyeraposibleaccederaunatexturatambiéndesdeel shader devértices. En cualquier caso, debido a que rara vez el tamaño de un fragmento se corresponde con el de un téxel de la textura, el acceso a la textura conlleva dos problemas:
Magnificación:cuandoaunfragmentolecorrespondeuntrocitodeuntéxel delatextura.
Minimización:cuandoaunfragmentolecorrespondenvariostéxelesdela textura.


José Ribelles y Ángeles López
978-84-17429-87-4
Informática Gráfica (2ª edición) DOI: http://dx.doi.org/10.6035/Sapientia151
José Ribelles y
6.2.1.Magnificación
Paratrataresteproblema,WebGLproporcionadostiposdefiltrado:


Filtrocaja:seutilizaeltéxelmáscercano.Pordesgracia,aunqueesmuy rápido,produceeltípicoefectodepixeladoqueobtenemosalampliaruna imagen(véasefigura6.10).
• gl.texParameteri(gl.TEXTURE_2D, gl.TEXTURE_MAG_FILTER,gl.NEAREST);
Filtrobilineal:utilizacuatrotéxelescuyosvaloresseinterpolanlinealmente. Estefiltroproduceunefectodeborrosidad(véasefigura6.11).
• gl.texParameteri(gl.TEXTURE_2D, gl.TEXTURE_MAG_FILTER,gl.LINEAR);
Figura6.10:FiltrocajadeWebGL,devuelveelvalordeltéxelmáscercanoyproduceelefectode pixelado
Figura6.11:FiltrobilinealdeWebGL,devuelvelainterpolaciónlinealdecuatrotéxelesyproduce elefectodeborrosidad
6.2.2.Minimización
WebGLproporcionaunmétodomásdefiltradoparaelproblemadelaminimización,ademásdelfiltrocajaydelbilinealcomentadosenlasecciónanterior.Se denomina mipmapping yconsisteenproporcionar,ademásdelatexturaoriginal,
López
Informática Gráfica (2ª edición) DOI: http://dx.doi.org/10.6035/Sapientia151
unconjuntodeversionesmáspequeñasdelatextura,cadaunadeellasuncuarto máspequeñaquelaanterior. A este conjunto de texturas de distintos tamaños se le llama pirámide de texturas.
Filtrocajaybilineal,respectivamente:
• gl.texParameteri(gl.TEXTURE_2D, gl.TEXTURE_MIN_FILTER,gl.NEAREST);
• gl.texParameteri(gl.TEXTURE_2D, gl.TEXTURE_MIN_FILTER,gl.LINEAR);
Mipmapping:entiempodeejecución,la GPU seleccionalatexturacuyotamañoseacercamásaldelatexturaenlapantalla(véasefigura6.12).WebGL puedegenerarlapirámidedetexturasdemaneraautomática:


• gl.generateMipmap(gl.TEXTURE_2D);
Utilizandoestemétododefiltrado, WebGL también puederealizarunfiltradotrilinealseleccionandodostexturas,muestreandocadaunautilizandoun filtrobilineal,einterpolandolosdosvaloresobtenidos:
• gl.texParameteri(gl.TEXTURE_2D, gl.TEXTURE_MIN_FILTER,gl.LINEAR_MIPMAP_LINEAR);
ParapoderaplicarunatexturaenWebGLesnecesario:
1.crearunobjetotexturayestablecertodossusdatos,y
2.asignarloaunaunidaddetextura.
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
Figura6.12:Ejemplodeescenacon Mipmapping (izquierda)ysolofiltrobilineal(derecha).EnWebGLlastexturasserepresentanmedianteobjetosconnombre.Elnombrenoesmásqueunenterosinsignodondeelvalor0estáreservado.Paracrear unobjetotexturaesnecesarioobtenerenprimerlugarunnombrequenoseesté utilizando.Estasolicitudserealizaconlaorden gl.createTexture.Sehandesolicitartantosnombrescomoobjetostexturanecesitemos,teniendoencuentaqueun objetotexturaalmacenaunaúnicatextura.
Unavezcreadoesteobjeto,hayqueespecificartantolatextura(laimagen 2Dennuestrocaso)comolosdiferentesparámetrosderepeticiónyfiltrado.Para especificarlatexturaseutilizalasiguienteorden:
gl.texImage2D(GLenum objetivo,GLint nivel, GLenum formatoInterno,GLsizei ancho,
GLsizei alto,GLint borde,GLenum formato, GLenum tipo,TexImageSource datos);
dondeelobjetivoserá gl.TEXTURE_2D.Elparámetro formatoInterno seutiliza paraindicarcuálesdelascomponentes R, G, B y A seempleancomotéxelesde laimagen.Losparámetros formato, tipo y datos especifican,respectivamente,el formatodelosdatosdelaimagen,eltipodeesosdatosyunareferenciaalosdatos delaimagen.Elparámetro nivel seutilizasoloenelcasodeusardiferentesresolucionesdelatextura,siendo0encualquierotrocaso.Yporúltimo,losparámetros ancho, alto y borde serefierenalanchoyaltodelatextura,yaltamañodelborde quehadesercero.Paraqueestaordenylasquepermitendefinirlosparámetrosde repeticiónyfiltradotenganefectosobrelatextura,hacefaltausar gl.bindTexture sobrelatexturacreadacon gl.createTexture.Ellistado6.3muestraunejemploque incluyelacreacióndelatexturayelestablecimientodesusdatosypropiedades.
Listado6.3:CreacióndeunatexturaenWebGL2.0
//Creaunobjetotextura texture=gl.createTexture(); gl.bindTexture(gl.TEXTURE_2D,texture);
//EspecificalatexturaRGB gl.texImage2D(gl.TEXTURE_2D,0,gl.RGB,image.width, image.height,0,gl.RGB,gl.UNSIGNED_BYTE,image);
//Repitelatexturatantoenscomoent gl.texParameteri(gl.TEXTURE_2D,gl.TEXTURE_WRAP_S,gl.REPEAT); gl.texParameteri(gl.TEXTURE_2D,gl.TEXTURE_WRAP_T,gl.REPEAT);
//Filtrado
gl.texParameteri(gl.TEXTURE_2D,gl.TEXTURE_MIN_FILTER, gl.LINEAR_MIPMAP_LINEAR); gl.texParameteri(gl.TEXTURE_2D,gl.TEXTURE_MAG_FILTER, gl.LINEAR); gl.generateMipmap(gl.TEXTURE_2D);
José Ribelles y Ángeles López ISBN: 978-84-17429-87-4
Informática Gráfica (2ª edición) DOI: http://dx.doi.org/10.6035/Sapientia151
Yasoloquedaasignarelobjetotexturaaunaunidaddetextura.Estasunidades sonfinitasysunúmerodependedel hardware. El consorcio ARB fija que al menos 16 unidades de textura deben existir en WebGL 2.0, pero es posible que nues tro procesador gráfico disponga de más.Laorden gl.activeTexture especificael selectordeunidaddetexturaactiva.Así,porejemplo,laorden: gl.activeTexture(gl.TEXTURE3); seleccionalaunidaddetextura 3.Acontinuación,hayqueespecificarelobjetotexturaautilizarpordichaunidadconlaorden gl.bindTexture.Acadaunidaddetexturasoloselepuedeasignarunobjetotexturapero,durantelaejecución,podemos cambiartantasvecescomoqueramoselobjetotexturaasignadoaunadeterminada unidad. El listado 6.4 muestra un ejemplo que incluye ambas órdenes.
Listado6.4:Asignacióndeunobjetotexturaaunaunidaddetextura
//Seleccionalaunidaddetextura0 gl.activeTexture(gl.TEXTURE0);
//Asociaunobjetotexturaalaunidadseleccionada gl.bindTexture(gl.TEXTURE_2D,texture);
Unavezcreadalatexturanohayqueolvidarasignaralavariabledetipo sampler del shader launidaddetexturaquehadeutilizar(véaselistado6.5).
Listado6.5:Asignacióndeunidadaun sampler2D
//Obtieneelíndicedelavariabledelshaderdetiposampler2D program.textureIndex= gl.getUniformLocation(program,’myTexture’);
//IndicaqueelsamplermyTexturedelshaderuse //launidaddetextura0 gl.uniform1i(program.textureIndex,0);
Comoseexplicóenelprimerpuntodeestecapítulo,losvérticeshandeproporcionarunnuevoatributo:lascoordenadasdetextura.Enconsecuencia,hayque habilitarelatributo(véaselistado6.6)ytambiénespecificarcómoseencuentra almacenado(véaselistado6.7).
Listado6.6:Habilitacióndelatributodecoordenadadetextura
//seobtienelareferenciaalatributo program.vertexTexcoordsAttribute= gl.getAttribLocation(program,"VertexTexcoords");
//sehabilitaelatributo gl.enableVertexAttribArray(program.vertexTexcoordsAttribute);
José Ribelles y Ángeles López
Informática Gráfica (2ª edición)
DOI: http://dx.doi.org/10.6035/Sapientia151
Listado6.7:Especificacióndetresatributos:posición,normalycoordenadasdetextura gl.bindBuffer(gl.ARRAY_BUFFER,model.idBufferVertices); gl.vertexAttribPointer(program.vertexPositionAttribute,3, gl.FLOAT,false,8
4,0); gl.vertexAttribPointer(program.vertexNormalAttribute,3, gl.FLOAT,false,8
4); gl.vertexAttribPointer(program.vertexTexcoordsAttribute,2, gl.FLOAT,false,8
Ejercicios
4,3
4,6
4);
6.9 Ejecutaelprograma c06/aplicaTextura.html.Experimentaypruebaacargardiferentestexturas.Comoresultado,obtendrásimágenessimilaresalasdelafigura6.13. Después,edita aplicaTextura.html y aplicaTextura.js ycompruebacómosehanincorporadotodosloscambiosnecesariosparapoderutilizartexturas2D.
Figura6.13:EjemplosobtenidosutilizandotexturasenWebGL
6.4.Texturas3D
Unatextura3Ddefineunvalorparacadapuntodelespacio.Estetipodetexturasresultaperfectaparaobjetosquesoncreadosapartirdeunmediosólidocomo unatallademaderaounbloquedepiedra.Sonunaextensióndirectadelastexturas2Denlasqueahoraseutilizantrescoordenadas (s,t,r),ydondeenlugarde téxelestenemosvóxeles.

Laprincipalventajadeestetipodetexturasesqueelpropioatributodeposicióndelvérticesepuedeutilizarcomocoordenadadetextura.Sinembargo,son carasdealmacenarytambiéndefiltrar.Tambiénsonineficientescuandoseutilizan conmodelosdesuperficies,yaquelamayorpartedelainformaciónquelatextura almacenanuncaseutiliza. Por último, cabe señalar que WebGL soporta este tipo de texturas a partir de la versión 2.0.
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
6.5.Mapasdecubo

Unmapadecubosonseisimágenescuadradasdondecadaunadeellasseasociaaunacaradelcubodistintayquejuntascapturanundeterminadoentorno(véase figura6.14).Losmapasdecuboseutilizanprincipalmenteparatresaplicaciones:
6.5.1. Reflectionmapping

Estatécnicadeaplicacióndetexturasirveparasimularobjetosquereflejansu entorno.Enlaliteraturatambiénaparececonelnombrede environmentmapping Elobjetivoesutilizarunatexturaquecontengalaescenaquerodeaalobjetoy,en tiempodeejecución,determinarlascoordenadasdetexturaquevanadependerdel vectordireccióndelobservadoro,mejordicho,desureflexiónencadapuntode lasuperficie.Deestamanera,lascoordenadasdetexturacambianalmoverseel observador,consiguiendoqueparezcaqueelobjetoreflejasuentorno.
A la textura o conjunto de texturas que se utilizan para almacenar el entorno de un objeto se le denomina mapa de entorno. Este mapa puede estar formado por solo una textura, a la cual se accede utilizando coordenadas esféricas, o por un conjunto de seis texturas cuadradas formando un mapa de cubo. Este último es el caso que se describe en esta sección.
El cálculo de las coordenadas de textura se realiza de la siguiente manera.Para cadapuntodelasuperficiedelobjetoreflejanteseobtieneelvectordereflexión R respectoalanormal N enesepuntodelasuperficie(véasefigura6.15).Las coordenadasdeestevectorsevanautilizarparaaccederalmapadecuboyobtener elcolor.Enprimerlugar,hayquedeterminarcuáldelasseistexturassehade
Informática
utilizar.Paraello,seeligelacoordenadademayormagnitud.Sieslacoordenada x,seutilizanlacaraderechaoizquierdadelcubo,dependiendodelsigno.Deigual forma,siesla y seutilizanladearribaoladeabajo,oladedelanteodedetrássi esla z.Después,hayqueobtenerlascoordenadas s y t paraaccederalatextura seleccionada.Porejemplo,silacoordenada Rx delvectordereflexióneslade mayormagnitud,lascoordenadasdetexturasepuedenobtenerasí:
Figura6.15:Vectoresinvolucradosen reflectionmapping
EnWebGLunatexturamapadecubosedeclaradetipo samplerCube.Elcálculodelascoordenadasdetexturaserealizademaneraautomáticaalaccederala texturamediantelafunción texture,queserealizahabitualmenteenel shader de fragmentos,igualquecuandoseaccedíaaunatextura2D.Elvectordereflexión R secalculaparacadavérticemediantelafunción reflect,yelprocesadorgráfico haráquecadafragmentorecibaelvector R convenientementeinterpolado. El lis tado 6.8 muestra el uso de estas funciones en un shader. La figura 6.16 muestra un ejemplo del resultado obtenido.

Figura6.16:Elmapadecubo(quesemuestraaladerechaenlafigura6.14)sehautilizadopara simularqueeltoroestáreflejandosuentorno
José Ribelles y Ángeles López
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151

reflectionmapping
invec3 VertexNormal
//vectordereflexiónenelvértice
void main(){
vec4 ecPosition=modelViewMatrix
N=normalize(normalMatrix
V=normalize(
samplerCubemyCubeMapTexture;
main(){
6.5.2. Refractionmapping
Estatécnicadeaplicacióndetexturaseutilizaparasimularobjetosquelaluz atraviesacomohielo,agua,vidrio,diamante,etc.(véasefigura6.17).Lascoordenadasdetexturasecorrespondenconelvectorderefracciónparacadapuntode lasuperficie.Elvectorderefracciónsecalculaapartirdelosvectores V y N utilizandolaleydeSnell.Estaleyestablecequelaluzsedesvíaalcambiardeun medioaotro(delairealagua,porejemplo)enbaseauníndicederefracción.El vectorderefracciónsecalculaconlafunción refract paracadavérticeenel shader devérticesyelprocesadorgráficoharáquecadafragmentorecibaelvectorconvenientementeinterpolado.Enellistado6.9semuestraelusodeestasfunciones enambos shaders.Además,secombinaelresultadodelareflexiónylarefracción, yaqueeshabitualquelosobjetosrefractantestambiénseanreflejantes.Elpesose balanceautilizandolavariable refractionFactor
6.5.3. Skybox
Un skybox esuncubomuygrandesituadoalrededordelobservador.Elobjetivo deestecuboesrepresentarelfondodeunaescenaquehabitualmentecontiene elementosmuydistantesalobservador,comoporejemploelsol,lasmontañas,las nubes,etc.Comotexturaseutilizaunmapadecubo.Lascoordenadasdetexturase
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
establecenenel shader devértices,simplementeapartirdelatributodeposición decadavérticedel Skybox.Elprocesadorgráficoharáquecadafragmentoreciba lascoordenadasdetexturaconvenientementeinterpoladas.Enellistado6.10se muestranlosprincipalescambiosparadibujarel skybox
Listado6.9:Cambiosenel shader para refractionmapping
//Shaderdevértices
invec3 VertexNormal; outvec3 RefractDir,ReflectDir;
void main(){
ReflectDir=reflect( V,N);
RefractDir=refract( V,N,material.refractionIndex);

}
//Shaderdefragmentos
uniform samplerCubemyCubeMapTexture; invec3 RefractDir,ReflectDir;
void main(){
fragmentColor=mix(texture(myCubeMapTexture,RefractDir), texture(myCubeMapTexture,ReflectDir), material.refractionFactor);
}
Informática
Listado6.10:Cambiosenel shader para skybox
//Shaderdevértices

invec3 VertexPosition; outvec3 tcSkybox; //coordenadasdetexturadelSkybox
void main(){
//simplementeasignaatcSkyboxlascoordenadasdelvértice tcSkybox=VertexPosition;
...
}
//Shaderdefragmentos
... uniform samplerCubemyCubeMapTexture; invec3 tcSkybox; //coordenadasdetexturainterpoladas
void main(){
fragmentColor=texture(myCubeMapTexture,tcSkybox);
}
Ejercicios
6.10 El listado 6.11 contiene el shader para que un modelo refleje su entorno y ade más se pinte el skybox Observa que con el mismo shader se pinta tanto el cubo como el modelo. La variable skybox se utiliza para saber si se está pintando uno u otro. Por otra parte, la matriz invT es la inversa de la matriz modelo vista del skybox. Recuerda que el skybox ha de estar centrado en la posición de la cámara. Los archivos c06/cubeMap.html y c06/cubeMap.js implementan la creación de una textura de mapa de cubo. Edítalos y estúdialos. Observa también las imágenes de la figura 6.18 para ver los resultados que po drías obtener. Interesantes, ¿verdad? Sin duda, un ejemplo inspirado en Fiat Lux de Paul Debevec.

José Ribelles y Ángeles López
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151

Listado6.11: Shader para skybox y reflectionmapping
uniform boolskybox; uniformmat3 invT; outvec3 R;
void main(){
vec3 N=normalize(normalMatrix
ecPosition=modelViewMatrix
if (skybox)
R= vec3 (VertexPosition);
VertexNormal);
vec4 (VertexPosition,1.0);
ecPosition;
(ecPosition)),N);
//Shaderdefragmentos
uniform samplerCubemyCubeMapTexture; invec3 R;
void main(){
6.11 Añaderefracciónalejercicioanterior(véasefigura6.19).Utilizaíndicesderefracciónmenoresque1(estoesdebidoalaimplementacióndelafunción refract en GLSL). Paracadafragmento,utilizalafunción mix paraqueelcolorfinalseaun15%elvalordel reflejoyun85%elvalorderefracción.

Figura6.19:Ejemplosobtenidosutilizando refraction y reflectionmapping enWebGL.Elíndicede refracciónes,deizquierdaaderecha,de0,95y0,99
José Ribelles y Ángeles López
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151

6.6. Normalmapping
Estatécnicaconsisteenmodificarlanormaldelasuperficieparadarlailusión derugosidadosimplementedemodificacióndelageometríaamuypequeñaescala. Aestatécnicaseleconocetambiéncomo bumpmapping.Elcálculodelavariación delanormalsepuederealizarenelpropio shader demaneraprocedural(véase imagen6.20), o también se puede precalcular y proporcionar al procesador gráfico como una textura, conocida con el nombre de mapa de normales o bump map
Elcálculodelailuminaciónsehaderealizarenelespaciodelatangente.Este espacioseconstruyeparacadavérticeapartirdesunormal,elvectortangentea lasuperficieendichopuntoyelvectorresultantedelproductovectorialdeesos dosvectores,quesedenominavectorbinormal.Conlostresvectoressecreala matrizquepermiterealizarelcambiodebase.Comoresultado,lanormalcoincide coneleje Z,latangenteconeleje X ylabinormalconeleje Y .Entoncesse operanlosvectores L y V conestamatrizyhacemosqueelprocesadorgráficolos interpoleparacadafragmento.Enel shader defragmentosseaccedealatextura quealmacenaelmapadenormalesyapartirdeestanormalylosvectores L y V interpoladosseaplicaelmodelodeiluminación.
Figura6.20:Objetostexturadosconlatécnicade bumpmapping.Lamodificacióndelanormal producequeaparentementelasuperficietengabultos
6.7. Displacementmapping


Estatécnicaconsisteenaplicarundesplazamientoencadavérticedelasuperficiedelobjeto.Elcasomássencilloesaplicareldesplazamientoenladirección delanormaldelasuperficieendichopunto.Eldesplazamientosepuedealmacenarenunatexturaalaqueseleconocecomomapadedesplazamiento.Enel shader devérticesseaccedealatexturaquealmacenaelmapadedesplazamientoysemodificalaposicióndelvértice,sumándoleelresultadodemultiplicarel desplazamientoporlanormalenelvértice(véasefigura6.21).
José Ribelles y Ángeles López
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
6.8. Alphamapping
Estatécnicaconsisteenutilizarunatexturaparadeterminarquépartesdeun objetosonvisiblesyquépartesnoloson.Estopermiterepresentarobjetosque geométricamentepuedentenerciertacomplejidaddeunamanerabastantesencilla apartirdeunabasegeométricasimpleydelatexturaquehacelafuncióndemáscara.Esenel shader defragmentosdondeseaccedealatexturaparatomaresta decisión.Porejemplo,lafigura6.22muestraunatexturaydosresultadosdecómo sehautilizadosobreelmismoobjeto.Enelprimercaso,sehautilizadoparaeliminarfragmentos,produciendounobjetoagujereadocuyomodeladoseríabastante máscomplejodeobtenerutilizandométodostradicionales.Enelsegundocaso,el valordel alphamap sehautilizadoparadecidirelcolordefinitivodelfragmento. Conelmismomodeloycambiandoúnicamentelatexturaesmuysencilloobtener acabadosmuydiferentes(véasefigura6.23).


Ejercicios
6.12 Conlaayudadeuneditorgráfico,creaun alphamap obúscaloeninternet.Cárgalocomounanuevatexturayutilízaloparaobtenerresultadoscomolosquesemuestran enlasfiguras6.22y6.23.
Informática Gráfica (2ª edición)



José
Figura6.23:Ejemplosdeaplicacióndediferentes alphamaps sobreelmismoobjeto
CUESTIONES
6.1 ¿Enquérangovaríanlascoordenadasdetexturaenelespaciodelatextura?¿Qué ocurresiunacoordenadadetexturatomaunvalormayorqueuno?
6.2 ¿Cómoseconsiguequecadafragmentotengasuscoordenadasdetexturacuando estasseespecificanporvértice?
6.3 ¿Dequétipoeslavariablequeseutilizaparaaccederaunaunidaddetextura?
6.4 ¿Quéesunaunidaddetextura?¿Yunobjetotextura?
6.5 Lavariabledetipo sampler2D contieneunidentificadordel¿objetotexturao delaunidaddetextura?
6.6 ¿Dóndeseasignaunobjetotexturaaunaunidaddetextura,enel shader oenel ladodelaaplicación?
6.7 ¿Esposiblequedesdeel shader sepuedaaccederavariastexturasalavez? ¿Cómoloharías?
6.8 ¿Esposibleaccederaunatexturadesdeel shader devérticesosolosepuede desdeeldefragmentos?
6.9 ¿Cuántasunidadesdetexturahaydisponiblesenelequipoenelqueestáshaciendolosejercicios?Recuerdaqueenelcapítulo1semuestraunejemplodecómoconocer estetipodeinformación.
6.10 ¿Quévectoresintervienenenelcálculodelascoordenadasdetexturaenelmétodode Reflection-Mapping?¿Yenelde Refraction-Mapping?
6.11 Aldibujarun Skybox conWebGL,¿esnecesarioqueseproporcionencoordenadas detexturacomounatributomásdelosvérticesdelcubo?

6.12 Sideseasutilizarunatexturademapadecuboparasimularelefectoderefracción, ¿cómoproporcionasal shader elíndicederefracciónnecesarioparaobtenerelcorrespondientevectorderefracción,comounatributodelvértice,comovariable uniform,como variable in/out ocomounaconstante?
6.13 Enelmétodoconocidocomo NormalMapping,indicaenqué shader (vérticeso fragmentos)seaccedealatexturaquealmacenaelmapadenormales.
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
Texturasprocedurales
Índice
turalageneraunprocedimientoentiempodeejecución,esdecir,latexturanose encuentrapreviamentealmacenadatalycomoseexplicóenelcapítulo6.Ahora, existeunafunciónqueimplementalatexturayaestafunciónselellamadesdeel shader para,apartirdeunascoordenadasdetextura,computarydevolverunvalor. Lafunciónpuededevolvertantounvalordecolorcomocualquierotrovalorque sepuedautilizarparadeterminarelaspectofinaldelmodelo(véasefigura7.1).Sin duda,elusodetexturasproceduralesesunadelasgrandesvirtudesqueofrecenlos actualesprocesadoresgráficosprogramables.

porlafuncióndetexturaseutilizaparadeterminarsihayqueeliminarundeterminadofragmento
Sonvariaslasventajasqueofreceelusodelastexturasprocedurales.Porejemplo,unatexturaprocedural,engeneral,vaaconsumirmenosmemoria,yaqueal
noestardiscretizadanopresentalosproblemasderivadosdetenerunaresolución fijaycualquieraspectoclavedelatexturasepuedeparametrizarparaobtenerefectosmuydiversosutilizandolamismafunción.Porejemplo,lascopasdelafigura 7.1sehanobtenidoutilizandoexactamentelamismatexturaprocedural,peroparacadaunasehanasignadovaloresdiferentesalasvariables o parámetrosque gobiernanelnúmeroytamañodelosagujeros.
Tambiénesciertoquenotodosonventajas.Porejemplo,computacionalmente sonmáscarasylosalgoritmosquehayqueimplementaravecessonmuycomplejos,inclusotambiénpodríaocurrirquelosresultadosfuerandiferentessegúnel procesadorgráficoqueseutilice.
Endefinitiva,combinartexturasbasadasenimágenesjuntocontexturasproceduralesserácasisiempreloideal(véasefigura7.2).
Figura7.2:Ejemplodecombinacióndetextura2Dytexturaprocedural.Alaizquierdaelobjetoes dibujadosintextura,enelcentroselehaaplicadounatextura2D,yaladerechasehacombinadola textura2Dconunatexturaprocedural
7.1.Rayado
Elobjetivodeestetipodetexturaproceduralesmostrarunrayadosobrela superficiedelobjeto(véasefigura7.3).Seutilizaunacoordenadadetexturayel rayadoqueseobtienesiempreseráenladireccióndelacoordenadaelegida.Se aplicaunfactordeescalasobrelacoordenadadetexturaparaestablecerelnúmero derayas.Laparterealdelacoordenadadetexturasecomparaconunavariable quecontrolaelanchodelarayaparasabersielfragmentosehadecolorearcon elcolordelarayaoconeldelmaterialdelmodelo.Ellistado7.1muestraestas operaciones.
Ejercicios
7.1 Ejecutaelejemplo c07/rayado.html.Pruebaamodificarlosparámetrosquegobiernanelrayado. Estudia cómo gobiernan el aspecto del rayado y cómo se opera con ellos. ¿Qué coordenada de textura se está interpolando para cada fragmento? No dejes de averiguar el significado de las funciones fract, step y mix

José Ribelles y Ángeles López
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
7.2 Modifícael shader defragmentosen c07/rayado.html paraqueahoraseinterpole laotracoordenadadetextura(véasefigura7.4).







7.3 Enlafigura7.5semuestrandosimágenesdondelasrayasseobtienenutilizando lafunciónseno.Piensacómopodríasconseguirlo.Silointentas,esmuyprobableque consigasotrosresultadosmuyinteresantesporelcamino.

Listado7.1: Shader derayado
//Shaderdevértices
outfloat texCoord; void main(){
texCoord=VertexTexcoords.s;
}
//Shaderdefragmentos
... uniformvec3 StripeColor; //colordelaraya uniformfloat Scale; //númeroderayas uniformfloat Width; //anchodelaraya
infloat texCoord; outvec4 fragmentColor;
void main(){
float scaledT=fract(texCoord ∗ Scale); float s=step(Width,scaledT); vec3 newKd=mix(StripeColor,Kd,s);
fragmentColor= vec4 (phong(newKd,N,L,V),1.0);
}
7.2.Damas
Estetipodetexturaproceduralconsisteenpresentarlasuperficiedeunobjeto comoladeltablerodeljuegodelasdamas(véasefigura7.6).Seutilizaunfactor deescalasobrelascoordenadasdetexturaparaestablecerelnúmerodecuadrados, enprincipioelmismoenambasdirecciones.Laparteenteradelascoordenadasde texturaescaladasseutilizaparasaberaquéfilaycolumnapertenececadafragmento.Sumandoambasyobteniendoelmódulodosseaveriguasielresultadoespar oimpary,enconsecuencia,sesabesielfragmentoperteneceaunacasillablanca onegra.Ellistado7.2recogeloscambiosnecesarios.
Ejercicios
7.4 Ejecutaelejemplo c7/damas.html.Pruebaamodificarelparámetroquegobierna elnúmerodecuadrados.Ahora,editaelcódigoymodifícaloparaquesepuedaestablecer unfactordeescaladiferenteencadadirección(véasefigura7.7).
7.5 Enellistado7.2,¿conquéfinalidadseutilizalafunción floor enel shader de fragmentos?
José Ribelles y Ángeles López
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
Listado7.2: Shader dedamas
//Shaderdevértices




outvec2 texCoord; void main(){ texCoord=VertexTexcoords;
//Shaderdefragmentos

uniformfloat Scale; //númerodecuadrados invec2 texCoord; outvec4 fragmentColor; void main(){

float row=floor(texCoord.s
Scale); float col=floor(texCoord.t
Scale); float res=mod(row+col,2.0); vec3 newKd=Kd+(res
fragmentColor= vec4 (phong(newKd,N,L,V),1.0);
José Ribelles y Ángeles López
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
7.3.Enrejado
Elenrejadoconsisteenutilizarlaorden discard paraeliminarfragmentos,produciendoenconsecuenciaagujerosenlasuperficiedelobjeto(véansefiguras7.1y 7.8).Lascoordenadasdetexturaseescalanparadeterminarelnúmerodeagujeros, utilizandounfactordeescaladistintoparacadadirección.Laparterealseutiliza paracontrolareltamañodelagujero.Ellistado7.3recogelospasosnecesarios.
Figura7.8:Ejemplosdel shader deenrejado

Listado7.3: Shader deenrejado
... outvec2 TexCoord;
void main(){
TexCoord=VertexTexcoords;
uniformvec2 Scale; uniformvec2 Threshold; invec2 TexCoord; outvec4 fragmentColor;

void main(){
José Ribelles y Ángeles López
float ss=fract(TexCoord.s
Scale.t);
Scale.s); float tt=fract(TexCoord.t
((ss>Threshold.s)&&(tt>Threshold.t)) discard;
fragmentColor= vec4 (phong(N,L,V),1.0);
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151

Ejercicios
7.6 Ejecutaelejemplo c07/enrejado.html.Pruebaamodificarlosparámetrosque gobiernanelnúmerodeagujerosysutamaño.
7.7 Ahora,editaelcódigoymodifícaloparaqueseeliminenlosfragmentosqueno pertenecenalasuperficiedeuncírculo.Fíjateenlosresultadosquesemuestranenlas imágenesdelafigura7.9.




Figura7.9:Ejemplosdeenrejadoscirculares
7.8 Denuevorealizalasmodificacionesnecesariasparaqueahoraseeliminenlos fragmentosquepertenecenalasuperficiedeuncírculo.Fíjateenelresultadoquesemuestraenlaimágendelafigura7.10.
Figura7.10:Ejemplodeenrejadocircularenelquesehaeliminadolasuperficiedelcírculo
7.4.Ruido
Entérminosgenerales,elusoderuidoeninformáticagráficaresultamuyútil parasimularefectosatmosféricos,materialesosimplementeimperfeccionesenlos objetos.Lafigura7.11muestraalgunosejemplosenlosquesehautilizadouna funciónderuidocomométododetexturaprocedural.Adiferenciadeotrasáreas, lafunciónderuidoquenosinteresahadeserrepetible,esdecir,queproduzca
José Ribelles y Ángeles López
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
Figura7.11:Ejemplosobtenidosutilizandounafunciónderuidocomotexturaprocedural
La función de ruido se ha de implementar en el propio shader. También se po dría implementar en un programa externo, ejecutarlo y almacenar el resultado para proporcionarlo en forma de textura al procesador gráfico, pero en este caso ya no se puede hablar de textura procedural. Por ejemplo, la figura 7.12 muestra diversos ejemplos de objetos en los que se ha utilizado una función de ruido de Perlin en el shader de fragmentos para a partir de la posición interpolada de cada fragmento, obtener un valor de ruido y combinarlo de diferentes formas con los valores de material.


Figura7.12:EjemplosobtenidosmedianteelusodelafunciónderuidodePerlinenel shader de fragmentos

Ejercicios

7.9 Ejecuta los ejemplos c07/nubes.html y c07/sol.html y prueba a modificar los pa rámetros que gobiernan el aspecto final de los modelos. Después, edita el código y prueba a realizar modificaciones a partir de los valores de ruido obtenidos, seguro que consigues resultados interesantes. Algunos ejemplos de los resultados que se pueden conseguir se muestran en la figura 7.13.
 siemprelamismasalidaparaelmismovalordeentradayquealmismotiempo aparentealeatoriedad,esdecir,quenomuestrepatronesregulares.
siemprelamismasalidaparaelmismovalordeentradayquealmismotiempo aparentealeatoriedad,esdecir,quenomuestrepatronesregulares.
CUESTIONES
7.1 ¿QuéopcionestenemosparautilizarunvalorderuidoenWebGL2.0?

7.2 ¿Quédesventajapresentautilizartexturasderuidofrenteautilizarfuncionesde ruido?
7.3 Sideseasutilizartexturasprocedurales,¿estásdeacuerdoenquenuncaesnecesarioproporcionarcoordenasdetexturacomoatributoporcadavértice?
7.4 Estudiaelsiguiente shader defragmentosquepintaunasuperficiecomoeltablero delasdamas.Modifícaloparaqueelefectogobernadoporlavariable Scale puedaser diferenteencadaunadelasdosdireccionesdelatextura.





7.5 Estudiaelsiguiente shader defragmentosqueeliminaalgunosfragmentosproduciendoagujeroscuadradosenlasuperficiedelosobjetos.Propónlasmodificaciones oportunasparaqueenlugardeagujeroscuadradosseobservenagujeroscircularesyqueel radio(válidoenelrango [0, 0 5])seaunparámetroqueseestablezcadesdelaaplicación. uniformfloatScale; uniformfloatThreshold; outvec4fragmentColor; voidmain(){ floatss=fract(TexCoord.s * Scale); floattt=fract(TexCoord.t * Scale); if((ss<Threshold)&&(tt<Threshold)) discard; fragmentColor=vec4(phong(),1.0); }
7.6 Estudiaelsiguiente shader defragmentosquepintaunasuperficiecomoeltablero delpopularjuegodelasdamas.Modifícaloparaqueambostiposdecasillassepinten utilizandolamismaKdyquelasqueinicialmenteerandecolormásclaroseanahora transparentesconungradodeopacidaddel20%(ylascasillasqueinicialmenteerande colormásoscurosigansiendoopacasal100%). uniformfloatScale; invec2TexCoord; outvec4fragmentColor;
voidmain(){
floatrow=floor(TexCoord.s * Scale); floatcol=floor(TexCoord.t * Scale); floatres=mod(row+col,2.0); vec3newKd=Kd+(res * 0.4); fragmentColor=vec4(phong(newKd),1.0); }
7.7 Estudiaelsiguiente shader defragmentosquepintaunasuperficiearayas.Modifícaloparaqueahoraseproduzcauncambiogradualentreelcolordelaraya StripeColor yla Kd.
uniformvec3StripeColor; uniformfloatScale; uniformfloatWidth; infloatTexCoord;//coordenadadetexturat outvec4fragmentColor;
voidmain(){
floatscaledT=fract(TexCoord * Scale); floats=step(Width,scaledT); vec3newKd=mix(StripeColor,Kd,s); fragmentColor=vec4(phong(newKd),1.0); }
José Ribelles y Ángeles López
ISBN:
Informática Gráfica (2ª edición)
DOI: http://dx.doi.org/10.6035/Sapientia151
7.8
Estudiaelsiguiente shader defragmentosymodifícaloparaquelarayaaparezca endiagonal.Haztambiénloscambiosnecesariosparaquesepuedaestablecerelnúmero derayasdeseado. uniformvec3StripeColor; infloatTexCoord;//coordenadadetexturas outvec4fragmentColor;
voidmain(){ floats=step(0.5,TexCoord); vec3newKd=mix(StripeColor,Kd,s); fragmentColor=vec4(phong(newKd),1.0); }
Necesitaselmodelodemediaesferaparaincluirloentuescena.Sinembargo, solodisponesdelmodelodeunaesferacompletaqueteproporcionatresatributospor vértice:posición,normalycoordenadasdetextura.Desarrollaunatexturaproceduralque comoresultadodeordenareldibujadodelaesferacompletaproduzcaquesolosemuestre lamitaddeellayqueestamitadsiempresecorrespondaconelmismotrozodelaesfera (esdecir,lomismoqueobtendríassidispusierasdelmodelodemediaesfera).
7.9
José Ribelles y Ángeles López ISBN: 978-84-17429-87-4
Informática Gráfica (2ª edición) DOI: http://dx.doi.org/10.6035/Sapientia151
José
Realismovisual Índice
Estecapítulopresentatresaspectosbásicosenlabúsquedadelrealismovisualenimágenessintéticas:transparencia,reflejosysombras.Enlaliteraturase hanpresentadonumerososmétodosparacadaunodeellos.Aligualqueencapítulosanteriores,sevanapresentaraquellosmétodosque, aun siendo sencillos, consiguenunamejoraimportanteenlacalidadvisualconpocoesfuerzodeprogramación.
8.1.Transparencia
Losobjetostransparentessonmuyhabitualesenelmundoquenosrodea.Suele ocurrirqueestosobjetosproducenunefectoderefraccióndelaluz,oquelaluz cambiealgunadesuspropiedadesalatravesarlos.Todoestohacequelainclusión deobjetostransparentesenunmundovirtualseaunproblemacomplejoderesolver. Enestasección,sevaaabordarelcasomássencillo,esdecir,suponerqueelobjeto transparenteesmuyfinoynovaaproducirelefectoderefraccióndelaluzni vaamodificarlaspropiedadesdelasfuentesdeluz.Quizápuedaparecerquese simplificamuchoelproblema,locualescierto,peroaúnasílagananciavisualque sevaaobteneresmuyalta.
Cuandounaescenaincluyeunobjetotransparente,elcolordelospíxelescubiertospordichoobjetodepende,ademásdelaspropiedadesdelobjetotransparente,
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
delosobjetosquehayandetrásdeél.Unmétodosencilloparaincluirobjetostransparentesennuestraescenaconsisteendibujarprimerotodoslosobjetosquesean opacosydibujardespuéslosobjetostransparentes.Elgradodetransparenciase suministraalprocesadorgráficocomounacuartacomponenteenlaspropiedades dematerialdelobjeto,conocidacomocomponente alfa.Si alfa es1,elobjetoes totalmenteopaco,ysies0significaqueelobjetoestotalmentetransparente(véase figura8.1).Así,elcolorfinalsecalculaapartirdelcolordel framebuffer ydel colordelfragmentodeestamanera:
Figura8.1:Tresejemplosdetransparenciacon,deizquierdaaderecha, alfa = 0 3, 0 5 y 0 7
Aldibujarunobjetotransparente,eltestdeprofundidadsetienequerealizar deigualmaneraquealdibujarunobjetoopacoyasíasegurarqueelproblemade lavisibilidadseresuelvecorrectamente.Sinembargo,yaqueunobjetotransparentedejaveratravésdeél,paracadaunodelosfragmentosquesupereeltest deberáactualizarseel buffer decolor,peronoeldeprofundidad,yaquedehacerlo evitaríaqueotrosobjetostransparentessituadosdetrásfuesenvisibles.Ellistado 8.1recogelasecuenciadeórdenesdeWebGLnecesariaparapoderincluirobjetos transparentesenlaescena. Sin embargo, se ha de tener en cuenta que el navegador compone el resultado de WebGL con la página y que al utilizar el canal alfa puede producir un efecto blanquecino en toda la escena. Una forma sencilla de evitarlo es especificar en el fichero .html el color negro como color de fondo del canvas:
<style> canvas {...; background: black;} </style>
En el caso de que varios objetos transparentes se solapen en la proyección, elcolorfinalenlazonasolapadaesdiferentedependiendodelordenenelque sehayandibujado(véasefigura8.2).Enestecaso,habríaquedibujarlosobjetos transparentesdemaneraordenada,pintandoenprimerlugarelmáslejanoy,en últimolugar,elmáscercanoalobservador.Sinembargo,enocasioneslaordenaciónnoestrivial,como,porejemplo,cuandounobjetoatraviesaotro.Enestos
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
 C
C
Listado8.1:Secuenciadeoperacionesparadibujarobjetostransparentes
//dibujaenprimerlugarlosobjetosopacos
//activaelcálculodelatransparencia gl.enable(gl.BLEND);
//especificalafunciondecálculodelatransparencia gl.blendFunc(gl.SRC_ALPHA,gl.ONE_MINUS_SRC_ALPHA);
//impidelaactualizacióndelbufferdeprofundidad gl.depthMask(false);
//dibujalosobjetostransparentes
...
//desactivaelcálculodelatransparencia gl.disable(gl.BLEND);
//permiteactualizarelbufferdeprofundidad gl.depthMask(true);
casos,unaformadeevitaresteproblemaesestablecerlaoperacióndecálculode latransparenciacomounincrementosobreelcoloracumuladoenel framebuffer:
Cfinal = alfa Cfragmento + Cframebuffer (8.2)
Figura8.2:Dosresultadosdiferentesenlosqueúnicamentesehavariadoelordeneneldibujadode losobjetostransparentes
EnWebGL,estoseconsigueespecificandocomofuncióndecálculo gl.ONE enlugarde gl.ONE_MINUS_SRC_ALPHA (que sería la que corresponde a la ecua ción 8.1).Deestamanera,elordenenelquesedibujenlosobjetostransparentesya noinfluyeenelcolorfinaldelaszonassolapadas.Porcontra,laszonasvisiblesa travésdelosobjetostransparentessonmásbrillantesqueenelresto,produciendo unadiferenciaqueengeneralresultademasiadonotable (véase figura 8.3).

José Ribelles y Ángeles López
Informática Gráfica (2ª edición)
DOI: http://dx.doi.org/10.6035/Sapientia151
Figura8.3:Losplanostransparentesdelaizquierdasehanpintadoutilizandolafunción gl.ONE mientrasqueenlosdeladerechasehautilizado gl.ONE_MINUS_SRC_ALPHA
Hastaelmomentosehanutilizadocomoobjetostransparentespolígonossimples,loqueresultasuficienteparasimular,porejemplo,unaventana.Pero,¿qué ocurresiesunobjetoenelqueloqueseveatravésdeélesaélmismo?En esoscasos,sedebeprestaratenciónespecialalordendedibujado.Dadounobjeto transparente,unasoluciónmuysencillaconsisteendibujarprimerolascarastraserasdelobjeto(quedependendelaposicióndelobservador)ydespuéslascaras dedelantedelobjeto.Porsuerte,elprocesadorgráficoimplementaensu pipeline laeliminacióndecarasdemaneraautomática.Elprogramadordebehabilitarlo (gl.enable(gl.CULL_FACE))eindicarquécarasquiereeliminar,esdecir,si quiereeliminarlascarasdelapartetrasera(gl.cullFace(gl.BACK)),olas deladelantera(gl.cullFace(gl.FRONT)).
Listado8.2:Objetostransparentes //Primeropintalosobjetosopacos
//Despuéslostransparentes gl.blendFunc(gl.SRC_ALPHA,gl.ONE_MINUS_SRC_ALPHA); gl.enable(gl.BLEND); //habilitalatransparencia gl.enable(gl.CULL_FACE); //habilitaelfaceculling gl.depthMask(false); //impideactualizarelbufferdeprof.
gl.cullFace(gl.FRONT); //seeliminaránlosdecaraalobservador drawSolid(exampleCube); //sedibujaelobjetotransparente

gl.cullFace(gl.BACK); //seeliminaránlosdelapartetrasera drawSolid(exampleCube); //sevuelveadibujarelobjeto
gl.disable(gl.CULL_FACE); gl.disable(gl.BLEND); gl.depthMask(true);
Ellistado8.2recogelasecuenciadeórdenesdeWebGLnecesariaparapoder visualizardemaneracorrectaestetipodeobjetostransparentes.Además,sueleser convenienteaplicarlailuminaciónporambascaras,yaquelapartetraseraahorase
José Ribelles y Ángeles López
ISBN:
Informática Gráfica (2ª edición) DOI: http://dx.doi.org/10.6035/Sapientia151
iluminagraciasalatransparenciadelpropioobjeto.Lafigura8.4muestraalgunos resultadosobtenidosconestatécnica.
Ejercicios
8.1 Observalasdosesferasdelafigura8.2alasqueseleshancolocadodosplanos transparentesdelantedeellas,cadaplanodeuncolordistinto,ycuyaúnicadiferenciaesel ordendedibujadodedichosplanos.¿Cuáldeellasteparecemásrealista?,¿porqué?,¿en quéordencreesquesehanpintadolosobjetostransparentesqueaparecendelantedecada esfera?
8.2 Consultalainformacióndel pipeline deWebGL2.0yaveriguadóndetienenlugar lasoperacionesde faceculling y blending.

8.3 Ejecutaelprograma c08/transparencia.html.Compruebaqueenelcódigofigura todolonecesarioparadibujarelobjetodemaneratransparente.Observalaescenamoviendolacámaraycontesta,¿creesqueelobjetotransparenteseobservadeformacorrecta desdecualquierpuntodevista?Sinoesasí,¿porquécreesqueocurre?
8.4 Edita c08/transparencia.js,establececomofuncióndecálculo gl.ONE enlugarde gl.ONE_MINUS_SRC_ALPHA yobservaelnuevoresultado.
Figura8.4:Ejemplodeobjetotransparentecon,deizquierdaaderecha, alfa= 0 3, 0 5 y 0 7,pintado utilizandoelcódigorecogidoenellistado8.2.
8.2.Espejos
Losobjetosreflejantes,aligualquelostransparentes,sontambiénmuyhabitualesencualquierescenario.Esfácilencontrardesdeespejospurosaobjetosque, porsuspropiedadesdematerialytambiéndesuprocesodefabricación,comoel mármol,porejemplo,reflejanlaluzyactúancomoverdaderosespejos. Sin em bargo, el cálculo del reflejo es realmente complejo, por lo que en esta sección se muestra un truco muy habitual para conseguir añadir superficies planas reflejantes a nuestra escena (véase figura 8.5) y que de una manera sencilla nos va a permitir obtener muy buenos resultados visuales.
Elmétodoconsisteendibujarlaescenadeformasimétricarespectoalplano quecontieneelobjetoreflejante(elobjetoenelquesevayaaobservarelreflejo).
Ribelles
Informática Gráfica (2ª edición)

http://dx.doi.org/10.6035/Sapientia151

Haydostareasprincipales:laprimeraesobtenerlatransformacióndesimetría;la segundaesevitarquelaescenasimétricaseobservefueradeloslímitesdelobjeto reflejante.
Para obtener la matriz de simetría hay que calcular el resultado de la siguiente secuencia de transformaciones: trasladar el plano de simetría al origen, girarlo para hacerlo coincidir con, por ejemplo, el plano

=0
escalar con un factor de 1 en la dirección
último, deshacer
giro
la translación anteriores. La matriz resultante
es la siguiente, donde
es
punto que pertenece al objeto plano reflejante
8.2.2.Evitardibujarfueradeloslímites
Paralasegundatarea,ladenodibujarfueradeloslímitesdelobjetoreflejante (véansefiguras8.6y8.7),hayvariosmétodos.Unodeellosconsisteenutilizarel buffer deplantilladelasiguienteforma.Enprimerlugar,sedibujaelobjetoreflejantehabiendopreviamentedeshabilitadolos buffers decolorydeprofundidad, ytambiénhabiendoconfiguradoel buffer deplantilla,paraquesepongana1los píxelesdedicho buffer quecorrespondanconlaproyeccióndelobjeto.Después, sehabilitanlos buffers deprofundidadycoloryseconfigurael buffer deplantilla pararechazarlospíxelesqueenel buffer deplantillanoesténa1.Entonces,se
Informática
edición)
dibujalaescenasimétrica.Después,sedeshabilitael buffer deplantillaysedibujalaescenanormal.Porúltimo,demaneraopcional,hayquedibujarelobjeto reflejanteutilizandotransparencia.Ellistado8.3muestracómoserealizanestos pasosconWebGL.Elejemplo c08/espejos.html recogetodaslasoperacionesdescritas,produciendoimágenescomoladelafigura8.7. Una última observación, en el momento de obtener el contexto es necesario solicitar la creación del buffer de plantilla ya que este no se crea por defecto: canvas.getContext(..., {stencil:true});
Figura8.6:Aldibujarlaescenasimétricaesposibleobservarlafueradeloslímitesdelobjetoreflejante(izquierda).El


Informática

José
Listado8.3:Secuenciadeoperacionesparadibujarobjetosreflejantes gl.clear(gl.COLOR_BUFFER_BIT|gl.DEPTH_BUFFER_BIT| gl.STENCIL_BUFFER_BIT);
//Desactivalosbuffersdecoloryprofundidad gl.disable(gl.DEPTH_TEST); gl.colorMask(false,false,false,false);
//Establececomovalordereferenciael1 gl.enable(gl.STENCIL_TEST); gl.stencilOp(gl.REPLACE,gl.REPLACE,gl.REPLACE); gl.stencilFunc(gl.ALWAYS,1,0xFFFFFFFF);
//Dibujaelobjetoreflejante
//Activadenuevolosbuffersdeprofundidadydecolor gl.enable(gl.DEPTH_TEST); gl.colorMask(true,true,true,true);
//Configuraelbufferdeplantilla gl.stencilOp(gl.KEEP,gl.KEEP,gl.KEEP); gl.stencilFunc(gl.EQUAL,1,0xFFFFFFFF);
//Dibujalaescenareflejada
//Desactivaeltestdeplantilla gl.disable(gl.STENCIL_TEST);
//Dibujalaescenanormal
//Dibujaelobjetoreflejantecontransparencia
Informática Gráfica (2ª edición)
DOI: http://dx.doi.org/10.6035/Sapientia151
8.3.Sombras
Enelmundoreal,sihayfuentesdeluz,habrásombras.Sinembargo,enel mundodelainformáticagráficapodemoscrearescenariosconfuentesdeluzysin sombras.Pordesgracia,laausenciadesombrasenlaescenaesalgoque,además deincidirnegativamenteenelrealismovisualdelaimagensintética,dificultade maneraimportantesucomprensión,sobretodoenescenariostridimensionales. Por ejemplo, observa las dos imágenes de la figura 8.8 en la que al añadir la som bra entendemos que el plano está en el aire y no pegado al suelo.Estohahecho queenlaliteraturaencontremosnumerososymuydiversosmétodosquetratan deaportarsoluciones.Porsuerte,prácticamentecualquiermétodoquenospermita añadirsombras,porsencilloquesea,puedesermásquesuficienteparaaumentar elrealismoyqueelusuariosesientacómodoalobservarelmundo3D.

Unmétodosimpleparaelcálculodesombrassobresuperficiesplanasesel conocidoconelnombredesombrasproyectivas.Consisteenobtenerlaproyección delobjetosituandolacámaraenelpuntodeluzyestableciendocomoplanode proyecciónaquelenelquequeramosqueaparezcasusombra.Elobjetosombra, esdecir,elresultadodelaproyección,sedibujacomounobjetomásdelaescena, perosinpropiedadesdematerialniiluminación,simplementedecoloroscuro. Dadaunafuentedeluz
=0,lamatrizde proyección

eslasiguiente:
yunplanodeproyección N ·
José
Comoelobjetosombraescoplanarconelplanoquesehautilizadopara elcálculodelaproyección,habríaqueañadirunpequeñodesplazamientoa unodeellosparaevitarelefectoconocidocomo stitching (véasefigura8.9). WebGLproporcionalaorden gl.polygonOffset paraespecificareldesplazamiento,quesesumaráalvalordeprofundidaddecadafragmentosiemprey cuandosehayahabilitadocon gl.enable(gl.POLYGON_OFFSET_FILL)
Figura8.9:Ejemplode stiching producidoporsercoplanareselsueloyelobjetosombra
Hayquecontrolarqueelobjetosombranovayamásalládelasuperficie sobrelaquerecae(véasefigura8.10).Aligualqueenlarepresentación de espejos (véase sección 8.2),el buffer deplantillasepuedeutilizarpara asegurarelcorrectodibujadodelaescena.
Figura8.10:Elobjetosombrasuperaloslímitesdelasuperficiesobrelaquerecae
Lassombrassonmuyoscuras,peroutilizandotransparenciasepuedeconseguirunresultadomuchomásagradable,yaquedejaentreverelplanosobre elqueseasientan(véasefigura8.11).
Esmuycomplejoparasuperficiescurvasopararepresentarlassombrasque caensobreelpropioobjeto.
Informática Gráfica (2ª edición)

http://dx.doi.org/10.6035/Sapientia151

8.3.2. Shadowmapping
Silaescenaseobservadesdelaposicióndondeseubicalafuentedeluz,lo queseconsigueesverjustoloquelafuentedeluzilumina,porlotanto,secumple tambiénqueestaráensombraloquelaluznove.Estemétodosebasaendibujar primerolaescenavistadesdelafuentedeluzconelobjetivodecrearunmapade profundidadyalmacenarlocomotextura.Después,sedibujalaescenavistadesde laposicióndelobservadorperoconsultandolatexturadeprofundidadparasaber siunfragmentoestáensombraypintarlodemaneraacorde.
ParaobtenerdichomapadeprofundidadconWebGL2.0,esnecesariodibujar laescenacontraun framebufferobject (FBO).Elprocesadorgráficopuededibujar enun FBO diferentedelcreadopordefecto,yenesecasosucontenidonoesvisible alusuario. Este FBO debe tener asociado una textura de profundidad puesto que esa información es la única que nos interesa.Trascrearel FBO,sedibujalaescenay enel shader defragmentos no hay que establecer un color de fragmento(véase imagendelaizquierdaenlafigura8.12).


Tras el primer dibujado se consigue que la información de profundidad quede almacenada en la textura de profundidad que se había asociado al FBO.Aldibujar laescenavistadesdelaposicióndelobservador,cadavérticedelmodelosehade operartambiénconlamatrizdetransformacióndelacámarasituadaenlafuente deluz.Deestamanera,paracadafragmentosepuedecompararsuprofundidad conlaalmacenadaenlatexturaysabersielfragmentoestáensombraono.La figura8.12muestraunejemplodeestatécnica,dondesepuedeobservarelmapa deprofundidadobtenidodesdelaposicióndelafuentedeluzylavistaconsombras desdelaposicióndelacámara.
Ejercicios
8.5 Ejecutaelprograma c08/sombras.html.Observalaescenamientrasmuevesla cámaraycontesta,¿detectasalgúntipodeproblemaeneldibujadodelassombras?,¿aqué creesquesedebe?Modificaelcódigoparaqueladimensióndelatexturadeprofundidad seadeuntamañomuchomáspequeño,¿quéocurreahora?,¿porqué?
José Ribelles y
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
Figura8.12:Ejemplode shadowmapping.Alaizquierdaseobservaelmapadeprofunidadobtenido desdelafuentedeluz;aladerechasemuestralaescenaconsussombras

CUESTIONES
8.1 Enelcálculodelatransparenciamedianteeloperador over seutilizandosvalores decolor,¿cuálesson?
8.2 EnWebGL2.0,¿cómoseestablecelatransparenciaaniveldefragmento?

8.3 ¿Conquéobjetivoseutilizalaorden depthMask alahoradetrabajarconescenas queincluyenobjetostransparentes?Explicatambiénporquéesnecesario,esdecir,qué tipodeproblemaspuedenocurrirsinolautilizas.
8.4 Enel shader defragmentosimplementadoenelejemplo transparencia.html se realizaelcálculodelailuminaciónparaambascarasenelcasodelosobjetostransparentes, ¿sabríasexplicarporqué?
8.5 Dadaunaescenaquecontieneunaúnicafuentedeluzydadounobjetoque perteneceadichaescena,sisehaceusodelmétododesombrasproyectivas¿cuántasveces sehadeobtenerydibujarelcorrespondienteobjetosombra?
8.6 Siquieroimplementarelmétododesombrasproyectivas,¿porquéyenquécasos necesitoutilizarun buffer deplantilla?
8.7 Enelmétododesimulacióndeespejosmediantesimetría,argumentalanecesidad onodeaplicarlamatrizdetransformacióndesimetríaalascoordenadas,alasnormalesy alascoordenadasdetexturaparaqueelreflejoobtenidoseacorrecto.
8.8 Enelmétodode shadowmapping,¿porquéenelprimerdibujadonoesnecesarioestableceruncolordelfragmento?Escribeelcódigodelcorrespondiente shader de fragmentosparaelprimerdibujado.
José Ribelles y Ángeles López
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
Interacciónyanimacióncon shaders Índice
Estecapítulojuntatécnicasdeinteracciónconmétodosbásicosdeanimación con shaders.Esuncapítulodeíndolemuyprácticaqueseacompañadeejemplos quecomplementanlosmétodosexplicados.
9.1.Seleccióndeobjetos
Enunaaplicacióninteractivaesfácilqueelusuariopuedaseñalarobjetosde laescenayque,portanto,laaplicaciónnecesitesaberdequéobjetosetrata.Habitualmente,elusuarioutilizaelratónparamoverelpunteroymedianteelbotón izquierdorealizalaselecciónalpresionarlo,perotambiénpuedehacerloconeldedoenelcasodeutilizardispositivosmóvilesconpantallatáctil.Encualquiercaso, comoresultadodelainteracciónseproduceuneventoqueesnecesarioatender paraaveriguarlascoordenadasdelpíxelsobreelquesehizoelclic.
Paraaveriguarlascoordenadasdelpíxelseleccionadohayquetenerencuenta queelorigendecoordenadasenelnavegadorestáenlaesquinasuperiorizquierda
Gráfica (2ª
http://dx.doi.org/10.6035/Sapientia151
delapágina.Porlotanto,alhacerelclic,elmanejadordeeventosnosproporcionalascoordenadasrespectoadichoorigen.Sinembargo,loquenecesitamos conocersonlascoordenadasrespectoalorigendeWebGLquesecorrespondecon laesquinainferiorizquierdadelcanvas.Ellistado9.1muestracómoobtenerlas coordendascorrectasparaserutilizadasenWebGL.
Listado9.1:ConversióndecoordenadasparaserutilizadasenWebGL rectangle=event.target.getBoundingClientRect(); x_in_canvas=(event.clientX rectangle.left); y_in_canvas=(rectangle.bottom event.clientY);


A partir de aquí hay dos maneras de averiguar de qué objeto se trata, una utili zando solo el canvas y la otra utilizando además un FBO
9.1.1.Utilizandoelpropiocanvas
Este método consiste en dibujar dos veces la escena de manera consecutiva. En el primer dibujado se pinta cada objeto seleccionable de un color diferente y plano (véase figura 9.1(a)). De esta manera, si tras el primer dibujado se accede al canvas en las coordenadas elegidas por el usuario, se puede averiguar el color del píxel correspondiente, y sabiendo el color se sabe a qué objeto pertenece. Solo quedaría borrar el canvas y pintar de nuevo la escena pero ya con el aspecto final que se ha de mostrar al usuario. Por supuesto, el usuario nunca llega a ver la escena pintada con colores planos, simplemente se dibuja para después acceder al framebuffer y conocer el color del píxel.
Ellistado9.2muestralaoperacióndeaccesoalcolordeunpíxelqueserealiza mediantelafunción gl.readPixels.Lavariable pixels contendráenconsecuenciael valordecolorbuscado.Después,yasolorestacompararelvalorleídoconlosutilizadosaldibujarlosobjetos,borrarel framebuffer conlaorden gl.clear ydibujar laescena,estavezconlastécnicashabituales,yaqueestenuevodibujadosíque seráelquefinalmenteterminemostrándosealusuario.
Listado9.2:Accesoalcolordeunpíxelenel framebuffer varpixels=newUint8Array(4); gl.readPixels(x_in_canvas,y_in_canvas,1,1,gl.RGBA, gl.UNSIGNEDBYTE,pixels);
Para implementar esta técnica es habitual utilizar un flag en el shader de frag mentos que indique si el objeto se ha de dibujar o no utilizando un color plano. Este flag sería una variable de tipo uniform bool que será puesta a verdadero o falso se gún el caso. Como color plano es buena idea, por ejemplo, aprovechar la propia componente difusa del material del objeto ya que este valor es muy probable que se encuentre disponible en el shader El listado 9.3 muestra un ejemplo muy simple de cómo implementar esta técnica en el shader de fragmentos.
Listado9.3:Usodeun flag paradecidirsidibujaronoconuncolorplano fragmentColor=(flag==false)? vec4 (phong(n,L,V),1.0) : vec4 (Material.Kd,1.0);
Ejercicios
9.1 Ejecutaelejemplo c09/seleccion.html queimplementaelmétododeselección descritoenestasección.Compruebasufuncionamiento.Examinalaatencióndelevento, laobtencióndelascoordenadasdelpíxelseleccionadoycómosedeterminalaprimitiva seleccionadaenbasealcolorleído. Modifícalo para que el plano del suelo también sea seleccionable.
9.2 ¿Quévaloresdecolorseobtienenalseleccionarcadaunodelosobjetos?Compruebacómoestosvalorescoincidenconlosespecificadosenlascomponentesdifusasde losrespectivosmateriales.
9.1.2.Utilizandoun FBO
Elmétodoanteriordibujalaescenadecoloresplanosparaaveriguarelobjeto seleccionadoapartirdelmomentoenqueelusuariorealizalaselección.Sila escenamuestraobjetosestáticos,estonoentrañamayorproblema.Sinembargo, silosobjetosseleccionablesestánanimados,puedeocurrirquelaseleccióndel usuarioyloleídoenel framebuffer nocoincidadebidoalpasodeltiempoyla correspondienteactualizacióndelosobjetosdelaescena.Unamaneradeevitarlo estenerlaescenadecoloresplanosalmacenada,demaneraquealrealizarelclic seaposiblerealizarlaconsultasobrelaescenaqueseestámostrandoalusuarioy nosobreunanueva.
Estosepuedeconseguirutilizandounnuevoobjeto framebuffer (FBO)paradibujarenéllaescenaconcoloresplanos.Lacondiciónesqueeste FBO almacene coloryprofundidadyquetengaelmismotamañoqueelcanvas.Cuandoelusuario realizalaselección,el FBO yacontienelaimagendibujada,puestoqueenélseha
José Ribelles
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
dibujadolamismaescenaqueelusuarioestáviendo,soloqueconcoloresplanos. Deestamanera,loqueseconsigueespoderrealizarlaconsultasobreloyadibujado.Ellistado9.4muestralaoperacióndeaccesoalcolordeunpíxel.Sepuede observarquelaúnicavariaciónesqueantesdellamaralafunción gl.readPixels seactivael FBO creadoaprópositoydespuéssevuelveaestablecerel framebuffer pordefecto.
Listado9.4:Accesoalcolordeunpíxelenel FBO gl.bindFramebuffer(gl.FRAMEBUFFER,myFbo); //seleccionaelFBO varpixels=newUint8Array(4); gl.readPixels(x_in_canvas,y_in_canvas,1,1,gl.RGBA, gl.UNSIGNEDBYTE,pixels); gl.bindFramebuffer(gl.FRAMEBUFFER,null); //framebuffernormal
Ejercicios
9.3 Ejecutaelejemplo c09/seleccionFbo.html queimplementaelmétododeselección queutilizaunobjeto framebuffer
Compruebasufuncionamiento. Examinacómosedeterminalaprimitivaseleccionadaenbasealcolorleídoapartir delaescenayadibujada.
¿Hayalgúncambioenel shader defragmentosrespectoalimplementadoenel métodoanterior?
¿Dequétamañoesel FBO?,¿yelcanvas?,¿quéocurriríasinocoincidiesenambos tamaños?
9.2.Animación
Realizaranimaciónatravésde shaders puederesultarmuysencillo.Solonecesitamosunavariableuniformeenel shader yqueestaseactualicedesdelaaplicaciónconelpasodeltiempo.Enel shader seutilizarádichavariableparamodificar cualquieradelaspropiedadesdelosobjetos.
Porejemplo,sisemodificaelvalor alfa quecontrolalaopacidaddeunobjeto, podemosconseguirqueesteaparezcaosedesvanezcadeformagradual;también modificarparámetrosdelasfuentesdeluzhaciendoque,porejemplo,laintensidad delaluzaumenteodecaigadeformagradualoquelosobjetoscambiensucolor. Porsupuesto,tambiénpodemosmodificarlamatrizdetransformacióndelmodelo cambiandolaposición,eltamañoolaorientacióndealgúnobjetodelaescenao, porquéno,añadirdosmaterialesaunobjetoyhacerqueunobjetocambiede materialconunasimpleinterpolaciónlineal.
Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
9.2.1.Eventosdetiempo
JAVASCRIPT proporcionaunaordenparaespecificarqueunadeterminadafunciónseaejecutadatranscurridounciertotiempo.Ladisponibilidaddeunafunción deestetipoesfundamentalparaactualizarlavariabledel shader queseutilizapara generarlaanimación.Lafuncióneslasiguiente:
myVar=setTimeout(updateStuff,40);
Elvalornuméricoindicaelnúmerodemilisegundosquehandetranscurrir paraquesellamealafunción updateStuff.Unaveztranscurridodichotiempo,esa funciónseejecutaráloantesposible.Sisedeseaquelafunciónseejecuteotravez alcabodeunnuevoperiododetiempo,ellamismapuedeestablecerlollamando alafunción setTimeout antesdefinalizar.Otraalternativaesutilizarlasiguiente orden,queproducelaejecuciónde updateStuff cada40ms: myVar=setInterval(updateStuff,40);
Y para suspender la ejecución: clearInterval(myVar);
9.2.2.Encendido/apagado
Unefectomuysimpledeanimaciónconsisteenqueunapropiedadtomedos valoresdiferentesquevanalternándosealolargodeltiempo,comopodríanserla simulacióndelparpadeodeunaluzalencenderseoelmalfuncionamientodeun tubofluorescente. Para implementar esta técnica es habitual utilizar un flag en el shader de fragmentos que indique si el objeto se ha de dibujar de una manera u otra. Este flag sería una variable de tipo uniform bool que será puesta a verdadero o falso según el caso. Por ejempo, es buena idea aprovechar la propia componente ambiente del material del objeto para el estado de apagado ya que este valor es muy probable que se encuentre disponible en el shader. El listado 9.5 muestra un ejemplo muy simple de cómo implementar esta técnica en el shader de fragmentos en el que la variable apagado indica el estado, es decir, si encendido o apagado).
Listado9.5: Shader paraencendido/apagado
uniform boolapagado; //almacenaelestado
Informática Gráfica
edición)
José
Enlaaplicacióneshabitualquedichavariableestégobernadaporunsimple procesoaleatorio.Porejemplo,lafunción setFlickering enellistado9.6recibeun valorcomoparámetroquesecomparaconunnúmeroaleatorio.Deestamanera, sepuedecontrolarlapreferenciahaciaunodelosdosestadosposibles.
Listado9.6:Funciónquecontrolaelencendido/apagado functionsetFlickering(value){ if (Math.random()>value) //Math.randomen[0..1] gl.uniform1i(program.apagadoIndex,false); else gl.uniform1i(program.apagadoIndex,true);
}
Ejercicios
9.4 Ejecutaelejemplo c09/onOff.html queimplementaelmétododeanimaciónde encendido/apagado.Compruebasufuncionamiento.Examinacómoseestableceunvalor diferentedeparpadeoparacadaprimitiva,demaneraquealgunassevenmástiempoencendidasyotrasmástiempoapagadas.Realizalasmodificacionesnecesariasparaque,en lugardeencendido/apagado,seaencendido/sobreiluminado.
9.2.3.Texturas
Modificarlascoordenadasdetexturaconeltiempoesalgosencilloydelo quesepuedenobtenerresultadosmuyinteresantes.Porejemplo,enelcasode serunatextura2D,sepodríasimularunpanelpublicitariorotativo.Enelcaso deutilizarunatexturaprocedural,porejemplo,el shader denubesutilizadoen elejemplo c07/nubes.html,modificarlascoordenadasdetexturapermitequesu aspectocambiesuavementeconeltiempo.Encualquiercaso,soloesnecesario utilizarunavariablequeseincrementeconelpasodeltiempo(véaselistado9.7) yqueasuvezseutiliceparaincrementarlascoordenadasdetexturaenel shader, comosemuestraenellistado9.8.Deestamanera,acadainstantedetiempolas coordenadasdetexturadecadavérticesondiferentes,produciéndoseelefectode animación.
Ejercicios
9.5 Ejecutaelejemplo c09/nubes.html queimplementaelmétododeanimaciónbasadoenmodificarlascoordenadasdetexturaconeltiempo.Compruebasufuncionamiento. Examinacómosemodificanlascoordenadasdetexturaparaaccederalafunciónderuido. Ahoraponloenpráctica.Partedelejemplo c06/aplicaTexturas.html ymodifícaloparaque latexturasedesplacesobrelasuperficiedelasprimitivasconelpasodeltiempo.
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
Listado9.7:Funciónqueactualizaeldesplazamientodelatexturaconeltiempo vartexCoordsOffset=0.0,Velocity=0.01; functionupdateTexCoordsOffset(){ texCoordsOffset+=Velocity; gl.uniform1f(program.texCoordsOffsetIndex,texCoordsOffset); requestAnimationFrame(drawScene);
} functioninitWebGL(){ setInterval(updateTexCoordsOffset,40);
}
Listado9.8: Shader paraactualizarlascoordenadasdetexturaconeltiempo //Shaderdefragmentos
uniformfloat texCoordsOffset;
void main(){
vec2 newTexCoords=texCoords; newTexCoords.s+=texCoordsOffset; fragmentColor=texture(myTexture,newTexCoords);
}
9.2.4.Desplazamiento
Enlasección6.7seexplicóelmétodoquepermiteutilizarunatexturacomo mapadedesplazamientoparaqueentiempodeejecucióncadavérticesedesplace apartirdelvalorleídodelmapa.Ahora,loquesepersigueesanimarlageometría, haciendoqueeldesplazamientodecadavérticenoseasiempreelmismo,sino quecambieconeltiempo.Lafigura9.2(a)muestradosejemplosenlosqueenel shader devérticessehautilizadolafunciónsenocondiferenteamplituddeonda paracalculareldesplazamientoenfuncióndeltiempotranscurrido.Enlafigura 9.2(b)semuestraelresultadodeutilizarunafunciónderuidoparadeterminarel desplazamiento.Elvalordetiemposeutilizacomoparámetrodeentradadela funciónderuido,obteniéndoseelefectodeunabanderaalviento.
Ejercicios
9.6 Elejemplo c09/vd.html implementaelmétododeanimaciónbasadoendesplazamiento.Ejecútaloy,porejemplo,pruebaaescalarelvalordeldesplazamiento.
José Ribelles y Ángeles López
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
9.3.Sistemasdepartículas
Lossistemasdepartículassonunatécnicademodeladoparaobjetosqueno tienenunafronterabiendefinidacomo,porejemplo,humo,fuegoounespray. Estosobjetossondinámicosyserepresentanmedianteunanubedepartículasque, enlugardedefinirunasuperficie,definenunvolumen.Cadapartículanace,vive ymueredemaneraindependiente.Ensuperiododevida,unapartículacambiade posiciónydeaspecto.Atributoscomoposición,color,transparencia,velocidad, tamaño,formaotiempodevidaseutilizanparadefinirunapartícula.Durantela ejecucióndeunsistemadepartículas,cadaunadeellassedebeactualizarapartir desusatributosydeunvalordetiempoglobal.
Lasfiguras9.3y9.4muestranejemplosdeunsistemaenelquecadapartícula esuncuadradoypretendenmodelarrespectivamenteunmosaicoypequeñasbanderasenunescenariodeportivo.Enamboscasos,acadapartículaseleasignaun instantedenacimientoaleatoriodemaneraquelaspiezasdelmosaico,olasbanderas,apareceneninstantesdetiempodiferentes.Mientrasestánvivas,paracada partículaseaccedeaunatexturaderuidoutilizandolavariablequerepresentael pasodeltiempoyasínoaccedersiemprealmismovalordelatexturaconelfinde actualizarsuposición.Acadapartículatambiénseleasignadeformaaleatoriaun valordetiempofinalquerepresentaelinstanteenquelapartículadebedesaparecer.
Informática Gráfica (2ª edición)


http://dx.doi.org/10.6035/Sapientia151

Figura9.3:Animacióndeunmosaicoimplementadocomosistemadepartículas
Figura9.4:Animacióndebanderasimplementadacomosistemadepartículas

Todaslaspartículas,juntoconsusatributos,puedenseralmacenadasenun bufferobject.Deestamanera,enel shader devérticessedeterminaelestadode lapartícula,esdecir,siaúnnohanacido,siestávivaosiporelcontrarioya hamuerto.Enelcasodeestarviva,esendicho shader dondeseimplementasu comportamiento.Porlotanto,lavisualizacióndeunsistemadepartículasserealiza totalmenteenelprocesadorgráficosincargaalgunaparala CPU.Parasimplificar eldibujadodeunsistemadepartículasseasumequelaspartículasnocolisionan entresí,noreflejanluzynoproducensombrassobreotraspartículas.


Unejemplodecreacióndeunsistemadepartículassemuestraenellistado9.9. Enconcretosecreandiezmilpartículas;acadapartículaseleasignaunavelocidad yunaposiciónalolargodeleje X,ambasaleatorias,yunvalordenacimiento.Esta informaciónsealmacenaenelvector particlesInfo,elcualsetransfiereaun buffer object.
Ellistado9.10muestracómoseordenaeldibujadodelsistemadepartículas. Enesteejemplo,cadapartículaconstadedosatributos,posicióneinstantedenacimiento,yelsistemasedibujacomounacoleccióndepuntos.
Porútltimo,enel shader devérticessecompruebasilapartículahanacido y,siesasí,secalculasuposiciónapartirdelvalordeposición X yelvalorde velocidadalmacenadoenlaposición Y ,juntoconelvalordeltiempotranscurrido. Ellistado9.11muestraesteúltimopaso.Lafigura9.5muestradosejemplosenlos queúnicamentecambiaeltamañodelpunto.
Listado9.9:Cortinadepartículas varnumParticles=10000; functioninitParticleSystem(){ varparticlesInfo=[]; for (vari=0;i<numParticles;i++){
//velocidad
varalpha=Math.random(); varvelocity=(0.1
alpha)+(0.5
//posición varx=Math.random(); vary=velocity; varz=0.0;
(1.0 alpha));
particlesInfo[i
4+0]=x; particlesInfo[i
4+1]=y; particlesInfo[i
4+2]=z; particlesInfo[i
4+3]=i
0.00075; //nacimiento }
program.idBufferVertices=gl.createBuffer(); gl.bindBuffer(gl.ARRAY_BUFFER,program.idBufferVertices); gl.bufferData(gl.ARRAY_BUFFER, newFloat32Array(particlesData), gl.STATIC_DRAW); } Listado9.10:Dibujadodelsistemadepartículas functiondrawParticleSystem(){ gl.bindBuffer(gl.ARRAY_BUFFER,program.idBufferVertices); gl.vertexAttribPointer(program.vertexPositionAttribute, 3,gl.FLOAT,false,4 ∗ 4,0); gl.vertexAttribPointer(program.vertexStartAttribute, 1,gl.FLOAT,false,4 ∗ 4,3 ∗ 4); gl.drawArrays(gl.POINTS,0,numParticles); }
Ejercicios
9.7 Elejemplo c09/particulas.html implementalaanimacióndeunsistemadepartículas.Ejecútaloyexperimentaconélparacomprenderlomejor.
9.8 Modificaelejemploparaqueelsistemadepartículastengaprofundidad.Tendrás quemodificartantoel js comoel shader.Elefectoqueseconsigueesmuyinteresante.
José Ribelles y Ángeles López
Informática Gráfica (2ª edición) DOI: http://dx.doi.org/10.6035/Sapientia151
Listado9.11: Shader devérticesparaelsistemadepartículas

invec3 VertexPosition; infloat VertexStart; void main(){
vec3 pos= vec3 (0.0); if (Time>VertexStart){ //sihanacido float t=Time VertexStart; if (t<2.0){ //siaúnvive pos.x=VertexPosition.x; pos.y=VertexPosition.y
t; alpha=1.0 t/2.0;
}
}
(pos,1.0); gl_Position=projectionMatrix

vec4 ecPosition=modelViewMatrix
ecPosition; gl_PointSize=6.0;
Figura9.5:Ejemplodesistemadepartículasdibujadocontamañosdepuntodiferentes
CUESTIONES
9.1 Justodespuésdequeunusuariorealicelaaccióndeseleccióndeunobjetoes necesarioaveriguardequéobjetosetrata,¿cuáldelosdosmétodosvistosenestecapítulo nonecesitadibujarlaescenajustoacontinuacióndel clic paraaveriguardequéobjetose trata?
9.2 Deentrelosdosmétodosvistosenestecapítuloparaseleccióndeobjetos,¿cuáles laprincipalventajaqueproporcionaelmétodoqueusaun FBO yenquécasosseproduce?
José Ribelles y Ángeles López
978-84-17429-87-4
Informática Gráfica (2ª edición) DOI: http://dx.doi.org/10.6035/Sapientia151
José Ribelles y
Enelprocesodeseleccióndeunobjeto,¿porquénopuedoutilizardirectamente lascoordenadasobtenidasatravésdelavariable event conlaorden gl.readPixels?
9.3
9.4
Enunsistemadepartículasgenérico,¿cómoseproporcionaal shader elvalorde nacimientodecadapartícula?
9.5 Supónqueentuescenariovirtualdeseasincluirunavallapublicitaria.Estavalla hademostrardosimágenesalternaseneltiempo,intercambiándolascada10segundos. Elcambiodeunaimagenaotraserealizamedianteundesplazamientoverticalyduraun segundo.Detallacómoloharías,tantoenlapartede javascript comoenel shader.Trata deserlomásespecificoposible(cómomodelaríaslavalla,quévariablesnecesitasparala animación,cómocontrolaríaseltiempo,etc).
Estásmodelandounplanetayquieresanimarlohaciendoquegiresobresímismo. Quizálomássencilloseautilizarunatransformaciónderotación,demaneraqueelángulo degiroseincrementeconeltiempo.Propónunaalternativaautilizartransformacionesque consigaelmismoefectovisual(dequeelplanetagiraalrededordesimismo),detallala respuestatodoloquepuedascomosiuntercerotuviesequeimplementarloapartirdetu explicación.
9.6
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
Procesamientodeimagen
pipeline la posibilidaddemanipularimágenessinasociarlegeometríaalguna.Sinembargo, noeshastaqueseproducelaaparicióndelosprocesadoresgráficosprogramables
deimágenes,consiguiendoaumentardemaneradrásticalacapacidaddeanalizar ymodificarimágenes,asícomodegenerarunaampliavariedaddeefectos(véase figura10.1).
10.1.Aparienciavisual
Antialiasing
sutérminoeninglés
tidadescontinuasadiscretas.Porejemplo,alvisualizarunsegmentodelínease
Figura10.1:Ejemplodeprocesadodeimagen.Alaimagendelaizquierdaselehaaplicadoun efectoderemolino,generandolaimagendeladerecha
convierteaunasecuenciadepíxelescoloreadosenel framebuffer,siendoclaramenteperceptibleelproblema,exceptosilalíneaeshorizontalovertical(véase figura10.2).Esteproblemaestodavíamásfácildepercibir,ytambiénmuchomás molesto,silosobjetosestánenmovimiento.
Figura10.2:Enlaimagendelaizquierdaseobservaclaramenteelefectoescalera,quesehacemás suaveenlaimagendeladerecha
Nosreferimoscon antialiasing alastécnicasdestinadasaeliminareseefecto escalera.Hoyendía,lapotenciadelosprocesadoresgráficospermitequedesdeel propiopaneldecontroldelcontroladorgráficoelusuariopuedasolicitarlasolución deesteproblemaeinclusoestablecerelgradodecalidad.Hayquetenerencuenta que,amayorcalidaddelresultado,mayorcosteparala GPU,pudiendollegara producirciertaralentizaciónenlainteracciónconnuestroentornográfico.Poreste motivo,lasaplicacionesgráficasexigentesconel hardware gráficosuelenofrecer alusuariolaposibilidaddeactivarlocomounaopción.


Supersampling
Elmétodode supersampling sebasaentomarmásmuestrasporcadapíxel.De estamanera,elvalorfinaldeunpíxel p seobtienecomoresultadodelacombinacióndetodassusmuestras.Hayquedefinirunpatróndemuestreoytambiénse puedeasignarunpesodiferenteacadamuestra.
Lafigura10.3muestraunejemplodelfuncionamientodelmétododonde,en lugardeutilizarunaúnicamuestra,seutilizancuatro.Eneseejemplo,dosdelas muestrasquedancubiertasporlaproyeccióndelaprimitivagráficayelcolorfinal delpíxeleselvalormedioponderadodelosvaloresobtenidosparalascuatro muestrasrealizadas.
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
Figura10.3:Ejemplodefuncionamientodel supersampling
Laimplementaciónmáspopulardeestemétodoseconoceconelnombrede fullsceneanti-aliasing, FSAA.Alutilizarestatécnicaesnecesariodisponerdeun framebuffer cuyotamañosea n vecesmayor,donde n eselnúmerodemuestras, yanosoloparaalmacenarelcolor,sinotambién,porejemplo,paraguardarlaprofundidaddecadamuestra.Estemétodoprocesacadamuestrademaneraindependiente,porloqueesbastantecostoso,dadoqueelnúmerodepíxelessemultiplica fácilmenteporcuatro,ochooinclusodieciséis.

Multisampling
Elmétodoconocidopor multi-samplinganti-aliasing, MSAA,sebasaenmuestrearcadapíxel n vecesparaaveriguarelporcentajedelpíxelcubiertoporlaprimitiva.El shader defragmentossoloseejecutaunavezporfragmento,adiferencia delmétodo fullsceneanti-aliasing,dondedicho shader seejecutabaparacada muestra. WebGL 2.0 implementa este método (véase figura 10.4) y por defecto es tá habilitado. En el caso de no quererlo hay que desactivarlo de manera específica al obtener el contexto:


Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
Losmonitoresnoproporcionanunarespuestalinealrespectoalosvaloresde intensidaddelospíxeles.Estoproducequeveamoslasimágenesunpocomás oscurasonotanbrillantescomorealmentedeberíanobservarse.Enciertasaplicaciones,eshabitualqueseofrezcacomoopciónalusuariopoderrealizaresteajuste demaneramanualyasícorregirelproblema.Enlafigura10.5,lacurva CRT gammamuestralarespuestadelmonitorparacadavalordeintensidaddeunpíxel.La curvacorreccióngammarepresentalaintensidaddelpíxelnecesariaparaqueel monitorpresentelarespuestalineal,representadaporlalínearecta.
Figura10.5:Esquemadefuncionamientodelacorrecióngamma



Silaintensidadpercibidaesproporcionalalaintensidaddelpíxelelevadoa
,porloquelacorrecióngammaconsisteencontrarrestaresteefectoasí:
Listado10.1: Shader defragmentosparalacorrecióngamma
uniformfloat Gamma; void main(){

vec3 myColor=phong(n,L,V); float gammaFactor=1.0/Gamma;
myColor.r=pow(myColor.r,gammaFactor); myColor.g=pow(myColor.g,gammaFactor); myColor.b=pow(myColor.b,gammaFactor);
fragmentColor= vec4 (myColor,1.0);
}
10.2.Posprocesodeimagen
Enestasecciónseconsideranalgunastécnicasdetratamientodeimágenes queserealizanamododeposprocesodelresultadodesíntesis.Porejemplo,las imágenesquesemuestranenlafigura10.7sonelresultadodelmismoproceso desíntesisyladiferenciaesque,unavezobtenidoelcolordelfragmento,seha realizadoalgunaoperaciónqueseaplicaporigualatodoslosfragmentosdela imagen.


10.2.1.Brillo
Lamodificacióndelbrillodeunaimagenesunefectomuysencillo.Consiste enescalarelcolordecadafragmentoporunvalor Brillo.Sidichovalores1, laimagennosealtera,siesmayorque1seaumentaráelbrillo,ysiesmenor sedisminuirá(véasefigura10.8).Ellistado10.2muestraelcódigoquehabría queincluirenel shader defragmentosparamodificarelbrillo(véaseejemplo c10/postproceso.html).
José Ribelles y Ángeles López ISBN: 978-84-17429-87-4
Informática Gráfica (2ª edición)
DOI: http://dx.doi.org/10.6035/Sapientia151
Figura10.7:EjemplosdeposprocesodeimagenListado10.2:Modificacióndelbrillodeunaimagen
fragmentColor= vec4 (miColor ∗ Brillo,1.0);
Figura10.8:Ejemplosdemodificacióndelbrillodelaimagenconfactoresdeescala 0 9, 1 2 y 1 5
10.2.2.Contraste
Laalteracióndelcontrastedelaimagenseobtienecomoresultadodemezclar doscolores,unoeselcolorobtenidocomocolordelfragmentoyelotroeselvalor deluminanciamedia(véasefigura10.9).Lavariable Contraste seutilizaparadar máspesoaunvaloruotro(véaselistado10.3yelejemplo c10/postproceso.html).
Listado10.3:Modificacióndelcontrastedeunaimagen



vec3 LumiMedia= vec3 (0.5,0.5,0.5); fragmentColor= vec4 (mix(LumiMedia,miColor,Contraste),1.0);
10.2.3.Saturación
Lasaturaciónesunamezcladelcolordelfragmentoconunvalordeintensidad específicodecadapíxel(véasefigura10.10).Observaenellistado10.4lasoperacioneshabitualesparamodificarlasaturaciónquesepuedenencontrartambiénen elejemplo c10/postproceso.html
Listado10.4:Modificacióndelasaturacióndelaimagen vec3 lumCoef= vec3 (0.2125,0.7154,0.0721); vec3 Intensidad= vec3 (dot(miColor,lumCoef)); fragmentColor= vec4 (mix(Intensidad,miColor,Saturacion),1.0);
10.2.4.Negativo
Otroejemplomuysencilloeslaobtencióndelnegativodeunaimagen(véase figura10.11).Únicamentehayqueasignarcomocolorfinaldelfragmentoelresultadoderestarlea1suvalordecolororiginal.Enellistado10.5semuestrael códigocorrespondientealcálculodelnegativodelfragmento.
José Ribelles y Ángeles López
ISBN: 978-84-17429-87-4
Informática Gráfica (2ª edición)
DOI: http://dx.doi.org/10.6035/Sapientia151







10.2.5.Escaladegrises
Tambiénesmuyfácillaobtencióndelaimagenenescaladegrises(véasefigura10.12).Lomássencilloseríaasignarcomocolorfinaldelfragmentoelresultado delamediadesustrescomponentes. Sin embargo, lo habitual es combinar las componentes de color con
determinados pesos siguiendo la recomendación ITU R BT.709 El listado 10.6 muestra
código correspondiente al cálculo del color
Listado10.6:Cálculodelaimagenenescaladegrises float

Figura10.12:Ejemplodelresultadodelaimagenenescaladegrises
10.2.6.Convolución
Laconvoluciónesunaoperaciónmatemáticafundamentalenprocesamiento deimágenes.Consisteencalcularparacadapíxellasumadeproductosentrela imagenfuenteyunamatrizmuchomáspequeñaalaquesedenominafiltrode convolución.Loquelaoperacióndeconvoluciónrealicedependedelosvalores
RealizarestaoperaciónconWebGLrequierequelaimagensintéticasegenereenprimerlugarysealmacenedespuéscomotexturaparaqueenunsegundo dibujadosepuedaaplicarlaoperacióndeconvoluciónsobrelaimagenyagenerada. Por otra parte, si la operación de la convolución sobrepasa los límites de la imagen, se utilizan los mismos parámetros que se indicaron para especificar el comportamiento de la aplicación de texturas fuera del rango [0, 1].
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
Lasoperacionesmáshabitualessonel blurring,el sharpening yladetección debordes,entreotras.Latabla10.1muestraejemplosdefiltrosdesuavizadoo blurring,nitidezo sharpening ydeteccióndebordes(véasefigura10.13).Elejemplo c10/bordes.html
Tabla10.1:Filtrosdeconvolución:(a)suavizado,(b)nitidezy(c)deteccióndebordes
Figura10.13:Ejemploderesultadodelaoperacióndeconvoluciónconelfiltrodedetecciónde bordesenlaparteizquierdadelaimagen
Ejercicios
10.1 Entrelasoperacionestípicasparaelprocesadodeimágenesseencuentranlas operacionesdevolteohorizontalyvertical.¿Cómoimplementaríasdichasoperaciones?
10.2 Combinalaoperacióndedeteccióndebordesjuntoconelsombreadocómic vistoenlasección5.6paraobtenerunresultadoaúnmássimilaraldeunverdaderocómic.
10.3.Transformaciones
Latransformacióngeométricadeunaimagenserealizaentrespasos:
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151

3.Escribirun shader devérticesquerealicelaoperacióngeométricadeseada.

Elpaso1hasidodescritoenelcapítulo6.Pararealizarelpaso2,unsimplecuadradodeladounidadessuficiente,noimportasilaimagennotieneesta proporción.Enelpaso3,el shader devérticesdebetransformarlosvérticesdel rectángulodeacuerdoalatransformacióngeométricarequerida.Porejemplo,paraampliarlaimagensolohayquemultiplicarlosvérticesporunfactordeescala superiora1,yparareducirlaelfactordeescaladebeestarentre0y1.Eseneste pasodondetambiénsedebedarlaproporciónadecuadaalpolígonodeacuerdoa laproporcióndelaimagen.
Otratransformaciónarealizarenel shader devérticesesel warping,esdecir,la modificacióndelaimagendemaneraqueladistorsiónseaperceptible.Estatécnica serealizadefiniendounamalladepolígonosenlugardeunúnicorectánguloy modificandolosvérticesdemaneraconveniente(véasefigura10.14).
Figura10.14: Warping deunaimagen:imagenoriginalenlaizquierda,mallamodificadaenla imagendelcentroyresultadoenlaimagendeladerecha
Comounaextensióndelatécnicaanteriorsepodríarealizarel morphing de dosimágenes.Dadasdosimágenesdeentrada,hayqueobtenercomoresultado unasecuenciadeimágenesquetransformaunadelasimágenesdeentradaenla otra.Paraestosedefineunamalladepolígonossobrecadaunadelasimágenesyel morphing seconsiguemediantelatransformacióndelosvérticesdeunamallaalas posicionesdelosvérticesdelaotramalla,almismotiempoqueelcolordefinitivo decadapíxelseobtieneconunafuncióndemezcla.
CUESTIONES
10.1 Enelmétodode antialiasingFull-SceneAnti-Aliasing o FSAA,¿cuántasvecesse ejecutaráel shader defragmentosparacadapíxeldelaimagenfinal?¿porqué?
10.2 Sial shader defragmentosqueestemosutilizandoleañadimoslacorrección gammayfijamosunvalordegammaiguala 1.0,¿cómocreesqueafectaráalaimagen final?
10.3 Utilizando GLSL sedeseaimplementarunfiltrodesuavizadodeimágenesmediantelaoperacióndeconvoluciónytamaño5 × 5.¿Quéocurrecuandoalaplicarla operacióndeconvoluciónalospíxelesdelosbordesdelaimagenseintentaaccedera píxelesqueseencuentrenmásalládelaspropiasdimensionesdelaimagen?
Ribelles y Ángeles López
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
José
10.4
SequiereproporcionaralusuariolaposibilidaddemodificarelbrillodelasimágenesgeneradasconWebGL.Seimplementaunmétodoendospasosqueconsisteen dibujarcontraun FBO enelprimerpaso,yutilizaresteresultadocomotexturadeunúnico polígonoquesedibujaenunsegundopasoyaal framebuffer pordefecto.¿Quéatributos porvérticesehandeproporcionaralahoradedibujaresteúnicopolígono?Indicaaquellos atributosqueresultenestrictamentenecesariosyjustificalarespuesta.
10.5 Imaginaquedeseasmodificarelbrillodelaimagen.Duranteelprocesodecreacióndelaimagendefinesenel shader defragmentosunavariable uniform quecontendrá elfactordebrillo.Situescenacontieneobjetostransparentes,¿quécuidadohasdetenera lahoradeoperarconelfactordebrillo?
Laoperacióndeconvoluciónnosepuedehaceralmismotiempoqueseobtiene laimagensintética,sehaderealizarsobrelaimagensintéticacompletamentecalculada, ¿porqué?
10.6
Informática Gráfica (2ª edición)
http://dx.doi.org/10.6035/Sapientia151
