UŚciskdziekański
Jednodniówka,2024r./One-offissue,2024
UŚciskdziekański
Jednodniówka,2024r./One-offissue,2024
Redaktorzy/Editors:
MaciejSabliki/andEkaterinaShulman
Redaktorjęzykowy/Languageeditor: ThomasZürcher
Redakcjatechnicznaiprojektokładki/Technicaleditorandcoverdesign: AleksandraHankus
Przygotowaniedodruku/Preparationforprinting: AgataKołodziejczyk
Wstęp/Introduction
Thispublicationisanimplementationoftheproject“Popularizationofscience”,which weproposedinacompetitionannouncedbytheEuropeanCityofScienceKatowice2024. LastyearthesecondeditorofthispublicationhadclassesofAcademicEnglishwithPhD students.Sheproposedthemtodescribetopicsoftheirresearchinapopularway.Then shesharedtheideawiththefirsteditor,andinspiredhimtowriteaprojectproposaland submitittothecompetition.Sowesubmittedtheproposal,andtheprojecthasbeen qualifiedforthefinancingbytheECSK2024.
Wewroteinthejustification,amongothers,thattheprojectofthepublicationisin asenseacontinuationoftheirregularpaper“Macierzator”,whichusedtobepublished bytheStudents’MathematicalSocietyoftheUniversityofSilesia.Ontheotherhand, popularizationofresearchhasalwaysbeencherishedbytheauthoritiesofbothfaculties ofMathematics,PhysicsandChemistryandScienceandTechnology,whichhasorganized thecelebrated“PiDay”since2007.
Wedohopethatthispublicationwillfindfollowers,andthefirstthreeauthorswill beconsideredpioneersofwritingaboutscienceinapopularway.Inthepresentissuewe havepapersbyMgrMagdalenaMamcarz,MgrAleksanderBies(bothPhDstudentsatthe UniversityofSilesia)andDr.ThomasZürcher,ascholarintheInstituteofMathematics. Mamcarzsubmittedanarticlepresentingpuremathematicalquestionsofinfinity,while BiesandZürcherdealwith“hot”subjectssuchasAIortherecentalgaebloom.
Dr.Zürcherwasalsoresponsibleforthelinguisticcorrections,whileMgrAleksandra Hankuswasthecomputertypesetter.WearealsoindebtedtoMgrAgataKołodziejczyk, whoengagedintheproductionoftheone-offissue.OurthanksgotoProfessorAgnieszka Nowak-Brzezińska,thevice-deanoftheFacultyofScienceandTechnology,whosupported theproject.Inasenseshehasbeenagodmotherofthejournal“Uściskdziekański”,which translatesto“TheDeans’hug”.Actually,therearetwodeansinvolvedintheproject:Prof. Nowak-Brzezińska,andthefirsteditor,whousedtoserveasadeanoftheformerFaculty ofMathematics,PhysicsandChemistry.
Ofcourse,itisneedlesstosaythatourgratitudegoestotheEuropeanCityofScience Katowice2024.WithouttheidealaunchedbyECSK2024andtheirfinancialsupport, thisprojectwouldnotbepossible.
MaciejSablikandEkaterinaShulman
Spistreści/Contents
Wstęp/Introduction, MaciejSablik3
Let’snotbeafraidofAI!WhatpossibilitiesdoesArtificialIntelligenceofferus?, AleksanderBies...............................................................7 Infinity, MagdalenaMamcarz.................................................21
Algaeandhowtocountthem, ThomasZürcher................................25
Let’snotbeafraidofAI!Whatpossibilitiesdoes
ArtificialIntelligenceofferus?
AleksanderBies
InstituteofComputerScience,FacultyofScienceandTechnology,UniversityofSilesia aleksander.bies@us.edu.pl
Abstract
ArtificialIntelligencehasemergedasatransformativetechnologywiththepotentialto revolutionizevariousaspectsofhumanlife.ThisarticleexploresthefundamentalsofAI, includingitsdefinition,types,andhistoricalmilestones.Itdelvesintothekeyconcepts ofmachinelearning,highlightingitsroleasaprogrammingparadigmanditsvarious subfieldssuchassupervised,unsupervised,semi-supervised,andreinforcementlearning. Theimportanceofdatapreprocessinginmachinelearningisalsoemphasized,alongwith adetaileddescriptionofitssteps.Furthermore,thearticlediscussesthebenefitsofAI anditssafetyconsiderations,emphasizingtheneedforethicalframeworks,regulations, andhumanoversighttoensureresponsibleAIdevelopmentanddeployment.Through collaborationandadherencetoethicalprinciples,AIhasthepotentialtobringabout significantpositiveimpactswhileminimizingrisks,thuspavingthewayforasaferand moreprosperousfuture.
WhatisAI?
Artificialintelligence(AI)isafieldofcomputersciencethatfocusesoncreatingcomputersystemscapableofperformingtasksthattypicallyrequirehumanintelligence.AI isabroadfieldencompassingmanydifferenttechniques,methods,andapproaches,and itsprimarygoalistodevelopsoftwareandsystemsthatcananalyzedata,understand context,makedecisions,learnfromexperience,andcommunicateinamannersimilarto humanintelligence,[1].GeneralAI,alsoknownasArtificialGeneralIntelligence(AGI), referstotherepresentationofhumanintellectualabilitiesacrossthefullrangeofhuman activities,aimingforamaximallyuniversalsystem,[2].Auniversalsystemisonethat hasthecapabilitytosolveawiderangeofproblemsandperformvarioustasks,regardless ofthecontextorfield.Thismeansthatthesystemcanadapttonewchallenges,acquire newskills,andmakedecisionsincomplex,changingconditions.Inthecontextofartificialintelligence,thepursuitofcreatingauniversalsysteminvolvesdevelopingtechnology
capableofperformingintellectualtasksatalevelcomparabletohumanintelligence,regardlessofthespecificityofagivenfieldofknowledge.
Figure1:Achartdepictingtypesofartificialintelligenceasitssubgroups
Artificialintelligencecanalsobedividedintoweakandstrong.WeakArtificialIntelligencereferstosystemsthatareprogrammedtoperformspecifictasksandmayappear intelligentwithinthatnarrowcontext,butdonotdemonstrategeneralunderstanding orself-awareness.StrongArtificialIntelligencereferstoatheoreticaltypeofartificial intelligenceinwhichsystemshavetheabilityforgeneralunderstanding,learning,understandingtheworld,andevenself-improvement.Theycansimulateintellectualfunctions attributedtohumanintelligence,[3]and[4].
Figure2:Typesofartificialintelligence
Referringtothechart(Figure2):
• WeakAIreferstoAIsystemsthatarelimitedtoperformingspecifictasksanddo notdemonstrategeneralunderstandingorself-awareness.
• StrongAI,ontheotherhand,referstosystemsthathavetheabilityforgeneral understanding,learning,understandingtheworld,andevenself-improvement.
• ExpertSystemsarerule-basedapproachestoartificialintelligenceanddecisionmaking,inwhichexpertscreateasetofrulesusedformakingdecisionsandsolving specificproblems.
• MachineLearningisamethodinwhichsystemslearnfromdatawithouttheneed forexplicitprogramming.
• ArtificialNeuralNetworksareatypeofmachinelearningthatmimicsthefunctioningofhumanneurons.
• GeneralIndependentLearningistheideathatAIcanlearnindependentlyofhuman supervisionordata.
Machinelearningasaprogrammingparadigm
Machinelearning(ML)asaprogrammingparadigmrepresentsashiftinhowsoftware systemsaredeveloped,allowingcomputerstolearnfromdataratherthanbeingexplicitly programmedforeverytask.Itisasubfieldofartificialintelligence(AI)thatfocuseson thedevelopmentofalgorithmsandmodelsthatenablecomputerstolearnpatternsand makepredictionsordecisionsbasedondata.Theessenceofmachinelearningliesin theabilityofalgorithmstoimprovetheirperformanceovertimeastheyareexposedto moredata.Thisprocess,knownastraining,involvesfeedingthealgorithmwithlabeled examples(insupervisedlearning)orlettingitexplorepatternsindata(inunsupervised learningorreinforcementlearning).Throughrepeatediterations,thealgorithmadjusts itsinternalparameterstominimizeerrorsormaximizerewards,ultimatelyimprovingits abilitytomakeaccuratepredictionsordecisions,[5].Oneofthekeystrengthsofmachine learningisitsabilitytohandlecomplexandlarge-scaledatasets,extractingmeaningful insightsthatmightnotbeimmediatelyapparenttohumanobservers.Thiscapabilityhas ledtoadvancementsinvariousdomains,includinghealthcare,finance,transportation, andmarketing,whereMLmodelsareusedfortaskssuchasmedicaldiagnosis,fraud detection,autonomousdriving,andpersonalizedrecommendations.Machinelearning (ML)andclassicalprogrammingrepresenttwodistinctapproachestosolvingproblems incomputerscience,eachwithitsownstrengthsandweaknesses.Inclassicalprogramming,developersexplicitlywritealgorithmsandrulestosolveaproblem.Theserules arebasedonlogicaldeductionsandhumanexpertiseinthedomain.Classicalprograms
producedeterministicoutputsforgiveninputs.Thebehavioroftheprogramisentirely predictableandfollowstherulesdefinedbytheprogrammer.Traditionalprogramming canbecomecomplexanddifficulttomaintain,especiallyforlarge-scaleproblemsorthose withevolvingrequirements.Programsaretailoredtosolvespecifictasksandareoften noteasilyadaptabletoneworunseenscenarioswithoutsignificantre-engineering.Machinelearningalgorithmslearnpatternsandrelationshipsdirectlyfromdata.Insteadof writingexplicitrules,themodelistrainedonlabeledexamplesorrawdata,allowingitto generalizeandmakepredictionsonunseendata.Machinelearningmodelscanadaptand improvetheirperformanceovertimeastheyareexposedtomoredata.Theycanhandle complex,high-dimensionaldataandlearnintricatepatternsthatmightbechallengingfor humanstoarticulateexplicitly.MLmodelscangeneralizetounseendata,makingthem suitableforawiderangeoftasks.Oncetrained,theycanmakepredictionsordecisions onnewinstanceswithoutneedingtobereprogrammed.MLtechniquescanscalewellto largedatasetsandcomplexproblems,oftenleveragingparallelprocessinganddistributed computingtotrainmodelsefficiently.
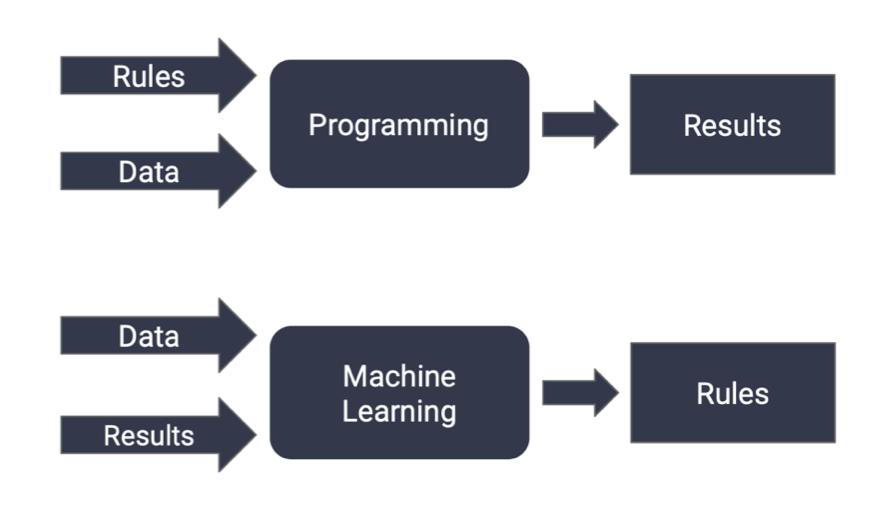
Classicalprogrammingmayoffermorecontrolandtransparency,allowingdevelopersto preciselydefinethebehaviorofthesystem.However,itrequiresadeepunderstandingof theproblemdomainandmaystrugglewithcomplexoruncertainenvironments.Machine learning,ontheotherhand,canhandlemoreambiguoustasksandadapttochanging circumstanceswithoutrequiringexplicitreprogramming.Insomecases,classicalalgorithmsmayoutperformmachinelearningmodels,especiallyfortaskswheretheproblem structureiswell-definedandthedataislimitedornoisy.Machinelearningexcelsintasks involvingpatternrecognition,prediction,anddecision-making,wheretherelationships
Figure3:Programmingvs.MachineLearning
betweeninputsandoutputsarecomplexandmaynotbeeasilycapturedbytraditional algorithms.Classicalprogramsaretypicallyeasiertointerpretanddebugsincedevelopershavefullvisibilityintothelogicandrulesgoverningthesystem.Machinelearning models,particularlydeeplearningmodels,canbemoreopaque,makingitchallenging tounderstandhowtheyarriveattheirdecisions.However,effortsareunderwaytoimprovetheinterpretabilityofMLmodelsthroughtechniquessuchasfeatureimportance analysisandmodelvisualization.Classicalprogrammingandmachinelearningrepresent complementaryapproachestoproblem-solving,eachwithitsownadvantagesandlimitations.Thechoicebetweenthemdependsonfactorssuchasthenatureoftheproblem,the availabilityandqualityofdata,andthedesiredlevelofinterpretabilityandadaptability.
Somehistory...
Thefirstartificialintelligencewasnottheworkofonespecificprogrammerbuttheresult oftheeffortsofmanypeopleandadvancementsinthefieldofcomputerscience.The conceptofartificialintelligenceemergedinthe1950s.Oneofthepioneersinthefield ofAIwasAlanTuring,whodevelopedtheconceptof"Turingmachines".Thiswasa theoreticalconceptratherthanafullimplementationofAI.Thefirstcomputerprogram consideredtobeanimplementationofAIisthe"LogicTheorist",createdin1955byAllen NewellandHerbertA.Simon.Thisprogramhadtheabilitytosolvelogicalproblemsand provetheoremsinmathematicallogic.
ThehistoryofArtificialIntelligenceismarkedbysignificantmilestonesthathaverevolutionizedthefieldandreshapedourunderstandingofmachineintelligence.Itbeganwith
Figure4:Fathersofartificialintelligence.
AlanTuring’sproposalofthe"TuringTest",abenchmarkforevaluatingamachine’s abilitytoexhibitintelligentbehaviorindistinguishablefromthatofahuman.SubsequentdevelopmentsintroducedkeyconceptsliketheNaiveBayesianClassifierandthe perceptronalgorithm,layingthegroundworkformodernmachinelearningtechniques. Breakthroughssuchasbackpropagationfurtheradvancedthefieldbyprovidingamethod fortrainingcomplexneuralnetworks.Intherealmofgamingandstrategicthinking,AI madeheadlineswhenDeepBlue,acomputerdevelopedbyIBM,defeatedGarryKasparov,oneofthegreatestchessplayersofalltime.Thislandmarkeventhighlightedthe powerofmachineintelligenceinstrategicdecision-makinganddemonstratedthepotentialofAItocompetewithhumanexpertiseincomplextasks.IBM’sWATSON’striumph onagameshowdemonstratedAI’scapabilitytoprocessvastamountsofinformation andcompetewithhumancontestantseffectively.However,perhapsthemostsignificant leapcamewithAlphaGo’svictoryovertheworldchampioninGo,agameofimmense complexityandstrategicdepth.ThiseventshowcasedtheabilityofAItotacklechallengesoncethoughttobeexclusivelyhumandomains.Morerecently,theemergence ofChatGPT-3haspushedtheboundariesofAIevenfurther.Itsremarkableabilityto generatehuman-liketexthassparkedconversationsaboutthefutureofnaturallanguage processingandhuman-AIinteraction.Theseachievementsrepresentkeymomentsinthe richandevolvinghistoryofAI,highlightingitstransformativepotentialandtheongoing questtounlockthefullcapabilitiesofintelligentmachines.
Figure5:AtimelineshowingkeyAIevents.
Typesofmachinelearning
Machinelearning,asubsetofartificialintelligence,encompassesvarioustechniquesand approachesthatenablecomputersystemstolearnfromdataandimprovetheirperformanceovertimewithoutbeingexplicitlyprogrammed.Insupervisedlearning,thealgorithmlearnsfromlabeleddata,whereeachexampleispairedwithacorrespondingtarget label.Thegoalistolearnamappingfrominputvariablestooutputlabels,makingpredictionsonunseendatabasedonthislearnedrelationship.Commonsupervisedlearning algorithmsincludelinearregression,decisiontrees,supportvectormachines,andneural networks.Unsupervisedlearningdealswithunlabeleddata,wherethealgorithmtriesto findpatternsorstructureinthedatawithoutexplicitguidance.Itisoftenusedfortasks likeclustering,dimensionalityreduction,andanomalydetection.Clusteringalgorithms likek-meansandhierarchicalclustering,aswellasdimensionalityreductiontechniqueslike principalcomponentanalysis(PCA)andt-SNE,areexamplesofunsupervisedlearning. Semi-supervisedlearningisacombinationofsupervisedandunsupervisedlearning,where thealgorithmlearnsfrombothlabeledandunlabeleddata.Itcanbeusefulwhenlabeled dataisscarceorexpensivetoobtain,asthealgorithmleveragestheadditionalunlabeled datatoimproveperformance.Techniqueslikeself-training,co-training,andmulti-view learningarecommonlyusedinsemi-supervisedlearning.Reinforcementlearninginvolves anagentinteractingwithanenvironmentandlearningtomakedecisionsbyreceiving feedbackintheformofrewardsorpenalties.Theagentlearnstomaximizecumulative rewardovertimethroughtrialanderror.Reinforcementlearningiswidelyusedinfields suchasrobotics,gaming,andautonomoussystems,andalgorithmslikeQ-learningand deepQ-networks(DQN)arepopularinthisdomain.
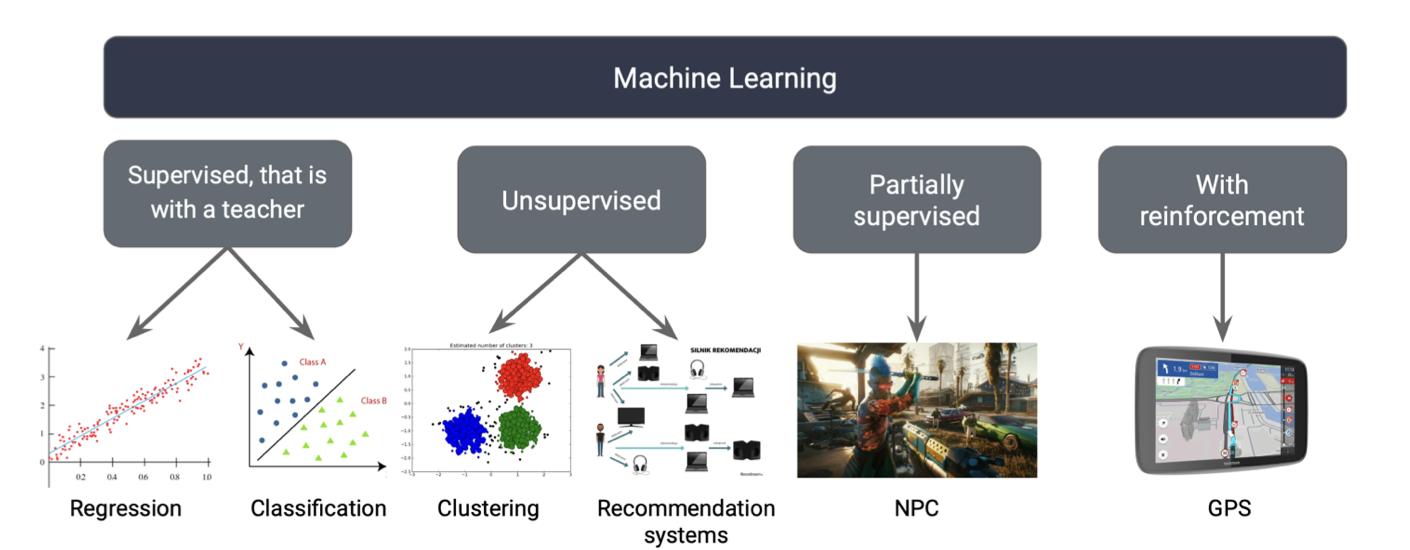
Figure6:Examplesoftheuseofparticulartypesofartificialintelligence
Howdomachineslearn?Whatdeterminessuccessinmachine learning?Howdoweknow"howmuch"amachinecando?
Machinelearningcanbecomparedtoachild’slearningprocess.Ahumancanmakedecisionsonlyaftergainingacertainamountofexperiencefromwhichitcandrawconclusions. Inthecaseofmachinelearningalgorithms,dataservesastheequivalentofexperiences, withthemachineprocessingthisdatatodrawconclusions.Inmachinelearning,thereare manyimportantaspects,butitcanbesaidthatthekeyonesaredataandtheirpreparation(preprocessing).Successinmachinelearninglargelydependsonthequalityofthe availabledata.Gooddatashouldbeaccurate,comprehensive,andrepresentativeofthe problembeingaddressed.Themoredata,thebetter.Largedatasetsallowforbettergeneralizationandoverfittingreduction.Overfittingisoneofthemostsignificantproblems inmachinelearninganddeeplearning.Thisphenomenonoccurswhenamachinelearning modelbecomesoverlytailoredtothetrainingdata,therebylosingitsabilitytogeneralize welltonew,unseendata.Overfittingistypicallyundesirablebecausethemodelbecomes toospecificandperformswellonthetrainingdatabutpoorlyontestdataorreal-world applications.Preprocessing,alsoknownasdatapreprocessingordatapreparation,isthe processofmanipulatingandpreparingsourcedatabeforeanalysis,machinelearning,or otherdataprocessingtechniques.Thegoalofpreprocessingistomakethedatasuitable foranalysis,modeling,andotheranalyticaloperations,[6]and[7].
Datapreprocessingisacriticalstageinthepipelineofanydata-drivenproject,particularlyinmachinelearning.Itinvolvesaseriesofstepsaimedatcleaning,transforming, andpreparingrawdataforanalysisormodeltraining.Datacleaningistheinitialphase ofpreprocessing,focusingonhandlingmissingvaluesandoutliers.Missingvaluescan distortanalysisandmodeltraining,requiringtechniquessuchasimputationordeletion. Outliers,ontheotherhand,canskewresultsandaffectmodelperformance,necessitating detectionandappropriatetreatmentbasedondomainknowledge.Thetransformation stepinvolvespreparingthedataformodelingbyscalingnumericalfeaturesandencoding
Figure7:Howtoperformpreprocessing?Stepbystepdiagram
categoricalvariables.Featurescalingensuresthatfeaturesareonasimilarscaletoprevent dominancebythosewithlargevalues.Categoricalvariablesareencodedintonumerical representationssuitableformachinelearningalgorithms,facilitatingtheirincorporation intomodels.Dimensionalityreductionandsamplingtechniquesareemployedinthedata reductionsteptostreamlinethedataset.DimensionalityreductionmethodslikePCAor t-SNEreducethenumberoffeatureswhilepreservingessentialinformation.Sampling techniquesaddressimbalanceddatasetsbybalancingclassdistributionsthroughundersamplingoroversamplingstrategies.Normalizationensuresuniformityinthescaleor distributionoffeatures,enhancingtheperformanceandconvergenceofmachinelearning algorithms.Techniqueslikemin-maxscalingorz-scorenormalizationareappliedtonormalizethedata,makingitconducivetomodeltrainingandanalysis.Featureselection isthefinalpreprocessingstep,focusingonidentifyingandselectingthemostrelevant featuresformodeltraining.Byreducingdimensionalityandeliminatingirrelevantorredundantfeatures,featureselectionimprovesmodelefficiencyandinterpretability.Various techniques,includingfilter,wrapper,andembeddedmethods,areemployedforfeature selectionbasedonspecificprojectrequirements.Datapreprocessinglaysthefoundation forsuccessfuldataanalysisandmodeldevelopmentinmachinelearningprojects.By meticulouslycleaning,transforming,andpreparingrawdata,practitionerscanenhance thequalityandreliabilityofmachinelearningmodels,ultimatelyleadingtomoreaccurate andinsightfulresults.Understandingthesignificanceofeachpreprocessingstepiscrucial forachievingoptimalmodelperformanceandunlockingthefullpotentialofdata-driven solutions.Insupervisedlearningalgorithms,learningisbasedonexamples.Supervised learningmodelsconsistofpairsof"input"and"output"data,wheretheoutputdatais labeledwiththetargetvalue.Withinthealgorithm,thesystemcompilestrainingdata andgraduallybeginstoidentifycorrelationalsimilarities,differences,andotherlogical elements.Eventually,itbecomescapableofautonomouslyrecognizingdata.
So,howdoesthe"training"phaseofamachinelearningmodelwork?Ihaveaverysimple example.WeshowthemachinemanypicturesofvariousT-shirts,whichserveasinput data.Eachpictureislabeledas"T-shirt".Themachine"views"moreandmorepictures andcreatesasetofcharacteristicfeaturesforaT-shirt,suchasshortsleeves.
Toverifyifthemachinehas"learned"whataT-shirtlookslike,weshowitvariousimages ofclothing,includingT-shirts,withoutanylabels.Theseimagesaredifferentfromthe onesthemachinewastrainedon.ThetaskofthemachineistoidentifytheT-shirt.The
Figure8:Stepsofsupervisedlearning
Figure9:Trainingstepofsupervisedlearning
computercomparestheimagesitseeswithwhatitlearnedduringtraining,andthemore similarfeaturesitfinds,themoreconfidentlyitwilldeterminethatsomethingisaT-shirt. IfthemachinecorrectlyidentifiestheT-shirteachtime,wecansaythatthelearningwas successful.
Howdoesunsupervisedlearningwork?Atthebeginning,letusassumethatastorepurchased2000piecesofvariousclothingitems"blindly".Nooneinthestoreknowswhatis intheshipment.Nobodyinthestorehastimetogothroughit.However,thewholesaler sentpicturesoftheseclothes,whichcanbeusedformachinelearning.Themachinethen looksthroughthepicturesandsearchesforcharacteristicfeatures.Itcreatesgroupsof similar-lookingclothes,butcannotassignlabels.TheresultsareshowninFigure11.
Inunsupervisedlearning,[8]and[9],themachinedoesnotreceivefeedbackonwhetherit hasperformedthetaskcorrectlybecausethehumanthemselvesmaynotknow.Unsupervisedlearningistypicallyusedinsituationswherehumanscannotpredictoutcomeswell.
Semi-supervisedlearningissomewhatlikecookingwithahintofarecipeandatouchof improvisation.Inshort,itinvolveshavingsomelabeleddatabutalsoabitofmystery intheformofunlabeleddata.Itislikesolvingapuzzlewhereyouhaveafewpieces ofthepuzzleandyouhavetoguesstherest.Interesting,isn’tit?Agoodexampleof semi-supervisedlearningisindependentcharactersincomputergames.Theprogrammer indicatestosuchanNPC(Non-PlayerCharacter)whattheterrainis,whatobstaclesare, andwhatthegoalis,fortheNPCtonavigate.Suchan"agent",aswecallartificialintelligenceingames,autonomouslymakesdecisions,interpretingonlycertaindataprovided bytheprogrammer.
Reinforcementlearningisaformoflearningwhereyoudealwithanagentthatmakes decisionsinaspecificenvironmenttomaximizeacertainreward.Itisliketeachingadog
Figure10:Testingstepofsupervisedlearning
Figure11:Resultofunsupervisedmachinelearningalgorithm
atrickusingrewardsandpunishments.Theagentexploresdifferentactions,observes theoutcomes,andreceivesrewardsorpunishmentsbasedonthedecisionsitmakes.Itis somewhatlikeplayingchess,butwithamoredynamicandinteractiveapproach.Agood exampleofreinforcementlearningiscarnavigation.GPSguidesseveraldriversthrough traffic,butaftersometime,itbeginstoreacttotrafficjamsandredirectssubsequent driversondetours.
BenefitsofArtificialIntelligence–WhyisAIsafe?
Ensuringthesafetyofartificialintelligencesystemsisacrucialaspectoftheirdevelopmentanddeployment.WhileAIoffersnumerousbenefitsandopportunities,italso posespotentialrisksandchallenges.AIsystemsundergorigoroustestingandvalidation processestoidentifyandmitigatepotentialsafetyconcerns.Thisincludestestingthe systemundervariousscenarios,includingedgecasesandadversarialinputs,toensure itsreliabilityandrobustness.ThereisgrowingrecognitionoftheimportanceofethicalconsiderationsinAIdevelopment.Organizations,governments,andindustrybodies areestablishingethicalframeworksandguidelinestoensurethatAIsystemsprioritize safety,fairness,transparency,andaccountability.Governmentsandregulatorybodiesare increasinglyinvolvedinoverseeingthedevelopmentanddeploymentofAItechnologies. Regulationsandstandardsarebeingputinplacetoaddresssafety,privacy,andsecurity concernsassociatedwithAIsystems,therebypromotingtheirsafeandresponsibleuse. ManyAIsystemsaredesignedwithmechanismsforhumanoversightandcontrol.This allowshumanoperatorstointervene,whennecessary,monitorthesystem’sbehavior,and ensurethatitoperatessafelyandinaccordancewithestablishedguidelines.Ensuring transparencyandexplainabilityinAIsystemsisessentialforunderstandinghowthey makedecisionsandensuringthatthosedecisionsalignwithethicalandsafetyconsiderations.TechniquesforexplainingAIdecisions,suchasinterpretabilitymethodsandmodel transparency,arebeingdevelopedtoenhancetrustandaccountability.AIsystemsare subjecttocontinuousmonitoringandimprovementthroughouttheirlifecycle.Thisincludesmonitoringtheirperformanceinreal-worldsettings,collectingfeedbackfromusers, andupdatingthesystemtoaddressanysafetyconcernsoremergingrisks.Addressing thesafetyofAIrequirescollaborationacrossvariousstakeholders,includingresearchers, developers,policymakers,ethicists,andend-users.Byworkingtogether,thesestakeholderscanidentifypotentialrisks,sharebestpractices,anddevelopstrategiesforensuring thesafeandresponsibleuseofAItechnologies.WhileAIholdstremendouspromisefor improvingourlivesandadvancingsociety,itisessentialtoapproachitsdevelopmentand deploymentwithcautionandresponsibility.Byprioritizingsafety,ethics,andhuman values,wecanharnessthefullpotentialofAIwhileminimizingrisksandmaximizing benefitsforall.
Conclusion
Inconclusion,ArtificialIntelligence(AI)standsasabeaconofinnovationandpotential, offeringamyriadofpossibilitiestorevolutionizeourworld.Throughoutthisexploration, wehavedelvedintothefundamentalsofAI,fromitsdiversetypestoitshistoricalmilestones.Wehavediscussedtheparadigmshiftrepresentedbymachinelearning,illustratinghowitempowerscomputerstolearnfromdataratherthanrelysolelyonexplicit programming.Fromsupervisedandunsupervisedlearningtoreinforcementandsemisupervisedlearning,thespectrumofAItechniquesoffersversatilesolutionstoavast arrayofchallenges.Moreover,wehavetracedtheevolutionofAIthroughhistory,from thetheoreticalconceptsofAlanTuringtothegroundbreakingachievementsofAlphaGo andbeyond.Eachmilestonerepresentsastepforwardinourquesttounderstandandharnessthepowerofintelligentmachines.Yet,withgreatpromisecomestheresponsibilityto ensuresafety,ethics,andaccountabilityinAIdevelopmentanddeployment.Aswehave discussed,robustethicalframeworks,regulations,andhumanoversightareimperativeto mitigaterisksandpromoteresponsibleAIusage.Byprioritizingtransparency,fairness, andcontinuousimprovement,wecannavigatethecomplexitiesofAIwithconfidenceand clarity.Ultimately,thejourneyintoAI’spossibilitiesisoneofcollaboration,innovation, andethicalstewardship.AsweembracethetransformativepotentialofAI,letusdoso withacommitmenttobuildingasafer,moreprosperousfutureforall.Throughcollective effortandconscientiousdecision-making,wecanharnessthefullpotentialofAItodrive progress,inspireinnovation,andenrichlivesaroundtheglobe.
References
[1] Z.–H.Zhou, Machinelearning,Springernature,2021.
[2] B.Mahesh, Machinelearningalgorithms–areview,InternationalJournalofScience andResearch.(Online),vol.9,np.1,pp.381–386,2020.
[3] J.Biamonte,P.Wittek,N.Pancotti,P.Rebentrost,N.Wiebe,andS.Lloyd, Quantummachinelearning,Nature,vol.549,no.7671,pp.195–202,2017,
[4] C.Molnar, Interpretablemachinelearning,Lulu.com,2020.
[5] E.Alpaydin, Introductiontomachinelearning,MITpress,2020.
[6] J.J.Grefenstette, Geneticalgorithmsandmachinelearning,inProceedingsofthe sixthannualconferenceonComputationallearningtheory,1993,pp.3–4.
[7] T.G.Dietterich, Ensemblemethodsinmachinelearning,inInternationalworkshop onmultipleclassifiersystems,Springer,2000,pp.1–15.
[8] T.Hastie,R.Tibshirani,J.Friedman, Unsupervisedlearning,Theelementsofstatisticallearning:Datamining,inference,andprediction,pp.485–585,2009.
[9] H.U.Dike,Y.Zhou,K.K.Deveerasetty,andQ.Wu, Unsupervisedlearningbased onartificialneuralnetwork:Areview,in2018IEEEInternationalConferenceon CyborgandBionicSystems(CBS),IEEE,2018,pp.322–327.
Infinity
MagdalenaMamcarz
InstituteofMathematics,FacultyofScienceandTechnology,UniversityofSilesia magdalena.mamcarz@us.edu.pl
ThemathematicalparadoxlinkedtoHilbert’snameimaginesahotelwithacountably infinitenumberofrooms,meaningeachroomcanbematchedwithauniquenatural number.Althougheveryroomisoccupied,anewguestarrives–canavacantroombe foundforthem?
1Zeno’sparadoxes
Theconceptofinfinityhasbeeninterestingtopeopleforthousandsofyears. Aristotlewasthefirsttoscientificallyapproachtheproblemofinfinity.Scientistswere afraidofinfinitybecauseinfinityleadstoparadoxes.Themostfamousofwhicharethe paradoxesofZenoofElea.Ipresentsomeoftheparadoxes.
1.1Dichotomyparadox
Asprinterhasafinitedistancetorun.However,beforeitcoversthewholedistance,it mustfirstreach 1 2 ofthelength,butbeforeitreaches 1 2 ,itmustfirstreach 1 4 ,butbefore itreaches 1 4 ,itmustfirstreach 1 8 ,adinfinitum.Thismeansthattherunnerhastocover infinitelymanysegmentseachoffinitedistance.Sinceitisimpossibletocoveraninfinite numberofsectionsinafinitetime,therunnerwillneverfinishtherace.
Moreover,therunnercannotevenstartrunning,becausethesameparadoxalsoapplies toanydistance:justasitisimpossible(accordingtotheabovereasoning)torun 100 m, itisalsoimpossibletorunadistanceofonemeteroronemillimeter.
1.2Achillesandthetortoise
Achillesandthetortoiseareatthestartinglineofaraceoveranyfinitedistance.Achilles canruntwiceasfastasthetortoiseandtherefore,atthestart,heallowsthetortoiseto move 1 2 ofthedistanceaway.Achilles,asherunstwiceasfastasthetortoise,willreach 1 2 ofthedistancewhentheturtlereaches 3 4 ofthedistance.Intheinitialphase,when Achillesruns 3 4 ofthedistance,thetortoisewill"escape"himagain,covering 7 8 ofthe
distance.WhenAchillesreachesthisplace,thetortoisewillagainbe 1 16 ofthedistance awayfromhim,andsoonindefinitely.Result:Achilleswillnevercatchupwiththe tortoiseeventhoughherunstwiceasfastbecausetheirdistancewillalwaysbedecreasing butstillremainpositive.
InthecaseofthedichotomyandAchillesparadoxes,itcanbemathematicallyproven thatthesumofaninfinitenumberofsegmentscangiveasegmentoffinitelength,and thereforethetimeneededtoovercomeitisalsofinite(convergentseries).
2GeorgeCantorandsettheory
GeorgCantorwasbornin1845inSaintPetersburg,RussianEmpire.Herelocatedto Germanyin1856.In1860,Cantorcompletedhisschooling.In1862,hegraduatedfrom the"HöhereGewerbeschuleDarmstadt"andenrolledattheSwissFederalPolytechnicin Zurich.InJune1863,CantortransferredtotheUniversityofBerlin.Hespentthesummer of1866attheUniversityofGöttingen,aprominenthubformathematicalresearchatthe time.Cantorexcelledinhisstudiesandearnedhisdoctoraldegreein1867.
Cantor’sworkbetween1874and1884laidthefoundationforsettheory.Itwasnot recognizedthatsettheoryhadanysignificantdepth.BeforeCantor,onlyfinitesetswere wellunderstood,while"theinfinite"wasthoughttobelongmoretophilosophythanto mathematics.Cantor’sproofthatinfinitesetscanhavedifferentsizesrevolutionizedthis view,showingthatsettheorywasfarfromtrivialandwarrantedseriousstudy.Today, settheoryservesasafoundationalframeworkinmodernmathematics.
Inoneofhisearlypapers,Cantordemonstratedthatthesetofrealnumbersis"larger" thanthesetofnaturalnumbers,revealingforthefirsttimethatinfinitesetscandiffer insize.Hedividedinfinitesetsintocountablyinfinite(denumerable)anduncountably infinite(nondenumerable)sets.
TheContinuumHypothesisisaconjectureconcerningthepossiblesizesofinfinite sets.Itassertsthat: "Nosetexistswithacardinalitythatfallsbetweenthatoftheintegersandthereal numbers."
TheContinuumHypothesis,proposedbyCantor,washighlightedbyDavidHilbertas thefirstofhistwenty-threeunresolvedproblemsduringhisspeechatthe 1900 InternationalCongressofMathematiciansinParis.Cantor’sworkreceivedattentionandpraise notonlyfromHilbertbutalsofromothermathematicians.
3Hilbert’sparadoxoftheGrandHotel
Hilbert’sparadoxoftheGrandHotelisathoughtexperimentthathighlightsasurprising characteristicofinfinitesets.Itshowsthatahotelwithaninfinitenumberoffully
occupiedroomscanstillaccommodatemoreguests,evenaninfinitenumberofthem,and thisprocesscanberepeatedindefinitely.DavidHilbertintroducedthisconceptina 1925 lecturetitled"ÜberdasUnendliche"("OntheInfinite").
Hilbertenvisionsahypotheticalhotelwithroomsnumbered 1, 2, 3, Thissetupis knownasacountablyinfinitenumberofrooms.Initially,eachroomisoccupied,butnew guestscontinuetoarrive,eachneedingaroom.
Howcanthisbemanaged?Thesolutioninvolvesshiftingthecurrentguests:theguest inroom 1 movestoroom 2,theguestinroom2movestoroom 3,andsoon,witheach guestmovingfromroom n toroom n +1.Sincethereisnolastroominthisinfinite hotel,everyonehasaplacetogo.Afterthisshift,room 1 becomesvacant,allowingthe newguesttotakethatroom.Byrepeatingthisprocess,thehotelcanaccommodateany finitenumberofnewguests.Specifically,if m newguestsarrive,thehotelcanmoveeach guestfromroom n toroom n + m,makingspaceforthem.
Itispossibletomakeroomforacountablyinfinitenumberofnewguests.Todothis, movethepersoninroom 1 toroom 2,thepersoninroom 2 toroom 4,andgenerally, movethepersoninroom n toroom 2n (twicetheircurrentroomnumber).Thiswillfree upalltheodd-numberedrooms,whicharecountablyinfinite,forthenewguests.
Therearemultiplewaystoaccommodateacountablyinfinitenumberofcoaches,each carryingacountablyinfinitenumberofpassengers.
3.1Primepowersmethod
Imagineanendlessstreamofcoaches,eachcarryinganendlessstreamofnewguests.Let ussimplifythingsbynumberingthecoachesas 1, 2, 3,andsoon,andtheseatswithin eachcoachas 1, 2, 3,andsoforth.Initially,weaskeachexistingguesttomovetoaroom whosenumberistwicethenumberoftheircurrentroom.Thisleavesallroomswithodd numbersvacant.Then,weinstructthepassengersofcoach 1 tomovetospecificrooms: passenger 1 toroom 31,passenger 2 toroom 32,passenger 3 toroom 33,andsoforth. Howaboutthepassengersfromthenextcoach?Wehandlethemsimilarly,ensuringeach personfindsavacantroom.Forinstance,thefirstpassengerofcoach 2 goestoroom 51 , thesecondtoroom 52,andsoon.Wecontinuethispattern,assigningpassengersofeach subsequentcoachtoroomsbasedonthenextprimenumberinsequence.
3.2Primefactorizationmethod
Weassigneachpersonsittinginseat s ofcoach c toroom 2s 3c.Sinceeachnumberhas auniqueprimefactorization,thisensuresthateverypersongetstheirownroom,withno twopeoplesharingthesameone.
Asintheprimepowersmethod,thisapproachleavessomeroomsunoccupied.
References
[1] DavidHilbert, ÜberdasUnendliche,MathematischeAnnalen,vol.95,pp.161–190.
[2] GeorgCantor, BeiträgezurBegründungdertransfinitenMengenlehre(1),MathematischeAnnalen,46(4):481-–512.
[3] GeorgCantor, EinBeitragzurMannigfaltigkeitslehre ,JournalfürdieReineund AngewandteMathematik,84:242-–248.
[4] GeorgeGamow, OneTwoThree...Infinity:FactsandSpeculationsofScience. New York:VikingPress.p.17.
[5] HelgeKragh, TheTrue(?)StoryofHilbert’sInfiniteHotel. arXiv:1403.0059.
[6] NickHuggett, Zeno’sParadoxes:5.Zeno’sInfluenceonPhilosophy. StanfordEncyclopediaofPhilosophy.
[7] WilliamDunham, JourneythroughGenius:TheGreatTheoremsofMathematics, PenguinBooks,ISBN978-0140147391.
[8] "Zeno’sParadoxes–InternetEncyclopediaofPhilosophy", https://iep.utm.edu/ zenos-paradoxes/.
Algaeandhowtocountthem
ThomasZürcher
InstituteofMathematics,FacultyofScienceandTechnology,UniversityofSilesia thomas.zurcher@us.edu.pl
1Countingalgae
Algae!Welltheydidit.Notonlydidtheymanagetoshowupinamathematicalarticle, buttheywereabletoraiseinpopularityandinnumberstoevenmakeittothevery beginningofthearticle.Buthowdidtheydoit?Tofindout,wehavetoresorttothe workofAristidLindenmayer.Wemayfollowhisinsightofwhathappenstoacell.Given acellofanalga,aftersometime,thecelldividesintotwocells.However,thedivision processdoesnotleadtotwoequalcells,rathertoayoungoneandanoldone.Whilethe oldonecandivideafteronetimestep,thenewoneisnotyetreadytodivideaftersucha timeinterval.However,afteronemoretimeunitpasses,theyoungcellisnowgrownup, anddivideshenceforthineachtimestep.Actually,thereisafurtherdistinctionbetween thecells.Whenacelldivides,theyoungcellmightendupontheleftorontheright. Thisgivesusfourcelltypesintotal.Letusthinkaboutagoodnotation.First:foryoung andold,wecanuse Y and O,respectively.Furthermore,weaddsomedistinctionforleft andright: Y ←, Y →, O ←,and O→.Soforexamplein O ←,theletter O meansthatitisanoldcell, andthearrowpointingtotheleftmeansthattheyoungcellwillendupontheleft-hand side.Ontheotherhand,in Y →,theletter Y denotesayoungcell,andthearrowtothe rightmeansthatonceitgetsoldanddivides,theyoungcellwillbeontheright.
Lindenmayerproposedthefollowingmodel,meaningwestartwith Y →,andthenapply ineachsteptheappropriatereplacementrulestoallthecellsseparately:
Hence,weobtain
andsoforth.
Onenicethingtonoticeisthatthepositionofthenewcellsisalternating.Ifanold cellsplitsandthenewcellisontheright,theninthenextstep,whentheoldcellsplits again,thenewcellisontheleft.
Letuscountthenumberofcellsintheindividualsteps: 1, 1, 2, 3, 5, 8.Fansofrabbits mayrecognizethatatleastthestartisthesameasthesequencefoundbyFibonacci whenhestudiedthegrowthofpopulationsofrabbits.Givenanonnegativeinteger n and denotingby Fn thenumberofrabbitsinstep n,Fibonaccifoundthefollowing: F0 =1, F1 =1 andforall n ∈ N0 (allnaturalnumberswith 0 included,thatisallnonnegative integers)
Now,wearereadytoattackourformulaforthenumberofcellsinstep n.However, whiletheleftandrightpolaritydonotplayarolehere,thedistinctionbetweenyoungand oldisimportant.Hence,weneedtocontrolthenumberofoldandyoungcellsseparately. Letusintroducethefollowingnotions:
• Cn:thenumberofcellsinstep n,
• Yn:thenumberofyoungcellsinstep n,
• On:thenumberofoldcellsinstep n.
Wehave
Wheredotheyoungcellsinstep n +1 comefrom?Eachofthemwasformedfromexactly oneoldcellinthepreviousstep,hence
Fortheoldcells,itisabitmorecomplicated.Eacholdcellinthepreviousstepproduces anoldcell,butsodoeseachyoungcell:
Therefore,wehave
Thisway,wecertainlycancomeupwiththenumberofcellsineachstep.However,todo so,weneedtosimulatethewholesystemthegivennumberofsteps.Isthereaformula, wherewejustcanpluginthestepandobtainthenumberofcells?
Next,weworktowardsobtainingsuchaformula.Letusdefine f : R2 → R2 by f (x,y)=(y,x + y).Thus, f (Yn,On)=(On,Yn + On)=(Yn+1,On+1)
Hence,wehaveencodedhowthesystemmovesfromonesteptothenextone.Letus investigate f next.Ithasapeculiarpropertycalled linearity.Namely,given (x,y), (u,v) ∈ R2 and α ∈ R,wehave
f (α(x,y))= f (αx,αy)=(αy,αx + αy)= α(y,x + y)= αf (x,y) and f ((x,y)+(u,v))= f (x + u,y + v)=(y + v,x + u + y + v) =(y,x + y)+(v,u + v)= f (x,y)+ f (u,v).
Itturnsoutthatwheneverweknow f (1, 0) and f (0, 1),thenwealsoknow f (x,y): f (x,y)= f (x(1, 0)+ y(0, 1))= f (x(1, 0))+ f (y(0, 1))= xf (1, 0)+ yf (0, 1).
Tobemoreinlinewithstandardnotation,letusfromnowonwritetheelementsof R2 bystackingthetwocoefficientsverticallyinsteadofwritingthemhorizontally.Further, tounburdennotation,wealsooftenwrite f x y insteadofthemorecumbersome f x y
Letusassumethat
and
forsomerealnumbers a11, a12, a21,and a22.Thus,wecanencode f asatable,herecalled matrix : a11 a12 a21 a22 .
Wecanrecoverwhat f doesto (x,y) asfollows:
Itturnsoutthatif α ∈ R and f,g : R2 → R2 arebothlinear,thensoare f + g and αf If A and B arethematricescorrespondingto f and g,respectively,wemayaskwhich matricescorrespondto f + g and αf .Writing A = a11 a12 a21 a22 and B = b11 b12 b21 b22 , thecorrespondingmatricesare
+
respectively.Whatabout f f ?Well,thatisnotreallydefined.However,thereisone moreprominentmatrixthatwemaylookfor:theonecorrespondingto g ◦ f ,meaning thatfirstweapply f andthen g.Usingtheaboveencoding,wehave
Furthermore,
Thus,weobtain
Thereisquitesomecomputationgoingon!However,therearesomeexampleswherewe havelesstocompute.Forexample
Now,wecancomebacktotheproblemofcountingthecells.Wecanwrite
and
Actually,weobtain
Well,thisseemscomplicated,itwouldbemucheasierifthematrixwhosepowerwetake hadzeroentriesoutsidethediagonal.Thereisatricktoachievethis,whichdoesnot alwayswork,butwilldothejobhere.Assumethatwefindamatrix S suchthatthere existsacorrespondingmatrixdenotedby S 1 suchthat SS 1 = S 1S andtheseproducts equalthe identitymatrix (thatisthematrixwith 1 onthediagonaland 0 otherwise)and amatrix
suchthat
Weneedonemoretrick,orpropertyofmatrices.Having 2 × 2-matrices A, B,and C,we have (AB)C = A(BC) Thus
andmoregenerally,
Buthowcanweidentify α and β?
Multiplying(1)fromtheleftby S 1 andfromtherightby S,weobtain
Thus
, yielding
Weseethat α isspecialinthesensethatthereexistsavector
Justlookingatthisequation,weseethatthevectorwith x = y =0 isacandidate. However,wewanttoarguenextthatas x y = S 1 0 , thecase x =0 cannotoccur.Todoso,wefirstshowthat x =0 impliesthat y =0:
andindeed y =0.Next,
yielding,
acontradiction.
Withthegainedknowledgethat x =0,wegobackto(2):
Weendupwith
As x =0,thisleadsto
or,otherwisestated,
Fromthis,weseethat
Wehavethusidentified α and β.Wecouldalsofind S and S 1,butletustakeashortcut here.Namely,wearejustlookingfor A,B ∈ R suchthat
For n =0,wehave
andfor n =1,weseethat
Thistransformsto
Tobehonest,aswehavenotbeenahundredpercentstrictwhenderivingourformula, wecannotbesurethatitisreallycorrect.Buthowcanwenonethelessguaranteethe
correctness?Whatdoespreventagenerationtobecomerevolutionariesandchangethe rules?Letusassumebycontradictionthattheformuladoesnothold.Wehavetofocus notontherevolutionaries,butonthegenerationbefore.Ifwecanprovethattheydo producewell-behavedoffspring,thenweruninacontradiction,thatisallgenerations behaveaccordingtotherule.Thisprincipleisnicelyencodedinthefollowingjoke:all nonnegativeintegersareinteresting.Well, 0 iscertainlyinterestingaswhenwemultiply anumberwithit,weobtain 0 again.Also, 1 isinterestingforsimilarreasons.Assume nowbycontradictionthattherearenumbersthatarenotinteresting.Thereiscertainly aminimalone.However,theminimalnumberthatisnotinteresting,canitbecome moreinterestingthanthat!Wehavefoundaninterestingnumberthatisnotinteresting, acontradiction.Hence,allnumbersareinteresting.Atthecoreofthisliesacharacterizationofthenonnegativeintegers.Acharacterizationthatisofteneasytohandle.Namely, asubset A ofthenonnegativeintegersactuallyagreeswiththesetofallnonnegativeintegersifitcontains 0 andforeachnumber n ∈ A,wealsohave n +1 ∈ A.Thisdescription, orrathertheproceduretoverifyitforaset,iscalled induction.Itisaveryusefultool. Hence,toensurethattheformulaiscorrect,itissufficienttoshowthat C0 = C1 =1 (whichwebasicallydidwhencomputing A and B)andthatforall n ∈ N0
Letusdothework.First,wehavetoshowthatthecase n =0 iscorrect.Bywhat weknowalready,thismeansthatwehavetoprovethat C2 =2.Wehave
Therefore,wenowassumethat Cn+2 = Cn+1 + Cn holdsforsome n ∈ N0.Whatwe needtoproveisthat Cn+3 = Cn+2 + Cn+1.Hence,
Wehave
Thisnowindeedshowsthat
Figure12:Cantorset
1.1Additionalcomments
Here,welookedatmatriceswithtworowsandtwocolumns.Thisisonlyasmallsubsetof possiblematrices.Wecanvarythenumberofrowsandthenumbercolumnsindividually. However,onlycertaincombinationsallowfortheaddition/multiplicationofthem,among themarematriceswhosenumberofrowsandcolumnsagreeandarefixed.Asmentioned before,itisnotalwayspossibletotransformamatrixinadiagonaloneaswecould dohere.Whensettingupthematrix,welookedatwhathappensto 1 0 and 0 1 However,wecouldhavechosendifferentvectors.Insomesensetheroleofthematrices S and S 1 isthechangefromonesuchsystemtoanother.
2AnotherL-system
LetusnowlookatadifferentL-system:
Letusinterpret F asadrawnlinesegmentofagivenlength,and f ajumpofthesame length.Then,wecandrawthefollowingapproximationoftheCantorset,Figure12.
3Discussionofsomeliterature
ConcerningtheLindenmayersystems,oneimportantsourceis[PL90]writtenbyPrzemysławPrusinkiewiczandthelateAristidLindenmayer.Thewebpageoftheresearch groupofthefirstauthorcanbefoundhere: http://algorithmicbotany.org/.ItcontainsawealthofinformationaswellassoftwareforsimulatingL-systems.Theapproach takenhereisrathercomputational.Adifferentapproachtodescribecelldevelopmentis pursuedin[Mei09],wherethelanguageofpartialdifferentialequationsisused.
Thelinearalgebrapartcanprobablybefoundinanyintroductorylinearalgebratext. However,personallyIamveryfondof[Mey00].
Theendofthearticleleadustofractalgeometry.There,Iwouldofcourseliketo mentiononeofthebooksbyBenoitMandelbrot,sometimestermedthe fatheroffractal geometry:[Man82].Amoremathematicaltakeis[Fal14].
References
[Fal14] KennethFalconer, Fractalgeometry.Mathematicalfoundationsandapplications, JohnWiley&Sons,Ltd.,Chichester,thirdedition,2014.
[Man82] BenoitB.Mandelbrot, Thefractalgeometryofnature,W.H.FreemanandCo., SanFrancisco,Calif.,1982.SchriftenreihefürdenReferenten.[SeriesfortheReferee].
[Mei09] HansMeinhardt, TheAlgorithmicBeautyofSeaShells,TheVirtualLaboratory. SpringerBerlinHeidelberg,4edition,2009.
[Mey00] CarlMeyer, Matrixanalysisandappliedlinearalgebra.SocietyforIndustrialand AppliedMathematics(SIAM),Philadelphia,PA,2000.With1CD-ROM(Windows, MacintoshandUNIX)andasolutionsmanual(iv+171pp.).
[PL90] PrzemysławPrusinkiewiczandAristidLindenmayer, Thealgorithmicbeautyof plants.TheVirtualLaboratory.Springer-Verlag,NewYork,1990.WiththecollaborationofJamesS.Hanan,F.DavidFracchia,DeborahR.Fowler,MartinJ.M.de BoerandLynnMercer.
FB:https://www.facebook.com/wnsit mail:wnst@us.edu.pl
promocja.wnst@us.edu.pl
