WPS Math Curriculum 6-8

WaterfordPublicSchools

MATHEMATICS

Grades6-8

MathematicsCurriculumRevision

2023

Table of Contents

Curriculum Revision Committee

Grades 6-8 Mathematics

MichaelEllis MathematicsDepartmentChair

WaterfordHighSchoolMathematicsTeacher

HeatherJoyner

KellyBarnes

KirstenEident

CristinadeCastro

JayGionet

Grades6-8MathematicsDepartmentCurriculumLeader

ClarkLaneMiddleSchoolMathematicsTeacher

ClarkLaneMiddleSchoolMathematicsTeacher

ClarkLaneMiddleSchoolMathematicsTeacher

ClarkLaneMiddleSchoolMathematicsTeacher

ClarkLaneMiddleSchoolMathematicsTeacher

CourseName:Grade6Unit1Title:AreaandSurfaceAreaEst.#ofLessons:18

UnitOverview:

Inthisunit,studentswilldivemoredeeplyintotheconceptofareabyextendingtheirknowledgeof rectanglestocalculatingtheareaofparallelograms,triangles,andpolygons,includinggeneralizingandusing formulas.Oncethatfoundationisbuilt,wewillextendinto3-dimensionalshapestocalculatesurfacearea.

STAGE1:DESIREDRESULTS

EstablishedGoals

CSDEContentStandards:

6.EE.A.2.a: Writeexpressionsthatrecord operationswithnumbersandwithlettersstanding fornumbers.

6.EE.A.2.c: Evaluateexpressionsatspecificvalues oftheirvariables.Includeexpressionsthatarise fromformulasusedinreal-worldproblems. Performarithmeticoperations,includingthose involvingwhole-numberexponents,inthe conventionalorderwherethereareno parenthesestospecifyaparticularorder.

6.G.A.1: Findtheareaofrighttriangles,other triangles,specialquadrilaterals,andpolygonsby composingintorectanglesordecomposinginto trianglesandothershapes;applythesetechniques inthecontextofsolvingreal-worldand mathematicalproblems.

6.G.A.4: Representthree-dimensional figuresusing netsmadeupofrectanglesandtriangles,anduse thenetsto findthesurfaceareaofthese figures. Applythesetechniquesinthecontextofsolving real-worldandmathematicalproblems.

Understandings

● Howtodecomposeashapeandrearrange thepiecestokeeptheareathesame.

● Makingageometricargumentrequires referencingdefinitionsandfacts.

TransferGoals

CSDEMathPractices(MP)in Blue toverifysignificance

● COMMUNICATION: Createalogicaland evidence-basedargumenttosupportideas. MP #3Constructviableargumentsandcritiquethe reasoningofothers;MP#6:Attendtoprecision

● CRITICALTHINKING: Demonstrate flexibility anddeterminationwhensolvingproblems. MP#1 Makesenseandperseverethroughchallenges; MP#2Reasonabstractlyandquantitatively;MP #4Modelwithmathematics.

● CRITICALTHINKING: Analyzedatainorderto drawconclusions. MP#6:Attendtoprecision;MP #8:Lookforandexpressregularityinrepeated reasoning.

EssentialQuestions

● HowdoIdeterminehowmuchmaterialIneed tocoverthisspace?

● HowdoIjustifymyargumentusingprecise mathlanguageandthestrategyIused?

Knowledge Skills(FramedasLearningTargets)

● Howtodefineandcalculatearea.

● Howtodefineandcalculatesurfacearea.

● Icanexplainwhatareais.

● Icanusedifferentstrategiestodeterminethe areaofaparallelogram.

Grade6Unit1EndofUnitAssessment

● Icanidentifyabaseandheightofatriangle withoutagrid.

● Icancalculatetheareaofanytriangle..

○ Problem1

● Icandescribethefacesofapolyhedron.

● Icancompareandcontrastprismsand pyramids.

● Iknowwhatanetisandhowitisrelatedto apolyhedron.

○ Problem2

● Icanusedifferentstrategiestodetermine theareaofaparallelogram.

● Icanidentifythebaseandheightofa

● Icanidentifythebaseandheightofa parallelogramonagrid.

● Icanexplainhowtocalculatetheareaofany parallelogramusingitsbaseandheight.

● Icanidentifyabaseandheightofatriangle withoutagrid.

● Icancalculatetheareaofanytriangle.

● Icandescribethecharacteristicsofapolygon.

● Icancalculatetheareaofapolygon.

● Icanidentifyandexplaincommonmistakesor misconceptionsrelatedtoarea.

● Icanexplainwhatsurfaceareais.

● Icancalculatethesurfaceareaofa rectangularprismandexplainmystrategy.

● Icandescribethefacesofapolyhedron.

● Icancompareandcontrastprismsand pyramids.

● Iknowwhatanetisandhowitisrelatedtoa polyhedron.

● Icanmatchapolyhedronwithitsnet.

● Icancalculatethesurfaceareaofaprismor pyramidfromadrawinganddescribemy strategy.

● Icandesignanetforathree-dimensional object.

● Icancalculatesurfaceareatoanswer problemsincontext

● Icanidentifyandexplaincommonmistakesor misconceptionsrelatedtosurfacearea.

Grade6Unit1MidUnitAssessment

Ongoingassessments:IMsynthesisandcooldowns asappropriate Frayermodel(blanktemplateandrationale)

● Area

● SurfaceArea

parallelogramonagrid.

● Icanexplainhowtocalculatetheareaof anyparallelogramusingitsbaseandheight.

○ Problem3

● Icandescribethecharacteristicsofa polygon.

● Icancalculatetheareaofapolygon.

○ Problem4

● Icanexplainwhatsurfaceareais.

● Icancalculatethesurfaceareaofa rectangularprismandexplainmystrategy.

○ Problem5

● Icanmatchapolyhedronwithitsnet.

● Icancalculatethesurfaceareaofaprismor pyramidfromadrawinganddescribemy strategy.

○ Problem6

● Icanidentifyabaseandheightofatriangle withoutagrid.

● Icancalculatetheareaofanytriangle.

○ Problem7

PerformanceTask

● I’lltakeittogo! Designatake-outfood containergiventheconstraintsthatthe teacherprovidesbasedonthecarryout food.

○ Icandesignanetfora three-dimensionalobject.

○ Icancalculatesurfaceareato answerproblemsincontext

● Lights,Camera,Action! Makeavideotutorial explainingwhatareaorsurfaceareais. Thenshowhowtotakeaneasyproblem andsolveit.Andthenamorecomplex problemandsolveit.Sharesomecommon mistakes/misconceptions.

○ Icanexplainwhatareais.

○ Icanexplainwhatsurfaceareais.

○ Icanidentifyandexplaincommon mistakesormisconceptionsrelated toarea.

○ Icanidentifyandexplaincommon mistakesormisconceptionsrelated tosurfacearea.

Understandings 1&2

LearningTargets 1,9,10,19

TransferSkills: CommunicationandCritical Thinking

STAGE3:LEARNINGPLAN

Previousmathconnections

Thefollowingconceptsfrompreviousgradesmay supportstudentsinmeetinggrade-levelstandards inthisunit:

● Calculatingareaofrectangles.(3.MD.C, 3.MD.C.6,3.MD.C.7.B,4.MD.A.3, 5.NF.B.4B)

● Classifyingshapessuchasrighttriangles andparallelograms.(4.G.A.2,5.G.B.4)

● Calculatingthevolumeofarectangular prism.(5.MD.C.4)

Diagnosticassessmentquestions/problemsbasedon priorgradelevelexperience

FromReadinessCheck

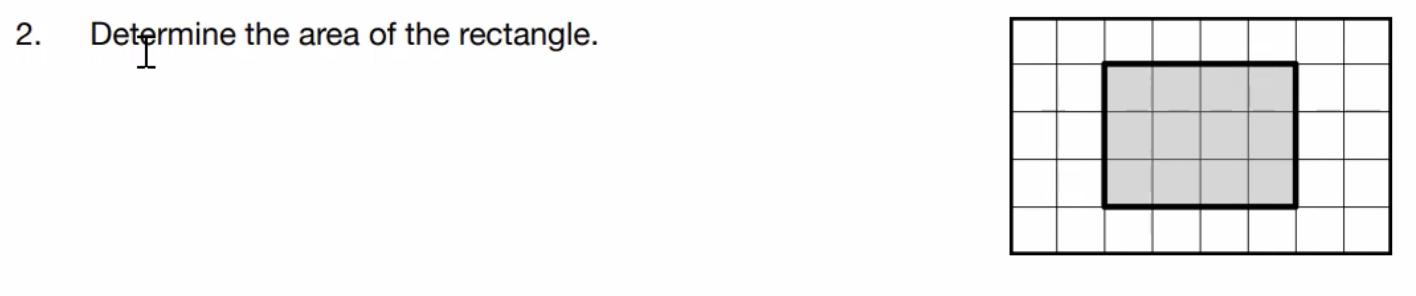
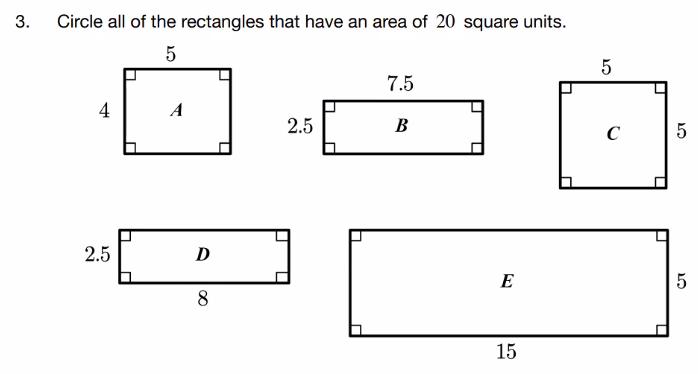
Studentswill firstsolvethetwoproblemsandbeprepared tosharetheirthinkingwithothers.Studentsthenshare withotherstosolidifytheconceptofareaandbeable explainitintheirownwords.

FirstTopic:Area

LearningTargets:

● Icanexplainwhatareais.

● Icanusedifferentstrategiestodetermine theareaofaparallelogram.

● Icanidentifythebaseandheightofa parallelogramonagrid.

● Icanexplainhowtocalculatetheareaof anyparallelogramusingitsbaseandheight.

● Icanidentifyabaseandheightofatriangle withoutagrid.

● Icancalculatetheareaofanytriangle.

● Icandescribethecharacteristicsofa polygon.

● Icancalculatetheareaofapolygon.

● Icanidentifyandexplaincommonmistakes ormisconceptionsrelatedtoarea.

Estimated#ofLessons:10

EssentialQuestions: HowdoIdeterminehowmuchmaterialIneedto coverthisspace?

LearningActivities:

● Studentsdevelopstrategiesfordeterminingtheareaofnot-rectangularshapes.

● Studentsdevelopandnamestrategiesforcalculatingtheareaofmorecomplexshapes.

● Studentsdevelopstrategiesforcalculatingtheareaandapplyaformulafortherelationship betweenthebase,height,andareaofallparallelograms.

● Studentscalculatetheareaofparallelogramswithoutagrid.

● Studentsgenerate,discuss,andapplyseveraldifferentstrategiesforcalculatingtheareaoftriangles onagrid

● Studentsmakeconnectionsbetweentheareasoftrianglesandtheareaofparallelograms

● Studentscalculatetheareasoftriangleswithoutagrid.

● Studentsapplywhattheyhavelearnedaboutcalculatingtheareasofparallelogramsandtrianglesto anewcategoryofshapes:polygons.

SecondTopic:SurfaceArea

LearningTargets:

● Icanexplainwhatsurfaceareais.

● Icancalculatethesurfaceareaofa rectangularprismandexplainmystrategy.

● Icandescribethefacesofapolyhedron.

● Icancompareandcontrastprismsand pyramids.

● Iknowwhatanetisandhowitisrelatedto apolyhedron.

● Icanmatchapolyhedronwithitsnet.

● Icancalculatethesurfaceareaofaprismor pyramidfromadrawinganddescribemy strategy.

● Icandesignanetforathree-dimensional object.

● Icancalculatesurfaceareatoanswer problemsincontext

● Icanidentifyandexplaincommonmistakes ormisconceptionsrelatedtosurfacearea.

LearningActivities:

Estimated#ofLessons:8

EssentialQuestions:

HowdoIjustifymyargumentusingprecisemath languageandthestrategyIused?

● Studentsdevelopaconceptualunderstandingofthemeaningofsurfacearea.

● Studentsbegintovisualizethreedimensionalobjectsknownaspolyhedra.

● Studentsareintroducedtothenamesofpolyhedraandpracticeidentifyingpolyhedrafromtheir nets.

● Studentscalculatethesurfaceareasofprismsandpyramids.

● Studentsusetheircreativity,personalexperiences,andtheconceptstheylearnedinthisunitto designatake-outcontainer.

CourseName:Grade6Unit2Title:IntroducingRatios

UnitOverview:

Inthisunit,studentswilllearnwhatratiosare,howtodescribethemandhowtogenerateequivalentratios. Studentsareintroducedtodoublenumberlinesandtablesastoolsforsolvingproblemswithequivalent ratios.Studentswilluseequivalentratiostocompareratiosandsolvemorecomplexproblems.

STAGE1:DESIREDRESULTS

EstablishedGoals

CSDEContentStandards:

6.RP.A.1: Understandtheconceptofaratioand useratiolanguagetodescribearatiorelationship betweentwoquantities.

6.RP.A.2: Understandtheconceptofaunitrate associatedwitharatiowith,anduse ��/�� ��:�� ��≠0 ratelanguageinthecontextofaratiorelationship.

6.RP.A.3: Useratioandratereasoningtosolve real-worldandmathematicalproblems,e.g.,by reasoningabouttablesofequivalentratios,tape diagrams,doublenumberlinediagramsor equations.

6.RP.A.3.a: Maketablesofequivalentratios relatingquantitieswithwhole-number measurements, findmissingvaluesinthetables, andplotthepairsofvaluesonthecoordinate plane.Usetablestocompareratios.

6.RP.A.3.b: Solveunitrateproblemsincluding thoseinvolvingunitpricingandconstantspeed.

Understandings

● Alimitedsetofsymbolscanbeusedto representnumericaldescriptionsand relationships.

● Mathematicsisauniversallanguagethat usesassumedandlogicalstatementsto describetheworld.

Knowledge

● Aratioisacomparisonoftwoquantities.

● Tworatiosareequivalentifyoucan multiplyeachofthevaluesinthe firstratio bythesamenumbertogetthevaluesinthe secondratio.

TransferGoals

CSDEMathPractices(MP)in Blue toverifysignificance

● CRITICALTHINKING:Demonstrate flexibility anddeterminationwhensolvingproblems. MP#1 Makesenseandperseverethroughchallenges; MP#2Reasonabstractlyandquantitatively;MP #5Useappropriatetoolsstrategically

EssentialQuestions

● Whatisthisnumber/relationshipexpressing? HowcanIrepresentitindifferentways?

● Howdoweuseratiostrategiestoidentifyand describerelationshipstohelpmesolve problems?

Skills(FramedasLearningTargets)

● Icanexplainwhataratioisandidentifythem inthreedifferentrepresentations.

● Icanexplainwhatequivalentratiosareand createthembasedongivenratios.

● Icanexaminewhethertworatiosare equivalentandjustifymyreasoning.

● Icanexplainwhataunitrateisandusethatto interpret,compare,andsolveratioproblems.

● Icandeterminewhichobjectismovingfaster andexplainhowIknow.

● Icanusedifferentstrategies(doublenumber line,tapediagram,tables)tosolveproblems involvingratios.

STAGE2:DETERMINEACCEPTABLEEVIDENCE

SummativeAssessment

Grade6Unit2EndUnitAssessment

● Icanexplainwhataratioisandidentify theminthreedifferentrepresentations

Problem1-7

● Icanexplainwhatequivalentratiosareand createthembasedongivenratios.

Problem1,2,3,4,6

● Icanexaminewhethertworatiosare equivalentandjustifymyreasoning.

Problem4,6

● Icanexplainwhataunitrateisandusethat tointerpret,compare,andsolveratio problems.

Problem4,5

● Icandeterminewhichobjectismoving fasterandexplainhowIknow.

Problem5

● Icanusedifferentstrategies(double numberline,tapediagram,tables)tosolve problemsinvolvingratios.

Problem:6,7

PerformanceTask

● Howmuchwaste? Studentsuseratio relationshipstodeterminehowmuchtrash iscreatedataschoolinadayandinayear. Studentsthenmakeaplantoreducethe amountofwastegenerated,

○ Icanusedifferentstrategies (doublenumberline,tapediagram, tables)tosolveproblemsinvolving ratios.

Understanding#1and2

LearningTarget#6

TransferSkills:CriticalThinking

FormativeAssessment

Grade6Unit2MidunitAssessment

Ongoingassessments:IMsynthesisandcooldowns asappropriate

Frayermodel(blanktemplateandrationale)

● Ratio

● UnitRate

Previousmathconnections

STAGE3:LEARNINGPLAN

Thefollowingconceptsfrompreviousgradesmay supportstudentsinmeetinggrade-levelstandards inthisunit:

● Creatingandinterpretingnumberline diagrams.(2.MD.B.6)

● Recognizingandgeneratingequivalent fractions.(4.NF.A.1)

● Understandingmultiplicativerelationships, includingtherelationshipbetween multiplyingbyaunitfractionanddividing byawholenumber.(4.OA.A.1,4.OA.A.2, 4.NF.B.3,5.NF.B.4,5.NF.B.5)

FirstTopic:IntroducingRatios

LearningTargets:

● Icanexplainwhataratioisandidentify theminthreedifferentrepresentations.

● Icanexplainwhatequivalentratiosareand createthembasedongivenratios.

● Icanexaminewhethertworatiosare equivalentandjustifymyreasoning.

● Icanexplainwhataunitrateisandusethat tointerpret,compare,andsolveratio problems.

LearningActivities:

● Studentsinformallyexploreratiosincontext.

Diagnosticassessmentquestions/problemsbasedon priorgradelevelexperience

FromReadinessCheck

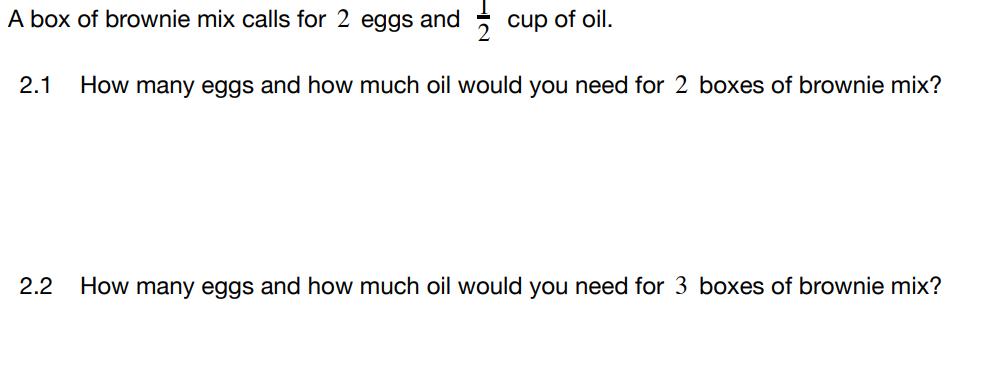
Studentswill firstsolvethetwoproblemsandbe preparedtosharetheirthinkingwithothers. Studentsthensharewithotherstosolidifythe conceptofmultiplicativerelationshipsandscaling recipes.

Estimated#ofLessons:8

EssentialQuestions:

Whatisthisnumber/relationshipexpressing?How canIrepresentitindifferentways?

● Studentsexplainwhataratioisusingmathematicallanguage,

● Studentsexplainwhatequivalentratiosareand findthembydoubling,tripling,andhalvingin context.

● Studentsgenerateequivalentratiosandjustifythattheyareequivalent.

● Studentsuseadoublenumberlinetogenerateequivalentratios.

● Studentsuseunitpricestosolveproblems.

SecondTopic:SolvingProblemswithRatios Estimated#ofLessons:11

RelevantLearningTargets(fromStage1):

● Icanexplainwhataunitrateisandusethat tointerpret,compare,andsolveratio problems.

● Icandeterminewhichobjectismoving fasterandexplainhowIknow.

● Icanusedifferentstrategies(double numberline,tapediagram,tables)tosolve problemsinvolvingratios.

EssentialQuestions: Howdoweuseratiostrategiestoidentifyand describerelationshipstohelpmesolveproblems?

LearningActivities:Studentsdevelopstrategiesforcomparingratiosincontext.

● Studentscalculatethespeedofanobjectasaunitrate.

● Studentsusetablesofequivalentratiostodeterminelargeunknownvaluesincontext.

● Studentssolveproblemsbyreasoningabouttablesofequivalentratiosanddoublenumberline diagrams.

● Studentsusedifferentstrategiestosolveproblemsandtodeterminewhetherornotyoucanuse equivalentratiostosolveaproblem.

● Studentsuseandinterprettapediagramstosolveproblemsinvolvingpart-part-wholeratios.

● Studentscreateandusetapediagramsandtablestohelpsolveproblemsinvolvingpart-part-whole ratios.

● StudentsapplythestrategiestheylearnedinLesson12tosolveproblemsinvolvingpart-part-whole ratiosinthecontextofhousingandgreenspaceinneighborhoods.

● Studentsapplyratioreasoningtoanswerquestionsaboutareal-worldsituation.

UnitOverview:

Inthisunit,studentswilluseratioreasoningtoconvertbetweenunitsofmeasurementbothwithinand acrosssystemsofmeasurement.Studentsrecognizethateachratiorelationshiphastwounitrates,anduse eachofthoseunitratestosolveproblemsinvolvingtablesofequivalentratios.Studentsmakeconnections betweenpercentages,ratios,andrates,thenusethisratioreasoningtodetermineunknownparts,wholes, andpercentages.

CSDEContentStandards:

6.RP.A.2: Understandtheconceptofaunitratea/b associatedwitharatioa:bwithbanduserate ≠0, languageinthecontextofaratiorelationship.

6.RP.A.3: Useratioandratereasoningtosolve ● CRITICALTHINKING:Demonstrate flexibility anddeterminationwhensolvingproblems. MP#2 Reasonabstractlyandquantitatively;MP#5Use

real-worldandmathematicalproblems,e.g.,by reasoningabouttablesofequivalentratios,tape diagrams,doublenumberlinediagrams,or equations.

6.RP.A.3.b: Solveunitrateproblemsincludingthose involvingunitpricingandconstantspeed.

6.RP.A.3.c: Findapercentofaquantityasarateper 100(e.g.,30%ofaquantitymeans30/100times thequantity);solveproblemsinvolving findingthe whole,givenapartandthepercent.

6.RP.A.3.d: Useratioreasoningtoconvert measurementunits;manipulateandtransform unitsappropriatelywhenmultiplyingordividing quantities. appropriatetoolsstrategically;MP#7Lookfor andmakeuseofstructure.

Understandings

● Ratioscanbeusedtoconvertbetween differentunitsofmeasurements.

● Unitratescompareto1.

● Percentsareratiosthatcompareto100.

Knowledge

● Findequivalentratiosandpercentages

● Recognizeandcalculatetwounitratesfor thesameratiorelationship.Useunitrates tosolveproblemsinvolvingtablesof equivalentratios.

● Makeconnectionsbetweenpercentages, ratiosandrates.Useratioreasoningto determineunknownparts,wholes,and percentages.

EssentialQuestions

● Howdoweuseratiostrategiestoidentifyand describerelationships?Howdoesthathelp mesolvetheproblem?

● Howdoweuseratiosandpercentagesto solverealworldproblems?

Skills(FramedasLearningTargets)

● Icanconvertmeasurementsfromoneunitto anotherindifferentmeasurementsystems

● Icanusethewordpertodescribeunitrates.

● Icancompareratesthatarewrittenin differentunits.

● Icancalculateandinterpretthetwounitrates forthesamerelationship.

● Icanchoosewhichunitratetousetosolvea problemandexplainmychoice.

● Icanmakecomparisonsandcalculate unknownquantitiesusingunitrates.

● Icanmakeconnectionsbetweenpercentages andratios.

● Icanuseadoublenumberline,tapediagram, ortabletodetermineunknownpartsor wholes.

● Icancreatetapediagrams,doublenumber linediagrams,ortablestodetermineunknown parts,percentages,orwholes.

● Icancalculateanypercentageofanumber.

● Icanexplaintwodifferentexpressionsfor calculatingapercentageofanumber.

● Icancalculateanunknownpercentage.

● Icanexplaindifferentexpressionsfor calculatinganunknownpercentage.

● Icanuseratesandpercentagestoanalyze characteristicsofacountry’spopulation.

STAGE2:DETERMINEACCEPTABLEEVIDENCE

SummativeAssessment

Grade6Unit3EndofUnitAssessment

● Icanmakeconnectionsbetween percentagesandratios.

● Icanuseadoublenumberline,tape diagram,ortabletodetermineunknown partsorwholes.

○ Problem1

● Icancalculateandinterpretthetwounit ratesforthesamerelationship.

● Icanchoosewhichunitratetousetosolve aproblemandexplainmychoice.

○ Problem2

● Icanmakecomparisonsandcalculate unknownquantitiesusingunitrates.

○ Problem3

● Icancalculateanypercentageofanumber.

● Icanexplaintwodifferentexpressionsfor calculatingapercentageofanumber.Ican calculateanunknownpercentage.

○ Problem4

● Icanconvertmeasurementsfromoneunit toanotherindifferentmeasurement systems

○ Problem5

● Icanusethewordpertodescribeunit rates.

● Icancompareratesthatarewrittenin differentunits.

● Icancalculateanunknownpercentage.

● Icanexplaindifferentexpressionsfor calculatinganunknownpercentage.

○ Problem6

● Icancreatetapediagrams,doublenumber linediagrams,ortablestodetermine unknownparts,percentages,orwholes.

● Icancalculateanypercentageofanumber.

● Icanexplaintwodifferentexpressionsfor calculatingapercentageofanumber.

FormativeAssessment

Grade6Unit3MidUnitAssessment

Ongoingassessments:IMsynthesisandcooldowns asappropriate

Frayermodel(blank templateandrationale)

● UnitsandMeasurement

● UnitRates

● Percentages

○ Problem7

PerformanceTask:

● ACountryasaVillage:Studentswillchoose acountryandlookatsomefactsaboutit. Theywillthencreateaposterpretending thatthecountryisavillageof100people. Theywillneedtoconvertallofthe informationtobehowmanyoutof100.

○ Icanuseratesandpercentagesto analyzecharacteristicsofa country’spopulation.

Understanding 3

LearningTarget 14

TransferSkills:CriticalThinking

STAGE3:LEARNINGPLAN

Previousmathconnections

Thefollowingconceptsfrompreviousgradesand unitsmaysupportstudentsinmeetinggrade-level standardsinthisunit:

● Measuringandestimatinglengths, volumes,andmasses/weightsinstandard units.(2.MD.A,3.MD.A)

● Multiplicationofwholenumbersby fractionsandfractionsbyfractions. (4.NF.B.4,5.NF.B.4)

● Understandingtheconceptofaratioand usingratioreasoningtosolveproblems. (6.RP.A.1)

Diagnosticassessmentquestions/problemsbasedon priorgradelevelexperience

FromReadinessCheck:

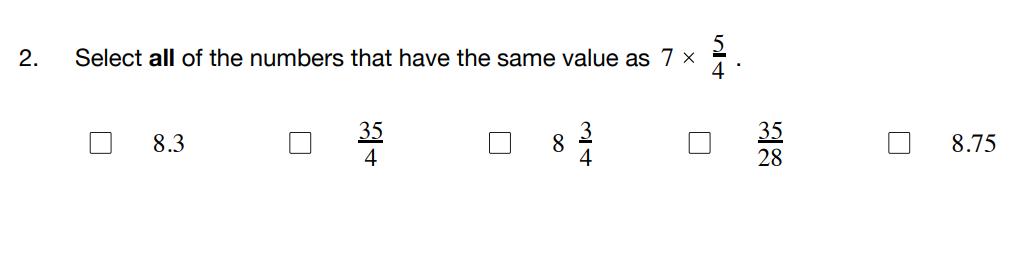
Studentswill firstsolvethetwoproblemsandbe preparedtosharetheirthinkingwithothers. Studentsthensharewithotherstosolidifythe conceptsofunitsformeasuringlengthandvolumeas wellasmultiplyingawholenumberbyafraction.

FirstTopic:Unitsandmeasurement Estimated#ofLessons:3(1-3)

LearningTargets:

EssentialQuestions:

toanotherindifferentmeasurement systems describerelationships?Howdoesthathelp mesolvetheproblem?

LearningActivities:

● Studentsdescribedifferentunitsofmeasurementandconnectthemwithmeasurementsof everydayobjects,suchasthewidthofa fingerortheweightofasliceofbread.

● Studentsconvertmeasurementsfromoneunittoanother.

● Studentsconvertmeasurementsbasedoninformationfrompenpalsaroundtheworld.

SecondTopic:UnitRates

RelatedLearningTargets:

● Icanusethewordpertodescribeunit rates.

● Icancompareratesthatarewrittenin differentunits.Icancalculateandinterpret thetwounitratesforthesamerelationship.

● Icanchoosewhichunitratetousetosolve aproblemandexplainmychoice.

● Icanmakecomparisonsandcalculate unknownquantitiesusingunitrates.

LearningActivities:

Estimated#ofLessons:7

EssentialQuestions: Howdoweuseratiostrategiestoidentifyand describerelationships?Howdoesthathelpmesolve theproblem?

● Studentscomparethespeedsofmodeltrainsanddiscussunitratesusingtheword per

● Studentslearnthateveryratiorelationshiphastwoassociatedunitratesandthateachunitrateis usefulforsolvingdifferentproblems.

● Studentsrecognizethatinatableofequivalentratios,theycanmultiplybyaunitratetogofromone columntoanother.

● Studentspracticeusingwhatthey’velearnedaboutunitratestomakecomparisonsandcalculate unknowns.

ThirdTopic:Percentages

RelatedLearningTargets:

● Icanmakeconnectionsbetween percentagesandratios.

● Icanuseadoublenumberline,tape diagram,ortabletodetermineunknown partsorwholes.

● Icancreatetapediagrams,doublenumber linediagrams,ortablestodetermine unknownparts,percentages,orwholes.

● Icancalculateanypercentageofanumber.

● Icanexplaintwodifferentexpressionsfor calculatingapercentageofanumber.Ican calculateanunknownpercentage.

● Icanexplaindifferentexpressionsfor calculatinganunknownpercentage.

● Icanuseratesandpercentagestoanalyze

Estimated#ofLessons:9

RelatedEssentialQuestions: Howdoweuseratiosandpercentagestosolvereal worldproblems?

characteristicsofacountry’spopulation.

LearningActivities:

● Studentsbuildontheirexperienceswithpercentagesinordertoreasonaboutthesebenchmark percentages:10%,25%,50%,75%.

● Studentsmakeconnectionsbetweentapediagramsanddoublenumberlinesthatrepresent percentages,andthenusedoublenumberlinesandtablestosolveproblemsinvolvingfriendly percentages.

● Studentscreatetapediagrams,doublenumberlines,andtablestosolveproblemswithpercentages.

● Studentsdevelopandusestrategiesforcalculatinganypercentofanumber.

● Studentsdevelopanduseoneormorestrategiestocalculateunknownpercentages.

● Studentsusewhatthey’velearnedaboutratesandpercentagestoanalyzecharacteristicsof countries’populations.

UnitOverview:

Inthisunit,studentsdevelopmultiplestrategiesfordividingfractionsandapplythosestrategiestosolve problemsaboutareasandvolumeswithfractionaldimensions.Studentsreasonaboutwhatitmeansto dividebyafractionandmakeconnectionsbetweencontexts,tapediagrams,andexpressions.Students developstrategiesforcalculatingquotientsoftwofractions,includingtheuseofcommondenominators. Studentsthenusewhattheyknowaboutdividingfractionstosolveproblems.

STAGE1:DESIREDRESULTS

EstablishedGoals

CSDEContentStandards:

6.NS.A.1: Interpretandcomputequotientsof fractions,andsolvewordproblemsinvolving divisionoffractionsbyfractions(e.g.,byusing visualfractionmodelsandequationstorepresent theproblem).

6.G.A: Solvereal-worldandmathematical problemsinvolvingarea,surfacearea,andvolume.

6.G.A.2: Findthevolumeofarightrectangular prismwithfractionaledgelengthsbypackingit withunitcubesoftheappropriateunitfraction edgelengths,andshowthatthevolumeisthesame aswouldbefoundbymultiplyingtheedgelengths oftheprism.Applytheformulasand ��=����ℎ to findvolumeofrightrectangularprisms ��=��ℎ withfractionaledgelengthsinthecontextof solvingreal-worldandmathematicalproblems.

TransferGoals

CSDEMathPractices(MP)in Blue toverifysignificance

● CRITICALTHINKING:Demonstrate flexibility anddeterminationwhensolvingproblems. MP#2Reasonabstractlyandquantitatively.

● COMMUNICATION:Createalogicaland evidence-basedargumenttosupportideas. MP#6Attendtoprecision;MP#7Lookfor andmakeuseofstructure

Understandings EssentialQuestions

Afractionisadivisionproblemthatcanbe manipulatedandrepresentedindifferentways.

Knowledge

● Dividingtwofractionsisthesameas multiplyingthe firstfractionbythe reciprocalofthesecondfraction.

● Areaandvolumewithfractionaldimensions

Howdoweusefractionstosolverealworld problems?

Skills(FramedasLearningTargets)

● Icandecideifquotientsofdivisionsituations aregreaterthan1,lessthan1,orequalto1.

● Icanconnectsituations,expressions,andtape diagramsthatrepresentthesamesituation.

● Icanusetapediagramstorepresentandsolve divisionproblemswhentheanswerisa fraction.

● Icandecideifthenumberofgroupsina divisionproblemisgreaterthanorlessthan1.

● Icanusetapediagramswithcommon denominatorstosolvedivisionproblems.

● Icanexplainwhyitisequivalentto. 12 5 ÷ 3 5 =12÷3

● Icanusecommondenominatorstodivide fractions.

● Icancalculatethequotientoftwofractions andexplainmystrategy.

● Icancompareandcontrasttwostrategiesfor dividingfractions.

● Icansolveproblemsinvolvingdivisionof fractionsbyfractionsincontext.

● Icanwritemyownproblemtorepresenta divisionexpression.

● Icanuseadivisionexpressiontorepresenta questionlike“Howmanytimesaslong?”

● Icandividefractionstosolveproblemsabout comparinglengths.

● Icancalculatetheareaofarectanglewith lengthsthatarefractions.

● Icanusedivisionandmultiplicationtosolve problemsaboutareasofrectangleswith lengthsthatarefractions.

● Icancalculatethevolumeofarectangular prismwithlengthsthatarefractions.

● Icanusedivisionandmultiplicationtosolve problemsaboutvolumesofrectangularprisms withlengthsthatarefractions.

● Icanusefractiondivisionandmultiplicationto solveproblemsaboutareaandvolumein context.

STAGE2:DETERMINEACCEPTABLEEVIDENCE

SummativeAssessment

Grade6Unit4EndofUnitAssessment

● Icandecideifquotientsofdivision situationsaregreaterthan1,lessthan1,or equalto1.

○ Problem1

● Icandecideifthenumberofgroupsina divisionproblemisgreaterthanorlessthan 1.

● Icanusetapediagramswithcommon denominatorstosolvedivisionproblems

○ Problem2

● Icanexplainwhyitisequivalentto.

● 12 5 ÷ 3 5 =12÷3

● Icanusecommondenominatorstodivide fractions.

● Icancalculatethequotientoftwofractions andexplainmystrategy.

● Icancompareandcontrasttwostrategies fordividingfractions.

○ Problem3

● Icanuseadivisionexpressiontorepresent aquestionlike“Howmanytimesaslong?”

● Icandividefractionstosolveproblems aboutcomparinglengths.

○ Problem4

● Icanconnectsituations,expressions,and tapediagramsthatrepresentthesame situation.

● Icanusetapediagramstorepresentand solvedivisionproblemswhentheansweris afraction.

○ Problem5

● Icancalculatetheareaofarectanglewith lengthsthatarefractions.

● Icanusedivisionandmultiplicationtosolve problemsaboutareasofrectangleswith lengthsthatarefractions.

● Icancalculatethevolumeofarectangular prismwithlengthsthatarefractions.

● Icanusedivisionandmultiplicationtosolve problemsaboutvolumesofrectangular prismswithlengthsthatarefractions.

○ Problem6

FormativeAssessment

Grade6Unit4MidUnitAssessment

Ongoingassessments:IMsynthesisandcooldowns asappropriate

Frayermodel(blanktemplateandrationale)

● DividingFractions

● AreaandVolumewithFractions

● Icansolveproblemsinvolvingdivisionof fractionsbyfractionsincontext.

● Icanwritemyownproblemtorepresenta divisionexpression.

○ Problem7

PerformanceTask: PlanterPlanner. Studentsare giveninformationregardingareaneededand servingsizeaboutdifferentplantsthattheycan growintheirgarden.Theywillusethisinformation toanswerquestionsandultimatelydesigntheir ownplanter.

● Icanusefractiondivisionandmultiplication tosolveproblemsaboutareaandvolumein context.

Understanding #2 LearningTargets 18 TransferSkills: CommunicationandCritical Thinking

STAGE3:LEARNINGPLAN

Previousmathconnections

Thefollowingconceptsfrompreviousgradesand unitsmaysupportstudentsinmeetinggrade-level standardsinthisunit:

● Understandingdivisionasanunknown factorproblem.(3.OA.B.6)

● Explainingwhytwofractionsareequivalent andgeneratingequivalentfractions. (4.NF.A.1)

● Makingconnectionsbetweendivisionand fractions(i.e.,that �� ÷ �� =).(5.NF.B.3) ��

● Multiplyingfractionsbywholenumbersand fractionsbyfractions.(5.NF.B.4)

● Calculatingthevolumeofarectangular prismwithwholenumbersidelengths. (5.MD.C.5.B)

Diagnosticassessmentquestions/problemsbasedon priorgradelevelexperience

FromReadinessCheck:

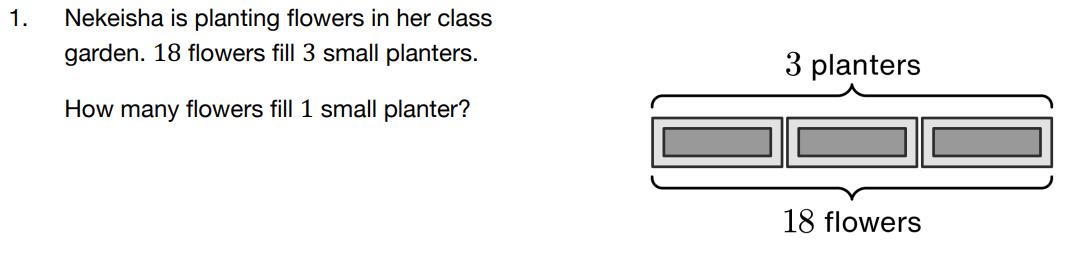
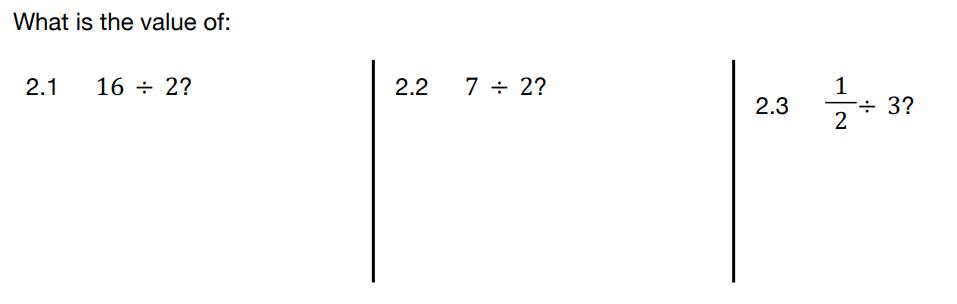
Studentswill firstsolvethetwoproblemsandbe preparedtosharetheirthinkingwithothers. Studentsthensharewithotherstosolidifythe conceptofdivisionincludingdividingfractionsby wholenumbers.

FirstTopic:IntroductiontoDividingFractions Estimated#ofLessons:4

LearningTargets:

● Icandecideifquotientsofdivision situationsaregreaterthan1,lessthan1,or equalto1.

LearningActivities:

EssentialQuestions:

Howcandividingbyafractionbeimplementedina realworldsituation?Exhowmanybatchesofcookies canImakeifIhave3cupsof flourandeachbatch requires ⅔ acup.

● Studentsestimatequotientsbydeterminingiftheyaregreaterthan`1`,lessthan`1`,orequalto`1`.

● Studentsinterpretandcreatetapediagramsthatrepresentdivisionsituationswithwholenumber dividendsanddivisors.

● Studentsmakeconnectionsbetweendrawings,tapediagrams,andmultiplicationanddivision expressionstoanswerthequestion"Howmanygroups?"

● Studentsextendwhattheyknowaboutwholenumberstoanswerthequestion“Howmanyin`1` group?”whenthenumberofgroupsisafraction.

SecondTopic:DividingFractions

LearningTargets:

● Icanconnectsituations,expressions,and tapediagramsthatrepresentthesame situation.

● Icanusetapediagramstorepresentand solvedivisionproblemswhentheansweris afraction.

● Icandecideifthenumberofgroupsina divisionproblemisgreaterthanorlessthan 1.

● Icanusetapediagramswithcommon denominatorstosolvedivisionproblems.

● Icanexplainwhyitisequivalentto.

● 12 5 ÷ 3 5 =12÷3

● Icanusecommondenominatorstodivide fractions.

● Icancalculatethequotientoftwofractions andexplainmystrategy.

● Icancompareandcontrasttwostrategies fordividingfractions.

● Icansolveproblemsinvolvingdivisionof fractionsbyfractionsincontext.

● Icanwritemyownproblemtorepresenta divisionexpression.

LearningActivities:

Estimated#ofLessons:8

EssentialQuestions:

Howcandividingbyafractionbeimplementedina realworldsituation?Exhowmanybatchesofcookies canImakeifIhave3cupsof flourandeachbatch requires ⅔ acup.

● Studentsmakeconnectionsbetweensituations,expressions,andtapediagramsthatrepresentthe samesituation.

● Studentsdeterminewhetherthenumberofgroupsinadivisionproblemisgreaterthanorlessthan `1`.

● Studentsdevelop fluencyinusingcommondenominatorstodividefractions.

● Studentsexploreastrategyfordividingbyaunitfractionbyaskingthequestion“Howmanyin`1` group?”

● Studentsdevelop fluencywithatleastonemethodfordividingfractions.

● Solveproblemsinvolvingdivisionoffractionsbyfractionsincontext.

ThirdTopic:AreaandVolumewithFractions

LearningTargets:

● Icandividefractionstosolveproblems aboutcomparinglengths.

● Icancalculatetheareaofarectanglewith lengthsthatarefractions.

● Icanusedivisionandmultiplicationtosolve problemsaboutareasofrectangleswith lengthsthatarefractions.

● Icancalculatethevolumeofarectangular prismwithlengthsthatarefractions.

● Icanusedivisionandmultiplicationtosolve problemsaboutvolumesofrectangular prismswithlengthsthatarefractions.

LearningActivities:

Estimated#ofLessons:7

EssentialQuestions:

HowdoIdeterminehowmuchmaterialIneedto coverthisspacewhenthedimensionsarenotwhole numbers?

● Studentspracticedividingfractionsbycomparinglengthsandansweringquestionsoftheform “Howmanytimesaslong?”

● Studentsapplywhattheyknowaboutmultiplyinganddividingfractionstoafamiliarcontext: calculatingarea.

● Studentsextendwhattheyhavelearnedtocalculatevolumesofrectangularprismswithfractional dimensions.

● Studentsapplywhattheyhavelearnedaboutfractiondivision,area,andvolumetosolveproblems aboutbuildingagarden.

UnitOverview:

Inthisunit,studentsdevelopanduseavarietyofstrategiesforadding,subtracting,multiplying,anddividing decimals.Theyalsoexploretheleastcommonmultipleandgreatestcommonfactoroftwonumbers.

CSDEContentStandards:

6.RP.A.3.B: Solveunitrateproblemsincluding thoseinvolvingunitpricingandconstantspeed.

6.RP.A.3.C: Findapercentofaquantityasarate per100;solveproblemsinvolving findingthe whole,givenapartandthepercent.

6.NS.B: Compute fluentlywithmulti-digitnumbers and findcommonfactorsandmultiples.

6.NS.B.2: Fluentlydividemulti-digitnumbersusing thestandardalgorithm.

6.NS.B.3: Fluentlyadd,subtract,multiply,and dividemulti-digitdecimalsusingthestandard algorithmforeachoperation.

6.NS.B.4: Findthegreatestcommonfactoroftwo wholenumberslessthanorequalto100andthe leastcommonmultipleoftwowholenumbersless thanorequalto12.Usethedistributiveproperty toexpressasumoftwowholenumbers1-100with acommonfactorasamultipleofasumoftwo wholenumberswithnocommonfactor.For example,expressas 36+8 4(9+2).

● COMMUNICATION:Createalogicaland evidence-basedargumenttosupportideas. MP #3Constructviableargumentsandcritiquethe reasoningofothers;MP#6:Attendtoprecision

● CRITICALTHINKING:Analyzedatainorderto drawconclusions. MP#6:Attendtoprecision;MP #8:Lookforandexpressregularityinrepeated reasoning.

Understandings EssentialQuestions

● Estimationcanhelpyoudetermineifyour answertoamultiplication/divisionproblem isreasonable.

● Determiningthegreatestcommonfactor andleastcommonmultiplemakesyoua moreefficientproblemsolver.

Knowledge

● Howtocomputeoperationswithdecimals.

● Howtoidentifytheleastcommonmultiple andgreatestcommonfactor.

● HowdoIuseestimationtoseeifmy calculationsmakesense?

● HowdoIbuildonmypriormathknowledgeto findcommonfactorsandmultiples?

Skills(FramedasLearningTargets)

● Icanusediagrams,verticalcalculations,and placevaluetoaddandsubtractdecimals.

● Icanaddandsubtractdecimalsusingdifferent strategies.

● Icanuseareatoreasonaboutdecimal multiplication.

● Icanusefractionstomultiplydecimals.

● Icanusetheproductofwholenumbersto calculatetheproductofdecimals.

● Icanmultiplydecimalsusingdifferent strategies.

● Icanuseahundredthschartandreasoningto dividedecimals.

● Icanmakeconnectionsbetweendecimal divisionanddividingfractionswithcommon Denominators.

● Icanuselongdivisionorotherstrategiesto dividedecimalswithnoremainders.

● Icanwriteanequivalentdivisionexpressionin ordertodividedecimals.

● Icandividedecimalstosolveproblemsabout moviespeedsanddurations.

● Icanadd,subtract,multiply,anddivide decimalstosolveproblemsincontext.

● Icanexplainwhattheleastcommonmultiple oftwonumbersmeans.

● Icandeterminetheleastcommonmultipleof twonumbers

● Icanexplainwhatthegreatestcommonfactor oftwonumbersmeans.

● Icandeterminethegreatestcommonfactor oftwonumbers.

STAGE2:DETERMINEACCEPTABLEEVIDENCE

SummativeAssessment

Grade6Unit5EndofUnitAssessment

● Icanexplainwhattheleastcommon multipleoftwonumbersmeans.

● Icandeterminetheleastcommonmultiple oftwonumbers

○ Problem1

● Icanuseahundredthschartandreasoning todividedecimals.

● Icanmakeconnectionsbetweendecimal divisionanddividingfractionswithcommon Denominators.

○ Problem2

● Icanaddandsubtractdecimalsusing differentstrategies.

● Icanusetheproductofwholenumbersto calculatetheproductofdecimals.

● Icanmultiplydecimalsusingdifferent strategies.

● Icanuselongdivisionorotherstrategiesto dividedecimalswithnoremainders.

● Icanwriteanequivalentdivision expressioninordertodividedecimals.

FormativeAssessment

Grade6Unit5MidUnitAssessment

Ongoingassessments:IMsynthesisandcooldowns asappropriate Frayermodel(blanktemplateandrationale)

● AddingandsubtractingDecimals

● Multiplyinganddividingdecimals

● Solvingproblemswithdecima;s

● Leastcommonmultipleandgreatestcommon factor

○ Problem3

● Icanusediagrams,verticalcalculations,and placevaluetoaddandsubtractdecimals.

○ Problem4

● Icanuseareatoreasonaboutdecimal multiplication.

● Icanusefractionstomultiplydecimals.

○ Problem5

● Icanexplainwhatthegreatestcommon factoroftwonumbersmeans.

● Icandeterminethegreatestcommon factoroftwonumbers.

○ Problem6

● Icandividedecimalstosolveproblems aboutmoviespeedsanddurations.

○ Problem7

PerformanceTasks: BudgetVehicles Studentsare giveninformationaboutdifferenttypesofcars. Theyneedtodecidewhichtypeofcarwouldbe besttopurchasebasedoncost,gasefficiencyor electricityuse.

● Icanadd,subtract,multiply,anddivide decimalstosolveproblemsincontext.

Understanding: 1

LearningTarget: 13

TransferSkills: CommunicationandCritical Thinking

Previousmathconnections

Thefollowingconceptsfrompreviousgradesmay supportstudentsinmeetinggrade-levelstandards inthisunit:

● Representingdecimalsusingtenthsand hundredths.(5.NBT.A.3.A)

● Adding,subtracting,multiplying,and dividingwholenumbers.(3.NBT.A.2, 4.NBT.B.6, 5.NBT.B.5, 5.NBT.B.7)

● Determiningfactorsandmultiplesofa number.(4.OA.B, 4.OA.B.4)

Diagnosticassessmentquestions/problemsbasedon priorgradelevelexperience

FromReadinessCheck:

STAGE3:LEARNINGPLAN

FirstTopic:AddingandSubtractingDecimals

LearningTargets:

● Icanusediagrams,verticalcalculations,and placevaluetoaddandsubtractdecimals.

● Icanaddandsubtractdecimalsusing differentstrategies.

LearningActivities:

Studentswill firstsolvethetwoproblemsandbe preparedtosharetheirthinkingwithothers. Studentsthensharewithotherstosolidifythe conceptofworkingwithdecimalsinregardtoplace value(tenthsandhundredths)andmoney.

Estimated#ofLessons:5

EssentialQuestions:

● HowdoIuseestimationtoseeifmy calculationsmakesense?

● Studentsmakeestimatesandroughcalculationsabouttheamountitwillcosttomakevarious dishesandcreateadishoftheirown.

● Studentsrevisitwhattheyhavelearnedaboutplacevalueinpreviousgradesandmakeconnections betweenplacevalueandthedecimalrepresentationofnumbers.Studentsthenusethese relationshipstoaddandsubtractdecimals.

● Studentsaddandsubtractdecimalsbymakingconnectionsbetweenplacevaluethinking,diagrams, andverticalcalculations.

● Studentsdevelop fluencywithaddingandsubtractingdecimalsusingverticalcalculations.They practiceaddingandsubtractingmulti-digitdecimalsbycompletingaseriesofmissingdigitpuzzles.

SecondTopic:MultiplyingandDividingDecimals

LearningTargets:

● Icanuseareatoreasonaboutdecimal multiplication.

● Icanusefractionstomultiplydecimals.

● Icanusetheproductofwholenumbersto calculatetheproductofdecimals.

● Icanmultiplydecimalsusingdifferent strategies.

● Icanuseahundredthschartandreasoning todividedecimals.

● Icanmakeconnectionsbetweendecimal divisionanddividingfractionswithcommon Denominators.

● Icanuselongdivisionorotherstrategiesto dividedecimalswithnoremainders.

● Icanwriteanequivalentdivision expressioninordertodividedecimals.

● Icandividedecimalstosolveproblems aboutmoviespeedsanddurations.

Estimated#ofLessons:9

EssentialQuestions: HowdoIuseestimationtoseeifmycalculations makesense?

LearningActivities:

● Studentsusewhattheyknowaboutahundredthscharttoreasonaboutplacevaluewhen multiplyingdecimals.

● Studentsuseareamodelstohelpthemmultiplydecimalsthathavemorethanonenon-zerodigit.

● Studentsareintroducedtoonemorestrategyformultiplyingdecimalsandhavetheopportunityto develop fluencybycompletingascavengerhuntactivity.

● Studentsmakesenseofdividingdecimalsusingahundredthschart.Studentswilluseastrategy similartowhattheylearnedfordividingfractions:writinganequivalentdivisionproblem.

● Inthislesson,studentsbeginbydividingwholenumberswithnoremainders,makingconnectionsto astrategytheymayhaveseeninearliergrades:longdivision.Laterinthelesson,studentswilldivide decimalsbywritingequivalentdivisionexpressionswithwholenumbers.

● Inthislesson,studentsuselongdivisionandvisualmodelstodividedecimalswhenthereisa remainder.Studentscontinuetobuild fluencywithdividingdecimalsbywritingequivalent expressionsandusinglongdivision.

● Studentspracticedividingdecimalstosolveproblemsandanswerthequestion“Howlongwillthis movietakeifIplayitatadifferentspeed?”

ThirdTopic:SolvingProblemswithDecimals

LearningTargets:

● Icanadd,subtract,multiply,anddivide decimalstosolveproblemsincontext.

LearningActivities:

Estimated#ofLessons:2

EssentialQuestions: HowdoIuseestimationtoseeifmycalculations makesense?

● Studentspracticetheskillstheyhavelearnedaroundoperationswithdecimalstohelpthemmake decisionsaboutpurchasingacar.

● Inthislesson,studentsusewhattheyhavelearnedaboutpercentagesandoperationswithdecimals tocomparethepricesofgroceriesindifferentplacesaroundtheU.S.

FourthTopic:LeastCommonMultipleandGreatest CommonFactor

LearningTargets:

● Icanexplainwhattheleastcommon multipleoftwonumbersmeans.

● Icandeterminetheleastcommonmultiple oftwonumbers

● Icanexplainwhatthegreatestcommon factoroftwonumbersmeans.

● Icandeterminethegreatestcommon factoroftwonumbers.

Estimated#ofLessons:4

EssentialQuestions: HowdoIbuildonmypriormathknowledgeto find commonfactorsandmultiples?

LearningActivities:

● Studentslearnhowtodeterminetheleastcommonmultiple(LCM)oftwonumbers.

● Studentslearnhowtodeterminethegreatestcommonfactor(GCF)oftwonumbers.

CourseName:Grade6Unit6Title:ExpressionsandEquationsEst.#ofLessons:21

UnitOverview:

Inthisunitstudentswriteandsolveequationsoftheform andinandoutofcontext. ��+��=�� ����=�� Studentsexplorewhatequivalentexpressionswithvariablesareandusethedistributivepropertytowrite equivalentexpressions.Studentsextendtheirworkwithexpressionstoevaluatenumericalandvariable expressionswithwholenumberexponents.Studentsareintroducedtodifferentwaysofrepresenting relationships:usingtables,equations,andgraphs.

STAGE1:DESIREDRESULTS

EstablishedGoals

CSDEContentStandards:

6.RP.A.1: Understandtheconceptofaratioanduse ratiolanguagetodescribearatiorelationship betweentwoquantities.

6.RP.A.2: Understandtheconceptofaunitrate �� �� associatedwitharatioa:bwith,anduserate ��≠0 languageinthecontextofaratiorelationship.

6.RP.A.3: Useratioandratereasoningtosolve real-worldandmathematicalproblems,e.g.,by reasoningabouttablesofequivalentratios,tape diagrams,doublenumberlinediagrams,or equations.

6.RP.A.3.A: Maketablesofequivalentratios relatingquantitieswithwhole-number measurements, findmissingvaluesinthetables, andplotthepairsofvaluesonthecoordinate plane.Usetablestocompareratios.

6.NS.B.2: Fluentlydividemulti-digitnumbersusing thestandardalgorithm.

6.EE.A.1: Writeandevaluatenumerical expressionsinvolvingwhole-numberexponents.

6.EE.A.2: Write,read,andevaluateexpressionsin

● CRITICALTHINKING:Demonstrate flexibility anddeterminationwhensolvingproblems. MP#2 Reasonabstractlyandquantitatively;MP#7Look forandmakeuseofstructure.

● COMMUNICATION:Createalogicaland evidence-basedargumenttosupportideas. MP #3Constructviableargumentsandcritiquethe reasoningofothers.

whichlettersstandfornumbers.

6.EE.A.2.A: Writeexpressionsthatrecord operationswithnumbersandwithlettersstanding fornumbers.

6.EE.A.2.B: Identifypartsofanexpressionusing mathematicalterms(sum,term,product,factor, quotient,coefficient);viewoneormorepartsofan expressionasasingleentity.

6.EE.A.2.C: Evaluateexpressionsatspecificvalues oftheirvariables.Includeexpressionsthatarise fromformulasusedinreal-worldproblems. Performarithmeticoperations,includingthose involvingwhole-numberexponents,inthe conventionalorderwhentherearenoparentheses tospecifyaparticularorder(Orderofoperations).

6.EE.A.3: Applythepropertiesofoperationto generateequivalentexpressions.

6.EE.A.4: Identifywhentwoexpressionsare equivalent.

6.EE.B.5: Understandsolvinganequationor inequalityasaprocessofansweringaquestion: whichvaluesfromaspecifiedset,ifany,makethe equationorinequalitytrue?USesubstitutionto determinewhetheragivennumberinaspecified setmakesanequationorinequalitytrue.

6.EE.B.6: Usevariablestorepresentnumbersand writeexpressionswhensolvingareal-worldor mathematicalproblem;understandthatavariable canrepresentanunknownnumber,or,depending onthepurposeathand,anynumberinaspecified set.

6.EE.B.7: Solvereal-worldandmathematical problemsbywritingandsolvingequationsofthe form andforcasesinwhichp,q ��+��=�� ����=�� andxareallnonnegativerationalnumbers.

6.EE.C.9: Usevariablestorepresenttwoquantities inareal-worldproblemthatchangeinrelationship tooneanother;writeanequationtoexpressone quantity,thoughtofasthedependentvariable,in termsoftheotherquantity,thoughtofasthe independentvariable.Analyzetherelationship betweenthedependentandindependentvariables usinggraphsandtables,andrelatethesetothe equation.

6.G.A.1: Findtheareaofrighttriangles,other triangles,specialquadrilaterals,andpolygonsby composingintorectanglesordecomposinginto trianglesandothershapes;applythesetechniques

inthecontextofsolvingreal-worldand mathematicalproblems.

6.G.A.2: Findthevolumeofarightrectangular prismwithfractionaledgelengthsbypackingit withunitcubesoftheappropriateunitfraction edgelengths,andshowthatthevolumeisthesame aswouldbefoundbymultiplyingtheedgelengthof theprism.Applytheformulasand ��=����ℎ ��=��ℎ to findvolumesofrightrectangularprismswith fractionaledgelengthsinthecontextofsolving real-worldandmathematicalproblems.

Understandings

● Inanequation,avariablerepresentsone number,andanygivensolutionmaybe checkedforprecision.

● Equationsmaybeusedasmodelstosolve real-worldproblems.

Knowledge

● Howtowriteandsolveexpressionsand equationsinvolvingrationalnumbersand exponents.

● Howtorepresentrelationshipsintable, graph,andequationform.

EssentialQuestions

● Howcanwesolvemultistepequationsand checkthatsolutionsarecorrect?

● Howcanrepresentingthesamemathematical relationshipindifferentwaysallowusto modelreal-worldscenariosandsolve problems?

Skills(FramedasLearningTargets)

● Icansolveequationsthatincludewhole numbers,decimals,andfractions.

● Icanexplainwhatthesolutiontoanequation meansinasituation.

● Icanjustifywhethertwoexpressionsare equivalent.

● Icanuseanareamodeltowriteequivalent expressions.

● Icandecidewhethertwoexpressionsthat includeexponentsareequivalent.

● Icandeterminethevalueofanexpression thathasanexponentandaddition, subtraction,multiplication,ordivision.

● Icandeterminethevalueofanexpression thathasavariable,anexponent,andaddition, subtraction,multiplication,ordivisionfora specificvalueofthevariable.

● Icanuseatableoranequationtorepresenta relationship.

● Icanconnecttables,graphs,andequations thatrepresentthesamerelationship.

● Icanusetables,graphs,andequationsto analyzeanissueinsociety.

STAGE2:DETERMINEACCEPTABLEEVIDENCE

SummativeAssessment

Grade6Unit6EndofUnitAssessment

● Icansolveequationsthatincludewhole numbers,decimals,andfractions.

○ Problem3

● Icanexplainwhatthesolutiontoan equationmeansinasituation.

○ Problem1

● Icanjustifywhethertwoexpressionsare equivalent.

○ Problem2

● Icanuseanareamodeltowriteequivalent expressions.

○ Problem7

● Icandecidewhethertwoexpressionsthat includeexponentsareequivalent.

○ Problem4

● Icandeterminethevalueofanexpression thathasanexponentandaddition, subtraction,multiplication,ordivision.

○ Problem7

● Icandeterminethevalueofanexpression thathasavariable,anexponent,and addition,subtraction,multiplication,or divisionforaspecificvalueofthevariable.

○ Problem7

● Icanuseatableoranequationtorepresent arelationship.

○ Problem5,6

● Icanconnecttables,graphs,andequations thatrepresentthesamerelationship.

○ Problem5,6

● Icanusetables,graphs,andequationsto analyzeanissueinsociety.

○ Problem6

PerformanceTask: SubwayFares Studentsare giveninformationaboutsubwaytransportation. Theyrepresenttheinformationingraphs,tables andequationsandusethemtomakedecisions aboutthebestchoicesoftickettopurchase.

● Icanusetables,graphs,andequationsto analyzeanissueinsociety.

FormativeAssessment

Grade6Unit6MidUnitAssessment

Ongoingassessments:IMsynthesisandcooldowns asappropriate

Frayermodel(blanktemplateandrationale)

● SolvingEquations

● Equivalentexpressions

● Exponents

Understanding 2 LearningTargets 13

TransferSkills: CommunicationandCritical Thinking

STAGE3:LEARNINGPLAN

Previousmathconnections

Thefollowingconceptsfrompreviousgradesor earlierinGrade6maysupportstudentsinmeeting grade-levelstandardsinthisunit:

● Adding,subtracting,multiplying,and dividingdecimalsandfractions.(6.NS.A.1, 6.NS.B.3)

● Usingwholenumberexponentsto representpowersof10.(5.NBT.A.2)

● Evaluatingexpressionswithaddition, subtraction,multiplication,division,and parenthesesorbrackets.(5.OA.A.1)

● Graphingpointsinthe firstquadrantofthe coordinateplane.(5.G.A.2)

FirstTopic:SolvingEquations

LearningTargets:

● Icansolveequationsthatincludewhole numbers,decimals,andfractions.

● Icanexplainwhatthesolutiontoan equationmeansinasituation.

LearningActivities:

Diagnosticassessmentquestions/problemsbasedon priorgradelevelexperience

FromReadinessCheck:

Studentswill firstsolvethetwoproblemsandbe preparedtosharetheirthinkingwithothers. Studentsthensharewithotherstosolidifythe conceptsofusingtapediagramstorepresent relationshipsbetweenwholenumbersand determiningunknownnumbersinadditionand multiplicationequations.

Estimated#ofLessons:5

EssentialQuestions:

Howcanwesolvemultistepequationsandcheckthat solutionsarecorrect?

● Studentsusereasoning,equations,andtapediagramstodetermineunknownweightsonasee-saw.

● Thislessonintroducessituationsdescribedinwords.Studentsconnecttapediagrams,equations, andsituations,andusethemastoolstoanswerquestionsincontext.

● Studentsusehangerstorepresentequationsandthendetermineunknownvaluesthatbalanceeach hanger.

● Studentsdevelop fluencywithsolvingequations,particularlywithequationsthatincludedecimals andfractions.

● Studentsconnectequationstosituationsbywritingtheirownsituationstomatchequationsand

thentradesituationswithclassmates.

SecondTopic:EquivalentExpressions

LearningTargets:

● Icanjustifywhethertwoexpressionsare equivalent.

● Icanuseanareamodeltowriteequivalent expressions.

LearningActivities:

Estimated#ofLessons:6

EssentialQuestions: Howcanwesolvemultistepequationsandcheckthat solutionsarecorrect?

● Studentsuseexpressionswithvariablestorepresentsituations(inthiscase,thecostofsome numberofpoundsoffruit).

● Studentsexploretheconceptof equivalentexpressions (twodifferentexpressionsthatdescribethe samething)inthecontextofthenumberoftilesthatborderasquare.

● Studentsusevariableexpressionstorepresentareasofrectanglesintwodifferentways:asthesum oftwoareasandastheproductofthetwosidelengths.

● Studentsstrengthentheworktheydidinthepreviouslessonaswellasextendtheirthinkingto expressionsthatinvolvesubtractionorexpressionsinwhichthecommonfactorisavariable.

ThirdTopic:Exponents

LearningTargets:

● Icandecidewhethertwoexpressionsthat includeexponentsareequivalent.

● Icandeterminethevalueofanexpression thathasanexponentandaddition, subtraction,multiplication,ordivision.

● Icandeterminethevalueofanexpression thathasavariable,anexponent,and addition,subtraction,multiplication,or divisionforaspecificvalueofthevariable.

LearningActivities:

Estimated#ofLessons:3

EssentialQuestions: Howcanwesolvemultistepequationsandcheckthat solutionsarecorrect?

● Studentsmakesenseofexponents,bothwhenthebaseisawholenumberandwhenitisafraction.

● Studentsuseareastomakesenseofmorecomplexexpressionswithexponents,particularly evaluatingexpressionsthatincludeanexponentandoneotheroperation.

● Studentsextendwhattheyhavelearnedaboutnumericalexpressionswithexponentstoevaluate variableexpressionsthatinvolveexponentsandotheroperations.

FourthTopic:Relationships

LearningTargets:

● Icanuseatableoranequationtorepresent

Estimated#ofLessons:7

EssentialQuestions:

● Howcanrepresentingthesamemathematical

arelationship.

● Icanconnecttables,graphs,andequations thatrepresentthesamerelationship.

● Icanusetables,graphs,andequationsto analyzeanissueinsociety.

LearningActivities:

relationshipindifferentwaysallowusto modelreal-worldscenariosandsolve problems?

● Studentsextendtheirworkwithvariableexpressionsinearlierlessonstoexplorerelationships betweentwovariables.Studentsusebothtablesandequationstorepresentrelationshipsandlearn theterms independentvariable and dependentvariable todescribeeachpartofarelationship.

● Studentsareintroducedtographsasawayofrepresentingrelationshipsbetweentwovariables.

● Studentsfocusonmakingconnectionsbetweendifferentrepresentationsofthesamerelationship.

● Studentsusetables,graphs,andequationstohelpcustomersmakedecisionsaboutwhattypeof transportationtickettobuy.

CourseName:Grade6Unit7Title:PositiveandNegativeNumbers

UnitOverview:

Inthisunit,studentsexplorepositiveandnegativenumbersinseveralcontexts:onanumberline, representedasinequalities,andinthecoordinateplane.Studentsdescribelocationsonthenumberline andsituationsincontextusingpositiveandnegativenumbers.Theyalsocompareandorderpositiveand negativenumbersandtheirabsolutevalues.Studentsrepresentinequalities,suchas , usingsymbols, ��>3 words,andgraphs,andidentifysomeoftheirsolutions.Studentssolvereal-worldandmathematical problemsbygraphingpoints,anddrawpolygonsgivencoordinatesforthevertices.

STAGE1:DESIREDRESULTS

EstablishedGoals

CSDEContentStandards:

6.NS.C.5: Understandthatpositiveandnegative numbersareusedtogethertodescribequantities havingoppositedirectionsorvalues;usepositive andnegativenumberstorepresentquantitiesin real-worldcontexts,explainingthemeaningof0in eachsituation.

6.NS.C.6: Understandarationalnumberasapoint onthenumberline.Extendnumberlinediagrams andcoordinateaxestorepresentpointsontheline andintheplanewithnegativenumbercoordinates.

6.NS.C.6.A: Recognizeoppositesignsofnumbersas indicatinglocationsonoppositesidesof0onthe numberline;recognizethattheoppositeofthe oppositeofanumberisthenumberitself,andthat 0isitsownopposite.

TransferGoals

CSDEMathPractices(MP)in Blue toverifysignificance

● COMMUNICATION:Createalogicaland evidence-basedargumenttosupportideas. MP #3Constructviableargumentsandcritiquethe reasoningofothers;MP#6:Attendtoprecision

● CRITICALTHINKING:Demonstrate flexibility anddeterminationwhensolvingproblems. MP#2 Reasonabstractlyandquantitatively.

6.NS.C.6.B: Understandsignsofnumbersin orderedpairsasindicatinglocationsinquadrants ofthecoordinateplane;recognizethatwhentwo orderedpairsdifferonlybysigns,thelocationsof thepointsarerelatedbyreflectionsacrossoneor bothaxes.

6.NS.C.6.C: Findandpositionintegersandother rationalnumbersonahorizontalorvertical numberlinediagram; findandpositionpairsof integersandotherrationalnumbersona coordinateplane.

6.NS.C.7: Understandorderingandabsolutevalue ofrationalnumbers.

6.NS.C.7.A: Interpretstatementsofinequalityas statementsabouttherelativepositionoftwo numbersonanumberlinediagram.

6.NS.C.7.B: Write,interpret,andexplain statementsoforderforrationalnumbersin real-worldcontexts.

6.NS.C.7.C: Understandtheabsolutevalueofa rationalnumberasitsdistancefrom0onthe numberline;interpretabsolutevalueasmagnitude forapositiveornegativequantityinareal-world situation.

6.NS.C.7.D: Distinguishcomparisonsofabsolute valuefromstatementsaboutorder.

6.NS.C.8: Solvereal-worldandmathematical problemsbygraphingpointsinallfourquadrantsof thecoordinateplane.Includeuseofcoordinates andabsolutevalueto finddistancesbetween pointswiththesame firstcoordinateorthesame secondcoordinate.

6.EE.B.5: Understandsolvinganequationor inequalityasaprocessofansweringaquestion: whichvaluesfromaspecifiedset,ifany,makethe equationorinequalitytrue?Usesubstitutionto determinewhetheragivennumberinaspecified setmakesanequationorinequalitytrue.

6.EE.B.6: Usevariablestorepresentnumbersand writeexpressionswhensolvingareal-worldor mathematicalproblem;understandthatavariable canrepresentanunknownnumber,or,depending onthepurposeathand,anynumberinaspecified set.

6.EE.B.8: Writeaninequalityoftheformor ��>�� torepresentaconstraintorconditionina ��<�� real-worldormathematicalproblem.Recognize thatinequalitiesoftheformorhave ��>�� ��<��

infinitelymanysolutions;representsolutionsof suchinequalitiesonnumberlinediagrams.

6.G.A.3: Drawpolygonsinthecoordinateplane givencoordinatesforthevertices;usecoordinates to findthelengthofasidejoiningpointswiththe same firstcoordinateorthesamesecond coordinate.Applythesetechniquesinthecontext ofsolvingreal-worldandmathematicalproblems.

Understandings

● Signednumberscanbeusedinreal-world situations.

● Equationsandinequalitiesusesymbolsto representquantitiesandtheirrelationships.

Knowledge

● Howtocompareandordersignednumbers.

● Howtoreadandinterpretorderedpairson thecoordinateplane.

EssentialQuestions

Whatdosignednumbers(positiveandnegative) meaninrealworldcontexts?

Skills(FramedasLearningTargets)

● Icanidentifyandplotpositiveandnegative numbersonthenumberline.

● Icancomparepositiveandnegativenumbers usingwordsandsymbols.

● Icanuseanumberlinetoorderpositiveand negativenumbers.

● Iunderstandwhattheabsolutevalueisand howtowriteitinsymbols.

● Icanshowthesameinformationaboutan inequalityusingwords,symbols,andanumber line.

● Icanwriteandinterpretinequalitiesto describeunbalancedhangers.

● Icandrawandlabelanumberlinediagram thatrepresentsthesolutiontoaninequality.

● Icanexplainhowmanysolutionsaninequality canhave.

● Icanjustifywhetherornotavalueisa solutiontoagiveninequality.

● Icanexplainwhatthecoordinateplanelooks likewithpositiveandnegativenumbers.

● Icanwritecoordinatesforpointsinthe coordinateplane.

● Icanplotpointsincoordinateplanes.

● Icandrawapolygoninthecoordinateplane.

● Icandeterminehorizontalandverticalside lengthsofapolygoninthecoordinateplane.

● Icanuseagraphtotellastoryabouta solution. ●

SummativeAssessment

Grade6Unit7EndofUnitAssessment

● Icanidentifyandplotpositiveandnegative numbersonthenumberline.

○ Problem1

● Icandrawandlabelanumberlinediagram thatrepresentsthesolutiontoan inequality.

● Icanjustifywhetherornotavalueisa solutiontoagiveninequality.

● Icanexplainhowmanysolutionsan inequalitycanhave.

○ Problem2

● Icancomparepositiveandnegative numbersusingwordsandsymbols.

● Icanuseanumberlinetoorderpositive andnegativenumbers.

○ Problem3

● Iunderstandwhattheabsolutevalueisand howtowriteitinsymbols.

○ Problem4

● Icanshowthesameinformationaboutan inequalityusingwords,symbols,anda numberline.

● Icanwriteandinterpretinequalitiesto describeunbalancedhangers.

○ Problem5

● Icanplotpointsincoordinateplanes.

● Icandrawapolygoninthecoordinate plane.

● Icandeterminehorizontalandverticalside lengthsofapolygoninthecoordinate plane.

○ Problem6

● Icanexplainwhatthecoordinateplane lookslikewithpositiveandnegative numbers.

● Icanwritecoordinatesforpointsinthe coordinateplane.

● Icanuseagraphtotellastoryabouta solution.

○ Problem7

FormativeAssessment

Grade6Unit7MidUnitAssessment

Ongoingassessments:IMsynthesisandcooldowns asappropriate

Frayermodel(blanktemplateandrationale)

● NegativenumbersandAbsoluteValue

● Inequalities

● TheCoordinateplane

PerformanceTask: GraphTelephone:Studentsplot andinterpretcoordinatestomakesenseof situationsincontext.Theythencreategraphsthat representsituationsandtellstoriesbasedonthe graphs.

● Icanuseagraphtotellastoryabouta solution.

Understanding 2 LearningTargets 15

TransferSkills: CommunicationandCritical Thinking

STAGE3:LEARNINGPLAN

Previousmathconnections

Thefollowingconceptsfrompreviousgradesmay supportstudentsinmeetinggrade-levelstandards inthisunit:

● Representingfractionsanddecimalsonthe numberlineandcomparingfractionsand decimals.(3.NF.A.2.b, 4.NF.A.2, 4.NF.C.6)

● Identifyingandplottingpointswithpositive coordinatesonthecoordinateplane. (5.G.A.1, 5.G.A.2)

Diagnosticassessmentquestions/problemsbasedon priorgradelevelexperience

FromReadinessCheck:

Studentswill firstsolvethetwoproblemsandbe preparedtosharetheirthinkingwithothers. Studentsthensharewithotherstosolidifythe conceptsofmeasuringdistancesinopposite directionsandestimatingthelocationsoffractions anddecimalsonanumberline.

FirstTopic:NegativeNumbers

Estimated#ofLessons:7

LearningTargets: EssentialQuestions:

● Icanidentifyandplotpositiveandnegative numbersonthenumberline.

● Icancomparepositiveandnegative numbersusingwordsandsymbols.

● Icanuseanumberlinetoorderpositive andnegativenumbers.

● Iunderstandwhattheabsolutevalueisand howtowriteitinsymbols.

LearningActivities:

Whatdosignednumbers(positiveandnegative) meaninrealworldcontexts?

● Studentsareintroducedtonumberslessthan`0`onthenumberline.

● Studentsdescribeandusestrategiesforidentifyingandplottingnegativerationalnumbersonthe numberline.Thislessonalsointroduceswhatitmeansfortwonumberstobeoppositeswhenthey arethesamedistancefromzeroonanumberline.

● Studentspracticecomparingpositiveandnegativenumbersinasocialway.

● Studentsapplywhattheyhavelearnedaboutpositiveandnegativenumbersinthecontextsof elevationsandtemperaturesaroundtheworld.

● Thislessonintroducestheconceptofabsolutevalue.Itisalsoanopportunityforstudentsto practicewhatthey'velearnedsofarinthisunitbysolvingaseriesofpuzzles.

SecondTopic:Inequalities

LearningTargets:

● Icanshowthesameinformationaboutan inequalityusingwords,symbols,anda numberline.

● Icanwriteandinterpretinequalitiesto describeunbalancedhangers.

● Icandrawandlabelanumberlinediagram thatrepresentsthesolutiontoan inequality.

● Icanexplainhowmanysolutionsan inequalitycanhave.

● Icanjustifywhetherornotavalueisa solutiontoagiveninequality.

●

LearningActivities:

Estimated#ofLessons:3

EssentialQuestions: Whatdosignednumbers(positiveandnegative) meaninrealworldcontexts?

● Thepurposeofthislessonistointroduceinequalitieswithvariablesandconnectverbal descriptions,symbols,andnumberlinerepresentationsofinequalities.

● Studentsdevelopadeeperunderstandingofusinginequalitysymbolstodescribeunknownvalues. Studentsusethehangerrepresentationtointerpretandwriteinequalitiesthatinvolveonevariable andmorethanonevariable.

● Studentsconsolidateandapplywhattheyhavelearnedaboutinequalitiesonthenumberlineand

learntheterm solutiontoaninequality.

ThirdTopic:TheCoordinatePlane

LearningTargets:Icanexplainwhatthecoordinate planelookslikewithpositiveandnegative numbers.

● Icanexplainwhatthecoordinateplane lookslikewithpositiveandnegative numbers.

● Icanwritecoordinatesforpointsinthe coordinateplane.

● Icanplotpointsincoordinateplanes.

● Icandrawapolygoninthecoordinate plane.

● Icandeterminehorizontalandverticalside lengthsofapolygoninthecoordinate plane.

● Icanuseagraphtotellastoryabouta solution.

LearningActivities:

Estimated#ofLessons:7

EssentialQuestions: Whatdosignednumbers(positiveandnegative) meaninrealworldcontexts?

● Studentsdevelopanunderstandingofnegativenumbersinthecoordinateplane.

● StudentspracticewhattheylearnedaboutcoordinatesinLesson9inthecontextofsolvingmazes. Thislessonalsointroducesgridsthatusedifferentscalesfortheaxesandpatternsincoordinates thatdifferonlybythesign.

● Studentsapplywhatthey'velearnedaboutcoordinateswithpositiveandnegativenumbersto createpolygonsanddeterminedistancesinthecoordinateplane.

● Studentsplotandinterpretcoordinatesinordertomakesenseofsituationsincontext.

CourseName:Grade6

UnitOverview: Inthisunit,studentswillbeintroducedtostatisticsbyvisualizingdata,usingdotplots,histograms,andbox plots,aswellascalculatingmeasuresofcenterandspread.

CSDEContentStandards:

6.SP.A.1: Recognizeastatisticalquestionasone thatanticipatesvariabilityinthedatarelatedtothe questionandaccountsforitintheanswers.

6.SP.A.2: Understandthatasetofdatacollectedto answerastatisticalquestionhasadistribution whichcanbedescribedbyitscenter,spread,and overallshape.

6.SP.A.3: Recognizethatameasureofcenterfora numericaldatasetsummarizesallofitsvalueswith asinglenumber,whileameasureofvariation describeshowitsvaluesvarywithasinglenumber.

6.SP.B.4: Displaynumericaldatainplotsona numberline,includingdotplots,histograms,and boxplots.

6.SP.B.5: Summarizenumericaldatasetsinrelation totheircontext.

6.SP.B.5.A: Reportthenumberofobservations.

6.SP.B.5.B: Describethenatureoftheattribute underinvestigation,includinghowitwasmeasured anditsunitsofmeasurement.

6.SP.B.5.C: Givingquantitativemeasuresofcenter (medianand/ormean)andvariability(interquartile rangeand/ormeanabsolutedeviation),aswellas describinganyoverallpatternandanystriking deviationsfromtheoverallpatternwithreference tothecontextinwhichthedataweregathered.

6.SP.B.5.D: Relatingthechoiceofmeasuresof centerandvariabilitytotheshapeofthedata distributionandthecontextinwhichthedatawere gathered.

● CRITICALTHINKING:Demonstrate flexibility anddeterminationwhensolvingproblems. MP#2 Reasonabstractlyandquantitatively.

● COMMUNICATION: Createalogicaland evidence-basedargumenttosupportideas. MP #3Constructviableargumentsandcritiquethe reasoningofothers.

● CRITICALTHINKING: Analyzedatainorderto drawconclusions. MP#6:Attendtoprecision

Understandings EssentialQuestions

● Graphicalrepresentationsandstatistics allowustoidentifyandrepresentkey featuresofdata.

● Identifyandappropriatelyutilizemeasures ofcentraltendencies.

Howcanstatisticsbecollected,displayed,and analyzed?

Knowledge

● Howtorepresenttwovariabledatain multipleways(graphically,frequency tables,lists)

● Howtocalculatemeasuresofcentral tendencies.

Skills(FramedasLearningTargets)

● Icandescribeandinterpretadotplottohelp answerastatisticalquestion.

● Icancreateadotplottovisualizedata.

● Icanusedotplotstocompareandcontrast datasets.

● Icandescribeandinterpretahistogramthat representsadataset.

● Icancalculatethemeanofadataset.

● Icancalculatethemeanabsolutedeviation (MAD)ofadataset.

● Icandetermineandinterpretthemedianofa dataset.

● Icandetermineandinterpretthequartilesof adataset.

● Icandeterminetherangeandinterquartile range(IQR)ofadataset.

● Icanuseboxplotstocompareandcontrast datasets.

● Icancreateadotplot,histogram,orboxplot tovisualizeadataset.

● Icanchooseandcalculateeitherthemeanand MADormedianandIQRforadataset.

● IcanusemeanandMADormedianandIQR tocomparereal-worlddatasets.

STAGE2:DETERMINEACCEPTABLEEVIDENCE

SummativeAssessment

Grade6Unit8EndofUnitAssessment

● Icandescribeandinterpretadotplotto helpanswerastatisticalquestion.

● Icandetermineandinterpretthemedianof adataset.

○ Problem1

● Icandescribeandinterpretahistogram thatrepresentsadataset.

○ Problem2

● Icancalculatethemeanofadataset.

○ Problem3

● Icancreateadotplottovisualizedata.

● Icanusedotplotstocompareandcontrast datasets.

● Icandetermineandinterpretthequartiles ofadataset.

○ Problem4

Grade6Unit8MidUnitAssessment

Ongoingassessments:IMsynthesisandcooldowns asappropriate

Frayermodel(blanktemplateandrationale)

● VisualizingData

● MeasuringData:MeanandMAD

● MeasuringData:MedianandIQR

● Icandeterminetherangeandinterquartile range(IQR)ofadataset.

○ Problems4&5

● Icancalculatethemeanabsolutedeviation ofadataset.

○ Problem5

● Icanuseboxplotstocompareandcontrast datasets.

○ Problem6

● Icancreateadotplot,histogram,orbox plottovisualizeadataset.

○ Problem7

PerformanceTask: Hollywood(Part3) Studentsuse whattheyhavelearnedaboutmeasuresofcenter andspreadtocomparethepercentageofwords spokenbywomenandmenintop-grossingmovies. Inparticular,studentsconsiderwhetherornotthe differencesaregettinglargerorsmallerovertime. Studentswillcreateavisualrepresentation includingagraph,ameasureofcenterandtheir analysisoftheinformationthattheychoose.

● Icancreateadotplot,histogram,orbox plottovisualizeadataset.

● Icanchooseandcalculateeitherthemean andMADormedianandIQRforadataset.

● IcanusemeanandMADormedianandIQR tocomparereal-worlddatasets.

Understanding 2 LearningTargets 11,12,13

TransferSkills: CommunicationandCritical Thinking

STAGE3:LEARNINGPLAN

Previousmathconnections

Thefollowingconceptsfrompreviousgradesor earlierinGrade6maysupportstudentsinmeeting grade-levelstandardsinthisunit:

● Positioningfractionsanddecimalsona numberline.(3.NF.A.2, 4.MD.B.4)

● Visualizingdatausinglineplots(another namefordotplots).(5.MD.B.2)

● Calculatingdistancesonanumberline. (4.MD.A.2)

Diagnosticassessmentquestions/problemsbasedon priorgradelevelexperience

FromReadinessCheck:

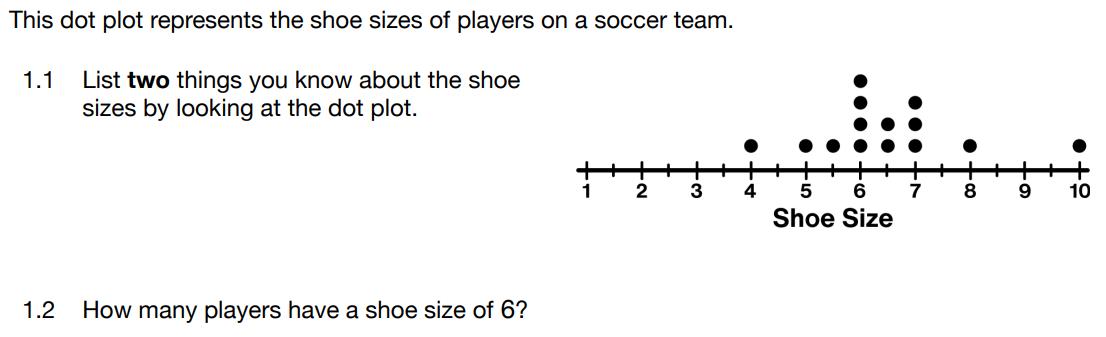
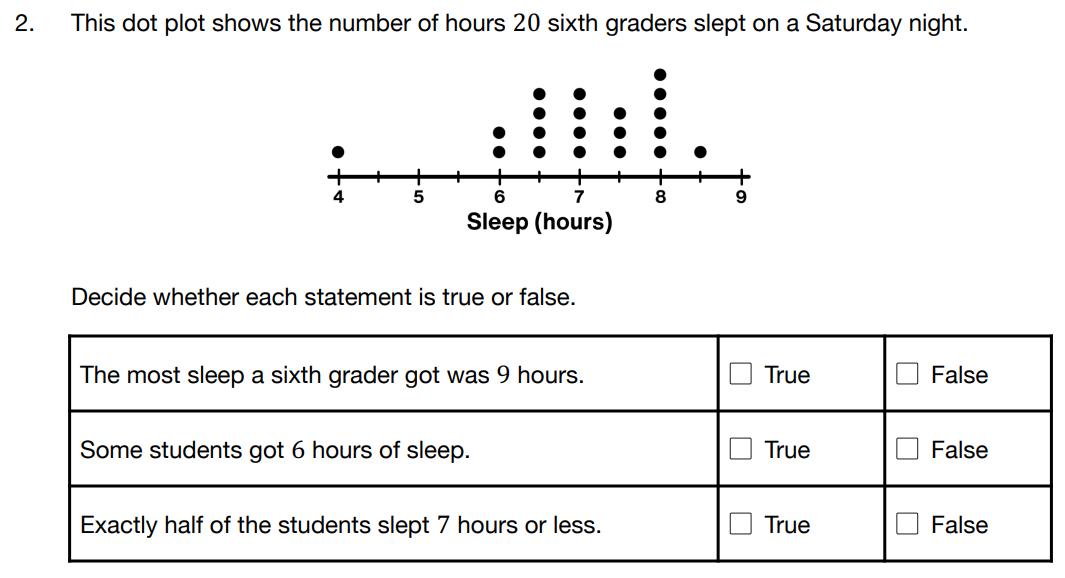
Studentswill firstsolvethetwoproblemsandbe preparedtosharetheirthinkingwithothers. Studentsthensharewithotherstosolidifytheir abilitytomakesenseofinformationpresentedina dotplot(calledalineplotinGrades4–5).

FirstTopic:VisualizingData Estimated#ofLessons:6

LearningTargets:

● Icandescribeandinterpretadotplotto helpanswerastatisticalquestion.

● Icancreateadotplottovisualizedata.

● Icanusedotplotstocompareandcontrast datasets.

● Icandescribeandinterpretahistogram thatrepresentsadataset.

LearningActivities:

EssentialQuestions: Howcanstatisticsbecollected,displayed,and analyzed?

● Studentsmakeconnectionsbetweenquestions,claims,anddataastheybegintheunit.

● Studentsmakesenseofdotplotsandlearntheterm statisticalquestion.

● Studentsfocusoncreatingdotplotstovisualizedatasets.

● Studentslearnabout center and spread aswaystodescribeadatasetandusethosetermsto comparedataaboutminimumhourlywages.

● Studentslearnanotherwaytovisualizedata:inahistogram.

● Studentspracticecreatinghistogramsbyhandandusehistogramstocomparedatasets.

SecondTopic:MeasuringData:MeanandMAD Estimated#ofLessons:7

LearningTargets:

● Icancalculatethemeanofadataset.

● Icancalculatethemeanabsolutedeviation ofadataset.

LearningActivities:

EssentialQuestions: Howcanstatisticsbecollected,displayed,and analyzed?

● Studentslearnabout mean asanequalshareandasanumberthatcanbeusedtodescribethe centerofadataset.

● Studentslearnapropertyofthemean:thesumsofthedistancesfromeachpointtothemean (absolutedeviations)areequalontheleftandontheright.

● Studentslearnwhatmeanabsolutedeviation(MAD)isandhowtocalculatetheMADofadataset.

● Studentsusewhattheyhavelearnedaboutmeanandmeanabsolutedeviation(MAD)tocompare thesalariesofthe fivetop-earningactorsofdifferentgendersindifferentyears.

ThirdTopic:MeasuringData:MedianandIQR Estimated#ofLessons:9

LearningTargets:

● Icandetermineandinterpretthemedianof adataset.

● Icandetermineandinterpretthequartiles ofadataset.

● Icandeterminetherangeandinterquartile range(IQR)ofadataset.

● Icanuseboxplotstocompareandcontrast datasets.

● Icancreateadotplot,histogram,orbox plottovisualizeadataset.

LearningActivities:

EssentialQuestions: Howcanstatisticsbecollected,displayed,and analyzed?

● Studentslearnhowtodetermineanewmeasureofcenter:themedian.

● Studentsconsiderhowtheshapeofadatasetaffectsthemeanandmedian,andthendecidewhich measureofcentermoreaccuratelydescribesthedata.

● Studentslearnwhat quartiles areandwhytheymaybeusefulwhendescribingdata.

● Studentsareintroducedtoanewwaytovisualizedata(asaboxplot)andtwonewwaystomeasure spread(rangeandIQR).Studentsalsomakeconnectionsbetweendatasets,boxplots,interquartile range,andrange.

● Studentsinterpretandcompareboxplotsinordertomakeandevaluateclaimsaboutoriginal animatedmoviesandsequels.

● Studentsusewhattheyhavelearnedaboutmeasuresofcenterandspreadtocomparethe percentageofwordsspokenbywomenandmenintop-grossingmovies.

CourseName:Grade7Unit1Title:ScaleDrawings

UnitOverview:

Est.#ofLessons:18

Inthisunit,studentsexaminethescalefactor(theamountitisenlargedorreduced)ofpicturesandplane figures,thenapplywhattheyhavelearnedtoverify/createscaledrawings,e.g.,mapsand floorplans.

STAGE1:DESIREDRESULTS

EstablishedGoals

ContentMathStateStandards:

7.G.A.1: Solveproblemsinvolvingscaledrawings ofgeometric figures,includingcomputingactual lengthsandareasfromascaledrawingand reproducingascaledrawingatadifferentscale.

7.G.B.6: Solvereal-worldandmathematical problemsinvolvingarea,volume,andsurfacearea oftwo-andthreedimensionalobjectscomposedof triangles,quadrilaterals,polygons,cubes,andright prisms.

Understandings

Scalefactorsmaintainproportionalitywhen creatingdesignsforobjectswhicharetobe manufactured.

Knowledge

● Objectsarescalecopiesofeachotherwhen alldimensionsusethesamescalefactor.

● Scaleisusedtorepresentthecommonratio betweentwodrawings.

● CRITICALTHINKING: Demonstrate flexibility anddeterminationwhensolvingproblems. MP#2Reasonabstractlyandquantitatively; MP#4Modelwithmathematics.

● COMMUNICATION: Createalogicaland evidence-basedargumenttosupportideas. MP#3Constructviableargumentsandcritique thereasoningofothers;MP#6Attendto precision.

EssentialQuestions

Howisscalefactorusedinrealworldscenarios?

Skills(FramedasLearningTargets)

● Icantellwhetherornota figureisascaledcopy ofanother figureanddescribesomeofthe characteristics

● Icandrawascaledcopyofa figureusingagiven scalefactor.

● Icandescribehowscalefactorimpactsthearea ofascaledcopyandcalculatetheareaofa scaledcopy.

● Icanexplainandinterpretthescaleofa drawing.

● Icanuseascaledrawingandascaletocalculate actualandscaleddistances.

● Icancreateascaledrawinggivenascale.

● Icancalculateadistanceononescaledrawing

basedonanotherdrawingwithadifferent scale.

● Icanchooseanappropriatescaletomakea scaledrawing.

STAGE2:DETERMINEACCEPTABLEEVIDENCE

SummativeAssessment

Grade7Unit1EndUnitAssessment:

● Icantellwhetherornota figureisascaled copyofanother figureanddescribesomeof thecharacteristics

○ Problem1

● Icandescribehowscalefactorimpactsthe areaofascaledcopyandcalculatethearea ofascaledcopy.

○ Problems2,3

● Icandrawascaledcopyofa figureusinga givenscalefactor.

○ Problem4

● Icanuseascaledrawingandascaleto calculateactualandscaleddistances.

○ Problem5

● Icancalculateadistanceononescale drawingbasedonanotherdrawingwitha differentscale.

○ Problem6

PerformanceTask

RoomRedesign:Studentspracticechoosingan appropriatescaleforascaledrawingandcreatinga drawingusingthatscale.

Understanding#1 LearningTargets

● Icanexplainandinterpretthescaleofa drawing.

● Icanchooseanappropriatescaletomakea scaledrawing.

● Icanuseascaledrawingandascaleto calculateactualandscaleddistances.

FormativeAssessment

Grade7Unit1MidUnitAssessment

Ongoingassessments:IMsynthesisandcooldowns asappropriate

Frayermodel(blanktemplateandrationale)

● ScaledCopies

● ScaleDrawings

● Icancreateascaledrawinggivenascale TransferSkills:CriticalThinkingand Communication

STAGE3:LEARNINGPLAN

Previousmathconnections

Thefollowingconceptsfrompreviousgradesmay supportstudentsinmeetinggrade-levelstandards inthisunit:

● Measuringandestimatinglengthsand anglesingeometric figures.(4.MD.C.5)

● Relativesizesofmeasurementunitswithin onesystemofunits,suchasinchesandfeet, orgramsandkilograms.(4.MD.A.1)

● Multiplicationanddivisionoffractions. (6.NS.A.1)

● Findingtheareaofpolygonsby decomposingintorectanglesandtriangles. (6.G.A.1)

FirstTopic:ScaledCopies

LearningTargets:

● Icantellwhetherornota figureisascaled copyofanother figureanddescribesomeof thecharacteristics

● Icandrawascaledcopyofa figureusinga givenscalefactor.

● Icandescribehowscalefactorimpactsthe areaofascaledcopyandcalculatethearea ofascaledcopy.

LearningActivities:

Diagnosticassessmentquestions/problemsbasedon priorgradelevelexperience

FromReadinessCheck:

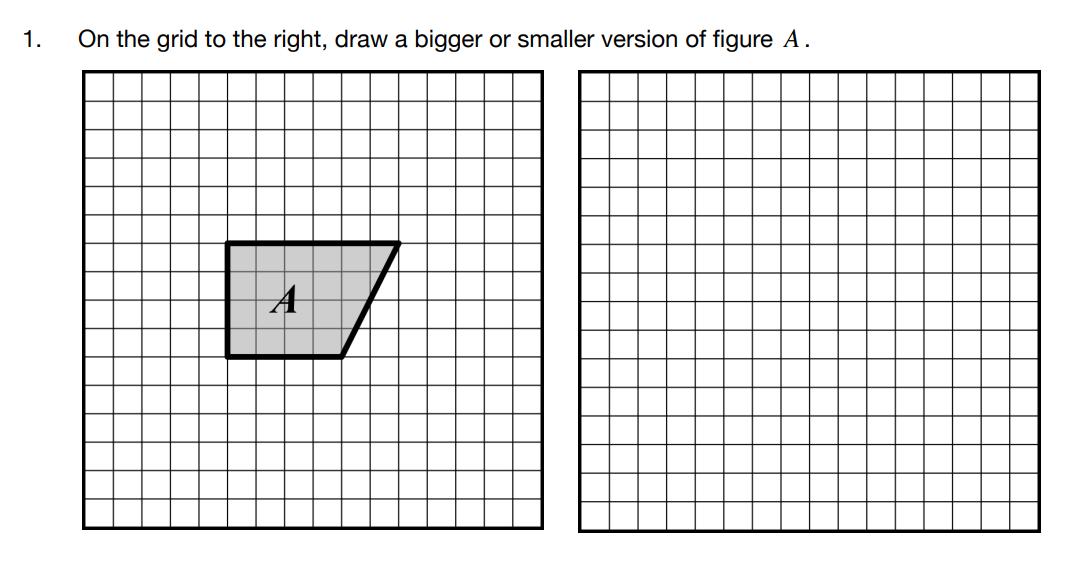
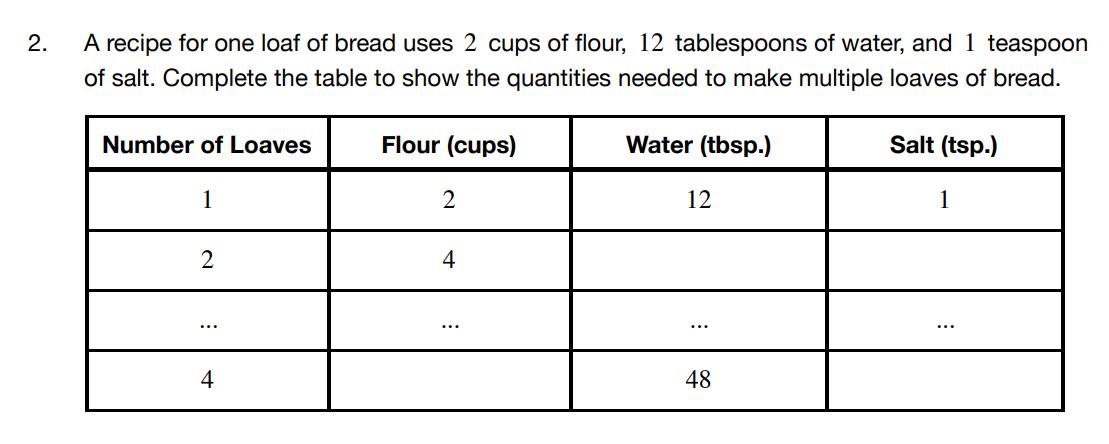
Studentswill firstsolvethetwoproblemsandbe preparedtosharetheirthinkingwithothers. Studentsthensharewithotherstosolidifythe conceptofscalingusingbothgridpaperandtables.

Estimated#ofLessons:9

EssentialQuestions

● Howisscalefactorusedinrealworld scenarios?

● Studentsdevelopanunderstandingofwhatscaledcopiesareanddescribecharacteristicsofscaled copiesusinginformallanguage.

● Studentsunderstandhowlengthsinanoriginal figureandinascaledcopyarerelatedandlearna newphrase:scalefactor.

● Studentsdrawscaledcopiesofshapesonandoffagridandstrengthentheirunderstandingthatthe samescalemustbeappliedtoalllengthsinascaledcopy.

● Studentsunderstandhowscalefactorsaffectthesizeofscaledcopies.

● Studentsusepatternsandstructuretomakesenseofhowscalefactorimpactstheareaofascaled copy.

SecondTopic:ScaleDrawings

LearningTargets:

● Icanexplainandinterpretthescaleofa drawing.

● Icanuseascaledrawingandascaleto calculateactualandscaleddistances.

● Icancreateascaledrawinggivenascale.

● Icancalculateadistanceononescale drawingbasedonanotherdrawingwitha differentscale.

● Icanchooseanappropriatescaletomakea scaledrawing.

LearningActivities:

Estimated#ofLessons:9

EssentialQuestions: Howisscalefactorusedinrealworldscenarios?

● Studentstransitionfromthinkingaboutscalingusingscalefactortothinkingaboutscalingusing scale.Studentsusescalestoreasonaboutscaledrawingsfortheremainderoftheunit.

● Studentsanalyzescaledrawings(scaledtwo-dimensionalrepresentationsofactualobjectsor places).

● Studentsusereal-worlddistancestocalculatescaleddistancesandcreatetheirownscaledrawings.

● Studentsreasonaboutmultiplescaledrawingsofthesameobjectusingdifferentscales.

● Studentschooseanappropriatescaleforascaledrawingandcreatingadrawingusingthatscale.

CourseName:Grade7Unit2Title:IntroducingProportionalRelationshipEst.#ofLessons:19

UnitOverview:

Inthisunit,studentsbuildontheirknowledgeofscalefactorandunitratestodeveloptheideaofa proportionalrelationship.Studentswillexaminearangeofrealworldscenariostosetupequationsand determinesolutions.

EstablishedGoals

ContentMathStateStandards:

7.RP.A.2: Recognizeandrepresentproportional relationshipsbetweenquantities.

7.RP.A.2.A: Decidewhethertwoquantitiesareina proportionalrelationship(e.g.,bytestingfor equivalentratiosinatableorbygraphingona coordinateplaneandobservingwhetherthegraphis astraightlinethroughtheorigin).

7.RP.A.2.B:Identifytheconstantofproportionality (unitrate)intables,graphs,equations,diagrams,and verbaldescriptionsofproportionalrelationships.

7.RP.A.2.C: Representproportionalrelationships withequations.

7.RP.A.2.D: Explainwhatpoint(x,y)onthegraphof aproportionalrelationshipmeansintermsofthe situation,withspecialattentiontothepoints(0,0) and(1, r)where r istheunitrate.

Understandings

Thecorrectratioinagivensituationisbasedonan understandingofproportionality.

TransferGoals

CSDEMathPractices(MP)in Blue toverifysignificance

● CRITICALTHINKING: Demonstrate flexibilityanddeterminationwhensolving problems. MP#2Reasonabstractlyand quantitatively;MP#4Modelwith mathematics.

● COMMUNICATION: Createalogicaland evidence-basedargumenttosupportideas. MP#3Constructviableargumentsand critiquethereasoningofothers;MP#6 Attendtoprecision.

EssentialQuestions

HowcanIuseproportionalityinanauthentic contexttodetermineaprecisesolution?

Knowledge Skills(FramedasLearningTargets)

● Howcanaproportionalrelationshipbe representedusingatable,equation,or graph?

● HowcanIcalculateandapplytheconstantof proportionality?

● Icanuseatabletocalculateunknown quantitiesinaproportionalrelationship.

● Icanexplainwhyarelationshipis proportionalornotbylookingatthe equation.

● Icanexplainwhataproportional relationshiplookslikewhenrepresented withagraph.

● Icaninterpretpointsonthegraphofa proportionalrelationshipandidentifythe constantofproportionality.

● Icanwriteanequationofaproportional relationshipfromapointonagraph.

● Icancomparerelatedproportional relationshipsbasedontheirgraphs.

● Icanmodelareal-worldsituationby

decidingwhatinformationisimportantand makingassumptions.

● Icanuseproportionalrelationshipsto answeraquestionaboutareal-world situation.

STAGE2:DETERMINEACCEPTABLEEVIDENCE

SummativeAssessment

Grade7Unit2EndUnitAssessment:

● Icanexplainwhataproportional relationshiplookslikewhenrepresented withagraph.

○ Problem1

● Icaninterpretpointsonthegraphofa proportionalrelationshipandidentifythe constantofproportionality.

○ Problem2

● Icanwriteanequationofaproportional relationshipfromapointonagraph.

○ Problem3

● Icancomparerelatedproportional relationshipsbasedontheirgraphs.

○ Problem4

● Icanuseatabletocalculateunknown quantitiesinaproportionalrelationship.

○ Problem5

● Icanexplainwhyarelationshipis proportionalornotbylookingatthe equation.

○ Problem6

● Icanwriteanequationofaproportional relationshipfromapointonagraph.

○ Problem7

PerformanceTask

WaterEfficiency:Studentsusetheirunderstanding ofproportionalrelationshipstoexplorewhether bathsorshowersusemorewater.

Understanding#1

LearningTargets:

● Icanmodelareal-worldsituationby decidingwhatinformationisimportantand makingassumptions.

● Icanuseproportionalrelationshipsto answeraquestionaboutareal-world

FormativeAssessment

Grade7Unit2MidUnitAssessment

Ongoingassessments:IMsynthesisandcooldowns asappropriate

Frayermodel(blanktemplateandrationale)

● Proportionalrelationshipsintables

● Proportionalrelationshipsinequations

● Proportionalrelationshipsinequations

● Usingproportionalrelationships

TransferSkills:CriticalThinkingand Communication

PreviousMathConnections

● Understandingandusingratioandrate languageinavarietyofcontexts.(6.RP.A.1, 6.RP.A.2)

● Findingequivalentratiosusingascalefactor. (6.RP.A.2,6.RP.A.3)

● Findingunitratesincontext.(6.RP.A.3.band 6.RP.A.2)

● Givenonevalueofaratio,usetheunitrate to findtheother.(6.RP.A.3.b)

● Representingequivalentratiosinatable. (6.RP.A.1,6.RP.A.3.a)

● Graphingpointsinthecoordinateplane. (6.RP.A.3.a)

Diagnosticassessmentquestions/problemsbased onpriorgradelevelexperience

From ReadinessCheck:

Studentswill firstsolvethetwoproblemsandbe preparedtosharetheirthinkingwithothers. Studentsthensharewithotherstosolidifythe conceptofUnitRateandProportionalRelationships.

FirstTopic:ProportionalRelationshipsinTables Estimated#ofLessons:4

LearningTargets:

● Icanuseatabletocalculateunknown quantitiesinaproportionalrelationship.

LearningActivities:

EssentialQuestions: HowcanIuseproportionalityinanauthentic contexttodetermineaprecisesolution?

● Studentssurfaceinitial,informalthinkingaboutthekeyideasinproportionalrelationships.

● Studentsareintroducedtotheconceptofaproportionalrelationshipbylookingattablesof equivalentratios

● Studentsdetermine,interpret,anduseconstantsofproportionalitytomakesenseofproportional relationships.

SecondTopic:ProportionalRelationshipsin Estimated#ofLessons:6

STAGE3:LEARNINGPLAN

Equations

LearningTargets:

● Icanexplainwhyarelationshipis proportionalornotbylookingatthe equation.

LearningActivities:

EssentialQuestions: HowcanIuseproportionalityinanauthentic contexttodetermineaprecisesolution?

● Studentsaresupportedinwritingequationsforproportionalrelationships.Thismaybeoneofthe firsttimesthatstudentsencounterequationswithtwovariables.

● Studentsdevelop fluencywritingandusingequationstomakesenseofproportionalrelationshipsin avarietyofcontexts.

● Students findthetwoconstantsofproportionalityforaproportionalrelationship,andexplainhow thoseconstantsarerelated.

● Studentsdevelopstrategiesfordecidingwhetherarelationshipisproportionalornotbasedonthe structureofitsequation.

ThirdTopic:ProportionalRelationshipsinGraphs Estimated#ofLessons:4

LearningTargets:

● Icanexplainwhataproportional relationshiplookslikewhenrepresented withagraph.

● Icaninterpretpointsonthegraphofa proportionalrelationshipandidentifythe constantofproportionality.

● Icanwriteanequationofaproportional relationshipfromapointonagraph.

● Icancomparerelatedproportional relationshipsbasedontheirgraphs.

LearningActivities:

EssentialQuestions: HowcanIuseproportionalityinanauthentic contexttodetermineaprecisesolution?

● Studentsexplorewhataproportionalrelationshiplookslikegraphically.

● Studentsdevelop fluencyworkingwithgraphsofaproportionalrelationshipandidentifythe constantofproportionalityusingagraph.

● Studentsusegraphsandequationstocompareproportionalrelationships.

FourthTopic:UsingProportionalRelationships Estimated#ofLessons:5

LearningTargets:

● Icanmodelareal-worldsituationby

EssentialQuestions: HowcanIuseproportionalityinanauthentic contexttodetermineaprecisesolution?

decidingwhatinformationisimportantand makingassumptions.

● Icanuseproportionalrelationshipsto answeraquestionaboutareal-world situation.

LearningActivities:

● Studentscreateandconnectdescriptions,tables,equations,andgraphsofproportional relationships.

● Studentsusetheirunderstandingofproportionalrelationshipstoexplorewhetherbathsorshowers usemorewater.

CourseName:Grade7Unit3Title:MeasuringCircles

UnitOverview:

Inthisunit,studentsexplorepropertiesofcirclesbyapplyingtheirknowledgeofproportionalrelationships. Studentswilluseradius,diameter,andpitodevelopformulasforareaandcircumference.Theyapplythese formulastosolverealworldproblems.

STAGE1:DESIREDRESULTS

EstablishedGoals

ContentMathStateStandards:

7.RP.A.2.A: Decidewhethertwoquantitiesareina proportionalrelationship(e.g.,bytestingfor equivalentratiosinatableorbygraphingona coordinateplaneandobservingwhetherthegraph isastraightlinethroughtheorigin).

7.G.B.4: Knowtheformulasfortheareaand circumferenceofacircle,andusethemtosolve problems.Giveaninformalderivationofthe relationshipbetweenthecircumferenceandarea ofacircle.

7.G.B.6: Solvereal-worldandmathematical problemsinvolvingarea,volume,andsurfacearea oftwo-andthree-dimensionalobjectscomposedof triangles,quadrilaterals,polygons,cubes,andright prisms.

Understandings

● Circumferenceandareaofacircleare

TransferGoals

CSDEMathPractices(MP)in Blue toverifysignificance

● CRITICALTHINKING: Identifyaproblem,ask keyquestions,andmakepredictions. MP#2 Reasonabstractlyandquantitatively;MP#4 Modelwithmathematics.

● COMMUNICATION:Createalogicaland evidence-basedargumenttosupportideas. MP#3Constructviableargumentsand critiquethereasoningofothers;MP#6 Attendtoprecision.

EssentialQuestions

● Whatmakesacircleacircle?

dependentontheradiusofthecircle.

Knowledge

● Howtocalculatecircumferenceandareaof acirclegivenadimensionofacircle,orvice versa.

● HowcanIusecircumferenceandareaofa circletosolvereal-worldproblems?

Skills(FramedasLearningTargets)

● Icandescribetherelationshipbetweenthe radius,diameter,andcircumferenceofacircle.

● Giventheradius,diameter,orcircumference ofacircle,Icancalculatetheothertwo measurements.

● Icancalculatetheperimeterofacomplex shapethatincludespartsofcircles.

● Icanwriteperimeterasanexpressionthat includesπ,suchas20π+50.

● Icancalculatetheareaofacircle.

● Icancalculatetheareaofacomplexshape thatincludespartsofcircles.

● Icanexpressthevalueofareaasan expressionthatincludesπ,suchas20π+50.

● Icancalculatetheareaofacirclegivenits circumference.

● Icanevaluateasituationanddetermineifit involvescircumferenceorareaofacircle.

STAGE2:DETERMINEACCEPTABLEEVIDENCE

SummativeAssessment

Grade7Unit3EndUnitAssessment

● Icancalculatetheareaofacircle.

○ Problem1

● Icandescribetherelationshipbetweenthe radius,diameter,andcircumferenceofa circle.

○ Problems2,3

● Giventheradius,diameter,or circumferenceofacircle,Icancalculatethe othertwomeasurements.

○ Problems2,3

● Icanevaluateasituationanddetermineifit involvescircumferenceorareaofacircle.

○ Problem4

● Icancalculatetheareaofacomplexshape thatincludespartsofcircles.

○ Problem5

● Icanexpressthevalueofareaasan expressionthatincludesπ,suchas20π+ 50.

FormativeAssessment

MidUnitAssessmentGrade7Unit3Quiz

Ongoingassessments:IMsynthesisandcooldowns asappropriate

Frayermodel(blanktemplateandrationale)

● Circumferenceofacircle

● Areaofacircle

○ Problem5

● Icancalculatetheperimeterofacomplex shapethatincludespartsofcircles.

○ Problem5

● Icanwriteperimeterasanexpressionthat includesπ,suchas20π+50.

○ Problem5

● Icancalculatetheareaofacirclegivenits circumference.

○ Problem6

PerformanceTask

● Stained-GlassWindows-Students determinethecircumferenceandareaof partsofcirclesinastainedglasswindowto determinetheamountandcostofmaterials needed.(OpenUpResourceslink)

Understanding#1 LearningTargets:

○ Icancalculatetheperimeterofa complexshapethatincludesparts ofcircles.

○ Icanwriteperimeterasan expressionthatincludesπ,suchas 20π+50.

○ Icancalculatetheareaofacomplex shapethatincludespartsofcircles.

○ Icanexpressthevalueofareaasan expressionthatincludesπ,suchas 20π+50.

TransferSkills:CriticalThinkingand Communication

PreviousMathConnections

● Writingandusingequationsofproportional relationships.(7.RP.A.2.C)

● Calculatingtheareaofrectanglesand triangles,includingtheareaofcomplex polygons.(6.G.A.1)

● Evaluatingexpressionsforspecificvaluesof theirvariables,(e.g.,evaluatingπ·4). (6.EE.A.2.C)

Diagnosticassessmentquestions/problemsbasedon priorgradelevelexperience

FromReadinessCheck:

STAGE3:LEARNINGPLAN

FirstTopic:CircumferenceofaCircle

LearningTargets:

● Icandescribetherelationshipbetweenthe radius,diameter,andcircumferenceofa circle.

● Giventheradius,diameter,or circumferenceofacircle,Icancalculatethe othertwomeasurements.

● Icancalculatetheperimeterofacomplex shapethatincludespartsofcircles.

● Icanwriteperimeterasanexpressionthat includesπ,suchas20π+50.

LearningActivities:

Studentswill firstsolvethetwoproblemsandbe preparedtosharetheirthinkingwithothers. Studentsthensharewithotherstosolidifythe conceptofwritingandusingequationsof proportionalrelationshipsandbeabletoexplainitin theirownwords.

Estimated#ofLessons:8

EssentialQuestions:

● Whatmakesacircleacircle?

● Studentsexaminetherelationshipbetweenthesidelengthofasquareanditsperimeter,aswellas therelationshipbetweenthediagonalofasquareanditsperimeter,bothofwhichareproportional.

● Studentsgeneratecharacteristicsthatdefineacirclebeforeexploringthecircumferenceandareaof circleslaterintheunit.

● Studentsmakesenseoftherelationshipbetweenthediameterofacircleanditscircumference.

● Studentspracticecalculatingtheperimeterofshapescomposedofsquaresandpartsofcircles.

SecondTopic:AreaofaCircle

LearningTargets:

● Icancalculatetheareaofacircle.

● Icancalculatetheareaofacomplexshape thatincludespartsofcircles.

Estimated#ofLessons:8

EssentialQuestions:

● HowcanIusecircumferenceandareaofa circletosolvereal-worldproblems?

● Icanexpressthevalueofareaasan expressionthatincludesπ,suchas20π+ 50.

● Icancalculatetheareaofacirclegivenits circumference.

● Icanevaluateasituationanddetermineifit involvescircumferenceorareaofacircle.

LearningActivities:

● Studentssurfaceandusestrategiesforreasoningabouttheareaofcomplexshapesandestimate theareaofshapeswithcurvededges.

● Studentsestimateanduserepeatedreasoningtomakesenseoftherelationshipbetweentheradius ofacircle,thesquareoftheradius,andtheareaofthecircle.

● Studentsunderstandwhytheformulafortheareaofacirclemakessensebyconnectingittothe formulaforthecircumferenceofacircle.

● Studentspracticecalculatingtheareaofshapescomposedofsquaresandpartsofcircles.

● Studentsusewhatthey’velearnedaboutcircumferenceandareatosolvechallengeslikecalculating theareaofasquareandacirclebasedontheirperimeters.

UnitOverview:

Inthisunit,studentsextendtheirgrade6knowledgeofequivalentratios(tapediagrams,tables,anddouble numberlines)andtheirUnit2knowledgeofproportionalrelationshipstosolveproblemsinvolving fractionalquantitiesandpercentchange.Studentsinterpretandsolveproblemsaboutdailysituations involvingproportionalrelationshipsandpercentchange.

ContentMathStateStandards:

7.RP.A.1: Computeunitratesassociatedwithratios offractions,includingratiosoflengths,areas,and otherquantitiesmeasuredinlikeordifferentunits.

7.RP.A.2: Recognizeandrepresentproportional relationshipsbetweenquantities.

7.RP.A.3: Useproportionalrelationshipstosolve multistepratioandpercentproblems(e.g.,simple interest,tax,markupsandmarkdowns,gratuities andcommissions,fees,percentincreaseand decrease,andpercenterror).

● CRITICALTHINKING: Identifyaproblem,ask keyquestions,andmakepredictions. MP#2 Reasonabstractlyandquantitatively;MP#4 Modelwithmathematics.

● COMMUNICATION: Createalogicaland evidence-basedargumenttosupportideas. MP#3Constructviableargumentsand critiquethereasoningofothers.

● CRITICALTHINKING: Analyzedatainorder todrawconclusions. MP#6Attendto

STAGE1:DESIREDRESULTS

7.EE.A.2: Understandthatrewritinganexpression indifferentformsinaproblemcontextcanshed lightontheproblemandhowthequantitiesinit arerelated.

7.EE.B.4: Usevariablestorepresentquantitiesina real-worldormathematicalproblem,andconstruct simpleequationsandinequalitiestosolveproblems byreasoningaboutthequantities.

precision;MP#8Lookforandexpress regularityinrepeatedreasoning.

Understandings EssentialQuestions

Aconsumer,user,orwageearnerexpectsavalueto increaseordecreasebasedontheadvertised percentchange.

Knowledge

● Howtodevelopapercentequationandits solution

● Howtoevaluatesituationsforwhich percentagescanbeusedtodescribea changerelativetoaninitialamount

HowcanIuseproportionalrelationshipsandpercent ofchangetoanalyzeasituationinarealworld setting?

Skills(FramedasLearningTargets)

● Icanusetheconstantofproportionalityto solveproblemsthatinvolvefractions

● Icanuseatabletodetermineanunknown valueinaproportionalrelationship.

● Icanusetapediagramsandtablesto representaddingorsubtractingapercentage from100%.

● IcandeterminethenewamountifIknowthe originalamountandthepercentchange

● Icanwriteanequationtorepresentaddingor subtractingapercentagefrom100%.

● Icanusedoublenumberlinestorepresent addingorsubtractingapercentagefrom 100%.

● IcandeterminetheoriginalamountifIknow thenewamountandthepercentchange.

● IcandeterminetheoriginalamountifIknow thenewamountandthepercentchangefor one-stepandmultistepproblems.

● Icansolvemultistepproblemsaboutsalestax andtip.

● Icanwriteequationstorepresentthecostof collegeovertime.

● Icansolveproblemsaboutthecostofcollege overtime.

● Icanexplainwhatpercenterrorisandhowto calculateit.

● Icandecidewhetheravalueiswithinan acceptablepercenterror.

STAGE2:DETERMINEACCEPTABLEEVIDENCE

SummativeAssessment

Grade7Unit4EndofUnitAssessment

● Icanusetapediagramsandtablesto representaddingorsubtractinga percentagefrom100%.

○ Problems1,5,6

● IcandeterminethenewamountifIknow theoriginalamountandthepercentchange

○ Problems1,5,6

● Icanusetheconstantofproportionalityto solveproblemsthatinvolvefractions

○ Problem2

● Icanuseatabletodetermineanunknown valueinaproportionalrelationship.

○ Problem2

● Icanexplainwhatpercenterrorisandhow tocalculateit.

○ Problem3

● Icandecidewhetheravalueiswithinan acceptablepercenterror.

○ Problem3

● IcandeterminetheoriginalamountifI knowthenewamountandthepercent changeforone-stepandmultistep problems.

○ Problem4

● Icanwriteanequationtorepresentadding orsubtractingapercentagefrom100%.

○ Problem6

● Icanwriteequationstorepresentthecost ofcollegeovertime.

○ Problem7

● Icansolveproblemsaboutthecostof collegeovertime.

○ Problem7

PerformanceTask

● RestaurantPercentProject-Studentswill explorehowpercentagesareusedina restaurantsettinginregardstopricing, taxesandtips.

Understanding#1 LearningTargets:

FormativeAssessment

Grade7Unit4MidUnitAssessment

Ongoingassessments:IMsynthesisandcooldowns asappropriate

Frayermodel(blanktemplateandrationale)

● PercentagesasProportionalrelationships

● Applyingpercentages

○ Icansolvemultistepproblems aboutsalestaxandtip.

○ IcandeterminethenewamountifI knowtheoriginalamountandthe percentchange

○ Icandeterminetheoriginalamount ifIknowthenewamountandthe percentchange.

○ Icandeterminetheoriginalamount ifIknowthenewamountandthe percentchangeforone-stepand multistepproblems.

TransferSkills:CriticalThinkingand Communication

STAGE3:LEARNINGPLAN

PreviousMathConnections

● Usingunitratestosolveaproblem, includingratesthatinvolvefractions. (6.RP.A.2,6.RP.A.3)

● Recognizingrelationshipsbetween fractions,percentages,anddecimals. (6.RP.A.3.C)

● Calculatingapercentageofanumber. (6.RP.A.3.C)

● Recognizingequivalentexpressionsandthe distributiveproperty. (6.EE.A.3)

● Representingrelationshipsusingdouble numberlines. (6.RP.A.3)

FirstTopic:PercentagesasProportional Relationships

LearningTargets:

● Icanusetheconstantofproportionalityto solveproblemsthatinvolvefractions

● Icanuseatabletodetermineanunknown valueinaproportionalrelationship.

● Icanusetapediagramsandtablesto representaddingorsubtractinga

Diagnosticassessmentquestions/problemsbasedon priorgradelevelexperience

FromReadinessCheck

Studentswill firstsolvethetwoproblemsandbe preparedtosharetheirthinkingwithothers. Studentsthensharewithothersjtosolidifythe conceptofunitratesandratiosandbeabletoexplain itintheirownwords.

Estimated#ofLessons:9

EssentialQuestions:

● HowcanIuseproportionalrelationshipsand percentofchangetoanalyzeasituationina realworldsetting?

percentagefrom100%.

● IcandeterminethenewamountifIknow theoriginalamountandthepercentchange

● Icanwriteanequationtorepresentadding orsubtractingapercentagefrom100%.

● Icanusedoublenumberlinestorepresent addingorsubtractingapercentagefrom 100%.

● IcandeterminetheoriginalamountifI knowthenewamountandthepercent change.

● IcandeterminetheoriginalamountifI knowthenewamountandthepercent changeforone-stepandmultistep problems.

LearningActivities:

● Studentsdiscoverwhattheyalreadyknowabouttherelationshipsbetweenpercentsandfractions.

● StudentsusestrategiesfromUnit2tocomparerelationshipsthatinvolvefractionalquantities.

● Studentsuseconstantsofproportionalitytodetermineunknownvaluesinproportional relationships,someofwhichinvolvefractionalquantities

● Studentsvisualizewhatitmeanstoincreaseordecreasebyapercentage,andusethatvisualtohelp themcalculateunknownvalues.

● Studentsrepresentsituationsinvolvingpercentincreaseordecreaseusingequationsandmake connectionsbetweendifferentwaystowritethatequation.

● Studentspracticecalculatingtheoriginalamount,thenewamount,orthepercentchangegiventhe othertwoquantities.

● Studentspracticecalculatingtheoriginalvalue,thenewvalue,orthepercentchangegiventheother twoquantities.

SecondTopic:ApplyingPercentages Estimated#ofLessons:11

LearningTargets:

● Icansolvemultistepproblemsaboutsales taxandtip.

● Icanwriteequationstorepresentthecost ofcollegeovertime.

● Icansolveproblemsaboutthecostof collegeovertime.

● Icanexplainwhatpercenterrorisandhow tocalculateit.

● Icandecidewhetheravalueiswithinan acceptablepercenterror.

LearningActivities:

EssentialQuestions:

● HowcanIuseproportionalrelationshipsand percentofchangetoanalyzeasituationina realworldsetting?

● Studentsapplywhatthey'velearnedinthe firstsectionoftheunittosolvemultisteppercent problemsinacommoncontext:salestaxandtip.

● Studentsusewhatthey’velearnedaboutproportionalrelationshipsandpercentchangetoanalyze anissueinsociety.

● Studentsusewhatthey’velearnedaboutcalculatingpercentincreasetosolveproblemsabout increasesinminimumwageandthecostofcollegeovertime.

● Studentsareintroducedtoreal-worldcontextsinwhicherroroccurs.Theyconsiderwhypercent errorisuseful,andtheypracticecalculatingpercenterroranddecidingwhetherornota measurementiswithinanacceptablerange.

● Studentsapplywhatthey'velearnedaboutincreasinganddecreasingbyapercentagetogenerate andanswerquestionsaboutthesocietyinwhichwelive.

● Studentsconvertfractionstodecimalsusinglongdivision. CourseName:Grade7Unit5Title:RationalNumberArithmetic

UnitOverview:

Inthisunit,studentsinterpretsignednumbersincontexts(e.g.,temperature,elevation,depositand withdrawal,position,direction,speedandvelocity,percentchange)togetherwiththeirsums,differences, products,andquotients.

STAGE1:DESIREDRESULTS

EstablishedGoals

ContentMathStateStandards:

7.NS.A.1 Applyandextendprevious understandingsofadditionandsubtractiontoadd andsubtractrationalnumbers.Representaddition andsubtractiononahorizontalorverticalnumber linediagram.

7.NS.A.1.A Describesituationsinwhichopposite quantitiescombinetomake0.

7.NS.A.1.B Understand p+q asthenumberlocated adistanceof|q|from p inthepositiveornegative directiondependingonwhether q ispositiveor negative.Showthatanumberanditsoppositehave asumof0(areadditiveinverses).Interpretsumsof rationalnumbersbydescribingreal-world contexts.

7.NS.A.1.C Understandsubtractionofrational numbersasaddingtheadditiveinverse, p-q=p+(-q). Showthatthedistancebetweentworational

TransferGoals

CSDEMathPractices(MP)in Blue toverifysignificance

● CRITICALTHINKING: Demonstrate flexibility anddeterminationwhensolvingproblems. MP#2Reasonabstractlyandquantitatively; MP#4Modelwithmathematics.

● COMMUNICATION: Createalogicaland evidence-basedargumenttosupportideas. MP#3Constructviableargumentsand critiquethereasoningofothers.

● CRITICALTHINKING: Analyzedatainorder todrawconclusions. MP#6Attendto precision;MP#8Lookforandexpress regularityinrepeatedreasoning.

numbersonthenumberlineistheabsolutevalue oftheirdifference,andapplythisprinciplein real-worldcontexts.

7.NS.A.1.D Applypropertiesofoperationsas strategiestoaddandsubtractrationalnumbers.

7.NS.A.2 Applyandextendprevious understandingsofmultiplicationanddivisionof fractionstomultiplyanddividerationalnumbers.

7.NS.A.2.A Understandthatmultiplicationis extendedfromfractionstorationalnumbersby requiringthatoperationscontinuetosatisfythe propertiesofoperations,particularlythe distributiveproperty,leadingtoproductssuchas (-1)(-1)=1andtherulesformultiplyingsigned numbers.Interpretproductsofrationalnumbers bydescribingreal-worldcontexts.

7.NS.A.2.B Understandthatintegerscanbe divided,providedthatthedivisorisnotzeroand everyquotientofintegers(withanon-zerodivisor) isarationalnumber.If p and q areintegers,then -(p/q)=(-p)/q=p/(-q).Interpretquotientsofrational numbersbydescribingreal-worldcontexts.

7.NS.A.2.C Applypropertiesofoperationsas strategiestomultiplyanddividerationalnumbers.

7.NS.A.2.D Convertarationalnumbertoadecimal usinglongdivision.Knowthatthedecimalformofa rationalnumberterminatesinzerosoreventually repeats.

7.NS.A.3 Solvereal-worldandmathematical problemsinvolvingthefouroperationswith rationalnumbers.

7.EE.B.3 Solvemultistep,real-life,and mathematicalproblemsposedwithpositiveand negativerationalnumbersinanyform(whole numbers,fractions,anddecimals)usingtools strategically.Applypropertiesofoperationsto calculatenumbersinanyform.Convertbetween formsasappropriate,andassessthe reasonablenessofanswersusingmental computationandestimationstrategies.

Understandings EssentialQuestions

● Computationswithsignednumbersfollow thesamefractionanddecimalrulesthat youhavebeenusingsince4thgrade.

● Calculationsandsolutionswithsigned numbersfollowtheintegerrules.

Knowledge

● “Signednumbers”includeallrational numbers,writtenasdecimalsorintheform

● Howtoapplytheintegerruleswhen computingwithintegers,fractionsand decimals.

● HowdoIuseprecisemathematicalnumbers andsymbolstodescribegivensituations?

● Howcantheuseofoperationswithpositive andnegativenumbersbeusedinrealworld situations?

Skills(FramedasLearningTargets)

● Icanconnectaddingandremoving floatsand anchorstoaddingandsubtractingintegers.

● Icanidentifydifferentexpressionsthathave thesamevalue.

● Icanaddandsubtractintegers,decimals,and fractionsonanumberline.

● Icandeterminethevalueofavariablethat makesanequationtrue.

● Icandrawanumberlinetoaddandsubtract positiveandnegativenumbers.

● Icancompareandcontrastsimilar expressions(e.g.,2.5−3.5and3.5−2.5).

● Icanmakeargumentsaboutadditionand subtractionwithvariables.

● Icanuseposition,rate,andtimetorepresent multiplyingpositiveandnegativenumbers.

● Icanexplainwhymultiplyingtwonegative numbershasapositivevalue.

● Icanmultiplyanddividepositiveandnegative numbers.

● Icanidentifydifferentexpressionsthathave thesamevalue.

● Icanreasonaboutexpressionsthatinvolve variables.

● Icanadd,subtract,multiply,anddivide integersincomplicatedexpressions.

● Icansolveproblemsandmakepredictions usingpositiveandnegativerates.

● Icancomparechangesinthevalueof differentstocks,includingthedollaramount andthepercentageofthepreviousvalue.

● Icaninterprettablesthatrepresentthe valuesofdifferentstocksinthestockmarket.

Grade7Unit5EndofUnitAssessment

● Icanaddandsubtractintegers,decimals, andfractionsonanumberline.

○ Problems1,2,6

● Icandeterminethevalueofavariablethat makesanequationtrue.

○ Problems1,2,6

● Icanconnectaddingandremoving floats andanchorstoaddingandsubtracting integers.

○ Problem2

● Icanidentifydifferentexpressionsthat havethesamevalue.

○ Problem2

● Icandrawanumberlinetoaddand subtractpositiveandnegativenumbers.

○ Problem3

● Icancompareandcontrastsimilar expressions(e.g.,2.5−3.5and3.5−2.5).

○ Problem3

● Icanmakeargumentsaboutadditionand subtractionwithvariables.

○ Problem3

● Icanreasonaboutexpressionsthatinvolve variables.

○ Problem3

● Icanadd,subtract,multiply,anddivide integersincomplicatedexpressions.

○ Problem4

● Icanmultiplyanddividepositiveand negativenumbers.

○ Problems5,6

● Icanidentifydifferentexpressionsthat havethesamevalue.

○ Problems5,6

● Icanuseposition,rate,andtimeto representmultiplyingpositiveandnegative numbers.

○ Problem7

● Icanexplainwhymultiplyingtwonegative numbershasapositivevalue.

○ Problem7

● Icansolveproblemsandmakepredictions usingpositiveandnegativerates.

○ Problem7

PerformanceTask:

TheStockMarket-

Grade7Unit5MidUnitAssessments (2)

Ongoingassessments:IMsynthesisandcooldowns asappropriate

FrayerModel(blanktemplateandrationale)

● AddingandSubtractingrationalnumbers

● MultiplyingandDividingrationalnumbers

● Applyingoperations

Studentsapplytheirknowledgeofoperationswith rationalnumberstocalculateastock’snewvalue, changeinvalue,orchangeexpressedasasigned percentageofthepreviousvalue.(OpenUp Resourceslink)

Understanding#1 LearningTargets:

● Icancomparechangesinthevalueof differentstocks,includingthedollar amountandthepercentageoftheprevious value.

● Icaninterprettablesthatrepresentthe valuesofdifferentstocksinthestock market.

TransferSkills:CriticalThinkingand Communication

STAGE3:LEARNINGPLAN

PreviousMathConnections

● Usingpositiveandnegativenumbersto representquantitiesinreal-worldcontexts. (6.NS.C.5)

● Plottingpositiveandnegativenumbersona numberline. (6.NS.C.6)

● Identifyingwhentwoexpressionsor equationshavethesamevalue. (6.EE.A.4)

● Determiningthevalueofavariableinan equationoftheformx+p=qandpx=q. (6.EE.B.7)

Diagnosticassessmentquestions/problemsbasedon priorgradelevelexperience

FromReadinessCheck:

Studentswill preparedtosharetheirthinkingwithothers. Studentsthensharewithotherstosolidifytheir abilitytoreasonwithnegativenumbersandcompare signednumbers.

FirstTopic:AddingandSubtracting

LearningTargets:

● Icanconnectaddingandremoving floats andanchorstoaddingandsubtracting integers.

● Icanidentifydifferentexpressionsthat havethesamevalue.

● Icanaddandsubtractintegers,decimals, andfractionsonanumberline.

● Icandeterminethevalueofavariablethat makesanequationtrue.

● Icandrawanumberlinetoaddand subtractpositiveandnegativenumbers.

● Icancompareandcontrastsimilar expressions(e.g.,2.5−3.5and3.5−2.5).

● Icanmakeargumentsaboutadditionand subtractionwithvariables.

LearningActivities:

Estimated#ofLessons:8

EssentialQuestions:

● HowdoIuseprecisemathematicalnumbers andsymbolstodescribegivensituations?

● Studentsdevelopamodelforaddingandsubtractingpositiveandnegativeintegers.

● Studentstransitionfrommanipulating floatsandanchorstousing floatsandanchorstoreason aboutaddingandsubtractingintegers.

● Studentsextendwhattheylearnedaboutrepresentingaddingandsubtractingintegersonanumber linetoaddingandsubtractingdecimalsandfractions.

● Studentsreasonaboutrepresentingsubtractionofsignednumbersonanumberlineandpractice drawingtheirownnumberlines.

● Studentspracticereasoningaboutthesignsandvaluesofexpressions.

SecondTopic:MultiplyingandDividing

LearningTargets:

● Icanuseposition,rate,andtimeto representmultiplyingpositiveandnegative numbers.

● Icanexplainwhymultiplyingtwonegative numbershasapositivevalue.

● Icanmultiplyanddividepositiveand negativenumbers.

● Icanidentifydifferentexpressionsthat havethesamevalue.

● Icanreasonaboutexpressionsthatinvolve variables.

● Icanadd,subtract,multiply,anddivide integersincomplicatedexpressions.

LearningActivities:

Estimated#ofLessons:7

EssentialQuestions:

● HowdoIuseprecisemathematicalnumbers andsymbolstodescribegivensituations?

● Studentsextendthe floatsandanchorsmodeltomakesenseofmultiplyingpositiveandnegative integers.

● Studentsmakesenseofadifferentmodelformultiplyingpositiveandnegativenumbers(rateof change·time=position).

● Studentsmakesenseofdivisionofsignednumbersusingthecontextofposition,rate,andtimeasa model.

● Studentsreasonaboutvariableexpressionsinvolvingadding,subtracting,multiplying,anddividing signednumbers.Studentsalsogeneralizepatternsforthevalueofvariableexpressions.

● Studentspracticereasoningaboutthesignsandvaluesofexpressionsthatincludeallfour operationsandpositiveandnegativenumbers.

ThirdTopic:ApplyingOperations

LearningTargets:

● Icansolveproblemsandmakepredictions usingpositiveandnegativerates.

LearningActivities:

Estimated#ofLessons:5

EssentialQuestions:

● Howcantheuseofoperationswithpositive andnegativenumbersbeusedinrealworld situations?

● Studentsusewhattheyhavelearnedabouttheadditionandsubtractionofpositiveandnegative numberstomakesenseofchangingtemperaturesaroundtheworldandseaicemelt.

● Studentsusewhattheyhavelearnedaboutpositiveandnegativeratestounderstandtheeffectsof climatechangeonArcticseaiceandrisingsealevels.

● Studentsusewhattheyhavelearnedaboutallfouroperationswithpositiveandnegativenumbers tounderstandsolarpanelsandcarbonfootprints.

CourseName:Grade7Unit6Title:Expressions,Equations,andInequalitiesEst.#ofLessons:24

UnitOverview:

Inthisunit,studentsextendwhattheylearnedinGrade6aboutsolvingone-stepequationstosolve multi-stepequationsthatincludeexpanding,factoring,oraddingtermsto findasolution.Sometimesa situationhasmanysolutionswhichcanberepresentedasinequalities.

STAGE1:DESIREDRESULTS

EstablishedGoals

ContentMathStateStandards:

7.EE.A.1 Applypropertiesofoperationsas strategiestoadd,subtract,factor,andexpand linearexpressionswithrationalcoefficients.

7.EE.B.3 Solvemultistep,real-life,and mathematicalproblemsposedwithpositiveand negativerationalnumbersinanyform(whole

Blue toverifysignificance

● COMMUNICATION: Createalogicaland evidence-basedargumenttosupportideas. MP#3Constructviableargumentsand critiquethereasoningofothers.

● CRITICALTHINKING: Analyzedatainorder todrawconclusions. MP#6Attendto

numbers,fractions,anddecimals)usingtools strategically.Applypropertiesofoperationsto calculatewithnumbersinanyform.Convert betweenformsasappropriate,andassessthe reasonablenessofanswersusingmental computationandestimationstrategies.

7.EE.B.4 Usevariablestorepresentquantitiesina real-worldormathematicalproblem,andconstruct simpleequationsandinequalitiestosolveproblems byreasoningaboutthequantities.

7.EE.B.4.A Solvewordproblemsleadingto equationsoftheform`px+q=r`and`p(x+q)=r`, where`p`,`q`,and`r`arespecificrationalnumbers. Solveequationsoftheseforms fluently.Compare analgebraicsolutiontoanarithmeticsolution, identifyingthesequenceoftheoperationsusedin eachapproach.

7.EE.B.4.B Solvewordproblemsleadingto inequalitiesoftheform`px+q>r`or`px+q<r`, where`p`,`q`,and`r`arespecificrationalnumbers. Graphthesolutionsetoftheinequalityand interpretitinthecontextoftheproblem.

Understandings

● Realisticsolutionstoequationsorinequalities requireunderstandingofwhatthereal-world scenariolookslikeregardlessoftheform(i.e., table,graph,oralgebraically)

● Leveragingtechnologytodemonstratethe relationshipbetweenequationsand inequalitiescreatesadynamicrepresentation ofthereal-worldscenarioforfurther possibilities.

Knowledge

● Howtoconstructandsolveequationsto modelreallifeproblems.

precision;MP#8Lookforandexpress regularityinrepeatedreasoning.

EssentialQuestions

● Howdowewriteandsolveequationsand inequalitiestomakesenseofreal-world problems?

● Whatdoestheequationorinequalitylooklikeon thegraph?Howdoesthatrevealpossible solutionstothereal-worldproblem?

Skills(FramedasLearningTargets)

● Icandrawtapediagramstorepresent situationsinwhichthevariablerepresenting

● Howtoconstructinequalitiestomodelreal lifeproblems.

theunknownisspecified.(Foundational)

● Icansolveequationsthatinvolveexpanding.

● Icancomparedifferentstrategiesforsolving thesameequation.

● Icanwriteequivalentexpressions.

● Icanexplainwhetherornottwoexpressions areequivalent.

● Icanconnectbalancingmovesonhangersto solvingequations.

● Icansolveequationswithpositivenumbers.

● Icanwriteequivalentexpressionswithfewer terms.

● Icanexpandandfactorexpressions.

● Icanexplainwhetherornotfractionsor negativenumbersmakesenseassolutionsto aninequality.

● Icanwriteandsolveaninequalitytoanswera questionaboutasituation.

● Ican figureoutthesolutionstoaninequality.

● Icanexplainthedifferencebetweenthe solutiontoanequationandthesolutionstoan inequality.

● Icanwriteaninequalitytorepresenta context.

● Icansolveaninequalityincontextbyusinga relatedequation. STAGE2:DETERMINEACCEPTABLEEVIDENCE SummativeAssessment

Grade7Unit6EndofUnitAssessment

● Ican figureoutthesolutionstoan inequality.

○ Problem1

● Icanexplainthedifferencebetweenthe solutiontoanequationandthesolutionsto aninequality.

○ Problem1

● Icanwriteaninequalitytorepresenta context.

○ Problems2,6

● Icansolveaninequalityincontextbyusing arelatedequation.

○ Problems2,6

● Icanexpandandfactorexpressions.

Grade7Unit6MidUnitAssessment

Ongoingassessments:IMsynthesisandcooldowns asappropriate

FrayerModel(blanktemplateandrationale)

● EquationsandTapeDiagrams

● SolvingEquations

● Inequalities

○ Problem3

● Icansolveequationsthatinvolve expanding.

○ Problem3

● Icancomparedifferentstrategiesfor solvingthesameequation.

○ Problem3

● Icanwriteequivalentexpressions.

○ Problem3

● Icanexplainwhetherornottwo expressionsareequivalent.

○ Problem3

● Icanconnectbalancingmovesonhangers tosolvingequations.

○ Problem4

● Icansolveequationswithpositive numbers.

○ Problem4

● Icanwriteequivalentexpressionswith fewerterms.

○ Problem5

● Icanexplainwhetherornotfractionsor negativenumbersmakesenseassolutions toaninequality.

○ Problem6

● Icanwriteandsolveaninequalityto answeraquestionaboutasituation.

○ Problem6

PreviousMathConnections

STAGE3:LEARNINGPLAN

● Generatingequivalentexpressionsbyusing thedistributivepropertyandbyadding terms.(6.EE.A.3)

● Usingsubstitutiontodetermineifavalueis asolutiontoanequationoraninequality. (6.EE.B.5)

● Writingandsolvingone-stepequationsof theform �� + �� = �� and ���� = ��.(6.EE.B.7)

● Writingandgraphinginequalitiesofthe form �� > �� and �� < ��.(6.EE.B.8)

Diagnosticassessmentquestions/problemsbasedon priorgradelevelexperience.

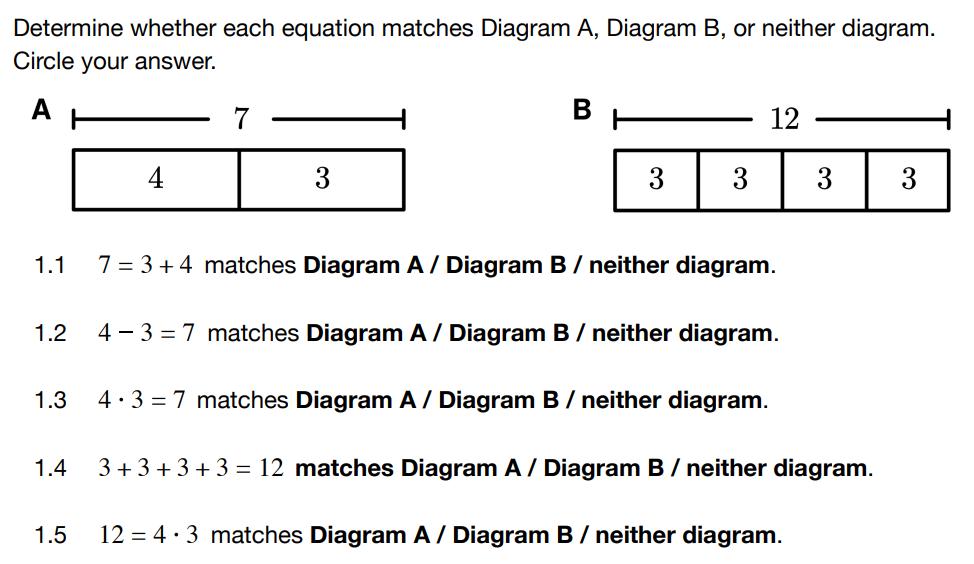
FirstTopic:EquationsandTapeDiagrams

LearningTargets:

● Icandrawtapediagramstorepresent situationsinwhichthevariable representingtheunknownisspecified. (Foundational)

LearningActivities:

Studentswill firstsolvethetwoproblemsandbe preparedtosharetheirthinkingwithothers. Studentsthensharewithotherstosolidifythe conceptoftapediagramsandwritingandsolving equationsrelatingtotherealworld.

Estimated#ofLessons:6

EssentialQuestions:

● Howdowewriteandsolveequationsand inequalitiestomakesenseofreal-world problems?

● Studentsextendwhattheyknowaboutproportionalrelationshipstoexplorepatternsinothertypes ofrelationships.

● Studentsrevisittapediagramsandsurfacestrategiesforusingtapediagramstodetermineunknown valuesinsituations.

● Studentsusewhattheyknowabouttapediagramsandsituationstomakesenseofequationsof nonproportionalrelationships.Studentsbothconnectdifferentrepresentationsofthesame situationandcreatetheirownrepresentations.

● Studentsusestructuretoanalyzeandsolveaquestionincontextandinterpretthemeaningofits solution.

SecondTopic:SolvingEquations

LearningTargets:

● Icanexpandandfactorexpressions.

● Icansolveequationsthatinvolve expanding.

● Icancomparedifferentstrategiesfor solvingthesameequation.

● Icanwriteequivalentexpressions.

● Icanexplainwhetherornottwo expressionsareequivalent.

● Icanconnectbalancingmovesonhangers tosolvingequations.

Estimated#ofLessons:11

EssentialQuestions:

● Howdowewriteandsolveequationsand inequalitiestomakesenseofreal-world problems??

● Icansolveequationswithpositive numbers.

● Icanwriteequivalentexpressionswith fewerterms.

LearningActivities:

● Studentsdevelopstrategiesfor figuringoutanunknownweightbycreatingbalancedhangerswith fewerobjects.

● Studentsunderstandstrategiesforsolvinganequationandconnectthosetobalancedmovesona hanger.

● Studentsdescribeandusestrategiesforsolvingequationsoftheforms

and

)= �� that involvepositiveandnegativenumbers.

● Studentsextendwhattheyknowaboutdistributingandsolvingtofactorandexpandexpressions, andthensolveequationsinmultiplewaysandcomparetheresults.

● Studentsunderstandthatequivalentexpressionshavethesamevalueforanyvalueofthevariable. Studentswillreasonaboutequivalentexpressionsthatinvolvefactoring,expanding,andreordering terms

● Studentspracticewritingexpressionswithfewertermsbyaddingandexpandingterms.

● Studentspracticesolvingequationsthatinvolveaddingtermsandexpandingexpressions.

● Studentsuseeverythingthey’velearnedsofarintheunittorepresentandanswerquestionsabout situationsincontext.

ThirdTopic:Inequalities

LearningTargets:

● Ican figureoutthesolutionstoan inequality.

● Icanexplainthedifferencebetweenthe solutiontoanequationandthesolutionsto aninequality.

● Icanwriteaninequalitytorepresenta context.

● Icansolveaninequalityincontextbyusing arelatedequation.

● Icanexplainwhetherornotfractionsor negativenumbersmakesenseassolutions toaninequality.

● Icanwriteandsolveaninequalityto answeraquestionaboutasituation.

LearningActivities:

Estimated#ofLessons:7

EssentialQuestions:

● Whatdoestheequationorinequalitylook likeonthegraph?Howdoesthatreveal possiblesolutionstothereal-worldproblem?

● StudentsbuildontheirknowledgefromGrade6aboutgraphinginequalitiesandareintroducedto twonewsymbols:≥and≤.

● Studentsmakesenseofsolvinginequalitiesusinghangerdiagrams.

● Studentsusewhattheyhavelearnedtowriteandsolveinequalitiesrelatedtosituationsabout budgetingandspendingmoney.

● Studentspracticesolvinginequalitieswithbothpositiveandnegativecoefficients,andconnectthe solutionsofinequalitiestotheirgraphs.

● Studentspracticewritingandsolvinginequalitiesandcriticallyexaminewhatthesolutionstothose inequalitiesmeanincontext.

CourseName:Grade7Unit7Title:Angles,Triangles,andPrismsEst.#ofLessons:19

UnitOverview:

Inthisunit,studentsextendtheir6thgradeworkonrectangularsurfaceareaandvolumetotriangular prisms.Studentssolveequationsbasedongeometricproperties(complementary,supplementary,vertical). Studentsalsoexplorewhetheritispossibletodrawnotriangles,onetriangle,ormorethanonetriangle giventhreemeasuresofsidesorangles.

STAGE1:DESIREDRESULTS

EstablishedGoals

ContentMathStateStandards:

7.G.A.2 Draw(byhand,witharulerandprotractor, andwithtechnology)geometricshapeswithgiven conditions.Focusonconstructingtrianglesfrom threemeasuresofanglesorsidesandnoticewhen theconditionsdetermineauniquetriangle,more thanonetriangle,ornotriangle.

7.G.A.3 Describethetwo-dimensional figuresthat resultfromslicingthree-dimensional figures,asin planesectionsofrightrectangularprismsandright rectangularpyramids.

7.G.B.5 Usefactsaboutsupplementary, complementary,vertical,andadjacentanglesina multistepproblemtowriteandsolvesimple equationsforanunknownangleina figure.

7.G.B.6 Solvereal-worldandmathematical problemsinvolvingarea,volume,andsurfacearea oftwo-andthree-dimensionalobjectscomposedof triangles,quadrilaterals,polygons,cubes,andright prisms.

7.EE.A.2 Understandthatrewritinganexpression indifferentformsinaproblemcontextcanshed lightontheproblemandhowthequantitiesinit arerelated.

7.EE.B.4 Usevariablestorepresentquantitiesina

TransferGoals

CSDEMathPractices(MP)in Blue toverifysignificance

● CRITICALTHINKING: Identifyaproblem,ask keyquestions,andmakepredictions. MP#2 Reasonabstractlyandquantitatively;MP#4 Modelwithmathematics.

real-worldormathematicalproblem,andconstruct simpleequationsandinequalitiestosolveproblems byreasoningaboutthequantities.

Understandings

● Recognizingdifferentrelationsbetween anglescanassistin findinganunknown angle.

● Thechangeindimensionsofaprismaffects thesurfaceareaandvolumeofanobject.

Knowledge

● Howtodifferentiateandapplydifferent anglerelationships.

● Howtoconstructatriangleusinggivenside lengthsandangles.

● Howtoevaluatetheeffectsonvolume givenchangestoanydimension.

EssentialQuestion

● Whatanglerelationshipsareformedwith intersectinglines?

● Howdoesmypriorknowledgeofrectangles helpmedeterminethepropertiesoftriangles?

Skills(FramedasLearningTargets)

● Icandescribewhatcomplementaryand supplementaryanglesare.

● IcandetermineunknownanglesusingwhatI knowaboutcomplementaryand supplementaryangles.

● Icanconnectananglediagramwithan equationthatrepresentsit.

● Icandescribewhatverticalanglesare.

● Icanwriteanduseequationstodetermine unknownangles.

● IcansolvemultistepproblemsusingwhatI knowaboutcomplementary,supplementary, andverticalangles.

● Icandecidewhetherornotthreesidelengths willmakeatriangle.

● Icanbuildtrianglesgiventhree measurements.

● Icanexplainwhythereissometimesmore thanonepossibletrianglegiventhree measurements.

● Icandescribecrosssectionsofasolid.

● Icancompareandcontrastcrosssectionsof prismsandpyramids.

● Icanexplainhowthevolumeofaprismis relatedtotheareaofitsbaseanditsheight.

● Icancalculatethevolumeofrectangularand triangularprisms.

● Icancalculatethesurfaceareaofaprism.

● Icancompareandcontrastdifferent strategiesforcalculatingsurfacearea.

● Icandecidewhethervolumeorsurfaceareais moreusefultoansweraquestionabouta situation.

● Icanansweraquestionaboutareal-world situationusingmyknowledgeofsurfacearea andvolume.

STAGE2:DETERMINEACCEPTABLEEVIDENCE

SummativeAssessment

Grade7Unit7EndofUnitAssessment

● Icandescribewhatcomplementaryand supplementaryanglesare.

○ Problem3

● Icandetermineunknownanglesusingwhat Iknowaboutcomplementaryand supplementaryangles.

○ Problem3

● Icanconnectananglediagramwithan equationthatrepresentsit

○ Problem3

● Icandescribewhatverticalanglesare.

○ Problem3

● Icanwriteanduseequationstodetermine unknownangles

○ Problem3

● Icandecidewhetherornotthreeside lengthswillmakeatriangle.

○ Problem1

● Icandescribecrosssectionsofasolid.

○ Problem2

● Icancompareandcontrastcrosssections ofprismsandpyramids.

○ Problem2

● Icanbuildtrianglesgiventhree measurements.

○ Problem4

● Icanexplainwhythereissometimesmore thanonepossibletrianglegiventhree measurements.

○ Problem4

● Icanexplainhowthevolumeofaprismis relatedtotheareaofitsbaseanditsheight.

○ Problem5

● Icancalculatethevolumeofrectangular andtriangularprisms.

○ Problem5

● Icancalculatethesurfaceareaofaprism.

○ Problem5

FormativeAssessment

Grade7Unit7MidUnitAssessment

Ongoingassessments:IMsynthesisandcooldowns asappropriate

Frayermodel(blanktemplateandrationale)

● AngleRelationships

● DrawingTriangles

● SolidGeometry

● Icancompareandcontrastdifferent strategiesforcalculatingsurfacearea.

○ Problem5

● IcansolvemultistepproblemsusingwhatI knowaboutcomplementary, supplementary,andverticalangles.

○ Problem6

● Icandecidewhethervolumeorsurface areaismoreusefultoansweraquestion aboutasituation.

○ Problem7

● Icanansweraquestionaboutareal-world situationusingmyknowledgeofsurface areaandvolume.

○ Problem7

FirstTopic:AngleRelationships

LearningTargets:

● Icandescribewhatcomplementaryand supplementaryanglesare.

● Icandetermineunknownanglesusingwhat Iknowaboutcomplementaryand supplementaryangles.

● Icanconnectananglediagramwithan equationthatrepresentsit.

● Icandescribewhatverticalanglesare.

● Icanwriteanduseequationstodetermine unknownangles.

● IcansolvemultistepproblemsusingwhatI knowaboutcomplementary, supplementary,andverticalangles.

LearningActivities:

Estimated#ofLessons:6

EssentialQuestions:

● Whatanglerelationshipsareformedwith intersectinglines?

● Studentsrecallwhattheyknowaboutanglesandhowtoestimatethemeasure.Thentheyusewhat theyknowaboutangleslike90°and360°toreasonaboutanglemeasurementsaroundacircle.

● Studentscontinuetoexploreanglemeasurementsandtheirrelationships.Theylearnformalwaysto describetwospecificanglerelationships:complementaryanglesandsupplementaryangles.They alsorevisitwhattheylearnedinUnit6astheyconnectanglediagramstoequations.

● Studentsapplywhatthey’velearnedsofartounderstandtherelationshipbetweenverticalangles. Theywritetheirownequationstorepresentcomplexdiagramsandusethoseequationsto determineunknownanglemeasures.

● Thislessonconcludesstudents’explorationofanglerelationshipsinGrade7.Studentssolve multistepproblemsanddeterminemissinganglemeasuresonpaper.Theyalsocreatetheirown

STAGE3:LEARNINGPLAN

challengestotradewiththeirclassmates.

SecondTopic:DrawingTriangles

LearningTargets:

● Icandecidewhetherornotthreeside lengthswillmakeatriangle.

● Icanbuildtrianglesgiventhree measurements.

● Icanexplainwhythereissometimesmore thanonepossibletrianglegiventhree measurements.

LearningActivities:

Estimated#ofLessons:6

EssentialQuestions:

● Whatanglerelationshipsareformedwith intersectinglines?

● Thislessoninvitesstudentstonoticethatnotallcombinationsofthreesidescreateatriangleandto reasonaboutcharacteristicsofsidelengthsthatdoanddonotcreatetriangles.

● Studentscontinuetostudythesidelengthsofpolygons.Studentsmakeconnectionsbetweenside lengthsandcircles,andusethosecirclestocreatetriangleswithspecificsidelengths.Thislesson alsointroducestheideathatalltriangleswiththesamesidelengthsareidenticalcopies,butall quadrilateralswiththesamesidelengthsarenot.

● Studentsareaskedtoconsiderboththelengthsandtheanglesoftriangles.Theyrecognizethattwo triangleswithtwoanglemeasuresandonesidelengthincommon(ortwosidelengthsandoneangle measureincommon)arenotnecessarilyidenticalcopies.Studentsalsocometounderstandthat knowingtheorderofthemeasurementscanhelpcreateidenticaltriangles.

● Studentsareinvitedtotakethethinkingtheyweredoingindigitallessons5–7andapplyittopaper. Theyuserulersandprotractorstodrawtrianglesgiventhreemeasurementsandcontinuetoanswer questionslike: Isitpossibletodrawatrianglewiththesemeasurements?Isitpossibletodrawmorethan one?

ThirdTopic:SolidGeometry

LearningTargets:

● Icandescribecrosssectionsofasolid.

● Icancompareandcontrastcrosssections ofprismsandpyramids.

● Icanexplainhowthevolumeofaprismis relatedtotheareaofitsbaseanditsheight.

● Icancalculatethevolumeofrectangular andtriangularprisms.

● Icancalculatethesurfaceareaofaprism.

● Icancompareandcontrastdifferent strategiesforcalculatingsurfacearea.

● Icandecidewhethervolumeorsurface areaismoreusefultoansweraquestion

Estimated#ofLessons:7

EssentialQuestions:

● Howdoesmypriorknowledgeofrectangles helpmedeterminethepropertiesoftriangles?

aboutasituation.

● Icanansweraquestionaboutareal-world situationusingmyknowledgeofsurface areaandvolume.

LearningActivities:

● Studentsexploreanddescribepossiblecrosssectionsofsolids.Theyalsoexploreideasaboutcross sectionsofprismsandpyramids.

● Studentsusepriorknowledgeaboutvolumeofrectangularprismstohelpthemcalculatethevolume oftriangularprismsusingthebaseareaandheight.

● Studentsextendthisworktocalculatethevolumeofmorecomplicatedprisms.Studentsusea varietyofstrategiestodeterminetheareasofcomplicatedbases,includingdecomposingintomore familiarshapesorsurroundingandsubtracting.

● StudentsbuildontheworktheyhavedonecalculatingsurfaceareaofrectangularprismsinGrade6 inordertocalculatethesurfaceareaofmorecomplicatedprisms.

● Studentswrapupthisunitbyapplyingtheirknowledgeofsurfaceareaandvolumetosolvea complexprobleminvolvingfoldingan8.5-by-11-inchsheetofpaper.Studentsdeterminewhetheror notfoldingthepaperinonedirectionortheotheraffectstheamountofpopcornaboxcanholdor theamountofmaterialneededtocreatethebox. CourseName:Grade7Unit8Title:ProbabilityandSamplingEst.#ofLessons:22

UnitOverview:

Inthisunit,studentsexploretheconceptofprobabilitytodescribethelikelihoodofunknowneventsand usesimulationstoestimatetheprobabilityofreal-worldsituations.Astheybecomemoresophisticated, studentsusesamplestocalculateprobabilitiesandmakepredictionsaboutthepopulation(ex.peopleor things).

STAGE1:DESIREDRESULTS

EstablishedGoals

ContentMathStateStandards:

7.SP.A.1 Understandthatstatisticscanbeusedto gaininformationaboutapopulationbyexamininga sampleofthepopulation.Generalizationsabouta populationfromasamplearevalidonlyifthe sampleisrepresentativeofthatpopulation. Understandthatrandomsamplingtendsto producerepresentativesamplesandsupportvalid inferences.

TransferGoals

CSDEMathPractices(MP)in Blue toverifysignificance

● CRITICALTHINKING: Identifyaproblem,ask keyquestions,andmakepredictions. MP#2 Reasonabstractlyandquantitatively;MP#4 Modelwithmathematics.

● CRITICALTHINKING: Analyzedatainorder todrawconclusions. MP#6Attendto

7.SP.A.2 Usedatafromarandomsampletodraw inferencesaboutapopulationwithanunknown characteristicofinterest.Generatemultiple samples(orsimulatedsamples)ofthesamesizeto gaugethevariationinestimatesorpredictions.

7.SP.B.3 Informallyassessthedegreeofvisual overlapoftwonumericaldatadistributionswith similarvariabilities,measuringthedifference betweenthecentersbyexpressingitasamultiple ofameasureofvariability.

7.SP.B.4 Usemeasuresofcenterandmeasuresof variabilityfornumericaldatafromrandomsamples todrawinformalcomparativeinferencesabouttwo populations.

7.SP.C.5 Understandthattheprobabilityofa chanceeventisanumberbetween0and1that expressesthelikelihoodoftheeventoccurring. Largernumbersindicategreaterlikelihood.A probabilitynear0indicatesanunlikelyevent,a probabilityaround1/2indicatesaneventthatis neitherunlikelynorlikely,andaprobabilitynear1 indicatesalikelyevent.

7.SP.C.6 Approximatetheprobabilityofachance eventbycollectingdataonthechanceprocessthat producesitandobservingitslong-runrelative frequency,andpredicttheapproximaterelative frequencygiventheprobability.

7.SP.C.7 Developaprobabilitymodelanduseitto findprobabilitiesofevents.Compareprobabilities fromamodeltoobservedfrequencies.Ifthe agreementisnotgood,explainpossiblesourcesof thediscrepancy.

7.SP.C.7.A Developauniformprobabilitymodelby assigningequalprobabilitytoalloutcomes,anduse themodeltodetermineprobabilitiesofevents.

7.SP.C.7.B Developaprobabilitymodel(whichmay notbeuniform)byobservingfrequenciesindata generatedfromachanceprocess.

7.SP.C.8 Findprobabilitiesofcompoundevents

precision;MP#8Lookforandexpress regularityinrepeatedreasoning.

usingorganizedlists,tables,treediagrams,and simulation.

7.SP.C.8.A Understandthat,justaswithsimple events,theprobabilityofacompoundeventisthe fractionofoutcomesinthesamplespaceforwhich thecompoundeventoccurs.

7.SP.C.8.B Representsamplespacesforcompound eventsusingmethodssuchasorganizedlists, tables,andtreediagrams.Foraneventdescribedin everydaylanguage(e.g.,"rollingdoublesixes"), identifytheoutcomesinthesamplespacewhich composetheevent.

7.SP.8.C Designanduseasimulationtogenerate frequenciesforcompoundevents.

Understandings

Theaccuracy/effectivenessofasampleiscentralto thevalidityofaprediction.

Knowledge

● Howtodeterminetheprobabilityofan event.

● Howtodecidethepropersamplingmethod andanalysisofagivensituation.

EssentialQuestions

● HowcanIuseprobabilitytounderstandor predictanoutcome?

● Isthisagoodsample?

Skills(FramedasLearningTargets)

● Icandeterminetheprobabilityofanevent usingitssamplespace.

● Icancompareprobabilitieswrittenas fractions,decimals,andpercentages.

● Icanexplainwhytheresultsofarepeated experimentmaynotexactlymatchthe probabilityoftheevent.

● Icanexplainhowtheresultsofarepeated experimentarerelatedtotheprobabilityof theevent.

● Icancalculatetheprobabilityofamultistep event.

● Icanwriteoutthesamplespacefora multistepexperimentusingalist,table,ortree diagram.

● Icancalculatethemeanandmeanabsolute deviation(MAD)foradataset.

● Icancompareandcontrastpopulationsusing meanandMAD.

● Icanexplainwhyasamplingmethodisoris notlikelytoproduceabiasedsample.

● Icanusemeasuresofcenterandthe variabilityoftwosamplestodecideiftwo populationsareverydifferent.

● Icanuseameasureofvariabilitytoexplain thedifferencebetweenmeasuresofcenter.

● Icancomparetwogroupsbytakingrandom samples,thencalculatingandinterpretingthe statistics.

● Icanuseproportionalreasoningandasample toestimateinformationaboutapopulation.

STAGE2:DETERMINEACCEPTABLEEVIDENCE

Grade7Unit8EndofUnitAssessment

● Icandeterminetheprobabilityofanevent usingitssamplespace.

○ Problem1

● Icancompareprobabilitieswrittenas fractions,decimals,andpercentages.

○ Problem1

● Icanexplainwhyasamplingmethodisoris notlikelytoproduceabiasedsample.

○ Problem2

● Icancalculatethemeanandmeanabsolute deviation(MAD)foradataset.

○ Problem3

● Icancompareandcontrastpopulations usingmeanandMAD.

○ Problem3

● Icanexplainhowtheresultsofarepeated experimentarerelatedtotheprobabilityof theevent.

○ Problem4

● Icanexplainwhytheresultsofarepeated experimentmaynotexactlymatchthe probabilityoftheevent.

○ Problem4

● Icanwriteoutthesamplespacefora multistepexperimentusingalist,table,or treediagram.

○ Problem5

● Icancalculatetheprobabilityofamultistep event.

○ Problem5

Grade7Unit8MidUnitAssessment

Ongoingassessments:IMsynthesisandcooldowns asappropriate

FrayerModel(blanktemplateandrationale)

● Probability

● Sampling

● Icanuseproportionalreasoninganda sampletoestimateinformationabouta population.

○ Problem6

● Icanusemeasuresofcenterandthe variabilityoftwosamplestodecideiftwo populationsareverydifferent.

○ Problem7

● Icanuseameasureofvariabilitytoexplain thedifferencebetweenmeasuresofcenter.

○ Problem7

PerformanceTask:

AsthmaRates-Studentsanalyzerealdataabout asthmaratesbygeneratingrandomsamplesand usingthesamplestocompareasthmaratesin differentplacesinNewYork.

Understanding#2 LearningTargets:

● Icancomparetwogroupsbytakingrandom samples,thencalculatingandinterpreting thestatistics.

TransferSkill:CriticalThinking

STAGE3:LEARNINGPLAN

PreviousMathConnections

Writingequivalentfractions,decimals,and percentages.(6.RP.A.3.C)

● Understandingwhatthecenter,variability,and shapedescribeaboutasetofdata.(6.SP.A.2, 6.SP.A.3)

● Calculatingquantitativemeasuresofcenter (meanandmedian)andvariability(meanabsolute deviationandinterquartilerange). (6.SP.B.5.c)

Diagnosticassessmentquestions/problemsbasedon priorgradelevelexperience

FromReadinessCheck

Studentswill firstsolvethetwoproblemsandbe preparedtosharetheirthinkingwithothers. Studentsthensharewithotherstosolidifytheir understandingofconceptsofchance,benchmark fractions,anddecimalsbetween0and1.

FirstTopic:Probability

LearningTargets:

● Icandeterminetheprobabilityofanevent usingitssamplespace.

● Icancompareprobabilitieswrittenas fractions,decimals,andpercentages.

● Icanexplainwhytheresultsofarepeated experimentmaynotexactlymatchthe probabilityoftheevent.

● Icanexplainhowtheresultsofarepeated experimentarerelatedtotheprobabilityof theevent.

● Icancalculatetheprobabilityofa multistepevent.

LearningActivities:

Estimated#ofLessons:12

EssentialQuestins:

● HowcanIuseprobabilitytounderstandor predictanoutcome?

● Studentsconductexperimentsandusephrasessuchas“likely”and“equallylikelyasnot”todescribe thelikelihoodofdifferentevents.

● Studentsconnecttheconceptoflikelihoodwithprobabilityusingnumbersbetween0and1.They alsousesamplespacestohelpdeterminetheseprobabilities.

● Studentsuserepeatedexperimentsandproportionalitytopredictthecontentsofamysterybag, recognizingthatthenumberofrepeatedexperimentsaffectstheaccuracyofyourprediction.

● Studentsrecognizethatifyouperformanexperimentrepeatedly,theresultswillapproach,butmay notexactlymatch,theprobabilityoftheevent.

● Studentschallengetheirassumptionsaboutprobabilitytoolssuchascoinsandnumbercubes.They decidewhetherornotanobjectisfairbycomparingprobabilitiesfromamodeltotheresultsofa repeatedexperiment.

● Studentsmakesenseofprobabilitiesofmultistepevents.Theylearnaboutanduselists,tables,and treediagramstorepresentthesamplespaceofeventswithmultiplepenniesorspinners.Theythen usethesetoolstodeterminetheprobabilitiesofmultistepeventsandconsiderwhetherornot different

● Studentsusespinnersandblocksinbagstosimulatethechancesthatitrainsbasedonprobabilities fromaweatherforecast.gamesarefair.

● Studentsdesignandperformsimulationstoestimatetheprobabilitiesofmultistepreal-world situations.

SecondTopic:Sampling

LearningTargets:

● Icanwriteoutthesamplespacefora multistepexperimentusingalist,table,or treediagram.

● Icancalculatethemeanandmeanabsolute deviation(MAD)foradataset.

● Icancompareandcontrastpopulations usingmeanandMAD.

● Icanexplainwhyasamplingmethodisoris

Estimated#ofLessons:10

EssentialQuestions: ● Isthisagoodsample?

notlikelytoproduceabiasedsample.

● Icanusemeasuresofcenterandthe variabilityoftwosamplestodecideiftwo populationsareverydifferent.

● Icanuseameasureofvariabilitytoexplain thedifferencebetweenmeasuresofcenter.

● Icancomparetwogroupsbytakingrandom samples,thencalculatingandinterpreting thestatistics.

● Icanuseproportionalreasoninganda sampletoestimateinformationabouta population.

LearningActivities:

● Studentscalculatethemeanandmeanabsolutedeviation(MAD),andusethesemeasuresto compareandcontrastdatarepresentedbydotplots.

● Studentslearnthetermssampleandpopulation,andexploretheadvantagesanddisadvantagesof usingsamplestoansweraquestionaboutapopulation.

● Studentsreviewheadlinesproducedfromdifferentsamplesofdataandexplainwhetherornota givensamplingmethodislikelytoproducedatathatisrepresentativeofthepopulation.

● Studentsrevisitproportionalrelationshipsandpercentagesusingdatafromasampletoestimate thenumberofmarigoldsinalarge flowergarden.

● Studentsestimateameasureofcenterofapopulationbasedononeormoresamplesofthe population.Theyalsoexplainwhyanestimateforthecenterofapopulationismorelikelytobe accuratewhenitisbasedonarandomsamplewithlessvariability.

● Studentscomparetwopopulationsbasedonsamples.Thislessonintroducestheideathatyoucan determineifthereisabigdifferencebetweentwopopulationsbylookingatthedifferencebetween thecentersofsamplesandcomparingthedifferencetothemeasureofvariability.

● Studentsanalyzerealdataaboutasthmarates.Theygeneraterandomsamplesandusethemto comparetheasthmaratesofdifferentplacesinNewYork.

CourseName:Grade8Unit1Title:RigidTransformationsandCongruenceEst.#ofLessons:20

UnitOverview:

Inthisunit,studentswillinvestigate translations, rotations,and reflections,andusethesetransformationsto makeinformalargumentsaboutcongruence.Theyalsoexploreanglerelationshipsonparallellinesandthe trianglesumtheorem.

STAGE1:DESIREDRESULTS

EstablishedGoals

ContentMathStateStandards:

8.G.A Understandcongruenceandsimilarityusing physicalmodels,transparencies,orgeometry software.

8.G.A.1: Verifyexperimentallythepropertiesof rotations,reflections,andtranslations.

8.G.A.1.A Linesaretakentolines,andline segmentstolinesegmentsofthesamelength.

8.G.A.1.B Anglesaretakentoanglesofthesame measure.

8.G.A.1.C Parallellinesaretakentoparallellines.

8.G.A.2 Understandthatatwo-dimensional figure iscongruenttoanotherifthesecondcanbe obtainedfromthe firstbyasequenceofrotations, reflections,andtranslations;giventwocongruent figures,describeasequencethatexhibitsthe congruencebetweenthem.

8.G.A.3: Describetheeffectofdilations, translations,rotations,andreflectionson two-dimensional figuresusingcoordinates.

8.G.A.5 Useinformalargumentstoestablishfacts abouttheanglesumandexteriorangleoftriangles, abouttheanglescreatedwhenparallellinesarecut byatransversal,andtheangle-anglecriterionfor similarityoftriangles.

TransferGoals

CSDEMathPractices(MP)in Blue toverifysignificance

● COMMUNICATION:Createalogicaland evidence-basedargumenttosupportideas. MP #3Constructviableargumentsandcritiquethe reasoningofothers;MP#5:Useappropriatetools strategically;MP#6:Attendtoprecision.

● CRITICALTHINKING:Analyzedatainorderto drawconclusions. MP#:1Makesenseofproblems andpersevereinsolvingthem;MP#5:Use appropriatetoolsstrategically;MP#6:Attendto precision;MP#7:Lookforandmakeuseof structure.

Understandings EssentialQuestions

● Partsofcongruent figuresdonotchangeno matterthetransformationapplied.

Knowledge

● Howtotranslate,reflect,androtatea congruent figurefromonepositionto another.

● Howtodeterminewhethertwo figuresare congruent.

Howcanyouusetranslations,rotations,and reflectionstoprovecongruence?

Skills(FramedasLearningTargets)

● Icandescribehowtomoveonepartofa figure toanotherusingarigidtransformation.

(Foundational)

● Icandecidewhichtypeoftransformations willworktomoveone figuretoanother.

● Icanusegridstocarryouttransformationsof figures.

● Icanapplytransformationstopointsonagrid ifIknowtheircoordinates.

● Icandescribetheeffectsofarigid transformationonapairofparallellines.

● IfIhaveapairofverticalanglesandknowthe anglemeasureofoneofthem,Ican findthe anglemeasureoftheother.

● Ican findmissingsidelengthsorangle measuresusingpropertiesofrigid transformations.

● Icanuseprecisemathematicalknowledgein communicatingthetransformation.

● Icandecidevisuallywhetherornottwo figuresarecongruent.

● Icandecideusingrigidtransformations whetherornottwo figuresarecongruent.

STAGE2:DETERMINEACCEPTABLEEVIDENCE

SummativeAssessment

EndUnitAssessment

● Icandecidewhichtypeoftransformations willworktomoveone figuretoanother.

○ Problem2

● Icanusegridstocarryouttransformations of figures.

○ Problem2

● Icanapplytransformationstopointsona gridifIknowtheircoordinates.

○ Problem1

● Icandescribetheeffectsofarigid transformationonapairofparallellines.

○ Problem3,4,5

● IfIhaveapairofverticalanglesandknow

FormativeAssessment

MidunitGradeAssessment 8Unit7Quizzes1and2

Ongoingassessments:IMsynthesis,cooldownsand practicedaysasappropriate.

Frayermodel(rationale)

● Transformations

● DefiningCongruence

● ApplyingCongruence

theanglemeasureofoneofthemIcan find theanglemeasureoftheother.

○ Problem3,4,5

● Ican findmissingsidelengthsorangle measuresusingpropertiesofrigid transformations.

○ Problem7

● Icandecidevisuallywhetherornottwo figuresarecongruent.

○ Problem7

● Icandecideusingrigidtransformations whetherornottwo figuresarecongruent.

○ Problem6,7

PerformanceTask TransformationGolf:

● Studentsidentifyanddescribesequences oftransformationsthattakeone figureto anotherinthecontextofseveral TransformationGolfchallenges.

Understanding#1

LearningTargets#1&2 TransferSkills:CriticalThinkingand Communication

AretheyCongruent?

● Studentsuserigidtransformationstomake argumentsforwhytwo figuresareorare notcongruent.Theylearnthattwo figures withcommonalities,suchashavingthe sameareaorhavingcorrespondingside lengthsthatareequal,doesnotguarantee congruence.

Understanding#2

LearningTargets#8,9,10 TransferSkills:CriticalThinkingand Communication

Previousmathconnections

Thefollowingconceptsfrompreviousgradesmay supportstudentsinmeetinggrade-levelstandards inthisunit:

STAGE3:LEARNINGPLAN

● Identifyingparallelandperpendicularlines. (4.G.A.1)

● Graphingpointsanddrawingpolygonsin thecoordinateplane.(5.G.A.1,6.G.A.3)

● Identifyingverticalandadjacentangles. (7.G.B.5)

● Drawinggeometricshapeswithgiven conditions,payingspecialattentiontothe anglesoftriangles.(7.G.A.2)

● Calculatingtheareaoftrianglesand quadrilaterals.(6.G.A.1)

Studentswill firstsolvethetwoproblemsandbe preparedtosharetheirthinkingwithothers. Studentsthensharewithotherstosolidifythe conceptsofrigidmotionsintheplaneaswellas parallelandperpendicularlines.

FirstTopic:Transformations

LearningTargets:

● Icandecidewhichtypeoftransformations willworktomoveone figuretoanother.

● Icanusegridstocarryouttransformations of figures.

● Icanapplytransformationstopointsona gridifIknowtheircoordinates.

LearningActivities:

Estimated#ofLessons:8

EssentialQuestions:

● Whatarecongruent figuresandhowarethey translated,rotated,andreflectedaboutthe coordinateplane?

● Studentsareintroducedtotransformationsof figuresanddescribethesemovementsusing everydaylanguage.

● Studentsbegintodescribeagiventranslation,rotation,orreflectionwithgreaterprecision.

● Studentsidentifyanddescribesequencesoftransformationsthattakeone figuretoanotherinthe contextofseveralTransformationGolfchallenges.

● Studentsusethetermstranslation,rotation,andreflectiontodescribeanddrawtransformationson agrid.

● Studentsusecoordinatestodescribe figuresandtheirimagesundertransformationsinthe coordinateplane.

● Studentscommunicatepreciselyabouttransformationsofpolygonsonacoordinategrid.

SecondTopic:DefiningCongruence

LearningTargets:

● Icandescribetheeffectsofarigid transformationonapairofparallellines.

● IfIhaveapairofverticalanglesandknow theanglemeasureofoneofthem,Ican find theanglemeasureoftheother.

● Ican findmissingsidelengthsorangle measuresusingpropertiesofrigid transformations.

LearningActivities:

Estimated#ofLessons:6

EssentialQuestions:

● Whatarecongruent figuresandhowarethey translated,rotated,andreflectedaboutthe coordinateplane?

● Studentsexplorewhatitmeansforshapestobe“thesame”andtolearnthetermcongruent.

● Studentsbegintoseethattranslations,rotations,andreflectionspreservelengthsandangle measures,andusethetermrigidtransformationsforthe firsttime.

● Studentsuserigidtransformationstomakeargumentsforwhytwo figuresareorarenotcongruent.

ThirdTopic:ApplyingCongruence

LearningTargets:

● Icandecidevisuallywhetherornottwo figuresarecongruent.

● Icandecideusingrigidtransformations whetherornottwo figuresarecongruent.

LearningActivities:

Estimated#ofLessons:6

EssentialQuestions:

● Whatarecongruent figuresandhowarethey translated,rotated,andreflectedaboutthe coordinateplane?

● Studentsseethatparallellinesaretakentoparallellinesunderanyrigidtransformations.They justifythatpairsofverticalanglesandalternateinterioranglesonparallellinesarecongruent.

● Studentsobservethatthesumoftheinterioranglesofanytriangleisalways180degrees.

● Studentsapplywhatthey'velearnedaboutanglerelationshipsinpreviouslessonsandinformally establishthetrianglesumtheorem.

● Studentsexamineandcreatedifferentpatternsofshapes,includingtessellationsandcomplex designsthatexhibitrotationalsymmetry.

UnitOverview:

Inthisunit,studentswillinvestigatetheconceptsofdilation,similarity,andslopeinorderinorderto discoverhowtoenlargeorreducethesizeofaplane figure.Thisdiscoverywillallowthestudentstowork with“slopetriangles”andusethesimilarityofslopetrianglesonthesamelinetounderstandthatanytwo distinctpointsonalinedeterminethesameslope.

EstablishedGoals

ContentMathStateStandards:

STAGE1:DESIREDRESULTS

8.G.A: Understandcongruenceandsimilarityusing physicalmodels,transparencies,orgeometry software.

8.G.A.2: Understandthatatwo-dimensional figure iscongruenttoanotherifthesecondcanbe obtainedfromthe firstbyasequenceofrotations, reflections,andtranslations;giventwocongruent figures,describeasequencethatexhibitsthe congruencebetweenthem.

8.G.A.3: Describetheeffectofdilations, translations,rotations,andreflectionson two-dimensional figuresusingcoordinates.

8.G.A.4: Understandthatatwo-dimensional figure issimilartoanotherifthesecondcanbeobtained fromthe firstbyasequenceofrotations, reflections,translations,anddilations.Giventwo similartwo-dimensional figures,describea sequencethatexhibitsthesimilaritybetween them.

8.G.A.5: Useinformalargumentstoestablishfacts abouttheanglesumandexteriorangleoftriangles, abouttheanglescreatedwhenparallellinesarecut byatransversal,andtheangle-anglecriterionfor similarityoftriangles

8.EE.B.6: Usesimilartrianglestoexplainwhythe slope`m`isthesamebetweenanytwodistinct pointsonanon-verticallineinthecoordinate plane.Derivetheequation`y=mx`foraline throughtheoriginandtheequation`y=mx+b`fora lineinterceptingtheverticalaxisat`b`.

TransferGoals

CSDEMathPractices(MP)in Blue toverifysignificance

● COMMUNICATION:Createalogicaland evidence-basedargumenttosupportideas. MP #3Constructviableargumentsandcritiquethe reasoningofothers;MP#5:Useappropriatetools strategically.

● CRITICALTHINKING:Analyzedatainorderto drawconclusions. MP#5:Useappropriatetools strategically;MP#8Lookforandexpress regularityinrepeatedreasoning.

Understandings EssentialQuestions

● Whenyoushrinkorenlargea figure,the anglesstaythesamebutthesidelengths change.

● Theslopeofalineisfoundthroughthe

● Howdo figureschangewhentheyarereduced orenlarged?

● Howdosimilartriangleshelprevealtheslope ofaline?

explorationofthepropertiesofsimilar triangles.

Knowledge

● Howtoreduceorenlargeaplane figure throughdilationsinordertoconstruct similar figures.

● Howtodeterminetheslopeofalineusing theconceptofsimilartriangles.

Skills(FramedasLearningTargets)

● Icanapplyadilationtoapolygonusingagrid.

● Icanapplydilationstopolygonsona rectangulargridifIknowthecoordinatesof theverticesandofthecenterofdilation.

● Icanapplyasequenceoftransformationsto one figuretogetasimilar figure.

● Icanuseasequenceoftransformationsto explainwhytwo figuresaresimilar.

● Icanuseanglemeasuresandsidelengthsto concludethattwopolygonsarenotsimilar.

● Iknowtherelationshipbetweenangle measuresandsidelengthsinsimilarpolygons.

● Iknowhowtodecideiftwotrianglesare similarjustbylookingattheiranglemeasures.

● Icandecideiftwotrianglesaresimilarby lookingatquotientsoflengthsof correspondingsides.

● Ican findmissingsidelengthsinapairof similartrianglesusingquotientsofside lengths.

● Icandrawalineonagridwithagivenslope.

● Ican findtheslopeofalineonagrid.

SummativeAssessment

EndofUnitAssessment

● 1.Icanapplyadilationtoapolygonusinga grid.

○ Problem4

● 2.Icanapplydilationstopolygonsona rectangulargridifIknowthecoordinatesof theverticesandofthecenterofdilation.I knowhowtodecideiftwotrianglesare similarjustbylookingattheirangle measures.

○ Problem7

● 3.Icanapplyasequenceof transformationstoone figuretogeta similar figure.

○ Problem2,4

● 4.Icanuseasequenceoftransformations

FormativeAssessment

MidunitassessmentsGrade8Unit2

Ongoingassessments:IMsynthesisandcooldowns asappropriate.

Frayermodel(rationale)

● Dilations

● Similarity

● Slope

toexplainwhytwo figuresaresimilar.

○ Problem2,4

● 5.Icanuseanglemeasuresandside lengthstoconcludethattwopolygonsare notsimilar.

○ Problem3

● 6.Iknowtherelationshipbetweenangle measuresandsidelengthsinsimilar polygons.

○ Problem3

● 7.Iknowhowtodecideiftwotrianglesare similarjustbylookingattheirangle measures.

○ Problem5

● 8.Icandecideiftwotrianglesaresimilarby lookingatquotientsoflengthsof correspondingsides.

○ Problem1

● 9.Ican findmissingsidelengthsinapairof similartrianglesusingquotientsofside lengths.

○ Problem1

● 10.Icandrawalineonagridwithagiven slope.

○ Problem7

● 11.Ican findtheslopeofalineonagrid

○ Problem7

Previousmathconnections

STAGE3:LEARNINGPLAN

Thefollowingconceptsfrompreviousgradesmay supportstudentsinmeetinggrade-levelstandards inthisunit:

● Graphingpointsinallfourquadrantsofthe coordinateplane.(6.NS.C.8)

● Usingproportionalrelationshipsto determineunknownvalues.(7.RP.A.2)

● Graphingproportionalrelationships. (7.RP.A.2.d)

● Dividingvaluesintofractionalparts. (6.NS.A.1)

● Computinglengthsandscalefactorsof scaledcopies.(7.G.A.1)

Diagnosticassessmentquestions/problemsbasedon priorgradelevelexperience

FromReadinessCheck:

FirstTopic:Dilations

LearningTargets:

● Icanapplyadilationtoapolygonusinga grid.

● Icanapplydilationstopolygonsona rectangulargridifIknowthecoordinatesof theverticesandofthecenterofdilation.I knowhowtodecideiftwotrianglesare similarjustbylookingattheirangle measures.

LearningActivities:

Studentswill firstsolvethetwoproblemsandbe preparedtosharetheirthinkingwithothers. Studentsthensharewithotherstosolidifythe conceptsofplottingpointsonthecoordinateplane, locatingthey-axis,and findingdistancesonaplane.

Estimated#ofLessons:6

EssentialQuestions:

● Whataresimilar figuresandhowarethey usedtohelpdeterminetheslopeofaline?

● Studentsareinformallyintroducedtotheconceptsofdilationandsimilarityandexploredilationas aprocessthatproducesscaledcopies.

● Studentsperformdilations,movingfrominformaltoformalwaysofmeasuringtodeterminethe distancesbetweenthecenter,pre-image,andimageinadilation.

● Studentsapplydilationstopolygonsonagridandexploretheimpactofscalefactorsbetween0and 1.Studentsdiscoverthatdilationsmaplinesegmentstolinesegments,andpolygonstopolygons.

● Studentsworkonacoordinategridtopreciselycommunicatetheinformationneededtoperform dilations.

SecondTopic:Similarity

LearningTargets:

● Icanapplyasequenceoftransformations toone figuretogetasimilar figure.

● Icanuseasequenceoftransformationsto

Estimated#ofLessons:5

EssentialQuestions:

● Whataresimilar figuresandhowarethey usedtohelpdeterminetheslopeofaline?

explainwhytwo figuresaresimilar.

● Icanuseanglemeasuresandsidelengthsto concludethattwopolygonsarenotsimilar.

● Iknowtherelationshipbetweenangle measuresandsidelengthsinsimilar polygons.

● Iknowhowtodecideiftwotrianglesare similarjustbylookingattheirangle measures.

● Icandecideiftwotrianglesaresimilarby lookingatquotientsoflengthsof correspondingsides.

● Ican findmissingsidelengthsinapairof similartrianglesusingquotientsofside lengths.

LearningActivities:

● Studentsidentifyanddescribesequencesoftransformations,includingdilations,thattakeone figuretoanotherinthecontextofTransformationGolf.

● Studentsexaminethesidelengthsandanglemeasuresofpolygonsinordertounderstandsimilarity.

● Studentsexamineanglemeasurementsintrianglestodeterminewhetherornottwotrianglesare similar.

● Studentsdiscoverthatthequotientoftwosidelengthsinonetriangleisequaltothequotientofthe correspondingsidelengthsinasimilartriangle.

ThirdTopic:Slope Estimated#ofLessons:5

LearningTargets:

● Icandrawalineonagridwithagivenslope.

● Ican findtheslopeofalineonagrid.

LearningActivities:

EssentialQuestions

● Whataresimilar figuresandhowarethey usedtohelpdeterminetheslopeofaline?

● Studentsareintroducedtotheslopeofthelineasthequotientoftheverticalsidelengthandthe horizontalsidelength.

● Studentsuseslopetohelpdetermineifpointslieonaparticularline.

CourseName:Grade8Unit3Title:LinearRelationships Est.#ofLessons:16

UnitOverview:

Inthisunit,studentswilldeepentheirunderstandingofslopeaslinearequationstranslateverticallyalong they-axis.Theymakeconnectionsamongrateofchange,slope,andconstantofproportionality,and betweenlinearandproportionalrelationships.

EstablishedGoals

ContentMathStateStandards:

8.EE.B: Understandtheconnectionsbetween proportionalrelationships,lines,andlinear equations.

8.EE.B.5: Graphproportionalrelationships, interpretingtheunitrateastheslopeofthegraph. Comparetwodifferentproportionalrelationships representedindifferentways.Forexample, compareadistance-timegraphtoadistance-time equationtodeterminewhichoftwomoving objectshasgreaterspeed.

8.EE.B.6: Usesimilartrianglestoexplainwhythe slopemisthesamebetweenanytwodistinct pointsonanon-verticallineinthecoordinate plane;derivetheequationy=mxforalinethrough theoriginandtheequationy=mx+bforaline interceptingtheverticalaxisatb.

8.EE.C: Analyzeandsolvelinearequationsand pairsofsimultaneouslinearequations.

8.EE.C.8.A: Understandthatsolutionstoasystem oftwolinearequationsintwovariablescorrespond topointsofintersectionoftheirgraphs,because pointsofintersectionsatisfybothequations simultaneously.

8.F.A.2: Comparepropertiesoftwofunctionseach representedinadifferentway(algebraically, graphically,numericallyintables,orbyverbal descriptions).Forexample,givenalinearfunction representedbyatableofvaluesandalinear functionrepresentedbyanalgebraicexpression, determinewhichfunctionhasthegreaterrateof change.

8.G.A.1: Linesaretakentolines,andlinesegments tolinesegmentsofthesamelength

Understandings

● Understandingthatslopeisarateof changebetweenthexandyvariableshelps

TransferGoals

CSDEMathPractices(MP)in Blue toverifysignificance

● COMMUNICATION:Createalogicaland evidence-basedargumenttosupportideas.MP #3:Constructviableargumentsandcritiquethe reasoningofothers;MP#4:Modelwith Mathematics.

● CRITICALTHINKING:Analyzedatainorderto drawconclusions. MP#2:Reasonabstractlyand quantitatively;MP#6:Attendtoprecision.

EssentialQuestions

● Howdoesthegraphofalineconnecttoreal worldscenarios?

initsapplicationinrealworldscenarios.

● Alineismadeupofallthepossible solutionstoanequationintwovariables whichcanberepresentedintable, equation,orgraphform.

● They-interceptadjustsasthecontextof therealworldscenariochanges.

Knowledge

● Howtocalculatearateofchangefora linearrelationshipgivenitsgraph,pointson thegraph,oratableofitsvalues.

● Howtographaline,onthecoordinate plane,givenitsslopeandy-intercept.

● Keyvocabulary:

a.rateofchange

b.linearrelationship

c.verticalintercept

● Howtoidentifythesolutionofatwo variableequation.

● WhatinformationdoIneedtodetermine whetherit’salinearrelationship?HowcanI representthatusingprecisemathlanguage?

Skills(FramedasLearningTargets)

● Icanidentifythemeaningofslope.

● Ican findtherateofchangeofalinear relationshipfromatable,graphorequationby figuringouttheslopeofthelinerepresenting therelationship.

● Icanscaleandlabelacoordinategridinorder tography=mx+b.

● Icanexplainwhereto findtheslopeand verticalinterceptinbothanequationandits graph.

● Icangiveanexampleofasituationthatwould haveanegativeslopewhengraphed.

● Icanwriteequationsoflinesusingy=mx+b.

● Icanwritelinearequationstoreasonabout real-worldsituations.

● Iunderstandwhatthesolutiontoanequation intwovariablesis. STAGE2:DETERMINEACCEPTABLEEVIDENCE

SummativeAssessment

EndofUnitAssessment

● Icanidentifythemeaningofslope.

○ Problem3

● Ican findtherateofchangeofalinear relationshipfromatable,graphorequation by figuringouttheslopeoftheline representingtherelationship.

○ Problem5,7

● Icanscaleandlabelacoordinateaxesin ordertography=mx+b.

○ Problem7

● Icanexplainwhereto findtheslopeand verticalinterceptinbothanequationand itsgraph.

○ Problem2

FormativeAssessment

MidunitGrade8Unit3Quiz

Ongoingassessments:IMsynthesisandcooldowns asappropriate

Frayermodel(rationale)

● Proportionalityrevisited

● SlopeInterceptform

● SolutioninStandardform

● Icangiveanexampleofasituationthat wouldhaveanegativeslopewhengraphed

○ Problem2

● Icanwriteequationsoflinesusingy=mx+b.

○ Problem4

● Icanwritelinearequationstoreasonabout real-worldsituations.

○ Problem7

● Iunderstandwhatthesolutiontoan equationintwovariablesis.

○ Problem1,6,7

PerformanceTask

● Lesson3-Posters-Comparing ProportionalRelationships-Inthislesson onproportionalrelationships,students expandontheworkofthepreviouslessons bycomparingtwosituationsrepresentedin differentways.

Understanding#1 LearningTargets#1&2 TransferSkills:CriticalThinkingand Communication

Previousmathconnections

Thefollowingconceptsfrompreviousgradesmay supportstudentsinmeetinggrade-levelstandards inthisunit:

● Decidingwhetherornotquantitiesareina proportionalrelationship.(7.RP.A.2.a)

● Usingproportionalrelationshipstosolve problems.(7.RP.A.3)

● Writingequationstodescribeproportional relationships.(7.RP.A.2.c)

● Solvingproblemswithpositiveand negativenumbers.(7.EE.B.3)

● Applyingtransformationstolines. (8.G.A.1.aand8.G.A.1.c)

Diagnosticassessmentquestions/problemsbasedon priorgradelevelexperience

FromReadinessCheck:

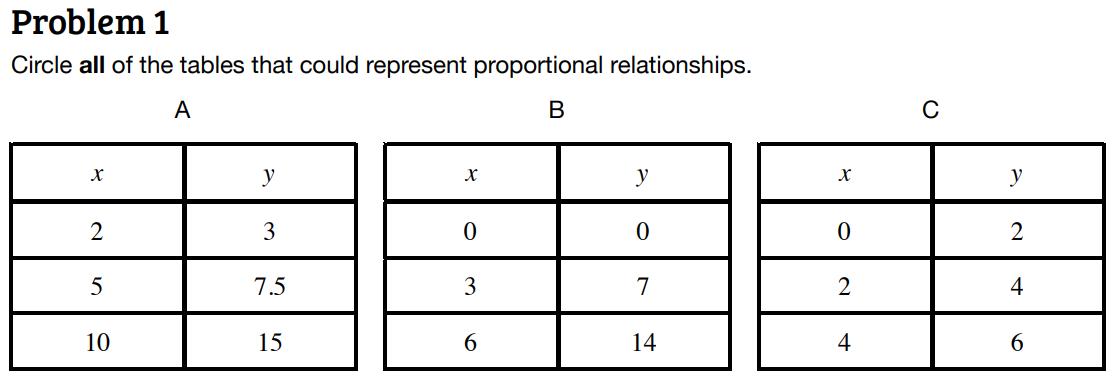
Studentswill firstsolvethetwoproblemsandbe preparedtosharetheirthinkingwithothers. Studentsthensharewithotherstosolidifythe conceptofproportionalrelationships.

STAGE3:LEARNINGPLAN

FirstTopic:ProportionalityRevisited

LearningTargets:

● Icanidentifythemeaningofslope.

● Ican findtherateofchangeofalinear relationshipfromatable,graphorequation by figuringouttheslopeoftheline representingtherelationship.

LearningActivities:

Estimated#ofLessons:4

EssentialQuestions:

● Howdoesthegraphofalineconnecttoreal worldscenarios?

● WhatinformationdoIneedtodetermine whetherit’salinearrelationship?HowcanI representthatusingprecisemathlanguage?

● Studentsmakeconnectionsbetweenthedifferentrepresentationsofproportionalrelationships.

● Studentsscaleaxesinmultiplewaysinordertographproportionalrelationships.

● Studentscomparetwodifferentproportionalrelationshipsgivendifferentrepresentationsofthem.

SecondTopic:SlopeInterceptForm

LearningTargets:

● Icanscaleandlabelacoordinategridin ordertography=mx+b.

● Icanexplainwhereto findtheslopeand verticalinterceptinbothanequationand itsgraph.

● Icangiveanexampleofasituationthat wouldhaveanegativeslopewhengraphed.

● Iunderstandwhatthesolutiontoan equationintwovariablesis.

● Icanwriteequationsoflinesusingy=mx+b.

● Icanwritelinearequationstoreasonabout real-worldsituations.

LearningActivities:

Estimated#ofLessons:7

EssentialQuestions:

● Howdoesthegraphofalineconnecttoreal worldscenarios?

● WhatinformationdoIneedtodetermine whetherit’salinearrelationship?HowcanI representthatusingprecisemathlanguage?

● Studentsmovefromproportionalrelationshipstolinearrelationshipswithpositiveratesofchange.

● Studentswriteandinterpretequationsoflinesbyconsideringtheslopeandverticalintercept.

● Studentswriteequationsoflinesusingtheideathatanylineinaplaneisaverticaltranslationofa linethroughtheorigin.

● Studentsreflectonsimilaritiesanddifferencesbetweenlineswithpositiveandnegativeslopes.

● Studentsdevelopamethodforcalculatingtheslopeofanylinegiventhecoordinatesoftwopoints ontheline.

● Studentswriteequationsofhorizontalandverticallinesinadditiontolineswithpositiveand negativeslopes.

ThirdTopic:SolutionsandStandardForm

LearningTargets:

● Iunderstandwhatthesolutiontoan equationintwovariablesis.

Estimated#ofLessons:5

EssentialQuestions:

● Howdoesthegraphofalineconnecttoreal worldscenarios?

● WhatinformationdoIneedtodetermine whetherit’salinearrelationship?HowcanI representthatusingprecisemathlanguage?

LearningActivities:

● Studentscometounderstandthatthegraphofanequationisavisualrepresentationofallsolutions totheequation.

● Studentsinterpretmultiplerepresentationsofnon-proportionallinearrelationshipsincontext, includingslopes,intercepts,andsolutions.

CourseName:Grade8Unit4Title:LinearEquationsandLinearSystemsEst.#ofLessons:20

UnitOverview:

Inthisunit,studentsbuilduponUnit3wheretheyarenowusingmultiplelinearequationsonacoordinate plane.Theylookattheintersections(orlackthereof)tosolvelinearequationswithrationalcoefficients (decimals,fractions,andintegers)anddeterminethenumberofpossiblesolutions.Studentsalsolearnto recognizethatsolutionscanbefoundbysolvingasystemofequationsalgebraically.

STAGE1:DESIREDRESULTS

CSDEMathPractices(MP)in Blue toverifysignificance

ContentMathStateStandards:

8.EE.C: Analyzeandsolvelinearequationsand pairsofsimultaneouslinearequations.

8.EE.C.7: Solvelinearequationsinonevariable.

8.EE.C.7.A: Giveexamplesoflinearequationsin onevariablewithonesolution,infinitelymany solutions,ornosolutions.Showwhichofthese possibilitiesisthecasebysuccessively transformingthegivenequationintosimplerforms untilanequivalentequationoftheform`x=a`, `a=a`,or`a=b`results(where`a`and`b`are differentnumbers).

8.EE.C.7.B: Solvelinearequationswithrational numbercoefficients,includingequationswhose solutionsrequireexpandingexpressionsusingthe distributivepropertyandcollectingliketerms.

8.EE.C.8: Analyzeandsolvepairsofsimultaneous

● CRITICALTHINKING:Analyzedatainorderto drawconclusions. MP#2:Reasonabstractlyand quantitatively;MP#5:UseAppropriatetools strategically;MP#7:Lookforandmakeuseof structure.

linearequations.

8.EE.C.8.A: Understandthatsolutionstoasystem oftwolinearequationsintwovariablescorrespond topointsofintersectionoftheirgraphsbecause pointsofintersectionsatisfybothequations simultaneously.

8.EE.C.8.B: Solvesystemsoftwolinearequationsin twovariablesalgebraically,andestimatesolutions bygraphingtheequations.Solvesimplecasesby inspection.

8.EE.C.8.C: Solvereal-worldandmathematical problemsleadingtotwolinearequationsintwo variables.

Understandings

● Realisticsolutionstoequationsorsystems ofequationsrequireunderstandingofwhat real-worldscenariolookslikeregardlessof theform(i.e.,table,graph,oralgebraically)

● Leveragingtechnologytodemonstratethe relationshipbetweenequationsand systemsofequationscreatesadynamic representationofthereal-worldscenario forfurtherpossibilities.

Knowledge

● Howtoconstructandsolveequationsand systemsofequationstomodelreallife problems.

EssentialQuestions

● Howdoweconstructandsolvelinear equationsorsystemsoflinearequationsto makesenseofreal-worldproblems?

Skills(FramedasLearningTargets)

● Icanvisuallybalanceanequation.

● Icanmakesenseofmultiplewaystosolvean equation.

● Icansolveanequationwherethevariable appearsonbothsides.

● Icanuseanexpressionto findwhentwo things,likeheight,arethesameinareal-world situation.

● Icanexplainthesolutiontoasystemof equationsinareal-worldcontext.

● Icanexplainwhatasystemofequationsis.

● Icanmakegraphsto findanorderedpairthat tworeal-worldsituationshaveincommon.

● Icangraphasystemofequations.

● Icansolvesystemsofequationsusingalgebra.

● Icancalculateasolutiontoasystemof equationsincontext.

● Icanusethestructureofequationstohelpme figureouthowmanysolutionsasystemof equationshas.

● Icanidentifyandinterpretpointsthatsatisfy tworelationshipsatthesametimeusing graphs.

STAGE2:DETERMINEACCEPTABLEEVIDENCE

SummativeAssessment

EndofUnitAssessment

● Icanvisuallybalanceanequation.

○ Problem1

● Icanmakesenseofmultiplewaystosolve anequation.

○ Problem4

● Icansolveanequationwherethevariable appearsonbothsides.

○ Problem4

● Icanuseanexpressionto findwhentwo things,likeheight,arethesameina real-worldsituation.

○ Problem6

● Icanexplainthesolutiontoasystemof equationsinareal-worldcontext.

○ Problem6

● Icanexplainwhatasystemofequationsis.

○ Problem2

● Icanmakegraphsto findanorderedpair thattworeal-worldsituationshavein common.

○ Problem6

● Icangraphasystemofequations.

○ Problem3

● Icansolvesystemsofequationsusing algebra

○ Problem3

● Icancalculateasolutiontoasystemof equationsincontext.

○ Problem7

● Icanusethestructureofequationstohelp me figureouthowmanysolutionsasystem ofequationshas.

○ Problem3

FormativeAssessment

Grade8Unit4MidUnitAssessment

Ongoingassessments:IMsynthesis,cooldownsand practicedaysasappropriate.

Frayermodel(rationale)

● SolvingLinearequations

● SystemsofLinearEquations

STAGE3:LEARNINGPLAN

Previousmathconnections

Thefollowingconceptsfrompreviousgradesmay supportstudentsinmeetinggrade-levelstandards inthisunit:

● Applyingthedistributivepropertyto generateequivalentexpressions.(6.EE.A.3)

● Combiningliketermstogenerate equivalentexpressions.(6.EE.A.3,7.EE.A.1)

● Solvingproblemsbywritingandsolving equationswithvariablesononesideofthe equation.(6.EE.B.7,7.EE.B.4.a)

● Understandingwhatitmeansforavalueto beasolutiontoanequation.(6.EE.B.5)

Diagnosticassessmentquestions/problemsbasedon priorgradelevelexperience

FromReadinessCheck:

Studentswill firstsolvethetwoproblemsandbe preparedtosharetheirthinkingwithothers. Studentsthensharewithotherstosolidifythe conceptsofdistributivepropertyandnegative numbers.

FirstTopic:SolvingLinearEquations

LearningTargets:

● Icanvisuallybalanceanequation..

● Icanmakesenseofmultiplewaystosolve anequation.

● Icansolveanequationwherethevariable appearsonbothsides.

LearningActivities:

Estimated#ofLessons:12

EssentialQuestions:

● Howdoweconstructandsolvelinear equationsorsystemsoflinearequationsto makesenseofreal-worldproblems?

● Studentscreateandsolvenumberpuzzlesthatcanberepresentedbylinearequationsinone variable.

● Studentsusehangerdiagramstocalculateunknownweightsofobjectsbyaddingandremoving equalitemsfromeachside.

● Studentsmovefromusinghangerstousingequationstorepresentaproblem.

● Studentsreviewandcritiquesolvingstrategiesbeforesolvingcomplexequationsindependently.

● Studentsmovetowardgeneralmethodsforsolvinglinearequations.

● Studentscategorizelinearequationsinonevariablebasedontheirstructure,andsolveequations fromeachcategory.

● Studentsencounterequationsthathavenosolutionsandequationsforwhicheverynumberisa

solution.

● Studentsencounterequationsthathavenosolutionsandequationsforwhicheverynumberisa solution.

SecondTopic:SystemsofLinearEquations Estimated#ofLessons:8

LearningTargets:

● Icanuseanexpressionto findwhentwo things,likeheight,arethesameina real-worldsituation.

● Icanexplainthesolutiontoasystemof equationsinareal-worldcontext.

● Icanexplainwhatasystemofequationsis.

● Icanmakegraphsto findanorderedpair thattworeal-worldsituationshavein common.

● Icangraphasystemofequations.

● Icansolvesystemsofequationsusing algebra.

● Icancalculateasolutiontoasystemof equationsincontext.

● Icanusethestructureofequationstohelp me figureouthowmanysolutionsasystem ofequationshas.

LearningActivities:

EssentialQuestions:

● Howdoweconstructandsolvelinear equationsorsystemsoflinearequationsto makesenseofreal-worldproblems?

● Studentsinterpretpointsthatlieonone,both,orneitherlineonagraphoftwosimultaneous equationsincontext.

● Studentscreateandinterpretagraphoftwolinesincontext.

● Studentsunderstandthatsolvingasystemofequationsmeans findingvaluesofthevariablesthat makebothequationstrue.

● Studentssolveasystemofequationsusingalgebraicmethods.

● Studentsconsidertherelationshipbetweenthestructureoftheequationsinasystemandthe numberofsolutions.

● Studentsidentify,describe,andemploystrategiesforsolvinglinearsystemsofequationswith differentfeaturesorstructures.

UnitOverview:

Inthisunit,studentsareintroducedtotheconceptofafunctionasarelationshipbetweeninputsand outputs.ThistakesthembacktotheirGrade6explorationofindependentanddependentvariablesand asksthemtomakeconnectionstoinputsandoutputsofafunction.Studentsthenmanipulateequationsto isolatetheoutputtosolveformissingpartsoftheformula.

Thisfoundationalknowledgewillbedeepenedthroughoutmostoftheirhighschoolmathcurriculum.for

the firsttime,analyzerepresentationsoffunctions,andexaminefunctionsinthecontextofthevolumeof cylinders,cones,andspheres.

STAGE1:DESIREDRESULTS

ContentMathStateStandards:

8.F.A.1: Understandthatafunctionisarulethat assignstoeachinputexactlyoneoutput.Thegraph ofafunctionisthesetoforderedpairsconsisting ofaninputandthecorrespondingoutput.

8.F.A.2: Comparepropertiesoftwofunctionseach representedinadifferentway(algebraically, graphically,numericallyintables,orbyverbal descriptions).

8.F.A.3: Interprettheequation`y=mx+b`as definingalinearfunctionwhosegraphisastraight line.Giveexamplesoffunctionsthatarenotlinear.

8.F.B.4: Constructafunctiontomodelalinear relationshipbetweentwoquantities.Determine therateofchangeandinitialvalueofthefunction fromadescriptionofarelationshiporfromtwo`(x, y)`values,includingreadingthesefromatableor fromagraph.Interprettherateofchangeand initialvalueofalinearfunctionintermsofthe situationitmodels,andintermsofitsgraphora tableofvalues.

8.F.B.5: Describequalitativelythefunctional relationshipbetweentwoquantitiesbyanalyzinga graph(e.g.,wherethefunctionisincreasingor decreasing,linearornonlinear).Sketchagraphthat exhibitsthequalitativefeaturesofafunctionthat hasbeendescribedverbally.

8.G.C.9: Describequalitativelythefunctional relationshipbetweentwoquantitiesbyanalyzinga graph(e.g.,wherethefunctionisincreasingor decreasing,linearornonlinear).Sketchagraphthat exhibitsthequalitativefeaturesofafunctionthat hasbeendescribedverbally.

● COMMUNICATION:Createalogicaland evidence-basedargumenttosupportideas. MP #3Constructviableargumentsandcritiquethe reasoningofothers;MP#4Modelwith Mathematics;MP#6:Attendtoprecision.

● CRITICALTHINKING:Demonstrate flexibility anddeterminationwhensolvingproblems. MP#1 Makesenseofproblemsandpersevereinsolving them;MP#2ReasonAbstractlyand Quantitatively;MP#5Useappropriatetools strategically.

Modelingofreal-worldscenarios,withtheuseofa function,allowsforpredictionstobemadeinthe pastorinthefuture.

Knowledge

● Howtoconstructthemodelofafunction sothatpredictionscanbemadeby evaluatingthefunction.

● Howtousefunctionstodeterminevolume orgiventhevolumedetermineamissing dimension.

Howarefunctionsdefinedtomodelandpredict behaviorofreal-worldscenarios?

Skills(FramedasLearningTargets)

● Icanexplainthestrengthsandweaknessesof differentrepresentations.

● Icancompareinputsandoutputsoffunctions thatarerepresentedindifferentways.

● Icanusedatapointstomodelalinear function.

● Icandecidewhenalinearfunctionisagood modelfordataandwhenitisnot.

● Icanexplainthestorytoldbythegraphofa function.

● Ican findandinterpretpointsonthegraphof afunction.

● Icandeterminewhetherafunctionis increasingordecreasingbasedonwhetherits rateofchangeispositiveornegative.

● Icanexplainwhyagraphdoesordoesnot representafunction.

● Icanusepreciselanguagetodescribe functions(e.g.,“isafunctionof”or “determines”).

● Icanusedatapointstomodelalinear function.

● Icandecidewhenalinearfunctionisagood modelfordataandwhenitisnot.

● Icanexplainthestrengthsandweaknessesof differentrepresentations.

● Icancompareinputsandoutputsoffunctions thatarerepresentedindifferentways.

● Icanexplaintherelationshipbetweenthe volumeofaconeandthevolumeofacylinder.

● Icanusetheformulaforthevolumeofacone.

● Ican findmissinginformationaboutacylinder orconeifIknowitsvolumeandother information.

● Icancompareandcontraststrategiesfor findinginformationaboutaconeorcylinder.

● Icananalyzetherelationshipbetweenthe heightorradiusofacylinderanditsvolume.

● Icanexplainwhytherelationshipbetween heightandvolumeislinearbutthe relationshipbetweenradiusandvolumeis not.

STAGE2:DETERMINEACCEPTABLEEVIDENCE

SummativeAssessment

EndofUnitAssessment

● Icanexplainthestrengthsandweaknesses ofdifferentrepresentations.

○ Problem1

● Icancompareinputsandoutputsof functionsthatarerepresentedindifferent ways.

○ Problem1

● Icanusedatapointstomodelalinear function.

○ Problem1

● Icandecidewhenalinearfunctionisagood modelfordataandwhenitisnot.

○ Problem1

● Icanexplainthestorytoldbythegraphofa function.

○ Problem3

● Ican findandinterpretpointsonthegraph ofafunction.

○ Problem3

● Icandeterminewhetherafunctionis increasingordecreasingbasedonwhether itsrateofchangeispositiveornegative.

○ Problem3

● Icanexplainwhyagraphdoesordoesnot representafunction.

○ Problem5

● Icanusepreciselanguagetodescribe functions(e.g.,“isafunctionof”or “determines”).

○ Problem5

● Icanusedatapointstomodelalinear function.

○ Problem5

● Icandecidewhenalinearfunctionisagood modelfordataandwhenitisnot.

○ Problem5

● Icanexplainthestrengthsandweaknesses ofdifferentrepresentations.

○ Problem7

● Icancompareinputsandoutputsof functionsthatarerepresentedindifferent ways.

○ Problem7

FormativeAssessment

Grade8Unit5MidUnitAssessments(2)

Ongoingassessments:IMsynthesis,cooldownsand practicedaysasappropriate.

Frayermodel(rationale)

● IntroductiontoFunctions

● RepresentingandInterpretingFunctions

● Volume

● Icanexplaintherelationshipbetweenthe volumeofaconeandthevolumeofa cylinder.

○ Problem2

● Icanusetheformulaforthevolumeofa cone.

○ Problem2

● Ican findmissinginformationabouta cylinderorconeifIknowitsvolumeand otherinformation.

○ Problem4

● Icancompareandcontraststrategiesfor findinginformationaboutaconeor cylinder.

○ Problem4

● Icananalyzetherelationshipbetweenthe heightorradiusofacylinderandits volume.

○ Problem6

● Icanexplainwhytherelationshipbetween heightandvolumeislinearbutthe relationshipbetweenradiusandvolumeis not.

○ Problem6

PerformanceTask Charge!:

● Studentsuselinearfunctionstomodela real-worldsituation(MP4).Theyaregiven dataforarelationshipthatisalmostlinear, andfromthat,theydevelopalinearmodel. Theyusetheirmodeltomakepredictions andtodeterminewhetheralinear approximationisreasonableandforwhich valuesitwouldbereasonable.Students begintoseeboththevalueandthe limitationsoflinearmodels.Onesuch limitation—thatsomedatasetscannotbe modeledwellbyasingleline—leadsintothe nextlessonwherestudentsmodel nonlinearscenarioswithpiecewiselinear functions.

Understanding#1

LearningTarget#1

TransferSkills:CriticalThinkingand Communication

Previousmathconnections

STAGE3:LEARNINGPLAN

Thefollowingconceptsfrompreviousgradesmay supportstudentsinmeetinggrade-levelstandards inthisunit:

● Readingandplottingcoordinatepointson graphs.(6.NS.C.6.c)

● Calculatingtherateofchangeoflines. (7.RP.A.2.b,8.EE.B.5)

● Orderofoperationsandcalculation techniques(e.g.,evaluatingπ·42 ·7). (4.OA.A.3,6.EE.A.2.c)

● Workingwithdecimalsorfractions(e.g., usingtheequation ).(5.NF.B.4, ��= 4 3 π�� 3 5.NBT.B.5)

Diagnosticassessmentquestions/problemsbasedon priorgradelevelexperience

FromReadinessCheck:

Studentswill firstsolvethetwoproblemsandbe preparedtosharetheirthinkingwithothers. Studentsthensharewithotherstosolidifythe conceptsofwritingequationstorepresentthe relationshipbetweenquantitiesaswellas representationsofproportionalandnon-proportional relationships.

FirstTopic:IntroductiontoFunctions Estimated#ofLessons:6

LearningTargets:

● Icanexplainwhyagraphdoesordoesnot representafunction.

● Icanusepreciselanguagetodescribe functions(e.g.,“isafunctionof”or “determines”).

LearningActivities:

EssentialQuestions:

● Howarefunctionsdefinedtomodeland predictbehaviorofreal-worldscenarios?

● Studentsbegintomakeconnectionsbetweenscenariosandgraphsthatrepresentthem.

● Studentswriterulesbasedoninput-outputpairsrepresentedintables,andareintroducedtothe conceptoffunction.

● Studentsdeterminewhetherornotagraphrepresentsafunctionandexplaintheirreasoning.

● Studentsexploretherelationshipbetweenequationsandfunctions,andunderstandthatan equationmaylookdifferentdependingonhowtheindependentanddependentvariablesare defined.

SecondTopic:RepresentingandInterpreting Functions

LearningTargets:

● Icanexplainthestrengthsandweaknesses ofdifferentrepresentations.

● Icancompareinputsandoutputsof functionsthatarerepresentedindifferent ways.

● Icanusedatapointstomodelalinear function.

● Icandecidewhenalinearfunctionisagood modelfordataandwhenitisnot.

● Icanexplainthestorytoldbythegraphofa function.

● Ican findandinterpretpointsonthegraph ofafunction.

● Icandeterminewhetherafunctionis increasingordecreasingbasedonwhether itsrateofchangeispositiveornegative.

● Icanusedatapointstomodelalinear function.

● Icandecidewhenalinearfunctionisagood modelfordataandwhenitisnot.

● Icanexplainthestrengthsandweaknesses ofdifferentrepresentations.

● Icancompareinputsandoutputsof functionsthatarerepresentedindifferent ways.

LearningActivities:

Estimated#ofLessons:7

EssentialQuestions:

● Howarefunctionsdefinedtomodeland predictbehaviorofreal-worldscenarios?

● Studentsinterpretqualitativefeaturesofafunctionandspecificpointsincontext.Studentsalso considerthemeaningofrateofchangeovergivenintervals.

● Studentsdrawthegraphofafunctionthatrepresentsareal-worldsituation.

● Studentscompareandcontrastthreecalorie-burningrelationshipsrepresentedindifferentways.

● Studentsusedatapointstomodelalinearfunctionanddecidewhenitisreasonabletomodelthe relationshipwithalinearfunction.

● Studentsusepiecewisefunctionstomodelreal-worlddatasetspresentedasgraphs.

ThirdTopic:Volume

Estimated#ofLessons:9

LearningTargets:

● Icanexplaintherelationshipbetweenthe volumeofaconeandthevolumeofa cylinder.

● Icanusetheformulaforthevolumeofa cone.

● Ican findmissinginformationabouta cylinderorconeifIknowitsvolumeand otherinformation.

● Icancompareandcontraststrategiesfor findinginformationaboutaconeor cylinder.

● Icananalyzetherelationshipbetweenthe heightorradiusofacylinderandits volume.

● Icanexplainwhytherelationshipbetween heightandvolumeislinearbutthe relationshipbetweenradiusandvolumeis not.

LearningActivities:

EssentialQuestions:

● Howarefunctionsdefinedtomodeland predictbehaviorofreal-worldscenarios?

● Studentsestimatethevolumesofcylinders,cones,cubes,andspheres.

● Studentsexploreanduseastrategytocalculatethevolumeofacylinder.

● Studentsusefunctionstoexplorehowchangingacylinder’sradiusorheightimpactsitsvolume.

● Studentsrecognizethatthevolumeofaconeisthevolumeofacylinderwiththesameradiusand 1 3 thesameheight.

● Studentscalculatemissingdimensionsofcylindersandconesgiventheirvolumeandanother dimension.

● Studentsdevelopanduseaformulaforthevolumeofasphere.

UnitOverview:

Inthisunit,studentsbuildontheirpreviousexperienceinearlierunitswiththecoordinateplaneandlinear functionstofocusondataintwovariables.Theyusescatterplotsand fittedlinestoanalyzenumericaldata. Theyalsousetwo-waytables,bargraphsandsegmentedbargraphstoanalyzecategoricaldata.

ContentMathStateStandards:

8.SP.A.1: Constructandinterpretscatterplotsfor bivariatemeasurementdatatoinvestigatepatterns ofassociationbetweentwoquantities.Describe patternssuchasclustering,outliers,positiveor negativeassociation,andlinearassociationor nonlinearassociation.

8.SP.A.2: Knowthatstraightlinesarewidelyused tomodelrelationshipsbetweentwoquantitative variables.Forscatterplotsthatsuggestalinear association,informally fitastraightlineandassess themodel fitbyjudgingtheclosenessofthedata pointstotheline.

8.SP.A.3: Usetheequationofalinearmodelto solveproblemsinthecontextofbivariate measurementdata,interpretingtheslopeand intercept.

8.SP.A.4: Understandthatpatternsofassociation canalsobeseeninbivariatecategoricaldataby displayingfrequenciesandrelativefrequenciesina two-waytable.Constructandinterpretatwo-way tablesummarizingdataontwocategorical variablescollectedfromthesamesubjects.Use relativefrequenciescalculatedforrowsorcolumns todescribepossibleassociationbetweenthetwo variables.

Understandings

● Graphicalrepresentationsandstatistics allowustoidentifyandrepresentkey featuresofdata.

● Modelsmayallowustopredictresponses tochangesinavariable.

● COMMUNICATION:Createalogicaland evidence-basedargumenttosupportideas. MP #4ModelwithMathematics;MP#7Lookforand makeuseofstructure.

● CRITICALTHINKING:MP#1Makesenseof problemsandpersevereinsolvingthem; MP#2 ReasonAbstractlyandQuantitatively;MP#5Use appropriatetoolsstrategically.

EssentialQuestions

● HowdoIusemypriormathematical knowledgetodeepenmyconnectionsin statistics?

● Howcanyoudeterminetheeffectivenessofa linearmodel?

Knowledge Skills(FramedasLearningTargets)

● Howtorepresenttwovariabledatain multipleways(graphically,frequencytable, lists)

● Howtodescribetwovariabledata (direction,outliers,strength)

● Icanorganizedatatonoticepatternsmore clearly.(Foundational)

● Icancompareandcontrasttwodifferent waystodisplaydata(adotplotandascatter plot)(Foundational)

● Icanuserelativefrequenciesintablesandin segmentedbargraphstodecideifthereisan associationbetweentwovariables.

● Icanidentifyandrepresentthesamedatain bargraphsandintwo-wayfrequencytables.

● Icanuserelativefrequenciesintablesandin segmentedbargraphstodecideifthereisan associationbetweentwovariables.

● Icanexplainwhetherdatainascatterplothas apositiveassociation,anegativeassociation, orneither.

● Icaninterprettheslopeofaline fittodataina real-worldsituation.

● Icanuseascatterplottodecideiftwo variableshavealinearassociationandmake connectionstowhatthedatarepresents.

● Icanpickoutclustersindataandmake connectionstowhatthedatarepresents.

● Icanusealineof fittopredictvaluesnotin thedata.

● Icanidentifyoutliersonascatterplot.

● Icandrawalineto fitdatainascatterplot.

● Icandescribefeaturesofalinethat fitsdata well.

STAGE2:DETERMINEACCEPTABLEEVIDENCE

SummativeAssessment

EndofUnitAssessment

● Icanuserelativefrequenciesintablesand insegmentedbargraphstodecideifthere isanassociationbetweentwovariables.

○ Problem2

● Icanidentifyandrepresentthesamedata inbargraphsandintwo-wayfrequency tables.

○ Problem5

● Icanuserelativefrequenciesintablesand insegmentedbargraphstodecideifthere isanassociationbetweentwovariables.

○ Problem6

● Icanexplainwhetherdatainascatterplot hasapositiveassociation,anegative association,orneither.

○ Problem1

● Icaninterprettheslopeofaline fittodata inareal-worldsituation.

○ Problem1

● Icanuseascatterplottodecideiftwo variableshavealinearassociationand

FormativeAssessment

Grade8Unit6MidUnitAssessment

Ongoingassessments:IMsynthesis,cooldownsand practicedaysasappropriate.

Frayermodel(rationale)

● Organizingnumericaldata

● Analyzingnumericaldata

● Categoricaldata

makeconnectionstowhatthedata represents.

○ Problem3,4

● Icanpickoutclustersindataandmake connectionstowhatthedatarepresents.

○ Problem3,4

● Icanusealineof fittopredictvaluesnotin thedata.

○ Problem7

● Icanidentifyoutliersonascatterplot.

○ Problem7

● Icandrawalineto fitdatainascatterplot.

○ Problem7

● Icandescribefeaturesofalinethat fits datawell.

○ Problem7

PerformanceTask FindingAssociations

UsingDataDisplaystoFindAssociations

● Studentsuserelativefrequenciesdisplayed intablesandinsegmentedbargraphsto identifypossibleassociationsbetween variablesindatarelatedtothesinkingof theRMSTitanic.TransformationGolf:

Understanding#2 LearningTarget#3

TransferSkills:CriticalThinkingand Communication STAGE3:LEARNINGPLAN

Previousmathconnections

Thefollowingconceptsfrompreviousgradesmay supportstudentsinmeetinggrade-levelstandards inthisunit:

● Determiningtherateofchangeofalinear functiongiventwopoints.(8.F.B.4)

● Makingconnectionsbetweenalinear relationshipandacontext,including calculatingaunitrate.(6.RP.A.3.b,8.EE.B.6)

● Drawingbargraphsandinterpreting informationpresentedinabargraph. (2.MD.D.10,3.MD.B.3)

Diagnosticassessmentquestions/problemsbasedon priorgradelevelexperience

FromReadinessCheck:

FirstTopic:OrganizingNumericalData

LearningTargets:

● Icanorganizedatatonoticepatternsmore clearly.(Foundational)

● Icancompareandcontrasttwodifferent waystodisplaydata(adotplotanda scatterplot)(Foundational)

LearningActivities:

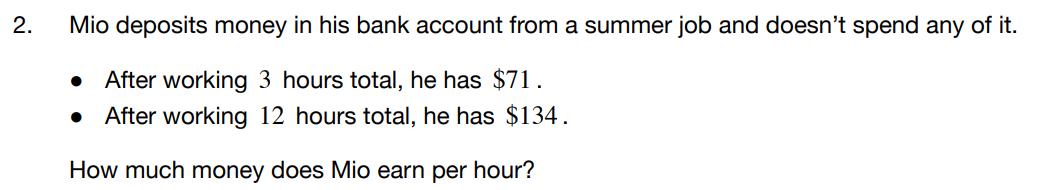
Studentswill firstsolvethetwoproblemsandbe preparedtosharetheirthinkingwithothers. Studentsthensharewithotherstosolidifythe conceptsofslopeofalinewhengiventwopointsand calculatingarateusingcontext.

Estimated#ofLessons:3

EssentialQuestions:

● Whatstatisticalmeasurementscouldbeused todescribeadataset?

● Howcanyoudeterminetheeffectivenessofa linearmodel?

● Studentsparticipateina"clicking"challengetogeneratedatathattheywillorganizeandthenuseto recognizepatternsandmakepredictions.

● Studentscompareandcontrastthesamedatarepresentedbyadotplotandbyascatterplot.

SecondTopic:AnalyzingNumericalData

LearningTargets:

● Icanexplainwhetherdatainascatterplot hasapositiveassociation,anegative association,orneither.

● Icaninterprettheslopeofaline fittodata inareal-worldsituation.

● Icanuseascatterplottodecideiftwo variableshavealinearassociationand makeconnectionstowhatthedata represents.

Estimated#ofLessons:8

EssentialQuestions:

● Howcanyoudeterminetheeffectivenessofa linearmodel?

● Icanpickoutclustersindataandmake connectionstowhatthedatarepresents.

● Icanusealineof fittopredictvaluesnotin thedata.

● Icanidentifyoutliersonascatterplot.

● Icandrawalineto fitdatainascatterplot.

● Icandescribefeaturesofalinethat fits datawell.

LearningActivities:

● Studentsinterpretpointsonascatterplotintermsofacontextandaddpointstoascatterplotgiven informationaboutanindividualinthepopulation.

● Studentsbegintoseeasetofdatapointsasasinglethingthatcanbeanalyzed,notjustabunchof disconnectedpoints.

● Studentspracticecreatinglinearmodelsthatmatchtheassociationofsetsofdata.

● Studentsinterprettheslopeofalineof fitincontext.

● Studentsvisualizeclusteringandassociationsindata.

● Studentsanalyzeandinterpretbivariatedataincontext.

ThirdTopic:CategoricalData

LearningTargets:

● Icanuserelativefrequenciesintablesand insegmentedbargraphstodecideifthere isanassociationbetweentwovariables.

● Icanidentifyandrepresentthesamedata inbargraphsandintwo-wayfrequency tables.

● Icanuserelativefrequenciesintablesand insegmentedbargraphstodecideifthere isanassociationbetweentwovariables.

LearningActivities:

Estimated#ofLessons:6

EssentialQuestions:

● Whatstatisticalmeasurementscouldbeused todescribeadataset?

● Studentsstudycategoricaldatadisplayedintwo-waytablesandinbargraphs.Thedifferent graphicalrepresentationshelpstudentsvisualizethefrequencies.

● Studentsuserelativefrequenciesdisplayedintablesandinsegmentedbargraphstoidentify possibleassociationsbetweenvariablesindatarelatedtothesinkingoftheRMSTitanic.

● Studentsusetwo-waytables,bargraphs,andsegmentedbargraphstodecidewhetherthereis evidenceofanassociationincategoricaldata.

UnitOverview: Inthisunit,studentsgain fluencywithexpressionsinvolvingexponents(anextensionof6thgrade)andnow

extendtopowersof`10`andscientificnotation.Then,theyperformoperationsonnumberswrittenin scientificnotation.Finally,theyapplytheseconceptstothebase-tensystemlearningaboutordersof magnitudeandscientificnotationtorepresentandcomputewithverylargeandverysmallquantities.

STAGE1:DESIREDRESULTS

EstablishedGoals

ContentMathStateStandards:

8.EE.A.1: Knowandapplythepropertiesofinteger exponentstogenerateequivalentnumerical expressions.

8.EE.A.3: Usenumbersexpressedintheformofa singledigittimesanintegerpowerof`10`to estimateverylargeorverysmallquantities,andto expresshowmanytimesasmuchoneisasthe other.

8.EE.A.4: Performoperationswithnumbers expressedinscientificnotation,includingproblems wherebothdecimalandscientificnotationare used.Usescientificnotationandchooseunitsof appropriatesizeformeasurementsofverylargeor verysmallquantities.Interpretscientificnotation thathasbeengeneratedbytechnology.

Understandings

● Rulesofexponentsallowustosimplify complexexpressions.

● ScientificNotationallowsustoworkwith verylargeorverysmallnumbersina manageablefashion.

Knowledge

● Howtouseexponentsandscientific notationtosolvereal-worldscenarios involvinglargeorsmallnumbers.

TransferGoals

CSDEMathPractices(MP)in Blue toverifysignificance

● COMMUNICATION:Createalogicaland evidence-basedargumenttosupportideas. MP #4ModelwithMathematics.

● CRITICALTHINKING:Demonstrate flexibility anddeterminationwhensolvingproblems. MP#1 Makesenseofproblemsandpersevereinsolving them;MP#2ReasonAbstractlyand Quantitatively.

● CRITICALTHINKING:Identifyaproblem,askkey questions,andmakepredictions. MP#5Use appropriatetoolsstrategically;MP#6Attendto precision;MP#7Lookforandmakeuseof structure;MP#8Lookforandexpressregularity inrepeatedreasoning.

EssentialQuestions

● Howcanrepresentingthesamemathematical relationshipindifferentwaysallowusto modelreal-worldscenariosandsolve problems?

Skills(FramedasLearningTargets)

● Icandescribewhatitmeansfortwo expressionswithexponentstobeequivalent.

● Icancreateequivalentexpressionswith exponents.

● Icanrewriteexpressionswithpositive exponentsasasinglepower.

● Icanexplainwhatitmeansforanumbertobe raisedtoazerooranegativeexponent.

● Icandetermineiftwoexpressionswith positive,zero,andnegativeexponentsare equivalent.

● Icandivideexpressionswithexponentsthat havethesamebase.

● IcanapplywhatIlearnedaboutpowersof10 toanswerquestionsaboutreal-world situations

● Icanrepresentlargeandsmallnumbersas multiplesofpowersof10usingnumberlines.

● Icanaddandsubtractnumbersgivenin scientificnotation.

● Icanusescientificnotationandestimationto compareverylargeorverysmallnumbers

● Icanmultiplyanddividenumbersgivenin scientificnotation.

● Icanusescientificnotationtocompare differentquantitiesandanswerquestions aboutreal-worldsituations.

STAGE2:DETERMINEACCEPTABLEEVIDENCE

SummativeAssessment

EndofUnitAssessment

● Icandescribewhatitmeansfortwo expressionswithexponentstobe equivalent.

○ Problem1

● Icancreateequivalentexpressionswith exponents.

○ Problem1

● Icanrewriteexpressionswithpositive exponentsasasinglepower.

○ Problem6

● Icanexplainwhatitmeansforanumberto beraisedtoazerooranegativeexponent.

○ Problem6

● Icandetermineiftwoexpressionswith positive,zero,andnegativeexponentsare equivalent.

○ Problem6

● Icandivideexpressionswithexponents thathavethesamebase.

○ Problem6

● IcanapplywhatIlearnedaboutpowersof 10toanswerquestionsaboutreal-world situations

○ Problem2

● Icanrepresentlargeandsmallnumbersas multiplesofpowersof10usingnumber

FormativeAssessment

Grade8Unit7MidUnitAssessment

Ongoingassessments:IMsynthesis,cooldownsand practicedaysasappropriate.

Frayermodel(rationale)

● ExponentRules

● ScientificNotation

lines.

○ Problem4

● Icanaddandsubtractnumbersgivenin scientificnotation.

○ Problem3

● Icanusescientificnotationandestimation tocompareverylargeorverysmall numbers

○ Problem5

● Icanmultiplyanddividenumbersgivenin scientificnotation.

○ Problem5

● Icanusescientificnotationtocompare differentquantitiesandanswerquestions aboutreal-worldsituations.

○ Problem7

PerformanceTask

WriteaRule:

● Studentswriterulesforsimplifying exponentialexpressions.

Understanding#1

LearningTargets#8

TransferSkills:CriticalThinkingand Communication

StarPower:

● Inthisunit-culminatinglesson,studentsuse scientificnotationasatoolforcomparing, combining,andoperatingonthenetworth ofdifferentcelebrities.Studentsidentify theessentialfeaturesofthequestionsand reasonquantitativelyandabstractlyin ordertoanswerthemincontext(MP2, MP4).

Understanding#1

LearningTargets#9,10,11,12

TransferSkills:CriticalThinkingand Communication

STAGE3:LEARNINGPLAN

Previousmathconnections

Thefollowingconceptsfrompreviousgradesmay

Diagnosticassessmentquestions/problemsbasedon priorgradelevelexperience

supportstudentsinmeetinggrade-levelstandards inthisunit:

● Writingandevaluatingnumerical expressionsinvolvingwhole-number exponents.(6.EE.A.1)

● Multiplyinganddividingmulti-digitwhole numbersanddecimals.(6.NS.B.2,6.NS.B.3)

● Reading,writing,andcomparingdecimals. (5.NBT.A.3)

FromReadinessCheck:

Studentswill firstsolvethetwoproblemsandbe preparedtosharetheirthinkingwithothers. Studentsthensharewithotherstosolidifythe conceptsofestimation,placevalue,decimalsand quotients.

FirstTopic:ExponentRules

LearningTargets:

● Icandescribewhatitmeansfortwo expressionswithexponentstobe equivalent.

● Icancreateequivalentexpressionswith exponentsthathavethesamebase.

● Icanrewriteexpressionswithpositive exponentsasasinglepower.

● Icanexplainwhatitmeansforanumberto beraisedtoazerooranegativeexponent.

● Icandetermineiftwoexpressionswith

Estimated#ofLessons:9

EssentialQuestions:

● Howcanrepresentingthesamemathematical relationshipindifferentwaysallowusto modelreal-worldscenariosandsolve problems?

positive,zero,andnegativeexponentsare equivalent.

LearningActivities:

● Studentsreviewtheconceptsofwholenumberexponents

● Studentsdiscoverwaystowriteequivalentexponentialexpressionsinvolvingtheproductofpowers andpowersofpowers.

● Studentslookforandmakeuseofstructuretoidentifyequivalentexponentexpressionsthatuse powersofpowersandproductsofpowers.

● Studentsrewriteproductsofpowers,quotientsofpowers,andpowersofpowersassinglepowers.

● Studentsdevelopanunderstandingofthemeaningofzeroandnegativeexponents.

● Studentswriterulesforsimplifyingexponentialexpressions.

SecondTopic:ScientificNotation

LearningTargets:

● Icandivideexpressionswithexponents thathavethesamebase.

● IcanapplywhatIlearnedaboutpowersof 10toanswerquestionsaboutreal-world situations

● Icanrepresentlargeandsmallnumbersas multiplesofpowersof10usingnumber lines.

● Icanaddandsubtractnumbersgivenin scientificnotation.

● Icanusescientificnotationandestimation tocompareverylargeorverysmall numbers.

● Icanmultiplyanddividenumbersgivenin scientificnotation.

● Icanusescientificnotationtocompare differentquantitiesandanswerquestions aboutreal-worldsituations.

LearningActivities:

Estimated#ofLessons:10

EssentialQuestions:

● Howcanrepresentingthesamemathematical relationshipindifferentwaysallowusto modelreal-worldscenariosandsolve problems?

● Studentsrepresentlargeandsmallnumbersusingmultiplesofpowersof10.

● Studentsusenumberlinestorepresentlargeandsmallnumbersasmultiplesofpowersof10.

● Studentsapplypowersof10andexponentrulestosolveproblemsincontext.

● Studentsusescientificnotationtoexpressverylargenumbersandverysmallnumbers.

● Studentsmultiplyanddividenumbersexpressedinscientificnotation,andexpresshowmanytimes asmuchonequantityisastheother.

● Studentsaddandsubtractnumbersexpressedinscientificnotationandexpresstheresultingsums anddifferencesinscientificnotation.

● Studentsusescientificnotationasatoolforcomparing,combining,andoperatingonthenetworth ofdifferentcelebrities.

CourseName:Grade8Unit8Title:PythagoreanTheoremandIrrationalNumbers Est.#ofLessons:20

UnitOverview:

Inthisunit,studentsexplorethePythagoreantheoremanddifferenttypesofnumbers(squarerootsand cuberoots,rationalandirrationalnumbers).Thisdeepenstheirmathematicalunderstandingthatthereare irrationalsolutionstoproblemsandhowthatimpactsrealworldscenarios. STAGE1:DESIREDRESULTS EstablishedGoals

ContentMathStateStandards:

8.EE.A.2: Usesquarerootandcuberootsymbolsto representsolutionstoequationsoftheform �� 2 =�� and,where`p`isapositiverationalnumber. �� 3 =�� Evaluatesquarerootsofsmallperfectsquaresand cuberootsofsmallperfectcubes.Knowthatis 2 irrational.

8.G.B: UnderstandandapplythePythagorean theorem.

8.G.B.6: ExplainaproofofthePythagorean theoremanditsconverse.

8.G.B.7: ApplythePythagoreantheoremto determineunknownsidelengthsinrighttriangles inreal-worldandmathematicalproblemsintwo andthreedimensions.

8.G.B.8: ApplythePythagoreantheoremto findthe distancebetweentwopointsinacoordinate system.

8.NS.A: Knowthattherearenumbersthatarenot rationalandapproximatethembyrational numbers.

8.NS.A.1: Knowthatnumbersthatarenotrational arecalledirrational.Understandinformallythat everynumberhasadecimalexpansion.Forrational numbers,showthatthedecimalexpansionrepeats eventually,andconvertadecimalexpansionwhich repeatseventuallyintoarationalnumber.

● COMMUNICATION:Createalogicaland evidence-basedargumenttosupportideas. MP #4ModelwithMathematics;MP#7Lookforand makeuseofstructure.

● CRITICALTHINKING:Identifyaproblem,askkey questions,andmakepredictions. MP#2Reason AbstractlyandQuantitatively;MP#3Construct viableargumentsandcritiquethereasoningof others;MP#5Useappropriatetoolsstrategically.

● CRITICALTHINKING:Demonstrate flexibility anddeterminationwhensolvingproblems. MP#1 Makesenseofproblemsandpersevereinsolving them;MP#2Reasonabstractlyandquantitatively; MP#4Modelwithmathematics.

8.NS.A.2: Userationalapproximationsofirrational numberstocomparethesizeofirrationalnumbers, locatethemapproximatelyonanumberline diagram,andestimatethevalueofexpressions.

Understandings

Irrationalnumbersallowustosolvereal-world problemsinvolvingroots.

Knowledge

● Howtosolvereal-worldproblemsinvolving squareandcuberoots.

● HowtousethePythagoreanTheoremto solveformissingsidelengthsinright triangles.

EssentialQuestions

Whatroledoirrationalnumbersplayassolutionsto real-worldscenarios?

Skills(FramedasLearningTargets)

● Icanexplainthemeaningofacuberoot,like ,intermsofitsedgelengthandvolume. 35

● Icanidentifythetwowholenumbersacube rootisbetweenandexplainwhy.

● Icanwritearepeatingdecimalasafraction.

● Iunderstandthateverynumberhasadecimal expansion.

● Iknowwhatarationalnumberisandcangive anexample.

● Iknowwhatanirrationalnumberisandcan giveanexample.

● Icanplotsquarerootsonanumberline.

● Icanidentifythetwowholenumbersasquare rootisbetweenandexplainwhy.

● Icanexplainwhyitistruethatiftheside lengthsofatrianglesatisfytheequation thenitmustbearighttriangle �� 2 +��2 =�� 2

● Icandeterminewhetheratriangleisaright triangleifIknowitssidelengths.

● Icanidentifywhichsideisthehypotenuseand whichsidesarethelegsinarighttriangle.

● IcanusethePythagoreantheoremto find unknownsidelengthsinrighttriangles.

● Icancalculatethedistancebetweentwo pointsinthecoordinateplane.

● Icancalculatethelengthofadiagonalline segmentinthecoordinateplane.

● IcanusethePythagoreantheoremtosolve problems.

● Icanexplainthemeaningofacuberoot,like ,intermsofitsedgelengthandvolume.

35

○ Problem1

● Icanidentifythetwowholenumbersacube rootisbetweenandexplainwhy.

○ Problem1

● Icanwritearepeatingdecimalasafraction.

○ Problem3

● Iunderstandthateverynumberhasa decimalexpansion.

○ Problem3

● Iknowwhatarationalnumberisandcan giveanexample.

○ Problem3

● Iknowwhatanirrationalnumberisandcan giveanexample.

○ Problem3

● Icanplotsquarerootsonanumberline.

○ Problem5

● Icanidentifythetwowholenumbersa squarerootisbetweenandexplainwhy.

○ Problem5

● Icanexplainwhyitistruethatiftheside lengthsofatrianglesatisfytheequation thenitmustbearight �� 2 +��2 =�� 2 triangle.

○ Problem2

● Icandeterminewhetheratriangleisaright triangleifIknowitssidelengths.

○ Problem2

● Icanidentifywhichsideisthehypotenuse andwhichsidesarethelegsinaright triangle.

○ Problem4

● IcanusethePythagoreantheoremto find unknownsidelengthsinrighttriangles.

○ Problem4

● Icancalculatethedistancebetweentwo pointsinthecoordinateplane.

○ Problem6

● Icancalculatethelengthofadiagonalline segmentinthecoordinateplane.

○ Problem6

● IcanusethePythagoreantheoremtosolve problems.

○ Problem7

Ongoingassessments:IMsynthesis,cooldownsand practicedaysasappropriate. Frayermodel(rationale)

● Squarerootsandcuberoots

● ThePythagoreanTheorem

● Rationalandirrationalnumbers

PerformanceTask

PondHopperFindingDistancesintheCoordinate Plane StudentscontinuetoapplythePythagorean theoremto finddistancesbetweenpointsinthe coordinateplane:

● Studentsidentifyanddescribesequences oftransformationsthattakeone figureto anotherinthecontextofseveral TransformationGolfchallenges.

Understanding:

● Irrationalnumbersallowustosolve real-worldproblemsinvolvingroots. LearningTargets

● Icancalculatethedistancebetweentwo pointsinthecoordinateplane.

● Icancalculatethelengthofadiagonalline segmentinthecoordinateplane.

● IcanusethePythagoreantheoremtosolve problems.

TransferSkills:CriticalThinkingand Communication

Previousmathconnections

Thefollowingconceptsfrompreviousgradesmay supportstudentsinmeetinggrade-levelstandards inthisunit:

● Writingandevaluatingnumerical expressionsinvolvingwhole-number exponents.(6.EE.A.1)

● Reading,writing,andcomparingdecimals. (5.NBT.A.3)

● Calculatingtheareasofrighttrianglesand otherpolygons.(6.G.A.1)

● Determiningdistancesinthecoordinate plane.(6.G.A.3)

Diagnosticassessmentquestions/problemsbasedon priorgradelevelexperience

FromReadinessCheck:

STAGE3:LEARNINGPLAN

FirstTopic:SquareRootsandCubeRoots

LearningTargets:

● Icanexplainthemeaningofacuberoot,like ,intermsofitsedgelengthandvolume. 35

Problem1

● Icanidentifythetwowholenumbersacube rootisbetweenandexplainwhy.Problem1

● Icanplotsquarerootsonanumberline. Problem5

● Icanidentifythetwowholenumbersa squarerootisbetweenandexplainwhy. Problem5

LearningActivities:

Studentswill firstsolvethetwoproblemsandbe preparedtosharetheirthinkingwithothers. Studentsthensharewithotherstosolidifythe conceptsofcalculatingdistancebetweentwopoints andcalculatingsquaresandcubesofrational numbers.

Estimated#ofLessons:8

EssentialQuestions:

● Whatroledoirrationalnumbersplayinthe solutionstoreal-worldscenarios?

● Studentsestimatesidelengthsofsquareswithknownareasandreviewstrategiesforcalculating areas.

● Studentsdevelopanunderstandingofsquarerootsandsquarerootnotation.

● Studentsapproximatethevalueofsquarerootsbydeterminingthetwointegervaluesitlies betweenandbydrawingasquare.

● Studentslearnaboutrepresentingasquarerootasapointonanumberline.

● Studentsexploretherelationshipbetweentheedgelengthandthevolumeofacube.

SecondTopic:ThePythagoreanTheorem

LearningTargets:

● Icanexplainwhyitistruethatiftheside lengthsofatrianglesatisfytheequation

● thenitmustbearight �� 2 +��2 =�� 2 triangle.Problem2

● Icandeterminewhetheratriangleisaright triangleifIknowitssidelengths. Problem2

● Icanidentifywhichsideisthehypotenuse andwhichsidesarethelegsinaright triangle. Problem4

● IcanusethePythagoreantheoremto find unknownsidelengthsinrighttriangles. Problem4

● Icancalculatethedistancebetweentwo

Estimated#ofLessons:7

EssentialQuestions:

● Whatroledoirrationalnumbersplayinthe solutionstoreal-worldscenarios?

pointsinthecoordinateplane. Problem6

● Icancalculatethelengthofadiagonalline segmentinthecoordinateplane. Problem6

● IcanusethePythagoreantheoremtosolve problems. Problem7

LearningActivities:

● Studentsidentifypatternsintherelationshipbetweenthesquaresofsidelengthsoftrianglesand learnthattherelationshipbetweenthesidelengthsofarighttriangleisthePythagoreantheorem.

● StudentsstudyadiagramthattheywillusetoprovethePythagoreantheoremandthenapplythe Pythagoreantheoremintherestofthelesson.

● StudentspracticeusingthePythagoreantheoremtocalculatesidelengthsofrighttriangles.

● StudentsdevelopandapplytheirunderstandingoftheconverseofthePythagoreantheorem.

● StudentsusethePythagoreantheoremasatooltosolveproblemsinvolvingdiagonaldistances.

● StudentsapplythePythagoreantheoremto finddistancesbetweenpointsinthecoordinateplane.

STAGE3:LEARNINGPLAN

ThirdTopic:RationalandIrrationalNumbers Estimated#ofLessons:5

LearningTargets:

● Icanwritearepeatingdecimalasafraction.

● Iunderstandthateverynumberhasa decimalexpansion.

● Iknowwhatarationalnumberisandcan giveanexample.

LearningActivities:

EssentialQuestions:

● Whatroledoirrationalnumbersplayinthe solutionstoreal-worldscenarios?

● Studentsexploreconnectionsbetweenunitfractionsandtheirdecimalrepresentationsusinglong divisiontoconvertfractionstodecimals.

● Studentsdevelopastrategyforrewritingrepeatingdecimalsasfractions.

● Studentsbuildontheirworkwithsquareroots,fractions,anddecimalrepresentationsto understandirrationalnumbers.