5.4 Loh. Constructing a Very Special Circle through Six Very Special Points

5.4 Loh. Constructing a Very Special Circle through Six Very Special Points 55

References [1] Quantum Physics Lady. What is wave function collapse? is it a physical event? 2020. URL: http : / / www . quantumphysicslady . org / what is - wave - function - collapse - is - it - a physical- event/ (cited on page 54).

5.4 Constructing a Ver y Special Circle through Six Ver y Special Points (ft. weird angle chasing and magical tornadoes)

By Vivian Loh ’24

noindent The following proof is the proof of Lemma 3.11 in the book EGMO [1]

“The Nine-Point Circle"

What the heck even is that diagram?

First of all, given a triangle, these three blue lines are the altitudes, AKA the lines from opposite corners forming 90 degree angles with the sides.

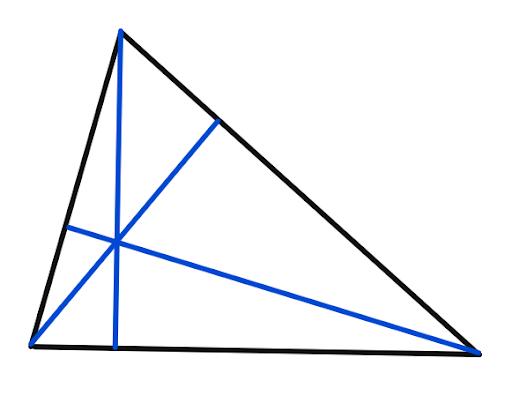
And these three red points are the midpoints of the sides.

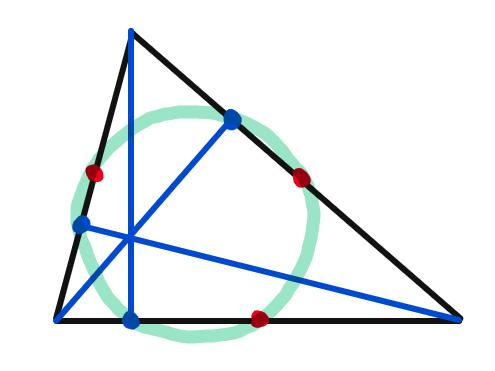
We claim that there is a circle passing through the 3 blue points AND the 3 red points, like this:

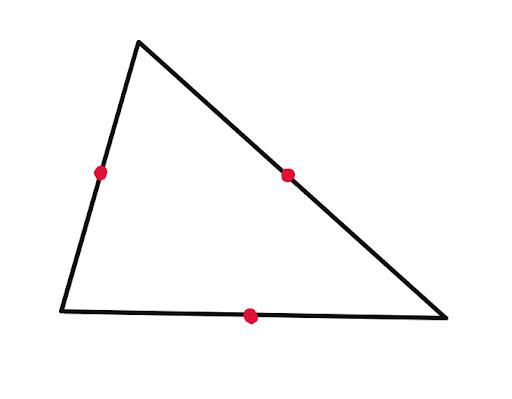
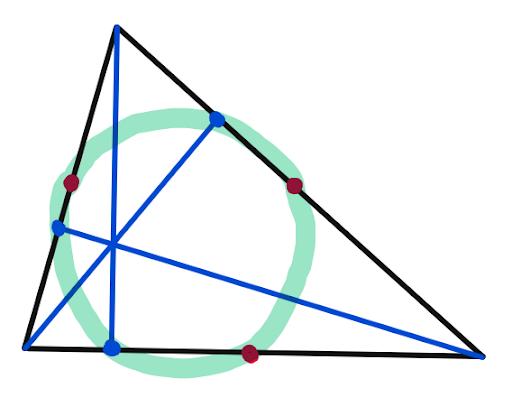
(Not all sets of 6 points can have a circle drawn through them, for example these 6 points do not.)

56

First, we can draw a circle through the vertices of the triangle, like this:

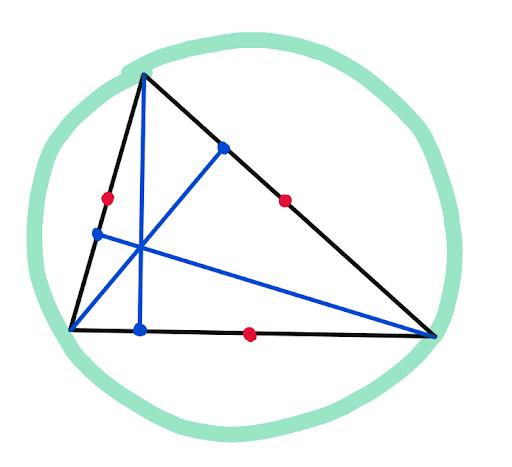
This is called the circumcircle of the big triangle. Now we make the following claim:

Claim 1: The reflections of the intersection of the blue lines over the 3 sides lie on the circumcircle.

“Intersection of the blue points” is just a fancy name for this purple point in the middle. Chapter 5. Mathematics

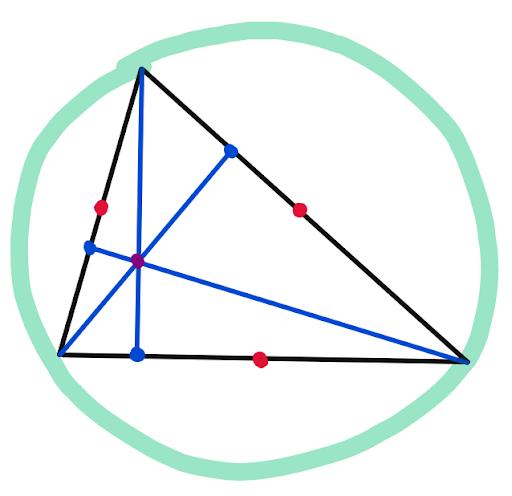
So we just want to show that the yellow triangles, which are just reflections of the purple triangles, also have vertices lying on the circumcircle.

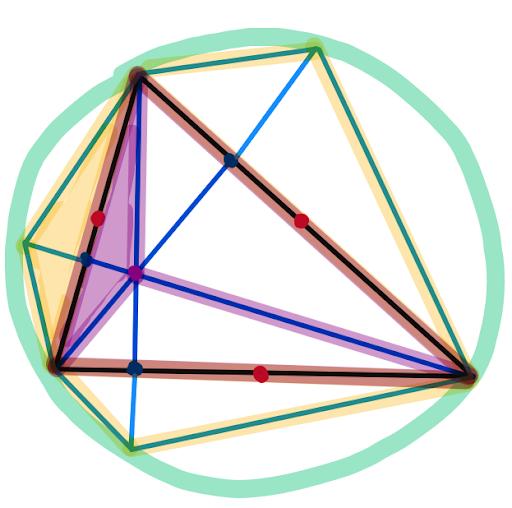
Now we’ll do a bit of geometry, using a technique called angle chasing. It is known that if you have 4 lines such that the blue angles are equal, then we can draw a circle through these 4 points:

5.4 Loh. Constructing a Very Special Circle through Six Very Special Points 57

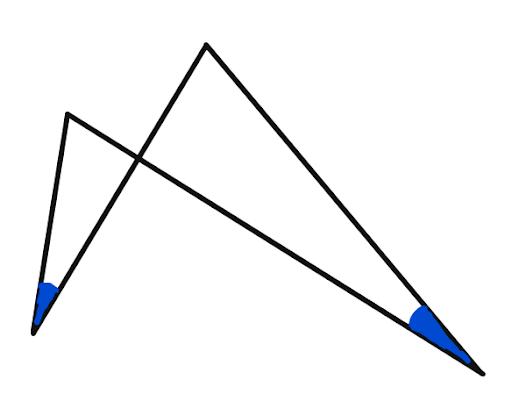
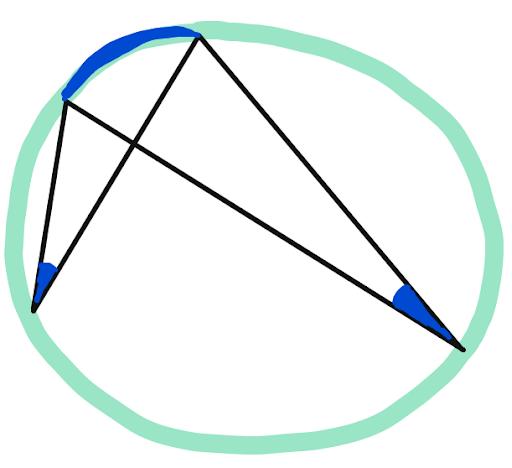
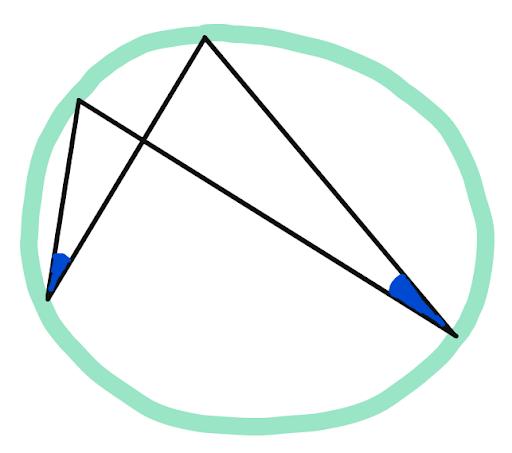
This is because of the Inscribed Angle Theorem, which says that the arc inscribed by an angle has twice the measure of the angle. And both of these angles inscribe the same arc of the circle:

Now back to the original problem. Because the altitudes create right triangles, the blue angles have measures equal to 90 degrees minus the red angles, correct?

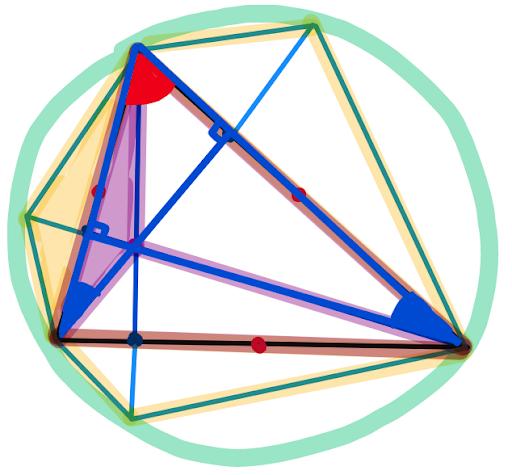
And since the yellow triangle is just a reflection of the purple triangle, this third angle is also blue:

58

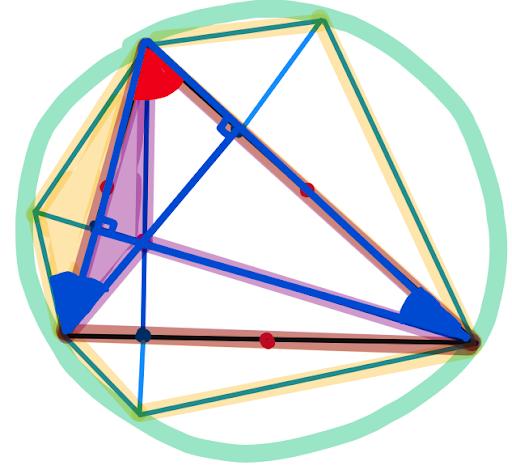
Now we just use the fact we proved earlier: Since these two angles are both blue, there is a circle drawn through the 3 vertices of the triangle and one of the yellow reflection points!

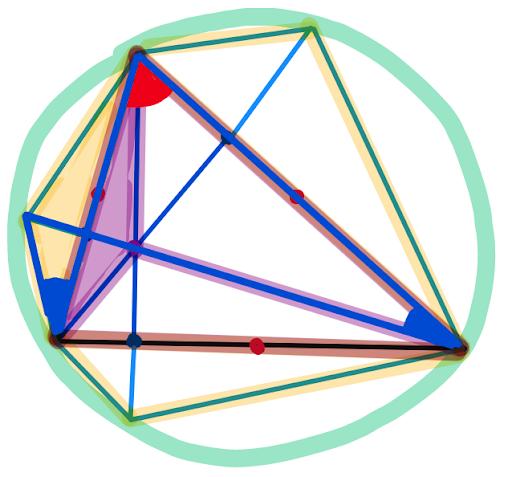
Applying this to the other 2 reflection points, we have shown that all three yellow reflection points lie on the circumcircle! Good news: We’re basically done with the geometry.

Claim 2: The reflections of the intersection of the blue lines over the red points also lie on the circumcircle.

This is much easier now that we know Claim 1 is true. Chapter 5. Mathematics

When you reflect a triangle over the midpoint of one side, you get a parallelogram.

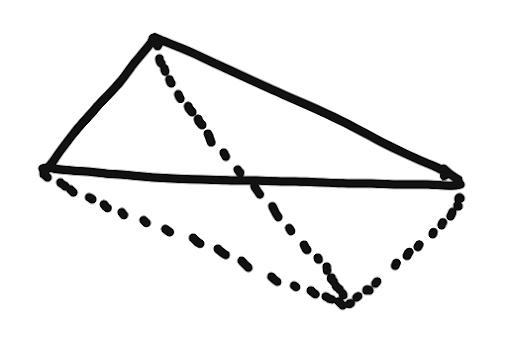
So, the reflection of the original triangle over the midpoint (purple triangle) is just the reflection of the green triangle over the perpendicular bisector of the horizontal segment.

And clearly, if the 3rd vertex of the green triangle lies on the circumcircle, then so must the purple triangle, because of symmetry.

5.4 Loh. Constructing a Very Special Circle through Six Very Special Points 59

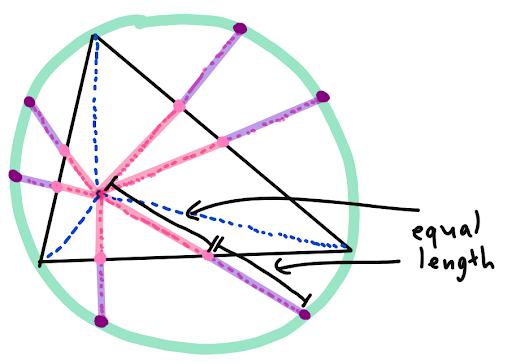
So, the reflections of the intersection of the blue lines over the midpoints of the sides lie on the circumcircle, too, and Claim 2 is proven!

Now for the punchline:

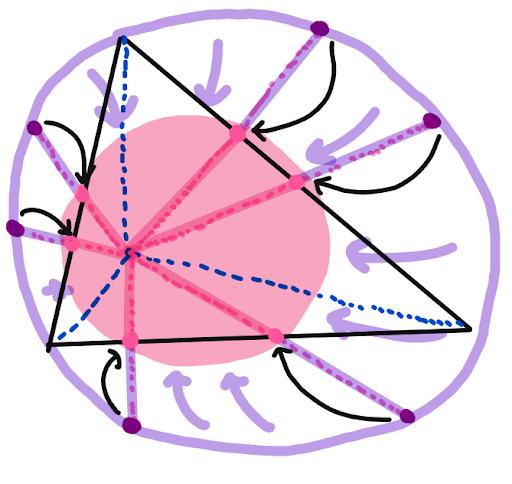
Which means we can “shrink” the green circle down by a factor of two, AT the intersection of the blue lines, almost like a magical tornado-like vortex. The purple points will “travel” to the pink points, and we end up with the following overcomplicated diagram:

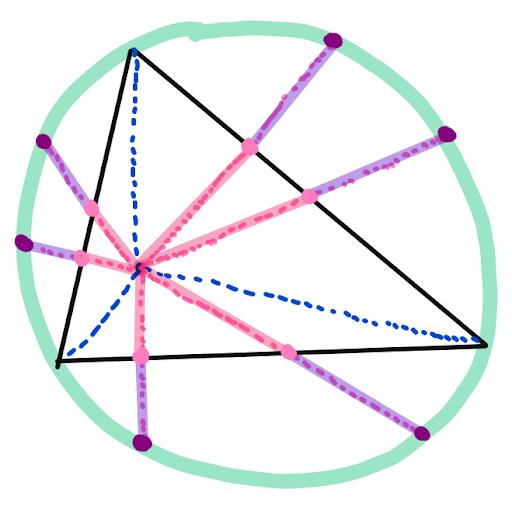
Look at this diagram here: The reflections of the intersection of the blue lines over all six pink points are the purple points, which lie on the green circle. Thus the pink segments and their corresponding purple segments are the same length, as shown:

So because every point in the diagram is “mapped” to a point half as far from the “origin”, which is the intersection of the blue lines, the purple circle (the circumcircle) “maps” to a circle passing through all six pink points, so indeed, the six points lie on a circle, as desired!!!

Reference [1] Evan Chen. Euclidean Geometry in Mathematical Olympiads. MAA Press, 2016 (cited on page 55).