5.6 Simhan, Bandi. The Fermi Estimate

5.6 Simhan, Bandi. The Fermi Estimate 63

5.6 The Fermi Estimate

By Jay Simhan ’23 and Kush Bandi ’22

Abstract

Many questions have been proposed which are physically unanswerable by our current technology. Often, scientists and mathematicians have no basis or starting point on how to proceed in answering a certain question. However, having the ability to make educated and justified guesses is extremely significant in nearly all fields involving numbers. These are Fermi Problems and their solutions are counter-intuitive. The more estimates one makes regarding a certain proposition, the further they approach the true answer. The solutions to Fermi Problems involve several calculus-based concepts. Specifically, functions and equations that fluctuate around a certain value, which then converge to that value, exemplify the premise behind why Fermi Problems are equatable. Through our analysis of converging functions representing error in estimations, we exhibit how the nature of educated estimations concentrates to a single value as extra guesses are added. Though most Fermi Problems are generally not provable by current data, those which have been mathematically computed result in values extremely close to the estimates made in solving with minimal real data. These types of accurate estimations can help further humanity’s knowledge on abstract concepts we have yet to understand, and can potentially allow us to progress further in all regards.

Introduction

Have you ever wondered how many piano tuners there are in Chicago? Probably not - but how would one go about answering such a proposition? An approximation could be severely incorrect, acutely precise, or anywhere in between. These types of indeterminable problems which can’t be determined by mathematical or scientific deduction are known as Fermi Problems [3].

Enrico Fermi, whom these questions are named after, was known for having the ability to make extremely approximate calculations with minimal data [3]. He solved these problems by making numerous justified and educated guesses about quantities. Figure 1: Enrico Fermi [4]

The reason Fermi’s estimations work in these problems is because the approximations of individual terms are generally close to correct, and the overestimates and underestimates help cancel each other out. Broadly, if bias is excluded, a Fermi calculation that involves calculations on several levels of different approximations will continuously become more accurate, and eventually will be more accurate than first supposed.

This paper will discuss the theory behind Fermi Problems, famous examples and solutions to these problems, and finally, the mathematical notation and calculations proving why infinite Fermi estimates result in accurate determinations of seemingly unanswerable questions.

Methods/problems The most noted example of Fermi’s Estimate comes from the question posed above – how many piano tuners are there in Chicago [1]? To take on this broad yet oddly specific inquiry, let us start with something a little bit easier to grasp. How many people are in Chicago? We don’t know the exact number, but we could assume somewhere between 2 and 3 million since it is probably less than one-third of the New York population (Which is somewhere around 8.5 million). Lets assume there are 2.5 million people in Chicago. An average household has about 4 people, so we can say there are about 625,000 households in Chicago. Of course not all households have pianos, so let us assume 1 5 houses has a piano. This gives us about 125,000 pianos in Chicago. Pianos need to be tuned about once a year, so we need to find how many people it takes to service all 125,000 pianos per year. Consider a piano tuner who works full time. They

64 Chapter 5. Mathematics

could likely tune about 3 pianos a day, and work a 5 day week. This would be about 15 pianos tuned per day, multiplied by 50 weeks (let us take two off for vacation days, sick days, or other absences) to get 750 pianos tuned per year. Divide the number of pianos in Chicago that we calculated earlier (125,000) by the number of pianos serviced per year for every one piano tuner (750) and we get about 167 piano tuners in Chicago. Here, we have no way of checking if this is absolutely correct, but the goal is to understand the magnitude and proportion of the answer using common sense alone.

To summarize the equation described above, consider:

Pre-calculating the number of pianos a piano tuner could service each year:

3 days · 5 days/week · 50 weeks = 750 pianos tuned per year

Next, using the calculation above with the other estimations supposed earlier:

Number of households 2, 500, 000 4

Households with pianos 1 5 ≈ 167 piano tuners in Chicago

Pianos tuned per year 1 750

We used a series of parameters increasing in specificity in our estimate to narrow down our number into something more realistic and likely to occur. As seen above, the more restrictions we put on the number, the closer to correct (or the correct magnitude) our estimate became. This phenomenon seems to be counter intuitive –how can more numbers result in a more accurate estimate?

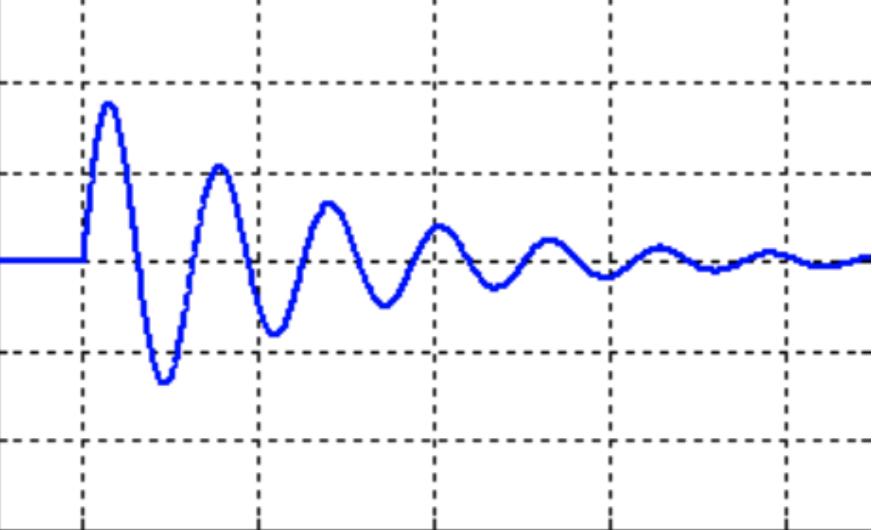
Figure 2: Positive and Negative Errors Converging to 0 [2]

This curve seen in Figure 2 is known as a decaying sine wave, and helps represent the errors accumulated while solving a Fermi Problem. By taking the integral from 0 to infinity of the decaying sine wave, we get 0. The individual waves in the curve represent positive or negative error in an estimated guess, and the graph exemplifies that infinite guesses result in an overall error of 0, equating to a hyper-accurate result.

We see this occurrence in calculus as well, in something called a converging series. In this series, an infinite sum of positive and negative values add to approximately 0. If we call each of these values an “error" in our estimate, the converging series shows that the more numbers totalling to the overall sum, the more accurately the function approaches its true value. Say we assume 1 million people live in Chicago– an underestimate. Then, we assume 6 people live in each household on average–an overestimate. Eventually, as modeled by the series pictured above, these positive and negative errors will even out to an approximation of the correct magnitude and near-correct value [3]. The ability to balance out errors by increasing the number of parameters seems illogical, but with calculus we can see that Fermi’s Estimate follows a similar pattern [5]. Fermi’s method of understanding bypasses complex mathematical calculations for “unsolvable" scientific questions and instead uses conceptual theories to narrow down guesses to a fairly accurate estimation.

Conclusion While you may not need to know how many piano tuners are in Chicago at any given moment, Fermi’s Estimate can be helpful for any excessively difficult calculations at hand in which data and measurements are not an option. Although Fermi calculations are not acutely precise (due to non-infinite amounts of estimations), this analysis often produces results that are beneficial for many purposes. For example, if you wanted to pursue piano tuning in Chicago, the general estimate of competing businesses may be enough information. If the lack of precision is too risky, the value attained using this estimate at least provides a better understanding of where to look for more precise answers – perhaps our errors were made in the approximate number of pianos in the city, and that is something that we could look further into for details. Despite the “unsolvable" nature of Fermi Problems, the ability to calculate a value that would be impossible with true mathematical methods is significant due to the accuracy with minimal real data and limited substantial knowledge of the subject. Now, with the knowledge of this fascinating concept, consider a question that could have true environmental impact (if it was possible to plant that many trees): how many trees would need to be planted to lower the average global temperature by one degree?