Cracking Muon G-2 Using Mimicry to Solve

Cracking Muon g-2

Andy Yin

The date is February 25 of this year. 170 physicists gather in a Zoom call and intently watch two of their number rip open an envelope.

Both of them hold up a sheet of paper to the screen. Each has the same number written on it - a number that has been kept secret for three years. Someone else types it into a formula in Python, and a single graph appears on the screen. There are just four points on it - it seems like too little to get excited over - but the call erupts into applause in an instant.

What these physicists were waiting to see is a quantity called the muon g-2. Their anticipation is well justified - their efforts to measure it have been nine years in the making, and the last time it was measured was 20 years ago.

These physicists are members of the muon g-2 collaboration at Fermi National Accelerator Laboratory, better known as Fermilab, in Illinois.

On April 8, the world learned what they found, and shared in their excitement: their measurements conflicted with theoretical expectations. It strengthens the possibility of a gap in the Standard Model (SM) of particle physics - our best current model of the fundamental particles of reality - and hints at the existence of hitherto undescribed particles.

The star of the story is the muon - it’s a fundamental particle, meaning it isn’t divided into any smaller objects - sometimes called the heavier cousin of the electron. Muons have the same negative electric charge as the electron, but have about 207 times the mass. The reason that electrons are found in atoms, and muons are not, is that their mass makes them unstable - they quickly decay into lighter subatomic particles. As a consequence, experiments on muons are a lot more challenging, because it’s difficult to get hold of a large number of them before they decay.

The quantity measured at Fermilab is the muon’s g-factor. This is a number that describes how a particle behaves in a magnetic field.

As an analogy, swap out the magnetic field for a field that we experience constantly: the gravitational field. Swap the muon for a spinning top. If you spin a top, it will spin around its point, but if you tilt the top first, the direction of tilt will also spin. This rotation is called precession. Anything that spins around an axis, if that axis isn’t perfectly vertical, will experience this.

Spinning things in a magnetic field behave the same way. The curious difference is that a fundamental particle - such a muon - has a quantity called spin which makes it behave in a way that would be expected of a rotating object, without rotating at all. A particle with spin has an axis of spin - an imaginary line through the particle - and it behaves like a tiny bar magnet.

For example, if a charged particle is placed in a magnetic field, and its axis of spin is tilted away from the direction of the field, then the direction of tilt will precess just as it would for a top. In other words, the spin axis itself spins! How fast it processes depends on a quantity called the g-factor of the particle (Think of ‘g’ as in ‘gyroscopic’). We think of the energy in the universe as an eternal constant, something that can’t be created or destroyed. But quantum mechanics tells us that the physical properties of things cannot be exactly determined.

That means, for just a small period of time, the amount of energy in the universe is uncertain, and an energetic particle can pop into existence. That means that a muon or electron in a magnetic field really behaves like this: A virtual particle such as a photon (the horizontal squiggly line) is spontaneously emitted from the muon or electron and later reabsorbed - giving it just a little kick, changing its motion. It contributes to the muon or electron’s g-factor deviating a bit from 2.

However, as the electron has the same charge as a muon but is a lot lighter, it feels the electromagnetic force more strongly, so most virtual particles don’t give it much of a kick. Except for photons, physicists ignored most of them in their calculations, and they estimated values of g that matched up extremely well with experimental measurements - the electron g-factor is said to be one of the best-determined quantities in physics.

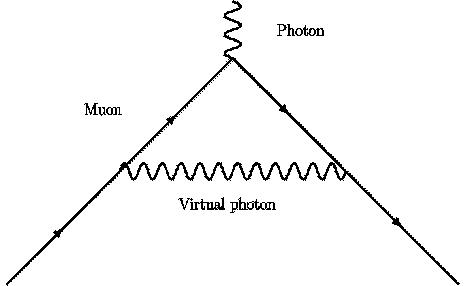
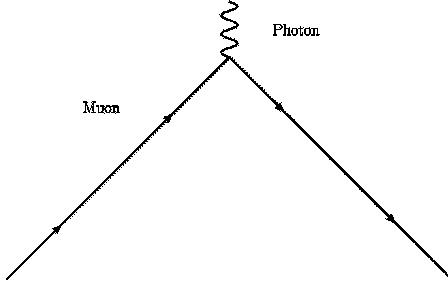
The celebrated Dirac equation predicts that both the electron and the muon have a g-factor of 2. In practice, this turns out to be wrong. That’s because the Dirac equation essentially assumes that the magnetic field affects the muon like this:

The effect of the magnetic field is represented by a photon - a particle of electromagnetic radiation - colliding with the muon. The arrows represent the trajectory of the muon, and the squiggly line represents the photon.

But the muon doesn’t just interact with the magnetic field. Even if it’s in a vacuum, it will interact with other particles, because - astonishingly - energetic particles can spontaneously appear from empty space.

The muon is where theory and experiment diverge. The muon g-factor is so hard to calculate because, unlike the lighter electron, many different types of virtual particles have an appreciable effect on it.

In 2001, researchers at Brookhaven National Laboratory on Long Island, New York, measured the muon g-2 and found it to be 2.0023318416 (in other words, g-2 = 0.0023318416). That didn’t agree with the number predicted by theory, which was 2.0023318362 (in other words, g-2 = 0.0023318362).

Because the experimental and theoretical values of g-2 were both accurate to 0.7 parts per million, this seemingly tiny difference was actually quite sizable. Using statistical terminology, the difference between is 2.7σ, where σ stands for the uncertainty. Physicists use statistics to test whether a disparity between prediction and reality is large enough to mean the prediction is wrong, or small enough that it could have happened by random chance. 2.7σ means that the chance this disparity was just down to chance would be about 0.35%.

Using statistical terminology, the difference between them is 2.7σ. This translates to a 0.35% chance that a disparity of this size could have been caused by random error. So, either the measurement disparity was an unlikely fluke, or something is missing from the theory of the muon. As unlikely as 0.35% is, the physics community did not jump to the second conclusion. In physics, the standard for rejecting a theory set high at the 5σ level, which translates to a 1 in a million chance of a fluke. This is a guard against false discoveries, and encourages experimental repetition and review.

But, even if 2.7σ doesn’t constitute a discovery of new science, it’s a good hint of it. The muon g-factor is different from 2 because of virtual particles, and, in calculating g, theorists have accounted for every type of particle in the Standard Model. If the value they predicted was wrong, then it could mean that there exist exciting particles yet to be described, outside the Standard Model.

Spurred by the prospect of new science, over the past twenty years, theorists and experimentalists each worked to sharpen the precision of their respective values of g-2. In other words, they were working to shrink the uncertainty σ. As σ shrinks, the gap becomes a bigger multiple of σ, growing towards the tantalising 5σ.

The muon g-2 experiment at Fermilab is the experimentalists’ side of the deal. Efforts lay dormant for some time after the experiment at Brookhaven ended in 2001. In 2012, physicists at Fermilab proposed reviving the experiment. The idea was to retool Fermilab’s particle accelerator complex, previously used to generate antimatter, to generate larger quantities of muons than were possible at Brookhaven. Quantity is crucial, because of how fast muons decay.

The other piece of the puzzle is an enormous ring-shaped muon container with a powerful magnetic field inside - 1.45 tesla, about 30,000 times the strength of our planet’s magnetic field. The ring already existed - it had been built for the experiments at Brookhaven. You can’t move an accelerator so easily, but you can move a huge magnet. So, the ring, weighing more than 600 tonnes and 7 metres in radius, was transported by barge and truck from Brookhaven in Illinois to Fermilab in New York over 35 days in 2013.

After arrival, the muon g-2 team spent four years calibrating the magnet. To make their experiment exceed the precision of Brookhaven’s, and bring down σ as much as they could, they made the ring’s magnetic field as uniform as possible. If you used a magnetometer to measure the magnetic field inside the ring, you would find that it is almost exactly the same everywhere, to within a few parts in a million.

The Fermilab accelerator was hooked up to the Brookhaven muon ring, producing a stream of muons. Subjected to a strong magnetic field, the muons circle the chamber. At the same time, each muon’s spin-axis is precessing, at a rate determined by g.

A muon whose spin axis is pointing away from its direction of movement tends to emit lower-energy positrons than a muon whose spin axis is aligned with its direction of movement. By comparing the positron energies recorded at different points along the ring, it’s possible to work out the frequency at which the muons’ spin axes precess. Once you know that, you can calculate g. There’s one catch - the measurement apparatus at Fermilab did not measure frequency in hertz or any other known unit of frequency. The apparatus’s internal clock was set to a unit of time that was decided randomly, and known to just two Fermilab physicists, neither of whom were part of the muon g-2 team.

This ‘blinding’ measure was a precaution against unconscious bias. The muon g-2 experiment might have corroborated the Brookhaven result or reveal it was just a fluke. Whatever the team at Fermilab hoped for or expected, they didn’t want it to cloud their judgement. If the experimentalists knew the frequencies they measured as they finetuned the equipment, perhaps they would have unconsciously calibrated the magnet to bias the results towards what they expected to see.

Instead, the team collected data and calculated numbers that would mean nothing to them until the secret unit of time was revealed. Three years after the experiment, with all the data collected and processed, all that was left to do was plug the secret number into a formula.

“This was our Mars rover moment,” said Chris Polly, co-spokesperson for the muon g-2 project, at a public seminar. “Ten years, thousands of people, years of effort, suddenly in one moment being revealed to the collaboration.”

The team revealed their measurement of g: 2.0023318408 (that is, g-2 = 0.0023318408). This number is close enough to agree with the Brookhaven number, and once again differs starkly from what theory tells us to expect.

With two measurements averaged together, σ becomes low enough for the gap to be 4.2σ - close, but still not quite there. The team knew that it would take multiple measurements to raise their certainty to meet the 5σ bar, so the muon g-2 project is still ongoing. The number that was publicly revealed on 8 April was only the result of their first run. The results and analysis of two more runs can be expected to release within a year, and a fourth run is ongoing as of May 2021. So, if things go smoothly, this won’t be the last of the interesting news out of Fermilab.