


ناك اذإ ص،س ( ددع امهل نيريغتم ن) يب نوسيب طابترا لماعم نإف ميقلا نم نييغتملا ص،س وه =ر : ةظحلام ناكاذإ ص ، ؛س ميقل ناطسوتملا امه ص،س ، بيتيلا لىع ن : نإف ميقلا ددع


1( نييغتملا يب نوسيبل طابترلأا لماعم دجوأ ) ص،س ناكاذإ هعون ددحو ى =س 68 ، ى =ص 36 ، ى =صس 348 ، ىس 2620= ، ىص 2204= =ن ، 8 ةباجلإا =1 ىدرط مات


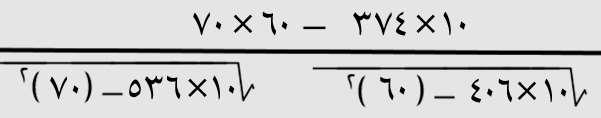
)2( نييغتملا يب طىخلا طابترلاا لماعم ص،س : ثيح................ وه س6= ، ى =ص 70 ، ى =صس 374 ،ىس 2406= ، ىص 2536= =ن ، 10 )أ( 1 )ب( – 1 )ـج( 5 , 0 )د( -0,5 ةباجلإا ىس=6×1060= =ر =ر -=1

ــل بترلا طابترا لماعم ناميبســـ نييغتم يب ناميبسـل بترلا طابترا لماعم ص،س ثيح ف ، نييغتملا بتر يب قرفلا هى ن نييغتملا نم لكميق ددع
3( : تناكاذإ ) ف نييغتملل ةرظانتملا ميقلا بتر يب قرفلا هى ص،س ناكو ىف2 0= طابترلأا لماعم نإف ]ر[يب ص،س سي .................... ىوا )أ( – 1 )ـج( رفص )ب( 1 2 )د( 1 ةباجلإا =ر-1 ف1 2 ى6 (1− ن1 2 )ن =-1رفص =1
)4( هعون انيبم ناميبسل بترلا طابترا لماعم لىاتلا لودجلا تانايب نم س ديج ادج زاتمم ديج ادج ديج لوبقم ص زاتمم ادج ديج لوبقم ادج ديج لوبقم )أ( 1 )ب( 75 , 0 )ـج( ,57 0 )د( – 75 , 0
ةباجلإا =ر-1 ف1 2 دغ 6 (1− ن1 2 )ن -1=ر 5×6 24×5 =,750 س ص بتر س بتر ص ف ف2 ادجديج زاتمم ,53 5 ,5-1 ,252 زاتمم ادجديج 5 ,53 ,51 ,252 ديج لوبقم 2 51, ,5 ,25 ادجديج ادجديج ,53 ,53 رفص رفص لوبقم لوبقم 1 ,51 ,5- ,25 ف1 2 دغ ⟵ 5
5( ل طابترلأا لماعم بسحا ) : هتجردو هعون انيبم تلأا لودجلل ) بترلا ( ناميبس س 3 9 5 11 15 ص 12 8 10 6 5
ةباجلإا =ر-1 ف1 2 دغ 6 (1− ن1 2 )ن -1= 40×6 24×6 =ر1- مات سىكع س ص بتر س بتر ص ف ف2 3 12 1 5 -4 16 9 8 3 3 0 0 5 10 2 4 -2 4 11 6 4 2 2 4 15 5 5 1 4 16 رفص 40
رادــــحــــــنلإا طـــــخ ةـــــلداعم لىع ص رادحنلإا طخ ةلداعم س هى "ص سب+ا= =ب ص دغ س دغ −ص س دغ ن (س دغ ) 1 2 − س1 2 دغ ن ثيح ب رادحنا لماعم ص لىع س رادحنلاا طخ ليم هىو =ا س دغ ب−ص دغ ن
6( رادحنا طخ ةلداعم تناكاذإ ) ص لىع س هى ص ̂ – =س 9 يب طابترلإا نإف ميق س ميقو ، ص .................... نوكي امات ايدرط )ب( امدعنم )أ( ايسكع )د( ايدرط )ـج( ةباجلإا ص ̂ +س= 9 >ب0 ∴ >ر 0 ايدرط طابترلاا
7( رادحنا طخ ةلداعم ف ) ص لىعص[س ̂ ]ا+سب= لماعم ناكاذإ س رفص نم لقأ نييغتملا يب طابترلإا نإف ص،س ......... نوكي .............. امات )د( ايدرط )ج( امدعنم )ب( ايسكع )أ( ةباجلإا ايسكع
8( رادحنا ةلداعم تناكاذإ ) ص لىع س هىص ̂ = 0,2 +س 3 ةميق تناكو ص ةيلودجلا امدنع =س5 هى 4,6 ةميق فأطخلا رادقم نإف ص واست ................. ى )أ( 0,2 )ب( 0,4 )ـج( 0,6 )د( 0,8 ةباجلإا دنع =س 5 =ص,20×+53=4 | = أطخلا رادقم ,64–4 | =,60
9( ( ناتطقنلا تعقو اذإ ) 5 ، 13 ) ( ، 4 ، 14 رادحنا طخ لىع ) ص لىع س .......................... ةطقنلا ادعام طخلا سفن لىع عقت ةيلاتلا طاقنلا عيمج نإف ( )أ( 15 ، 5 ( )ب( ) 10 ، 8 ( )ـج( ) 6 ، 12 ( )د( ) 5 ، )13 ةباجلإا ليملا = 13−14 5−4 =113−ص 5−س =1=13-ص5+س18+س-=ص ( ادعام عفت طاقنلا عيمج 15 ، 5 )
10( ( ناتطقنلا تعقو اذإ ) 6 ، 5 ( ، ) 3 ، 8 يب طابترلأا عون نإف رادحنلإا طخ لىع ) ص،س ........................... مدعنم )ـج( سىكع )ب( ىدرط )أ( مات ىدرط )د( ةباجلإا = ليملا 5−8 6−3 = 3 3− = -1 سىكع
11( ( ناتطقنلا تعقو اذإ ) 2 ، 8 ( ، ) 7 3، رادحنا طخ لىع ) ص لىع س طابترلاا ناكو ................. ىواسي طىخلا طابترلاا لماعم نإف امات )أ( – 1 )ب( )ـج( رفص 1 2 )د( 1 ةباجلإا =ر مات طابترلاا نلأ ليملا =ر 3−8 7−2 = 5 5− =-1
ثدح لكل أ ( ةيئاوشع ةبرجتل ةنيعلا ءاضف نم ف ( ل : نوكي ) ا = ) ا رصانع ددع ف رصانع ددع : لامتحلإا نيناوقو تاملسم )1 0 ( ل ا ) 1 2 =)ف( ل ) 1 ( ل ، ∅ رفص = ) 3 ( ل ) ا)/ = 1– ( ل ا) 4 ( ل ) بلآبا) = ( ل ا ( ل + ) ب) – ( ل بلابا) 5 ( ل ) ب-ا) = ( ل ا) – ( ل بلابا) 6 ناك اذإ ) اe ب نإف ( ل بلابا ( ل = ) ا ( ل ، ) بلآبا ( ل = ) ب)
طىشلا لامتحلإا ( ل ا|ب = ) (بلابا)ل (ب)ل ( ل ثيح ب > ) 0 ( ل ب|ا = ) (بلابا)ل (ا)ل ( ل ثيح ا) 0> نأ ىأ ( ل بلابا) = = ( ل ب) . ( ل ا|ب ) = ( ل ا) . ( ل ب|ا ) : نأ نعي اذهو ( عوقو لامتحا ب،أ و لامتحإ = ) عوق ا × عوقو لامتحا ب عوقو طشب ا عوقو لامتحا = ب × عوقو لامتحا ا عوقو طشب ب ( ل ا/|ب = ) 1- ( ل ا|ب)
ةلقتسم يغلاو ةلقتسملا ثادحلأا : نلاقتسملا ناثدحلا رثؤي لا يثدحلا دحأ عوقو ناكاذإ يلقتسم ناثدحلا نوكي . رخلآا ثدحلا عوقو لامتحا ف نأ ىأ ناكاذإ : ب،ا ( ل نإف يلقتسم يثدح امه ا|ب ( ل = ) ا ) َ ( ل ا|ب = ) (ب لاب ا ) ل ( ب ) ل ً ( ل ا = ) (ب لاب ا ) ل ( ب ) ل ً ( ل ا لابب = ) ( ل ا × ) ( ل ب) : نأ ىأ اعم يلقتسم يثدح عوقو لامتحإ لامتحإ = (( لولأا ثدحلا عوقو )) × لامتحإ (( تاثلا ثدحلا عوقو )) يثدحلا نإ لاقي : فيرعت ب،ا ناكاذإ طقفو اذإ نلاقتسم ( ل ا لابب = ) ( ل ا × ) ( ل ب) سم يغلا ثادحلاا ةلقت
نوكي ب،ا ناكاذإ يلقتسم يغ يثدح ل (ا لابب) ≠ ( ل ا × ) ( ل ب) 12( : ناكاذإ ) ب،ا نم يلقتسم يثدح ف ثيح =]ب[ل 6, 0 =]بِا[ل، 12, 0 نإف =]ا[ل ...................... )أ( 0,5 )ب( 0,4 )ـج( 0,3 )د( 0,2 ةباجلإا ]ا[ل=]بِا[ل ×]ب[ل ,120 ]ا[ل= ×,60 ∴ =]ا[ل ,20
(13 ناكاذإ ) ب،ا ةيئاوشع ةبرجتل ةنيع ءاضف نم يثدح ف ناكو =]ا[ل ,6 0 =]ب[ل5 , 0 ، ]بٍا[ل = ,8 0 ................ : يثدح نانوكي ....... يلقتسمو ييفانتم )د( ييفانتم )ج( يلقتسم يغ )ب( يلقتسم )أ( ةباجلإا ]ب[ل+]ا[ل=]بِا[ل – ]بٍا[ل =]بِا[ل 6 +, ,5,8-0 ∴,3=]بِا[ل ×]ا[ل =]ب[ل 6 ×, 5 =, ,3 ]ا[ل=]بِا[ل × ]ب[ل ب،ا يلقتسم ناثدح
14( ناكاذإ ) =ف { ج،ب،ا تناكو } ج،ب،ا ثيح ةيفانتم ثادحأ =]ا[ل 0.25 ، =]ب[ل 0,4 نإف ]ج[ل .......................= )أ( 0,1 )ب( 0,15 )ـج( 0.35 )د( 0,65 ةباجلإا =]ج[ل+]ب[ل+]ا[ل 1 25 +, ,4 =]ج[ل+ 1 ,35=]ج[ل
15( ناكاذإ ) ب،ا ، نايفانتم ناثدح =]ا[ل 0,3 ب[ل، / =] 0,4 نإف =]بٍا[ل ................... )أ( 0,3 )ب( 0,7 )ـج( 0,9 )د( 0,6 ةباجلإا =]ا[ل ,3 =]ب[ل ,6 ]ب[ل+]ا[ل=]بٍا[ل =]بٍا[ل 3 +, 6 =, ,9
16( ناكاذإ ) ب،ا ناكو نلاقتسم ناثدح =]ا[ل 3, 0 س=]ب[ل، ]بٍا[ل ، =,720 ةميق دجوأف س ةباجلإا ]ب[ل+]ا[ل=]بٍا[ل –]بِا[ل 72 =, 3 س+, 3- س, 42 =, 7 س, =س,6
17( ناكاذإ ) =]ا[ل 1 2 =]ب[ل، 1 4 =]بٍا[ل، 5 8 دجوأف بِا[ل / ل ، ] بٍا[ /] ةباجلإا ]ب[ل+]ا[ل=]بِا[ل –]بٍا[ل 1 2 + 1 45 8 = 1 8 بِا[ل/-]ا[ل=] =]بِا[ل 1 21 8 = 3 8 بٍا[ل / =] -1 ]بِا[ل+]ب[ل -1=1 4+ 1 8 = 7 8
18( ناكاذإ ) ب،ا نم ييفانتم يثدح ف ناك ، =]ا[ل 37, 0 ل ، =]ب[ 44, 0 دجوأ ا[ل / بِا[ل، ]بِا[ل ، ] / ا[ل، ]بٍا[ل، ] / بِ /] ةباجلإا ب،ا نايفانتم ناثدح =]بِا[ل 0 ا[ل / =] -1 =]ا[ل 37-1 =, ,63 بِا[ل / ]ا[ل=] – =]بِا[ل ,37-رفص,37= =]ب[ل+]ا[ل=]بٍا[ل، 37 +, 44 =, ,81 ا[ل / بِ / ]بٍا[ل=] /=-1 ]بٍا[ل -181[ ] , =,19
19( ناكاذإ ) ب،ا ناكو يلقتسم يثدح =]ا[ل 25, 0 =]ب[ل، 4, 0 نإف ا[ل - =]ب ...................... )أ( 0.1 )ب( 0,15 )ـج( 0,3 )د( 0,65 ةباجلإا ا[ل - ]ا[ل=]ب – ]بِا[ل ,25=-25 ×, 4 =, ,15
20( ناكاذإ ) ب،ا نم يلقتسم يثدح ف ثيح =]ب[ل 0,6 =]بٍا[ل، 0,68 نإف =]ا[ل ................... )أ( 0,2 )ب( 0,3 )ـج( 0,4 )د( 0,5 ةباجلإا ]ب[ل+]ا[ل=]بٍا[ل – ]بِا[ل 68 +س=, ×س-,6,6 ,080=4 س, =س 1 5 ]ا[ل= 1 5 =]ا[ل ,2
21( ددعلا روهظ لامتحإ ، ةدحاو ةرم مظتنم درن رجح ءاقلإ هبرجت ف ) 3 ب املع نأ ..................... وه ىدرفلارهاظلا ددعلا )أ( 1 4 )ب( 1 3 )ـج( 3 4 )د( 1 2 ةباجلإا { =ف ،1 2 ، 3 ، 4 ، 5 ، 6 } =ا }3{ =ب 1{ ، 3 ، 5 } ا⋂ =ب }3{ ( ل ا|ب=) (ب ِ ا)ل (ب)ل = 1 6 1 2 = 1 3
22( : ناكاذإ ) =]ا[ل 7, 0 =]ب[ل ، 4, 0 =]بِا[ل، 2, 0 نإف ا[ل │ب / =] ................... )أ( 1 2 )ب( 5 6 )ـج( 1 )د( 3 4 ةباجلإا ا[ل│ب1 / =] ( بِا1 / )ل ( ب1 / )ل = ( ب−ا)ل (ب)ل−1 = ( بِ ا)ل−(ا)ل (ب)ل−1 = ,2− ,7 ,4−1 = 5 6
23( ةيمرلا ف ةباتكروهظ لامتحا ، يتيلاتتم يترم ةمظتنم دوقن ةعطق ءاقلإ ةبرجت ف ) ا ..................... ىواسي لىولأا ةيمرلا ف ةروص ترهظ اذإ ةيناثل )أ( 1 2 )ب( 1 4 )ـج( 1 )د( 3 4 ةباجلإا }]ك،ك[،]ص،ك[،]ك،ص[،]ص،ص[{=ف }]ك،ك[،]ك،ص[{=ا ]ص،ص[،]ك،ص[{=ب } ا⋂ }]ك،ص[{=ب ا[ل| =]ب ( ب⋂ا)ل (ب)ل = 1 4 1 2 = 1 2
(24 لىوأ جوز ددع روهظ لامتحا ، ةدحاو ةرم مظتنم درن رجح ءاقلإ ةبرجت ف ) نم يكأ ددع رهظ اذإ 1 ...................... وه )أ( 1 5 )ب( 2 5 )ـج( 3 5 )د( 4 5 ةباجلإا ،1{=ف2،34،،56،} {=ا2} ،2{=ب3،45،}6، {=بِا }2 ا[ل|=]ب (ب ِ ا) (ب)ل = 1 6 5 6 = 1 5
طسوتلما باسح ، نيابتلا و يرايعلما فارنحلإا )1( طسوتلما μ = ن دغ 1 = ر سر.(دسر) )2( نيابتلا σ 2 = ن دغ 1 = ر سر 2 . (دسر)-μ 2 )3( رايعلما فارنحلإا ى σ = ة نيابتلا ىأ نأ رايعملا فارحنلإا : ى σ = ة σ2 )4( فلاتخلإا لماعم = ىرايعملا فارحنلأا طسوتملا × 100 % ىأ نأ : = فلاتخلإا لماعم σ μ × 100 %
25( : لىاتلا لىامتحلإا عــيزوتلل عقوتلا ناكاذإ ) ىواسي 2 نإف =ك .............................. )أ( 3 )ب( 4 )ـج( 5 )د( 6 ةباجلإا μ= 2 ∴ ,1 0 + ,6 1 + ,1 ك 2= ك3= سر 1 2 ك دس[ر] 1, 0 8, 0 1, 0
26( ىواسي تاوشع يغتمل تاسحلا طسوتملا ناكاذإ ) 4 هل فلاتخلإا لماعم ناكو ىواسي 79 .....................= هل ىرايعملا فارحنلإا نإف % )أ( 10 )ب( 100 )ـج( 6 , 31 )د( 16 3, ةباجلإا μ4= = فلاتخلاا لماعم �� �� × 100 % 79 = % �� 4 × 100 % �� = ,16 3
27( : ناكاذإ ) س ىواسي عقوتلا ناكو ايئاوشع ايغتم ،3 ىس 2 ر. دس[ر =] 14,5 حنلإا نإف ................. ىواسي ىرايعملا فار )أ( 4,8 )ب( 2,35 )ـج( 11,5 )د( 5,5 ةباجلإا μ = 3 σ 2 = ىس 2 ر. دس[ر-]μ 2 =,5149-=,55 σ = ,35 2
28( تاوشعلا يغتملل لىامتحلأا عــيزوتلا ناكاذإ ) سوه ({ ،0 0,25 ( ، ) 1 ، 0,5 ( ، ) 2 ، 0,25 ) تاسحلا طسولا( عقوتلا نإف } ) ......................... ىواسي )أ( 0,5 )ب( 1 )ـج( 1,25 )د( 1,5 ةباجلإا μ=×025, 01+×5 +, 2×,2501=
ةفاثكلا ةلاد : ناكاذإ س نلا د ةيقيقحلا ةلادلا نإف لاصتم ايئاوشع ايغتم بلاس يغ اهادم مىست : اعم نايتلآا ناطشلا ققحت تناكاذإ ةيلامتحلإا ةفاثكلا ةلاد 1( نحنم ) أ تانيسلا روحم قوف عقي د ةلادلا ى : نأ د 0 ميق عيمجب س نلا مىتنت . ةلادلا لاجمل 2( نحنم لفسأ ةقطنملا ةحاسم ) قوفو د ةلادلا واست تانيسلا روحم ى حيحصلا دحاولا
29( ناكاذإ ) س هى هل لامتحلإا ةفاثكةلاد لاصتم ايئاوشع ايغتم د]س[ 4 ≥ س ≥ 1 ، 1+س 2 18 كلذ ادع اميف رفص } : نإف س[ل ≤3 =] ............................ )أ( 1 9 )ب( 4 9 )ـج( 1 3 )د( 5 9 ةباجلإا س[ل ≤3 [ل=] 3≥س≥4 =] 1 2 (د [ 3 (د + ) 4 ( ] ) 4-)3 = 1 2 [ 7 18 + 9 18 × ] 1 = 4 9
30( تاوشعلا يغتملل لىامتحلإا عــيزوتلا ناكاذإ ) س هى د=]س[ 4 ≥ س ≥ 2 ، سك كلذ ادع اميف رفص} : نإف =ك ............................ )أ( 1 6 )ب( 3 4 )ـج( 1 2 )د( 1 3 ةباجلإا د=]س[ 4 ≥ س ≥ 2 ، سك كلذ ادع اميف رفص} 2[ل≥س≥4 =] 1 1 2 (د [ 2 (د + ) )4 ( ] 4-1=)2 1 2 [2 +ك ك4 × ] 2 = 1 =ك 1 6
31( ناكاذإ ) س هى هل لامتحلاا ةفاثكةلاد ، لصتم تاوشع يغتم د]س[ 4 > س > 4 − ، ك كلذ ادع اميف رفص } : نإف =ك ............................ ةباجلإا 4-[ل <س< 1=]4 1 2 (د[-4 (د + ) 4 ( ] ) 4-(-4 = ] ) 1 1 2 [ ك+ك × ] =8 1 1=ك8 =كً 1 8
32( تاوشعلا يغتملل لىامتحلأا عــيزوتلا ناكاذإ ) س وه د]س[= 3 > س > 3 − 1 6 كلذ ادع اميف رفص } ل نإف 2>س[] ....................= رفص )أ( )ب( 1 6 )ـج( 1 3 )د( 1 2 ةباجلإا >س[ل2 [ل=] 2 <س< ]3 = 1 2 2(د[ (د + ) 3 ( ] ) 3-2 = ) 1 2 [ 1 6 + 1 6 × ] 1 = 1 6
عيبط يرغتلم تلاامتحلإا باسح ى رايعم يرغ ى ناكاذإ س يغتم هطسوتم ايعيبط ا μ ىرايعملا هفارحناو σ يغتملا اذه لوحن اننإف ىرايعم عىيبط يغتم لىإ ص : ةدعاقلاب ص= μ−س σ نوكيو ل ( اسب = ) ل ( μ−ا σ ص μ−ب σ )
33( طسوتمب ايعيبط اعيزوت ةعزوم تاناحتملإا دحأ ف بلاطلا تاجرد تناكاذإ ) 50= ىرايعم فارحناو =2 ىواست بلاطلا دحلأ ةيرايعملا ةجردلا تناكاذإف 2 .................... ىواست ناحتملإا اذه ف اهيلع لصح نلا هتجرد نإف )أ( 54 )ب( 98 )ـج( 46 )د( 102 ةباجلإا μ=50 σ2= = ةيرايعملا ةجردلا ��−ةيلعفلا ةجردلا �� ∴=2 50−س 2 =س54
34( ناكاذإ ) س هطسو ايعيبط ايغتم μ 6= هل ىرايعملا فارحنلااو σ3= ................ وه ىرايعم عىيبط عــيزوتل عضخي ىذلا يغتملا نإف )أ( س−3 6 )ب( 6−س 3 )ـج( س−6 3 )د( 3−س 6 ةباجلإا μ 6= σ3= 6−س 3

)35( ناكاذإ س ةطسوتم ايعيبط ايئاوشع ايغتم μ ىرايعملا هفارحناو س نإف س[ل -μ< 1,5 س=]................... )أ( 4332 , 0 )ب( 0668 , 0 )ـج( 5668 , 0 )د( 9332 , 0 لحلا ( ل ��−س �� < �� 1,5 �� ( ل =) <ص 5,1 ) = 5 ( ل + , 0 < ص < 5 , 1 ) = 5 , 0 + ,4332 0 = 9332 , 0

36( ويح نم هعومجم نازوأ تناكاذإ ) طسوتمب ايعيبط اعيزوت عبتت براجتلا تانا μمارج ىرايعم فارحناو 10 ناكو تامارج س[ل ≤180 =] 1587 , 0 طسوتملا نإف μ مج............... = )أ( 160 )ب( 170 )ـج( 180 )د( 190 ةباجلإا ص[ل≤ ��−180 10 =] ,1587 ,5- [ل 0 <ص< ��−180 10 =] ,1587 3413 [ل=, 0 <ص< ��−180 10 ] ��−180 10 1= μ∴=170مج
37( : ناكاذإ ) ص ثيحب ايرايعم ايعيبط ايغتم [ل ا-≥ص≥ =]ا 796, 0 نإف =ا ................. )أ( 398 , 0 )ب( ,2 1 )ـج( ,27 1 )د( 27 , 0 ةباجلإا [ل ا-≥ص≥ =]ا 796, 0 [ل2رفص≥ص≥ =]ا 796, 0 ∴ [لرفص≥ص≥ =]ا 3980, 0 ,27=ا1
38( ناكاذإ ) س هطسو عىيبط يغتم μ 4= هنيابتو 25 نإف س[ل ≤14 =] ................. )أ( 0,4772 )ب( 0,9772 )ـج( 0,0228 )د( 0,5 ةباجلإا ص[ل ≤ 4−14 5 ] >ص[ل= ]2 =,5-4772 =, ,02280
