)1( نحنملل سامملا ه=ص ن اجن ، س ه= ن اتجن اهدنع نلا ةطقنلا دنع =ن 1 4 �� ............ اهسايق ةيواز تانيسلا روحمل بجوملا هاجتلاا عم عنصي )أ( 1 4 �� )ـج( رفص )ب( 1 2 �� )د( 1 3 ��
ةباجلإا ه=ص ن اجن ، س ه= ن اتجن ص د ن د = هن اتجن+هن اجن ه= ن[اتج +ن اج]ن س د ن د =-هن اجن+هن اتجن ه= ن[اتجن–اج]ن ص د ن د = ن اج+ن اتج ن اج−ن اتج امدنع ن = 1 4 �� =م ص د س د = 2ة 0 ∴ = ةيوازلا سايق 1 2 ��
2( (د تناكاذإ ) س = ) ه[ ك س2 – ه2س3+ ] ةيلحملا ىرغصلا ةميقلا نإف ..................... ىواست د ةلادلل )أ( 1 )ب( 2ك )ـج( 3ك 4)د(
لحلا (دس = ) ه[ ك س2 – ه2س3+ ] د/(س = ) ه21 س − ه 2 1 س 2 3+ ه21 س − ه1 س 2 د عضوب /(س = ) 0 2هس2 – ه2س 0= هس ه[س0=]1هس 0= ضوفرم هس0=10=س (د0 = ) ك =]3+2-1[ 2ك ةلادلل ةيلحملا ىرغصلا ةميقلا 2ك

3( كاذإ : لباقملا لكشلا ف ) ميقتسملا نا با ⃡ نحنملل سامم ص[ ك = س 2 1- ] ثيح ص > 1 دنع ةطقن ا حطس ةحاسم دجوأف ، باوي .
لـــــــــــــــــحلا دنع =س 0 ة=ص 2 [ا 0 ة، 2 ] =س ك ص[ 21-] =1 ص د س د ص 2 1− ص1 2 ص د س د = 1− ص1 2 ص 2 [ صد س د] = 1 2ة 2 ةلداعم با ⃡ 2ة−ص س = 1 2ة 2 ة=ص 2 =س2ة2 4-ص 4-[ب0،] =]باوي[م 1 2 ×4×2ة =2ة2 ةعبرم ةدحو
)4( ناكاذإ =ص 1 س وله 1 ه3س نإف ص د س د ...............= )أ( 3 )ب( هس رفص )ـج( )د( وله 1 س ةباجلإا =ص 1 س وله 1 ه3س = 1 س 3=س3× ص د س د =رفص
5( (د تناكاذإ ) س) = 1 3 +س سـ2 صقانت د ةلادلا نإف لكل ةي س ∋.................... ] )أ( 0 ، 8 ] )ب( [ -8 ، ∞ ] )ـج( [ -8 0، )د( [ ح[–-8 0، ] لـــــــــــــــــحلا د]س[ = 1 3+سس1 2 3 د/]س[ = 1 3+ 2 3 س1 1 3 − = 1 3+ 2 سـ 3 عضوب 1 3+ 2 سـ 3 0= + سـ 20= =سـ 2- 8-=س امدنع 0=س د/ ]س[ ةفرعم يغ دنع ةجرحلا طاقنلا =س 0 ، =س -8 ةيصقانت ةلادلا س ]∋ 8-، 0 [
6( ناكاذإ ) ج ه=س ص 0 <س< π ص د س د = ................... )أ( – س ظ )ب( – س ط )ـج( س ظ )د( س ط لــــــــــــــــــــحلا ه = سح ص ص د س د ص د س د = س ح ه1 ص = س ح سج سط =
)7( اذإ د تناك س=]س[ 2 =]س[ر، اتج س تناكو [=]س[ق د∘ ]س[]ر نإف ق/[π 12 =] ................. )أ( 3ة 2 )ب(3ة 2 )ـج(1 2 )د( 1 2 ةباجلإا [=]س[ق د∘ ]س[]ر د =]]س[ر[ د [ اتج =]س اتج2 س ق/[π 12 ]=2-اتج س× اج =س -اج س2 ق/[π 12 ]=-اج 2[× π 12 ] ق/[π 12 ]=-اج [π 6 =]1 2
8( ثيح ح لىع ةلصتم ةيجوز ةلاد د تناكاذإ ) 1 3 − ئ3 �� +ا[د =سد]]س[ 30 ، 1 0 ئ 3 − �� د =سد]س[ 6 نإف =ا ........................ )أ( 9 )ب( 3 )ـج( 7 )د( 7,5 لحلا 1 3 − ئ3 �� +ا[د =سد]]س[ 30 [سا] 3− 3 + 2 1 3 − ئ 0 ��د30=سد]س[ 12-]ا3-[-ا330= 42=ا6 7=ا
)9( ناكاذإ =ص وله 1 اق س : نإف ص د1 2 س1 2 د .................= )أ( اتج س )ب( – اتظ2 س )ـج( – اج س اق )د( 2 س ةباجلإا =ص وله 1 اق س لىإ ةبسنلاب قاقتشلإاب س ص/ = س اظ س اق س اق اظ = س لىإ ةبسنلاب قاقتشلإاب س ص//= اق2 س
10( تناكاذإ ) ج = ص س4 ثيح ص1 // ص ا+ 2≤0 ، ص≠0 نإف ا∋................ ] )أ( -4 4، [ )ب( [ -4 ، 4 ] )ـج( -ح ]-4 ، 4 د( [ ح ) – [-4 ، 4 ] لحلا ص / = ح4 4 ص س // = 16- س4ج ص1 // ص ا+ 2≤0 س 4ج 16− س 4ج ا+ 2≤0 ا2≤16 ا∋-ح ]4 ، 4 −[
11( ةلادلا نحنم يب ةروصحملا ةقطنملا نارود نم ئشانلا مسجلا مجح ) سة=ص ميقتسملاو =س4 ................. ىواسي ةرود فصن تانيسلا روحم لوح )أ( π8 )ب( 6 π )ـج( 4 π )د( 3 π لـــــحلا 0=ص ، سة=ص ح = 1 2 π 1 0 ئ4 1 ص 2 سد = 1 2 π 1 0 ئ4 1 ص 2 سد = 1 2 π [ س1 2 2 ] 4 0 = 1 2 π ( 0 − 16 2 ) = 1 2 π×8=4π
)12( ناكاذإ هص س= اقس نإف ص/= ............... )أ( π )ب( π − )ـج( 1 �� )د( 1− ��
ةباجلإا هص س= اقس ∴ وله 1 هص = وله 1 س اقس ص وله 1 =ه اقس وله 1 س =ص اقس وله 1 س لىإ ةبسنلاب قاقتشلإاب س ص/= اقس× 1 س ول+ه 1 س اق س اظ س ص/= اقس [ 1 س + اظ س ولهس ] [ ص1 / ] ��=س 1 =- [رفص + 1 π] = 1− π
)13( ئ 2ج ح س س3 سد+ ئ س3جس2ح سد ث+.................. = )أ( 1− 5 س5ح )ب( 1 5 س5ح )ـج( 1− 6 س3حس2ج )د( 1− 6 س2حس3ج لحلا ئ +س2[ج ]س3 سد= ئ س5ج سد = 1− 5 س5حث+
14( د تناكاذإ ) ]س[ = ��ح−2 س ط د نإف /]س[ ...........................= )ب( رفص )أ( سظسق3 )ـج( ق32 س )د( 3- ق2 س لحلا د=]س[ 3 سطسظ3= د/ق3=]س[2 س
)15( د ةلادلا نحنمل ناكاذإ =]س[ اتج س– سك 2 بلاقنا ةطقن دنع =س 1 3 π نإف =ك ................ )أ( 1 4 )ب( 1 4 − )ـج( 2 )د( – 1 ةباجلإا د =]س[ اتج س– سك 2 د/ =]س[ -اج س2- سك د// =]س[ -اتج سك2د// [π 3 =] -اتج π 3 ك2=01 2 ك2- اهنمو =ك 1 4 −

)16( ةللظملا ةقطنملا نارود نم ئـشانلا مسجلا ناكاذإ م لوح ةلماكةرود ىواسي تانيسلا روح π12 ةدحو نإف مجح ك ................= )أ( 8 )ب( 7 )ـج( 6 )د( 5
لـــــــــــــــــــحلا ح 12= π ⇐ π 1 ئ1ك 1 ص 2 =سد 12π 1 ئ1ك 1 سدس =12 ⇐ [ س1 2 2 ] ك 1 =12 ك1 2 21 2 =12 ⇐ ك1 2 –1 =24 ك1 2 =25 =ك 5
)17( تناكاذإ 1 ئ3ن 1 س د س = وله 1 5 نإف =ن................... )أ( 8 )ب( 16 )ـج( 15 )د( 20
ةباجلإا 1 ئ3ن 1 س د س = وله 1 5 [وله 1 |س| ]ن 3 = وله 1 5 [وله 1 ن - وله 1 3] = وله 1 5 وله 1 =نوله 1 3 + وله 1 5 وله 1 =نوله 1 [3 × 5] وله 1 =ن وله 1 15 =نً 15
)18( تناكاذإ =ص ج ب 3 ث ، ا = س ح3 ث ثيح ث ∋ 0] ، π 2 [ ، ا ح + 0=ثظ2 نإف ب .........................= )أ( -2 )ب( 2 )ـج( 4 )د( -4 لحلا صد دث ]ثج[ب3=2 جب3=]ثح[2 ثح ث سد دث ]يثح[3=2 حا3-=]ثج-[2 ثجث صد سد -= ب ا ثظ اصد سد + 20=ثظ ∴+ثظب-20=ثظ =ب2
19( ةطقنلا كرحتت ) ا ( ص،س ةلادلا نحنم لىع ) س=ص 2 +س+ 5 ثيحب سد ند = 1 ةحاسم ف يغتلا لدعم نإف ث/ ةدحو بواي ةطقن و ثيح ، ب ( 3 ، 3 دنع ث/ هعبرم ةدحو ......... ىواسي ) س = 1 )أ( 4 )ب( 3 )ـج( 2 )د( 1
لحلا |1 0 0 1 3 3 1 5 + س س1 2 س| =س32 +15+س3س3=س3-215+ =م1 2 |15 + س 3 1 2 | = 3 2 س 2 + 15 2 صد سد =س3سد ند دنع=س1 سد ند 1= ن 2 ند 3= ث / ةعبرم ةدحو
)20( 1 ئ 0 (دس) =سد 5 نإف π 2 ئ π 4 ح2س (د.ج2س) =سد.................. )أ( 5− 2 )ب( 5 2 )ـج( 5 )د( – 5 لحلا س2ج=ص د = ص س2ح2دس π 2 ئ π 4 س2ح د]س2ج[د = س 0 ئ 1 1 2 د]ص[دص -= 1 2 1 ئ 0 د]ص[د = ص1 2 5× -= 5 2
21( = ص تناكاذإ ) سج كم لىضافت نإف ص = ............. )أ( قس )ب( سدص )ج( .سطدس )د( سظ لحلا ل=صه سج لىضافت =ص سح سجدس سط=دس
)22( دادزت هردق تباث لدعمب ةركحطس ةحاسم مس22 اهيف نوكي نلا ةظحللا دنع ث/ ةركلا رطق فصن لوط 7 مس............= ةركلا مجح ف ةدايزلا لدعم نإف مس 3 ث/ )أ( 6 )ب( 7 )ـج( 8 )د( 9
ةباجلإا ةركلا حطس ةحاسم =م 4πغ2 م د ن د = 8 π غ× غ د ن د =2 8 π ×7× غ د ن د غ د ن د = 1 ��28 ةركلا مجح ح = 4 3 π غ3 اب لىإ ةبسنلاب قاقتشلإ ن ح د ن د = 4 π غ2× غ د ن د =4 ×π 49 × 1 ��28 = 7 مس 3 ث /
)23( ئ ه1 س ظ س ح 2 1 2 سد ث+.................. = )أ( ه21 س ظ )ب( 1 2 ه1 س ظ )ـج( 1 2 س ق ه1 س ظ )د( 2 ق2 هس1 س لحلا ئ ه1 س ظ س ح 2 1 2 سد = ئ 1 2 ق2هس1 س ظ سد = 1 2 ه1 س ظ ث+
)24( اــــــــــــــــــــــــــــــــــــــــهـــــن 0 ← س 1− 31 س 3 س ج .......................= )أ( ك 9 )ب( ك 3 )ـج( ك 6 ( )د( ك 3 )2 لحلا اــــــــــــــــــــــــــــــــــــــــهـــــن 0 ← س 2 1− 31 س 2 س 2 × اــــــــــــــــــــــــــــــــــــــــهـــــن 0 ← س س 2 س ج = ك 2×3 = 2ك 3 = ك 9
25( لا ليم ناكاذإ ) ( هيلع ةطقن ىأ دنع نحنمل سامم س، ص ةقلاعلاب طىعي ) ح = س ص ق1 2 +1 نإف لصلأا ةطقنب رمي نحنملا ناكو صظ+ص ............= )أ( س 2 )ب( 1 2 س 2 )ـج( س–2 )د( 1− 2 س 2
لحلا ئ 1[ ص ق1 2 + ]د=ص ئ سدس = صظ+ص 1 2 س 2 +ث لصلأا ةطقنب ضيوعتلاب ∴ 0=ث = صظ+ص 1 2 س 2
26( ( تناكاذإ ) 1 ، - 6 نحنملل بلاقنا ةطقن هى ) س=ص 3 سا+ 24-سب+ نإف ب ........................= )أ( – 3 )ـج( رفص )ب( 1 )د( 3 لحلا صد سد س3=2 +ب+سا2 ص د1 2 س1 2 د =ا2+س6 دنع =س 1 ص د1 2 س1 2 د 0= 2+6 =ا 0 3-=ا س=ص 3+س324-سب+ وعتلاب ( ضي 1،-6 ) 6-3-1=4-ب+ ∴ب رفص =
27( ، د تناكاذإ ) ر ، دودح ةيثكلاود د = سج 2 +ر(س ناكو ، ) ر(1) ك= ، ر//(1) =6 ( هى بلاقنإ ةطقن د ةلادلا نحنمل ناكو 1 ، 5 ) ثيح ، ك،ج ةميق دجوأ تباوث ك–ج لحلا د = سج 2 +ر(س) 1(د = ) 5 د/ =]س[ 2 ر+سج /]س[ [ر+ج 5=]1 د// =]س[ ر+ج2//]س[ 3-5=ك+ د//)1(0= 8=ك ر+ج2//1[ =] 0 3+8=ج-ك11= 6+ج20= 3-=ج
28( د ، قاقتشلأل ةلباق ةلاد د تناكاذإ ) 3[ س=]س س د نإف / ]3[ ........................= )أ( 1 3 )ب( 2 3 )ـج( 1 )د( 3 لحلا د3[ س=]س س دنع 1=س كمن دسكس=]س3[ د1=]3[ (س3) د1 / 3 (س 3)د +سك= 1 س س× عضوب 1=س (3) د1 / 3 ( 3)د 1+1ك= ∴ 3 د/3( = ) 1 د/ 3( = ) 1 3
29( ناكاذإ ) ه س صس ص = ج+2 س سامملا ليم نإف هعطاقت ةطقن دنع نحنملل ...................... ىواسي تاداصلا روحم عم )أ( 1 )ب( – 1 )ـج( ه رفص )د( لحلا ه س صس ص = ج+2 س عضوب=س0 0=ص ،0[]0 هصس ه+ صسس+ص[صد سد ×] =س صد سد +2 سح سج =1صد سد
)30( ئ (س ك)ح س سد ث +................... = )أ( ك |س| × ]س ك[ ج )ب( – ] س ك[ج )ـج( ]س ك[ج قبس امم ىأ سيل )د( لحلا ئ 1 س ]س ك[ ح د + ] س ك[ ج = س ث
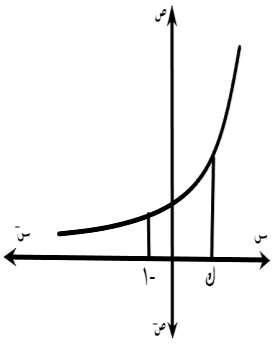
)31( لباقملا لكشلا ف ةلادلا نحنم ه=ص س شانلا مسجلا مجح ناكاذإ لوح ةلماكةرود ةللظملا ةقطنملا نارود نم ملاو تانيسلا روحم ميقتس =س -1، ك=س ىواسي π 2 ه[10 –ه2-] نإف ةبعكم ةدحو ك ............ = )أ( 2 )ب( 1 )ـج( 10 )د( 5
لحلا π 2 ه[10 –ه2-=]π ا 1 − ك ا هس2سد π 2 ه[10 –ه2-=]π [ ه 1 2 1 س 2 ] 1− ك ه10 –ه2=هك2 –ه2∴5=ك
32( تناكاذإ ) د(س ، ) ر(س) قاقتشلإل يتلباق يتلاد د ثيح /2( = ) 4 ، ر /3=)1( ، ر=)1( 2 نإف د سد ( س 2 + (د رهه ()س ) ) امدنع ........ = س = 1 )أ( 12 )ب( 14 )ج( 18 )د( 24
لحلا = ص ( س 2 + (د رهه ()س ) ) = ص س 2 [د + ر(س]) =ح 2 +س د/ [ر(س × ]) ر/(س) دنع 1=س =ح 2×1+4×3=14

33( ةقتشملا نحنم لثمي رواجملا لكشلا ناكاذإ ) ىرغص ةميق اهل د ةلادلا نإف د ةلادلل لىولأا دنع ةيلحم س∋ .................. { )أ( 4 ، 4- { )ب( } }2 { )ـج( 2- }رفص{ )د( } لحلا دنع ةيلحم ىرغصةميق اهل ةلادلا س∋4{ ، 4- }
34( (د تناكاذإ ) 1+ص س=) 3 (د تناكو ، 5 = ) 8 د ، /5( = ) 4 ةميق نإف ح دنع ....... = =ص 4 )أ( 4 )ب( 3 )ـج( 12 )د( 48 لحلا د/(ص1+ × ) =ح 3س 2 5(د = ) 8 د/( 5 × ) =ح 12 ص4= 4 × =ح 12 س2= =ح 3
(35 (ةطقنلا دنع د ةلادلا نحنمل موسرملا سامملا ناكاذإ ) 1-،2 ةيواز عنصي ) 135° روحمل بجوملا هاجتلإا عم س نإف اهن 2س (2)د−(س)د 4–س 2 ............. = ....... لحلا 1 2 اهن 2س (2)د−(س)د 2–س = 1 2 × د/ 2( = ) 1 2 × - 1 = 1− 2
)36( جباي هيف ا ( 1،2 ، ) ب ( +س 1،3 ، ) ج ( 0 +س، 3 نإف ) ةميق س ةحاسملا لعجت نلا جباي ............ هى نكمي ام رغصأ )أ( 1− 2 )ب( 1 3 )ـج( 3 4 )د( 1 2
لحلا |1 2 1 1 3 1 + س 1 3 + س 0 | = س-س2-3+]1-س-1[]3+س[س= 21+س2-س3+ س= 21+س+ =م1 2 |1 + س + س1 2 | = 1 2 س[2]1+س+ مد سد +س= 1 2 عضوب +س 1 2 0= -=س 1 2
37( لدعمب دادزي علاضلأا ىواستم ثلثم علض لوط ناكاذإ ) ة3 ثيحب ث/ مس ثلثملل ةجراخلا ةرئادلا حطس ةحاسم يغت لدعم نإف ةلكشب اظفتحم لظي ث/ مس................ ىواسي 2 ثلثملا هعلض لوط اهيف نوكي نلا ةظحللا ف ىواسي 2 مس )أ( 3 ة 3 )ب( 3 )ـج( 3 2 )د( π4 3ة
لحلا سد ند 3ة= ث/ مس س 60 ج غ2= =غ س 60 ج2 = س 3ة =غ 1 3ةس =مπ 1 3 س 2 = π 3 س 2 مد ند = π2 3 س سد ند ∴ مد ند = π2 3 3ة×2× = 3ةπ4 30 = π4 3ة ث/ مس 2
)38( ئ هسة =سد ه2سة ث+).........................( )أ( 1-سة )ب( 1–سة )ـج( سة+1 )د( –1[ ]سة+ لحلا ئ هسة =سد ئسة2× 1 س ة 2 هسة سد 2= هسة سة –ئ ×2 1 س ة 2 هسةسد ( ه1 سة 1 س ة 2 سة2 ه 1 سة 1 س ة 2 × 2) 2= هسة سة –ه2سة +ث =ه2سة سة[1- +] ث
