3.4.3 Grid-sensitivity analysis

48 Chapter 3

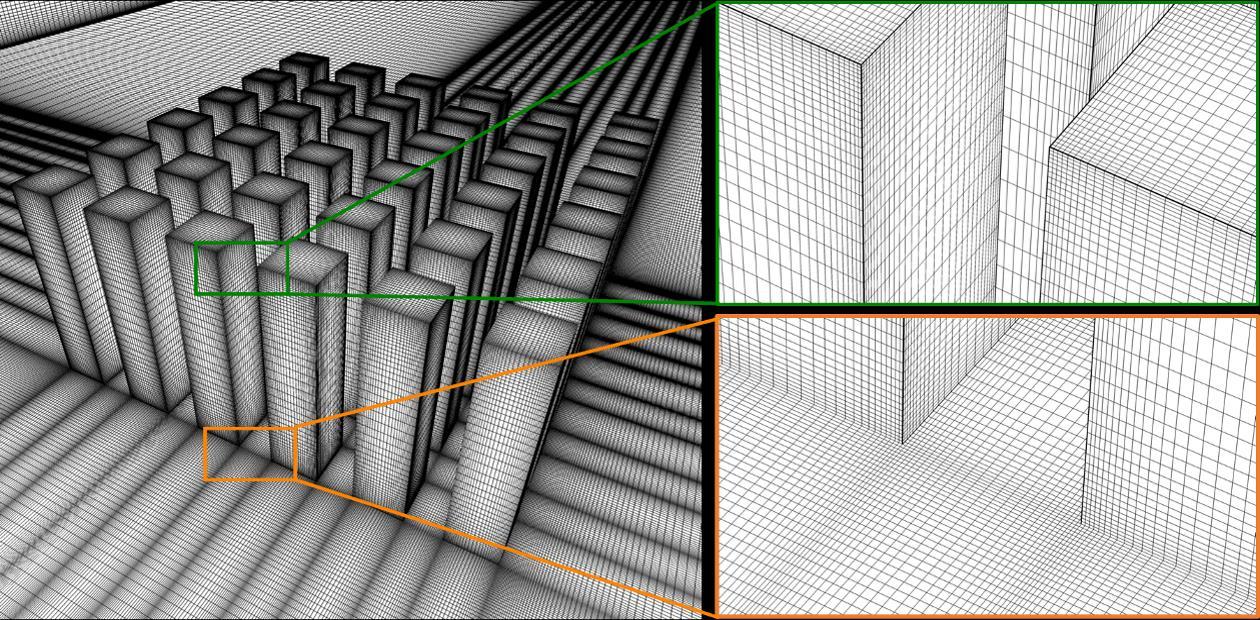
Figure 3.5. (a) Coarse (11.3 million cells), (b) medium (18.0 million cells), and (c) fine grids (47.8 million cells) for Case R3. Enlarged views show the grid near the ground and roof.

3.4.3 Grid-sensitivity analysis

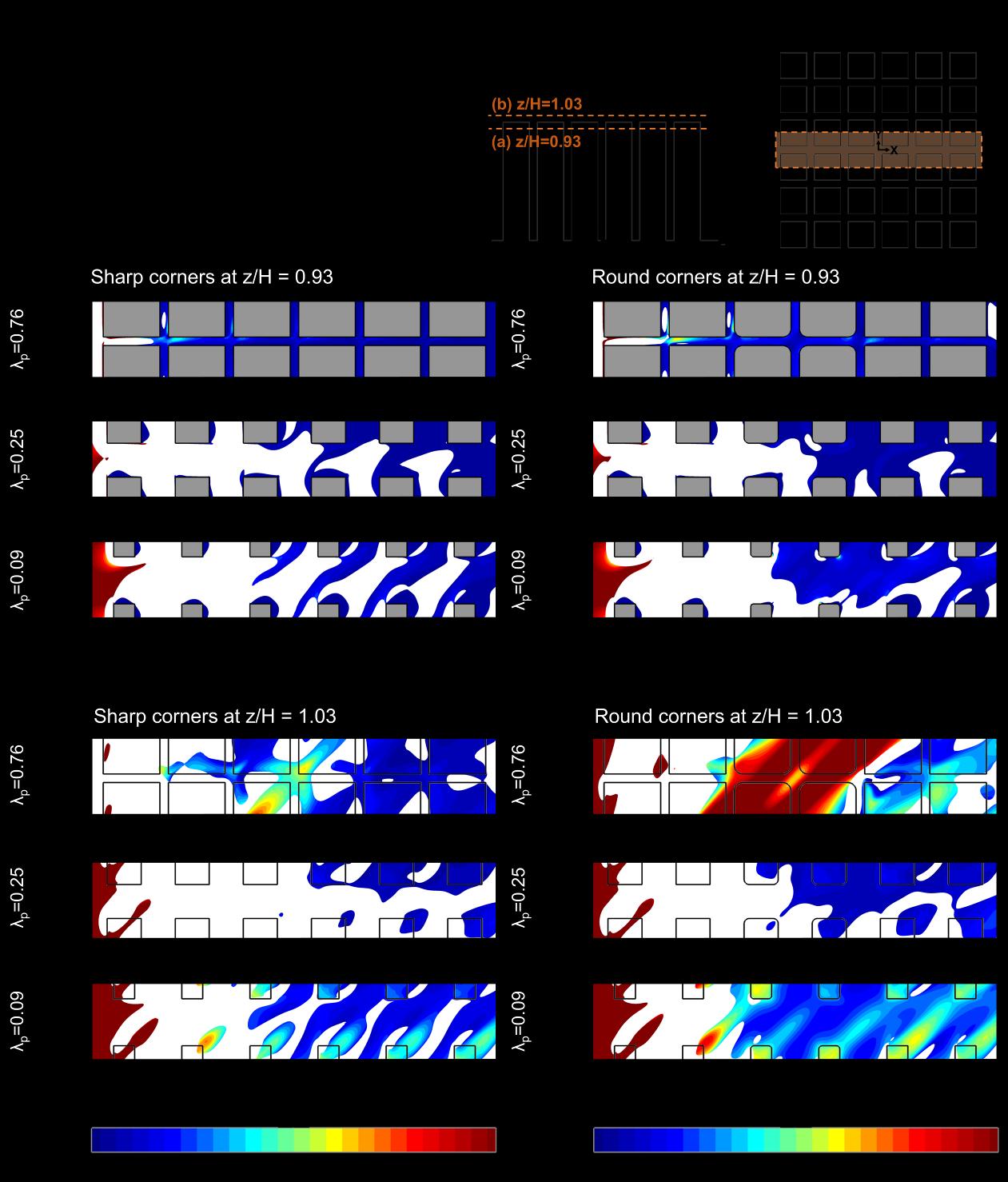
A grid-sensitivity analysis is performed using three uniformly refined grids with a refinement factor of √2. The analysis is performed for case R3 (r = 0.15B). The rounded corner shape is selected. The three grids are shown in Fig. 3.5. The number of cells for the coarse, medium and fine grids is 11,277,645, 18,023,086 and 47,785,776, respectively. Fig. 3.6 compares U/Uref and TI/TIref along the vertical centerline (y/B = 0) at z/H = 0.93 (just below the roof) for the three grids. The results indicate that the average deviation of U/Uref and TI/TIref between the coarse and

Urban wind energy potential: Impacts of building corner modifications 49

medium grids is 7%, while it is less than 1% between the base and the fine grids. The gridconvergence index (GCI) proposed by Roache [101] is used to estimate the errors of U/Uref on the medium grid, given by Eq. 3.6:

������ =���� |����[(����������−���������� 1−���� )/��������]|×100% (3.6)

here Fs is the safety factor of 1.25 as the recommended value when more than three grids are considered, RP is the linear grid refinement factor of √2, P is the formal order of the accuracy (= 2 based on the use of second-order discretization schemes). The average GCI of U/Uref and TI/TIref along the horizontal centerline at z/H = 0.93 between the medium and fine grids is 3.3% and 8%, respectively. Therefore, the medium grid is considered for the rest of this study.

Figure 3.6. Grid-sensitivity analysis: (a) dimensionless mean streamwise velocity component and (b) turbulence intensity along centerline at z/H = 0.93.