Dino Sauro 3 - Matematica

Centro

di Ricerca Didattica Ardea Editrice

Tiziana Trotta

MATEMATICA

ESERCIZIARIO

ESERCIZI DI LOGICA

CODING PROBLEM SOLVING

Centro di Ricerca Didattica Ardea Editrice

Tiziana Trotta 2 3

MATEMATICA

INDICE

PER RICOMINCIARE

4 Il nostro sistema...

5 ... di numerazione

Lo zero

6 I numeri fino a 99

7 Il numero 100

TRUCCHI MATEMAGICI

31 Sottrazioni flash

32 Operazioni inverse

RAGIONA... MENTE!

33 È logico!

34 VERIFICA

NUMERI

8 Numeri sull’abaco

9 I numeri fino a 999

10 Il migliaio

14 Comporre e...

15 ... Scomporre

16 Confrontare

RAGIONA... MENTE!

17 Indovina i numeri

18 VERIFICA

OPERAZIONI

20 L’addizione

21 L’addizione in colonna

22 L’addizione con le migliaia

23 Le proprietà dell’addizione

TRUCCHI

30

36 La moltiplicazione

37 Tabelline, che magia!

38 Le proprietà della moltiplicazione

40 La moltiplicazione in colonna

41 Moltiplicazioni per 10, 100 e 1 000

42 La moltiplicazione a due cifre

TRUCCHI MATEMAGICI

44 Le tabelline

45 La divisione

TRUCCHI MATEMAGICI

46 Divisioni al volo

47 La divisione in colonna

48 Con tre cifre al dividendo

50 Operazioni inverse

51 La prova della divisione

53 Divisioni per 10, 100 e 1 000

54 VERIFICA

PROBLEM SOLVING

56 I problemi

58 I dati inutili

59 I dati nascosti

60 Problemi con due domande

61 Problemi con domanda nascosta

62 I dati mancanti

63 Mi esercito con i problemi

64 Ancora diagrammi

65 Problemi senza numeri

RAGIONA... MENTE!

66 Alleniamo la logica

67 VERIFICA

FRAZIONI E NUMERI DECIMALI

68 Le frazioni

70 Le frazioni decimali

71 Dalla frazione decimale al numero decimale

72 I decimi

74 I centesimi

76 I millesimi

78 I numeri decimali

79 Decimali a confronto

80 L’euro L'EURO

82 Costo unitario e costo totale L'EURO

84 VERIFICA

MISURE

87 Misurare

88 Le misure di lunghezza

90 Le equivalenze

91 Equivalenze con le misure di lunghezza

92 Le misure di capacità

93 Equivalenze con le misure di capacità

94 Le misure di peso o massa

95 I sottomultipli del grammo

96 Equivalenze con le misure di peso

97 Peso lordo, peso netto, tara

99 Problemi di misura

100 Le misure di tempo

RAGIONA... MENTE!

101 Giochi e indovinelli per “misurare”

102 VERIFICA

SPAZIO E FIGURE

104 I solidi

105 Scopriamo i solidi

106 Lo sviluppo dei solidi

107 Le linee

108 Retta, semiretta e segmento

109 La posizione delle rette nel piano

110 Gli angoli

112 I poligoni

113 Gli elementi del poligono

114 Classifichiamo i poligoni

115 Il perimetro dei poligoni

116 Problemi con il perimetro

117 Superficie e area dei poligoni

118 La simmetria

CODING

120 Algoritmi

122 Istruzioni e percorsi

RAGIONA... MENTE!

123 La frase nascosta

124 VERIFICA

RELAZIONI, DATI E PREVISIONI

126 Classificazioni

IL NOSTRO SISTEMA...

Il nostro sistema numerico è allo stesso tempo decimale e posizionale .

È decimale perché le quantità sono raggruppate in base 10 Utilizza dieci cifre: 0, 1, 2, 3 , 4 , 5, 6, 7, 8, 9.

Combinate in modi diversi possono formare infiniti numeri.

Le quantità si raggruppano per dieci

10 unità (u)

10 decine (da)

1 Completa le uguaglianze.

5 da = .............. u

20 u = .............. da

50 u = .............. da

100 u = .............. da

8 da = .............. u

90 u = .............. da

60 u = .............. da

9 da = u

20 da = u

700 u = h

40 da = h

600 u = da

3 h = u

500 u = h

1 decina (da)

Un gruppo di 10 unità forma 1 decina.

u da 0 1

1 centinaio (h)

Un gruppo di 10 decine forma 1 centinaio.

u da h

0 0 1

LO SAPEVI CHE...

Nel 1202 il matematico italiano Leonardo Fibonacci pubblicò il Liber abbaci, opera con la quale introdusse per la prima volta in Europa le nove cifre, da lui chiamate indiane, e il segno 0, chiamato zephirus (adattamento dell’arabo sifr).

... DI NUMERAZIONE

Il nostro sistema è definito poi posizionale perché, a seconda della posizione occupata nel numero, ogni cifra può assumere valori diversi : unità, decina o centinaio.

1 Osserva gli abachi.

u 1 u da 0 1 u da h 0 0 1

LO SAPEVI CHE...

La parola abaco indica una tavoletta con delle scanalature affiancate in cui scorrono piccole pietre o altri oggetti. Gli esperti ritengono che l’uso dell’abaco risalga al III millennio a.C. e per questo la sua invenzione viene attribuita ai Sumeri. Questo strumento di calcolo è rimasto in uso nel mondo per millenni.

La cifra zero è molto importante, perché indica l’assenza di quantità e quindi la posizione vuota sull’abaco.

2 Cerchia in rosso le decine e in blu le unità . Poi inverti le cifre, come nell’esempio, e scrivi il nuovo numero che hai formato.

• I numeri sono cambiati? SÌ NO

• Cambiando posizione, è cambiato il valore della cifra? SÌ NO

I NUMERI FINO A 99

1 Rappresenta i numeri sull’abaco e scrivili in parola.

2 Completa la tabella, componendo o scomponendo il numero.

Ricordi i simboli > (maggiore) , < (minore) e = (uguale) ?

La “bocca” è aperta sempre verso il numero più grande.

3 Confronta le coppie di numeri e inserisci correttamente i simboli > , < o = , come nell’esempio.

100 unità

100 u

IL NUMERO 100

10 decine 10 da 1 centinaio 1 h = =

1 Colora solo i cartellini che valgono 100.

1 h 10 u 10 da 1 h e 0 da 1 da 20 da 50 u

2 Unisci con una linea le coppie che formano il 100.

100 u

3 Scrivi in ogni nuvola il numero che manca per formare il 100.

NUMERI SULL’ABACO

In un numero a tre cifre, la cifra di destra indica le unità ( u ), la cifra di mezzo le decine ( da ) e la cifra di sinistra le centinaia ( h ).

1 Conta, rappresenta sull’abaco e scrivi in parola e in cifre.

u da h 5 2 1

u da h u da h

u da h

u da h u da h u da h

I NUMERI FINO A 999

1 Scrivi il numero rappresentato sull’abaco e rispondi.

u da h u da h u da h

• Quanto vale la cifra 2 nel numero 214?

• Quanto vale nel 421? ............

2 Rappresenta sull’abaco i numeri scritti in tabella.

3 Indica in ogni numero il valore posizionale della cifra evidenziata. Osserva l’esempio.

4 Colora allo stesso modo il cartellino del numero e quello della scomposizione corrispondente.

IL MIGLIAIO

Che cosa succede se al numero 9 9 9 aggiungi 1 unità ? Osserva gli abachi.

u da h k

u da h k u da h k

u da h k

1 000 u = 100 da = 10 h = 1 k

Ricorda che il simbolo del migliaio è k . Quando scrivi i numeri grandi, la cifra delle k va separata con uno spazio o un puntino dalle cifre di h , da e u

1 Completa.

• Hai aggiunto una pallina blu alle 9 unità. Sono diventate 1 da.

• Hai aggiunto una pallina rossa alle 9 da. Sono diventate 1

• Hai aggiunto una pallina verde alle 9 h. Sono diventate 1 ................

IL MIGLIAIO

1 Scrivi in tabella il numero rappresentato sull’abaco .

u da h k u da h k u da h k u da h k

2 Rappresenta sull’abaco il numero indicato.

da

u

da

da

3 Quanto manca per arrivare a 1 000? Scrivi l’addendo mancante.

500 + = 1 000

600 + = 1 000

700 + ................ = 1 000

250 + = 1 000

900 + = 1 000

450 + = 1 000

980 + ................ = 1 000

100 + = 1 000

4 Completa le equivalenze, come nell’esempio.

• 3 h = 300 u

• 7000 u = ................ k

• 20 h = k

• 8 k = da

• 4 000 u = da

• 100 da = ................ k

• 30 da = h

• 5 000 u = k

• 700 u = h

• 600 da = ................ k

• 80 da = u

• 70 h = u

IL MIGLIAIO

1 Osserva il disegno e registra sull’abaco, come nell’esempio.

u 5 da 2 h 2 k 1

u da h k

u da h k

u da h k

u da h k

u da h k

u da h k

u da h k

COMPORRE E...

1 Componi e scrivi il numero come nell’esempio.

1 000 + 200 + 10 + 9 1 289 milleduecentottantanove

1 000 + 300 + 50 + 1

1 000 + 400 + 30 + 3

1 000 + 100 + 80 + 4

1 000 + 700 + 40 + 2

1 000 + 500 + 60

1 000 + 90 + 9

1 000 + 600 + 5

2 Collega con una freccia ogni somma al risultato corrispondente.

1

2

1

3 Componi e scrivi il numero in cifre.

1 k , 3 h , 6 da , 2 u 1 362

3 k , 4 h , 0 da , 2 u

4 k , 0 h , 2 da , 7 u

2

3

1 k , 9 h , 9 da , 1 u

6 k , 7 h , 5 da , 1 u

4 k , 4 h , 4 da , 1 u

1 Scomponi come nell’esempio.

1 256 1 000 + 200 + 50 + 6

2 157

4 632

6 270

3 014

7 137

3 286

8 261

2 Scomponi i numeri nella tabella.

numero k h da u

1 503

3 491

2 480

1 258 1 k + 2 h + 5 da + 8 u

3 814

1 325

2 441

1 036

8 274

4 836

6 459

numero k h da u

9 620

4 610

2 380

3 Collega il sole alla sua scomposizione.

3

2

4

5 Colora solo le equivalenze esatte.

40

300

4

20

8

2

13

INDOVINA I NUMERI

ᄗ Leggi gli indizi e scopri i numeri.

INDIZI

• Ha 3 cifre uguali

• È un numero pari

• Se sommi le sue cifre ottieni 12

• È compreso tra 400 e 500

• È un numero compreso tra 901 e 915

• Non è un numero dispari

• Se sommi le sue cifre ottieni una decina

• Se lo sommi a 90 ottieni un migliaio

INDIZI

• Non è un numero pari

• Se sottrai le u dalle da ottieni 3

• Se sottrai le da dalle h ottieni 3

È il numero

• È minore di 999 e maggiore di 900

INDIZI

• Ha 2 cifre uguali

• È un numero pari

• È compreso tra 145 e 238

• Ha 0 da e 0 u

È il numero

ᄗ In piccolo gruppo pensate ad un numero e scrivete gli indizi per trovarlo, poi sfidate i vostri compagni ad indovinarlo. Vince la squadra che ne indovina di più al primo colpo.

1 Quanto manca per arrivare a 100? Completa l’addizione.

3 da 5 u + = 100

10 u + = 100

9 da + = 100

2

6 da 9 u + = 100

4 da + = 100

9 da 8 u + = 100

7 da 2 u + = 100

5 da + = 100

1 da 1 u + = 100

3 Scomponi i numeri in tabella. Osserva l’esempio.

4 Per ogni numero scrivi il precedente e il successivo.

5 In ogni serie numerica cerchia di blu il numero maggiore e di rosso il numero minore .

6 Completa le tabelle.

7 Colora solo le uguaglianza corrette.

1 Leggi e completa.

L’ADDIZIONE

Dall’albero sono cadute 12 foglie gialle e 14 foglie marroni. Quante foglie in tutto?

OPERAZIONE

......... ......... = .........

RISPOSTA In tutto sono cadute foglie.

In classe di Oscar c’erano 11 maschi e 10 femmine. Quest’anno sono arrivate 2 nuove compagne.

Quante sono ora complessivamente le femmine in classe di Oscar?

OPERAZIONE

Ricorda

L’addizione è l’operazione che unisce , mette insieme , somma , aggiunge , trova il totale

Risponde alle domande: quanti in tutto? Quanti complessivamente?

Il segno dell’addizione è il + ( più ).

I termini dell’addizione si chiamano

12 + 27 = 39

= RISPOSTA Le femmine ora sono . addendo addendo somma o totale

L’ADDIZIONE IN COLONNA

Hai già imparato a calcolare in colonna, ma ora conosci numeri più grandi. Il procedimento è lo stesso, basta stare attenti a incolonnare bene.

Ricorda di scrivere le unità sotto le unità , le decine sotto le decine e le centinaia sotto le centinaia

• Somma prima le unità 5 + 3 = 8;

• poi le decine 3 + 4 = 7;

• infine le centinaia 1 + 2 = 3

Quando fai una somma e il risultato supera il 9, ricorda di fare il cambio. Attenzione! Il cambio può essere alle decine o alle centinaia oppure a entrambi come nell'esempio.

L’ADDIZIONE CON LE MIGLIAIA

k h da u

1345+

1214=

2559

Per fare l’addizione in colonna con le migliaia, vale sempre la stessa regola. Incolonna le unità sotto le unità , le decine sotto le decine , le centinaia sotto le centinaia e infine le migliaia sotto le migliaia . Calcola sempre partendo dalle unità e fai attenzione ai cambi, quando la somma supera il 9. I cambi possono essere più di 2.

1 Esegui le addizioni con 2 cambi. Osserva l’esempio.

k h da u

1 +1 7 +1 3 1 +

1 3 8 3 =

2 Esegui le addizioni con più di 2 cambi. Osserva l’esempio.

k h da u 1

3 Esegui le addizioni in colonna sul quaderno.

LE PROPRIETÀ DELL’ADDIZIONE

1 Osserva e rispondi.

da u 3

5

La proprietà commutativa

Proprietà commutativa: cambiando l’ordine degli addendi, il risultato non cambia.

La proprietà commutativa si usa per fare la prova dell’addizione.

2 Osserva e completa.

• I risultati sono uguali? SÌ NO

• Se sono uguali, l’addizione è esatta.

3 Esegui le addizioni in colonna con la prova sul quaderno. Attenzione ai cambi.

158

237

426

243

1

6

•

LE PROPRIETÀ DELL’ADDIZIONE

1 Osserva e rispondi.

Osserva l’addizione.

22 + 8 + 7 = 37

30 + 7 = 37

La proprietà associativa

• Il risultato delle due addizioni è cambiato? SÌ NO

Hai applicato la proprietà associativa.

Proprietà associativa: in un’addizione con tre o più addendi, se sostituisci due addendi con la loro somma il risultato non cambia.

2 Prova tu! Calcola a mente le seguenti addizioni, applicando la proprietà associativa. Segui i comandi delle frecce.

3 Calcola a mente, applicando la proprietà associativa. Somma prima gli addendi evidenziati.

ADDIZIONI FLASH

CON QUESTI TRUCCHI, CALCOLARE VELOCEMENTE SARÀ FACILISSIMO.

Scomponi gli addendi, poi somma, le da alle da e le u alle u.

21 15 36 + =

20 + 1 + 10 + 5

20 + 10 + 1 + 5

30 6 36 + =

21 + 15 = (20 + 10) + (1 + 5) = ....... + ....... = .......

18 + 21 =

54 + 33 = ..................................................................................

71 + 26 =

81 + 14 = ...................................................................................

Per aggiungere 9, somma 1 da e togli 1 u.

43 + 9 K 43 +10

38 + 9 K

136 + 9 K

215 + 9 K

Per aggiungere 11, somma prima 1 da e poi 1 u.

56 + 11 K 56 +10

96 + 11 K

199 + 11 K

287 + 11 K

Ricorda

ADDIZIONIAMO

Ricorda di usare i trucchi matemagici.

1 Calcola a mente.

200 + 8 + 11 = ................

110 + 11 + 9 = ................

15 + 5 + 9 = ................

230 + 10 + 9 = ................

29 + 11 + 20 = ................

32 + 20 + 9 = ................

110 + 34 + 11 =

450 + 15 + 11 =

1 220 + 20 + 9 =

1 003 + 100 + 9 =

1 089 + 10 + 11 =

73 + 1 200 + 11 =

2 Scomponi gli addendi e calcola a mente, come nell’esempio.

45 + 51 = (40 + 50) + (5 + 1) = .................... + .................... = ....................

83 + 14 =

42 + 56 = ............................................................................................................................... .............................

63 + 36 =

44 + 55 = ............................................................................................................................... .............................

3 Completa le catene di addizioni calcolando a mente.

4 Applica la proprietà associativa alle seguenti addizioni, sottolinea gli addendi da unire, e calcola.

• 23 + 62 + 8 = .........

• 64 + 9 + 6 =

• 48 + 25 + 5 = .........

• 42 + 7 + 13 =

• 121 + 9 + 18 =

• 135 + 13 + 7 = .........

• 18 + 20 + 2 = .........

• 227 + 30 + 3 =

• 436 + 29 + 1 = .........

LA SOTTRAZIONE

1 Leggi e completa.

Nel cesto ci sono 23 uova, ma 11 di esse hanno il guscio rotto. Quante sono le uova intere?

OPERAZIONI

=

RISPOSTA Le uova intere sono .

Luisa ha collezionato 24 fermagli per capelli, la sua amica Lyn ne ha invece 15. Quanti fermagli di differenza ci sono?

OPERAZIONI =

RISPOSTA I fermagli di differenza sono

Ricorda

La sottrazione è l’operazione che ti permette di conoscere il resto o la differenza .

Risponde alle domande: quanti in più? Quanti in meno? Quanto resta? Quanto manca?

Il segno della sottrazione è il – ( meno ).

I termini della sottrazione si chiamano

18 – 7 = 11

minuendo sottraendo resto o differenza

SOTTRAZIONE IN COLONNA

Hai già imparato a calcolare in colonna, ma ora conosci numeri più grandi. Il procedimento è lo stesso, basta stare attenti ad incolonnare bene.

h da u

4 8 9 −

1 4 6 =

3 4 3

Ricorda di scrivere le unità sotto le unità , le decine sotto le decine e le centinaia sotto le centinaia . Sottrai i numeri partendo sempre prima dalle unità.

Se la cifra del minuendo è minore di quella del sottraendo, chiedi un prestito e ricorda di fare il cambio. Attenzione! Puoi chiedere il prestito per il cambio alle decine o alle centinaia oppure a entrambi come negli esempi.

h da u

4 5 13 4 10 −

2 7 5 =

2 6 5

1 Esegui le sottrazioni in colonna sul quaderno.

SENZA

791 – 520

872 – 451

346 – 132

987 – 276

231 – 101

417 – 305

999 – 354

CON

371 – 32

690 – 247

851 – 236

547 – 38

387 – 49

706 – 264

680 – 327

CON

SOTTRAZIONE CON LE MIGLIAIA

Per fare la sottrazione in colonna con le migliaia, vale sempre la stessa regola. Incolonna le unità sotto le unità , le decine sotto le decine , le centinaia sotto le centinaia e infine le migliaia sotto le migliaia . Calcola sempre partendo dalle unità e fai attenzione ai prestiti, quando la cifra del minuendo è minore di quella del sottraendo.

I prestiti possono essere più di 2.

1 Esegui le sottrazioni con 2 prestiti.

2 Esegui le sottrazioni con 3 prestiti.

3 Esegui le sottrazioni in colonna sul quaderno.

LA PROPRIETÀ DELLA SOTTRAZIONE

La proprietà invariantiva

Per rendere i calcoli più semplici, puoi applicare la proprietà invariantiva della sottrazione. Aggiungendo o sottraendo lo stesso numero al minuendo e al sottraendo, il risultato non cambia.

1 Osserva e rispondi.

35 − 16 = 19

+4 +4

39 − 20 = 19

102 − 82 = 20

−2 −2

100 − 80 = 20

• Abbiamo aggiunto il 4 al minuendo e al sottraendo. Il risultato è cambiato? SÌ NO

• Abbiamo sottratto il 2 al minuendo e al sottraendo. Il risultato è cambiato? SÌ NO

• È stato più facile trovare il risultato applicando la proprietà? SÌ NO

2 Applica la proprietà invariantiva alle seguenti sottrazioni, come nell’esempio.

OPERAZIONI INVERSE

Ricorda

L’addizione e la sottrazione sono operazioni inverse.

1 Esegui le seguenti operazioni inverse.

Esegui le sottrazioni in colonna con la prova sul quaderno.

Con un prestito

519 − 327

780 − 65

456 − 183

281 − 157

848 − 288

751 − 116

411 − 263

954 − 667

LA MOLTIPLICAZIONE

1 Leggi e osserva.

Nel pollaio ci sono 4 nidi.

In ogni nido ci sono 5 uova.

Quante uova in tutto?

Ricorda

Puoi risolvere questo problema in due modi:

∞ con l’addizione: 5 + 5 + 5 + 5 = 20

∞ con la moltiplicazione: 5 × 4 = 20

Nell’addizione gli addendi sono tutti uguali , quindi moltiplico il 5 per 4 volte.

La moltiplicazione è l’operazione che ripete più volte la stessa quantità

Risponde alla domanda: quanti in tutto?

Nel testo fai attenzione alle paroline: ogni, ciascuno, volte, in tutto . Il segno della moltiplicazione è × ( per ).

I termini della moltiplicazione si chiamano

5 × 4 = 20

(moltiplicando moltiplicatore) prodotto FATTORI

2 Trasforma le addizioni in moltiplicazioni, come nell’esempio.

• 10 + 10 + 10 + 10 + 10 = 10 × 5 = 50

• 6 + 6 + 6 + 6 + 6 + 6 =

• 9 + 9 + 9 + 9 + 9 + 9 + 9 =

• 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 =

3 Trasforma le moltiplicazioni in addizioni, come nell’esempio.

• 5 × 4 = 5 + 5 + 5 + 5 = 20

• 6 × 3 =

• 2 × 5 =

• 3 × 4 =

• 9 × 3 =

• 8 × 4 =

• 5 × 5 =

• 3 × 6 =

TABELLINE, CHE MAGIA!

1 Cancella solo le caselle dei numeri che non appartengono alla tabellina indicata.

2 Completa con il fattore mancante.

3 Colora allo stesso modo i cartellini delle moltiplicazioni che danno lo stesso prodotto.

4

4 Cancella con una X il prodotto sbagliato. •

5 Collega con una freccia ogni moltiplicazione al suo risultato.

LE PROPRIETÀ DELLA MOLTIPLICAZIONE

1 Osserva e completa.

3 × 4 =

4 × 3 =

• Hanno lo stesso risultato? SÌ NO

La proprietà commutativa

• 4 × 5 = 20 K 5 × 4 = 20

• 8 × 2 = K × =

• 8 × 9 = K × =

Per la proprietà commutativa della moltiplicazione, cambiando l’ordine dei fattori il risultato non cambia. Puoi applicare questa proprietà per fare la prova della moltiplicazione.

• 6 × 7 = K × =

• 4 × 3 = K × =

• 5 × 10 = K × =

• 9 × 7 = K × =

2 Esegui le moltiplicazioni e applica la proprietà commutativa, per verificare se il risultato è corretto.

• 2 × 5 = ......... K ...... × ...... = .........

• 3 × 6 = ......... K ...... × ...... = .........

• 7 × 5 = ......... K ...... × ...... = .........

• 9 × 4 = ......... K ...... × ...... = .........

• 3 × 8 = ......... K ...... × ...... = .........

• 6 × 9 = ......... K ...... × ...... = .........

• 4 × 8 = ......... K ...... × ...... = .........

3 Conta il numero delle bandierine.

Puoi calcolare anche così:

2 bandierine 3 panini 2 vassoi × ×

6 bandierine in un vassoio × 2 vassoi = 12 bandierine

La proprietà associativa

Per la proprietà associativa della moltiplicazione, se a due o più fattori sostituisci il loro prodotto, il risultato non cambia.

4 Esegui le moltiplicazioni, applicando la proprietà associativa come nell’esempio. Moltiplica prima i fattori evidenziati.

• 3 × 4 × 2 = 12 × 2 = 24

• 5 × 6 × 2 = × =

• 3 × 7 × 2 = × =

• 9 × 4 × 5 = ×

• 2 × 5 × 10 = ×

• 4 × 6 × 2 = ×

La proprietà distributiva

Per calcolare velocemente una moltiplicazione, puoi usare un piccolo trucco.

Osserva l’esempio.

15 × 7 = 105

(10 + 5) × 7 = 105

(10 × 7) + (5 × 7) = 70 + 35 = 105

È la proprietà distributiva , che ti permette di scomporre un fattore nella somma dei suoi addendi.

Ciascun addendo è poi moltiplicato per il secondo fattore e infine si sommano gli addendi ottenuti.

5 Esegui le moltiplicazioni, applicando la proprietà distributiva, come nell’esempio.

• 13 × 4

• 16 × 3

• 27 × 3

• 19 × 5

• 22

• 18

• 15 × 6

LA MOLTIPLICAZIONE IN COLONNA

Per eseguire la moltiplicazione in colonna, devi moltiplicare il moltiplicatore per ogni cifra del moltiplicando. Moltiplica prima le unità , poi le decine ed infine le centinaia

Osserva.

1 Prova tu. Esegui in colonna sul quaderno.

• 132 × 3

• 210 × 2

• 142 × 2

• 231 × 3

Fase 1

• 313 × 2

• 122 × 4

• 322 × 3

• 324 × 2

• 131 × 3

• 112 × 2

MOLTIPLICAZIONI CON IL CAMBIO

Fase 2

• 222 × 3

•

2

Fase 3

Moltiplica le unità per le unità , scrivi l’unità al risultato e riporta le decine nella casella delle decine .

h da u 1

Moltiplica per le decine , somma le decine che hai riportato e scrivi il risultato, riporta poi le centinaia nella loro casella. h da u +1

Moltiplica ora per le centinaia , somma le centinaia che hai riportato e scrivi il risultato. h da u +1

2 Prova tu. Esegui in colonna sul quaderno.

MOLTIPLICAZIONI PER 10, 100 E 1000

Quando moltiplichi un numero per 10, 100, 1 000, il suo valore aumenta di 10, 100, 1 000 volte.

k h da u

6 6 0 × 10

k h da u

6

6 0 0 × 100

k h da u

6

6 0 0 0 × 1 000

Quando moltiplichi per 10, aggiungi uno 0 all’ unità e il 6 diventa decina

Quando moltiplichi per 100, aggiungi uno 0 all’ unità , uno 0 alla decina e il 6 va nella casella delle centinaia

Quando moltiplichi per 1 000, aggiungi uno 0 all’ unità , uno 0 alla decina , uno 0 al centinaio e il 6 va nella casella delle migliaia

Per moltiplicare per 10, 100, 1 000 aggiungi 1, 2, 3 zeri a destra del numero.

LA MOLTIPLICAZIONE A DUE CIFRE

Per eseguire la moltiplicazione con il moltiplicatore a due cifre devi eseguire alcuni passaggi. Osserva le fasi.

Fase 1

Moltiplica l’unità del moltiplicatore per il moltiplicando. Hai ottenuto il 1° prodotto parziale : 24 × 2 = 48

Fase 2

Scrivi uno 0 segnaposto al posto dell’unità del 2° prodotto parziale . Moltiplica poi la decina del moltiplicatore per il moltiplicando.

Hai ottenuto il 2° prodotto parziale: 24 × 10 = 240

Fase 3

Somma ora i due prodotti parziali e scrivi il prodotto totale : 48 + 240 = 288

h da u

2 4 × 1 2 = 4 8

h da u

2 4 × 1 2 = 4 8

2 4 0

h da u

2 4 × 1 2 = 4 8 +

2 4 0 =

2 8 8

moltiplicando moltiplicatore

1° prodotto parziale

moltiplicando moltiplicatore

1° prodotto parziale

2° prodotto parziale

moltiplicando moltiplicatore

1° prodotto parziale

2° prodotto parziale prodotto totale

Ricorda

Per eseguire la moltiplicazione con due cifre, devi eseguire due moltiplicazioni e sommare i loro risultati. Non dimenticare lo 0 segnaposto Anche nelle moltiplicazioni a due cifre, potresti trovare dei cambi da fare: non dimenticare il riporto.

1 Esegui le moltiplicazioni in colonna con la prova.

Prova

k h da u

3 4 × 1 6 = + =

k h da u

2 9 × 3 2 = + =

k h da u

1 8 ×

5 6 = + =

k h da u

1 6 × 3 4 = + =

Prova

k h da u × = + =

Prova

k h da u × = + =

k h da u

2 2 × 1 6 = + =

k h da u

4 2 × 3 1 = + =

k h da u

6 6 × 1 7 = + =

Prova

k h da u × = + =

Prova

k h da u × = + =

2 Esegui in colonna sul quaderno con la prova.

21 × 14

13 × 22

15 × 21

16 × 11

33 × 12

Prova

k h da u × = + =

90 × 17

LE TABELLINE

RICORDA DI RIPETERE SEMPRE LE TABELLINE.

Quando un numero finisce con 0, la moltiplicazione è un gioco da ragazzi.

3 3 15

× × ×

50 5 10

= × =

10 150

1 Ora prova tu!

70 × 3 =

× ............. × 3

• Scomponi il 50 in una moltiplicazione per 10;

• moltiplica i due fattori che non finiscono per 0;

• moltiplica il risultato per 10 (basta aggiungere uno 0!).

5 × 50 = 5 × ............. ×

80 × 6 =

E quando il numero finisce con due zeri? Il matetrucco è lo stesso, basta togliere due zeri e aggiungerli al prodotto!

2 Osserva gli esempi e continua da solo. Occhio agli zeri evidenziati!

7 × 4 00 = 2 8 00

200 × 9 =

4 × 3 00 =

500 × 4 =

2 × 700 =

6 00 × 6 =

Quando un fattore ha due cifre e la moltiplicazione ti sembra difficile, basta “fare a pezzi” il numero, applicando la proprietà distributiva.

24 3 × =

20 + 4

3 Ora prova tu.

27 × 5 = (20 × ) + ( × 5) = + =

52 × 3 = ( × ) + ( × ) = + =

12 60

20 × 3 4 × 3 + + = 72

19 × 4 = ( × ) + ( × ) = + =

LA DIVISIONE

1 Leggi e completa.

Jenny ha 12 biscotti per cani e vuole distribuirli ai suoi 4 amici pelosetti in parti uguali. Quanti biscotti avrà ogni cagnolino?

Distribuisci con una freccia i biscotti in parti uguali ai cagnolini.

OPERAZIONI

12 : 4 =

RISPOSTA Ogni cagnolino avrà biscotti.

Jenny ha preparato poi 20 biscotti per i suoi amici gatti e ne mette 5 in ogni piattino. Quanti piattini le serviranno?

Raggruppa i biscotti e disegna i piattini.

OPERAZIONI

20 : 5 = .........

RISPOSTA Le serviranno .......... piattini.

La divisione è l’operazione che ti permette di dividere o distribuire (divisione di ripartizione) in parti uguali o di raggruppare una quantità in gruppi uguali (divisione di contenenza).

Risponde alle domande: quanti ciascuno? Quanti per ogni…? Il segno della divisione è : (diviso ). I termini della divisione sono

8 : 2 = 4

Ricorda dividendo divisore quoto (resto 0)

Se la divisione ha il resto, il risultato si chiama quoziente

LA DIVISIONE IN COLONNA

Per eseguire le divisioni che non riesci a calcolare a mente, puoi metterle in colonna. Osserva le fasi del procedimento.

da u

7 2 2

1 3

Fase 1

Considera le decine : il 2 sta nel 7 3 volte (2 × 3 = 6) con il resto di 1.

da u

7 2 2

1 2 3 6 0

Fase 2

Considera le unità e scrivile accanto al resto 1. Si è formato il 1 2 . Il 2 sta nel 1 2 6 volte (2 × 6 = 12) e non c’è resto.

1 Metti in colonna e calcola sul quaderno.

Osserva questa divisione O 32 : 4 La prima cifra del dividendo è minore del divisore ( 3 < 4 ).

Considera sia le decine che le unità . Il 4 sta nel 3 2 8 volte ( 4 × 8 = 32) con il resto di 0.

2 Metti in colonna e calcola sul quaderno.

da u

3 2 4

0 8

CON TRE CIFRE AL DIVIDENDO

Quando il dividendo è formato da 3 cifre, il procedimento è lo stesso che hai imparato, è solo più lungo. Osserva le fasi.

Fase 1

Considera le centinaia : il 2 sta nel 2 , 1 volta (2 × 1 = 2) con il resto di 0.

Fase 2

Considera le decine e scrivi il 3 sotto il 3 .

Il 2 sta nel 3 1 volta (2 × 1 = 2) con il resto di 1.

Fase 3

Considera le unità e scrivi il 6 sotto il 6. Accanto all’1 delle decine si è formato il numero 1 6

Il 2 sta nel 1 6 8 volte (2 × 8 = 16) con il resto di 0.

1 Adesso prova tu! Calcola in colonna sul quaderno.

• 936 : 3

• 825 : 5

• 704 : 2

• 845 : 5

• 627 : 3

• 849 : 4

• 768 : 4

• 926 : 6

• 278 : 2

• 432 : 2

• 347 : 3

• 542 : 4

•

•

•

•

CON TRE CIFRE AL DIVIDENDO

Anche nella divisione a 3 cifre, quando la prima cifra del dividendo è minore del divisore, si considerano subito le prime due cifre. Osserva.

h da u

1 4 4 3 2 4

Fase 1

Considera le centinaia e le decine : il 3 sta nel 1 4 4 volte ( 3 × 4 = 12) con il resto di 2.

h da u

1 4 4 3 2 4 4 8 0

Fase 2

Considera le unità e scrivi il 4 sotto il 4 . Accanto al 2 delle decine si è formato il numero 24 . Il 3 sta nel 24 8 volte ( 3 × 8 = 24) con il resto di 0.

1

•

2

in colonna sul quaderno.

OPERAZIONI INVERSE

La divisione è l’operazione inversa della moltiplicazione: questa caratteristica della divisione ti permette di eseguire la prova

1 Completa.

2 Utilizza la moltiplicazione per fare la prova della divisione, come nell’esempio.

LA PROVA DELLA DIVISIONE

Hai già imparato che la moltiplicazione e la divisione sono operazioni inverse. Puoi dunque usare la moltiplicazione per fare la prova della divisione e verificare se il tuo calcolo è esatto. Osserva gli esempi.

h da u

1 4 4 3

2 4 4 8 0

Prova

h da u

4 8 × 3 =

1 4 4

Moltiplicando il risultato della divisione per il divisore, dovrai ottenere il dividendo.

h da u

1 4 6 3

2 6 4 8 2

Prova

h da u

4 8 ×

3 = 1 4 4 +

2 = 1 4 6

Se la divisione ha il resto, basta sommarlo al prodotto della moltiplicazione.

1 Esegui le divisioni in colonna con la prova aiutandoti con i colori.

Prova

Prova

h da u

1 2 8 4 h da u

h da u

3 0 8 5

2 Metti in colonna e calcola sul quaderno con la prova.

• 858 : 5

• 668 : 4

• 692 : 4

• 908 : 6

• 274 : 4

• 756 : 2

• 917 : 8

• 258 : 3

• 772 : 3

h da u

• 765 : 5

• 926 : 2

• 174 : 6

LA PROPRIETÀ DELLA DIVISIONE

Per rendere i calcoli più semplici, puoi applicare la proprietà invariantiva della divisione. Moltiplicando o dividendo per uno stesso numero (tranne lo 0) sia il dividendo che il divisore, il risultato non cambia.

1 Osserva e rispondi.

30 : 10 = 3

:2 :2

15 : 5 = 3

45 : 5 = 9

×2 ×2

90 : 10 = 9

• Abbiamo diviso per 2 il dividendo e il divisore.

Il risultato è cambiato? SÌ NO

• Abbiamo moltiplicato per 2 il dividendo e il divisore.

Il risultato è cambiato? SÌ NO

• È stato più facile trovare il risultato applicando la proprietà? SÌ NO

2 Esegui le divisioni applicando la proprietà invariantiva, come nell’esempio.

40 : 8 = 5

:4 :4

10 : 2 = 5

25 : 5 = × ×

30 : 6 = : :

18 : 6 = : :

3 Esegui le divisioni sul quaderno applicando la proprietà invariantiva.

• 150 : 30

•

•

:

:

:

DIVISIONI PER 10, 100 E 1 000

Quando dividi un numero per 10, 100, 1 000, il suo valore diminuisce di

10, 100, 1 000 volte.

k h da u

4 0 4 : 10

k h da u

4 0 0

4

: 100

Quando dividi per 10 , togli uno 0 all’ unità e il 4 diventa unità .

k h da u

4 0 0 0

4 : 1 000

Quando dividi per 100 , togli uno 0

all’ unità , uno 0 alla decina e il 4 va nella casella delle unità

Quando dividi per 1 000 , togli uno 0

all’ unità , uno 0 alla decina , uno 0 al centinaio e il 4 va nella casella delle unità

2

Ho la febbre. Che cosa posso fare?

I PROBLEMI

Il problema è una situazione che richiede una soluzione

Abbiamo € 8. Quanti bastoncini di zucchero filato possiamo comprare?

€ 2

Quando nel problema ci sono i numeri e puoi risolverlo eseguendo operazioni, allora il problema è matematico.

Leggi il testo facendo attenzione alla domanda e alle parole chiave

Cerca e trascrivi i dati , cioè le informazioni numeriche. Scegli l’ operazione adatta ed esegui il calcolo. Puoi aiutarti con il diagramma.

Trascrivi la risposta

Quanti bastoncini?

€ 8 = euro a disposizione € 2 = costo di un bastoncino

8 : 2 = 4

:

8 2 4

Si possono comprare 4 bastoncini di zucchero filato.

I PROBLEMI

Il testo del problema ci fornisce le informazioni (i dati numerici) necessarie per risolverlo. Alla domanda possiamo rispondere eseguendo operazioni

1 Leggi con attenzione il testo, sottolinea i dati numerici e indica con una X la domanda alla quale devi rispondere.

a. Gino e Mario giocano ai videogames. Mario con 150 punti batte Gino che ne totalizza 103.

A. Quanti punti di differenza?

B. Quale console di gioco hanno usato?

b. Al teatro il biglietto di ingresso per lo spettacolo serale costa € 25 a persona. Bea vuole vedere lo spettacolo con le sue due sorelle.

A. A che ora comincia lo spettacolo?

B. Quanto spenderà in tutto Bea?

2 Leggi con attenzione il testo del problema, sottolinea i dati numerici e scrivi tu una domanda adatta.

a. A l mercato un venditore ha esposto 150 modellini d’auto d’epoca. A fine mattinata ne ha vendute 85.

b. Per l’abbonamento allo stadio Leo ha speso 230 euro e potrà assistere a 10 partite.

3 Osserva l’immagine e inventa il testo del problema, tenendo presente la domanda.

Quanti punti hanno totalizzato in tutto?

I DATI INUTILI

In un problema a volte ci sono informazioni superflue, non necessarie alla soluzione: sono i dati inutili. Per trovarli, devi capire bene la domanda.

Michael è nato nel 2012. Sta per imbarcarsi per New York con la sua famiglia. Sono in fila con il numero 87 e al check-in stanno controllando i documenti del numero

45. Tra quante persone toccherà a Michael?

• Che cosa devo trovare? La differenza tra il numero di Michael e il numero delle persone servite

• Quali dati mi servono? 87 e 45

• Qual è il dato inutile? 2012

1 Leggi il testo del problema e cerchia in verde i dati utili e in rosso i dati inutili . Poi risolvi con il diagramma e l’operazione sul quaderno.

a. Lorenzo e i suoi 2 amici hanno collezionato 2 700 figurine di animali. Decidono di regalarne 500 al loro amico Mario, che ha 2 album dei calciatori. Quante figurine restano nella collezione?

b. Samira deve leggere un libro di 250 pagine, che costa € 12. Paga con una banconota da € 20. Quanto riceve di resto?

c. N el parcheggio di un centro commerciale ci sono 6 piani e su ogni piano ci sono 45 posti auto. Nel centro commerciale ci sono 120 negozi, 6 bar e 4 ristoranti. Quanti posti auto ci sono in tutto?

I DATI NASCOSTI

Il testo del problema a volte ci dà delle informazioni che non sembrano numeriche, ma che sono utili invece alla soluzione. Sono i dati nascosti. Fai attenzione alle parole metà, doppio, triplo, alle parole del tempo come settimana, mese, o a informazioni che fanno parte delle nostre conoscenze come il numero di zampe di un animale.

1 Leggi con molta attenzione il testo dei problemi, sottolinea la parola del dato nascosto e trasformalo in dato numerico. Poi risolvi sul quaderno con il diagramma e l’operazione.

a. L a famiglia di Ruben consuma di solito 2 litri di latte al giorno. Quanti litri in una settimana?

Dato nascosto:

K Dato numerico:

b. S amuele ha 12 anni e suo padre ha due dozzine di anni in più di lui. Quanti anni ha il padre di Samuele?

Dato nascosto:

c. In una scuderia posso contare 36 occhi. Quanti cavalli ci saranno?

Dato nascosto:

MATE

ᄗ Prova a risolvere l’indovinello. Ci sono solo dati nascosti

K Dato numerico:

K Dato numerico:

“Quale numero ottengo se moltiplico le zampe di un cane per i ladroni di Ali Babà?”

TUTTI INSIEME

ᄗ Lavorando in coppia, inventate indovinelli con dati nascosti e sfidate i vostri compagni.

PROBLEMI CON DUE DOMANDE

I problemi possono avere due domande alle quali bisogna rispondere eseguendo due operazioni.

1 Leggi, rifletti e completa.

Alla mensa dell’ospedale ci sono 18 tavoli con 6 sedie ciascuno. Quanti sono in tutto i posti disponibili? Al secondo piano nella mensa ci sono 22 tavoli con 8 sedie ciascuno. Quanti sono i posti nella mensa del secondo piano? DATI

PROBLEMI CON DOMANDA NASCOSTA

A volte la domanda è una, ma ce n’è un’altra nascosta che ci serve per ricavare un dato. Per rispondere alla domanda finale bisogna dunque eseguire due operazioni.

1 Leggi, rifletti e completa.

I 18 alunni della III C hanno realizzato ciascuno 3 oggetti per una mostra di beneficenza. Sono già stati esposti 26 lavori. Quanti devono ancora essere esposti?

DATI 18 3 26 Dato da ricavare

OPERAZIONI

I DATI MANCANTI

Non sempre i problemi sono risolvibili. Accade quando il testo non ci dà tutte le informazioni necessarie, cioè quando ci sono dati mancanti

1 Leggi, rifletti e completa.

Il proprietario di un negozio di articoli sportivi realizza alcune confezioni contenenti ciascuna

48 magliette. Quante sono in tutto le magliette?

Puoi risolvere il problema? SÌ NO

Quale dato manca?

Il numero

2 Riscrivi il testo del problema sul quaderno, inventa il dato mancante e risolvi.

In un’enoteca sono disposte 12 bottiglie su ciascuna delle mensole dello scaffale del vino rosso. Quante bottiglie in tutto? Il cartolaio ha sistemato 200 quaderni in alcuni scatoloni. Quanti quaderni in ogni scatolone?

Mattia sistema le sue automobiline, mettendole su 3 ripiani. Quante macchinine sistema su ogni ripiano? Simone ha 238 figurine. Ne regala alcune ai suoi compagni. Quante figurine ha ora Simone?

MI ESERCITO CON I PROBLEMI

1 Risolvi sul quaderno con operazione e diagramma. Ricorda il procedimento.

Con una domanda ed un’operazione

1. In un garage posso contare 36 ruote di motocicletta e 61 di automobili. Quante motociclette sono parcheggiate?

2. In fila all’ufficio postale la signora Giovanna ha il numero 134. È il turno del numero 95. Quante persone ci sono in fila prima di lei?

Ricorda

Con due domande e due operazioni

3. In una fattoria ci sono 12 galline, 12 cavalli e 6 oche. Quanti animali in tutto? Nella conigliera ci sono 35 conigli. Quante zampe conto nella conigliera?

4. In pasticceria spendo € 24 per una torta e pago con una banconota da € 50. Quanto ricevo di resto? Il pasticciere aveva esposto in vetrina 40 muffins alla ciliegia, 50 bignè al cioccolato e 36 croissant alla crema. Quanti dolci in tutto?

Con una domanda e due operazioni

5. L a bibliotecaria ha conservato 30 libri in ciascuno dei 6 scatoloni a disposizione. Di questi 45 sono libri di storia. Quanti libri non sono di storia?

6. A l teatro “Manzoni” ci sono 24 file da 16 posti ciascuna. Allo spettacolo di ieri sera erano presenti 195 spettatori. Quanti posti erano liberi?

ANCORA DIAGRAMMI

1 Risolvi sul quaderno i problemi, poi collega ciascuno di essi al diagramma a blocchi che ne rappresenta la soluzione.

Per la festa di compleanno, Giorgio gonfia 54 palloncini rossi e 28 verdi. Quanti palloncini in tutto?

Nella scatola c’erano 100 palloncini. Quanti palloncini sono rimasti?

Un fruttivendolo ha 320 fragole e ne mette 10 in ogni cestino. Quanti cestini prepara? Vende ogni cestino a € 4 l’uno. Quanto incassa dalla vendita di tutti i cestini?

La classe III A è composta da 23 alunni. Ognuno ritaglia 4 bandierine blu e 3 gialle. Quante bandierine prepara ogni alunno? Quante bandierine ritaglia tutta la classe?

2 Osserva i diagrammi e inventa sul quaderno un problema per ciascuno di essi.

Su ciascun ripiano di uno scaffale ci sono 24 libri. Lo scaffale ha 5 ripiani. Quanti libri in tutto? La maestra distribuisce 18 libri agli alunni. Quanti libri restano sullo scaffale?

PROBLEMI SENZA NUMERI

Non sempre servono i numeri per risolvere i problemi. Basta ragionare.

LA GARA DI CORSA CAMPESTRE

ᄗ Nadia, Filippo, Niko, Ilaria e Francesco hanno partecipato a un torneo di bowling. Nadia è arrivata ultima; Filippo prima di Nadia ma dopo Ilaria; Niko dopo Filippo ma prima di Francesco; Francesco subito prima di Nadia. Chi ha vinto?

Ilaria Nadia Niko Francesco Filippo

LA PAROLA MANCANTE

ᄗ Trova la chiave di questa sequenza di parole e indica quella che potrebbe entrare nello spazio vuoto.

uva → casa → palla → ? → tamburo → girasole → bacchetta

delfino balena dinosauro

LE CINQUE SORELLE

ᄗ Flora è più alta di Lia, ma è più bassa di Simona. Marta e Karol hanno la stessa altezza, ma sono più basse di Flora. Chi è la più alta?

Flora Simona

Karol

Lia Marta

SUDOKU

ᄗ Inserisci i seguenti simboli nella griglia, in modo che non si ripetano mai nella stessa riga e nella stessa colonna.

ALLENIAMO LA LOGICA

ᄗ Leggi, rifletti e rispondi.

Dopodomani andrò in piscina e oggi, che è il giorno che precede il mercoledì e segue il lunedì, andrò al cinema con i miei amici. In quale giorno della settimana andrò in piscina?

RISPOSTA

Immagina di partecipare ad una gara di tuffi. A un certo punto in classifica superi il quarto. In quale posizione ti troveresti se con un magnifico tuffo superassi il terzo in classifica?

RISPOSTA

ᄗ Osserva le immagini e forma la frase da scrivere sui puntini. Fai attenzione al numero di lettere indicato in parentesi.

CE (6,6)

M NE R (8,5)

STRO R (8,5)

GR RAN (6,8)

1 Leggi il testo, scrivi i dati e risolvi il problema.

Per la sua festa Gianluca ha chiesto alla mamma di acquistare 60 ciambelline zuccherate, 4 crostate al cioccolato e 45 dolcetti alla marmellata. Quanti dolci in tutto?

DATI

OPERAZIONE =

RISPOSTA

2 Scrivi la domanda adatta e risolvi il problema sul quaderno con il diagramma.

Ai corsi di inglese sono iscritti in tutto 136 bambini di scuola primaria. Oggi sono arrivate altre 18 domande di iscrizione.

DOMANDA

ᄗ

ᄗ

LE FRAZIONI

Tommy, Gaia e Anna vogliono dividere la tavoletta di cioccolata in parti uguali, in modo da avere la stessa quantità.

1 Osserva l’immagine e completa, indicando con una X la risposta esatta.

• La tavoletta è divisa in parti uguali? Sì No

• In quante parti è stata divisa la tavoletta? 1 2 3

• Quante parti riceverà ciascuno di loro? 1 2 3

La tavoletta è stata divisa in parti uguali, cioè è stata frazionata

Ogni parte in cui è stata divisa si chiama unità frazionaria

Ognuno ha avuto 1 fetta su 3 , cioè 1 3 (si legge un terzo).

2 Osserva le immagini e indica con una X le crostate che sono state frazionate correttamente.

3 Osserva e scrivi in quante parti è stata frazionata l'immagine.

8 parti parti parti

Una frazione indica una parte dell’intero.

2 5 numeratore denominatore

linea di frazione

Si scrive 2 5 si legge due quinti

Il numeratore è il numero sopra la linea di frazione e mi dice quante parti dell’intero sono state considerate (2 fette di torta).

Ricorda

La linea di frazione indica la divisione in parti uguali.

Il denominatore è il numero sotto la linea di frazione e mi dice in quante parti uguali è stato diviso l’intero (5 fette di torta).

• Per il numeratore si usano i numeri cardinali : 1, 2, 3 …

• Per il denominatore si usano i numeri ordinali : terzo, quarto, quinto… Attenzione al 2! Si legge mezzo e non secondo.

COSTRUIAMO LE FRAZIONI

ᄗ Giochiamo con i mattoncini delle costruzioni. Usando mattoncini di diverse misure come frazioni, divertitevi a ricostruire gli interi.

Osserva

corrispondente, in cifre e in parola.

5

le immagini e scrivi la frazione

4 Colora la parte indicata dalla frazione.

LE FRAZIONI DECIMALI

1 Osserva e completa.

• L'intero è stato frazionato in parti.

• È stata colorata solo 1 parte su 10, cioè 1

• Si legge un

• L'intero è stato frazionato in ................. parti.

• È stata colorata solo 1 parte su 100, cioè 1

• Si legge un

• L'intero è stato frazionato in parti.

• È stata colorata solo 1 parte su 1 000, cioè 1 ............

• Si legge un ...............................

Ricorda

Le frazioni che al denominatore hanno 10, 100, 1 000 si chiamano frazioni decimali

2 Colora la frazione indicata.

DALLA FRAZIONE DECIMALE

AL NUMERO DECIMALE

1 Le frazioni decimali possono essere scritte anche sotto forma di numeri decimali. Osserva, rifletti e rispondi.

• In quante parti è diviso l’intero?

• Quante sono le parti colorate?

• A quale frazione corrisponde la parte colorata? ......

Possiamo scriverla anche così:

Ricorda

, 4 parte intera parte decimale

È un numero decimale e si legge zero virgola quattro Lo 0 indica le unità e il 4 i decimi.

Le frazioni decimali possono essere trasformate in numeri decimali. La virgola separa la parte intera dalla parte decimale.

2 Completa la linea dei numeri da 0 a 1, trasformando la frazione nel corrispondente numero decimale.

3 Colora seguendo le indicazioni, poi scrivi in cifre la frazione e il corrispondente numero decimale. Segui l’esempio.

cinque decimi sei decimi quattro decimi

tre decimi otto decimi due decimi

I DECIMI

Il decimo è la decima parte dell’unità. Il suo simbolo è d.

10 decimi formano 1 unità 10 d = 1 u

Per rappresentarlo sull’abaco, mettiamo un’asta a destra dell’unità.

1 decimo (1 d) si scrive 0,1 1 10 = 0,1

L’1 è scritto a destra della virgola.

, u 0 da h k d 1

1 Rappresenta i numeri decimali sull’abaco, come nell’esempio.

2 Scrivi il numero decimale che manca per arrivare al numero intero.

• 0,3 + .............. = 1

• 0,8 + .............. = 1

• 0,1 + .............. = 1

• 0,2 + .............. = 1

• 0,7 + = 1

• 0,9 + = 1

•

•

•

•

•

•

• 2,9

• 2,5

• 2,7

• 3,8

• 3,6

• 3,1

= 3

4

= 4

3 Trasforma le frazioni decimali in numeri decimali, come nell’esempio.

4 Componi i numeri sotto forma di numero decimale, come nell’esempio.

• 2 unità e 6 decimi → 2,6

• 3 unità e 4 decimi →

• 1 unità e 9 decimi →

• 7 unità e 3 decimi →

• 1 unità e 4 decimi →

• 3 unità e 7 decimi →

• 4 unità e 8 decimi →

• 7 unità e 6 decimi → .............

• 8 unità e 3 decimi → .............

• 5 unità e 3 decimi →

• 9 unità e 3 decimi →

• 6 unità e 6 decimi →

• 6 unità e 8 decimi →

• 8 unità e 9 decimi →

5 Scomponi ciascun numero decimale, come nell’esempio.

• 0,6

0 unità e 6 decimi

I CENTESIMI

Il centesimo è la centesima parte dell’unità. Il suo simbolo è c

100 centesimi formano 1 unità 100 c = 10 d = 1 u

Per rappresentarlo sull’abaco, mettiamo un’asta a destra dei decimi.

1 centesimo (1 c) si scrive 0,01 1

100 = 0,01

L’1 è scritto al secondo posto, a destra della virgola. ,

1 Rappresenta i numeri decimali sull’abaco, come nell’esempio.

2 Colora la frazione indicata e scrivi il suo valore sotto forma di numero decimale, come nell’esempio.

=

3 Completa le equivalenze, come nell’esempio.

• 1 u = 10 d

• 2 u = d

• 3 d = c

• 20 d = u

• 1 u = .............. c

• 2 u = .............. c

• 3 u = .............. d

• 600 c = .............. u

• 1 d = .............. c

• 2 d = .............. c

• 3 u = .............. c

• 90 c = .............. d

4 Completa la tabella componendo o scomponendo i numeri.

numero u , d c scomposizione 0,23

centesimi ,

centesimi

I MILLESIMI

Il millesimo è la millesima parte dell’unità. Il suo simbolo è m

1 000 millesimi formano 1 unità 1 000 m = 100 c = 10 d = 1 u

Per rappresentarlo sull’abaco, mettiamo un’asta a destra dei centesimi.

1 millesimo (1 m) si scrive 0,001 1

1 000 = 0,001

L’1 è scritto al terzo posto, a destra della virgola.

1 Rappresenta i numeri decimali sull’abaco, come nell’esempio. tre

2 Trasforma le seguenti frazioni in numeri decimali.

3 Completa, come nell’esempio.

• 1 u = 1 000 m

• 6 d = m

• 400 c = m

• 40 d c

• 3 d = m

• 4 d = .............. m

• 70 c = d

• 500 c = u

• 2 c = m

• 8 d = m

• 5 000 m = u

• 7 000 m = u

4 Scomponi come nell’esempio.

• 1,234 = 1 u, 2 d, 3 c, 4 m

• 3,275 =

• 0,357 =

• 7,057 =

• 1,439 =

tenth decimo

hundredth centesimo

thousandth millesimo

• 4 c = m

• 9 d = m

• 2 000 m = u

• 50 d = m

• 8 000 m = u

• 1 200 c = u

• 5,136 = ......................................................................................................

• 1,009 = ......................................................................................................

• 4,506 = ......................................................................................................

5 Componi come nell’esempio.

• 0 u, 4 d, 3 c, 5 m = 0,435

• 1 u, 6 d, 5 c, 9 m =

• 1 u, 7 d, 8 c, 9 m =

• 0 u, 7 d, 8 c, 9 m =

• 0 u, 8 c, 9 m = ................................

• 6 u, 7 d, 3 m = ................................

• 3 u, 4 d, 6 m = ................................

• 0 u, 1 m = ...........................................

I NUMERI DECIMALI

I numeri decimali sono formati da una parte intera e da una decimale. La virgola separa le due parti.

1 Cerchia di azzurro la parte intera e di rosso la parte decimale di ciascun numero. 27,456

2 Scomponi in tabella, come nell’esempio.

3 Scrivi il valore di ogni cifra evidenziata, come nell’esempio.

5 140,001

3 267,554

147,296

54,3

66,48

•

4 Scrivi quanto manca per raggiungere il numero intero, come nell’esempio.

• 3,7 + 0,3 = 4

• 2,45 + = 3

• 4,999 + = 5

• 8,6 + = 9

• 0,05 + = 1

• 0,994 + = 1

• 0,9 + = 1

•

• 0,001 + = 1

•

• 2,75 + = 3

•

1 Osserva e confronta prima la parte intera poi la parte decimale.

12 è maggiore di 6, quindi 12 ,5 è maggiore di 6,8.

Se la parte intera dei due numeri è uguale, allora confronto la parte decimale: 38,47 è minore di 38,95.

2 Leggi e completa con > o

12,5 > 6,8

38,47 < 38,95

3 Riscrivi i numeri in ordine crescente.

4 Riscrivi i numeri in ordine decrescente.

L’EURO

In Italia e in molti Paesi dell’Unione Europea la moneta è l’ euro È coniato in 8 monete e 6 banconote. Il suo simbolo è € .

2 Completa come nell’esempio.

7 euro e 20 centesimi = €

1 Osserva lo schema.

3 Scrivi come si leggono i seguenti numeri. Segui l’esempio.

€ 8,35 → 8 euro e 35 centesimi

€ 12,73 →

€ 0,75 →

€ 37,80 →

€ 172,75 →

€ 350,05 →

4 Leggi e completa con > o <.

€ 0,10 ............ € 0,18

€ 0,05 ............ € 0,50

€ 1 ............ € 0,50

€ 2 ............ € 20

€ 225,99 → ......................................................

€ 500,00 → ......................................................

€ 1,50 → ......................................................

€ 125,10 → ......................................................

€ 27,00 → ......................................................

€ 470,35 →

€ 4,70 € 47

€ 13,50 € 1,35

€ 5,50 € 55

€ 20,50 € 2,50

€ 12,50 € 1,25

€ 25,15 € 2,15

€ 3,60 € 0,36

€ 50,50 € 55

5 Mauro ha nel portafogli € 40,00. Vuole comprare per la sua mamma almeno 3 romanzi. Quali tra i seguenti libri potrebbe acquistare? Indica con una X poi completa la frase.

€ 10,00

Ho scelto questi tre libri perché

IL DOMINO DELL’EURO

€ 38,00 € 31,50

ᄗ In gruppo costruite tessere del domino raffigurando una moneta e una banconota sul cartoncino. Giocate in coppia o in gruppo al “domino dell’euro”.

COSTO UNITARIO E COSTO TOTALE

1 Leggi e rifletti.

Lisa compra 4 album di adesivi

Ogni album costa € 5,00.

Quanto spende in tutto?

€ 5,00

= ×

costo unitario quantità

4 costo totale

€ 20,00

Lisa acquista anche 10 bustine di adesivi. Paga in tutto € 2,00. Quanto costa un pacco di figurine?

€ 2,00

10 costo totale

= :

€ 0,20 costo unitario quantità

Compra poi i gelati e spende € 12,00.

Ogni gelato costa € 3,00.

Quanti gelati acquista Lisa? = : € 3,00

€ 12,00

costo totale

4

costo unitario quantità

Ricorda :

Ricorda queste semplici formule per eseguire i tuoi calcoli sui costi.

quantità

costo unitario :

× costo totale

costo totale quantità costo unitario

costo totale quantità

costo unitario

2 Completa la tabella.

costo totale costo unitario quantità operazione

€ 2,00 6

€ 84,00 3

€ 18,00 € 2,00

3 Risolvi i problemi sul quaderno, con il diagramma e l’operazione.

1) Giacomo compra 2 paia di jeans e spende in tutto € 130,00. Quanto ha pagato per ogni paio di jeans?

2) Il signor Lobotka acquista alcuni libri usati spendendo in tutto € 120,00. Se per ogni libro ha speso € 6,00, quanti ne ha acquistati?

3) Una busta di popcorn costa € 2,00. Quanto spenderà Luana per acquistarne 13?

4) Thiago acquista 20 confezioni di merendine. Ogni confezione costa € 3,00. Quanto costano in tutto le merendine?

1 Per ogni figura colora e scrivi l’unità frazionaria, come nell’esempio.

2 Collega ogni frazione al disegno corrispondente.

3 Osserva le parti colorate e scrivi le frazioni corrispondenti.

4

•

5

6 Scomponi il numero.

• 0,12 =

• 252,3 = ........................................................

• 92,345 =

• 6,294 =

• 0,004 = ........................................................

• 0,8 =

• 41,3 =

• 12,25 = ........................................................

• 3,007 =

• 11,014 =

7 Scomponi e componi il numero.

• 8 u , 6 d , 3 c , 7 m =

• 0 u , 0 d , 3 c , 6 m = ......................

• 1 da , 3 u , 9 d , 0 c , 1 m =

• 9 u , 1 d , 7 c =

• 1 da , 1 u , 0 d , 0 c , 4 m = ......................

• 7 u , 4 d, 0 c , 9 m =

• 2 da ,0 u , 5 d , 0 c , 6 m =

• 3 da , 8 u , 0 d , 4 c = ......................

• 0 u , 5 d , 2 c , 2 m =

• 1 da , 8 u , 9 d , 8 c =

€ 2,65

8 Disegna il minor numero possibile di monete per formare la somma indicata.

9 Qual è il valore totale di queste monete?

6 euro e 30 cent

8 euro e 30 cent

6 euro e 50 cent

9 euro e 80 cent

10 Risolvi i problemi sul quaderno, con il diagramma e l’operazione.

Una scatola di 6 pastelli costa € 12,00. Quanto costa un pastello?

Il biglietto del traghetto da Napoli a Capri costa € 14,00 a persona. Quanto spende in tutto una famiglia composta da 5 persone?

ᄗ

Lucas ha speso € 24,00 per acquistare dei sacchetti di crocchette per il suo cane. Ha speso € 4,00 per ogni sacchetto. Quanti sacchetti di crocchette ha acquistato?

ᄗ

MISURARE

Sin dai tempi più lontani l’uomo ha avvertito il bisogno di misurare , cioè di calcolare ad esempio la lunghezza di un campo da coltivare, la quantità di raccolto, l’altezza di un monumento, il passare del tempo.

Per fare queste misurazioni, gli uomini usavano parti del loro corpo: il pollice , il piede , la spanna , il cubito .

Allora in Francia, nel 1775, si riunì una commissione di scienziati con lo scopo di creare un unico insieme di unità di misura, uguale per tutti, da usare per le misure di lunghezza, di peso, di capacità, e così via.

Il nuovo sistema fu chiamato SISTEMA METRICO DECIMALE .

La parola metrico deriva dal greco metría (misura), mentre la parola decimale indica che il sistema è in base 10 , formato da multipli e sottomultipli che si ottengono moltiplicando o dividendo per 10, 100, 1 000.

inch pollice span spanna feet piedi cubit cubito

Ricorda

La misura è quella parte della matematica che misura le grandezze, usando unità di misura convenzionali.

Una grandezza è tutto ciò che possiamo misurare.

Compito di REALTÀ

Divisi in gruppi, provate a misurare con pollice, piede, spanna e cubito le dimensioni della palestra e dei vari attrezzi ginnici. Poi confrontate le misure con quelle registrate dai compagni di squadra. Che cosa noterete?

SPANNA

CUBITO PIEDE POLLICE

LE MISURE DI LUNGHEZZA

Con le misure di lunghezza puoi misurare quanto è lungo, largo, alto un oggetto o quanto distano due punti tra loro. L’unità di misura della lunghezza è il metro, il cui simbolo è m. Per misurare grandezze più grandi o più piccole del metro si usano i suoi multipli e sottomultipli.

multipli

Unità di misura sottomultipli

chilometro ettometro decametro metro decimetro centimetro millimetro km hm dam m dm cm mm

1 000 m 100 m 10 m 1 0,1 m 0,01 m 0,001 m

I sottomultipli del metro si usano per misurare lunghezze più piccole del metro.

Il decimetro (dm) è la decima parte del metro → 1 dm = 1 10 di m = 0,1 m

Il centimetro (cm) è la centesima parte del metro → 1 cm = 1 di m = 0,01 m

Il millimetro (mm) è la millesima parte del metro

Uno strumento utile per misurare in dm, cm e mm è il

1 Prova a misurare con il righello gli oggetti del tuo corredo scolastico e registra le misure nella tabella.

gomma cm quaderno cm libro .......... cm temperamatite cm astuccio cm

Ricorda

I simboli con cui indichiamo le misure si chiamano marche e corrispondono sempre alla cifra delle unità Si scrivono dopo il numero e senza il punto (esempio 1 dm).

2 Osserva e indica con una X l’unità di misura adatta.

dm cm mm dm cm mm

dm cm mm

dm cm mm

I multipli del metro servono a misurare lunghezze più grandi del metro.

Il decametro (dam) è 10 volte più grande del metro → 1 dam = 10 m

L’ettometro (hm) è 100 volte più grande del metro → 1 hm = 100 m

Il chilometro (km) è 1 000 volte più grande del metro → 1 km = 1 000 m

3 Indica con una X le misure adatte per le seguenti lunghezze.

campo da calcio

km hm dam

scogliera

km hm dam

autostrada

km hm dam

4 Scomponi le misure ricordando che il simbolo della marca corrisponde alla cifra dell’unità. Segui l’esempio.

142 m → 1 hm, 4 dam, 2 m

56 m →

298 dm →

349 mm →

Compito di REALTÀ

12 cm →

155 dam →

3 211 dm →

76 hm →

ᄗ In coppia costruite un metro usando una fettuccia di cotone, indicando decimetri e centimetri con colori differenti.

LE EQUIVALENZE

Per passare da una misura all’altra bisogna compiere un’ equivalenza

Per passare da un’unità di misura maggiore ad una minore , devi moltiplicare:

per 10 se ti sposti di 1 posto; per 100 se ti sposti di 2 posti; per 1 000 se ti sposti di 3 posti.

Per passare da un’unità di misura minore ad una maggiore , devi dividere:

per 10 se ti sposti di 1 posto; per 100 se ti sposti di 2 posti; per 1 000 se ti sposti di 3 posti.

1 Completa le tabelle delle equivalenze, come nell’esempio.

EQUIVALENZE CON LE MISURE DI LUNGHEZZA

1 Completa la tabella, come nell’esempio.

km hm dam m dm cm mm

135 m

45 hm

3 678 mm

125 dam

36 cm

458 dm

5 476 m

1 3 5

Ricorda

La marca corrisponde sempre all’ unità.

2 Esegui le equivalenze, come nell’esempio.

• 32 dam = 320 m

• 4 cm = ................. mm

• 25 m = cm

• 5 km = dam

• 300 m = ................. hm

• 5 000 mm = dm

• 1 200 m = dam

• 35 dm = ................. mm

• 700 dam = km

3 Indica a quale marca corrisponde la cifra evidenziata.

324 m K 3 hm

250 cm K .................

4 520 dm K

408 mm K

2 789 m K .................

28 hm K

4 Indica con una X se le equivalenze sono vere (V) o false (F).

• 4 km = 400 dam V F

• 340 cm = 3 400 m V F

• 1 200 mm = 12 dm V F

• 700 km = 7 dam V F

• 3 800 m = 38 hm V F

• 965 cm = 9 650 mm V F

• 410 cm = 41 dm V F

• 2 000 m = 200 hm V F

1 087 cm K

326 dam K .................

976 m K

5 Colora allo stesso modo i cartellini delle misure equivalenti.

6 km 600 m

6 dam 60 mm

6 cm

6 000 m

6 hm 600 dm

LE MISURE DI CAPACITÀ

Con le misure di capacità puoi misurare quanto liquido può contenere un recipiente. La sua unità di misura è il litro ( [l ). Il litro ha multipli e sottomultipli.

multipli

Unità di misura sottomultipli

ettolitro decalitro litro decilitro centilitro millilitro h [l da [l [l d [l c [l m [l

100 [l 10 [l 1 0,1 [l 0,01 [l 0,001 [l

I sottomultipli del litro si usano per misurare capacità minori del litro.

Il decilitro ( d [l ) è la decima parte del litro → 1 d [l = 1 10 di [l = 0,1 [l

Il centilitro ( c [l ) è la centesima parte del litro → 1 c [l = 1 100 di [l = 0,01 [l

Il millilitro ( m [l ) è la millesima parte del litro → 1 m [l = 1 1 000 di [l = 0,001 [l

I multipli del litro servono a misurare capacità maggiori del litro.

Il decalitro (da [l ) è 10 volte più grande del litro → 1 da[l = 10 [l

L’ ettolitro ( h [l ) è 100 volte più grande del litro → 1 h[l = 100 [l

1 Indica con una X la misura di capacità adatta.

[l da [l h [l [l da [l

EQUIVALENZE CON LE MISURE DI CAPACITÀ

1 Completa le tabelle delle equivalenze, come nell’esempio.

x 10 x 100 x 1 000 : 10 : 100

[l d [l c [l m [l

3 30 300 3 000

2 8 7

2 Completa la tabella, inserendo le misure al posto giusto, come nell’esempio.

h [l da [l [l

9 90 900 400 500 600

h [l da [l [l d [l c [l m [l

7 234 d[l 7 2 3 4

64 da[l

367 c[l

458 [l

852 m[l

1 854 c[l

3 Esegui le equivalenze, come nell’esempio.

• 2 da[l = 20 [l

• 45 [l = c[l

• 235 h[l = da[l

• 6 h[l = ................. [l

• 8 000 m[l = [l

• 7 000 m[l = [l

• 300 m[l = ................. d[l

• 24 d[l = m[l

• 3 400 da[l = h[l

4 Osserva le capacità dei contenitori ed esegui le equivalenze.

........ c

3 [l

200 c [l

........ d

[l m[l

d[l

[l

2 h [l 2 d [l

da[l d[l

........ c[l ........ m[l

LE MISURE DI PESO O MASSA

L’unità di misura del peso è il chilogrammo (kg) con i suoi multipli e sottomultipli

multipli

Unità di misura sottomultipli

megagrammo 100 chilogrammi 10 chilogrammi chilogrammo ettogrammo decagrammo grammo Mg - - kg hg dag g

1 000 kg 100 kg 10 kg 1 0,1 kg 0,01 kg 0,001 kg

L’ettogrammo (hg) è la decima parte del chilogrammo → 1 hg = 1 10 di kg = 0,1 kg

Il decagrammo (dag) è la centesima parte del chilogrammo → 1 dag = 1 100 di kg = 0,01 kg

Il grammo (g) è la millesima parte del chilogrammo → 1 g = 1 1 000 di kg = 0,001 kg

Ricorda

I multipli del chilogrammo servono a misurare capacità maggiori del chilogrammo. Il megagrammo (Mg) è l’unico multiplo del chilogrammo ed è 1 000 volte più grande del chilogrammo 1 Mg = 1 kg × 1 000 = 1 000 kg

LO SAPEVI CHE...

Il Sistema Internazionale di misura ha abolito il miriagrammo, che valeva 10 kg, e il quintale (100 kg), che viene però usato ancora nella vita di tutti i giorni.

1 Disegna alcuni oggetti che hanno il peso indicato.

1 kg più di 1 kg meno di 1 kg

I SOTTOMULTIPLI DEL GRAMMO

Unità di misura sottomultipli

grammo decigrammo centigrammo milligrammo g dg cg mg

1 0,1 g 0,01 g 0,001 g

Per misurare pesi più piccoli del grammo usiamo i sottomultipli del grammo

Il decigrammo (dg) è la decima parte del grammo → 1 dg = 1 10 di g = 0,1 g

Il centigrammo (cg) è la centesima parte del grammo → 1 cg = 1 100 di g = 0,01 g

1 Indica con una X la misura di peso adatta.

kg Mg kg cg g mg hg dg

Il milligrammo (mg) è la millesima parte del grammo → 1 mg = 1 1 000 di g = 0,001 g mg dag

EQUIVALENZE CON LE MISURE DI PESO

1 Completa le tabelle delle equivalenze, come nell’esempio.

x 10 x 100 x 1 000 : 10 : 100 : 1 000

kg hg dag g

6 60 600 6 000

4 7

5

g dg cg mg

1 10 100

1 000

3 000

8 000

9 000

2 Completa la tabella, inserendo le misure al posto giusto. Osserva l’esempio.

Mg 100 kg 10 kg kg hg dag g dg cg mg

1 467 kg 1 4 6 7

2 180 g

498 mg

3 567 hg

305 dag

98 cg

765 dg

3 Completa le equivalenze.

• 80 dg = g

• 96 g = dg

• 2 Mg = ............... kg

• 40 dag = hg

• 8 kg = g

• 36 hg = ............... dag

• 16 kg = hg

• 500 g = hg

• 300 cg = mg

• 75 g = mg

• 480 hg = ............... kg

• 61 dag = dg

• 4 000 kg = Mg

• 520 g = ........................... dag

• 2 100 mg = dg

• 45 kg ........................... dag

PESO LORDO, PESO NETTO, TARA

PESO LORDO 750 g

Il peso lordo è la somma del peso del contenuto (biscotti) e del contenitore (scatola)

PESO NETTO 730 g

Il peso netto è il peso del contenuto (biscotti)

TARA 20 g

La tara è il peso del contenitore (scatola)

Ricorda queste semplici formule per eseguire i tuoi calcoli sul peso.

peso netto tara

+

peso lordo

peso lordo peso netto

−

tara

peso lordo peso netto tara

−

.

1 Osserva le immagini e scrivi al posto giusto: peso lordo , peso netto , tara

PROBLEMI DI MISURA

Attenzione! Se le misure non sono espresse con la stessa marca, esegui un’equivalenza.

1 Risolvi i problemi sul quaderno.

MISURE DI LUNGHEZZA

1. Il corridoio che porta dalla cucina alla cameretta di Lucia è lungo 8 m. Se Lucia lo percorre 10 volte, quanti dam avrà percorso?

2. Milano dista da Parigi cir ca 850 km. Quanti km percorrerà un automobilista in un viaggio di andata e ritorno?

MISURE DI CAPACITÀ

1. Una piscina da giardino può contenere circa 14 h [l di acqua. Se viene riempita a metà, quanti litri di acqua vengono versati?

2. Per il mio raffreddore, il pediatra mi ha prescritto 40 m[l di sciroppo 5 volte al giorno. Quanti d [l di sciroppo prenderò in tutto al giorno?

MISURE DI PESO

1. Un panettier e inforna 30 kg di pane ogni notte. Oggi ne ha venduti 210 hg. Quanti kg di pane sono rimasti invenduti?

2. Alessia taglia una torta in 16 fette. Ogni fetta pesa 120 g. Quanti grammi pesa l’intera torta?

LE MISURE DI TEMPO

Anche il trascorrere del tempo si può misurare. Puoi misurare il tempo che impieghi a fare i compiti, la durata di una partita di calcio, delle vacanze estive.

1 Indica con una X gli strumenti che ti aiutano a misurare il tempo.

2 Osserva la tabella e completa le uguaglianze.

x 60 x 60 x 24

secondo (s) minuto (m) ora (h) giorno (d)

• 1 minuto = secondi

• 1 ora = minuti

• 1 giorno = ore

• 1 settimana = .......... giorni

• 1 mese = giorni

• 1 anno = giorni

Ricorda

Ricorda

L’unità di misura del tempo è il secondo ( s ). Le misure del tempo non seguono il sistema decimale.

x 7

x 30

x 365

una settimana un mese un anno

Nel linguaggio comune ci sono molte espressioni che indicano la durata del tempo.

Bimestre K 2 mesi; Trimestre K 3 mesi; Quadrimestre K 4 mesi;

Semestre K 6 mesi; Biennio K 2 anni;

Triennio K 3 anni; Quinquennio o lustro K 5 anni; Decennio K 10 anni; Secolo K 100 anni; Millennio K 1 000 anni.

GIOCHI E INDOVINELLI PER “MISURARE”

ᄗ Leggi, rifletti e rispondi.

Oggi è martedì. Che giorno sarà tra 68 giorni da oggi?

RISPOSTA

Orizzontali

3. è la misura di peso più piccola

5. è la centesima parte di un metro

Se sette ragni riescono a catturare sette mosche in sette minuti, quanto impiegherà un solo ragno a catturare una sola mosca?

RISPOSTA

Verticali

1. è formato da 1000 grammi

2. è la misura di capacità più piccola

4. è l’unità di misura della capacità

1 Completa le equivalenze.

• 80 dg = g

• 976 hg = ............... dag

• 2 500 cg = ............... g

• 143 dg = ............... mg

• 5 Mg = kg

• 7 dam = m

• 350 km = hm

• 47 dam = dm

• 180 m = ............... dam

• 65 hm = ............... m

• 71 h[l = [l

• 18 [l = c[l

• 32 da[l = d[l

• 390 m[l = ............... c[l

2 Quale freccia indica la strada più breve per raggiungere la biblioteca?

700 m 40 dam 5 hm 6 km

Freccia gialla

Freccia rossa

Freccia azzurra

Freccia verde

3 Scrivi l’unità di misura della cifra evidenziata.

4 Completa la tabella. peso lordo peso netto tara

.......... kg 5 kg 1 kg

5 È pomeriggio: Luca esce alle ore 14:30 e rientra all’ora indicata dall’orologio. Quanto tempo è rimasto fuori di casa?

500 g g

750 g g

100 g

6 Quanto devono pesare le pere perché la bilancia indichi lo stesso peso delle mele?

ᄗ PER ME LA PROVA

È STATA...

15 minuti

1 ora e 15 minuti

45 minuti

15 ore e 45 minuti

3 kg ?

300 g

30 dag

300 hg

30 hg

ᄗ CHE COSA DICE L'INSEGNANTE?

HAI SVOLTO CORRETTAMENTE LA PROVA

PUOI MIGLIORARE UN PO'

CI ESERCITEREMO INSIEME

altezza

I SOLIDI

I solidi sono figure geometriche che occupano uno spazio e hanno 3 dimensioni: lunghezza , larghezza e altezza . Per questo sono detti tridimensionali.

lunghezza larghezza

1 Collega ogni oggetto al solido corrispondente.

cono

sfera cilindro piramide cubo parallelepipedo

2 Colora i solidi come indicato.

cubo → verde parallelepipedo → blu cilindro → rosso

cono → giallo piramide → arancione sfera → viola

ᄗ In coppia osservate gli oggetti che vi circondano in aula e, sul quaderno, classificateli in base alla figura solida che vi ricordano.

SCOPRIAMO I SOLIDI

In ogni solido puoi riconoscere 3 elementi: faccia , spigolo e vertice .

• Le facce sono figure geometriche piane che racchiudono il solido.

• Lo spigolo è la linea che separa due facce.

• Il vertice è il punto in cui si incontrano tre o più spigoli.

spigolo

vertice

faccia

1 In ogni figura solida, colora in verde una faccia , in rosso uno spigolo e in azzurro un vertice .

2 Completa la tabella e rispondi.

• Osserva il numero degli spigoli, delle facce e dei vertici: a che cosa corrisponde il numero maggiore?

solido

nome

n. spigoli

n. facce

n. vertici

• Che cosa hanno in comune il cubo e il parallelepipedo?

FIGURE IN 3D

ᄗ Procuratevi cannucce, plastilina, forbici dalla punta arrotondata e righello. Divisi in gruppi, scegliete una figura solida e realizzatela con le cannucce, unite ai vertici dalle palline di plastilina. Prima di tagliare le cannucce, misuratele con il righello, per essere più precisi.

LO SVILUPPO DEI SOLIDI

• La scatola ha la forma di un cubo. Se la apri e la stendi sul banco otterrai lo sviluppo del solido.

• La scatola chiusa è un solido con 3 dimensioni. Lo sviluppo della scatola è un insieme di figure piane che hanno ..................... dimensioni: lunghezza e

1 Collega ogni solido al suo sviluppo.

Compito di REALTÀ

ᄗ Apri il cartone di una confezione di pastelli senza rompere le facce e disegna il suo sviluppo sul cartoncino. Traccia gli spigoli con la matita per separare le facce e costruisci una nuova scatola.

linea retta

LE LINEE

La linea è un insieme continuo e infinito di punti.

Ha una sola dimensione: la lunghezza

linea curva aperta

linea spezzata aperta

linea spezzata chiusa

linea curva chiusa

linea mista chiusa

Ricorda

• La linea retta va sempre nella stessa direzione.

• La linea curva cambia sempre direzione.

• Nella linea aperta l’inizio e la fine non si toccano.

• Nella linea chiusa l’inizio e la fine si incontrano.

• La linea spezzata è formata solo da tratti di linea retta.

• La linea mista è formata da tratti di linea retta e di linea curva.

TUTTI INSIEME

ᄗ In palestra, con l’aiuto dell’insegnante, giocate con le corde e rappresentate i vari tipi di linea che avete studiato.

RETTA, SEMIRETTA E SEGMENTO

1 Leggi e osserva con attenzione.

È una retta!

Una retta è una linea che procede sempre nella stessa direzione e non ha inizio né fine. Una retta si indica con una lettera minuscola. a

Sono due semirette!

Il punto O divide la retta in due semirette . Ciascuna delle due semirette inizia dal punto O ( origine ) e non finisce mai. Le due semirette si indicano con due lettere minuscole. O a b

È un segmento!

Il “ tratto ” di retta compreso tra i punti A e B si chiama segmento . Il segmento ha un inizio e una fine e si indica con due lettere maiuscole. A B

2 Osserva le linee con attenzione e scrivi il loro nome.

O a a

3 Leggi la frase e scrivi R se si riferisce alla retta, SR se si riferisce alla semiretta o SG per il segmento.

• Si indica con una sola lettera minuscola.

• È racchiuso tra due punti.

• Il suo punto di inizio si chiama origine.

• I suoi punti si indicano con le lettere maiuscole.

• Ha inizio ma non fine.

• Non ha né inizio né fine.

R SR SG

R SR SG

R SR SG

R SR SG

R SR SG

R SR SG

LA POSIZIONE DELLE RETTE NEL PIANO

In base alla sua posizione sul piano una linea retta può essere: obliqua verticale orizzontale

Due o più rette possono assumere tra loro posizioni diverse. Osserva.

a b a b

Due rette si dicono incidenti quando si incontrano in un punto. Talvolta, per scoprire se due rette sono incidenti, bisogna prolungarle.

a

Due rette si dicono parallele quando non si incontrano mai, neppure se si prova a prolungarle. b

Due rette si dicono perpendicolari , se due rette incidenti si incontrano in un punto e dividono il piano in 4 parti uguali. a b

1 Indica se la retta è verticale (V), orizzontale (OR), obliqua (OB).

2 Disegna 2 rette parallele, 2 rette incidenti e 2 rette perpendicolari.

GLI ANGOLI

ᄗ Osserva il percorso di Dino Sauro per arrivare alla bacchetta magica. Ogni volta che cambia direzione forma un angolo.

• Un angolo è una parte di piano compresa tra due semirette che hanno lo stesso punto di origine.

• Le semirette formano i lati dell’angolo.

• Il punto di origine si chiama vertice

• La parte di piano compresa tra i due lati è l’ ampiezza

lato

• L’ ampiezza di un angolo si misura in gradi . lato

1 Nei seguenti angoli colora in rosso i lati , in giallo l’ ampiezza e segna con il verde il vertice .

2 Colora

l’ampiezza di tutti gli angoli che trovi nel disegno poi rispondi.

• Quanti angoli hai trovato?

GLI ANGOLI

Due rette perpendicolari dividono il piano in 4 parti uguali e formano 4 angoli retti. Un angolo retto misura 90 gradi .

ANGOLO RETTO

90 gradi

Se prendi come riferimento l’angolo retto della tua squadra osserverai che:

ANGOLO ACUTO ha un’ampiezza minore dell’angolo retto (< 90 gradi).

ANGOLO PIATTO

180 gradi

ANGOLO OTTUSO ha un’ampiezza maggiore di quella dell’angolo retto (> 90 gradi).

ANGOLO GIRO

360 gradi

Se prendi come riferimento l’angolo retto della tua squadra osserverai che:

Due angoli retti vicini tra loro formano un angolo piatto . L’ampiezza dell’angolo piatto è il doppio dell’angolo retto (180 gradi).

Quattro angoli retti formano un angolo giro. L’ampiezza dell’ angolo giro è il quadruplo dell’angolo retto (360 gradi).

I POLIGONI

Il poligono è una parte di piano delimitata da una linea spezzata chiusa . È una figura piana e ha due dimensioni: lunghezza e larghezza

Le figure piane delimitate da una linea chiusa mista o curva sono NON poligoni

1 Osserva il quadro di August

Herbin e colora solo i poligoni.

2 Osserva i poligoni e in ognuno ripassa con il verde la lunghezza e con il blu la larghezza.

GLI ELEMENTI DEL POLIGONO

vertice

angolo

lato

superficie

I lati sono i segmenti che racchiudono il poligono.

Il vertice è il punto in cui si incontrano due lati e formano un angolo .

Il contorno del poligono è l’insieme dei lati.

La parte di piano racchiusa dai lati si chiama superficie.

1 In ogni figura colora di azzurro i lati , di verde i vertici , di viola gli angoli .

2 Ripassa con l'azzurro il contorno delle figure e colora di giallo la superficie .

CLASSIFICHIAMO I POLIGONI

Ricorda

I poligoni hanno tante forme diverse. Prendono il nome dal numero dei lati e degli angoli .

1 Osserva le figure, poi conta e completa la tabella, come nell’esempio.

NOME FIGURE

CARATTERISTICHE

Triangolo 3 lati, 3 angoli, 3 vertici

Quadrilatero ....... lati, ....... angoli, ....... vertici

Pentagono lati, angoli, vertici

Esagono lati, angoli, vertici

Ettagono ....... lati, ....... angoli, ....... vertici

Ottagono lati, angoli, vertici

2 Con il righello disegna le seguenti figure:

1 triangolo 1 quadrilatero 1 pentagono 1 esagono

IL PERIMETRO DEI POLIGONI

Procurati 3 cannucce di colore diverso e dello spago, poi segui le istruzioni.

1. Taglia le cannucce in modo che siano lunghe 4 , 3 e 5 cm.

2. Inf ila lo spago nelle cannucce e annoda le estremità.

Quale poligono hai ottenuto?

Quanto misura il suo contorno?

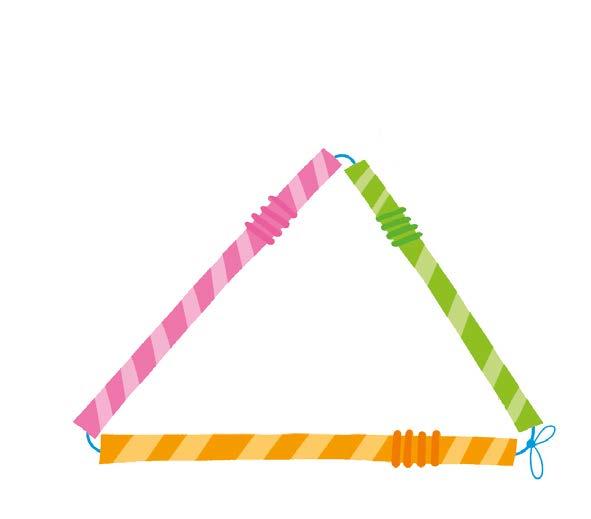
Hai ottenuto il perimetro, cioè la misura del contorno del poligono.

1 Misura i lati di ogni poligono con il righello, poi calcola il perimetro.

Il perimetro ( P ) è la misura del contorno . Si calcola sommando la misura di tutti i lati.

Ricorda

Quando due poligoni hanno lo stesso perimetro, si dicono isoperimetrici

PROBLEMI CON IL PERIMETRO

1 Risolvi i problemi sul quaderno.

Prima di risolvere il problema, ti sarà utile disegnare la figura geometrica.

1. Una tavoletta r ettangolare di legno ha un lato di 18 cm e l’altro lato è la metà del primo. Quanto misura il suo perimetro?

2. Un fazzoletto quadrato ha il lato di 25 cm. Quanti cm di pizzo sono necessari per decorare tutto il bordo del fazzoletto?

3. Un orto di forma quadrata ha il lato di 3 dam. Quanti metri di steccato occorreranno per recintarlo tutto?

4. Una piastr ella di forma pentagonale ha tutti i lati uguali. Ogni lato misura 12 cm. Quale sarà il perimetro della piastrella?

5. Un segnale stradale triangolar e, con i lati tutti uguali, ha il lato di 90 cm. Quanto misura il suo perimetro?

6. Il cortile r ettangolare di una scuola è largo 30 m e lungo 45 m. Quanti metri di recinzione metallica servono per recintarlo?

SUPERFICIE E AREA DEI POLIGONI

La superficie di un poligono è la parte di piano che sta dentro il suo contorno. superficie

L’ area è la misura della superficie. Per calcolarla bisogna scegliere un’unità di misura, in questo caso il quadratino.

• Quanti quadratini sono stati utilizzati per ricoprire la superficie di questo poligono?

1 Conta i quadratini in ogni figura e rispondi.

• Quali poligoni hanno la stessa area?

• Quale poligono ha l’area maggiore? ....................................................

• Quale ha l’area minore?

Ricorda

Due poligoni di forma diversa ma con la stessa area si dicono equiestesi

LA SIMMETRIA

ᄗ Osserva le immagini.

Ogni figura è composta da due parti che, ribaltate l’una sull’altra, si sovrappongono perfettamente. Queste due parti si dicono simmetriche perché si ottengono con un movimento di ribaltamento, cioè con una simmetria.

La linea che divide la figura in due parti simmetriche si chiama asse di simmetria.

1 Costruisci e colora la parte o la figura simmetrica. asse

Quando l’asse di simmetria divide la figura in due parti simmetriche, si dice asse di simmetria interno.

Quando invece l’asse di simmetria ti permette di ottenere due figure simmetriche, si dice asse di simmetria esterno.

L’ asse di simmetria può essere in posizione verticale, orizzontale oppure obliqua.

2 Costruisci e colora la parte simmetrica di ciascuna figura. Poi rispondi.

• L’asse di simmetria è interno o esterno?

3 Costruisci e colora le figure simmetriche a quelle date. Poi rispondi.

• L’asse di simmetria è interno o esterno?

ALGORITMI

Per compiere molte azioni, ogni giorno, senza rendercene conto, seguiamo una sequenza di istruzioni.

Questa sequenza di istruzioni si chiama algoritmo .

Per rappresentare un algoritmo, puoi usare un diagramma di flusso : con simboli e frecce ti aiuta a rappresentare l’ordine da seguire nella sequenza di istruzioni.

1 Osserva l’algoritmo “Sbuccia la mela”.

INIZIO

Prendi una mela

Prendi un coltello

È pulito?

Sbuccia la mela

FINE

Puoi lavarlo?

start inizio

Lava il coltello

finish

fine

flow chart

diagramma di flusso

2 Seguendo lo stesso schema, scrivi il diagramma di flusso per “temperare la matita”.

INIZIO

FINE

Il diagramma di flusso può essere molto utile nella soluzione dei problemi di matematica. Ti aiuta a mettere in ordine i pensieri!

ISTRUZIONI E PERCORSI

1 Osserva le istruzioni per disegnare il percorso di Dino Sauro.

Disegna una linea retta

Ruota di un angolo a sinistra

Ruota di un angolo a destra

2 Completa il disegno del percorso di Dino Sauro, chiudendo il rettangolo. Poi scrivi nel riquadro le istruzioni corrispondenti.

LA FRASE NASCOSTA

ᄗ Seguendo le frecce indicate nel codice, trova la frase nascosta.

PARTENZA:

B, 1 CODICE:

Frase nascosta:

1 Ripassa con il rosso la linea retta , con il verde la semiretta , con il blu il segmento .

B A O a a

2 Sotto ogni coppia di rette scrivi se sono incidenti, perpendicolari o parallele.

b e c d O O f a

3 Disegna un angolo retto, un angolo acuto, un angolo ottuso, un angolo giro, un angolo piatto.

4 Completa le affermazioni e disegna la figura corrispondente.

Ha 3 lati, 3 angoli e 3 vertici, è un

Ha 4 lati, 4 angoli e 4 vertici, è un

Ha 5 lati, 5 angoli e 5 vertici, è un

5 Misura i lati del poligono con il righello, poi calcola il perimetro.

P = cm + cm + cm + cm = cm

6 Calcola l’area dei seguenti poligoni, usando un quadratino come unità di misura.

ᄗ Quale figura ha l'area maggiore?

ᄗ

ha

ᄗ

ᄗ CHE COSA DICE L'INSEGNANTE?

Figura 1

Figura 2

Figura 3

CLASSIFICAZIONI

Classificare vuol dire raggruppare elementi in base ad una o più caratteristiche.

1 Osserva i bambini e scrivi i loro nomi nel diagramma in base alle caratteristiche date.

MARCO FABIO CARLO REMO GIANNI LUCA

MARIO TOMMY

bambini con jeans bambini con occhiali

bambini con jeans e occhiali

Ricorda

Questa rappresentazione si chiama diagramma di Venn .

2 Rappresenta la stessa situazione con il diagramma di Carroll e con il diagramma ad albero.

DIAGRAMMA DI CARROLL

CON OCCHIALI

SENZA OCCHIALI

CON JEANS SENZA JEANS

BAMBINI

DIAGRAMMA AD ALBERO CON JEANS SENZA JEANS

CON OCCHIALI

CON OCCHIALI

SENZA OCCHIALI

SENZA OCCHIALI

RELAZIONI

La relazione è un legame logico che unisce gli elementi di due insiemi. , cioè un diagramma

1 Osserva gli animali e mettili in relazione completando il diagramma

lumaca

mosca

coniglio

leone

Quale animale ha più

• Perché? .................................................

• Quale non ha x ? ...................................................................

• Perché?

2 Indica con una X quale relazione indica la freccia.

È frutto di È di colore Mangia

3 Sul quaderno trasforma il diagramma sagittale dell’esercizio 2 in una tabella a doppia entrata.

INDAGINI STATISTICHE

Gli alunni della III A devono fare un’uscita didattica.

La maestra vuole conoscere la meta preferita dalla maggior parte degli alunni. Decide dunque di fare un’indagine per capire le loro preferenze. Chiede loro “Dove vorreste fare un’uscita didattica?” e raccoglie i dati in una tabella di frequenza.

1 Conta le preferenze e scrivi il numero corrispondente.

Destinazione preferenze numero agriturismo museo

teatro acquario zoo

Ricorda

2 Rappresenta i dati della tabella precedente in un istogramma e rispondi alla domanda.

ogni rettangolino corrisponde ad una preferenza

Qual è la moda?

PREVISIONI E PROBABILITÀ

È certo che uscirà un numero da 1 a 6.

È impossibile che esca 10.

È possibile che esca 3.

Ricorda

Un evento è certo , quando accadrà sicuramente. È possibile , quando potrebbe accadere o non accadere. È impossibile , quando sicuramente non si verificherà.

1 Immagina di lanciare un dado e indica con una X se le affermazioni sono vere (V) o false (F).

• È certo che uscirà un numero. V F

• È certo che uscirà il 6. V F

• È possibile che esca lo 0. V F

• È possibile che esca un numero dispari. V F

• È impossibile che esca un numero pari. V F

• È impossibile che esca un numero maggiore di 6. V F

2 Leggi le frasi e completa scrivendo: certo, possibile, impossibile.

• Un asino vola.

• Domani riderò.

• Stasera il sole tramonterà. ..............................................

• L’aquila abbaia.

• Il mare è agitato.

• Ci sono le nuvole: forse pioverà. ..............................................

• Dopo gennaio c’è febbraio.

• I pesci nuotano con maschera e boccaglio.

PROBABILITÀ

La probabilità è il rapporto tra casi favorevoli e casi possibili.

1 Rifletti e rispondi.

ᄗ Nel cassetto della maestra ci sono 7 gessetti bianchi e 3 colorati. La maestra apre il cassetto e senza guardare ne prende uno.

• Quale gessetto ha più probabilità di prendere? ................................................

• Perché? ............................................................................................................................... ................

• Quante probabilità ci sono che prenda un gessetto colorato? ..............................

ᄗ Immagina che nel cassetto siano rimasti un gessetto bianco e due colorati.

• Quale gessetto ha più probabilità di prendere?

• Perché?

• Quante probabilità ci sono che prenda il gessetto bianco?

probability probabilità

favourable case caso favorevole

unfavourable case caso sfavorevole

2 Prendi un dado e lancialo: che cosa uscirà? Scegli la frase adatta con una X .

È certo che esca: un numero da 1 a 6 un numero maggiore di 6

È possibile che esca: il numero 7 un numero pari

È impossibile che esca: il numero 1 un numero minore di 1

1 Leggi e completa il diagramma di Carroll. con cappello senza cappello

Jenny roberto

nella sergio

maschio

femmina

2 Indica con una X la risposta esatta.

In un acquario ci sono 6 pesciolini rossi, 4 verdi e 2 a righe.

Immagina di raccoglierli con un retino.

• Quale tipo di pesce hai più probabilità di pescare?

Rosso Verde A righe

• Quale frazione indica la probabilità di pescare un pesce a righe?

2

ᄗ PER ME LA PROVA

ᄗ CHE COSA DICE L'INSEGNANTE?

È STATA... HAI SVOLTO CORRETTAMENTE LA PROVA

PUOI MIGLIORARE UN PO'

CI ESERCITEREMO INSIEME

A1. Carlo va allo zoo con i suoi 3 figli per festeggiare l’undicesimo compleanno dell’ultimogenito. Il biglietto costa € 12,00, i bambini fino a 10 anni pagano € 6,00. Quanto spende in tutto Carlo?

A. € 42,00

B. € 36,00

C. € 48,00

A2. Osserva le offerte nei due volantini.

VOLANTINO 1

VOLANTINO 2

Quale volantino ha l’offerta più vantaggiosa?

3 BOTTIGLIE DI

DETERSIVO DA 1 l

Costo 4,50 € 1 l 1 l 1 l

1 BOTTIGLIA DI DETERSIVO DA 2 l

Costo 2,90 € 2 l

A. 1

B. 2 Perché? …...........................................……

A3. Quale delle seguenti moltiplicazioni ha il risultato sbagliato?

A. 36 × 12 = 432

B. 16 × 15 = 235

C. 81 × 9 = 729

A4. Sara ogni sera va a letto alle 21:30 e si sveglia il mattino successivo alle 7:30. Quante ore dorme?

A. 9 ore

B. 10 ore

C. 15 ore

A5. Completa le sequenze, eseguendo le operazioni indicate dalle frecce.

A6. Quale serie è scritta correttamente in ordine crescente?

A. 12,3 • 13,2 • 13,6 • 14

B. 14 • 13,6 • 13,2 • 12,3

C. 14 • 12,3 • 13,2 • 13,6

A7. Quale numero è nascosto dalla macchia?

A. 8,55

B. 8,45

C. 8,50

A8. A quale frazione decimale corrisponde il numero 3,45?

A9. Quale immagine rappresenta correttamente la frazione

A10. Ho comprato un sacchetto di noci che pesa 0,5 kg. Il sacchetto vuoto pesa 100 g. Voglio sapere quanto pesano le noci. Che cosa voglio sapere?

A. Il peso lordo

B. Il peso netto

C. La tara

Per conoscere la risposta quale formula devi applicare?

A11. Quale relazione indica la freccia?

A. È fatto di

B. Si usa per

C. Si rompe con

A12. È stata svolta un’indagine sul genere di film preferito. Osserva la tabella di frequenza e completa le frasi.

Fantascienza

Commedia

Avventura

Amore

Thriller

Quale genere ha una maggiore frequenza?

Quante preferenze sono state raccolte in tutto? ...................................

A13. In una scatola ci sono 20 palline: 10 blu e 10 rosse. Due amici, bendati, estraggono a turno 5 palline dalla scatola.

Se il primo amico ha estratto 1 pallina blu e 4 rosse…

A. È certo che il secondo amico estrarrà una pallina rossa

B. È certo che il secondo amico estrarrà una pallina blu

C. È più probabile che il secondo amico estragga una pallina blu

A14. Quale tra le seguenti figure non è un poligono? A. B. C.

NUMERI

INDICE ESERCIZIARIO

136 I numeri fino a 100

137 I numeri fino a 999

138 Comporre e scomporre

139 Il migliaio

140 Comporre e scomporre

142 Confrontare

OPERAZIONI

143 L’addizione

144 Le proprietà dell’addizione

145 Addizioni matemagiche

146 La sottrazione

147 La proprietà della sottrazione

148 Sottrazioni matemagiche

149 Operazioni inverse

150 Moltiplicazioni in colonna

151 Le proprietà della moltiplicazione

153 Moltiplicazioni per 10, 100, 1 000

154 Moltiplicazioni a due cifre

155 La divisione con le tabelline

156 Ancora divisioni

157 Divisioni in colonna

158 La divisione con tre cifre al dividendo

159 Operazioni inverse

160 La proprietà della divisione

161 Divisioni per 10, 100, 1 000

PROBLEM SOLVING

162 Problemi

163 I dati inutili e nascosti

164 Problemi con due domande

165 I dati mancanti

166 Risolviamo

FRAZIONI E NUMERI DECIMALI

167 Le frazioni

168 Le frazioni decimali

169 Dalla frazione decimale al numero decimale

170 I numeri decimali

172 Il pigiama party

173 Costo unitario e costo totale

MISURE

174 Le misure di lunghezza

175 Le misure di capacità

176 Le misure di peso

177 Equivalenze

178 Peso lordo, peso netto, tara

179 Le misure di tempo

SPAZIO E FIGURE

180 Lo sviluppo dei solidi

181 Rette, semirette e segmenti

183 Gli angoli

184 I poligoni

185 Il perimetro dei poligoni

186 Problemi con il perimetro

187 L’area dei poligoni

188 La simmetria

RELAZIONI, DATI E PREVISIONI

189 Classificazioni

190 Relazioni

191 Indagini statistiche

192 Previsioni e probabilità

I NUMERI FINO A 100

1 Scomponi i numeri, come nell’esempio, usando decine e unità.

34 = 10 + 10 + 10 + 4

62 = ...............................................................................................................................

50 =

43 =

70 =

85 = 90 =

2 Riscrivi i numeri in parola, poi scomponili in decine e unità. Segui l’esempio.

3 Scomponi e componi come nell’esempio.

35 = 30 + 5 = 3 da 5 u

28 = ..............................................................................................

79 =

84 =

4 da 3 u = 40 + 3 = 43

9 da 1 u =

6 da 9 u =

5 da 7 u =

4 Quanto manca per arrivare a 100? Completa le uguaglianze.

Comporre e scomporre

1

I NUMERI FINO A 999

Osserva l’esempio.

COMPORRE E SCOMPORRE

1 Scomponi i numeri in tabella, inserendo ogni cifra al posto giusto.

h da u 254 2 5 4 351

2 Componi come nell’esempio.

1 h 4 da 5 u = 100 + 40 + 5 = 145

7 h 7 da 9 u =

3 h 8 da 2 u = ..............................................................................................

4 h 5 da 6 u = ..............................................................................................

1 h 4 da 8 u =

9 h 5 da 2 u =

da u

8 h 6 da 9 u =

6 h 4 da 7 u = ..............................................................................................

6 h 0 da 1 u =

7 h 3 da 6 u =

9 h 7 da 0 u =

8 h 9 da 2 u = ..............................................................................................

3 Completa le

IL MIGLIAIO

Ricorda

Sull’abaco aggiungiamo una quarta asta a sinistra delle centinaia.

1 Quale numero è rappresentato sull’abaco? Scrivilo in cifre.

2 Rappresenta sull’abaco i seguenti numeri.

3 Colora allo

modo i cartellini dei numeri che, sommati tra loro, formano il 1 000.

Conoscere il migliaio.

4 Quanto manca al 1 000? Completa.

stesso

COMPORRE E SCOMPORRE

1 Completa la tabella, componendo o scomponendo i numeri.

2 Componi come nell’esempio.

1 k 5 h 2 da 8 u = 1 000 + 500 + 20 + 8 = 1 528

1 k 5 h 0 da 8 u = ............................................................................................................................................................................................................................

3 k 6 h 9 da =

2 k 3 h 7 da 7 u =

3 k 5 h 8 da 3 u = ............................................................................................................................................................................................................................

2 k 4 h 9 da 1 u = ............................................................................................................................................................................................................................

3 k 9 h 3 da 2 u =

6 k 7 h 5 da 9 u =

3 Scomponi i numeri come nell’esempio.

1 936 = 1 000 + 900 + 30 + 6 = 1 k 9 h 3 da 6 u

3 625 =

4 270 =

1 362 =

2 480 = ............................................................................................................................................................................................................................

3 104 =

1 783 =

2 930 =

•

1

2

5

L’ADDIZIONE

Ricorda

L’addizione è l’operazione che ti permette di unire due o più quantità.

1 Esegui le addizioni a mente e collega ogni addizione al suo risultato.

620 + 80

2 Esegui le addizioni in colonna.

350 + 2 463

k h da u

+ 824 k h da u

k h da u

1 680 + 2 196 k h da u

3 072 + 924 k h da u

3 Esegui le addizioni in colonna sul quaderno.

• 139 + 258

• 329 + 276

• 218 + 56

• 106 + 245

Eseguire

• 18 + 809 + 76

• 465 + 39 + 136

• 2 139 + 196 + 17

• 8 + 74 + 389

• 251 + 3 + 195

• 365 + 2 645 + 2 393

• 243 + 1 236 + 198

• 1 048 + 9 + 507

LE PROPRIETÀ DELL’ADDIZIONE

Ricorda

Proprietà commutativa : cambiando l’ordine degli addendi, il risultato non cambia. La proprietà commutativa si usa per fare la prova dell’addizione.

1 Esegui la prova delle addizioni, applicando la proprietà commutativa.

2 586 + 203

k h da u + =

623 + 1 459

k h da u

PROVA

k h da u + =

PROVA

k h da u

4 197 + 3 412

k h da u + =

1 607 + 2 408

k h da u

2 Esegui le addizioni in colonna con la prova sul quaderno.

• 225 + 430

• 217 + 330

Ricorda

• 528 + 252

• 1 327 + 175

• 366 + 415

• 471 + 169

PROVA

k h da u + =

PROVA

k h da u

• 208 + 350

• 2 140 + 1 560

Proprietà associativa : in un’addizione con tre o più addendi, se sostituisci due addendi con la loro somma il risultato non cambia.

3 Applica la proprietà associativa come nell’esempio e calcola a mente.

13 + 7 + 9 = 29

5 + 15 + 36 =

13 + 17 + 45 =

32 + 18 + 126 =

20 + 9 = 29

Conoscere e applicare le proprietà dell’addizione.

ADDIZIONI MATEMAGICHE

1 Scomponi i numeri e poi somma tutti gli addendi.

• 56 + 24 = (50 + 20) + (6 + 4) = 70 + 10 = 80

• 76 + 19 =

• 46 + 39 =

• 28 + 56 =

Ricorda

Ricorda i “ trucchi matemagici ”!

• 49 + 66 = ......................................................................................................................................................................................................................................

2 Per aggiungere 9, somma 10 e togli 1. Completa come nell’esempio.

• 33 + 9 = 33 + 10 − 1 = 42

• 66 + 9 =

• 53 + 9 =

• 9 + 27 =

• 9 + 64 = ....................................................................

• 9 + 82 = ....................................................................

3 Per aggiungere 11, somma prima 10, poi 1. Completa come nell’esempio.

• 47 + 11 = 47 + 10 + 1 = 58

• 82 + 11 =

• 99 + 11 = ....................................................................

• 11 + 89 =

• 11 + 121 =

• 11 + 136 = 4

LA SOTTRAZIONE

1 Completa la tabella, calcolando a mente.

−

3 450

1 893

2 728

4 536

2 159

2 Esegui le sottrazioni in colonna.

1 359 − 247

k h da u

2

k h da u

1 690 − 1 530

k h da u

La sottrazione è l’operazione che ti permette di conoscere il resto o la differenza.

2 345 − 1127

k h da u

2 499 − 1 845

k h da u

3

k h da u

3

k h da u

3 Esegui le sottrazioni in colonna sul quaderno.

Con un prestito

3 456 – 2 076

4 356 – 824

2 840 – 1 632

2 387 – 1 915

Con due prestiti

6 042 –

5

3 508 – 2 299

9 182 –

2

k h da u

Con tre prestiti

9 012 – 6 048

2 000 – 1 327

6 201 – 3 453

4 305 – 1 697

LA PROPRIETÀ DELLA SOTTRAZIONE

Ricorda

Proprietà invariantiva : aggiungendo o sottraendo lo stesso numero al minuendo e al sottraendo, il risultato non cambia.

1 Applica la proprietà invariantiva, come nell’esempio.

2 Calcola sul quaderno, applicando la proprietà invariantiva.

3 Inventa tu le sottrazioni, a cui applicare la proprietà invariantiva, seguendo gli indicatori dati.

Conoscere e applicare la proprietà della sottrazione.

SOTTRAZIONI MATEMAGICHE

Ricorda i “ trucchi matemagici ” per calcoli veloci! Ricorda

1 Quando il sottraendo è 9, sottrai 10 e aggiungi 1. Calcola a mente.

• 34 − 9 = (34 − 10) + 1 = 25

• 66 − 9 =

• 85 − 9 = .........................................................................................

• 163 − 9 =

• 214 − 9 = .........................................................................................

• 360 − 9 =

2 Quando il sottraendo è 11, sottrai prima 10, poi 1. Completa come nell’esempio.

• 67 − 11 = (67 − 10) − 1 = 56

• 71 − 11 = .........................................................................................

• 59 − 11 =

• 46 − 11 =

• 138 − 11 = ........................................................................................

• 236 − 11 =

• 520 − 11 =

• 436 − 11 =

3 Quando il sottraendo è 90, sottrai 100 e aggiungi 10. Completa come nell’esempio.

• 236 − 90 = (236 − 100) + 10 = 146

• 235 − 90 =

• 184 − 90 =

• 332 − 90 = ........................................................................................

4

• 857 − 90 =

• 471 − 90 =

• 548 − 90 = ........................................................................................

• 633 − 90 =

5 Completa le

di

Usare

OPERAZIONI INVERSE

1 Completa i diagrammi.

2 Completa l’operazione con il numero mancante.

• 15 + = 65

• ............ + 12 = 48

• 63 + = 75

• 156 – = 100

• – 90 = 200

• 365 – ............ = 55

• + 56 = 97

• 123 + ............ = 148

• 151 + = 160

• – 60 = 240

• 418 – = 310

• 677 – ............ = 610

• + 93 = 195

• ............ + 61 = 90

• + 120 = 260

• – 48 = 112

• – 124 = 250

• ............ – 150 = 430

3 Esegui in colonna sul quaderno le sottrazioni e verifica i risultati con la prova.

• 832 – 717

• 307 – 219

• 2 394 – 1 328

• 3 870 – 1 529

• 643 – 427

• 794 – 675

• 2 668 – 1 388

• 1 544 – 1 336

• 998 – 677

• 529 – 268

• 7 815 – 4 319

• 8 012 – 3 616

MOLTIPLICAZIONI IN COLONNA

Ricorda

La moltiplicazione è l’operazione che ripete più volte la stessa quantità.

1 Esegui in colonna le moltiplicazioni senza il cambio.

2 Esegui in colonna le moltiplicazioni con il cambio.

3 Esegui in colonna sul quaderno. SENZA CAMBIO 113

LE PROPRIETÀ DELLA MOLTIPLICAZIONE

Ricorda

Proprietà commutativa: cambiando l’ordine dei fattori il risultato non cambia.

Puoi applicare questa proprietà per fare la prova della moltiplicazione.

1 Applica la proprietà commutativa come nell’esempio.

2 Applica la proprietà commutativa come prova della moltiplicazione e verifica il risultato.

• 10 × 6 = 60 6 × 10 = 60

• 7 × 9 = .................

• 6 × 6 =

• 10 × 4 =

• 8 × 10 = .................

• 10 × 5= .................

• 3 × 7 =

Conoscere e applicare le proprietà della moltiplicazione.

• 9 × 6 =

• 3 × 5 =

• 10 × 2 =

• 4 × 9 =

• 7 × 6 =

• 5 × 6 =

• 4 × 3 =

Ricorda

Proprietà associativa: se a due o più fattori sostituisci il loro prodotto, il risultato non cambia.

3 Applica la proprietà associativa come nell’esempio. Unisci i fattori evidenziati.

• 2 × 5 × 2 = 10 × 2 = 20

• 5 × 5 × 2 =

• 3 × 2 × 10 =

• 2 × 5 × 9 = .....................................................................

• 2 × 3 × 9 =

• 7 × 2 × 3 =

• 5 × 7 × 3 =

• 6 × 4 × 2 = .....................................................................

Ricorda

• 9 × 2 × 4 =

• 3 × 4 × 5 =

• 6 × 2 × 5 = .....................................................................

• 4 × 7 × 10 =

• 3 × 3 × 9 =

• 8 × 2 × 4 =

• 7 × 2 × 5 = .....................................................................

• 10 × 4 × 9 = .....................................................................

Proprietà distributiva: posso scomporre un fattore nella somma dei suoi addendi.

Ciascun addendo è poi moltiplicato per il secondo fattore e si sommano gli addendi ottenuti. È utile per semplificare i calcoli.

4 Applica la proprietà distributiva, come nell’esempio.

• 12 × 8 = (10 × 8) + (2 × 8) = 80 + 16 = 96

• 22 × 4 = .........................................................................................................................................

• 66 × 2 =

• 15 × 5 =

• 52 × 2 =

• 18 × 6 = .........................................................................................................................................

• 32 × 2 = .........................................................................................................................................

• 25 × 5 =

• 24 × 4 =

Conoscere e applicare le proprietà della moltiplicazione.

MOLTIPLICAZIONI PER 10, 100, 1 000

Ricorda

Quando moltiplichi un numero per 10, 100, 1 000, il suo valore aumenta di 10, 100,1 000 volte. Aggiungi 1, 2, 3 zeri a destra del numero.

1 Calcola in riga.

PER 10

132 × 10 =

65 × 10 =

147 × 10 = ...................................

777 × 10 = ...................................

6 × 10 =

39 × 10 =

PER 100

23 × 100 =

8 × 100 =

96 × 100 = ...................................

14 × 100 = ...................................

86 × 100 =

15 × 100 =

2 Indica con una x se l’uguaglianza è vera (V) o falsa (F).

• 21 × 100 = 210 V F

• 56 × 10 = 560 V F

• 1 × 1 000 = 1 000 V F

• 541 × 10 = 541 V F

• 30 × 1 000 = 3 000 V F

3 Completa la tabella.

× 10 100 1 000

4 1 7 6 3

PER 1 000

5 × 1 000 =

9 × 1 000 =

3 × 1 000 = ...................................

4 × 1 000 = ...................................

2 × 1 000 =

8 × 1 000 =

• 32 × 100 = 3 200 V F

• 453 × 10 = 4 530 V F

• 2 × 1 000 = 200 V F

• 34 × 10 = 340 V F

• 25 × 100 = 250 V F

4 Completa con il numero mancante.

• 5 × .................. = 5 000

• 45 × = 450

• 11 × .................. = 1 100

• 66 × = 6 600

• 7 × .................. = 7 000

• 2 × = 200

• 123 × .................. = 1 230

• .................. × 100 = 500

• × 1 000 = 9 000

• .................. × 10 = 30

• × 100 = 4 800

• .................. × 10 = 320

• × 10 = 440

• ............... × 10 = 1 000

Ricorda

MOLTIPLICAZIONI A DUE CIFRE

Per eseguire la moltiplicazione con due cifre, devi eseguire due moltiplicazioni e sommare i loro risultati. Non dimenticare lo 0 segnaposto. Anche nelle moltiplicazioni a due cifre, potresti trovare dei cambi da fare: non dimenticare il riporto.

1 Esegui le moltiplicazioni in colonna.

× 22

k h da u

× 13

h da u

k h da u

12 × 33

× 55 k h da u

k h da u

× 29 k h da u

k h da u

× 26 k h da u

2 Riscrivi nelle stelle, in ordine decrescente, i risultati dell’esercizio 1.

3 Esegui le moltiplicazioni in colonna con la prova sul quaderno.

Eseguire moltiplicazioni con due cifre al moltiplicatore.

LA DIVISIONE CON LE TABELLINE

Ricorda

La divisione è l’operazione che ti permette di dividere o distribuire in parti uguali o di raggruppare una quantità in gruppi uguali.

Per eseguire le divisioni possono aiutarti le tabelline.

1 Esegui le divisioni.

10 : 2 = 5

• 16 : 2 = ........................

• 20 : 4 =

• 18 : 2 =

• 30 : 6 =

• 12 : 3 = ........................

• 24 : 4 = ........................

• 14 : 7 =

• 18 : 9 =

• 15 : 5 =

• 24 : 6 = ........................

• 40 : 8 = ........................

• 27 : 9 =

• 32 : 8 =

• 40 : 5 =

• 18 : 6 = ........................

2 Esegui le divisioni e indica il resto quando c’è.

14 : 3 = 4 resto 2

• 31 : 6 = r

• 24 : 3 = .......... r ..............

• 54 : 7 = r

• 28 : 4 = r

• 12 : 9 = r

• 33 : 6 = r

• 16 : 6 = .......... r ..............

• 17 : 7 = r

• 12 : 3 = r

• 26 : 8 = r

Eseguire divisioni a mente con e senza resto.

• 48 : 8 = ........................

• 24 : 3 =

• 36 : 9 =

• 21 : 7 =

• 14 : 2 = ........................

• 49 : 9 = r

• 49 : 7 = .......... r ..............

• 51 : 7 = r

• 23 : 9 = r

• 50 : 8 = r

• 34 : 5 = r

• 29 : 3 = .......... r ..............

• 45 : 5 = r

• 20 : 4 = r

• 36 : 5 = r

1

ANCORA DIVISIONI

Il divisore è ................

Il divisore è

Il divisore è

3 Indica con una X se il risultato è vero (V) o falso (F)

• 60 : 10 = 6 V F

• 24 : 3 = 6 V F

• 18 : 2 = 9 V F

• 32 : 8 = 7 V F

• 12 : 2 = 3 V F

• 81 : 9 = 8 V F

• 45 : 5 = 8 V F

• 72 : 8 = 9 V F

Il divisore è ................

Il divisore è ................

• 36 : 6 = 4 V F

• 54 : 6 = 9 V F

• 20 : 2 = 10 V F

• 15 : 5 = 3 V F

DIVISIONI IN COLONNA

Il resto deve essere sempre minore del divisore! Ricorda

1 Esegui in colonna.

Usa la moltiplicazione per fare la prova della divisione. Ricorda

Metti

2

in colonna e calcola sul quaderno con la prova.

LA DIVISIONE CON TRE CIFRE AL DIVIDENDO

1 Esegui in colonna.

2 Riscrivi nei cuori, in ordine crescente, i risultati dell’esercizio 1.

3 Esegui in colonna sul quaderno.

• 756 : 4

• 917 : 8

• 450 : 3

• 607 : 5

• 853 : 8

• 917 : 6

• 484 : 4

• 489 : 3

• 812 : 7

• 930 : 3

Eseguire divisioni con tre cifre al dividendo.

• 238 : 8

• 169 : 6

• 428 :

• 309 : 7

• 626 :

OPERAZIONI INVERSE

1 Completa gli schemi.

Ricorda

La divisione è l’ operazione inversa della moltiplicazione: questa caratteristica della divisione ti permette di eseguire la prova.

2 Completa con il numero mancante.

• 6 × = 36

• 7 × ............... = 21

• 6 × ............... = 48

• 4 × = 20

• 3 × = 12

• × 6 = 42

• 907 : 5

• 373 : 8

• 157 : 6

• × 8 = 16

• ............... × 7 = 28

• ............... × 6 = 48

• × 8 = 56

• 16 : = 4

• 72 : = 8

• 639 : 5

• 850 : 5

• 286 : 4

• 741 : 3

• 218 : 7

• 965 : 5

• 20 : = 2

• 27 : ............... = 3

• 40 : ............... = 5

• : 2 = 4

• : 4 = 2

• : 9 = 6

• 456 : 3

• 750 : 6

• 384 : 8

3 Esegui in colonna con la prova sul quaderno.

LA PROPRIETÀ DELLA DIVISIONE

Ricorda

Per rendere i calcoli più semplici, puoi applicare la proprietà invariantiva della divisione. Moltiplicando o dividendo per lo stesso numero (tranne lo 0) il dividendo e il divisore, il risultato non cambia.

1 Applica la proprietà invariantiva e completa. Osserva l’esempio.

30 : 6 = 5 :2 :2

60 : 15 = :3 :3

: 14 = :7 :7 36 : 12 = :6 :6 15 :

5 = 3

:

(20 : 10)

: ..........) : (.......... : ..........) = .......... : .......... = ..........

:

) : ( : ) = : =

:

27 : 9 = (27 × 2) : (9 × 2)

300 : 50 = (300 : 10) : (50 : 2)

140 : 20 = (140 : 10) : (20 × 10)

Conoscere e applicare la proprietà della divisione.

28 : 14 = (28 : 7) : (14 : 7)

48 : 12 = (48 : 6) : (12 : 6)

81 : 27 = (81 : 9) : (27 : 3)

20 : 5 = (20 × 2) : (5

× 2)

DIVISIONI PER 10, 100, 1 000

Ricorda

Per dividere per 10,

1 Completa le tabelle.

2 Esegui le divisioni.

PER

3 Indica con una X i risultati

4 Completa con il numero mancante.

•

•

•

•

2, 3 zeri a destra del numero.

PROBLEMI

1 Leggi e rispondi alle domande.

a. In un acquario ci sono 19 pesci rossi, 3 stelle marine, 4 granchietti e 15 conchiglie rosa. Quanti animali ci sono in tutto?

• Qual è l’argomento del problema? .........................................................

• Quali e quanti animali sono presenti?

Ci sono

Ci sono

Ci sono

Ci sono ..............................................................................................................................

• Che cosa chiede la domanda?

• Quale operazione devi eseguire per rispondere?

b. Giusy sta preparando 12 torte. Se utilizza 3 uova per ogni torta, quante uova le serviranno? Alla fine le avanzano 6 uova. Quante uova aveva acquistato?

• Qual è l’argomento del problema? .........................................................

• Quante torte deve preparare Giusy?

• Che cosa le serve per ogni torta?

• Che cosa chiede la prima domanda?

• Cosa le sono avanzate? ...............................................................................................

• Che cosa chiede la seconda domanda? ...............................................................................................

• Quante operazioni devi eseguire?

• Quali operazioni?

Analizzare

I DATI INUTILI E NASCOSTI

Ricorda

Nei problemi possono esserci informazioni superflue, i dati inutili . A volte invece ci sono dati nascosti nelle parole.

1 Leggi il testo, sottolinea e scrivi i dati, compresi quelli inutili o nascosti, e risolvi con il diagramma e l’operazione.

Carlo, dopo 6 mesi, finalmente è riuscito a completare l’album delle figurine. L’album è composto da 124 pagine e in ogni pagina Carlo ha incollato 6 figurine. Quante figurine in tutto?

DATI

RISPOSTA

h da u =

2 Leggi il testo, sottolinea i dati inutili o nascosti e risolvi sul quaderno con il diagramma e l’operazione.

a. Nico nuota 2 ore ogni giorno dal lunedì al venerdì. Quante ore in una settimana? E in 4 settimane?

c. Lisa acquista 3 confezioni di panini al latte. Se in ogni confezione ci sono una dozzina di panini, quanti panini acquista Lisa?

b. Il signor Biagio ha 54 anni, cioè il doppio di suo figlio Mario. Quanti anni ha Mario?

d. Michele è andato al cinema con 2 amici. Il biglietto costava € 10,00 e ognuno di loro ha speso € 5,00 per il popcorn e una bibita. Quanto hanno speso in tutto per i biglietti di ingresso?

Riconoscere dati inutili o nascosti nel testo di un problema.

PROBLEMI CON DUE DOMANDE

Ricorda

I problemi possono avere due domande alle quali bisogna rispondere eseguendo due operazioni . A volte la domanda è una, ma ce n’è un’altra nascosta che ci serve per ricavare un dato . Per rispondere alla domanda finale bisogna dunque eseguire due operazioni .

1 Leggi, rifletti e risolvi con il diagramma e l’operazione.

Luigi ha regalato 23 figurine a Dario e 34 ad Alberto. Gli restano ora 240 figurine. Quante ne aveva prima?

DATI

23 = ........................................................................................

34 =

240 =

DATO DA RICAVARE

OPERAZIONI

1

2 Leggi, rifletti e risolvi sul quaderno, con il diagramma e l'operazione.

Sullo scuolabus per la gita ci sono 45 posti.

Se gli alunni partecipanti sono 36, quanti posti restano liberi?

Se sullo scuolabus salgono anche 4 insegnanti, quanti posti saranno occupati in tutto?

Risolvere

problemi con due o più operazioni.

I DATI MANCANTI

Ricorda

Quando il testo non ci dà tutte le informazioni necessarie, cioè quando ci sono dati mancanti , il problema non è risolvibile.

1 Inventa il dato mancante e risolvi i problemi.

Per la festa di compleanno la mamma di Stefania ha acquistato dei palloncini da gonfiare. Li distribuisce in parti uguali fra i 7 bambini presenti. Quanti palloncini vengono consegnati a ciascun bambino?

Puoi risolvere il problema? Quale dato manca? Il numero

DATI =

RISPOSTA

Alla fine della partita di bowling, Saverio ha totalizzato 63 punti ma Luis ha vinto con alcuni punti di differenza. Quanti punti ha totalizzato Luis?

Puoi risolvere il problema? Quale dato manca? Il numero

DATI

RISPOSTA

Comprendere se il testo di un problema fornisce tutti i dati necessari alla soluzione.

RISOLVIAMO

1 Leggi il testo e risolvi sul quaderno, con il diagramma e l’operazione.

a. Lungo il viale principale della villa comunale ci sono 2 file di 36 alberi. Quanti alberi in tutto?

b. Nicola ha conservato i suoi francobolli in un raccoglitore ad anelli formato da 8 cartelle. I francobolli sono in tutto 678. Quanti francobolli in ogni cartella? Quanti resteranno fuori?

c. Il gattino di Sara mangia 2 scatolette di paté al giorno. Quante scatolette in 2 settimane? E in un mese?

d. Al luna park Gianni e Franco giocano al tiro a bersaglio. Gianni totalizza 36 punti e Franco 42. Per vincere il pupazzo gigante servono 150 punti. Quanti punti mancano per vincere il premio?

e. Marcella festeggia il compleanno il 9 novembre. Se è nata nel 1998, quanti anni ha oggi?

LE FRAZIONI

Ricorda

Una frazione indica una parte dell’intero.

1 Osserva l’immagine e la frazione e rispondi alle domande.

• Come si legge la frazione? .....................................................................................................................

• Qual è il numeratore?

• Qual è il denominatore?

3 8

• Che cosa indica la linea frazionaria? ............................................................................................................................................................................................................................

• In quante parti è stato diviso l’intero? ...........................................................................

• Quante parti sono state colorate?

2 Leggi la frazione e colora la parte corrispondente. Poi scrivila in parola.

3 Scrivi le frazioni corrispondenti in cifre e in parola.

LE FRAZIONI DECIMALI

Le frazioni che al denominatore hanno 10, 100, 1 000 si chiamano frazioni decimali .

1 Osserva le immagini, scrivi le frazioni corrispondenti e dividile in tabella.

Frazioni decimali

Frazioni non decimali

2 Indica con una X se l’affermazione è vera (V) o falsa (F).

• Le frazioni decimali hanno 10, 100 o 1 000 al denominatore.

• La frazione 3 1 000 si legge tre millesimi.

• Se coloro 4 quadratini di una riga di 10, ne ho colorati i 10 4 .

• La frazione 1 1 000 è un’unità frazionaria.

• Se leggo 19 pagine di un libro di 1 000 pagine, ne leggo i 19 100 .

Ricorda Conoscere

DALLA FRAZIONE DECIMALE

AL NUMERO DECIMALE

Le frazioni decimali possono essere trasformate in numeri decimali. La virgola separa la parte intera dalla parte decimale. Ricorda

1 Trasforma in numeri decimali le seguenti frazioni, come nell’esempio.

•

2 Trasforma i seguenti numeri decimali in frazioni, come nell’esempio. • 0,12

3 Colora allo stesso modo il cartellino della frazione e del numero decimale corrispondente.

1

I NUMERI DECIMALI

2 Scrivi sotto forma di frazione e di numero decimale, come nell’esempio.

4

3

•

4

Ricorda

Anche i numeri decimali si possono confrontare e ordinare.

5 Leggi e completa in modo da rendere vera la relazione.

• 3,6 <

• 5,9 > .................................

• 3,17 <

• 41,91 =

• 22,30 <

• 90,78 = .................................

• 15,5 =

• 80,013 <

• 77,01 >

• 4,374 < .................................

• 6,951 >

• 12,118 =

6 Riscrivi i numeri in ordine crescente, dal minore al maggiore.

7 Riscrivi i numeri in ordine decrescente, dal maggiore al minore.

IL PIGIAMA PARTY

Laura e Denith fanno acquisti per il pigiama party che hanno organizzato.

1 Osserva le immagini e completa.

COSTO UNITARIO

COSTO TOTALE PAGO CON RESTO

€

COSTO UNITARIO E COSTO TOTALE

1 Completa i diagrammi, mettendo il segno giusto.

costo totale quantità

..........

costo unitario

costo totale quantità

costo unitario

costo unitario

quantità

costo totale

2 Completa la tabella.

oggetto costo totale costo unitario quantità operazione

3 Risolvi i problemi sul quaderno, con il diagramma e l’operazione.

a. Maura compra 4 paia di calze e spende in tutto € 16,00. Quanto costa un paio di calze? Paga con una banconota da € 50,00. Quanto riceve di resto?

b. Giordana ha regalato 5 mazzi di fiori alle sue amiche. Ogni mazzo le è costato € 4,00. Quanto ha pagato in tutto?

c. Zoe spende € 28,00 per acquistare delle confezioni di latte. Ogni confezione costa € 4,00. Quante confezioni acquista?

Conoscere

Ricorda

LE MISURE DI LUNGHEZZA

L’unità di misura della lunghezza è il metro , il cui simbolo è m .

1 Completa la tabella delle misure di lunghezza con i multipli e i sottomultipli. multipli Unità di misura sottomultipli ............................. ............................. ............................. m ............................. ............................. ............................. 1 000 m 100 m 10 m 1 0,1 m 0,01 m 0,001 m

2 Collega correttamente con una freccia ogni misura al righello.

Ricorda

Due misure sono equivalenti quando hanno lo stesso valore.

3 Unisci tra loro, con una freccia i cartellini delle misure equivalenti.

4 Esegui le equivalenze.

• 17 m = dm

• 25 dm = cm

• 124 km = hm

• 8 km = ............................. m

• 1 500 cm = dm

• 320 hm = km

• 200 m = hm

• 66 hm = ........................ dam

Conoscere le misure di lunghezza e operare con esse.

Ricorda

LE MISURE DI CAPACITÀ

L’unità di misura della capacità è il litro , il cui simbolo è [l .

1 Completa la tabella delle misure di capacità con i multipli e i sottomultipli.

multipli Unità di misura sottomultipli [l

100 [l 10 [l 1 0,1 [l 0,01 [l 0,001 [l

2 Completa la tabella, scomponendo le misure.

h[l da[l [l d[l c[l m[l

32 da [l

526 m [l

3 789 d [l

144 c [l

357 m [l

725 [l

3 Quanto manca per formare…? Completa.

6

4 Esegui le equivalenze.

• 300 [l = h [l

• 230 da [l = h [l

• 530 m [l = c [l

• 9 000 m [l = .................................................. [l

Conoscere le misure di capacità e operare con esse.

• 510 c [l d [l

• 2 400 [l = h [l

• 730 [l = da [l

• 21 da [l = .................................................. d [l

LE MISURE DI PESO

L’unità di misura del peso è il chilogrammo , il cui simbolo è kg . Ricorda

1 Completa la tabella delle misure di peso con i multipli e i sottomultipli.

2 Colora allo stesso modo i cartellini delle misure equivalenti. 4

3 Scomponi le misure, come nell’esempio.

• 345 g = 3 hg, 4 dag, 5 g

• 167 cg =

• 54 hg =

• 1 456 g = .......................................................................................

4 Quanto manca per formare…? Completa.

• 384 mg =

• 95 dg =

• 785 dag =

• 532 g = ...........................................................................................

Conoscere le misure di peso e operare con esse.

EQUIVALENZE

1 Esegui le equivalenze completando le tabelle.

MISURE DI LUNGHEZZA

km hm dam m

1 000 m 100 m 10 m 1

3 km m

8 hm dm

5 m .................... mm

7 dam .................... cm

5 km hm

12 m dm

54 cm .................... mm

31 dam .................... m

dm cm mm

0,1 m 0,01 m 0,001 m

9 600 m hm

400 cm m

300 dam .................... km

1 500 dm .................... dam

MISURE DI CAPACITÀ

h [l da [l [l d [l c [l m [l

100 [l 10 [l 1 0,1 [l 0,01 [l 0,001 [l

52 [l .................... d [l

400 da [l [l

784 h [l da [l

9 c [l m [l

32 d [l .................... m [l

4 h [l [l

50 da [l d [l

9 [l c [l

MISURE DI PESO

700 [l .................... h [l

4 000 d [l da [l

300 c [l [l

8 000 m [l [l

1 000 g 100 g 10 g 1

dg cg mg 0,1 g 0,01 g 0,001 g kg hg dag g

3 kg g

4 hg dg

6 g mg

9 kg g

96 g cg

3 dag dg

8 kg dag 7 dg mg

7 800 dag kg

1 250 g dag

1 200 dg dag

3 000 g kg

PESO LORDO, PESO NETTO, TARA

1 Completa i diagrammi.

peso netto peso lordo

+

peso lordo

peso lordo −

tara −

tara

2 Completa la tabella, eseguendo equivalenze dove necessario.

peso lordo peso netto tara

420 g 3 500 dg g

............ kg 5 kg 1 kg

50 dag 475 g ............ g

............ hg 35 hg 5 hg

1 500 g hg 500 g

15 cg mg 30 mg

LAVORO IN COPPIA

3 Osservate le immagini e inventate un problema da risolvere sul quaderno.

3 kg 28 hg ............... hg

4 Risolvi i problemi sul quaderno, con diagramma e operazione.

a. Un pacco di biscotti pesa 500 g. I biscotti pesano 490 g. Qual è la tara in centigrammi?

b. Un portapastelli di alluminio pesa 150 g e contiene 390 g di penne e pastelli. Qual è il peso lordo in decagrammi?

c. Il contenitore pieno di carta da riciclare pesa 13 kg e vuoto pesa 10 hg. Calcola il peso netto in chilogrammi.

Operare in contesti reali con i concetti di peso lordo, peso netto, tara.

LE MISURE DI TEMPO

Ricorda

1 minuto (m) = 60 secondi (s)

1 ora (h) = 60 minuti (m)

1 giorno (d) = 24 ore (h)

1 Completa le equivalenze del tempo, come nell’esempio.

• 2 m = 120 s

• 3 h = ............... m

• 180 s = m

• 240 m = h

• 45 m = ............... s

• 2 d = h

2 Osserva le vignette e rispondi alle domande.

SONO LE 17.45. HO COMINCIATO I COMPITI 2 ORE FA.

• 3 000 s = m

• 120 h = ............... d

• 3 d = h

studiare?

SONO LE 11.30. LA CAMPANELLA SUONERÀ TRA 3 ORE.

3 Colora il cartellino corrispondente al periodo indicato.

Conoscere e usare le misure di

LO SVILUPPO DEI SOLIDI

1 Colora allo stesso modo ogni solido e il suo sviluppo sul piano.

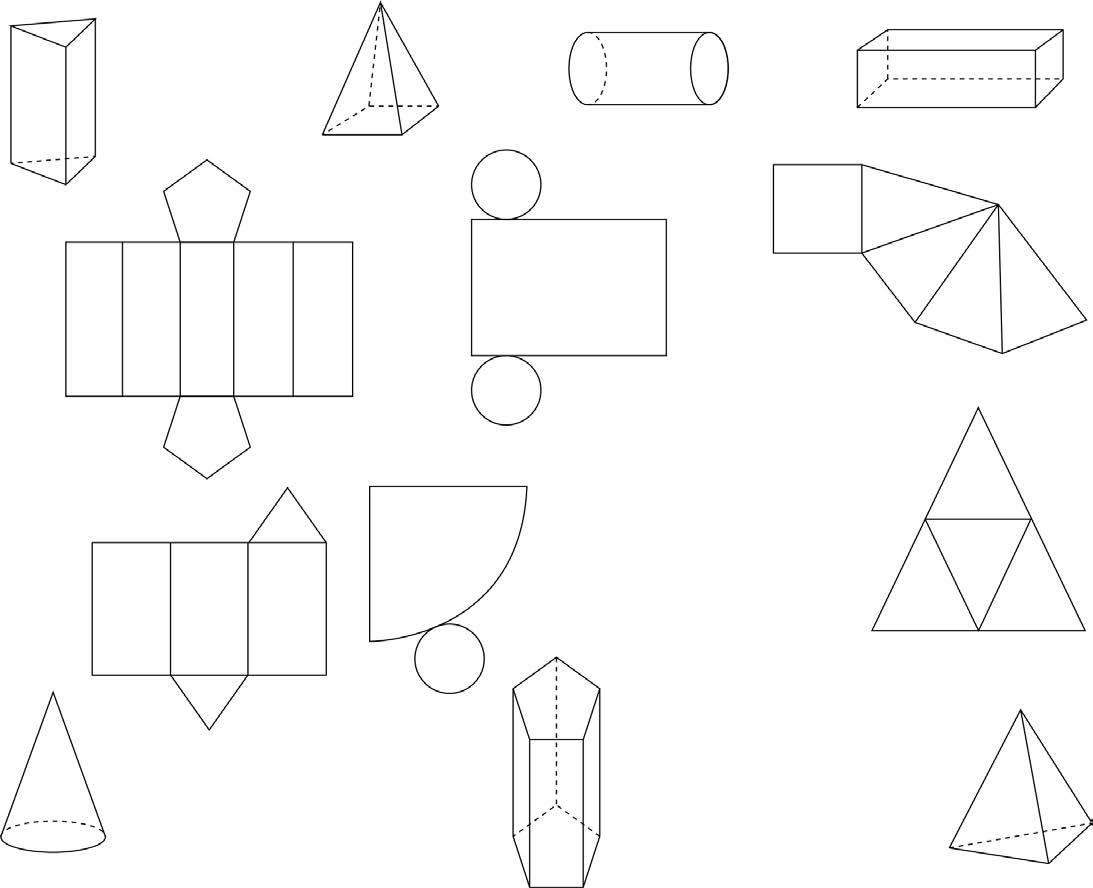
2 Osserva le immagini e indica con una X qual è lo sviluppo corretto della piramide.

Riconoscere lo sviluppo di un solido sul piano.

RETTE, SEMIRETTE E SEGMENTI

1 Collega ogni figura al riquadro giusto.

Retta: non ha inizio né fine

Semiretta: ha un inizio ma non ha una fine

Segmento: parte di retta compresa tra due punti

2 Ripassa con il rosso le rette, con il verde le semirette, con il blu i segmenti.

3 Scrivi accanto a ogni linea il nome adatto scegliendolo tra: retta, semiretta, segmento.

4 Indica con una X la giusta definizione per ogni coppia di rette.

f e a b g h c d

rette incidenti

rette parallele

5 Disegna quanto indicato nei riquadri, usando il righello.

Due segmenti paralleli

Due rette incidenti

Tre rette parallele

Due rette orizzontali

Tre segmenti verticali

Due semirette oblique

Conoscere rette, semirette e segmenti e le loro caratteristiche.

GLI ANGOLI

1 Usa l’angolo retto della tua squadra, sovrapponilo agli angoli qui sotto e colora di rosso gli angoli acuti e di verde gli angoli ottusi.

2 Collega ogni angolo al suo nome e scrivi la sua ampiezza in gradi.

Acuto: < Ottuso: > Piatto: Giro:

Retto:

3 Disegna in ciascun “orologio” la seconda lancetta in modo da formare l’angolo indicato. Poi colora l’ampiezza di ciascun angolo.

PIATTO

RETTO GIRO

Conoscere gli angoli e la loro classificazione.

1 Scrivi nella tabella il numero di lati di ciascun poligono; poi colora nello stesso modo i poligoni che hanno un numero uguale di lati. poligono

2 Completa i poligoni, aiutandoti con il righello.

Sono tutti triangoli

Sono tutti quadrati

Sono tutti trapezi

Sono tutti rettangoli

Conoscere e classificare i poligoni. Distinguerne gli elementi.

Ricorda

IL PERIMETRO DEI POLIGONI

Il perimetro è la misura del contorno di un poligono e si indica con P. Si calcola sommando le misure di tutti i lati.

1 Usate il righello per misurare i lati dei poligoni e calcolate il perimetro.

LAVORO IN COPPIA

Misurare i lati e calcolare il perimetro di un poligono.

PROBLEMI CON IL PERIMETRO

1 Risolvi i problemi sul quaderno. Ricorda di disegnare la figura ed esegui le equivalenze se necessario.

a. Un tavolino è largo 90 cm e lungo 75 cm. Quanti dm misura il suo perimetro?

b. Uno stendardo triangolare ha i lati che misurano 35 cm, 40 cm, 25 cm. Qual è il suo perimetro in millimetri?

c. Un campo esagonale ha il lato di 9 dam. Quanti metri misura il suo perimetro?

d. Il piazzale del parcheggio ha una forma rettangolare, lungo 180 m e largo 50 m. Calcola il perimetro.

e. Una cornice pentagonale ha il lato di 45 m. Calcola il perimetro della cornice.

f. Un foglio di carta in formato A4 ha i lati di circa 21 cm e 30 cm. Quanto misura il suo perimetro? Quanto misura il perimetro di 4 fogli uguali?

g. Calcola il perimetro di un tavolo rettangolare la cui larghezza misura 120 cm e la cui lunghezza è il doppio della lunghezza.

2 Quanto misura il perimetro di questo poligono?

Risolvere problemi con il perimetro, eseguendo anche equivalenze.

Ricorda

L’AREA DEI POLIGONI

L’area di un poligono è la misura della superficie , cioè della parte di piano racchiusa dal contorno.

1 Calcola l’area dei poligoni e rispondi alle domande.

• Ci sono poligoni con la stessa area?

• Quali sono? ..................................................................................................................................................................................................

• Come vengono detti due poligoni di forma diversa ma con la stessa area?

2 Disegna dei poligoni aventi le aree indicate.

LA SIMMETRIA

1 Osserva le figure e indica con una X quale delle due è correttamente divisa dall’asse di simmetria.

2 Completa le figure in modo simmetrico e ripassa di rosso l’asse di simmetria.

Ricorda

Se la figura è divisa in due parti perfettamente uguali, si dice che le due parti sono simmetriche

3 Disegna la figura simmetrica a quella data.

CLASSIFICAZIONI

1 Inserisci nel diagramma di Venn i risultati delle tabelline del 5 e del 10. Attento ai numeri in comune.

Diagramma di Venn

TABELLINA

DEL 5

TABELLINA

DEL 10

NUMERI IN COMUNE

2 Completa i due diagrammi inserendo i numeri da 90 a 110.

Diagramma di Carroll Diagramma ad albero

NUMERI DA 90 A 110

NUMERI PARI A 2 CIFRE A 3 CIFRE

NUMERI DISPARI A 2 CIFRE A 3 CIFRE

NUMERI PARI NUMERI DISPARI A 2 CIFRE A 3

CIFRE

RELAZIONI

1 Osserva l’insieme degli animali e l’insieme degli ambienti. Scrivi la relazione sulle frecce.

2 Osserva la tabella a doppia entrata, completala e trasformala in un diagramma sagittale.

colore preferito rosso giallo arancione verde viola

Simona

Camilla Lyn

Brenda Mercy

La relazione è

Simona ....................................................................

Camilla

Lyn

LAVORO IN COPPIA

Brenda ....................................................................

Mercy

3 Trovate una relazione che riguardi la frutta e rappresentatela sul quaderno in una tabella a doppia entrata.

Riconoscere e rappresentare relazioni.

INDAGINI STATISTICHE

1 In una terza primaria è stata svolta un’indagine sulla bevanda preferita dai bambini. Osserva i dati della tabella di frequenza e registrali nell’istogramma.

succo di frutta

latte

bibita gassata

spremuta

tè

acqua

Legenda:

= 1 preferenza

succo di frutta latte bibita gassata spremuta tè acqua

Rispondi: Qual è la moda?

LAVORO IN COPPIA

2 Provate a svolgere la stessa indagine nella vostra classe. Raccogliete i dati e rappresentateli in un ideogramma e in un istogramma.

Ricorda

1 Da un mazzo di carte prendi i 4 assi e forma un mazzetto. Immagina di estrarne una: come sarà? Indica con una X se l’affermazione è vera o falsa.

• È certo che sia l’asso di cuori. V F

• È possibile che esca l’asso di fiori. V F

• È impossibile che esca un re. V F

• È certo che esca un asso. V F

• È possibile che esca una regina. V F

• È impossibile che esca l’asso di quadri. V F

• È possibile che esca l’asso di picche. V F

2 Colora di rosso gli eventi certi, di verde gli eventi possibili e di azzurro gli eventi impossibili.

Frequento la scuola primaria. Se piove la strada si bagna.

Il mare è agitato. Allo zoo posso vedere i dinosauri. Sabato andremo al parco giochi.

A Natale ci sono le vacanze scolastiche. Gli uccelli hanno quattro zampe.

Discriminare