– forenklet
Ørnulf Borgan
John Engeseth
Odd Heir
Håvard Moe
Tea Toft Norderhaug
Sigrid Melander Vie
Ørnulf Borgan
John Engeseth
Odd Heir
Håvard Moe
Tea Toft Norderhaug
Sigrid Melander Vie
– forenklet
Bokmål
Innhold
1 Prosent
Prosent – brøk – desimaltall 5
Prosentandel 6
Prosentpoeng 7
Vekstfaktor 8
Regning med vekstfaktor 9
Prosentendring i flere perioder 12
Eksponentiell vekst 13
Modellering med eksponentialfunksjoner 15
Eksamensoppgaver 17
2 Statistikk
Frekvens 20
Relativ frekvens 21
Stolpediagram (søylediagram) 22
Klasser og klassebredde 23
Histogram 25
Sektordiagram (sirkeldiagram) 26
Kumulativ frekvens 27
Kumulativ relativ frekvens 28
Gjennomsnitt 29
Median 30
Gjennomsnitt og median med regneark 31
Typetall 32
Variasjonsbredde 32
Standardavvik 33
Eksamensoppgaver 34
3 Likninger og ulikheter
Grafisk løsning av likninger 37
Grafisk løsning av ulikheter 39
Løsning ved tegning 40
Løsning av likninger ved regning 41
Løsning av ulikheter ved regning 42
Løsning med CAS 43
Grafisk løsning av likningssystemer 44
Likningssystemer med CAS 45
Kryssmultiplisering 46
Eksamensoppgaver 47
4 Geometri
Omkrets 49
Areal 50
Overflate av prisme 52
Volum 53
Volum av sylinder 54
Pytagorassetningen 55
Formlikhet 58
Målestokk 59
Eksamensoppgaver 60
5 Økonomi
Lønn 64
Konsumprisindeksen 66
Kroneverdi 68
Reallønn 68
Sparing 69
Kredittkort 71
Budsjett 72
Regnskap 73
Eksamensoppgaver 74
Fasit 77
Om Matematikk 2P – forenklet
Matematikk 2P – forenklet er én av komponentene i Matematikk 2P, som består av
Forenklet bok
grunnleggende emner innføres med et minimum av teori og med tilpassede
vi mener bør løses med hjelpemidler, er merket med
Når du mestrer oppgavene i denne boka, bør du prøve deg på oppgavene
Vi håper at Matematikk 2P – forenklet hjelper deg på veien til å mestre
Vi setter stor pris på kommentarer og innspill, så send oss gjerne en e-post til
Vi ønsker deg lykke til med faget!
Hilsen forfatterne Ørnulf Borgan, John Engeseth, Odd Heir, Håvard Moe, Tea Toft Norderhaug og Sigrid Melander Vie, og redaktørene Harald Øyen Kittang og Bjørn Johannes Neef
Prosent – brøk – desimaltall 5
Prosentandel 6
Prosentpoeng 7
Vekstfaktor 8
Regning med vekstfaktor 9
Prosentendring i flere perioder 12
Eksponentiell vekst 13
Modellering med eksponentialfunksjoner 15
Eksamensoppgaver 17
Prosent – brøk – desimaltall
Prosent betyr hundredeler.
EKSEMPEL 1
Skriv 5 % som a en brøk med 100 som nevner
b et desimaltall
Prosentandel
EKSEMPEL 3
Hvor mange prosent av elevene liker musikken til Kygo?
107
Hvor mange prosent av elevene liker musikken til Alan Walker?
108
Hvor mange prosent av elevene liker musikken til Beatles?
109
Alle bortsett fra tre av dem liker
Hvor mange prosent av elevene liker musikken til Tiësto?
EKSEMPEL 4
Hvor mange har en iPhone?
10 av 28 svarer til 10 28 0,3636%
Regn her:
Andelen er 10 28
Prosentandelen er 36 %.
Vi skriver 54 % som desimaltall: 54 % = Vi ganger med innbyggertallet, og får
65300,543526,2 ⋅=
Regn her: 110
Hvor mange har en iPhone?
111
På en skole med 385 elever svarer
Hvor mange av elevene ser daglig på Netflix?
Prosentpoeng
EKSEMPEL 5
a Hvor stor var økningen i prosentpoeng?
b Hvor mange prosent var økningen?
112
Andelen som spiser sunt, økte fra 65 %
a Hvor stor var økningen i prosentpoeng?
b Hvor mange prosent var økningen?
113
I en meningsmåling gikk et parti fram fra 8,0 %
a Hvor stor var økningen i prosentpoeng?
b Hvor mange prosent gikk partiet fram?
Et annet parti gikk tilbake fra 10,0 % til 8,0 %
c Hvor stor var nedgangen i prosentpoeng?
d Hvor mange prosent gikk partiet tilbake?
e Hvorfor er ikke svaret på oppgave b og oppgave d likt?
114
a Hvor mange prosentpoeng gikk andelen dagligrøykere
ned fra 2007 til 2019?
b Hvor mange prosentpoeng høyere var andelen
dagligrøykere i 2012 enn i 2017?
c Hvor mange prosentpoeng lavere var andelen
dagligrøykere i 2019 enn i 2012?
d enn i 2007?
Vekstfaktor
En vekstfaktor er et tall vi kan gange med for å finne den nye verdien ved prosentvis økning eller nedgang.
EKSEMPEL 6
a Hva er vekstfaktoren ved en økning på 23 %?
b Hva er vekstfaktoren ved en nedgang på 23 %?
115
a 100 % + 23 % = 123 % = 1,23
b 100 % 23 % = 77 % = 0,77
a Hva er vekstfaktoren ved en økning på 25 %?
b Hva er vekstfaktoren ved en nedgang på 25 %?
c Hvordan kan vi ut fra vekstfaktoren avgjøre om det er snakk om økning eller nedgang?
116 EndringVekstfaktor
Regn her:
Regning med vekstfaktor
ny verdi = gammel verdi vekstfaktor N = G V
EKSEMPEL 7
Hva blir den nye husleia?
Vekstfaktoren er 100 % + 6 % = 106 % = Vi bruker N = G ⋅ V med G = 8700 og V =
117
Hva blir den nye husleia?
118
Hva blir den nye husleia?
EKSEMPEL 8
Hva blir den nye husleia?
Vekstfaktoren er 100 % 6 % = 94 % = Vi bruker N = G V med G = 8700 og V =
119
Hva blir den nye husleia?
120
Hva blir den nye husleia?
Regn her:
Regn her:
EKSEMPEL 9
Husleia økte med 6 %, og er
Hva var den gamle husleia?
121
Husleia til Pelle økte med 12 %, og er nå på 8400 kr
Hva var den gamle husleia?
122
Husleia til Pernille økte med 3 %, og er nå på 12 000 kr
Hva var den gamle husleia?
EKSEMPEL 10
Husleia gikk ned med 6 %, og er nå på 8700 kr
Hva var den gamle husleia?
123
Husleia til Pjotr gikk ned med 10 %, og er nå på
Hva var den gamle husleia?
124
Husleia til Perle gikk ned med 5 %, og er nå på
Hva var den gamle husleia?
Vekstfaktoren er 100 % + 6% = 106 % = Vi bruker N = G V med N = 8700 og V =
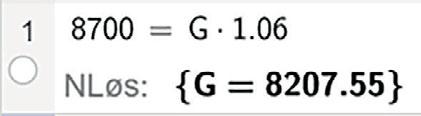
Regn her:
Vekstfaktoren er 100 % 6 % = 94 % = Vi bruker N = G ⋅ V med N = 8700 og V =
Regn her:
Vi runder av til nærmeste hele krone.
EKSEMPEL 11
Husleia økte fra 8700 kr til 9000 kr per måned Hvor mange prosent økte husleia?
Vekstfaktoren er 1,03 =
125
Husleia til Pål økte fra 8400 kr til 10 000 kr
Hvor mange prosent økte husleia?
126
Husleia til Poletta økte fra 6900 kr til 9600 kr
Hvor mange prosent økte husleia?
EKSEMPEL 12
Husleia gikk ned fra 8700 kr til 8000 kr
Hvor mange prosent sank husleia?
127
Husleia til Pavlov gikk ned fra 8400 kr til 8000 kr
Hvor mange prosent sank husleia?
128
Husleia til Pamela gikk ned fra 9000 kr til 6000 kr
Hvor mange prosent endret husleia seg?
her: Vi bruker N = G V med N = 9000 og G = Vi bruker N = G V med N = 8000 og G =
Vekstfaktoren er 0,92 = Én desimal ekstra gir 1,034 og 3,4 %.
Regn her:
Regn
Prosentendring i flere perioder
Når vi har flere prosentendringer etter hverandre, finner vi sluttverdien ved å gange den opprinnelige verdien med vekstfaktoren for hver endring.
EKSEMPEL
13
Verdien av et kunstverk var 825 000 kr i 1995
I 2005 var verdien 5 % høyere enn i 1995
I dag er verdien 10 % lavere enn i 2005
Hvor mye er kunstverket verdt i dag?
129
Verdien av et kunstverk var 825 000 kr i 1995
I 2005 var verdien 10 % lavere enn i 1995. I dag er verdien 5 % høyere enn i 2005
a Hvor mye er kunstverket verdt i dag?
b Sammenlikn med svaret i eksempel 13.
Formuler det du observerer.
130
Verdien av et kunstverk var 825 000 kr i 1995
I 2005 var verdien 5 % lavere enn i 1995. I dag er verdien 10 % høyere enn i 2005
a Hvor mye er kunstverket verdt i dag?
b Sammenlikn med svaret i eksempel 13.
Formuler det du observerer.
131
Den 1. august 2020 var det totalt 9309 meldte tilfeller av covid-19 i Norge. Deretter økte antallet med 19 % til 1. september. Videre økte det med 29 % til 1. oktober. Så økte det med 50 % til 1. november.
a Hvor mange meldte tilfeller av covid-19 var det 1. september?
b Hvor mange meldte tilfeller av covid-19 var det 1. oktober?
c Hvor mange meldte tilfeller av covid-19 var det 1. november?
d Regn ut 1,19 1,29 1,5. Hva forteller svaret?
Vekstfaktoren for perioden med økning er 100 % + 5 % = 105 % = 1,05
Vekstfaktoren for perioden med nedgang er 100 % 10 % = 90 % = 0,9.
825 000 1,05 0,9 = 779 625
I dag er kunstverket verdt 779 625 kr.
Regn her:
Eksponentiell vekst
Når noe øker eller avtar med like mange prosent i hver periode, sier vi at det øker eller avtar eksponentielt
ny verdi = gammel verdi ⋅ vekstfaktorantall perioder
EKSEMPEL 14
Verdien av et kunstverk var
Verdien har deretter økt med Hvor mye var kunstverket verdt i 2020?
Vekstfaktoren for økningen per år er 100 % + 2 % = 102 % = Vi bruker N = G V t med G = 755 000, V = 1,02 og t =
132
Verdien av et kunstverk var 236 700 kr
Verdien har deretter økt med 8 %
a Hvor mye var kunstverket verdt i 2012?
b Hvor mye var kunstverket verdt i 2016?
c Regn ut 1,0812
133
Verdien har deretter minket med 15 %
a Hvor mye var bilen verdt i 2015?
b Hvor mye var bilen verdt i 2018?
c Regn ut 0,8513
Regn her:
EKSEMPEL 15
Verdien av et kunstverk var
I årene før økte verdien med
Hvor mye var kunstverket verdt i 2012?
134
Verdien av et kunstverk var 53 750 kr i
Vekstfaktoren for økningen per år er
a Hvor mye var kunstverket verdt i 2004?
b Hvor mye var kunstverket verdt i 1999?
135
Hvor mye var bilen verdt i 2015?
EKSEMPEL 16
Verdien av et kunstverk økte fra 187 000 kr i 2013 til
Hvor mange prosent økte verdien i gjennomsnitt per år?
Vekstfaktoren er 1,03 =
136
Verdien av et kunstverk økte fra
Hvor mange prosent økte verdien i gjennomsnitt per år?
137
Verdien av en bil sank fra 598 000 kr
Hvor mange prosent sank verdien i gjennomsnitt per år?
Regn her:
Regn her:
EKSEMPEL 17
Verdien av et kunstverk
øker med 9 % per år.
Verdien er 425 000 kr i dag.
Hvor lang tid tar det før verdien er én million kroner?
138
Vi bruker N = G V t med N = 1 000 000, G = 425 000 og V = 1,09.
Verdien er én million kroner om ca. 10 år.
Verdien av et kunstverk øker med 16 % per år. Verdien er 259 000 kr i dag.
a Hvor lang tid tar det før verdien er dobbelt så stor?
b Hvor lang tid tar det før verdien er én million kroner?
Modellering med eksponentialfunksjoner
Når noe vokser eksponentielt (prosentvis), kan vi bruke en funksjon på formen fxab () x = =⋅⋅ som modell.
fx a b N G V () x t = =⋅⋅
EKSEMPEL 18
Verdien av et kunstverk var 755 000 kr i 1998. Fram til 2020 økte verdien med 2 % hvert år.
Lag en modell for verdien f(x) kr x år etter 1998.
Vekstfaktoren er 100 % + 2 % = 102 % = 1,02. Modellen er derfor gitt ved
fx()755 0001,02x =⋅
139
Verdien av et kunstverk var 236 700 kr i 2008. Fram til 2020 økte verdien med 8 % per år.
Lag en modell for verdien f(x) kr x år etter 2008.
140
Verdien av en bil var 895 000 kr i 2013. Fram til 2021 sank verdien med 15 % per år.
Lag en modell for verdien av bilen, V(t) kr, t år etter 2013.
EKSEMPEL 19
Verdien av en bil har utviklet seg slik tabellen viser.
Lag en modell for verdien f(x) kr x år etter januar 2012.
År (januar) 20122014201620182020 x 02468
Verdi (kr) 690 000 510 000375 000280 000205 000
❶ Klikk på , «Vis» og «Regneark».
❷ Legg inn x-verdiene i kolonne A og funksjonsverdiene i kolonne B.
❸ Marker cellene ved å venstreklikke i A1 og dra nedover til B5
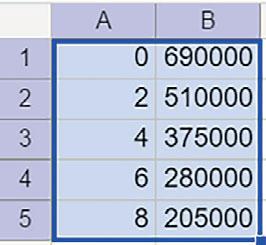
141
Verdien av en bil har utviklet seg slik tabellen viser.
❹ Velg «Regresjonsanalyse»
❺ Velg «Eksponentiell» i rullegardinmenyen under «Regresjonsmodell».
Vi ser at modellen er gitt ved fx()6899110,86 x =⋅
År (januar) 20122014201620182020
Verdi (kr) 899 000680 000 515 000390 000295 000
Lag en modell for verdien f(x) kr x år etter januar 2012.
Eksamensoppgaver
142 (2P våren 2019)
Hvor mye kostet varen før prisen ble satt ned?
143 (2P høsten 2019)
I 2018 var det totalt 487 000 passasjerer på
a Hvor mange prosent økte antall anløp med fra 2017 til 2018?
b Hvor mange passasjerer var det totalt på cruiseskipene i 2017?
144 (2P våren 2020)
145 (2P våren 2020)
Svein fikk 4 % lønnsøkning i 2018 og 6 %
Tore fikk 8 % lønnsøkning i 2018 og 2 %
Hvem av de to hadde høyest lønn i 2019?
Regn her:
Regn her:
Odd Heir har i en årrekke vært lærer, lærebokforfatter og kursholder i matematikk for videregående skole.
Håvard Moe har bred realfaglig utdanning og har skrevet lærebøker i matematikk i flere år. Han er lærer ved Sandnessjøen videregående skole og underviser i matematikk, fysikk og kjemi.
Ørnulf Borgan er professor emeritus ved Matematisk institutt, Universitetet i Oslo, der han arbeider med utvikling og anvendelser av statistiske metoder. Han har vært lærebokforfatter i mange år og har gitt en rekke kurs og foredrag for lærere i videregående skole.
Matematikk 2P følger fagfornyelsens læreplan i Matematikk 2P (LK20) og består av lærebok, forenklet tilleggsbok, og digitale elev- og lærerressurser på Aunivers.no
Forenklet bok
Denne engangsboka har de samme kapitlene som læreboka. Utvalgte, grunnleggende emner innføres med teori og med oppgaver tilpasset teorien. Eleven loses gjennom fagstoffet med tydelige eksempler, via delvis løste oppgaver til mer selvstendig arbeid. Til slutt i hvert kapittel er det noen eksamensoppgaver. Boka er laget for innskriving.
John Engeseth har bred undervisningspraksis og underviser til daglig ved Elvebakken videregående skole. Han har vært forfatter av matematikkbøker for videregående skole i mange år.
Tea Toft Norderhaug har mastergrad i matematikk fra NTNU. Hun er lærer ved Bjørknes privatskole og underviser i matematikk, kjemi og naturfag. Tea har i flere år bidratt til Aschehougs læreverk i matematikk for videregående skole.
Sigrid Melander Vie er utdannet sivilingeniør fra NTNU. Hun jobber som lærer ved Rud videregående skole og underviser i matematikk og fysikk. Sigrid har i flere år bidratt til Aschehougs læreverk i matematikk for videregående skole.
Digitale ressurser
Aunivers.no inneholder blant annet: •opplæringsressurser til GeoGebra, regneark og Python •interaktive oppgaver •eksamensløsninger
Som lærer får du også tilgang til: •lærerveiledning •kapittelprøver •terminprøver •aktivt klasserom
Den digitale elevressursen er inkludert i lærerressursen, og er tilgjengelig med FEIDE-innlogging.
ISBN 978-82-03-31963-1