Matemagisk 9: Grunnbok by Aschehoug Utdanning

Matemagisk

Asbjørn Lerø Kongsnes

Anne Karin Wallace

Matemagisk

Asbjørn Lerø Kongsnes

Anne Karin Wallace

Matemagisk9–10Lærebok er en del av læremiddelet Matemagisk1–10. Læremiddelet følger læreplanen i matematikk for 1.–10. årstrinn.

Materialet er vernet etter åndsverkloven. Uten uttrykkelig samtykke er eksemplarfremstilling, som utskrift og annen kopiering, bare tillatt når det er hjemlet i lov (kopiering til privat bruk, sitat o.l.) eller i avtale med Kopinor (www.kopinor.no).

Utnyttelse i strid med lov eller avtale kan medføre erstatnings- og straffansvar.

Redaktør: Kari Kleivdal

Grafisk formgiving: Marit Jakobsen og Type-it AS Omslag: Marit Jakobsen

Bilderedaktør: Nina Hovda Johannesen

Tekniske tegninger: Arnvid Moholt

Illustrasjoner: Erik Ødegård, Kari Sortland og Martin Hvattum Ombrekking: ord og form, Gudbrand Klæstad

Grunnskrift: Frutiger LT Std, 10/14 pkt.

Papir: 100 g G-print 1,0

Trykk: Merkur Grafisk AS Innbinding: Bokbinderiet Johnsen AS, Skien

ISBN 978-82-03-40775-8

Aunivers.no

Foto og tegninger

s. 6 Bartosz Hadyniak/iStock , s. 44 johnnorth/iStock, s. 82 Yusufozluk/iStock, s. 120 NTB Scanpix / Sipa Asia, s. 150 Caroline Brundle Bugge/iStock, s. 184 Shuoshu/iStock

Oppgave 14.6 på s. 128 er laget med inspirasjon i en video, GeoGebra. En ressurs utviklet av Matematikksenteret (matematikksenteret.no).

www.aschehoug.no

SVANEMERKET

Forfatterne har mottatt stipend fra det faglitterære fond.

Innhold

11 Figurtall og tallmønster

11A

12 Statistikk

12A Tabeller og diagrammer 46

12B Sentralmål og spredningsmål .....

13 Sannsynlighet

13A Grunnleggende sannsynlighet 84

13B Store talls

13C Sammensatte forsøk

15 Areal og omkrets

15A Arealenheter

15C Areal og omkrets av sirkler og sirkelsektorer

16 Pytagoras’ setning og formlikhet

14 Linjer, figurer og vinkler

14A Definisjoner og egenskaper .....

14B Vinkler i mangekanter

17 Volum og overflate

Velkommen til Matemagisk 9

Matemagisk9 legger til rette for at dere som elever får være aktive, utforske og oppdage matematiske sammenhenger. Vi ønsker at dere skal snakke matte med hverandre, utvikle forståelse og bli gode problemløsere. Boka legger opp til at dere kan samarbeide om matematikken. I boka finner dere varierte oppgaver knyttet til virkeligheten som gjør matematikken meningsfull og relevant. Boka kan brukes alene eller i kombinasjon med Matemagisk8-10Elevhåndbok

Fellesløypa

Hvert delkapittel begynner med en fellesløype. Denne er designet for arbeid i fellesskap i klassen. Den består av teori, eksempler, utforskende oppgaver, snakke matte oppgaver, spill, aktiviteter og andre varierte oppgaver. Programmering og andre digitale verktøy er integrert i delkapitlene der det er relevant.

Nøkkelhull

Oppgaver som viser spesielt viktige ideer og tenkemåter.

Oppgaver der dere skal snakke matte med hverandre. Her trener dere på å forklare hvordan dere tenker.

Følg stien

Oppgaver der du får trent mer på det klassen har arbeidet med i fellesskap. Her trener du på én ting om gangen. Følg stien dekker det mest sentrale faginnholdet og finnes i slutten av hvert delkapittel.

Terrengløypa

Oppgaver som bygger videre på det klassen har arbeidet med i fellesskap. Her kan du få sammensatte utfordringer, også fra flere temaer på en gang. Terrengløypa finner du i slutten av hvert delkapittel.

SNAKKE MATTE

Topptur

Oppgaver som er svært utfordrende og som går utover det som kan forventes på dette trinnet. Jobb med toppturen hvis du mestrer oppgavene i terrengløypa godt. Toppturen finner du i slutten av hvert kapittel.

Ekspedisjon

Oppgaver som går langt utover det som kan forventes på dette trinnet. Oppgavene gir særlig god trening i abstraksjon, generalisering og avansert problemløsing. Fire ekspedisjoner er plassert på strategiske steder i boka.

Noen ganger jobber jeg bare i «følg stien».

Noen få ganger jobber jeg bare i «terrengløypa».

Jeg gjør noen ganger «toppturen», men jeg gjør alltid «terrengløypa» først.

Noen ganger jobber jeg litt i «følg stien» og litt i «terrengløypa».

Hiyanna

Henrik

Tuva

Yonas

Figurtall og tallmønster

11A Å multiplisere to par enteser

• Utforske og begrunne hvordan vi multipliserer to parenteser.

• Multiplisere to parenteser og trekke sammen uttrykk.

På 8. trinn lærte vi at:

Vi kan sette inn tall for variabler og regne ut verdien av algebraiske uttrykk.

Vi kan forenkle algebraiske uttrykk ved å trekke sammen ledd av samme type.

For alle tall a, b og c er a(b + c) = ab + ac

Når vi programmerer i Python, kan vi opprette variabler og gi dem verdi. Vi kan bruke print() for å få skrevet noe til skjermen.

Python følger vanlig regnerekkefølge.

Eksempel

navn = "Heidi" print(navn)

Addisjon: +

Subtraksjon:

Multiplikasjon: *

Divisjon: /

OPPGAVE 11.1

Her ser du et regneark.

a Kopier regnearket og lag en formel i celle E2 som regner ut ab + ac

b Endre tallene i celle A2, B2 og C2. Hva oppdager du? Prøv gjerne med negative tall og desimaltall også.

c Lag et pythonprogram som henter inn tall a, b og c fra brukeren, og som skriver svaret på de to regnestykkene a(b + c) og ab + ac. Kjør programmet flere ganger. Hva oppdager du?

OPPGAVE 11.2

Forklar at a(b + c) = ab + ac for alle tall a, b og c. For å støtte forklaringen din kan du tegne figurer, lage en regnefortelling eller lage en figurtallsoppgave som kan illustrere dette.

OPPGAVE 11.3

Her ser du to ulike rektangler.

a For hvert av rektanglene, regn ut arealet på følgende to måter:

Måte 1: Regn direkte ut totalt antall ruter

Måte 2: Regn ut hvor mange ruter det er av hver farge, og legg sammen til slutt.

b La a, b, c og d være positive tall. Bruk de samme tenkemåtene som i oppgave a, og lag to algebraiske uttrykk for arealet av rektanglet uttrykt ved a, b, c og d

b c d

OPPGAVE 11.4

I hver av deloppgavene skal du regne ut svaret på to forskjellige måter. Tegn rektangler som viser hvordan du tenker til hver oppgave. a (2 + 1) (3 + 1) b (4 + 1) (2 + 2) c (3 + 2) (1 + 1)

OPPGAVE 11.5

Lag et regneark eller et pythonprogram som kan brukes til å undersøke om (a + b)(c + d) = ac + ad + bc + bd for tall a, b, c og d

Prøv gjerne med tilfeller der noen av tallene er desimaltall eller negative tall.

SNAKKE MATTE

Martin er glad i å løpe og løper både morgenøkter og kveldsøkter. Morgenøktene er 6 km lange, mens kveldsøktene er 3 km lange. Martin løper både morgen- og kveldsøkter 4 hverdager og 1 helgedag hver uke. Han lurer på hvor langt han løper til sammen hver uke.

Henriks løsning

Martin løper 4 + 1 = 5 dager i løpet av en uke. Hver dag løper han 6 + 3 = 9 km.

Til sammen løper han (4 + 1) (6 + 3) = 5 9 = 45 km i uka.

Hiyannas løsning

Martin løper 4 6 = 24 km til sammen på morgenen på hverdagene.

Han løper 4 3 = 12 km til sammen på kvelden på hverdagene.

Han løper 1 6 = 6 km til sammen på morgenen i helgene.

Han løper 1 3 = 3 km til sammen på kvelden i helgene.

Til sammen løper han 4 6 + 4 3 + 1 6 + 1 3 = 24 + 12 + 6 + 3 = 45 km i uka.

Forklar hvordan Henrik og Hiyannas løsning illustrerer at vi kan multiplisere to parenteser med hverandre på følgende måte: (a + b)(c + d) = ac + ad + bc + bd

OPPGAVE 11.6

Her ser du de tre første figurene i et mønster.

Figur nr. 1Figur nr. 2

a Fyll ut tabellen.

Figur nr. 3

b Bruk tabellen og lag et algebraisk uttrykk for antall brikker i figur nr. n

De samme figurene er tegnet med andre farger.

Figur nr. 1Figur nr. 2

Figur nr. 3

c Lag et algebraisk uttrykk for antall grønne brikker i figur nr n

d Lag et algebraisk uttrykk for antall blå brikker i figur nr. n

e Lag et algebraisk uttrykk for antall lilla brikker i figur nr. n

f Hvor mange oransje brikker er det i hver figur?

g Legg sammen uttrykkene fra oppgave c–f for å lage et algebraisk uttrykk for antall brikker i figur nr. n

h Forklar hvorfor uttrykket fra oppgave b og oppgave g alltid har samme verdi.

a Hvis disse uttrykkene var ledd i et algebraisk uttrykk, hvilke ville vært ledd av samme type?

b Forklar med egne ord hva det vil si at ledd er av samme type.

SNAKKE MATTE

EKSEMPEL 2

Å multiplisere to parenteser

Skriv uttrykket (a + 4)(2a 3) så enkelt som mulig.

Vi skriver om 3 som + ( 3).

Vi må gange alle ledd i den første parentesen med alle ledd i den andre parentesen.

Til slutt trekker vi sammen ledd av samme type.

OPPGAVE 11.7

Regn ut og trekk sammen så mye som mulig.

a (2 + x)(4 x)

b (2a + 3)(5 a)

c 6 + (a + 2)(a 3)

d (4x + 2y)(x + y) 2xy

Minus foran parentesene

Skriv uttrykket 4x2 (x + 4)(x 3) så enkelt som mulig.

Vi ganger først sammen de to parentesene. Svaret setter vi inn i en stor parentes.

Vi trekker sammen ledd av samme type inne i parentesen.

Vi løser opp parentesen.

Vi trekker sammen ledd av samme type til slutt.

SNAKKE MATTE

OPPGAVE 11.8

Skriv så enkelt som mulig.

a 4x 2(x + 2)

b 3(4a 6) + 3a

c 2x(xy) (2x + y)(xy)

d 4(a2 + 3) (a + 6)(4a 2)

Hvordan kan vi gå fram når vi skal multiplisere tre parenteser med hverandre?

Hvordan kan vi gå fram når vi skal multiplisere fire parenteser med

Følg stien

OPPGAVE 11.9

Løs opp parentesene. a 5(x + 2) b 3(a + 4) c 6(y 8)

OPPGAVE 11.10

Regn ut og trekk sammen så mye som mulig.

a 12 + 3(x 4) b 10 2(a 5) c 4 6(3 + n)

OPPGAVE 11.11

Regn ut og trekk sammen så mye som mulig.

5(7 − n)

4(x + 2) 4(x − 1)

a (x + 2)(x + 3) b (a + 5)(a + 1) c (n + 4)(n + 3) d (t + 1)(t + 1)

OPPGAVE 11.12

Regn ut og trekk sammen så mye som mulig.

a (a + 1)(a 2) b (x 2)(x + 4) c (x 3)(4 x) d (n + 1)(n 1)

OPPGAVE 11.13

Regn ut og trekk sammen så mye som mulig.

a (4a + 2)(a 5) b (5 3x)(2x + 7) c (s + t)(st) d (2ab)(ba)

OPPGAVE 11.14

Skriv så enkelt som mulig.

a 15 + (x 3)(x + 5) b 6a + (a + 2)(a 8)

c 4n2 + (n + 2)(n 3) + 6 d (t 3)(t 6) + 2t2 2(t + 1)

OPPGAVE 11.15

Skriv så enkelt som mulig.

a 12 (a + 3)(a + 4) b 2n (n + 3)(5 n)

c 4a (3a + 2)(a 1) + 3a2 d (x + 2)(x 6) (x + 4)(x 3)

Terrengløypa

OPPGAVE 11.16

Tidligere har vi funnet ut at (a + b)c = ac + bc. La nå c = (r + s).

a Forklar hvorfor (a + b)c = (a + b)(r + s).

b Forklar hvorfor (a + b)c = ac + bc = a(r + s) + b(r + s).

c Forklar hvorfor a(r + s) = ar + as

d Forklar hvorfor b(r + s) = br + bs

e Forklar hvorfor a(r + s) + b(r + s) = ar + as + br + bs

f Forklar hvorfor (a + b)(r + s) = ar + as + br + bs

OPPGAVE 11.17

Bruk framgangsmåten fra forrige oppgave til å forklare at (x + y)(uv) = xuxv + yuyv

EKSEMPEL 3

Å regne ut en parentes opphøyd i andre

Skriv uttrykket ()() +− + xxx 22 2 2 så enkelt som mulig.

Vi skriver først ut hva det betyr at parentesen er opphøyd i andre.

Vi ganger sammen de to første parentesene.

Vi forenkler uttrykket i den første parentesen og ganger 2x inn i den siste parentesen.

Vi løser opp parentesene.

Vi trekker sammen ledd av samme type.

OPPGAVE 11.18

Regn ut og trekk sammen så mye som mulig. a () a 4 2 b aaa32 3 2 () () −+ + c () () +− aa4222 d () () ++ −+ ssstst 13 34 2 2 2

OPPGAVE 11.19

Ingeborg, Susanne og Reda diskuterer hvordan de kan regne ut uttrykket 3(x + 1)(2x 4). Her ser du hvordan de tre har regnet.

Ingeborg: 3(x + 1)(2x 4) = (3x + 3)(2x 4) = 6x2 12x + 6x 12 = 6x2 6x 12

Susanne: 3(x + 1)(2x 4) = (3x + 3)(6x 12) = 18x2 36x + 18x 36 = 18x2 18x 36

Reda: 3(x + 1)(2x 4) = 3(2x2 4x + 2x 4) = 3(2x2 2x 4) = 6x2 6x 12

Forklar framgangsmåten Ingeborg, Susanne og Reda har brukt. Hvorfor blir svaret til Susanne feil?

OPPGAVE 11.20

Skriv så enkelt som mulig. a 4(x + 2)(x 3) + 4x b 2x3 x(x 4)2x c 4a 3(2a + 5)(2 4a) d (a + 2)(a 1)(2a 4) 2a3 8 e x 2 + 4 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ x 1 4 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ x 2 2 1 ⎛ ⎝ ⎜ ⎞ ⎠ ⎟ f 4 a 3a2 + 1 2

⎜ ⎞ ⎠ ⎟ 12aa + 2 () a 2 ()

11B Figurtall

• Utforske og beskrive mønstre i arbeid med figurtall.

• Lage algebraisk uttrykk for rektangeltall, trekanttall og kvadrattall

• Lage algebraiske uttrykk for antall brikker i figur nr. n når figuren er sammensatt av ulike deler.

På 8. trinn brukte vi følgende strategier i arbeid med figurtall:

• Bruke farger.

• Tegne neste figur

• Beskrive mønstret med ord.

• Sette opp en systematisk tabell.

OPPGAVE 11.21

Her ser du figurer satt sammen av blå og oransje brikker.

nr. 1Figur nr. 2

Figur nr. 3

a Tegn figur nr. 4 og figur nr. 5. Bruk farger. Skriv hvor mange blå brikker det er i hver figur. b Lag et algebraisk uttrykk for antall brikker i figur nr. n.

c Lag et algebraisk uttrykk for antall blå brikker i figur nr. n

Tallene vi får når vi ser på antall brikker i hver figur, kalles rektangeltall. Tallene vi får når vi ser på antall blå brikker i hver figur, kalles trekanttall. Tallene kalles trekanttall fordi figurene ser ut som nettopp trekanter. Disse tallene dukker opp mange steder og er ofte nyttige når vi utforsker mønstre.

Figur

d Fyll ut tabellen. RegnestykkeSum 1 1

1 + 2 3

1 + 2 + 3

1 + 2 + 3 + 4

1 + 2 + 3 + 4 + 5

e Hvilken sammenheng finner du mellom summene i tabellen og trekanttallene? Kan du forklare hvorfor det blir slik?

f Regn ut 1 + 2 + 3 + + 99 + 100.

g Lag et program eller en regnearkmodell som finner summen av de 100 første naturlige tallene ved å summere. La også programmet regne ut den samme summen ved hjelp av uttrykket du kom fram til i oppgave c

OPPGAVE 11.22

Her ser du de fire første figurene i et mønster.

Figur nr. 1

Figur nr. 2

Figur nr. 3

Figur nr. 4

a Hvor mange brikker trenger du for å lage figur nr. 5?

b Lag et algebraisk uttrykk for antall brikker i figur nr. n

Her ser du de samme figurene fargelagt på en annen måte.

Figur nr. 1

Figur nr. 2

Figur nr. 3

c Forklar hvordan figur nr. 3 viser at 1 + 3 + 5 = 9.

Figur nr. 4

d Forklar med utgangspunkt i figurene at summen av de n første oddetallene er n2 .

e Regn ut 1 + 3 + 5 + 7 + … + 97 + 99.

OPPGAVE 11.23

På hver figur er det kvadratiske fliser som danner et stort kvadrat. La n være antall fliser langs en av kantene. n = 5

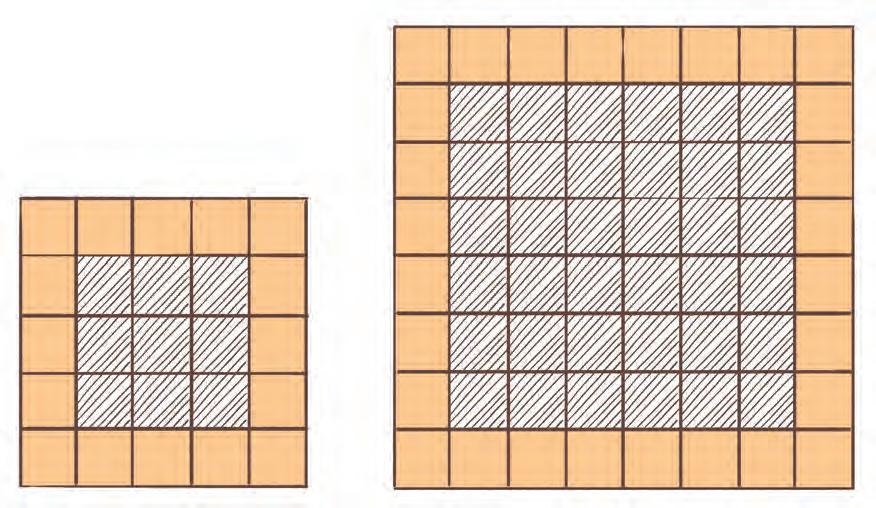
Hvor mange små kvadrater består rammen av når det er

a 5 fliser langs kanten?

b 8 fliser langs kanten?

c 10 fliser langs kanten?

n = 8 n = 8

d Lag et algebraisk uttrykk for hvor mange små kvadrater rammen består av når det er n fliser langs kanten. Du kan gå ut fra at n > 2. Kan du tenke på ulike måter? Illustrer de ulike tenkemåtene med tegninger, og lag algebraiske uttrykk som passer til tenkemåtene.

e Vis ved regning at verdien av de algebraiske uttrykkene alltid er den samme.

Kvadrattall

Figur nr. 1

Figur nr. 2

Figur nr. 3

De første kvadrattallene er 1, 4, 9, 16, 25, 36, …

Algebraisk uttrykk: n2

Rektangeltall

Figur nr. 1

Figur nr. 2

Figur nr. 3

De første rektangeltallene er 2, 6, 12, 20, 30, 42, …

Algebraisk uttrykk: n(n + 1)

Trekanttall

Figur nr. 1

Figur nr. 2

Figur nr. 3

De første trekanttallene er 1, 3, 6, 10, 15, 21, …

Algebraisk uttrykk: nn(1) 2 +

Figur nr. 4

EKSEMPEL 4

Her ser du de fire første figurene i et mønster.

nr. 1

Figur nr. 2

nr. 3

nr. 4

For å lage et algebraisk uttrykk for antall brikker i figur nr. n kan vi dele opp figurene i mindre enheter.

Figur nr. n består av en illustrasjon av kvadrattall nr. n + trekanttall nr. n

Et algebraisk uttrykk for antall brikker i figur nr. n blir dermed + + n nn(1) 2 2 .

Jeg deler opp figurene i kvadrattall og trekanttall. Jeg viser dette med blå og oransje brikker.

Figur nr. 1

Figur nr. 2

Figur nr. 3

Vi trekker sammen dette uttrykket. +

Figur nr. 4

Vi utvider den første brøken så brøkene får samme nevner, og løser opp parentesen.

Vi setter på felles brøkstrek.

Vi trekker sammen ledd av samme type i telleren.

Figur

OPPGAVE 11.24

Her ser du de tre første figurene i et mønster.

Figur nr. 1Figur nr. 2

Figur nr. 3

a Vis med farger hvordan du kan dele opp figurene i mindre enheter.

b Lag et algebraisk uttrykk for antall brikker i figur nr. n Skriv uttrykket så enkelt som mulig.

OPPGAVE 11.25

Lag en figurtallsoppgave. Bytt oppgave med en annen elev, og løs hverandres oppgave.

Følg stien

OPPGAVE 11.26

Lag et algebraisk uttrykk for antall brikker i figur nr. n a

Figur nr. 1Figur nr. 2Figur nr. 3

Figur nr. 1Figur nr. 2

Figur nr. 3

Figur nr. 1Figur nr. 2

Figur nr. 3

Figur nr. 1Figur nr. 2

Figur nr. 3

Figur nr. 1

Figur nr. 2

Figur nr. 3

Figur nr. 1Figur nr. 2Figur nr. 3

OPPGAVE 11.27

Her ser du de tre første figurene i et mønster.

Figur nr. 1Figur nr. 2 Figur nr. 3

a Fyll ut tabellen.

Figur nr.Antall brikker i nederste radAntall brikker i figuren 1 3 9 2 3 4

b Hvor mange brikker trenger du for å lage figur nr. 10?

c Lag et algebraisk uttrykk for antall brikker i den nederste raden i figur nr. n

d Lag et algebraisk uttrykk for antall brikker i figur nr. n

OPPGAVE 11.28

Her ser du de tre første figurene i et mønster.

Figur nr. 1Figur nr. 2Figur nr. 3

a Hvor mange sirkler trenger du for å lage figur nr. 4? Hva med figur nr. 5?

b Hvor mange sirkler trenger du for å lage figur nr. 8?

c Lag et algebraisk uttrykk for antall sirkler i figur nr. n

Terrengløypa

OPPGAVE 11.29

Her ser du de fire første figurene i et mønster.

Figur nr. 1Figur nr. 2

Figur nr. 4 Figur nr. 3

a Lag et algebraisk uttrykk for antall brikker i figur nr. n

Her ser du de fire første figurene i et mønster.

Figur nr. 1

Figur nr. 2

Figur nr. 3

nr. 4

b Hva er likt, og hva er ulike i dette og det forrige mønstret?

c Lag et algebraisk uttrykk for antall brikker i figur nr. n

OPPGAVE 11.30

Her ser du de tre første figurene i et mønster.

a Forklar hvordan mønstret utvikler seg.

b Forklar med utgangspunkt i figurene at alle kvadrattall er summen av to påfølgende trekanttall.

nr. 1Figur nr. 2

c Lag et algebraisk uttrykk for antall blå brikker i figur nr. n

d Lag et algebraisk uttrykk for antall oransje brikker i figur nr. n

e Vis ved regning at summen av to påfølgende trekanttall er et kvadrattall.

n2 + 2n + 1 = (

nr. 3

Figur

Å dele opp figurer i mindre enheter

Her ser du de fire første figurene i et mønster.

Figur nr. 1

Figur nr. 2

Figur nr. 3

De oransje brikkene illustrerer rektangeltallene.

Antall oransje brikker i figur nr. n er dermed n(n + 1)

Figur nr. 4

nr. 1

Figur nr. 2

nr. 3

nr. 4

De blå brikkene illustrerer «det forrige trekanttallet». Antall blå brikker i figur nr. 2 er trekanttall 1, antall blå brikker i figur nr. 3 er trekanttall 2, osv. Vi bytter derfor ut n med n 1 i det algebraiske uttrykket for trekanttallene. Antall blå brikker i figur nr. n er dermed nn(1) 2

Antall brikker i figur nr. n er + + = + + = ++ = ++ = + nn nnnnnn nnnn nnnn nn (1) (1) 2 2( 1) 2 (1) 2 2( 1) (1) 2 22 2 3 2 22 2

Figur

OPPGAVE 11.31

Figurene illustrerer de tre første «hundetallene». De oransje boksene er hodet, de blå er beina, de grå er kroppen, og de grønne er halen.

Hund nr. 1

Hund nr. 2

Hund nr. 3

Lag et algebraisk uttrykk for antall brikker du trenger for å lage

a halen i figur nr. n b beina i figur nr. n c hodet i figur nr. n d kroppen i figur nr n

e Lag et algebraisk uttrykk for antall brikker du trenger for å lage hund nr n Skriv uttrykket så enkelt som mulig.

Her illustreres de tre første «hundetallene» på nytt. Denne gangen er alle brikkene i samme farge.

nr. 1

Hund nr. 2

nr. 3

f Del opp figurene på en eller flere andre måter. Lag algebraiske uttrykk for antall brikker i hund nr. n ut fra oppdelingene dine. Forenkle de algebraiske uttrykkene, og vis at alle uttrykkene har samme verdi.

Hund

OPPGAVE 11.32

Her ser du de tre første figurene i et mønster.

Figur nr. 1Figur nr. 2 Figur nr. 3

a Beskriv hvordan du kan tegne figur nr n

b Lag et algebraisk uttrykk for antall røde streker i figur nr. n

c Lag et algebraisk uttrykk for antall grønne streker i figur nr. n

Alle de blå kvadratene er laget av 4 svarte streker.

d Lag et algebraisk uttrykk for antall svarte streker i figur nr n

e Lag et algebraisk uttrykk for antall streker til sammen (røde, grønne og svarte) i figur nr. n.

Skriv uttrykket så enkelt som mulig.

Her ser du to eksempler på T-kryss.

f Lag et algebraisk uttrykk for antall T-kryss i figur nr n

Matematikk for 8.–10. trinn

Matemagisk oppfordrer elevene til å utforske og diskutere fra første stund. Læremiddelets struktur ivaretar fellesskapet i klasserommet. Fellesdelene i hvert kapittel er laget for at elevene skal lære sammen. Dette gjør de gjennom «Snakke matte», spill, aktiviteter og utforskende samarbeidsoppgaver.

Den unike differensieringsmodellen i Matemagisk gir elevene individuelle tilpasninger innenfor samme tema. Slik lærer elevene matematikk på sitt nivå, men likevel i takt med hverandre.

Matemagisk er utviklet av fagpersoner og lærere med nærhet til klasserommet.

Matemagisk 9 består av:

• Lærebok

• Matemagisk 8–10. Elevhåndbok

• Matemagisk 8–10 Digital, med elevressurser og lærerveiledning

Digitale ressurser ﬁnner du på Aunivers.no