

Sinus T MATEMATIKK
STUDIEFORBEREDENDE VG1
BOKMÅL
Oldervoll | Svorstøl | Jacobsen
Foto og grafikk:
Bildene er fargemanipulert.
Omslagsfoto: Andreafidone / Getty Images
Kapittel 1: adaask / Getty Images
Kapittel 2: BlueBackIMAGES / Shutterstock
Kapittel 3: helloabc / Getty Images
Kapittel 4: Jia Na / Getty Images
Kapittel 5: mf-guddyx / Getty Images
Kapittel 6: nuchao / Getty Images
Kapittel 7: nuchao / Getty Images
Oppgavedel: araho / Adobe Stock
Side 52: Cappelen Damm, side 353: Farbai / iStock
© Cappelen Damm AS, Oslo 2024
Sinus1T følger læreplan (LK20) i teoretisk matematikk fellesfag 1T fra 2020, for vg1 studieforberedende utdanningsprogram.
Materialet i denne publikasjonen er omfattet av åndsverklovens bestemmelser. Uten særskilt avtale med Cappelen Damm AS er enhver eksemplarfremstilling og tilgjengeliggjøring bare tillatt i den utstrekning det er hjemlet i lov eller tillatt gjennom avtale med Kopinor, interesseorgan for rettighetshavere til åndsverk. Enhver bruk av hele eller deler av utgivelsen som input eller som treningskorpus i generative modeller som kan skape tekst, bilder, film, lyd eller annet innhold og uttrykk, er ikke tillatt uten særskilt avtale med rettighetshaverne.
Bruk av utgivelsens materiale i strid med lov eller avtale kan føre til inndragning, erstatningsansvar og straff i form av bøter eller fengsel.
Kilde for alle eksamensoppgaver er Utdanningsdirektoratet. Disse oppgavene er merket og er gjengitt med tillatelse.
Grafisk formgiver: BØK og Cappelen Damm
Omslagsdesign: Cappelen Damm
Frihåndstegninger: Per Ragnar Møkleby
Tekniske tegninger: Terje Sundby, Keops / Cappelen Damm
Redaktør: Bjørn-Terje Smestad
Sats: Have a Book, Polen 2024
Trykk og innbinding: Livonia Print, Latvia 2024
Utgave nr. 5
Opplag nr. 1
ISBN 978-82-02-82583-6
www.cdu.no
sinus.cdu.no
Forord
Sinus er et matematikkverk utviklet etter læreplanene fra 2024. Boka Sinus1T er skrevet for faget 1T i den videregående skolen. Boka legger vekt på tradisjonell matematikk og legger opp til grundig forståelse av faget, blant annet ved at eleven ser på matematiske problemer fra flere synsvinkler. I teoridelen har hvert kapittel, hvert delkapittel og hver oppgavesekvens økende vanskegrad. Et sammendrag av regler og metoder samt en kapitteltest står bakerst i hvert kapittel.
Læreplanene fra 2020 inneholder krav om at elevene skal kunne kommunisere ideer og drøfte matematiske problemer, strategier og løsninger med andre. Boka inneholder derfor mange diskusjonsoppgaver der elevene skal øve på dette.
Utforskende matematikk er sentralt i læreplanen. Flere steder i boka er det utforskende opplegg der elevene skal oppdage egenskaper og regler. Disse oppleggene er plassert før temaet blir behandlet i teoridelen. Boka er skrevet slik at det også er mulig å lese teoridelen uten å gjøre utforskingsoppleggene. De er best egnet som gruppearbeid, men kan også gjøres individuelt.
Til slutt i hvert kapittel finner elevene et sammendrag av viktige regler og metoder i kapittelet. Der finner de også en større prosjektoppgave. I noen av disse prosjektoppgavene får elevene bruke stoffet i kapittelet innenfor andre fagfelt. I andre oppgaver får elevene lære ny og spennende matematikk. Hvert kapittel blir avsluttet med et oppgavesett som er egnet til repetisjon av stoffet.
Boka inneholder grundige forklaringer på bruk av GeoGebra som grafisk verktøy og som CAS-verktøy. I tillegg lærer elevene å bruke programmeringsspråket Python. Til verket hører også et eget nettsted: sinus.cdu.no. Her finner vi tilleggsstoff, blant annet løsninger av oppgavene i teoridelen.
Oppgavedelen i boka er delt i tre deler: «Øv mer», «Blandede oppgaver» og «Åpne oppgaver». «Øv mer» er repetisjonsoppgaver ordnet etter delkapitlene i teoridelen. «Blandede oppgaver» inneholder både eksamensoppgaver og varierte oppgaver med passende utfordringer for alle elever. Oppgavene er merket, slik at læreren vet hvilke oppgaver elevene kan løse når de er ferdig med et delkapittel. «Åpne oppgaver» inneholder morsomme og utfordrende oppgaver som ikke har noe fast løsningsmønster. Her får elevene brukt kreativiteten sin.
Helt til slutt i boka finner vi fasit og stikkordregister.
I arbeidet med å få fram best mulige læremidler er det viktig å ha god kontakt med brukerne av boka. Vi vil gjerne ha tilbakemeldinger og innspill til forbedringer.
ToreOldervoll–OttoSvorstøl–RobinBjørnetunJacobsen




TALL OG VARIABLER
Mål for opplæringen er at eleven skal kunne
•formulere og løse problemer ved hjelp av algoritmisk tenkning, ulike problemløsingsstrategier, digitale verktøy og programmering
•identifisere variable størrelser i ulike situasjoner, sette opp formler og utforske disse ved hjelp av digitale verktøy
•utforske strategier for å løse likninger, likningssystemer og ulikheter og argumentere for tenkemåtene sine
•forklare forskjellen på en identitet, en likning, et algebraisk uttrykk og en funksjon
•lese, hente ut og vurdere matematikk i relevante tekster om ulike tema og presentere relevante beregninger og analyser av resultatene
EKSEMPEL
LØSNING
1.1 Regnerekkefølge
DISKUSJON
Her har vi regnet noen oppgaver på to måter. Forklar hva vi har gjort. Hvilken utregning tror dere er riktig?
a) 44202214 325 4312
b) 2 214 3318 4312 246
c) 12210 236 3330 12126
d) 44 2 3317 532 4520
e) 2 35 39 25 2211 22 2
f) 2 36 39 36 2218 22 2
g) 422 24 44 4 1 22 2 : ::
h) 55 25 25 2 2
Lag regler som gjelder for slike uttrykk.
Når vi skal regne ut et uttrykk, gjør vi det i denne rekkefølgen:
1 Regn først ut parentesene.
2 Regn deretter ut potensene.
3 Utfør deretter multiplikasjonene og divisjonene.
4 Utfør til slutt addisjonene og subtraksjonene.
Vi viser nå med et eksempel hvordan vi går fram.
Regn ut 231624423 : . 23162442 248442 248448 8232 2 3 3 : : : 22
Regn ut parentesene først.
Regn deretter ut potensene.
Utfør så ganging og deling. Trekk sammen leddene.
Legg spesielt merke til hvordan vi regner ut 4 ∙ 23. Det er ikke det samme som 83. Når vi skriver 4 ∙ 23, er det bare 2-tallet som skal opphøyes i tredje potens, slik at 424832 3
Hvis vi vil at 4-tallet også skal opphøyes i tredje potens, må vi sette en parentes og skrive
428512 3 3
Når vi skriver 32, er det bare tallet 3 som skal opphøyes i andre potens, ikke tallet 3. Dermed er
32 9
Hvis vi vil opphøye tallet 3 i andre potens, må vi skrive 3 2 .
39 2
Uttrykket i eksempelet kan vi regne ut digitalt.
Kalkulator
På gode kalkulatorer kan vi regne ut uttrykket uten å dele det opp. Vi taster inn hele uttrykket på én gang.
M Prøv å få til det på din kalkulator.
Python
Med Python bruker vi «/» som delingstegn. For potensen 23 skriver vi 2**3.
Programmet kan da se slik ut:
print(-2*(3+1) - (6+2)/4 + 4*2**3) 1 2
Det gir denne utskriften:
22.0
CAS Vi åpner GeoGebra, klikker på øverst i høyre hjørne og velger Vis . Der merker vi av for CAS. Der skriver vi uttrykket slik det står. Som delingstegn bruker vi tegnet «/» på tastaturet. Vi bruker tegnet «*» som multiplikasjonstegn. For å få fram eksponenten 3 i 23 taster vi Alt+3. Vi kan også taste tegnet «^» etterfulgt av 3. Svaret kommer fram når vi trykker på

Legg merke til at GeoGebra ikke skiller mellom delingstegn og brøkstrek.
?
OPPGAVE 1.10
Regn ut uten og med digitale hjelpemidler.
a) 422 b) 42 2
c) 532 d) 53 2
e) 2322 22 f) 232 22 2
g) 3536 2 h) 3452 3 3
OPPGAVE 1.11
Regn ut uten og med digitale hjelpemidler. a) 2 752 b) 3412232
c) 843 2 d) 231733425 4222
OPPGAVE 1.12
Regn ut uten digitale hjelpemidler.
a) 2 222 2 b) 22 6 6
c) 432323 33 d) 423323 2 5 32 5
UTFORSK PARENTESREGLER
Her skal dere ikke bruke kjente regneregler for parenteser. Dere skal prøve å forstå reglene.
STEG 1
Her har vi regnet ut noen uttrykk på flere måter. Forklar hva vi har gjort i hvert tilfelle. En av utregningene er riktig ut fra det vi lærte i kapittel 1.1. Hvilken er det? Bruk denne til å finne ut hvilke utregninger som må være feil, og hvilke som kan være riktige.
a) 753729
75 37531239
b) 753781
75 3753235
753753231
c) 753725
75 3753231
75 3753235
Hvilke regneregler kan være riktige ut fra dette?
STEG 2
Her har vi regnet ut noen uttrykk på flere måter. Forklar hva vi har gjort i hvert tilfelle. En av utregningene er riktig ut fra det vi lærte i kapittel 1.1.
Hvilken er det? Bruk denne til å finne ut hvilken utregning som må være feil, og hvilke som kan være riktige.
a) 2 5310313
2 532816
2 53252310616
b) 253224
25325310313
2532522310 64
25325231064
c) 2 5321530
2 53252310660
2 53253 1 10330
2 535325630
1.2 Variabler og parenteser
En variabel er et tall med ukjent verdi. Når vi skal arrangere en fotballkamp, vet vi ikke hvor mange som kommer for å se på. Vi kan la x være antallet.
Da er x en variabel. Hvis billettene koster 100 kr, gir uttrykket 100x inntektene i kroner.
Bokstavuttrykk eller tall med plusstegn eller minustegn mellom kaller vi ledd. Uttrykket 2x 4x består av to ledd, 2x og 4x. Disse to leddene er av samme type, og dermed kan vi trekke dem sammen:
2 46 xxx
I uttrykket
42131 22 aaaa
er det seks ledd. Leddene 4a 2 og –a 2 er av samme type, og vi kan trekke dem sammen. Leddene 4a 2 og 2a er ikke av samme type og kan derfor ikke trekkes sammen.
EKSEMPEL
Vi sorterer leddene slik at ledd av samme type står samlet og trekker sammen: 42131 42311 35 22 22 2 aaaa aaaa
Når vi regner med bokstavuttrykk, får vi bruk for å løseoppparenteser. Når vi løser opp en parentes, fjerner vi parentesen. Da bruker vi disse reglene:
Når vi skal løse opp en parentes som har et minustegn foran, må vi skifte fortegn på alle leddene inne i parentesen. En parentes med et plusstegn foran kan vi fjerne uten å endre noen fortegn inne i parentesen.
LØSNING
Trekk sammen.
a) aabaab 223233
b) 2 222223 xxxyxy
a) aabaabaaaabb ab 222 2 2 32332333 34
b) 2 222322223
OPPGAVE 1.20
Trekk sammen ledd av samme type.
a) 2 537 1 xyxy
b) aaaa 222331
c) 2 22 222 xxyxy
d) 2 2 222 xyxyxyxyyx
OPPGAVE 1.21
Løs opp parentesene og trekk sammen.
a) 52xyxy
b) abab 2
c) xxxx 222121
d) 233 22 aaaa
EKSEMPEL
Når vi multipliserer parentesuttrykk, bruker vi disse reglene:
Når vi skal multiplisere et tall og et parentesuttrykk, må vi multiplisere tallet med hvert ledd som står inne i parentesen.
Når vi skal multiplisere to parentesuttrykk, må vi multiplisere hvert ledd i den første parentesen med hvert ledd i den andre.
LØSNING
Regn ut.
a) 2 34 x
b) 34225 xx
c) xxxx121211
a) 2()34232468 xxx
b) Denne oppgaven kan vi løse på to måter. En måte er først å gange tallene uten fortegn inn i parentesene og beholde parentesene:
34225312410312410 2 xxxxxxx
Vi kan også gange tallene med fortegn med tallene i parentesen slik:
34225342253124102 xxxxxxx
Når vi bruker denne metoden, tar vi vanligvis ikke med den første mellomregningen. Vi fører utregningen slik: 342253124102 xxxxx
c) Her multipliserer vi først parentesene og beholder parentesene om produktet: xxxx
Regn ut.
a) 2 4 x b) 23 t
c) 321231 xx d) 53251 22 xxx
?
OPPGAVE 1.23
Trekk sammen.
a) 2 2323 abab
b) 2 2 22 aabbbaab
c) xx123
d) 3221 tt
OPPGAVE 1.24
Trekk sammen.
a) 21314 xxxx
b) xxxx3412123
c) 2 123xx
I CAS kan vi regne ut alle slike algebraiskeuttrykk. Her har vi regnet ut 34225 xx fra eksempelet på forrige side:

OPPGAVE 1.25
Løs oppgave 1.24 i CAS.
DISKUSJON
Det er ikke riktig at 2 1341 () . Klarer du å få regnestykket til å bli riktig ved å sette inn en parentes? Hvor mange måter kan du gjøre det på?
UTFORSK BRØK
STEG 1
a) Bruk figuren nedenfor til å forklare at 1 2 2 4 .
b) Bruk figuren nedenfor til å forklare at 2 3 6 9 .
c) Lag en figur som forklarer hvorfor 3 5 9 15 .
d) Forklar ut fra oppgave a, b og c at du kan gange eller dele telleren og nevneren i en brøk med det samme tallet uten at brøken skifter verdi.
STEG 2
a) Bruk figuren til å bestemme 2 7 3 7 . 2 7 3 7
b) Hvordan summerer vi etter dette brøker med samme nevner?
c) Hva må vi gjøre med denne figuren hvis vi skal bruke den til å regne ut 2 7 5 14 ? 2 7 5 14
d) Hva må vi gjøre når vi skal summere brøker som ikke har samme nevner?
STEG 3
1Å regne ut 1 3 6 er det samme som å finne en tredel av 6, som er 2.
Dermed er 1 3 62
2 1 3 6 7 er en tredel av 6 7 , som er 2 7 . Altså er 1 3 6 7 2 7 .
3To tredeler av 6 7 er dobbelt så mye som en tredel, altså lik 2 2 7 4 7 .
Dermed er 2 3 6 7 4 7 .
EKSEMPEL LØSNING
Denne tankegangen kan vi bruke til å gange brøker i hodet.
a) Regn ut 1 2 4, 1 2 4 5 og 3 2 4 5 med tankegangen ovenfor.
b) Regn ut 1 4 12 , 1 4 12 13 og 3 4 12 13 på tilsvarende måte som ovenfor.
c) Bruk tankegangen ovenfor og regn ut 1) 2 3 9 7 2) 2 5 10 11
1.3 Brøkregning
Vi har disse regnereglene for brøker:
• Når vi vil utvide en brøk, multipliserer vi med det samme tallet i telleren og i nevneren.
• Når vi vil forkorte en brøk, dividerer vi med det samme tallet i telleren og i nevneren.
• Når vi skal summerebrøker, må vi først finne fellesnevneren. Deretter utvider vi alle brøkene så de får den samme nevneren. Til slutt summerer vi tellerne og lar nevneren stå som den er.
• Når vi skal multiplisereethelttallogenbrøk, multipliserer vi det hele tallet med telleren og lar nevneren stå som den er.
• Når vi skal multipliseretobrøker, multipliserer vi telleren med telleren og nevneren med nevneren. Vi trenger ikke å finne fellesnevneren.
• Når vi skal divideremedenbrøk, multipliserer vi med den omvendte brøken.
a) Utvid brøken 5 8 slik at nevneren blir 56.
b) Forkort brøken 18 30
a) Ettersom 8 756 , multipliserer vi telleren og nevneren med 7. 5 8 5 8 35 56 7 7
EKSEMPEL
b) 6 er det største tallet som går opp i både 18 og 30. Vi dividerer derfor telleren og nevneren med 6.
LØSNING
a) Fellesnevneren er 24.
b) Fellesnevneren for de to brøkene er 18.
Legg merke til hvordan vi gjør om tallet 3 til en brøk ved å skrive tallet som 3
Det er lurt å forkorte før vi multipliserer tallene i telleren og i nevneren.
Vi forkorter brøken før vi multipliserer tallene i telleren og i nevneren.
Svarene i eksempelet på forrige side lar vi stå som uekte brøk. For eksempel trenger vi ikke gjøre om 45 16 til 2 13 16 . I den videregående skolen bruker vi slike
blandedetall svært lite. Grunnen er at det er vanlig å utelate multiplikasjonstegn. Vi vet at 2x betyr 2 x . Da er det rimelig å tro at 2 13 16 betyr 2 13 16 i stedet for 2 13 16 , som er det rette.
Du trenger altså ikke gjøre uekte brøker om til blandede tall, men du må passe på å forkorte alle svar.
OPPGAVE 1.30 Forkort brøkene mest mulig.
Brøkstykkene ovenfor kan vi regne ut digitalt. Vi skriver inn regnestykkene med tallene på brøkform. Svaret blir da ferdig forkortet på brøkform.
Kalkulator
CAS

Med Python får vi fram svarene som desimaltall og ikke som brøk.
EKSEMPEL
LØSNING
Et rasjonaltuttrykk er en brøk som kan inneholde en variabel. Men ettersom en variabel er et tall med ukjent verdi, kan vi bruke de vanlige regnereglene for brøker når vi regner med slike uttrykk.
Regn ut.
a) Fellesnevneren for x, 2x og 4 er 4x. Vi utvider brøkene slik at alle får nevneren 4x.
b) Vi multipliserer telleren med telleren og nevneren med nevneren.
c) Når vi dividerer med en brøk, multipliserer vi med den omvendte brøken.
OPPGAVE 1.33
Trekk sammen.
OPPGAVE 1.34
Regn ut.
LØSNING
Hvis tellerne inneholder en sum eller en differanse, må vi sette parentes når vi setter uttrykkene på felles brøkstrek.
Regn ut.
Oppgavene i eksempelet kan vi også gjøre i CAS. Som brøkstrek bruker vi tegnet «/» på tastaturet. Vi bruker piltastene for å flytte markøren mellom telleren og nevneren og for å komme ut av brøken. Til slutt trykker vi på .

DISKUSJON
Ovenfor skriver ikke CAS svarene slik vi gjorde det i eksempelet. Forklar hvorfor svarene er like.
OPPGAVE 1.35
Regn ut uten og med digitale hjelpemidler.
UTFORSK LIKNINGER
STEG 1
Hvor mange løsninger har likningene?
a) 520 x
b) 3211 x
c) 0 4 x
d) 0 0 x
STEG 2
Hvor mange løsninger har likningene?
a) 2 13xx
b) 2 123xx
c) 3125 xx
d) 313 1 xx
STEG 3
Nå ser vi på likningen axbcxd
Hva kan dere si om tallene a,b,c og d når likningen har
a) ingen løsninger
b) uendelig mange løsninger
c) nøyaktig én løsning
1.4 Likninger og identiteter
Å løse likningen 312 x er det samme som å finne alle verdiene for variabelen x som er slik at 3x blir 12. Vi ser at den eneste løsningen er x 4 , for 3412, og det er ikke noen andre verdier for x som passer. Vi kan føre løsningen slik: 312 4 x x
At likningen 2 17 x har løsningen x 3, ser vi umiddelbart, for 2 317.
Dette er den eneste løsningen, for ingen andre verdier for x passer. Vi kan gjerne løse likningen slik:
2 17 3 x x
EKSEMPEL
Når vi skal løse vanskeligere likninger, trenger vi disse regnereglene:
• Vi kan trekke fra eller legge til det samme tallet på begge sidene av likhetstegnet.
• Vi kan multiplisere eller dividere med det samme tallet på begge sidene av likhetstegnet dersom tallet ikke er null.
• Vi kan flytte et ledd over på den andre siden av likhetstegnet hvis vi samtidig skifter fortegn på leddet.
• Når vi har løst en likning, kan vi sette prøve på svaret. Vi setter da inn løsningen i likningen og kontrollerer at begge sidene av likhetstegnet har samme verdi.
LØSNING ?
Løs likningen og sett prøve på svaret.
72310 xx
72310 73102
412 3 xx xx x x
Vi setter prøve på svaret ved å sette inn x 3 på begge sidene i likningen i oppgaven.
Venstre side: 7273219 x
Høyre side: 310331019 x
Venstre og høyre side er like. Løsningen er derfor riktig.
OPPGAVE 1.40
Løs likningene og sett prøve på svaret.
a) 2 15 x b) 312 xx
c) 2222 xx d) 2 237xx
OPPGAVE 1.41
Løs likningene.
a) 12139 7 xx b) 71123 xx
c) 0 020700302 ,,,, xx
EKSEMPEL
Når vi skal løse en noe mer sammensatt likning, kan det ofte svare seg å bruke denne framgangsmåten:
1 Løs opp parenteser.
2 Multipliser med fellesnevneren på begge sidene av likhetstegnet hvis det finnes brøker.
3 Trekk sammen leddene på begge sidene av likhetstegnet.
4 Samle alle leddene med den ukjente på venstre side og alle andre ledd på høyre side.
5 Trekk sammen leddene på begge sidene av likhetstegnet.
6 Finn løsningen ved å dividere med det tallet som står foran den ukjente.
En slik punktvis framgangsmåte kaller vi algoritme.
Løs likningen.
LØSNING
x 6 632 44 1 x x x
OPPGAVE 1.42 Løs likningene.
Fellesnevneren er 6.
I CAS kan vi løse alle slike likninger. Da skriver vi likningen i CAS. Når vi skal skrive 2 3 x , kan det være lurt å skrive brøkstreken først og så flytte markøren mellom telleren og nevneren ved hjelp av piltastene. Når vi trykker på , får vi fram løsningen på neste side.
?

Når vi skal løse en likning, trykker vi på og ikke på . Når vi trykker på , blir likningen forenklet og ikke løst.
OPPGAVE 1.43
Løs oppgave 1.42 i CAS.
Hvis to uttrykk gir likt svar for alle verdier for variabelen x, sier vi at uttrykkene er identiske. Når vi bruker regnereglene i kapittel 1.2, får vi identiske uttrykk. Uttrykkene 321 x og 6x 3 er identiske. Begge uttrykkene gir samme svar uansett hvilke x-verdier vi setter i uttrykkene. I likningen 32163 xx er alle mulige verdier av x en løsning. En slik likning kaller vi en identitet.
Hvordan kan vi finne ut om en likning er en identitet?
EKSEMPEL
LØSNING
Undersøk om likningen er en identitet.
a) 2 315321 xx
b) 43122514 xx
a) Vi omformer hver side av likningen. 2 315321 6 2563 6 363 xx xx xx
Nå har vi fått det samme uttrykket på hver side av likhetstegnet, og alle verdier for x passer da i likningen.
Dette er en identitet.
b) 43122514 12 421024 122102 2 4 2 xx xx xx x x
Det er bare én verdi for x som passer.
Dette er ikke en identitet.
EKSEMPEL
Nå løser vi de to likningene i eksempelet i CAS:

CAS skriver {xx} når alle verdier for x passer i en likning, det vil si når likningen er en identitet.
OPPGAVE 1.44
Finn ut ved regning og i CAS om likningen er en identitet.
a) 2 4182 xx
b) 32123312 xxxx
c) 52222332xxxx
d) 3215223 xxxx
Til nå har vi løst ferdig oppstilte likninger. Noen ganger har vi oppgaver som ikke inneholder noen variabel, men som vi likevel kan løse ved hjelp av en likning. Da velger vi selv en variabel.
Anne, Berit og Cathrine har til sammen 1450 kr. Berit har 50 kr mer enn
Anne. Cathrine har dobbelt så mye som Anne. Hvor mye penger har hver av dem?
LØSNING
Her er det lurt å sette kronebeløpet til Anne som en variabel x, for da kan vi enkelt finne uttrykk for beløpene til de to andre. Kronebeløpet til Berit blir x 50, og beløpet til Cathrine blir 2x. Til sammen skal dette bli 1450.
Anne har
kr, Berit har 400 kr, og Cathrine har 700 kr.
OPPGAVE 1.45
a) Anne, Berit og Cathrine er 42 år til sammen. Berit er dobbelt så gammel som Anne. Cathrine er 2 år eldre enn Berit.
Hvor gamle er hver av jentene?
b) Abel, Bjarne, Cato og David er 36 år til sammen. Bjarne er 2 år yngre enn Abel. Cato er dobbelt så gammel som Bjarne. Alderen til David er 2 7 av summen av alderen til Bjarne og Cato.
Hvor gamle er hver av guttene?
c) Adam er 10 år eldre enn Xeres. Om 4 år er Adam dobbelt så gammel som Xeres. Hvor gammel er Xeres?
OPPGAVE 1.46
Faren til Xeres og Yasep ba dem velge ett felles tall.
Så sa han til Xeres: Legg 2 til tallet og gang deretter svaret med 3. Legg 4 til det tallet du nå har, og gang så svaret med 2.
Til Yasep sa han: Legg 1 til tallet dere valgte, og gang svaret med 2. Legg så 1 til det tallet du nå har, og gang svaret med 3. Til slutt legger du til tallet 11. Xeres og Yasep gjorde som faren sa, og de ble veldig forundret da de fikk samme svar.
Forklar hvorfor svarene ble like.
1.5 Lineære ulikheter
I mange praktiske sammenhenger har vi bruk for å vite om en størrelse er større enn eller mindre enn en annen størrelse. I matematikken kaller vi slike problemer ulikheter.
Vi har fire forskjellige ulikhetssymboler. Det er (mindre enn), (mindre enn eller lik), (større enn) og (større enn eller lik).
Når vi skriver x 3, betyr det at x er et tall som er mindre enn 3. Uttrykket x 5 forteller at x er et tall som er større enn eller lik 5. Legg merke til at åpningen i ulikhetstegnet alltid peker mot det største tallet.
Ulikheter løser vi omtrent på den samme måten som likninger. Men det finnes ett viktig unntak: Når vi multipliserer på begge sidene av en ulikhet med et negativt tall, må vi snu ulikhetstegnet. Det kan vi forklare på denne måten:
Vi har et tall x som er større enn et tall y, altså er xy.
Hvis vi dobler x, får vi et større tall enn når vi dobler y. Altså må 2x være større enn 2y. Da er 2x 2y
Dermed kan vi gange med 2 på begge sidene av ulikhetstegnet uten å endre ulikhetstegnet. Men hva skjer hvis vi ganger med 2 på begge sidene av ulikhetstegnet? Det kan vi finne ut på denne måten:
EKSEMPEL
At xy, er det samme som at xy er et positivt tall. Når vi ganger dette positive tallet med 2, må vi få et negativt tall. Altså er 20 220 22 () xy xy xy
Hvis xy , er altså 22xy . Når vi ganger med 2, må vi snu ulikhetstegnet. Det samme gjelder når vi ganger med andre negative tall.
Her er regnereglene for ulikheter:
• Vi kan legge til og trekke fra det samme tallet på hver side av ulikhetstegnet.
• Vi kan flytte et ledd over på den andre siden av ulikhetstegnet hvis vi skifter fortegn på leddet.
• Vi kan multiplisere og dividere med et tall som ikke er null på begge sidene av ulikhetstegnet. Hvis tallet er negativt, må vi snu ulikhetstegnet.
LØSNING
Løs ulikhetene.
a) 348 xx b) xxx2452
a) Vi bruker reglene ovenfor.
Nå dividerer vi med 2 på begge sidene av ulikhetstegnet. Da må vi snu tegnet.
EKSEMPEL
Også ulikheter kan vi løse digitalt. Her viser vi hvordan vi løser ulikheten xxx2452
ved hjelp av GeoGebra CAS. Når vi skal skrive ulikhetstegnet , kan vi åpne tastaturet i GeoGebra ved å trykke på i nederste venstre hjørne og finne der. Men vi kan også bruke det vanlige tastaturet og skrive etterfulgt av .
Løsningen får vi fram ved å trykke på .

OPPGAVE 1.50
Løs ulikhetene uten digitale hjelpemidler.
a) 328 x
b) 251 xx
c) xx 33 1
d) 2136 xx
OPPGAVE 1.51
Løs ulikhetene uten og med digitale hjelpemidler.
a) 2 541xx
b) 2 3231 xx
c) 2 361 2 0 x x
d) 2 3 5 2 1 3 xx
e) 5 2 1 6 7 6 9 2 xx
Til nå har vi arbeidet med ferdig oppsatte ulikheter. I praktiske oppgaver må vi stille opp ulikhetene selv.
Didrik har 5000 kr og bruker 200 kr per uke. Etter x uker er antallet kroner som Didrik har, gitt ved
yx 5000200
Johannes har 3500 kr og bruker 100 kr per uke. Beløpet Johannes har etter x uker, er gitt ved
yx 3500100
Når har Didrik mest penger av de to?
Didrik har mest penger når
50002003500100
10020035005000
1001500
100 100 xx xx x x 1500 100 15 x
De 15 første ukene har Didrik mest penger.
OPPGAVE 1.52
La x være lengden av en drosjetur målt i kilometer. Prisen U i kroner er gitt ved Ux3050
a) Hvor langt kan vi kjøre med drosjen hvis prisen skal være mindre enn 380 kr?
b) Hvor langt kan vi kjøre med drosjen hvis prisen skal være over 500 kr?
OPPGAVE 1.53
Temperaturen i ei bestemt termosflaske er 86 C og synker med 2,5 C per time.
a) Når er temperaturen over 61 °C?
b) Når er temperaturen under 71 °C?
1.6 To lineære likninger med to ukjente
DISKUSJON
a) Petter kjøper brus og sjokolade. Brusflaskene koster 30 kr per stykk, og sjokoladeplatene koster 40 kr per stykk. Han betaler 170 kr til sammen. La x være antallet brusflasker og y antallet sjokoladeplater.
Sett opp en likning med x og y som ukjente. Vis ved prøving og feiling at denne likningen har nøyaktig én løsning.
b) Mari kjøper epler og pærer. Eplene koster 30 kr per kilogram og pærene 40 kr per kilogram. Hun betaler 170 kr til sammen for eplene og pærene. La x og y være vekta av henholdsvis eplene og pærene i kilogram.
Sett opp en likning med x og y som ukjente. Forklar at denne likningen har mange løsninger.
c) Hva er det som gjør at likningen i oppgave a har én løsning mens likningen i oppgave b har mange løsninger?
En likning av typen axbyc
der a, b og c er tall, kaller vi en lineærlikning. Likningen 524 xy er et eksempel på en lineær likning. Likningen 524 2 xy er derimot ikke lineær, fordi den inneholder x 2 og ikke bare x.
Nå skal vi løse to lineære likninger med to ukjente. Når vi har flere likninger der flere variabler skal passe, kaller vi det et likningssett eller et likningssystem. Her er et eksempel på et slikt likningssett:
524 5 xy xy
Å løse et likningssett med to ukjente er det samme som å finne verdier for x og y som passer i begge likningene samtidig.
Når vi skal løse likningssettet
524 5 xy xy
ved regning, kan vi bruker en metode som vi kaller innsettingsmetoden. Da finner vi først et uttrykk for enten x eller y i en av likningene og setter dette uttrykket inn i den andre likningen. Her velger vi å finne et uttrykk for x fra likning nr. 2 fordi det gir et enkelt uttrykk.
xy xy 5 5
Deretter setter vi inn dette uttrykket for x i likning nr. 1:
524
5524
25524 7425 721 3 xy yy yy y y y
Til slutt finner vi x ved å sette inn y 3 i uttrykket xy 5 .
xy5532
Løsningen blir x 2 og y 3. At dette er riktig, ser vi når vi setter løsningen inn i de to likningene.
5252231064
235 xy xy
Løsningen stemmer.
LØSNING
Løs likningssettet ved hjelp av innsettingsmetoden.
28 341 xy xy
Her velger vi å finne et uttrykk for y fra likning nr. 1 da det gir et uttrykk uten brøker.
2 8 28 28 xy yx yx
Dette uttrykket for y setter vi inn i likning nr. 2.
341 34281 3 8321 1133 3 xy xx xx x x
Vi finner y ved å sette x 3 inn i uttrykket for y. yx28238682
Løsningen er x = 3 og y = –2.
Multipliser alle leddene med –1. ?
OPPGAVE 1.60
Løs likningssettet ved hjelp av innsettingsmetoden.
xy xy 24 23
OPPGAVE 1.61
Mari og Knut kjøper epler og pærer i en butikk. Mari kjøper 3 kg epler og 2 kg pærer. Hun betaler 170 kr til sammen. Per kjøper 2 kg epler og 2,5 kg pærer. Han betaler 160 kr.
Finn kiloprisen for epler og for pærer.
OPPGAVE 1.62
Bruk innsettingsmetoden og løs likningssettene. a) xy xy 25 2 b) 3 41 67 xy xy c) xy xy 24 33 d) xy xy 22 1 2 1
Nå skal vi løse likningssettet
524 5 xy xy
ved hjelp av addisjonsmetoden. Her ganger vi den andre likningen med 2.
524 5 524 2210 2 xy xy xy xy
Ettersom 524 xy og 2 210xy , må
5222410 52 2214 714 2 xyxy xyxy x x
Her ser vi hvorfor vi ganget den andre likningen med 2. Det var for at y-leddene skulle forsvinne når vi la sammen likningene.
Til vanlig fører vi den siste utregningen slik:
524 2 210 714 2 xy xy x x
I raden under streken har vi summert de to radene over streken.
Nå setter vi inn x 2 i en av likningene for å finne y. xy y y 5 2 5 3
Løsningen er x 2 og y 3.
DISKUSJON
Hvis vi hadde satt inn x 2 i likningen 524 xy , hvilken verdi hadde vi da fått for y? Hvorfor var det lurere å sette inn x 2 i likningen xy 5?
Løs likningssettene ved hjelp av addisjonsmetoden.
a) xy xy 29 2 313 b) 7311 328 xy xy
a) Her kan vi gange den første likningen med 2. xy xy 292 2 313 |
Da får vi dette likningssettet: 2418 2313 5 5 xy xy y y
Nå setter vi inn y 5 i den første likningen.
xy x x x 29 259 109 1
Løsningen er x 1 og y 5.
b) Her kan vi gange den første likningen med 2 og den andre med 3.
73112 3283 xy xy | |
Det gir dette settet:
Til slutt setter vi x 2 inn i den andre likningen.
Løsningen er x 2 og y 1.
OPPGAVE 1.63
Løs likningssettet ved hjelp av addisjonsmetoden.
xy xy 24 23
OPPGAVE 1.64
Bruk addisjonsmetoden og løs likningssettene.
a) xy xy 25 2 b) 3 41 67 xy xy
c) xy xy 24 33 d) 3 46 438 xy xy
I GeoGebra CAS kan vi løse likningssett. Her viser vi framgangsmåten ved å løse likningssettet 524 5 xy xy
Der skriver vi først inn de to likningene i hver sin rad.

Deretter markerer vi de to radene. Da holder vi inne venstre musetast og drar musepekeren over de to radene. Til slutt trykker vi på og får svaret på denne måten:
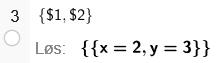
Løsningen er xy23 og
OPPGAVE 1.65
Løs likningssettene i CAS. a) 2 1 1 2 3 2 xy xy b) xy xy 22 2
c) xy xy 27 2 5 2 d) 0124 0434 ,, ,, xy xy
OPPGAVE 1.66
Vil du bruke innsettingsmetoden eller addisjonsmetoden for å løse likningssettene? Begrunn valget ditt før du løser dem.
a) xy xy 35 532 b) 430 1 xy xy
c) 2 2 1032 xy xy
1.7 Formler
d) 3 42 562 xy xy
En formel gir oss verdien av en variabel ved hjelp av verdien av en eller flere andre variabler. Volumet V av ei kule er gitt ved
Vr 4 3 3

I denne formelen finner vi verdien for V når vi kjenner verdien av variabelen r, som er radien. Variabelen r kaller vi den uavhengigevariabelen, og V kaller vi den avhengigevariabelen. Vi velger verdier for den uavhengige variabelen og regner ut verdien for den avhengige variabelen. Formelen ovenfor inneholder også konstanten 314 , .
Noen ganger trenger vi verdier for to variabler for å regne ut den tredje. Volumet V av en sylinder er gitt ved
Vrh 2

Her må vi kjenne både radien r og høyden h for å kunne finne volumet V. I dette tilfellet har vi to uavhengige variabler og én avhengig. h
Elfrid har nettopp ladet opp elsparkesykkelen sin. Strømmengden på sykkelen er da 600 Wh (wattimer). Når hun har kjørt x kilometer, er strømmengden i wattimer gitt ved
y 600 – 12x
a) Hvor mye strøm er det på batteriet når hun har kjørt 15 km?
b) Hvor langt har hun kjørt når det er 300 Wh igjen på batteriet?
c) Hvor langt kan hun kjøre før batteriet er tomt?
a) Når hun har kjørt 15 kilometer, er x 15. Strømmengden er da y 6001215600180420
Det er 420 Wh igjen på batteriet.
b) Når det er 300 Wh igjen på batteriet, er y 300. Det gir denne likningen:
Elfrid har kjørt 25 km.
c) Batteriet er tomt når strømmengden er 0 Wh. Det gir denne likningen:
Hun kan kjøre 50 km.
OPPGAVE 1.70
Elbjørg leier en elsparkesykkel. Prisen i kroner for en tur er gitt ved
Pt25010 ,
der t er tida i minutter.
a) Hva koster en tur på 10 minutter?
b) Hvor lenge kan Elbjørg kjøre for 50 kr?
c) Hva koster det å ta i bruk sparkesykkelen, og hva er prisen per minutt?
OPPGAVE 1.71
Elbjørg vurderer å kjøpe en elsparkesykkel som koster 7200 kr. Hun må i tillegg betale for vedlikehold, forsikring og strøm. Hun regner med at de samlede utgiftene i kroner er gitt ved
Ux 72005
der x er antallet turer.
a) Hva har elsparkesykkelen kostet henne når hun har kjørt 60 turer?
b) Hvor mange turer har hun kjørt når utgiftene er 8000 kr?
b) Elbjørg regner med at turene er på 10 minutter i gjennomsnitt. Hvor mange turer må hun da kjøre for at det skal lønne seg å eie i stedet for å leie, når leieprisen er gitt ved Pt25010 , , der t er tida i minutter? Hvor mange dager går det hvis hun i gjennomsnitt kjører 4 turer per dag?
OPPGAVE 1.72
Elbjørg kjøper elsparkesykkelen som koster 7200 kr. Hun regner med at verdien minker med 200 kr per måned.
a) Finn en formel for verdien V av sparkesykkelen om t måneder.
b) Bruk formelen til å finne verdien om 2 år.
c) Hvor lang tid går det før verdien av sykkelen er halvert?
OPPGAVE 1.73
Elfrid har kjørt med elsparkesykkelen sin til venninna Elbjørg. Så begynner hun på hjemveien. Etter t minutter er avstanden s hjemmefra målt i kilometer gitt ved
st 1203 ,
a) Hvor langt hjemmefra er Elfrid etter 20 minutter?
b) Hvor lang tid går det før hun er 3 km hjemmefra?
c) Hvor lang tid bruker hun hjem?
d) Hvor langt er det til venninna?
e) Finn farten i kilometer per time.
EKSEMPEL
LØSNING
Ved hjelp av en formel kan vi lage nye formler. Vi bruker da regnereglene for likninger.
Elbjørg leier en elsparkesykkel. Prisen i kroner for en tur er da gitt ved Pt25010 , der t er tida i minutter. På en tur kjører Elbjørg med farten 15 km/h.
a) Finn en formel for prisen uttrykt med lengden x av kjøreturen i kilometer.
b) Finn en formel for kjørelengden x uttrykt med prisen P.
c) Hvor langt har Elbjørg kjørt når prisen ble 30 kr?
a) I løpet at 1 time kjører Elbjørg 15 km. Antallet kilometer hun kjører på ett minutt er da 15 60 025 ,
Antallet kilometer hun kjører på t minutter er da xt 025 , . Dette er en formel for avstanden x uttrykt med tida t. Vi vil finne en formel for tida t uttrykt med avstanden x. Det kan vi gjøre slik:
xt tx 0254 4 4 ,|
Dette setter vi inn i formelen for prisen.
b) Vi kan nå finne en formel for x uttrykt med P slik:
c) Når prisen er 30 kr, er kjørelengden x 3010 10 20 10 2
Elbjørg har kjørt 2 km.
OPPGAVE 1.74
Elbjørg leier en elsparkesykkel. Prisen i kroner for en tur er gitt ved
Pt25010 ,
der t er tida i minutter. På en tur kjører Elbjørg med farten 18 km/h.
a) Finn en formel for prisen uttrykt med lengden x av kjøreturen i kilometer.
b) Finn en formel for kjørelengden x uttrykt med prisen P
c) Hvor langt har Elbjørg kjørt når prisen ble 30 kr?
OPPGAVE 1.75
Elfrid har kjørt med elsparkesykkelen sin til en venn som bor 10 km unna. Så begynner hun på hjemveien. Hun kjører i 20 km/h.
a) Vis at etter t minutter er avstanden s hjemmefra målt i kilometer gitt ved
s t 10 3
b) Finn en formel for tida t uttrykt med s.
c) Bruk formelen til å finne ut hvor lang tid hun har kjørt når det er 2 km igjen hjem.
d) Bruk formelen til å finne ut hvor lang tid hun bruker hjem.
Når vi leier en sparkesykkel, betaler vi en startpris og en minuttpris. Hvis startprisen er 10 kr og minuttprisen 2,50 kr, blir prisen y i kroner gitt ved
yt25010 ,
Hvis vi lar s være startprisen og m minuttprisen, får vi denne formelen: ymts
Denne formelen inneholder 4 variabler. I matematikk bruker vi én bokstav som navn på en variabel. I programmering kan vi bruke ord som navn på variabler. Da blir formelen enklere å forstå. Formelen ovenfor kan se slik ut i programmering:
pris = minuttpristid + startpris
Her er et program i Python som bestemmer prisen når vi leier en elsparkesykkel i 15 minutter når startprisen er 10 kr og minuttprisen er 1,50 kr.
startpris = 10 minuttpris = 2.50 tid = 15
pris = minuttpris*tid + startpris
er", pris, "kr.")
Legg merke til at vi bruker punktum som desimaltegn. Vi må skrive 2.50 og ikke 2,50.
Når vi kjører dette programmet, får vi denne utskriften:
Prisen er 47.5 kr.
Vi kan endre variablene startpris, minuttpris og tid i programmet og kjøre programmet på nytt. Men vi kan også lage programmet slik at vi kan skrive inn verdiene når vi kjører programmet. Da bruker vi kommandoen input. Men når vi skriver inn verdier på denne måten, blir det vi skriver tolket som en tekst som programmet ikke kan regne med. Vi bruker da kommandoen float for å gjøre teksten om til et tall.
startpris = float(input("Hva er startprisen?")) minuttpris = float(input("Hva er minuttprisen?")) tid = float(input("Hvor mange minutter?"))
pris = minuttpris*tid + startpris
print("Prisen er", pris, "kr.")
Når vi kjører dette programmet, kan det se slik ut:
Hva er startprisen? 10
Hva er minuttprisen? 2.5
Hvor mange minutter? 15
Prisen er 47.5 kr.
OPPGAVE 1.76
Bruk programmet ovenfor til å finne hvor mye det koster å leie en elsparkesykkel i 20 minutter når startprisen er 5 kr og minuttprisen 3,20 kr.
OPPGAVE 1.77
I USA måler de temperaturen i fahrenheitgrader og ikke i celsiusgrader.
Vi kan bruke denne formelen når vi regner om: fahrenheitgrader 1,8 celsiusgrader 32
a) Lag et pythonprogram som regner om fra celsiusgrader til fahrenheitgrader. Bruk programmet til å finne ut hvor mange fahrenheitgrader det er når temperaturen er 30 °C.
b) Lag et program som regner om fra fahrenheitgrader til celsiusgrader. Bruk programmet til å regne ut hvor mange celsiusgrader det er når det er 100 fahrenheitgrader. ?
1.8 Kvadratrøtter og røtter av høyere orden
Vi vet at 93 fordi 39 2 . Vi skulle tro at 9 kunne være –3, for 39 2 , men kvadratrota av et tall skal aldri være negativ.
Kvadratrota av x er det ikke-negative tallet som opphøyd i andre er lik x
xaaxa dersom 2 0 og
Det finnes ikke noe tall a slik at a 2 4, fordi a 2 0 for alle verdier av a.
Dermed kan vi ikke finne kvadratrota av 4. x er bare definert når x 0
Etter definisjonen av kvadratrot må
fordi og
Vi får rett svar om vi regner slik: 4 9 4 9 2 3
Vi finner kvadratrota av en brøk ved å finne kvadratrota av telleren og nevneren hver for seg. Vi har disse regnereglene for kvadratrøtter:
La a og b være to positive tall. Da er
Det finnes ingen tilsvarende regel for en sum. Legg for eksempel merke til at 169437 ikke er lik. For 16925 5.
Bruk regnereglene for kvadratrøtter til å vise at 5052
Vi utnytter at 50252 . Dermed er
5025225252
OPPGAVE 1.80
Regn ut uten å bruke kalkulator. a) 16 25 b) 49 64 c) 1 121 d) 18 98
OPPGAVE 1.81
Bruk regnereglene for kvadratrøtter til å vise at a) 1832 b) 1223 c) 4843
OPPGAVE 1.82
Skriv kvadratrøttene ved hjelp av kvadratrota av et mindre tall. a) 27 b) 75 c) 162
OPPGAVE 1.83
a) Et kvadrat har arealet 18 cm2. Hvor lange er sidene i kvadratet?
b) En sirkel har arealet 12,56 m2
Hvor stor er radien i sirkelen?
c) En sirkel har det samme arealet som et kvadrat der sidene er 5 cm lange. Finn radien i sirkelen.
Vi vet at 2 8 3 . Tallet 2 kaller vi da tredjerota eller kubikkrota av 8. Vi skriver
82 3
Tredjerota definerer vi på denne måten: x 3 er det tallet som opphøyd i tredje potens er lik x. x 3 =a dersom a 3 =x
Legg merke til at vi kan finne tredjerota av negative tall:
82 3 fordi 28 3
Kalkulator
Vår kalkulator har en egen tast med tredjerota 3 (SHIFT + ). Den gir dette resultatet:
CAS
I GeoGebra CAS kan vi finne tredjerota slik:

I kapittel 5 lærer vi å finne tredjerøtter ved hjelp av Python.
Vi kan også finne røtter av høyere orden. Ettersom 381 4 , kaller vi 3 for fjerderota av 81 og skriver
813 4
Nå er også 381 4 . Likevel sier vi ikke at –3 er fjerderota av 81. Fjerderota skal alltid være et positivt tall.
Vi vet at 2 32 5 . Tallet 2 er dermed femterota av 32. Vi skriver
322 5
Slike røtter kan vi finne digitalt.
Kalkulator
På vår kalkulator trykker vi 4, så på (SHIFT + x ) etterfulgt av 81. M
CAS
I GeoGebra CAS går vi fram på denne måten:

EKSEMPEL
LØSNING
EKSEMPEL
En femmerball har volumet 5 dm3. Finn radien i en femmerball.





Når volumet er 5 dm3, får vi denne likningen:
, Vi fant r i GeoGebra CAS på denne måten:

Radien er 1,06 dm, som er 10,6 cm.
OPPGAVE 1.84
Regn ut uten og med digitale hjelpemidler. a) 27 3 b) 1000 3 c) 64 3 d) 8000 3 e) 625 4 f) 243 5
OPPGAVE 1.85
Når vindstyrken er målt i meter per sekund, er effekten P i kilowatt av ei vindmølle på Storheia gitt ved
Pv 32 3 , Finn vindstyrken når effekten er 2000 kW.
DISKUSJON
For hvilke verdier av n kan vi finne n-te-rota av negative tall?
1.9 Figurtall
Et figurtall er en følge av tall som vi kan få fram ved hjelp av geometriske figurer eller mønstre. Her ser vi de fire minste trekanttallene:


T1 = 1



T2 = 3






T3 = 6









T4 = 10
Vi ser at for eksempel det tredje trekanttallet, T3, består av 3 kuler i bredden og 3 i høyden. Hvis vi summerer radvis fra toppen, ser vi at
T T T 2 3 4 123 1236 123410
Når vi skal finne T5, kan vi legge en ny rad med 5 kuler under figuren med T4. Da blir
T T 5 1234515 4
Tallene 1, 2, 3, 4, … kaller vi de naturligetallene. Vi bruker symbolet om mengden av dem. Trekanttall nr. n blir summen av de naturlige tallene opp til og med n.
Tn n 1234...
Vi lager nå et pythonprogram som skriver ut de 10 minste trekanttallene.
sum = 0
print("Ferdig") 1 2 3 4 5 6 7 8
for n in range(1, 11):
sum += n
print(f"Trekanttall nr. {n} er {sum}.")
Her har vi ei for-løkke. I linje 3 blir n alle hele tall som er større enn eller lik 1 og mindre enn 11. Den største verdien til n blir dermed 10. Programmet går så gjennom de to linjene med innrykk med n-verdier fra og med 1 til og med 10. I linje 4 legger programmet n til variabelen sum. I linje 5 skriver vi ut nummeret og trekanttallet. Linje 7 blir først utført etter at programmet har gått gjennom linje 3 til 5 ti ganger.
Programmet gir denne utskriften:
Trekanttall nr. 1 er 1.
Trekanttall nr. 2 er 3.
Trekanttall nr. 3 er 6.
Trekanttall nr. 4 er 10.
Trekanttall nr. 5 er 15.
Trekanttall nr. 6 er 21.
Trekanttall nr. 7 er 28.
Trekanttall nr. 8 er 36.
Trekanttall nr. 9 er 45.
Trekanttall nr. 10 er 55.
Ferdig
Vi kan også lage et program som skriver ut alle trekanttallene som er mindre enn 100.
n = 1
sum = 1
while sum < 100:
print(f"Trekanttall nr. {n} er {sum}.")
n += 1
sum += n
print(f"Ferdig, for neste trekanttall er {sum}.") 1 2 3 4 5 6 7 8 9 10
Her har vi ei while-løkke. Her blir linjene med innrykk som kommer etter linja med while, utført så lenge variabelen sum er mindre enn 100. I linje 6 øker n med 1. I linje 7 øker sum med n.
Her er siste delen av utskriften:
Trekanttall nr. 11 er 66.
Trekanttall nr. 12 er 78.
Trekanttall nr. 13 er 91.
Ferdig, for neste trekanttall er 105.
DISKUSJON
Endre tallet 100 til 104 i linje 4 i koden over og kjør programmet. Endre så til 105, og til 106.
Forklar hva som skjer.
Rektangeltallene kan vi få fram ved å ordne kuler i rader og kolonner slik at antallet rader er én mer enn antallet kolonner. Figuren nedenfor viser de fire minste rektangeltallene.












R1 = 2 R2 = 6







R3 = 12















R4 = 20


Det tredje rektangeltallet, R3, består av 3 rader og 4 kolonner. Antallet kuler er dermed R3 3412. Av samme grunn er R4 4520. Generelt er
Rnn n 1
Av figuren ovenfor ser vi at rektangeltallene er sammensatt av to like trekanttall. Vi ser for eksempel at RT 33 2 , og at RT 44 2 . Dette gjelder for alle rektangeltallene slik at 2 TR nn . Da blir
T Rnn n n 2 1 2
Vi vet at T n er summen av de naturlige tallene opp til og med n. Dermed er 1234 1 2 ... n nn
Denne formelen kan vi kontrollere ved hjelp av programmet på side 44.
sum = 0 for n in range(1, 11):
sum += n y = n*(n + 1)/2
print(f"Trekanttall nr. {n} er {sum}. Formelen gir {y}")
Her er utskriften:
Trekanttall nr. 1 er 1. Formelen gir 1.0.
Trekanttall nr. 2 er 3. Formelen gir 3.0.
Trekanttall nr. 3 er 6. Formelen gir 6.0.
Trekanttall nr. 4 er 10. Formelen gir 10.0.
Trekanttall nr. 5 er 15. Formelen gir 15.0.
Trekanttall nr. 6 er 21. Formelen gir 21.0.
Trekanttall nr. 7 er 28. Formelen gir 28.0.
Trekanttall nr. 8 er 36. Formelen gir 36.0.
Trekanttall nr. 9 er 45. Formelen gir 45.0.
Trekanttall nr. 10 er 55. Formelen gir 55.0.
OPPGAVE 1.90
a) Lag et program som finner summen 1 2 3 100.
b) Finn summen 50 51 52 … 100.
c) Finn det minste hele tallet n som er slik at 1 2 3 … n 10 000.
OPPGAVE 1.91
a) Bestem de 10 minste rektangeltallene.
b) Lag et program i Python som finner summen av de n minste positive partallene for alle naturlige tall n 10.
c) Sammenlikn svarene i oppgave a og b.
Hva ser du?
d) Figuren nedenfor viser de fire minste rektangeltallene, men nå er de fargelagt på en annen måte.

































R1 = 2 R2 = 6 R3 = 12 R4 = 20
Bruk figuren til å forklare det du fant i oppgave c.
OPPGAVE 1.92
a) Hvis n er et naturlig tall, er K n n 2 et kvadrattall. Finn de 10 minste kvadrattallene.




b) Lag et program i Python som finner summen av de n minste positive oddetallene for alle naturlige tall n ≤10.
c) Sammenlikn svarene i oppgave a og b.
Hva ser du?
d) De fire minste kvadrattallene kan vi illustrere på denne måten:





























K1 = 1 K2 = 4 K3 = 9 K4 = 16
Bruk figuren til å forklare det du fant i oppgave c.

Nå skal vi se på noen andre figurtall der vi kan finne en generell formel for tallene. Her lager vi kvadratiske figurer ut fra et senter.








































F1 = 5 F2 = 13 F3 = 25
Vi legger merke til at
Figurtall nr. n er gitt ved denne summen: Fn n 1442434
DISKUSJON
Forklar leddene 4∙2, 4∙3 og 4∙ n ut fra figurene.
Vi kan nå lage et pythonprogram som bestemmer de fem første figurtallene.
sum = 1 for n in range(1, 6): sum += 4*n print(f"Figurtall nr. {n} er {sum}.")
Det gir dette resultatet:
Figurtall nr. 1 er 5.
Figurtall nr. 2 er 13.
Figurtall nr. 3 er 25.
Figurtall nr. 4 er 41.
Figurtall nr. 5 er 61.
Nå skal vi finne en generell formel for disse figurtallene. Da faktoriserer vi deler av uttrykket for F n
Fn n 14123...
På side 46 viste vi at 123 1 2 n nn
Dermed blir F nn nnnn Fnn n n 14 1 2 121122 221 2 2
Med denne formelen blir
F3 2 23231186125
Det stemmer med det vi fant foran.
OPPGAVE 1.93
Forklar ut fra figurene på forrige side at figurtallene består av éi sentral kule og fire like trekanttall.
Bruk forklaringen til å bevise den generelle formelen for F n.
OPPGAVE 1.94
Utvid programmet foran slik at det bestemmer de 20 første av figurtallene fra forrige side.
Få programmet til å kontrollere formelen for figurtallene.
OPPGAVE 1.95
Nedenfor har vi tegnet noen figurtall som vi kan kalle sekskanttallene.










S1 = 7












S2 = 19
a) Finn sekskanttallet S4.








S3 = 37
b) Finn et sumuttrykk for sekskanttallet S n.
c) Finn en formel for sekskanttallet S n.





Få programmet til å kontrollere formelen fra oppgave c. ?
d) Forklar denne formelen ved hjelp av trekanttall.
e) Lag et program i Python som bestemmer de 10 første sekskanttallene.
SAMMENDRAG
Regnerekkefølge
1.Regn ut parentesene.
2. Regn ut potensene.
3.Gjør deretter multiplikasjonene og divisjonene.
4.Gjør til slutt addisjonene og subtraksjonene.
Regneregler ved brøkregning
Når vi forkorter en brøk, dividerer vi med det samme tallet i telleren og i nevneren. Brøken endrer ikke verdi.
Vi utvider en brøk ved å multiplisere med det samme tallet i telleren og i nevneren. Brøken endrer ikke verdi.
Når vi skal summere brøker, må vi først finne fellesnevneren. Deretter utvider vi alle brøkene så de får den samme nevneren. Til slutt summerer vi tellerne og lar nevneren stå som den er.
Når vi skal multiplisere et helt tall og en brøk, multipliserer vi det hele tallet med telleren og lar nevneren stå som den er.
Når vi skal multiplisere to brøker, multipliserer vi telleren med telleren og nevneren med nevneren. Vi trenger ikke finne fellesnevneren.
Når vi skal dividere med en brøk, multipliserer vi med den omvendte brøken.
Kvadratrot
Kvadratrota av x er det positive tallet som opphøyd i andre potens er lik x.
xaaxa dersom 2 0 og
Tredjerot
Tredjerota av x er det tallet som opphøyd i tredje potens er lik x.
xaax 3 3 dersom
Å løse opp parenteser
Når vi løser opp en parentes med minustegn foran, må alle leddene inne i parentesen skifte fortegn.
En parentes med plusstegn foran kan vi fjerne uten å endre noen fortegn inne i parentesen.
Multiplikasjon med parentes
Når vi skal multiplisere et tall med et uttrykk i en parentes, må vi multiplisere tallet med hvert ledd i parentesen.
Når vi skal multiplisere to parentesuttrykk, må vi multiplisere hvert ledd i den første parentesen med hvert ledd i den andre.
Identitet
I en identitet har venstre og høyre side av likhetstegnet samme verdi for alle verdier av variabelen.
Likning
Når vi løser en likning, finner vi den eller de verdiene for variabelen som gjør at uttrykkene på venstre og høyre side av likhetstegnet blir like.
Regneregler for likninger
Vi kan legge til eller trekke fra det samme tallet på begge sidene av likhetstegnet.
Vi kan multiplisere eller dividere med det samme tallet på begge sidene av likhetstegnet dersom tallet ikke er null.
Vi kan skifte et ledd over på den andre siden av likhetstegnet hvis vi samtidig skifter fortegn på leddet.
Regneregler for ulikheter
Vi kan legge til og trekke fra det samme tallet på hver side av ulikhetstegnet.
Vi kan flytte et ledd over på den andre siden av ulikhetstegnet hvis vi skifter fortegn på leddet.
Vi kan multiplisere og dividere med et tall som ikke er null, på begge sidene av ulikhetstegnet. Hvis tallet er negativt, må vi snu ulikhetstegnet.
Innsettingsmetoden
Når vi skal løse to likninger med to ukjente x og y med innsettingsmetoden, finner vi et uttrykk for x eller y fra en av likningene. Dette uttrykket setter vi inn i den andre likningen. Det gir oss én likning med én ukjent, som vi da løser.
Addisjonsmetoden
Når vi skal løse to likninger med to ukjente x og y med addisjonsmetoden, multipliserer vi om nødvendig likningene med hvert sitt tall slik at en av variablene forsvinner når vi legger sammen likningene.
Figurtall
Et figurtall er en følge av tall som vi kan få fram ved hjelp av geometriske figurer eller mønstre.
MATEMATIKK VED
VALG
I Norge har vi valg hvert andre år. I 2025, 2029, … er det stortingsvalg, og i 2027, 2031, … er det kommunestyre- og fylkestingsvalg. Landet blir delt opp i valgkretser der hver valgkrets har et bestemt antall mandater. Et mandat er for eksempel en plass på Stortinget. Når alle stemmene er talt opp, blir mandatene fordelt etter stemmetallene til partiene i valgkretsen. Mange land bruker Sainte-Laguës metode til å bestemme fordelingen av mandater.
Sainte-Laguës metode
For å fordele mandater med Sainte-Laguës metode lager vi en tabell. I tabellen har hvert parti en kolonne med navnet på partiet og stemmetallet øverst. Nedover i kolonnen deler vi stemmetallet med 1, 3, 5 og så videre. Vi deler altså med oddetallene. Deretter finner vi de største tallene i tabellen.
Vi ser på et valg der vi skal fordele 5 mandater blant de tre partiene A, B og C. Parti A fikk 60 000 stemmer, B fikk 26 000 stemmer, og C fikk 14 000 stemmer. Tabellen blir slik:
Deletall 60 00026 00014 000 1160 00026 00014 000 2 3
Mandatfordeling i Norge
I Norge bruker vi Sainte-Laguës metode med en liten endring. Det første deletallet er 1,4 i stedet for 1.
Ved kommunevalg kan velgerne også gi personstemmer. Dette påvirker vanligvis bare hvilke personer som skal representere et parti, og ikke hvor mange mandater et parti får.
Ved stortingsvalg har vi utjevningsmandater i tillegg til de vanlige mandatene. Utjevningsmandatene fordeles slik at det blir større samsvar mellom antall stemmer og antall mandater et parti får i landet sett under ett. Et parti kan bare få utjevningsmandater hvis det kommer over en sperregrense. Ved stortingsvalget i 2021 var sperregrensa 4 %, som betyr at et parti må ha minst 4 % av stemmene i landet for å få utjevningsmandater.
6115 4552 36 4 1 273 7134 6152 0001 077
I kolonnen til A står stemmetallet 60 000 i rosa. Den oransje delen i kolonnen starter med 60 000, 20 000 og 12 000. Tallene får vi ved å dele stemmetallet 60 000 med henholdsvis 1, 3 og 5.
Nå ser vi på den oransje delen av tabellen for alle partiene. Det største tallet er 60 000. Det står i kolonnen til A. Da får A det første mandatet. Det andre mandatet går til B fordi 26 000 er det nest største tallet. De siste tre mandatene går til A (20 000), C (14 000) og A (12 000).
Totalt ender altså A med 3 mandater. B og C får 1 mandat hver.

Sainte-Laguës metode har navn etter den franske matematikeren André Sainte-Lagüe (1882–1950).
PROSJEKTOPPGAVE 1
Se på eksempelet i teksten. Se bort fra personstemmer og utjevningsmandater.
a) Hvilke partier hadde fått det 6. og 7. mandatet hvis det var 7 mandater i valgkretsen?
b) Hvor mange mandater måtte det vært totalt for at C skulle fått minst to mandater?
c) Hvordan ser tabellen ut hvis vi bruker den norske varianten av Sainte-Laguës metode? Får vi en annen fordeling av mandatene i valgkretsen da?
PROSJEKTOPPGAVE 2
Lag et regneark eller et program dere kan bruke for å regne ut mandatfordeling i en valgkrets ved kommunevalg i Norge. Dere kan for eksempel starte et regneark slik:

Bruk regnearket eller programmet på en valgkrets ved det forrige valget i Norge.
PROSJEKTOPPGAVE 3
I et valg skal 7 mandater fordeles. Parti A får over halvparten av stemmene med 52 %, parti B får 25 %, og parti C får 23 %.
Bruk regnearket eller programmet til å regne ut fordelingen av mandater i dette valget. Hvorfor tror dere parti A vil mene at denne fordelingen ikke er rettferdig?
PROSJEKTOPPGAVE 4
I Norge bruker vi varianten av Sainte-Laguës metode der det første deletallet er 1,4 i stedet for 1.
Er dette en fordel for små partier eller for store partier?
PROSJEKTOPPGAVE 5
Mandater kan også fordeles proporsjonalt med stemmetallene: Et parti som får 30 % av stemmene, får også 30 % av mandatene. Hvordan ville mandatfordelingen blitt i eksempelet i teksten da? Ser dere noen ulemper med denne metoden?
PROSJEKTOPPGAVE 6
I noen land bruker man D’Hondts metode for å bestemme fordelingen av mandater. Metoden er som Sainte-Laguës metode, men med deletallene 1, 2, 3 og så videre. Sammenlikn D’Hondts metode med de to variantene av Sainte-Laguës metode.
PROSJEKTOPPGAVE 7
Ordningen med utjevningsmandater ved stortingsvalg bygger også på matematiske beregninger med stemmetallene. Finn ut mer om ordningen og lag en presentasjon der dere forklarer hovedtrekkene.
REPETISJONSOPPGAVER
OPPGAVE 1
Løs likningene ved regning.
a) 42533 xxx
b) 3 2 1 1 2 12 xx c) 1 2 2 1 3 1 1 3 1 2 4 xxx
OPPGAVE 2
En elev har løst en likning på denne måten:
OPPGAVE 5
Når Sander skal besøke Sandra, tar han buss halve strekningen. Det er 1 km å gå hjemmefra og til bussholdeplassen. Etter at han går av bussen, gjenstår 1 6 av avstanden mellom dem.
Hvor langt unna bor Sandra?
OPPGAVE 6
Bestem a slik at likningen blir en identitet. 21365 2 xxaxxa
OPPGAVE 7
Løs likningssettet ved å bruke både innsettingsmetoden og addisjonsmetoden. 3222 431 xy xy
3x - 12 - 2x + 2 = 4x - 1 + 1x 3x - 2x - 4x - 1x = 12 - 2 - 1 -4x = 9 = - x
Finn feil i løsningen. Løs likningen riktig.
OPPGAVE 3
Lise og Henrik er foreldrene til Grete. Til sammen er familien 108 år. Lise er fire år yngre enn Henrik, og Henrik er akkurat tre ganger så gammel som Grete. Hvor gamle er de enkelte familiemedlemmene?
OPPGAVE 4 Løs ulikheten ved regning.
OPPGAVE 8
Finn a uttrykt ved de andre størrelsene i formelen. A abh 2
OPPGAVE 9
a) Løs likningssettet ved regning og i CAS.
b) Ved en videregående skole opplyste 1 3 av jentene og 1 4 av guttene at de hadde snust, mens 373 av elevene svarte at de aldri hadde snust. På skolen var det 24 flere jenter enn gutter. Vis at likningssettet i oppgave a kan brukes til å finne hvor mange gutter og jenter det er på skolen.
OPPGAVE 10
a) Lag et program i Python som regner ut lengden av hypotenusen i en rettvinklet trekant når lengdene av katetene er gitt.
b) Lag et program i Python som regner ut lengden av en katet når både lengden av hypotenusen og lengden av den andre kateten er gitt.
OPPGAVE 11
Regn ut uten bruk av hjelpemidler.
OPPGAVE 12
Regn ut og skriv svaret så enkelt som mulig uten bruk av hjelpemidler.
OPPGAVE 13
En elev løste ulikheten
på denne måten:
+4x-3x
Vurder besvarelsen og løs ulikheten riktig.
OPPGAVE 14
Tenk på et tall. Legg til 5.
Gang svaret med 2. Trekk fra 4.
Del på 2. Trekk fra tallet du tenkte på.
a) Hvilket tall får du?
b) Begynn med et negativt tall.
Hvilket svar får du nå?
c) Begynn med en brøk.
Hvilket svar får du nå?
d) Kall det tallet du tenker på, for x, og bevis at du alltid vil få det samme svaret til slutt.
OPPGAVE 15
Oscar bruker grønne brikker for å lage figurer etter et bestemt mønster. Nedenfor ser du figur nr. 2, nr. 3 og nr. 4.
Figur 2Figur 3Figur 4
a) Hvor mange brikker vil det være i figur nr. 5, figur nr. 6 og figur nr. 7? Forklar.
b) Sett opp en formel som forteller hvor mange brikker det er i figur nr. n.
c) Lag et program i Python som skriver ut hvor mange brikker det er i hver av de ti første figurene.
d) Gjør endringer i programmet slik at du kan regne ut hvor mange brikker det er til sammen i de ti første figurene.
e) Hvor mange figurer kan Oskar lage til sammen hvis han har 3000 brikker? Hvor mange brikker har han da til overs?
