Y ESTADÍSTICA

MENDENHALL – BEAVER – BEAVER Introducción
PROBABILIDAD
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
a la
This is an electronic version of the print textbook. Due to electronic rights restrictions, some third party content may be suppressed. Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. The publisher reserves the right to remove content from this title at any time if subsequent rights restrictions require it. For valuable information on pricing, previous editions, changes to current editions, and alternate formats, please visit www.cengage.com/highered to search by ISBN#, author, title, or keyword for materials in your areas of interest.
Important Notice: Media content referenced within the product description or the product text may not be available in the eBook version.
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
Introducción a la PROBABILIDAD Y ESTADÍSTICA
William Mendenhall, III
1925–2009
Robert J. Beaver
University of California, Riverside, Emeritus
Traducción
RaquelArcosBulos
Maestra en Demografía y Traductora técnica
Revisión técnica
LuisMedinaGual
Universidad Iberoamericana
AlbinoRodríguezDíaz
TecNM, Instituto Tecnológico de Tepic
AndreaOviedoBautista
Universidad Anáhuac de Querétaro
AzucenaMinervaGarcíaLeón
Universidad Autónoma de Nuevo León
BeatrizAdrianaHernándezHernández
UNITEC campus Atizapán
CarlosAugustoJiménezZárate
Universidad Autónoma de Nuevo León
DeydraCelesteLópezPiñón
Universidad Autónoma de Nuevo León
DianaLizetteBecerraPeña
Universidad de Guadalajara
EdgarEduardoMendozaVelázquez
Universidad Autónoma de Chihuahua
ErickEscobedoRodríguez
Universidad Anáhuac de Querétaro
ErnestinaMacíasLópez
Universidad Autónoma de Nuevo León
FélixFernándezMéndez
Universidad Anáhuac México
FiladelfoLeón-Cázares
Universidad de Guadalajara
Barbara M. Beaver
University of California, Riverside, Emeritus
GilbertoGamalielDíazMonroy
Instituto Politécnico Nacional
GracielaGonzálezPerales
Universidad Autónoma de Nuevo León
JönsSánchezAguilar
TecNM campus Querétaro
JosédeJesúsCedilloBarco
UNITEC campus León
LuisArturoSilvaGarnica
UNITEC campus Querétaro
LuzMaríaTrinidadPérezAlvarado
TecNM campus León
MaríadelCarmenGarzaSalazar
Universidad Autónoma de Nuevo León
MaríaTeresaTovarMorales
Universidad Autónoma de Nuevo León
MarioCruzVargas
Universidad Autónoma de Nuevo León
SergioRamírezEspinosa
Instituto Politécnico Nacional
SoniaGuadalupeAnguianoRostro
Universidad Autónoma de Nuevo León
YadiraValdiviesoDíaz
Universidad de las Américas Puebla
Australia • Brasil • Canadá • Estados Unidos • México • Reino Unido • Singapur
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
Introducción a la probabilidad y estadística
Primera edición
William Mendenhall, III, Robert J. Beaver, Barbara M. Beaver
Directora Higher Education
Latinoamérica:
Lucía Romo Alanís
Gerente editorial Latinoamérica:
Jesús Mares Chacón
Editora:
Cinthia Chávez Ceballos
Coordinador de manufactura: Rafael Pérez González
Diseño de portada:
Karla Paola Benítez García
Imagen de portada: © YesPhotographers / Shutterstock.com
Composición tipográfica: Ediciones OVA
© D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Av. Andrés Molina Enríquez 354, Primer piso, Oficina “A”, Colonia Ampliación Sinatel, Delegación Iztapalapa, Ciudad de México, C.P. 09479. Cengage Learning® es una marca registrada usada bajo permiso.
DERECHOS RESERVADOS. Ninguna parte de este trabajo amparado por la Ley Federal del Derecho de Autor, podrá ser reproducida, transmitida, almacenada o utilizada en cualquier forma o por cualquier medio, ya sea gráfico, electrónico o mecánico, incluyendo, pero sin limitarse a lo siguiente: fotocopiado, reproducción, escaneo, digitalización, grabación en audio, distribución en internet, distribución en redes de información o almacenamiento y recopilación en sistemas de información a excepción de lo permitido en el Capítulo III, Artículo 27 de la Ley Federal del Derecho de Autor, sin el consentimiento por escrito de la Editorial.
Traducido del libro Introduction to Probability and Statistics, Fifteenth Edition, Metric Version de William Mendenhall, III, Robert J. Beaver y Barbara M. Beaver. Publicado en inglés por Cengage Learning © 2020
ISBN: 978-0-357-11446-9
Datos para catalogación bibliográfica: Mendenhall, III, William, Robert J. Beaver, Barbara M. Beaver Introducción a la probabilidad y estadística
Primera edición
ISBN: 978-607-570-166-0
Visite nuestro sitio web en: latam.cengage.com
Publicado en México 1 2 3 4 5 6 26 25 24 23 MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
Tabla de contenido breve
INTRODUCCIÓN: ¿QUÉ ES LA ESTADÍSTICA? 1
1 DESCRIPCIÓN DE DATOS CON GRÁFICOS 7
2 DESCRIPCIÓN DE DATOS CON MEDIDAS NUMÉRICAS 54
3 DESCRIPCIÓN DE DATOS BIVARIADOS 96
4 PROBABILIDAD 126
5 DISTRIBUCIONES DE PROBABILIDAD DISCRETAS 167
6 LA DISTRIBUCIÓN DE PROBABILIDAD NORMAL 212
7 DISTRIBUCIONES MUESTRALES 245
8 ESTIMACIÓN CON MUESTRAS GRANDES 288
9 PRUEBAS DE HIPÓTESIS CON MUESTRAS GRANDES 335
10 INFERENCIA A PARTIR DE MUESTRAS PEQUEÑAS 380
11 EL ANÁLISIS DE VARIANZA 445
12 REGRESIÓN LINEAL SIMPLE Y CORRELACIÓN 503
13 ANÁLISIS DE REGRESIÓN LINEAL MÚLTIPLE 555
14 ANÁLISIS DE DATOS CATEGÓRICOS 599
15 ESTADÍSTICA NO PARAMÉTRICA 633
APÉNDICE I 681
FUENTES DE DATOS 714
RESPUESTAS A EJERCICIOS SELECCIONADOS 727
ÍNDICE 745
iii MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
Contenido
Introducción: ¿Qué es la estadística? 1
Poblaciones y muestras 3
Estadística descriptiva e inferencial 3
Lograr el objetivo de la estadística inferencial: los pasos necesarios 4 Claves para un aprendizaje exitoso 5
Descripción de datos con gráficos 7
1.1 Variables y datos 8 Tipos de variables 9
Ejercicios 11

1.2 Gráficos para datos categóricos 12 Ejercicios 15
1.3 Gráficos para datos cuantitativos 17
Gráficas circulares y gráficas de barras 17 Gráficas de líneas 19

Gráficas de puntos 20
Diagramas de tallo y hoja 20
Interpretación de gráficas con ojo crítico 22 Ejercicios 24
1.4 Histogramas de frecuencia relativa 27 Ejercicios 31
Revisión del capítulo 35
Tecnología actual 35
Revisar lo que ha aprendido 47
ESTUDIO DE CASO: ¿Cómo está su presión arterial? 53

Descripción de datos con medidas numéricas 54
Introducción 55
2.1 Medidas de tendencia central 55 Ejercicios 59
2.2 Medidas de variabilidad 61 Ejercicios 66
iv
1
2
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
3 4
2.3 Comprensión e interpretación de la desviación estándar 67
Teorema de Chebyshev 67
La regla empírica 69
Aproximación de s mediante el rango 71
Ejercicios 73
2.4 Medidas de posición relativa 76
Puntaje z 76
Percentiles y cuartiles 77
El resumen de cinco números y el diagrama de caja 80
Ejercicios 83
Revisión del capítulo 86
Tecnología actual 87
Revisar lo que ha aprendido 91
ESTUDIO DE CASO: Los chicos del verano 95
Descripción de datos bivariados 96
Introducción 97
3.1 Descripción de datos categóricos bivariados 97
Ejercicios 99
3.2 Descripción de datos cuantitativos bivariados 101
Diagramas de dispersión 101
Coeficiente de correlación 104
La línea recta de mínimos cuadrados 106
Ejercicios 109

Revisión del capítulo 112
Tecnología actual 112
Revisar lo que ha aprendido 118
ESTUDIO DE CASO: Su ropa, ¿está realmente limpia? 124

Probabilidad 126
Introducción 127
4.1 Eventos y el espacio muestral 127
Ejercicios 130
4.2 Cálculo de probabilidades mediante eventos simples 131
Ejercicios 134
4.3 Reglas de conteo útiles 137
Uso de la calculadora TI-83/84 Plus 142
Contenido v
Ejercicios 142 MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
4.4 Reglas para calcular probabilidades 144
Cálculo de probabilidades para uniones y complementos 146

Cálculo de probabilidades para intersecciones 148
Ejercicios 155
4.5 Regla de Bayes 158 Ejercicios 161
Revisión del capítulo 163
Revisar lo que ha aprendido 163
ESTUDIO DE CASO: Probabilidad y toma de decisiones en el Congo 166
Distribuciones de probabilidad discretas 167
5.1 Variables aleatorias discretas y sus distribuciones de probabilidad 168 Variables aleatorias 168
Distribuciones de probabilidad 168
La media y la desviación estándar de una variable aleatoria discreta 170 Ejercicios 174
5.2 La distribución de probabilidad binomial 176 Ejercicios 185
5.3 La distribución de probabilidad de Poisson 189 Ejercicios 194
5.4 La distribución de probabilidad hipergeométrica 196 Ejercicios 198
Revisión del capítulo 200
Tecnología actual 201
Revisar lo que ha aprendido 206
ESTUDIO DE CASO: Un misterio: casos de cáncer cerca de un reactor 211

La distribución de probabilidad normal 212
6.1 Distribuciones de probabilidad para variables aleatorias continuas 213
La distribución de probabilidad uniforme continua 215
La distribución de probabilidad exponencial 216
Ejercicios 217
6.2 La distribución de probabilidad normal 218
La variable aleatoria normal estándar 219
Calcular probabilidades para una variable aleatoria normal general 222
Ejercicios 225
6.3 La aproximación normal a la distribución de probabilidad binomial 228
Ejercicios 232
Contenido vi
6 5 MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
Revisión del capítulo 235
Tecnología actual 235
Revisar lo que ha aprendido 241
ESTUDIO DE CASO: “¿Va a calificar por curva?” 244
Distribuciones muestrales 245
Introducción 246
7.1 Planes de muestreo y diseños experimentales 246
Ejercicios 249
7.2 Estadísticas y distribuciones muestrales 252
Ejercicios 254
7.3 El teorema del límite central y la media muestral 255
El teorema del límite central 255
La distribución muestral de la media muestral 258
Error estándar de la media muestral 259
Ejercicios 262
7.4 Pruebas de normalidad 264
7.5 La distribución muestral de la proporción muestral 268
Ejercicios 271
7.6 Una aplicación del muestreo: control estadístico de procesos (opcional) 273
Una gráfica de control para la media del proceso: la gráfica x 274
Una gráfica de control para la proporción de piezas defectuosas: la gráfica p 276 Ejercicios 278
Revisión del capítulo 280

Tecnología actual 281
Revisar lo que ha aprendido 284
ESTUDIO DE CASO: Muestreo con la ruleta en Monte Carlo 287

Estimación con muestras grandes 288
8.1 Dónde hemos estado y hacia dónde vamos 289
Inferencia estadística 289
Tipos de estimadores 290
8.2 Estimación puntual 291
Ejercicios 296
8.3 Estimación por intervalos 298
Construir un intervalo de confianza 298
Intervalo de confianza con muestras grandes para una media poblacional 300
Contenido vii
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
7 8
Interpretar el intervalo de confianza 301
Intervalo de confianza para una proporción poblacional p con muestras grandes 303
Usar la tecnología 304
Ejercicios 304
8.4 Estimar la diferencia entre dos medias poblacionales 307
Ejercicios 311
8.5 Estimar la diferencia entre dos proporciones binomiales 313
Usar la tecnología 316
Ejercicios 316
8.6 Límites de confianza unilaterales 319
Ejercicios 320
8.7 Elegir el tamaño de la muestra 322
Ejercicios 325
Revisión del capítulo 326
Tecnología actual 327
Revisar lo que ha aprendido 330
ESTUDIO DE CASO: ¿Qué tan confiable es esa encuesta? CBS News: cómo y dónde comen los estadounidenses 333
Pruebas de hipótesis con muestras grandes 335

Introducción 336
9.1 Una prueba estadística de hipótesis 336
Ejercicios 339
9.2 Una prueba para la media poblacional, con muestra grande 340
Lo esencial de la prueba 340
Calcular el valor p 344
Dos tipos de errores 348
El poder (potencia) de una prueba estadística 349
Ejercicios 352
9.3 Una prueba de hipótesis para la diferencia entre dos medias poblacionales, con muestras grandes 354
Pruebas de hipótesis e intervalos de confianza 356
Ejercicios 357
9.4 Una prueba de hipótesis para una proporción binomial, con muestra grande 360 Significancia estadística e importancia práctica 362
Ejercicios 363
9.5 Una prueba de hipótesis para la diferencia entre dos proporciones binomiales, con muestras grandes 365
Ejercicios 367
Contenido viii
9 MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
9.6 Comentarios finales sobre las pruebas de hipótesis 369
Revisión del capítulo 370
Tecnología actual 371
Revisar lo que ha aprendido 375
ESTUDIO DE CASO: ¿Una aspirina al día...? 378
Inferencia a partir de muestras pequeñas 380
Introducción 381
10.1 Distribución t de Student 381 Supuestos detrás de la distribución t de Student 384 Ejercicios 385
10.2 Inferencias respecto a una media poblacional a partir de una muestra pequeña 386
Ejercicios 390
10.3 Inferencias respecto a la diferencia entre dos medias poblacionales a partir de muestras pequeñas: muestras aleatorias independientes 394 Ejercicios 400
10.4 Inferencias respecto a la diferencia entre dos medias a partir de muestras pequeñas: una prueba de diferencias por pares 404
Ejercicios 409

10.5 Inferencias respecto a una varianza poblacional 413
Ejercicios 419
10.6 Comparar dos varianzas poblacionales 421
Ejercicios 427
10.7 Revisión de los supuestos a partir de muestras pequeñas 429
Revisión del capítulo 430
Tecnología actual 431
Revisar lo que ha aprendido 439
ESTUDIO DE CASO: Responsabilidad escolar: ¿lo estamos haciendo mejor? 443

El análisis de varianza 445
11.1 El diseño de un experimento 446 Definiciones básicas 446 ¿Qué es un análisis de varianza? 447
Los supuestos para un análisis de varianza 448
Ejercicios 448
11.2 El diseño completamente aleatorio: una clasificación en una dirección 449
Dividir la variación total en el experimento 450
Contenido ix
10 11 MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
Probar la igualdad de las medias de tratamientos 453
Estimación de diferencias en las medias de tratamientos 455
Ejercicios 458
11.3 Clasificación de las medias poblacionales 461
Ejercicios 464
11.4 El diseño aleatorio en bloques: una clasificación en dos direcciones 465
Dividir la variación total en el experimento 466
Probar la igualdad de las medias de tratamientos y de bloques 469
Identificación de diferencias en las medias de tratamientos o de bloques 471
Algunos comentarios de advertencia sobre el bloqueo 472
Ejercicios 473
11.5 El experimento factorial a 3 b: una clasificación en dos direcciones 477
El análisis de varianza para un experimento factorial a 3 b 479
Ejercicios 483
11.6 Revisión de los supuestos del análisis de varianza 486
Gráficas residuales 487
11.7 Un breve resumen 489
Revisión del capítulo 490
Tecnología actual 490
Revisar lo que ha aprendido 497
ESTUDIO DE CASO: ¡Cómo ahorrar dinero en comestibles! 502
Regresión lineal simple y correlación 503
Introducción 504
12.1 Regresión lineal simple 504
Un modelo lineal simple 505
El método de mínimos cuadrados 507
Ejercicios 509
12.2 Un análisis de varianza para regresión lineal 511
Ejercicios 514
12.3 Prueba de la utilidad del modelo de regresión lineal 516

Inferencias respecto a b, la pendiente de la recta de medias 516
La prueba F del análisis de varianza 519
Medir la fuerza de la relación: el coeficiente de determinación 520
Interpretar los resultados de una regresión significativa 521
Ejercicios 522
Contenido x
12 MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
12.4 Herramientas de diagnóstico para comprobar los supuestos de regresión 525
Términos de error dependientes 525
Gráficas de residuos 525
Ejercicios 526
12.5 Estimación y predicción mediante la recta ajustada 530
Ejercicios 534
12.6 Análisis de correlación 537
Ejercicios 540
Revisión del capítulo 543
Tecnología actual 544
Revisar lo que ha aprendido 549
ESTUDIO DE CASO: ¿Su automóvil es “hecho en Estados Unidos”? 553

Análisis de regresión lineal múltiple 555
Introducción 556
13.1 El modelo de regresión múltiple 556
13.2 Análisis de regresión múltiple 558
El método de mínimos cuadrados 558
El análisis de varianza 559
Probar la utilidad del modelo de regresión 561
Interpretar los resultados de una regresión significativa 562
Regresión de los mejores subconjuntos 563
Verificar los supuestos de regresión 564
Uso del modelo de regresión para estimación y predicción 564
Ejercicios 565
13.3 Un modelo de regresión polinomial 567
Ejercicios 570
13.4 Uso de variables predictoras cuantitativas y cualitativas en un modelo de regresión 573
Ejercicios 578
13.5 Prueba de conjuntos de coeficientes de regresión 582
13.6 Otros temas en la regresión lineal múltiple 584
Interpretación de las gráficas de residuos 584
Análisis de regresión por pasos 586
Regresión logística binaria 587
Interpretación incorrecta de un análisis de regresión 587
13.7 Pasos que deben seguirse al construir un modelo de regresión múltiple 589
Contenido xi
13 MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
Revisión del capítulo 589
Tecnología actual 590
Revisar lo que ha aprendido 592
ESTUDIO DE CASO: “Hecho en Estados Unidos”: otra mirada 598
Análisis de datos categóricos 599
14.1 El experimento multinomial y la estadística ji-cuadrada 600
14.2 Prueba de probabilidades para celdas específicas: la prueba de bondad de ajuste 602
Ejercicios 604
14.3 Tablas de contingencia: una clasificación en dos direcciones 606

La prueba de independencia ji-cuadrada 607
Ejercicios 611
14.4 Comparación de varias poblaciones multinomiales: una clasificación en dos direcciones con totales de fila o de columna fijos 614

Ejercicios 616
14.5 Otros temas del análisis de datos categóricos 619
La equivalencia de pruebas estadísticas 619
Otras aplicaciones de la prueba ji-cuadrada 620
Revisión del capítulo 621
Tecnología actual 622
Revisar lo que ha aprendido 627
ESTUDIO DE CASO: ¿Quién es el sostén principal de su familia? 631
Estadística no paramétrica 633
Introducción 634
15.1 La prueba de suma de rangos de Wilcoxon: muestras aleatorias independientes 634
Aproximación normal a la prueba de suma de rangos de Wilcoxon 638 Ejercicios 641
15.2 La prueba de signos para un experimento pareado 643
Aproximación normal para la prueba de signos 644
Ejercicios 646
15.3 Comparación de pruebas estadísticas 648
15.4 La prueba de rangos con signo de Wilcoxon para un experimento pareado 648
Aproximación normal para la prueba de rangos con signo de Wilcoxon 652
Ejercicios 653
Contenido xii
14 15 MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
15.5 La prueba H de Kruskal-Wallis para diseños completamente aleatorios 655
Ejercicios 658
15.6 La prueba F r de Friedman para diseños aleatorios en bloques 660
Ejercicios 663
15.7 Coeficiente de correlación de rangos 666
Ejercicios 670
15.8 Resumen 672
Revisión del capítulo 672
Tecnología actual 673
Revisar lo que ha aprendido 676
ESTUDIO DE CASO: Segunda sede de Amazon 680
Apéndice I 681
Tabla 1 Probabilidadesbinomialesacumuladas 682
Tabla 2 ProbabilidadesdePoissonacumuladas 688
Tabla 3 Áreasbajolacurvanormal 690
Tabla 4 Valorescríticosde t 692
Tabla 5 Valorescríticosdeji-cuadrada 694
Tabla 6 Puntosporcentualesdeladistribución F 696
Tabla 7 Valorescríticosde T paralapruebadesumaderangosdeWilcoxon, n1 # n2 704
Tabla 8 Valorescríticosde T paralapruebaderangosconsigno deWilcoxon, n 5 5(1)50 706
Tabla 9 Valorescríticosdelcoeficientedecorrelaciónderangos deSpearmanparaunapruebadeunacola 707
Tabla 10 Númerosaleatorios 708
Tabla 11 PuntosporcentualesdelrangodeStudent, q.05(k, df ) 710
Fuentes de datos 714
Respuestas a ejercicios seleccionados 727
Índice 745
Contenido xiii
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
Cada vez que lee un periódico o una revista, ve la televisión o navega por Facebook encuentra estadísticas. Cada vez que llena un cuestionario, se registra en un sitio de internet o ingresa su tarjeta de puntos por compras en un escáner electrónico, sus datos personales pasan a formar parte de una base de datos que contiene su información estadística personal. ¡No puede evitarlo! En esta era digital, la recopilación y el análisis de datos forman parte de nuestras actividades diarias. Si quiere ser un consumidor y un ciudadano educado, necesita entender cómo se usan las estadísticas de manera correcta e incorrecta en nuestra vida diaria. Esta versión métrica internacional está diseñada para las escuelas y los estudiantes que se encuentran fuera de Estados Unidos. Las unidades de medida que se usan en los ejemplos y ejercicios seleccionados se han cambiado, de las unidades habituales en Estados Unidos a unidades métricas. No actualizamos los problemas que son específicos de las unidades habituales estadounidenses, como las yardas por pase en el futbol o los datos relacionados con publicaciones específicas.
El secreto de nuestro éxito
En el primer curso universitario de introducción a la estadística que nosotros tomamos usamos el texto Introducción a la probabilidad y estadística, de William Mendenhall. Desde entonces, este texto (actualmente en la decimoquinta edición en inglés) ha ayudado a generaciones de estudiantes a entender en qué consiste la estadística y cómo se puede usar como una herramienta en sus áreas de aplicación particular. El secreto del éxito de Introducción a la probabilidad y estadística es su capacidad para combinar lo antiguo con lo nuevo. Con cada revisión intentamos basarnos en los puntos fuertes de las ediciones anteriores y buscar nuevas formas de motivar, animar e interesar a los estudiantes usando nuevas tecnologías.
Características distintivas de esta edición
Esta edición fue traducida de la decimoquinta edición en inglés, la cual mantiene el esquema tradicional de cobertura de la estadística descriptiva e inferencial que se ha empleado en las ediciones anteriores. Esta revisión mantiene la presentación sencilla de la decimocuarta edición en inglés. Continuamos con la simplificación del idioma para que el texto sea más legible, sin sacrificar la integridad estadística de la presentación. Queremos que los estudiantes entiendan cómo aplicar los procedimientos estadísticos y también que entiendan:
• Cómo describir de manera significativa conjuntos de datos reales.
• Cómo explicar los resultados de las pruebas estadísticas en forma práctica.
• Cómo saber si los supuestos en los que se basan las pruebas estadísticas son válidos.
• Qué hacer cuando estos supuestos se infringen.
Ejercicios
Como en todas las ediciones anteriores en inglés, la variedad y la cantidad de aplicaciones reales en los conjuntos de ejercicios son uno de los puntos fuertes principales de esta edición. Hemos revisado los conjuntos de ejercicios para ofrecer nuevas e interesantes situaciones del mundo real y conjuntos de datos reales, muchos de los cuales provienen de publicaciones
Contenido xv
xv MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
Prefacio
periódicas y revistas actuales. Esta edición contiene más de 1900 ejercicios, muchos de los cuales son nuevos. Los ejercicios se gradúan según el nivel de dificultad; algunos, que solo incluyen técnicas básicas, pueden ser resueltos por casi todos los estudiantes, mientras que otros, que involucran aplicaciones prácticas e interpretación de resultados, desafían a los alumnos para que apliquen un razonamiento estadístico y una comprensión más sofisticados. Los ejercicios se han reorganizado para ofrecer una distribución más uniforme de los problemas al interior de cada capítulo, además, se ha introducido un nuevo sistema de numeración que inicia con cada nueva sección.
Organización y cobertura
Creemos que los capítulos 1 a 10 (con la posible excepción del capítulo 3) deben abordarse en el orden en que se presentan. Los capítulos restantes se pueden cubrir en cualquier orden. El capítulo de análisis de varianza precede al de regresión, de tal forma que el docente pueda presentar el análisis de varianza como parte de un análisis de regresión. Por lo tanto, la presentación más efectiva sería ordenar también estos tres capítulos.
Los capítulos 1 a 3 presentan el análisis descriptivo de datos para una y dos variables con MINITAB 18, Microsoft Excel 2016 ® y las calculadoras TI-83/84 Plus. El capítulo 4 incluye una presentación completa de la probabilidad. La última sección del capítulo 4 en la decimocuarta edición en inglés del texto, “Variables aleatorias discretas y sus distribuciones de probabilidad”, se reubicó para convertirse en la primera sección del capítulo 5. Al igual que en la decimocuarta edición en inglés, los capítulos sobre análisis de varianza y regresión lineal incluyen, en la presentación básica del texto, tanto las fórmulas de cálculo como salidas de programas de cómputo. Los docentes que deseen emplear el enfoque de cálculo “manual” de la regresión lineal y del ANOVA pueden usar estos capítulos con la misma facilidad que aquellos que opten por centrarse en la interpretación de las salidas estadísticas generadas por computadora. Esta edición incluye una cobertura ampliada de las distribuciones uniforme y exponencial en el capítulo 5, gráficas de probabilidad normal para evaluar la normalidad en el capítulo 7, además de una tabla t ampliada (tabla 4 del apéndice I). Los nuevos temas del capítulo 13 incluyen los procedimientos de regresión de mejores subconjuntos y la regresión logística binaria.
Una característica importante en los capítulos sobre pruebas de hipótesis es el énfasis en los valores p y su uso para evaluar la significancia estadística. Con la llegada de los valores p generados por computadora, estas probabilidades se han vuelto esenciales al momento de presentar los resultados de un análisis estadístico. Así, el valor observado de la estadística de prueba y su valor p se estudian de manera conjunta al principio de nuestro análisis sobre las pruebas de hipótesis estadísticas como herramientas equivalentes para la toma de decisiones. La significancia estadística se define en términos de valores preasignados de , y el enfoque del valor p se presenta como una alternativa al enfoque del valor crítico para probar una hipótesis estadística. Los ejemplos se explican usando ambos enfoques, el del valor p y el del valor crítico, para la prueba de hipótesis. En los ejemplos prácticos del texto se hace hincapié en la discusión sobre la interpretación práctica de los resultados estadísticos, junto con la diferencia entre las significancias estadística y práctica.
Características especiales de esta edición
• NECESITO SABER : en esta edición se incluyen las secciones destacadas denominadas “NECESITO SABER…” que se identifican con este icono Necesito saber... ? . Estas secciones proporcionan información que consiste en definiciones, procedimientos o instrucciones paso a paso para la resolución de problemas asociados con preguntas específicas, por ejemplo “NECESITO SABER... ¿Cómo construir un histograma de frecuencia relativa?” o “NECESITO SABER... ¿Cómo decidir qué prueba utilizar?”.
• La descripción gráfica y numérica de los datos incluye tanto métodos tradicionales como el análisis exploratorio de datos (EDA, por sus siglas en inglés), usando gráficas generadas con los programas de cómputo MINITAB 18 para Windows y MS Excel 2016
• En varios ejemplos se usan capturas de pantalla de la calculadora TI-84 Plus, lo que permite a los estudiantes tener acceso a esta opción para el análisis de los datos.
Prefacio xvi
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
• Todos los ejemplos y ejercicios del texto que incluyen impresiones o capturas de pantalla de calculadoras se basan en MINITAB 18,MS Excel 2016 o la calculadora TI-84 Plus. Para algunos ejercicios se proporcionan estos resultados, mientras que otros problemas requieren que el estudiante obtenga soluciones sin usar una computadora.




NombreLongitud (km)NombreLongitud (km)







Superior560Titicaca195
Victoria334Nicaragua163
Huron330Athabasca333
Michigan491Reindeer229
MardeAral416TonleSap112
Tanganyika672Turkana246
Baykal632IssykKul184
GreatBear307Torrens208
Nyasa576Vänern146
GreatSlave477Nettilling107










Erie386Winnipegosis226
Winnipeg426Albert160
Ontario309Nipigon115
Balkhash602Gairdner144
Ladoga198Urmia144
Maracaibo213Manitoba224
Onega232Chad280
Eyre144
Fuente:The World Almanac and Book of Facts 2017
a. Use un diagrama de tallo y hoja para describir la longitud de los principales lagos del mundo.
b. Utilice un histograma para mostrar estos datos. ¿Cómo se compara con el diagrama de tallo y hoja del inciso a?
c. ¿Estos datos son simétricos o se encuentran sesgados? Si la distribución está sesgada, ¿cuál es la dirección de la inclinación?
DATA SET DS0128


6. Limpieza de derrames de petróleo El 20 de abril de 2010 hubo en Estados Unidos un gran desastre ambiental cuando la plataforma de perforación
Deepwater Horizon explotó en el Golfo de México. El personal ocupado y el equipo que se utilizó en la limpieza del derrame de petróleo en el Golfo, desde el 2 de mayo de 2010 (día 13) hasta el 9 de junio de 2010 (día 51) se indica en la siguiente tabla.17
d. Utilice una gráfica de barras para mostrar el porcentaje de áreas de pesca federales del Golfo cerradas.
e. Use una gráfica de líneas para mostrar las cantidades de dispersantes utilizadas. ¿Hay alguna relación de línea recta subyacente a lo largo del tiempo?
DATA SET
DS0129
7. Resultados electorales Las elecciones de 2016 en Estados Unidos fueron una contienda en la que Donald Trump derrotó a Hillary Clinton y otros candidatos al ganar 304 votos electorales, o 57% de los 538 disponibles. Sin embargo, Trump solo ganó 46.1% del voto popular, mientras que Clinton obtuvo 48.2%. El voto popular (en miles) para Donald Trump en cada uno de los 50 estados se enlista a continuación:18
AL1319HI129MA1091NM320SD228
AK163ID409MI2280NY2820TN1523
AZ1252IL2146MN1323NC2363TX4685
AR685IN1557MS701ND217UT515
CA4484IA801MO1595OH2841VT95
CO1202KS671MT279OK949VA1769
CT673KY1203NE496OR782WA1222
DE185LA1179NV512PA2971WV489
FL4618ME336NH346RI181WI1405
GA2089MD943NJ1602SC1155WY174
a. Con solo mirar la tabla, ¿qué forma cree que tendrá la distribución del voto popular por estado?
b. Trace un histograma de frecuencia relativa para describir la distribución del voto popular para el presidente Trump en los 50 estados.
c. ¿El histograma del inciso b confirmó su suposición del inciso a? ¿Hay valores atípicos? ¿Cómo puede lil?
Prefacio xvii 0
Figura 9.9
Salida de la calculadora TI-84 Plus, para el ejemplo 9.7
Frecuencia relativa Puntuaciones 8.5 14.5 20.5 26.5 32.5 6/25 4/25 2/25 0
Figura 2.11 Histograma de frecuencia relativa para el ejemplo 2.8
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
TECNOLOGÍA ACTUAL
El papel de las computadoras y de las calculadoras en esta edición: tecnología actual
Las computadoras y las calculadoras científicas o graficadoras ahora son herramientas comunes para los estudiantes universitarios de todas las disciplinas. La mayoría de ellos son usuarios expertos de procesadores de texto, hojas de cálculo y bases de datos, y no tienen problemas para navegar por los programas de cómputo en el entorno Windows. Muchos tienen una calculadora científica o graficadora, a menudo una de aquellas que fabrica Texas InstrumentsTM. Sin embargo, creemos que los avances en la tecnología de cómputo no deberían convertir los análisis estadísticos en una “caja negra”. Más bien, optamos por aprovechar las facilidades de cálculo que la tecnología moderna ofrece con el fin de tener más tiempo para reforzar el razonamiento estadístico, además de comprender e interpretar los resultados estadísticos.
En esta edición, los estudiantes podrán utilizar las computadoras para efectuar análisis estadísticos estándar y como herramienta para reforzar y visualizar los conceptos estadísticos. MS Excel2016 y MINITAB18 se emplean exclusivamente como programas de cómputo para el análisis estadístico, junto con los procedimientos disponibles en las calculadoras TI-83 o TI-84 Plus. Sin embargo, hemos decidido aislar las instrucciones para generar las salidas de computadora o de calculadora en secciones independientes denominadas “Tecnología actual ”, al final de cada capítulo. En cada análisis se usan ejemplos numéricos para guiar al estudiante a través de los comandos y opciones de MS Excel necesarios en los procedimientos que se estudian en ese capítulo y, a continuación, se presentan los pasos y comandos equivalentes necesarios para obtener los mismos resultados o algunos similares con MINITAB y las calculadoras TI-83/84 Plus. Hemos incluido capturas de pantalla de MS Excel, MINITAB18 y la TI-84 Plus para que el estudiante pueda trabajar en estas secciones como “minilaboratorios”.
Si usted no necesita conocimientos “prácticos” sobre MINITAB, MS Excel o las calculadoras TI-83/84 Plus, o si utiliza otra calculadora o programa de cómputo, puede omitir estas secciones y usar las impresiones como guía para una comprensión básica de los resultados generados por computadora o calculadora.
Medidas numéricas descriptivas en Excel






















MS Excel proporciona la mayoría de las estadísticas descriptivas básicas que se presentaron en el capítulo 2 mediante un solo comando en la pestaña Data. Es posible calcular otras estadísticas descriptivas mediante el grupo Function Library en la pestaña Formulas
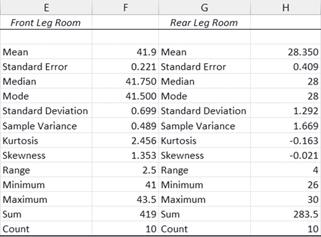
EJEMPLO . Los siguientes datos son los espacios (en pulgadas) para las piernas en los asientos delanteros y traseros de 10 vehículos utilitarios deportivos compactos diferentes:13
Marca y modelo Espacio para piernas en asientos delanteros Espacio para piernas en asientos traseros
ChevroletEquinox42.530.0
FordEscape41.528.0
HyundaiTucson41.528.0 JeepCherokee43.530.0
Medidas numéricas descriptivas en MINITAB MINITAB proporciona la mayoría de las estadísticas descriptivas básicas presentadas en el capítulo 2 mediante un solo comando en los menús desplegables.
EJEMPLO .







Los siguientes datos son los espacios (en pulgadas) para las piernas en los asientos delanteros y traseros de 10 vehículos utilitarios deportivos compactos diferentes:13
Marca y modelo Espacio para piernas en asientos delanteros Espacio para piernas en asientos traseros
ChevroletEquinox42.530.0
FordEscape41.528.0
HyundaiTucson41.528.0
Medidas numéricas descriptivas en las calculadoras TI-83/84 Plus Las calculadoras TI-83/84 Plus pueden utilizarse para calcular estadísticas descriptivas y crear diagramas de caja con los comandos stat ➤ CALC y 2nd ➤ stat plot
EJEMPLO . Los siguientes datos son los espacios (en pulgadas) para las piernas en los asientos delanteros y traseros de 10 vehículos utilitarios deportivos compactos diferentes:13
Marca y modelo Espacio para piernas en asientos delanteros Espacio para piernas en asientos traseros
ChevroletEquinox42.530.0
FordEscape41.528.0 HdiT415280
Prefacio xviii
TECNOLOGÍA ACTUAL MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
Apoyos de estudio
Los numerosos y variados ejercicios del texto son la mejor herramienta de aprendizaje para los estudiantes que emprenden un primer curso de estadística. Las respuestas a todos los ejercicios impares se incluyen al final del libro. Cada ejercicio de aplicación tiene un título, lo que facilita a los alumnos y a los profesores identificar de inmediato tanto el contexto del problema como el área de aplicación. Todos los ejercicios básicos se reescribieron y todos los ejercicios de aplicación se reestructuraron en orden creciente de dificultad. Se añadieron nuevos ejercicios, se eliminaron los obsoletos y se introdujo un nuevo sistema de numeración en cada sección.
Técnicas básicas
¿Aproximación normal? ¿Se puede emplear la aproximación normal para aproximar las probabilidades de la variable aleatoria binomial x, con los valores de n y p dados en los ejercicios 1 a 4? Si no, ¿hay alguna otra aproximación que pueda usar?



1. n = 25 y p = .6 2. n = 45 y p = .05
3. n = 25 y p = .3 4. n = 15 y p = .5












Uso de la aproximación normal Encuentre la media y la desviación estándar de la variable aleatoria binomial x con la información de los ejercicios 5 a 11. Posteriormente, use la corrección por continuidad y calcule las probabilidadesmediantelaaproximaciónnormal
12. P(x ≥ 6) y P(x > 6) cuando n = 15 y p = .5
13. P(4 ≤ x ≤ 6) cuando n = 25 y p = .2
14. P(x ≥ 7) y P(x = 5) cuando n = 20 y p = .3
15. P(x ≥ 10) cuando n = 20 y p = .4
Aplicación de los conceptos básicos
16. Día de la Tierra Una instantánea en la revista USA Today encontró que 47% de los estadounidenses asocia el “reciclaje” con el Día de la Tierra.9 Suponga que se aplica una encuesta a una muestra aleatoria de n = 50 adultos y que la cifra de 47% es correcta. Use la curva normal para aproximar a las probabilidades de los siguientes eventos.
Se debe animar a los estudiantes para que usen las secciones “NECESITO SABER...” en cuanto aparecen en el texto. La ubicación de estas secciones tiene el objetivo de responder las preguntas tal como se plantearían normalmente en los debates. Además, hay numerosos consejos denominados “CONSEJO PRÁCTICO” que aparecen en los márgenes del texto. Estos consejos son breves y concisos.
● Consejo práctico Parámetro ⇔ Población Estadística ⇔ Muestra
En los tres capítulos anteriores usted aprendió mucho sobre distribuciones de probabilidad, como las distribuciones binomiales y normales. La forma de la distribución normal está determinada por su media m y su desviación estándar s, mientras que la forma de la distribución binomial está representada por p. Estas medidas numéricas descriptivas, a las que se llama parámetros, son necesarias para calcular la probabilidad de observar resultados muestrales.
En la práctica usted puede decidir qué tipo de distribución de probabilidad usará como modelo, pero los valores de los parámetros que especifican su formaexacta se desconocen. He aquí dos ejemplos:
Por último, las secciones denominadas “Conceptos y fórmulas clave” aparecen en cada capítulo como un resumen del material cubierto en ese capítulo.
Conceptos y fórmulas clave
I. Medidas de tendencia central de una distribución de datos
1. Media aritmética (media) o promedio
a. Población: m
b. Muestra de n mediciones: x x n i 5
2. Mediana; posición de la mediana n 1 .5(1)
3. Moda
4. Se prefiere la mediana sobre la media si los datos están muy sesgados.
II. Medidas de variabilidad 1R R láilíi
2. La regla empírica solo puede emplearse para conjuntos de datos relativamente en forma de montículo. Aproximadamente 68%, 95% y 99.7% de las mediciones se ubican dentro de una, dos y tres desviaciones estándar de la media, respectivamente.
IV. Medidas de posición relativa
1. Puntaje z muestral: z xx s
2. p-ésimo percentil; p% de las mediciones son menores, y p (100)% son mayores.
3. Cuartil inferior, Q1 ; posición de Q n 51.25(1) 1
4. Cuartil superior, Q3; posición de Q3 = .75(n + 1)




















5. Rango intercuartil: QQ52 IQR 31
V. El resumen de cinco números y los diagramas de caja
Prefacio xix
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
REVISIÓN DEL CAPÍTULO
Recursos para el docente (disponibles solo en inglés)
WebAssign
WebAssign para el texto Introducción a la probabilidad y estadística, de Mendenhall/Beaver/ Beaver, 15.ª edición versión métrica, es una solución didáctica en línea, flexible y totalmente personalizable que pone a disposición de los profesores poderosas herramientas que les permiten implementar las tareas, evaluar al instante el rendimiento individual de los alumnos y del grupo, así como ayudar a sus alumnos a dominar los conceptos del curso. Con la potente plataforma digital WebAssign y el contenido específico de Introducción a la probabilidad y estadística, puede personalizar su curso, mediante una amplia gama de configuraciones de tareas, añadir sus propias preguntas y contenido, y tener acceso a herramientas de análisis y comunicación de los estudiantes y del curso.
MindTap Reader
Disponible a través de WebAssign, MindTap Reader es el libro electrónico de próxima generación de Cengage. El lector MindTap ofrece sólidas herramientas para que los estudiantes subrayen, tomen notas, naveguen e interactúen con el texto. Los profesores pueden editar el texto y los recursos en el lector, así como añadir videos o hipervínculos.
Cognero
La herramienta de pruebas de Cengage, desarrollada por Cognero, es un sistema en línea flexible que le permite importar, editar y manejar contenido del banco de exámenes creado para el texto, o de otros lugares (incluidas sus preguntas de examen favoritas); además le permite crear varias versiones de examen rápidamente y entregar los exámenes a través de su sistema de gestión de aprendizaje, en su salón de clases u otro lugar.
Manual
de
soluciones
para el docente
Este manual en línea que ahorra un valioso tiempo a los docentes ofrece soluciones completas a todos los problemas del texto. Puede descargar el manual de soluciones en el sitio web de acompañamiento para los docentes.
Sitio web de acompañamiento para los docentes
¡Todo lo que necesita para su curso en un solo lugar! Esta colección de herramientas de clase específicas para un libro está disponible en línea en www.cengage.com/login. Ingrese y descargue presentaciones de PowerPoint, imágenes, el Manual de soluciones para el docente, conjuntos de datos y más.
SnapStat
Cuente la historia detrás de las cifras con SnapStat en WebAssign. Diseñado con el apoyo de estudiantes para dar vida a las estadísticas, SnapStat usa imágenes interactivas para efectuar complejos análisis en línea. Los Laboratorios y Proyectos de WebAssign permiten a los estudiantes analizar sus propios datos o bien elegir entre conjuntos de datos preexistentes con el fin de familiarizarse con la tecnología y comprobar, por sí mismos, que la estadística es mucho más que solo números.
WebAssign
WebAssign para el texto Introducción a la probabilidad y estadística, de Mendenhall/Beaver/ Beaver, 15.ª edición versión métrica, le permite prepararse con confianza para la clase. Esta
Prefacio xx
Recursos para el estudiante (disponible solo en inglés y el acceso se vende por separado)
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
plataforma de aprendizaje en línea, para sus cursos de matemáticas, estadística y ciencias, le ayuda a practicar y asimilar lo que estudia. Los videos y tutoriales le explican los conceptos cuando tiene dificultades; la retroalimentación y las calificaciones que se generan al instante le permiten saber dónde se encuentra, de modo que puede enfocar su tiempo de estudio y obtener mejores resultados en sus tareas. ¡Estudie de forma más inteligente con WebAssign!
MindTap Reader
Disponible a través de WebAssign, MindTap Reader es el libro electrónico de próxima generación de Cengage. El lector MindTap ofrece sólidas herramientas para que los estudiantes subrayen, tomen notas, naveguen e interactúen con el texto. Las anotaciones escritas en MindTap se vinculan automáticamente con la aplicación Bloc de notas, donde se pueden ver cronológicamente, de forma lineal y convincente.
SnapStat
Aprenda la historia detrás de las cifras con SnapStat en WebAssign. Diseñado con el apoyo de estudiantes con el objetivo de dar vida a las estadísticas, SnapStat usa imágenes interactivas para efectuar complejos análisis en línea. Los Laboratorios y Proyectos de WebAssign permiten a los estudiantes analizar sus propios datos, o bien elegir entre conjuntos de datos preexistentes con el fin de familiarizarse con la tecnología y comprobar, por sí mismos, que la estadística es mucho más que solo números.
Reconocimientos
Los autores agradecen a Catherine Van Der Laan y al equipo editorial de Cengage Learning por su paciencia, ayuda y cooperación en la preparación de esta edición.
También agradecemos a los revisores de la decimoquinta edición en inglés, Olcay Akman, Matt Harris, Zhongming Huang, Bo Kai, Sarah Miller y Katie Wheaton. Queremos dar las gracias a los autores y a las organizaciones por permitirnos reimprimir material seleccionado; dondequiera que dichos materiales aparecen en el texto, se incluyen las citas y menciones correspondientes.
Robert J. Beaver Barbara M. Beaver
Prefacio xxi
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
¿Qué es la estadística?
¿Qué es la estadística? ¿Alguna vez ha conocido a un experto en esta materia? ¿Sabe usted qué hace? Tal vez piense en la persona que se sienta en la cabina de transmisión del Tazón de las Rosas (Rose Bowl) y registra el número de pases completos, yardas recorridas o intercepciones lanzadas el día de Año Nuevo. O tal vez la simple mención de la palabra estadística le produce temor. Usted quizá piense que no sabe nada de estadística, pero prácticamente cada vez que vea los noticieros o consulte su aplicación de noticias favorita, ¡se encontrará con la estadística de una forma u otra! Estos son algunos ejemplos que encontramos justo antes de las elecciones de noviembre de 2017:

• Northam encabeza la contienda por la gubernatura de Virginia con una ligera ventaja. Las primeras elecciones estatales importantes desde la toma de posesión del presidente Trump se llevarán a cabo en martes... Y aunque el resultado final de la contienda, por sí solo, no nos diga mucho sobre el entorno político nacional, es probable que tenga un gran efecto en las elecciones intermedias de 2018. Las encuestas muestran una contienda bastante reñida, con Northam ligeramente favorecido para ganar [sobre Ed Gillespie]. Un promedio de las últimas 10 encuestas concede a Northam una ventaja de 46 a 43%. Durante el último mes la contienda se endureció, pues el candidato Gillespie logró remontar lo que había sido una ventaja de seis puntos. Sin embargo, hay una dispersión bastante amplia entre las encuestas individuales. Se ha estimado la ventaja de Northam en 17 puntos porcentuales (una encuesta de la Universidad de Quinnipiac) y, por otra parte, ha quedado atrás de su oponente hasta en 8 puntos porcentuales (una encuesta de la Universidad de Hampton).1
—www.fivethirtyeight.com
• ¿Por qué Trump tiene asegurada la nominación del Partido Republicano para 2020? En entrevistas con casi tres docenas de estrategas y recaudadores de fondos del Partido Republicano en las acaloradas últimas semanas, casi todo el mundo me dijo que... esperan que Trump alcance la nominación del Partido Republicano en el año 2020... los obstáculos que sus opositores enfrentarán en las elecciones primarias de 2020 son evidentes si se considera una encuesta reciente del Washington Post/ABC News, que indica que 91% de los votantes de Trump dijo que volvería a votar por él... Esta encuesta de ABC News/Washington Post se realizó por teléfono fijo y celular del 29 de octubre al 1 de noviembre de 2017, en inglés y español, con base en una muestra aleatoria nacional compuesta por 1005 adultos. El margen de error de muestreo es de 3.5 puntos, incluido el efecto de diseño.2
1
—www.cnn.com 1
Introducción
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
Andrea Ricordi, Italy/Moment/Getty Images
¿Qué es la estadística?
Artículos semejantes a estos son comunes en todos los medios de comunicación y se publica una nueva encuesta casi todos los días, justo antes de una elección presidencial o legislativa. Estos artículos nos son muy familiares; sin embargo, pueden dejar algunas preguntas sin respuesta. ¿Cómo se seleccionó a las personas que participaron en la encuesta? ¿Estas personas darán la misma respuesta mañana? ¿Responderán lo mismo el día de las elecciones? ¿Votarán siquiera? ¿Estas personas son representativas de todos los que votarán el día de las elecciones? El trabajo de un experto en estadística es hacer estas preguntas y encontrar respuestas en el lenguaje de la encuesta.
La mayoría cree en el “encubrimiento” de los hechos en el asesinato de JFK
La mayoría del público cree que el asesinato del presidente John F. Kennedy fue parte de una conspiración mayor y no el acto de un solo individuo. Además, la mayoría de los estadounidenses piensa que diversos hechos sobre el tiroteo del año 1963 fueron encubiertos. Casi 50 años después del asesinato de JFK, una encuesta de FOX News indica que muchos estadounidenses están en desacuerdo con las conclusiones del gobierno acerca de ese hecho. La Comisión Warren concluyó que Lee Harvey Oswald actuó solo cuando disparó a Kennedy; no obstante, 66% del público actualmente piensa que el asesinato fue “parte de una conspiración mayor”, mientras que únicamente 25% piensa que fue el “acto de un individuo”.
“Para los estadounidenses de mayor edad, el asesinato de Kennedy fue una experiencia traumática que inició una pérdida de confianza en el gobierno”, comentó John Gorman, presidente de Opinion Dynamics. “Las personas más jóvenes han crecido con películas y documentales que han promocionado la línea de la ‘conspiración’. Por lo tanto, no sorprende que haya un consenso nacional, bastante sólido, de que aún no se sabe la verdad”.
(En la encuesta se preguntó): “¿Cree que conocemos todos los hechos acerca del asesinato del presidente John F. Kennedy o cree que hubo un encubrimiento?”
Conocemos todos los hechos (%) Hubo un encubrimiento (No está seguro)
—www.foxnews.com3
Cuando usted ve un artículo como este, ¿simplemente lee el título y el primer párrafo, o lee más allá y trata de entender el significado de las cifras? ¿Cómo obtuvieron los autores estas cifras? ¿De verdad entrevistaron a todos los estadounidenses con cada afiliación política? Es tarea del experto en estadística responder algunas de estas preguntas.
Noticias de última hora: 98.6 ºF no es normal
Después de creer durante más de un siglo que 98.6 °F era la temperatura corporal humana normal, los investigadores ahora afirman que lo normal ya no es normal.
Para algunas personas, a ciertas horas del día, 99.9 °F podría estar bien mientras que lecturas tan bajas como 96 °F resultan ser muy “humanas”.
El estándar 98.6 °F proviene de cálculos que realizó un médico alemán en 1868. Algunos médicos han sospechado siempre de la investigación de este buen médico, en particular sobre su afirmación: un millón de lecturas, en una época sin computadoras.
Así que Mackowiak & Co. registraron las lecturas de temperatura de 148 personas sanas durante un periodo de tres días y descubrieron que la temperatura media era de 98.2 °F. Únicamente 8% de las lecturas fueron de 98.6 °F.
—The Press-Enterprise4
¿Qué preguntas le vienen a la mente cuando lee este artículo? ¿Cómo seleccionaron los investigadores a las 148 personas y cómo podemos estar seguros de que los resultados obtenidos de estas son precisos cuando se refieren a la población general? ¿Cómo llegaron los investigadores a las temperaturas normales “altas” y “bajas” que se presentan en el artículo? ¿Cómo registró el médico alemán un millón de temperaturas en 1868? Este es otro ejemplo de un problema estadístico con aplicación en la vida cotidiana.
INTRODUCCIÓN
2
Todos 147412 Demócratas 11818 Republicanos 186913 Independientes 127117
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
La estadística es una rama de las matemáticas que tiene aplicaciones en casi todos los aspectos de nuestra vida diaria. Para la mayoría de las personas es un lenguaje nuevo y desconocido; sin embargo, como cualquier lenguaje nuevo, la estadística puede resultar abrumadora a primera vista. Pero una vez que se aprende y se entiende su lenguaje, proporciona una poderosa herramienta para el análisis de datos en muchos campos de aplicación diferentes.
Poblaciones y muestras
En el lenguaje de la estadística, uno de los conceptos fundamentales es el muestreo. En la mayoría de los problemas estadísticos, se extrae un número específico de mediciones o datos (una muestra) de un conjunto de mediciones mucho más grande, llamado población.
En el experimento de la temperatura corporal, la muestra consiste en el conjunto de mediciones de temperatura corporal de las 148 personas sanas seleccionadas por el experimentador. Esperamos que la muestra sea representativa de un conjunto de mediciones mucho más grande: la población, ¡la temperatura corporal de todas las personas sanas del mundo!
¿Qué es más importante para nosotros, la muestra o la población? En la mayoría de los casos nos interesa principalmente la población, pero identificar a cada miembro de la población puede ser difícil o imposible. ¡Imagine que trata de registrar la temperatura corporal de cada persona sana en el mundo o la preferencia presidencial de todos los votantes registrados en Estados Unidos! En cambio, tratamos de describir o predecir el comportamiento de la población con base en la información contenida en una muestra representativa de esa población.
Los términos muestra y población tienen dos significados para la mayoría de las personas. Por ejemplo, usted leyó que una encuesta de Gallup que se aplicó en Estados Unidos se basó en una muestra de 1823 personas. Se supone que a cada persona entrevistada se le plantea una pregunta en particular, y su respuesta representa una sola medición en la muestra. ¿La muestra consiste en el conjunto de 1823 personas o en las 1823 respuestas que dan?
En estadística distinguimos entre el conjunto de objetos en los que se toman las mediciones y las propias mediciones. Para los experimentadores, los objetos en los que se toman las mediciones se denominan unidades experimentales. Quienes se dedican al estudio de las encuestas por muestreo los llaman elementos de la muestra.
Estadística descriptiva e inferencial
Cuando usted tiene ante sí cierto conjunto de mediciones por primera vez, ya sea una muestra o una población, debe encontrar una manera de organizarlo y resumirlo. La rama de la estadística que proporciona herramientas para describir conjuntos de mediciones se denomina estadística descriptiva. Usted ha visto estadísticas descriptivas de muchas formas: gráficas de barras, gráficas circulares y gráficas de líneas que son presentadas, por ejemplo, por algún candidato político; tablas numéricas en los medios de comunicación, o la cantidad promedio de precipitaciones en su aplicación meteorológica favorita. Las gráficas y los resúmenes numéricos generados por computadora son habituales en nuestra comunicación diaria.
Estadística descriptiva e inferencial 3
Población
Muestra
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
DEFINICIÓN
La estadística descriptiva comprende los procedimientos que se usan para resumir y describir las características importantes de un conjunto de mediciones.
Si el conjunto de mediciones es toda la población usted solo necesita obtener conclusiones basadas en las estadísticas descriptivas. Sin embargo, identificar a cada miembro de la población puede resultar demasiado costoso o consumir bastante tiempo. Incluso, aplicar cierta prueba en todas las unidades experimentales de una población las destruiría, por ejemplo, al medir la cantidad de fuerza necesaria para provocar la rotura de un casco de futbol. Por estas u otras razones, es posible que solo cuente con una muestra de la población. Para estudiar la muestra necesitará responder preguntas sobre la población en su conjunto. La rama de la estadística que se ocupa de este problema se denomina estadística inferencial
DEFINICIÓN
La estadística inferencial comprende procedimientos que se usan para hacer inferencias (es decir, obtener conclusiones, hacer predicciones, tomar decisiones) acerca de una población a partir de la información contenida en una muestra extraída de dicha población.
El objetivo de la estadística inferencial es hacer inferencias acerca de una población, a partir de la información contenida en una muestra.
Lograr el objetivo de la estadística inferencial: los pasos necesarios
¿Cómo puede hacer inferencias acerca de una población usando la información contenida en una muestra? La tarea se simplifica si organiza el problema en una serie de pasos lógicos.
1. Especifique las preguntas por responder e identifique la población de interés. En la encuesta electoral de Virginia, el objetivo es determinar quién recibirá más votos el día de las elecciones. Por lo tanto, la población de interés es el conjunto de todos los votos en las elecciones de Virginia. Al seleccionar una muestra es importante que esta última sea representativa de esta población, no de la población que consiste en las preferencias de los votantes algún día previo a la elección.
2. Decida cómo seleccionar la muestra. Esto se denomina diseño del experimento o diseño muestral. ¿La muestra es representativa de la población de interés? Por ejemplo, si se selecciona una muestra de los votantes registrados en la ciudad de San Francisco, ¿sería representativa de todos los votantes del estado de California? ¿Será igual a una muestra de “votantes posibles” (aquellos que probablemente sí votarán en las elecciones)? ¿La muestra es suficientemente grande para responder las preguntas formuladas en el paso 1 sin perder tiempo y dinero en información adicional? Un buen diseño muestral responderá las preguntas planteadas con un costo mínimo para el experimentador.
3. Seleccione y analice la información de la muestra. Al margen de la cantidad de información que contenga la muestra, debe usar un método de análisis adecuado para extraerla. Muchos de estos métodos, que dependen del diseño muestral del paso 2, se explican en el texto.
INTRODUCCIÓN ¿Qué
estadística? 4
es la
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
4. Use la información del paso 3 para hacer inferencias acerca de la población. Es posible usar muchos procedimientos diferentes para hacer estas inferencias, algunos son mejores que otros. Por ejemplo, 10 métodos distintos para estimar la respuesta humana a un fármaco experimental podrían estar disponibles, pero un procedimiento puede ser más preciso que otros. Debe usar el mejor procedimiento de inferencia disponible (muchos de ellos se explican en el texto).
5. Determine la confiabilidad de la inferencia. Puesto que usted está usando solo una fracción de la población para obtener las conclusiones descritas en el paso 4, ¡podría equivocarse! Si una agencia realiza una encuesta estadística para usted, en la que estima que el producto de su empresa ganará 34% del mercado este año, ¿cuánta confianza depositaría en esta estimación? ¿La precisión de la estimación será de 1, 5 o 20 puntos porcentuales?
¿Es suficientemente confiable para que usted la use en el establecimiento de los objetivos de producción? Cada inferencia estadística debe incluir una medida de confiabilidad que indique cuánta confianza se tiene en ella.
Ahora que ha aprendido algunos términos y conceptos básicos, planteamos de nuevo la pregunta que se hizo al principio de esta discusión: ¿sabe lo que hace un experto en estadística? Pues bien, su trabajo es llevar a cabo todos los pasos anteriores.
Claves para un aprendizaje exitoso
A medida que avance en el estudio de la estadística, descubrirá que hay muchos términos y conceptos nuevos por aprender y dominar. Puesto que la estadística es una rama aplicada de las matemáticas, muchos de estos conceptos fundamentales son matemáticos, se basan en los resultados del cálculo o las matemáticas superiores. Sin embargo, no es necesario ser capaz de probar los resultados para aplicarlos de forma lógica. En este texto, usamos ejemplos numéricos y argumentos de sentido común para explicar conceptos estadísticos, en lugar de argumentos matemáticos más complicados.
Actualmente hay computadoras y calculadoras que están disponibles para los estudiantes y que representan una herramienta invaluable. En el estudio de la estadística, incluso el estudiante que inicia puede utilizar programas de cómputo para efectuar análisis estadísticos con un alto grado de velocidad y precisión. Algunos de los programas estadísticos más comunes disponibles en los laboratorios de cómputo son MINITABTM, SAS y SPSS. MINITAB, MS Excel, JMP y otros pueden instalarse tanto en las computadoras de escritorio como en las portátiles. Muchos estudiantes están familiarizados con las calculadoras TI-83 o TI-84 Plus, que incluyen numerosas funciones estadísticas. Incluso hay programas estadísticos en línea y “applets” interactivos que los estudiantes pueden usar.
Estos programas, denominados software estadístico, difieren en los tipos de análisis disponibles, las opciones dentro de los programas y las formas de los resultados impresos (denominados resultados o salidas). Sin embargo, todos son similares. En este libro se utilizarán MINITAB y Microsoft Excel como herramientas estadísticas. Comprender los resultados o las salidas básicas de estos programas le ayudará a interpretar los de otros programas. Del mismo modo, entender los resultados que se muestran en su calculadora TI-83 o TI-84 Plus facilitará mucho la comprensión de una calculadora diferente.
Al final de la mayoría de los capítulos encontrará una sección llamada “Tecnología actual ”. Estas secciones presentan ejemplos numéricos con el fin de guiarlo a través de los comandos y opciones de MINITAB, MS Excel y TI-83/84 Plus necesarios en los procedimientos de ese capítulo. Si utiliza MINITAB, MS Excel o su calculadora TI-83/84 Plus en un laboratorio o en su hogar, tal vez quiera trabajar esta sección con su propia computadora o calculadora para familiarizarse con los métodos prácticos. Si no necesita conocimientos prácticos sobre MINITAB, MS Excel o las calculadoras TI-83/84 Plus, puede omitir esta sección y simplemente usar las imágenes de la computadora o las capturas de pantalla de la calculadora para el análisis, tal como aparecen en el texto.
Claves
5
para un aprendizaje exitoso
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
Lo más importante es que el uso exitoso de la estadística requiere sentido común y pensamiento lógico. Por ejemplo, si queremos encontrar la estatura promedio de todos los estudiantes de una universidad en particular, ¿seleccionaríamos toda nuestra muestra de los miembros del equipo de basquetbol? En el ejemplo de la temperatura corporal, un pensador lógico cuestionaría un promedio con base en un millón de mediciones que se efectuaron en 1868, cuando las computadoras aún no se habían inventado.
A medida que aprenda nuevos términos, conceptos y técnicas estadísticas, recuerde ver cada problema con una mirada crítica y asegúrese de aplicar la regla del sentido común. A lo largo del texto, le recordaremos las dificultades y los peligros del uso o mal uso de la estadística. Benjamin Disraeli dijo una vez que hay tres tipos de mentiras: ¡mentiras, malditas mentiras y estadísticas! Nuestro propósito es demostrar que esta afirmación es errónea, ¡le mostraremos cómo hacer que la estadística trabaje para usted y no mienta por usted!
A medida que avance en el libro, consulte esta introducción de vez en cuando. Cada capítulo aumentará sus conocimientos de estadística y, de alguna manera, debería ayudarlo a lograr uno de los pasos descritos aquí. Cada uno de estos pasos es importante para lograr el objetivo general de la estadística inferencial: hacer inferencias acerca de una población con base en la información contenida en una muestra extraída de esa población.
INTRODUCCIÓN
6
¿Qué es la estadística?
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
Descripción de datos con gráficos
¿Cómo está su presión arterial?

¿Su presión arterial es normal o se encuentra demasiado alta o baja? El estudio de caso al final de este capítulo examina un amplio conjunto de datos sobre la presión arterial. Utilizará gráficas para describir estos datos y comparar su presión arterial con la de otras personas de su misma edad y sexo.
OBJETIVOS DE APRENDIZAJE
Muchosconjuntosdemedicionessonmuestrasseleccionadasdepoblacionesmásgrandes.Otros conjuntosconformantodaunapoblación,comoenelcasodeuncensonacional.Enestecapítulo aprenderáquéesuna variable,cómoclasificarlasvariablesenvariostiposycómosegeneranmedicionesodatos.Posteriormenteserácapazdeusargráficasparadescribirconjuntosdedatos.
ÍNDICE DEL CAPÍTULO
● Distribucionesdedatosysusformas(1.1,1.3)
● Gráficasdepuntos(1.3)
● Gráficascirculares,gráficasdebarras,gráficasdelíneas(1.2,1.3)
● Variablescualitativasycuantitativas:discretasycontinuas(1.1)
● Histogramasdefrecuenciarelativa(1.4)
● Diagramasdetalloyhoja(1.3)
● Datosunivariadosybivariados(1.1)
● Variables,unidadesexperimentales,muestrasypoblaciones,datos(1.1)
● Necesito saber...
Cómo construir un diagrama de tallo y hoja
Cómo construir un histograma de frecuencia relativa
7 1 MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
© Photographee.eu/Shutterstock.com
1.1 Variables y datos
En los capítulos 1 y 2 presentaremos algunas técnicas básicas en estadística descriptiva, la rama de la estadística que se ocupa de describir conjuntos de mediciones, tanto de muestras como de poblaciones. Una vez que haya recopilado un conjunto de datos, ¿cómo puede mostrarlos de forma clara, comprensible y legible? En primer lugar, debe ser capaz de definir qué se entiende por mediciones o “datos” y clasificar los tipos de datos que probablemente encuentre en la vida real. Empezaremos por presentar algunas definiciones.
DEFINICIÓN
Una variable es una característica que cambia o varía con el tiempo y para diferentes personas u objetos en consideración.
Por ejemplo, la temperatura corporal es una variable que cambia con el tiempo en una sola persona; también varía de una persona a otra. La afiliación religiosa, el origen étnico, los ingresos, la estatura, la edad y el número de hijos son variables, características que varían según la persona seleccionada.
En la “Introducción” definimos una unidad experimental o un elemento de la muestra como el objeto en el que se toma una medición. Es lo mismo que decir que una unidad experimental es el objeto sobre el que se mide una variable. Cuando una variable se mide en un conjunto de unidades experimentales se obtiene un conjunto de mediciones o datos
DEFINICIÓN
Una unidad experimental es el individuo o el objeto en el que se mide una variable. Se produce una sola medición o valor de dato cuando una variable se mide en la realidad en una unidad experimental.
Si se obtiene una medición para cada unidad experimental en toda la colección, el conjunto de datos resultante constituye la población de interés. Cualquier subconjunto más pequeño de mediciones es una muestra
DEFINICIÓN
Una población es el conjunto de todas las mediciones de interés para el investigador.
DEFINICIÓN
Una muestra es un subconjunto de mediciones seleccionado de la población de interés.
EJEMPLO . De todos los estudiantes de pregrado de una universidad grande se selecciona un subconjunto de cinco y las mediciones se registran en una hoja de cálculo, como se muestra en la figura 1.1. Identifique los diversos elementos que intervienen en la obtención de este conjunto de datos.
Solución La unidad experimental en la que se miden las variables es un estudiante universitario del campus en particular, esto se muestra en la columna A. Para cada estudiante se miden cinco variables: promedio de calificaciones (GPA, grade point average), género, nivel en la universidad, especialidad y número actual de unidades matriculadas. Cada una de estas
CAPÍTULO Descripción de datos con gráficos 8
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
Figura 1.1
Mediciones en cinco estudiantes de pregrado
Estudiante Género Especialidad Número de unidades Psicología Matemáticas
características varía de un estudiante a otro. Si consideramos que los GPA de todos los estudiantes de esta universidad son la población de interés, los cinco promedios de la columna B representan una muestra de esta población. Si se hubiera medido el promedio de cada estudiante de pregrado de la universidad, tendríamos toda la población de mediciones para esta variable.
La segunda variable que se mide en los estudiantes es el género, en la columna C. Esta variable es algo diferente del GPA porque normalmente toma uno de dos valores: masculino (M) o femenino (F). Si pudiéramos identificar a cada miembro de la población, esto consistiría en un conjunto de M y F, uno para cada estudiante de la universidad. La tercera y cuarta variables, nivel y especialidad, también involucran datos no numéricos: el nivel tiene cuatro categorías (primero, segundo, tercero y último año) y la variable especialidad tiene una categoría para cada especialidad de pregrado ofrecida en el campus. La última variable, el número actual de unidades matriculadas, se valora numéricamente y consiste en un conjunto de números en lugar de un conjunto de cualidades o características.
Aunque hemos analizado cada variable de manera individual, recuerde que hemos medido cada una de estas cinco variables en una sola unidad experimental: el estudiante. Por lo tanto, en este ejemplo, una “medición” en realidad consiste en cinco observaciones, una para cada variable medida. Por ejemplo, la medición tomada en el estudiante 2 produce esta observación: (2.3, F, segundo, Matemáticas, 15)
Hay una diferencia entre una sola variable medida en una sola unidad experimental y múltiples variables medidas en una sola unidad experimental como en el ejemplo 1.1.
DEFINICIÓN
Se obtienen datos bivariados cuando se mide una sola variable en una sola unidad experimental.
DEFINICIÓN
Se obtienen datos bivariados cuando se miden dos variables en una sola unidad experimental.

Se obtienen datos multivariados cuando se miden más de dos variables.
Si se mide la temperatura corporal de 148 personas, los datos resultantes son univariados. En el ejemplo 1.1 se midieron cinco variables en cada estudiante, lo que dio como resultado datos multivariados.
■ Tipos de variables
Las variables pueden clasificarse en dos tipos: cualitativas o cuantitativas.
DEFINICIÓN
Las variables cualitativas miden una cualidad o característica en cada unidad experimental. Las variables cuantitativas miden una cantidad numérica en cada unidad experimental.
. Variables y datos 9
Inglés Inglés Negocios Nivel Primero Segundo Segundo Primero Tercero
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
● Consejo práctico
Cualitativo ⇔ “calidad” o característica
Cuantitativo ⇔ “cantidad” o número
Las variables cualitativas producen datos que se pueden separar en categorías. Por lo tanto, se denominan variables categóricas y producen datos categóricos. Las variables género, año y especialidad en el ejemplo 1.1 son variables cualitativas que producen datos categóricos. Estos son otros ejemplos:
• Afiliación política: republicana, demócrata, independiente.
• Clasificación de sabor: excelente, buena, regular, mala.
• Color de un caramelo: café, amarillo, rojo, naranja, verde, azul.
Las variables cuantitativas, que a menudo se representan con la letra x , producen datos numéricos como los que se enlistan a continuación:
• x = tasa de interés preferencial
• x = número de pasajeros en un vuelo de Los Ángeles a Nueva York
• x = peso de un paquete listo para enviar
• x = volumen del jugo de naranja en un vaso
Observe la diferencia en los tipos de valores numéricos que toman estas variables cuantitativas. El número de pasajeros, por ejemplo, solo puede ser x 5 0, 1, 2, . . ., mientras que el peso de un paquete puede ser cualquier valor superior a cero, o x . 0. Para dar cuenta de esta diferencia, definimos dos tipos de variables cuantitativas: discretas y continuas.
DEFINICIÓN
Una variable discreta solo puede tomar un número finito o contable de valores. Una variable continua puede tomar los valores infinitos que corresponden a los puntos que hay en un intervalo de recta.
● Consejo práctico
Discreto ⇔ “es posible enlistar los valores”
Continuo ⇔ “no es posible enlistar los valores”
El término discreto se refiere a los espacios discretos entre los valores posibles que la variable puede tomar. Variables como el número de miembros de una familia, el número de automóviles nuevos vendidos y el número de neumáticos defectuosos devueltos para su reemplazo son ejemplos de variables discretas. Por otro lado, variables como la altura, el peso, el tiempo, la distancia y el volumen son continuas porque pueden tomar valores en cualquier punto a lo largo de un intervalo de recta. En este caso, ¡para cualesquiera dos valores que se elijan siempre se puede encontrar un tercer valor entre ellos!
Identifique cada una de las siguientes variables como cualitativa o cuantitativa:
1. El uso más frecuente de su horno microondas (recalentar, descongelar, calentar, otros).
2. El número de consumidores que se niegan a responder una encuesta telefónica.
3. La puerta elegida por un ratón en un experimento de laberinto (A, B o C).
4. El tiempo ganador para un caballo que corre en el Derby de Kentucky.
5. El número de niños en una clase de quinto grado que leen al nivel de su grado o por encima de él.
● Consejo práctico
Las variables discretas a menudo consisten en el “número de” elementos en un conjunto.
Solución Las variables 1 y 3 son cualitativas porque solo se mide una cualidad o característica de cada individuo u objeto; las categorías para estas dos variables se muestran entre paréntesis. Las otras tres variables son cuantitativas. Las variables 2 y 5 son discretas porque pueden tomar cualquiera de los valores x 5 0, 1, 2, . . ., con un valor máximo en función del número de consumidores a quienes se llamó o del número de niños en la clase, respectivamente. La variable 4, el tiempo ganador para un caballo que corre en el Derby de Kentucky, es la única variable continua de la lista. El tiempo ganador, si puede medirse con suficiente precisión, podría ser de 121 segundos, 121.5 segundos, 121.25 segundos o cualquier valor entre dos tiempos cualesquiera que se hayan elegido.
CAPÍTULO Descripción de datos con gráficos 10
EJEMPLO .
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
¿Por qué preocuparse por los diferentes tipos de variables (que se muestran en la figura 1.2) y los datos que generan? Porque los diferentes tipos de datos requieren métodos distintos para su descripción, de modo que puedan presentarse de forma clara y comprensible para el público.
Datos
1.1 E JERCICIOS
Técnicas básicas
Unidades experimentales Defina las unidades experimentales para las variables descritas en los ejercicios 1 a 5.
1. Género de un estudiante.
2. Número de errores en un examen parcial.
3. Edad de un paciente con cáncer.
4. Número de flores en una planta de azalea.
5. Color de un automóvil que entra a un estacionamiento. ¿Cualitativa o cuantitativa? Las variables de los ejercicios
6 a 9 ¿son cualitativas o cuantitativas?
6. Cantidad de tiempo que toma armar un rompecabezas sencillo.
7. Número de estudiantes en un aula de primer grado.
8. Calificación de un político recién elegido (excelente, bueno, regular, malo).
9. Estado en el que vive una persona.
¿Discreta o continua? Las variables de los ejercicios 10 a
18, ¿son discretas o continuas?
10. Población en un área determinada de Estados Unidos.
11. Peso de los periódicos reciclados en un día.
12. Número de reclamos presentados a una compañía de seguros durante un día.
13. Número de consumidores en una encuesta de 1,000 entrevistados que consideran importante el etiquetado nutricional de los productos alimenticios.
14. Número de accidentes de navegación en un tramo de 80 kilómetros del río Colorado.
15. Tiempo necesario para completar un cuestionario.
16. Costo de una lechuga.
17. Número de hermanos y hermanas que usted tiene.
18. Rendimiento del trigo (en toneladas) de una parcela de una hectárea.
¿Poblaciones o muestras? En los ejercicios 19 a 22, determine si los datos recopilados representan una población o una muestra.
19. Un investigador utiliza una base de datos estatal para determinar el porcentaje de conductores de Michigan que han tenido un accidente en los últimos cinco años.
20. Se entrevistó a mil ciudadanos y se registraron sus opiniones sobre el control de armas.
21. Veinte animales reciben una nueva dieta y se registra su aumento de peso durante tres meses.
22. La distribución de ingresos de 10% de la población que percibe los salarios más altos en Estados Unidos se determina mediante datos del Servicio Interno de Impuestos.
. Variables y datos 11
Continuo
CualitativoCuantitativo Discreto
Figura 1.2 Tipos de datos
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
Aplicación de los conceptos básicos
23. Estacionamiento en el campus Seis vehículos seleccionados de una base de datos de automóviles del campus se muestran en la tabla.
VehículoTipoMarca¿Colectivo?
25. Actitudes de los votantes Usted es un candidato para la legislatura de su estado y desea aplicar una encuesta para conocer las actitudes de los votantes hacia sus posibilidades de ganar.
Distancia de viaje en una dirección (kilómetros)
a. ¿Cuál es la población que le interesa y de la que desea elegir su muestra?
Antigüedad (años)
1AutoHondaNo37.86
2AutoToyotaNo27.53
3CamiónToyotaNo16.24
4CamionetaDodgeSí50.72
5MotocicletaHarleyDavidson No40.81
6AutoChevroletNo 8.69
a. ¿Cuáles son las unidades experimentales?
b. Enliste las variables que se están midiendo, ¿de qué tipo son?
c. ¿Se trata de datos univariados, bivariados o multivariados?
24. Expresidentes de Estados Unidos Un conjunto de datos proporciona información sobre las edades, al momento de la muerte, de los 38 expresidentes de Estados Unidos que han fallecido hasta ahora.
a. Este conjunto de datos, ¿es una población o una muestra?
b. ¿Cuál es la variable que se mide?
c. ¿La variable del inciso b es cuantitativa o cualitativa?
b. La población en el inciso a, ¿cómo depende del tiempo?
26. Tiempos de supervivencia al cáncer Un investigador desea estimar el tiempo de supervivencia de un paciente enfermo de cáncer después de un ciclo de radioterapia.
a. ¿Cuál es la variable de interés para el investigador?
b. La variable en el inciso a, ¿es cualitativa, cuantitativa discreta o cuantitativa continua?
c. ¿Cuál es la población de interés?
d. ¿Cómo podría el investigador seleccionar una muestra de la población?
e. ¿Qué problemas pueden ocurrir en el muestreo de esta población?
27. Nuevos métodos de enseñanza Una investigadora quiere saber si una nueva forma de enseñar a leer a estudiantes sordos es eficaz. Mide la puntuación de los estudiantes en un examen de lectura antes y después de enseñarles con el nuevo método.
a. ¿Cuál es la variable que se mide? ¿Qué tipo de variable es?
b. ¿Cuál es la unidad experimental?
c. ¿Cuál es la población de interés?
1.2 Gráficos para datos categóricos
Una vez recopilados los datos, estos se pueden consolidar y resumir para mostrar la siguiente información:
• Los valores de la variable que se han medido.
• La frecuencia con la que se ha producido cada valor. En primer lugar, elabore una tabla estadística y, a continuación, úsela para crear una gráfica denominada distribución de datos. El tipo de gráfica que elija depende del tipo de variable que haya medido.
Cuando la variable de interés es cualitativa o categórica, la tabla estadística incluye una lista de las categorías junto con una medida de la frecuencia con la que se produjo cada categoría. Puede medir “con qué frecuencia” se ha producido cada valor de tres maneras diferentes:
• La frecuencia o el número de mediciones en cada categoría.
• La frecuencia relativa o proporción de mediciones en cada categoría.
• El porcentaje de mediciones en cada categoría.
CAPÍTULO Descripción de datos con gráficos 12
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
Sea n el número total de mediciones en el conjunto, puede encontrar la frecuencia relativa y el porcentaje mediante estas relaciones:
● Consejo práctico
Tres pasos para la distribución de datos:
(1) Datos brutos ⇒
(2) Tabla estadística ⇒
(3) Gráfico
La suma de las frecuencias siempre es n, la suma de las frecuencias relativas es 1 y la suma de los porcentajes es 100%.
Cuando la variable es cualitativa, las categorías deben elegirse de tal manera que:
• una medición se clasifique en una y solo una categoría, y
• haya una categoría a la que pertenezca cada medición. Por ejemplo,
• Para clasificar los productos cárnicos según el tipo de carne utilizada, podría usar las categorías: carne de res, pollo, mariscos, cerdo, pavo u otros.
• Para clasificar los rangos de los profesores universitarios, podría emplear las categorías: profesor, profesor asociado, profesor asistente, instructor, conferencista, otros.
La categoría “otros” se incluye en ambos casos para permitir la posibilidad de que una medición no entre en alguna de las categorías definidas.
Una vez que las mediciones se han resumido en una tabla estadística, puede usar una gráfica circular o una de barras para mostrar la distribución de los datos. Una gráfica circular es la que se conoce como gráfica de pay o pastel, y que muestra cómo se distribuyen los datos entre las categorías. Una gráfica de barras muestra la misma distribución de datos entre las categorías, y la altura de las barras mide la frecuencia con la que se observa cada categoría en particular.
EJEMPLO . En una encuesta sobre educación pública se pidió a 400 administradores de escuelas que calificaran la calidad de la educación en Estados Unidos. Sus respuestas se resumen en la tabla 1.1. Elabore una gráfica circular y una gráfica de barras para este conjunto de datos.
Solución Para crear una gráfica circular, asigne un sector del círculo a cada categoría. El ángulo de cada sector está determinado por la proporción de mediciones (o frecuencia relativa) en esa categoría. Como un círculo tiene 360°, puede usar la siguiente ecuación para encontrar el ángulo:
Ángulo 5 Frecuencia relativa 3 360°
■ Tabla 1.1 Calificación de la educación en Estados Unidos hecha por 400 educadores
CalificaciónFrecuencia
A35 B260
C93 D12
Total400
● Consejo práctico
Las proporciones suman 1. Los porcentajes suman 100. Los ángulos de sector suman 360°.
La tabla 1.2 muestra las calificaciones junto con las frecuencias, las frecuencias relativas, los porcentajes y los ángulos de sector necesarios para elaborar la gráfica circular que se muestra en la figura 1.3. Mientras que en las gráficas circulares se emplean los porcentajes para determinar los tamaños relativos de los “sectores circulares”, en las gráficas de barras por lo general se emplean las frecuencias de las categorías. En la figura 1.4 se muestra una gráfica de barras para estos datos.
. Gráficos para datos categóricos 13
Frecuenciasrelativas Frecuencia Porcentaje100 Frecuenciarelativa 5 53 n
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
EJEMPLO .
■ Tabla 1.2 Cálculos necesarios para crear la gráfica circular del ejemplo 1.3 CalificaciónFrecuenciaFrecuencia relativaPorcentajeÁngulo
El aspecto de estas dos gráficas es muy diferente. La gráfica circular muestra la relación de las partes con el todo; la gráfica de barras, en cambio, muestra la cantidad o frecuencia real de cada categoría. Como las categorías de este ejemplo están ordenadas como “calificaciones” (A, B, C y D), no se quiere reordenar las barras de la gráfica para cambiar su forma. En una gráfica circular el orden de presentación es irrelevante.
Una bolsa de cacahuates M&M’s® contiene 21 piezas con los colores que se indican en la tabla 1.3. La variable “color” es cualitativa, por lo que la tabla 1.4 enumera las seis categorías junto con el conteo del número de chocolates por cada color. Las tres últimas columnas de la tabla 1.4 muestran la frecuencia con la que se produjo cada categoría. Como las categorías son colores y no tienen un orden en particular, puede crear gráficas de barras con muchas formas diferentes simplemente reordenando las barras. Para enfatizar que el café es el color más frecuente, seguido del azul, el verde y el naranja, se ordenan las barras de mayor a menor frecuencia y se elabora la gráfica de barras de la figura 1.5. Una gráfica de barras donde las barras se ordenan de mayor a menor altura se denomina diagrama de Pareto
14
CAPÍTULO Descripción de datos con gráficos
A3535/400 5 .099% 358.09360324 B260260/400 5 .6565% 8234.0 C9393/400 5 .2323% 882.8 D1212/400 5 .033% 8 10.8 Total4001.00100% 8360 D 3.0% A 8.8% B 65.0% C 23.3% Figura 1.3 Gráfica circular para el ejemplo 1.3 Figura 1.4 Gráfica de barras para el ejemplo 1.3 250 200 150 100 50 0 ABCD Calificación Frecuencia
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
■ Tabla 1.3 Datos brutos: colores de 21 chocolates confitados
1.2 EJERCICIOS
E JERCICIOS
■ Tabla 1.4 Tabla estadística: datos de chocolates confitados para el ejemplo 1.4
CategoríaConteoFrecuenciaFrecuencia relativaPorcentaje
CaféIIIII 66/2128%
VerdeIII 33/2114
NaranjaIII 33/2114
AmarilloII 22/2110
RojoII 22/2110
AzulIIII 55/2124
Total211100%
Técnicas básicas
Gráficas circulares y de barras Los datos de los ejercicios 1 a 3 representan diferentes formas de clasificar a un grupo de 100 estudiantes de una clase de estadística. Elabore una gráfica de barras y una gráfica circular para describir cada conjunto de datos.
Calificación finalFrecuencia
A31
B36
C21 D9
Primeraño32
Segundoaño34
Terceraño17
Últimoaño 9
Graduado 8
Facultad Frecuencia
Humanidades,ArtesyCiencias43
CienciasNaturalesyAgronomía32
Negocios17
4. Grupos de personas Cincuenta personas se agrupan en cuatro categorías: A, B, C y D, y el número de personas que pertenecen a cada categoría se muestra en la tabla:
CategoríaFrecuencia
a. Elabore una gráfica circular para describir los datos.
b. Elabore una gráfica de barras para describir los datos.
c. ¿Cambia la forma de la gráfica de barras del inciso b según el orden de presentación de las cuatro categorías?
¿Es importante el orden de presentación?
d. ¿Qué proporción de personas están en las categorías B, C o D?
e. ¿Qué porcentaje de personas no están en la categoría B?
.
Gráficos para datos categóricos 15
RojoRojoVerdeCafé AmarilloNaranjaVerdeAzul CaféAzulAzulCafé NaranjaAzulCaféNaranja
CaféVerdeCaféAzul
Amarillo
Figura 1.5
6 5 4 3 2 1 0
Diagrama de Pareto para el ejemplo 1.4
Frecuencia
Café Azul Verde Naranja Amarillo Rojo Color
F3
Otras8 1. 3.
B14 C20
A11
D5
2. Nivel Frecuencia
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
5. Pantalones de mezclilla Un fabricante de pantalones de mezclilla tiene plantas de manufactura en California, Arizona y Texas. Se seleccionan al azar 25 pantalones de la base de datos computarizada y se registra el estado en el que se produce cada uno:
9. Elabore una gráfica de barras para describir el nivel de aprobación de Barack Obama según la edad.
10. ¿Qué efecto, si lo hay, tienen las variables de género, origen étnico, edad y afiliación de partido en las calificaciones de aprobación?
a. Use una gráfica circular para describir los datos.
b. Use una gráfica de barras para describir los datos.
c. ¿Qué proporción de pantalones se fabrica en Texas?
d. ¿Qué estado produjo la mayor cantidad de pantalones?
e. Si quiere saber si las tres plantas produjeron la misma cantidad de pantalones, ¿cómo puede usar las gráficas de los incisos a y b para averiguarlo? ¿Qué conclusiones puede obtener a partir de estos datos?
Aplicación de los conceptos básicos
Popularidadpresidencial Después de las elecciones de 2016 se aplicó una encuesta para estudiar los niveles de aprobación de los expresidentes George W. Bush y Barack Obama. En la encuesta, que incluyó a 1,009 adultos estadounidenses de 18 años o más que viven en Estados Unidos y el Distrito de Columbia, se obtuvieron calificaciones de aprobación por género, origen étnico, edad y afiliación de partido.1 Use estos datos para los ejercicios 6 a 10.
Categoría George W. BushBarack Obama

11. ¿Le gustaría ser presidente? En una encuesta de opinión realizada por ABC News, casi 80% de los adolescentes dijo que no estaba interesado en ser presidente de Estados Unidos.2 Cuando se les preguntó: “¿Cuál es la razón principal por la que no querría ser presidente?”, mencionaron las siguientes respuestas:
Otrosplanesdecarrera/noleinteresa40% Demasiadapresión20% Demasiadotrabajo15% Noseríabuenoenello14% Demasiadasdiscusiones5%
a. ¿Se incluyen todos los motivos en esta tabla? Añada otras categorías si lo considera necesario.
b. ¿Usaría una gráfica circular o una gráfica de barras para describir visualmente los datos? ¿Por qué?
c. Dibuje la gráfica que eligió en el inciso b.
d. Si usted fuera la persona que aplicó la encuesta de opinión, ¿qué otras cuestiones querría investigar?
Adultos
estadounidenses 5963
Género Hombre5660
Mujer6066
Origen étnico
Caucásico6455


Nocaucásico4782
Edad
18a344275
35a546462
551 6555
Afiliación de partido
Republicanos8222
Independientes5665
Demócratas4195
6. Elabore una gráfica de barras para describir el nivel de aprobación de George W. Bush según la afiliación de partido.
7. Elabore una gráfica de barras para describir el nivel de aprobación de George W. Bush según la edad.
8. Elabore una gráfica de barras para describir el nivel de aprobación de Barack Obama según la afiliación de partido.
Usuarios de Facebook La red social Facebook ha crecido rápidamente en los últimos 10 años. La siguiente tabla muestra el número promedio de usuarios diarios (en millones) a medida que ha crecido de 2010 a 2017, en diferentes regiones del mundo.3 Use estos datos para resolver los ejercicios 12 a 15.
Región
20102017
EstadosUnidos/Canadá99183
Europa107271
Asia64453
Restodelmundo58419
Total3281,326
Fuente: Reportes de la compañía | A partir del segundo trimestre de 2017.
12. Use una gráfica circular para describir la distribución de los usuarios diarios promedio en las cuatro regiones en 2017.
13. Use una gráfica de barras para describir la distribución de los usuarios diarios promedio en las cuatro regiones en 2010.
14. Use una gráfica de barras para describir la distribución de los usuarios diarios promedio en las cuatro regiones en 2017.
15. ¿Cómo describiría los cambios en la distribución de los usuarios diarios promedio durante este periodo de siete años?
CAPÍTULO Descripción de datos con gráficos 16
DATA SET DS0101
CACATXTXTX AZAZCAAZTX CAAZTXTXTX CAAZAZCACA
CAAZAZTXCA
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
16. Regreso al trabajo ¿Cuánto tiempo le lleva adaptarse a su rutina laboral normal después de volver de vacaciones? Aquí se muestra una gráfica de barras con datos de USA Today:
a. ¿Se tienen en cuenta todas las opiniones en la gráfica? Añada otra categoría si lo considera necesario.
b. ¿La gráfica de barras se dibujó con precisión? Es decir, ¿las tres barras están en la proporción correcta entre sí?
c. Use una gráfica circular para describir las opiniones. ¿Cuál gráfica resulta más interesante?
Adaptación después de vacaciones
Participación mundial en los ingresos por diamantes
17. Dibuje una gráfica circular para describir las distintas participaciones de los ingresos mundiales por producción de diamantes.
18. Dibuje una gráfica de barras para describir las distintas participaciones de los ingresos mundiales por producción de diamantes.
19. Dibuje un diagrama de Pareto para describir las distintas participaciones de los ingresos mundiales por producción de diamantes.
20. ¿Cuál de las gráficas es la más eficaz para describir los datos?
DATA SET DS0102



¡Los diamantes son para siempre! Gran parte de la industria minera de diamantes del mundo se encuentra en África, Rusia y Canadá. A continuación se muestra una representación visual de la participación de los ingresos mundiales derivados de la producción de diamantes, adaptada de la revista Time Magazine 4 Use esta información para responder las preguntas de los ejercicios 17 a 20.
21. Colores de automóviles Los colores más populares para autos compactos y deportivos en los últimos años se muestran en la tabla.5
Color PorcentajeColor Porcentaje Plata14Blanco/blanco perla
21 Negro/efecto negro21Beige/café4 Gris17Amarillo/dorado2 Azul9Verde1 Rojo11Otro ,1
Fuente:The World Almanac and Book of Facts 2017 Use una gráfica apropiada para describir estos datos.
1.3 Gráficos para datos cuantitativos
Las variables cuantitativas miden una cantidad en cada unidad experimental. Si la variable solo puede tomar un número finito o contable de valores, se trata de una variable discreta. Una variable que puede tomar el número infinito de valores correspondientes a los puntos en un intervalo de recta se denomina continua
■ Gráficas circulares y gráficas de barras
A veces una variable cuantitativa puede medirse en diferentes segmentos de la población o para diferentes categorías de clasificación. Por ejemplo, usted puede medir los ingresos promedio de personas de diferentes grupos de edad y géneros, o que viven en áreas geográficas distintas del país. En esos casos puede usar gráficas circulares o de barras para describir los datos, utilizando la cantidad medida en cada categoría. La gráfica circular muestra cómo se distribuye la cantidad total entre las categorías y la gráfica de barras se vale de la altura de cada barra para mostrar la cantidad en una categoría en particular.
. Gráficos para datos cuantitativos 17
Botsuana Otros 8–13% Zimbabwe 10% Angola 10% Sudáfrica 18% Canadá 20% Rusia
26%
40 30 20 10 0 Porcentaje 40 34 19
UndíaVariosdías Sintiempo
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
Fuente: Kimberley Process.
EJEMPLO .
La cantidad de dinero gastada en el año fiscal 2016 por el Departamento de Defensa de Estados Unidos en varias categorías se muestra en la tabla 1.5.6 Utilice tanto una gráfica circular como una de barras para describir los datos. Compare las dos formas de presentación.
■ Tabla 1.5 Gastos por categoría
Categoría
Cantidad (miles de millones de dólares)
Personalmilitar138.6
Operaciónymantenimiento244.4
Adquisiciones118.9
Investigaciónydesarrollo69.0
Construcciónmilitar6.9
Otro2.5
Total 580.3
Solución Se están midiendo dos variables: la categoría del gasto (cualitativa) y la cantidad del gasto (cuantitativa). La gráfica de barras de la figura 1.6 muestra las categorías en el eje horizontal y las cantidades en el eje vertical.
OperaciónAdquisicionesPersonalymantenimiento militar
Para la gráfica circular de la figura 1.7, cada “sector circular” representa la proporción de los gastos totales ($580.3 mil millones) correspondiente a su categoría particular. Por ejemplo, para la categoría de investigación y desarrollo, el ángulo del sector es
CAPÍTULO Descripción de datos con gráficos 18
250 200 150 100 50 0 Cantidad (miles de millones de dólares)
InvestigaciónydesarrolloConstrucciónmilitar Otro
3858 69.0 580.3 36042.8 Construcción militar 6.9 Otro 2.5 Personal militar 138.6 Operación y mantenimiento 244.4 Adquisiciones 118.9 Investigación y desarrollo 69.0
barras
ejemplo 1.5
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
Figura 1.6
Gráfica de
para el
Figura 1.7
Gráfica
circular para el ejemplo 1.5
EJEMPLO .
Ambas gráficas muestran que las mayores cantidades de dinero se gastaron en personal y operaciones. Como no hay un orden particular para las categorías, puede reorganizar las barras o los sectores de las gráficas en la forma que desee. La forma de la gráfica de barras no influye en su interpretación.
■ Gráficas de líneas
Cuando una variable cuantitativa se registra a lo largo del tiempo a intervalos equidistantes (como diario, semanal, mensual, trimestral o anual), el conjunto de datos forma una serie de tiempo. Los datos de series de tiempo se presentan de forma más eficaz en una gráfica de líneas con el tiempo representado en el eje horizontal. La idea es tratar de encontrar un patrón o tendencia que probablemente continúe en el futuro, y luego usar ese patrón para hacer predicciones precisas para el futuro inmediato.
En 2025, los baby boomers de edad más avanzada (nacidos en 1946) tendrán 79 años, y los integrantes de la Generación X de edad más avanzada (nacidos en 1965) estarán a dos años de ser elegibles para jubilarse. ¿Cómo afectará esto las tendencias de los consumidores en los próximos 40 años? ¿Habrá fondos suficientes para que los baby boomers reciban los beneficios del Seguro Social? La Oficina del Censo de Estados Unidos realiza proyecciones acerca de la población estadounidense que tendrá 85 años o más en los próximos años, como se muestra en la tabla 1.6.5 Utilice una gráfica de líneas para representar los datos. ¿Cuál es el efecto de estirar o encoger el eje vertical de la gráfica de líneas?
■ Tabla 1.6 Proyecciones de crecimiento demográfico
Fuente: The World Almanac and Book of Facts 2017, p. 618
Solución La variable cuantitativa “85 y más” se mide en cuatro intervalos, creando una serie de tiempo que puede representarse visualmente mediante una gráfica de líneas. Los intervalos están marcados en el eje horizontal y las proyecciones en el eje vertical. Los puntos de datos se conectan para formar las gráficas de líneas de la figura 1.8. Observe la diferencia en las escalas verticales de las dos gráficas. Encoger la escala en el eje vertical hace que los cambios grandes parezcan pequeños y viceversa. Para evitar conclusiones equivocadas, observe cuidadosamente las escalas de los ejes vertical y horizontal. Sin embargo, a partir de ambas gráficas se obtiene una imagen clara del número cada vez mayor de personas de 85 años y más en los próximos 40 años.
. Gráficos
19
para datos cuantitativos
Año 20202030204020502060 85ymás(millones)6.79.114.619.019.7
2050 2060 2040 2030 2020 Año 20.0 17.5 15.0 12.5 10.0 7.5 5.0 85 y más (millones) Figura 1.8 Gráficas de líneas para el ejemplo 1.6 100 80 60 40 20 85 y más (millones) 2050 2060 2040 2030 2020 Año MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
• Consejo práctico ¡Tenga cuidado de estirar o encoger los ejes cuando elabore o analice una gráfica!
Figura 1.9
Gráficas de puntos para conjuntos de datos pequeños y grandes
■ Gráficas de puntos
Muchos conjuntos de datos cuantitativos consisten en números que no se pueden separar fácilmente en categorías o intervalos. ¡Necesita una forma diferente de graficar este tipo de datos!
La gráfica más sencilla para los datos cuantitativos es la gráfica de puntos. Para un conjunto pequeño de datos (por ejemplo, el conjunto 2, 6, 9, 3, 7, 6) puede simplemente trazar los datos como puntos en un eje horizontal, como se muestra en la figura 1.9(a). Sin embargo, para un conjunto de datos grande, como el de la figura 1.9(b), la gráfica de puntos puede ser difícil de interpretar.
■ Diagramas de tallo y hoja
Otra forma sencilla de mostrar la distribución de un conjunto de datos cuantitativos es el diagrama de tallo y hoja. Esta gráfica utiliza los valores numéricos de cada punto de datos.
Necesito saber...
Cómo construir un diagrama de tallo y hoja
1. Divida cada dato en dos partes: el tallo y la hoja.
2. Enliste los tallos en una columna, con una línea vertical a la derecha.
3. Para cada dato, registre la parte de la hoja en la misma fila que su tallo correspondiente.
4. En cada tallo, ordene las hojas de menor a mayor.
5. Proporcione una clave para la codificación del tallo y de la hoja de tal forma que el lector pueda volver a generar los datos originales si es necesario.
EJEMPLO . La tabla 1.7 muestra los precios (en dólares) de 19 marcas diferentes de zapatos para caminar. Utilice un diagrama de tallo y hoja para representar los datos.
■ Tabla 1.7 Precios de zapatos para caminar 907070707570 656860747095
Solución Para crear el tallo y la hoja, divida cada observación entre las unidades y las decenas. El número de la izquierda es el tallo y el número de la derecha es la hoja. Por lo tanto, para los zapatos que cuestan $65, el tallo es 6 y la hoja es 5. Los tallos, que van de 4 a 9, se enlistan en la figura 1.10, junto con las hojas para cada uno de los 19 datos. Si indica que la unidad de hoja es 1, el lector sabrá que el tallo 6 y la hoja 8, por ejemplo, representan el número 68, registrado al dólar más cercano.
CAPÍTULO Descripción de datos con gráficos 20
2 3 4 5 6 7 8 9 Conjunto de datos pequeño (a) 0.98 1.05 1.12 1.19 1.26 1.33 1.40 1.47 Conjunto de datos grande (b)
?
70
757068654065
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
EJEMPLO .
A veces, las opciones de tallos disponibles dan como resultado un diagrama que contiene muy pocos tallos y una gran cantidad de hojas en cada tallo. En esta situación puede extender los tallos dividiendo cada uno en varias líneas, según los valores de hoja que se les asignen. En general los tallos se dividen de dos maneras:
• En dos líneas, con la hojas de 0 a 4 en la primera línea y las hojas de 5 a 9 en la segunda línea.
• En cinco líneas, con las hojas 0-1, 2-3, 4-5, 6-7 y 8-9 en las cinco líneas, respectivamente.
Los datos de la tabla 1.8 son los pesos al nacer, en libras, de 30 recién nacidos a término en un hospital metropolitano; los pesos se registraron hasta la décima de libra más cercana.7 Elabore un diagrama de tallo y hoja para mostrar la distribución de los datos.
■ Tabla 1.8 Pesos al nacer, en libras, de 30 recién nacidos a término
Solución Aunque los datos se registran con la precisión de solo un decimal, son mediciones de la variable continua x 5 peso, que puede tomar cualquier valor positivo. Si observa los datos de la tabla 1.8 verá que los pesos más alto y más bajo son 9.4 y 5.6 libras, respectivamente. Pero, ¿cómo se distribuyen los pesos restantes? Si utiliza el punto decimal como línea divisoria entre el tallo y la hoja, solo tendrá cinco tallos, lo que no proporciona una imagen suficientemente buena. Si, en cambio, divide cada tallo en dos líneas, habrá ocho tallos, ¡porque la primera línea del tallo 5 y la segunda línea del tallo 9 están vacías! Este es un diagrama más descriptivo, como se muestra en la figura 1.11. Para estos datos, la unidad de hoja es .1, y el lector puede deducir que el tallo 8 y la hoja 2, por ejemplo, representan el dato x 5 8.2.
Si gira el diagrama de tallo y hoja hacia un lado, de modo que la línea vertical sea un eje horizontal, verá que los datos se han “amontonado” o “distribuido” a lo largo del eje en un patrón que puede describirse como “en forma de montículo”, como un montón de arena en la playa. Este diagrama muestra de nuevo que los pesos de estos 30 recién nacidos oscilan entre 5.6 y 9.4; muchos pesos están entre 7.5 y 8.0 libras.
. Gráficos para datos cuantitativos 21
5 140 55 6580855Reordenamiento6055588 7000504050070000000455 88 905905
40Unidaddehoja
Figura 1.10
Diagrama de tallo y hoja para los datos de la tabla 1.7
● Consejo práctico Tallo | Hoja
7.27.86.86.28.2 8.08.25.68.67.1 8.27.77.57.27.7 5.86.86.88.57.5 6.17.99.49.07.8 8.59.07.76.77.7
Figura 1.11
586568 612612 68887Reordenamiento67888 72217122 78795775877557777889 8022280222 85658556 9040Unidaddehoja=.19004
Diagrama de tallo y hoja para los datos de la tabla 1.8
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
■ Interpretación de gráficas con ojo crítico
Una vez que haya creado una o varias gráficas para un conjunto de datos, ¿qué debe buscar al intentar describir los datos?
• Primero, compruebe las escalas horizontal y vertical para que tenga claro lo que se está midiendo.
• Observe la ubicación de la distribución de datos. ¿En qué parte del eje horizontal se ubica el centro de la distribución? Si compara dos distribuciones, ¿están ambas centradas en el mismo lugar?
• Observe la forma de la distribución. ¿Tiene un “pico”, es decir un punto más alto que cualquier otro? Si es así, esta es la medición o categoría que se produce con más frecuencia. ¿Hay más de un pico? ¿Hay aproximadamente el mismo número de datos a la izquierda y a la derecha del pico?
• Busque medidas excepcionales o valores atípicos. Es decir, ¿hay alguna medida mucho más grande o más pequeña que todas las demás? Es posible que estos valores atípicos no sean representativos de los demás valores del conjunto.
Las distribuciones se describen a menudo según su forma.
DEFINICIÓN
Una distribución es simétrica si los lados izquierdo y derecho, cuando se dividen a la altura del valor medio, forman imágenes espejo.
Una distribución está sesgada a la derecha si una mayor proporción de las mediciones se encuentra a la derecha del valor máximo. Las distribuciones que están sesgadas a la derecha contienen algunas mediciones excepcionalmente grandes.
Una distribución está sesgada a la izquierda si una mayor proporción de las mediciones se encuentra a la izquierda del valor máximo. Las distribuciones que están sesgadas a la izquierda contienen algunas mediciones excepcionalmente pequeñas.
Una distribución es unimodal si tiene un pico; una distribución bimodal tiene dos picos. Las distribuciones bimodales a menudo representan una mezcla de dos poblaciones diferentes en el conjunto de datos.
EJEMPLO . Observe las cuatro gráficas de puntos que se muestran en la figura 1.12. Describa las ubicaciones y formas de estas distribuciones.
CAPÍTULO Descripción de
con
22
datos
gráficos
Figura 1.12
2 3 5 7 9 1468
Formas de distribuciones de datos para el ejemplo 1.9
1234567 1234567
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
● Consejo
Solución La primera gráfica de puntos muestra una distribución relativamente simétrica con un solo pico ubicado en x 5 4. Si doblara la página en este punto máximo o pico, las mitades izquierda y derecha serían casi imágenes espejo. A veces a esta forma se le llama “forma de montículo” porque los puntos de datos parecen acumularse como un montículo de arena. La segunda gráfica de puntos también es simétrica, pero es plana o “uniforme” en lugar de tener forma de montículo. La tercera gráfica de puntos, no obstante, está lejos de ser simétrica. Tiene una “cola derecha” larga, lo que significa que hay algunas observaciones excepcionalmente grandes. Si doblara la página en el pico o valor máximo, en el lado derecho habría una proporción de datos mayor que la del izquierdo. Esta distribución está sesgada a la derecha. De manera similar, la cuarta gráfica de puntos con la “cola izquierda” larga está sesgada a la izquierda
EJEMPLO .
Un asistente administrativo del departamento de atletismo de una universidad local da seguimiento a los GPA de ocho miembros del equipo femenino de voleibol. El asistente ingresa los GPA en una base de datos pero, por accidente, coloca mal el punto decimal de la última entrada.
2.83.03.03.32.43.43.0.21
Utilice una gráfica de puntos para describir los datos y descubrir el error del asistente.
Solución La gráfica de puntos de este pequeño conjunto de datos se muestra en la figura 1.13(a). Claramente se distingue el valor atípico o excepcional generado por el asistente al capturar los datos. Una vez corregido el error, como en la figura 1.13(b), se aprecia la distribución correcta del conjunto de datos. Como se trata de un conjunto muy pequeño, es difícil describir la forma de la distribución, pero parece tener un valor máximo en 3.0 y ser relativamente simétrica.
Al comparar las gráficas creadas para dos conjuntos de datos debe comparar sus escalas de medición, ubicaciones y formas, y buscar valores excepcionales o atípicos. Recuerde que los valores atípicos no siempre se deben a errores o al registro de datos incorrecto. A veces proporcionan información muy valiosa que no debe ignorarse. Es posible que tenga que investigar si un valor atípico es una medición válida que simplemente es excepcionalmente grande o pequeña, o si ha habido algún error en la recopilación de datos. Si las escalas difieren mucho, ¡tenga cuidado al hacer comparaciones o sacar conclusiones que podrían ser inexactas!
. Gráficos para datos cuantitativos 23 2 3 5 7 9 1468
ejemplo 1.10 0.51.01.52.02.53.03.5 GPA 2.22.42.62.83.03.23.4 GPA
práctico Simétrico ⇔ imágenes espejo Sesgada a la derecha ⇔ cola derecha larga Sesgada a la izquierda ⇔ cola izquierda larga Figura
1.13
Distribuciones del GPA para el
● Consejo práctico Los valores atípicos se encuentran lejos del cuerpo principal de datos.
(b) MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
(a)
1.3 EJERCICIOS
Técnicas básicas
Gráficas de puntos Elabore una gráfica de puntos para los datos que se proporcionan en los ejercicios 1 y 2. Describa la forma de la distribución y busque valores atípicos.
11. Describa la forma de la distribución. ¿Observa algún valor atípico?
12. Compare la gráfica de puntos y el diagrama de tallo y hoja. ¿Transmiten aproximadamente la misma información?
1. 2.0 , 1.0 ,
0.9,
1.1,
,
,
1.0 , 0.9, 1.4 , 0.9, 1.0 , 1.0
2. 53, 61, 58 , 56 , 58 , 60 , 54 , 54 , 62 , 58 , 60 , 58 , 56 , 56 , 58
Diagrama de tallo y hoja I Elabore un diagrama de tallo y hoja para estas 50 mediciones y responda las preguntas de los ejercicios 3 a 5.
3.14.92.83.62.54.53.53.74.14.9
2.92.13.54.03.72.74.04.43.74.2
3.86.22.52.92.85.11.85.62.23.4
2.53.65.14.81.63.66.14.73.93.9
4.35.73.74.64.05.64.94.23.13.9
3. Describa la forma de la distribución. ¿Observa algún valor atípico?




4. Utilice el diagrama de tallo y hoja para encontrar la observación más pequeña.
5. Encuentre la octava y la novena observaciones más grandes. DATA SET
DS0104
Diagrama de tallo y hoja II Utilice el siguiente conjunto de datos para responder las preguntas de los ejercicios 6 a 8.
4.53.23.53.93.53.9
4.34.83.63.34.34.2
3.93.74.34.43.44.2
4.44.03.63.53.94.0
6. Dibuje un diagrama de tallo y hoja, utilice como tallo el número en la posición de las unidades.
7. Dibuje un diagrama de tallo y hoja, utilice dos veces cada número en la posición de las unidades para formar los tallos.
8. ¿El diagrama de tallo y hoja del ejercicio 7 mejora la presentación de los datos?
Comparación de gráficas Una variable discreta solo puede tomar los valores 0, 1 o 2. Use el conjunto de 20 mediciones de esta variable para responder las preguntas de los ejercicios 9 a 12. 12102
Gráficas de líneas Elabore una gráfica de líneas para describir los datos y responder las preguntas de los ejercicios 13 y 14.
13. Atravesar un laberinto Un psicólogo midió el tiempo que tardaba una rata en atravesar un laberinto cada día durante un periodo de cinco días. ¿Cree que está ocurriendo algún aprendizaje?
Día12345
Tiempo(segundos)4543463225
9. Trace una gráfica de puntos para describir los datos.
10. ¿Cómo podría definir el tallo y la hoja de este conjunto de datos? Dibuje el diagrama de tallo y hoja.
DATA SET DS0105
14. Medición a lo largo del tiempo Una variable cuantitativa se mide una vez al año durante un periodo de 10 años. ¿Qué indica la gráfica de líneas acerca de los datos?
Aplicación de los conceptos básicos
15. Hamburguesas con queso Elabore una gráfica de puntos para el número de hamburguesas con queso que 10 estudiantes universitarios comen en una semana determinada.
45421
33427
a. ¿Cómo describiría la forma de la distribución?
b. ¿Qué proporción de los estudiantes comió más de cuatro hamburguesas con queso esa semana?
DATA SET DS0106









16. Puntuaciones en pruebas Se registraron las puntuaciones de 20 estudiantes en una prueba de 100 puntos.
61939186556386827657
94896762728768657584
a. Describa los datos mediante un diagrama de tallo y hoja.
b. Describa la forma y la ubicación de las puntuaciones.
c. ¿La forma de la distribución es excepcional? ¿Se le ocurre alguna razón por la que las puntuaciones tienen esa forma?
CAPÍTULO Descripción de datos con gráficos 24
1.1,
1.0
1.2
1.3,
0.9,
22110 01211
21100
DATA SET DS0103
161.5658.2 262.3757.5 360.7857.5 459.8956.1 558.01056.0
AñoMediciónAñoMedición
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
17. Recuento de glóbulos rojos El recuento de glóbulos rojos de una persona sana se midió cada día durante un periodo de 15 días. El valor registrado se mide en millones de células por microlitro (μL).
5.45.25.05.25.5
5.35.45.25.15.3
5.34.95.45.25.2
a. Describa los datos mediante un diagrama de tallo y hoja.
b. Describa la forma y la ubicación de los recuentos de glóbulos rojos.
c. Si el día de hoy se midiera el número de glóbulos rojos de la persona y el resultado fuera 5.7 millones de células por microlitro, ¿este valor sería excepcional? ¿Qué conclusiones puede obtener?
de Hershey's®
a. ¿Los tamaños, alturas y volúmenes de los seis productos representan con precisión la cantidad de calorías que contienen?
b. Elabore una gráfica de barras para describir el número de calorías en estos seis alimentos.
DATA SET
DS0110
DATA SET
DS0108
18. Contenido de calcio El contenido de calcio (Ca) de una sustancia mineral en polvo se analizó 10 veces con los siguientes porcentajes de composición registrados.
2.712.822.792.812.68
2.712.812.692.752.76
a. Dibuje una gráfica de puntos para describir los datos. (Sugerencia: La escala del eje horizontal debe comprender entre 2.60 y 2.90).





b. Dibuje un diagrama de tallo y hoja para los datos. Emplee como tallos los números en las posiciones de las centésimas y las milésimas.
c. ¿Alguno de los datos es inconsistente con el resto de las mediciones? Esto indicaría que el técnico pudo haber cometido un error en el análisis.
21. ¡La educación vale la pena! La educación vale la pena, de acuerdo con algunos datos de la Oficina de Estadísticas Laborales. La mediana de los ingresos semanales y las tasas de desempleo para ocho niveles educativos diferentes se muestran en la tabla.10
Nivel de estudios
Tasa de desempleo (%)
Mediana de los ingresos semanales habituales ($)










Títulodedoctorado1.61,664 Títulodeespecialidad1.61,745
Títulodemaestría2.41,380
Títulodelicenciatura2.71,156 Títulotécnico3.6819 Licenciaturainconclusa,sintítulo4.4756 Graduadodebachillerato5.2692 Menosquediplomade bachillerato
7.4504
Nota:Losdatosaplicanparapersonasde25añosomás.Losingresosson paratrabajadoresasalariadosdetiempocompleto.
DATA SET
DS0109
19. Correr en el agua Se ha sugerido que correr en el agua es un buen ejercicio para los atletas lesionados y otras personas que desean practicar un programa de aeróbicos de bajo impacto. Un estudio publicado en la revista Journal of Sports Medicine informó sobre las frecuencias cardiacas de 20 voluntarios sanos a una cadencia de 96 pasos por minuto.8 A continuación se enlistan los datos:
871097980969590929698
10191781129498941078196
a. Elabore un diagrama de tallo y hoja para describir los datos.
b. Analice las características de la distribución de datos.
20. El gran debate sobre las calorías ¿Quiere perder peso? ¡Puede hacerlo si reduce las calorías, siempre y cuando obtenga suficiente valor nutricional de los alimentos que come! Esta es una imagen que muestra la cantidad de calorías que contienen algunos de los alimentos favoritos en Estados Unidos, adaptada de un artículo en The Press-Enterprise 9
Fuente: Encuestadepoblaciónactual,DepartamentodeTrabajodeEstadosUnidos,OficinadeEstadísticasLaboralesdeEstadosUnidos,20de abrilde2017.
a. Elabore una gráfica de barras para describir las tasas de desempleo por nivel educativo.
b. Elabore una gráfica de barras para describir la mediana de los ingresos semanales medios por nivel educativo.
c. Resuma la información con base en las gráficas de los incisos a y b.
22. Religiones organizadas Las estadísticas de las religiones del mundo son solo aproximadas porque muchas de ellas no llevan un registro del número de sus miembros. En la tabla se muestra una estimación de estos números (en millones).11
. Gráficos para datos cuantitativos 25
DATA SET DS0107
Religión Miembros (millones)Religión Miembros (millones) Budismo376Judaísmo14 Cristianismo2,100Sijismo23 Hinduismo900Chinatradicional394 Islam1,500Otra61 Indígenasprimitivasy africanastradicionales 400 Númerodecalorías 26 Kisses
53
140
145 Botella
330 Una
800
DATA SET DS0111 MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
Galleta Oreo®
Lata
de refresco de cola de 350 mL
de cerveza Budweiser® de 350 mL
rebanada de pizza de pepperoni de Papa John's®
Hamburguesa Whopper con queso de Burger King®
a. Describa el número total de miembros de las religiones organizadas del mundo mediante una gráfica circular.
b. Describa el número total de miembros de las religiones organizadas del mundo mediante una gráfica de barras.
c. Ordene los grupos religiosos según el número de miembros, del número menor al mayor. Utilice un diagrama de Pareto para describir los datos. ¿Cuál de las tres visualizaciones considera más eficaz?
2.
3.
23. Residuos peligrosos ¿Qué tan seguro es su vecindario? ¿Hay algún sitio con residuos peligrosos cerca? La tabla y el diagrama de tallo y hoja muestran el número de sitios con residuos peligrosos en cada uno de los 50 estados y el Distrito de Columbia en Estados Unidos en 2016.5
DS0112
AL15HI3MA33NM16SD2



AK6ID9MI67NY87TN17
AZ9IL49MN25NC39TX53
AR9IN40MS9ND0UT18
CA99IA13MO33OH43VT12
CO21KS13MT19OK8VA31
CT15KY13NE16OR14WA51
DE14LA15NV1PA97WV10
DC1ME13NH21RI12WI38
FL54MD21NJ115SC25WY2
GA17
Fuente: The World Almanac and Book of Facts 2017, p. 335.
a. Describa la forma de la distribución. Identifique a qué estados pertenecen las mediciones excepcionalmente grandes marcadas como “altas” en el diagrama.






b. ¿Se le ocurre alguna razón por la que estos estados tendrían una gran cantidad de sitios con residuos peligrosos? ¿Qué otra variable podría medir para explicar por qué los datos se comportan de esta manera?
Diagrama de tallo y hoja de residuos peligrosos N 5 51
a. Dibuje un diagrama de tallo y hoja para los datos. Describa la forma de la distribución y busque valores atípicos.
b. Dibuje una gráfica de puntos para los datos. ¿Cuál de las dos gráficas es más informativa? Explique por qué.
24. Las 20 mejores películas La siguiente tabla muestra los ingresos brutos (en millones de dólares) por la venta de boletos de cine para ver las 20 mejores películas durante el fin de semana del 25 al 28 de agosto de 2017:12
DATA SET

DS0114
25. Presidentes estadounidenses La siguiente tabla muestra las edades, en el momento de la muerte, de los 38 presidentes estadounidenses fallecidos, desde George Washington hasta Ronald Reagan:5
Washington67Arthur57
J.Adams90Cleveland71
Jefferson83B.Harrison67
Madison85McKinley58
Monroe73T.Roosevelt60
J.Q.Adams80Taft72
Jackson78Wilson67
VanBuren79Harding57
W.H.Harrison68Coolidge60
Tyler71Hoover90
Polk53F.D.Roosevelt63
Taylor65Truman88
Fillmore74Eisenhower78
Pierce64Kennedy46
Buchanan77L.Johnson64
Lincoln56Nixon81
A.Johnson66Ford93
Grant63Reagan93
Hayes70
Garfield49
a. Antes de graficar los datos, piense en la distribución de las edades de los presidentes en el momento de la muerte. ¿Qué forma tendrá?
CAPÍTULO Descripción de datos con gráficos 26
DATA SET
120689999
212111 18255 163133 13389 11403 949 85134 55 56 567 Unidad de hoja 5 1 HI 87, 97, 99, 115
6 0011223
211022333344 (9)1555667789
Película Ingresos brutos de fin de semana ($ millones) Película Ingresos brutos de fin de semana ($ millones)
$2.4
1. Duro de cuidar $10.311. Viaje de chicas
Anabelle
7.712.
2.3
2: la creación
Locos por las nueces 2
Bailarina 4.713.
3 1.8 4. Viento salvaje 4.614. La torre oscura 1.7 5. La estafa de los Logan 4.215. Mujer maravilla 1.7 6. Dunkerque 3.916. El milagro de todos los santos 1.5 7. Spiderman: de regreso
casa 2.817. Desaparecido 1.5 8. El nacimiento del dragón 2.718. El castillo de cristal 1.4 9. Mayweather vs. McGregor 2.619. Baby: el aprendiz del crimen 1.2 10. Emoji: la película 2.520. El planeta de los simios: la guerra 0.9
Mi villano favorito
a
DATA SET
DS0113
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
b. Dibuje un diagrama de tallo y hoja para los datos. Describa la forma. ¿Le sorprende?
c. Los cinco presidentes más jóvenes en el momento de la muerte aparecen en la “cola” inferior de la distribución. Identifique a estos cinco presidentes.
d. Tres de los cinco presidentes más jóvenes en el momento de la muerte tienen una característica en común. ¿Cuál es?
1.4 Histogramas de frecuencia relativa
Un histograma de frecuencia relativa se parece a una gráfica de barras, pero se usa para representar visualmente datos cuantitativos en lugar de cualitativos. Los datos de la tabla 1.9 son los pesos al nacer, en libras, de 30 recién nacidos a término, reproducidos del ejemplo 1.8 y representados mediante una gráfica de puntos en la figura 1.14(a). En primer lugar, divida el intervalo que comprende de la medición más pequeña a la más grande en subintervalos o clases de igual longitud. Si apila los puntos en cada subintervalo (figura 1.14(b)) y dibuja una barra sobre cada pila, habrá creado un histograma de frecuencia o un histograma de frecuencia relativa, según la escala del eje vertical.
■ Tabla 1.9 Pesos al nacer, en libras, de 30 recién nacidos a término
Estas son algunas definiciones y términos que se usan comúnmente al construir histogramas de frecuencia relativa.
DEFINICIONES
• Una clase es un subintervalo que se crea al dividir el intervalo que comprende de la medición más pequeña a la más grande.
• Los límites o fronteras de clase son los números que marcan los límites superior e inferior de la clase.
• El ancho de clase es la diferencia entre los límites de clase superior e inferior.
• La frecuencia de clase es el número de mediciones que caen dentro de esa clase en particular.
• Un histograma de frecuencia relativa para un conjunto de datos cuantitativos es una gráfica de barras en la que la altura de la barra muestra “con qué frecuencia” (medida como proporción o frecuencia relativa) las mediciones caen en cada subintervalo o clase. Las clases o subintervalos se trazan a lo largo del eje horizontal.
. Histogramas de frecuencia relativa 27
7.27.86.86.28.2 8.08.25.68.67.1 8.27.77.57.27.7 5.86.86.88.57.5 6.17.99.49.07.8 8.59.07.76.77.7
6.06.67.27.88.49.0 Pesos al nacer (a) 9.0 8.5 8.0 7.5 7.0 6.5 6.0 9.5 Pesos al nacer
(b)
Figura 1.14
Cómo construir un histograma
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
● Consejo práctico Las frecuencias relativas suman 1; las frecuencias suman n
La forma en que se crean las clases o subintervalos es una cuestión de elección personal. Sin embargo, como regla general, el número de clases debe oscilar entre 5 y 12; cuantos más datos disponibles haya, más clases se necesitan. Elija las clases de tal forma que cada medición se incluya en una y solo una clase. Puede usar la tabla 1.10 como guía para seleccionar el número aproximado de clases para un conjunto de datos en particular. Sin embargo, recuerde que esto es solo una guía; puede usar más o menos clases si esto hace que la gráfica sea más descriptiva.
■ Tabla 1.10 Elección del número de clases
Tamañodelamuestra2550100200500
Númerodeclases678910
Para los pesos al nacer de la tabla 1.9, se ha decidido usar ocho intervalos de igual longitud. Puesto que el rango total de los pesos al nacer es
25 9.45.63.8
el ancho mínimo de clase necesario para cubrir el rango de los datos es (3.8 ÷ 8) = .475. Por conveniencia se redondea este ancho aproximado a .5. El primer intervalo comienza en el valor más bajo, 5.6; a partir de ese punto se forman subintervalos de 5.6 hasta 6.1, pero sin incluir este último; de 6.1 hasta 6.6, pero sin incluir este último, y así sucesivamente. Al emplear el método de inclusión izquierda en el que se incluye el punto límite de clase izquierdo pero no el punto límite de clase derecho se elimina cualquier confusión sobre dónde colocar una medición que se ubica exactamente en un límite de clase.
La tabla 1.11 muestra las ocho clases, etiquetadas del 1 al 8 para su identificación. Los límites o fronteras de las ocho clases, junto con un recuento del número de mediciones que caen en cada clase, también se muestran en la tabla. Al igual que con las gráficas de la sección 1.3, ahora es posible medir la frecuencia con la que cada clase ocurre utilizando ya sea la frecuencia o la frecuencia relativa
Para construir el histograma de frecuencia relativa, trace los límites o fronteras de clase a lo largo del eje horizontal. Dibuje una barra sobre cada intervalo de clase, con una altura igual a la frecuencia relativa de esa clase. El histograma de frecuencia relativa para los datos de peso al nacer (figura 1.15) muestra, de un vistazo, cómo se distribuyen los pesos al nacer en el intervalo que va de 5.6 a 9.4.
■ Tabla 1.11 Frecuencias relativas para los datos de la tabla 1.9
ClaseLímites de claseRegistro Frecuencia de clase
Frecuencia relativa de clase
15.6a ,6.1II22/30
26.1a ,6.6II22/30
36.6a ,7.1IIII44/30
47.1a ,7.6IIII55/30
57.6a ,8.1IIIIIII88/30
68.1a ,8.6IIII55/30
78.6a ,9.1III33/30
89.1a ,9.6I11/30
CAPÍTULO Descripción de datos con gráficos 28
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
EJEMPLO . Veinticinco clientes de una cafetería son entrevistados para una encuesta de mercadotecnia en la que se les pregunta: “¿Con qué frecuencia visita la cafetería en una semana típica?”. En la tabla 1.12 se enlistan las respuestas de estos 25 clientes. Utilice un histograma de frecuencia relativa para describir los datos.
■ Tabla 1.12 Número de visitas en una semana típica para 25 clientes 67156
Solución La variable que se mide es “número de visitas a la cafetería”, una variable discreta que solo toma valores enteros. En este caso, lo más sencillo es elegir las clases o subintervalos como valores enteros en el rango de valores observados: 1, 2, 3, 4, 5, 6 y 7. Los intervalos podrían escribirse como .5 a <1.5, 1.5 a <2.5, y así sucesivamente, pero note que los únicos valores que realmente pueden aparecer son los valores enteros, 1, 2,..., 8. La tabla 1.13 muestra las clases así como sus frecuencias y frecuencias relativas correspondientes. El histograma de frecuencia relativa se muestra en la figura 1.16.
. Histogramas de frecuencia relativa 29
Histograma de frecuencia relativa 8/30 7/30 6/30 5/30 4/30 3/30 2/30 1/30 0 5.66.16.67.17.68.18.69.19.6 Frecuencia relativa Pesos al nacer
Figura 1.15
46468 65634 55576 35755
Número de visitas a la cafetería Límites de claseFrecuencia Frecuencia relativa 1.5a ,1.51.04 21.5a ,2.5— 32.5a ,3.52.08 43.5a ,4.53.12 54.5a ,5.58.32 65.5a ,6.57.28 76.5a ,7.53.12 87.5a ,8.51.04 MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
■ Tabla 1.13 Tabla de frecuencias para el ejemplo 1.11
Necesito saber... ?
Cómo construir un histograma de frecuencia relativa
1. Elija el número de clases, normalmente entre 5 y 12. Cuantos más datos tenga, más clases debe usar.
2. Encuentre el ancho aproximado de clase, para ello divida la diferencia entre los valores más grande y más pequeño entre el número de clases.
3. Redondee el ancho de clase aproximado a un número conveniente.
4. Si los datos son discretos, puede asignar una clase para cada valor entero. Para un gran número de valores enteros, es posible que tenga que agruparlos en clases.
5. Enliste los límites o fronteras de clase. La primera clase debe incluir la medición más pequeña. A continuación, defina las clases restantes; incluya el punto límite izquierdo pero no el derecho.
6. Elabore una tabla estadística que contenga las clases, sus frecuencias y sus frecuencias relativas.
7. Dibuje el histograma como una gráfica de barras, con los intervalos de clase en el eje horizontal y las frecuencias relativas como la altura de las barras.
Se puede utilizar un histograma de frecuencia relativa para describir la ubicación y la forma de un conjunto de datos, y para comprobar si hay valores atípicos. Por ejemplo, los datos de peso al nacer resultaron relativamente simétricos, sin mediciones excepcionales, mientras que los datos sobre las visitas a la cafetería estaban sesgados a la izquierda. Dado que la barra dibujada sobre cada clase representa la frecuencia relativa o proporción de las mediciones en esa clase, estas alturas se pueden utilizar para calcular lo siguiente:
• La proporción de las mediciones que caen en una clase o grupo de clases en particular.
• La probabilidad de que una medida extraída al azar del conjunto caiga en una clase o grupo de clases en particular.
Observe el histograma de frecuencia relativa para los datos de peso al nacer en la figura 1.15. ¿Qué proporción de los recién nacidos tienen un peso al nacer de 7.6 libras o mayor? Esto implica a todas las clases más allá de 7.6 en la tabla 1.11. Puesto que hay 17 recién nacidos en esas clases, la proporción de bebés que tienen un peso al nacer de 7.6 o mayor es de 17/30, o aproximadamente 57%. Este es también el porcentaje del área total bajo el histograma de la figura 1.15 que se encuentra a la derecha de 7.6.
CAPÍTULO Descripción de datos con gráficos 30 La distribución está sesgada a la izquierda y hay un espacio entre 1 y 3. Figura 1.16 Histograma de frecuencia relativa para el ejemplo 1.11 0.30 0.35 0.25 0.20 0.05 0.10 0.15 0 12345678 Visitas Frecuencia relativa
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
Suponga que usted escribió cada uno de los 30 pesos al nacer en un pedazo de papel, puso los pedazos en un sombrero y extrajo uno al azar. ¿Cuál es la probabilidad de que en este pedazo de papel esté escrito un peso al nacer de 7.6 o mayor? Como 17 de los 30 pedazos de papel cumplen con esta característica, hay 17 oportunidades de 30; es decir, la probabilidad es de 17/30. La palabra probabilidad no es desconocida para usted; se discutirá con más detalle en el capítulo 4.
Aunque solo estamos describiendo el conjunto de n = 30 pesos al nacer, también puede interesarnos la población de la que se extrajo la muestra, que es el conjunto de pesos al nacer de todos los bebés nacidos en este hospital. O, si nos interesan los pesos de los recién nacidos en general, podemos considerar nuestra muestra como representativa de la población de pesos al nacer de los recién nacidos en hospitales similares. Un histograma de la muestra o muestral proporciona información valiosa sobre el histograma de la población o poblacional, la gráfica que describe la distribución de toda la población. No obstante, recuerde que diferentes muestras de la misma población producirán histogramas diferentes, incluso si usa los mismos límites de clase. Sin embargo, puede esperar que los histogramas de la muestra y de la población sean similares. A medida que agrega más y más datos a la muestra, los dos histogramas se parecen cada vez más. Si amplía la muestra para incluir a toda la población, ¡los dos histogramas serán idénticos!
1.4 E JERCICIOS
Técnicas básicas
Elaborar histogramas de frecuencia relativa Elabore un histograma de frecuencia relativa con la información de las tablas estadísticas de los ejercicios 1 y 2. ¿Cómo describiría la forma de la distribución?
1.
Límites de clase Frecuencia relativa
100a ,120.08
120a ,140.22
140a ,160.49
160a ,180.17
180a ,200.04
2.
Número de animales de compañía Frecuencia
3. 33 o mayor
5. Menor que 31
4. 32 a <33.5
6. Mayor o igual que 33.5
7. Por lo menos 34 8. Por lo menos 31.5 pero menor que 33.5
Límites de clase En los ejercicios 9 a 12, use la información proporcionada para encontrar un ancho de clase conveniente. A continuación haga una lista de los límites o fronteras de clase que se pueden usar para crear un histograma de frecuencia relativa.
Interpretación de histogramas de frecuencia relativa Use el histograma de frecuencia relativa a continuación para calcular la proporción de mediciones que caen dentro de los intervalos dados en los ejercicios 3 a 8. Recuerde que las clases incluyen el punto límite izquierdo, pero no el derecho.
9. 7 clases para n 5 50 mediciones; valor mínimo = 10; valor máximo = 110
10. 6 clases para n 5 20 mediciones; valor mínimo = 25.5; valor máximo = 76.8
11. 10 clases para n 5 120 mediciones; valor mínimo = 0.31; valor máximo = 1.73
. Histogramas de frecuencia relativa 31
013
21
119
2 34 41 50 61
0.4 0.3 0.2 0.1 0 30.531.031.532.032.533.033.534.0 34.5 x Frecuencia relativa MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
12. 8 clases para n 5 75 mediciones; valor mínimo = 0; valor máximo = 192
21. Describa la forma y la ubicación de las puntuaciones.
22. ¿La forma de la distribución es excepcional? ¿Se le ocurre alguna razón por la que los datos tengan esa forma?
DS0115
Histograma de frecuencia relativa I Elabore un histograma de frecuencia relativa para las siguientes 50 mediciones, defina clases que comiencen en 1.6 con un ancho de clase de .5. Posteriormente, responda las preguntas de los ejercicios 13 a 16.
3.14.92.83.62.54.53.53.74.14.9
2.92.13.54.03.72.74.04.43.74.2
3.86.22.52.92.85.11.85.62.23.4
2.53.65.14.81.63.66.14.73.93.9
4.35.73.74.64.05.64.94.23.13.9
13. ¿Cómo describiría la forma de la distribución?




14. ¿Qué fracción de las mediciones es menor que 5.1?
15. ¿Cuál es la probabilidad de que una medición tomada al azar de este conjunto sea mayor o igual que 3.6?
16. ¿Qué fracción de las mediciones va desde 2.6 hasta 4.6, pero sin incluir 4.6?
Histograma de frecuencia relativa II Elabore un histograma de frecuencia relativa para las siguientes 20 mediciones en una variable discreta que solo pueda tomar los valores 0, 1 y 2. Posteriormente, responda las preguntas de los ejercicios 17 a 20. 12102
23. Compare la forma del histograma con el diagrama de tallo y hoja del ejercicio 16, sección 1.3. ¿Las formas son aproximadamente las mismas?
Aplicación de los conceptos básicos
17. ¿Qué proporción de las mediciones es mayor que 1?
18. ¿Qué proporción de las mediciones es menor que 2?
19. Si se selecciona al azar una medición de las 20 mostradas, ¿cuál es la probabilidad de que sea un 2?
20. Describa la forma de la distribución. ¿Observa algún valor atípico?




DATA SET
DS0116
Puntuaciones en pruebas Se registraron las puntuaciones de 20 estudiantes en una prueba de 100 puntos. Elabore un histograma de frecuencia relativa para los datos, utilice seis clases de ancho 8 que inicien en el valor 52. Posteriormente, responda las preguntas de los ejercicios 21 a 23.
61939186556386827657
94896762728768657584
DATA SET
DS0117
24. Tiempos de supervivencia En un estudio, Altman y Bland informaron sobre los tiempos de supervivencia de pacientes con hepatitis activa; la mitad fueron tratados con prednisona y la otra mitad no recibió tratamiento.13 Los datos a continuación son una adaptación de los datos de los investigadores y corresponden a los pacientes que fueron tratados con prednisona. Los tiempos de supervivencia se registran en el mes más cercano:
887127147
1193133148

5297139157
57109142162
65120144165
a. Observe los datos. ¿Puede suponer cuál sería la forma aproximada de su distribución?
b. Elabore un histograma de frecuencia relativa para los datos. ¿Cuál es la forma de la distribución?
c. ¿Hay valores atípicos en el conjunto? Si es así, ¿qué tiempos de supervivencia son excepcionalmente cortos?
25. Una enfermedad recurrente Se registró el tiempo (en meses) entre el inicio de una enfermedad particular y su recurrencia para n = 50 pacientes:
a. Construya un histograma de frecuencia relativa para los datos.




b. ¿Describiría la forma como aproximadamente simétrica, sesgada a la derecha o sesgada a la izquierda?
c. Encuentre la fracción de tiempos de recurrencia que son menores o iguales a 10 meses.
CAPÍTULO Descripción de datos con gráficos 32
DATA SET
21100 22110 01211
DATA SET DS0118
2.14.42.732.39.99.02.06.63.91.6 14.79.616.77.48.219.26.94.33.31.2 4.118.4.26.113.57.4.28.3.31.3 14.11.02.42.418.08.724.01.48.25.8 1.63.511.418.026.73.712.623.15.6.4
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
26. Preescolar Las edades (en meses) en las que 50 niños fueron inscritos por primera vez en preescolar se enlistan a continuación.
38403035394048363136
47353443413641434840
32344130463540304637
55393332324542413650
42503739334538463631
a. Elabore un histograma de frecuencia relativa para estos datos. Establezca el límite inferior de la primera clase en 30 y utilice un ancho de clase de cinco meses.





b. ¿Qué proporción de niños tenía una edad igual o mayor que 35 meses pero menor que 45 meses al momento de ser inscritos por primera vez en preescolar?
c. Si un niño fuera seleccionado al azar de este grupo, ¿cuál es la probabilidad de que tuviera menos de 50 meses al momento de ser inscrito por primera vez en preescolar?
a. Elabore un histograma de frecuencia relativa para describir los promedios de bateo de estos 20 campeones.
DATA SET
DS0120
27. ¿Qué tan larga es la fila? Para decidir el número de mostradores de servicio necesarios para las tiendas que se construirán en el futuro, una cadena de supermercados recopiló información sobre el tiempo (en minutos) necesario para atender a los clientes; para ello empleó una muestra de 60 tiempos de servicio al cliente, que se muestran a continuación:
b. Si eligiera al azar uno de los 20 nombres, ¿qué posibilidades hay de que elija a un jugador cuyo promedio esté por encima de .400 en su año de campeonato?
a. Elabore un histograma de frecuencia relativa para los tiempos de servicio en las tiendas.
b. Describa la forma de la distribución. ¿Observa algún valor atípico?
c. Si se asumiera que los valores atípicos de este conjunto de datos son observaciones válidas, ¿cómo los explicaría a la gerencia de la cadena de supermercados? DATA SET DS0121
28. Campeones de bateo Los oficiales de las Grandes Ligas de Béisbol han coronado a un campeón de bateo en la Liga Nacional cada año desde 1876. En la tabla14 se presenta una muestra de los promedios de bateo de algunos de estos campeones:
DATA SET DS0122











29. Antigüedad de monedas de un centavo Se recolectaron 50 centavos estadounidenses y se registró su antigüedad mediante el siguiente cálculo: ANTIGÜEDAD = AÑO ACTUAL – AÑO GRABADO EN LA MONEDA.
5191220025017
144302533828
521199050210
011902020162210
a. Antes de elaborar cualquier gráfica, ¿cómo piensa que será la distribución de la antigüedad de las monedas de un centavo? ¿Tendrá forma de montículo, simétrica, sesgada a la derecha o sesgada a la izquierda?
b. Trace un histograma de frecuencia relativa para mostrar la antigüedad de las monedas de un centavo. ¿Cómo describiría la forma de la distribución?
30. Antigüedad de monedas de un centavo, continuación Aquí los datos representan la antigüedad de un conjunto distinto de 50 monedas de un centavo, nuevamente mediante el siguiente cálculo: ANTIGÜEDAD = AÑO ACTUAL – AÑO GRABADO EN LA
. Histogramas de frecuencia relativa 33 DATA SET DS0119
3.61.92.1.3.8.21.01.41.81.6 1.11.8.31.1.51.2.61.1.81.7 1.4.21.33.1.42.31.84.5.9.7 .62.82.51.1.41.2.41.3.81.3 1.11.2.81.0.9.73.11.71.12.2 1.61.95.2.51.8.31.1.6.7.6
19362301176050
DATA SET DS0123
419043038213 2104014025122419 311472445120 1493530817160 0735237281792 Año Nombre Promedio 2000ToddHelton.372 2017CharlieBlackmon.331 1917EddRoush.341 1934PaulWaner.362 1911HonusWagner.334 1898WillieKeeler.379 1924RogerHornsby.424 1963TommyDavis.326 1992GarySheffield.330 1954WillieMays.345 1975BillMadlock.354 1958RichieAshburn.350 1942ErnieLombardi.330 1948StanMusial.376 1971JoeTorre.363 1996TonyGwynn.353 1961RobertoClemente.351 1968PeteRose.335 1885RogerConnor.371 2009HanleyRamirez.342 MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
MONEDA.
a. Trace un histograma de frecuencia relativa para mostrar las antigüedades de las monedas de un centavo. ¿La forma es similar a la forma del histograma de frecuencia relativa del ejercicio 29?
b. ¿Hay alguna medida excepcionalmente grande o pequeña en el conjunto?
31. Ciudades con viento ¿Hay ciudades con más viento que otras? ¿La ciudad de Chicago merece ser apodada como “la ciudad del viento”? Estos datos se refieren a la velocidad media del viento (en kilómetros por hora) para 54 ciudades seleccionadas de Estados Unidos:5
13.112.215.411.011.212.018.112.012.5
11.218.416.816.511.856.216.014.912.6
13.316.515.811.812.511.414.912.316.3
11.713.315.715.213.412.89.814.614.4
9.912.615.29.816.310.612.613.418.4
15.015.87.010.615.515.712.817.013.6

Fuente: The World Almanac and Book of Facts 2017, p. 343
a. Elabore un histograma de frecuencia relativa para los datos. (Sugerencia: Elija los límites de la clase sin incluir el valor x = 56.2 en el rango de valores).






b. El valor x = 56.2 se registró en la ciudad de Mt. Washington, Nuevo Hampshire. ¿La geografía de esa ciudad explica la observación?
c. La velocidad media del viento en Chicago se registra en 15.8 kilómetros por hora. ¿Cree que ahí hace mucho viento?
32. Estaturas de estudiantes Las estaturas declaradas por 105 estudiantes de una clase de bioestadística se describen en el histograma de frecuencia relativa que se muestra a continuación.
a. Describa la forma de la distribución.
b. ¿Observa alguna característica excepcional en este histograma?
c. ¿Se le ocurre alguna explicación para los dos picos o máximos locales del histograma? ¿Hay algo que ocasione que las estaturas se aglutinen en dos picos o máximos locales separados? ¿Qué es?
33. Starbucks® ¡Los estudiantes de la Universidad de California, Riverside (UCR), al igual que muchos otros californianos, adoran su Starbucks®! Aquí se muestran las distancias en kilómetros desde el campus a las 39 cafeterías Starbucks® que se localizan en un radio de 16 kilómetros de la UCR:15
a. Construya un histograma de frecuencia relativa para describir las distancias desde el campus de la UCR; utilice ocho intervalos de clase de ancho 2, inicie en 0.0.
b. ¿Cuál es la forma del histograma? ¿Observa alguna característica excepcional?
c. ¿Puede explicar por qué el histograma tiene ese aspecto?
A medida que continúe trabajando en los ejercicios de este capítulo, aprenderá a reconocer mejor los diferentes tipos de datos y a elegir cuál es la mejor gráfica para utilizar. Recuerde que el tipo de gráfica que emplee no es tan importante como la interpretación que acompaña a la imagen. Busque estas características importantes:



• Ubicación del centro de los datos.
• Forma de la distribución de los datos.
• Observaciones excepcionales en el conjunto de datos.
Con estas características como guía puede interpretar y comparar conjuntos de datos mediante gráficas, que son solo las primeras de muchas herramientas estadísticas con las que pronto tendrá que trabajar.
CAPÍTULO Descripción de datos con gráficos 34
DATA SET DS0125
0.61.01.61.84.55.85.96.16.46.4 7.07.28.58.58.89.39.49.810.210.6 11.212.012.212.212.513.013.313.813.914.1 14.114.214.214.614.715.015.415.515.7
DATA SET DS0126 10/105 5/105 0 152.5160.0167.5175.0182.5190.0 Estaturas Frecuencia relativa
DATA SET DS0124 MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
Conceptos clave
I. Cómo se generan los datos
1. Unidades experimentales, variables y mediciones
2. Muestras y poblaciones
3. Datos univariados, bivariados y multivariados
II. Tipos de variables
1. Cualitativa o categórica
2. Cuantitativa
a. Discreta
b. Continua
III. Gráficos para distribuciones de datos univariados
1. Datos cualitativos o categóricos
a. Gráficas circulares
b. Gráficas de barras
Introducción a Microsoft Excel
2. Datos cuantitativos
a. Gráficas circulares y de barras
b. Gráficas de líneas
c. Gráficas de puntos
d. Diagramas de tallo y hoja
e. Histogramas de frecuencia relativa
3. Descripción de las distribuciones de datos
a. Formas: simétricas, sesgadas a la izquierda, sesgadas a la derecha, unimodales y bimodales
b. Proporción de mediciones en determinados intervalos
c. Valores atípicos
MS Excel está diseñado para una variedad de aplicaciones, incluidas las estadísticas. Asumiremos que está familiarizado con el sistema operativo Windows y que conoce las técnicas básicas necesarias para ejecutar comandos desde las pestañas, los grupos y los menús desplegables en la parte superior de la pantalla. Si no es así, quizás un asistente de laboratorio o un profesor pueda ayudarle a dominar los conceptos básicos. La versión de MS Excel que se muestra en esta sección a lo largo de la obra es Excel 2016, que se utiliza en el ambiente Windows 10. Cuando se abre el programa aparece una hoja de cálculo (véase la figura 1.17) que contiene filas y columnas en las que puede introducir datos. Las pestañas de la parte inferior de la pantalla identifican las hojas de cálculo disponibles para su uso; cuando se guardan varias hojas de cálculo como una colección, estas se denominan libro de trabajo.
Tecnología actual 35
TECNOLOGÍA ACTUAL
REVISIÓN DEL CAPÍTULO
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
Figura 1.17
Graficar con Excel
En MS Excel es posible crear gráficas circulares, gráficas de barras y gráficas de líneas. Los datos se introducen en la hoja de cálculo, incluidas las etiquetas, si es necesario. Resalte los datos que se van a representar en la gráfica y, a continuación, haga clic en el tipo de gráfica que desee en la pestaña Insert del grupo Charts. Una vez creada la gráfica se puede editar de varias formas para cambiar su aspecto.
EJEMPLO . (Gráficas circulares y de barras) Se registró la variable cualitativa “nivel cursado en la universidad” para cada uno de los 105 estudiantes en una clase de Introducción a la Estadística; las frecuencias se registran en la tabla 1.14.
■ Tabla 1.14. Nivel que cursan estudiantes universitarios que actualmente estudian la materia de Estadística
Nivel Primer añoSegundo añoTercer año Último añoGraduado Frecuencia523323510
1. Introduzca las categorías en la columna A y las frecuencias en la columna B de la primera hoja de cálculo. Debe tener dos columnas con datos, incluidas las etiquetas.
2. Resalte los datos; para ello haga clic en el botón izquierdo del mouse y arrastre desde la celda A1 hasta la celda B6 (este rango puede expresarse como A1:B6). A continuación dé clic en la pestaña Insert y haga clic en el icono Pie en el grupo Charts. En la lista desplegable verá una variedad de estilos para elegir. Seleccione la primera opción de la sección Gráfico 2D para producir la gráfica circular. Haga doble clic en el título “Frequency” y cambie el título a “Nivel del estudiante”.
3. Edición de la gráfica circular: una vez que haya creado la gráfica, utilice el mouse para asegurarse de que esté seleccionada; aparecerá un cuadro con controladores de tamaño alrededor de ella. Debería ver una pestaña con la etiqueta “Chart Tools” en color verde. Haga clic en la pestaña Design y consulte las listas desplegables de los grupos Chart Layout y Chart Styles. Estas listas le permiten modificar la apariencia de la gráfica. En la figura 1.18(a), la gráfica circular se modificó utilizando el diseño 6 en Quick Layout (en el grupo Chart Layout) para que los porcentajes se muestren en los sectores apropiados y la leyenda aparezca a la derecha. Para que la leyenda se muestre más cerca de la gráfica circular la hemos arrastrado con un clic.
4. Haga clic en varias partes de la gráfica circular (leyenda, área de la gráfica, sector) y aparecerá un cuadro con controladores de tamaño alrededor. Haga doble clic y aparecerá un menú de formato en la parte derecha de la pantalla. Puede ajustar la apariencia del objeto o la región seleccionada en este menú. Cuando haya terminado, para cerrar el menú de formato, haga clic en la “X” que se encuentra en la esquina superior derecha.
CAPÍTULO Descripción de datos con gráficos 36
Nivel del estudiante Primeraño Segundoaño Terceraño Últimoaño Graduado 5% Nivel del estudiante Frecuencia Primeraño 40 35 30 25 20 15 10 5 0 SegundoGraduado añoTercerañoÚltimoaño
Figura 1.18
(a) (b) MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
5. Aún en la pestaña Design, pero en el grupo Type, haga clic en Change Chart Type y elija el tipo de Column más simple. Haga clic en OK para crear una gráfica de barras para el mismo conjunto de datos.
6. Edición de la gráfica de barras: de nuevo, puede experimentar con las distintas opciones de los grupos Chart Layouts y Chart Styles para cambiar el aspecto de la gráfica. Puede hacer clic en toda la gráfica de barras (“chart area”) o en el interior (“Plot area”) para estirar la gráfica. Puede cambiar los colores al hacer doble clic en la región correspondiente. Se ha elegido el diseño 9 en Quick Layout (en el grupo Charts Layout) que incorpora los títulos de los ejes (se han editado) y se eliminó la leyenda “frequency”. También se han reducido los espacios entre las barras; para ello, haga clic con el botón derecho en una de las barras, enseguida seleccione la opción Format Data Series en el menú contextual y cambie Gap Width a 50%. La gráfica de barras editada se muestra en la figura 1.18(b).
EJEMPLO . (Gráficas de líneas) Se dio seguimiento al promedio industrial Dow Jones (PIDJ) al cierre de la negociación durante 10 días en un año reciente; los resultados se muestran en la tabla 1.15.
■ Tabla 1.15 Promedio Industrial Dow Jones
1. Haga clic en la pestaña de la parte inferior de la pantalla marcada con “+” para abrir una nueva hoja de cálculo. Introduzca el Día en la columna A y el PIDJ en la columna B. Debe tener dos columnas con datos, incluidas las etiquetas.
2. Resalte los datos del PIDJ en la columna B; para ello haga clic en el botón izquierdo del mouse y arrastre desde la celda B1 hasta la celda B11 (este rango puede expresarse como B1:B11). Haga clic en la pestaña Insert y dé clic en el icono Line del grupo Charts Seleccione la primera opción de la sección 2D Line para producir la gráfica de líneas.
3. Edición de la gráfica de líneas: de nuevo, puede experimentar con las distintas opciones de los grupos Charts Layout y Charts Styles para cambiar el aspecto de la gráfica. Se ha elegido un diseño (Layout 10 desde el grupo Quick Layout) que incorpora los títulos de ambos ejes y los hemos cambiado a “Día” y “PIDJ”. Además, se ha eliminado el título y la leyenda del lado derecho. La gráfica de líneas se muestra en la figura 1.19.
4. Nota: Si la serie de tiempo involucra periodos que no están igualmente espaciados, es mejor usar un gráfico de dispersión con puntos conectados para formar una gráfica de líneas. Este procedimiento se describe en la sección Tecnología actual del capítulo 3.
Tecnología actual 37
PIDJ Día 21700 21600 21500 21400 21300 21200 21100 12345678910
Figura 1.19
Día12345678910 PIDJ21,47921,47821,32021,41421,40921,53221,55321,63821,63021,575
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
EJEMPLO . (Histogramas de frecuencia) Las 50 principales acciones extrabursátiles (OTC, over-thecounter) de un año reciente se encontraron utilizando una ponderación igual del rendimiento total a 1 año y el crecimiento promedio del volumen diario en dólares. Estas 50 ponderaciones o promedios se muestran a continuación:16
■ Tabla 1.16 Clasificación de las 50 principales acciones OTC
1. Muchos de los procedimientos estadísticos que se usan en este libro de texto requieren la instalación del complemento Analysis ToolPak. Para cargar este complemento, haga clic en File ➤ Options ➤ Add-ins. En la parte inferior del cuadro de diálogo, dé clic en el botón Go ubicado justo a la derecha de la lista desplegable Manage Excel Add-ins Seleccione las casillas Analysis ToolPak, Analysis ToolPak VBA y, a continuación, haga clic en OK
2. Haga clic en la pestaña marcada con “+” en la parte inferior de la pantalla para añadir una nueva hoja de cálculo. Introduzca los datos en la primera columna e incluya la etiqueta “Promedio” en la primera celda.
3. Excel se refiere al valor máximo de cada intervalo de clase como límite de clase. Esto significa que Excel utiliza un método de inclusión derecha, que es ligeramente diferente del método presentado en la sección 1.4. Para este ejemplo, se ha elegido usar los intervalos de clase 0-150, >150-300, >300-450, etc. Introduzca los valores de límite de clase (150, 300, 450, ..., 1500) en la segunda columna de la hoja de cálculo, incluya la etiqueta “Límites de clase” en la celda B1
4. Seleccione Data ➤ Data Analysis➤ Histogram y haga clic en OK. Aparecerá el cuadro de diálogo Histogram, como se muestra en la figura 1.20.

5. Resalte o escriba los rangos de entrada y de límites de clase apropiados para los datos. Note que puede dar clic en el botón Minimizar a la derecha del cuadro antes de dar clic y arrastrar para resaltarlo. De nuevo haga clic en el botón minimizar para ver todo el cuadro de diálogo. El rango de entrada aparecerá como $A$1:$A$51, con el signo de dólar que indica un rango de celdas absoluto. Asegúrese de hacer clic en las casillas de verificación “Labels” y “Chart Output”. Elija una celda conveniente para la ubicación de la salida (aquí se ha elegido E1) y a continuación dé clic en OK. La tabla de frecuencias y el histograma aparecerán en la hoja de cálculo. El histograma (figura 1.21(a)) no aparece exactamente como se esperaba.
6. Edición del histograma: dé clic en la leyenda frecuencia y en el título del histograma y oprima la tecla Eliminar. A continuación, seleccione la Serie de datos dando doble clic en una barra. En el menú de Formato que aparece, cambie Gap Width a 0% (sin espacio) y haga clic en la “X” en la esquina superior derecha para cerrar el menú. Agrande el gráfico arrastrando la esquina inferior derecha y edite los colores, el título y las etiquetas, si es necesario, para completar el histograma, como se muestra en la figura 1.21(b). Recuerde que los números que se muestran a lo largo del eje horizontal son los límites de clase, es decir los límites superiores de los intervalos de clase, no los puntos medios de los intervalos.
CAPÍTULO Descripción de datos con gráficos 38
1395.27 1196.82 1147.05 1138.47 832.23 807.73 780.16 729.44 642.91 598.51 515.74 392.52 374.27 350.20 350.13 305.59 297.60 268.97 258.30 246.19 245.39 231.13 195.94 194.91 189.79 176.81 166.09 165.73 152.97 147.95 143.70 142.82 135.82 135.47 124.06 113.52 112.60 105.74 105.10 103.15 95.75 88.73 88.38 85.02 83.48 83.44 80.85 78.67 78.20 76.48
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
Figura 1.20
FrecuenciaFrecuencia
TECNOLOGÍA ACTUAL
Introducción a MINITABTM
El software MINITAB es un programa de computadora basado en Windows diseñado específicamente para aplicaciones estadísticas. Asumiremos que está familiarizado con el ambiente Windows y que conoce las técnicas básicas necesarias para ejecutar comandos desde las pestañas y los menús desplegables en la parte superior de la pantalla. Si no es así, quizás un asistente de laboratorio o profesor pueda ayudarle a dominar los conceptos básicos. La versión actual de MINITAB que se muestra en esta sección a lo largo de la obra es MINITAB 18, que se utiliza en el ambiente Windows 10. Cuando se abre el programa se muestra la pantalla principal (véase la figura 1.22) que contiene dos ventanas: la ventana Datos, similar a una hoja de cálculo de Excel, y la ventana Sesión, en la que aparecerán los resultados. Al igual que con MS Excel, MINITAB permite guardar hojas de cálculo (similares a las hojas de cálculo de Excel), proyectos (colecciones de hojas de cálculo) o gráficos.
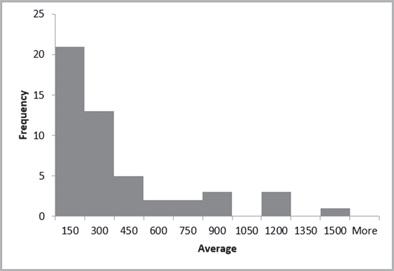
Tecnología actual 39
Límitesdeclase Más Histograma
7. Puede guardar el libro de Excel para utilizarlo más adelante mediante los comandos File ➤ Save o File ➤ Save As y llámelo “Capítulo 1”.
Frecuencia Promedio Más
Figura 1.21
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
Figura 1.22
Representación gráfica con MINITAB

Todos los métodos gráficos que hemos revisado en este capítulo se pueden crear en MINITAB Los datos se ingresan en una hoja de cálculo de MINITAB, con etiquetas en las celdas grises justo debajo del nombre de la columna (C1, C2, etc.) en la ventana Datos. EJEMPLO
(Gráficas circulares y de barras) Se ha registrado la variable cualitativa “nivel cursado en la universidad” para cada uno de los 105 estudiantes en una clase de Introducción a la Estadística y las frecuencias se muestran en la tabla 1.17.
■ Tabla 1.17 Nivel que cursan estudiantes universitarios que actualmente estudian la materia de Estadística
NivelPrimerañoSegundoañoTercerañoÚltimoañoGraduado Frecuencia523323510
1. Introduzca las categorías en la columna C1, con su propio nombre descriptivo, quizás “Nivel (Status)” en la celda gris. Observe que el nombre C1 ha cambiado a C1-T porque está introduciendo texto en lugar de números. Introduzca las cinco frecuencias numéricas en C2 y asígnele el nombre “Frecuencia (Frequency)”.
2. Para crear una gráfica circular para estos datos, dé clic en Graph Pie Chart y aparecerá un cuadro de diálogo (véase la figura 1.23). Dé clic en el botón de opción marcado Chart values from a table. A continuación, coloque el cursor en el cuadro marcado como “Categorical variable”. O bien (1) resalte C1 en la lista de la izquierda y elija Select, (2) haga doble clic en C1 en la lista de la izquierda o (3) escriba C1 en el cuadro “Categorical variable”. Del mismo modo, coloque el cursor en el cuadro marcado “Summary variables” y seleccione C2. Haga clic en Labels y seleccione la pestaña marcada Slice Labels. Verifique las casillas marcadas como “Category names” y “Percent”. Al hacer dos veces clic en OK, MINITAB creará la gráfica circular de la figura 1.24(a). La leyenda se eliminó al seleccionarla y borrarla.
3. A medida que vaya mejorando en el uso del comando de gráfico circular, podrá aprovechar algunas de las opciones disponibles. Una vez que haya creado la gráfica, dé clic con el botón derecho en la gráfica circular y seleccione Edit pie. Puede cambiar los colores y el formato de la gráfica, “separar” sectores importantes del círculo y cambiar el orden de las categorías. Si hace clic con el botón derecho en la gráfica circular y selecciona Update Graph Automatically, la gráfica circular se actualizará en forma automática cuando cambie los datos en las columnas C1 y C2 de la hoja de cálculo de MINITAB.
4. Para construir una gráfica de barras, utilice el comando Graph Bar Chart. En el cuadro de diálogo que aparece, seleccione Simple. Elija una opción en la lista desplegable “Bars represent”, según la forma en que se hayan introducido los datos en la hoja de cálculo. Para los datos de la tabla 1.17, se elige “Values from a table” y se da clic en OK Cuando aparezca el cuadro de diálogo, coloque el cursor en el cuadro “Graph variables”
CAPÍTULO Descripción de datos con gráficos 40
.
Figura 1.23
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
y seleccione C2, en el cuadro “Categorical variable” seleccione C1. Haga clic en OK para terminar la gráfica de barras, que se muestra en la figura 1.24(b). Una vez creada la gráfica, haga clic con el botón derecho en varias partes de la gráfica de barras y elija Edit para cambiar su aspecto.
EJEMPLO . (Gráficas de líneas) Se dio seguimiento al promedio industrial Dow Jones al cierre de la negociación durante 10 días en un año reciente con los resultados que se muestran en la tabla 1.18.
■ Tabla 1.18
Promedio Industrial Dow Jones
1. Aunque podríamos simplemente introducir estos datos en la tercera y cuarta columnas de la hoja de cálculo actual, vamos a crear una nueva con los comandos File ➤ New ➤ Worksheet. Introduzca los Días en la columna C1 y el PIDJ en la columna C2.
2. Para crear la gráfica de líneas, utilice Graph ➤ Time Series Plot ➤ Simple. En el cuadro de diálogo que aparece, coloque el cursor en el cuadro “Series” y seleccione “PIDJ” en la lista de la izquierda. En Time/Scale, elija “Stamp” y seleccione la columna C1 (“Día”) en el cuadro denominado “Stamp Columns”. Haga clic dos veces en OK para obtener la gráfica de líneas que se muestra en la figura 1.25.

Tecnología actual 41
Gráficacirculardelnivel GraduadoPrimeraño Segundoaño Terceraño Últimoaño (a) PrimerañoSegundoañoTercerañoÚltimoañoGraduado Nivel Frecuencia (b)
Figura 1.24
Día12345678910 PIDJ21,47921,47821,32021,41421,40921,53221,55321,63821,63021,575
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
EJEMPLO . (Gráficas de puntos, diagramas de tallo y hoja, histogramas) Las 50 principales acciones extrabursátiles (OTC) de un año reciente se encontraron mediante una ponderación igual del rendimiento total de 1 año y el crecimiento promedio del volumen diario en dólares. Estas 50 ponderaciones o promedios se enlistan en la tabla 1.19.16 Cree una nueva hoja de cálculo (File ➤ New ➤ Worksheet). Introduzca los datos en la columna C1 y asígnele el nombre “Promedio” en la celda gris justo debajo de C1.
■ Tabla 1.19 Clasificación de las 50 principales acciones OTC
1. Para crear una gráfica de puntos, utilice Graph ➤ Dotplot. En el cuadro de diálogo que aparece, elija One Y Simple y haga clic en OK. Para crear un diagrama de tallo y hoja, utilice Graph ➤ Stem-and-Leaf. Para cualquiera de las gráficas, coloque el cursor en el cuadro “Graph variables” y seleccione “Promedio” en la lista de la izquierda (véase la figura 1.26).
2. Puede elegir entre una variedad de opciones de formato antes de hacer clic en OK. La gráfica de puntos aparece como un gráfico, mientras que el diagrama de tallo y hoja aparece en la ventana Session. Para imprimir ya sea una ventana de Graph o la ventana de Session, haga clic en la ventana para activarla y utilice File ➤ Print Graph (o Print Session Window).
CAPÍTULO Descripción de datos con gráficos 42
Figura 1.25
Día
PIDJ
GráficadeseriedetiempodePIDJ
Figura 1.26
1395.27807.73515.74305.59245.39176.81143.70113.5295.7583.44 1196.82780.16392.52297.60231.13166.09142.82112.6088.7380.85 1147.05729.44374.27268.97195.94165.73135.82105.7488.3878.67 1138.47642.91350.20258.30194.91152.97135.47105.1085.0278.20 832.23598.51350.13246.19189.79147.95124.06103.1583.4876.48
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
3. Para crear un histograma, utilice Graph Histogram. En el cuadro de diálogo que aparece, elija Simple y haga clic en OK, seleccionando “Promedio” en el cuadro “Graph variables”. Seleccione Scale Y-Scale Type y haga clic en el botón de opción marcado como “Frequency”. (Puede editar el histograma más adelante para mostrar las frecuencias relativas). Haga clic dos veces en OK. Una vez creado el histograma, haga clic con el botón derecho en el eje y y elija Edit Y-Scale. En la pestaña marcada “Scale”, puede hacer clic en el botón de opción marcado como “Position of ticks” y escribir 0 5 10 15 20. A continuación, haga clic en la pestaña “Labels”, marque el botón de opción “Specified” y escriba 0 5/50 10/50 15/50 20/50. Haga clic en OK. Esto reducirá el número de marcas en el eje y y las cambiará a frecuencias relativas. Por último, haga doble clic en la palabra “Frequency” a lo largo del eje y. Cambie la casilla marcada como “Text” para que diga “Frecuencia relativa” y haga clic en OK
4. Para ajustar los límites o fronteras de clase del histograma, haga clic con el botón derecho en las barras del histograma y elija Edit Bars. Use la pestaña marcada como “Binning” para elegir “Cutpoints” o “Midpoints” para el histograma; puede especificar las posiciones del punto de corte o el punto medio si lo desea. En este mismo cuadro Edit, puede cambiar los colores, el tipo de relleno y el estilo de fuente del histograma. Si da clic con el botón derecho en las barras y selecciona Update Graph Automatically, el histograma se actualizará en forma automática cuando cambie los datos de la columna “Promedio”.
A medida que se familiarice con MINITAB, podrá explorar las distintas opciones disponibles para cada tipo de gráfica. Es posible trazar más de una variable a la vez, cambiar los ejes, elegir los colores y modificar las gráficas de muchas maneras. Sin embargo, incluso con los comandos básicos por defecto, está claro que la distribución de las acciones OTC en la figura 1.27 está muy sesgada a la derecha.
TECNOLOGÍA ACTUAL
Introducción a las calculadoras TI-83/84 Plus
Muchos estudiantes están familiarizados con las calculadoras TI-83 o TI-84 Plus. Estas dos calculadoras funcionan casi de la misma manera y pueden utilizarse para diversas aplicaciones, incluida una gran cantidad de aplicaciones estadísticas. Cuando la calculadora esté encendida, verá una pantalla con un cursor parpadeante, donde puede realizar muchos cálculos numéricos. Sin embargo, para usar muchas de las funciones estadísticas, primero deben introducirse los datos en las listas del Editor de listas de estadísticas. Una vez que se han registrado los datos, se dará cuenta de que hay muchas gráficas diferentes disponibles.
Tecnología actual 43
Frecuencia relativa 20/50 15/50 10/50 5/50 0 030060090012001500 Histogramadepromedio Promedio HistogramofAverage
Figura 1.27
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
Crear gráficas con la calculadora TI-83/84 Plus
Primero, borre cualquier gráfico, función o dibujo no deseado de la calculadora. Oprima 2nd ➤ stat plot. Use las flechas de dirección (o presione 4) para seleccionar 4:PlotSoff y oprima enter dos veces. La calculadora responderá con Done. Puede activar un gráfico en el menú stat plot cuando lo necesite. Borre las funciones no deseadas presionando y = y el botón clear. Por último, oprima 2nd ➤ draw ➤ 1:ClrDraw para borrar los dibujos no deseados.
EJEMPLO . (Gráficas de barras) Se ha registrado la variable cualitativa “nivel cursado en la universidad” para cada uno de los 105 estudiantes en una clase de Introducción a la Estadística, y las frecuencias se muestran en la tabla 1.20.
■ Tabla 1.20 Nivel que cursan estudiantes universitarios que actualmente estudian la materia de Estadística
Nivel PrimerañoSegundoañoTercerañoÚltimoañoGraduado
Frecuencia 523323510
1. Introduzca los datos en el editor de la lista de estadísticas presionando stat. El cursor (resaltado en negro) debe estar en el comando EDIT y 1:Edit... y, al oprimir enter, aparecerá el editor de la lista de estadísticas (figura 1.28).

La variable cualitativa “año en la universidad” se codifica numéricamente como Primero = 1, Segundo = 2, ..., Graduado = 5, y luego se introduce en las primeras cinco filas de la lista L1 con las flechas de dirección para navegar por la tabla. Las cinco frecuencias se incluyen en la lista L2.
2. Para crear la gráfica de barras, presione 2nd ➤ stat plot. El cursor estará en 1:Plot 1, presione enter. Hay cuatro opciones que se pueden elegir en la siguiente pantalla (figura 1.29), presione enter después de cada elección y utilice las flechas de dirección para navegar por la pantalla.
CAPÍTULO Descripción de datos con gráficos 44
Figura 1.28
Figura 1.29
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
Elija activar el gráfico (On) y después Histogram (la tercera opción). La opción Xlist especifica los datos del eje horizontal (x), en este caso L1. La opción Ylist muestra los datos del eje vertical (y), en este caso L2. Como el valor predeterminado para Ylist es 1, tendrá que cambiarlo con 2nd ➤ L2. Ahora presione zoom y 9:ZoomStat para ver la gráfica de barras, creada automáticamente por la calculadora, que se muestra en la figura 1.30(a).
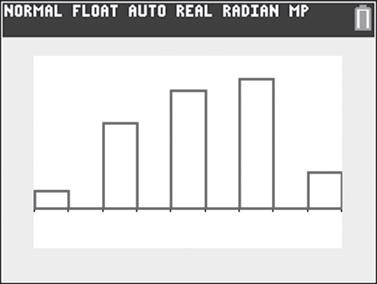
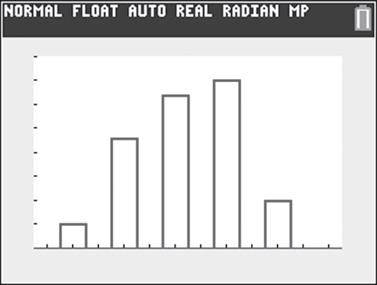
3. Observe que no hay etiquetas en ninguno de los ejes. Puede entender mejor la gráfica presionando la tecla trace y moviendo el cursor parpadeante de izquierda a derecha con las flechas direccionales. La barra “Primer año” comienza en 1, termina en <1.5 y su altura es 5. La brecha entre la primera y la segunda barras comienza en 1.5 y termina en 2, donde comienza la barra “Segundo año”. Es decir, la calculadora está creando clases “inclusivas a la izquierda”.
4. Edición de la gráfica de barras: presione window para ver los ajustes exactos de la gráfica (figura 1.30(b)). Es posible cambiar cualquiera de estos ajustes. Los valores mínimo y máximo para los ejes x y y son Xmin, Xmax, Ymin y Ymax. El ancho de cada intervalo a lo largo de los ejes x y y es Xscl y Yscl, respectivamente. Para la figura 1.30(a), el límite inferior de la primera clase es 1 y el límite superior de la última clase es 5.5; cada barra mide 0.5 unidades de ancho y la distancia entre las marcas de graduación del eje es de 59 unidades. Si se cambia la configuración de la ventana como se muestra en la figura 1.31(a) y presiona la tecla graph, la gráfica de barras aparecerá como en la figura 1.31(b). Ahora, las barras están centradas sobre los valores de “nivel en la universidad”, 1, 2, 3, 4 y 5. [Nota: Si presiona zoom ➤ 9:ZoomStat en lugar de graph en este punto, la configuración de la calculadora volverá a la configuración predeterminada y la gráfica de barras aparecerá como en la figura 1.30(a)].
Tecnología actual 45
Figura 1.31
(a)
(b)
(a)
Figura 1.30
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
(b)
EJEMPLO . (Gráficas de líneas) Se dio seguimiento al promedio industrial Dow Jones, al cierre de la negociación durante 10 días en un año reciente, y los resultados se muestran en la tabla 1.21.
■ Tabla 1.21 Promedio Industrial Dow Jones
1. En el editor de listas de estadísticas, borre las listas L1 y L2, para ello coloque el cursor sobre el nombre de la lista y oprima clear y enter. Después ingrese los datos en la tabla 1.21, con los Días en la lista L1 y el PIDJ en la lista L2.
2. Siga un procedimiento similar al que se utilizó para crear la gráfica de barras. Presione 2nd stat plot 1: Plot1. En la pantalla que aparece, asegúrese de que el gráfico esté activado y elija el tipo de gráfico Line Chart (la segunda opción). Luego Xlist = L1 (días) y Ylist = L2 (PIDJ). Presione zoom 9:ZoomStat (o simplemente zoom 9) para obtener la gráfica de líneas que se muestra en la figura 1.32.
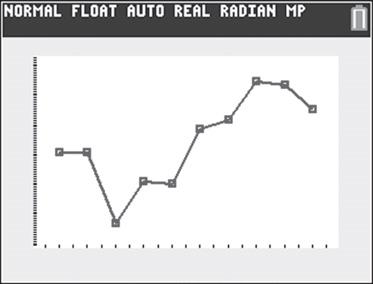
3. Del mismo modo que con la gráfica de barras, puede usar la tecla trace para navegar por la pantalla y ver los valores de PIDJ de los 10 días. También puede utilizar la pantalla window para modificar la configuración de los ejes x y y. De nuevo, no hay etiquetas en ninguno de los ejes, pero aún se puede ver la tendencia del PIDJ durante los 10 días.
(Histogramas de frecuencia) Las 50 principales acciones extrabursátiles (OTC) de un año reciente se encontraron utilizando una ponderación igual del rendimiento total de 1 año y el crecimiento promedio del volumen diario en dólares. Estas 50 ponderaciones o promedios se muestran aquí:16
■ Tabla 1.22 Clasificación de las 50 principales acciones OTC
1. De nuevo se utilizará el tipo de gráfico Histogram en el menú de gráficos de estadísticas (stat plot), pero en este caso cada observación ocurre solo una vez, por lo que las frecuencias (Freq) serán 1. Introduzca los datos en la lista L1 en el editor de listas de estadísticas.
2. Para crear el histograma, presione 2nd stat plot 1:Plot1. En la pantalla que aparece, asegúrese de que la gráfica esté activada (On), elija el tipo Histogram (la tercera opción) y Xlist = L1 (promedios). Escriba el número “1” en Ylist y presione zoom 9:ZoomStat (o simplemente zoom 9) para mostrar el histograma.
CAPÍTULO Descripción de datos con gráficos 46
Día12345678910
PIDJ21479214782132021414214092153221553216382163021575
Figura 1.32
1395.27807.73515.74305.59245.39176.81143.70113.5295.7583.44 1196.82780.16392.52297.60231.13166.09142.82112.6088.7380.85 1147.05729.44374.27268.97195.94165.73135.82105.7488.3878.67 1138.47642.91350.20258.30194.91152.97135.47105.1085.0278.20 832.23598.51350.13246.19189.79147.95124.06103.1583.4876.48
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
EJEMPLO .
3. Edición del histograma: una vez creado el histograma, utilice la ventana (window) para ajustar los límites o fronteras de clase y el ancho de las clases. La pantalla window se muestra en la figura 1.33(a). Hemos optado por usar clases de ancho 150, que comienzan en 0 y terminan justo por encima del valor más grande en 1500. Recuerde que las calculadoras TI utilizan el método de “inclusión a la izquierda” tal como se presenta en la sección 1.4. Una vez que haya cambiado la configuración de la ventana, presione graph para mostrar el histograma de la figura 1.33(b). La distribución de las acciones OTC está muy sesgada a la derecha, con algunas mediciones excepcionalmente grandes.
REVISAR LO QUE HA APRENDIDO
1. ¿Cuantitativa o cualitativa? Identifique cada variable como cuantitativa o cualitativa:
a. Origen étnico de un candidato a un cargo público.
b. Puntuación (0-100) en un examen de colocación.
c. Restaurante de comida rápida preferido por un estudiante (McDonald’s®, Burger King® o Carl’s Jr.®).
d. Concentración de mercurio en una muestra de atún.
2. ¿Simétrica o sesgada? ¿Espera que las distribuciones de las siguientes variables sean simétricas o sesgadas? Explique.
a. Precio de una lata de chícharos de 250 gramos.
b. Estatura en centímetros de las estudiantes de primer año en su universidad.
c. Número de tostadas rotas en un paquete de 100 tostadas.
d. Número de garrapatas encontradas en cada uno de 50 conejos de rabo blanco atrapados.
3. ¿Continua o discreta? Identifique cada variable como continua o discreta:


a. Periodo entre llegadas de pacientes a una clínica médica.
b. Tiempo necesario para terminar un examen.
c. Peso de dos docenas de camarones.
d. La temperatura corporal de una persona.
e. Número de personas que esperan atención en la sala de emergencias de un hospital.
4. Continua o discreta, de nuevo Identifique cada variable como continua o discreta:

a. Número de propiedades en venta por una agencia inmobiliaria.
b. Profundidad de una nevada.
c. Periodo para que un conductor responda cuando está a punto de sufrir un choque.
d. Número de aviones que llegan al aeropuerto de Atlanta en una hora determinada.
DATA SET

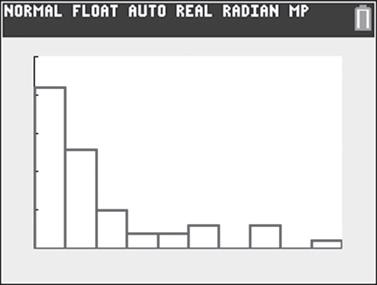
DS0127
5. Los principales lagos del mundo Un lago es una masa de agua rodeada de tierra. Por lo tanto, algunos cuerpos de agua llamados “mares”, como el mar Caspio, son en realidad lagos salados. En la siguiente tabla se indica la longitud en kilómetros de los principales lagos naturales del mundo, excepto el mar Caspio, que tiene una longitud de 1,216 kilómetros.5
Revisar lo que ha aprendido 47
(a) (b)
Figura 1.33
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
NombreLongitud (km)NombreLongitud (km)
Superior560Titicaca195
Victoria334Nicaragua163
Huron330Athabasca333
Michigan491Reindeer229
MardeAral416TonleSap112
Tanganyika672Turkana246
Baykal632IssykKul184
GreatBear307Torrens208
Nyasa576Vänern146
GreatSlave477Nettilling107
Erie386Winnipegosis226
Winnipeg426Albert160
Ontario309Nipigon115
Balkhash602Gairdner144









Ladoga198Urmia144
Maracaibo213Manitoba224
Onega232Chad280
Eyre144
Fuente:The World Almanac and Book of Facts 2017
a. Use un diagrama de tallo y hoja para describir la longitud de los principales lagos del mundo.
b. Utilice un histograma para mostrar estos datos. ¿Cómo se compara con el diagrama de tallo y hoja del inciso a?
c. ¿Estos datos son simétricos o se encuentran sesgados? Si la distribución está sesgada, ¿cuál es la dirección de la inclinación?
6. Limpieza de derrames de petróleo El 20 de abril de 2010 hubo en Estados Unidos un gran desastre ambiental cuando la plataforma de perforación
Deepwater Horizon explotó en el Golfo de México. El personal ocupado y el equipo que se utilizó en la limpieza del derrame de petróleo en el Golfo, desde el 2 de mayo de 2010 (día 13) hasta el 9 de junio de 2010 (día 51) se indica en la siguiente tabla.17
d. Utilice una gráfica de barras para mostrar el porcentaje de áreas de pesca federales del Golfo cerradas.
e. Use una gráfica de líneas para mostrar las cantidades de dispersantes utilizadas. ¿Hay alguna relación de línea recta subyacente a lo largo del tiempo?
7. Resultados electorales Las elecciones de 2016 en Estados Unidos fueron una contienda en la que Donald Trump derrotó a Hillary Clinton y otros candidatos al ganar 304 votos electorales, o 57% de los 538 disponibles. Sin embargo, Trump solo ganó 46.1% del voto popular, mientras que Clinton obtuvo 48.2%. El voto popular (en miles) para Donald Trump en cada uno de los 50 estados se enlista a continuación:18
AL1319HI129MA1091NM320SD228
AK163ID409MI2280NY2820TN1523
AZ1252IL2146MN1323NC2363TX4685
AR685IN1557MS701ND217UT515
CA4484IA801MO1595OH2841VT95
CO1202KS671MT279OK949VA1769
CT673KY1203NE496OR782WA1222
DE185LA1179NV512PA2971WV489
FL4618ME336NH346RI181WI1405
GA2089MD943NJ1602SC1155WY174
a. Con solo mirar la tabla, ¿qué forma cree que tendrá la distribución del voto popular por estado?
b. Trace un histograma de frecuencia relativa para describir la distribución del voto popular para el presidente Trump en los 50 estados.
c. ¿El histograma del inciso b confirmó su suposición del inciso a? ¿Hay valores atípicos? ¿Cómo puede explicarlos?
Barrerascolocadas(kilómetros)7450410301454
Dispersantesusados(miles delitros)
590189332934326
Barcosdesplegados(cientos)1.06.014.035.0
a. ¿Qué tipos de gráficas podría utilizar para mostrar estos datos?
b. Antes de trazar las gráficas, ¿qué tendencias observa en cada una de las variables?
c. Use una gráfica de líneas para mostrar el personal ocupado durante este periodo de 51 días.
DATA SET
DS0130
8. Resultados electorales, continuación Consulte el ejercicio 7. A continuación se muestra el porcentaje del voto popular que el presidente Trump recibió en cada uno de los 50 estados:18
CAPÍTULO Descripción de datos con gráficos 48
DATA SET DS0129
DATA SET DS0128
AL62HI30MA33NM40SD62 AK51ID59MI47NY37TN61 AZ49IL39MN45NC50TX52 AR61IN57MS58ND63UT46 CA32IA51MO57OH52VT30 CO43KS57MT56OK65VA44 CT44KY63NE59OR39WA37 DE42LA58NV46PA48WV68 FL49ME45NH46RI39WI47 GA51MD34NJ41SC55WY68
Númerodepersonal(miles)3.017.520.024.0 Áreasdepescafederales cerradasenelGolfo 3%8%25%32%
Día
13Día 26Día 39Día 51
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
a. Con solo mirar la tabla, ¿qué forma cree que tendrá la distribución del porcentaje del voto popular por estado?
b. Trace un histograma de frecuencia relativa para describir la forma de la distribución y busque los valores atípicos.
¿La gráfica confirma su respuesta del inciso a?
9. Resultados electorales, continuación Consulte los ejercicios 7 y 8. Los diagramas de tallo y hoja que aquí se muestran se generaron con el software MINITAB para las variables denominadas “voto popular” y “porcentaje de voto”.



Diagrama de tallo y hoja: Voto popular Diagrama de tallo y hoja: Porcentaje
Diagrama de tallo y hoja de voto popular N 5 50
Diagrama de tallo y hoja de porcentaje N 5 50
600111115300234
12022233310377999
17044455164012344
22066677(10)45566677899
250899245011122
251011185567778899
22122223396112233
161455536588
12167
Unidad de hoja = 1 101 10201 8223 62 62 62889
Unidad de hoja = 100 HI 44, 46, 46
a. Describa las formas de las dos distribuciones. ¿Hay valores atípicos?
b. ¿Se parecen los diagramas de tallo y hoja a los histogramas de frecuencia relativa construidos en los ejercicios 7 y 8?






c. Explique por qué la distribución del voto popular para el presidente Trump por estado es sesgada, mientras que el porcentaje de votos populares por estado tiene forma de montículo. DATA SET
a. ¿Por qué todas las medidas son números pares?
b. Dibuje un diagrama de tallo y hoja para describir los datos, divida cada tallo en dos líneas.
c. Construya un histograma de frecuencia relativa para los datos.
d. Escriba un párrafo breve que describa la distribución de las frecuencias del pulso de los estudiantes.
DATA SET
DS0132
11. Energía eólica La energía eólica es el uso del flujo del viento a través de turbinas para propulsar generadores de energía eléctrica. El siguiente mapa muestra la generación neta del viento (en megavatios hora) por estado en Estados Unidos a finales de 2017.19
a. Para los estados que cuentan con capacidad de generación de energía eólica instalada, utilice un histograma de frecuencia relativa para describir su capacidad de generación eólica a finales de 2017.
b. ¿Cuál es la forma del histograma? ¿Hay alguna característica excepcional? Si hay algún valor atípico, ¿puede explicarlo?
c. ¿Se le ocurre alguna razón para la falta de generadores eólicos en los estados del sureste?
DATA SET
DS0133
10. Pulso Un grupo de 50 estudiantes de biomédica registró su pulso, para ello los estudiantes contaron el número de latidos durante 30 segundos y lo multiplicaron por 2.
12. Un hallazgo arqueológico Un artículo en la revista científica Archaeometry describió 26 muestras de cerámica romano-británica, encontradas en cuatro hornos diferentes en Reino Unido.20 El porcentaje de óxido de aluminio en cada una de las 26 muestras se expone en la siguiente tabla.
DS0131
Revisar lo que ha aprendido 49 2222 3944 3379 0 471 0 0 0 NS = No significativo 0 0 0 67,092 24,404 0 18,501 5237 3154 10,987 2150 4398 9567 4542 588 935 361 13,971 6506 7481 2453 30 0 0 1563 4742 11,297 1949 20,816 10,885 1529 5072 221 414 279 153 NS 20 5 511 164 643 80708870846684826642 52729070968496866278 608288546666808856104 84846084885872846874 8472629072847211010058
LlanederynCaldicotIsland ThornsAshley Rails 14.411.611.818.317.7 13.811.111.615.818.3 14.613.418.016.7 11.512.418.014.8 13.813.120.819.1 10.912.7 10.112.5
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
a. Use un histograma de frecuencia relativa para describir el contenido de óxido de aluminio en las 26 muestras de cerámica.
b. ¿Qué característica excepcional observa en esta gráfica? ¿Se le ocurre una explicación para esta característica?
c. Dibuje una gráfica de puntos para los datos, use las letras (L, C, I o A) para ubicar el punto de datos en la escala horizontal. ¿Ayuda esto a explicar la característica excepcional del inciso b? DATA
22,50010,0006,300
14,0008,3706,000
14,0006,8096,000
13,8606,4005,850
11,2346,4005,616
Fuente: The World Almanac and Book of Facts 2017, p. 726.
a. Construya un diagrama de tallo y hoja para los datos.
b. ¿Cómo describiría la forma de esta distribución?
DS0134
13. Impuesto a la gasolina A continuación se muestran los impuestos estatales a la gasolina en 2017, expresados en centavos por galón para los 50 estados de Estados Unidos y el Distrito de Columbia.21
DATA SET DS0136
15. ¿Qué es normal? El valor estándar de 37.0 grados para la temperatura corporal humana fue derivado por un médico alemán en 1868. Para comprobar esta afirmación, Allen Shoemaker22 registró la temperatura corporal de 130 personas sanas. A continuación se muestra el histograma de frecuencia relativa de estos datos.
0.25
0.20
0.15
0.10
AL22.91HI44.39MA26.54NM18.88SD30.00
AK12.25ID33.00MI40.44NY43.88TN21.40
AZ19.00IL34.01MN28.60NC34.55TX20.00
AR21.80IN33.59MS18.79ND23.00UT29.41
CA38.13IA30.70MO17.30OH28.01VT30.46
CO22.00KS24.03MT27.75OK17.00VA22.39












CT39.85KY26.00NE28.20OR31.12WA49.40
DC23.50LA20.01NV33.52PA58.20WV32.20
DE23.00ME30.01NH23.83RI34.00WI32.90
FL36.80MD33.50NJ37.10SC16.75WY24.00
GA31.09
a. Dibuje un diagrama de tallo y hoja para los datos.
b. ¿Cómo describiría la forma de esta distribución?
c. ¿Hay estados con impuestos a la gasolina excepcionalmente altos o bajos? Si es así, ¿qué estados son?
DATA SET
a. Describa la forma de la distribución de temperaturas.
b. ¿Hay alguna observación excepcional? ¿Se le ocurre alguna explicación para esto?
c. Ubique el valor estándar de 37.0 grados en el eje horizontal de la gráfica. ¿Parece estar cerca del centro de la distribución?
Por su cuenta
DATA SET
14. Centrales hidroeléctricas Los siguientes datos representan las capacidades instaladas en megavatios (millones de vatios) para las 15 centrales hidroeléctricas más grandes del mundo.5 0.05
16. Vetos presidenciales A continuación se presenta una lista de los 44 presidentes de Estados Unidos junto con el número de vetos regulares para cada uno de ellos:5
DS0137
Washington2B.Harrison19
J.Adams0Cleveland42
Jefferson0McKinley6
Madison5T.Roosevelt42
Monroe1Taft30
J.Q.Adams0Wilson33 (Continúa)
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
CAPÍTULO Descripción de datos con gráficos 50
SET
ME 30.01¢ NY 43.88¢ PA 58.20¢ VA 22.39¢ NC 34.55¢ SC 16.75¢ GA 31.09¢ FL 36.80¢ AL 22.91¢ MS 18.79¢ LA 20.01¢ TX 20.00¢ OK 17.00¢ AR 21.80¢ KS 24.03¢ NE 28.20¢ SD 30.00¢ ND 23.00¢ MT 27.75¢ WY 24.00¢ CO 22.00¢ NM 18.88¢ AZ 19.00¢ UT 29.41¢ NV 33.52¢ CA 38.13¢ OR 31.12¢ WA 49.4¢ ID 33.00¢ TN 21.40¢ KY 26.00¢ WV 32.20¢ OH 28.01¢ IN 33.59¢ IL 34.01¢ MO 17.30¢ IA 30.70¢ MN 28.60¢ WI 32.90¢ MI 40.44¢ NH 23.83¢ AK 12.25¢ HI 44.39¢ VT 30.46¢ MA 26.54¢ RI 34.00¢ CT 39.85¢ NJ 37.10¢ DE 23.00¢ MD 33.50¢ DC 23.50¢
DS0135 Frecuencia relativa Temperatura 37.037.4 37.8 38.2 38.639.0 0
Jackson5Harding5
VanBuren0Coolidge20
W.H.Harrison0Hoover21
Tyler6F.D.Roosevelt372
Polk2Truman180
Taylor0Eisenhower73
Fillmore0Kennedy12
Pierce9L.Johnson16
Buchanan4Nixon26
Lincoln2Ford48
A.Johnson21Carter13
Grant45Reagan39
Hayes12G.H.W.Bush29
Garfield0Clinton36
Arthur4G.W.Bush12
Cleveland304Obama12
Fuente: The World Almanac and Book of Facts 2017.
Emplee una gráfica apropiada para describir el número de vetos emitidos por los 44 presidentes. Escriba un resumen de un párrafo que describa este conjunto de datos.



17. Derby de Kentucky El siguiente conjunto de datos muestra los tiempos ganadores (en segundos) para las carreras del Derby de Kentucky de 1950 a 2017.23
podían usar computadoras en casa. Aquí se muestran los resultados de los exámenes finales de las dos clases.
Con computadora portátil Sin computadora portátil
†Tiemporécordestablecidoporelsecretariadoen1973
Fuente: https://www.kentuckyderby.com/history/kentucky-derby-winners
a. ¿Piensa que habrá una tendencia en los tiempos ganadores a lo largo de los años? Elabore una gráfica de líneas para verificar su respuesta.
b. Use una gráfica para describir la distribución de los tiempos ganadores. Comente la forma de la distribución y busque cualquier tiempo ganador excepcional.
Escriba un resumen de un párrafo que describa y compare las puntuaciones del examen final de los dos grupos de estudiantes. DATA SET






19. Old Faithful Los siguientes datos son los tiempos de espera entre las erupciones del géiser Old Faithful en el Parque Nacional de Yellowstone.25 Use una gráfica para describir los tiempos de espera. Si hay alguna característica excepcional en su gráfica, reflexione sobre si existe alguna explicación práctica para ella.
DATA SET

DS0139
18. Las computadoras portátiles y el aprendizaje En una escuela secundaria de Nueva Jersey se llevó a cabo un experimento informal para investigar el uso de computadoras portátiles como herramienta para el aprendizaje en el estudio del álgebra.24 A 20 estudiantes de una clase de primer año se les dieron computadoras portátiles para que las usaran en la escuela y en el hogar, mientras que a 27 estudiantes de otra clase de primer año no se les proporcionaron; sin embargo, muchos de estos estudiantes
Revisar lo que ha aprendido 51
9884638397 9793935274 8857836388 10084868184 10081999149 7883808189 6884782964 4793747289 9057678970 9483
(1950)121.3122.3121.3122.0123.0121.4123.2122.1125.0122.1 (1960)122.2124.0120.2121.4120.0121.1122.0120.3122.1121.4 (1970)123.2123.1121.4119.2†124.0122.0121.3122.1121.1122.2 (1980)122.0122.0122.2122.1122.2120.1122.4123.0122.1125.0 (1990)122.0123.0123.0122.0123.3121.1121.0122.2122.1123.29 (2000)121.00119.97121.13121.19124.06122.75121.36122.17121.82122.66 (2010)124.45122.04121.83122.89123.66123.02121.31123.59
Con computadora portátil Frecuencia relativa Sin computadora portátil 0.40 0.30 0.20 0.10 0 30 40506070809010030405060708090100
Los histogramas a continuación muestran la distribución de las puntuaciones en los exámenes finales de los dos grupos.
56895179588252885278 69757753805479746578 55875385619354768081 59867871778945937271 76947550838272777565 79727877797282748049 75786480494988517885 65757769929153864979 68876181559353847073 93508777748987765980 DATA SET DS0138 MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
DS0140
20. ¿Qué tan cara es su universidad? Los datos a continuación representan una muestra de instituciones educativas terciarias que ofrecen carreras con duración de cuatro años y universidades en Estados
Unidos; se incluyen sus costos de matrícula y cuotas por alojamiento y alimentación en 2016.5 ¿Cómo se compara su institución educativa con esta muestra?
Nombre
Pública o privada Matrícula y cuotas
Alojamiento y alimentaciónName
Pública o privada Matrícula y cuotas
Alojamiento y alimentación
AmericanUniv.,DCPrivada$44,593$14,526NorthParkUniv.,ILPrivada$25,860$8,460 AuburnUniv.,ALPública10,42412,584OhioState,OHPública10,03711,666 BelmontUniv.,TNPrivada30,00010,970PacificLutheran,WAPrivada37,95010,330 BradleyUniv.,ILPrivada31,4809,700PrairieViewA&M,TXPública9,7458,419 CalStateBakersfield,CAPública6,81112,561RobertMorrisUniv.,ILPrivada25,95012,600 CarletonCollege,MNPrivada49,26312,783St.John’sUniv.,MNPrivada40,2269,604 TheCitadel,SCPública13,0246,381SanFranciscoState,CAPública6,47612,234 CollegeoftheHolyCross,MAPrivada48,94013,225SouthDakotaState,SDPública8,1727,462 ConcordiaUniv.,ILPrivada30,6409,172SouthwesternUniv.,TXPrivada39,06012,288 DePauwUniv.,INPrivada44,67811,700StetsonUniv.,FLPrivada43,24012,326 EasternMichiganUniv.,MIPública10,4179,398TowsonUniv.,MDPública9,18211,638 EndicottCollege,MAPrivada30,49214,112Univ.atAlbany,SUNY,NYPública8,99612,422 FordhamUniv.,NYPrivada47,31716,350Univ.ofCentralFlorida,FLPública6,3689,300 GeorgiaStateUniv.,GAPública10,68613,646Univ.ofIllinoisatUrbana-Champaign,ILPública15,62611,000 HampshireCollege,MAPrivada48,81013,274Univ.ofMiami,CoralGables,FLPrivada47,00413,310 IdahoStateUniv.,IDPública6,7846,338Univ.ofNorthCarolina,NCPública8,59110,902 IthacaCollege,NYPrivada40,65814,674Univ.ofRedlands,CAPrivada44,90013,090 KentState,OHPública10,0129,908Univ.ofSouthernCalifornia,CAPrivada50,21013,855 LehighUniv.,PAPrivada46,23012,280Univ.ofUtah,UTPública8,1979,000 LoyolaMarymount,CAPrivada42,56914,470ValparaisoUniv.,INPrivada36,16010,520 MarquetteUniv.,WiPrivada38,47011,440WartburgCollege,IAPrivada38,3809,460 MiamiUniv.,OHPública14,28711,644WashingtonStateUniv.,Pullman,WAPública11,96711,356 MonroeCollege,NYPrivada14,1489,400WesternOregonUniv.,ORPública8,7969,638 MuhlenbergCollege,PAPrivada45,87510,770WorcesterStateUniv.,MAPública8,85711,560
Fuente: The World Almanac and Book of Facts 2017
Utilice cualquiera de las gráficas que se han estudiado en este capítulo para describir los costos de las universidades en la tabla. Si observa alguna característica excepcional en las gráficas o detecta algún valor atípico, ¿puede explicar estos resultados?



CAPÍTULO Descripción de datos con gráficos 52
SET DS0141
DATA
MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.
¿Cómo está su presión arterial?
La presión arterial es la presión que la sangre ejerce contra las paredes de las arterias. Cuando los médicos oenfermeros miden la presión arterial, toman dos lecturas. La presión arterial sistólica es la presión cuando el corazón se contrae y, por lo tanto, bombea. La presión arterial diastólica es la presión en las arterias cuando el corazón se relaja. La lectura de la presión arterial diastólica es siempre la más baja de las dos lecturas. La presión arterial varía de una persona a otra; también variará para una sola persona de un día a otro e incluso en un mismo día.
Si la presión arterial es demasiado alta puede provocar un derrame cerebral o un infarto. Si es demasiado baja la sangre no llegará a las manos ni a los pies y es posible que se sienta mareado. Por lo general, la presión arterial baja no es grave.
Entonces, ¿cuál debería ser su presión arterial? Una presión arterial sistólica de 120 se consideraría normal; una de 150 sería alta. Pero, puesto que la presión arterial varía entre los géneros y aumenta con la edad, se obtendrá un mejor indicador de la posición relativa de la presión arterial al compararla con la población de la presión arterial de todas las personas de su género y edad en Estados Unidos. Por supuesto, no es posible proporcionar ese conjunto de datos, pero sí presentar una muestra muy grande seleccionada a partir de este. Los datos de la presión arterial de 1,910 personas, 965 hombres y 945 mujeres de entre 15 y 20 años, forman parte de una encuesta de salud realizada por los National Institutes of Health (NIH). Las observaciones para cada persona incluyen su edad y su presión arterial sistólica y diastólica en el momento en que se registró la presión arterial. Utilice un paquete estadístico para responder las siguientes preguntas.
1.¿Cuáles son las variables que se midieron en esta encuesta? ¿Las variables son cuantitativas o cualitativas? ¿Discretas o continuas? ¿Los datos son univariados, bivariados o multivariados?
2.¿Qué tipos de gráficas se pueden usar para describir este conjunto de datos? ¿Qué tipos de preguntas se pueden responder con diferentes tipos de gráficas?




3.Elabore un histograma de frecuencia relativa con los datos de presión arterial sistólica para los 965 hombres y otro para las 945 mujeres. Compare ambos histogramas.
4.Considere a los 965 hombres y 945 mujeres como la totalidad de la población de interés. Seleccione una muestra de n 5 50 hombres y n 5 50 mujeres, y registre tanto los datos de la presión arterial sistólica como de las edades. Dibuje dos histogramas de frecuencia relativa para mostrar gráficamente la presión arterial sistólica en las dos muestras. ¿Se parecen las formas de los histogramas a los histogramas de población del inciso 3?
5.¿Cómo se compara su propia presión arterial con la de otras personas de su mismo sexo? Verifique su presión arterial sistólica con el histograma apropiado de los incisos 3 o 4 para determinar si su presión arterial es “normal” o si es excepcionalmente alta o baja.

Estudio de caso 53 DATA SET BLOOD PRESSURE
ESTUDIO DE CASO MUESTRA ISSUU © D.R. 2023 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Cengage Learning® es una marca registrada usada bajo permiso. DERECHOS RESERVADOS.













































































































