Pensamiento matemático III
Verónica Flores Cortés Arturo Flores Cortés
Australia Brasil Canadá Estados Unidos México Reino Unido Singapur
Pensamiento matemático III, primera edición
Verónica Flores Cortés Arturo Flores Cortés
Director Higher Education
Latinoamérica: Lucía Romo Alanís
Gerente editorial Latinoamérica: Jesús Mares Chacón
Editor:
Alejandro Nava Alatorre
Coordinador de manufactura: Rafael Pérez González
Diseño de portada y diseño de interiores: Punto 5
Imagen de portada: benjaminec / Punto 5
Composición tipográfica: Mariana Sierra Enríquez
© D.R. 2024 por Cengage Learning Editores, S.A. de C.V., una Compañía de Cengage Learning, Inc. Av. Andrés Molina Enríquez 354, Primer piso, Oficina “A”, Colonia Ampliación Sinatel, Delegación Iztapalapa, Ciudad de México, C.P. 09479. Cengage Learning® es una marca registrada usada bajo permiso.
DERECHOS RESERVADOS. Ninguna parte de este trabajo amparado por la Ley Federal del Derecho de Autor, podrá ser reproducida, transmitida, almacenada o utilizada en cualquier forma o por cualquier medio, ya sea gráfico, electrónico o mecánico, incluyendo, pero sin limitarse a lo siguiente: fotocopiado, reproducción, escaneo, digitalización, grabación en audio, distribución en internet, distribución en redes de información o almacenamiento y recopilación en sistemas de información a excepción de lo permitido en el Capítulo III, Artículo 27 de la Ley Federal del Derecho de Autor, sin el consentimiento por escrito de la Editorial.
Datos para catalogación bibliográfica: Flores Cortés, Verónica, Arturo Flores Cortés
Pensamiento matemático III
Primera edición.
ISBN: 978-607-570-224-7
Visite nuestro sitio en: http://latam.cengage.com
Impreso en México 1 2 3 4 5 6 7 24 23 22 21



Unidad 1. Variación y sus consecuencias .......................................2 Diagnóstico ....................................................................... 4 Activación ......................................................................... 6 Progresión 1 .........................................................................................7 Tema 1. Variación promedio y variación instantánea ......................................13 Progresión 2 .......................................................................................21 Tema 2. El problema de construir una recta tangente ....................................21 Progresión 3 ......................................................................................29 Tema 3. Aritmética de funciones ............................................................29 CIERRE ............................................................................. 34 Valoración ........................................................................ 37 Progreso .......................................................................... 41 Unidad 2. Funciones ...................................................................42 Diagnóstico ...................................................................... 44 Activación ........................................................................ 46 Progresión 4 ......................................................................................49 Tema 1. Algunas propiedades de las funciones............................................49 Progresión 5 ......................................................................................63 Tema 2. Estudio de funciones por medio del límite .......................................63 Progresión 6 ......................................................................................73 CIERRE ............................................................................. 77 Valoración ........................................................................ 80 Progreso .......................................................................... 85 Unidad 3. La derivada .................................................................86 Diagnóstico ...................................................................... 88 Activación ........................................................................ 90 Desarrollo ...........................................................................................91 Progresión 7 ......................................................................................94 Tema 1. La derivada y algunas interpretaciones ..........................................94 Progresión 8 .....................................................................................108 Tema 2. Propiedades de la derivada .......................................................108 CIERRE ............................................................................ 120 Valoración ....................................................................... 122 Progreso ......................................................................... 125 Contenido v Contenido


Unidad 4. Aplicación de la derivada ............................................126 Diagnóstico .................................................................... 128 Activación ...................................................................... 130 Progresión 9 ......................................................................................131 Progresión 10 ....................................................................................133 Tema 1. Aplicación de la derivada: Máximos y mínimos ..................................121 Progresión 11 .....................................................................................147 Tema 2. Optimización ........................................................................147 Progresión 12 ....................................................................................160 Tema 3. Funciones exponencial y logarítmica............................................160 CIERRE ........................................................................... 166 Valoración ...................................................................... 168 Progreso ........................................................................ 173 Unidad 5. Fenómenos periódicos y modelación .............................174 Diagnóstico .................................................................... 176 Activación ...................................................................... 178 Progresión 13 ....................................................................................178 Tema 1. Funciones periódicas ...............................................................180 Progresión 14 .....................................................................................191 Tema 2. Modelación: el costo marginal .....................................................191 Progresión 15 ....................................................................................195 CIERRE ........................................................................... 199 Valoración ...................................................................... 201 Progreso ........................................................................ 205 Pensamiento matemático II vi
CONOCE TU LIBRO

Entrada de unidad.
Conocerás las progresiones de aprendizaje que serán abordadas en la unidad correspondiente.
La evaluación diagnóstica será útil para identi car tus conocimientos previos.


Encontrarás varias actividades donde tendrás e es acio s ciente ara escribir tus respuestas o realizar tus operaciones.
Conoce tu libro vii

Podrás orientarte con los ejemplos.
Las actividades PARA PRACTICAR serán útiles para reforzar tus conocimientos adquiridos y descubrir lo que todavía no tienes claro respecto a algún concepto.


La sección CONEXIÓN puntualiza la interacción con otras áreas del conocimiento, es decir, lo que se denomina transversalidad.
Pensamiento matemático II viii
Responder las preguntas de la sección VALORACIÓN te ayudará a valorar lo que has aprendido para aprovecharlo mejor durante tu proceso educativo.
Conoce tu libro


Progreso
Registra cuánto has aprendido. Pon una en el porcentaje de comprensión que tienes de cada aspecto.
AspectoAl100%Entre80%y90%Entre60y79%Deborepasarlo
Comprendo conceptos como: variación promedio, variación instantánea, procesos in nitos y movimiento.
Aplico procedimientos y lenguaje matemático para la solución de problemas.
Modelos fenómenos aplicando conocimientos básicos de funciones reales de variable real.
Comparte tu valoración con un compañero, platiquen acerca de la comprensión que cada uno tiene de los aspectos mencionados y entre ambos definan las respuestas a las siguientes preguntas.
1. ¿Qué es la variación directa?
2. Describan una situación cotidiana donde se aplica el conocimiento de la variación directa.
3. ¿Creen que un modelo matemático podría ayudar a definir soluciones para combatir alguna forma de desigualdad social? Habilidades Socioemocionales
Registrar en la sección PROGRESO lo que consideras que has aprendido, te ayudará a autoevaluarte y de nir los aspectos donde puedes mejorar.
Recuerda que compartir tus valoraciones permitirá que obtengas retroalimentación para entender mejor cómo va tu aprendizaje.
Habilidades socioemocionales
En estas actividades se exponen aspectos socioemocionales acerca del trabajo realizado, con el n de retroalimentar el aprendizaje considerando la diversidad de ideas, equidad de género y otros aspectos importantes que fomentan un aprendizaje integral y humanista.
Habilidades Socioemocionales
Variación y sus consecuencias 41
ix
Conocer las raíces de una idea nos da una visión más amplia de su significado y de sus repercusiones. Saber las causas que motivaron a los científicos a realizar sus investigaciones nos hace entender sus aplicaciones, tanto en el momento histórico que se develaron, como en el mundo contemporáneo. Aún más, nos motiva a preguntarnos en qué más podemos utilizar esas ideas y qué otras aplicaciones pueden tener.
Por tal motivo, en este libro se hace énfasis en conocer la historia del cálculo. Estudiarás a los personajes que le dieron vida al cálculo variacional y algunos de los problemas que en otro momento fueron insolubles y que después de algún tiempo pudieron resolverse gracias a la construcción de varias definiciones y teoremas. También aprenderás conceptos de suma importancia en las matemáticas: el concepto de función, continuidad, límite y derivada.
¿Qué sería de las matemáticas sin sus aplicaciones? El cálculo en particular tiene múltiples aplicaciones en diversas áreas, esa es la razón por la cual en este libro les proponemos resolver problemas sobre fenómenos físicos. Así que, aprenderás varios conceptos matemáticos a la par de que conocerás cómo se comportan los cuerpos en movimiento. Te darás de cuenta que puedes entender el mundo que te rodea haciendo uso del lenguaje abstracto del cálculo.
Ser un experto en todas las áreas es algo imposible; sin embargo, entender conceptos fundamentales que se construyeron hace décadas y utilizarlos para resolver problemas reales es algo completamente alcanzable. Asimismo, siempre es posible tener la capacidad de impresionarse por todo lo que podemos resolver y saber del mundo en el que vivimos.
Será una tarea colectiva, tanto de nosotros los autores, como de los docentes y estudiantes, buscar las motivaciones que inspiren a seguir aprendiendo y creando.
Introducción
Pensamiento matemático II x
En este libro, las progresiones que dirigirán tu aprendizaje durante este semestre son:
1. Genera intuición sobre conceptos como variación promedio, variación instantánea, procesos in nitos y movimiento a través de la revisión de las contribuciones que desde la losofía y la matemática hicieron algunas y algunos personajes históricos en la construcción de ideas centrales para el origen del cálculo.
2. Analiza de manera intuitiva algunos de los problemas que dieron origen al cálculo diferencial, en particular el problema de determinar la recta tangente a una curva en un punto dado.
3. Revisa situaciones y fenómenos donde el cambio es parte central en su estudio, con la nalidad de modelarlos aplicando algunos conocimientos básicos de funciones reales de variable real y las operaciones básicas entre ellas.
4. Analiza la grá ca de funciones de variable real buscando simetrías, y revisa conceptos como continuidad, crecimiento, decrecimiento, máximos y mínimos relativos, concavidades, entre otros, resaltando la importancia de éstos en la modelación y el estudio matemático.
5. Conceptualiza el límite de una función de variable real como una herramienta matemática que permite comprender el comportamiento local de la grá ca de una función.
6. Identi ca y contextualiza la continuidad de funciones utilizadas en la modelación de situaciones y fenómenos y hace un estudio, utilizando el concepto de límite, de las implicaciones de la continuidad de una función tanto dentro del desarrollo matemático mismo, como de sus aplicaciones en la modelación.
7. Interpreta, a partir de integrar diferentes perspectivas y métodos, el concepto central del cálculo diferencial, “la derivada , de forma intuitiva e intenta dar una de nición formal, así como la búsqueda heurística para encontrar la derivada de la función constante, lineal y algunas funciones polinomiales.
8. Encuentra de manera heurística algunas reglas de derivación como la regla de la suma, la regla del producto, la regla del cociente y la regla de la cadena y las aplica en algunos ejemplos.
9. Selecciona una problemática en la que el cambio sea un factor fundamental en su estudio para aplicar el concepto de la derivada como razón de cambio instantánea.
10. Explica y socializa el papel de la derivada para analizar una función (donde crece/decrece, máximo/mínimos locales, concavidades y traza su grá ca.
11. Resuelve problemas de su entorno o de otras áreas del conocimiento empleando funciones y aplicando la derivada (e.g. problemas de optimización), organiza su procedimiento y lo somete a debate.
12. Examina la grá ca de funciones logarítmicas con diferentes bases y las grá cas de las funciones exponenciales para describirlas y realizar a rmaciones sobre el signi cado de que la función exponencial y logarítmicas de base “a sean funciones inversas entre sí.
13. Analiza y describe un fenómeno en el que la periodicidad sea un constituyente fundamental a través del estudio de propiedades básicas funciones trigonométricas.
14. Selecciona una problemática, situación o fenómeno tanto real como cticio para modelarlo utilizando funciones derivables.
15. Considera y revisa algunas ideas subyacentes al teorema fundamental del cálculo.
1

Activación
En esta primera unidad aprenderás sobre el origen de una de las piedras fundamentales del conocimiento matemático: el cálculo. No solamente leerás sobre sus inventores, Newton y Leibniz, sino también reconocerás a muchos científicos y matemáticos que les antecedieron y propusieron algunos problemas fundamentales que hicieron imprescindible la invención de un lenguaje que les permitiera resolver y explicar esos dilemas.
Saber sobre la historia de la ciencia es importante porque nos permite conocer cuáles fueron las necesidades de las personas en diferentes épocas que motivaron a las y los científicos a hacer sus investigaciones y obtener los resultados que hoy en día conocemos. También saber las dificultades y los obstáculos que se encontraron y que provocaron que no avanzaran más en sus estudios, o los métodos que siguieron para llegar a sus conclusiones. No solo es importante conocer la teoría, sino también aprender sobre los procesos de razonamiento, el o los métodos usados, las preguntas que se hicieron, las herramientas que utilizaron o que tuvieron que crear para avanzar con sus investigaciones. Es decir, observar el panorama completo. De una situación o fenómeno físico se desarrollará la teoría matemática.

Con esa actividad serás capaz de observar, analizar, investigar y construir los conceptos necesarios para entender algunos fenómenos, así como visualizar la aplicación y la importancia del cálculo en otras áreas del conocimiento. Conforme vayas avanzando en la unidad, comprenderás temas cada vez más abstractos como: variación promedio, variación instantánea y procesos infinitos. Sin embargo, con apoyo de la “Actividad” y los ejercicios “Para practicar”, adquirir estos nuevos conocimientos será un proceso intuitivo.
Pensamiento matemático III 6
Utilizarás conceptos que estudiaste en el semestre anterior y ampliarás ese conocimiento para ahora verlo desde la perspectiva del cálculo.
Progresión 1
El cálculo se utiliza en muchas áreas del conocimiento, desde la medicina hasta la física, y es precisamente en el área de la cinemática donde el cálculo diferencial tiene sus orígenes.
El célebre físico, astrónomo, ingeniero y matemático Galileo Galilei (1564-1642) de Pisa, Italia, es el creador de la cinemática, una rama de la física que estudia el movimiento de los objetos sin tomar en cuenta las causas que lo generan.
Para estudiar el movimiento hizo muchos experimentos, entre los cuales están los siguientes: dejar caer objetos en un plano inclinado, subir a la torre Pisa y dejar caer dos objetos de masas diferentes, el estudio de las oscilaciones de las lámparas de la Catedral, entre otros. Sin embargo, el experimentador Galileo se dio cuenta que necesitaba un lenguaje más avanzado para describir con mayor precisión el movimiento de los cuerpos.
Otro de los precursores del cálculo diferencial fue el gran matemático Pierre de Fermat. A él se le ocurrió la idea de hallar la recta tangente en un punto arbitrario de una curva. De ahí se planteó la pregunta “¿cómo se puede calcular la pendiente en un punto dado?”. Pero no se encontraría la respuesta hasta algunos años después.
¿Qué problemas motivaron el desarrollo del cálculo? Uno de ellos fue justamente el problema de las tangentes, era necesario resolverlo tanto para el diseño de lentes ópticas como para saber la dirección instantánea de un movimiento curvo. Otro fue el problema de los máximos y mínimos para saber el alcance de un proyectil en el movimiento planetario, en problemas de integración, para determinar longitudes de curvas, áreas encerradas por curvas, etc., y también para hallar la trayectoria recorrida por un cuerpo. Otras dudas surgieron a partir de las necesidades de la navegación y el manejo del infinito.










Éstas y otras cuestiones planteadas, como la necesidad del ser humano de entender su entorno, de explorar


ton Variación y sus consecuencias 7
Isaac Ne
 Gottfried Leibniz
Gottfried Leibniz
y aprender de él, fueron las ideas que motivaron a Isaac Newton (1643-1727) y a Gottfried Leibniz (16461716) a inventar el cálculo infinitesimal. Es importante aclarar que Newton parte de problemas físicos y Leibniz, de problemas filosóficos y de su búsqueda de los infinitesimales.
Dos eruditos trabajando en la misma época, en dos lugares diferentes del mundo, Inglaterra y Alemania respectivamente; ambos con motivaciones diferentes crearon el cálculo, el lenguaje más avanzado del que hablaba y que necesitaba Galileo Galilei y otros científicos para entender mejor la dinámica de los cuerpos y los procesos infinitos.
Otras personas que contribuyeron al desarrollo del cálculo infinitesimal fueron Joseph Raphson (1648-1715), Rolle (1652-1719), los hermanos Bernouilli, Leonhard Euler (1707-1783), entre otros.
ACTIVIDAD
Para realizar la actividad, formen equipos de 3 o personas.
A modo de introducción, presentamos un brevísimo resumen sobre el origen y el desarrollo del cálculo, y mencionamos a los personajes más relevantes que participaron en su invención. Así que, para que conozcan más sobre la historia del cálculo, buscarán un texto en la página eb o libro de su preferencia sobre alguno de los siguientes temas:
1. Origen del cálculo
2. uién fue Isaac Ne ton
3. uién fue Gottfried Leibniz
4. Aplicaciones del cálculo
5. Procesos in nitos
Sigan los siguientes pasos para llevar a cabo un círculo de estudio:
a) El an el tema que más les llame la atención.
b) usquen información en fuentes con ables.
Pensamiento matemático III 8
continuación
c) Lean el texto de forma individual y escriban un resumen de las ideas más importantes. Anoten además las preguntas que les hayan surgido.
d) Reúnanse en equipos y el an a un moderador. espués, cada uno tendrá que compartir alguna o algunas de las ideas escritas. Posteriormente, planteen sus preguntas y comenten si se cuestionaron lo mismo, si pensaron o investigaron alguna respuesta a sus preguntas, o justo en ese momento intenten darle solución.
e) inalmente, escriban en conjunto las conclusiones a las que hayan llegado. Por ejemplo, la relevancia del trabajo de Isaac Ne ton en la física o la importancia de las aplicaciones del cálculo después de muchos a os de su invención.
f) Entreguen su escrito a su docente.
ACTIVIDAD
Para esta parte de la actividad te plantearemos dos problemas donde tendrás que analizar el movimiento de un cuerpo, uno que viaja a velocidad constante y otro que no. Con base en tu observación, conocimientos previos de la física y los conceptos aprendidos en esta unidad, resolverás y contestarás cada pregunta. Serás capaz de resolver un problema físico con la teoría matemática.
Situación1:
n ciclista que viaja en la ciudad de Puebla a velocidad constante y recorre 3 metros en 6 segundos. tilizando estos datos, haz lo que se te pide en cada inciso.

Variación y sus consecuencias 9
a) Completa la siguiente tabla:
(segundos)Distancia (metros)
b) Elabora la grá ca de su movimiento (tiempo contra distancia).
Con base en tu grá ca, responde lo siguiente:
c) etermina la velocidad del ciclista.
d) Tomando en cuenta tu respuesta anterior, cómo son las grá cas de tiempo contra distancia de un objeto que se mueve con una velocidad como la del ciclista
6 12 18 2 3
Tiempo
t d
continuación Pensamiento matemático III 10
e) Cómo has decidido que esto que dices es cierto
Situación2:
Se analizará el cambio en la velocidad de un cuerpo deslizándose sobre un plano inclinado. Para este análisis, formen equipos y hagan lo que se pide en cada inciso:
a) Construyan un plano inclinado con un ángulo de (como el que se muestra en la imagen) y una rampa de longitud de 1 m, de manera que puedan deslizar una pelota. Pueden utilizar un riel para que ésta se deslice en una sola dirección. 45°




b) na vez que hayan construido su plano, utilicen un exómetro o regla y tracen una línea cada 25 cm sobre el plano.
c) Consigan un cronómetro o descarguen uno en sus celulares para medir el tiempo cada vez que la pelota pase por las marcas que trazaste en el inciso b). Pueden hacer el experimento varias veces y sacar el promedio de los tiempos para tener un resultado más aproximado al real.
Tiempo (s)Distancia (m) .25 .5 . 5 1. continuación Variación y sus consecuencias 11
d) Elaboren la grá ca del movimiento de la pelota (distancia contra tiempo).
Con base en sus resultados, respondan lo siguiente:
e) Expliquen por qué la velocidad cambia.
f) El movimiento de la pelota es un Movimiento Rectilíneo niforme o Movimiento Rectilíneo niformemente Acelerado Argumenta tu respuesta.
g) En ausencia de fricción, qué pasaría con la pelota que se desliza a un ángulo de °
h) Cuál crees que sea el propósito de este experimento
d
t
continuación Pensamiento matemático III 12
Tema 1. Variación promedio y variación instantánea
Uno de los temas que se tocan cuando se estudia matemáticas es sobre la aplicación de la teoría en nuestra vida diaria, con el propósito de saber si lo que se está estudiando sirve para lo cotidiano o son simples hipótesis que solo hacen sufrir a quien las estudia.
Es cierto que algunas de las teorías que se han concebido a lo largo de la historia de las matemáticas son creadas para existir por sí solas, sin importar si se pueden aplicar o no para resolver problemas en nuestro entorno. Sin embargo, la gran mayoría de las teorías que se han inventado (o descubierto), obedecen a preguntas o necesidades que la humanidad se ha planteado, desde la construcción de los sistemas numéricos hasta estructuras algebraicas cada vez más complejas.
En ese sentido, cuando se quiere utilizar a las matemáticas para explicar o entender nuestro entorno, habría que plantearse primero cuál es la naturaleza de los fenómenos que se desean explicar o entender. En general, cuando se observan los fenómenos en nuestro contexto, se puede concluir que en su gran mayoría estos fenómenos son del tipo dinámico, es decir, fenómenos que no están inmóviles y que evolucionan con el


Algunos ejemplos de este tipo de fenómenos dinámicos son el crecimiento de una planta, el rendimiento de una atleta, la frecuencia cardiaca de una persona, calentar una sopa instantánea en el microondas, el ación de la moneda de un






Variación y sus consecuencias 13
ACTIVIDAD
1. Responde: Las situaciones 1 y 2 que se plantearon en la actividad son del tipo dinámico Por qué
Ejemplo
Consideremos el fenómeno de estudiar el crecimiento de una planta. n biólogo a lo largo de cinco meses mide y anota su altura obteniendo los datos de la siguiente tabla:
e los datos se pueden sacar algunas conclusiones:
1. Cada mes, la planta crece a diferente ritmo, es decir, que entre mes y mes la planta no aumenta los mismos centímetros. el mes cero al mes uno creció 21 cm mientras que del mes uno al mes dos fue de 22 cm.
2. En promedio, la planta se agranda 2 .2 cm por mes. Escrito en términos matemáticos:
1 1 cm
5 meses 2 .2 cm mes
A pesar de que la variación del crecimiento de la planta con respecto a los meses no es constante, se puede ver que la variación es directa. En otras palabras, cuando la cantidad de meses aumenta, la altura de la planta también lo hace.
Observa que esta variación la podríamos pensar como una razón (el cociente de la altura obtenida y los meses transcurridos), por lo que, podemos interpretar a la variación del crecimiento como la razón (o cociente) entre la altura de la planta y el tiempo transcurrido.
MesAltura (cm) 121 243 363 482 51 1
Pensamiento matemático III 14
Así, si queremos ver cuál es la variación de crecimiento entre el mes dos y el mes cuatro habrá que calcular la razón entre la altura de la planta (el crecimiento de la planta es la resta de la altura en el mes cuatro menos la altura en el mes dos) y el tiempo transcurrido, esto es:
Lo anterior se puede interpretar como “entre los meses dos y cuatro, en promedio la planta creció 1 .5 cm por mes .
Diremos que la variación entre y y x es directa si, para alguna k constante se cumple: y kx
Diremos que la variación entre y y x es inversa si, para alguna k constante se cumple: y k 1 x
Observa que cuando existe una variación directa, a medida que x crece también lo hace y. Sin embargo, cuando hay una variación inversa, a medida que x crece, y disminuye.
Los dos tipos de variaciones anteriores son variaciones del tipo lineal, pero las variaciones entre dos cantidades, x y y, no necesariamente es lineal.
Cuando la variación es lineal, la gráfica que se obtiene al graficar x contra y, es una recta. De lo contrario decimos que la variación no es lineal.
ACTIVIDAD
1. Responde: En las situaciones 1 y 2 de la actividad anterior, qué tipo de variación se presenta, directa o inversa Son relaciones lineales Argumenta tu respuesta.
Crecimiento Tiempo transcurrido 82 cm 43 cm 4 meses 2 meses 3 cm 2 meses 1 .5 cm mes
Variación y sus consecuencias 15
Otra forma de darnos cuenta si la variación en un fenómeno dinámico es lineal, es comparando la variación en intervalos de tiempo distintos ([ti, t f ]). Si esta variación es la misma, la variación es lineal.
Naturalmente que este criterio se puede extender para fenómenos que no dependan necesariamente del tiempo, para formalizarlo, escribiremos esto en términos matemáticos. Supongamos que a cada x n la asociamos con yn , por lo tanto, se puede expresar la variación de y con respecto a x en el intervalo ([x n 1, x n]) como:
yn x n
Donde:
x n x n x n 1
yn yn yn 1
Cuando hablemos de fenómenos dinámicos cambiaremos la notación, sustituiremos a x n x n x n 1 por t n t n t n 1, la única razón es para hacer hincapié en que el fenómeno cambia con respecto al tiempo.
Ejemplo
Supongamos que y representa el costo de fabricar x televisores y y n representa el costo para fabricar n televisores planos, por lo que x n n . Así, el cociente: yn x n , representará el cambio en el costo de fabricar el televisor número n 1 y el televisor n .

A este número también se le conoce como razón de cambio. Por lo tanto, concluimos que una variación es lineal si la razón de cambio es constante.
Pensamiento matemático III 16
ACTIVIDAD
1. Tomando los datos de las situaciones de la actividad 1 y 2, haz lo que se te pide en cada inciso.
a) Identi ca a t n y yn.
b) Calcula la velocidad promedio: vpromedio yn t n .
c) Para cada n, concluye si las variaciones son lineales o no. sa el recuadro para hacer las operaciones necesarias.
En la situación 1 de la actividad principal, el valor: yn t n , representará el cambio de la posición, yn yn 1, entre los segundos n y n 1. De los cursos de física aprendiste que el cambio de la posición con respecto al tiempo es la velocidad, por lo que, el valor yn t n representará la velocidad promedio entre el segundo n y el segundo n 1.
En general, la velocidad promedio de un objeto en el intervalo de tiempo, está dada por el cociente:
v prom yf yi
tf ti
Donde yf es la posición del objeto en el tiempo t f .
Si bien este cociente ya nos ofrece información acerca de cómo se mueve el objeto, no precisa qué fue lo que pasó en cada momento del intervalo de tiempo [ti, t f ], pudo haber pasado que, en algún momento, el objeto bajó la velocidad y después la subió, para que al final su velocidad promedio fuera:
Variación y sus consecuencias 17
v prom yf yi tf ti . Por lo que surge una pregunta: ¿cómo podemos saber la velocidad en el tiempo ti ? Una forma de saberlo puede ser, tomar intervalos de tiempo cada vez más pequeños.
El intervalo de tiempo es cada vez más pequeño, siempre que la diferencia tf ti también sea más pequeña. Observa que, si esta diferencia es cercana al cero, la velocidad promedio se acerca a la velocidad instantánea en el tiempo ti .
Este proceso siempre se puede hacer, ya que, siempre podemos tomar t f ti , con t f muy cercano a ti , pero sin que sean iguales.
Ejemplo
Si quisiéramos tomar números cercanos a 3, podemos tomar a 3.1, 3. 1, 3. 1, 3. 1, etc. Esto nos sugiere que este proceso se puede hacer de forma in nita, una consecuencia es que el tama o del intervalo de tiempo es cada vez menor, por lo que, se puede concluir que el intervalo de tiempo se puede hacer tan peque o como se desee.
ACTIVIDAD
1. tiliza los datos de la situación sobre el ciclista que viaja a velocidad constante y completa la tabla.
m)
1
1
2. Recuerda que el valor v prom yt y12 t 12 , representa la velocidad en el intervalo . Con esta información, responde lo que se pide:
v
yt
12.5 12.1 12.
12.
t (s) yt (
prom
y12 t 12 (m/s)
Pensamiento matemático III 18
continuación
a) La velocidad promedio en cada intervalo de tiempo se acerca a algún valor jo Cuál
b) Cuál debería ser la velocidad instantánea en el segundo 12
En las situaciones que se analizaron anteriormente se pudieron ver ejemplos en el que las variables son del tipo discreto o continuo, para evitar confusiones en la notación y hacer más evidente cuándo un fenómeno es del tipo discreto (el costo de fabricar televisores) y cuándo es uno continuo (la posición en la que se encuentra un ciclista en un tiempo ), usaremos las siguientes notaciones:
Cuando x es del tipo discreto: x n y yn denotará la variación de x y y respectivamente; cuando x cambia de n 1 a n. Y para denotar la variación de y con respecto a x de n 1 a n usaremos: yn x n .
Cuando es del tipo continuo: x y y denotará la variación de x y y respectivamente en un determinado intervalo [a , b]. Y para denotar la variación de y con respecto a x en [a , b] usaremos: y x .
Observa que cuando tenemos variables continuas es necesario decir en qué intervalo se está calculando la variación. De aquí en adelante se precisará el intervalo en el que se está haciendo el estudio, además que en general, se usará n variables del tipo continuo.
1. Escribe tres ejemplos de razones de cambio.
a)
b)
c) PARA PRACTICAR
Variación y sus consecuencias 19
2. Analiza la siguiente tabla que contiene los datos del entrenamiento de un nadador profesional. espués contesta las preguntas.
a) Es la variación constante
b) Es la variación directa usti ca tu respuesta.
c) Calcula la velocidad promedio.
d) Traza la grá ca distancia contra tiempo. t d
Tiempo (s)Distancia (m) 1 2 2 4 3 6 4 8 5 1
Pensamiento matemático III 20
continuación
e) Al observar la grá ca, puedes concluir que la variación es lineal Explica por qué. continuación
Progresión 2
Tema 2. El problema de construir una recta tangente
En el tema anterior se propuso una forma de poder intuir la velocidad instantánea de un objeto en un transcurso dado, parte de esta forma consistía en tomar intervalos de tiempo ([a , b]) cada vez más pequeños, esto equivale a decir que la distancia entre a y b es cada vez menor, o bien, a decir que a se acerca “mucho” a b En este tema usaremos esta idea para intentar dar respuesta al problema de construir una recta tangente a una curva dada.
Para plantear el problema de la construcción de una recta tangente a una curva tenemos que aclarar algunos conceptos previos.
La recta tangente a una curva es una recta que solo “toca” a la curva en un solo punto, llamado punto de tangencia.
Esta definición se conocía desde los tiempos de los griegos, fue planteada por Euclides (325 a.C.-265 a.C) y de hecho, Apolonio (262 a.C.-190 a.C.) planteó un método para la construcción de una recta tangente a una parábola. Este método es el siguiente:
Método 1
Consideremos una parábola con vértice en v y cuyo eje de simetría es la recta l .
Supongamos que se quiere trazar la recta tangente a la parábola cuyo punto de tangencia es p.
Variación y sus consecuencias 21
Trazamos el segmento ap, de tal manera que ap sea perpendicular a l . Luego, sobre l trazamos el punto b, tal que av vp, es decir, la distancia de a a v es igual a la distancia de v a b. v p b
La recta que pasa por los puntos p y b, es tangente a la parábola. Es cierto que el método de construcción se puede repetir para cualquier parábola, sin embargo, solo sirve para este tipo de curvas. Para dar una técnica más general para la construcción de dicha recta, haremos uso de la geometría analítica y los conceptos desarrollados en el tema anterior.
Método 2
Recordemos que en la geometría analítica, una recta son todos los puntos (x, y) que cumplen: y mx b. Para cualquier x, con m y b números reales. Y representa la pendiente de la recta. Sabemos también que la pendiente se calcula de la forma:
m y1 y0
x1 x0
Con (x 0, y 0) y (x 1, y1) dos puntos distintos de la recta.
Ahora bien, consideremos a una curva cualquiera y un punto p sobre ella. Queremos encontrar y trazar una recta que sea tangente a esta curva y que pase por el punto p: (x 0, y 0). Para esto, consideramos a un punto cualquiera q: (x, y) y trazamos la recta que pasa por los puntos p y q, analíticamente podemos encontrar la pendiente de esta recta secante y, por lo tanto, la ecuación de esta recta.
l a
Pensamiento matemático III 22
Observa que a medida que x 1 se acerca a x 0, la recta que pasa por los puntos p y q se aproximan a ser una recta tangente en el punto p. Por otro lado, p y q no pueden, ni deben, ser los mismos, ya que, el denominador del cociente: m y1 y0 x1 x0 sería cero. Sin embargo, siempre es posible aproximar x 1 a x 0. La noción de acercarse tanto como se quiera puede parecer un poco confusa, ya que, pareciera que esta idea depende de lo que el lector decida hacer. En este sentido estamos suponiendo que la idea de aproximarse está basada en que, por lo menos teóricamente, siempre es posible encontrar un punto cada vez más cercano a uno dado, por ejemplo, el punto medio.
q:( x1, y1)
y1
y0 p:( x0, y0)
x1, y1) x0 x1 y1
y0 p:( x0, y0) q:(
x0 x1
Variación y sus consecuencias 23
La imagen anterior muestra cómo a medida que x 1 se acerca a x 0, la recta secante se convierte en recta tangente. En este caso, la idea de tangencia es un poco distinta a la que planteaba Euclides. Él definía a la recta tangente como la recta que toca a una curva en un solo punto; sin embargo, como se puede ver, la recta “toca” a la curva en más de un punto, por lo que, nosotros entenderemos a la recta tangente como la recta que se construye por el proceso de aproximarse tanto como se desee.
y0 p:( x0, y0)
y1
q:( x1, y1)
Como podemos ver, es posible obtener información de la curva a partir de la recta tangente, por ejemplo, si la pendiente de dicha recta es positiva podemos pensar que la curva asciende y si la pendiente es negativa, la curva desciende, esto puede ofrecer información valiosa.
Supongamos que la pendiente de la recta es positiva y de un momento a otro se convierte en negativa, o viceversa, que pasó de ser positiva a negativa. Podemos concluir que existe un punto en el que la curva alcanzó un máximo o bien un mínimo, por lo menos localmente.
x0 x1
Pensamiento matemático III 24
y0 p:( x0, y0)
y1
q:( x1, y1)
x0 x1
y0 p:( x0, y0)
y1
x0 x1
q:( x1, y1)
Las gráficas anteriores muestran cómo la pendiente de la recta cambia de positiva a negativa, cuando existe este cambio podemos observar que la curva tiene un valor máximo o bien un valor mínimo.
ACTIVIDAD
1. Gra ca las curvas de las situaciones 1 y 2 de la Actividad. Elige un punto donde quieras trazar una recta tangente, aleatoriamente escoge otro punto de la curva y traza la recta que pasa por estos puntos. Aproxímate a la marca de tangencia cada vez más y observa qué pasa.
Variación y sus consecuencias 25
a) Grá ca de la Situación 1 d t
b) Grá ca de la Situación 2 d t
c) ué se puede decir de las curvas que se obtienen
e) Si la curva alcanza un máximo o un mínimo, cómo es la pendiente de la recta tangente en este punto continuación
d) En la situación 1, la grá ca es una recta, la pendiente de la recta tangente cambia
Pensamiento matemático III 26
Como puedes observar, el comportamiento de la pendiente de la recta tangente a una curva nos puede ofrecer información de dicha curva. Por ejemplo, supongamos que se tiene una curva que representa el volumen de una botella y nos interesa saber cuáles son las dimensiones de la botella para contener el mayor volumen, por lo que, estamos interesados en encontrar el máximo de dicha curva.
En el ejemplo anterior estamos interesados en encontrar las dimensiones de la botella donde el volumen es mayor, por lo que hemos visto, parece que ese punto es en el que la pendiente se hace cero. Más adelante daremos condiciones necesarias y suficientes para dicho objetivo.
1. Traza la grá ca de tiempo contra distancia utilizando los datos de la tabla. Luego, haz lo que se te pide en cada inciso.
a) Elige un punto sobre la recta y márcalo con la letra A.
b) ibuja la recta tangente que pasa por ese punto.
c) bica otros dos puntos, y C, que se aproximen al punto A.
d) Traza las rectas secantes que pasan por y A, y por C y A.
e) ado que la grá ca es una recta, la pendiente de la recta tangente cambia
Tiempo (s)Distancia (m) 1 2 2 4 3 6 4 8 5 1
d t Variación y sus consecuencias 27
PARA PRACTICAR
continuación
f) Si la pendiente de la recta tangente no cambia, qué implica físicamente hablando
2. Observa la siguiente grá ca y analízala con las preguntas que se te plantean:
a) Elige un punto sobre la recta y márcalo con la letra A.
b) ibuja la recta tangente que pasa por ese punto.
c) bica otros dos puntos, y C, que se aproximen al punto A.
d) Traza las rectas secantes que pasan por y A, y por C y A.
e) La pendiente de la recta tangente cambia
f) Si la curva alcanza un máximo o un mínimo, cómo es la pendiente de la recta tangente en este punto
200 180 160 140 120 100 80 60 40 20 0 25710 14
Pensamiento matemático III 28
Tema 3. Aritmética de funciones
En apartados anteriores estudiaste anteriormente que es posible analizar una curva a partir de la pendiente de la recta tangente en un punto dado. Esto se puede saber si la curva es creciente o decreciente observando únicamente la pendiente de la recta tangente.
Para hacer un análisis más profundo es necesario dejar claro qué es lo que vamos a entender por curva, para lo que definiremos antes lo que entenderemos por función.
Una función es una asociación única entre elementos de dos conjuntos a los que llamaremos dominio y codominio. Esto es si A es dominio y B el codominio; a cada elemento de A se asocia, por medio de f , un único elemento de B. Esto lo representaremos como:
f : A B
Diremos que la función es de variable real si A y B son subconjuntos de los números reales. Por lo tanto, la gráfica de una función serán los puntos en el plano cartesiano de la forma (x , f (x)). Dicho lo anterior, a cada función de variable real le podemos asociar una gráfica. Esto nos servirá para poder estudiar las funciones por medio de sus gráficas.
Al igual que en los números reales, podemos definir operaciones, pero en lugar de que estas operaciones sean entre números serán entre funciones.
Suma de funciones: La suma de dos funciones será otra función, de tal forma que: (
3
Progresión
f g )(x) f (x) g (x) Variación y sus consecuencias 29
Ejemplo
Si f (x) x2 4 y g (x) x 2. Calcular (f g) (x) y evaluar en x 2.
Primero calculemos (f g) (x):
(f g) (x) f (x) g (x)
(x2 4) (x 2)
x2 x 2
Evaluando en x 2, tenemos:
(f g) (2) f (2) g (2)
(2)2 4) (2 2) 8
Como se puede ver, es posible definir la resta de funciones de la misma forma que la suma. Esto es:
( f g )(x) f (x) g (x)
Producto de funciones: El producto de funciones es otra función, tal que la función producto es el producto de las funciones, es decir:
( f g )(x) f (x) g (x)
Como las funciones son de variable real, f y g toman valores reales, por lo tanto, las propiedades que tienen son las mismas que existen para los números reales.
Ejemplo
Si f (x) x 2 y g (x) x2 1, calcular (f g) (x) y evaluar en x 1.
(f g) (x) f (x) g (x)
(x 2) (x2 1)
x3 2x2 x 2
Al determinar en x 1, tenemos:
(f g) (1) 13 2(1)2 1 2
Pensamiento matemático III 30
Como es de esperarse también se puede definir el cociente de funciones, para valores en los que g (x) 0.
Cociente de funciones: El cociente de funciones es otra función, tal que la función cociente es el cociente de funciones, es decir:
f g (x) f (x) g (x)
Para los valores en los que la función g (x) es distinta de cero.
Ejemplo
Si f (x) x 1 y g (x) x2 1, calcular f g (x) y evaluar en x 2.
f g (x) x 1 x2 1
Evaluando en x 2, tenemos:
Composición de funciones: La composición de funciones es otra función de tal manera que se evalúa la primera en x y el resultado se usa como argumento para la segunda:
( f g )(x) f ( g (x))
Esto se lee como “g seguida de f o bien f de g (x)”. Observa que en esta operación entre funciones es importante que el dominio de f sea el mismo que el codominio de g, de lo contrario puede ser que la composición no esté bien definida.
x 1
x
1 x 1
(
1) (x 1)
g
1 2 1 1 Variación y sus consecuencias 31
f
(2)
Ejemplo
Si f (x) x y g(x) x2 1, calcular (f g)(x) y evaluar en x 3.
Al hacer la composición tenemos:
(f g)(x) f (g (x))
f (x2 1)
(x2 1)
Al evaluar en x 3, tenemos
(f g)(3) 32 1) 8
Al definir estas operaciones entre funciones, el objetivo principal es poder dar una interpretación de fenómenos en nuestra vida cotidiana, por ejemplo, si f representa la altura de un terreno y g la base de éste, el producto ( f g )(x), representará el área de dicho terreno.
Otro ejemplo de esta interpretación puede ser la siguiente: supongamos que f (x) determina el valor de comercializar un cierto producto, y g (x) la variación del precio de la gasolina. Es sabido que para contemplar el costo de comercializar un producto el costo de la gasolina puede interferir en el costo final de dicho producto, así, podemos interpretar a ( f g ) (x) como el valor de comercializar el producto cuando cambia el valor de la gasolina.
Existen muchas y variadas interpretaciones del entorno por medio de funciones, nuestro objetivo en lo siguiente es poder dar la interpretación correcta a fenómenos que sucedan en nuestro alrededor y con esto crear una herramienta que nos ayude a comprender dichos fenómenos.
PARA PRACTICAR
adas las funciones: f (x) x2 5x 6 y g (x) x 2 resuelve las operaciones que se te indican y utiliza los recuadros en blanco para hacer tus cálculos.
1. (f g) (x)
Pensamiento matemático III 32
2. (f g) (x)
3. (g f) (x)
4. (f g) (x)
5. (g f) (x)
6. f g (x)
7. g f (x)
continuación Variación y sus consecuencias 33
8. (f g) (x)
9. (g f) (x)
CIERRE
Como te puedes dar cuenta, cuando se quiere estudiar el comportamiento de una curva, la pendiente de la recta tangente a dicha curva puede ofrecernos información valiosa. En las siguientes unidades se intentará formalizar esta construcción, no solo desde el punto de vista geométrico sino también desde el punto algebraico.
Esta construcción se hace desde lo dinámico, es decir, procesos en los que el movimiento es fundamental, más adelante formalizaremos la noción de acercarnos tanto como se desea. Priorizaremos la idea de repetir un cierto proceso de manera infinita, así como el concepto de infinitamente pequeño.
El concepto central será la construcción de un método para calcular y trazar una recta tangente a una curva dada y con esto saber si la recta “asciende” o “desciende”. Naturalmente que lo que buscaremos es hacer esto de manera formal y por supuesto, encontrar una aplicación en nuestra vida diaria.
continuación Pensamiento matemático III 34
CONEXIÓN
Para poder entender de mejor manera cómo se construye la recta tangente a una curva, construiremos este proceso de forma dinámica en el soft are libre, GeoGebra.
1. Traza una curva, no importa cuál sea, puedes escribir una ecuación en el apartado “entrada .
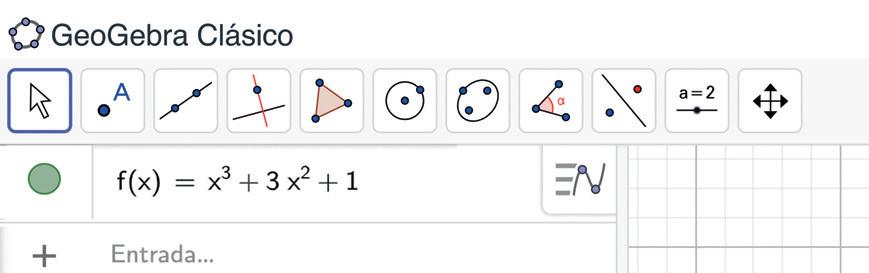
2. Al escribir esto se generará automáticamente una curva, en nuestro caso generará una curva cúbica. En el eje X, selecciona dos puntos, A y . Estos puntos se pueden mover a lo largo del eje X, observa que el punto se puede acercar “tanto como se desee al punto A.
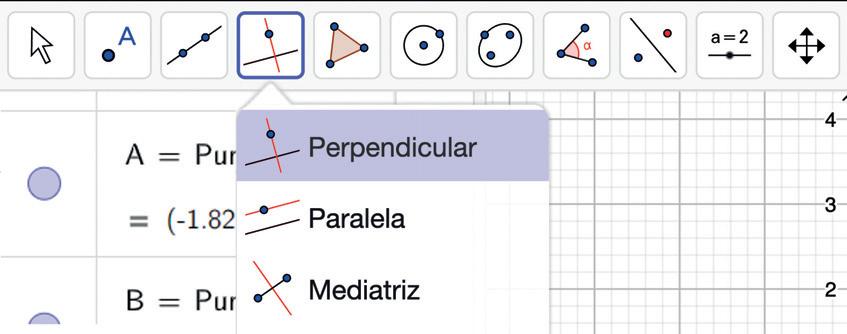
3. Selecciona la opción recta perpendicular y traza la perpendicular al eje X que pasa por los puntos
A y .
Variación y sus consecuencias 35
4. Selecciona la opción intersección para generar dos puntos, C y , de intersección de las perpendiculares con la curva inicial. Traza la recta que pasa por estos puntos, se obtendrá una recta secante que pasa por C y . Observa cómo a medida que el punto se acerca al punto A la recta secante se convierte en una recta tangente. Puedes mover este punto para ver con mayor facilidad.
i j D B A -4 -3 -2 -101 1 2 3 4 5 23 c Pensamiento matemático III 36
Valoración
1. Encierra en un círculo aquellos enunciados que sí sean ejemplos de razones de cambio:
a) La cantidad de ilómetros recorridos por litros de gasolina.
b) na atleta corre 21 ilómetros en hora y media.
c) La distancia de la tierra a la Luna.
d) La aceleración de la gravedad es de .8 metros por segundo al cuadrado.
e) Las temperaturas diurnas en Marte pueden llegar hasta los °C.
f) La velocidad de propagación de una epidemia en una determinada ciudad.
2. Observa la siguiente tabla que contiene los datos de la cantidad de ilómetros recorridos por litros de gasolina que necesita un automóvil.
a) Es la variación constante
b) Es directa o inversa
c) Es lineal
Litros de gasolinaKilómetros recorridos 115 23 345 46 5 5
Variación y sus consecuencias 37
d) Calcula la razón de cambio:
3. Observa la siguiente grá ca de personas contra la cooperación que les corresponde (en pesos) para comprar un pastel. espués, contesta las preguntas de los incisos.
a) Es la variación directa o inversa
b) Es la variación lineal
c) Si fueran 2 personas las que cooperarán para la compra del pastel, de cuánto le tocaría a cada uno
175 70 50 35 25 180 160 140 120 100 80 60 40 20 0 25710 14
Pensamiento matemático III 38
4. ué es una línea tangente
5. ué es una línea secante
6. En la grá ca, traza la o las rectas tangentes a la curva donde su pendiente sea igual a cero.
7. Completa los siguientes enunciados:
a) Si la pendiente es positiva, la curva .
b) Si la pendiente es , la curva desciende.
c) Si la pendiente de la recta tangente no cambia, decimos que la variación es .
d) Si la curva alcanza un mínimo o un máximo, la pendiente es .
e) Cuando la variación es inversa, sucede que mientras una variable aumenta, la otra .
f) Cuando la variación es directa, sucede que mientras una variable aumenta, la otra .
8. En la grá ca, dibuja lo siguiente:
a) na recta tangente a la curva donde la pendiente sea positiva.
b) na recta tangente a la curva donde la pendiente sea negativa.
1 0 2 345 -5 -4 -3 -2 -1 -1 -2 2 1
Variación y sus consecuencias 39
9. En tus palabras, de ne qué es una función:
Sean f (x) x2 2x 8 y g (x) x 2. Encierra en un círculo la opción correcta para cada operación entre funciones:
10. f g (x)
a) x 4
b) x 4
c) x2 2x 4
11. (f g) (x)
a) x2 2x 4
b) x2 2x 4
c) x2 2x 8
12. (g f) (x)
a) x2 2x 1
b) x2 2x 1
c) x2 2x 4
0.5 0.5111.51.5222.52.5333.53.5444.54.5555.5 5.5 -1 -0.5 0.5 1 0
Pensamiento matemático III 40


























 Gottfried Leibniz
Gottfried Leibniz













