






Hoe krijg je een ei in een fles met een nauwe opening? Dat is de vraag die aan enkele kandidaten in een tv-quiz gesteld werd. Benieuwd naar het antwoord?
Scan de QR-code en bekijk het videofragment.


























Eén van de aggregatietoestanden waarin materie kan voorkomen, is gas. Voor deze toestand gelden specifieke wetten: de gaswetten.
Volgens het deeltjesmodel bestaat een gas uit kleine deeltjes die voortdurend door elkaar bewegen. In een gas hebben de gasdeeltjes zoveel warmte opgenomen dat ze los van elkaar gaan bewegen en zich verspreiden in de ruimte die ze tot hun beschikking hebben. De gasdeeltjes zijn daardoor zeer sterk verspreid, waardoor ze meestal onzichtbaar zijn voor het menselijk oog. De cohesiekrachten tussen de gasdeeltjes zijn daarbij heel klein.
We beperken ons in deze module tot een ideaal gas. Dit model stelt volgende voorwaarden:
De gasdeeltjes trekken elkaar niet aan;
De gasdeeltjes hebben een verwaarloosbaar volume ten opzichte van het totale gasvolume; De gasdeeltjes bewegen door elkaar, volgens een rechte lijn en met een constante snelheid. De botsingstijd is verwaarloosbaar klein, een botsing met de wand verandert de grootte van de snelheid niet.
Geen enkel gas voldoet in werkelijkheid aan deze eigenschappen, maar de meeste reële gassen zoals zuurstofgas, lucht en stikstofgas kunnen we zeer nauwkeurig benaderen als ideale gassen. Enkel bij heel lage temperaturen of bij hoge dichtheden volgen ze de ideale gaswet niet meer.
In tegenstelling tot een vloeistof is een gas goed samendrukbaar. We kunnen het volume van een gas dus gemakkelijk veranderen. Gassen hebben dus geen vast volume. Als ze bewaard worden, gebeurt dat in een afgesloten vat, het gas neemt dan automatisch het volume van het vat aan.


Een gas heeft een aantal toestandsfactoren die de toestand van een gas ondubbelzinnig bepalen. Dat zijn: het volume V de druk p de temperatuur T het aantal gasdeeltjes
Laten we ervan uitgaan dat we een vast aantal gasdeeltjes in ons gas hebben, dus een constante hoeveelheid gas. Dan resten ons dus drie toestandsfactoren:
het volume V de druk p de temperatuur T
Deze toestandsfactoren zijn niet onafhankelijk van elkaar. Als we twee van de toestandsfactoren kiezen, dan is de derde automatisch bepaald.
WIST-JE-DAT
Gassen kunnen zuivere gassen zijn of een gasmengsel. Zuivere gassen kunnen bestaan uit atomen van één element (dit is het geval bij een edelgas zoals neon Ne), ze kunnen ook uit moleculaire enkelvoudige verbindingen bestaan (een voorbeeld daarvan is zuurstofgas O2), of ze kunnen uit een samengestelde verbinding van meerdere atoomsoorten bestaan (een voorbeeld daarvan is koolstofdioxide CO2).
Lucht is dan weer een voorbeeld van een gasmengsel, dat is samengesteld uit verschillende gassen.
In het heelal komt bijna alle materie voor in de vorm van een gas.
Het woord 'gas' is afgeleid uit het Griekse woord voor chaos en werd reeds in de 17de eeuw door de Vlaamse alchemist Jan Baptista van Helmont geïntroduceerd. De reden van zijn keuze is duidelijk, de gasdeeltjes bewegen immers kriskras en dus chaotisch door elkaar.
Broeikasgassen zijn oorspronkelijk van nature voorkomende gassen in de atmosfeer. Door een deel van het zonlicht en van de door de aarde uitgestraalde warmte te absorberen, garanderen zij de voorwaarden voor het leven op onze planeet. Het broeikaseffect dat zij veroorzaken is dus een natuurlijk verschijnsel
Maar de menselijke activiteiten hebben de concentratie van een aantal van deze gassen gevoelig doen toenemen en hebben ook een aantal synthetische stoffen in de atmosfeer gebracht, wat het natuurlijke broeikaseffect versterkt en de aarde doet opwarmen, met tal van nefaste gevolgen.
Wil je graag meer weten over broeikasgassen en het broeikaseffect? Scan dan deze QR-code.
We willen nu natuurlijk het verband tussen de verschillende toestandsfactoren vinden.
Om dat te doen gaan we telkens het verband tussen twee toestandsfactoren zoeken, terwijl we de derde toestandsfactor constant houden.
In een wetenschappelijk onderzoek wordt immers meestal het verband tussen twee grootheden gezocht. Daarbij is het belangrijk om de andere invloedfactoren constant te houden zodat die geen invloed hebben.
We krijgen zo dus drie gaswetten, die we één voor één gaan bekijken.
drukwet van Gay-Lussac, ook wel wet van Regnault genoemd
volumewet van Gay-Lussac
Deze wet onderzoekt de verandering van de gasdruk met het volume, bij een constante temperatuur en voor een constante massa gas.
Volgens het deeltjesmodel bewegen de gasmoleculen vrij door elkaar. Als we het volume van een afgesloten hoeveelheid gas laten afnemen, neemt de kans op botsingen tussen de gasmoleculen onderling toe, alsook de kans op botsingen met de wand. Het aantal onderlinge botsingen zal dus toenemen en dus zal ook de gasdruk toenemen.
Omgekeerd, als we het volume van het gas laten toenemen, zal de gasdruk dalen.
Ga zelf even na hoe dit gebeurt door gebruik te maken van onderstaande applet (kies voor de optie ‘Ontdek’). Scan hiervoor de QR-code.


Het volume kan je aanpassen door het handvat links te verschuiven, de gasdruk kan je aflezen. Let goed op de bewegingen van de gasdeeltjes.


We zien dat, voor een constant aantal gasdeeltjes, een afname van het volume een drukverhoging teweegbrengt en, omgekeerd, dat een toename van het volume een drukdaling veroorzaakt.
We vermoeden dus dat er een omgekeerd evenredig verband is tussen het volume en de gasdruk, voor een constant aantal gasdeeltjes bij een constante temperatuur.
Experimenteel onderzoek bevestigt dit vermoeden.
Voor een constante massa gas bij een constante temperatuur geldt:
⋅
p is omgekeerd evenredig met V
p is recht evenredig met
Het product van druk en volume is constant voor een constante massa gas waarvan de temperatuur niet verandert.
Als 1 en 2 twee toestanden van het gas zijn, wordt deze wet: ⋅
Als het product van twee grootheden constant is, dan zeggen we dat die twee grootheden omgekeerd evenredig zijn.
We kunnen dus het volgende besluiten.
De gasdruk is omgekeerd evenredig met het volume, voor een constant aantal gasdeeltjes en bij een constante temperatuur.
Het p(V)-diagram geeft ook dit omgekeerd evenredig verband weer.
Deze kromme is een kromme van constante temperatuur, zo’n kromme noemen we een isotherm.
( )
In een -diagram zien we het recht evenredig verband tussen p en . Zo tonen we ook het omgekeerd evenredig verband tussen p en V aan.
( )
In een p(V)-diagram zijn de isothermen van een gas hyperbolen. We noemen een toestandsverandering bij constante temperatuur dan ook een isotherme toestandsverandering.
Beschouwen we hetzelfde gas bij twee verschillende temperaturen, dan zullen we voor elk van de temperaturen een isotherm vinden in het p(V)-diagram. Voor twee temperaturen T1 en T2, waarbij T2 > T1 krijgen we bijvoorbeeld onderstaande grafiek. Hoe lager de temperatuur, hoe lager de hyperbool in het p(V)-diagram komt te liggen.
In het p(V)-diagram zijn de isothermen hyperbolen. Hoe hoger de temperatuur, hoe hoger de hyperbool in het p(V)-diagram ligt.
p (hPa) V (ml)





Leerlingenlabo: experimenteel onderzoek van de wet van Boyle-Mariotte
Voor dit labo sluiten we een bepaald volume gas af in een meetspuit. Tijdens het experiment veranderen (en meten) we het volume en bepalen we telkens de bijhorende druk van het gas. De temperatuur van het gas blijft hierbij constant.










Scan de QR-code om het onderzoek naderbij te bekijken of zelf het experiment uit te voeren.
Er is een omgekeerd evenredig verband tussen de druk en het volume van een constante massa gas bij een constante temperatuur.
Hierbij geldt dat als het volume x-aantal keer kleiner wordt, de druk x-aantal keer groter wordt.
Bij dit verband geldt dat p · V een constante is.
Het p(V)-diagram van het omgekeerd evenredig verband is een hyperbool.
Het -diagram van het recht evenredig verband is een schuine rechte.
Deze wet onderzoekt de verandering van de gasdruk met de temperatuur bij een constant volume en voor een constante massa gas.
Volgens het deeltjesmodel bewegen de gasmoleculen vrij door elkaar.
Als we de temperatuur van een afgesloten hoeveelheid gas laten toenemen, neemt de beweging van de gasmoleculen toe. Hierdoor nemen de onderlinge botsingen tussen de gasmoleculen toe en stijgt dus ook de gasdruk.
Omgekeerd, als we de temperatuur laten afnemen, zal de gasdruk ook dalen.
Ga dit zelf even na met behulp van onderstaande applet (kies voor de optie ‘Ontdek’). Scan hiervoor de QR-code.

In de emmer kan je vuur maken om de temperatuur te laten toenemen of ijs plaatsen om de temperatuur te laten dalen. Let goed op de beweging van de gasdeeltjes.
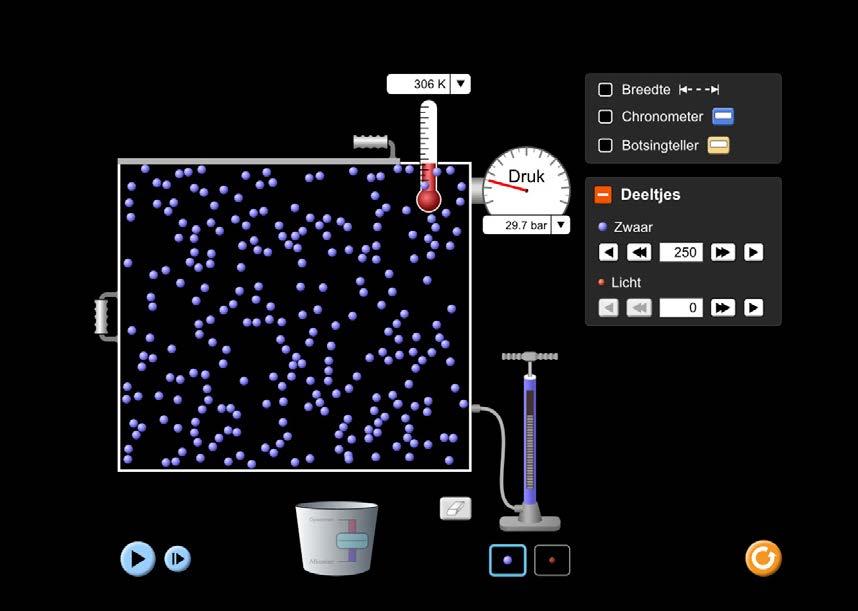


We zien dat, voor een constant aantal gasdeeltjes, een toename van de temperatuur een drukverhoging teweegbrengt en, omgekeerd, dat een afname van de temperatuur een drukdaling veroorzaakt.
We vermoeden dus dat er een recht evenredig verband bestaat tussen de temperatuur en de gasdruk voor een constant aantal gasdeeltjes in een constant volume.
Experimenteel onderzoek bevestigt dit vermoeden.
Voor een constante massa gas in een constant volume geldt:
p is recht evenredig met T
Als 1 en 2 twee toestanden van het gas zijn, dan wordt deze wet:
Het p(T)-diagram geeft een schuine rechte door de oorsprong, het absolute nulpunt.
Deze lijn is een lijn van constant volume, zo’n lijn noemen we een isochoor.
) ( )
In een p(T)-diagram zijn de isochoren van een gas rechten die door het absolute nulpunt gaan.
We noemen een toestandsverandering bij constant volume dan ook een isochore toestandsverandering.
Beschouwen we hetzelfde gas bij twee verschillende volumes, dan zullen we voor elk van de volumes een isochoor vinden in het p(T)-diagram. Voor twee volumes V1 en V2, waarbij V1 > V2 krijgen we bijvoorbeeld onderstaande grafiek. Hoe kleiner het volume, hoe hoger de rechte in het p(T)-diagram komt te liggen.
( ) <
( )
In het p(T)-diagram zijn de isochoren rechten die door de oorsprong gaan.
Hoe groter het volume, hoe lager de rechte in het p(T)-diagram ligt.
Leerlingenlabo: experimenteel onderzoek van de drukwet van Gay-Lussac


In het derde jaar leidden we in de module Druk reeds het verband tussen de gasdruk en de temperatuur experimenteel af.
We bespraken daarbij ook uitvoerig de link met de absolute temperatuur. We herhalen dit experiment hier kort en gebruiken hier onmiddellijk de absolute temperatuur in plaats van de temperatuur in graden Celsius.
De onderzoeksvraag luidt:
Wat is het verband tussen de temperatuur en de gasdruk voor een constant aantal gasdeeltjes in een constant volume?
Om een antwoord te vinden op de onderzoeksvraag voeren we volgend labo uit.
We brengen een hoeveelheid gas in een erlenmeyer en bevestigen een temperatuursensor en druksensor (of thermometer en manometer (drukmeter)) in de dop. We sluiten de erlenmeyer af zodat het volume en het aantal gasdeeltjes constant blijven.
Door de erlenmeyer op te warmen, veranderen (en meten) we de temperatuur θ van een hoeveelheid gas en bepalen we telkens de bijhorende druk p.












Scan de QR-code om het onderzoek naderbij te bekijken of zelf het experiment uit te voeren.
De absolute temperatuur is recht evenredig met de gasdruk voor een constant aantal gasdeeltjes in een constant volume.
Deze wet onderzoekt de verandering van het volume met de temperatuur bij een constante druk en voor een constante massa gas.
Volgens het deeltjesmodel bewegen de gasmoleculen vrij door elkaar.
Als we de temperatuur van een afgesloten hoeveelheid gas laten toenemen, neemt de beweging van de deeltjes toe. Als de gasdruk dezelfde moet blijven, dan moet het volume toenemen.
Omgekeerd, als we de temperatuur laten afnemen, zal het volume ook dalen.
We vermoeden dus dat V en T recht evenredig zijn met elkaar.
Experimenteel onderzoek bevestigt dit vermoeden.
Voor een constante massa gas bij een constante druk geldt:
V is recht evenredig met T
Als 1 en 2 twee toestanden van het gas zijn, wordt deze wet:
Het V(T)-diagram geeft een schuine rechte door de oorsprong, het absolute nulpunt.
Deze lijn is een lijn van constante druk, zo’n lijn noemen we een isobaar. ( ) ( )
In een V(T)-diagram zijn de isobaren van een gas rechten die door het absolute nulpunt gaan.
We noemen een toestandsverandering bij constante druk dan ook een isobare toestandsverandering.
Beschouwen we hetzelfde gas bij twee verschillende drukken, dan zullen we voor elke druk een isobaar vinden in het V(T)-diagram. Voor twee drukken p1 en p2, waarbij p1 > p2 krijgen we bijvoorbeeld onderstaande grafiek. Hoe kleiner de druk, hoe hoger de rechte in het V(T)-diagram komt te liggen.
( ) <
( )
In het V(T)-diagram zijn de isobaren rechten die door de oorsprong gaan.
Hoe groter de druk, hoe lager de rechte in het V(T)-diagram ligt.
Bij elk van de drie gaswetten, die we net hebben gezien, hoort een formule. Hieronder vind je een overzicht.
VERBAND TUSSEN ...BIJ CONSTANTE ... WET FORMULE
p en V T wet van Boyle-Mariotte =
p en T V drukwet van Gay-Lussac, wet van Regnault =
V en T p volumewet van Gay-Lussac =
WIST-JE-DAT
Jullie kennen allemaal de Eiffeltoren in Parijs, maar jullie weten misschien niet dat aan de vier zijden van de toren telkens 18 namen van Franse wetenschappers, ingenieurs … aangebracht werden. Tussen deze 72 namen kan je, in vergulde letters van 60 cm hoog, ook de namen Joseph Louis GayLussac en Henri Victor Regnault terugvinden.


Deze drie wetten voegen we nu samen tot de ideale gaswet
De ideale gaswet wordt ook wel de algemene gaswet of universele gaswet genoemd.
Het samenvoegen van deze drie wetten geeft ons:
⋅ = (voor een bepaalde hoeveelheid gas)
Als 1 en 2 twee toestanden van het gas zijn, dan wordt deze wet:
De constante in ⋅ = hangt samen met de stofhoeveelheid n van het gas. Hoe groter de stofhoeveelheid, hoe groter de constante:
Dus: =
Deze constante heeft voor alle gassen dezelfde waarde.
We noemen deze constante daarom de gasconstante R, ook algemene gasconstante of molaire gasconstante genoemd.
Experimenteel vinden we = ⋅ mol
De ideale gaswet
Dat geeft ons als formule voor de ideale gaswet:
De ideale gaswet geldt voor ideale gassen en is een goede benadering voor reële gassen.
Het model van het ideale gas is een fysisch-mathematische model met een beperkte reikwijdte.
Bij hoge druk of nabij het condensatiepunt komen de moleculen dichter bij elkaar en zijn de cohesiekrachten tussen de moleculen niet meer verwaarloosbaar. Het reële gasvolume wordt dan lager dan de ideale gaswet aangeeft.
We controleren nog even de eenheden:
Eenheid van m = m m = m =
Eenheid van ⋅ ⋅ ⋅ ⋅ ⋅ =
We kunnen de stofhoeveelheid ook uitdrukken in functie van de massa gas, in functie van het aantal deeltjes N en in functie van het volume V:
= M
Voor de massa van een gas geldt immers: = ⋅ M
=
Voor het aantal deeltjes van een gas geldt immers: = ⋅
=
Voor het volume van een gas geldt immers: = ⋅ m
Hierbij gebruiken we een aantal grootheden uit de chemie, de eenheden kunnen verschillen van wat we gewoon zijn:
• m = massa gas (g)
• M = de molaire massa van het gas g mol
• N = aantal deeltjes
• NA = het getal van Avogadro =
• V = volume (l)
• Vm = het molair volume
We kunnen de ideale gaswet dus ook omvormen tot onderstaande vorm voor het bepalen van het molair volume:
⟺ m = ⋅
Berekenen we het molair volume onder norm-omstandigheden ( = ( ) en = ), dan vinden we:
⋅ = =
Onder norm-omstandigheden (standaardomstandigheden) is het volume van 1 mol ideaal gas gelijk aan 22,4136 liter.
Inleiding
Een bepaalde massa gas heeft drie toestandsfactoren. Som deze op.
Een ideaal gas is een geïdealiseerde voorstelling (model) van een werkelijk gas. Geef de voorwaarden waaraan een werkelijk gas moet voldoen opdat dit gas kan voorgesteld worden als een ideaal gas.
Verbanden tussen de toestandsfactoren p, V en T
Als we telkens één toestandsfactor constant houden (voor een constante massa gas), kunnen we het verband tussen de andere twee onderzoeken. Dat geeft ons dus drie gaswetten. Vul onderstaande tabel aan.
VERBAND TUSSEN …BIJ CONSTANTE …FORMULENAAM VAN DE WET
Bij –273,15 °C gebeurt er iets speciaals met moleculen.
Hoe noemen we deze temperatuur? Noteer.
Wat kan je zeggen over de beweging van moleculen bij deze temperatuur? Noteer.
Naast de eenheid °C gebruiken we dus ook vaak een andere eenheid om temperatuur in uit te drukken. Welke eenheid is dat? Geef de naam en het symbool.
Wat is het verband tussen de temperatuur uitgedrukt in de eenheid uit puntje c en de temperatuur uitgedrukt in °C? Noteer.
Hoe kan je het verband tussen druk en volume van een constante massa gas met een constante temperatuur voorstellen? Maak een grafiek en leg uit.
Gegeven: onderstaande grafieken
Grafiek A
) ( )
Grafiek C
Grafiek B
) (m3 )
Grafiek D (m3 ) ( ) ( ) ( )
Grafiek E
) (m3 )
Grafiek G
Grafiek F
) ( )
Grafiek H (m3 ) ( ) (m3 ) ( )
Welke grafieken horen bij een isochore toestandsverandering? Leg uit.
Welke grafieken horen bij een isobare toestandsverandering? Leg uit.
Welke grafieken horen bij een isotherme toestandsverandering? Leg uit.
Waarom wordt de temperatuur –273,15 °C het absolute nulpunt genoemd? Leg uit.
Een leerling heeft drie grafieken gemaakt die horen bij de drie gaswetten. Hij is echter vergeten de assen te benoemen. Doe jij dat even? Kies uit:
Een meetspuit wordt gevuld met een gas en nadien afgesloten. Als je de meetspuit probeert in te duwen, voel je duidelijk een druk. Leg uit hoe dat komt.
In welke van de onderstaande gevallen geldt de wet van Boyle-Mariotte? Duid het juiste antwoord aan.
We pompen een fietsband op waardoor de druk in de band toeneemt. De omgevingstemperatuur blijft hierbij constant.
De fiets staat in de zon waardoor de druk in de fietsband toeneemt.
We laten wat lucht uit de fietsband waardoor de druk in de fietsband afneemt.
We drukken de fietsband op een bepaalde plaats in waardoor de druk in de band toeneemt.
De ideale gaswet
Gegeven: de gaswet =
Een ideaal gas ondergaat echter een isobare toestandsverandering. Tot welke vorm kan de gaswet dan vereenvoudigd worden? Duid het juiste antwoord aan.
een vereenvoudiging is niet mogelijk, we moeten = blijven gebruiken.
Als je jouw fiets met goed opgeblazen banden in de felle zon laat staan, dan kan het dat jouw banden ontploffen. Leg uit hoe dit kan.
Een duiker blaast vanop zekere diepte een paar luchtbellen. Beschrijf hoe het volume van deze luchtbellen verandert tijdens het opstijgen.
Verbanden tussen de toestandsfactoren p, V en T
3 4 5 6 7 8
Het volume van de opblaasbare pop is 560,0 ml bij het begin van het experiment (bij de standaarddruk). Bij het aanzetten van de vacuümpomp neemt het volume van de opblaasbare pop toe tot 780,0 ml Welke druk heerst er op dat moment onder de glazen stolp? Bereken. 1
Duid het juiste antwoord aan. 30 °C komt overeen met:
243 K
303 K
273 K
30 K
Duid het juiste antwoord aan. 293 K komt overeen met:
220 °C
23 °C
30 °C
20 °C
Bij atmosferische druk neemt een ideaal gas, bij een bepaalde temperatuur, 40 cm3 in. Bepaal de druk die heerst in een ruimte van 240 cm3 als die gevuld wordt met dezelfde hoeveelheid van dat ideaal gas, bij dezelfde temperatuur.
Een hoeveelheid waterstof wordt bij 1,0 atm en 20 °C in een container met een constant volume gebracht en wordt vervolgens opgewarmd tot 300 °C. Bereken de einddruk in de container.
Bij 1 atm en 21 °C neemt een bepaalde massa zuurstof een volume van 785 liter in. Bereken het volume dat het zuurstofgas inneemt bij 28 °C als je weet dat de druk onveranderd blijft.
Een meetspuit, gevuld met lucht, heeft oorspronkelijk een volume van 15,0 ml. De druk in de meetspuit bedraagt op dat moment 1000 hPa. De meetspuit wordt vervolgens uitgerekt tot een volume van 25,0 ml waardoor het gas kan uitzetten. Bereken de druk van het gas in deze toestand.
113 liter heliumgas bij 27,0 °C wordt afgekoeld tot –78,0 °C onder constante druk. Bereken het nieuwe volume van het heliumgas.
Je bent benieuwd naar de druk onder de glazen stolp bij het aanzetten van de vacuümpomp. Je plaatst daarom een opblaasbare pop onder de stolp en bekijkt hoe die verandert als de vacuümpomp aangezet wordt.

Een staal heliumgas neemt een volume van 3,8 l in bij –45 °C. Welk volume zal het staal innemen bij 45 °C? Bereken.
Een staal stikstofgas neemt een volume van 250 ml in bij 25 °C. Welk volume zal het staal innemen bij 95 °C? Bereken.
Een staal zuurstofgas neemt een volume van 250 ml bij een druk van 98,7 kPa. Welk volume zal het staal innemen bij 106,7 kPa? Je mag ervan uitgaan dat de temperatuur constant gehouden wordt.
Als het volume van een bepaalde hoeveelheid gas verdriedubbelt bij een constante temperatuur, wat gebeurt er dan met de druk? Bereken.
Als de temperatuur van een bepaalde hoeveelheid gas verdubbelt bij een constant volume, wat gebeurt er dan met de druk? Bereken.
Een spuitbus wordt leeggespoten tot het enkel nog het drijfgas bevat, die dan nog onder een druk van 1,77 atm bij 23 °C in de bus zit.
De spuitbus wordt in een kampvuur gegooid (θ = 475 °C), bereken de druk in de spuitbus op dat moment.
Een frisdrankfles is zo flexibel dat het volume van de fles kan veranderen zonder ze te openen. Een lege fles heeft een volume van 2,0 liter bij kamertemperatuur (25 °C). Welk volume zal de fles hebben als ze in de koelkast gestopt wordt bij een temperatuur van 4,0 °C? Bereken.
Een staal CO2 gas neemt een volume van 3,50 liter in bij 125 kPa. Als je ervan uitgaat dat de temperatuur constant gehouden wordt, welke druk wordt dan uitgeoefend op het gas op het moment dat het een volume heeft van 2,00 liter? Bereken.
In een afgesloten vat zit een hoeveelheid ideaal gas bij 10 °C. Duid het juiste antwoord aan. Om de druk in het vat te verdubbelen, moeten we de temperatuur laten stijgen tot:
20 °C
293 °C
283 K
293 K
Een meetspuit bevat 80 cm3 lucht bij 10 °C. De lucht wordt, bij constante druk, opgewarmd van 10 °C tot 40 °C. Bereken het volume dat de lucht inneemt bij 40 °C
Bij 27 °C bedraagt de druk in een met gas gevulde gloeilamp 15 hPa. Als de lamp brandt, bedraagt de druk in de lamp echter 30 hPa. Bepaal de temperatuur van de brandende lamp.
Op een koude dag, bij 10 °C, bedraagt de druk in een autoband 3,20 bar. Bereken de druk in de autoband op een zomerse dag bij 50 °C.
8,2 liter lucht bevindt zich onder een druk van 110 kPa. De lucht wordt isotherm samengeperst tot de druk 185 kPa bedraagt. Bereken het volume dat de lucht op dat moment inneemt.
Een aerosol bevat 400,0 ml samengeperst gas bij 5,2 atm. Het gas wordt in een grote plastiek zak gespoten en neemt daar een volume van 2,14 liter in. Bereken de druk van het gas in de plastiek zak.
Duikboten moeten bestand zijn tegen de enorm hoge druk die het water van de oceaan op hen uitoefent. In een experimenteel onderzoek wordt een duikboot met een volume van 15000 liter onderworpen aan een inwendige druk van 1,2 atmosfeer. Als de duikboot het zou begeven onder de waterdruk van de oceaan zou er een druk van 250 atm op de ontstane luchtbel uitgeoefend worden. Bereken het volume van de ontstane luchtbel.
Bij 23,0 °C en 1,00 atm neemt CO2 een volume van 20,0 liter in. Bereken welk volume het zou innemen bij 23,0 °C en 0,830 atm
Een volleybal heeft een volume van 2,00 liter onder een druk van 1,0 atm en een temperatuur van 20,0 °C. Je gaat duiken en neemt een volleybal mee onder water naar een plaats waar de druk 3,91 atm is en de temperatuur 0,245 °C. Bereken het volume van de volleybal op dat moment.
Een bolvormige weerballon heeft een straal van 1,0 m op zeeniveau bij 1,0 atm en 20 °C De ballon wordt losgelaten en tot zijn maximum hoogte gebracht. De weerballon heeft op dat moment een straal van 3,0 m bij een temperatuur van –20,0 °C. Bereken de druk in de weerballon op zijn maximale hoogte.
De ideale gaswet
Een airconditioning systeem bevat een koelgas bij 28 °C, in een volume van 500 ml en bij een druk van 92,0 kPa. Bereken de druk die het koelgas, gekoeld tot –5,0 °C, zal uitoefenen als het wordt samengedrukt tot een volume van 300 ml.
Gegeven zijn onderstaande waarden behorende bij een ideaal gas, bereken het volume.
p = 1,01 atm
n = 0,00831 mol
θ = 25 °C
Gegeven zijn onderstaande waarden behorende bij een ideaal gas, bereken de druk.
V = 0,602 l
n = 0,00801 mol
T = 311 K
Bij welke temperatuur zit 2,10 molN2 gas onder een druk van 1,25 atm in een tank van 25,0liter? Bereken.
Welk volume neemt 2,35 mol He bij 25 °C en bij een druk van 0,980 atm in? Bereken.
Bereken welk volume 1,00 mol gas inneemt onder standaardomstandigheden (θ = 0,0 °C, p = 1,0 atm).
Welk volume heeft 18 g waterstofgas bij 1013 hPa en 20 °C? Bereken.
M( )=
Voor een groot feest worden 300 ballonnen gevuld met helium bij 295 K tot hun volume 8liter en de druk Pa bedraagt. Hoeveel kilogram helium werd hiervoor gebruikt? Bereken.
M( )=
De totale longinhoud bedraagt bij vrouwen ongeveer 4,2 liter en bij mannen ongeveer 5,8liter
Vergelijk het aantal mol gas in de longen van een man met het aantal mol gas in de longen van een vrouw. Ga er hierbij van uit dat de longen een druk van 1,00 atm ondervinden en de temperatuur 37 °C bedraagt.
Een onbekend gas neemt een volume van 3,0 liter in bij 1013 hPa en 27,0 °C . Bereken de molaire massa van 2,40 g van dat onbekend gas.
Bereken het volume dat 5,03 g O2 gas inneemt bij 28 °C en een druk van 0,998 atm
Bereken de druk in een gastank van 212 liter gevuld met 23,3 kg argon gas bij 25 °C
Bij welke temperatuur heeft 16,3 g stikstofgas een druk van 1,25 atm in een tank van 25,0liter? Bereken.
Welke massa CO2 is nodig om een tank van 80,0 l te vullen onder een druk van 150,0 atm bij 27,0 °C? Bereken.
Bij welke temperatuur neem 5,00 g H2 een volume van 50,0 liter in bij 1,01 atm? Bereken.
Een staal zuurstofgas heeft een volume van 36,7 l bij 145 kPa en 65 °C. Welk volume zal het staal innemen onder standaardomstandigheden? Bereken.
Een vat van 20 liter bevat stikstofgas bij 15 °C en 400 kPa. Na gebruik is de temperatuur in de fles gedaald tot –13 °C en de druk tot 200 kPa. Welke massa stikstofgas is verbruikt? Bereken.
Een hoeveelheid ideaal gas ondergaat bovenstaande toestandsverandering. In toestand C bedraagt het volume van het gas 2,0 l. Bereken en duid het juiste antwoord aan.
Het volume van het ideaal gas in toestand A bedraagt:
Het volume van het ideaal gas in toestand B bedraagt:
Welke grootheid bleef constant tijdens de toestandsverandering van toestand B naar toestand C? Noteer.
Welke vereenvoudigde formule kan je dus gebruiken bij het oplossen? Noteer.
Heb je deze formule gebruikt? Kruis aan.
Bij de chemische reactie 2 NaN3 (s) ⟶ 2 Na (s) + 3 N2 (g) wordt natriumazide (NaN3) omgezet in vast natrium (Na) en stikstofgas (N2)
Een airbag van een auto maakt gebruik van deze chemische reactie. Het stikstofgas dat hierbij vrijkomt zorgt ervoor dat de airbag zich opblaast.
(s) staat hierbij voor 'solid' = vaste toestand.
(g) staat hierbij voor 'gas' = gasvormige toestand.
Bereken hoeveel liter N2 er uit 40,0 g NaN3 kan gevormd worden bij 32 °C en 1125 hPa. Bereken het aantal mol NaN3 uit de massa NaN3 Bereken het aantal mol N2 dat gevormd wordt. Bereken de hoeveelheid stikstofgas (in gram) die hierbij geproduceerd wordt.
200 mol methaan (CH4) wordt in een gasopslagtank gebracht, de druk in de tank bedraagt hierdoor 1,20 atm. Even later wordt nog eens 100 mol methaangas in de tank toegevoegd. Bereken de einddruk in de tank. Je mag ervan uitgaan dat de temperatuur tijdens het proces constant blijft.
Vroeger werd het beeld in televisie- en computerschermen gevormd met behulp van een kathodestraalbuis. Bereken de druk in dergelijke buis bij 23 °C als je weet dat deze 0,10 µg stikstofgas bevatte en een volume had van 5,0 liter.


Eucalyptusolie wordt geproduceerd uit de bladeren van eucalyptus en bevat daardoor de vluchtige organische component eucalyptol.
Eucalyptoldamp heeft een massadichtheid van 0,320 kg m3 bij 190 °C en 8000 Pa
Bereken de molaire massa van eucalyptol.
Per dag produceert een cementbedrijf 100 ton cement. Het cement bevat 62 % CaO, welke als volgt bereid wordt: CaCO3 (s) ⟶ CaO (s) + CO2 (g) Bereken welk volume CO2 gas hierdoor dagelijks in de atmosfeer gestuurd wordt, bij een gemiddelde temperatuur van 20 °C en een luchtdruk van 980 hPa. (s) staat hierbij voor 'solid' = vaste toestand. (g) staat hierbij voor 'gas' = gasvormige toestand.
Bij het vullen van een weerballon met gas, moet er rekening mee gehouden worden dat het gas veel zal uitzetten naarmate de weerballon stijgt en de druk afneemt.
Als we een weerballon vullen met 10,0 mol He gas aan de grond, dan is de ballon met een volume van 5000 liter niet vol. De ballon wordt opgelaten tot een hoogte waar de temperatuur –10,0 °C is en de ballon volledig met gas gevuld is. Bereken de druk op die hoogte.
In rust verbruikt een gemiddelde man van 70 kg 14 liter zuiver O2 per uur bij 25 °C en 100 kPa. Hoeveel mol O2 verbruikt deze man als hij gedurende 1,0 uur rust? Bereken.
Verbanden tussen de toestandsfactoren p, V en T
In dit experiment voer je zelf het onderzoek naar de wet van Boyle-Mariotte uit en zoek je het verband tussen druk en volume van een constante massa gas bij een constante temperatuur.

manometer (op 0,1 bar meetspuitnauwkeurig) (op 1 ml nauwkeurig)

















Je kan het experiment rond de wet van Boyle-Mariotte virtueel uitvoeren met behulp van de applet ‘Eigenschappen van gassen’ die je eerder al gebruikt hebt. Scan hiervoor de QR-code. Stel de temperatuur in op K en de druk op kPa.
Klik breedte aan zodanig dat de breedte van het vat weergegeven wordt. Kies een aantal gasdeeltjes en laat dat gedurende het experiment ongewijzigd. Verander tijdens het experiment de breedte, en dus ook het volume van het vat, en meet telkens de druk in kPa.
In dit experiment voer je zelf het onderzoek naar de drukwet van Gay-Lussac uit en onderzoek je het verband tussen de temperatuur en de gasdruk voor een constant aantal gasdeeltjes in een constant volume.

erlenmeyer thermometer manometer dop voor de bunsenbrandererlenmeyer


















Je kan het experiment rond de drukwet van Gay-Lussac virtueel uitvoeren met behulp van de applet ‘Eigenschappen van gassen’ die je eerder al gebruikt hebt. Scan hiervoor de QR-code. Stel de temperatuur in op K en de druk op kPa
Kies een aantal gasdeeltjes en laat dat gedurende het experiment ongewijzigd. Warm het gas op of koel het gas af en meet de absolute temperatuur in kelvin. Meet ook telkens de bijhorende druk in kPa
De ideale gaswet
Toepassing op de wet van Boyle-Mariotte

BENODIGDHEDEN

2 elektriciteitsbuizen, een dikke en een dunne, die juist in elkaar passen, (de dunne buis neem je best iets langer dan de dikke), lengte bv ongeveer 60 cm en 70 cm aardappel




Duw de aardappel op een uiteinde van de dikke buis, en trek die er vervolgens weer af, maar zorg ervoor dat er een stuk aardappel vast blijft zitten in de buis.
Herhaal dit bij de andere kant van de dikke buis.
Er zit nu een hoeveelheid lucht in de buis afgesloten, tussen de twee stukken aardappel.
Duw nu de dunne buis in de dikke buis.
Wat neem je waar? Noteer. Hoe kan je dit verklaren? Bespreek.
Toepassing op de wet van Boyle-Mariotte

petfles met een klein gaatje ballon






Bevestig de ballon aan de dop van de petfles zoals op bovenstaande foto.
Zet je vinger op het gaatje dat onderaan de fles zit. Blaas de ballon op.
Verplaats je vinger, laat het gaatje dat in de fles is dus open. Blaas de ballon op.
Bespreek onderstaande vragen.
a b
Wat neem je waar? Hoe kan je dit verklaren?
Toepassing op de drukwet van Gay-Lussac
BENODIGDHEDEN


fles met trechtervormige hals (bv type karaf) ballon water




Vul de ballon met water, zorg hierbij dat er net voldoende water in de ballon zit zodat die niet door de hals van fles valt.
Giet heet water in de fles en giet de fles daarna volledig leeg.
Leg de ballon op de hals van de fles.
Bespreek onderstaande vragen.
a b c d e
Wat neem je waar?
Hoe kan je dit verklaren?
Welke toestandsfactoren veranderen hier, welke blijven constant?
Welke gaswet is hier van toepassing?
Bedenk een manier om de ballon uit de fles te halen. Leg uit.















Implosie van een afkoelend blikje

leeg blikje bak met ijskoud water of bak gevuld met water en ijs heet water houten tang bunsenbrander





Vul het blikje met wat heet water. Hou het blikje met de tang boven de bunsenbrander tot het water kookt.
Draai het blikje om (opening naar onder), en dompel het blikje geheel onder in het koude water. Doe dit voldoende snel.
Bespreek onderstaande vragen.
Wat neem je waar?
Hoe kan je dit verklaren?
Welke toestandsfactoren veranderen hier, welke blijven constant?
Welke gaswet is hier van toepassing?














ik ken het!
Ik ken de drie voorwaarden voor een ideaal gas. Ik zie in dat een ideaal gas een model is dat een reëel gas onder bepaalde voorwaarden beschrijft en ik weet wanneer een reëel gas door een ideaal gas kan worden benaderd.
paginanummer
p. 4, p. 16
Ik weet dat een bepaalde massa gas bepaald wordt door drie toestandsfactoren, namelijk druk, volume en temperatuur. p. 4-5
Ik kan het onderscheid tussen een ideaal en een reëel gas beschrijven. p. 4-5
Ik kan het verband (recht en omgekeerd evenredig verband) tussen twee grootheden, terwijl de overige constant blijft, op kwantitatieve wijze onderzoeken (verband tussen druk, volume en temperatuur).
p. 6-14, p. 26-31
Ik kan grafisch het verband tussen de toestandsgrootheden druk, volume en absolute temperatuur zien. p. 6-14
Ik kan grafieken, die de toestand en de toestandsverandering van een gas beschrijven, opstellen en interpreteren. Ik kan het recht en omgekeerd evenredig verband tussen twee grootheden, terwijl de overige constant blijft, grafisch weergeven (verband tussen druk, volume en temperatuur).
p. 6-14, p. 18-25
Ik kan een temperatuur in graden Celsius omzetten naar kelvin en omgekeerd. p. 18-25
Ik kan de ideale gaswet opbouwen vanuit de afzonderlijke gaswetten. p. 15-17
Ik kan het verband tussen de toestandsgrootheden druk, volume en absolute temperatuur gebruiken om de toestand van een ideaal gas en de veranderingen ervan te beschrijven.
Ik ken de ideale gaswet, inclusief formule =
p. 15-17, p. 18-25
en kan deze toepassen in vraagstukken. p. 15-17, p. 21-25
Ik ken de begrippen stofhoeveelheid, molaire massa en molair volume. p. 16-17
Ik kan de stofhoeveelheid uitdrukken in functie van de massa gas, in functie van het aantal deeltjes N en in functie van het volume V p. 16-17
Ik kan de ideale gaswet omvormen voor het bepalen van het molair volume. p. 16-17
Ik kan formules omvormen (één variabele uitdrukken in functie van de andere). Ik kan de ideale gaswet opzoeken in een formularium en deze omvormen om volume, druk of temperatuur van een gas te bepalen als de andere twee grootheden gegeven zijn. p. 21-25
Ik kan de ideale gaswet toepassen in stoichiometrische berekeningen. p. 21-25
Auteur Freya Vermeiren
Met medewerking van Anke Van Roy
Eerste druk 2024
SO 0188/2024
Bestelnummer 90 808 0458
Module 3 van ISBN 978 90 4865 010 1
KB D/2024/0147/252
NUR 126
Thema YPMP5
Verantwoordelijke uitgever die Keure, Kleine Pathoekeweg 3, 8000 Brugge
RPR 0405 108 325 - © die Keure, Brugge
Niets uit deze uitgave mag verveelvoudigd en/of openbaar gemaakt worden door middel van druk, fotokopie, microfilm of op welke wijze ook zonder voorafgaande schriftelijke toestemming van de uitgever. No parts of this book may be reproduced in any form by print, photoprint, microfilm or any other means without written permission from the publisher. De uitgever heeft naar best vermogen getracht de publicatierechten volgens de wettelijke bepalingen te regelen. Zij die niettemin menen nog aanspraken te kunnen doen gelden, kunnen dat aan de uitgever kenbaar maken.
Die Keure wil het milieu beschermen. Daarom kiezen wij bewust voor papier dat het keurmerk van de Forest Stewardship Council® (FSC®) draagt.
Dit product is gemaakt van materiaal afkomstig uit goed beheerde, FSC®-gecertificeerde bossen en andere gecontroleerde bronnen.