Kadet 3 - Sloep (onthoudboekje)

3 3 p p e oe o loe l Sl S

Getallenkennis

Denk aan de kleuren van het MAB-materiaal of aan de zin: Dolfijn Hanna Tuimelt Eens.

Maak een tabel als je twijfelt.

Getallen tot 1 000 op de getallenas

Kijk goed naar de richting van de pijl.

Kijk goed naar de getallen.

Kijk goed naar de sprongen.

Kijk goed naar de waarde H, T, E.

900

Denk aan Henk: Henk hapt altijd naar het meeste.

Doortellen en terugtellen tot 1 000 met sprongen Met sprongen van 2

Met sprongen van 10

Teken pijlen bij de sprongen en schrijf de bewerking erbij.

Tel dan eens in de andere richting om te controleren.

Getallen tot 1 000 afronden

Afronden naar het dichtstbijzijnde tiental

We zoeken het tiental dat het dichtste bij ons getal ligt�

Kleur het tiental groen!

Is het laatste cijfer 0, 1, 2, 3 of 4?

➔ Het tiental blijft, de eenheden worden 0. = We ronden af naar beneden.

Is het laatste cijfer 5, 6, 7, 8 of 9?

➔ Het tiental krijgt er één bij, de eenheden worden 0. = We ronden af naar boven.

Afronden naar het dichtstbijzijnde honderdtal

We zoeken het honderdtal dat het dichtste bij ons getal ligt�

Kleur het honderdtal blauw!

Zijn de laatste twee cijfers < 50?

➔ Het honderdtal blijft, TE wordt 00. = We ronden af naar beneden.

Zijn de laatste twee cijfers ≥ 50?

➔ Het honderdtal krijgt er één bij, TE wordt 00. = We ronden af naar boven.

Even en oneven getallen

Even getallen

• eindigen op 0, 2, 4, 6 of 8�

• hebben geen rest na deling door 2�

➔ Dus: we kunnen steeds de helft nemen van een even getal

Oneven getallen

• eindigen op 1, 3, 5, 7 of 9

• hebben steeds rest 1 na deling door 2�

Negatieve getallen

Negatieve getallen zijn getallen onder nul�

Bijvoorbeeld: in een lift, op een thermometer, in een parkeergarage

Functies van getallen

We gebruiken getallen:

➔ als een hoeveelheid� (We tellen hoeveel keer iets voorkomt�)

We tellen 12 vissen

➔ in een bewerking

We tellen 7 ballen

Een bewerking is een oefening waarbij we optellen, aftrekken, vermenigvuldigen of delen� We maakten er al veel in ons werkboek�

30 + 50 = 80

➔ als een code�

20 – 5 = 15

Een code is een aantal cijfers die (soms in combinatie met letters) samen een betekenis hebben�

➔ als een maatgetal (bij een maateenheid)

Het maatgetal geeft aan hoeveel keer de maateenheid voorkomt�

➔ in een rangorde (in een rij)�

Een rangorde staat in een rij� We kunnen ons afvragen ‘de hoeveelste’, op welke plaats in de rij

Jonas

Super simpel!

Hoeveel? ➔ hoeveelheid

+, –, x, : ➔ bewerking

Hoeveel keer een maateenheid? ➔ maatgetal

Hoeveelste?

➔ rangorde

En de code, die onthouden we gewoon!

Sofie

Ik weeg 37 kg

Ik drink 2 dl chocomelk

Jonas staat als derde in de rij

Sofie is de eerste van de loopwedstrijd

• In het derde leerjaar leren we tot 1 000�

• Lees vaak samen met je kind getallen in het dagelijkse leven: in kranten en tijdschriften, op de tablet, bij reclames Laat deze zowel luidop zeggen als opschrijven Dicteer bijvoorbeeld een telefoonnummer�

• Zoek met je kind naar het juiste huisnummer als je in een straat rijdt en vraag aan je kind in welke richting er gereden moet worden

• Splits samen getallen met je kind, bijvoorbeeld 467 is 4 keer 100 en 67 (want tot 100 kunnen ze al goed)�

• Gebruik vaak de begrippen tussen, net voor / na, juist voor / na in de dagelijkse context, zonder wiskundige bijbedoeling

➔ Neem het boek dat tussen de plant en de tekening ligt

➔ Neem eens de pot uit de keukenkast die achter de suiker staat� Besteed hierbij ook aandacht aan de omgekeerde verwoording, want dat vinden kinderen moeilijk Ze zien het woord voor, maar moeten hetgeen dat erachter staat benoemen of omgekeerd

➔ Het zoutvat staat voor …

➔ In de zwemwedstrijd kwam Lotte net achter …

• De woorden die we vaak gebruiken zijn: minder, meer, verminderen, vermeerderen, helft, dubbel, aantal keer … Oefen deze in met je kind tijdens het bakken en koken Daar moet je vaak het aantal porties en de ingrediënten halveren of verdubbelen en werk je vaak met de getallen 125, 250 en 500�

Bijvoorbeeld: We hebben 750 gram nodig: drie keer een pakje boter van 250 gram is 750 gram

• Veel gezelschapsspelletjes gaan over getallen: UNO, Regenwormen, in kaartspelen ordent je kind kaarten, in Monopoly gaat het afronden en schatten of het genoeg geld

Tips voor de ouders om getallen thuis te oefenen

GETALLENKENNIS

Breuken

Hoe zeg ik het? 2

5

teller = bovenste deel van een breuk

De teller zegt hoeveel delen we van iets/een geheel nemen� breukstreep

noemer = onderste deel van een breuk

De noemer zegt in hoeveel delen we iets/een geheel verdelen�

Ik lees:

• twee vijfde�

• twee van de vijf gelijke delen�

• 2 delen van het geheel dat in 5 verdeeld is

Stambreuken

= breuken waarvan de teller 1 is�

bijvoorbeeld: 1 of 1 � 2 4

Denk aan taarten.

De teller vertelt hoeveel stukken taart we eten.

De noemer vertelt in hoeveel gelijke stukken we de taart gesneden hebben.

We eten 3 van de 8 gelijke stukken. ➔

Er blijven 5 van de 8 gelijke stukken over. ➔

3 8

Een hele taart is 8 van de 8 gelijke stukken. ➔ = het geheel = 1

5 8 8 8

of 3 8 of

Breukenladder

Op de breukenladder zien we:

Denk opnieuw aan de taart:

Van welke taart krijg je het liefst een stuk?

Een stuk van de taart verdeeld in 4 gelijke stukken?

Een stuk van de taart verdeeld in 7 gelijke stukken?

Van de taart verdeeld in 4 gelijke stukken, want is groter dan , dus dan hebben we meer

Breuk nemen van een getal

1 van 20 is 5

1) 20 : 5 = 4

2) 1 x 4 = 4

20 gedeeld door vijf is gelijk aan vier� Ik noteer ‘4’� Dan kijk ik naar mijn teller�

Hoeveel keer moet ik dit groepje van vier nemen? Eén keer

Eén keer vier is gelijk aan vier� Ik noteer ‘4’ als uitkomst�

x 4� 4 : x 8 � 4 :

2 van 20 is 5

1) 20 : 5 = 4

2) 2 x 4 = 8

20 gedeeld door vijf is gelijk aan vier Ik noteer ‘4’ Dan kijk ik naar mijn teller

Hoeveel keer moet ik dit groepje van vier nemen? Twee keer�

Twee keer vier is gelijk aan acht� Ik noteer ‘8’ als uitkomst�

Ik neem altijd eerst één deel (delen door de noemer) en vermenigvuldig dan met de teller.

We gaan verder met de mandarijnen�

Bijvoorbeeld: 5 van 28 = 7

Hoeveel mandarijnen hebben we? 28

In hoeveel gelijke delen moeten we verdelen? 7

Hoeveel is één deel? 28 : 7 = 4

Hoeveel keer moeten we dat deel nemen? 5 keer

Hoeveel mandarijnen zijn dat dan? 5 x 4 = 20

➔ 5 van 28 mandarijnen zijn 20 mandarijnen� 7

• Breuken zijn moeilijk� Hoe meer breuken je kind visueel voorgesteld krijgt, hoe sneller het de leerstof onder de knie heeft Als je kind een breuk van een getal moet nemen, kan dit ook met jetons of centjes gebeuren Gebruik hiervoor altijd dezelfde stappen, zoals op p� 18�

• Bij het aansnijden van een taart of pizza, kan je je kind het aantal gelijke delen laten tellen (noemer) Neem bijvoorbeeld twee stukken van de taart / pizza weg

Dit zijn 2 van de 8 gelijke delen of (twee achtste)

• Bij het opdienen van het eten kan je kind benoemen hoeveel iedereen neemt� Nadien kan je kind vertellen wie meer at�

Bijvoorbeeld: papa at en ik maar �

Tips voor de ouders om breuken thuis te oefenen

Tabellen en grafieken

Van enkelvoudige tabel naar turflijst

Welke huisdieren hebben de kadetten en de kapitein?

Amke kat

Saar konijn

Miel hond

Obe konijn

Cor konijn

Tara kat

Ali hond

Jack goudvis

Zeynep hond

Joppe goudvis

Leen hond

Finn hond

kapitein papegaai

kolom

huisdier aantal

kat II

konijn III

hond IIII

goudvis II

papegaai I

• Wat staat er op de horizontale as? het aantal huisdieren

• Wat staat er op de verticale as? de soorten huisdieren

• Van welk huisdier zijn er het meest? de hond

• Hoeveel konijnen zijn er?

Kansberekening Begrippen

Wat is de kans dat je een rode snoep uit de zak neemt?

Dat is zeker

Want: er zitten alleen maar rode snoepen in de zak�

Wat is de kans dat je een rode snoep uit de zak neemt?

Dat is niet zeker

Dat is mogelijk�

Dat kan

Dat lukt misschien�

Want: er zitten rode en gele snoepen in de zak

Wat is de kans dat je een rode snoep uit de zak neemt?

Dat kan zeker niet�

Dat is onmogelijk�

Dat kan niet

Want: er zitten geen rode snoepen in de zak

Kans omzetten naar een breuk

Wat is de kans dat je een rode snoep neemt?

Tel alle snoepen�

Dat zijn er vijf�

Dit getal noteren we bij de noemer

Tel nu de rode snoepen

Dat zijn er drie�

Dit getal noteren we bij de teller�

De kans dat je een rode snoep neemt, is

Wat is de kans dat je een gele snoep neemt?

Tel alle snoepen�

Dat zijn er vijf

Dit getal noteren we bij de noemer�

Tel nu de gele snoepen�

Dat zijn er twee�

Dit getal noteren we bij de teller

De kans dat je een gele snoep neemt, is �

Bewerkingen

BEWERKINGEN

Rekentaal Optellen

33 + 15 = 48 Dit is een optelling�

het plusteken

het gelijkheidsteken

33 + 15 = 48

33 is het opteltal� 15 is de opteller�

33 en 15 zijn de termen

Ik tel 15 op bij 33�

Ik vermeerder 33 met 15

Ik doe 15 bij 33�

Aftrekken

85 – 31 = 54 Dit is een aftrekking

het minteken

85 – 31 = 54

85 is het aftrektal� 31 is de aftrekker�

De uitkomst van een optelling is de som�

De uitkomst van een aftrekking is het verschil�

85 en 31 zijn de termen�

Ik verminder 85 met 31�

Ik trek 31 af van 85�

Ik doe 31 weg van 85

BEWERKINGEN

Vermenigvuldigen

het maalteken

De uitkomst van een vermenigvuldiging is het product

3 is de vermenigvuldiger

3 x 25 = 75 25 is het vermenigvuldigtal�

3 en 25 zijn de factoren�

25 + 25 + 25 = 75

Ik neem 3 keer 25�

Ik doe 3 maal 25�

Delen

het deelteken

100 : 5 = 20

100 is het deeltal� 5 is de deler� 100 en 5 zijn de factoren �

Ik verdeel 100 in 5 gelijke delen�

100 gedeeld door 5 is 20

De uitkomst van een deling is het quotiënt�

BEWERKINGEN

Hoofdrekenen: optellen en aftrekken

Optellen tot 100 met brug over T

TE + TE = TE + T + E

47 + 36 = 47 + 30 + 6 = 83

77 3 3

Het eerste getal houden we heel, het tweede getal doen we er in stappen bij.

Aftrekken tot 100 met brug over T

TE – TE = TE – T – E

62 – 29 = 62 – 20 – 9 = 33

42 2 7

Het eerste getal houden we heel, het tweede getal doen we er in stappen af.

Met de verticale strepen is het een makkie!

De tussenoplossing komt altijd voor de streep, zo moeten we niet alles onthouden.

➔ Eerst doen we de T erbij / eraf.

➔ Daarna doen we de E erbij / eraf.

BEWERKINGEN

Optellen en aftrekken tot 1 000 zonder brug

HTE + HTE = HTE + H + T + E

151 + 136 = 151 + 100 + 30 + 6 = 287 2 5 1 281

HTE - HTE = HTE - H - T - E 258 - 124 = 258 - 100 - 20 - 4 = 134 158 138

Met de verticale strepen is het een makkie!

De tussenoplossing komt altijd voor de streep, zo moeten we niet alles onthouden.

➔ Eerst doen we de H erbij / eraf.

➔ Dan doen we de T erbij / eraf.

➔ Tenslotte doen we de E erbij / eraf.

BEWERKINGEN

Optellen tot 1 000 met brug over H en T

HTE + HTE = HTE + H + T + E

477 + 167 = 477 + 100 + 60 + 7 = 644 577 30 30 3 4 607 637

• Het eerste getal houden we heel. Het tweede getal doen we er in stappen bij.

• We tellen er eerst de honderdtallen bij. 477 + 100 = 577

• Daarna tellen we de tientallen erbij.

Opletten! We moeten er ‘60’ bijtellen.

We tellen er eerst 30 bij en daarna nog eens 30. 577 + 60 = 637

30 30 607

• Als laatste tellen we de eenheden erbij.

Opletten! We moeten er '7' bijtellen.

We tellen er eerst 3 bij en daarna nog eens 4. 637 + 7 = 644

3 4

BEWERKINGEN

Aftrekken tot 1 000 met brug over H en T

HTE – HTE = HTE – H – T – E 345 – 259 = 345 – 200 – 50 – 9 = 86

• Het eerste getal houden we heel. Het tweede getal doen we er in stappen af.

• We trekken eerst de honderdtallen af. 345 – 200 = 145

• Daarna trekken we de tientallen eraf.

Opletten! We moeten er ‘50’ aftrekken. We trekken eerst 40 af en daarna nog eens 10. 145 – 50 = 95

40 10 105

• Als laatste trekken we de eenheden eraf.

Opletten! We moeten er '9' aftrekken. We trekken eerst 5 af en daarna nog eens 4. 95 – 9 = 86

5 4

BEWERKINGEN

Flexibel rekenen

Compenseren: waar ligt het dichtbij?

564 – 99 = 564 – 100 + 1 = 465

➔ 99 ligt dicht bij 100� Ik trek er 100 af en tel er dan terug één bij

564 + 198 = 564 + 200 – 2 = 762

➔ 198 ligt dicht bij 200� Ik doe er 200 bij en trek er dan terug twee af

Als ik er te veel bijdoe (+), dan moet ik dat ook weer wegdoen (–).

Als ik er te veel wegdoe (–), dan moet ik dat er ook weer bijdoen (+).

Wisselen: wat vormt samen een afgerond getal?

140 + 267 + 360 = 140 + 360 + 267 = 500 + 267 = 767

➔ 140 en 360 vormen samen 500 Ik tel er dan nog 267 bij

➔ Zijn er meerdere getallen om op te tellen?

Zoek altijd naar de getallen die goed samen passen en tel die eerst op�

• Bij plus mag alles: van plaats wisselen en termen samen nemen.

• Bij min mag niets: laat alles staan en werk van links naar rechts.

Haakjes

54 + (49 – 13 ) = 54 + 36 = 90

Wanneer er haakjes staan, lossen we deze altijd eerst op.

Hoofdrekenen: vermenigvuldigen en delen

Maaltafels oefenen

Hoe meer ik oefen, hoe beter het gaat.

Als ik dat kan, wordt rekenen een makkie!

Denk goed na, met deze tips lukt het zeker: • Wat is het dubbel ?

BEWERKINGEN

Vermenigvuldigen tot 1 000

Maal 10 en maal 100

10 x 30 = 300

10 x 14 = 140

100 x 2 = 200

➔ 10 x = één nul bij

➔ 100 x = twee nullen bij

Naar analogie met de tafels

5 x 70 = 350

8 x 30 = 240

➔ Denk aan de tafels om deze oefeningen op te lossen�

bijvoorbeeld: 5 x 70 ➔ (5 x 7) x 10 = 350 35

Als ik bij maal bij de factoren de nullen weg denk, dan moet ik die terugzetten bij het product.

Splitsen en vermenigvuldigen

E x TE = (E x T) + (E x E)

3 x 26 = (3 x 20) + (3 x 6) = 78 60 18

E x HTE = (E x H) + (E x T) + (E x E)

4 x 137 = (4 x 100) + (4 x 30) + (4 x 7) = 548 400 120 28

➔ We houden één factor heel, de andere factor splitsen we op�

We doen eerst maal en dan plus�

Ik kan ook altijd splitsbeentjes plaatsen als hulp.

BEWERKINGEN

Delen tot 1 000 zonder rest

Gedeeld door 10 en door 100

240 : 10 = 24

600 : 10 = 60

1 000 : 100 = 10

➔ : 10 = één nul weg

➔ : 100 = twee nullen weg

Naar analogie met de tafels

280 : 4 = 70

180 : 2 = 90

➔ Denk aan de tafels om deze oefeningen op te lossen� bijvoorbeeld 28 : 4 = 7 ➔ 280 : 4 = 70

Als ik bij gedeeld door in het deeltal de nul weg denk, dan moet ik die terugplaatsen in het quotiënt.

Splitsen en delen

HTE : E = H(T) : E + (H)TE : E

621 : 3 = (600 : 3) + ( 21 : 3) = 207 200 7

600 21

720 : 6 = (600 : 6) + (120 : 6) = 120 100 20

600 120

We houden de deler heel en splitsen het deeltal op in gekende veelvouden. We delen elk veelvoud door de deler en tellen dan op. De deler mag je nooit splitsen!

BEWERKINGEN

Delen tot 1 000 met rest

47 : 6 = 7 rest 5 ➔ want (7 x 6) + 5 = 42 + 5 = 47

644 : 8 = 80 rest 4 ➔ want (80 x 8) + 4 = 640 + 4 = 644

Denk aan de tafels. Neem het veelvoud dat net onder het getal komt. Schrijf dat op en kijk hoeveel je over hebt.

Flexibel rekenen

Schakelen: welke tafel vormt samen een afgerond getal?

5 x 12 x 2 = (5 x 2) x 12 = 10 x 12 = 120

➔ 5 x 2 = 10, daarna vermenigvuldig ik met 12

➔ Zijn er meerdere getallen om te vermenigvuldigen?

Zoek altijd naar de getallen die goed samen passen en vermenigvuldig die eerst

Onthoud goed:

• bij maal mag alles: van plaats wisselen en factoren samen nemen.

• bij gedeeld door mag niets: laat alles staan en werk van links naar rechts.

• Als hoofdrekenen nog moeilijk gaat, stimuleer dan om telkens de tussenstappen te gebruiken Zeg dat je kind tijdens het huiswerk de tussenstappen luidop moet verwoorden of opschrijven

• In de winkel kan je kind de prijzen afronden en optellen� Hoeveel zal het ongeveer kosten?

• De tafels moet je kind paraat kennen Deze zijn nodig in tal van oefeningen Er bestaan heel veel computerspelletjes of apps waarmee je kind kan oefenen Maak ook gebruik van de minigames die de methode voorziet�

• Het is beter om elke dag 10 minuten tafels te oefenen dan één keer in de week een uur�

• Je kunt oefenen tijdens een wandeling, bijvoorbeeld bij elke stap een tafel opzeggen of als je kind de trap oploopt bij elke trede

• Hang een tafelrooster aan de koelkast of op een krijtbord� Je kind vult de tafels in en geeft de moeilijke gevallen een kleurtje� Blijf de tafels inoefenen�

• De tafels kun je oefenen met kleurplaten of flitskaarten Beloon en moedig je kind aan, want hoe beter de tafels gekend zijn, hoe beter het hoofdrekenen zal lukken De tafels vind je op pagina 32 tot en met 34�

Tips voor de ouders om hoofdrekenen thuis te oefenen

Cijferen: rekentaal en cijferrichting

Vermenigvuldigen

kladblok

BEWERKINGEN

Cijferen

Optellen tot 1 000

Schatten

We schatten eerst onze oefening Dit doen we door af te ronden bijvoorbeeld: 204 + 143 ➔ schatting: 200 + 140 = 340

Daarna vergelijken we onze schatting met de uitkomst

We beginnen altijd rechts bij de eenheden (E), bij de rode hulplijn�

4 E + 3 E = 7 E

Daarna de tientallen (T)�

0 T + 4 T = 4 T

Als laatste de honderdtallen (H)�

2 H + 1 H = 3 H

De som lezen we af onder de cijferstreep: 347�

We beginnen altijd bij de eenheden (E), bij de rode hulplijn�

3 E + 9 E = 12 E

We schrijven de 2 (E) en onthouden de 10 of 1 T in de volgende kolom, die van de T�

Nu de tientallen (T)�

1 T + 7 T + 6 T = 14 T

We schrijven de 4 (T) en onthouden de 100 of 1 H in de volgende kolom, die van de H

Als laatste de honderdtallen (H)�

1 H + 2 H + 1 H = 4 H

De som lezen we af onder de cijferstreep: 442

BEWERKINGEN

Aftrekken tot 1 000

zonder lenen met lenen

We beginnen altijd rechts bij de eenheden (E), bij de rode hulplijn�

3 E – 1 E = 2 E

Daarna de tientallen (T)

5 T – 2 T = 3 T

Als laatste de honderdtallen (H)

8 H – 5 H = 3 H

Het verschil lezen we af onder de cijferstreep: 332

We beginnen altijd bij de eenheden (E), bij de rode hulplijn

3 E – 7 E =

Dat gaat niet! Ik ga lenen bij de tientallen Eén tiental van de 6 T ga ik lenen, dat zijn 10 eenheden�

10 E + 3 E = 13 E

13 E – 7 E = 6 E

Nu de tientallen (T)� Er blijven nog 5 T over�

5 T – 3 T = 2 T

Als laatste de honderdtallen (H)�

7 H – 5 H = 2 H

Het verschil lezen we af onder de cijferstreep: 226�

Cijferen? Denk aan een kadet die zijn bestemming moet bereiken, zo lukt het altijd!

Ik zoek mijn bestemming. ➔ Ik maak eerst een schatting.

Ligt mijn boot juist? ➔ Staan mijn getallen juist in het rooster? E onder de E.

Ik plaats mijn boot tegen de rode lijn en start met varen.

➔ Ik cijfer en begin altijd aan de kant van de rode lijn. Bij optellen en aftrekken is dat bij de eenheden (E).

Heb ik goed gevaren? Ik kijk naar mijn bestemming.

➔ Ik vergelijk mijn ligplaats, de uitkomst met mijn schatting.

BEWERKINGEN

Vermenigvuldigen tot 1 000

1

Bij vermenigvuldigen beginnen we altijd rechts, bij de kleinste rang, bij de rode hulplijn�

3 x 2 = 6

Dan schuiven we één rang op en komt het volgende getal aan de beurt� 3 x 0 = 0

Tenslotte lossen we de laatste rang op� 3 x 1 = 3

Het product we af onder de cijferstreep:

We beginnen altijd rechts, bij de kleinste rang, bij de rode hulplijn�

3 x 5 = 15

Er kunnen geen twee getallen in één hokje, we moeten onthouden

We schrijven de 5 en onthouden 1� We noteren 1 op het kladblok� De 5 noteren we rechts tegen de rode lijn

Dan schuiven we één rang op en komt het volgende getal aan de beurt: 3 x 1 = 3, maar we hebben nog 1 op ons kladblok dus 3 + 1 = 4

We noteren 4 en doorstrepen de 1�

Tenslotte lossen we de laatste rang op 3 x 2 = 6

Het product lezen we af onder de cijferstreep: 645�

Cijferen? Denk aan een kadet die zijn bestemming moet bereiken, zo lukt het altijd!

• Ik zoek mijn bestemming. ➔ Ik maak eerst een schatting.

• Ligt mijn boot juist? ➔ Staan mijn getallen juist in het rooster? Vermenigvuldiger en vermenigvuldigtal tegen de rode lijn.

• Ik plaats mijn boot tegen de rode lijn en start met varen.

➔ Ik cijfer en begin altijd aan de kant van de rode lijn. Bij vermenigvuldigen is dat bij de kleinste rang.

• Heb ik goed gevaren? Ik kijk naar mijn bestemming.

➔ Ik vergelijk mijn ligplaats, de uitkomst met mijn schatting.

BEWERKINGEN

Delen tot 1 000 Richtlei

De richtlei helpt ons bij het zoeken naar de juiste tafel van de deler� Zo schrijven we eerst 5 keer en 10 keer de deler op� Zo weten we waar de tafel van de deler tussen ligt� Handig toch?

Vul de richtlei altijd eerst in�

Bij delingen beginnen we altijd links, bij de grootste rang, bij de rode hulplijn

Hoeveel keer kan 3 in 3? 1 keer

We noteren ‘1’ bij het quotiënt, onder de streep

Nu moeten we terugkeren� Dit doen we door te vermenigvuldigen.

1 x 3 = 3

We noteren ‘3’ onder de 3 in het grote cijfervak�

We zijn nog niet klaar Nu moeten we nog aftrekken.

3 – 3 = 0

We kijken naar de volgende rang

We laten de 6 zakken tot aan de laatste oplossing�

We werken verder zoals de eerste keer

Hoeveel keer kan 3 in 6? 2 keer

2 x 3 = 6 ➔ 6 – 6 = 0

We laten de 9 zakken tot aan de 0�

Hoeveel keer kan 3 in 9? 3 keer

3 x 3 = 9 ➔ 9 – 9 = 0

Mijn quotiënt is 123, de rest is 0�

5 x 9 = 45 10 x 9 = 90

Bij delingen beginnen we altijd links, bij de grootste rang, bij de rode hulplijn

Hoeveel keer kan 9 in 4?

9 kan niet in 4, het eerste getal is kleiner dan de deler�

We nemen de eerste twee getallen samen met een boogje�

Hoeveel keer kan 9 in 48? 5 keer

5 x 9 = 45 ➔ 48 – 45 = 3

We laten de 5 zakken tot aan de laatste oplossing Samen vormen ze een nieuw getal: 35�

Hoeveel keer kan 9 in 35? 3 keer

3 x 9 = 27 ➔ 35 – 27 = 8

Het quotiënt is 53, de rest is 8�

• Als je kind bij cijferen systematisch de stappen volgt, dan lukt het zeker! Vraag eens om de stappen bij het cijferen luidop te verwoorden Dit helpt bij het memoriseren van de stappen én zo leer je de denkwijze van je kind kennen en ontdek je eventuele fouten�

• Je kind moet heel netjes cijferen� Geef hiervoor altijd een geruit blad papier�

• Tafels zijn essentieel bij het cijferen De tips bij de tafels kun je hier zeker ook gebruiken

• Laat je kind eens een rekening van de bakker of de slager controleren, daar zijn de getallen ook vaak onder elkaar geordend�

• Geef je kind het gevoel dat eens het kan cijferen, een rekenmachine helemaal niet meer nodig is in huis!

Tips voor de ouders om cijferen thuis te oefenen

Problemen oplossen: verhoudingen

De verhoudingstabel

Kijk hoeveel schelpen je nodig hebt voor één mandala�

Voor twee mandala’s vermenigvuldig je alle getallen met 2�

Voor drie mandala’s vermenigvuldig je alle getallen met 3�

Voor vijf mandala’s vermenigvuldig je alle getallen met 5

mandala's

mandala's

Recht evenredige verhoudingen

Als het aantal mandala’s meer wordt, wordt het aantal schelpen ook meer�

1 mandala 5 mandala's

Als het aantal mandala’s minder wordt, wordt het aantal schelpen ook minder�

3 mandala's 1 mandala

Meten en metend rekenen

METEN EN METEND REKENEN

Tijd Kloklezen

1 uur = 60 minuten

= 2 keer een half uur

= 4 keer een kwartier

De grote wijzer gaat helemaal rond�

1 half uur = 30 minuten

= 2 keer een kwartier

Je hebt er twee in een uur, een half uur is de helft van een uur

1 kwartier = 15 minuten

Je hebt er vier in een uur, een kwartier is een kwart van een uur�

METEN EN METEND REKENEN

Analoge klok

Hoe lees ik de analoge klok af?

1) Staat de minutenwijzer, de grote wijzer, in het veld ‘over’ of het veld ‘voor’?

2) Hoeveel minuten staat de grote wijzer ‘over’ of ‘voor’ het uur, de 12?

3) Nu kijken we naar de uurwijzer, de kleine wijzer: welk uur zijn we voorbij of moet nog komen?

Kijk goed naar de grote wijzer: staat de grote wijzer VOOR of OVER de 12?

• grote wijzer ➔ minuten

• kleine wijzer ➔ uren

Hoe noteer ik het uur op de digitale klok?

1) We kijken eerst naar de kleine wijzer. Die toont het uur. Welk uur is het geweest? De kleine wijzer is voorbij de 7. We noteren 07. Let op: we noteren altijd twee cijfers.

2) Nu kijken we naar de grote wijzer. Die toont de minuten. Hoeveel minuten voorbij het uur is het? De grote wijzer staat 10 streepjes (minuten) voorbij de twaalf. We noteren 10. Het is 07 : 10.

24 uren in een dag

Tijdstippen na de middag krijgen getallen boven de 12!

Ella gaat slapen om kwart over 7 ’s avonds�

➔ 19 : 15

TIP

Tel ‘12’ bij het gewone uur� ➔ 7 + 12 = 19

1 uur = 13 uur

2 uur = 14 uur

3 uur = 15 uur

4 uur = 16 uur

5 uur = 17 uur

6 uur = 18 uur

7 uur = 19 uur

8 uur = 20 uur

9 uur = 21 uur

10 uur = 22 uur

11 uur = 23 uur

12 uur = 24 uur of 00 uur

METEN EN METEND REKENEN

Tijdsduur

Van 03 : 48 naar 04 : 16

Hoeveel minuten liggen hiertussen? We rekenen eerst tot het volgende uur�

Plaats boogjes en werk in stappen. Denk vooraf na over welke stap je kan helpen.

METEN EN METEND REKENEN

Maateenheden omzetten: algemene werkwijze en verwoording

Regel: De E staan in de kolom van de maateenheid.

6 m = cm

Met welke maateenheid werken we? m

We werken dus in de kolom van de m�

Hier moet ook de eenheid van het getal komen

We schrijven de 6 in de kolom van de m�

Hoeveel cm is dit nu?

We vullen aan met nullen tot aan de kolom van de cm

Wat lezen we af?

600 cm

Dus 6 m = 600 cm

50 cm = dm

Met welke maateenheid werken we? cm

We werken dus in de kolom van de cm� Hier moet ook de eenheid van het getal komen�

Wat is de eenheid bij 50? 0

We schrijven 0 in de kolom van de cm De 5 komt in de kolom van de dm�

Hoeveel dm is dit nu?

We werken in de kolom van de dm, want dit is nu de maateenheid

Wat lezen we af? 5 dm

Dus 50 cm = 5 dm�

METEN EN METEND REKENEN

Dit is altijd:

1 km = de afstand van school tot aan ?

100 m = de lengte van een voetbalveld

10 m = de lengte van een klaslokaal

1 m = de breedte van onze open armen

1 dm = de afstand tussen de buitenste hoeken van onze ogen

1 cm = de breedte van onze duimnagel

Regel: De E staan in de kolom van de maateenheid.

Met de tabel lukt het altijd!

De meter hebben we nodig bij vragen over lengte, hoogte, diepte, breedte, omtrek, dikte en afstand. Als je rekent met maten, zorg er dan voor dat ze in een gelijke maateenheid staan.

METEN EN METEND REKENEN

Inhoud

l dl cl

1 l = 10 dl = 100 cl

1 dl = 10 cl

Referentiematen

Dit is altijd:

1 dl

100 l = de inhoud van een bad

10 l = de inhoud van een gewone emmer

1 l = de inhoud van een karton melk

1 dl = de inhoud van een half brikje

1 cl = de inhoud van een koffielepel

Maten omzetten

l dl cl

2 0

3 0 8 5

Regel: De E staan in de kolom van de maateenheid.

2 l = 20 dl

3 dl = 30 cl

85 cl = 8 dl en 5 cl

Met de tabel lukt het altijd! Met de maatbeker kun je een inhoud meten. Als je rekent met maten, zorg er dan voor dat ze in een gelijke maateenheid staan.

METEN EN METEND REKENEN

Gewicht/massa

kg 100 g 10 g g

1 kg = 1 000 g

Referentiematen

Dit is altijd: 10 kg 1 kg 100 g 10 g 1 g

100 kg = het gewicht/de massa van een scooter

10 kg = het gewicht/de massa van een zware boekentas

1 kg = het gewicht/de massa van een pak suiker

100 g = het gewicht/de massa van een halve appel

10 g = het gewicht/de massa van een suikerklontje

1 g = het gewicht/de massa van een paperclip

Maten omzetten

kg 100 g 10 g g

Regel: De E staan in de kolom van de maateenheid.

1 0 0 0 1 kg = 1 000 g

5 0 0

5 x 100 g = 500 g

Onze armen kunnen we gebruiken als weegschaal.

Doe je ogen dicht: Wat is er zwaarder ? Wat weegt er meer ?

METEN EN METEND REKENEN

Omtrek

omtrek = de som van alle zijden

4 cm

De omtrek berekenen we door de lengte van alle zijden samen te tellen

3 cm

Oppervlakte

4 cm

3 cm

4 cm + 3 cm + 4 cm + 3 cm = 14 cm

De omtrek is 14 cm�

De oppervlakte van een vlakke figuur is datgene waarover we kunnen wrijven

In dit geval alles wat groen gekleurd is�

De donkergroene figuur heeft de grootste oppervlakte�

Met mijn vinger ga ik over de rand van een figuur, dat is de omtrek Met mijn hand wrijf ik over de hele figuur, dat is de oppervlakte.

Geld Geldwaarden

€ 2 en 55 c�

➔ Dit lezen we als 2 euro en 55 cent

Let op de notatie!

€ 2 (het euro-teken komt VOOR het cijfer)

55 c. (cent wordt afgekort als c� en komt NA het cijfer)

Gepast teruggeven

Papa koopt een paar schoenen van 89 euro en 55 cent�

Hij betaalt met een biljet van € 100�

Hoeveel krijgt hij terug?

45 c� + € 10

€ 89 en 55 c�

€ 90 € 100

€ 10 en 45 c�

De prijs is 89 euro en 55 cent

Papa betaalt met 100 euro�

Papa krijgt 10 euro en 45 cent terug�

Hoeveel krijg je terug? Werk altijd in twee stappen:

1) Tel bij tot de volgende euro (100 cent).

2) Tel bij tot het gegeven bedrag.

Temperatuur

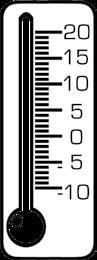
Op een thermometer lees je de temperatuur af� De temperatuur duidt aan hoe warm of koud het is� We drukken de temperatuur uit in Celsius (°C)�

Het verschil in temperatuur is hier 7 °C

Het verschil in temperatuur is hier 20 °C�

• Oefen thuis met een klein winkeltje, kassa en een set munten en biljetten� Laat je kind in de winkel eens zelf betalen

• Je kind kan sparen en tellen hoeveel het nog te weinig heeft voor wat het wilt kopen

• Veel gezelschapsspellen waarin je zaken kunt kopen en verkopen, helpen met het leren betalen en teruggeven�

• Als je gaat wandelen of rijden, dan kan je kind afstanden schatten Gebruik hiervoor de referentiematen van p 54

• Je kind kan helpen bij het koken, wegen, meten … en de maatbeker gebruiken� Hierbij kun je ook de gegeven maten laten omzetten�

Bijvoorbeeld: 1 kg is hetzelfde als hoeveel gram? (1 000 g)

• Lees vaak samen het je kind het uur Vraag regelmatig hoe laat het is, zowel op de analoge als de digitale klok� Je kind kan ook in het dagelijkse leven veel over tijdsduur leren: bij het gebruiken van de microgolf, de lengte van liedjes ���

• Stel ook vragen om het besef van tijd aan te leren Bijvoorbeeld: Het is nu zeven uur, je gaat slapen om kwart voor acht/7 uur 45 Hoelang mag je nog opblijven?

• Bij het nemen van de bus, tram of trein kan je kind zelf de uurtabel raadplegen� Met wat hulp lukt het zeker

Tips voor de ouders om meten en metend rekenen thuis te oefenen

Meetkunde

Patronen

Herhalend patroon

Dit is de patrooneenheid�

Dit is het patroon�

Bij herhalende patronen wordt de patrooneenheid steeds herhaald.

Groeiend patroon

Dit is de patrooneenheid�

Dit is het patroon�

Bij groeiende patronen wordt de patrooneenheid steeds met het laatste element uitgebreid.

3 3 p p epoe o loe l Sl S

Patronen omzetten naar letters

Herhalende patronen

• Zoek de patrooneenheid

• Zet de patrooneenheid om naar letters

Geef het eerste element van de letter B ���

• Zet vervolgens het hele patroon om naar letters Bij twijfel kan je terugkijken naar de patrooneenheid�

Groeiende patronen

• Zoek de patrooneenheid�

• Zet de patrooneenheid om naar letters�

MEETKUNDE A B C A B C A B C A B C A A B A B A B B A B B B

Geef het eerste element van de patrooneenheid de letter A, het tweede element de letter B ���

Ruimtelijke oriëntatie: blokkenbouwsels

grondplan 2 2 1 1

vooraanzicht achteraanzicht

zijaanzicht rechts zijaanzicht links

Een plan zegt hoe we moeten bouwen. ➔ cijfers

Een aanzicht zegt hoe het bouwsel eruit ziet. ➔ tekenen

Ruimtelijke oriëntatie: coördinatenrooster

In een rooster met coördinaten kun je gemakkelijk dingen aanduiden of zoeken�

Een coördinaat bestaat uit een letter en een cijfer� We noteren eerst de letter en daarna het cijfer�

De meeuw vliegt in vak D3�

De krab zit in vak E2�

De schelp ligt in vak G9

Vormleer

Rechte f staat loodrecht op rechte g/ rechte f en rechte g staan loodrecht op elkaar

Lijnstuk JK is evenwijdig met lijnstuk HI/ lijnstuk JK en lijnstuk HI staan even wijd/even ver van elkaar

Hoeken

hoekpunt been been

hoek

rechte hoek scherpe hoek stompe hoek

A B C

De benen staan loodrecht/ recht op elkaar

Deze hoek is kleiner dan de rechte hoek

Deze hoek is groter dan de rechte hoek

Denk goed aan de bovenste hoek van je geodriehoek, die vertelt ons alles. ➔ Dat is een rechte hoek.

• Is de hoek kleiner? ➔ scherpe hoek

• Is de hoek groter? ➔ stompe hoek

Vlakke figuren en ruimtefiguren

Vlakke figuren kunnen we onder de deur schuiven

Veelhoeken hebben allemaal rechte zijden�

driehoeken vierhoeken vijfhoeken

Vlakke figuren die geen veelhoek zijn hebben één of meerdere gebogen zijden�

ruimtefiguren

Driehoeken

We kijken naar de zijden�

gelijkzijdige driehoek

➔ drie gelijke zijden

gelijke zijden = even lange zijden

gelijkbenige driehoek

➔ twee gelijke zijden

Wij hebben twee gelijke benen, dus een gelijkbenige driehoek heeft ook twee gelijke zijden.

ongelijkzijdige/ ongelijkbenige driehoek

➔ drie verschillende zijden

We kijken naar de hoeken�

scherphoekige driehoek

➔ drie scherpe hoeken

rechthoekige driehoek

➔ één rechte hoek + twee scherpe hoeken

Vierhoeken

• vier gelijke rechte hoeken

• vier gelijke zijden

• overstaande/tegenoverliggende zijden zijn gelijk

• overstaande/tegenoverliggende zijden zijn evenwijdig

vierhoeken

• vier gelijke rechte hoeken

• overstaande/tegenoverliggende zijden zijn gelijk

• overstaande/tegenoverliggende zijden zijn evenwijdig

➔ een vierkant ➔ een rechthoek

Meetinstrumenten gebruiken: de geodriehoek

rechte hoek

loodlijn

tekenzijde evenwijdige lijnen

Meetkundige relaties

Evenwijdigheid en loodrechte stand

Evenwijdige lijnen tekenen

1 Kies één van de evenwijdige lijnen op je geodriehoek�

2 Leg deze lijn gelijk met de getekende lijn op je blad�

3 Teken zelf een lijn met potlood langs de tekenzijde van de geodriehoek

4 Dit is nu lijn k, evenwijdig aan de gegeven lijn j�

Loodrechte lijnen tekenen

1 Leg de loodlijn van de geodriehoek precies op de getekende lijn op het blad�

2 Teken nu zelf een lijn met potlood langs de tekenzijde van de geodriehoek

Tekenen

3 Dit is nu een lijn f, loodrecht op de gegeven lijn d�

doen we ALTIJD met een tekenpotlood.

Symmetrie

Deze figuur is symmetrisch�

Ze is aan beide zijden van de (symmetrie)as gelijk

Dit is een symmetrieas�

Als ik mijn figuur plooi op de symmetrieas, dan liggen beide delen perfect op elkaar. Een figuur kan meer dan één symmetrieas hebben!

Deze figuur heeft oneindig veel symmetrieassen!

Spiegelbeelden

Beeld en spiegelbeeld:

• staan even ver van de spiegel�

• zijn even groot�

• hebben dezelfde vorm

• links wordt rechts en omgekeerd�

spiegelas

beeld

spiegelbeeld

Vraag een spiegel als je twijfelt.

Controleer eerst de hoekpunten van de figuren: staan die allemaal even ver van de spiegelas?

Niet dezelfde vorm

Deze figuren zijn gelijk van vorm en grootte�

Ze hebben dezelfde vorm en grootte�

Deze figuren zijn gelijk van vorm, maar niet van grootte

Ze hebben dezelfde vorm, maar niet dezelfde grootte�

Ze zijn gelijkvormig�

oefenen

• Verwijs regelmatig naar vlakke figuren in het dagelijkse leven� Vraag je kind om die te omschrijven Laat bijvoorbeeld eens de vorm van verkeersborden benoemen

• Laat je kind op de computer eens een figuur uitrekken en vraag of de figuur gelijk blijft van vorm of niet�

• Sommige gezelschapsspelletjes laten vormen en kleuren sorteren, idem bij memoryspelletjes

• Laat je kind soorten lijnen zoeken in de dagelijkse omgeving

Tips voor de ouders om meetkunde thuis te